Prerpints.org logo
Preprint
Article

3D Reconstruction of Indoor Scenes Based on Neural Implicit

Altmetrics

Downloads

108

Views

63

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

28 August 2024

Posted:

29 August 2024

You are already at the latest version

Alerts
Abstract
Reconstructing 3D indoor scenes from 2D images has always been an important task in computer vision and graphics applications. For indoor scenes, traditional 3D reconstruction methods suffer from the lack of surface details, poor reconstruction of large flat surface textures and areas with uneven lighting, and many falsely reconstructed floating debris noises in the reconstructed models. We add adaptive normal priors to the neural implicit reconstruction process to optimize the network, and improve the accuracy of volume density prediction by adding regularization terms to the neural radiation field to constrain the volume density obtained by weight distribution, and learn a smooth SDF surface from the network to obtain an explicit mesh model. Experiments show that the method proposed in this paper outperforms the state-of-the-art methods on ScanNet, Hypersim, and Replica datasets.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Vision and Graphics

1. Introduction

The goal of 3D reconstruction of indoor scenes is to reconstruct and restore an accurate scene model from 2D images of indoor scenes from multiple angles to reflect the geometry, structure, and appearance characteristics of the actual scene [1]. This process can obtain an explicit 3D model observed from any perspective. This task has been a hot topic and an important task in computer vision and graphics research in recent years, and has broad application prospects in house interior restoration, interior design, virtual reality, augmented reality, indoor navigation, etc. [2].
Unlike object-level reconstruction, indoor environments usually include large and small objects, different materials, and complex spatial layouts, which puts higher demands on feature extraction and scene understanding. Indoor lighting conditions are also complex and changeable, and may include natural light, artificial light, and shadow areas. These factors will affect the quality of the reconstructed model and the difficulty of reconstruction. In addition, occlusion between objects is more common in indoor scenes, which makes it more difficult to obtain complete scene information from a limited perspective. Existing methods often have poor effects on uneven lighting (as shown in Figure 1(a)) and partial planar texture processing (as shown in Figure 1(b)). There are many floating noises in the air of the reconstructed indoor 3D model (as shown in Figure 1(c)). The recently proposed neural radiance fields (NeRF) reconstruction method can achieve good results, but the computation is large and it cannot directly obtain a 3D mesh model. We strengthen surface learning by adding normal priors and use SDF, a compact and continuous multi-layer perceptron (MLP) to parameterize the representation of the implicit model, and finally obtain a high-quality 3D mesh model. In summary, this paper has the following main contributions:
1) Propose a new indoor 3D reconstruction method that combines neural radiation field and SDF scene expression, which not only preserves the high-quality geometric information of the neural radiation field, but also uses SDF to generate an explicit mesh with a smooth surface.
2) By adding adaptive normal priors to provide globally consistent geometric constraints, the reconstruction quality of planar texture areas and details is significantly improved.
3) By introducing a new regularization term, the problem of uneven distribution of neural radiation field density is alleviated, and the effect of removing floating debris is achieved in the final generated model, which improves the look and feel of the visualization results.

2. Related works

2.1. 3D reconstruction of indoor scenes based on MVS

traditional multi-view stereo (MVS) method first estimates the depth map of each image based on multiple views, and then performs depth fusion to obtain the final reconstruction result. These methods can reconstruct relatively accurate 3D shapes and have been used in many downstream applications, such as new view synthesis. However, it is difficult to handle planar texture areas, such as indoor scenes. The main reason is that planar texture areas make dense feature matching difficult to handle. Schoenberger proposed a new general image 3D reconstruction method, which uses SIFT features and FLANN matching algorithms to improve the accuracy and efficiency of SFM, and open-sourced the project as COLMAP [3] software for use by a large number of enthusiasts, which can perform dense point cloud reconstruction and surface reconstruction. Based on this, researchers at Stanford University proposed the Pixelwise View Selection [4] method, which improves the poor reconstruction effect and efficiency problems caused by the inconsistent input image specifications (such as different input image sizes, different lighting, etc.). This method regards the view selection problem as a binary classification problem and selects the best view for each pixel, so that the information from all perspectives can be used for better stereo matching. However, these methods perform poorly in large planar texture areas or areas with sparse textures because their optimization is highly dependent on the photometric process. In Indoor scenes with planar texture areas, the inherent uniformity makes photometric measurement invalid, which makes it difficult to accurately estimate depth [5].
In recent years, learning-based MVS methods have achieved good results. These methods can be divided into two categories: depth-based methods and TSDF (truncated signed distance function)-based methods. Depth-based methods [6-9] first estimate the depth map of the image separately, and then use additional filtering and fusion processes to reconstruct the scene. Such methods are often incomplete, with noisy surfaces and scale blurring caused by inconsistent separate estimates of the depth map. To alleviate these problems, some methods directly regress the input image to the TSDF. Atlas [10] proposed a volume design to regress a 3D global feature volume constructed from a series of images to the TSDF. Limited by the global design and computational resources, Atlas can only process a limited number of images, and its reconstruction results lack details. To reduce the computational burden, unlike Atlas, which processes the entire image sequence at once, NeuralRecon [11] proposed a coarse-to-fine framework to reconstruct the entire scene by incrementally processing local fragments. However, due to its local estimation design, NeuralRecon has difficulty in obtaining global reconstructions with fine details.

2.2. Indoor 3D reconstruction based on neural implicit

Coordinate-based implicit neural networks, which encode a field by regressing 3D coordinates to output values via an MLP, have become a popular approach for representing scenes due to their compactness and flexibility. The Dist [12] model proposed a method to learn 3D shapes from 2D images. IDR [13] models rely on view appearance and can be applied to non-Lambertian surface reconstruction. Despite achieving impressive performance, they require mask information to obtain reconstructions. NeRF encode scene geometry via volume density and are suitable for the novel view synthesis task of volume rendering. However, due to the lack of surface constraints, volume density cannot represent high-fidelity surfaces. Inspired by NeRF, Neus [14] and VolSDF [15] attached volume rendering techniques to IDR and eliminated the need for mask information. While these methods achieve impressive reconstruction results on small-scale, texture-rich scenes, we found in our experiments that these methods often perform poorly on large-scale indoor scenes with untextured planar regions. Mip -NeRF360 [16] improves upon the original NeRF’s problems with details and scale imbalance at near and far distances, as well as the limited nature of synthesized scenes, and is able to render unbounded scenes more realistically. Later, NeRF was no longer limited to static scenes, but was further extended to run in dynamic scenes. To address the slow convergence of the original NeRF training process, NSVF [17] uses a sparse voxel octree to assist in spatial modeling, which has achieved significant improvements in training time. Traditional NeRF requires input from multiple views to estimate volume representation. If multi-view data is insufficient, the generated scene can easily collapse into a plane. To address this problem, Google researchers proposed LOLNeRF [18], which can train a NeRF model from a single viewpoint for the same type of object, without adversarial supervision, thereby enabling a single 2D image to generate a 3D model. The above are all advances made by NeRF in new viewpoint synthesis. In recent years, researchers have gradually turned their attention to using NeRF for 3D reconstruction. Guy et al. [19] applied NeRF to facial reconstruction and achieved the generation of high-quality 3D facial models from a single RGB image. By introducing the time dimension, this method can model and reconstruct the dynamic changes of facial shape and expression. However, the above NeRF research is limited to object-level reconstruction. When the reconstructed object is expanded to indoor scenes, the generated 3D model often contains a lot of noise and topological errors.

3. Methodology

This paper proposes a method for indoor scene 3D reconstruction that combines neural radiation field and SDF implicit expression. The volume density of the neural radiation field is used to provide geometric information for the SDF field, and the learning process is optimized by adding normal priors to strengthen the learning of geometric shapes and surfaces. The overall framework of the method proposed in this paper is shown in Figure 2. Multiple 2D images of indoor scenes are used as input, and the explicit 3D model mesh of the corresponding scene is output.

3.1. Optimization of indoor 3D reconstruction based on adaptive normal prior

Normal map is an important type of image, which represents the surface normal direction of each pixel in the image through the color of the pixel. In 3D graphics and computer vision, the normal is a vector perpendicular to the surface of an object, which can be used to describe the direction and shape of the surface. In the normal map, RGB color channels are generally used to represent the X, Y, and Z components of the normal vector respectively. Normal information helps to correct errors in the reconstruction process and improve the reconstruction quality.
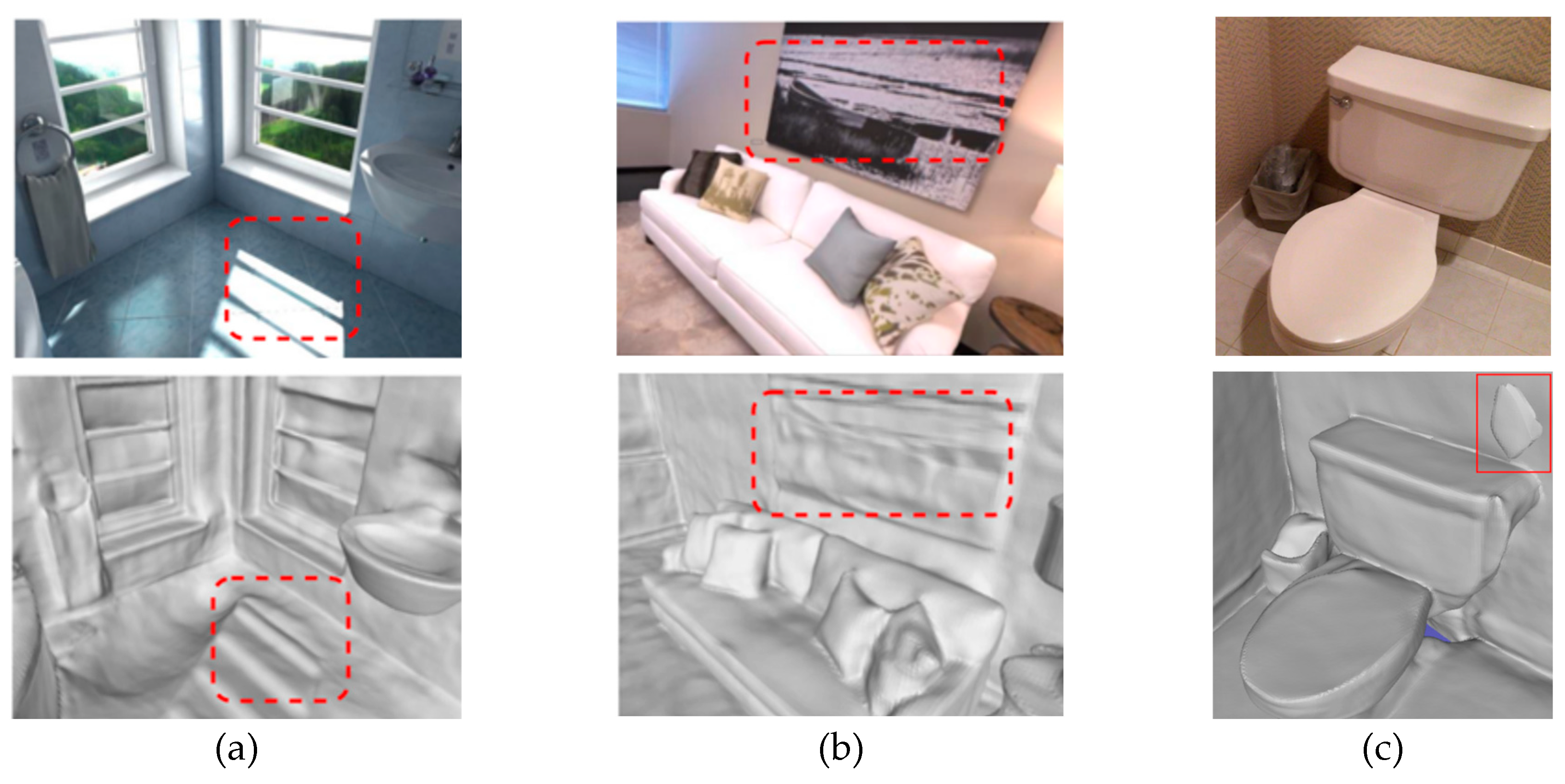
Currently, many monocular normal estimation methods have achieved high accuracy under clear image input. However, considering that indoor scene images often have small blur and tilt, this paper selects TiltedSN [20] as the normal estimation module. Because the estimated normal map is usually over-smoothed, there are problems of inaccurate estimation on some fine structures, such as the chair legs in Figure 3(a). Therefore, we adopt an adaptive method to use normal priors, using a mechanism based on the consistency of multiple views of the input image to evaluate the reliability of the normal prior. As shown in Figure 3(b), this process is also called geometric checking. For areas that do not meet the consistency of multiple images, the normal prior is not applied. Instead, the appearance information is used for optimization to avoid the negative effects of incorrect normal maps that lead to misjudgment in reconstruction.
Given a reference image I i , evaluate the consistency of the surface observed from pixel q . Define a local 3D plane p p T n = d v T n   in the camera space associated with q , where v is the viewing direction, d is the distance to pixel q , and n is the normal estimate. Next, find a set of adjacent images, assuming that one of the adjacent images is I j . The homography change from I i to I j can be calculated by the following formula:
H n , d = K j R j R i − 1 − t i − t j n T d v T n K i − 1
where K * ,   R * ,   t * is the intrinsic parameter matrix, the rotation and translation camera parameters. For pixel q in I i , find a square block P centered on it as the neighborhood, and warp the block to its adjacent view I j using the calculated homography matrix. The block matching method (Patchmatch) can be used to find similar image blocks on adjacent views, and the Normalized Cross-Correlation (NCC) method is used to evaluate the visual consistency of ( n , d ). NCC is a method for measuring the similarity between two images. It evaluates the similarity between the two images by calculating the degree of correlation between them. Compared with simple cross-correlation, normalized cross-correlation is insensitive to changes in brightness and contrast, so it is more reliable in practical applications. The applied NCC formula is as follows:
N C C j P , n = ∑ q ∈ P I ^ i q I ^ j H n , d q ∑ q ∈ P I ^ i q 2 ∑ q ∈ P I ^ j H n , d q 2
where I ^ * q = I * q − I ¯ * q , I i q and I j q represent two image regions to be compared, I ¯ * q is the average value of I * q , I ^ * q is the difference between them, the numerator calculates the sum of the products of the differences between the two image blocks, and the denominator calculates the square root of the product of the sum of the squares of the differences between the two image blocks. This process ensures the normalization of the results, making the NCC range in (-1, 1). The closer the NCC value is to 1, the more similar the two image regions are; the closer the NCC value is to -1, the less similar they are; the closer the NCC value is to 0, the less obvious linear relationship there is between them.
If the reconstructed geometry is not accurate at the sampling pixel, it cannot meet the multi-view photometric consistency, which means that its related normal prior cannot provide help for the overall reconstruction. Therefore, a threshold ϵ is set, and by comparing the NCC at the sampling block with ϵ, the following indicator function can be used to adaptively determine the training weight of the normal prior.
Ω q n ^ = 1         i f ∑ j N C C j P , n ^ ≥ ϵ 0         i f ∑ j N C C j P , n ^ < ϵ
The normal prior is used for supervision only when Ω q n ^ = 1 . If Ω q n ^ = 0 , the normal prior of the region is considered unreliable and will not be used in subsequent optimization processes.

3.2. Neural implicit reconstruction

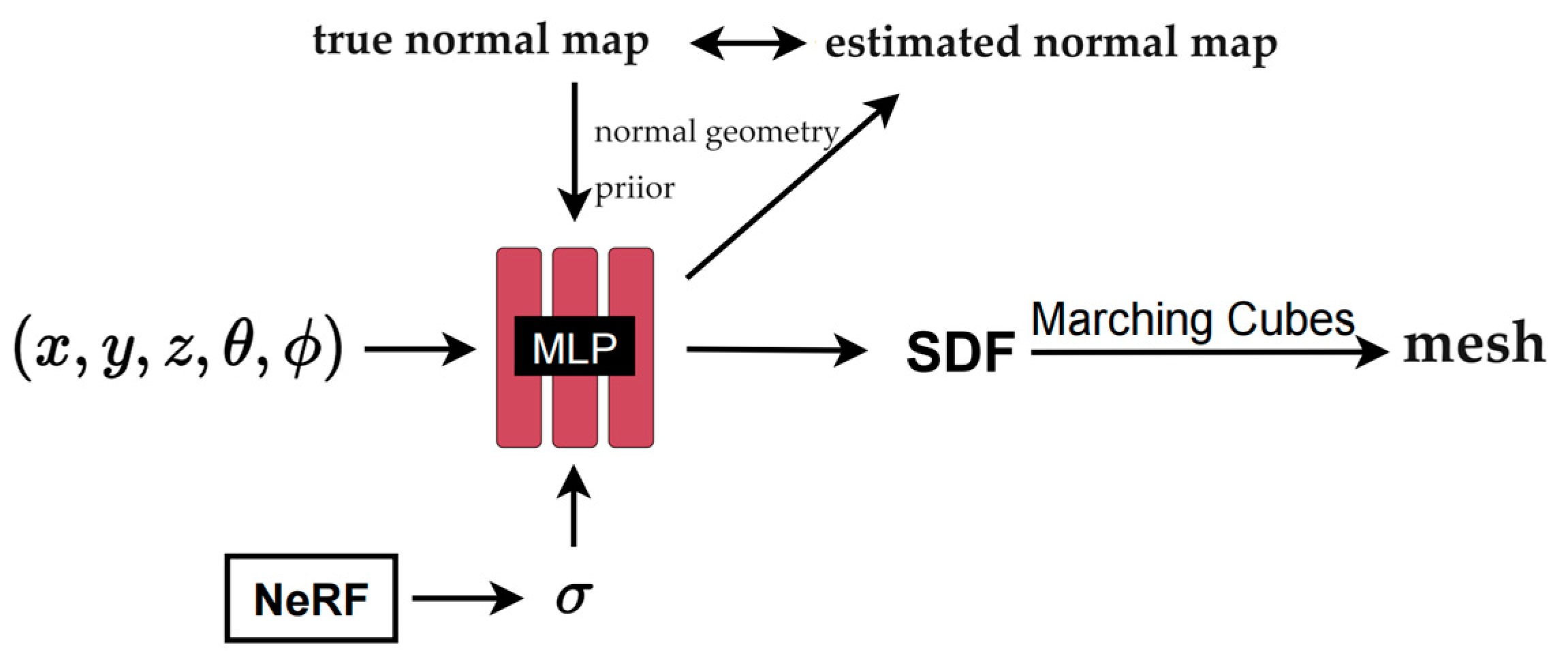
Since the neural radiation field cannot express the surface of the object well, we are looking for a new implicit expression. The signed distance function (SDF) can represent the surface information of objects and scenes and achieve better surface reconstruction. Therefore, we choose SDF as the implicit scene representation.3.3.1 Scene Representation

3.2.1. Scene Representation

We represent the scene geometry as a SDF. A SDF is a continuous function f that, for a given 3D point, returns the distance from that point to the nearest surface:
f : R 3 → R x ⟼ s = f ( x )
Here, x represents a 3D point and s is the corresponding SDF value, thus completing the mapping from a 3D point to a signed distance. We define the surface S as the zero level set of the SDF, expressed as follows:
S = x f x = 0
By using the Marching Cubes algorithm on the zero horizontal plane of the SDF, that is, the surface of the object or scene, we can obtain a 3D mesh with a relatively smooth surface.
Using the SDF to get the mesh has the following advantages:
1) Clear surface definition: SDF provides the distance to the nearest surface for each spatial point, where the surface is defined as the location where the SDF value is zero. This representation is well suited for extracting clear and precise surfaces, making the conversion from SDF to mesh relatively direct and efficient.
2) Geometric accuracy: SDF can accurately represent sharp edges and complex topological structures, which can be maintained when converted to meshes, thereby generating high-quality 3D models.
3) Optimization-friendly: The information provided by SDF can be directly used to perform geometry optimization and mesh smoothing operations, which helps to further improve the quality of the model when generating the mesh.

3.2.2. Implicit indoor 3D reconstruction based on normal prior

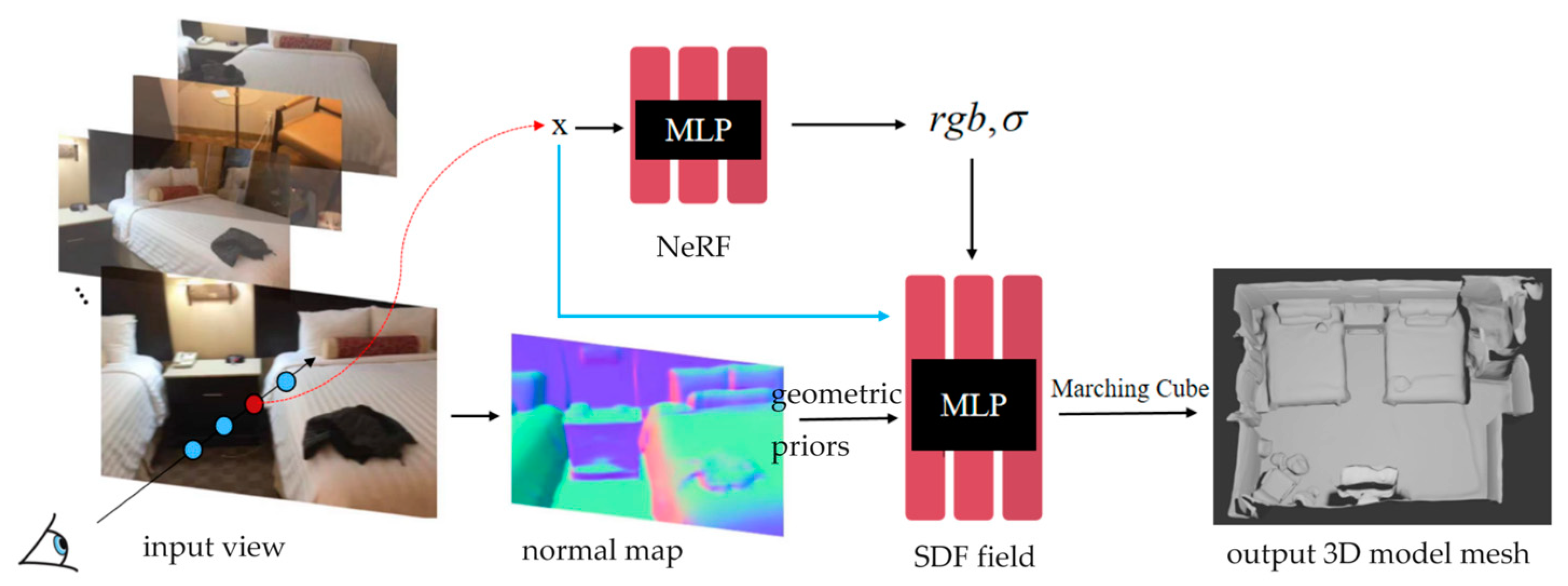
The reconstruction process based on normal prior is shown in Figure 4. The input mainly consists of three parts.
The first part is a five-dimensional vector representing the information of the sampling point ( x , y , z , θ , ϕ ) . The second part is the volume density we obtained previously through the neural radiation field σ . Given that we use SDF as a surface expression, the volume density obtained by NeRF can represent more comprehensive scene geometry information. Because the scene contains multiple objects and air, it is difficult to represent a complex scene only through surface information. Traditional SDF-based methods are often limited to object reconstruction. The constraints of NeRF volume density combined with SDF reconstruction can reconstruct richer scene geometry. The third part is the normal geometry prior. The normal map here is obtained by the monocular normal estimation method mentioned earlier. The normal map provides the orientation information of the object surface, which is conducive to enhancing detail reconstruction.
The network used here is an improved neural radiation field, which also contains 2 MLPs. Like NeRF, there is a color network f c , and the other grid has become an SDF network f θ g , which can get the SDF value of the point through the 3D coordinates of the point.
Here we will use volume rendering technology to get the predicted image, and optimize it with the input real image through the loss function. Specifically, for each pixel, we sample a set of points along the corresponding emission light, denoted as p i = o + d i v , where p i   is the sampling point, o is the camera center, and v is the direction of the light. The color value can be accumulated by the following volume rendering formula.
c ^ = ∑ i = 1 n T i α i c ( p i , v )
where T i = ∏ j = 1 i − 1 ( 1 − α j ) is the cumulative transmittance, i.e., the probability that of no object occlusion, c is the color value, α i = 1 − e x p ⁡ ( − ∫ t i t i + 1 ρ ( t ) d t ) is the discrete opacity, and ρ ( t ) is the opacity corresponding to the volume density σ in the original NeRF. Since the rendering process is fully differentiable, we learn the weights of f c and f θ g by minimizing the difference between the rendering result and the reference image.
In addition to generating the appearance, the above volume rendering scheme can also obtain the normal vector. We can approximate the surface normal observed from a viewpoint by volume accumulation along this ray:
n ^ = ∑ i = 1 n T i α i n i
where n i = ∇ f ( p i ) is the gradient at point p i .
At this time, we compare the true normal map obtained by the monocular method with the estimated normal map obtained by the volume rendering process, and further optimize the parameters of the MLP by calculating the loss to obtain a more accurate normal map and geometric structure.

3.3. Floating debris removal

The neural radiation field initially acts on the generation of new perspectives on objects, maintaining a high degree of clarity and realism. This is mainly due to volume rendering. However, when the neural radiation field is used for 3D reconstruction, some floating debris in the air often appear. These floating debris refer to small disconnected areas in the volume space and translucent substances floating in the air. In view synthesis work, these floating debris are often not easy to detect. However, if an explicit 3D model needs to be generated, these floating debris will seriously affect the quality and appearance of the 3D model. Therefore, it is very necessary to remove the floating debris in these incorrectly reconstructed places.
These floating debris often do not appear in object reconstruction. However, in scene-level reconstruction, due to the significant increase in environmental complexity and the lack of relevant constraints on the neural radiation field, there is a phenomenon of inaccurate local area density prediction. Therefore, this paper proposes a new regularization term to constrain the weight distribution of the neural radiation field.
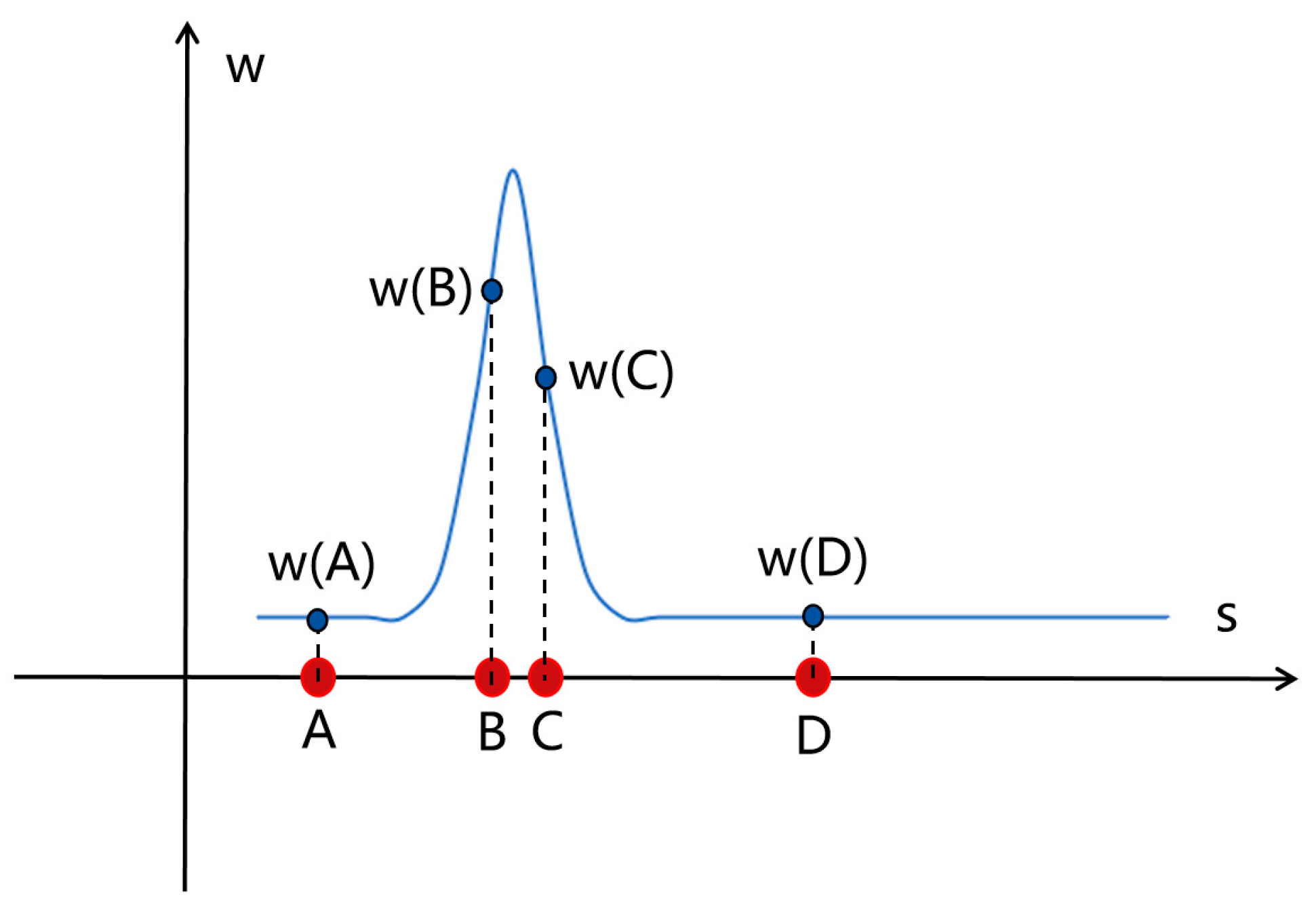
First, simulate the sampling process of the neural radiation field. In a scene, assume that there are only rigid objects, excluding the existence of translucent objects. After a ray is shot out, there will be countless sampling points on this ray. The weight value of the sampling point before the ray encounters the object should be extremely low (close to 0). When the ray contacts the rigid object, the weight value here should soar, much higher than other values. After the object, the weight value returns to a lower range. This is the desired weight distribution in an ideal state, which is a relatively compact unimodal distribution. This method defines a regularization term, which is a step function defined by a set of standardized ray distances s and the weight w after parameterizing each ray:
L d i s t s , w = ∬ − ∞ ∞ w s u w s v u − v d u d v
Here u and v refer to points on the sampling ray, that is, points on the x-axis in the weight distribution diagram, u − v is the distance between the two points, w s u and w s v are the weight values at point u and point v, respectively. Since all particle combinations from negative infinity to positive infinity need to be exhausted, integration is performed in the front. If you want to make the loss function as small as possible, there are mainly two situations:
1) If the distance between point u and point v is relatively far, that is, the value of u − v is large, if you want to ensure that the value of L d i s t s , w is as small as possible, then one of w s u and w s v needs to be small and close to zero. That is, as shown in Figure 5, (A, B), (B, D), (A, D), etc. all satisfy that u − v   is large and the weight value of at least one point is extremely small (close to zero);
2) If the values of w s u and w s v are both large, if you want to ensure that the value of L d i s t s , w is as small as possible, then the value of u − v needs to be small, that is, the distance between points u and v is very close. As shown in figure 5, only the combination of (B, C) satisfies the condition that the values of w s u and w s v are both large, and at this time, points u and v just meet the condition that the distance is very close.
Therefore, through the analysis of the above two cases, it can be found that the properties of the regularization term can constrain the density distribution to the ideal single-peak distribution with good central tendency proposed before. The purpose of this regularization term is to minimize the sum of the normalized weighted absolute values of all samples along the ray, and encourage each ray to be as compact as possible, which is specifically reflected in:
1. Minimize the width of each interval;
2. Bring the intervals that are far apart closer to each other;
3. Make the weight distribution more concentrated.
The regularization term above cannot be used directly for calculation because it is in integral form. In order to facilitate calculation and use, it is discretized as:
L d i s t s , w = ∑ i , j w i w j s i + s i + 1 2 − s j + s j + 1 2 + 1 3 ∑ i w i 2 ( s i + 1 − s i )
This discretized form also provides a more intuitive understanding of the behavior represented by this regularization, where the first term minimizes the weighted distance between points in all intervals, and the second term minimizes the weighted size of each individual interval.

3.4. Training and loss function

During the training phase, we sample a batch of pixels and adaptively minimize the difference between the color and normal estimates and the true normal map. We sample m pixels { q k } and their corresponding reference colors { I ( q k ) } and normals { N ( q k ) } in each iteration. For each pixel, we sample n points in the world coordinate system along the corresponding ray, and the total loss is defined as:
L = λ c L c + λ n L n + λ e L e i k + λ d L d i s t
Among them λ c , λ n , λ e and λ d are the hyperparameters of color loss, normal loss, Eikonal loss and distortion loss respectively.
Color loss L c is used to measure the difference in color between the reconstructed image and the real image:
L c = 1 m ∑ k I q k − c ^ ( q k )
In the training phase, a batch of pixels need to be sampled. Each iteration samples m pixels { q k } and the corresponding reference color { I q k }, where c ^ ( q k ) represents the pixel color predicted by volume rendering.
The normal prior loss L n is to render the reconstructed 3D mesh of the indoor scene as a normal map, and compare it with the real normal map generated by the monocular method to obtain a loss:
L n = ∑ k N q k − n ^ ( q k ) 1 · Ω q k ( n ^ q k )
where N q k is the true normal information, and n ^ ( q k ) is the normal information predicted by the gradient. Ω q k ( n ^ q k ) is an indicator function used to judge the accuracy of the normal prior. Here, some data with inaccurate normal estimation are eliminated. The normal loss is mainly calculated by cosine similarity, because the direction of the normal vector is more important than its length. Cosine similarity is a good measure of the similarity of the two vectors in direction.
The Eikonal loss L e i k [31] of the regularized SDF is
L e i k = ∑ x ∈ Χ ( ∇ f θ x 2 − 1 ) 2
where Χ is a set of sampling points in the 3D space and the area near the surface, and x represents one of the sampling points. The reason why the gradient ∇ f θ x needs to be close to 1 is that the ideal SDF represents the shortest distance from the current point to the surface, so the gradient direction is the direction in which the distance field changes the steepest. Assuming that x moves toward the surface along this direction by ∆d, the SDF should also change by ∆d. Therefore, in the ideal state, ∇ f θ x = ∂ D x = ∆ D x / ∆ x = ∆ d / ∆ d = 1 , where D x is the original Eikonal equation. By introducing the Eikonal loss, the properties of the SDF can be well constrained, thereby ensuring the smoothness and continuity of the reconstructed surface.

4. Experimentation

4.1. Dataset

This paper conducts experimental analysis on the ScanNet[21], Hypersim[22] and Replica [23] datasets. The ScanNet dataset is the main dataset used for indoor scene 3D reconstruction tasks. At the same time, data from Hypersim and Replica are selected to test the generalization of this method in large-scale scenes.

4.2. Comparative Experiment

five evaluation indicators are used: accuracy (Acc), completeness (Comp), precision (Prec), recall (Recall) and F1 score (F-score). As shown in Table 1, the method in this paper is significantly better than the state-of-art methods, and performs well in most indicators, far exceeding the traditional MVS method and TSDF-based reconstruction method.
Among the neural implicit reconstruction methods, Neus and VolSDF mainly focus on object-level reconstruction, so they perform poorly on the ScanNet dataset; the first generation NeRF is mainly used for new perspective synthesis, and no algorithm for extracting grids is proposed. Therefore, direct use of Marching Cubes to extract grids will result in large-scale collapse. This article only draws on many modules of NeRF, so it is compared here; the I2-SDF method has good results in the synthetic dataset proposed in this article, but it does not have generalization ability and does not work well on the ScanNet dataset with more noise and motion blur.
MonoSDF and Manhattan-SDF are second only to this method in terms of quantitative results. Manhattan-SDF is based on the Manhattan World hypothesis, which assumes that the world is mainly composed of planes aligned with the coordinate axes. It is easily affected by the complexity of indoor scenes. Strict reliance on planes aligned with the coordinate axes for reconstruction may lead to missing or inaccurate details. Therefore, the overall accuracy is lower than this method. MonoSDF has achieved good performance in various indicators, especially accuracy. This is because MonoSDF weakens the reconstruction of complex structures that are difficult to handle during the reconstruction process. Therefore, the reconstructed part is highly overlapped with the scene itself, but some parts of the reconstruction will be lost. Therefore, compared with other evaluation indicators, there is some gap between its recall rate and this method, because the recall rate measures the ratio of the real model that is reconstructed.
In addition to quantitative analysis, this chapter visualizes the reconstruction results and makes qualitative comparisons with the most advanced MonoSDF and Manhattan-SDF. As shown in Figure 6(a), compared with GT, this method fills some holes that were not scanned at the time. Compared with Manhattan-SDF, this method has higher accuracy and smoother reconstruction effect on the surface of objects. Compared with MonoSDF, this method has more accurate reconstruction in many structures (shown by the red dashed line). The specific details in the red dashed box in Figure 6(a) are shown in Figure 6(b). Manhattan-SDF has low reconstruction accuracy. After zooming in on the detail image, larger triangular facets can be seen. From the visualization point of view, the details are far inferior to those of this method. MonoSDF has better overall detail reconstruction, especially the wall area is relatively smooth, but there are many missing objects. In the right picture of Figure 6(b) , MonoSDF did not correctly reconstruct the lamp on the table, and only reconstructed a small part of the outline of the objects placed on the bookshelf, while this method restored these details of the real scene well. In the left picture of Figure 6(b), MonoSDF and Manhattan-SDF are largely missing chair legs and armrests, while the method in this paper restores the chair structure in the real scene to a large extent.

4.3. Ablation Experiment

4.4.1. Normal geometry prior ablation experiment

This section will demonstrate the effectiveness of the adaptive normal prior scheme added in this paper through quantitative and qualitative ablation experimental analysis. There are three settings in this ablation experiment: (1) no normal prior is added, denoted as w/o N; (2) normal prior is added, but the adaptive scheme is not used, denoted as w/ N, w/o A; (3) the adaptive scheme is used with normal prior, denoted as Ours. All settings are tested on the ScanNet dataset, Hypersim dataset and Replica dataset. The evaluation indicators of each setting are shown in Table 2. It can be seen that the reconstruction quality can be significantly improved by adding geometric prior, because it provides additional geometric constraints and alleviates many ambiguity problems caused by the lack of texture information in the original image. On this basis, the adaptive scheme can remove the incorrectly estimated normal map and further improve the reconstruction quality.
The following will verify the effectiveness of the adaptive normal prior module used in this section through qualitative visualization results. This module has a certain improvement in the reconstruction of all indoor scenes, but the improvement in thin structure areas and reflective areas is particularly obvious, so these two areas are selected as visualization displays. As shown in Figure 7, a qualitative analysis of the chair leg structure is performed. Figure 7(a) is the input RGB image, i.e., the reference image, and figure 7(b) is the model reconstructed without using the normal prior. The overall reconstruction accuracy is not high, which is reflected in the fact that the reconstruction effect of the surrounding floor and walls is not flat enough, and the surface of the chair is not smooth enough. Figure 7(c) adds the normal prior, but does not use the adaptive scheme. Although the reconstruction effect of the wall and chair surface is improved, the chair leg part is not reconstructed due to the wrong normal estimation. Figure 7(d) is the method used in this paper, that is, the adaptive scheme uses the normal prior, which not only greatly improves the accuracy, but also completely reconstructs the thin structure area such as the chair leg.
In addition to having a good visual improvement effect in thin structure areas, the adaptive normal prior scheme is also effective in some areas due to lighting or specular reflection. As shown in Figure 8(a) is a reference image. The sunlight projected from the window forms regular white light and shadows on the ground. These light and shadows usually affect the reconstruction of the flatness of the entire ground because the network will understand them as independent geometric structures. Figure 8(b) is a model reconstructed without using normal prior. A more obvious step structure is reconstructed in the light and shadow area, which is not the result of correct reconstruction. The reconstruction granularity in other areas is also obviously insufficient. Figure 8(c) adds normal prior but does not use the adaptive scheme. Since most of the normal priors have weakened the erroneous impact of this area on the reconstruction, the erroneous outline of this area is already vague and not as obvious as in Figure 8(b). However, there are also a few normal maps closer to the light and shadow area that estimate this area as a geometric structure different from the floor. Therefore, after adding the adaptive scheme, these few normal estimates can be removed, and the reconstruction effect is as smooth as the ground area, as shown in Figure 8(d).
Through the above quantitative and qualitative results, it is not difficult to find that the normal prior can significantly improve the reconstruction effect and geometric details in the indoor scene reconstruction task. The use of adaptive normal prior can reduce the erroneous reconstruction of many geometric structures and regions, and has a good correction effect on thin structures and partially reflective areas, making the reconstruction of these parts more robust and reasonable and close to the real scene, further proving the effectiveness and usability of the adaptive normal prior module in this section.

4.4.2. Ablation experiment of distortion loss function

the effectiveness of the new regularization term, the distortion loss function, proposed in this paper through quantitative and qualitative ablation experimental analysis. Since the distortion loss function L d i s t is only applicable to scenes with floating debris, the ablation experiment is also conducted on these scene datasets. There are two different settings in this ablation experiment: (1) without adding the distortion loss function, denoted as w/o L d i s t ; (2) after adding the distortion loss function, denoted as Ours. By ablating it in 5 scenes with floating debris noise in ScanNet, the quantitative indicators shown in Table 3 can be obtained.
As can be seen from Table 3, Acc and Prec have been significantly improved, which means that the distortion loss function removes some erroneous reconstruction parts and achieves more accurate reconstruction, while Comp and Recall have not changed much, because the method in this paper does not produce too many additional areas for supplementary reconstruction.
Figure 9 shows a visual comparison of a scene with a large number of floating debris. There are a large number of incorrectly reconstructed floating debris in Figure 9(a). After adding the distortion loss function, most of these floating debris in Figure 9(b) are eliminated.
In addition, it also has a good removal effect on single floating debris in some scenes. As shown in Figure 10, there are single floating debris in both scenes in Figure 10(a), which are successfully removed in Figure 10(b).
The ablation experiment results on the distortion loss function show that, both qualitatively and quantitatively, the distortion loss function proposed in Chapter 3 of this paper can effectively remove floating object noise in the 3D model and improve the overall quality of the 3D model.

4.4. Limitations

The comparative experiment part illustrates that the proposed method has advantages over the benchmark model in both quantitative indicators and visualization results, which fully proves the superiority of the proposed method. The ablation experiment part proves the effectiveness of each module of the proposed method. Nevertheless, the proposed method still has some limitations in some specific scenarios.
For scenes with messy objects, the reconstruction effect of this method is not perfect. Because in the 3D reconstruction task of indoor scenes, the arrangement and combination of objects will greatly affect the reconstruction process. As shown in Figure 11 , there are many irregularly shaped objects on the table in the input image, and they are placed in overlapping and mutually occluding situations. For soft and transparent objects, such as plastic bags, it is difficult to accurately estimate their surface details because their appearance features are not easy to capture. Although this method can reconstruct its general outline, it is difficult to judge that this is a plastic bag based on the outline. The reconstruction of such soft and non-solid objects in the scene has always been a difficult problem, and even the GT model obtained by scanning has not been able to restore this part well.
In addition, the fuzziness of the input image is also crucial to the reconstruction result. If the input image has a certain amount of camera blur as shown in Figure 5-8 , many details of the object will be lost in the image, and the loss of these details increases the difficulty of reconstruction. This blur can also lead to inaccurate feature point detection, affecting the feature extraction and feature matching process. This blur can also affect the reconstruction of some areas with insufficient texture features, such as the dividing line and gap between the drawers in Figure 11. Due to the image blur, the area is incorrectly reconstructed.

5. Conclusions

This paper proposes a neural implicit 3D reconstruction method. Based on the implicit expression of neural radiation field and SDF, a method for indoor scene reconstruction based on adaptive normal prior is proposed. The adaptive normal prior optimizes the geometric learning process. The entire indoor scene is reconstructed to obtain a high-quality explicit 3D mesh model. In the future, the scene can be deblurred while maintaining geometric consistency to enhance the effect of 3D reconstruction of blurred scenes. In addition, when there are many objects and elements in the scene and they are irregular, more priors are introduced to allow the neural network to obtain more useful information to accurately learn and understand the elements in the scene, thereby improving the reconstruction effect of irregular objects.

Author Contributions

Conceptualization, Zhaoji Lin and Yutao Huang; methodology, Zhaoji Lin and Yutao Huang; validation, Zhaoji Lin and Yutao Huang; formal analysis, Zhaoji Lin, Yutao Huang and Li Yao; investigation, Zhaoji Lin, Yutao Huang and Li Yao; resources, Zhaoji Lin and Yutao Huang; data curation, Zhaoji Lin and Yutao Huang; writing—original draft preparation, Zhaoji Lin and Yutao Huang; writing—review and editing, Zhaoji Lin and Li Yao; visualization, Zhaoji Lin and Yutao Huang; supervision, Li Yao; project administration, Li Yao.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

The dataset used in this study is open access and can be found here: scanNet dataset: http://www.scan-net.org/; Hypersim dataset: https://github.com/apple/ml-hypersim; Replica dataset: https://github.com/facebookresearch/Replica-Dataset/releases

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. KANG Z, YANG J, YANG Z, et al. A review of techniques for 3d reconstruction of indoor environments. ISPRS International Journal of Geo-Information, 2020, 9(5):330. [CrossRef]
  2. LI J, GAO W, WU Y, et al. High-quality indoor scene 3d reconstruction with rgb-d cameras: A brief review. Computational Visual Media, 2022, 8(3):369-393. [CrossRef]
  3. SCHONBERGER J L, FRAHM J M. Structure-from-motion revisited. Proceedings of the IEEE conference on computer vision and pattern recognition. 2016. 4104-4113.
  4. SCHÖNBERGER J L, ZHENG E, FRAHM J M, et al. Pixelwise view selection for unstructured multi-view stereo. Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, October 11-14, 2016, Proceedings, Part III 14. Springer, 2016. 501-518. [CrossRef]
  5. XU Q, TAO W. Planar prior assisted patchmatch multi-view stereo. Proceedings of the AAAI conference on artificial intelligence: volume 34. 2020. 12516-12523.
  6. YU Z, GAO S. Fast-mvsnet: Sparse-to-dense multi-view stereo with learned propagation and gauss-newton refinement. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2020. 1949-1958.
  7. DING Y, YUAN W, ZHU Q, et al. Transmvsnet: Global context-aware multi-view stereo network with transformers. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2022. 8585-8594.
  8. XU H, ZHOU Z, QIAO Y, et al. Self-supervised multi-view stereo via effective cosegmentation and data-augmentation. Proceedings of the AAAI Conference on Artificial Intelligence: volume 35. 2021. 3030-3038. ttps://doi.org/10.1609/aaai.v35i4.16411.
  9. Yang H, Chen R, An S P, Wei H and Zhang H. The growth of image-related three dimensional reconstruction techniquesin deep learning-driven era: a critical summary. Journal of Image and Graphics. 2023, 28(08):2396-2409.
  10. MUREZ Z, VAN AS T, BARTOLOZZI J, et al. Atlas: End-to-end 3d scene reconstruction from posed images. Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part VII 16. Springer, 2020. 414-431.
  11. SUN J, XIE Y, CHEN L, et al. Neuralrecon: Real-time coherent 3d reconstruction from monocular video. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2021. 15598-15607.
  12. Liu S, Zhang Y, Peng S, et al. Dist: Rendering deep implicit signed distance function with differentiable sphere tracing[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020: 2019-2028.
  13. Yariv L, Kasten Y, Moran D, et al. Multiview neural surface reconstruction by disentangling geometry and appearance. Advances in Neural Information Processing Systems, 2020, 33: 2492-2502.
  14. Wang P, Liu L, Liu Y, et al. Neus: Learning neural implicit surfaces by volume rendering for multi-view reconstruction. arXiv preprint. arXiv:2106.10689, 2021.
  15. Yariv L, Gu J, Kasten Y, et al. Volume rendering of neural implicit surfaces. Advances in Neural Information Processing Systems, 2021, 34: 4805-4815.
  16. Barron, Jonathan T., et al. "Mip-nerf 360: Unbounded anti-aliased neural radiance fields." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2022.
  17. Liu L, Gu J, Zaw Lin K, et al. Neural sparse voxel fields. Advances in Neural Information Processing Systems, 2020, 33: 15651-15663.
  18. Rebain, Daniel, et al. "Lolnerf: Learn from one look." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2022.
  19. Gafni, Guy, et al. "Dynamic neural radiance fields for monocular 4d facial avatar reconstruction." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2021.
  20. Do T, Vuong K, Roumeliotis SI, et al. Surface normal estimation of tilted images via spatial rectifier[C]//Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part IV 16. Springer International Publishing, 2020: 265-280.
  21. DAI A, CHANG A X, SAVVA M, et al. Scannet: Richly-annotated 3d reconstructions of indoor scenes. Proceedings of the IEEE conference on computer vision and pattern recognition. 2017. 5828-5839.
  22. ROBERTS M, RAMAPURAM J, RANJAN A, et al. Hypersim: A photorealistic synthetic dataset for holistic indoor scene understanding. Proceedings of the IEEE/CVF international conference on computer vision. 2021. 10912-10922.
  23. STRAUB J, WHELAN T, MA L, et al. The replica dataset: A digital replica of indoor spaces. arXiv preprint. arXiv:1906.05797, 2019.
  24. Mildenhall B, Srinivasan PP, Tancik M, et al. Nerf: Representing scenes as neural radiance fields for view synthesis. Communications of the ACM, 2021, 65(1): 99-106.
  25. GUO H, PENG S, LIN H, et al. Neural 3d scene reconstruction with the Manhattan-world assumption. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2022. 5511-5520.
  26. YU Z, PENG S, NIEMEYER M, et al. Monosdf: Exploring monocular geometric cues for neural implicit surface reconstruction. Advances in neural information processing systems, 2022, 35:25018-25032.
  27. Zhu J, Huo Y, Ye Q, et al. I2-SDF: Intrinsic Indoor Scene Reconstruction and Editing via Raytracing in Neural SDFs[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2023: 12489- 12498.
Preprints 116510 g001
Figure 1. (a) Distortion of reconstructed 3D models under uneven lighting conditions; (b) Distortion of 3D reconstruction of smooth planar texture areas; (c) Floating debris noise in 3D reconstruction.
Figure 1. (a) Distortion of reconstructed 3D models under uneven lighting conditions; (b) Distortion of 3D reconstruction of smooth planar texture areas; (c) Floating debris noise in 3D reconstruction.
Preprints 116510 g001
Preprints 116510 g002
Figure 2. overall framework of the method.
Figure 2. overall framework of the method.
Preprints 116510 g002
Preprints 116510 g003
Figure 3. (a)The normal estimation is inaccurate in some fine structures, such as chair legs based on TiltedSN normal estimation module; (b) Use an adaptive normal prior method to derive accurate normal based on the consistency of adjacent images.
Figure 3. (a)The normal estimation is inaccurate in some fine structures, such as chair legs based on TiltedSN normal estimation module; (b) Use an adaptive normal prior method to derive accurate normal based on the consistency of adjacent images.
Preprints 116510 g003
Preprints 116510 g004
Figure 4. Neural implicit reconstruction process.
Figure 4. Neural implicit reconstruction process.
Preprints 116510 g004
Preprints 116510 g005
Figure 5. Distribution diagram of distance and weight values between sampling points.
Figure 5. Distribution diagram of distance and weight values between sampling points.
Preprints 116510 g005
Preprints 116510 g006
Figure 6. (a)Comparison of 3D models; (b) Comparison of the specific details in the red dashed box.
Figure 6. (a)Comparison of 3D models; (b) Comparison of the specific details in the red dashed box.
Preprints 116510 g006
Preprints 116510 g007
Figure 7. Qualitive comparison for thin structure areas: (a) reference image; (b) a model reconstructed without using normal prior; (c)a model reconstructed with normal prior and without adaptive scheme;(d) a model reconstructed with normal prior and adaptive scheme.
Figure 7. Qualitive comparison for thin structure areas: (a) reference image; (b) a model reconstructed without using normal prior; (c)a model reconstructed with normal prior and without adaptive scheme;(d) a model reconstructed with normal prior and adaptive scheme.
Preprints 116510 g007
Preprints 116510 g008
Figure 8. Qualitive comparison for reflective areas: (a) reference image; (b) a model reconstructed without using normal prior; (c)a model reconstructed with normal prior and without adaptive scheme;(d) a model reconstructed with normal prior and adaptive scheme.
Figure 8. Qualitive comparison for reflective areas: (a) reference image; (b) a model reconstructed without using normal prior; (c)a model reconstructed with normal prior and without adaptive scheme;(d) a model reconstructed with normal prior and adaptive scheme.
Preprints 116510 g008
Preprints 116510 g009
Figure 9. visual comparison for a scene with a large number of floating debris (a) reconstruction result without adding distortion loss function; (b) reconstruction result with distortion loss function.
Figure 9. visual comparison for a scene with a large number of floating debris (a) reconstruction result without adding distortion loss function; (b) reconstruction result with distortion loss function.
Preprints 116510 g009
Preprints 116510 g010
Figure 10. visual comparison for a scene with single floating debris; (a) reconstruction result without adding distortion loss function; (b) reconstruction result with distortion loss function.
Figure 10. visual comparison for a scene with single floating debris; (a) reconstruction result without adding distortion loss function; (b) reconstruction result with distortion loss function.
Preprints 116510 g010
Preprints 116510 g011
Figure 11. The limitations of this method in the 3D reconstruction of scenes with clutter, occlusion, soft non-solid objects, and blurred images.
Figure 11. The limitations of this method in the 3D reconstruction of scenes with clutter, occlusion, soft non-solid objects, and blurred images.
Preprints 116510 g011
Table 1. Quantitative comparison with other methods.
Table 1. Quantitative comparison with other methods.
Method Acc ↓ Comp ↓ Prec ↑ Recall ↑ F - score ↑
Colmap [3] 0.047 0.235 0.711 0.441 0.537
Atlas [10] 0.211 0.070 0.500 0.659 0.564
NeuralRacon [11] 0.056 0.081 0.545 0.604 0.572
Neus [14] 0.179 0.208 0.313 0.275 0.291
VolSDF [15] 0.414 0.120 0.321 0.394 0.346
NeRF [24] 0.735 0.177 0.131 0.290 0.176
Manhattan-SDF [25] 0.072 0.068 0.621 0.586 0.602
MonoSDF [26] 0.035 0.048 0.799 0.681 0.733
I2-SDF [27] 0.066 0.070 0.605 0.575 0.590
Ours 0.037 0.048 0.801 0.702 0.748
Table 2. Normal geometry prior ablation experiment.
Table 2. Normal geometry prior ablation experiment.
Method Acc ↓ Comp ↓ Prec ↑ Recall ↑ F - score ↑
w/o N 0.183 0.152 0.286 0.290 0.284
w/ N, w/o A 0.050 0.047 0.759 0.699 0.727
Ours 0.037 0.048 0.805 0.709 0.753
Table 3. Distortion loss function ablation experiment.
Table 3. Distortion loss function ablation experiment.
Method Acc ↓ Comp ↓ Prec ↑ Recall ↑ F - score ↑
w / o   L d i s t 0.055 0.052 0.742 0.701 0.721
Ours 0.047 0.052 0.795 0.704 0.746
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated