Prerpints.org logo
Preprint
Article

Advanced Stock Price Prediction with xLSTM-Based Models: Improving Long-Term Forecasting

Altmetrics

Downloads

748

Views

819

Comments

0

This version is not peer-reviewed

Submitted:

29 August 2024

Posted:

29 August 2024

You are already at the latest version

Alerts
Abstract
Stock price prediction has long been a critical area of research in financial modeling. The inherent complexity of financial markets, characterized by both short-term fluctuations and long-term trends, poses significant challenges in accurately capturing underlying patterns. While Long Short-Term Memory (LSTM) networks have shown strong performance in short-term stock price prediction, they struggle with effectively modeling long-term dependencies. In this paper, we propose an advanced stock price prediction model based on the Extended Long Short-Term Memory (xLSTM) algorithm, designed to enhance predictive accuracy over both short and long-term periods. We conduct extensive experiments by building and evaluating models based on xLSTM and LSTM architectures for multiple stocks. Our results demonstrate that the xLSTM model consistently outperforms the LSTM model across all stocks and time horizons, with the performance gap widening as the prediction period extends. The observations underscore the superior capability of the xLSTM-based model to capture long-term patterns in financial data, offering a promising approach for more accurate and reliable stock price predictions.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Predicting stock prices has long been a central focus in financial modeling due to its profound impact on investment strategies, risk management, and market efficiency. The complexity and volatility of financial markets, driven by both short-term fluctuations and long-term trends, make accurate stock price prediction a particularly challenging task [1]. The unpredictable nature of stock prices is further compounded by numerous factors, including economic indicators, market sentiment, and external events, all contributing to the intricate dynamics of financial markets [2,3,4].
Over the years, various machine learning techniques, such as K-Nearest Neighbors (k-NN) [5], AutoRegressive Integrated Moving Average (ARIMA) [6], and XGBoost [7], have been employed to address the problem of stock price prediction. While these methods have provided valuable insights and demonstrated effectiveness in specific contexts, they often fall short of fully capturing the complex and dynamic nature of financial markets. The limitations of these models, particularly in dealing with non-linear relationships and long-term dependencies, have prompted researchers to explore more advanced approaches.
Recent advancements in deep learning have led to the development of more sophisticated models capable of capturing the non-linear relationships inherent in time series data[8]. Among these, Long Short-Term Memory (LSTM) networks have gained prominence for their ability to model temporal dependencies and effectively manage sequential data [9,10,11]. LSTM networks have demonstrated significant improvements in stock price prediction, particularly in capturing short-term market trends [12,13,14]. However, despite their effectiveness, LSTM models face considerable limitations in modeling long-term dependencies, which are crucial for accurate long-term predictions [15,16]. This limitation can result in reduced prediction accuracy, especially when forecasting stock prices over extended periods. A recent innovation, Extended Long Short-Term Memory (xLSTM) architecture, builds upon the traditional LSTM by incorporating mechanisms to better manage and retain information over longer sequences and refining the gating mechanisms to allow for more effective processing of relevant information across sequences of various lengths[17]. xLSTM has demonstrated competitive performance in handling long sequences and large contexts compared to some prominent large language models [18]. However, its potential in financial time series forecasting remains largely unexplored.
In this work, we aim to develop and evaluate an advanced stock price prediction model based on the xLSTM architecture to address the limitations of current approaches in modeling long-term trends. While some studies have leveraged Large Language Models that incorporate news and market sentiment to enhance financial modeling [19,20,21], our focus in this paper is on non-text-based deep learning approaches. We conduct extensive experiments to compare the performance of xLSTM and LSTM models across multiple stocks and a range of prediction horizons. LSTM is chosen as the benchmark for comparison due to its established success in short-term stock price prediction in previous studies. The results demonstrate that our xLSTM model consistently outperforms the traditional LSTM model in both short-term and long-term stock price predictions. These findings underscore the strong potential of xLSTM in financial time series forecasting, offering more accurate and reliable predictions that can enhance decision-making processes in the financial industry.

2. Related Work

2.1. Traditional Methods

Traditional statistical and machine learning models have been extensively studied and applied to a wide range of prediction tasks in both financial [22,23,24] and non-financial domains [25,26,27]. For time-series forecasting tasks, including stock price predictions, Autoregressive Integrated Moving Average (ARIMA) [6], Generalized Autoregressive Conditional Heteroskedasticity (GARCH) [28], and Exponential Smoothing (ETS) [29] have been widely used. These models were effective in capturing linear relationships and volatility clustering, which are typical in financial time series data. However, their performance was limited by their inability to model complex non-linear patterns that are often present in stock market movements. Other machine learning methods such as Support Vector Machines (SVM) [30] and Random Forests [31] have also been applied for stock price predictions, with varying degrees of success, but they still face challenges in effectively capturing the temporal dynamics of financial data.

2.2. Deep Learning Approaches

Deep learning has revolutionized various fields by offering powerful models capable of capturing complex patterns in data. Its applications span numerous domains including but not limited to healthcare [32,33,34,35,36], retail[37], civil-engineering[38], psychology [39] and finance[40]. For stock price predictions, Recurrent Neural Networks (RNNs) have been particularly effective due to their ability to handle sequential data leveraging a hidden state that captures information from previous time steps. However, traditional RNNs suffer from issues such as vanishing and exploding gradients, which limits their ability to capture long-term dependencies in time series data [41]. Long Short-Term Memory (LSTM) networks are developed to overcome some of these limitations [42]. Specifically, the featuring memory cells and gating mechanisms of LSTM, enable it to retain information over longer sequences, making it particularly effective for time series forecasting. It has been shown that LSTM networks significantly outperform traditional models in predicting stock prices by effectively capturing complex temporal dependencies, especially in short-term forecasts [43,44].

2.3. Limitations of LSTM

Despite its success, LSTM is not without limitations, particularly when applied to long-term stock price prediction. Studies have shown that while LSTM models are robust for short to medium-term predictions, their performance tends to degrade when predicting over longer horizons. [41]. To address the limitations of LSTM, several advancements and alternative methods have been introduced. Gated Recurrent Units (GRU), for example, offers a simplified architecture with fewer parameters compared to LSTM, making them easier to train while still capturing long-term dependencies [45]. Attention mechanisms, as seen in Transformer models, have also been applied to time series forecasting, allowing models to focus on the most relevant parts of the input sequence and improving performance in tasks like stock price prediction [46]. Among the advancements in RNNs, xLSTM has emerged as a promising extension of LSTM, designed to improve the model’s capacity to handle complex, long-range dependencies through architectural modifications like enhanced gradient flow and multi-scale temporal processing [17]. In stock price prediction, short-term and long-term forecasts serve different strategic purposes. Short-term predictions are often driven by recent market movements and are critical for day trading and high-frequency trading strategies, whereas long-term predictions rely on capturing broader market trends, which are more relevant for investment strategies with extended time horizons. Given the fundamentally different drivers for short-term and long-term stock price changes, there is a clear need for prediction models that are robust for predictions across different time horizons.

3. Methodology

3.1. xLSTM

The Extended Long Short-Term Memory (xLSTM) model extends the standard LSTM by incorporating additional mechanisms, such as enhanced memory cells and gating modifications. These improvements help the model better focus on relevant parts of the input sequence, making xLSTM particularly effective in scenarios where the relationship between past and future values is complex and non-linear. This is especially useful for stock price prediction across varying time horizons, where market conditions can shift rapidly. Some relevant innovations are explained below.
  • Enhanced Memory Cells: The xLSTM introduces modifications that allow memory cells to operate with more flexibility and efficiency. Specifically, xLSTM includes two variants of LSTM, sLSTM and mLSTM. The sLSTM variant uses scalar memory updates, which simplify the memory operations, allowing for faster and more efficient computation. On the other hand, mLSTM employs a matrix memory structure that can handle more complex dependencies across longer sequences. The matrix memory enables the model for parallel computations, significantly improving its ability to manage and retain information across extended periods, which is particularly beneficial in scenarios such as long-term stock price forecasting.
  • Exponential Gating: Gating is central to the operation of LSTM networks, controlling the flow of information through input, forget, and output gates. In xLSTM, these gates are modified to include exponential gating and advanced normalization techniques, as shown in Equation (1).
    g t = exp ( W g · x t + U g · h t − 1 + b g )
    where g t represents the input or forget gate at time t, W g and U g are weight matrices, and b g is the bias. The exponential function exp provides a more flexible and dynamic adjustment of gate values, allowing for a more stable gradient flow during training. Exponential gating helps manage the vanishing gradient problem more effectively by dynamically adjusting how much past information is retained or forgotten during the training process. The adjustment ensures that relevant information is preserved over long sequences, while less important data is filtered out, making the model more efficient in learning and predicting complex patterns. This is crucial in financial applications where retaining key market trends while discarding noise can significantly enhance prediction accuracy.

3.2. Dataset

Data Collection These enhancements make xLSTM particularly well-suited for scenarios involving complex, non-linear relationships and long-term dependencies, which are prevalent in stock markets.
This study employs historical stock price data sourced from Yahoo Finance [47] for three major companies: Apple, Johnson & Johnson, and Nike. The data spans from January 1, 2014, to December 31, 2023, covering a broad range of market conditions including bullish, bearish, and volatile phases. These companies are selected based on their significant market capitalization, industry leadership, and consistent trading volumes, which ensure that the data is representative of different sectors, i.e. consumer goods, healthcare, and technology, and is robust for time series analysis. We select the daily `Close’ price as the prediction target. The `Close’ price is a critical indicator of market sentiment and is widely used in financial forecasting due to its ability to encapsulate the outcome of daily trading activities.
Data Pre-processing Given the sequential nature of stock prices, the dataset is structured into sequences of 60 consecutive days. This sequence length is strategically chosen to capture sufficient historical context, balancing the need to model relevant market dynamics without introducing excessive noise. This approach is aligned with best practices in financial time series forecasting, where similar window lengths effectively capture meaningful patterns in stock price movements. Additionally, multiple future time points are selected in our work: t+1, t+3, t+5, t+10, and t+15 days to allow for a comprehensive analysis of predictive performance across both short-term and long-term horizons. Furthermore, to standardize the data and facilitate effective training of models, the ’Close’ prices are normalized using a MinMaxScaler, with a range from 0 to 1. Normalization is crucial in time series modeling, especially when using neural networks, as it ensures consistent input data and improves model convergence and stability.

4. Experiments

4.1. Experiment Setup

We conduct a series of experiments across multiple stocks and prediction horizons to evaluate the effectiveness of the xLSTM model in comparison to the traditional LSTM model.
Model Training Both the xLSTM and LSTM models are trained using the pre-processed dataset described in the Methodology section. For each stock, the data was split into three sets: 60% for training, 20% for validation, and 20% for testing. Each model is trained separately on a per-stock and per-time horizon basis to ensure that the models are tailored to the unique characteristics of each stock and the specific prediction horizons. For example, the xLSTM and LSTM models are independently trained on the NIKE stock for each of the following prediction horizons: t+1, t+3, t+5, t+10, and t+15 days.
Hyperparameter Tuning To ensure a fair and thorough comparison between the xLSTM and LSTM models, we implement a hyperparameter tuning process that was carefully tailored to optimize each model individually. We choose a fixed value or range for some hyperparameters shared by both models across all prediction horizons to maintain fairness and consistency. Specifically, a consistent dropout rate of 0.1 is applied to both models to prevent overfitting, with early stopping based on validation performance to ensure that neither model is over-trained. Additionally, we set the learning rate uniformly at 0.001 across all training tasks to ensure stable and comparable training dynamics. The number of layers is explored in the range of 2 to 4, while the hidden size is varied between 32, 64, and 128. We also include key hyperparameters that are unique and critical to the xLSTM model, including the number of heads and kernel sizes for both the sLSTM and mLSTM components, as well as the mLSTM projection block sizes. We implement Random Search to fine-tune all hyperparameters to optimize the performance of both models over each stock and each prediction horizon. The best-performing model configuration is selected based on its performance on the validation set for final evaluation.
Model Evaluation We evaluate the trained and tuned xLSTM and LSTM models by assessing prediction accuracy on the test set for each stock over each prediction horizon. This comparison provides a comprehensive understanding of how well each model performs on diverse stocks as well as in short-term and long-term predictions. Specific evaluation metrics are documented in the following section.

4.2. Evaluation Metrics

To thoroughly evaluate the performance of the xLSTM and LSTM models, we employed three key metrics: Root Mean Squared Error (RMSE), R-squared ( R 2 ), and Net Error Reduction (NER). Each of these metrics provides a unique perspective on models’ predictive accuracy and ability to capture both short-term and long-term trends in stock prices.
RMSEis a standard metric used to measure the average magnitude of prediction errors. RMSE is particularly useful for understanding the overall accuracy of the model, as it penalizes larger errors more heavily. A lower RMSE indicates higher predictive accuracy. RMSE is calculated as follows:
RMSE = 1 n ∑ i = 1 n ( y ^ i − y i ) 2
where y ^ i represents the predicted stock price, y i represents the actual stock price, and n is the total number of observations.
R 2 is a statistical measure that represents the proportion of variance in the dependent variable (stock prices) that can be explained by the model. R 2 indicates how well the model’s predictions match the actual data, with values closer to 1 indicating a better fit. The R 2 is calculated as follows:
R 2 = 1 − ∑ i = 1 n ( y i − y ^ i ) 2 ∑ i = 1 n ( y i − y ¯ ) 2
where y ¯ is the mean of the actual stock prices.
ERis a metric introduced to quantify the net difference in predictive accuracy between the xLSTM and LSTM models across various stocks and prediction horizons. This metric is particularly useful for understanding how the performance gap between the two models changes as the prediction window increases. A positive ER indicates that the xLSTM model outperforms the LSTM model by reducing the error, while a negative ER suggests that the LSTM model has better predictive accuracy. By analyzing ER across different prediction horizons, we can gain insights into how the relative performance of the models evolves with the length of the forecast period. ER is calculated as:
ER = RMSE LSTM − RMSE xLSTM

5. Results

5.1. Stock-Specific Performance

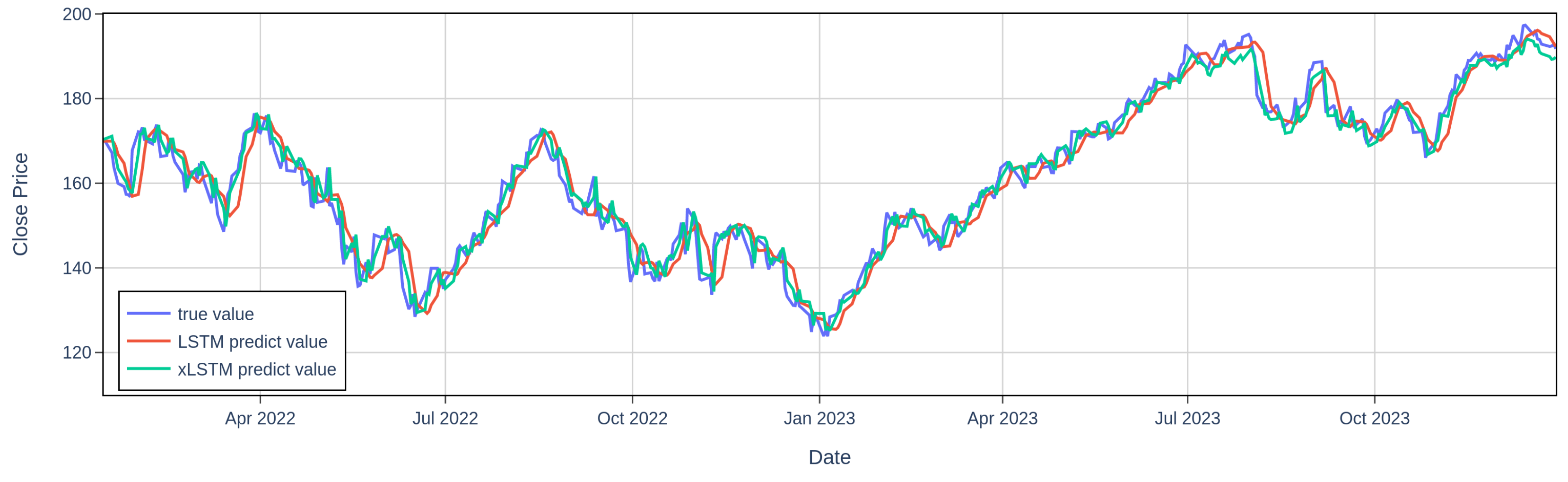
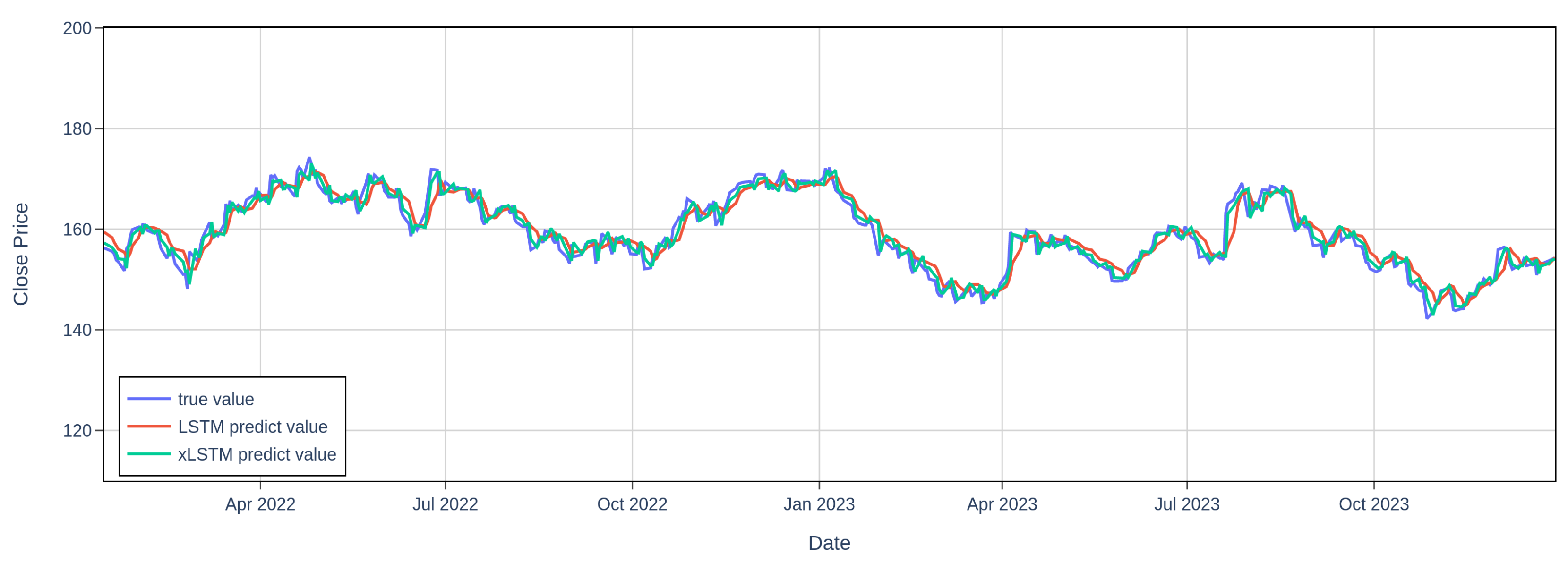
Table 1 on page 4 reveals clear differences in the predictability of the three stocks due to different magnitudes in market volatility. For example, as illustrated in Figure 1 and Figure 2 on page 4, AAPL exhibits higher market volatility than JNJ from 2022 to 2023. For the results, AAPL consistently exhibits the highest RMSE and the lowest R 2 across all models and prediction horizons, reflecting the challenges both LSTM and xLSTM face in forecasting highly volatile stocks. In contrast, JNJ, consistently shows the lowest RMSE and the highest R 2 , indicating that both models are more effective at forecasting less volatile stocks where price movements are more stable. Despite the varying levels of volatility, xLSTM consistently outperforms LSTM across all stocks and time horizons. Even for the more volatile AAPL, xLSTM reduces prediction errors more effectively, demonstrating its superior ability to handle complex market conditions. This consistent outperformance underscores xLSTM’s robustness and adaptability across different market environments.

5.2. Model Performance across Prediction Horizons

Table 1 also shows that both LSTM and xLSTM models experience a decline in predictive accuracy, reflected in increasing RMSE and decreasing R 2 , as the prediction horizon extends from 1 to 15 days. This trend is consistent across all stocks and highlights the common challenge of maintaining accuracy over longer time horizons in time series forecasting. However, the xLSTM model consistently outperforms LSTM across all stocks and prediction horizons. The xLSTM’s lower RMSE and higher R 2 demonstrate its enhanced capability to model complex temporal dependencies, particularly over extended periods. The superior performance is likely due to xLSTM’s advanced architecture, which includes improved gating mechanisms and memory management, enabling it to retain and utilize relevant information more effectively than LSTM as the forecast horizon lengthens.

5.3. Performance Gap across Time Horizons

Table 2 highlights the increasing performance gap between xLSTM and LSTM, measured by Error Reduction (ER), as the prediction horizon lengthens. The gap becomes more pronounced as the forecasting task grows more challenging with longer time horizons. While both models show increased RMSE as the horizon extends from 1 to 15 days, the rate of increase is notably slower for xLSTM. This suggests that xLSTM is more resilient to the typical degradation in predictive accuracy that accompanies longer forecasting periods. The widening gap underscores LSTM’s limitations in handling long-term dependencies, where its accuracy declines significantly. In contrast, xLSTM manages these dependencies more effectively, maintaining a more stable error profile across different prediction horizons.

5.4. Practical Implications

LSTM models have long been recognized for their strong performance in time series forecasting, especially in financial contexts, where they have outperformed traditional models. However, our study demonstrates that xLSTM not only builds on these strengths but also significantly enhances predictive accuracy, particularly as the forecast horizon extends. The practical implications of xLSTM’s superior performance are profound for financial analysts and investors. In scenarios where long-term forecasts are critical, xLSTM’s enhanced accuracy can lead to more reliable predictions, reducing uncertainty, improving decision-making, and potentially enhancing financial outcomes. Moreover, xLSTM’s robustness across different stocks and market conditions suggests it is a versatile and dependable tool for a wide range of financial forecasting applications. Whether dealing with volatile markets or stable trends, xLSTM’s ability to maintain lower prediction errors over extended periods positions it as a valuable asset in the financial industry.

6. Conclusions

In this work, we build an enhanced stock price prediction model using xLSTM to address the limitations of traditional LSTM models in managing long-term dependencies. Through extensive experiments conducted across three major stocks, Apple, Johnson & Johnson, and Nike, and various prediction horizons, we demonstrate that the xLSTM model consistently outperforms the standard LSTM. Furthermore, as the prediction horizon extends, the performance gap between xLSTM and LSTM becomes increasingly evident, underscoring xLSTM’s ability to maintain accuracy where traditional models tend to falter.
Despite the promising results, several limitations of our study warrant further exploration. For example, our work focuses exclusively on historical stock prices without incorporating external factors such as macroeconomic indicators, news sentiment, or market volatility indices. Including these variables could improve the model’s predictive accuracy, particularly in volatile markets. Future work should explore how the integration of such external factors can further enhance xLSTM’s performance. Meanwhile, our study focuses on specific prediction horizons of 1, 3, 5, 10, and 15 days. This approach may not fully capture the performance of xLSTM across other relevant time frames, such as intraday predictions or longer-term forecasts extending to months or years. Expanding the range of prediction horizons could provide deeper insights into the model’s applicability to different investment strategies. Lastly, our experiments are conducted on a small set of three stocks. While these stocks are chosen for their market significance, the findings may not generalize across a broader range of financial instruments or different market conditions. Future research should validate these results using a more extensive and diverse dataset, encompassing stocks from various sectors and international markets.

References

  1. Ma, F.; Wang, J.; Wahab, M. I. M.; Ma, Y. Stock market volatility predictability in a data-rich world: A new insight. International Journal of Forecasting 2023, 39, 1804–1819. [Google Scholar] [CrossRef]
  2. Feng, F.; He, X.; Wang, X.; Luo, C.; Liu, Y.; Chua, T. S. Temporal relational ranking for stock prediction. ACM Transactions on Information Systems (TOIS) 2019, 37, 1–30. [Google Scholar] [CrossRef]
  3. Baker, M.; Wurgler, J. Investor sentiment and the cross-section of stock returns. The journal of Finance 2006, 61, 1645–1680. [Google Scholar] [CrossRef]
  4. Naeem, M. A.; Qureshi, F.; Farid, S.; Tiwari, A. K.; Elheddad, M. Time-frequency information transmission among financial markets: evidence from implied volatility. Annals of Operations Research 2024, 334, 701–729. [Google Scholar] [CrossRef]
  5. Alkhatib, K.; Najadat, H.; Hmeidi, I.; Shatnawi, M. K. A. Stock price prediction using k-nearest neighbor (knn) algorithm. International Journal of Business, Humanities and Technology 2013, 3, 32–44. [Google Scholar]
  6. Khanderwal, S.; Mohanty, D. Stock price prediction using arima model. International Journal of Marketing & Human Resource Research 2021, 2, 98–107. [Google Scholar]
  7. Yun, K. K.; Yoon, S. W.; Won, D. Prediction of stock price direction using a hybrid ga-xgboost algorithm with a three-stage feature engineering process. Expert Systems with Applications 2021, 186, 115716. [Google Scholar] [CrossRef]
  8. Ismail Fawaz, H.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P. A. Deep learning for time series classification: a review. Data mining and knowledge discovery 2019, 33, 917–963. [Google Scholar] [CrossRef]
  9. Hochreiter, S. Long short-term memory; Neural Computation MIT-Press, 1997. [Google Scholar]
  10. Sundermeyer, M.; Ney, H.; Schlüter, R. From feedforward to recurrent lstm neural networks for language modeling. IEEE/ACM Transactions on Audio, Speech, and Language Processing 2015, 23, 517–529. [Google Scholar] [CrossRef]
  11. Ni, H.; Meng, S.; Geng, X.; Li, P.; Li, Z.; Chen, X.; Wang, X.; Zhang, S. Time series modeling for heart rate prediction: From arima to transformers. arXiv 2024, arXiv:2406.12199. [Google Scholar]
  12. Sunny, M.A.I.; Maswood, M.M.S.; Alharbi, A.G. Deep learning-based stock price prediction using lstm and bi-directional lstm model. In 2020 2nd novel intelligent and leading emerging sciences conference (NILES); IEEE, 2020; pp. 87–92. [Google Scholar]
  13. Mehtab, S.; Sen, J.; Dutta, A. Stock price prediction using machine learning and lstm-based deep learning models. In Machine Learning and Metaheuristics Algorithms, and Applications: Second Symposium, SoMMA 2020, Chennai, India, October 14–17, 2020, Revised Selected Papers 2; Springer, 2021; pp. 88–106. [Google Scholar]
  14. Md, A.Q.; Kapoor, S.; AV, C.J.; Sivaraman, A.K.; Tee, K.F.; Sabireen, H.; Janakiraman, N. Novel optimization approach for stock price forecasting using multi-layered sequential lstm. Applied Soft Computing 2023, 134, 109830. [Google Scholar] [CrossRef]
  15. Gers, F.A.; Schraudolph, N.N.; Schmidhuber, J. Learning precise timing with lstm recurrent networks. Journal of machine learning research 2002, 3, 115–143. [Google Scholar]
  16. Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
  17. Beck, M.; Pöppel, K.; Spanring, M.; Auer, A.; Prudnikova, O.; Kopp, M.; Klambauer, G.; Brandstetter, J.; Hochreiter, S. xlstm: Extended long short-term memory. arXiv 2024, arXiv:2405.04517. [Google Scholar]
  18. Alharthi, M.; Mahmood, A. xlstmtime: Long-term time series forecasting with xlstm. AI 2024, 5, 1482–1495. [Google Scholar] [CrossRef]
  19. Ni, H.; Meng, S.; Chen, X.; Zhao, Z.; Chen, A.; Li, P.; Zhang, S.; Yin, Q.; Wang, Y.; Chan, Y. Harnessing earnings reports for stock predictions: A qlora-enhanced llm approach. arXiv 2024, arXiv:2408.06634. [Google Scholar]
  20. Mo, K.; Liu, W.; Xu, X.; Yu, C.; Zou, Y.; Xia, F. Fine-tuning gemma-7b for enhanced sentiment analysis of financial news headlines. arXiv 2024, arXiv:2406.13626. [Google Scholar]
  21. Gu, W.; Zhong, Y.; Li, S.; Wei, C.; Dong, L.; Wang, Z.; Yan, C. Predicting stock prices with finbert-lstm: Integrating news sentiment analysis. arXiv 2024, arXiv:2407.16150. [Google Scholar]
  22. Yan, Y. Influencing factors of housing price in new york-analysis: Based on excel multi-regression model. In Proceedings of the International Conference on Big Data Economy and Digital Management; 2022. [Google Scholar] [CrossRef]
  23. Zhao, S.; Dong, Z.; Cao, Z.; Douady, R. Hedge fund portfolio construction using polymodel theory and itransformer. arXiv 2024, arXiv:2408.03320. [Google Scholar]
  24. Yan, C.; Weng, Y.; Wang, J.; Zhao, Y.; Zou, Y.; Li, Z.; Baltimore, U.S. Enhancing credit card fraud detection through adaptive model optimization. 2024. [Google Scholar] [CrossRef]
  25. Hu, T.; Zhu, W.; Yan, Y. Artificial intelligence aspect of transportation analysis using large scale systems. In Proceedings of the 2023 6th Artificial Intelligence and Cloud Computing Conference; 2023; pp. 54–59. [Google Scholar]
  26. Chen, J.; Xu, W.; Wang, J. Prediction of car purchase amount based on genetic algorithm optimised bp neural network regression algorithm. Preprints 2024. [Google Scholar] [CrossRef]
  27. Zhao, S.; Lu, J.; Yang, J.; Chow, E.; Xi, Y. Efficient two-stage gaussian process regression via automatic kernel search and subsampling. arXiv 2024, arXiv:2405.13785. [Google Scholar]
  28. Engle, R.F. Autoregressive conditional heteroscedasticity with estimates of the variance of united kingdom inflation. Econometrica: Journal of the econometric society 1982, 987–1007. [Google Scholar] [CrossRef]
  29. Gardner, E.S., Jr. Exponential smoothing: The state of the art. Journal of forecasting 1985, 4, 1–28. [Google Scholar] [CrossRef]
  30. Lin, Y.; Guo, H.; Hu, J. An svm-based approach for stock market trend prediction. In The 2013 international joint conference on neural networks (IJCNN); IEEE, 2013; pp. 1–7. [Google Scholar]
  31. Khaidem, L.; Saha, S.; Dey, S.R. Predicting the direction of stock market prices using random forest. arXiv 2016, arXiv:1605.00003. [Google Scholar]
  32. Wu, C.; Yang, X.; Gilkes, E.G.; Cui, H.; Choi, J.; Sun, N.; Liao, Z.; Fan, B.; Santillana, M.; Celi, L.; Silva, P. De-identification and obfuscation of gender attributes from retinal scans. In Workshop on Clinical Image-Based Procedures; Springer, 2023; pp. 91–101. [Google Scholar]
  33. Zhong, Y.; Liu, Y.; Gao, E.; Wei, C.; Wang, Z.; Yan, C. Deep learning solutions for pneumonia detection: Performance comparison of custom and transfer learning models. medRxiv 2024, 2024–06. [Google Scholar]
  34. Zhang, Q.; Qi, W.; Zheng, H.; Shen, X. Cu-net: a u-net architecture for efficient brain-tumor segmentation on brats 2019 dataset. arXiv 2024, arXiv:2406.13113. [Google Scholar]
  35. Dang, B.; Ma, D.; Li, S.; Qi, Z.; Zhu, E.Y. Deep learning-based snore sound analysis for the detection of night-time breathing disorders. Applied and Computational Engineering 2024, 76, 109–114. [Google Scholar] [CrossRef]
  36. Dang, B.; Zhao, W.; Li, Y.; Ma, D.; Yu, Q.; Zhu, E.Y. Real-time pill identification for the visually impaired using deep learning. arXiv 2024, arXiv:2405.05983. [Google Scholar]
  37. Tan, L.; Liu, S.; Gao, J.; Liu, X.; Chu, L.; Jiang, H. Enhanced self-checkout system for retail based on improved yolov10. arXiv 2024, arXiv:2407.21308. [Google Scholar]
  38. Dan, H.C.; Lu, B.; Li, M. Evaluation of asphalt pavement texture using multiview stereo reconstruction based on deep learning. Construction and Building Materials 2024, 412, 134837. [Google Scholar] [CrossRef]
  39. Li, P.; Abouelenien, M.; Mihalcea, R. Deception detection from linguistic and physiological data streams using bimodal convolutional neural networks. arXiv 2024, arXiv:2311.10944. [Google Scholar]
  40. Yu, C.; Xu, Y.; Cao, J.; Zhang, Y.; Jin, Y.; Zhu, M. Credit card fraud detection using advanced transformer model. arXiv 2024, arXiv:2406.03733. [Google Scholar]
  41. Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE transactions on neural networks 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
  42. Schmidhuber, J.; Hochreiter, S.; et al. Long short-term memory. Neural Comput 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
  43. Fischer, T.; Krauss, C. Deep learning with long short-term memory networks for financial market predictions. European journal of operational research 2018, 270, 654–669. [Google Scholar] [CrossRef]
  44. Bao, W.; Yue, J.; Rao, Y. A deep learning framework for financial time series using stacked autoencoders and long-short term memory. PloS one 2017, 12, e0180944. [Google Scholar] [CrossRef] [PubMed]
  45. Cho, K. Learning phrase representations using rnn encoder-decoder for statistical machine translation. arXiv 2020, arXiv:1406.1078. [Google Scholar]
  46. Vaswani, A. Attention is all you need. Advances in Neural Information Processing Systems 2017. [Google Scholar]
  47. Finance, Y. Yahoo finance historical stock data. 15 July. Available online: https://finance.yahoo.com (accessed on 15 July 2024).
Preprints 116611 g001
Figure 1. AAPL 1-Day Stock Predictions by xLSTM and LSTM Models
Figure 1. AAPL 1-Day Stock Predictions by xLSTM and LSTM Models
Preprints 116611 g001
Preprints 116611 g002
Figure 2. JNJ 1-Day Stock Predictions by xLSTM and LSTM Models
Figure 2. JNJ 1-Day Stock Predictions by xLSTM and LSTM Models
Preprints 116611 g002
Table 1. Overall Performance Across Time Horizons.
Table 1. Overall Performance Across Time Horizons.
STOCK MODEL T = 1 T = 3 T = 5 T = 10 T = 15
RMSE↓ R2 ↑ RMSE↓ R2 ↑ RMSE↓ R2 ↑ RMSE↓ R2 ↑ RMSE↓ R2 ↑
AAPL LSTM 4.341 0.887 6.513 0.768 7.839 0.665 10.416 0.464 12.433 0.261
xLSTM 3.020 0.941 5.155 0.831 6.347 0.875 8.750 0.742 10.500 0.376
JNJ LSTM 2.381 0.941 3.613 0.882 4.340 0.834 5.429 0.712 6.413 0.601
xLSTM 1.716 0.972 2.915 0.917 3.605 0.875 4.670 0.568 5.616 0.659
NKE LSTM 3.516 0.926 5.364 0.835 6.614 0.763 9.094 0.515 11.128 0.320
xLSTM 2.522 0.962 4.334 0.886 5.474 0.818 7.817 0.625 9.690 0.419
AVG LSTM 3.413 0.918 5.163 0.828 6.264 0.754 8.313 0.564 9.991 0.394
xLSTM 2.419 0.958 4.135 0.878 5.142 0.812 7.079 0.652 8.602 0.484
Table 2. Error Reduction Across Time Horizons.
Table 2. Error Reduction Across Time Horizons.
STOCK T = 1 T = 3 T = 5 T = 10 T = 15
AAPL 1.321 1.358 1.492 1.666 1.933
JNJ 0.665 0.698 0.735 0.759 0.797
NKE 0.994 1.030 1.140 1.277 1.438
AVG 0.993 1.029 1.122 1.234 1.389
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated