Prerpints.org logo
Preprint
Article

Optimization of Solar-Assisted CCHP Systems: Enhancing Efficiency and Reducing Emissions through Harris Hawks-Based Mathematical Modeling

Altmetrics

Downloads

72

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

28 August 2024

Posted:

29 August 2024

You are already at the latest version

Alerts
Abstract
The increasing demand for energy, driven by technological advances, population growth, and economic expansion, has intensified the focus on efficient energy management. Tri-generation systems, such as Combined Cooling, Heating, and Power (CCHP) systems, are of particular interest due to their efficiency and sustainability. Integrating renewable energy sources like solar power with traditional fossil fuels further optimizes CCHP systems. This study presents a novel method for enhancing CCHP system efficiency by identifying optimal design parameters and assisting decision-makers in selecting the best geometric configurations. A mathematical programming model using the Harris Hawks optimizer was developed to maximize net power and exergy efficiency while minimizing CO2 emissions in a solar-assisted CCHP system. The optimization resulted in 100 Pareto optimal solutions, offering various choices for performance improvement. This method achieved higher net power output, satisfactory exergy efficiency, and lower CO2 emissions compared to similar studies. The study shows that maximum net power and exergy efficiency, with reduced CO2 emissions, can be achieved with a system having a low compression ratio and low combustion chamber inlet temperature. The proposed approach surpassed the response surface method, achieving at least a 4.2% reduction in CO2 emissions and improved exergy values.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Energy is a fundamental factor in attaining the economic, social, and environmental growth of any country. The rise in energy consumption in recent times, instilled by economic development and population growth, has exacerbated the emission of greenhouse gases (GHGs). Hence, it is crucial to employ fundamental techniques geared towards improving the design of power generation systems to increase their efficiency and reduce pollution to the environment.
Multi-generation systems are born out of the need for more sustainable generation of one or more forms of energy as output. They are mainly categorized, according to the number of outputs, into co-generation and tri-generation systems. Co-generation, or combined heat and power (CHP) system, involves the use of a power-generating unit to produce both power and thermal energy simultaneously. In conventional separate power generation systems, the heat energy would have been dissipated immediately to the atmosphere but is recovered in CHP systems to provide heating power thus enabling savings in fuel and GHG emission reduction [1]. Irrespective of the fact that CHP systems have glaring advantages over conventional separate heat and power generation systems, they are susceptible to fluctuations in their system’s overall efficiency especially during summer seasons when heating loads are at a minimum [2]. A stable and constant power and thermal energy demand profile is essential to achieve maximum overall system efficiency all year round. Therefore, it is ideal to incorporate cooling systems into a CHP system to boost its efficiency hence the concept of CCHP systems.
Tri-generation systems, often referred to as CCHP systems, are an expansion of CHP systems in which a single energy source is used to create electricity, cooling, and heating power. It typically comprises a power generation unit/prime mover, cooling system, and heat recovery systems [3]. The prime mover generates mechanical power which is used to rotate the shaft of an electric motor for the generation of electricity. The thermal energy generated during power generation is utilized to operate heating and cooling systems, such as the absorption chiller, heat recovery generation unit, or to generate more power through the organic Rankine or Kalina cycle.
Renewable sources, especially solar thermal technologies, have been extensively researched as visible solar harvesting options for power generation in a bid to reduce fossil fuel consumption. Solar thermal collectors are predominantly employed to operate side-by-side with fossil fuels because of their relatively lower cost and higher conversion efficiency when compared to solar photovoltaic technologies [4]. Solar-assisted CCHP systems offer a sustainable approach to energy production by reducing carbon emissions and operational costs, while also enhancing the system’s overall energy efficiency. These systems ensure the reliability and availability of various energy sources. [5]. However, its performance can be further improved through optimization and hence the search for even better thermodynamic performance metrics is underway.
The optimization domain has applied several use cases in solving the challenge associated with rapid advancement in industrial technology [6]. According to Hansen, Muller & Koumoutsakos [7], there are generally two types of optimizations: deterministic and metaheuristic algorithms. In the deterministic/heuristic approach, the gradient of the objective function is required, and a constant output is obtained for a given input. The metaheuristic, on the other hand, can solve several types of optimization problems by tuning its parameters and it does not yield a constant output for a given input. Two common types of metaheuristic optimization are the evolutionary and swarm optimization techniques [8]. The evolutionary algorithm is driven by the principles of mutation, crossover, and survival of the fittest, as proposed by Charles Darwin. On the other hand, the swarm algorithm aims to mimic the foraging behavior of a specific group of animals in order to achieve a certain objective. The genetic algorithm, genetic programming, and differential evolution are valid examples of evolutionary algorithms, and these are presented in Figure 1. Prominent examples of swarm-intelligence algorithms are the Harris hawk, Greywolf, moth flame, ant colony, ant-lion optimization, etc.
Typically, practical engineering scenarios involve many objectives that often conflict with each other, as indicated by [9]. Multi-objective problems can be resolved by either decomposing them into a single-objective function or by calculating the Pareto optimal solutions while maintaining the multi-objective formulation. This research study will employ the latter approach. Other research studies have described various optimization methods, including the response surface method (RSM) [10], non-dominated sorting genetic algorithm-II (NSGA-II) [11], particle swarm optimization (PSO) [12], Harris hawk optimization (HHO) [13], grasshopper optimization (GOA) [14], ant-lion optimization [15], moth flame optimization (MFO) [16], and grey wolf optimization (GWO) [17].
Prior optimization research has shown that the optimization of Combined Cooling, Heating, and Power (CCHP) systems primarily depends on three key evaluation categories: exergetic, economic, and environmental variables [18]. These criteria form a comprehensive framework for assessing CCHP system optimization, addressing efficiency, cost-effectiveness, financial feasibility, and environmental impact. Achieving an optimal CCHP system involves balancing these criteria to achieve efficiency, cost-effectiveness, and environmental sustainability. This study demonstrates the application of HHO in formulating and solving a problem associated with a solar-integrated CCHP system. Based on the information provided, the proposed research seeks to achieve the following goals:
  • To develop a mathematical model using the Harris Hawks algorithm on a solar-assisted CCHP system.
  • Optimize the net power output and exergy efficiency, while simultaneously limiting CO2 emissions, in a solar energy-integrated CCHP system utilizing the Harris Hawks optimizer.

2. Literature Review

The pursuit of continual improvement in Combined Cooling, Heating, and Power (CCHP) systems through the use of different optimization approaches is a forward-thinking trend in energy conservation and management research. A thorough literature study examines efforts aimed at optimizing specific performance parameters in solar-based CCHP systems.
A comprehensive examination revealed that a substantial proportion of researchers have employed the genetic algorithm to optimize the CCHP system assisted with solar energy. For example, Cao et al. [19] presented a revised solar-powered CCHP system that utilized the genetic algorithm to enhance electricity generation, exergy performance, and overall cost per unit exergy. Their parametric study investigated the influence of decision variables, such as the proportion of oil mass, the inlet pressure of the Rankine cycle, and operating temperature, on performance metrics. This technique exhibited enhanced results across several performance metrics, surpassing conventional methodologies.
Wang et al. [20] performed a thermodynamic assessment and efficiency improvement of a combined cooling, heating, and power (CCHP) system that integrates solar and natural gas. They utilized a genetic optimization technique to maximize the system’s energetic and exergetic capacities. Furthermore, Wang et al. [21] devised a multi-objective optimization model that utilizes the genetic algorithm to improve energy and cost efficiency, reduce CO2 emissions, and boost grid integration of the CCHP system. Although their suggested operational flexibility strategy enhanced the ability to respond to changing situations, it resulted in decreased levels of grid contact, as well as reduced exergetic efficiency, cost-effectiveness, and environmental impacts.
Song, Liu, and Lin [22] utilized the NSGA-II algorithm to conduct multi-objective optimization of a solar-powered CCHP system across three different operational configurations. The decision variables considered were the capacity of the gas turbine, the area of the photovoltaic (PV) system, and the size of the solar collector. The objective was to optimize the ratio of cost-saving and energy-saving. The findings highlighted the significant impact of energy costs and the performance of the PV panels, solar collectors, and gas turbines on the CCHP system.
The multi-objective Harris hawk method has been utilized to optimize a variety of multi-generation systems. Abba et al. [23] suggested a hybrid optimization strategy that used Harris Hawks and particle swarm optimization, along with support vector regression (SVR), to estimate load requirements and optimize the sizing of a hybrid renewable energy system, with the goal of minimizing annual cost. The findings demonstrated that the suggested HHO-based optimization technique surpassed the single SVR in several performance indicators, such as the coefficient of correlation, coefficient of determination, mean squared error, and root mean squared error.
Yousri, Babu, and Fathy [24] introduced the Harmony Search algorithm as a means to optimize the parameters of a proportional-integral controller within a renewable energy-based system. The optimization of the system focuses on minimizing the integral time absolute error and maximizing the tie-line power. The system includes thermal plants, photovoltaic plants, wind turbines, and other components. The resulting results were validated using the greywolf optimizer, multi-verse optimizer, and sine cosine algorithm.
Zhao et al. [25] described the enhancement of a fuel cell-based combined cooling, heating, and power (CCHP) system by optimizing the use of HHO (hydrogen and oxygen) with the introduction of the singer mechanism. The CCHP system was optimized to maximize exergy performance, system performance, greenhouse gas reduction, and cost efficiency. The computed results were assessed using both the conventional HHO and the NSGA-II algorithms. The updated HHO approach exhibited reduced exergy efficiency and increased greenhouse gas reduction.
Song, Tan, and Mizzi [26] introduced an adapted HHO method to optimize a proton exchange membrane fuel cell. The HHO method underwent modifications by incorporating the quasi-oppositional concept and a logistic map mechanism. These modifications were aimed at enhancing the system’s speed and robustness. This approach was implemented in three case studies and assessed by comparing it with the krill herd method, grass fibrous root optimization, and a conventional HHO algorithm. The objective of reducing the squared deviation between the output voltage and predicted data was successfully accomplished as the proposed approach yielded satisfactory outcomes.
In addition, Pandey & Jadoun [27] investigated the optimal scheduling strategies for a virtual power plant consisting of photovoltaic solar collectors, a wind energy source, a fuel cell, and a combined cooling, heating, and power (CCHP) system. A modified HHO system was used to reduce both financial gains and emissions. The optimization technique was enhanced by augmenting the step duration of the hawks and incorporating a chaotic mapping mechanism to amplify the algorithm’s diversity. The acquired solutions were verified using data from the Particle Swarm Optimization (PSO) and mixed linear programming.
Mahalekshmi and Maruthupandi (2018) utilized the Harmony Search algorithm to address the issues of economic and emission dispatch in power systems. The proposed method utilized a fuzzy-based technique to control the size of the Pareto optimal solutions. The overall system was then optimized for emission dispatch and total cost. The acquired findings were evaluated for quality using set spacing, hyper volume, and CM, and were compared with results derived from the PSO technique.
Mahdavi, Mojaver & Khalilarya [29] have developed an innovative solar-powered CCHP system. The researchers utilized Response Surface Methodology (RSM) to perform multi-objective optimization, specifically targeting net power output, CO2 emission reduction, and exergy efficiency. In this system, waste heat generated between the compression stages is captured by a cooling unit to drive a chiller system. By analyzing the combined impacts of several key parameters, a set of six optimal configurations were identified. The TOPSIS approach was utilized to determine the most favorable solution, yielding ideal outcomes for net power output, CO2 emission reduction, and exergy efficiency, respectively.
This section has examined literary works that have showcased the efficacy of solar-integrated CCHP systems. Furthermore, this literature analysis emphasized the increasing enthusiasm for utilizing these optimization techniques in multi-generation systems, such as the CCHP. Furthermore, the author found no evidence of the HHO being utilized in a solar-assisted CCHP system, to the best of their knowledge. Therefore, the objective of this research is to utilize the HHO to optimize a solar-assisted CCHP system, based on the insights gained from previous studies.
Table 1. Overview of relevant studies.
Table 1. Overview of relevant studies.
S/N Source Methods for
Optimization		 Renewable energy employed Metrics for Performance Improvement System Analyzed
1 Cao et al. [19] Genetic algorithm Solar Exergy efficiency, net output electricity and cost per unit exergy Tri-generation
2 Wang et al. [20] Genetic algorithm Solar, natural gas Energy efficiency, exergy efficiency Tri-generation
3 Wang et al. [21] Genetic algorithm Solar Primary energy saving ratio, CO2 emission reduction ratio, annual cost saving rate Tri-generation
4 Song Liu & Lin [22] NSGA-II Solar Annual cost saving ratio, primary energy saving ratio Tri-generation
5 Abba et al.
[23]		 HHO, PSO & SVR Solar Annual capital and maintenance cost Power generation
6 Yousri, Babu & Fathy [24] HHO Solar, wind Integral time absolute error, tie-line power Power generation
7 Zhao et al. [25] HHO N/A GHG emission reduction, exergy efficiency, annual cost rate Tri-generation
8 Song, Tan & Mizzi [26] HHO N/A Squared deviation between actual and true output voltage Power generation
9 Pandey & Jadoun [27] HHO N/A Net profit, GHG emission reduction Co-generation
10 Mahalekshmi & Maruthupandi [28] HHO Wind Total cost, emission dispatch Power
generation

3. Materials and Methods

3.1. Description of the System

This study specifically examines the solar-assisted CCHP system described in the research conducted by Mahdavi et al. [29]. The system depicted in Figure 1 comprises three gas turbines, two compressors, a Kalina cycle, an absorption chiller, solar collectors, a Heat Recovery Steam Generator unit (HRSG), and a hot water generator.
The system presented functions using a specific sequence that includes multiple components. The air is compressed using two-stage compressors with a cooling unit positioned between them. The waste heat generated by the cooling unit is utilized to power an absorption chiller, which aids in the heat transfer process within a desorber. Afterwards, the warmed air, which has been heated by both solar energy and exhaust gases from a gas turbine in air preheaters, combines with methane fuel in the combustion chamber to produce high-temperature gases. These gases are utilized to operate three gas turbines, with the third turbine being responsible for driving a generator that produces electrical power. In addition, the waste gases from the third gas turbine are used to heat the Heat Recovery Steam Generator (HRSG), the Kalina cycle via an evaporator (Eva-1), and a household water heat exchanger before being discharged into the ambient.
In the Kalina cycle, a mixture of ammonia and water, known as the working fluid, is pumped to increase its pressure. It then flows through two heat exchangers, namely the low-temperature recuperator and the high-temperature recuperator, to increase its heat content. This process helps to reduce the amount of energy needed for Eva-1. The resultant mixture is divided into saturated vapor and liquid phases, with the vapor utilized to provide work output in a steam turbine. Simultaneously, the fully saturated liquid is sent back to the High Temperature Reactor (HTR) in order to recover heat energy, prior to being directed through Expansion Valve-1 (Ev-1), which reduces its pressure. Afterwards, the low-pressure saturated liquid is mixed with the steam turbine output. The mixture is then transported through the LTR to disperse its energy before being expelled into the environment through Condenser-1 (cond-1), thus concluding the cycle.
The single-effect absorption chiller utilizes a series of operations to extract energy at the desorber by utilizing the discarded gases from the intercooler. The obtained energy is subsequently used to generate cooling load at the corresponding evaporator (Eva-2). Pump-2 is used to transport the working fluid, which is initially in a saturated LiBr-H2O liquid state, to the solution heat exchanger (SHE). In the SHE, the working fluid absorbs thermal energy. The working fluid, in a gaseous state, flows from the desorber into the condenser (cond-2), where it undergoes condensation and transforms into a saturated liquid. Afterwards, it flows via the expansion valve (Ev-3) and enters Eva-2. During the Eva-2 process, energy is collected and converted into a saturated vapor state. This vapor is then absorbed into the solution in Ev-2, reverting to its original saturated liquid state at the start of the cycle.
The system’s operation was based on several assumptions, including constant operating conditions, minimal fluctuations in kinetic and potential energy, and insignificant thermal losses from components other than the combustion chamber.

3.2. Response Surface Method

The Response Surface Method (RSM) is an analytical approach used to optimize and model complex systems by examining the relationship between input variables and output results. RSM involves creating regression models to describe the link between a specific outcome and its influencing factors. The main procedures include:
  • Experimental design: This stage entails establishing the circumstances for the experiment. It involves choosing pertinent input factors that may influence the response variable. Constraints are subsequently identified to evaluate the design variables during the experiment.
  • Experimental testing: This involves the execution of tests according to a predetermined experimental strategy. Data pertaining to the outcome variable is gathered across different combinations of design factor levels. These tests are carefully performed to minimize the influence of less significant design variables.
  • Regression model fitting: This involves the development of models utilizing data collected from experiments. This is accomplished using techniques such as the least squares or maximum likelihood estimation. The resulting regression models are evaluated to determine their level of conformity to the initial model assumptions.
  • Validation of the regression model: This occurs after successful fitting of the model by predicting outcomes using new, unused data from further experimental tests. This stage guarantees the dependability and precision of the established model.
Mahdavi, Mojaver, and Khalilarya [29] employed the response surface methodology to develop regression models that can estimate the net power, CO2 emission, and exergy efficiency of the system presented in Section 3.1. Table 2 and equations 10-12 display the decision variables, constraints, and objectives.
This study entails the examination of three separate objective functions:
  • Net power output: This refers to the combined power created by the gas turbine and the Kalina cycle, taking into account the work generated from both systems. The mathematical expression can be represented using the formula proposed by Mahdavi, Mojaver, and Khalilarya [29].
P ˙ net = P ˙ net ,   GT + P ˙ net ,   KC
P ˙ net ,   GT = P ˙ GT - 1 + P ˙ GT - 2 + P ˙ GT - 3 - (   P ˙ AC - 1 -   P ˙ AC - 2   )
P ˙ net ,   KC = P ˙ ST - P ˙ pump - 2
P ˙ GT - 1 = m ˙ p h 7 - h 8 = P ˙ AC - 1
P ˙ GT - 2 = m ˙ p h 8 - h 9 = P ˙ AC - 2
P ˙ GT - 3 = m ˙ p h 9 - h 10
where,
P ˙ net = net power output
P ˙ net ,   GT ,   P ˙ net ,   KC = net power generated by gas turbines and kalina cycle respectively,
P ˙ GT - 1 ,   P ˙ GT - 2 , P ˙ GT - 3 = net power generated by the three gas turbines,
P ˙ AC - 1 ,   P ˙ AC - 2 = net power delivered to the two,
P ˙ ST , P ˙ pump - 2 = net power generated steam turbine and pump2,
h 7 , h 8 ,   h 9 ,   h 10 = specific enthalpies at the respective states
  m ˙ p = mass flow rate of the combustion gases exiting the combustion chamber
2.
Exergy efficiency: This is a useful and effective measure used to evaluate the extent, size, and positions of irreversibilities in a thermodynamic system [31]. The efficiency is mathematically defined as the quotient of the output exergy divided by the input exergy.
ℇ = P ˙ net + E ˙ 45 -   E ˙ 44 + E ˙ 50 - E ˙ 51 + ( E ˙ 47 - E ˙ 46 )   E ˙ in
E ˙ in   = E ˙ fuel + E ˙ coll
where,
E ˙ 44 ,   E ˙ 45 , E ˙ 46 , E ˙ 47 , E ˙ 50 , E ˙ 51 = Exergy at state 44, 45, 46, 47, 50 and 51,
E ˙ in Input exergy
E ˙ fuel = Exergy of fuel
E ˙ coll = Exergy of solar collector
3.
CO2 Emission: The discharge of CO2 into the atmosphere poses adverse environmental impacts, emphasizing the ongoing need for its mitigation within thermal energy systems. Emission, a metric assessing the level of CO2 production, is defined as the ratio of the mass flow rate of CO2 to the overall output energy, as defined by Mahdavi and Khalilarya [29].
Emission = m ˙ CO 2 P ˙ net + Q ˙ heating + Q ˙ cooling
where,
Q ˙ heating   and   Q ˙ cooling = Heating and cooling loads of the CCHP system
P ˙ n e t M W = 62.19 + 0.4573 . X 1 + 0.0259 . X 2 − 0.02421 . X 3 + 0.03638 . X 4           − 0.010867 . X 1 . X 1 − 0.000029 . X 2 . X 2 + 0.000005 . X 3 . X 3           − 0.000009 . X 4 . X 4 − 0.0003 . X 1 . X 2 + 0.00022 . X 1 . X 3           − 0.00042 . X 1 . X 4 − 0.000005 . X 2 . X 3           − 0.000005 . X 2 . X 4 − 0.000003 . X 3 . X 4
E m i s s i o n g r M J           = 13.1 + 3.722 . X 1 + 0.2003 . X 2 − 0.0122 . X 3 + 0.0451 . X 4           − 0.03047 . X 1 . X 1 + 0.0000296 . X 2 . X 2 + 0.00004 . X 3 . X 3           + 0.000052 . X 4 . X 4 + 0.0049 . X 1 . X 2 − 0.00294 . X 1 . X 3           + 0.00286 . X 1 . X 4 − 0.000285 . X 2 . X 3 + 0.000285 . X 2 . X 4           − 0.000099 . X 3 . X 4
ℇ % = − 29 − 0.36 . X 1 + 0.287 . X 2 + 0.0659 . X 3 + 0.0133 . X 4 − 0.01807 . X 1 . X 1           − 0.000029 . X 2 . X 2 − 0.000011 . X 3 . X 3 − 0.000009 . X 4 . X 4           − 0.0125 . X 1 . X 2 + 0.0003 . X 1 . X 3 + 0.00086 . X 1 . X 4           − 0.000205 . X 2 . X 3 + 0.000195 . X 2 . X 4 − 0.000009 . X 3 . X 4

3.3. Harris Hawk Optimization

This optimization technique is inspired by one of the smartest birds, usually located in South Arizona USA, known as Harris’ hawk [32]. These hawks have a peculiar behavior of carrying out coordinated exploration, attacking, and feeding off the prey while in groups. They mainly employ the ‘surprise pounce’ or ‘seven kills’ tactics to catch their prey. This involves a situation where a group of hawks, emerging from different angles, simultaneously converge on the fleeing prey.
The harris hawk optimization (HHO), proposed by Heidari et al. [33], is a common nature-inspired meta-heuristic algorithm that mimics the exploration and attacking behaviour of the harris’ hawk. Figure 3.4 shows the stages of the HHO in capturing the prey and can modelled using the following equations.
A = 2 A 0 ( 1 − r R )
A 0 = 2 t 1 − 1
where,
A = flight energy of the prey
r = number of initial repetitions
R = number of maximum repetitions
A 0 = initial flight energy of the prey and is a random number in [-1, 1]
t 1 = random value in [0, 1]
The value of A steadily reduces with each iteration since it is correlated with the prey’s flight energy. The prey is said to be physically exhausted when A 0 reduces from 0 to -1 and strengthened when A 0 is increased from 0 to 1. Hence, when A ≥1, the hawks are still in the process of searching in various areas for the prey’s whereabouts and this is called the exploration phase. This process is transitioned to the exploitation phase when A<1 indicating that the hawks are prepared to capture the prey. The subsequent section will provide a more detailed explanation of these stages.

3.3.1. Exploration Stage

This is the first stage of the hunting process whereby the hawks (also known as candidate solutions) monitor, track and locate a prey (also known as target) using their powerful eyes. If an equal likelihood, t for each waiting strategy is considered, m<0.5 depicts the condition for the first waiting method while m≥0.5 depicts the condition for second waiting method. Both methods are modelled in equation 15.
Y r + 1 = Y r a n d r − t 2 Y r a n d r − 2 t 3 Y r   m ≥ 0.5 Y p r e y r − Y n r − t 4 L B + t 5 U B − L B   m < 0.5  
where,
Y r + 1 = new position of the hawks based on r repetitions
Y p r e y = position of the prey
Y n = average position of the current hawk’s population
Y r a n d r = arbitrarily chosen hawk from the hawk’s population
Y r = the present position of the hawk
t 2 , t 3 , t 4 , t 5 , m = random values in (0, 1) updated in each repetition, r.
L B = lower bund of the variable
U B = upper bound of the variable

3.3.2. Exploitation Stage

This step is known as the “surprise pounce” phase, in which the hawks employ tactical maneuvers to capture the prey they have spotted after the exploring phase. During the exploitation stage, the HHO models four different methods based on the prey’s avoidance behavior and the assault method of the Harris’ hawks. These tactics rely on the likelihood of finding the desired solution and the energy of the prey. The options consist of the soft besiege, hard besiege, soft besiege with progressive rapid dives, and hard besiege with progressive rapid dives.

3.3.3. Single-Objective Harris Hawk Optimization

Based on the above-mentioned equations, a mathematical model was developed, and it followed the following methodology:
  • Problem definition: The objective functions and the HHO parameters such as upper and lower boundaries of the decision variables, maximum number of iterations, etc. were defined.
  • Initialization: The initial population size of solutions was initialized. The initialization function was created to ensure that the initialized values do not exceed the defined boundaries of the decision variables.
  • Evaluation: The prey’s energy, calculated using equations 13 and 14, determined if the HHO algorithm employed exploration or exploitation. For any of the two methods employed, the prey’s energy was employed to calculate the fitness value of the hawks (objective value) while the prey’s location was regarded as the solution for the decision variable. The prey’s location and hawks’ fitness value were updated at each iteration until the maximum number of iterations was attained. The prey’s location at the final iteration became the optimal decision variable solution returned by the algorithm and the corresponding objective value was obtained.

3.3.4. Multi-Objective Harris Hawk Optimization

The multi-objective Harris Hawks optimization (MOHHO) is inspired by the multi-objective greywolf technique to perform organized hunting by the Harris hawks. The MOHHO utilizes an archive repository and a roulette wheel approach to store non-dominated Pareto solutions in the archive. During each iteration, newly discovered non-dominated solutions are compared with the existing ones before updating the archive. Once the archive reaches its maximum capacity, the most densely populated solutions are discarded to make space for new entries. The likelihood of removing a solution from the archive is governed by:
P i = N i c ,   c > 1  
where,
c = constant value,
N i = number of solutions around the i t h   solutions.
To develop the mathematical model for the multi-objective HHO, additional components were integrated into the model for single-objective HHO. The model comprised the following:
  • Problem definition: All three objective functions as well as the upper and lower boundaries of the decision variables were defined. Additionally, parameters such as the inertia weight, global learning coefficient, inflation rate, leader selection pressure, mutation rate, etc., were defined.
  • Initialization: The initial population size, number of iterations, and archive/repository size were initialized to store the non-dominated solutions.
  • Iteration improvement: The leader selection approach was employed in this algorithm to maintain the diversity of the repository. The leader selection pressure parameter (beta) and the non-dominated solution were passed as arguments to the ‘leader’ function and yielded the fittest non-dominated solution as output. This output was subsequently employed to guide the algorithm in performing exploration and exploitation. The roulette wheel was employed to select the leader of the MOHHO where each solution’s probability of being selected as a leader depended on their fitness value.
  • Evaluation: During the evaluation process, the Pareto dominance was used to determine the domination of the solutions. During each iteration, a solution was included in the archive if it outperformed one or more of the existing solutions in the archive, and if neither the new solution nor the existing solutions in the archive outperformed each other. However, a recently acquired solution was excluded from the archive if it was surpassed by at least one of the existing solutions. When a solution was added to the archive, a resident solution was deleted to maintain the pre-defined archive size. Within each iteration, non-dominated solutions and objective values were obtained and updated until the maximum m number of iterations was attained. The Pareto fronts were used to represent the optimal solutions and their accompanying objective values.
The developed models were implemented on MATLAB R2023a for single and multi-objective optimization. Table 3 shows the MOHHO parameters employed. Figure 2 and Figure 3 display the flowcharts for single and multi-objective optimization using Harris Hawks.

3.4. Mathematical Formulation

The mathematical expression for optimizing net power is as follows:
Maximize   F = { P net ( X 1 ,   X 2 ,   X 3 ,   X 4 ) }
Similarly, the process of optimizing CO2 emission with a single target can be expressed as follows:
Maximize   F =   { ( − emission   ( X 1 ,   X 2 ,   X 3 ,   X 4 ) }
The single-objective optimization of exergy efficiency can be expressed as follows:
Maximize   F =   { ℇ   ( X 1 ,   X 2 ,   X 3 ,   X 4 ) }
The multi-objective optimization problem is defined as follows:
Maximize   F =   { P net ( X 1 ,   X 2 ,   X 3 ,   X 4 ) ,   ℇ   ( X 1 ,   X 2 ,   X 3 ,   X 4 ) , − emission   ( X 1 ,   X 2 ,   X 3 ,   X 4 ) }
Equations (17)–(20) are subject to constraints stated in Table 2.

4. Results and Discussion

4.1. Single-Objective Optimization

A single-objective HHO algorithm was executed on each objective function for 100 iterations, employing a search agent population size of 100. The MATLAB codes were run on a laptop that has an Intel Core i3-5005U CPU running at a speed of 2.00GHz and 8GB of RAM.

4.1.1. Net Power, CO2 Emission, Exergy Efficiency and Optimization

The solutions for Equation (10)–(12) were derived utilizing the decision variables and the respective values listed in Table 2, utilizing the HHO algorithm. The outcomes, shown in Table 4, highlight the necessary steps to enhance net power and exergy efficiency while simultaneously reducing CO2 emissions. The key optimization steps for net power and CO2 emission are as follows:
  • Lower the compression ratio, pinch point temperature difference, and the combustion chamber inlet temperature.
  • Increase the turbine inlet temperature.
To enhance the exergy efficiency, the implementation of the following procedures is necessary:
  • Decrease the compression ratio, pinch point temperature difference, and turbine inlet temperature.
  • Increase the combustion chamber inlet temperature to its highest possible level.

4.1.2. Analysis of the Single-Objective Optimization Outcomes

The results obtained in Table 4 have been summarized in Table 5, which shows the behavior of the optimal solutions. As shown in Table 5, an upward trend is represented by ↑, a downward trend is represented by ↓ while a conflict between the parameters is indicated by ≠. It could be seen that for decision variables Cr and Pp, all three objective functions are in harmony. However, for the Gt and Ct decision variables, the exergy efficiency conflicts with the net power and CO2 emission. Thus, a simultaneous optimization of the three objectives is required to determine the Pareto optimal solutions.

4.2. Multi-Objective Optimization

The optimization algorithm has produced a hundred non-dominated solution sets, in the Pareto front as shown in Figure 4. The ensuing optimal solution sets provide the best feasible trade-offs despite the inherent conflicts between the three objectives. Each solution on the Pareto front represents a potential optimal, with the final selection determined by the judgment of the decision-maker.
An analysis was conducted on three scenarios to have a deeper comprehension of the correlation between each objective function. This study examined the correlations between CO2 emissions and net power output, exergy efficiency and net power output, and exergy efficiency and CO2 emissions in various situations. For clarity, the overall outcomes have been condensed into three two-dimensional Pareto fronts that emphasize crucial aspects. Figure 5 shows the Pareto front, highlighting the trade-off between net power and CO2 emissions during the decision-making process. Maximizing net power will unavoidably result in increasing CO2 emissions, which may have detrimental consequences on the environment. In the CCHP system under study, the net power output is significantly influenced by the power generated by the GT-3 and then the Kalina cycle. As a result, the system can be configured to ensure the combustion gases entering from APH-2 are hotter when they reach the unfired HRSG than when they enter the combustion chamber. Furthermore, it is feasible to simultaneously reduce the rate of fuel consumption and improve the output of the photovoltaic thermal collectors. The principal power source of the system, the GT-3, produces less net power as a result of these modifications, which are intended to minimize CO2 emissions. However, there will be an increase in the cleaner, non-combustible power output from the Kalina cycle. Even if in the end this method lowers the net power generated, it is optimized to minimize CO2 emissions.
Figure 6 demonstrates the relationship between exergy efficiency and CO2 emissions, indicating a compatibility between the two. An increased exergy efficiency is correlated with a lower CO2 emission value. The graph also shows that in order to significantly boost energy efficiency, CO2 emissions must be reduced to a certain extent. Additional study reveals that by reducing fuel use, there would be a corresponding drop in the input exergy of the fuel. Consequently, this would enhance the exergy outputs and usable work produced by the Kalina cycle, water heat exchanger, and absorption chiller, so greatly optimizing the exergy efficiency. As a result, there would be minimal CO2 emissions.
Additionally, Figure 7 illustrates a negative correlation between exergy efficiency and net power. This indicates that a system can have a high net power output yet still lack efficiency. Instead, the highest exergy efficiency is defined by the effectiveness of utilizing the energy provided by the CCHP system. Therefore, it is recommended to run and construct bottom systems (such as the Kalina cycle and absorption chiller) in a way that maximizes the use of waste heat and minimizes the loss of exergy.
The constraints placed on the HHO optimization techniques and the convergence of each choice variable are shown in Figure 8’s scatter plot distribution. The results show that lower compression ratios and pinch point temperatures are preferred by the suggested HHO optimization strategy. However, values in the range between the minimum and the midpoint were selected, by the optimization method, for the combustion chamber inlet temperature. The scatter plot for the gas turbine inlet temperature is distributed between the constraint’s upper and lower bounds.
The MOHHO was designed to produce six ideal solutions, which were then compared with the outcomes of similar research that utilized the RSM. The data gathered, detailed in Table 9, indicates the MOHHO, generally produced CO2 emissions ranging from 50.33 gr/MJ to 50.66 gr/MJ, which is at least 4.2% lower than CO2 emission values produced by the RSM. Overall, the MOHHO yielded decision variable configurations that produced higher net power (61.91 MW), higher exergy efficiency (45.28%), and a relatively lower CO2 emission (50.33 gr/MJ) as highlighted in Table 6. Therefore, the proposed MOHHO outperformed the RSM in optimizing net power, CO2 emission, and exergy efficiency.

5. Conclusions

This study aimed to maximize the efficiency of a solar-assisted CCHP system through multi-objective optimization using the Harris Hawks approach. The optimization sought to minimize greenhouse gas emissions, which have detrimental effects on human health and contribute to global warming while increasing net power and energy efficiency. This study emphasizes how important it is to slow down the rate at which fossil fuels are depleting as demonstrated by the optimized solar-assisted CCHP system. In addition, this work introduces a new optimization strategy, whereas previous studies have utilized different methods to achieve multi-objective optimization of the solar-powered CCHP system. being studied. The research’s results and findings are described in the subsequent section.
  • The most effective parameter configuration for the thermodynamic design of the solar-powered CCHP system is identified using a multi-objective optimization technique with decision variables including compression ratio, pinch point temperature difference, turbine inlet temperature, and combustion chamber inlet temperature.
  • The net power, CO2 emissions, and exergy efficiency serve as objective functions for evaluating the efficacy of the CCHP system by assessing how effectively the decision variables meet the restrictions.
  • The Harris-Hawk technique is utilized to accomplish multi-objective optimization by generating non-dominated Pareto optimum solutions. This study calculates a collection of Pareto optimal solutions, which are then presented as alternative choices to the decision maker. The objective is to empower the decision-makers to exercise their judgment and improve the efficiency of the CCHP system. The convergence of the individual decisions streamlines the decision-making process.
  • Interestingly, the mutual reliance among the four decision variables, within the CCHP system under study, signifies that alterations to a single variable will invariably influence the remaining three. Consequently, employing a multi-objective optimization methodology is recommended for the comprehensive assessment of the system’s operational efficacy.
  • The research identified a conflict within decision-making processes concerning the optimization of net power and CO2 emissions. Maximizing net power tends to correlate with increased CO2 emissions, presenting a trade-off as higher net power often leads to elevated CO2 emissions, which is undesirable.
  • Another significant observation pertains to the correlation between exergy efficiency and CO2 emissions. It suggests that a system characterized by minimal CO2 emissions tends to exhibit high exergy efficiency. This indicates compatibility wherein a system with minimal CO2 emissions tends to be highly efficient. The study’s findings challenge the assumption that a system with high net power production invariably guarantees high efficiency. This assertion is supported by the inverse relationship observed between net power and exergy efficiency. Hence, it is important to note that attaining a high level of net power does not always result in higher efficiency, as there exists a negative correlation between net power and exergy efficiency.
  • The analysis of the convergence of decision variables reveals that optimizing the objective values can be achieved by minimizing the compression ratio, pinch point temperature difference, and inlet combustion chamber temperature. However, it’s noteworthy that the ranges for the gas turbine temperature are spread across the upper and lower bounds of the constraints. This dispersion suggests challenges in achieving convergence for this variable, hinting at potential difficulties in its optimization. Consequently, additional techniques may be necessary to address these challenges and achieve convergence for the gas turbine temperature within the defined constraints.

Author Contributions

Conceptualization, methodology, formal analysis, writing—original draft preparation, U.U.; writing—review and editing, supervision, L.T, C.W.L; All authors have read and agreed to the published version of the manuscript.

Data Availability Statement

The MATLAB codes employed in this study can be downloaded at: www.mdpi.com/xxx/s1.

Acknowledgments

The authors wish to express their gratitude to the University of Johannesburg Research Committee and the Commonwealth Scholarship Fund for their support and sponsorship of this research.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ortiga, J.; Bruno, J.C.; Coronas, A. Operational optimization of a complex trigeneration system connected to a district heating and cooling network. Applied Thermal Engineering 2013, 50, 1536–1542. [Google Scholar] [CrossRef]
  2. Lozano, M.A.; Carvalho, M.; Serra, L.M. Allocation of economic costs in trigeneration systems at variable load conditions. Energy and Buildings 2011, 43, 2869–2881. [Google Scholar] [CrossRef]
  3. Wang, L.; Lu, J.; Wang, W.; Ding, J. Energy, environmental and economic evaluation of the CCHP systems for a remote island in south of China. Applied Energy 2016, 183, 874–883. [Google Scholar] [CrossRef]
  4. Sharma, M.K.; Bhattacharya, J. Finding optimal operating point for advection-cooled concentrated photovoltaic system. Sustainable Energy Technologies and Assessments 2022, 49, 101769. [Google Scholar] [CrossRef]
  5. Dincer, I.; Zamfirescu, C. Renewable-energy-based multigeneration systems. Int. J. Energy Res. 2012, 36, 1403–1415. [Google Scholar] [CrossRef]
  6. Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S.; Zamani, H.; Bahreininejad, A. GGWO: Gaze cues learning-based grey wolf optimizer and its applications for solving engineering problems. J. Comput. Sci. 2022, 61, 101636. [Google Scholar] [CrossRef]
  7. N. Hansen, S.D. Muller, P. Koumoutsakos, Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (CMA-ES). Evol. Comput. 2003, 11, 1–18. [CrossRef]
  8. Abualigah, L. Multi-verse optimizer algorithm: A comprehensive survey of its results, variants, and applications. Neural Comput. Appl. 2020, 32, 12381–12401. [Google Scholar] [CrossRef]
  9. Mirjalili, S.; Saremi, S.; Mirjalili, S.M.; Coelho, L.D.S. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization. Expert Syst. Appl. 2016, 47, 106–119. [Google Scholar] [CrossRef]
  10. Hasanzadeh, R.; Mojaver, M.; Azdast, T.; Park, C.B. A novel systematic multi-objective optimization to achieve high-efficiency and low-emission waste polymeric foam gasification using response surface methodology and TOPSIS method. Chem. Eng. J. 2022, 430, 132958. [Google Scholar] [CrossRef]
  11. Ren, F.; Wang, J.; Zhu, S.; Chen, Y. Multi-objective optimization of combined cooling, heating and power system integrated with solar and geothermal energies. Energy Convers. Manag. 2019, 197, 111866. [Google Scholar] [CrossRef]
  12. Azaza, M.; Wallin, F. Multi objective particle swarm optimization of hybrid micro-grid system: A case study in Sweden. Energy 2017, 123, 108–118. [Google Scholar] [CrossRef]
  13. Shehab, M.; Mashal, I.; Momani, Z.; Shambour, M.K.Y.; Al-Badareen, A.; Al-Dabet, S.; Bataina, N.; Alsoud, A.R.; Abualigah, L. Harris Hawks Optimization Algorithm: Variants and Applications. Arch. Comput. Methods Eng. 2022, 29, 5579–5603. [Google Scholar] [CrossRef]
  14. Sharifian, Y.; Abdi, H. Solving multi-zone combined heat and power economic emission dispatch problem considering wind uncertainty by applying grasshopper optimization algorithm. Sustain. Energy Technol. Assess. 2022, 53, 102512. [Google Scholar] [CrossRef]
  15. Ji, J.; Wang, F.; Zhou, M.; Guo, R.; Ji, R.; Huang, H.; Zhang, J.; Nazir, M.S.; Peng, T.; Zhang, C.; et al. Evaluation Study on a Novel Structure CCHP System with a New Comprehensive Index Using Improved ALO Algorithm. Sustainability 2022, 14, 15419. [Google Scholar] [CrossRef]
  16. Xu, L.; Luo, X.; Wen, Y.; Wu, T.; Wang, X.; Guan, X. Energy Management of Hybrid Power Ship System Using Adaptive Moth Flame Optimization Based on Multi-Populations. IEEE Trans. Power Syst. 2023, 1–15. [Google Scholar] [CrossRef]
  17. Ukaegbu, U.; Tartibu, L.; Lim, C.W. Multi-Objective Optimization of a Solar-Assisted Combined Cooling, Heating and Power Generation System Using the Greywolf Optimizer. Algorithms 2023, 16, 463. [Google Scholar] [CrossRef]
  18. Wang, J.; Han, Z.; Guan, Z. Hybrid solar-assisted combined cooling, heating, and power systems: A review. Renew. Sustain. Energy Rev. 2020, 133, 110256. [Google Scholar] [CrossRef]
  19. Cao, Y.; Dhahad, H.A.; Togun, H.; Haghghi, M.A.; Athari, H.; Mohamed, A.M. Exergetic and economic assessments and multi-objective optimization of a modified solar-powered CCHP system with thermal energy storage. J. Build. Eng. 2021, 43, 102702. [Google Scholar] [CrossRef]
  20. Wang, J.; Lu, Y.; Yang, Y.; Mao, T. Thermodynamic performance analysis and optimization of a solar-assisted combined cooling, heating and power system. Energy 2016, 115, 49–59. [Google Scholar] [CrossRef]
  21. Wang, J.; Liu, Y.; Ren, F.; Lu, S. Multi-objective optimization and selection of hybrid combined cooling, heating and power systems considering operational flexibility. Energy 2020, 197, 117313. [Google Scholar] [CrossRef]
  22. Song, Z.; Liu, T.; Lin, Q. Multi-objective optimization of a solar hybrid CCHP system based on different operation modes. Energy 2020, 206, 118125. [Google Scholar] [CrossRef]
  23. Abba, S.I.; Rotimi, A.; Musa, B.; Yimen, N.; Kawu, S.J.; Lawan, S.M.; Dagbasi, M. Emerging Harris Hawks Optimization based load demand forecasting and optimal sizing of stand-alone hybrid renewable energy systems–A case study of Kano and Abuja, Nigeria. Results in Engineering 2021, 12, 100260. [Google Scholar] [CrossRef]
  24. Yousri, D.; Babu, T.S.; Fathy, A. Recent methodology based Harris Hawks optimizer for designing load frequency control incorporated in multi-interconnected renewable energy plants. Sustainable Energy, Grids and Networks 2020, 22, 100352. [Google Scholar] [CrossRef]
  25. Zhao, L.; Li, Z.; Chen, H.; Li, J.; Xiao, J.; Yousefi, N. A multi-criteria optimization for a CCHP with the fuel cell as primary mover using modified Harris Hawks optimization. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, 2020, pp.1-16.
  26. Song, Y.; Tan, X.; Mizzi, S. Optimal parameter extraction of the proton exchange membrane fuel cells based on a new Harris Hawks Optimization algorithm. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, 2020, pp.1-18.
  27. Pandey, A.K.; Jadoun, V.K. Real-time and day-ahead risk averse multi-objective operational scheduling of virtual power plant using modified Harris Hawk’s optimization. Electric Power Systems Research 2023, 220, 109285. [Google Scholar] [CrossRef]
  28. Mahalekshmi, T.; Maruthupandi, P. Multiobjective Economic/Environmental Dispatch Using Harris Hawks Optimization Algorithm. Intelligent Automation And Soft Computing 2023, 36, 445–460. [Google Scholar] [CrossRef]
  29. Mahdavi, N.; Mojaver, P.; Khalilarya, S. Multi-objective optimization of power, CO2 emission and exergy efficiency of a novel solar-assisted CCHP system using RSM and TOPSIS coupled method. Renew. Energy 2022, 185, 506–524. [Google Scholar] [CrossRef]
  30. Costa, E.; Almeida, M.F.; Alvim-Ferraz, C.; Dias, J.M. Otimization of Crambe abyssinica enzymatic transesterification using response surface methodology. Renewable Energy 2021, 174, 444–452. [Google Scholar] [CrossRef]
  31. Kumar, R. A critical review on energy, exergy, exergoeconomic and economic (4-E) analysis of thermal power plants. Engineering Science and Technology, an International Journal 2017, 20, 283–292. [Google Scholar] [CrossRef]
  32. Bednarz, J.C. Cooperative hunting Harris’ hawks (Parabuteo unicinctus). Science 1988, 239, 1525–1527. [Google Scholar] [CrossRef]
  33. Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future generation computer systems 2019, 97, 849–872. [Google Scholar] [CrossRef]
Preprints 116591 g001
Figure 1. An illustration the solar-assisted CCHP system.
Figure 1. An illustration the solar-assisted CCHP system.
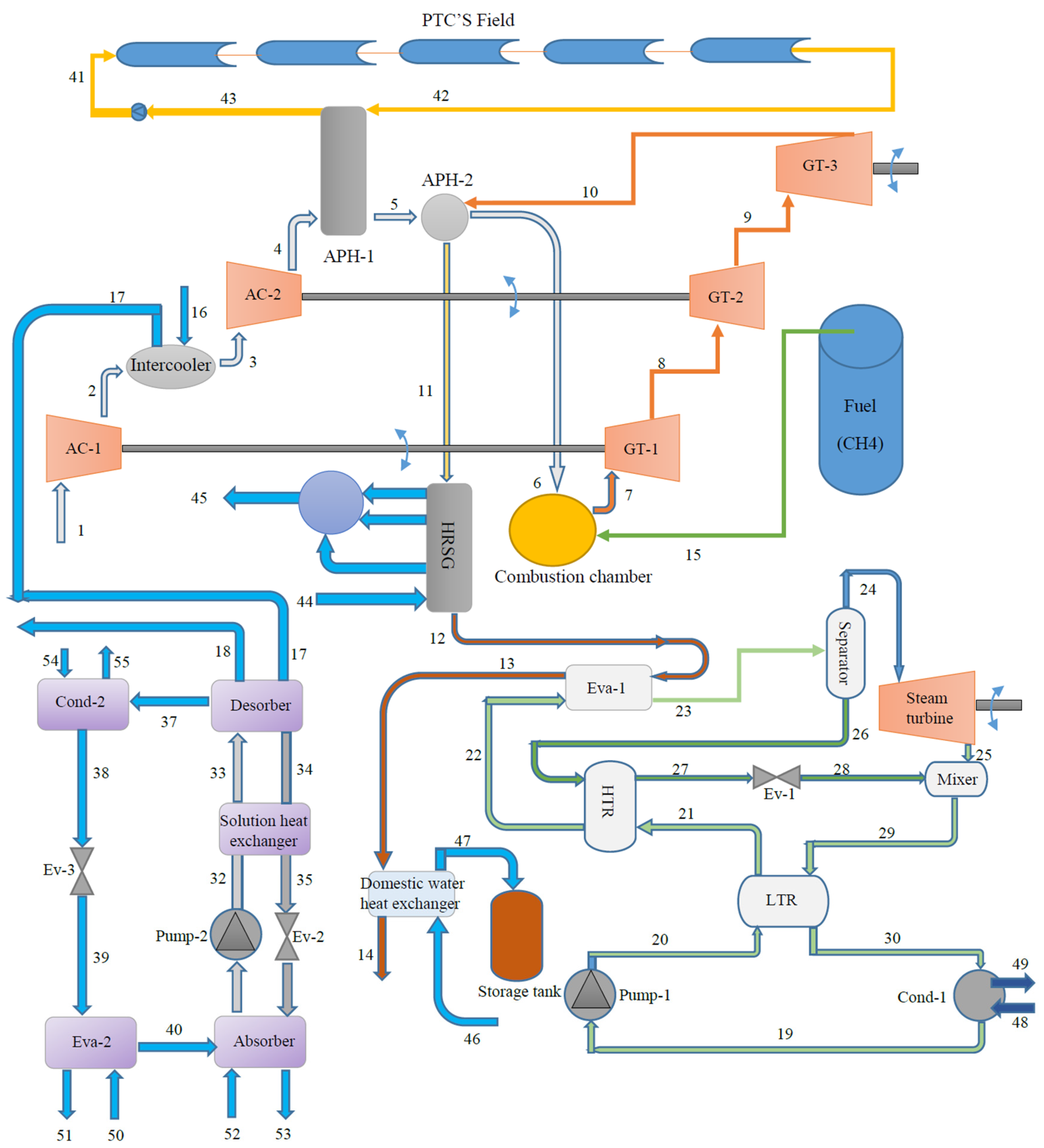
Preprints 116591 g001
Preprints 116591 g002
Figure 2. Flowchart for single-objective harris hawk optimization.
Figure 2. Flowchart for single-objective harris hawk optimization.
Preprints 116591 g002
Preprints 116591 g003
Figure 3. Flowchart for multi-objective harris hawk optimization.
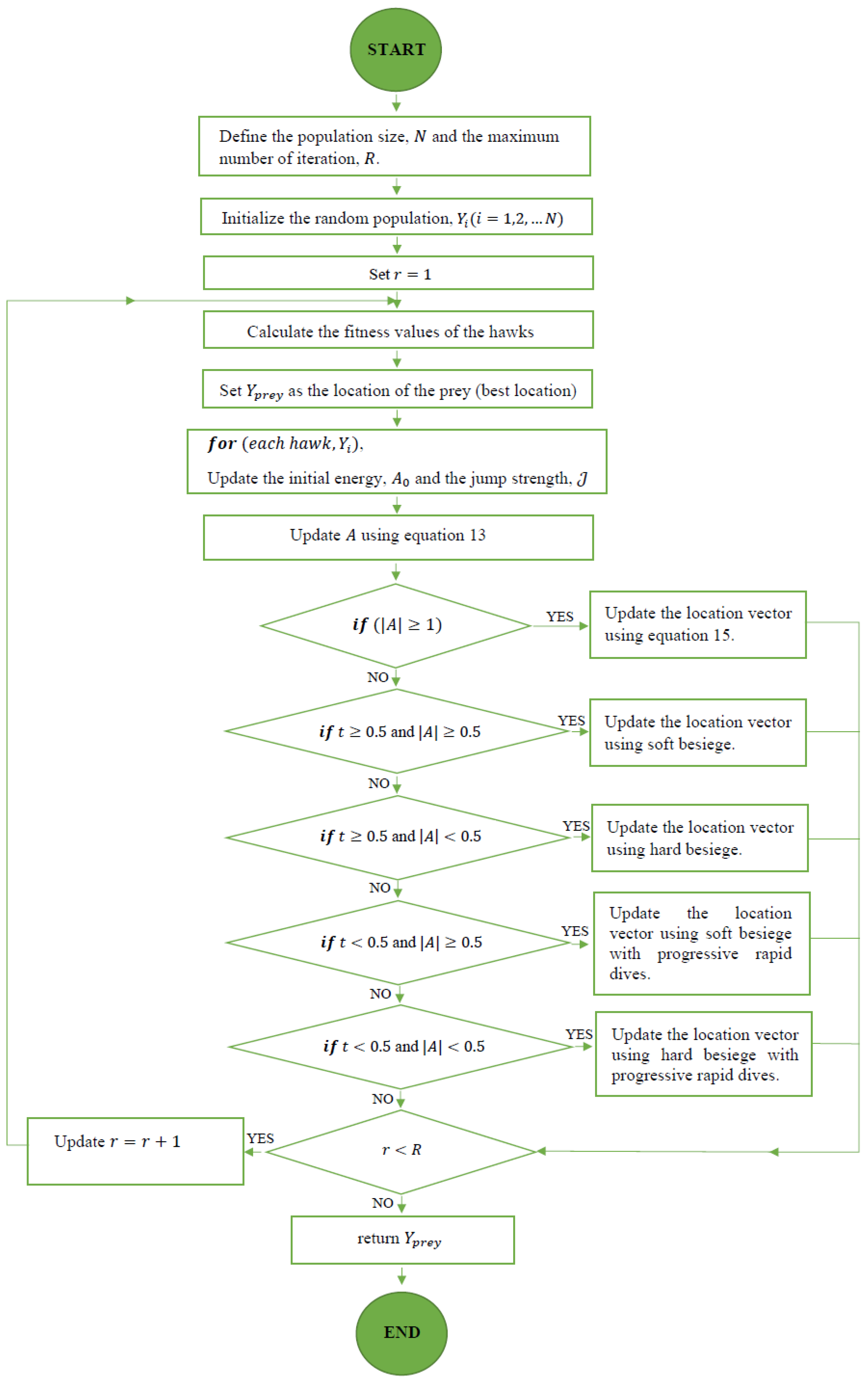
Figure 3. Flowchart for multi-objective harris hawk optimization.
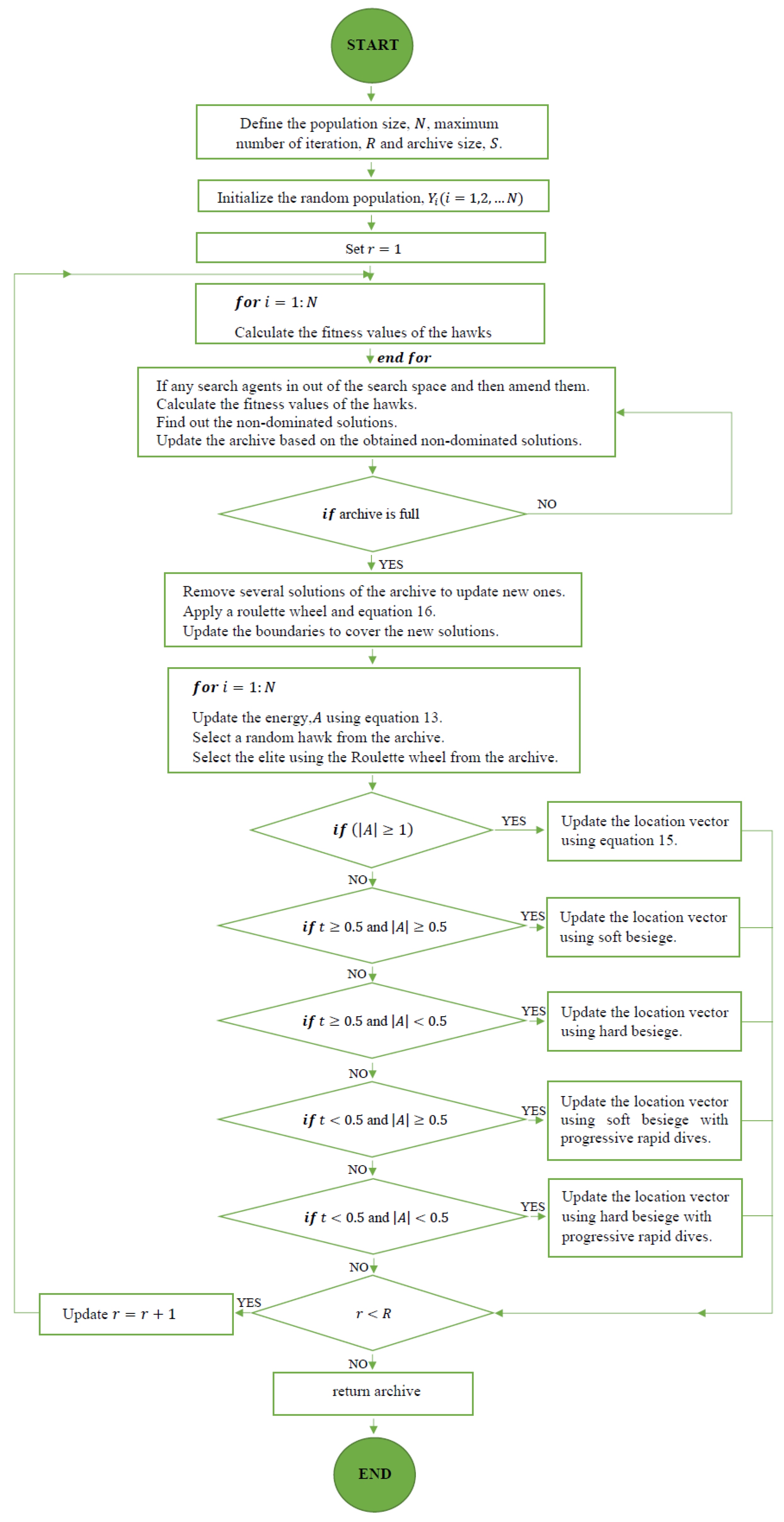
Preprints 116591 g003
Preprints 116591 g004
Figure 4. Pareto front illustrating the relationship between CO2 emissions, net power, and exergy efficiency.
Figure 4. Pareto front illustrating the relationship between CO2 emissions, net power, and exergy efficiency.
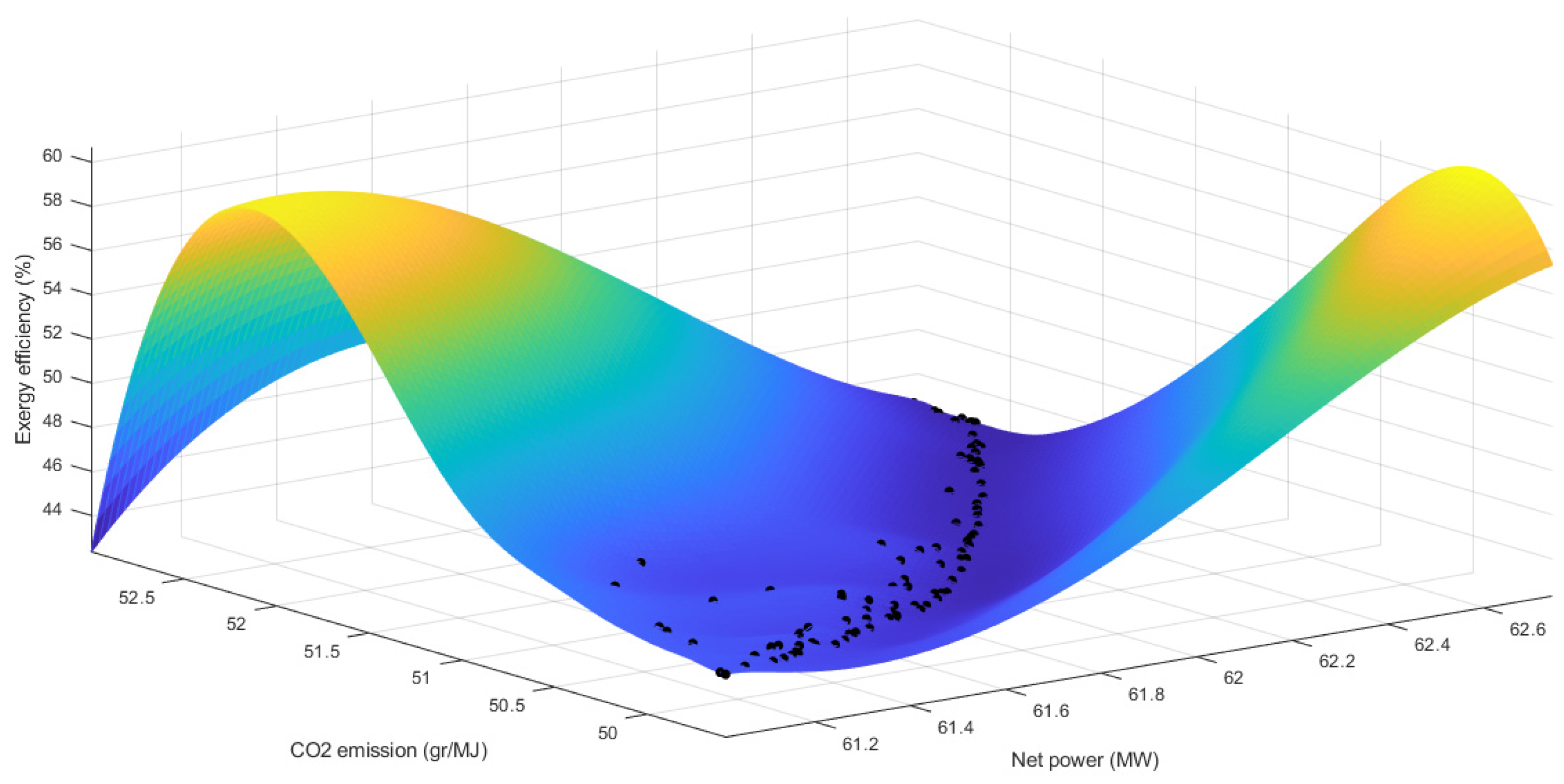
Preprints 116591 g004
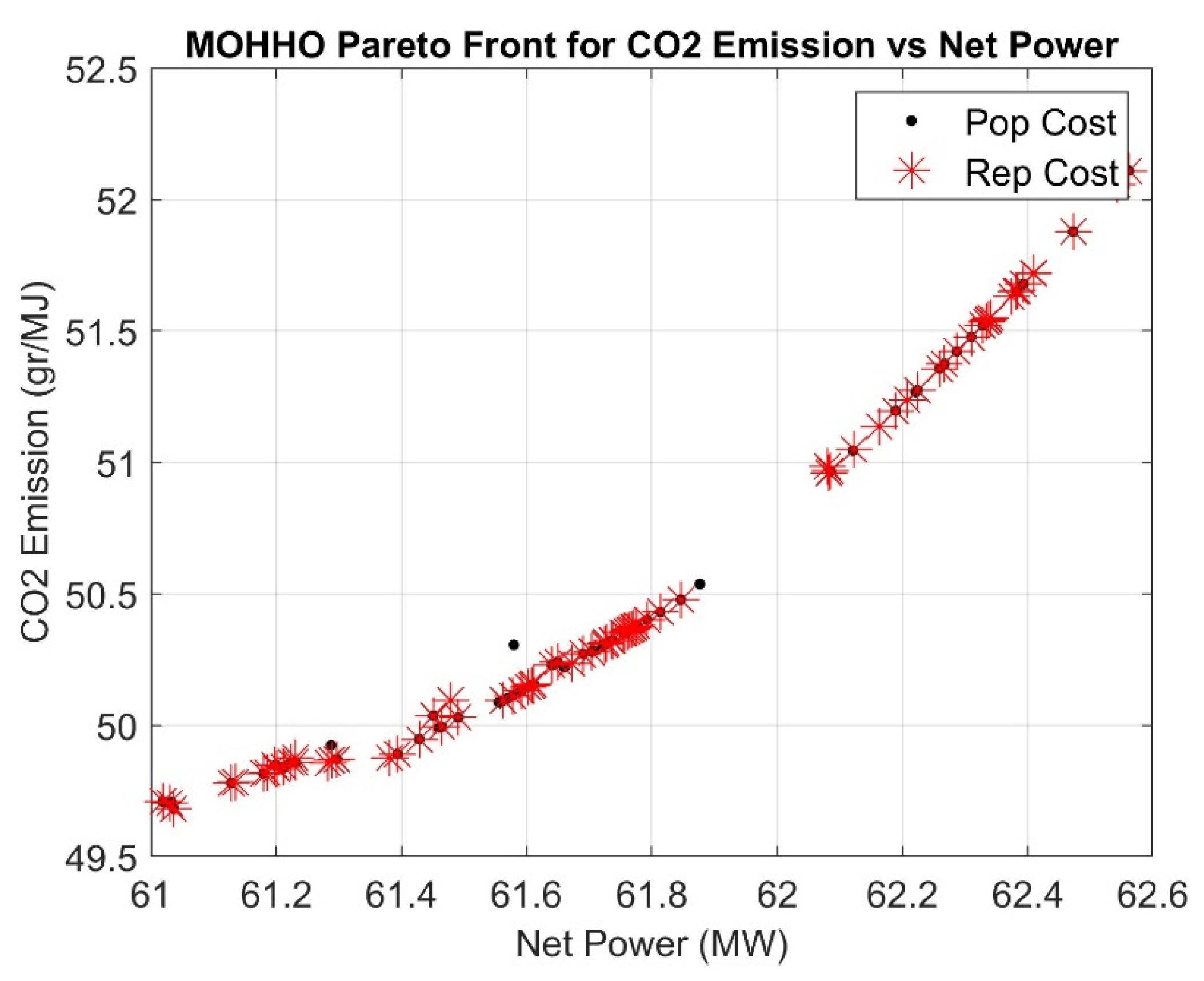
Preprints 116591 g005
Figure 5. Pareto front showing the trade-off between CO2 emissions and net power.
Figure 5. Pareto front showing the trade-off between CO2 emissions and net power.
Preprints 116591 g005
Preprints 116591 g006
Figure 6. Pareto front showing the trade-off between exergy efficiency and CO2 emissions.
Figure 6. Pareto front showing the trade-off between exergy efficiency and CO2 emissions.
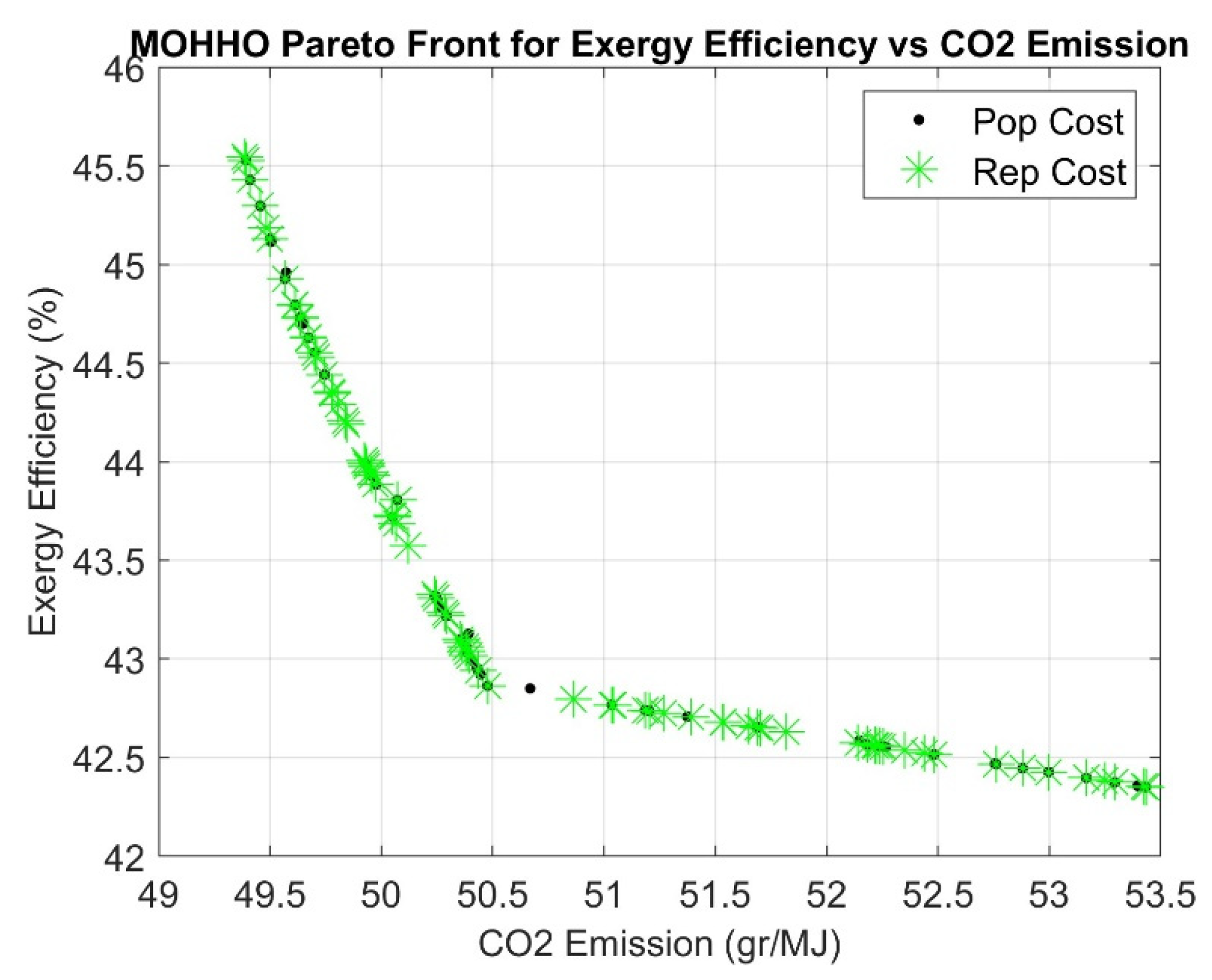
Preprints 116591 g006
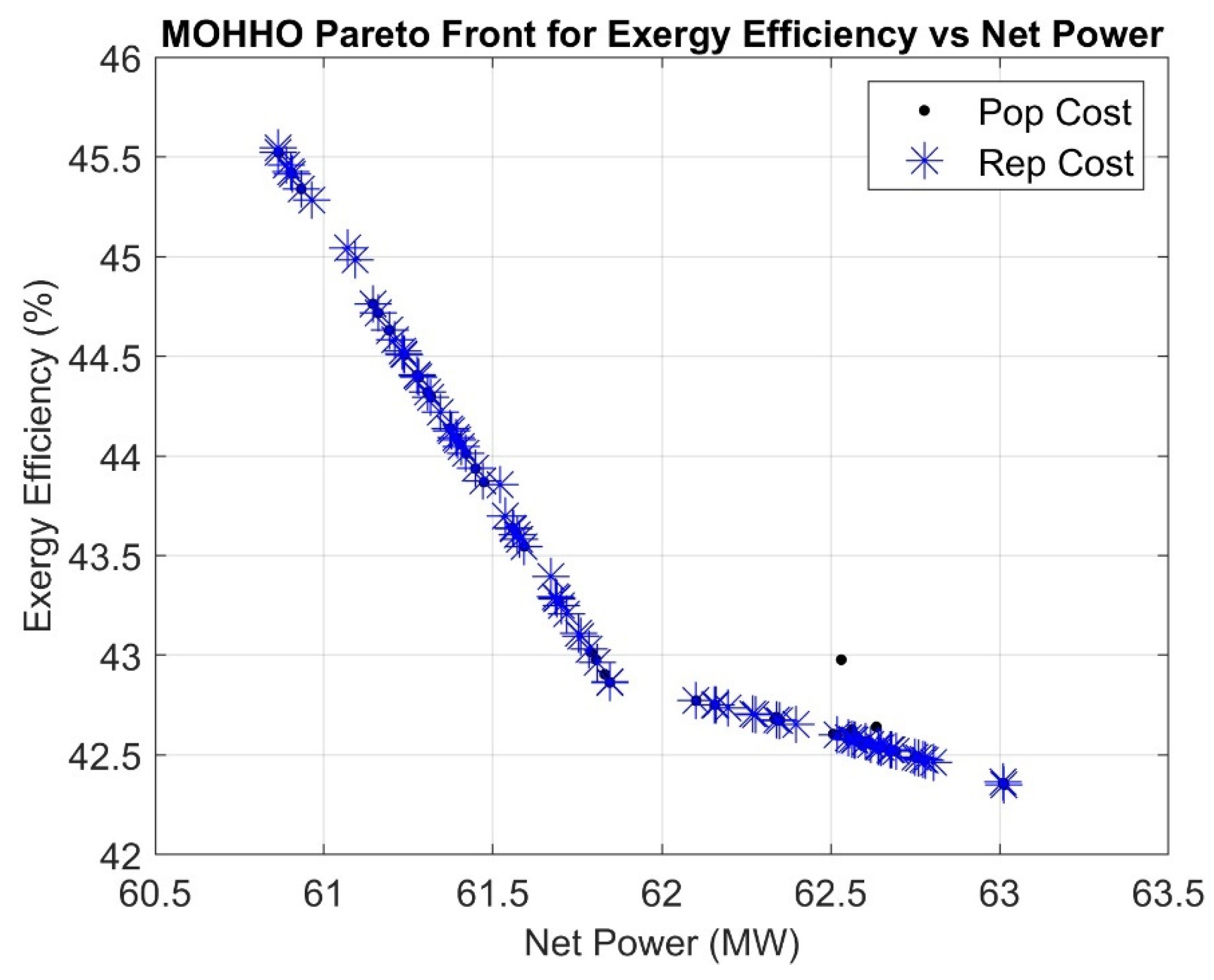
Preprints 116591 g007
Figure 7. Pareto front showing the trade-off between exergy efficiency and net power.
Figure 7. Pareto front showing the trade-off between exergy efficiency and net power.
Preprints 116591 g007
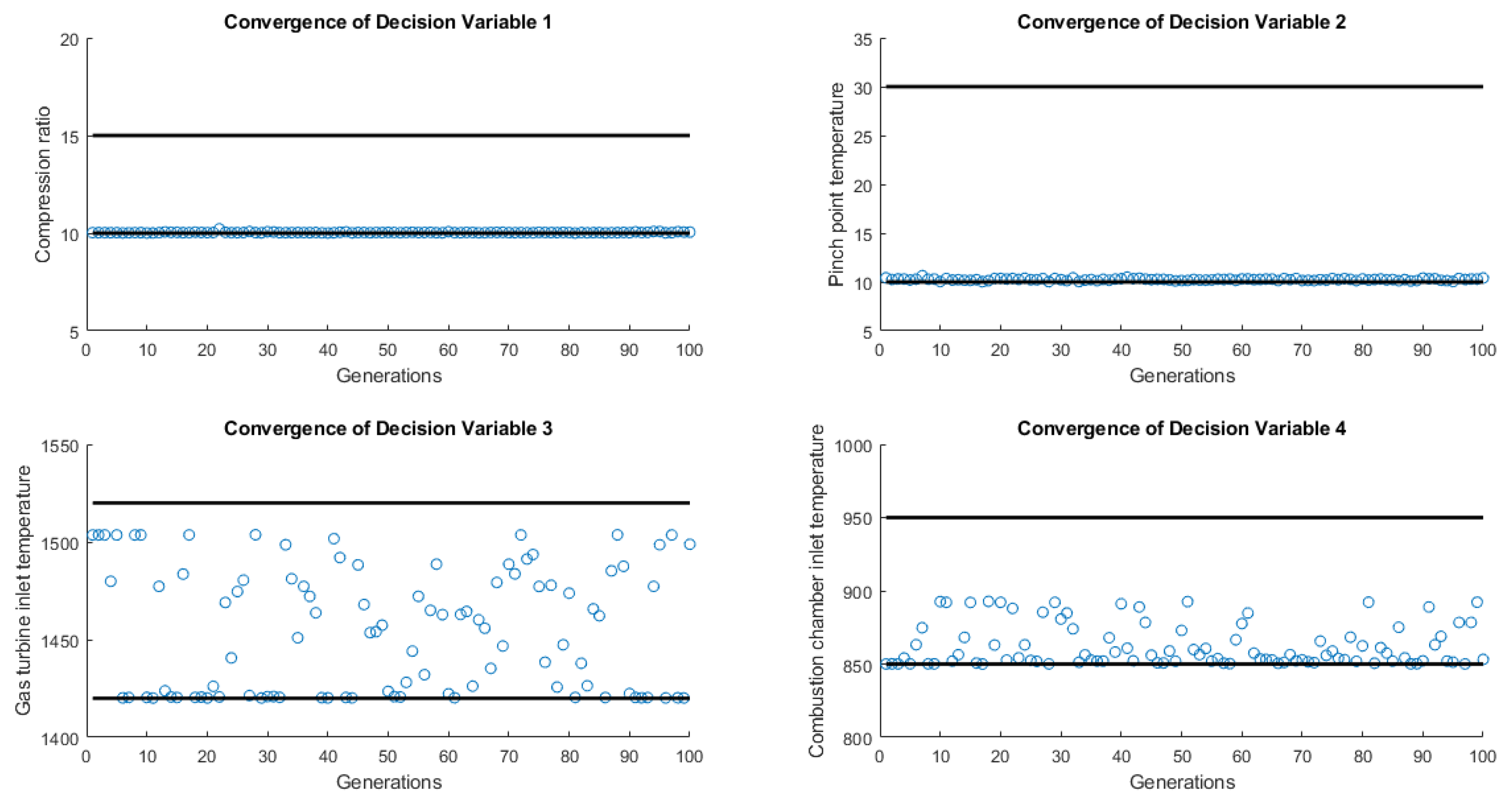
Preprints 116591 g008
Figure 8. Scatter Pattern of Decision Variables.
Figure 8. Scatter Pattern of Decision Variables.
Preprints 116591 g008
Table 2. Decision variables.
Table 2. Decision variables.
Decision variable Constraints
Compression ratio 10≤ X1≤15
Pinch point temperature differential 10≤ X2 ≤30
Turbine inlet temperature 1420≤ X3≤1520
Combustion chamber inlet temperature 850≤ X4≤950
Table 3. Hyperparameter values for MOHHO.
Table 3. Hyperparameter values for MOHHO.
S/N Parameter Value
1 Maximum Iterations (MaxIt) 100
2 Population Count (nPop) 100
3 Repository Capacity (nRep) 100
4 Inertia Weight 0.5
5 Inertia Weight Damping Factor 0.99
6 Personal Learning Factor 1
7 Global Learning Factor 2
8 Grids per Dimension (nGrid) 4
9 Inflation Factor (alpha) 0.1
10 Leader Selection Pressure (beta) 2
11 Deletion Selection Pressure (gamma) 2
12 Mutation Rate (mu) 0.1
Table 4. Optimal solutions optimizing the net power, CO2 emission, and exergy efficiency.
Table 4. Optimal solutions optimizing the net power, CO2 emission, and exergy efficiency.
Objective X1 X2 X3 X4 Optimal Objective Value
Maximum Power 10 10 1520 850 60.8552
Minimum CO2 10 10 1520 850 49.3771
Maximum Exergy Efficiency 10 10 1420 950 42.3507
Table 5. Illustration of the trend of the objective functions.
Table 5. Illustration of the trend of the objective functions.
Decision variable Net power CO2 emission Exergy efficiency
X1 ↓ ↓ ↓
X2 ↓ ↓ ↓
X3 ↑ ↑ ↓ ≠
X4 ↓ ↓ ↑ ≠
Table 6. Comparison of Optimization Results with a Related Study.
Table 6. Comparison of Optimization Results with a Related Study.
Optimization technique Best-Performing Decision Variables Optimal Performance Metrics
X1 X2 X3 X4 Net Power CO2
Emission		 Exergy
Efficiency
MOHHO 10 10 1420 855.34 61.91 50.61 42.84
10 10 1422.67 850 61.82 50.44 42.94
10.28 11.14 1514.57 896.17 61.52 50.66 45.28
10 10 1426.26 850 61.78 50.38 43.04
10.01 10.77 1469.76 870.77 61.60 50.33 44.15
10.28 11.14 1514.31 896.01 61.52 50.66 45.28
RSM
(Mahdavi, Mojaver & Khalilarya [29])		 11.66 11.96 1470 900 61.73 52.87 44.22
11.11 20.00 1470 900 61.73 52.99 44.09
11.98 20.00 1470 890 61.75 53.84 44.12
12.50 16.10 1484 900 61.75 54.07 44.58
12.50 15.72 1470 891 61.79 54.07 44.10
12.50 20.00 1468 882 61.75 54.28 44.30
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated