Quantum Security of A Compact Multi-Signature

Preprint

Article

Quantum Security of A Compact Multi-Signature

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Shaoquan Jiang^*

This version is not peer-reviewed

Submitted:

29 August 2024

Posted:

30 August 2024

You are already at the latest version

Alerts

Abstract

With the rapid advance in quantum computing, quantum security is now an indispensable property for any cryptographic system. In this paper, we study how to prove the security of a complex cryptographic system in the quantum random oracle model. We first give a variant of Zhandry’s compressed quantum random oracle (CStO), called compressed quantum random oracle with adaptive special points (CStOs). Then, we extend the on-line extraction technique of Don et al (EUROCRYPT’22) from CStO to CStOs. We also extend the random experiment technique of Liu and Zhandry (CRYPTO’19) for extracting the CStO query that witnesses the future adversarial output. With these preparations, a systematic security proof in the quantum random oracle model can start with a random CStO experiment (that extracts the witness for the future adversarial output) and then convert this game to one involving CStOs. Next, the on-line extraction technique for CStOs can be applied to extract the witness for any on-line commitment. With this strategy, we give a security proof of our recent compact multi-signature framework that is converted from any weakly secure linear ID scheme. We also prove the quantum security of our recent lattice realization of this linear ID scheme, by iteratively applying the weakly collapsing protocol technique of Liu and Zhandry (CRYPTO 2019). Combining these two results, we obtain the first quantum security proof for a compact multi-signature.

Keywords:

Subject: Computer Science and Mathematics - Security Systems

1. Introduction

A multi-signature scheme allows a group of signers to jointly generate a signature while any subset of them can not represent the group. This mechanism was introduced by Itakura and Nakamura [22] with the motivation to reduce the signature size. In the blockchain application [41], it is also demanded that the aggregated public-key that represents the group should also have a small size, as it will be part of the transaction and the network storage. The blockchain has no control over a user and hence one should be able to freely decide his public-keys. Accordingly, we must make sure that it is secure against a rogue key attack: the attacker might choose his public-key after seeing other signers’ public-keys. In a poorly designed scheme, an attacker could manage to decide the secret key of the aggregated public-key. In addition, with the advance of quantum computer, the quantum attack places a major threat to any cryptographic system. Especially, the RSA based multi-signature (such as [5]) is no longer secure [45]. In this paper, we investigate the multi-signature security in the quantum random oracle model, where the attacker has an internal quantum computer and also can access to the quantum random oracle. We aim to develop quantum random oracle techniques that enable a security proof of a complex cryptographic system. We then apply it to prove the security of our recent compact multi-signature.

1.1. Related Works

A multi-signature scheme [22] is a special case of aggregate signature [8] where each signer of the latter can sign a possibly different message. Since it was introduced by Itakura and Nakamura [22], it has been intensively studied in the literature [2,3,5,7,32,36,38,39,42,46]. However, most of schemes are based on some variants of discrete logarithm assumption which does not hold under a quantum attack [45]. There are multi-signatures that are based on quantum mechanics only (i.e., without a computational hardness assumption) [21,25]. However, their schemes are certainly not what is understood in the crypto community: (1) signers need to share a private key with a trusted party; (2) the verification is completely done by the trusted party; (3) signer has no public-key.

Constructions from lattice assumptions such as (ring-)LWE are potentially the solutions for the quantum secure multi-signature problem. However, currently there are only very few schemes [10,19,26,27,31,37] from this. In addition, some schemes [26,27] are known insecure [23,31]. Schemes [10,14,17–19,23,37] did not consider a quantum attacker. Fukumitsu and Hasegawa [20] is the only previous scheme that considered the quantum security. Their construction is based on Dilithium signature [28]. However, their scheme only allows a constant number of signers and the verification requires all signers’ public-keys. Their proof technique (also that of Dilithium [28]) seems to rely on the statistical lossy property of the underlying ID scheme and is unclear if it can be generally usable in other security analysis. In this paper, we investigate general quantum random oracle techniques that are useful in proving a wide class of random oracle based systems. With this, we prove the quantum security of our recent multi-signature framework [23].

The random oracle basically models a hash function as a completely random function. It was first proposed by Bellare and Rogaway [4]. This methodology has a heuristic assumption: when the random oracle is replaced by a cryptographic hash function, the security will preserve. This generally is not true [11]. However, the counter example does not seem realistic. So the crypto community still widely believes that this methodology is practically meaningful. Furthermore, it greatly simplifies the construction of many cryptographic systems and the proof in the classic random oracle is usually amazingly simple. However, it is not true for the quantum world. The great advantage of a classic random oracle is that the simulator can easily record the attacker’s query history. In the quantum setting, this is difficult as an attacker can query a superposition. If the simulator makes a measurement on the query, it will destroy the quantum state. Zhandry [49] proposed new techniques to record the oracle query which is called compressed random oracle (

C S t O

). Essentially, if the oracle is only queried q times, then the oracle can be compactly represented into a superposition of database with the basis record only containing at most q non-trivial values. Don et al. [15] showed a simulation that can extract an oracle query of a (classic) commitment on the fly. The impact of this feature is that if an adversary outputs a commitment value, we can immediately extract his query input that matches this commitment. This will not destroy the quantum state essentially because when an attacker outputs his classic commitment, he must have already made the measurement. Hence, this gives us a very useful tool, especially when a simulator needs to know the query in order to continue the simulation. However, this is not enough in some proofs. For example, in our multi-signature scheme, the adversary will receive a honest user’s public-key

p k_{1}

and then generate two public-key

p k_{2}, p k_{2}

. At the end, he will try to forge a signature w.r.t. a combined public-key

F (p k_{1}, p k_{2}, p k_{3})

that is computed from

H (p k_{i} | p k_{1} | p k_{2} | p k_{3})

for

i = 1, 2, 3

and H is the random oracle. The problem is that

p k_{2}, p k_{3}

will reveal only at the end of the game. If the simulator wishes to know it in advance, it is impossible using the techniques in [15]. Liu and Zhandry [30] presented a measurement technique to extract

p k_{2}, p k_{3}

during the game involving

C S t O

. Essentially, it chooses a random query and measures it. Then, the outcome is

p k_{i} | p k_{1} | p k_{2} | p k_{3}

for some i with a good probability. Further, the adversary success probability for the forgery will be degraded only by a polynomial fraction. For technique reasons, it is desired that the simulator can set the random oracle value of the measure outcome

p k_{i} | p k_{1} | p k_{2} | p k_{3}

(called special point) to a value of his favorite. To take the advantage of both extraction techniques, one might consider the simulation of [15] with the measurement techniques in [30]. However, there are two issues. First, Some verification measurements in [30] will be done on the random oracle database and hence the extraction theorems in [15] will no longer hold. Second, the special input measurement [30] is operated only once. This sometimes is insufficient to produce a witness for the final adversary output. Our work in this paper is to propose an improved

C S t O

that addresses the two issues and then apply the improved random oracle techniques to prove the security of our recent compact multi-signature scheme [23].

1.2. Contribution

In this paper, we study how to improve

C S t O

so that it still has a simulator (similar to [15]) that allows to extract a query input of any given commitment on the fly but additionally also allows to adaptively specify a small number of special points and set their random oracle values to our own choices. The improved random oracle is called compressed random oracle with adaptive special points (

{CStO}_{s}

). We generalize the simulator and extraction theorem in [15] to the

{CStO}_{s}

setting. We also generalize the experiment sampling technique in [30] to allow samplings for several times. This allows us to extract the witness of the final adversary output, where this witness might depend on several random oracle queries (that are measured during the game). This random experiment can be easily converted to an interaction with

{CStO}_{s}

oracle and hence the foregoing on-line extraction technique can be applied. With this improved random oracle technique, we show that our recent multi-signature framework (which is converted from any weakly secure linear identification) is provably secure in the quantum random oracle model. The proof strategy is to use the sequence of game technique. It starts the adversary with a standard quantum random oracle and then continues with the compressed quantum random oracle (CStO) while preserving the same adversary success probability. It next applies the random experiment sampling techniques which degrades the adversary success only by a polynomial fraction but it can extract the witness for the final adversary output. Then, we convert the random experiment (with

CStO

) to one involving

{CStO}_{s}

. Finally, the online extraction technique is used to simulate the interaction without the knowledge of the secret of an ID scheme. This allows to reduce the adversary success to the security of the ID scheme. We also prove the quantum security of the JAK ID scheme in [23]. The main tool to achieve this is to use the collapsing sigma protocol technique in [30] that was originally proposed by Unruh [47]. Our security proof essentially is to formulate the JAK ID security game into two public-coin protocols, each of which uses the collapsing property to guarantee the non-negligibility of the adversary success probability. This two-step analysis allows us to reduce the adversary success probability in attacking the JAK ID scheme to break the underlying ring-SIS assumption.

2. Preliminaries

Notations. We will use the following notations.

$x \leftarrow S$ samples x uniformly random from a set S.
For a randomized algorithm A, $u = A (x; r)$ denotes the output of A with input x and randomness r, while $u \leftarrow A (x)$ denotes the random output (with unspecified randomness).
Min-entropy $H_{\infty} (X) = - log ({max}_{x} log P_{X} (x))$ .
A concatenating with B is represented by $A | B$ and also by $(A, B)$ (if the context is clear).
negl $(λ)$ is negligible: ${lim}_{λ \to \infty} p o l y (λ) negl (λ) = 0$ for any polynomial $p o l y (λ) .$
$[ν]$ denotes set ${1, \dots, ν} .$
$| | | ν 〉 | |$ is the Euclidean norm: $| | | v 〉 | | = \sqrt{〈 v | v 〉} .$
$Y^{X}$ denotes the set of vector $y : = {y_{x}}_{x \in X}$ . We use $y (x)$ to denote $y_{x} .$

2.1. Ring and Module

In this section, we review math concepts: ring and module (for details, see [29]). A ring A is a set, associated with multiplication and addition operators, respectively written as a product and a sum, satisfying the following conditions:

-: R-1. A is a commutative group under addition operator + with identity element 0.
-: R-2. A is associative under multiplication operator: for $a, b, c \in A$ , (ab)c=a(bc). Also, it has a unit element 1: 1a=a.
-: R-3. It satisfies the distributive law: for $a, b, c \in A$ , $a (b + c) = a b + a c$ and $(b + c) a = b a + c a .$

In this paper, we only consider a commutative ring: if

a, b \in A

, then

a b = b a

. When we say ring, it always means a commutative ring. If A is a commutative ring with

0 \neq 1

and every non-zero element in A has an inverse, then A is a field.

Definition 1.

Let R be a ring. An Abelian group M (with group operator ⊞) is a R-module , if (1) it has defined a multiplication operator • between R and M: for any

r \in R, m \in M

r • m \in M

; (2) the following conditions are satisfied: for any

r, s \in R

and

x, y \in M

1.: $r • (x ⊞ y) = (r • x) ⊞ (r • y)$ ;
2.: $(r + s) • x = (r • x) ⊞ (s • x)$
3.: $(r s) • x = r • (s • x)$
4.: $1_{R} • x = x$ , where $1_{R}$ is the multiplicative identity of R.

Note that if R is a field, then R-module M in fact is the well-understood concept - vector space, where M consists of vectors and R is the coefficient field.

2.2. Elements in Quantum Computing

In this section, we give a brief introduction to quantum computing. Details can be found in [43]. A quantum system is a finite-dimensional complex Hilbert space

H

with an inner product

〈 \cdot | \cdot 〉

. We use standard bra-ket notations to denote vectors in

H

and its dual space. The state of a quantum system is a unit vector

| ψ 〉

. Let

Y

be a finite Abelian group. We use

{| y 〉}_{y \in Y}

to represent an orthonormal basis for

H = C^{| Y |}

. We also write this

H

C [Y]

to emphasize that

H

is expanded by

{| y 〉}_{y \in Y}

. For two quantum systems

H_{1}

and

H_{2}

, the joint system is a tensor product

H_{1} \otimes H_{2}

. For

| ψ_{1} 〉 \in H_{1}

and

| ψ_{2} 〉 \in H_{2}

, their product state is

| ψ_{1} 〉 | ψ_{2} 〉 .

For an ordered set

X = {x_{1}, \dots, x_{n}}

C {[\bar{Y}]}^{\otimes X}

represents the tensor product of

| X |

copies of

C [\bar{Y}]

with the ith copy labeled by

x_{i} .

A quantum system

H

has an orthonormal basis

{| ψ_{1} 〉, \dots, | ψ_{n} 〉}

. With this, a quantum state

| ψ 〉 \in H

can be represented as

| ψ 〉 = \sum_{i = 1}^{n} λ_{i} | ψ_{i} 〉

with

\sum_{i} {| λ_{i} |}^{2} = 1 .

Quantum operations on

H

consist of unitaries and measurements. A unitary U on

H

is an operator from

H

H

with

U U^{†} = I

, where

U^{†}

is the conjugate of U. Measurement

M = {M_{i}}_{i}

on a quantum state

| ψ 〉 \in H

is the operator for extracting the classic information from

| ψ 〉

, where each

M_{i}

must be Hermitian (i.e.,

M_{i}^{†} = M_{i}

) and satisfies the completeness condition

\sum_{i} M_{i}^{†} M_{i} = I .

After the measurement, the post-measurement state will be

M_{i} | ψ 〉 / | | M_{i} | ψ 〉 | |

, which occurs with probability

| | M_{i} {| ψ 〉 | |}^{2}

. A quantum algorithm A is represented by a list of unitaries/measurements. Due to deferred measurement principle [43, pp. 186], the measurement can be deferred to the end of operations of A. Hence, whenever applicable, we assume that A before the final measurement is represented by a list of unitaries

U_{1}, \dots, U_{ℓ} .

Let

L (H)

denote the linear operator from

H

H

. For

A, B \in L (H)

, their commuter is defined as

[A, B] = A B - B A .

The norm of linear operator A on

H

is defined as

| | A | | = {max}_{v} | | A | v 〉 | |

, where

| v 〉

goes over all the possible unit vectors in

H .

By the singular value decomposition theorem, we can write

A = \sum_{i} λ_{i} | v_{i} 〉 〈 y_{i} |

, where

{v_{i}}_{i}

and

{y_{i}}_{i}

are respectively a set of orthonormal vectors in

H

and

{λ_{i}}_{i}

is the set of positive singular values of A. Hence,

| | A | | = {max}_{i} λ_{i}

. The trace distance between two states

ρ, σ

is defined as

D_{t} (ρ, σ) = \frac{1}{2} tr (| ρ - σ |),

where

| A | : = \sqrt{A^{†} A}

2.3. Multi-Signature

In this section, we introduce the multi-signature and its security model. A multi-signature scheme is a protocol that allows a group of signers to jointly generate a signature. The signature should be valid against an aggregated public-key determined from all signers’ public-keys. The protocol proceeds in rounds. Signers are pair-wise connected but the channel is not secure. The target is to generate a short signature. It is desired that the aggregated public-key should be short too.

Definition 2.

A multi-signature scheme is a quadruple of algorithms (Setup, KeyGen, Sign, Verify), described as follows.

Setup. Given

1^{λ}

, it generates a system parameter param. Note: param should be part of the input for KeyGen, Sign, Verify. But we usually omit it for brevity.

KeyGen. It takes param as input and generates a private key

s k

and a public-key

p k

Sign. Given public-keys

(p k_{1}, \dots, p k_{n})

and a message

M,

user i has the private key

s k_{i}

w.r.t.

p k_{i}

. Then, they interact with each other and finally output a signature σ, with respect to an aggregated public-key

\bar{p k} : = F (p k_{1}, \dots, p k_{n})

, where F is called an aggregation function.

Verify. Upon

(σ, M)

and an aggregated public-key

\bar{p k} = F (p k_{1}, \dots, p k_{n})

, verifier outputs either 1 (for accept) or 0 (for reject).

Remark 1.

The aggregated key

\bar{p k}

carries the information of the signers’ public-keys. It is desired that it has a size independent of n. But this is not enforced in the definition.

2.3.1. Security Model

In the following, we define the existential unforgeability of a multi-signature in the quantum random oracle model. Essentially, it says that no quantum adversary can forge a valid signature on a new message as long as the signing group contains an honest member. Toward this, the attacker can access to a signing oracle and quantum random oracle and create fake public-keys at will. The security is defined through a game between a challenger

CHAL

and a quantum attacker

A

that has oracle access to quantum random oracle maintained by CHAL.

Initially, CHAL generates param and a challenge public-key

p k^{*}

with a private key

s k^{*}

. It then provides

p k^{*} | param

A

who has an initial state

| ψ 〉 = \sum_{x y w} λ_{x y w} {| x 〉}_{X} {| y 〉}_{Y} {| w 〉}_{W}

, where

X, Y, W

represents query register, response register and working register respectively. Next,

A

interacts with CHAL through signing oracle and random oracle

R O

and finally generates a forgery.

Sign

(P K, M)

. Here

P K

is a set of distinct public-keys with

p k^{*} \in P K

. Upon this query, CHAL represents the signer of

p k^{*}

and

A

represents signers of

P K - {p k^{*}}

to run the signing protocol on message M. Finally, it outputs the multi-signature

σ

(if it succeeds) or ⊥ (if it fails).

RO.

A

can query random oracle

R O

by providing his

X Y

registers to

CHAL

who applies

R O

X Y D

so that

{R O | x 〉}_{X} {| y 〉}_{Y} {| H 〉}_{D} = | x 〉 | y + H (x) 〉 | H 〉,

where H is the random function and D is the random oracle register. Finally, it returns registers

X Y

back to

A

. See Section 4.1 for details.

Forgery. Finally,

A

outputs a signature

σ^{*}

for a message

M^{*}

, w.r.t. a set of distinct public-keys

(p k_{1}^{*}, \dots, p k_{N}^{*})

s.t.

p k^{*} = p k_{i}^{*}

for some i.

A

succeeds if (a)

Verify (\bar{p k^{*}}, σ^{*}, M^{*}) = 1

and (b)

((p k_{1}^{*}, \dots, p k_{N}^{*}), M^{*})

was not issued to

Sign

oracle. Denote a success forgery event by

succ

Definition 3.

A multi-signature scheme (Setup, KeyGen, Sign, Verify) is existentially unforgeable against chosen message attack (or EU-CMA for short) in the quantum random oracle model, if the following holds.

Correctness.For $(s k_{1}, p k_{1}), \dots, (s k_{n}, p k_{n})$ generated by KeyGen, the signature generated by signing algorithm on a message M will pass the verification, except for a negligible probability.
Existential Unforgeability.For any quantum polynomial time adversary $A$ in the above forgery game, $Pr (succ (A))$ is negligible.

2.4. Canonical Linear Identification

A canonical identification system is a 3-round public coin protocol where the first round message has a super logarithmic min-entropy. It is formally defined as follows (also see Figure 1).

Definition 4.

A canonical identification scheme with parameter

τ \in N

is a quadruple of algorithms

ID = (Setup, KeyGen, P, V_{τ})

, where Setup takes security parameter λ as input and generates a system parameter param; KeyGen is a key generation algorithm that takes

param

as input and outputs a public key

p k

and a private key

s k

; P is an algorithm, executed by prover;

V_{τ}

is an algorithm parameterized by τ, executed by Verifier.

ID

is a three-round protocol, where Prover starts with a committing message

CMT

with

H_{\infty} (CMT) = ω (log λ)

, and then Verifier replies with a challenge

CH \leftarrow Θ

and finally Prover finishes with a response

Rsp

which will be either rejected or accepted by

V_{τ}

The domains of

s k

p k

, CMT, Rsp are respectively denoted by

SK, PK, CMT, RSP .

We are interested in a canonical ID scheme with linearity [23] and simulability in the following sense.

Linearity. A canonical ID scheme

ID = (Setup, KeyGen, P, V_{τ})

is linear if it satisfies the following conditions.

i.: $SK, PK, CMT, RSP$ are $R$ -modules for some ring $R$ with $Θ \subseteq R$ (as a set);
ii.: For any $λ_{1}, \dots, λ_{t} \in Θ$ and public/private pairs $(s k_{i}, p k_{i})$ ( $i = 1, \dots, t$ ), we have that $\bar{s k} = \sum_{i = 1}^{t} λ_{i} • s k_{i}$ is a private key of $\bar{p k} = \sum_{i = 1}^{t} λ_{i} • p k_{i}$ .

Note: Operator • between $R$ and $SK$ (resp. $PK, CMT, RSP$ ) might be different. But we will use the same symbol • as long as it is clear from the context.
iii.: Let $λ_{i} \leftarrow Θ$ and $(p k_{i}, s k_{i}) \leftarrow KeyGen (1^{λ}),$ for $i = 1, \dots, t .$ If ${C M T}_{i} | C H | {R s p}_{i}$ is a faithfully generated transcript of the ID scheme w.r.t. $p k_{i}$ , then

$V_{τ} (\bar{p k}, \bar{C M T} | C H | \bar{R s p}) = 1,$

(1)

where $\bar{p k} = \sum_{i = 1}^{t} λ_{i} • p k_{i}, \bar{C M T} = \sum_{i = 1}^{t} λ_{i} • {C M T}_{i}$ and $\bar{R s p} = \sum_{i = 1}^{t} λ_{i} • {R s p}_{i}$ .

Note: we require Equation (1) to hold only if the keys and transcripts are faithfully generated. If some are contributed by attacker, this equality might fail.

Simulability.

ID

is simulatable if there exists a polynomial time algorithm SIM s.t. for

(s k, p k) \leftarrow KeyGen (1^{λ})

CH \leftarrow Θ

and

(CMT, Rsp) \leftarrow SIM (CH, p k, param)

, it holds that

CMT | CH | Rsp

is indistinguishable from a real transcript, even if the quantum distinguisher is given

p k | param

and has access to oracle

O_{i d} (s k, p k)

, where

O_{i d} (s k, p k)

acts as follows:

(s t, CMT) \leftarrow P (param)

;

CH \leftarrow Θ

;

Rsp \leftarrow P (s t | s k | p k, CH)

; output

CMT | CH | Rsp .

Now we define the security for a linear ID scheme. Essentially, it is desired that an attacker is unable to impersonate a prover w.r.t. an aggregated public-key, where at least one of the participating public-keys is not generated by attacker. Here we use the aggregated public-key as the challenge public-key in order to relate it to the security of the multi-signature later.

Definition 5.

A canonical identification scheme

ID = (Setup, KeyGen, P, V_{τ}, Θ)

with linearity and

τ \in N

is secure if it satisfies correctness and security below.

Correctness. When no attack presents, Prover will convince Verifier.

Soundness. For any quantum polynomial time algorithm

A

Pr ({EXP}_{ID, A} = 1)

is negligible, where

{EXP}_{ID, A}

is defined below with

p k_{i} \in PK

for

i \in [t]

and

\bar{p k} = \sum_{i = 1}^{t} λ_{i} • p k_{i}

Experiment

{Exp}_{ID, A} (λ)

param

\leftarrow Setup (1^{λ})

;

(p k_{1}, s k_{1}) \leftarrow KeyGen (param)

;

(| s t_{0} 〉, p k_{2}, \dots, p k_{t}) \leftarrow A (param, p k_{1})

λ_{1}, \dots, λ_{t} \leftarrow Θ

(| s t_{1} 〉, C M T) \leftarrow A (| s t_{0} 〉, λ_{1}, \dots, λ_{t})

;

C H \leftarrow Θ

;

R s p \leftarrow A (| s t_{1} 〉, C H)

;

b \leftarrow V_{t} (\bar{p k}, C M T | C H | R s p)

;

output

b .

3. Basic Properties in Quantum Computing

In this section, we give some fundamental properties in quantum computing. The first result is trivial and can be verified by simple calculations. We thus state it without a proof.

Lemma 1.

Let

A, B, C \in L (H) .

Then, the following holds.

1.: $[A B, C] = A [B, C] + [A, C] B$ ;
2.: $[A B C, D] = A B [C, D] + A [B, D] C + [A, D] B C;$
3.: $[A^{n}, B] = \sum_{i = 0}^{n - 1} A^{i} [A, B] A^{n - i - 1} .$

The next lemma was stated in [15] with a proof omitted. We give a proof for completeness.

Lemma 2.

Let

A, B, A_{1},, A_{2} \in L (H) .

Then, the following holds.

1.: If $A_{1}, A_{2} \in L (H)$ , then $| | A_{1} \otimes A_{2} | | = | | A_{1} | | \cdot | | A_{2} | | .$
2.: If $A^{†} B = 0$ and $A B^{†} = 0$ , then $| | A + B | | \leq max (| | A | |, | | B | |) .$ Especially, if $A = \sum_{x} | x 〉 〈 x | \otimes A^{x}$ , then $| | A | | \leq {max}_{x} | | A^{x} | | .$

Proof. 1. Let

A_{1} = U_{1} D_{1} V_{1}

and

A_{2} = U_{2} D_{2} V_{2}

for

D_{i} = diag (μ_{i 1}, \dots, μ_{i t_{i}})

with

μ_{i j} \geq 0

and unitary

U_{1}, U_{2}, V_{1}, V_{2}

. Then,

A_{1} \otimes A_{2} = (U_{1} \otimes U_{2}) (D_{1} \otimes D_{2}) (V_{1} \otimes V_{2}) .

Hence,

| | A_{1} \otimes A_{2} | | = ({max}_{t} μ_{1 t}) ({max}_{j} μ_{2 j}) = | | A_{1} | | \cdot | | A_{2} | |

U_{1} \otimes U_{2}

and

V_{1} \otimes V_{2}

are unitary.

2. By the singular value decomposition theorem, we can write

A = \sum_{i = 1}^{s} λ_{i} | x_{i} 〉 〈 y_{i} |

and

B = \sum_{i = 1}^{t} β_{i} | u_{i} 〉 〈 v_{i} |

, where

{| x_{i} 〉}_{i}, {{〈 y_{i} |}}_{i}, {| u_{i} 〉}_{i}, {{〈 v_{i} |}}_{i}

are respectively orthonormal sets of vectors in

H

and

λ_{j}, β_{i} > 0

. Then, from

A^{†} B = 0

, we have

\sum_{i, j} λ_{i}^{*} β_{j} 〈 x_{i} | u_{j} 〉 \cdot | y_{i} 〉 〈 v_{j} | = 0 .

〈 y_{i} | A^{†} B | v_{j} 〉 = 0

, we know that

〈 x_{i} | u_{j} 〉 = 0

for

i = 1, \dots, s

and

j = 1, \dots, t .

Similarly, from

A B^{†} = 0

, we have

〈 y_{i} | v_{j} 〉 = 0 .

Hence,

{| y_{i} 〉 {}_{i = 1}^{s}, {| v_{i} 〉}}_{i = 1}^{t}

are disjoint and together orthonormal states. They together can be extended to an orthonormal basis. Let

| x 〉

be any normalized state represented under this basis with coordinate vector

(w_{1}, \dots, w_{n}) .

Then,

(A + B) | x 〉 = \sum_{i = 1}^{s} λ_{i} w_{i} | x_{i} 〉 + \sum_{j = 1}^{t} β_{j} w_{s + j} | u_{j} 〉 .

Its norm is upper bounded by

{max}_{i j} (| λ_{i} |, | β_{j} |) = max (| | A | |, | | B | |),

desired! This result implies the second claim as

(| x 〉 {〈 x | \otimes A^{x})}^{†} (| y 〉 〈 y | \otimes A^{y}) = 0

for any

x \neq y .

□

Definition 6.

W D

, if B can be written as

B = \sum_{y} B_{y} \otimes {| y 〉 〈 y |}_{D}

for an orthonormal basis

{| y 〉}_{y}

, where

B_{y}

works on W.

Remark 2.

This definition is very loose. If B does not operate on D, by default, it is understood as

B \otimes I_{D} = \sum_{x} B \otimes | x 〉 〈 x |

for a basis

{| x 〉}_{x}

and so D is a control register for B. The following lemma is shown by simple verifications.

Lemma 3.

Let

X Y D

be three quantum registers. The following properties hold.

1.: If A operates on $X D$ while B operates on $Y D$ with D being a control register in the same basis ${| y 〉}_{y \in D}$ for both A and B, then $[A, B] = 0 .$
2.: If A is a projector on D in basis ${| y 〉}_{y}$ and B operates on $Y D$ with D being a control register in the same basis, then $[A, B] = 0 .$

Lemma 4.

Let

| ψ 〉 = \sum_{y} t_{y} | ψ_{y} 〉 | y 〉

be a joint state for register

X Y

with

{| y 〉}_{y \in Y}

orthonormal basis of register Y. Let

P = {| y 〉 {〈 y |}}_{y}

be the projective measurement on register Y. Let

Q = {Q_{x}}_{x}

be the measurement on register X. Let

U_{y}

be a unitary on register X, labelled with

y \in Y

. Consider procedure A: apply

\sum_{y \in Y} U_{y} \otimes | y 〉 〈 y |

| ψ 〉

and then apply measurement Q on X to output x. Also consider procedure

A^{'}

which starts with measurement P on Y and continues with procedure A with the final output denoted by

x^{'}

. Then, the distributions of x and

x^{'}

are identical.

Proof. Procedure A outputs x with probability

| | \sum_{y} t_{y} Q_{x} U_{y} | ψ_{y} {〉 | y 〉 | |}^{2} .

The procedure

A^{'}

outputs y, resulting in the collapsed state

U_{y} | ψ_{y} 〉 | y 〉

with probability

| | t_{y} {| |}^{2}

. Following the measurement Q, it outputs x with probability

| | t_{y} Q_{x} U_{y} | ψ_{y} {〉 | y 〉 | |}^{2}

. So the overall probability to output x with probability

\sum_{y} | | t_{y} Q_{x} U_{y} | ψ_{y} {〉 | y 〉 | |}^{2} = | | \sum_{y} t_{y} Q_{x} U_{y} | ψ_{y} {〉 | y 〉 | |}^{2},

{| y 〉}_{y}

is orthogonal, desired. □

Remark 3.

There are two points to clarify.

(1) In Lemma 4, it is important that projective measurement

P = {| y 〉 {〈 y |}}_{y}

uses the same basis as

{| y 〉}_{y}

as in

\sum_{y} U_{y} \otimes | y 〉 〈 y |

. That is, the unitary needs to use register Y as a control register in the basis of the projective measurement P. Otherwise, the result will be incorrect. For example, let

| ψ 〉 = | 0 〉 | + 〉,

where

| + 〉 = \frac{| 0 〉 + | 1 〉}{\sqrt{2}}

and

| - 〉 = \frac{| 0 〉 - | 1 〉}{\sqrt{2}} .

Define

U_{+} = | 1 〉 〈 0 | + | 0 〉 〈 1 |

and

U_{-} = I .

Let

Q = {| 0 〉 〈 0 |, | 1 〉 〈 1 |}

on register X and

P = Q

but on register Y. Let

U = U_{+} \otimes | + 〉 〈 + | + U_{-} \otimes | - 〉 〈 - |

. Then, for procedure A, the state before measurement Q is

| 1 〉 | + 〉

and hence the outcome of Q is 1 with probability 1. But procedure

A^{'}

, after measurement P, the state is

| 0 〉 | 1 〉

| 0 〉 | 0 〉

, each with probability 1/2. Since

| 1 〉 = \frac{| + 〉 - | - 〉}{\sqrt{2}}

and

| 0 〉 = \frac{| + 〉 + | - 〉}{\sqrt{2}}

, after applying U, the result is

\frac{1}{\sqrt{2}} (| 1 〉 | + 〉 \pm | 0 〉 | - 〉)

(± depending 1 or 0 on Y register) and next the measurement Q on register X gives the outcome 1 with probability

1 / 2 \cdot 1 / 2 + 1 / 2 \cdot 1 / 2 = 1 / 2 .

This is different from the procedure A.

(2) This counter example can also be regarded as the evidence that starting with a different projective measurement on the same register will result in a different final output distribution. Indeed, Procedure A in our example can also be regarded as starting with a projective measurement

P^{'} = {| + 〉 〈 + |, | - 〉 〈 - |}

as it does not change

| ψ 〉

, while procedure

A^{'}

remains unchanged (starting with measurement P). But x and

x^{'}

are distributed differently.

Summarizing the example, if we insert a measurement into the quantum algorithm, the output could be disturbed. But the following result states that the probabilities w/o a measurement are actually related. This result was given by Boneh and Zhandry [9] but it seems only valid for the case where M is a projective (instead of general) measurement.

Lemma 5.

Let A be a quantum algorithm and

Pr [x]

be the probability that A outputs x. Let

A^{'}

be the algorithm that runs A till some stage and then performs a projective measurement M which gives an outcome m (out of k possible choices) and next continues the execution of A with post-measurement state. Let

{Pr}^{'} [x]

be the probability that

A^{'}

outputs x. Then,

{Pr}^{'} [x] \geq Pr [x] / k .

Proof. Let

M = {M_{i}}_{i = 1}^{k}

be the measurement. Let

| ϕ 〉

be the state right before this measurement. Then, the probability of partial measurement outcome m occurs with probability

p_{m} = 〈 ϕ | M_{m}^{*} M_{m} | ϕ 〉

and the post-measurement has the state

| ϕ_{m} 〉 = M_{m} | ϕ 〉 / \sqrt{p_{m}} .

By deferred measurement principle, we can assume that A after this consists of a unitary U and a final projective measurement

{P_{i}}_{i}

be the final measurement. Then

\begin{matrix} {Pr}^{'} [x] = & \sum_{m} p_{m} 〈 ϕ_{m} | U^{†} P_{x}^{†} P_{x} U | ϕ_{m} 〉 = \sum_{m} 〈 ϕ | M_{m}^{†} U^{†} P_{x}^{†} P_{x} U M_{m} | ϕ 〉 \end{matrix}

(2)

\begin{matrix} = & \sum_{m} | | P_{x} U M_{m} {| ϕ 〉 | |}^{2} \geq | | \sum_{m} P_{x} U M_{m} {| ϕ 〉 | |}^{2} / k \end{matrix}

(3)

\begin{matrix} = & | | P_{x} {U | ϕ 〉 | |}^{2} / k = Pr [x] / k . \end{matrix}

(4)

where the inequality follows from Cauchy-Schwarz inequality and Equation (4) uses the fact that M is the projective measurement so

\sum_{m} M_{m} = \sum_{m} M_{m}^{†} M_{m} = I

. □

Lemma 6.

Let

| u 〉, | v 〉

be two states for a quantum system.

D_{t} (| u 〉 〈 u |, | v 〉 〈 v |) \leq | | | u 〉 - | v 〉 | | .

Proof. Let

| 0 〉 = | u 〉

and take

| 1 〉

as a unit orthogonal state of

| 0 〉

so that

| v 〉 = ω (cos (θ) | 0 〉 + sin (θ) | 1 〉)

with

θ \in [0, π / 2]

, by absorbing the complex unit factor (if any) into

| 1 〉,

where

ω

is a complex unit factor. By calculation,

D_{t} (| u 〉 〈 u |, | v 〉 〈 v |) = | sin (θ) | .

On the other hand,

| | | u 〉 - | v 〉 | | = \sqrt{{| 1 - ω cos (θ) |}^{2} + {sin}^{2} (θ)} \geq \sqrt{{(1 - cos (θ))}^{2} + {sin}^{2} (θ)} = 2 | sin (θ / 2) | .

Since

| sin (θ) | = 2 | sin (θ / 2) \cdot cos (θ / 2) | \leq 2 | sin (θ / 2) |,

the result follows. □

The following property states that an intermediate measurement by a quantum algorithm is not necessary (in the sense that we can replace it with a certain unitary) if we are only concerned with the final output. This is essentially the deferred measurement principle [43].

Lemma 7.

Let

| ϕ 〉

be a quantum state. We apply the following operators on register A: first a unitary U, then a measurement

M = {M_{y}}_{y}

that results in y, next a unitary

V_{y}

and finally a measurement

N_{y} = {N_{y x}}_{x}

that results in x. Then, there exist a unitary W on A and additional registers

B C

and a projective measurement P on C that results x with the same probability.

Proof. It can be seen that the original procedure outputs x with probability

\sum_{y} | | N_{y x} V_{y} M_{y} {U | ϕ 〉 | |}^{2} .

Then, define a unitary operator

U_{M}

so that

U_{M} {| ϕ 〉}_{A} {| 0 〉}_{B} = \sum_{y} M_{y} {| ϕ 〉}_{A} {| y 〉}_{B}

([43]). Also define unitary V on

A B

with

V = \sum_{y} V_{y} \otimes {| y 〉 〈 y |}_{B} .

Also define unitary

U_{N}

so that

U_{N} {| u 〉}_{A} {| y 〉}_{B} {| 0 〉}_{C} = \sum_{x} \sum_{r} (N_{r x} \otimes | r 〉 〈 r |) {| u 〉}_{A} {| y 〉}_{B} {| x 〉}_{C} .

Finally, define P to be the projective measurement

P = {| x 〉 {〈 x |}}_{x} .

Then, consider

U_{N} V U_{M} {U | ϕ 〉}_{A} {| 0 〉}_{B} {| 0 〉}_{C}

followed by P on C. Then, the probability of outcome x, by first applying

W = U_{N} V U_{M}

, followed by measurement P on C, is

\begin{matrix} {Pr}^{'} (x) = & | | \sum_{r} (N_{r x} \otimes | r 〉 〈 r |_{B}) \cdot \sum_{y^{'}} V_{y^{'}} \otimes | y^{'} 〉 〈 y^{'} |_{B} \cdot \sum_{y} M_{y} {| ϕ 〉}_{A} {| y 〉}_{B} {| x 〉}_{C} {| |}^{2} \\ = & | | \sum_{y} N_{y x} V_{y} M_{y} {U | ϕ 〉 | y 〉 | |}^{2} \\ = & \sum_{y} | | N_{y x} V_{y} M_{y} {U | ϕ 〉 | |}^{2}, desired! □ \end{matrix}

Remark 4.

In this lemma, register B is a control register in the basis

{{| y 〉}_{B}}_{y}

for other operators; register C is a control register in the basis

{{| x 〉}_{C}}_{x}

for other operators. Hence, the projective measurement

{| x 〉 {〈 x |}}_{x}

on B commutes with other operators and so can be moved to the end of the operations (especially, after measurement P on C) and hence does not affect the distribution of outcome x of P, and hence it can be removed. This justifies the proof idea of the above lemma. With this in mind, the following generalization corollary of the lemma is straightforward.

Corollary 1.

Let

| ϕ 〉

be a quantum state of register A. For

ℓ = 1, \dots, N

, run a unitary

U_{ℓ},

measurement

M_{y^{ℓ - 1}} = {M_{y^{ℓ}}}_{y_{ℓ}}

that results in

y_{ℓ}

, followed by unitary

V_{y^{ℓ}}

, where

y^{i}

represents the sequence

y_{1} \dots y_{i}

. Finally, it applies measurement

N_{y^{N}} = {N_{y^{N} x}}_{x}

that results in x. Then, there is unitary W and projective measurement P that applies to the initial state

{| ϕ 〉 | 0 〉}_{1} {\dots | 0 〉}_{N} | 0 〉

and results in x with the same probability.

4. Quantum Random Oracle

In this section, we will introduce the quantum random oracle. We use bold font to represent the random oracle (e.g.,

RO

) and the italic font (e.g.,

R O

) to represent the operator for the random oracle query. We distinguish an oracle and its operator because some oracle could offer more operators.

4.1. Standard Random Oracle

In the random oracle model, a cryptographic hash function

H : X \to {0, 1}^{n}

is treated as an external oracle so that whenever one needs to compute

H (x)

, he queries x to this oracle and receives

H (x)

. We assume

X

has a finite bit-length. The oracle uses a random function from

X

Y

to answer the queries. Let

X = {x_{1}, \dots, x_{N}}

be an ordered set with

x_{1} < x_{2} < \dots < x_{N} .

Function H can be represented by its truth table

H (x_{1}), H (x_{2}), \dots, H (x_{N})

. In the quantum random oracle model, H is represented by state

| H 〉

(using its truth table). An algorithm

A

can query a superposition to random oracle

RO

. For query

| x 〉 | y 〉

R O

maps

| x 〉 | y 〉 | H 〉

| x 〉 | y \oplus H (x) 〉 | H 〉

The standard random oracle

StO

has an initial state in a uniform superposition

\frac{1}{\sqrt{2^{n | X |}}} \sum_{H} | H 〉 .

For query

| x 〉 | y 〉

S t O

maps

\frac{1}{\sqrt{2^{n | X |}}} \sum_{H} | x 〉 | y 〉 | H 〉

\frac{1}{\sqrt{2^{n | X |}}} \sum_{H} | x 〉 | y \oplus H (x) 〉 | H 〉

. Notice that

RO

can be obtained from

StO

by starting with a projective measurement on oracle register (resulting in

| H 〉

). Even though

RO

and

StO

are different, no adversary can distinguish them. This can be seen from Lemma 3(2) by observing that oracle register is a control register in the computational basis for adversarial operators (which do not operate on oracle register) and

S t O

. Hence, the projective measurement on oracle register can be moved to after

A

makes the final measurement.

Fact 1.

Let

A

be a quantum algorithm with oracle access to the quantum random oracle. Then,

Pr (A^{RO} () = 1) = Pr (A^{StO} () = 1)

4.2. Compressed Random Oracle

The compressed random oracle

CStO

was introduced in [49] and our exposition mainly follows [15]. It is a powerful tool for security proof in the quantum random oracle model (QROM). Let

Y = {0, 1}^{n}

and

\bar{Y} = Y \cup {⊥}

. Let H be the quantum Walsh-Hadamard transform over

C [Y]

. Define

ϕ_{y} = H | y 〉

for

y \in {0, 1}^{n}

. Since

{| y 〉}_{y \in {0, 1}^{n}}

is orthonormal and

H^{2} = I

{| ϕ_{y} 〉}_{y \in {0, 1}^{n}}

is orthonormal either. Then, we define an unitary operator F over

C [\bar{Y}]

such that

\begin{matrix} F | ⊥ 〉 = | ϕ_{0} 〉, F | ϕ_{0} 〉 = | ⊥ 〉, F | ϕ_{y} 〉 = | ϕ_{y} 〉, \forall y \in Y - {0} . \end{matrix}

(5)

It is Hermitian (i.e.,

F^{†} = F

) because

F = | ϕ_{0} 〉 〈 ⊥ | + | ⊥ 〉 〈 ϕ_{0} | + \sum_{y \neq 0} | ϕ_{y} 〉 〈 ϕ_{y} | .

Further, notice that

| y 〉 = 2^{- n / 2} \sum_{η \in {0, 1}^{n}} {(- 1)}^{y \cdot η} | ϕ_{η} 〉 .

This implies that

F | y 〉 = | y 〉 + 2^{- n / 2} (| ⊥ 〉 - | ϕ_{0} 〉) .

We consider the multi-register

D = {D_{x}}_{x \in X}

for the random oracle, where

D_{x}

has a state space

C [\bar{Y}]

, spanned by the computational basis

{| y 〉}_{y \in Y} \cup {| ⊥ 〉} .

The initial state of D is

\otimes_{x} {| ⊥ 〉}_{D_{x}}

. We assume that the adversary has a query register X, response register Y and a work register

W .

To query the oracle, adversary provides

X Y

registers to oracle who then applies unitary

\begin{matrix} C S t O_{X Y D} & = \sum_{x \in X} {| x 〉 〈 x |}_{X} \otimes C S t O_{Y D_{x}} \end{matrix}

(6)

X Y D

, where

C S t O_{Y D_{x}} = F_{D_{x}} \cdot {C N O T}_{Y D_{x}} \cdot F_{D_{x}}

and

{C N O T | y 〉}_{Y} {| u 〉}_{D_{x}} = {| y + u 〉}_{Y} {| u 〉}_{D_{x}} .

Then, the following result holds. It must be pointed out that the result holds only if no operator other than

C S t O

(resp.

S t O

) is applied on D; otherwise, the result might fail.

Lemma 8.

[49] Let

A

be a quantum algorithm with oracle access to the quantum random oracle. Then,

Pr (A^{StO} () = 1) = Pr (A^{CStO} () = 1) .

4.3. Compressed Random Oracle with Adaptive Special Points

Compressed random oracle with adaptive special points (denoted by

{CStO}_{s}

) is a natural generalization of

CStO

. Liu and Zhandry [30] briefly introduced CStO with non-adaptive special points. But we believe that

{CStO}_{s}

(which has adaptive special points) is very useful in applications. It allows to register special points on the fly. In fact, it seems the Fiat-Shamir based signature proof in [30] also seems to require this adaptivity as the adversary’s signing query can not be guessed or predicted before the query. The oracle has the initial state

\otimes_{x} {| ⊥ 〉}_{D_{x}} .

We maintain two initially empty set

Ξ_{0}

and

Ξ_{1}

to record the special points at different stages. We also allow the oracle to abort after certain measurements and the motivation will be discussed later. The oracle can be accessed through three types of queries below.

PointReg0 Query. One can send a new point $x \in X$ to oracle. If $x \in Ξ_{0} \cup Ξ_{1}$ , it does nothing; otherwise, the oracle updates $Ξ_{0} = Ξ_{0} \cup {x} .$
Random Oracle Query. One can issue a random oracle query by providing a query register X and a response register Y to oracle. If this is the ith random oracle query, the oracle applies a projective measurement $Λ_{i} = (Λ_{i 0}, Λ_{i 1})$ in the computational basis to oracle register $D_{Ξ_{0}}$ ( $Λ_{i}$ can be determined by i and some parameters that are determined before the oracle starts). If the outcome is 1, it aborts; otherwise, it applies $C S t O_{s} = \sum_{x \in X} | x 〉 〈 x | \otimes C S t O_{s Y D_{x}}$ to $X Y D$ registers, where

$C S t O_{s Y D_{x}} = \{\begin{matrix} C S t O_{Y D_{x}}, & x \notin Ξ_{1} \\ {C N O T}_{Y D_{x}}, & o t h e r w i s e . \end{matrix}$

Finally, it returns register $X Y$ .
PointReg1 Query. One can send $x \in Ξ_{0}$ to oracle. If $x \notin Ξ_{0}$ , it does nothing. Otherwise, it measures $D_{x}$ with $Π = (Π_{0}, Π_{1})$ , where $Π_{0} = | ⊥ 〉 〈 ⊥ |, Π_{1} = I - Π_{0}$ . If the outcome is 1, it aborts; otherwise, it updates ${| ⊥ 〉}_{D_{x}}$ with $| r 〉$ for a random $r \in Y$ (this can be done as ${| ⊥ 〉}_{D_{x}}$ is now classic; or, we can apply unitary $| ⊥ 〉 〈 r | + | r 〉 〈 ⊥ | + \sum_{v \in Y - {r}} | v 〉 〈 v |$ ). Finally, it updates $Ξ_{1} = Ξ_{1} \cup {x}$ and $Ξ_{0} = Ξ_{0} - {x} .$

Remark 5.

It is time to justify this strange random oracle. It is in fact motivated by the requirements in the security proof. The main motivation is to find a modified random oracle so that the randomly sampled experiment (with

CStO

) in Section 5 can be easily converted into a game with this modified random oracle. The idea is that we want to define some special points and set their random oracle values to our own choices, just as I can do in the classical random oracle.

In the classic random oracle, a simulator can set the random oracle values of special queries to his own choices. In the ${CStO}_{s}$ , a special point will be first recorded in $Ξ_{0}$ and later set to a planned value (when a PointReg1 query on this point is issued). We handle special points in two stages for technical reasons (See the remark after Theorem 5) only. Essentially, if we define the random oracle value of a special point early (e.g., at the time of adding into $Ξ_{0}$ ), it could make the previously selected experiment change to a different one.
${CStO}_{s}$ is to formulate the selected experiment in Section 5 as a well-defined random oracle model. Especially, measurement $Λ_{i}$ in a random oracle query is to make sure the interaction with oracle follows the restriction of the selected experiment. If the measurement outcome is 1, it indicates that the game is not consistent with the selected experiment and hence it can stop now; otherwise, it continues. This randomly selected but consistent experiment can guarantee the adversary to have a good success probability, compared with the original game.
In the classic random oracle, a simulator can pay attention to each query to make sure that each special point is not queried before it is set to the designated value. In the quantum setting, recording each query is difficult as one can query $\frac{1}{| X |} \sum_{x} {| x 〉}_{X} {| 0 〉}_{Y}$ which indicates that every x is actually queried. To overcome this, we need to confirm that $O R (x)$ is not defined by measurement Π on $D_{x}$ . If measurement is successful, then $D_{x}$ will have ${| ⊥ 〉}_{D_{x}}$ now and non-⊥ components in the superposition are pruned and we can define the random oracle value for this x; if the measurement fails, we have no way to set the random oracle value for x and so abort.

We define

{CStO}^{'}

to be a variant of

{CStO}_{s}

so that

C S t O_{s}

in the random oracle query is replaced by

C S t O

and also in PointReg1 query, in case the measurement outcome 0, it leaves

{| ⊥ 〉}_{D_{x}}

as it is (instead of replacing it by

| r 〉

). Essentially,

{CStO}^{'}

is the same as

CStO

, except it applies

Λ_{i}

and

Π

measurements on D. The following lemma shows that

{CStO}_{s}

is perfectly indistinguishable from

{CStO}^{'}

, conditional on that the abort event in the oracle does not occur.

Lemma 9.

Let

A

be a quantum algorithm with access to quantum random oracle and

abort

be the oracle abortion event. Then,

\begin{matrix} Pr (A^{{CStO}^{'}} () = 1 \land \neg abort) = Pr (A^{{CStO}_{s}} () = 1 \land \neg abort) . \end{matrix}

(7)

Proof. We use the hybrid argument with a variant

{CStO}_{s}^{'}

{CStO}_{s}

to bridge

{CStO}_{s}

and

{CStO}^{'}

Oracle

{CStO}_{s}^{'}

. We modify

{CStO}_{s}

{CStO}_{s}^{'}

so that upon PointReg1 query x with

D_{x}

measured with outcome 0 (i.e.,

| ⊥ 〉

), it updates

{| y 〉}_{D}

\frac{1}{2^{n / 2}} \sum_{r} {| y \cup {(r)}_{x} 〉}_{D}

(instead of

{| y \cup (r)}_{x} 〉_{D}

for a random r), where

y \cup {(r)}_{x}

(which is well defined as

y_{x} = ⊥

) is the vector with

y_{x^{'}}

at index

x^{'} \neq x

and r at index x. Notice that right after this,

x \in Ξ_{1}

. Further,

D_{x}

for this x is a control register (Def. 6) in the computational basis for adversary operations,

Π_{0}, Π_{1}, Λ_{i 0}, Λ_{i 1}

and

C S t O_{s Y D_{u}}

. To see this, it suffices to check

C S t O_{s Y D_{x}}

only as other cases are clear (e.g.,

C S t O_{s Y D_{u}}

for

u \neq x

does not operate on

D_{x}

at all). Since

x \in Ξ_{1}

, we know that

C S t O_{Y D_{x}} = {C N O T}_{Y D_{x}}

which obviously can be written as a format of

\sum_{y \in \bar{Y}} B_{y} \otimes {| y 〉 〈 y |}_{D_{x}}

. Further,

{CStO}_{s}

is obtained from

{CStO}_{s}^{'}

by projective measurement on

D_{x}

in the computational basis for every

x \in Ξ_{1}

(right after x is put in

Ξ_{1}

). By Lemma 3(2), the projective measurement on

D_{x}

can be moved to the end of the interaction (after

A

outputs). Thus, the output of

A

with access to

{CStO}_{s}^{'}

is the same as with access to

{CStO}_{s}

Oracle

{CStO}^{'}

. We show that under the event

\neg abort

, if the final (unnormalized) state after interacting with

{CStO}_{s}^{'}

| ψ 〉

, then the final state (unnormalized) after interacting with

{CStO}^{'}

will be

F_{D_{Ξ_{1}}} | ψ 〉 .

This can be shown by induction on the query. It is correct initially, as

Ξ_{1} = \emptyset

initially and hence

F_{D_{Ξ_{1}}}

is identity. Then, if it is correct after query

i - 1

, consider query

i .

Before query i,

A

will operate on

X Y W

registers (for simplicity, assume it is a unitary). But since adversary does not operate on D, if the state right before query i (when interacting with

{CStO}_{s}^{'}

) is

| ψ 〉

, then the state right before query i (when interacting with

{CStO}^{'}

) will be

F_{D_{Ξ_{1}}} | ψ 〉

If query i is a PointReg0 query, then the claim still holds after the query as no operation on the quantum state is executed.

If query i is a PointReg1 query x, then it suffices to consider

x \in Ξ_{0}

. Since

x \notin Ξ_{1}

and the outcome of

Π

is 0 (otherwise,

abort

occurs, contradiction to the probability condition) so x will be added to

Ξ_{1}

, the conclusion holds after the query as

F | ⊥ 〉 = | ϕ_{0} 〉

(while, after the query,

D_{x}

in case of

{CStO}_{s}^{'}

will have

| ⊥ 〉

and

D_{x}

in case of

{CStO}^{'}

will

| ϕ_{0} 〉

If query i is a random oracle query, we show that the induction still holds. First,

[F_{D_{Ξ_{1}}}, Λ_{i b}] = 0

for both

b = 0, 1

Λ_{i}

only operates on register

D_{Ξ_{0}}

. Thus, after the measurement (with the same outcome), the relation still holds. Second, the relation still holds after operator

C S t O_{s}

(in case of

{CStO}_{s}^{'}

) and operator

C S t O

(in case of

{CStO}^{'}

): for query

{| x 〉}_{X} {| y 〉}_{Y}

with

x \notin Ξ_{1}

, both oracles use

C S t O_{Y D_{x}}

to respond and hence their states after the query maintain the same relation (as

D_{Ξ_{1}}

is untouched); for query

{| x 〉}_{X} {| y 〉}_{Y}

with

x \in Ξ_{1}

{CStO}^{'}

uses

C S t O_{Y D_{x}}

and

{CStO}_{s}^{'}

uses

{C N O T}_{Y D_{x}}

but two applications of

F_{D_{x}}

{C S t O}_{Y D_{x}}

will cancel out. So after the query the relation still holds. The induction holds too.

Let

| ψ 〉

be the final unnormalized state under

\neg abort

and the final measurement of

A

(P_{0}, P_{1})

with

P_{1}

corresponding to outcome 1. Then,

Pr (A^{{CStO}_{s}^{'}} () = 1 \land \neg abort)

| | P_{1} {| ψ 〉 | |}^{2}

, while

Pr (A^{{CStO}^{'}} () = 1 \land \neg abort)

| | P_{1} \cdot F_{D_{Ξ_{1}}} {| ψ 〉 | |}^{2}

. However,

| | P_{1} \cdot F_{D_{Ξ_{1}}} {| ψ 〉 | |}^{2} = | | P_{1} {| ψ 〉 | |}^{2}

F_{D_{Ξ_{1}}}

commute with

P_{1}

(since they operate on disjoint registers) and

F^{2} = I

. □

The following lemma essentially states that if

x^{*}

has large min-entropy and we measure

D_{x^{*}}

of the adversary-oracle joint state, then, with high probability, the post-measurement state with outcome ⊥ is close to the original state.

Lemma 10.

Let the current adversary-oracle joint state be

| ψ 〉 = \sum_{z y} λ_{z y} {| z 〉 | y 〉}_{D}

after q queries to

{CStO}_{s}

(or CStO ). Let

| ψ_{x} 〉 = \sum_{z y : y_{x} = ⊥} λ_{z y} {| z 〉 | y 〉}_{D}

and

x^{*}

is a random variable over

X

with min-entropy at least μ. Then, with probability

1 - 2^{- μ / 2}

(over

x^{*}

| | | ψ 〉 - | ψ_{x^{*}} 〉 | | \leq q^{1 / 2} 2^{- μ / 4}

Proof. Let

| ψ_{x}^{'} 〉 = \sum_{z y : y_{x} \neq ⊥} λ_{z y} {| z 〉 | y 〉}_{D} .

Then,

| ψ 〉 = | ψ_{x}^{'} 〉 + | ψ_{x} 〉 .

Consider

L : = \sum_{x} | | | ψ_{x}^{'} {〉 | |}^{2}

. Let

N_{y}

be the number of x so that

y_{x} \neq ⊥

y

. Then, given

y

| y 〉

appears in

| ψ_{x}^{'} 〉

for exactly

N_{y}

possible x’s. Thus,

L = \sum_{z y} {| λ_{z y} |}^{2} N_{y} .

Since each

y

| ψ 〉

has at most q possible non-⊥ entries, it follows that

N_{y} \leq q

and hence

L \leq q .

Hence, there are at most

2^{μ / 2}

choices for x so that

| | | ψ_{x}^{'} 〉 | | \geq q^{1 / 2} 2^{- μ / 4} .

Since

x^{*}

has min-entropy

μ

, we have that

| | | ψ_{x^{*}}^{'} 〉 | | < q^{1 / 2} 2^{- μ / 4}

with probability at least

1 - 2^{- μ / 2}

. The lemma follows. □

4.4. Measurement $U_{R}$

Let

R \subset X \times Y

be a fixed and efficiently verifiable relation with

R (x, y) = 1

if and only if

(x, y) \in R

. Especially,

R (x, y) = 0

for any

(x, y) \notin X \times Y

. We assume that

0 \notin X

and so

R (0, y) = 0

. Further,

R (x, ⊥) = 0

⊥ \notin Y

. Let

\bar{X} = X \cup {0} .

We define function

f_{R} : {\bar{Y}}^{| X |} \to \bar{X}

so that

f_{R} (y_{1}, \dots, y_{N}) = \{\begin{matrix} x_{i}, & (x_{j}, y_{j}) \notin R f o r j < i b u t (x_{i}, y_{i}) \in R \\ 0, & i d o e s n o t e x i s t . \end{matrix}

where

X = {x_{1}, \dots, x_{N}}

is an ordered set with

x_{1} < x_{2} < \dots < x_{N} .

In other words,

f_{R} (y_{1}, \dots, y_{N})

is the smallest

x_{i}

so that

(x_{i}, y_{i}) \in R .

It is easy to verify that

\begin{matrix} f_{R} (y_{1}, \dots, y_{| X |}) = \sum_{i = 1}^{| X |} x_{i} \cdot \bar{R} (x_{1}, y_{1}) \cdot \dots \cdot \bar{R} (x_{i - 1}, y_{i - 1}) \cdot R (x_{i}, y_{i}) . \end{matrix}

(8)

Here we emphasize that we do not require

\bar{X}

itself to be a group but we implicitly assume that it can be regarded as a subset of an Abelian group

\tilde{X}

(e.g.,

\bar{X} = {0, 1, 2, 4}

can be regarded as a subset of

Z_{5}

). Next, we define

U_{R}

to be a unitary on

C {[\bar{Y}]}^{\otimes X} \otimes C [\tilde{X}]

for register

D P

so that

\begin{matrix} U_{R} {| y 〉}_{D} {| w 〉}_{P} = {| y 〉}_{D} {| w + f_{R} (y_{1}, \dots, y_{| X |}) 〉}_{P}, \end{matrix}

(9)

where

{| y 〉}_{D} : = | y_{1} 〉_{D_{x_{1}}} \dots {| y_{| X |} 〉}_{D_{x_{| X |}}}

. Let

Γ_{R} = max_{x} | {y ∣ (x, y) \in R} | a n d Γ_{x} = | {y ∣ (x, y) \in R} | .

(10)

Notice that our

U_{R}

is an alternative specification but identical to

U_{R}

in [15]. The following lemma was proved in [15] (we can obtain the same bound by a proof for our specification).

Lemma 11.

For any

x \in X

| | [F_{D_{x}}, U_{R}] | | \leq 4 \sqrt{2 Γ_{R} / 2^{n}} .

Lemma 12.

[{C N O T}_{X Y D}, U_{R}] = 0 .

Proof. It can be seen that

{C N O T}_{X Y D} = \sum_{y} (\sum_{x, y} | x, y_{x} + y 〉 〈 x, y |) \otimes {| y 〉 〈 y |}_{D}

and also that

U_{R} = \sum_{y} (\sum_{w} | w + f_{R} (y) 〉 〈 w |_{P}) \otimes {| y 〉 〈 y |}_{D}

. Therefore, D is a control register for

U_{R}

and

{C N O T}_{X Y D}

in the computational basis. By Lemma 3(1), they commute. □

Theorem 1.

| | [C S t O_{s}, U_{R}] | | \leq 8 \cdot 2^{- n / 2} \sqrt{2 Γ_{R}} .

Proof. Notice that

C S t O_{s} = \sum_{x \in X} | x 〉 〈 x | \otimes C S t O_{s Y D_{x}}

and for

x \in Ξ_{1}

C S t O_{s Y D_{x}} = {C N O T}_{Y D_{x}}

. Hence, by Lemma 12,

[C S t O_{s}, U_{R}] = \sum_{x \notin Ξ_{1}} {| x 〉 〈 x |}_{X} \otimes [F_{D_{x}} \otimes {C N O T}_{Y D_{x}} \otimes F_{D_{x}}, U_{R}],

where we also use

[| x 〉 〈 x |_{X}, U_{R}] = 0 .

By Lemma 1(3) and Lemma 2(2),

| | [C S t O_{s}, U_{R}] | | \leq 2 max_{i} | | [F_{D_{x_{i}}}, U_{R}] | | + | | [C N O T, U_{R}] | | .

By Lemma 11 and Lemma 12, the result follows. □

4.5. Bounding the Probability for Relation Search through Oracle Queries

We are interested in finding an entry

y_{x}

for some x in the oracle (through oracle queries) so that

R (x, y_{x}) = 1

for a relation R. The following lemma upper bounds the probability for this. The proof idea is that

R (x, y_{x}) = 1

can be detected by applying

U_{R}

and measuring P register with outcome

\hat{x} \neq 0 .

If we apply

U_{R}

and measure P at the beginning of the interaction, then

\hat{x} = 0

because the initial oracle state is dummy. Hence, the success probability with

U_{R}

at the end of interaction, is bounded by the squared norm of the commuter of operators (throughout the interaction) with

U_{R}

Lemma 13.

Let

A

be a quantum algorithm with access to

{CStO}_{s}

, incurring

L_{0}

random oracle queries and

q - L_{0}

PointReg1 queries. The final state goes through

U_{R}

of relation R and a projective measurement on register P in the computational basis with outcome

\hat{x} \in \bar{X}

. Then,

\begin{matrix} Pr (\hat{x} \neq 0 \land \neg abort) \leq 128 q^{2} Γ_{R} / 2^{n} . \end{matrix}

(11)

Proof. Let

| ψ 〉

be the initial state of

A

with registers

X Y Z

. The joint initial state with oracle is then

| ω_{0} {〉 = | ψ 〉}_{X Y Z} \otimes {(\otimes_{x} | ⊥ 〉}_{D_{x}} {) \otimes | 0 〉}_{P}

(after register P added). Then,

A

has access to

{CStO}_{s}

, incurring

L_{0}

random oracle queries with intermediate operator

V_{X Y Z}

, where, for simplicity, we assume that

V_{X Y Z}

remains unchanged throughout the game. Finally, oracle applies

U_{R}

D P

and projective measurement

P

on P, outputting the outcome

\hat{x}

. The final state before measurement

P

| ω 〉 = U_{R} {(V \cdot {CStO}_{s})}^{L} | ω_{0} 〉

for some L, where

{CStO}_{s}

is PointReg0 query or PointReg1 query or random oracle query. If the query is PointReg0, it does not operate on the state and so commutes with

U_{R}

; if it is PointReg1, then we only consider the case

x \in Ξ_{0}

. Under

\neg abort

, it consists of projector

Π_{0}

and

U_{⊥, r} = | r 〉 〈 ⊥ | + | ⊥ 〉 〈 r | + \sum_{v \neq r} | v 〉 〈 v |

for uniformly random r over

Y

. We notice that

[Π_{0}, U_{R}] = 0

. Further, it is not hard to verify that

U_{⊥, r} Π_{0}

in PointReg1 commutes with

U_{R}

(x, r) \notin R

(as

(x, ⊥) \notin R

). If it is a random oracle query, we notice that

[Λ_{i}, U_{R}] = 0

as D is control register for both

Λ_{i}

and

U_{R}

in the computational basis. Therefore,

\begin{matrix} Pr (\hat{x} \neq 0 \land \neg abort) \\ \leq E_{r} (| | (I - | 0 〉 〈 0 |_{P}) {| ω 〉 | |}^{2}) / * r^{'} s from PointReg1; state | ω 〉 is consistent with \neg abort * / \\ = E_{r} (| | (I - | 0 〉 〈 0 |_{P}) [U_{R}, {(V \cdot {CStO}_{s})}^{L}] | ω_{0} 〉 + (I - | 0 〉 〈 0 |_{P}) {(V \cdot {CStO}_{s})}^{L} U_{R} | ω_{0} {〉 | |}^{2}) \\ / * {CStO}_{s} requires the operator for measurement outcome (e . g ., Π_{0}, Λ_{i 0}) consistent with \neg abort * / \\ = E_{r} (| | (I - | 0 〉 〈 0 |_{P}) [U_{R}, {(V \cdot {CStO}_{s})}^{L}] | ω_{0} {〉 | |}^{2}) \\ / * as V and {CStO}_{s} {do not operate on P and so part 2 has | 0 〉}_{P} before applying I - | 0 〉 〈 0 | * / \\ \leq E_{r} (| | [U_{R}, {(V \cdot CStO)}^{L}] {| |}^{2}) \leq E_{r} {(L_{0} | | [U_{R}, C S t O_{s}] | | + \sum_{i} | | [U_{R}, U_{⊥, r_{i}}] {| |)}^{2}} \\ / * Lemma 1(3) and [Λ_{i}, U_{R}] = [Π_{0}, U_{R}] = [V, U_{R}] = 0 and L_{0} i s ♯ of C S t O_{s} queries \\ and r_{i} corresponds to r in the i th PointReg1 query . * / \\ \leq E_{r} {{(8 L_{0} \cdot 2^{- n / 2} \sqrt{2 Γ_{R}} + 2 N_{r})}^{2}} . \\ / * N_{r} is the number of r_{i} in i th PointReg1 (x_{i}) so that (x_{i}, r_{i}) \in R * / \\ / * [U_{R}, U_{⊥, r}] = 0 for (x, r) \notin R; | | [U_{R}, U_{⊥, r}] | | \leq 2 a s | | U_{R} | | = | | U_{⊥, r} | | = 1 * / \\ \leq 128 q^{2} Γ_{R} / 2^{n}, \end{matrix}

where the last inequality follows from the calculation with the observation:

N_{r}

is the result of Bernouli trial with probability

Γ_{R} / 2^{n}

for

q - L_{0}

times;

E {(a + N_{r})}^{2} = V a r (N_{r}) + {[a + E (N_{r})]}^{2}

;

V a r (N_{r}) = (q - L_{0}) Γ_{R} / 2^{n} (1 - Γ_{R} / 2^{n})

and

E (N_{r}) = (q - L_{0}) Γ_{R} / 2^{n}

. The lemma follows. □

4.6. Simulating ${CStO}_{s}$ with Extraction

In this section, we adapt the simulation of

CStO

with the extraction capability in [15] to the

{CStO}_{s}

setting. Essentially, the simulator simulates the oracle and also provides an interface for extracting the attacker’s oracle query x that, together with y in

D_{x}

, is a witness of a target “commitment”. Let

θ (x, y)

be an arbitrary but fixed function from

X \times Y

T .

For

t \in T

, define relation

R_{t} = {(x, y) ∣ θ (x, y) = t}

and

U_{t}

denotes unitary

U_{R_{t}}

. Then, the simulator is described in Figure 2.

In the following, we prove that if

A

uses x and

y = O R (x)

to generate t, then the extracted

\hat{x}

from

S . E (t)

will equal to x. This is useful in a security proof where an attacker generates an output and we need to find out the witness of this output. We first prove a weaker version of this: if

\hat{x}

is extracted at the end of game, the claim is true. Then, we extend to the case that

\hat{x}

is extracted on-the-fly (i.e., right after

A

outputs t).

4.6.1. Extraction at the End of Game

We begin with a collision event in a computational basis

{| y 〉}_{D}

in the oracle state w.r.t. a function f in the sense that

f (x, y_{x}) = f (x^{'}, y_{x^{'}})

for some

x^{'} \neq x

. We give a result which says that after q oracle queries, the probability of collision in the oracle is small. It is extended from [49] in the setting of

CStO

{CStO}_{s}

(see Appendix C for details).

Lemma 14.

Let

f : X \times Y \to T

. Then, for any quantum algorithm

A

with access to

{CStO}_{s}

, incurring q oracle queries of either PointReg1 or random oracle,

Pr (col \land \neg abort) \leq 16 q^{3} Γ_{f} / 2^{n},

(12)

where

col

is the collision event in the final state

ρ_{q}

and

Γ_{f} = {max}_{x^{'} \neq x, y^{'}} | {y ∣ f (x, y) = f (x^{'}, y^{'})} |

Now we give an extraction theorem, where

\hat{x}

is extracted at the end of oracle access. It states that if attacker computes t from x so that

t = f (x, R O (x))

, then

S . E (t)

at the end of game will most likely have

\hat{x} = x

. The idea is as follows. Assume

\hat{x} \neq x

. After attacker’s oracle access to

{CStO}_{s}

, we apply a classical oracle query on x with result

y_{x}

. Assume this state (right before

S . E (t)

) is

\sum_{y : y_{x} f i x e d} λ_{y} | ω_{y} {〉 | y 〉}_{D_{X - {x}}} F | y_{x} 〉_{D_{x}} {| 0 〉}_{P}

. Further, notice that

F | y_{x} 〉 = | y_{x} 〉 + | δ 〉

. If

y

in the sum measures with outcome

\hat{x}

(i.e., after

S . E (t)

), then it has a collision (since

f (\hat{x}, y_{\hat{x}}) = t = f (x, y_{x})

). This probability is small (by Lemma 15) and we can ignore it. If

{| y 〉}_{D_{X - {x}}} | y_{x}^{'} 〉

for

y_{x}^{'} \neq y_{x}

under

S . E (t)

gives

\hat{x}

, then

y_{x}^{'}

must come from

δ

. However,

| | δ | |

is very small. So this is unlikely too. This idea is from [15] in the

C S t O

case and can be generalized to prove a vector

(t, x)

case.

Theorem 2.

Consider quantum algorithm

A

with access to

S

(via interfaces other than

S . E

), including q random oracle queries or PointReg1 queries and outputting

t \in T^{ℓ}

and

x \in X^{ℓ} .

Let

h_{i}

be the output for an additional classical query

x_{i}

S . R O

and

{\hat{x}}_{i} = S . E (t_{i})

. Then,

\begin{matrix} Pr (\exists i : x_{i} \neq {\hat{x}}_{i}, f (x_{i}, h_{i}) = t_{i} \land \neg abort) \leq 2^{- n + 1} ℓ + 16 {(q + ℓ)}^{3} Γ_{f} / 2^{n} . \end{matrix}

(13)

Proof. Let the adversary-oracle joint state be

| ψ_{0} 〉

after queries to

S

(including q random oracle queries or PointReg1 queries). In the following, we always assume that random oracle query does not abort. Then,

A

measures and outputs

t, x

. Each

x_{i}

is then classically queried to

S . R O

and results in a joint state

| ψ_{1} 〉

. We assume that

x \cap Ξ_{1} = \emptyset

(the other case is similar). Hence,

| ψ_{1} 〉

can be written as

| ψ_{1} {〉 = | r 〉}_{D_{Ξ_{1}}} \otimes F_{D_{x}} {| h 〉}_{D_{x}} \otimes \sum_{ω u : u \in {\bar{Y}}^{A}} λ_{ω u} {| ω 〉}_{X Y Z} {| u 〉}_{D_{A}},

where

Ξ_{1} \cup x \cup A

is a decomposition of

X .

Finally, it applies the projective measurement

Π_{D} = {| y 〉 {〈 y |}}_{y \in {\bar{Y}}^{X}}

in the computational basis on D and applies

U_{t_{i}}, i = 1, \dots, ℓ

followed by (projective) measurement on register P as well as measurement

(Π_{c o l}, I - Π_{c o l})

to the resulting state (assuming the collision measurement writes the result in a new register C), where

Π_{c o l}

is a projection into a space spanned by

{| y 〉}_{D}

with

y \in {\bar{Y}}^{X}

satisfying

f (x, y_{x}) = f (x^{'}, y_{x^{'}})

for some

x^{'} \neq x

and

y_{x}, y_{x^{'}} \in Y .

Notice that D is a control register in the computational basis for

Π_{D}, P U_{t_{i}}

, and collision measurement, where

P

is the projective measurement on P. Hence, by Lemma 3, they all commute. Hence, both collision probability and

Pr (\exists i : x_{i} \neq {\hat{x}}_{i}, f (x_{i}, h_{i}) = t_{i})

will remain the same as the original game. For collision probability, it is the same as we move

P U_{t_{i}}

and

Π_{D}

to after collision measurement; for

Pr (\exists i : x_{i} \neq {\hat{x}}_{i}, f (x_{i}, h_{i}) = t_{i})

, it is similar by keeping

P U_{t_{i}}

while moving other two operators to the end of game. Let

c o l

be the output 0 of measurement

(Π_{c o l}, I - Π_{c o l})

. Notice that

\begin{matrix} Pr (\exists i : x_{i} \neq {\hat{x}}_{i}, f (x_{i}, h_{i}) = t_{i} | | ψ_{1} 〉) \end{matrix}

(14)

\begin{matrix} \leq & Pr (\exists i : x_{i} \neq {\hat{x}}_{i} \land f (x_{i}, h_{i}) = t_{i} \land \neg c o l | | ψ_{1} 〉) + Pr (c o l | | ψ_{1} 〉) \end{matrix}

(15)

Notice that register

D_{x_{i}}

| ψ_{1} 〉

| h_{i} 〉 + 2^{- n / 2} (| ⊥ 〉 - | ϕ_{0} 〉) .

Since

f (x_{i}, h_{i}) = t_{i}

, it follows that under

\neg c o l

condition,

x_{i} \neq {\hat{x}}_{i}

implies that after measurement on P (that results in

{\hat{x}}_{i}

in the ith component on register P), the post-measurement joint state

| ψ^{'} 〉_{X Y Z D} {| \hat{x} 〉}_{P}

must have

D_{x_{i}}

content different from

h_{i}

(that is,

〈 h_{i} | ψ^{'} 〉 = 0

). Since

| ψ_{1} 〉

has

F | h_{i} 〉

D_{x_{i}}

, this has a probability

1 - | 〈 h_{i} | (| h_{i} 〉 + 2^{- n / 2} | ϕ_{0} {〉) |}^{2} = 1 - {(1 - 2^{- n})}^{2} \leq 2^{- n + 1} .

There are at most ℓ possible i’s. So the first item in Equation (15) is at most

2^{- n + 1} ℓ

. On the other hand,

| ψ_{1} 〉

is obtained by measurements. Averaging over the choices of

| ψ_{1} 〉

satisfying

\neg abort

(due to intermediate measurements) gives

Pr (\exists i : x_{i} \neq {\hat{x}}_{i} \land f (x_{i}, h_{i}) = t_{i} \land \neg c o l \neg abort) \leq 2^{- n + 1} ℓ

. By Lemma 14,

Pr (c o l \land \neg abort) \leq 16 {(q + ℓ)}^{3} Γ_{f} / 2^{n}

. Thus,

Pr (\exists i : x_{i} \neq {\hat{x}}_{i}, f (x_{i}, h_{i}) = t_{i} \land \neg abort) \leq 2^{- n + 1} ℓ + 16 {(q + ℓ)}^{3} Γ_{f} / 2^{n} .

□

4.6.2. Extraction on the Fly

We have showed the extraction result where the extractions occur only at the end of the game. To be useful, it is expected that we can extract them “on-the-fly" (i.e., right after each commitment is given during the game). In the following, we consider this. The result is extended from [15] from the

CStO

setting to the

{CStO}_{s}

setting.

Let us consider a function

f : X \to T \cup {\emptyset}

with some special set

Ξ \subset X

so that

f (Ξ, Y) = \emptyset

and

f (\bar{Ξ}, Y) \subseteq T

. Consider the following games, where

S . {CStO}_{s}

S . R O

S . P R_{0}

S . P R_{1}

Game

Γ_{0} .

A

, with

q_{1}^{'}

queries to

{CStO}_{s}

, outputs

t \in T

and then with

q_{2}^{'}

queries to

{CStO}_{s}

, outputs

x \in X

and auxiliary output

W .

Finally, x is classically issued to

{CStO}_{s}

with response h.

Game

Γ_{1}

A

, with

q_{1}^{'}

queries to

S . {CStO}_{s}

, outputs

t \in T

and

S . E (t)

is executed to output

\hat{x}

. Then,

A

continues

q_{2}^{'}

queries to

S . {CStO}_{s}

and finally outputs

x \in X

and auxiliary output W. Finally, x is classically issued to

S . {CStO}_{s}

with response h.

Let

q_{1}

be the number of random oracle queries or PointReg1 queries in the first

q_{1}^{'}

queries to

S . {CStO}_{s}

. Similarly, we can define

q_{2} .

The pair

{(X, Y)}_{Γ}

denotes

(X, Y)

in game

Γ

. Define

Δ ({(X, Y = y)}_{Γ_{0}}, {(X, Y = y)}_{Γ_{1}}) \overset{d e f}{=} \frac{1}{2} \sum_{x} | P_{X Y} (x, y) - Q_{X Y} (x, y) |

(a partial sum in the statistical distance), where

P_{X Y}

(resp.

Q_{X Y})

is the joint distribution of

X Y

Γ_{0}

(resp.

Γ_{1}

In the following, we show that adversarial outputs from

Γ_{0}

and

Γ_{1}

are close. Also, the extraction

\hat{x}

from

S . E (t)

Γ_{1}

will be mostly identical to x. The idea is that

Γ_{0}

can be regarded as the simulated game with extraction occurring at the end because the extraction at the end does not affect the adversarial output. Then, we try to shift

S . E (t)

toward the end of game step-by-step and quantify the change of the quantum state. We find that the change throughout this shift process is small. The second claim

x = \hat{x}

follows from the foregoing argument and Theorem 2.

Theorem 3.

Let

{(α)}_{Γ}

be the random variable α w.r.t. game

Γ .

Let

A

be a quantum algorithm with access to

{CStO}_{s}

s.t.

Ξ_{1} \subseteq Ξ

. Let

q = q_{1} + q_{2} .

Then,

\begin{matrix} Δ ({(t, x, h, W, abort = 0)}_{Γ_{0}}, {(t, x, h, W, abort = 0)}_{Γ_{1}}) \leq 8 (q_{2} + 1) \sqrt{2 Γ_{f} / 2^{n}}, \end{matrix}

(16)

\begin{matrix} Pr (x \neq \hat{x} \land f (x, h) = t \land abort = 0) \leq 8 (q_{2} + 1) \sqrt{2 Γ_{f} / 2^{n}} + 2^{- n + 1} + \frac{16 {(q + 1)}^{3} Γ_{f}}{2^{n}} . \end{matrix}

(17)

Proof. Let

U_{t}

be the unitary measurement on

D P

, following which, the projective measurement

{P_{x}}_{x \in \bar{X}}

on register P is applied, resulting in

\hat{x}

. Assume that

{T_{t}}_{t}

is the measurement for t. Let

V_{X Y W}

be the unitary operator of

A

between queries, and

{M_{x w}}_{x, w}

be the measurement for

(x, w) .

The initial state is

| γ_{0} {〉 = | ω 〉}_{X Y W} \otimes {(\otimes_{x} | ⊥ 〉}_{D_{x}} {) \otimes | 0 〉}_{P} .

Then, the final unormalized state in

Γ_{1}

\begin{matrix} | γ_{1} 〉 = & P_{h} \cdot S . R O \cdot M_{x w} \cdot {(S . {CStO}_{s} \cdot V)}^{q_{2}} \cdot S . E (t) \cdot T_{t} \cdot {(S . {CStO}_{s} \cdot V)}^{q_{1}} | γ_{0} 〉 \end{matrix}

(18)

\begin{matrix} = & P_{h} \cdot {CStO}_{s} \cdot M_{x w} \cdot {({CStO}_{s} \cdot V)}^{q_{2}} \cdot P_{\hat{x}} \cdot U_{t} \cdot T_{t} \cdot {({CStO}_{s} \cdot V)}^{q_{1}} | γ_{0} 〉, \end{matrix}

(19)

where the last

{CStO}_{s}

in Equation (19) is a random oracle query and

P_{\hat{x}} = | \hat{x} 〉 〈 \hat{x} |_{P}

. Further, if

A

makes a random oracle query, then under

abort = 0

S . {CStO}_{s}

C S t O_{s} \cdot Λ_{i 0}

; if

A

makes PointReg1 query x and

abort = 0

, then oracle applies

Π_{0}

and then

U_{⊥, r}

D_{x}

. A PointReg0 query does not impact on the quantum state and hence does not occur in the above equation but it is implicit to maintain

Ξ_{0}

. We assume that the operators other than the measurements mentioned are unitary (which can be made up with some auxiliary registers). Then, the probability of

x h w \hat{x} t Ξ_{1}

with

abort = 0

Γ_{1}

(denoted by

p_{x h w \hat{x} t Ξ_{1}}

) is

| | γ_{1} {| |}^{2}

. Further, since

P_{\hat{x}}

can be moved to the end of game (as variable

\hat{x}

and register P are not related to operators currently on the left to

P_{\hat{x}}

p_{x h w \hat{x} t Ξ_{1}} = | | γ_{2} {| |}^{2}

, where

\begin{matrix} | γ_{2} 〉 = P_{\hat{x}} P_{h} \cdot {CStO}_{s} \cdot M_{x w} \cdot {({CStO}_{s} \cdot V)}^{q_{2}} \cdot U_{t} \cdot T_{t} \cdot {({CStO}_{s} \cdot V)}^{q_{1}} | γ_{0} 〉 . \end{matrix}

(20)

If we remove

P_{\hat{x}} U_{t}

from Equation (19), then

| γ_{1} 〉

becomes the final state of

Γ_{0}

. Then, the probability of

x h w \hat{x} t Ξ_{1}

Γ_{0}

with

abort = 0

(denoted by

q_{x h w \hat{x} t Ξ_{1}}

) is

| | γ_{2}^{'} {| |}^{2}

(if further applying

U_{t}

and projective measurement

{P_{\hat{x}}}_{\hat{x}}

at the end of

Γ_{0}

), where

\begin{matrix} | γ_{2}^{'} 〉 = P_{\hat{x}} U_{t} P_{h} \cdot {CStO}_{s} \cdot M_{x w} \cdot {({CStO}_{s} \cdot V)}^{q_{2}} \cdot T_{t} \cdot {({CStO}_{s} \cdot V)}^{q_{1}} | γ_{0} 〉 . \end{matrix}

(21)

By triangle inequality, Equation (17) is bounded by

\begin{matrix} \frac{1}{2} \sum_{x h w \hat{x} t Ξ_{1}} | | | | γ_{2} {〉 | |}^{2} - | | | γ_{2}^{'} {〉 | |}^{2} | \leq \frac{1}{2} \sum_{i = 0}^{q_{2}} \sum_{x h w \hat{x} t Ξ_{1}} | | | | γ_{2 (i + 1)} {〉 | |}^{2} - | | | γ_{2 i} {〉 | |}^{2} |, \end{matrix}

(22)

where

| γ_{2 i} 〉

is the variant of

| γ_{2} 〉

with

U_{t}

relocated (starting from the leftmost) to right after the ith

{CStO}_{s}

operator in

| γ_{2} 〉

(that is either random oracle query or PointReg1 query) and thus

γ_{2}^{'} = | γ_{20} 〉

and

| γ_{2} 〉 = | γ_{2 (q_{2} + 1)} 〉

We consider the inner summation at Equation (23) for a fixed i. We can separate

x h w \hat{x} t Ξ_{1}

A B

, where A is the subset of variables obtained by measurements in

| γ_{2 i} 〉

after

U_{t}

and B is the remaining variables. Denote

| ψ_{B} 〉

be the state right before

U_{t}

and

M_{A}^{'}

be the product of operators after

U_{t}

and the ith

{CStO}_{s}

| γ_{2 i} 〉

. Then,

| γ_{2 i} 〉 = M_{A}^{'} \cdot U_{t} \cdot {CStO}_{s} | ψ_{B} 〉

and,

| γ_{2 (i + 1)} 〉 = M_{A}^{'} \cdot {CStO}_{s} \cdot U_{t} | ψ_{B} 〉

[U_{t}, V] = 0

. It is well-known that the measurement can be made at the end of operation without changing the measurement outcome distribution. Hence, we can assume

M_{A}^{'} = M_{A} S

for projection

M_{A}

of A and unitary S. That is, we can assume that

| γ_{2 i} 〉 = M_{A} \cdot S \cdot U_{t} \cdot {CStO}_{s} | ψ_{B} 〉

and

| γ_{2 (i + 1)} 〉 = M_{A} \cdot S \cdot {CStO}_{s} \cdot U_{t} | ψ_{B} 〉

. Let

| ψ_{B}^{'} 〉

be the normalized

| ψ_{B} 〉

. Then,

\begin{matrix} \frac{1}{2} \sum_{x h w t b Ξ} | | | | γ_{2 (i + 1)} {〉 | |}^{2} - | | | γ_{2 i} {〉 | |}^{2} | \end{matrix}

(23)

\begin{matrix} = & \sum_{B} | | | ψ_{B} {〉 | |}^{2} \cdot \frac{1}{2} \sum_{A} | | | M_{A} \cdot S \cdot U_{t} \cdot {CStO}_{s} | ψ_{B}^{'} {〉 | |}^{2} - | | M_{A} \cdot S \cdot {CStO}_{s} \cdot U_{t} | ψ_{B}^{'} {〉 | |}^{2} | \end{matrix}

(24)

{CStO}_{s}

is a random oracle query, then the inner sum is the statistical distance between measurement outcomes from

S \cdot U_{t} \cdot C S t O_{s} \cdot Λ | ψ_{B}^{'} 〉

and

S \cdot C S t O_{s} \cdot U_{t} \cdot Λ | ψ_{B}^{'} 〉

(note: Here

Λ

is some

Λ_{i 0}

and

[U_{t}, Λ] = 0

). By [43], it is no more than their trace distance. Further, by Lemma 6, trace distance of two states is no more than their Euclidean distance which is further bounded by

| | [C S t O_{s}, U_{t}] | | .

Hence, by Theorem 1,

\begin{matrix} E q u a t i o n (24) \leq \sum_{B} | | | ψ_{B} {〉 | |}^{2} \cdot | | U_{t}, {CStO}_{s} | | = | | U_{t}, {CStO}_{s} | | \leq 8 \cdot 2^{- n / 2} \sqrt{2 Γ_{f}} . \end{matrix}

(25)

{CStO}_{s}

is PointReg1 query

x \in Ξ_{0}

with

abort = 0

, this will apply

Π_{0}

and

U_{⊥, r} {= | r 〉 〈 ⊥ |}_{D_{x}}

to register

D_{x}

. Note that

U_{t}

commutes with

U_{⊥, r}

f (x, r) \neq t

(that is,

{| ⊥ 〉}_{D_{x}}

replaced by

{| r 〉}_{D_{x}}

will not change

\hat{x}

). By Lemma 3,

[Π_{0}, U_{t}] = 0 .

Thus,

{CStO}_{s}

(i.e., PointReg1) commutes with

U_{t}

f (x, r) \neq t

. By our assumption,

A

satisfies

Ξ_{1} \subseteq Ξ

. Hence,

f (x, r) = \emptyset

and so

f (x, r) = t

will never hold. Hence, PointReg1 commutes with

U_{t} .

Hence, Equation (24) is 0 for this query.

Finally, since there are at most

q_{2}

random oracle queries after t is measured, Equation (22) is bounded by

8 (q_{2} + 1) \sqrt{2 Γ_{f} / 2^{n}} .

Now we consider the second claim. Notice that Z is defined as boolean variable

(x \neq \hat{x} \land f (x, h) = t \land abort = 0)

(x, h, \hat{x}, t)

. We still use

p_{Z}

to denote the distribution in

Γ_{1}

and

q_{Z}

to denote the distribution of Z in

Γ_{0}

. Then, by the forgoing argument,

p_{Z} (1) \leq q_{Z} (1) + 8 (q_{2} + 1) \sqrt{2 Γ_{f} / 2^{n}} .

Then, by Theorem 2,

q_{Z} (1) \leq 2^{- n + 1} + 16 {(q + 1)}^{3} Γ_{f} / 2^{n} .

The result follows. □

The above theorem can be extended to the vector case, where

M_{x w}, U_{t}

are replaced with several

M_{x_{i} w_{i}}, U_{t_{i}}

at location

i .

Then, we switch

U_{t_{i}}

with each

{CStO}_{s}

after

t_{i}

is measured as in the above theorem. Denote the number of this kind of

{CStO}_{s}

(that is either random oracle query or PointReg1 query) by

q_{2 i}

. Then,

q_{2 i} < q

. For each i, we obtain the similar bound as the above theorem. Summarizing the argument for

i = 1, \dots, ℓ

, the extension of the first claim can be obtained. For the extension of the second claim is very similar to the second claim of the above theorem.

Corollary 2.

Let q be the total number of random oracle queries or PointReg1 queries and

Ξ_{1} \subseteq Ξ

. If

(x, t, h, \hat{x})

with vector length ℓ is the vector corresponding to

(x, t, h, \hat{x})

in Theorem 3, then

\begin{matrix} Δ ({(t, x, h, W, abort = 0)}_{Γ_{0}}, {(t, x, h, W, abort = 0)}_{Γ_{1}}) \leq 8 (q + ℓ) ℓ \sqrt{2 Γ_{f} / 2^{n}} \\ Pr (\exists i : x_{i} \neq {\hat{x}}_{i} \land f (x_{i}, h_{i}) = t_{i} \land abort = 0) \leq 8 (q + ℓ) ℓ \sqrt{\frac{2 Γ_{f}}{2^{n}}} + \frac{2 ℓ}{2^{n}} + \frac{16 {(q + ℓ)}^{3} Γ_{f}}{2^{n}} . \end{matrix}

(26)

Remark 6.

Theorem 3 requires

Ξ_{1} \subset Ξ

. If this is not satisfied, then the proof can not get through. However, this condition is only used in the PointReg1 query to guarantee that

f (x, r) \neq t

. Since r is taken uniformly randomly after x is fixed, this condition holds for

2^{n} - Γ_{t}

choices of

r .

Since there are at most

q_{s}

PointReg1 queries, this holds for every PointReg1 query with probability at least

1 - q_{s} Γ_{t} / 2^{n} .

When this holds, the proof of Theorem 3 remains valid. Furthermore, this argument extends to the vector case in Corollary 2 with further observation that Equation (26) holds with q replaced by

q - q_{s}

as that is the bound from the number of the random oracle queries. Notice that

Γ_{t} / 2^{n} < 8 ℓ \sqrt{2 Γ_{t} / 2^{n}} .

Hence, with this tighter analysis, we have the following corollary that preserves the same bound.

Corollary 3.

Let q be the number of random oracle queries or PointReg1 queries. If

(x, t, h, \hat{x})

with vector length ℓ is the vector corresponding to

(x, t, h, \hat{x})

in Theorem 3. Let

A

be a quantum algorithm with access to

{CStO}_{s}

with at most

q_{s}

PointReg1 queries. Then,

\begin{matrix} Δ ({(t, x, h, W, abort = 0)}_{Γ_{0}}, {(t, x, h, W, abort = 0)}_{Γ_{1}}) \leq 8 (q + ℓ) ℓ \sqrt{2 Γ_{f} / 2^{n}}, \\ Pr (\exists i : x_{i} \neq {\hat{x}}_{i} \land f (x_{i}, h_{i}) = t_{i} \land abort = 0) \leq 8 (q + ℓ) ℓ \sqrt{\frac{2 Γ_{f}}{2^{n}}} + \frac{ℓ}{2^{n - 1}} + \frac{16 {(q + ℓ)}^{3} Γ_{f}}{2^{n}} . \end{matrix}

4.7. Efficient Encoding of $CStO$ and ${CStO}_{s}$

Notice that so far the oracle state is represented via basis states

{| y 〉}_{D} \in {\bar{Y}}^{X}

with at most q non-⊥ entries. However, we need to show how operators used so far can be efficiently implemented. Zhandry [49] showed how to efficiently encode and compute

O_{X Y D}

. In our work, more operators on D are introduced. It is necessary to show that Zhandry’s encoding can be extended. In Appendix B, we detail how these operators can be efficiently executed on the encoded oracle state.

5. Extracting Queries to $CStO$ that Witness the Future Adversarial Output

In this section, we introduce and extend the techniques of Liu and Zhandry [30] for extracting an adversarial query that matches the adversary’s final output which is unknown at the time of the extraction. This extraction technique is very useful in a security proof when the final adversary output is the final solution of the attack while the query input to be extracted is a certain witness of this solution. In the classical world, we can find this witness query by guessing, which has the polynomial fraction of the success probability. In the quantum world, this guessing strategy does not quite work as the query could be a superposition. Liu and Zhandry [30] showed that we can randomly guess which superposition query will contain the witness and then measure it. Then, the measurement outcome is the witness to the final output with a good probability. In the following, we adapt their technique to the setting of multiple extractions (but still interacting with

CStO

). This modified game can be used to extract multiple queries that are collectively used to derive a witness for the final adversary output. This game can be easily converted to one where the random oracle is

{CStO}_{s}

and so our extraction theorems in the previous sections can be used.

Assume that adversary

A

makes at most q oracle queries to

CStO

oracle. In the end, we measure the adversary-oracle joint state and obtain

(w, y)

so that D has the collapsed state

F_{D} {| y 〉}_{D}

(i.e., measuring the final state on D using

{{F_{D} | y 〉}_{D}}_{y}

basis). Let

λ_{w, y}

denote the probability of outcome

(w, y) .

We define game

{Exp}_{i, j, k}

(with either

i = j = k

i < j < k

for

i, j, k \in [q]

). Before this, we define

\underset{̲}{x}

as an equivalence class (which is a subset of

X

, including x and also determined by x) in the sense that

\underset{̲}{x} = \underset{̲}{u}

for any

u \in \underset{̲}{x} .

We assume that the cardinality of

\underset{̲}{x}

is polynomially bounded. For

y \in Y^{X}

y (\underset{̲}{x}) = \vec{⊥}

denotes that

y_{u} = ⊥

for

\forall u \in \underset{̲}{x} .

{Exp}_{i, i, i}

: In this game, it proceeds normally until the ith oracle query. Assume the attacker-oracle state is

\sum_{x u z y} α_{x u z y} | x, ϕ_{u}, z, y 〉,

where we remind that Y register is represented using Fourier basis

{ϕ_{u}}_{u \in Y}

. Then, we measure1 the query input to output

{\underset{̲}{x}}^{*}

and further we measure to test (by two measurements) whether it holds:

D ({\underset{̲}{x}}^{*}) = \vec{⊥}

before the oracle query2but

D ({\underset{̲}{x}}^{*}) \neq \vec{⊥}

after the oracle query3. If both test measurements succeed, then the resulting state before applying

C S t O

oracle will be

\begin{matrix} \sum_{x^{'} u z y : y_{x^{'}} = ⊥, u \neq 0, x^{'} \in {\underset{̲}{x}}^{*}} α_{x^{'} u z y} | x^{'}, ϕ_{u}, z, y 〉 . \end{matrix}

(27)

In this case, the state after the

C S t O

query will become

\begin{matrix} \sum_{x^{'} u z y : y_{x^{'}} = ⊥, u \neq 0, x^{'} \in {\underset{̲}{x}}^{*}} α_{x^{'} u z y} | x^{'}, ϕ_{u}, z 〉 \frac{1}{\sqrt{2^{n}}} \sum_{y \in Y} {(- 1)}^{u \cdot y} | y \cup {(y)}_{x^{'}} 〉 . \end{matrix}

(28)

Then, the game proceeds normally. If one or both measurements fails, the game aborts.

{Exp}_{i, j, k}

with

i < j < k

: In this game, it proceeds normally until the ith oracle query. Let the attacker-oracle state be

\sum_{x u z y} α_{x u z y} | x, ϕ_{u}, z, y 〉 .

Then, we measure the query input to output

{\underset{̲}{x}}^{*}

and further we measure (similar to that in

{Exp}_{i, i, i}

) to test whether the followings are satisfied throughout the ith oracle query to the kth oracle query (using footnotes 2 and 3):

right before the ith query, $D ({\underset{̲}{x}}^{*}) = \vec{⊥}$ ; but after it, $D ({\underset{̲}{x}}^{*}) \neq \vec{⊥}$ .
after ith query and before the jth query, it remains that $D ({\underset{̲}{x}}^{*}) \neq \vec{⊥}$ .
after jth query and before the kth query, $D ({\underset{̲}{x}}^{*}) = \vec{⊥} .$
right after the kth query, $D ({\underset{̲}{x}}^{*}) \neq \vec{⊥} .$

If the test measurement fails, the game aborts; otherwise, it proceeds normally. It should be emphasized that we do not care if

D ({\underset{̲}{x}}^{*}) = \vec{⊥}

after any other query than those listed above.

We remark that

{Exp}_{i, i, i}

in fact is a special case of

{Exp}_{i, j, k}

with

i = j = k

as “after ith query and before the j query" and “after jth query and before the k query" in

{Exp}_{i, j, k}

are both null statements in this setting.

Further, although

{Exp}_{i, j, k}

is defined in the game between adversary and

CStO

, by inspecting its definition, we can see that

{Exp}_{i^{'}, j^{'}, k^{'}}

{Exp}_{i, j, k}

is also well-defined (as the conducted measurements are well-defined). It is not hard to see that the game

{Exp}_{i, j, k}

{Exp}_{i^{'}, j^{'}, k^{'}}

and the game

{Exp}_{i^{'}, j^{'}, k^{'}}

{Exp}_{i, j, k}

are the same. By iteration, we can define

{Exp}_{i^{t}, j^{t}, k^{t}}

as game

{Exp}_{i_{t}, j_{t}, k_{t}}

{Exp}_{i^{t - 1}, j^{t - 1}, k^{t - 1}}

, where

v^{t}

is the sequence

v_{1}, \dots, v_{t} .

Let

U_{I J K}

be the distribution of

(i, j, k)

that is uniformly random in

{(i, i, i) ∣ i \in [q]} \cup {(i, j, k) ∣ 1 \leq i < j < k \leq q} .

Further,

U_{I J K}^{c}

is the product distribution of

U_{I J K}

of c copies.

The following is the main result in this section. This is an extension of [30, Corollary 6] with the proof mainly extending [30, Theorem 9]. The details can be found in Appendix D.

Theorem 4.

Let

c > 0

be a constant. Take

(i^{c}, j^{c}, k^{c}) \leftarrow U_{I J K}^{c}

. Let S be a subset of the possible output

(w, y)

in the game with

C S t O

oracle. Define the measurement

(P_{0}, P_{1})

with

P_{0} = \sum_{(w, y) \in S} | w, \tilde{y} 〉 〈 w, \tilde{y} |

(where we use the basis

F_{D} | y 〉 = | \tilde{y} 〉

for the consistency with the measurement at the beginning of this section) and

P_{1} = I - P_{0} .

Let

x_{w, y, t} \in X

for

t = 1, \dots, c

be representatives for c (possibly repeating) classes, determined by

(w, y)

with

y ({\underset{̲}{x}}_{w, y, t}) \neq ⊥

. Let λ be the probability in the random game

{Exp}_{i^{c}, j^{c}, k^{c}}

that gives

{\underset{̲}{x}}_{w, y, t}

for some

(w, y) \in S

from the measurement on the

i_{t}

th oracle query for

t = 1, \dots, c

and the final measurement

(P_{0}, P_{1})

gives outcome 0. Let γ be the probability that the final measurement in the normal game gives outcome 0. Then,

λ \geq \frac{γ}{{(q + (\binom{q}{3}))}^{3 c}} .

6. Quantum Security of the JAK Multi-Signature Framework

Jiang et al. [23] proposed a framework that converts a linear ID scheme into a compact multi-sinagure scheme and proved its security in the classic random oracle model. In this section, we prove its security in the quantum random oracle model.

6.1. Review of JAK Mutli-Signature Framework

Let

ID = ({Setup}_{i d}, {KeyGen}_{i d}, P, V_{τ}, Θ)

be a canonical linear ID with parameter

τ \in N

. Let

H_{0}, H_{1}

be two random oracles from

{0, 1}^{*}

Θ

with

Θ \subseteq R

, where

R

is the ring defined for the linearity property of

ID

. The JAK multi-signature scheme

(Setup, KeyGen, Sign, Verify)

is as follows.

Setup. Sample and output

param \leftarrow {Setup}_{i d} (1^{λ})

KeyGen. Sample

(p k, s k) \leftarrow {KeyGen}_{i d} (param)

; output a public-key

p k

and private key

s k

Sign. Assume that signers with public-keys

{p k_{i}}_{i = 1}^{t}

want to jointly sign message M. Let

λ_{i} = H_{0} (p k_{i}, P K)

and

\bar{p k} = \sum_{i = 1}^{t} λ_{i} • p k_{i}

, where

P K = (p k_{1}, \dots, p k_{t}) .

They execute the following.

R-1. Signer i takes $(s t_{i}, {C M T}_{i}) \leftarrow P (param)$ and sends $r_{i} : = H_{0} ({C M T}_{i} | p k_{i})$ to all signers.
R-2. Upon $r_{j}$ for all j (we don’t restrict $j \neq i$ for brevity), signer i sends ${C M T}_{i}$ to all signers.
R-3. Upon ${C M T}_{j}, j = 1, \dots, t$ , signer i checks if $r_{j} = H_{0} ({C M T}_{j} | p k_{j})$ for all j. If no, it rejects; otherwise, it computes $\bar{C M T} = \sum_{j = 1}^{t} λ_{j} • {C M T}_{j}$ , $C H = H_{1} (\bar{p k} | \bar{C M T} | M)$ and ${R s p}_{i} = P (s t_{i} | s k_{i} | p k_{i}, C H)$ . Finally, it sends ${R s p}_{i}$ to all signers.
Output. Upon ${R s p}_{j}, j = 1, \dots, t$ , signer i computes $\bar{R s p} = \sum_{j = 1}^{t} λ_{j} • {R s p}_{j}$ , and outputs the aggregated public-key $\bar{p k} | t$ and multi-signature $\bar{C M T} | \bar{R s p}$ .

Verify. Upon signature

(\bar{C M T}, \bar{R s p})

on message M with the aggregated public key

\bar{p k} | t

, it outputs

V_{t} (\bar{p k}, \bar{C M T} | C H | \bar{R s p})

, where

C H = H_{1} (\bar{p k} | \bar{C M T} | M) .

6.2. Security Theorem

In this section, we prove the security of the JAK framework in the quantum random oracle model. Our proof strategy is to use the sequence of game techniques. We first replace two random oracles

| H_{0} 〉

and

| H_{1} 〉

with a single one

| H 〉

so that

H (0 | x) = H_{0} (x)

and

H (1 | x) = H_{1} (x) .

Since the distributions of

H (b | x)

and

H_{b} (x)

are identical, adversary success does not decrease. Then, we replace

| H 〉

CStO

and this will not change the adversary success by Fact 1 and Lemma 8. Next, we sample experiment

{Exp}_{i^{2}, j^{2}, k^{2}}

so that the

i_{1}

th query has measurement outcome

{\underset{̲}{x}}_{1}^{*}

with

x_{1}^{*} = 0 | p k_{1}^{'} | P K^{'}

where

P K^{'}

is the signature group in the attacker’s forgery and the measurement outcome for the

i_{2}

th query is

{\underset{̲}{x}}_{2}^{*}

with

x_{2}^{*} = 1 \bar{p k^{'}} | \bar{{CMT}^{'}} | M

being the attacker’s input to compute

{CH}^{'}

in its forgery. By Theorem 4, the adversary success in this experiment is degraded only by a polynomial fraction. Then, we consider the signing oracle in

{Exp}_{i^{2}, j^{2}, k^{2}}

. We will try to confirm (by measurement) that the query input

x = 1 | \bar{p k} | \bar{CMT} | M

to compute

CH

, is not recorded in

CStO

(so that we can set this

C H

by ourselves). Since

\bar{CMT}

contains the challenger’s committing message (that has super-logarithmic min-entropy), this confirmation measurement will succeed with high probability (Lemma 10). Then, we reformulate

{Exp}_{i^{2}, j^{2}, k^{2}}

as the game with

{CStO}^{'}

and further change to a game with

{CStO}_{s}

. The format of

{Exp}_{i^{2}, j^{2}, k^{2}}

is very compatible with

{CStO}^{'}

and so this switch is just a simple formatting problem. Now under the game with

{CStO}_{s}

, we can use the extraction technique to extract the committing messages from adversary in a signing oracle and treat

x = 1 | \bar{p k} | \bar{C M T} | M

as a special point. We also treat

{\underset{̲}{x}}_{1}^{*}, {\underset{̲}{x}}_{2}^{*}

as special points. We can set the random oracle value of these special points by ourselves. With this benefit, we use the ID simulator to simulate the honest signer’s messages in a signing oracle without its secret. Finally, we can reduce the adversary success to break the ID scheme by setting the CH in attacker’s forgery as the challenge from the ID challenger. So the attacker’s forgery will help us to break the ID security.

Theorem 5.

Assume that

h \leftarrow Θ

is invertible in

R

with probability

1 - negl (λ)

. Let

ID = ({Setup}_{i d}, {KeyGen}_{i d}, P, V_{τ})

be a secure ID scheme with linearity and simulability. Then, the JAK multi-signature scheme is EU-CMA secure in the quantum random oracle model.

Proof. Our proof follows the sequence of game strategy. The game consists of quantum polynomial time adversary

D

and a challenger

C

who maintains the quantum random oracle and the signing oracle that jointly signs a message M with

D .

We use

Succ (G)

to denote the adversary success probability in game

G .

Game

G_{0} .

This is the real forgery game. Challenger runs Setup

(1^{λ})

to generate

param

and executes

KeyGen (param)

to generate a challenge key pair

(p k^{*}, s k^{*})

. Then, it provides

(p k^{*}, param)

D

and maintains two quantum random oracles

| H_{0} 〉, | H_{1} 〉

and signing oracle

O_{s}

to interact with

D

. Finally,

D

outputs a forgery

(σ^{*}, M^{*})

with a set of public keys

(p k_{1}^{*}, \dots, p k_{N}^{*})

where

p k^{*} = p k_{1}^{*} .

He succeeds if

Verify (\bar{p k^{*}}, σ^{*}, M^{*}) = 1

and no query

(p k_{1}^{*}, \dots, p k_{N}^{*}, M^{*})

was issued to

O_{s} .

Game

G_{1} .

We modify

G_{0}

G_{1}

so that

H_{0} (x) = H (0 | x)

and

H_{1} (x) = H (1 | x)

for a random oracle

H .

This does not reduce the adversary success probability as the tables for

H (0 | \cdot), H (1 | \cdot)

and the tables for

H_{0} (\cdot), H_{1} (\cdot)

jointly are identically distributed (i.e., purely random in both cases). Any query

| ψ 〉

H_{b} (\cdot)

is a special case of query

| b 〉 | ψ 〉

| H 〉

. Thus,

Pr (Succ (G_{1}) \geq Pr (Succ (G_{0}))

Game

G_{2} .

We modify

G_{1}

G_{2}

so that the random oracle is implemented using

CStO .

By Fact 1 and Lemma 8, the success probabilities of

D

G_{1}

and

G_{2}

are identical.

Game

G_{3} .

We modify

G_{2}

G_{3}

so that it selects the game (involving

D

)

{Exp}_{i^{2}, j^{2}, k^{2}}

for

(i^{2}, j^{2}, k^{2}) \leftarrow U_{I J K}^{2}

. Let the measurement at the

i_{t}

th oracle query be

{\underset{̲}{x}}_{t}^{*}

for some

x_{t}^{*}

for

t = 1, 2 .

At the end of game, let

(w, y)

be the measurement output, where w is the forgery

(α, β, P K^{'}, M)

measured by

D

on register

X Y W

and

y

is the measurement outcome on D (which represents the quantum state

F_{D} {| y 〉}_{D}

and hence

y

satisfies

y_{x} = R O (x)

). Define

x_{w, y, 1} = 0 | p k_{1}^{'} | P K^{'}

for

P K^{'} = (p k_{1}^{'}, \dots, p k_{n}^{'})

. Further, define

{\underset{̲}{x}}_{w, y, 1} = {0 | p k_{v}^{'} | P K^{'} : v = 1, \dots, n}

and

\underset{̲}{x} = {x}

(for any x that can not be written in

0 | p k_{v} | P K

with

p k_{v} \in P K

). Hence, the equivalence class is well-defined. In addition, define

x_{w, y, 2} = 1 | \bar{p k^{'}} | α | M

. We consider the case

x_{t}^{*} = x_{w, y, t}

for

t = 1, 2

. Define S in Theorem 4 as the set of all pairs

(w, y)

so that w is a valid forgery under random oracle assignments

y_{x} = R O (x)

. Since the probability

(w, y) \in S

is the success probability of

D

G_{2}

, by Theorem 4, the success probability of

D

G_{3}

will be at least

\frac{ϵ}{{(q + (\binom{q}{3}))}^{6}} .

Game

G_{4} .

We modify

G_{3}

G_{4}

so that in the signing oracle, right before the classic oracle query

x = 1 | \bar{p k} | \bar{C M T} | M

to generate

C H,

it does a measurement

(| ⊥ 〉 〈 ⊥ |, I - | ⊥ 〉 〈 ⊥ |)

to the register

D_{x}

of the oracle. If it gives the outcome 0, it aborts with

Fail

(indicating the failure of the simulation); otherwise, it continues normally. By Lemma 11, this Fail occurs only with a negligible probability (recall that

H_{\infty} (C M T)

is super-logarithmic for randomly generated

C M T

) and hence the success probability

D

G_{4}

is at least

\frac{ϵ}{{(q + (\binom{q}{3}))}^{6}} - negl (κ)

Game

G_{5} .

We re-format

G_{4}

as a game between an adversary

D

and challenger

C^{'}

that has oracle access to

{CStO}^{'}

(ref. Section 4.3) so that

D

G_{5}

has the success probability exactly identical to that of

D

G_{4} .

The code of

C^{'}

as follows. It follows

C

to set up

G_{4}

to invoke

D

with the public parameters and then interacts with

D

C^{'}

also follows

C

to choose the random game

{Exp}_{i^{2}, j^{2}, k^{2}}

Whenever a random oracle query is issued, $C^{'}$ does as follows. Assume this is the ℓth random oracle query. If $ℓ = i_{1}$ or $i_{2}$ , then $C^{'}$ (like challenger $C$ in $G_{4}$ ) will apply a projective measurement on X register in the computational basis and results in ${\underset{̲}{x}}_{1}^{*}$ or ${\underset{̲}{x}}_{2}^{*}$ and then it issues a PointReg0 query with each $x \in {\underset{̲}{x}}_{1}^{*}$ or ${\underset{̲}{x}}_{2}^{*}$ to ${CStO}^{'}$ . If $ℓ = k_{t}$ (for $t = 1$ or 2), it issues a $P o i n t R e g 1$ query with $x^{'} \in {\underset{̲}{x}}_{t}^{*}$ (which does measurement $Π$ on $D_{x^{'}}$ like challenger in $Γ_{4}$ ). Then (no matter what is ℓ), recall that, in $G_{4}$ , the challenger will conduct a projective measurement $Λ^{'}$ (determined by ℓ and $i_{1}, j_{1}, k_{1}$ ) on D and another projective measurement $Λ^{''}$ (still determined by $ℓ, i_{2}, j_{2}, k_{2})$ on D. These measurements are described in ${Exp}_{i^{2}, j^{2}, k^{2}}$ and can be seen that they are only applied on $D_{Ξ_{0}}$ as desired by ${CStO}^{'}$ . These two measurements can be combined into one projective measurement $Λ_{ℓ} = (Λ_{ℓ 0}, I - Λ_{ℓ 0})$ in the computational basis on $D_{Ξ_{0}}$ . Then, to be consistent with $G_{4}$ , $D^{'}$ in $G_{5}$ issues the random oracle query with its register $X Y$ to ${CStO}^{'}$ which will handle it first with measurement $Λ_{ℓ}$ and then with $C S t O$ (if it does not abort). Under this reformatting, the action on the joint state is the same as in $G_{4}$ .
When $D$ issues a signing query $(P K, M)$ so that $P K$ contains $p k_{1}^{*}$ , $C^{'}$ in $G_{5}$ computes $\bar{p k}$ , $\bar{C M T}$ and $x = 1 | \bar{p k} | \bar{C M T} | M$ normally as in $G_{4}$ , with possibly random oracle access to ${CStO}^{'}$ as in the previous item. Next, it issues $P o i n t R e g 0$ query and then $P o i n t R e g 1$ query both with x to ${CStO}^{'}$ , and finally a classic random oracle query with x (if it does not abort), where the random oracle queries are handled as the above reformatting. In turn, if ${CStO}^{'}$ does not abort, $C^{'}$ receives the reply $y = R O (x)$ and it continues normally as in $G_{4}$ to generate the signature. Note that $C^{'}$ together with ${CStO}^{'}$ acts the same as $C$ together with $CStO$ in $G_{4}$ . Thus, this does not change the view of $D$ and the joint quantum state.

From our description, we can see that

D

G_{4}

and

G_{5}

has the same view, as it is just a reformatting of

G_{4}

. Hence,

D

G_{5}

has the same success probability as in

G_{4} .

Game

G_{6} .

We modify

G_{5}

G_{6}

s.t.

{CStO}^{'}

is replaced by

{CStO}_{s}

. By Lemma 9, the success probability of

D

G_{6}

is the same as in

G_{5}

by checking the output of

C^{'}

which is defined as 1 if and only if

D

succeeds (

\neg abort

can be removed in the lemma as

C^{'}

outputting 1 indicates

\neg abort = 1

Game

G_{7} .

We modify

G_{6}

G_{7}

so that

{CStO}_{s}

is now simulated by

S

. Since

S . E

is not used, the adversary success probability is identical to

G_{6} .

Game

G_{8} .

We modify

G_{7}

G_{8}

so that in the signing query

O_{s} (p k_{1}, \dots, p k_{n}, M)

, after receiving

r_{i}

, challenger extracts

{C M T}_{i}^{'} = S . E (r_{i})

and later in round R-3, when it receives

{C M T}_{i}

, if

{C M T}_{i} \neq {C M T}_{i}^{'}

but

S . R O ({C M T}_{i}) = r_{i}

, it terminates with Fail. By Corollary 2, this occurs negligibly. Thus, the success probability of

D

G_{8}

is negligibly close to that in

G_{7} .

Game

G_{9} .

We modify

G_{8}

G_{9}

so that in

O_{s} (p k_{1}, \dots, p k_{n}, M)

with

p k_{t} = p k^{*}

for some t, it generates

({C M T}_{t}, {R s p}_{t}) \leftarrow SIM (C H, p k^{*}, param)

, where

C H \leftarrow Θ

. It does the same as

G_{8}

: measure

(| ⊥ 〉 〈 ⊥ |, I - | ⊥ 〉 〈 ⊥ |)

D_{x}

(specified since

G_{4}

), issues

P o i n t R e g 0

query, then

P o i n t R e g 1

queries with

x = 1 | \bar{p k} | \bar{C M T} | M

{CStO}_{s}

, where

P o i n t R e g 1

will define r in

{CStO}_{s}

for

D_{x}

(if it does not abort) as the random oracle value for x. In

G_{9}

, it defines this r as

C H

. By the simulability of ID, this has the same distribution as

G_{8}

. So the adversary success probability remains the same as in

G_{8}

(specifically, any non-negligible difference in this success probability can be straightforwardly reduced through hybrid argument on

({C M T}_{t}, {R s p}_{t}, {C H}_{t})

in the signing queries to break the ID simulability; details are omitted). We remind that the secret key

s k

is no longer used in

G_{9}

Game

G_{10} .

We modify

G_{9}

G_{10}

so that it will embed the ID challenges into the attack. Specially,

C^{'}

sets up the game so that

p k_{1}^{*}

is the ID challenge key. In addition, after obtaining

{\underset{̲}{x}}_{1}^{*}

(by measuring the

i_{1}

th random oracle query) with

x_{1}^{*} = 1 | p k_{1}^{*} | {p k_{1}^{*}, \dots, p k_{n}^{*}}

, it sends

p k_{2}^{*}, \dots, p k_{n}^{*}

as its response of group keys to its own ID challenger and in turn will receive

λ_{1}, \dots, λ_{n}

. Upon

P o i n t R e g 1

queries

x_{u} \in {\underset{̲}{x}}_{1}^{*}

(from

C^{'}

{CStO}_{s}

sets its random oracle value4

S . R O (x_{u})

λ_{u}

(

u = 1, \dots, n

), provided by ID challenger. In addition, later for

x_{2}^{*} = 1 | \bar{p k^{'}} | α | M

, in

P o i n t R e g 1

query

x_{2}^{*}

, it sets the hash value

r = C H

, provided by ID challenger. This will not change the distribution of the game because

λ_{u}

for any u as well as this

C H

are all uniformly random and hence remains the same distribution as in

G_{9}

. When

D

outputs its forgery, if the output

(w, y) \in S

, then it sends the response

R s p

in w to ID challenger as its response. Obviously,

C^{'}

succeeds in its ID challenge session if and only if

D

succeeds with

(w, y) \in S

(that is, the forgery is valid). Thus, the adversary success probability is the same as in

G_{9}

and hence

C^{'}

has a success probability negligibly close to

\frac{ϵ}{{(q + (\binom{q}{3}))}^{6}}

. This contradicts the security of ID scheme. □

Remark 7.

G_{5}

, we convert the game with

CStO

to the game with

{CStO}^{'}

, where we register

{\underset{̲}{x}}_{t}^{*}

Ξ_{0}

at the

i_{t}

th oracle random oracle query while it registers to

Ξ_{1}

only at the

k_{t}

th random oracle query. This generally is the routine to convert

{Exp}_{i^{c}, j^{c}, k^{c}}

to a game with

{CStO}^{'}

. One might wonder why we register

{\underset{̲}{x}}_{t}^{*}

twice. The issue in fact comes from the switch from

{CStO}^{'}

{CStO}_{s}

G_{6}

{CStO}_{s}

requires that after registration in

Ξ_{1}

, no measurement for testing

D (x) = ⊥

will be performed. If we register it once, this should happen at the

i_{t}

th query for

{\underset{̲}{x}}_{t}^{*}

. But in this case, we can not guarantee that

G_{5}

(with

{CStO}^{'}

) will be indistinguishably switched to

G_{6}

with

{CStO}_{s}

: after the

i_{t}

th query, we still need to measure if

D ({\underset{̲}{x}}_{t}^{*}) = ⊥

. But in

G_{6}

, this will never be true as

| ⊥ 〉

is replaced by

| r 〉

, while in

G_{5}

(with

{CStO}^{'}

), it is still possible. This distinguishing event does not violate Lemma 9 because this test is no longer performed in

{CStO}_{s}

after updating

| ⊥ 〉

| r 〉 .

7. Quantum Security of The JAK ID Scheme

In this section, we prove the quantum security of the lattice-based ID scheme in [23] (which we call it the JAK ID scheme). Together with Theorem 5, it gives a secure lattice-based multi-signature in the quantum random oracle model. We will use the following notations.

As a convention for lattice over ring, the security parameter is denoted by n (a power of 2);
q is a prime with $q \equiv 3$ mod 8;
$R = Z [x] / (x^{n} + 1)$ ; $R_{q} = Z_{q} [x] / (x^{n} + 1)$ ; $R_{q}^{*}$ is the set of invertible elements in $R_{q}$ ;
A vector $w$ is implicitly a column vector and the ith component is $w_{i}$ or $w [i]$ ;
for a matrix or vector X, $X^{T}$ is its transpose;
$1$ denotes the all-1 vector ${(1, \dots, 1)}^{T}$ of dimension clear only in the specific context;
for $u = \sum_{i = 0}^{n - 1} u_{i} x^{i} \in R$ , ${| | u | |}_{\infty} = {max}_{i} | u_{i} |;$
$α \in Z_{q}$ always uses the default representative with $- (q - 1) / 2 \leq α \leq (q - 1) / 2$ and similarly, for $u \in R_{q}$ , each coefficient of u by default belongs to this range;
$e = 2.71828 \dots$ is the Euler’s number;
$C = {c \in R ∣ | | c | |_{\infty} \leq log n, deg (c) < n / 2}$
$Y = {y \in R ∣ | | y | |_{\infty} \leq n^{1.5} σ {log}^{3} n}$
$Z = {z \in R ∣ | | z | |_{\infty} \leq (n - 1) n^{1 / 2} σ {log}^{3} n}$ .

7.1. Ring-LWE and Ring-SIS

In the following, we introduce the ring-LWE and ring-SIS assumptions (see [33,35,44] for details). For

σ > 0

, distribution

D_{Z^{n}, σ}

assigns the probability proportional to

e^{- {π | | y | |}^{2} / σ^{2}}

for any

y \in Z^{n}

and 0 for other cases. As in [1],

y \leftarrow D_{R, σ}

samples

y = \sum_{i = 0}^{n - 1} y_{i} x^{i}

from R by taking

y_{i} \leftarrow D_{Z, σ} .

The Ring Learning With Error (

{Ring-LWE}_{q, σ, 2 n}

) problem over R with standard deviation

σ

is defined as follows. Initially, it takes

s \leftarrow D_{R, σ}

as secret. It then takes

a \leftarrow R_{q}, e \leftarrow D_{R, σ}

and outputs

(a, a s + e)

. The problem is to distinguish

(a, a s + e)

from a tuple

(a, b)

for

a, b \leftarrow R_{q} .

The

{Ring-LWE}_{q, σ, 2 n}

assumption [16,34] is to say that no quantum polynomial time algorithm can solve

{Ring-LWE}_{q, σ, 2 n}

problem with a non-negligible advantage.

The Small Integer Solution problem with parameters

q, m, β

over ring R (

{Ring-SIS}_{q, m, β}

) is as follows: given m uniformly random elements

a_{1}, \dots, a_{m}

over

R_{q}

, find

(t_{1}, \dots, t_{m})

so that

| | t_{i} {| |}_{\infty} \leq β

and

a_{1} t_{1} + \dots + a_{m} t_{m} = 0

. We consider the case

m = 3

. We assume that

q = 3

mod 8, in which case, by [6],

x^{n} + 1 = Φ_{1} (x) Φ_{2} (x)

for irreducible polynomials

Φ_{1} (x), Φ_{2} (x)

of degree

n / 2

. So by Chinese remainder theorem,

a_{i}

is invertible, except for probability

2 q^{- n / 2}

. Hence, ring-SIS is equivalent to the case of invertible

a_{2}

which is further equivalent to problem

a_{1} t_{1} + t_{2} + a_{3} t_{3} = 0

, as we can multiply it by

a_{2}^{- 1}

. The quantum hardness of ring-SIS can be found in [13,33].

7.2. The JAK ID Scheme

We now review the JAK ID scheme [23]. Initially, take

s_{1}, s_{2} \leftarrow D_{R, σ}, a_{1}, a_{2} \leftarrow R_{q}^{*}

and compute

u = a_{1} s_{1} + a_{2} s_{2}

. The system parameter is

(a_{1}, a_{2})

; the public key is u and the private key is

(s_{1}, s_{2}) .

The ID scheme is as follows (also see Figure 3).

1.: Prover generates $y_{1}, y_{2} \leftarrow Y^{μ}$ and computes $v = a_{1} y_{1} + a_{2} y_{2}$ and sends $v$ to Verifier, where $μ \geq {log}^{2} n .$
2.: Receiver samples $c \leftarrow C$ and sends it to Prover.
3.: Upon c, Prover computes $z_{1} = s_{1} c + \sum_{j} y_{1 j}, z_{2} = s_{2} c + \sum_{j} y_{2 j} .$
4.: Upon $z_{1}, z_{2}$ , Verifier checks if $\sum_{i = 1}^{μ} v_{i} \overset{?}{=} a_{1} z_{1} + a_{2} z_{2} - u c$ and $| | z_{b} {| |}_{\infty} \overset{?}{\leq} η_{t}$ for $b = 1, 2,$ where $η_{t} = 5 σ n^{2} \sqrt{t μ} {log}^{6} n$ and t is a positive integer (that represents the number of signers when converted to a signature scheme) and recall that (as a convention) $v_{i}$ is the ith component of $v$ . If all are valid, it accepts; otherwise, it rejects.

The above specification uses the public-key

u = a_{1} s_{1} + a_{2} s_{2}

while the original protocol uses

u = a s_{1} + s_{2} .

This change is only for convenience for our proof for Lemmas A3 (that is needed for the ID security). It will not affect other properties: correctness, simulatability, linearity and classical security, as if we define

a = a_{1} a_{2}^{- 1}

, the current version is different from the original one only by a scaling factor

a_{2}

and all the proofs go through. Further, Step 3 in the above specification is a simplified but equivalent version of the original protocol (see the remark after the scheme description in [23]). The proofs of the correctness and linearity do not involve the adversary and hence remain unchanged as in [23]. The simulability given in [23] holds statistically. It hence holds against a quantum attacker, where the model is the same except that the attacker can also internally run the quantum operations.

It remains to prove the quantum security of this ID scheme under Definition 5. The idea is to implement the classic rewinding technique in the quantum world. We start with the security game below with

u_{1}

the honest signer’s public key. We first make the change that

λ_{2}, \dots, λ_{t}

are provided by attacker (which will increase the attacker A’s success probability only).

1 . a_{1}, a_{2} \leftarrow Setup (1^{λ})

;

2 . (| s t_{0} 〉, λ_{2}, u_{2}, \dots, λ_{t}, u_{t}) \leftarrow A (a_{1}, a_{2}, u_{1})

3 . λ_{1} \leftarrow C

4 . (| s t_{1} 〉, v) \leftarrow A (| s t_{0} 〉, λ_{1})

;

5 . c \leftarrow C

;

z_{1} | z_{2} \leftarrow A (| s t_{1} 〉, c)

;

6. Check:

\sum_{j = 1}^{μ} v_{j} \overset{?}{=} a_{1} z_{1} + a_{2} z_{2} - \bar{u} c, | | z_{1} {| |}_{\infty} < η_{t}, | | z_{2} {| |}_{\infty} < η_{t}

In the classic proof, we first obtain a valid transcript

({λ_{i} | u_{i}}_{i = 2}^{t}, λ_{1}, v, c, z_{1} | z_{2})

and then rewind A to line 5 and produce another valid transcript

({λ_{i} | u_{i}}_{i = 2}^{t}, λ_{1}, v, c^{'}, z_{1}^{'} | z_{2}^{'})

. This allows us to derive a short solution

(o_{1}, o_{2}, o_{3}) = (z_{1} - z_{1}^{'}, z_{2} - z_{2}^{'}, c - c^{'})

for equation

a_{1} o_{1} + a_{2} o_{2} - \bar{u} o_{3} = 0 .

In the quantum world, this rewinding strategy is not quite working because when A produces

z_{1}, z_{2}

, it might do a measurement which is not reversible. If it only uses unitary (e.g., U), then the rewinding can be done by applying

U^{†} .

Unruh [47] introduced a notion of collapsing property for a protocol: even with the measurement, the rewinding still can produce a successful new transcript with a good probability. In our quantum security proof, we will guarantee this property is satisfied. Next, we rewind A to step 3 with a new challenge

λ_{1}^{'}

and repeat the above procedure to obtain a new solution

(o_{1}^{'}, o_{2}^{'}, o_{3}^{'})

satisfying

a_{1} o_{1}^{'} + a_{2} o_{2}^{'} - \bar{u^{'}} o_{3}^{'} = 0

, where

\bar{u^{'}}

is updated as

u_{1} λ_{1}^{'} + \sum_{i = 2}^{t} λ_{i} u_{i} .

Combining these two solutions allows us to derive a short solution

(x_{1}, x_{2}, x_{3})

for

a_{1} x_{1} + a_{2} x_{2} + u_{1} x_{3} = 0 .

u_{1}

is uniformly random in

R_{q}

, this is the solution for Ring-SIS. However, even though

u_{1}

is sampled as

a_{1} s_{1} + a_{2} s_{2}

, it is indistinguishable from the uniformly random

u_{1}

by Ring-LWE assumption. Since the secret

(s_{1}, s_{2})

is never used in the above game, if we use the uniformly random

u_{1}

in the game, we can obtain the solution

(x_{1}, x_{2}, x_{3})

with the similar probability. This contradicts the Ring-SIS assumption. The detailed implementation of this strategy is given Appendix A.

Theorem 6.

Under

{ring-LWE}_{q, σ, 2 n}

and

{ring-SIS}_{3, q, β}

assumptions, the JAK ID scheme is secure (under Definition 5), where

β \geq 16 η_{t} \sqrt{n} {log}^{2} n

Applying the compiler theorem to the JAK ID scheme, it gives a quantum-secure multi-signature scheme (denoted by RLWE-Multisig scheme). For a complete description of this scheme, see [23]. The following is a summary of its security.

Corollary 4.

Under

{Ring-LWE}_{q, σ, 2 n}

and

{Ring-SIS}_{3, q, β}

assumptions,RLWE-MultiSigis EU-CMA secure in the quantum random oracle model, where

β \geq 16 η_{t} \sqrt{n} {log}^{2} n

8. Conclusions

In this paper, we investigated the security analysis techniques in the quantum random oracle model. We combined and extended three existing techniques to form a model called compressed random oracle with adaptive special points (

{CStO}_{s}

). We extended the query extractions from previous models to

{CStO}_{s}

. We can simulate this random oracle so that we can extract the query for a given commitment and we can also extract a query that is a witness for the future (unknown) adversary output. To see the power of this simulated oracle, we proved the security of our previous compact multi-signature scheme. This gives the first compact mult-signature provable secure in the quantum random oracle model. We hope that this oracle technique will be useful to prove the post-quantum security of many cryptographic systems.

Funding

This research received no external funding

Institutional Review Board Statement

not applicable

Informed Consent Statement

not applicable

Data Availability Statement

not applicable

Acknowledgments

Conflicts of Interest

The author declares no conflict of interest.

Appendix A. Proof of Theorem 6

In the following, we first introduce the notion of a public-coin protocol, which is a straightforward generalization of a sigma protocol.

Definition A1.

A n-round public-coin protocol Σ is a tuple of algorithms

(Gen, P, V)

that executes as follows.

Initially, $(p k, s k) \leftarrow Gen$ is executed to generate a public-key $p k$ for $P$ and $V$ and a private key $s k$ for $P$ . $P$ has an initial state $s t_{P} = p k | s k$ while $V$ has an initial state $s t_{V} = p k .$ Let $c_{0} = n i l$ .
The protocol proceeds in n rounds. In round $ℓ = 1, \dots, n$ , $P$ executes $a_{ℓ} \leftarrow P . {c o m}_{ℓ} (s t_{P}, c_{ℓ - 1})$ and sends it to $V$ . For $ℓ < n$ , $V$ replies with a challenge $c_{ℓ} \leftarrow Θ_{ℓ}$ . For $ℓ = n$ , $V$ runs $V . v e r (p k, a_{1} | c_{1} | \dots | a_{n})$ and outputs 0 (for reject) or 1 (for accept).

Appendix A.1. Collapsing Public-Coin Protocol

For any quantum polynomial time distinguisher

D

, we define a collapsing game

clpsExp (D)

between

D

and a challenger

Chal

with respect to a n-round public-coin protocol

Σ = (Gen, P, V)

Initially, Chal generates $p k$ and gives it to $D$ .
Then, $D$ (in the role of $P$ ) and Chal (in the role of $V$ ) executes the protocol $Σ$ except for round n. At round n, $D$ generates a quantum superposition $| ϕ 〉$ (over the response $a_{n}$ ) which might be entangled with states in extra registers. He then provides $| ϕ 〉$ to Chal.
Upon $| ϕ 〉$ , $Chal$ uses a measurement to check if $a_{n}$ in $| ϕ 〉$ is a valid response for $a_{1} | c_{1} | \dots | a_{n - 1} | c_{n - 1}$ . If the verification fails, Chal aborts; otherwise, let $| ϕ^{'} 〉$ be the superposition containing all the valid $a_{n}$ ’s. Then, $Chal$ flips a coin $b \leftarrow {0, 1}$ . If $b = 0$ , it does nothing; otherwise, it measures $| ϕ^{'} 〉$ in the computational basis. Finally, it sends the resulting superposition back to $D .$
Finally, $D$ outputs a guess bit $b^{'}$ for b, which is also set as the output of the game.

We use

{clpsExp}_{D}^{b}

to denote the game with challenge bit

b .

Definition A2.

A Σ-protocol is collapsing if

\begin{matrix} Pr ({clpsExp}_{D}^{1} = 0) = Pr ({clpsExp}_{D}^{0} = 0) + negl (λ) . \end{matrix}

(A1)

It is γ-weakly collapsing if

\begin{matrix} Pr ({clpsExp}_{D}^{1} = 0) \geq γ \cdot Pr ({clpsExp}_{D}^{0} = 0) - negl (λ) . \end{matrix}

(A2)

Remark. This definition was extended from [30] for the Sigma protocol to a general public coin protocol. In this definition, the collapsing property states that no attacker can detect whether the final round is a superposition or a classic response by measuring the former. This property is concerned only with the last round and all the previous

n - 1

prover messages are still classic.

Appendix A.2. Two Public-Coin Protocols from Our ID Scheme

We define two public-coin protocols

Σ_{1}

and

Σ_{2}

between quantum algorithm A and challenger, which are derived from the JAK ID protocol. We keep the notations in Section 7.2 unless specified.

Appendix A.2.1. Protocol Σ 1 .

Let

u_{1}, a_{1}, a_{2} \leftarrow R_{q}

. A interacts with challenger as follows.

1.: A sends $(λ_{2}, u_{2}, \dots, λ_{t}, u_{t})$ to challenger and holds a state $| ψ_{1} 〉$ , where $λ_{i} \leftarrow Θ$ .
2.: Challenger sends $λ_{1} \leftarrow Θ$ to A.
3.: A applies a unitary $U_{λ_{1}}$ to $| ψ_{1} 〉$ and results in $\sum_{o, ψ_{o}} | o, ψ_{o} 〉$ . It measures $o = (o_{1}, o_{2}, o_{3})$ in the computational basis and sends it to challenger.
4.: Challenger accepts if $a_{1} o_{1} + a_{2} o_{2} - \bar{u} o_{3} = 0$ and $| | o_{i} {| |}_{\infty} \leq 2 η_{t}$ for $i = 1, 2, 3$ , where $\bar{u} = \sum_{i = 1}^{t} λ_{i} u_{i}$ .

Appendix A.2.2. Protocol Σ 2 .

Let

u_{1}, a_{1}, a_{2} \leftarrow R_{q}

. A interacts with challenger as follows.

1.: A sends $(λ_{2}, u_{2}, \dots, λ_{t}, u_{t})$ to challenger, where $λ_{i} \leftarrow Θ$ .
2.: Challenger sends $λ_{1} \leftarrow Θ$ to A.
3.: A sends $v \in R_{q}^{μ}$ to challenger and prepares a state $| ψ_{1} 〉$ .
4.: Challenger replies with $c \leftarrow Θ$ .
5.: A applies a unitary $V_{λ_{1} c}$ to its state $| ψ_{1} 〉$ and results in $\sum_{z, ψ_{z}} | z, ψ_{z} 〉$ , where, although not stated, $V_{λ_{1} c}$ also depends on the previous messages. It measures $z = (z_{1}, z_{2})$ in the computational basis and sends it to challenger.
6.: Challenger accepts if $\sum_{i = 1}^{μ} v_{i} = a_{1} z_{1} + a_{2} z_{2} - \bar{u} c$ and $| | z_{1} {| |}_{\infty} \leq η_{t}, | | z_{2} {| |}_{\infty} \leq η_{t}$ .

Appendix A.3. Security of the JAK ID Scheme when Σ 1 and Σ 2 are Weakly Collapsing

In the following we prove that the JAK ID is secure (w.r.t. Def. 5) based on the assumptions that

Σ_{1}

and

Σ_{2}

are both weakly collapsing. This proof is threaded by two observations.

First, in

Σ_{2}

, if we can rewind the execution to the beginning of Step 4, then we can obtain two tuples (

z_{1}, z_{2}, c)

and

(z_{1}^{'}, z_{2}^{'}, c^{'})

with

z_{1}, z_{2}, z_{1}^{'}, z_{2}^{'}

short, satisfying

\begin{matrix} \sum_{i = 1}^{μ} v_{i} = a_{1} z_{1} + a_{2} z_{2} - \bar{u} c, \sum_{i = 1}^{μ} v_{i} = a_{1} z_{1}^{'} + a_{2} z_{2}^{'} - \bar{u} c^{'} . \end{matrix}

(A3)

This gives a solution

(o_{1}, o_{2}, o_{3})

with short

o_{i}

(as

c, c^{'}

are also short) so that

a_{1} o_{1} + a_{2} o_{2} - \bar{u} o_{3} = 0

If A executes Step 5 by unitary operator

U_{c}

on its state (i.e., without measuring

(z_{1}, z_{2})

), then the rewinding is just to apply

U_{c}^{†}

. The weakly collapsing property of

Σ_{2}

assures that even if it measure

(z_{1}, z_{2})

, the rewinding technique by

U^{†}

still produces two accepting tuples

(z_{1}, z_{2}, c)

and

(z_{1}^{'}, z_{2}^{'}, c^{'})

with a good probability.

Second, in

Σ_{1}

, if we can rewind the execution to the beginning of Step 2, we obtain two solutions

(o_{1}, o_{2}, o_{3}, λ_{1})

and

(o_{1}^{'}, o_{2}^{'}, o_{3}^{'}, λ_{1}^{'})

so that

\begin{matrix} a_{1} o_{1} + a_{2} o_{2} - \bar{u} o_{3} = 0, a_{1} o_{1}^{'} + a_{2} o_{2}^{'} - \bar{u^{'}} o_{3}^{'} = 0, \end{matrix}

(A4)

where

\bar{u^{'}} = λ_{1}^{'} u_{1} + \sum_{i = 2}^{t} λ_{i} u_{i}

. This allows us to derive a short solution

(t_{1}, t_{2}, t_{3})

for

a_{1} t_{1} + a_{2} t_{2} + u t_{3} = 0

, contradiction to the ring-SIS assumption. Again, due to the weakly collapsing property of

Σ_{1}

, this rewinding with measuring

(o_{1}, o_{2}, o_{3})

can still succeed with good probability, compared with the rewinding without measuring

(o_{1}, o_{2}, o_{3})

With these observations, we can now return the ID security game (Def. 5). We notice that this game can be formulated as

Σ_{2}

. On the other hand,

Σ_{1}

can be regarded as the internal execution of

Σ_{2}

after step 2, the rewinding of which gives a solution

(o_{1}, o_{2}, o_{3}) .

This leads to an attack for ring-SIS: the attacker runs A to run

Σ_{2}

to produce

(o_{1}, o_{2}, o_{3})

and with rewinding, it produces another

(o_{1}^{'}, o_{2}^{'}, o_{3}^{'}) .

As seen above, this gives a solution to the ring-SIS problem.

Lemma A1.

Σ_{1}

γ_{1}

-weakly collapsing and

Σ_{2}

γ_{2}

-weakly collapsing, then under

{ring-LWE}_{q, σ, 2 n}

and

{ring-SIS}_{3, q, β}

assumptions, the JAK ID scheme is secure, where

β \geq 16 η_{t} \sqrt{n} {log}^{2} n

Proof. Assume that A has a success probability

ϵ

in the security game of an ID scheme (see Definition 5). We revise the game so that

u_{1}

is uniformly random over

R_{q}

(instead of

u_{1} = a_{1} s_{1} + a_{2} s_{2}

which is indistinguishable from uniformly random over

R_{q}

under ring-LWE assumption, as

a_{2}

is invertible in

R_{q}

except for a negligible probability). Then, by ring-LWE assumption, the success of A is changed only negligibly. Further, we change the game so that A chooses

λ_{2}, \dots, λ_{t}

. This will only increase the success of A. Finally, we change the game so that A is unitary (whenever operating on its quantum state) except when it needs to measure its state to produce a protocol message (in the computational basis). This does not change the success probability of A as any A can always be made into this kind without changing its output distribution by adding more ancilla registers and also applying the deferred measurement principle. Now the security game is simply

Σ_{2}

. For brevity, we still assume A can succeed with probability

ϵ .

Let

τ

be the partial transcript

(u_{1}, a_{1}, a_{2}, {u_{i}, λ_{i}}_{i = 2}^{t}, λ_{1}, v)

. Let

ω_{τ}

be the probability of

τ .

For fixed

τ

, let

P_{τ c}

be the projection to the subspace from all

| z_{1}, z_{2} 〉 〈 z_{1}, z_{2} |

so that

(v, c, (z_{1}, z_{2}))

is accepting. Further, let

ϵ_{τ}

be the accepting probability (over c), given the partial transcript

τ

. We modify

Σ_{2}

Σ_{2}^{'}

so that A does not measure

(z_{1}, z_{2})

and instead it only measures

P_{τ c} .

It is not hard to see that A in

Σ_{2}^{'}

and

Σ_{2}

has the same success probability

ϵ

(by Lemma 3(2)). Let

| ψ_{τ} 〉

be the normalized state after A sending

v

. Then,

ϵ_{τ} = \frac{1}{| Θ |} \sum_{c \in Θ} | | V_{τ c}^{†} P_{τ c} V_{τ c} | ψ_{τ} {〉 | |}^{2}

and

ϵ = \sum_{τ} ω_{τ} ϵ_{τ} .

Define

{\tilde{P}}_{τ c} = V_{τ c}^{†} P_{τ c} V_{τ c} .

Before moving on, we give a claim from [47, Lemma 7].

Claim 1.

Let E be a set. Let

{(Q_{e})}_{e \in E}

be orthogonal projectors on Hilbert space

H

. Let

| Φ 〉 \in H

be a unit vector. Let

V = \sum_{e \in E} \frac{1}{| E |} | | Q_{e} {| Φ 〉 | |}^{2}

and

F = \sum_{e_{1}, e_{2} \in E} \frac{1}{| E |} | | Q_{e_{1}} Q_{e_{2}} {| Φ 〉 | |}^{2} .

Then,

F \geq V^{3} .

From this claim, we have that

\frac{1}{{| Θ |}^{2}} \sum_{c^{'}, c \in Θ} | | {\tilde{P}}_{τ c^{'}} {\tilde{P}}_{τ c} | ψ_{τ} {〉 | |}^{2} \geq ϵ_{τ}^{3} .

This is the probability that we rewind A in

Σ_{2}^{'}

, after

P_{τ c}

projection, to produce a second response

(z_{1}^{'}, z_{2}^{'})

using challenge

c^{'}

. If we require

c^{'} \neq c

, then this probability will change to

ϵ_{τ}^{3} - ϵ_{τ} / | Θ |

, as

{\tilde{P}}_{τ c^{'}} {\tilde{P}}_{τ c} = {\tilde{P}}_{τ c}

when

c^{'} = c

Now consider this success probability in

Σ_{2}

(not

Σ_{2}^{'}

) when

c^{'} \neq c

, where the projective measurement for

(z_{1}, z_{2})

after

P_{τ c}

and the projective measurement for

(z_{1}^{'}, z_{2}^{'})

after

P_{τ c^{'}}

will be applied. By

γ

-weakly collapsing property of

Σ_{2}

, it is easy to show that this probability is at least

γ_{2}^{2} (ϵ_{τ}^{3} - ϵ_{τ} / | Θ |)

(similar to [30, Lemma 5] and the analysis right after it). Therefore,

Σ_{2}

rewindings produce two accepting transcripts

(c, z_{1}, z_{2})

and

(c^{'}, z_{1}^{'}, z_{2}^{'})

for

c^{'} \neq c

, with probability at least

γ_{2}^{2} (ϵ_{τ}^{3} - ϵ_{τ} / | Θ |) .

Notice that these two accepting transcripts will result in a witness

(o_{1}, o_{2}, o_{3}) = (z_{1} - z_{1}^{'}, z_{2} - z_{2}^{'}, c - c^{'})

so that

a_{1} o_{1} + a_{2} o_{2} - \bar{u} o_{3} = 0 .

When

τ^{'} = (u_{1}, a_{1}, a_{2}, {u_{i}, λ_{i}}_{i = 2}^{t})

is fixed, this occurs with probability at least

\sum_{λ_{1} v} P_{λ_{1} v | τ^{'}} γ_{2}^{2} (ϵ_{τ^{'} λ_{1} v}^{3} - ϵ_{τ^{'} λ_{1} v} / | Θ |) \geq γ_{2}^{2} (ϵ_{τ^{'}}^{3} - ϵ_{τ^{'}} / | Θ |)

by Cauchy-Schwarz inequality, where

ϵ_{τ^{'}} = E_{λ_{1} v} (ϵ_{τ^{'} λ_{1} v} | τ^{'})

and marginal probability

P_{τ^{'}} = \sum_{λ_{1} v} P_{τ^{'} λ_{1} v}

is the occurrence of

τ^{'}

We then modify A in

Σ_{2}

to an attacker

A^{'}

for

Σ_{1}

: in

Σ_{1}

A^{'}

follows A to prepare Step 1 message and after receiving

λ_{1}

, it makes use of A in

Σ_{2}

in the above rewinding technique (where the challenge

c^{'}, c

are sampled randomly) to produce

(o_{1}, o_{2}, o_{2}) .

We then modify

A^{'}

so that it defers the measurements (after receiving

λ_{1}

) other than measuring

(o_{1}, o_{2}, o_{3})

to the end of the game (where

A^{'}

has already produced

(o_{1}, o_{2}, o_{3})

). This does not change the success probability of

A^{'}

by the deferred measurement principle (with some ancilla registers as in Corollary 1, extended from Lemma 7). Next, we modify

A^{'}

so that

A^{'}

does not do the deferred measurements mentioned above. This does not change the success probability of

A^{'}

as the deferred measurements are done after

(o_{1}, o_{2}, o_{3})

are obtained. Let

ϵ_{τ^{'}}^{'}

be the success probability of this

A^{'}

that produces

(o_{1}, o_{2}, o_{3})

with short

(o_{1}, o_{2}, o_{3})

so that

a_{1} o_{1} + a_{2} o_{2} - \bar{u} o_{3} = 0

with

| | o_{i} {| |}_{\infty} \leq 2 η_{t}

. By our foregoing argument,

ϵ_{τ^{'}}^{'} \geq γ_{2}^{2} (ϵ_{τ^{'}}^{3} - ϵ_{τ^{'}} / | Θ |) .

Let

| ψ_{τ^{'} λ_{1}} 〉

be the state right before the projective measurement that results in

(o_{1}, o_{2}, o_{3})

and

Q_{τ^{'} λ_{1}}

be the test measurement on

| ψ_{τ^{'} λ_{1}} 〉

to check if

a_{1} o_{1} + a_{2} o_{2} - \bar{u} o_{3} = 0 .

Let

A^{''}

be the variant of

A^{'}

so that projective measure resulting in

(o_{1}, o_{2}, o_{3})

is not made and instead it makes only the test measurement

Q_{τ^{'} λ_{1}} .

Under this,

A^{''}

still has the success probability

ϵ_{τ^{'}}^{'}

. Let the unitary that produces

| ψ_{τ^{'} λ_{1}} 〉

U_{τ^{'} λ_{1}}

. Then, using Claim above, we similarly have that

\frac{1}{{| Θ |}^{2}} \sum_{λ_{1}, λ_{1}^{'}} | | {\tilde{Q}}_{τ^{'} λ_{1}^{'}} {\tilde{Q}}_{τ^{'} λ_{1}} | ψ_{τ^{'}} {〉 | |}^{2} \geq {ϵ^{'}}_{τ^{'}}^{3},

where

{\tilde{Q}}_{τ^{'} λ_{1}} = U_{τ^{'} λ_{1}}^{†} Q_{τ^{'} λ_{1}} U_{τ^{'} λ_{1}} .

Further, if we require

λ_{1} \neq λ_{1}^{'}

, then

\frac{1}{{| Θ |}^{2}} \sum_{λ_{1} \neq λ_{1}^{'}} | | {\tilde{Q}}_{τ^{'} λ_{1}^{'}} {\tilde{Q}}_{τ^{'} λ_{1}} | ψ_{τ^{'}} {〉 | |}^{2} \geq {ϵ^{'}}_{τ^{'}}^{3} - {ϵ^{'}}_{τ^{'}} / | Θ | .

Again, by applying weakly-collapsing property of

Σ_{1}

, if

A^{''}

does the measurement for

(o_{1}, o_{2}, o_{3})

after

Q_{τ^{'} λ_{1}}

and the measurement for

(o_{1}^{'}, o_{2}^{'}, o_{3}^{'})

after

Q_{τ^{'} λ_{1}^{'}}

, then the success probability producing successful

(o_{1}, o_{2}, o_{3})

and

(o_{1}^{'}, o_{2}^{'}, o_{3}^{'})

with probability at least

γ_{1}^{2} ({ϵ^{'}}_{τ^{'}}^{3} - {ϵ^{'}}_{τ^{'}} / | Θ |) \geq γ_{1}^{2} ({ϵ^{'}}_{τ^{'}}^{3} - 1 / | Θ |) .

Since

{ϵ^{'}}_{τ^{'}} \geq γ_{2}^{2} (ϵ_{τ^{'}}^{3} - ϵ_{τ^{'}} / | Θ |)

, averaging over

τ^{'}

and using Cauchy-Schwarz inequality, the success probability to produce two accepting

(o_{1}, o_{2}, o_{3})

and

(o_{1}^{'}, o_{2}^{'}, o_{3}^{'})

with

λ_{1} \neq λ_{1}^{'}

is at least

γ_{1}^{2} (γ_{2}^{6} (ϵ^{3} - ϵ / {| Θ |)}^{3} - 1 / | Θ |) .

Since

γ_{1}, γ_{2}

and

ϵ

are all non-negligible, this lower bound is non-negligible either. However,

(o_{1}, o_{2}, o_{3})

and

(o_{1}^{'}, o_{2}^{'}, o_{3}^{'})

with

λ_{1} \neq λ_{1}^{'}

leads to a solution

(x_{1}, x_{2}, x_{3})

for Ring-SIS problem

a_{1} x_{1} + a_{2} x_{2} + u_{1} x_{3} = 0

(see Eqs (36)-(38) in [23] where our length bound

β

for

| | x_{i} {| |}_{\infty}

is summarized from there). This contradicts the

{ring-SIS}_{q, n, β}

assumption! □

Appendix A.4. Σ 2 and Σ 1 are Weakly Collapsing

We introduce the notation of compatible lossy function of a n-round public-coin protocol (as a straightforward generalization of the same notion in [30] for a sigma protocol).

Definition A3.

A compatible lossy function for a n-round public-coin protocol

Σ = (Gen, P, V)

is an efficiently computable function generator

CLF . gen (λ, p k, s k, {a_{i} | c_{i}}_{i = 1}^{n - 1}, mode)

which takes λ (security parameter),

p k, s k,

partial transcript

{a_{i} | c_{i}}_{i = 1}^{n - 1}

in Σ and mode (either constant or injective) and outputs an efficiently computable function f so that

constantmode: Let the domain of f be all r with ${a_{i} | c_{i}}_{i = 1}^{n - 1} | r$ being a valid transcript when $a_{n} = r$ . Then, the probability that f has an image of size at most p, is at least $γ .$ That is, ${Pr}_{f} (I m (f) \leq p) \geq γ$ , for $f \leftarrow CLF . gen (λ, p k, s k, {a_{i} | c_{i}}_{i = 1}^{n - 1}, constant)$ .
injectivemode: for $f \leftarrow CLF . gen (λ, p k, s k, {a_{i} | c_{i}}_{i = 1}^{n - 1}, injective)$ , f is injective over all r s.t. $({a_{i} | c_{i}}_{i = 1}^{n - 1} | r)$ is a valid transcript when $a_{n} = r$ , except for a negligible probability.
indistinguishability. We first define game ${clfExp}_{D, p k, s k}^{b}$ for $b = 0, 1 .$

-

$D$ is given $p k$ and challenge $Chal$ has $p k, s k$ .

-

$D$ (in the role of $P$ ) andChal(in the role of $V$ ) execute Σ in the first $n - 1$ rounds, resulting in the partial transcript ${a_{i} | c_{i}}_{i = 1}^{n - 1}$ .

-

If $b = 0,$ let $mode = constant$ ; otherwise,mode=injective. Then, challenger samples

$f \leftarrow CLF . gen (λ, p k, s k, {a_{i} | c_{i}}_{i = 1}^{n - 1}, mode)$

and provides it to $D .$ Then, $D$ outputs a guess bit $b^{'}$ for b, which is also defined as the output of the game.

The function generator $CLF . gen$ is $(p, γ)$ -compatible w.r.t. Σ if for any polynomial time quantum algorithm $D$ and for $(p k, s k) \leftarrow Gen (1^{λ})$ , we have

$\begin{matrix} Pr ({clfExp}_{D, p k, s k}^{0} = 0) = Pr ({clfExp}_{D, p k, s k}^{1} = 0) + negl (λ) . \end{matrix}$

(A5)

The following lemma is adapted from Liu and Zhandry [30], which shows that the existence of a compatible function for

Σ

implies that

Σ

is weakly collapsing. The result is stated with respect to a quantum secure sigma protocol. But their proof does not require the quantum security of the sigma protocol and can also be trivially extended to a n-round public-coin protocol. Thus, we state it without a proof.

Lemma A2.

If A n-round public-coin protocol Σ has a

(p, γ)

-compatible lossy function, then Σ is

γ / p

-weakly collapsing.

In the following, we prove that

Σ_{2}

has a compatible lossy function.

Lemma A3.

Let

F_{0}

and

F_{1}

w.r.t.

a_{1} | a_{2} | {u_{i} | λ_{i}}_{i = 1}^{t} | v | c

Σ_{2}

be two distributions of function families: for each valid

(z_{1}, z_{2}) \in R_{q}^{2}

(w.r.t.

{u_{i} | λ_{i}}_{i = 1}^{t} | v | c

\begin{matrix} F_{0} & = {f ∣ f (z_{1}, z_{2}) = {⌊ (s (a_{1}, a_{2}) + e) {(z_{1}, z_{2})}^{T} + r ⌉}_{θ}, s \leftarrow R_{q}^{2 log n}, e \leftarrow D_{R, σ}^{2 log n \times 2}, r \leftarrow R_{q}^{2 log n}} \\ F_{1} & = {f ∣ f (z_{1}, z_{2}) = {⌊ B {(z_{1}, z_{2})}^{T} + r ⌉}_{θ}, B \leftarrow R_{q}^{2 log n \times 2}, r \leftarrow R_{q}^{2 log n}}, \end{matrix}

where

8 σ n η_{t}^{1.5} log n < θ < \frac{q}{n log n}

and

{⌊ x ⌉}_{θ}

for

x \in R_{q}^{2}

rounds each coefficient

x_{i} \in F_{q}

(when representing

x

as a vector in

F_{q}^{2 n}

) using the

{⌊ x ⌉}_{θ}

function: it first repsents

x = k θ + y

with

y \in (- θ / 2, θ / 2]

and

k \in Z

and then outputs

k θ

. Then,

F_{0}

and

F_{1}

are

(\frac{2^{6}}{3^{6}}, 1)

-compatible w.r.t.

Σ_{2}

Proof. First, we show that

F_{0}

is a constant function family; second, we show that

F_{1}

is an injective function family; finally, we show that they are indistinguishable. In

Σ_{2}

, the message flows in order are

{λ_{i} | u_{i}}_{i = 2}^{t}

λ_{1}

v

, c and

(z_{1}, z_{2})

. The transcript is valid if

| | z_{1} {| |}_{\infty} < η_{t}

and

| | z_{2} {| |}_{\infty} < η_{t}

and

\sum_{i = 1}^{μ} v_{i} = a_{1} z_{1} + a_{2} z_{2} - \bar{u} c

, where

\bar{u} = \sum_{i = 1}^{t} λ_{i} u_{i}

To show

F_{0}

is a constant function family, we first show that

\begin{matrix} F_{0}^{'} = {f ∣ f (z_{1}, z_{2}) = {⌊ s (a_{1}, a_{2}) {(z_{1}, z_{2})}^{T} + r ⌉}_{θ}, s \leftarrow R_{q}^{2 log n}} \end{matrix}

(A6)

is a constant function family for

Σ_{2}

. Indeed, since transcript is valid,

f (z_{1}, z_{2}) = {⌊ r + s (\sum_{i} v_{i} + \bar{u} c) ⌉}_{θ}

(invariant). Then, we continue to show that

F_{0}

is a constant function family. The strategy is to show that there is a constant probability that

{⌊ r + s (\sum_{i} v_{i} + \bar{u} c) ⌉}_{θ} = {⌊ s (a_{1}, a_{2}) {(z_{1}, z_{2})}^{T} + r + e {(z_{1}, z_{2})}^{T} ⌉}_{θ}, \forall valid (z_{1}, z_{2}) .

(A7)

Since the left side is constant,

F_{0}

is a constant family. Now we implement this strategy.

Claim. Let

σ > ω (\sqrt{n})

. For

e \leftarrow D_{R, σ}

and

z \in R_{q}

with

{| | z | |}_{\infty} < η_{t}

, then

{Pr (| | e z | |}_{\infty} \geq η_{t}^{1.5} σ) < n \cdot exp (- π η_{t}) .

Proof. Notice that ith component of

e z \in R_{q}

\sum_{j = 0}^{n - 1} \pm e_{j} z_{i - j}

, where

i - j

means

(i - j)

mod n and the sign is - when

i < j

and is + otherwise. By [40, Lemma 4.4],

Pr (| \sum_{j = 0}^{n - 1} \pm e_{j} z_{i - j} {| > σ | | z | |}_{\infty} \sqrt{η_{t}}) < e^{- π η_{t}} .

The union bound on i gives the result. □

Back to our proof, the above claim implies that

Pr (| | e_{b 1} z_{1} + e_{b 2} z_{2} {| |}_{\infty} > 2 σ η_{t} \sqrt{η_{t}} : \exists b \in [2 log n]) < 2 n log n \cdot exp (- π η_{t}) .

(A8)

The space of

x \in R_{q}

with

{| | x | |}_{\infty} \leq η_{t}

has a size at most

{(2 η_{t})}^{n}

. Since

| | z_{1} {| |}_{\infty} \leq η_{t}

and

| | z_{2} {| |}_{\infty} \leq η_{t}

(z_{1}, z_{2})

has at most

{(2 η_{t})}^{2 n}

choices. By union bound,

| | e_{b 1} z_{1} + e_{b 2} z_{2} {| |}_{\infty} > 2 σ η_{t} \sqrt{η_{t}}

for some

(z_{1}, z_{2}, b)

only has an exponentially small probability (over

(e_{1}, e_{2})

), as

η_{t} = ω (n log n)

. Assume that

| | e_{b 1} z_{1} + e_{b 2} z_{2} {| |}_{\infty} \leq 2 σ η_{t}^{1.5}

holds for any

(b, z_{1}, z_{2})

. Notice that

w : = s (a_{1}, a_{2}) {(z_{1}, z_{2})}^{T} + r

is uniformly random in

R_{q}^{2 log n}

(as

r

is). For

x \in R_{q}

, we use

\underset{̲}{x}

to denote the coeffient vector of x over

F_{q}

. Similarly, for a vector

x \in R_{q}^{ℓ}

, we still use

\underset{̲}{x}

to denote the concatenated vector from

{\underset{̲}{x}}_{i}

for all

i = 1, \dots, ℓ

and use

\underset{̲}{x} [j]

to denote the jth coordinate in

\underset{̲}{x} .

Then,

\underset{̲}{w}

is uniformly random over

F_{q}^{2 n log n} .

If all

\underset{̲}{w} [i]

mod

θ

belong to

(- θ / 2 + 2 σ η_{t}^{1.5}, θ / 2 - 2 σ η_{t}^{1.5})

, then

{⌊ \underset{̲}{w} [i] ⌉}_{θ} = {⌊ \underset{̲}{w} [i] + \underset{̲}{(e_{1}, e_{2}) {(z_{1}, z_{2})}^{T}} [i] ⌉}_{θ}

for all i. By a simple calculation, the statistical distance between

\underset{̲}{w} [i]

mod

θ

and the uniform distribution over

(- θ / 2, θ / 2)

is at most

\frac{θ}{2 q} .

Hence,

\underset{̲}{w} [i]

mod

θ

is in that interval for all i with probability at least

{(1 - \frac{4 σ η_{t}^{1.5}}{θ} - \frac{θ}{2 q})}^{2 n log n} \geq {(1 - \frac{1}{n log n})}^{2 n log n}

, which is at least

2^{6} / 3^{6}

by our assumption on

θ

due to the fact that

{(1 - 1 / x)}^{x}

is increasing when

x \geq 3

. This indicates that

(e_{1}, e_{2}) {(z_{1}, z_{2})}^{T}

does not change the value of

f (z_{1}, z_{2})

. In addition,

w

is unchanged over all valid

(z_{1}, z_{2})

(as seen in

F_{0}^{'}

). Hence, f is constant, which occurs with probability at least

2^{6} / 3^{6} .

Next, we prove that

F_{1}

is injective. That is,

B (z_{1}, z_{2}) + r

is injective. Indeed,

B

is invertible if

det (B)

is invertible in

R_{q}

, where B is

B_{i} \in R_{q}^{2 \times 2}

for some i while

B = {(B_{i})}_{i = 1}^{log n}

. Let

B = {(a_{i j})}_{i, j = 1, 2}

. Represented using Chinese Remainder basis,

det (B) = a_{11} ⊙ a_{22} - a_{12} ⊙ a_{21}

, where ⊙ is the coordinate-wise multiplication over

F_{q}

and x is the coordinate vector of

x \in R_{q}

under Chinese Remainder basis (for background on this, see [24,35]). Notice that

x \in R_{q}

is invertible if and only if each coordinate of x is non-zero. Since

a_{i j}

is uniformly random over

R_{q}

, a calculation shows that

det (B)

is invertible with probability

{(1 - 1 / q - 1 / q^{2} + 1 / q^{3})}^{n}

and so

det (B)

is not invertible with probability at most

n / q + O (n^{2} / q^{2})

. Thus, the statement that no

B_{i}

is invertible, has a probability at most

{(n / q + O (n^{2} q^{- 2}))}^{log n} = O (2^{- {log}^{2} n}),

negligible.

Finally, we prove that

F_{0}

and

F_{1}

are indistinguishable. This directly follows from ring-LWE assumption as

s_{b} (a_{1}, a_{2}) + (e_{b 1}, e_{b 2})

for

s_{b} \leftarrow R_{q}, e_{b 1}, e_{b 2} \leftarrow D_{R, σ}

is indistinguishable from

(B_{b 1}, B_{b 2}) \leftarrow R_{q}^{2}

for

b = 1, 2, \dots, 2 log n

. This concludes our proof. □

Next, we consider the compatible function families

F_{0}

and

F_{1}

for

Σ_{1}

Lemma A4.

Assume that

ℓ = log n

. Let

F_{0}

and

F_{1}

be the two families of function distributions w.r.t.

a_{1} | a_{2} | {u_{i} | λ_{i}}_{i = 1}^{t}

Σ_{1}

defined as follows.

\begin{matrix} F_{0} & = {f ∣ f (o_{1}, o_{2}, o_{3}) = {⌊ (s (a_{1}, a_{2}, - \bar{u}) + e) {(o_{1}, o_{2}, o_{3})}^{T} + r ⌉}_{θ}, s \leftarrow R_{q}^{3 ℓ \times 1}, e \leftarrow D_{R, σ}^{3 ℓ \times 3}, r \leftarrow R_{q}^{3 ℓ}} \\ F_{1} & = {f ∣ f (o_{1}, o_{2}, o_{3}) = {⌊ B {(o_{1}, o_{2}, o_{3})}^{T} + r ⌉}_{θ}, B \leftarrow R_{q}^{3 ℓ \times 3}, r \leftarrow R_{q}^{3 ℓ}}, \end{matrix}

where

12 σ n {η^{'}}_{t}^{1.5} log n \leq θ \leq \frac{q}{n log n}

and

η_{t}^{'} = 2 η_{t}

. Then,

F_{0}

and

F_{1}

are

(\frac{2^{9}}{3^{9}}, 1)

-compatible w.r.t.

Σ_{1}

Proof. The proof is very similar to Lemma A3. We only sketch the main changes: (1) we use

(a_{1}, a_{2}, - \bar{u}) {(o_{1}, o_{2}, o_{3})}^{T} = 0

(fixed) instead of

(a_{1}, a_{2}) {(z_{1}, z_{2})}^{T} = \sum_{i} v_{i} + u c

(fixed), and hence

F_{0}^{'}

consists only of a constant function r; (2)

η_{t}

is replaced by

η_{t}^{'}

. Further, the injective property of

B (o_{1}, o_{2}, o_{3}) + r

is reduced to the invertibility of

B = {(a_{i j})}_{i, j = 1, 2, 3}

(instead of order 2 matrix) when

a_{i j}

is random in

R_{q}

. By Gaussian elimination, if

a_{11}

is invertible, then we make the entries (1, 2) and (1, 3) in B as zero. This updates

a_{22}

a_{22}^{'}

and

a_{33}

a_{33}^{'}

while

a_{22}^{'}

and

a_{33}^{'}

are still uniformly random in

R_{q}

. If

a_{22}^{'}

is invertible, then we can make

a_{23}^{'}

zero similarly that updates

a_{33}^{'}

a_{33}^{''}

while preserving its uniformity. So B is invertible if

a_{11}, a_{22}^{'}

and

a_{33}^{''}

are all invertible, which has a probability at least

{(1 - 1 / q)}^{3 n}

. So for

B = {(B_{i})}_{i = 1}^{ℓ}

B (o_{1}, o_{2}, o_{3}) + r

is invertible if some

B_{i}

is invertible. This is violated with probability at most

{(3 n / q + O (n^{2} / q^{2}))}^{log n} \leq 2^{- {log}^{2} n}

, negligible. □

From Lemmas A2, A3 and A4, we can immediately conclude the following corollary.

Corollary A1.

Σ_{2}

\frac{2^{6}}{3^{6}}

-weakly collapsing and

Σ_{1}

\frac{2^{9}}{3^{9}}

-weakly collapsing.

Proof of Theorem 6. From Corollary A1, we know that

Σ_{1}

and

Σ_{2}

are both weakly collapsing. Then, Lemma A1 gives our desired result. □

Appendix B. Encoding of CStO or CStO s and Efficient Operations on Oracle State

In this section, we detail how to efficiently encode

C S t O

(or

C S t O_{s}

) and efficiently implement operations (such as

U_{R}

and projective measurements) on oracle register. Since

C S t O

is a special case of

{C S t O}_{s}

, we only need to consider

{C S t O}_{s}

. Let q be a polynomial upper bound on the number of random oracle queries to

C S t O_{s}

. Let

X = {x_{1}, \dots, x_{N}}

be an ordered set with

x_{1} < \dots < x_{N}

and

| X | = N

, with

0 \notin X .

Let

D_{q}

be the set of

y \in {\bar{Y}}^{X}

that contains at most q non-⊥ entries, where

\bar{Y} = Y \cup {⊥}

. For

y \in D_{q}

{| y 〉}_{D}

represents

| y_{1} 〉_{D_{x_{1}}} \dots {| y 〉}_{D_{x_{N}}}

. We can encode it as

| x_{1}^{'} 〉 | y_{1}^{'} 〉 \dots | x_{ℓ}^{'} 〉 | y_{ℓ}^{'} 〉 (| 0 〉 | ⊥ {〉)}^{q - ℓ}

(denoted it by

| (x^{'}, y^{'}) 〉

and in this case the number of records in the encoded D as

| D | : = ℓ

) where

x_{1}^{'} < x_{2}^{'} < \dots < x_{ℓ}^{'}

are all the indices in

y

with

D (x_{i}^{'}) = y_{i}^{'} \neq ⊥

. Denote this encoding by

e n c

. Let

L_{q} \subset X \times Y

be the set of all the possible pairs

(x^{'}, y^{'})

of cardinality at most q (sorted according to the first coordinate). Since

| (x^{'}, y^{'}) 〉

represents

| x_{1}^{'} 〉 | y_{1}^{'} 〉 \dots | x_{ℓ}^{'} 〉 | y_{ℓ}^{'} 〉 (| 0 〉 | ⊥ {〉)}^{q - ℓ}

for

(x^{'}, y^{'}) = {(x_{i}^{'}, y_{i}^{'})}_{i = 1}^{ℓ}

with

x_{1}^{'} < x_{2}^{'} < \dots < x_{ℓ}^{'}

and

ℓ \leq q

e n c

is a unitary between

H (D_{q})

and

H (L_{q})

(indeed,

e n c

is one-one and onto mapping between the two sets of orthonormal basis states).

With

e n c

in mind, we claim that our results in this paper holds when the quantum state in D is encoded (via

e n c

). Specifically, if originally an operator O is applied (with the state on D not encoded), it now applies

e n c \cdot O \cdot e n c^{†}

(with the state on D encoded), where

e n c

operates on D. Since

e n c^{†} \cdot e n c = I

, the final (adversary-oracle) state with or without encoding on D are related by

e n c

unitary. This will not change the final adversary output (from measurement, say

M = {M_{t}}_{t}

), as

〈 ψ | \cdot e n c^{†} \cdot M_{t}^{†} M_{t} \cdot e n c | ψ 〉 = 〈 ψ | M_{t}^{†} M_{t} | ψ 〉

(recall that adversary does not operate on D and so

e n c

and

M_{t}

operate on disjoint registers and commute and also that

e n c

is unitary).

However, this is not enough as we need an efficient implementation of

e n c

. Our next step is to deal with this. We first introduce some notations. If D has a state

| (x, y) 〉

with

| D | = ℓ < q

, define

| (x, y) \cup (x, y) 〉

with

x \neq x_{i}

for any

i = 1, \dots ℓ

, as sorted pairs

| (x^{'}, y^{'}) 〉

(w.r.t. the first coordinate), updated from

(x, y)

with

(x, y)

inserted. This operation is undefined for

ℓ \geq q

. Similarly, we can define

| (x, y) ∖ (x_{i}, y_{i}) 〉

as removing

(x_{i}, y_{i})

from D and sorting the remaining pairs. Next, we introduce the encoding operator COD on

X D

. For

x \in X

{COD}_{x}

is a unitary from

H ({\bar{L}}_{q})

H ({\bar{L}}_{q})

, where

{\bar{L}}_{q} \subset X \times \bar{Y}

is similar to

L_{q}

, except that

(x, y) \in {\bar{L}}_{q}

means

y_{i} \in \bar{Y}

(instead of

y \in Y

). For basis state

{| (x, y) 〉}_{D}

with

(x, y) \in {\bar{L}}_{q}

and

| D | = ℓ

, we use

D (x_{i})

to denote

y_{i}

and

D (x) = n i l

x \neq x_{i}

for any

i = 1, \dots, ℓ

. Essentially,

{COD}_{x}

operates on

D_{x}

(by trying to clean up or adding entry

(x, ⊥)

) and then sorts the updated

| (x, y) 〉

on D. Specifically, it operates as follows.

-: If $D (x) \in Y$ , then ${COD}_{x} {| (x, y) 〉}_{D} = | (x, y) 〉$ .
-: If $D (x) = ⊥$ , then ${COD}_{x} {| (x, y) 〉}_{D} = | (x, y) ∖ (x, ⊥) 〉$ (this implies $| D | < q$ after the operation).
-: If $D (x) = n i l$ (i.e., x is not in D) and $| D | < q$ , then ${COD}_{x} {| (x, y) 〉}_{D} = | (x, y) \cup (x, ⊥) 〉 .$
-: If $D (x) = n i l$ and $| D | = q$ , then ${COD}_{x} {| (x, y) 〉}_{D} = | (x, y) 〉$ .

Note that

{COD}_{x}

is unitary as it maps from orthonormal basis to orthonormal basis in

H ({\bar{L}}_{q}) .

Further,

{COD}_{x}

is obviously Hermitian. Finally, we define

COD = \sum_{x \in X} {| x 〉 〈 x |}_{X} \otimes {COD}_{x} .

Note this

COD

can be implemented in a polynomial size of quantum gates as it can be described in polynomial and hence the known techniques (e.g., [48]) can be applied.

We know that without encoding, the initial state of D is

\otimes_{x} {| ⊥ 〉}_{D_{x}}

and hence after encoding, the initial state is

{(| 0 〉 | ⊥ 〉)}^{q} .

In the following, we show

e n c \cdot O \cdot e n c^{†}

for any original operator O in this paper can be implemented in polynomial time. This can be seen through the following cases.

1.: O does not operate on D. For example, attacker’s operator and projective measurements on P belong to this category. In this case, since $e n c$ and O operates on disjoint registers and $e n c \cdot e n c^{†} = I,$ $e n c \cdot O \cdot e n c^{†} = O$ . So instead of $e n c \cdot O \cdot e n c^{†}$ , it suffices to apply O.
2.: $C S t O_{s X Y D}$ . Recall that $C S t O_{s X Y D} = \sum_{x \in X} | x 〉 〈 x | \otimes C S t O_{s Y D_{x}}$ and $C S t O_{s Y D_{x}} = F_{D_{x}} \cdot {C N O T}_{Y D_{x}} \cdot F_{D_{x}}$ for $x \notin Ξ$ and $C S t O_{s Y D_{x}} = {C N O T}_{Y D_{x}}$ for $x \in Ξ$ . We implement $e n c \cdot C S t O_{s} \cdot e n c^{†}$ with $COD \cdot C S t O_{s} \cdot COD = \sum_{x \in X} | x 〉 〈 x | \otimes {COD}_{x} \cdot C S t O_{s Y D_{x}} \cdot {COD}_{x}$ . The validity of this implementation can be verified through the basis state $| (x, y) 〉 .$ The verification is tedious but straightforward and hence omitted here.
3.: $U_{R}$ . Recall that for $y \in D_{q}$ , there exists $x_{1}^{'} < x_{2}^{'} < \dots < x_{ℓ}^{'}$ so that $y_{x_{i}^{'}} \in Y$ and $y_{x} = ⊥$ for $x \neq x_{i}^{'}$ for any $i \in [ℓ] .$ Then, $y$ is encoded as $(x^{'}, y^{'})$ , where $y^{'} = (y_{x_{1}^{'}}, \dots, y_{x_{ℓ}^{'}})$ . Define ${\tilde{f}}_{R} ((x_{1}^{'}, y_{1}^{'}), \dots, (x_{q}^{'}, y_{q}^{'})) = \sum_{i} x_{i}^{'} \cdot \bar{R} (x_{1}^{'}, y_{1}^{'}) \dots \bar{R} (x_{i - 1}^{'}, y_{i - 1}^{'}) \cdot R (x_{i}^{'}, y_{i}^{'}),$ where $x_{i}^{'} = 0$ and $y_{i}^{'} = ⊥$ for $i > ℓ .$ We remind that $f_{R} (y) = {\tilde{f}}_{R} (x^{'}, y^{'}) .$ Define unitary ${\tilde{U}}_{R}$ so that ${\tilde{U}}_{R} | (x^{'}, y^{'}) {〉 | 0 〉}_{P} = | (x^{'}, y^{'}) 〉 | {\tilde{f}}_{R} (x^{'}, y^{'}) 〉 .$ Then, $e n c \cdot U_{R} \cdot e n c^{†}$ can be implemented by ${\tilde{U}}_{R},$ by directly operating ${\tilde{U}}_{R}$ on $D P$ without decoding D.
4.: Measurement $Π = (Π_{0}, Π_{1}) = (| ⊥ 〉 〈 ⊥ |, I - | ⊥ 〉 〈 ⊥ |)$ on $D_{x}$ (in PointReg1 query). In this case, we implement $e n c \cdot Π_{b} \cdot e n c^{*}$ as $COD \cdot Π_{b} \cdot COD$ . For any $(x^{'}, y^{'}) \in L_{q}$ , let $e n c^{*} | (x^{'}, y^{'}) 〉 = | y 〉$ . It suffices to verify ${COD}_{x} \cdot Π_{b} \cdot {COD}_{x} | (x^{'}, y^{'} 〉 = e n c \cdot Π_{b} | y 〉 .$ This can be checked for cases $D (x) = n i l, ⊥, y$ for $y \in Y$ . Tedious details are omitted.
5.: Measurement on D. In this paper, measurement property on D with $| y 〉$ only depends on the non-⊥ entries. That is, the property $f (y)$ equals to $\tilde{f} ((x^{'}, y^{'}))$ for some $\tilde{f}$ , where $e n c (y) = (x^{'}, y^{'}) .$ Hence, measurement on uncompressed D for property f can be done on compressed D for property $\tilde{f}$ . For example, f is a collision property on $y$ for non-⊥ is equivalent to the collision property $\tilde{f}$ on encoded $y$ (i.e., $(x^{'}, y^{'})$ ). Since $\tilde{f}$ on the encoded D can be implemented efficiently, measurement of property f can be done efficiently.

Based on the analysis above, we can conclude that our computation with the oracle state un-encoded can be implemented by applying efficient operations with oracle state encoded, preserving the same adversary success probability and the resulting joint-state related only by the unitary encoding on the oracle state.

Appendix C. Proof of Lemma 14

Proof. Our strategy is to relate the collision probabilities before and after one oracle query, when the

abort

event does not happen. Since there are at most q queries of either

P o i n t R e g 1

C S t O_{s}

{CStO}_{s}

and the initial state

\otimes_{x} {| ⊥ 〉}_{D_{x}}

has no collision, this will allow us to bound the collision probability in the final state. We use

μ

to represent the collision probability after the next operation and

μ^{'}

to the collision probability before the query. We will show

\sqrt{μ} \leq \sqrt{μ^{'}} + ϵ

for some

ϵ .

We assume that the current state is a pure state

| ψ 〉 = \sum_{x y z y} λ_{x y z y} | x 〉 | ϕ_{y} {〉 | z 〉 | y 〉}_{D}

(the mixed state will be handled later), where we use basis

{ϕ_{y}}_{y}

on response register Y for the ease of adapting the phase oracle based proof in [49] to

{CStO}_{s}

. If the next query is

P o i n t R e g 0

, then the state is unchanged and hence

μ^{'} = μ .

Then, we consider the other two cases: random oracle query and PointReg1 query.

Next operation is random oracle query. We classify basis

{| x, ϕ_{y}, z, y 〉}_{x y z y}

into four sets:

P, Q, R, S .

P: It consists of the basis states so that $y$ contains a collision.
Q: It consists of the basis states satisfying: (1) $y$ has no collision; (2) $y \neq 0$ ; (3) $y_{x} = ⊥$ .
R: It consists of the basis states satisfying: (1) $y$ has no collision; (2) $y \neq 0$ ; (3) $y_{x} \neq ⊥$ .
S: It consists of the basis states satisfying: (1) $y$ has no collision; (2) $y = 0$ .

We also use

P, Q, R, S

to denote the projection into the space spanned by the basis states in the respective category. Then,

P + Q + R + S = I .

Since the attacker only makes at most q random oracle queries, D contains at most q non-⊥ entries. In this case, the square root of collision probability (when abort does not occur) is

| | P \cdot C S t O_{s} \cdot Λ_{i 0} | ψ 〉 | |

, which is at most

\begin{matrix} | | P \cdot C S t O_{s} \cdot Λ_{i 0} P | ψ 〉 | | + | | P \cdot C S t O_{s} \cdot Λ_{i 0} Q | ψ 〉 | | + | | P \cdot C S t O_{s} \cdot Λ_{i 0} R | ψ 〉 | | + | | P \cdot C S t O_{s} \cdot Λ_{i 0} S | ψ 〉 | | . \end{matrix}

Notice that

C S t O_{s}

has two cases: if

x \in Ξ_{1}

, then

C S t O_{s Y D_{x}} = {C N O T}_{Y D_{x}}

; if

x \notin Ξ_{1}

, then

C S t O_{s Y D_{x}} = C S t O_{Y D_{x}} .

Let’s write

| ψ 〉 = \sum_{x} | ψ_{x} 〉

where

ψ_{x} = {| x 〉}_{X} \dots

We first consider the case

x \notin Ξ_{1}

. In this case,

{C S t O}_{s} | ψ_{x} 〉 = C S t O | ψ_{x} 〉

Case $P | ψ_{x} 〉$ . In this case,

| | P \cdot C S t O \cdot Λ_{i 0} P | ψ_{x} 〉 | | \leq | | C S t O \cdot Λ_{i 0} P | ψ_{x} 〉 | | = | | Λ_{i 0} \cdot P | ψ_{x} 〉 | | \leq | | P | ψ_{x} 〉 | | .

Case $Q | ψ_{x} 〉$ .

C S t O

| x, z 〉 | ϕ_{y} {〉 \otimes | y 〉}_{D}

(in Q) gives

| x, z 〉 | ϕ_{y} 〉 \otimes \frac{1}{\sqrt{2^{n}}} \sum_{w} {(- 1)}^{y \cdot w} | y \cup {(w)}_{x} 〉

y_{x} = ⊥

. Hence, further after operator P, it has a norm of at most

\sqrt{q Γ_{f} / 2^{n}}

, as

| D | \leq q

and the collision implies that

f (x, w) = f (x^{'}, y_{x^{'}})

for some

x^{'} \neq x

(recall that

y

has no collision) because each

(x^{'}, y_{x^{'}})

collides with

(x, w)

for at most

Γ_{f}

possible w’s. Since distinct

| x, z 〉 | ϕ_{y} 〉 \otimes | y 〉

(in Q) gives orthogonal images, it follows that

P \cdot C S t O \cdot Λ_{i 0} Q | ψ_{x} 〉

has a norm at most

\sqrt{q Γ_{f} / 2^{n}} | | Λ_{i 0} Q | ψ_{x} 〉 | | \leq \sqrt{q Γ_{f} / 2^{n}} | | Q | ψ_{x} 〉 | |

(as

Λ_{i 0}, Q

are projectors on D in the computational basis).

Case $R | ψ_{x} 〉$ . For category R, consider that D has a state

{| y \cup (w)}_{x} 〉

with

y_{x} = ⊥

and

w \neq ⊥

. By a tedious calculation (also in [49, Theorem1]), we can show that

C S t O | x, z 〉 | ϕ_{y} 〉 | y \cup {(w)}_{x} 〉

\begin{matrix} | x, z 〉 | ϕ_{y} {〉 ((- 1)}^{y \cdot w} {(| y \cup (w)}_{x} 〉 + \frac{1}{2^{n / 2}} | y 〉) + \frac{1}{2^{n}} \sum_{y^{'}} (1 - {(- 1)}^{y \cdot w} - {(- 1)}^{y \cdot y^{'}}) | y \cup {(y^{'})}_{x} 〉) . \end{matrix}

After applying P, since

| x, ϕ_{y}, z 〉 | y \cup {(w)}_{x} 〉

is in R and so

| x, ϕ_{y}, z 〉 | y 〉

is in Q, it becomes

\begin{matrix} | x, z 〉 | ϕ_{y} 〉 \otimes \frac{1}{2^{n}} \sum_{y^{'} : \exists x^{'}, f (x, y^{'}) = f (x^{'}, y_{x^{'}})} (1 - {(- 1)}^{y \cdot w} - {(- 1)}^{y \cdot y^{'}}) P | y \cup {(y^{'})}_{x} 〉 . \end{matrix}

(A9)

Now we relate the different states of form

| x, z 〉 | ϕ_{y} 〉 | y \cup {(w)}_{x} 〉

in category R . If they have different

(x, z, y, y)

tuples, then their results in (A9) are orthogonal (as they all have

y_{x} = ⊥

by definition and thus their tuple

(x, z, y, {y_{t}}_{t \neq x})

are different). So we only need to consider the setting of the same

(x, z, y, y)

for the norm in this category. In this case, there are at most

2^{n}

choices of w. By Chauchy-Schwardz inequality, the norm of the superposition of Equation (A9) over w, is at most

\sqrt{2^{n}}

times of its maximum over

w .

It remains to upper bound the norm of Equation (A9) for a given

w .

In this case, notice that for each

(x^{'}, y_{x^{'}})

with

y_{x^{'}}

non-⊥, there are at most

Γ_{f}

possible

y^{'}

in Equation (A9) so that

f (x, y^{'}) = f (x^{'}, y_{x^{'}})

. There are at most q non-⊥

y_{x^{'}}

y

. Equation (A9) has a norm of at most

3 \sqrt{q Γ_{f}} \cdot 2^{- n}

. Hence, the superposition of Equation (A9) has a norm at most

3 \sqrt{q Γ_{f} / 2^{n}} .

Thus,

| | P \cdot C S t O \cdot Λ_{i 0} R | ψ_{x} 〉 | | \leq 3 \sqrt{q Γ_{f} / 2^{n}} | | Λ_{i 0} R | ψ_{x} 〉 | | \leq 3 \sqrt{q Γ_{f} / 2^{n}} | | R | ψ_{x} 〉 | |

(as

Λ_{i 0}, R

are projectors on D in the computational basis).

Case $S | ψ_{x} 〉$ . In this case,

C S t O \cdot | x, z 〉 | ϕ_{0} 〉 | y 〉 = | x, z 〉 | ϕ_{0} 〉 | y 〉

, which has no collision.

Summarizing the four cases, we have

\begin{matrix} | | P \cdot C S t O \cdot Λ_{i 0} | ψ_{x} 〉 | | \leq | | P \cdot | ψ_{x} 〉 | | + 4 \sqrt{q Γ_{f} / 2^{n}} | | | ψ_{x} 〉 | | . \end{matrix}

(A10)

Second, we consider case

x \in Ξ_{1}

and so

C S t O_{s} = C N O T

. In this case, notice that

P \cdot C N O T \cdot Λ_{i 0} | ψ_{x} 〉 = P^{2} \cdot C N O T \cdot Λ_{i 0} | ψ_{x} 〉 = P \cdot C N O T \cdot Λ_{i 0} P | ψ_{x} 〉

, as P commutes with

C N O T

and

Λ_{i 0}

. Further,

| | P \cdot C N O T \cdot Λ_{i 0} P | ψ_{x} 〉 | | \leq | | C N O T \cdot Λ_{i 0} P | ψ_{x} 〉 | | = | | Λ_{i 0} P | ψ_{x} 〉 | | \leq | | P | ψ_{x} 〉 | |,

C N O T

is unitary and

Λ_{i 0}

is a projector in the computational basis (as is for P).

Summarizing both

x \in Ξ_{1}

and

x \notin Ξ_{1}

cases and noticing that their images are orthogonal (as

{| x 〉}_{X}

will remain unchanged after the operation), we have

\begin{matrix} | | P \cdot C S t O_{s} \cdot Λ_{i 0} | ψ 〉 | | \leq | | P \cdot | ψ 〉 | | + 4 \sqrt{q Γ_{f} / 2^{n}} \end{matrix}

(A11)

For the mixed state, suppose

| ψ 〉

has the probability

λ_{ψ}

. Then averaging the square of the above inequality and expanding the right side and using the Cauchy-Schwarz inequality

\sum_{i} λ_{i} x_{i} \leq {(\sum_{i} λ_{i} x_{i}^{2})}^{1 / 2}

with

λ_{i}, x_{i} \geq 0

and

\sum_{i} λ_{i} = 1,

we have

\begin{matrix} \sqrt{μ} \leq \sqrt{μ^{'}} + 4 \sqrt{q Γ_{f} / 2^{n}} . \end{matrix}

(A12)

Next operation is PointReg1. Still we assume the current adversary-oracle joint state is a pure state

| ψ 〉

. In this case, under event

\neg abort

, projection

Π_{0}

| ψ 〉

is applied and

{| ⊥ 〉}_{D_{x}}

is replaced by

{| r 〉}_{D_{x}}

. Since r is random, the resulting state

ρ_{0}

is the mixed state (over r) and so the collision probability is

t r (P \cdot ρ_{0} \cdot P)

. We write the current state

| ψ 〉 = \sum_{y z y} α_{y z y} | x, z 〉 | ϕ_{y} {〉 | y 〉}_{D} .

We classify the basis states

| x, z, ϕ_{y} {〉 | y 〉}_{D}

into 3 categories

P, Q^{'}, R^{'}

, similar to the

C S t O_{s}

case. But different from

Q, R

, here

Q^{'}, R^{'}

respectively removes condition 2 (the restriction on y). It is not hard to show5 that

\sqrt{t r (P \cdot ρ_{0} \cdot P)}

for any mixed state

ρ_{0}

that starts from

| ψ 〉

and through some quantum algorithm, can be upper bounded by

\begin{matrix} \sum_{V \in {P, Q^{'}, R^{'}}} \sqrt{t r (P \cdot ρ_{0 V} \cdot P)}, \end{matrix}

(A13)

where

ρ_{0 V}

is the mixed state

ρ_{0}

with the input state

V | ψ 〉

(instead of

| ψ 〉

Case $P | ψ 〉$ . In this case, after applying

Π_{0}

, only the basis states

| x, z 〉 | ϕ_{y} 〉 | y 〉

P | ψ 〉

, with

y_{x} = ⊥

and

y

containing a collision, are left and after the query, this state becomes

| x, z 〉 | ϕ_{y} 〉 | y \cup {(r)}_{x} 〉

for a uniformly random r. Note

y \cup {(r)}_{x}

for any r still contains a collision. Therefore,

t r (P \cdot ρ_{0 P} \cdot P) = \sum_{r} 2^{- n} 〈 ψ | P Π_{0} U_{⊥, r} P P U_{⊥, r} Π_{0} P | ψ 〉 = 〈 ψ | P Π_{0} Π_{0} P | ψ 〉 = | | Π_{0} {P | ψ 〉 | |}^{2} \leq {| | P | ψ 〉 | |}^{2}

, where

U_{⊥, r} = | r 〉 〈 ⊥ | + | ⊥ 〉 〈 r | + \sum_{s \neq r} | s 〉 〈 s |

. Thus the collision probability of

P | ψ 〉

after the query is at most

{| | P | ψ 〉 | |}^{2} .

Case $Q^{'} | ψ 〉$ . In this case, since

D_{x}

in this category always has ⊥,

Π_{0} Q^{'} | ψ 〉 = Q^{'} | ψ 〉

, which, after applying

U_{⊥, r}

and P, changes the basis state

| x, z 〉 | ϕ_{y} 〉 | y 〉

Q^{'} | ψ 〉

(where

y_{x} = ⊥

) to

| x, z 〉 | ϕ_{y} 〉 | y \cup {(r)}_{x} 〉

(if

(x, r)

collides with

(x^{'}, y_{x^{'}})

(for some

x^{'} \neq x

)) or 0 (if

(x, r)

does not collide with any

(x^{'}, y_{x^{'}})

). Notice that for different

(x, z, y, y)

| x, z 〉 | ϕ_{y} 〉 | y \cup {(r)}_{x} 〉

in this category will be orthogonal to each other. Therefore,

\begin{matrix} t r (P \cdot ρ_{0 Q^{'}} \cdot P) \leq \frac{q Γ_{f}}{2^{n}} | | Q^{'} {| ψ 〉 | |}^{2}, \end{matrix}

(A14)

as there are at most q choices of

(x^{'}, y_{x^{'}})

y

and that

y

itself has no collision by definition.

Case $R^{'} | ψ 〉$ . In this case, since

D (x) \neq ⊥

, under

\neg abort

event,

Π_{0} R^{'} | ψ 〉 = 0

(no collision).

Summarizing the three cases, we have that

\begin{matrix} \sqrt{t r (P \cdot ρ_{0} \cdot P)} \leq | | P | ψ 〉 | | + \sqrt{\frac{q Γ_{f}}{2^{n}}} | | ψ | | . \end{matrix}

(A15)

If the current state is a mixed state so

| ψ 〉

has a probability

λ_{ψ}

and

ρ_{ψ}

P \cdot ρ_{0} \cdot P

from

| ψ 〉

, then

\sqrt{\sum_{ψ} λ_{ψ} t r (ρ_{ψ})} \leq \sqrt{\sum_{ψ} λ_{ψ} (| | P | ψ 〉 | | + \sqrt{\frac{q Γ_{f}}{2^{n}}} {| | | ψ 〉 | |)}^{2}},

which is upper bounded by

\begin{matrix} \sqrt{\sum_{ψ} λ_{ψ} {| | P | ψ 〉 | |}^{2}} + \sqrt{\sum_{ψ} λ_{ψ} \sqrt{\frac{q Γ_{f}}{2^{n}}} {| | | ψ 〉 | |}^{2}} = \sqrt{μ^{'}} + \sqrt{q Γ_{f} / 2^{n}}, \end{matrix}

(A16)

where the first part of Equation (A16) uses

\sqrt{\sum_{i = 1}^{n} {(a_{i} + b_{i})}^{2}} \leq \sqrt{\sum_{i = 1}^{n} | | a_{i} {| |}^{2}} + \sqrt{\sum_{i = 1}^{n} | | b_{i} {| |}^{2}} .

This gives

\sqrt{μ} \leq \sqrt{μ^{'}} + \sqrt{\frac{q Γ_{f}}{2^{n}}} .

Let

μ_{q}

be the collision probability of the final state. Since there are at most q queries (either PointReg1 or random oracle query) to

{CStO}_{s}

\sqrt{μ_{q}} \leq 4 q \sqrt{\frac{q Γ_{f}}{2^{n}}} .

This gives our lemma. □

Appendix D. Proof of Theorem 4

For constant

c > 0

, define

λ_{i^{c}, j^{c}, k^{c}, {\underset{̲}{x}}^{c}, w, y}

to be the probability that the measurement in the

i_{t}

th oracle query in

{Exp}_{i^{c}, j^{c}, k^{c}}

has outcome

{\underset{̲}{x}}_{t}

(for

t = 1, \dots, c

) and the final measurement outcome is

(w, y)

, where

{\underset{̲}{x}}^{c} = ({\underset{̲}{x}}_{1}, \dots, {\underset{̲}{x}}_{c}) .

For

v \in Y

, we use

{v}_{x}

to denote the vector in

Y^{X}

so that the coordinate at index x is v and the remaining coordinates are all 0 (do not confuse with

{(v)}_{x}

where it is v at coordinate x and ⊥ otherwise). For

v \in Y^{X}

, we use

| ϕ_{v} 〉_{D}

to denote the oracle state with

| ϕ_{v_{x}} 〉_{D_{x}}

. Then,

C S t O

oracle has the following property (which is an alternative description of Fourier oracle’s essential property in [49] but in the language of

C S t O

Fact 1.

{| x 〉}_{X} | ϕ_{y} 〉_{Y} F_{D} {| ϕ_{v} 〉}_{D}

under

C S t O

oracle will be mapped to

{| x 〉}_{X} | ϕ_{y} 〉_{Y} F_{D} {| ϕ_{v + {y}_{x}} 〉}_{D}

The following lemma is extended from [30, Theorem 9] through translating their proof on compressed Fourier oracle using

C S t O

oracle and generalizing it from

{Exp}_{i j k}

{Exp}_{i^{c}, j^{c}, k^{c}}

Lemma A5.

For any

w, y, x^{c}

with

D ({\underset{̲}{x}}_{t}) \neq ⊥

(

t = 1, \dots, c

) and

γ_{w, y}

is the probability in the normal game with output

(w, y)

. Then, there exists

(i^{c}, j^{c}, k^{c})

so that

λ_{i^{c}, j^{c}, k^{c}, {\underset{̲}{x}}^{c}, w, y} \geq γ_{w, y} / {(q + (\binom{q}{3}))}^{2 c}

Proof. Let

\sum_{x, y, z} α_{x, y, z} | x, ϕ_{y}, z 〉

be the state of the adversary before the first query. Let

U_{x, y, z, x^{'}, y^{'}, z^{'}}^{(i)}

be the transition function from

| x, ϕ_{y}, z 〉

| x^{'}, ϕ_{y^{'}}, z^{'} 〉

, starting from the ith query to

C S t O

but right before

(i + 1)

th query, where the

C S t O

is represented under basis

F_{D} {| ϕ_{v} 〉}_{D}

. By Fact 1 above, this is well-defined for a fixed adversary quantum algorithm (as adversarial algorithm is not acting on D). For any vector

x, y, z

and w, let

\begin{matrix} α_{x, y, z, w} = α_{x_{1}, y_{1}, z_{1}} U_{x_{1}, y_{1}, z_{1}, x_{2}, y_{2}, z_{2}}^{(1)} \dots U_{x_{q}, y_{q}, z_{q}, w}^{(q)} . \end{matrix}

(A17)

Then, we can write the final adversary-oracle joint state as

\begin{matrix} \sum_{x, y, z, w} α_{x, y, z, w} | w 〉 \otimes F_{D} {| ϕ_{{y_{1}}_{x_{1}} + \dots + {y_{q}}_{x_{q}}} 〉}_{D} . \end{matrix}

(A18)

(Note: here the oracle uses basis

F_{D} | ϕ_{y} 〉

and will switch to

| y 〉

later). For any

v \in Y^{X}

with at most q non-zero coordinates, define set

S_{v}

: it contains

x, y

so that

\sum_{i = 1}^{q} {y_{i}}_{x_{i}} = v

, where the addition is the coordinate-wise addition in group

Y

If we measure D using basis

F_{D} | ϕ_{v} 〉

for

v \in Y^{X}

and measure w normally, then the measurement outcome

(w, v)

has a probability

γ_{w, v} = {| γ_{w, v}^{'} |}^{2}

, where

γ_{w, v}^{'} = \sum_{(x, y, z) : (x, y) \in S_{v}} α_{x, y, z, w} .

Next, starting with

S_{v, i^{0}, j^{0}, k^{0}} : = S_{v}

, we iteratively define

S_{v, i^{t}, j^{t}, k^{t}}

as a subset of

S_{v, i^{t - 1}, j^{t - 1}, k^{t - 1}}

. For vector

(x^{'}, y^{'})

and x, we say that $\underset{̲}{x}$ is in the database after the tth query, we mean

F_{D} | ϕ_{{y_{1}^{'}}_{x_{1}^{'}} + \dots + {y_{t}^{'}}_{x_{t}^{'}}} 〉

is orthogonal to

{| ⊥ 〉}_{D_{u}}

at some coordinate

u \in \underset{̲}{x}

(i.e., at coordinate u, it is

| ϕ_{y} 〉_{D_{u}}

for some

y \neq 0

). We fix

x^{c}

with

v ({\underset{̲}{x}}_{t}) \neq 0, \forall t \in [c] .

Then,

S_{v, i^{t}, j^{t}, k^{t}}

is defined as follows.

Case $i_{t} = j_{t} = k_{t}$ : It contains all $(x^{'}, y^{'})$ in $S_{v, i^{t - 1}, j^{t - 1}, k^{t - 1}}$ so that

1. ${\underset{̲}{x}}_{t}$ is not in $F_{D} | ϕ_{{y_{1}^{'}}_{x_{1}^{'}} + \dots + {y_{i_{t} - 1}^{'}}_{x_{i_{t} - 1}^{'}}} 〉$ (i.e., every index $u \in {\underset{̲}{x}}_{t}$ has coordinate $| ⊥ 〉$ ).

2. ${\underset{̲}{x}}_{t} = {\underset{̲}{x}}_{i_{t}}^{'}$ and $y_{i_{t}}^{'} \neq 0 .$
Case $i_{t} < j_{t} < k_{t}$ : It contains all $(x^{'}, y^{'})$ in $S_{v, i^{t - 1}, j^{t - 1}, k^{t - 1}}$ so that

1. ${\underset{̲}{x}}_{t}$ is not in the database before the $i_{t}$ th query

2. ${\underset{̲}{x}}_{t}$ is in the database after the $i_{t}$ th query and befire $j_{t}$ th query

3. ${\underset{̲}{x}}_{t}$ is not in the database after the $j_{t}$ th query and befire $k_{t}$ th query

4. ${\underset{̲}{x}}_{t}$ is in the database after the $k_{t}$ th query.

Then, we define

\begin{matrix} γ_{i^{t}, j^{t}, k^{t}, w, v}^{'} = \sum_{(x, y, z) : (x, y) \in S_{v, i^{t}, j^{t}, k^{t}}} α_{x, y, z, w}, \end{matrix}

(A19)

where we remind

x^{c}

is fixed and implicit in

γ^{'}

and S variables. Then, we have the following claim.

Claim. For any

x^{c}, w, v

with

v ({\underset{̲}{x}}_{t}) \neq 0

(

t = 1, \dots, c

), it holds that

\begin{matrix} \sum_{i_{t} : i_{t} = j_{t} = k_{t}} γ_{i^{t}, j^{t}, k^{t}, w, v}^{'} - \sum_{i_{t} < j_{t} < k_{t}} γ_{i^{t}, j^{t}, k^{t}, w, v}^{'} = γ_{i^{t - 1}, j^{t - 1}, k^{t - 1}, w, v}^{'} \end{matrix}

(A20)

Proof. Given

(x, y) \in S_{v, i^{t - 1}, j^{t - 1}, k^{t - 1}}

and

z

, consider the first

i_{t}

queries in the process toward

α_{x, y, z, w} | w 〉 F_{D} {| ϕ_{v} 〉}_{D}

. Assume that

{\underset{̲}{x}}_{t}

is inserted ℓ times into the database (i.e., the change from not in the database to being in the database). Then,

ℓ \geq 1

; otherwise,

v (x_{t}) = 0

(contradiction). On the left side,

α_{x, y, z, w}

will appear in

\sum_{i_{t} : i_{t} = j_{t} = k_{t}} γ_{i^{t}, j^{t}, k^{t}, w, v}^{'}

for ℓ times (by the meaning of insertion: before it, it is not in while it is in after it) while appearing in

\sum_{i_{t} < j_{t} < k_{t}} γ_{i^{t}, j^{t}, k^{t}, w, v}^{'}

for

ℓ - 1

times (as each

(x, y)

α_{x, y, z, w}

in this sum requires at least two insertions). This can be seen from the specification of

S_{v, i^{t}, j^{t}, k^{t}}

. So

α_{x, y, z, w}

on the left side appears exactly once. By definition of

γ_{i^{t - 1}, j^{t - 1}, k^{t - 1}, w, v}^{'}

, it appears on the right side exactly once. Finally, for every

α_{x, y, z, w}

on the left or right side, it must have

(x, y) \in S_{v, i^{t - 1}, j^{t - 1}, k^{t - 1}}

, by definition of

γ_{i^{u}, j^{u}, k^{u}, w, v}^{'}

for

u = t, t - 1

. The foregoing argument applies again. The claim follows. ▪

Back to our lemma proof, Equation (A20) for

t = 1, \dots, c

can be combined into one equation with right side

γ_{w, v}^{'}

while the left side being a sum of

γ_{i^{c}, j^{c}, k^{c}, w, v}^{'}

over all

{(q + (\binom{q}{3}))}^{c}

possible

(i^{c}, j^{c}, k^{c})

. Notice that

γ_{i^{t}, j^{t}, k^{t}, w, v}^{'}

over

(t, i^{t}, j^{t}, k^{t})

has a dependency in a tree structure. Therefore,

\begin{matrix} γ_{w, v}^{'} = \sum_{(i^{c}, j^{c}, k^{c})} \pm γ_{i^{c}, j^{c}, k^{c}, w, v}^{'}, \end{matrix}

(A21)

where ± can only be one of + and − but is not important to be precise here. Either of the two sides of Equation (A21) is the coefficient of

| w 〉 F_{D} | ϕ_{v} 〉 .

Let the superposition before the final measurement be

| ψ 〉 = \sum_{w^{'}, v} γ_{w^{'}, v}^{'} | w^{'} 〉 F_{D} {| ϕ_{v} 〉}_{D}

. Let

v

v_{x_{i}^{'}}

x_{i}^{'}

for

i = 1, \dots, L

while it is 0 at any other index. Thus, by definition of Walsh-Hadamard transform,

| ψ 〉

can be expanded as

\begin{matrix} | ψ 〉 = \frac{1}{{| Y |}^{L / 2}} \sum_{w^{'}, v} \sum_{u_{x_{1}^{'}}, \dots, u_{x_{L}^{'}}} {(- 1)}^{u_{x_{1}^{'}} v_{x_{1}^{'}} + \dots + u_{x_{L}^{'}} v_{x_{L}^{'}}} γ_{w^{'}, v}^{'} | w^{'} {〉 | u 〉}_{D}, \end{matrix}

(A22)

where

u_{x_{j}^{'}}

for

j > L

is ⊥. Thus,

| w^{'} {〉 | u 〉}_{D}

| ψ 〉

has coefficient

\begin{matrix} γ_{w^{'}, u}^{''} \overset{d e f}{=} \frac{1}{{| Y |}^{L / 2}} \sum_{w^{'}, v : v_{x_{j}^{'}} \neq 0, j \in [L]} {(- 1)}^{u_{x_{1}^{'}} v_{x_{1}^{'}} + \dots + u_{x_{L}^{'}} v_{x_{L}^{'}}} γ_{w^{'}, v}^{'} . \end{matrix}

(A23)

Let

γ_{i^{t}, j^{t}, k^{t}, w^{'}, u}^{''}

be the coefficient of

| w^{'} {〉 | u 〉}_{D}

| ψ 〉

from

{Exp}_{i^{c}, j^{c}, k^{c}}

. Then,

\begin{matrix} γ_{i^{t}, j^{t}, k^{t}, w^{'}, u}^{''} = \frac{1}{{| Y |}^{L / 2}} \sum_{w^{'}, v : v_{x_{j}^{'}} \neq 0, j \in [L]} {(- 1)}^{u_{x_{1}^{'}} v_{x_{1}^{'}} + \dots + u_{x_{L}^{'}} v_{x_{L}^{'}}} γ_{i^{t}, j^{t}, k^{t}, w^{'}, v}^{'} . \end{matrix}

(A24)

From Equation (A21), we have

\begin{matrix} γ_{w, u}^{''} = \sum_{(i^{c}, j^{c}, k^{c})} \pm γ_{i^{c}, j^{c}, k^{c}, w, u}^{''} . \end{matrix}

(A25)

Hence, at least one

| γ_{i^{c}, j^{c}, k^{c}, w, u}^{''} | \geq | γ_{w, u}^{''} | / {(q + (\binom{q}{3}))}^{c} .

Since

λ_{i^{c}, j^{c}, k^{c}, {\underset{̲}{x}}^{c}, w, u} = {| γ_{i^{c}, j^{c}, k^{c}, w, u}^{''} |}^{2}

and

λ_{w, u} = {| γ_{w, u}^{''} |}^{2}

, the lemma follows. □

Proof of Theorem 4. We take the implicit

x^{c} = x_{w, y, 1}, \dots, x_{w, y, c} .

Let

λ_{{\underset{̲}{x}}^{c}, w, y}

λ_{i^{c}, j^{c}, k^{c}, {\underset{̲}{x}}^{c}, w, y}

for a random

(i^{c}, j^{c}, k^{c})

. There are

{(q + (\binom{q}{3}))}^{c}

possible

(i, j, k)

in the support of

U_{I J K}^{c}

. Then, by Lemma A5,

λ_{{\underset{̲}{x}}^{c}, w, y} \geq λ_{w, y} / {(q + (\binom{q}{3}))}^{3 c} .

Hence,

\begin{matrix} λ \geq \sum_{(w, y) \in S} λ_{{\underset{̲}{x}}^{c}, w, y} \geq \sum_{(w, y) \in S} \frac{γ_{w, y}}{{(q + (\binom{q}{3}))}^{3 c}} = \frac{γ}{{(q + (\binom{q}{3}))}^{3 c}}, \end{matrix}

(A26)

desired! □

References

Michel Abdalla, Pierre Alain Fouque, Vadim Lyubashevsky, Mehdi Tibouchi, Tightly-Secure Signatures from Lossy Identification Schemes. EUROCRYPT 2012, 572-590.
H. K. Alper and J. Burdges. Two-round trip schnorr multi-signatures via delinearized witnesses. In T. Malkin and C. Peikert, editors, CRYPTO 2021, Part I, volume 12825 of LNCS, pages 157-188, Virtual Event, Aug. 2021. Springer, Heidelberg.
Ali Bagherzandi, Jung Hee Cheon and Stanislaw Jarecki, Multisignatures secure under the discrete logarithm assumption and a generalized forking lemma. CCS 2008, pp. 449-458, 2008.
Mihir Bellare, Phillip Rogaway: Random Oracles are Practical: A Paradigm for Designing Efficient Protocols. CCS 1993: 62-73, 1993.
Mihir Bellare, Gregory Neven: Multi-signatures in the plain public-Key model and a general forking lemma. CCS 2006: 390-399.
Ian F. Blake, Shuhong Gao and Ronald C. Mullin, Explicit Factorization of x^2k+1 over F_p with Prime p≡3 mod 4. Appl. Algebra Eng. Commun. Comput. 4:89-94 (1993).
Alexandra Boldyreva, Threshold Signatures, Multisignatures and Blind Signatures Based on the Gap-Diffie-Hellman-Group Signature Scheme. Public Key Cryptography 2003: 31-46.
D. Boneh, C. Gentry, B. Lynn, and H. Shacham. Aggregate and verifiably encrypted signatures from bilinear maps. In E. Biham, editor, EUROCRYPT 2003, volume 2656 of LNCS, pages 416-432. Springer-Verlag, 2003.
Dan Boneh, Mark Zhandry, Secure Signatures and Chosen Ciphertext Security in a Quantum Computing World. CRYPTO (2) 2013: 361-379.
Cecilia Boschini, Akira Takahashi, and Mehdi Tibouchi. Musig-L: Lattice-based multi-signature with single-round online phase, CRYPTO’22.
Ran Canetti, Oded Goldreich, Shai Halevi: The Random Oracle Methodology, Revisited. STOC 1998: 209-218.
Kai-Min Chung, Serge Fehr, Yu-Hsuan Huang, Tai-Ning Liao: On the Compressed-Oracle Technique, and Post-Quantum Security of Proofs of Sequential Work. EUROCRYPT (2) 2021: 598-629.
Ronald Cramer, Léo Ducas, and Benjamin Wesolowski. Short stickelberger class relations and application to ideal-svp. Eurocrypt 2017.
Ivan Damgård, Claudio Orlandi, Akira Takahashi, and Mehdi Tibouchi. Two-round n-out-of-n and multisignatures and trapdoor commitment from lattices. PKC 2021, LNCS 12710, pages 99-130, 2021.
Jelle Don, Serge Fehr, Christian Majenz, Christian Schaffner: Online-Extractability in the Quantum Random-Oracle Model. EUROCRYPT’22.
Léo Ducas and Alain Durmus. Ring-lwe in polynomial rings. In PKC 2012, LNCS 7293, pages 34-51. Springer, 2012.
Rachid El Bansarkhani and Jan Sturm. An efficient lattice-based multisignature scheme with applications to bitcoins, CANS’16, pages 140-155.
Nils Fleischhacker, Mark Simkin, Zhenfei Zhang: Squirrel: Efficient Synchronized Multi-Signatures from Lattices. CCS 2022, papges 1109-1123, 2022.
Masayuki Fukumitsu and Shingo Hasegawa. A tightly-secure lattice-based multisignature. The 6th Asia Public-Key Cryptography Workshop 2019, page 3-11, 2019.
Masayuki Fukumitsu and Shingo Hasegawa. A lattice-based provably secure multisignature scheme in quantum random oracle model, ProvSec 2020.
Qianqian He, Xiangjun Xin and Qinglan Yang, Security analysis and improvement of a quantum multi-signature protocol, Quantum Information Processing, 20:26, 2021.
K. Itakura and K. Nakamura, A public-key cryptosystem suitable for digital multisignatures. NEC Research & Development, 71:1-8, 1983.
S. Jiang, D. Alhadidi and H. F. Khojir, Key-and-Signature Compact Multi-Signatures for Blockchain: A Compiler with Realizations, IEEE Transactions on Dependable and Secure Computing, accepted, 2024. [CrossRef]
S. Jiang, G. Gong, J. He, K. Nguyen and H. Wang, PAKEs: New Framework, New Techniques and More Efficient Lattice-Based Constructions in the Standard Model, The International Conference on Practice and Theory in Public-Key Cryptography (PKC’20), A. Kiayias, M. Kohlweiss, P. Wallden, V. Zikas (Eds.), LNCS 12110, IACR, pp. 396-427, 2020.
D. H. Jiang, Q. Z. Hu, X. Q. Liang, G. B. Xu, A novel quantum multi-signature protocol based on locally indistinguishable orthogonal product states. Quantum Inf. Process. 18(9), 268 (2019). [CrossRef]
Meenakshi Kansal, Amit Kumar Singh, Ratna Dutta, Efficient Multi-Signature Scheme Using Lattice. Comput. J. 65(9): 2421-2429 (2022).
Meenakshi Kansal and Ratna Dutta, Round Optimal Secure Multisignature Schemes from Lattice with Public Key Aggregation and Signature Compression. AFRICACRYPT 2020, pages 281-300, 2020.
Eike Kiltz, Vadim Lyubashevsky, and Christian Schaffner. A concrete treatment of Fiat-Shamir signatures in the quantum random-oracle model, J. B. Nielsen and V. Rijmen (Eds.), EUROCRYPT 2018, Springer, pages 552-586, 2018.
Serge Lang, Algebra, GTM 211, Springer-Verlag, 2002.
Qipeng Liu and Mark Zhandry, Revisiting Post-quantum Fiat-Shamir. CRYPTO (2) 2019: 326-355.
Zi-Yuan Liu, Yi-Fan Tseng, and Raylin Tso. Cryptanalysis of a round optimal lattice-based multisignature scheme. Cryptology ePrint Archive, Report 2020/1172, 2020.
Steve Lu, Rafail Ostrovsky, Amit Sahai, Hovav Shacham, Brent Waters: Sequential Aggregate Signatures and Multisignatures Without Random Oracles. EUROCRYPT 2006: 465-485.
Vadim Lyubashevsky and Daniele Micciancio, Generalized Compact Knapsacks Are Collision Resistant. ICALP 2006, part 2, pages 144-155, 2006.
Vadim Lyubashevsky, Chris Peikert, and Oded Regev. On ideal lattices and learning with errors over rings. J. ACM, 60(6):43:1-43:35, 2013.
Vadim Lyubashevsky, Chris Peikert, and Oded Regev. A toolkit for Ring-LWE cryptography. In EUROCRYPT 2013, volume 7881 of LNCS, pages 35–54. Springer, 2013.
Changshe Ma, Jian Weng, Yingjiu Li, Robert H. Deng: Efficient discrete logarithm based multi-signature scheme in the plain public key model. Des. Codes Cryptogr. 54(2): 121-133 (2010).
Changshe Ma, Mei Jiang, Practical Lattice-Based Multisignature Schemes for Blockchains. IEEE Access 7: 179765-179778 (2019).
Maxwell, G., Poelstra, A., Seurin, Y., Wuille, P.: Simple schnorr multi-signatures with applications to bitcoin. Cryptology ePrint Archive, Report 2018/068 (2018).
Silvio Micali, Kazuo Ohta, Leonid Reyzin: Accountable-subgroup multisignatures: extended abstract. CCS 2001: 245-254.
D. Micciancio and O. Regev. Worst-case to average-case reductions based on gaussian measures. SIAM J. Comput., 37(1): 267-302, 2007.
Satoshi Nakamoto. Bitcoin: A Peer-to-Peer Electronic Cash System, 2008. Available at http://bitcoin.org/bitcoin.pdf.
J. Nick, T. Ruffing, and Y. Seurin. MuSig2: Simple two-round Schnorr multi-signatures. CRYPTO 2021, Part I, LNCS 12825, pp. 189-221, Springer, 2021.
Michael A. Nielsen and Isaac L. Chuang, Quantum Computation and Quantum Information, Cambridge University Press, New York, 2010.
Chris Peikert, Alon Rosen, Efficient Collision-Resistant Hashing from Worst-Case Assumptions on Cyclic Lattices. TCC 2006, pages 145-166, 2006.
Peter W. Shor, Algorithms for Quantum Computation: Discrete Logarithms and Factoring. FOCS 1994, pp. 124-134.
Ewa Syta, Iulia Tamas, Dylan Visher, David Isaac Wolinsky, Philipp Jovanovic, Linus Gasser, Nicolas Gailly, Ismail Khoffi, and Bryan Ford. Keeping authorities “honest or bust” with decentralized witness cosigning. IEEE Symposium on Security and Privacy 2016, pp. 526-545. IEEE Computer Society Press, May 2016.
Dominique Unruh, Quantum Proofs of Knowledge. EUROCRYPT 2012: 135-152.
John Watrous, Quantum Computing, Lecture notes, 2006. Available at https://cs.uwaterloo.ca/ watrous/QC-notes/.
Mark Zhandry, How to Record Quantum Queries, and Applications to Quantum Indifferentiability, CRYPTO 2019, part II, pages 239-268.

1	Let $rep (\underset{̲}{x}) \in X$ be the representative of $\underset{̲}{x}$ and assume that it can be efficiently computed from any $u \in \underset{̲}{x}$ . Let $U_{C}$ be a unitary with ${\| x 〉}_{X} {\| 0 〉}_{C} \mapsto \| x 〉 \| rep (\underset{̲}{x}) 〉$ ; measuring register C in the computational basis gives $rep (\underset{̲}{x})$ .
2	$D ({\underset{̲}{x}}^{}) = \vec{⊥}$ can be tested by a projective measurement $Π_{⊥} = (Π_{⊥}^{0}, I - Π_{⊥}^{0})$ with $Π_{⊥}^{0} = \sum_{y : y ({\underset{̲}{x}}^{}) = \vec{⊥}} \| y 〉 〈 y \|$ , which can be implemented by writing bit $y ({\underset{̲}{x}}^{*}) = = \vec{⊥}$ onto a new register and measuring it.
3	If $D (x^{'}) = ⊥$ before the oracle query, then it remains $D (x^{'}) = ⊥$ after the oracle query (i.e., after applying $C S t O$ ) if and only if Y register is currently $\| ϕ_{0} 〉$ . Thus, to test if $D (x^{'}) = ⊥$ after the oracle query, we can simply apply the unitary $\| ϕ_{y} 〉_{Y} {\| 0 〉}_{Q} \mapsto \| ϕ_{y} 〉_{Y} {\| y 〉}_{Q}$ and measure if Q register has 0. That is, we can make the test without applying the $C S t O$ operation.
4	Recall that in $G_{5}$ - $G_{9}$ , PointReg1 query for $x \in {\underset{̲}{x}}_{1}^{*}$ occurs when $D$ issues the $k_{1}$ th random oracle query, where the test measurement $Π$ has outcome ${\| ⊥ 〉}_{D_{x}}$ (since it does not abort) and hence $D (x) = ⊥$ .
5	Let $ρ_{0} = \sum_{i}^{n} M_{i}^{†} \| ψ 〉 〈 ψ \| M_{i}$ . Let $\| a_{i} 〉 = P M_{i} P \| ψ 〉, \| b_{i} 〉 = P M_{i} Q^{'} \| ψ 〉, \| c_{i} 〉 = P M_{i} R^{'} \| ψ 〉$ . Then, Equation (A13) becomes $\sqrt{\sum_{i = 1}^{n} \| \| \| a_{i} 〉 + \| b_{i} 〉 + \| c_{i} {〉 \| \|}^{2}} \leq \sqrt{\sum_{i = 1}^{n} \| \| \| a_{i} {〉 \| \|}^{2}} + \sqrt{\sum_{i = 1}^{n} \| \| \| b_{i} {〉 \| \|}^{2}} + \sqrt{\sum_{i = 1}^{n} \| \| \| c_{i} {〉 \| \|}^{2}}$ . Further, define $a$ as the long vector $(\| a_{1} 〉, \dots, \| a_{n} 〉)$ and $b$ , $c$ similarly. Then, Equation (A13) becomes $\| \| a + b + c \| \| \leq \| \| a \| \| + \| \| b \| \| + \| \| c \| \|$ , which is evident.

Figure 1. Canonical Identification Protocol.

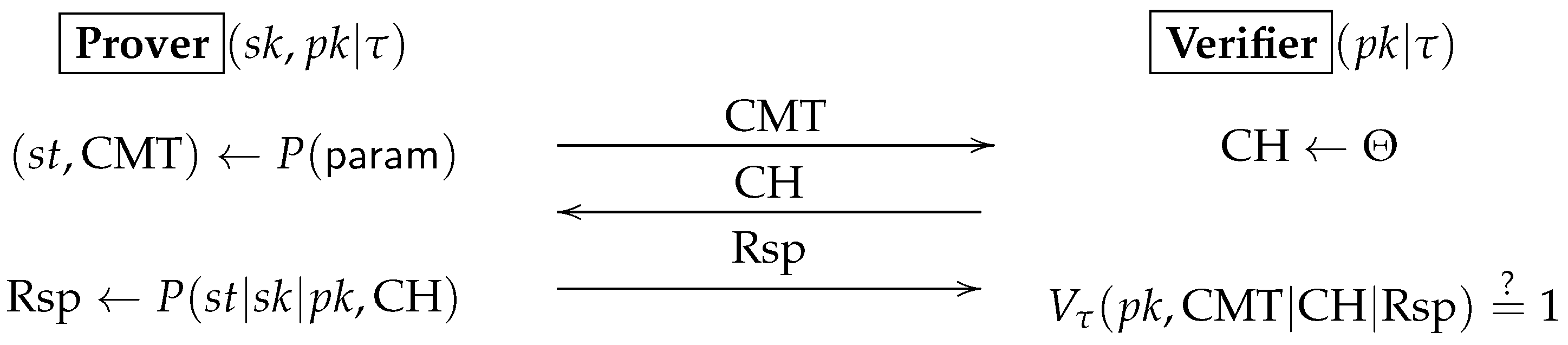
Figure 2. Simulator

S

Figure 2. Simulator

S

Figure 3. The JAK ID Scheme

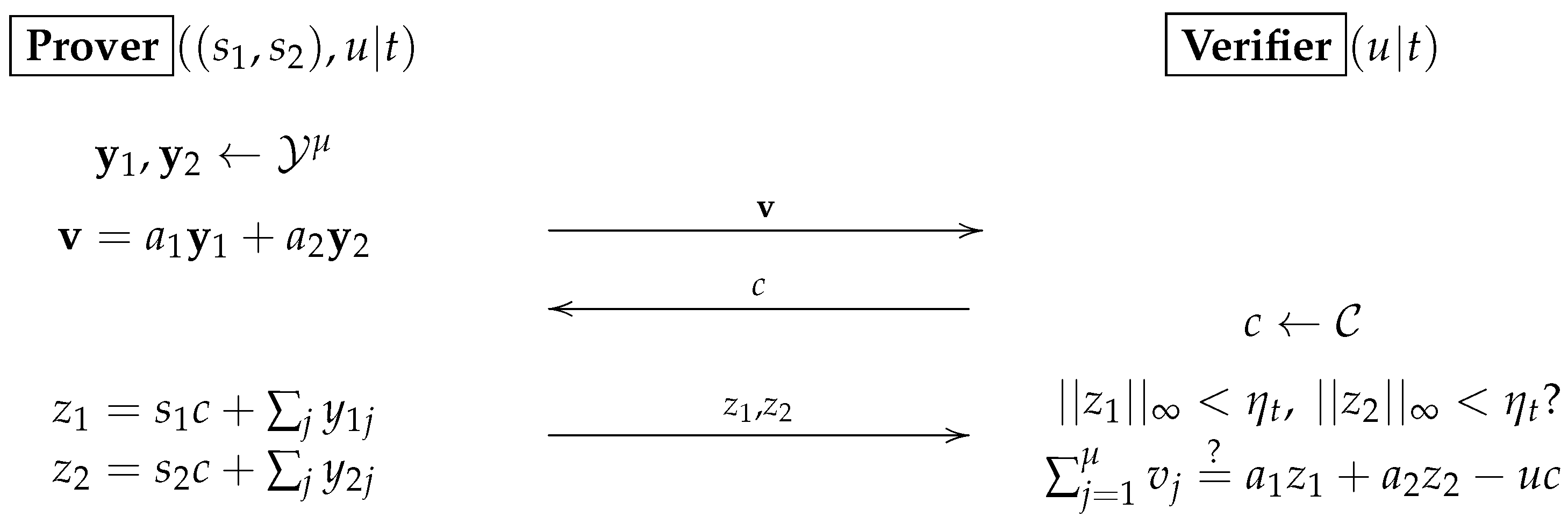
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

1	Let $rep (\underset{̲}{x}) \in X$ be the representative of $\underset{̲}{x}$ and assume that it can be efficiently computed from any $u \in \underset{̲}{x}$ . Let $U_{C}$ be a unitary with ${\| x 〉}_{X} {\| 0 〉}_{C} \mapsto \| x 〉 \| rep (\underset{̲}{x}) 〉$ ; measuring register C in the computational basis gives $rep (\underset{̲}{x})$ .
2	$D ({\underset{̲}{x}}^{}) = \vec{⊥}$ can be tested by a projective measurement $Π_{⊥} = (Π_{⊥}^{0}, I - Π_{⊥}^{0})$ with $Π_{⊥}^{0} = \sum_{y : y ({\underset{̲}{x}}^{}) = \vec{⊥}} \| y 〉 〈 y \|$ , which can be implemented by writing bit $y ({\underset{̲}{x}}^{*}) = = \vec{⊥}$ onto a new register and measuring it.
3	If $D (x^{'}) = ⊥$ before the oracle query, then it remains $D (x^{'}) = ⊥$ after the oracle query (i.e., after applying $C S t O$ ) if and only if Y register is currently $\| ϕ_{0} 〉$ . Thus, to test if $D (x^{'}) = ⊥$ after the oracle query, we can simply apply the unitary $\| ϕ_{y} 〉_{Y} {\| 0 〉}_{Q} \mapsto \| ϕ_{y} 〉_{Y} {\| y 〉}_{Q}$ and measure if Q register has 0. That is, we can make the test without applying the $C S t O$ operation.
4	Recall that in $G_{5}$ - $G_{9}$ , PointReg1 query for $x \in {\underset{̲}{x}}_{1}^{*}$ occurs when $D$ issues the $k_{1}$ th random oracle query, where the test measurement $Π$ has outcome ${\| ⊥ 〉}_{D_{x}}$ (since it does not abort) and hence $D (x) = ⊥$ .
5	Let $ρ_{0} = \sum_{i}^{n} M_{i}^{†} \| ψ 〉 〈 ψ \| M_{i}$ . Let $\| a_{i} 〉 = P M_{i} P \| ψ 〉, \| b_{i} 〉 = P M_{i} Q^{'} \| ψ 〉, \| c_{i} 〉 = P M_{i} R^{'} \| ψ 〉$ . Then, Equation (A13) becomes $\sqrt{\sum_{i = 1}^{n} \| \| \| a_{i} 〉 + \| b_{i} 〉 + \| c_{i} {〉 \| \|}^{2}} \leq \sqrt{\sum_{i = 1}^{n} \| \| \| a_{i} {〉 \| \|}^{2}} + \sqrt{\sum_{i = 1}^{n} \| \| \| b_{i} {〉 \| \|}^{2}} + \sqrt{\sum_{i = 1}^{n} \| \| \| c_{i} {〉 \| \|}^{2}}$ . Further, define $a$ as the long vector $(\| a_{1} 〉, \dots, \| a_{n} 〉)$ and $b$ , $c$ similarly. Then, Equation (A13) becomes $\| \| a + b + c \| \| \leq \| \| a \| \| + \| \| b \| \| + \| \| c \| \|$ , which is evident.

Quantum Security of A Compact Multi-Signature

Abstract

1. Introduction

1.1. Related Works

1.2. Contribution

2. Preliminaries

2.1. Ring and Module

2.2. Elements in Quantum Computing

2.3. Multi-Signature

2.3.1. Security Model

2.4. Canonical Linear Identification

3. Basic Properties in Quantum Computing

4. Quantum Random Oracle

4.1. Standard Random Oracle

4.2. Compressed Random Oracle

4.3. Compressed Random Oracle with Adaptive Special Points

4.4. Measurement U R

4.5. Bounding the Probability for Relation Search through Oracle Queries

4.6. Simulating CStO s with Extraction

4.6.1. Extraction at the End of Game

4.6.2. Extraction on the Fly

4.7. Efficient Encoding of CStO and CStO s

5. Extracting Queries to CStO that Witness the Future Adversarial Output

6. Quantum Security of the JAK Multi-Signature Framework

6.1. Review of JAK Mutli-Signature Framework

6.2. Security Theorem

7. Quantum Security of The JAK ID Scheme

7.1. Ring-LWE and Ring-SIS

7.2. The JAK ID Scheme

8. Conclusions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

Appendix A. Proof of Theorem 6

Appendix A.1. Collapsing Public-Coin Protocol

Appendix A.2. Two Public-Coin Protocols from Our ID Scheme

Appendix A.2.1. Protocol Σ 1 .

Appendix A.2.2. Protocol Σ 2 .

Appendix A.3. Security of the JAK ID Scheme when Σ 1 and Σ 2 are Weakly Collapsing

Appendix A.4. Σ 2 and Σ 1 are Weakly Collapsing

Appendix B. Encoding of CStO or CStO s and Efficient Operations on Oracle State

Appendix C. Proof of Lemma 14

Appendix D. Proof of Theorem 4

References

MDPI Initiatives

Important Links

Subscribe

4.4. Measurement $U_{R}$

4.6. Simulating ${CStO}_{s}$ with Extraction

4.7. Efficient Encoding of $CStO$ and ${CStO}_{s}$

5. Extracting Queries to $CStO$ that Witness the Future Adversarial Output