Achieving Robust Learning Outcomes in Autonomous Driving with DynamicNoise Integration in Deep Reinforcement Learning

Preprint

Article

Achieving Robust Learning Outcomes in Autonomous Driving with DynamicNoise Integration in Deep Reinforcement Learning

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Haotian Shi,Jiale Chen,Feijun Zhang,

Mingyang Liu^*,

Mengjie Zhou

Haotian Shi,Jiale Chen,Feijun Zhang,

Mingyang Liu^*,

Mengjie Zhou

This version is not peer-reviewed

Submitted:

29 August 2024

Posted:

30 August 2024

You are already at the latest version

Alerts

Abstract

The advancement of autonomous driving technology is becoming increasingly vital in the modern technological landscape, promising notable enhancements in safety, efficiency, traffic management, and energy use. Despite these benefits, conventional deep reinforcement learning algorithms often struggle to navigate complex driving environments effectively. To tackle this challenge, we propose a novel network called DynamicNoise, designed to significantly boost algorithmic performance by introducing noise into the Deep Q-Network (DQN) and Double Deep Q-Network (DDQN). Drawing inspiration from the NoiseNet architecture, DynamicNoise uses stochastic perturbations to improve the exploration capabilities of these models, leading to more robust learning outcomes. Our experiments demonstrate a 57.25% improvement in navigation effectiveness within a 2D experimental setting. Moreover, by integrating noise into the action selection and fully connected layers of the Soft Actor-Critic (SAC) model in the more complex 3D CARLA simulation environment, our approach achieved an 18.9% performance gain, substantially surpassing traditional methods. These results confirm that the DynamicNoise network significantly enhances the performance of autonomous driving systems across various simulated environments, regardless of their dimensionality and complexity, by improving their exploration capabilities rather than just their efficiency.

Keywords:

Subject: Engineering - Control and Systems Engineering

1. Introduction

The emergence of autonomous driving technology marks a pivotal shift in the transportation sector, with profound implications for road safety [1], efficiency [2], and accessibility [3]. Utilizing advanced sensors, machine learning, and artificial intelligence, autonomous vehicles have been designed to minimize human error—the primary cause of road accidents. This reduction is expected to substantially decrease the incidence of collisions, injuries, and fatalities. Beyond enhancing safety, autonomous driving technology promises to transform access for populations with limited mobility, such as the elderly and disabled, thus providing increased independence. Additionally, these vehicles are engineered to optimize routing and traffic management [4], which could [5] alleviate congestion and lower environmental impacts through the promotion of more efficient fuel usage and accelerating the adoption of electric vehicles. The potential applications of autonomous driving are extensive, encompassing personal and public transport, logistics, and delivery services, transforming urban environments and fundamentally altering our interaction with travel.

To advance the development of vehicles that can navigate and operate autonomously without human intervention, traditional control methodologies such as [6,7] Proportional–Integral–Derivative (PID) controllers and Model Predictive Control (MPC) [8] provide distinct approaches to automation. PID controllers are lauded for their simplicity, which minimizes the discrepancy between the desired trajectory and the actual position of the vehicle. This method is easy to implement and performs effectively under stable conditions, making it ideal for straightforward applications such as cruise control. However, its reactive nature is less effective in dynamic, complex environments, where the ability to anticipate future conditions is crucial. In contrast, MPC is distinguished by its capacity to incorporate future states and constraints, thus optimizing control inputs across a predictive horizon. This forward-thinking approach enables MPC to proficiently manage intricate driving situations, such as obstacle avoidance and adaptive cruise control. Despite its benefits, the computational intensity of MPC presents challenges for real-time implementation, underscoring a significant trade-off between predictive accuracy and computational efficiency.

In traditional reinforcement learning tasks [9], the deep Q-Network (DQN) has gained widespread application [14] due to its benefits in end-to-end learning, stability, and efficiency, making it valuable for addressing problems in environments with discrete action spaces [15]. However, DQN only applies to discrete action spaces; other schemes are needed for continuous action spaces. The Soft Actor–Critic (SAC) algorithm [16] is characterized by its high sampling efficiency, and better stability and convergence can be achieved through both value and policy functions. In addition, SAC is particularly effective for tasks with a continuous action space, making it suitable for applications such as autonomous driving. However, these methods face common challenges, including slow convergence rates, insufficient exploration, issues with time delays, and sub-optimal reward outcomes.

To address these issues, we propose a network framework named DynamicNoise, which introduces an innovative approach to enhance network performance. One of the critical challenges in reinforcement learning is balancing exploration and exploitation effectively. Traditional methods such as the

ε

-greedy algorithm often fall short in facilitating sufficient exploration, leading to sub-optimal policies. Our DynamicNoise network employs a straightforward strategy to balance exploration and exploitation [17] through the incorporation of noise into the network architecture. This modification, achieved with a singular adjustment of the weight vector, induces a consistent yet complex alteration in the policy, which is dependent on the state over multiple time steps, contrasting sharply with jittering strategies that insert uncorrelated noise, such as the

ε

-greedy strategy, at each decision point.

The main contributions of our work are as follows:

1. Enhanced Exploration in 2D Environments: We employ Markov models for environmental inputs (e.g., vehicle speed, location, and destination) and action decisions (including acceleration and turning) in DQN and DDQN networks, respectively, in a 2D setting. Subsequently, we introduce random-valued noise to optimize the vehicle turning process, significantly improving exploration and policy robustness.

2. Application in Realistic 3D Scenarios: To validate the applicability of our framework in more realistic scenarios, as well as with different network architectures, we introduce noise into the action selection and fully-connected layers of the SAC model in a 3D environment to optimize the process of actual0 vehicle driving. This approach enhances the exploration capabilities of the SAC model, leading to better performance in complex driving environments.

3. Comprehensive Validation and Future Implications: We first validate the feasibility of the algorithm in a two-dimensional scenario and then demonstrate the superiority of the algorithm in a more realistic three-dimensional scenario. The results indicate that our DynamicNoise framework can more effectively accomplish the autonomous driving navigation task. The application of the DynamicNoise framework could be extended to similar operating environments, suggesting broad implications for future research and applications of autonomous systems.

The remainder of this paper is organized as follows: Section 2 reviews the related literature. Section 3 describes the methodology. Section 4 presents the experimental setup. Section 5 discusses the results. Finally, Section 6 concludes the paper and suggests future research directions.

2. Related Work

While autonomous driving has many challenges regarding its complexity and dynamics, riding on the development of machine learning techniques, reinforcement learning has led to breakthroughs in the field.

Alizadeh et al. [18] established a decision-making and planning model based on the DQN algorithm, which had better performance than the traditional method in a noisy environment with different noise levels. Unfortunately, DQN networks are not without their challenges: one major drawback of such an approach is the slow convergence rate, which may not allow for real-time adaptation in dynamic driving scenes. Furthermore, poor exploration may result from poor policy learning when using a DQN.

Some of the limitations of DQNs have been addressed by creating the DDQN algorithm. Double Q-learning, proposed by Hasselt et al. [19], mitigates the overestimation bias in Q-learning and acts as the genesis point for the development of DDQN, which has been commonly used in the context of autonomous driving. Liao et al. [20] used DDQN to address high-level decision-making problems with large state spaces and obtained good safety results and performance. DDQN can still lead to high-time decision delays under binary action spaces, offering sub-optimal reward outcomes.

Seong et al. [21] employed the SAC method to propose a spatio-temporal attention mechanism to assist in the decision-making method for managing autonomous driving at intersections. SAC algorithms, which are highly sample-efficient and stable, perform well in complex driving scenarios. Nevertheless, similar to DQN and DDQN, SAC also needs to improve its convergence and exploration problems, which can become ineffective, especially when considering a quickly changing environment.

Lillicrap et al. [22] proposed continuous control with deep reinforcement learning, which has been instrumental in developing algorithms such as DDPG for more granular control in autonomous driving tasks. Schulman et al. [23] developed Proximal Policy Optimization (PPO), another popular RL algorithm used for continuous control tasks in autonomous driving.

Chen et al. [24] developed a safe reinforcement learning approach that integrates human driver behavior, utilizing regret theory to determine whether to change lanes or maintain the current lane. This composite model allows agents to learn safe and stable driving strategies, mimicking human decision-making processes. Although this method still needs to improve its inefficiencies, it laid the groundwork for improved approaches by enhancing the safety and stability of autonomous driving strategies by incorporating human decision-making models.

Building on this, He et al. [25] adopted a constrained observation-robust Markov decision process to simulate lane-changing behaviour in autonomous vehicles. Employing Bayesian optimization for black-box attacks, they effectively approximated optimal adversarial observation perturbations. Their algorithm demonstrated excellent generality and robustness in the face of observational perturbations, further enhancing the stability of autonomous driving systems in complex and uncertain environments. However, they did not verify continuous action spaces and, thus, could not address longitudinal decision-making problems in autonomous vehicles.

To further mitigate driving risks, Li et al. [26] proposed a new method based on risk assessment, using a probabilistic model to evaluate the risk and apply it to reinforcement learning driving strategies. This approach aimed to minimize driving risks during lane-changing maneuvers, ensuring safer decision-making processes. This research builds on previous work by focusing on risk management and safety enhancement. However, such methods still need to consider integrating different decision-making layers with various approaches, increasing the complexity of decision-making tasks.

Peng et al. [27] decoupled speed and lane-changing decisions, training them separately using different reinforcement learning methods to address the complexity of decision-making in driving tasks. This separation helped to overcome the training difficulties caused by the coupling of these tasks, leading to more efficient learning and strategy optimization. However, this method does not allow for the simultaneous inclusion of lane-change trajectories during the research process. Additionally, the model performs poorly in situations characterized by high speeds and small distances between vehicles.

Hoel et al. [28] combined Bayesian reinforcement learning with a Random Prior Function (RPF) to estimate the confidence of actions, yielding more reliable action outputs at intersections under high uncertainty and reducing the likelihood of collisions. This study enhanced the reliability of decision-making under uncertain environments through confidence evaluation. However, how to set the parameter values systematically was not specified, nor could these parameter values be automatically updated during the training process.

Finally, Zhang et al. [29] incorporated traffic rules into a reinforcement learning algorithm, integrating the priority of surrounding vehicles into the state space. Combining this with Responsibility-Sensitive Safety (RSS) detection, they were able to control the longitudinal speed more effectively, assisting vehicles in ensuring their safe driving in various traffic scenarios. This study further enhanced the practicality and safety of autonomous driving systems by combining rules and safety detection.

Despite these successes, balancing exploration and exploitation remains a challenge [30]. Studies have explored value penalty factors and policy normalization to align the learned policies with expert behaviors. Lillicrap et al. [31] explored techniques for training exploration strategies using correlated noise, but these techniques may face difficulties under more variable conditions. Plappert et al. [32] introduced a technique involving constant Gaussian noise in the network. Unlike these works, the method proposed in this study allows for dynamic adjustment of noise applications over time, not limited to the Gaussian mode, thereby enhancing its adaptability and effectiveness in different driving environments.

Adding noise introduces new exploration opportunities, and while it can effectively handle uncertainties within the training environment, it may struggle to address novel, unseen uncertainties in real-world scenarios. To overcome this issue, Hunmin et al. [33] proposed an active, robust adaptive control architecture for autonomous vehicles across various environments. This architecture estimates unknown cornering stiffness using weather forecasts and vehicle network data, effectively balancing performance and robustness. Currently, systems increasingly rely on machine learning. Although many scholars have proposed effective techniques to demonstrate the robustness of predictions against adversarial input perturbations, these techniques have often diverged from the downstream control systems that use these predictions. Jinghan et al. [34] address this by providing robust certification of control against adversarial input perturbations through robust control of the original input disturbances. This enhances certification security, ensuring reliable operation under a broader range of unpredictable conditions.

3. Methods

3.1. Markov Decision Process Modeling

The usefulness of the MDP has led to its continuous use in reinforcement learning. The MDP is characterized by the tuple (S, R, A,

γ

, T), where S denotes the state space, R the reward function, A the action space,

γ

the discount factor, and T the transition model, which describes the probability of transitioning from one state to another.

3.1.1. State Space

State space in DQN Variants

The most critical aspect of successful autonomous driving is determining the state of the vehicle itself and its surrounding environment. Relying on a single state makes it difficult for each vehicle to make optimal decisions. Therefore, we introduce a multi-dimensional state. In our model, the state configuration includes the observation information of the autonomous vehicles. Specifically, the observation type is "Kinematics," and the number of observed vehicles is 15. We selected a series of features to describe the state of each vehicle, including the presence of the vehicle, x-coordinate (measured in meters, m), y-coordinate (measured in meters, m), velocity in the x-direction (measured in meters per second, m/s,

v_{x}

), velocity in the y-direction (measured in meters per second, m/s,

v_{y}

), and the cosine (

c o s_{h}

) and sine (

s i n_{h}

) of the heading angle.

The value ranges for these features are as follows: the x-coordinate ranges from -100 to 100 meters, the y-coordinate ranges from -100 to 100 meters, the velocity in the x-direction ranges from -20 to 20 meters per second, and the velocity in the y-direction ranges from -20 to 20 meters per second.

Additionally, we use absolute coordinates to describe these features without flattening the observation matrix or considering the intentions of other vehicles. The number of controlled vehicles is set to 1, the initial vehicle count is 10, and the probability of spawning a new vehicle is 0.6. This multi-dimensional state representation helps the model to make more accurate and effective decisions in various traffic scenarios.

State space in SAC

An RGB image is created by stitching together outputs from three 60-degree cameras mounted on the car roof, resulting in a 180° wide-angle view. This stitched RGB image has a size of 3 × 84 × 252. For training purposes, three consecutive images were stacked to capture temporal information, making the final input to the model a tensor with a shape of 9 × 84 × 252. This configuration allows the model to utilize both spatial and temporal features for more robust learning.

3.1.2. Action Space

Actions in DQN Variants

In our model, the action configuration defines the operations that autonomous vehicles can undertake. We set the action type to DiscreteMetaAction, meaning the vehicles can select from predefined discrete actions. The action space includes the following three operations:

Decelerate (target velocity: 0 units);
Maintain Speed (target velocity: 4.5 units);
Accelerate (target velocity: 9 units).

These actions primarily control the vehicle’s longitudinal movement, allowing it to adjust its speed in response to different driving scenarios. While the action space does not explicitly include lateral actions such as turning, the vehicle’s ability to navigate intersections and perform turns is achieved through the manipulation of its velocity components (

v_{x}

and

v_{y}

) and heading direction (represented by

c o s_{h}

and

s i n_{h}

). This approach enables the vehicle to change direction smoothly by adjusting the direction of its velocity vector within the physical simulation of the environment.

By focusing on these essential longitudinal actions with specific target velocities, the model ensures operational stability and responsiveness while maintaining the flexibility to perform complex manoeuvres, such as turning at intersections, through the underlying kinematic adjustments. This design reduces unnecessary complexity and allows the model to effectively control the movement of the vehicle in diverse and dynamic driving environments.

Actions in SAC

The action space is composed of two amplitude control dimensions: steering amplitude control and brake (acceleration) amplitude control. The steering amplitude control is normalized to the continuous interval [0,1], and in practice, it operates within a continuous range of continuous_steer_range [-0.3, 0.3] radians (approximately -17.19 to 17.19 degrees). This allows the vehicle to adjust its direction within this range.

The brake amplitude control, also normalized to the [0,1] interval, corresponds to the vehicle’s acceleration control, defined by the continuous_accel_range of [-3.0, 3.0] m/s². Positive values of this control result in acceleration, while negative values manage braking or deceleration.

3.1.3. Reward Function

Reward in DQN Variants

In our task, vehicles traveling at high speeds, staying in their designated lanes, avoiding collisions, and successfully reaching the destination will be rewarded. The reward function is defined according to Formula 1:

R = (W_{c o l l i s i o n} \times R_{c o l l i s i o n} + W_{s p e e d} \times R_{s p e e d} + W_{a r r i v e d} \times R_{a r r i v e d}) \times R_{l a n e},

(1)

where R is the total reward,

R_{c o l l i s i o n}

is the collision reward,

R_{s p e e d}

is the speed reward, and

R_{l a n e}

is the lane reward.

R_{c o l l i s i o n}

R_{s p e e d}

, and

R_{l a n e}

are computed according to Formulas 2, , and 4, respectively:

R_{c o l l i s i o n} = \{\begin{matrix} - 5, if the car crashed, \\ 0, otherwise, \end{matrix}

(2)

R_{speed} = \{\begin{matrix} 1, & if Speed > 9, \\ \frac{Speed - 7}{2}, & if 7 < Speed \leq 9, \\ 0, & otherwise . \end{matrix}

(3)

R_{l a n e} = \{\begin{matrix} 1, if the car is on road, \\ 0, if the car is not on road . \end{matrix}

(4)

If arrived_reward is True, then we get Formulas 5 and 6.

R = R_{a r r i v e d},

(5)

R_{a r r i v e d} = \{\begin{matrix} 1, if the car arrives, \\ 0, if the car does not arrive . \end{matrix}

(6)

In the above formulas,

W_{c o l l i s i o n}

W_{s p e e d}

, and

W_{l a n e}

are hyperparameters used to determine the importance of speed, lane adherence, and safety. Each vehicle is represented as a rectangle (5 meters long and 2 meters wide) in this environment. A collision occurs if there is an overlap between the rectangle corresponding to the autonomous vehicle and those corresponding to other vehicles.

Reward in SAC

The reward is described by Formula 7.

r_{t} (s, a) = v^{T} \hat{u} * Δ t - C_{i} * I - C_{s} * ∣ steer ∣,

(7)

where

v^{T} \hat{u}

represents the actual speed of the vehicle projected onto the road’s effective speed. This term encourages the vehicle to maintain an optimal speed along the direction of the road, maximizing the effective distance travelled during the time step

Δ t

I is the impact force (N/s) obtained through sensors, representing the external forces acting on the vehicle. A higher impact force results in a greater penalty, discouraging aggressive or unsafe driving behaviours. The coefficient

C_{i}

determines the severity of this penalty.

∣ steer ∣

is the magnitude of the steering control, reflecting the extent of steering input. Excessive steering, which could lead to instability, is penalized more heavily. The penalty is scaled by the coefficient

C_{s}

, which adjusts the impact of steering control on the overall reward.

This reward function is designed to balance the trade-offs between maintaining efficient speed, minimizing impact forces, and avoiding erratic steering, thereby promoting stable and safe driving behaviours.

3.1.4. Discount Factor: $γ$

In the context of autonomous vehicles, particularly when considering models focused on turning and obstacle avoidance, the discount factor (

γ

) is instrumental in shaping the learning process. This factor is crucial for balancing immediate and long-term goals, thereby enhancing the efficiency and stability of learning outcomes. An appropriately calibrated discount factor not only prompts the vehicle to execute safe and effective maneuvers in critical situations but also enhances the overall efficiency and comfort of the journey. Doing so ensures that the developed driving strategies are optimal regarding safety and practical usability. Therefore, carefully selecting the discount factor is vital for achieving efficient and secure autonomous driving operations.

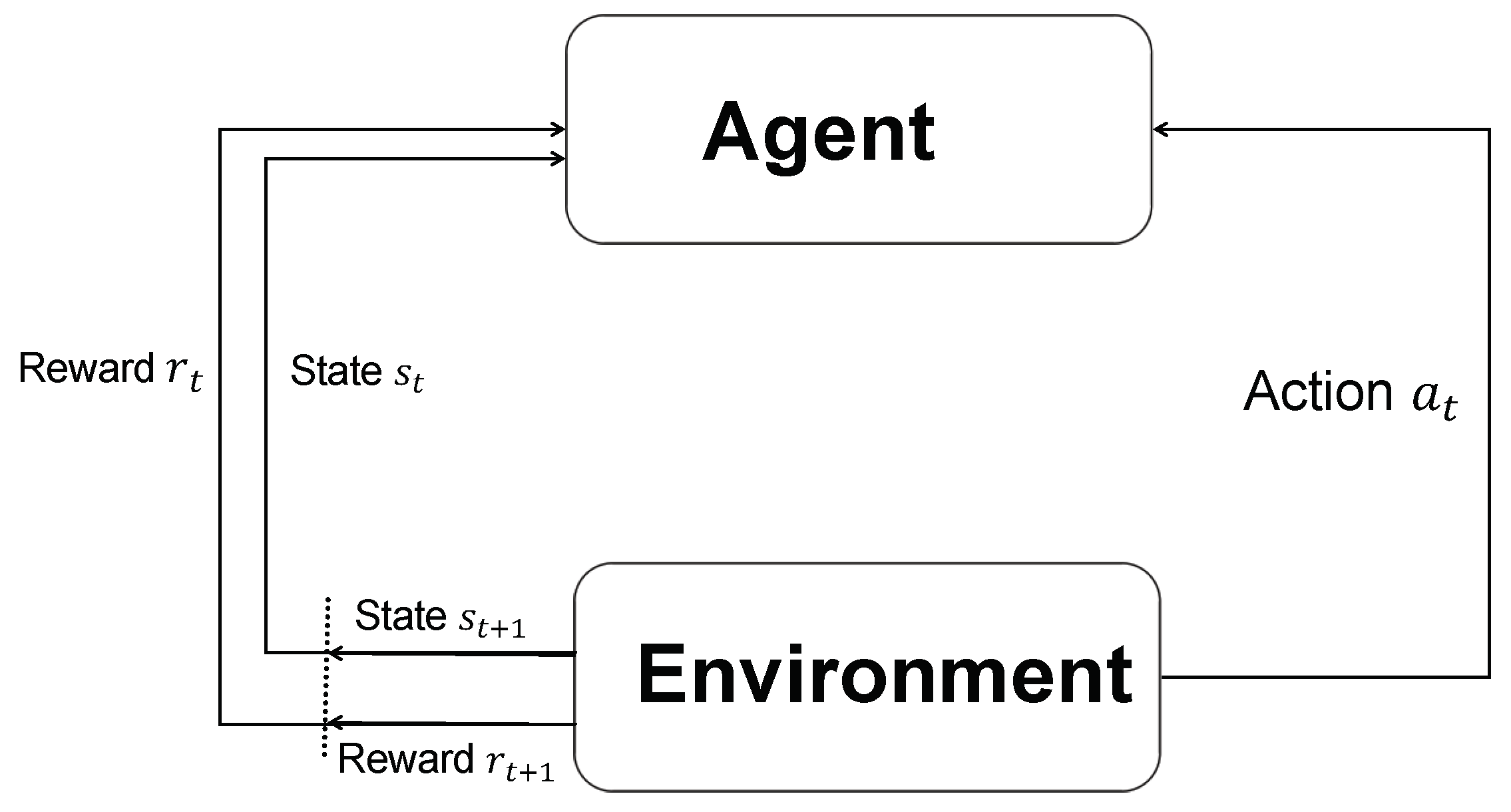
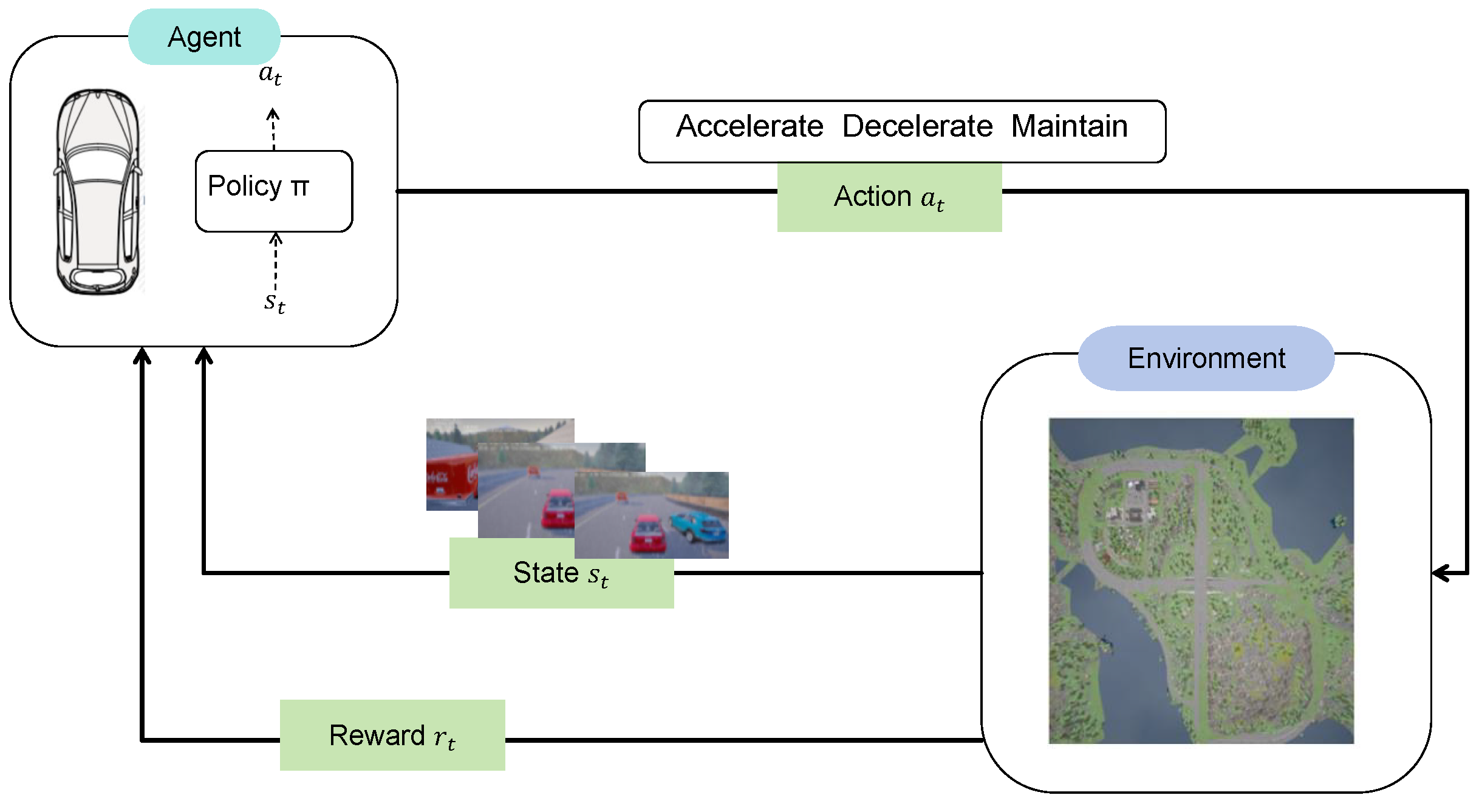
In the MDP, the action space

A_{t}

and reward function

R_{t}

are incorporated into the foundational structure of a Markov process. We can conceptualize

A_{t}

as the input of the system and

R_{t}

as its output. In this framework, as shown in Figure 1, the state transitions within the MDP are influenced externally rather than solely by internal processes; that is, they are determined by the current state

S_{t}

and the input

A_{t}

. Consequently, the subsequent state

S_{t + 1}

is dictated by the transition probability model

P (S_{t + 1} | S_{t})

and, similarly,

R_{t}

is defined by the probability distribution

P (R_{t} | S_{t}, A_{t})

; which, for simplicity, can be denoted as

R_{t} (S_{t}, A_{t})

In the realm of RL, the environment responds by assigning a reward according to the action of the agent and the current state. The RL model aims to discover the optimal policy by maximizing this reward. For example, the policy for navigating intersections, as shown in Figure 2, represents a specific type of MDP where the autonomous vehicle (AV) acts as an intelligent agent. This agent enhances performance through dynamic interactions with other vehicles, continuously learning and adapting. The delineation of a policy within the context of this MDP involves precise definitions of these interactions and the resultant learning mechanisms.

3.2. The Proposed Framework

3.2.1. Overview

The DynamicNoise framework represents a comprehensive approach to enhancing deep reinforcement learning capabilities to cope with complex dynamic environments. At the core of the framework is the integration of high-level variants of standard DQN models and SAC models to better address the challenges faced by autonomous systems, with a particular focus on increasing exploration and improving the accuracy of decision-making.

The proposed DynamicNoise framework consists of two modules: NoisyNet based on the DQN model and NoisyNet based on the SAC model, where NoisyNet based on the DQN model consists of the DQN and the DDQN. Each of these components is designed to take advantage of the intrinsic strengths of the basic model while, at the same time, introducing a noise mechanism that enhances the exploration through the injection of noise.

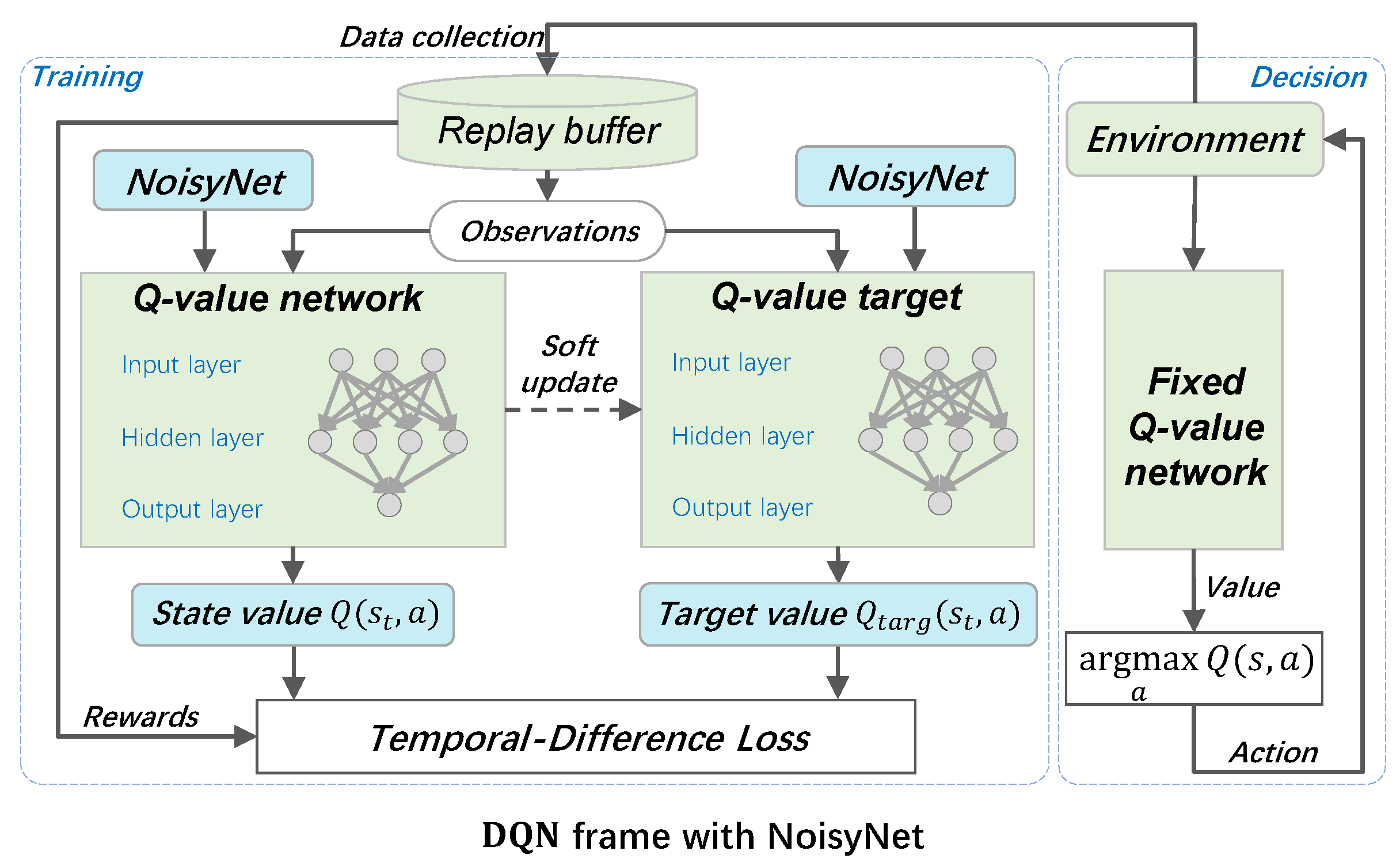
1. DQN Model: This component modifies the traditional DQN by adding NoisyNet and introducing parameter noise into the network weights. The flowchart of the network is represented in Figure 3. This noise enriches the policy exploration, allowing the network to explore a more diverse set of actions without explicitly exploring specific hyperparameters, similar to

ε

in the

ε

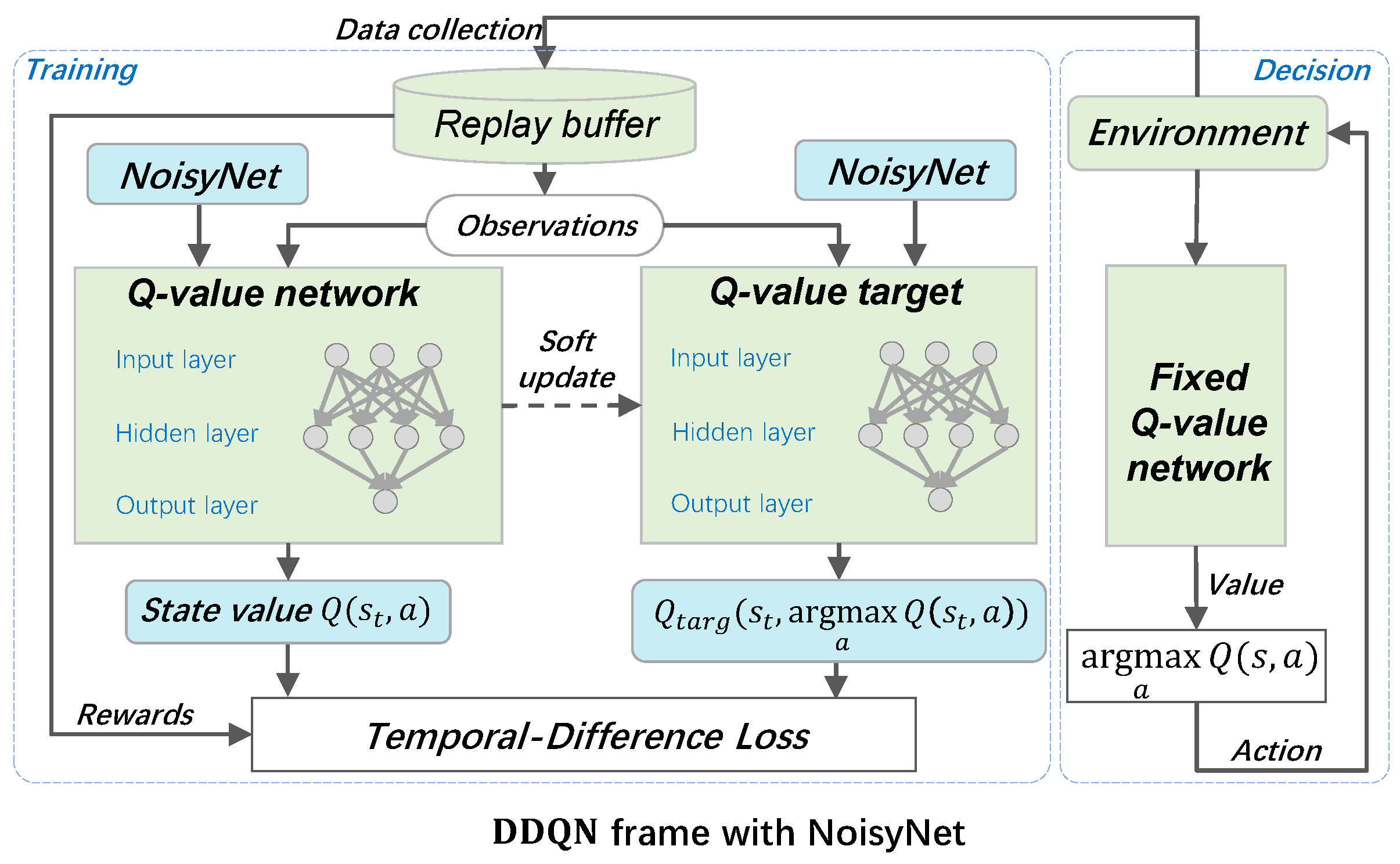
-greedy policy. Building on the DQN using NoisyNet, the DDQN using NoisyNet is made more efficient and effective by using two separate networks to extend the framework, as in the traditional DDQN approach. This setup helps to reduce the overestimation of action values, which often occurs in standard DQN models. The flowchart of this network is simply represented in Figure 4. Adding NoisyNet to the policy and target networks can further facilitate exploration and help speed up convergence by providing a wider range of experience during training.

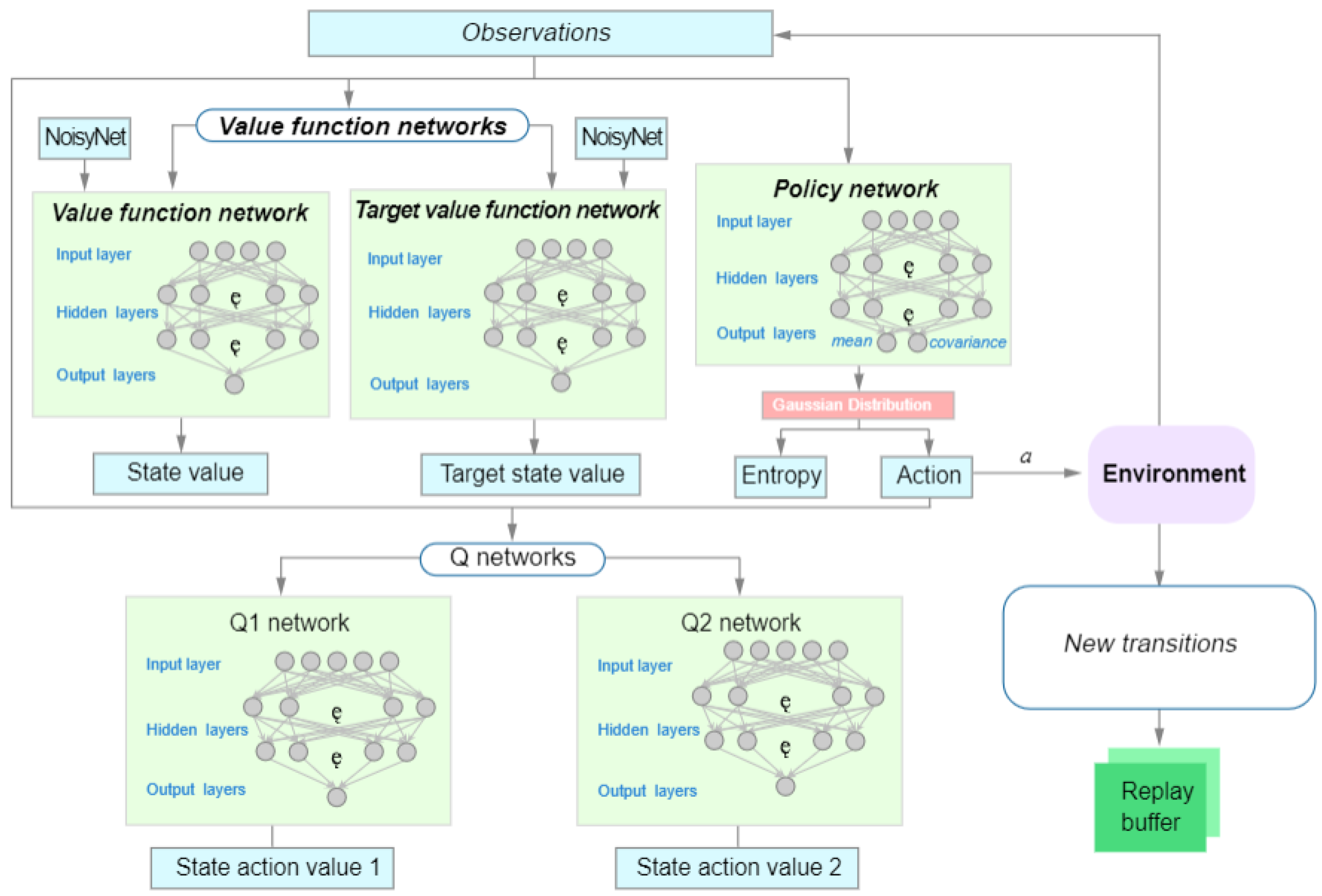
2. SAC Model: This component modifies the traditional SAC by adding NoisyNet and introducing parameter noise into the network weights. The network flow is represented in Figure 5. This noise enriches the exploration of strategies, making the NoisyNet SAC framework more efficient and effective. This setup helps reduce the bias in value estimation that often occurs when using standard SAC models.

3.2.2. DQN with NoisyNet

Through practical research, we found that the exploitation capability of DQN alone was insufficient. Therefore, we modified the DQN network to enhance its exploitation abilities.

We changed the traditional exploration mechanism by enhancing DQN by introducing parametric noise into its network weights. Specifically, in the neural network of DQN, each weight is no longer a fixed value but a random variable determined by a fixed mean parameter and a learnable variance parameter. In this way, each forward propagation of the network produces a different result, depending on the randomness of the weights, thus introducing exploration ability into the decision-making process of agents. Unlike traditional

ε

-greedy exploration or noise-adding strategies, NoisyNet allows the exploration behaviour of the agent to adapt along with the learning process, which is achieved by optimizing the variance parameters of the weighted noise.

When the noise layer replaces the linear layer, the parametric action value function

Q (x, a, ε; ζ)

can be considered a random variable. In particular, a dense neural network layer that inputs p dimensions and outputs q dimensions is expressed as

y = ω \cdot x + b

. The respective noisy layer is characterized by Formula 8.

y = (μ^{ω} + ϵ^{ω} ⊙ σ^{ω}) x + (μ^{b} + ϵ^{b} ⊙ σ^{b}),

(8)

where

μ^{ω}, σ^{ω} \in R^{p \times q}, σ^{b}, μ^{b} \in R^{q}

are trainable parameters, and

ϵ^{ω} \in R^{p \times q}, ϵ^{b} \in R^{q}

are noises. Given that the loss of a noisy network is represented as an expectation over noise, the gradient can be calculated using

L (ζ) = E [L (θ)]

. In noisy networks, the parameters of the original DQN can be replaced with trainable parameters, as shown in Formula 9:

\bar{L} (ζ) = E [E_{(x, a, r, y) \sim D} {[r + γ max_{b \in a} Q (y, b, ϵ^{'}; ζ) - Q (y, a, ϵ^{'}; ζ)]}^{2}] .

(9)

DQN stands out as a typical algorithm in the field of value-based reinforcement learning [35]. It leverages the Temporal Difference (TD) error as the loss function for the neural network, incorporating techniques such as convolution, an experienced buffer, and random experience replay. DQN has achieved human-level performance in the domain of Atari games. At each time step, as shown in Algorithm 1, the environment offers the agent an observation

s_{t}

. Initially, the agent selects an action following the

ε

-greedy strategy and receives a response

r_{t}

and the subsequent state

s_{t + 1}

from the environment. Subsequently, the tuple

(s_{t}, a_{t}, r_{t}, s_{t + 1})

is added to the experience buffer, and we obtain Formula 10:

L (θ) = E [{(r_{t} + γ max_{a} Q^{π} (s_{t + 1}, a^{'}; θ^{-}) - Q^{π} (s_{t}, a_{t}; θ))}^{2}],

(10)

where

θ

represents the parameters of the online network, while

θ^{-}

denotes the parameters of the target network. The parameters

θ^{-}

are periodically updated to match

θ

at regular intervals.

Algorithm 1 DQN with NoisyNet.

Input:: Env: Environment $ε$ : a set of random variables for the network B: initialized as an empty replay buffer $ξ$ : initial parameters of the network $ζ^{-}$ : initial parameters of the target network $N_{B}$ : capacity of the replay buffer $N_{T}$ : batch size for training $N^{-}$ : interval for updating the target network
Output:: $Q (\cdot, ε; ξ)$
1:: for episode $e \in \{1, . . ., M\}$ do
2:: Initialize state sequence $x_{0} \sim E n v$
3:: for $t \in \{1, . . .\}$ do
4:: Set $x \leftarrow x_{0}$
5:: Draw a noisy network sample $ξ \sim ε$
6:: Choose an action $a \leftarrow a r g m a x_{b \in a} Q (x, b, ξ; ζ)$
7:: Draw the next state $y \leftarrow P (\cdot | x, a)$ , obtain reward $r \leftarrow R (x, a)$ , and set $x_{0} \leftarrow y$
8:: Receive reward B[-1] $\leftarrow (x, a, r, y)$
9:: if $|B| > N B$ then
10:: Remove the oldest transition from B
11:: end if
12:: Sample a minibatch of NT transitions ${((x_{j}, a_{j}, r_{j}, y_{j}) \sim D)}_{j = 1}^{N^{T}}$
13:: Draw the noisy variable for the online network $ξ \sim ε$
14:: Generate the noisy variables for the target network. $ζ_{0} \sim ε$
15:: for $j \in \{1, . . ., N_{T}\}$ do
16:: if $y_{j}$ represents an ultimate state then
17:: $\hat{Q} \leftarrow y_{j}$
18:: else
19:: $\hat{Q} \leftarrow r_{j} + γ arg {max}_{b \in A} Q (y_{j}, b, ξ^{''}; ζ^{-})$
20:: Perform a gradient update using the loss ${(\hat{Q} - Q (x_{j}, a_{j}, ξ^{''}; ζ))}^{2}$
21:: end if
22:: if $t \equiv 0 (m o d N^{-})$ then
23:: Generate the noisy variables for the target network: $ζ^{-} \leftarrow ξ$
24:: end if
25:: end for
26:: end for
27:: end for

3.2.3. DDQN with NoisyNet

Building upon the DynamicNoiseDQN framework, we further explored incorporating a noise layer into the DDQN structure to enhance the exploration capabilities of the network in complex autonomous driving scenarios, particularly for tasks involving turning and avoiding other vehicles.

DDQN improves upon the traditional DQN method by addressing the issue of overestimated value estimations. This is achieved through two separate networks: one for action selection and the other for evaluating the value of that action. Thus, we obtain the Formula 11.

Q_{t a r g e t} = r + γ Q (s^{'}, {argmax}_{a^{'}} Q (s^{'}, a^{'}; θ); θ^{-}),

(11)

where r represents the reward,

γ

is the discount factor,

s^{'}

is the next state,

θ

denotes the current network parameters, and

θ^{-}

denotes the target network parameters.

To further enhance exploration in DDQN, we introduced noise into the fully connected layers. The parameters of these layers are defined by the following Formula 12, where the noise component provides random perturbations to the parameters during training, facilitating the exploration of different strategies.

w = σ^{w} ⊙ ϵ^{w} + μ^{w}, b = σ^{b} ⊙ ϵ^{b} + μ^{b},

(12)

where

μ^{w}

and

σ^{w}

are the mean and standard deviation of the weights, respectively, and

ϵ^{w}

is noise sampled from a probability distribution. A similar setup is applied to the bias b.

During training, the noise vector

ϵ

is resampled at each training step, ensuring that each forward pass of the network slightly differs. This dynamic change in network parameters, as shown in Algorithm 2, not only enhances environmental exploration but also improves the network’s adaptability to changing conditions. This is particularly valuable considering the variable conditions encountered in autonomous driving.

Algorithm 2 DDQN with NoisyNet.

Input:: Env: Environment $ε$ : a set of random variables for the network B: initialized as an empty replay buffer $ξ$ : initial parameters of the network $ζ^{-}$ : initial parameters of the target network $N_{B}$ : capacity of the replay buffer $N_{T}$ : batch size for training $N^{-}$ : interval for updating the target network
Output:: $Q (\cdot, ε; ξ)$
1:: for episode $e \in \{1, . . ., M\}$ do
2:: Initialize state sequence $x_{0} \sim E n v$
3:: for $t \in \{1, . . .\}$ do
4:: Set $x \leftarrow x_{0}$
5:: Draw a noisy network sample $ξ \sim ε$
6:: Choose an action $a \leftarrow a r g m a x_{b \in a} Q (x, b, ξ; ζ)$
7:: Draw the next state $y \leftarrow P (\cdot | x, a)$ , obtain reward $r \leftarrow R (x, a)$ , and set $x_{0} \leftarrow y$
8:: Receive reward B[-1] $\leftarrow (x, a, r, y)$
9:: if $|B| > N B$ then
10:: Remove the oldest transition from B
11:: end if
12:: Sample a minibatch of NT transitions ${((x_{j}, a_{j}, r_{j}, y_{j}) \sim D)}_{j = 1}^{N^{T}}$
13:: Draw the noisy variable for the online network $ξ \sim ε$
14:: Generate the noisy variables for the target network. $ζ_{0} \sim ε$
15:: for $j \in \{1, . . ., N_{T}\}$ do
16:: if $y_{j}$ represents an ultimate state then
17:: $\hat{Q} \leftarrow y_{j}$
18:: else
19:: $Q_{o n l i n e} \leftarrow a r g m a x_{b \in A} Q (y_{j}, b; ξ^{''})$
20:: $\hat{Q} \leftarrow r_{j} + γ Q (y_{j}, Q_{o n l i n e}; ζ^{-})$
21:: end if
22:: Perform a gradient update using the loss ${(\hat{Q} - Q (x_{j}, a_{j}, ξ^{''}; ζ))}^{2}$
23:: end for
24:: if $t \equiv 0 (m o d N^{-})$ then
25:: Update the parameters of the target network: $ζ^{-} \leftarrow ξ$
26:: end if
27:: end for
28:: end for

Through these improvements, the noise-enhanced DDQN model demonstrates superior performance in handling complex autonomous driving tasks, effectively learning and adapting to different driving situations better than the traditional DDQN.

3.3. Soft Actor–Critic with Noisy Critic

To further validate the performance of our Noisynet in real-world autonomous driving scenarios, we compared SAC+Noisynet with the existing SAC framework. SAC is a reinforcement learning framework commonly used in high-dimensional continuous control scenarios with high efficiency and stability. The SAC framework consists of two main components: the Critic and Actor networks. The Critic network is responsible for learning Q-valued functions, while the Actor-network is responsible for learning strategies. Critic networks evaluate the quality of the current policy by minimizing the error of the Q-value function, while Actor networks update the policy by maximizing the expected reward.

The purpose of the SAC algorithm is to maximize the future cumulative reward value and entropy, such that the strategy is as random as possible; that is, the probability of the output of each action is as scattered as possible rather than concentrated on one action. The objective function of the SAC algorithm can be expressed as Formula 13:

J (π) = \sum_{t = 0}^{T} E_{(s_{t}, a_{t}) \sim ρ^{π}} [r (s_{t}, a_{t}) + α H (π (\cdot ∣ s_{t}))],

(13)

where T represents the total number of time steps of the interaction between the agent and the environment,

p^{π}

represents the distribution under the strategy

π (s_{t}, a_{t})

H (\cdot)

represents the entropy, and

α

is a hyperparameter, the purpose of which is to control the randomness of the optimal strategy and weigh the importance of entropy relative to the reward.

In our experiments, we integrated Noisynet into the SAC framework, as shown in Algorithm 3, to evaluate its performance in autonomous driving tasks. Noisynet enhances exploration by adding noise into neural networks to help find better strategies in complex environments. Our extensive experiments on multiple simulation environments and real-world driving data revealed that SAC+Noisynet outperforms the standard SAC framework in several performance metrics.

Algorithm 3 Soft Actor-Critic with Noisy Critic.

Input:: Initial policy parameters $θ$ , Q-function parameters $ϕ_{1}, ϕ_{2}$ , empty replay buffer $D$
1:: Set target parameters equal to main parameters $ϕ_{targ, i} \leftarrow ϕ_{i}$ , $ϕ_{targ, 2} \leftarrow ϕ_{2}$
2:: repeat
3:: Observe state s and select action $a \sim π_{θ} (\cdot | s)$
4:: Execute a in the environment
5:: Observe next state $s^{'}$ , reward r, and done signal d to indicate whether $s^{'}$ is terminal
6:: Store $(s, a, r, s^{'}, d)$ in replay buffer $D$
7:: if $s^{'}$ is terminal then
8:: Reset environment state
9:: end if
10:: if it’s time to update then
11:: for j in range(however many updates) do
12:: Randomly sample a batch of transitions, $B = {(s, a, r, s^{'}, d)}$ from $D$
13:: Compute targets for the Q functions:

$y (r, s^{'}, d) = r + γ (1 - d) (min_{i = 1, 2} Q_{ϕ_{targ, i}} (s^{'}, a^{'}) - α log π_{θ} (a^{'} | s^{'})), a^{'} \sim π_{θ} (\cdot | s^{'})$
14:: Update Q-functions by one step of gradient descent using

$\nabla_{ϕ_{i}} \frac{1}{| B |} \sum_{(s, a, r, s^{'}, d) \in B} {(Q_{ϕ_{i}} (s, a) - y (r, s^{'}, d))}^{2} for i = 1, 2$

where $Q_{ϕ_{i}} (s, a)$ includes noisy layers:

$Q_{ϕ_{i}} (s, a) = Q_{noisy_fc} (s, a)$
15:: Define $Q_{noisy_fc}$ :

$Q_{noisy_fc} (x) = (W + σ_{W} ⊙ ϵ_{W}) x + (b + σ_{b} ⊙ ϵ_{b})$

with $ϵ_{W}, ϵ_{b} \sim N (0, 1)$ .
16:: Update policy by one step of gradient ascent using

$\nabla_{θ} \frac{1}{| B |} \sum_{s \in B} (min_{i = 1, 2} Q_{ϕ_{i}} (s, {\tilde{a}}_{θ} (s)) - α log π_{θ} ({\tilde{a}}_{θ} (s) | s)),$

where ${\tilde{a}}_{θ} (s)$ is a sample from $π_{θ} (\cdot | s)$ which is differentiable with respect to $θ$ via the reparameterization trick.
17:: Update target networks with

$ϕ_{targ, i} \leftarrow ρ ϕ_{targ, i} + (1 - ρ) ϕ_{i} for i = 1, 2$
18:: end for
19:: end if
20:: until convergence

4. Experiment

4.1. Experiment in Highway_env

To evaluate the objectives outlined in the introduction, we implemented the noise-enhanced DynamicNoiseDQN network within a car turning scenario at an intersection utilizing the open-source highway_env [36] simulation platform. Specifically, the intersection-v0 environment was employed to simulate intersection dynamics, where Vehicle trajectories were created using the kinematic bicycle model. This setting enables vehicles to execute continuous-valued steering and throttle control actions, thereby closely replicating real-life driving scenarios.

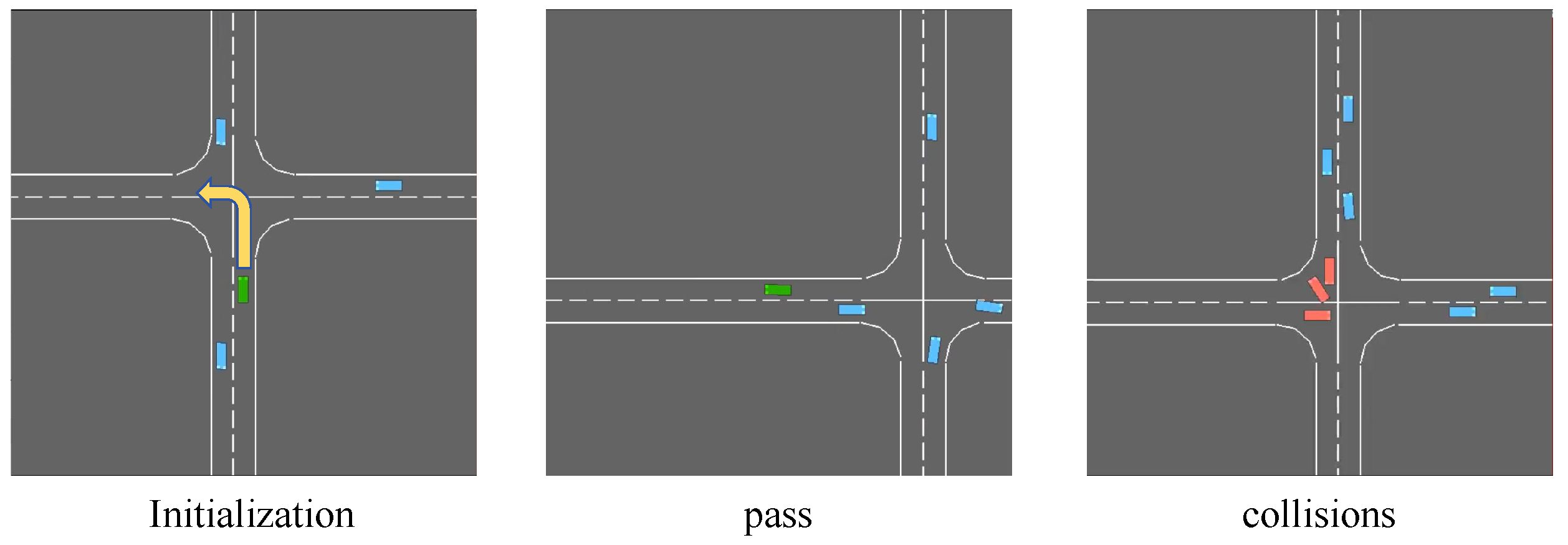
In the intersection scenario shown in Figure 6, the agent being tested (represented by a green vehicle) was tasked with executing a collision-free, unprotected left turn at a two-lane intersection in the presence of another vehicle (represented by a blue vehicle). A collision in this context is considered a rare event, with the adversarial policy reflecting the behavior of the surrounding vehicle. The primary goal is to evaluate stationary deterministic strategies, which include maintaining a constant speed and adhering to lane protocols. This involves following standard rules at intersections without traffic signals, such as yielding to vehicles approaching from the right, maintaining a safe distance, avoiding arbitrary acceleration or deceleration, and not changing lanes unpredictably. To compare the performance of the noise-enhanced network with that of a conventional DQN network, ten independent and distinct experiments were conducted for each model.

To showcase the effectiveness of our proposed approach, we compared our method with contemporary, state-of-the-art traditional RL strategies, and the performance was assessed across multiple dimensions using a variety of metrics.

a) Speed of convergence: We compared the efficiency of our model by examining the number of episodes required to reach convergence for two data sets. This was performed by calculating the average number of episodes over ten experiments and assessing whether our model demonstrated a significant improvement in efficiency.

b) Success rate: In an autonomous driving system, safety is the primary performance indicator. In our framework, the success rate and average passing time served as general metrics for performance assessment. The success rate directly reflects how the RL agent handles the specified task. Our framework defines the success rate according to Formula 14.

s u c c e s s r a t e = \frac{S u c c e s s C o u n t s}{T o t a l N u m b e r s} \times 100 %,

(14)

c) Time for completion of tasks: In our analysis of successfully completed journeys, we meticulously documented the time each vehicle took to traverse from the starting point to the designated destination. The efficacy of our network strategy was directly correlated with the efficiency exhibited by vehicles, as reflected in the average time required to accomplish the task.

For training of the DQN network, we adopted a discount factor of 0.95 and set the batch size to 64. To avoid overfitting, we limited the number of training episodes to 2000. We choose a target update value of 256 for training the noise network, with the batch size remaining at 64 and the discount factor set to 0.9. Our DynamicNoiseDQN network structure was a 128 × 128 fully connected network, and the target memory_capacity value was set to 15,000. When training the DQN network with the

ε

-greedy strategy, we set the value of

ε

to 0.5. In the training task for NoisyNet with DDQN, we kept the other settings unchanged and set the value of double to 1.

In our implementation of NoisyNet, the noise is generated by sampling from a standard normal distribution and applying a non-linear transformation. Specifically, the noise

ϵ

is calculated as

ϵ = sign (x) \cdot \sqrt{| x |}

, where

x \sim N (0, 1)

. This approach ensures that the noise retains the properties of the normal distribution while providing more stable variance, thereby enhancing the model’s exploration capabilities during training.

4.2. Experiment in CARLA

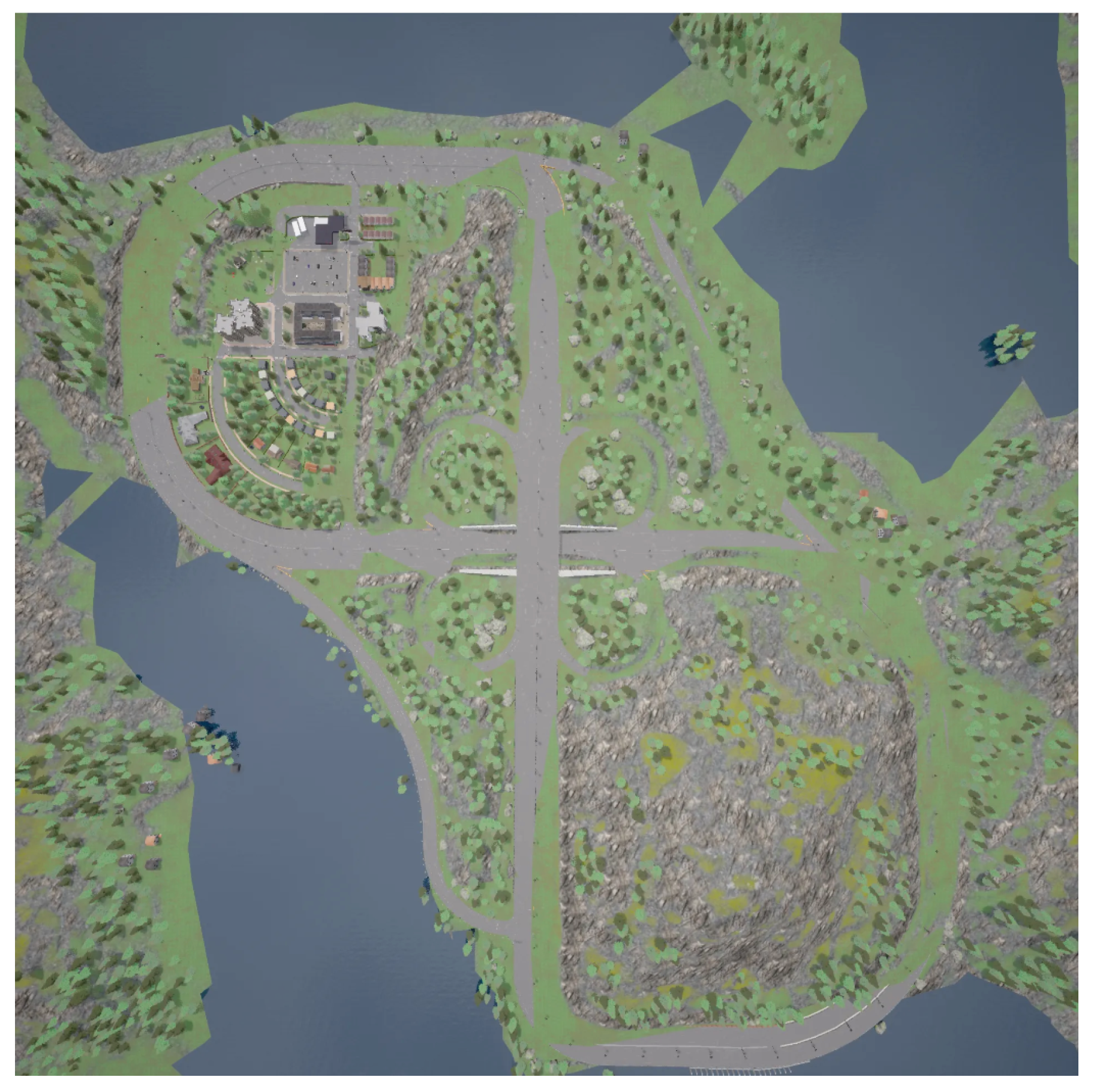
To verify the superiority and reliability of our algorithm, we performed additional validation in a 3D scene. We simulated realistic scenarios using the CARLA[37] simulator. This open-source autonomous driving simulator was built from scratch as a modular and flexible API to solve various tasks involved in autonomous driving problems. Town 4, as shown in Figure 7, is a small town with a backdrop of snow-capped mountains and conifers. As seen in Figure 8, a multi-lane road circumnavigates the town. The road network consists of a small network of short streets and junctions between commercial and residential buildings, with a "figure of 8"-style ring road circumnavigating the buildings and a nearby mountain. The crossing of the road is designed as an underpass/overpass with circular slip roads.

In our task setup, our objective was to maximize the effective distance travelled by the vehicle agent within a fixed 1000 environment steps. The metrics for evaluating the performance of this task were the driving distance and reward. The greater the driving distance and reward, the better the model was considered to have performed.Further hyperparameters are described in Table 1.

5. Results

5.1. Result in Highway_env

5.1.1. Rewards

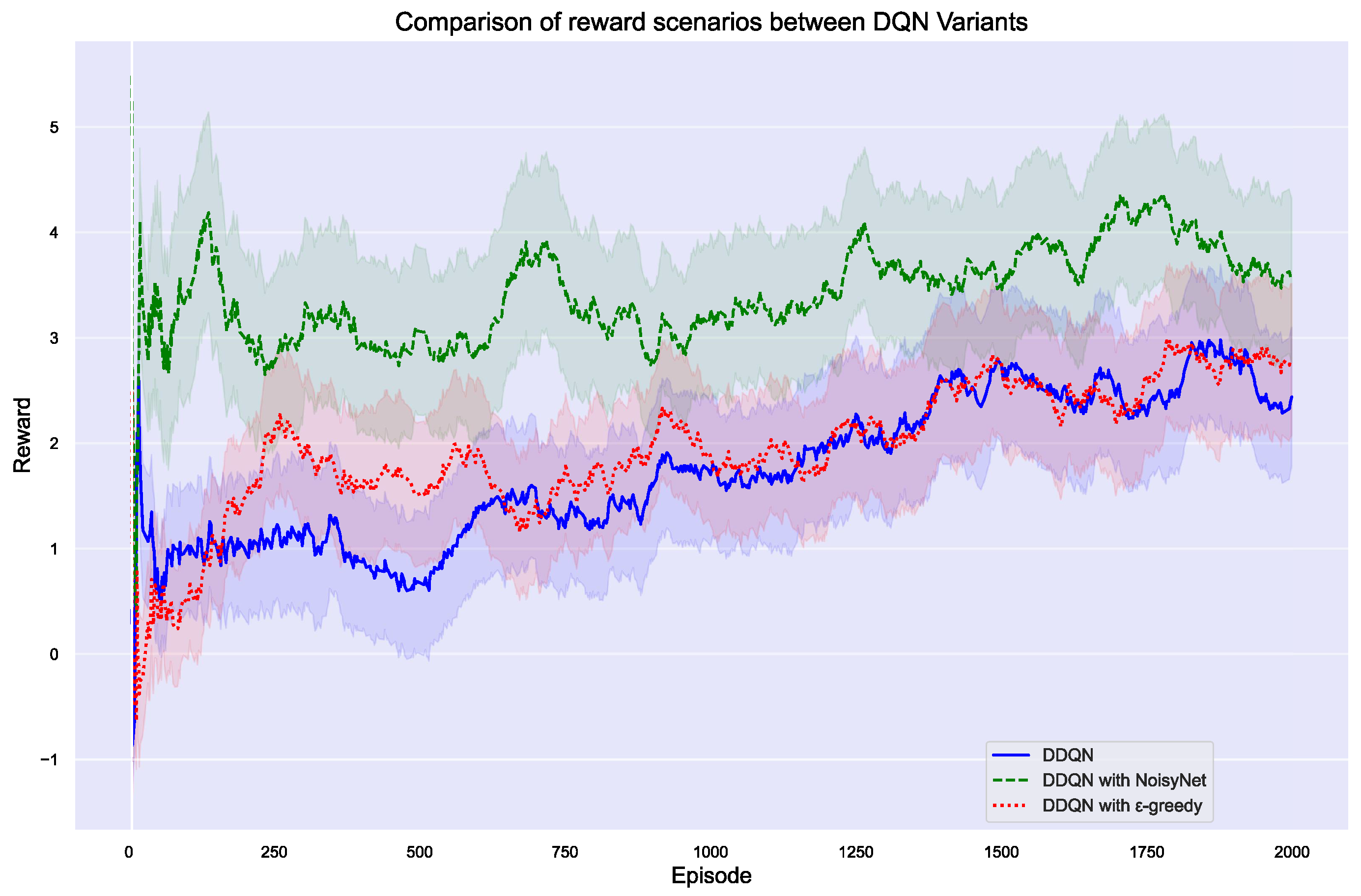
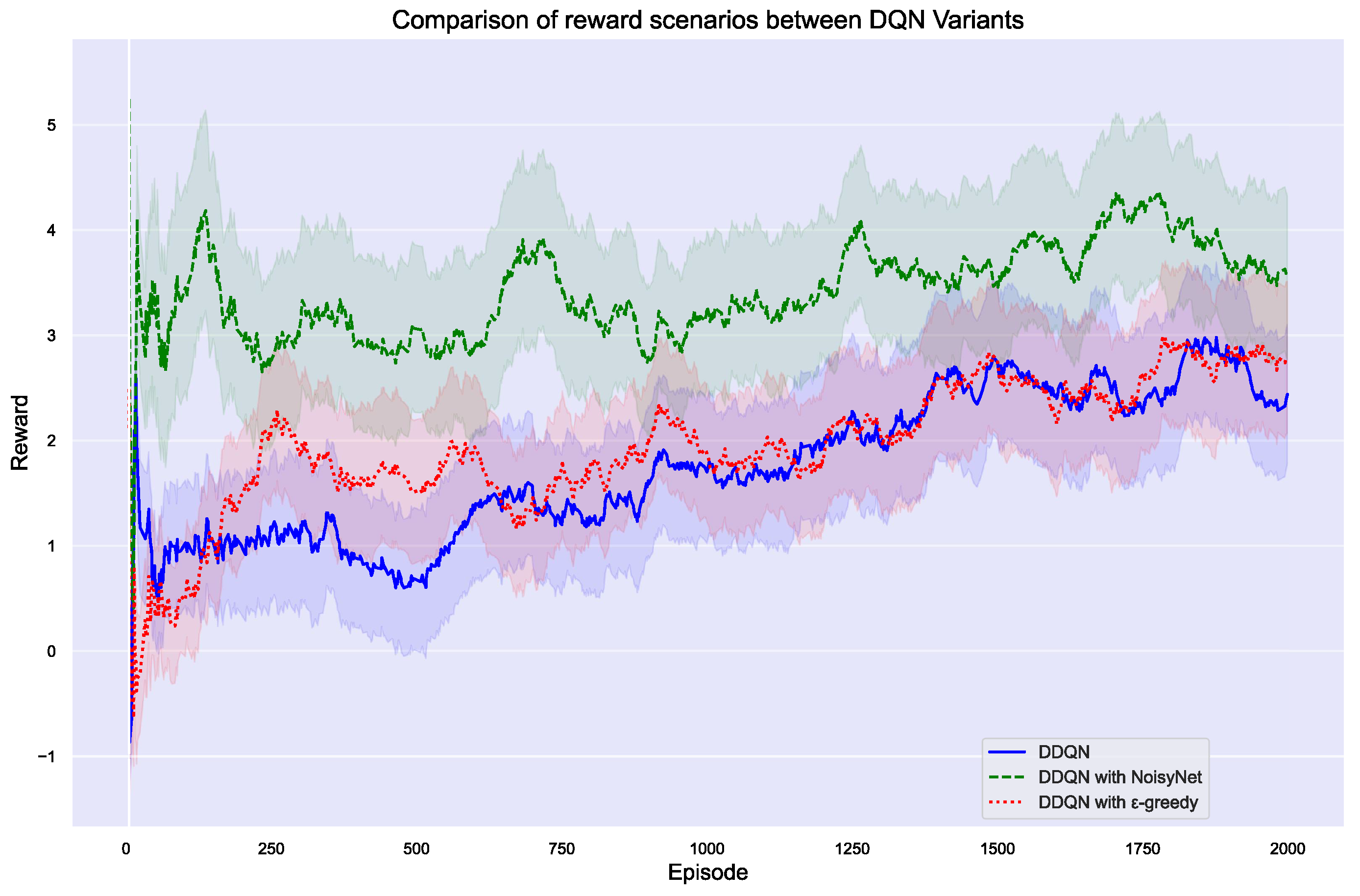
We analyzed the reward values from 2000 episodes collected across three experimental sets. After averaging these values, we applied a smoothing technique to the data and plotted the resulting curves. The reward comparison graphs (Figure 9 and Figure 10) reveal important insights into the performance of different DQN and DDQN variants across episodes. In Figure 9, DQN with NoisyNet clearly outperforms both the standard DQN and DQN with

ϵ

-greedy, highlighting the effectiveness of NoisyNet in enhancing exploration and achieving higher rewards. The

ϵ

-greedy variant shows some improvement over the standard DQN, but it doesn’t reach the level of performance seen with NoisyNet. In contrast, Figure 10 shows that while DDQN with NoisyNet initially performs well, the standard DDQN eventually surpasses it as training progresses. This suggests that although NoisyNet provides early benefits, the standard DDQN may offer better long-term stability and higher rewards. The DDQN with the

ϵ

-greedy variant demonstrates more consistent performance than NoisyNet but still falls short of the standard DDQN. These figures collectively underscore the complex dynamics of exploration strategies in reinforcement learning, with NoisyNet offering strong early performance, while the standard DDQN shows superior long-term results in certain cases.

Figure 9. Comparison of reward scenarios between DQN, DQN with

ε

-greedy, and DQN with NoisyNet

Figure 9. Comparison of reward scenarios between DQN, DQN with

ε

-greedy, and DQN with NoisyNet

Figure 10. Comparison of reward scenarios between DDQN, DDQN with

ε

-greedy, and DDQN with NoisyNet

Figure 10. Comparison of reward scenarios between DDQN, DDQN with

ε

-greedy, and DDQN with NoisyNet

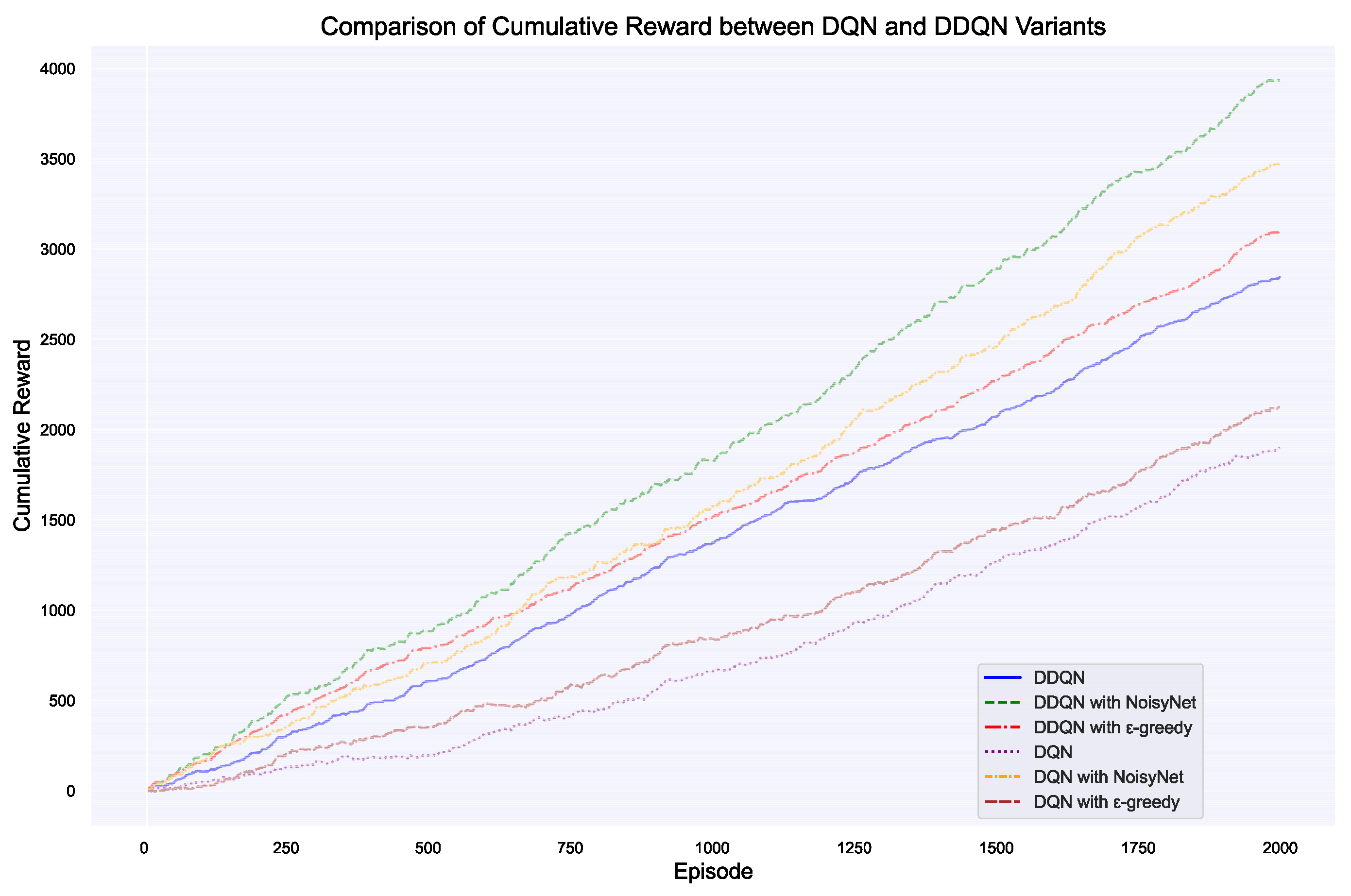
Figure 11. Cumulative rewards across episodes for different DQN and DDQN variants.

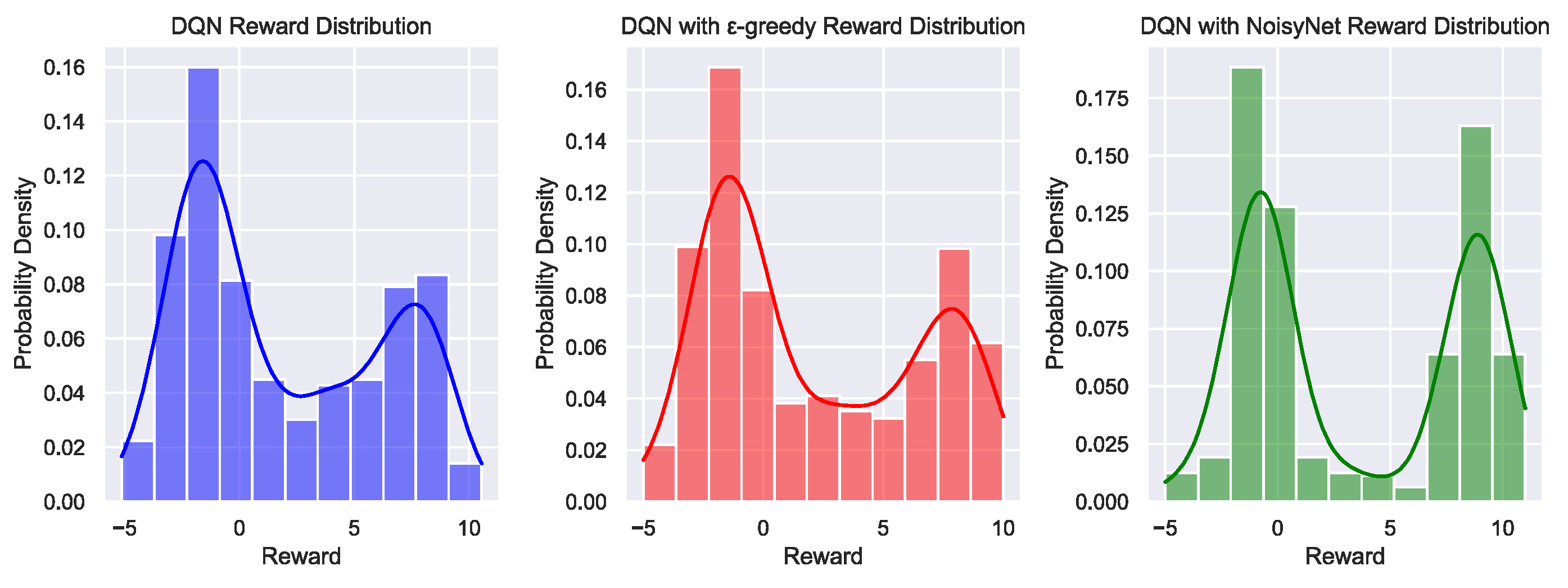
The reward distribution charts in Figure 12 reveal significant differences in how DQN and its variants perform in terms of reward distribution. The standard DQN shows a bimodal distribution, with rewards mainly concentrated around 0 and close to 10. This indicates that DQN can achieve high rewards in certain states, but overall, the reward values remain relatively low, reflecting inconsistent learning effectiveness across different states. The DQN with

ϵ

-greedy strategy exhibits a more pronounced peak in the reward distribution, primarily around 0, with a noticeable spread in the positive reward range (between 5 and 10). This suggests that the

ϵ

-greedy strategy enhances DQN exploration capability, leading to a more balanced distribution of rewards, though still leaning towards lower values. In contrast, the reward distribution for DQN with NoisyNet is more dispersed. Although the bimodal structure persists, the reward values are more evenly spread, covering a range from -5 to 10. This indicates that NoisyNet significantly boosts DQN exploration ability, preventing rewards from being overly concentrated in a specific range, thus demonstrating stronger exploration capabilities and broader reward coverage. Overall, these distribution charts clearly reflect the impact of different strategies on DQN exploration and exploitation balance. In particular, the introduction of NoisyNet results in a more diversified reward distribution, highlighting its advantages in enhancing learning performance.

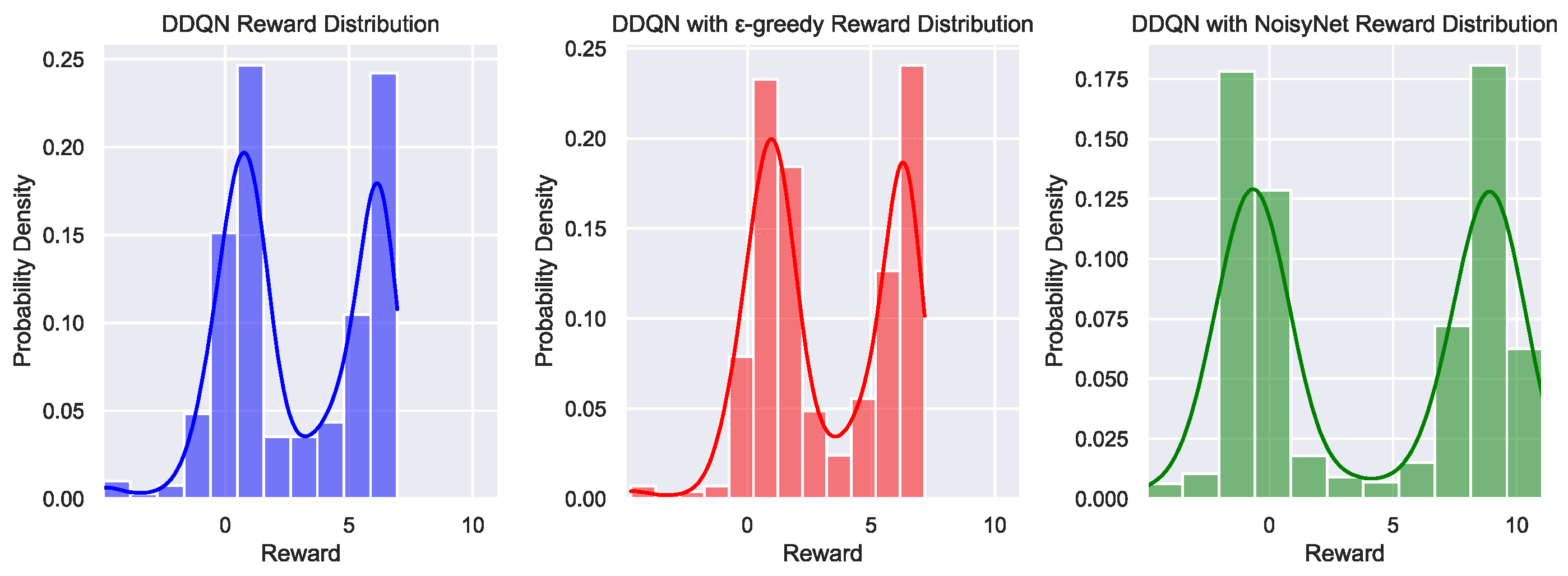
The analysis of the reward distribution charts in Figure 13 indicates that DDQN and DDQN with

ϵ

-greedy exhibit more concentrated reward values compared to other variants, with no occurrence of particularly low rewards. This suggests that both algorithms maintain stable performance during training, effectively avoiding the pitfall of extremely low rewards. This characteristic is confirmed by the reward distribution charts, where the smaller shaded areas (variance) further demonstrate the reduced reward fluctuations, highlighting the consistency and reliability of these algorithms. Specifically, the rewards for DDQN and DDQN with

ϵ

-greedy are primarily concentrated in the mid-range. Although they fail to explore rewards above 7, they successfully avoid the trap of low reward regions. This indicates that these algorithms can effectively enhance overall performance while maintaining relatively stable learning outcomes. However, this stability might come at the cost of exploring higher reward regions, but overall, they show more consistent performance and reduce the risk of extremely low rewards.

NoisyNet-DDQN, on the other hand, manages to retain the advantages of DDQN and DDQN with

ϵ

-greedy while also effectively exploring high-value regions. Specifically, NoisyNet-DDQN not only exhibits a reward distribution similar to the other two algorithms, characterized by stable and mid-range reward values that avoid extremely low rewards but also demonstrates a strong exploratory capability, more frequently reaching reward regions above 7. This indicates that the random perturbation mechanism introduced by NoisyNet enhances the diversity of exploration, enabling the algorithm to break out of local optima and discover and exploit higher rewards, all while maintaining overall performance stability.

The cumulative rewards graph (Figure 11) clearly illustrates the significant differences in performance among various DQN and DDQN variants. The combination of DDQN with NoisyNet performs the best, achieving the highest cumulative rewards, indicating its superior ability to balance exploration and exploitation, leading to better long-term learning outcomes. While DDQN with

ϵ

-greedy also outperforms standard DDQN, it does not reach the levels of the NoisyNet variant, suggesting that NoisyNet is more effective in reducing overestimation bias and enhancing learning robustness. In contrast, although DQN with NoisyNet outperforms other DQN variants, it still falls short of the DDQN combinations, further highlighting the advantages of the DDQN architecture when paired with exploration strategies like NoisyNet. Overall, the combination of NoisyNet with DDQN demonstrates the most significant improvement in cumulative rewards in complex reinforcement learning tasks.

5.1.2. Success Rate

The success rate of vehicle passage is a crucial metric reflecting the effectiveness of our models. We computed the success rates for the traditional DQN, DDQN, and our DynamicNoise-enhanced algorithms across ten experiments and then determined their average values. The success rate for the conventional DQN was 52.8%, while the

ϵ

-greedy modification achieved 62.5%. The DDQN algorithm achieved a success rate of 68.6%, with the

ϵ

-greedy variation reaching 74.5%. Both were still significantly lower than the 88.9% success rate recorded for DQN with NoisyNet and 91.2% for DDQN with NoisyNet. Analysis of the reward distribution revealed that the rewards obtained by the algorithms using the DynamicNoise framework were mainly concentrated in higher values, indirectly affirming their excellent success rates and suggesting that their network architectures are more efficient.

Moreover, we analyzed the variance of rewards for all methods across the ten data sets, computing average values. The variance of the traditional DQN network was 18.46, while the

ϵ

-greedy method had a variance of 19.32. In contrast, DQN with NoisyNet had a higher variance value of 23.26, and DDQN with NoisyNet showed a similar trend with a variance of 23.61, indicating their enhanced exploratory capabilities. However, the DDQN algorithm and its

ϵ

-greedy variation, known for more conservative exploration strategies, exhibited lower variance values of 14.14 and 15.26, respectively. This lower variance reflects the DDQN-based methods’ tendency towards stability and reduced exploration, compared to the more aggressive exploration in the NoisyNet-enhanced strategies. Overall, the higher variance observed in the DynamicNoiseDQN-based methods confirms their superior exploratory capabilities, while the lower variance in the DDQN methods underscores their focus on stability and consistent performance.

5.1.3. Number of Iterations at Convergence

To further assess the task completion efficiency, we compared the minimum number of episodes required by all networks to achieve their objectives. DDQN with NoisyNet particularly stood out, requiring only 210 attempts to succeed, a drastic reduction from the original 1220 attempts with DQN, representing an improvement of 82.79%. The DDQN algorithm required 370 attempts, and its

ϵ

-greedy variation further improved to 290 attempts, both significantly fewer than the traditional DQN and its

ϵ

-greedy variant, which required 1240 episodes. This comparison underscores the effectiveness of integrating advanced strategies such as NoisyNet and doubling techniques into both DQN and DDQN networks. Such enhancements not only boost the efficiency of the learning process but also significantly increase the speed and reliability of reaching optimal solutions in dynamic environments.

5.1.4. Time for Completion of Tasks

The comparative data showcase significant advancements in time efficiency across various DQN configurations. From Table 2, it can be seen that the original DQN model required an average of 6.58 seconds per episode, which is indicative of the baseline performance. When incorporating the

ε

-greedy strategy, the time was slightly reduced to 6.41 seconds, indicating a marginal improvement in processing efficiency.

However, the integration of DDQN and the DynamicNoiseDQN framework presented more notable time reductions. The standard DDQN model required 6.40 seconds, while the DDQN with

ε

-greedy strategy further reduced this to 6.25 seconds. DQN with NoisyNet reduced the average time to 6.01 seconds, and DDQN with NoisyNet achieved the most efficient time of 5.93 seconds, representing a 10.96% improvement over the original DQN model. These results highlight the effectiveness of using NoisyNet in combination with DDQN, demonstrating significant improvements in both time efficiency and overall task performance.

These results demonstrate that integrating advanced strategies such as NoisyNet and the doubling technique enhances the time efficiency of the network. This reduction in time not only indicates quicker decision-making capabilities but also highlights the ability of models to handle dynamic environments more effectively.

5.2. Result in CARLA

We report the comparison data regarding the episode distance and episode reward for the vehicle over 1000 fixed environment steps in Table 3, while the obstacle avoidance ability of the vehicle is visualized in Figure 14. The average steering control magnitude percentage per step was recorded throughout the training.

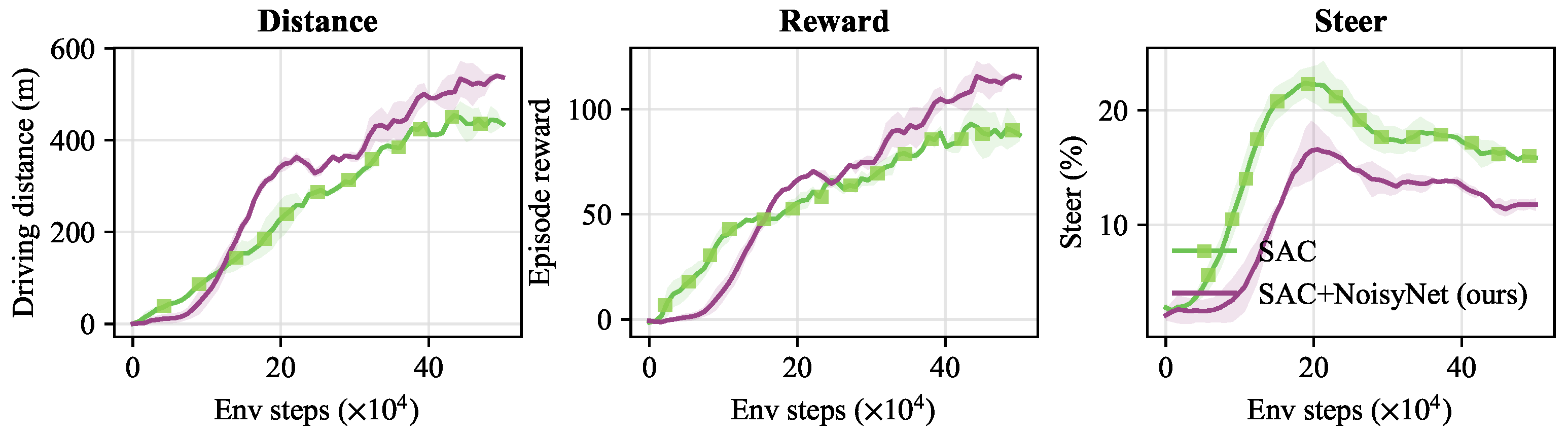
The experiments demonstrate that the proposed method, when integrated into the SAC reinforcement learning framework, can effectively enhance driving performance to the base framework. The results obtained with the two algorithms are shown in Figure 15. Specifically, on the one hand, the proposed method (SAC+NoisyNet) achieved the optimal episode driving distance of 540.5 meters, an improvement of nearly 18.9% compared to the 454.1 meters achieved by the original SAC method (as shown in Table 3). On the other hand, as shown on the right side of the Figure, the proposed method performed better in steering control, maintaining a stable steering magnitude, effectively enhancing the overall driving distance. Overall, these qualitative experiments strongly prove the control performance of the proposed method in the context of autonomous driving.

6. Conclusion

We proposed the NoisyNet framework to address slow convergence, instability, and low exploration efficiency in high-dimensional state spaces of reinforcement learning algorithms, particularly in complex driving scenarios. By introducing noise parameters, NoisyNet effectively balances exploration and exploitation, enhancing decision-making and adaptability. Integrated with DQN and SAC algorithms, NoisyNet has been experimentally validated, demonstrating significant improvements in both performance and stability. This framework shows great promise for optimizing the intelligence and reliability of autonomous driving systems, improving their ability to manage complex traffic environments, enhancing decision-making and control efficiency, and optimizing the collaborative operation of autonomous vehicle fleets to increase overall traffic efficiency and safety.

Despite its strong performance in laboratory settings, NoisyNet may encounter challenges when applied to real-world environments, where complexity and interference can affect its effectiveness. To address this, our future work will focus on enhancing the robustness of the framework through extensive testing on autonomous vehicles and UGVs in various real-world traffic scenarios, including urban, highway, and rural environments. We will refine NoisyNet for seamless integration with existing autonomous driving systems, ensuring real-time processing and adherence to safety standards required for deployment. Additionally, we plan to validate the performance of NoisyNet under practical conditions, collaborating with industry partners to ensure it meets the rigorous demands of real-world applications. By expanding its application to intelligent transportation systems, we aim to develop more resilient and efficient traffic management solutions, ultimately bridging the gap between simulation and real-world deployment.

7. Patents

This research is supported by the Jilin Province Transportation Science and Technology project. (NO.2018ZDGC-4).

Conflicts of Interest

The funding sources did not influence the study design, data collection, analysis, interpretation, manuscript writing, or the decision to publish the findings.

Abbreviations

The following abbreviations are used in this manuscript:

RL	Reinforcement Learning
SAC	Soft Actor–Critic
KDE	Kernel Density Estimate
DQN	Deep Q-Network
DDQN	Double DQN
MPC	Model Predictive Control
PID	Proportional–Integral–Derivative
MDP	Markov Decision Process
UAV	unmanned aerial vehicles

References

M. Althoff and S. Lutz, “Automatic generation of safety-critical test scenarios for collision avoidance of road vehicles,” in 2018 IEEE Intelligent Vehicles Symposium (IV). IEEE, 2018, pp. 1326–1333.
F. Gao, J. Duan, Z. Han, and Y. He, “Automatic virtual test technology for intelligent driving systems considering both coverage and efficiency,” IEEE Transactions on Vehicular Technology, vol. 69, no. 12, pp. 14 365–14 376, 2020.
Z. Li, A. Zhou, J. Pu, and J. Yu, “Multi-modal neural feature fusion for automatic driving through perception-aware path planning,” IEEE Access, vol. 9, pp. 142 782–142 794, 2021.
J. James, W. Yu, and J. Gu, “Online vehicle routing with neural combinatorial optimization and deep reinforcement learning,” IEEE Transactions on Intelligent Transportation Systems, vol. 20, no. 10, pp. 3806–3817, 2019.
Y. Zhang, W. Macke, J. Cui, S. Hornstein, D. Urieli, and P. Stone, “Learning a robust multiagent driving policy for traffic congestion reduction,” Neural Computing and Applications, pp. 1–14, 2023.
L. Zhu, J. Gonder, E. Bjarkvik, M. Pourabdollah, and B. Lindenberg, “An automated vehicle fuel economy benefits evaluation framework using real-world travel and traffic data,” IEEE Intelligent Transportation Systems Magazine, vol. 11, no. 3, pp. 29–41, 2019.
T. Le-Anh and M. De Koster, “A review of design and control of automated guided vehicle systems,” European journal of operational research, vol. 171, no. 1, pp. 1–23, 2006.
F. A. A. Cheein, C. De La Cruz, T. F. Bastos, and R. Carelli, “Slam-based cross-a-door solution approach for a robotic wheelchair,” International Journal of Advanced Robotic Systems, vol. 6, no. 3, p. 20, 2009.
J. Suh, H. Chae, and K. Yi, “Stochastic model-predictive control for lane change decision of automated driving vehicles,” IEEE Transactions on Vehicular Technology, vol. 67, no. 6, pp. 4771–4782, 2018.
B. R. Kiran, I. Sobh, V. Talpaert, P. Mannion, A. A. Al Sallab, S. Yogamani, and P. Pérez, “Deep reinforcement learning for autonomous driving: A survey,” IEEE Transactions on Intelligent Transportation Systems, vol. 23, no. 6, pp. 4909–4926, 2021.
X. Xu, L. Zuo, X. Li, L. Qian, J. Ren, and Z. Sun, “A reinforcement learning approach to autonomous decision making of intelligent vehicles on highways,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 50, no. 10, pp. 3884–3897, 2018.
Y. Shan, B. Zheng, L. Chen, L. Chen, and D. Chen, “A reinforcement learning-based adaptive path tracking approach for autonomous driving,” IEEE Transactions on Vehicular Technology, vol. 69, no. 10, pp. 10 581–10 595, 2020.
A. Garg, H.-T. L. Chiang, S. Sugaya, A. Faust, and L. Tapia, “Comparison of deep reinforcement learning policies to formal methods for moving obstacle avoidance,” in 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2019, pp. 3534–3541.
P. Wang, C.-Y. Chan, and A. de La Fortelle, “A reinforcement learning based approach for automated lane change maneuvers,” in 2018 IEEE Intelligent Vehicles Symposium (IV). IEEE, 2018, pp. 1379–1384.
S. Aradi, “Survey of deep reinforcement learning for motion planning of autonomous vehicles,” IEEE Transactions on Intelligent Transportation Systems, vol. 23, no. 2, pp. 740–759, 2020.
T. Haarnoja, A. Zhou, K. Hartikainen, G. Tucker, S. Ha, J. Tan, V. Kumar, H. Zhu, A. Gupta, P. Abbeel et al., “Soft actor-critic algorithms and applications,” arXiv preprint arXiv:1812.05905, 2018.
J. Li, Y. Chen, X. Zhao, and J. Huang, “An improved dqn path planning algorithm,” The Journal of Supercomputing, vol. 78, no. 1, pp. 616–639, 2022.
A. Alizadeh, M. Moghadam, Y. Bicer, N. K. Ure, U. Yavas, and C. Kurtulus, “Automated lane change decision-making using deep reinforcement learning in dynamic and uncertain highway environments,” in 2019 IEEE Intelligent Transportation Systems Conference (ITSC), 2019, pp. 1399–1404.
H. Van Hasselt, A. Guez, and D. Silver, “Deep reinforcement learning with double q-learning,” in Proceedings of the AAAI Conference on Artificial Intelligence, vol. 30, no. 1, 2016.
J. Liao, T. Liu, X. Tang, X. Mu, B. Huang, and D. Cao, “Decision-making strategy on the highway for autonomous vehicles using deep reinforcement learning,” IEEE Access, vol. 8, pp. 177 804–177 814, 2020.
H. Seong, C. Jung, S. Lee, and D. H. Shim, “Learning to drive at unsignalized intersections using attention-based deep reinforcement learning,” in 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), 2021, pp. 559–566.
T. P. Lillicrap, J. J. Hunt, A. Pritzel, N. Heess, T. Erez, Y. Tassa, ..., and D. Wierstra, “Continuous control with deep reinforcement learning,” arXiv preprint arXiv:1509.02971, 2015.
J. Schulman, F. Wolski, P. Dhariwal, A. Radford, and O. Klimov, “Proximal policy optimization algorithms,” arXiv preprint arXiv:1707.06347, 2017.
D. Chen, L. Jiang, Y. Wang, and Z. Li, “Autonomous driving using safe reinforcement learning by incorporating a regret-based human lane-changing decision model,” in 2020 American Control Conference (ACC). IEEE, 2020, pp. 4355–4361.
X. He, H. Yang, Z. Hu, and C. Lv, “Robust lane change decision making for autonomous vehicles: An observation adversarial reinforcement learning approach,” IEEE Transactions on Intelligent Vehicles, vol. 8, no. 1, pp. 184–193, 2022.
G. Li, Y. Yang, S. Li, X. Qu, N. Lyu, and S. E. Li, “Decision making of autonomous vehicles in lane change scenarios: Deep reinforcement learning approaches with risk awareness,” Transportation research part C: emerging technologies, vol. 134, p. 103452, 2022.
J. Peng, S. Zhang, Y. Zhou, and Z. Li, “An integrated model for autonomous speed and lane change decision-making based on deep reinforcement learning,” IEEE Transactions on Intelligent Transportation Systems, vol. 23, no. 11, pp. 21 848–21 860, 2022.
C.-J. Hoel, T. Tram, and J. Sjöberg, “Reinforcement learning with uncertainty estimation for tactical decision-making in intersections,” in 2020 IEEE 23rd international conference on intelligent transportation systems (ITSC). IEEE, 2020, pp. 1–7.
C. Zhang, K. Kacem, G. Hinz, and A. Knoll, “Safe and rule-aware deep reinforcement learning for autonomous driving at intersections,” in 2022 IEEE 25th International Conference on Intelligent Transportation Systems (ITSC). IEEE, 2022, pp. 2708–2715.
L. Chen, X. Hu, B. Tang, and Y. Cheng, “Conditional dqn-based motion planning with fuzzy logic for autonomous driving,” IEEE Transactions on Intelligent Transportation Systems, vol. 23, no. 4, pp. 2966–2977, 2020.
G. Li, S. Li, S. Li, Y. Qin, D. Cao, X. Qu, and B. Cheng, “Deep reinforcement learning enabled decision-making for autonomous driving at intersections,” Automotive Innovation, vol. 3, pp. 374–385, 2020.
Y. Wu, G. Tucker, and O. Nachum, “Behavior regularized offline reinforcement learning,” arXiv preprint arXiv:1911.11361, 2019.
H. Kim, W. Wan, N. Hovakimyan, L. Sha, and P. Voulgaris, “Robust vehicle lane keeping control with networked proactive adaptation,” Artificial Intelligence, vol. 325, p. 104020, 2023.
J. Yang, H. Kim, W. Wan, N. Hovakimyan, and Y. Vorobeychik, “Certified robust control under adversarial perturbations,” in 2023 American Control Conference (ACC). IEEE, 2023, pp. 4090–4095.
M. Plappert, R. Houthooft, P. Dhariwal, S. Sidor, R. Y. Chen, X. Chen, T. Asfour, P. Abbeel, and M. Andrychowicz, “Parameter space noise for exploration,” arXiv preprint arXiv:1706.01905, 2017.
E. Leurent, “An environment for autonomous driving decision-making,” https://github.com/eleurent/highway-env, 2018.
A. Dosovitskiy, G. Ros, F. Codevilla, A. Lopez, and V. Koltun, “CARLA: An open urban driving simulator,” in Proceedings of the 1st Annual Conference on Robot Learning, 2017, pp. 1–16.

Figure 1. MDP flow diagram.

Figure 2. Schematic diagram of how the model works.

Figure 3. Flowchart of DQN with NoisyNet.

Figure 4. Flowchart of DDQN with NoisyNet.

Figure 5. Flowchart of SAC with NoisyNet.

Figure 6. Environment in highway_env, showing the initial state, the collision state, and the passage state.

Figure 7. Overhead view of town 4. A multi-lane road circumnavigates the town in a "figure of 8" shape.

Figure 8. The network also features an underpass and overpass with circular slip roads.

Figure 12. Reward distribution of DQN, DQN with

ε

-greedy and DQN with NoisyNet

Figure 12. Reward distribution of DQN, DQN with

ε

-greedy and DQN with NoisyNet

Figure 13. Reward distribution of DDQN, DDQN with

ε

-greedy and DDQN with NoisyNet

Figure 13. Reward distribution of DDQN, DDQN with

ε

-greedy and DDQN with NoisyNet

Figure 14. The red car in the middle represents the agent. This sequence of observations indicates that the algorithm can effectively avoid other cars and complete the driving task.

Figure 15. Comparison of Performance Metrics in CARLA Autonomous Driving.

Table 1. Key hyperparameters used in training stage.

Hyperparameter	Value
Camera number	3
Full FOV angles	$3 \times 60$ degree
Observation downsampling	$84 \times 252$
Initial exploration steps	100
Training frames	500,000
Replay buffer capacity	30,000
Batch size	64
Action repeat	4
Stacked frames	3
$Δ$ t	0.05 seconds
$C_{i}$	0.0001
$C_{s}$	1.0
Learning rate	0.0005
Optimizer	Adam

Table 2. Experimental results for DQN Variants

	Reward	Success rate	Minimum number of times to complete	Time for completion of tasks
DQN	2.62	52.8%	1220	6.58 s
DQN with $ε$ -greedy	3.05	62.5%	1240	6.41 s
DQN with NoisyNet	3.72	88.9%	240	6.01 s
DDQN	2.85	68.6%	370	6.40 s
DDQN with $ε$ -greedy	3.17	74.5%	290	6.25 s
DDQN with NoisyNet	4.12	91.2%	210	5.93 s
Improvement	57.25%	72.73%	82.79%	10.96%

Table 3. Comparison of Performance Metrics in CARLA Autonomous Driving Evaluation.

Methods	Distance	Eval Reward	Steer(%)
SAC	454.1±13.6	92.9±7.0	22.4±1.3
SAC+noisynet(Ours)	540.5±2.7	115.8±1.5	16.6±2.0

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Achieving Robust Learning Outcomes in Autonomous Driving with DynamicNoise Integration in Deep Reinforcement Learning

Abstract

1. Introduction

2. Related Work

3. Methods

3.1. Markov Decision Process Modeling

3.1.1. State Space

3.1.2. Action Space

3.1.3. Reward Function

3.1.4. Discount Factor: γ

3.2. The Proposed Framework

3.2.1. Overview

3.2.2. DQN with NoisyNet

3.2.3. DDQN with NoisyNet

3.3. Soft Actor–Critic with Noisy Critic

4. Experiment

4.1. Experiment in Highway_env

4.2. Experiment in CARLA

5. Results

5.1. Result in Highway_env

5.1.1. Rewards

5.1.2. Success Rate

5.1.3. Number of Iterations at Convergence

5.1.4. Time for Completion of Tasks

5.2. Result in CARLA

6. Conclusion

7. Patents

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe

3.1.4. Discount Factor: $γ$