Short-Term Forecasting of Total Aggregate Demand in Uncontrolled Residential Charging with Electric Vehicles Using Artificial Neural Networks

1. Introduction

One of the options to support the development of a cleaner and more sustainable world is to reduce polluting gases such as $C{O}_2$ that are emitted into the atmosphere. This gas strongly contributes to pollution that causes climate change, environmental crises, and global crises, causing great global concern [1].

The transportation sector is associated with a country’s economic base, where they are responsible and contributors to$C{O}_2$ [2] emissions. Allied to this, the current scenario of combustion transportation has been proliferating, increasing its contribution to climate change and energy crises [3].

The focus is on more significant global incentives for policies that accelerate the adoption of electric vehicles (EVs) and reduce and encourage transport decarbonization [4].

These new additions to EVs will cause a growing increase in power demand in distribution networks caused by the high and constant need to connect and charge their batteries. It is understood that this increase could generate serious problems for the electrical system [5] since batteries require high load demands during charging, meaning that the current electrical grid is not capable, in some cases, of meeting the required demand [6].

These new EV connections pose a significant challenge to the electrical power system, as EVs can be charged in private homes, buildings, companies, and private and public charging stations [7].

In this context, ensuring projections and forecasts of electrical loads in the short term has become a timely and relevant topic for concessionaires, the electrical energy market, and academic research. Load forecasting is not easy, as loads correlate not only between hours, days, weeks, or months but also with human behavior and exogenous variables, such as humidity, temperature, and seasons [8].

Introducing Artificial Neural Networks (ANNs) means that electrical charge prediction problems can be solved more efficiently and accurately, as this technique learns from past data, saving certain information for later use [9], which has motivated us to use an ANN model in this research. Learning models with ANNs are currently widely used in this topic in charging demand forecasting and simultaneous VES charging problems, among others.

The present work aims to apply ANN based on the multilayer feedforward perceptron (MLP) [10] architecture using hybrid supervised training backpropagation with Bayesian regularization [11] to forecast the total demand generated by charging EVs plugged into homes. Forecasts were made for the next 24 hours of total aggregate demand in each year’s season for comparative purposes.

2. Uncoordinated Residential EV Charging and Impacts

In uncoordinated residential charging, EVs begin charging instantly when plugged into an outlet, and charging can happen at any time, 24 hours a day. These loads have a highly random profile and behavior. Currently, the electricity sector does not recommend it. It does not have much incentive for this type of charging, as they do not present the necessary usage information for scheduled or delayed managed charging, ensuring the optimization of EV charges. By delaying the start of charging, EVs are charged at off-peak times [17].

This charging does not present information on energy prices and is without any control or strategy. EV users can plug and unplug at any time or even charge the battery altogether [12].

The high integration of EVs into the electrical power system will present challenges due to the uncoordinated increase in EV connections in homes, particularly to the distribution system. These loads from residential charging combined with EVs can lead to a significant peak increase, creating a lack of power, grid congestion, voltage and frequency instability, and electrical component failures [13].

Specifically, in this scenario, EV loads require a high connection for an extended period, coinciding with peak residential demand. As the current system is not designed for high EV penetration rates, the high rate of uncoordinated EV charging may negatively impact the electrical power system’s distribution, generation, and transmission infrastructure [14,15].

Generally, energy utilities represent demands through customer profiles for each behavior, using load curves over time [17]. Each curve is represented by a different profile, which can be public, residential, commercial, or industrial [16].

The impacts generated by EVs are significant due to the high power required in aggregate charging and the mass implementation of EVs that the electric mobility sector is going through [18]. The charging of Plugable Electric Vehicles VEPs and Plugable Hybrid Electric Vehicles VEHP will affect the electrical energy system with the additional load on residential demand, generating a new total aggregate demand. These batteries are charged mainly in residential plugs with power levels 1 and 2 when the VEPs are parked in garages in the morning and evening [19].

The high rates of connections by VEPs in the electrical distribution network lead to operation problems [14]. The distribution systems were designed for conventional load traffic capacity, such as residential or commercial, based on the profiles of each consumer. When VEPs are connected, there is a significant change in these profiles and energy demand due to the high power delivered in a shorter space of time for residential charging, buildings, commercial locations, and public charging stations [20].

3. EV Charging Demand Forecast

EV loads have specific characteristics distinct from residential loads, with different spatial and temporal distribution profiles. This charging requires high power due to its highly periodic and fluctuating behavior. EV charging curves show several power peaks, especially in small time intervals throughout the day [21].

Traditionally, time series forecasts are made using historical data or modeling simulations. In this way, they play a decisive role in forecasting. However, predictions with EVs involve several uncertainties and volatility because they are new types of load with the characteristics previously described. Such load profiles have growth rules and non-stationary and stochastic characteristics. With this, it was observed that for time series data in which the output has a certain degree of correlation to time, ANNs are more appropriate, as models based on ANNs consider previous information in the past to make new future projections [22].

The main difficulties in forecasting the total charging demand for VEPs can be cited as volatile loads, availability of public data, spatial and temporal distribution characteristics, different charging modes, varying penetration rates of EVs in the network, uncontrolled growth of charging, and demand spikes [22]. With the increase in EV adoptions, EV charging is predicted to impact the power grid notably.

Furthermore, the need for a constant high power supply demonstrates a critical degree for charging EVs. The high power requirement for charging EVs causes enormous constraints on the grid. For this purpose, the need arose to accurately predict the charging load of EVs simultaneously with residential charging, and this will help grid operators to properly manage power distribution and make certain decisions [23].

4. Multilayer Perceptron Artificial Neural Network

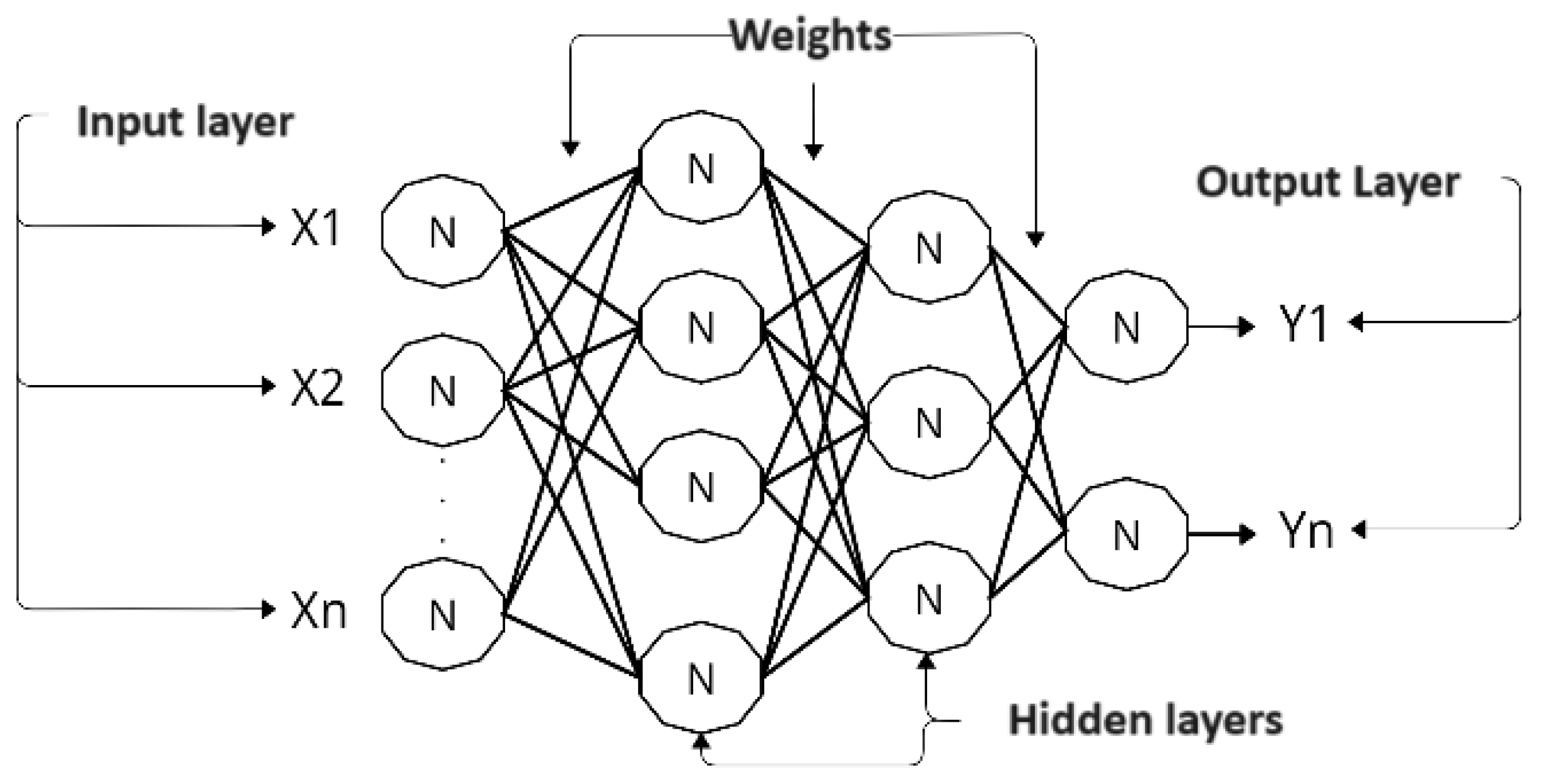
Multilayer perceptron (MLP) [10] ANNs are fully connected layered architecture networks. Neurons in any network layer are always connected to all other neurons in the previous layer, which are interconnected directly in an input layer through weights. This type of network has layers in levels, $i.e.$, an input layer containing one or more neurons, one or several hidden layers, and an output layer containing one or more neurons. Each layer has nodes, and each node is directly connected by weights with nodes in the next layer (Figure 1), being $[X_1,X_2,\dots ,X_n]$ network input signals; N neurons; $weights$ weights the synaptic weights of neuron N; $[Y_1,Y_2,\dots ,Y_n]$ output signals from N neurons.

MLP transforms its linear inputs through a non-linear activation function (1) [9]:

$$x_o=f\left(\sum _{h=1}^H\left(x_h{w}_{h,o}\right)\right)$$

(1)

where f is the activation function of the o-th neuron of the output layer; $x_h$ the output of the h-th hidden layer neuron; $w_{h,o}$ the interconnection between the h-th neuron of the hidden layer and the o-th neuron of the output layer, and H the size of the hidden layer.

The transfer function or also called activation defines the type of output of a neuron. The most common activation functions are the relay-type functions, the semi-linear function, the sigmoid function and the hyperbolic tangent [24]. We can exemplify the hyperbolic tangent type sigmoid function (2):

$$f\left(x\right)={\displaystyle \frac{(1-e^{-\lambda x})}{(1+e^{-\lambda x})}}$$

(2)

where $\lambda$ is the slope of the curve.

5. Backpropagation Training with Bayesian Regularization

The $backpropagation$ (BP) training algorithm with Bayesian regularization (BR) minimizes a combination of quadratic errors and weights and then determines the correct combination to produce training output with high generalization ability [11].

This BR training aims to avoid training overfittings and improve generalization capacity. This training adds a new coefficient to the optimization process, which penalizes the objective function F by increasing the number of [11] coefficients.

In [11] regularization, the objective function F is modified using the sum of the mean squared errors coming from backpropagation, called $E_D$, and, subsequently, the objective function is increased by the term additional $E_w$, which is the sum of the squared errors of the network weights bias (3):

$$F=\beta E_D+\alpha E_w$$

(3)

with $\alpha$ and $\beta$ being the regularization parameters of the objective function, these variables control the training emphasis. While $\alpha \ll \beta$ training will focus on minimizing errors in the trained data. And while $\alpha \gg \beta$, training will prioritize minimizing the values of the weights generated by network errors.

The main training challenge is how the terms $\alpha$ and $\beta$ are defined to control the objective function. In the Bayesian process, weights are treated as random variables. After obtaining the training data, the weight density function is updated by the Bayes theorem (4).

$$P\left(W\right|D,\alpha ,\beta ,M)={\displaystyle \frac{P\left(D\right|W,\beta ,M\left)P\right(W|\alpha ,M)}{P\left(D\right|\alpha ,\beta ,M)}}$$

(4)

on what M is the network architecture used; D the training matrix; W the weight matrix; $P\left(W\right|\alpha ,M)$ the prior density, representing knowledge of the weights before any data was collected; $P\left(D\right|,W|,\beta ,M)$ the likelihood function, which is the probability of a certain event occurring, considering the weights W; and $P\left(D\right|,\alpha ,\beta ,M)$ the normalization factor, which guarantees that the total probability is 1.

If it is assumed that the data in the training set is of type Gaussian and its prior distribution for the weights is Gaussian, then probability densities can be written (5) in the following way:

$$\begin{array}{c}\hfill P\left(W\right|D,\alpha ,\beta ,M)={\displaystyle \frac{1}{Z_D^{\beta }}}{e}^{(-\beta E_D)}\\ \hfill \\ \hfill P\left(W\right|\alpha ,M)={\displaystyle \frac{1}{Z_W^{\alpha }}}{e}^{(-\alpha E_W)}\end{array}$$

(5)

being $Z_D^{\beta }={\left({\displaystyle \frac{\pi }{\beta )}}\right)}^{n/2}$ e $Z_W^{\alpha }={\left({\displaystyle \frac{\pi }{\alpha }}\right)}^{N/2}$.

Replacing these probabilities in (4), we can rewrite the calculation as follows (6):

$$\begin{array}{ccc}\hfill P\left(W\right|D,\alpha ,\beta ,M)& =& {\displaystyle \frac{\frac{1}{Z_W^{\alpha }}\frac{1}{Z_D^{\beta }}{e}^{(-(\beta E_D+\alpha E_W))}}{FN}}\hfill \\ \hfill \\ & =& \left({\displaystyle \frac{1}{Z_F(\alpha ,\beta )}}{e}^{-F\left(W\right)}\right)\hfill \end{array}$$

(6)

where $FN$ is the normalization factor.

In this Bayesian step, the optimal weights maximize the posterior probability $P\left(W\right|D,\alpha ,\beta ,M)$. Then, maximizing the posterior probability is equivalent to minimizing the regularized objective function $F=\beta E_D+\alpha E_W$.

5.0.1. Optimization of Regularization Parameters

In this step, the application of Bayes theorem is demonstrated to calculate the optimization of the parameters $\alpha$ and $\beta$ of the objective function F (7):

$$P(\alpha ,\beta |D,M)={\displaystyle \frac{P\left(D\right|\alpha ,\beta ,M\left)P\right(\alpha ,\beta \left|M\right)}{P\left(D\right|M)}}$$

(7)

According to the uniform prior density $P(\alpha ,\beta |M)$ for the regularization parameters $\alpha$ and $\beta$, then maximizing the posterior density is possible by calculating its likelihood function $P\left(D\right|\alpha ,\beta ,M)$. It is observed that this function is the normalization factor for (4). Assuming that all probabilities have a Gaussian form, the form for the given posterior density (4) is known. It was demonstrated in (6) and it can be solved (4) for the normalization factor (8):

$$\begin{array}{ccc}\hfill P\left(D\right|\alpha ,\beta ,M)& =& {\displaystyle \frac{P\left(D\right|W,\beta ,M\left)P\right(W|\alpha ,M)}{P\left(W\right|D,\alpha ,\beta ,M)}}\hfill \\ & =& {\displaystyle \frac{\left(\left[\frac{1}{Z_D^{\left(\beta \right)}}{e}^{(-\left(\beta E_D\right))}\right]\left[\frac{1}{Z_W^{\left(\alpha \right)}}{e}^{(-\left(\alpha E_W\right))}\right]\right)}{\frac{1}{Z_F^{(\alpha ,\beta )}}{e}^{(-\left(\alpha E_W\right))}}}\hfill \\ & =& {\displaystyle \frac{Z_F^{(\alpha ,\beta )}}{Z_D^{\left(\beta \right)}{Z}_W^{\left(\alpha \right)}}}{\displaystyle \frac{e^{(-\beta E_D-\alpha E_W)}}{e^{(-FW)}}}\hfill \\ & =& {\displaystyle \frac{Z_F^{(\alpha ,\beta )}}{Z_D^{\left(\beta \right)}{Z}_W^{\left(\alpha \right)}}}\hfill \end{array}$$

(8)

We can observe that the constants $Z_D^{\left(\beta \right)}$ and $Z_W^{\left(\alpha \right)}$ calculated in (5) are known. The only unknown constant is $Z_F^{(\alpha ,\beta )}$. Caused by Taylor series expansion. One can expand $F\left(W\right)$ around the minimum point of the posterior density $W^{MP}$, where the gradient calculation is null. Calculating the normalization constants:

$$Z_F\approx {\left(2\pi \right)}^{{\displaystyle \frac{N}{2}}}{(det\left({\left(H^{MP}\right)}^{-1}\right))}^{{\displaystyle \frac{1}{2}}}{e}^{(-F\left(W^{MP}\right))}$$

(9)

where $H=\beta {\nabla }^2{E}_D+\alpha {\nabla }^2{E}_D$ is a Hessian matrix of the objective function F.

With the result of the calculation in (8) it is possible to calculate the optimal values for $\alpha$ and $\beta$ at the minimum point. Taking the derivative with respect to each of the log of (8) and setting them equal to zero will result in (10):

$$\begin{array}{c}\hfill {\alpha }^{MP}={\displaystyle \frac{\gamma }{2E_W\left(W^{MP}\right)}}\\ \hfill \\ \hfill {\beta }^{MP}={\displaystyle \frac{n-\gamma }{2E_D\left(W^{MP}\right)}}\end{array}$$

(10)

where $\gamma =N-2{\alpha }^{MP}{\left(H^{MP}\right)}^{-1}$ called the effective number of parameters and N is the total number of parameters in the network. The $\gamma$ parameter is a measure of how many neural network parameters are effectively used to minimize the error objective function. It can range from zero to N.

5.0.2. Calculation of the Gauss-Newton Approximation for the Hessian matrix

BR training requires calculating the Hessian matrix (H) of the objective function $F\left(W\right)$ for the minimum point $W^{MP}$. This approximation can be calculated using the Levenberg-Marquardt optimization algorithm to find the minimum point [25].

6. Materials and Methods

To apply the proposed method, the data set proposed is in reference [19]. The data are from 200 private residences in the Midwest region of the United States (USA). The household composition included 502 individuals and 348 EVs. The load profiles were measured regarding electrical power in Watts (W), with a resolution of 10 minutes over one year. VEPs with 60% load and Pluggable Hybrid Electric Vehicles (PHEV) with 40% load were considered, all charged with a level 1 plugged with a power of 1920 W.

6.0.3. Pre–Processing and Processing

As the original data has a resolution of 10 minutes in the very-short term, it was decided to group the measurements for a resolution of 1 hour in the short term. All home measurements and all EV charging were added together each hour, forming measurements from 00:00 to 23:00. The transformation was done by reducing 144 measurements (10-minute resolution) to 24 measurements (1-hour resolution) each day.

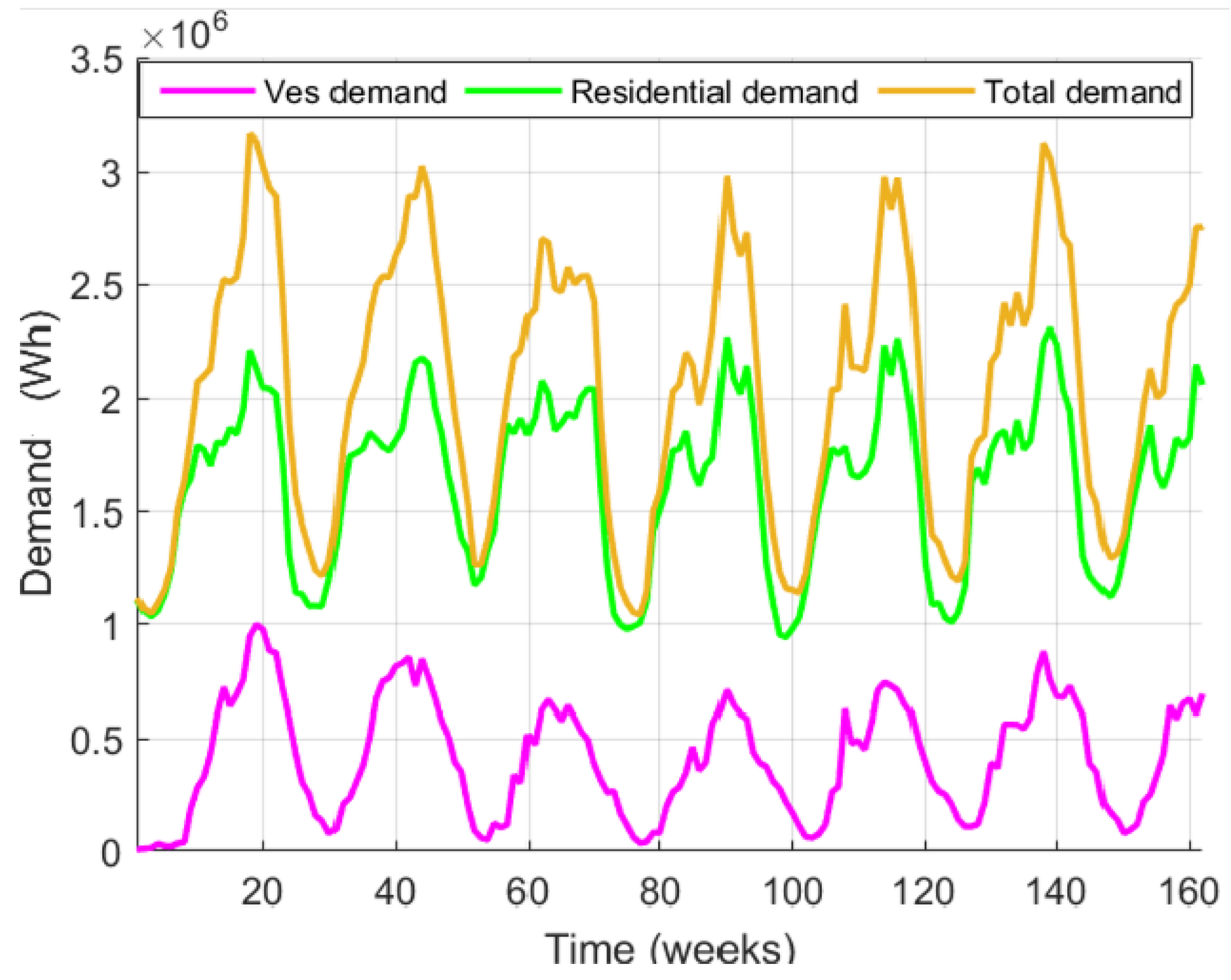
The data was separated into two demands: the first represented by residential demand and the second by EV demand. A single column containing all measurements was generated for each demand by adding the 200 homes and 348 vehicles, forming vectors of 8760×1, data from the two consumptions over one year. The total demand (11) was obtained by the sum of all respective loads every hour, day, and month between the two demands, residential and EVs (Figure 2):

$$D_{total}=D_{residential}+D_{vehicles}$$

(11)

where $D_{total}$ is the total aggregate demand for forecasting; $D_{residential}$ total residential demand; $D_{vehicles}$ total EV demand.

6.1. Separation of Training and Testing Data Sets

When separating the training and testing data sets, total aggregate demand was used. The total set made up of 8760 measurements was divided into the 4 seasons of the year, for the purpose of comparisons and analysis of seasonality. In this way, 4 forecasts were proposed for the next 24 hours, one for each season of the year. The input and test matrices are composed of the variables:

• Days: $[1\dots 31]$ = day variables;
• Weeks: $[1\dots 7]$ = variables for the weeks from Monday to Sunday;
• Months: $[1\dots 12]$ = variables from the months of January to December;
• Times: $[00\dots 23]$ = variables in hours $\left(h\right)$ in the 24-hour period;
• Loads $\left(h\right)$: [total aggregate demand] = load variables referring to the hour $\left(h\right)$ in Watts.

The ANN output set is composed of the total aggregate demand variable, with $(h+1)$ representing the load measurements for the following hour $(h+1)$, in Watts.

The dataset was separated into 83% for training and 17% for testing. The dimensions of the datasets are presented in Table I.

6.2. Configuration and Architecture of the ANN

Initially, it was decided to divide the 1-year database into the year’s four seasons, as climate change has direct links to consumption patterns and profiles of EVs and homes. With this, predictions become more realistic and perform better. To obtain a better configuration for the ANN architecture, exhaustive tests were carried out by varying the number of hidden layers and the number of neurons in the hidden layers. The best configuration found was the one with six neurons in the first hidden layer, 2 in the second hidden layer, and 1 in the third hidden layer. The hyperbolic tangent activation function was used.

6.3. Prediction Performance Evaluation

The methodology used to evaluate forecast successes and errors was the mean absolute percentage error (MAPE) (12) [26].

$$MAPE={\displaystyle \frac{1}{Num}}\sum _{h=1}^{Num}\left(\left|{\displaystyle \frac{C_{\left(h\right)}-C_{forecast\left(h\right)}}{C_{\left(h\right)}}}\right|\right)*100$$

(12)

where $Num$ is the total number of hours; $C_{\left(h\right)}$ the actual value at time h and $C_{forecast\left(h\right)}$ the value predicted by the network at time h.

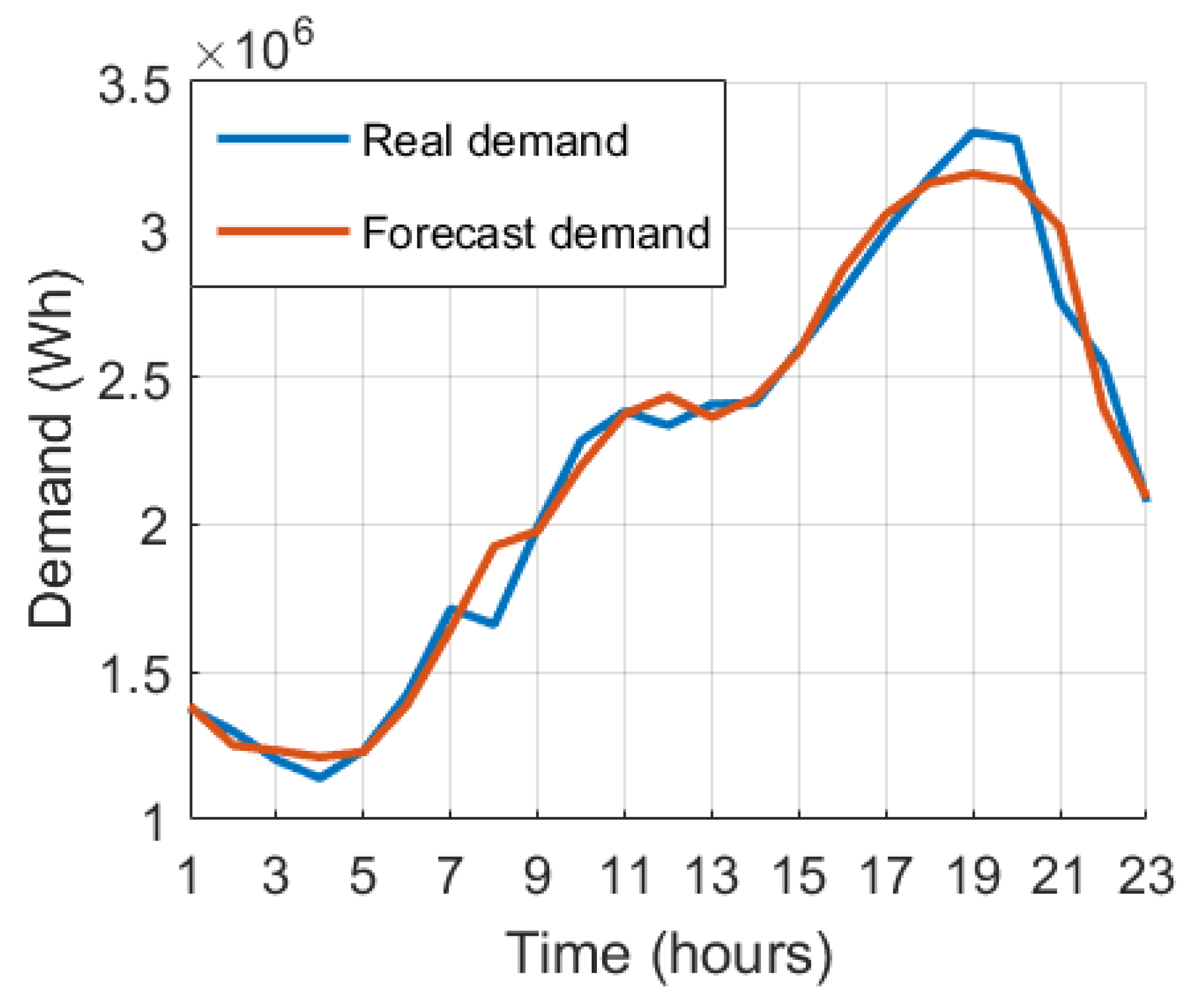
Figure 3. 24-hour winter demand forecast.

Figure 3. 24-hour winter demand forecast.

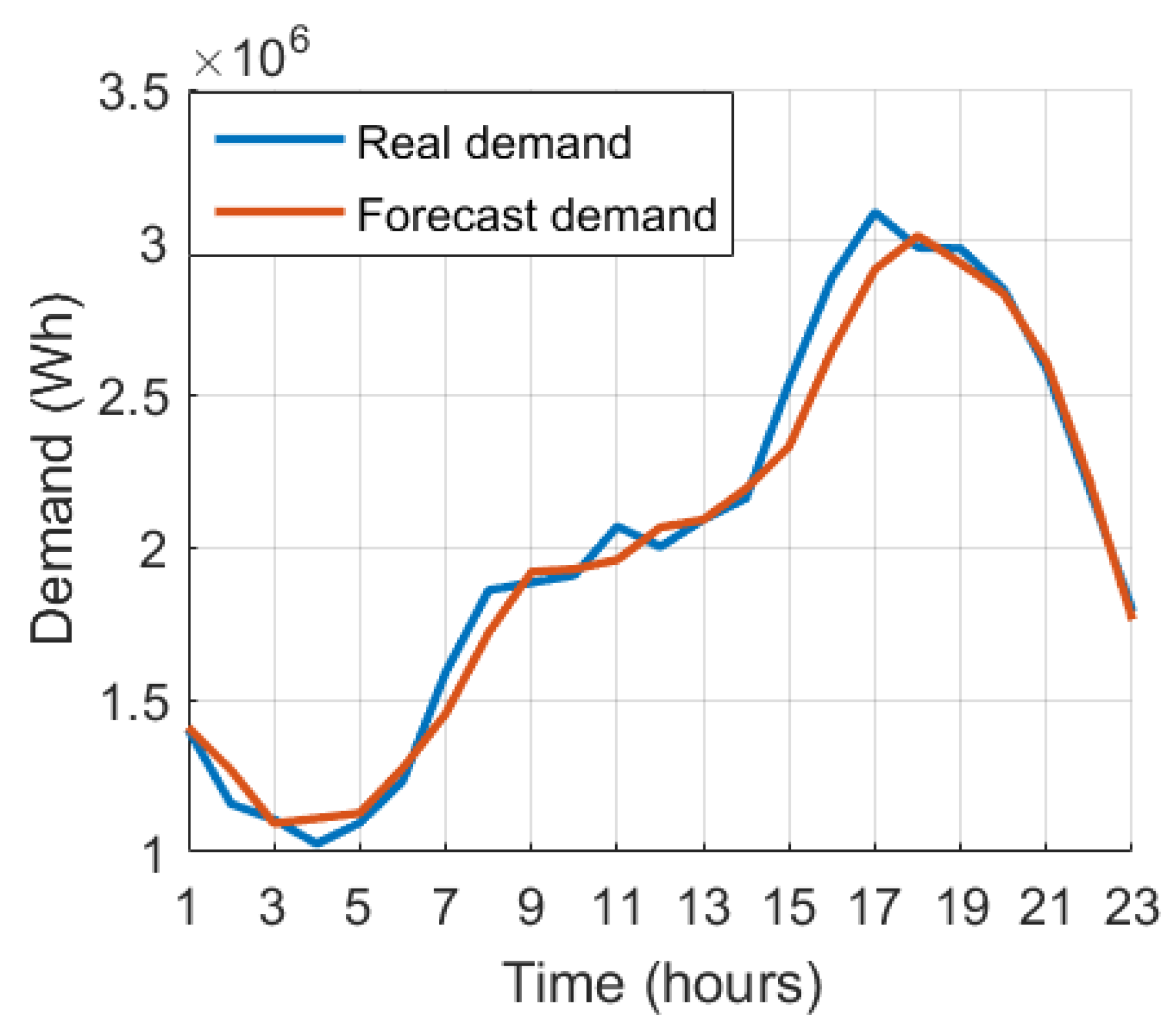
Figure 4. 24-hou r fall demand forecast.

Figure 4. 24-hou r fall demand forecast.

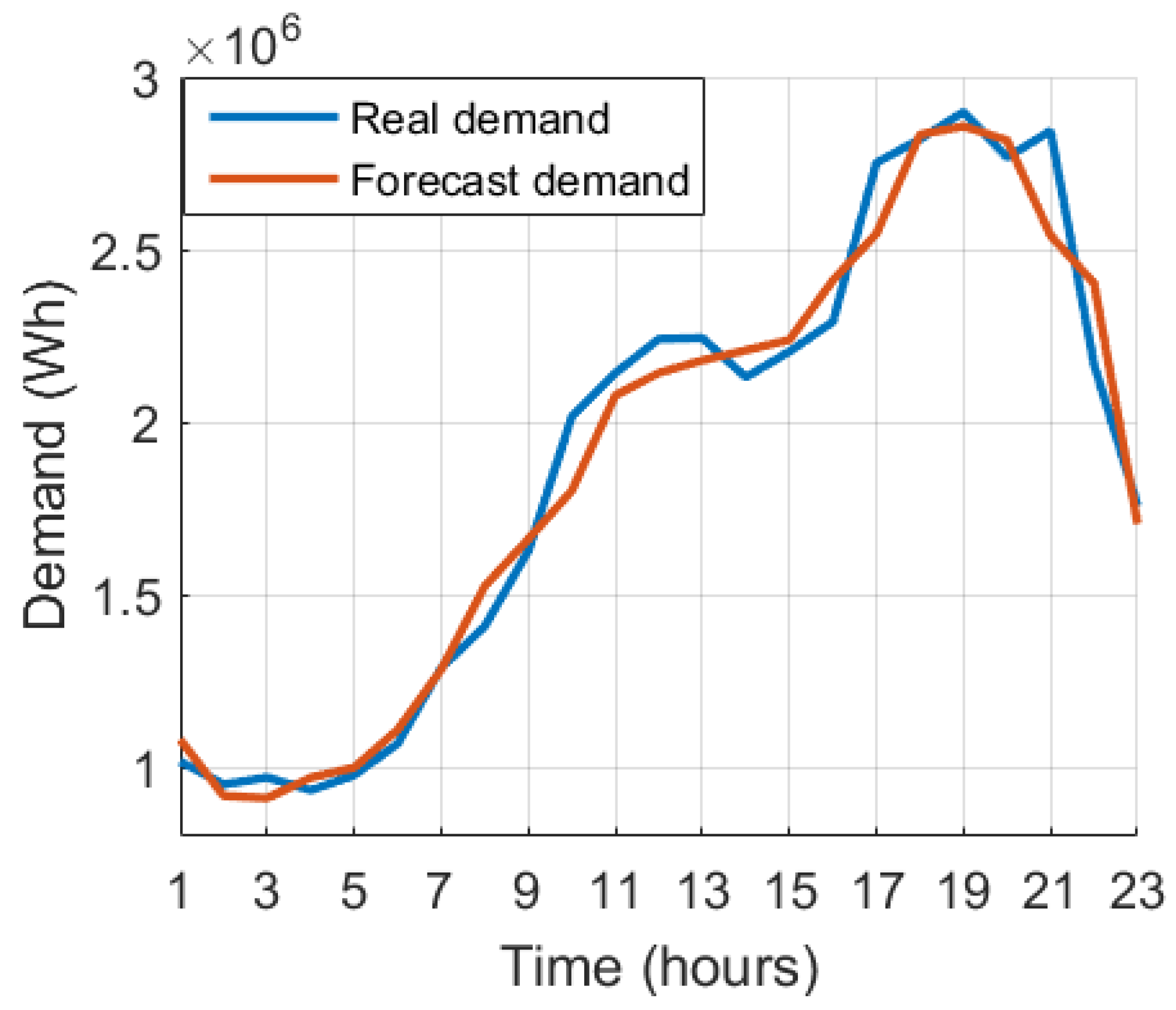
Figure 5. 24-hour spring demand forecast.

Figure 5. 24-hour spring demand forecast.

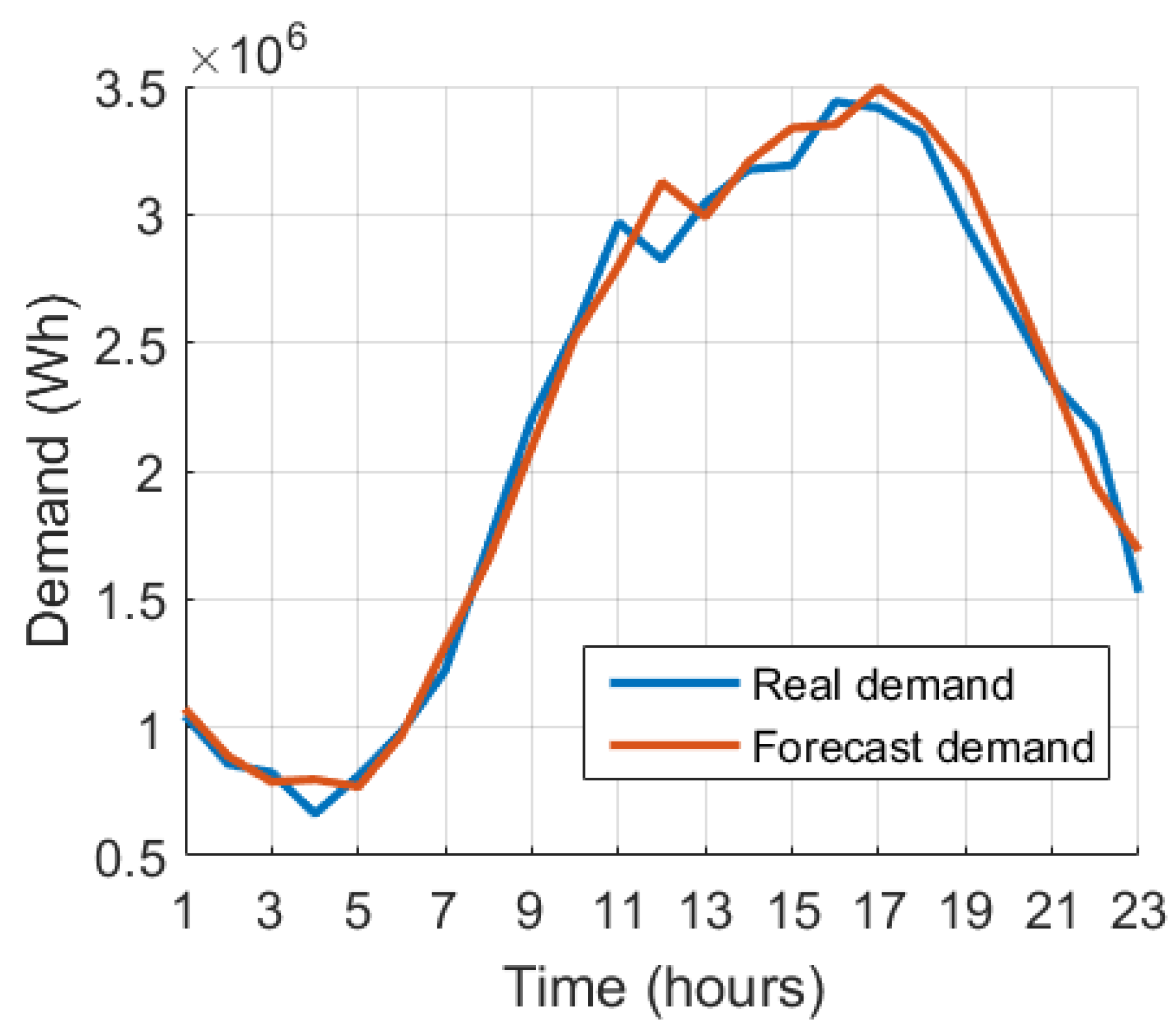
Figure 6. 24-hour summer demand forecast.

Figure 6. 24-hour summer demand forecast.

7. Results

The software used for modeling, training, and prediction was Matlab 2023b. In training, the data set is divided randomly by default; even when splitting the set into 83 %, the algorithm divides this value in random order to make the training process more robust without being associated with a single answer.

Tests were carried out on the configurations of the hidden layers and their number of neurons, and it was observed that the best configuration of the network is with three hidden layers. This configuration was the best performing due to the accuracy and stability of the training response. It was noted that, with fewer than three hidden layers, the network loses precision, demonstrating a limitation of the network in training, and with more than three layers, the network loses training stability. The architecture of the proposed model achieved a significant improvement in the learning process, finding the best configuration of the numbers of neurons and hidden layers.

Table II presents the MAPE results obtained for each season of the year.

8. Discussion

It was possible to observe that using only backpropagation training the response is not satisfactory, that is because a hybrid training with Bayesian Regularization is used. With the union of the two training sessions, the network obtained a significant improvement in results, as Bayesian regularization determines the probability of an event happening given the saved learning. With these improvements, the proposed architecture and technique increase its effectiveness.

In the spring forecast, the biggest errors were found during the night, between 7 pm and 9 pm, with average errors of $\pm 10\%$. This is due to the peak generated by EVs during this period. It was also seen that in the morning, at precisely 9 am, the network showed an error of $10,644\%$.

It was observed that the highest load peaks due to the penetration of EVs are found in the morning (between 7 am and 12 pm) and also at night (between 6 pm and 9 pm). With these peaks in residential demand, the maximum errors are found at these times. It was observed that between 1 pm and 6 pm the forecasts had low errors, caused by the low charge of the EVs.

The forecast for summer presented the biggest errors when compared to the other three seasons, with three very pronounced error times: in the morning with a $20\%$ error (largest error), in the lunch period with $10\%$ of error and at night with $10\%$ of error (between 9 and 10 pm).

For the winter period, the network obtained the lowest errors compared to the other seasons. However, it obtained a maximum error of $15.9345\%$ in the morning peak hour and at this point the network was optimistic, that is, it overestimated the demand at the predicted time.

The fall forecast resulted in the MAPE being just above the winter forecast. At peak loading times the maximum error was $9,540\%$.

It is also observed that due to the amount of trained data from the winter and summer seasons being greater than the others, this division generated greater maximum errors than the others, arround 15.934% in the winter and 20.228% in the summer.

The growth in the adoption of EVs in residential charging had a major impact on the electrical power system. The forecast of total loading demand presents itself as an important strategic tool in a scenario with a broad growth trend and with great openness for exploration and investigation.

The MLP network and the proposed training showed good generalization capacity, with satisfactory results and fast convergence, with training time between 5 and 15 seconds and 200 to 500 iterations. The use of three hidden layers was of great importance for the training generalization process, increasing the quality of the results. The proposed model showed an improvement in learning due to hybrid training, which resulted in more realistic responses, satisfying the need for reliable predictions with more precision and robustness.

9. Conclusions

Total demand forecasting presented itself as a promising option for future projections, having the ability to estimate new demands based on EV loads added to residential load, instead of just making forecasts in EVs. In this way, the ANN learned the behavior of residential loads, EVs and both being used simultaneously.

The proposed methodology presented promising answers to a topic in high and rapid expansion, relatively recent and with great potential for practical application in future research. The proposal, due to its efficiency and reliability in results, has the possibility of being implemented in order to assist in the development of a robust strategy, preparing the power system for new EV penetration rates. This work also has the potential to assist in the development of strategies for smart charging, optimizing the EV charging process.