Prerpints.org logo
Preprint
Article

Design and Implementation of an Ultra-Wideband Water Immersion Antenna for Underwater Ultrasonic Sensing in Microwave Induced Thermoacoustic Tomography

Altmetrics

Downloads

75

Views

21

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

29 August 2024

Posted:

30 August 2024

You are already at the latest version

Alerts
Abstract
Microwave-induced thermoacoustic tomography (MITAT) holds significant promise in biomedical applications. It creates images using ultrasonic sensors to detect thermoacoustic signals induced by microwaves. The key to generating thermoacoustic signals that accurately reflect the fact is to achieve sufficient and uniform microwave power absorption of the testing target, which is closely tied to the microwave illumination provided by the antenna. In this article, we introduce a novel design and implementation of an ultra-wideband water immersion antenna for an MITAT system. We analyze and compare the advantages of selecting water as the background medium. Simulations are conducted to analyze the ultra-wideband characteristics in impedance matching, axial ratio, and radiation pattern of the proposed antenna. The measured |S11| shows good agreement with the simulated results. We also simulate the microwave power absorption of tumor and brain tissue, and the uniform microwave power absorption and high contrast between the tumor and brain indicate the excellent performance of the proposed antenna in the MITAT system.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Cancer is a large group of diseases that starts in almost any organ or tissue of the body, and the key to improving cancer outcomes and cancer survival is early detection [1,2]. Various methods have been evaluated as cancer screening tools. Among these, medical imaging technology occupies an important place [3,4,5,6,7]. However, different imaging methods are appropriate for different medical needs. X-ray computed tomography (CT) is mature and widely used, but its ionizing radiation makes it unsuitable for broad screening and frequent use [8,9]. Magnetic resonance imaging (MRI) is non-ionizing and obtains clearer images of soft tissues such as the brain, ovary, and liver. However, it is time-consuming and expensive, which brings limitations to routine cancer screening [10,11]. Ultrasound imaging (UT) is one of the conventional medical examination methods in present hospitals [12,13]. It is non-ionizing, has a low cost, and has a high resolution. However, it does not apply to tumor cell detection when the acoustic impedance difference between a tumor and the surrounding tissue is small, such as the tumor in the brain and breast. Microwave imaging (MWT) is an emerging research field that avoids using ionizing radiation and would be inexpensive, quick, and comfortable for patients [14,15]. When the human body is illuminated with microwave radiation, tumors, and the surrounding tissues induce different reflections and scatterings due to the differences in dielectric properties [16]. However, two main challenges of low resolution and difficulty in identifying received signals from same-frequency transmitted signals have limited its use.
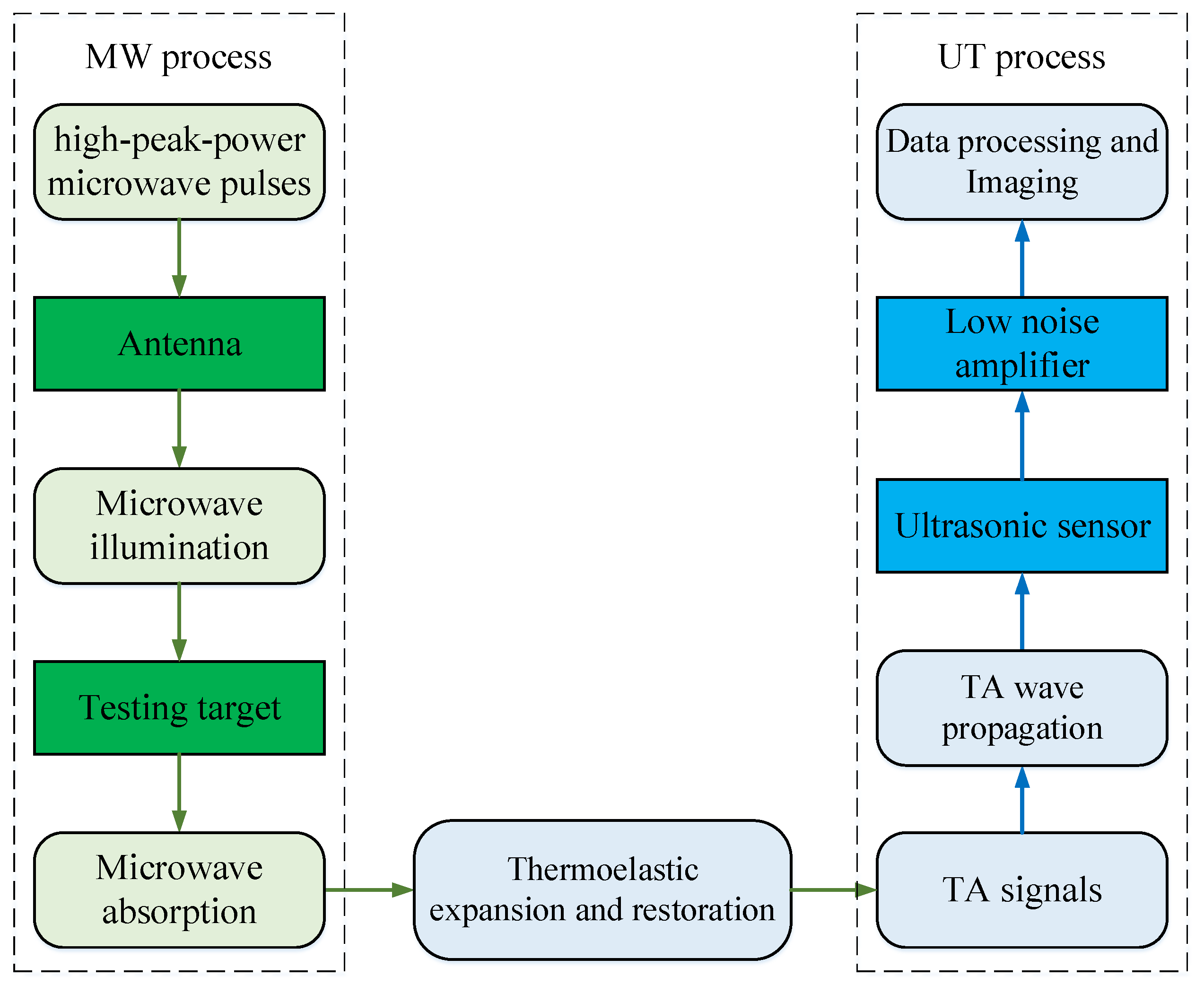
Based on the interdisciplinary research of electromagnetics, acoustics, biology, and medical science, microwave-induced thermoacoustic tomography (MITAT) has become another potential alternative technique for medical imaging [17,18,19]. The physical mechanism is based on the thermoacoustic phenomenon. When the tissue is illuminated by high-peak-power microwave pulses, it absorbs microwave energy and generates microwave-induced thermoacoustic signals (TA signals) due to thermoelastic expansion. The TA pressure amplitude PMIT is proportional to the quantity of the absorbed microwave power PMW, and PMW has a functional relationship with the electrical property of the tissue. The relationship between PMIT and PMW is shown in Equation (1), α is the attenuation coefficient. When the testing target contains different kinds of tissues, such as tumors and the surrounding healthy tissues, it generates different values of PMIT. After that, an ultrasonic sensor runs a full scan of electric machinery and transmits the data to the computer to complete data processing; then, the microwave power absorption distribution map is reconstructed, which is the image of the testing target. The detection of ultrasonic signals is also run by a sensor array [20].
P M I T ∝ 2 α P M W
The block diagram of the whole process of the MITAT system is shown in Figure 1. The system is divided into two parts: the MW process and the UT process. The former contributes similar high contrast with MWT due to the large difference in dielectric conductivity between a tumor and the surrounding tissue, the latter contributes high resolution with UT. The integration of the advantages of MWT and UT extends the application range of MITAT.
The data source of computer processing and imaging is obtained from ultrasonic sensor detection, whose accuracy and reliability determine the image quality [21]. One of the solutions to obtain satisfied sensor detection results is to improve the accuracy of the microwave power absorption condition of the target, which is closely related to the microwave illumination from the antenna.
In this work, in order to meet the requirements mentioned above, the following three issues are concerned with the design of the proposed antenna. Firstly, the core circuits are designed using microstrip lines with the advantages of low profile, low fabrication cost, high radiation efficiency, and ease of manufacturing. Secondly, the antenna is circularly polarized. A common problem in the MITAT is the nonuniform microwave power absorption resulting from the inhomogeneous microwave illumination [22,23,24]. Using a circularly polarized antenna has been demonstrated to be useful in achieving more uniform microwave power absorption in tumors by Yu He et al. [25], thereby reducing the adverse effect of inhomogeneous illumination. Lastly, the antenna is operating underwater. As shown in Figure 1, microwave and ultrasonic waves flow in the system simultaneously, and water is the conditioner that decreases the power propagation losses and return losses of both. Other materials may also be used as the background medium, but water has the advantage of lower power loss and is readily available.
In recent years, underwater wireless communication has drawn the attention of the research community due to its broad applications, including underwater wireless sensor networks [26], remote-operated vehicles, and diver-to-diver communications. To develop reliable and efficient underwater communication, significant effort has been devoted to the designing of water immersion antennas [27,28,29,30]. Most of the reported antennas are electrically small, which either have low radiation efficiency due to high ohmic loss or use inefficient nonresonant size that leads to huge power consumption [31,32,33]. The magnetoelectric antennas that radiate electromagnetic waves by physically moving, rotating, or oscillating the electric charges or magnetic dipole moments have provided a possible way to miniaturize the antenna[34,35,36,37], but the problems of power inefficient and not easily packaged in water could not meet the challenge of high peak power radiation in the MITAT system [38,39,40,41].
Evangelia A. Karagianni proposed a bow-tie microstrip antenna for a wireless sensor network (WSN) that is used to monitor environmental or physical phenomena of the sea and cooperatively disseminate the data through the network of sensors to a shore access point [42]. The antenna is omnidirectional with a gain of 1.2 dBi. The input reflection coefficients under seawater are -12 dB and -16 dB at the S and C bands, respectively. Majid Ostadrahimi et al. made an array that contains 24 dipole elements for microwave imaging [43]. The impedance matching condition is optimized by adjusting the salinity of the background medium. David Gibbins et al. proposed a wide-slot UWB antenna for an MWT system [44], of which the background medium is specially prepared and has similar dielectric properties with human breast tissue in order to reduce reflections by eliminating the air/skin interface. However, this leads to additional preparation for experiments and limits the application of the system.
This article proposed a water immersion antenna for the MITAT system that features a simple structure, small size, easy fabrication, ultra-wide bandwidth, and circular polarization.

2. Power Loss Analysis

The special feature of the MITAT system is that there are two kinds of waves in the background medium when it is imaging, as shown in Figure 1. Therefore, the background medium should be friendly to both waves, which means the power losses related to it must be low. To simplify the analysis, we ignore the power losses induced by the antenna radiation angle, as well as some other power losses, like the possible impurities in the background medium and the scattering. Thus, the power losses of both waves occur only in two ways: the power transmission loss in the background medium and the reflection loss on the interface of the tissue. Table 1 shows the parameters related to three common background media and four types of biological tissues. The power attenuation mechanisms of microwave and acoustic waves are different and are discussed separately in the following sections.

2.1. Ultrasonic Wave Power Loss

The ultrasonic wave transmission loss is analyzed by Equation (2), in which pz is the pressure amplitude at a distance of z meters from the source, p0 is the sound pressure of the source, αu is the ultrasonic attenuation coefficient of the background medium. On referring to the αu values in Table 1, it decreases from air, mineral oil to water, and there is almost no attenuation in water. Therefore, the ultrasonic wave propagation loss is the lowest in water.
p z = p 0 e − α u z
The reflection loss of the ultrasonic wave on the interface of the tissue is qualitatively analyzed by the acoustic impedance difference |ΔZ| between the tissue and the background medium. Reflection occurs when |ΔZ| is bigger than 0.1%, and larger |ΔZ| means stronger reflection and higher power loss. Acoustic impedance Z of a material is calculated by Equation (3), in which P is the density, and C is the sound speed in the material. The |ΔZ| of the four tissues in Table 1 have been calculated, and the results are shown in Figure 2 (a). For breast fat, the values of |ΔZ| with the two kinds of background medium are close, indicating similar power losses. For the brain, skull, and muscle, using water as the background medium has clearly smaller values of |ΔZ|, indicating that the reflection losses are smaller in water.
Z = P × C

2.2. Microwave Power Loss

Under the hypothesis above, the microwave power loss occurs only in two ways: the transmission loss PL in the background medium and the reflection loss RL on the interface of the tissue. Therefore, the total power loss L is calculated by Equation (4).
L = P L + R L
To calculate the PL in the background medium, the incident signal is considered a plane electromagnetic wave, where the electric field is given by Equation (5):
E → ( z , t ) = e x → E x m e − a z e j ( ω t − β z )
In (5), E → ( z , t ) is the electric field intensity vector along the direction of propagation, e x → is the unit vector in the x direction, Exm is the amplitude of the electric field, α is the microwave attenuation coefficient, β is phase constant, z is the transmission distance, ω is the angular frequency. The related formulas of α and β are shown in Equations (6) and (7), in which μ is magnetic permeability and is set to be the same as that of vacuum for all of the materials in Table 1. Therefore, the PL is calculated using Equation (8), which is derived from (5).
α = ω μ ε 2 [ 1 + ( σ ω ε ) 2 − 1 ]
β = ω μ ε 2 [ 1 + ( σ ω ε ) 2 + 1 ]
P L ( d B ) = 10 log ( e 2 a z )
The microwave return loss RL on the interface of the tissue is calculated by Equations (9)–(11), in which Γ is the voltage reflection coefficient.
R L ( d B ) = − 20 log | Γ |
Γ = η 2 − η 1 η 2 + η 1
η = μ ε
Above all, the total microwave power losses of the four tissues in water and mineral oil are calculated, and the results are shown in Figure 2(b). The value of distance z between the antenna and the tissue makes no difference for the purpose of comparison between different background media, which is set to be 100 mm in this study. According to Figure 2(b), the total microwave power loss changes with the medium and the tissue. By definition, the value of L is negatively correlated to the total power loss. In other words, the bigger the value of L, the less the total power loss. The result shows that the microwave power loss is less with mineral oil when the target tissue is breast fat, while it is less with water when the target tissue is one of the other three tissues.
Above all, the background medium has a great influence on both microwave and ultrasonic power losses. Considering synthetically from the ultrasonic and microwave sides, this work selects water as the background medium. Moreover, water has some other advantages in medical applications, such as cleanliness, lack of prior preparation, and higher comfort and acceptance to the patients.

3. Antenna Design

3.1. Antenna Structure

The overall structure and the perspective view of the proposed antenna are shown in Figure 3. Viewing from the outside, it is a cube with a coaxial port at the bottom. The dimensions of the cube are 55 mm◊55 mm◊60 mm. The antenna is made up of four parts: the radiating element, the balun, the shelter, and the reflector.
The reflector is a copper-clad board that is the same size as the radiating element. It reflects the radiation side lobes of the radiating element to concentrate the radiation beams, and improves the directivity.
The shelter is a dielectric cavity that wraps up the balun between the radiating element and the reflector. It keeps the balun and the inner sides of the radiating element and the reflector free of water to avoid electric leakage and rust. Its dielectric constant is 6, which is close to the substrates of the microstrip circuits. Without the shelter, the electric conduction of water may cause higher power loss, and the great difference in dielectric constant between water and the substrate brings more difficulties to the work of impedance matching.
Both of the radiating element and the balun are designed with microstrip lines on the substrate with permittivity of 4 and thickness of 1.6 mm. The specific design processes are described in the following sections.

3.2. Radiating Element Design

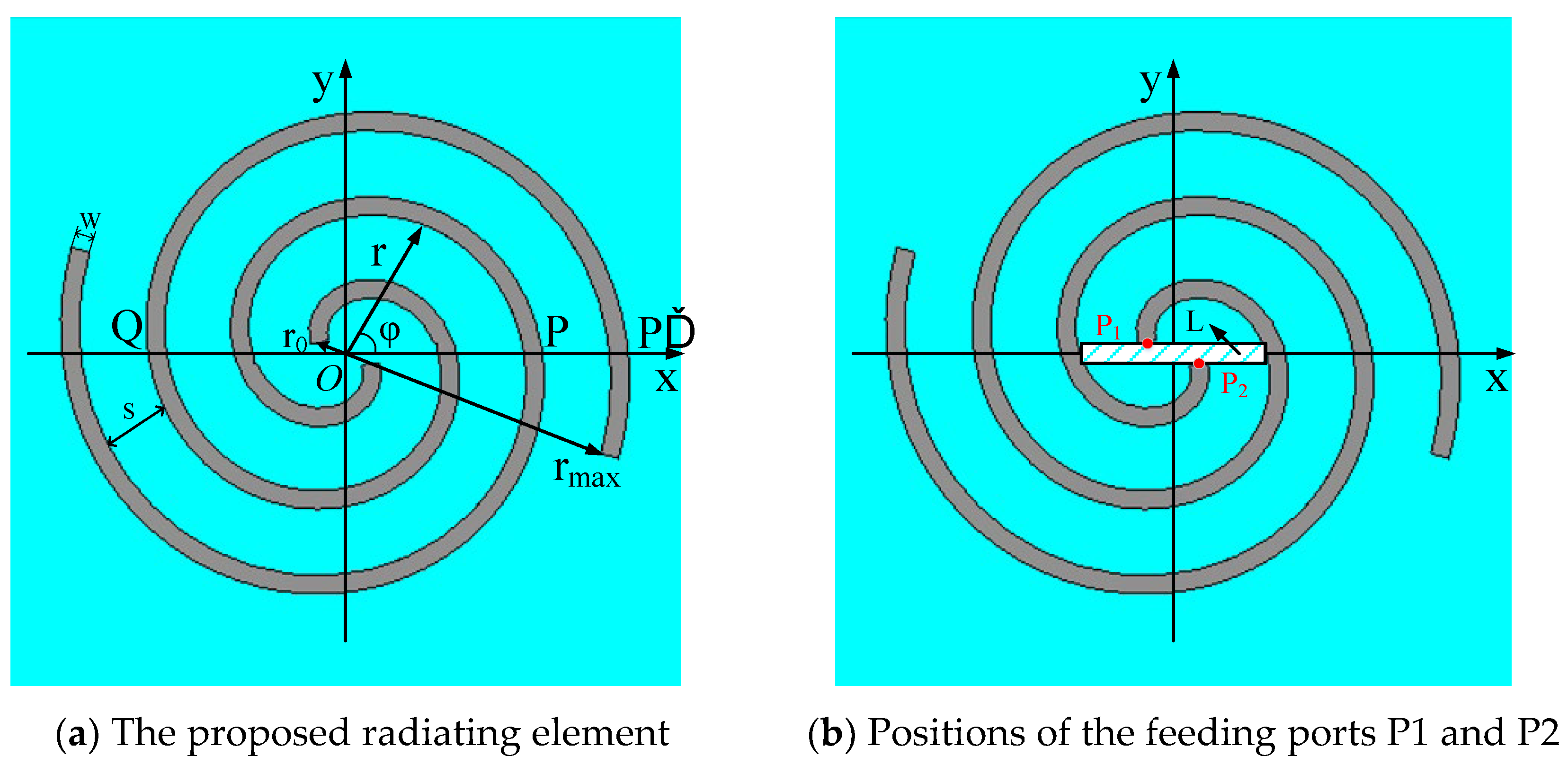
The front view of the proposed radiating element is shown in Figure 4(a), while there is no metal layer coated on the other side of the substrate.
The two spirals constitute one kind of bifilar Archimedean spiral antenna, which is obtained by rotating the two arms of a dipole in the same direction under the equation of the Archimedean spiral, as shown in Equation (12).
r = r 0 + k ( φ − φ 0 )
c = λ f
Referring to Figure 4(a), r is the distance from center point O to an arbitrary point at the spiral, r0 is the distance from point O to the starting point of either arm, φ is the azimuth angle, φ0 is the starting angle, k is the growth rate of the spiral. The key to efficient radiation is to make currents on the two arms in-phase stack. In order to achieve this, r should be λ/2π, and λ is the wavelength. Points P and Q are two symmetrical points on the two spiral lines, respectively, and O P ¯ = O Q ¯ . The input currents at the starting points of the two arms are equal and opposite, namely, the phase difference between point P and Q is π. The current path from point Q to P’ is approximately equal to a semicircle arc with a radius of r. As a result, the current phase difference between point P and P’ is Δϕ=π+(2π/λ)πr. When Δϕ=2π, namely, r=λ/2π, the radiations of the two arms realize an in-phase stack.
Above all, the main radiating area is the spiral ring with radius r=λ/2π. Since λ is inversely proportional to frequency f, the range of r corresponds to the range of working frequency. For the proposed antenna, r ranges from r0 to rmax which is 2 to 21 mm, which corresponds to a theoretical frequency range of 0.26 to 2.71 GHz. The relationship between λ and f is shown in Equation (13), in which c is the light speed in the vacuum.
The growth rate k determines the value of r and thereby influences the radiation condition. Taking one spiral as an example, when the total length is a constant, k is negatively correlated with the number of spiral rings. A small k indicates more rings in the main radiation area, which leads to stronger radiation capacity and a smooth radiation pattern. However, this causes additional transmission loss and lower gain. On the other hand, large k means lower radiation capacity, which leads to an increase of terminal reflection at the end of the spiral and a deterioration of the circular polarization characteristic of the antenna. In this work k is 0.022.
The arm width W and arm spacing S are related to the input impedance of the proposed radiating element. Normally, more stable impedance matching conditions are achieved by making the values of W and S, and they are usually to be set between 0.007λ to 0.01λ if they radiate in the air as common applications. However, the wavelength underwater is shorter, and the calculated values of W and S are too small, which may cause more insertion loss and difficulties in fabrication. The wavelength underwater is calculated by Equations (14) and (15). β is the phase constant. In this work, W is 1.5 mm, and S is 5.5 mm.
λ = 2 π β
β = π f μ σ
The relative position of the starting points P1 and P2 of the two spiral arms has a significant influence on the impedance matching condition, as shown in Figure 4(b). The rectangle L is a section of the balun, and its dimensions are 15 mm by 1.6 mm. P1 and P2 are connected to the balun and are symmetrically located on the two sides of L. The distance in the x direction between them is 4 mm.

3.3. Balun Design

The proposed spiral radiating element is a balanced structure and wants equal currents along the two arms. However, the fed-coaxial cable does not necessarily meet the requirement directly since some of the current may travel down the outside of the outer coax and lead to unbalanced operation. The balun is designed to solve this problem and achieve impedance matching simultaneously.
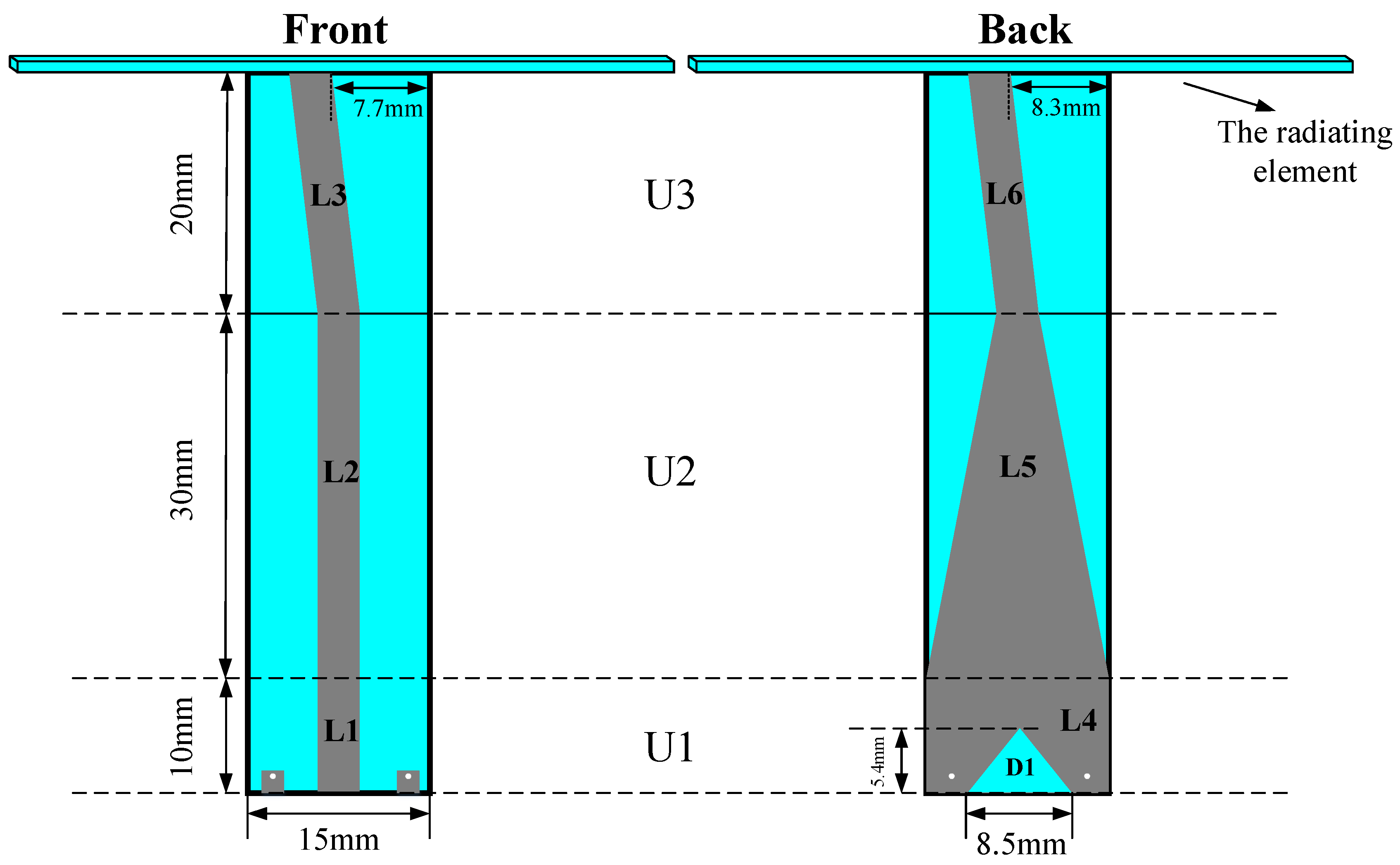
The proposed balun and the dimensional information are shown in Figure 5. The width of L1, L2, and L6 is 3 mm. The shape of L3 is a trapezoid, and the top and bottom lengths are 3.6 mm and 3 mm, respectively. The gap D1 under L4 is an isosceles trapezoid, and the upper length is 0.2 mm.
The theoretical total length of the balun is a quarter wavelength of 1.1 GHz, while there is a small amount of change in simulation and optimization. According to Equation (16), the input impedance ZIN of a quarter wavelength microstrip line is defined by the characteristic impedance Z0 and the load ZL. Z0 is closely related to the microstrip line width. Therefore, the input impedance of the balun is optimized mainly by changing the line widths.
Z I N = Z 0 2 Z L
The proposed balun comprises three units: U1, U2 and U3. U1 is the microwave input unit and is designed to be a coplanar waveguide, which is balanced by nature and can force the unbalanced fed-coaxial line to be balanced. The source power is input from L1, and the two metal squares on both sides of L1 at the bottom are connected to the ground by two vials coated with a metal conductor. To achieve good grounding conditions, the metal area of L4 on the other side of the substrate is larger. The gap D1 under L4 helps to add more variables for easy optimization. U2 is the transition unit, which contains L2 and L5. L5 is a tapered line that is introduced to gradually convert L4 to L6 in case the impedance mismatch problem is caused by the large width difference between the two lines. U3 is the linking-up unit that connects the balun with the spiral radiating element. The upper ends of L3 and L6 tilt to the left to connect with points P1 and P2 in Figure 4(b).

4. Antenna Performance

4.1. Antenna Simulation

To illustrate the proposed antenna’s working performance, the S11, axial ratios, and radiation patterns at different frequencies have been simulated and analyzed.
The simulated results of S11 are shown in Figure 6. The 10 dB impedance bandwidth is 1.91 GHz, from 0.84 to 2.75 GHz. This fits the theoretical result analyzed in the previous section, which is from 0.26 to 2.71 GHz. The subtle variation between them is due to the truncation effect of the radiating element. The terminals of the two spiral lines are truncated, and the small amounts of current that aren’t radiated as expected are reflected at the terminals, which causes destruction to the traveling wave state of the currents flowing along the spiral lines. According to the simulated results, the influence of the truncation effect is very small, and the proposed antenna performs well in impedance matching.
The characteristic of circular polarization is described by axial ratio. The average axial ratios at different frequencies of the proposed antenna are shown in Figure 7. It is less than 2 from 0.91 to 3.97 GHz, indicating the good and stable circular polarization characteristic in an ultra-wide band of the proposed antenna.
The radiation patterns at 6 sample frequencies are shown in Figure 8. For all frequencies, the main lobes point to the direction z accurately, and there are very few side lobes. The radiation pattern bandwidth of the proposed antenna is from 0.6-1.8 GHz. When the frequency is over this range, the main lobe deviates to the side of more than 10 degrees, and the directivity may decrease. The directivities and 3 dB angular widths at the sample frequencies are listed in Table 2. With the increase of frequency, the directivity increases, and the 3 dB angular width decreases. This is due to the corresponding change in the electric dimension of the balun. From 0.9 to 1.8 GHz, the directivity is greater than 11 dBi.
The 3 dB beam angle reflects the microwave beam focusing condition, which is related to the microwave illumination performance in the MITAT system. Narrow angle means strong beam focusing, which may lead to imperfect power coverage on the target tissue and cause damage. A wide beam angle makes it easy to provide full cover, but the illumination power may be insufficient. On the other hand, the testing target is put in the far field area of the antenna in order to achieve stable radiation illumination, which is R meters away and is calculated by Equation (17). L is the largest dimension of the antenna, λ is the wavelength underwater. As an example, the calculated R is 70.6 mm at 1.1 GHz for the proposed antenna. The 3 dB beam angle is 45 degrees, according to Table 2, and it covers a circle area with a radius of 82.8 mm at a distance of 100 mm. If the cross-sectional area of the testing target is larger than this, the illumination performance is not satisfied, and the power absorption distribution cannot reflect the real substance distribution. This is validated by the simulation of the effective microwave absorption area of brain tissue in the later section. However, the relative position of the antenna and the target tissue is adjusted to get the best microwave illumination condition during the experiment.
R = 2 L 2 λ
Above all, the frequency bandwidths defined by impedance matching, axial ratio and radiation pattern of the proposed antenna are calculated in Table 3, the antenna is ultra-wide band in all the three aspects.

4.2. Antenna Fabrication

The fabricated antenna is shown in Figure 9. The radiating element and the balun are fabricated on the FR4 substrates, both with permittivity of 4 and thickness of 1.6 mm. The black object is the shelter, and its material is epoxy resin, with a permittivity of approximately 6. To achieve leak tight and tight wrapping performance, a cube-shaped cavity mold is printed by a 3D printer in advance. The inner circuit is put in the mold, and the epoxy resin liquid is injected into it. After 12 hours, the liquid is solidified, and the mold is easy to take off.

4.3. Antenna Measurement

The diagram of the testing system is shown in Figure 10. The microwave vector network analyzer is used to measure the S11. The tank is plastic and used to retain water. During the testing, the external surface of the reflector of the proposed antenna must stay free of water in case of electrical leakage from the feed port. The other parts of the proposed antenna should be fully immersed in water. The distances from the antenna to the tank walls should be larger than the far field distance R in order to reduce the negative effects in impedance matching and radiation performance caused by the reflected power at the walls. In this study, the tank dimensions are 75 cm◊60 cm◊45 cm. In order to ensure compliance with the far field requirement, the antenna is held in the center of the cross-section of the tank during the testing, and the water depth is 40 cm.
The measured S11 is presented in Figure 6, showing good agreement with the simulated result at frequencies from 0-1.87 GHz. The minor differences between them are due to the increased radiation losses in testing, the insertion loss caused by errors in the manufacturing process, and the parasitic effects of discontinuous components. At frequencies above 1.87 GHz, the measured data fluctuations are higher, indicating that the insertion loss becomes higher at high frequencies. The measured 10 dB frequency bandwidth is 2 GHz corresponding to the frequency range of 0.9 to 2.9 GHz.
For the confined condition, the radiation pattern of the proposed antenna is not measured. However, the radiation performance is proved from the side by analyzing the microwave power absorption distribution of the target tissue. This is studied in the following section.

5. Microwave Power Absorption Under the Illumination of the Proposed Antenna

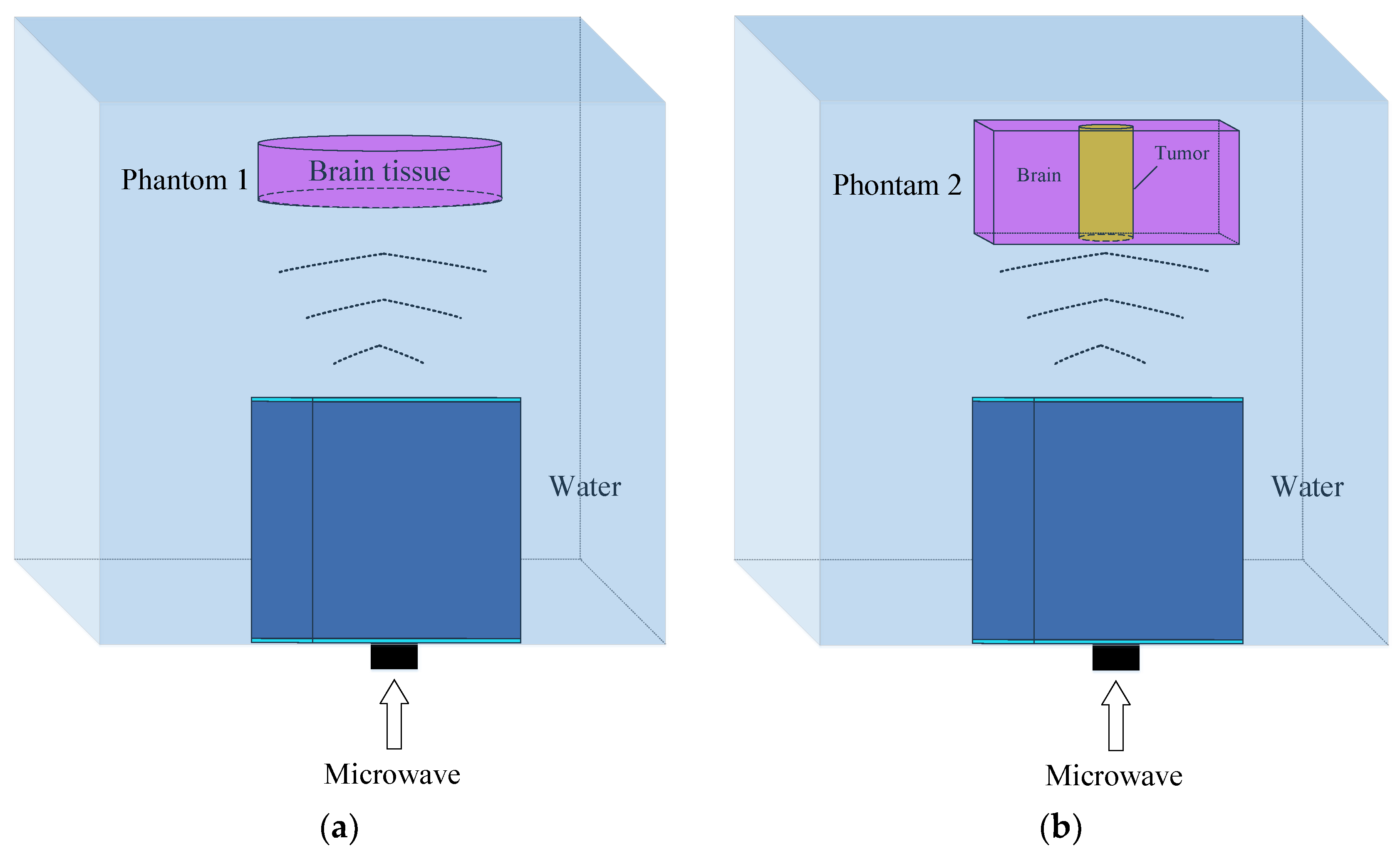
As described in the introduction, the microwave power absorption distribution reflects the substance distribution of the testing target. The high degree of conformity between the two implies good microwave illumination from the antenna. In this study, we build models to simulate the microwave power absorptions of two tissue phantoms under illumination from the proposed antenna. The models and phantoms are shown in Figure 11.
The input microwave power is 50 kW at 1.1 GHz. The pulse frequency is 10 Hz with a pulse width of 0.5 μs. The distance between the antenna and the phantom is 100 mm. Theoretically, the 3 dB power beam of the proposed antenna covers a circular area of 82.8 mm in diameter at this distance. 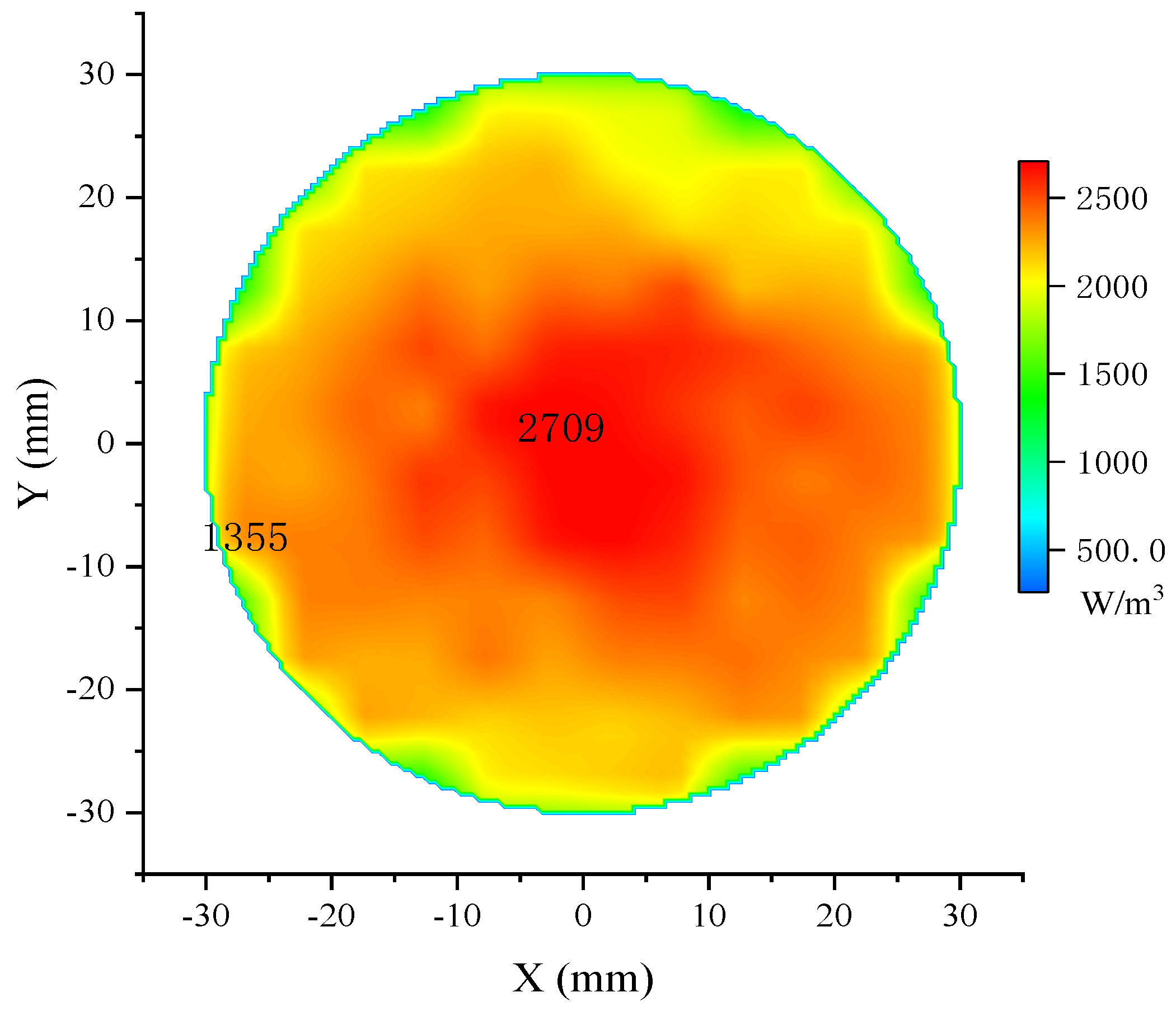Phantom 1 is the model of the cylindrical brain tissue; the diameter is 60 mm, and the height is 2 mm; the electrical parameters are listed in Table 1. The 2-dimensional bird’s eye view of the microwave absorption distribution is shown in Figure 12, and the energy value per cubic meter is represented in different colors.
The maximum amount of absorbed power is in the center and gradually decreases to half at the edge of the phantom, as shown in the two markers in Figure 12. This distribution pattern conforms to the radiation pattern of the proposed antenna, and the resulting uneven molecular thermal motions further induce the mild uneven distribution on the same radius. Besides, the reflections at the boundaries cause more apparent fluctuations near the phantom edge. However, highly uneven distribution will decrease the accuracy of the blur identification and the quality of the restored image. According to Figure 12, the effective microwave absorption area of phantom 1 is defined as a circle 40 mm in diameter.
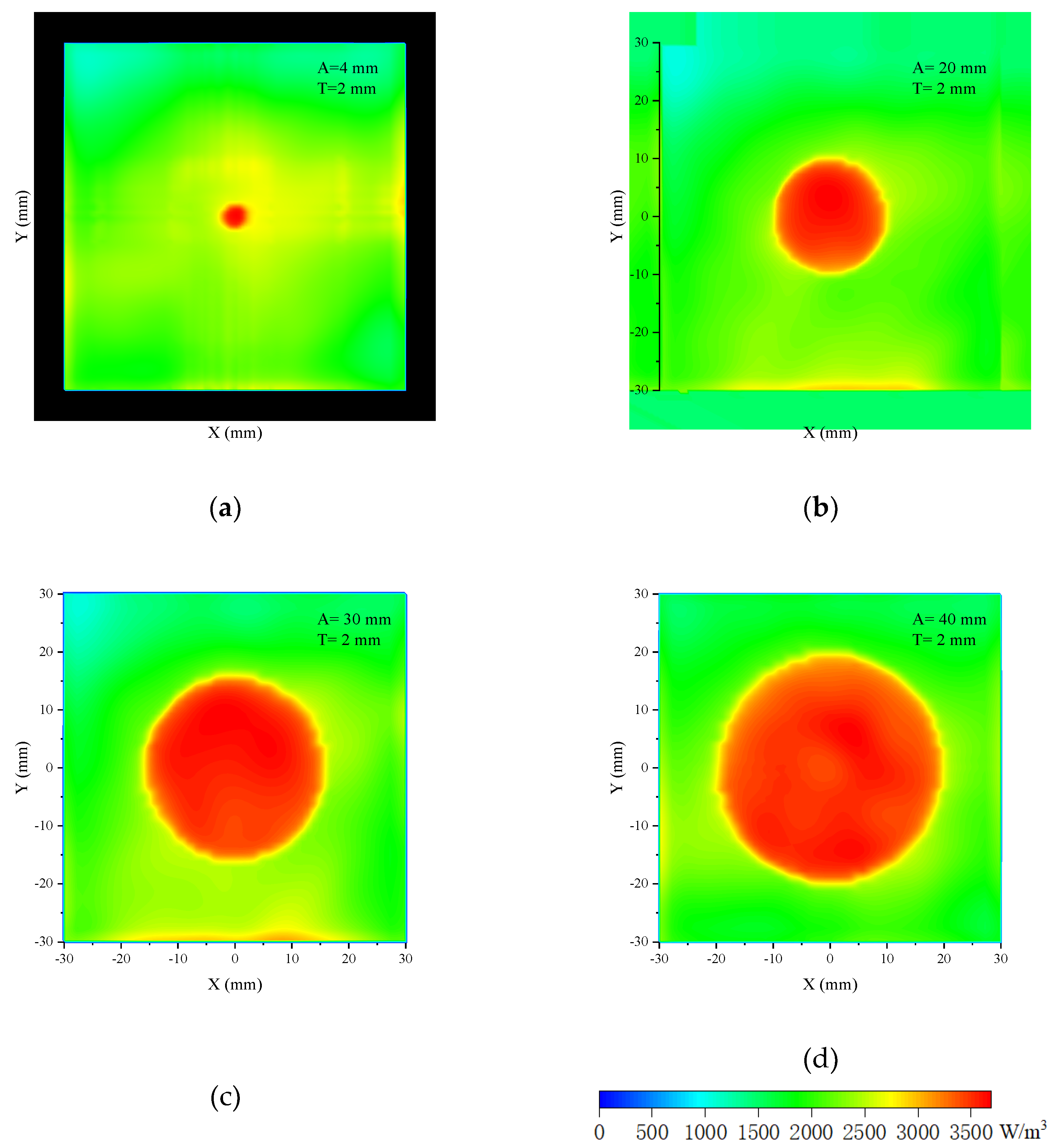
Phantom 2 in Figure 11(b) is the model in which a cylindrical tumor is inserted in the cubic brain tissue. The dimensions of the cross section of the cubic are 30 mm◊30 mm, and the height varies with that of the cylinder. The relative permittivity of the tumor is close to the muscle and is set to be 70; the conductivity is 2 S/m. Set the phantom height to 2 mm and change the tumor diameter from 4 mm, 10 mm, 20 mm, and 30 mm to 40 mm; the related 2-dimensional bird’s eye views of the microwave absorption distributions are shown in Figure 13 and Figure 14. When the tumor diameter is 4 mm, the outline of the tumor has a slight deformation, and the microwave absorption distribution of the brain tissue near the tumor is nonuniform. When the tumor diameter is larger, the outline of the tumor is clear and smooth, with almost no deformation. Moreover, the power absorption distribution inside the tumor is uniform. In this case, the contrast of the tumor and brain tissue is significant. The minor fluctuations near the edge of the brain tissue are caused by the boundary effect and the slight inhomogeneous illumination of the antenna. This only appears at the boundary, and the power intensity is much less than in the tumor; therefore, it makes no difference to the tumor image identification.
D = ( ω μ ε 2 ( 1 + ( σ ω ε ) 2 − 1 ) ) − 1
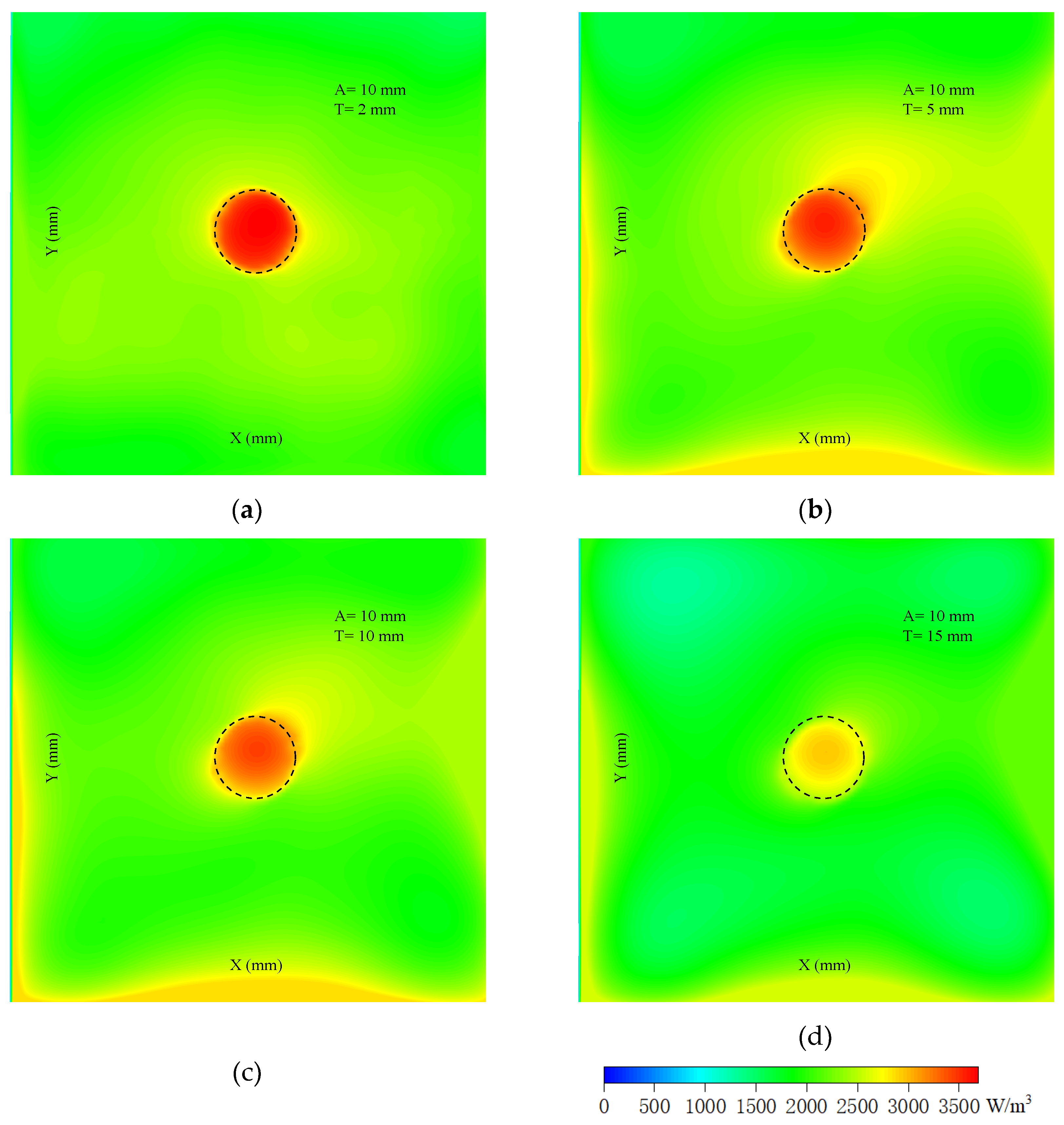
The imaging depth is also studied. Theoretically, the microwave penetrating depth D is calculated by Equation (18) [47], ω is the angular frequency, μ is magnetic permeability, ε is the dielectric constant, σ is conductivity. Therefore, the calculated microwave penetrating depth D in the tumor is 32 mm. Due to the difference in dielectric properties between the tumor and the surrounding healthy tissue and the stray loss, the effective penetrating depth for a high-quality image should be less than the calculated value. The simulated results are shown in Figure 14. The diameter of the phantom is 10 mm. When the height is 2 mm, the tumor outline is clear, and the energy distribution inside the tumor is uniform. When the height exceeds 5 mm, more energy gathers in the middle, and two small sidelobes appear at the edge of the tumor. Further increasing the height, the sidelobes become bigger, and the total amount of microwave absorption decreases. When the height comes to 10 mm, the absorbed energy at the center of the tumor is less by a third compared with the 2 mm case. It is even worse for the 15 mm case; though the tumor is still recognizable, the contrast becomes very low.
Above all, under the microwave illumination provided by the proposed antenna under water, brain tissue and tumors within the dimensions of 5 mm in thickness and 40 mm in diameter absorb microwave power sufficiently and uniformly, which induces strong ultrasonic signals. When the tumor is inside brain tissue, there is a huge difference in absorbed microwave power between both, and the microwave absorption distribution map is in high contrast and accurately reflects the fact. Assuming the ultrasonic part of the MITAT system is ideal, the final images should have no difference from the microwave absorption distribution map, indicating the availability and potentiality of the proposed antenna in brain tumor detection.

6. Conclusion

In this article, an ultra-wideband water immersion antenna for underwater thermoacoustic sensing in biomedical imaging applications has been designed. The power losses of microwave and ultrasonic waves in water and mineral oil of the MITAT system have been analyzed and compared. Theoretical analysis, simulations, and experiments have been made to analyze and verify the good working performance of the proposed antenna. As a result, it has ultra-wide bandwidth in impedance matching, axial ratio, and radiation pattern, indicating stability, flexibility, and reliability in biomedical applications. The simulations on microwave absorption distribution of brain tissue and tumor have been made; the results indicate that the proposed antenna provides satisfactory illumination and thereby achieve uniform microwave absorption distribution inside the tumor and high contrast between the tumor and the surrounding healthy brain tissues. In general, this work proves the proposed antenna has the advantages of ultra-wideband, stable performance, lightweight, antirust, and low cost, which work cooperatively with the ultrasonic sensor to make the MITAT efficient in biomedical imaging. This work would also provide a basis for further development and optimization of water immersion antennas for various applications, such as underwater sensor networks and underwater communications.

Author Contributions

Conceptualization, F. T.; data curation, F. T.; Formal analysis, investigation, F. T.; methodology, F. T.; software, F. T.; validation, F. T.; visualization, F. T.; writing-original draft, F. T.; writing-review & editing, F. T.; Funding acquisition, F. T. and H. W.; project administration, F. T. and H. W.; resources, F. T. and H. W.; supervision, F. T. and H. W. All authors have read and agreed to the published version of the manuscript.”

Funding

This research was funded by the China Scholarship Council, grant number 201808515091; the Talent Introduction Project of Chengdu University of Information Technology, grant number KYTZ201818; the Major Science and Technology Projects of Sichuan Province, grant number 2023ZDZX0013.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors on request.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. McKinney, S.M.; Sieniek, M.; Godbole, V.; Godwin, J.; Antropova, N.; Ashrafian, H.; Back, T.; Chesus, M.; Corrado, G.S.; Darzi, A.; et al. International evaluation of an AI system for breast cancer screening. Nature 2020, 577, 89–94. [Google Scholar] [CrossRef]
  2. Hassan, E.M.; DeRosa, M.C. Recent advances in cancer early detection and diagnosis: Role of nucleic acid based aptasensors. TrAC Trends Anal. Chem. 2020, 124, 115806. [Google Scholar] [CrossRef]
  3. Lyu, S.; Cheung, R.C.C. Efficient and Automatic Breast Cancer Early Diagnosis System Based on the Hierarchical Extreme Learning Machine. Sensors 2023, 23, 7772. [Google Scholar] [CrossRef] [PubMed]
  4. Harmsen, S.; A Wall, M.; Huang, R.; Kircher, M.F. Cancer imaging using surface-enhanced resonance Raman scattering nanoparticles. Nat. Protoc. 2017, 12, 1400–1414. [Google Scholar] [CrossRef] [PubMed]
  5. Cheon, H.; Yang, H.-J.; Son, J.-H. Toward Clinical Cancer Imaging Using Terahertz Spectroscopy. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 1–9. [Google Scholar] [CrossRef]
  6. De Visschere, P.J.; Standaert, C.; Fütterer, J.J.; Villeirs, G.M.; Panebianco, V.; Walz, J.; Maurer, T.; Hadaschik, B.A.; Lecouvet, F.E.; Giannarini, G.; et al. A Systematic Review on the Role of Imaging in Early Recurrent Prostate Cancer. Eur. Urol. Oncol. 2019, 2, 47–76. [Google Scholar] [CrossRef]
  7. Baran, P.; Pacile, S.; I Nesterets, Y.; Mayo, S.C.; Dullin, C.; Dreossi, D.; Arfelli, F.; Thompson, D.; Lockie, D.; McCormack, M.; et al. Optimization of propagation-based x-ray phase-contrast tomography for breast cancer imaging. Phys. Med. Biol. 2017, 62, 2315–2332. [Google Scholar] [CrossRef]
  8. Gergeľ, T.; Hamza, J.; Ondrejka, V.; Němec, M.; Vanek, M.; Drugdová, J. Radiation Protection of a 3D Computer Tomography Scanning Workplace for Logs—A Case Study. Sensors 2023, 23, 8937. [Google Scholar] [CrossRef]
  9. Han, B.K.; Garcia, S.; Aboulhosn, J.; Blanke, P.; Martin, M.H.; Zahn, E.; Crean, A.; Overman, D.; Craig, C.H.; Hanneman, K.; et al. Technical recommendations for computed tomography guidance of intervention in the right ventricular outflow tract: Native RVOT, conduits and bioprosthetic valves:. J. Cardiovasc. Comput. Tomogr. 2024, 18, 75–99. [Google Scholar] [CrossRef]
  10. Willke, P.; Yang, K.; Bae, Y.; Heinrich, A.J.; Lutz, C.P. Magnetic resonance imaging of single atoms on a surface. Nat. Phys. 2019, 15, 1005–1010. [Google Scholar] [CrossRef]
  11. Neugut, A.I.; Sackstein, P.; Hillyer, G.C.; Jacobson, J.S.; Bruce, J.; Lassman, A.B.; Stieg, P.A. Magnetic Resonance Imaging-Based Screening for Asymptomatic Brain Tumors: A Review. Oncol. 2018, 24, 375–384. [Google Scholar] [CrossRef] [PubMed]
  12. Avery, J.C.; Deslandes, A.; Freger, S.M.; Leonardi, M.; Lo, G.; Carneiro, G.; Hull, M.L.; Hull, L.; O’hara, R.; Condous, G.; et al. Noninvasive diagnostic imaging for endometriosis part 1: a systematic review of recent developments in ultrasound, combination imaging, and artificial intelligence. Fertil. Steril. 2024, 121, 164–188. [Google Scholar] [CrossRef]
  13. Wen, L.; Tan, C.; Dong, F. Design of Ultrasonic Tomography System for Biomedical Imaging. IEEE international instrumentation and measurement technology conference, Auckland, New Zealand, 20-23 May 2019. [CrossRef]
  14. Zaatar, O.; Zakaria, A.; Qaddoumi, N. A Novel Switch for Microwave Imaging Systems. IEEE Access 2024, 12, 26978–26990. [Google Scholar] [CrossRef]
  15. Wu, L.; Cheng, Z.; Ma, Y.; Li, Y.; Ren, M.; Xing, D.; Qin, H. A Handheld Microwave Thermoacoustic Imaging System With an Impedance Matching Microwave-Sono Probe for Breast Tumor Screening. IEEE Trans. Med Imaging 2021, 41, 1080–1086. [Google Scholar] [CrossRef] [PubMed]
  16. Wang, B.; Zhang, X.; Zhang, L.; Li, C.; Wu, T.; Wang, X. Investigation of Transducer Distribution in Compressive Thermoacoustic Tomography for Breast Cancer Detection. IEEE Sensors J. 2023, 24, 788–797. [Google Scholar] [CrossRef]
  17. Luo, Z.; Li, C.; Liu, D.; Wang, B.; Zhang, L.; Ma, Y.; Xu, K.; Wang, X. Quantitative Reconstruction of Dielectric Properties Based on Deep-Learning-Enabled Microwave-Induced Thermoacoustic Tomography. IEEE Trans. Microw. Theory Tech. 2023, 71, 2652–2663. [Google Scholar] [CrossRef]
  18. Yan, A.; Lin, L.; Liu, C.; Shi, J.; Na, S.; Wang, L.V. Microwave-induced thermoacoustic tomography through an adult human skull. Med Phys. 2019, 46, 1793–1797. [Google Scholar] [CrossRef] [PubMed]
  19. Machado, A. Prospects of Photo-and Thermoacoustic Imaging in Neurosurgery. Neurosurgery 2020, 87, 24–24. [Google Scholar]
  20. Liang, M.; Yang, K.; Feng, M.; Mu, K.; Jiao, M.; Li, L. Acoustic Imaging Method for Gas Leak Detection and Localization Using Virtual Ultrasonic Sensor Array. Sensors 2024, 24, 1366. [Google Scholar] [CrossRef]
  21. Liu, S.; Zhang, R.; Zheng, Z.; Zheng, Y. Electromagnetic–Acoustic Sensing for Biomedical Applications. Sensors 2018, 18, 3203. [Google Scholar] [CrossRef]
  22. Li, C.; Pramanik, M.; Ku, G.; Wang, L.V. Image distortion in thermoacoustic tomography caused by microwave diffraction. Phys. Rev. E 2008, 77, 031923–031923. [Google Scholar] [CrossRef] [PubMed]
  23. Huang, L.; Yao, L.; Liu, L.; Rong, J.; Jiang, H. Quantitative thermoacoustic tomography: Recovery of conductivity maps of heterogeneous media. Appl. Phys. Lett. 2012, 101, 244106. [Google Scholar] [CrossRef]
  24. He, Y.; Shen, Y.; Liu, C.; Wang, L.V. Suppressing excitation effects in microwave induced thermoacoustic tomography by multi-view Hilbert transformation. Appl. Phys. Lett. 2017, 110. [Google Scholar] [CrossRef]
  25. He, Y.; Liu, C.; Lin, L.; Wang, L.V. Comparative Effects of Linearly and Circularly Polarized Illumination on Microwave-Induced Thermoacoustic Tomography. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 1593–1596. [Google Scholar] [CrossRef]
  26. Ali, M.F.; Jayakody, D.N.K.; Chursin, Y.A.; Affes, S.; Dmitry, S. Recent Advances and Future Directions on Underwater Wireless Communications. Arch. Comput. Methods Eng. 2019, 26, 1–34. [Google Scholar] [CrossRef]
  27. Kelley, B.; Manoj, K.; Jamshidi, M.; et al. Broadband RF communications in underwater environments using multi-carrier modulation. IEEE press 2009, 2303–2308. [Google Scholar]
  28. Hao, Z.; Dawei, G.; Guoping, Z.; Gulliver, T.A. The impact of antenna design and frequency on underwater wireless communications. IEEE pacific rim conference on signal processing, Victoria, Canada, 23-26 August 2011.
  29. Aboderin, O.; Pessoa, L.M.; Salgado, H.M. Wideband dipole antennas with parasitic elements for underwater communications. IEEE Oceans, Aberdeen, United Kingdom, 17-66 June 2017.
  30. Smolyaninov, I.I.; Balzano, Q.; Davis, C.C.; Young, D. Surface Wave Based Underwater Radio Communication. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 2503–2507. [Google Scholar] [CrossRef]
  31. Zoksimovski, A.; Sexton, D.; Stojanovic, M.; Rappaport, C. Underwater electromagnetic communications using conduction – Channel characterization. Ad Hoc Networks 2015, 34, 42–51. [Google Scholar] [CrossRef]
  32. Aboderin, O.; Pessoa, L.M.; Salgado, H.M. Wideband dipole antennas with parasitic elements for underwater communications. IEEE Oceans, Aberdeen, United Kingdom, 17-66 June 2017.
  33. Smolyaninov, I.I.; Balzano, Q.; Davis, C.C.; Young, D. Surface Wave Based Underwater Radio Communication. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 2503–2507. [Google Scholar] [CrossRef]
  34. Domann, J.P.; Carman, G.P. Strain powered antennas. J. Appl. Phys. 2017, 121, 044905. [Google Scholar] [CrossRef]
  35. Bickford, J.A.; Duwel, A.E.; Weinberg, M.S.; McNabb, R.S.; Freeman, D.K.; Ward, P.A. Performance of Electrically Small Conventional and Mechanical Antennas. IEEE Trans. Antennas Propag. 2019, 67, 2209–2223. [Google Scholar] [CrossRef]
  36. Cui, Y.; Wu, M.; Song, X.; Huang, Y.-P.; Jia, Q.; Tao, Y.-F.; Wang, C. Research progress of small low-frequency transmitting antenna. Acta Phys. Sin. 2020, 69, 208401–208401-13. [Google Scholar] [CrossRef]
  37. Chen, H.; Liang, X.; Dong, C.; He, Y.; Sun, N.; Zaeimbashi, M.; He, Y.; Gao, Y.; Parimi, P.V.; Lin, H.; et al. Ultra-compact mechanical antennas. Appl. Phys. Lett. 2020, 117, 170501. [Google Scholar] [CrossRef]
  38. Du, Y.; Xu, Y.; Wu, J.; Qiao, J.; Wang, Z.; Hu, Z.; Jiang, Z.; Liu, M. Very-Low-Frequency Magnetoelectric Antennas for Portable Underwater Communication: Theory and Experiment. IEEE Trans. Antennas Propag. 2023, 71, 2167–2181. [Google Scholar] [CrossRef]
  39. Fereidoony, F.; Nagaraja, S.P.M.; Santos, J.P.D.; Wang, Y.E. Efficient ULF Transmission Utilizing Stacked Magnetic Pendulum Array. IEEE Trans. Antennas Propag. 2021, 70, 585–597. [Google Scholar] [CrossRef]
  40. Niu, Y.; Ren, H. Transceiving Signals by Mechanical Resonance: A Miniaturized Standalone Low Frequency (LF) Magnetoelectric Mechanical Antenna Pair With Integrated DC Magnetic Bias. IEEE Sensors J. 2022, 22, 14008–14017. [Google Scholar] [CrossRef]
  41. Zhang, Y.; Jing, L.; Shi, P.; Hou, J.; Yang, X.; Peng, Y.; Chen, S. Research on a miniaturized VLF antenna array based on a magnetoelectric heterojunction. J. Mater. Sci. Mater. Electron. 2022, 33, 4211–4224. [Google Scholar] [CrossRef]
  42. Karagianni, E.A. ELECTROMAGNETIC WAVES UNDER SEA: BOW-TIE ANTENNAS DESIGN FOR WI-FI UNDERWATER COMMUNICATIONS. Prog. Electromagn. Res. M 2015, 41, 189–198. [Google Scholar] [CrossRef]
  43. Ostadrahimi, M.; Mojabi, P.; Zakaria, A.; LoVetri, J.; Shafai, L. Enhancement of Gauss–Newton Inversion Method for Biological Tissue Imaging. IEEE Trans. Microw. Theory Tech. 2013, 61, 3424–3434. [Google Scholar] [CrossRef]
  44. Gibbins, D.; Klemm, M.; Craddock, I.J.; Leendertz, J.A.; Preece, A.; Benjamin, R. A Comparison of a Wide-Slot and a Stacked Patch Antenna for the Purpose of Breast Cancer Detection. IEEE Trans. Antennas Propag. 2009, 58, 665–674. [Google Scholar] [CrossRef]
  45. Wells, P.N.T. Ultrasonic imaging of the human body. Rep. Prog. Phys. 1999, 62, 671–722. [Google Scholar] [CrossRef]
  46. Liang, S.; Lashkari, B.; Choi, S.S.S.; Ntziachristos, V.; Mandelis, A. The application of frequency-domain photoacoustics to temperature-dependent measurements of the Grüneisen parameter in lipids. Photoacoustics 2018, 11, 56–64. [Google Scholar] [CrossRef] [PubMed]
  47. Vorst, A.V.; Rosen, A.; Kotsuka, Y. RF/Microwave Interaction with Biological Tissues; Wiley-IEEE Press: Hoboken, NJ, USA, 2006; pp. 63–91. [Google Scholar]
Preprints 116640 g001
Figure 1. Block diagram of the process of MITAT.
Figure 1. Block diagram of the process of MITAT.
Preprints 116640 g001
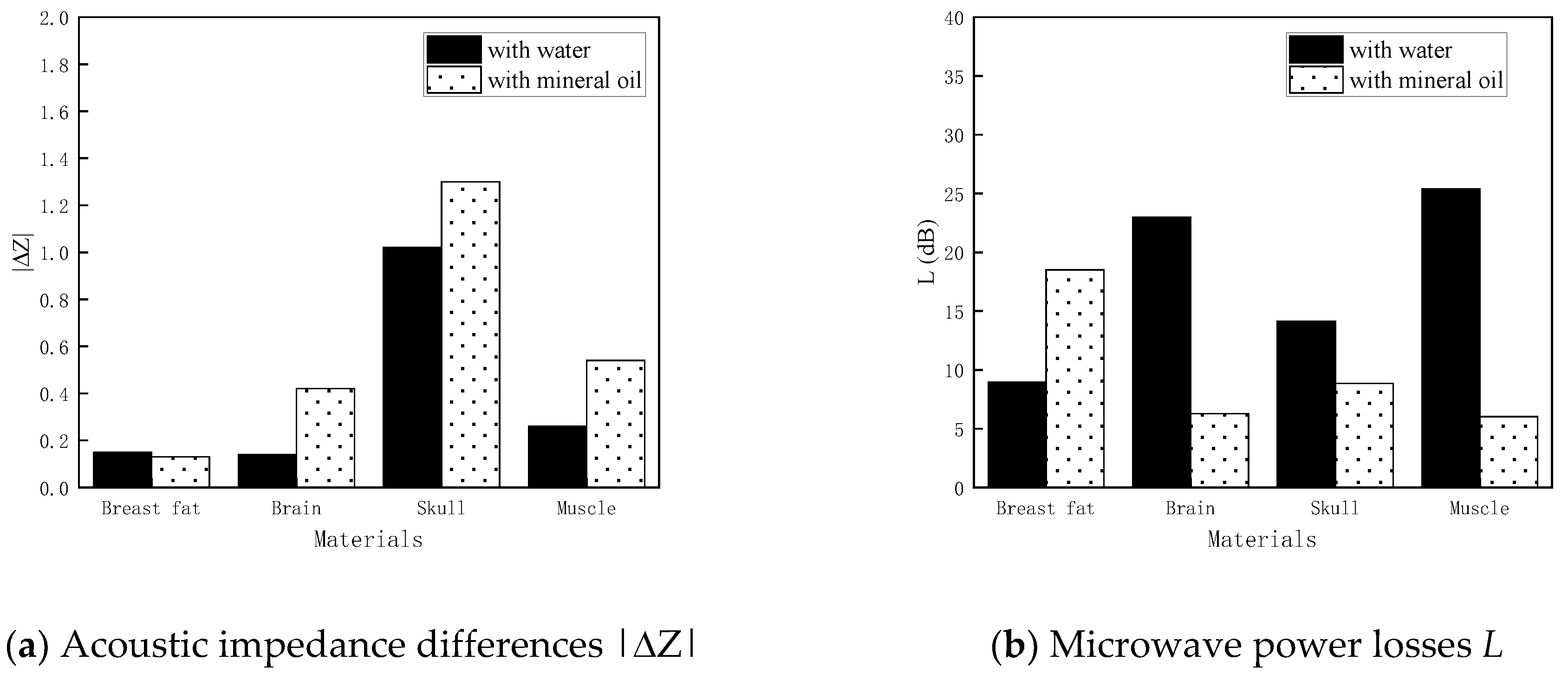
Preprints 116640 g002
Figure 2. Histograms of acoustic impedance differences and microwave power losses when the four tissues are illuminated in mineral oil and water, respectively.
Figure 2. Histograms of acoustic impedance differences and microwave power losses when the four tissues are illuminated in mineral oil and water, respectively.
Preprints 116640 g002
Preprints 116640 g003
Figure 3. Schema of the decomposed structures for the proposed antenna.
Figure 3. Schema of the decomposed structures for the proposed antenna.
Preprints 116640 g003
Preprints 116640 g004
Figure 4. Front views of the proposed radiating element.
Figure 4. Front views of the proposed radiating element.
Preprints 116640 g004
Preprints 116640 g005
Figure 5. Front and back views of the proposed balun.
Figure 5. Front and back views of the proposed balun.
Preprints 116640 g005
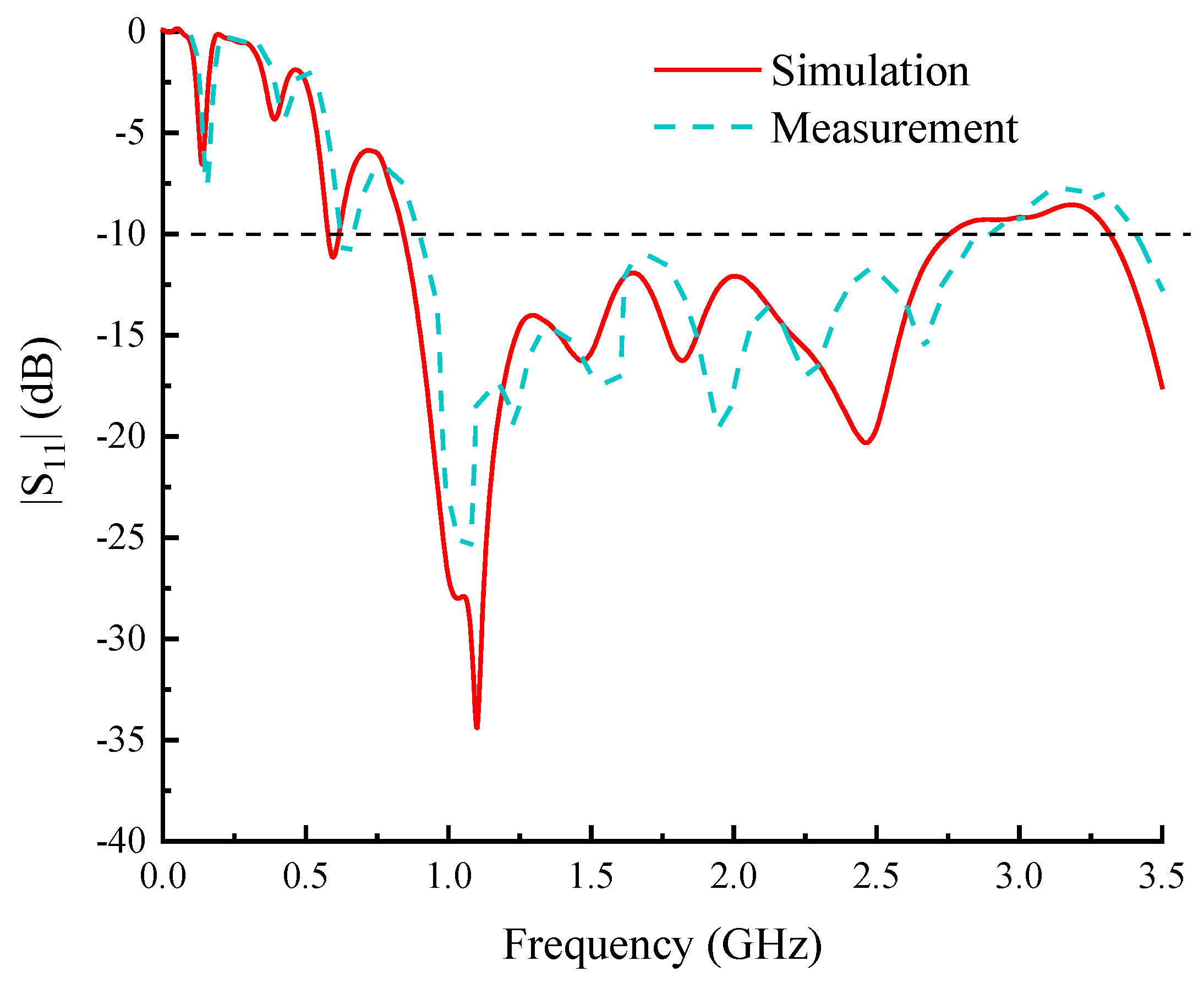
Preprints 116640 g006
Figure 6. S parameters of the proposed antenna.
Figure 6. S parameters of the proposed antenna.
Preprints 116640 g006
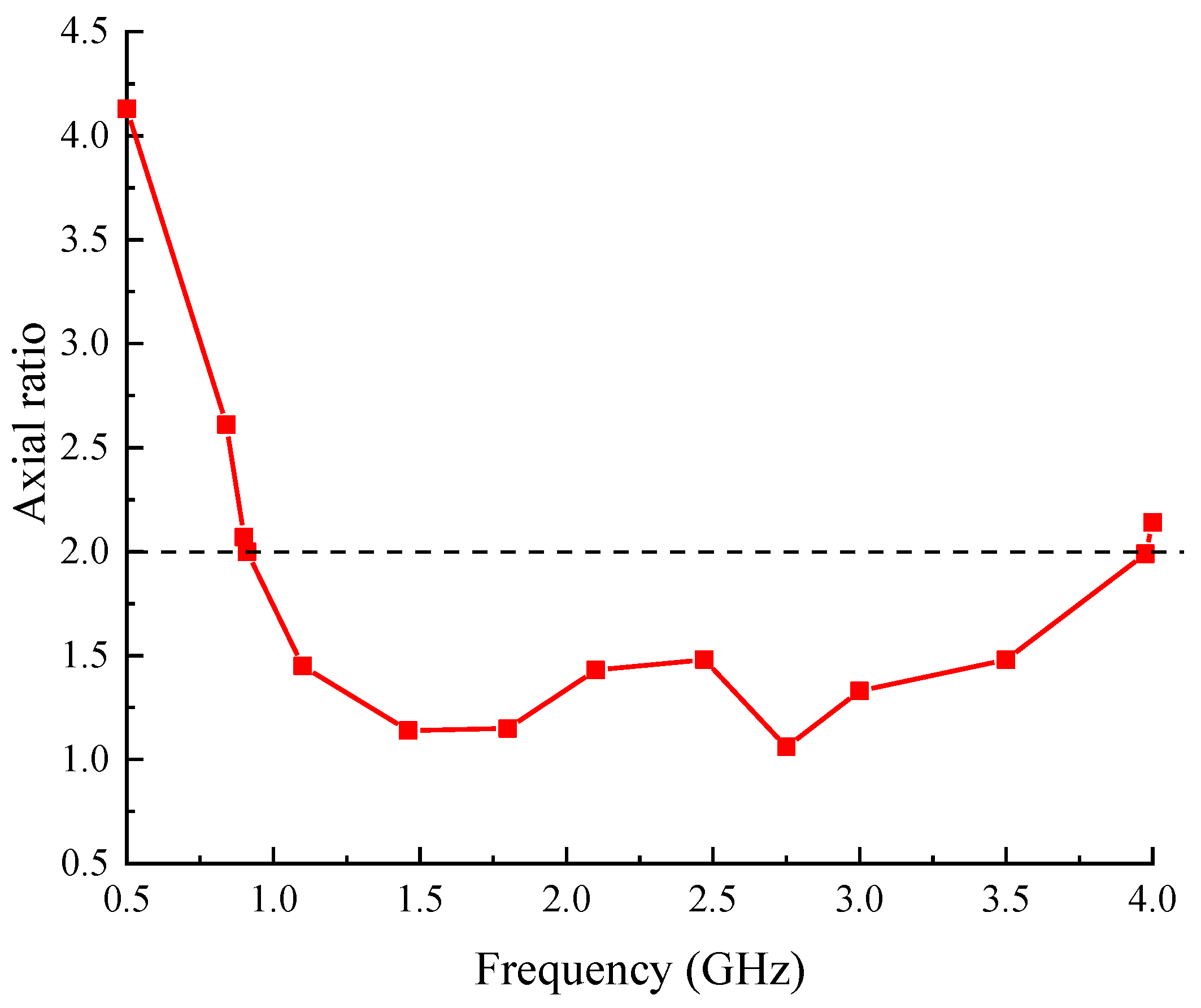
Preprints 116640 g007
Figure 7. Axial ratios of the proposed antenna.
Figure 7. Axial ratios of the proposed antenna.
Preprints 116640 g007
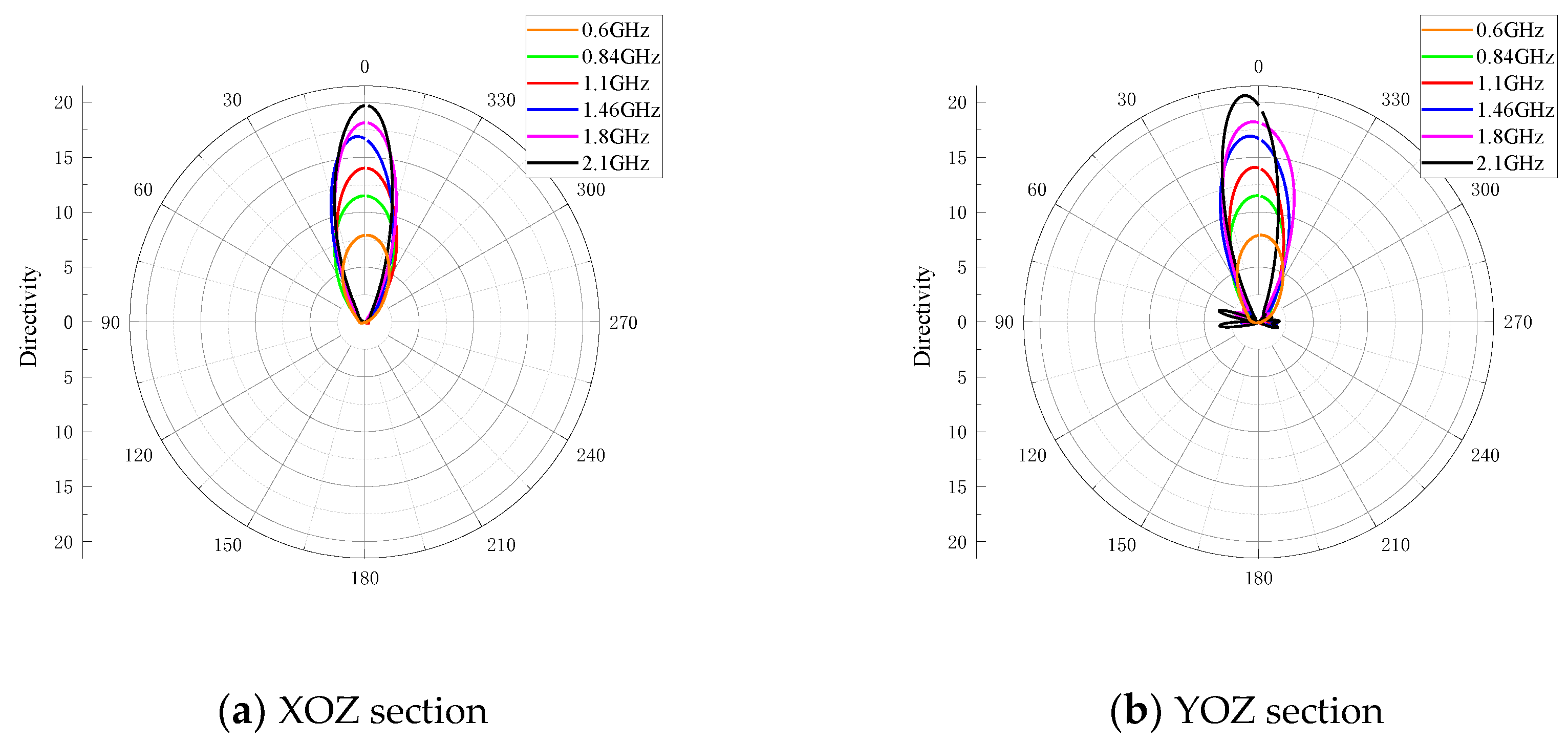
Preprints 116640 g008
Figure 8. Radiation patterns of XOZ and YOZ sections of the proposed antenna.
Figure 8. Radiation patterns of XOZ and YOZ sections of the proposed antenna.
Preprints 116640 g008
Preprints 116640 g009
Figure 9. Photographs of the proposed antenna. (a) is the inner circuits that contains the fabricated radiation element and balun, (b) is the full view of the fabricated antenna, the black object is the shelter.
Figure 9. Photographs of the proposed antenna. (a) is the inner circuits that contains the fabricated radiation element and balun, (b) is the full view of the fabricated antenna, the black object is the shelter.
Preprints 116640 g009
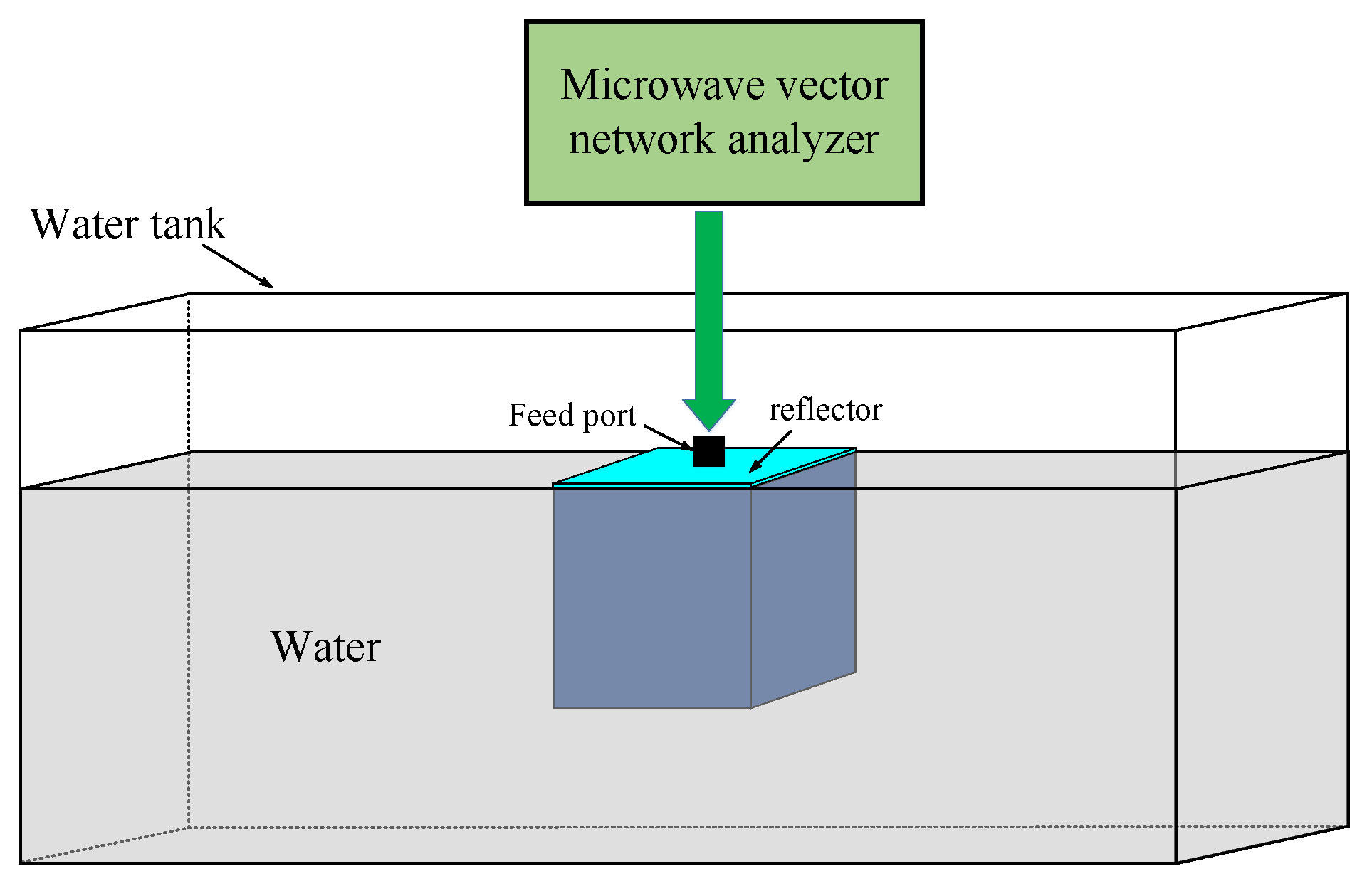
Preprints 116640 g010
Figure 10. Diagram of the testing system.
Figure 10. Diagram of the testing system.
Preprints 116640 g010
Preprints 116640 g011
Figure 11. Diagrams of the microwave absorption simulation models of the phantoms.
Figure 11. Diagrams of the microwave absorption simulation models of the phantoms.
Preprints 116640 g011
Preprints 116640 g012
Figure 12. Microwave absorption distribution map of phantom 1.
Figure 12. Microwave absorption distribution map of phantom 1.
Preprints 116640 g012
Preprints 116640 g013
Figure 13. The microwave absorption distribution maps of phantom 2 with different tumor diameters. A is tumor diameter, and T is phantom height.
Figure 13. The microwave absorption distribution maps of phantom 2 with different tumor diameters. A is tumor diameter, and T is phantom height.
Preprints 116640 g013
Preprints 116640 g014
Figure 14. The microwave power absorption distribution maps of phantom 2 with different phantom heights. A is the tumor diameter, and T is the phantom height.
Figure 14. The microwave power absorption distribution maps of phantom 2 with different phantom heights. A is the tumor diameter, and T is the phantom height.
Preprints 116640 g014
Table 1. Acoustic and electric parameters of different materials [45,46].
Table 1. Acoustic and electric parameters of different materials [45,46].
Category Material Density
kg/m3 		Sound speed
m/s		 Acoustic
impedance
106kg/m2⋅s		 αu *
Np/m		 εr * σ *
S/m
Background medium Air 1 330 0.00033 13.81 1 0
Mineral oil 825 1440 1.19 3.63 3 0.02
Water 994 1480 1.47 0.02 78 0.23
Target
tissue		 Breast fat 911 1450 1.32 4.36 5.41 0.1
Skull cancellous 1178 2117 2.49 47 20.6 0.364
Brain 1046 1540 1.61 10.36 48.9 1.31
muscle 1090 1590 1.73 7.11 54.8 0.978
* αu is the ultrasonic attenuation coefficient at 1 MHz; εr is the relative permittivity; σ is the conductivity.
Table 2. Directivity and 3dB angular width at different frequencies.
Table 2. Directivity and 3dB angular width at different frequencies.
Frequency
(GHz)		 Directivity
(dBi)		 3dB Angular width
(degree)
0.6 8.98 62.3
0.84 10.6 53.9
0.9 11 51.3
0.91 11 50.8
1.1 11.5 45
1.46 12.3 37.9
1.8 12.6 34.8
Table 3. The bandwidths of impedance, axial ratio, and radiation pattern of the proposed antenna.
Table 3. The bandwidths of impedance, axial ratio, and radiation pattern of the proposed antenna.
Category Absolute
Bandwidth
(GHz)		 Relative
Bandwidth		 Center
Frequency
(GHz)
Impedance 1.91 106.4% 1.795
Axial ratio 3.06 125.4% 2.44
Radiation pattern 1.2 100% 1.2
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated