A Novel Robust Hybrid Control Strategy for a Quadrotor Trajectory Tracking Aided with Bioinspired Neural Dynamics

Preprint

Article

A Novel Robust Hybrid Control Strategy for a Quadrotor Trajectory Tracking Aided with Bioinspired Neural Dynamics

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Jianqi Li^*,Xin Li,

Jianquan Lu,Binfang Cao,

Jian Sun

Jianqi Li^*,Xin Li,

Jianquan Lu,Binfang Cao,

Jian Sun

This version is not peer-reviewed

Submitted:

29 August 2024

Posted:

30 August 2024

You are already at the latest version

Alerts

Abstract

This paper proposes a novel hybrid control strategy for quadrotor unmanned aerial vehicles (UAVs) based on bio-inspired neural dynamics. This strategy addresses the velocity jump issue prevalent in traditional backstepping control and the control signal chattering problem common in traditional sliding mode control. The control system comprises an outer-loop bio-inspired backstepping controller and an inner-loop bio-inspired sliding mode controller, ensuring smooth trajectory tracking even in the presence of external disturbances. The stability of the quadrotor UAV control system is rigorously analyzed using Lyapunov stability theory. Extensive comparative simulation experiments are conducted to assess the robustness and effectiveness of the control system. Results demonstrate superior trajectory tracking performance of the proposed control system compared to other control systems for quadrotor UAVs.

Keywords:

Subject: Engineering - Automotive Engineering

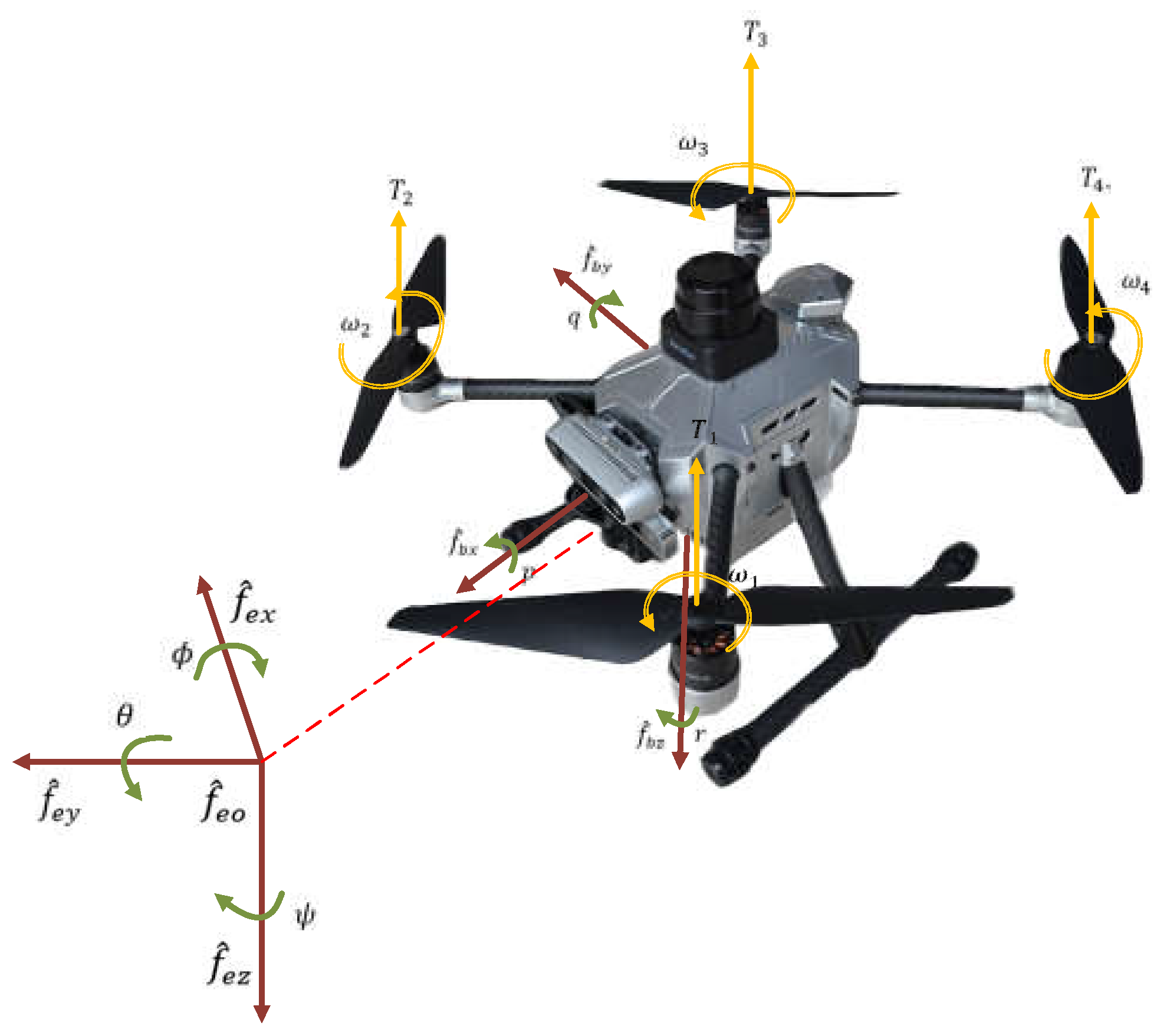
1. Introduction

Quadrotor unmanned aerial vehicles (UAVs) are well-suited for various applications, including vertical take-off and landing [1] and flexible trajectory tracking [2]. Consequently, they have garnered significant attention from developers worldwide, stimulating extensive research in this field. Consequently, quadrotor UAVs have found extensive utilization across various civilian domains [3-7]. Nevertheless, the design of a UAV flight control system, be it for autonomous or non-autonomous flight, often presents challenges concerning sensor technology, hardware, and software design. The quadrotor UAV represents a highly complex nonlinear control system that has garnered considerable interest among researchers in the field of automatic control.

Trajectory tracking control has consistently been a focal point of research in the autonomous flight control of quadrotor UAVs. Among the commonly utilized control methods, linear control strategies [8] offer simplicity and ease of design and implementation. However, the inherent nonlinear and strongly coupled characteristics of quadrotor UAV dynamics impose numerous limitations on the effectiveness of these linear control strategies. Moreover, quadrotor UAVs are consistently exposed to external and internal disturbances during autonomous flight operations in complex scenarios, rendering the existing linear control strategies challenging to apply in practical settings.

To address the limitations of linear control strategies, previous studies have proposed various nonlinear control strategies [9-14]. Robust nonlinear control techniques, in general, enhance flight stability, ensuring satisfactory performance even in the face of unpredictable environmental changes. They enable flexible maneuverability and precise trajectory tracking. Initially, nonlinear control techniques were employed to govern the vertical takeoff and landing (VTOL) of three-degree-of-freedom helicopters [15]. Controller design for quadrotor UAVs poses greater challenges due to the inherent strong coupling between the body frame dynamics and the yaw, pitch, and roll motion, in contrast to helicopters. Numerous studies have explored different nonlinear controllers for diverse autonomous flight control tasks of quadrotor UAVs, including backstepping controllers [10-11], sliding mode controllers [12-13], and other related adaptive nonlinear controllers [14].

The pioneering work of Reference [16] introduced a nonlinear controller for quadrotor aircraft. The authors developed a dynamic feedback controller for hovering flight, utilizing a technique known as exact feedback linearization. The simulation results presented in the paper demonstrated acceptable performance, even in the presence of external disturbances. However, the design of controllers using feedback linearization necessitates an exact model with stable zero dynamics to compensate for the nonlinear terms. However, in practice, the dynamic uncertainty and external disturbances that are inherent in quadrotor flight pose challenges in achieving accurate model predictions, rendering the feedback linearization control strategy infeasible for real-time trajectory tracking control. Consequently, to apply this feedback linearization control strategy in practical applications, it should be augmented with another control strategy that incorporates quadrotor model prediction, as suggested in Reference [17].

The backstepping control strategy [11] is widely employed in robot control as one of the most commonly used methods. Its fundamental principle involves recursively stabilizing a closed-loop backstepping system. Analysis and design of this strategy can be carried out using Lyapunov stability theory. When designing controllers for quadrotor unmanned aerial vehicles using the backstepping control strategy [18], the design of control laws is dependent on the tracking error. Consequently, a significant tracking error leads to a substantial speed jump in the control signal. The power system of the unmanned aerial vehicle cannot immediately realize such an unrealistic speed change. Employing a fuzzy logic control strategy [19] is a practical solution to address the speed jump issue within the aforementioned backstepping control strategy. Nevertheless, the design of fuzzy logic controllers relies on the designer's prior knowledge, posing challenges in formulating satisfactory fuzzy rules tailored to specific environments. Neural network optimization strategy has been employed as a viable solution for addressing similar issues in unmanned aerial vehicles, enabling the computation of complex nonlinear relationships. However, this approach necessitates online learning training, costly computational resources, and a substantial volume of experimental data. Previous studies have explored the implementation of the backstepping control strategy to achieve position tracking control in quadrotor unmanned aerial vehicles; however, the majority of controller designs overlooked the presence of external disturbances.

Previous studies have focused on the development of robust controllers to mitigate the impact of external and internal disturbances on quadrotor unmanned aerial vehicles (UAVs) and ensure stable autonomous flight in challenging environments. One robust control method, the sliding mode control strategy [12], is known for its insensitivity to parameter variance, thereby enhancing the system's resilience to disturbances. However, the control signals generated by the sliding mode control strategy exhibit significant shaking, which can lead to high-frequency variations detrimental to onboard hardware. While attempts have been made to address the shaking problem in existing methods by substituting the shaking term with saturation and tanh functions [20], these solutions compromise robustness to disturbances and necessitate meticulous parameter tuning to mitigate shaking. Furthermore, given the susceptibility of both backstepping control and sliding mode control to noise, control strategies inspired by biological systems can offer smoother control signals, thus effectively resolving the challenges associated with backstepping control and sliding mode control, which is particularly crucial in the context of limited actuators.

Biological neural dynamics, initially proposed by Hodgkin and Huxley [21], refers to the utilization of electrical circuit elements in a patch of membrane within a biological neural system. Yang [22] introduced this bioinspired neural dynamics to the field of robotics, while Zhu [23] subsequently applied it to the motion control of an underwater unmanned submarine. The overall control design was based on bioinspired neural dynamics and employed a hybrid control approach. A bioinspired backstepping control strategy was employed to address the velocity jump issue in traditional backstepping control, resulting in smooth position control. Additionally, a bioinspired sliding mode control strategy was utilized to tackle the control signal chattering problem in traditional sliding mode control, thereby minimizing the impact on onboard actuators.

The control system for quadrotor unmanned aerial vehicles (UAVs) typically consists of two sub-systems: an outer-loop position control subsystem and an inner-loop attitude control subsystem. In their previous work [11,24], the authors introduced a PID controller for position control and an integral sliding mode controller for attitude control of the quadrotor UAV. Another study [25] presented a terminal sliding mode position controller and a sliding mode attitude controller. Motivated by the characteristics of neural dynamics, this paper presents a robust nonlinear hybrid control strategy based on neural dynamics for quadrotor UAVs. The overall design of the control system includes based on biological neural dynamics backstepping position control subsystem and based on biological neural dynamics sliding mode attitude control subsystem. These subsystems are built upon the dual-loop control structure introduced in [26,27]. The proposed neural dynamics mitigate the speed jump issue commonly encountered in traditional backstepping control methods. Moreover, leveraging the filtering capability of neural dynamics, the control system effectively handles external noise and produces smooth velocity control signals. Furthermore, the integration of neural dynamics with the sliding mode control strategy addresses the control signal chattering problem inherent in traditional sliding mode control, resulting in continuous, smooth, and chattering-free torque control signals.

The paper is organized as follows: Section 2 introduces the kinematic and dynamic models of the quadrotor unmanned aerial vehicle (UAV). In Section 3, a bioinspired neural dynamics model is presented as the foundation for the development of the bioinspired backstepping position controller and the bioinspired sliding mode attitude controller for the quadrotor UAV. The stability analysis of the proposed control system is conducted in Section 3 as well. 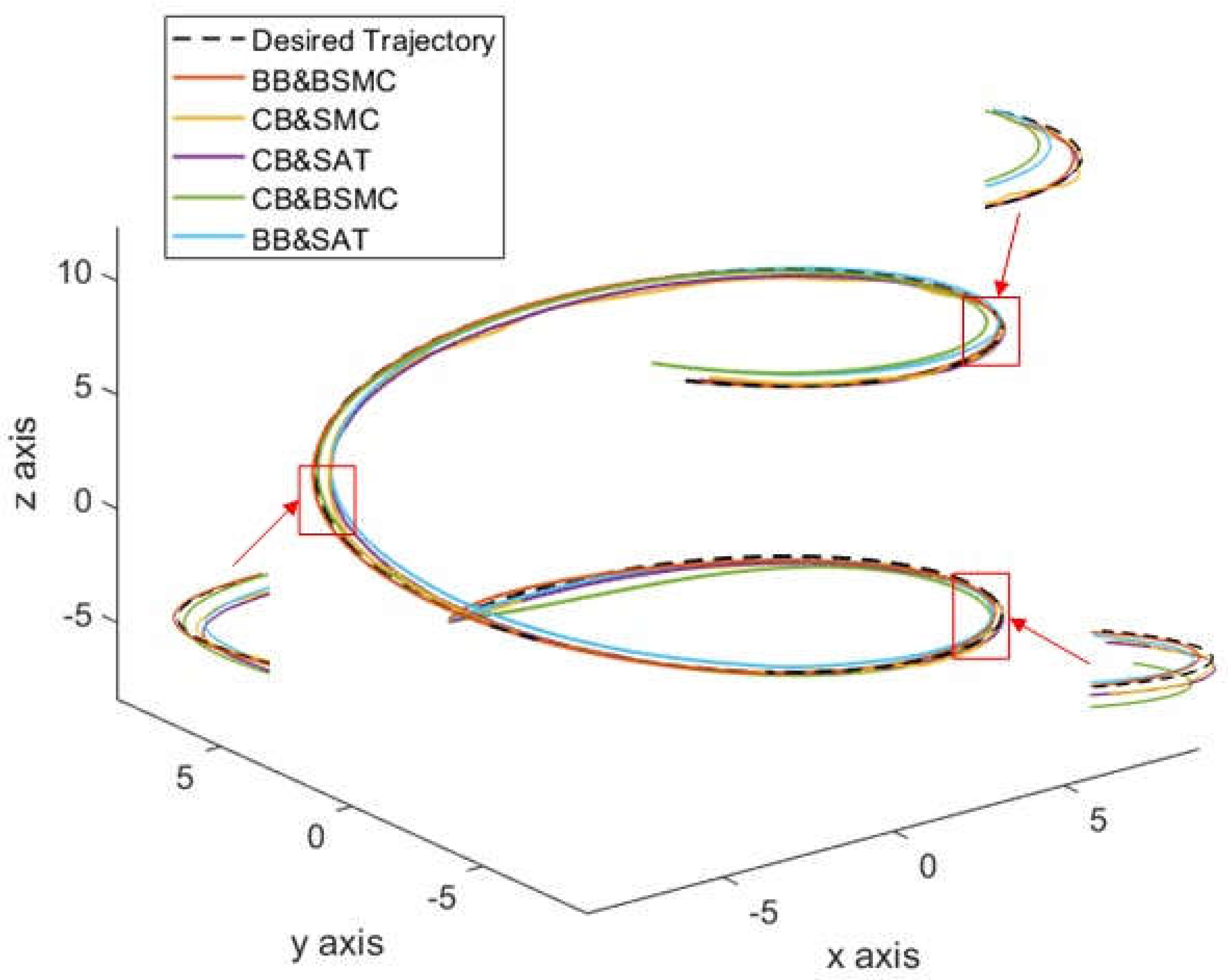Section 4 provides the numerical simulation results, which are compared with other control systems to showcase their advantages and effectiveness. Finally, Section 5 summarizes the development philosophy and justifies the superiority of the proposed hybrid control strategy for quadrotor UAVs. The conclusion also includes suggestions for areas of improvement.

2. Dynamical Model

2.1. Quadrotor Model

Using the Newton-Euler equations, the kinematic and dynamic models of the quadrotor unmanned aerial vehicle (UAV) are formulated in two coordinate reference frames: the inertial frame and the body frame [28]. In this study, the inertial frame, denoted as frame

{\hat{F}}_{E} = \{\begin{matrix} \begin{matrix} {\hat{f}}_{e o,} & {\hat{f}}_{e x,} \end{matrix} & \begin{matrix} {\hat{f}}_{e y,} & {\hat{f}}_{e z} \end{matrix} \end{matrix}\}

, while the body frame, denoted as frame

{\hat{F}}_{B} = \{\begin{matrix} \begin{matrix} {\hat{f}}_{b o,} & {\hat{f}}_{b x,} \end{matrix} & \begin{matrix} {\hat{f}}_{b y,} & {\hat{f}}_{b z} \end{matrix} \end{matrix}\}

. Here,

{\hat{f}}_{e o}

represents the origin of the inertial coordinate system, and

{\hat{f}}_{b o}

represents the center of mass of the quadrotor UAV. These definitions are illustrated in Figure 1. The Euler angles of the quadrotor, denoted as

Θ^{E} = {[\begin{matrix} ϕ & θ & ψ \end{matrix}]}^{T} \in R^{3 \times 1}

, represent its roll angle (

ϕ

), pitch angle (

θ

), and yaw angle (

ψ

). These angles satisfy the conditions

|ϕ| < \frac{π}{2}, |θ| < \frac{π}{2}, |ψ| < π

.The angular velocities of the drone, denoted as

Ω^{B} = {[p q r]}^{T} \in R^{3 \times 1}

, correspond to its rotations along the X, Y, and Z axes of the body coordinate system, respectively. The position of the quadrotor in the world coordinate system

{\hat{F}}_{E}

is defined as

P^{E} = {[\begin{matrix} p_{x}^{e} & p_{y}^{e} & p_{z}^{e} \end{matrix}]}^{T} \in R^{3 \times 1}

, while the velocity of the quadrotor's movement in the inertial coordinate system

{\hat{F}}_{E}

is defined as

V^{E} = {[\begin{matrix} v_{x}^{e} & v_{y}^{e} & v_{z}^{e} \end{matrix}]}^{T} \in R^{3 \times 1}

. Consequently, the kinematic and dynamic model of the quadrotor's displacement and rotation can be expressed as follows:

{\dot{P}}^{E} = V^{E} {\dot{V}}^{E} = m^{- 1} [R_{B}^{E} T_{B} + F_{d} + d v] {\dot{Θ}}^{E} = R_{Θ} \cdot Ω^{B} \begin{matrix} {\dot{Ω}}^{B} = I^{- 1} [τ_{b} + G_{a} - Ω^{B} \times (I \cdot Ω^{B}) + M_{d}] \end{matrix}

(1)

Where

m

represents the mass of the quadrotor,

I

denotes the inertial matrix of the quadrotor in the inertial coordinate system, given by

I = d i a g (I_{x x}, I_{y y}, I_{z z})

R_{B}^{E}

signifies the rotation matrix between the body-fixed coordinate system and the inertial coordinate system for the quadrotor's translation, and

R_{Θ}

represents the rotation matrix for the quadrotor's rotation. These matrices satisfy the following conditions:

R_{B}^{E} = [\begin{matrix} \begin{matrix} c o s θ c o s ψ & s i n ϕ s i n θ - c o s ϕ s i n ψ & s i n ϕ s i n ψ + c o s ϕ s i n θ c o s ψ \end{matrix} \\ \begin{matrix} c o s θ s i n ψ & c o s ϕ c o s ψ + s i n ϕ s i n θ s i n ψ & c o s ϕ s i n θ s i n ψ - c o s ψ s i n ϕ \end{matrix} \\ \begin{matrix} - s i n θ & s i n ϕ c o s θ & c o s ϕ c o s θ \end{matrix} \end{matrix}]

(2)

R_{Θ} = [\begin{matrix} \begin{matrix} 1 & s i n ϕ t a n θ & c o s ϕ t a n θ \end{matrix} \\ \begin{matrix} 0 & c o s ϕ & - s i n ϕ \end{matrix} \\ \begin{matrix} 0 & s i n ϕ / c o s θ & c o s ϕ / c o s θ \end{matrix} \end{matrix}]

(3)

d v

represents step-like increasing values of external disturbances. The variables

F_{d}

and

M_{d}

represent bounded variations of aerodynamic force and moment, respectively.

T_{B}

satisfies

T_{B} = T_{K} E_{3} - m g {(R_{B}^{E})}^{T} E_{3}

, where

g

denotes the gravitational constant.

T_{K}

represents the total thrust generated by the quadrotor at time

t_{0}

, and it can be expressed as

T_{K} = T_{1} + T_{2} + T_{3} + T_{4}

. Each

T_{i} (i = 1,2, 3,4)

represents the thrust

T_{i} = k_{ω} ω_{i}^{2}

generated by the i-th motor, where

k_{ω}

is a positive constant. The variable

τ_{b}

describes external torques acting on the x, y, and z axes of the body frame, which satisfy:

τ_{b} = [\begin{matrix} l_{b} b (T_{1} - T_{2} - T_{3} + T_{4}) \\ l_{b} b (T_{1} + T_{2} - T_{3} - T_{4}) \\ k_{τ} (T_{1} - T_{2} + T_{3} - T_{4}) \end{matrix}]

(4)

Where,

l_{b}

and

k_{τ}

represent the body radius and the conversion factor from force to torque, respectively.

2.2. Control Problem Description

In the above,

P_{d}^{E} = {[\begin{matrix} p_{d x}^{e} & p_{d y}^{e} & p_{d z}^{e} \end{matrix}]}^{T}

and

V_{d}^{E} = {[\begin{matrix} v_{d x}^{e} & v_{d y}^{e} & v_{d z}^{e} \end{matrix}]}^{T}

represent the desired position and velocity of the quadrotor in the inertial frame, respectively.

Θ_{d}^{E} = {[\begin{matrix} ϕ_{d} & θ_{d} & ψ_{d} \end{matrix}]}^{T}

represents the desired Euler angles of the quadrotor, and

Ω_{d}^{B} = {[\begin{matrix} p_{d} & q_{d} & r_{d} \end{matrix}]}^{T}

represents the desired angular velocity of the quadrotor in the body frame. Among these variables,

P_{d}^{E}

and

ψ_{d}

serve as inputs to the entire control system. The desired roll angle

ϕ_{d}

and pitch angle

θ_{d}

are obtained by the outer loop bioinspired backstepping position control system to achieve trajectory tracking. Specifically, the desired position

P_{d}^{E}

and yaw angle

ψ_{d}

of the quadrotor are determined based on the tracking trajectory at time

t_{0}

. Figure 3 depicts the relationship between tracking errors in the body and inertial coordinate systems during the tracking process. Here, the position error is represented by

e_{P} = P_{d}^{E} - P^{E}

, the velocity error by

e_{V} = V_{d}^{E} - V^{E}

, the Euler angle error by

e_{Θ} = Θ_{d}^{E} - Θ^{E}

, and the body angle error by

e_{Ω} = Ω_{d}^{B} - Ω^{B}

. The outputs of the relevant controllers are denoted as

u_{P} = [u_{p i}] \in R^{3 \times 1}

u_{V} = [u_{v i}] \in R^{3 \times 1}

u_{Θ} = [u_{Θ i}] \in R^{3 \times 1}

, and

u_{Ω} = [u_{Ω i}] \in R^{3 \times 1}

. Specifically,

u_{P}

u_{Θ}

, and

u_{v i} (i = 1,2)

correspond to the inputs of the velocity controller, angle controller, and angular velocity controller, respectively. They satisfy

V_{d}^{E} = u_{P}

ϕ_{c d} = u_{v 1}

θ_{c d} = u_{v 2}

, and

Ω_{d}^{B} = u_{Θ}

u_{v 3}

and

u_{Ω}

represent the control signal inputs for the quadrotor, which drive the four motors to generate total thrust and torque for following the desired trajectory. In this paper, the actual quadrotor dynamical system is treated as a nominal system with the addition of an equivalent disturbance. Therefore, the quadrotor dynamical model can be rewritten as follows:

{\dot{P}}^{E} = u_{P} + Δ_{p} {\dot{V}}^{E} = G_{V} u_{V} - G + Δ_{v} {\dot{Θ}}^{E} = u_{Θ} + Δ_{Θ} \begin{matrix} {\dot{Ω}}^{B} = G_{Ω} u_{Ω} + I^{- 1} [G_{a} {- Ω^{B} \times (I \cdot Ω^{B})}_{}] + Δ_{Ω} \end{matrix}

(5)

Where,

G = {[\begin{matrix} 0 & 0 & g \end{matrix}]}^{T}

；

G_{V} = d i a g (g, - g, k_{t} / m)

;

G_{Ω} = I^{- 1} d i a g (k_{σ p}, k_{σ q}, k_{σ r})

；

k_{t}

k_{σ p}

k_{σ q}

, and

k_{σ r}

are gain constants of the controller satisfying

T_{K} = k_{t} u_{v z}

τ_{b p} = k_{σ p} u_{Ω p}

τ_{b q} = k_{σ q} u_{Ω q}

, and

τ_{b r} = k_{σ r} u_{Ω r}

;

Δ_{i} (i = p, v, Θ, Ω)

represents external disturbances and aerodynamics, satisfying:

Δ_{p} = V^{E} - u_{P} Δ_{v} = \frac{1}{m} (F_{d} + d v) Δ_{Θ} = R_{Θ} Ω^{B} - u_{Θ} \begin{matrix} Δ_{Ω} = I^{- 1} M_{d} \end{matrix}

(6)

3. Quadrotor Control Design Aided with Bioinspired Neural Dynamics

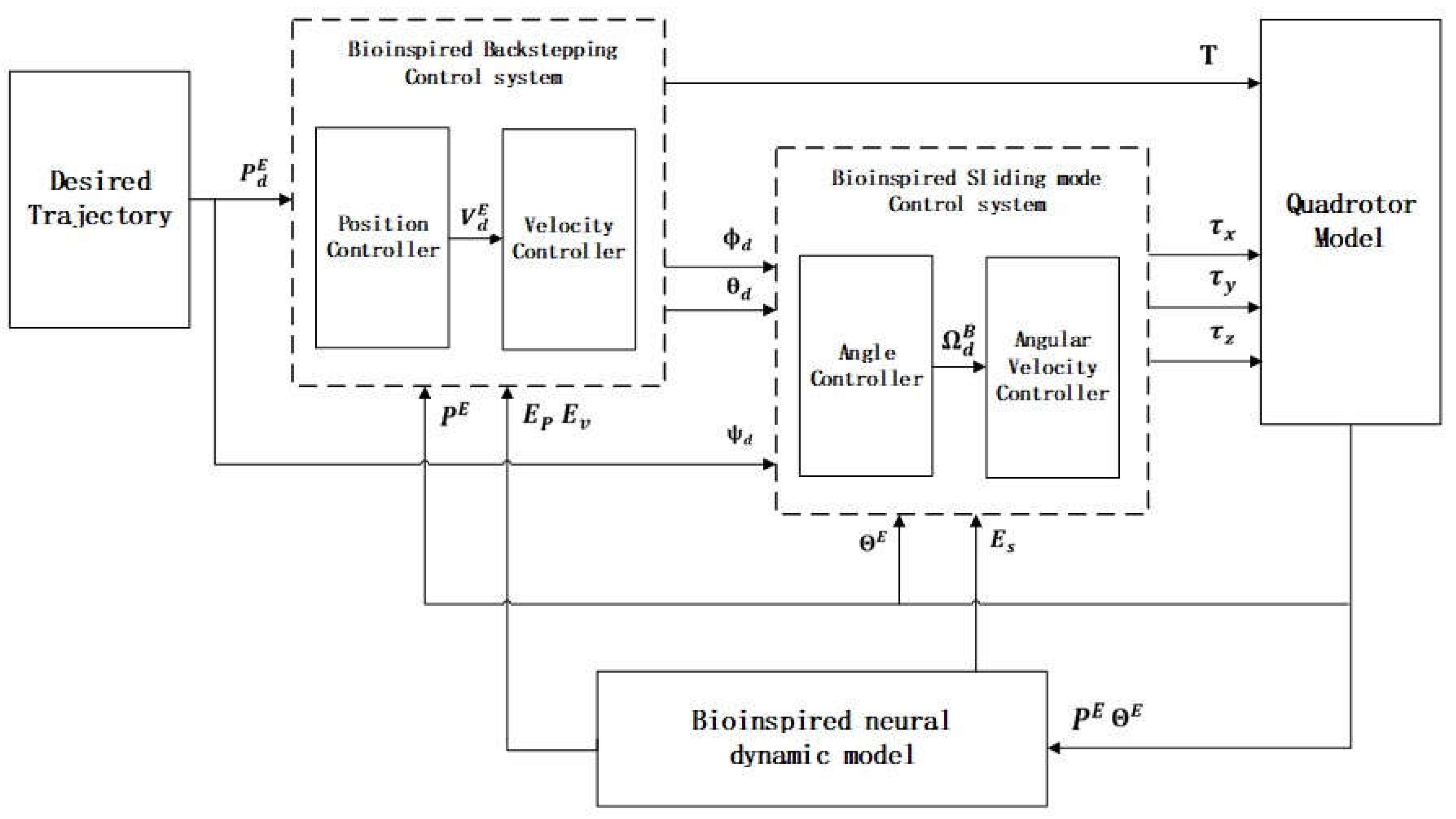
In this section, a hybrid control strategy is developed for a quadcopter drone to address the issues of velocity jumps and control signal chattering in backstepping control and sliding mode control. Figure 3 illustrates the closed-loop control framework, comprising two cascaded control systems. The outer-loop position control system consists of a bioinspired backstepping position controller and velocity controller. The position controller generates smooth velocity commands to prevent abrupt velocity jumps caused by significant tracking errors and external disturbances, while the velocity controller provides desired angular commands. The inner-loop attitude control system utilizes the output angular commands from the outer-loop control system to generate torque control signals for trajectory tracking. To mitigate the control signal chattering problem encountered in traditional sliding mode control, the inner-loop attitude control system incorporates a sliding mode controller with bioinspired neural dynamics.

3.1. Bioinspired Neural Dynamic Model

Hodgkin and Huxley initially proposed a membrane model that utilized electrical elements to describe the behavior of a membrane [26]. Subsequently, Grossberg [30] further advanced this model to capture real-time adaptive behavior in individuals. Yang and Meng [22] were pioneers in applying this model to robots, enabling real-time collision-free motion planning in dynamic environments without the need for prior learning. Over time, this model has been extended to various other robot applications. Referred to as the shunting model, the bioinspired neural dynamics model is expressed as follows:

{\dot{x}}_{i} = - A_{i} x_{i} + (B_{i} - x_{i}) S_{i}^{+} - (D_{i} + x_{i}) S_{i}^{-}

(7)

In this model,

x_{i}

denotes the neural activity of the i-th neuron.

A_{i}

represents the passive decay rate, while

B_{i}

and

D_{i}

represent the upper and lower bounds of the i-th neuron, respectively. The variables

S_{i}^{+}

and

S_{i}^{-}

indicate the excitatory and inhibitory inputs to the i-th neuron. By utilizing equation (7), the shunting model for the quadcopter can be defined as follows:

\begin{matrix} {\dot{E}}_{i} = - A_{i} E_{i} + (B_{i} - E_{i}) f (e_{i}) - ({E_{i} - D}_{i}) g (e_{i}) \end{matrix}

(8)

Where,

e_{i} (i = P, V, S)

represents the inputs to the shunting model, which signifies the error between the desired pose and the quadrotor's state. The functions

f (e_{i})

and

g (e_{i})

are defined as

f (e_{i}) = \max (e_{i}, 0) a n d g (e_{i}) = m a x (- e_{i}, 0)

respectively.

E_{i}

denotes the output of the shunting model, and for any input

e_{i}

E_{i}

is constrained within the limits of

{(B}_{i}, D_{i})

. Given the specific characteristics of the quadcopter drone model, we assume

|B_{i}| = |D_{i}|

. Moreover, it is important to highlight that the shunting model exhibits properties similar to those of a low-pass filter, imparting robustness against aerodynamic forces and external disturbances. Subsequent sections will delve into a detailed explanation of the design process for the entire control system.

3.2. Bioinspired Backstepping Position Control System

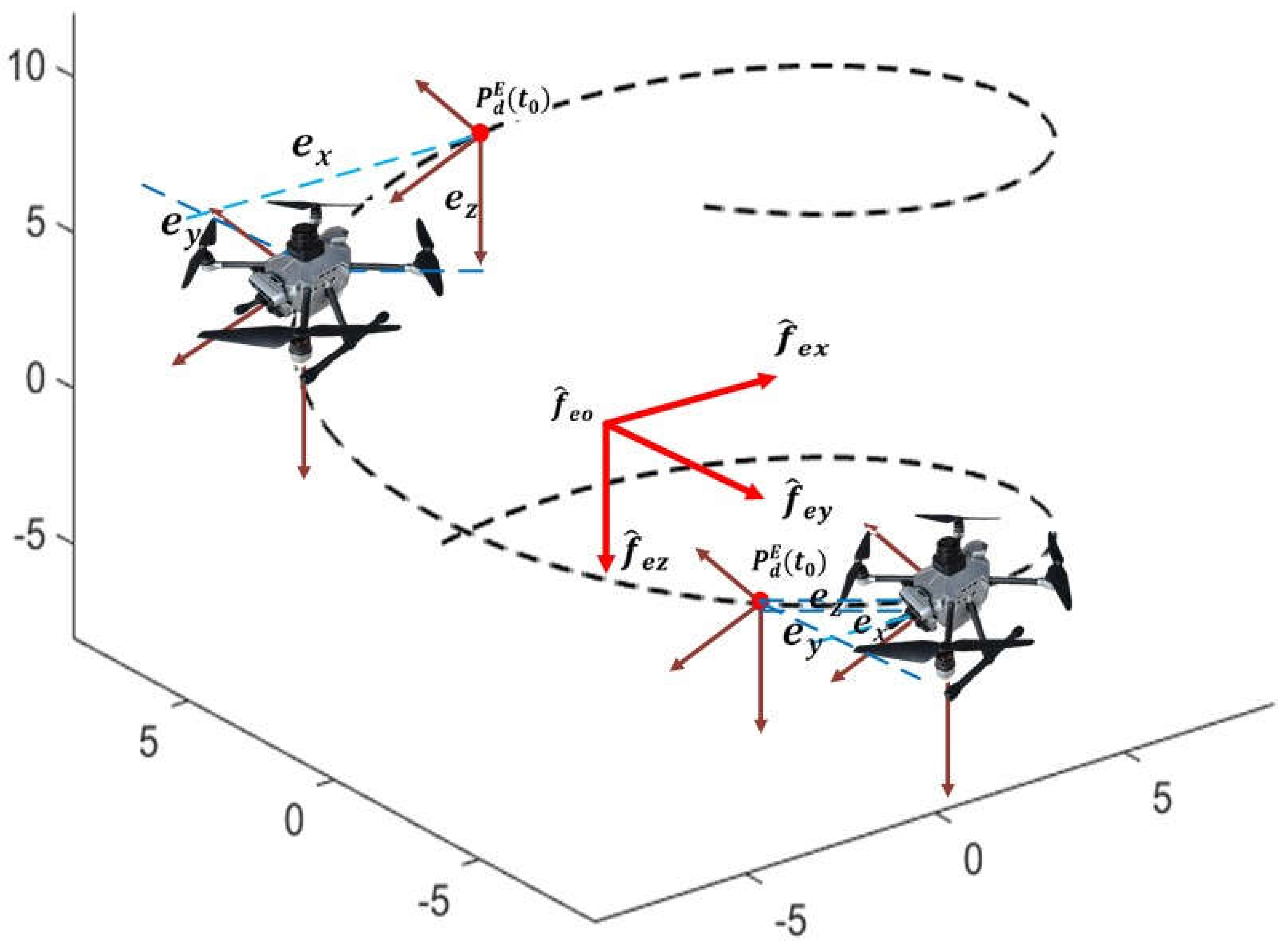
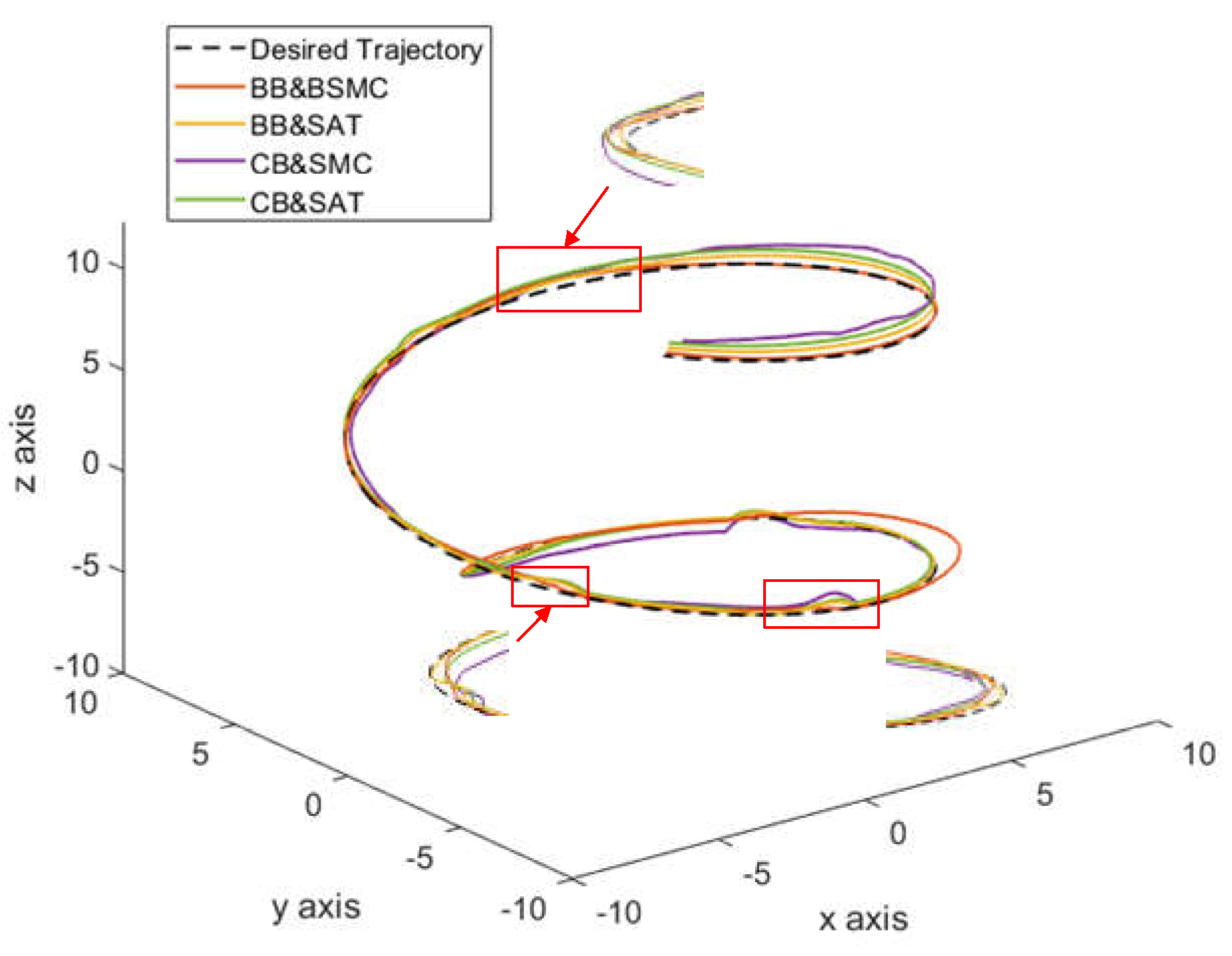
Designing a backstepping position controller for a quadcopter using Lyapunov functions is relatively straightforward. However, the drone's state and external disturbances can cause unrealistic velocity changes that are not achievable for a drone with limited inputs. To address this issue, this section proposes a bioinspired backstepping position controller that combines the shunting model (Equation 8) with the backstepping control strategy. The focus of this article is primarily on controlling the quadcopter drone to track a spiral ascent trajectory in three-dimensional space, as shown in Figure 2. Therefore, the relationship between the desired position state and the desired velocity state for the drone's trajectory tracking is expressed as:

[\begin{matrix} v_{d x}^{e} \\ v_{d y}^{e} \\ v_{d z}^{e} \end{matrix}] = [\begin{matrix} {\dot{x}}_{d} \\ {\dot{y}}_{d} \\ {\dot{z}}_{d} \end{matrix}]

(9)

The objective of the outer-loop position control system is to produce control inputs for the thrust, roll angle, and pitch angle. The position controller in the system generates velocity control inputs to drive the quadcopter to a certain speed, thus minimizing the tracking error towards zero. Figure 2 shows the tracking position error in the X, Y, and Z-axis directions of the inertial coordinate system as

e_{P} = {[\begin{matrix} e_{x} & e_{y} & e_{z} \end{matrix}]}^{T}

, combined with the velocity error obtained from equation (9) as

e_{V} = {[\begin{matrix} e_{v x} & e_{v y} & e_{v z} \end{matrix}]}^{T}

. Consequently, the position control inputs for the quadcopter, based on the backstepping control approach, are as follows:

u_{V} = G_{V}^{- 1} [{\ddot{P}}_{d}^{E} + G + k_{V} e_{V}] {\dot{V}}_{}^{E} = {\ddot{P}}_{d}^{E} + k_{V} e_{V} \begin{matrix} {\dot{P}}_{}^{E} = V^{E} = {\dot{P}}_{d}^{E} + k_{P} e_{P} \end{matrix}

(10)

k_{P}

and

k_{V}

, respectively. These parameters are defined as

k_{P} = d i a g (k_{p 1}, k_{p 2}, k_{p 3})

and

k_{V} = d i a g (k_{v 1}, k_{v 2}, k_{v 3})

. Equation (10) reveals that in scenarios where the drone is in its initial stage or affected by external disturbances, resulting in significant tracking errors in position and velocity, the terms

k_{V} e_{V} a n d {k_{P} e}_{P}

may lead to abrupt changes in velocity during displacement motion. To mitigate this issue, a backstepping control strategy combined with the bioinspired neural dynamics model is proposed. The new virtual control commands are defined as follows:

u_{V} = G_{V}^{- 1} [{\ddot{P}}_{d}^{E} + G + {k_{V} E}_{V}]

(11)

Where

E_{P}

and

E_{V}

represent the outputs of the shunting model for the quadcopter, replacing the position and velocity error inputs,

e_{P}

and

e_{V}

. The error terms in the virtual control commands must satisfy the following inequality:

k_{P} D_{P} < k_{P} E_{P} < k_{P} B_{P}, {k_{V} D}_{V} < k_{V} E_{V} < + k_{V} B_{V}

(12)

B_{P}

and

B_{V}

represent positive constants, while

D_{P} = {- B}_{P}

and

D_{V} = {- B}_{V}

. Consequently, by carefully selecting appropriate desired velocity

{\dot{P}}_{d}^{E}

and desired acceleration

{\ddot{P}}_{d}^{E}

, the virtual control command

u_{V}

remains within its dynamic constraints and is bounded. Furthermore, thanks to the filtering capability of the bioinspired neural dynamics model, the bioinspired backstepping controller can provide smooth control inputs, even in the presence of noise. The stability of the bioinspired backstepping controller is demonstrated in Section 3.4.

3.3. Bioinspired Sliding Attitude Control System

In this section, we present the development of a robust sliding mode control strategy for a quadcopter drone. The proposed attitude control system combines traditional sliding mode control with the bioinspired neural dynamics model (8) to effectively address the issue of signal chattering commonly encountered in traditional sliding mode controllers. The angle commands

u_{v 1}, u_{v 2}

generated by the bioinspired backstepping position control system, along with the desired yaw angle

ψ_{d}

, are utilized as inputs to the attitude control system. Subsequently, the bioinspired sliding mode controller generates torque control signals

u_{Ω}

to guide the quadcopter drone model towards the desired state.

The defined sliding surface is expressed as follows:

S = {\dot{e}}_{Ω} + a_{1} e_{Ω} + a_{2} \int e_{Ω}

(13)

Where

a_{1}

and

a_{2}

are defined as positive constants. Taking the derivative of equation (13), we have:

\dot{S} = {\ddot{e}}_{Ω} + a_{1} {\dot{e}}_{Ω} + a_{2} e_{Ω}

(14)

From equation (14), we can see that when the system operates on the sliding surface

\dot{S} = 0

, we have:

{\ddot{e}}_{Ω} + a_{1} ({\dot{Ω}}_{d}^{B} - {\dot{Ω}}_{}^{B}) + a_{2} e_{Ω} = 0

(15)

By substituting the quadcopter dynamics model (5) into equation (15), we obtain:

{\ddot{e}}_{Ω} + a_{1} ({\dot{Ω}}_{d}^{B} - (G_{Ω} u_{Ω} + I^{- 1} [G_{a} {- Ω^{B} \times (I \cdot Ω^{B})}_{}] + ∆_{Ω})) + a_{2} e_{Ω} = 0

(16)

Therefore, the design of the equivalent control law is given by:

u_{q} = G_{Ω}^{- 1} (\frac{1}{a_{1}} ({\ddot{e}}_{Ω} + a_{2} e_{Ω}) + {\dot{Ω}}_{d}^{B} - I^{- 1} [G_{a} {- Ω^{B} \times (I \cdot Ω^{B})}_{}] - D_{Ω})

(17)

Where

D_{Ω}

represents the compensation for aerodynamic moments by the sliding mode controller, satisfying:

D_{Ω} = d_{Ω 2} - d_{Ω 1} s g n (S)

(18)

d_{Ω 1} = (δ_{U} + δ_{L}) / 2

and

d_{Ω 2} = (δ_{L} - δ_{U}) / 2

, where

δ_{U}

represents the upper bound of the aerodynamic moment and

δ_{L}

represents the lower bound. Due to the computational challenges in calculating

{\ddot{e}}_{Ω}

as stated in equation (17), an approximation can be made by defining

{\ddot{e}}_{Ω} = k_{e} {\dot{e}}_{Ω}

, where

k_{e}

represents a feedback control gain. The conventional sliding mode control law can be expressed as follows:

u_{Ω} = u_{q} + k_{s} s g n (S)

(19)

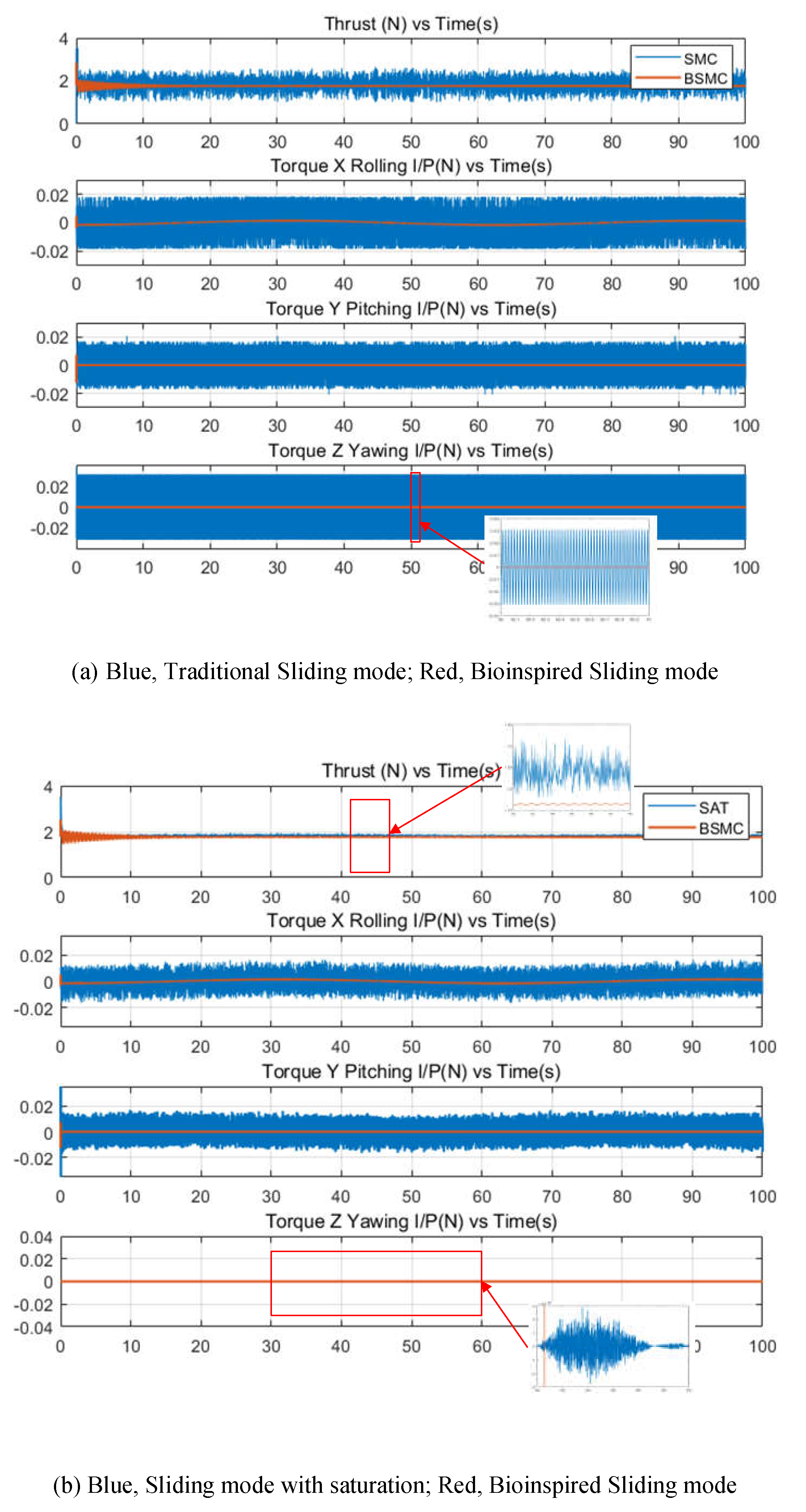
Chattering in traditional sliding mode control signals is a result of the sign function sgn(·). To mitigate this issue, a commonly used approach is to substitute the sign function with a saturation function. Consequently, the sliding mode control law incorporating the saturation function can be expressed as follows:

u_{Ω} = u_{q} + k_{s} s a t (S) \begin{matrix} s a t (S) = \{\begin{matrix} B_{S}, k_{s} S > B_{S} \\ k_{s} S, B_{S} \geq k_{s} S \geq \\ D_{S}, {D_{S} > k}_{s} S \end{matrix} B_{S} \end{matrix}

(20)

Where

B_{S}

and

D_{S}

denote the upper and lower bounds of the saturation function, respectively. Although the saturation function effectively reduces control signal chattering in the presence of small control signals, it may not be suitable for all applications in complex operating environments where larger control signals are necessary to ensure stable flight. To address this limitation, a combination of biologically inspired neural dynamics (equation 8) and sliding mode control is proposed. The resulting biologically inspired sliding mode control commands are defined as follows:

u_{Ω} = u_{q} + E_{S}

(21)

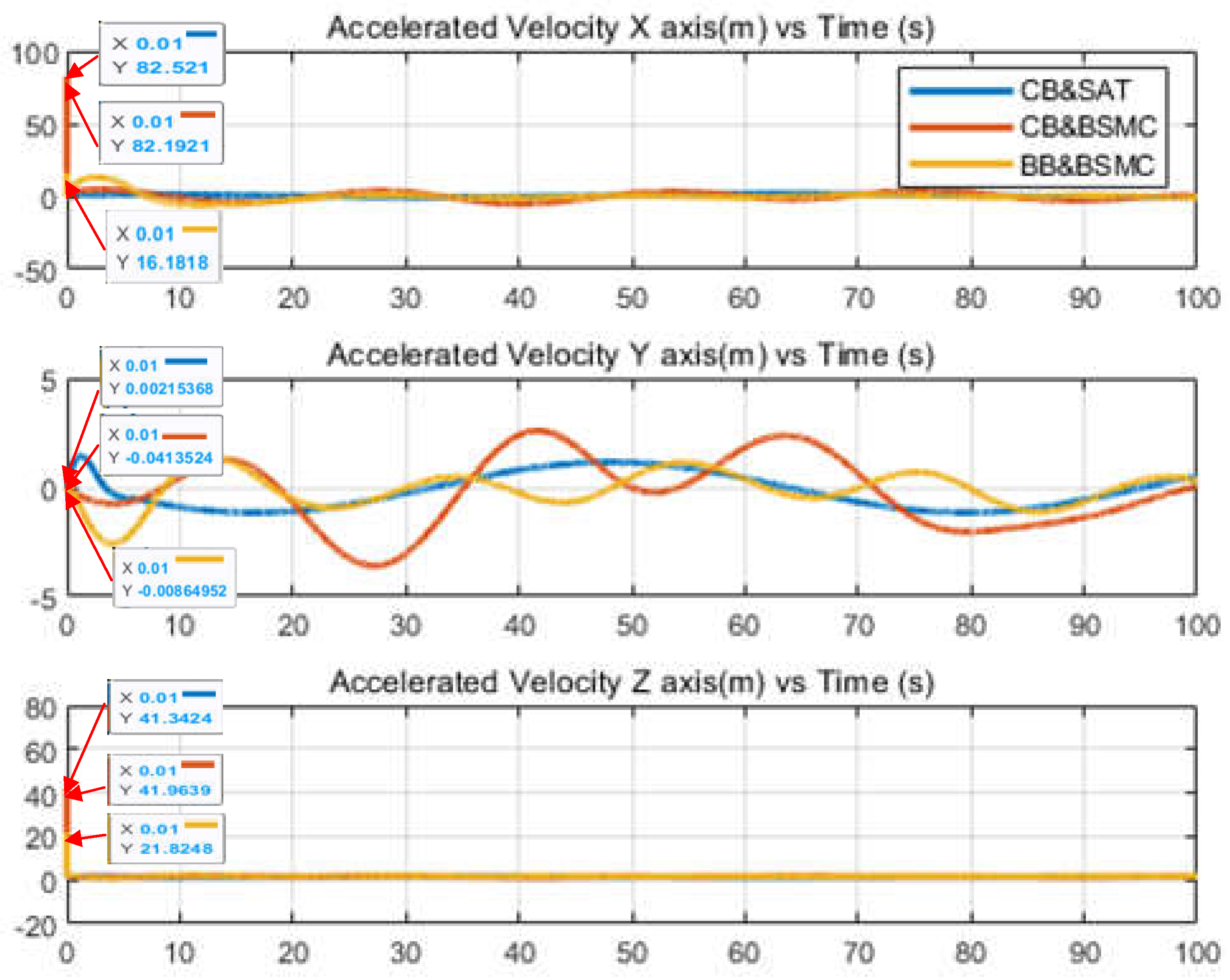
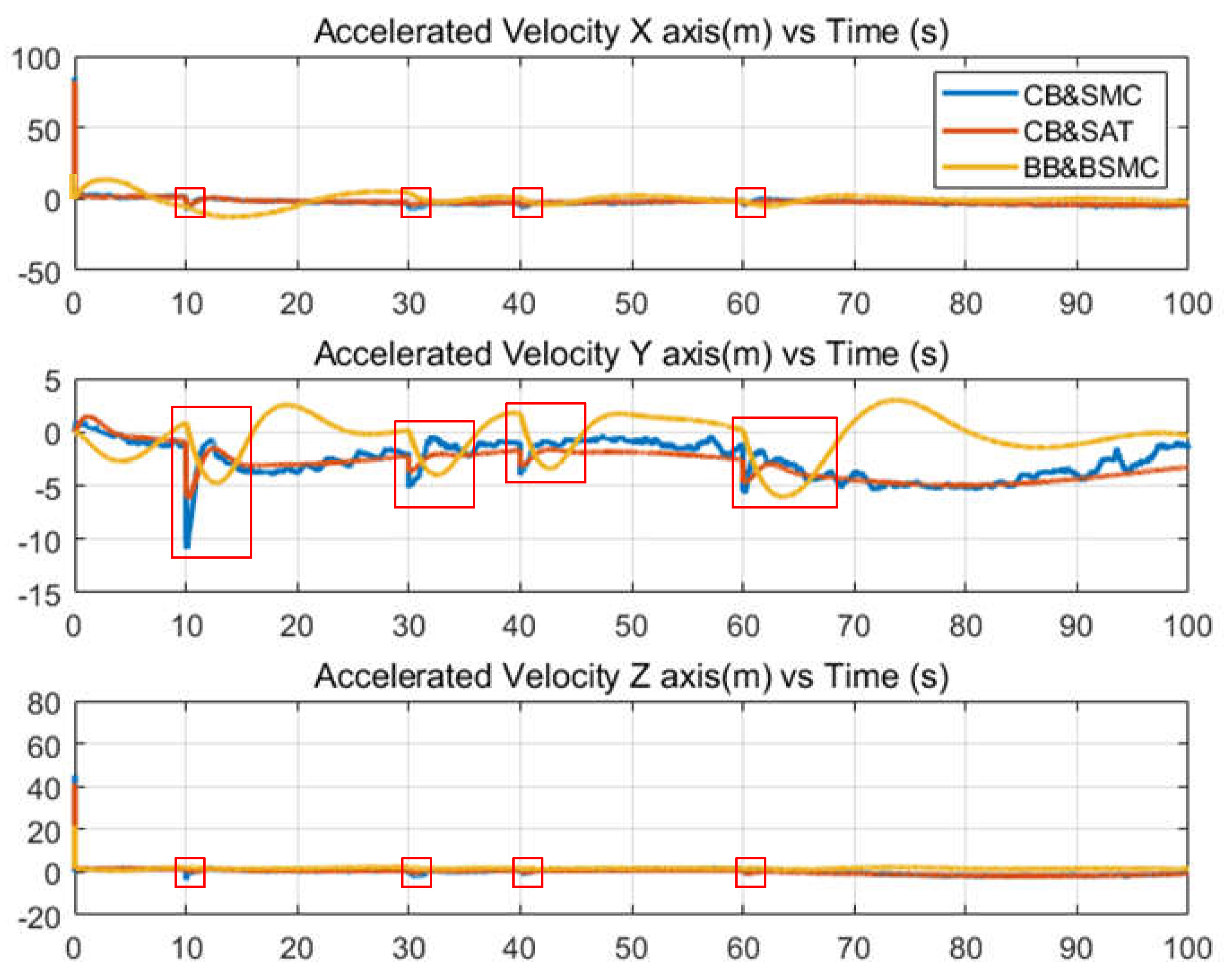
The proposed biologically inspired sliding mode controller in this paper effectively mitigates the problem of control signal chattering that is commonly encountered in traditional sliding mode control methods. Moreover, it demonstrates excellent trajectory tracking performance even in complex scenarios.

3.4. Stability Analysis

This paper presents a novel approach to achieve progressive trajectory tracking control by integrating a bioinspired neural network control strategy with the aerodynamics and external disturbances of a quadrotor unmanned aerial vehicle. The asymptotic stability of both control systems is verified through rigorous Lyapunov stability analysis. Additionally, by constructing a global Lyapunov candidate function, the study establishes the global asymptotic stability of the proposed control system.

To demonstrate the stability of the bioinspired backstepping controller, the Lyapunov function is defined as follows:

V_{P} = \frac{1}{2} e_{P}^{2} + \frac{1}{2} e_{V}^{2} + \frac{k_{P}}{2 B_{P}} E_{P}^{2} + \frac{k_{V}}{2 B_{V}} E_{V}^{2}

(22)

Then, the derivative of

V_{P}

is denoted as:

{\dot{V}}_{P} = {e_{P} {\dot{e}}_{P} + e}_{V} {\dot{e}}_{V} + \frac{k_{P}}{B_{P}} E_{P} {\dot{E}}_{P} + \frac{k_{V}}{B_{V}} E_{V} {\dot{E}}_{V}

(23)

Splitting the time derivative expression (23) of the candidate function into two components, we have:

{e_{P} {\dot{e}}_{P} + e}_{V} {\dot{e}}_{V}

and

\frac{k_{P}}{B_{P}} E_{P} {\dot{E}}_{P} + \frac{k_{V}}{B_{V}} E_{V} {\dot{E}}_{V}

. Based on the tracking errors and equation (10),

{e_{P} {\dot{e}}_{P} + e}_{V} {\dot{e}}_{V}

can be written as:

{e_{P} {\dot{e}}_{P} + e}_{V} {\dot{e}}_{V} = e_{P} ({\dot{P}}_{d}^{E} - {\dot{P}}_{}^{E}) + e_{V} ({\dot{V}}_{d}^{E} - {\dot{V}}_{}^{E}) \begin{matrix} = {- {k_{P} E}_{P} e}_{P} {- k_{V} E_{V} e}_{V} \end{matrix}

(24)

For the second part, ，

\frac{k_{P}}{B_{P}} E_{P} {\dot{E}}_{P} + \frac{k_{V}}{B_{V}} E_{V} {\dot{E}}_{V}

, of the Lyapunov function, considering the specific characteristics of the quadrotor unmanned aerial vehicle model, let's assume

B_{P} = {- D}_{P}

and

B_{V} = {- D}_{V}

. Based on the biological neural dynamics model equation (8), the second part can be written as:

\frac{k_{P}}{B_{P}} E_{P} {\dot{E}}_{P} + \frac{k_{V}}{B_{V}} E_{V} {\dot{E}}_{V} = \frac{k_{P}}{B_{P}} E_{P} (- A_{P} E_{P} + (B_{P} - E_{P}) f (e_{P}) - (E_{P} - D_{P}) g (e_{P})) + \frac{k_{V}}{B_{V}} E_{V} (- A_{V} E_{V} + (B_{V} - E_{V}) f (e_{V}) - (E_{V} - D_{V}) g (e_{V})) \begin{matrix} = \frac{k_{P}}{B_{P}} E_{P}^{2} (- A_{P} - f (e_{P}) - g (e_{P})) + {k_{P} E}_{P} (f (e_{P}) - g (e_{P})) \end{matrix} \begin{matrix} + \frac{k_{V}}{B_{V}} E_{V}^{2} (- A_{V} - f (e_{V}) - g (e_{V})) + {k_{V} E}_{V} (f (e_{V}) - g (e_{V})) \end{matrix}

(25)

Combining equations (24) and (25), we can infer that:

{\dot{V}}_{P} = \frac{k_{P}}{B_{P}} E_{P} (- A_{P} E_{P} + (B_{P} - E_{P}) f (e_{P}) - (E_{P} - D_{P}) g (e_{P})) + \frac{k_{V}}{B_{V}} E_{V} (- A_{V} E_{V} + (B_{V} - E_{V}) f (e_{V}) - (E_{V} - D_{V}) g (e_{V})) \begin{matrix} = \frac{k_{P}}{B_{P}} E_{P}^{2} (- A_{P} - f (e_{P}) - g (e_{P})) + {k_{P} E}_{P} (f (e_{P}) - g (e_{P}) - e_{P}) \end{matrix} \begin{matrix} + \frac{k_{V}}{B_{V}} E_{V}^{2} (- A_{V} - f (e_{V}) - g (e_{V})) + {k_{V} E}_{V} (f (e_{V}) - g (e_{V}) - e_{V}) \end{matrix}

(26)

According to the equation (8), we can conclude that:

\{\begin{matrix} f (e_{i}) = e_{i} g (e_{i}) = 0, e_{i} \geq 0 \\ f (e_{i}) = 0 g (e_{i}) = - e_{i}, e_{i} < 0 \end{matrix}

(27)

By using formula (27), we obtain:

- A_{i} - f (e_{i}) - g (e_{i}) < 0 \begin{matrix} f (e_{i}) - g (e_{i}) = e_{i} \end{matrix}

(28)

From equations (22), (26), and (28), it can be inferred that as

t \to \infty

V_{P} \to 0

and

{\dot{V}}_{P}

is negative definite.

V_{P}

can only be zero when

e_{i} = 0^{3 \times 1}

. Therefore, the bioinspired backstepping position control system designed in this paper is asymptotically stable.

To prove the stability of the bioinspired sliding mode controller, the designed Lyapunov function is defined as follows:

V_{Θ} = - \frac{1}{2} S^{T} S + \frac{1}{2 B_{S}} E_{S}^{T} E_{S}

(29)

Differentiating the Lyapunov equation, we obtain:

{\dot{V}}_{Θ} = - S^{T} \dot{S} + \frac{1}{B_{S}} {\dot{E}}_{S}^{T} E_{S}

(30)

Combining the biological neural dynamics model (8) with equation (30), we have:

{\dot{V}}_{Θ} = {- S}^{T} ({\ddot{e}}_{Ω} + a_{1} {\dot{e}}_{Ω} + a_{2} e_{Ω}) \begin{matrix} + \frac{1}{B_{S}} E_{S} (- {A_{S}}^{T} {E_{S}}^{T} + ({B_{S}}^{T} - {E_{S}}^{T}) f^{T} (S) - ({E_{S}}^{T} - {D_{S}}^{T}) g^{T} (S)) \\ = {- S}^{T} ({\ddot{e}}_{Ω} + a_{1} {\dot{e}}_{Ω} + a_{2} e_{Ω}) + \frac{1}{B_{S}} E_{S} {E_{S}}^{T} (- {A_{S}}^{T} - f^{T} (S) - g^{T} (S)) \\ + \frac{1}{B_{S}} E_{S} ({B_{S}}^{T} f^{T} (S) + {D_{S}}^{T} g^{T} (S)) \end{matrix}

(31)

Combining formulas (5), formula (31) can be written as:

\begin{matrix} {\dot{V}}_{Θ} = - S^{T} E_{S} + \frac{1}{B_{S}} E_{S} {E_{S}}^{T} (- {A_{S}}^{T} - f^{T} (S) - g^{T} (S)) \\ + \frac{1}{B_{S}} E_{S} ({B_{S}}^{T} f^{T} (S) + {D_{S}}^{T} g^{T} (S)) \end{matrix}

(32)

Where,

{B_{S}}^{T} = - {D_{S}}^{T} a n d {{B_{S}}^{T} = B}_{S}

, rewriting equation (32), we have:

{\dot{V}}_{Θ} = \frac{1}{B_{S}} E_{S} {E_{S}}^{T} (- {A_{S}}^{T} - f^{T} (S) - g^{T} (S)) + E_{S} (f^{T} (S) - g^{T} (S) - S^{T})

(33)

Based on formulas (27) and (28), we can also observe that

\frac{1}{B_{S}} E_{S} {E_{S}}^{T} (- {A_{S}}^{T} - f^{T} (S) - g^{T} (S)) < 0 a n d E_{S} (f^{T} (S) - g^{T} (S) - S^{T}) = 0

. From the biological neural dynamics model (8), as

t \to \infty

S \to 0

, and

E_{S}

also tends to 0. It follows that

V_{Θ} \to 0

{\dot{V}}_{Θ}

is negative definite, and

V_{Θ}

can only be zero when

S = 0

. Therefore, the designed bioinspired sliding mode attitude control system is asymptotically stable.

To demonstrate the stability of the entire control system, the Lyapunov function of the system and its time derivative are designed as follows:

V_{} = V_{P} + V_{Θ} \begin{matrix} \dot{V_{}} = {\dot{V}}_{P} + {\dot{V}}_{Θ} \end{matrix}

(34)

The results obtained from equations (26) and (33) can prove that the entire control system is asymptotically stable.

4. Results

In this study, we validate the efficacy of the proposed hybrid control strategy through comprehensive numerical simulations conducted using MATLAB/Simulink. We employ the quadrotor unmanned aerial vehicle model described in equation (1), and the specific model parameters are documented in Table 1. To evaluate the robustness and effectiveness of our control approach, we examine two scenarios: an ideal environment devoid of disturbances and a more intricate application setting featuring step-wise ascending disturbances. The simulations are conducted over a duration of 100 seconds.

4.1. Undisturbed Trajectory Tracking

To assess the trajectory tracking capabilities of our proposed hybrid control strategy, we assume a continuous and differentiable desired tracking trajectory. The chosen trajectory is defined as

x_{d} = 8 s i n (0.1 t), y_{d} = 8 s i n (0.1 t + \frac{1}{2} π), z_{d} = - 8 + 0.2 t

, with a constant desired yaw angle

ψ_{d}

of zero. Initially, the body is positioned at

P^{E} = {[0 - 0 - - 8]}^{T}

, while the velocities

V^{E} = Θ^{E} = Ω^{B} = 0^{3 \times 1}

. We conduct numerical simulations in the absence of disturbances, utilizing the control parameters listed in Table 2. Figure 4 illustrates the performance of our proposed control method, which exhibits slight deviations compared to other control methods [31-33].

In comparison to other control methods, the proposed approach demonstrates superior trajectory tracking performance. While the traditional backstepping control strategy results in a shorter time for the unmanned aerial vehicle to reach the desired trajectory compared to the bioinspired backstepping control strategy, Figure 5 shows that the velocity commands generated by the former exhibit abrupt changes. On the other hand, the bioinspired hybrid control method produces smoother velocity commands without any jumps. The abrupt change in velocity commands is a crucial issue for practical applications of unmanned aerial vehicles because it demands the immediate attainment of unrealistic velocities and torques when there is a significant initial error, which is not achievable with existing actuators. Furthermore, this issue may pose a risk of crashes during flight. Therefore, the bioinspired backstepping control strategy effectively addresses this problem.

Furthermore, from Figure 6a, it can be observed that the traditional sliding mode control strategy suffers from control signal chattering, which imposes a significant burden on the onboard actuators. In contrast, the proposed bio-inspired sliding mode controller effectively avoids this issue and provides smooth torque control inputs. The combination of saturation function and sliding mode control is a common approach that can effectively mitigate the chattering problem associated with some traditional sliding mode control methods. However, when the tracking error

e_{Ω}

is outside the interval defined by

B_{Ω}

and

D_{Ω}

, the control signal may still exhibit chattering. When the unmanned aerial vehicle operates in a complex environment, it is challenging to tune the control parameters of the saturation function to achieve satisfactory performance under varying flight conditions. As shown in Figure 6b, although the chattering problem is partially addressed, some chattering still persists. Hence, the saturation function alone cannot fully resolve the chattering issue in traditional sliding mode control, while the bio-inspired sliding mode control strategy, as observed from Figure 6, demonstrates good performance in handling chattering.

4.2. Disturbed Trajectory Tracking

In this section, we investigate an application scenario characterized by step-wise ascending external disturbances as shown in Figure 7, which are caused by adverse weather conditions such as gusts directly impacting the aircraft's center of mass. This scenario aims to assess the robustness of the proposed hybrid control strategy. The control parameters remain consistent with those presented in Table 2, demonstrating reduced reliance on parameters compared to conventional backstepping and sliding mode control approaches. From Figure 8, Figure 9 and Figure 10, it is evident that the proposed control strategy exhibits smoother tracking trajectories and velocity changes in the presence of external disturbances, while maintaining consistent tracking performance thereafter.

5. Conclusions

This paper introduces a novel hybrid control strategy for quadrotor unmanned aerial vehicles (UAVs) based on bioinspired neural dynamics. The control system comprises an outer-loop bioinspired backstepping controller and an inner-loop bioinspired sliding mode controller, addressing the challenges of velocity jumps in traditional backstepping control and control signal chattering in traditional sliding mode control. Furthermore, the proposed control system ensures smooth tracking trajectories even in the presence of external disturbances. The stability of the quadrotor UAV control system is rigorously analyzed using Lyapunov stability theory. Extensive comparative simulation experiments are conducted to assess the robustness and effectiveness of the control system. The results unequivocally demonstrate superior trajectory tracking performance of the proposed control system compared to other control systems for quadrotor UAVs. Future research should include the incorporation of precise state estimation techniques to account for the impact of actuator delays on trajectory tracking.

Funding

This work was supported by the National Natural Science Foundation of China (No. 62273142), the Hunan Province Natural Science Foundation, China (No. 2023JJ30437) and the science and technology innovation Program of Hunan Province (No. 2021GK2010).

References

B. Erginer and E. Altug, "Modeling and PD Control of a Quadrotor VTOL Vehicle," 2007 IEEE Intelligent Vehicles Symposium, Istanbul, Turkey, 2007, pp. 894-899. [CrossRef]
Y. Wu, J. Sun and Y. Yu, "Trajectory tracking control of a quadrotor UAV under external disturbances based on linear ADRC," 2016 31st Youth Academic Annual Conference of Chinese Association of Automation (YAC), Wuhan, China, 2016, pp. 13-18. [CrossRef]
Grzonka, Slawomir, Giorgio Grisetti, and Wolfram Burgard. "A fully autonomous indoor quadrotor." IEEE Transactions on Robotics 28.1 (2011): 90-100. [CrossRef]
Ghadiok, Vaibhav, Jeremy Goldin, and Wei Ren. "On the design and development of attitude stabilization, vision-based navigation, and aerial gripping for a low-cost quadrotor." Autonomous Robots 33.1-2 (2012): 41-68.
Mohd Basri, Mohd Ariffanan, Abdul Rashid Husain, and Kumeresan A. Danapalasingam. "Enhanced backstepping controller design with application to autonomous quadrotor unmanned aerial vehicle." Journal of Intelligent & Robotic Systems 79 (2015): 295-321. [CrossRef]
Shauqee, Mohamad Norherman, Parvathy Rajendran, and Nurulasikin Mohd Suhadis. "An effective proportional-double derivative-linear quadratic regulator controller for quadcopter attitude and altitude control." Automatika: časopis za automatiku, mjerenje, elektroniku, računarstvo i komunikacije 62.3-4 (2021): 415-433. [CrossRef]
Dydek, Zachary T., Anuradha M. Annaswamy, and Eugene Lavretsky. "Adaptive control of quadrotor UAVs: A design trade study with flight evaluations." IEEE Transactions on control systems technology 21.4 (2012): 1400-1406. [CrossRef]
Koivo, A., and Ten-Huei Guo. "Adaptive linear controller for robotic manipulators." IEEE Transactions on Automatic Control 28.2 (1983): 162-171. [CrossRef]
Mokhtari, Abdellah, Abdelaziz Benallegue, and Boubaker Daachi. "Robust feedback linearization and GH/sub/spl infin//controller for a quadrotor unmanned aerial vehicle." 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2005.
Chen, Fuyang, et al. "A novel nonlinear resilient control for a quadrotor UAV via backstepping control and nonlinear disturbance observer." Nonlinear Dynamics 85 (2016): 1281-1295. [CrossRef]
Thanh, Ha Le Nhu Ngoc, et al. "Quadcopter UAVs Extended States/Disturbance Observer-Based Nonlinear Robust Backstepping Control." Sensors 22.14 (2022): 5082. [CrossRef]
Weidong, Zhou, et al. "Position and attitude tracking control for a quadrotor UAV based on terminal sliding mode control." 2015 34th Chinese control conference (CCC). IEEE, 2015.
Noordin, Aminurrashid, et al. "Adaptive PID controller using sliding mode control approaches for quadrotor UAV attitude and position stabilization." Arabian Journal for Science and Engineering 46 (2021): 963-981. [CrossRef]
Mohammadi, Mostafa, and Alireza Mohammad Shahri. "Adaptive nonlinear stabilization control for a quadrotor UAV: Theory, simulation and experimentation." Journal of Intelligent & Robotic Systems 72 (2013): 105-122.
Isidori, Alberto, et al. "Robust nonlinear motion control of a helicopter." Robust Autonomous Guidance: An Internal Model Approach (2003): 149-192.
Mistler, V., Abdelaziz Benallegue, and N. K. M'sirdi. "Exact linearization and noninteracting control of a 4 rotors helicopter via dynamic feedback." Proceedings 10th IEEE international workshop on robot and human interactive communication. Roman 2001 (Cat. no. 01th8591). IEEE, 2001.
Zhang, Yanjun, Gang Tao, and Mou Chen. "Relative degrees and adaptive feedback linearization control of T–S fuzzy systems." IEEE Transactions on Fuzzy systems 23.6 (2015): 2215-2230. [CrossRef]
Mian, Ashfaq Ahmad, and Wang Daobo. "Modeling and backstepping-based nonlinear control strategy for a 6 DOF quadrotor helicopter." Chinese Journal of Aeronautics 21.3 (2008): 261-268. [CrossRef]
Abro, Ghulam E. Mustafa, et al. "Fuzzy Based Backstepping Control Design for Stabilizing an Underactuated Quadrotor Craft under Unmodelled Dynamic Factors." Electronics 11.7 (2022): 999. [CrossRef]
Wei, Yuhao, Li Sun, and Zhongxian Chen. "An improved sliding mode control method to increase the speed stability of permanent magnet synchronous motors." Energies 15.17 (2022): 6313. [CrossRef]
Hodgkin, Alan L., and Andrew F. Huxley. "A quantitative description of membrane current and its application to conduction and excitation in nerve." The Journal of physiology 117.4 (1952): 500. [CrossRef]
Yang, Simon X., and Max Meng. "An efficient neural network approach to dynamic robot motion planning." Neural networks 13.2 (2000): 143-148. [CrossRef]
Zhu, Daqi, and Bing Sun. "The bio-inspired model based hybrid sliding-mode tracking control for unmanned underwater vehicles." Engineering Applications of Artificial Intelligence 26.10 (2013): 2260-2269. [CrossRef]
Mu, Bingxian, Yuanyang Pei, and Yang Shi. "Integral sliding mode control for a quadrotor in the presence of model uncertainties and external disturbances." 2017 American control conference (ACC). IEEE, 2017.
Xiong, Jing-Jing, and En-Hui Zheng. "Position and attitude tracking control for a quadrotor UAV." ISA transactions 53.3 (2014): 725-731. [CrossRef]
Xu, Zhe, et al. "A hybrid tracking control strategy for an unmanned underwater vehicle aided with bioinspired neural dynamics." IET Cyber-Systems and Robotics 4.3 (2022): 153-162. [CrossRef]
Almakhles, Dhafer J. "Robust backstepping sliding mode control for a quadrotor trajectory tracking application." IEEE Access 8 (2019): 5515-5525. [CrossRef]
Zhao, Wanbing, Hao Liu, and Xinlong Wang. "Robust visual servoing control for quadrotors landing on a moving target." Journal of the Franklin Institute 358.4 (2021): 2301-2319. [CrossRef]
Zhang, Xu, et al. "Autonomous flight control of a nano quadrotor helicopter in a GPS-denied environment using on-board vision." IEEE Transactions on Industrial Electronics 62.10 (2015): 6392-6403. [CrossRef]
Grossberg, Stephen. "Nonlinear neural networks: Principles, mechanisms, and architectures." Neural networks 1.1 (1988): 17-61.
Abro, Ghulam E. Mustafa, et al. "Review of hybrid control designs for underactuated quadrotor with unmodelled dynamic factors." Emerging Technologies in Computing: Third EAI International Conference, iCETiC 2020, London, UK, August 19–20, 2020, Proceedings 3. Springer International Publishing, 2020.
Wang, Ning, et al. "Hybrid finite-time trajectory tracking control of a quadrotor." ISA transactions 90 (2019): 278-286. [CrossRef]
Maaruf, Muhammad, Waleed M. Hamanah, and Mohammad A. Abido. "Hybrid Backstepping Control of a Quadrotor Using a Radial Basis Function Neural Network." Mathematics 11.4 (2023): 991. [CrossRef]
Raffo, Guilherme V., Manuel G. Ortega, and Francisco R. Rubio. "Robust nonlinear control for path tracking of a quad-rotor helicopter." Asian Journal of Control 17.1 (2015): 142-156. [CrossRef]
Jia, Zhenyue, et al. "Integral backstepping sliding mode control for quadrotor helicopter under external uncertain disturbances." Aerospace Science and Technology 68 (2017): 299-307. [CrossRef]

Figure 1. Quadrotor unmanned aerial vehicle (UAV) coordinates in body fixed and inertial frame.

Figure 2. Coordinate conversion for quadrotor unmanned aerial vehicle (UAV).

Figure 3. Control system framework for UAV based on the bioinspired hybrid control strategy.

Figure 4. Trajectory tracking performance. CB, Traditional Backstepping [12]; SMC, Traditional Sliding mode [32] SAT, Sliding mode with saturation [19]; BB, Bioinspired Backstepping; BSMC, Bioinspired Sliding mode.

Figure 5. Acceleration Commands. Blue, Traditional Backstepping and Sliding mode with saturation; Red, Traditional Backstepping and Bioinspired Sliding mode; Yellow, Bioinspired Backstepping and Bioinspired Sliding mode.

Figure 6. Thrust and Torque Commands.

Figure 7. Step-wise ascending Disturbance signal.

Figure 8. Trajectory tracking performance with disturbance. CB, Traditional Backstepping [35]; SMC, Traditional Sliding mode [35] SAT, Sliding mode with saturation [19]; BB, Bioinspired Backstepping; BSMC, Bioinspired Sliding mode.

Figure 9. Acceleration Commands with disturbance. Blue, Traditional Backstepping and Sliding mode with saturation; Red, Traditional Backstepping and Bioinspired Sliding mode; Yellow, Bioinspired Backstepping and Bioinspired Sliding mode.

Figure 10. Thrust and Torque Commands with disturbance.

Table 1. Quadrotor model Parameters.

Symbol	Value
m	0.18 kg
g	9.81 m/ $s^{2}$
$l_{b}$	0.225 m
b	2.9× $10^{- 6}$ N $s^{2} / {r a d}^{2}$
$k_{τ}$	1.779× $10^{- 7}$ N $s^{2} / {r a d}^{2}$
$I_{x x}$	2.5× $10^{- 4}$ m/ $s^{2}$
$I_{y y}$	2.5× $10^{- 4}$ m/ $s^{2}$
$I_{z z}$	3.738× $10^{- 4}$ m/ $s^{2}$

Table 2. Controller Parameters.

Symbol	Value
$k_{t}$	0.6
$G_{Ω}$	$I^{- 1} d i a g (1, 1, 1)$
$A_{P}$	$d i a g (- 0.4, - 0.4, - 0.4)$
$B_{P}$	$d i a g (0.8, 0.8, 0.8)$
$D_{P}$	$d i a g (- 0.8, - 0.8, - 0.8)$
$A_{V}$	$d i a g (- 0.25, - 0.25, - 0.25)$
$B_{V}$	$d i a g (1, 1, 1)$
$D_{V}$	$d i a g (- 1, - 1, - 1)$
$A_{S}$	$d i a g (- 0.825, - 0.825, - 0.825)$
$B_{S}$	$d i a g (1.8, 1.8, 1.8)$
$D_{S}$	$d i a g (- 1.8, - 1.8, - 1.8)$
$K_{P}$	$d i a g (1.48, 1.48, 1.2)$
$K_{V}$	$d i a g (6, 6, 4.8)$
$a_{1}$	$d i a g (0.1, 0.1, 0.1)$
$a_{2}$	$d i a g (0.01, 0.01, 0.01)$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Novel Robust Hybrid Control Strategy for a Quadrotor Trajectory Tracking Aided with Bioinspired Neural Dynamics

Abstract

1. Introduction

2. Dynamical Model

2.1. Quadrotor Model

2.2. Control Problem Description

3. Quadrotor Control Design Aided with Bioinspired Neural Dynamics

3.1. Bioinspired Neural Dynamic Model

3.2. Bioinspired Backstepping Position Control System

3.3. Bioinspired Sliding Attitude Control System

3.4. Stability Analysis

4. Results

4.1. Undisturbed Trajectory Tracking

4.2. Disturbed Trajectory Tracking

5. Conclusions

Funding

References

MDPI Initiatives

Important Links

Subscribe