Prerpints.org logo
Preprint
Article

Nature of Charge Transfer Effects in Complexes of Dopamine Derivatives Adsorbed on Graphene-Type Nanostructures

Altmetrics

Downloads

76

Views

27

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.pdf (16.41MB )

This version is not peer-reviewed

Submitted:

29 August 2024

Posted:

30 August 2024

You are already at the latest version

Alerts
Abstract
Continuing the investigation already started (See Farcaş, A.-A.; Bende, A. PCCP 2024, 26, 14937), the light absorption and charge-transfer properties of the dopamine (DA), dopamine zwitterion (called as dopamine-semi-quinone or DsQ) and dopamine-o-quinone (DoQ) adsorbed on the graphene nanoparticle surface have been investigated using the ground state and linear-response time-dependent density functional theories, considering the B97X-D3BJ/def2-TZVPP level of theory. In terms of the strength of molecular adsorption on the surface, the DsQ form has 50 % higher binding energy than that for the DA or DoQ cases (-20.24 kcal/mol vs. -30.41 kcal/mol). The results obtained for electronically excited states and UV-Vis absorption spectra show that the photochemical behavior of DsQ is more similar to DA than that observed for DoQ. Of the three systems analyzed, the DsQ-based complex showed the most active CT phenomenon, both in terms of the number of CT-like states and the amount of charge transferred. Of the first thirty electronically excited states computed for the DsQ case, eleven are purely CT-type and nine are mixed CT and localized (or Frenkel) excitations. By varying the adsorption distance between the molecule and the surface vertically, the amount of charge transfer obtained for DA decreases significantly as the distance increases, for DoQ it remains stable, while for DsQ there are states for which little change is observed, while for others there is a significant change. Furthermore, the mechanistic compilation of the electron orbital diagrams of the individual components cannot describe in detail the nature of the excitations inside the complex.
Keywords: 
Subject: Physical Sciences  -   Chemical Physics

1. Introduction

Charge transfer (CT) effects govern the functional principle of many more complex physical phenomena found in photovoltaic [1,2,3,4,5], photocatalytic [6,7,8] or other optoelectronic materials [9,10]. The basic concept of the CT phenomenon was first introduced by Mulliken [11,12,13], but since then the physical model has progressed considerably as it has become increasingly important in the development of materials with special properties [14,15,16,17].
In general, the theoretical description of CT effects can be formulated based on the first order rate equation in the framework of Marcus theory [18,19,20]. However, in order to understand the global picture of CT effects in biological, molecular electronics and photonics processes it is important to assume the so-called multifaceted nature of charge transfer phenomenon [21,22,23,24,25]. One of these special cases is when the CT effects are induced through the photon absorption by one of the constituents of the system, and either a photoinduced electron transfer (PET) or a hole transfer (PHT) is generated [22]. The resulting photoelectron (or hole) is than the trigger for phenomena such as photocatalysis [26,27,28], photosensitization [29,30] or photovoltaics [5,31].
Energy transfer and its dynamics based on charge carriers at the molecule-semiconductor interface play a fundamental role in almost all the elementary steps required for surface chemistry [32]. Recently, in a previous study [33], we showed that the light-induced charge transfer effects between the graphene nanoparticle (GrNP) surface and the dopamine (DA) molecule adsorbed on it depend on the oxidative state of dopamine (catechol or o-quinone forms). Namely, the charge transfer excitations were characterised as molecule-surface charge transfer (or MSCT) for the GrNP – DA complex and as the reverse, i.e. surface-to-molecule charge transfer (or SMCT) for the GrNP – dopamine-o-quinone (or DoQ) complex. The difference between the two cases is due to the presence of an energetically low-lying unoccupied orbital (LUMO+1 of the complex) in the case of DoQ, which allows charge transfer from the surface to the molecule. This means that the nature of the electron orbitals formed within a complex system is crucial for the charge transfer between subsystems. On the other hand, the photochemical behavior of the isolated dopamine strongly dependents on its the concentration and tautomer forms as well as on the nature and the pH of the solvent environment [34,35]. Moreover, DA through the self-polymerization process can form thin, surface-adherent polydopamine films (PDA) [36,37], where different tautomers or quinone forms of DA build the polymer hetero structure chain. In this regard, it is worth studying not only the surface adsorption and light-absorption properties of the two extremes of the oxidation process [38], but also of the intermediates, such as the protonated dopamine-semi-quinone (DsQ) called as DA-zwitterion [34] (See Figure 1c).
The aim of our study is to give a detailed description of the nature of electron transitions induced by electromagnetic radiation in the case of graphene – DsQ and of the nature of charge transfer as a function of the distance between the molecule and the surface in all three cases (GrNP – DA, GrNP – DsQ and GrNP – DoQ).

2. Results and Discussion

2.1. DsQ Adsorbed on the GrNP Surface

Structure: As a first step, the fully aromatic hydrocarbon structure containing three zig-zag and seven armchair edges as model system for GrNP was fully optimized considering the ωB97X-D3BJ/def2-TZVPP/CPCM level of theory (For details see Section 3). The geometry optimization leads to an irregular honeycomb lattice for GrNP, where the C–C bond length varies between 1.38–1.47 Å. Hereafter, the geometry of the GrNP was kept fixed, on which the DsQ molecule was superimposed, and the relative position of the molecule with respect to the GrNP was optimized using the same theoretical method. The geometry configuration of the DsQ adsorbed on the GrNP surface can be seen in Figure 2. In the equilibrium geometry configuration of the binary complex, the DsQ lies almost parallel with the graphene sheet, distances between the graphene plane and the heavy atoms of the catechol fragment are between 3.369 – 3.463 Å, and the N atom of the amine group is at 3.63 Å far from the plane (see Figure 2b). The adsorption energy, defined as the difference between the energy of the binary complex and the sum of the energies of the individual fragments, is -30.41 kcal/mol, which is more than 50% higher than the adsorption energies obtained for DA (-20.24 kcal/mol) and DoQ (-20.11 kcal/mol), respectively (See Ref. [33]). This also means that DsQ adheres better to the graphene surface than either DA or DoQ molecules. As for the ground state charge distribution, there is a charge transfer from DsQ to the surface of 0.070e (so-called molecular-surface charge transfer or MSCT), which is very close to the value obtained for DA (0.068e, see Ref. [33]). As for the difference in conformational energy between DA and DsQ adsorbed on graphene, it was found that the GrNP – DA complex is more stable than GrNP – DsQ with an energy value of 10.55 kcal/mol. However, in a very recent study, it was shown that the PCM model incorrectly prefers the neutral form to the zwitterion [39], which may, for example, give a discrepancy between DA and DsQ results in the present case. In this respect, e.g. the CANDLE solvent model could give more accurate results [39,40].
UV absorption: In order to better understand the UV absorption spectrum of the binary system and the fingerprints of the different components, the first 30 electronically excited states were calculated both for the binary system and the components separately (See the black, red and blue curves in Figure 3). Taking into account that the results for DsQ have already been reported (see results for dopamine zwitterion (or DAzw) presented in Ref. [34]), only a brief summary of its photochemical behavior is given. In the present case, a slightly different result was obtained, since instead of the DLPNO-STEOM-CCSD method developed at coupled-cluster theory level, the calculations were performed with TDDFT. Accordingly, DsQ presents spectral characteristics with peak maxima at 259 nm (S1) and 224 nm (S2). See the blue spectral curve in Figure 3. The one-electron molecular as well as the natural difference orbitals involved in the electronic excitations of DsQ molecule can be found in the Supplementary Material (SM) file (see Tables S1 and S2)
The geometry optimization of the first excited electron state (S1) leads to a shortening of the C–O bonds (from 1.371 Å to 1.367 Å and from 1.298 Å to 1.270 Å) and to a stretching of the carbon ring, with all six bonds being longer than 1.4 Å (the bond values are 1.427, 1.456, 1.400, 1.414, 1.400 and 1.424, respectively in Å). The fluorescence emission wavelength is 308 nm.
Graphene is a 2D solid that has interesting physics due to its unusual electronic band structure [41]. Of course, this is accompanied by unusual optical properties characterized by a broad absorption spectral range, given by intra-band transitions (π –π *) at low photon energies (0.0-5.0 eV in the far-infrared spectral range) and inter-band transitions ((π – σ*) at higher energies (more than 5.0 eV from the mid-infrared to the ultraviolet) [42,43]. As described in more detail in Section 3, the simplified 0-dimensional GrNP model is able to reproduce most of the spectral features observed in the 2D model. The UV absorption spectrum for GrNP is shown with red line in Figure 3. In this case, two characteristic peaks are observed, one at 566 nm and the other at 270 nm. The first one appears as an effect of a GrNP finite dimensional model, while the second one is the absorption maximum typical of a 2D graphene sheet [33,43].
The UV absorption spectrum of the GrNP – DsQ complex is shown in black in the same Figure 3, while the electronic excited state energies oscillator strengths, amount of charge transfers between the subsystems and the nature of the electronic states (either localized on one of the subsystems or CT state) for the first thirty electronic excited states are collected in Table 1. For the spectrum of the binary system, it is observed that both peaks seen at 566 nm and 270 nm for the pristine GrNP system are almost identically preserved. A very small intensity increase is observed for the S0 → S2 electronic transition (λ(S2) = 471 nm). As for the nature of the excited states, ten are localized on the GrNP, eleven are CT-type, while nine are mixed, i.e. containing both localized and CT-type excitation (See data in Table 1 and the natural difference orbitals (NDO) collected in Table S3 in the SM file). Compared to the GrNP – DA and GrNP – DoQ cases where seventeen and eighteen electron excitations are localized on GrNP, respectively, DsQ is characterized by fewer localized and more CT-type electron transitions, with no pure DsQ-like excitations. Interestingly, it was observed that excitations localized on GrNP have lower (exception S0→ S2), while pure CT-type excitations are characterized by higher energy (upper than S0→ S12) transitions. The strongest CT nature of the excited electron states for DsQ is also confirmed by the amount of charge transferred between the two subsystems. While in the case of GrNP–DA there were only three cases where the transferred charge was greater than 0.3e and only one case greater than 0.7e, for the present system there are eleven states having CT greater than 0.3e, three cases greater than 0.7e, and for the S2 state even one unitary charge is transferred from the DsQ to the graphene nanoparticle (called as molecule-to-surface charge transfer or MSCT effects). To understand the reason for this significant charge transfer, it is necessary to see what the nature of the highest occupied and lowest unoccupied electron orbitals are. Accordingly, based on the fragment orbital contribution analysis, the molecular orbital scheme of the joined GrNP – DsQ system was built. Its graphics can be seen in Figure 4. By comparison with the GrNP – DA case, it can be observed that since the HOMO energy of the individual DsQ molecule is higher than that of the DA and thus approaches the HOMO energy of GrNP, not only the HOMO - 1 orbital of the GrNP – DsQ complex will contain a DsQ contribution (more than 80% DsQ), but also the HOMO (18% DsQ). And, of course, not only the HOMO and HOMO - 1 orbitals contain smaller or larger DsQ contributions, but also the other lower lying occupied orbitals. As for the unoccupied orbitals, the first eleven are almost entirely localized on GrNP, but also the subsequent three orbitals contain only a small proportion of DsQ contributions (Figure 4).
Accordingly, in the molecular orbital excitation scheme the lowest electronic excitation partially localized on DsQ (S0 → S25) involves the LUMO + 15 unoccupied orbitals (See Table S3 in SM file). Overall, it can be concluded that the nature of the electronic transitions observed in GrNP – DsQ is very similar to that seen in GrNP – DA, with the addition that in the first case, charge-transfer electronic excitations appear to be more pronounced.
Excited state relaxation: From the analyses carried out so far, it can be concluded that excited states can be localised on one or the other component of the molecule-surface complex, or charges can easily migrate from the molecule to the surface, or vice versa [33]. It can therefore be assumed that relaxation processes for different electronic excited states can occur either on the components separately or even inside the binary system. It has already been shown that non-radiative relaxation can occur either on the graphene surface itself [44] or in the binary complex [45,46,47,48,49,50], while excited states can also decay via fluorescence phenomena in the case of slightly modified GrNP [51,52]. Furthermore, it was also shown that for the S1 excited state, there was no significant geometric change for DA adsorbed on GrNP, whereas for DoQ, significant changes appeared for both C=O and aromatic C–C bonds due to excitation [33]. To see exactly what effect the excitation has on the DsQ molecule adsorbed on GrNP, the geometry of the molecule was optimized in the first excited state. Similar approaches as for DA and DoQ have been considered in the present case. Namely, i) non-radiative phenomena were neglected due to the very complex theoretical framework and huge computation resources; ii) positions of the carbon atoms forming the surface have been frozen. When comparing the ground and first excited state geometries, it can be observed that there is a slightly more pronounced change in the molecular bonds than was seen for DA, but not nearly as significant as was obtained for DoQ. Accordingly, the C–O- and C–OH bonds stretch from 1.283 Å and 1.359 Å to 1.302 Å and 1.372 Å, respectively, while the aromatic C–C bond lengths oscillate from 1.411-1.383-1.395-1.398-1.374-1.429 Å to 1.405-1.397-1.388-1.404-1.377-1.426 Å. As regarding the relative position of the DsQ, the plane defined by the aromatic ring fragment comes closer to the GrNP surface and appears to be tilted, with the six carbon atoms between 3.08–3.27 Å away from the plane of the surface, the O atoms at 3.00 Å and 3.04 Å, respectively, as well as the N atom of the amine group at 3.36 Å. At the same time, the wavelength of the S0 → S1 excitation changes from 570 nm to 627 nm. In conclusion, it can be stated that no significant geometric change occurs in the DsQ molecule during the relaxation of the S1 excited state, unlike in DoQ (See Ref. [33]).

2.2. Charge Transfer and Distance from Surface

The effects of changing the separation distance on the charge transfer interactions between luminescent QD and proximal dopamine (in QD–dopamine assemblies) has been already demonstrated by steady-state and time-resolved fluorescence measurements considering different lengths of poly(ethylene glycol) (PEG) as bridge [53]. In light of this, the question arises as to what extent the perpendicular shift between the plane of the DA, DoQ and DsQ molecules and the GrNP surface affects the charge transfer phenomenon in these assemblies. Accordingly, the molecules have been moved along the z-coordinate axis by different values (Δz = -0.3, -0.2, -0.1, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.8 and 1.0 Å) relative to the equilibrium distance (z0) from the surface. Separately for each of these geometries, the Löwdin electron population was calculated for the first thirty electronic excited states, based on the electron density of the given state. Amounts of charge transfer calculated for different plane distances relative to the equilibrium geometry for the DA, DoQ and DsQ adsorbed on the GrNP surface are presented in Figure 5. Molecular orbital energy schemes (in eV) built based on the fragment orbital contribution analysis of the individual, GrNP, DA, DoQ and DsQ components and of the mixed GrNP – DA, GrNP – DoQ and GrNP – DsQ binary complexes computed for Δz = -0.3, 0.0 and +1.0 relative stacking distances values are shown in Figure 6.
DA: It was already shown that, the nature of the charge transfer between the DA and the GrNP substrate is MSCT (or metal-to-surface charge transfer) [33]. For the present case, at the equilibrium geometry configuration (z0 + Δz, where Δz = 0.0) it can be observed three distinct sets of electronic excited states with significant CT character (See Figure 5a). The first set is formed by S6, S7 and S9, the second group is formed by S15, S16 and S17, while the third set is defined by S25 – S29 states. When the DA plane approaches the surface (Δz = -0.3, -0.2 and -0.1 Å) it is observed that the number of CT-like electronically excited states increases, but the charge transfer amount of the existing CT states decreases and that of the newly created CT states increases. For Δz = -0.3, only S1, S3 and S5 showed a charge transfer lower than 0.1e, but for S6, for example, the 0.4e CT obtained at Δz = 0.0 Å for -0.3 Å decreases to 0.18e. Furthermore, a shift of the CT peaks also can be observed as the distance between the planes decreases. For example, the peak of S7 at Δz = 0.0 Å becomes S6 at -0.3 Å, S16 becomes S15, and S26 mainly bifurcates into S25 and S27. As the distance between the planes increases, the opposite effect is observed. That is, the number of CT states decreases, but the amount of charge transfer increases. The first set of excited states (S6, S7 and S9) collapses as S14 for Δz = +1.0 Å, the second group as S26, while the third group moves out of the S1–S30 interval proposed for the present analysis. However, for S14 and S26, the amount of charge transfer is 0.87e and 0.95e, respectively. Fragment orbital contribution analysis reveals that the amount of this charge transfer as a function of Δz depends on the degree of overlap of the individual molecular orbitals. Indeed, for Δz = -0.3, the HOMO and HOMO – 1 orbitals contain larger DA-type contribution, which means stronger CT effects between the DA and the GrNP substrate, while in the case of Δz = +1.0 there are hardly any mixed molecular orbitals and therefore the number of CT-type excited electron states is significantly reduced. In the latter case, the S12 electron excitation is characterized by HOMO –2 → LUMO, while S26 is characterized by HOMO – 8 → LUMO and HOMO – 9 –> LUMO one-electron transitions, respectively (See Figure 6a).
DoQ: For the CT states of the complex formed by the DoQ molecule in adsorption on GrNP surface the charge is mostly transferred from the surface to the molecule (called as SMCT or surface-to-molecule charge transfer) [33], in contrast to the previous DA case. At the equilibrium geometry position, for Δz = 0.0 Å, also three distinct sets of electronic excited states with significant CT character can be observed (See Figure 5b). The first set is made up of the S3 state alone, the second is formed by the S16, S18 and S21 states, and the third is the S30 state. In the decreasing distance direction between the planes (Δz = -0.3, -0.2 and -0.1 Å), no substantial change in the charge transfer phenomenon is observed. Rather, the transferred charge is slightly dispersed in other states (see S9 – S15), but the position of states with high CT values in the excitation spectrum does not change. A similar trend can be observed for the increasing distance direction between the planes. The S3 excited state still behaves as a CT state even at Δz = +1.0 Å, the set of S16 – S21 are slightly rearranged, here states S20 and S23 will show the strongest charge transfer character, while state S30 moves out from the interval proposed for the present analysis. Basically, it can be said that for DoQ – GrNP, the CT phenomenon does not show any significant change in the distance interval of -0.3 Å and +0.1 Å. This can also be explained by the fact that, based on the fragment orbital contribution analysis, LUMO + 1 is essentially a DoQ-type molecular orbital and by varying the distance (Δz), the orbital nature almost remain the same (See Figure 6b). For ex. the CT-type S3 state is defined by the HOMO → LUMO + 1 one-electron transitions.
DsQ: It has already been shown in the previous subSection 2.1 that the photochemical behavior of DsQ is similar to that of DA since the nature of the CT effects is the same MSCT-type transition as that observed for DA. The difference is that the number of pure CT-type transitions or their mixing with localized GrNP-type excitation within the first thirty excited states is significantly higher for DsQ than for DA, and on average the magnitude of charge transfer is also higher (Compare Figure 5a,c). At the equilibrium geometry position of the DsQ, i.e. with Δz = 0.0 Å, significant CT transitions are seen for the S2 state and for all other excited states starting from S13. For a molecular configuration approaching to the surface, e.g. Δz = -0.3 Å, the intensity of charge transfer increases and the CT nature is already observed at S11. When the molecule starts to move away from the surface, the opposite happens, i.e. intensities decrease and, for example, at Δz = +0.4 Å the S13 – S15 states hardly contain any CT nature. At Δz = +1.0 Å only S2, S16 and S30, and partially the groups of S20 – S27, show CT character. Similar to DA, the CT transitions for DsQ are strongly dependent on the distance between the molecule and the surface, but the number of CT states is still larger than that observed for DA. Compared to DA, the change is that for Δz = +1.0 Å, the DsQ-type orbital is no longer HOMO – 2, but HOMO – 1 with lower orbital energy (See Figure 6c).

3. Materials and Methods

The equilibrium geometries were computed in the framework of density functional theory (DFT) considering the ωB97X-D3BJ exchange–correlation (XC) functional [54,55] by including the Grimme’s empirical dispersion correction scheme [56,57] and using the def2-TZVPP triple-ξ basis set of the Karlsruhe group [58] as implemented in the Orca program suite [59,60]. The water solvent environment was taken into account through the conductor-like polarizable continuum (CPCM) model [61,62]. The electronically excited state calculations were performed using the time-dependent version of the same DFT framework considering the Tamm–Dancoff approximation (TDA) approximation [63]. The RIJCOSX approximation [64,65,66,67,68] designed to accelerate Hartree–Fock and hybrid DFT calculations were considered together with the Def2/J [69] auxiliary basis set for Coulomb fitting and the def2-TZVPP/C [70] auxiliary basis set for correlation fitting in the case of TD-DFT calculations. The amount of transferred charge between the complex constituents was obtained based on the analysis of the charge population (Löwdin atomic charges) of a given electronically excited state density computed in the TDDFT framework. The molecular geometries were built, analyzed and further manipulated using Multiwfn [71], Gabedit [72] and Avogadro [73] programs, while the molecular graphics were created using the GaussView [74] software.
For the GrNP model a two-dimensional (three zig-zag and seven armchair edges) rectangular graphene nano-sheet with fully aromatic hexagonal rings was considered. Most features of the experimental UV absorption spectra of GrNPs [42,43,75] can already be theoretically reproduced by the TDDFT method considering the above mentioned 0-dimensional aromatic hydrocarbon structure model [33]. This simplified surface model with its discrete electron states can act as an environment for interacting with adsorbed molecules, where these electron states can combine appropriately with the molecule’s electron states and realistically reproduce the electron excitation behavior of the molecule on the surface. Of course, this model tends to describe only the electron states of the adsorbed molecule more accurately, if one wants to follow the changes in the electronic band structure of graphene, the simplified model described here is no longer suitable, it needs for solid-state model [76,77].

4. Conclusions

In the present work, the equilibrium geometry structure and light absorption properties of the dopamine-semi-quinone (DsQ) adsorbed on the graphene surface has been compared with the results obtained for the dopamine (DA) and dopamine-o-quinone (DoQ) [33] using the ground state and linear-response time-dependent density functional theories at ωB97X-D3BJ/def2-TZVPP level. Computing the adsorption energies between the individual molecules and the graphene substrates it has been shown that, the DsQ form has with 50 % higher binding energy than that found for the DA or DoQ cases (-30.41 kcal/mol vs. -20.24 kcal/mol and -20.11 kcal/mol). Furthermore, analyzing the natural difference orbital profiles characteristic for the vertical electronic excitation three different types of electronic transitions were identified, i.e. locally excited on graphene, locally excited on the molecule and charge transfer (CT) states characteristic for the charge migration induced by the excitation. In terms of the nature of charge transfer, DA and DsQ-based complexes show a high degree of similarity, i.e. in both cases the transfer is from the molecule to the surface, whereas for DoQ the transfer direction is the opposite. As for the comparison between DA and DsQ-based complexes, in the latter case the number of CT-type electronic transitions and the amount of charge transfer is significantly higher. By varying vertically the adsorption distance between the molecule and the surface, the amount of charge transfer obtained for DA and DsQ decrease significantly as the distance increases, while for DoQ this dependence is much weaker. Based on these findings, it can be emphasized that a mechanistic compilation of the electron orbital diagrams of the individual components (for ex. see Figure 1 in Ref. [4] or Figure 4 in Ref. [5]) cannot describe in detail the nature of the excitations inside the complex, since the electronic excitations occur directly between different mixed molecular-surface one-electron orbitals. In general, for the three complexes studied, the number of CT-type electron transitions, the amount of charge transferred and the direction of transfer between the molecule and the substrate are different from one to another dopamine derivative. In this way, if one can control the protonation state of dopamine units, it is possible to influence charge transfer phenomena between the dopamine polymer and the graphene substrate.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org

Author Contributions

Conceptualization, A.B.; methodology, A.B.; validation, A.B.; investigation, A.-A. F. and A.B.; resources, A.B.; writing—original draft preparation, A.B.; writing—review and editing, A.B.; visualization, A.B.; supervision, A.B.; project administration, A.B.; funding acquisition, A.B. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by Romanian Ministry of Research, Innovation and Digitization (MCID) through the “Nucleu” Program within the National Plan for Research, Development and Innovation 2022-2027, project code PN 23 24 01 02.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data available in a publicly accessible repository.

Acknowledgments

The authors also thank INCDTIM, Cluj-Napoca Data Center, for providing computer facilities.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Bakulin, A.A.; Dimitrov, S.D.; Rao, A.; Chow, P.C.Y.; Nielsen, C.B.; Schroeder, B.C.; McCulloch, I.; Bakker, H.J.; Durrant, J.R.; Friend, R.H. Charge-Transfer State Dynamics Following Hole and Electron Transfer in Organic Photovoltaic Devices. J. Phys. Chem. Lett. 2013, 4, 209–215. [Google Scholar] [CrossRef] [PubMed]
  2. Stoltzfus, D.M.; Donaghey, J.E.; Armin, A.; Shaw, P.E.; Burn, P.L.; Meredith, P. Charge Generation Pathways in Organic Solar Cells: Assessing the Contribution from the Electron Acceptor. Chem. Rev. 2016, 116, 12920–12955. [Google Scholar] [CrossRef] [PubMed]
  3. Holliday, S.; Li, Y.; Luscombe, C.K. Recent advances in high performance donor-acceptor polymers for organic photovoltaics. Prog. Polym. Sci. 2017, 70, 34–51. [Google Scholar] [CrossRef]
  4. Li, Y.; Huang, W.; Zhao, D.; Wang, L.; Jiao, Z.; Huang, Q.; Wang, P.; Sun, M.; Yuan, G. Recent Progress in Organic Solar Cells: A Review on Materials from Acceptor to Donor. Molecules 2022, 27, 1800. [Google Scholar] [CrossRef] [PubMed]
  5. Solak, E.K.; Irmak, E. Advances in organic photovoltaic cells: A comprehensive review of materials, technologies, and performance. RSC Adv. 2023, 13, 12244. [Google Scholar] [CrossRef]
  6. Buzzetti, L.; Crisenza, G.E.M.; Melchiorre, P. Mechanistic Studies in Photocatalysis. Angew. Chem. Int. Ed. 2019, 58, 3730–3747. [Google Scholar] [CrossRef]
  7. Yuan, Y.q.; Majumder, S.; Yang, M.h.; Guo, S.r. Recent advances in catalyst-free photochemical reactions via electron- donor-acceptor (EDA) complex process. Tetrahedron Lett. 2020, 61, 151506. [Google Scholar] [CrossRef]
  8. Tasnim, T.; Ayodele, M.J.; Pitre, S.P. Recent Advances in Employing Catalytic Donors and Acceptors in Electron Donor Acceptor Complex Photochemistry. J. Org. Chem. 2022, 87, 10555–10563. [Google Scholar] [CrossRef]
  9. Ostroverkhova, O. Organic Optoelectronic Materials: Mechanisms and Applications. Chem. Rev. 2016, 116, 13279–13412. [Google Scholar] [CrossRef]
  10. Mathur, C.; Gupta, R.; Bansal, R.K. Organic Donor-Acceptor Complexes As Potential Semiconducting Materials. Chem. Eur. J. 2024, 30, e202304139. [Google Scholar] [CrossRef]
  11. Mulliken, R.S. Molecular Compounds and their Spectra. II. J. Am. Chem. Soc. 1952, 74, 811–824. [Google Scholar] [CrossRef]
  12. Mulliken, R.S. Molecular Compounds and their Spectra. III. The Interaction of Electron Donors and Acceptors. J. Phys. Chem. 1952, 56, 801–822. [Google Scholar] [CrossRef]
  13. Mulliken, R.S.; Person, W.B. Donor-Acceptor Complexes. Ann. Rev. Phys. Chem. 1962, 13, 107–126. [Google Scholar] [CrossRef]
  14. Cabellos, J.L.; Mowbray, D.J.; Goiri, E.; El-Sayed, A.; Floreano, L.; de Oteyza, D.G.; Rogero, C.; Ortega, J.E.; Rubio, A. Understanding Charge Transfer in Donor - Acceptor/Metal Systems: A Combined Theoretical and Experimental Study. J. Phys. Chem. C 2012, 116, 17991–18001. [Google Scholar] [CrossRef]
  15. Chen, X.K.; Coropceanu, V.; Brédas, J.L. Assessing the nature of the charge-transfer electronic states in organic solar cells. Nat. Commun. 2018, 9, 5295. [Google Scholar] [CrossRef]
  16. Crisenza, G.E.M.; Mazzarella, D.; Melchiorre, P. Synthetic Methods Driven by the Photoactivity of Electron Donor–Acceptor Complexes. J. Am. Chem. Soc. 2020, 142, 5461–5476. [Google Scholar] [CrossRef] [PubMed]
  17. Wortman, A.K.; Stephenson, C.R. EDA photochemistry: Mechanistic investigations and future opportunities. Chem 2023, 9, 2390–2415. [Google Scholar] [CrossRef]
  18. Marcus, R.A. Chemical and electrochemical electron-transfer theory. Annu. Rev. Phys. Chem. 1964, 15, 155–196. [Google Scholar] [CrossRef]
  19. Piechota, E.J.; Meyer, G.J. Introduction to Electron Transfer: Theoretical Foundations and Pedagogical Examples. J. Chem. Educ. 2019, 96, 2450–2466. [Google Scholar] [CrossRef]
  20. Marcus, R.A. Reflections on electron transfer theory. J. Chem. Phys. 2020, 153, 210401. [Google Scholar] [CrossRef]
  21. Taylor, N.B.; Kassal, I. Generalised Marcus theory for multi-molecular delocalised charge transfer. Chem. Sci. 2018, 9, 2942–2951. [Google Scholar] [CrossRef]
  22. Derr, J.B.; Tamayo, J.; Clark, J.A.; Morales, M.; Mayther, M.F.; Espinoza, E.M.; Rybicka-Jasińska, K.; Vullev, V.I. Multifaceted aspects of charge transfer. Phys. Chem. Chem. Phys. 2020, 22, 21553–22118. [Google Scholar] [CrossRef] [PubMed]
  23. Nazmutdinov, R.R.; Shermokhamedov, S.A.; Zinkicheva, T.T.; Ulstrup, J.; Xiao, X. Understanding molecular and electrochemical charge transfer: Theory and computations. Chem. Soc. Rev. 2023, 52, 6223–6588. [Google Scholar] [CrossRef] [PubMed]
  24. Hashemi, A.; Peljo, P.; Laasonen, K. Understanding Electron Transfer Reactions Using Constrained Density Functional Theory: Complications Due to Surface Interactions. J. Phys. Chem. C 2023, 127, 3398–3407. [Google Scholar] [CrossRef] [PubMed]
  25. Liu, Z.; Sun, X. Instantaneous Marcus theory for photoinduced charge transfer dynamics in multistate harmonic model systems. J. Phys. Condens. Matter 2024, 36, 315201. [Google Scholar] [CrossRef]
  26. Henderson, M.A. A surface science perspective on TiO2 photocatalysis. Surf. Sci. Rep. 2011, 66, 185–297. [Google Scholar] [CrossRef]
  27. Xu, C.; Anusuyadevi, P.R.; Aymonier, C.; Luque, R.; Marre, S. Nanostructured materials for photocatalysis. Chem. Soc. Rev. 2019, 48, 3868–3902. [Google Scholar] [CrossRef]
  28. Wang, L.; Zhu, W. Organic Donor-Acceptor Systems for Photocatalysis. Adv. Sci. 2024, 11, 2307227. [Google Scholar] [CrossRef]
  29. Quina, F.H.; Silva, G.T.M. The photophysics of photosensitization: A brief overview. J. Photochem. Photobiol. 2021, 7, 100042. [Google Scholar] [CrossRef]
  30. Zhao, X.; Liu, J.; Fan, J.; Chao, H.; Peng, X. Recent progress in photosensitizers for overcoming the challenges of photodynamic therapy: From molecular design to application. Chem. Soc. Rev. 2021, 50, 4185–4219. [Google Scholar] [CrossRef] [PubMed]
  31. Sun, L.; Chen, Y.; Sun, M.; Zheng, Y. Organic Solar Cells: Physical Principle and Recent Advances. Chem. Asian J. 2023, 18, e202300006. [Google Scholar] [CrossRef]
  32. Wodtke, A.M.; Matsiev, D.; Auerbach, D.J. Energy transfer and chemical dynamics at solid surfaces: The special role of charge transfer. Prog. Surf. Sci. 2008, 83, 167–214. [Google Scholar] [CrossRef]
  33. Farcaş, A.A.; Bende, A. Theoretical insights into dopamine photochemistry adsorbed on graphene-type nanostructures. Phys. Chem. Chem. Phys. 2024, 26, 14937–14947. [Google Scholar] [CrossRef] [PubMed]
  34. Falamaş, A.; Petran, A.; Hada, A.M.; Bende, A. Dopamine Photochemical Behaviour under UV Irradiation. Int. J. Mol. Sci. 2022, 23, 5483. [Google Scholar] [CrossRef]
  35. Hirata, K.; Kasai, K.I.; Yoshizawa, K.; Grégoire, G.; Ishiuchi, S.I.; Fujii, M. Excited state dynamics of protonated dopamine: Hydration and conformation effects. Phys. Chem. Chem. Phys. 2022, 24, 10737–10744. [Google Scholar] [CrossRef]
  36. Liebscher, J.; Mrówczyński, R.; Scheidt, H.A.; Filip, C.; Hădade, N.D.; Turcu, R.; Bende, A.; Beck, S. Structure of Polydopamine: A Never-Ending Story? Langmuir 2013, 29, 10539–10548. [Google Scholar] [CrossRef]
  37. Lyu, Q.; Hsueh, N.; Chai, C.L.L. Unravelling the polydopamine mystery: Is the end in sight? Polym. Chem. 2019, 10, 5771–5777. [Google Scholar] [CrossRef]
  38. Bacil, R.P.; Chen, L.; Serrano, S.H.P.; Compton, R.G. Dopamine oxidation at gold electrodes: Mechanism and kinetics near neutral pH. Phys. Chem. Chem. Phys. 2020, 22, 607–614. [Google Scholar] [CrossRef] [PubMed]
  39. Adasme-Carreño, F.; Ochoa-Calle, A.; Galván, M.; Ireta, J. Conformational preference of dipeptide zwitterions in aqueous solvents. Phys. Chem. Chem. Phys. 2024, 26, 8210–8218. [Google Scholar] [CrossRef]
  40. Sundararaman, R.; III, W.A.G. The charge-asymmetric nonlocally determined local-electric (CANDLE) solvation model. J. Chem. Phys. 2015, 142, 064107. [Google Scholar] [CrossRef]
  41. Castro-Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
  42. Mak, K.F.; Sfeir, M.Y.; Wu, Y.; Lui, C.H.; Misewich, J.A.; Heinz, T.F. Measurement of the Optical Conductivity of Graphene. Phys. Rev. Lett. 2008, 101, 196405. [Google Scholar] [CrossRef] [PubMed]
  43. Mak, K.F.; Ju, L.; Wang, F.; Heinz, T.F. Optical spectroscopy of graphene: From the far infrared to the ultraviolet. Solid State Commun. 2012, 152, 1341–1349. [Google Scholar] [CrossRef]
  44. Chen, S.; Ullah, N.; Zhao, Y.; Zhang, R. Nonradiative Excited-State Decay via Conical Intersection in Graphene Nanostructures. ChemPhysChem 2019, 20, 1–6. [Google Scholar] [CrossRef]
  45. Dou, W.; Nitzan, A.; Subotnik, J.E. Surface hopping with a manifold of electronic states. II. Application to the many-body Anderson-Holstein model. J. Chem. Phys. 2015, 142, 084110. [Google Scholar] [CrossRef]
  46. Dou, W.; Nitzan, A.; Subotnik, J.E. Surface hopping with a manifold of electronic states. III. Transients, broadening, and the Marcus picture. J. Chem. Phys. 2015, 142, 234106. [Google Scholar] [CrossRef] [PubMed]
  47. Dou, W.; Nitzan, A.; Subotnik, J.E. Erratum: "Surface hopping with a manifold of electronic states. III. Transients, broadening and the Marcus picture" [J. Chem. Phys. 142, 234106 (2015)]. J. Chem. Phys. 2015, 143, 189902. [Google Scholar] [CrossRef]
  48. Chen, J.; Jin, Z.; Dou, W.; Subotnik, J. Electronic Structure for Multielectronic Molecules near a Metal Surface. J. Phys. Chem. C 2021, 125, 2884–2899. [Google Scholar] [CrossRef]
  49. Bende, A.; Farcaş, A.A.; Falamaş, A.; Petran, A. New insight into catechol photochemistry: The role of different monomer and dimer configurations in radiation-less decay of the S1 electronic excited state. Phys. Chem. Chem. Phys. 2022, 24, 29165–29175. [Google Scholar] [CrossRef]
  50. Bende, A.; Farcaş, A.A. Intermolecular-Type Conical Intersections in Benzene Dimer. Int. J. Mol. Sci. 2023, 24, 2906. [Google Scholar] [CrossRef]
  51. Lui, C.H.; Mak, K.F.; Shan, J.; Heinz, T.F. Ultrafast Photoluminescence from Graphene. Phys. Rev. Lett. 2010, 105, 127404. [Google Scholar] [CrossRef] [PubMed]
  52. Wang, J.; Cao, S.; Ding, Y.; Ma, F.; Lu, W.; Sun, M. Theoretical Investigations of Optical Origins of Fluorescent Graphene Quantum Dots. Sci. Rep. 2016, 6, 24850. [Google Scholar] [CrossRef] [PubMed]
  53. Ji, X.; Wang, W.; Mattoussi, H. Effects of separation distance on the charge transfer interactions in quantum dot–dopamine assemblies. Phys. Chem. Chem. Phys. 2015, 17, 10108–10117. [Google Scholar] [CrossRef]
  54. Chai, J.D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
  55. Lehtola, S.; Steigemann, C.; Oliveira, M.; Marques, M. Recent developments in Libxc - A comprehensive library of functionals for density functional theory. Software X 2018, 7, 1–5. [Google Scholar] [CrossRef]
  56. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
  57. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
  58. Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
  59. Neese, F. Software update: The ORCA program system–Version 5.0. WIREs Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
  60. Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA quantum chemistry program package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef]
  61. Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
  62. Garcia-Rates, M.; Neese, F. Effect of the Solute Cavity on the Solvation Energy and its Derivatives within the Framework of the Gaussian Charge Scheme. J. Comput. Chem. 2020, 41, 922–939. [Google Scholar] [CrossRef] [PubMed]
  63. Hirata, S.; Head-Gordon, M. Time-dependent density functional theory within the Tamm-Dancoff approximation. Chem. Phys. Lett. 1999, 314, 291–299. [Google Scholar] [CrossRef]
  64. Neese, F.; Wennmohs, F.; Hansen, A.; Becker, U. Efficient, approximate and parallel Hartree-Fock and hybrid DFT calculations. A ’chain-of-spheres’ algorithm for the Hartree-Fock exchange. Chem. Phys. 2009, 356, 98–109. [Google Scholar] [CrossRef]
  65. Izsák, R.; Neese, F. An overlap fitted chain of spheres exchange method. J. Chem. Phys. 2011, 135, 144105. [Google Scholar] [CrossRef]
  66. Izsák, R.; Neese, F.; Klopper, W. Robust fitting techniques in the chain of spheres approximation to the Fock exchange: The role of the complementary space. J. Chem. Phys. 2013, 139, 094111. [Google Scholar] [CrossRef]
  67. Helmich-Paris, B.; de Souza, B.; Neese, F.; Izsák, R. An improved chain of spheres for exchange algorithm. J. Chem. Phys. 2021, 155, 104109. [Google Scholar] [CrossRef]
  68. Neese, F. The SHARK Integral Generation and Digestion System. J. Comp. Chem. 2022, 44, 381–396. [Google Scholar] [CrossRef]
  69. Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef] [PubMed]
  70. Hellweg, A.; Hättig, C.; Höfener, S.; Klopper, W. Optimized accurate auxiliary basis sets for RI-MP2 and RI-CC2 calculations for the atoms Rb to Rn. Theor. Chem. Acc. 2007, 117, 587–597. [Google Scholar] [CrossRef]
  71. Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
  72. Allouche, A.R. Gabedit–A graphical user interface for computational chemistry softwares. J. Comput. Chem. 2011, 32, 174–182. [Google Scholar] [CrossRef] [PubMed]
  73. Hanwell, M.D.; Curtis, D.E.; Lonie, D.C.; Vandermeersch, T.; Zurek, E.; Hutchison, G.R. Avogadro: an advanced semantic chemical editor, visualization, and analysis platform. J. Cheminformatics 2012, 4, 17. [Google Scholar] [CrossRef] [PubMed]
  74. Dennington, R.; Keith, T.; Millam, J. Gaussview 6.1.1, 2009. Semichem Inc., Shawnee Mission, KS.
  75. Cayambe, M.; Zambrano, C.; Tene, T.; Guevara, M.; Usca, G.T.; Brito, H.; Molina, R.; Coello-Fiallos, D.; Caputi, L.S.; Gomez, C.V. Dispersion of graphene in ethanol by sonication. Materials Today: Proceedings 2021, 37, 4027–4030. [Google Scholar] [CrossRef]
  76. Yang, L.; Deslippe, J.; Park, C.H.; Cohen, M.L.; Louie, S.G. Excitonic Effects on the Optical Response of Graphene and Bilayer Graphene. Phys. Rev. Lett. 2009, 103, 186802. [Google Scholar] [CrossRef]
  77. Trevisanutto, P.E.; Holzmann, M.; Côté, M.; Olevano, V. Ab initio high-energy excitonic effects in graphite and graphene. Phys. Rev. B 2010, 81, 121405. [Google Scholar] [CrossRef]
Preprints 116652 g001
Figure 1. The 2D chemical structure of: (a) dopamine (or DA), (b) dopamine-o-quinone (or DoQ) and (c) dopamine-semiquinone (or DsQ).
Figure 1. The 2D chemical structure of: (a) dopamine (or DA), (b) dopamine-o-quinone (or DoQ) and (c) dopamine-semiquinone (or DsQ).
Preprints 116652 g001
Preprints 116652 g002
Figure 2. The geometry configuration of the dopamine-semi-quinone (or DsQ) adsorbed on the GrNP surface computed at ωB97X-D3BJ/def2-TZVPP/CPCM level of theory.
Figure 2. The geometry configuration of the dopamine-semi-quinone (or DsQ) adsorbed on the GrNP surface computed at ωB97X-D3BJ/def2-TZVPP/CPCM level of theory.
Preprints 116652 g002
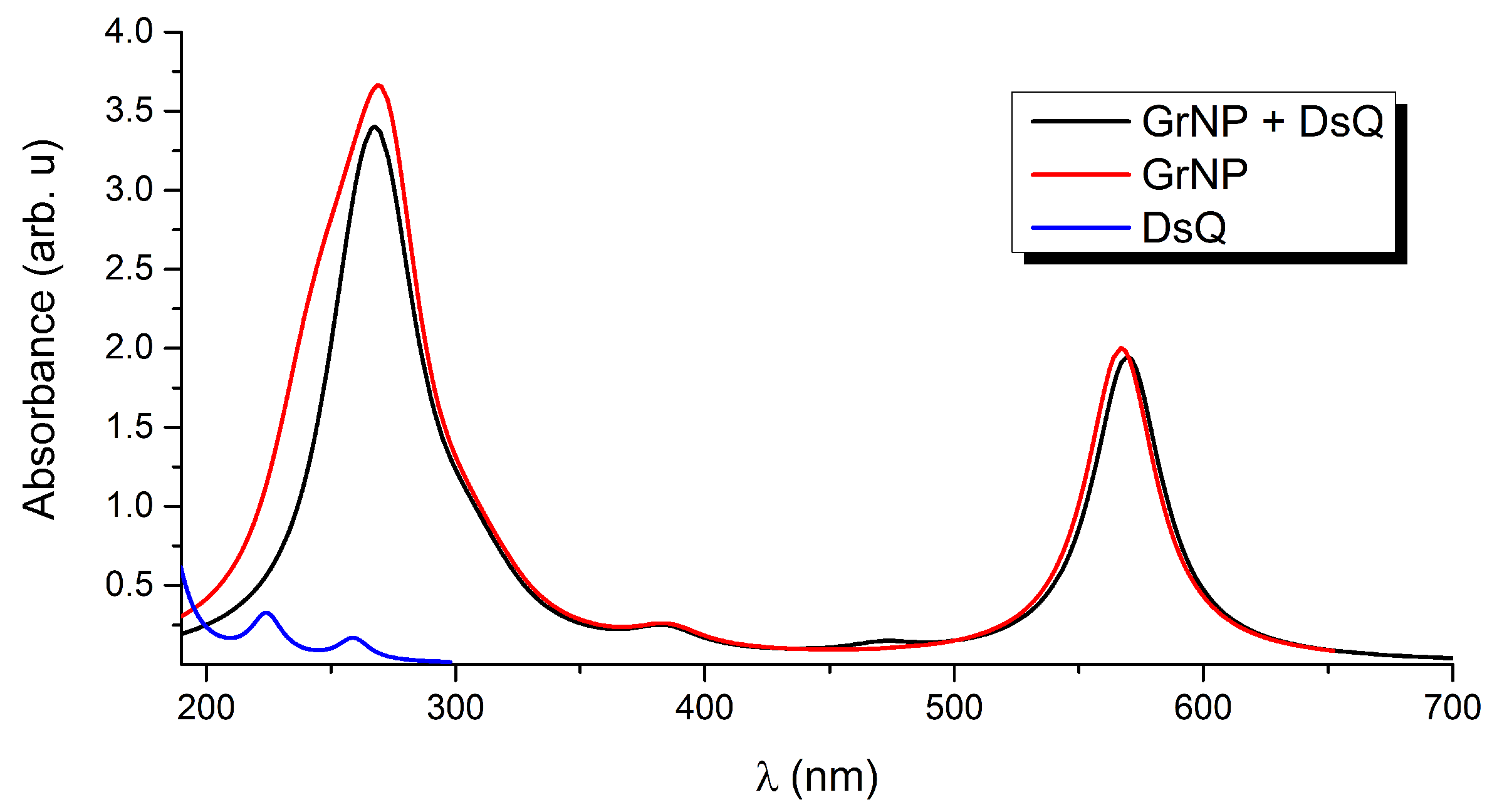
Preprints 116652 g003
Figure 3. Theoretical UV absorption spectra of the graphene – DsQ binary complex and the individual constituents computed at TDDFT/ωB97X-D3BJ/def2-TZVPP/CPCM level of theory.
Figure 3. Theoretical UV absorption spectra of the graphene – DsQ binary complex and the individual constituents computed at TDDFT/ωB97X-D3BJ/def2-TZVPP/CPCM level of theory.
Preprints 116652 g003
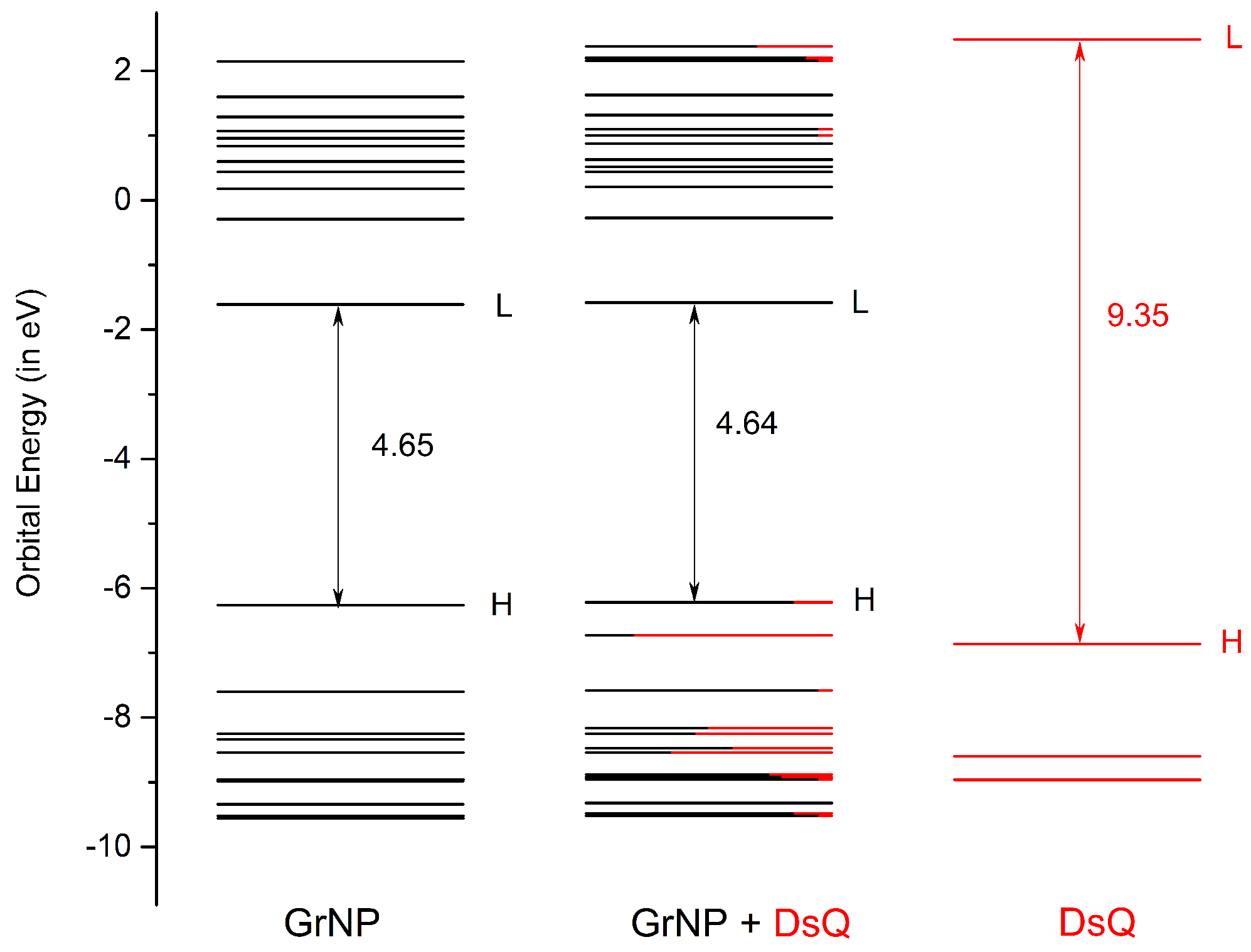
Preprints 116652 g004
Figure 4. The molecular orbital energy scheme (in eV) of the individual, GrNP and DsQ components and of the mixed GrNP – DsQ binary complex (H = HOMO, L = LUMO) based on the fragment orbital contribution analysis.
Figure 4. The molecular orbital energy scheme (in eV) of the individual, GrNP and DsQ components and of the mixed GrNP – DsQ binary complex (H = HOMO, L = LUMO) based on the fragment orbital contribution analysis.
Preprints 116652 g004
Preprints 116652 g005
Figure 5. The transferred charge units calculated for different plane distances relative to the equilibrium geometry (z0 + Δz, Δz between -0.3 Å and +1.0 Å) for DA (a), DoQ (b) and DsQ (c), respectively, adsorbed on the GrNP surface, computed at TDDFT/ωB97X-D3BJ/def2-TZVPP level of theory.
Figure 5. The transferred charge units calculated for different plane distances relative to the equilibrium geometry (z0 + Δz, Δz between -0.3 Å and +1.0 Å) for DA (a), DoQ (b) and DsQ (c), respectively, adsorbed on the GrNP surface, computed at TDDFT/ωB97X-D3BJ/def2-TZVPP level of theory.
Preprints 116652 g005
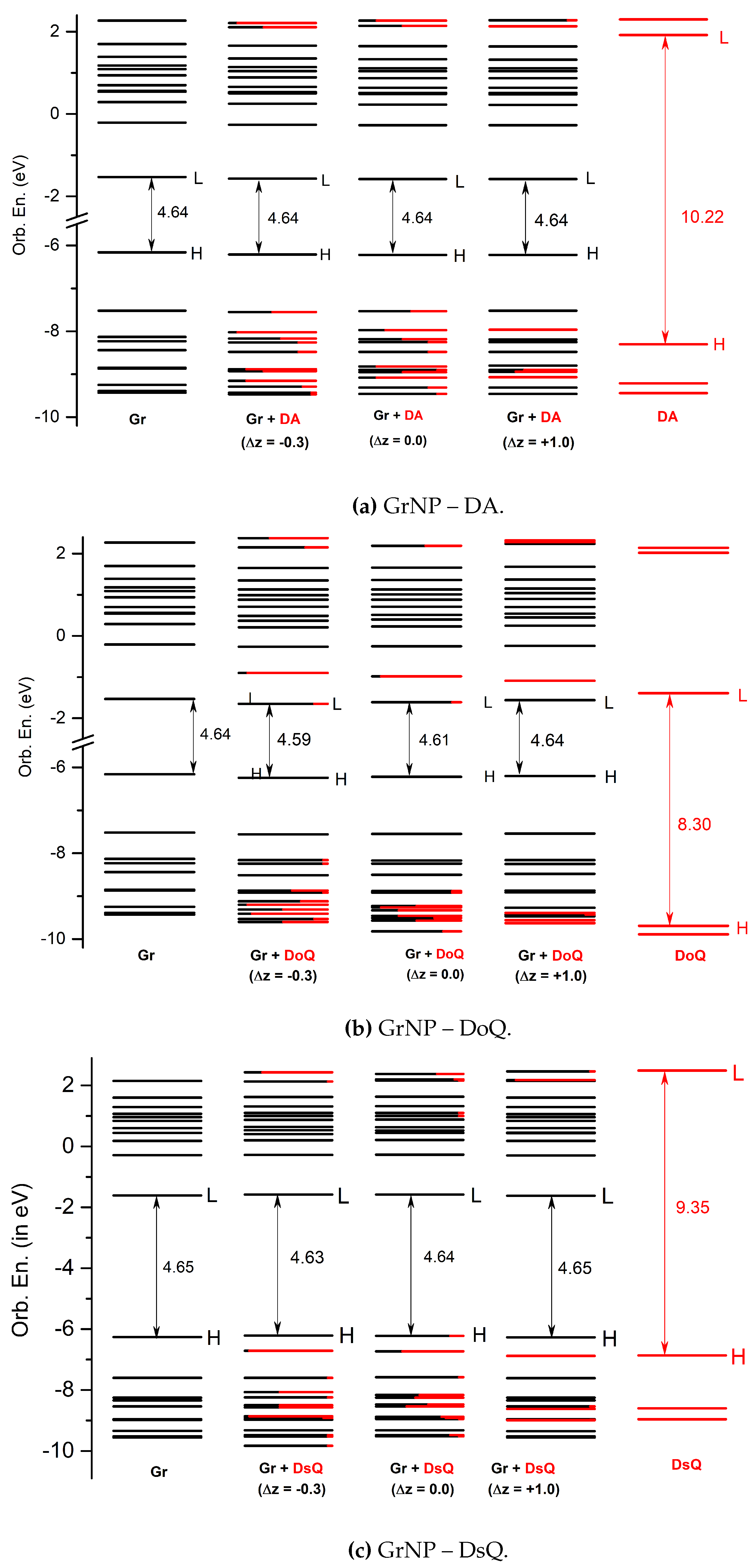
Preprints 116652 g006
Figure 6. Molecular orbital energy schemes (in eV) built based on the fragment orbital contribution analysis of the individual, GrNP (1st col.), DA, DoQ and DsQ (last col.) components and of the mixed a): GrNP – DA, b): GrNP – DoQ and c): GrNP – DsQ binary complexes (H = HOMO, L = LUMO) computed for Δz = -0.3 (2nd col.), 0.0 (3rd col.) and +1.0 (4th col.) relative stacking distances.
Figure 6. Molecular orbital energy schemes (in eV) built based on the fragment orbital contribution analysis of the individual, GrNP (1st col.), DA, DoQ and DsQ (last col.) components and of the mixed a): GrNP – DA, b): GrNP – DoQ and c): GrNP – DsQ binary complexes (H = HOMO, L = LUMO) computed for Δz = -0.3 (2nd col.), 0.0 (3rd col.) and +1.0 (4th col.) relative stacking distances.
Preprints 116652 g006
Table 1. The first thirty electronic excited state energies (in nm), their oscillator strengths, transferred charges and electronic transition types (either located on the GrNP and on DsQ fragments or charge transfer states between the fragments) of the GrNP – DsQ binary complex, computed at TDDFT/ωB97X-D3BJ/def2-TZVPP level of theory.
Table 1. The first thirty electronic excited state energies (in nm), their oscillator strengths, transferred charges and electronic transition types (either located on the GrNP and on DsQ fragments or charge transfer states between the fragments) of the GrNP – DsQ binary complex, computed at TDDFT/ωB97X-D3BJ/def2-TZVPP level of theory.
Si 1 2 3 4 5 6 7 8 9 10
λ (nm) 570 471 384 375 364 357 340 325 322 314
Osc. Str. 1.9323 0.0573 0.1312 0.0004 0.0000 0.0025 0.0023 0.0035 0.0144 0.1213
Charge tr. (e) 0.085 1.000 0.075 0.066 0.074 0.070 0.068 0.083 0.069 0.064
Type GrNP CT GrNP GrNP GrNP GrNP GrNP GrNP GrNP GrNP
Si 11 12 13 14 15 16 17 18 19 20
λ (nm) 305 304 301 297 295 290 285 284 282 273
Osc. Str. 0.2109 0.0050 0.0313 0.0253 0.0410 0.0020 0.0406 0.0407 0.0819 0.9082
Charge tr. (e) 0.110 0.190 0.576 0.505 0.569 0.930 0.233 0.478 0.604 0.429
Type GrNP + CT GrNT + CT CT CT CT CT GrNP + CT CT CT CT
Si 21 22 23 24 25 26 27 28 29 30
λ (nm) 270 268 266 262 261 260 259 258 256 254
Osc. Str. 0.6146 0.2963 0.5778 0.1547 0.4897 0.0171 0.0570 0.0121 0.2461 0.1927
Charge tr. (e) 0.651 0.107 0.099 0.227 0.237 0.095 0.215 0.828 0.148 0.690
Type CT GrNP + CT GrNP + CT GrNP + CT DsQ + CT GrNP GrNP + CT CT GrNP + CT CT
CT = Charge transfer character; sign “-” means charge transfer from GrNP to DsQ.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated