Prerpints.org logo
Preprint
Article

Design of Differential Loudspeaker Line Array for Steerable Frequency-Invariant Beamforming

Altmetrics

Downloads

101

Views

37

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

29 August 2024

Posted:

01 September 2024

You are already at the latest version

Alerts
Abstract

Differential beamforming has attracted much research since it can utilize the array with small aperture size to form frequency-invariant beampatterns and achieve high directional gains. It has recently been applied to the linear loudspeaker array to produce a broadside frequency-invariant radiation pattern. However, designing steerable frequency-invariant beampatterns for the linear loudspeaker array has yet to be explored. This paper proposes a method to design the steerable differential beamformer with the linear loudspeaker array. We first determine the target differential beampatterns according to the desired direction, the main lobe width, and the beampattern order. Then, we transform the target beampattern into the modal domain for representation. The Jacobi-Anger expansion is subsequently used to design the beamformer so that the resulting beam pattern matches the target differential beam pattern. Furthermore, based on the criterion of minimizing the mean square error between the synthesized beam pattern and the ideal one, a multi-constraint optimization problem is formulated to calculate the optimal desired weighting vector. Simulations and experimental results show that the proposed method can achieve steerable frequency-invariant beamforming over 300 Hz – 4 kHz.

Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Beamforming is a fundamental technique in array signal processing and has garnered significant attention in research [1,2,3,4,5,6]. In microphone arrays, beamforming suppresses spatial interferences and improves the output signal-to-noise ratio [7,8,9,10,11,12]. In loudspeaker arrays, beamforming creates highly directional beam patterns, reducing room reflections and enhancing the desired sound's delivery [13,14,15,16,17,18]. Array systems can be classified into two categories: additive arrays and differential arrays. Additive arrays generate directional beam patterns through the synchronize-and-add principle [19]. However, they cannot achieve high directivity at low frequencies with limited array aperture. In contrast, differential arrays, which respond to the spatial derivatives of the sound field, can generate narrow beam patterns and achieve high directional gains even with small apertures [20].
Differential arrays offer advantages in compact size, frequency-invariant beampatterns, and high spatial directivity, and have been extensively studied in microphone array applications over the last two decades. Differential microphone arrays can be implemented in various geometric shapes, including line-shaped [20,21,22,23,24,25], planar [26,27,28,29,30,31], and volumetric designs [32,33,34,35]. Among these, the line-shaped differential microphone array (LDMA) is particularly well-studied due to its ease of integration with electronic devices. While most research focuses on directing the main lobe in the endfire direction, this is often unsuitable for applications like smart TVs or tablets, where beam steering is needed, e.g., to accurately pick up voice commands from users speaking from different positions.
Efforts have been made to design first- and second-order steerable LDMAs [36,37], including the development of general conditions for steerable differential beamformers [38]. However, the ideal beam pattern can become ineffective due to improper null position selection. To address this, extremum and interference suppression constraints have been used in designing steerable LDMAs [39]. Nonetheless, selecting the optimal trade-off parameter between the directivity factor (DF) and interference suppression energy remains challenging. Recently, a novel method was proposed using both omnidirectional and directional microphones to design fully steerable LDMAs, achieving steering- and frequency-invariant beampatterns with a linear super array (LSA) [40,41]. However, mismatches between omnidirectional and directional microphones can impact beamformer performance in practical applications.
Differential beamformers have also been applied to linear loudspeaker arrays to produce highly directional patterns [42,43,44,45,46,47,48,49]. For example, a three-element line array with a second-order differential broadside beam has been studied to create a near-field sound zone in car cabins [44]. For higher-order broadside differential beampatterns, a null-constrained method has been proposed as a convenient approach for designing differential beamformers [45]. However, its frequency-invariant beampattern is limited, which may be undesirable for certain applications. Our recent research extends the null-constrained method using a series expansion approach for broadside linear loudspeaker arrays, enhancing the beamformer's robustness and better preserving the frequency-invariant beam pattern [48,49]. In the study of beam steering for differential loudspeaker arrays (DLAs), A linear loudspeaker array composed of miniature omnidirectional speakers and dipole speakers is used to design the steerable first-order DLAs [47]. Our recent study develops steerable frequency-invariant differential beampatterns using a circular loudspeaker array with a rigid baffle [46]. However, miniature loudspeakers and circular arrays are not widely applicable, such as in public broadcasting and outdoor sound reinforcement scenarios. Therefore, there is a need to explore beam steering with loudspeaker line arrays.
In this paper, we propose a method for designing steerable differential beamformers using a loudspeaker line array. The key contributions include: 1) calculating the target steerable differential beampattern based on the desired direction, main lobe width, and beampattern order; 2) formulating the desired differential beampattern in the modal domain for representation; and 3) developing a multi-constraint optimization problem to design a steerable frequency-invariant beamformer using the Jacobi-Anger expansion, while minimizing the mean square error (MSE) between the synthesized and ideal beampatterns. Both simulation and experimental studies are provided. Although this work focuses on differential loudspeaker line arrays, the proposed method is also applicable to differential microphone arrays, making it suitable for designing LDMAs with steerable differential beampatterns for high-quality acoustic signal acquisition.
The paper is organized as follows: Section 2 introduces the signal model, problem formulation, and key definitions. Section 3 details the proposed method for designing steerable frequency-invariant beampatterns with a linear array. Section 4 presents simulations with design examples and discusses the impacts of constraint parameters and element mismatch, as well as a performance comparison with existing methods. Section 5 provides experimental results that align with the simulations, validating the proposed method. Finally, Section 6 concludes the paper.

2. Problem Formulation

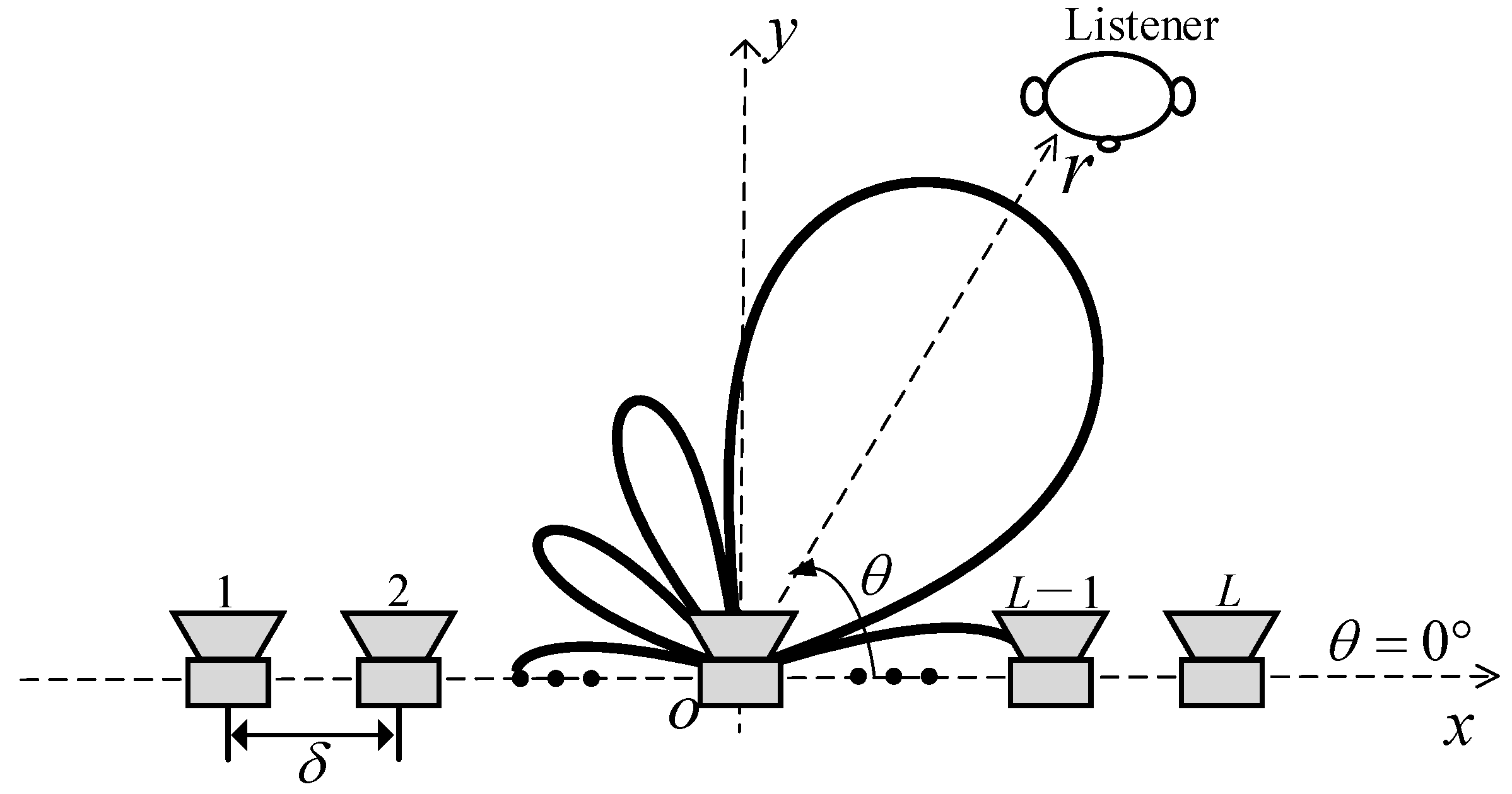
Figure 1 illustrates a loudspeaker array designed to radiate a steerable differential beampattern towards a listener. The line array consisting of L loudspeakers with an interelement spacing δ lies on the x axis. The loudspeaker array is centers at the origin of the coordinate system. Each loudspeaker is modelled as omnidirectional point source, and the far-field sound pressure at a listener position ( r , θ ) generated by the loudspeaker array can be expressed as
p ( k , r , θ ) ≈ e i k r 4 π r ∑ l = 1 L w l * ( k ) e − i k x l cos θ
where i is the imaginary unit, with i 2 = − 1 , k = 2 π f / c is the wave number, f denotes the frequency, c is the speed of sound in air, the superscript · * is the complex-conjugate operator, w l ( k ) denotes the weight of the l-th loudspeaker at ( x l , 0 ) , where x l = − ( L + 1 ) δ / 2 + l δ , l is the loudspeaker index, l = 1, 2, …, L, r is the distance from the origin of the coordinate system to the listener, the angle θ is defined with the respect to the positive x axis.
In the far-field, the directivity of the loudspeaker array does not change with the distance r. To evaluate the directivity of radiation, the normalized far-field radiation pattern is
B ( k , θ ) = p ( k , r , θ ) / ( e i k r / 4 π r ) = ∑ l = 1 L w l * ( k ) e − i k x l cos θ ,
which can be written in a vector form
B ( k , θ ) = w H ( k ) g ( k , θ ) ,
where
w ( k ) = [ w 1 ( k ) , ... , w L ( k ) ] T ,
g ( k , θ ) = [ e − i k x 1 cos θ , ⋯ , e − i k x L cos θ ] T ,
where the superscripts · H and · T are the conjugate-transpose operator and the transpose operator respectively, w is the beamforming filter to be designed to achieve a steerable differential radiation pattern.
Apart from the normalized far-field radiation pattern, there are two commonly used metrics to evaluate the performance of a beamformer: white noise gain (WNG) and directivity factor (DF). The WNG quantifies the robustness of the beamformer against the white noise that
WNG ( k ) = B ( k , θ s ) 2 w H ( k ) w ( k ) ,
where θ s is the desired radiation direction. For the loudspeaker array, the WNG also represents the radiation efficiency of the array.
The DF evaluates the directional characteristics of the beamformer. The 2-dimensional DF is defined as the ratio of the sound power radiated in the desired direction to the average sound power across the half-plane in front of the loudspeaker array, and is expressed as
D F ( k ) = π B ( k , θ s ) 2 ∫ 0 π B ( k , θ ) 2 d θ = B ( k , θ s ) 2 w H ( k ) Γ ( k ) w ( k ) ,
where
Γ ( k ) = 1 π ∫ 0 π g H ( k , θ ) g ( k , θ ) d θ
is a L × L square matrix, whose elements are Γ m , n ( k ) = J 0 [ k ( i − j ) δ ] , m , n ∈ { 1 , 2 , ... , L } . Here, J 0 ( ⋅ ) is the zero order Bessel function of the first kind. For brevity, we will omit the dependence on k in the following text.

3. Methods

The objective of the proposed method is to form a directional steerable loudspeaker array such that the energy radiated by the array is mainly concentrated in the main lobe area while minimizing the output energy of the sidelobe area. It is achieved in three steps: (1) calculating the target radiation pattern according to the radiation steering angle, main lobe area and sidelobe area; (2) formulating the target radiation pattern in the modal domain; (3) designing the steerable differential beamformer using the modal matching with Jacobi-Anger expansion.

3.1. Target Radiation Pattern with the Mainlobe Steering

The ideal N-th order differential beampattern for a differential microphone array is
B ˜ ( N ) ( θ ) = ∑ n = 0 N α N , n cos n θ ,
  • which assumes the microphone spacing is much smaller than the wavelength, and
  • α N , n , n = 0 , 1 , ... , N are real coefficients. To allow mainlobe steering to the desired direction
  • θ s , two conditions should be satisfied, that B ˜ ( N ) ( θ s ) = 1 and ∂ B ˜ ( N ) ( θ s ) / ∂ θ s = 0 . In the vector form,
A T α N = b
Where
A = 1 cos θ s … cos N θ s 0 sin θ s … N cos N − 1 θ s sin θ s T ,
α N = α N , 0 α N , 1 … α N , N T , b = 1 0 T .
Also, (9) in the vector form is
B ˜ ( N ) ( θ ) = α N T c N ,
where
c N = [ 1 cos θ … cos N θ ] T .
The corresponding beam power can be expressed as
B ˜ ( N ) ( θ ) 2 = α N T c N c N T α N = α N T C α N ,
where
C = c N c N T .
Due to the acoustic reciprocity principle, our proposed method applies equation (13) as the ideal N-th order differential radiation pattern for a differential loudspeaker array, enabling precise steering of sound propagation towards the desired direction θ s . Additionally, it is necessary to minimize the radiation of sound energy in the sidelobe area, defined as
Θ S L ∈ 0 ∘ ， θ s − Δ / 2 ∪ θ s + Δ / 2 , 180 ∘ ,
where Δ is the mainlobe width. Therefore, once the desired direction and mainlobe width are determined, the optimal solution α N can be obtained by solving the following optimization problem
min α N B ˜ ( N ) ( Θ S L ) 2 s . t . A T α N = b .
This can be solved using the CVX toolbox [50]. Moreover, the selection of the mainlobe width and the desired direction θ s must satisfy
Δ ≤ 2 ⋅ min ( θ s , 180 ∘ − θ s )
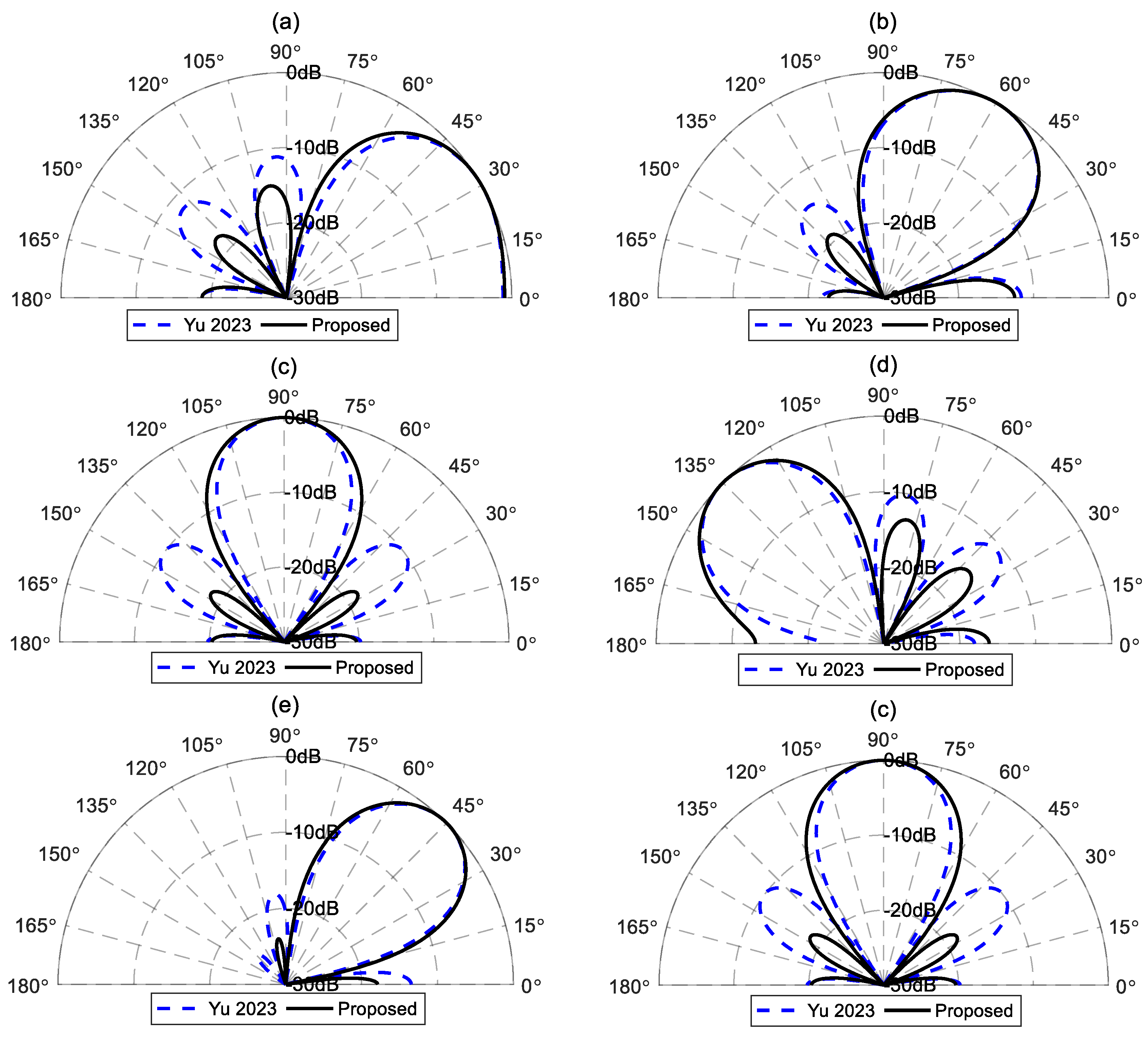
The optimal target radiation pattern can be obtained by substituting the resultant into (13). Figure 2 provides examples of target radiation patterns designed using the above method at different desired angles. This indicates that the proposed method can design effective radiation patterns for different orders in various desired directions. Figure 2 also presents the target radiation patterns of the same order and desired directions designed using the method stated in Ref [39]. Yu's method finds the optimal vector α N by maximizing the directivity factor of the beampattern under the constraints of the distortionless constraint and the extremum constraint in the desired direction [as (10)]. This method needs a regularization parameter to trade off the radiation power in the end-fire direction and the spatial average of the radiated power over the entire space. The regularization parameter is set to 0.15, as given in Ref [39] and applied in the following simulation.
Figure 2a–Figure 2d present the comparison results of the fourth-order target differential radiation patterns at desired angles of 30°, 60°, 90°, and 135°, using Yu's method and the proposed method, respectively. Though both methods can design effective fourth-order differential radiation patterns at the desired angles, the proposed method has smaller sidelobes (excluding that in the end-fire direction). This is because Yu's method designs the target radiation pattern by adjusting the regularization parameter to balance the array's energy radiated in the end-fire direction and the average energy radiated into the entire space. Since this method does not account for the energy distribution of sidelobes other than the end-fire direction, it can result in excessively large sidelobes. Thus, the regularization parameter selection is required for different desired directions. However, selecting the appropriate regularization parameter is quite challenging, which hinders the practical application of this method. In contrast, the proposed method designs the target radiation patterns by minimizing the total energy in the sidelobe area, which includes the end-fire direction. As a result, the target beampattern radiates less energy into the sidelobe area. Additionally, once the desired direction and main lobe width are determined, we can design the optimal radiation pattern without adjusting other parameters, facilitating practical applications.
Figure 2e-Figure 2f further compare the fifth-order target radiation patterns by Yu’s and the proposed methods, with the desired directions of θ s = 45 ∘ and θ s = 90 ∘ , respectively. The above findings hold. In addition, when the desired direction is in the broadside direction, θ s = 90 ∘ , the 5th-order target radiation pattern (Figure 2f) is the same as the 4th-order target pattern (Figure 2c). This occurs because the target radiation pattern in the broadside direction is symmetric about the y axis. As a result, the odd terms of the optimal vector α N are zero, leading to pairs of nulls in the target beampattern that are symmetrically distributed about the y axis. Therefore, when designing N-th order broadside radiation patterns (where N is odd), the process automatically reduces to designing an (N−1)-th order pattern.

3.2. Formulating the Target Radiation Pattern in the Modal Domain

Using the N-th order target radiation pattern obtained in Section 3.1, we will transform the ideal radiation pattern from equation (9) into the modal domain, depending on the parity of N.

3.2.1.N. is Even

Let N = 2 N ˜ and α N , − 1 = 0 , (9) will be
B ˜ ( N ) ( θ ) = ∑ n = 0 N α N , n cos n θ = ∑ n = 0 N ˜ α N , 2 n cos 2 n θ + ∑ n = 0 N ˜ α N , 2 n − 1 cos 2 n − 1 θ .
According to the following relations [51]:
cos 2 n θ = 1 2 2 n ∑ t = 0 n − 1 2 2 n t cos 2 n − t θ + 2 n n ,
cos 2 n − 1 θ = 1 2 2 n − 2 ∑ t = 0 n − 1 2 n − 1 t cos 2 n − t − 1 θ ,
where · · is combinations. Combining the Euler’s formula, i.e.,
cos ( n θ ) = e i n θ + e − i n θ 2 ,
then (20) can be expressed as
B ˜ ( N ) ( θ ) = ∑ n = − N N γ n e i n θ .
where
γ n = ∑ p = n + 1 2 N ˜ α N , 2 p − 1 η ˜ n + sgn ( n ) 2 ( p ) n = ± 1 , ± 3 , ... , ± ( 2 N ˜ − 1 ) , ∑ p = n / 2 N ˜ α N , 2 p η n / 2 ( p ) n = 0 , ± 2 , ± 4 , ... , ± 2 N ˜ ,
η ˜ t ( n ) = 0 t = 0 , 1 2 2 n − 1 2 n − 1 n − t t = ± 1 , ± 2 , ... , ± n ,
sgn ( t ) = 1 t > 0 , 0 t = 0 , − 1 t < 0 ,
η t ( n ) = 1 2 2 n 2 n n − t t = 0 , ± 1 , ... , ± n .
where · represents absolute value.

3.2.2.N. is odd

Let N ' = ( N + 1 ) / 2 , and
α 2 N ' , n = α N , n n = 0 , 1 , ... , N , 0 n = N + 1 ,
then we can express the odd (N-th) order target radiation pattern as a form of the even ( 2 N ' ) order target beampattern:
B ˜ ( N ) ( θ ) = B ˜ ( 2 N ' ) ( θ ) = ∑ n = 0 2 N ' α 2 N ' , n cos n θ = ∑ n = 0 N ' α 2 N ' , 2 n cos 2 n θ + ∑ n = 0 N ' α 2 N ' , 2 n − 1 cos 2 n − 1 θ ,
Similar to the derivation steps in Section 3.2.1, we can formulate (30) in the modal domain with a symmetric form
B ˜ ( N ) ( θ ) = B ˜ ( 2 N ' ) ( θ ) = ∑ n = − 2 N ' 2 N ' γ n e i n θ
where
γ n = ∑ p = n + 1 2 N ' α 2 N ' , 2 p − 1 η ˜ n + sgn ( n ) 2 ( p ) n = ± 1 , ± 3 , ... , ± ( 2 N ' − 1 ) ∑ p = n / 2 N ' α 2 N ' , 2 p η n / 2 ( p ) n = 0 , ± 2 , ± 4 , ... , ± 2 N ' ,
where η ˜ t ( n ) , sgn ( t ) and η t ( n ) are defined in (26), (27) and (28), respectively.

3.3. Beamformer Design

The objective is to determine the loudspeaker weighting so that the array’s radiation pattern closely approximates the target radiation pattern. Based on (2) and (24), we use the Jacobi-Anger series expansion method to accomplish this task.

3.3.1. Modal Matching Method with Maximum WNG

In the series expansion method, the Jacobi–Anger expansion is used to decompose the resulting radiation pattern into a linear combination of circular harmonics. The Jacobi-Anger expansion is
e − i σ cos θ = ∑ n = − ∞ + ∞ β n ( σ ) e i n θ ,
where β n ( σ ) = ( − i ) n J n ( σ ) , and J n ( ⋅ ) is the nth-order Bessel function of the first kind. Substituting (33) into (2), we obtain
B ( θ ) = ∑ l = 1 L w l * ∑ n = − ∞ + ∞ β n ( k x l ) e i n θ .
In order to obtain a Nth-order target radiation pattern, the infinite summation in (34) is truncated to the order N, that
B ( θ ) ≈ ∑ n = − N N e i n θ ∑ l = 1 L β n ( k x l ) w l * .
When the normalized far-field radiation pattern in (35) is in consistent with the target radiation pattern in (24), there is
∑ l = 1 L β n ( k x l ) w l * = γ n n = 0 , ± 1 , ... , ± N . .
For the design of a steerable differential beamformer, the distortionless constraint in the desired direction is needed
w H g ( θ s ) = 1 .
Combing (36) and (37) yields
Φ w = ν .
where
Φ = β − N … β N g ( θ s ) H ,
β n = [ β n ( k x 1 ) ⋯ β n ( k x L ) ] T ,
and
ν = γ − N ... γ 0 ... γ N 1 T .
Using the symmetric property of the Bessel function, i n J n ( ⋅ ) = i − n J − n ( ⋅ ) , (38) can be simplified to
  Φ ˜   w =   ν ˜ ,
where
  Φ ˜ = β 0 ⋯ β N g ( θ s ) H
is N + 2 × L full matrix and
  ν ˜ = [ γ 0 ... γ N 1 ] T .
With L > N + 2 loudspeakers to generate Nth-order steerable target radiation pattern, one approach to design the beamformer is to maximize WNG with the constraints of (42). Due to (37) holds, The WNG, defined in (6), can be written as WNG = 1 / w H w .
The optimization problem can be formulated as
min w w H w s . t .   Φ ˜   w =   ν ˜ .
The solution is
w =   Φ ˜ H (   Φ ˜   Φ ˜ H ) − 1   ν ˜ .

3.3.2. Modal Matching Method with WNG Constraint

Since the resulting beamformer (46) is obtained with some approximations, the mean square error (MSE) is adopted to evaluate the accuracy of these approximations. The MSE of the approximations of the beamformer to the Nth-order target differential radiation pattern is defined as
d ( w ) = 1 π ∫ 0 π w H g ( θ ) − B ˜ ( N ) ( θ ) 2 d θ .
Substituting (9) into (47), the MSE can be written as a quadratic function,
d ( w ) = w H Γ w − w H q − q H w + ξ
where
q = 1 π ∫ 0 π g ( θ ) B ˜ ( N ) ( θ ) d θ = Q α N ,
Q = 1 π ∫ 0 π g ( θ ) c N T d θ ,
ξ = ∫ 0 π B ˜ ( N ) ( θ ) 2 d θ = α N T   C ˜ α N ,
  C ˜ = 1 π ∫ 0 π c N c N T d θ .
The matrix Γ is the array spatial correlation matrix, which is defined in (8). Q is an complex matrix. Its (m, n + 1)th (m = 1, 2, …, L; n = 0, 1, …, N) element is
Q m , n + 1 = 1 2 n − 1 ∑ p = 0 n / 2 n p i n − 2 p J n − 2 p ( − k x m ) − 1 2 n δ 0 , n − 2 n / 2 n n / 2 i n − 2 n / 2 J n − 2 n / 2 ( − k x m ) ,
where ⋅ represents the floor function applied to a real number, J n ( ⋅ ) is the nth-order Bessel function of the first kind and δ m , n represents the Kronecker delta.   C ˜ is an ( L + 1 ) × ( L + 1 ) real matrix, whose (m + 1, n + 1)th element is
  C ˜ m + 1 , n + 1 = 1 π ∫ 0 π cos m + n θ d θ = ( 1 + ( − 1 ) ( m + n ) ) Γ ( 1 + m + n ) / 2 2 π Γ ( 2 + m + n ) / 2 m = 0 , 1 , ... , N ; n = 0 , 1 , ... , N
where Γ ( ⋅ ) is the Euler’s Gamma function.
After calculating the optimal coefficients of the target differential beampattern (9) according to the actual requirements, the objective for designing the beamformer are twofold. On the one hand, we aim to design the resulting beampattern approaches the target one as much as possible. On the other hand, we hope the system is robust enough to against unknown channel mismatch in real applications. The MSE, defined in (47), measures how closely the synthesized beampattern approximates the target beampattern. The WNG, defined in (6), is a metric for measuring the robustness of the designed beamformer. Therefore, attention should be paid to these two metrics when designing the beamformer.
The solution in (46) gives the maximum WNG. The higher the value of WNG, the more robust is the radiation. However, it does not consider the MSE in the design of the beamformer. In practice, the WNG greater than a suitable value should be ensured. It indicates the beamformer is robust enough for usage. In addition, the degrees of freedom provided by the weighting functions can be used to minimize MSE. The optimization problem can be described as follows
min w w H Γ w − w H q − q H w s . t . Φ ˜ w =   ν ˜ , w H w ≤ ε WNG .
The parameter ε WNG represents the lower limit of the WNG of the designed beamformer. It is noteworthy that ε WNG must not exceed ε WNG max , which is the WNG obtained from the solution in (46). The optimal weighting vector w can be obtained by solving the optimization problem in (55) using the CVX toolbox [50].

4. Simulations

In this section, we will verify the effectiveness of the proposed method and investigate the performance of the beamformer through simulations. A linear array of 21 loudspeakers with a spacing of 0.04 m is used in the following simulation. The frequency range of interest is from 300 Hz to 4 kHz, which covers the frequency range of speech.

4.1. Performance Study and Comparison

We first conduct the simulations to verify the effectiveness of the proposed method. For ease of identification, we refer to the method proposed in Section 3.3.1 as the proposed method I and the method proposed in Section 3.3.2 as the proposed method II. The parameter ε WNG used in the proposed method II is set to 0 dB in this simulation.
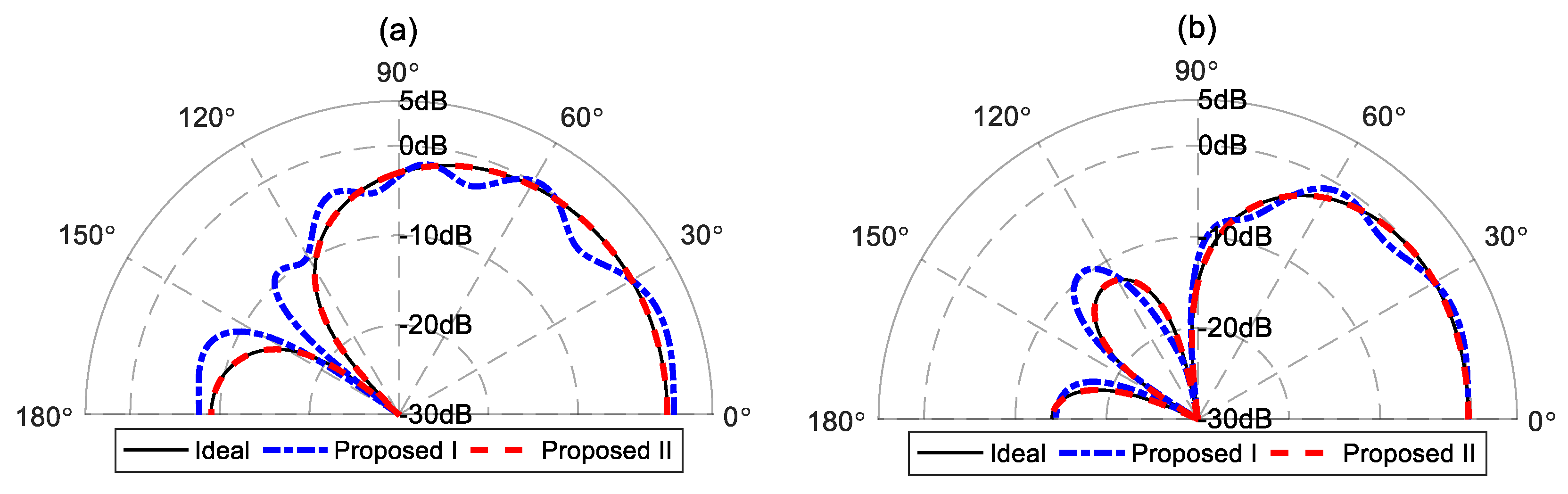
The second-order and third-order target radiation pattern, with the desired direction is set as θ s = 30 ° and the main lobe width Δ = 60 ° , are synthesized by the proposed method I and the proposed method II, respectively. Figure 3 presents comparisons between the beam patterns synthesized using the two proposed methods and the target beampattern at 2 kHz. The target beampatterns have maximum values of one, which located at the preset angle θ s = 30 ° . The second-order target beampattern has a null at 138 ° . The third-order target beampattern has two nulls at 100 ° and 154 ° . Figure 3a shows the comparison result of the second-order beampattern. It is observed that the beampattern synthesized using the proposed method I deviates from the target beampattern. Despite the value of the synthesized beampattern is one at the preset direction, the values of the resulting beampattern near 20 ° and 60 ° are both greater than one. This indicates that although the distortionless constraint is satisfied in the proposed method I, the finite orders of modal matching cannot ensure the maximum value of the generated beampattern in the preset direction. However, the beampattern of the proposed method II matches well the target beampattern shown with a black solid line. The same results can be seen in the comparison of the third-order beampattern shown in Figure 3b. It is noteworthy that, compared to the second-order synthesized beampattern, the third-order beampattern of the proposed method I is closer to the target beampattern. This is because the truncation error caused by (35) decreases as the order of the target beampattern increases.
The broadband synthesized radiation patterns are shown in Figure 4. Figure 4a-Figure 4b shows the broadband beampatterns of the second-order and third-order synthesized beampatterns of the proposed method I. There are two issues with the beampattern generated by the proposed method I: Firstly, the beampatterns cannot maintain consistent, as both the main lobe width and the null positions change with frequency. Secondly, the maximum values of the generated beampatterns deviate from the desired direction, which means that the generated beampattern does not closely approximate the desired beampattern. Figure 4c-4d plot the broadband beampatterns synthesized using the proposed method II. As seen, the proposed method II can design the different orders of target radiation patterns. The resulting beampatterns maintain almost frequency-invariant across the evaluated frequency range.
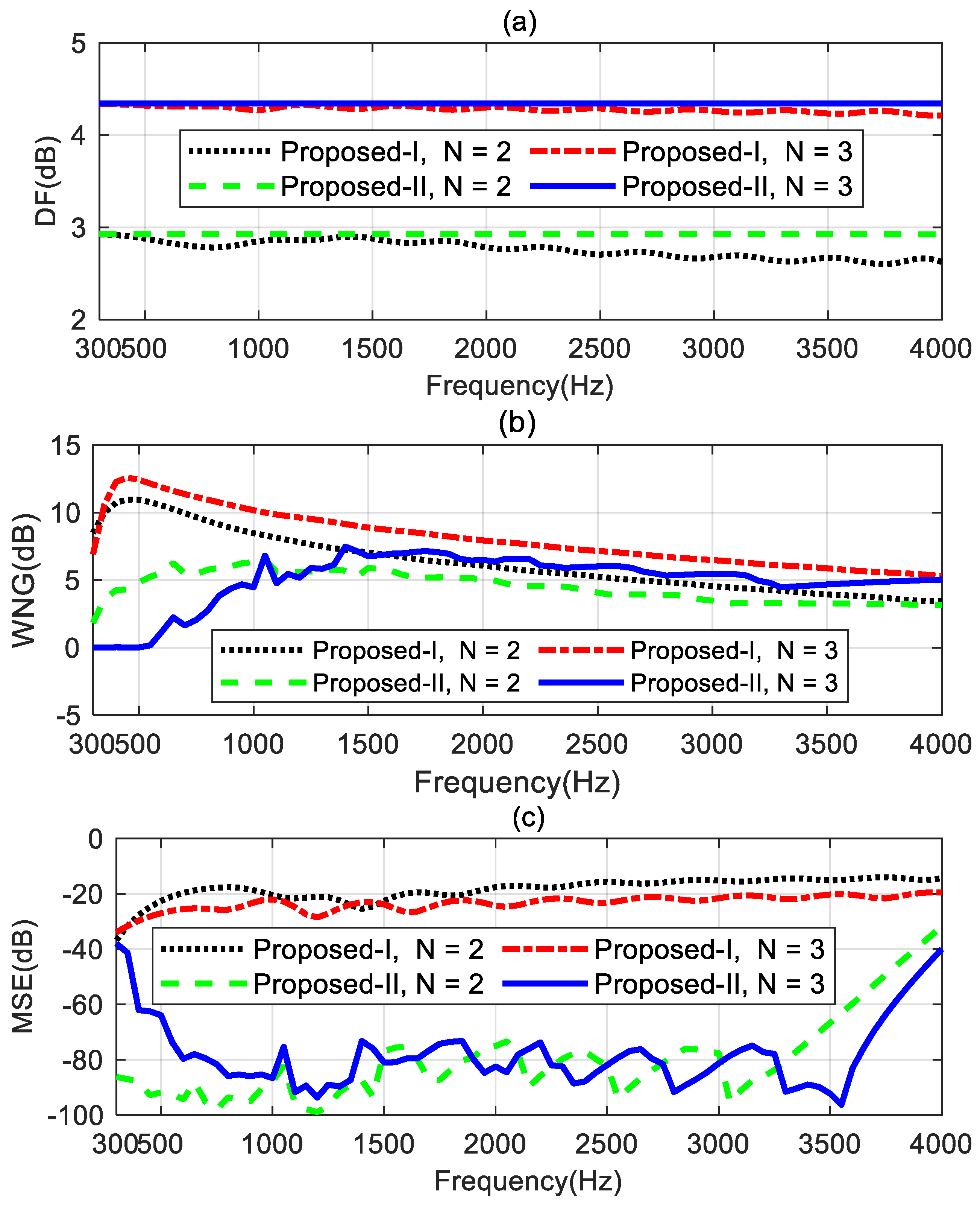
The performance comparisons of the two proposed methods for designing the second- and third order target differential beampatterns are shown in Figure 5. The performance measures are DF, WNG and MSE. Figure 5a shows the DF increases with the order of target beampattern increases. the DF of the proposed method I cannot remain constant values and exhibits some fluctuations at certain frequencies. However, the proposed method II can maintain constant DF values over the frequency range of interest (300 Hz – 4 kHz) for designing the different order target beampatterns. This indicates the proposed method II can achieve the frequency-invariant beampatterns in the whole evaluated frequency range. From Figure 5b, the WNGs of the proposed method II is smaller than that of the proposed method I. This is because the proposed method I uses all the remaining degrees of freedom of the array to optimize the WNG while satisfying the linear constraints. Therefore, the proposed method I has the highest WNG. The proposed method II, while meeting the linear constraints and ensuring the WNG exceeds ε WNG , uses the remaining degrees of freedom of the array to optimize the MSE. The preset value ε WNG plays a role in a tradeoff between the WNG and the MSE. As can be seen in Figure 5c, The MSE of the proposed method II is significantly lower than that of the proposed method I. Especially in the range of 1-3.5 kHz, compared to the proposed method I, the proposed method II achieves a reduction of over 40 dB in MSE by only slightly decreasing the WNG value. It is interesting to note that the performance of the proposed method I in designing the third-order target beampattern is superior to its performance in designing the second-order target beampattern. It has a larger DF factor, higher WNG, and lower MSE. This means that the beamformer of the third-order ideal beampattern has stronger directivity, higher robustness, and lower mean square error. Nevertheless, the MSEs of the proposed method I are still only around -20 dB, which does not meet the requirements for practical applications. However, the proposed method II can significantly improve the mean square error by sacrificing a slight degree of robustness, which is highly valuable in real applications. Therefore, we will only study the performance of the proposed method II in the following sections. Any mentioned the proposed method hereafter refers to the beamformer obtained by solving the optimization problem (55).

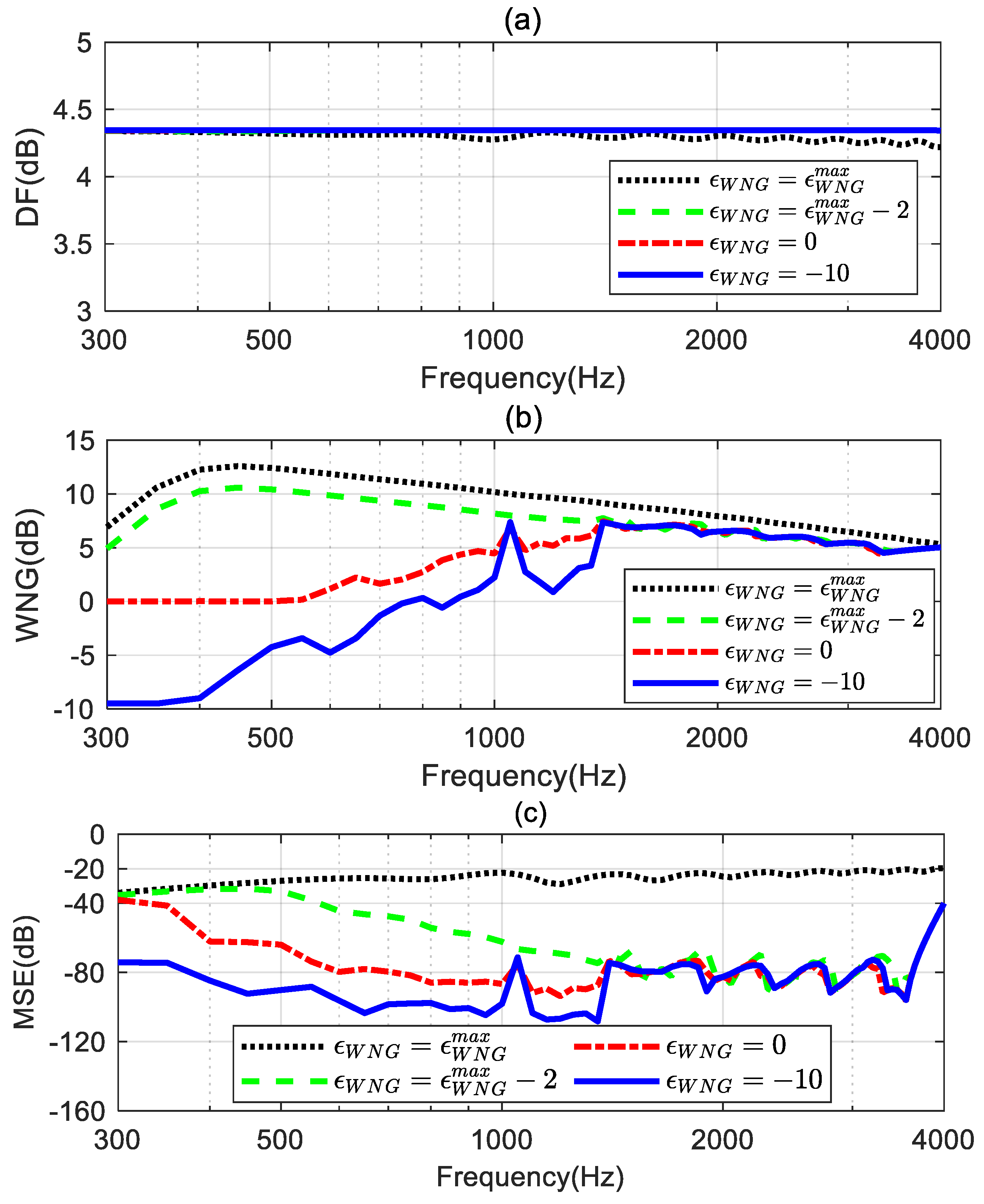
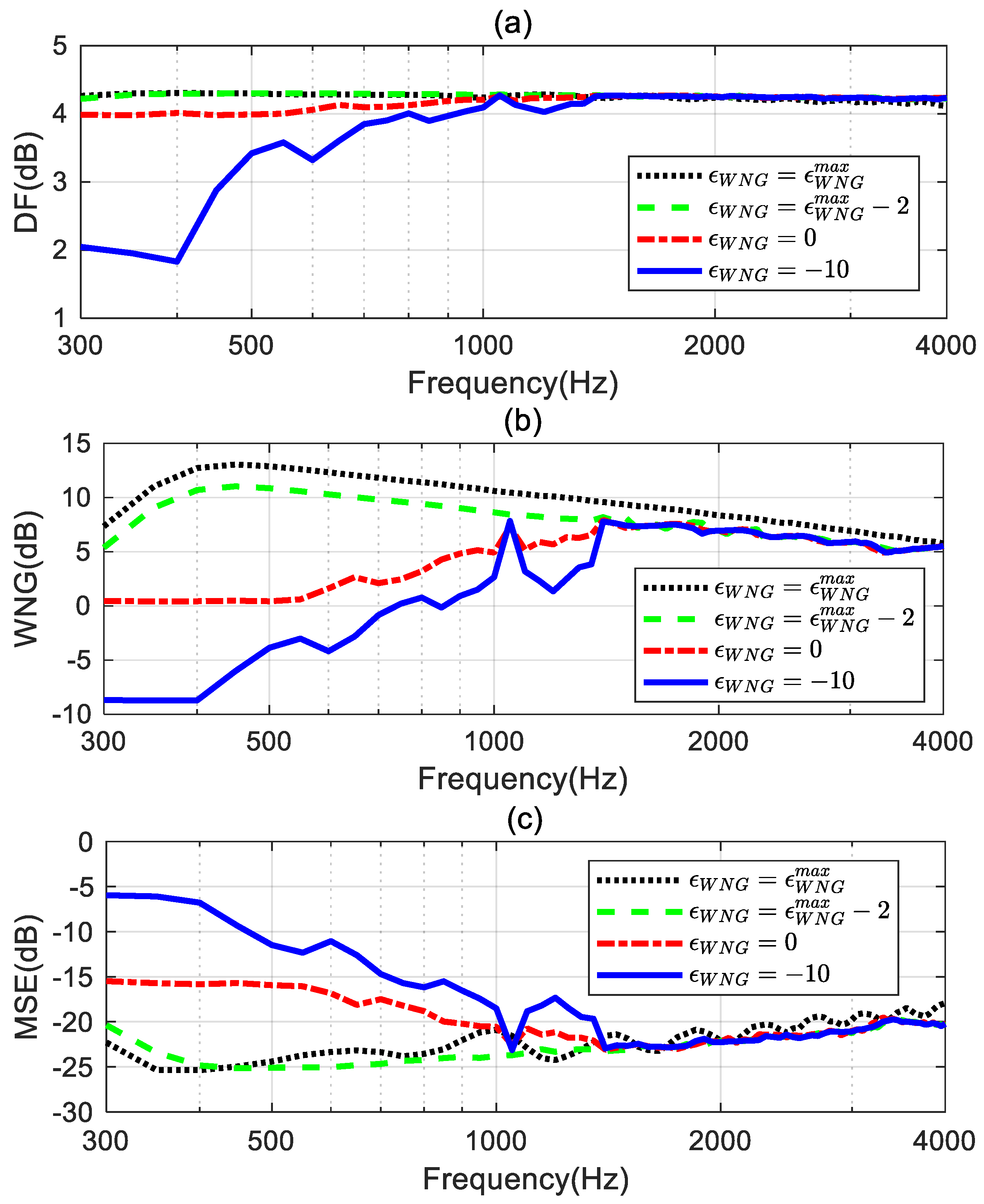
4.2. Impact of the Parameter ε WNG

ε WNG is a key parameter to trade off the robustness and the approximation error of the proposed method. This simulation study the impact of the value of ε WNG on the performance of the proposed method with the third-order differential beampattern (see in Figure 3b) being the ideal radiation pattern. The level of ε WNG is set to four different values: 1) ε WNG = ε WNG max dB; 2) ε WNG = ( ε WNG max − 2 ) dB; 3) ε WNG = 0 dB; and 4) ε WNG = − 10 dB.
The corresponding broadband radiation patterns of the proposed method are shown in Figure 6. Figure 6a presents the synthesized beampattern when ε WNG equals ε WNG max dB. It gives the same result shown in Figure 4b, indicating the solutions obtained by solving the optimized problem in (55) equal to the solution in (46) when ε WNG = ε WNG max dB. Figure 6b displays the synthesized beampattern when ε WNG = ( ε WNG max − 2 ) dB. With a slight decrease in the value of ε WNG , the mean square error (MSE) between the synthesized beampattern and the ideal beampattern is reduced above 500 Hz (shown in Figure 6c), resulting in an improvement of the synthesized beampattern, although there is a slight deviation from the ideal beampattern at low frequencies. Furthermore, from Figure 6c and 6d, we can observe that as the value of ε WNG is further reduced, the synthesized beampattern can be closer to the ideal one across the entire evaluated frequency range.
Table 7. Figure 7a shows that the DF of the beamformer with ε WNG = ε WNG max fluctuates at certain frequencies and the DFs of the beamformers with other ε WNG values can maintain a constant over the whole evaluated frequencies range. This indicates that the frequency-invariant beampattern can be achieved by the proposed method with an appropriate ε WNG value. Figure 7b and 7c plot the WNG and the MSE of the proposed method with different ε WNG values. It can be observed that at low frequencies, especially below 1.4 kHz, the WNG and MSE of the beamformer decrease as ε WNG decreases. This means that, with the decrease in the value of ε WNG , the synthesized beampattern more closely approaches the target beampattern, but this improvement comes at the expense of a decrease in the WNG. Above 1.4 kHz, the WNG of these beamformers dose not differ significantly. However, the MSE of the beamformers when ε WNG = ε WNG max − 2 , ε WNG = 0 , and ε WNG = − 10 is much smaller than the MSE of the beamformer when ε WNG = ε WNG max . Hence, we can tune the tradeoff between the WNG and MSE of the beamformer by setting ε WNG to slightly less than ε WNG max .

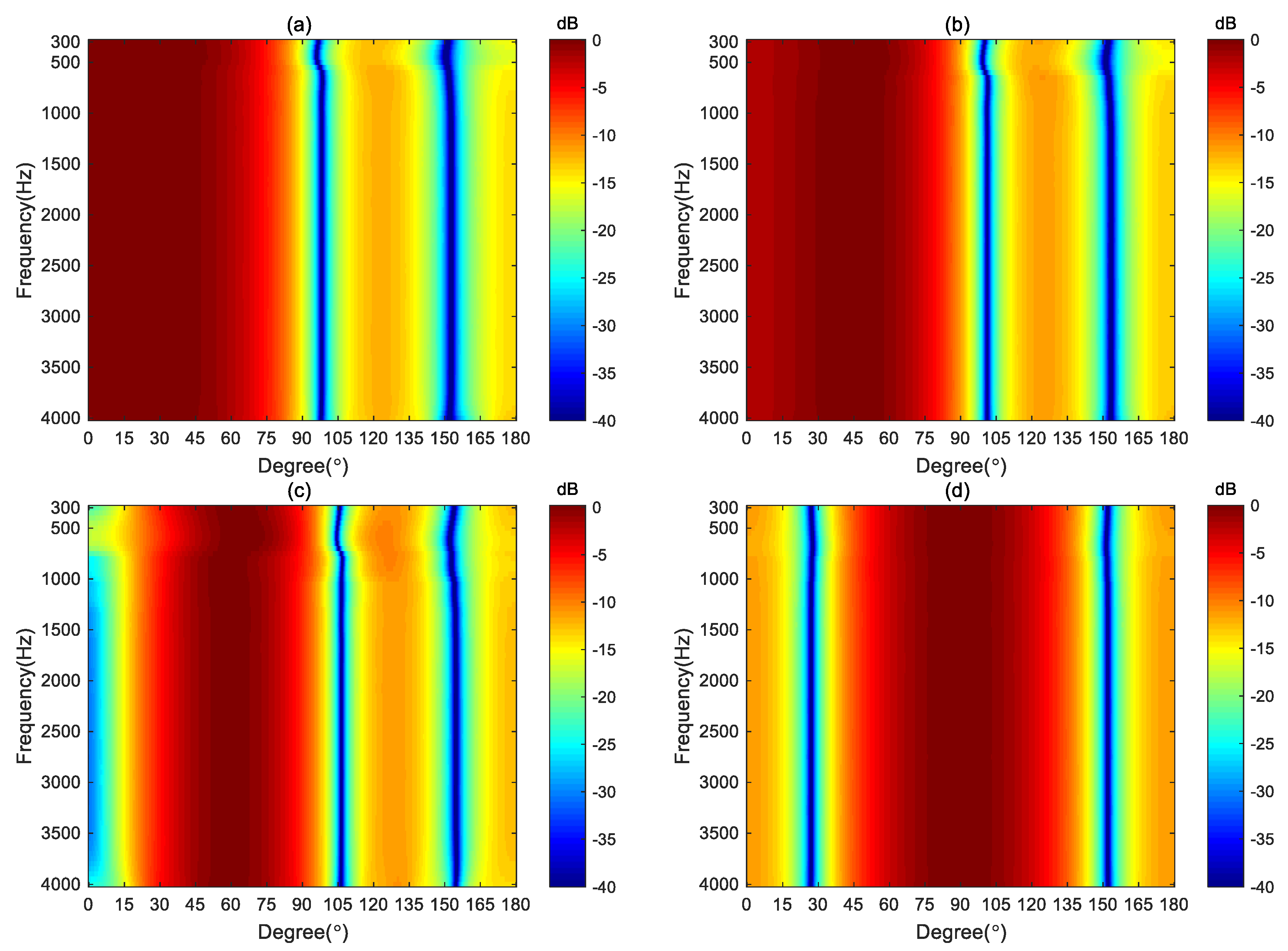
4.3. Impact of Loudspeaker Mismatch

It was assumed in the previous section that the loudspeakers used for designing the beamformer are ideal, without any mismatch issues among the loudspeaker units. However, in practice, there exists the uncertainty in the loudspeaker characteristics (magnitude, phase and position) due to the variations in the response of the drivers. This simulation investigates the impact of the driver mismatch on the proposed method with different ε WNG values. The target beampattern and ε WNG values are set the same as in Section 4.2. The perturbations are added to the spatial responses of the loudspeakers, for which the error has a multiplicative form with uniform distribution between −3 and +3 dB in magnitude and uniform distribution between −10° and +10° in phase. The performance measures are averaged over 1000 Monte Carlo trails.
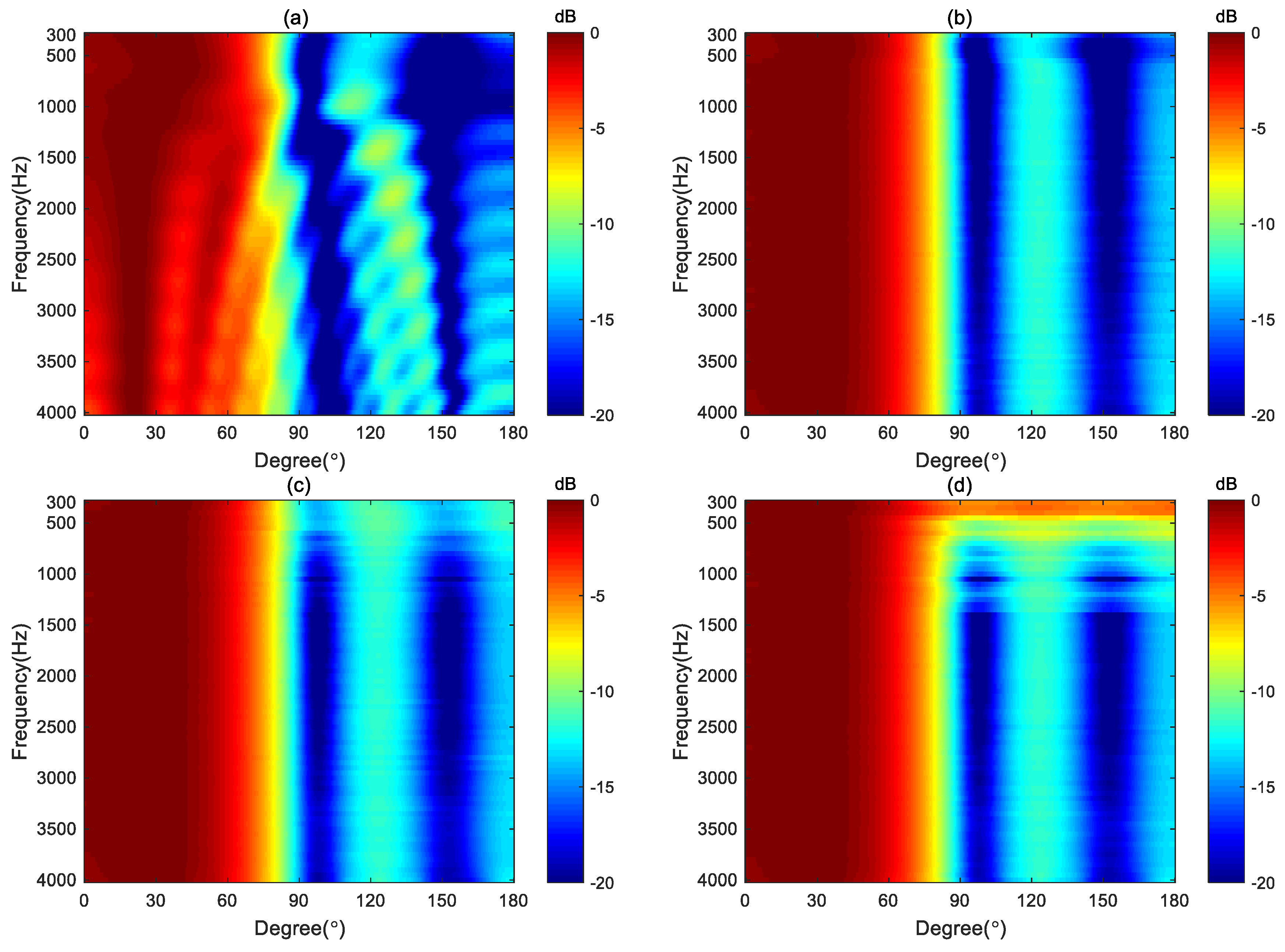
Broadband beampatterns are plotted in Figure 8. By comparing Figure 8a and Figure 8b with Figure 6a and Figure 6b, we can observe that, aside from the difference in amplitude range, the basic shape of the beampattern remains unchanged. This indicates that when ε WNG = ε WNG max and ε WNG = ε WNG max − 2 , the beamformer is robust enough to against the perturbations in the frequency response of the loudspeaker. However, Figure 8c and Figure 8d show significant differences from Figure 6c and Figure 6d at low frequencies, suggesting that when ε WNG = 0 and ε WNG = − 10 , the beamformer’s robustness is reduced, causing the synthesized beampattern to deviate from the target beampattern due to the errors added to the loudspeaker.
Figure 9 shows the averaged DF, WNG and MSE of the beamformers. Figure 9a shows that the DF of the beamformers with ε WNG = ε WNG max and ε WNG = ε WNG max − 2 are almost identical over the whole evaluated frequency range. When ε WNG = 0 and ε WNG = − 10 , the DFs decrease with the ε WNG value decrease below 1 kHz. Figure 9b and 9c plot the WNG and MSE, respectively. Unlike the conclusion drawn in Section 4.2 that a smaller WNG of the beamformer results in a smaller MSE, when there exists a mismatch in the drivers, a smaller WNG value leads to a larger MSE which means large deviations from the target beampattern at low frequencies. Hence, the appropriate selection of the ε WNG value is crucial for the proposed method in practical applications.

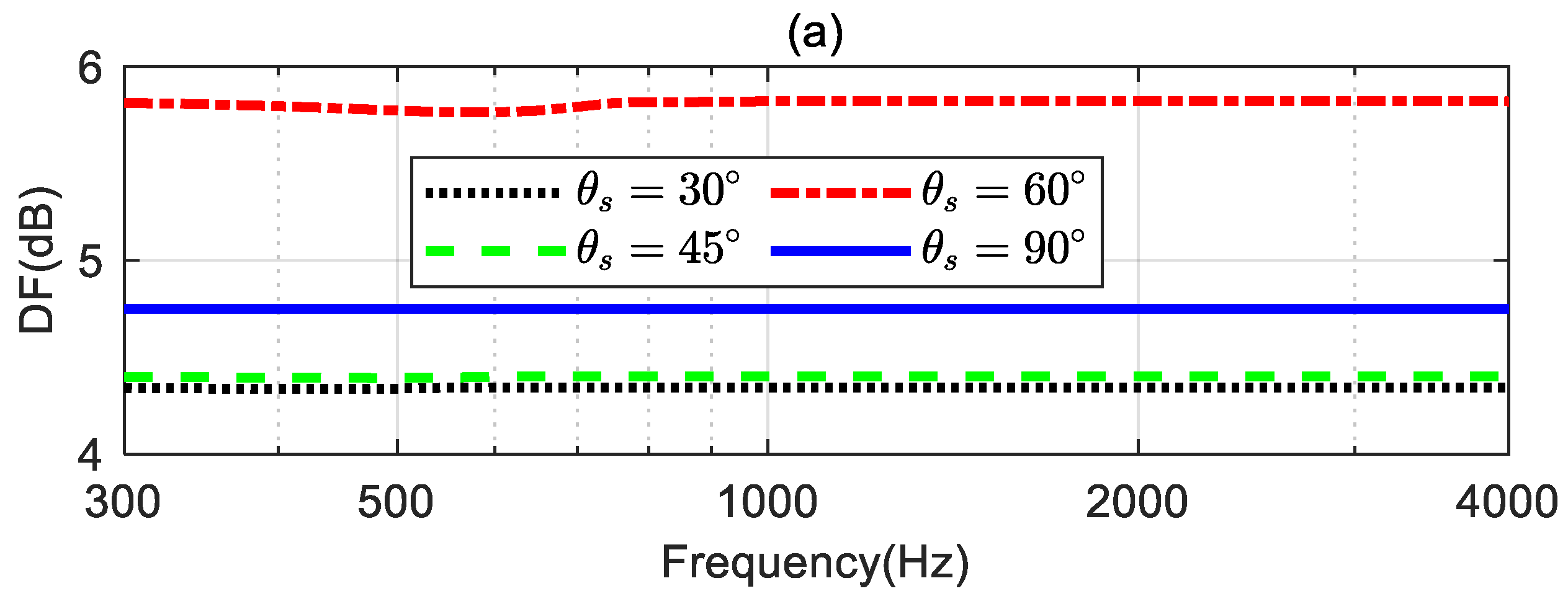
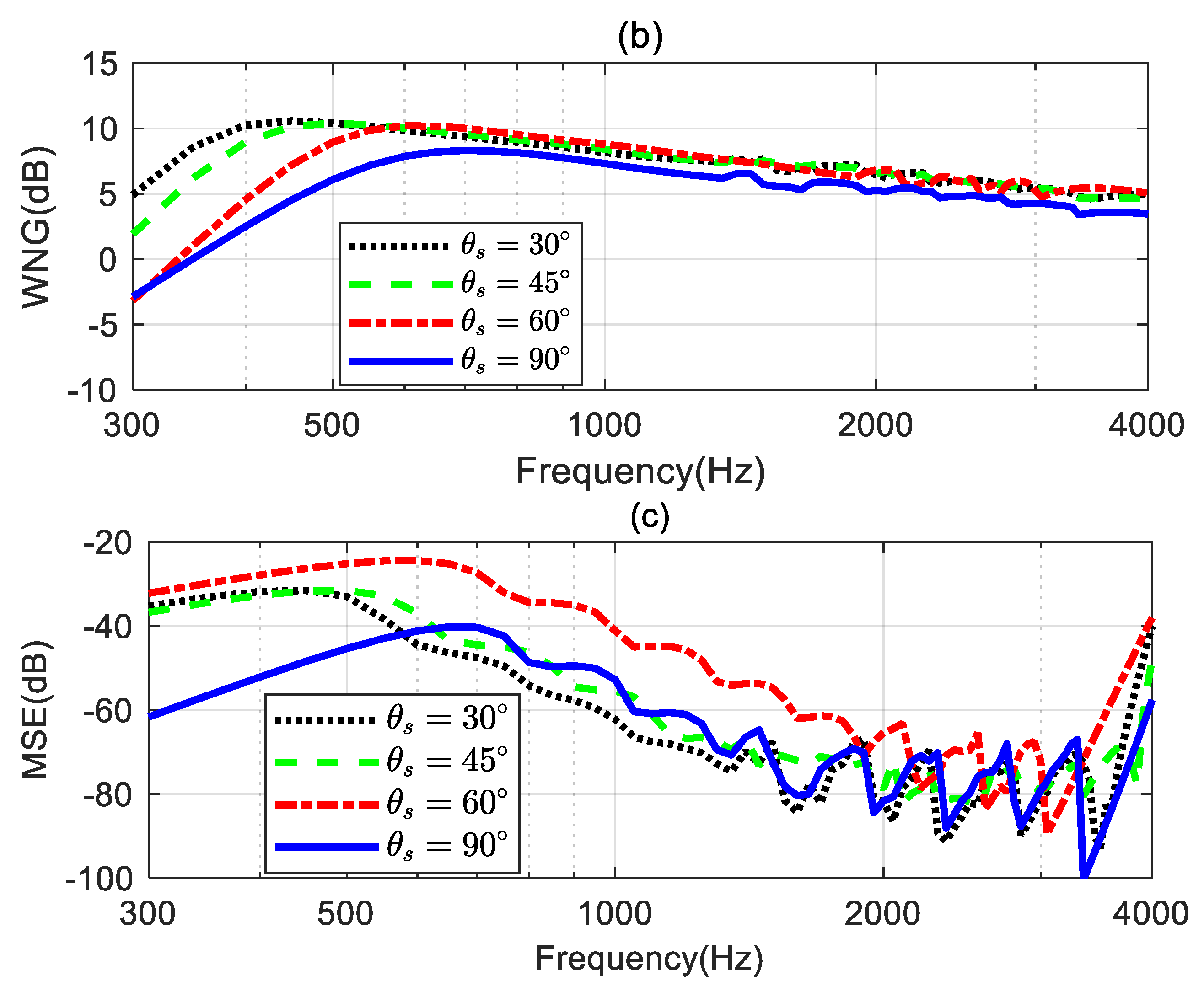
4.4. Validation of the Steering Flexibility

In this simulation, we investigate the steering flexibility of the proposed method. For the broadside array illustrated in Figure 1, we consider four different desired directions: θ s = 30 ∘ , θ s = 45 ∘ , θ s = 60 ∘ and θ s = 90 ∘ . The coefficients of the third-order differential beampattern with mainlobe width equals 60° and the different desired directions need to be determined by solving (18) first, and then the synthesized beampattern is obtained using the proposed method. The parameter ε WNG used in the simulation is set to ( ε WNG max − 2 ) dB.
Figure 10 shows the synthesized broadband beampatterns. As seen, the mainlobe of the synthesized beampatterns can be steered to the desired directions. This indicates that the proposed method can design steerable different beamformers with a linear array. The synthesized beampatterns slightly deviate from the ideal beampatterns at low frequencies for θ s = 30 ∘ , θ s = 45 ∘ , θ s = 60 ∘ and θ s = 90 ∘ . When θ s = 90 ∘ , the proposed method can achieve frequency-invariant beampattern over the whole evaluated frequency range.
Figure 11 shows the DF, WNG and MSE of the beamformers with different desired directions. As seen from Figure 11a, when θ s are 30°, 45°, and 60° respectively, the DF of the beamformer increases as θ s increases. However, when the desired direction θ s is 90°, the DF does not increase as expected. That is because, in this case, the ideal beampattern is symmetric with respect to the direction , the coefficient of the ideal beampattern satisfies α N , m = 0 when m is odd, leading to a reduction in the DF value. From Figure 11b, the WNG decrease as θ s increases at low frequencies. Figure 11c shows that when θ s = 90 ∘ , the MSE is below -40 dB over the whole evaluated frequency range, which is considered the ideal beampattern has been well approximated.

4.5. Comparison with Other Steerable Beamforming Methods

To demonstrate the advantages of the proposed method in designing the steerable broadband differential beampattern with linear array, we compare the performance of the proposed method with three other steerable beamforming methods: (i) the Delay and Sum (DS) method, which increases the acoustic energy in the desired direction by phase-aligning [43]. (ii) the Minimum Variance Distortionless Response (MVDR) method, which aims to minimize the output power of the array while maintaining a distortionless response in the desired direction [52]. (iii) the Null Constrained (NC) method, which utilizes the null position for the ideal beampattern to design the differential beamformer [38]. The MVDR method requires a regularization parameter during the solving process. We set the regularization parameter to 0.001 in the simulation. The steerable differential beamformer we designed aims to approach the fourth-order differential beampattern with the mainlobe width of 60° and the desired direction being steered to 120°.
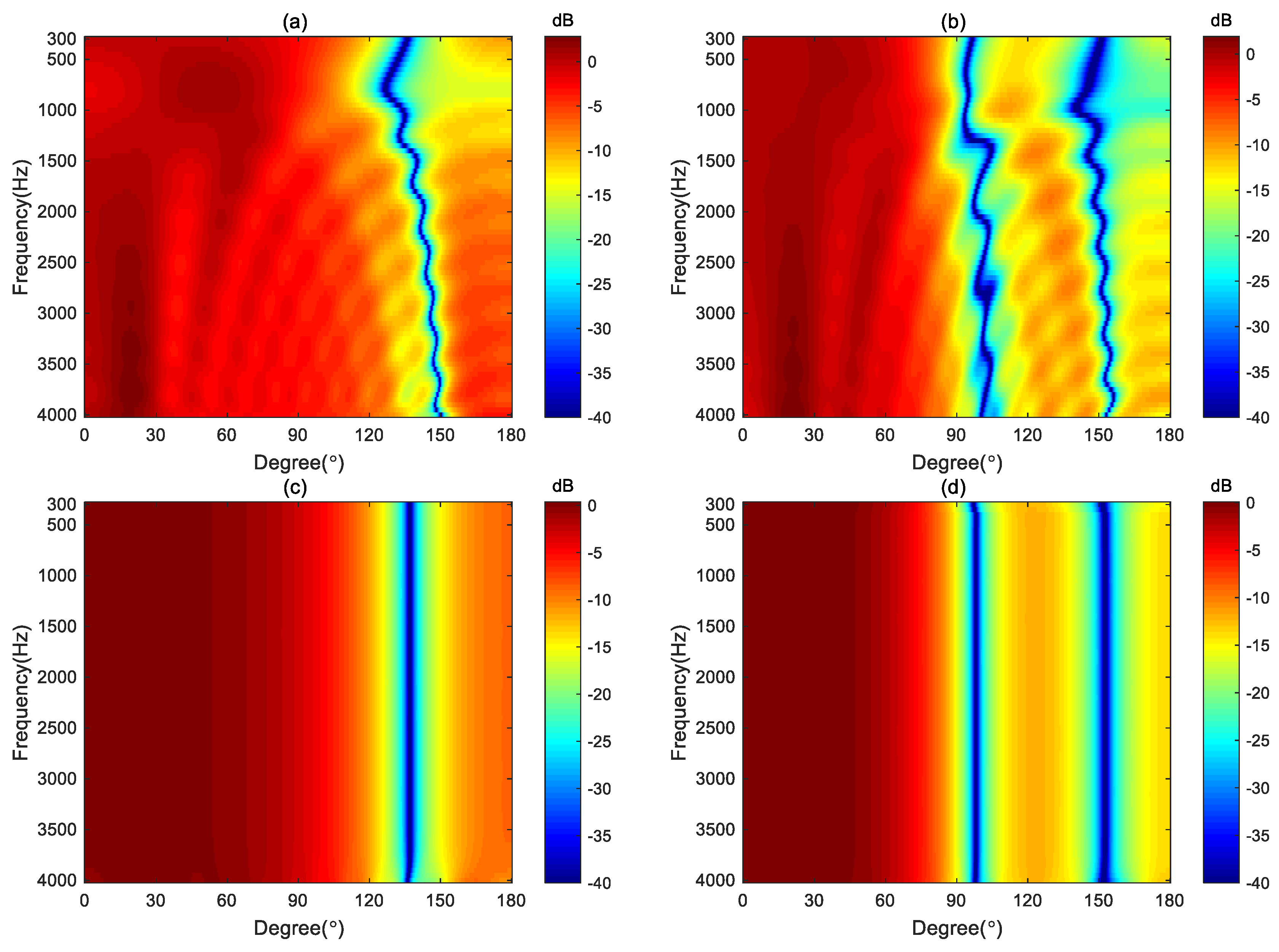
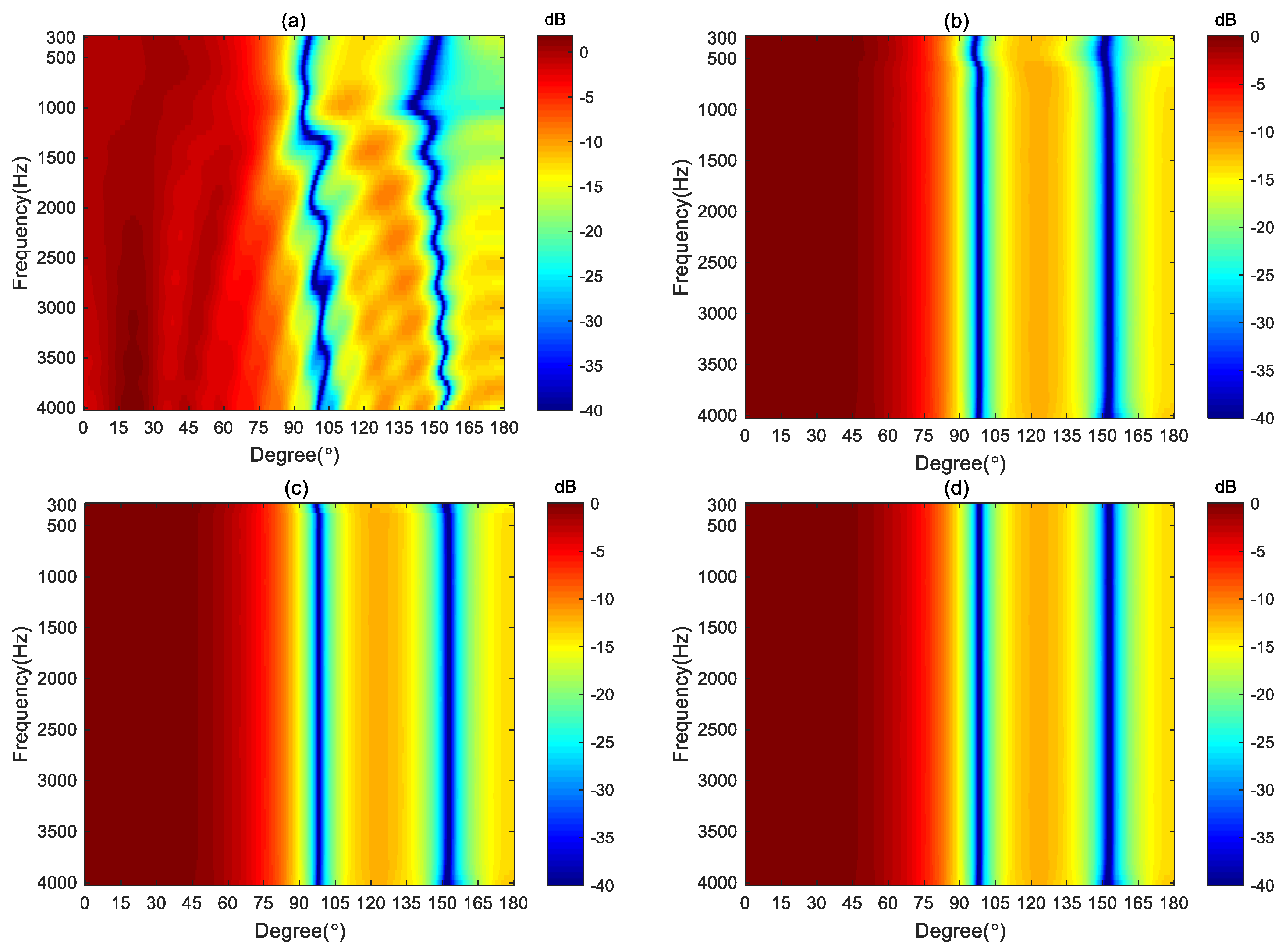
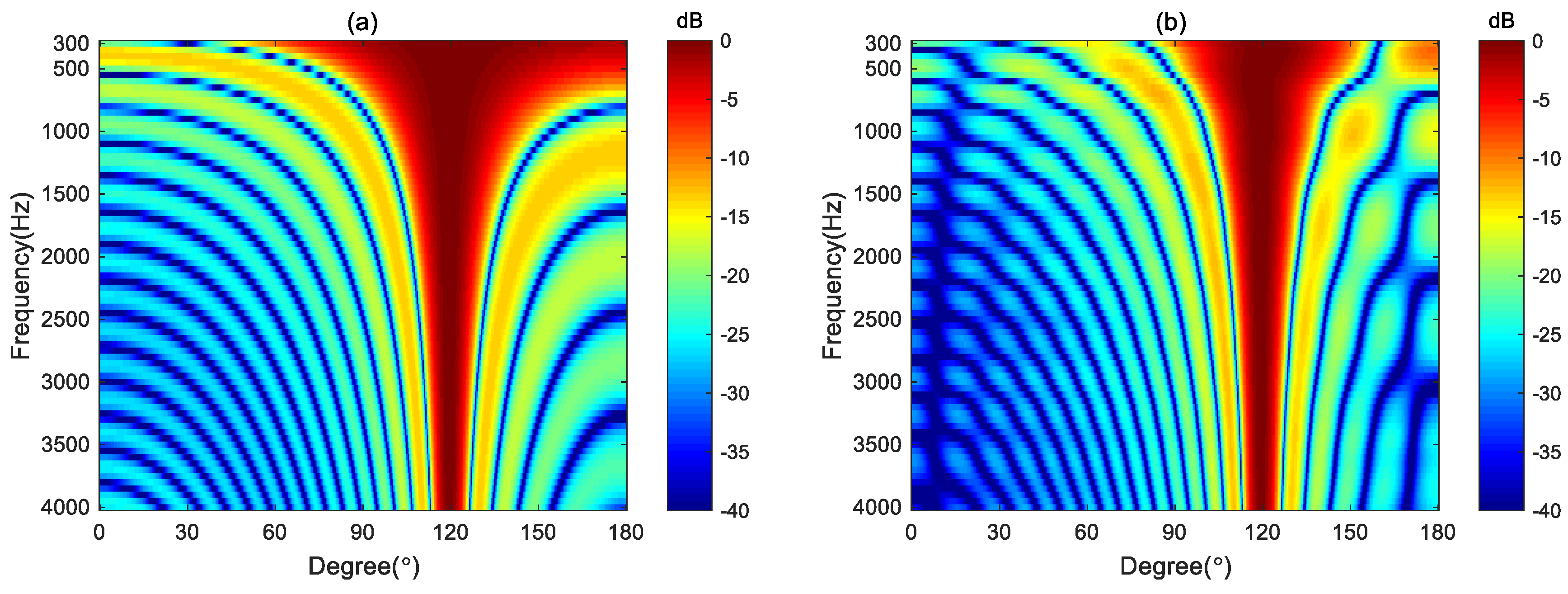
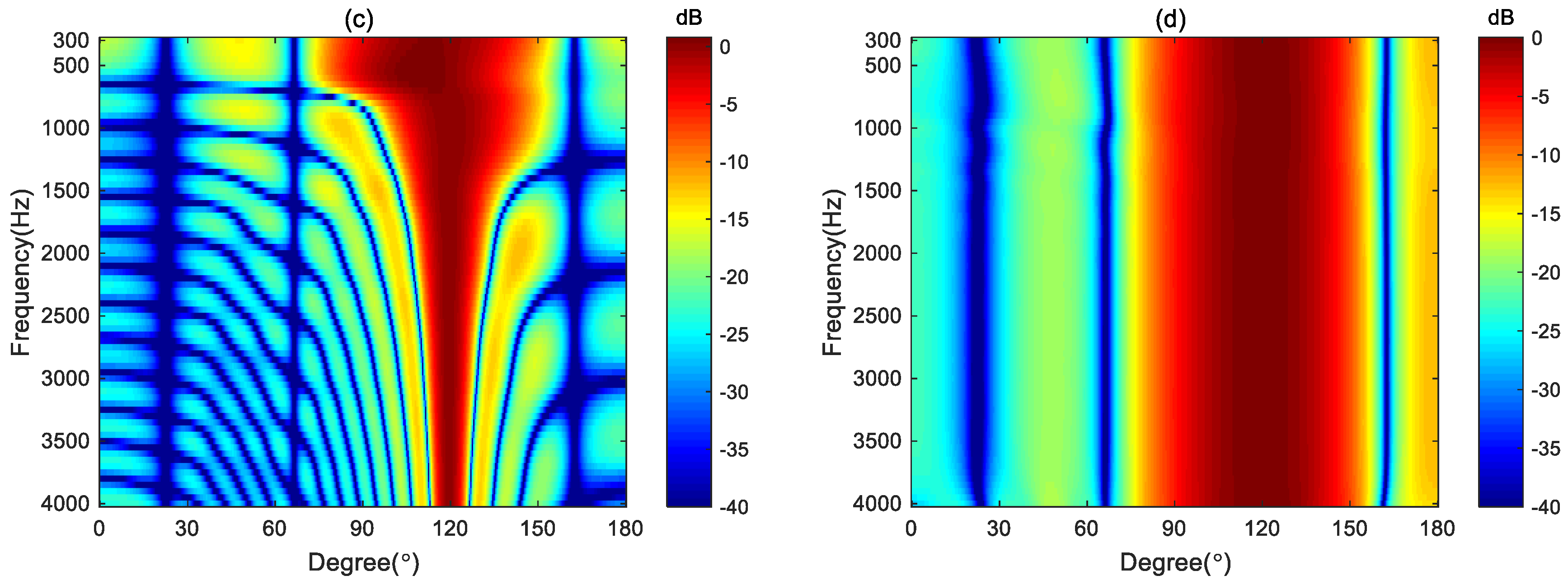
Figure 12 plots the broadband beampatterns synthesized by these four methods. As seen, the mainlobes of the DS and MVDR methods become narrower as the frequencies increases. The NC method can only maintain a constant main lobe width at low frequencies. Above 600 Hz, like the DS method, its mainlobe width also narrows as the frequency increases. In contrast, the proposed method maintains the frequency-invariant beampattern over the whole frequency range.
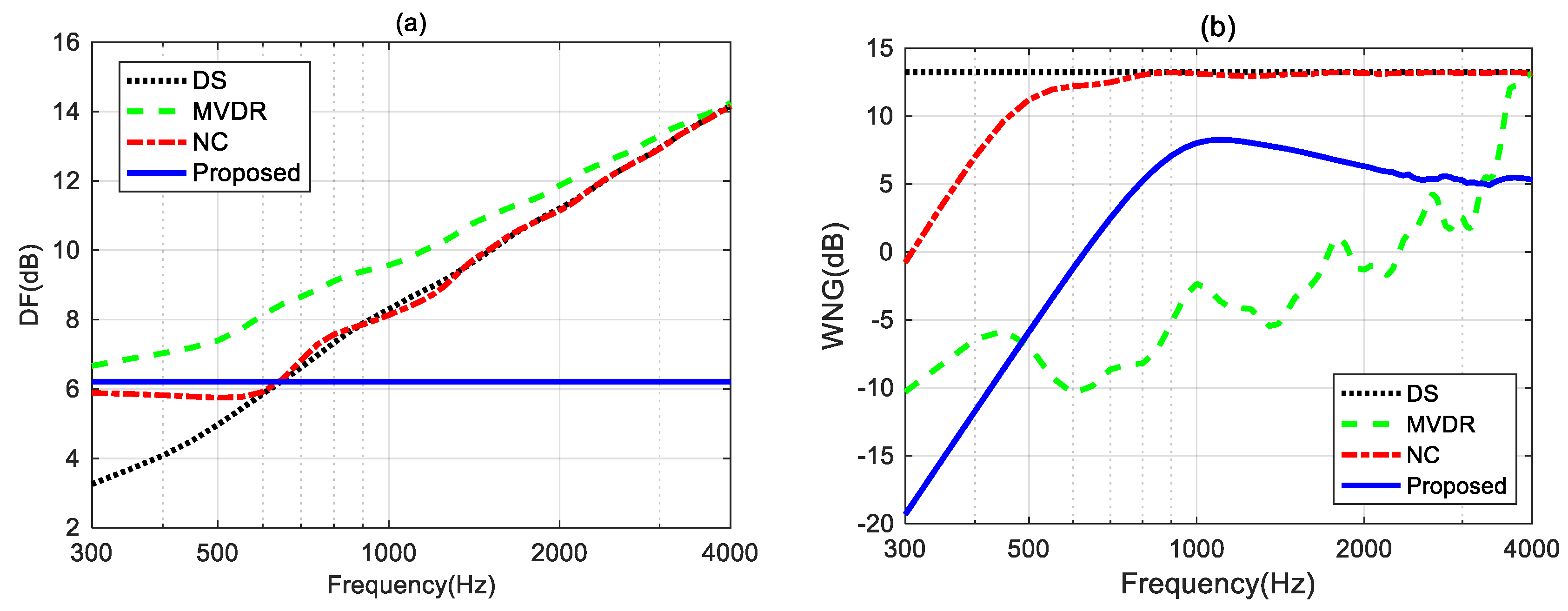
The DF and WNG of the different beamforming methods are plotted in Figure 13. Figure 13a shows the DF of DS and MVDR increase with frequency. DF of NC maintains almost the same below 600 Hz but increases with frequencies above 600 Hz. The DF of the proposed method can maintain a constant across the whole frequency range, indicating the frequency-invariant pattern can be achieved by the proposed method. In Figure 13b, DS has the maximum WNG and remains constant across the entire frequency range. The WNG of the NC method increases with frequency at low frequencies, and at high frequencies, its value matches that of the DS. In the 500-3k Hz frequency range, the MVDR method has the lowest WNG, indicating the worst anti-perturbation ability within this frequency band. Above 1 kHz，the WNG of the proposed method is lower than that of the DS and NC methods, but it still greater than 5 dB, which is considered a proper level of robustness for practical usage.

5. Experiment and Discussion

Experiments were carried out in an anechoic chamber using a linear loudspeaker array shown in Figure 14a consisting of 31 moving-coil speaker units (B1S of HiVi Inc.) spaced 3.8 cm apart. The experimental setup is illustrated in Figure 14b. The array was mounted on a turntable and positioned in the front when the turntable angle was 0°. An omni-directional microphone (BSWA MPA201) was placed at 3 m from the geometrical center of the array. Both the microphone and the linear array were placed at a height of 2 m from the floor.
A linear swept sine signal in the frequency range of 300-4k Hz with a resolution of 5 Hz was reproduced by each loudspeaker to measure its transfer function. The signals recorded by the microphone were processed by an AP2720 audio analyzer to obtain the transfer function at a specific angle. The turntable was then rotated by 5° in the counter-clockwise direction, and the same measurement procedure was repeated. This process was repeated when the array was rotated from 0° to 180°, giving a total of 37 positions with 31 measurements each. Finally, the transfer functions were used to calculate the measured beampattern to evaluate the performance of the proposed method.
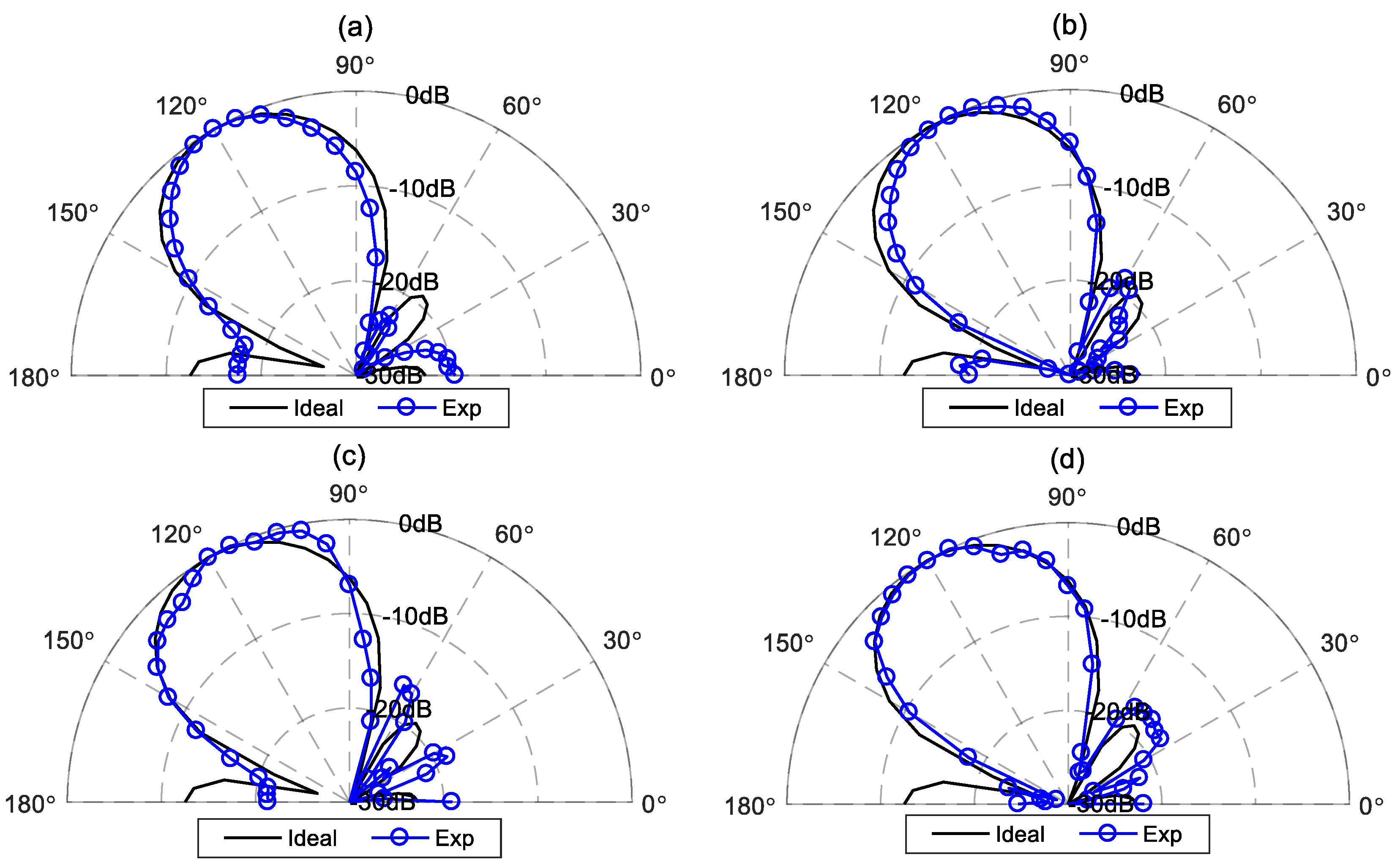
Figure 15 illustrates comparisons between the measured beampatterns and the ideal beampattern at frequencies: 500 Hz, 1 kHz, 2 kHz and 4 kHz. As can be seen, the measured beampatterns closely resemble the ideal beampattern, although there exist some minor differences due to array imperfections and measurement errors.
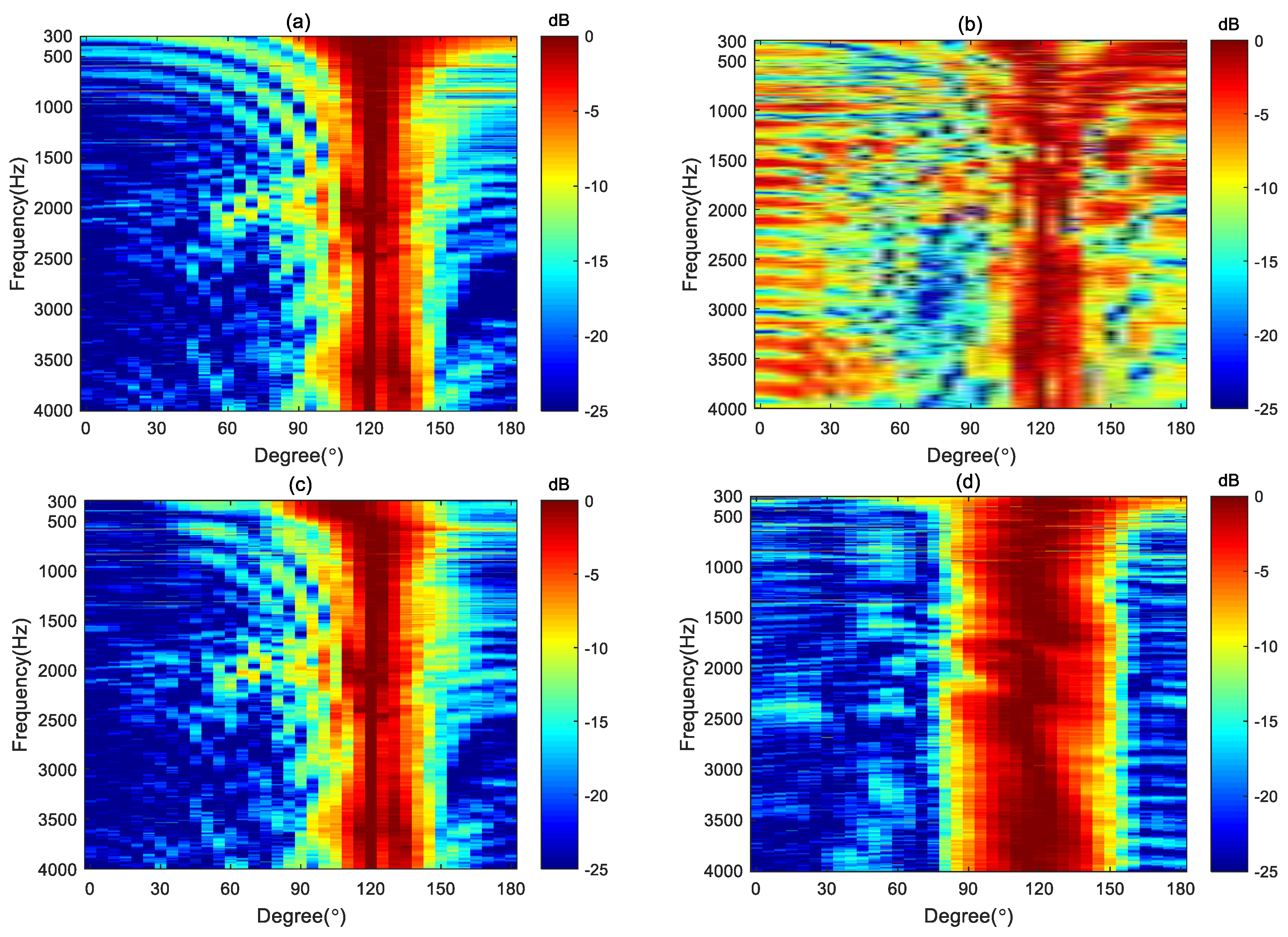
To further demonstrate the good performance of the proposed method, Figure 16 gives the measured broadband beampatterns of the four different methods: DAS, MVDR, NC and the proposed method. The regularization parameter used in the MVDR method is 0.001 and the WNG constraint value of the proposed method is set to ε WNG max − 2 over the whole evaluated frequency range. It can be observed that the main lobe of the beampattern generated by the DS method became narrower as the frequency increases. The MVDR method cannot generate an effective beampattern due to its poor robustness. The main lobe of the NC method is well-maintained at low frequencies. However, at high frequencies, its beampattern becomes similar to that of the DS method, with the main lobe narrowing as the frequency increases. In contrast, the main lobe of the proposed method kept almost the same in the evaluated frequency range of up to 4 kHz, which demonstrates that the frequency-invariant beampattern can be synthesized by the proposed method in a broadband of frequencies.

6. Conclusions

In this paper, we propose a method for designing the steerable frequency-invariant beamformer using a differential loudspeaker line array. The design process begins by determining the target differential beampatterns based on the desired direction, mainlobe width, and beampattern order. These target beampatterns are then represented in the modal domain. The Jacobi-Anger series expansion is employed to design the beamformer, ensuring that the resulting beampattern closely aligns with the target differential beampattern. To further enhance beampattern matching and robustness, a multi-constraint optimization problem is formulated. This approach introduces a white noise gain constraint value, enabling a trade-off between the white noise gain performance and the mean square error of the synthesized beampatterns. We also derive the upper limit for the proposed constraint value. Simulation results demonstrate that setting the proposed constraint value slightly below this upper limit can significantly improve the mean square error performance. Both simulations and experimental results demonstrate that the proposed method outperforms existing steerable beamforming techniques, achieving steerable frequency-invariant beamforming across the frequency range of 300 Hz to 4 kHz.

Author Contributions

Conceptualization, Y.Z.; methodology, Y.Z.; software, Y.Z.; validation, Y.Z. and Q.X.; formal analysis, Y.Z. and Q.Z.; investigation, Y.Z. and Q.X.; resources, Y.Z.; data curation, Y.Z. writing—original draft preparation, Y.Z.; writing—review and editing, Q.Z.; visualization, Y.Z.; supervision, Y.Z.; project administration, Y.Z.; funding acquisition, Y.Z. All authors have read and agreed to the published version.

Funding

This research was funded by Natural Science Research Project of Anhui Educational Committee (Grant No. 2023AH050422), Open Project of Anhui Digital Intelligent Engineering Research Center for Agricultural Products Quality Safety under the Peak Cultivation Discipline of Electronic Information (Grant No. APDI202304).

Data Availability Statement

Data are available upon request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Don H. Johnson, D.E.D. Array Signal Processing Concepts and Techniques; Prentice-Hall: New Jersey, USA, 1993.
  2. G.W.Elko. "Superdirectional microphone arrays" in Acoustic Signal Processing for Telecommunication; Springer-Verlag: Berlin, Germany, 2000.
  3. Van Trees, H.L. Optimum array processing: Part IV of detection, estimation, and modulation theory; John Wiley & Sons: New Jersey, USA, 2002.
  4. Liu, W.; Weiss, S. Wideband Beamforming Concepts and Techniques John Wiley& Sons: New Jersey, USA, 2010.
  5. Benesty, J.; Cohen, I.; Chen, J. Fundamentals of signal enhancement and array signal processing; John Wiley & Sons: New Jersey, USA, 2017.
  6. Yan, S. Broadband array processing; Springer-Verlag: Berlin, Germany, 2019.
  7. Benesty, J.; Chen, J.; Huang, Y. Microphone array signal processing; Springer Science & Business Media: Berlin, Germany, 2008.
  8. Chen, H.; Ser, W. Design of Robust Broadband Beamformers With Passband Shaping Characteristics Using Tikhonov Regularization. IEEE Transactions on Audio, Speech, and Language Processing 2009, 17, 665-681. [CrossRef]
  9. Cohen, I.; Benesty, J.; Chen, J. Differential Kronecker product beamforming. IEEE/ACM Transactions on Audio, Speech,Language Processing 2019, 27, 892-902.
  10. Yu, G.; Qiu, Y.; Wang, N. A Robust Wavenumber-Domain Superdirective Beamforming for Endfire Arrays. IEEE Transactions on Signal Processing 2021, 69, 4890-4905. [CrossRef]
  11. Hao, X.; Wang, Y.; Zhang, Y.; Yang, Y. An optimization method for frequency-invariant beamforming with arbitrary sensor arrays. Applied Acoustics 2023, 207. [CrossRef]
  12. Zhang, J.; Gong, P.; Wu, Y.; Li, L.; Yu, L. Frequency-invariant beamformer design via ADPM approach. Signal Processing 2023, 204. [CrossRef]
  13. Mabande, E.; Kellermann, W. Towards superdirective beamforming with loudspeaker arrays. In Proceedings of the Conf. Rec. International Congress on Acoustics, Madrid, Spain, 2-7 September, 2007.
  14. Boone, M.M.; Cho, W.-H.; Ih, J.-G. Design of a highly directional endfire loudspeaker array. J. Audio Eng. Soc. 2009, 57, 309-325.
  15. Bai, M.R.; Hsieh, Y.H. Point focusing using loudspeaker arrays from the perspective of optimal beamforming. The Journal of the Acoustical Society of America 2015, 137, 3393. [CrossRef]
  16. Zhao, S.; Qiu, X.; Burnett, I. Acoustic contrast control in an arc-shaped area using a linear loudspeaker array. The Journal of the Acoustical Society of America 2015, 137, 1036-1039.
  17. Gölles, L.; Zotter, F.; Merkel, L. Miniature line array for immersive sound reinforcement. In Proceedings of the Audio Engineering Society Conference: AES 2023 International Conference on Spatial and Immersive Audio, 2023.
  18. Pan, K.; Huang, J.; Cheng, J.; Shen, Y. Loudspeaker array beamforming for sound projection in a half-space with an impedance boundary. The Journal of the Acoustical Society of America 2023, 153, 1626-1636.
  19. Benesty, J.; Chen, J. Study and Design of Differential Microphone Arrays Springer-Berlin: Heidelberg,Germany, 2012.
  20. Chen, J.; Benesty, J.; Pan, C. On the design and implementation of linear differential microphone arrays. J. Acoust. Soc. Am 2014, 136, 3097-3113. [CrossRef]
  21. Pan, C.; Chen, J.; Benesty, J. Theoretical Analysis of Differential Microphone Array Beamforming and an Improved Solution. IEEE/ACM Transactions on Audio, Speech, and Language Processing 2015, 23, 2093-2105. [CrossRef]
  22. Pan, C.; Chen, J.; Benesty, J. Reduced-order robust superdirective beamforming with uniform linear microphone arrays. IEEE/ACM Transactions on Audio, Speech, Language Processing 2016, 24, 1548-1559.
  23. Zhao, L.; Benesty, J.; Chen, J. Design of robust differential microphone arrays with the Jacobi–Anger expansion. Applied Acoustics 2016, 110, 194-206. [CrossRef]
  24. Chen, Z.; Chen, H.; Tu, Q. Sensor Imperfection Tolerance Analysis of Robust Linear Differential Microphone Arrays. IEEE/ACM Transactions on Audio, Speech, and Language Processing 2021, 29, 2915-2929. [CrossRef]
  25. Wang, J.; Yang, F.; Hu, X.; Yang, J. Theoretical Analysis of Maclaurin Expansion based Linear Differential Microphone Arrays and Improved Solutions. IEEE/ACM Transactions on Audio, Speech, and Language Processing 2024, 1-14. [CrossRef]
  26. Wang, Y.; Yang, Y.; He, Z.; Ma, Y.; Li, B. Robust Superdirective Frequency-Invariant Beamforming for Circular Sensor Arrays. IEEE Signal Processing Letters 2017, 24, 1193-1197. [CrossRef]
  27. Huang, G.; Chen, J.; Benesty, J. Insights Into Frequency-Invariant Beamforming With Concentric Circular Microphone Arrays. IEEE/ACM Trans. Audio Speech Lang. Proc 2018, 26, 2305-2318. [CrossRef]
  28. Itzhak, G.; Benesty, J.; Cohen, I. Multistage approach for steerable differential beamforming with rectangular arrays. Speech Communication 2022, 142, 61-76. [CrossRef]
  29. Albertini, D.; Bernardini, A.; Borra, F.; Antonacci, F.; Sarti, A. Two-Stage Beamforming With Arbitrary Planar Arrays of Differential Microphone Array Units. IEEE/ACM Transactions on Audio, Speech, and Language Processing 2023, 31, 590-602. [CrossRef]
  30. Wang, J.; Yang, F.; Li, J.; Sun, H.; Yang, J. Mode matching-based beamforming with frequency-wise truncation order for concentric circular differential microphone arrays. The Journal of the Acoustical Society of America 2023, 154, 3931-3940. [CrossRef]
  31. Shi, Q.; Wang, J.; Yang, F.; Yang, J. A note on the design of frequency-invariant beamforming with uniform concentric circular microphone array. Applied Acoustics 2024, 217. [CrossRef]
  32. Wang, X.; Benesty, J.; Chen, J.; Huang, G.; Cohen, I. Beamforming with Cube Microphone Arrays Via Kronecker Product Decompositions. IEEE/ACM Transactions on Audio, Speech, and Language Processing 2021, 29, 1774-1784. [CrossRef]
  33. Itzhak, G.; Cohen, I. Differential constant-beamwidth beamforming with cube arrays. Speech Communication 2023, 149, 98-107. [CrossRef]
  34. Zhao, X.; Huang, G.; Chen, J.; Benesty, J. Design of 2D and 3D Differential Microphone Arrays With a Multistage Framework. IEEE/ACM Transactions on Audio, Speech, and Language Processing 2023, 31, 2016-2031. [CrossRef]
  35. Zhao, X.; Luo, X.; Huang, G.; Chen, J.; Benesty, J. Differential Beamforming with Null Constraints for Spherical Microphone Arrays. In Proceedings of the 2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Korea, 14-19 April 2024, 2024; pp. 776-780.
  36. Borra, F.; Bernardini, A.; Antonacci, F.; Sarti, A. Uniform Linear Arrays of First-Order Steerable Differential Microphones. IEEE/ACM Transactions on Audio, Speech, and Language Processing 2019, 27, 1906-1918. [CrossRef]
  37. Tu, Q.; Chen, H. On Mainlobe Orientation of the First- and Second-Order Differential Microphone Arrays. IEEE/ACM Transactions on Audio, Speech, and Language Processing 2019, 27, 2025-2040. [CrossRef]
  38. Jin, J.; Huang, G.; Wang, X.; Chen, J.; Benesty, J.; Cohen, I. Steering Study of Linear Differential Microphone Arrays. IEEE/ACM Transactions on Audio, Speech, and Language Processing 2021, 29, 158-170. [CrossRef]
  39. Yu, G. Eigenbeam-space transformation based steerable differential beamforming for linear arrays. Signal Processing 2023, 212. [CrossRef]
  40. Luo, X.; Jin, J.; Huang, G.; Chen, J.; Benesty, J. Design of Steerable Linear Differential Microphone Arrays With Omnidirectional and Bidirectional Sensors. IEEE Signal Processing Letters 2023, 30, 463-467. [CrossRef]
  41. Luo, X.; Jin, J.; Huang, G.; Chen, J.; Benesty, J. Design of Fully Steerable Differential Beamformers With Linear Superarrays. IEEE/ACM Transactions on Audio, Speech, and Language Processing 2024, 32, 3076-3089. [CrossRef]
  42. Choi, J.-W.; Kim, Y.; Ko, S.; Kim, J. A differential approach for the implementation of superdirective loudspeaker array. In Proceedings of the Audio Engineering Society Convention 128, London, UK., 2010.
  43. Kim, Y.-H.; Choi, J.-W. Sound visualization and manipulation; John Wiley & Sons: 2013.
  44. Choi, J.W. Generation of a Near-field Sound Zone Using Broadside Differential Array. In Proceedings of the 2021 Immersive and 3D Audio: from Architecture to Automotive (I3DA), Bologna, Italy, 08-10 Sept, 2021.
  45. Wang, J.; Zhang, W.; Pan, C.; Chen, J.; Benesty, J. On the design of differential loudspeaker arrays with broadside radiation patterns. JASA Express Letters 2021, 1, 084804. [CrossRef]
  46. Zhang, Y.; Mao, J.; Cai, Y.; Ye, C. Sound reproduction with a circular loudspeaker array using differential beamforming method. In Proceedings of the 2022 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Chiang Mai, Thailand, 2022; pp. 143-148.
  47. Miotello, F.; Bernardini, A.; Albertini, D.; Antonacci, F.; Sarti, A. Steerable First-Order Differential Loudspeaker Arrays with Monopole and Dipole Elements. In Proceedings of the Convention of the European Acoustics Association, Forum Acusticum, Turin, Italy, 2023; pp. 11-15.
  48. Zhang, Y.; Mao, J.; Cai, Y.; Ye, C.; Zhu, Q. Broadband frequency-invariant broadside beamforming with a differential loudspeaker array. In Proceedings of the 2023 31st European Signal Processing Conference (EUSIPCO), Helsinki, Finnland, 2023; pp. 1728-1732.
  49. Zhang, Y.; Wei, H.; Zhu, Q. Design of Robust Broadband Frequency-Invariant Broadside Beampatterns for the Differential Loudspeaker Array. Applied Sciences 2024, 14. [CrossRef]
  50. Grant, M.C.; Boyd, S.P. The CVX Users’ Guide; CVX Research, Inc.: 2020.
  51. Gradshteyn, I.S.; Ryzhik, I.M. Table of integrals, series, and products; Academic press: 2014.
  52. Bitzer, J.; Simmer, K.U. Superdirective microphone arrays. In Microphone arrays: Signal processing techniques and applications; Springer: 2001; pp. 19-38.
Preprints 116665 g001
Figure 1. The loudspeaker line array with a steerable differential radiation pattern.
Figure 1. The loudspeaker line array with a steerable differential radiation pattern.
Preprints 116665 g001
Preprints 116665 g002
Figure 2. Comparison of the N-th order target radiation patterns designed by the method stated in Ref [39] and the proposed method at different desired angels: (a) N = 4 , θ s = 30 ∘ , (b) N = 4 , θ s = 60 ∘ , (c) N = 4 , θ s = 90 ∘ , (d) N = 4 , θ s = 135 ∘ , (e) N = 5 , θ s = 45 ∘ and (f) N = 5 , θ s = 90 ∘ .
Figure 2. Comparison of the N-th order target radiation patterns designed by the method stated in Ref [39] and the proposed method at different desired angels: (a) N = 4 , θ s = 30 ∘ , (b) N = 4 , θ s = 60 ∘ , (c) N = 4 , θ s = 90 ∘ , (d) N = 4 , θ s = 135 ∘ , (e) N = 5 , θ s = 45 ∘ and (f) N = 5 , θ s = 90 ∘ .
Preprints 116665 g002
Preprints 116665 g003
Figure 3. Comparisons between the different order beampatterns synthesized by the two proposed methods and the target beampattern at 2 kHz (a) Second-order (b) Third-order.
Figure 3. Comparisons between the different order beampatterns synthesized by the two proposed methods and the target beampattern at 2 kHz (a) Second-order (b) Third-order.
Preprints 116665 g003
Preprints 116665 g004
Figure 4. Different order target beampatterns synthesized by the proposed methods: (a) Second-order, Proposed I (b) Third-order, Proposed I (c) Second-order, Proposed II (d) Third-order, Proposed II.
Figure 4. Different order target beampatterns synthesized by the proposed methods: (a) Second-order, Proposed I (b) Third-order, Proposed I (c) Second-order, Proposed II (d) Third-order, Proposed II.
Preprints 116665 g004
Preprints 116665 g005
Figure 5. Performance comparison of the proposed methods for designing different order target beampatterns: (a) DF, (b) WNG and (c) MSE.
Figure 5. Performance comparison of the proposed methods for designing different order target beampatterns: (a) DF, (b) WNG and (c) MSE.
Preprints 116665 g005
Preprints 116665 g006
Figure 6. Broadband beampatterns of the third-order differential beampattern with a line array for different ε WNG values: (a) ε WNG = ε WNG max , (b) ε WNG = ε WNG max − 2 , (c) ε WNG = 0 , and (d) ε WNG = − 10 .
Figure 6. Broadband beampatterns of the third-order differential beampattern with a line array for different ε WNG values: (a) ε WNG = ε WNG max , (b) ε WNG = ε WNG max − 2 , (c) ε WNG = 0 , and (d) ε WNG = − 10 .
Preprints 116665 g006
Preprints 116665 g007
Figure 7. Performance comparison of the proposed methods with different ε WNG values: (a) DF, (b) WNG, and (c) MSE.
Figure 7. Performance comparison of the proposed methods with different ε WNG values: (a) DF, (b) WNG, and (c) MSE.
Preprints 116665 g007
Preprints 116665 g008
Figure 8. The averaged broadband beampatterns of the third-order differential beampattern with loudspeaker mismatch for different ε WNG values: (a) ε WNG = ε WNG max , (b) ε WNG = ε WNG max − 2 , (c) ε WNG = 0 , and (d) ε WNG = − 10 .
Figure 8. The averaged broadband beampatterns of the third-order differential beampattern with loudspeaker mismatch for different ε WNG values: (a) ε WNG = ε WNG max , (b) ε WNG = ε WNG max − 2 , (c) ε WNG = 0 , and (d) ε WNG = − 10 .
Preprints 116665 g008
Preprints 116665 g009
Figure 9. Performances of the proposed methods with different ε WNG values considering the loudspeaker mismatch: (a) DF, (b) WNG, and (c) MSE
Figure 9. Performances of the proposed methods with different ε WNG values considering the loudspeaker mismatch: (a) DF, (b) WNG, and (c) MSE
Preprints 116665 g009
Preprints 116665 g010
Figure 10. Broadband beampatterns of the third-order differential beampatterns for different steering directions: (a) θ s = 30 ∘ , (b) θ s = 45 ∘ , (c) θ s = 60 ∘ and (d) θ s = 90 ∘ .
Figure 10. Broadband beampatterns of the third-order differential beampatterns for different steering directions: (a) θ s = 30 ∘ , (b) θ s = 45 ∘ , (c) θ s = 60 ∘ and (d) θ s = 90 ∘ .
Preprints 116665 g010
Preprints 116665 g011aPreprints 116665 g011b
Figure 11. Performances of the proposed method with different desired directions: (a) DF, (b) WNG and (c) MSE.
Figure 11. Performances of the proposed method with different desired directions: (a) DF, (b) WNG and (c) MSE.
Preprints 116665 g011aPreprints 116665 g011b
Preprints 116665 g012aPreprints 116665 g012b
Figure 12. Broadband synthesized beampatterns of different beamforming methods: (a) the DS method, (b)the MVDR method, (c)the NC method and (d)the proposed method.
Figure 12. Broadband synthesized beampatterns of different beamforming methods: (a) the DS method, (b)the MVDR method, (c)the NC method and (d)the proposed method.
Preprints 116665 g012aPreprints 116665 g012b
Preprints 116665 g013
Figure 13. Performances of the different beamforming methods: (a) DF and (b) WNG.
Figure 13. Performances of the different beamforming methods: (a) DF and (b) WNG.
Preprints 116665 g013
Preprints 116665 g014
Figure 14. A photo of the linear array with 31 loudspeakers and experimental setup of the measurement:(a) the linear array and (b) the experimental setup.
Figure 14. A photo of the linear array with 31 loudspeakers and experimental setup of the measurement:(a) the linear array and (b) the experimental setup.
Preprints 116665 g014
Preprints 116665 g015
Figure 15. The measured beampattern of the proposed method and the ideal fourth-order differential beampattern at different frequencies for Δ = 60 ° ， θ s = 120 ° : (a) 500 Hz, (b) 1 kHz, (c) 2 kHz and (d) 4 kHz.
Figure 15. The measured beampattern of the proposed method and the ideal fourth-order differential beampattern at different frequencies for Δ = 60 ° ， θ s = 120 ° : (a) 500 Hz, (b) 1 kHz, (c) 2 kHz and (d) 4 kHz.
Preprints 116665 g015
Preprints 116665 g016
Figure 16. The measured broadband beampatterns of different beamforming methods: (a) the DS method, (b) the MVDR method, (c) the NC method and (d) the proposed method.
Figure 16. The measured broadband beampatterns of different beamforming methods: (a) the DS method, (b) the MVDR method, (c) the NC method and (d) the proposed method.
Preprints 116665 g016
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated