Prerpints.org logo
Preprint
Article

Comparative Study of Temperature and Pressure Variation Patterns in Hydrogen and Natural Gas Storage in Salt Cavern

Altmetrics

Downloads

70

Views

23

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

29 August 2024

Posted:

02 September 2024

You are already at the latest version

Alerts
Abstract
Clarifying the distribution of temperature and pressure in the wellbore and cavern during hydrogen injection and extraction is crucial for quantitatively assessing cavern stability and wellbore integrity. This paper establishes an integrated flow and heat transfer model for the cavern and wellbore during hydrogen injection and production, analyzing the variations in temperature and pressure in both the wellbore and the cavern. The specific conclusions are as follows. (1) The temperature and pressure parameters of hydrogen and natural gas within the chamber and wellbore were compared. Under identical injection and production conditions, the temperature of hydrogen in the chamber was 10°C higher than that of natural gas, and 16°C higher in the wellbore. The pressure of hydrogen in the chamber was 2.9 MPa greater than that of natural gas, and 2.6 MPa higher in the wellbore. (2) A comparative analysis was conducted on the impact of surrounding rock’s horizontal and numerical distance on temperature during hydrogen and natural gas injection processes. As the distance from the cavity increases, from 5 to 15 meters, the temperature fluctuation in the surrounding rock diminishes progressively, with the temperature effect in the hydrogen storage chamber extending at least 10 meters. (3) The influence of rock thermal conductivity parameters on temperature during the processes of hydrogen injection and natural gas extraction is compared. The better the thermal conductivity, the deeper the thermal effects penetrate the rock layers, with the specific heat capacity having the most significant impact.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction

The process of hydrogen injection and extraction in salt cavern storage involves complex gas flow and heat transfer, resulting in unclear temperature and pressure variations within the cavern and wellbore. During hydrogen injection and extraction, the temperature and pressure within the cavern and wellbore not only influence the stress conditions of the cavern and the tubing but also significantly impact cavern leakage and wellbore corrosion rates. Clarifying the distribution of temperature and pressure in the wellbore and cavern during hydrogen injection and extraction is crucial for quantitatively assessing cavern stability and wellbore integrity[1,2,3,4] .
In the practical engineering of underground salt cavern gas storage, the thermo-hydro-mechanical coupling effects of the surrounding rock mass are increasingly receiving widespread attention [5,6,7] . Researchers both domestically and internationally have conducted studies on the thermodynamic properties of in-cavity gases. Kushnir et al. [8,9] proposed two methods for analyzing temperature and pressure variations within a reservoir based on the equations of mass conservation, energy conservation, and the thermal conductivity of rocks. Xia et al. [10] proposed a simplified analytical solution for calculating the temperature and pressure of the cavity air building upon Kushnir’s analytical solution. Jiang et al. [11] validated the accuracy of the thermodynamic process calculation method for compressed air by relying on the quality of compressed air and the principles of energy conservation. Niu et al. [12] developed a non-steady-state dynamic mathematical model for the coupling of salt cavern storage and wellbores in gas storage, taking into account the properties of real gases and the convective heat transfer between the gas and the surrounding rock at the cavern walls. Li et al. [13,14] developed a thermal model for the conditions of injection and production, investigating the effects of gas extraction rate on the temperature of the cavity. Yan et al. [15] conducted a thermal analysis of cavernous natural gas storage facilities, determining the temperature, pressure within the salt caverns, and the distribution of the thermal field within the rock mass, while also analyzing various sensitivity factors. Zhang[16] developed a numerical model for compressed air cavern storage, analyzing the variations in temperature and pressure within the cavern over a single operational cycle. Yin et al. [17]conducted a comprehensive numerical simulation analyzing the long-term variations in temperature and pressure at the Jintan Salt Mine’s old gas storage facility. Wang et al. [18,19] investigated the high-temperature creep characteristics of salt rock under various loading paths and the long-term stability of salt rock gas storage. Chen et al. [20] utilized finite element numerical simulation to couple the surrounding rock temperature field with the stress field, establishing a thermal stress model. He et al. [21] derived the functional relationship between gas temperature and pressure within the salt cavity as a function of time when the injection and extraction gas rates are constant based on variable mass thermodynamics theory.
The aforementioned studies primarily focus on the storage of natural gas in salt caverns, with insufficient research on the thermo-mechanical coupling effects in the wells and cavern cavities during hydrogen cyclic injection and production. This paper establishes an integrated flow and heat transfer model for the cavern and wellbore during hydrogen injection and production, analyzing the variations in temperature and pressure in both the wellbore and the cavern. The findings provide a theoretical foundation for hydrogen storage projects in salt caverns.

2. Integrated Flow and Heat Transfer Model for Cavity and Wellbore

2.1. Model Assumptions

In the context of hydrogen injection and extraction, the following assumptions are made regarding the flow and heat transfer model for salt caverns used as hydrogen storage facilities [22,23,24].
(1) The hydrogen gas within the wellbore and cavity exhibits one-dimensional steady-state flow, with temperature, pressure, and velocity uniformly distributed across any cross-section.
(2) The geothermal gradient remains constant, and the thermal conductivity of the formation does not vary with depth.
(3) The heat transfer modes within both the wellbore and cavity are steady-state, adhering to the dimensionless time function as defined by Ramey.
(4) The contact thermal resistance between structural material interfaces is neglected, and radiative heat transfer effects are disregarded.

2.2. The Thermal Transfer Model for Wellbore Flow

Research indicates that during the hydrogen injection and production cycle, temperature variations occur due to the compression and release of hydrogen. Given the temperature difference between the hydrogen within the wellbore and the surrounding rock, thermal exchange between the hydrogen and the surrounding formation ensues. Throughout the hydrogen injection and production process, this thermal exchange manifests through convective heat transfer within the wellbore and radial conductive heat transfer.
A steady-state hydrogen flow model is established a within the wellbore for the hydrogen injection and production process based on the assumptions stated earlier. The fluid control model for hydrogen within the wellbore is derived, encompassing the mass continuity equation, momentum principle, and energy conservation equation.
The quality continuity equation:
ρ d v d z + v d ρ dz = 0
The gas momentum equation:
dp dz = ρ g sin θ − f ρ v | v | 2 d − ρ v dv dz
The energy conservation equation：
Q + A ρ v ( dh dz + vdv dz − g ) = 0
In equations (1) to (3), ρ the fluid density, kg/m³; v the fluid velocity, m/s; z the depth of the wellbore, m; p the fluid pressure, Pa; g the gravitational acceleration, 9.81 m/s²; θ the well deviation angle, °; f the friction coefficient, dimensionless; d the internal diameter of the wellbore, m; Q the heat transfer rate of the fluid per unit length of the wellbore, J/(m·s); h the specific enthalpy, J/kg; T the temperature, K; A the cross-sectional area of the tubing, m².
Heat transfer between hydrogen gas and the inner walls of the well is governed by convective heat transfer. According to Newton’s Law of Cooling, the heat transfer equation for hydrogen gas within the well can be defined based on the rate of heat transfer between the hydrogen gas and the well’s inner wall.：
Q = 2 π r t i h f ( T f − T t i ) Δ L
In equation (4), hf denotes the forced convective heat transfer coefficient for hydrogen gas within the borehole and its walls:
h f = k f N u f 2 r t i
In equation (5), Nuf denotes the Nusselt number for hydrogen.：
N u f = 0.023 Re 0.8 Pr f 0.4
In equation (6), Prf denotes the Prandtl number of the injected fluid：
Pr f = c p f μ f k f
In equations (7) to (10): rti the radius of the borehole, m; kf the thermal conductivity of hydrogen, W/(m·K); μf the dynamic viscosity of hydrogen, Pa·s; cpf the specific heat capacity of hydrogen at constant pressure, J/(kg·K).
The radial heat conduction equation for the wellbore and surrounding rock：
Q = − 2 π r k d T d r Δ L
The convective heat transfer equation for hydrogen：
Q = 2 π r t o h a ( T t o − T s i ) Δ L
In equation (9), ha represents the natural convective heat transfer coefficient for hydrogen:
ha = 0.049 ( G r a Pr a ) 1 / 3 Pr a 0.074 k a r t 0 ln ( r s i / r t 0 )
Pr a = c p a μ a k a
In equations (9) to (11): ka the thermal conductivity of hydrogen, W/(m·K); μa the dynamic viscosity of hydrogen, Pa·s; cpa the specific heat capacity of hydrogen at constant pressure, J/(kg·K).

2.3. Turbulent Heat Transfer Model in Cavities

The mass continuous equation for hydrogen：
∂ ρ ∂ t + ρ ( u ⋅ ∇ ) = 0
In the equation (12), ρ the density of hydrogen gas at various points within the chamber, g/cm3; t the time, s; u the velocity vector of hydrogen gas at various points within the chamber.
The turbulent kinetic energy equation for hydrogen.：
ρ ∂ k ∂ t + ρ ( u ⋅ ∇ ) k = ∇ ⋅ ( μ + μ Τ ∇ k ) + p k
In equation (13), p the pressure of compressed air at various locations, Pa; μ the dynamic viscosity of hydrogen, Pa·s; μT the turbulent viscosity of hydrogen; k the turbulent kinetic energy.
The energy conservation equation for hydrogen.：
ρ C p ∂ T ∂ t + ρ C p u ⋅ ∇ + ∇ ⋅ ( − λ ∇ T ) = Q
In the equation (14): Cp the specific heat capacity of materials, J/(g·K); λ the thermal conductivity of materials, W/(m·°C); T the temperature of materials, K.
Integrating the aforementioned wellbore pipe flow model and cavity turbulence model, we establish a unified flow and heat transfer model for the hydrogen injection and extraction process, as illustrated in Equation (15). This model innovatively incorporates the convective heat transfer of hydrogen in the wellbore, radial heat transfer, the temperature-pressure coupling effects within the cavity, and the turbulent heat transfer effects within the cavity.
d p d z = ρ g sin θ − f ρ v | v | 2 d − ρ v d v d z Q + A ρ v ( d h d z + v d v d z - g ) = 0 Q 1 = 2 π r t i h f ( T f − T t i ) Δ L           Q 2 = − 2 π r k d T d r Δ L           Q 3 = 2 π r t o h a ( T t o − T s i ) Δ L ρ ∂ ε ∂ t + ρ ( u ⋅ ∇ ) ε = ∇ ⋅ [ ( μ + μ Τ σ ε ) ∇ k ] + C 1 ρ 2 S : S − C 2 ρ C p ∂ T ∂ t + ρ C p u ⋅ ∇ + ∇ ⋅ ( − λ ∇ T ) = Q 2 ∂ u ∂ t + ( u ⋅ ∇ ) u = g 1 ρ ∇ ⋅ [ − ρ I + 2 ( μ + μ Τ ) S − 2 3 ( μ + μ Τ ) ( ∇ ⋅ u ) I − 2 3 ρ k I ]

3. Numerical Simulation Computation

3.1. Engineering Background and Geometric Model

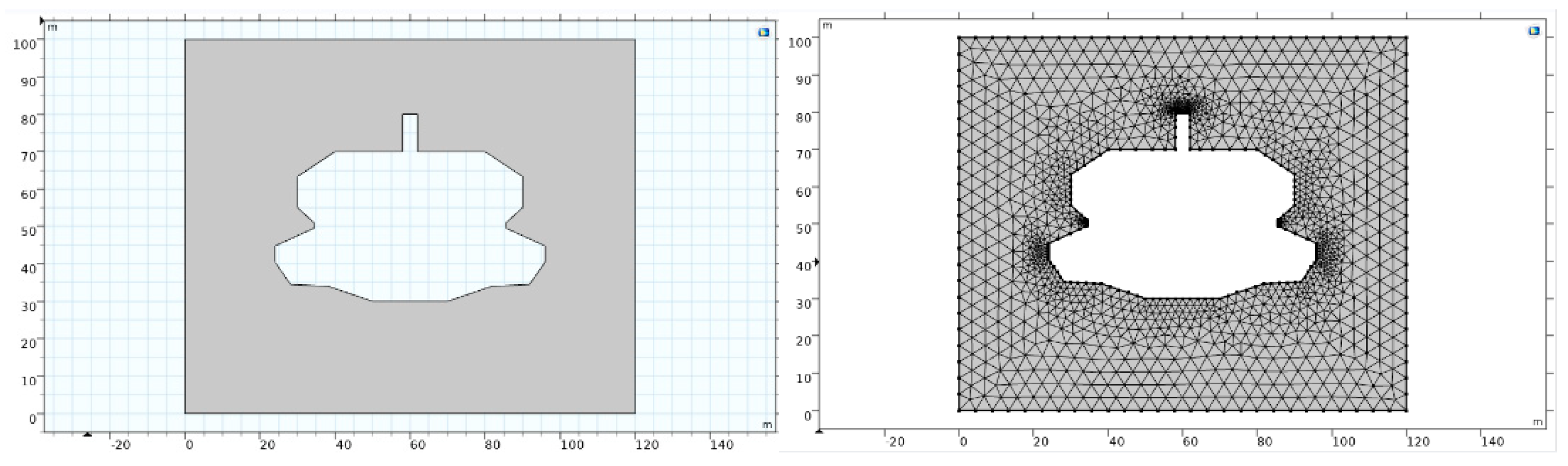
The salt cavern in this paper is J106 in Jintan, Jiangsu Province of China. An axisymmetric geological model as shown in Figure 1 is established, and the simplified cavern shape is applied.

3.2. Parameter Configuration

In order to simplify the calculations, all formations with less than 45 % mud content are uniformly treated as salt rock formations in the numerical model. The physical and mechanical parameters of the surrounding rock are shown in Table 1
Parameters Salt rock
Density (kg/m3) 2100
Elastic modulus (GPa) 3.6
Bulk modulus (GPa) 2.75
Poisson’s ratio 0.282
Initial permeability (m2) 5.47×10-21
Initial porosity 0.01
Biot’s coefficient 0.12
Cohesion (MPa) 3.69
Internal friction angle (°) 38.76

3.3. Software Settings and Boundary Conditions

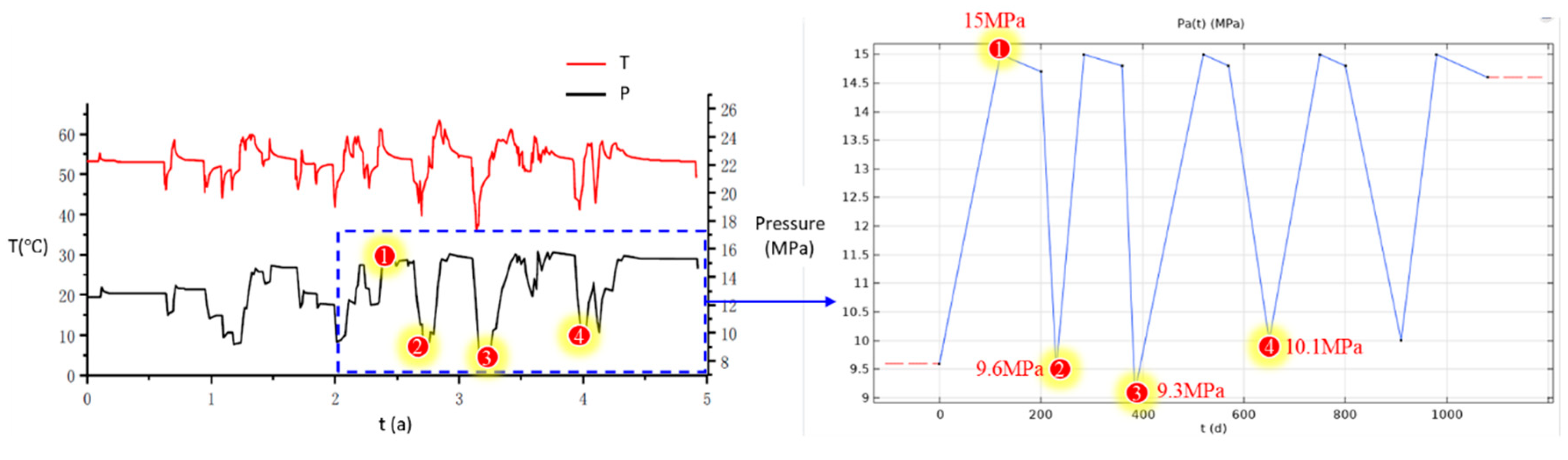
The numerical model was solved in the software COMSOL Multiphysics. The solid mechanics interface is used to solve the stress and deformation fields of the surrounding rock. The initial ground stress is solved in advance and applied as prestress. Based on the actual operating curve of the injection and extraction process, simulations are conducted for the stable operation phase from the 2nd to the 5th year, with a reasonable simplification of the pressure curve. The simplified pressure curve will serve as the boundary condition for the cavity gas pressure, as illustrated in Figure 2. The initial temperature of the gas within the cavity is set to 40°C, corresponding to the pressure.

3.4. Software Settings and Simulation of Working Conditions

4. Results and Discussion

4.1. Simulation Results of Natural Gas Storage

Figure 3 illustrates the variation in natural gas pressure within the salt cavern storage over a period of 1080 days. During the gas injection phase, the compression of the gas within the cavern generates heat, resulting in an increase in the temperature of the gas as the injection proceeds. Conversely, during the storage phase, the temperature of the gas slightly decreases due to thermal exchange with the surrounding formation. The principal reason for the decrease in gas temperature during the withdrawal phase is the reduction in gas pressure. Over the course of 1080 days, the gas temperature rises to 59.5°C during the initial injection phase, then slightly decreases to 58.3°C during the first storage period. Subsequently, the gas temperature rapidly drops to approximately 40°C during the withdrawal phase. Each injection and withdrawal cycle exhibits a pattern of “sharp rise - decrease - steep drop” in temperature. Overall, throughout the three-year cycle, there is a positive correlation between the gas temperature and pressure within the cavern. The simulated gas temperatures align closely with the actual measured temperatures, thereby validating the accuracy and feasibility of the model.

4.2. Comparison of Natural Gas and Hydrogen

4.2.1. Comparison of the Thermodynamic Properties of Gases in Cavity

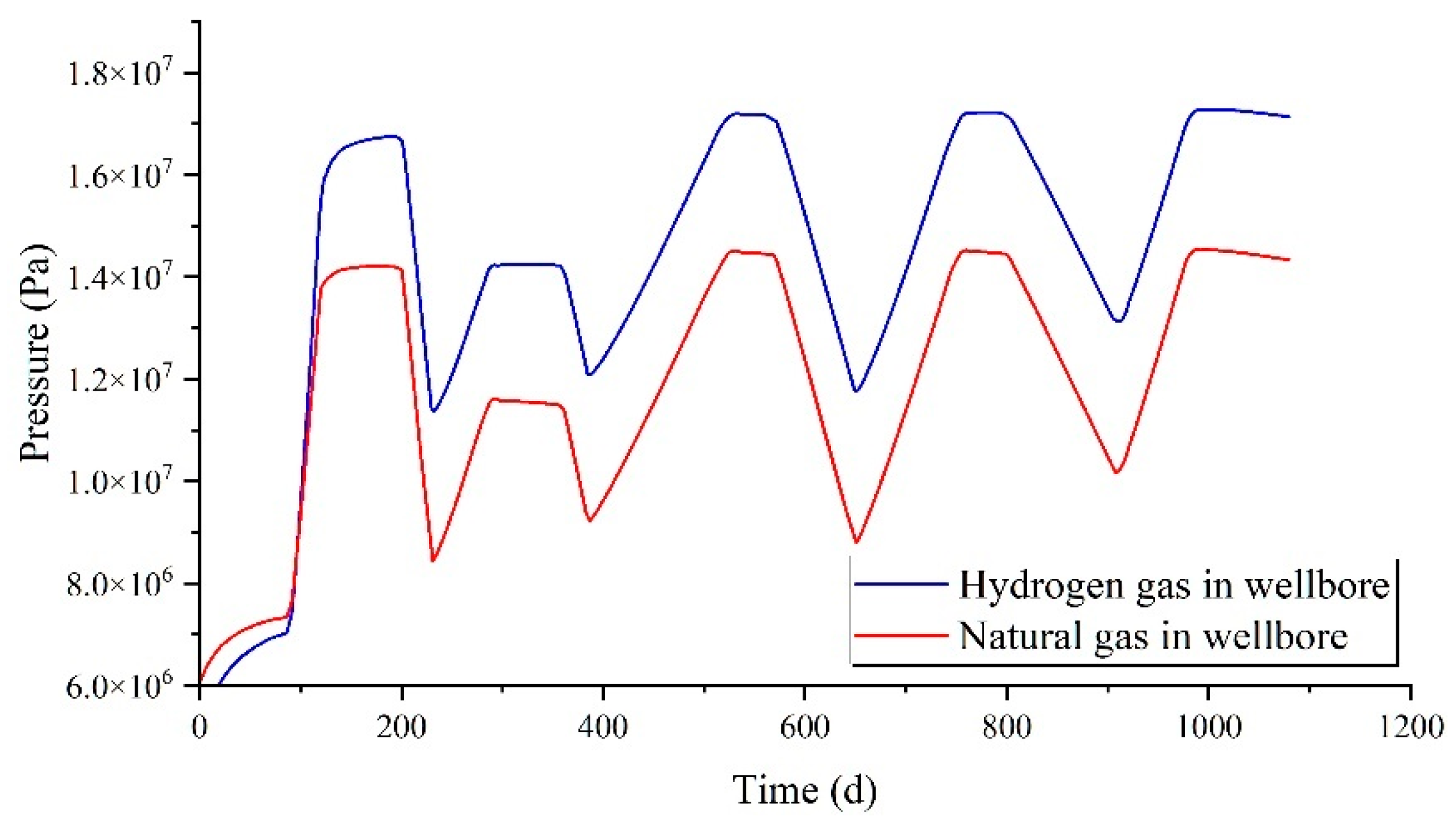
Under the same injection and production parameters, the variation in cavity pressure over a three-year injection-production cycle is illustrated in Figure 4. The pressure fluctuation patterns of the two gases within a single injection-production cycle are strikingly similar, yet the pressure differences are substantial. Under identical injection and production parameters, the cavity pressure of hydrogen can reach up to 17.9 MPa, while the maximum pressure of natural gas is approximately 15 MPa.
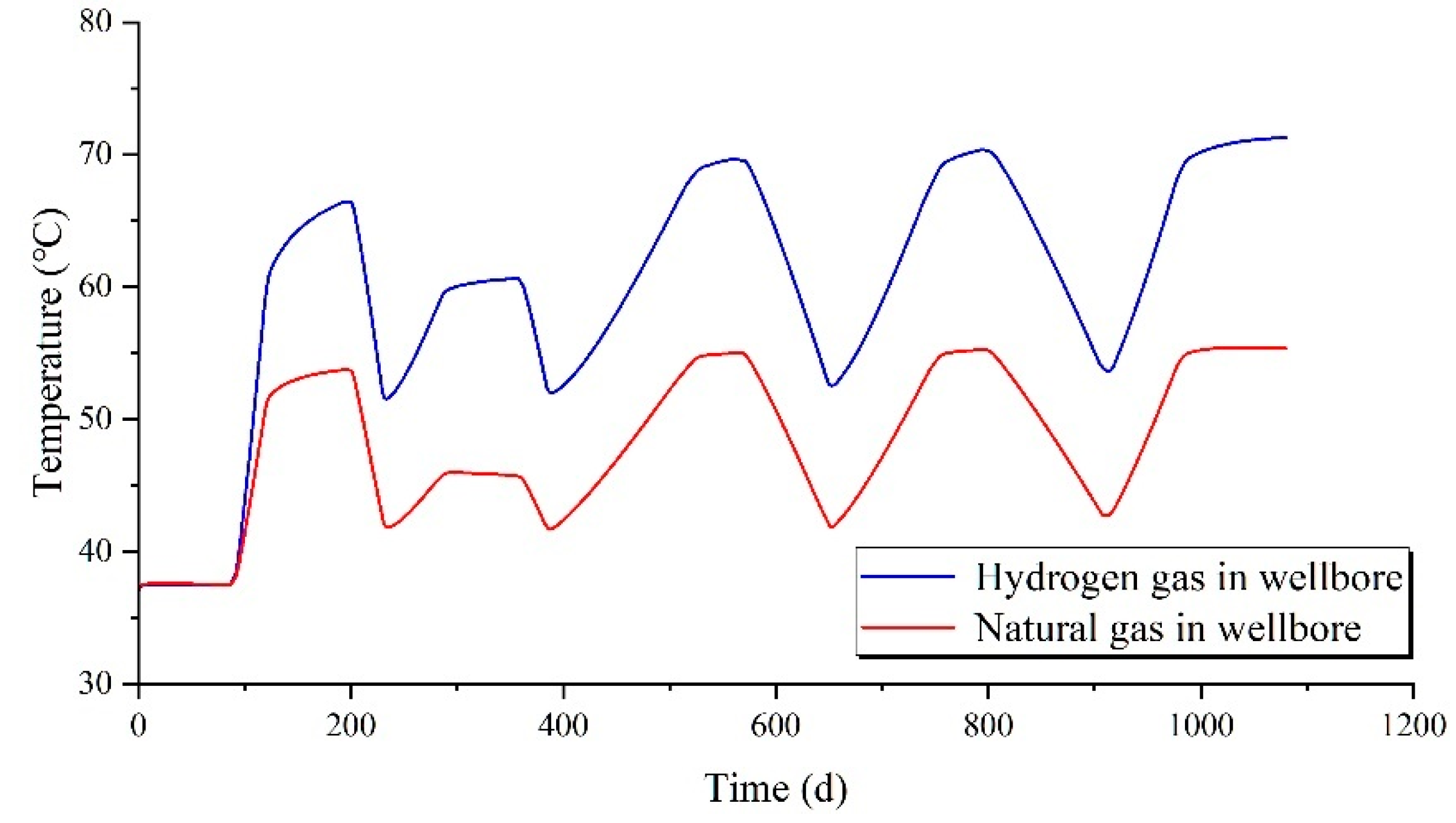
The temperature variations of hydrogen during a three-year injection-production cycle are illustrated in Figure 5. The temperature fluctuation of hydrogen within a single injection-production cycle bears striking resemblance to that of natural gas. However, due to differences in thermodynamic parameters such as specific heat capacity and thermal conductivity between hydrogen and natural gas, their temperature discrepancies are substantial. At identical injection-production pressures, the temperature of hydrogen can reach up to 76°C, while the maximum temperature of natural gas is approximately 60°C, a difference of around 16°C. During the production process, the temperature drop of hydrogen is generally more pronounced than that of natural gas, amounting to approximately 5°C.

4.2.2. Comparison of the Thermodynamic Properties of Gases in Wellbores

Under identical injection and production parameters, the variations in gas pressure within the wellbore over a three-year injection and production cycle are illustrated in Figure 6. Similar to the cavity pressure, the pressure changes of the two gases within the wellbore during a single injection and production cycle exhibit strikingly similar patterns, though with substantial differences in pressure levels. Under the same injection and production parameters, the pressure of hydrogen within the wellbore can reach up to 17.1 MPa, whereas the maximum pressure of natural gas is approximately 14.5 MPa.
The variation in gas temperature within the wellbore over a three-year injection-production cycle under identical parameters is illustrated in Figure 7. The pattern of gas temperature changes within the wellbore during a single injection-production cycle closely resembles that within the chamber. Under the same injection-production parameters, the temperature of hydrogen within the wellbore can reach up to 71°C, whereas the maximum temperature of natural gas is approximately 55°C.

4.2.3. Surrounding Rock Temperatures at Varying Distances from the Cavity

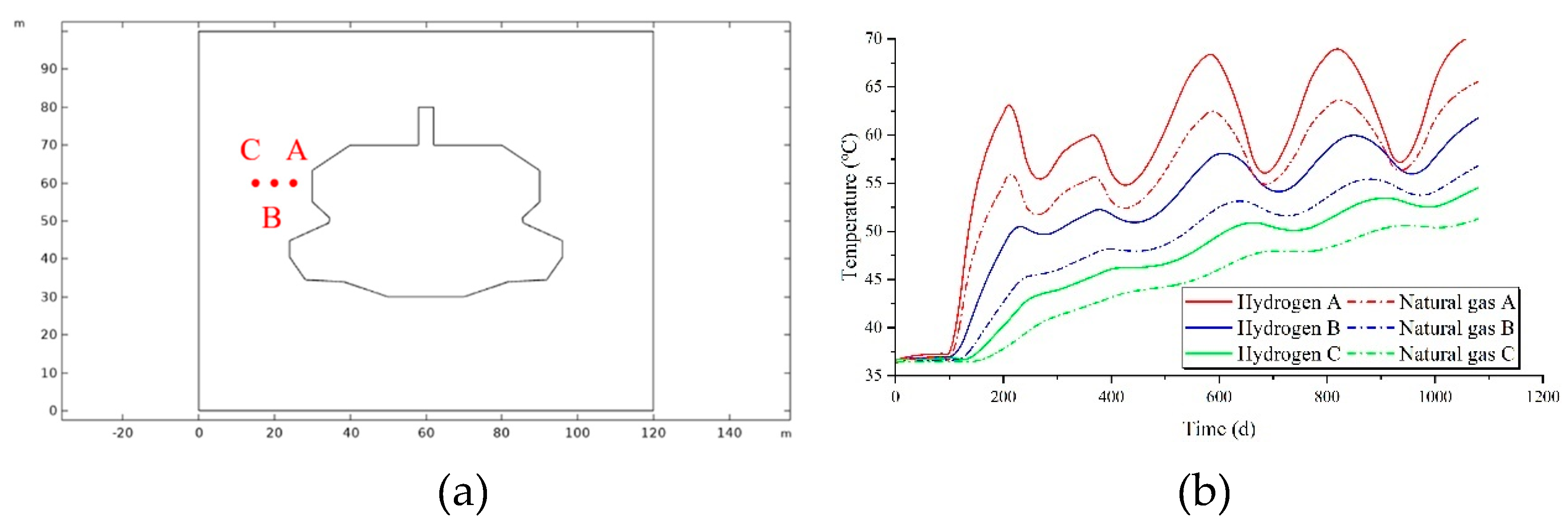
As illustrated in Figure 8a, three monitoring points are established at varying horizontal distances from the cavity, designated as A, B, and C, in order from nearest to farthest. The temperature variations at these horizontal monitoring points during the injection and production operation are depicted in Figure 8b. The temperature of the surrounding rock changes in accordance with the temperature of the gas within the cavity during the injection and production cycle. As the distance from the cavity increases, the amplitude of temperature change in the surrounding rock diminishes. For the same monitoring point, the temperature of the surrounding rock when storing hydrogen is higher than that when storing natural gas. Additionally, the rate of temperature increase and decrease is more pronounced for hydrogen storage compared to natural gas, indicating a more significant thermal exchange effect between hydrogen and the surrounding rock.

4.2.4. Temperature Variations in Surrounding Rock at Different Burial Depth

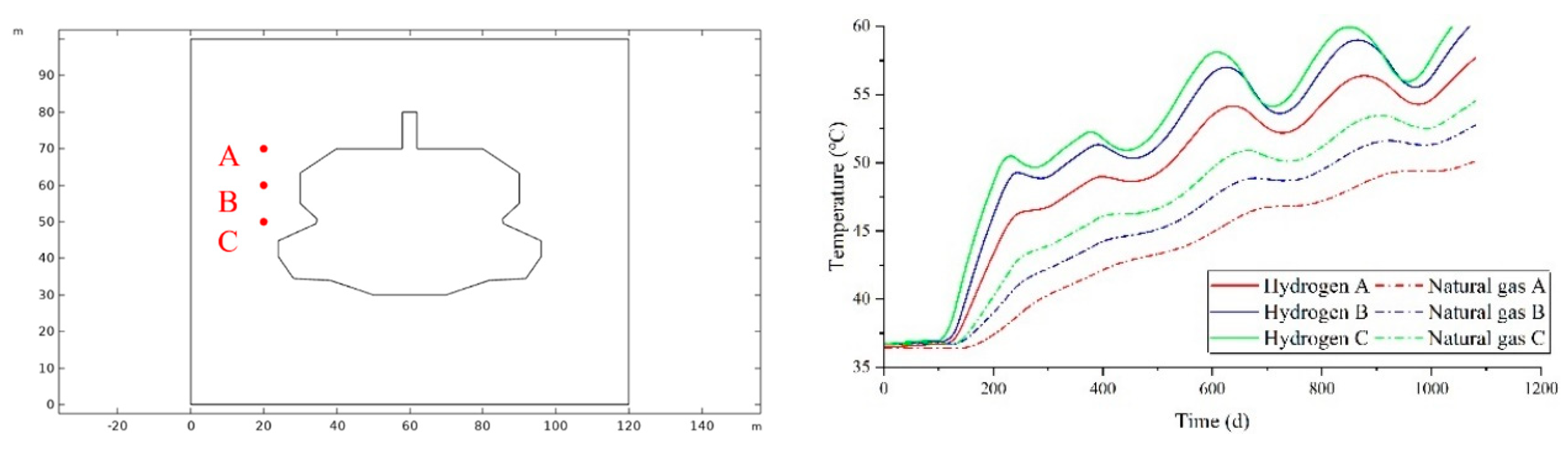
As illustrated in Figure 9(a), three monitoring points are established at varying distances horizontally from the cavity, designated as A, B, and C, progressing from closest to farthest. The temperature variations at these horizontal monitoring points during the injection and extraction process are depicted in Figure 9(b). The temperature of the surrounding rock fluctuates in response to changes in the gas temperature within the cavity during the injection and extraction cycle; as the distance from the cavity increases, the amplitude of temperature fluctuations in the surrounding rock diminishes. For the same monitoring point, the temperature of the surrounding rock storing hydrogen is consistently higher than that storing natural gas. When storing hydrogen, the rate of increase or decrease in the surrounding rock temperature is greater compared to natural gas, indicating a more pronounced thermal exchange effect between hydrogen and the surrounding rock.

4.2.5. Thermal Conductivity of Surrounding Rock

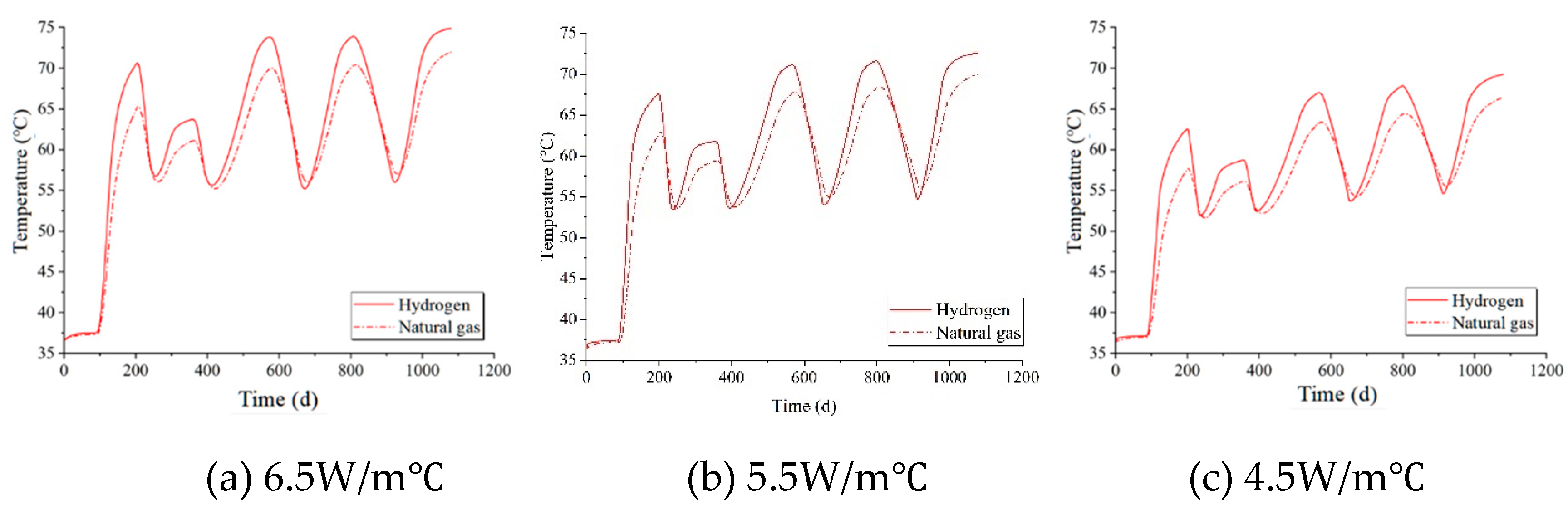
Set the thermal conductivity of the salt rock to 6.5 W/m°C, 5.5 W/m°C, and 4.5 W/m°C respectively. The temperature variations around the cavity under these three different thermal conductivities are depicted in Figure 10. For both hydrogen and natural gas, as the thermal conductivity of the surrounding rock decreases, the peak and valley temperatures around the cavity progressively diminish. At the same thermal conductivity, the temperatures during hydrogen storage are consistently higher than those observed during natural gas storage.
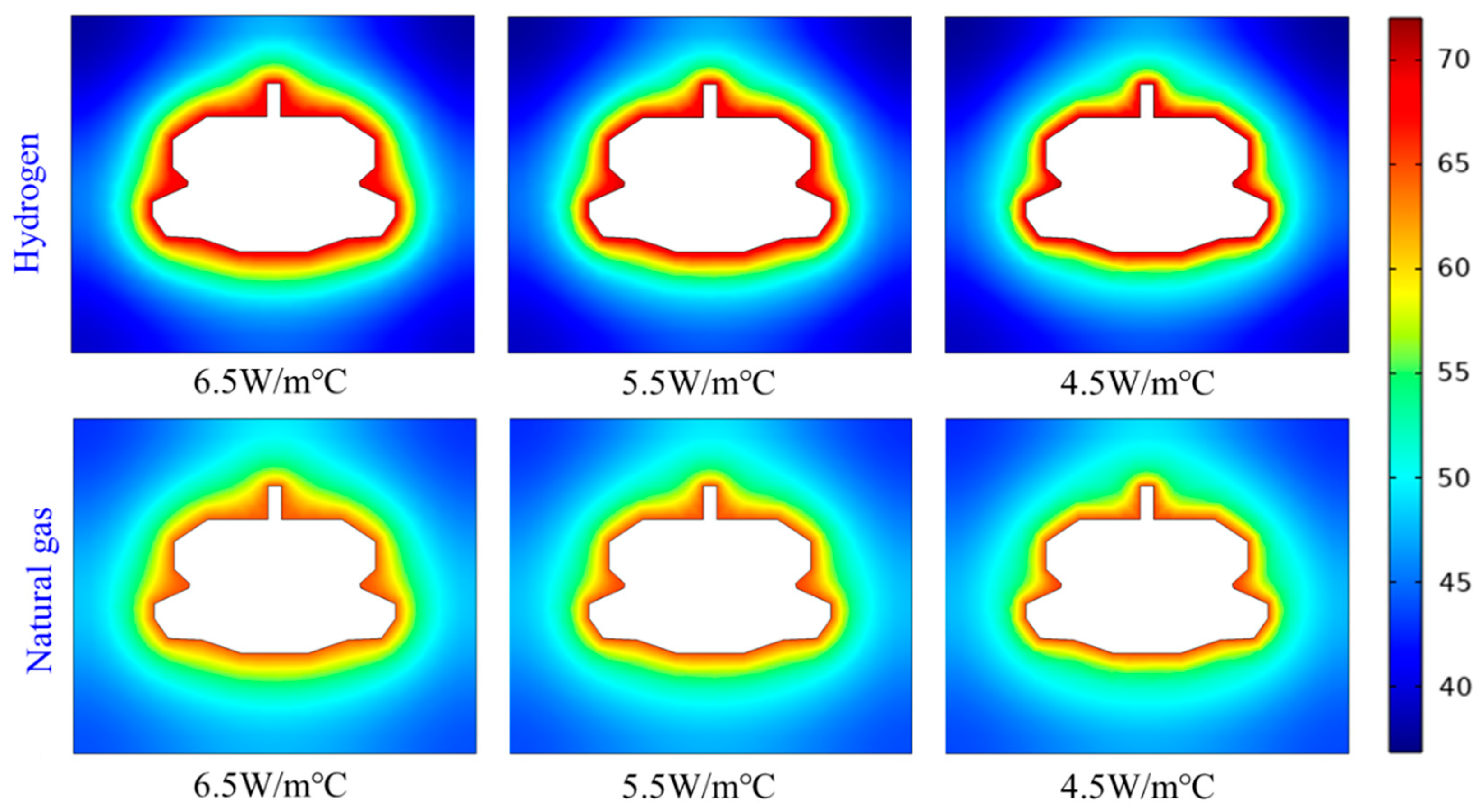
Figure 11 presents the thermal distribution contours of surrounding rock after three years of injection and production cycles with varying thermal conductivity coefficients. When storing the same type of gas, variations in thermal conductivity affect the extent of thermal effects; a higher thermal conductivity results in a deeper penetration of thermal effects into the rock strata, although the overall trend of thermal influence remains unchanged. The thermal effects of hydrogen are generally greater than those of natural gas, and the thermal exchange with the surrounding rock is also more pronounced.

4.2.6. Thermal Capacity of Surrounding Rock

Set the specific heat capacities of the salt rock to 920 J/kg·℃, 820 J/kg·℃, and 720 J/kg·℃, respectively. The temperature variations around the cavity under these three different specific heat capacities are illustrated in Figure 12. For both hydrogen and natural gas, as the specific heat capacity of the surrounding rock decreases, the peak and trough temperatures around the cavity progressively rise. Under the same specific heat capacity of the surrounding rock, the temperature is consistently higher when storing hydrogen compared to storing natural gas.
Figure 13 illustrates the temperature distribution maps of surrounding rock with different specific heat capacities after three years of injection and production cycles. When storing the same type of gas, variations in specific heat capacity also alter the extent of thermal effects; a lower specific heat capacity results in a deeper penetration of thermal effects into the rock. The reduction in specific heat capacity has a similar effect to an increase in thermal conductivity, as both influence temperature by affecting heat transfer. Generally, the thermal effect of hydrogen is higher than that of natural gas.

4.2.7. Coefficient of Thermal Expansion

Set the thermal expansion coefficients of salt rock to 5×10⁻⁵/K⁻¹, 4.5×10⁻⁵/K⁻¹, and 4×10⁻⁵/K⁻¹ respectively. The temperature distribution maps of the surrounding rock after three years of injection and production cycles with different thermal expansion coefficients are shown in Figure 14. The temperature distributions around the cavity with different thermal expansion coefficients are generally consistent. Variations in the thermal expansion coefficient do not alter the range of thermal effects, similar to the thermal conductivity and specific heat capacity. For the same thermal expansion coefficient, the thermal effect of hydrogen is generally higher than that of natural gas.

5. Conclusions

(1) A unified flow and heat transfer model is established for the hydrogen injection and extraction process. This model innovatively incorporates the convective heat transfer of hydrogen in the wellbore, radial heat transfer, the temperature-pressure coupling effects within the cavity, and the turbulent heat transfer effects within the cavity.
(2) The temperature and pressure parameters of hydrogen and natural gas within the chamber and wellbore were compared. Under identical injection and production conditions, the temperature of hydrogen in the chamber was 10°C higher than that of natural gas, and 16°C higher in the wellbore. The pressure of hydrogen in the chamber was 2.9 MPa greater than that of natural gas, and 2.6 MPa higher in the wellbore.
(3) A comparative analysis was conducted on the impact of surrounding rock’s horizontal and numerical distance on temperature during hydrogen and natural gas injection processes. As the distance from the cavity increases, from 5 to 15 meters, the temperature fluctuation in the surrounding rock diminishes progressively, with the temperature effect in the hydrogen storage chamber extending at least 10 meters.
(4) The influence of rock thermal conductivity parameters on temperature during the processes of hydrogen injection and natural gas extraction is compared. The better the thermal conductivity, the deeper the thermal effects penetrate the rock layers, with the specific heat capacity having the most significant impact.

Author Contributions

Conceptualization, L.ZZ; methodology, L.YX; validation, W.ZH; All authors have read and agreed to the published version of the manuscript.

Funding

This study was sponsored by the Basic Research Funding for Central Universities of China (Grant No. 2024KYJD1010).

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors on request.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Bachand, A.; Doyon, B.; Raymond, J. Thermo-physical numerical model for hydrogen storage in underground tanks and caverns. INTERNATIONAL JOURNAL OF HYDROGEN ENERGY 2024, 66, 66–80. [Google Scholar] [CrossRef]
  2. Carro, A.; Carneiro, J.; Ortiz, C.; et al. Assessment of carbon dioxide transcritical cycles for electrothermal energy storage with geological storage in salt cavities. APPLIED THERMAL ENGINEERING 2024, 255. [Google Scholar] [CrossRef]
  3. Song, R.; Song, Y.; Liu, J.; et al. Multiscale experimental and numerical study on hydrogen diffusivity in salt rocks and interlayers of salt cavern hydrogen storage. INTERNATIONAL JOURNAL OF HYDROGEN ENERGY 2024, 79, 319–334. [Google Scholar]
  4. Zhao, T.; He, Y.; Deng, J. Effect of geothermal heat transfer on performance of the adiabatic compressed air energy storage systems with the salt cavern gas storage. APPLIED THERMAL ENGINEERING 2024, 249. [Google Scholar]
  5. Wang, J.; Wang, Z.; Zeng, Q.; et al. Modeling and Parameter Optimization of Multi-Step Horizontal Salt Cavern Considering Heat Transfer for Energy Storage. APPLIED SCIENCES-BASEL 2024, 14. [Google Scholar] [CrossRef]
  6. Xie, D.; Wang, T.; Li, L.; et al. Modeling debrining of an energy storage salt cavern considering the effects of temperature. ENERGY 2023, 282. [Google Scholar] [CrossRef]
  7. Li, P.; Kang, H.; Zhu, Q.; et al. Numerical and experimental investigations of concrete lined compressed air energy storage system. JOURNAL OF CLEANER PRODUCTION 2023, 390. [Google Scholar] [CrossRef]
  8. Kushnir, R.; Dayan, A.; Ullmann, A. Temperature and pressure variations within compressed air energy storage caverns. INTERNATIONAL JOURNAL OF HEAT AND MASS TRANSFER 2012, 55, 5616–5630. [Google Scholar] [CrossRef]
  9. Kushnir, R.; Ullmann, A.; Dayan, A. Thermodynamic and hydrodynamic response of compressed air energy storage reservoirs: A review. REVIEWS IN CHEMICAL ENGINEERING 2012, 28, 123–148. [Google Scholar] [CrossRef]
  10. Xia, C.; Zhou, Y.; Zhou, S.; et al. A simplified and unified analytical solution for temperature and pressure variations in compressed air energy storage caverns. RENEWABLE ENERGY 2015, 74, 718–726. [Google Scholar] [CrossRef]
  11. Jiang, T.; Cao, D.; Xie, D.; et al. Preventing clogging of debrining tubing in a gas storage salt cavern during construction. GAS SCIENCE AND ENGINEERING 2024, 123. [Google Scholar] [CrossRef]
  12. Niu, C.; Tan, Y.; Li, J.; et al. Model validation and stability analysis for operation projects in Jintan Salt Cavern for strategic oil storage of China. JOURNAL OF PETROLEUM SCIENCE AND ENGINEERING 2015, 127, 44–52. [Google Scholar]
  13. Li, W.; Chen, G.; Ding, S.; et al. A method for assessing the gas capacity based on thermodynamic state analysis for salt cavern during operation. JOURNAL OF ENERGY STORAGE 2022, 50. [Google Scholar] [CrossRef]
  14. Li, W.; Miao, X.; Wang, J.; et al. Study on thermodynamic behaviour of natural gas and thermo-mechanical response of salt caverns for underground gas storage. ENERGY 2023, 262. [Google Scholar]
  15. Yan, Z.; Wang, Z.; Wu, F.; et al. Stability analysis of Pingdingshan pear-shaped multi-mudstone interbedded salt cavern gas storage. JOURNAL OF ENERGY STORAGE 2022, 56. [Google Scholar]
  16. Zhang, N.; Liu, X.; Zhang, Y.; et al. Investigating the Mechanism of Land Subsidence Due to Water Network Integration at the Guangzhou Longgui Salt Mine and Its Impact on Adjacent Subway. WATER 2024, 16. [Google Scholar] [CrossRef]
  17. Yin, H.; Yang, C.; Ma, H.; et al. Stability evaluation of underground gas storage salt caverns with micro-leakage interlayer in bedded rock salt of Jintan, China. ACTA GEOTECHNICA 2020, 15, 549–563. [Google Scholar]
  18. Wang, J.; Wang, X.; He, M.; et al. Long-term stability analysis and evaluation of horizontal salt cavern gas storage. JOURNAL OF ENERGY STORAGE 2023, 66. [Google Scholar]
  19. Wang, X.; Wang, J.; Zhao, P.; et al. Study on the long-term airtightness of salt cavern gas storage considering the permeability variation of surrounding rock. COMPUTERS AND GEOTECHNICS 2024, 168. [Google Scholar]
  20. Chen, X.; Xiong, T.; Li, Y. Research on the helium seepage mechanism in the strata surrounding bedded salt cavern helium storage and its tightness evaluation. GEOENERGY SCIENCE AND ENGINEERING 2024, 238. [Google Scholar] [CrossRef]
  21. He, T.; Wang, T.; Yang, X.; et al. Leakage path prediction model and gas tightness assessment method for gas storage salt cavern wellbores. COMPUTERS AND GEOTECHNICS 2024, 171. [Google Scholar] [CrossRef]
  22. Derakhshani, R.; Lankof, L.; Ghaseminejad, A.; et al. A Novel Sustainable Approach for Site Selection of Underground Hydrogen Storage in Poland Using Deep Learning. ENERGIES 2024, 17. [Google Scholar] [CrossRef]
  23. Naderi, H.; Hekmatnejad, A.; Aftab, A.; et al. Integrating 1D and 3D geomechanical modeling to ensure safe hydrogen storage in bedded salt caverns: A comprehensive case study in canning salt, Western Australia. INTERNATIONAL JOURNAL OF HYDROGEN ENERGY 2024, 81, 1073–1090. [Google Scholar] [CrossRef]
  24. Wang, J.; Wang, Z.; Zeng, Q.; et al. Modeling and Parameter Optimization of Multi-Step Horizontal Salt Cavern Considering Heat Transfer for Energy Storage. APPLIED SCIENCES-BASEL 2024, 14. [Google Scholar] [CrossRef]
Preprints 116646 g001
Figure 1. Shape of the salt cavern J106.
Figure 1. Shape of the salt cavern J106.
Preprints 116646 g001
Preprints 116646 g002
Figure 2. Boundary conditions of the numerical model.
Figure 2. Boundary conditions of the numerical model.
Preprints 116646 g002
Preprints 116646 g003
Figure 3. Variation in natural gas pressure within the salt cavern storage.
Figure 3. Variation in natural gas pressure within the salt cavern storage.
Preprints 116646 g003
Preprints 116646 g004
Figure 4. Variation in cavity pressure over a three-year injection-production cycle.
Figure 4. Variation in cavity pressure over a three-year injection-production cycle.
Preprints 116646 g004
Preprints 116646 g005
Figure 5. Variation in cavity temperature over a three-year injection-production cycle.
Figure 5. Variation in cavity temperature over a three-year injection-production cycle.
Preprints 116646 g005
Preprints 116646 g006
Figure 6. Variation in wellbore pressure over a three-year injection-production cycle.
Figure 6. Variation in wellbore pressure over a three-year injection-production cycle.
Preprints 116646 g006
Preprints 116646 g007
Figure 7. Variation in wellbore temperature over a three-year injection-production cycle.
Figure 7. Variation in wellbore temperature over a three-year injection-production cycle.
Preprints 116646 g007
Preprints 116646 g008
Figure 8. Horizontal monitoring points setting and temperature variations.
Figure 8. Horizontal monitoring points setting and temperature variations.
Preprints 116646 g008
Preprints 116646 g009
Figure 9. Vertical monitoring point setting and temperature variations.
Figure 9. Vertical monitoring point setting and temperature variations.
Preprints 116646 g009
Preprints 116646 g010
Figure 10. Temperature variations around the cavity with different thermal conductivities.
Figure 10. Temperature variations around the cavity with different thermal conductivities.
Preprints 116646 g010
Preprints 116646 g011
Figure 11. Temperature distribution of surrounding rock with different thermal conductivities.
Figure 11. Temperature distribution of surrounding rock with different thermal conductivities.
Preprints 116646 g011
Preprints 116646 g012
Figure 12. Temperature variation around the cavity with different thermal capacities.
Figure 12. Temperature variation around the cavity with different thermal capacities.
Preprints 116646 g012
Preprints 116646 g013
Figure 13. Temperature distribution of surrounding rock with different thermal capacities.
Figure 13. Temperature distribution of surrounding rock with different thermal capacities.
Preprints 116646 g013
Preprints 116646 g014
Figure 14. Temperature distribution with different thermal expansion coefficients.
Figure 14. Temperature distribution with different thermal expansion coefficients.
Preprints 116646 g014
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated