Probabilistic Power and Energy Balance Risk Scheduling Method Based on Distributed Robust Optimization

The volatility and uncertainty associated with the high proportion of wind and PV output in the new power system significantly impact power and energy balance, making it challenging to accurately assess the risks related to renewable energy abandonment and supply guarante. Therefore, a probabilistic power and energy balance risk analysis method based on distributed robust optimization is proposed. Firstly, the affine factor and the flexible ramp reserve capacity of thermal power are combined to establish a probabilistic index, which serves to characterize the risk associated with power and energy balance. Drawing upon the principles of conditional value at risk theory, the risk indexes of load shedding power and curtailment power under a certain confidence probability are proposed. Secondly, the probability distribution fuzzy sets of uncertain variables are constructed using the distributionally robust method to measure the Wasserstein distance between different probability distributions. Finally, aiming at minimizing the operation cost of thermal power, the risk cost of power abandonment and the risk cost of load shedding, a distributed robust optimal scheduling model based on flexible ramp reserve of thermal power is established.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

0. Introduction

The advancement of new energy technologies is a crucial pathway to realizing the objectives of "carbon peak and carbon neutrality", addressing environmental pollution, and resolving energy crisis issues. The rapid progress in new energy technology has led to a significant increase in the integration of new energy into the power grid, marking a distinctive characteristic of the modern power system. By the end of 2023, China's installed capacity of wind power and photovoltaics reached 440 million kW and 610 million kW respectively. The proportion of new energy installed capacity has reached 36%, making it the second largest power source in China [1].

When analyzing the traditional power system dominated by thermal power generation, the larger controllable range of thermal power generation often leads to an oversight of the temporal coupling relationship of operating constraints, and a segmented description of unit outage limits. Furthermore, with relatively small variance in load forecast errors, deterministic reserve rules effectively mitigate power imbalance risk to a low level [2]. The structural and operational characteristics of high-proportion renewable energy power systems exhibit substantial differences from traditional systems. Factors such as generation, demand, and storage collectively contribute to achieving power balance, and the temporal coupling characteristics result in interdependencies among viable solutions for power equilibrium at various time intervals [3,4]. The significant random fluctuations in wind and solar power have emerged as the primary source of electricity within the system, characterized by intricate and variable operating conditions that defy representation through a limited set of typical scenarios. There is an urgent imperative for probabilistic analysis of power quantity balance. Conventional time-series simulation-based methods rely on specific operational points to analyze power quantity balance, yet these operational points are uncertain under ambiguous conditions, leading to analytical challenges. Mere augmentation of simulated scenarios or introduction of segmented probability balance analysis does not effectively resolve the aforementioned issue. Consequently, traditional methods for analyzing power quantity balance are increasingly inadequate in addressing the need for temporal coupling and probability balance analysis in contexts where wind and solar energy penetration rates are escalating, necessitating a reevaluation of the matter concerning power quantity balance in power systems.

The analysis of power quantity balance is a fundamental cornerstone for designing power distribution and formulating operational strategies, serving as the central and primary concern in establishing new power systems. Presently, research on deterministic power quantity balance has achieved a significant level of maturity, with key areas of emphasis including optimized allocation of regulating resources, balanced analysis across multiple time scales within the system, and rapid solution algorithms for production simulation [5,6]. Document [7] established the groundwork for power and energy balance analysis calculations, introducing a table-based analysis method based on typical days. However, this approach is only suitable for early power systems dominated by thermal power plants. Additionally, Document [8] addressed the power and energy balance of systems with complex power supply structures, considering internal section limitations, external AC/DC power receiving operating conditions, and different resource attributes in each division to achieve inter-regional power and energy balance. With the increasing integration of fluctuating renewable energy sources, scholars are prompted to consider the evolving power and energy balance characteristics of systems with high proportions of renewable energy. Document [9] examines the variability of wind and photovoltaic energy generation across multiple time scales, as well as the complementary characteristics of new energy generation among different provinces, based on actual data from regional and provincial grids. Additionally, it assesses the absorption and supply risks faced by the power system in a high proportion of new energy sources scenario using future grid operation data. Document [10] proposes a power balance mechanism suitable for China's Northwest region that accounts for the uncertainty of new energy sources. To capture the temporal characteristics of new energy generation, time-series production simulation technology is extensively employed to analyze supply-demand balance in high-proportion new energy systems. Document [11] introduces a generator scheduling optimization algorithm that considers fluctuations in wind power generation output by pre-arranging starting modes of generators based on deterministic wind power generation scenarios in the main problem, and adjusting rescheduling plans of thermal power generation units in sub-problems to accommodate the intermittent nature of wind power generation. The final result is achieved through a hierarchical iterative solution method. Document [12] presents a fully parallelized stochastic generator scheduling method that decomposes the stochastic optimization problem into modules for generator configuration, optimal power flow calculation, and connection module; it calculates operation modes of each generator within the system under multiple wind power generation scenarios simultaneously, effectively enhancing simulation speed for large-scale transmission, distribution, transformation networks as well as direct current/alternating current hybrid transmission and distribution networks. There are several commonly used production simulation calculation software available both domestically and internationally, including the power system planning and decision-making software developed by Tsinghua University (referred to as grid optimization planning tools, GOPT) [13], and the new energy evaluation and optimization system (NEOS) [14] developed by State Grid Energy Research Institute Co., Ltd. Nevertheless, existing methods and software for analyzing power generation balance do not fully account for the significant uncertainty associated with high levels of new energy output. The decision-making units' operational modes fail to encompass the output characteristics during extreme weather scenarios, resulting in a heightened risk of compromised power supply reliability and curtailment of renewable energy within the power system.

Stochastic optimization and robust optimization are effective methods for dealing with the high uncertainty of renewable energy output, which can help achieve multi-source coordinated optimization. Among them, stochastic optimization methods aim to minimize the expected value of system operating costs by constructing models that satisfy specific probability level constraints. Document [15] considered the randomness of wind power output and optimized the unit combination based on the reliability index of wind power; Document [16] proposed a two-layer stochastic optimization model that takes into account the potential risks brought by the uncertainty of new energy output and determines the optimal standby capacity for participating in reserve auxiliary services; Document [17] applied stochastic optimization methods to the power market and achieved economic dispatch of traditional fossil-fuel power plants. The robust optimization method, when addressing the uncertainty of renewable energy output, does not necessitate explicit probability distribution of uncertain variables. Instead, it converts the uncertainty optimization problem into a deterministic optimization problem under extreme scenarios. This approach is currently extensively utilized in integrated energy systems [18], unit combinations [19], and optimal power flow [20] optimization models. To tackle the challenges associated with obtaining probability distribution information for wind and solar power output errors and excessively conservative results from robust optimization, experts have proposed the distributionally robust optimization (DRO) method. DRO establishes fuzzy sets for all potential distributions of uncertain variables based on historical data, effectively managing the uncertainty of renewable energy output. Document [21] considers the intra-provincial/inter-provincial coupled scheduling operation mode and establishes an uncertainty set of source-load power matrix based on distributionally robust optimization method, achieving the cross-province and cross-region integration of clean energy. Document [22] fully exploits the flexible regulation capability of the power system, establishing a two-stage distributionally robust optimization model to achieve economic dispatch of flexible ramping reserves. However, these models do not quantitatively evaluate the power balance risk in new-type power systems or provide probabilistic risk assessment indicators that adapt to high proportions of new energy access while considering strong uncertainty characteristics. Document [23], based on a time-varying probability model for clustered wind turbine virtual units, proposes a quantitative method for risk indicators considering the scheduling characteristics of clustered wind turbine virtual units; however, it does not consider the adjustment capability of fossil fuel-based flexible ramping reserves in response to risks. In summary, existing studies on uncertainty balance often characterize balanced risks based on deterministic probability distributions or intervals without providing probabilistic indicators with clear physical meanings for power balance risks and without considering flexibility resources' ability to respond to risks within the system, leading to biased risk assessment results.

This paper presents a method for probabilistic power balance risk analysis based on distributionally robust optimization. Initially, it integrates the affine factor and the flexible ramping reserve capacity of thermal power to define probabilistic metrics that characterize power balance risk. By leveraging conditional value-at-risk theory, it introduces risk metrics for shedding load and curtailed energy at a specified confidence level. Subsequently, employing the distributionally robust approach to measure Wasserstein distance between different probability distributions, fuzzy sets are constructed for the probability distributions of uncertain variables. Finally, in order to minimize thermal generation operating costs, curtailment risk costs, and shedding load risk costs, this study establishes a distributionally robust optimization scheduling model based on flexible ramping reserves of thermal power.

1. Assessment of Probabilistic Power and Energy Balance Characteristics and Risk Indicators for Supply-Demand Equilibrium

1.1. Analysis of Probability Balance Characteristics

In conventional power systems, achieving power and energy equilibrium relies on 'load balancing source,' where regulating load fluctuations becomes pivotal for maintaining system stability. However, within high-penetration renewable energy frameworks, wind and photovoltaic generation display significant stochastic traits that limit their regulatory capacity. Instead, numerous adaptable loads contribute to supply-demand equilibrium as an emerging form of regulatory asset—ushering in an innovative paradigm characterized by 'interconnected equilibrium across all facets of the power network.' Consequently, analyzing power-energy equilibrium has evolved into assessing adjustable resources alongside regulatory needs to better reflect operational realities. Table 1 illustrates key adjustable resources and regulatory requisites within high-penetration systems.

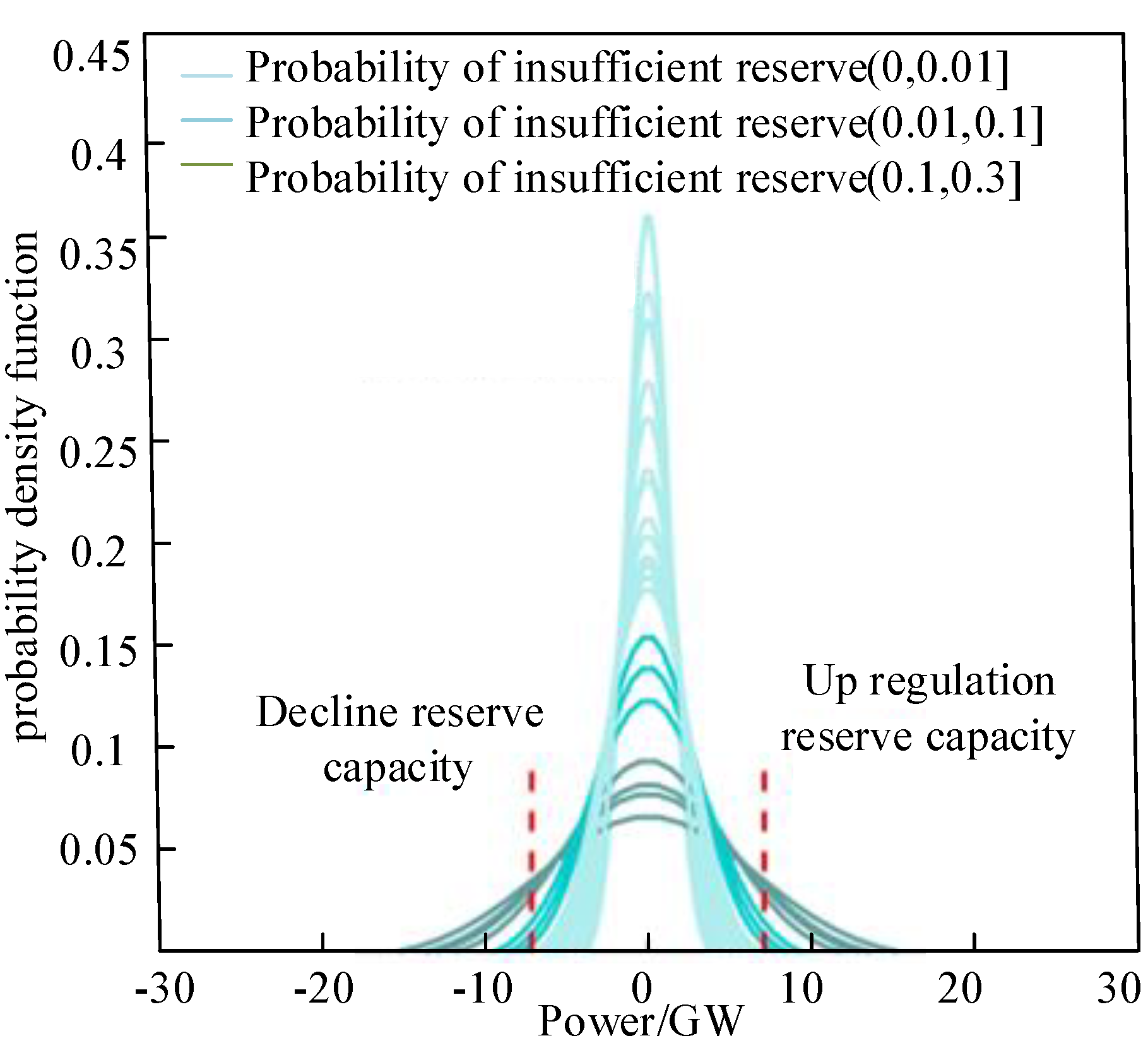
The probabilistic balance characteristics of power and energy arise from the stochastic variations in non-adjustable loads, wind/solar generation, and other sources. In comparison, the uncertainty associated with wind/solar generation surpasses that of load uncertainty, leading to significant disparities in prediction error levels across different time periods. Fixed reserve capacities struggle to ensure reliable balance across all time periods due to these differences, making the analysis of probabilistic balance characteristics a focal point of concern.

In a significant portion of renewable energy power system planning for a specific region, the determination of system standby capacity is based on the 10% peak load. The probability of standby deficiency for each time slot was calculated using the error distribution of net load forecast for a particular day. The error distribution was color-coded to represent the range of standby deficiency probability, as illustrated in Figure 1. It is evident from the figure that due to substantial variations in net load error distribution across different time slots, there are also considerable fluctuations in standby deficiency probability, with values reaching up to 0.3. Therefore, it is imperative to incorporate probabilistic characteristic analysis into power and energy balance assessments to effectively capture the impact of uncertainty on the system and address reliability and economic challenges stemming from standby deficiencies.

It is evident that the structure and operational characteristics of high-penetration renewable energy power systems differ significantly from traditional systems. Various adjustable resources in the sources, loads, and storage sectors collectively participate in achieving power and energy balance. The temporal coupling characteristics lead to mutual influences on the existence of feasible solutions for power and energy balance across different time periods. Wind/solar power sources with strong stochastic fluctuations have become the primary source of electricity generation for these systems. Their complex and variable operating conditions are challenging to represent using a limited number of typical scenarios, emphasizing the urgent need for probabilistic characteristic analysis in power and energy balance assessments.

1.2. Indicators of Supply and Demand Equilibrium Risk

According to the analysis of probability balance characteristics, it can be inferred that the high level of uncertainty in predicting errors for new energy is the primary factor contributing to power and energy balance risks in a significant portion of new energy power systems. The combined error in wind and solar predictions is represented as follows,

{\tilde{ψ}}_{t} = {\tilde{ω}}_{t}^{wind} + {\tilde{ω}}_{t}^{pv}

(1)

In the equation,

{\tilde{ω}}_{t}^{wind}

{\tilde{ω}}_{t}^{pv}

denotes the forecast errors of the wind farm and photovoltaic power station at time t.

The affine strategy is utilized as a method of adjustment for thermal power units to mitigate the forecast errors associated with wind and solar power. The actual output of the thermal power units is represented by an affine function, incorporating the forecast errors of wind and solar power as variables. The specific value of this affine function can only be computed once the actual outputs of wind and solar energy are determined.

\begin{array}{l} {\tilde{P}}_{i, t}^{G} = P_{i, t}^{G} + α_{i, t}^{G} {\tilde{ψ}}_{t} \\ = P_{i, t}^{G} + {\bar{α}}_{i, t}^{G} \max {{\tilde{ψ}}_{t}, 0} + {\underline{α}}_{i, t}^{G} \min {{\tilde{ψ}}_{t}, 0} \end{array}

(2)

P_{i, t}^{G} - R_{i, t}^{down} \leq {\tilde{P}}_{i, t}^{G} \leq P_{i, t}^{G} + R_{i, t}^{up}

(3)

In the equation,

α_{i, t}^{G}

represents the participation factor of the thermal power unit;

{\bar{α}}_{i, t}^{G}

{\underline{α}}_{i, t}^{G}

represent the upward/downward adjustment factors of thermal power unit i at time t;

R_{i, t}^{up}

、

R_{i, t}^{down}

represent the upward and downward spinning reserve capacities of thermal power unit i at time t.

Combined with the affine factor and the total forecast error of wind and solar power,

α_{i, t}^{G} {\tilde{ψ}}_{t}

and

{\underline{α}}_{i, t}^{G} {\tilde{ψ}}_{t}

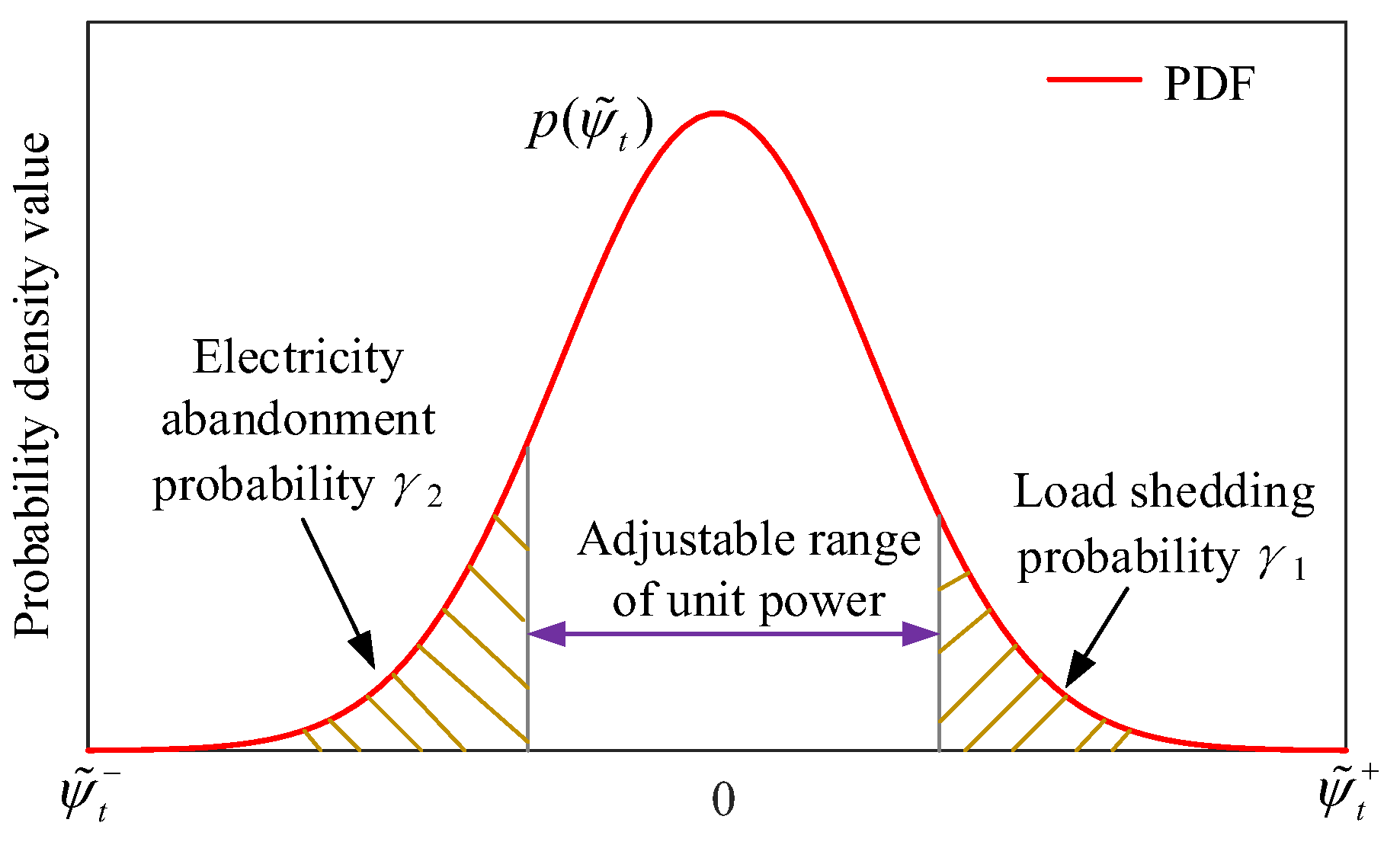
respectively represent the system's upward and downward regulation requirements. When the thermal power's upward ramping reserve regulation capacity is insufficient to cover the fluctuation adjustment demand of forecasted wind and solar outputs, there exists a risk of load shedding in the system. Similarly, when the thermal power's downward ramping reserve regulation capacity is inadequate to cover the fluctuation adjustment demand of forecasted wind and solar outputs, there exists a risk of curtailment as illustrated in Figure 2.

If the forecast error of wind and solar power is a stochastic variable, then the expression for the system's probabilistic electricity balance risk is as follows.

\{\begin{cases} \inf_{P_{t}^{ψ} \in ℜ_{t}^{ψ}} P_{t}^{ψ} [{\bar{α}}_{i, t}^{G} {\tilde{ψ}}_{t} \leq R_{i, t}^{up}] \geq 1 - γ_{1} = β_{1} \\ \inf_{P_{t}^{ψ} \in ℜ_{t}^{ψ}} P_{t}^{ψ} [- R_{i, t}^{down} \leq {\underline{α}}_{i, t}^{G} {\tilde{ψ}}_{t}] \geq 1 - γ_{2} = β_{2} \end{cases}

(4)

In equation (4),

γ_{1}

γ_{2}

represents the allowable loss-of-load/curtailment probability of the system. Equation (4) describes that, even when the wind and solar prediction error distribution

P_{t}^{ψ}

is in the worst distribution of

ℜ_{t}^{ψ}

, there is a probability less than

γ_{1}

γ_{2}

that the constraint cannot be satisfied, as shown in Figure 2.

According to the expression for probabilistic electricity balance risk in equation (4), random variables for load shedding and curtailed power can be defined as follows,

{\tilde{P}}_{t}^{cut} = \sum_{i = 1}^{G} {({\bar{α}}_{i t}^{G} {\tilde{ψ}}_{t} - R_{i t}^{up})}^{+}

(5)

{\tilde{S}}_{t}^{re} = \sum_{i = 1}^{G} {(- R_{i t}^{down} - {\underline{α}}_{i t}^{G} {\tilde{ψ}}_{t})}^{+}

(6)

In the equation,

{\tilde{P}}_{t}^{cut}

represents the random variable for load shedding, and

{\tilde{S}}_{t}^{re}

represents the random variable for curtailed power.

In accordance with the Value at Risk (VaR) definition, the threshold expressions for the random variables of load shedding and curtailed power can be delineated at a specific confidence level.

θ_{t}^{cut} = \min [b_{1} : ℙ {{\tilde{P}}_{t}^{cut} \leq b_{1}} \geq 1 - γ_{1} = β_{1}]

(7)

θ_{t}^{S} = \min [b_{2} : ℙ {{\tilde{S}}_{t}^{re} \leq b_{2}} \geq 1 - γ_{2} = β_{2}]

(8)

The variables

θ_{t}^{cut}

and

θ_{t}^{S}

denote the threshold values of the random variables corresponding to load shedding and curtailed power at time t, respectively.

The physical interpretation of

θ_{t}^{cut}

is the minimum threshold for load shedding power at a confidence level of β1, indicating the potential imbalance between supply and demand when the dispatch instruction for thermal power reserve exceeds

\sum_{i = 1}^{G} R_{i t}^{up}

with a probability greater than β₁ at time t. The physical interpretation of

θ_{t}^{cut}

aligns closely with this concept.

In the optimization strategy for balancing probabilistic power supply and demand in the power system, the objective is to identify the optimal balance point for dispatching thermal power standby capacity. This takes into consideration both safety and economic efficiency, aiming to minimize the likelihood of significant load shedding or curtailment during actual operation while ensuring effective implementation of dispatch instructions. The conditional value-at-risk (CVaR) theory is utilized to quantify the risk associated with large load shedding or curtailment caused by prediction errors in the probability distribution of new energy sources on both upper and lower tails. This study quantifies risk indicators for supply and demand balance in a high proportion new energy power system based on CVaR, expressing risk indicators for load shedding power and curtailment power at confidence levels β1 and β2 as average VaR values,

φ_{t}^{cut} = \frac{1}{1 - β_{1}} \int_{{\tilde{P}}_{t}^{cut} \geq θ_{t}^{cut}} {\tilde{P}}_{t}^{cut} p ({\tilde{ψ}}_{t}) d {\tilde{ψ}}_{t}

(9)

φ_{t}^{S} = \frac{1}{1 - β_{2}} \int_{{\tilde{S}}_{t}^{re} \geq θ_{t}^{S}} {\tilde{S}}_{t}^{re} p ({\tilde{ψ}}_{t}) d {\tilde{ψ}}_{t}

(10)

The variables

φ_{t}^{cut}

and

φ_{t}^{S}

represent the risk indicators for load shedding power and curtailed wind power, respectively, at time t.

p ({\tilde{ψ}}_{t})

denotes the probability distribution function of wind and solar forecasting errors.

φ_{t}^{cut}

can be interpreted physically as the conditional expectation value of the load shedding power exceeding its threshold

θ_{t}^{cut}

, and a similar physical interpretation applies to

φ_{t}^{S}

In fact, by minimizing

φ_{t}^{cut}

φ_{t}^{S}

, a small

θ_{t}^{cut}

θ_{t}^{S}

is also obtained due to the constraint that

θ_{t}^{cut}

θ_{t}^{S}

does not exceed

φ_{t}^{cut}

φ_{t}^{S}

. An auxiliary function

F_{β, t}^{cut}

F_{β, t}^{S}

is introduced to represent

φ_{t}^{cut}

φ_{t}^{S}

, which is defined as follows,

F_{β, t}^{cut} = b_{1} + \frac{1}{1 - β_{1}} \int_{{\tilde{ψ}}_{t} \in ℜ} {[{\tilde{P}}_{t}^{cut} - b_{1}]}^{+} p ({\tilde{ψ}}_{t}) d {\tilde{ψ}}_{t}

(11)

F_{β, t}^{S} = b_{2} + \frac{1}{1 - β_{2}} \int_{{\tilde{ψ}}_{t} \in ℜ} {[{\tilde{S}}_{t}^{re} - b_{2}]}^{+} p ({\tilde{ψ}}_{t}) d {\tilde{ψ}}_{t}

(12)

In this formula,

{[\cdot]}^{+}

represents

\max {\cdot, 0}

F_{β, t}^{cut}

F_{β, t}^{S}

can be estimated using sample data of random variables

{\tilde{ψ}}_{t}^{j}

(j=1,2,...M) as follows,

{\tilde{F}}_{β, t}^{cut} = b_{1} + \frac{1}{M (1 - β_{1})} \sum_{j = 1}^{M} {[{\tilde{P}}_{t}^{cut} ({\tilde{ψ}}_{t}^{j}) - b_{1}]}^{+}

(13)

{\tilde{F}}_{β, t}^{S} = b_{2} + \frac{1}{M (1 - β_{2})} \sum_{j = 1}^{M} {[{\tilde{S}}_{t}^{re} ({\tilde{ψ}}_{t}^{j}) - b_{2}]}^{+}

(14)

Furthermore, let,

H_{β, t}^{cut} = \max {b_{1}, \frac{1}{1 - β_{1}} {\tilde{P}}_{t}^{cut} - \frac{β_{1} b_{1}}{1 - β_{1}}}

(15)

H_{β, t}^{S} = \max {b_{2}, \frac{1}{1 - β_{2}} {\tilde{S}}_{t}^{re} - \frac{β_{2} b_{2}}{1 - β_{2}}}

(16)

Moreover, we can acquire,

F_{β, t}^{cut} = b_{1} + \frac{1}{1 - β_{1}} E_{{\hat{P}}_{M}} ({[{\tilde{P}}_{t}^{cut} - b_{1}]}^{+}) = E_{{\hat{P}}_{M}} (H_{β, t}^{cut})

(17)

F_{β, t}^{S} = b_{2} + \frac{1}{1 - β_{2}} E_{{\hat{P}}_{M}} ({[{\tilde{S}}_{t}^{re} - b_{2}]}^{+}) = E_{{\hat{P}}_{M}} (H_{β, t}^{S})

(18)

2. Probabilistic Balancing Analysis Model for New Energy Power Systems Based on Distributed Robust Optimization

2.1. A New Energy Power System Balance Analysis Model Based on Risk Assessment Indicators

(1): The objective function

The objective function aims to minimize the cost of thermal power generation, standby capacity expenses, and the potential loss costs under extreme distribution conditions for system load shedding and wind curtailment.

\min (\sum_{t = 1}^{T} \sum_{i = 1}^{G} (F_{i, t}^{G} + F_{i, t}^{R}) + \sup_{ℙ \in B ε ({\hat{ℙ}}_{M})} E_{ℙ} (C L + C E))

(19)

Among them,

\{\begin{cases} F_{i, t}^{G} = a_{i} {(P_{i, t}^{g})}^{2} + b_{i} P_{i, t}^{g} + c_{i} \\ F_{i, t}^{R} = ρ_{i}^{G} R_{i, t}^{up} + ρ_{i}^{G} R_{i, t}^{down} \end{cases}

(20)

\begin{array}{l} C L = c^{l} F_{β, t}^{cut} = c^{l} (b_{1} + \frac{1}{1 - β_{1}} E_{{\hat{ℙ}}_{M}} ({[{\tilde{P}}_{t}^{cut} - b_{1}]}^{+})) \\ = c^{l} E_{{\hat{ℙ}}_{M}} (H_{β, t}^{cut}) \end{array}

(21)

\begin{array}{l} C E = c^{e} F_{β, t}^{S} = b_{2} + \frac{1}{1 - β_{2}} E_{{\hat{ℙ}}_{M}} ({[{\tilde{S}}_{t}^{re} - b_{2}]}^{+}) \\ = E_{{\hat{ℙ}}_{M}} (H_{β, t}^{S}) \end{array}

(22)

In the equation,

ρ_{i}^{G}

denotes the cost of spinning reserve capacity for thermal power units; ai, bi, ci denote the coefficients of a polynomial;

P_{i, t}^{G}

denotes the power output of unit i at time t; CL represents load shedding costs; CE represents curtailment costs; cl is the penalty cost for unit capacity load shedding and ce is the penalty cost for unit capacity curtailment.

(2): Equations governing power flow

\begin{array}{l} P_{i, t} = \sum_{j \in B} G_{i, j} V_{i, t} V_{j, t} \cos θ_{i, j, t} + \\ \sum_{j \in B} B_{i, j} V_{i, t} V_{j, t} \sin θ_{i, j, t} \begin{matrix} , & i \in B \end{matrix} \end{array}

(23)

P_{i, t} = P_{i, t}^{g} + P_{i, t}^{wind} + P_{i, t}^{pv} - P_{i, t}^{d}

(24)

\begin{array}{l} Q_{i, t} = - \sum_{j \in B} B_{i, j} V_{i, t} V_{j, t} \cos θ_{i, j, t} + \\ \sum_{j \in B} G_{i, j} V_{i, t} V_{j, t} \sin θ_{i, j, t} \begin{matrix} , & i \in B \end{matrix} \end{array}

(25)

Q_{i, t} = Q_{i, t}^{r} - Q_{i, t}^{d}

(26)

P_{i, j, t}^{l} = - V_{i, t}^{2} G_{i, j} + V_{i, t} V_{j, t} (G_{i, j} \cos θ_{i, j, t} + B_{i, j} \sin θ_{i, j, t})

(27)

- {\bar{P}}^{l} \leq P_{i, j, t}^{l} \leq {\bar{P}}^{l} \begin{matrix} , & (i, j) \end{matrix} \in L

(28)

{\underline{V}}_{i} \leq V_{i, t} \leq {\bar{V}}_{i}

(29)

{\underline{Q}}_{i}^{r} \leq Q_{i, t}^{r} \leq {\bar{Q}}_{i}^{r}

(30)

In the equations, B and L represent the sets of buses and lines respectively;

P_{i, t}^{wind}

and

P_{i, t}^{pv}

denote the forecasted output of wind farms and photovoltaic fields at time period t;

P_{i, t}^{g}

represents the thermal power output at node i;

P_{i, t}^{d}

denotes the conventional load in the system;

Q_{i, t}^{d}

represents reactive power demand in the system;

Q_{i, t}^{r}

{\underline{Q}}_{i}^{r}

{\bar{Q}}_{i}^{r}

respectively represent reactive power generation, lower bound of reactive power output, upper bound of reactive power output;

P_{i, j, t}^{l}

represents line power flow;

V_{i, t}

{\bar{V}}_{i}

{\underline{V}}_{i}

respectively represent node voltage, upper bound of node voltage, lower bound of node voltage.

(3): Limitations on the Commencement and Termination of Operations for Thermal Power Units.

\{\begin{cases} [t_{i (t - 1)}^{on} - T_{i \min}^{on}] [X_{i (t - 1)} - X_{i t}] \geq 0 \\ [t_{i (t - 1)}^{off} - T_{i \min}^{off}] [X_{i t} - X_{i (t - 1)}] \geq 0 \end{cases}

(31)

In the equation,

T_{i \min}^{on}

T_{i \min}^{off}

represents the minimum start-up/shut-down time for unit i;

t_{i (t - 1)}^{on}

t_{i (t - 1)}^{off}

represents the duration of operation/shut-down from unit i to time period t-1;

X_{i t}

is a binary integer variable representing the start-up/shut-down status of unit i in time period t, with a value of 1 indicating start-up and a value of 0 indicating shut-down.

(4): Restrictions on the Output Limitation of Thermal Power Units

X_{i t} P_{i}^{G, \min} \leq P_{i, t}^{G} \leq X_{i t} P_{i}^{G, \max}

(32)

In the equation,

P_{i}^{G, \max}

and

P_{i}^{G, \min}

represent the upper and lower bounds of unit i's output, respectively.

(5): Limitations on the Spinning Reserve Capacity of Thermal Power Units

\{\begin{cases} P_{i, t}^{G} - R_{i, t}^{down} \geq X_{i t} P_{i}^{G, \min} \begin{matrix} , & R_{i, t}^{down} \geq 0 \end{matrix} \\ P_{i, t}^{G} + R_{i, t}^{up} \leq X_{i t} P_{i}^{G, \max} \begin{matrix} , & R_{i, t}^{up} \geq 0 \end{matrix} \end{cases}

(33)

In the equation,

R_{i, t}^{up}

and

R_{i, t}^{down}

represent the upper and lower spinning reserve capacity of thermal power unit i in time period t, respectively.

(6): Limitations on the Ramp Rate of Thermal Power Units

\{\begin{cases} P_{i, t}^{G} + R_{i, t}^{up} - (P_{i, t - 1}^{G} - R_{i, t - 1}^{down}) \leq r_{i}^{up} \\ P_{i, t - 1}^{G} + R_{i, t - 1}^{up} - (P_{i, t}^{G} - R_{i, t}^{down}) \leq r_{i}^{down} \end{cases}

(34)

In the equation,

r_{i}^{up}

and

r_{i}^{down}

represent the ramp-up rate and ramp-down rate of thermal power unit i, respectively.

2.2. Wasserstein Fuzzy Sets for Characterizing Uncertainty in Wind and Solar Resources

In the objective function of the model presented in Equation (19), the expected value of system contingency load shedding and curtailment condition risk loss is approximated based on the empirical distribution

{\hat{ℙ}}_{M}

of wind and solar prediction errors. However, this approach only considers historical sample data and cannot accurately represent the true distribution

ℙ

of wind and solar prediction errors. The fundamental challenge in robust optimization with distribution lies in constructing a fuzzy set that can authentically reflect the uncertain prediction error distribution of new energy sources. In this paper, we propose a fuzzy set based on Wasserstein distance, which effectively measures differences between probability distributions. Specifically, given two distributions

ℚ

and

ℙ

within a compact support spaceΞ, the Wasserstein distance is defined as,

W (ℚ, ℙ) = \inf_{π \in m (E \times E)} {\int_{E \times E} d (ξ^{q}, ξ^{p}) Π (d ξ^{q}, d ξ^{p})}

(35)

(d ξ^{q}, d ξ^{p}) = ‖ξ^{q} - ξ^{p}‖

(36)

In the equation,

ξ^{q}

and

ξ^{p}

represent stochastic variables;

Π

denotes the joint distribution of

ℚ

and

ℙ

; Equation (36) defines the distance between

ξ^{q}

and

ξ^{p}

;

‖\cdot‖

represents a norm operation, with this paper utilizing the

\infty

-norm to enhance model solvability. The fuzzy set based on Wasserstein distance is defined as,

B_{ε} (ℚ) = {ℙ | W (ℙ, ℚ) \leq ε}

(37)

The variable

ε

represents a constant derived from historical data, while

B_{ε} (ℚ)

denotes a Wasserstein ball with a radius of

ε

and centered at

ℚ

The fuzzy set based on the Wasserstein distance should be centered around a specific distribution

ℚ

, as indicated by Equation (37). However, due to the unknown nature of the error distribution in wind and solar power generation, this center should be determined based on relevant historical data to ensure alignment with the actual distribution of uncertain output errors. Assuming we have a finite historical sample dataset

\{ψ^{1}, ψ^{2}, \dots, ψ^{M}\}

for an uncertain variable

ψ

following a certain distribution

ℙ

, we can construct an empirical distribution

{\hat{ℙ}}_{M}

to approximate the true distribution. Given that the true distribution typically does not deviate significantly from the empirical one, we select the empirical distribution as the center of our Wasserstein ball for estimating the unknown true distribution. The expression for this empirical distribution is as follows,

{\hat{ℙ}}_{M} = \frac{1}{M} \sum_{j = 1}^{M} δ_{ψ^{j}}

(38)

In the equation, M represents the sample size,

δ_{ψ^{j}}

is the Dirac measure (if

ψ^{j} \in A

, then

δ_{ψ^{j}} (A) = 1

; otherwise

δ_{ψ^{j}} (A) = 0

, A denotes any set belonging to

σ (Ξ)

, and

Ξ

signifies the support set of

ψ

. As M approaches infinity,

{\hat{ℙ}}_{M}

should tend toward the true distribution

ℙ

. In other words, as more data becomes available, the "distance" between

{\hat{ℙ}}_{M}

and

ℙ

will become smaller. The Wasserstein fuzzy set centered around an empirical distribution

{\hat{ℙ}}_{M}

can be expressed as,

B_{ε} ({\hat{ℙ}}_{M}) = {ℙ | W (ℙ, {\hat{ℙ}}_{M}) \leq ε}

(39)

In this equation, the parameter A can regulate the level of conservatism in the model, which significantly influences its performance based on the Wasserstein distance. A potential choice is suggested in literature [24],

ε = D \sqrt{\frac{2}{M} \log (\frac{1}{1 - η})}

(40)

In the equation,

η

represents the confidence level, and D denotes the diameter of the support points of the random variable. Nevertheless, literature [25] suggests that

ε

derived from Equation (40) is excessively conservative and proposes a new alternative as follows,

P {W (ℙ, {\hat{ℙ}}_{M}) \leq ε} \geq 1 - \exp (- M \frac{ε^{2}}{c^{2}})

(41)

The calculation method for

ε

can be derived by setting the right-hand side of Equation (41) equal to the confidence level

η

of the given fuzzy set.

ε = C \sqrt{\frac{1}{M} \ln (\frac{1}{1 - η})}

(42)

In the equation, C represents a constant. If

C = \sqrt{2} D

is true, then Equation (42) transforms into Equation (40). The value of C can be estimated using historical data, and the calculation formula is as follows,

\begin{array}{l} C \leq 2 \min_{ρ > 0} (\frac{1}{2 ρ} (1 + \ln E_{ℙ} [e^{ρ {‖λ - \hat{μ}‖}_{1}^{2}}])) \\ \approx \min_{ρ > 0} 2 \sqrt{\frac{1}{2 ρ} (1 + \ln (\frac{1}{M} \sum_{j = 1}^{M} e^{ρ {‖λ - \hat{μ}‖}_{1}^{2}}))} \end{array}

(43)

In this equation,

\hat{μ}

represents the average of the historical sample, specifically defined as

\hat{μ} = \frac{1}{M} \sum_{j = 1}^{M} ψ^{j}

3. Transformation of the Model

3.1. Linearization of Trends

In the aforementioned model, the power flow equations for AC systems exhibit non-convex and nonlinear characteristics, rendering direct solutions impractical. Consequently, linearizing the power flow equations for AC systems becomes imperative. The expansion of Equations (23) and (25) results in,

\begin{array}{l} P_{i, t} = g_{i, i} V_{i, t}^{2} + \sum_{j \in B, j \neq i} [g_{i, j} V_{i, t} (V_{i, t} - V_{j, t} \cos θ_{i, j, t}) - \\ b_{i, j} V_{i, t} V_{j, t} \sin θ_{i, j, t}] \begin{matrix} , & i \in B \end{matrix} \end{array}

(44)

\begin{array}{l} Q_{i, t} = - b_{i, i} V_{i, t}^{2} - \sum_{j \in B, j \neq i} [b_{i, j} V_{i, t} (V_{i, t} - V_{j, t} \cos θ_{i, j, t}) + \\ g_{i, j} V_{i, t} V_{j, t} \sin θ_{i, j, t}] \begin{matrix} , & i \in B \end{matrix} \end{array}

(45)

Approximate the non-linear terms in Equations (44) and (45) as outlined below,

\{\begin{cases} V_{i, t}^{2} \approx V_{i, t} \\ V_{i, t} V_{j, t} \sin θ_{i, j, t} \approx θ_{i, t} - θ_{j, t} \\ V_{i, t} (V_{i, t} - V_{j, t} \cos θ_{i, j, t}) \approx V_{i, t} - V_{j, t} \end{cases}

(46)

The ultimate outcome produces the subsequent decoupled linear power flow.

\{\begin{cases} P_{i, t} = \sum_{j \in B} G_{i, j} V_{j, t} - \sum_{j \in B} B_{i, j}^{'} θ_{j, t} \\ Q_{i, t} = - \sum_{j \in B} B_{i, j} V_{j, t} - \sum_{j \in B} G_{i, j}^{'} θ_{j, t} \end{cases} \begin{matrix} , & i \in B \end{matrix}

(47)

Likewise, the formula for line power is as follows.

P_{i, j, t}^{l} = G_{i, j} (V_{i, t} - V_{j, t}) - B_{i, j} (θ_{i, t} - θ_{j, t}) \begin{matrix} , & (i, j) \end{matrix} \in L

(48)

3.2. The Dual Transformation of a Distribution Robust Model

Distributionally robust optimization combines the principles of stochastic optimization and robust optimization, typically framed as a minimax problem. The model is outlined as follows,

\inf_{x} \sup_{P \in Ω_{P} (\tilde{ω})} E_{P} {f (x, \tilde{ω})}

(49)

In this formula,

Ω_{P} (\tilde{ω})

represents the fuzzy set of uncertain quantity

\tilde{ω}

;

\sup_{P \in Ω_{P} (\tilde{ω})}

represents the worst-case distribution of uncertain quantity

Ω_{P} (\tilde{ω})

within fuzzy set

\sup_{P \in Ω_{P} (\tilde{ω})}

; and

\inf_{x}

represents the lower bound of the expected value of

f (x, \tilde{ω})

under the worst-case distribution of

\tilde{ω}

Distributionally robust optimization utilizes fuzzy set

Ω_{P} (\tilde{ω})

to represent the higher-order uncertainty of uncertain quantity

\tilde{ω}

, encompassing both the intrinsic uncertainty of the quantity and the ambiguity in its probability distribution information.

The extreme distribution problem of model (49) can be reformulated in accordance with the strong duality theory [27] as follows,

\begin{array}{l} \inf_{x} \sup_{P \in Ω_{P} (\tilde{ω})} E_{P} {f (x, \tilde{ω})} = \\ \inf_{κ \geq 0} \{κ \cdot ε + \frac{1}{M} \sum_{m = 1}^{M} \sup_{\tilde{ω} \in Ξ} (f (x, \tilde{ω}) - κ ‖\tilde{ω} - {\hat{ω}}_{m}‖)\} \end{array}

(50)

The model (50) can be further reformulated as follows,

\{\begin{cases} \inf_{κ \geq 0} κ \cdot ε + \frac{1}{M} \sum_{m = 1}^{M} τ_{m} \\ s . t . f (x, \bar{ω}) - κ \cdot (\bar{ω} - {\hat{ω}}_{m}) \leq τ_{m} \\ f (x, \underline{ω}) + κ \cdot (\underline{ω} - {\hat{ω}}_{m}) \leq τ_{m} \\ f (x, {\hat{ω}}_{m}) \leq τ_{m} \end{cases}

(51)

In this equation, κ represents a dual variable;

\bar{ω}

and

\underline{ω}

denote the vectors formed by the boundaries of

{\tilde{ω}}^{i}

4. Simulation Study

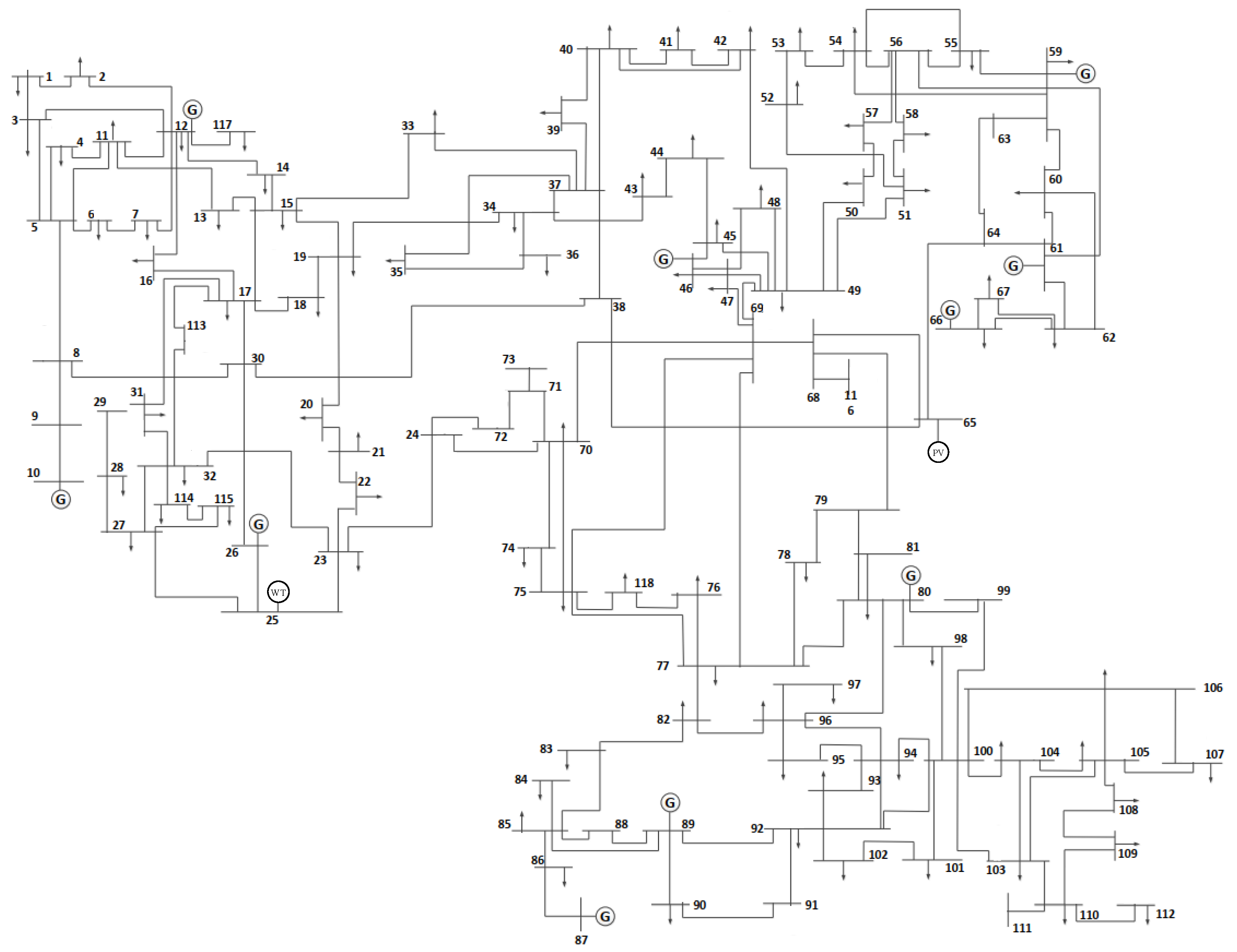
The proposed method was validated by testing it on the IEEE118 node system with an enhanced structure as a case study. The system structure utilized in the case study is depicted in Figure A1 of Appendix A. It comprises 11 thermal power units (G1 - G11) with specific parameters detailed in Table A1 of Appendix A. The installed capacity for wind power is 900 MW, connected to node 25, while the installed capacity for photovoltaic power is 1500 MW, connected to node 65. New energy accounts for a substantial 47% of the total installed capacity, signifying a significant proportion within the system. Additionally, each node's maximum load in the system has been limited to 75% of that in the original IEEE118 node system.

Utilizing the actual and predicted values of historical wind and solar power output, this study modeled the empirical distribution of errors in wind and solar power output. Subsequently, 1000 samples of errors in wind and solar power output were randomly generated at each time point based on the historical empirical distribution.

4.1. Systematic Probabilistic Analysis of Supply and Demand Balance

The paper conducts a probabilistic risk analysis of power generation balance in a high-proportion new energy power system, utilizing proposed load shedding and curtailed power conditions. For instance, the system dispatch optimization results at a 95% confidence level are illustrated in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12.

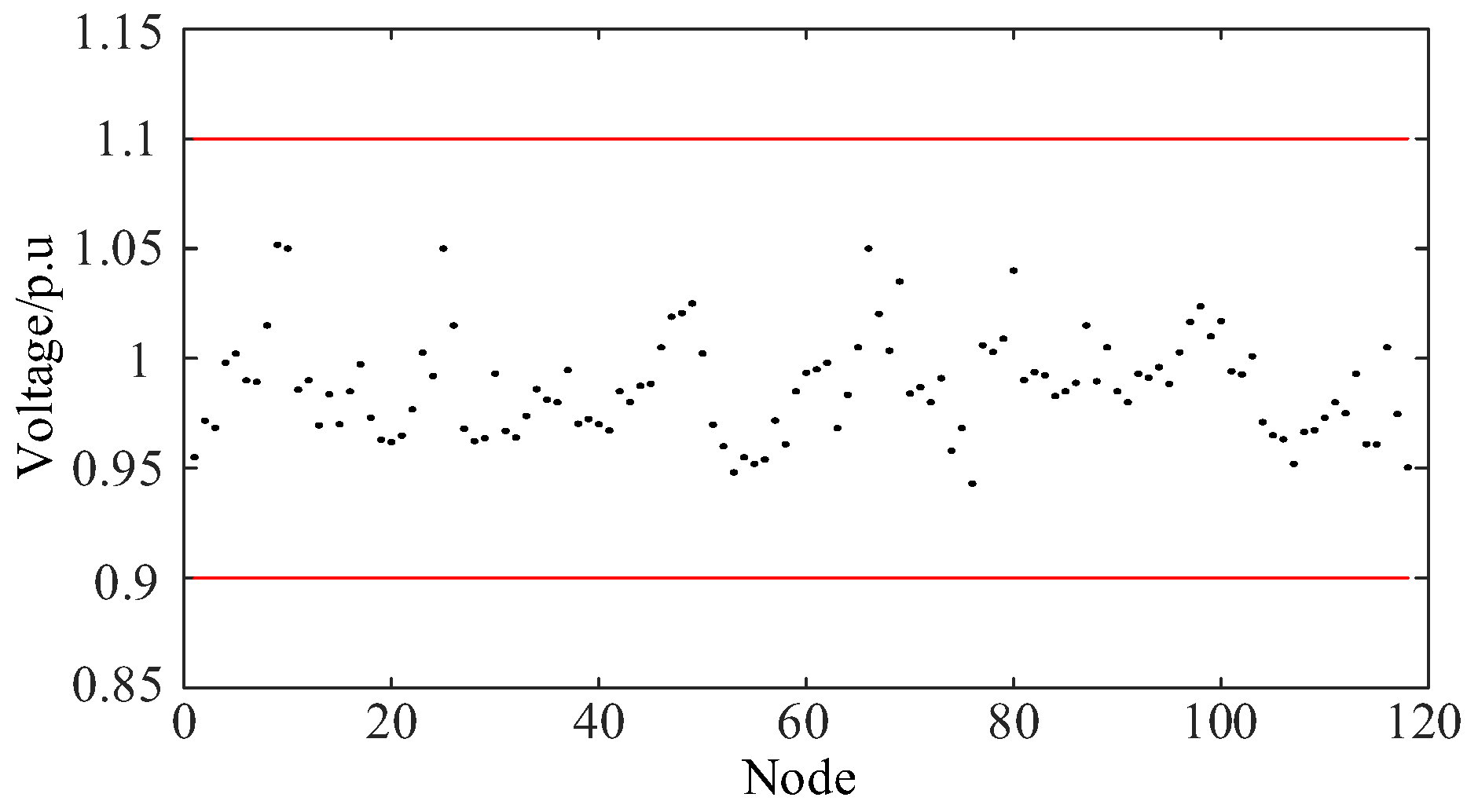
Figure 3 depicts the voltage levels at system nodes at a specific time, demonstrating that the system's voltage levels are within permissible limits. This validates the effectiveness of the power flow model proposed in this paper.

As depicted in Figure 4, the output of new energy sources reaches its minimum value in the early morning. Due to the lower limit on the output of new energy sources, downward fluctuations are constrained by uncertainty. Consequently, at this time, the total upward ramping reserve is at its daily nadir.

The system encounters insufficient climbing reserve capacity around the 19th hour, leading to a potential risk of load shedding. This means that relying solely on the regulation capacity of thermal power plants at this time is no longer adequate to manage the uncertainty of new energy output. Therefore, it is advisable to utilize a risk value for the probabilistic supply-demand balance cut-load condition as a guide for configuring storage, load demand response, and other flexible resources.

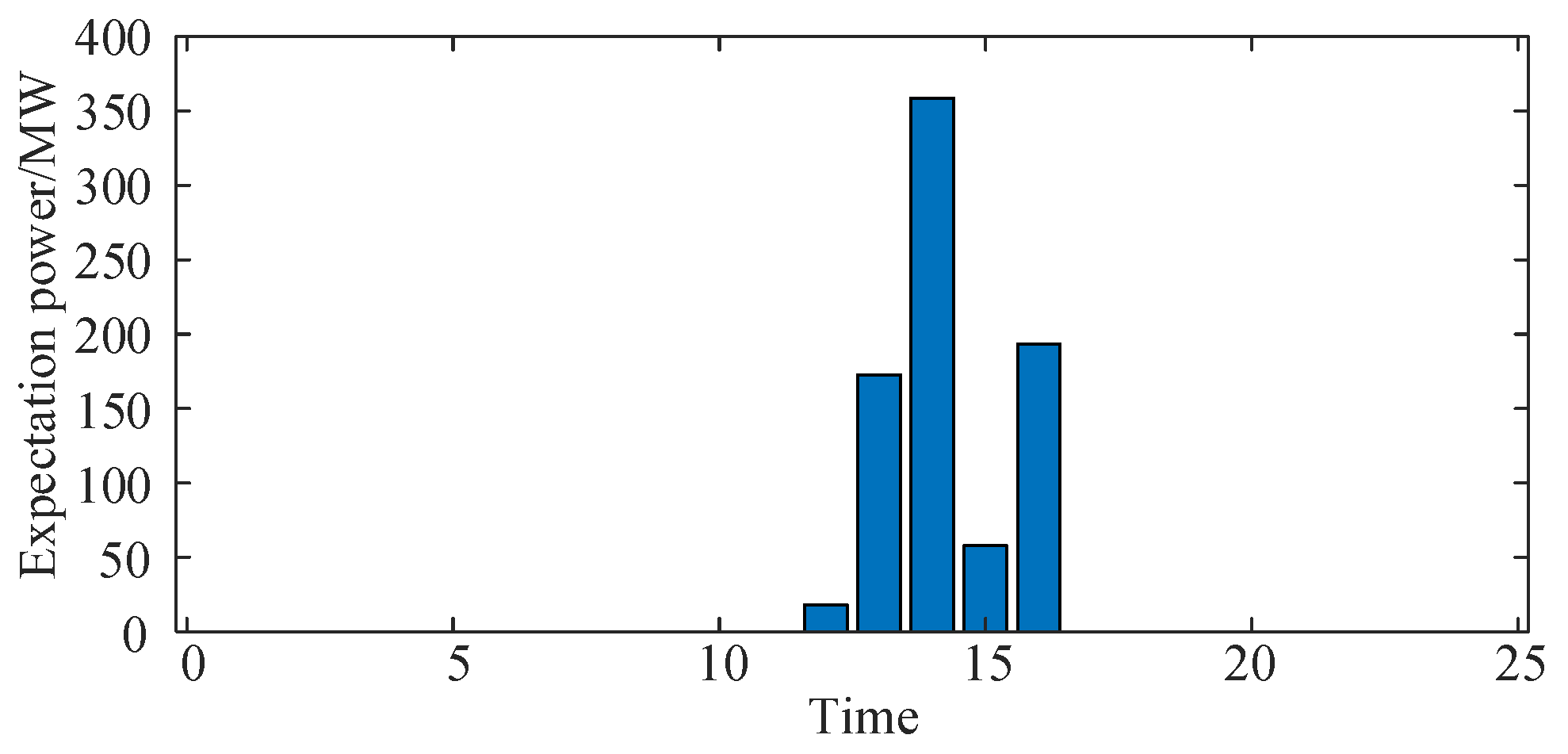
The risk assessment results for curtailed power under different time periods, as illustrated in Figure 7, indicate that insufficient downward ramping reserve capacity is experienced by the system during the 14th hour, leading to a significant risk of curtailed power.

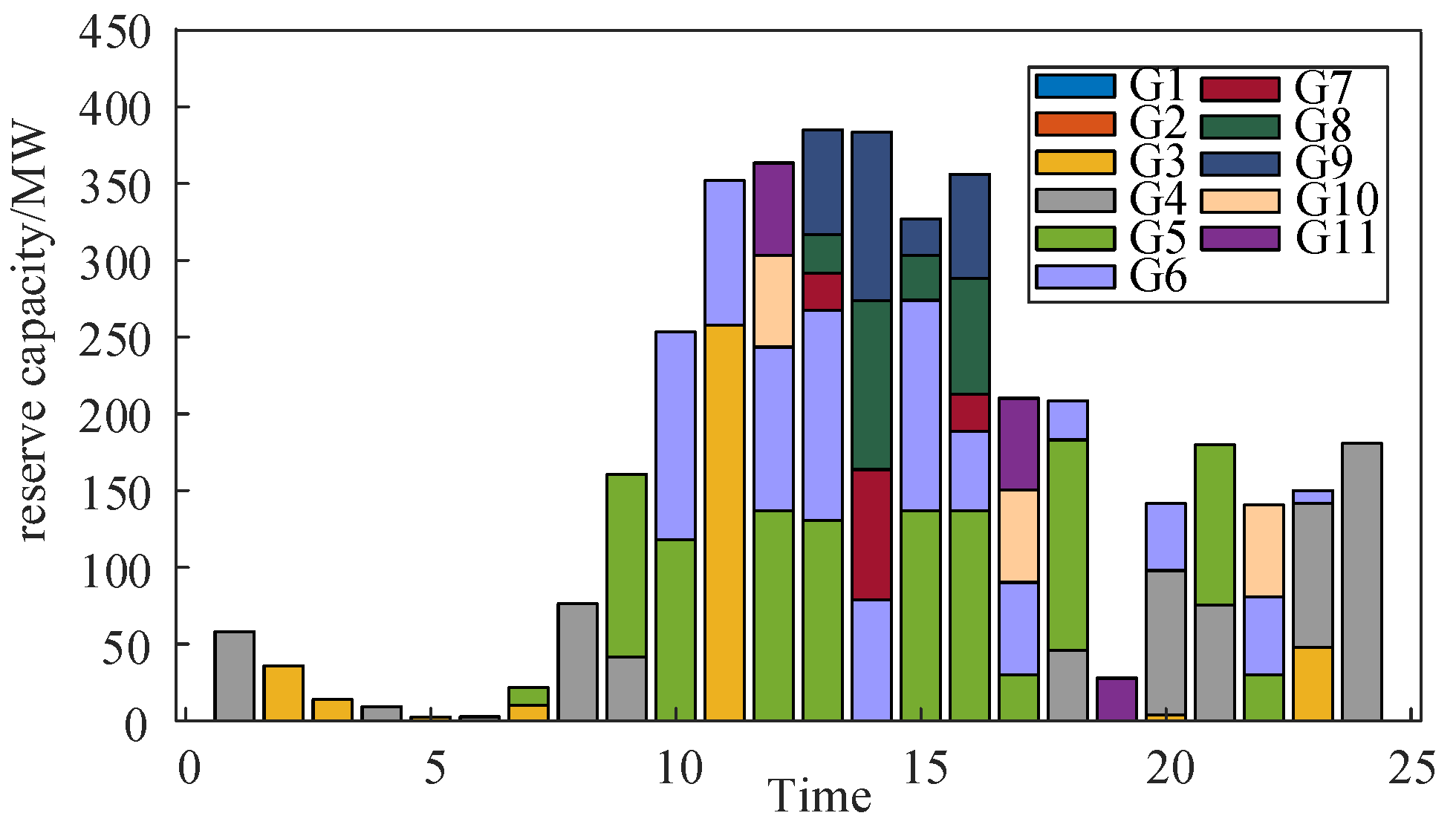
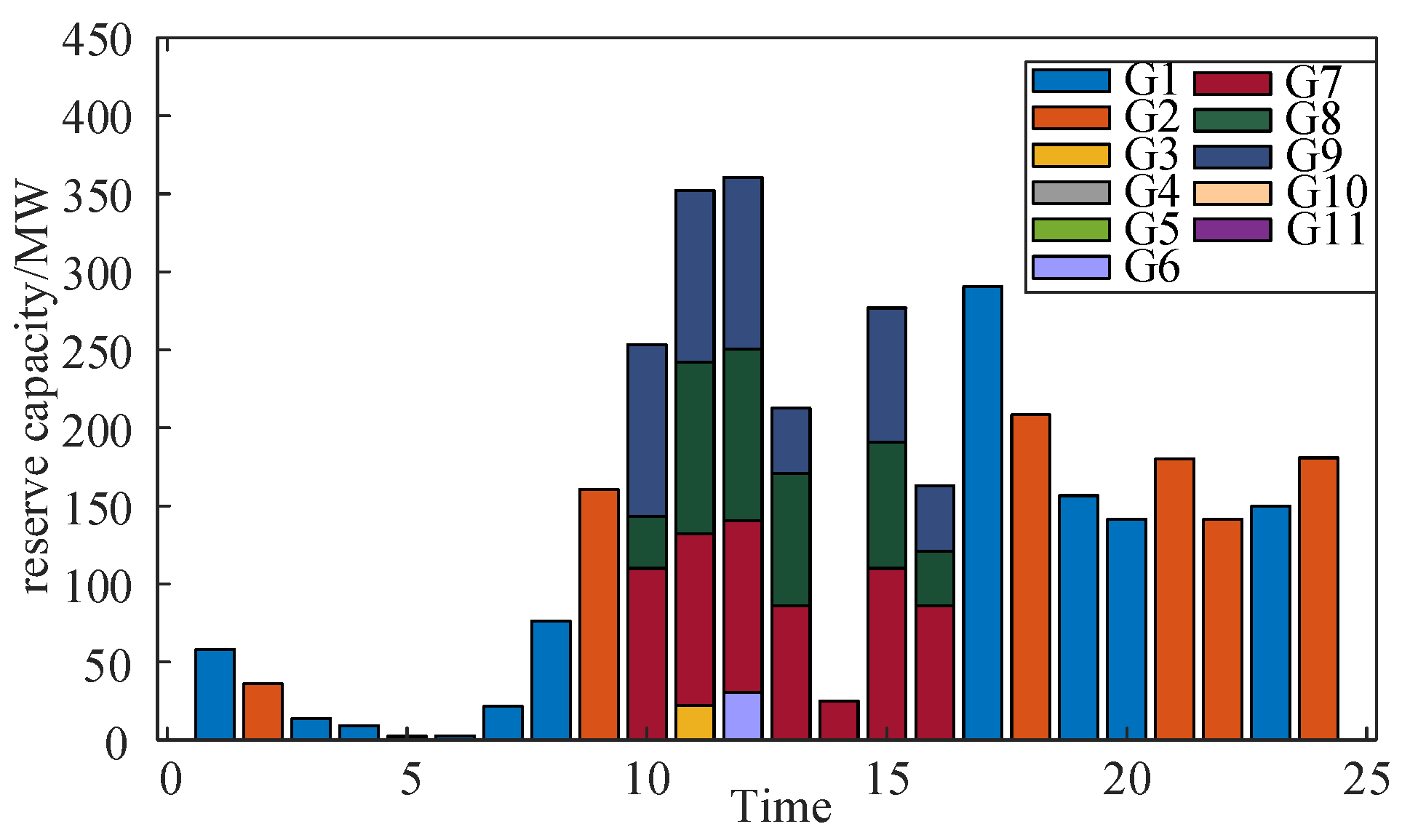
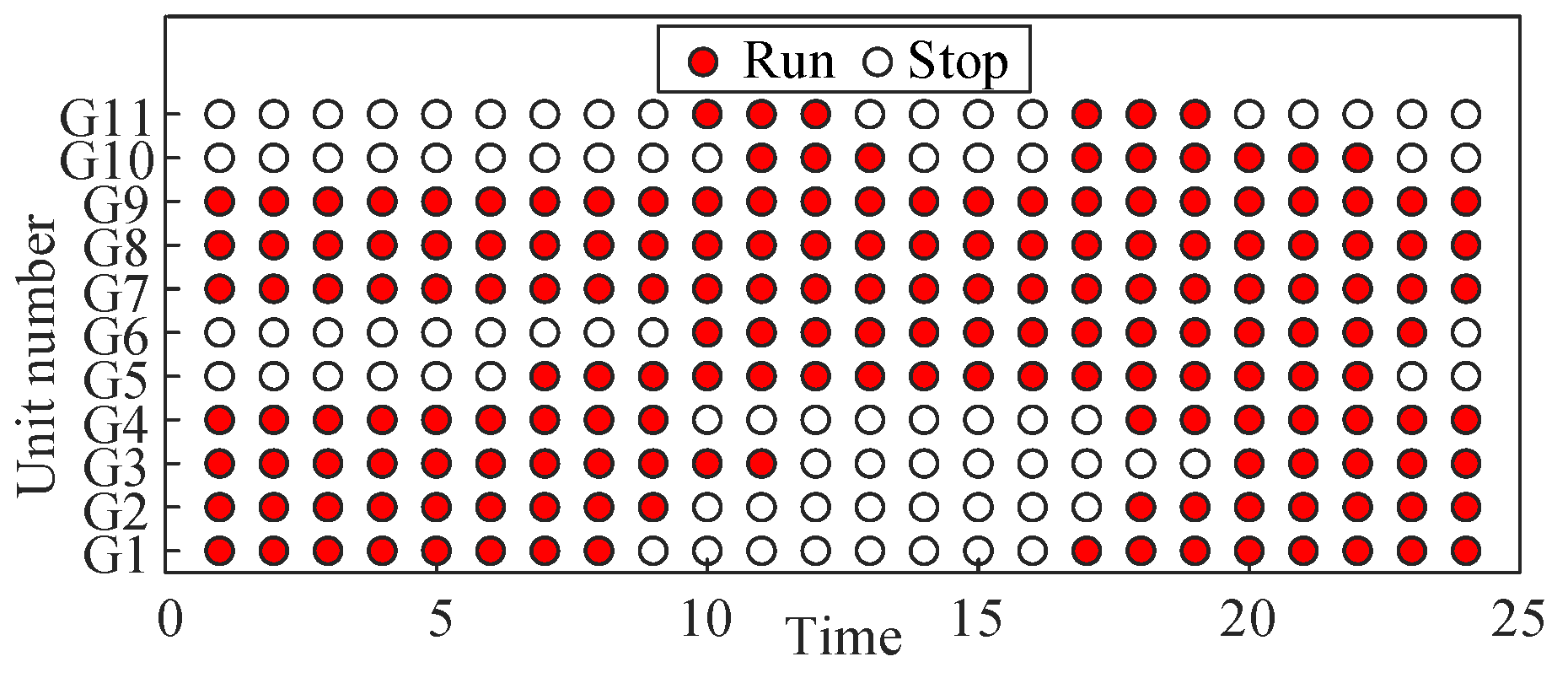
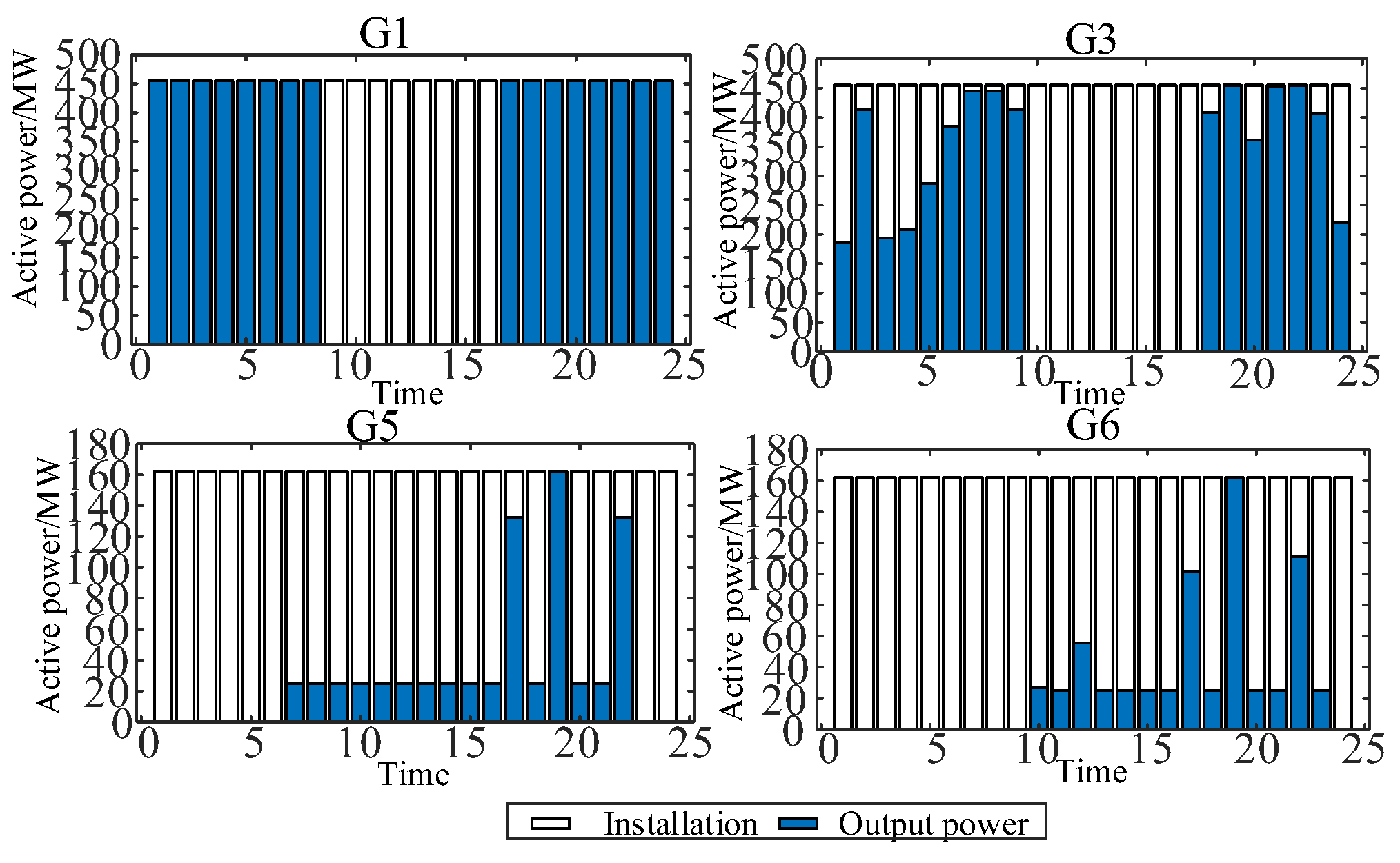
Moreover, by integrating the operational status and output outcomes of each thermal power unit depicted in Figure 8 and Figure 9, it is evident that during the time intervals of 0-10 and 17-24 hours, thermal power units G1-G4 are in operation. Conversely, during the period of 10-17 hours, units G5, G6, G10, and G11 are active. The operational state of these units is predominantly influenced by their operating cost coefficients. Consequently, during the time slots of 0-10 and 17-24 hours, reliance primarily rests on thermal power units G1-G4 to furnish reserves for managing uncertainties in new energy output; whereas during the period of 10-17 hours reliance mainly shifts to G5, G6, G10, and G11 for providing upward ramping reserves.

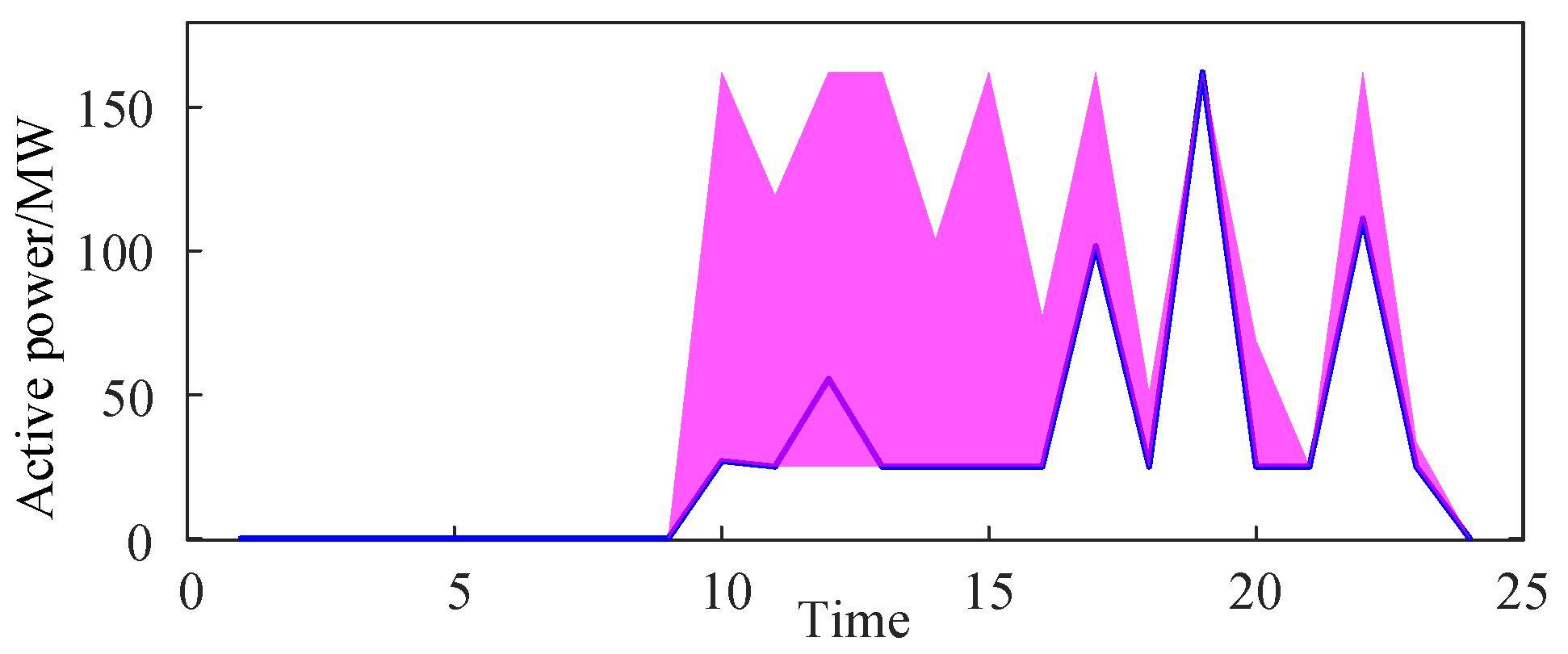
For instance, during the 10-17 time period, the active power generated by thermal power units G5 and G6 is notably below their installed capacity. Consequently, they are able to provide a higher upward ramping reserve capacity. The output and reserve capacity configuration of unit G6 is depicted in Figure 11.

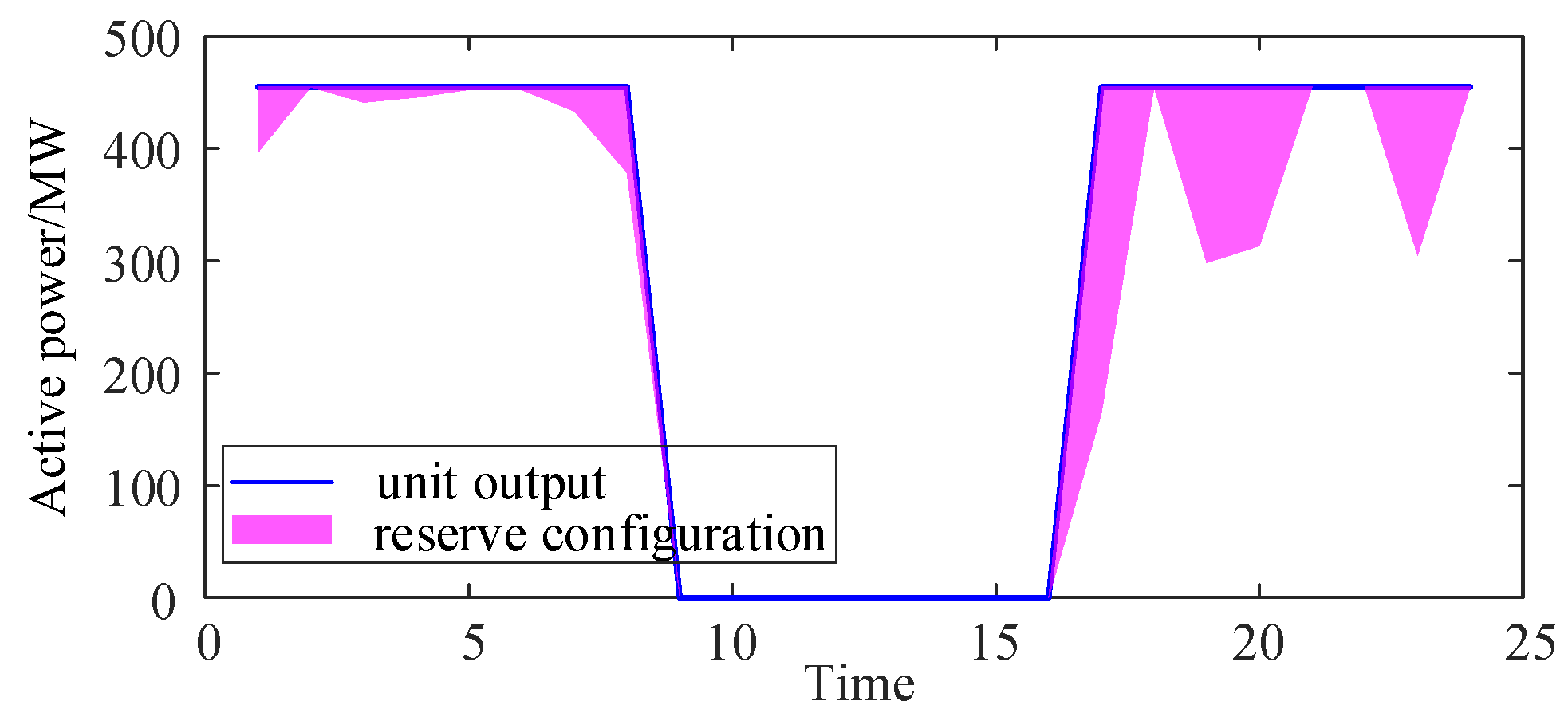
The output and reserve configuration of thermal power unit G1 are depicted in Figure 10. During the peak load period from 17 to 24 hours, in the decision-making process of power system dispatch, G1 operates at full capacity to optimize economic benefits, primarily providing downward ramping reserve capacity.

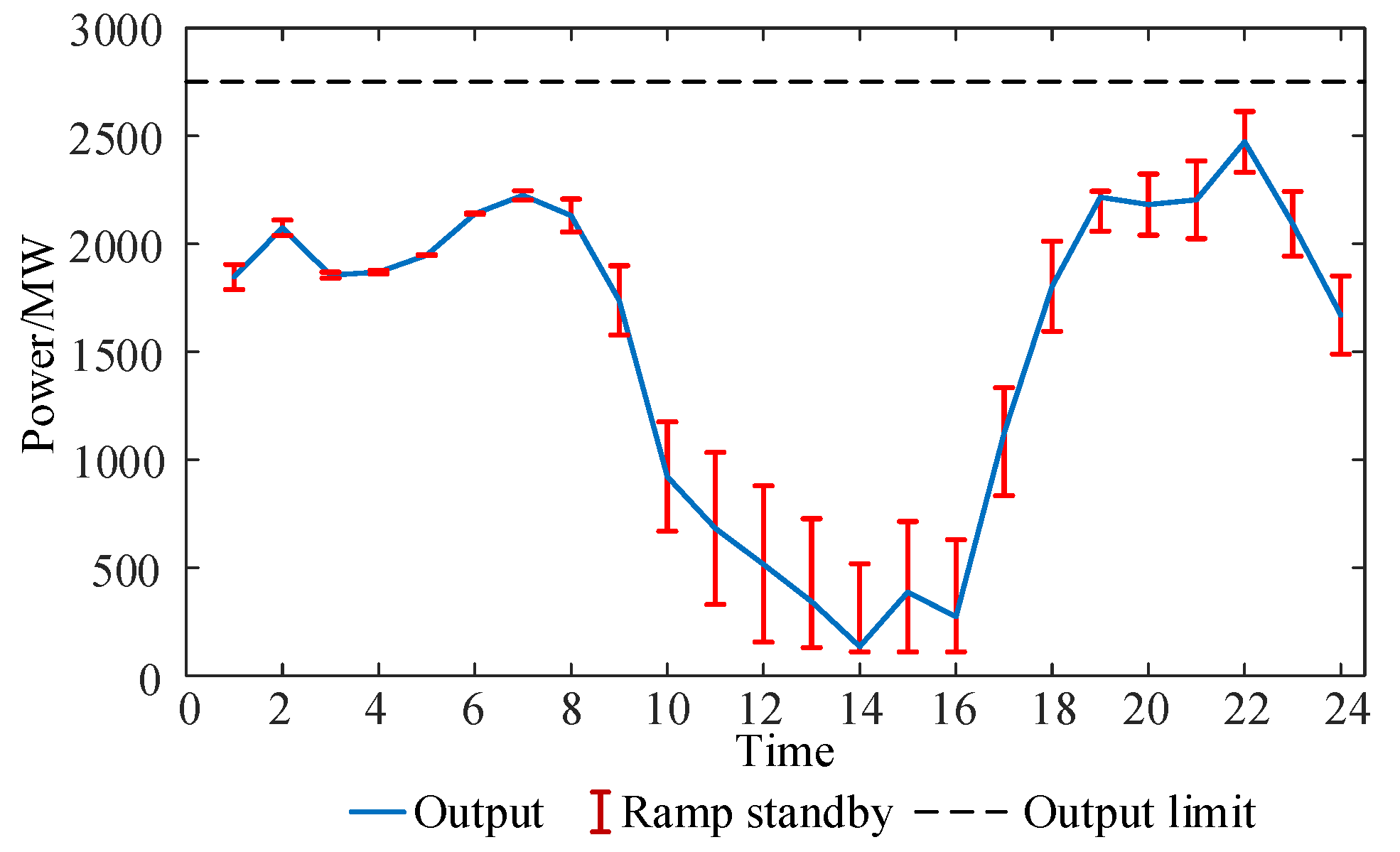
Figure 12 illustrates the correlation between the total output of the power plant and the ramp reserve. During the 1-8 hour period in the early morning, there is minimal fluctuation in the output of new energy sources, leading to a small allocation of reserve capacity by the system. However, during the 9-24 hour period, significant fluctuations in new energy source output necessitate a larger allocation of reserve capacity to manage uncertainty. At 14 hours, when the system's thermal power output reaches its lowest point, it provides ample up reserve capacity but insufficient down reserve capacity.

4.2. Analyzing the Influence of Varying Confidence Levels on Scheduling Outcomes

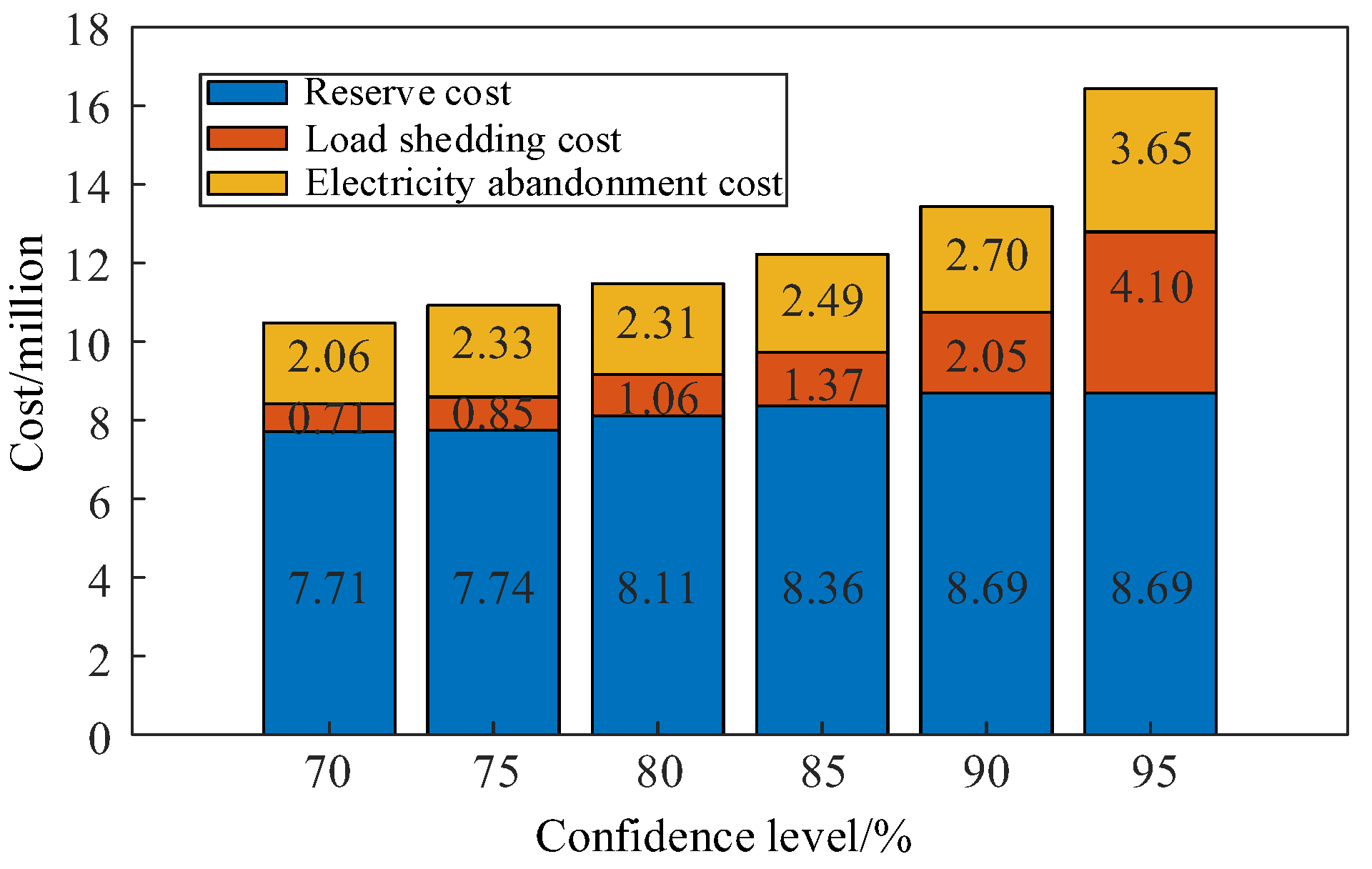
In order to validate the proposed distributed robust coordinated optimization scheduling model under various levels of confidence in load shedding and curtailed wind power risk, this study sets six distinct confidence levels. The corresponding optimized scheduling results are obtained and presented in Figure 13.

Based on Figure 13, it is evident that as the confidence level increases while maintaining the same thermal power regulation capacity, the associated risks also escalate. The expenses related to curtailed wind power and load shedding gradually mount. At a confidence level of 95%, the costs for curtailed wind power and load shedding amount to 36,500 yuan and 41,000 yuan respectively.

The higher the confidence level, the greater the need for adjustable resources that the system must allocate in order to manage fluctuations in new energy power and mitigate uncertainty at its source. Simultaneously, system reserve costs also increase as confidence levels rise, reaching 86,900 yuan when the confidence level is 95%.

To assess the scheduling performance of the proposed distributed robust coordinated optimization scheduling model under various levels of fuzzy set confidence, this study establishes six distinct fuzzy set confidence levels. The corresponding optimized scheduling results are computed and presented in Figure 14.

Based on the findings illustrated in Figure 14, it is evident that a higher fuzzy set confidence level corresponds to a larger Wasserstein ball radius and increased uncertainty in new energy output. Consequently, as the fuzzy set confidence level rises, so does the expected cost of tail risk for the system. At a 95% confidence level, the costs of curtailment and load shedding are RMB 36,500 and RMB 41,000 respectively.

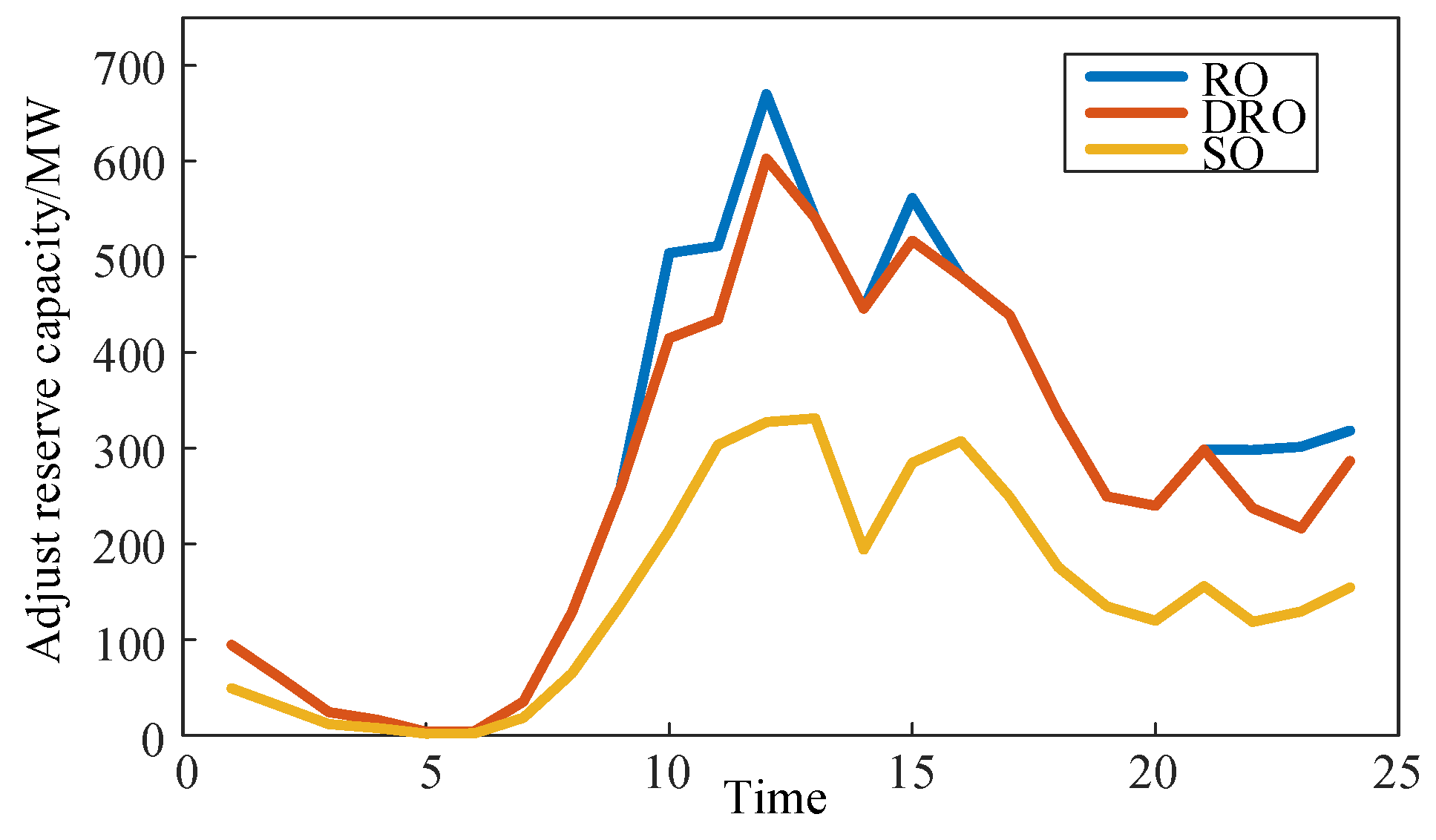
4.3. Analyzing Scheduling Outcomes Employing Various Optimization Techniques

The distributed robust optimization method proposed in this paper is further compared with the robust optimization method and stochastic optimization. In the robust optimization method, the new energy output error at each time is used as the boundary of the sample for new energy output errors at each time; in distributed robust optimization, a conditional risk confidence level of β=80% and a fuzzy set confidence level of η=95% are set; for the stochastic optimization model, the confidence parameter value is set to

β (—)

=80%. Subsequently, based on historical empirical distribution of wind and solar power output errors, 2000 samples are randomly generated to simulate external random scenarios for experimentation. The curtailment probability and load shedding probability for each optimization method are then statistically analyzed. The results of these three methods are presented in Table 2, while adjustments made for reserve allocation are illustrated in Figure 15.

According to Table 2, it is evident that the distributed robust optimization method based on conditional value-at-risk proposed in this paper has led to an approximate increase of 81.4% and 0.7% in total ramping requirements and total scheduling costs respectively, compared to the stochastic optimization method. However, it has significantly reduced the probabilities of load shedding and curtailment. In contrast, while the robust optimization method can further reduce supply-demand balance risk, it also results in an approximately 7.2% increase in total ramping requirements compared to our proposed approach. The comparative results suggest that our proposed method effectively balances safety and economic demands by enhancing optimization robustness without incurring excessive additional costs due to overly conservative measures.

5. Conclusions

In order to effectively evaluate the potential risk of power and energy balance disruption resulting from the variability of wind and solar power generation, as well as mitigate the likelihood of curtailment and supply shortages in modern power systems, this study introduces a probabilistic index for assessing power and energy balance risk based on conditional value at risk (CVaR) theory. Additionally, it develops a robust optimization dispatch model that incorporates flexible ramping reserves from coal-fired power plants. The key findings are as follows,

Tailored safety and economic risk indicators for modern power systems' power and energy balance have been proposed, which can be used in scheduling decisions to achieve operational equilibrium between safety and economic risks.
By fully considering the flexible ramping reserves provided by coal-fired power plants, the results of probabilistic risk assessment can guide the rational planning of flexible resources such as energy storage and demand-side response within the system.

Author Contributions

Conceptualization, Q.J.; methodology, J.S. and Q.J.; software, L.Z.; validation, L.Z.; formal analysis, J.S.; investigation, J.S. and Y.G.; resources, L.Z. and L.L.; data curation, Y.G.; writing—original draft preparation, J.S.; writing—review and editing, Q.J. and L.L; visualization, Q.J. and L.H.; supervision, L.H. and L.L.; funding acquisition, J.S and L.L. All authors have read and agreed to the published version of the manuscript.

Funding

The authors greatly acknowledge the financial support from the Science and Technology Project of State Grid Jiangsu Electric Power Co., Ltd (Grant No. Research on supply and demand assessment and auxiliary decision-making technology in complex scenarios of new power system J2023115).

Data Availability Statement

The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author/s.

Acknowledgments

This work was supported by the Science and TechnologyProject of State Grid jiangsu Electric Power Co. Ltd (Grant No. Research on supply and demand assessment and auxiliary decision-making technology in complex scenarios of new power system J2023115).

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

Figure A1. Improved IEEE118 node wiring diagram.

Table A1. Thermal power unit parameters.

Unit number	Access node	a_i/(CNY/MW².h)	b_i/(CNY/MWh)	c_i/(CNY/MW.h)	r_i^up、r_i^down/(MW/h)	$P_{G i . \max}$ /MW	$P_{G i . \min}$ /MW	T_i^on、T_i^off/h
G1	10	0.003264	110.092	6800	200	455	150	8
G2	12	0.003264	110.092	6800	200	455	150	8
G3	26	0.002108	117.368	6596	200	455	150	8
G4	46	0.002108	117.368	6596	200	455	150	8
G5	49	0.027064	133.96	3060	100	162	25	6
G6	59	0.027064	133.96	3060	100	162	25	6
G7	61	0.014348	112.2	4624	80	130	20	5
G8	66	0.0136	112.88	4760	80	130	20	5
G9	80	0.0136	112.88	4760	80	130	20	5
G10	87	0.048416	151.368	2516	72	80	20	3
G11	89	0.005372	188.632	3264	80	85	25	3

References

National Energy Administration The National Energy Administration released the statistical data of the national power industry in 2023 [EB/OL] [2024-01-26]. https, //www.nea.gov.cn/2024-01/26/c_1310762246.htm.
LIU chun, HUANG yuehui, SHI wenhui, et al. Production simulation of new energy power system [M]. Beijing, China Electric Power Press, 2019.
ZHUO Zhenyu, ZHANG Ning, XIE Xiaorong, et al. Key Technologies and Development Challenges of High Ratio Renewable Energy Power Systems [J]. Autom. Electr. Power Syst. 2021, 45, 171–191. [Google Scholar] [CrossRef]
CHEN Guoping, DONG Yu, LIANG Zhifeng．Analysis and reflection on high-quality development of new energy with Chinese characteristics in energy transition[J]．Proc. CSEE 2020, 40, 5493–5505.
WEI Lisen, AI Xiaomeng, FANG Jiakun, et al．Review on applications and solving techniques of time series production simulation for new power system [J]．Autom. Electr. Power Syst. 2024, 1–19.
CHEN Dian, LU runzhao, ZHANG songtao, et al. Review of power and electricity balance calculation and analysis technology of new power system [J]. power grid technology 2023, 47, 3952–3970. [Google Scholar]
TAN yongcai. Power system planning and design technology [M]. Beijing, China Electric Power Press, 2012.
LI Chenghao, ZHANG Jiawei, YAO Degui, et al．Power balance method of provincial power system with complex generation structure[J]. High Volt Eng. 2023, 1–17.
LI Mingjie, CHEN Guopin, DONG Cun et al．Research on Power Balance of High Proportion Renewable Energy System[J]. Power Syst. Technol. 2019, 43, 3979–3986.
REN Jing, GAO Min, CHENG Song, et al．A Balance Method for Power Supply-Demand Adapting to High Uncertainties of Renewable Energy in Northwest Power Grid. Electr. Power 2023, 56, 66–78.
Wang J, Shahidehpour M, Li Z．Security-constrained unit commitment with volatile wind power generation. IEEE Trans. Power Syst. 2008, 23, 1319–1327. [CrossRef]
Wang C, Fu Y．Fully parallel stochastic security-constrained unit commitment. IEEE Trans. Power Syst. 2016, 31, 3561–3571. [CrossRef]
Power planning decision support system gopt. Beijing, Tsinghua University, 2005-01-01.
LU Gang, R&D and application of full scenario power planning and operation decision-making platform (GEsP, Neos software system), Beijing, State Grid Energy Research Institute Co., Ltd., June 23, 2021.
ZHANG Ningyu, GAO Shan, ZHAO Xin．An unit commitment model and algorithm with randomness of wind power. Trans. China Electrotech. Soc. 2013, 28, 22–29.
WANG Jun, XU Jian, WABG Jingjing, et al．Bi-level Stochastic Optimization for A Virtual Power Plant Participating in Energy and Reserve Market Based on Conditional Value At Risk. Power Syst. Technol. 2024, 1–13.
JIANG Zhnegting, WANG Jianxue, XIAO Yunpeng, et al．Market Clearing Model and Pricing Methods Based on Two-stage Stochastic Optimization of Energy and Deep Peak Shaving Regulation Transactions[J]．Power Syst. Technol. 2023, 47, 3597–3613.
ZHOU Lihong, YU Hao, LI Peng, et al．Stochastic Robust Operation Optimization for Park-level Integrated Energy System in Multi-stakeholder Market. 2023, 47, 100–109.
ZHOU Bo, AI Xiaomeng, FANG Jiakun．Continuous time modeling based robust unit commitment considering beyond-the-resolution wind power uncertainty. Trans. China Electrotech. Soc. 2021, 36, 1456–1467.
ZHENG Liqin, XIE Dongmei, BAI Xiaoqing．Robust optimal power flow based on Predictive & Prescriptive framework[J]. Electr. Power Autom. Equip. 2023, 43, 175–181.
YANG Hongming, YI Bangzhe, MENG Ke, et al．Distributed Robust Optimal Scheduling of the New Interconnected Power System with the Inter-province and Intra-province Considering Moment Uncertainty of Source Load Power. Electr. Power Constr. 2023, 44, 98–110.
WANG Haoyuan, BIE Chaohong．Distributionally robust economic dispatch of flexible ramping reserve considering physical boundaries of uncertainty[J]. Autom. Equip. 2023, 43, 59–68.
YE Xi, LU Zongxiang, Qiao Ying, et al．Time-varying probabilistic model and dispatch performance indices for wind farm cluster virtual power generator—Part II, dispatch performance indices[J]. Proc. CSEE 2015, 35, 5395–5404.
Yang Y, Wu W．A distributionally robust optimization model for real-time power dispatch in distribution networks[J]. IEEE Trans. Smart Grid 2018, 10, 3743–3752. [CrossRef]
Zheng X, Chen H, Xu Y, et al．A mixed-integer SDP solution to distributionally robust unit commitment with second order moment constraints[J]. CSEE J. Power Energy Syst. 2020, 6, 374–383. [CrossRef]
ZHANG Yuchao, WU Wenchuan, Li Zhengshuo, et al．Hierar-chical load shedding method considering influence of distributed generat tors[J]. Power Syst. Technol. 2019, 43, 998–1005.
Zhao Chaoyue, Guan Yongpei．Data-driven risk-averse stochastic optimization with wasserstein metric. Oper. Res. Lett. 2018, 46, 262–267. [CrossRef]

Figure 1. Net load forecasting error distribution and reserve shortage probability of each hour on one day.

Figure 2. Power and energy balance risk diagram.

Figure 3. System voltage level at a given time.

Figure 4. The optimization outcomes of the uphill reserve capacity for each thermal power unit.

Figure 5. The risk assessment of power outages during load shedding in each time period.

Figure 6. The optimization outcomes of the downhill reserve capacity for each thermal power unit.

Figure 7. The conditional risk assessment of decommissioned power in each time period.

Figure 8. The operational status of each thermal power unit.

Figure 9. The active output of each thermal power unit.

Figure 10. The output and reserve configuration of the thermal power G1.

Figure 11. The output and reserve configuration of the thermal power G6.

Figure 12. The aggregate production of thermal power units and the overall allocation of climbing reserve capacity.

Figure 13. System operating cost at different confidence levels.

Figure 14. System operating cost at different confidence levels of wasserstein.

Figure 15. Multiple uncertainty optimization methods to adjust standby capacity curves.

Table 1. The main adjustable resources and adjustment demand sources of high proportion of new energy system.

Interconnection	Adjustable resources	Adjust the source of demand
Mains side	Thermal power and hydropower	New energy output prediction error
Load side	Adjustable load	Non-adjustable load
Energy storage side	Short-term and long-term energy storage	/

Table 2. Optimization results of different uncertainty optimization methods.

Case	Costs of scheduling/Ten thousand yuan	Reserve requirements on/MW	Reserve requirements under/MW	Electricity abandonment probability/%	Load shedding probability/%	Expected to discard electricity/MWh	Expected load shedding/MWh
RO	560.00	3661.48	3161.74	0.38	2.25	45.48	3.16
SO	555.09	1860.27	1649.25	9.13	11.46	104.84	63.38
RSO	559.38	3656.45	2711.23	0.46	2.83	50.98	3.24

Disclaimer/Publisher’s Note, The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Probabilistic Power and Energy Balance Risk Scheduling Method Based on Distributed Robust Optimization

Abstract

0. Introduction

1. Assessment of Probabilistic Power and Energy Balance Characteristics and Risk Indicators for Supply-Demand Equilibrium

1.1. Analysis of Probability Balance Characteristics

1.2. Indicators of Supply and Demand Equilibrium Risk

2. Probabilistic Balancing Analysis Model for New Energy Power Systems Based on Distributed Robust Optimization

2.1. A New Energy Power System Balance Analysis Model Based on Risk Assessment Indicators

2.2. Wasserstein Fuzzy Sets for Characterizing Uncertainty in Wind and Solar Resources

3. Transformation of the Model

3.1. Linearization of Trends

3.2. The Dual Transformation of a Distribution Robust Model

4. Simulation Study

4.1. Systematic Probabilistic Analysis of Supply and Demand Balance

4.2. Analyzing the Influence of Varying Confidence Levels on Scheduling Outcomes

4.3. Analyzing Scheduling Outcomes Employing Various Optimization Techniques

5. Conclusions

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

Appendix A

References

MDPI Initiatives

Important Links

Subscribe