Prerpints.org logo
Preprint
Article

Modulating Pain Signaling: The Impact of Tefluthrin, Telmisartan, and KB-R7943 on Voltage-Gated Na+ Currents

Altmetrics

Downloads

64

Views

31

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

31 August 2024

Posted:

02 September 2024

You are already at the latest version

Alerts
Abstract
Tefluthrin (Tef) is categorized as a type-I pyrethroid insecticide, telmisartan (Tel) functions as an angiotensin II receptor blocker, and KB-R7943 was identified as an inhibitor of Na+-Ca2+ exchange process. However, the influence of these compounds on the amplitude and gating properties of voltage-gated Na+ current (INa) in neurons associated with pain signaling remains unclear. In cultured dorsal root ganglion (DRG) neurons, whole-cell current recordings revealed that Tef or Tel increased the peak amplitude of INa, concomitant with an elevation in the time constant of INa inactivation, particularly in the slow component. Conversely, exposure to KB-R7943 resulted in a depression in INa, coupled with a decrease in the slow component of the inactivation time constant of INa. Theoretical simulations and bifurcation analyses were performed on a modeled interneuron in the spinal dorsal horn. The occurrence of INa inactivation accentuated the subthreshold oscillations (SO) in the membrane potential. With an increase in applied current, SO became more pronounced, accompanied by the emergence of high-frequency spiking (HF) with a frequency of approximately 150 Hz. Moreover, an elevation in INa conductance further intensified both SO and HF. Consequently, through experimental and in silico studies, this work reflects that Tef, Tel, or KB-R7943 significantly impacts the magnitude and gating properties of INa in neurons associated with pain signaling. The alterations in INa magnitude and gating in these neurons suggest a close relationship with pain transmission.
Keywords: 
Subject: Biology and Life Sciences  -   Biophysics

1. Introduction

It is established that nine isoforms, specifically NaV1.1-1.9 (or SCN1A-SCN5A and SCN8A-SCN11A), of voltage-gated Na+ (NaV) channels are distributed in mammalian excitable tissues, encompassing the central or peripheral nervous system, as well as the endocrine or neuroendocrine system (Catterall, 2012; de Lera Ruiz and Kraus, 2015; Shen et al., 2017; Bennett et al., 2019). These NaV channel proteins in eukaryotes have a single subunit, each containing four six-transmembrane pseudomains (Shen et al., 2017).
Upon rapid depolarization, NaV channels, which encode macroscopic voltage-gated Na+ currents (INa), undergo swift transitions from the resting (closed) state to the open state. Subsequently, there is a rapid shift to the inactivated state of the channel (Catterall, 2012; de Lera Ruiz and Kraus, 2015). The inactivation of INa can also accumulate before being triggered during repetitive brief depolarizing pulses (Taddese and Bean, 2002; Carter and Bean, 2011; Huang et al., 2015; Navarro et al., 2020). Once evoked, the increased magnitude of INa can depolarize the cell membrane through a positive feedback cycle, thereby eliciting the upstroke of the action potentials (APs) and governing the amplitude, frequency, and/or pattern of AP firing in different excitable cells such as sensory neurons (Catterall, 2012; de Lera Ruiz and Kraus, 2015; Bennett et al., 2019).
Tefluthrin (Tef) is a synthetic type-I pyrethroid insecticide that is characterized by the presence of a cyano group at the α-position of the alcohol moiety. It is recognized as an activator of INa and a slowing in current inactivation (So et al., 2018; Lin et al., 2022). Permethrin or λ-cyhalothrin, another pyrethroid, has been previously noticed to influence pain signaling (Jiang et al., 2013; Silwal et al., 2023). Telmisartan is a medication belonging to the class of angiotensin II receptor blockers. Despite its primary therapeutic effects on cardiovascular function, there is some evidence to reflect that Tel has additional effects on pain signaling (Hegazy et al., 2020). Whether the presence of Tef or Tel alters the amplitude and gating kinetics of INa in sensory or dorsal root ganglion (DRG) neurons is unclear. Alternatively, KB-R7943, an inhibitor of Na+-Ca2+ exchange process (Schröder et al., 1999; Amran et al., 2003), has been reported to cause antinociceptive effect in neuropathic pain model (Huang et al., 2019; Andreeva-Gateva et al., 2024). However, how KB-R7943 can cause any perturbations on INa linked to nociceptive signaling is unknown.
Therefore, the primary aim of this study was to examine the impact of three compounds―Tef, Tel, and KB-R7943―on cultured dorsal root ganglion (DRG) neurons. Specifically, the investigation focused on determing whether and how these compounds affect the magnitude and gating kinetics of INa. Additionally, a computational model of an interneuron, originally derived from the spinal dorsal horn (Ma et al., 2023), was utilized to investigate the influence of variations in INa inactivation and conductance, both individually and in combination, on dynamic changes in membrane potential. This investigation also employed the generation of bifurcation diagrams (White et al., 1995; Enns-Ruttan and Miurea, 2000; Chang et al., 2018).

2. Materials and Methods

2.1. Chemicals, Reagents, and Solutions Used in This Study

KB-R7943 (2-[2-[4-(4-nitrobenzyloxy)phenyl]ethyl]isothiourea, 2-[4-[(4-nitrophenyl)methoxy]phenyl]ethyl ester carbamimidothioic acid, C16H17N3O3S·CH3SO3H) was acquired from Cayman (Excel Biomedical, Tainan, Taiwan). Ranolazine (Ranexa®) and telmisartan (Micardis®, Tel) were supplied by Tocris (Bristol, UK), while tefluthrin (Tef), tetraethylammonium chloride (TEA), and tetrodotoxin (TTX) were by Sigma (Merck, Taipei, Taiwan).
The extracellular solution, specifically HEPES-buffered normal Tyrode’s solution, had the following compositions (mM): NaCl 136.5, KCl 5.4, CaCl2 1.8, MgCl2 0.53, glucose 5.5, and HEPES 5.5 (pH 7.4). In order to assess macroscopic K+ currents or membrane potential, we utilized a recording electrode filled with a solution containing (in mM): K-aspartate 130, KCl 20, MgCl2 1, Na2ATP 3, Na2GTP 0.1, EGTA 0.1, and HEPES 5 m (pH 7.2). For recording INa, K+ ions within the intracellular solution were substituted with equimolar Cs+ ions, and the pH was then adjusted to 7.2 with CsOH.

2.2. Cell Preparation

The rat dorsal root ganglion (DRG) neurons (neonatal) were high-quality sensory neuron suspension acquired from Lonza Walkersville, Inc. (R-DRG-505; Walkersville, MD) available at https://bioscience.lonza.com/lonza_bs/TW/en/document/27607 (accessed on 15 July 2024). Following the recommended conditions, the cells were cultured using the PNBMTM BulletKitTM (Lonza), which includes a 200 ml bottle of primary neuron basal medium (PNBMTM) and PNGMTM SingleQuotsTM. The cells were incubated at 37 °C in monolayer cultures within a humidified environment containing 5% CO2/95% air. Experiments were conducted five or six days after subculturing the cells, at a confluence of 60-80%.

2.3. Electrophysiological Measurements

Before the experiments, we dispersed DRG neurons using a 1% trypsin/EDTA solution. A small volume of cell suspension was transferred to a specially crafted chamber affixed on the stage of an inverted microscope. Cells were bathed at room temperature (20-25 °C) in the standard Tyrode’s solution. Prior to each measurement, the cells were allowed to settle at the chamber’s bottom. The patch pipettes were fashioned from Kimax®-51 borosilicate glass tube (#DWK34500-99; Kimble®, Merck, Tainan, Taiwan) and polished to attain a resistance ranging between 2 and 4 MΩ. Recordings of INa or other ionic currents were conducted in the whole-cell mode using a modified patch-clamp technique, employing an RK-400 amplifier (Bio-Logic, Claix, France) (Wu and Yu, 2023).
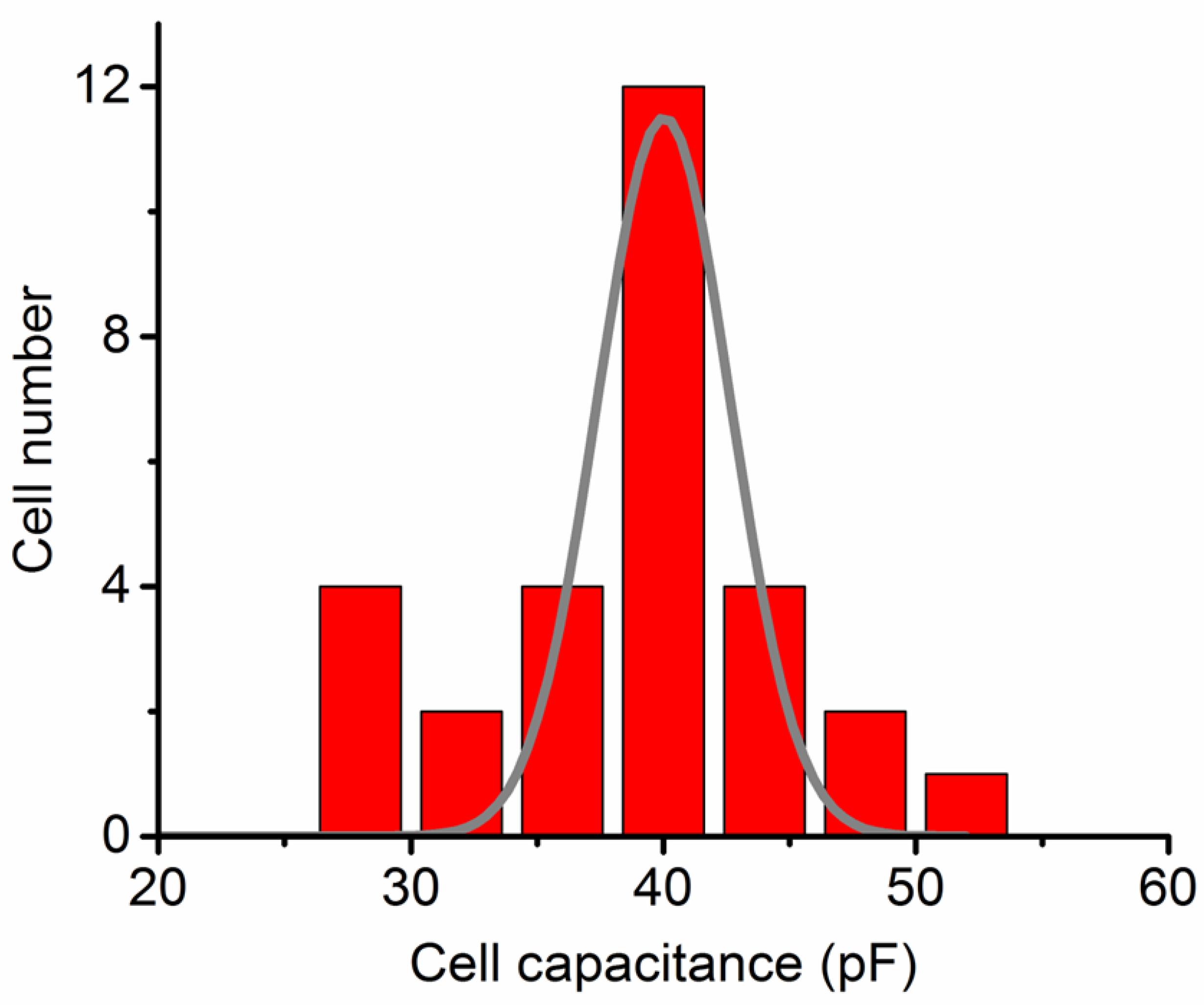
To nullify liquid junction potentials resulting from disparities between the composition of the pipette solution and that of the bath, adjustments were made before giga-Ω formation, and subsequent corrections were applied to the whole-cell data. The capacitive transients induced during INa elicitation were counteracted by applying a hyperpolarizing pulse of equal magnitude. Cell-membrane capacitance of 28-49 pF (37.3 ± 5.6 pF; n = 29) was compensated. Figure 1 illustrates a histogram showing the relationship between cell number and cell capacitance.

2.4. Data Recordings

The data were stored online on a laptop computer at 5 kHz or higher. The computer was equipped with Digidata® 1440A device (Molecular Devices; Bestgen Biotech, New Taipei City, Taiwan), facilitating analog-to-digital and digital-to-analog conversions controlled by pCLAMP® 10.6 (Molecular Devices). Off-line analyses of the acquired signals were performed using various analytical tools, including OriginPro® 2021 (OriginLab Corp.; Scientific Formosa, Kaohsiung, Taiwan), and custom-made macros developed in Excel® 2022 (Redmond, WA).

2.5. Curve-Fitting Procedures for INa Inactivation Time Course

The decay of the inactivation time course of INa is elucidated through a family of exponential functions. This family can be defined as
y t = ∑ i = 1 n A i × e x p − t τ i
Here, y(t) symbolizes the inactivation trajectory of INa over time, and the index i commonly takes on two values corresponding to the fast and slow components in the observed inactivation of INa. The nonlinear curve-fitting was performed to extract the parameters for the fast (τinact(F)) and slow component (τinact(S)) of the inactivation time constant (τinact).

2.6. Statistical Analyses

The experimental results are expressed as the means±SEM with sample sizes (n) indicating the cell number from which the data were taken. The paired or unpaired Student’s t-test and one- or two-way analysis of variance (ANOVA) followed by post-hic Fisher’s least-significant difference test were made for the evaluation of differences among means. Statistical analyses were performed using IBM SPSS Statistics 24.0 (Armonk, New York). The significance was determined at a P value of <0.05.

2.7. Computer Simulations

To explore the influence of changes in the amplitude and/or inactivation characteristics of INa on action potential (AP) firing related to pain signaling, we utilized a theoretical model of AP firing derived previously (Ma et al., 2023). This model is based on the biophysical properties of parvalbumin-expressing interneurons (PVINs) situated within the dorsal horn of the spinal cord. Voltage-gated Ca2+ current with concurrent changes in intracellular Ca2+ concentrations ([Ca2+]i) were also included in the model (Brown, 2003; Ma et al., 2023). The detailed descriptions of the modeled neuron were provided previously (Ma et al., 2023). The mathematical model is given by the following:
C m · d V d t = − I N a − I K − I A − I K D R − I l e a k + I a p p x ˙ = x ∞ − x τ x ,   x = m N a , h N a , n K , n A , I A , n K D R , h K D R
To simulate changes in the rate of INa inactivation, we mathematically constructed a modified Hodgkin-Huxley (HH) type model. The detailed framework utilized in this work was previously described (Ma et al., 2023), and the biophysical characteristics of INa were noted to closely resembled those from earlier studies (Wu et al., 2015; Ghovanloo et al., 2024). For INa, the modified HH scheme was used according to the following equation:
I N a = g N a × m ∞ 3 × h × ( V − V N a )
The rate constants for INa activation used in the simulation are described by the following equations (Traub and Miles, 1991; Ma et al., 2023):
m ∞ = 1 1 + e x p V + 17.5 − 11.4
The inactivation variable h in the paper of Ma et al. (2023) satisfies the dynamic equation
d h d t = α h · 1 − h − β h · h ,
where
α h = 0.0025 e x p V − 23 10
β h = 0.094 · ( V + 31 ) 1 − e x p V + 31 − 5.5
Moreover, an arbitrarily incorporated adjustable βh-inactivation parameter of INa, represented as ϕ, was integrated into the simulated neuron to mimic how variations in the inactivation time course of INa and current conductance (gNa) can influence the patterns of subthreshold oscillation (SO) or AP firing. This, in turn, leads to modifications in the bifurcation diagram through AUTO implementation (Winslow, 1989; White et al., 1995; Enns-Ruttan and Miura, 2000; Chang et al., 2018).
In particular, the inactivation parameter of INa used for mimicking the increase or decrease in current inactivation is reformulated by
d h d t = α h · 1 − h − ∅ · β h · h
where h is inactivation gating variable, αh and βh are the rate constants for inactivation gating variable, and the parameter ϕ represents the magnitude of NaV-channel inactivation embedded in the βh inactivation component. As the value of ϕ is decreased, the time course of NaV channel inactivation elicited by membrane depolarization becomes slowed.
For detailed information on other onic currents involved in simulated changes in membrane potential, such as voltage-gated Ca2+ current, KV1.3 K+ current, KV3.1 K+ current, and small-conductance Ca2+-activated K+ current., please refer to the previous work by Ma et al., 2023.

2.8. Numerical Simulation Technique Employed in This Study

The XPPAUT simulation package, accessible at https://sites.pitt.edu/~phase/bard/bardware/xpp/xpp.html (accessed on 2023, Dec 27), was utilized to conduct analyses related to linear stability and bifurcation. The term “bifurcation” refers to points in parameter space where the system undergoes a qualitative change in its dynamics, leading to the emergence of new solutions or the alteration of existing ones (Winslow, 1989; White et al., 1995). XPPAUT, a software tool for simulating and analyzing dynamical systems, provides a platform for conducting bifurcation analyses. The AUTO function in XPPAUT refers to a utility within the software that is used for bifurcation analysis (Winslow, 1989; White et al., 1995; Enns-Ruttan and Miura, 2000; Chang et al., 2018).

3. Results

3.1. Effects of Either Tefluthrin (Tef), Telmisartan (Tel), or KB-R7943 on Voltage-Gated Na+ Current (INa) Measured from Rat Dorsal Root Ganglion (DRG) Neurons

The initial series of experiments aimed to explore the possible impact of Tef, Tel, or KB-R7943 on INa elicited in response to short step depolarizations in these cells. The cells were bathed in Ca2+-free Tyrode’s solution supplemented with 0.5 mM CdCl2 and 10 mM tetraethylammonium chloride (TEA). The whole-cell voltage-clamp experiments were conducted using a pipette solution containing Cs+. As shown in Figure 2, the tested cell was depolarized from -100 to -10 mV for 30 msec, and the INa, which was sensitive to block by tetrodotoxin (1 μM, TTX), could be readily elicited in these neurons. As shown in Figure 2A, further addition of TTX (1 μM) completely blocks the INa amplitude observed during continued exposure to 10 μM Tef.
Upon exposure to Tef or Tel exhibited an enhancement in the peak amplitude of INa, accompanied by a progressive slowing of the inactivation time course of the current (Figure 1A,B). For instance, during a step depolarization from -100 to -10 mV, the addition of Tef (10 μM) or Tel (10 μM) increased the peak INa amplitude from 1.3 ± 0.3 to 2.2 ± 0.8 nA (n = 8, paired t-test, df = 7, P = 0.031) or from 1.1 ± 0.3 to 2.2 ± 0.9 nA (n = 8, paired t-test, df = 7, P = 0.032), respectively. After washout of Tef or Tel, INa amplitude returned to the control level. Additionally, during cell exposure to 10 μM Tef or 10 μM Tel, the slow component of the inactivation time constant of INa (τinact(S)) was prolonged, shifting from 12.1 ± 1.9 to 28.2 ± 2.1 msec (n = 8, paired t-test, df = 7, P = 0.023) and from 12.2 ± 2.0 to 27.4 ± 2.1 msec (n = 8, paired t-test, df = 7, P = 0.024), respectively. However, the value in the fast component of the inactivation time constant (τinact(F)) obtained in the presence of Tef or Tel was not changed (n = 8, paired t-test, df = 7, P = 0.063). Furthermore, when cells were exposed to 10 μM KB-R7943, the peak INa amplitude decreased, accompanied by a concurrent reduction in the τinact(S) value of the current (Figure 2C). The presence of 10 μM KB-R7943 significantly decreased the peak INa amplitude from 1.76 ± 0.05 to 1.51 ± 0.04 nA (n = 8, paired t-test, df = 7, P = 0.028). Concurrently, the value of τinact(S) decreased from 6.1 ± 0.2 to 2.1 ± 0.1 msec (n = 8, paired t-test, df = 7, P = 0.030). However, the τinact(F) value obtained with or without the KB-R7943 presence remained unaltered. We isolated neurons from the dorsal horn of the spinal cord in rats and found that Tef enhanced the INa amplitude. When cells were exposed to Tef (10 μM) the peak amplitude of INa increased from 0.45 ± 0.02 to 0.67 ± 0.03 nA (n = 6, paired t-test, df = 5, P = 0.039). Additionally, the inactivation time constant (τinact(S)) increased from 4.5 ± 0.1 to 8.9 ± 0.2 msec (n = 6, paired t-test, df = 5, P = 0.021).

3.2. Simulated INa Traces Created from a Modified Hodgkin-Huxley (HH) Model

In our endeavor to replicate the impact of Tef, Tel or KB-R7943 on INa in cultured DRG neurons, we undertook a detailed exploration into the modulation of both INa amplitude and gating. This work aimed to elucidate the influence on the electrical properties of neurons related to nociceptive signaling. The INa model employed in these simulations was developed based on a modified HH model (Wu, 2004; Chen et al., 2010; Chang et al., 2018; Ma et al., 2023). In this series of simulations, the values of gNa and VNa were set to be 120 nS and +58 mV, respectively. Other parameters are outlined in Table 1 and a recent paper (Ma et al., 2023).
Under the specified conditions, when the ϕ value, particularly within the βh inactivation component of h inactivation variable, was increased in a stepwise fashion, the inactivation time course of the simulated INa progressively became enhanced. This was accompanied by a reduction in the late component of INa during rapid step depolarization. It is established that a stepwise increase of the ϕ value (from 0.4 to 1.2) embedded in h inactivation variable is capable of increasing the inactivation rate of the current with a reduction in the sustained component of INa (Figure 3), although the amplitude in the transient component of the current was slightly changed. Therefore, the simulated INa trajectories within this modeled neuron aligned closely well with the experimentally observed results showing that the presence of Tef, Tel, or KB-R7943 altered the inactivation time course of this current in cultured DRG neurons (Figure 2).

3.3. Changes of Membrane Potential Caused by Different Value of ϕ

The variations in membrane potential resulting from different ϕ values were further investigated. In Figure 4A, ϕ was set at 1.0, with gNa and the applied current (Iapp) set at 400 nS and 300 pA, respectively, and the resulting changes in membrane potential were plotted over time. Under these simulations, a transient oscillatory spike followed by subthreshold oscillations (SOs) was observed. Notably, the amplitude and frequency of action potentials (APs) exhibited progressive decreases, indicative of spike-frequency adaptation (Chiesa et al., 1997; Wu et al., 2012). The emergence of SOs, as previously observed in interior olive neurons (Schweighofer et al., 1999), was evident.
However, when the gNa value was decreased 300 nS while maintaining the same values for Iapp and ϕ, both the amplitude and frequency of APs in response to current injection were reduced. Following the cessation of APs, the occurrence of SO was also observed (Figure 4B). Findings from these results highlight that changes in gNa alone can alter the electrical behavior of this modeled neurons.

3.4. Relationship of Changes in Steady-State Membrane Potential versus the Iapp Value

In this study, a bifurcation analysis was employed to explore alterations in the steady-state membrane potential in response to variations in the applied current (Iapp). A bifurcation diagraph is a graphical representation of the long-term behavior of a dynamical system as a parameter is changed (White et al., 1995; Schweighofer et al., 1999; Chang et al., 2018). Through these simulations, Iapp was considered a variable, while other parameters were maintained at default values (Table 1). With a constant value of ϕ set to 1, Figure 5 depicts the bifurcation diagram illustrating the correlation between Iapp and the change in membrane potential. Two critical values of Iapp, representing the subcritical and supercritical bifurcation points, were identified. Specifically, the Iapp values for these points at ϕ = 1 were noted to be 88 and 177 pA. Within the range of Iapp values between these two Hopf bifurcation points, a stable limit cycle emerged―a closed trajectory in the phase plane, indicating the SO occurrence in the modeled neuron, as demonstrated previously (White et al., 1995; Schweighofer et al., 1999). The range of membrane potential changes were found to be between -39.3 and -36.2 mV. The model therefore exhibits stability when Iapp is below the subcritical point or above the supercritical point. Conversely, self-sustained periodic oscillations, or SOs, occur when Iapp falls within the range between the subcritical and supercritical points.
However, a notable alteration in the bifurcation diagraph occurred when the ϕ value in the βh inactivation process of h inactivation variable decreased to 0.8 with a fixed gNa value of 300 nS, mimicking a slowing in the inactivation time course of INa (Figure 6A,B). Under these conditions, two types of periodical solutions were observed. The subcritical and supercritical points, determining the occurrence of preexisting SO, increased to 95 and 367 pA, respectively. Additionally, another phenomenon, namely somatic spiking (SS) or somatic AP firing, was noted during the existence of Iapp ranging between 52 and 98 pA. Within the domain of SS, the voltage of membrane potential was found to range between -40 and +15 mV. It is also noted from Figure 6B that as the SO domain overlapped with SS, the cell behavior was denoted to be SS/SO bistable in the system, when the Iapp amplitude ranged between 79 and 118 pA.

3.5. Further Modifications on Changes in Membrane Potential with the Increasing Iapp Value with a Fixe ϕ Value of 0.8

We made further adjustments to investigate how an additional large increase in Iapp amplitude, with the fixed ϕ and gNa values of 0.8 and 300 nS, influences changes in membrane potential, INa, and intracellular Ca2+ levels ([Ca2+]i) in the modeled neuron. As depicted in Figure 7A–C, setting the Iapp value of 700 pA resulted in high-frequency spiking (HS) of APs at a rate of 150 Hz. The membrane potential during this HS spiking exhibited periodical fluctuations with the range of -39 to +18 mV. Moreover, when HS occurred, the height of the AP gradually decreased over time, accompanied by a reduction of INa amplitude. This phenomenon corresponds to previous experimental reports, showing an accumulation of INa inactivation when excitable cells are subjected to high-frequency depolarizing stimuli (Taddese and Bean, 2002; Carter and Bean, 2011; Huang et al., 2015; Navarro et al., 2020). Alternatively, the [Ca2+]i level rose during AP firing. Over the 700-msec duration of Iapp, the [Ca2+]i level concurrently increased from 1.11 to 1.42 μM.

3.6. Bifurcation Analysis on the Relationship between Iapp and Membrane Potential at the Range between 0 and 1200 pA

As demonstrated in Figure 8, the bifurcation diagram, which illustrates the relationship between Iapp magnitude and membrane potential, was further examined. Three distinct periodic solutions, highlighted in red, are evident within the system. In these simulations, with gNa set at 300 nS and ϕ at 0.8, a gradual increase in Iapp amplitude within the 560 to 910 pA range leads to another self-sustained periodic solution of the system. That is, there appeared to be another closed trajectory in this phase plane. This result indicates the emergence of high-frequency spiking (HS), with a rate reaching 150 Hz (Figure 8). Notably, when both the inactivation time course of INa slowed down and the amplitude of Iapp were concurrently increased within the range of 560 to 910 nA, the modeled neuron became more predisposed to generate HS, namely high-frequency AP firing. Changes in membrane potential were noted to range between -35 and +4 mV during the HS occurrence in the bifurcation diagram. It is thus noted that as the gNa value increased to 400 nS, the range of limit cycles generated by both SO and HS was noted to increase. Moreover, the pattern of SO was noticeably amalgamated with that of HS, as observed in Figure 9, in comparison to the bifurcation diagram in Figure 8. Therefore, simulated alterations in both the INa amplitude and the inactivation time course of the current, as observed experimentally in the presence of Tef or Tel, makes the membrane potential susceptible to SO occurrence and even the HS emergence. Additionally, as found during cell exposure to KB-R7943, both decrease in INa amplitude and the inactivation time course of this current are anticipated to diminish the emergence of SO (subthreshold oscillation) or HS (high-frequency spiking).

4. Discussion

The results of this study demonstrate that in the presence of tefluthrin (Tef), telmisartan (Tel), or KB-R7943, the amplitude and gating of voltage-gated Na+ current (INa) in cultured dorsal root ganglion (DRG) neurons was affected. Tef or Tel increased the amplitude of INa while slowing down the inactivation time course of this current. The impact of Tel on INa is related to its effect on NaV channels and is not associated with its antagonistic action against angiotensin II receptors (Chang et al., 2018; Hegazy et al., 2020). Furthermore, in addition to suppression of the Na+-Ca2+ exchanging process (Schröder et al., 1999; Amran et al., 2003), KB-R7943 also inhibited the magnitude of INa while simultaneously accelerating the inactivation rate of INa in cultured DRG neurons.
This study shows that the presence of INa can be detected in cultured DRG neurons. However, these INa currents are blocked by tetrodotoxin (TTX). In these cells, we did not observe clear TTX-resistant (TTX-R) INa (Roy and Narahashi, 1992; Lee et al., 2003). The NaV1.6, NaV1.7, NaV1.8, and NaV1.9 isoforms were noticed to be expressed in DRG neurons. It is thus possible that the NaV1.8 expression in these cells (R-DRG-505 cells) could be relatively low (Szulczyk et al., 2022). However, we did observe that the current was enhanced by Tef or Tel and inhibited by KB-R7943, as reported previously (Kim et al., 2012; Chang and Wu, 2018; Chang et al., 2018; Lai et al., 2020; Lu and Wu, 2023). Additionally, the inactivation time course of these currents was also altered by these drugs (Figure 1). Our in silico study proposed that the inactivation time course of INa (indicated by the variable ϕ value), which is activated at depolarized potentials, contribute to the presence, amplitude and frequency of subthreshold oscillation (SO) and high-frequency spiking (SS) (White et al., 1995; Schweighofer et al., 1999; Taddese and Bean, 2002; Lee et al., 2003).
In our cultured DRG neurons, namely R-DRG-505 cells, we employed current-clamp voltage recordings to observe changes in membrane potential. However, we were unable to detect high-frequency spiking. Even in the presence of Tef or Tel, high-frequency spiking did not manifest. However, through our investigations using modeled interneurons in spinal dorsal horn (Ma et al., 2023), we found that enhancing the INa and slowing down the inactivation time course can simulate the exposure to Tef or Tel. The simulations suggest that these modeled neurons can generate SO and HS. Furthermore, when subjected to strong applied currents, HS with a rate of about 150 Hz was found to develop. The theoretical analyses of these scenarios are presented in the bifurcation diagrams provided herein.
In the modeled interneuron of this study, there were no parameters for the Na+-Ca2+ exchanging process. However, with the generation of AP firing, the level of [Ca2+]i also increased, as demonstrated in Figure 6C. Therefore, at least in excitable cells such as neuronal cells, changes in the magnitude of INa or the inactivation time course of the current might affect the level of [Ca2+]i without the need for the participation of the Na+-Ca2+ exchanging process. Indeed, KB-R7943, an inhibitor of Na+-Ca2+ exchanging process (Amran et al., 2003; Huang et al., 2019), was reported to inhibit the INa responsible for these effects (Wu and Yu, 2023).
Previous reports have indicated that ranolazine, a blocker of late INa, has an inhibitory effect on the INa in DRG neurons, concurrently demonstrating relief in painful sensations (Gould et al., 2014; Wu et al., 2015; Gould and Diamond, 2016). This study confirms this phenomenon and additionally reveals that KB-R7943, an inhibitor of Na+-Ca2+ exchanging process, can inhibit INa magnitude while accelerating the inactivation time course of the INa, as described recently (Wu and Yu, 2023). Therefore, KB-R7943 may alleviate a certain type of pain signaling (Huang et al., 2019). Furthermore, further investigations are needed to explore how Tef or Tel influences the biophysical properties of INa in DRG neurons or sensory neurons associated with pain signaling, consequently modulating the nociceptive transmission (Jiang et al., 2013; Castellanos et al., 2018; Karádi et al., 2023; Silwal et al., 2023).
The results of this study demonstrated that when the INa in DRG neurons increased and its inactivation time course simultaneously slowed down, as mimicked by the presence of Tef or Tel, the cell membrane of these neurons is prone to generating the occurrence of SO. Moreover, excessive stimulation with strong electrical currents easily induced the HS emergence. Conversely, when INa decreased and the inactivation time course accelerated (as mimicked by cell exposure to KB-R7943), these cells were less likely to exhibit the pattern of SOs and even resulted in the HS development (White et al., 1995; Schweighofer et al., 1999; Chen et al., 2010; Ma et al., 2023). Therefore, alterations in the biophysical properties of INa impact the cell excitability of DRG neurons in vivo, subject to biophysical, pharmacological, or toxicological modulation of INa.
The modeled neuron used in this study includes two types of different delayed-rectifier K+ currents, namely KV1.3 and KV3.1 currents (Ma et al., 2023). Previous reports have indicated that changes in the magnitude and inactivation process of these K+ currents significantly impact the HS emergence (Klemic et al., 2001; Lin et al., 2008; Wang et al., 2008; Wu et al., 2008; Hsiao et al., 2022). KCNQ channels have been also reported to enable reliable presynaptic spiking occurring at high frequency (Zhang et al., 2022). Therefore, further investigations are needed to understand how the modulation of these K+ currents may have effects on the HS emergence in the presence of Tef or Tel.
In this study, we employed a theoretical model of action potential (AP) firing, which was adapted from a previous study by Ma et al. (2023). This model is based on the biophysical properties of parvalbumin-expressing interneurons (PVINs) located in the dorsal horn of the spinal cord. Although there are some differences between this model neuron and the dorsal root ganglion neuron, both of these types of neurons contain abundant NaV channels. We thus believe that it is valuable to investigate how changes in the amplitude and/or inactivation characteristics of INa affect the patterns of AP firing related to pain signaling. However, the effects of these compounds on the AP firing in dorsal root ganglion neurons occurring in vivo still require further analysis and research.
Although our study found that TTX-R INa was not detected in cultured DRG neurons (R-DRG-505), it is established that nociceptive DRG neurons (≤30 μm in a diameter) express TTX-R NaV channels, such as NaV1.8 and NaV1.9, and that previous studies have emphasized the role of these channels in nociceptive transmission (Wolf and Ma, 2007; Szulczyk et al., 2022; Nascimento de Lima et al., 2024). However, the modified PVINs in lamina III of the spinal cord are very heterogeneous and mainly express NaV1.1, NaV1.2, and NaV1.6, and they do not express NaV1.7 abundant in nociceptive DRG neruons (Fukuoka et al., 2010; Petitjean et al., 2015; Gradwellet al., 2022). Nevertheless, the effects of three compounds on TTX-R NaV channels should be tested, possibly using native DRG neurons or other types of spinal neurons linked to pain transmission.
Plasma Tel concentration after intravenous administration of a single dose of 40 mg Tel was noted to reach about 2.32 μM (Stangier et al., 2000). As for Tel, it is a pyrethroid insecticide. Its concentration in the blood of organisms varies greatly, reaching up to several micromolar levels. After intravenous administration, KB-R7943 reached a concentration of about 0.12 μM (Miyata et al., 2002), which is lower than the concentration used in this study. However, recent reports have found that KB-R7943 can cross the blood-brain barrier, with concentrations in brain tissue reaching 5 to 10 times higher (Andreeva-Gateva et al., 2024).
The effects of these compounds on the dorsal root ganglia may extend beyond the necessity of the blood-brain barrier. However, in nociceptive transmission, the dorsal root ganglia is one of the first primary neuron; the nerve transmission also needs to reach the dorsal horn of the spinal cord, then pass and conduct through long fibers upward to the medulla oblongata, further up to the thalamus, and then to the cerebral cortex. In these regions, the blood-brain barrier is often present. Therefore, if these compounds, such as telmisartan, tefluthrin, or KB-7943, can easily pass through the blood-brain barrier across those areas, it is believed that they could have a regulatory effect on these pain-linked transmission pathways. Furthermore, neurons of the dorsal horn of the spinal cord, including parbalbumin-expressing interneurons, were reported to exhibit greater heterogeneity than DRG neurons (Gradwell et al., 2022). Nevertheless, the effects of Tel, Tef, or KB-R7943 may have implications for biological activity in the nervous system (So et al., 2018; Lin et al., 2022). Among these effects, the regulation of ion channels in the cell membrane might be one of the important mechanisms.
Of note, the model used in the current study is not perfect. Indeed, there are many different formulations for Na+ currents. The simulated firing of neuronal action potentials derived from dirrent regions linked to pain signaling can also be present in various possible forms, as detailed on the ModelDB website (http://modeldb.sicence/, accessed on 14 July 2024).
To ensure our experimental results are more substantial and effective in presentations, and to observe potential action potential firing patterns, we further explored this through bifurcation analysis. We indeed spent a significant amount of time searching for developments of various types of simulation models. Thus, we found the model developed by Ma et al. (2023) in PVINs to be more suitable for our needs. However, we still believe it is not perfect, and in the future, we will continue to develop more suitable computational models so that the experimentally observed and theoretical results can be more consistent.
Tefluthrin has previously been reported to inhibit voltage-gated Ca2+ current and mildly suppress delayed-rectifier K+ currents (Wu et al., 2009). Additionally, telmisartan has been shown to suppress erg-mediated K+ currents (Chang and Wu, 2018). However, there are no reports indicating that KB-R7943 affects K+ currents. This paper focuses solely on the changes these compounds induce in the amplitude and gating of Na+ currents. Further analysis is required to understand the effects of these agents on other ion currents, such as K+ and Ca2+ currents, is necessary. Therefore, additional research is necessary to provide further clarification in this area.

Funding

This work was partly supported by grants from the Ministry of Science and Technology (NSTC- 113-2923-B-906-001), Taiwan, from An Nan Hospital (ANHR-112-42, ANHR-112-43, and ANHR-112-44), and Ditmanson Medical Foundation Chia-Yi Christian Hospital Research Program. The funders were not involved in the study, design, data collection, analyses, or interpretation.

Data Availability Statement

The data will be made available upon request.

Acknowledgments

The authors of this study express gratitude to the late Professor Ching-Hsing Luo of the Department of Electrical Engineering at National Cheng Kung University, Tainan, Taiwan, for his assistance in the earlier work on bifurcation analyses.

Conflicts of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as potential conflicts of interest.

Abbreviations

AP, action potential; [Ca2+]i, intracellular Ca2+ concentration; df, degree of freedom; HH, Hodgkin-Huxley; HS, high-frequency spiking; DRG neuron, dorsal root ganglion neuron; Iapp, applied current; INa, voltage-gated Na+ current; NaV channel, voltage-gated Na+ channel; SK channel, small-conductance Ca2+-activated K+ channel; PVINs, parvalbumin-expressing interneurons; SO, subthreshold oscillation; SS, somatic spiking; τinact(F), fast component of inactivation time constant; τinact(S), slow component of inactivation time constant; Tef, tefluthrin; Tel, telmisartan; TTX, tetrodotoxin; TTX-R, tetrodotoxin-resistant. (The other abbreviations related to parameters used in the simulations are detailed in Table 1).

References

  1. Amran MS, Homma N, Hashimoto K. Pharmacology of KB-R7943: a Na+-Ca2+ exchange inhibitor. Cardiovasc Drug Rev 2003;21(4):255-76. [CrossRef]
  2. Andreeva-Gateva P, Hristov M, Strokova-Stoilova M, Ivanova N, Sabit Z, Surcheva S, Beliakov M, Karakashev G, Sukhov I, Belinskaya D, Shestakova N. Therapeutic potential of orally applied KB-R7943 in streptozotocin-induced neuropathy in rats. Heliyon 2024;10(6):e27367. [CrossRef]
  3. Bennett DL, Clark AJ, Huang J, Waxman SG, Dib-Hajj SD. The Role of Voltage-Gated Sodium Channels in Pain Signaling. Physiol Rev 2019;99(2):1079-1151. [CrossRef]
  4. Brown AM. A modeling study predicts the presence of voltage gated Ca2+ channels on myelinated central axons. Comput Methods Programs Biomed 2003;71(1):25-31. [CrossRef]
  5. Carter BC, Bean BP. Incomplete inactivation and rapid recovery of voltage-dependent sodium channels during high-frequency firing in cerebellar Purkinje neurons. J Neurophysiol 2011;105(2):860-71. [CrossRef]
  6. Casey GP, Roberts JS, Paul D, Diamond I, Gould HJ 3rd. Ranolazine attenuation of CFA-induced mechanical hyperalgesia. Pain Med 2010;11(1):119-26. [CrossRef]
  7. Castellanos A, Andres A, Bernal L, Callejo G, Comes N, Gual A, Giblin JP, Roza C, Gasull X. Pyrethroids inhibit K2P channels and activate sensory neurons: basis of insecticide-induced paraesthesias. Pain 2018;159(1):92-105. [CrossRef]
  8. Catterall WA. Voltage-gated sodium channels at 60: structure, function and pathophysiology. J Physiol 2012;590(11):2577-89. [CrossRef]
  9. Chang TT, Yang CJ, Lee YC, Wu SN. Stimulatory Action of Telmisartan, an Antagonist of Angiotensin II Receptor, on Voltage-Gated Na⁺ Current: Experimental and Theoretical Studies. Chin J Physiol 2018;61(1):1-13. [CrossRef]
  10. Chang WT, Wu SN. Activation of voltage-gated sodium current and inhibition of erg-mediated potassium current caused by telmisartan, an antagonist of angiotensin II type-1 receptor, in HL-1 atrial cardiomyocytes. Clin Exp Pharmacol Physiol 2018;45(8):797-807. [CrossRef]
  11. Chen BS, Lo YC, Lius YC, Wu SN. Effects of transient receptor potential-like current on the firing pattern of action potentials in the Hodgkin-Huxley neuron during exposure to sinusoidal external voltage. Chin J Physiol 2010;53(6):423-9. [CrossRef]
  12. Chiesa N, Rosati B, Arcangeli A, Olivotto M, Wanke E. A novel role for HERG K+ channels: spike-frequency adaptation. J Physiol 1997;501 ( Pt 2)(Pt 2):313-8. Erratum in: J Physiol (Lond) 1997 Aug 1;502(Pt 3):715. [CrossRef]
  13. de Lera Ruiz M, Kraus RL. Voltage-Gated Sodium Channels: Structure, Function, Pharmacology, and Clinical Indications. J Med Chem 2015;58(18):7093-118. [CrossRef]
  14. Enns-Ruttan JS, Miura RM. Spontaneous secondary spiking in excitable cells. J Theor Biol 2000;205(2):181-199. [CrossRef]
  15. Fukuoka T, Kobayashi K, Noguchi K. Laminae-specific distribution of alpha-subunits of voltage-gated sodium channels in the adult rat spinal cord. Neuroscience 2010;169(3):994-1006. [CrossRef]
  16. Ghovanloo MR, Tyagi S, Zhao P, Effraim PR, Dib-Hajj SD, Waxman SG. Sodium currents in naïve mouse dorsal root ganglion neurons: No major differences between sexes. Channels (Austin) 2024;18(1):2289256. [CrossRef]
  17. Gould HJ 3rd, Diamond I. Ranolazine: A potential treatment for refractory neuropathic pain. J Neurol Sci 2016;369:310-311. [CrossRef]
  18. Gould HJ 3rd, Soignier RD, Cho SR, Hernandez C, Diamond I, Taylor BK, Paul D. Ranolazine attenuates mechanical allodynia associated with demyelination injury. Pain Med 2014;15(10):1771-80. [CrossRef]
  19. Gradwell MA, Boyle KA, Browne TJ, Bell AM, Leonardo J, Peralta Reyes FS, Dickie AC, Smith KM, Callister RJ, Dayas CV, Hughes DI, Graham BA. Diversity of inhibitory and excitatory parvalbumin interneuron circuits in the dorsal horn. Pain 2022;163(3):e432-e452. [CrossRef]
  20. Hegazy N, Rezq S, Fahmy A. Renin-angiotensin system blockade modulates both the peripheral and central components of neuropathic pain in rats: Role of calcitonin gene-related peptide, substance P and nitric oxide. Basic Clin Pharmacol Toxicol 2020;127(6):451-460. [CrossRef]
  21. Hsiao HT, Wang JC, Wu SN. Inhibitory effectiveness in delayed-rectifier potassium current caused by vortioxetine, known to be a novel antidepressant. Biomedicines 2022;10(6):1318. [CrossRef]
  22. Huang CW, Hung TY, Wu SN. The inhibitory actions by lacosamide, a functionalized amino acid, on voltage-gated Na+ currents. Neuroscience 2015;287:125-36. [CrossRef]
  23. Huang Y, Wen LL, Xie JD, Ouyang HD, Chen DT, Zeng WA. Antinociceptive effectiveness of the inhibition of NCX reverse-mode action in rodent neuropathic pain model. Mol Pain 2019;15:1744806919864511. [CrossRef]
  24. Jiang N, Nutter TJ, Cooper BY. Molecular and cellular influences of permethrin on mammalian nociceptors at physiological temperatures. Neurotoxicology 2013;37:207-19. [CrossRef]
  25. Karádi DÁ, Galambos AR, Lakatos PP, Apenberg J, Abbood SK, Balogh M, Király K, Riba P, Essmat N, Szűcs E, Benyhe S, Varga ZV, Szökő É, Tábi T, Al-Khrasani M. Telmisartan Is a Promising Agent for Managing Neuropathic Pain and Delaying Opioid Analgesic Tolerance in Rats. Int J Mol Sci 2023;24(9):7970. [CrossRef]
  26. Kim HK, Youm JB, Lee SR, Lim SE, Lee SY, Ko TH, Long le T, Nilius B, Won du N, Noh JH, Ko KS, Rhee BD, Kim N, Han J. The angiotensin receptor blocker and PPAR-γ agonist, telmisartan, delays inactivation of voltage-gated sodium channel in rat heart: novel mechanism of drug action. Pflugers Arch 2012;464(6):631-43. [CrossRef]
  27. Klemic KG, Kirsch GE, Jones SW. U-type inactivation of Kv3.1 and Shaker potassium channels. Biophys J 2001;81(2):814-26. [CrossRef]
  28. Lai MC, Wu SN, Huang CW. Telmisartan, an antagonist of angiotensin II receptors, accentuates voltage-gated Na+ currents and hippocampal neuronal excitability. Front Neurosci 2020;14:902. [CrossRef]
  29. Lee HM, Kim HI, Shin YK, Lee CS, Park M, Song JH. Diclofenac inhibition of sodium currents in rat dorsal root ganglion neurons. Brain Res 2003;992(1):120-7. [CrossRef]
  30. Lin MH, Lin JF, Yu MC, Wu SN, Wu CL, Cho HY. Characterization in potent modulation on voltage-gated Na+ current exerted by deltamethrin, a pyrethroid insecticide. Int J Mol Sci 2022;23(23):14733. [CrossRef]
  31. Lin MW, Wang YJ, Liu SI, Lin AA, Lo YC, Wu SN. Characterization of aconitine-induced block of delayed rectifier K+ current in differentiated NG108-15 neuronal cells. Neuropharmacology 2008;54(6):912-23. [CrossRef]
  32. Lu TL, Wu SN. Investigating the impact of selective modulators on the renin-angiotensin-aldosterone system: unraveling their off-target perturbations of transmembrane ionic currents. Int J Mol Sci 2023;24(18):14007. [CrossRef]
  33. Ma X, Miraucourt LS, Qiu H, Sharif-Naeini R, Khadra A. Modulation of SK Channels via Calcium Buffering Tunes Intrinsic Excitability of Parvalbumin Interneurons in Neuropathic Pain: A Computational and Experimental Investigation. J Neurosci 2023;43(31):5608-5622. [CrossRef]
  34. Miyata A, Zipes DP, Hall S, Rubart M. Kb-R7943 prevents acute, atrial fibrillation-induced shortening of atrial refractoriness in anesthetized dogs. Circulation 2002;106(11):1410-9. [CrossRef]
  35. Nascimento de Lima AP, Zhang H, Chen L, Effraim PR, Gomis-Perez C, Cheng X, Huang J, Waxman SG, Dib-Hajj SD. Nav1.8 in small dorsal root ganglion neurons contributes to vincristine-induced mechanical allodynia. Brain. 2024 Mar 6:awae071. Epub ahead of print. [CrossRef]
  36. Navarro MA, Salari A, Lin JL, Cowan LM, Penington NJ, Milescu M, Milescu LS. Sodium channels implement a molecular leaky integrator that detects action potentials and regulates neuronal firing. Elife 2020;9:e54940. [CrossRef]
  37. Petitjean H, Pawlowski SA, Fraine SL, Sharif B, Hamad D, Fatima T, Berg J, Brown CM, Jan LY, Ribeiro-da-Silva A, Braz JM, Basbaum AI, Sharif-Naeini R. Dorsal Horn Parvalbumin Neurons Are Gate-Keepers of Touch-Evoked Pain after Nerve Injury. Cell Rep 2015;13(6):1246-1257. [CrossRef]
  38. Roy ML, Narahashi T. Differential properties of tetrodotoxin-sensitive and tetrodotoxin-resistant sodium channels in rat dorsal root ganglion neurons. J Neurosci 1992;12(6):2104-11. [CrossRef]
  39. Schröder UH, Breder J, Sabelhaus CF, Reymann KG. The novel Na+/Ca2+ exchange inhibitor KB-R7943 protects CA1 neurons in rat hippocampal slices against hypoxic/hypoglycemic injury. Neuropharmacology 1999;38(2):319-21. [CrossRef]
  40. Schweighofer N, Doya K, Kawato M. Electrophysiological properties of inferior olive neurons: A compartmental model. J Neurophysiol 1999;82(2):804-17. [CrossRef]
  41. Shen H, Zhou Q, Pan X, Li Z, Wu J, Yan N. Structure of a eukaryotic voltage-gated sodium channel at near-atomic resolution. Science 2017;355(6328):eaal4326. [CrossRef]
  42. Silwal P, Adhikari R, Yadav B, Sah SK, Bhatt A, Basnet S. Lambda-cyhalothrin ingestion: an infrequent yet concerning presentation of pyrethroid poisoning. Ann Med Surg (Lond) 2023;85(10):5250-5254. [CrossRef]
  43. So EC, Wu SN, Lo YC, Su K. Differential regulation of tefluthrin and telmisartan on the gating charges of INa activation and inactivation as well as on resurgent and persistent INa in a pituitary cell line (GH3). Toxicol Lett 2018;285:104-112. [CrossRef]
  44. Stangier J, Schmid J, Türck D, Switek H, Verhagen A, Peeters PA, van Marle SP, Tamminga WJ, Sollie FA, Jonkman JH. Absorption, metabolism, and excretion of intravenously and orally administered [14C]telmisartan in healthy volunteers. J Clin Pharmacol 2000;40(12 Pt 1):1312-22.
  45. Szulczyk B, Pasierski M, Gawlak M. Prefrontal cortex pyramidal neurons express functional Nav1.8 tetrodotoxin-resistant sodium currents. Clin Exp Pharmacol Physiol 2022;49(3):350-359. [CrossRef]
  46. Taddese A, Bean BP. Subthreshold sodium current from rapidly inactivating sodium channels drives spontaneous firing of tuberomammillary neurons. Neuron 2002;33(4):587-600. [CrossRef]
  47. Traub RD, Miles R. Multiple modes of neuronal population activity emerge after modifying specific synapses in a model of the CA3 region of the hippocampus. Ann N Y Acad Sci 1991;627:277-90. [CrossRef]
  48. Wang YJ, Lin MW, Lin AA, Peng H, Wu SN. Evidence for state-dependent block of DPI 201-106, a synthetic inhibitor of Na+ channel inactivation, on delayed-rectifier K+ current in pituitary tumor (GH3) cells. J Physiol Pharmacol 2008;59(3):409-23.
  49. White JA, Budde T, Kay AR. A bifurcation analysis of neuronal subthreshold oscillations. Biophys J 1995;69(4):1203-17. [CrossRef]
  50. Winslow RL. Bifurcation analysis of nonlinear retinal horizontal cell models. I. Properties of isolated cells. J Neurophysiol 1989;62(3):738-49. [CrossRef]
  51. Woolf CJ, Ma Q. Nociceptors--noxious stimulus detectors. Neuron 2007;55(3):353-64. [CrossRef]
  52. Wu SN. Simulations of the cardiac action potential based on the Hodgkin-Huxley kinetics with the use of Microsoft Excel spreadsheets. Chin J Physiol 2004;47(1):15-22.
  53. Wu SN, Chen BS, Lin MW, Liu YC. Contribution of slowly inactivating potassium current to delayed firing of action potentials in NG108-15 neuronal cells: experimental and theoretical studies. J Theor Biol 2008;252(4):711-21. [CrossRef]
  54. Wu SN, Wu YH, Chen BS, Lo YC, Liu YC. Underlying mechanism of actions of tefluthrin, a pyrethroid insecticide, on voltage-gated ion currents and on action currents in pituitary tumor (GH3) cells and GnRH-secreting (GT1-7) neurons. Toxicology 2009;258(1):70-7. [CrossRef]
  55. Wu SN, So EC, Liao YK, Huang YM. Reversal by ranolazine of doxorubicin-induced prolongation in the inactivation of late sodium current in rat dorsal root ganglion neurons. Pain Med 2015;16(5):1032-4. [CrossRef]
  56. Wu SN, Yeh CC, Huang HC, So EC, Lo YC. Electrophysiological characterization of sodium-activated potassium channels in NG108-15 and NSC-34 motor neuron-like cells. Acta Physiol (Oxf) 2012;206(2):120-34. [CrossRef]
  57. Wu SN, Yu MC. Inhibition of Voltage-Gated Na+ Currents Exerted by KB-R7943 (2-[2-[4-(4-nitrobenzyloxy)phenyl]ethyl]isothiourea), an Inhibitor of Na+-Ca2+ Exchanging Process. Int J Mol Sci 2023;24(2):1805. [CrossRef]
  58. Zhang Y, Li D, Darwish Y, Fu X, Trussell LO, Huang H. KCNQ channels enable reliable presynaptic spiking and synaptic transmission at high frequency. J Neurosci 2022;42(16):3305-3315. [CrossRef]
Preprints 116863 g001
Figure 1. Histogram depicting the relationship between cell number and cell capacitance. Each red bar represents the number of cells used in this study. A smooth line overlaid on the histogram illustrates the Gaussian distribution used for curve fitting.
Figure 1. Histogram depicting the relationship between cell number and cell capacitance. Each red bar represents the number of cells used in this study. A smooth line overlaid on the histogram illustrates the Gaussian distribution used for curve fitting.
Preprints 116863 g001
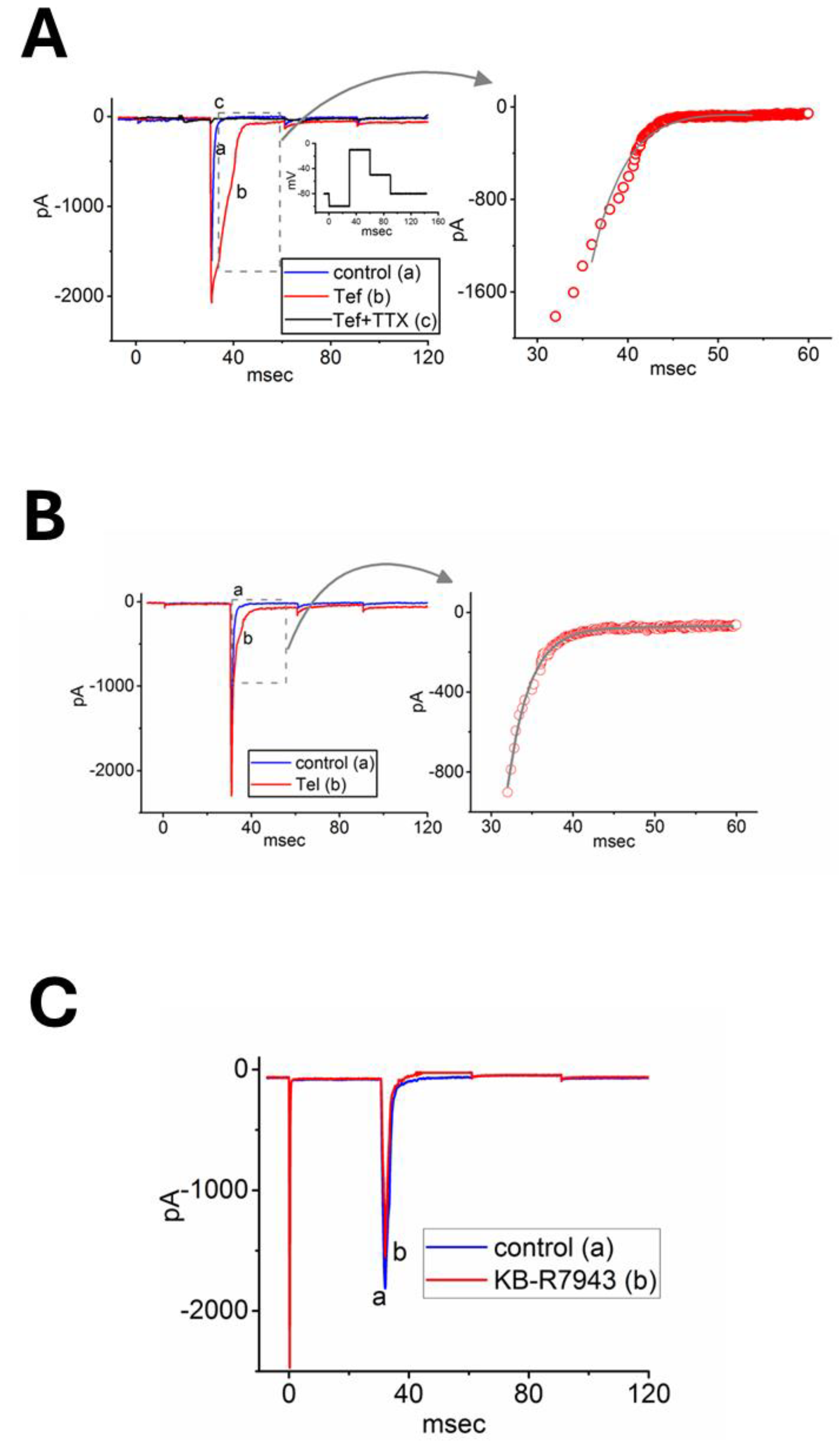
Preprints 116863 g002
Figure 2. Effects of tefluthrin (Tef), telmisartan (Tel), and KB-R7943 on voltage-gated Na+ current (INa) in rat dorsal root ganglion (DRG) neurons using whole-cell current recordings. These experiments were conducted in Ca2+-free Tyrode’s solution containing CdCl2 (0.5 mM) and tetraethylammonium chloride (TEA, 10 mM). Panel (A), (B), or (C) displays INa traces under the conditions: in the absence (a, blue color) and in the presence (b, red color) of Tef (10 μM), Tel (10 μM), or KB-R7943 (10 μM), respectively. Inset in the left side of panel (A) indicates the voltage-clamp protocol applied. The right graph of panels (A) and (B) shows an expanded view of the dashed box from the left side, with the red data points fitted to a two-exponential function (gray curve). Please note that in pane (A), the current trace labeled c (black color) indicates further addition of tetrodotoxin (TTX, 1 μM), in the continued presence of Tef (10 μM).
Figure 2. Effects of tefluthrin (Tef), telmisartan (Tel), and KB-R7943 on voltage-gated Na+ current (INa) in rat dorsal root ganglion (DRG) neurons using whole-cell current recordings. These experiments were conducted in Ca2+-free Tyrode’s solution containing CdCl2 (0.5 mM) and tetraethylammonium chloride (TEA, 10 mM). Panel (A), (B), or (C) displays INa traces under the conditions: in the absence (a, blue color) and in the presence (b, red color) of Tef (10 μM), Tel (10 μM), or KB-R7943 (10 μM), respectively. Inset in the left side of panel (A) indicates the voltage-clamp protocol applied. The right graph of panels (A) and (B) shows an expanded view of the dashed box from the left side, with the red data points fitted to a two-exponential function (gray curve). Please note that in pane (A), the current trace labeled c (black color) indicates further addition of tetrodotoxin (TTX, 1 μM), in the continued presence of Tef (10 μM).
Preprints 116863 g002
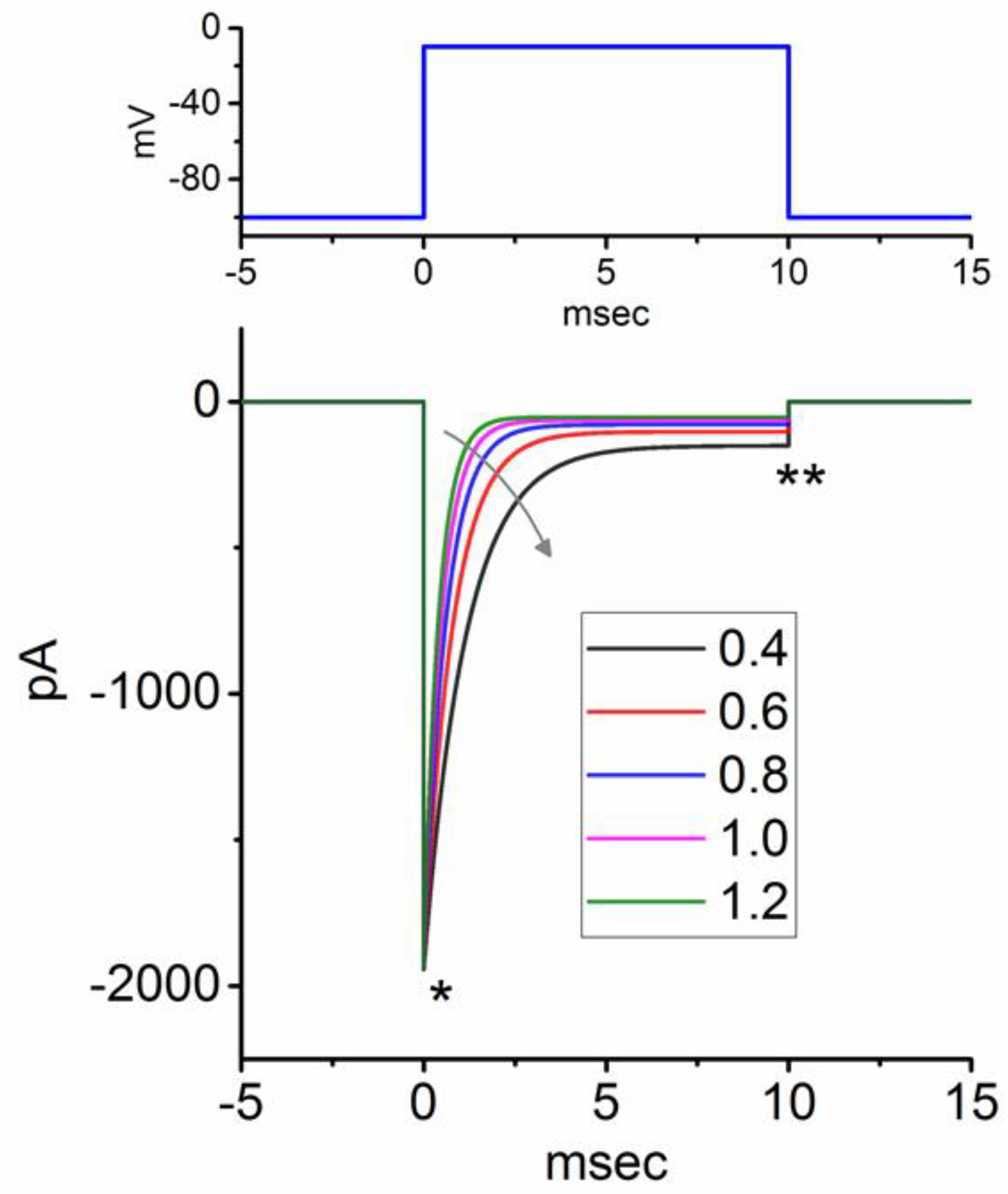
Preprints 116863 g003
Figure 3. Simulated INa traces in response to short depolarization from -100 to -10 mV for 10 msec. Detailed profile was described in the Materials and Methods section and a previous paper (Ma et al., 2023). INa traces were created when the ϕ value in the inactivation process (βh) of h variable decreased from 1.2 to 0.4 with 0.2 decrements (as indicated by curved arrow). The term “βh” in the HH kinetics refers to the rate at which the NaV channel undergoes inactivation in the h gating variable. * and ** represent the transient and late components of INa activated by an abrupt depolarizing pulse. The upper part illustrates the voltage-clamp protocol applied.
Figure 3. Simulated INa traces in response to short depolarization from -100 to -10 mV for 10 msec. Detailed profile was described in the Materials and Methods section and a previous paper (Ma et al., 2023). INa traces were created when the ϕ value in the inactivation process (βh) of h variable decreased from 1.2 to 0.4 with 0.2 decrements (as indicated by curved arrow). The term “βh” in the HH kinetics refers to the rate at which the NaV channel undergoes inactivation in the h gating variable. * and ** represent the transient and late components of INa activated by an abrupt depolarizing pulse. The upper part illustrates the voltage-clamp protocol applied.
Preprints 116863 g003
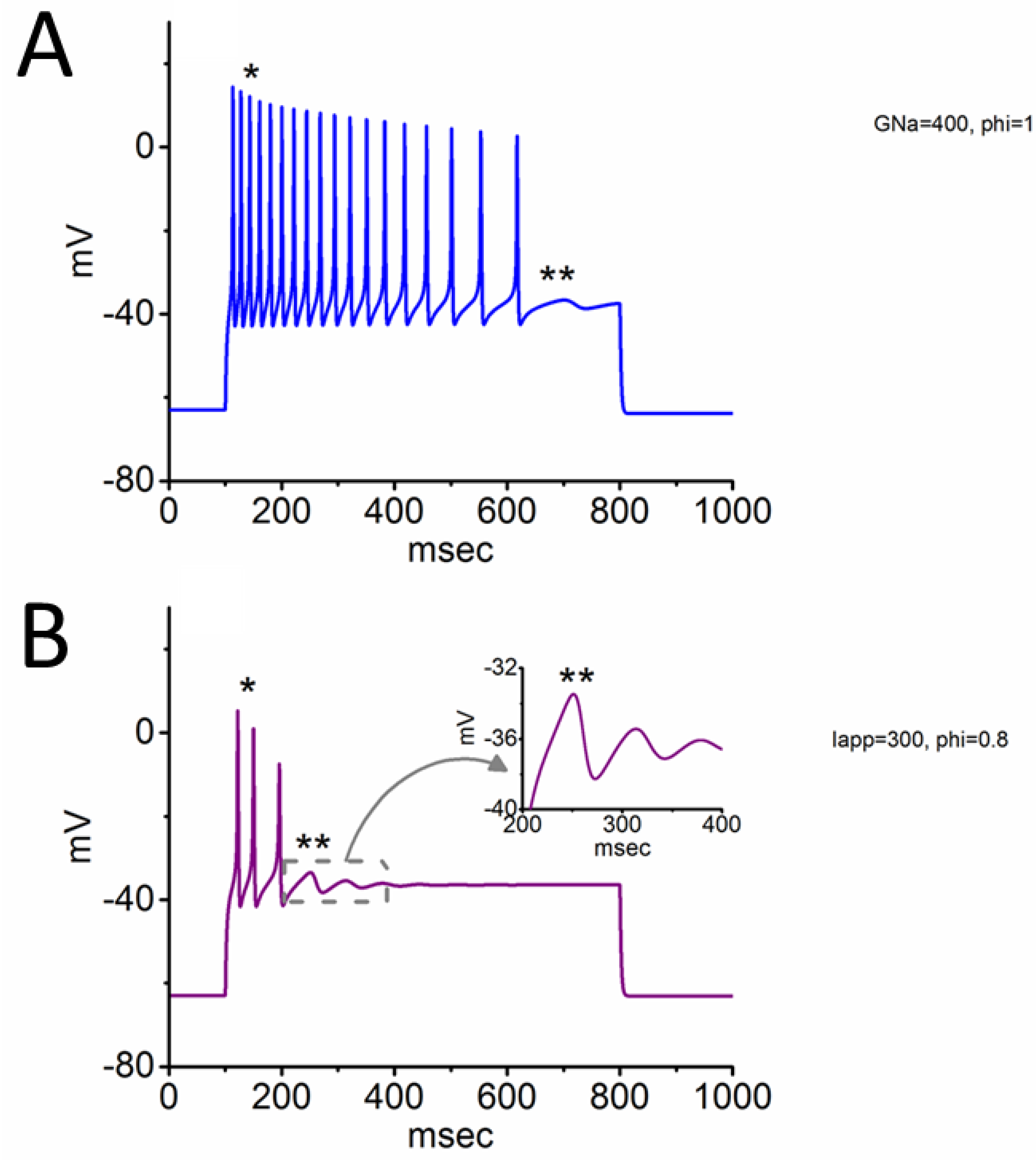
Preprints 116863 g004
Figure 4. Two distinct spiking patterns simulated from the modeled neuron. When a current injection (700 msec in duration) was applied to this modeled neuron, two different spike patterns emerged, namely somatic spike (SS) and subthreshold oscillation (SO). In panel (A), gNa = 400 nS, Iapp = 300 pA, ϕ = 1.0. In panel (B), gNa = 300 nS, Iapp = 300 pA, ϕ = 0.8. The symbols * and ** represent the occurrence of SS and SO, respectively. The inset in panel (B) is a magnified view from the dashed box in (B), highlighting the SO emergence.
Figure 4. Two distinct spiking patterns simulated from the modeled neuron. When a current injection (700 msec in duration) was applied to this modeled neuron, two different spike patterns emerged, namely somatic spike (SS) and subthreshold oscillation (SO). In panel (A), gNa = 400 nS, Iapp = 300 pA, ϕ = 1.0. In panel (B), gNa = 300 nS, Iapp = 300 pA, ϕ = 0.8. The symbols * and ** represent the occurrence of SS and SO, respectively. The inset in panel (B) is a magnified view from the dashed box in (B), highlighting the SO emergence.
Preprints 116863 g004
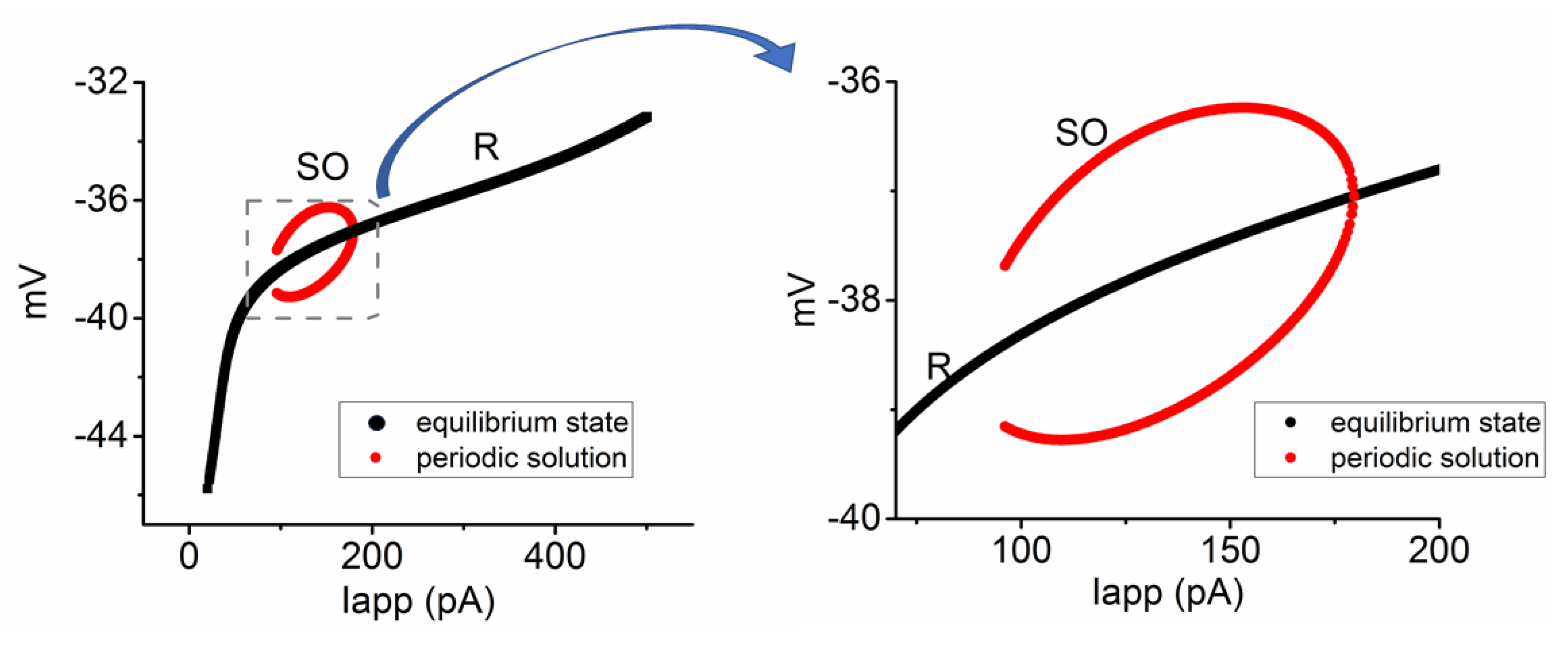
Preprints 116863 g005
Figure 5. Bifurcation diagram illustrating the relationship between Iapp and alterations in membrane potential in the modeled neuron. These simulations were conducted using default parameters detailed in Table 1, with a ϕ value of 1.0. Two types of solutions in the system were identified. That is, one is the resting, steady-state, or equilibrium state (R, black color), while the other is the unstable and periodic solution indicative of subthreshold oscillation (SO, red color). The enlarged graph on the right corresponds to the highlighted region within the dashed box on the left.
Figure 5. Bifurcation diagram illustrating the relationship between Iapp and alterations in membrane potential in the modeled neuron. These simulations were conducted using default parameters detailed in Table 1, with a ϕ value of 1.0. Two types of solutions in the system were identified. That is, one is the resting, steady-state, or equilibrium state (R, black color), while the other is the unstable and periodic solution indicative of subthreshold oscillation (SO, red color). The enlarged graph on the right corresponds to the highlighted region within the dashed box on the left.
Preprints 116863 g005
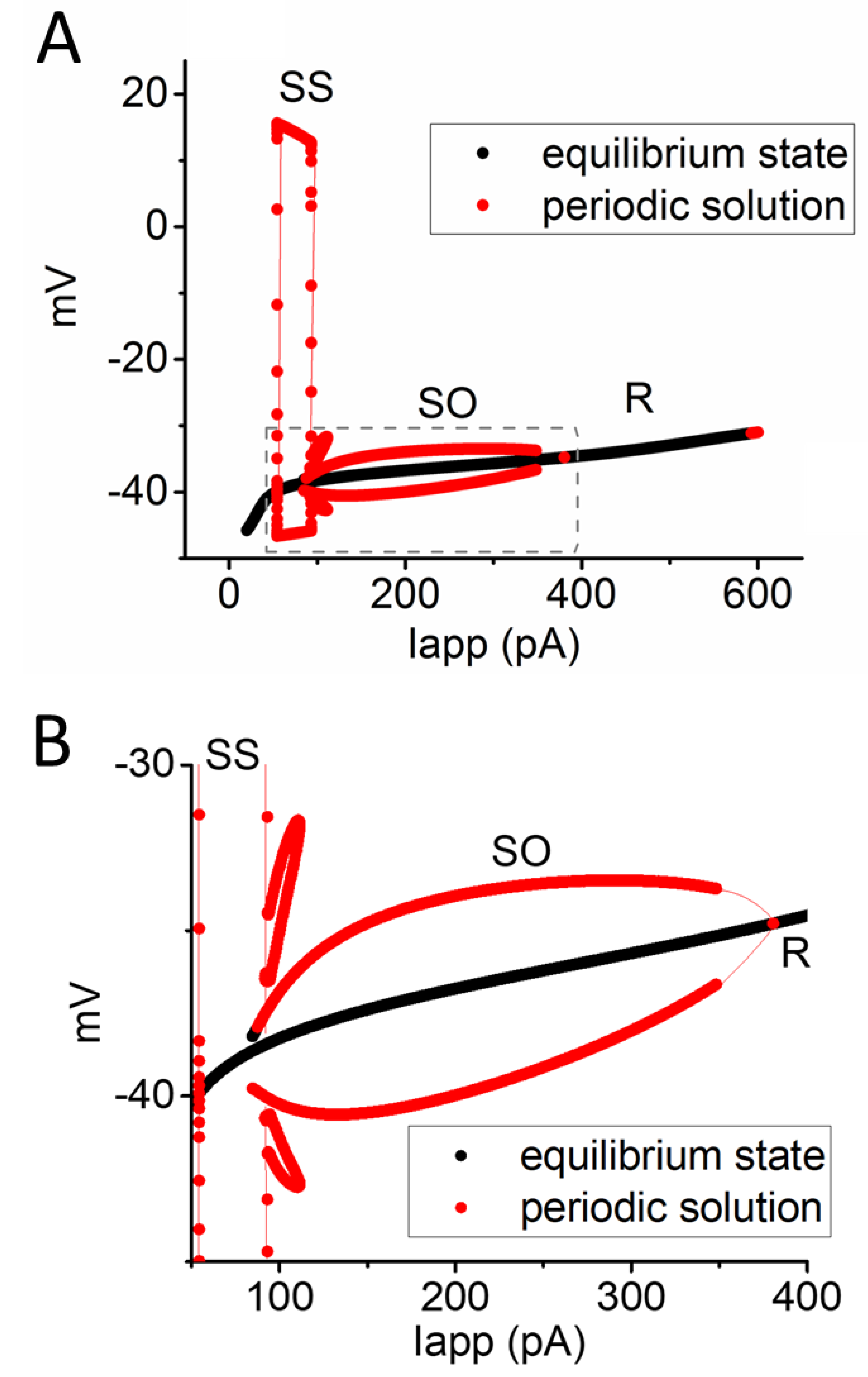
Preprints 116863 g006
Figure 6. Bifurcation diagram concerning the relationship between Iapp and membrane potential in the modeled neuron with a constant ϕ value of 0.8. Beside the equilibrium or resting state (R, in black color), two distinct types of periodic solutions (indicated in red color) were identified, namely somatic spiking (SS) occurring within the Iapp range of 52 to 97 pA and subthreshold oscillation (SO) at the Iapp range between 85 and 381 pA. Panel (B) is an enlarged view of the dashed box in panel (A).
Figure 6. Bifurcation diagram concerning the relationship between Iapp and membrane potential in the modeled neuron with a constant ϕ value of 0.8. Beside the equilibrium or resting state (R, in black color), two distinct types of periodic solutions (indicated in red color) were identified, namely somatic spiking (SS) occurring within the Iapp range of 52 to 97 pA and subthreshold oscillation (SO) at the Iapp range between 85 and 381 pA. Panel (B) is an enlarged view of the dashed box in panel (A).
Preprints 116863 g006
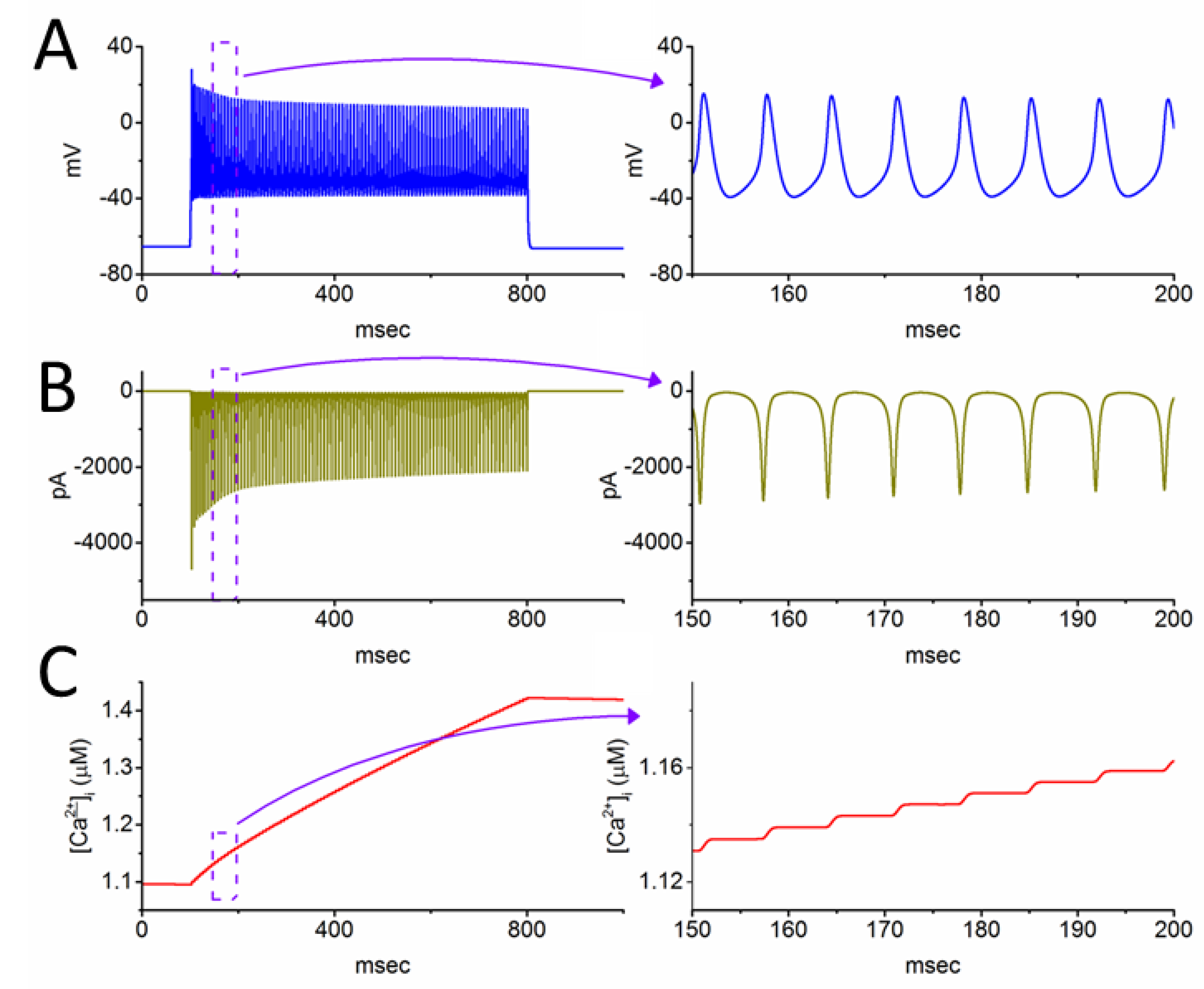
Preprints 116863 g007
Figure 7. Effect of elevated Iapp at 700 pA on spiking, INa, and intracellular Ca2+ concentration ([Ca2+]i) in the simulated neuron. Panels (A), (B), and (C) respectively depict membrane potential, INa amplitude, and [Ca2+]i induced by a 700-msec Iapp with 700 pA. Each corresponding panel on the right provides an enlarged view of the graph contained within the dashed box on the left.
Figure 7. Effect of elevated Iapp at 700 pA on spiking, INa, and intracellular Ca2+ concentration ([Ca2+]i) in the simulated neuron. Panels (A), (B), and (C) respectively depict membrane potential, INa amplitude, and [Ca2+]i induced by a 700-msec Iapp with 700 pA. Each corresponding panel on the right provides an enlarged view of the graph contained within the dashed box on the left.
Preprints 116863 g007
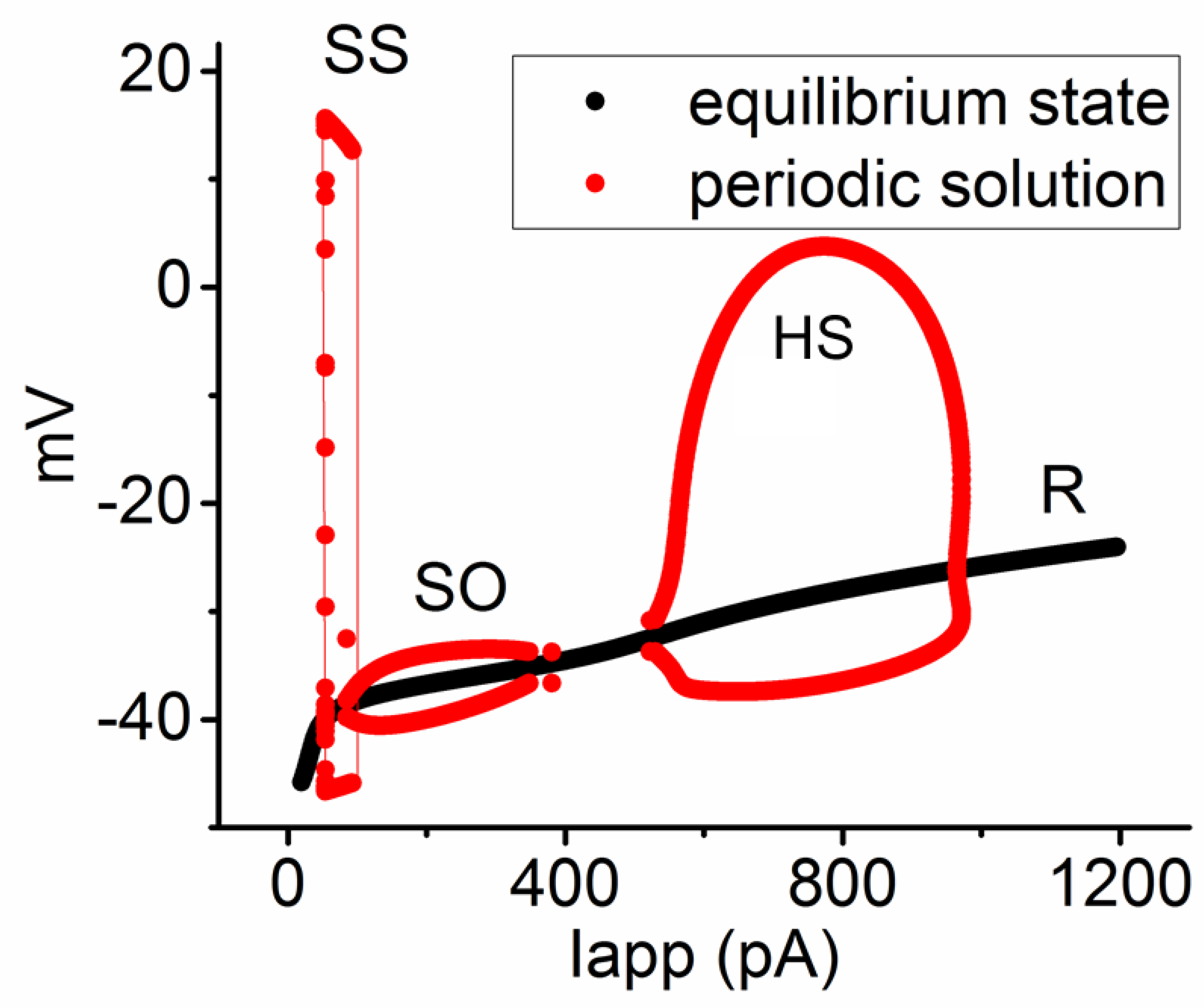
Preprints 116863 g008
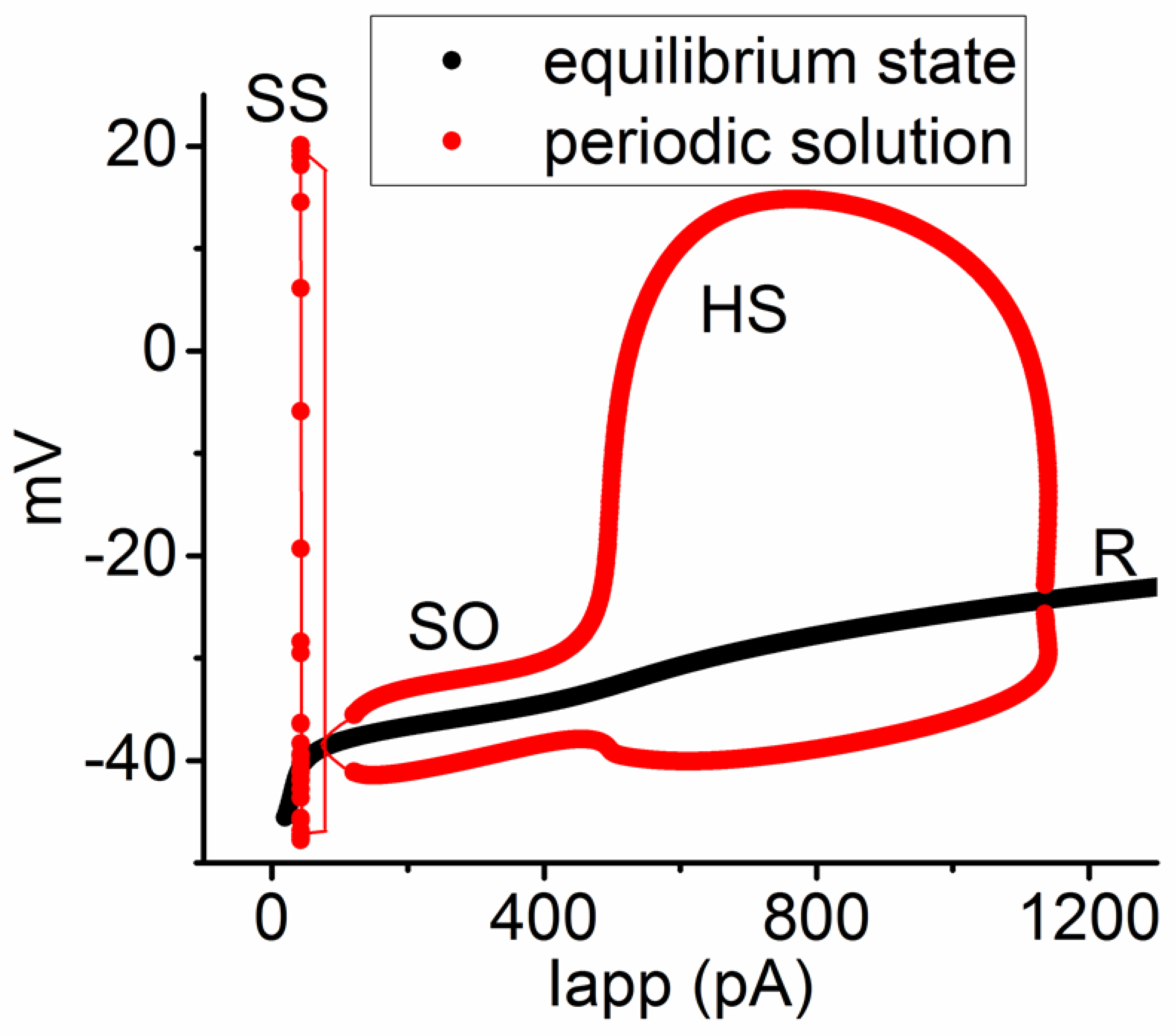
Figure 8. Bifurcation diagram showing the relationship between the applied current (Iapp) and membrane potential in the modeled neuron. The parameters were set at gNa = 300 nS and ϕ = 0.8, with the Iapp range spanning from 20 to 1300 pA. Three unstable bifurcations (indicated in red color) occur, namely SS with low frequency, SO, and a high-frequency spiking pattern (HS). This caption suggests that, in the presence of compounds like tefluthrin (Tef) or telmisartan (Tel), the modeled neuron exhibited HS occurrence, especially at higher intensities of applied current ranging between 500 and 950 pA. Red and black colors in this and the following Figures denote the periodic solutions (SS, SO, and HS) and the equilibrium or resting state (R), respectively.
Figure 8. Bifurcation diagram showing the relationship between the applied current (Iapp) and membrane potential in the modeled neuron. The parameters were set at gNa = 300 nS and ϕ = 0.8, with the Iapp range spanning from 20 to 1300 pA. Three unstable bifurcations (indicated in red color) occur, namely SS with low frequency, SO, and a high-frequency spiking pattern (HS). This caption suggests that, in the presence of compounds like tefluthrin (Tef) or telmisartan (Tel), the modeled neuron exhibited HS occurrence, especially at higher intensities of applied current ranging between 500 and 950 pA. Red and black colors in this and the following Figures denote the periodic solutions (SS, SO, and HS) and the equilibrium or resting state (R), respectively.
Preprints 116863 g008
Preprints 116863 g009
Figure 9. Phase diagram illustrating the impact of enhanced gNa coupled with a reduced ϕon the relationship of Iapp versus membrane potential. In this diagram, we set ϕ = 0.8, and increased gNa to 320 nS. With the increased Iapp, the coalescence of SO and HS became evident. No existence in the stable steady-state for Iapp ranging between 20 and 1100 pA was noted.
Figure 9. Phase diagram illustrating the impact of enhanced gNa coupled with a reduced ϕon the relationship of Iapp versus membrane potential. In this diagram, we set ϕ = 0.8, and increased gNa to 320 nS. With the increased Iapp, the coalescence of SO and HS became evident. No existence in the stable steady-state for Iapp ranging between 20 and 1100 pA was noted.
Preprints 116863 g009
Table 1. Default parametric values used for the modeling of interneurons in the dorsal horn of the spinal cord. For more detailed parameters of this model, please refer to Ma et al. (2023) paper.
Table 1. Default parametric values used for the modeling of interneurons in the dorsal horn of the spinal cord. For more detailed parameters of this model, please refer to Ma et al. (2023) paper.
Symbol or parameter Description* Value
Cm Membrane capacitance (pF) 30
gNa Maximum Na+ current conductance (nS) 300
gCa Maximum Ca2+ current conductance (nS) 8
gK1 Maximum KV1 current conductance (nS) 15
gK3 Maximum KV3 current conductance (nS) 180
gSK Maximum SK K+ current conductance (nS) 10
gleak Maximum leak current conductance (nS) 8
VNa Na+ reversal potential (mV) 58
VK K+ reversal potential (mV) -80
VCa Ca2+ reversal potential (mV) 68
VLeak Reversal potential for leak current (mV) -50
γ Ca2+ recovery rate (ms-1) 0.01
kSK Ca2+ sensitivity of SK channel (μM) 0.8
A Cell surface area (μm2) 3000
ϕ Adjustable βh-inactivation parameter of h gating variable (dimensionless) 1.0
* The parenthesis in each symbol or parameter indicates the unit.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated