Preprint
Article
A Unified Semiconductor-Device-Physics-Based Ballistic Model for the Threshold Voltage of Modern Multiple-gate MOSFETS
Altmetrics
Downloads
67
Views
27
Comments
0
This version is not peer-reviewed
Advances in Microelectronics and Semiconductor Engineering
Submitted:
29 August 2024
Posted:
02 September 2024
You are already at the latest version
Alerts
Abstract
Based on the minimum conduction band edge caused by the minimum channel potential resulting from the quasi-3D scaling theory and the 3D density of state (DOS) accompanied by the Fermi-Dirac distribution function on the source and drain sides, a unified semiconductor-device-physics-based ballistic model is developed for the threshold voltage of modern multiple-gate (MG) transistors, including FinFET, W-gate MOSFET, and Nanosheet (NS) MOSFET. It is shown that the thin silicon, thin gate oxide, and high work function will alleviate the ballistic effects and resist the threshold voltage degradation. Besides, as the device dimension is further reduced to give rise to the 2D/1D DOS, the lowest conduction band edge is hence increased to resist the threshold voltage degradation. The nanosheet MOSFET exhibits the largest threshold voltage among the three transistors due to the smallest minimum conduction band edge caused by the quasi-3D minimum channel potential. Compared to P-type MOSFET (P-FET), the N-FET shows more threshold voltage because the electron has a more effective mass than the hole
Keywords:
Subject: Engineering - Electrical and Electronic Engineering
1. Introduction
The modern multiple-gate (MG) MOSFET is superior to planar MOSFET in suppressing the short-channel effects (SCEs) and supporting a higher driving current and packing density. Among the MG transistors, the proposed triple-gate (TG) MOSFET (i.e., FinFET)[1,2,3] with the ultra-thin silicon body and 3D gate oxide coverage can enhance the switching speed and decrease more electrostatic power consumption than the double-gate (DG) MOSFET proposed as the first non-planar MOSFET with the unique volume conduction [4,5]. Meanwhile, to further increase the IC packing density to accommodate the future GPU for trillion transistor counts, the 3D IC has converted the conventional lateral CMOS layout into the vertical gate-stacked CFET [6,7,8]. The nanosheet MOSFET [9,10,11] comprising CFET has been recognized as an alternative to FinFET and served as the basic building block for the implementation of the next-generation 3D ULSI. As the device feature size is further reduced toward 3nm/2nm, semiconductor node, the free carriers can directly arrive in the drain side without backscattering due to the feature size being smaller than the mean free path. This implies that the traditional drift-diffusion model (DDM), based on the thermal equilibrium between the free carriers and the lattice, is no longer accurate for developing the model of device behavior. Instead of DDM, the ballistic transport model (BTM) should be applied to model the device. The threshold voltage is one of the essential semiconductor device parameters that must be carefully monitored when the 3D ULSI is evaluated for its electrostatic power consumption to achieve power saving. In this work, a unified threshold voltage model for the ballistic FinFET, Ω-gate MOSFET, and nanosheet transistor is achieved based on the quasi-3D scaling theory, the density of state (DOS), and the Fermia-Dirac distribution function. It is shown that the thin silicon, thin gate oxide, and high work function will alleviate the ballistic effects and resist the threshold voltage degradation. Besides, the nanosheet MOSFET exhibits the largest threshold voltage among the three transistors due to the smallest minimum conduction band edge. As the device height/width is further reduced to bring about 2D/1D DOS for the MG MOSFETs, the threshold voltage will be increased to some extent because the 2D/1D DOS can induce a smaller carrier concentration than the 3D DOS for the transistors.
Figure 1.
Typical schematic of the 3D modern multiple-gate MOSFETs composed of (A) nanosheet (NS) MOSFET, (B) W-gate MOSFET, and (C) FinFET. The channel direction is along with the z-axis. The channel length, height, and width are denoted by Lg, H, and W, respectively. The gate oxide thickness is denoted by tox.
Figure 1.
Typical schematic of the 3D modern multiple-gate MOSFETs composed of (A) nanosheet (NS) MOSFET, (B) W-gate MOSFET, and (C) FinFET. The channel direction is along with the z-axis. The channel length, height, and width are denoted by Lg, H, and W, respectively. The gate oxide thickness is denoted by tox.
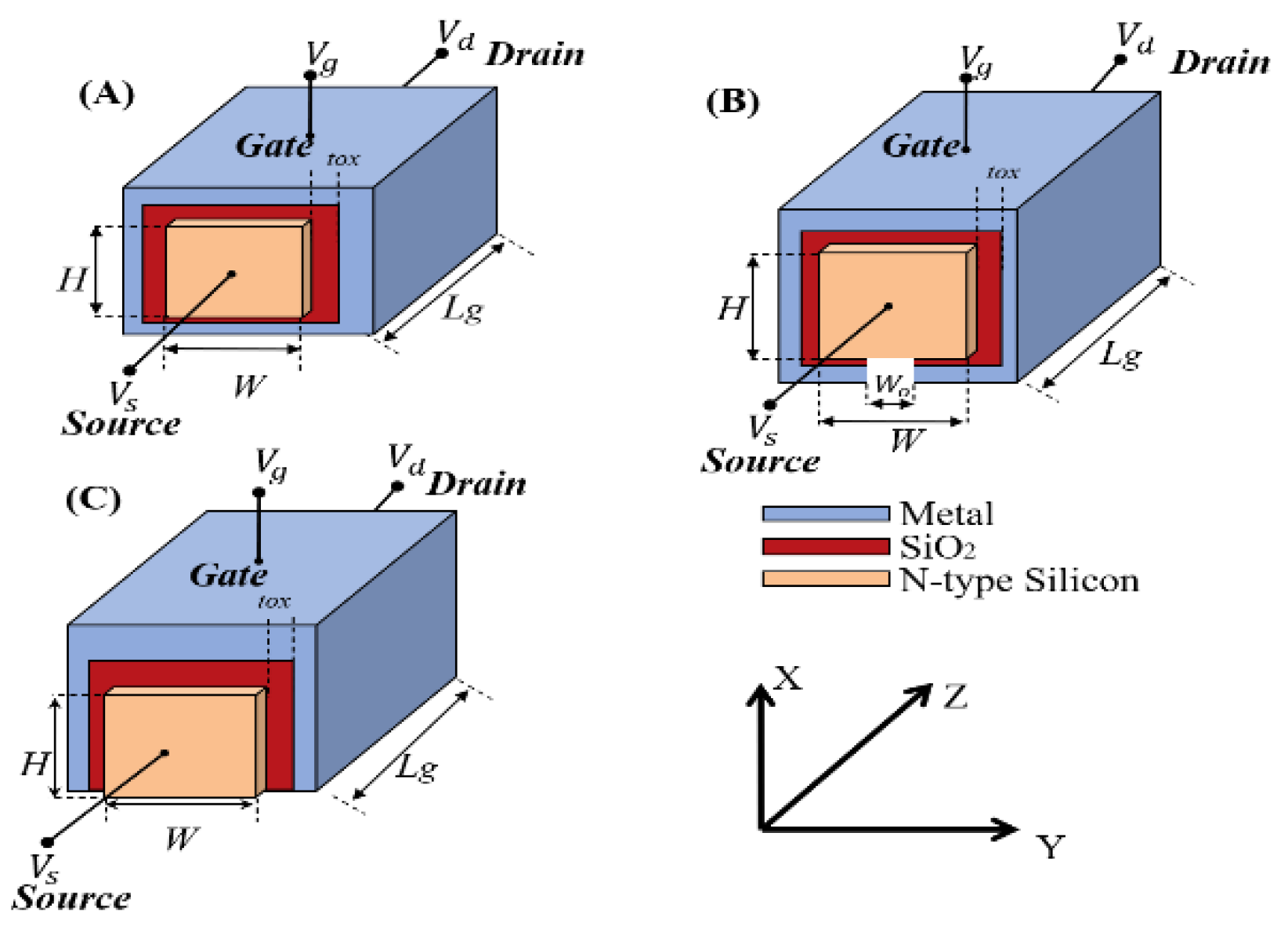
2. Model Description
- (A)
- Quasi-3D scaling theory for the ballistic MG MOSFETs:
As the device is further scaled down to work in the subthreshold regime, where the electrical field parallel to the channel direction strongly affects the device’s behavior, the channel potential of FMC can be governed by the quasi-3D scaling theory by accounting for the short-channel effects [12]:
with
where fMCL is the long-channel bulk potential. The 3D scaling length lMG in (1) can be expressed in (2), where lSG-x—z, lDG-x-z, and lDG-y-z are the 2D scaling lengths for the single-gate and double-gate MOSFETs residing in the x-z and y-z cut-plane, respectively.() considers the coupling effects between the x-z and y-z planes and a is the ratio of single-gate oxide to the entire gate oxide in the y-z cut plane. For nanosheet MOSFET, one obtains =0; for FinFET MOSFET, we have =1. However, 0< <1 should be used to develop the 3D scaling length for W-gate MOSFET, Wo is the opening at the bottom gate oxide of W-gate FET. The channel width, height, and gate oxide thickness in (3) are denoted by W, H, and tox. The difference in work function between the gate material and silicon body causes the flat-band voltage of Vfb in (4). The solution of (1) can be obtained as
With the boundary conditions of FMC(z=0)=Vbi, FMC(Z=Lg)=Vbi+Vds, the coefficients for T and U in (5) can be obtained as
where Vds and Vbi are the drain voltage and built-in potential at the junction between the source/drain and channel. With (6) and (7), the minimum channel potential for the ballistic MG MOSFETs can be expressed as
Both T and U in (8) can be linearized for Vgs, which leads to
with
- (B)
- Free electron concentration for the ballistic MG MOSFETs:
The free electron concentration for the MG MOSFETs by considering the ballistic transport mode (BTM) can be expressed as:
where gv is the silicon degeneracy, D(E) is the density of state (DOS), which has been divided by 2 by considering the electron per spin in calculating free electron concentration, fs(E) and fd(E) are the Fermin-Dirac distribution function on the source/drain sides, respectively. The 3D DOS in (12), by considering the 3D wave equation, can be obtained as
with
where m* is the effective mass of the electron and EC,min is the minimum conduction edge caused by the minimum channel potential of Fmin shown in (8). The Fermi-Dirac distribution function on the source/drain sides can be expressed as
with
where EFd and EFs are the quasi-Fermi levels on the drain/source sides, respectively. By substituting (13), (14), (15), and (16) into (12), the free electron concentration for the ballistic MG MOSFETs can be obtained as
with
and
where and are the fermi-Dirac integral of order 1/2. For the non-degenerate carrier statistics (i.e., Maxwell Boltzmann statistics), (17) can be further reduced as
because the Fermi-Dirac integral of any order can be reduced as exponential terms (i.e., Fi(h)=eh), which is shown as follows:
- (C)
- Criterion of threshold voltage for the ballistic MG MOSFETs:
To attain the threshold condition, the minority carrier concentration of n-FET should be equal to the majority carrier concentration of p-FET. This implies that the electron concentration of n in N-FET should be equal to Na of P-substrate by assuming the complete impurity ionization (i.e., pNa) in P-FET. According to the criterion of threshold condition, the threshold voltage of gate bias should satisfy the following criterion:
where Vth is the threshold voltage. By substituting (22) into (20), the minimum channel potential corresponding to the threshold criterion can be obtained as
From (8), (9), (10), (11), and (23), the threshold voltage can be achieved by solving for the quadratic equation of Vgs. This leads to
with
It should be noted that the BTM brings about the new minimum channel potential shown in (23), which can uniquely determine the threshold voltage for the ballistic MG MOSFETs.
- (D)
- Free electron concentration for the low-dimensional ballistic MG MOSFETs:
As the device height/weight is shrunk and compatible/smaller than the electron wavelength (~2nm), the 2D/1D DOS should be applied to derive the free electron concentration for the device. The 2D/1D DOS for the MG transistors can be obtained by solving the 2D/1D wave equation. This leads to
D2D(E) and D1D(E) have considered the spin per electron. According to the similar developing procedure as shown in (12), the 2D/1D free electron concentration can be expressed as
where F0(hF) and F-1//2(hF) are the Fermi-Dirac integral of order 0 and -1/2, respectively. They can be expressed as
Similarly, in terms of non-degenerate carrier statistics, (27) and (28) can be further reduced as
Criterion of threshold voltage for the low-dimensional ballistic MG MOSFETs:
By setting free electron density equal to the substrate doping concentration, as shown in (22), the criterion of threshold voltage for 2D and 1D MG devices can be shown as
By replacing Fmin,3D with Fmin,2D, and Fmin,1D, the threshold voltage for 2D and 1D MG MOSFETs can be obtained.
3. Results and Discussion
The 3D device simulator “SDEVICE” is employed to validate the proposed model [14]. Unless otherwise stated, the following device parameters are used to simulate the MG MOSFETs: the device structure’s square shape, the effective electron mass =1.08m0, and the valley degeneracy of the silicon gv=6. The graded density model is included to simulate the carrier density. Also, the quantum-potential model simulates the electrostatic potential, ensuring that the Poisson equation is self-consistent with the wave equation. Figure 2 plots the threshold voltage versus the channel length of FinFET for different silicon thicknesses. As the channel length decreases, the thin silicon can produce a larger threshold voltage than the thick silicon due to the alleviated ballistic effects that result in threshold voltage degradation. Figure 3 plots the threshold voltage versus the channel length of W-gate MOSFET for different oxide thicknesses. The thin gate oxide that effectively resists the ballistic effects can induce a smaller threshold voltage degradation than the thick gate oxide. Figure 4 shows how the work function affects the threshold voltage as the channel length is decreased for nanosheet MOSFET. The high work function can bring about a high threshold voltage as the channel length decreases, as opposed to the low work function, which reduces the threshold voltage due to the strong ballistic effects. To show how the different dimensionalities of the devices affect the threshold voltage. Figure 5 uses the different ratio of device width to device height (i.e., W H) by considering (2nm 2nm), (2nm 5nm), and (5nm5nm) cross-section area of FinFET with the channel length decreased from 20nm to 10nm. Note that as the device dimension is approaching the electron wavelength (~2nm), the 2D/1D density of state should be accounted for in calculating the electron concentration, as shown in Figure 5. It is shown that the 1D device with the cross-section area of 2nm 2nm can induce the largest threshold voltage as opposed to the 3D device with the cross-section area of 5nm 5nm, which results in the smallest threshold voltage because the high-dimensional device cannot effectively alleviate the ballistic effects that degrade the threshold voltage. Figure 6 shows the threshold voltage versus the channel length for different devices’ structures, including nanosheet MOSFET. W-gate MOSFET, and FinFET. The nanosheet MOSFET exhibits the largest threshold voltage and smallest threshold voltage degradation with the gate surrounding the channel regime. However, FinFET, with the smallest gate coverage, will show the smallest threshold voltage and largest threshold voltage degradation among the three devices. It is known that the scaling factor can provide the designing guidance for the threshold voltage of the MG devices. Figure 7 plots the threshold voltage versus the scaling factor for different silicon and oxide combinations of the FinFET. It can be seen that as the scaling factor is reduced below 3, the threshold voltage will be significantly degraded. Therefore, when designing the MG MOSFETs, the allowable silicon/oxide thickness combinations corresponding to the appropriate scaling factor should be carefully accounted for.
4. Conclusion
As for the modern multiple-gate (MG) transistors composed of FinFET, W-gate MOSFET, and nanosheet MOSFET, a unified ballistic model for the threshold voltage is proposed and validated. The model can also be applied for P-type MG devices by interchanging the device parameters between electron and hole. Accompanied by P-type MG MOSFET, the modern complementary gate-stacked MOSFET (i.e., CFET) can be integrated to simulate the subthreshold logic circuit for its low-power circuit application.
References
- M. Badaroglu and A. P. Gargini,”System and high-volume manufacturing driven more Moore scaling roadmap”, IEEE Electron Device Society News Lett.,vol. 28, no. 1, pp. 3-9,Jan. 2021.
- M. Raghavendra, S.K. Vamshi, and C. Rohini,” Low power high speed 4-dimension FinFET SRAM”, 3rd International Conference for Emerging Technology Belgaum, India, May, 2022. [CrossRef]
- M. H. Kahsani, H. Hsakiba, and A. Sheikholeslami,” A low-power high BW PAM4 VCSEL driver with three-tap FFE in 12-nm CMOS FinFET process, IEEE Journal of solid-state circuits, 2024. [CrossRef]
- F. Balestra, S. Cristoloveanu, M. Benachir, J. Brini, and T. Elewa,” Double-gate Silicon-On-Insulator transistor with volume inversion: A new device with greatly enhanced performance”, IEEE Electron Device Letters, vol. 8, no. 9, pp. 410-412, September, 1987. [CrossRef]
- Yuan Taur,” Analytical solution to a double-gate MOSFET with Undoped body”, IEEE Electron Device Letters, vol. 21, no. 9, pp. 245-247, September, , 2000. [CrossRef]
- Z, R. Xiao et al., “Vertical N-Type and P-Type Nanosheet FETs With C-Shaped Channel” IEEE Trans. Electron Devices. vol. 70, no.3, pp. 1380–1385, March, 2023. [CrossRef]
- X. Xiong, A. Tong, X. Wang, S. Liu, X. Li, R. Huang, and Y. Wu “Demonstration of Vertically-stacked CVD Monolayer Channels: MoS2 Nanosheets GAA-FET with Ion>700mA/mm and MoS2/WSe2 CFET”, International Electron Device Meeting, pp. 161-165, 2021. [CrossRef]
- P. J. Sung, et al., “Fabrication of Vertically Stacked Nanosheet Junctionless Field-Effect Transistors and Applications for the CMOS and CFET Inverters”, IEEE Trans. Electron Devices. vol. 67, no.9, pp. 3504–3509,Sept., 2020. [CrossRef]
- X. Yang, X. Li, Z. Liu, Y. Sun, Y. Liu, X. Li, and Y. Shi, “Impact of Process Variation on Nanosheet Gate-All-Around Complementary FET (CFET)”, IEEE Trans. Electron Devices. vol. 69, no.7, pp. 4029–4036,July, 2022. [CrossRef]
- X. Yang, Y. Sun, X. Li, Y. Shi, and Z. Liu, “Compact Modeling of Process Variations in Nanosheet Complementary FET (CFET) and Circuit Performance Predictions”, IEEE Trans. Electron Devices. vol. 70, no.7, pp. 3935–3942,July, 2023. [CrossRef]
- S. K. Kim et al. , “Heterogeneous 3-D Sequential CFETs With Ge (110) Nanosheet p-FETs on Si (100) Bulk n-FETs”, IEEE Trans. Electron Devices. vol. 71, no.1, pp. 393–399, Jan, 2024. [CrossRef]
- Juin J. Liou and Te-Kuang Chiang,” A Novel Effective-Conducting-Path-Induced Scaling Length Model and Its Application for Assessing Short-Channel Performance of Multiple-Gate MOSFETs”, IEEE Trans. Electron Devices. vol. 65, no.10, pp. 4535–4541, July 2018. [CrossRef]
- Mark Lundstrom, “Fundamentals of Nanotransistors”, Lessons from Nanoscience: A lecture note series, December 2015.
- SDEVICE: 3D device simulator, Sentaurus, Synopsis 2000.
Figure 2.
threshold voltage versus the channel length for different silicon thicknesses of the FinFET.
Figure 2.
threshold voltage versus the channel length for different silicon thicknesses of the FinFET.
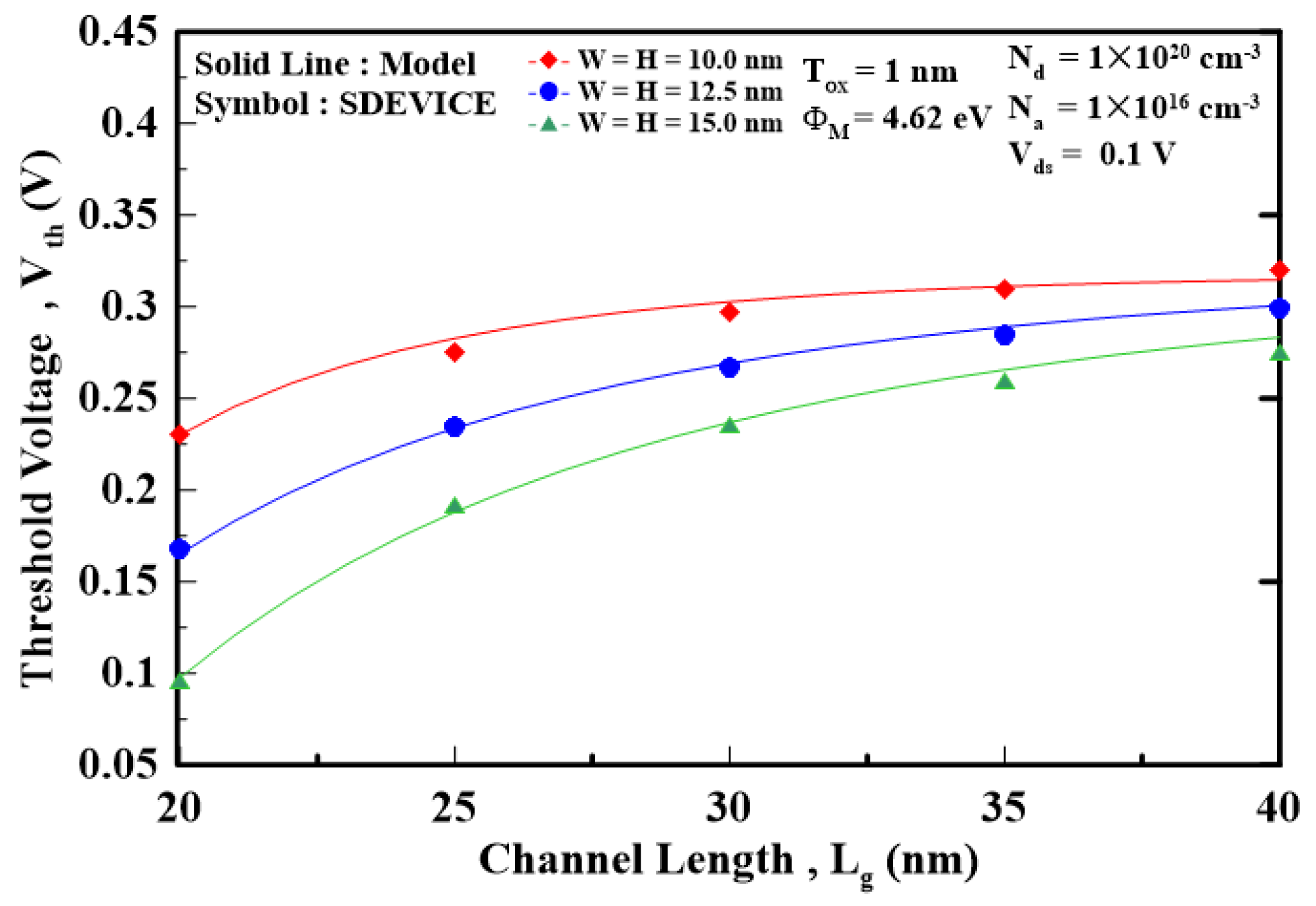
Figure 3.
threshold voltage versus the channel length for different gate oxide thicknesses of the W-gate MOSFET.
Figure 3.
threshold voltage versus the channel length for different gate oxide thicknesses of the W-gate MOSFET.
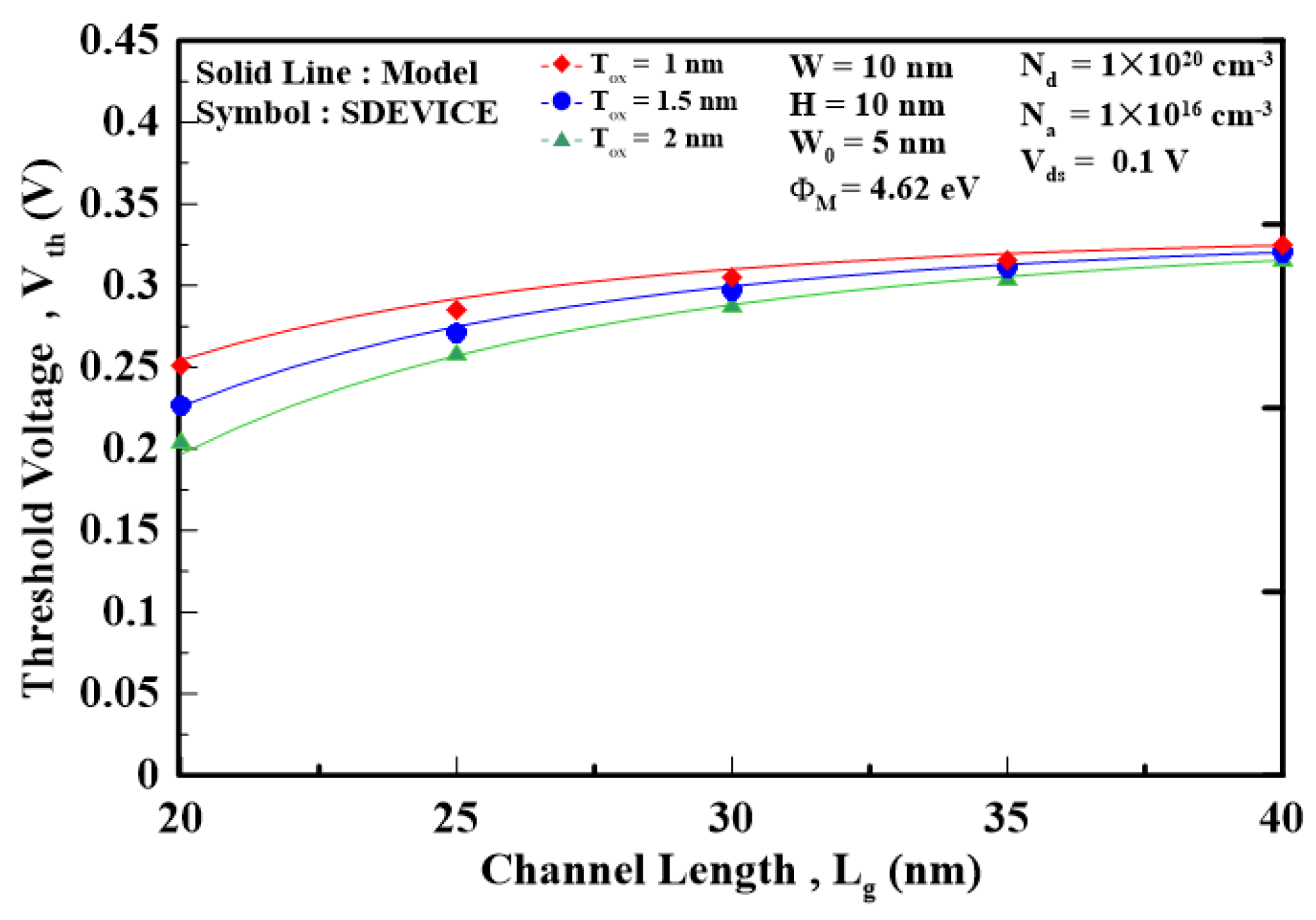
Figure 4.
threshold voltage versus the channel length for different work functions of the nanosheet MOSFET.
Figure 4.
threshold voltage versus the channel length for different work functions of the nanosheet MOSFET.
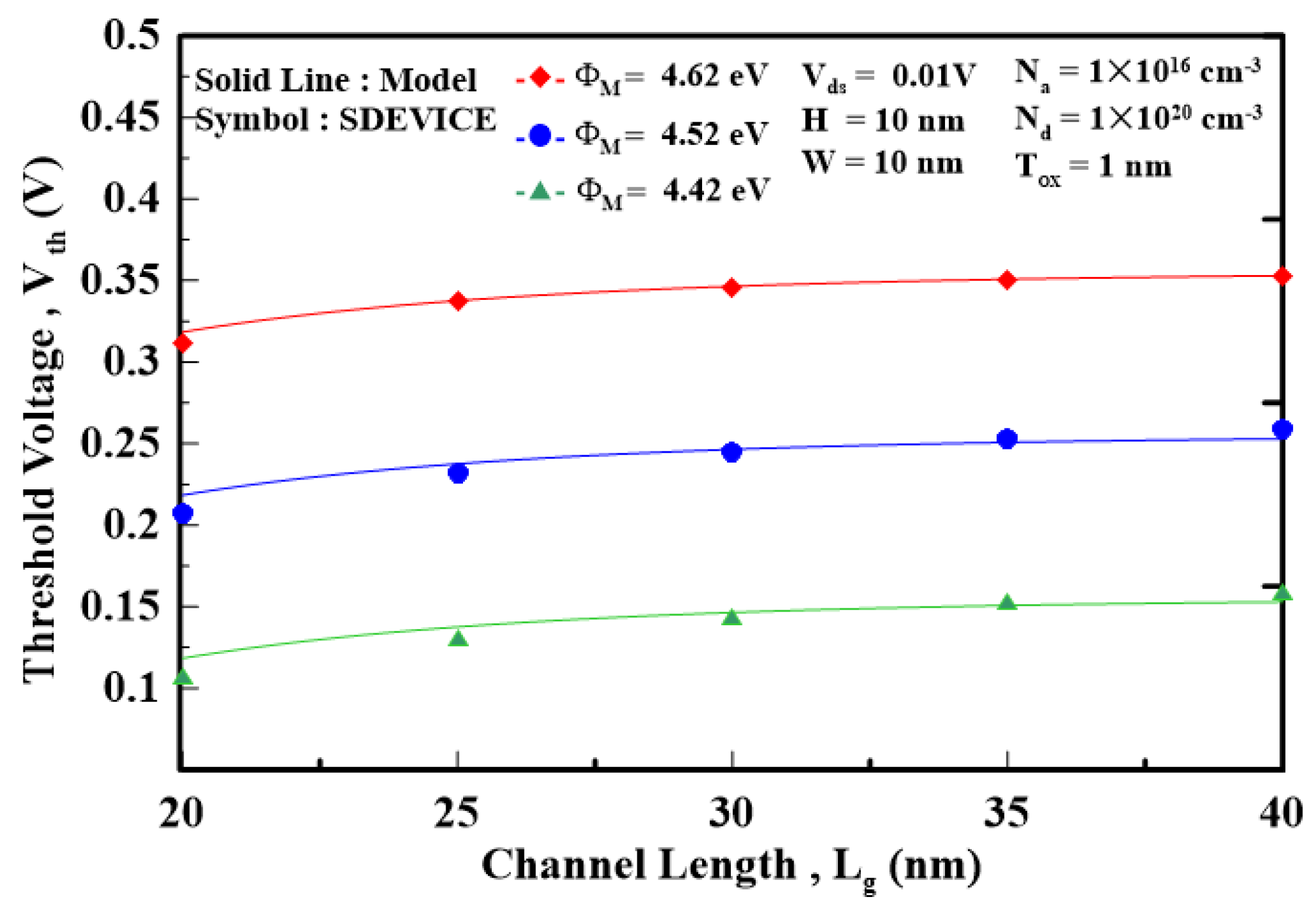
Figure 5.
threshold voltage versus the channel length for different dimensionalities of the FinFET.
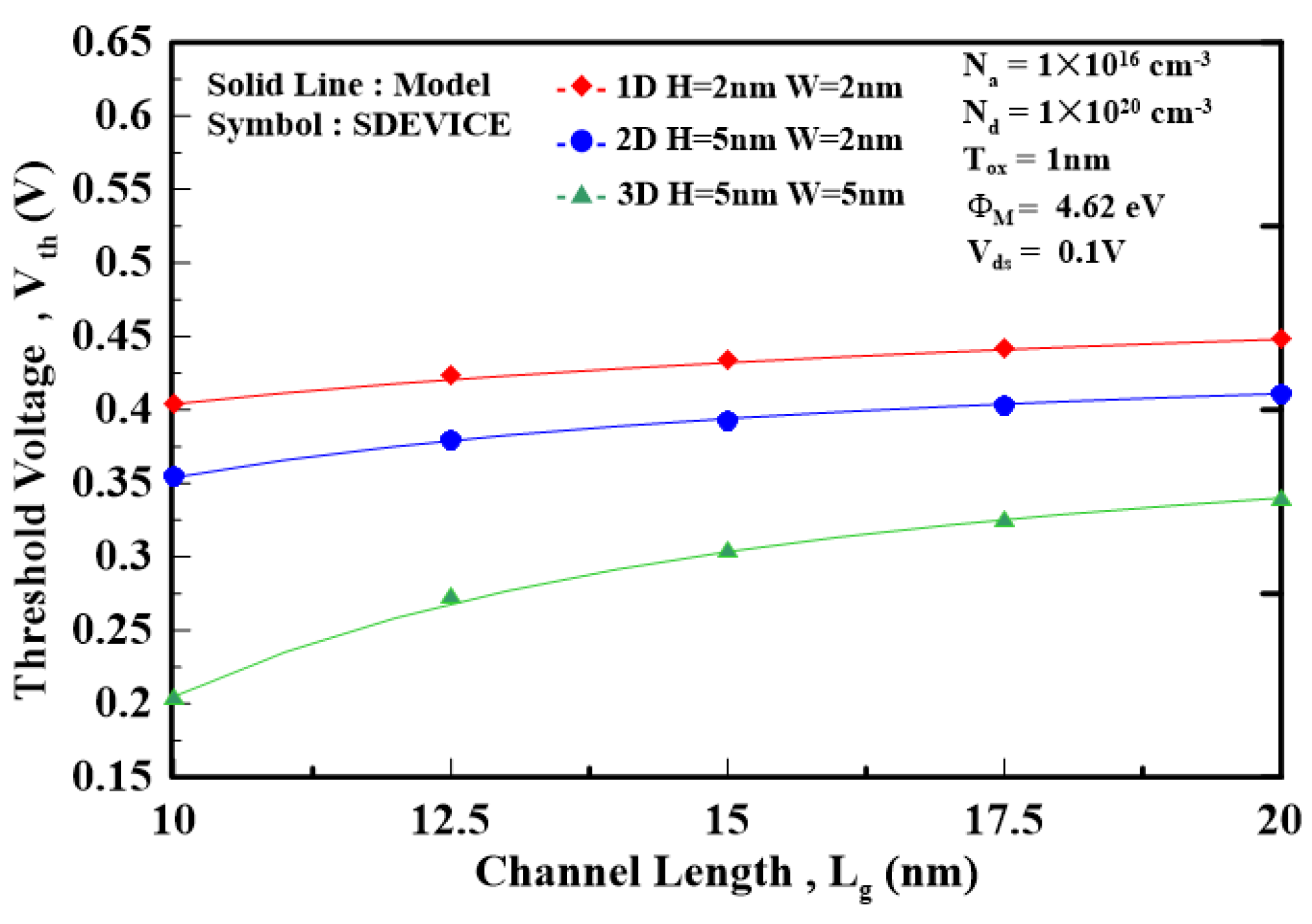
Figure 6.
threshold voltage versus the channel length for different MG FETs, including FinFET, W-gate MOSFET, and nanosheet MOSFET.
Figure 6.
threshold voltage versus the channel length for different MG FETs, including FinFET, W-gate MOSFET, and nanosheet MOSFET.
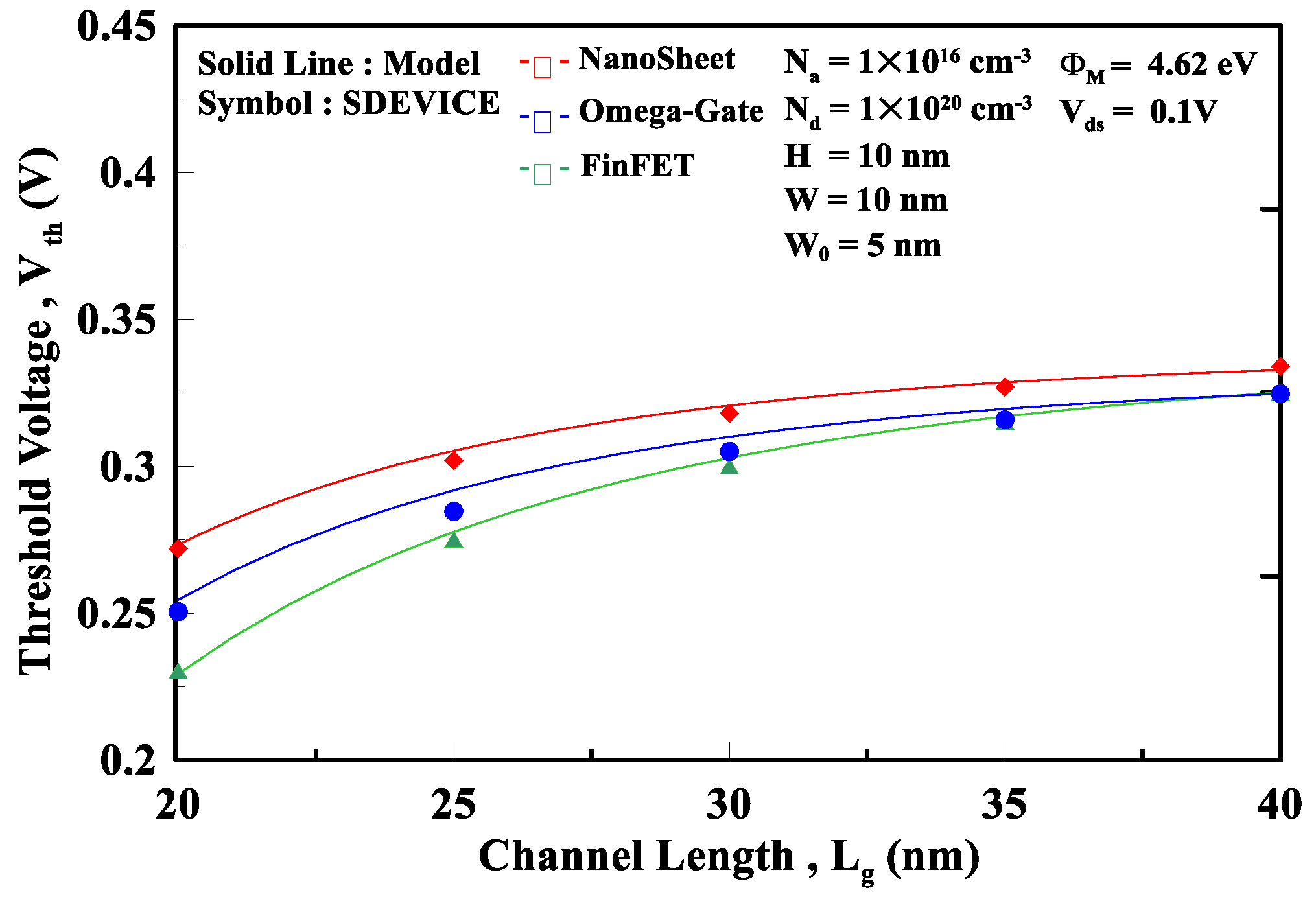
Figure 7.
threshold voltage versus the scaling factor for silicon/oxide thickness combinations of the FinFET.
Figure 7.
threshold voltage versus the scaling factor for silicon/oxide thickness combinations of the FinFET.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated




