The Cloud Model-Based Evaluation of Public Building Renewal Potential with the Game Theory Combination Weighting Methods-Case Study in China

Preprint

Article

The Cloud Model-Based Evaluation of Public Building Renewal Potential with the Game Theory Combination Weighting Methods-Case Study in China

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Zhang Jia Ying^*,Li Xi Sheng

This version is not peer-reviewed

Submitted:

02 September 2024

Posted:

02 September 2024

You are already at the latest version

Alerts

Abstract

Currently, urban renewal activities in China are booming. And promoting the renovation of public buildings is the key due to its large scale, high cost and significant impact to the nature and social environment. To reduce the ambiguity and uncertainty in evaluating the potential for renewal of existing public buildings, a renewal potential evaluation model combining game theory combination weighting method and cloud model theory is proposed. The paper constructs a comprehensive evaluation index system based on relevant standards and literature. Game theory is used to optimize the weights obtained by AHP and entropy weight methods to obtain a combined weight. MATLAB programming is used to calculate the comprehensive cloud parameters of the evaluation index for the potential renewal of existing public buildings and therefore generate cloud Graphs. Through case study in Nanjing of China, it has been demonstrated that the combination empowerment cloud model can objectively reflect the relationship between the fuzziness and randomness of evaluation indicators for public building renewal potential. The expression of cloud Graphs can intuitively reflect the magnitude of renewal and renovation potential and the degree of uncertainty in evaluation results. The research result provides useful references for the sustainable utilization of building resources in the era of building.

Keywords:

Subject: Engineering - Civil Engineering

1. Introduction

Urban renewal refers to a series of actions aimed at demolishing, rebuilding, and comprehensively improving areas that have experienced physical, functional, or social decline, as well as built environments that no longer meet current or future development needs [1]. As China shifts towards high-quality urbanization, urban renewal has transitioned from large-scale incremental development to smaller-scale, quality-focused improvements [2]. In 2020, the Fifth Plenary Session of the 19th Central Committee of the Communist Party of China approved the "Recommendations for Formulating the 14th Five-Year Plan for National Economic and Social Development and the Long-Range Objectives Through the Year 2035," explicitly proposing the implementation of urban renewal actions. Subsequently, the report of the 20th National Congress further emphasized the need to "enhance the Grades of urban planning, construction, and accelerate the transformation of development patterns in mega cities, as well as implement urban renewal actions." This has elevated urban renewal to an unprecedented national strategic priority [3].

According to the "Implementation Plan for Promoting the Renewal of Building and Municipal Infrastructure Equipment" [4] and the "Five-Year Action Plan for the In-Depth Implementation of a People-Centered New Urbanization Strategy" [5], which were issued by the Ministry of Housing and Urban-Rural Development and the State Council in 2024, public building renewal contents encompasses several aspects: infrastructure and equipment upgrades , improvements of safety and building energy efficiency, environmental facility upgrades , functional space modifications and the integration of intelligent and information systems, as well as cultural and historical preservation. As a critical component of urban renewal, public building renewal is characterized by large areas, high numbers, low design standards, and significant energy and environmental burdens [6]. Current research on public building renewal has made substantial progress in areas such as research of renewal implementation pathways, stakeholder rights and funding sources analysis during the renewal process [7,8,9]. However, there remain a gap between the theory and the practice, especially lacking of the research about the potential evaluation of public building renewal.

The potential of public building renewal is a practice that transforms latent utility into actual utility by leveraging external conditions, based on the existing conditions of public buildings in terms of cultural history, geographic location, structural safety, and user’s comfort [10]. Evaluating the renewal potential of existing buildings is fundamental to determining renewal plans (demolition, repair and renovation, or preservation and reconstruction). Current research about renewal potential evaluation primarily focuses on three fields. The first category involves evaluating urban area renewal potential from a intermediate perspective, based on land plots or regions. For example, Wang Jingli [11] evaluated the renewal potential of various administrative districts in Shenzhen using internet data; Han Huiran [12] proposed a conceptual model for spatial renewal and reproduction in the old industrial district of Yaohai, Hefei; Wang Xuefei [13] explored the renewal direction and implementation pathways of urban historical streets from the perspective of neighborhood memory. The second category focuses on evaluating the performance of existing buildings on specific aspects (usually carbon emissions [14], energy consumption [15], structural safety [16], etc.). The third category pertains to research on evaluation methods and models. Current methods for evaluating building renewal potential can be broadly categorized into two types: one is the commonly used multi-objective, multi-attribute decision-making methods based on fuzzy theory, which generally focus on establishing evaluation indicators, calculating indicator weights, and determining membership degrees [17,18,19]; the other type is converting multiple objectives into a single objective and deriving the renewal potential value by establishing an evaluation model to calculate a utility function, such as the ARP (Adaptive Reuse Potential) model [20] and the AdaptSTAR model [21].

The evaluation of the renovation potential of existing public buildings differs from that of land plots or single performance evaluations. As general, the performance of the building itself occupies a larger weight in the evaluation system with other multiple objectives and attributes. Although the fuzzy theory-based evaluation method is widely applied, the deficiency that weight value determining methods significantly affects the evaluation results. On the other hand, utility function evaluation methods, represented by ARP, provide a straightforward and intuitive expression with the challenging to obtain related data, and cannot clearly reflect the intrinsic relationship between evaluation results and evaluation indicators. A common issue with both methods is that the evaluation results cannot reflect the degree of uncertainty between the evaluation indicators and the outcomes. The cloud model proposed by Academician Li Deyi, which describes the randomness between uncertain linguistic values and precise numerical values, can realize the qualitative and quantitative transformation of uncertain concepts [22]. The cloud model has been widely applied in performance evaluation and prediction research. It also can visually and comprehensively reflect evaluation results and details through cloud Graphs which makes it as an effective tool for multi-objective, multi-attribute decision evaluation [23,24,25,26].

This paper takes the urban renewal project Military Club of Nanjing, China, as an example to establish an indicator system for evaluating the renewal potential of existing public buildings and a cloud model for potential evaluation. The indicator weights are calculated by the game theory-based combination weighting method. And the potential indicator membership degree and the relevant parameters of cloud model is calculated using MATLAB R2023b programming. The evaluation results are comprehensively analyzed to provide decision-making suggestions for the renovation of existing buildings.

2. Materials and Methods

2.1. Evaluation Index System for Public Building Renewal Potential

The establishment of a comprehensive evaluation index system should adhere to principles of systematic, scientific, and a combination of qualitative and quantitative approaches. Typically, methods such as literature review and expert consultation are employed to develop the index system. The factors influencing the renewal potential of existing public buildings are complex, and can be categorized from different dimensions depending on the evaluation method. Langston [27] categorized the influencing factors of urban building renewal potential into seven dimensions: "physical obsolescence, economic obsolescence, functional obsolescence, technological obsolescence, social obsolescence, legal obsolescence, and political obsolescence." Wu Hao [10] divided the influencing indicators for evaluating the renovation potential of public buildings into five categories: "building integrity, energy optimization, historical continuity, future profitability, and environmental benefits."

Given the dynamic nature of urban renewal across time and space dimensions, the renovation need to follow the principle of "one city, one strategy; one district, one policy" [28]. The evaluation indicators for the renewal of existing public buildings should reflect both the project’s generality and the individuality which capturing the uniqueness of each project. Based on previous studies [10,11,12,13,14,15,16,17,18,19] and industry standards such as Specification for Evaluation of Urban Traffic Operation Status GB/T 33171-2016 [29], Nanjing Urban Renewal Regulations [30], Regulations for the Classification and Grading of Urban Land GB/T 18507-2014[31], and Standards for the Reliability Appraisal of Civil Buildings GB 50292-2015[32], an initial index system was established. Subsequently, after gathering opining from functional departments responsible for construction management, universities, and property management experts, the final determination of a comprehensive evaluation system for public building renewal potential was developed. This system includes one target index, four criterion indices, and twenty-nine observational indices, as illustrated in Table 1.

The four criterion indices comprehensively consider the current state (C) and future development (D) of public buildings over a time dimension. It covers the land value (A) on which public buildings rely, the current state of the buildings themselves (C), and the surrounding environmental conditions associated with the public buildings (B) in the view of space dimension. Criterion A represents the attachment of the building to its site, as the value of any building is inherently linked to the value of the land it occupies. This criterion can be considered a latent variable, measured using observational indices (A1-A9). Criterion B reflects the impact of the external surrounding environment on the renewal potential of public buildings. Given the "public" nature of public buildings, the surrounding traffic conditions, among various environmental factors, most effectively reflect the potential value of public buildings, which can be measured using observational indices B1-B5. Criterion C represents the function, comfort and safety of the existing building itself, which is the most important influential criterion on renewal potential. According to relevant standards for the renovation of existing buildings, this criterion is measured using observational indices C1-C9. Criterion C primarily reflects the physical state of the building. Considering the actual situation in China, an additional indicator, C4 (property rights clarity), is added, as clear property ownership helps to reduce legal disputes and obstacles during the renewal process. Criterion D reflects the future value of existing public buildings from a time dimension. Observational indices D1-D5 indicate the subjective willingness for renewal (D2) and the objective expectations of the building's functional, safety, and historical value (D1, D3-D5).

2.2. Classification of Evaluation Standards

Based on the multi-criteria and multi-Grade evaluation system established in Table 1, the observational indicators layer employs a combination of qualitative and quantitative methods, incorporating fuzzy processing techniques to quantify qualitative information. Referring to relevant literature [10], the evaluation results of public building renewal potential are categorized into five semantic Grades: low potential, relatively low potential, moderate potential, relatively high potential, and high potential, corresponding to the evaluation set U = {I, II, III, IV, V} which divided into five equal intervals within [0,1]. Following similar principles, qualitative observational indicators are formed through the ratings provided by 12 experts in the fields of urban planning, land economics, and urban renewal. Basing on relevant evaluation standards and statistical data, different experts, drawing on their experience and knowledge, assign scores following the rule of 10-point scale and five equal intervals. For example, in order to get the indicator "Land Price Grade of Unit A2," we should firstly obtain the latest land transaction price of the adjacent plot (P1) and the average land price of the main urban area where the public building located (P0) . When P1/P0 < 50%, the corresponding score is within the interval [0,2), with a rating of "significantly low"; when 25% < P1/P0 < 50%, the corresponding score is within the interval [2,4), with a rating of "relatively low"; when 25% < P1/P0 < 1.25, the corresponding score is within the interval [4,6), with a rating of "average"; when 1.25 < P1/P0 < 1.5, the corresponding score is within the interval [6,8), with a rating of "relatively high"; when P1/P0 > 1.5, the corresponding score is within the interval [8,10), with a rating of "significantly high." For other observational indicators that cannot obtain quantitative evaluation data, the evaluation data can only be obtained based on expert subjective opinions. To eliminate the differences in expert evaluations, the expert linguistic assessments can be converted into triangular fuzzy numbers, and the mean area method can be employed to convert expert opinions into definite values. Furthermore, quantitative observations indicators follow the threshold divisions according to the industry standards outlined in Section 1.1, as detailed in Table 2.

3. Building a Cloud Evaluation Model

Combining probability theory and fuzzy set theory, the cloud model facilitates the transformation between qualitative and quantitative assessments through forward and backward cloud generators. The model describes linguistic values using three characteristic parameters: Expectation (Ex), Entropy (En), and Hyper Entropy (He). ‘Ex’represents the central point of the concept. ‘En’reflects the degree of uncertainty of the concept, and ‘He’measures the uncertainty of the entropy [33]. The evaluation index system for public building renovation potential is complex, with significant fuzziness and randomness inherent in various indicators. The cloud model not only considers the randomness of the membership degrees of each evaluation indicator but also accounts for the intrinsic relationship between randomness and fuzziness [34], making it well-suited for evaluating the renewal potential of existing public buildings.

After establishing the classification standards for the indicators as shown in Table 2, the evaluation based on the cloud model primarily involves two tasks: "determination of weights" and "cloud model evaluation." The specific process is illustrated in Figure 1.

3.1. Game Theory-Based Weight and Cloud Model Parameters Calculation

Scientifically determining the weights of evaluation indicators is a prerequisite for cloud model evaluation. Existing weighting methods can be categorized into subjective and objective approaches. Subjective weighting methods, such as the Analytic Hierarchy Process (AHP), can leverage the professional experience of decision-makers. However, due to differences in professional knowledge and background among respondents, these methods may lead to instability in the results. On the other hand, objective weighting methods, such as the entropy weight method, are based on sample data but often struggle to reveal the relative relationships between indicators. Considering the strengths and weaknesses of both AHP and the entropy weight method, the combination weighting method based on game theory facilitates the acquisition of comprehensive, balanced, and accurate integrated weights [35].

3.1.1. Analytic Hierarchy Process (AHP)

The 9-point scale method is used to invite experts to assign scores and construct a judgment matrix A_n_×_n. The square root method is then employed to combine and calculate the experts' judgment matrices to obtain the indicator weights, followed by a consistency check. The specific process is detailed in Equations (1)–(3).

\bar{A} = {(\prod_{k = 1}^{m} a_{i j}^{k})}^{\frac{1}{n}}

(1)

W_{i} = \frac{\bar{A}}{\sum_{i = 1}^{n} \bar{A}}

(2)

C R = \frac{C I}{R I} = \frac{λ_{m a x} - n}{(n - 1) R I} < 0.1

(3)

3.1.2. Entropy Weight Method

This method evaluates the importance of each factor based on the degree of variation of the indicators and information entropy. It calculates the entropy weights after data standardization, as detailed in Equations (4)–(6).

p_{i j} = \frac{x_{i j}}{\sum_{i = 1}^{n} X_{i j}}

(4)

e_{j} = - \frac{1}{l n (n)} \sum_{i = 1}^{n} p_{i j} l n （ p_{i j} ）

(5)

w_{j} = \frac{1 - e_{j}}{\sum_{j = 1}^{m} （ 1 - e_{j} ）} (j = 1, 2, \dots, m)

(6)

3.1.3. Game Theory-Based Combination Weighting

The essence of game theory-based combined weighting lies in aiming for Nash equilibrium, where the goal is to find the weight combination that minimizes the differences between the weight vectors of various indicators. The steps are as follows:

(1): The weight vectors of the subjective and objective indicators are linearly combined to obtain the comprehensive weight vector (In the formula, α1 and α2 represent the subjective and objective weight coefficients, respectively.):

W = α_{1} w_{1}^{T} + α_{2} {w_{2}}^{T}

(7)

(2): By minimizing the deviation as the objective, the two linear combination coefficients are optimized, resulting in the optimal weights:

\min {‖W - w_{k}‖}_{2}, k = 1, 2

(8)

(3): According to the properties of matrix differentiation, Equation (8) can be equivalently transformed into a system of linear equations based on the first-order optimality conditions:

(\begin{matrix} w_{1} w_{1}^{T} & w_{1} w_{2}^{T} \\ w_{2} w_{1}^{T} & w_{2} w_{2}^{T} \end{matrix}) [\begin{matrix} α_{1} \\ α_{2} \end{matrix}] = [\begin{matrix} w_{1} w_{1}^{T} \\ w_{2} w_{2}^{T} \end{matrix}]

(9)

(4): By normalizing the subjective and objective weight coefficients, the comprehensive weight ω is determined:

ω = α_{k} / \sum_{k = 1}^{2} α_{k}

(10)

3.2. Cloud Model Parameters and Membership Degree Calculation

Following the steps outlined above, after calculating the combined weights for each evaluation indicator, the calculation sequence for the cloud model's relevant parameters and membership degrees corresponds to Equations (11) through (14).

(1): Construct the Evaluation Standard Cloud.

$\{\begin{array}{l} E x = \frac{U_{\max} + U_{\min}}{2} \\ E n = \frac{U_{\max} - U_{\min}}{6} \\ H e_{0} = k \end{array}$

(11)
(2): Calculate the cloud parameters for each evaluation indicator.

$\{\begin{array}{l} \bar{X} = \frac{1}{n} \sum_{i = 1}^{n} x_{i} \\ S^{2} = \frac{1}{n - 1} \sum_{i = 1}^{n} {(x_{i} - \bar{X})}^{2} \\ E_{x} = \bar{X} \\ E_{n} = \sqrt{\frac{π}{2}} \cdot \frac{1}{n} \sum_{i = 1}^{n} | x_{i} - E_{x} | \\ H_{e} = \sqrt{| S^{2} - E_{n}^{2} |} \end{array}$

(12)
(3): Calculate the comprehensive cloud parameters for the evaluation object.

$\{\begin{array}{l} E x = \frac{\sum_{i = 1}^{n} ω_{i} E x_{i}}{\sum_{i = 1}^{n} ω_{i}} \\ E n = \frac{\sum_{i = 1}^{n} ω_{i}^{2} E n_{i}}{\sum_{i = 1}^{n} ω_{i}^{2}} \\ H e = \frac{\sum_{i = 1}^{n} ω_{i}^{2} H e_{i}}{\sum_{i = 1}^{n} ω_{i}^{2}} \end{array}$

(13)
(4): Calculate the membership degree of the evaluation object for each potential Grade.

$μ (x_{i}) = \exp (- \frac{{(x_{i} - E x)}^{2}}{2 y_{i}^{2}})$

(14)
(5): Generate the evaluation cloud Graph: By combining the evaluation cloud Graph with the standard cloud Graph, the area with the highest overlap between the two cloud Graphs indicates the evaluation Grade.

In Equation (11), ‘k’ is a constant, typically set between 0.005 and 0.01, adjusted according to the degree of fuzziness of the indicators. In Equation (13), ω_i represents the weight. In equation (14), y_i∼N(En,He²) and x_i∼N(Ex,y_i²).

4. Case Study

4.1. Case Overview

The Nanjing Military Club Building is a key project in the "2024 Nanjing Urban Renewal Project Implementation Plan" focusing on the transformation of production style. It is located at No. 105 Zhongshan North Road in the Gulou District of Nanjing, China. The project covers a land area of approximately 29,070.7 m², with a total building area of about 43,749.22 m². The site is bounded by Zhongshan North Road to the east, Fuzuo Road to the west, and is adjacent to Shanxi Road Department Store and Zhonghuan International Plaza to the north. The project includes 14 buildings, with Building No. 1 being a provincial-Grade cultural heritage site.

4.2. Data Sources

In this case, qualitative indicator data were collected through scores provided by 10 industry experts, while the "D2 Public Willingness to Update" data were gathered through surveys of residents living near the building. Quantitative indicators were obtained in two ways: firstly, through measurements and calculations based on professional standards such as the General Code for Building Environment GB 55016-2021 [36] and Acoustic Environment Quality Standards GB 3096-2008 [37]; and secondly, by querying relevant departments of Nanjing's urban construction management, specialized websites, and platforms like Gaode Graphs. After standardizing the collected qualitative and quantitative indicator data, MATLAB R2023b software was used to develop programs for calculating indicator weights, cloud model parameters, and membership degrees.

4.3. Model Implementation

4.3.1. Establishment of the Evaluation Standard Cloud

The rating intervals were divided based on five semantic Grades of building renewal potential. Setting the hyper-entropy (He) value to 0.005, the standard cloud parameters derived from Equation (11) are presented in Table 3. Using the cloud model code in MATLAB, 2000 cloud droplets were generated to plot the evaluation standard cloud Graph.

4.3.2. Calculation of Indicator Combination Weights and Cloud Parameters

Weight Calculation Using AHP Method: Based on the importance comparisons of indicator weights made by 10 experts, a judgment matrix was constructed. The subjective weights for the evaluation indicators of public building renewal potential were calculated using Equations (1)-(3). The results for the criterion layer are shown in Table 4-(1), and the indicator layer results are in Table 4-(7).

Weight Calculation Using the Entropy Method: Data from six public building renewal projects in Nanjing (including the Xinjiekou Art Building, Nanjing Normal University Xuanwu Science Park, Hanzhongmen Bus Station, etc.) similar to the Military Club building were collected. Using Equations (4)-(6), the objective weights for the indicators were calculated. The results for the criterion layer and indicator layer are shown in Table 4-(2) and Table 4-(8), respectively.

Combination Weight Calculation: Based on Equations (7)-(10), MATLAB code was written to calculate the game theory-based combination weight distribution coefficients for the criterion layer, resulting in α1=0.802 and α2=0.198. The final combination weights for the criterion layer ω are shown in Table 4-(3). Similarly, the combination weights for the indicator layer ω₀ were calculated, with results shown in Table 4-(9).

Cloud Parameter Calculation: The measured data from the case studies were substituted into Equation (12) to calculate the cloud parameters for the indicator layer, with results shown in Table 4-(10), (11), and (12). The criterion layer cloud parameters were then obtained by combining ω₀ and Equation (13), as shown in Table 4-(4), (5), and (6). Finally, Equation (13) was used again to calculate the comprehensive ·evaluation cloud parameters for the renewal potential at the target layer, resulting in (Ex, En, He) = (0.6551, 0.1900, 0.0320).

4.4. Membership Degree Calculation and Evaluation Cloud Graph Generation

Membership Degree Calculation: Based on the cloud parameters for the criterion layer and indicator layer in Table 4, the membership degrees for the target layer and criterion layer can be calculated using Equation (14). The results are shown in Table 5.

Cloud Graph Generation: By integrating the standard cloud parameters and evaluation cloud parameters, the comprehensive evaluation cloud Graph for renewal potential and the cloud Graphs for the criterion layer are plotted, as shown in Figure 2.

5. Results and Discussion

According to Figure 3.1, the comprehensive evaluation cloud Graph is primarily distributed between the Grade III and Grade IV standard cloud Graphs, closely aligning with the Grade IV standard cloud. Combined with the membership degree value in the target layer from the second row of Table 5 and following the principle of maximum membership degree, it is determined that the renewal potential of the Military Club building is Grade IV, indicating a high potential. This result aligns with the planning status of Nanjing’s second batch of urban renewal projects.

From Table 5, it can be seen that the membership degree evaluation results for criterion layers A, B, C, and D are all at Grade IV. Based on the relative positions of the criterion layer evaluation cloud Graphs compared to the evaluation standard clouds, only “D Future Benefits” (Figure 3.5) is located to the right of the Grade IV standard cloud, indicating that the future benefits after the building renewal will increase significantly. It can also be observed that the cloud droplets for “B Surrounding Traffic Conditions” (Figure 3.3) and “D Future Benefits” (Figure 3.5) are relatively dispersed, indicating a higher degree of uncertainty in the evaluation results. The reason for this could be that the former’s indicators were affected by factors such as holidays and weather during data collection, leading to significant data fluctuations, while the latter’s indicator layer consists of qualitative indicators that are highly influenced by the subjective judgments of respondents. The indicators under “A Land Space Value” (Figure 3.2) and “C Building Condition” (Figure 3.4) mainly reflect static data about the building, resulting in more stable data and higher certainty, leading to more convergent evaluation cloud Graphs.

The Ex values of the indicator layer cloud parameters in Table 4-(10) reflect the sensitivity of each indicator to the criterion layer. For positive indicators, higher Ex values are more beneficial for project renewal. Conversely, for negative indicators, higher Ex values indicate worse current conditions, highlighting the urgency for renewal. For example, in criterion layer C, the Ex value for “C1 Vacancy Grade” is 0.9050, the highest among all indicators, suggesting that this indicator has the highest potential and expectation for renewal. The reason lies in the fact that the Military Club was previously used as the Yangtze River Delta Publication Market, but due to outdated functionality and reduced social demand, the market closed in 2018, leaving most of the building vacant, thus leading to strong public demand for its renewal. The Ex value for “C2 Flexibility of Spatial Layout” is 0.8000, indicating the second-highest renewal potential, as the project was constructed a long time ago, and its design standards and concepts no longer meet contemporary needs, making it particularly urgent to optimize the spatial layout of the building.

The Ex values of the indicator layer reflect the building’s current conditions and renewal potential, but a higher Ex value does not necessarily imply prioritizing that aspect for renewal. For instance, the indicators under criterion layers A and B are more constrained by urban planning, construction, and traffic planning, meaning that individual public building renewals should adhere to the overall urban development layout. In summary, the suggested priority order for the renewal work of the Military Club is: C1, D4, A8, D1, A3, C2, D5, C8, C7, C9, C6. The renewal should first focus on transforming building functions and improving utilization rates while ensuring the protection and use of cultural heritage and historic buildings. Subsequently, the work should be carried out in the order of optimizing internal spatial structure, enhancing safety resilience, improving natural lighting, upgrading worn physical components, and improving sound insulation performance.

6. Conclusion and Outlook

(1): The application of the cloud model for evaluating the renewal potential of public buildings effectively captures the relationship between indicator fuzziness and randomness. The cloud Graph-based representation allows for a clear visualization of the renewal potential and the degree of uncertainty in the evaluation results. Additionally, the sensitivity of indicators is determined based on the expectation (Ex) parameter at the indicator Grade, providing insights that support the implementation and optimization of renovation plans. The combination weighting method based on game theory yields more balanced and accurate comprehensive weights, significantly influencing the calculation of cloud model parameters and the generation of backward clouds.
(2): In this study, qualitative indicators were assessed using the expert judgment method.And the arithmetic mean was used to obtain the average values, without accounting for the influence of expert experience and biases. Quantitative indicators were derived from literature or project inspection reports, with limited on-site measured data. Although a cloud model calculation program was developed based on MATLAB, the calculation process remains relatively complex, and user-friendliness is limited. Future research will focus on further advancements in the areas of intelligent renewal potential evaluation, automated data acquisition, and visualization of evaluation results.

Author Contributions

Conceptualization, X.L. and X.Z.; methodology, Y.Z. and .; software, Y.Z.; validation, X.L.; formal analysis, Y.Z.; investigation, Y.Z.; resources, Y.Z.; data curation, Y.Z.; writing—original draft preparation, Y.L.; writing—review and editing, X.L.; visualization, Y.Z.; supervision, X.L.; project administration, Y.Z.; funding acquisition, Y.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Science and Technology Program Project of the Ministry of Housing and Urban-Rural Development: Innovative Research on the Path of Mass Participation in the Renovation of Older Neighborhoods under the Concept of “Co-Creation”, grant number (2019-R-009)”.

Data Availability Statement

The data used in this paper come from actual sampling at the Nanjing Military Club building in Nanjing, Jiangsu Province, China.

Conflicts of Interest

The authors declare no conflict of interest.

References

Tang, Y. Dimensions and Strategies of Urban Renewal System Construction in China. International Urban Planning. 2022, 37, 1–8. (In Chinese) [Google Scholar] [CrossRef]
Yin, J.; Chen, Y.Z. Discourse Reconstruction of Urban Renewal from the Perspective of Spatial Production. Jiangsu Social Science. 2024, 169–177. (In Chinese) [Google Scholar] [CrossRef]
Yang, J.; Qin, B. Urban Renewal under the Perspective of Public Value--Realistic Dilemma, Theoretical Logic and Governance Path. City Planning. 2024, 48, 25–33. (In Chinese) [Google Scholar]
Su, T.; Peng, B.; Ma, X.Z.; Zhang, X.J.; Wang, Z.Z. The Establishment of Evaluation Indicator System for Functionality and Remodeling Potential of Urban Public Buildings. Heilongjiang Science. 2024, 15, 40–44+48. (In Chinese) [Google Scholar]
Liu, Z.Q. ; Steadily improving the quality and level of urbanization. People's Daily, 2024; 005. (In Chinese) [Google Scholar]
Qin, Y.H. Research on Post-Green Retrofit Assessment Indicator System for Existing Public Institution Buildings. Master, Shenyang Architecture University, 2020. (In Chinese)
Wang, F.H.; Zeng, X.K.; Zhang, C. Master Plan Implementation in the Age of Urban Renewal. City Planning. 2024, 48, 15–20. (In Chinese) [Google Scholar]
Manganelli, B.; Tataranna, S.; Pontrandolfi, P. A Model to Support the Decision-Making in Urban Regeneration. Land Use Policy 2020, 99, 104865. [Google Scholar] [CrossRef]
Rosa-Jiménez, C.; Márquez-Ballesteros, M.J.; García-Moreno, A.E.; Navas-Carrillo, D. Neighbourhood Cooperatives for the Integrated Urban Regeneration of Mass Housing Areas: Speculations on a Proposed Model. Soc. Enterp. J. 2023, 19, 575–597. [Google Scholar] [CrossRef]
Wu, H; Comprehensive Evaluation of Retrofitting Potential of Existing Public Buildings in Cities and Functional Remodeling Research. Master, Chongqing Jiaotong University, 2022. (In Chinese)
Wang, J.L.; Liu, Y.L.; Ma, H.X.; Long, S.Q.; Hu, Y.M. Evaluating the Potential of Urban Renewal and Reconstruction in Shenzhen City with the Support of Open Big Data. Geographic Research and Development. 2019, 38, 72–77. (In Chinese) [Google Scholar]
Han, H.R.; Xu, L.Y.; Yang, C.F. An investigation on the reproduction mechanism of old industrial area space in the context of urban renewal--The case of Yaohai old industrial area in Hefei City. Human Geography. 2024, 39, 59–67. (In Chinese) [Google Scholar] [CrossRef]
Wang, X.F.; Chen, Z.C.; Liao, S.Q.; Ma, D.W. Spatial Renewal Patterns of Historic Landmark Streets and Alleys from the Perspective of Neighborhood Memory. Urban Development Studies. 2023, 30, 25–30. (In Chinese) [Google Scholar]
Luo, X.; Ren, M.; Zhao, J.; Wang, Z.; Ge, J.; Gao, W. Life Cycle Assessment for Carbon Emission Impact Analysis for the Renovation of Old Residential Areas. J. Clean. Prod. 2022, 367, 132930. [Google Scholar] [CrossRef]
Li, L.Y.; Gu, H. Evaluation of the Comprehensive Benefits of Green Retrofitting in Older Neighborhoods Based on AHM-Toppable Evaluation Model. Ecological Economy. 2021, 37, 95–100+160. (In Chinese) [Google Scholar]
Jiang, J.; Tang, J.; Gan, Y.; Lan, Z.C.; Qin, T.Q. Structural safety evaluation of buildings based on combinatorial assignment method. Science Technology and Engineering. 2021, 21, 7278–7285. (In Chinese) [Google Scholar]
Chu, S.; Wei, J.F. Liu, Q.M.; Sun, L.N.; Xu, S.G. Comprehensive energy-saving retrofit and energy-efficiency assessment of a public building in Beijing. Building Energy Efficiency. 2024, 52, 88–94. (In Chinese) [Google Scholar]
Wang, Y.S.; Guo, Y.H.; Zhang, Y.Y. Ice Evaluation of the Comprehensive Benefits of Urban Village Renovation Based on Comprehensive Empowerment of Game Theory--Taking Guangzhou as an Example. Journal of Civil Engineering and Management. 2022, 39, 18–26. (In Chinese) [Google Scholar] [CrossRef]
Dong, J.; Guo, R.N.; Guo, F. Evaluation of regeneration potential and renewal strategy of urban abandoned railroads: A case study of the abandoned railroad of Dalian locomotive factory. Journal of Natural Resources. 2023, 38, 2672–2686. (In Chinese) [Google Scholar] [CrossRef]
Langston, C.; Wong, F.K.W.; Hui, E.C.M.; Shen, L.-Y. Strategic Assessment of Building Adaptive Reuse Opportunities in Hong Kong. Build. Environ. 2008, 43, 1709–1718. [Google Scholar] [CrossRef]
Conejos, S.; Langston, C.; Smith, J. Enhancing Sustainability through Designing for Adaptive Reuse from the Outset: A Comparison of adaptSTAR and Adaptive Reuse Potential (ARP) Models. Facilities 2015, 33, 531–552. [Google Scholar] [CrossRef]
Li, D.Y.; Liu, C.Y.; Du, Y.; Han, X. Uncertainty Artificial Intelligence. Journal of Software, 2004; 1583–1594. (In Chinese) [Google Scholar]
Li, J.; Pan, Y.H. Evaluation of energy-saving retrofit effect of existing public buildings based on cloud modeling: a case study in Chongqing. Journal of Engineering Management. 2021, 35, 89–94. (In Chinese) [Google Scholar] [CrossRef]
Qiao, H.; Pei, J. Urban Stormwater Resilience Assessment Method Based on Cloud Model and TOPSIS. Int. J. Environ. Res. Public. Health 2022, 19, 38. [Google Scholar] [CrossRef] [PubMed]
He, G.; Ruan, J. Study on Ecological Security Evaluation of Anhui Province Based on Normal Cloud Model. Environ. Sci. Pollut. Res. 2022, 29, 16549–16562. [Google Scholar] [CrossRef] [PubMed]
Liu, W.; Yuan, X. Research on the Resilience Evaluation of Urban Rail Transit Construction Organization Based on the Cloud Matter-Element Model: A Case Study of Nanchang West Station. Buildings 2024, 14, 616. [Google Scholar] [CrossRef]
Langston, C.; Yung, E.H.-K.; Chan, E.H.-W. The Application of ARP Modelling to Adaptive Reuse Projects in Hong Kong. Habitat Int. 2013, 40, 233–243. [Google Scholar] [CrossRef]
Journal Editorial Office. China Urban Renewal White Paper (2022) and Selected Typical Cases of China's Urban Renewal and Retrofitting of Existing Buildings in 2022 were released in Beijing. New Urbanization.
Chu, Y.C.; Zhang, H.J.; Ai, Y.B. Evaluation of Landside Traffic Operation Status of Capital International Airport. Journal of Chongqing Jiaotong University (Natural Science). 2024, 43, 78–85+9–85. (In Chinese) [Google Scholar]
Yang, J.Q.; Sun, L.P.; Zhu, Y.C. Identification and delineation of urban renewal areas. City Planning. 2024, 48, 4–14. (In Chinese) [Google Scholar]
Zhong, L.; Guo, X.; Zhao, L.H.; Han, Y.; Yi, D.; Zhu, Q. Dynamic grid algorithms taking into account obstacles in urban land classification. China Land Science. 2020, 34, 27–36. (In Chinese) [Google Scholar]
Li, D.B.; Zhang, H.C.; Lei, P.B.; Liu, J.P. Research on safety evaluation of raw soil buildings based on entropy weight method modification. Chinese Journal of Applied Mechanics. 2020, 37, 1656–1662+1867. (In Chinese) [Google Scholar]
Li, D. Knowledge Representation in KDD Based on Linguistic Atoms. J. Comput. Sci. Technol. 1997, 12, 481–496. [Google Scholar] [CrossRef]
Li, B.; Zhu, P.P; Xiao, R.M.; Li, Z.T.; Jin, Y.L. Application of combinatorial empowerment cloud model for freeway access adaptability evaluation. Journal of Traffic and Transportation Engineering. 2023, 23, 223–233. (In Chinese) [Google Scholar] [CrossRef]
Liu, Q.; Xu, J.; Wang, Q.; Li, W. Risk Assessment of Water Inrush from Coal Seam Roof Based on the Combined Weighting of the Geographic Information System and Game Theory: A Case Study of Dananhu Coal Mine No. 7, China. Water 2024, 16, 710. [Google Scholar] [CrossRef]
Wang, Y.; Huang, R.C. Optimization of Vertical Shading Elements in University Laboratories Based on Light Environment Simulation. Building Energy Efficiency. 2024, 52, 80–86. (In Chinese) [Google Scholar]
Pang, F.; Chen, Z.X.; Jin, P.; Sun, L.L.; Niu, F.F.; Wu, Z.J.; Yan, G. J.; Zhao, Q.Y.; Liu, Q.Y. Project Practice of Tranquil Housing Evaluation System. Building Science. 2024, 40, 173–177. (In Chinese) [Google Scholar] [CrossRef]

Figure 1. Evaluation Process for the Renewal Potential of Public Buildings.

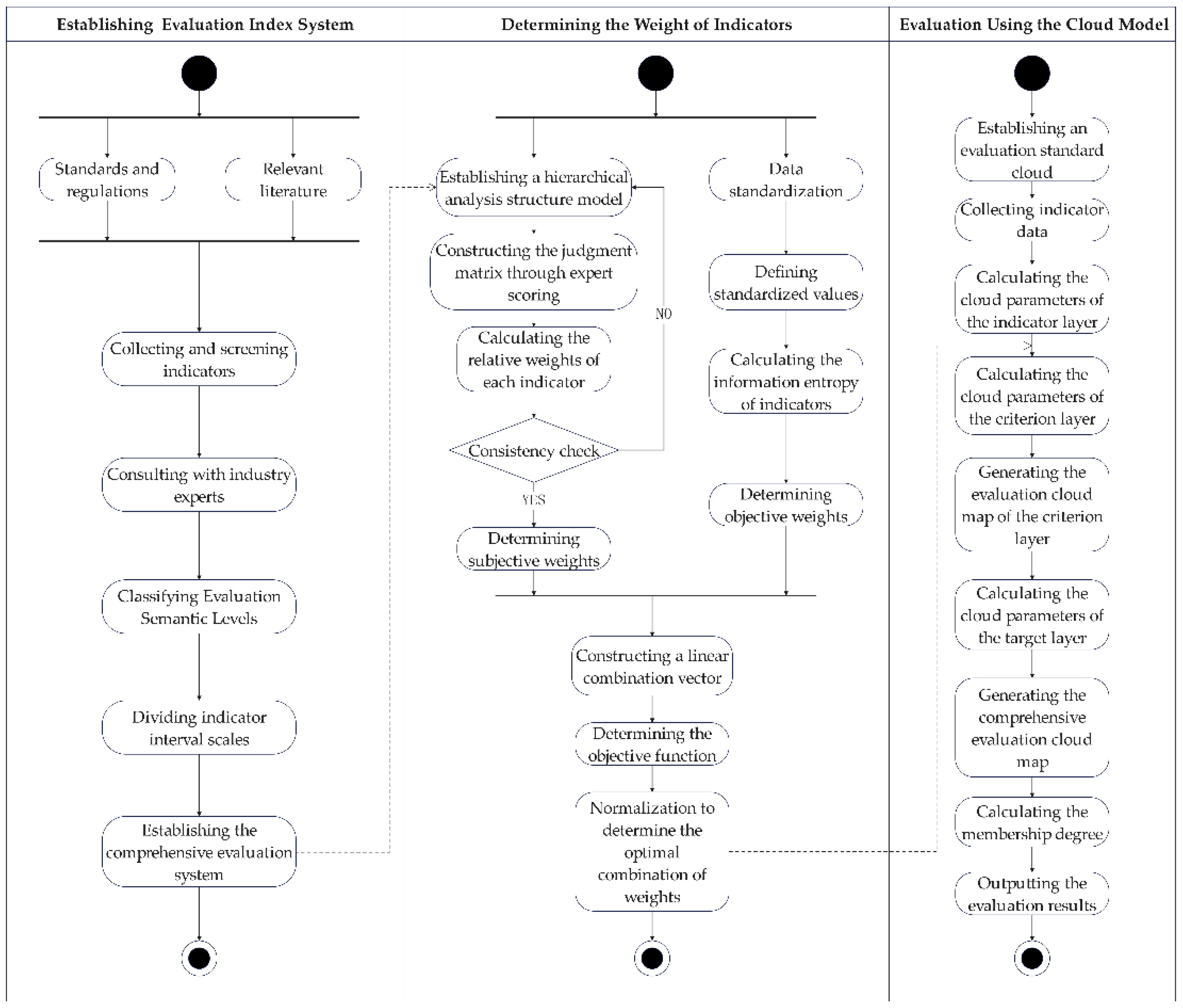
Figure 2. Comparison of Evaluation Cloud and Standard Cloud. (a) Comprehensive Project Evaluation; (b) Land Spatial Value; (c) Surrounding Traffic Operation Status; (d) Conditions of Building Itself; (e) Future Development.

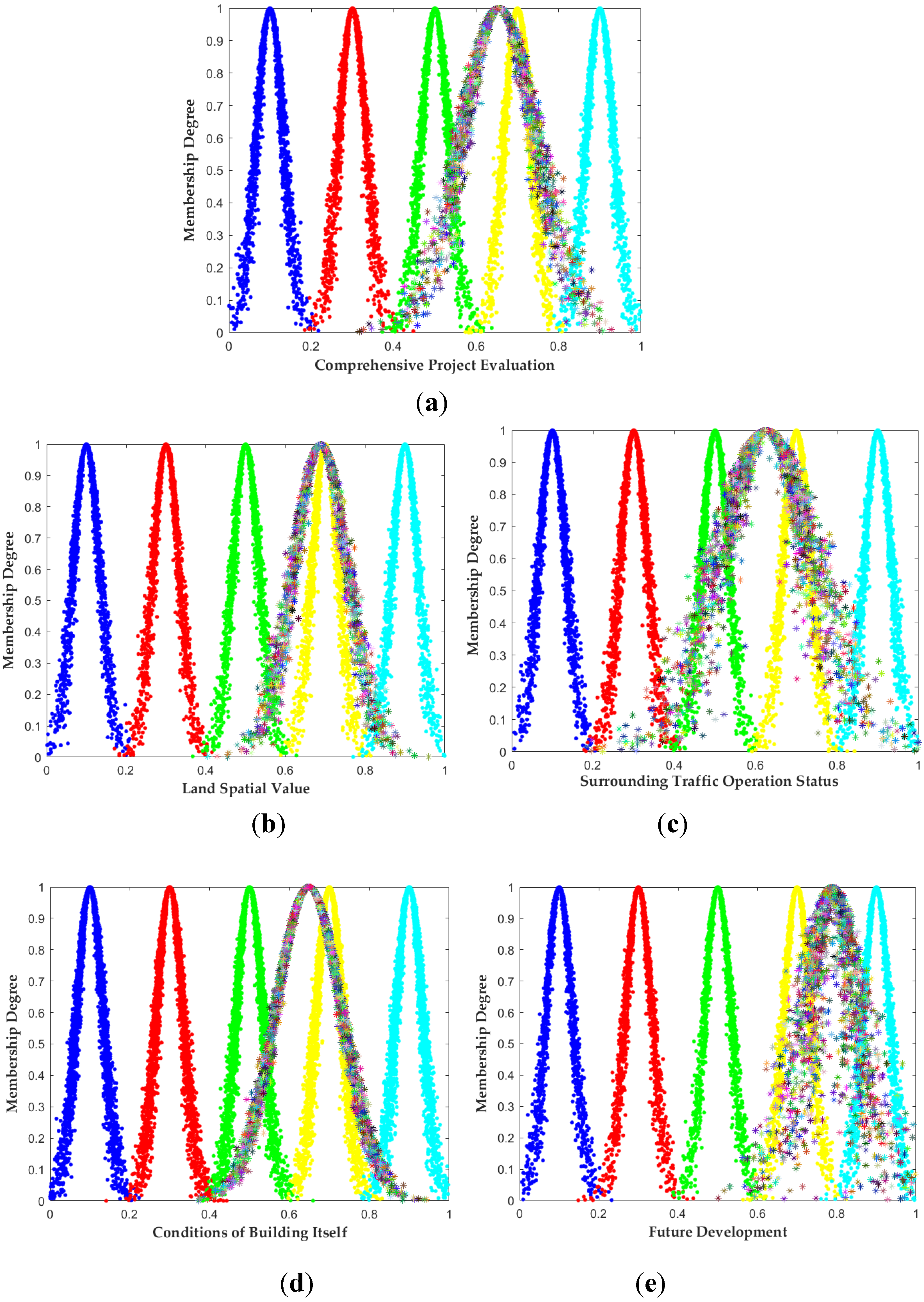
Table 1. Comprehensive Evaluation Index System for the Renewal Potential of Existing Public Buildings.

Target layer	Criterion Layer		Indicator Layer
Renewal Potential of Existing Public Buildings	(A)	Land Spatial Value	(A1)	Node Accessibility Coefficient
			(A2)	Land Price Grade of the Located Unit
			(A3)	Building Density Ratio
			(A4)	Density of Adjacent Buildings
			(A5)	Proportion of Nearby Low-Rise Buildings
			(A6)	Continuity Length of Block Facades
			(A7)	Accessibility to the Central Business District
			(A8)	Green Coverage Ratio
			(A9)	Commercial and Service Vibrancy
	(B)	Surrounding Traffic Operation Status	(B1)	Average Travel Speed
			(B2)	Delay Time Ratio
			(B3)	Travel Time Ratio
			(B4)	Traffic Saturation
			(B5)	Roadway Width
			(B6)	Road Function Index
	(C)	Conditions of Building Itself	(C1)	Degree of Vacancy
			(C2)	Spatial Layout Flexibility
			(C3)	Condition of Maintenance and Upkeep
			(C4)	Property Rights Clarity
			(C5)	Building Age
			(C6)	noise Grade.
			(C7)	indoor natural light illuminance
			(C8)	window-to-floor area ratio
			(C9)	component damage parameters
	(D)	Future Development	(D1)	degree of functional obsolescence
			(D2)	public willingness for renewal
			(D3)	compliance of the planned land use
			(D4)	value of historical and cultural heritage
			(D5)	safety resilience

Table 2. Classification Standards for Comprehensive Evaluation Indicators.

Secondary Indicators	Characteristics	Grades of Potential Evaluation
Secondary Indicators	Characteristics	Grade I [0, 0.2)	Grade II [0.2, 0.4)	Grade III [0.4, 0.6)	Grade IV [0.6, 0.8)	Grade V [0.8, 1)
(A1) Node Accessibility Coefficient	-	(1.6, 2]	(1.0, 1.6]	(0.6, 1.0]	(0.4, 0.6]	(0, 0.4]
(A2) Land Price Grade of the Located Unit	+	Low	Lower	Moderate	Higher	High
(A3) Building Density Ratio	-	[5.4, 6.0)	[4.5, 5.4)	[4.0, 4.5)	[2.5, 4.0)	[2.0, 2.5)
(A4) Density of Adjacent Buildings	-	(80%, 100%]	(60%, 80%]	(40%, 60%]	(20%, 40%]	(0, 20%]
(A5) Proportion of Nearby Low-Rise Buildings	+	(0, 20%]	(20%, 40%]	(40%, 60%]	(60%, 80%]	(80%, 100%]
(A6) Continuity Length of Block Facades	-	(600, 1000]	(400, 600]	(300, 400]	(100, 300]	(0, 100]
(A7) Accessibility to the Central Business District	-	(20000, 30000]	(17000, 20000]	(10000, 17000]	(5000, 10000]	(0, 5000]
(A8) Green Coverage Ratio	-	(35%, 60%]	(34%, 35%]	(33%, 34%]	(32%, 33%]	(25%, 33%]
(A9) Commercial and Service Vibrancy	+	(0, 0.10)	[0.10, 0.20)	[0.20, 0.40)	[0.40, 0.50)	[0.50, 0.70)
(B1) Average Travel Speed	+	[0, 0.30)	[0.30, 0.40)	[0.40, 0.50)	[0.50, 0.70)	[0.70, 1.00)
(B2) Delay Time Ratio	-	[0.70, 1.00)	[0.60, 0.70)	[0.50, 0.60)	[0.30, 0.50)	[0, 0.30)
(B3) Travel Time Ratio	-	[2.20, 7.00)	[1.90, 2.20)	[1.60, 1.90)	[1.30, 1.60)	[1.00, 1.30)
(B4) Traffic Saturation	-	[0.90, 1.00)	[0.75, 0.90)	[0.60, 0.75)	[0.40, 0.60)	[0, 0.40)
(B5) Roadway Width	+	[12, 20]	[25, 35]	[25, 50]	[35, 50]	[50, 80]
(B6) Road Function Index	+	(0, 0.40]	(0.40, 0.55]	(0.55, 0.75]	(0.60, 0.80]	(0.80, 1.00]
(C1) Degree of Vacancy	+	Low	Lower	Moderate	Higher	High
(C2) Spatial Layout Flexibility	+	Narrow	Relatively Narrow	Adequate	Relatively Spacious	Spacious
(C3) Condition of Maintenance and Upkeep	-	High	Higher	Moderate	Lower	Low
(C4) Property Rights Clarity	+	Complex	Relatively Complex	Moderate	Relatively Clear	Clear
(C5) Building Age	+	(0, 15)	[15, 25)	[25, 30)	[30, 40)	[40, 50)
(C6) noise Grade.	+	(15, 33]	(33, 40]	(40, 45]	(45, 55]	(45, 70]
(C7) indoor natural light illuminance	-	[600, 750)	[450, 600)	[300, 450)	[150, 300)	[100, 150)
(C8) window-to-floor area ratio	-	[1/3, 1/4)	[1/4, 1/5)	[1/5, 1/6)	[1/6, 1/10)	[1/10, 1/13)
(C9) component damage parameters	+	(0, 0.2]	(0.2, 0.4]	(0.4, 0.6]	(0.6, 0.8]	(0.8, 1)
(D1) degree of functional obsolescence	+	Low	Lower	Moderate	Higher	High
(D2) public willingness for renewal	+	Negative	Relatively Negative	Moderate	Relatively Positive	Positive
(D3) compliance of the planned land use	+	Unreasonable	Relatively Unreasonable	Adequate	Relatively Reasonable	Reasonable
(D4) value of historical and cultural heritage	+	Low	Lower	Moderate	Higher	High
(D5) safety resilience	-	Strong interference resistance, short recovery time	Relatively strong interference resistance, short recovery time	Moderate interference resistance, normal recovery time	Relatively low interference resistance, relatively long recovery time	Low interference resistance, long recovery time

Table 3. Scoring Intervals and Standard Cloud Parameters for Potential Grades.

Interval Division	Semantic Division	Potential Grade	Standard Cloud Parameters (Ex，En，He)
[0, 0.2)	low potential	Grade I	(0.1000, 0.0333, 0.0050)
[0.2, 0.4)	relatively low potential	Grade II	(0.3000, 0.0333, 0.0050)
[0.4, 0.6)	moderate potential	Grade III	(0.5000, 0.0333, 0.0050)
[0.6, 0.8)	relatively high potential	Grade IV	(0.7000, 0.0333, 0.0050)
[0.8, 1)	high potential	Grade V	(0.9000, 0.0333, 0.0050)

Table 4. Combination Weights and Cloud Parameters for Evaluation Indicators.

Criterion Layer
Code	ω₁₁ ¹	ω₁₂ ²	ω ³	Ex	En	He	Code	ω₂₁ ¹	ω₂₂ ²	ω₀ ³	Ex	En	He
Code	(1)	(2)	(3)	(4)	(5)	(6)	Code	(7)	(8)	(9)	(10)	(11)	(12)
A	0.2914	0.3283	0.2987	0.6263	0.1124	0.0382	A1	0.1964	0.0654	0.2495	0.5700	0.2478	0.0166
							A2	0.1486	0.1063	0.1658	0.7200	0.0426	0.0071
							A3	0.0330	0.0727	0.0169	0.8010	0.0000	0.0000
							A4	0.0687	0.0677	0.0691	0.7000	0.0000	0.0000
							A5	0.1011	0.1326	0.0883	0.8000	0.0000	0.0000
							A6	0.0202	0.0654	0.0019	0.6200	0.0000	0.0000
							A7	0.0426	0.1009	0.0190	0.6143	0.3760	0.1157
							A8	0.0120	0.1308	0.0181	0.8300	0.0000	0.0000
							A9	0.3774	0.2582	0.3715	0.5500	0.0752	0.0323
B	0.1990	0.1641	0.1920	0.6884	0.1604	0.0237	B1	0.1086	0.1301	0.1119	0.5900	0.0978	0.0232
							B2	0.0481	0.1741	0.0675	0.5059	0.3981	0.0515
							B3	0.0337	0.1435	0.0506	0.7040	0.3499	0.1123
							B4	0.2875	0.1887	0.2723	0.6478	0.3553	0.1172
							B5	0.1272	0.2345	0.1437	0.7333	0.0000	0.0000
							B6	0.3950	0.1291	0.3540	0.7650	0.0652	0.0279
C	0.4310	0.3725	0.4195	0.6480	0.2182	0.0292	C1	0.2892	0.0519	0.1875	0.9050	0.0589	0.0259
							C2	0.1508	0.0681	0.1153	0.8000	0.0627	0.0227
							C3	0.0339	0.1414	0.0800	0.5100	0.0677	0.0176
							C4	0.0751	0.0504	0.0645	0.9800	0.0401	0.0130
							C5	0.1115	0.2373	0.1654	0.6200	0.6200	0.0000
							C6	0.0141	0.1254	0.0618	0.4000	0.3008	0.0854
							C7	0.0462	0.1928	0.1090	0.5250	0.3509	0.0900
							C8	0.0186	0.0823	0.0459	0.5631	0.3855	0.0583
							C9	0.2606	0.0504	0.1705	0.4200	0.0852	0.0344
D	0.0786	0.1351	0.0898	0.7883	0.0643	0.0542	D1	0.4175	0.1754	0.4122	0.8050	0.0589	0.0259
							D2	0.0952	0.1992	0.0975	0.8750	0.0501	0.0000
							D3	0.1459	0.1890	0.1469	0.8650	0.0689	0.0085
							D4	0.0447	0.1890	0.0479	0.8400	0.0652	0.0050
							D5	0.2966	0.2473	0.2955	0.6900	0.0752	0.0280

¹ ω₁₁, ω₂₁ represents the criterion layer weight derived from the AHP method. ² ω₁₂, ω₂₂ represents the criterion layer weight derived from the entropy method. ³ ω, ω₀ represents the combined weight derived from the game theory method.

Table 5. Evaluation Results of Renewal and Renovation Potential Grades.

Evaluation Subject	The Membership Degree of Each Potential Grade					Evaluation Results
Evaluation Subject	Grade I	Grade II	Grade III	Grade IV	Grade V	Evaluation Results
Target layer	0.0000	0.0076	0.1592	0.2490	0.0191	IV
Land Spatial Value	0.0015	0.0133	0.0852	0.2155	0.0877	IV
Surrounding Traffic Operation Status	0.0073	0.0428	0.1350	0.1419	0.0811	IV
Conditions of Building Itself	0.0000	0.0000	0.0024	0.1973	0.1274	IV
Future Development	0.0047	0.0248	0.1149	0.1815	0.0652	IV

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

The Cloud Model-Based Evaluation of Public Building Renewal Potential with the Game Theory Combination Weighting Methods-Case Study in China

Abstract

1. Introduction

2. Materials and Methods

2.1. Evaluation Index System for Public Building Renewal Potential

2.2. Classification of Evaluation Standards

3. Building a Cloud Evaluation Model

3.1. Game Theory-Based Weight and Cloud Model Parameters Calculation

3.1.1. Analytic Hierarchy Process (AHP)

3.1.2. Entropy Weight Method

3.1.3. Game Theory-Based Combination Weighting

3.2. Cloud Model Parameters and Membership Degree Calculation

4. Case Study

4.1. Case Overview

4.2. Data Sources

4.3. Model Implementation

4.3.1. Establishment of the Evaluation Standard Cloud

4.3.2. Calculation of Indicator Combination Weights and Cloud Parameters

4.4. Membership Degree Calculation and Evaluation Cloud Graph Generation

5. Results and Discussion

6. Conclusion and Outlook

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe