Preprint
Article
Microwave Digital Twin Prototype for the Shoulder Injury Detection
Altmetrics
Downloads
66
Views
47
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
30 August 2024
Posted:
02 September 2024
You are already at the latest version
Alerts
Abstract
One of the most common shoulder injuries is rotator cuff tear (RCT). The risk of RCTs increases with age, with a prevalence of 9.7% in those under 20 years old to 62% in individuals aged 80 and older. In this article, we present first Microwave Digital Twin Prototype (MDTP) for RCT detection, based on machine learning (ML) and advanced numerical modeling of the system. We generate a generalizable dataset of scattering parameters through flexible numerical modeling, in order to bypass real-world data collection challenges. This involves solving the linear system in result of finite element discretization of the forward problem with use of domain decomposition method to accelerate the computations. We use support vector machine (SVM) to differentiate between injured and healthy shoulder models. This approach is more efficient in terms of required memory resources and computing time compared to the traditional imaging methods.
Keywords:
Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning
1. Introduction
The shoulder is the most mobile joint in the body, allowing rotation across multiple axes, with some capable of full rotation, as well as enabling arm elevation and overhead reaching. This mobility is facilitated by the rotator cuff, a complex group of muscles and tendons. With repetitive movements, the rotator cuff wears out eventually leading to rotator cuff tears (RCTs). This injury most commonly occurs with aging, but it also affects athletes and individuals in professions that involve frequent shoulder movements, such as manual labor or cleaning, making it one of the most prevalent shoulder injuries. According to [1], approximately 2 million people in the U.S. consult their physician each year for this condition. RCTs can advance to more serious conditions over time, reinforcing the relevance of early detection. Magnetic resonance imaging (MRI) is the golden standard imaging technique; however, its use is restricted to imaging centers and it does not always provide accurate depiction of the presence and severity of the tears [2,3].
With the RTC incidence, synovial fluid (SF) aspirates locally in the injury area [4,5]. This accumulation of SF changes the dielectric properties of the shoulder joint [6]. This change makes microwave imaging a credible alternative to MRI that we need to investigate. In [7], we introduced an alternative low-cost, portable and non-invasive electromagnetic imaging (EMI) system for the on-site diagnosis of RCTs. At that time, no EMI system for the shoulder existed (to the best of our knowledge, this remains true), so we had to start from scratch. To save time and resources during the initial design phase, we developed a virtual model of the shoulder and the imaging system to study and optimize the EMI system, as described in [7]. This model is the first step toward Microwave Digital Twin Prototype (MDTP).
The concept of the Digital Twin (DT) was originally proposed by Michael Grieves at the University of Michigan for monitoring Product Lifecycle Management. It involves creating a virtual model of a physical system, which is continuously updated with real-time data from the existing physical system. DTs are not intended for system design. However, in [8] the same authors introduce the Digital Twin Prototype (DTP), which exists in virtual space and is to be used in what the authors refer to as the creation phase. Since 2002, DTs have been widely used and developed for Industry 4.0 applications [9,10,11]. In the healthcare sector, a comprehensive review of Digital Twin for Health (DT4H) can be found in [11]. A wide range of applications are already investigated including detecting and monitoring cardiac pathologies, diabetes, breast or oropharyngeal cancers and Alzheimer’s diseases. DT4H often incorporates Machine Learning (ML) in order to enhance the performance of the illness detection as exemplified in [12] with the COVID-19. Very recently, DTs have been efficiently used for microwave ablation [13] and imaging purposes [14]. In this paper, we introduce the concept of Microwave Digital Twin Prototype as a virtual system that mimics the physical one and is capable of predicting the presence of the RCTs. The model not only includes the anthropomorphological model of the shoulder wether it is injured or not, but also the imaging system and the uncertainties due to its use, like noise, positioning errors and errors due to the RCTs itself like the synovial fluid’s variation that depends on the RCT’s severity.
Compared with our previous work [7], we aim to improve and systematize the detection of RCTs. So far, we have been solving an inverse problem for detecting the presence of RCTs. This process is time-consuming, requires extensive computing resources and is therefore not compatible with a large number of case studies. As an example, the final design consists of 32 ceramic () loaded open-ended waveguides. It requires 11 minutes and 27 seconds for image reconstruction of one shoulder model with the use of 480 computing cores. These amount of resources may not always be available and can limit the practical use of the device in real world. In this paper, we are going to address this issue by use of ML algorithms.
The rise of ML has led to the development of valuable tools in various medical applications, such as predicting sports injuries [15], simplifying medical imaging processes [16] and advancing stroke medicine [17]. Further, combining microwave imaging systems with ML algorithms has significantly improved stroke detection, stroke types classifications and localizing affected areas [18,19,20].
The dataset gathering is a crucial component of machine learning algorithms, particularly in medical applications, but it presents numerous challenges and limitations [21]. For example, insufficient or biased data can result in poor generalization that highly affect the algorithm’s accuracy in making predictions or diagnoses. To enhance generalization, large and diverse training datasets are necessary. Moreover, the effectiveness of ML algorithms heavily relies on the quality and quantity of the data. However, in the real world, obtaining data from patients involves privacy and authorization challenges and is a time-consuming process. Further, the limited available training data significantly impacts the performance of the classifiers. To address this issue, generating synthetic data through numerical simulations or various computer algorithms has emerged as a promising solution in recent years [22,23]. In [24], numerical simulations of a system are performed to investigate how integrating mathematical models with experimental datasets can enhance classification performance. It is important to note that while use of synthetic data can enhance continual and causal learning, it also carries the risk of introducing biases [25]. It emphasizes the importance of generating a reliable dataset.
In this work, we use numerical modeling to generate a generalizable dataset of scattering parameters. A parametric study is conducted, considering four main categories, outlined in Table 1. For the classification of injured and healthy models, we utilize a supervised machine learning support vector machine (SVM).
Note that the key indicator in differentiating the healthy and injured shoulder joint is the presence of RCTs because it is the most challenging case. The mean aspirate volume of SF is reported to correlates with the size of the tear. This volume for the small tears is , for medium tears is , and for large tears is [5]. In this study, we will consider the presence of a small tear in the injured shoulder model. The paper is structured as follows: Section presents the numerical modeling framework, including the numerical modeling of the system, its properties, and our methods for data generation and classification analysis using SVM. Section 3 discusses the numerical results for various scenarios, and the conclusion is provided in Section 4.
2. Mathematical Framework
2.1. Antropomorphic Model of the Shoulder
An accurate finite element modeling of the shoulder is first step to conduct a reliable numerical study to detect RCTs. Figure 1a shows a view of the the anatomy of the shoulder and Figure 1b shows anthropomorphic model of different tissues. To build this realistic shoulder model, we use Computer-Aided Design (CAD) models for the shoulder profile, scapula and humerus bones. These CAD models are achieved from a library of 3D anatomy models 1. The rotator cuff tendons are modeled to surround the shoulder joint and the skin with the thickness of is modeled to surround the shoulder structure. The injury is modeled by an ellipsoid with a volume of mL filled with SF which represent a small RCT [5]. The remaining space in the shoulder joint is filled with the muscle. Note that in the healthy shoulder model, the electrical properties of the injury area is changed to that of the muscle. In our simulations, we assign the complex permittivity values of each tissue at , reported in Table 2. In this Table, the SF value is based on our recent work in [7] and the values of other tissues are based on the reference websites2, 3. We consider the value of the complex permittivity of the matching medium is constant for all of the simulations and equal to that of the muscle (). If we consider the value of the matching medium as the reference, the wavelength in this medium is .
2.2. Numerical Model of the System
In this work, we use the optimized sensing system which was designed in our previous work [7], shown in Figure 2a. This configuration is designed to detect the smallest RCT with use of minimum number of antennas through differential imaging method. It consists an array of 32 ceramic () loaded open-ended waveguides that illuminates the shoulder from different angles. This multi-view approach helps in gathering a comprehensive and accurate data to represent the effect of internal tissues of the shoulder in the scattering parameters. The waveguides are arranged on 2 metallic fully-circular and 2 metallic half-circular layers. The width the rectangular waveguides are and and their height are . Their frequency bandwidth is and the operating frequency is chosen as . The two sides of the imaging chamber are open to let the insertion of the real shoulder, as shown in Figure 2b. A cross section of the finite element three dimensional (3D) mesh of the complete system including imaging system and the shoulder is shown in Figure 2c. In this mesh, the maximum diameter of the mesh cells is which gives . First order finite element discretization of this problem gives 1891259 number of degrees of freedom. We use open source FreeFEM software for the forward modeling of our problem.
The generated 3D domain (), including the sensing system and the shoulder, is heterogeneous dissipative non-magnetic medium of complex permittivity , where is the relative permittivity of each tissue, is the permittivity of free space, is the conductivity, and is the angular frequency. Each transmitting antenna emits a time periodic signal, where is the complex amplitude of the associated electric field at the space variable . We find is as the solution for each transmitting antenna by solving the boundary value problem defined in Equation (1).
where is the propagation constant along the waveguide, is the the unit outward normal to the boundaries, is the complex wavenumber of the inhomogeneous medium and is the permeability of the free space. We define the excitation term as . It imposes an incident wave that corresponds to the excitation of the dominant transverse electric mode (TE10) of the active waveguide. The boundaries are shown in Figure 2b and defined as it follows: presents the ports of receiving waveguides, presents the open sides of the chamber and the boundaries of shoulder profile which are outside of the chamber, presents the ports of the transmitting waveguide and presents the metallic surfaces of the chamber and the waveguides. Through solution of the boundary value problem for each transmitting antenna, we can compute the scattering matrix using Equation ().
where j represents the transmitting port and i represents the receiving port.
2.3. SVM
We chose SVM for our classification tasks due to its effectiveness in binary classification problems, which aligns with the nature of our dataset where we seek to detect whether the RCT is present or not. Given that our problem is straightforward and the dataset is relatively small, SVM is particularly well-suited as it offers a robust and interpretable approach. Its straightforward implementation and tuning processes also enable us to obtain dependable classification results without the need for more complex algorithms.
This supervised machine learning algorithm is designed to recognize patterns and relationships between features and the target variable within a dataset. This process, known as training or fitting, aims to prepare the algorithm to accurately predict labels for new, unseen data [26]. The SVM algorithm involves three main steps: training, validation, and testing. The training and validation phases together form the development phase. During the training step, the model learns the characteristics of the data to determine the best boundaries for class separation. The validation step involves using part of the training set to evaluate the model’s performance and make necessary adjustments to enhance its effectiveness on unseen data. Finally, the test phase uses an entirely new dataset to assess the model’s overall performance.
The performance of an SVM is highly dependent on the optimal selection of hyperparameters. For any type of SVM, the hyperparameter C needs to be optimized as it controls the margin that separates the two classes. A linear SVM kernel is used for linearly separable data, whereas more complex kernels, like radial basis function (RBF) kernels, are applied when the data is not linearly separable. For nonlinear kernels, the hyperparameter shapes the decision boundary and must also be optimized. This paper employs the grid search (GS) technique to choose the appropriate kernel method and determine the optimal hyperparameters.
2.4. Evaluation Metrics
A confusion matrix is frequently used to evaluate the performance of binary classification problems. In his work, samples obtained from healthy shoulder models are labeled as , while samples from injured models are marked as . It is a cross-table demonstrated in Table 3, that captures the occurrences of actual classifications versus predicted classifications. In this Table, is true negative, is true positive, is false positive and is false negative. These are numbers in set of .
The table assumes that there were healthy samples, of which only were correctly recognized as healthy, whereas were incorrectly recognized as injured. Similarly, there were injured models, of which only were correctly identified as injured, while were identified as healthy by mistake.
Accuracy (acr) is a widely recognized metric that measures the proportion of correctly classified samples out of the total number of samples. High acr values the classifier has strong classification capabilities [27]. It is defined as
Further we calculate the probability of correctly recognizing the healthy samples or true positives, as
and the probability of correctly recognizing the injured sample or true negatives, as
2.5. Dataset Processing
Different steps to numerically generate a sample with the use of the imaging system is illustrated in Figure 2. We need to solve the boundary value problem of Equation (1) to determine the scattering matrix. To calculate the scattered field, we first compute the scattering coefficients for the domain filled with only with the homogeneous matching medium (), and then subtract these from the scattering coefficients obtained with the shoulder present (). The difference between these two matrices is matrix of scattering parameters of size . Then to simulate a realistic experimental condition, we generate by adding multiplicative white Gaussian noise independently to the real and imaginary parts of each .
We build the complex nature dataset using the separate values of the real and imaginary parts of the that doubles the dimension of the scattering matrix into size 2048. This vector of synthetic data is introduced as an sample for the ML algorithm. The Figure 3 shows the steps of data preparation in our method.
The partitioning in the development set is as it follows: for the training set and for the validation set.
Throughout the paper, we will show the 3 most significant eigenvectors computed from the PCA applied to the training and test datasets separately. Note that the PCA is used to visually evaluate the differences and similarities between the classes [28] and not for classifying. Indeed, considering that SVM can work directly with the original features and to avoid loss of information, we choose to classify directly the raw data. In next sections, we will give a detailed description of the generated dataset for different scenarios.
3. Numerical Results
In this section, we introduce different scenarios to conduct a feasible numerical study of classifying healthy and injured shoulder models. We conduct our study using grid search and linear SVM to ensure faster testing. It helps us to establish baseline performance, gain insights into the data and efficiently explore hyperparameter spaces through grid search. Once we have a solid understanding of the data’s behavior and potential patterns, we can consider more complex models like nonlinear SVM for further refinement.
3.1. Influence of Noise
The classification of injured and healthy shoulder models using for the generated synthetic data with different noise levels is studied in this section. Studying the influence of very high noise levels, especially close to the Shannon limit (− 1.6 dB), is crucial for evaluating model robustness, understanding performance boundaries, and ensuring reliability in practical, noisy environments.
To consider a more realistic scenario, the noise levels among training and test data sets as well as healthy and injured samples are different. The detailed introduced noise levels for each category is mentioned in Table 4. For test set we consider 6 different noise levels and for training set we considered 5 different noise levels. Then for each noise level, we generate samples with 36 different seeds to build a large dataset. The number of samples for each category is presented in Table 5.
Let use GS method for optimization of C hyperparameter and report the results in Table 6. We can see that when , the accuracy of is achieved.
3.2. Dehydration Error in Complex Permittivity
In [29], it is reported that the dielectric properties can vary as a function of time at different temperatures due to the dehydration. This relative change is measured to be and we call it by . The effect of on the complex permittivity is reported in Table 7. Looking at this table we can see that the contrast between the dielectric properties of the SF and the muscle can become very small, specifically for cases that the dehydration error for the muscle is bigger than the one for the SF.
Considering that this contrast is the key element of differing between healthy and injured models, it is crucial to study the effect of this parameter. To build dataset for both healthy and injured shoulder models, we include three different variations of the muscle. Note that, for the case of injured model, we repeat the simulations in three groups, for each value of SF to be able to distinguish the dataset. For both healthy and injured models, we introduce 7 different noise levels from to and 48 number of seeds for each case. Table 8 explains the method of data generation for this scenario. The matrix for the injured model, holds for each group of generated dataset with different values of for the SF. Then we separate randomized 900 samples for training set and 108 samples for test, of each category, for healthy and injured models.
We repeat the classification, three different times with different values of SF. The result is reported in Table 9. It demonstrates that for all three values of SF, we can have accuracy in classifying healthy and injured models, when possible different values of for the muscle is also included in the dataset.
3.3. Positional Error of the Phantom
The location of the shoulder in the imaging system can vary due to the patient’s body habits, which can impact the values of the computed scattering parameters. In this section, the objective is to determine whether it is possible to detect injuries when the locations of the phantoms in the imaging system differ between the training and test datasets. In addition, we include all effects that have been previously introduced such as noise and dehydration. For each location, as far as the permittivity is concerned, we introduce the 3 values of the muscle’s permittivity that were used in the former section. For the injured model, we also include 3 values for the SF. In addition, we take 4 different level of noise comprised between 10 and 23 dB. Finally, we decide on the number of seeds for each model in order to have a balanced number of samples between the two classes in the training dataset : we include 12 seeds for each noise value, whereas we use only 4 for the injured model because the latter already includes 3 different SF values. . By this way, we generate 144 samples for healthy model and 144 samples for injured model, based on Table 10.
3.3.1. Translation Offset
In this section we investigate the maximum translation offset for which we still obtain optimal classification results. To start, we apply the offset along . The value of C has been optimized at with the grid search. The translation shift is exemplified on Figure 5 for a value of . The accuracy is 100% up to a shift in translation whereas it fails to 83.33% for with a sensitivity of 100% and a specificity of 66.67%. To draw a general conclusion, we have repeated this study along the and . The results are in line with those obtained for the shift along and show that is the maximal translation without loss of accuracy.
Note that in the real world, the anatomy of the shoulder limits extensive movement in translation without introducing rotation of the shoulder. So to simulate the realistic movements of the shoulder, we need to generate a larger dataset that includes various offsets and rotations of the phantoms inside the imaging system. This is investigated in the next section.
3.3.2. Effect of Rotation and Translation Offset
We generate 144 samples based on Table 10 for 31 different location of the phantoms for both healthy and injured models. Note that all the rotations are done along , and the shifts are done along and . Table 11, shows total number of dataset. In this study, we include the generated dataset for 30 locations of the phantoms for training (4320 samples) and we exclude one remaining dataset of different position for the test set (144 samples).
Figure 6, Figure 7 and Figure 8 show the geometries of 9 scenarios chosen for their diversity of the change in the position. They are indexed from to . Let us remind that both healthy and injured shoulder is considered for each scenario. For example is simulated two times, ones with the healthy shoulder (called -healthy) and one with the injured one (-injured).
To better understand the different included locations of the phantoms, we show the positions of the center of rotation for all the 31 scenarios in Figure 9. 9 out of the 31 scenarios are chosen for various test and specified in this figure with yellow points. The red point accounts for the reference position of the phantom in the absence of translation offset and with no rotation. We can see that these 9 chosen points are grouped 3 by 3, according to the value of the angle of rotation. For example, the location of M1, M2 and M3 are slightly different from each other but are nearby scenarios used for the training which are shown in grey. We have similar situation for , and . However, the third group, , and has larger distance from each other.
We examine different scenarios, with separating the test dataset for a specified position, explained in Table 12. The rest of the samples are included in the training dataset. Note that in this table, the accuracy is mentioned using linear kernel and . Let elaborate the result, for each scenario:
- In first case the dataset for M2 phantom for both healthy and injured (M2-healthy, M2-injured) is considered for the test. It shows the accuracy of in classifying healthy and injured models. This accuracy is due to the fact that the M2’s position is position is close to the phantoms used for training and belong to the group with small rotation angle (about ).
- Second case (with M2-healthy and M4-injured) is a little bit more challenging because both samples are apart considering their center of rotation. However, the similar positions for both exist in the training dataset. M2 belongs to the group with a small rotation (about ) angle whereas M4 belongs to the one with the middle value rotation angles (about 15°).
- Third case (M7-healthy, M3-injured) is the even more challenging, compared to the second case because the belongs to the group with large rotation (about 22°) and belongs to group of small rotation angle (about ). In this case, the classification accuracy drops to because the position of is apart from the rest of the positions in the training database. Indeed, the distance between M7 and the closest training point is . Note that all misclassified samples belong to the class of the healthy shoulder (M7-healthy) incorrectly classified as injured. This is in line with the fact that the position of M7 (which is healthy) is far away from the training phantoms which makes the classification more difficult.
- Scenario (M9-healthy, M6-injured) gathers samples belonging to the groups of large and medium rotation angles respectively but this time one sample (M9-healthy) is farther away from the positions that were in the training dataset. The distance between M9 and the closest training point is . As in the previous scenario this leads to a poorer classification performance that drops to and all misclassified samples are samples from the healthy shoulder incorrectly classified as injured.
As for the translation case, the results obtained from the two last scenarios show that there is a limitation in having a position of the patient that was not previously introduced in the training. We have found empirically that this limit is reached when the distance between the center of rotation and the closest point in the training is . In order to overcome this limitation, we now shuffle all the samples between the training and the test. Results are discussed in the next section.
3.3.3. Shuffled Large Dataset
To conduct further study, let shuffle all the samples that we generated for different locations 20 times. Let remind that our total number of samples is 4464. We separate samples for training and 1114 samples for test. The distribution of training and test dataset for a trial is shown in Figure 10. We have repeated this classification for 10 trials and the accuracy was always higher than using linear kernel and hyperparameter . The confusion matrix for a trial is shown in Table 13. The training time for this scenario is seconds whereas the test is in real time.
Further, we examine the effect of the C hyperparameter on the classification for this scenario. To do this, we vary its value and present the results in Table 14. We observe that increasing C reduces the classification error on the training dataset by allowing a smaller margin, which classifies all training points correctly. Conversely, a smaller C encourages a larger margin and a simpler decision function, resulting in lower accuracy. It’s important to note that increasing the C value results in a less complex model and an easier optimization problem, speeding up the training process. Additionally, it reduces the number of support vectors, which helps lower the overall computational time [30].
4. Conclusions
This study serves as a proof of concept for a Microwave Digital Twin Prototype for automatic, noninvasive, portable, and real-time detection of healthy and injured tendons in the shoulder. For this, we create a generalizable dataset using state-of-the-art numerical modeling and the proposed imaging system, considering various parameters: different noise levels, variations in complex permittivity due to dehydration effects, and different locations of the phantom in the imaging system. This parametric study leads us to several important conclusions:
- With flexible numerical modeling, we can construct a realistic dataset for classifying tendon injuries that addresses the challenge of obtaining real-world datasets.
- By incorporating noise levels into the training dataset, we can ensure accurate injury detection under varying noise conditions.
-
By accounting for changes in the measured complex permittivity of tissues due to dehydration, we can maintain high accuracy in injury detection. This is a key issue because it takes into account two important characteristics of human patients :
- −
- The small difference of dielectric properties from one patient to another for the same human tissue.
- −
- The variability in the Synovial Fluid (SF) values. We remind that SF which accounts for differentiating the healthy from the injured shoulder.
- Introducing various possible locations of the shoulder within the imaging system is critical for a realistic dataset. By generating datasets for different shifts and rotations, we can ensure high accuracy in classifying test data.
- When different shoulder locations are included in the training dataset, SVM classification achieves real-time detection of rotator cuff tears (RCTs) with accuracy provided that we train with positions close to those in test. We have found empirically that the training should not have positions further away than 0.5 cm from the test position. If the distance is larger, new positions have to be included in the training. This study will have to be pursued with statistical assessments once the system will be built in order to see what is the real dispersion in the different patient positions with respect to the imaging system.
The next step is to go from the Microwave Digital Twin Prototype to the Microwave Digital Twin by making tests using datasets measured from real-world shoulder models.
Acknowledgments
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 847581 and is co-funded by the Région Provence-Alpes-Côte d’Azur and IDEX and supported by National Research Agency (ANR) under reference number ANR-15-IDEX-01. The authors are grateful to the OPAL infrastructure from Université Côte d’Azur and the Université Côte d’Azur’s Center for High-Performance Computing for providing resources and support.
References
- of Orthopaedic Surgeons. (n.d.)., A.A. of Orthopaedic Surgeons. (n.d.)., A.A. Common Shoulder Injuries. https://orthoinfo.aaos.org/en/diseases–conditions/common-shoulder-injuries/.
- Teefey, S.A.; Rubin, D.A.; Middleton, W.D.; Hildebolt, C.F.; Leibold, R.A.; Yamaguchi, K. Detection and quantification of rotator cuff tears: comparison of ultrasonographic, magnetic resonance imaging, and arthroscopic findings in seventy-one consecutive cases. JBJS 2004, 86, 708–716. [Google Scholar] [CrossRef]
- Shibayama, Y.; Hirose, T.; Sugi, A.; Mizushima, E.; Watanabe, Y.; Tomii, R.; Iba, K.; Yamashita, T. Diagnostic accuracy of magnetic resonance imaging for partial tears of the long head of the biceps tendon in patients with rotator cuff tears. JSES international 2022, 6, 638–642. [Google Scholar] [CrossRef] [PubMed]
- Papatheodorou, A.; Ellinas, P.; Takis, F.; Tsanis, A.; Maris, I.; Batakis, N. US of the shoulder: rotator cuff and non–rotator cuff disorders. Radiographics 2006, 26, e23–e23. [Google Scholar] [CrossRef]
- Stone, M.; Jamgochian, G.; Thakar, O.; Patel, M.S.; Abboud, J.A. Synovial fluid volume at the time of arthroscopic rotator cuff repair correlates with tear size. Cureus 2020, 12. [Google Scholar] [CrossRef] [PubMed]
- Kiel, J.; Olwell, E. It might be a tumor: a unique presentation of a chronic rotator cuff tear. African Journal of Emergency Medicine 2020, 10, 288–290. [Google Scholar] [CrossRef]
- Borzooei, S.; Tournier, P.H.; Dolean, V.; Pichot, C.; Joachimowicz, N.; Roussel, H.; Migliaccio, C. Numerical Modeling for Shoulder Injury Detection Using Microwave Imaging. IEEE Journal of Electromagnetics, RF and Microwaves in Medicine and Biology, 2024; 1–8. [Google Scholar] [CrossRef]
- Grieves, M.; Vickers, J. Origins of the digital twin concept. Florida Institute of Technology 2016, 8, 3–20. [Google Scholar]
- Singh, M.; Fuenmayor, E.; Hinchy, E.P.; Qiao, Y.; Murray, N.; Devine, D. Digital twin: Origin to future. Applied System Innovation 2021, 4, 36. [Google Scholar] [CrossRef]
- Segovia, M.; Garcia-Alfaro, J. Design, modeling and implementation of digital twins. Sensors 2022, 22, 5396. [Google Scholar] [CrossRef]
- Wu, H.; Ji, P.; Ma, H.; Xing, L. A comprehensive review of digital twin from the perspective of total process: Data, models, networks and applications. Sensors 2023, 23, 8306. [Google Scholar] [CrossRef]
- Ahmed, I.; Ahmad, M.; Jeon, G. Integrating digital twins and deep learning for medical image analysis in the era of COVID-19. Virtual Reality & Intelligent Hardware 2022, 4, 292–305. [Google Scholar]
- Servin, F.; Collins, J.A.; Heiselman, J.S.; Frederick-Dyer, K.C.; Planz, V.B.; Geevarghese, S.K.; Brown, D.B.; Jarnagin, W.R.; Miga, M.I. Simulation of image-guided microwave ablation therapy using a digital twin computational model. IEEE Open Journal of Engineering in Medicine and Biology 2023. [Google Scholar] [CrossRef] [PubMed]
- Särestöniemi, M.; Singh, D.; Heredia, C.; Nikkinen, J.; von und zu Fraunberg, M.; Myllylä, T. Digital Twins for Development of Microwave-Based Brain Tumor Detection. Nordic Conference on Digital Health and Wireless Solutions. Springer, 2024, pp. 240–254.
- Amendolara, A.; Pfister, D.; Settelmayer, M.; Shah, M.; Wu, V.; Donnelly, S.; Johnston, B.; Peterson, R.; Sant, D.; Kriak, J.; others. An overview of machine learning applications in sports injury prediction. Cureus 2023, 15. [Google Scholar] [CrossRef]
- Akinbo, R.S.; Daramola, O.A. Ensemble machine learning algorithms for prediction and classification of medical images. Machine Learning-Algorithms, Models and Applications, 2021. [Google Scholar]
- Daidone, M.; Ferrantelli, S.; Tuttolomondo, A. Machine learning applications in stroke medicine: Advancements, challenges, and future prospectives. Neural Regeneration Research 2024, 19, 769–773. [Google Scholar] [CrossRef] [PubMed]
- Mariano, V. ; others. Microwave Imaging and Sensing Algorithms for Brain Stroke Diagnosis 2023. [Google Scholar]
- Zhu, G.; Bialkowski, A.; Guo, L.; Mohammed, B.; Abbosh, A. Stroke classification in simulated electromagnetic imaging using graph approaches. IEEE Journal of Electromagnetics, RF and Microwaves in Medicine and Biology 2020, 5, 46–53. [Google Scholar] [CrossRef]
- Salucci, M.; Polo, A.; Vrba, J. Multi-step learning-by-examples strategy for real-time brain stroke microwave scattering data inversion. Electronics 2021, 10, 95. [Google Scholar] [CrossRef]
- Frangi, A.F.; Tsaftaris, S.A.; Prince, J.L. Simulation and synthesis in medical imaging. IEEE transactions on medical imaging 2018, 37, 673–679. [Google Scholar] [CrossRef]
- Nikolenko, S.I. Synthetic data for deep learning; Vol. 174, Springer, 2021.
- Lu, Y.; Wang, H.; Wei, W. Machine Learning for Synthetic Data Generation: a Review. arXiv preprint arXiv:2302.04062, arXiv:2302.04062 2023.
- Lombardi, D.; Raphel, F. A method to enrich experimental datasets by means of numerical simulations in view of classification tasks. ESAIM: Mathematical Modelling and Numerical Analysis 2021, 55, 2259–2291. [Google Scholar] [CrossRef]
- McDuff, D.; Curran, T.; Kadambi, A. Synthetic Data in Healthcare. arXiv preprint arXiv:2304.03243, arXiv:2304.03243 2023.
- Gaspar, P.; Carbonell, J.; Oliveira, J.L. On the parameter optimization of Support Vector Machines for binary classification. Journal of integrative bioinformatics 2012, 9, 33–43. [Google Scholar] [CrossRef]
- Grandini, M.; Bagli, E.; Visani, G. Metrics for multi-class classification: an overview. arXiv preprint arXiv:2008.05756, arXiv:2008.05756 2020.
- Ringnér, M. What is principal component analysis? Nature biotechnology 2008, 26, 303–304. [Google Scholar] [CrossRef]
- Maenhout, G.; Santorelli, A.; Porter, E.; Ocket, I.; Markovic, T.; Nauwelaers, B. Effect of dehydration on dielectric measurements of biological tissue as function of time. IEEE Journal of Electromagnetics, RF and Microwaves in Medicine and Biology 2019, 4, 200–207. [Google Scholar] [CrossRef]
- Eitrich, T.; Lang, B. Efficient optimization of support vector machine learning parameters for unbalanced datasets. Journal of computational and applied mathematics 2006, 196, 425–436. [Google Scholar] [CrossRef]
| 1 | |
| 2 | |
| 3 |
Figure 1.
(a) Anatomy of the shoulder, (b) numerical model of the shoulder.
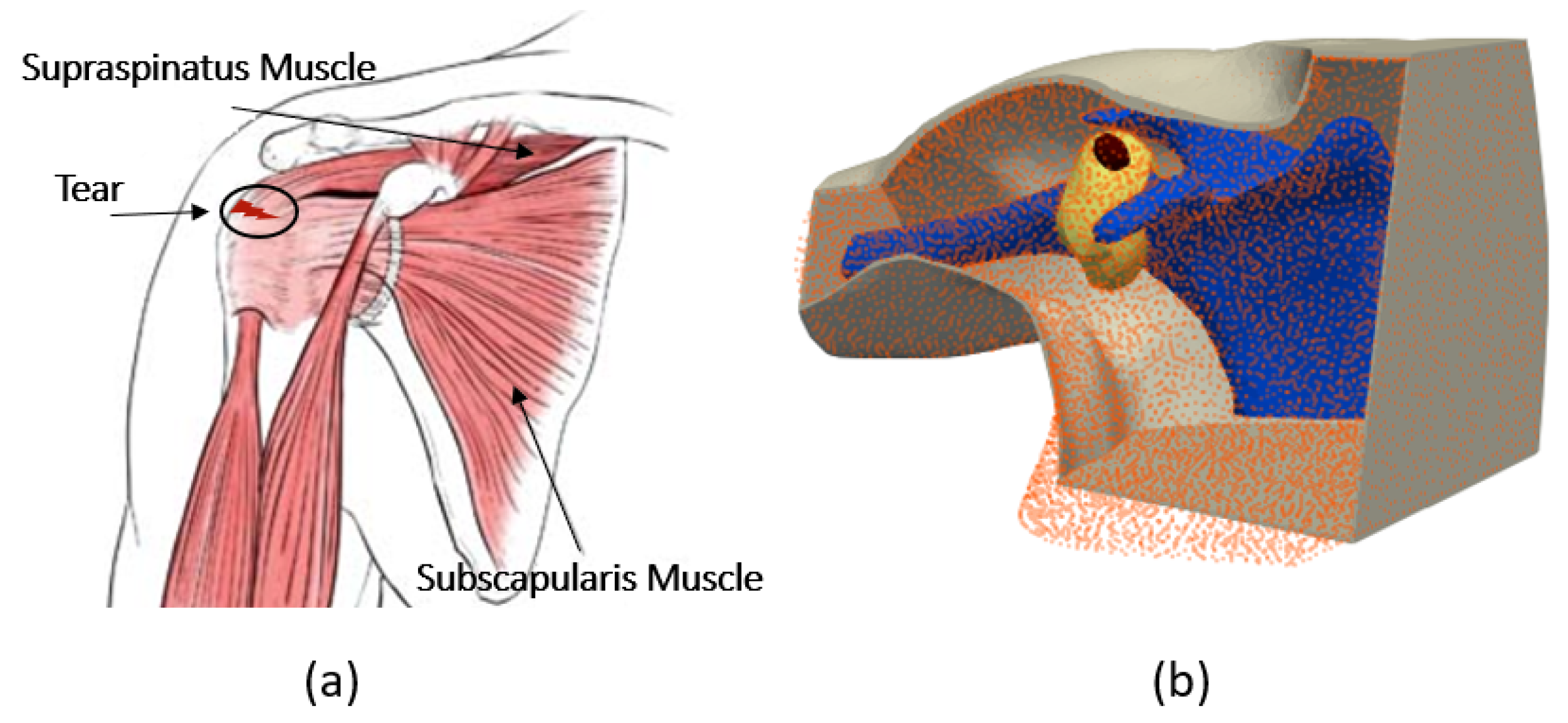
Figure 2.
(a): imaging system, (b) boundary conditions, (c) finite element mesh.
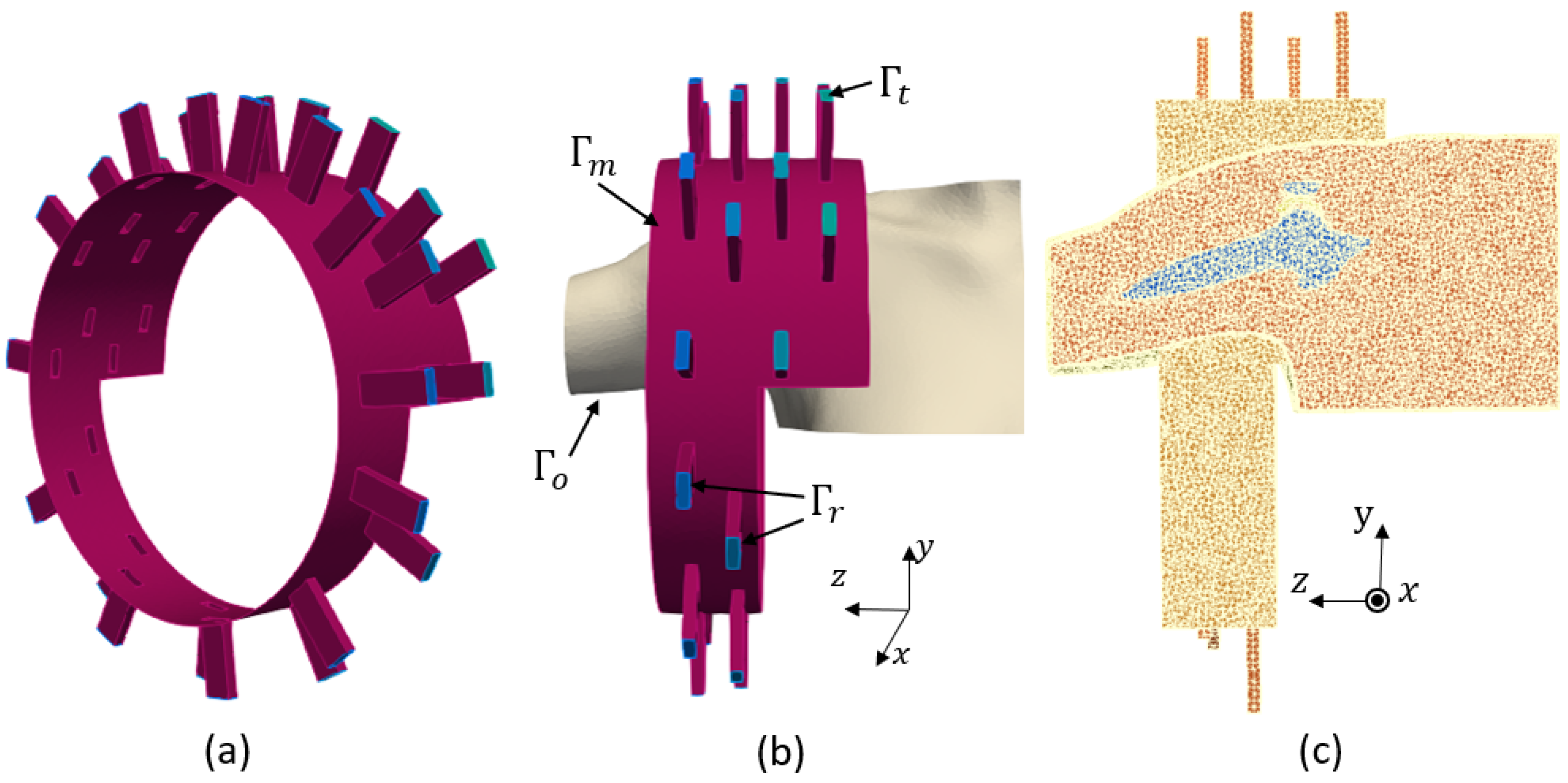
Figure 3.
The workflow of SVM classification.
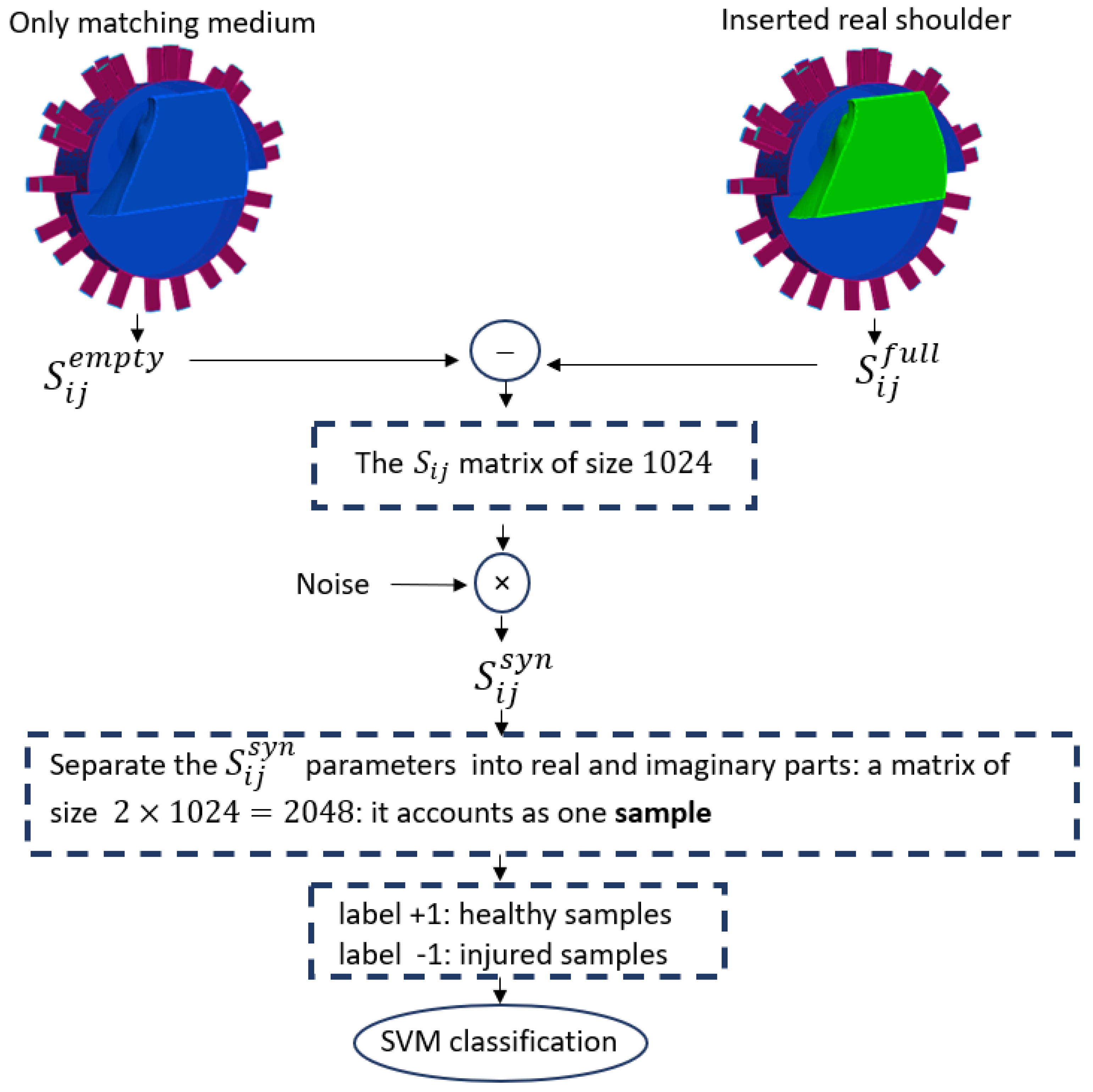
Figure 4.
Projection of the 3 most significant eigenvectors of the training dataset and test dataset when phantoms have a shift of along .
Figure 4.
Projection of the 3 most significant eigenvectors of the training dataset and test dataset when phantoms have a shift of along .
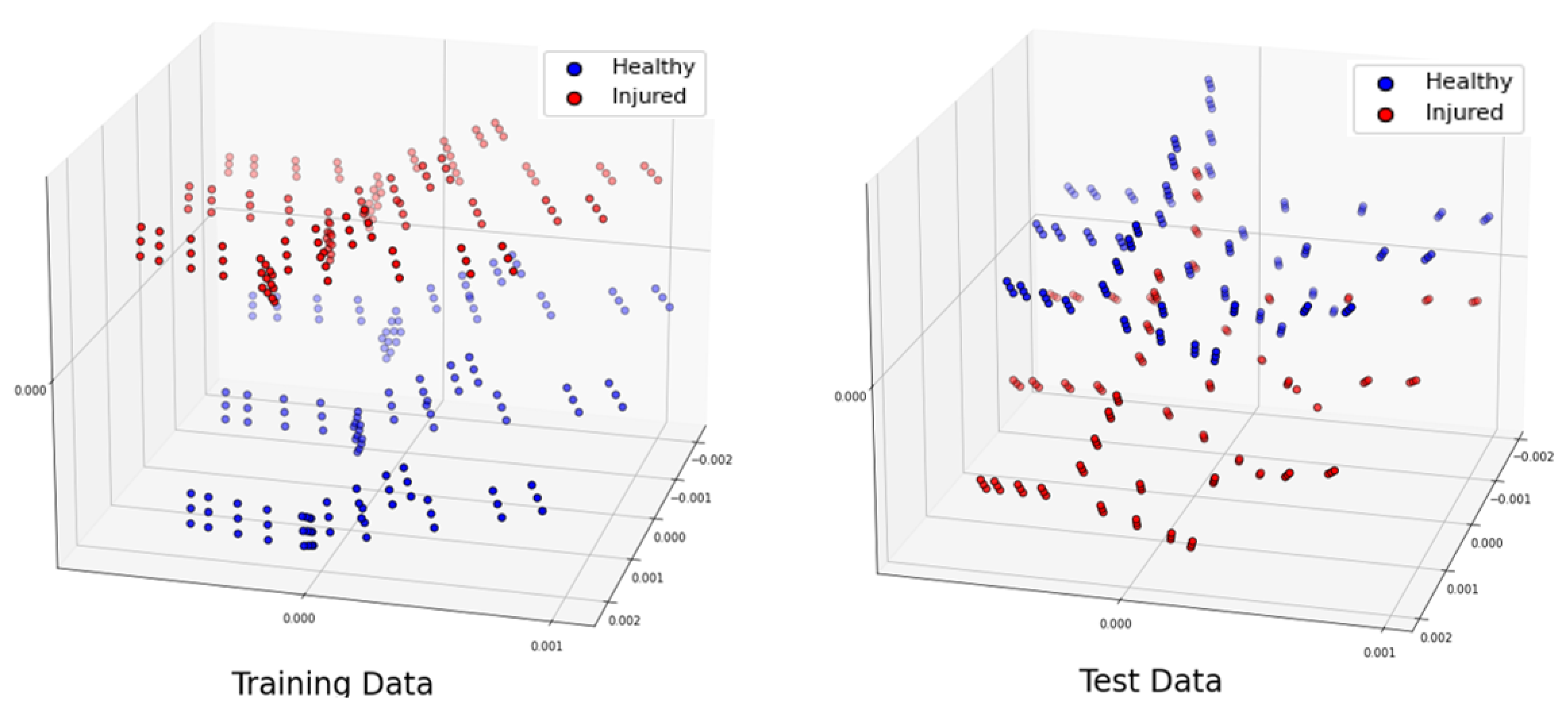
Figure 5.
The translation error of of cm along different axis between training and test dataset phantoms.
Figure 5.
The translation error of of cm along different axis between training and test dataset phantoms.
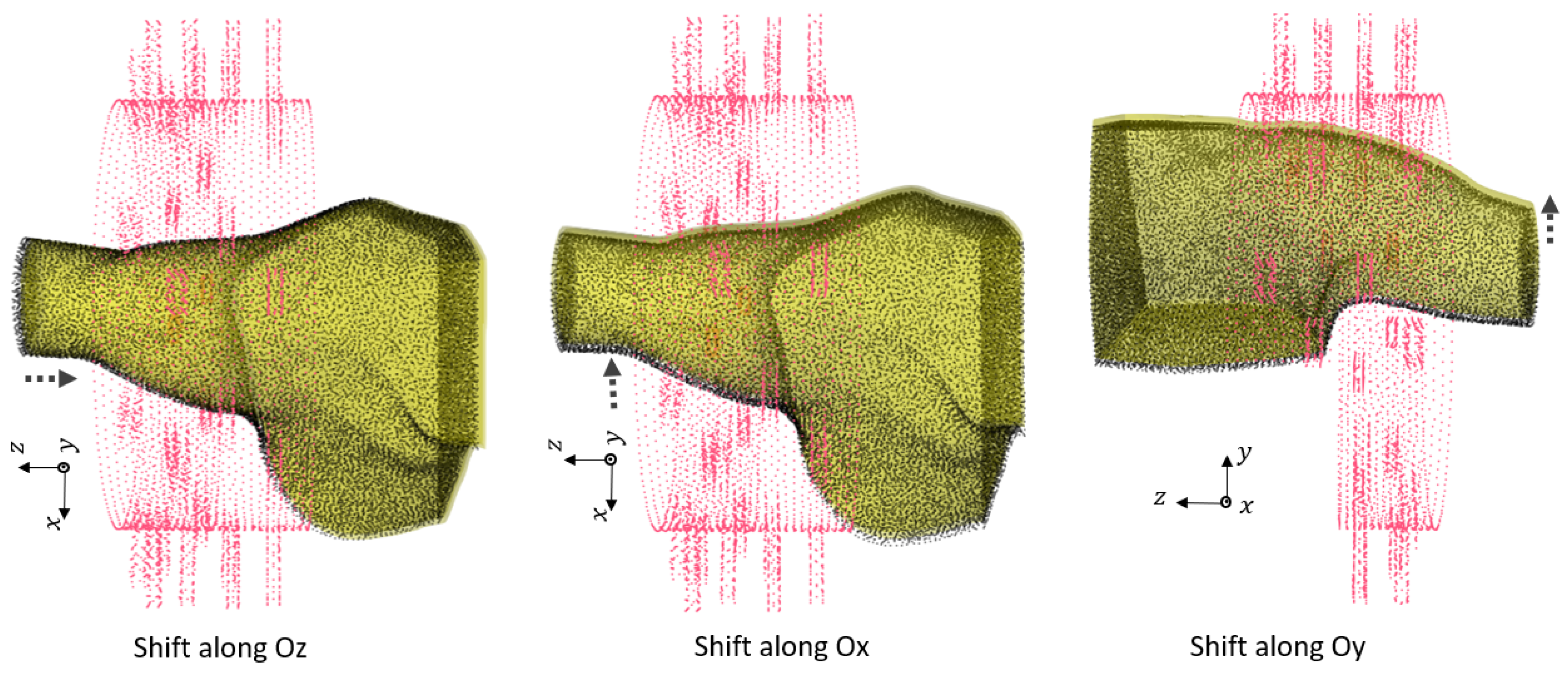
Figure 6.
First group of rotations. For : , for : and shift , for : .
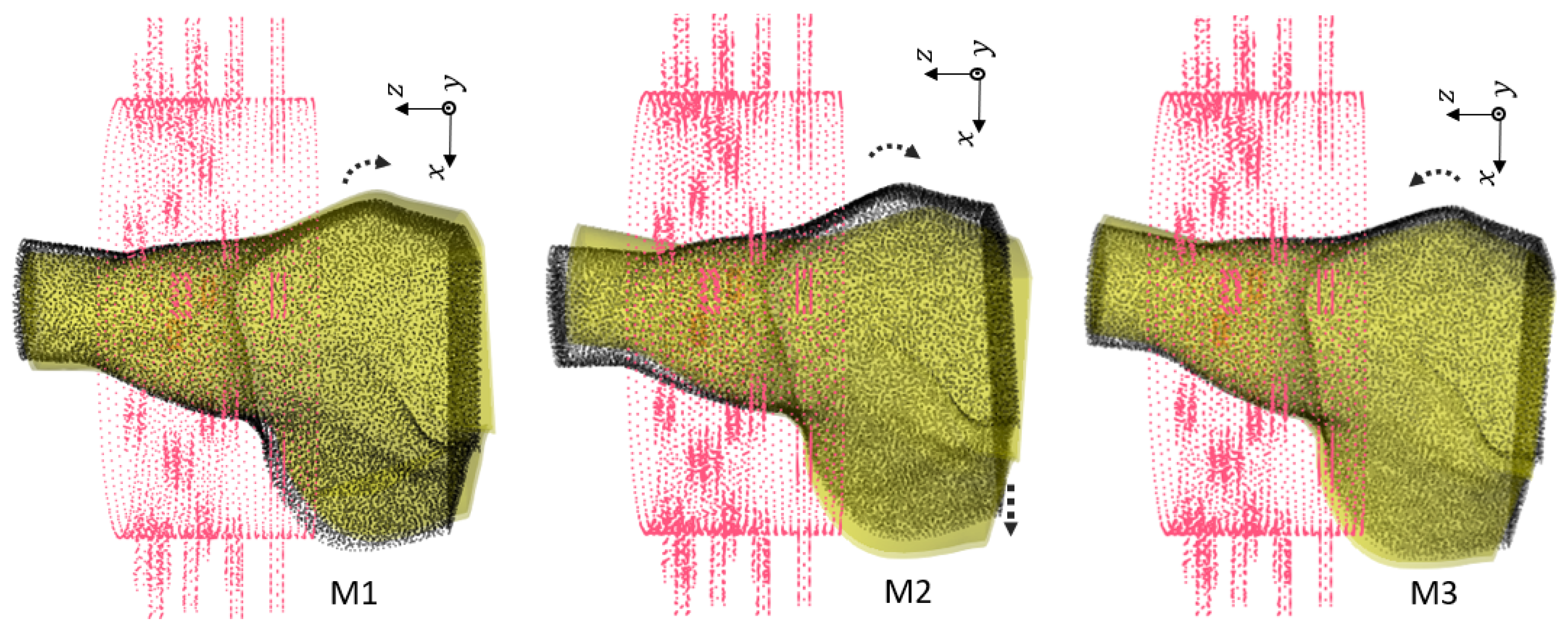
Figure 7.
Second group of rotations. For : . For : and shift . For : and shift .

Figure 8.
Third group of rotations. For : . For : , and . For : , and .
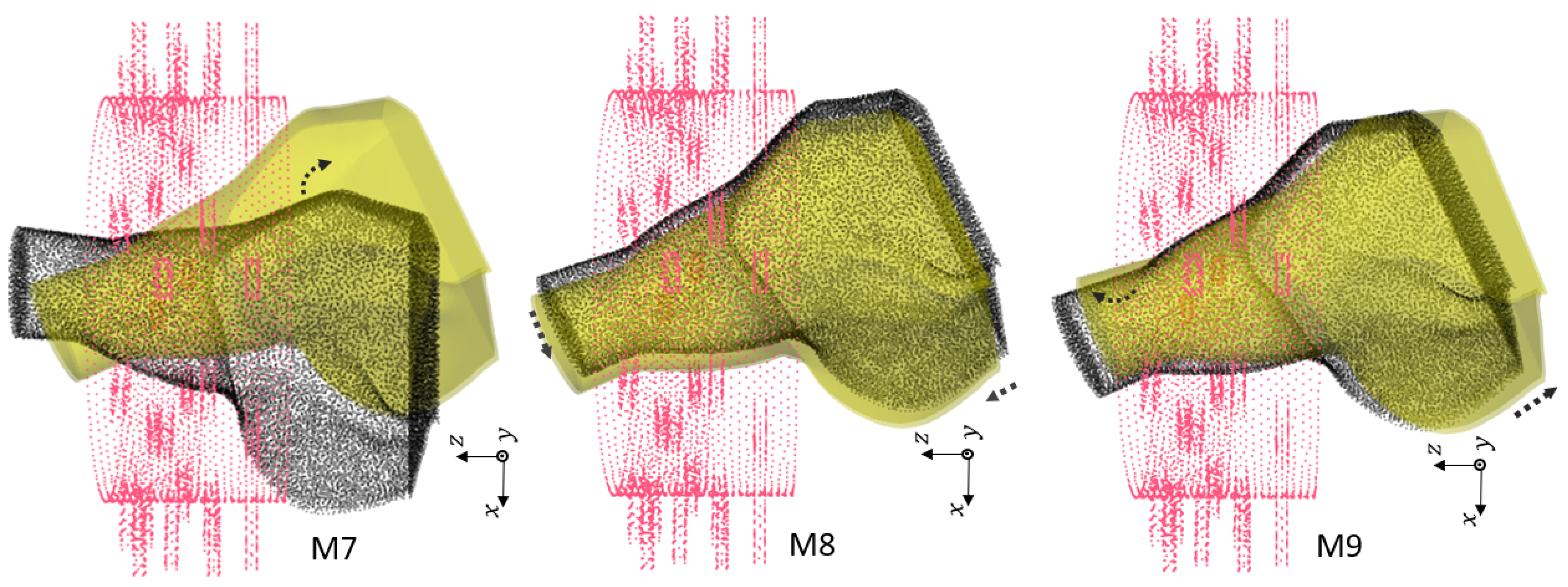
Figure 9.
Position of the center of the rotations for 31 different phantoms.
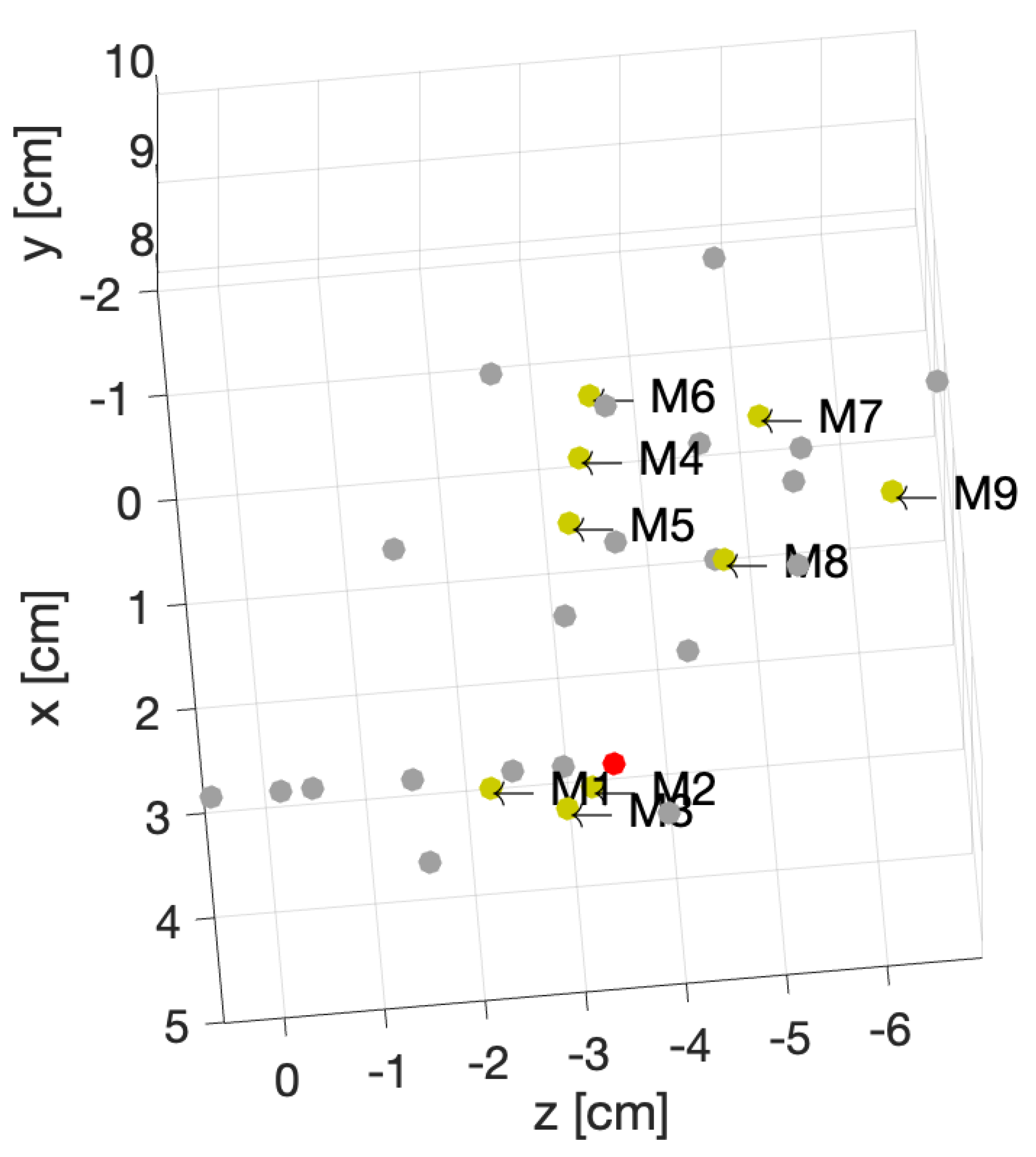
Figure 10.
Projection of the 3 most significant eigenvectors of the large dataset. Training dataset (left), test dataset (right).
Figure 10.
Projection of the 3 most significant eigenvectors of the large dataset. Training dataset (left), test dataset (right).
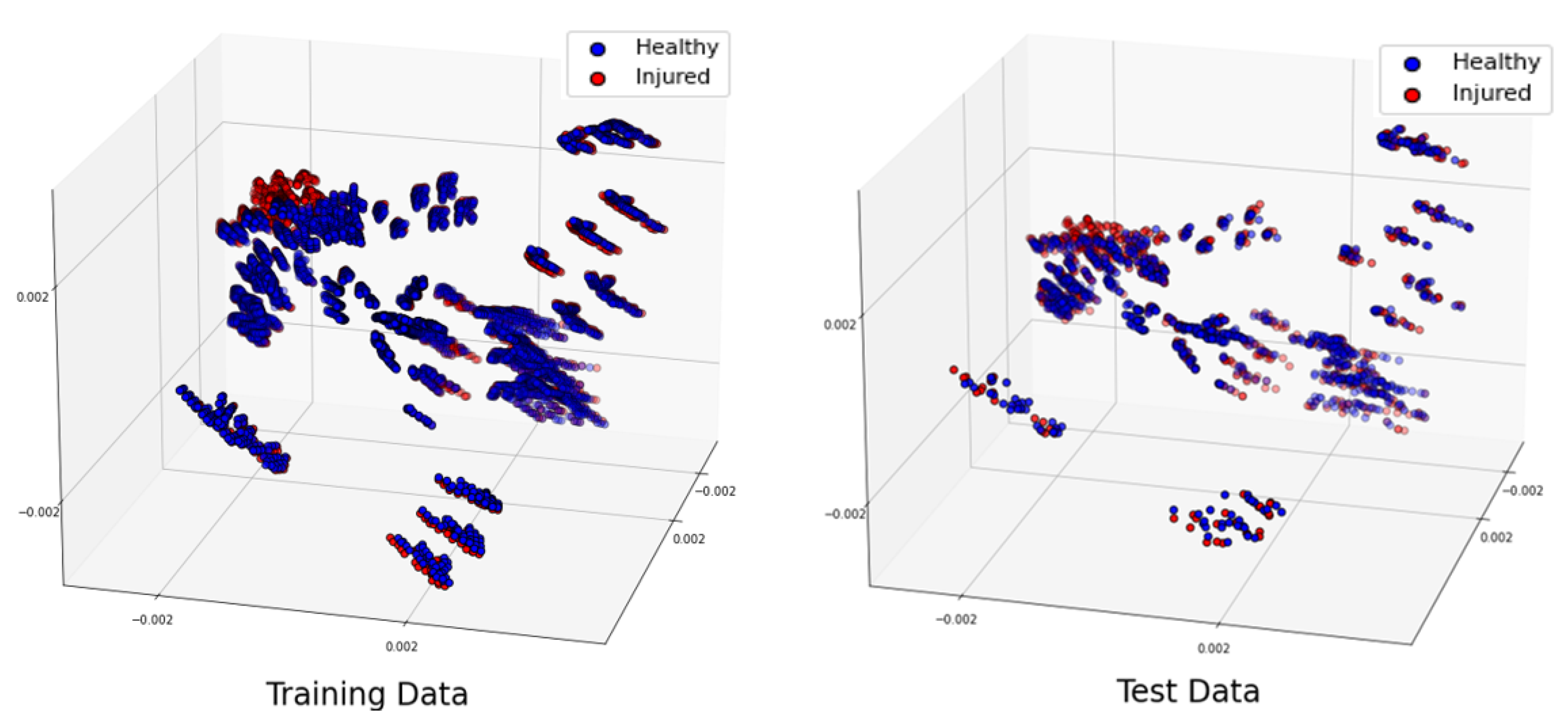
Figure 11.
Projection of the two most significant eigenvectors of classified test data for the random test case for different choice of C parameter.
Figure 11.
Projection of the two most significant eigenvectors of classified test data for the random test case for different choice of C parameter.
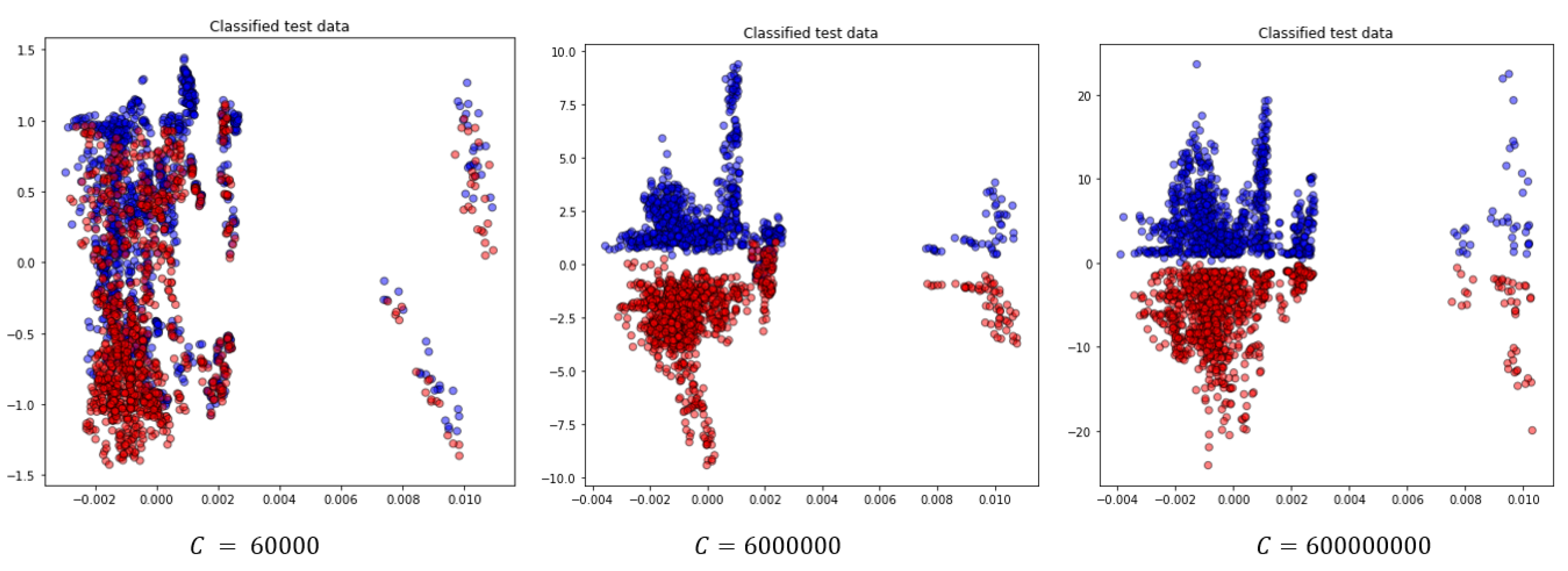
Table 1.
Parametric study for detection of RCTs.
| Scenario | Description |
|---|---|
| Noise level | Introducing different noise levels in synthetic data |
| Error in value of | Dielectric properties variations due to dehydration |
| Localization | Changes in the location of the shoulder |
| Randomized dataset | Shuffled training and test dataset |
Table 2.
Complex dielectric properties at 1 GHz.
| Different Tissues | Value of |
|---|---|
| Bone cortical | |
| Tendon | |
| Muscle | |
| Skin | |
| SF |
Table 3.
Confusion matrix interpretation
| Predicted class | |||
|---|---|---|---|
| Healthy | Injured | ||
| Actual class | Healthy | ||
| Injured | |||
Table 4.
The noise levels introduced in each sets of data. The values are in .
| Sample model | Training dataset | Test dataset |
|---|---|---|
| Healthy | ||
| Injured |
Table 5.
Number of generated training and test samples for healthy and injured model. We build the datasets with 36 number of seeds for each noise level.
Table 5.
Number of generated training and test samples for healthy and injured model. We build the datasets with 36 number of seeds for each noise level.
| Sample model | Training dataset | Test dataset |
|---|---|---|
| Healthy | ||
| Injured |
Table 6.
Classification results for different values of C in noise study.
| C | Acr | Spec | Sens |
|---|---|---|---|
| 6000 | |||
| 600000 | |||
| 6000000 |
Table 7.
The value of at with including the dehydration effect, compared to the original values ( )
| Tissue | Original values based on Table 2 | ||
|---|---|---|---|
| Bone cortical | |||
| Skin | |||
| Tendon | |||
| Muscle | |||
| SF |
Table 8.
Number of generated training and test samples for healthy and injured models. We build the datasets with 36 seeds for each noise level.
Table 8.
Number of generated training and test samples for healthy and injured models. We build the datasets with 36 seeds for each noise level.
| Sample Model | Total Dataset | Training Subset | Test Subset |
|---|---|---|---|
| Healthy | 900 | 108 | |
| Injured, 3 groups of SF value |
Table 9.
Classification accuracy for different values dehydration error, for .
| Value of SF | Accuracy |
|---|---|
Table 10.
Number of generated training and test samples for healthy and injured model, for each position of the phantom.
Table 10.
Number of generated training and test samples for healthy and injured model, for each position of the phantom.
| Sample model | Training dataset | Test dataset |
|---|---|---|
| Healthy | ||
| Injured |
Table 11.
Number of generated training and test samples for healthy and injured model, for 31 positioning of the shoulder inside sensing system, due to rotation and shift.
Table 11.
Number of generated training and test samples for healthy and injured model, for 31 positioning of the shoulder inside sensing system, due to rotation and shift.
| Sample model | Total dataset | Training subset | Test subset |
|---|---|---|---|
| Healthy | 4320 | 144 | |
| Injured | 4320 | 144 |
Table 12.
Different scenarios for various position of phantom in the imaging system.
| Healthy | Injured | Accuracy | Confusion matrix | |
|---|---|---|---|---|
| 1 | M2 | M2 | ||
| 2 | M2 | M4 | ||
| 4 | M7 | M3 | ||
| 5 | M9 | M6 |
Table 13.
Confusion matrix for randomized large dataset, with .
| Models | Healthy | Injured |
|---|---|---|
| Healthy | 1112 | 2 |
| Injured | 0 | 1114 |
Table 14.
The effect of C value in classification for the shuffled large dataset.
| C | Acr | Spec | Sens | Time (s) |
|---|---|---|---|---|
| 600 | ||||
| 6000 | ||||
| 60000 | ||||
| 600000 | ||||
| 6000000 | ||||
| 60000000 | ||||
| 600000000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






