Preprint
Article
Towards Hydraulic Design Optimization of Shaft Hydropower Plants: A 3D-CFD Application Based on Physical Models
Altmetrics
Downloads
79
Views
36
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
30 August 2024
Posted:
02 September 2024
You are already at the latest version
Alerts
Abstract
The shaft hydropower plant (SHPP) is a novel hydraulic concept for low-head hydropower sites with several environmental and operational advantages over conventional layouts. However, the first two projects implementing this concept have shown comparatively high construction costs and project risks. Therefore, further optimization is required to the economic attractiveness and enabling broader market adoption. Initial model tests recommend a square-shaped shaft inlet with a three-sided approach flow for low-loss and fish-friendly inflow conditions. Yet, this design requires significant space for structural implementation and may be unsuitable for use with multiple shafts or as an extension of non-powered dams and weirs. This research paper presents the application of a computational fluid dynamics simulation setup to evaluate the hydraulic per-formance of various design configurations, especially, alternative design layouts with one-sided approach flow without further physical model tests,. The simulation setup is calibrated against observations including head loss and velocity measurements from the physical model tests, and its satisfactory performance enables the analysis of alternative design layouts. This aims to derive the most significant design parameters for achieving the desired hydraulic conditions at the intake. Increasing the flow depth before the intake and enlarging the inlet area have the most significant impact, while increasing the overflow of the front gate has the least significant effect.. The chosen CFD application is deemed suitable for hydraulic design optimization and provides guidance on the key parameters to focus on for tailored site-specific design development.
Keywords:
Subject: Engineering - Civil Engineering
1. Introduction
In the context of climate change and the corresponding global need to increase the share of renewable generation in the energy mix, with >140 GW of estimated unexploited potential, small-scale hydropower – considering plants with an installed nominal capacity of ≤10 MW – offers a significant opportunity to get closer to this goal [1].
Small-scale hydropower is often referred to as having less negative ecological and social impacts than conventional large hydropower systems [2]; however, a distinguished and project-specific assessment is crucial, and a general statement should be considered carefully. SHP can come in various individual layouts, and determining impacts is often only possible after a thorough, specific assessment [3,4]. Evidently, no straightforward classification supports general statements, such as the claim that small-scale hydropower only has minor negative environmental impacts. Designing each facility using ecologically, technically, and economically viable concepts and tools is crucial to ensure the sustainable exploitation of the aforementioned untapped potential.
One innovative approach for harnessing hydropower in a sustainable way is the Shaft Hydropower Plant (SHPP). This type of plant is designed for low-head, in-river locations and features a unique hydraulic arrangement for its components. The design of the SHPP was developed based on physical model testing at the hydraulic laboratory of the Technical University of Munich (TUM). Initially, small-scale indoor model tests were conducted to explore different arrangements and derive a well-suited layout and basic dimensioning guidelines for its hydraulic design. Subsequent experiments were carried out at an outdoor prototype facility to further validate the concept and conduct comprehensive functionality tests. The conceptual scheme in Figure 1 illustrates a shaft chamber with a horizontal inlet area that is covered by a trash rack with narrow bar clearance (15-20 mm) and an incorporated rack cleaning mechanism. At this type of hydropower plant, the water withdrawal takes place vertically downwards, in contrast to conventional run-of-river hydropower plants. The water flow passes through the horizontal inlet plane, moves vertically through the shaft, drives the turbine, and then is released towards the tailwater through the draft tube. To ensure a vortex-free, low-loss, and uniform inflow into the shaft, it is important to have a relatively large intake area with a slow, three-sided upstream approach flow, adequate submergence of the inlet area (at least 1/4 of the intake length), and a continuous overflow of the vertically adjustable sluice gate [5,6]. In order to create a safe passage for fish swimming downstream near the intake, openings can be provided arranged in the gate. The tests with live fish have shown that this concept provides an effective fish protection measure and migration corridor. It combines the trash rack as a physical barrier and the vertical flow deflection as a behavioral barrier, along with permanently discharged openings at the downstream end of the intake.[7,8]
The SHPP concept offers further operational advantages. Since all electro-mechanical and hydraulic steelworks components are submerged, there is no need for a conventional powerhouse with complex flood protection requirements. This means that the system can withstand floods of any size without damaging the equipment. Additionally, positioning the inlet plane parallel to the riverbed promotes sediment continuity. When the water flow is high, sediment and debris are transported to and deposited on the trash rack. The submerged cleaning mechanism then pushes this material towards the downstream end of the gate, which is then raised, creating a flushing effect that moves the material towards the tailwater. Sediment fractions smaller than the spaces between the rack bars are discharged through the turbine into the tailwater. The gate can also be fully lowered to increase the flood discharge capacity.[5,6].
Despite the advantages of the concept, only two commercial-scale projects – SHPP Großweil and SHPP Dietenheim – have been implemented using it in the first decade since its development. Both implemented projects used hydraulic designs that relied on scaling up the dimensions of the physical model tests and prototype facility from TUM. These reference projects have proven the technical functionality of the SHPP concept but shared a common problem: they were very expensive to implement. These projects were financed in Germany due to high feed-in tariffs, low financing costs, and a substantial state grant in the case of Großweil. However, for countries with less attractive market framework conditions for hydropower financing and realization, it is necessary to significantly reduce the costs, complexity of implementation, and associated risks to enable the application of this technology while maintaining its proven advantages [9,10,11,12].
One of the main reasons for the high implementation costs (apart from site-specific constraints we won't go into) is the hydraulic layout with a three-sided upstream approach flow. This configuration requires a large amount of space and also restricts the use of this concept, as it cannot be implemented at certain sites with existing hydraulic infrastructure, such as weirs with fixed field widths. Additionally, it has the disadvantage that when the shaft needs to be drained for equipment maintenance, a three-sided massive stop log is needed, which requires large mobile cranes and limits maintenance work to low-flow periods [12].
The physical model test results from the SHPP prototype allow for upscaling this design while maintaining the relative dimensions of the SHPP arrangement. However, we cannot predict flow patterns that would occur when deviating from this base geometry. Despite this, it might be necessary to adapt the design accordingly due to the potential disadvantages of this basic configuration in certain site conditions. Therefore, it may not be possible to directly implement a scaled design similar to that of the prototype facility. When designing an SHPP layout with a significantly modified geometrical configuration, there is a risk of resulting flow conditions causing operational problems such as vortex formation with air entrainment, increased head loss, or unfavorable velocity distributions affecting fish protection. Additionally, conducting physical model tests for any new site would require substantial efforts at an early stage of project development.
Due to these reasons, it was important to apply and test a computer-based approach to accurately size SHPP layouts with alternative design configurations. Our approach is focused on a one-sided upstream approach flow. While such an approach should require less effort than physical model testing, it still has to provide sufficient certainty in predicting the resulting flow patterns. In our initial review, we examined various 3D computational fluid dynamics (CFD) approaches to establish a workflow that allows for predicting flow patterns and optimizing the design of SHPP arrangements for any suitable site. Previous studies have shown that applying a simplified representation of fine trash racks within such numerical models with a baffle or a porous medium is feasible to account for the pressure loss that occurs during flow through them. [13,14,15].
Based on the findings in the literature, we therefore utilized a 3D CFD approach to achieve the two main objectives of our study:
Replicating the flow conditions observed at the SHPP prototype by calibrating numerical parameters and validating them through quantitative comparison with physical results;
Applying the calibrated settings to analyze modified geometrical configurations with one-sided approach flow while determining relevant hydraulic parameters for assessing flow patterns and subsequent hydraulic design optimization.
2. Materials and Methods
2.1. Physical Model Testing
The presented study is centered around previous physical model testing at the prototype SHPP facility built and commissioned at the Oskar-von-Miller Hydraulic Research Institute of TUM in 2013. In accordance with objective (1) of our study, we are using the data and observations made during two different experimental setups for which we chose the following nomenclature for our study:
Experimental setup 01 (E01) is referred to when we describe observations with the basic hydraulic configuration of the prototype with a three-sided upstream approach flow.
Experimental setup 02 (E02) is referred to when we describe observations with a modified configuration of the prototype with a one-sided upstream approach flow.
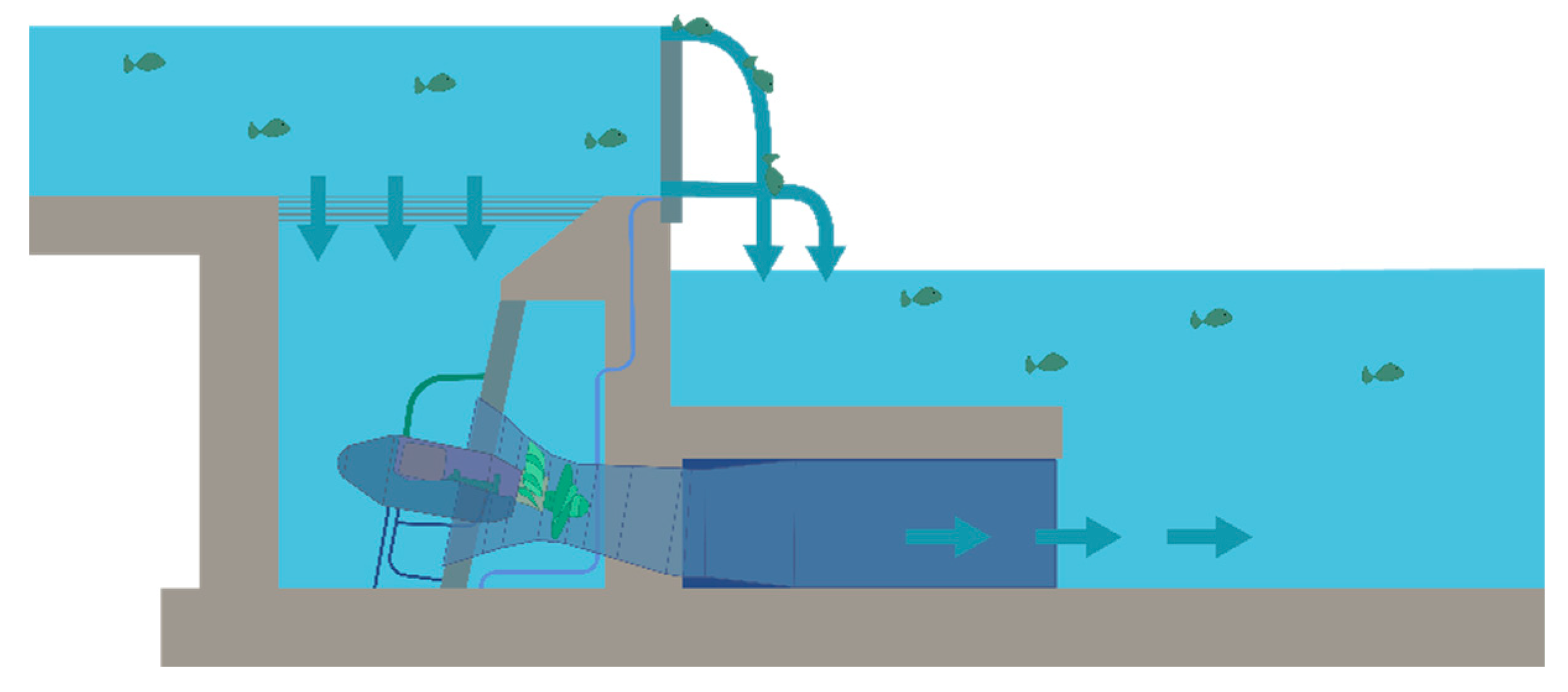
The overall arrangement of the prototype facility is displayed in Figure 2.
At this facility, experiments focused on analyzing fish behavior and assessing bypass functionality (E01) were carried out in 2013 using the basic arrangement of the SHPP concept with a three-sided upstream approach flow towards the shaft intake. As part of these experiments, flow velocity measurements were carried out to confirm the maximum velocities at the screen and the flow field distribution. These measurements utilized a 3D Nortek Field Acoustic Doppler Velocimeter (ADV) probe. The measurement grid had a lateral resolution of 39 cm in both directions (x and y), covering the entire intake plane, and was positioned 4.6 cm above the trash rack (see Figure 3). At each point, velocities for all three dimensions (x, y, z) were recorded for 60 seconds, and the time-averaged velocities were calculated [7].
Several discharges and configurations (i.e., with top or bottom bypass opening) were tested with this experimental setup. For the first objective of our study, only the case with full turbine discharge of 1.5 m3/s, an overflow height at the gate of 7.3 cm, and the bottom bypass in operation is relevant – as the physical measurements from this case are used for validation of the numerical model results. In the course of E01, the intake area exhibited a relatively smooth flow surface with minimal vortex activity. Irregular local vortices appeared sporadically in the areas where the sluice gate connected to the weir's corners. Nevertheless, this undesirable geometric feature did not impact the overall hydraulics of the intake [7]. Further data from the E01 setup includes measured head losses at the intake, including losses resulting both from the three-dimensional flow deflection above the intake as well as the losses resulting from the increased flow velocities and friction during the flow through the trash rack [16].
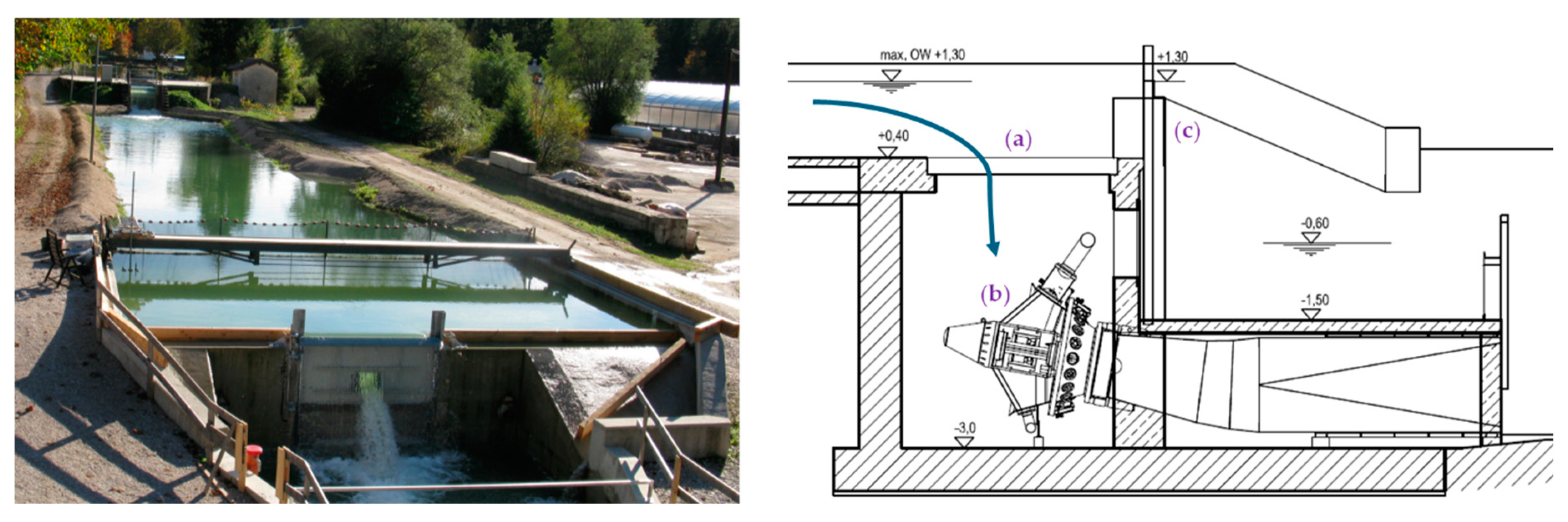
One further experiment (E02) was conducted at the same prototype facility in 2017. The objective of this experiment E02 was to find out how the inflow conditions and the overall efficiency of the power plant will change in the case of a one-sided upstream approach flow instead of the original design with a three-sided approach flow. For this experiment, they installed channel guide walls parallel to the main flow direction starting at the gate of the SHPP and reaching 7.5 m upstream, therefore creating a channeled approach flow towards the SHPP intake, as shown in Figure 4. The experiment was conducted at different flow rates, and the resulting conditions were recorded qualitatively by photos and quantitatively by ADV measurements following the same principle as during the experiments of E01 in 2013. The findings showed that the one-sided approach flow leads to an increased approach velocity and inhomogeneous flow patterns above the intake with the risk of vortex formation [17].
2.2. Numerical Model Testing
According to the first objective of the present study, the physically determined data from the two experimental setups, E01 and E02, at the prototype facility was used to set up, calibrate, and validate a numerical model of the two presented geometrically different arrangements. Following validation, the geometry of the model was modified to assess different configurations and their impact on the flow field. This forms the foundation for further design optimization of the SHPP concept. The numerical model testing process is organized into three simulation sets.
Simulation set M01 refers to all simulations we conducted to generate a calibrated and validated numerical model of the experimental setup E01 with a three-sided upstream approach flow.
In simulation set M02 we used the calibrated and validated model of the set M01 and added lateral guide walls in accordance with the experimental setup E02 with a one-sided up-stream approach flow.
Finally, in the simulation set M03, we conducted three further simulations with a one-sided upstream approach flow and additionally varying one relevant design parameter during each of them in order to determine their relevance and for subsequent hydraulic design optimization according to the second objective of our study.
For the 3D-CFD simulations, the commercial software FLOW-3D® HYDRO (Version 2023R1) was applied. It employs the finite difference and finite volume methods to solve the equations of motion for fluids and obtain three-dimensional solutions to flow problems. The software utilizes structured rectangular grids (i.e., computational mesh) to discretize the problem into a numerical model following the immersed boundary method, simplifying the process of importing diverse solid geometries and integrating the solid model into the software, as the base mesh can remain unchanged when importing an altered geometry. Within the computational mesh, the software solves the Reynolds-averaged Navier-Stokes equations, consisting of three-dimensional mass and momentum conservation equations to replicate the flow field. It also addresses the challenge of modeling free surfaces in computational environments by neglecting the inertia of gas adjacent to the liquid and replacing it with an empty space represented only by uniform pressure and temperature, defined as the Volume of Fluid (VOF) method [18,19]. The software offers the further advantage that sub-models can be easily added to the basic hydraulic-numerical model. For the presented cases, this is relevant for two reasons.
First, simulating the flow through the trash-rack with 20 mm bar spacing and 12 mm bar thickness would require an extremely fine resolution of the computational mesh with correspondingly long and unfeasible computation times. Instead, the trash rack was defined here as a porous medium with directional porosity characteristics, allowing the simplified yet accurate representation of the flow through it. The porous-media model is implemented as a sub-grid process by applying volume-averaged quantities to the porous region and calculating bulk fluid velocity and pressure drop with an appropriate drag model [13,18].
Second, the rotation of the turbine runner is represented in a simplified way as a fan model, which imparts momentum to the fluid in a region defined by a special type of geometry component. This model induces both swirl and axial velocity components to the fluid that enters the volume inside the fan component, which is defined by a cylinder of the actual turbine runner's dimensions (diameter, thickness) [18].
For the presented numerical model tests the following basic settings have been chosen within the software:
The turbulence model chosen was the Renormalized Group (RNG) k-epsilon model with dynamically computed mixing length.;
To represent the trash rack as a porous medium, the Forchheimer saturated drag model was applied with constant drag coefficient A throughout all simulations and variable drag coefficient B, which was modified for model calibration during simulation set M01 by varying the underlying -value. The drag coefficient B is calculated according to equation (1):
with being a roughness factor typically ranging between 1.8 and 4.0 (representing smooth through rough fibers), and the average equivalent spherical diameter of the porous medium´s fibers – i.e., in our case the trash rack bar depth of 6.5 mm [13,14,18]. The porosity, defined as the open volume divided by the total volume in each direction as well as the specific surface area, was determined based on the actual geometry of the trash rack (i.e., number of bars, their length, depth, thickness, and spacing). Once the numerical model during set M01 was calibrated and validated, we did not further vary the porosity settings for the subsequent sets M02 and M03.
For the representation of the turbine runner in motion, the fan model properties were set as follows: Spin rate 34.87 rad/s (333 rpm); Thickness 0.16 m; Blade tip thickness 0.014 m; Number of blades: 4.
2.2.1. Simulation Set M01–SHPP with Three-Sided Approach Flow
The first set of simulations, M01, aimed at determining the suitable numerical settings that are needed to replicate the physically measured flow fields as accurately as possible, aligning with objective (1) of this study. The geometry is generated as a 3D-CAD Model based on the technical drawings included in the Annex of [2]. The small-scale components not depicted with sufficient detail in these drawings (trash rack with cleaning mechanism, gate with bypass openings) were modeled based on their description and figures presented within that report.
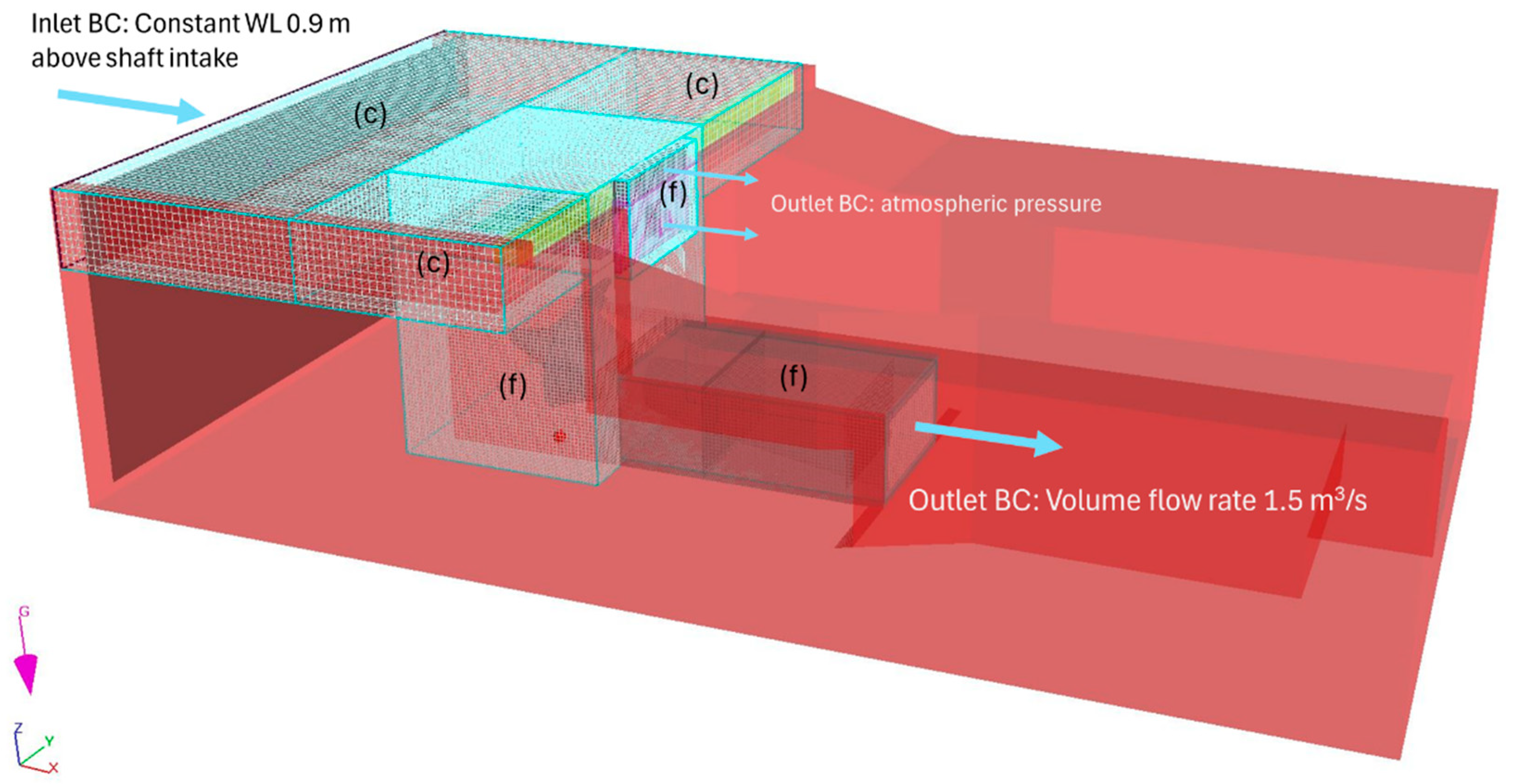
The measured head loss from the experimental setup E01 [16] was used for primary grid independence analysis and model calibration. The recorded (unpublished) data containing ADV-measured flow velocities of E01 has been made available by the authors of [7] and was subsequently used to validate the calibrated numerical model. The model was established using three mesh blocks with a coarser resolution for the upstream area and three mesh blocks with a finer resolution (factor 0.5 of the coarser resolution) surrounding the shaft, the gate, and the draft tube. To reduce the computation times during the calibration process, an initial model was simulated for 600 seconds in order to reach steady-state flow conditions. All further simulations were restarted using this first one as the initial hydraulic condition. The configuration of the M01 setup with mesh regions and relevant boundary conditions is shown in Figure 5:
The subsequently computed simulation set M01 contains five simulations and serves three purposes: to analyze the grid dependency, to calibrate the model by means of changing the drag coefficient B, and to validate the results of the calibrated model by means of statistical analysis. The five simulations with their decisive differences are listed in Table 1.
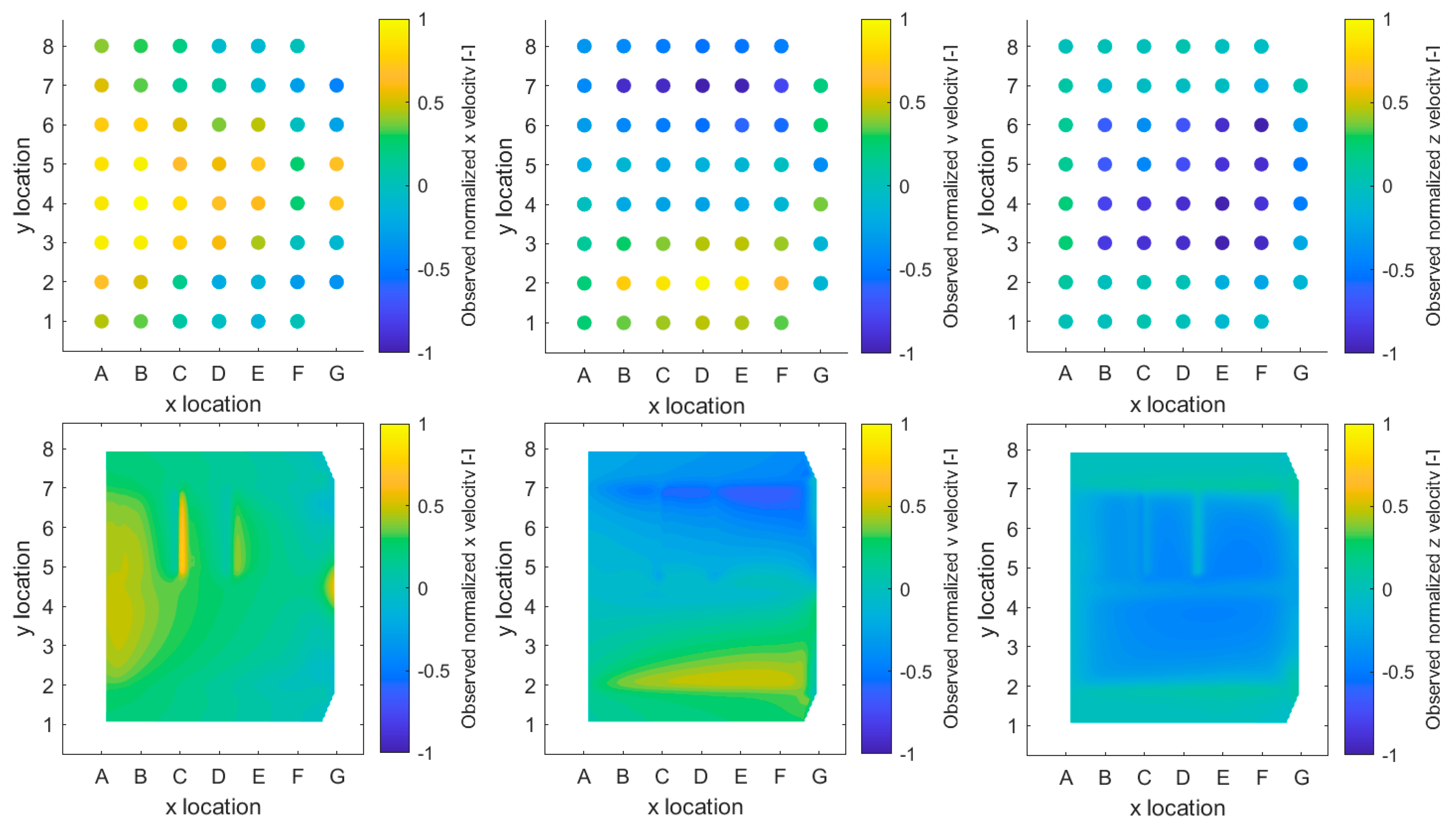
We chose the head loss along the flow section from the headwater area on the orographic left side to after the trash rack as the parameter for determining the grid dependency, as this value was also recorded at the prototype SHPP for different discharges. Further, the simulated head loss is also used to determine which porosity configuration, i.e., the simulation with which drag coefficient B, can approximate the measured head loss the closest. Within the simulation results, we then extracted velocities in x, y, and z directions along the prototype's measurement grid points (Figure 3), averaging the values within a 5 cm radius of each point. Additionally, we averaged the simulated velocities over time (60 s), similar to the ADV measurements at the physical prototype, to enable a better direct comparison between the measured and simulated velocities.
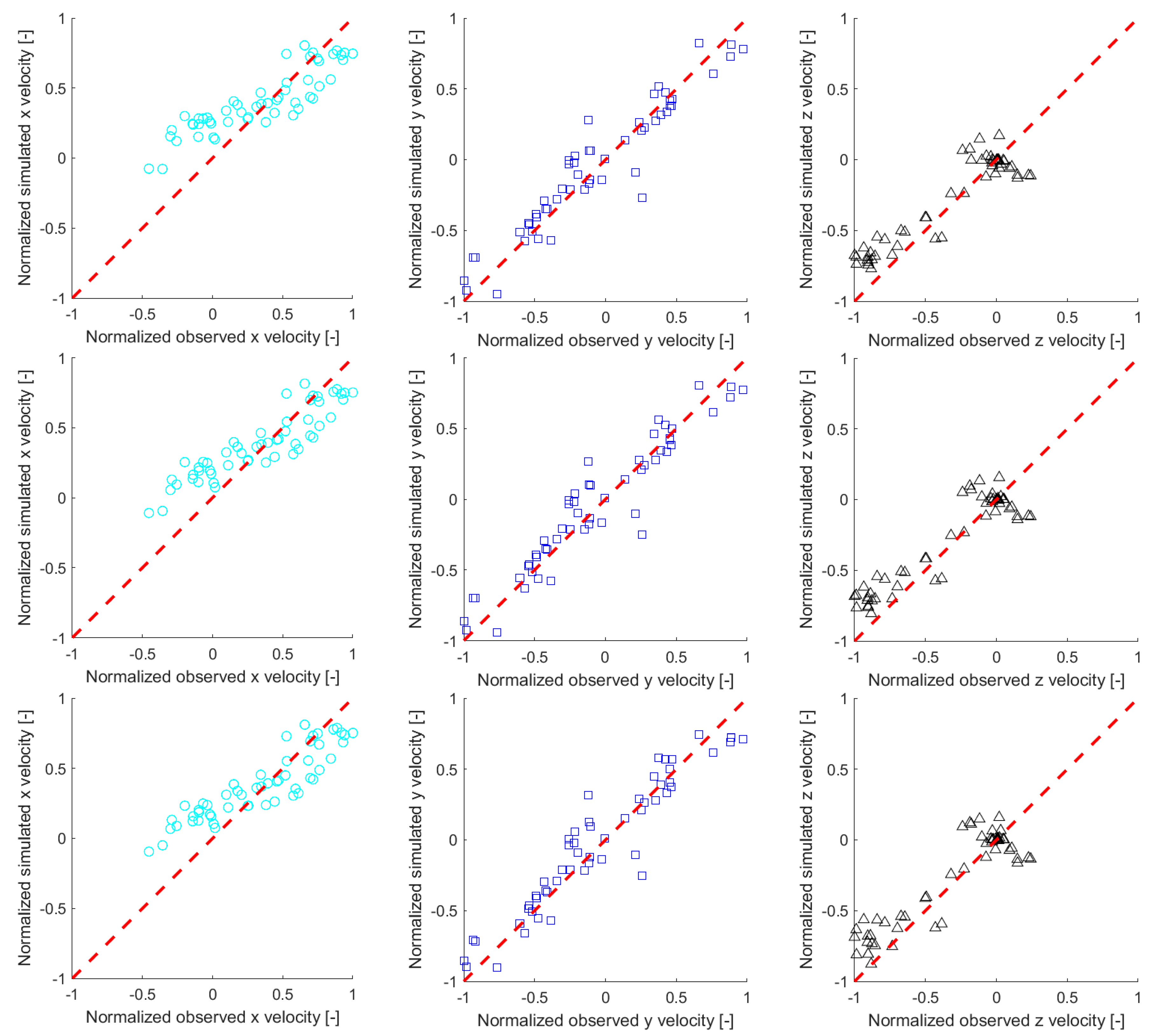
We compared the simulated and measured velocities both qualitatively and quantitatively. We assessed velocity deviations using statistical methods such as standard deviation and mean absolute error (MAE) for the quantitative analysis. These metrics provided insights into the absolute deviations between the two velocity datasets. We also used statistical evaluation metrics that normalize the datasets, including R-squared (R²) and Nash-Sutcliffe-Efficiency (NSE) to further contextualize the model results.
To enhance comparability, we normalized the x, y, and z velocities of both observed and simulated data against the respective maximum measured velocities. Scatter plots and 2D velocity plots were used to visually highlight the discrepancies between the simulated and observed velocities above the trash rack.
2.2.2. Simulation Set M02–SHPP with One-Sided Approach Flow
The second set of simulations (M02) within this study focused on reproducing the flow conditions at the SHPP prototype facility that were observed during the experimental setup E02 with a one-sided, channel-type approach flow. Our specific objective with this set was to prove that the calibrated model of the initial set M01 can also be used for a strongly modified upstream approach flow condition by only changing the relevant geometry – in this case, adding the two lateral channel walls – but leaving all other relevant settings (i.e., mesh resolution, hydraulic boundary conditions, porosity parameters) unchanged, therefore using the same simulation settings as in the simulation M01-mesh02-por02 (Table 1). Using these settings and the updated geometry with lateral walls for the simulations, we then qualitatively compared the resulting flow fields to the flow conditions recorded during experiment E02 at the prototype facility.
We simulated two cases with the following hydraulic boundary conditions per the physically tested settings during experiment E02 as shown in Table 2.
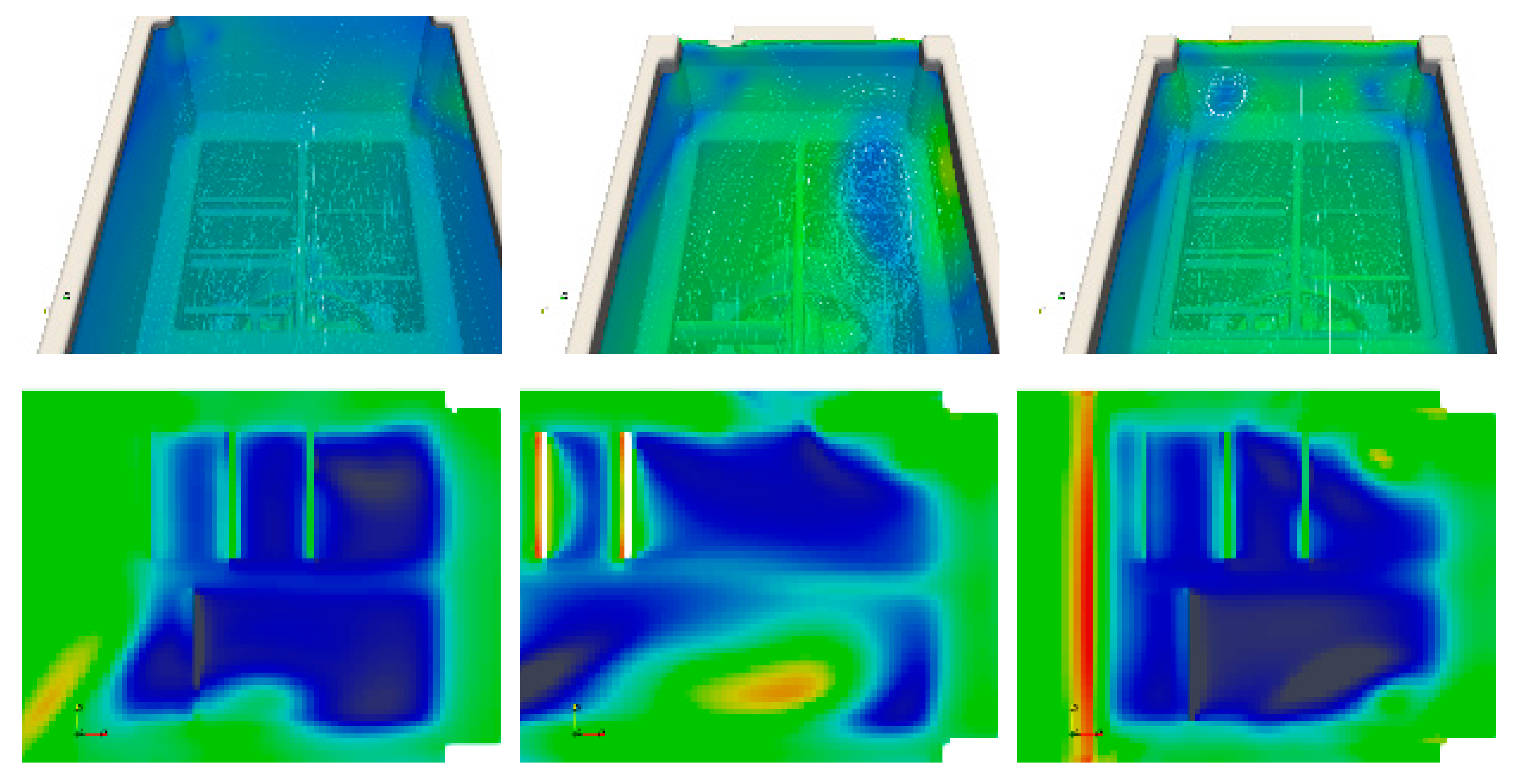
As the raw dataset containing the ADV measurements during E02 was unavailable for comparison with the simulation results, we only conducted a qualitative assessment based on the photos available in [17] related to E02. For this purpose, the flow field for the case with full turbine discharge (M02-C02) was visualized from a similar position and angle to compare the simulated and photo-documented case.
2.2.3. Simulation Set M03–One-Sided Approach Flow and Modified Design Parameters
With the third set of simulations (M03), we aimed to analyze alternative hydraulic designs for the case of a one-sided upstream approach flow previously not tested with physical experiments. The relevant settings (mesh resolution, porosity configuration, turbine discharge) within the numerical simulation setup remained unchanged compared to M02-C02-mesh02-por02 (Table 2). At the same time, three design parameters that are assumed to significantly influence the flow fields at the area of interest (i.e., at the shaft inlet) were individually increased by a factor of 1.5, targeting to reach optimized flow conditions. That means one parameter was increased while the other two remained unchanged in order to identify resulting effects individually, avoiding multiplier effects. The three chosen design parameters (DP) are:
DP01 = The length of the shaft intake (i.e., trash rack length). It is assumed that increasing the length and, therefore, the horizontal inlet area will lead to decreased z-velocities with more homogeneous, low-loss inflow conditions.
DP02 = The flow depth in the approach channel and above the shaft inlet. It is assumed that increasing the flow depth and, therefore, the cross-section of the channel will lead to reduced x-velocities and, therefore, more homogeneous, low-loss inflow conditions.
DP03 = The overflow height (and therefore discharge) over the front gate. It is assumed that increasing the permanent overflow height at the gate will lead to a decreased risk of vortex formation above the intake due to increased x-velocities in the surface near water layers towards the gate. This assumption is based on the findings during the experimental development of the initial three-sided approach flow variant, where the developers resumed that a permanent overflow over the spill gate contributes to a vortex-free inflow into the shaft [5].
In the same way as the previous two sets, we conducted an initial simulation using a coarse mesh setup for each case. We then restarted the simulation, running it for 90 seconds with a more detailed mesh configuration (mesh02). We evaluated the results based on the data captured at the final time step. The analyzed simulations in set M03 are shown in Table 3 with the modified DPs below M02-mesh02-por02 in the first row for comparison.
To classify the significance of the individual design modifications, we compared relevant resulting hydraulic parameters of the simulations within set M03 but for reference, also with those of the calibrated cases of M01 (three-sided approach flow) and M02 (one-sided approach flow. We chose the following parameters for the classification:
Head loss [m] – a lower value indicates optimized inflow conditions;
Average z-velocity above the trash rack vz-mean [m/s] – a lower value indicates optimized inflow conditions;
The share of the inlet area with z-velocities vz below a benchmark value [%] – a higher percentage indicates optimized inflow conditions;
Qualitative visual classification with focus on the tendency for vortex formation.
3. Results
3.1. Comparison of Simulated and Physically Determined Head Losses in Set M01
The results of the simulation set M01 shown in Table 4 suggest that the head loss determined with these simulations does not significantly change by only varying the mesh resolution. There is a slight decrease in head loss (0.2 cm / 4%) from the configuration mesh01 to mesh02, which is probably due to the fact that the coarsest resolution cannot completely dissolve the small-scale components of the geometry, which might have an influence on the head loss due to their position in the shaft inlet area. The mesh02 configuration with a cell size of 4 cm can already resolve this geometry sufficiently, and a slightly higher resolution with mesh03 (3 cm) no longer leads to any change in the analyzed parameter. Based on this finding, we decided to focus on the configuration mesh02 for the subsequent calibration process, considering that this configuration seems to be the best compromise between accurate geometry resolution and acceptable computation times. The findings presented in Table 4 also reveal a significant dependency between the head loss obtained from the simulations and the chosen calibration parameter: the drag coefficient B. The analysis indicates that a lower value results in a smaller head loss, as it was also determined in a previous study [14]. This is attributed to the fact that the drag coefficient B is derived from the β value, which, in turn, reflects the roughness of the porous material. At the SHPP prototype a head loss of 4.06 cm was measured along the same flow section for the same turbine discharge (1.5 m3/s), corresponding well with our simulation setup mesh02-por02. The calibrated porosity value of β =0.95 places us below its typical range [18].
To validate the calibrated model, we compare the flow fields of the simulations (focusing on those with configuration mesh02 and varied porosity settings) with those of the physical test recorded during experiment E01 [7]. Figure 6 shows scatter plots of the three velocity components for each M01-mesh02 simulation in direct comparison with the ADV measurements observed during the physical experiment.
The plots show that all three simulation results generally align well with the observed physical measurements without a clear indication of which of the porosity configurations fits best. The comparison of the x-velocities reveals a slightly higher deviation than the y- and z-velocities. Table 5 depicts statistical metrics of the velocity deviations.
Similar to the scatter plots, also these metrics don´t show a clear optimum but rather a generally satisfactory agreement between the three different simulation configurations and the physical observations, with the deviations of the x-velocities being consistently the highest. Looking at the normalized metrics R2 and NSE we can conclude that the configuration M01-mesh02-por02 fits best, which is validating the result of the calibration process, where we observed that this configuration can reproduce the physically determined head loss the closest. For a final visual comparison, the colored 2D velocity plots of the ADV-measured and simulated (M01-mesh02-por02) data sets are shown in Figure 7.
Upon visual comparison, it is evident that the general patterns appear similar, but the higher resolution of the simulation compared to the ADV measurements (4 cm grid vs. 39 cm grid) reveals more details, such as the small-scale trash rack cleaning mechanism on the orographic left side of the inlet. The slightly higher deviations in the x-velocities can be partially attributed to the difference in resolution, as the flow is significantly influenced by these small-scale structures, particularly in the main flow directions (x and z, with higher absolute velocities observed for x), leading to a higher error. Another probable factor is that the precise geometry and positioning of these small-scale mechanical components during the physical experiment were not recorded using a CAD model, but rather using only photographs and descriptions. This likely resulted in some inaccuracies during the process of recreating them for the simulation setup. Despite this, the overall agreement is satisfactory, and there is an excellent agreement in the y- and z-velocities. It can be inferred that the x-velocities of the simulation likely represent the real flow field more accurately than an interpolation between the ADV-measured points.
3.2. Qualitative Validation and Analysis of the Flow Fields with One-Sided Approach Flow
We utilized the outcomes obtained from simulation set M02 for further validation of our model settings developed during set M01 in contrast to the experimental results E02 conducted at the SHPP prototype and a subsequent qualitative assessment of the flow fields. This evaluation allowed us to analyze the flow conditions within the modified SHPP setup, characterized by a one-sided approach flow using lateral guide walls. The visual comparison for the case with full turbine discharge of 1.5 m3/s (C02) is shown in Figure 8.
Our simulation reveals an inhomogeneous velocity distribution around the area of interest. By employing streamlines for visualization, we have identified a strong tendency towards vortex formation associated with this design. Interestingly, the simulation projects the appearance of vortices on the right side of the intake. This contrasts sharply with the physical experiments, where only a vortex was observed on the left side. This discrepancy leads us to conclude that while our numerical model may not precisely mimic the observed flow condition in terms of the exact locations of induced vortices, it successfully signals the clear risk of vortex formation given the geometrical setup we have chosen.
3.3. Assessment of Alternative Geometry Configurations for One-Sided Approach Flow
Finally, we are examining the results of simulation set M03 with the goal of identifying the design parameters (DP) of the SHPP layout that could have a positive influence on flow conditions for a configuration with a one-sided approach flow upstream of the intake. The 3D flow fields for the three different cases are depicted in Figure 9.
For setup M03-C01, with increased flow depth across the approach channel and above the intake, a rather uniform flow is observed, showing no tendency for vortex formation and rather homogeneous z-velocity distribution above the inlet, indicating consistent flow.
In contrast, setup M03-C02, with increased intake / trash rack area, displays an inhomogeneous flow, leading to a strong tendency for vortex formation with uneven z-velocity distribution above the inlet. The 2D plot shows vortices reaching the trash rack plane with backflow within the vortex core, marked by positive z-velocities.
For setup M03-C03, with increased gate overflow, vortex formation is observed but less intense than in setup M03-C02. The velocity pattern above the intake highlights peak negative z-velocities concentrated on the intake's right side.
To complement this evaluation with a quantitative assessment, relevant hydraulic parameters were extracted from the simulation results, as shown in Table 6. This was done in order to better assess the significance of DPs with the objective of optimizing the flow conditions.
The comprehensive evaluation of these findings suggests that determining the superior design configuration is challenging, as it relies on the hydraulic parameter being assessed and its relative importance in our ranking process. When considering the head loss, which reflects pre-turbine energy conversion and intake area turbulence, adjusting the flow depth (DP01) has a notably positive impact on reducing head loss. The parameters mean z-velocity (vz mean) and minimum z-velocity (vz min) have less informative value due to their interpolated or punctual nature. Consequently, we have quantified the percentage of the inlet area where the z velocity falls below a threshold of - 0.5 m/s, as 0.5 m/s is the recommended maximum trash-rack normal approach velocity for consistency with established fish protection standards [7]. In terms of this parameter, the variant with increased trash rack length (DP02) yields the best result, with only 1% of the area exhibiting z velocities below the threshold, followed by variant DP01 with 7%. Based on these parameters and the qualitative assessment of vortex formation tendencies, it is evident that increasing DP01 and DP02 offers the most significant improvements in this optimization problem, while increasing DP03 does not enhance flow conditions as targeted. Additionally, raising the permanent overflow over the gate decreases the proportion of total flow available for energy production, making it an overall unsuitable choice for increase.
4. Discussion
The study involves using a 3D-CFD workflow to replicate existing physical models of the Shaft Hydropower Plant prototype facility (objective 1) with the calibration of numerical parameters and to evaluate alternative designs for an implementation with one-sided upstream approach flow deriving indications for future optimization of such configurations (objective 2). This is done using the commercial software Flow3D® HYDRO with specific sub-models activated, such as representing the trash rack as a porous medium and defining the turbine rotation using a fan-model.
The methodology partially builds on previously tested methods, such as studies on the general applicability of using porous media for trash-rack representation. While some studies found that trash racks at hydropower intakes can be represented using baffles instead of porous media due to ease of calibration and reproducing targeted pressure loss [13], for this study we chose porous media to more accurately represent the architecture of the trash rack in the model and assign directional porosity settings, similar to [14].
The study results demonstrate that it is feasible to accurately replicate the flow fields at a SHPP intake using the chosen method. This is particularly true for low-turbulent upstream flow conditions, such as those found in the three-sided approach flow in simulation set M01. Both the quantitative and qualitative comparisons with physically determined measurements indicate that the calibrated settings can be effectively used to predict similar flow patterns. Error analysis as part of the quantitative comparison of directional velocities show excellent agreement between numerical and physical models for the y-velocity, good agreement for the z-velocity, and satisfactory agreement for the x-velocity. The slightly larger deviation for the x-velocity can be attributed to differences in the upstream inlet boundary conditions. In the numerical model, we have an even inflow along the x-axis, while in reality, the water passes through a natural channel before reaching the head pond area. This presumably results in a not completely even velocity profile. Additionally, some small-scale geometry components could only be represented in a simplified manner based on photos and descriptions. Comparing our results of the simulation set M01 with the findings of [14] shows that our calibrated model settings, along with our 3D geometry including small-scale elements, allowed us to more accurately reproduce the physical experiment E01. For example, the R2 value of the compared z-velocities was 0.78 in [14] and 0.9 in our study.
Contrary the good agreement observed in the first set of simulations, we were unable to exactly replicate the flow pattern with higher turbulence in the second set of simulations using a one-sided approach flow with the tested settings. However, the results still provide useful indications for using the presented 3D CFD technique for hydraulic optimization of SHPP intakes. The results reveal important information about the flow quality, such as turbulence intensity, tendencies for vortex formation, and head loss. Although we couldn't precisely predict the location of the vortex observed during the physical experiment, it's important to note that the documentation for the second experiment with one-sided inflow is less detailed, which could be a factor contributing to the weaker agreement between numerical and physical observations, since there is uncertainty regarding whether the described flow state (i.e., steady/unsteady) correspond accurately with the image material used in the referenced report [17].
Regarding our second objective, which was to determine the relevant design parameters and their significance in optimizing the overall flow situation at the intake of a Shaft Hydropower Plant with one-sided approach flow, we have identified the relevant parameters and derived indications of which ones are important to focus on when aiming to improve the hydraulic design. It has become clear that increasing the permanent overflow over the gate does not have a significant beneficial effect on the design objective and, at the same time, reduces the total inflow available for energy production. Therefore, we do not recommend increasing the value of this parameter. However, the analysis of the other two parameters shows that modifying (i.e. increasing) them promises an improved flow situation. While it seems that reaching the objective with only modifying one of them is not possible, we conclude that both the trash rack area and the flow depth in the intake area should be increased compared to the values chosen for the originally developed SHPP configuration with three-sided approach flow. The reason why we have focused on altering the trash rack length instead of increasing the originally quadratic inlet area with equal proportions in the x and y directions is that the SHPP concept has significant potential for non-powered dams/weirs with movable gates and therefore fixed field widths. At such sites, like in the case of the 1.2 MW “At-Bashy” Shaft hydropower plant currently being developed in the Kyrgyz Republic [20,21,22], the SHPP concept can be integrated downstream of a weir field, but at the same time, it needs to be dimensioned considering the width limits given by the existing structure. As this case is expected to be the norm, we decided to focus on altering the length, as it can be more easily implemented in real-world situations.
When designing the intake of SHPP with one-sided approach flow, it is challenging to derive a rule-based methodology from our results. Instead, it is advisable to utilize the informative indicators we provided to guide the focus on specific parameters when developing the optimal hydraulic design for a site-specific SHPP layout using comparable numerical methods.
5. Conclusions
In conclusion, the 3D CFD application workflow presented here is a valuable tool for the future hydraulic design of SHPP intakes, even for heavily modified layouts compared to the original prototype setup. It enables the design of the facility with a focus on low-loss, uniform inflow conditions, and allows for detailed analysis with high resolution in areas of interest. This could be particularly relevant for assessing operational details, fish protection measures or sediment connectivity. The methodology presented will be applied to real-world cases in the future, leading to further validation and acceptance. Additionally, the application of the SHPP concept with one-sided approach flow layouts provides further opportunities for the exploitation of hydropower at existing hydraulic infrastructure, especially for non-powered dams and weirs with spillway gates. These SHPP modules can be implemented below the spillway gates without the need for diversion structures and without negative effects on the flood discharge capacities of such facilities
6. Patents
The study focuses on a hydraulic design application related to the Shaft Power Plant Concept. This concept is patented under the European patent number EP2499353B1. The authors of this study do not own the patents. The owner of all relevant SHPP patents is the Technical University of Munich.
Author Contributions
Conceptualization, B.A.; methodology, B.A. and N.G.; software, B.A and N.G.; validation, B.A. and N.G.; formal analysis, B.A.; investigation, B.A.; resources, N.R.; writing—original draft preparation, B.A.; writing—review and editing, N.G. and N.R.; visualization, B.A. and N.G.; supervision, N.R.; project administration, B.A.; funding acquisition, B.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was conducted as part of the project Hydro4U, which has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 101022905.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to ongoing investigations and planned publications.
Acknowledgments
Thanks to Franz Geiger, who has provided the unpublished data he and his former colleagues collected during their experiments (E01). We further thank for the support of the current colleagues at the chair of hydraulic engineering of TUM for valuable inputs during the preparation of this study. Finally, thanks to Prof. Peter Rutschmann and Albert Sepp, the co-inventors of the SHPP concept for the valuable and informative exchange and collaboration over the past years regarding this topic.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- UNIDO and ICSHP, "World Small Hydropower Development Report 2022.," 2022. [Online]. Available: www.unido.org/WSHPDR2022.
- T. Abbasi and S. A. Abbasi, "Small hydro and the environmental implications of its extensive utilization," Renewable and Sustainable Energy Reviews, vol. 15, no. 4, pp. 2134–2143, 2011. [CrossRef]
- M. Zeleňáková, R. Fijko, D. Diaconu, and I. Remeňáková, "Environmental Impact of Small Hydro Power Plant—A Case Study," Environments, vol. 5, no. 1, p. 12, 2018. [CrossRef]
- A. Alp, A. Akyüz, and S. Kucukali, "Ecological impact scorecard of small hydropower plants in operation: An integrated approach," Renewable Energy, vol. 162, pp. 1605–1617, 2020. [CrossRef]
- A. Sepp, F. Geiger, and P. Rutschmann, "Schachtkraftwerk – Konzept und Funktionskontrollen," Korrespondenz Wasserwirtschaft, vol. 9, no. 10, 2016. [CrossRef]
- A. Sepp and P. Rutschmann, "Ecological Hydroelectric Concept "Shaft Power Plant"," 2015. Accessed: Aug. 10 2024. [Online]. Available: https://hydroshaft.com/wp-content/uploads/2019/10/Ecological-hydrolelectric-concept-Shaft-power-plant_2014.pdf.
- S. Schäfer, F. Geiger, and P. Rutschmann, "Monitoring of downstream passage of small fish at the TUM-Hydro Shaft Power Plant Prototype: Test report no. 429," Institute of Hydraulic and Water Resources Engineering, Technical University Munich, Jun. 2016. Accessed: Aug. 7 2024. [Online]. Available: https://www.cee.ed.tum.de/fileadmin/w00cbe/wb/Versuchsanstalt_Obernach/Modellversuche_und_Forschung/V429_schlussbericht-fischabstieg-skw-vao.pdf.
- F. Geiger, M. Cuchet, and P. Rutschmann, "Experimental investigation of fish downstream passage and turbine related fish mortality at an innovative hydro power setup," La Houille Blanche, vol. 102, no. 6, pp. 44–47, 2016. [CrossRef]
- B. Alapfy and M. Reisenbüchler, "Hydroshaft Power Plant: a sustainable and simple design solution for existing as well as new lateral structures," World Small Hydropower Development Report 2022, 2022. [Online]. Available: www.unido.org/WSHPDR2022.
- B. Alapfy, "The Hydroshaft concept - eco-friendly, scalable and economic hydropower," Energetyka Wodna, no. 41, pp. 24–27, 2022.
- B. Alapfy, M. Klotz, and F. Böttger, "Schachtkraftwerk Dietenheim," Wasserwirtschaft, vol. 112, no. 10, pp. 69–70, 2022. [CrossRef]
- P. Rutschmann, A. Sepp, and C. Hackl, First experiences with a 420 kW TUM Hydroshaft power plant in the Bavarian Alps, 2019. Accessed: Oct. 10 2024. [Online]. Available: https://hydroshaft.com/wp-content/uploads/2019/10/First-Experience-with-a-420kW-TUM-Hydroshaft-Power-Plant-in-the-Bavarian-Alps_2019.pdf.
- M. Waldy, R. Gabl, J. Seibl, and M. Aufleger, "Alternative Methoden für die Implementierung von Rechenverlusten in die 3D-numerische Berechnung mit FLOW-3D," Österr Wasser- und Abfallw, vol. 67, 1-2, pp. 64–69, 2015. [CrossRef]
- M. Maldonado Lee and M. D. Bui, "Hydrodynamic modelling of a horizontal rack in a shaft power plant:alternative approch," Moosbacher Doktorandenkolloquium - Band 1, 2016. [Online]. Available: https://www.mosbach.dhbw.de/fileadmin/user_upload/dhbw/ressorts/forschung/dokumente/Schriftenreihe-Band-1_Doktorandenkolloquium.pdf.
- L. Rojas-Solorzano, Angela Arevalo, Gonzalo Montilla, Miguel Reyes, and Juan Carlos Marín, "CFD Modeling of Porous Media in the Study of the Flow at Penstock Intake of a 1:30 Model of Guri Hydro-Powerhouse," Unpublished, 2006. [Online]. Available: http://rgdoi.net/10.13140/2.1.4711.1201.
- A. Kratz, Wirkungsgradmessungen am Schachtkraftwerk: Unpublished Master´s Thesis at the chair of hydraulic engineering; Technical University Munich. Munich, 2015.
- M. Drexler, Geschwindigkeitsmessungen und Wirkungs-gradüberprüfung bei modifizierter Einlaufform am Schachtkraftwerk: Unpublished Bachelor´s Thesis at the faculty of mechanical engineering; Technical University Munich. Munich, 2017.
- Flow Science, Inc., Ed., "FLOW-3D® Version 2023R1 Users Manual," Santa Fe, NM, 2023. Accessed: Aug. 7 2024. [Online]. Available: https://www.flow3d.com/.
- C. Hirt and B. Nichols, "Volume of fluid (VOF) method for the dynamics of free boundaries," Journal of Computational Physics, vol. 39, no. 1, pp. 201–225, 1981. [CrossRef]
- M. Reisenbüchler, B. Alapfy, P. Rutschmann, and T. Siegfried, "Hydro4U - Nachhaltige Kleinwasserkraft in Zentralasien," Wasserwirtschaft, vol. 111, no. 12, pp. 10–15, 2021. [CrossRef]
- B. Alapfy et al., "Nachhaltige Kleinwasserkraft-Entwicklung in Zentralasien – Hydro4U in der Planungsphase," Wallgau, Germany, Jun. 29 2023. [Online]. Available: https://www.cee.ed.tum.de/wb/veranstaltungen/symposium-wallgau-2023/.
- B. Alapfy et al., "European Innovations in Kyrgyzstan - Development of the At-Bashi small hydro project," Kuala Lumpur, Malaysia, Mar. 15 2023.
Figure 1.
Conceptual section view of a Shaft Hydropower Plant. Figure recreation based on [5].
Figure 1.
Conceptual section view of a Shaft Hydropower Plant. Figure recreation based on [5].
Figure 2.
Left: Prototype SHPP in operation with overflown gate and lower fish bypass in open position (Photo by Albert Sepp, 2013). Right: Longitudinal section through the facility [7]: (a) inlet plane covered with trash-rack modules, (b) turbine-generator unit, (c) gate with fish bypass opening.
Figure 2.
Left: Prototype SHPP in operation with overflown gate and lower fish bypass in open position (Photo by Albert Sepp, 2013). Right: Longitudinal section through the facility [7]: (a) inlet plane covered with trash-rack modules, (b) turbine-generator unit, (c) gate with fish bypass opening.
Figure 3.
3D CAD Model of the Prototype SHPP with measurement grid above the inlet. Measurement points were defined by letters A – G on the x-axis and numbers 1 – 8 on the y-axis.
Figure 3.
3D CAD Model of the Prototype SHPP with measurement grid above the inlet. Measurement points were defined by letters A – G on the x-axis and numbers 1 – 8 on the y-axis.
Figure 4.
Modified SHPP prototype facility with lateral guide walls, overflown gate, and closed fish bypass openings during setup E02 [17].
Figure 4.
Modified SHPP prototype facility with lateral guide walls, overflown gate, and closed fish bypass openings during setup E02 [17].
Figure 5.
General model setup during simulation set M01. (c) indicates coarse mesh blocks, (f) indicates fine mesh blocks.
Figure 5.
General model setup during simulation set M01. (c) indicates coarse mesh blocks, (f) indicates fine mesh blocks.
Figure 6.
Scatter plots of normalized simulated vs. observed velocities for M02-mesh02 and three different porosity configurations. Top row: β =1.8; Middle row: β =0.95; Bottom row: β =0.1.
Figure 6.
Scatter plots of normalized simulated vs. observed velocities for M02-mesh02 and three different porosity configurations. Top row: β =1.8; Middle row: β =0.95; Bottom row: β =0.1.
Figure 7.
2D absolute x,- y- and z-velocities of the observed and simulated data sets in direct visual Top row: ADV-measurements; Bottom row: Simulation results (M01-mesh02-por02).
Figure 7.
2D absolute x,- y- and z-velocities of the observed and simulated data sets in direct visual Top row: ADV-measurements; Bottom row: Simulation results (M01-mesh02-por02).
Figure 8.
3D flow fields at the SHPP intake with one-sided approach flow. Left: Photo of the prototype SHPP; Right: 3D-velocity plot from the simulation result M02-C02-mesh02-por02 with streamlines indicating vortex regions.
Figure 8.
3D flow fields at the SHPP intake with one-sided approach flow. Left: Photo of the prototype SHPP; Right: 3D-velocity plot from the simulation result M02-C02-mesh02-por02 with streamlines indicating vortex regions.
Figure 9.
3D flow fields and 2D z-velocity plots at the SHPP intake with one-sided approach flow and modified design parameters. Left column: Modified DP01 – increased flow depth; Middle column: Modified DP02 – increased trash rack length; Right column: Modified DP03 – increased gate overflow.
Figure 9.
3D flow fields and 2D z-velocity plots at the SHPP intake with one-sided approach flow and modified design parameters. Left column: Modified DP01 – increased flow depth; Middle column: Modified DP02 – increased trash rack length; Right column: Modified DP03 – increased gate overflow.
Table 1.
Simulation set M01.
| Simulation | Mesh configuration (c/f) |
Cell count | Porosity configuration (β/B) |
|---|---|---|---|
| M01-mesh01-por01 | 10 cm / 5 cm | 659,900 | 1.8 / 22.5 |
| M01-mesh02-por01 | 8 cm / 4 cm | 1,283,880 | 1.8 / 22.5 |
| M01-mesh03-por01 | 6 cm / 3 cm | 3,033,732 | 1.8 / 22.5 |
| M01-mesh02-por02 | 8 cm / 4 cm | 1,283,880 | 0.95 / 11.875 |
| M01-mesh02-por03 | 8 cm / 4 cm | 1,283,880 | 0.1 / 1.25 |
Table 2.
Simulation set M02.
| Simulation | Turbine discharge |
Overflow height at gate | Discharge over gate |
|---|---|---|---|
| M02-C01-mesh02-por02 | 1.27 m3/s | 7.3 cm | 0.8 m3/s |
| M02-C02-mesh02-por02 | 1.5 m3/s | 7.3 cm | 0.8 m3/s |
Table 3.
Simulation set M03.
| Simulation | DP01 flow depth |
DP02 trash rack length |
DP03 gate overflow height |
|---|---|---|---|
| M02-mesh02-por02 | 0.9 m | 2.1 m | 7.3 cm |
| M03-C01-mesh02-por02 | 1.35 m | 2.1 m | 7.3 cm |
| M03-C01-mesh02-por02 | 0.9 m | 3.15 m | 7.3 cm |
| M03-C01-mesh02-por02 | 0.9 m | 2.1 m | 11.0 cm |
Table 4.
Results of simulation set M01.
| Simulation | Computational time | Head loss |
|---|---|---|
| M01-mesh01-por01 | 2:15 h | 4.6 cm |
| M01-mesh02-por01 | 6:25 h | 4.4 cm |
| M01-mesh03-por01 | 20:34 h | 4.4 cm |
| M01-mesh02-por02 | 6:47 h | 4.1 cm |
| M01-mesh02-por03 | 8:44 h | 3.6 cm |
Table 5.
Deviations between physically measured (E01) and simulated (M01) results.
| Simulation | Standard deviation | MAE | R2 | NSE |
|---|---|---|---|---|
| M01-mesh02-por01 | ||||
| x velocity | 0.140 | -0.044 | 0.775 | 0.633 |
| y velocity | 0.096 | -0.014 | 0.903 | 0.900 |
| z velocity | 0.094 | -0.031 | 0.863 | 0.814 |
| M01-mesh02-por02 | ||||
| x velocity | 0.127 | -0.031 | 0.818 | 0.707 |
| y velocity | 0.097 | -0.015 | 0.901 | 0.898 |
| z velocity | 0.094 | -0.030 | 0.857 | 0.816 |
| M01-mesh02-por03 | ||||
| x velocity | 0.129 | -0.027 | 0.806 | 0.703 |
| y velocity | 0.100 | -0.017 | 0.894 | 0.891 |
| z velocity | 0.098 | -0.029 | 0.829 | 0.804 |
Table 6.
Resulting hydraulic parameters for classification of the tested design parameters in M03.
| Simulation | Head loss | vz mean | vz min | % of inlet area with vz < - 0.5 m/s | vortex formation tendency |
|---|---|---|---|---|---|
| M01-mesh02-por02 | 4.1 | -0.38 | -0.62 | 6% | None |
| M02-mesh02-por02 | 7.9 | -0.34 | -0.68 | 14% | Medium |
| M03-C01-mesh02-por02 | 5.2 | -0.32 | -0.81 | 7% | Weak |
| M03-C01-mesh02-por02 | 7.4 | -0.21 | -0.53 | 1% | Strong |
| M03-C01-mesh02-por02 | 8.2 | -0.34 | -0.69 | 14% | Medium |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated