Prerpints.org logo
Preprint
Article

Development of Potential Slip Surface Identification Model for Active Deep-seated Landslide Sites: A Case Study in Taiwan

Altmetrics

Downloads

57

Views

28

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

01 September 2024

Posted:

03 September 2024

You are already at the latest version

Alerts
Abstract
Identifying locations of landslide slip surfaces provides critical information for understanding the volume of landslides and the scale of disasters, which is essential for formulating disaster preparedness and mitigation strategies. Based on hydrogeological survey data from 24 deep-seated landslide-prone sites in Taiwan's mountainous regions, this study first developed the hydraulic conductivity potential index (HCPI) using principal component analysis to quantify hydraulic properties of disturbed rock formation with six geological factors. Then, The regression analysis was performed to construct a permeability estimation model for the geological environment of landslides. Finally, the established model was utilized to develop an identification method for potential slip depths in landslide-prone sites. Results indicated a strong relation between HCPI and hydraulic conductivity with a determination coefficient of 0.895. The relation equation confirmed that its generated data concerning the depths of significant changes in hydraulic conductivity could be used to identify potential slip surfaces. Additionally, this study successfully establishes a rule for identifying potential slip zones by summarizing data concerning the generated hydraulic conductivity profiles, stratigraphic lithology, existing inclinometer slip depth records, and groundwater level of landslide sites. This identification method was then applied to predict potential slip depths for ten landslide sites where slip surfaces have not yet occurred. These findings offer a new alternative to having early information on potential sliding depths for timely disaster management and control implementation.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Deep-seated landslides often result in severe damage due to the greater depth to slip surface and volume of soil and debris mass movement [1]. The massive falling materials cause problems such as burying houses, blocking mountain roads, and obstructing downstream flood-prone areas by clogging river channels [2]. For example, one of Taiwan's most staggering deep-seated landslide disasters in the past decades occurred in August 2009 [3]. A rainfall event with a cumulative rainfall exceeding 2500 mm triggered a large-scale slope collapse disaster, leading to the destruction of the village of Xiaolin and the deaths of 474 people. This sudden and massive slope disaster had a slip surface depth of approximately 80 meters. As a result of such a significant rainfall event, the study of deep-seated landslides has become prevalent in Taiwan.
The failure area and depth of a landslide determine the magnitude of the disaster. When the depth of the slip surface is greater, the failure surface area will also expand with depth. Therefore, the confirmation of the depth of the slip surface plays a crucial role in predicting the scale of the disaster. In terms of mitigating such landslide disasters, having early knowledge of the depth of sliding and the affected surface area allows for the timely implementation of appropriate engineering remediation and disaster preparedness efforts. In order to obtain information concerning the locations of the slip surface, in engineering practice, the most common method for monitoring potential locations of the slip surface is to drill a borehole with the installation of an inclinometer [5]. The inclinometer is an in-situ instrument for displacement monitoring with time that can indicate when and where cumulative slope deformations could happen. Although the inclinometer has high measurement accuracy, this technique requires labor-intensive manual observation and does not have continuous monitoring with time. To overcome this drawback, techniques with real-time monitoring have been developed, including in-placed inclinometer (IPI) [5], ShapeAccelArray (SAA) [6], Time Domain Resistivity (TDR) [7], and Fiber Bragg Grating (FBG)[8]. Compared to the traditional sliding inclinometer, the above four types of instruments and techniques have been successfully introduced to the real-time and distributed monitoring of landslide displacement. However, there may be differences in measurement accuracy, resolution for larger shear deformations, and limitations in measurable deformations among these four methods [9].
Although the aforementioned on-site investigation methods can directly measure the depth of the sliding surface, information about the sliding surface depth is only obtained when the slope undergoes actual changes. Before the deformation trigger of the collapse mass, the scale of the landslide disaster cannot be determined. This situation leads to the inability to formulate prevention and preparation plans for disasters in advance to cope with potential disaster impacts and losses in the future. Therefore, some studies focused on the advance prediction of the disaster scale caused by landslides. The simplest method is the core drilling and visualizing method, which determines the occurrence of the sliding surface based on the lithology of the strata. According to the comparison of past landslide cases with the actual occurrence positions and lithology, it is usually found that the sliding surface is most likely to occur at the soil-rock interface or the location of sheared mud. This perspective is based on the significant differences in the permeability characteristics of the upper and lower formations of the sliding interface. When rainfall infiltrates the slope, groundwater accumulates above low-permeability formations, leading to increased soil weight and reduced internal friction. When the sliding force exceeds the shear strength of the soil, it triggers the sliding of the formation. Therefore, determining the sliding surface location based on the concept that the permeability of rock formations plays a crucial role in groundwater seepage can allow for an early understanding of the potential depth of the sliding surface. However, the drawback of this method is that it is prone to errors due to subjective experiential judgment, and visually determining the permeability characteristics of lithology may also lead to misjudgments.
Additionally, numerical analysis methods are common for predicting potential sliding surface locations in advance. Numerical methods have evolved over time and mainly include the limit equilibrium method (LEM) and numerical modeling methods (finite element, finite difference, and boundary element methods) [10,11,12,13]. However, these methods all have some basic assumptions and require the preparation of hydrogeological models for a collapse site, which consumes more time and human resources. Furthermore, the accuracy of predicting sliding surface locations highly depends on the accuracy of the hydrogeological models built from field investigation data. Therefore, some studies [14,15,16] proposed new methods for predicting sliding surfaces, attempting to overcome the limitations of numerical methods.
The basic concept of the newly proposed method was to integrate core sample record data and core testing data and to compare the data with the actual sliding surface positions, thereby confirming effective reference signal data for determining sliding surface positions. Furuya and Jiang [17] integrated various data, including RQD (rock quality designation), the Equotip hardness values, unit weight, the magnetic susceptibilities, orientation of geologic discontinuities, and digital imaging of core samples, from two deep-seated landslide sites in Japan for determining potential slip surfaces. The investigation results indicated that most data types, except for digital imaging data and magnetic susceptibility, appeared to have a distinct change near the observed slip surfaces for both sites. The Geological Survey and Mining Management Agency attempted to use instruments such as magnetic susceptibility meters and natural gamma ray meters to quantify the physical properties of core samples, aiming to study and evaluate their feasibility and applicability in identifying potential sliding surfaces [18]. Investigation results from a landslide site in southern Taiwan indicated that, regarding natural gamma ray measurements, there were slight variations in values depending on the composition of the rock mass, but overall, there was no significant difference. Additional data were needed to assess potential sliding surface locations if these measurements were to be used. In terms of magnetic susceptibility measurements, it was noted that variations in core magnetic susceptibility were observed due to differences in material composition; however, significant changes were not observed near the sliding depth in this particular case. Therefore, when the lithology of landslide sites was relatively homogeneous, the sensitivity of both instruments mentioned above was limited, posing challenges in evaluating potential sliding surfaces.
In addition to the emerging methods mentioned above for estimating the location of sliding surfaces, some scholars have observed a correlation between pore water pressure and the sliding surface of the stratum. For instance, Vassallo et al. [19] established a three-dimensional numerical model based on long-term rainfall data, pore water pressure, and permeability investigation results, finding that the permeability and pore water pressure of the sliding block are both higher than those of the stable layer beneath the sliding block. Park and Song [20] observed changes in rainfall and pore water pressure in a homogeneous sandy soil slope model, indicating that excessively high pore water pressure and hydrostatic pressure were more likely to cause slope failure. C. Di Maio et al. [21] studied the variation of pore water pressure and permeability in a mudstone landslide site using constant head tests and three-dimensional simulation methods (MODFLOW). The results showed a significant increase in pore water pressure in the sliding zone during rainfall, while the variation of pore water pressure below the sliding surface was stable. On the other hand, there was a significant difference in permeability between the sliding zone and the rock formation below the sliding surface. This variation in permeability can also be found in other landslide-sliding surfaces [22,23,24]. Therefore, these studies imply that if the vertical distribution of permeability characteristics in the strata can be obtained from locations with variations in the coefficient of permeability, this concept appears to have the potential to determine the occurrence location of the sliding surface.
If the use of borehole permeability profile data to predict potential sliding surface locations is a viable approach, the primary task is to address the method of obtaining profile data. Typically, the most direct and accurate method for obtaining such data is through dense-sampling double-packer hydraulic tests. However, this technique is associated with high costs, lengthy testing times, and substantial workforce requirements. To obtain permeability data continuously with depth at a lower cost and more efficiently, some scholars have proposed influential factors related to permeability and established relationships between these factors and permeability coefficients, thereby developing empirical formulas for quickly obtaining permeability profile data. A detailed review of various empirical formulas can be found in the study of Hsu [25]. Most empirical formulas are only applicable to single lithology sites and adopt fewer factors related to permeability characteristics, rendering them unsuitable for complex lithology sites. However, in recent years, Hsu [25] developed a rock mass permeability estimation model (HCB2 model) using composite geological indices applicable to various geological environments (sedimentary, igneous, and metamorphic rocks). Although this model can be applied to different lithology sites, the analysis data used to establish the model were not obtained from deep-seated landslide potential sites. The lithology of landslide sites mainly consists of fractured rock layers and colluvium, and the hydrogeological characteristics of these sites may differ from non-landslide sites, warranting further investigation and comparison.
Therefore, to obtain detailed and continuous hydrogeological information from deep-seated landslide potential sites and meet the needs of disaster prevention management, this study used borehole cores, downhole imaging, and double-packer hydraulic test data from 24 landslide-prone sites in Taiwan to construct a new rock mass permeability estimation model only applicable to deep-seated landslide potential sites. Prediction results from the new model were compared with the HCB2 model. Finally, based on the above results and with displacement data monitored by inclinometer meters, a new model for confirming sliding depth was developed to predict the scale of landslide disasters rapidly.

2. Description of Study Area and Data Preparation

Based on the needs of this study in establishing models for estimating the permeability of landslide rock masses and identifying the location of sliding surfaces, it is necessary to collect relevant data from investigation projects of potential deep-seated landslide areas in the mountainous regions of Taiwan to assist in the construction of the two models. The required data include (1) hydrogeological survey data of the strata where landslides occurred: drilling core samples, borehole imaging data, groundwater level data, and double-packer hydraulic test data, which can serve as the primary data for constructing models to assess the permeability characteristics of landslide rock masses; (2) underground displacement data: time-series monitoring data of inclinometers in landslide areas, serving as investigating the relationship between the simulated distribution of hydraulic conductivity and the actual occurrence locations of sliding surfaces.
Reviewing the current landslide investigation projects in Taiwan, the most comprehensive project is under the jurisdiction of the Geological Survey and Mining Management Agency (GSMMA). From 2007 to 2013 [26,27,28,29,30,31,32], the GSMMA implemented the project entitled "Investigation and Evaluation of Hydrogeological Impacts on Slope Stability in Watersheds across Taiwan." This project mainly focused on investigating and assessing hydrogeological impacts on slope stability in major watersheds across Taiwan. It aimed to strengthen field hydrogeological investigations to understand the extent of hydrogeological impacts on landslide occurrence. Furthermore, it conducted research on the correlation between landslides and related factors. The project targeted deep-seated landslide areas within major northern, central, southern, and eastern Taiwan watersheds. The 24 landslide sites were selected for investigation, experimentation, monitoring, and analysis to understand how infiltration during rainfall alters hydrogeological conditions, leading to a potential trend of recurring rockslides. At each landslide site, three geological boreholes were drilled with depths ranging from 50 to 80 meters, and geological descriptions were prepared based on core samples. Additionally, based on the results of borehole imaging surveys, representative sections of fractured rock masses were selected for double-packer hydraulic tests, totaling 169 test samples with a test section length of 1.5 meters each. Finally, an inclinometer was installed within the deepest borehole at each landslide site to monitor underground displacement, while other boreholes were set up as groundwater observation wells for monitoring groundwater levels. However, some inclinometer boreholes were constructed to monitor groundwater levels simultaneously.
Furthermore, the samples selected for constructing the specific rock mass permeability estimation model did not come from data of a single rock type but encompassed a variety of lithologies. The primary lithologies include sedimentary and metamorphic rocks, while sub-lithologies cover sandstone, shale, alternations of sandstone and shale, sandy shale, siltstone, muddy siltstone, mudstone, argillite, slate, and phyllite. Due to the wide range of lithologies covered by the data samples, the new rock mass permeability estimation model developed in this study possesses the characteristic of adapting to different geological environments.
Finally, the primary data collected for the 24 landslide sites, including inclinometer borehole number, landslide site name, primary lithology, regolith thickness (depth to rock mass), borehole depth, and normal groundwater level, are organized as shown in Table 1. Among them, normal groundwater levels are primarily collected from monitoring wells after the completion of inclinometer borehole installation and a few days of settling without any occurrence of heavy rain. If the inclinometer boreholes do not include groundwater monitoring capabilities, groundwater levels are estimated from data collected at nearby groundwater monitoring stations. Previous studies have suggested a correlation between groundwater levels and slope stability [33,34]. Therefore, this study also used the collected groundwater level data as one of the key factors for developing landslide slip surface identification models.
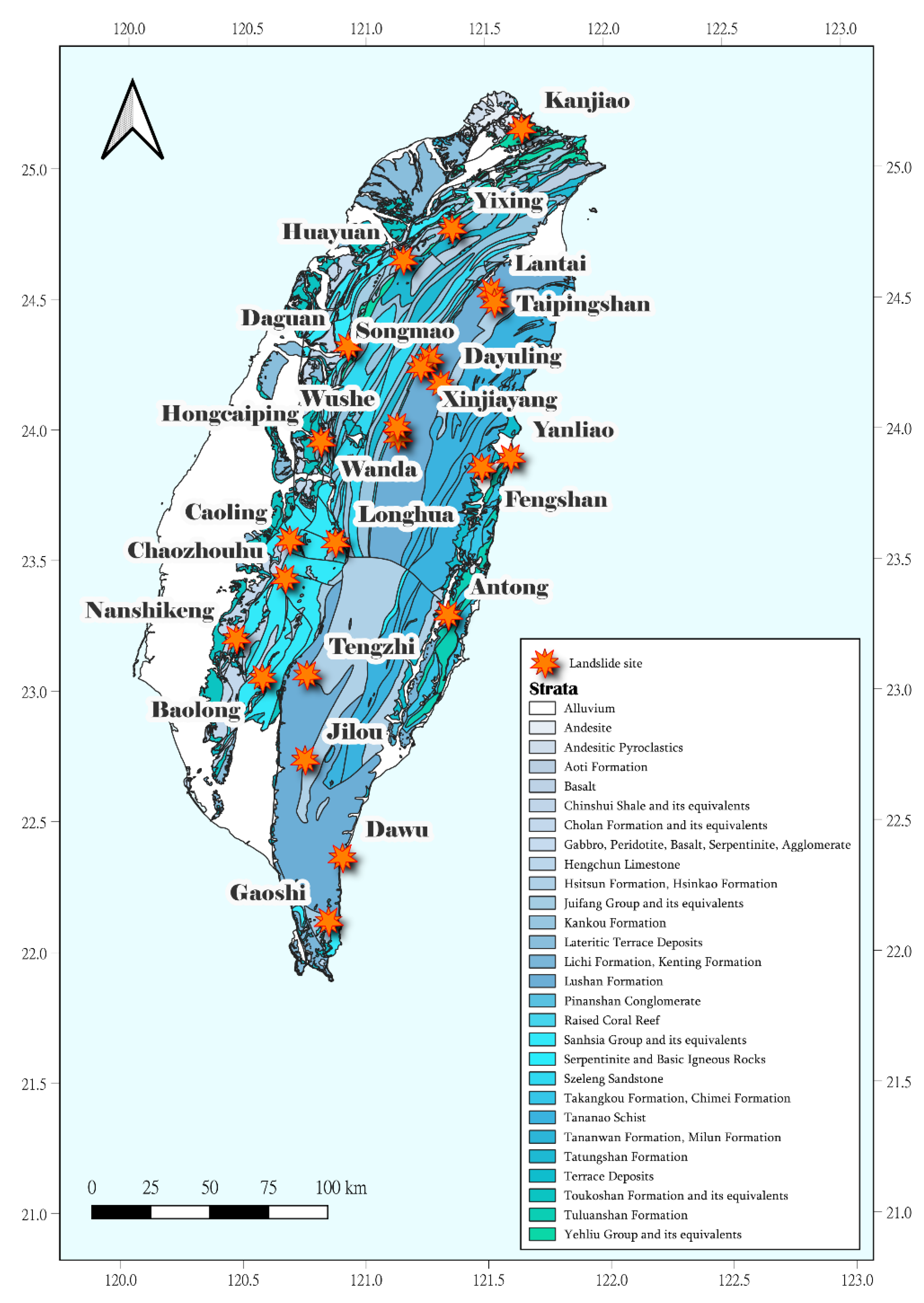
Preprints 116925 g001
Figure 1. Locations of the 24 landslide sites.
Figure 1. Locations of the 24 landslide sites.
Preprints 116925 g001

3. Methodology

This study targeted mountainous areas of Taiwan with deep-seated landslide potential. Utilizing past hydrogeological survey data, a model for estimating rock mass permeability was constructed. The aim was to reveal the distribution of permeability characteristics in the vertical direction of rock formations and attempt to explain the mechanism of landslide occurrence from the perspective of permeability distribution patterns. The research findings were expected to provide rapid feedback on disaster scale information for landslide-prone areas with deep-seated landslide potential, contributing to disaster prevention efforts. The associated approaches and procedures, including (1) selecting influential factors for characterizing the hydraulic properties of fractured rocks in active landslide sites; (2) multicollinearity analysis for the selected influential factors; (3) principal component analysis (PCA) for determining the weight of each factor; (4) model establishment and evaluations; (5) developing a rule for identifying potential slip surface, are provided as follows.

3.1. Selection of Influential Factors

Prior to developing a rock mass permeability estimation model for landslide sites, influential factors that may affect the permeability of disturbed rock mass must be considered. Based on the material composition and structural characteristics of fractured rock masses in landslide areas, this study referred to previous research [35,36,37,38,39,40,41,42,43,44] to select potential factors related to rock mass permeability characteristics. The most commonly considered factors include depth index (DI), rock quality designation (RQD), fracture aperture (FA), and fracture density (FD). Earlier models were developed based solely on individual influencing factors. However, subsequent research has considered multiple factors in model development [39,42,45], and the research results have demonstrated that predictive models using multiple factors outperform those using single factors. However, the models established above were often limited to application in single lithology sites. In recent years, Hsu [25] attempted to develop predictive models applicable to various geological environments, considering up to eight influencing factors. Eventually, six different combinations of factors were used to build predictive models. Although Hsu [25] has improved the accuracy and limitations of predictive models, the models were built using data collected from non-collapsible strata in the mountainous areas of Taiwan. However, hydrogeological characteristics are significantly more complex for sites with high collapsibility potential compared to non-disturbed strata conditions. Currently, there is no systematic construction of similar predictive models. Therefore, this study, based on survey data collected from sites with high collapsibility potential in Taiwan and referring to Hsu's [25] six-factor model, selected six influencing factors, including RQD, DI, FA, FD, gouge content designation (GCD), and lithology permeability index (LPI), to construct a predictive model for the permeability of disturbed strata.
In brief, RQD measures the quality of the rock mass, with lower values indicating more fractured rock, which correlates with higher permeability. DI represents the influence of in-situ stress on rock mass permeability, theoretically leading to decreased permeability with depth. GCD calculates the content of shear mud in a specific section of the rock mass, aiming to correct the drawback of RQD in neglecting shear mud, thereby identifying a critical factor in determining whether fractures have groundwater-conducting properties. LPI represents the overall permeability of the intact rock mass and is related to the rock's pore characteristics, excluding the influence of fracture characteristics on permeability. Finally, FA and FD describe the structural features of the rock mass and are crucial indicators of rock mass permeability, indirectly influencing the groundwater flow. Detailed scoring definitions and criteria in response to permeability for each influencing factor can be found in Hsu [25] and will not be repeated in this paper.
However, regarding the scoring system for the LPI factor across various lithologies, Hsu [25] initially designed it based on core samples obtained from relatively undisturbed rock mass sites. However, the sites of this study mainly consist of disturbed geological strata. According to the core investigation data from the collapse sites, lithologies such as weathered slate, weathered shale, weathered argillite, and argillite frequently appear, which were not accounted for in the original LPI scoring system. Therefore, this study made partial modifications to the LPI scoring system. In Table 2, in addition to the LPI score table developed by Hsu [25], additional rock mass scoring values specific to collapse sites were added (as shown in the last four rows of Table 2). The scoring ranges from 0 to 1, where a higher score indicates a higher permeability. Lastly, due to the complexity of lithologies in collapse areas, the calculation of LPI values in double-packer test sections may involve different lithological proportions, and therefore, the calculation was performed by combining various lithological ratios.

3.2. Multicollinearity Analysis for Selected Influencing Factors

Since this study employs multiple-factor statistical analysis, it is necessary to conduct multicollinearity tests on the selected influencing factors to examine whether there are multicollinearity issues among them. Multicollinearity can be assessed using one commonly used indicator-tolerance and variance inflation factor (VIF). Tolerance refers to the percentage of variance in a predictor variable that is not explained by other predictor variables, with values ranging from 0 to 1. A tolerance value close to 1 indicates the absence of multicollinearity, while values closer to 0 suggest multicollinearity issues. However, there is no formal threshold to determine the presence of multicollinearity among factors [46]. Although no universally accepted standards exist, some studies have explored the relationship between tolerance values and multicollinearity. For instance, Myers [47] suggested that tolerance values below 0.1 indicate severe multicollinearity issues, while Menard [48] proposed that values below 0.2 indicate potential multicollinearity problems.
Additionally, the reciprocal of tolerance, known as the variance inflation factor (VIF), is used to indicate the extent to which the variance of coefficient estimates is influenced by multicollinearity. Like tolerance, there is no formal cutoff value for VIF. However, VIF values exceeding ten indicate multicollinearity issues, although this criterion may require smaller values for weaker regression models. For example, Midi et al. [46] recommended that VIF values exceeding 2.5 in logistic regression analyses warrant attention to multicollinearity issues. Finally, this study conducted multicollinearity tests on the six influencing factors mentioned in Section 3-1 using the aforementioned diagnostic metrics to guide model construction.

3.3. Weights of Influential Factors through Principal Component Analysis

Theoretically, the permeability characteristics of rock masses are controlled by various influencing factors, and these factors may have different impacts on the permeability characteristics of fractured rock masses. By assigning appropriate weights to the influential factors and then combining the factors, better correlations with permeability characteristics may be obtained. To extract the weight values of each influential factor, this study adopted the Principal Component Analysis (PCA) method, a multivariate analysis technique.
PCA can be conducted using either an unstandardized covariance matrix or a standardized correlation matrix. When the units of the analyzed variables differ, using the correlation matrix is generally preferable. The eigenvalues and eigenvectors are then calculated from this matrix. The variance of each principal component is equal to its corresponding eigenvalue, with the first principal component having the most considerable variance, followed by the second principal component, and so on. The eigenvalues can also be used to compute the contribution proportion of each principal component (the percentage of total variance accounted for by that principal component), which reflects the explanatory power of the entire set of variables and serves as a basis for selecting principal components. The eigenvectors are the coefficients in the linear combinations of the principal components, and the coefficients can be derived from the loadings. Loadings are the correlation coefficients between the variables and the principal components., calculated using the eigenvalues, eigenvectors, and standard deviations. The loading formula is shown in Equation (1).
r y j x i = a j i λ j s i
where the loading r y j x i is the correlation coefficient between the j-th principal component and the i-th variable. A larger loading value indicates a greater influence of the principal components on the variables; λ j is the eigenvalue of the j-th principal component; s i is the standard deviation of the i-th variable; and a j i is the eigenvector coefficient.
Therefore, the eigenvector coefficient a j i can be derived from Equation (1) as follows.
a j i = r y j x i λ j s i
After obtaining the eigenvector coefficients, the linear combination coefficients of each principal component can be derived. The next step is to combine the linear combination coefficients of each principal component with their variance contribution ratios. Using the variance contribution ratio of each principal component as weights, the eigenvectors and variance contribution ratios of the more explanatory principal components are integrated to calculate the new coefficients of each variable in the new linear combination model.
The selection rule for the more explanatory principal components refers to selecting the first n principal components with the most significant variance contribution ratios among all j principal components, with the cumulative variance contribution rate of these n principal components exceeding 80%. Assuming that the first n principal components represent the original variable indicators, the new coefficients of the variables can be considered as a weighted average of the old coefficients of the variables in the linear combination of these n principal components, using their variance contribution ratios as weights. Therefore, the coefficient matrix b of all variables in the composite score model is given as follows:
b = b 1 b 2 ⋮ b i = a 1 × c 1 + a 2 × c 2 + … + a n × c n c 1 + c 2 + … + c n
where a n represents the eigenvector matrix of the n-th principal component; c n represents the contribution ratio of the n-th principal component.
Finally, since the sum of the coefficients (weights) for all variables i must equal one, all variable weights need to be normalized based on the variable coefficients in the composite score model. This results in the final weight score w i for each variable given as follows.
w i = b i b 1 + b 2 + … + b i
By using the above analysis process with available hydrogeological investigation data, the number of principal components with significant contributions can be selected and combined with the contribution proportions to calculate the weight value for each influencing factor. The determined weights can be utilized to establish the rock mass permeability index and further construct a rock mass permeability estimation model.

3.4. Model Establishment and Hypothesis Testing

As discussed in Section 3.1, six geological factors may influence the hydraulic properties of rock mass. Each factor impacts the permeability values differently. For example, if the RQD value of the rock core shows poor rock mass quality, theoretically, the permeability should be higher. However, if there is gouge filling in the fractures, the permeability of the rock mass may decrease. Similarly, suppose two core sections have the same RQD value but are at different depths. In that case, the deeper section may have reduced permeability due to increased stress closing the joints or rock matrix porosity. Therefore, a comprehensive permeability index for fractured rock masses may need to integrate various geological indicators. The six geological indicators (RQD, DI, GCD, LPI, FA, and FD) were integrated into this study. Considering the principal component analysis in Section 3.3 to obtain the weight of each geological factor, the factors were linearly combined by multiplying each factor by its corresponding weight value of wi. Equation (5) defines the hydraulic conductivity potential index (HCPI) for landslide-prone bedrock. The formula for HCPI is given as follows:
H C P I = [ ( 1 − R Q D 100 ) × w 1 ] + ( D I × w 2 ) + [ ( 1 − G C D ) × w 3 ] + ( L P I × w 4 ) + ( F D × w 5 ) + ( F A × w 6 )
HCPI can quantify the permeability of the rock mass with the scores of the given six factors, except for FA, ranging between 0 and 1. Higher values indicate a greater contribution of the corresponding parameter to increasing the rock mass permeability. A higher HCPI value represents permeable rock masses in the test section. Subsequently, different mathematical models (such as simple linear, logarithmic, exponential, or power law) can be selected, and regression analysis techniques can be applied to establish an estimation model for the permeability of fractured rock masses in landslide formations. The goodness of fit for each model can be determined by the R² value, the correlation coefficient between permeability and HCPI.
Additionally, two statistical analyses were conducted to ensure a reliable regression result for the best model. The first statistical analysis inspected the regression model’s assumptions for residuals (independence using the Durbin-Watson statistic, constant variance using Spearman’s rank correlation, and normality using the Kolmogorov–Smirnov test). In contrast, the second statistical analysis investigated the statistical significance of the regression analysis model using the F test statistic and p values. Based on the regression analysis outcomes, the best model for predicting the permeability of fractured rock masses was decided. The regression and statistical analyses mentioned above were carried out using the commercial software SigmaPlot.

3.5. Developing a Rule for Identifying Potential Slip Surface

To summarize and clarify whether the distribution pattern of permeability in a landslide area is related to the occurring location of the sliding surface, this study used the landslide-specific rock mass permeability estimation model established in Section 3.4 to create continuous hydraulic conductivity profiles for the 24 landslide sites, showing the variation with borehole depth meter by meter. Next, the observed inclinometer data from the 24 landslide sites, which had clear records of sliding, were superimposed onto the hydraulic conductivity bar charts (as illustrated in Figure 2). This work helped observe whether there were significant changes or other trends in hydraulic conductivity values near the monitored sliding depths. This process explored the feasibility of identifying sliding surface locations using information on the hydraulic conductivity profile. Subsequently, a more comprehensive method for estimating the potential sliding depth was established by combining borehole core data, groundwater level data, and the relationship between these data and the sliding surface locations. This method was then validated by applying it to sites with known sliding depths to check if it could correctly identify the sliding surface locations. Finally, the identification rule developed in this study can be applied when inclinometers have not yet detected significant displacement. This application can assist disaster prevention decision-making agencies in estimating the potential scale of deep-seated landslides in advance.

4. Results and Discussion

4.1. Descriptive Statistics for Six Influential Factors

Establishing the permeability estimation model requires first integrating the hydraulic conductivity of existing double-packer test sections and calculating the scores of the influential factors for each test section for subsequent principal component analysis and regression modeling. This study compiled 169 double-packer test section data from 48 boreholes in the 24 landslide areas. It sequentially calculated the RQD, DI, GCD, LPI, FA, and FD values for each double-packer section according to the method described in Section 3.2. The descriptive statistical results of the calculated factor scores are shown in Table 3. The overall average RQD value for all lithologies is approximately 0.479, with sedimentary rocks averaging 0.656 and metamorphic rocks averaging 0.291. According to Bieniawski's [49] rock core quality determination method, the overall rock core quality is poor, with fragmented metamorphic rock formations. Although the rock core quality of sedimentary rock formations is better than that of metamorphic rocks, it only reaches a fair level according to Bieniawski's [49] criteria. These results indicate that the overall rock core quality in landslide areas is generally poor, as expected.
Further observation of the statistical analysis results regarding FD and FA show that the average values for both parameters in metamorphic rock formations are greater than those in sedimentary rock formations, indicating a more developed fracture network in metamorphic rocks, which is consistent with the RQD results. Moreover, the descriptive statistics concerning GCD indicate that the gouge content in sedimentary and metamorphic rocks is comparable. Since DI and LPI represent the relative depth and lithology of the sampling section, their mean values and standard deviations have less physical significance and are not discussed here.
Finally, examining the six geological characteristic indicators selected for this study reveals that higher RQD and GCD values indicate better core quality and higher gouge content in the rock core section. Both higher values lead to lower hydraulic conductivity K, meaning RQD and GCD are negatively correlated with K. Conversely, the remaining four indicators are positively correlated with K. To ensure that all indicator factors have a positive correlation with K, this study transformed the RQD and GCD values to (1-RQD) and (1-GCD). This transformation changes the correlation to positive without affecting the order and spacing of the values. After the transformation, all factors show a positive correlation with K, thereby enhancing the convenience of interpreting the results of subsequent multicollinearity analysis and principal component analysis.

4.2. Multicollinearity Analysis Results of the Selected Factors

When establishing regression models using possible geological factors, checking for multicollinearity among them is vital to prevent redundancy in the independent variables. This could artificially enhance the explanatory and predictive power of certain variables, leading to inaccurate regression model predictions. Therefore, this study used the Variance Inflation Factor (VIF) to assess multicollinearity. The criteria for VIF are as follows: when VIF is greater than ten, it indicates a strong multicollinearity problem. The results of the multicollinearity analysis are shown in Table 4. Upon examining the VIF column in Table 4, it is evident that the VIF values for all factors are less than ten, indicating no strong multicollinearity among the indicator factors. Therefore, the regression model can directly include the six geological factors—RQD, DI, GCD, LPI, FA, and FD.

4.3. Results of PCA

This section presents the analysis results of calculating the weight values for each factor using PCA. First, the varimax method was used for axis rotation, and more influential factors were extracted based on principal components with eigenvalues greater than 1, aided by a scree plot to determine the number of components to extract (as shown in Figure 3). The analysis was performed with a cumulative contribution ratio of over 80%.
Table 5 shows the calculation results of each component in the principal component analysis, displaying the eigenvalues, contribution ratios, and cumulative contribution ratios of the principal components. Larger eigenvalues indicate greater importance. As shown in Table 5, the eigenvalues of the first three principal components are greater than 1, with a cumulative contribution ratio of 0.8152 for these three components. The cumulative contribution ratio explains 81.52% of the data variance.
Thus, the first three principal components with their variance contribution ratios were utilized to determine the weights of all factors. First, the factor loadings were derived according to Equation (1), as shown in the upper part of Table 6. Then, the eigenvector coefficients for the three principal components were calculated using Equations (2). The resulting linear combination equations for the three principal components are as follows:
F 1 = 0.589 × 1 − R Q D + 0.058 × D I + 0.116 × 1 − G C D − 0.068 × L P I + 0.505 × F A + 0.582 × F D
F 2 = − 0.14 × 1 − R Q D − 0.474 × D I + 0.602 × 1 − G C D + 0.622 L P I + 0.251 × F A + 0.015 × F D
F 3 = − 0.103 × 1 − R Q D + 0.685 × D I − 0.223 × 1 − G C D + 0.623 × L P I + 0.285 × F A − 0.047 × F D
Third, the weighted average of the linear combination coefficients of the three principal components was calculated to obtain the coefficient of the composite score model using Equation (3), as shown in Table 7. The composite model Equation is given as follows:
Y = 0.247 × 1 − R Q D + 0.049 × D I + 0.174 × 1 − G C D + 0.264 × L P I + 0.39 × F A + 0.296 × F D
Finally, based on the requirement that the weights of all factors need to be normalized in the composite score model, the weight values for each factor were obtained, as shown in Table 8.
The results of the weight analysis indicate that FA and FD have higher weight values, demonstrating that these two factors are the most significant in landslide areas, implying that the extent of the fracture network has a greater impact on assessing the hydraulic conductivity of fractured rock masses in landslides. Additionally, except for DI, which has a relatively low weight, the other factors are more balanced. The lower influence of DI in the principal component analysis suggests that, given the maximum borehole depth of 80 meters, the effect of tectonic stress is less significant within the limited depth range.

4.4. Establishment and Evaluation of the Predictive Model

Based on the results of the weight analysis on six geological factors through PCA in Section 4.3, each factor was multiplied by its respective weight and then linearly added to obtain the integrated permeability indicator HCPI. Next, by applying common mathematical models (including simple linear, logarithmic, exponential, or power law models) for regression analysis, the model was constructed using double-packer hydraulic test data and the HCPI data calculated from core samples. The coefficient of determination (R2) was used to identify the optimal regression mathematical model, thereby deriving the permeability estimation model for landslide-prone rock masses.
The regression analysis results, as shown in Figure 4, indicate that the power-law formula best fits the relationship between HCPI and K, with an R-squared value of 0.8953, demonstrating good predictive capability.
Furthermore, the optimal regression model underwent an F-test to examine the overall significance of the model and whether the error terms satisfy the assumptions of normality (Kolmogorov-Smirnov statistic), independence (Durbin-Watson statistic), and homoscedasticity (Spearman rank correlation coefficient).
The validation results of the best estimation model are shown in Table 9. The F-value and P-value from the regression analysis indicate that the independent variables of the hydraulic conductivity estimation model are significant predictors of the dependent variable, demonstrating predictive capability. Moreover, the model satisfies the three assumptions for the validation of error terms: the Durbin-Watson statistic of 1.5 (less than 2) indicates no autocorrelation in the residuals; the K-S normality test value is greater than 0.05, indicating the data follows a normal distribution; and the homoscedasticity value is 0.58, suggesting a good correlation between factors and permeability coefficient.
These five validation tests confirm the effectiveness of the permeability estimation model for landslide-prone rock masses. Therefore, in future applications, the developed landslide rock mass permeability estimation model can effectively and cost-efficiently obtain detailed and continuous hydraulic conductivity profiles. This work can be achieved at any active landslide site by obtaining six geological indicator parameters from core samples and double-packer hydraulic test data.

4.5. Comparisons of Previous and New Developed Models

In addition to developing a permeability estimation model for landslide-prone rock layers (named HCPI model), another research objective of this study was to test the differences in hydrogeological characteristics between disturbed and undisturbed fractured rock formations. The disturbed model is the HCPI model, while a brief introduction to the undisturbed model is provided here. Hsu [25] collected hydrogeological investigation data from boreholes in the mid and upper river basin of the Choshui river in Taiwan and developed an integrated permeability estimation model (named HCB2 model) using geological characteristic indicators and hydraulic conductivity data from double-packer test sections. This study successfully proposed a model applicable to the complex and fractured geological environments in the mountainous regions of Taiwan. While Hsu’s model [25] is applicable to sites of different lithologies with a wide application range, the data collected in their study did not specifically consider sites with the potential for stratum sliding. The hydrogeological characteristics of such potentially active landslide sites may differ from typical mountainous sites in Taiwan. Therefore, this study intented to compare hydrogeological properties between HCB2 and HCPI models. Before conducting this comparison, this study expanded the HCB2 model by incorporating more data points. In addition to the original 104 sample points, 352 data points from undisturbed strata in other major mountain basins of Taiwan were collected. The HCB2 model was then reconstructed to make the estimation of hydraulic conductivity more representative (named NHCB2).
Figure 5 shows the comparison of hydrogeological properties between NHCB2 and HCPI models. As shown in this figure, both models cover common metamorphic and sedimentary lithologies, indicating a wide range of lithologies. However, the HCPI model does not include samples of igneous rocks, suggesting potential for future enhancement by collecting similar lithologies to expand the model's applicability. In addition, both models have determination coefficients (R²) above 0.7, indicating a certain degree of explanatory power. The HCPI model performs better than the NHCB2 model, possibly due to the smaller sample size. The analysis samples for the two models differ by approximately three times, and the determination coefficient decreases with fewer samples. However, a larger sample size signifies a more statistically significant model. Future efforts can continue to collect landslide samples to build a more representative model while noting changes in the determination coefficient values with increasing sample size.
Finally, Figure 5 reveals differences in the estimated curve trends between the two integrated indices (HCPI and NHCB2) and K, with more pronounced differences when K is smaller. The NHCB2 model estimates higher values of permeability coefficient K, suggesting higher overall hydraulic conductivity in the major mountainous watersheds of Taiwan. In contrast, the hydraulic conductivity values estimated by the HCPI model are generally lower, implying a geological environment in landslide areas characterized by significant disturbance and more clay shear in geological strata, resulting in lower trends of hydraulic conductivity. Therefore, based on the comparison results, while both models can estimate the hydraulic conductivity of fractured rock masses using geological characteristic factors, the choice of model should consider whether the strata have been disturbed to obtain the required hydraulic characteristics of the site correctly.

4.6. The Relationship between Hydraulic Conductivity Distribution Patterns and the Locations Of Sliding Surfaces

Using the HCPI model, this study produced continuous distribution charts of hydraulic conductivity with depth per meter for each borehole equipped with an inclinometer in the 24 landslide sites. The results showed that most landslide sites exhibited certain invertals where the hydraulic conductivity values significantly increased or decreased with depth. Figure 6 illustrates the hydraulic conductivity profile of the Wanda landslide site, indicating significant variations in hydraulic conductivity values at depths above and below 34 meters (as highlighted in red boxes).
According to previous studies on deep-seated landslides [50,51,52], the upper and lower layers above the sliding surface often exhibit a trend where the upper layer is more permeable (K > 10-6 m/s,[53]) than the lower layer. The difference in hydraulic conductivity between the upper and lower layers typically falls within one to three orders of magnitude [50,51,52].
To verify whether the landslides collected in this study also exhibit similar trends reported in previous studies, cross-referencing can be done using existing inclinometer data showing clear deformation and hydraulic conductivity profiles. Reviewing the inclinometer monitoring data from the 24 landslide sites collected in this study, it was found that 14 landslide sites already have clear records of sliding in inclinometers. These sites include Caoling, Wanda, Yixing, Songmao, Xinjiayang, Longhua, Hongcaiping, Wushe, Huayuan, Baolong, Lantai, Kanjiao, Taipingshan, and Dayuling landslide sites. Therefore, the inclinometer data from the 14 sites were overlaid with the hydraulic conductivity distribution charts estimated by the HCPI model. Upon comparison, it was observed that for 12 inclinometer boreholes, there were clear interfaces of significant changes in hydraulic conductivity values corresponding to sliding depths. Figure 7 exemplifies the comparison results for the Longhua landslide site. The area within the red box, showing significant differences in hydraulic conductivity values above and below the depth of 44 meters, coincides precisely with the sliding depth recorded by the inclinometer.
Moreover, the average hydraulic conductivity values in the upper segments were greater than 10-6 m/s, indicating potential groundwater accumulation at the interface, leading to increased pore water pressure and decreased slope stability. However, for two inclinometer boreholes, the relationship between the predicted sliding depth and hydraulic conductivity variation estimated by the HCPI model was less clear, namely at the Yixing and Huayuan landslide sites. Further examination of the inclinometer data at these two sites revealed S-shaped displacement curves, as shown in Figure 8, which differed from the typical significant displacement at a certain depth. This suggests possible compression of the inclinometer due to thick layers of backfilled soil, thin layers of fractured rock, shear zones, or highly weathered rock layers, causing subsidence and negative frictional forces on the inclinometer, resulting in irregular S-shaped buckling phenomena. Additionally, irregularities in the S-shaped curve patterns may also arise from inadequate backfilling during inclinometer installation, as indicated by inconsistencies in multiple measurements of S-shaped curve patterns.
In summary, comparing the continuous distribution diagrams of hydraulic conductivity per meter with depth from boreholes at 14 landslide sites and inclinometer displacement data shows that the actual deformation at 12 landslide sites closely matches the estimated sliding results of the model. However, for two landslide sites, direct comparison was not feasible. Overall, the comparative results are generally consistent, verifying that the developed permeability estimation model can effectively predict potential sliding surfaces.

4.7. Establishment of Identification Rules for Sliding Surface Locations

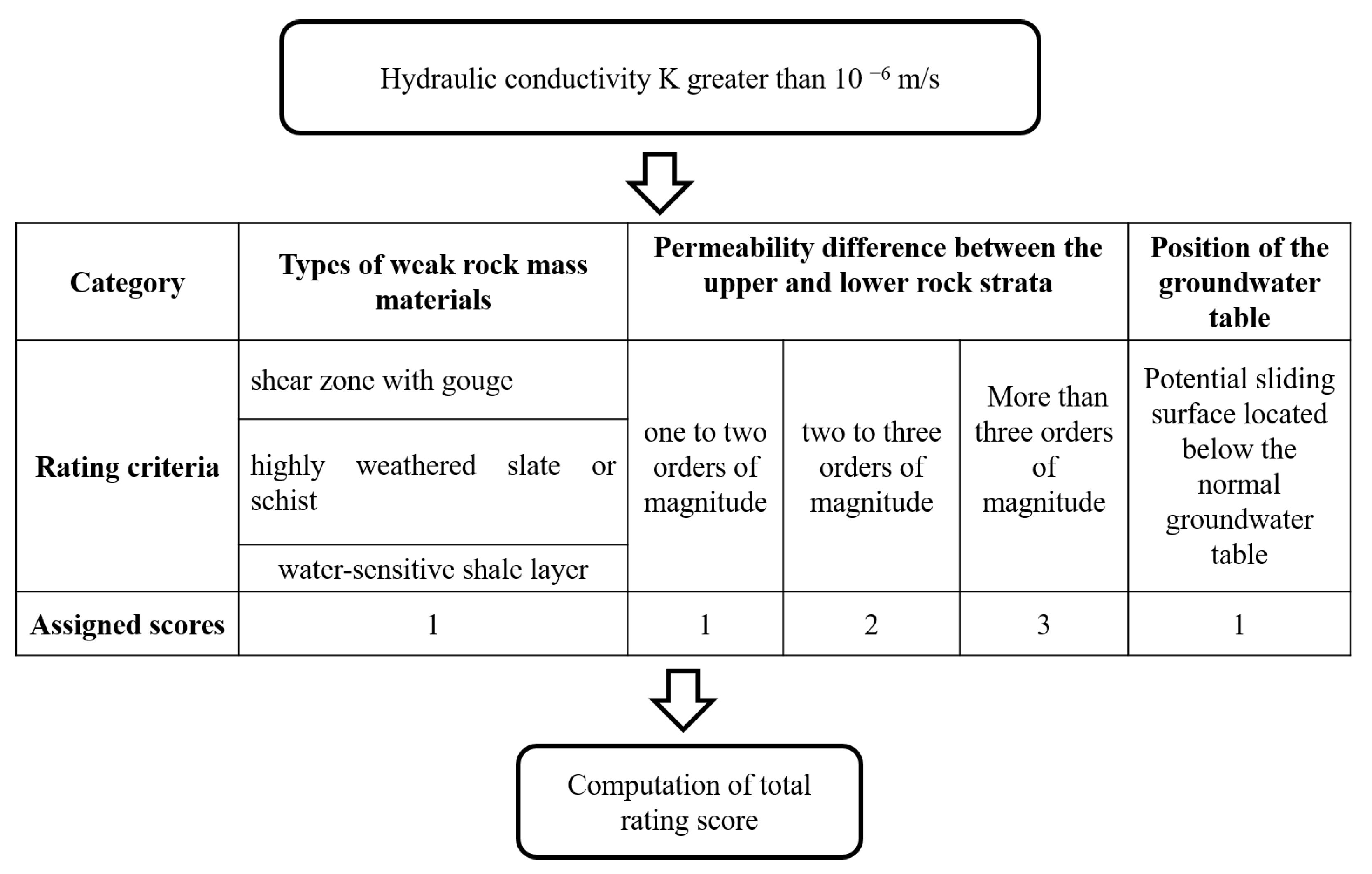
To more accurately estimate the potential sliding surface locations in landslide areas, this study integrates hydraulic conductivity profile information with literature-recommended weak sections of core samples related to the formation of sliding surfaces [34,52,54,55] and groundwater level data [33,34]. This newly proposed approach led to the establishment of an evaluation rule for identifying potential sliding surfaces. The evaluation method and steps are shown in Figure 9. First, it is necessary to determine whether the hydraulic conductivity profile indicates the presence of a rock layer with an average hydraulic conductivity value greater than 10-6 m/s and a thickness of more than 2 meters. If this condition is met, the process can proceed to the following evaluation step. The evaluation items can be divided into three categories, with each item's evaluation criteria described as follows:
  • The magnitude of hydraulic conductivity variation:
If the upper half of a rock mass interval is more permeable while the lower half is less permeable, groundwater may accumulate in the more permeable upper half of the rock medium. The greater the difference in permeability between the upper and lower sections, the higher the likelihood that water will concentrate in the more permeable upper section, thereby adding more groundwater weight to the upper rock layer. This can reduce the shear strength of the rock layer and lead to rock mass sliding. Therefore, this concept can be used as a basis for weighting the likelihood of sliding in the strata. If the permeability difference between the upper and lower rock strata is between one to two orders of magnitude, the water accumulation capacity is low, thus a weighting score of one is given. If the difference is between two to three orders of magnitude, the water accumulation capacity is higher, thus a weighting score of two is given. When the difference is more than three orders of magnitude, the water accumulation capacity is the highest, thus a weighting score of three is given.
2.
Presence of weak rock mass materials:
The occurrence of deep-seated sliding is often related to the degree of weakness in the properties of the rock material [34,52,54,55]. This study summarized the material properties of sliding surfaces from the 24 landslide sites and found that the materials at the sliding surface typically include shear zones with gouge, highly weathered slate or schist, and water-sensitive shale layers. Therefore, if the core sample contains 'shear zones with gouge,' 'highly weathered slate or schist,' or 'shale layers,' each is given a weighting score of one point.
3.
Position of the groundwater table:
Groundwater can induce weak layers in the strata to become sliding surfaces [33,34]. Therefore, if the potential sliding surface is located below the normal groundwater table, it is assigned a weighting score of one point.
Based on the aforementioned scoring rules, this study further calculated the sliding potential score for each sliding position from 12 landslide sites with clear sliding records. This results in data on sliding surface locations, hydraulic conductivity values for the upper and lower rock mass sections, and scoring results for the 12 borehole drilling records (as shown in Table 10). As shown in Table 10, the sliding potential scores of the 12 existing sliding sections all exceed three points, and all contain weak layers in the core samples. Therefore, this study concludes that if the sliding potential score of a rock layer section exceeds 3 points, it should be considered a potential sliding surface section. According to this conclusion, if future sites without installed inclinometers or sites where inclinometers have not yet detected signs of sliding are encountered, the evaluation rules proposed in this study can be applied. If the total score of a certain rock layer section exceeds 3 points after calculation, that section is likely to induce a sliding surface in the future, thereby predicting the occurrence location of the sliding surface in advance.
Preprints 116925 g009
Figure 9. Evaluation method and procedure for identification of potential sliding surfaces.
Figure 9. Evaluation method and procedure for identification of potential sliding surfaces.
Preprints 116925 g009

4.8. Application of the Evaluation Approach - Prediction of Potential Sliding Surfaces

Based on the evaluation method developed in this study for quickly assessing the locations of potential sliding surfaces, this method can then be used to estimate the potential sliding surface depths for the remaining ten landslides where no sliding has yet been detected during the monitoring period (due to the short monitoring period). Through the calculation process shown in Figure 9, a total of 12 potential sliding sections were identified in 9 landslide sites. The depths of each potential sliding surface, hydraulic conductivity values for the upper and lower sections, and scoring conditions of each potential sliding surface in each landslide site are summarized in Table 11. The results show that the sliding surface estimation method designed in this study can identify relatively less stable sliding surfaces in nine of the ten landslide sites, and these sliding depths are more likely to develop into sliding surfaces in the future.
Based on the proposed identification rules, Antong is the only landslide site where no potential sliding sections were identified. According to the rock core photos and core records of the landslide site, it was found that Antong lacks easily sliding-prone strata materials, such as shear mud zones and highly weathered strata. Therefore, when applying the identification method established in this study, the scores for strata materials could not be obtained, resulting in sliding potential scores for the sliding sections being below 3 points. This leads to the determination, based on the collected data, that there is no potential sliding risk. Consequently, the geological conditions of the landslide site are relatively more stable than the other nine landslide sites.

5. Conclusions

This study proposes a preliminary and efficient assessment method to predict the potential slip surface depth in landslide areas using geological characteristic data and the developed rock mass permeability estimation models, thereby reducing investigation time and economic costs. It also seeks to facilitate early preparation and formulation of remediation strategies in disaster prevention efforts, ultimately reducing the occurrence probability of slope disasters.The principal findings can be concluded as follows.
  • By collecting hydrogeological data from the 24 active landslide sites across Taiwan, a permeability estimation model (HCPI model) was established using six geological characteristic factors (RQD, DI, GCD, LPI, FA, and FD) related to rock permeability with the multicollinearity analysis, principal component analysis, and regression analysis. The coefficient of determination (R2) of the HPCI model is 0.895, meeting the practical application accuracy requirements. In addition, the HCPI model suits various lithological geological conditions and can be used to estimate the permeability variation per meter with depth along a borehole.
  • The HCPI model was compared with the non-disturbed rock mass permeability estimation model "NHCB2". Under the same geological characteristic conditions, the hydraulic conductivity estimated by the HCPI model is smaller than that of the NHCB2 model. This outcome can be attributed to the highly disturbed geological conditions of the landslide sites, and the overall geological environment contains more gouge content, resulting in smaller hydraulic conductivity. Thus, choosing a geologically compatible estimation model is crucial while estimating hydraulic conductivity in the geological environment of mountainous areas.
  • The concept of using abrupt changes in hydraulic conductivity data to estimate the depth of potential slip surfaces in landslide areas was feasible and confirmed by 12 landslide cases. According to the investigated landslide sites, the sliding surface occurred within a certain depth range of the strata, where the hydraulic conductivity of the upper layer was greater than that of the lower layer by one to three orders of magnitude. Additionally, the hydraulic conductivity of the upper layer is typically greater than 10-6 m/s.
  • An identification rule predicting sliding surface locations has been established through three criteria: the magnitude of hydraulic conductivity variation, the presence of weak rock mass materials, and the position of groundwater table. This identification rule has been applied to ten landslide sites to seek high-potential sliding zones, which can be used as valuable information for slope disaster prevention management.
  • Finally, the HCPI model was constructed based on sedimentary and metamorphic rock data samples, but no samples from igneous rocks. Future work can include igneous rock data and continue collecting more landslide data for analysis, enhancing the model's reliability and practical application value.

Author Contributions

Conceptualization, supervision, project administration, and funding acquisition, S.-M.H.; methodology, formal analysis, and investigation, S.-M.H., C.-C.H., Y.-F.L., andY.-J.C.; resources, Y.-J.C.; writing—original draft preparation, S.-M.H.; writing—review and editing, Y.-J.C.; visualization, S.-M.H., Y.-J.C., and J.-R.L. All authors have read and agreed to the published version of the manuscript.

Funding

This work was partially supported by the Ministry of Science and Technology of Taiwan (MOST 111-2116-M-019-003 -).

Acknowledgments

The authors express their gratitude to the Geological Survey and Mining Management Agency (GSMMA), Ministry of Economic Affairs (MOEA) of Taiwan for offering hydrogeological raw data used in this study.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Zhuang, J., Jia, K., Zhan, J. Zhu, Y., Zhang, C.L., Kong, J., Du, C.H., Wang, S., Cao, Y., Peng J.B. Scenario simulation of the geohazard dynamic process of large-scale landslides: a case study of the Xiaomojiu landslide along the Jinsha River. Nat. Hazards. 2022, 112, 1337–1357. [CrossRef]
  2. Nor Diana, M.I., Muhamad, N., Taha, M.R., Osman, A., Alam, M.M. Social vulnerability assessment for landslide hazards in Malaysia: a systematic review study. Land. 2021, 10, 315. [CrossRef]
  3. Tsai, T.T.; Tsai, Y.J.; Shieh, C.L., and John Wang, H.C. Triggering Rainfall of Large-Scale Landslides in Taiwan: Statistical Analysis of Satellite Imagery for Early Warning Systems. Water. 2022, 14, no. 21: 3358. [CrossRef]
  4. Stark, T.D., Choi, H. Slope inclinometers for landslides. Landslides. 2008, 5, 339–350. [CrossRef]
  5. Bordoni, M., Vivaldi, V., Bonì, R. et al. A methodology for the analysis of continuous time-series of automatic inclinometers for slow-moving landslides monitoring in Piemonte region, northern Italy. Nat Hazards. 2023, 115, 1115–1142. [CrossRef]
  6. Macciotta, R.; Hendry, M.; Martin, C.D. Developing an early warning system for a very slow landslide based on displacement monitoring. Nat Hazards. 2016, 81, 887–907. [Google Scholar] [CrossRef]
  7. Chung, C.C.; Lin, C.P. A Comprehensive Framework of TDR Landslide Monitoring and Early Warning Substantiated by Field Examples. Engineering Geology. 2019, 262(28), 105330. [Google Scholar] [CrossRef]
  8. Peng, H.; Chen, B.; Dong, P.; Chen, S.; Liao, L.; Guo, Q. Application of FBG Sensing Technology to Internal Deformation Monitoring of Landslide. 2020. [CrossRef]
  9. Han, H.; Shi, B.; Zhang, CC.; et al. Application of ultra-weak FBG technology in real-time monitoring of landslide shear displacement. Acta Geotech. 2023, 18, 2585–2601. [Google Scholar] [CrossRef]
  10. Li, S.H.; Wu, L.Z.; Luo, X.H. A novel method for locating the critical slip surface of a soil slope. Engineering Applications of Artificial Intelligence. 2020, 94, 103733. [Google Scholar] [CrossRef]
  11. Rotaru A.; Bejan F.; Almohamad D. Sustainable Slope Stability Analysis: A Critical Study on Methods. Sustainability. 2022, 14(14):8847. [CrossRef]
  12. Shin, J.; Baek, Y.; Song, J. Analysis of the Failure Area of the Slope Using the Slip Line Method. Appl. Sci. 2023, 13, 3863. [Google Scholar] [CrossRef]
  13. Ullah S.; Ullah Khan M.; Rehman G. A Brief Review of the Slope Stability Analysis Methods. Geological Behavior. 2020, 4(2): 73-77. [CrossRef]
  14. Furuya T.; Jiang J.C. Determination of slip surfaces in fracture zone landslides using oriented borehole core samples. Geomate Journal. 2015, 8 (15):1151-58.
  15. Wakizaka Y.; Kozuma M.; Watatani H.; Toyoguchi Y. Characteristics of crushed rocks in a landslide body: An example of a landslide located in the Shimanto Belt. Journal of the Japan Society of Engineering Geology. 2012, Vol. 52, No. 6, Feb. 2012, pp. 231-247. in Japanese.
  16. Kinoshita, A.; et al. Physical and chemicalproperties around slip surface by assaying samples of well-cared cores from crystalline schist area in Shikoku Islands, southwest Japan. Journal of the Japan Landslide Society. 2013, Vol. 50 No.4, Jul. 2013, pp. 1-9. in Japanese.
  17. Tsunataka Furuya ; Jiang, J.C. Determination of slip surfaces in fracture zone landslides using oriented borehole core samples. 2015, Vol. 8 No. 15, March 2015. 20 March.
  18. Geological Survey and Mining Management Agency. Development of landslide observation technique (2/4); Ministry of Economic Affairs: Taipei, Taiwan, 2016. [Google Scholar]
  19. Vassallo, R.; Grimaldi, G. M.; Di Maio, C. Pore water pressures induced by historical rain series in a clayey landslide: 3D modeling. Landslides. 2014, 12(4), 731–744. [Google Scholar] [CrossRef]
  20. Park, J.-Y.; Song, Y.-S. Laboratory Experiment and Numerical Analysis on the Precursory Hydraulic Process of Rainfall-Induced Slope Failure. Advances in Civil Engineering. 2020, 1–12. [Google Scholar] [CrossRef]
  21. Di Maio, C.; De Rosa, J.; & Vassallo, R. Pore water pressures and hydraulic conductivity in the slip zone of a clayey earthflow: Experimentation and modelling. Engineering Geology. 2021, 292.
  22. Perrone, A.; Vassallo, R.; Lapenna, V.; Maio, C. D. Pore water pressures and slope stability: a joint geophysical and geotechnical analysis. Journal of Geophysics and Engineering. 2008, 5(3), 323–337. [Google Scholar] [CrossRef]
  23. Zhang, S.; Xiahou, Y.; Tang, H.; Huang, L.; Liu, X.; Wu, Q. Study on the Spatially Variable Saturated Hydraulic Conductivity and Deformation Behavior of Accumulation Reservoir Landslide Based on Surface Nuclear Magnetic Resonance Survey. Advances in Civil Engineering. 2018, 1–15. [Google Scholar] [CrossRef]
  24. Rosa, J. D.; Pontolillo, D. M.; Caputo, V.; Di Maio, C.; Scaringi, G. Evaluation of hydraulic conductivity in the slip zone of an earthflow in clay shales. Proceedings of the XVII ECSMGE-2019. 2019.
  25. Hsu, S. M. Quantifying the hydraulic properties of fractured rock masses along a borehole using composite geological indices: A case study in the mid and upper Choshui River Basin in Central Taiwan. Engineering Geology. 2021. [Google Scholar] [CrossRef]
  26. Geological Survey and Mining Management Agency. Investigation and Evaluation of Hydrogeological Impacts on Slope Stability in Watersheds across Taiwan. Ministry of Economic Affairs: Taipei, Taiwan, 2007.
  27. Geological Survey and Mining Management Agency. Investigation and Evaluation of Hydrogeological Impacts on Slope Stability in Watersheds across Taiwan. Ministry of Economic Affairs: Taipei, Taiwan, 2008.
  28. Geological Survey and Mining Management Agency. Investigation and Evaluation of Hydrogeological Impacts on Slope Stability in Watersheds across Taiwan. Ministry of Economic Affairs: Taipei, Taiwan, 2009.
  29. Geological Survey and Mining Management Agency. Investigation and Evaluation of Hydrogeological Impacts on Slope Stability in Watersheds across Taiwan. Ministry of Economic Affairs: Taipei, Taiwan, 2010.
  30. Geological Survey and Mining Management Agency. Investigation and Evaluation of Hydrogeological Impacts on Slope Stability in Watersheds across Taiwan. Ministry of Economic Affairs: Taipei, Taiwan, 2011.
  31. Geological Survey and Mining Management Agency. Investigation and Evaluation of Hydrogeological Impacts on Slope Stability in Watersheds across Taiwan. Ministry of Economic Affairs: Taipei, Taiwan, 2012.
  32. Geological Survey and Mining Management Agency. Investigation and Evaluation of Hydrogeological Impacts on Slope Stability in Watersheds across Taiwan. Ministry of Economic Affairs: Taipei, Taiwan, 2013.
  33. Dou, H.Q.; Han,T.C.; Gong,X.N.; Qiu,Y.Z.; Li, Z.N. Effects of the spatial variability of permeability on rainfall-induced landslides. Engineering Geology, Volume. 2015, 192, p. 92-100.
  34. Han, T.; Liu, L.; Li, G. The Influence of Horizontal Variability of Hydraulic Conductivity on Slope Stability under Heavy Rainfall. Water. 2020, 12(9).
  35. Snow, D.T. The frequency and apertures of fractures in rock. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. 1970, 7, 23–40.
  36. Louis, C. Rock Hydraulics in Rock Mechanics; ed. L. Muller; Springer Verlag, Vienna, 1974.
  37. Carlsson, A.; Olsson, T. Hydraulic properties of Swedish crystalline rocks-hydraulic conductivity and its relation to depth. Bulletin of the Geological Institute, University of Uppsala. 1977, 71–84.
  38. Black, J. H. Flow and flow mechanisms in crystalline rock, in Fluid Flow in Sedimentary Basins and Aquifers. Geol. Soc. Special Publication. 1987, No. 34, pp. 186-200.
  39. Gates, W.C.B. The hydro-potential (HP) value: a rock classification technique for evaluation of the ground-water potential in fractured bedrock. Environ. Eng. Geosci. 1997, 3(2), 251–267. [Google Scholar] [CrossRef]
  40. Hamm, S.Y.; Kim, M.; Cheong, J.Y.; Kim, J.Y.; Son, M.; Kim, T.W. Relationship between hydraulic conductivity and fracture properties estimated from packer testsand borehole data in a fractured granite. Eng. Geol. 2007, 92 (1–2), 73–87. [CrossRef]
  41. Hsu, S.M.; Ke, C.C.; Lin, Y.T.; Hung, C.C. Ground-water exploration in regolith-bedrock aquifer: a case study in the basins of Mid-Jhuoshuei river and Beigang river, central Taiwan. EGU General Assembly 2011, Vienna, Austria. 2011a, Apr. 03–08, 13, EGU2011-3140.
  42. Hsu, S.M.; Lo, H.C.; Chi, S.Y.; Ku, C.Y. Rock mass hydraulic conductivity estimated by two empirical models. In: Dikinya, O. (ed.), Developments in Hydraulic Conductivity Research. IntechOpen. 2011b, p. 133–158.
  43. Hsu, S.-M.; Ke, C.C.; Lin, Y.T.; Huang, C.C.; Wang, Y.S. Unravelling preferential flow paths and estimating groundwater potential in a fractured metamorphic aquifer in Taiwan by using borehole logs and hybrid DFN/EPM model. ENVIRONMENTAL EARTH SCIENCES. 2019, 78, 150. [Google Scholar] [CrossRef]
  44. Hsu, S.-M.; Hsu, J.-P.; Ke, C.-C.; Lin, Y.-T.; Huang, C.-C. Rock mass permeability classification schemes to facilitate groundwater availability assessment in mountainous areas: a case study in Jhuoshuei river basin of Taiwan. Geosciences Journal. 2020, 24, 209–224. [Google Scholar] [CrossRef]
  45. El-Naqa, A. The hydraulic conductivity of the fractures intersecting Cambrian sandstone rock masses, Central Jordan. Environ. Geol. 2001, 40(8), 973–982. [Google Scholar] [CrossRef]
  46. Midi, H.; Sarkar, S.; Rana, S. Collinearity diagnostics of binary logistic regression model. Journal of Interdisciplinary Mathematics. 2013, 13. 253-267.
  47. Myers, R.H. Classical and modern regression with applications. PWS-Kent Publishing, Boston, 1990.
  48. Menard, S. Linear regression and the logistic regression model, Applied logistic regression analysis, SAGE Publications, Inc, 2002, pp. 2-17.
  49. Bieniawski, Z.T. The Geomechanics Classification in Rock Engineering Application. Proceedings 4th International Congress on Rock Mechanics, Montreux. 1979, 2-8, Vol. 2, 41-48.
  50. Perrone, A.; Vassallo, R.; Lapenna, V.; Di Maio, C. Pore water pressures and slope stability: a joint geophysical and geotechnical analysis. Journal of Geophysics and Engineering. 2008, 5(3):323. [CrossRef]
  51. Zhang, S.; Xiahou, Y.; Tang, H.; Huang, L.; Liu, X.; Wu, Q. Study on the Spatially Variable Saturated Hydraulic Conductivity and Deformation Behavior of Accumulation Reservoir Landslide Based on Surface Nuclear Magnetic Resonance Survey. 2018.
  52. Rosa, J. D.; D. M. Pontolillo, V. C.; C. Di Maio; Scaringi, G. Evaluation of hydraulic conductivity in the slip zone of an earthflow in clay shales. Proceedings of the XVII ECSMGE-2019. 2019.
  53. Struckmeier, W.F.; Margat, J. Hydrogeological maps: A guide and a standard legend. VERLAG HEINZ HEISE: HANNOVER, Germany. 1995.
  54. Terlien, M. T. J. Hydrological landslide triggering in ash-covered slopes of Manizales. Geomorphology. 1997, 20, 165–175. [Google Scholar] [CrossRef]
  55. Gomes, M. C. V.; Vieira, B. C. Saturated hydraulic conductivity of soils in a shallow landslide area in the Serra do Mar, São Paulo, Brazil. Zeitschrift für Geomorphologie. 2016, 60(1), 53-65.
Preprints 116925 g002
Figure 2. Schematic diagram for comparison of hydraulic conductivity profile and observed inclinometer data.
Figure 2. Schematic diagram for comparison of hydraulic conductivity profile and observed inclinometer data.
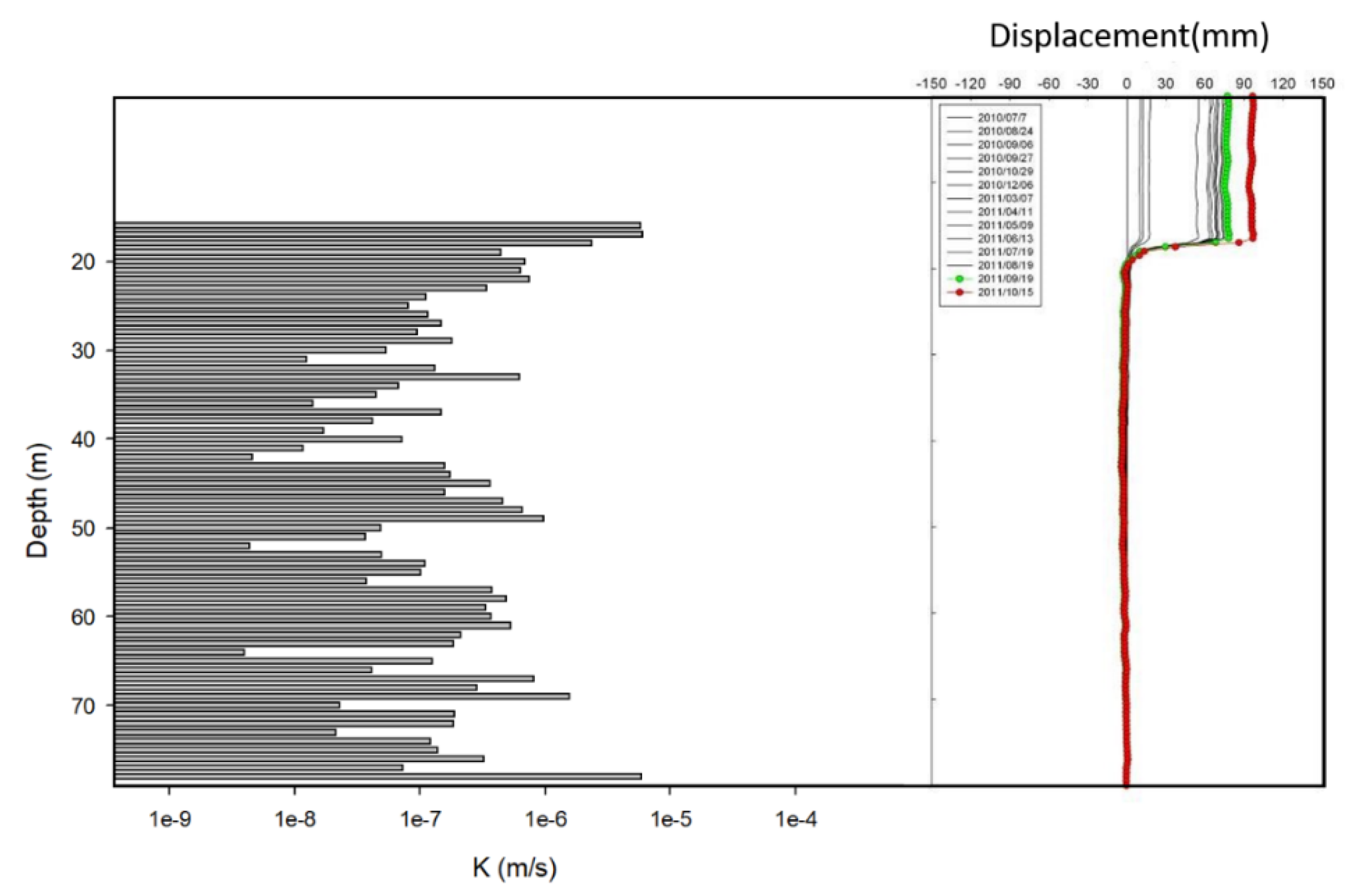
Preprints 116925 g002
Preprints 116925 g003
Figure 3. A scree plot.
Figure 3. A scree plot.
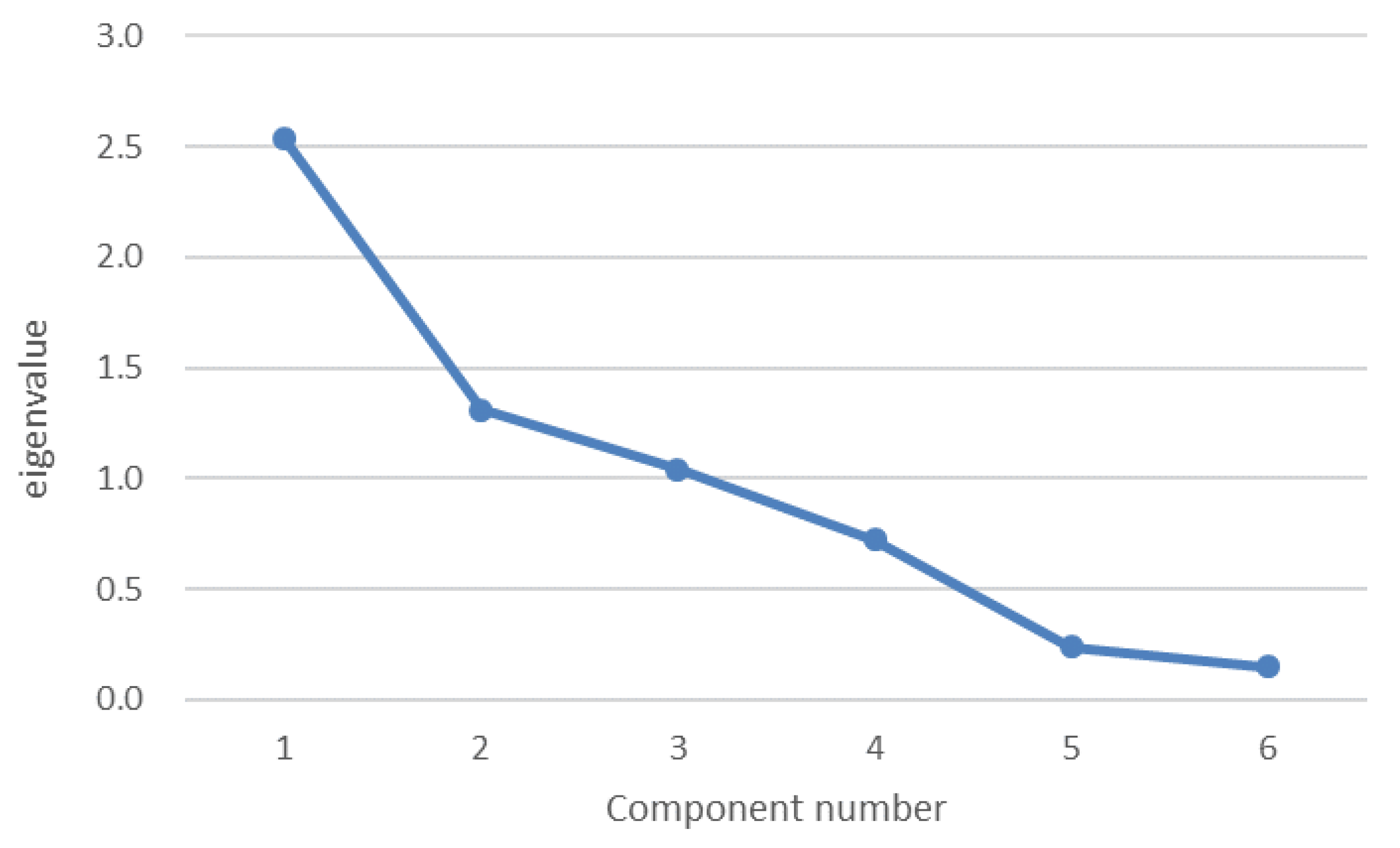
Preprints 116925 g003
Preprints 116925 g004
Figure 4. The regression model for estimating hydraulic conductivity.
Figure 4. The regression model for estimating hydraulic conductivity.
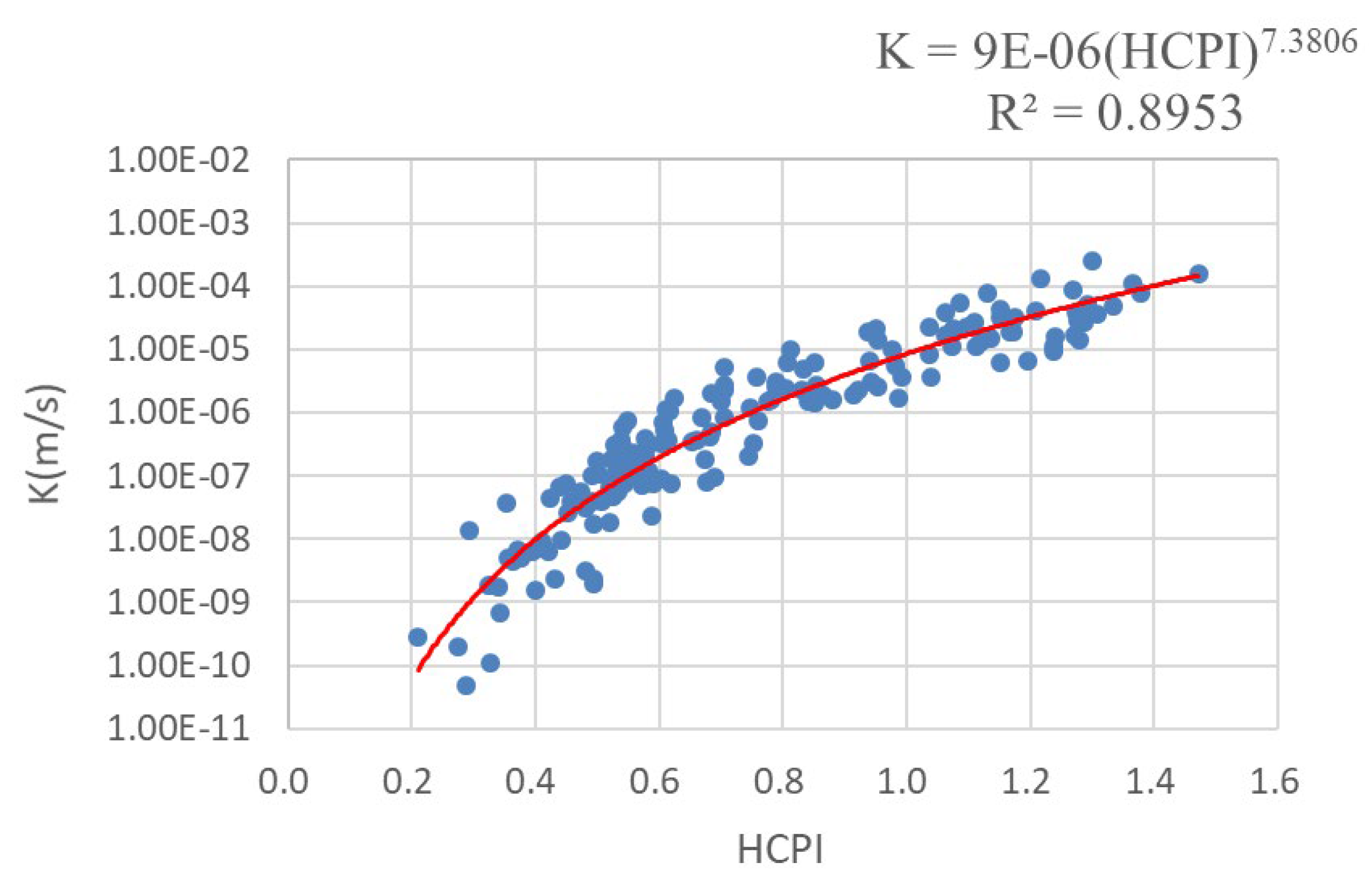
Preprints 116925 g004
Preprints 116925 g005
Figure 5. Comparison of HCPI and NHCB2 models.
Figure 5. Comparison of HCPI and NHCB2 models.
Preprints 116925 g005
Preprints 116925 g006
Figure 6. An abrupt changing zone for the hydraulic conductivity profile at the depths between 34 m and 36 m (an example of the Wanda landslide site).
Figure 6. An abrupt changing zone for the hydraulic conductivity profile at the depths between 34 m and 36 m (an example of the Wanda landslide site).
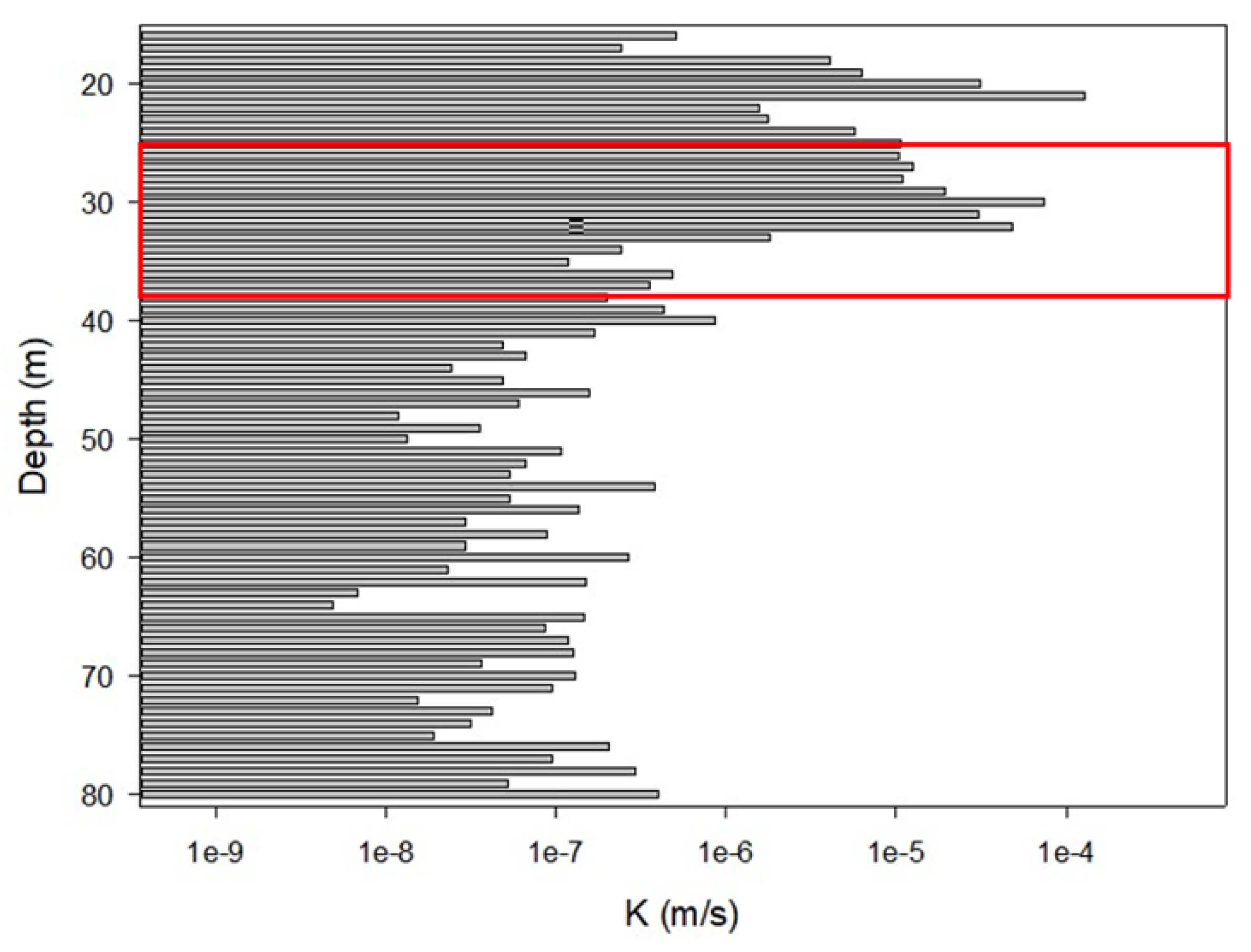
Preprints 116925 g006
Preprints 116925 g007
Figure 7. Comparison diagram for hydraulic conductivity profile and observed inclinometer data (an example of the Longhua landslide site).
Figure 7. Comparison diagram for hydraulic conductivity profile and observed inclinometer data (an example of the Longhua landslide site).
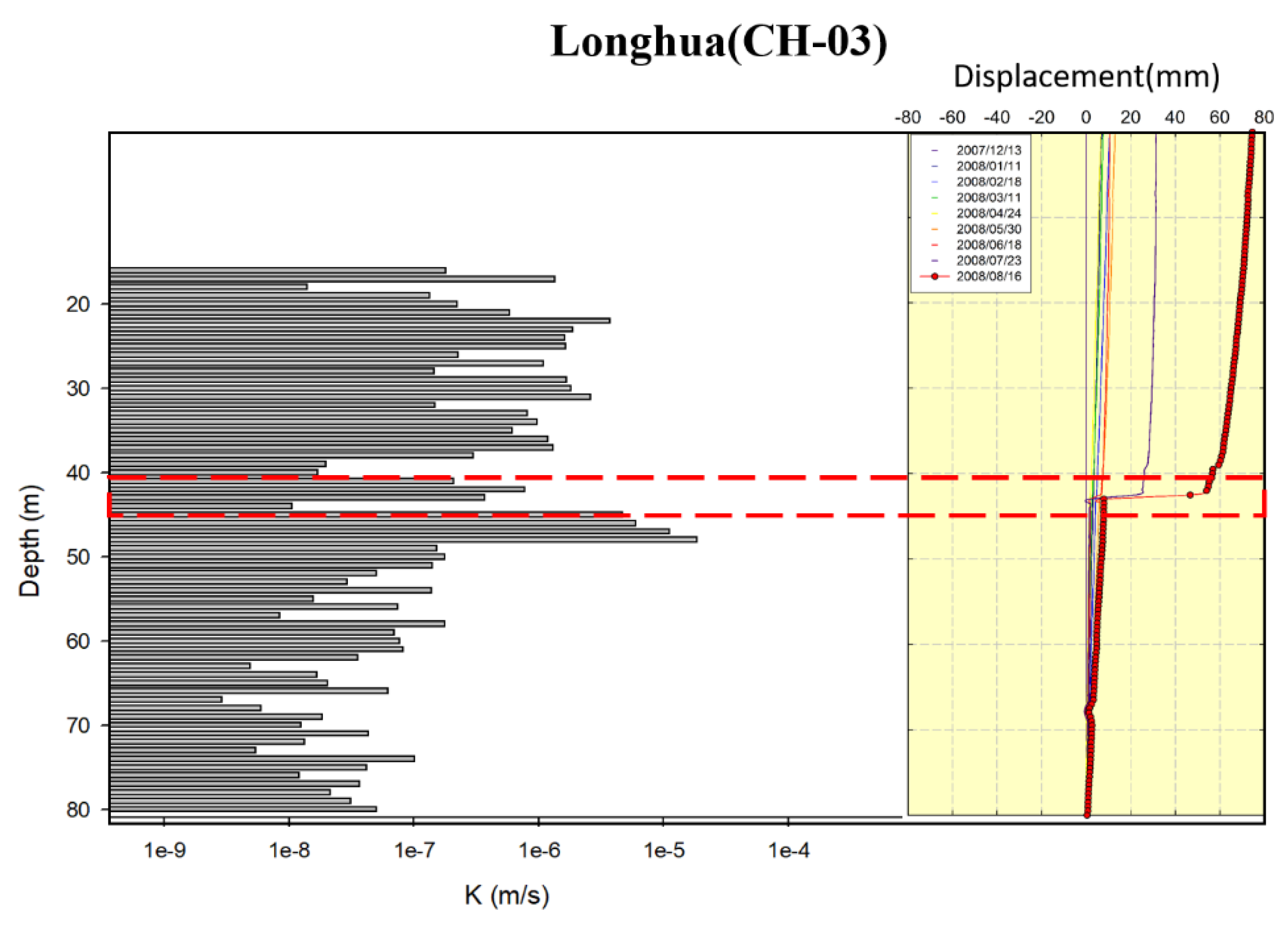
Preprints 116925 g007
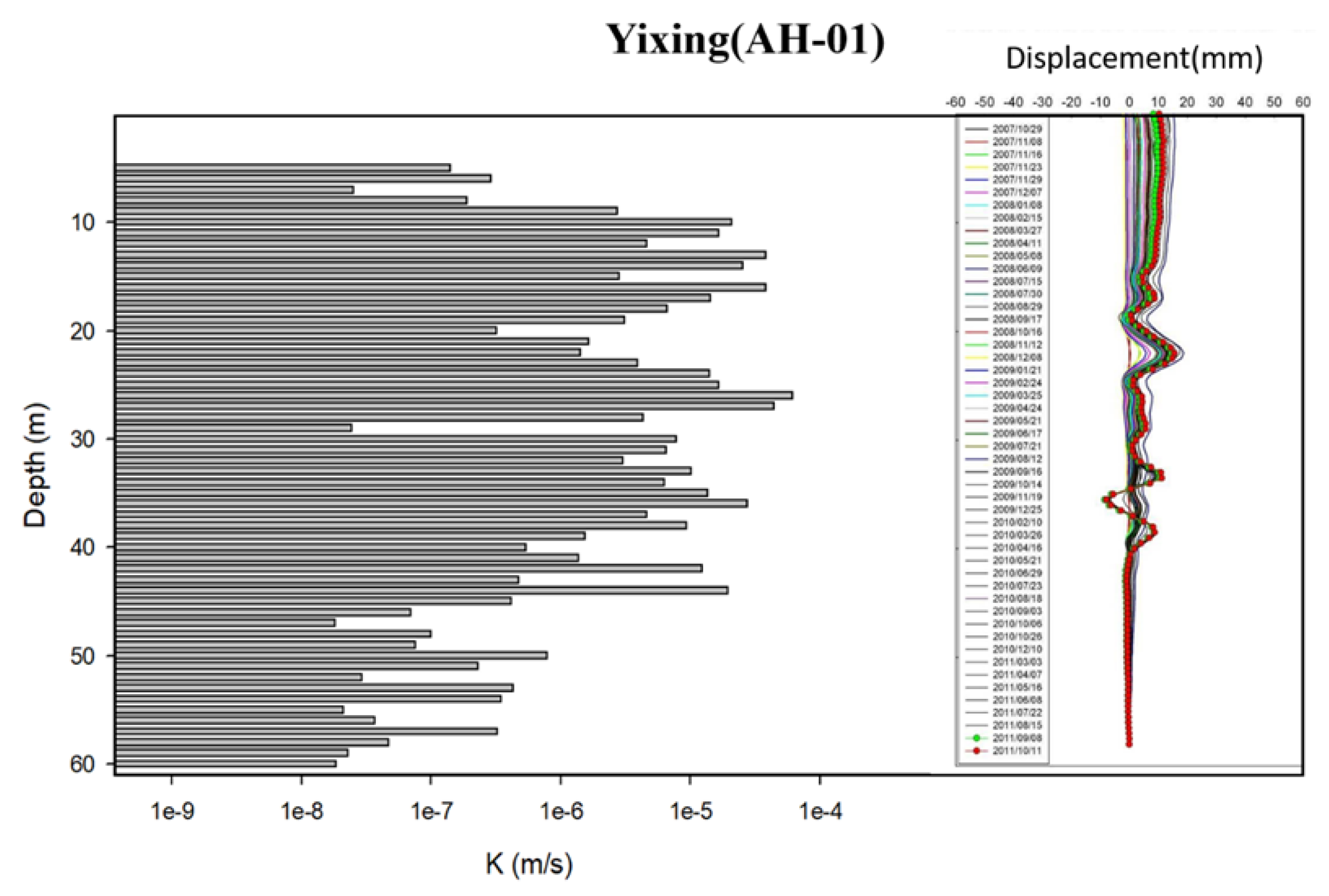
Preprints 116925 g008
Figure 8. Comparison diagram for hydraulic conductivity profile and observed S-shaped inclinometer data (an example of the Yixing landslide site).
Figure 8. Comparison diagram for hydraulic conductivity profile and observed S-shaped inclinometer data (an example of the Yixing landslide site).
Preprints 116925 g008
Table 1. Descriptions of collected inclinometer boreholes from the 24 Landslide Sites.
Table 1. Descriptions of collected inclinometer boreholes from the 24 Landslide Sites.
Inclinometer
Borehole Number		 Landslide Site
Name		 Main Lithology Borehole Depth(m) Regolith Thickness(m) Normal Groundwater Level(m)
QH-13 Dawu Argillite 60 7 18
OH-01 Antong Argillaceous Siltstone 80 5 50
QH-22 Gaoshi Sandy Shale 70 15 6.5
NH-15 Fengshan Schists 55 1 30
NH-01 Dayuling Slates 65 2 30
NH-21 Yanliao Alternations of Sandstone and Mudstone 70 2 6.5
JH-27 Daguan Argillaceous Siltstone 65 33 20
KH-01 Chaozhouhu Alternations of Sandstone and Shale 70 20 10
KH-11 Nanshikeng Mudstone 65 5 15
IH-23 Taipingshan Slates 80 14 34
HH-03 Kanjiao Sandstone interbedded with some shale 70 8 8*
IH-13 Lantai Argillite 80 16 10
FH-13 Tengzhi Slates 80 12 54.4
FH-21 Jilou Slates 70 16 41
FH-05 Baolong Shale interbedded with some sandstone 70 12 20
EH-06 Wushe Slates 80 10 51*
EH-05 Hongcaiping Shale 80 13 28.5*
DH-05 Huayuan Sandstone 80 19 46*
CH-04 Caoling Sandy Shale 80 3 50*
CH-09 Wanda Slates 80 15 45*
AH-01 Yixing Sandstone 60 4 45*
BH-09 Xinjiayang Slates 80 17 56*
CH-03 Longhua Sandy Shale 80 15 60*
BH-03 Songmao Slates 80 12 43*
* Groundwater levels were estimated from data collected at nearby groundwater monitoring stations.
Table 2. Description and ratings for lithology permeability index (LPI).
Table 2. Description and ratings for lithology permeability index (LPI).
Lithology Hydraulic Conductivity k (m/s) Range
Of
Rating		 Suggested
Rating
Reference1 Reference 2 Reference 3 Kaverage
Sandstone 10-6~10-9 10-7~10-9 10-7~10-9 10-7.5 0.9~1.0 0.92~1.0
Silty Sandstone 0.8~0.9 0.9
Argillaceous Sandstone 0.8~0.9 0.85
S.S. interbedded with some Sh. 0.7~0.8 0.75
Alternations of S.S & Sh. 0.6~0.7 0.65
Sh. interbedded with some S.S. 0.5~0.7 0.6
Alternations of S.S &
Mudstone		 0.5~0.6 0.55
Dolomite 10-6~10-10.5 10-7~10-10.5 10-9~10-10 10-8 0.6~0.8 0.7
Limestone 10-6~10-10.5 10-7~10-9 10-9~10-10 10-8 0.6~0.8 0.7
Shale 10-10~10-12 10-10~10-13 10-10.5 0.4~0.6 0.5
Sandy Shale 0.5~0.6 0.6
Siltstone 10-10~10-12 10-11 0.2~0.4 0.4
Sandy Siltstone 0.3~0.5 0.45
Argillaceous Siltstone 0.3~0.4 0.35
Claystone 10-9~10-13 10-11 0.2~0.3 0.2
Mudstone 0.2~0.4 0.3
Sandy Mudstone 0.3~0.4 0.4
Silty Mudstone 0.2~0.4 0.35
Granite 10-11~10-12 10-11.5 0.1~0.2 0.15
Basalt 10-6~10-10.5 10-10~10-13 10-11.5 0.1~0.2 0.15
Schists 0.25
Slates 0.35
Quartzite 0.3~1.0
Argillite(a) 0.4~0.5 0.4
Weathered Argillite(a) 0.45~0.5 0.5
Weathered Slates(a) 0.35~0.6 0.5
Weathered Schists(a) 0.5~0.75 0.6
1 B.B.S. Singhal & R.P. Gupta (1999) [44]；2 Karlheinz Spitz & Joanna Moreno (1996) [44]; 3 http://en.wikipedia.org/wiki/Hydraulic_conductivity(modified from Bear, 1972) [44] (a)Modified after Hus (2021) [25].
Table 3. Descriptive statistical results of indicative factors for both overall rock types and specific rock types.
Table 3. Descriptive statistical results of indicative factors for both overall rock types and specific rock types.
Factors RQD DI GCD LPI FF FW
All lithologies quantity 169 169 169 169 169 169
average 0.479 0.362 0.088 0.508 0.571 1.110
Standard deviation 0.300 0.226 0.146 0.176 0.275 0.742
Sedimentary rocks quantity 87 87 87 87 87 87
average 0.656 0.470 0.088 0.595 0.444 0.955
Standard deviation 0.238 0.243 0.154 0.180 0.232 0.773
Metamorphic rocks quantity 82 82 82 82 82 82
average 0.291 0.349 0.088 0.415 0.706 1.276
Standard deviation 0.239 0.219 0.138 0.113 0.252 0.673
Table 4. Multicollinearity analysis of the chosen controlling variables (dependent variable：K).
Table 4. Multicollinearity analysis of the chosen controlling variables (dependent variable：K).
Controlling Variables Tolerance VIF
1-RQD .242 4.136
DI .906 1.104
1-GCD .740 1.351
LPI .660 1.514
FA .322 3.103
FD .285 3.514
Table 5. Results of each component in the principal component analysis.
Table 5. Results of each component in the principal component analysis.
Component Number Eigenvalue Proportion of Variance
(%)		 Cumulative Proportion of Variance
(%)
1 2.539 42.316 42.316
2 1.312 21.868 64.184
3 1.041 17.344 81.528
4 0.722 12.041 93.569
5 0.239 3.986 97.555
6 0.147 2.445 100
Table 6. Factor loadings and linear combination coefficients for the first to third principal components.
Table 6. Factor loadings and linear combination coefficients for the first to third principal components.
Factor Loadings
factors PC1 PC2 PC3
1-RQD 0.939 -0.160 -0.105
DI 0.093 -0.543 0.699
1-GCD 0.185 0.689 -0.228
LPI -0.109 0.712 0.636
FW 0.804 0.288 0.291
FF 0.928 0.017 -0.048
Linear combination coefficients
factors PC1 PC2 PC3
1-RQD 0.589 -0.140 -0.103
DI 0.058 -0.474 0.685
1-GCD 0.116 0.602 -0.223
LPI -0.068 0.622 0.623
FW 0.505 0.251 0.285
FF 0.582 0.015 -0.047
Table 7. Composite scores model coefficients.
Table 7. Composite scores model coefficients.
Controlling Variables Tolerance
1-RQD 0.247
DI 0.049
1-GCD 0.174
LPI 0.264
FA 0.390
FD 0.296
Table 8. Weights for each factor.
Table 8. Weights for each factor.
Controlling Variables Tolerance
1-RQD 0.174
DI 0.034
1-GCD 0.123
LPI 0.186
FA 0.275
FD 0.209
Table 9. Evaluation results for the empirical model.
Table 9. Evaluation results for the empirical model.
Independence
(D-W Statistic)		 Normality
(K-S Statistic/P-Value)		 Constant of Variance
(Spearman/P-Value)		 F Test Statistic
F Ratio P-Value
1.5014 0.0910 0.5824 1419.1 <0.0001
Table 10. Sliding potential scores for each sliding position of 12 landslide sites.
Table 10. Sliding potential scores for each sliding position of 12 landslide sites.
Name of landslide site
(borehole No.)		 Sliding surface depth (m) K in the upper rock formation (m/s) Difference in K between upper and lower rock formation (m/s) Score for permeability difference Score for shear zone with gouge Score for highly weathered slate or schist Score for shale layer Score for position of groundwater table Overall score
Caoling
(CH-04)		 7 1.6×10-5 1.19×102 2 - - 1 - 3
Wanda
(CH-09)		 33 1.45×10-5 1.11×102 2 1 1 - - 4
Songmao
(BH-03)		 21 6.75×10-6 5.63×101 1 1 1 - - 3
Xinjiayang
(BH-09)		 25 2.35×10-6 2.61×101 1 1 1 - - 3
Longhua
(CH-03)		 41 1.50×10-6 1.71×102 2 1 - 1 - 4
Hongcaiping
(EH-05)		 20 7.38×10-6 9.79×101 1 1 - 1 - 3
Wushe
(EH-06)		 31 2.87×10-6 1.36×101 1 1 1 - - 3
Baolong
(FH-05)		 17 2.18×10-6 4.42×102 2 1 - - - 3
Lantai
(IH-13)		 21 1.67×10-6 7.63×100 - 1 - 1 1 3
Kanjiao
(HH-03)		 14 2.25×10-5 2.73×102 2 1 - - - 3
Taipingshan
(IH-23)		 27 1.33×10-5 5.19×101 1 1 1 - - 3
Dayuling
(MH-01)		 46 1.03×10-5 1.07×102 2 1 - - 1 4
Table 11. Sliding potential scores for each sliding position of 10 landslides with no sliding records detected.
Table 11. Sliding potential scores for each sliding position of 10 landslides with no sliding records detected.
Name of landslide site
(borehole No.)		 Sliding surface depth (m) K in the upper rock formation (m/s) Difference in K between upper and lower rock formation (m/s) Score for permeability difference Score for shear zone with gouge Score for highly weathered slate or Schist Score for shale layer Score for position of groundwater table Overall Score
Tengzhi
(FH-13)		 16 1.48×10-5 2.29×101 1 1 1 - - 3
Tengzhi
(FH-13)		 49 2.78×10-6 3.87×101 1 1 1 - - 3
Tengzhi
(FH-13)		 69 4.86×10-6 5.04×101 1 1 1 - 1 4
Jilou
(FH-21)		 45 3.59×10-6 4.83×101 1 1 - - 1 3
Chaozhouhu
(KH-01)		 24 3.47×10-5 6.39×102 2 1 - - 1 4
Daguan
(JH-27)		 46 4.54×10-6 1.42×102 2 1 - - 1 4
Nanshikeng
(KH-11)		 10 7.11×10-6 2.14×102 2 1 - - - 3
Yanliao
(NH-21)		 7 3.83×10-6 2.07×102 2 1 - - 1 4
Fengshan
(NH-15)		 50 3.55×10-6 6.18×100 - 1 1 - 1 3
Gaoshi
(QH-22)		 21 6.23×10-6 1.93×102 2 1 - 1 1 5
Antong
(OH-01)		 - - - - - - - - -
Dawu
(QH-13)		 14 6.09×10-6 1.96×101 1 1 - 1 - 3
Dawu
(QH-13)		 48 6.04×10-6 2.15×102 2 1 - 1 - 4
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated