Prerpints.org logo
Preprint
Article

A First Principles Study of Lithium Adsorption in Nanoporous Graphene

Altmetrics

Downloads

61

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

30 August 2024

Posted:

03 September 2024

You are already at the latest version

Alerts
Abstract
Nanoporous graphene structures have high accessible surface area for lithium-ion adsorption or intercalation. Here, we present theoretical investigations on lithium-ion adsorption mechanism in a graphene nanopore. Ab initio electronic structure calculations are performed based on density functional theory. We also study different lithium-ion distributions in graphene nanopores to determination multilayer lithium-nanoporous graphene structures for lithium-ion batteries. We believe, these multilayer nanoporous graphene nanostructures with more pores opening can offer improved capacity and better rate performance for energy storage applications.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

Lithium-ion batteries (LIBs) have tremendous popularity in recent years as promising renewable energy storage systems. The high capacity, relatively low cost and high power and energy density makes LIBs very desirable for electric vehicles and energy storage applications [1,2,3]. However, lower lithium density in batteries is a problem in battery production [4]. In LIBs production, a most commonly used anode materials is graphite oxide, however, it was not the answer considering the increasing storage capacity demands [8,9,10]. In search of a better anode material to increase the storage capacity recently LIBs manufacturers considered graphene and graphene-based materials as promising materials for energy storage in LIBs and supercapacitors [8,9,10].
Recent studies show that nanoporous and porous graphene can possess more spatial region for lithium-ions to increase the lithium density [11,12,13]. The pore formation of graphene provides the ability to create ion transfer channels in lithium-ion batteries. A recent study reported a high specific capacity of 1084 mAh g−1 at 0.2 A g−1 and an outstanding high-rate performance [14].
There are various theoretical investigations of graphene or graphene-based materials for lithium-ion battery anodes. Lee and Persson studied Li adsorption and intercalation in single layer graphene and a few layer graphene by performing density functional theory (DFT) calculations [15]. They considered metallic Li atoms energy as a base energy which is cohesive energy of metallic lithium. If adsorption energy or intercalation energy is lower than this cohesive energy, lithium ions would be on graphene or in between the graphene layers. They found that there exists no Li arrangement that stabilizes Li adsorption on the surface of a single layer graphene unless there are defects in graphene. Y. Liu et. al. performed DFT calculations of interactions of Li with a wide variety of sp2 C substrates including pristine, defective and strained graphene [16]. They also calculate work required to fill the unoccupied electronic states of the substrates. D. Datta et al. investigated enhanced lithiation of defective graphene with divacancy (DV) and Stone-Wales (SW) defects [17]. They stated that Li storage capacities up to 1675 mAh/g can be achieved. Y.J. Tsai and C.L. Kuo performed first principles calculations to study the effects of structural disorder in the graphene substrate on Li storage capacity[18]. They found that Li storage capacity is largely determined by the local geometry of the defect sites. Many of these studies were on defective graphene, however, lithium adsorption mechanism of nanoporous graphene is not clearly understood yet.
Here, we focus on lithium-ion adsorption mechanism in nanoporous graphene. Different lithium-ion distributions in a graphene nanopore are also studied. Ab initio electronic structures calculations were performed. The methods used in our calculations are presented in Section 2. In the 3rd section our results are presented. Lithium-ion transport through the nanopores for different pore sizes are presented in Section 3.1. Lithium-ion adsorption in a graphene nanopore is studied by investigating the effect of the graphene pore size, lithium-ion placement and the lithium height above the graphene surface which is presented in Section 3.2. Many lithium ions were distributed in graphene pores, and they were evaluated based on adsorption energy per lithium, adsorption energy per carbon and lithium density. Investigations of multilayer lithium – nanoporous graphene structures and their evaluation for lithium-ion battery anodes are in Section 3.3. Our conclusions are in Section 4.

2. Methods

Our electronic structure and geometry optimization calculations are based on density functional theory (DFT). The Quickstep module [19] in the CP2K software package was used. Periodic structures can be investigated using this module. The exchange-correlation term in the Kohn-Shams equations were approximated by the Perdew-Burke-Erznerhof (PBE) [20] functional with generalized gradient approximation (GGA). The DZVP-MOLOPT-SR-GTH [21] basis set and the Goedecker-Teter-Hutter (GTH) [22] pseudopotential were used with a cut-off energy of 900 Ry for the density grid. The Van der Waals interactions were included using the semi-empirical ‘DFT+D3’ term [23]. The LBFGS [24] optimizer was used for energy minimization to optimize the geometry.

3. Results

3.1. Lithium ion transport through graphene nanopores

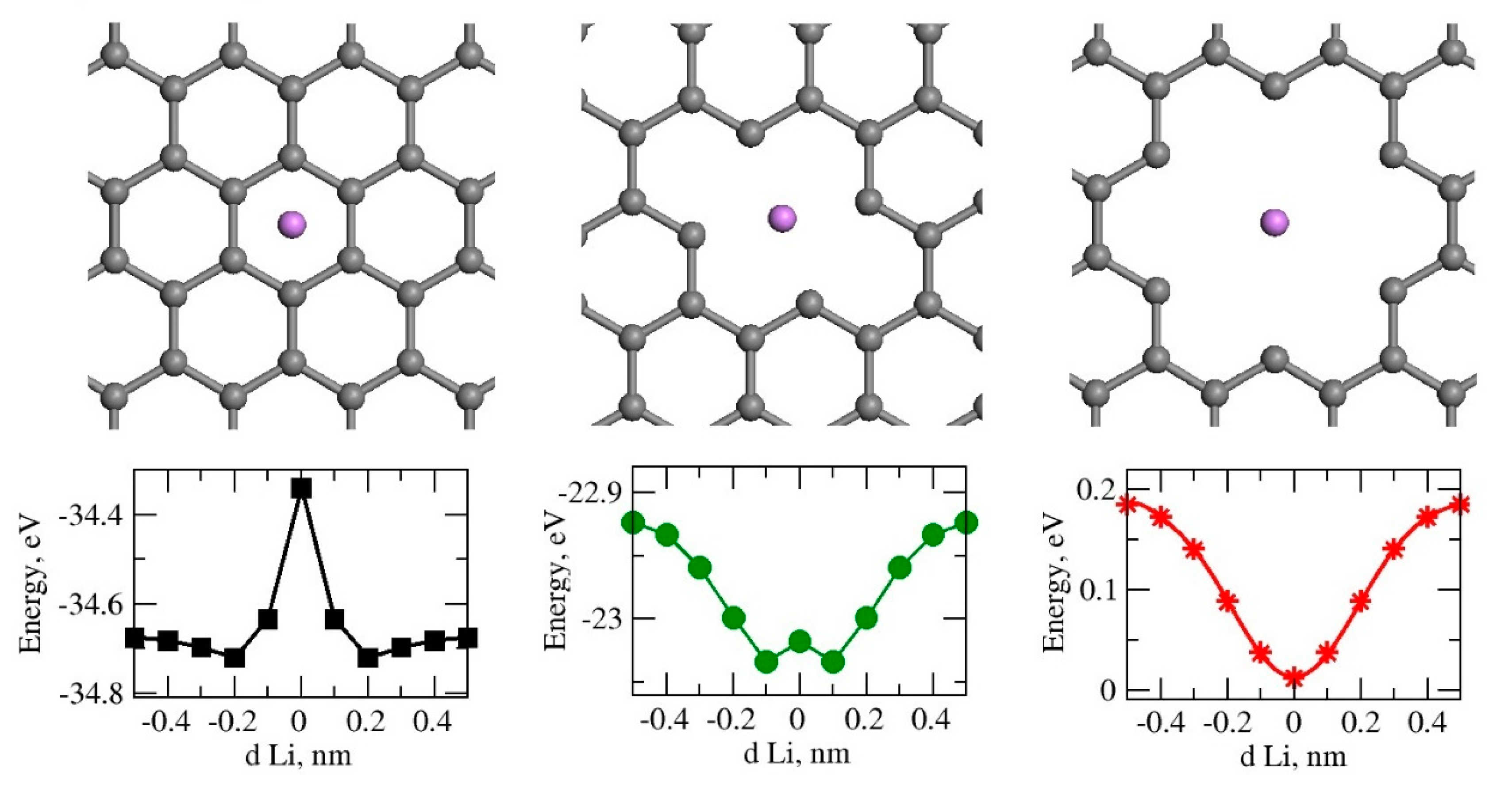
First, we studied lithium transport through graphene nanopores. By removing carbon atoms from the pristine graphene, pores of different sizes were created. The model structures labelled as C0H, C2H and C6H with zero, 2 or 6 carbon atoms removed from the graphene atomic structure are presented in Figure 1. The lithium atom was placed 0.5 nm above the graphene plane and it was translated towards the center of the pore in discrete steps. Ab initio total energy calculation was performed in each step. No potential energy barrier was observed when the lithium atom passed through the center in the C6H model. Therefore, we selected model C6H for part of the further studies.

3.2. Adsorption mechanism of lithium in a graphene nanopore

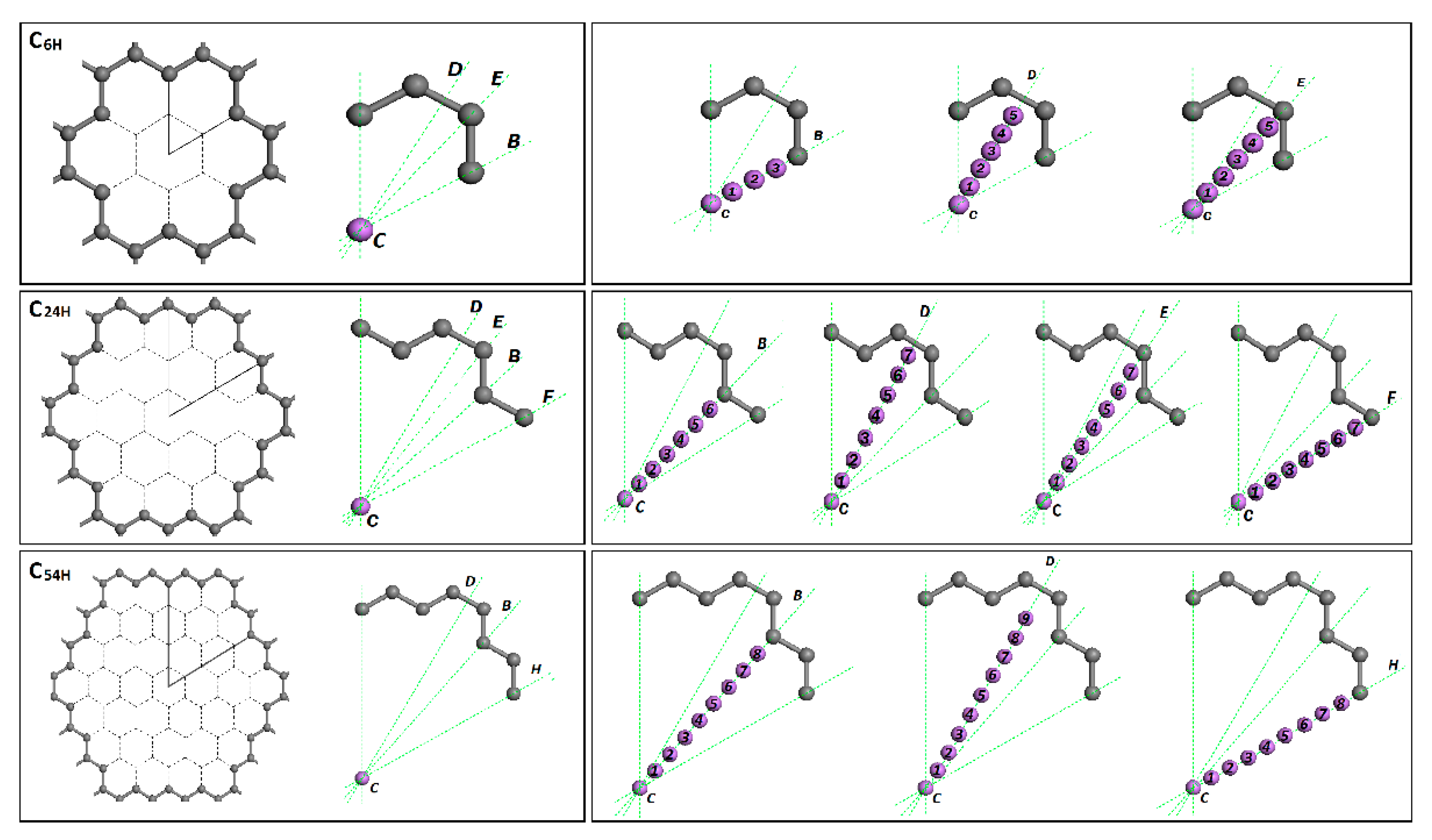
In addition to the model C6H, two new nanopore models (C24H and C54H) were created with 24 and 54 removed carbon atoms from the graphene structure. Using these three model structures, we investigated the lithium adsorption in a graphene nanopore. For all these three models, the symmetry of the graphene pore structure was studied and important translation lines or directions were identified. As it can be seen in Figure 2, these important translation lines start from the center (C) site of the graphene pore and ends at the pore edge. In the figure, B, E, F and H-lines end at carbon atoms, and the D-line ends at the carbon-carbon (C-C) bond.
Lithium ions were placed and translated along these lines. The variation of total energy was calculated for each line. During these calculations, the lithium ion was placed at 0.0 nm or 0.172 nm height above the graphene pore surface. 0.172 nm was found to be the optimized height of a lithium ion on the pristine graphene.
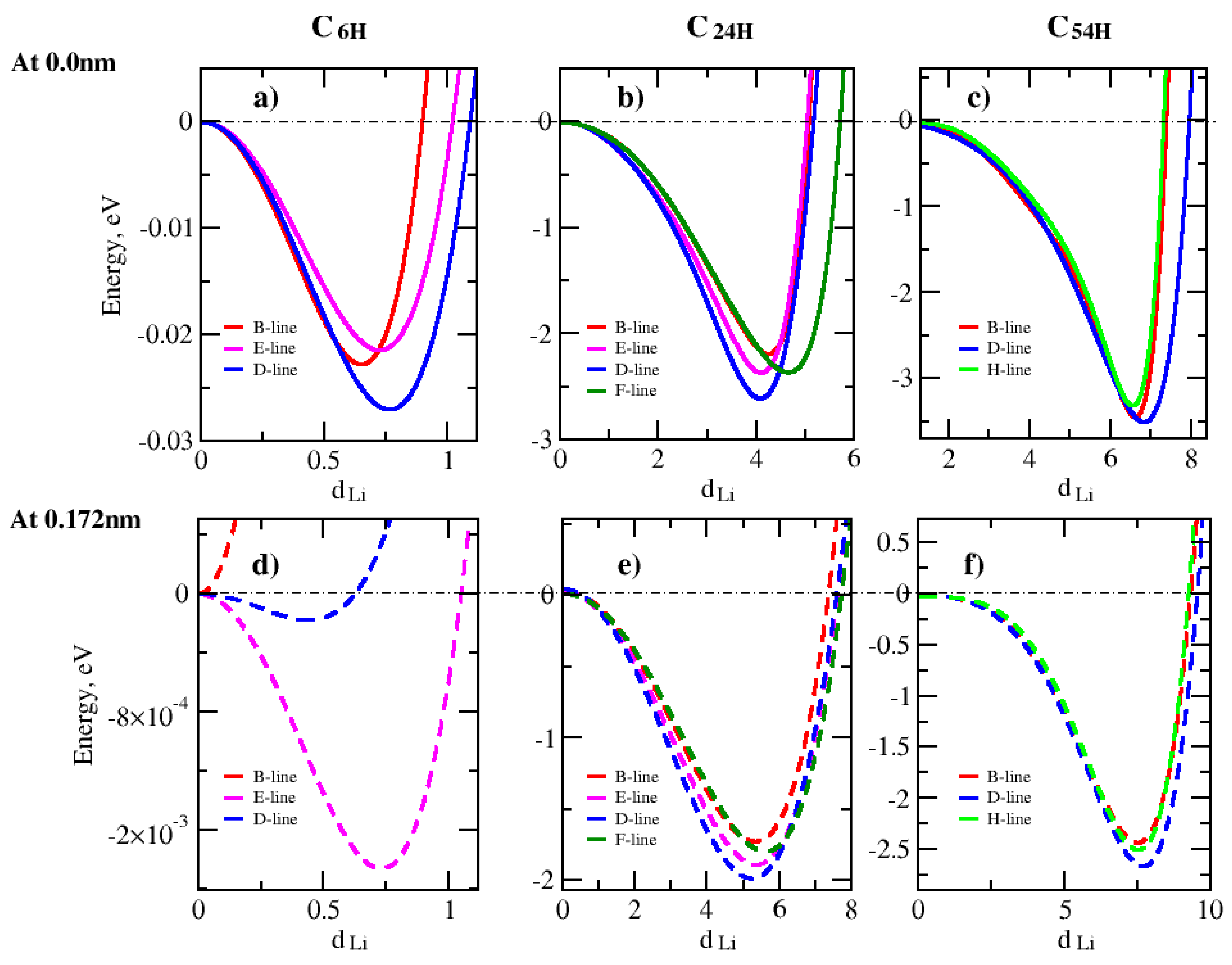
Lithium-ion adsorption in a graphene nanopore is studied by investigating the effect of the graphene pore size, lithium-ion placement and the lithium height above the graphene surface. First, we investigated the effect of graphene pore size on the lithium adsorption. Figure 3 presents the variation of total energy along the Li-ion translation lines for different pore sizes.
To determine the lowest energy positions for the lithium adsorption, various translation directions or lines were selected inside the graphene pores as they can be seen in Figure 2. The B, E, F and H-lines ends at carbon atoms, and the D-line ends at the carbon-carbon (C-C) bond. By comparing the results in Figure 3, it appeared that the directionality of lithium ions placement inside graphene pore has a direct impact on the lithium adsorption mechanism. The study shows that the lowest energy values are along the D-line in the C6H, C24H and C54H structures at distances from the center (dLi) = 0.75, 4 and 7 nm, respectively. The lithium height is 0.0 nm.
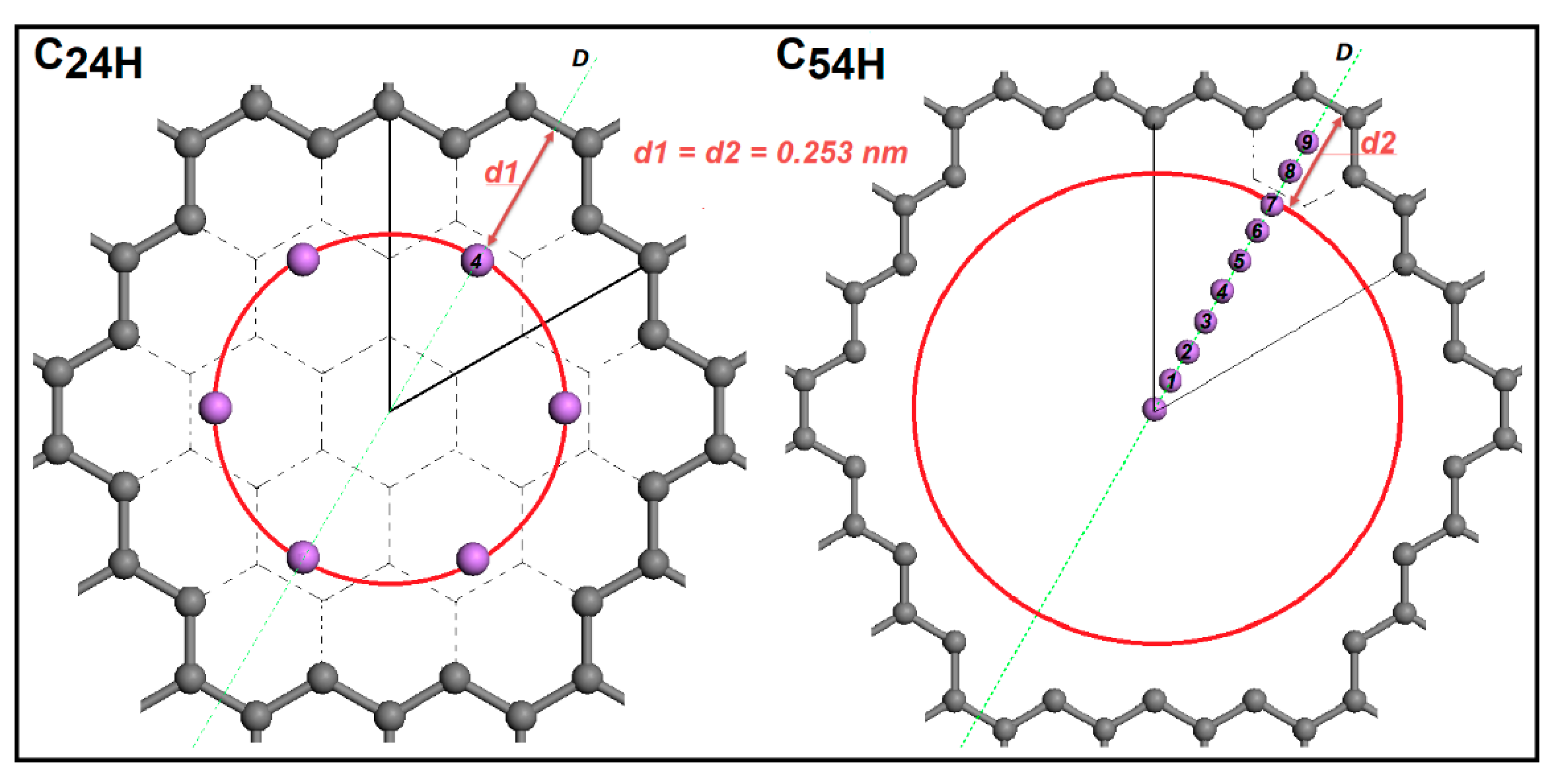
Another interesting result from these investigations is that the lowest energy position of the Li-ion relative to the center of the C-C bond is the same for different pore sizes. It is 0.253 nm away from the C-C bond in both C24H and C54H models. In Figure 4, d1 and d2 distances represent these distances and they are equal. This information gives us the opportunity to place multiple Li-ions in the pore. On the other side, lithium ion-ion repulsion may limit the number of ions placed in the pore.
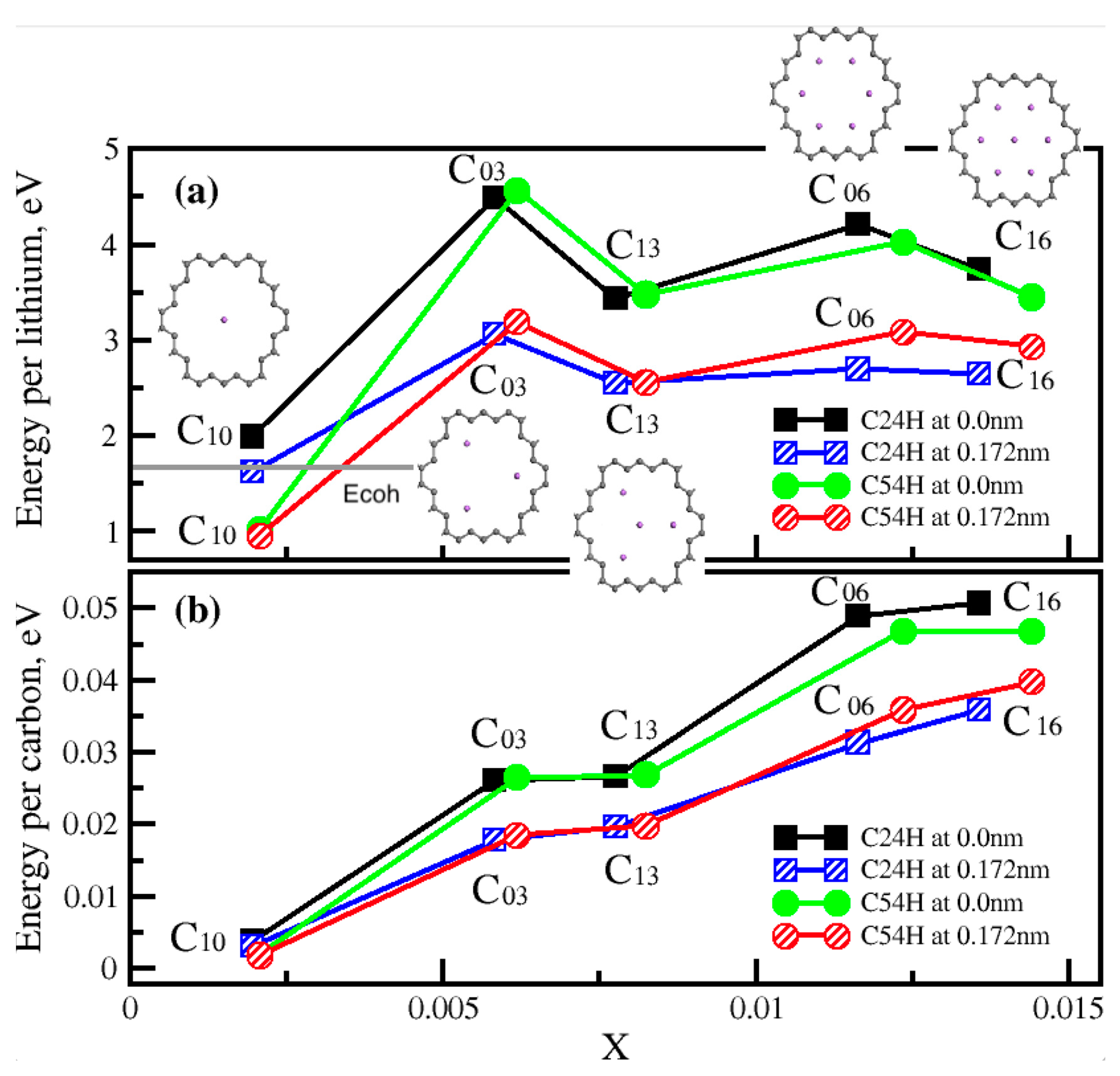
The lithium-ion distribution inside the C24H and C54H pores and their adsorption energies were studied. New models from C24H (C10, C03, C13, C06 and C16) were created and the D-lines were used to distribute the lithium ions. Figure 5 presents the models for the C24H pore size. In the same way we also created the new models for C54H.
The adsorption energies per lithium and per carbon atoms are determined next. The total adsorption energy is presented as:
E = -( EGLi - NLi*ELi - EG )
where EGLi – the total energy of the combined structure, NLi – the total number of lithium ions in the structure, ELi – the total energy of an isolated lithium ion, and EG – the total energy of an isolated mono- or bilayer graphene. In some of the theoretical investigations, cohesive energy of metallic lithium is used for ELi. We also consider cohesive energy of metallic lithium, Ecoh = 1.68 eV [25] and compare adsorption energy per Li atom in graphene nanopores with this value.
In Figure 5, adsorption energy per lithium and adsorption energy per carbon are presented. They are functions of lithium density, x, per carbon. Adsorption energy per carbon increases but energy per lithium saturates when we increase the lithium ion density and it does not decrease as long as we do not place a lithium ion at the center. Other lithium ions are symmetrically distributed facing the C-C bonds in the best lithium distribution model structures. The cohesive energy of metallic lithium is presented as a grey line in Figure 5(a). We found that energy per Li is higher than Ecoh in most cases, thus these nanopores can contain multiple Li ions. C03 and C06 are appeared to be the best lithium – nanoporous graphene structures in a single layer graphene.

3.3. Multilayer lithium - nanoporous graphene structures

After determining the best lithium distribution inside the graphene pore, we focused on creating lithium–nanoporous graphene combined structures. Ten new model structure models were created. Here, the idea is the optimize the lithium - nanoporous graphene combined structure for the highest lithium-ion density. The first four models are shown in Figure 6.
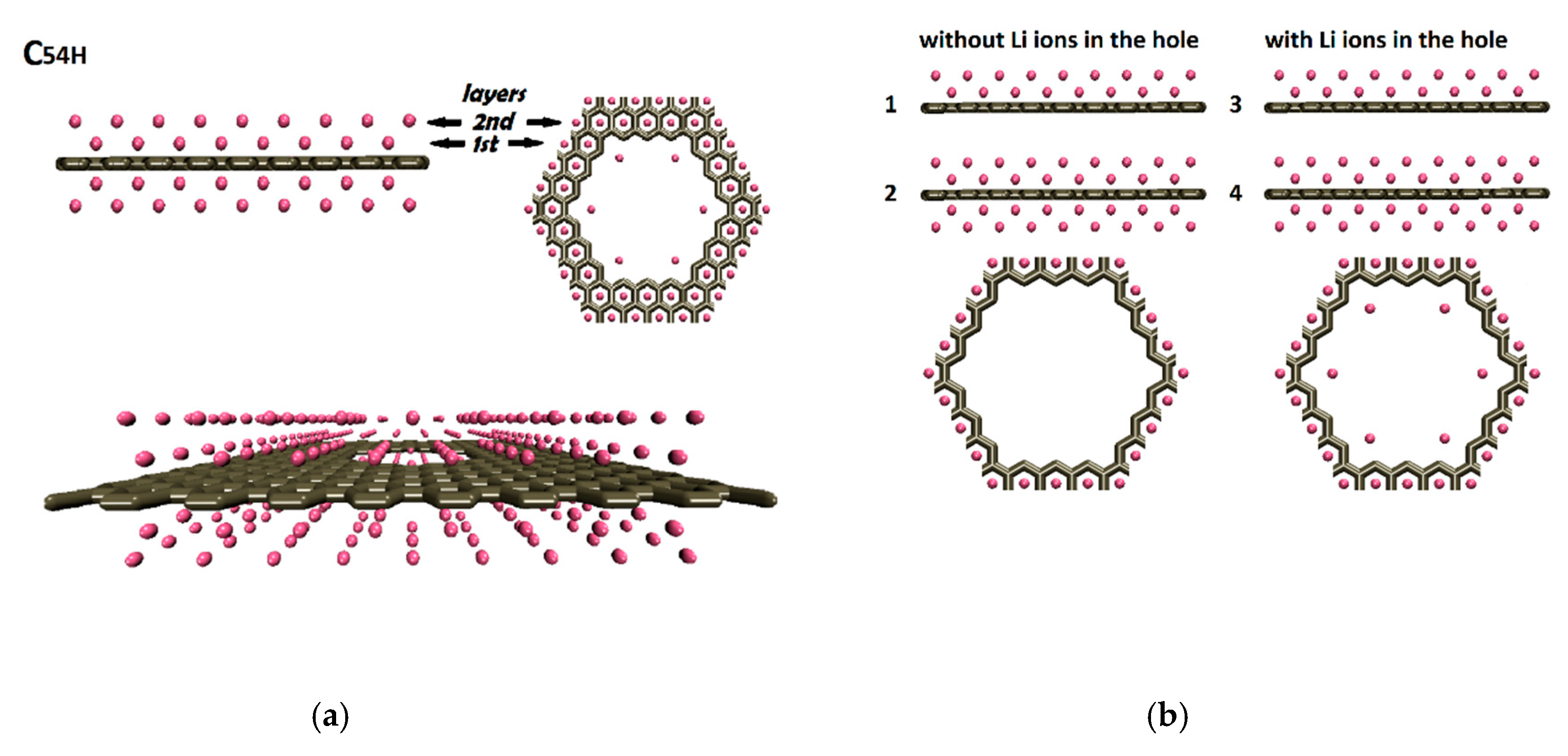
The C54H pore was used to create these model structures. The first lithium layer – graphene separation was 0.184 nm and the second lithium layer was placed 0.203 nm above the first lithium layer with respect to the data obtained from reference [26]. No lithium ions were distributed above and below the graphene pores (Figure 6a). These four models were divided into two categories: without Li ions inside the pore (models M1, M2) and with Li ions inside the pore (models M3, M4 which are based on C06 lithium assembly at 0.0 nm). Models M1 and M3 had only two lithium layers above the nanoporous graphene surface. Models M2 and M4 had an additional two layers of lithium at the bottom of the nanoporous graphene (Figure 6b).
The next two models created (M5 and M6) contained bilayer graphene structures. The combination of a nanoporous graphene and a pristine graphene was in model M5. A bilayer containing two identical nanoporous graphene layers are in model M6 as presented in Figure 7. Two additional lithium layers around the second pristine graphene layer were added in model M5, while model M6 still had four lithium layers distributed around the first nanoporous graphene layer.
Total energy calculations were performed to determine the correct separation distance between the graphene layers. For both structures the lowest energy was observed around 0.6 nm of the separation distance between the graphene layers and the distance between the bottom graphene and the lithium layer above it was 0.213 nm.
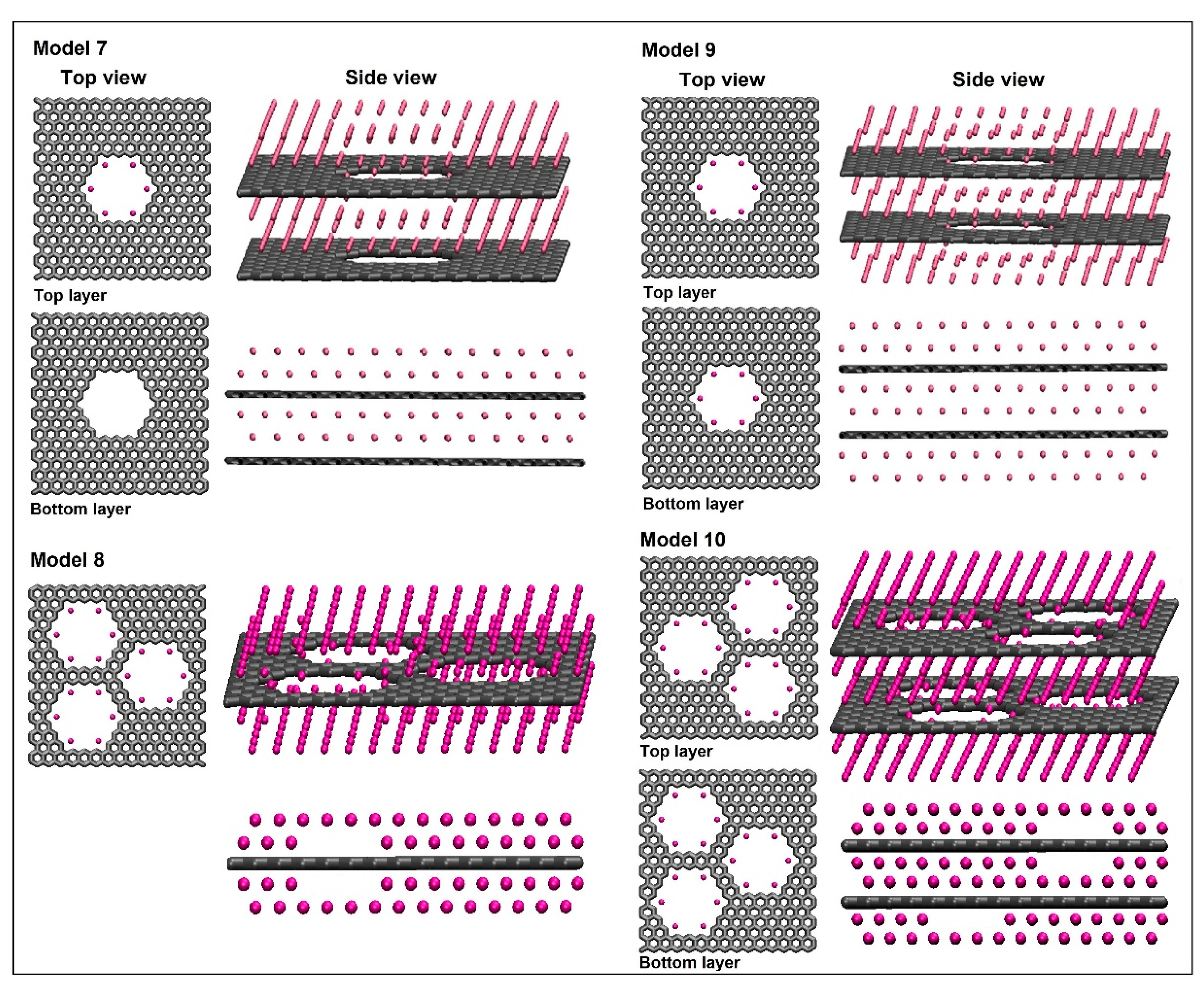
Models (M7-M10) are presented in Figure 8. Like M6, the lowest energy for models M7, M9 and M10 was found at the separation around 0.6 nm between graphene layers. Model M7 is like model M6, however, six lithium ions were distributed inside the top graphene pore. In model M9, we added another six lithium ions inside the bottom graphene pore and an additional two lithium layers below the second graphene sheet. In models M8 and M10, the number of pores in a single graphene layer is increased to three. Model M8 contains a single layer of nanoporous graphene with two lithium layers above and below it with additional lithium ions assembled inside all three pores. Model M10 contains a bilayer of nanoporous graphene with three pores in each graphene layer.
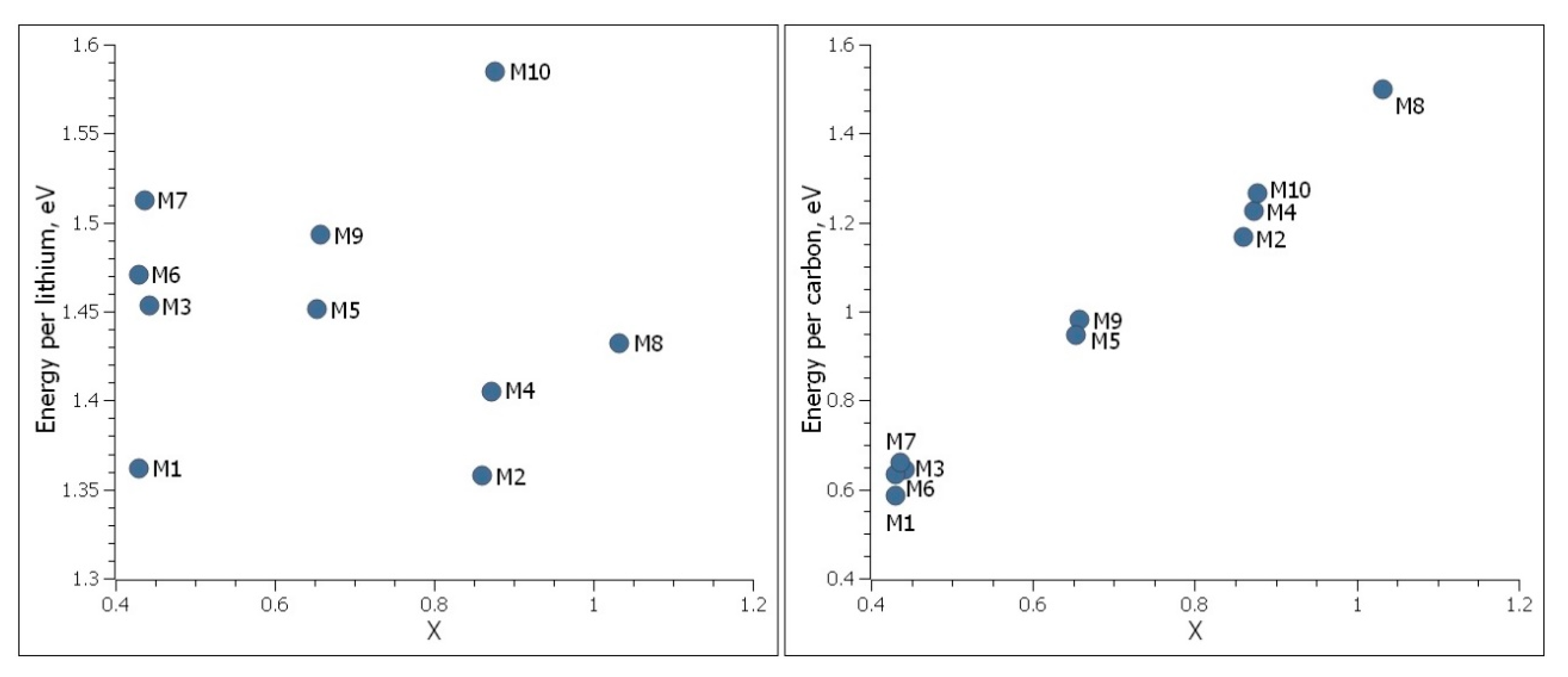
The adsorption energy per lithium and adsorption energy per carbon were calculated for these models and are shown in the Figure 9. We found that Model M10 is a better atomic structure considering all other models due to its highest energy per lithium with high lithium density. On the other side, its energy per lithium is still lower than the cohesive energy of metallic lithium. Next best structures are M7 and M9. Since M7 has two lithium layers missing at the bottom of the second nanoporous graphene sheet, it has a lower lithium density in comparison to M9. Model M8 has high lithium-ion density, however, it has significantly less adsorption energy per lithium as it contains only a single layer of nanoporous graphene.
These investigations show that structures containing Li in the pores and in between the graphene sheets have higher adsorption energy per lithium. Multilayer nanoporous graphene with pores are found to be more favorable. There are no favorable single layer nanoporous graphene structures if they do not contain many nanopores. Lithium ions will likely be only in the nanopores of single layer nanoporous graphene structures. Adding nanopores to single layer graphene may help to increase the Li capacity. Bilayer nanoporous graphene will contain more lithium due to intercalation between the layers. We believe, the best structures will be multilayer nanoporous graphene structures and adding more nanopores to multilayer nanoporous graphene can result with higher Li storage capacity.

4. Conclusions

Lithium adsorption mechanism a graphene nanopore was studied by performing first principles calculations. The lithium adsorption sites were 0.253 nm away from the center of the C-C bond at the edge of the pore and at 0.0 nm heights. More lithium ions were distributed in the pores considering the preferred adsorption sites. These lithium-ion distributions in graphene nanopores were evaluated based on adsorption energy per lithium. Most of these distributions have lithium adsorption energies higher than cohesive energy of metallic lithium. Final part of the study was on creation of multilayer lithium – nanoporous graphene model structures and their evaluations. We found that lithium ions will likely be only in the nanopores of single layer nanoporous graphene structures. On the other side, adding more nanopores to multilayer nanoporous graphene can result with higher Li storage capacity.

Author Contributions

The authors confirm contribution to the paper as follows: study conception and design: L.B, A.B; investigations: L.B.; analysis and interpretation of results: L.B, A.B.; draft manuscript preparation: L.B., A.B.; supervision: A.B. All authors reviewed the results and approved the final version of the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. P. Zhu, D. Gastol, J. Marshall, R. Sommerville, V. Goodship, E. Kendrick. A review of current collectors for lithium-ion batteries. Journal of Power Sources, 2021, 36, 229321. [CrossRef]
  2. J. Hou, S. Qu, M. Yang, J. Zhang. Materials and electrode engineering of high capacity anodes in lithium ion batteries. Journal of Power Sources, 2020, 450, 227697. [CrossRef]
  3. L. Zhang, X. Qin, S. Zhao, A. Wang, J. Luo, Z. L. Wang, F. Kang, Z. Lin, B. Li. Advanced Matrixes for Binder-Free Nanostructured Electrodes in Lithium-Ion Batteries. Advanced Materials, 2020, 32, 1908445.
  4. H. Zhang, Y. Yang, D. Ren, L. Wang and H. Xiangming. Graphite as anode materials: Fundamental mechanism, recent progress and advances. Energy Storage Materials, 2021, 36, 147-170. [CrossRef]
  5. B. Ding, Z. Cai, Z. Ahsan, Y. Ma, S. Zhang, G. Song, C. Yuan, W. Yang and C. Wen. A review of metal silicides for lithium-ion battery anode application. 2021, 34 (3), 291-308.
  6. M.M. Obeid, Q. Sun Recent advances in topological quantum anode materials for metal-ion batteries. J. Power Sources, 2022, 540, 231655. [CrossRef]
  7. N. Alam, A. Ullah, Y. Khan, W. C. Oh and K. Ullah. Fabrication and enhancement in photoconductive response of α-Fe2O3/graphene nanocomposites as anode material. J. Mater. Sci.: Mater. Eletron., 2018, 29 (20), 17786-17794.
  8. C. Choi, D.S. Ashby, D.M. Butts, R.H. DeBlock, Q. Wei, J. Lau, B. Dunn. Achieving high energy density and high power density with pseudocapacitive materials. Nat. Rev. Mater., 2020, 5, 5-19. [CrossRef]
  9. L. Peng, Z. Fang, Y. Zhu, C. Yan, G. Yu. Nanoporous 2D nanomaterials for electrochemical energy storage. Adv. Energy Mater., 2018, 8, 1702179. [CrossRef]
  10. S. Jia, J. Zang, P. Tian, S. Zhou, H. Cai, X. Tian, Y. Wang. A 3-D covalently crosslinked N-doped porous carbon/nanoporous graphene composite for quasi-solid-state supercapacitors. Microporous Mesoporous Mater, 2020, 293, 109796. [CrossRef]
  11. J. Bi, Z. Du, J. Sun, Y. Liu, K. Wang, H. Du, W. Ai, W. Huang. On the Road to the Frontiers of Lithium-Ion Batteries: A Review and Outlook of Graphene Anodes, 2023, 35, 16, 2210734. [CrossRef]
  12. X. Zhang, J. Zhou, C. Liu, X. Chen, H. Song. A universal strategy to prepare porous graphene films: binder-free anodes for high-rate lithium-ion and sodium-ion batteries. J. Mater. Chem. A, 2016, 4, 8837-8843. [CrossRef]
  13. M. Ye, H. Cheng, J. Gao, C. Li, L. Qu. A respiration-detective graphene oxide/lithium battery. J. Mater. Chem. A,2016, 4, 19154-19159. [CrossRef]
  14. Z. Mi, D. Hu, J. Lin, H. Pan, Z. Chen, Y. Li, Q. Liu, S. Zhu. Anchoring nanoarchitectonics of 1T’-MoS2 nanoflakes on nanoporous graphene sheets for lithium-ion batteries with outstanding high-rate performance. Electrochimica Acta, 2022, 403, 139711. [CrossRef]
  15. E. Lee and K. A. Persson. Li Absorption and Intercalation in Single Layer Graphene and Few Layer Graphene by First Principles. Nano. Lett. 2012, 12, 4624 – 4628.
  16. Y. Liu, Y. M. Wang, B. A. Yakobson, and B. C. Wood, Phys. Rev. Lett. 2014, 113, 028305.
  17. D. Datta, J. Li, N. Koratkar and V. B. Shoney, Carbon, 2014, 80, 305-310.
  18. Y. J. Tsai and C. L. Kuo, ACS Appl. Mater. Interfaces, 2020, 12, 22917-22929.
  19. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter QUICKSTEP: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach, Comput. Phys. Comm., 2005, 167, 103-128. [CrossRef]
  20. C. Wang, W. Zhang, H. Sun, R.M. van Horn, R.R. Kulkarni, C. Tsai, Hsu C., B. Lotz, X. Gong and S. Z. D. Cheng. Adv. Energy Mater, 2012, 2,1375.
  21. J. VandeVondele and J. Hutter. Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases. J. Chem. Phys., 2007, 127, 114105. [CrossRef]
  22. S. Goedecker, M. Teter and J. Hutter. Separable dual-space Gaussian pseudopotentials. Phys. Rev. B, 1996, 54, 1703. [CrossRef]
  23. S. Grimme, J. Antony, S. Ehrlich and H. Krieg. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys., 2010, 132,154104. [CrossRef]
  24. D.C. Liu and J. Nocedal. On the Limited Memory BFGS Method for Large Scale Optimization, Math.Prog., 1989, 45, 503-528.
  25. W.Y. Ching and J. Callaway, Phys. Rev. B. 1974, 9, 5115.
  26. Buldum, and G. Tetiker. First-principles study of graphene-lithium structures for battery applications, J. Appl. Phys., 2013, 113, 154312. [CrossRef]
Preprints 116803 g001
Figure 1. Top views of the pore structures and variation of total energy of as a function of Li-graphene pore separation dLi perpendicular to graphene plane for C0H, C2H and C6H graphene pore sizes are presented. Periodic boundary conditions are used in all three directions. There is a 30-angstrom gap in the perpendicular direction.
Figure 1. Top views of the pore structures and variation of total energy of as a function of Li-graphene pore separation dLi perpendicular to graphene plane for C0H, C2H and C6H graphene pore sizes are presented. Periodic boundary conditions are used in all three directions. There is a 30-angstrom gap in the perpendicular direction.
Preprints 116803 g001
Preprints 116803 g002
Figure 2. The graphene pore symmetric parts and important translation lines or directions for models C6H, C24H and C54H.
Figure 2. The graphene pore symmetric parts and important translation lines or directions for models C6H, C24H and C54H.
Preprints 116803 g002
Preprints 116803 g003
Figure 3. Total energy of the structure as a function of Li-graphene pore edge separation dLi parallel to graphene plane for C6H, C24H and C54H graphene pore sizes. The energy values are relative to the C-site energy in each model structure.
Figure 3. Total energy of the structure as a function of Li-graphene pore edge separation dLi parallel to graphene plane for C6H, C24H and C54H graphene pore sizes. The energy values are relative to the C-site energy in each model structure.
Preprints 116803 g003
Preprints 116803 g004
Figure 4. Li-graphene pore edge distance for C24H and C54H pore sizes along D-line with the lowest energy positions presented for C24H.
Figure 4. Li-graphene pore edge distance for C24H and C54H pore sizes along D-line with the lowest energy positions presented for C24H.
Preprints 116803 g004
Preprints 116803 g005
Figure 5. Adsorption energy per lithium and adsorption energy per carbon as a function of lithium density, x, of single layer nanoporous graphene with Li assembly inside the pore at 0.00 nm and 0.172 nm heights. Cohesive energy of metallic lithium is represented by a grey line in figure 5(a). Ecoh = 1.68 eV.
Figure 5. Adsorption energy per lithium and adsorption energy per carbon as a function of lithium density, x, of single layer nanoporous graphene with Li assembly inside the pore at 0.00 nm and 0.172 nm heights. Cohesive energy of metallic lithium is represented by a grey line in figure 5(a). Ecoh = 1.68 eV.
Preprints 116803 g005
Preprints 116803 g006
Figure 6. (a) Multilayer lithium-nanoporous graphene structures. (b) Side views of the atomic structures of the models M1-M4 and top views of the pores.
Figure 6. (a) Multilayer lithium-nanoporous graphene structures. (b) Side views of the atomic structures of the models M1-M4 and top views of the pores.
Preprints 116803 g006
Preprints 116803 g007
Figure 7. The atomic structures for models M5 and M6 with and without Li inside the pores, respectively.
Figure 7. The atomic structures for models M5 and M6 with and without Li inside the pores, respectively.
Preprints 116803 g007
Preprints 116803 g008
Figure 8. The structures for models M7-M10.
Figure 8. The structures for models M7-M10.
Preprints 116803 g008
Preprints 116803 g009
Figure 9. Adsorption energy per lithium and adsorption energy per carbon as a function of lithium density, x, of single and bilayer nanoporous graphene structures. Cohesive energy of metallic lithium is Ecoh = 1.68 eV.
Figure 9. Adsorption energy per lithium and adsorption energy per carbon as a function of lithium density, x, of single and bilayer nanoporous graphene structures. Cohesive energy of metallic lithium is Ecoh = 1.68 eV.
Preprints 116803 g009
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated