Preprint
Article
Timed Interpreted Systems as a New Agent-Based Formalism for Verification of Timed Security Protocols
Altmetrics
Downloads
50
Views
26
Comments
0
A peer-reviewed article of this preprint also exists.
Submitted:
01 September 2024
Posted:
03 September 2024
You are already at the latest version
Alerts
Abstract
This article introduces a new method for modelling and verifying the execution of timed security protocols (TSP) and their time-dependent security properties. The method, which is both novel and reliable, uses an extension of interpreted systems, accessible semantics in multi-agent systems, and timed interpreted systems (TIS) with dense time semantics to model TSP executions. We enhance the models of TSPs by incorporating delays and varying lifetimes to capture real-life aspects of protocol executions. To illustrate the method, we model a timed version of the Needham-Schroeder Public Key Authentication Protocol. We have also developed a new SMT-based bounded model checking reachability algorithm for the proposed structures and implemented it with the tool. The method comprises a new procedure for modelling TSP executions, a translation of TSP into TIS, and a translation of TIS's reachability problem into the SMT problem. The paper also includes thorough experimental results for nine protocols modelled by TIS and discusses the findings in detail.
Keywords:
Subject: Computer Science and Mathematics - Security Systems
1. Introduction
Security Protocols (SPs) play a fundamental role in ensuring the secure exchange of data across communication systems. The primary objectives of these protocols include achieving unilateral or bilateral authentication of the communicating parties, preserving the confidentiality and integrity of the transmitted information, and distributing new session keys that enable encrypted and secure communication channels. SPs, such as widely implemented communication protocols, are typically integral components of larger systems. However, both literature and practical network implementations have revealed numerous flaws in existing SP schemes, such as those found in the Needham-Schroeder Public Key Authentication protocol [1], CCITT X.509 [2], and the Wide Mouth Frog protocol [3], among others. Identifying these vulnerabilities underscores the critical need for robust methods to verify the properties of SPs to ensure their correctness and security.
Introducing temporal elements into SP schemes significantly increases the complexity of their modelling and verification processes but also enhances the model’s expressiveness by allowing the consideration of time-dependent security properties. However, modelling time accurately in the context of security protocols is inherently challenging, and addressing time-related security properties is even more complex.
Timed Interpreted Systems (TIS) offer an advanced framework for cryptographic protocol verification by incorporating the temporal dimension, which is crucial for accurately modelling and analyzing protocols that rely on time constraints. TIS extend traditional interpreted systems by enabling reasoning about the timing of actions, essential for detecting and mitigating time-based attacks, such as replay or delay attacks [4]. By explicitly modelling timing requirements, TIS can verify time-sensitive properties, such as the timely delivery or expiration of cryptographic tokens, ensuring that these properties are upheld throughout the execution of the protocol [5]. Additionally, TIS facilitate the verification of liveness properties, such as guaranteeing that a protocol completes within a specified time frame, which is critical for protocols requiring responsiveness [6].
TIS are particularly effective in analyzing scenarios where synchronization between agents is necessary, such as in multi-party cryptographic protocols, thereby enhancing resilience against synchronization-related vulnerabilities [7]. They provide a formal framework to model and reason about temporal aspects, including timeouts, delays, and deadlines, which are crucial in cryptographic operations like key exchange and session management [8]. By integrating time into epistemic logic, TIS enable the verification of temporal-epistemic properties, such as ensuring that ,,an agent knows within a certain time that a message has been securely received”, which is vital for secure communication protocols [9].
Furthermore, TIS improve the modelling of network delays and processing times, critical factors affecting real-world cryptographic protocols’ security [10]. They allow for a more realistic analysis of how time impacts protocol security under various environmental conditions, such as in mobile networks or high-latency settings, thereby providing more robust security guarantees [11]. TIS also ensures that security properties are maintained in logical terms and within the required time constraints, thus enhancing the practical security of cryptographic systems [12]. This comprehensive temporal modelling leads to more robust cryptographic protocol designs that are better equipped to withstand real-world, timing-based threats.
The primary objective of this paper is to present a novel method for modelling and analysing protocol executions, taking into account the temporal relationships and dependencies among the time primitives involved, such as ticket generation times, validity periods, and data transmission times within the network.
We require a description in the language specified by the tool to verify protocol properties formally using specific verification tools. It necessitates strict language rules that prevent the direct use of traditional protocol message descriptions. Our approach begins by describing the timed protocol using the well-established Alice-Bob notation. We then formalize it using a time-extended version of the ProToc specification language [13], which captures all external and internal actions performed during the protocol. This description is subsequently used to automatically create a model of protocol executions with time dependencies as a Timed Interpreted System (TIS). This system models the behaviours of honest agents, the intruder, and the environment, all represented as networks of synchronizing timed automata [14,15]. We selected TIS for modelling Timed Security Protocol (TSP) executions due to limitations in previous approaches that modelled TSPs as networks of timed automata [14,15]. These approaches could not separate users from their operational environment, relied on non-interleaved semantics of timed automata–preventing the modelling of real-world SP executions–and only considered a single delay and lifetime parameter.
Our proposed method addresses these limitations by expanding the number of analysed time parameters, thereby enabling a deeper analysis. Furthermore, our approach utilizes dense time semantics, which facilitates the analysis of a broader range of attacks [16].
To automatically verify the fundamental security properties of TSPs, we employ SMT-based bounded model checking (BMC) [17,18], a symbolic model-checking technique known for its efficiency in finding counterexamples and mitigating the state explosion problem. BMC operates by checking whether the negation of the property of interest holds in a pruned model up to a specific depth, reducing the problem to the satisfiability of a quantifier-free first-order formula.
The structures created and utilized in our BMC method encompass all elements necessary for modelling and verifying timed protocol primitives, including ticket generation times, validity periods, and data transmission times across the network. The results demonstrate the ability to establish characteristic time dependencies that determine the correct functioning of each protocol.
In conclusion, the primary contributions of this paper consist of a new formal verification approach for TSP security properties, which include:
- modelling TSP executions as timed interpreted systems with real-time, in which each agent (user) taking part in the protocol is modelled as a network of timed, synchronised automata – it is a more realistic solution compared with the previous ones;
- expressing times of actions performed during the protocol’s execution and the network delays (which includes message generation times, encryption, decryption and network transfer times) – using these, we can compute dependencies between these values and lifetimes of TSPs’ time primitives (time tickets), which is essential when considering the possibility of an attack;
- the ability to detect and prevent the existence in the network of a passive Intruder in Man-in-the-Middle configurations;
- considering a strongly monotonic version of dense timed semantics, and many different lifetimes, and their values;
- new, suitable implementation and experimental results.
These ideas will be further developed and discussed in the subsequent sections.
Related Work
The application of timed automata and timed multi-agent systems (MAS) in verifying cryptographic protocols has gained significant momentum in recent years, underscoring the critical importance of temporal aspects in securing communication protocols and systems. Recent studies reflect this evolution by addressing the challenges of time-sensitive attacks, enhancing security features, and ensuring system robustness under various operational conditions.
Since the 1990s, researchers have proposed numerous methodologies for verifying the properties of security protocols. Beyond basic real or virtual simulations, several mathematical approaches, including inductive and deductive methods, have been introduced [19,20]. These methods prove that a given protocol possesses a specific security property. Currently, the most effective methods in this domain involve model checking of transition systems that encode user behaviour, including their knowledge during the execution of a protocol [14,17,21,22,23,24,25].
In recent years, there has been an increasing need to consider the properties of time-dependent protocols, which is inherently challenging due to the complexity of time models. Only a few well-founded approaches address time dependencies between protocol parameters or user behaviours [26,27,28,29]. Several notable proposals utilise MAS for verification purposes within the extensive literature on the verification of timed security protocols (TSPs).
For example, [30] introduces a new MAS-based semantics for security protocol verification called LDYIS, which employs rewriting rules for the automatic generation of protocol runs, where certain temporal epistemic logic can be interpreted. In [31], the authors formalise the concept of attack detectability within MAS and demonstrate its application to a variant of the Kerberos protocol. These approaches have also been applied to more complex systems like e-voting protocols. In [32], the same authors propose a new technique for automatically verifying protocols specified in the CAPSL language [33]. They define translation models based on CAPSL descriptions into Interpreted Systems, the most widely used semantics for temporal-epistemic logic. The method also includes rewriting protocol goals expressed in CAPSL into temporal-epistemic formulas, which are then linked to the MCMAS symbolic model checker for verification.
The study presented in [34] addresses the analysis of security protocol properties for an unbounded number of sessions. The authors define a parameterised model-checking problem based on security requirements formulated in temporal-epistemic logic, focusing on authentication and key-establishment protocols. A specialised tool is proposed and utilised to verify the properties of the NSPK and ASRPC protocols. However, these MAS-based approaches must address the temporal aspects of security protocols.
The difficulty of modelling time has limited the development of solutions addressing the temporal properties of TSPs. Notable contributions include works such as [14,35,36,37], which incorporate time primitives into formal modelling systems to describe and verify temporal properties.
One of the earliest studies on TSP verification, [35] and [36], employed different types of Timed Automata for formal TSP modelling. In [14], the authors adapted Networks of Timed Synchronised Automata for TSP verification. In a subsequent study, [38], a systematic method was developed to formally specify and automatically verify timed security protocols with clock drift. In [26], a parametric verification approach for TSPs was proposed using a timed version of calculus for specification. This method defines its formal semantics as a transition structure constructed over timed logic rules, facilitating the efficient verification of TSP properties. The authors also introduced the concept of minimal network latency, describing the time required for message composition (including encryption) within the network.
Further contributions include [39], demonstrating how self-adaptive MAS can dynamically adjust to environmental changes using probabilistic timed automata to verify system behaviour and enhance operational stability. Similarly, [40] presents a methodology integrating automata learning to improve timed systems’ synthesis and verification processes, signalling a shift towards automated and scalable solutions. The article [41] focuses on symbolic approaches for verifying timed cryptographic primitives, providing new tools for ensuring time-limited security properties in protocols like sealed-bid auctions and contract signing. Moreover, studies such as [42] and [43] explore novel techniques for analysing communication protocols’ temporal behaviour and correctness by integrating new logical frameworks and model-checking tools. These advancements emphasise the critical role of temporal dimensions in cryptographic protocol analysis, fostering a new era of research where timing constraints and behaviours are central to the verification process, ultimately enhancing the security and reliability of cryptographic systems.
However, these approaches often need to adequately account for the time required to compose and decompose messages, which is crucial for cryptographic operation protocols. In complex cases, the time required for message generation may exceed the network delay time. Additionally, the existing literature often assumes that the lifetime values are consistent across all timestamps and that the minimal network latency remains constant throughout all protocol steps. Furthermore, these studies do not explicitly differentiate between protocol users. Our new approach addresses all of these limitations identified in previous works.
Paper Organisation
The remainder of the paper is structured as follows. Section 2 provides a brief overview of the theory behind timed interpreted systems. In Section 3, we discuss the theory of Security Protocols modelling and introduce our novel modelling approach. The subsequent section focuses on enhancing the SMT-based BMC reachability analysis for Timed Interpreted Systems. Section 5 presents an experimental evaluation of our SMT-based algorithm’s performance and the results of reachability analysis for Security Protocols modelled using TIS. Finally, we provide a concluding discussion in Section 6.
2. Timed Interpreted Systems
Interpreted systems (ISs) [44] were initially developed to model distributed systems. However, with the increasing interest in Multi-agent Systems (MASs) [45], the concept of ISs has evolved into a formalism for modelling, for example, communication between agents. Over the years, this formalism has been successfully extended [46,47,48]. The formalism of timed interpreted systems (TISs), as presented in [48], enhances ISs by enabling reasoning about the discrete time aspects of MASs. In our work, we have extended this capability to reason about the real-time aspects of MASs. The primary advantage of employing dense time semantics is that timed models with dense time allow for abstraction from the specific rate at which clocks may tick. In contrast, using discrete-time semantics results in timed models where each clock ticks and measures time in discrete units.
We begin by establishing some notation that will be used throughout the paper. Let denote the set of positive real numbers, denote the set of natural numbers, and denote a finite set of variables known as clocks. Each clock is a variable that ranges over the set of non-negative real numbers. For a clock and a constant , we define the set of clock constraints over , denoted by . These constraints, , are conjunctions of comparisons between a clock and a time constant c taken from the set of natural numbers, . Next, we recall the Timed Interpreted Systems (TIS) definition from [48]. Let represent a non-empty finite set of agents, and let represent a special agent used to model the environment in which these agents operate. Additionally, let be the set of propositional variables, where for all distinct agents . The set of agents, , and the environment, , form a multi-agent system (MAS).
A timed interpreted system is defined as a tuple:
The set denotes a non-empty set of clocks, ensuring that for all distinct agents . The function is a protocol function that models the program executed by the agent . Formally, for any agent , the actions are determined according to this local protocol.
A valuation function assigns to each location a set of atomic formulae that are considered true at that location. The set represents the collection of joint actions performed by all agents.
The evolution function specifies how local states ’evolve’ based on several factors: the local state of the agent, the actions of other agents, the local state of a special agent representing the environment, the clock constraints of the agent , and the set of clocks to reset. A function is a (partial) evolution function for agents, while a function is a (partial) evolution function for the environment.
We assume that the environment’s locations, actions, and clocks are ’public’, while the locations and clocks of any agent are considered ’private’. We further assume that if , then for , any , and any .
Each element t of is represented by a tuple , where denotes the source location, represents the target location, a is the action, is the enabling condition for , and is the set of clocks reset when performing t. The guard must be satisfied to enable the transition.
3. Modelling of TSP Executions
This section briefly overviews the foundational theory of security protocols and introduces our novel method for modelling the execution of Timed Security Protocols as Timed Interpreted Systems. Security Protocols (SPs) are distributed algorithms that define a sequence of data exchanges during communication within a network. During the execution of a protocol, the actions of the involved parties can be categorised into internal actions–such as generating new confidential information, encrypting and decrypting cryptograms, comparing data, or performing mathematical operations on locally stored data—and external actions, which involve the mutual transmission of information between the parties. To illustrate our new method clearly, we have selected an example involving the timed version of the Needham–Schroeder Public-Key Protocol (NSPKT) [49]. The NSPKT, presented in Alice-Bob notation, proceeds as follows:
In the first step, , user A initiates communication by sending an encrypted message to user B. This message includes the timestamp (ticket) generated by A and the identifier . User B decrypts the message to obtain the ticket . In response, during the second step, , user B generates their own ticket and combines it with the ticket in an encrypted message, which is then sent back to A. In this manner, it appears that B is authenticating to A. Subsequently, user A decrypts the received message and returns the timestamp to B. Again, this appears to authenticate user A to user B.
Since 1978, the NSPK protocol was widely used until 1995, when Gavin Lowe discovered an attack [50] that involved two interlaced executions of the protocol.
The executions and cannot occur independently. In the first execution, , an honest user A sends a message to the user I. Here, the Intruder I acts like a normal user. In the second execution, , the Intruder impersonates user A and relays information from A to B. In doing so, the Intruder deceives B by assuming the identity of A.
Before commencing the modelling process, several underlying assumptions must be considered. Firstly, honest users generate dedicated, confidential information only once for a given execution and do not reuse it. The Intruder, however, is capable of generating keys, timestamps, and messages for backup purposes, storing them, copying elements from others, presenting them as their own, impersonating users, and taking control. Encryption is assumed to be secure, and the Intruder cannot decrypt messages without the appropriate key. The Intruder may intercept communication and attempt to exploit any information gained after earning the trust of honest users. Additionally, it is essential to consider temporal dependencies, such as lifetimes and delays. All of these assumptions are incorporated into our modelling approach.
In this work, as in [14], we treat a Timed Security Protocol (TSP) as an abstract object. The hypothetical executions of the protocols specified in the ProToc language can be generated as composite substitutions of the abstract protocol within a defined finite space and structure, reflecting the actual operation of the network. For our experiments, we consider a space comprising two honest users, an Intruder, one key (or one pair of keys), and a one-time ticket per user. These hypothetical substitutions can be generated automatically using combinatorial techniques. By incorporating the Intruder in this manner, we can compute such executions as:
,
(Intruder as an ordinary user),
(Intruder impersonating B),
,
,
(Intruder impersonating A),
,
,
,
,
and several others of a similar nature. The executions mentioned above are translated into a product of synchronised automata. Given that we know in which execution the Intruder impersonates an honest user, our goal is to determine whether the final step of one of these executions can be performed in our experiments. To achieve this, we check the reachability of undesired states within our automata network. Our analysis is based on the Dolev-Yao model of the Intruder. This concept is illustrated in the following example and Figure 2.
3.1. TIS for NSPKT Executions Modelling
We now explain how the previously defined structures are utilised to build the TIS model for NSPKT executions. Translating the protocol specified in ProToc into a Timed Interpreted System extends the method presented in [13,14].
The so-called execution automata represent the transmission of messages within the network. Each execution of the protocol is modelled as a distinct automaton, where each transition corresponds to a single step of the protocol. Additionally, we introduce a separate automaton that models the system’s time clock. The collection of all such automata constitutes the environment of our TIS model. In real network scenarios, the execution of protocols depends on the user’s knowledge, as every step can only be executed with the user possessing the requisite knowledge. To represent this, we define and employ knowledge automata that model the knowledge of users [14]. For instance, an automaton models the knowledge of user A regarding the timestamp . These automata function similarly to characteristic functions over the set of knowledge primitives. They consist of two states: the first states indicate that the user lacks a particular piece of knowledge (such as ), while the second state represents the situation where the user has acquired that knowledge (). In such automata, the first transition model possesses the process of the proper primitive, and the loop in the second state models the necessity of knowing a primitive for executing a protocol’s step. These loops are specific guards for executing steps from the user’s knowledge point of view. In this way, we can model the protocol’s executions as the work of a TIS system that consists of three agents: a collection of automata that model the environment (executions automata [14] and clock automaton) and the users that execute the protocol (modelled by knowledge automata). For one, honest execution of NSPKT, we have the following structure (Figure 1).
This system involves three agents: one representing each honest user and one representing the environment. Within the model, we distinguish automata that map the execution of the protocol (the first one in Figure 1) and the clock automaton, which can reset each clock within the system. The product of these automata constitutes the environment . We also differentiate a network of synchronised automata that model the knowledge of individual agents, with blue representing agent A and green representing agent B. For the components of the environment depicted, we consider the locations: , , , , ; the actions associated with the protocol steps, ; and a set of clocks . The clock serves as a global clock, reflecting the passage of time between individual steps. Thus, to transition to the next state, a certain amount of time must elapse, where i denotes the step number. The value of corresponds to the time required for ticket generation, encryption, message creation, or decryption. In some steps of the protocol, encryption or decryption time is not considered; this occurs when users send encrypted messages they received earlier or need more knowledge to decrypt the message.
Therefore, each transition depends on the time condition – guard , and for every step, the global clock is reset . The agent used the other two clocks to check the validity of the generated data. They are reset in transitions, during which the appropriate ticket is generated. For example, the environment’s clock , corresponding to the ticket , is reset when transition labelled with the action is executed because is generated in this step.
We assume the following local evolution functions for the environment:
,
,
.
As previously noted, agents are modelled using knowledge models. Each automaton, , represents the process by which a given agent X gains knowledge about a specific piece of data Y. For instance, the automaton models the behaviour of agent A concerning the data . These automata have two possible states: – representing the absence of knowledge, and – representing possession of knowledge. Additionally, there are temporal conditions to consider. For example, in the case of , during the action , a check is performed to determine whether the validity period of the information has expired, specified by . It is important to note that we distinguish different lifetimes for different tickets, as the later a ticket is generated, the shorter its duration is during the protocol’s execution. The local evolution functions for and are:
,
,
,
,
,
,
.
Analysing a single execution typically does not suffice to identify an attack. It is necessary to consider multiple executions, including those involving the Intruder, who will intertwine these executions precisely as they would occur in reality. There are three steps for each execution, and we can intertwine all of them. The rule is that the order of the steps within a single execution must be preserved, and a step cannot be executed if the sender does not possess the necessary knowledge to perform it. The second condition significantly reduces the search space. For example, consider the analysis of step . This step cannot be executed immediately after step because the Intruder does not know the ticket (he cannot decode the information received from B). In our model, the Intruder can continue operations (allowing appropriate transitions in the automata) by either sending complete information (as in step ) or by gathering the necessary individual components during the interlacing steps (as in and ).
Three automata are required to model the attack on the NSPKT protocol in the form of a Timed Interpreted System (TIS) (Figure 2), where their combined product represents the environment. Two of these automata are utilised to model the protocol’s execution, while the third automaton is responsible for resetting the clocks.
Figure 2.
Timed Interpreted System for Lowe attack on NSPKT
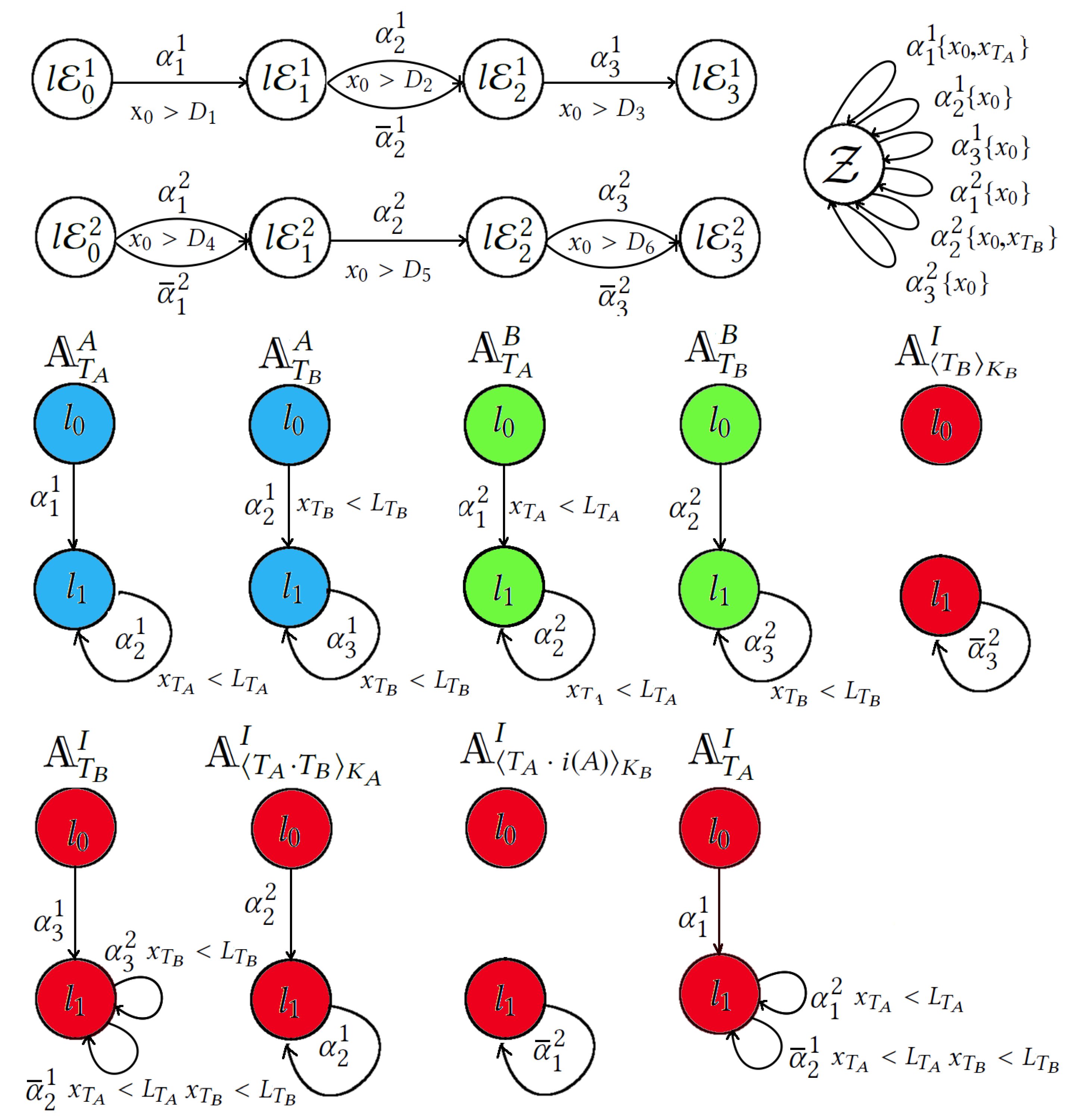
For these components of the environment, we define the locations as follows: , , , , actions , and a set of clocks . As observed, the superscript indicates the protocol execution number. Notably, there are no additional clocks, as the Intruder does not generate any new information. Instead, he merely duplicates the information that he has intercepted. The additional actions, denoted by , represent the Intruder’s enhanced capabilities. Specifically, he can retransmit the entire message if it has been intercepted previously or reconstruct it from individual components.
An additional agent is introduced to represent the Intruder in the version that includes an attack. Automata are also used to model the Intruder’s knowledge (depicted in red in Figure 2). For the Intruder, we have two standard automata, and , as well as an automaton that represents the possibility of the Intruder obtaining the entire message ().
The automata and , which lack transitions between states and (Figure 2), model the Intruder’s inability to proceed. We refer to these as blocking automata. Their inclusion allows the constructed interlacing model to be limited to only realistic behaviours. Thus, any path where the Intruder sends a message they could not formulate will not be represented.
We define the local evolution functions in a similar manner for the environment and the initial execution:
,
,
,
;
the second execution:
,
,
,
,
;
and the resetting automaton:
.
For the agents, we define the local evolution functions for the :
,
,
,
,
;
and for the ticket :
,
,
.
The intruder-specific automaton for a complete message can be described by the following functions:
,
;
and all the blocking automata:
,
The timed model induced by the above description of both NSPKT scenarios, as outlined in subsection 4.1, should be straightforward to infer.
4. Reachability Checking
Timed Interpreted Systems (TIS) provide computationally grounded semantics that enable the interpretation of time-bounded temporal modalities.
The transition system [51] that models the behaviour of TISs referred to as the timed model, consists of two types of transitions. The first type is action transitions, which are labelled with timeless joint actions representing the discrete evolutions of TIS. The second type is time transitions, labelled with non-negative real numbers corresponding to the passage of time. Due to the infinite nature of time, there are infinitely many possible time transitions.
Let us recall the necessary notations adopted from the theory of Timed Automata. A clock valuation v of is a total function mapping to the set of non-negative real numbers. The set of all clock valuations is denoted by . For a subset , the valuation that assigns the value 0 to all clocks in is defined as follows: and , and is denoted by . For and , is the clock valuation of that assigns the value to each clock x. A valuation v satisfies a clock constraint , denoted as if evaluates to true using the clock values provided by the valuation v.
4.1. Timed Model
For a given TIS, let the symbol denote the non-empty set of all the global states. Furthermore, for a specific global state , let the symbols and represent, respectively, the local component and the clock valuation of agent in the global state s.
We define a timed model (or simply a model) for a given TIS as a tuple , where: is the set of all initial global states; ; is a transition relation defined by action and time transitions. This relation is crucial in understanding how the system evolves, as it captures the possible transitions from one global state to another based on actions and time.
For an action , an action transition (denoted as ) holds if, for all , there exists a local transition such that and . Additionally, there must exist a local transition such that and . A time transition holds if, for all , we have and , where .
An infinite path in is defined as a sequence of states such that is an initial state, and for each even , there exists such that . For each odd , there exists a joint action such that .
Note that the above definition of a path ensures that the first transition is a time transition. Each action transition is followed by a time transition, and each time transition is followed by an action transition. Semantics in which every action transition is preceded by a time transition with is strongly monotonic. Strongly monotonic semantics require that no two events occur at the same time.
The transition system (timed model) of a timed interpreted system typically has infinitely many states and infinitely many labels. However, the reachability problem for can be reduced to a reachability problem for a transition system with finitely many states and finitely many labels.
Let be the largest constant c such that some clock x is compared with c in some constraint appearing in a guard of TIS. By , we denote the transition system for a timed interpreted system that differs from only in its set of labels: for the set of labels of , we take the set .
The region equivalence (the equivalence relation ≃) is defined over the set of all clock valuations for . For two clock valuations v and in , we say that if, for each , where n is the number of clocks, either and , or and and .
It is well-known that the relation ≃ is an equivalence relation, allowing for constructing a finite abstract model.
4.2. Reachability Analysis
The reachability problem for multi-agent systems (MAS) modelled by Timed Interpreted Systems (TISs) involves determining whether, for a specified set of target locations, a state containing a target location can be reached from some initial state. We assume that a propositional formula representing a particular property describes the set of target locations. To verify the reachability of a state that satisfies this property using the Bounded Model Checking (BMC) method, the model’s transition relation is initially unfolded iteratively to a certain depth k and encoded as a quantifier-free first-order formula of state variables. Subsequently, the property is converted into a quantifier-free first-order formula of state variables, and an SMT-solver is used to check the satisfiability of the conjunction of these two formulae.
If the conjunction (denoted in the algorithm by ) is satisfiable, it can be concluded that a path to a target location has been found. If not, the value of k is incremented by 2, as time transitions do not alter the global locations (Algorithm 1). The parameter n, which represents the number of steps in a given protocol, plays a crucial role in determining the depth of the model’s transition relation that needs to be unfolded.
| Algorithm 1 The standard bounded model checking algorithm for testing reachability |
|
The SMT encoding of the reachability problem for Timed Interpreted Systems (TIS) builds upon the encoding described in [52]. However, we have:
- refined the definitions for the encoding of the transition relation (as the definition in the cited paper lacked precision), and
- incorporated real-time aspects of multi-agent systems (MAS), whereas the previous SMT encoding was limited to discrete time.
Let be a model. To formulate and solve the reachability problem for TISs, we must define the unfolding of the transition relation up to depth . To this end, we define a k-path as a finite prefix of a path. Note that an arbitrary state s is reachable in if and only if it is reachable on a k-path for some .
Next, we define the formula , which symbolically encodes all the k-paths starting at the initial state of . The definition of the formula assumes that each global state of can be represented by a valuation of a symbolic state that consists of symbolic local states. Each symbolic local state is a pair of individual variables ranging over the natural numbers, which represent the local state of the agent and a clock valuation. Similarly, each action can be represented by a valuation of a symbolic joint action , which is a vector of individual variables ranging over natural numbers.
Let and be two symbolic states, a symbolic action, and a symbolic non-negative real number. We define the following quantifier-free first-order formulae:
- encodes the state s of the model ,
- encodes an action transition and ensures that every local action in is performed by each agent in which this action appears,
- encodes a time transition in .
For every even , we can now define the formula as follows:
Using the above formula and a quantifier-free first-order formula , which encodes the set of states that satisfy a given property, we aim to determine whether any state satisfying is reachable. It is achieved by verifying the satisfiability of the following formula:
Theorem 1.
The proof by induction on k is straightforward.Let be a model and s a state. Then, for every , the state s is reachable in via a path of length k if and only if the formula is satisfiable.
We terminate the unfolding of the transition relation if either the formula is satisfiable or if the SMT-solver cannot determine the satisfiability of the formula in question. Alternatively, termination could occur if the value of k equals the reachability diameter of the system–the minimum number of steps required to reach all reachable states. However, the reachability diameter cannot be calculated for many systems, and the available estimates often need more precise. This limitation results in BMC needing to be completed in practice.
5. Experimental Results
In this section, we present the experimental results and the implementation details.
5.1. Implementation.
We provide a complete end-to-end implementation1. All the protocols are specified using the ProToc language [13].
The first step of the method involves translating the executions of the TSP into TIS. The second step entails converting this model into a BMC problem, generating a file that encodes the transition relation as an SMT problem. The final step is to perform satisfiability checking using an SMT solver. Our SMT-based BMC reachability algorithm is implemented as a standalone program written in C++. For this purpose, we utilised the state-of-the-art SMT solver Z3 [53] (version 8.4.5).
5.2. SMT-Solvers
Given a quantifier-free first-order formula with variables defined in 4, the objective is to find an assignment for the variables that makes the formula satisfiable. Solving the SMT problem becomes particularly useful when restricted to specific logical theories, where existing tools, known as SMT solvers, are employed to find solutions. The most notable solvers include Z3 [53], Yices2 [54], and CVC4 [55].
For a given input, which is a conjunction of two quantifier-free first-order formulae, it denoted as , the SMT solver has three possible outcomes: sat: when the input is satisfiable; unsat: when the input is not satisfiable; unknown: when it is indeterminate whether is sat or unsat, as this determination exceeds the capabilities of the decision procedures.
Our choice for the Z3 SMT solver is motivated by several reasons. Z3 is used on an industrial scale; many experimental results for different systems, including MAS and timed automata, show that for reachability checking, Z3 gives the best results [37,56]. Z3 also can be trusted: when it answers sat, then it produces a witness (an assignment for variables) that makes the formula satisfiable; when it answers unsat, it produces proof that the formula is not satisfiable.
5.3. Performance Evaluation
Unfortunately, we could not compare our results with other approaches, as the executions of our TSP model are richer, capturing more time dependencies than the timed models mentioned in Section 1.
Our experiments were meticulously conducted on a high-performance computer, featuring an I7-5500U processor, 12 GB of RAM, and a Linux operating system running kernel 5.2.9. This robust setup ensured the reliability and accuracy of our results.
In our experiments, we examined the standard authentication and secrecy properties of TSP. In addition, we also detected and prevented situations where a passive intruder participates in the protocol execution by positioning themselves between the users and merely relaying all transmitted data. This scenario represents a Man-in-the-Middle (MitM) attack [57]. Although the intruder may not gain access to secret data or compromise the authentication process, the mere presence of the intruder in the network is undesirable. Such situations can be detected and prevented by selecting appropriate lifetime values.
We will discuss the experimental results and draw our conclusions based on nine timed versions of protocols well-known from the literature. We tested the following: the Needham-Schroeder Public Key Protocol (NSPKT) [49] and Lowe’s modification of NSPKT () [1,28]; the Denning-Sacco Protocol (DS) [58]; the Woo-Lam Pi Protocol (WLP) [37,59]; other versions of the Woo-Lam Pi protocol, WLP 1 and 3 [59]; the Andrew Protocol (AP) [60]; Lowe’s modification of the Andrew Protocol (P) [61]; and MobInfoSec (MIS) [62].
5.3.1. Andrew protocol
To present the experimental results, we assume the delay values: , , , and . For the Andrew protocol (Figure 3), we conducted a comprehensive analysis and identified two paths indicative of Man-in-the-Middle behaviour (though not a complete attack). In these paths, locations 74 or 94 were found to be reachable. Additionally, we observed two paths that correspond to honest executions (paths where location 4 or 9 was reachable) and eight paths representing executions involving the Intruder (paths where locations 14, 24, 34, 44, 54, 64, 84, or 104 were reachable). The term executions with the Intruder encompasses two scenarios: firstly, executions in which the Intruder behaves as a legitimate user (paths where one of the locations 14, 54, 64, or 104 is reachable); and secondly, executions in which the Intruder unsuccessfully attempts to impersonate honest users (paths where one of the locations 24, 34, 44, or 84 is reachable).
It was found that the minimum lifetime values for the assumed delay values that ensure only honest executions occur (i.e., values that prevent Man-in-the-Middle behaviour) are . The minimum values that permit Man-in-the-Middle behaviour to manifest at locations 74 and 94 are .
5.3.2. Lowe’s Modification of Andrew Protocol
For Lowe’s modification of the Andrew Protocol (Figure 4), we assumed the following delay values: , , and . With these delay settings, we identified two paths that indicate a Man-in-the-Middle behaviour (where locations 74 or 94 were reachable), two paths representing an honest execution (where locations 4 or 9 were reachable), and eight paths representing executions involving the Intruder (where locations 14, 24, 34, 44, 54, 64, 84, or 104 were reachable). The minimum lifetime values required to permit only honest executions are . The minimum values required to enable a Man-in-the-Middle behaviour (reachability of locations 74 and 94) are .
5.3.3. Denning–Sacco Protocol
In our analysis of the Denning–Sacco protocol (Figure 5), we assigned the following delay values: , , , . We found two paths that exhibit a Man-in-the-Middle behaviour, where locations 47 or 87 were reachable. Additionally, we discovered two paths representing an honest execution, with locations 3 or 7 being reachable, and two paths representing an execution involving the Intruder, with locations 43 or 83 being reachable. Our observations showed that for the Denning–Sacco protocol, under the assumed delays, the minimum value allowing both honest executions but not permitting a Man-in-the-Middle attack is . Furthermore, we determined that the minimum value enabling a Man-in-the-Middle behaviour for the given delays (reachability of locations 47 and 87) is .
5.3.4. Needham Schroeder Public Key Protocol
Within the NSPKT protocol (Figure 6), we assigned the following delay values: , , . Over the course of our analysis, we executed four scenarios, encompassing two instances of Intruder interventions, two Lowe’s attacks, and two instances of Man in the Middle behaviour. It’s important to note that, as outlined by the protocol structure, we were required to employ two distinct lifetime values, which play a crucial role in the protocol’s operation.
Lowe’s attacks were found to be possible at locations 23 or 55, while Man in the Middle behaviour could manifest at locations 47 or 71. Honest executions were feasible at locations 3 or 7. Intruder interventions were observed at locations 11, 15, 27, 31, 39, 43, 59, or 63.
Our investigation revealed that for the NSPKT protocol and the stipulated delays, the minimum values of ensured honest executions without enabling the Man in the Middle behaviour. To allow for the occurrence of the Man in the Middle behaviour at locations 47 and 71, the minimum required values were . These minimum values for honest executions and specific attacks are crucial for understanding the behaviour of the NSPKT protocol.
5.3.5. Lowe’s Modification of Needham Schroeder Public Key Protocol
In the NSPKT protocol (Figure 6), we assigned the following delay values: , , . During our analysis, we carried out four scenarios, including two Intruder interventions, two Lowe’s attacks, and two Man in the Middle behaviour. It is important to note that as per the protocol structure, we had to use two distinct lifetime values, which are crucial for the protocol’s operation.
Figure 7.
NSPKT Lowe’s modification
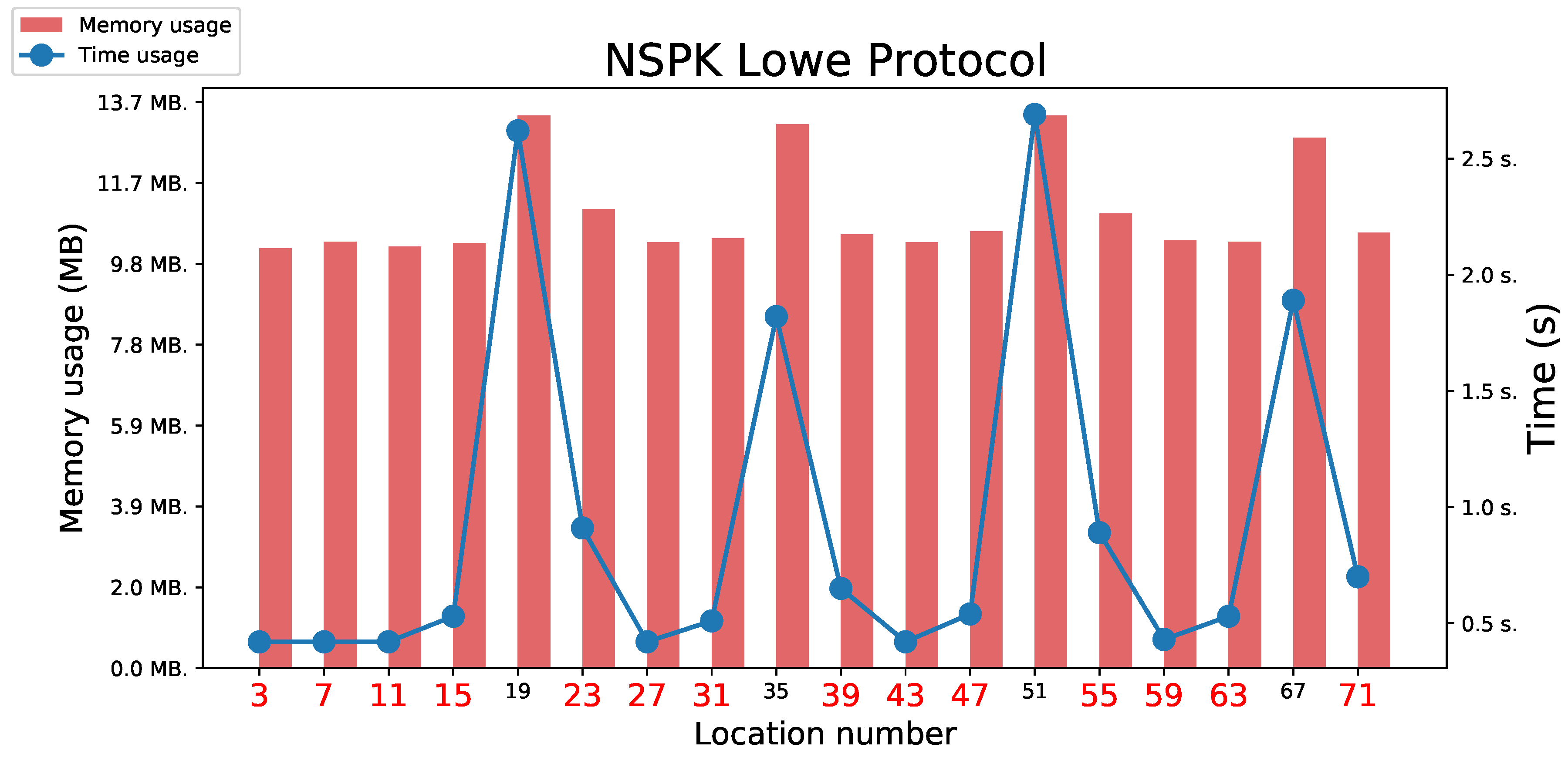
Lowe’s attacks were found to be possible at locations 23 or 55, while Man in the Middle behaviour could occur at locations 47 or 71. Honest executions were feasible at locations 3 or 7. Intruder interventions were observed at locations 11, 15, 27, 31, 39, 43, 59, or 63.
Upon investigation, we found that for the NSPKT protocol and the given delays, the minimum values of ensured honest executions without enabling the Man in the Middle behaviour. The minimum values that allow a Man in the Middle behaviour (the locations 47 and 71 are reachable) are . These minimum values for honest executions and specific attacks are crucial for understanding the behaviour of the NSPKT protocol.
5.3.6. Woo Lam Pi Protocol
We have established the following delay values for the WLP protocol (Figure 8): . Our analysis revealed two paths indicating potential Man in the Middle behaviour, with locations 71 or 131 being reachable. These two paths represent honest executions, with locations 5 or 11 being reachable, while ten other paths represent executions with an intruder, where locations 17, 29, 35, 41, 53, 77, 83, 89, 101 or 113 are reachable. Notably, for this protocol, the values are the minimum values allowing both honest executions. Furthermore, the minimum values that allow Man in the Middle behaviour to appear (locations 71 and 131 are reachable) are .
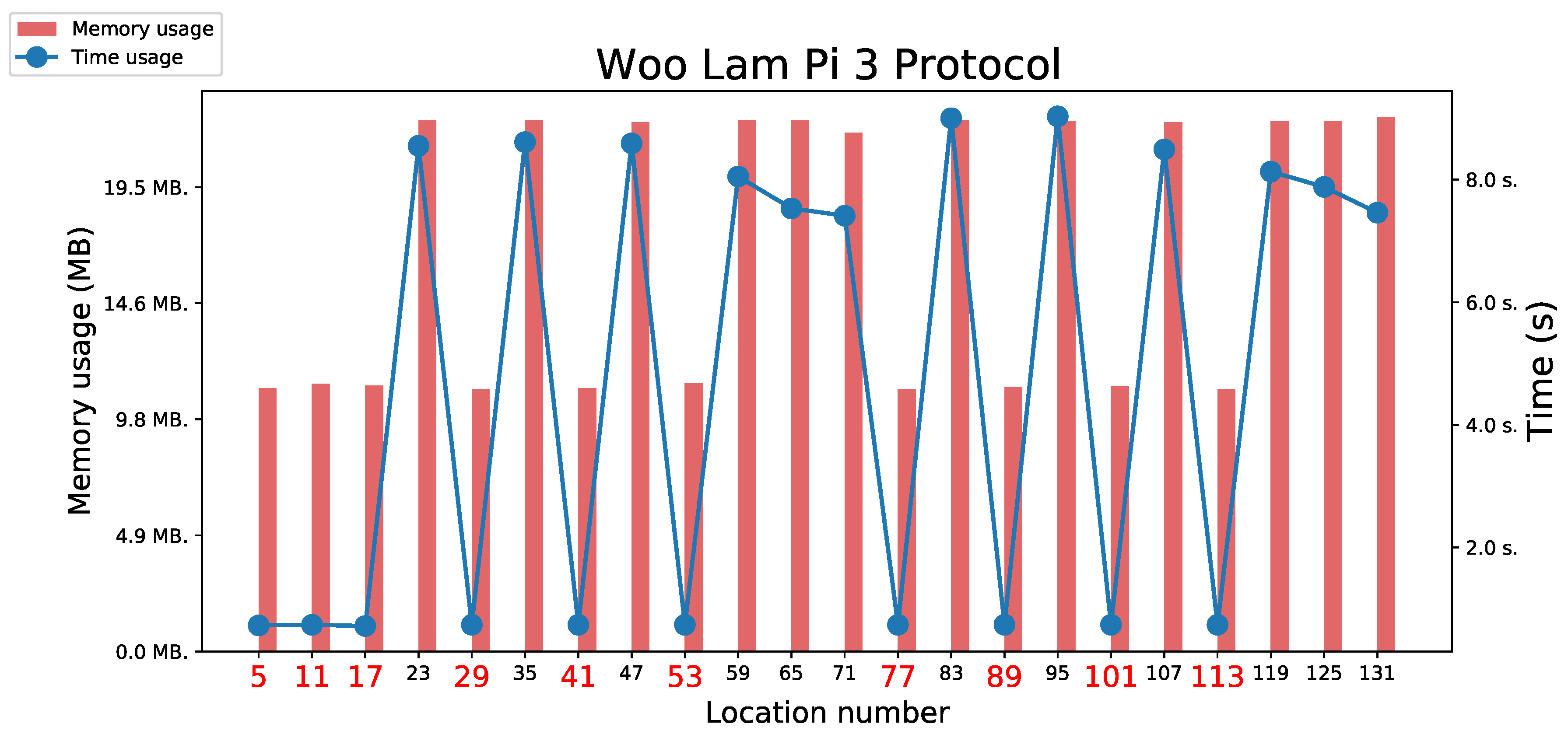
5.3.7. Woo Lam Pi 1 and 3
For the WLP1 and WLP3 protocols (Figure 9 and Figure 10), we assumed delay values as , , . We found two paths indicating a Man in the Middle behaviour (locations 53 or 113 are reachable). These two paths represent an honest execution (locations 5 or 11 are reachable), and six paths represent execution with the Intruder (locations 17, 29, 41, 77, 89 or 101 are reachable). For those protocols and the assumed delays, we observed that values are minimum values that allow us to perform honest executions and do not allow Man in the Middle behaviour. However, it was impossible to find the lifetime values that allow performing the executions to represent MitM behaviour for the assumed delays, highlighting the challenges in network security.
5.3.8. MobInfoSec Protocol
The MIS protocol has the following delay values: . We have identified four paths that indicate a Man in the Middle behaviour (locations 195, 1345, 1763, or 2463 are reachable), twenty-four paths representing an honest execution (locations from 1 to 24 are reachable), and 380 paths representing execution with the Intruder.
For this protocol, we have observed that values and are the only values that allow all the honest executions (these values do not allow a Man in the Middle behaviour). The minimum values that allow a Man in the Middle behaviour to appear (locations 1345, 1763, or 2463 are reachable) are .
The minimum values that allow all Man in the Middle behaviours to appear (locations 195, 1345, 1763, or 2463 are reachable) are .
5.4. Conclusions on Performance Evaluation
We have found the final results promising and would like to apply our approach further to validate more complex TSPs. Additionally, we aim to expand upon the algorithm presented in [37], which currently only considers a single lifetime value and does not account for system delays or the identification of time dependencies for when attacks occur. We plan to compare both approaches to assess their effectiveness.
6. Conclusions
This paper introduces Timed Interpreted Systems (TIS) with dense time semantics for modelling the execution of Timed Security Protocols (TSPs). We present the construction of the TIS model, a powerful tool that can capture changes in user behaviour and knowledge during protocol executions. Our model utilises specially designed time conditions to represent system delays and the intervals between executing specific protocol steps while adhering to time constraints based on timestamps and lifetime generation times.
The most recent method for verifying software systems [26] determines whether a system with specified parameter values functions correctly and identifies the relationships between parameters that must be satisfied for the system to operate correctly. These relationships can be established through testing or automated verification. Our research focuses on the latter goal.
We have introduced bounded model checking (BMC) for TIS. Our approach analyses the reachability properties of correctly specified model states. We applied the highly effective SMT-based BMC algorithm to nineteen security protocols, demonstrating its robustness and efficiency. Based on these promising preliminary results, we aim to model and verify more complex security protocols and properties in future work.
Author Contributions
Conceptualization, A.M.Z., A.Z., S.S., O.S-L. and M.K.; methodology, A.M.Z. and A.Z.; software, A.M.Z and A.Z.; validation, A.M.Z and A.Z.; formal analysis, A.M.Z, A.Z., S.S., O.S-L.; investigation, A.M.Z and A.Z.; resources, A.M.Z and A.Z.; writing—original draft preparation, A.M.Z and A.Z., S.S., O.S-L., M.K.; writing—review and editing, A.M.Z.; visualization, A.M.Z.; supervision, A.Z., and M.K.; project administration, A.M.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lowe, G. Breaking and Fixing the Needham-Schroeder Public-Key Protocol Using FDR. Proc. of TACAS’96; Springer-Verlag: London, UK, 1996; pp. 147–166. [Google Scholar]
- Burrows, M.; Abadi, M.; Needham, R. A Logic of Authentication. ACM Trans. Comput. Syst. 1990, 8, 18–36. [Google Scholar] [CrossRef]
- Dojen, R.; Jurcut, A.; Coffey, T.; Gyorodi, C. On Establishing and Fixing a Parallel Session Attack in a Security Protocol. Intelligent Distributed Computing, Systems and Applications. Springer, 2008, pp. 239–244.
- Boureanu, I.; Delicata, S.; Rasmussen, K. Timed Authentication in Security Protocols. International Journal of Information Security 2019, 18, 287–309. [Google Scholar]
- van der Meyden, R.; Su, K. Timed Epistemic Logic for Security Protocols. International Symposium on Trustworthy Global Computing. Springer, 2012, pp. 224–241. [CrossRef]
- Kremer, S.; Ryan, M.D.; Steel, G. A Compositional Proof System for Cryptographic Protocols with Time Constraints. In International Conference on Computer Aided Verification; Springer, 2018; pp. 110–128. [Google Scholar] [CrossRef]
- Dolev, D.; Halpern, J.Y.; Pinter, S. On Clocks and Messaging in Cryptographic Protocols. Journal of Cryptology 2004, 17, 41–58. [Google Scholar]
- Alur, R.; Dill, D.L. A Theory of Timed Automata. Theoretical Computer Science. Springer, 1994, pp. 116–135. [CrossRef]
- Halpern, J.Y.; Vardi, M.Y. Epistemic Logic for Distributed Protocols. Proceedings of the First Symposium on Logic in Computer Science. IEEE, 1989, pp. 250–260.
- Lomuscio, A.R.; Penczek, W.; Qu, H. Model Checking for Multi-Agent Systems with Time Constraints. Software and Systems Modeling 2017, 16, 425–444. [Google Scholar] [CrossRef]
- Herzberg, A.; Jarecki, S. Timed Communication Protocols in Adversarial Networks. International Workshop on Theory and Practice in Public Key Cryptography. Springer, 1995, pp. 73–89. [CrossRef]
- Kuhn, M.G.; Anderson, R.J. Timing Attacks on Cryptographic Protocols: Formal Analysis and Prevention. ACM Transactions on Information and System Security (TISSEC) 2010, 13, 47. [Google Scholar] [CrossRef]
- Grosser, A.; Kurkowski, M.; Piatkowski, J.; Szymoniak, S. ProToc - An Universal Language for Security Protocols Specifications. Soft Computing in Computer and Information Science. Springer, 2014, Vol. 342, Advances in Intelligent Systems and Computing, pp. 237–248.
- Kurkowski, M.; Penczek, W. Applying Timed Automata to Model Checking of Security Protocols. Handbook of Finite State Based Models and Applications, CRC Press, Taylor & Francis Group, 2016; 223–254. [Google Scholar] [CrossRef]
- Zbrzezny, A.M.; Siedlecka-Lamch, O.; Szymoniak, S.; Kurkowski, M. SMT Solvers as Efficient Tools for Automatic Time Properties Verification of Security Protocols. 20th Int’l Conf. PDCAT. IEEE, 2019, pp. 320–327.
- Kanovich, M.; Kirigin, T.; Nigam, V.; Scedrov, A.; Talcott, C. Discrete vs. Dense Times in the Analysis of Cyber-Physical Security Protocols. Proc. of 4th Conf. on Principles of Security and Trust, vol. 9036. Springer, 2015, p. 259–279.
- Basin, D.A.; Cremers, C.; Meadows, C.A. Model Checking Security Protocols. In Handbook of Model Checking; Springer, 2018; pp. 727–762. [Google Scholar]
- Biere, A.; Cimatti, A.; Clarke, E.M.; Fujita, M.; Zhu, Y. Symbolic Model Checking Using SAT Procedures instead of BDDs. Proc. of the 36th Conf. on Design Automation., 1999, pp. 317–320.
- Kurkowski, M.; Srebrny, M. A Quantifier-free First-order Knowledge Logic of Authentication. Fundam. Inform. 2006, 72, 263–282. [Google Scholar]
- Lomuscio, A.; Raimondi, F.; Wozna, B. Verification of the TESLA protocol in MCMAS-X. Fundam. Inform. 2007, 79, 473–486. [Google Scholar]
- Basin, D.A.; Cremers, C.; Dreier, J.; Sasse, R. Symbolically analyzing security protocols using tamarin. ACM SIGLOG News 2017, 4, 19–30. [Google Scholar] [CrossRef]
- Siedlecka-Lamch, O.; Szymoniak, S.; Kurkowski, M. A Fast Method for Security Protocols Verification. Proc. of 18th Int’l Conf. CISIM, 2019, pp. 523–534.
- Hess, A.V.; Mödersheim, S. Formalizing and Proving a Typing Result for Security Protocols in Isabelle/HOL. 30th IEEE Computer Security Foundations Symposium, CSF 2017, Santa Barbara, CA, USA, August 21-25, 2017. IEEE Computer Society, 2017, pp. 451–463. 21 August. [CrossRef]
- Mödersheim, S.; Viganò, L.; Basin, D.A. Constraint differentiation: Search-space reduction for the constraint-based analysis of security protocols. J. Comput. Secur. 2010, 18, 575–618. [Google Scholar] [CrossRef]
- Armando, A.; Carbone, R.; Compagna, L. SATMC: a SAT-based model checker for security protocols, business processes, and security APIs. Int. J. Softw. Tools Technol. Transf. 2016, 18, 187–204. [Google Scholar] [CrossRef]
- Li, L.; Sun, J.; Liu, Y.; Sun, M.; Dong, J. A Formal Specification and Verification Framework for Timed Security Protocols. IEEE Transactions on Software Engineering 2018, 44, 725–746. [Google Scholar] [CrossRef]
- Benerecetti, M.; Cuomo, N.; Peron, A. TPMC: A Model Checker For Time–Sensitive Security Protocols. Journal of Computers 2009, 4, 366–377. [Google Scholar] [CrossRef]
- Szymoniak, S.; Siedlecka-Lamch, O.; Kurkowski, M. On Some Time Aspects in Security Protocols Analysis. Proc. of 25th Int’l Conf. CN’18, 2018, pp. 344–356.
- Zbrzezny, A.M.; Zbrzezny, A.; Siedlecka-Lamch, O.; Szymoniak, S.; Kurkowski, M. VerSecTis - an agent based model checker for security protocols. Proc. of Int’l Conf. AAMAS’20. ACM, 2020, pp. 2123–2125.
- Lomuscio, A.; Penczek, W. LDYIS: a Framework for Model Checking Security Protocols. Fundam. Inform. 2008, 85, 359–375. [Google Scholar]
- Boureanu, I.; Cohen, M.; Lomuscio, A. Model checking detectability of attacks in multiagent systems. Proc. of 9th Int’l Conf. AAMAS’10, 2010, Vol. 1-3, pp. 691–698.
- Boureanu, I.; Jones, A.V.; Lomuscio, A. Automatic verification of epistemic specifications under convergent equational theories. Proc. of 11th Int’l Conf. AAMAS’12, 2012, Vol. 3, pp. 1141–1148.
- Millen, J.K. CAPSL: Common Authentication Protocol Specification Language. Proc. of the 1996 Workshop on New Security Paradigms, 1996, p. 132.
- Boureanu, I.; Kouvaros, P.; Lomuscio, A. Verifying Security Properties in Unbounded Multiagent Systems. Proc. AAMAS’16 Conf., 2016, pp. 1209–1217.
- Corin, R.; Etalle, S.; Hartel, P.H.; Mader, A. Timed analysis of security protocols. Journal of Computer Security 2007, 15, 619–645. [Google Scholar] [CrossRef]
- Jakubowska, G.; Penczek, W. Modelling and Checking Timed Authentication of Security Protocols. Fundam. Inform. 2007, 79, 363–378. [Google Scholar]
- Zbrzezny, A.M.; Szymoniak, S.; Kurkowski, M. Efficient Verification of Security Protocols Time Properties Using SMT Solvers. Proc. of 12th Int’l Conf. CISIS’19, 2019, pp. 25–35. [CrossRef]
- Li, L.; Sun, J.; Dong, J.S. Automated Verification of Timed Security Protocols with Clock Drift. FM 2016: Formal Methods - 21st International Symposium, Proceedings, 2016, Vol. 9995, Lecture Notes in Computer Science, pp. 513–530. [CrossRef]
- Mu, Y.; Juan, L.; Shen, G.; Zihao, W. Runtime verification of self-adaptive multi-agent system using probabilistic timed automata. Journal of Intelligent and Fuzzy Systems 2023. [Google Scholar] [CrossRef]
- Sankur, O. Timed Automata Verification and Synthesis via Finite Automata Learning. International Conference on Tools and Algorithms for Construction and Analysis of Systems, 2023, pp. 335–349. [CrossRef]
- Barthe, G.; Lago, U.D.; Malavolta, G.; Rakotonirina, I. Tidy: Symbolic Verification of Timed Cryptographic Protocols. Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security, 2022. [CrossRef]
- Middelburg, C. Dormancy-aware timed branching bisimilarity with an application to communication protocol analysis. Theoretical Computer Science 2024, 912, 114681. [Google Scholar] [CrossRef]
- Sahu, P. Automated Verification for Real-Time Systems. Lecture Notes in Computer Science, 2023. [CrossRef]
- Fagin, R.; Halpern, J.Y.; Moses, Y.; Vardi, M.Y. Reasoning about Knowledge; MIT Press: Cambridge, 1995. [Google Scholar]
- Wooldridge, M. An Introduction to Multi-Agent Systems - Second Edition, John Wiley & Sons, 2009.
- Lomuscio, A.; Sergot, M.J. Deontic Interpreted Systems. Studia Logica 2003, 75, 63–92. [Google Scholar] [CrossRef]
- Woźna-Szcześniak, B. SAT-Based Bounded Model Checking for Weighted Deontic Interpreted Systems. Proc. of Conf. EPIA’13, 2013, pp. 444–455.
- Woźna-Szcześniak, B.; Zbrzezny, A. Checking EMTLK Properties of Timed Interpreted Systems Via Bounded Model Checking. Studia Logica 2015, 1–38. [Google Scholar]
- Needham, R.; Schroeder, M. Using Encryption for Authentication in Large Networks of Computers. Commun. ACM 1978, 21, 993–999. [Google Scholar] [CrossRef]
- Lowe, G. An Attack on the Needham-Schroeder Public-Key Authentication Protocol. Inf. Process. Lett. 1995, 56, 131–133. [Google Scholar] [CrossRef]
- Baier, C.; Katoen, J.P. Principles of Model Checking; MIT Press, 2008; pp. I–XVII, 1–975. [Google Scholar]
- Zbrzezny, A.M.; Zbrzezny, A. Checking WECTLK Properties of Timed Real-Weighted Interpreted Systems via SMT-based Bounded Model Checking. Proc. of 17th Conf. EPIA’15. Springer, 2015, Vol. 9273, LNCS, pp. 638–650.
- Moura, L.D.; Bjørner, N. Z3: an Efficient SMT solver. Proc. of 14th Int’l Conf. TACAS’08. Springer-Verlag, 2008, Vol. 4963, LNCS, pp. 337–340.
- Dutertre, B. Yices 2.2. Proc. of CAV’14 Conf. Springer, 2014, Vol. 8559, LNCS, pp. 737–744.
- Barrett, C.; Conway, C.L.; Deters, M.; Hadarean, L.; Jovanovi’c, D.; King, T.; Reynolds, A.; Tinelli, C. CVC4. Proc. of the 23rd CAV Conf. Springer, 2011, Vol. 6806, LNCS, pp. 171–177.
- Zbrzezny, A.M.; Zbrzezny, A. SAT-Based BMC Approach to Verifying Real-Time Properties of Multi-Agent Systems. 15th IEEE/ACS Int’l Conf. AICCSA’18, 2018, pp. 1–8.
- Callegati, F.; Cerroni, W.; Ramilli, M. Man-in-the-Middle Attack to the HTTPS Protocol. IEEE Secur. Priv. 2009, 7, 78–81. [Google Scholar] [CrossRef]
- Denning, D.E.; Sacco, G.M. Timestamps in Key Distribution Protocols. Commun. ACM 1981, 24, 533–536. [Google Scholar] [CrossRef]
- Woo, T.Y.C.; Lam, S.S. A Lesson on Authentication Protocol Design. SIGOPS Oper. Syst. Rev. 1994, 28, 24–37. [Google Scholar] [CrossRef]
- Satyanarayanan, M. Integrating security in a large distributed system. ACM Trans. Comput. Syst. 1989, 7, 247–280. [Google Scholar] [CrossRef]
- Lowe, G. Some new attacks upon security protocols. Proceedings 9th IEEE Computer Security Foundations Workshop, 1996, pp. 162–169.
- Siedlecka-Lamch, O.; El Fray, I.; Kurkowski, M.; Pejas, J. Verification of Mutual Authentication Protocol for MobInfoSec System. Proc. of 14th Int’l Conf. CISIM, 2015, pp. 461–474.
| 1 | The implementation [29], along with instructions for installing the necessary software and the specifications of the tested protocols, can be found on GitHub (https://github.com/amz-research-veri/VerSecTis). |
Figure 1.
Timed Interpreted System for NSPKT
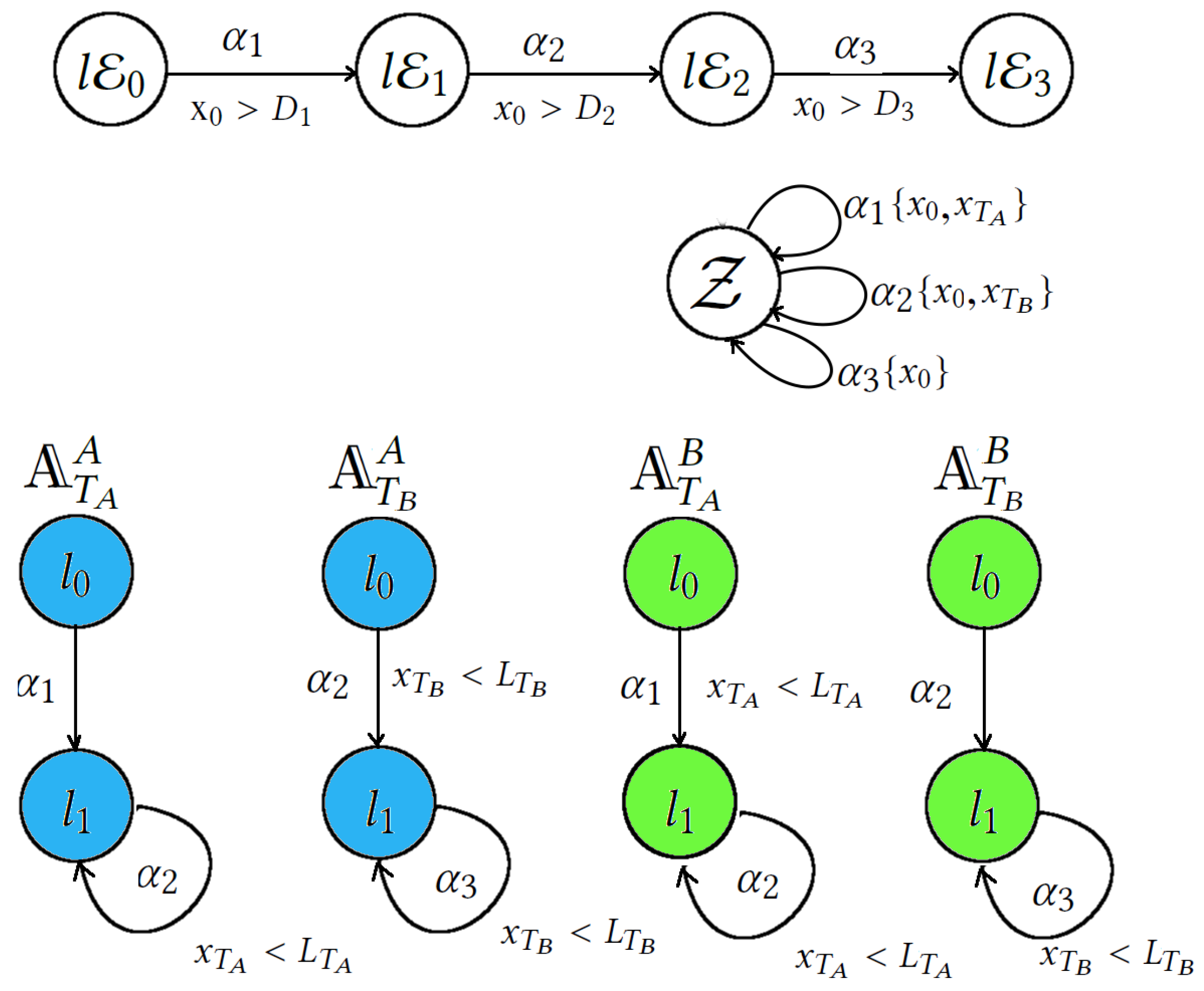
Figure 3.
Andrew Protocol
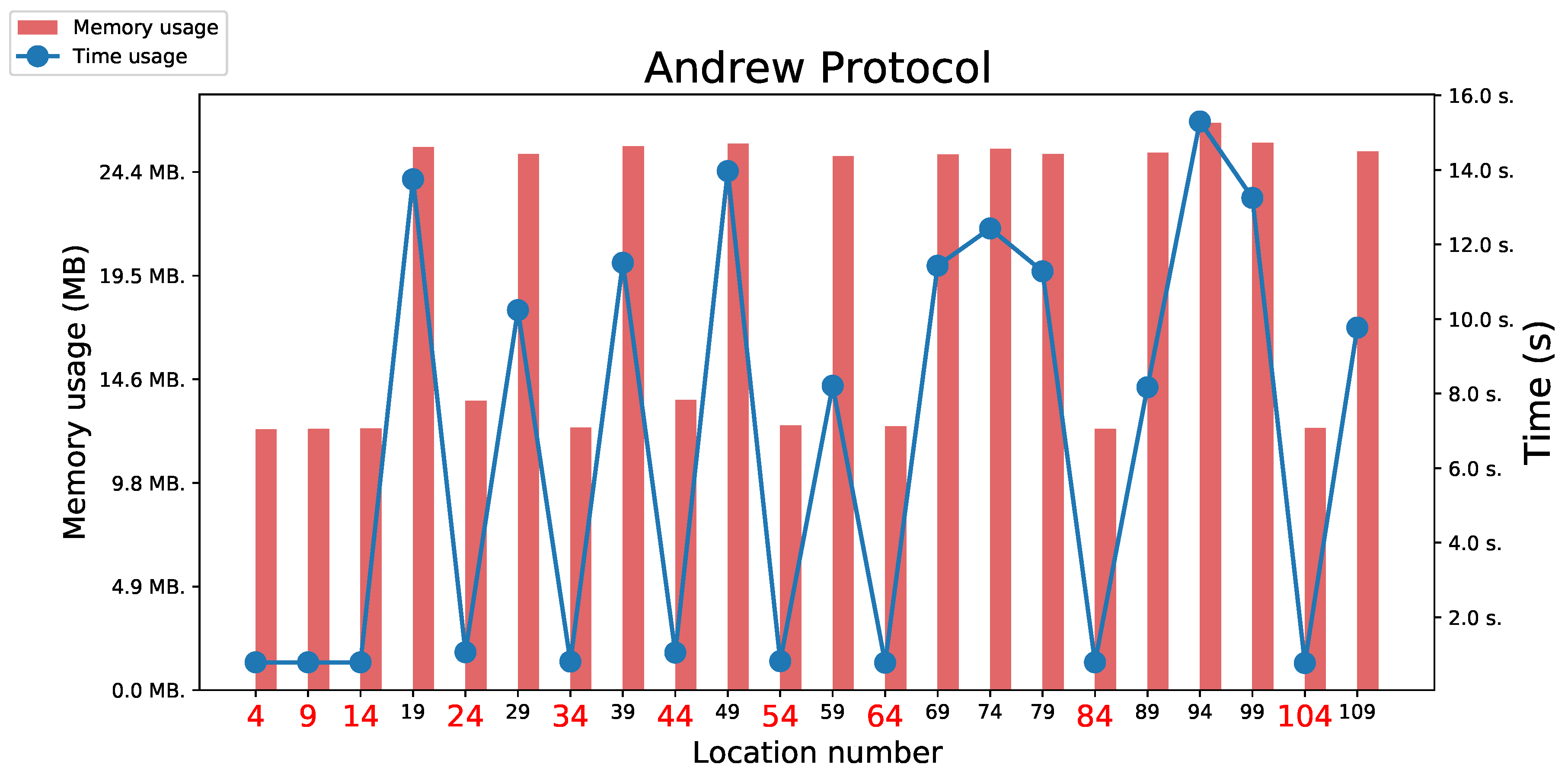
Figure 4.
Andrew Lowe Protocol
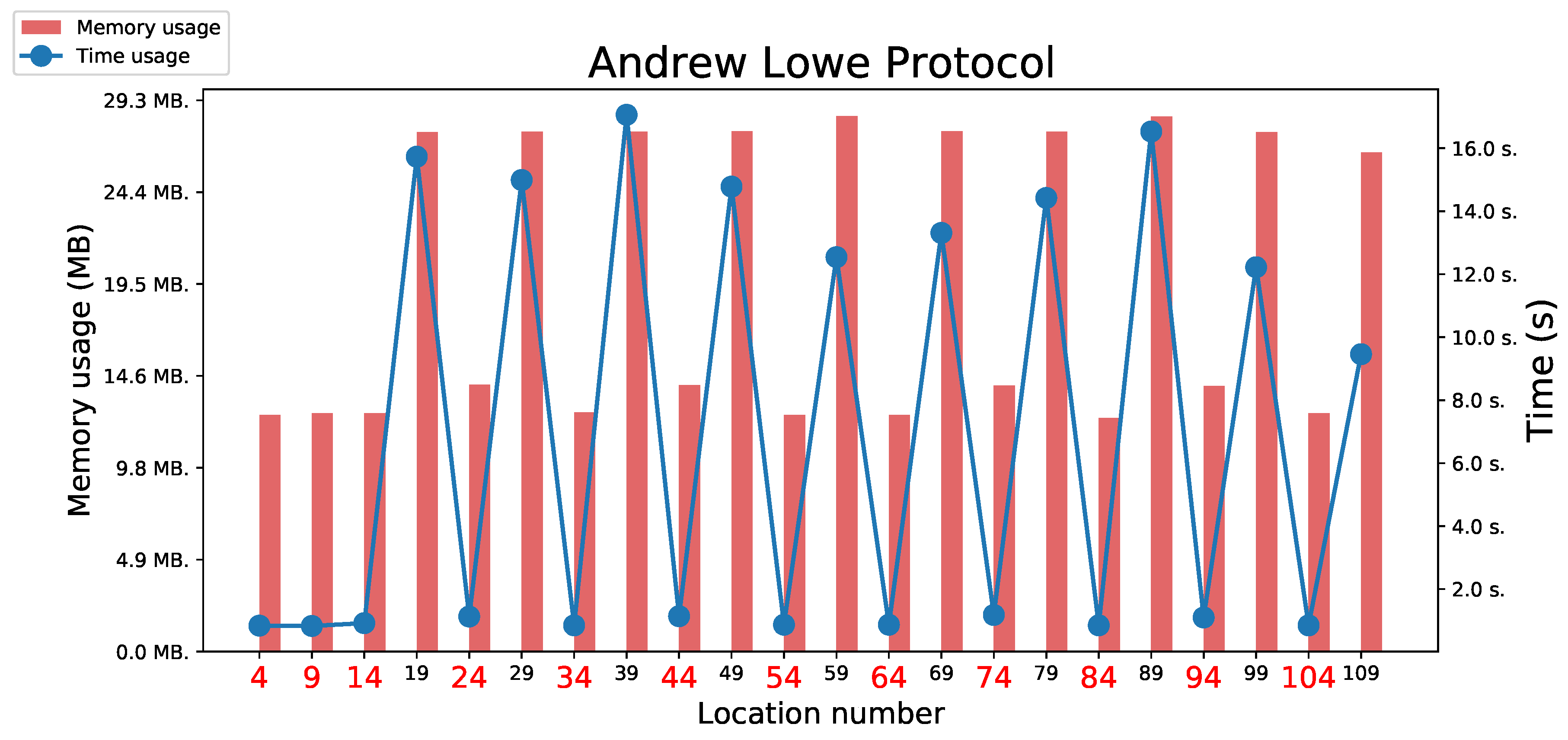
Figure 5.
Denning–Sacco
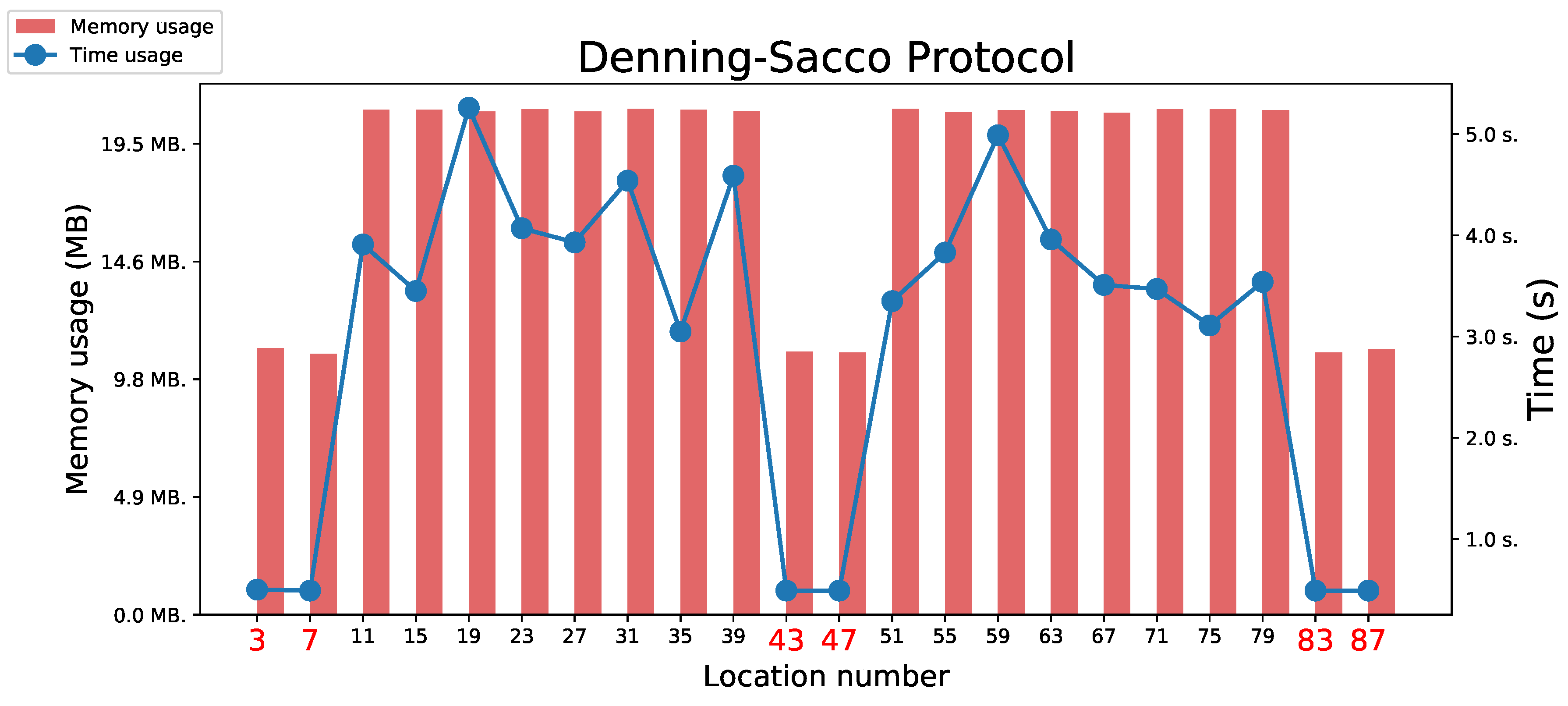
Figure 6.
NSPKT
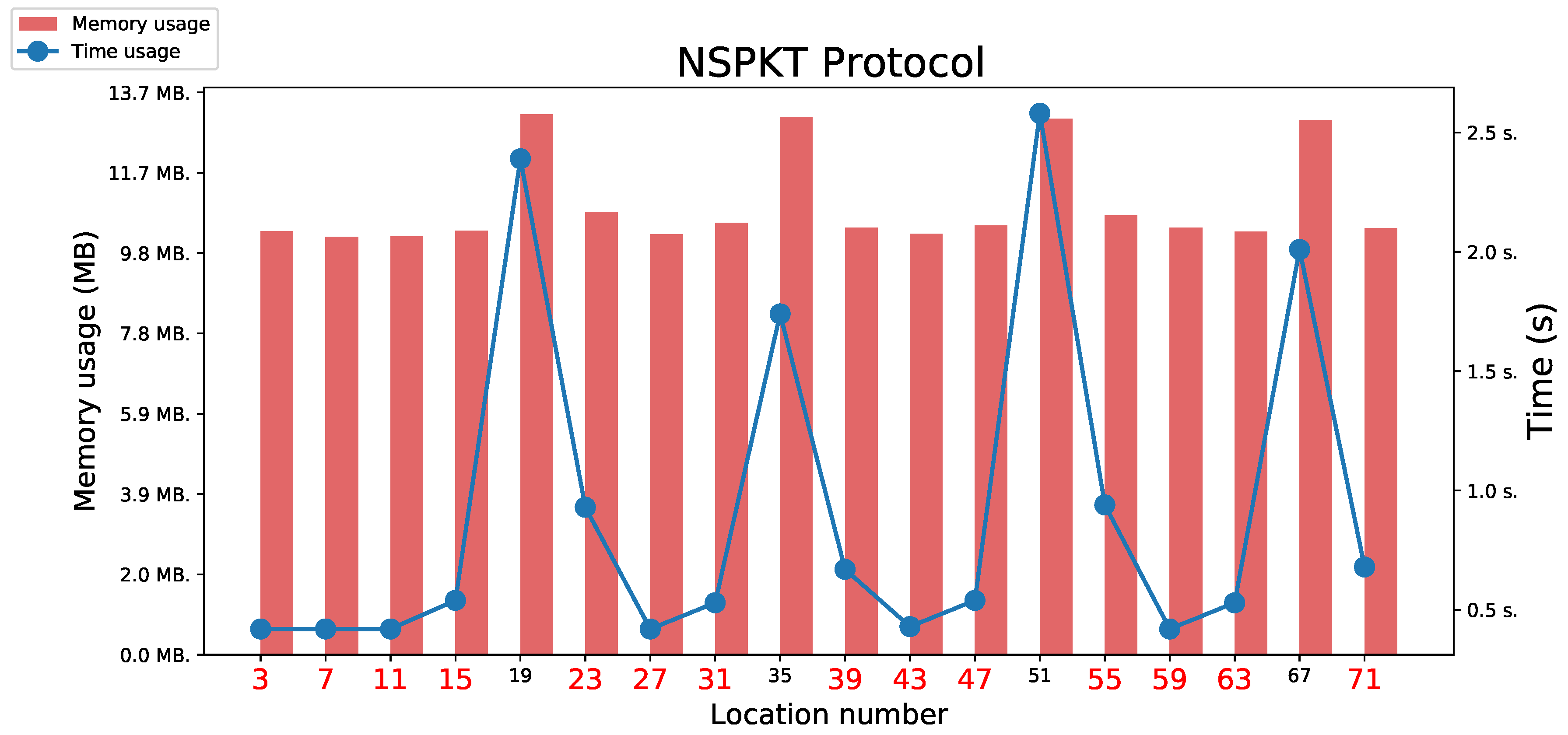
Figure 8.
Woo Lam Pi
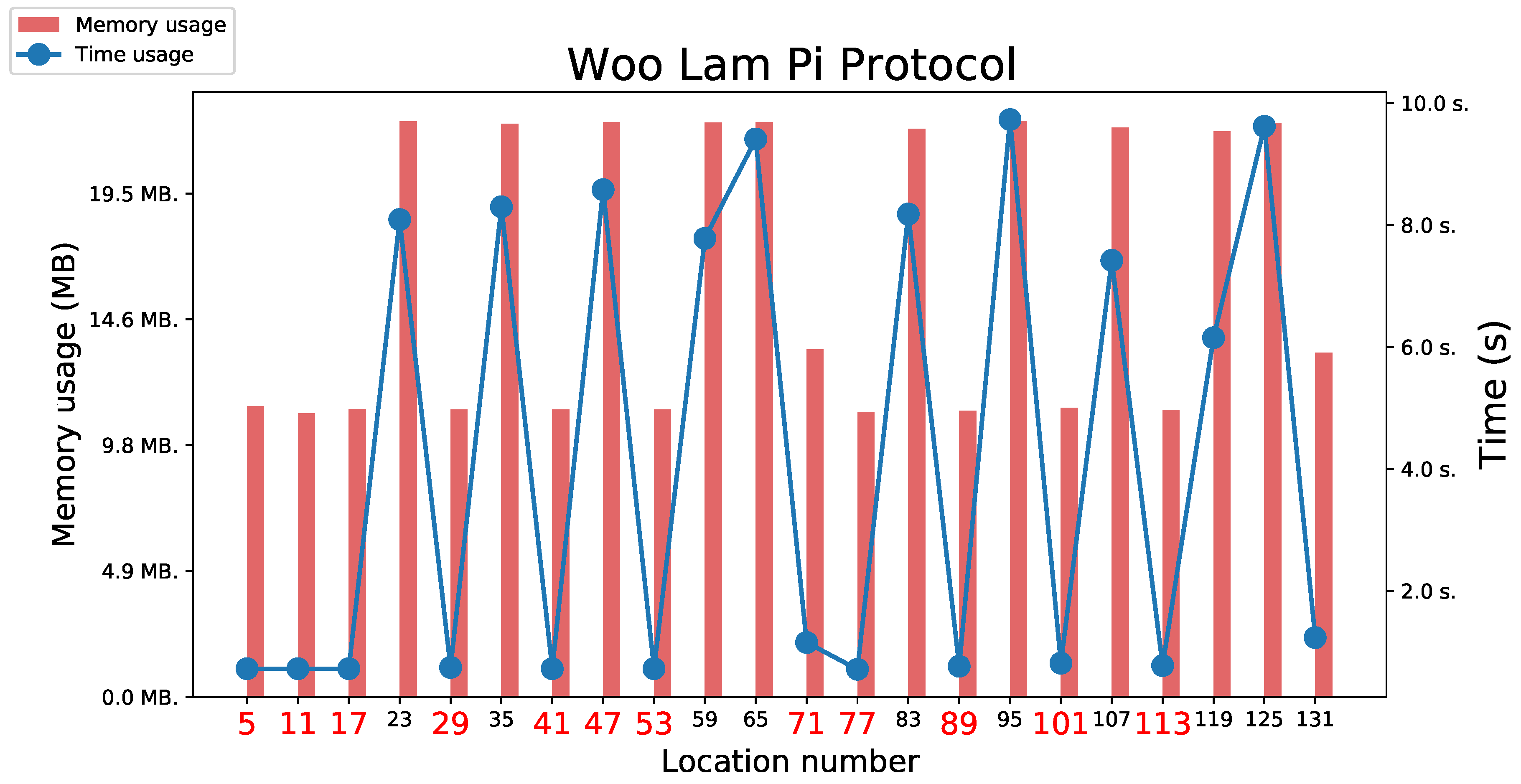
Figure 9.
Woo Lam Pi 1
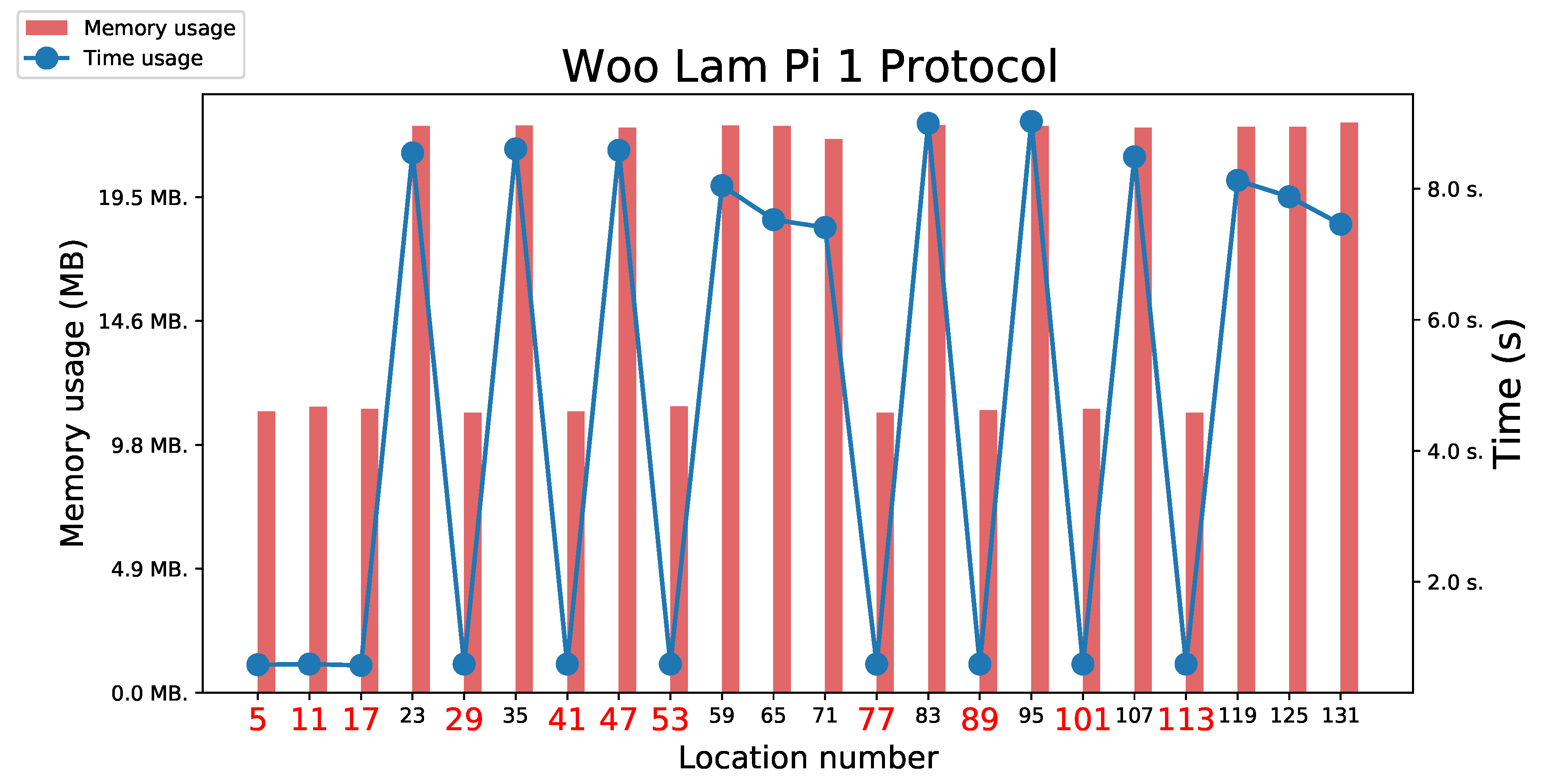
Figure 10.
Woo Lam Pi3
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






