Submitted:
02 September 2024
Posted:
03 September 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
2.1. Growth Curve Model
3. Results
3.1. Plant Cycle
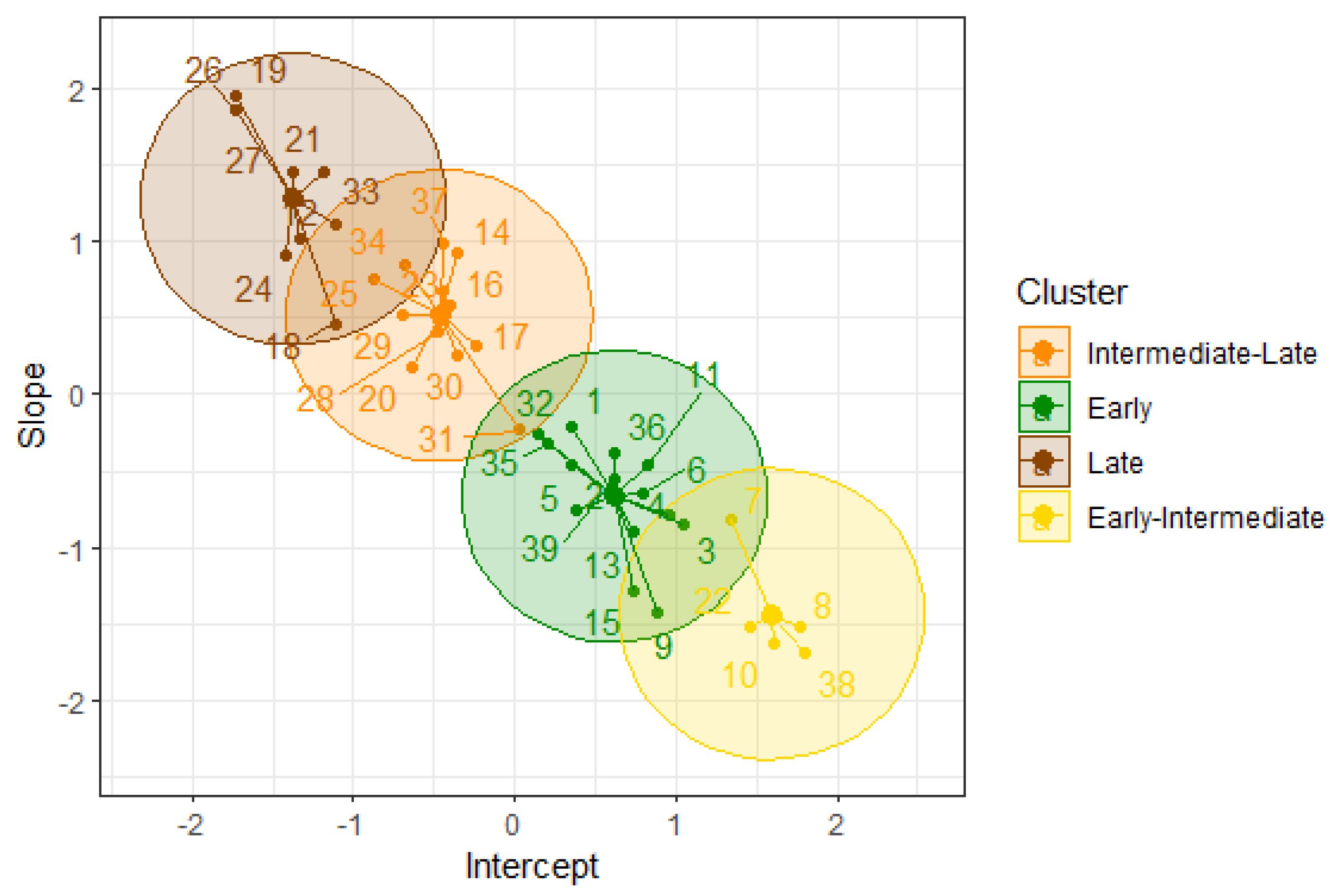
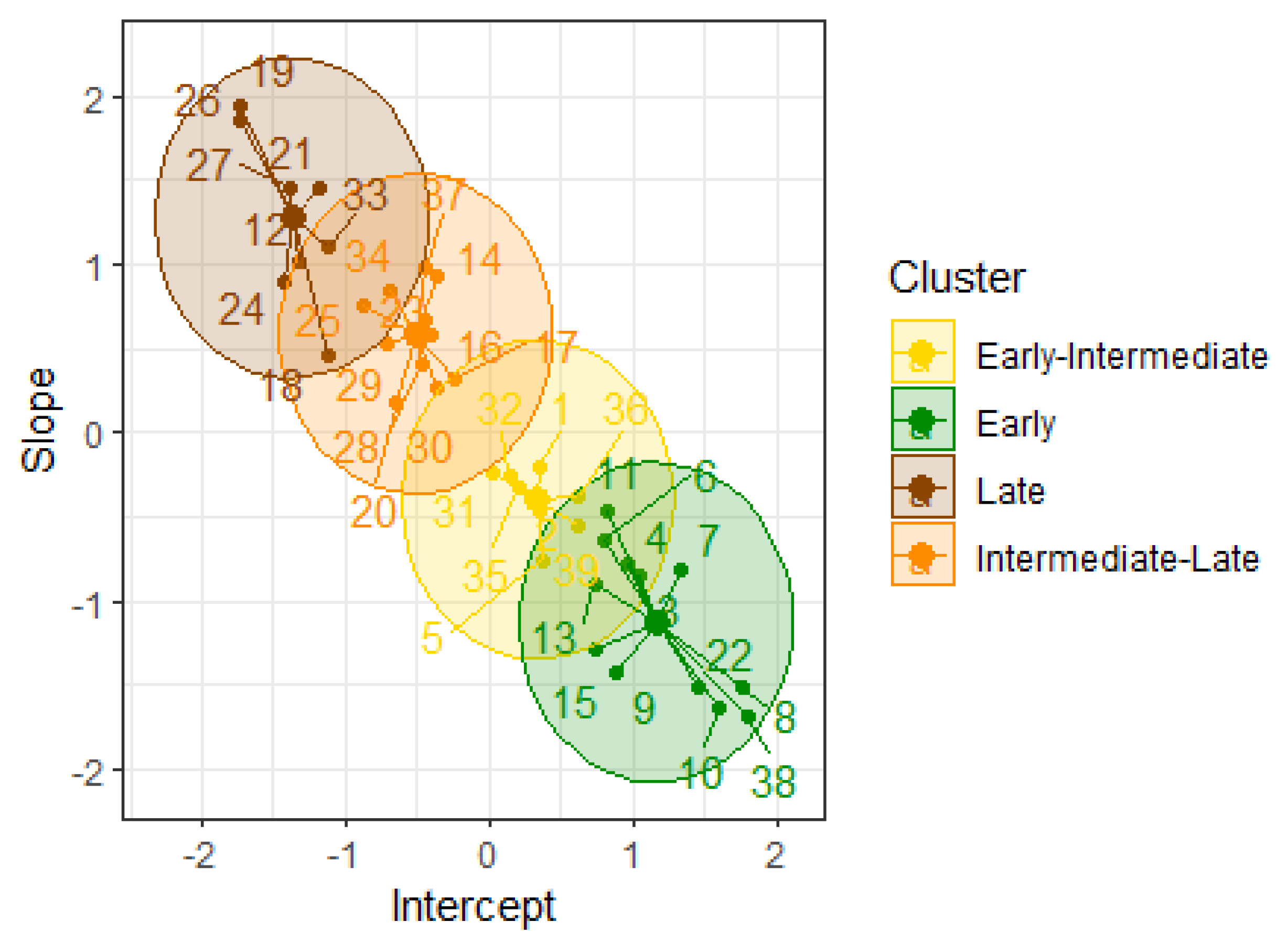
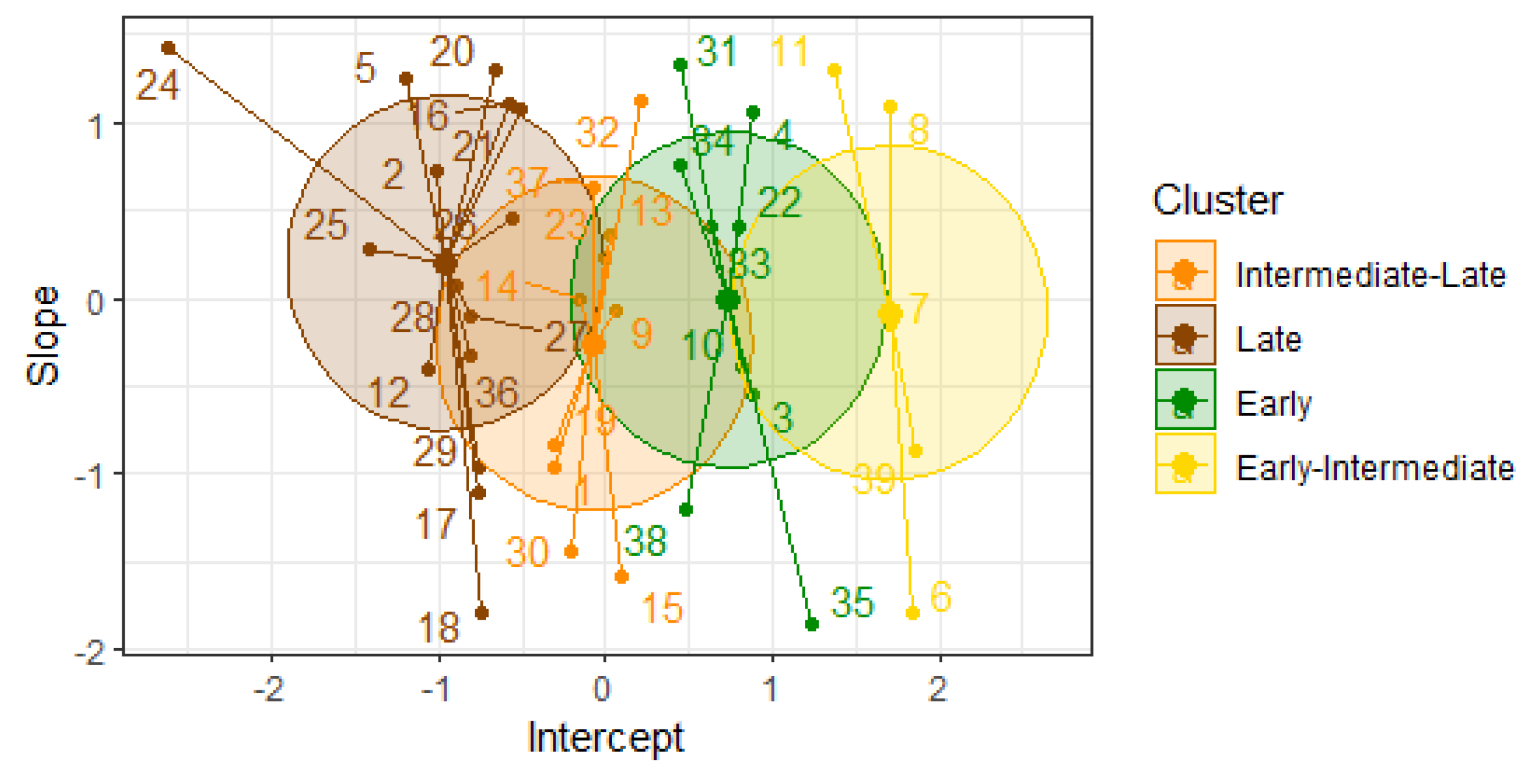
3.1.1. Clustering
3.2. Ratoon Cycle
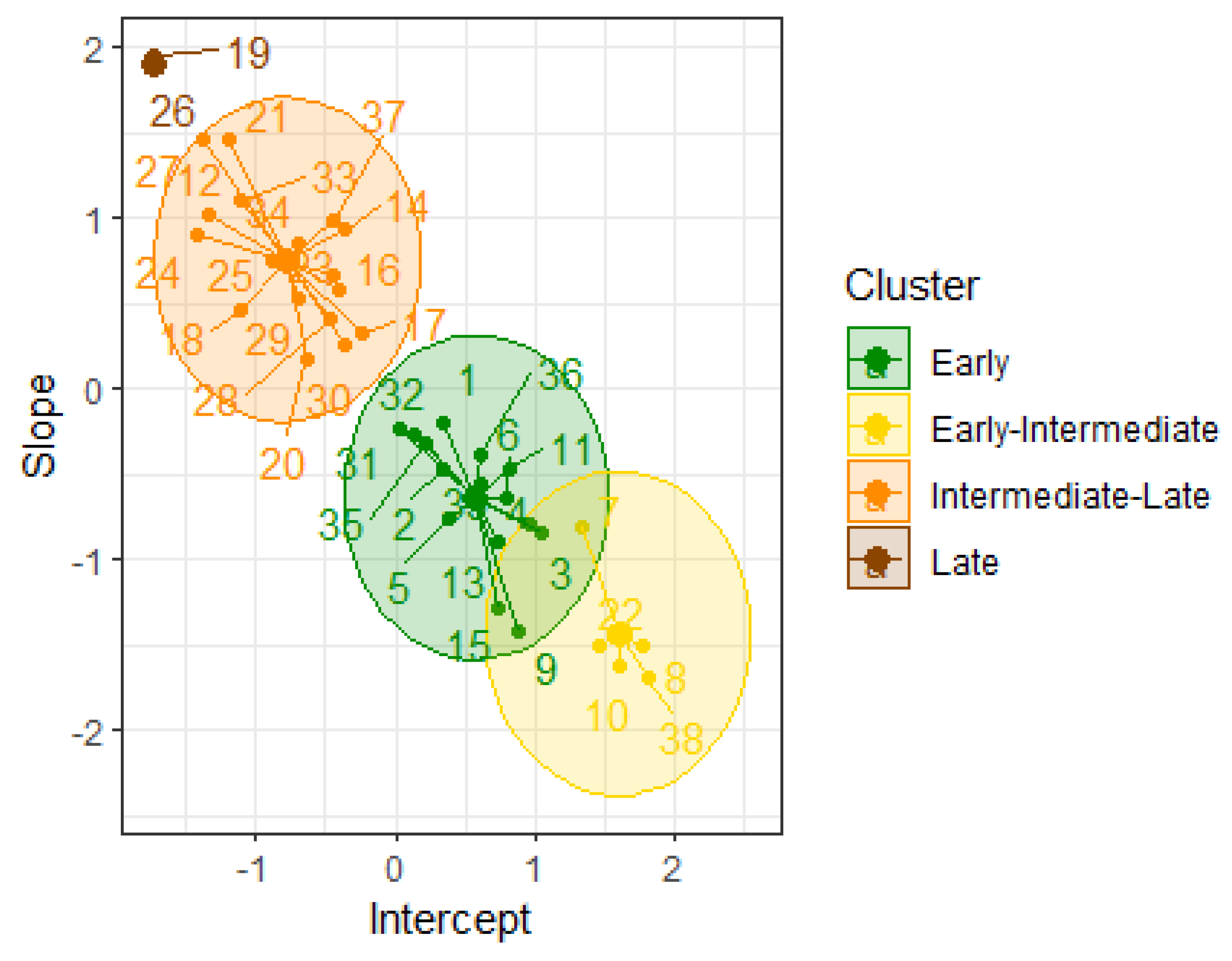
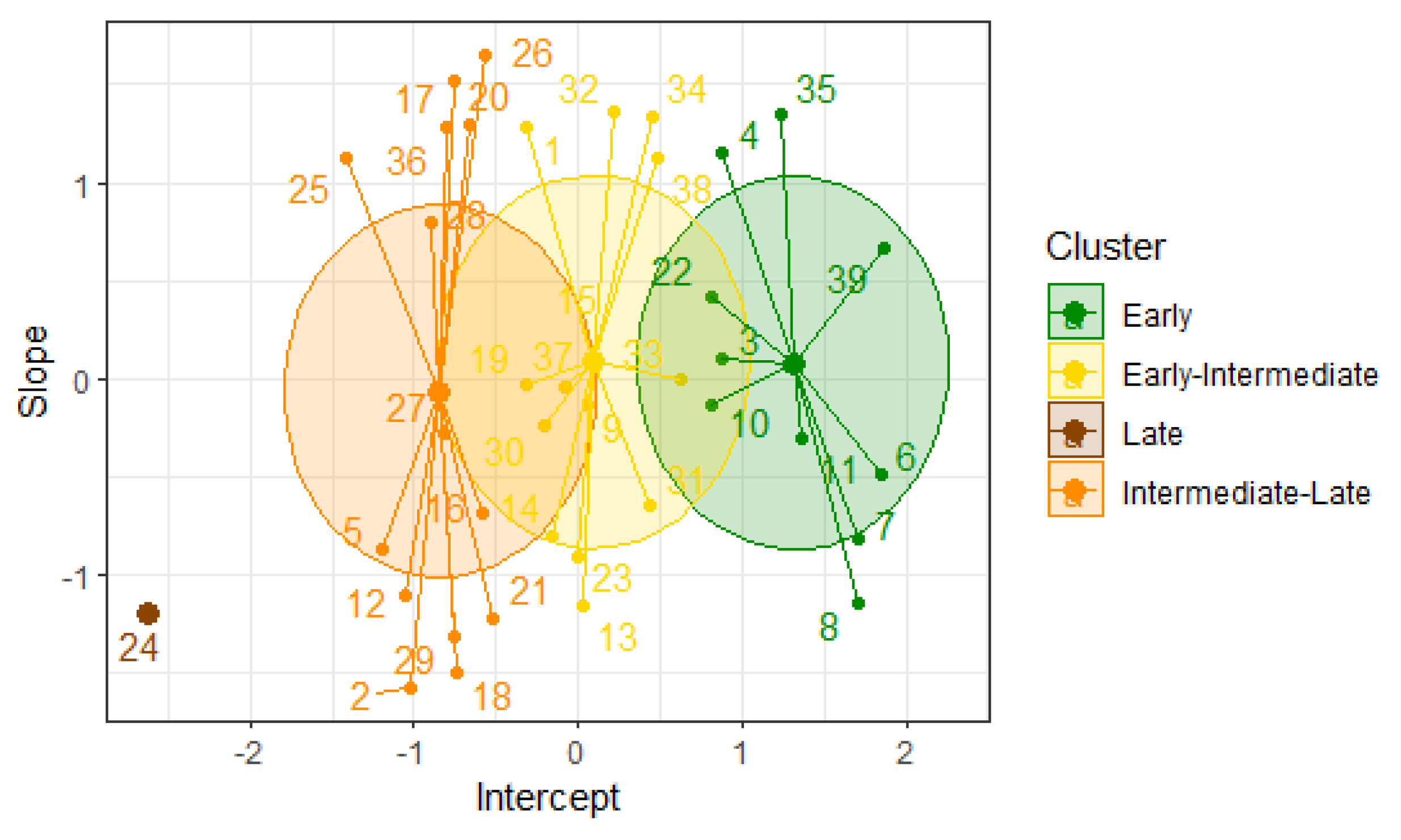
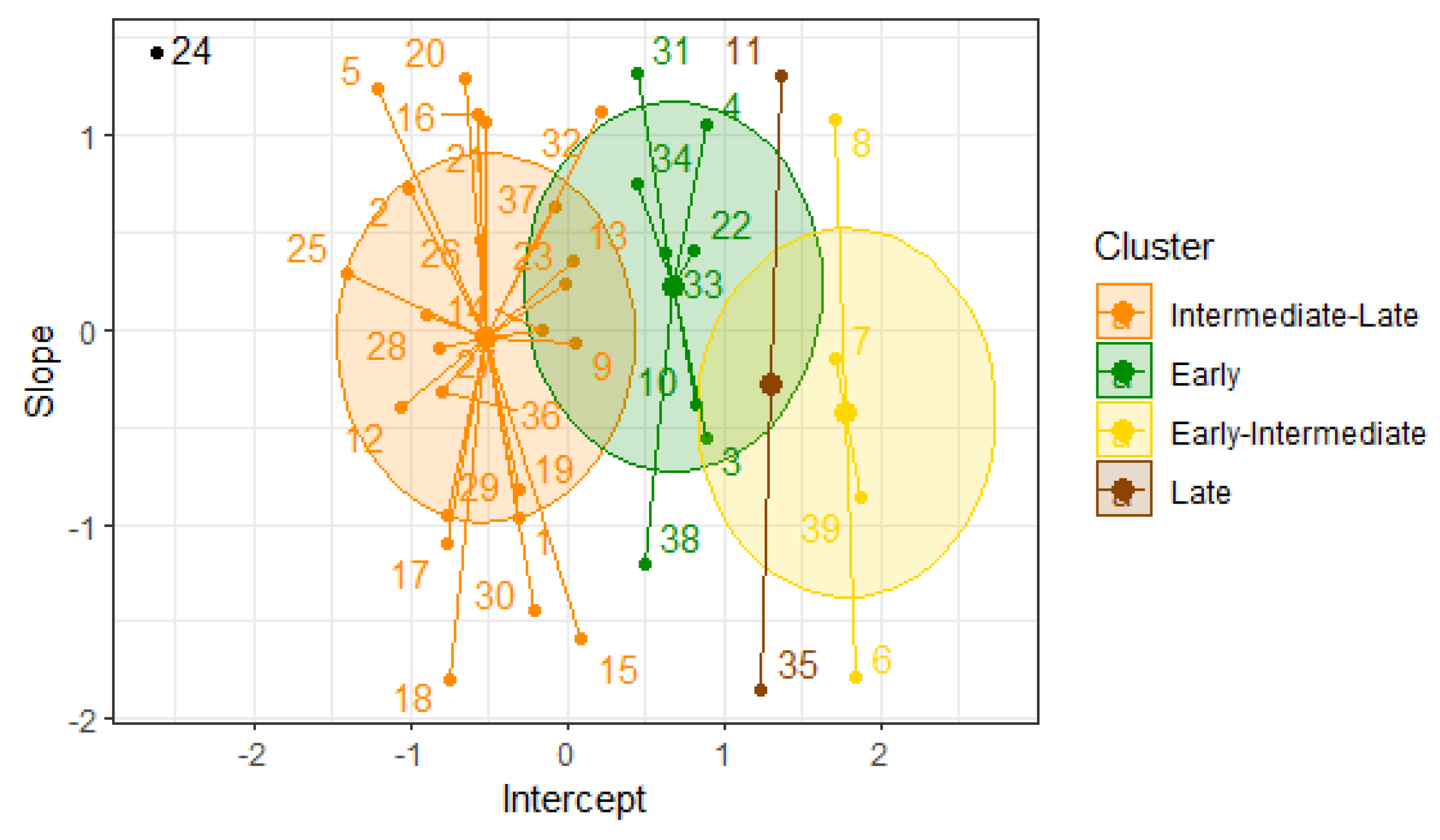
3.2.1. Clustering
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SP | Sucrose Percentage |
| PP | Polarization Percentage |
| INIFAP | National Institute of Forestry, Agriculture, and Livestock Research |
| Silhouette Index | |
| Dunn Index | |
| Connectivity Index |
References
- Alejandre Rosas, J.A.; Galindo Tovar, M.E.; Lee Espinosa, H.E.; Alvarado Gómez, O.G. Variabilidad genética en 22 variedades híbridas de caña de azúcar (Saccharum spp. Híbrido). Phyton (Buenos Aires) 2010, 79, 87–94. Available online: https://revistaphyton.fund-romuloraggio.org.ar/vol79/Alejandre-Rosas.pdf.
- Arntzen, C.J.; Ritter, E.M. Encyclopedia of agricultural science Volume 2: EL.; Academic Press: 1994. Available online: https://www.cabidigitallibrary.org/doi/full/10.5555/19951403738.
- CONADESUCA. Nota informativa sobre innovaciones en materia de productividad del sector. Nuevas variedades de caña de azúcar; Sagarpa: Ciudad de México, 2016. Available online: https://www.gob.mx/cms/uploads/attachment/file/136406/NotaNuevasVariedadesd_Cana_deAzucar.compressed.pdf.
- Que, Y.; Wu, Q.; Zhang, H.; Luo, J.; Zhang, Y. Developing new sugarcane varieties suitable for mechanized production in China: principles, strategies and prospects. Frontiers in Plant Science 2024, 14, 1337144. [Google Scholar] [CrossRef]
- Sentíes-Herrera, H. E.; Valdez-Balero, A.; Loyo-Joachin, R.; Gómez-Merino, F. C. Fases experimentales en el mejoramiento genético de la caña de azúcar (Saccharum spp.) en México. AgroProductividad 2017, 10, 93–99. [Google Scholar]
- García-Preciado, J. C. Evaluación de variables de calidad en híbridos de Saccharum spp. en diferentes ambientes agroecológicos de Jalisco, México. AgroProductividad 2017, 10, 11. [Google Scholar]
- Bastidas, L.; Rea, R.; Sousa Vieira, O. de; Hernández, E.; Briceño, R. Análisis de variables agronómicas en cultivares de caña de azúcar con fines azucareros, paneleros y forrajeros. Bioagro 2012, 24, 135–142. [Google Scholar]
- Rodríguez Gross, R.; Puchades Izaguirre, Y.; Abiche Maceo, W.; Rill Martínez, S.; Suarez, H. J.; Salmón Cuspineda, Y.; Gálvez, G. Estudio del rendimiento y modelación del período de madurez en nuevos cultivares de caña de azúcar. Cultivos Tropicales 2015, 36, 134–143. [Google Scholar]
- Hernández, O.L.; García, S.S.; Nataren, E.H.; Espinoza, L.C.L.; Oliva, A.C.; Sanchez, S.C.; Romero, E.R.; Zossi, S. La espectroscopía de infrarrojo cercano (NIRS) en el seguimiento de la madurez del cultivo de la caña de azúcar (Saccharum spp.). Agro Productividad 2019, 12. [Google Scholar] [CrossRef]
- Larrahondo, J. E.; Cassalett, C.; Torres, J.; Issacs, C. El cultivo de la caña de azúcar en la zona azucarera de Colombia. In Calidad de caña; Cassalett, C., Torres, J., Issacs, C., Eds.; Cenicaña: Cali, 1995; pp. 337–354. [Google Scholar]
- Ostengo, S.; Rueda Calderón, M. A.; Bruno, C.; Cuenya, M. I.; Balzarini, M. A protocol for identifying characteristic sucrose accumulation curves of sugarcane genotypes (Saccharum spp.). Sugar Tech 2021, 23, 519–523. [Google Scholar] [CrossRef]
- West, B. T.; Welch, K. B.; Galecki, A. T. Linear Mixed Models: A Practical Guide Using Statistical Software; Chapman and Hall/CRC: Boca Raton, FL, 2006; pp. 9–28. [Google Scholar] [CrossRef]
- Balaguera Carrasquilla, N. P. Modelo de curvas de crecimiento: Modelos lineales mixtos vs Datos funcionales. Ph.D. Thesis, Universidad Santo Tomás, 2020. Available online: http://hdl.handle.net/11634/22477.
- Gilbert, R. A.; Shine, J., Jr. M.; Miller, J. D.; Rice, R. W. Sucrose accumulation and harvest schedule recommendations for CP sugarcane cultivars. Crop Management 2004, 3, 1–7. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, J.; Huang, H.; Zan, F.; Zhao, P.; Zhao, J.; Deng, J.; Wu, C. Genetic improvement of sugarcane (Saccharum spp.) contributed to high sucrose content in China based on an analysis of newly developed varieties. Agriculture 2022, 12. [Google Scholar] [CrossRef]
- McCulloch, C. E.; Searle, S. R. Generalized, Linear, and Mixed Models; Wiley-Interscience: Hoboken, NJ, 2001. [Google Scholar] [CrossRef]
- Gałecki, A.; Burzykowski, T. Linear mixed-effects models using R; Springer: New York Heidelberg Dordrecht London, 2013; pp. 245–273. [Google Scholar] [CrossRef]
- Aguirre-Calderón, O.A. ¿Cómo corregir la heterocedasticidad y autocorrelación de residuales en modelos de ahusamiento y crecimiento en altura? Revista Mexicana de Ciencias Forestales 2018, 9, 49. [Google Scholar] [CrossRef]
- Zhang, C.; Huang, W.; Niu, T.; Liu, Z.; Li, G.; Cao, D. Review of Clustering Technology and Its Application in Coordinating Vehicle Subsystems. Automotive Innovation 2023, 1–27. [Google Scholar] [CrossRef]
- Khan, M. M. R.; Siddique, M. A. B.; Arif, R. B.; Oishe, M. R. ADBSCAN: Adaptive density-based spatial clustering of applications with noise for identifying clusters with varying densities. In 2018 4th International Conference on Electrical Engineering and Information & Communication Technology (iCEEiCT); IEEE: Dhaka, Bangladesh, 2018; pp. 107–111. [Google Scholar] [CrossRef]
- Ben Ncir, C.-E.; Hamza, A.; Bouaguel, W. Parallel and scalable Dunn Index for the validation of big data clusters. Parallel Computing 2021, 102, 102751. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P.J. Finding groups in data: an introduction to cluster analysis; John Wiley & Sons: New Jersey, 2009. [Google Scholar]
- Videla, M. E.; Bruno, C. Validación de agrupamientos para representar estructura genética poblacional. Agriscientia 2022, 39, 1–10. [Google Scholar] [CrossRef]
- Luna-Romera, J. M.; del Mar Martinez-Ballesteros, M.; Garcia-Gutierrez, J.; Riquelme-Santos, J. C. An approach to silhouette and dunn clustering indices applied to big data in spark. In Advances in Artificial Intelligence: 17th Conference of the Spanish Association for Artificial Intelligence, CAEPIA 2016, Salamanca, Spain, September 14-16, 2016. Proceedings 17; Springer: Cham, 2016; pp. 160–169. [Google Scholar] [CrossRef]
- Brock, G.; Pihur, V.; Datta, S.; Datta, S. clValid: An R package for cluster validation. Journal of Statistical Software 2008, 25, 1–22. [Google Scholar] [CrossRef]
- Gómez-Merino, F. C. Manual para la identificación varietal de caña de azúcar; Colegio de Postgraduados: Texcoco, Estado de México, 2015. [Google Scholar]
- Mendoza Batista, Y.; Cruz Sarmiento, R.; Vaillant Cáceres, Y.; Luis Martínez, O.; Céspedes Argota, M. Comportamiento de los cultivares de caña de azúcar C97-445 y C95-416 en localidades de la provincia Holguín. Centro Agrícola 2019, 46, 49–53. [Google Scholar]
- Mei, H.; Mao, L.; Zhang, Y.; Chen, M. BDT-ADBSCAN: Adaptive Density-Based Spatial Clustering of Applications with Noise Based on Bayesian Decision Theory for Identifying Clusters with Multi-Densities. In Proceedings of the 2022 IEEE 10th Joint International Information Technology and Artificial Intelligence Conference (ITAIC); 2022; pp. 1510–1516. [Google Scholar] [CrossRef]
- Cheavegatti-Gianotto, A.; De Abreu, H.M.C.; Arruda, P.; Bespalhok Filho, J.C.; Burnquist, W.L.; Creste, S.; di Ciero, L.; Ferro, J.A.; de Oliveira Figueira, A.V.; de Sousa Filgueiras, T.; et al. Sugarcane (Saccharum X officinarum): a reference study for the regulation of genetically modified cultivars in Brazil. Tropical plant biology 2011, 4, 62–89. [Google Scholar] [CrossRef]
- Marcano, M.; Manrique, U.; Garcia, M.; Salcedo, F. Prueba de ocho variedades de caña de azúcar (Saccharum sp.) bajo condiciones de secano en un suelo de sabana del estado Monagas, Venezuela. Revista Científica UDO Agrícola 2005, 5, 54–61. [Google Scholar]
- Vasantha, S.; Kumar, R.A.; Tayade, A.S.; Krishnapriya, V.; Ram, B.; Solomon, S. Physiology of sucrose productivity and implications of ripeners in sugarcane. Sugar Tech 2021, 1–17. [Google Scholar] [CrossRef]
- Jackson, P.A. Breeding for improved sugar content in sugarcane. Field Crops Research 2005, 92, 277–290. [Google Scholar] [CrossRef]
- Delgado Mora, I.; Jorge Suarez, H.; Vera, A.; Cornide Hernández, M.T.; Díaz Mujica, F.R.; Gómez Pérez, J.R.; Suárez Sanchez, O.; Puchades Isaguirre, Y. Influencia de la edad y cultivar de caña de azúcar en el momento de la cosecha. Centro Agrícola 2016, 43, 59–65. [Google Scholar]
- Espinoza, J. G. Maduración de la caña de azúcar y floración de la caña de azúcar y su manejo. Cengicaña. 2012, pp. 262–281. Available online: https://cengicana.org/files/20150828053619432.pdf.
- García, S.S.; Escobar, R.N.; Alanis, L.B. Determinación de la dosis óptima económica de fertilización en caña de azúcar. Terra latinoamericana 2003, 21, 267–272. [Google Scholar]
| ID | Material | Origin | Type | ID | Material | Origin | Type |
| 1 | COSTA JAL | Mexican | N | 21 | ITSAMEX 07-7259 | Mexican | N |
| 2 | RB 85-5035 | Foreign | N | 22 | ITSAMEX 06-6395 | Mexican | N |
| 3 | ITV 92-1424* | Foreign | C | 23 | ITSAMEX 06-4863 | Mexican | N |
| 4 | RB 85-5113* | Foreign | C | 24 | ITSAMEX 07-4954 | Mexican | N |
| 5 | LAICA 92-13 | Foreign | N | 25 | ITSAMEX 07-4387 | Mexican | N |
| 6 | CP 72-2086* | Foreign | C | 26 | ITSAMEX 07-121115 | Mexican | N |
| 7 | COLMEX 94-8* | Mexican | C | 27 | ITSAMEX 07-246 | Mexican | N |
| 8 | ATEMEX 99-48 | Mexican | N | 28 | ITSAMEX 07-12116 | Mexican | N |
| 9 | ATEMEX 99-1 | Mexican | N | 29 | ITSAMEX 07-12113 | Mexican | N |
| 10 | ATEMEX 99-61 | Mexican | N | 30 | ITSAMEX 07-2963 | Mexican | N |
| 11 | MEX 70-486 | Mexican | N | 31 | ITSAMEX 07-99711 | Mexican | N |
| 12 | TCP 89-3505 | Foreign | N | 32 | ITSAMEX 07-9886 | Mexican | N |
| 13 | MEX 80-1521 | Mexican | N | 33 | ITSAMEX 07-86810 | Mexican | N |
| 14 | MEX 69-290* | Mexican | C | 34 | ITSAMEX 07-12119 | Mexican | N |
| 15 | ITSAMEX 07-44814 | Mexican | N | 35 | ITSAMEX 07-1903 | Mexican | N |
| 16 | ITSAMEX 06-3049 | Mexican | N | 36 | ITSAMEX 07-44813 | Mexican | N |
| 17 | ITSAMEX 07-8681 | Mexican | N | 37 | ITSAMEX 07-12118 | Mexican | N |
| 18 | ITSAMEX 07-20810 | Mexican | N | 38 | CP 85-1382 | Foreign | N |
| 19 | ITSAMEX 07-7501 | Mexican | N | 39 | COLMEX 95-27* | Mexican | C |
| 20 | ITSAMEX 07-1107 | Mexican | N |
| Cycle | Period | Date 1 | Date 2 | Date 3 | Date 4 |
| Planting | |||||
| Plant | 03-04-2011 | 10-08-2011 | 11-08-2011 | 12-08-2011 | 01-11-2012 |
| Harvest | |||||
| >Ratoon | 05-21-2012 | 11-16-2012 | 12-19-2012 | 01-22-2013 | 02-25-2013 |
| Fixed effects | Random effects | ||||
| Parameter | CI | Parameter | CI | Parameter | CI |
| Material | Material | ||||
| COSTA JAL | 7.04 | 1.43 | ITSAMEX 07-7259 | 4.07 | 2.00 |
| RB 85-5035 | 7.05 | 1.34 | ITSAMEX 06-6395 | 9.19 | 0.98 |
| ITV 92-1424 * | 8.39 | 1.21 | ITSAMEX 06-4863 | 5.51 | 1.73 |
| RB 85-5113 * | 8.23 | 1.23 | ITSAMEX 07-4954 | 3.62 | 1.81 |
| LAICA 92-13 | 7.11 | 1.24 | ITSAMEX 07-4387 | 4.68 | 1.76 |
| CP 72-2086 * | 7.92 | 1.28 | ITSAMEX 07-121115 | 3.01 | 2.14 |
| COLMEX 94-8* | 8.97 | 1.22 | ITSAMEX 07-246 | 3.70 | 2.00 |
| ATEMEX 99-48 | 9.79 | 0.98 | ITSAMEX 07-12116 | 5.45 | 1.64 |
| ATEMEX 99-1 | 8.08 | 1.01 | ITSAMEX 07-12113 | 5.01 | 1.68 |
| ATEMEX 99-61 | 9.48 | 0.94 | ITSAMEX 07-2963 | 5.67 | 1.59 |
| MEX 70-486 | 7.97 | 1.34 | ITSAMEX 07-99711 | 6.43 | 1.42 |
| TCP 89-3505 | 3.79 | 1.85 | ITSAMEX 07-9886 | 6.65 | 1.41 |
| MEX 80-1521 | 7.79 | 1.19 | ITSAMEX 07-86810 | 4.21 | 1.88 |
| MEX 69-290* | 5.67 | 1.82 | ITSAMEX 07-12119 | 5.04 | 1.79 |
| ITSAMEX 07-44814 | 7.80 | 1.06 | ITSAMEX 07-1903 | 6.78 | 1.39 |
| ITSAMEX 06-3049 | 5.60 | 1.70 | ITSAMEX 07-44813 | 7.56 | 1.37 |
| ITSAMEX 07-8681 | 5.92 | 1.61 | ITSAMEX 07-12118 | 5.52 | 1.84 |
| ITSAMEX 07-20810 | 4.21 | 1.66 | CP 85-1382 | 9.86 | 0.92 |
| ITSAMEX 07-7501 | 3.03 | 2.17 | COLMEX 95-27* | 7.56 | 1.31 |
| ITSAMEX 07-1107 | 5.13 | 1.56 |
| ID | Material | k-means | k-medoids | DBSCAN |
| 1 | COSTA JAL | Early | Early-Intermediate | Early |
| 2 | RB 85-5035 | Early | Early-Intermediate | Early |
| 3 | ITV 92-1424* | Early | Early | Early |
| 4 | RB 85-5113* | Early | Early | Early |
| 5 | LAICA 92-13 | Early | Early-Intermediate | Early |
| 6 | CP 72-2086* | Early | Early | Early |
| 7 | COLMEX 94-8* | Early-Intermediate | Early | Early-Intermediate |
| 8 | ATEMEX 99-48 | Early-Intermediate | Early | Early-Intermediate |
| 9 | ATEMEX 99-1 | Early | Early | Early |
| 10 | ATEMEX 99-61 | Early-Intermediate | Early | Early-Intermediate |
| 11 | MEX 70-486 | Early | Early | Early |
| 12 | TCP 89-3505 | Late | Late | Intermediate-Late |
| 13 | MEX 80-1521 | Early | Early | Early |
| 14 | MEX 69-290* | Intermediate-Late | Intermediate-Late | Intermediate-Late |
| 15 | ITSAMEX 07-44814 | Early | Early | Early |
| 16 | ITSAMEX 06-3049 | Intermediate-Late | Intermediate-Late | Intermediate-Late |
| 17 | ITSAMEX 07-8681 | Intermediate-Late | Intermediate-Late | Intermediate-Late |
| 18 | ITSAMEX 07-20810 | Late | Late | Intermediate-Late |
| 19 | ITSAMEX 07-7501 | Late | Late | Late |
| 20 | ITSAMEX 07-1107 | Intermediate-Late | Intermediate-Late | Intermediate-Late |
| 21 | ITSAMEX 07-7259 | Late | Late | Intermediate-Late |
| 22 | ITSAMEX 06-6395 | Early-Intermediate | Early | Early-Intermediate |
| 23 | ITSAMEX 06-4863 | Intermediate-Late | Intermediate-Late | Intermediate-Late |
| 24 | ITSAMEX 07-4954 | Late | Late | Intermediate-Late |
| 25 | ITSAMEX 07-4387 | Intermediate-Late | Intermediate-Late | Intermediate-Late |
| 26 | ITSAMEX 07-121115 | Late | Late | Late |
| 27 | ITSAMEX 07-246 | Late | Late | Intermediate-Late |
| 28 | ITSAMEX 07-12116 | Intermediate-Late | Intermediate-Late | Intermediate-Late |
| 29 | ITSAMEX 07-12113 | Intermediate-Late | Intermediate-Late | Intermediate-Late |
| 30 | ITSAMEX 07-2963 | Intermediate-Late | Intermediate-Late | Intermediate-Late |
| 31 | ITSAMEX 07-99711 | Intermediate-Late | Early-Intermediate | Early |
| 32 | ITSAMEX 07-9886 | Early | Early-Intermediate | Early |
| 33 | ITSAMEX 07-86810 | Late | Late | Intermediate-Late |
| 34 | ITSAMEX 07-12119 | Intermediate-Late | Intermediate-Late | Intermediate-Late |
| 35 | ITSAMEX 07-1903 | Early | Early-Intermediate | Early |
| 36 | ITSAMEX 07-44813 | Early | Early-Intermediate | Early |
| 37 | ITSAMEX 07-12118 | Intermediate-Late | Intermediate-Late | Intermediate-Late |
| 38 | CP 85-1382 | Early-Intermediate | Early | Early-Intermediate |
| 39 | COLMEX 95-27* | Early | Early-Intermediate | Early |
| Fixed effects | Random effects | ||
| Parameter | CI | Parameter | CI |
| Material | Material | ||||
| COSTA JAL | 7.00 | 1.95 | ITSAMEX 07-7259 | 6.78 | 1.95 |
| RB 85-5035 | 6.23 | 1.95 | ITSAMEX 06-6395 | 8.22 | 1.95 |
| ITV 92-1424* | 8.30 | 1.95 | ITSAMEX 06-4863 | 7.33 | 1.95 |
| RB 85-5113* | 8.30 | 1.95 | ITSAMEX 07-4954 | 4.48 | 1.95 |
| LAICA 92-13 | 6.03 | 1.95 | ITSAMEX 07-4387 | 5.80 | 1.95 |
| CP 72-2086* | 9.35 | 1.95 | ITSAMEX 07-121115 | 6.73 | 1.95 |
| COLMEX 94-8* | 9.20 | 1.95 | ITSAMEX 07-246 | 6.45 | 1.95 |
| ATEMEX 99-48 | 9.20 | 1.95 | ITSAMEX 07-12116 | 6.36 | 1.95 |
| ATEMEX 99-1 | 7.40 | 1.95 | ITSAMEX 07-12113 | 6.51 | 1.95 |
| ATEMEX 99-61 | 8.23 | 1.95 | ITSAMEX 07-2963 | 7.11 | 1.95 |
| MEX 70-486 | 8.83 | 1.95 | ITSAMEX 07-99711 | 7.82 | 1.95 |
| TCP 89-3505 | 6.19 | 1.95 | ITSAMEX 07-9886 | 7.57 | 1.95 |
| MEX 80-1521 | 7.37 | 1.95 | ITSAMEX 07-86810 | 8.03 | 1.95 |
| MEX 69-290* | 7.16 | 1.95 | ITSAMEX 07-12119 | 7.83 | 1.95 |
| ITSAMEX 07-44814 | 7.44 | 1.95 | ITSAMEX 07-1903 | 8.69 | 1.95 |
| ITSAMEX 06-3049 | 6.71 | 1.95 | ITSAMEX 07-44813 | 6.46 | 1.95 |
| ITSAMEX 07-8681 | 6.51 | 1.95 | ITSAMEX 07-12118 | 7.26 | 1.95 |
| ITSAMEX 07-20810 | 6.53 | 1.95 | CP 85-1382 | 7.87 | 1.95 |
| ITSAMEX 07-7501 | 7.00 | 1.95 | COLMEX 95-27* | 9.37 | 1.95 |
| ITSAMEX 07-1107 | 6.62 | 1.95 |
| ID | Material | k-means | k-medoids | DBSCAN |
| 1 | COSTA JAL | Early-Intermediate | Intermediate-Late | Intermediate-Late |
| 2 | RB 85-5035 | Intermediate-Late | Intermediate-Late | Intermediate-Late |
| 3 | ITV 92-1424* | Early | Early | Early |
| 4 | RB 85-5113* | Early | Early | Early |
| 5 | LAICA 92-13 | Intermediate-Late | Late | Intermediate-Late |
| 6 | CP 72-2086* | Early | Early-Intermediate | Early-Intermediate |
| 7 | COLMEX 94-8* | Early | Early-Intermediate | Early-Intermediate |
| 8 | ATEMEX 99-48 | Early | Early-Intermediate | Early-Intermediate |
| 9 | ATEMEX 99-1 | Early-Intermediate | Intermediate-Late | Intermediate-Late |
| 10 | ATEMEX 99-61 | Early | Early | Early |
| 11 | MEX 70-486 | Early | Early-Intermediate | Late |
| 12 | TCP 89-3505 | Intermediate-Late | Late | Intermediate-Late |
| 13 | MEX 80-1521 | Early-Intermediate | Intermediate-Late | Intermediate-Late |
| 14 | MEX 69-290* | Early-Intermediate | Intermediate-Late | Intermediate-Late |
| 15 | ITSAMEX 07-44814 | Early-Intermediate | Intermediate-Late | Intermediate-Late |
| 16 | ITSAMEX 06-3049 | Intermediate-Late | Late | Intermediate-Late |
| 17 | ITSAMEX 07-8681 | Intermediate-Late | Late | Intermediate-Late |
| 18 | ITSAMEX 07-20810 | Intermediate-Late | Late | Intermediate-Late |
| 19 | ITSAMEX 07-7501 | Early-Intermediate | Intermediate-Late | Intermediate-Late |
| 20 | ITSAMEX 07-1107 | Intermediate-Late | Late | Intermediate-Late |
| 21 | ITSAMEX 07-7259 | Intermediate-Late | Late | Intermediate-Late |
| 22 | ITSAMEX 06-6395 | Early | Early | Early |
| 23 | ITSAMEX 06-4863 | Early-Intermediate | Intermediate-Late | Intermediate-Late |
| 24 | ITSAMEX 07-4954 | Late | Late | Null |
| 25 | ITSAMEX 07-4387 | Intermediate-Late | Late | Intermediate-Late |
| 26 | ITSAMEX 07-121115 | Intermediate-Late | Late | Intermediate-Late |
| 27 | ITSAMEX 07-246 | Intermediate-Late | Late | Intermediate-Late |
| 28 | ITSAMEX 07-12116 | Intermediate-Late | Late | Intermediate-Late |
| 29 | ITSAMEX 07-12113 | Intermediate-Late | Late | Intermediate-Late |
| 30 | ITSAMEX 07-2963 | Early-Intermediate | Intermediate-Late | Intermediate-Late |
| 31 | ITSAMEX 07-99711 | Early-Intermediate | Early | Early |
| 32 | ITSAMEX 07-9886 | Early-Intermediate | Intermediate-Late | Intermediate-Late |
| 33 | ITSAMEX 07-86810 | Early-Intermediate | Early | Early |
| 34 | ITSAMEX 07-12119 | Early-Intermediate | Early | Early |
| 35 | ITSAMEX 07-1903 | Early | Early-Intermediate | Late |
| 36 | ITSAMEX 07-44813 | Intermediate-Late | Late | Intermediate-Late |
| 37 | ITSAMEX 07-12118 | Early-Intermediate | Intermediate-Late | Intermediate-Late |
| 38 | CP 85-1382 | Early-Intermediate | Early | Early |
| 39 | COLMEX 95-27* | Early | Early-Intermediate | Early-Intermediate |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





