Flagellar Microswimmer with One-point Actuation: Effects of Non-uniform Mass and Elasticity on Propulsion

Preprint

Article

Flagellar Microswimmer with One-point Actuation: Effects of Non-uniform Mass and Elasticity on Propulsion

Altmetrics

Downloads

109

Views

Comments

Moisés Bolívar-Vivas,

Andrés Joaquín Serrano-Balbontín

Inés Tejado^*

Blas M. Vinagre

Moisés Bolívar-Vivas,

Andrés Joaquín Serrano-Balbontín

Inés Tejado^*

Blas M. Vinagre

This version is not peer-reviewed

Submitted:

03 September 2024

Posted:

03 September 2024

You are already at the latest version

Alerts

Abstract

Microscale swimmers have to face the dominance of viscous forces over inertial forces, the so-called low Reynolds number (hereafter Re) regime. The undulatory motion of an elastic tail is one of the few possible mechanisms for the self-propulsion of microswimmers in the particular conditions of low Re. Instead of using a complex arrangement of multiple actuators along the body of the swimmer, this work studies the propulsion of a swimming microrobot that is able to generate a non-reciprocal motion by moving a passive elastic tail with non-uniform properties using only a single actuator located at its head. A simulation model is developed in MATLAB to evaluate the effect of different mass and elasticity distributions in the tail on the microrobot propulsion. The results are used to observe the undulating motion of the tail and to optimize the design of the robotic microswimmers in terms of efficiency.

Keywords:

Subject: Engineering - Control and Systems Engineering

1. Introduction

Microrobotics has experienced great advances in recent years and is on its way to revolutionize many different fields of application such as medicine, biology and industry, among others, since the small size and weight of these robots not only allow them to access confined and/or hard-to-reach spaces where other devices cannot reach, but they can also interact in these areas with other entities, as well as transport elements to deposit in a specific location. Current reviews of the state of the art, mainly in the biomedical field, can be found in [1,2,3,4,5,6,7].

Most artificial microrobots are designed to reproduce the functionality of some biological systems or microorganisms, i.e., they are bio-inspired. In fact, biomimetics has been the main source of inspiration for robotics in general. Engineers have developed more efficient, versatile, and adaptable robots by studying how animals behave and solve problems. Among them, fish, larvae and bacteria inspire the development of aquatic robots that can move with both efficiency and agility, as demonstrated by their swimming abilities. For example, a multilink magnetic microrobot was developed in [8]. Highly efficient swimming locomotion was achieved by reproducing fish-inspired movements by passing a wave of bending along the length of the flexible body.

Small scale swimmers face big viscous forces in comparison with inertial forces. These conditions are identified by a low Reynolds number (hereafter

R e

). Two big groups of biological swimmers are identified when observing the microscale: helical swimmers, which advance in a fluid when reproducing a corkscrew motion, while many other microorganisms are propelled by one ore more flagella, a flexible structure that undergo beating motions, allowing them to move at such environments. The latter group has been the inspiration for the development of artificial swimming microrobots that are made up of a head and a slender filament attached to it, and it is the subject of this work.

Recent developments of oscillating microswimmers include the LarvaBot [9], which imitates the natural swimming of midge larvae. The prototype takes advantage of a non-uniform distribution of the magnetization of ferromagnetic particles that are embedded inside the hydrogel-based soft body.

Soft magnetic microswimmers inspired in bacteria, such as C. crescentus and Helicobacter pylori, were manufactured using magnetic hydrogel nanocomposites in [10]. Various shapes of artificial swimmers were compared, including combinations of tubular and helical shapes of their heads and tails. Microswimmers with flexible planar tail were found to be much faster, inside a solution with similar viscosity to blood, compared with the other prototypes using helical shapes. In addition, the elasticity of the tail was demonstrated to be useful for the microrobots to adapt to complex channels.

Simplifying the actuation methods can result in easier miniaturization. In addition, shape-adapting and power efficient microrobots can be obtained by taking advantage of the compliant properties of soft materials.

In order to achieve artificial microswimmers that are useful in the final application, it is necessary to achieve the best possible specifications regarding swimming performance. On one hand, some microswimmers, if not designed properly, can be very slow, which would result in long task-completion times. On the other hand, minimizing the power consumption of microswimmers is essential when using finite power sources, such as those based on chemical reactions, to extend its total operating time. In this sense, some works have paid special attention to swimming performance. In [11], a geometry optimization of helical swimmers was carried out using the resistive force theory. The propulsion efficiency was considered. In [12], larvae-inspired small scale swimmers were manufactured with different shapes and stiffness distributions. Initiating the study of nonuniform properties of flagella in the swimming efficiency at low Reynolds numbers. A general model to analyze the performance of flagella-driven artificial swimmer with several combinations of material, shape and stiffness distributions remains unexplored.

In this context, the aim of this work is to study the propulsion of a small swimming robot in a low

R e

medium, i.e., dominated by viscous forces. The robot is propelled by the traveling wave motion [13] of a passive flexible flagellum by using a non-uniform distribution of its properties, more specifically, its mass and elasticity. The contributions of this work are as follows:

Development of a simulation model of the robot based on a larval specimen of the zebra-fish (Danio Rerio) [12] by using rigid elements and viscoelastic joints [14];
Analysis of various flagellum designs, which differ from each other in mass distribution and elasticity;
Evaluation of these designs according to different performance indices; and
Recommendation of guidelines for the optimal design of a small-dimensional bacterial flagellum-type swimmer.

This work continues a path initiated by the research group Fractional Order Control & Robotics (FOC&ROB) of the University of Extremadura with works such as [15,16].

The remainder of this paper is organized as follows. Section 2 briefly describes the ways to generate traveling waves that enable propulsion in low

R e

environments. Section 3 is devoted to the swimmer simulation model that has been developed in the MATLAB/Simulink environment. Section 4 presents the propulsion performance of the robot under different conditions, namely excitation frequencies, and stiffness and mass distributions. Section 5 provides some guidelines for the optimal design of this type of microswimmer. Finally, the conclusions of this work are summarized in Section 6.

2. Traveling Waves

The number

R e

determines the influence of inertial and viscous forces on a moving Newtonian fluid by the following expression:

R e = \frac{v l ρ}{μ}

(1)

where v and l are the maximum velocity and characteristic dimension of the flow, respectively, and

ρ

and

μ

are the density and dynamic viscosity of the fluid, respectively.

The forms of propulsion of artificial swimmers with flexible flagella have their origin in the movement and flexibility of the flagella of eukaryotic cells. The basic movement of this type of swimmer is called traveling wave [17]. In essence, the flagellum of such swimmers describes a smooth curve that is propagated along its body. Usually, the front part of the body is almost still during the wave motion, and the distance traversed by each point of the flagellum increases as the rear portion is reached. In the continuous and smooth case, each point of the tail is forced to describe a sine wave that slightly changes in phase and amplitude with respect to the preceding neighboring point.

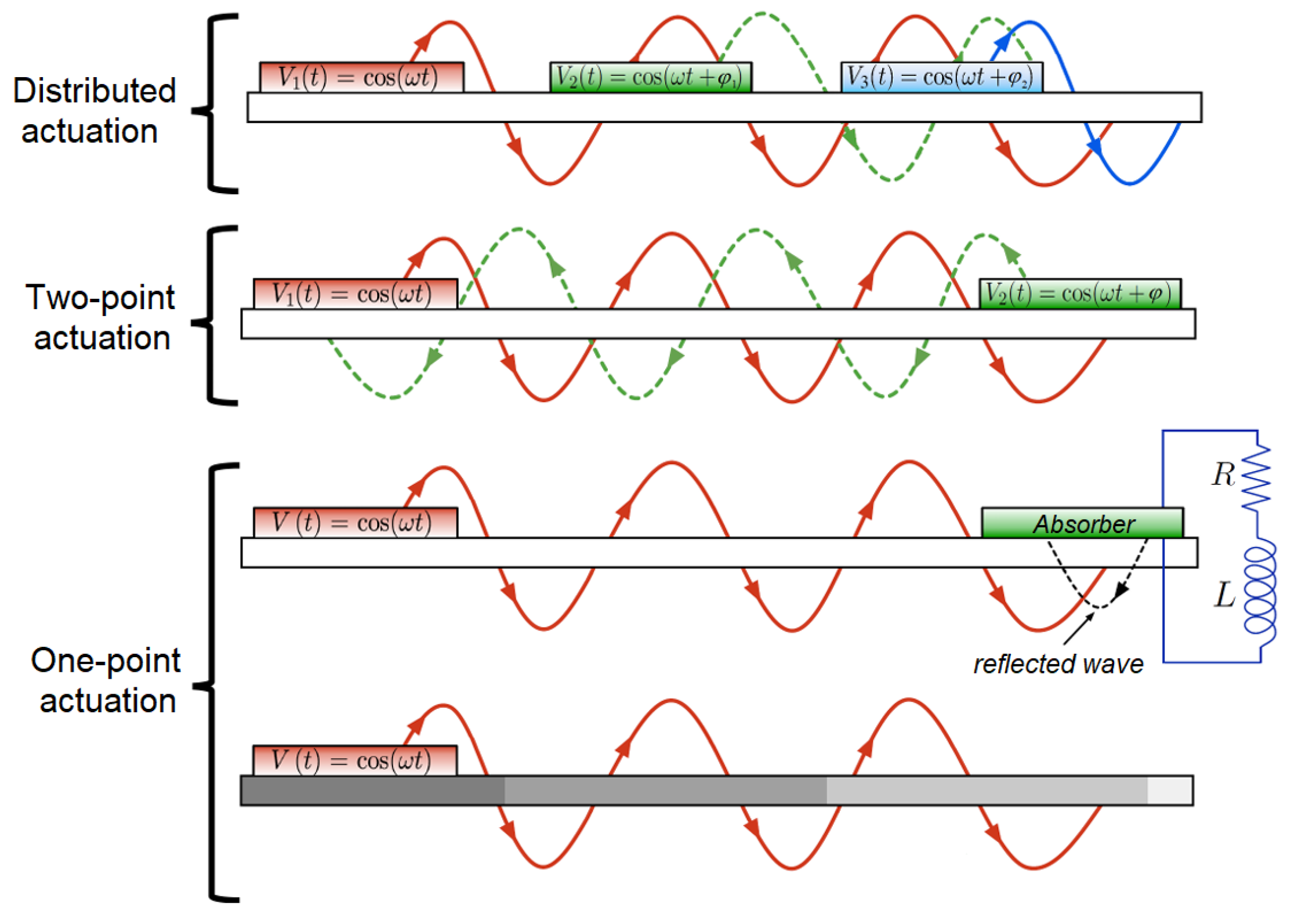
It is possible to generate traveling waves in a flexible flagellum using the methods described below (Figure 1):

By distributed actuation, so that each point on the flagellum is excited by a sinusoidal signal, with amplitude and phase matched so that the composition of all of them gives the desired progressive waveform.
By means of standing waves generated by excitation of two points of the flagellum in the following way: the first actuator generates a vibration on the flagellum whose reflected waves are compensated by the vibration generated by the second actuator, excited with different spatial and temporal phase. That is, assuming that the voltage applied to each actuator is $v_{1} (t) = cos (ω t)$ and $v_{2} (t) = cos (ω t + φ)$ , where $ω$ is the excitation frequency and $φ = π (n - m) / 2$ is the phase shift, where $m = \pm 2 K + 1$ and $n = \pm 2 K$ , with $K \in R$ . The wavelength of the generated progressive wave will be $λ = 4 d / (n + m)$ , where d is the distance between the actuators.
By exciting the flagellum at a single point, the reflected waves are eliminated by means of an element located at the end of it that acts as an absorber of the mechanical vibration, such as a piezoelectric that dissipates its energy through an electrical circuit formed by a resistance and an inductance connected in series with the same [18].
With single actuation, either transverse or angular [19], of a flagellum that may have a non-uniform distribution of masses [16] and/or elasticity [12]. This paper focuses on this method of generating traveling waves.

3. Swimmer Modeling

The swimmer is a robot with one degree of freedom consisting of a head and a flexible flagellum immersed in a viscous medium. Its model was developed in Simulink using the Simscape physical modeling tool, which allows the creation of system models from the elements that make it up, as well as 3D animations of the motion it performs. Likewise, it allows to obtain results fast in comparison with other models such as finite element methods that, despite being more accurate, in general, are more time consuming and computationally expensive.

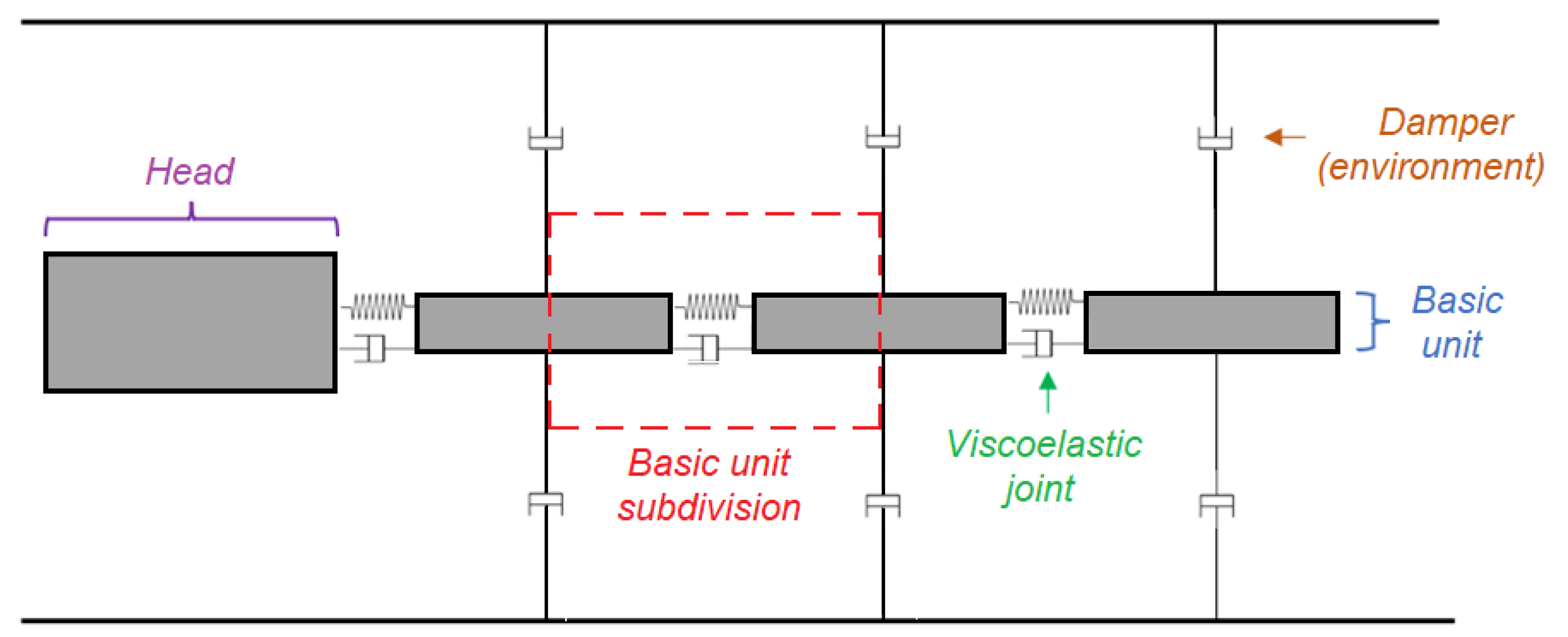
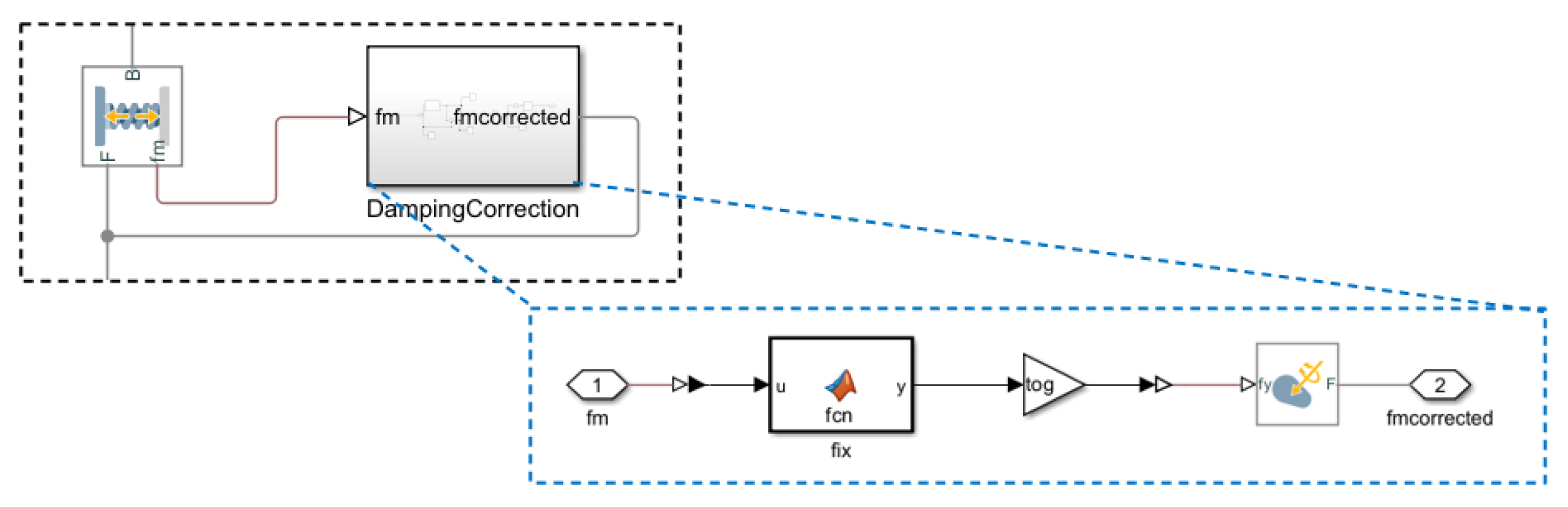
The robot model is essentially divided into two parts: the body of the swimmer, consisting of the head and the flagellum, and the environment in which it is immersed. The model also includes a block for analyzing the robot movement in the environment. It should be noted that since Simscape does not have blocks to simulate flexible elements, it was decided to model the robot flagellum as a series of rigid elements connected by viscoelastic joints, as shown in Figure 2. The model was configured to allow for variations in its geometry (mass distribution) and stiffness distribution. It also incorporates interactions with the medium in a simplified form through viscous forces acting on each rigid element of the flagellum. The following is a detailed description of all of the parts that make up the model of the robot.

3.1. Microswimmer Body

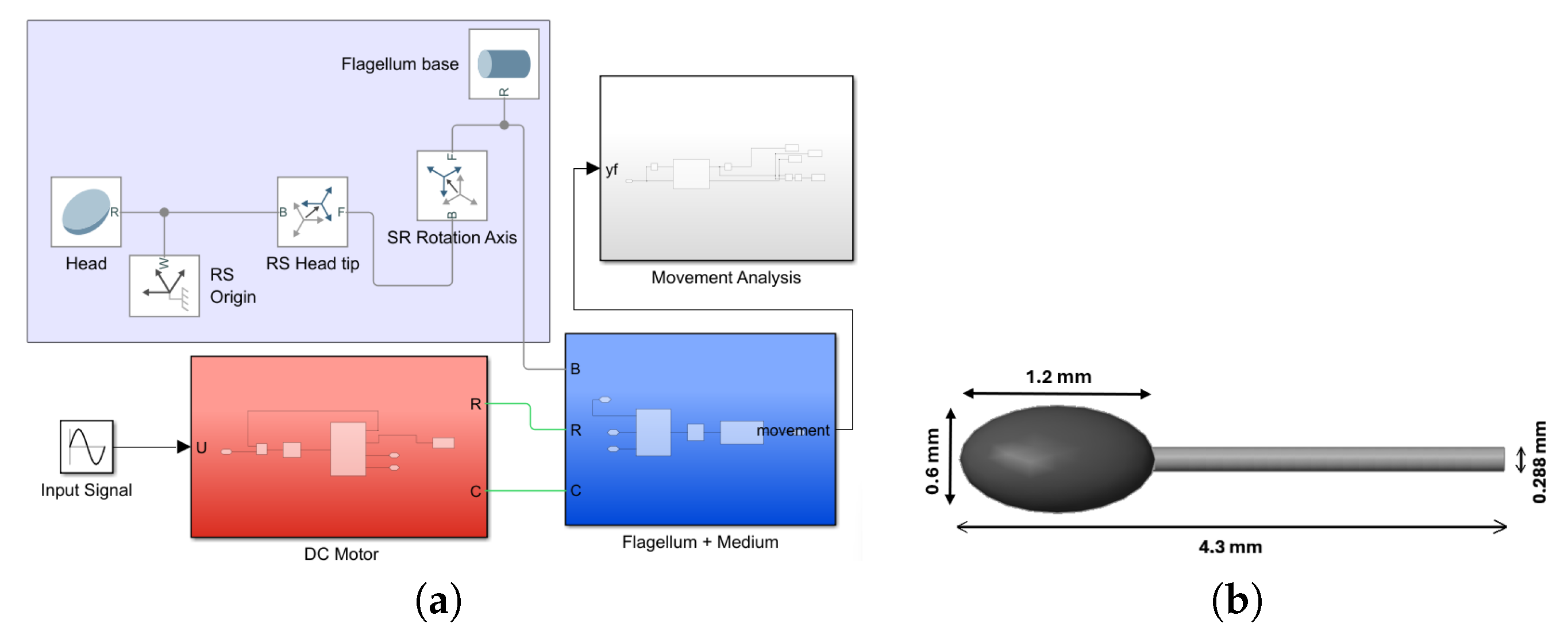
Figure 3 shows the model of the swimmer body, the implementation with Simulink blocks, and the appearance of the associated 3D animation. This last figure includes the robot dimensions.

The head is an ellipsoidal solid that serves as an anchor for the flagellum and is located at the origin of the simulation coordinates. It is therefore an immobile object in the model and serves as a reference point for various sensors used to measure flagellum displacement. It is connected to the flagellum by means of a DC motor acting as an actuator, modeled as an electromechanical converter with dimensions and specifications suitable for the correct operation of the robot specified in Table 1. In order for the flagellum to follow the desired sinusoidal signal, the motor is controlled by a compensator designed to obtain a phase margin of at least 45° and a bandwidth of 30 to 90 Hz in closed loop.

As mentioned earlier, there are two basic elements in the flagellum model: the basic units, which are the rigid elements into which the flagellum is divided, and the viscoelastic joints, which connect the basic units together and allow the mobility and flexibility of the flagellum. These two elements are present in what is called the “basic unit subdivision” in Figure 2. 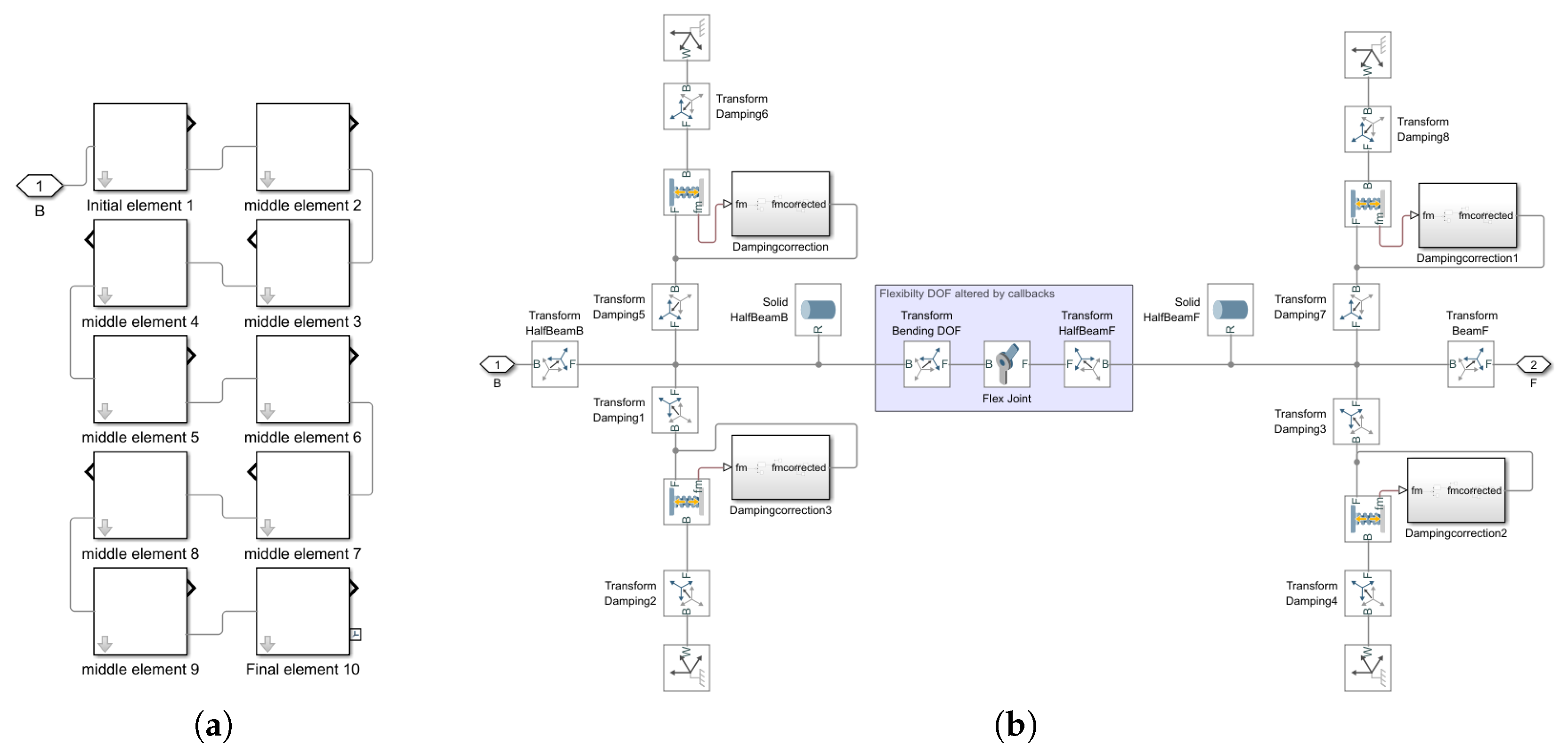Specifically, each of these subdivisions consists of two halves of basic units (solid-like blocks called “half beam”) connected by a viscoelastic element (Revolute Joint block called “Flex Joint”). Thus, the flagellum is obtained by connecting a given number of these subdivisions, as shown in Figure 4(a). As can be seen in Figure 4(b), the “half beam” blocks are attached to each other and to the viscoelastic joints by “Rigid Transform” blocks, which are used to change the position of the reference systems of the solids to which they are attached. By default, the reference system of each rigid element is located at its center of gravity, but with these blocks you can change the system to its extremes so that they can engage with viscoelastic joints and other rigid elements. For its part, the “Flex Joint” block has an elastic component, given by the elastic stiffness coefficient k (parameter Stiffness of the block), and a viscous component, defined by the damping

δ

(parameter Damping Coefficient of the block). For the former, although the value of k varies depending on the geometry of the flagellum, the reference value is given by [14]

k = \frac{E I_{z z}}{l}

(2)

where E is Young’s modulus of the flagellum material,

I_{z z}

is the area moment of inertia and l is the flagellum length. For the latter, the value

δ = 10^{- 6} \sqrt{4 k m}

was chosen to simulate the flexible and flaccid character of the flagellum. The Transform Sensor blocks are also responsible for collecting the flagellum displacement data.

Regarding the model of the microswimmer body, it should be noted that:

The material chosen for the flagellum is EcoFlex 00-30, a very strong and flexible vulcanized rubber with a Young’s modulus of $E = 0.125$ MPa and a density of $ρ_{f} = 1065.02$ kg/m³ [20]. These physical properties were added to the “half beam” blocks to simulate the flexible behavior of the flagellum).
In the simulations, the value of k and the mass distribution are varied in different flagellum geometries, keeping all other model parameters constant.
In choosing the number of rigid elements that make up the swimmer flagellum, it was considered that the model must have enough segments to see the effect of the parameter k in the simulations. And second, the study of the motion of a zebrafish pup reported in [3], in which 5 segments with different stiffness are proposed, i.e., changes in k occur at points located at $24.44$ %, $40.08$ %, $58.50$ %, and $76.74$ % of the total length of the flagellum. After an iterative process, it was concluded that 11 rigid elements and 10 junctions were sufficient to achieve a reasonable compromise between computational cost and fidelity of results. Figure 5 shows the comparison between our choice and the one proposed in [12].

3.2. Viscous Environment

As mentioned earlier, the simulation has a representation of the viscous medium in which the microrobot will be immersed. This medium is emulated by four dampers (Spring and Damper Force blocks) per each basic unit subdivision, as shown in Figure 2. This is intended to bring the simulation closer to a real case by acting as dampers on both sides of the center of mass of each “half beam” block, thus simulating the resistance to motion that the viscous fluid would cause on the flagellum. Specifically, they are placed perpendicular to the center of mass of each segment of the flagellum to more appropriately and accurately simulate the damping of the medium in each section of the length of the flagellum.

Based on Stokes’ law, it is possible to calculate the viscous friction in a low

R e

medium in terms of drag (

F_{d}

) from the velocity of a flagellum segment (v) as

F_{d} = 6 π R μ v

(3)

where R is the radius of the segment and

μ

is the dynamic viscosity of the medium. This expression is implemented by means the block parameter Spring Stiffness for each Spring and Damper Force block, so that a drag force is created against the movement of the flagellum. Due to the viscous nature of the medium, the block Spring and Damper Force is configured to emulate an overdamped system. This damping property is introduced thanks to the parameter Damping Coefficient of the block.The aforementioned Spring and Damper Force block creates both repulsive and attractive forces on the flagellum depending on the natural length of the virtual spring the system is using to emulate the viscous medium. Since the attractive component of the force is not desired, as can be seen in Figure 6, a small function has been added to the output of the block to keep only the positive/repulsive component of the force.

The robot is considered to be immersed in silicone oil. Its viscosity makes it ideal for use in experiments of this type to achieve low

R e

conditions. This fluid has a viscosity of

μ = 0.0964

kg/(m·s) and a density of

ρ = 864

kg/m³.

3.3. Motion Analysis

The developed swimmer model also has a block for calculating the propulsion force and the displacement velocity of the microrobot as a function of the flagellum geometry (more precisely, the flagellum length l and the wavelength of the generated progressive wave

λ

) and the chosen drag coefficients (head drag coefficient,

c_{h}

, and tangential and normal drag coefficients,

c_{l}

and

c_{n}

, respectively).

4. Propulsion Performance

This section deals with the simulations carried out with the described swimmer model under different conditions: excitation frequencies, and stiffness and mass distributions. The propulsion performance of the microswimmer is discussed in terms of the several indexes.

4.1. Preliminary Considerations

For this study, a total of 144 simulations were performed to evaluate the effects of the excitation frequency and both the stiffness and the mass distributions on the microswimmer propulsion. Details of each are given below:

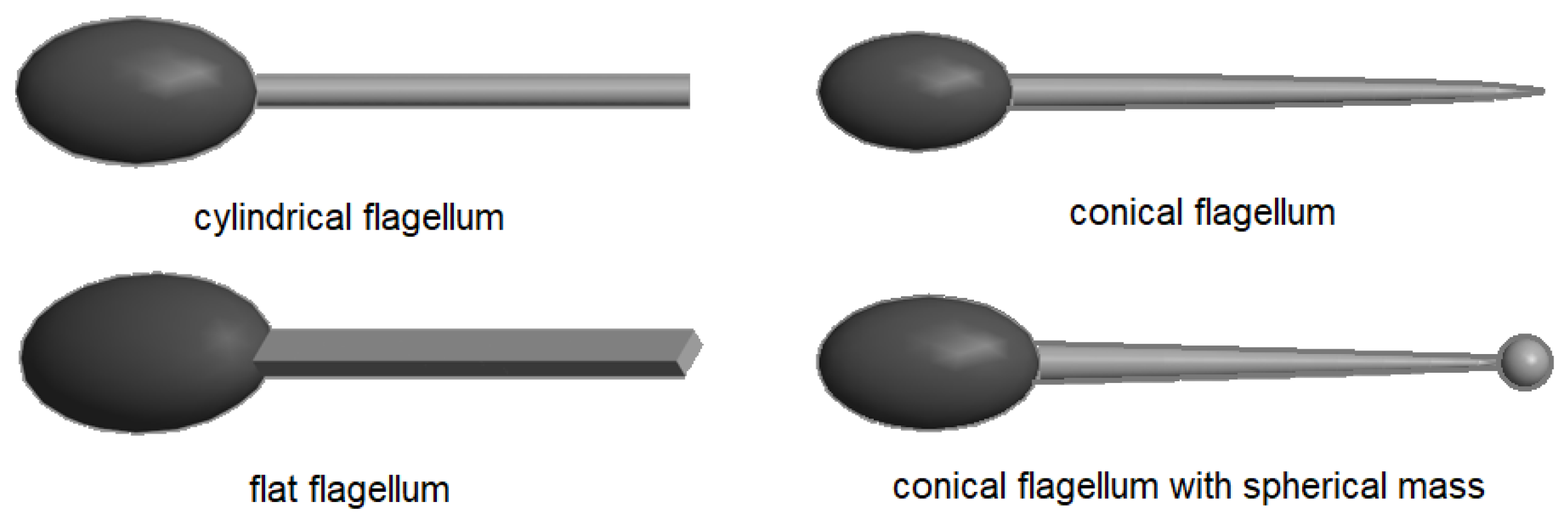
Four different mass distributions were chosen (Figure 7): cylindrical flagellum, conical flagellum, conical flagellum with a spherical mass at the end of the flagellum, and flat flagellum with a rectangular cross section. All four distributions have an identical mass, $0.202$ g, while the length of the flagellum has been adjusted for each geometry to accommodate the same amount of mass: $l = 4.3$ mm for the cylindrical and flat shape, while the flagellum is longer in its cylindrical and cylindrical with spherical mass reaching $6.6$ mm and $5.5$ mm, respectively.
Four different excitation frequencies are considered within the so-called ’biologically relevant frequency range’ [21], i.e., frequencies used by most living organisms to propel themselves in a liquid medium: 30, 50, 70 and 90 Hz.
The reference stiffness distribution is the uniform one, where the value of k varies in the interval $[10^{- 8}, 10^{- 9}]$ N·m depending on the shape of the flagellum according to eq. (2). In addition, other stiffness distributions characterized by variations of k are considered below:
- Group 1: ascending and descending logarithmic and linear distributions. With this first group of k distributions, it is intended to broadly study the effects of different distributions on the flagellum, as well as the effects of further variation of k within each distribution.
- Group 2: a descending exponential distribution defined by
  
  $k_{i} = k_{i - 1} e^{- a (l_{i} + 0.2)}$
  
  (4)
  
  where $k_{i}$ and $l_{i}$ are the stiffness and length of each flagellar segment, respectively, and a is the uniformity factor, which allows to increase or decrease the difference in stiffness between two consecutive flagellar segments. This expression is inspired by the natural stiffness distribution of a zebrafish (Danio Rerio) along its tail [12]. This second set of distributions aims to study smaller k variations between flagellar segments, which in turn are more realistic distributions due to their inspiration from the zebrafish body.
To evaluate and compare the results obtained in the simulations, four performance indexes are used: the forward speed $V_{x}$ (measured in mm/s), the thrust force $F_{x}$ (measured in N), the efficiency $ξ$ , defined as the ratio between the mechanical power developed by the flagellum and the electrical power supplied by the motor, and the transport cost per unit mass (CoTm), measured in W/m and defined as the quotient between the electrical power supplied to the DC motor and the distance traveled in the forward direction for a given time. The first two quantities are calculated by the motion analysis block described above and are used to quantify the robot forward motion. Efficiency and CoTm, on the other hand, allow us to evaluate the robot design in terms of load versus power consumption.

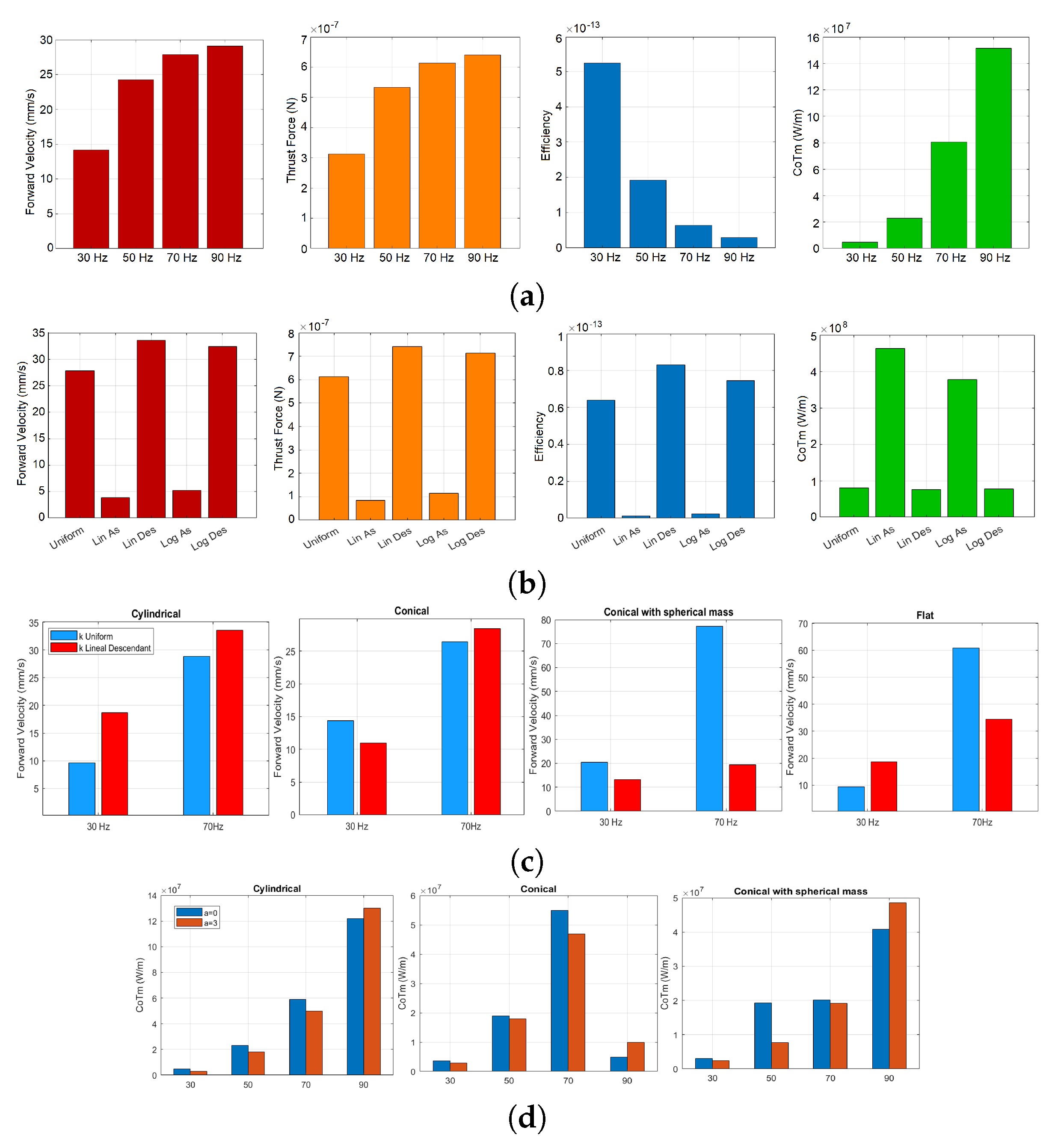
All the obtained results are shown in Figure 8; they will be explained in detail in the following subsections.

4.2. Effects of Excitation Frequencies

In the first set of simulations, both the stiffness and geometry of the flagellum are left unchanged, and only the excitation frequency of the flagellum is varied.

It can be seen that as the frequency is increased, the velocity and propulsive force improve, but the efficiency and transport cost deteriorate. This is consistent with what is expected in wave motion. The higher the frequency, the more speed it is obtained for a higher energy expenditure. The four mass distributions present this behavior when increasing the excitation frequency. The four rates at different frequencies can be seen for a cylindrical flagellum in Figure 8(a).

4.3. Effects of Stiffness Distributions

For this comparison, simulations are performed to vary the stiffness of the flagellum for the different flagellum geometries at the four study frequencies:

In the first group of distributions, it can be seen that the ascending distribution of stiffness is largely inferior to the rest. This is reflected in the results with the worst values for all established performance indexes. The descending distributions generally give the best performance indexes results for the conical and cylindrical flagella, while their conical and flat counterparts generally give better results with a uniform k distribution. This can be seen in Figure 8(b).
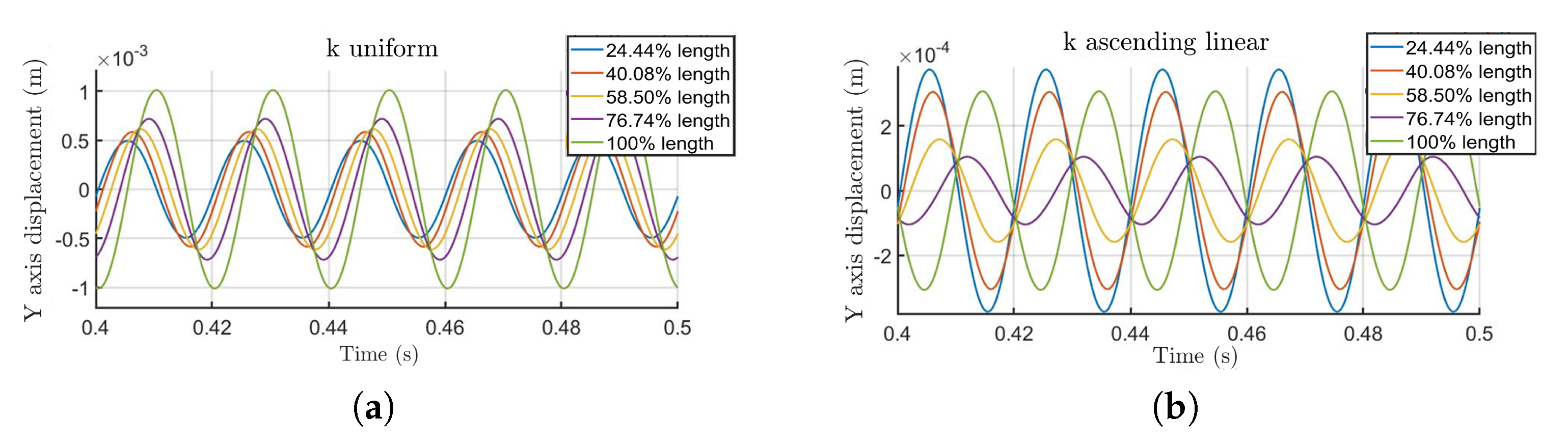
The traveling wave motion performed by the flagellum (Figure 9(a)) achieves better performance rates than in cases where it can perform a more chaotic motion (Figure 9(b)).
The behavior of the first two geometries can be found in nature. Most fish and aquatic animals have tails and fins that become more elastic as one approaches the tip [22]. In the case of the conical flagellum with ball, it can be deduced that uniform stiffness allows better tracking of the motion generated at the origin of the flagellum by the rest of the body. On the other hand, if the stiffness is reduced in the body approaching the sphere, the mass concentration in the sphere will be too great for the rest of the flagellum to pull, so the sphere will not move too far from its initial position, which would interfere with the wave motion.
In the case of the flat-section flagellum, the explanation can be found in a higher pulling force than in the other geometries. As a flat section flagellum, this less hydrodynamic design generates a higher drag force than the other three types of flagellum, which prevents it from moving easily, so when the stiffness is reduced as the end is approached, there are difficulties found in reproducing the wave motion. What is described for the geometries can be observed in Figure 8(c).
Regarding the second group of distributions, it can be seen how it gets better overall results as the non-uniformity of the stiffness along the flagellum is increased. There is only one scenario where it can be useful to have a uniform k distribution, and that is for high frequencies if the objective is to get better results in both the efficiency and transportation cost indexes.
As also shown in [12], for low frequencies the transport cost is lower for a non-uniform distribution than for a uniform one. However, the opposite is the case at high frequencies, where uniform distributions have lower transportation costs than non-uniform ones. In the current study, this behavior was replicated for all geometries except the planar geometry. This is likely due to the previously mentioned drag coefficients for the planar geometry. This behavior can be seen in Figure 8(d).

4.4. Effects of mass distributions

For this comparison, simulations are performed with the robot maintaining a uniform k distribution and the same frequency while varying among the four geometries of the flagellum.

In these simulations the geometries with the best results in performance indexes are the planar geometry and the conical geometry with ball.

The conical flagellum with ball, having a concentration of mass at the tip of the flagellum, creates an important inertia in the undulation that allows to generate a considerable movement. These good results are obtained as already mentioned for k distributions such as uniform, but not for all.

On the other hand the flat flagellum, having a less hydrodynamic section, its passage generates a higher fluid resistance but also a higher thrust. The results obtained with this geometry make sense if one takes into account the number of aquatic organisms that use flat fins and tails to propel themselves.

5. Guidelines for microswimmer optimal design

This section provides some guidelines for the optimal design of this type of microswimmer. Firstly, the best performances between the two stiffness distribution groups are discussed.

5.1. Results comparison

If the results obtained with the two sets of k distributions are compared side by side, it is apparent that the second set of distributions outperforms the first across all performance indexes (Table 2). This is consistent since the first group consists of distributions that have been found to be reasonable, but the first group always starts from a calculated stiffness value for each type of geometry and is inspired by the distribution found in the tail of a zebrafish pup.

5.2. Recommendations

From all the simulations performed, it has been seen that the most successful mass distributions for the flagellum have been the conical with ball and the planar. As for the k distributions, in general the descending stiffness distributions were the most successful. However, in some cases the uniform distribution may be more desirable, as was found in the second group, when exciting the flagellum at high frequencies in order to achieve a better efficiency.

Table 3 can be used as a reference as to which configurations may be the most interesting when designing a swimming microrobot for a specific flagellum mass distribution. For example, if a cylindrical geometry is selected for the flagellum, the desired propulsion performance will determine the type of stiffness distribution to implement. Specifically, if the objective is to maximize forward velocity and propulsion force, it is recommended to employ the descending linear stiffness distribution (the optimal values of such indexes would be

V_{x} = 28.83

mm/s and

F_{x} = 0.64

N); in case of efficiency and CoTm, it is recommended to use the exponential distribution with

a = 3

(in this case, the optimal values of the indexes would be

ξ = 4.34

and

CoT m = 0.64

W/m).

It should be noted that:

Priority has been given to achieving better results in both travel speed and transportation cost. This is due to the fact that, in the design of a microrobot, the travel speed is considered a more important indicator than the propulsion power, since it is important to know how fast it moves in the environment. On the other hand, transportation cost is considered a more interesting performance indicator than efficiency, since it represents the energy that must be supplied to the robot to travel a given distance.
These guidelines should only be taken into consideration when designing a microrobot with dimensions similar to those of the one under study. While the mass distribution and geometry of the flagellum are the primary factors influencing the microrobot performance, modifying the length or width of the flagellum could result in enhanced performance with a different stiffness distribution than that recommended here.
To replicate the varying stiffness values across the five segments of the flagellum, which is entirely made of Ecoflex, it is essential to focus on the stiffness distribution given by eq. (2). Since both the Young’s modulus, E, and the flagellum length, l, are fixed values and cannot be altered, the only way to adjust stiffness is through manipulation of the area moment of inertia ( $I_{x x}$ ). This parameter depends on the dimensions of the cross-section. Accordingly, to attain the requisite stiffness, gaps can be incorporated along the length of the flagellum, thereby facilitating modification of the cross-sectional dimensions. A detailed explanation of this method can be found in [12].

6. Conclusions

This work has evaluated the performance of one-point actuated artificial microswimmer with elastic tail. Different mass distributions (or geometries) and stiffness distributions of the flagellum have been tested. A simulation model was developed based on rigid elements and viscoelastic joints using fundamental libraries from Simscape in the MATLAB/Simulink environment.

The simulation model of this work made possible to evaluate several combinations of geometry, stiffness, mass distribution and excitation frequencies using four performance indices: forward average speed, thrust force, efficiency and transport cost of unit mass.

The results obtained here can be used to manufacture microrobots that achieve great swimming velocities, which is essential to perform tasks that require traveling long distances, for instance, traveling through blood vessels in the human body, or great swimming efficiencies necessary to achieve higher levels of autonomy, specially when using finite power sources. In this sense, a set of design recommendations were given.

In future work, the simulation model can be further complemented to include application-specific actuator models, such as the magnetic torque generated by Helmholtz coils or head oscillation caused by chemical reactions, as in our current research lines. In addition, control strategies appropriated to correctly induce the traveling waves can be explored.

Author Contributions

conceptualization, I.T.; methodology, I.T.; software, M.B.-V.; validation, M.B.-V.; investigation, M.B.-V., and I.T.; data curation, M.B.-V.; writing—original draft preparation, M.B.-V., A.J.S.-B., and I.T.; writing—review and editing, M.B.-V., A.J.S.-B., and I.T.; visualization, M.B.-V.; supervision, I.T., and B.M.V.; project administration, I.T.; funding acquisition, I.T., and B.M.V. All authors have read and agreed to the published version of the manuscript.

Funding

This work was partially funded by the Agencia Estatal de Investigación (Ministerio de Ciencia e Innovación) through the project PID2022-141409OB-C22/AEI/10.13039/501100011033/FEDER, UE, and by the European Regional Development Fund (FEDER) “A way to make Europe”.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Ahmad, B.; Gauthier, M.; Laurent, G.J.; Bolopion, A. Mobile Microrobots for In Vitro Biomedical Applications: A Survey. IEEE Transactions on Robotics 2022, 38, 646–663. [Google Scholar] [CrossRef]
Xu, Y.; Bian, Q.; Wang, R.; Gao, J. Micro/nanorobots for precise drug delivery via targeted transport andtriggered release: A review. International Journal of Pharmaceutics 2022, 616, 121551. [Google Scholar] [CrossRef] [PubMed]
Wang, B.; Kostarelos, K.; Nelson, B.J.; Zhang, L. Trends in micro-/nanorobotics: Materials development, actuation, localization, and system integration for biomedical applications. Advanced Materials 2021, 33, 2002047. [Google Scholar] [CrossRef] [PubMed]
Sun, B.; Wood, G.; Miyashita, S. Milestones for autonomous in vivo microrobots in medical applications. Surgery 2021, 169, 755–758. [Google Scholar] [CrossRef] [PubMed]
Ceylan, H.; Yasa, I.C.; Kilic, U.; Hu, W.; Sitti, M. Translational prospects of untethered medical microrobots. Progress in Biomedical Engineering 2019, 1, 012002. [Google Scholar] [CrossRef]
Li, J.; Esteban-Fernández de Ávila, B.; Gao, W.; Zhang, L.; Wang, J. Micro/nanorobots for biomedicine: Delivery, surgery, sensing, and detoxification. Science Robotics 2017, 2, eaam6431. [Google Scholar] [CrossRef] [PubMed]
Sitti, M.; Ceylan, H.; Hu, W.; Giltinan, J.; Turan, M.; Yim, S.; Diller, E. Biomedical applications of untethered mobile milli/microrobots. Proceedings of the IEEE 2015, 103, 205–224. [Google Scholar] [CrossRef] [PubMed]
Li, T.; Li, J.; Zhang, H.; Chang, X.; Song, W.; Hu, Y.; Shao, G.; Sandraz, E.; Zhang, G.; Li, L.; Wang, J. Magnetically Propelled Fish-Like Nanoswimmers. Small 2016, 12, 6098–6105. [Google Scholar] [CrossRef] [PubMed]
Xia, N.; Jin, B.; Jin, D.; Yang, Z.; Pan, C.; Wang, Q.; Ji, F.; Iacovacci, V.; Majidi, C.; Ding, Y.; Zhang, L. Decoupling and Reprogramming the Wiggling Motion of Midge Larvae Using a Soft Robotic Platform. Advanced Materials 2022, 34, 2109126. [Google Scholar] [CrossRef] [PubMed]
Huang, H.W.; Uslu, F.E.; Katsamba, P.; Lauga, E.; Sakar, M.S.; Nelson, B.J. Adaptive locomotion of artificial microswimmers. Science Advances 2019, 5, eaau1532. [Google Scholar] [CrossRef] [PubMed]
Miao, J.; Li, X.; Liang, B.; Wang, J.; Xu, X. Enhancing Swimming Performance by Optimizing Structure of Helical Swimmers. Sensors 2021, 21. [Google Scholar] [CrossRef] [PubMed]
Wang, T.; Ren, Z.; Hu, W.; Li, M.; Sitti, M. Effect of body stiffness distribution on larval fish–like efficient undulatory swimming. Science Advances 2021, 7. [Google Scholar] [CrossRef] [PubMed]
Gray, J.; Hancock, G.J. The Propulsion of Sea-Urchin Spermatozoa. Journal of Experimental Biology 1955, 32, 802–814. [Google Scholar] [CrossRef]
Chudnovsky, V.; Kennedy, D.; Mukherjee, A.; Wendlandt, J. Modeling Flexible Bodies in SimMechanics and Simulink, 2006.
Traver, J.E.; Tejado, I.; Nuevo-Gallardo, C.; López, M.A.; Vinagre, B.M. Performance study of propulsion of N-link artificial Eukaryotic flagellum swimming microrobot within a fractional order approach: From simulations to hardware-in-the-loop experiments. European Journal of Control 2021, 58, 340–356. [Google Scholar] [CrossRef]
López, M.A.; Prieto, J.; Traver, J.E.; Tejado, I.; Vinagre, B.M.; Petrás, I. Testing non reciprocal motion of a swimming flexible small robot with single actuation. 19th International Carpathian Control Conference (ICCC2018), 2018, pp. 312–317. [CrossRef]
Alberts, B.; Bray, D.; Hopkin, K.; Johnson, A.; Lewis, J.; Raff, M.; Roberts, K.; Walter, P. Essential Cell Biology, fourth ed.; Taylor & Francis Group, 2013.
Hariri, H.; Bernard, Y.; Razek, A. A traveling wave piezoelectric beam robot. Smart Materials and Structures 2013, 26, 2577–2590. [Google Scholar] [CrossRef]
Yu, T.S.; Lauga, E.; Hosoi, A.E. Experimental investigations of elastic tail propulsion at low Reynolds number. Physics of Fluids 2006, 18, 091701. [Google Scholar] [CrossRef]
Ecoflex 00-30 Product Information Smooth-On Inc.
J.L van Leuuwen, C.J. Voesenek, U.M. How body torque and Strouhal number change with swimming speed and developmental stage in larval zebrafish. Journal of the Royal Society Interface 2015, 12, 237–252. [Google Scholar] [CrossRef]
Sfakiotakis, M.; Lane, D.; Davies, J. Review of fish swimming modes for aquatic locomotion. IEEE Journal of Oceanic Engineering 1999, 24, 237–252. [Google Scholar] [CrossRef]

Figure 1. Methods for generating traveling waves with a flexible flagellum.

Figure 2. Representation of the microrobot model in the medium.

Figure 3. Microswimmer body: (a) block diagram in Simulink, (b) appearance of the 3D animation with dimensions.

Figure 4. Model of the microswimmer flagellum: (a) connection of “basic unit subdivision” blocks, (b) details of a “basic unit subdivision” block.

Figure 5. Illustration of the distribution of the 5 segments of k along the 11 basic units of the flagellum.

Figure 6. Model of the viscous environment in which the microswimmer is immersed.

Figure 7. Illustrations of the mass distributions simulated.

Figure 8. Results of various simulations: (a) variation of the four performance indexes for the different frequencies (cylindrical flagellum), (b) performance indexes for the different k distributions in group 1 (cylindrical flagellum), (c) average forward speed for uniform and descending linear k in the four geometries, and (d) effect of increasing the frequency (in Hz) in the CoTm index for group 2 for various geometries.

Figure 9. Displacement on the axis and at different points of the cylindrical flagellum in a traveling wave motion at an excitation frequency of 50 Hz with: (a) uniform stiffness, (b) ascending linear stiffness.

Table 1. DC motor parameters.

Parameter (Unit)	Value
Inertia (kg·m²)	$2 \times 10^{- 4}$
Damping (N·m/(rad/s))	$5 \times 10^{- 6}$
Electromotive force constant (V/(rad/s))	$0.036$
Stator resistance ( $Ω$ )	$6.42$
Stator inductance (H)	$2.3 \times 10^{- 5}$

Table 2. Best performances between the two stiffness distribution groups.

Group 1	Group 2
Forward velocity	Forward velocity
$58.9$	$64.39$
k uniform, conical flagellum with mass	k exponential with $a = 3$ , flat flagellum
Propulsion force	Propulsion force
$1.13$	$1.42$
k uniform, conical flagellum with mass	k exponential with $a = 3$ , flat flagellum
Efficiency	Efficiency
$15.03$	$15.03$
k uniform, flat flagellun	k exponential with $a = 1$ , flat flagellum
CoTm	CoTm
$2.06$	$1.82$
k uniform, conical flagellum	k exponential with $a = 1$ , conical flagellum with mass

Table 3. Guidelines for an optimal design of a flagellar microswimmer with one-point actuation. The optimal values of the performance indexes for each option are indicated in parentheses.

Desired properties		Recommended stiffness distribution
Mass distribution	Performance
Cylindrical	Forward velocity and propulsion force	Descending linear ( $V_{x} = 28.83$ and $F_{x} = 0.64$ )
	Efficiency and CoTm	Exponential with $a = 3$ ( $ξ = 4.34$ and $CoT m = 0.64$ )
Conical	Forward velocity and propulsion force	Logarithmic descending ( $V_{x} = 28.74$ and $F_{x} = 0.63$ )
	Efficiency and CoTm	Exponential with $a = 1$ ( $ξ = 2.47$ and $CoT m = 2.07$ )
Conical with spherical mass	Forward velocity and propulsion force	Exponential with $a = 2$ ( $V_{x} = 60.53$ and $F_{x} = 1.34$ )
	Efficiency and CoTm	Exponential with $a = 3$ ( $ξ = 11.31$ and $CoT m = 1.95$ )
Flat	Forward velocity and propulsion force	Exponential with $a = 3$ ( $V_{x} = 64.39$ and $F_{x} = 1.42$ )
	Efficiency and CoTm	Exponential with $a = 3$ ( $ξ = 12.01$ and $CoT m = 1.89$ )

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Flagellar Microswimmer with One-point Actuation: Effects of Non-uniform Mass and Elasticity on Propulsion

Abstract

1. Introduction

2. Traveling Waves

3. Swimmer Modeling

3.1. Microswimmer Body

3.2. Viscous Environment

3.3. Motion Analysis

4. Propulsion Performance

4.1. Preliminary Considerations

4.2. Effects of Excitation Frequencies

4.3. Effects of Stiffness Distributions

4.4. Effects of mass distributions

5. Guidelines for microswimmer optimal design

5.1. Results comparison

5.2. Recommendations

6. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe