Preprint
Article
Harmonizing Quantum Gravity with Thermodynamics: Determination of the EUP Parameter by Prigogine’s Law
Altmetrics
Downloads
124
Views
73
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
11 September 2024
Posted:
12 September 2024
You are already at the latest version
Alerts
Abstract
In 1974, Stephen Hawking made the groundbreaking discovery that black holes emit thermal radiation, characterized by a specific temperature now known as the Hawking temperature. While his original derivation is intricate, retrieving the exact expressions for black hole temperature and entropy in a simpler, more intuitive way without losing the core physical principles behind Hawking's assumptions is possible. This is obtained by employing the Heisenberg uncertainty principle which is known to be connected to the vacuum fluctuation. This exercise allows us to easily perform more complex calculations involving the effects of quantum gravity. This work aims to answer the following question: \textit{Is it possible to reconcile Prigogine's second law of thermodynamics for open systems and the second law of black hole dynamics with Hawking radiation}? Due to quantum gravity effects, the Heisenberg uncertainty principle has been extended to the Generalized Uncertainty Principle (GUP) and successively to the Extended Uncertainty Principle (EUP). The expression for the EUP parameter is obtained by conjecturing that Prigogine's second law of thermodynamics and the second law of black holes are not violated by Hawking thermal radiation mechanism. The modified expression for the entropy of a Schwarzschild black hole is also derived.
Keywords:
Subject: Physical Sciences - Astronomy and Astrophysics
1. Introduction
Hawking radiation, proposed by physicist Stephen Hawking, is a phenomenon predicted by quantum mechanics that describes black holes’ gradual loss of mass and energy. In the past, it was very difficult to accept that black holes had a temperature because they would then have to emit radiation, which went against the definition of a black hole. In 1974, S. Hawking theoretically discovered that a static black hole located in a vacuum must emit from its horizon in all directions a type of thermal radiation known as Hawking radiation [1]. According to Hawking’s mechanism, radiation occurs near the event horizon of a black hole and it arises from the steady conversion of quantum vacuum fluctuations into pairs of particles, one of which escapes at infinity while the other is trapped inside the black hole horizon. In Hawking’s most famous book, A Brief History of Time [2,3], he makes the analogy that space is filled with particle-antiparticle pairs and that one member can escape, carrying positive energy, while the other falls in, with negative energy. Since these pairs of particles were present outside the black hole, the flow of positive energy particles appears as radiation while the flow of negative energy particles reduces its mass leading to black hole decay. There are, however, two main issues to address: one of a pedagogical nature (i) and the other of a fundamental nature (ii).
(i) Hawking’s original derivation of black hole radiation involves complex mathematics due to the need to handle quantum fields in curved spacetime and solve intricate equations. Simplifying and intuitively explaining these concepts helps in making the ideas more accessible and comprehensible. Such approaches can provide a clearer understanding of the fundamental physics behind Hawking radiation and black hole thermodynamics without requiring advanced mathematical tools. Additionally, an intuitive approach can highlight the physical principles behind Hawking radiation - such as vacuum fluctuations and particle creation near the event horizon - without getting lost in technical details. This helps in grasping why and how black holes emit radiation.
(ii) At first glance, the Hawking radiation process seems to contradict both Prigogine’s second law of thermodynamics for open systems [4,7] and the second law of black hole dynamics [8]. Prigogine’s second law for open systems states that "During the evolution, the entropy production of the system is always positive". The second law of black hole dynamics states that "In any classical process involving black holes, the total area of the event horizon of the black hole cannot decrease". So, in the standard picture, since Hawking radiation causes a black hole to lose mass over time, Prigogine’s law and the second law of black holes are violated. The generalized second law (GSL) of black holes incorporates the entropy of both the black hole and the surrounding radiation, ensuring the total entropy (black hole entropy plus radiation entropy) never decreases (see for instance [9]). However, this all seems like a "gimmick, since a black hole that emits energy is an open system and must still satisfy Prigogine’s law.
This work deals with the above issues i) and ii). More specifically, the standard Hawking radiation mechanism will be revisited through the Generalized Uncertainty Principle (GUP) [10,11,12] or the Extended Uncertainty Principe (EUP) [13,14]. The GUP is a theoretical framework in quantum mechanics that extends the Heisenberg Uncertainty Principle by incorporating the effects of quantum gravity. The GUP modifies this principle by including terms that account for gravitational effects, particularly those that become significant at extremely small (Planck-scale) distances. These modifications suggest that at such scales, the uncertainties in position and momentum are influenced not just by quantum mechanical factors, but also by gravitational effects. The GUP suggests the existence of a minimal measurable length, typically on the order of the Planck length. This contrasts with the standard quantum mechanics view, where smaller and smaller distances could, in theory, be probed with higher momentum. The GUP has implications for black hole physics, particularly for the end stages of black hole evaporation. It suggests modifications to the Hawking radiation process and could imply that black holes do not evaporate completely but leave behind a Planck-sized remnant. The EUP addresses the possibility of both positive and negative values of the so-called EUP deformation parameter while still maintaining a minimum length scale. This flexibility in the EUP deformation parameter is significant because it broadens the range of possible physical interpretations and applications of the uncertainty principle in quantum gravity scenarios. We shall see that contrary to GUP, the possibility of a negative EUP parameter opens up the opportunity to set the Hawking temperature to zero. This adjustment can address the conflicts between Prigogine’s second law of thermodynamics and the second law of black hole mechanics. Indeed, by choosing a negative EUP parameter value such that the Hawking temperature becomes zero, the black hole ceases to radiate. However. even when the Hawking temperature is set to zero by adjusting the EUP parameter the black hole’s entropy does not vanish because entropy is primarily tied to the geometry of the black hole (its horizon area), not directly to the temperature. The entropy represents the number of hidden microstates or the information content of the black hole, which remains finite as long as the black hole has a non-zero mass and horizon area. This stabilization implies that the black hole’s mass and entropy would no longer decrease, thereby aligning with both the area theorem (second law of black hole mechanics) and Prigogine’s law of non-negative entropy production in open systems. This leads also to the situation where black hole entropy continues to increase despite no radiation. The increase in entropy without radiation suggests that the black hole is still evolving in some way, even if it is not losing mass through radiation.
The manuscript is organized as follows. Before starting our analysis, in Section 2 we shall revisit the steps leading to the determination of the Hawking temperature. This will allow us to focus on the main assumptions adopted by Hawking for getting the expression of the temperature of a black hole. In Section 3 we shall derive the exact expressions of the Hawking Temperature and Entropy for a Schwarzschild black hole. To do this task, we shall follow J. Pinochet’s arguments [15]. However, it should be stressed that we shall follow some of his mathematical steps but we shall not adopt his physical interpretation of the black hole radiation mechanism, remaining faithful to the original Hawking’s picture of the mechanism responsible for the thermal emission. For easy reference, Prigogine’s second law for open systems and the second law of black holes are recalled in Section 4. The connection between these two laws is shown in subSection 4.3. The method suggested by Pinochet will allow us to deal with more complex situations without resorting to complex mathematical methods. In particular, it will allow us to deal with, and resolve, the conflict between Hawking radiation and the second law of black holes. This will be the subject of Section 5. In Section 6 we determine the GUP and EUP deformation parameters that can reconcile Hawking radiation with Prigogine’s law and Bekenstein thermodynamic analogy. Concluding remarks can be found in Section 7.
2. The Hawking Radiation Mechanism
In 1974 [1] Stephen W. Hawking published his celebrated result stating that if one takes quantum theory into account, black holes are not quite black, but they emit radiation consisting of photons, neutrinos, and to a lesser extent all sorts of massive particles. The Hawking radiation mechanism describes hypothetical particles and antiparticles formed by a black hole’s boundary, and it is based on the assumption that the horizon is the radiating surface. This radiation implies black holes have temperatures that are inversely proportional to their mass. Below, we resume in a few bullets the main assumptions made by Hawking to explain the mechanism of black hole radiation:
i) The universe is filled with particle-antiparticle pairs popping in and out of existence;
ii) These pairs of particle-antiparticle exist even in empty space, as a consequence of quantum field theory and the Heisenberg uncertainty relations;
iii) These pairs always find one another and re-annihilate after a very small time interval;
iv) Hawking radiation arises from quantum effects near the event horizon of a black hole. The strong gravitational field near the event horizon causes quantum vacuum fluctuations to become real particles;
v) This mechanism leads to a situation where one member of the pair falls in while a real particle escapes and is emitted with positive mass/energy from just outside the horizon itself;
vi) The paired member that falls into the event horizon must have negative energy that subtracts from the black hole’s total mass. The flow of particles of negative energy into the black hole reduces its mass until it disappears completely in a final burst of radiation;
Figure 1 illustrates the Hawking radiation process.
The Hawking radiation mechanism is a purely quantum effect. Hawking’s findings are practically irrelevant for classical black holes.
Vacuum Fluctuations and Time-Energy Heisenberg’s Uncertainty Relation
The Quantum Field Theory (QFT) states that the vacuum is not so empty: there are fluctuations in the vacuum field that produce measurable macroscopic effects. The vacuum, even in the absence of particles and photons, has vacuum energy (zero point energy): that is, virtual photons and virtual particle-antiparticle pairs that are created and destroyed in very short times, in such a way as to conserve energy and respect the Heisenberg uncertainty principle. The main effects affected by “vacuum fluctuations” are the Casimir effect, the Lamb shift, Blackbody radiation, Hawking radiation, and the inhibition and acceleration of spontaneous emission. Vacuum fluctuations arise due to the quantum uncertainty in energy over short time intervals, as described by the time-energy Heisenberg uncertainty relation. Heisenberg’s uncertainty principle states that it is not possible to simultaneously measure the position and the velocity of a particle with absolute precision, the same is true for energy and time. From this principle, it follows that in a vacuum it is possible to create a virtual boson (for example a photon) as long as the vacuum reabsorbs it after a very short time interval. Or it is possible to create two virtual fermions (always in the particle-antiparticle composition) as long as they annihilate in a small time interval. The Heisenberg uncertainty principle, through the energy uncertainty , permits vacuum fluctuations where virtual particles momentarily appear. Near a black hole’s event horizon, these fluctuations can lead to the creation of real particles via Hawking radiation. The escaping particles are observed as radiation, while the black hole loses mass due to the infall of particles with negative energy, leading to its gradual evaporation.
3. A (Heuristic) Derivation of the Exact Expressions of Temperature and Entropy for a Schwarzschild Black Hole
Stephen Hawking’s original work on Hawking radiation is mathematically complex for several reasons. Hawking’s derivation involves applying quantum field theory in the curved spacetime of a black hole. This requires complex calculations involving the behavior of quantum fields in a non-flat (curved) spacetime, which is inherently complicated. Additionally, Hawking used the semi-classical approximation where the spacetime is treated classically (using general relativity), but the fields are treated quantum mechanically. Combining these two frameworks is non-trivial and requires sophisticated mathematical tools. Hawking’s method involves decomposing the quantum fields into modes that interact with the black hole’s event horizon. Calculating the contributions of these modes to the radiation is mathematically intensive. The derivation involves evaluating complex integrals and solving differential equations that describe the behavior of fields near the event horizon. This requires advanced techniques from mathematical physics. Finally, showing that the radiation emitted by the black hole is thermal, and finding the exact temperature involves intricate calculations related to black body radiation and quantum statistics. So, deriving the exact expressions for Hawking temperature and entropy more simply and intuitively is necessary as simplifying and intuitively explaining these concepts helps in making the ideas more accessible and comprehensible. In our derivation of Hawking’s temperature, we shall follow the arguments of J. Pinochet [15]. However, this work differs conceptually from that of J. Pinochet. As the six points above state, we utilize the quantum vacuum fluctuation. In our derivation, according to Hawking’s assumption, the radiation does not come directly from within the black hole but near the horizon event. If particles are subject to the uncertainty principle, then we cannot know both the time and energy of a particle with perfect accuracy. Hawking radiation represents a situation where the energy-time uncertainty principle plays a crucial role in determining the characteristics of the emitted radiation. Denoting with the uncertainty in the time of the particle, the process effectively "chooses" the emission of particles with energy corresponding to the minimum value that the product of these quantities can take [16,17]
with ℏ denoting the reduced Planck constant. In our energy situation, , with c denoting the speed of light and the momentum uncertainty, respectively. So, the Heisenberg Uncertainty Principle relating the uncertainties in position and momentum implies . In quantum field theory, the quantum vacuum state is the quantum state with the lowest possible energy . Since and are inversely proportional, the minimum value , compatible with Eq. (1), corresponds to the maximal uncertainty in the position of the particle . Taking into account this observation, Eq. (1) leads to
Assuming that the black hole event horizon is spherically symmetric with a radius equal to Schwarzschild’s radius , it is easily checked that corresponds to the maximal uncertainty in the coordinate x (or y) of the particle on the event horizon. Hence, by taking into account that:
with (with ) and (with ) denoting the spherical coordinates, we get:
as the maximum indetermination is obtained for , , and at the coordinate values . So,
By plugging in Eq. (5) the expression for the Schwarzschild’s radius [8]
with M denoting the mass of the black hole and G is the universal gravitational constant, respectively, we get the Hawking expression for the black hole emitted energy:
As said, Hawking radiation is a theoretical prediction that black holes can emit radiation due to quantum effects near the event horizon. This radiation has a thermal spectrum, and its associated temperature is known as the Hawking temperature. The energy of the particles (usually photons, but also other particles) emitted in Hawking radiation is directly related to the Hawking temperature by the relation [18,19,20]:
with denoting the Boltzmann constant. This equation makes sense in this scenario because the emitted radiation is thermal, similar to black body radiation, but with Hawking temperature. So, the particles emitted by the black hole have an average energy that is proportional to the Hawking temperature through Boltzmann’s constant . We finally get
We note the subtlety implicit in Eq. (9). The temperature of a classical black hole is . According to Hawking’s radiation mechanism, due to the quantum effect, the black hole emits energy in the form of escaping matter showing a very weak temperature given by Eq. (9). The energy that the black hole loses is equal to the negative energy of the antimatter it has captured i.e., . In the absence of work, the first law of thermodynamics reads
with denoting the black hole entropy. Hawking radiation propagates away from the event horizon, and since real radiation carries energy, the only place where that energy can be taken from is from the mass of the black hole itself, via the classic Einstein’s equation, . In this case, the mass lost by the black hole has to balance the energy of the emitted radiation. So,
where Eq. (9) has been taken into account. The integration yields
where is an arbitrary constant of integration. In physical contexts like black hole thermodynamics, typically corresponds to the minimal entropy or entropy at a particular reference point.
- Black Holes and Generalized Second Law (GSL) of Thermodynamics
Expression (9) shows that a black hole loses mass through evaporation. This seems in disagreement with the law of thermodynamics expressed as The total entropy of an isolated system always increases. We soon realize that this disagreement is only apparent. Indeed, after simple calculations, we have that the total entropy change of the isolated system, composed of the black hole plus reservoir (i.e., the the rest of Universe) reads [9]
with and denoting the original mass and the final mass of the black hole, respectively. Since the initial mass is greater than the final mass , the result is a positive quantity showing an increase in entropy.
4. Prigogine’s Second Law of Thermodynamics and the Second Law of the Black Hole Dynamics
According to Hawking in [3] since the average temperature of the universe is about , most black holes absorb more energy than they emit and will not begin to evaporate for some time until the universe has expanded and cooled below their temperature. So, the expression for the total entropy (13) is valid only when the black hole is at thermodynamic equilibrium with the Universe. It is not applicable during the transition phase in which the black hole and the Universe tend to reach thermodynamic equilibrium. However, we know that a body with a temperature above absolute zero will emit radiation by Planck’s law. As said, during the transitional phase Eq. (13) does not apply and this is a big limitation of the demonstrations shown above. Briefly, what needs to be demonstrated is that a radiating black hole in non-equilibrium conditions satisfies Prigogine’s second law of thermodynamics. This is the subject of the next section.
4.1. Prigogine’s Second Law of Thermodynamics for Open Systems
The verification that the entropy of matter outside the black hole plus the entropy of the black hole never decreases does not satisfactorily answer the question about the validity of the second law of black hole thermodynamics. Indeed, some important questions remain open. The first reaction is that having demonstrated that the total entropy of an isolated system (in this case the black hole plus external environment) is always increasing sounds as a sort of escamotage rather than a convincing demonstration. This is because for open systems, as is the case of radiating black holes, the correct formulation of the second law of thermodynamics is expressed by Ilya Prigogine’s law. In 1971, Prigogine proposed to split the total differential of entropy of an open system into two components [4,7]:
with denoting the entropy production produced inside the system, and is the outflow or inflow of entropy into the system from the outside, respectively. The sign of depends on the situation whereas is always a non-negative quantity. Notice that Eq. (14) can describe an open system in which the total entropy decreases (i.e., ) when and . In general, Eq. (14) does not contain indications of the factors on which the sign and quantity of depend whereas the sign of is known. Prigogine proved the following inequality:
Notice that Eqs (14) and (15) generalize Boltzmann’s law as for isolated systems we have , so i.e., the entropy of isolated systems can never decrease.
4.2. The Second Law of the Black Hole Dynamics
In [21] and [22] it is shown that the mass-energy formula of a Kerr Newmann black hole of mass M can be expressed in terms of the irreducible mass as well as a function of the charge Q, and of the angular momentum L1
The black hole exists if
The surface area of the event horizon A is also related to the irreducible mass according to the equation [21]
The fact that the irreducible mass monotonically increases implies that the black hole event horizon surface also monotonically increases as shown by Hawking [22]. In Bekenstein-Hawking definition, the entropy of the black hole is proportional to the event horizon’s area A according to the formula [23]:
with denoting Planck’s length (). The second law of black hole dynamics states [8]: "No black-hole transformation can ever reduce its surface of the event horizon or, equivalently, its irreducible mass". In other words:
4.3. Link between the Second Law of the Black Hole Dynamics and Prigogine’s Second Law of Thermodynamics
Bekenstein noted that by differentiating Eq. (16) we obtain an expression that strongly resembles the first law of thermodynamics [24,27]:
where
and and a are the horizon location in the Kerr-Newman geometry and the angular momentum per unit mass, respectively [8]:
Bekenstein proposed Eq. (21) as the first law of thermodynamics for a black hole in analogy with the first law of thermodynamics. Bekenstein identified E with M and the sum of the last two contributions in Eq. (21) as the work W done on the black hole. and play the role of the rotational angular frequency and the electric potential of the black hole, respectively. Additionally, Bekenstein and Wheeler identified as the entropy of the black hole and as its characteristic temperature2. In this way, Eq. (21) takes the familiar form of the first law of thermodynamics:
For an isolated Schwarzschild black hole (i.e., , , and ), it is easily checked that Eq (21) and (24) reduce to:
where, in Planck units (, , , and ), the Schwarzschild black hole entropy production reads 3:
Prigogine’s second law of thermodynamics states that which, by Eq. (26), implies that, for an isolated black hole, also . Therefore, Prigogine’s second law of thermodynamics and the second law of black holes are intimately connected. In other words, for an isolated black hole, violating Prigogine’s law implies violating the second law of black hole dynamics and vice-versa. Coming back to Hawking’s radiation mechanism the following questions arise now spontaneously:
Does a radiating black hole, seen as an open system, satisfy the second law of thermodynamics as formulated by I. Prigogine? or, equivalently
Is the variation of the event horizon area of an isolated black hole always increasing?
Up to now, we have ignored the quantum gravitational effects. To answer the above questions we have to take into account the so-called Extended Uncertainty Principle (EUP). We shall see that it is possible to conciliate both Prigogine’s second law of thermodynamics and the second law of black holes [8] with the Hawking temperature radiation mechanism.
5. EUP and Conciliation with Prigogine’s Second Law of Thermodynamics and the Second Law of Black Hole Dynamics
5.1. GUP and Prigogine’s Second Law of Thermodynamics
The Generalized Uncertainty Principle (GUP) is a theoretical framework in quantum mechanics that extends the Heisenberg Uncertainty Principle by incorporating the effects of quantum gravity. The GUP is often expressed as (see, for example, [28]):
with and denoting the uncertainty in momentum and the Planck mass, respectively. is a dimensionless GUP deformation parameter that encodes the strength of quantum gravitational effects. Eq. (27) modifies both the Hawking expressions for the temperature and the entropy of a black hole. The great advantage of the method presented in Section 3 is that we can easily determine Hawking’s corrections for temperature and entropy without having to resort to the sophisticated and complex calculations performed by Hawking. By performing the same procedure illustrated in the Section 3, we obtain
where we have taken into account that for a black hole, the uncertainty in energy is related to the uncertainty in momentum by the relation , and . At the first order in Eq. (28) reads:
Since has not been measured experimentally, it is often treated as a free parameter that can be varied to explore different physical implications of the GUP [29]. For instance, in [30], the value of the GUP parameter is obtained by conjecturing that the GUP-deformed black hole temperature of a Schwarzschild black hole and the modified Hawking temperature of a quantum-corrected Schwarzschild black hole are the same. Here, we aim to set the expression for in such a way that both Prigogine’s second law of thermodynamics and the second law of black holes are not violated. From Eq. (29), we see that these conditions are satisfied if
However, a negative GUP parameter leads to several counterintuitive and potentially problematic physical consequences. For instance, a negative could lead to calculations’ instabilities, divergences, or singularities. These unphysical behaviors would make applying the GUP to realistic scenarios difficult. While there have been some speculative models exploring negative , they often face significant challenges and are not widely accepted within the physics community. Hence, it is generally believed that the GUP parameter must be positive to ensure consistency with the principles of quantum mechanics and avoid unphysical consequences. Finally, solution (30) must be discarded.
5.2. EUP and Prigogine’s Second Law of Thermodynamics
The work of Du and Long [13], as well as the subsequent consideration by Song-Shan Luo and Zhong-Wen Feng [14], introduces a novel perspective on the deformation parameter in the uncertainty principle, specifically addressing the possibility of both positive and negative values for the parameter , which is referred to as the Extended Uncertainty Principle (EUP) parameter. The model proposed by Du and Long allows the deformation parameter to take on either positive or negative values while still maintaining a minimum length scale. This flexibility in is significant because it broadens the range of possible physical interpretations and applications of the uncertainty principle in quantum gravity scenarios. The most important feature of this theory is that, unlike traditional models where a positive is associated with a minimal length scale and a negative might imply its absence or different implications, this novel model preserves the concept of a minimum length regardless of the sign of . This suggests that the deformation of the uncertainty principle is symmetric with respect to the sign of , and the physical implications are adapted accordingly. In GUP a contradiction arises when the parameter is negative as the GUP no longer includes a minimum length, which contradicts the model-independent existence of the minimum length. To address this issue, Du and Long [13] introduced a novel uncertainty principle model, which can be expressed as
with denoting the deformation parameter EUP. The most important features of the inequality (31) are that the EUP parameter can be assigned positive or negative values and that it maintains a fixed and uniform minimum length regardless of whether the parameter is positive or negative. Furthermore, it is easily checked that if ignoring the higher-order corrections Eq. (31) reduces to Eq. (27). By performing the same calculations as in Section 3, and by taking into account that , , and , we get
We are interested in exploring the case of black holes with very small masses. This leads to ignoring higher-order terms in (see the forthcoming Eq. (35)). So, at the leading contributions, we find 4
Notice that Eqs (33) are compatible with the Generalized Gravitational Uncertainty Principle (GGUP) as expressed in [31,32]:
with the parameters and set to zero and of negative value 5. The modification in temperature due to the EUP introduces a correction term that depends on the EUP parameter and the mass M of the black hole. Additionally, the entropy expression includes a logarithmic correction term, common in quantum gravity scenarios, suggesting a modification in the black hole’s microstates. These expressions give insight into how the EUP affects the thermodynamic properties of black holes, particularly in the context of quantum gravity effects near the Planck scale. By choosing a negative value such that the Hawking temperature becomes zero, the black hole ceases to radiate. This happens if, and only if,
which is valid only for small black hole masses. With Hawking radiation effectively turned off by given by Eq. (35), the entropy of the black hole stabilizes, eliminating the decrease that would otherwise violate both Prigogine’s second law and the area theorem (second law of black hole dynamics). This approach thus provides a novel resolution to the apparent conflict between these two fundamental thermodynamic principles. Hence, for a Schwarzschild black hole, due to EUP and Prigogine’s second law of thermodynamics, for black holes with very small masses, we have:
The entropy receives a logarithmic correction term, a common feature in many quantum gravity scenarios, which becomes significant for small black hole masses.
5.3. Determination of the Constant
To complete our calculations, we need to determine the value of . In the case of the irreducible mass, from Eq. (17), a lower limit to the value of can be deduced by imposing a lower limit in the value of the angular momentum from quantum mechanics considerations [33]:
From Eq. (17) we have
So,
However, from Eq. (16), we have
By taking into account Eq. (38), we get
The black hole does not exist for (it is a naked singularity), and we can set as . Consequently, even mast vanish as . This implies
To summarize, for small Schwarzschild black holes, Prigogine’s second law of thermodynamics is satisfied if (and only if):
In summary, by the Extended Uncertainty Principle, we get a modification of the standard Heisenberg uncertainty principle motivated by quantum gravity considerations at very small scales. In this regime, if the deformation parameter is sufficiently negative, the Hawking temperature could potentially be zero leading to no radiation. For black holes with large mass (i.e., when ) we may argue that EUP (31) reads:
For large black holes, where , the Hawking radiation process resembles black body radiation in many ways. The black hole emits radiation, and while the black hole’s entropy decreases, the emitted radiation increases the total entropy of the universe. In this regime, the process can be treated as quasi-static and near-equilibrium, and Prigogine’s law is trivially satisfied because the variation of the entropy production of the black hole is almost zero and the total entropy of the universe increases (see the above subsection Black Holes and Generalized Second Law (GSL) of Thermodynamics). The black hole’s evaporation aligns with Prigogine’s law when considering the total entropy of the system, which approximates the classical area law. However, as the black hole’s mass approaches the Planck mass (), quantum fluctuations become significant, and the process is no longer quasi-static or near-equilibrium. The evaporation process becomes more complex. In this regime, the black hole is an open system out of equilibrium due to significant quantum fluctuations. To reconcile Prigogine’s law with the Hawking radiation process, one approach is to assume that the Hawking temperature is zero or negligible, thus avoiding significant entropy production and aligning with the laws of the thermodynamics of irreversible processes. To sum up, the EUP has implications for black hole physics, particularly for the end stages of black hole evaporation. According to our model, due to Hawking radiation, a black hole tends to evaporate by infinitesimal quasi-static transformations until it reaches a mass of the order of the Planck mass. Due to Prigogine’s second law of thermodynamics for open systems, black holes do not evaporate completely but leave behind a Planck-sized remnant. The black hole, in this case, could act as a stable object that does not radiate and therefore persists indefinitely.
5.4. Discussion
If we choose the parameter in the Extended Uncertainty Principle (EUP) so that the Hawking temperature is zero, an important question is raised: Why does the entropy of the black hole not also vanish? We already mentioned that the Hawking temperature and the entropy of a black hole are related by the first law of black hole thermodynamics (10). If , this implies that for any (see Eq. (10)). In other words, no energy (or mass) is radiated away by the black hole because the temperature is zero. Normally, for a system with , one might expect the entropy to be constant (i.e., ), which implies is at a minimum, potentially zero. However, in the case of a black hole, represents the number of microstates of the black hole, a measure of the hidden information or the event horizon’s area. The entropy is proportional to the event horizon’s area, not the temperature according to the formula (19):
where A is the area of the event horizon. This entropy is a geometric property of the black hole and is non-zero as long as the black hole has a finite horizon area. The Generalized Uncertainty Principle (or its extended form, EUP) modifies the temperature and entropy, but the entropy still reflects the area of the event horizon. If is chosen so that , the black hole essentially stops radiating. However, this does not imply the event horizon area vanishes or the microstates disappear, hence the entropy does not go to zero. The black hole might retain a residual entropy because it still has a finite event horizon, even if it does not radiate. This residual entropy can be interpreted as the ground state entropy of the black hole. In brief, Even when the Hawking temperature is set to zero by adjusting , the black hole’s entropy does not vanish because entropy is primarily tied to the geometry of the black hole (its horizon area), not directly to the temperature. The entropy represents the number of hidden microstates or the information content of the black hole, which remains finite as long as the black hole has a non-zero mass and horizon area. Thus, the black hole would still possess a significant amount of entropy, even at zero temperature.
6. Conciliation of Hawking Radiation with Prigogine’s Law and Bekenstein Thermodynamic Analogy
Eqs (43) reconciles Hawking Radiation with Prigogine’s law but not with the thermodynamic analogy proposed by Bekenstein and Wheeler (see Eq. (21) in Section 4.3). For this to happen, the Hawking temperature must be zero (to satisfy Prigogine’s law). At the same time, the entropy of the black hole must be identical to that calculated by Bekenstein and Wheeler. It is easily checked that these two conditions are satisfied simultaneously by appropriately choosing the expressions for the GUP and EUP parameters. For this, let us consider the complete uncertainty principle (34) written in the following form:
where is set to zero and the GUP and EUP parameters (i.e., and , respectively) of positive value. We consider black holes with small mass near Planck’s mass. So, we may approximate forms of and that are valid for small deviations from . and are therefore assumed to be a constant, or at least weakly dependent on the black hole mass. After simple algebra, we get:
where we have taken into account that and . At the first order in and , Eq. (47) reads:
and
Hence, Prigogine’s second law of thermodynamics and the Bekenstein-Wheeler thermodynamic interpretation of the horizon black hole surface are satisfied simultaneously by setting the EUP and GUP parameters respectively as
with final result
7. Conclusions
Even the most extreme objects in the universe, like black holes, are bound by certain rules. G. Gibbons and S. Hawking demonstrated that black hole thermodynamics extends beyond black holes themselves, revealing that cosmological event horizons also possess entropy and temperature [34]. In 1974, Hawking further showed that when quantum mechanics is considered, black holes can emit light and particles through a process known as Hawking radiation. Since quantum black holes emit energy and light, they must have a temperature, in addition to mass, charge, and rotation. This makes them subject to the laws of thermodynamics. Hawking’s mechanism hinges on quantum vacuum fluctuations, suggesting that the radiation originates near the event horizon rather than from within the black hole itself. However, Hawking’s original derivation of this radiation is mathematically intricate, involving quantum fields in curved spacetime and complex equations. From a pedagogical standpoint, it’s beneficial to explain these concepts more intuitively, making them accessible without sacrificing the core physical principles underlying Hawking radiation. This work aims to offer a clearer understanding of the fundamental physics of Hawking radiation and black hole thermodynamics, without relying on advanced mathematical techniques. To achieve this goal, we have rederived the exact expressions of the Hawking temperature and entropy for a Schwarzschild black hole following the indications of J. Pinochet in [15] with the addition, however, of new elements and physical considerations that have allowed us to overcome the vulnerable aspects present in the original work of J. Pinochet. The way suggested by J. Pinochet allowed us to deal with more complex situations. In particular, we have shown that it is possible to ensure consistency with both Prigogine’s second law and black hole thermodynamics. The second law of black holes states that even if black holes merge or matter falls into a black hole, the total event horizon area of the resulting black hole(s) will be greater than or equal to the sum of the event horizon areas of the original black holes. The second law of black hole dynamics applies classically. In quantum mechanics, Hawking radiation introduces the possibility of black holes losing mass and thereby shrinking in area, which would appear to violate this law. With Hawking radiation effectively turned off by the negative EUP parameter, the entropy of the black hole stabilizes, eliminating the decrease that would otherwise violate Prigogine’s second law. So, when gravitational quantum effects are considered, black holes still obey the non-decreasing law, preserving the analogy with Prigogine’s second law of thermodynamics. While the classical interpretation of suggests that when , the inclusion of EUP and quantum gravitational effects may lead to a scenario where entropy can still increase. This reflects a more complex interaction between the microstates of the black hole and quantum gravity, beyond what is described by classical thermodynamics alone. So, the key idea is that the traditional relation might not fully capture the behavior of entropy under the influence of the EUP, particularly when ,. In non-equilibrium thermodynamics, especially when considering open systems or systems influenced by quantum gravity, entropy can increase due to other processes, such as quantum fluctuations or interactions with external fields, even if the black hole is not radiating. We finally derived the modified entropy for a Schwarzschild black hole, which includes a logarithmic correction term, common in quantum gravity scenarios. In passing, we have shown that it is possible to determine the GUP and EUP deformation parameters such that Hawking radiation is turned off and the black hole entropy is the one proposed by Bekenstein and Wheeler in their thermodynamic analogy.
Acknowledgments
The author is very grateful to Prof. Jorge Pinochet from Universidad Metropolitana de Ciencias de la Educación for his encouragement and fruitful discussions held in December 2023 in Santiago de Chile.
References
- S.W. Hawking, Nature, 248, 30 (1974).
- S. W. Hawking, A Brief History of Time: From the Big Bang to Black Holes, (1988), Bantam Books. ISBN 978-0-553-38016-3.
- S. W. Hawking, The Illustrated Brief History of Time, (1986), updated and expanded ed. (Bantam Books, New York.
- I. Prigogine 1954 Thermodynamics of Irreversible processes, (John Wiley & Sons).
- I. Prigogine Etude Thermodynamique des Phénomènes Irréversibles, (Desoer, Liège, 1947).
- I. Prigogine and R. Hansen, Bull. classe sci. Acad. roy. Belg., 28, 301 (1942).
- I. Prigogine, Bull. classe sci. Acad. roy. Belg., 32, 30 (1946).
- C.W. Misner, K.S. Thorne, and J.A. Wheeler, Gravitation, W. H. Freeman and Company, San Francisco (1973).
- M. C. LoPresto, Some Simple Black Hole Thermodynamics, The Physics Teacher, 4 (2003). Available online: https://web.stanford.edu/ oas/SI/SRGR/lib/BlackHoleThermoShort.pdf.
- L. Buoninfante, G. G. Luciano, L. Petruzziello, Eur. Phys. J. C 70, 663 (2019).
- F. Scardigli, J. Phys. Conf. Ser, 1275, 012004 (2019).
- X. Calmet, M. Graesser, Phys. Rev. Lett. 93, 211101 (2004).
- X.-D. Du and C.-Y. Long, J. High Energy. Phys., 63, (2022).
- S.-S. Luo and Z.-W. Feng, The gravitational baryogenesis and a new higher-order extended uncertainty principle with parameter adaptability for the minimum length, ArXiv 2023. Available online: https://arxiv.org/pdf/2306.10078.
- J. Pinochet, The Hawking temperature, the uncertainty principle, and quantum black holes, Physics Education, (2018).
- M.F. Wondrak, W. D. van Suijlekom, and H. Falcke, Gravitational Pair Production and Black Hole Evaporation, (May 2023). Available online: https://arxiv.org/pdf/2305.18521.pdf.
- K. Krane (2012), Modern Physics, 3 ed., John Wiley and Sons, Hoboken.
- S. W. Hawking and G. F. R. Ellis, The Large Scale Structure of Space-Time, Cambridge University Press, (1973).
- K. S. Thorne, Black Holes and Time Warps: Einstein’s Outrageous Legacy, WW Norton & Co (1995).
- V. Mukhanov and S. Winitzki, Introduction to Quantum Effects in Gravity, Cambridge University Press, (2007).
- D. Christodoulou and R. Ruffini, Phys. Rev. D, 4, (1971) (received 1st 1971).
- S. Hawking, Phys. Rev. Lett., 26, (1971) (received 11th 1971).
- J. Bekenstein, Physics Today, 25 (1980).
- J. Bekenstein, (1972a), Baryon Number, Entropy, and Black Holes Physics, Ph.D. Thesis, Princeton University.
- J. Bekenstein, Lett. Nuovo Cimento. 4, 737, (1972b).
- J. Bekenstein, Phys. Rev. D, 7(8), 2333 (1973).
- J. Bekenstein, Physics. Phys. Rev. D, 9(12), 3292 (1974).
- R. J. Adler and D. I. Santiago, Modern Physics Letters A. 14(20), 1371 (1999).
- S. Giardino and V. Salzano, The European Physical Journal C, 81(110), (2021).
- E. C.Vagenas, S. M. Alsaleh, and A. F. Ali, ArXiv 2018 GUP parameter and black hole temperature. Available online: https://arxiv.org/pdf/1801.03670.
- A. N. Tawfik and A. M. Diab, Rep. Prog. Phys. 78 126001 (2015).
- M. J. Lake, M. Miller, and S.-D. Liang, Universe, 6(4), 56 (2020). [CrossRef]
- R. Ruffini, Private Communication, ICRANet (2023).
- G. W. Gibbons and S.W. Hawking, Phys. Rev.D., 15(10), 2738 (1977).
| 1 | Here, they set and . |
| 2 | Recall that we are in Planck units , , , and . |
| 3 | It is easily checked that in Kerr-Newman geometry the entropy production for an isolated black hole is, in Planck units, . |
| 4 | Here, we consider approximate forms of that are valid for small deviations from . So, is assumed to be a constant, or at least weakly dependent on the black hole mass. |
| 5 | We have . |
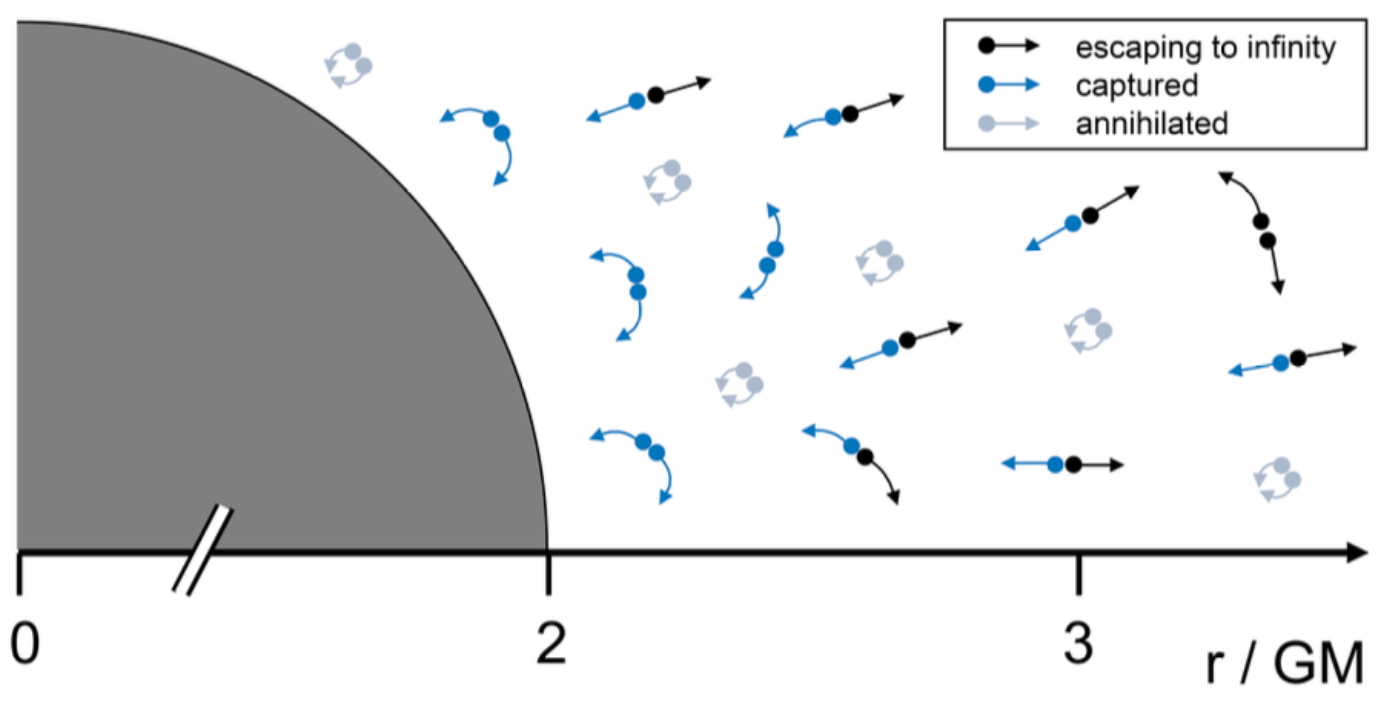
Figure 1.
The mechanism of Hawking radiation. To an outside observer, it looks as if the black hole has radiated a particle. Indeed, to conserve energy, the energy it took to create the particle and shoot it off to infinity must have come from the black hole. The particle that did not escape possesses a negative energy.
Figure 1.
The mechanism of Hawking radiation. To an outside observer, it looks as if the black hole has radiated a particle. Indeed, to conserve energy, the energy it took to create the particle and shoot it off to infinity must have come from the black hole. The particle that did not escape possesses a negative energy.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





