Prerpints.org logo
Preprint
Article

Reaction Thermodynamic and Kinetics for Esterification of Propylene Glycol Monomethyl Ether and Acetic Acid over Ion-exchange Resin

Altmetrics

Downloads

89

Views

33

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

03 September 2024

Posted:

04 September 2024

You are already at the latest version

Alerts
Abstract
The esterification of propylene glycol methanol (PM) and acetic acid (AA) is an important reaction for the production of propylene glycol methyl ether acetate (PMA). Herein, we used macroporous ion exchange resin Amberlyst-35 as a catalyst to explore the effects of reaction conditions on the reaction rate and equilibrium yield of PMA. Under the optimized conditions of reaction temperature of 353 K, initial reactant PM/AA molar ratio of 1:3, and catalyst loading of 10 wt%, PMA equilibrium yield reached 78%, which is the highest equilibrium yield so far. The reaction equilibrium constants and activity coefficients were estimated to obtain reaction thermodynamic properties, indicating the exothermicity of the reaction. Furthermore, Pseudo-homogeneous (PH), Eley-Rideal (ER), and Langmuir-Hinshelwood-Hogen-Watson (LHHW) kinetic models were fitted based on experimental reaction kinetic data. The results demonstrate that the LHHW model is the most consistent with experimental data, indicating surface reaction controlled process and exhibiting an apparent activation energy of 62.0 kJ/mol. This work represents a valuable example of calculating the reaction thermodynamic and kinetics, which are particularly essential for promising industrial reactor design.
Keywords: 
Subject: Chemistry and Materials Science  -   Applied Chemistry

1. Introduction

Methoxy propyl acetate, also known as propylene glycol methyl ether acetate (PMA), is widely used in paints, inks, dyes, cleaning agents, and photoresist [1,2]. Moreover, its high solvency, thermal stability, and low toxicity make it gradually replace ethylene glycol-based products [3,4,5] that have toxic effects on human metabolism [6,7,8,9]. Currently, ester exchange reaction and direct esterification are mainly considered methods for the synthesis of PMA. The catalyst for ester exchange between propylene glycol methyl ether (PM) and methyl acetate [1] (or ethyl acetate [10]) is methoxide sodium [11], which is difficult to separate and highly susceptible to decompose with water, resulting in a reduction in catalytic activity. The direct esterification of PM with acetic acid (AA) is industrially catalyzed by sulfuric acid, which has gradually been ruled out owing to its environmental unfriendly and equipment corrosive. Thus, some environmental-friendly catalysts such as p-toluenesulfonic acid, titanium sulfate, and cation exchange resins have been developed for PMA synthesis [3],12,13,14]. In addition, the direct esterification for PMA synthesis is reversible and limited by thermodynamic equilibrium [12,13,14,15,16,17,18,19,20,21]. Oh et al. indicated that in a batch reactor, the maximum conversion of PM is only 46% due to the limitation of chemical equilibrium [13].
In comparison with homogeneous catalyst, solid acid catalysts offer a number of advantages, including low corrosiveness and facile separation, and therefore are excellent alternative to traditional liquid acid catalysts [22,23,24]. Currently, solid acids are widely used in a variety of chemical reactions, including esterification [25,26,27], alkane isomerization [28,29], aldol condensations [30,31,32], hydrogenation[33] and formylations [34,35]. For the direct esterification in synthesizing PMA, Huang et al. conducted solid acid SO42-/TiO2 with a pseudo-homogeneous kinetic model [3], obtaining an apparent activation energy (Ea+) of 65.7 kJ/mol. Gadekar-Shinde et al. utilized ion exchange resin Amberlyst 15 as a catalyst [12] and developed a concentration-based pseudo-homogeneous kinetic model with an Ea+ value of 66.5 kJ/mol. Wang et al. employed ion exchange resin NKC-9 as a catalyst to obtain a maximum PM conversion of 46% in a batch reaction [14] and the Ea+ was determined to 60.5 kJ/mol based on second-order reaction kinetic model. However, these studies tend to focus on pseudo-homogeneous (PH) kinetic models, which are unable to reveal the real reaction mechanism related to surface adsorption and reaction.
Langmuir-Hinshelwood-Hougen-Watson (LHHW) and Eley-Rideal (ER) models have been extensively employed in the kinetic studies of heterogeneous catalytic systems. The LHHW model describes the surface reaction between adsorbed reaction species and has been successfully employed to predict numerous reactions catalyzed by heterogeneous acid catalysts. As evidenced by previous reports, the reaction kinetic data, such as esterification of benzoic acid with ethanol [36], oligomerization of 1-decene [37], liquid-phase hydrogenation of 1-indanone [38], esterification of lactic acid with ethanol [39], synthesis of tert-butyl methyl ether [40], and catalytic hydrogenation of d-lactose to lactitol [41], are well-fitted to the LHHW model. Conversely, the ER model postulates the potential for a reaction to occur between an adsorbed reactant molecule and another reactant molecule in the bulk phase. Catalytic reactions such as cyclohexene hydration [42], esterification of acetic acid with butanol [43], dehydration of 1-octanol to di-n-octyl ether[44], and oximation of cyclohexanone [45] are illustrated to follow the ER mechanism. It is noted that the model of the reaction catalyzed by heterogeneous catalysts is rather ambiguous from case to case, which should be dependent on the catalyst and reactants involved [42].
At present, the reaction kinetics of the esterification of PM with AA with a developed heterogeneous kinetic model is lacking. Herein, ion-exchange resin Amberlyst-35 was used as the catalyst and kinetic data were obtained through the esterification of pure AA with PM in a stirred batch reactor. The effects of operating parameters, including temperature, reactant ratio, and catalyst loading were investigated. Subsequently, reaction thermodynamic properties were evaluated and several kinetic models to describe a wide range of operating conditions were identified from the current work.

2. Experimental

2.1. Material

Acetic acid (AA, ≥99%), 1-methoxy-2-propanol (PM, ≥99%) and propylene glycol methyl ether acetate (PMA, ≥99%) were supplied by Shanghai Aladdin Biochemical Technology Co., Ltd. The chemicals were directly used as received without further purification. The ion-exchange resin Amberlyst-35 was supplied by Rohm & Haas Co., Ltd. Before use, the catalyst was placed in a muffle furnace at 110 °C for 8 h to remove moisture and impurities.

2.2. Esterification Reaction

The esterification reaction was conducted in a three-necked round-bottom flask with a volume of 100 mL. A condenser was attached to the top of the flask to prevent the loss of components with an anti backflow suction. The solid acid catalyst and a fixed molar ratio of AA and PM were loaded into the flask. Once the seal has been confirmed, the flask was placed in a preheated oil bath with specific temperature under continuous stirring. The acid-to-ether ratio was within the range of 1:1 to 1:4, and the temperature was within the range of 333 to 363 K. The catalyst Amberlyst-35 was employed in quantities from 5% to 12% in the total mass of AA and PM. Subsequent to the initiation of the reaction, sample was collected at a regular interval. A precise quantity of 0.5 mL of liquid sample was then taken using a syringe, which was immediately cooled in order to prevent further reaction and filtered using a needle filter.
In order to determine the adsorption equilibrium constants of the solid acid catalyst with each component, a series of independent experiments were conducted. The catalyst Amberlyst-35 was added to test tubes containing AA, PM, PMA, and H₂O, which were then vigorously stirred at room temperature using a constant-temperature oscillator (SD2-100, China) at 800 rpm for 8 hours. After adsorption was complete, the supernatant was collected and prepared for analysis.

2.3. Product Analysis

The concentrations of AA, PM, and PMA were determined using an Agilent 7890A gas chromatograph (USA) equipped with a flame ionization detector (FID) and an HP-FFAP chromatographic column (30 m×0.32 mm×0.25 μm). The analysis was conducted under the following conditions: nitrogen gas with a purity of 0.999 was used as carrier gas, and the injector and detector temperatures were maintained at 150 °C. The column temperature was increased at a rate of 10 °C/min to 90 °C, kept for 1 minute, and then rapidly heated to 230 °C at a rate of 30 °C/min. Toluene was used as an internal standard for quantitative analysis.

3. Results and Discussion

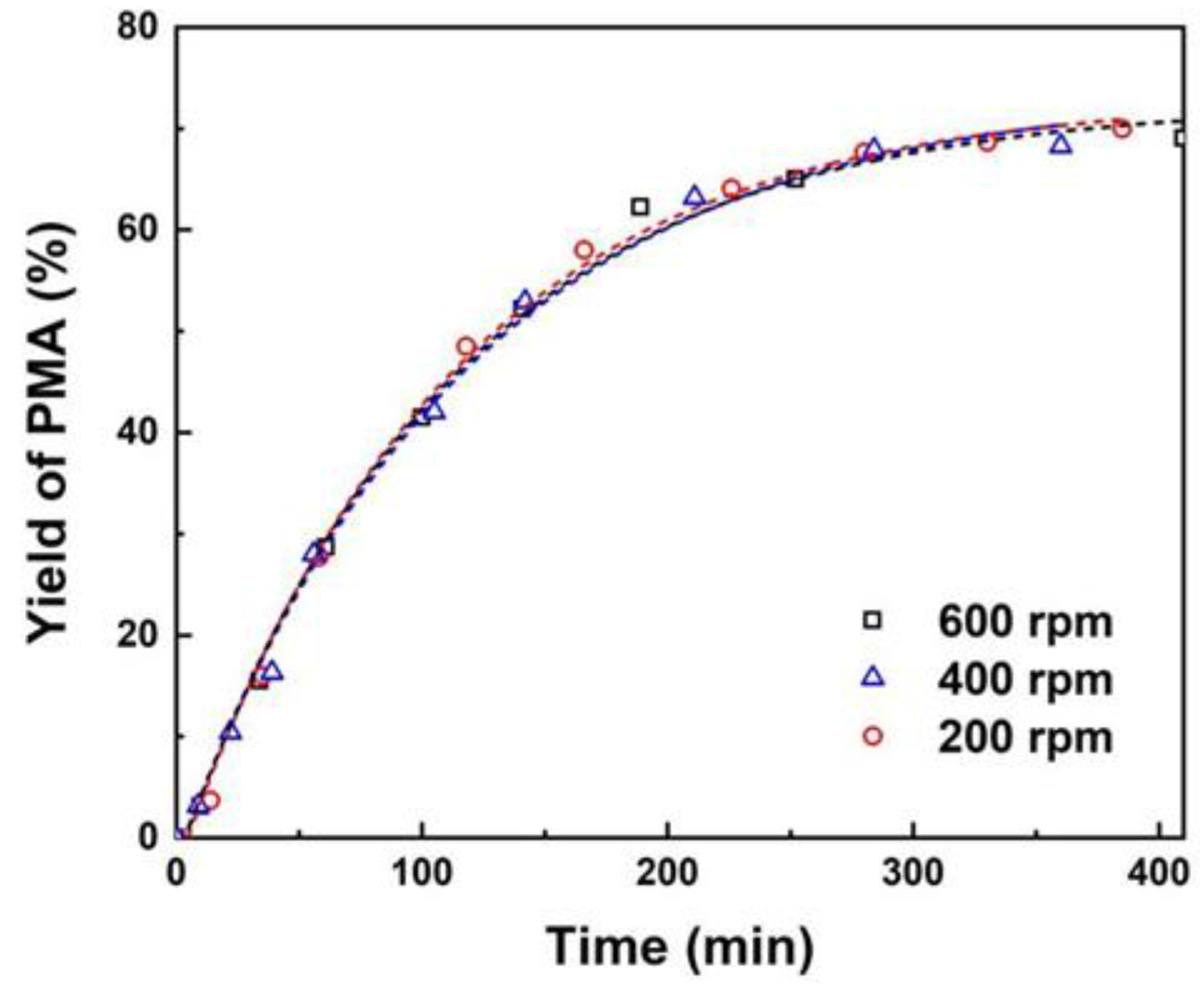
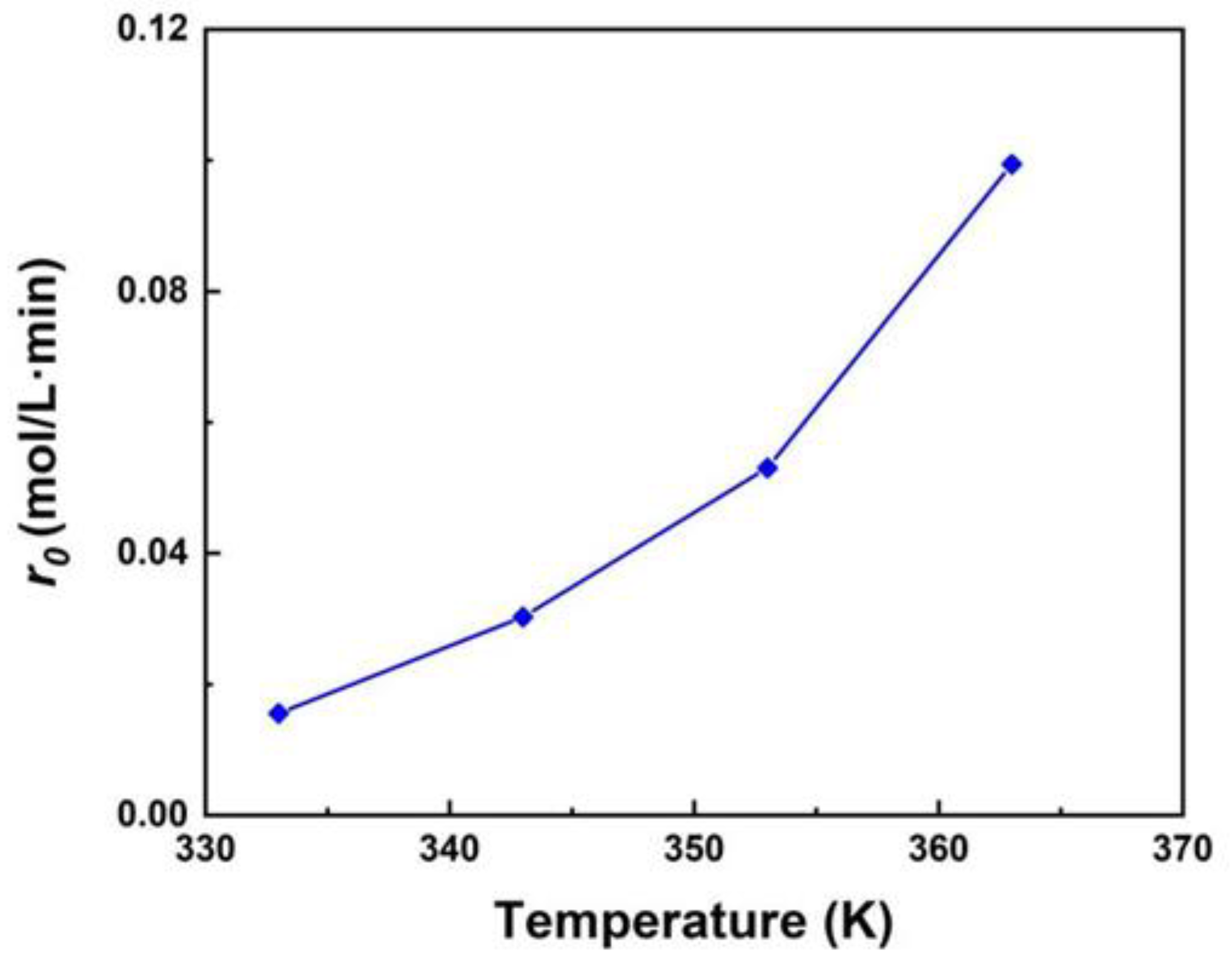
3.1. Effect of Mass Transfer

As indicated, the external and internal mass transfer limitations of resin catalysts in catalytic esterification reactions can be ruled out through varying stirring speed and particle sizes of catalysts [3,13,14]. As presented in Figure 1, it can be observed that varying stirring speeds within ranges of 200 to 600 rpm have no significant impact on the yield of PMA, indicating that the influence of external diffusion can be disregarded. Nevertheless, elevated rotational speeds may result in increased wear between the rotor and catalyst particles, which is detrimental to the recovery and reuse of the catalyst. Consequently, a stirring speed of 300 rpm can be established as the optimal setting for subsequent reaction process.
The particle diameter of the catalyst has a direct impact on internal diffusion. Previous studies have employed the method of varying catalyst particle diameter to investigate the effects of internal diffusion [13,14,46,47,48]. The particle size of the cation exchange resin Amberlyst-35 is not homogeneous, making it difficult to study the effects of internal diffusion by particle size screening. In theory, the Weisz-Prater number (Cwp) can be employed to assess the influence of internal diffusion on mass transfer in a reaction system catalyzed by a cation exchange resin [49]. When Cwp is much less than 1, the effect of internal diffusion on the mass transfer resistance of the reaction is negligible. Cwp is calculated by
C wp = − r obs ρ c R c 2 C s D e
where -robs represents the apparent rate of reaction, Cs is the concentration of reactants on the catalyst surface, De represents the effective diffusion coefficient, ρc is the density of catalyst, and Rc is the radius of catalyst particles (according to the manufacturer, ρc is 0.75 g/cm3 and Rc is 0.035 cm). De is calculated by
D e = ε c D A τ
where εc and τ represent the porosity and tortuosity factor of catalyst particles (where εc is assumed to be 0.35 and τ is 1/εc), respectively, and DA is the infinite dilution diffusion coefficient. DA can be calculated using the Wilke-Chang empirical correlation
D A = 7.4 × 10 − 8 ( φ 2 M 2 ) 0.5 T μ 2 V 1 0.6
where Φ2 is the association factor of PM, M2 is the molar mass of PM, μ2 is the viscosity of PM, and V1 is the molar volume of AA at normal boiling point.
Table 1 exhibits the calculated results of the Weisz-Prater parameter at different temperatures. Within the temperature ranges of 333.15 to 363.15 K, the Cwp values are significantly smaller than 1, indicating that the influence of internal diffusion can be neglected.

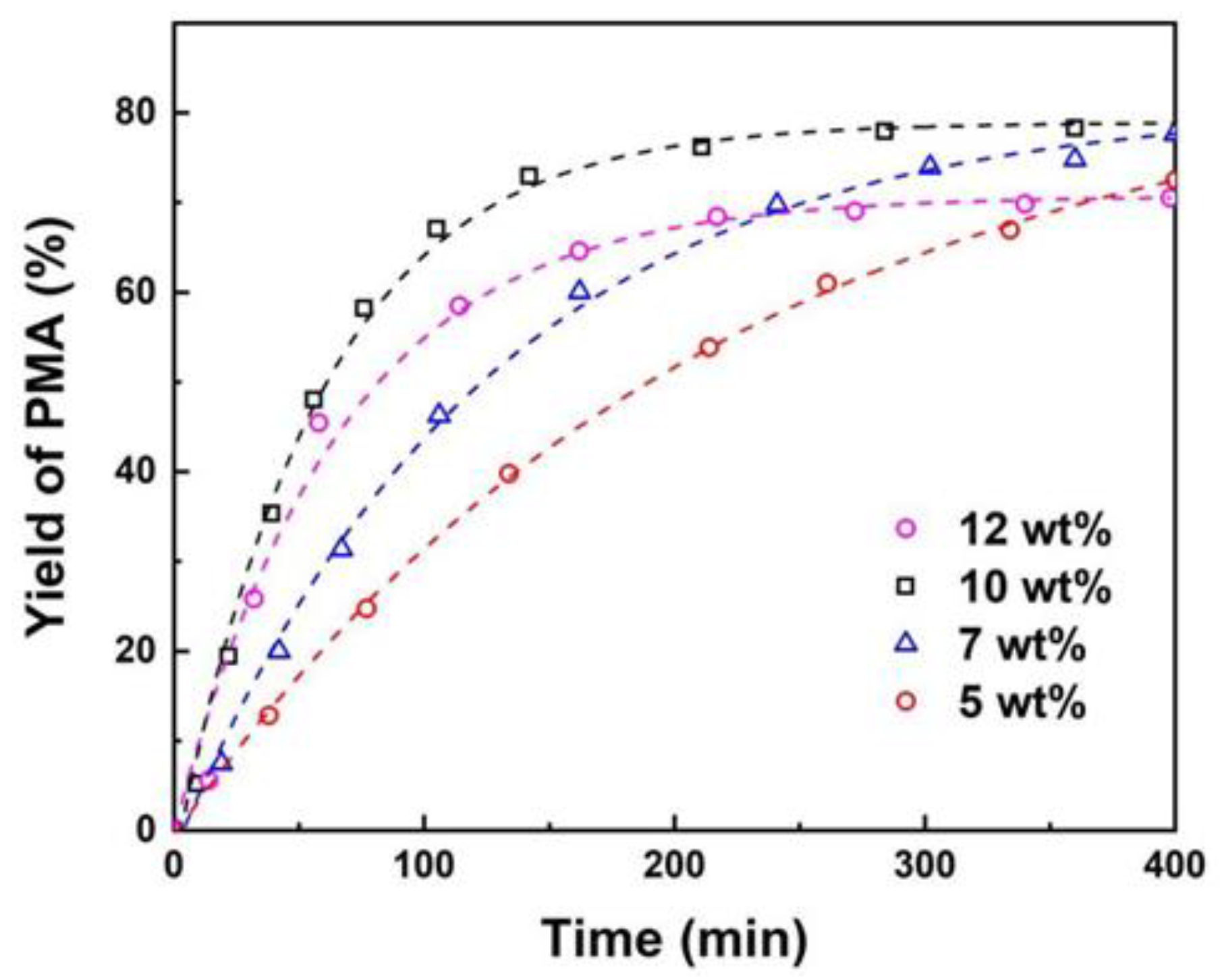
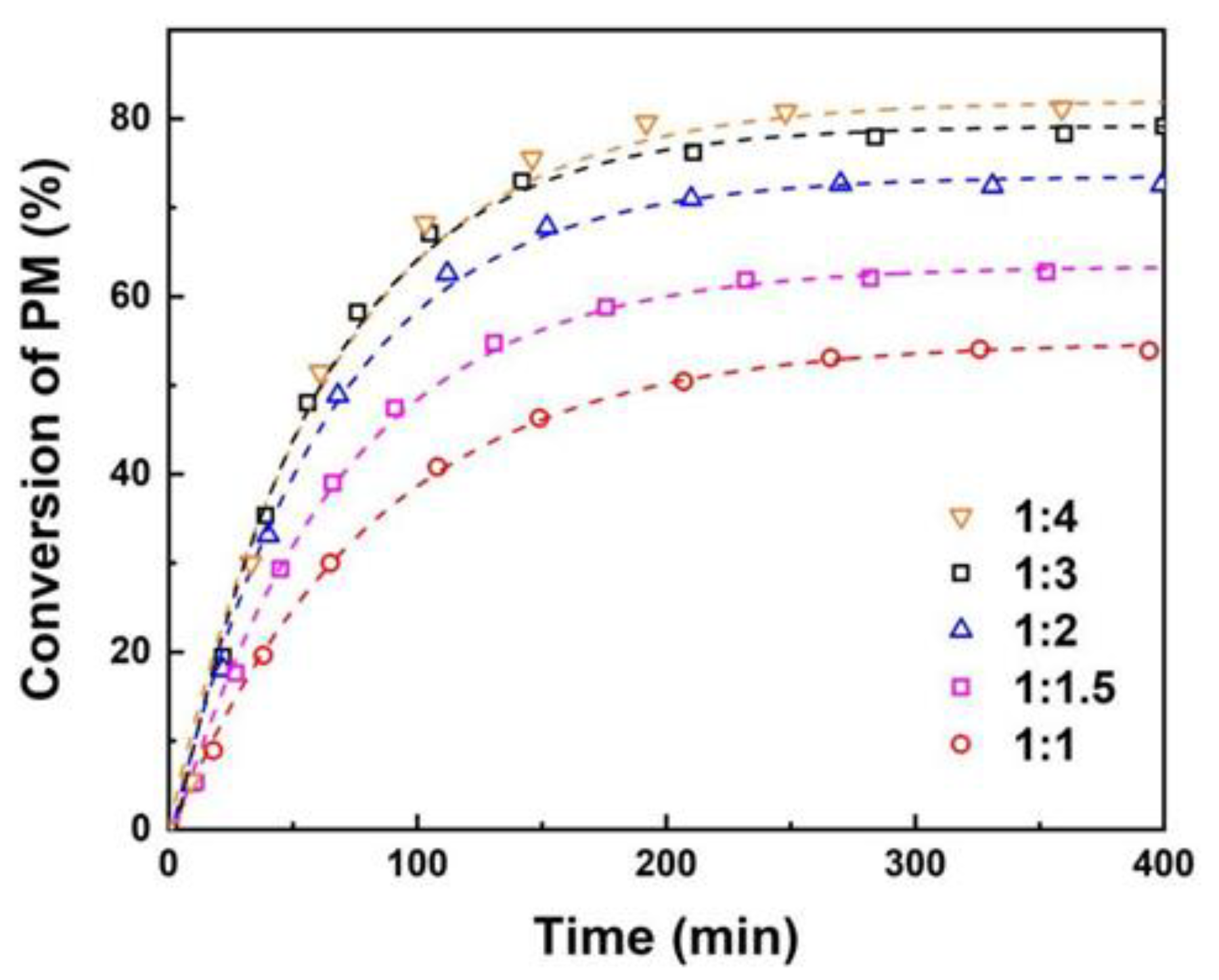
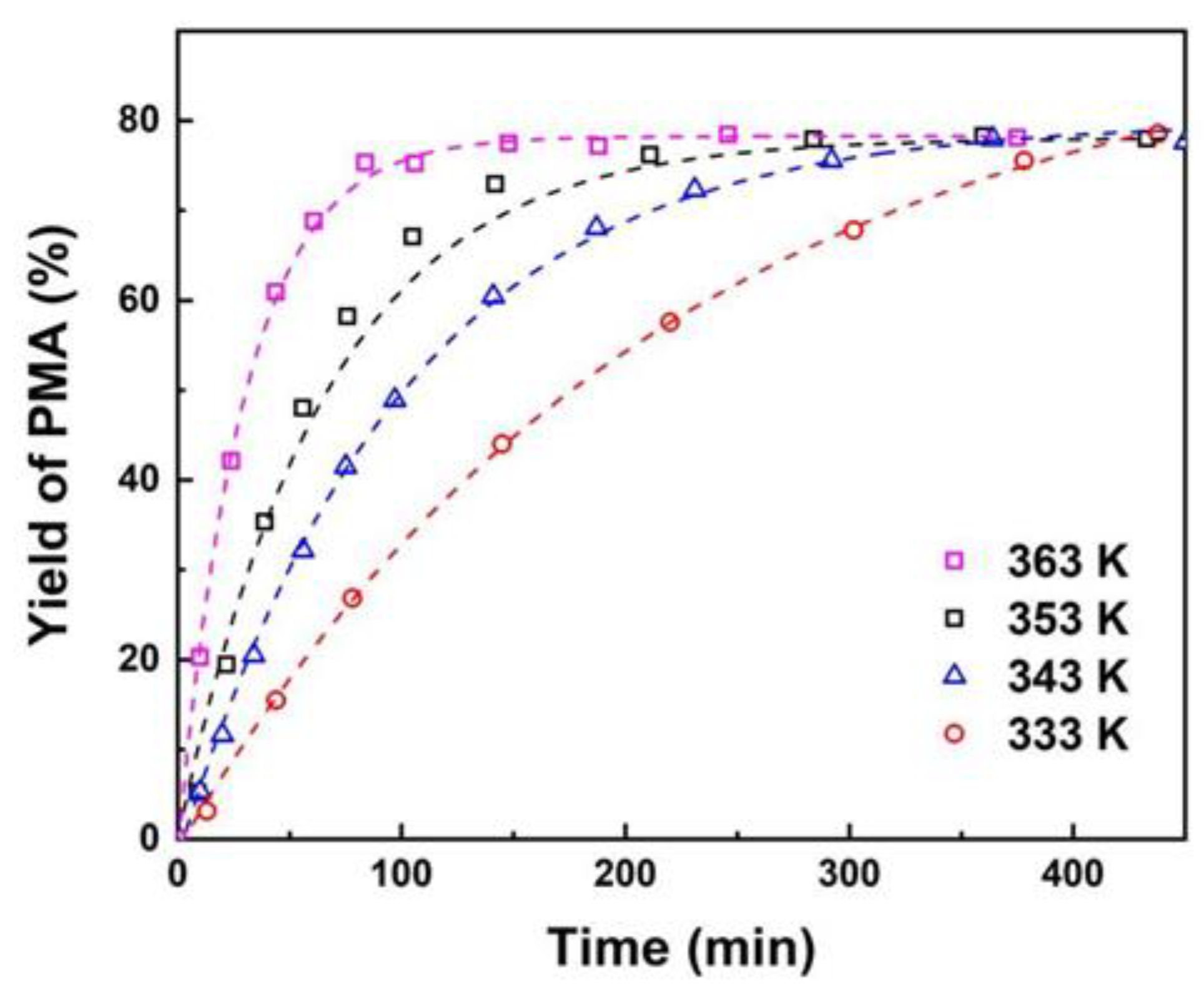
3.2. The Effect of Reaction Conditions

The impacts of various reaction parameters, including catalyst loading, temperature and reactant molar ratio on the esterification of PM and AA were investigated. The effect of the amount of catalyst on the PMA yield was studied by varying catalyst loading from 5 to 12 wt% while all other reaction parameters kept identical. The results as illustrated in Figure 2 demonstrate that when catalyst loading is below 10 wt%, an increase in the catalyst dosage leads to an acceleration in reaction rate. The maximum equilibrium yield of PMA is 78% when catalyst loading is 10 wt%. This indicates that the catalyst amount exerts an influence on the reaction rate, but not on the reaction equilibrium, which is well consistent with previous report [50].
However, with a high catalyst amount of 12 wt%, the reaction rate is found to be lower than that observed with a 10 wt% catalyst loading. The reason for this phenomenon may be that as the catalyst loading increases, the catalyst particles aggregate, reducing the effective surface area and thereby decreasing the number of active sites that actually participate in the reaction, which lowers the reaction rate [51]. Furthermore, the utilization of an excess of catalyst increases the cost of the reaction system. Consequently, a catalyst loading of 10 wt% is deemed to be the optimal catalyst amount for the esterification reaction between AA and PM.
The effect of initial molar ratio of PM to AA on the reaction was studied by varying the molar ratios of PM to AA from1:1 to 1:4, as shown in Figure 3 with catalyst loading of 10 wt% and reaction temperature of 353 K. The results reveal that the conversion of PM significantly improves as the initial molar ratio of PM to AA increases from 1:1 to 1:3. Similar results have been observed in previous studies of esterification of benzyl acetate [47]. Nevertheless, as the initial molar ratio of PM to AA continues to increase to 1:4, the increased trend of PM conversion becomes slower. This is due to the fact that within a certain range, an increase in the amount of AA results in an acceleration of collision frequency between reactant molecules, thereby increasing reaction rate. Furthermore, AA is also acted as a solvent to dilute the concentration of PM, which in turn results in a decrease in PM conversion. In consideration of subsequent separation issues, an excessively high concentration of AA would render separation more challenging, and consequently the optimal initial molar ratio of PM to AA is set at 1:3.
In order to investigate the effect of temperature on the reaction, the molar ratio of PM to AA was fixed to 1:3 and the catalyst loading was fixed to 10 wt%. Figure 4 illustrates the relationship between reaction rate and temperature within the studied temperature range. As the reaction temperature increases from 333 to 363 K, the reaction rate accelerates, while the equilibrium yield of PMA remains relatively constant at different reaction temperatures. The experimental results indicate that the temperature has a more significant impact on the initial reaction rate than on the final reaction rate, which is consistent with previous reports [13]. An increase in temperature facilitates the free movement of molecules, thereby enhancing the frequency of collisions between reactant molecules, which in turn leads to an increase in the reaction rate [52]. Nevertheless, an increase in temperature also results in elevated energy consumption and safety concerns and 353 K is identified as the optimal reaction temperature.
Figure 5 illustrates that the initial reaction rate exhibits exponential growth with temperature. The calculation of the initial reaction rate is represented by
r 0 = ( d C PM d t ) t = 0
For every 10-degree increase in temperature, the initial reaction rate doubles. The substantial impact of temperature on the reaction rate suggests that the reaction is regulated by either internal diffusion or surface reaction. The result has demonstrated that the esterification reaction between PM and AA is not limited by internal diffusion as shown in Figure 1. Consequently, the surface reaction is considered to be the limiting step of the esterification reaction.

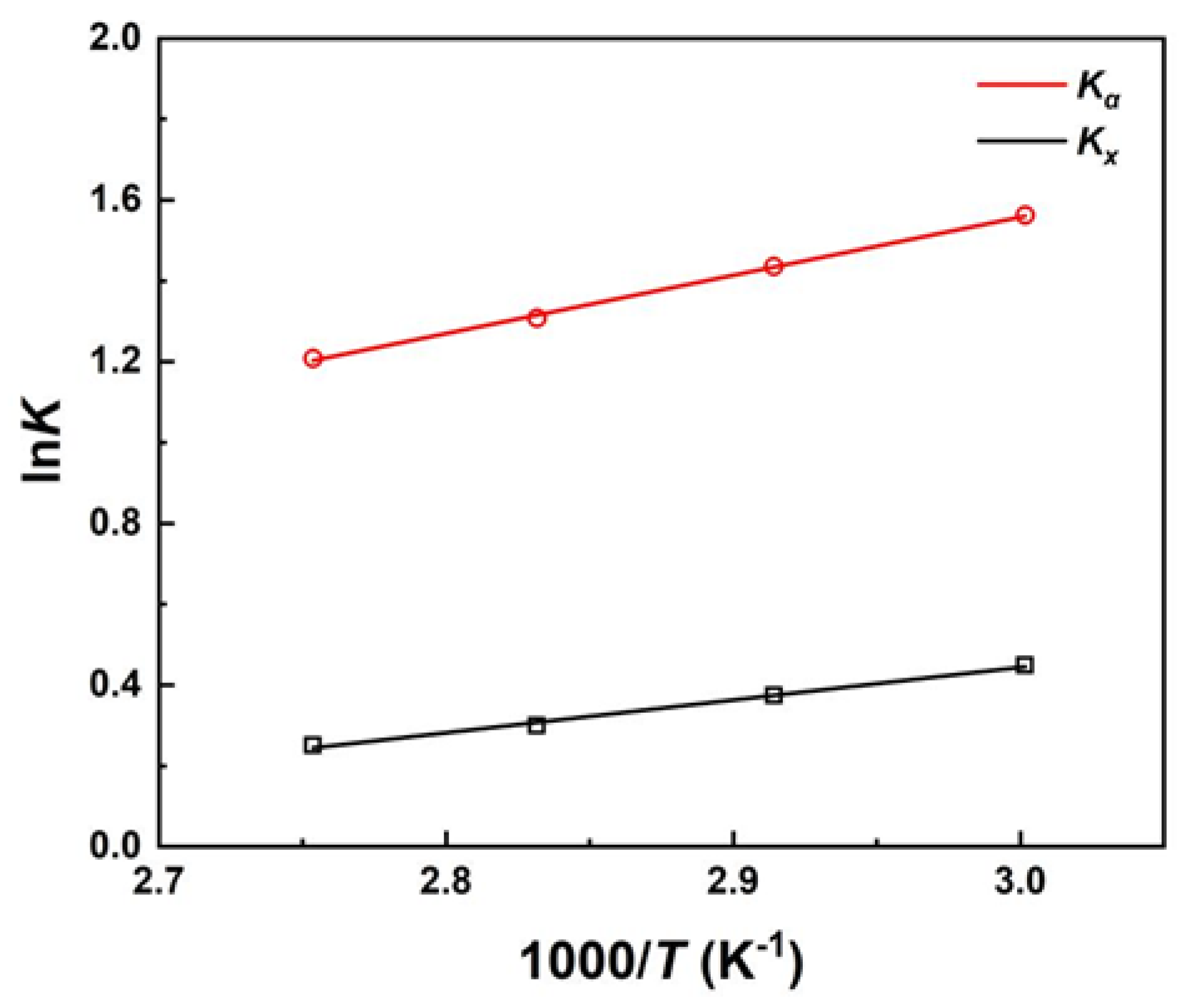
3.3. Chemical Reaction Thermodynamic Equilibrium

In general, the non-ideality of liquid phase mixture necessitates the use of an activity-based model. In accordance with Equation (5), the activity αi of component i is proportional to its mole fraction xi:
α i = γ i x i
where γi represents the activity coefficient of component i. The activity coefficient approach is applicable to liquid mixture based on COSMO model. This method enables the prediction of interaction energies and activity coefficients of complex liquid systems without the need for experimental data. The COSMO-RS model is capable of calculating chemical potential of any solute in any pure or mixed solvent, thereby enabling prediction of thermodynamic properties such as activity coefficients and solubilities.
The activity coefficient is calculated by
ln   γ i = ( μ i sol − μ i p ) / R T
where μisol represents the chemical potential of solute i in the solvent, and μip represents the chemical potential of solute i in the pure solute.
The chemical reaction for the esterification of AA and PM is represented by
This reaction is an acid-catalyzed esterification and is subject to thermodynamic equilibrium. The reaction equilibrium constant based on mole fractions (Kx) is given by
K x = ∏ x i ν i = x PMA x H 2 O x PM x AA
The reaction equilibrium constant based on activities (Kα) is predicted by
K α = ∏ α i ν i = ∏ ( x i γ i ) ν i = x PMA x H 2 O x PM x AA γ PMA γ H 2 O γ PM γ AA
The calculated activity coefficients for each component corresponding to the experimental mole fraction at equilibrium within the temperature range of 333 to 363 K are listed in Table 2. The values of Kx and Kα are calculated using Equations (8) and (9). According to the Van't Hoff equation, the relationship between the reaction equilibrium constant and temperature is given by
ln   K = − Δ r H θ R T + Δ r S θ R
A linear fit was performed by the ln of calculated equilibrium constants Kx and Kα versus the inverse of experimental temperature values. The fitting results are shown in Figure 6 and the calculated values of the reaction enthalpy change (ΔrHθ) and reaction entropy change (ΔrSθ) are presented in Table 3:
The expressions relating Kx and Kα to temperature (T) are given by
ln   K x = 809.92 T − 1.98584
ln   K α = 1440.27 T − 2.7631
The Gibbs free energy of the reaction can be calculated by
Δ r G θ = Δ r H θ − T Δ r S θ
The standard enthalpy of the reaction is determined to be -11.97 kJ/mol (Kα) based on activity-based calculations, while based on mole fraction calculations, the standard enthalpy of the reaction is determined to be -6.73 kJ/mol (Kx). The reaction enthalpy based on activity calculation considers the intricate interactions between molecules in the solution, thereby enhancing the accuracy of the resulting data. Previous studies have indicated that the relationship between the equilibrium constant of the reaction and temperature is not particularly strong, suggesting a relatively low value for ΔrH [13,53], which is consistent with our results. These results indicate that the influence of temperature on the initial reaction rate is more significant than its impact on the equilibrium conversion rate and the reaction is exothermal. A negative reaction entropy value indicates a reduction in the degree of chaos within the system. The standard Gibbs free energy of the reaction is calculated as -5.70 kJ/mol using Equation (13), indicating that the reaction is spontaneous, however the reaction couldn’t take place owing to the very slow reaction rate at standard state.

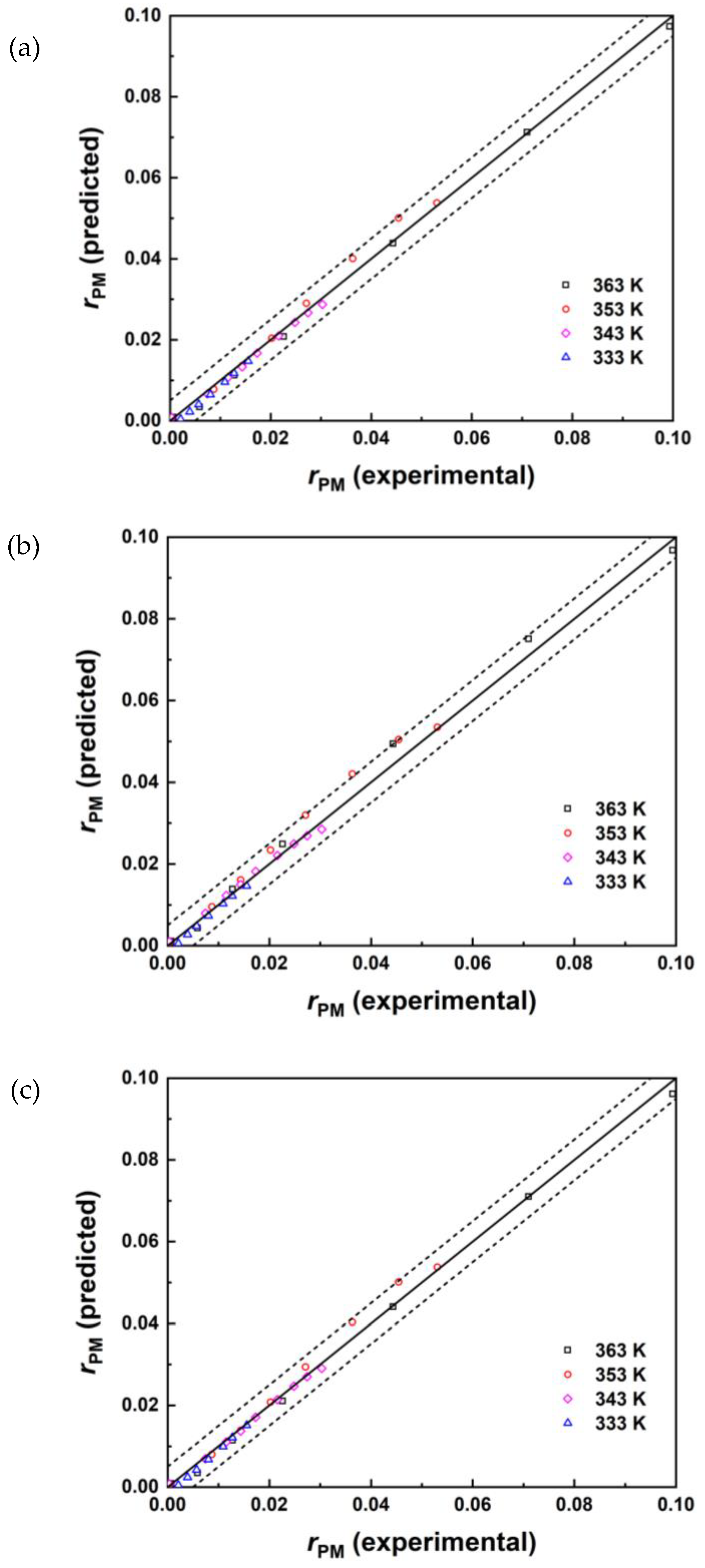
3.4. Reaction Kinetic Modelling

Both internal and external mass transfer resistances have been eliminated as shown in Figure 1 and Table 1, and thus the reaction rate is dependent on the adsorption of the reaction components on heterogeneous catalyst. The pseudo-homogeneous (PH), Eley-Rideal (ER), and Langmuir-Hinshelwood-Hougen- Watson (LHHW) kinetic models are frequently employed for correlating kinetic data pertaining to esterification reactions.
The PH model is widely applied in esterification systems, where the adsorption and desorption of all components can be neglected [52,54,55,56,57,58]. The PH model assumes that the catalyst swells completely upon contact with a polar solvent, and the cation exchange resin is equivalent to a liquid acid center, treating the entire reaction system as a homogeneous phase. Both the LHHW and ER models are suitable and applicable for multiphase catalytic reactions when the surface reaction is the controlling step. The LHHW model is effective in describing surface reactions between adsorbed molecules, while the ER model is well-suited to describe surface reactions between an adsorbed substance and a free substance in the liquid phase.
The esterification reaction between AA and PM is reversible and an excess amount of AA is added in order to enhance the conversion of PM. Consequently, the reaction rate is expressed as the consumption rate of PM. The formulations for the PH, ER, and LHHW models are presented in Equations (14)–(16):
r PM = d C PM d t = k + ( C PM C AA − 1 K x C PMA C H 2 O )
r PM = d C PM d t = k + ( C PM C AA − ( 1 / K x ) C PMA C H 2 O ) ( 1 + K PM C PM + K H 2 O C H 2 O )
r PM = d C PM d t = k + ( C PM C AA − ( 1 / K x ) C PMA C H 2 O ) ( 1 + K AA C AA + K PM C PM + K PMA C PMA + K H 2 O C H 2 O ) 2
where CPM, CAA, CPMA, and CH2O are molar concentrations of PM, AA, PMA, and H2O, respectively. Kx is the reaction equilibrium constant based on mole fractions, Ki represents the adsorption equilibrium constant of component i, and k+ is the rate constant of the forward reaction.
In consideration of the non-ideality of the liquid phase, the activity-based kinetic models are represented by Equations (17-19):
r PM = d C PM d t = k + ( α PM α AA − 1 K α α PMA α H 2 O )
r PM = d C PM d t = k + ( α PM α AA − ( 1 / K α ) α PMA α H 2 O ) ( 1 + K PM α PM + K H 2 O α H 2 O )
r PM = d C PM d t = k + ( α PM α AA − ( 1 / K α ) α PMA α H 2 O ) ( 1 + K AA α AA + K PM α PM + K PMA α PMA + K H 2 O α H 2 O ) 2
where αPM, αAA, αPMA, and αH2O represent the activities of PM, AA, PMA, and H2O, respectively, and Kα is the reaction equilibrium constant based on activities.
The adsorption equilibrium amount (qe, mg/g) of each component on the solid acid catalyst is calculated according to Equation (20):
q e = V ( C 0 − C e ) m
where C0 and Ce (g/L) represent the mass concentrations of the solution before adsorption and at equilibrium, respectively, V (L) is the volume of the solution, and m (g) is the mass of the catalyst.
The Langmuir adsorption isotherm model is employed with relevant expression provided by Equation (21):
1 q e = 1 q m K i 1 C e + 1 q m
where Ki is the adsorption equilibrium constant, Ce (g/L) is the mass concentration of the solution at adsorption equilibrium, and qm (g/g) represents the theoretical maximum adsorption capacity of the solid acid catalyst.
According to the Arrhenius equation, the relationship between k+ and reaction temperature (T) is given by Equation (22):
k + = k 0 + exp ( − E a + R T )
where k0+ is the pre-exponential factor of the reaction, Ea+ is the activation energy of the reaction, and R is the gas constant.
As both the ER model and LHHW model involve the adsorption of components from the liquid phase onto solid acid catalysts, adsorption experiments are conducted as a preliminary step. The Langmuir adsorption isotherm model is employed, and its expression is given by Equation (20). The qm of the solid acid catalyst and Ki obtained from the Langmuir model are presented in Table 4.
The experimentally obtained adsorption equilibrium constants exhibit considerable error, rendering them unsuitable for quantitative analysis. They can, however, be employed as qualitative references. Consequently, these parameter values are employed as initial values for the fitting calculations of the kinetic models, rather than being directly utilized as the adsorption equilibrium constant terms in the ER and LHHW models.
Python is a high-level programming language that is widely used in scientific computing and data analysis. The Python 3.8 programming language was employed to fit the kinetic models, with the kinetic parameters and error indicators presented in Table 5. Although all models exhibit similar values for root mean square error (RMSE) and coefficient of determination (R2), the LHHW model has the smallest mean absolute error (MAE). Consequently, among the three models employed, the LHHW model exhibits the most favorable correlation. The parity plot for the experimental and predicted rate of reaction is shown in Figure 7, indicating that the predicted concentration values of the three models are in good agreement with the experimental values.
According to the fitting results of the LHHW model, the apparent activation energy for the esterification reaction between AA and PM catalyzed by Amberlyst-35 is determined to be 62.0 kJ/mol. This result is in close agreement with the reported value of 60.5 kJ/mol for the forward reaction activation energy by Wang B et al. [14]. The satisfactory correlation between the experimental data and LHHW model suggests that the reaction is governed by surface reaction, which is in accordance with the findings in Section 3.2 regarding the impact of temperature on the esterification reaction. According to the LHHW model, PM and AA are independently adsorbed on the catalyst surface, after which a surface reaction occurs to form PMA. Finally, PMA is desorbed and diffuses into the liquid phase.

4. Conclusions

The ion exchange resin Amberlyst-35 was employed as a catalyst for the esterification reaction of PM and AA to form PMA. The impacts of varying reaction parameters, including temperature, catalyst dosage, initial molar ratio of reactants, and stirring speed on the reaction were investigated. Under optimized reaction conditions of initial reactant PM to AA molar ratio of 1:3 and catalyst loading of 10 wt% for a period of 3 h at 353 K, the equilibrium yield of PMA could reach 78%. Reaction thermodynamic equilibrium model was considered to analyze reaction enthalpy and entropy changes. Furthermore, reaction kinetic models including PH, ER, and LHHW were fitted and the LHHW model was demonstrated to be the most favorable correlation, indicating that the reaction was controlled by surface reactions. The reaction thermodynamic equilibrium and kinetic models serve as a promising foundation to support further efforts for the development of economical and environmentally friendly PMA industrial production routes through the application of ion exchange resin catalysts.

Data Availability Statement

The data presented in this study are available in this article.

Acknowledgments

The financial support from National Natural Science Foundation of China (22278134, 22472055) is greatly acknowledged.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hussain, A.; Chaniago, Y. D.; Riaz, A.; Lee, M. Process design alternatives for producing ultra-high-purity electronic-grade propylene glycol monomethyl ether acetate. Ind. Eng. Chem. Res. 2019, 58, 2246. [Google Scholar] [CrossRef]
  2. Chaniago, Y. D.; Hussain, A.; Andika, R.; Lee, M. Reactive pressure-swing distillation toward sustainable process of novel continuous ultra-high-purity electronic-grade propylene glycol monomethyl ether acetate manufacture. ACS Sustainable Chem. Eng. 2019, 7, 18677. [Google Scholar] [CrossRef]
  3. Huang, Z.; Lin, Y.; Li, L.; Ye, C.; Qiu, T. Preparation and shaping of solid acid SO42−/TiO2 and its application for esterification of propylene glycol monomethyl ether and acetic acid. Chin. J. Chem. Eng. 2017, 25, 1207. [Google Scholar] [CrossRef]
  4. Ye, C. S.; Dong, X. L.; Zhu, W. J.; Cai, D. R.; Qiu, T. Isobaric vapor-liquid equilibria of the binary mixtures propylene glycol methyl ether plus propylene glycol methyl ether acetate, methyl acetate plus propylene glycol methyl ether and methanol plus propylene glycol methyl ether acetate at 101.3 kPa. Fluid Phase Equilib. 2014, 367, 45. [Google Scholar] [CrossRef]
  5. Chaniago, Y. D.; Lee, M. Distillation design and optimization of quaternary azeotropic mixtures for waste solvent recovery. J. Ind. Eng. Chem. 2018, 67, 255. [Google Scholar] [CrossRef]
  6. Jyothi, M. S.; Nagarajan, V.; Chandiramouli, R. Adsorption properties of glycol ethers on cubic germanane nanosheets: A first-principles study. J. Phys. Chem. Solids. 2024, 188. [Google Scholar] [CrossRef]
  7. Kelsey, J. R. Ethylene oxide derived glycol ethers: A review of the alkyl glycol ethers potential to cause endocrine disruption. Regul. Toxicol. Pharmacol. 2022, 129. [Google Scholar] [CrossRef]
  8. Kelsey, J. R.; Cnubben, N. H. P.; Bogaards, J. J. P.; Braakman, R. B. H.; van Stee, L. L. P.; Smet, K. The urinary metabolic profile of diethylene glycol methyl ether and triethylene glycol methyl ether in Sprague-Dawley rats and the role of the metabolite methoxyacetic acid in their toxicity. Regul. Toxicol. Pharmacol. 2020, 110. [Google Scholar] [CrossRef]
  9. Wang, Y.-W.; Li, X.-X.; Zhang, Z.-L.; Liu, Q.; Li, D.; Wang, X. Volumetric, viscosimetric and spectroscopic studies for aqueous solution of ethylene glycol monoethyl ether. J. Mol. Liq. 2014, 196, 192. [Google Scholar] [CrossRef]
  10. Oh, J.; Sreedhar, B.; Donaldson, M. E.; Frank, T. C.; Schultz, A. K.; Bommarius, A. S.; Kawajiri, Y. Transesterification of propylene glycol methyl ether in chromatographic reactors using anion exchange resin as a catalyst. J. Chromatogr. A. 2016, 1466, 84. [Google Scholar] [CrossRef]
  11. Oh, J.; Sreedhar, B.; Donaldson, M. E.; Frank, T. C.; Schultz, A. K.; Bommarius, A. S.; Kawajiri, Y. Transesterification of propylene glycol methyl ether by reactive simulated moving bed chromatography using homogeneous catalyst. Adsorpt.-J. Int. Adsorpt. Soc. 2018, 24, 309. [Google Scholar] [CrossRef]
  12. Gadekar-Shinde, S.; Reddy, B.; Khan, M.; Chavan, S.; Saini, D.; Mahajani, S. Reactive distillation for the production of methoxy propyl acetate: experiments and simulation. Ind. Eng. Chem. Res. 2017, 56, 832. [Google Scholar] [CrossRef]
  13. Oh, J.; Agrawal, G.; Sreedhar, B.; Donaldson, M. E.; Schultz, A. K.; Frank, T. C.; Bommarius, A. S.; Kawajiri, Y. Conversion improvement for catalytic synthesis of propylene glycol methyl ether acetate by reactive chromatography: Experiments and parameter estimation. Chem. Eng. J. 2015, 259, 397. [Google Scholar] [CrossRef]
  14. Wang, B.; Cai, X.; Lu, L.; Ma, J. A combination of low-temperature reactive and extractive distillation for methoxy-2-propyl acetate synthesis and separation process: simulations and experiments. J. Chem. Technol. Biotechnol. 2019, 94, 3292. [Google Scholar] [CrossRef]
  15. Cho, M.; Han, M. Dynamics and control of entrainer enhanced reactive distillation using an extraneous entrainer for the production of butyl acetate. J. Process Control. 2018, 61, 58. [Google Scholar] [CrossRef]
  16. Kiss, A. A. Novel catalytic reactive distillation processes for a sustainable chemical industry. Top. Catal. 2019, 62, 1132. [Google Scholar] [CrossRef]
  17. Rodriguez, M.; Li, P. Z.; Diaz, I. A control strategy for extractive and reactive dividing wall columns. Chem. Eng. Process. 2017, 113, 14. [Google Scholar] [CrossRef]
  18. Simasatitkul, L.; Kaewwisetkul, P.; Wiyaratn, W.; Assabumrungrat, S.; Arpornwichanop, A. Optimal design and performance analyses of the glycerol ether production process using a reactive distillation column. J. Ind. Eng. Chem. 2016, 43, 93. [Google Scholar] [CrossRef]
  19. Wang, R. Z.; Chen, G. Z.; Qin, H.; Cheng, H. Y.; Chen, L. F.; Qi, Z. W. Systematic screening of bifunctional ionic liquid for intensifying esterification of methyl heptanoate in the reactive extraction process. Chem. Eng. Sci. 2021, 246. [Google Scholar] [CrossRef]
  20. Zeng, Q.; Hu, B.; Cheng, H. Y.; Chen, L. F.; Huang, J. M.; Qi, Z. W. Liquid-liquid equilibrium for the system of ionic liquid [BMIm][HSO4] catalysed isobutyl isobutyrate formation. J. Chem. Thermodyn. 2018, 122, 162. [Google Scholar] [CrossRef]
  21. Zeng, Q.; Song, Z.; Qin, H.; Cheng, H. Y.; Chen, L. F.; Pan, M.; Heng, Y.; Qi, Z. W. Ionic liquid [BMIm][HSO4] as dual catalyst-solvent for the esterification of hexanoic acid with n-butanol. Catal. Today. 2020, 339, 113. [Google Scholar] [CrossRef]
  22. Zhang, C.; Liu, T.; Wang, H.-J.; Wang, F.; Pan, X.-Y. Synthesis of acetyl salicylic acid over WO3/ZrO2 solid superacid catalyst. Chem. Eng. J. 2011, 174, 236. [Google Scholar] [CrossRef]
  23. Gao, A.; Chen, H.; Tang, J.; Xie, K.; Hou, A. Efficient extraction of cellulose nanocrystals from waste Calotropis gigantea fiber by SO42-/TiO2 nano-solid superacid catalyst combined with ball milling exfoliation. Ind. Crops Prod. 2020, 152. [Google Scholar] [CrossRef]
  24. Hassan, M. A.; Wang, W.; Chang, Z.; Li, M.; Dong, B.; Ndonfack, K. I. A.; Li, W.; Sun, C. TiO2/SO42- solid superacid catalyst prepared by recovered TiO2 from waste SCR and its application in transesterification of ethyl acetate with n-butanol. Waste Biomass Valorization. 2023, 14, 4035. [Google Scholar] [CrossRef]
  25. Kuwahara, Y.; Kaburagi, W.; Nemoto, K.; Fujitani, T. Esterification of levulinic acid with ethanol over sulfated Si-doped ZrO2 solid acid catalyst: Study of the structure-activity relationships. Appl. Catal., A 2014, 476, 186. [Google Scholar] [CrossRef]
  26. Lokman, I. M.; Goto, M.; Rashid, U.; Taufiq-Yap, Y. H. Sub- and supercritical esterification of palm fatty acid distillate with carbohydrate-derived solid acid catalyst. Chem. Eng. J. 2016, 284, 872. [Google Scholar] [CrossRef]
  27. Sheikh, R.; Choi, M.-S.; Im, J.-S.; Park, Y.-H. Study on the solid acid catalysts in biodiesel production from high acid value oil. J. Ind. Eng. Chem. 2013, 19, 1413. [Google Scholar] [CrossRef]
  28. Firouzjaee, M. H.; Taghizadeh, M. n-Butane isomerization over 0.5 Pt/HPA/MCM-41 catalyst: Optimization study using central composite design. Chem. Eng. Technol. 2024, 47, 887. [Google Scholar] [CrossRef]
  29. Li, L.; Liu, Y.; Wu, K.; Liu, C.; Tang, S.; Yue, H.; Lu, H.; Liang, B. Catalytic solvent regeneration of a CO2-loaded MEA solution using an acidic catalyst from industrial rough metatitanic acid. Greenh. Gases. 2020, 10, 449. [Google Scholar] [CrossRef]
  30. Yati, I.; Yeom, M.; Choi, J.-W.; Choo, H.; Suh, D. J.; Ha, J.-M. Water-promoted selective heterogeneous catalytic trimerization of xylose-derived 2-methylfuran to diesel precursors. Appl. Catal., A 2015, 495, 200. [Google Scholar] [CrossRef]
  31. Xu, W.; Ollevier, T.; Kleitz, F. Iron-modified mesoporous silica as an efficient solid lewis acid catalyst for the mukaiyama aldol reaction. Acs Catalysis. 2018, 8, 1932. [Google Scholar] [CrossRef]
  32. Orabona, F.; Capasso, S.; Perez-Sena, W. Y.; Taddeo, F.; Eränen, K.; Verdolotti, L.; Tesser, R.; Di Serio, M.; Murzin, D.; Russo, V.; Salmi, T. Solvent-free condensation of ethyl levulinate with phenol promoted by Amberlyst-15: Kinetics and modeling. Chem. Eng. J. 2024, 493. [Google Scholar] [CrossRef]
  33. Badia, J. H.; Soto, R.; Ramírez, E.; Bringué, R.; Fité, C.; Iborra, M.; Tejero, J. Role of ion-exchange resins in hydrogenation reactions. Catalysts. 2023, 13. [Google Scholar] [CrossRef]
  34. Jiang, T.; Zhao, Q.; Li, M.; Yin, H. Preparation of mesoporous titania solid superacid and its catalytic property. J. Hazard. Mater. 2008, 159, 204. [Google Scholar] [CrossRef] [PubMed]
  35. Huang, H.; Mu, J.; Liang, M.; Qi, R.; Wu, M.; Xu, L.; Xu, H.; Zhao, J.; Zhou, J.; Miao, Z. One-pot synthesis of MoO3-ZrO2 solid acid catalyst for solvent-free solketal production from glycerol. Mol. Catal. 2024, 552. [Google Scholar] [CrossRef]
  36. Waldron, C.; Pankajakshan, A.; Quaglio, M.; Cao, E.; Galvanin, F.; Gavriilidis, A. Closed-Loop Model-Based Design of Experiments for Kinetic Model Discrimination and Parameter Estimation: Benzoic Acid Esterification on a Heterogeneous Catalyst. Ind. Eng. Chem. Res. 2019, 58, 22165. [Google Scholar] [CrossRef]
  37. Echaroj, S.; Asavatesanupap, C.; Chavadej, S.; Santikunaporn, M. Kinetic study on microwave-assisted oligomerization of 1-decene over a HY catalyst. Catalysts. 2021, 11. [Google Scholar] [CrossRef]
  38. Bertero, N. M.; Apesteguia, C. R.; Marchi, A. J. Selective synthesis of 1-indanol by 1-indanone liquid-phase hydrogenation over metal-based catalysts: A LHHW kinetic approach. Chem. Eng. Sci. 2022, 254. [Google Scholar] [CrossRef]
  39. Delgado, P.; Sanz, M. T.; Beltran, S. Kinetic study for esterification of lactic acid with ethanol and hydrolysis of ethyl lactate using an ion-exchange resin catalyst. Chem. Eng. J. 2007, 126, 111. [Google Scholar] [CrossRef]
  40. Mao, W.; Wang, X.; Wang, H.; Chang, H.; Zhang, X.; Han, J. Thermodynamic and kinetic study of tert-amyl methyl ether (TAME) synthesis. Chem. Eng. Process. 2008, 47, 761. [Google Scholar] [CrossRef]
  41. Kuusisto, J.; Mikkola, J.-P.; Sparv, M.; Waerna, J.; Karhu, H.; Salmi, T. Kinetics of the catalytic hydrogenation of D-lactose on a carbon supported ruthenium catalyst. Chem. Eng. J. 2008, 139, 69. [Google Scholar] [CrossRef]
  42. Shan, X.; Cheng, Z.; Yuan, P. Reaction kinetics and mechanism for hydration of cyclohexene over ion-exchange resin and H-ZSM-5. Chem. Eng. J. 2011, 175, 423. [Google Scholar] [CrossRef]
  43. Sert, E.; Atalay, F. S. Kinetic study of the esterification of acetic acid with butanol catalyzed by sulfated zirconia. React. Kinet., Mech. Catal. 2010, 99, 125. [Google Scholar] [CrossRef]
  44. Casas, C.; Bringué, R.; Fité, C.; Iborra, M.; Tejero, J. Kinetics of the Liquid Phase Dehydration of 1-Octanol to Di-n-Octyl Ether on Amberlyst 70. AIChE J. 2017, 63, 3966. [Google Scholar] [CrossRef]
  45. Yip, A. C. K.; Hu, X. Catalytic Activity of Clay-Based Titanium Silicalite-1 Composite in Cyclohexanone Ammoximation. Ind. Eng. Chem. Res. 2009, 48, 8441. [Google Scholar] [CrossRef]
  46. Akyalcin, S.; Altiokka, M. R. Kinetics of esterification of acetic acid with 1-octanol in the presence of Amberlyst 36. Appl. Catal., A 2012, 429, 79. [Google Scholar] [CrossRef]
  47. Ali, S. H.; Merchant, S. Q. Kinetic study of Dowex 50 Wx8-catalyzed esterification and hydrolysis of benzyl acetate. Ind. Eng. Chem. Res. 2009, 48, 2519. [Google Scholar] [CrossRef]
  48. Patel, D.; Saha, B. Esterification of Acetic Acid with n-Hexanol in Batch and Continuous Chromatographic Reactors Using a Gelular Ion-Exchange Resin as a Catalyst. Ind. Eng. Chem. Res. 2012, 51, 11965. [Google Scholar] [CrossRef]
  49. Martinez, A. F.; Sanchez, C. A.; Orjuela, A.; Gil, I. D.; Rodriguez, G. Isobutyl acetate by reactive distillation. Part II. Kinetic study. Chem. Eng. Res. Des. 2020, 160, 447. [Google Scholar] [CrossRef]
  50. Son, Y. R.; Park, J. K.; Shin, E. W.; Moon, S. P.; Park, H. E. Synthesis of propylene glycol methyl ether acetate: Reaction kinetics and process simulation using heterogeneous catalyst. Processes. 2024, 12. [Google Scholar] [CrossRef]
  51. Yan, H.; Zhao, X.; Guo, N.; Lyu, Z.; Du, Y.; Xi, S.; Guo, R.; Chen, C.; Chen, Z.; Liu, W.; Yao, C.; Li, J.; Pennycook, S. J.; Chen, W.; Su, C.; Zhang, C.; Lu, J. Atomic engineering of high-density isolated Co atoms on graphene with proximal-atom controlled reaction selectivity. Nat. Commun. 2018, 9. [Google Scholar] [CrossRef] [PubMed]
  52. Chin, S. Y.; Ahmad, M. A. A.; Kamaruzaman, M. R.; Cheng, C. K. Kinetic studies of the esterification of pure and dilute acrylic acid with 2-ethyl hexanol catalysed by Amberlyst 15. Chem. Eng. Sci. 2015, 129, 116. [Google Scholar] [CrossRef]
  53. Ali, S. H. Kinetics of catalytic esterification of propionic acid with different alcohols over Amberlyst 15. Int. J. Chem. Kinet. 2009, 41, 432. [Google Scholar] [CrossRef]
  54. Li, K.; Xue, W.; Zeng, Z.; Shi, X. Kinetics of the reaction of ethanol and lauric acid catalyzed by deep eutectic solvent based on benzyltrimethylammonium chloride. Can. J. Chem. Eng. 2019, 97, 1144. [Google Scholar] [CrossRef]
  55. Qin, H.; Hu, X.; Wang, J.; Cheng, H.; Chen, L.; Qi, Z. Overview of acidic deep eutectic solvents on synthesis, properties and applications. Green Energy Environ. 2020, 5, 8. [Google Scholar] [CrossRef]
  56. Wang, R.; Qin, H.; Wang, J.; Cheng, H.; Chen, L.; Qi, Z. Reactive extraction for intensifying 2-ethylhexyl acrylate synthesis using deep eutectic solvent Im:2PTSA. Green Energy Environ. 2021, 6, 405. [Google Scholar] [CrossRef]
  57. Yang, J.; Zhou, L.; Guo, X.; Li, L.; Zhang, P.; Hong, R.; Qiu, T. Study on the esterification for ethylene glycol diacetate using supported ionic liquids as catalyst: Catalysts preparation, characterization, and reaction kinetics, process. Chem. Eng. J. 2015, 280, 147. [Google Scholar] [CrossRef]
  58. Yang, Z.; Cui, X.; Jie, H.; Yu, X.; Zhang, Y.; Feng, T.; Liu, H.; Song, K. Kinetic study and process simulation of transesterification of methyl acetate and isoamyl alcohol catalyzed by ionic liquid. Ind. Eng. Chem. Res. 2015, 54, 1204. [Google Scholar] [CrossRef]
Preprints 117123 g001
Figure 1. Effect of stirring speeds on yields of PMA. Reaction conditions: PM:AA=1:3 (mole ratio) and 10 wt% catalyst loading of total reactant mass at 353 K.
Figure 1. Effect of stirring speeds on yields of PMA. Reaction conditions: PM:AA=1:3 (mole ratio) and 10 wt% catalyst loading of total reactant mass at 353 K.
Preprints 117123 g001
Preprints 117123 g002
Figure 2. Effect of catalyst loadings on yield of PMA (wt% of total reactant mass). Reaction conditions: PM:AA=1:3 (mole ratio) at 353 K.
Figure 2. Effect of catalyst loadings on yield of PMA (wt% of total reactant mass). Reaction conditions: PM:AA=1:3 (mole ratio) at 353 K.
Preprints 117123 g002
Preprints 117123 g003
Figure 3. Effect of initial molar ratio of PM to AA. Reaction conditions: 10 wt% catalyst loading of total reactant mass at 353 K.
Figure 3. Effect of initial molar ratio of PM to AA. Reaction conditions: 10 wt% catalyst loading of total reactant mass at 353 K.
Preprints 117123 g003
Preprints 117123 g004
Figure 4. Effect of temperature on yield of PMA. Reaction conditions: PM:AA=1:3 (mole ratio), 10 wt% catalyst loading.
Figure 4. Effect of temperature on yield of PMA. Reaction conditions: PM:AA=1:3 (mole ratio), 10 wt% catalyst loading.
Preprints 117123 g004
Preprints 117123 g005
Figure 5. Effect of reaction temperature on the initial rate of reaction. Reaction conditions: PM:AA=1:3 (mole ratio), 10 wt% catalyst loading.
Figure 5. Effect of reaction temperature on the initial rate of reaction. Reaction conditions: PM:AA=1:3 (mole ratio), 10 wt% catalyst loading.
Preprints 117123 g005
Preprints 117123 g006
Figure 6. Relationship between lnKx/lnKα and 1000/T.
Figure 6. Relationship between lnKx/lnKα and 1000/T.
Preprints 117123 g006
Preprints 117123 g007
Figure 7. Parity plot for the experimental and predicted rate of reaction of (a) PH, (b) ER, and (c) LHHW.
Figure 7. Parity plot for the experimental and predicted rate of reaction of (a) PH, (b) ER, and (c) LHHW.
Preprints 117123 g007
Table 1. Calculated infinite dilution diffusion coefficient (DA), effective diffusion coefficient (De), and Weisz-Prater criterion (Cwp) at different temperatures.
Table 1. Calculated infinite dilution diffusion coefficient (DA), effective diffusion coefficient (De), and Weisz-Prater criterion (Cwp) at different temperatures.
T (K) DA (cm2/s) De (cm2/s) Cwp
333.15 2.31×10-5 2.42×10-6 0.06
343.15 2.58×10-5 2.71×10-6 0.11
353.15 2.84×10-5 2.98×10-6 0.18
363.15 3.10×10-5 3.25×10-6 0.30
Table 2. Mole fractions and the evaluated activity coefficients of components in the equilibrium state of the reaction at various temperatures.
Table 2. Mole fractions and the evaluated activity coefficients of components in the equilibrium state of the reaction at various temperatures.
T (K) PM AA PMA H2O
xPM αPM xAA αAA xPMA αPMA xH2O αH2O
333.15 0.0547 0.8870 0.5516 0.9333 0.1969 1.1870 0.1969 1.8158
343.15 0.0530 0.8433 0.5504 0.9239 0.1983 1.1794 0.1983 1.8119
353.15 0.0502 0.7963 0.5493 0.9135 0.2002 1.1685 0.2002 1.8000
363.15 0.0470 0.7447 0.5504 0.9033 0.2013 1.1521 0.2013 1.7772
Table 3. Thermodynamic parameters of the reaction.
Table 3. Thermodynamic parameters of the reaction.
Equilibrium constant ΔrHθ (kJ·mol-1) ΔrSθ (J·mol-1·K-1) R2
Kx -6.734 -16.51 0.9942
Kα -11.97 -22.97 0.9988
Table 4. Fitting calculation results of Langmuir adsorption isotherm models.
Table 4. Fitting calculation results of Langmuir adsorption isotherm models.
Component qm (g/g) Ki R2
PM 0.4768 0.0271 0.995
AA 0.3582 0.0250 0.833
PMA 2.1921 0.0001 0.926
H2O 0.7357 0.0071 0.953
Table 5. Kinetic parameters for different models.
Table 5. Kinetic parameters for different models.
Model k0+ Ea+(kJ/mol) KPM KAA KPMA KH2O MAE RMSE R2
PH 2.88×106 63.2 / / / / 1.26×10-3 1.59×10-3 0.9964
ER 4.25×106 63.3 0.12 / / 0.01 1.22×10-3 1.57×10-3 0.9947
LHHW 6.84×106 62.0 0.13 0.04 8.2×10-4 0.15 1.13×10-3 1.59×10-3 0.9946
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated