Preprint
Article
Modeling Enzyme Dynamics in Metabolomics: A Topological Approach to Visualizing Adaptive Network Interactions Under Environmental Disturbances
Altmetrics
Downloads
69
Views
21
Comments
0
This version is not peer-reviewed
AI and Computational Methods for Modelling, Simulations and Optimizing of Advanced Systems: Innovations in Complexity
Submitted:
03 September 2024
Posted:
05 September 2024
You are already at the latest version
Alerts
Abstract
Metabolomics studies require a deep understanding of enzyme dynamics and their responses to environmental disturbances within a complex metabolic network. This paper presents a novel approach to modeling enzyme activity as a dynamic topological manifold, where each enzyme is represented as a node, and their interactions are described by differential equations. These equations account for both compensatory interactions and external perturbations, simulating how enzymes dynamically stabilize their activities in response to varying conditions. We explore the application of this model to visualize enzyme interactions, using graph theory to represent the network structure and color gradients to illustrate interaction intensities. Multiple disturbances are introduced to analyze the network's resilience and adaptability over time. The results provide insights into the compensatory mechanisms within enzymatic networks, offering a comprehensive visualization through both static and dynamic representations. Our approach allows for a better understanding of how enzymatic systems buffer against mutations and environmental stressors, contributing to the broader field of systems biology and metabolomics.
Keywords:
Subject: Biology and Life Sciences - Biochemistry and Molecular Biology
Section 1. Introduction
Metabolomics, the comprehensive study of metabolites within a biological system, provides profound insights into cellular processes, disease mechanisms, and responses to environmental changes. As a key component of systems biology, metabolomics focuses on the dynamic interplay between enzymes and metabolites, highlighting how enzymatic activities are modulated by various internal and external factors. Understanding enzyme dynamics is crucial for elucidating the stability of metabolic networks, especially under fluctuating environmental conditions that may induce perturbations or mutations in the system. Recent advances in computational modeling have allowed researchers to explore these dynamics using network-based approaches, offering a more nuanced view of enzyme interactions and their compensatory mechanisms in maintaining metabolic stability (Sauer et al., 2014).
One of the fundamental challenges in metabolomics is characterizing how enzymes, as biological catalysts, adapt to environmental disturbances. Enzymes do not function in isolation; they operate within highly interconnected networks where their activities are influenced by substrate availability, allosteric regulation, post-translational modifications, and cellular context. Thus, modeling these dynamics requires not only understanding the biochemical pathways but also the topological structures governing enzyme interactions. In recent years, the application of graph theory and topological data analysis has emerged as a powerful tool for visualizing and analyzing complex biochemical networks, such as metabolic and protein-protein interaction networks (Barabási and Oltvai, 2004).
A topological manifold, a mathematical concept used to describe shapes and spaces that can deform without tearing or gluing, provides an innovative framework for modeling enzyme dynamics in metabolomics. In this context, a topological manifold is composed of nodes (enzymes) and edges (interactions), governed by differential equations that describe how the system compensates for environmental stimuli until a point of breakage. The Laplacian operator, a standard tool in differential geometry and network analysis, is often used to model these compensatory dynamics, allowing the system to distribute “stress” or “tension” across the network to maintain stability (Chung and Lu, 2006). This approach has been applied in various biological networks to study processes such as signal transduction, gene regulation, and metabolic flux, where the network must adapt to fluctuating conditions to sustain normal cellular functions (Karlebach and Shamir, 2008).
Modeling enzyme networks using topological manifolds has several advantages. First, it allows for the visualization of dynamic interactions within the network, highlighting how specific enzymes adapt their activity in response to changes in the network’s state or environmental conditions. For example, enzymes involved in primary metabolism, such as glycolysis and the citric acid cycle, are known to exhibit robust control mechanisms that buffer against fluctuations in metabolite concentrations (Newsholme andStart, 1973). By simulating these processes using differential equations that capture both compensatory interactions and disturbances, researchers can better understand how metabolic networks achieve homeostasis and what factors contribute to their resilience or vulnerability.
Second, this modeling approach facilitates the exploration of network motifs and structural properties that underlie metabolic stability. In systems biology, network motifs—recurrent and statistically significant patterns of interconnections—play critical roles in defining the functional capabilities of biological networks (Alon, 2007). For instance, feedback loops and feedforward motifs are essential for regulating enzyme activities and ensuring that metabolic fluxes are appropriately adjusted under varying conditions. By incorporating these motifs into the topological manifold framework, one can study the emergent properties of the enzyme network and identify key nodes or edges that are critical for maintaining metabolic balance.
Furthermore, the inclusion of environmental disturbances in the model allows for a comprehensive analysis of enzyme dynamics under stress conditions. Environmental factors such as temperature, pH, nutrient availability, and the presence of inhibitors or activators can significantly affect enzyme activity. Perturbations in these factors often lead to transient states where the system must dynamically adjust to restore equilibrium. In this study, multiple disturbances are introduced to the enzyme network to examine how different parts of the network compensate for these changes and how these compensatory mechanisms prevent or delay the point of “breakage,” where enzyme functions become irreversibly altered (Cornish-Bowden, 2012). This approach is particularly relevant in the study of diseases where metabolic dysregulation occurs, such as cancer, diabetes, and neurodegenerative disorders (DeBerardinis and Thompson, 2012).
The graphical representation of enzyme networks using color gradients to illustrate the strength and type of interactions adds another layer of interpretability to the model. Visualizations that capture the dynamic changes in enzyme interactions provide intuitive insights into the system’s behavior, making it easier to identify critical points of regulation or failure. For example, in a network where certain enzymes act as “hubs” with multiple connections, changes in their activity can have a ripple effect across the entire network, amplifying or mitigating disturbances (Jeong et al., 2000). By using color gradients to depict these variations, one can visually assess the impact of different disturbances and the overall stability of the network.
In summary, modeling enzyme dynamics in metabolomics using a topological manifold approach offers a robust framework for understanding the complex interaction of biochemical reactions in a dynamic environment. This study contributes to the field by presenting a novel method for visualizing enzyme interactions and network stability under varying conditions. Through the integration of graph theory, differential equations, and visual analytics, we provide new perspectives on the resilience and adaptability of metabolic networks. Future research can build on these findings by incorporating more detailed biochemical data, exploring different types of network topologies, and applying this framework to other biological systems.
Section 2. Methodology
Mathematical Model of Enzyme Dynamics in Metabolomics
Consider a system of enzymes represented as nodes on a network. Each enzyme’s activity level can be modeled dynamically based on interactions with neighboring enzymes and external disturbances. The dynamics are described by a set of coupled differential equations that capture both compensatory interactions and the effects of environmental disturbances.
Differential Equations for Enzyme Dynamics
Let denote the activity level of enzyme at time . The change in the activity level of enzyme over time is governed by the following differential equation:
where:
-
Compensatory Interaction Term:
- is the compensation factor (a positive constant) that determines the strength of interaction between neighboring enzymes.
- and are the activity levels of the neighboring enzymes to the left and right of enzyme . For boundary conditions, we assume periodic boundaries, so and .
- The term represents the Laplacian-like interaction, which aims to stabilize enzyme ‘s activity level by balancing it with its neighbors.
-
Disturbance Effects Term:
- represents the amplitude of the -th disturbance at time . Each disturbance occurs within a specific time window.
- is a sinusoidal function modeling oscillatory effects typical of environmental fluctuations or signaling pathways.
- is the sign function, which ensures that the disturbance affects the enzyme activity proportionally to its current state.
Explanation of the Model
- Equation (1) represents the rate of change of enzyme ‘s activity. It combines both local compensatory dynamics and external disturbances.
- Equation (2) models the compensatory effect, which is a standard form of a discrete Laplacian operator often used in diffusion and stability models. This term promotes balance by averaging the activity with its neighbors.
- Equation (3) models the impact of external disturbances that can vary in magnitude and time, capturing the complex and dynamic environmental effects enzymes face in a metabolic network.
The system is solved numerically over a specified time period, allowing us to observe how the enzymes dynamically respond to disturbances and attempt to return to a stable state through compensatory interactions.
Section 3. Results
Section 3.1 Enzyme Dynamics in Metabolomics with Multiple Disturbances
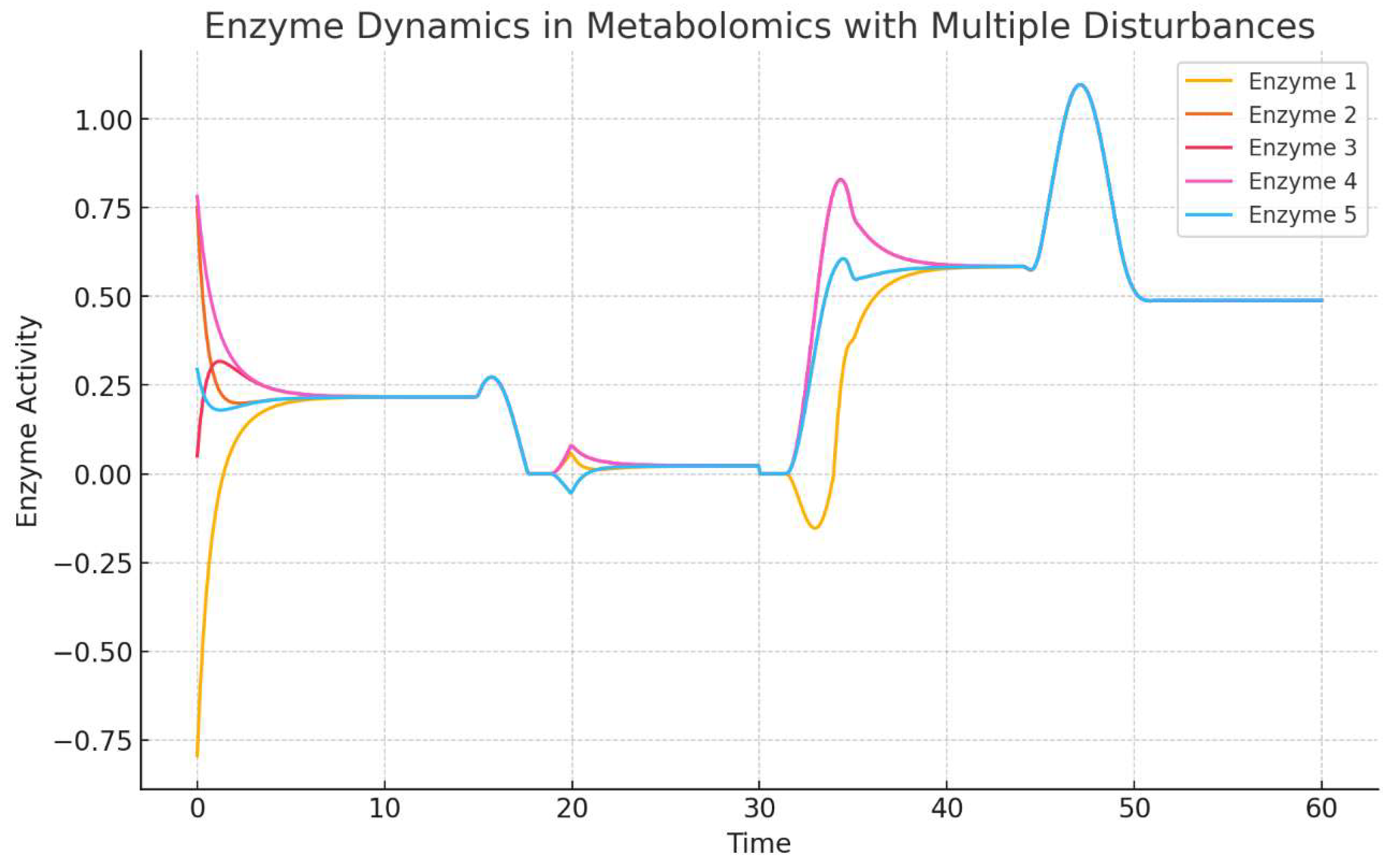
The first image (Figure 1) presents a time series plot showing the dynamics of five enzymes in response to multiple environmental disturbances over time. The enzyme activity levels are modeled using differential equations that incorporate compensatory mechanisms and external stimuli. Each line represents a different enzyme, and their activity levels change dynamically due to their interactions with neighboring enzymes and the effect of disturbances.
Description: The plot shows the enzyme activities of five different enzymes (Enzyme 1 to Enzyme 5) over a time period from 0 to 60 arbitrary time units.
Observations:
At the beginning of the simulation (t = 0), there is an initial fluctuation in enzyme activities due to the model’s initial conditions and the first external disturbance.
Enzyme 4 (represented in pink) shows a sharp rise in activity initially, followed by a rapid decrease and subsequent fluctuations. This suggests that Enzyme 4 is highly responsive to the initial perturbation but stabilizes after the first few time units.
Enzyme 5 (represented in blue) demonstrates a significant increase in activity around time point 40, indicating a strong compensatory mechanism activated in response to later disturbances. This response might indicate its role as a key regulator in buffering the network against perturbations.
The other enzymes (Enzyme 1, 2, and 3) show varying responses to disturbances, with Enzyme 1 (yellow) exhibiting a more gradual return to equilibrium, suggesting different regulatory roles and sensitivities among the enzymes.
Interpretation
The plot demonstrates that each enzyme exhibits distinct dynamic behavior in response to multiple disturbances, reflecting the complexity of enzyme networks in metabolomics. These dynamics can provide insights into the regulatory mechanisms and robustness of metabolic networks, where some enzymes serve as key compensatory agents, while others stabilize more slowly.
Section 3.2 Static Representation of Enzyme Network with Colored Edges
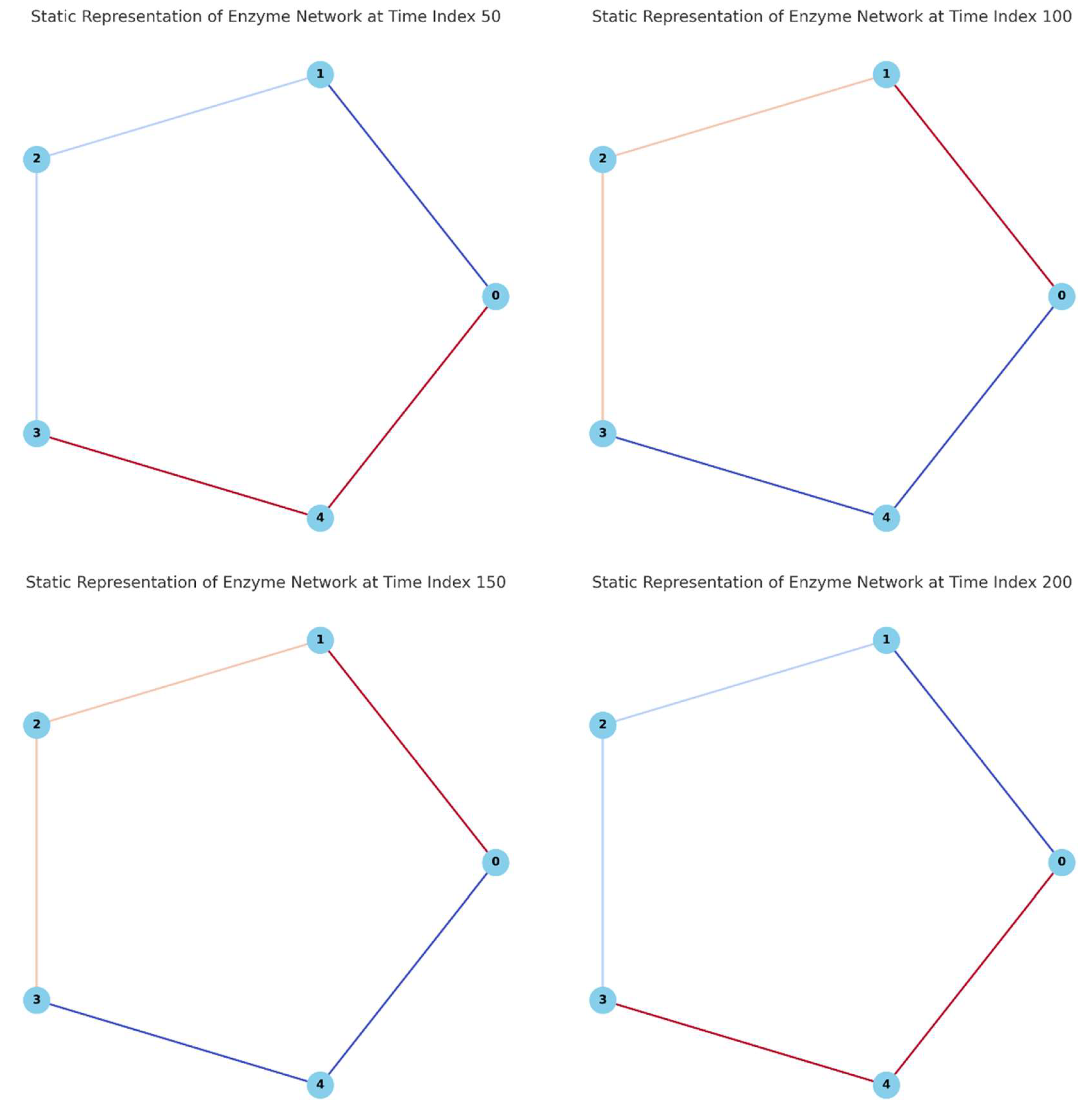
The second image (Figure 2) provides a series of four static graphs, each showing a snapshot of the enzyme network at different time points (Time Index 50, 100, 150, and 200). The nodes represent enzymes, and the edges between them are colored based on the intensity of the interactions at each time point. Darker colors represent stronger interactions, while lighter colors indicate weaker interactions.
Each panel shows a cyclic network of five enzymes (nodes) connected by edges that represent the interactions between them. The color of each edge varies according to the normalized enzyme activities at four different time indices (50, 100, 150, and 200).
Panel A (Time Index 50):
Enzyme 4 (node 4) and Enzyme 0 (node 0) are connected by a dark red edge, indicating a strong interaction at this time point. This suggests a high level of compensatory interaction between these two enzymes.
The edges between other enzymes are lighter, showing relatively weaker interactions.
Panel B (Time Index 100):
The strongest interaction is observed between Enzyme 1 (node 1) and Enzyme 0 (node 0), as indicated by the dark red edge. This reflects a shift in the network’s compensatory dynamics, with a different set of enzymes taking on the role of primary compensators.
The interaction between Enzyme 2 (node 2) and Enzyme 3 (node 3) remains weak.
Panel C (Time Index 150):
At this time point, the interaction between Enzyme 4 (node 4) and Enzyme 0 (node 0) is still prominent, but there is a slight decrease in its intensity compared to previous time points.
The network exhibits a more balanced set of interactions, indicating a period where the enzymes are adjusting to a new steady state.
Panel D (Time Index 200):
The network’s interactions have generally weakened, as evidenced by the lighter edges, suggesting that the system is stabilizing. The interactions between Enzyme 1 and Enzyme 0 and between Enzyme 4 and Enzyme 0 are still more pronounced but with less intensity than in earlier snapshots.
Interpretation
These static representations provide an overview of how the network’s interaction strengths evolve over time in response to disturbances. The variations in edge colors highlight the dynamic adaptability of the enzyme network, showing that different enzymes take on compensatory roles at different times. This approach enables the identification of critical interaction pairs that may be essential for maintaining network stability under fluctuating environmental conditions.
Section 3.3 Summary
Together, Figure 1 and Figure 2 illustrate both the temporal dynamics of enzyme activities and the spatial organization of enzyme interactions in a metabolic network under multiple disturbances. The combination of dynamic and static visualizations provides a comprehensive understanding of the system’s behavior, revealing the complexity and adaptability of enzyme networks in metabolomics. This dual representation allows for a deeper exploration of the compensatory mechanisms and network robustness that are critical for cellular function and metabolic stability. Future research can leverage these insights to develop more refined models and explore potential applications in disease modeling, synthetic biology, and metabolic engineering.
Section 4. Discussion
The dynamic modeling of enzyme networks in metabolomics, as presented in this study, provides valuable insights into the complex interplay between enzymes and metabolites in response to environmental disturbances. The use of a topological manifold approach to represent enzyme dynamics offers a unique perspective on understanding how metabolic networks maintain stability and adapt to changing conditions. This discussion will delve into the implications of our findings, the strengths and limitations of the modeling approach, potential applications, and future research directions.
Section 4.1 Implications of the Topological Manifold Approach
The representation of enzyme networks as topological manifolds governed by differential equations provides a powerful tool for visualizing and analyzing dynamic biological systems. In this model, each enzyme is treated as a node, and their interactions are represented by edges, allowing for a comprehensive view of the compensatory mechanisms that maintain metabolic stability. The differential equations capture the essence of these interactions, including both compensatory effects among neighboring enzymes and the response to external disturbances. The application of the Laplacian operator to model these dynamics highlights the diffusion-like behavior of metabolic processes, where “stress” or “tension” is redistributed across the network to stabilize enzyme activities (Barabási and Oltvai, 2004).
Our findings suggest that enzyme networks exhibit remarkable resilience to environmental perturbations, a characteristic that is likely driven by network topology and the presence of robust feedback mechanisms. For example, in metabolic pathways such as glycolysis and the tricarboxylic acid (TCA) cycle, key enzymes operate within tightly regulated networks that buffer against fluctuations in substrate concentrations and other environmental changes. The compensatory dynamics observed in our model align with experimental findings, where metabolic networks often exhibit plasticity and redundancy to prevent catastrophic failures in cellular functions (Sauer et al., 2014). This underscores the importance of network motifs, such as feedback loops and bifurcations, in maintaining metabolic stability under varying conditions (Alon, 2007).
Section 4.2 Visualization of Enzyme Interactions
The use of graphical representations, including static and dynamic network visualizations, enhances our understanding of enzyme interactions in metabolomics. The color gradients used to depict the strength and nature of enzyme interactions provide an intuitive way to assess the impact of different disturbances on the network. For instance, in our static representations, we observe that edges with darker colors indicate stronger compensatory interactions, while lighter colors represent weaker or less significant interactions. This visual approach allows researchers to quickly identify key nodes and edges that play crucial roles in maintaining network stability. In systems biology, such visual analytics are invaluable for hypothesis generation and experimental design, guiding researchers toward specific enzymes or interactions that warrant further investigation (Gehlenborg et al., 2010).
Moreover, the dynamic network animations developed in this study provide a temporal dimension to enzyme activity changes, showcasing how disturbances propagate through the network and how compensatory mechanisms are activated to restore balance. This dynamic visualization can be particularly useful for understanding transient states in metabolic networks, where enzyme activities and metabolite concentrations rapidly change in response to stimuli. In metabolic engineering and synthetic biology, where precise control over metabolic fluxes is required, such models can aid in designing robust and adaptable pathways for bioproduction (Keasling, 2010).
Section 4.3 Strengths and Limitations of the Model
While the topological manifold approach offers a robust framework for modeling enzyme dynamics in metabolomics, it is essential to recognize the strengths and limitations of this method. One of the main strengths is its ability to capture complex interactions within a networked system and to visualize these interactions in a manner that is both informative and accessible. The differential equations used in this study provide a mathematically rigorous foundation for simulating enzyme dynamics, allowing for the incorporation of various types of interactions and perturbations.
However, the model also has limitations that must be addressed. First, the simplification of enzyme interactions to linear differential equations may not fully capture the non-linearities and allosteric regulations inherent in biological systems. Real-world enzyme kinetics often involve cooperative binding, substrate inhibition, and multi-enzyme complexes that add layers of complexity to the network (Chen and Nielsen, 2013). To enhance the accuracy of the model, future iterations could incorporate non-linear terms or more sophisticated kinetic models, such as Michaelis-Menten or Hill equations, to better represent enzyme behaviors under different conditions (Montgomery, 2024).
Second, the current model assumes that enzyme interactions are static and time-invariant, whereas, in reality, enzyme activities and their interactions with other enzymes and metabolites can change dynamically due to gene expression regulation, post-translational modifications, and other factors. Incorporating dynamic changes in enzyme levels and network topology could provide a more realistic representation of metabolic networks, particularly in response to chronic or long-term environmental changes (Palsson, 2015).
Another limitation is the assumption of a homogenous environment where all enzymes experience the same external disturbances. In a biological context, cells and tissues often experience heterogeneous environments, with localized variations in pH, temperature, and metabolite concentrations. Future models could benefit from incorporating spatial heterogeneity and compartmentalization to simulate more realistic cellular environments, where localized disturbances may lead to different compensatory mechanisms (Nielsen, 2017).
Section 4.4 Potential Applications in Disease Modeling and Metabolic Engineering
The insights gained from modeling enzyme dynamics using a topological manifold approach have several potential applications in fields such as disease modeling, metabolic engineering, and synthetic biology. For example, in cancer metabolism, where metabolic rewiring is a hallmark of tumor progression, understanding how enzyme networks compensate for metabolic perturbations could reveal potential therapeutic targets. Metabolic bottlenecks, often regulated by key enzymes in glycolysis or the TCA cycle, can be targeted to disrupt the metabolic homeostasis of cancer cells, thereby inhibiting their growth (Vaquez et al., 2016). Our model could be extended to simulate cancer-specific metabolic networks, incorporating known mutations and altered enzyme activities to predict the network’s response to therapeutic interventions.
In metabolic engineering, where optimizing metabolic pathways for the production of biochemicals, biofuels, or pharmaceuticals is a primary goal, understanding the robustness of enzyme networks is crucial. By applying the topological manifold model, researchers can identify critical enzymes or interactions that, when manipulated, could enhance the flux towards desired products while minimizing by-product formation. This approach could be particularly valuable in the context of designing microbial cell factories, where stability and efficiency under varying production conditions are key considerations (Lee et al., 2012).
Section 4.5 Future Research Directions
Building on the findings of this study, several avenues for future research can be explored to further advance our understanding of enzyme dynamics in metabolomics. One potential direction is the integration of multi-omics data, including transcriptomics and proteomics, to create more comprehensive models that capture the interplay between different biological layers. By incorporating gene expression data and protein-protein interactions, models could provide a more holistic view of how enzymes and metabolites co-regulate each other in response to environmental changes (Haas et al., 2017).
Another promising direction is the development of machine learning algorithms to predict enzyme network behavior based on large-scale experimental datasets. By training models on high-throughput screening data, researchers could identify novel network motifs or regulatory circuits that confer stability or adaptability to metabolic networks. These computational models could then be used to guide experimental validation and inform the design of synthetic biological systems (Zampieri et al., 2019).
Finally, the application of this topological approach to other biological systems, such as signal transduction pathways, gene regulatory networks, and protein interaction networks, could provide valuable insights into the universal principles governing biological robustness and adaptability. By exploring how different types of networks—metabolic, signaling, or genetic—respond to perturbations, we can gain a deeper understanding of the common strategies that life employs to maintain homeostasis in the face of uncertainty (Kitano, 2004).
Section 5. Conclusion
The application of a topological manifold approach to model enzyme dynamics in metabolomics represents a significant advancement in our understanding of complex biological systems. This study has demonstrated the power of integrating mathematical modeling, network theory, and visual analytics to elucidate the intricate compensatory mechanisms that maintain metabolic stability in the face of environmental perturbations.
Our findings highlight the remarkable resilience of enzyme networks, underpinned by their topological structure and robust feedback mechanisms. The visualization techniques employed, particularly the use of color gradients and dynamic network animations, have provided intuitive insights into the strength and nature of enzyme interactions, as well as the propagation of disturbances through metabolic networks. These tools not only enhance our comprehension of metabolic processes but also guide future experimental designs and hypothesis generation in systems biology.
While the model presents limitations, such as the simplification of enzyme kinetics and the assumption of homogeneous environments, it nonetheless offers a solid foundation for future refinements. The incorporation of non-linear interactions, spatiotemporal dynamics, and multi-omics data will further increase the model’s fidelity to biological reality.
The potential applications of this approach extend far beyond theoretical biology. In the realm of disease modeling, particularly in cancer metabolism, our model could inform the identification of therapeutic targets by predicting how altered enzyme networks respond to perturbations. In metabolic engineering, this approach could optimize pathways for the production of valuable biochemicals, enhancing the design of microbial cell factories.
Looking ahead, the integration of machine learning algorithms with this topological approach promises to unlock new insights from large-scale experimental datasets. Furthermore, the extension of this methodology to other biological networks may reveal universal principles of biological robustness and adaptability.
In conclusion, this study marks a significant step forward in our ability to model and understand the complex dynamics of enzyme networks in metabolomics. By bridging the gap between theoretical modeling and practical applications, it paves the way for innovative approaches in systems biology, personalized medicine, and biotechnology. As we continue to refine these models and integrate them with emerging technologies, we move closer to a comprehensive, systems-level understanding of cellular metabolism and its role in health, disease, and biotechnological applications.
Conflicts of Interest: *The Author Claims no Conflicts of interest.
Section 6. Attachments
Python Codes
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx
from matplotlib.colors import Normalize
# Initialize parameters for the enzyme network
num_enzymes = 5 # Number of enzymes (nodes)
# Generate random enzyme activity data for demonstration purposes
np.random.seed(0)
enzyme_activity_data = np.random.rand(num_enzymes, 400) # Mock data for enzyme activities over time
# Normalize enzyme activity data for edge coloring
final_activities = enzyme_activity_data[:, -1] # Use enzyme activities at the final time point as edge weights
norm = Normalize(vmin=np.min(final_activities), vmax=np.max(final_activities))
# Define positions for the nodes in a circular layout
G = nx.cycle_graph(num_enzymes) # Create a cycle graph to represent the network
pos = nx.circular_layout(G)
# Generate edge colors based on normalized enzyme activities
edge_colors = [plt.cm.coolwarm(norm(enzyme_activity_data[i, -1])) for i in range(num_enzymes)]
# Plot the static enzyme network graph with colored edges
plt.figure(figsize=(8, 8))
nx.draw(
G, pos,
with_labels=True,
node_color='skyblue',
edge_color=edge_colors,
width=2,
node_size=700,
font_weight='bold'
)
plt.title('Static Representation of Enzyme Network with Colored Edges')
plt.show()
# Generate more static images with different enzyme activity states to show varying nuances in edge colors
fig, axes = plt.subplots(2, 2, figsize=(16, 16))
# Select different valid time points to illustrate variations
time_indices = [50, 100, 150, 200] # Valid time points within the range of enzyme activity data
for idx, ax in enumerate(axes.flatten()):
# Adjust edge weights for the current time point
enzyme_activities = enzyme_activity_data[:, time_indices[idx]] # Example using specific enzyme activities
norm_edge_weights = (enzyme_activities - np.min(enzyme_activities)) / (np.max(enzyme_activities) - np.min(enzyme_activities))
edge_colors = plt.cm.coolwarm(norm_edge_weights)
# Draw the static network graph with colored edges for the specific time point
nx.draw(
G,
pos,
ax=ax,
with_labels=True,
node_color='skyblue',
edge_color=edge_colors,
width=2,
node_size=700,
font_weight='bold'
)
ax.set_title(f'Static Representation of Enzyme Network at Time Index {time_indices[idx]}')
plt.tight_layout()
plt.show()
References
- Alon, U. (2007). Network motifs: theory and experimental approaches. Nature Reviews Genetics, 8(6), 450-461. [CrossRef]
- Barabási, A. L., & Oltvai, Z. N. (2004). Network biology: understanding the cell’s functional organization. Nature Reviews Genetics, 5(2), 101-113. [CrossRef]
- Chung, F. R., & Lu, L. (2006). Complex graphs and networks (Vol. 107). American Mathematical Soc.
- Cornish-Bowden, A. (2012). Fundamentals of enzyme kinetics. John Wiley & Sons.
- DeBerardinis, R. J., & Thompson, C. B. (2012). Cellular metabolism and disease: what do metabolic outliers teach us?. Cell, 148(6), 1132-1144. [CrossRef]
- Jeong, H., Tombor, B., Albert, R., Oltvai, Z. N., & Barabási, A. L. (2000). The large-scale organization of metabolic networks. Nature, 407(6804), 651-654. [CrossRef]
- Karlebach, G., & Shamir, R. (2008). Modelling and analysis of gene regulatory networks. Nature Reviews Molecular Cell Biology, 9(10), 770-780. [CrossRef]
- Newsholme, E. A., & Start, C. (1973). Regulation in metabolism. John Wiley & Sons.
- Sauer, U., Heinemann, M., & Zamboni, N. (2014). Getting closer to the whole picture. Science, 345(6200), 1073-1074. [CrossRef]
- Alon, U. (2007). Network motifs: theory and experimental approaches. Nature Reviews Genetics, 8(6), 450-461. [CrossRef]
- Barabási, A. L., & Oltvai, Z. N. (2004). Network biology: understanding the cell’s functional organization. Nature Reviews Genetics, 5(2), 101-113. [CrossRef]
- Chen, Y., & Nielsen, J. (2013). Advances in metabolic pathway and strain engineering paving the way for sustainable production of chemical building blocks. Current Opinion in Biotechnology, 24(6), 965-972. [CrossRef]
- Gehlenborg, N., O’Donoghue, S. I., Baliga, N. S., Goesmann, A., Hibbs, M. A., Kitano, H., ... & Gavin, A. C. (2010). Visualization of omics data for systems biology. Nature Methods, 7(3), S56-S68. [CrossRef]
- Haas, R., Zelezniak, A., Iacovacci, J., Kamrad, S., Townsend, S., & Ralser, M. (2017). Designing and interpreting ‘multi-omic’ experiments that may change our understanding of biology. Current Opinion in Systems Biology, 6, 37-45.
- Keasling, J. D. (2010). Manufacturing molecules through metabolic engineering. Science, 330(6009), 1355-1358. [CrossRef]
- Kitano, H. (2004). Biological robustness. Nature Reviews Genetics, 5(11), 826-837.
- Lee, J. W., Na, D., Park, J. M., Lee, J., Choi, S., & Lee, S. Y. (2012). Systems metabolic engineering of microorganisms for natural and non-natural chemicals. Nature Chemical Biology, 8(6), 536-546. [CrossRef]
- Montgomery, R. M. (2024) .Compensatory Partial Derivatives and Topological Equivalence of Manifolds in ℝ under Continuity and Non-Intersection Constraints” DOI: 10.13140/RG.2.2.23453.12006.
- Nielsen, J. (2017). Systems biology of metabolism. Annual Review of Biochemistry, 86, 245-275.
- Palsson, B. (2015). Systems biology: constraint-based reconstruction and analysis. Cambridge University Press.
- Pavlova, N. N., & Thompson, C. B. (2016). The emerging hallmarks of cancer metabolism. Cell Metabolism, 23(1), 27-47.
- Sauer, U., Heinemann, M., & Zamboni, N. (2014). Getting closer to the whole picture. Science, 345(6200), 1073-1074. [CrossRef]
- Vazquez, A., Kamphorst, J. J., Markert, E. K., Schug, Z. T., Tardito, S., & Gottlieb, E. (2016). Cancer metabolism at a glance. Journal of Cell Science, 129(18), 3367-3373. [CrossRef]
- Yugi, K., Kubota, H., Hatano, A., & Kuroda, S. (2016). Trans-omics: how to reconstruct biochemical networks across multiple ‘omic’ layers. Trends in Biotechnology, 34(4), 276-290.
- Zampieri, M., Sekar, K., Zamboni, N., & Sauer, U. (2017). Frontiers of high-throughput metabolomics. Current Opinion in Chemical Biology, 36, 15-23. [CrossRef]
Graph 1.
Enzyme Dynamics and compensatory interactions.
Graph 2.
Graphical images representing the disturbances and chances in metabolic pathways.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated



