On the Calibration of the Kennedy Model

Preprint

Article

On the Calibration of the Kennedy Model

Altmetrics

Downloads

Views

Comments

This version is not peer-reviewed

Submitted:

03 September 2024

Posted:

05 September 2024

You are already at the latest version

Alerts

Abstract

The Kennedy model offers a robust framework for modeling forward rates, leveraging Gaussian random fields to accommodate emerging phenomena such as negative rates. In our study, we employ maximum likelihood estimations to determine the parameters of the Kennedy field, utilizing Radon-Nikodym derivatives for enhanced accuracy. We introduce an efficient simulation method for the Kennedy field and develop a Black-Scholes-like analytical pricing formula for diverse financial assets. Additionally, we present a novel parameter estimation algorithm grounded in numerical extreme value optimization, enabling the recalibration of parameters based on observed financial product prices. To validate the efficacy of our approach, we assess its performance using real-world par swap rates in the latter part of this article.

Keywords:

Subject: Computer Science and Mathematics - Probability and Statistics

1. Introduction

In the 2010s, a new phenomenon, the negative rates, appeared in the financial markets, which brought extreme uncertainty to the world, resulting in the mathematical models used to describe the dynamics of the interest rates being reconsidered. The model, defined by Kennedy in the 1990s, describes the dynamics of the forward rates with Gaussian random fields [1,2]. This approach contains several advantages; for example, it offers a solution to handle the negative rates naturally and can be connected to the industry standard Heath-Jarrow-Morton (HJM) framework [3]. Additionally, maximum likelihood estimations of the parameters and analytical Black-Scholes-like pricing formulas for different financial assets can be derived due to the standard distribution properties of the Gaussian random fields.

This article summarizes the most critical issues related to using the Kennedy model in the financial world. In Section 2, we present the term structure model for describing forward interest rates based on Gaussian random fields proposed by Kennedy. Among other things, we present the condition for the martingale property of the discounted bond price and show in which cases coincide with the Gaussian Heath-Jarrow-Morton framework. Section 3 introduces the theoretical background of the parameter estimations. The results of the Radon-Nikodym derivative of Gaussian measures with different means are shown. This section derives the maximum likelihood and probability one estimation for the parameters in the Kennedy field. Section 4 shows a practical, simple, and fast way to simulate the Kennedy field with the help of the Brownian sheet. The following section (5) contains the analytical, fair price of various financial products (caplet, floorlet, and swap). Section 6 summarizes the calibration method for different financial products, in our case, the optimization algorithm, which is based on numerical extreme value search to estimate the parameters of the field. Finally, the previously presented calibration algorithm on real swap par rate data can be found in Section 7.

2. Kennedy Model

The development of the forward rates in the model proposed by Kennedy is described in the upcoming equation.

F (s, t) = α (s, t) + X (s, t)

(1)

where

X (s, t)

is a centered Gaussian random field with the covariance structure specified by

c o v [X (s_{1}, t_{1}), X (s_{2}, t_{2})] = c (s_{1} \land s_{2}, t_{1}, t_{2}), 0 \leq s_{i} \leq t_{i}, i = 1, 2 .

(2)

The function c is given and satisfies

c (0, t_{1}, t_{2}) = 0

. Assume that the drift function

α (s, t)

is deterministic and continuous in

0 \leq s \leq t

and that the initial term structure of

α (0, t), (t \geq 0)

is specified, also

E F (0, t) = α (0, t), (t \geq 0)

. The covariance function

c (s_{1} \land s_{2}, t_{1}, t_{2})

is symmetric in

t_{1}

and

t_{2}

, and is nonnegative definite in

(s_{1}, t_{1})

and

(s_{2}, t_{2})

. The dependency of the

s_{1} \land s_{2}

ensures that the Gaussian random field

X (s, t)

has independent increments.

A sufficient condition on the drift surface is derived to ensure that the discounted bond prices of zero-coupon bonds are martingales. Therefore, the model can be used to price financial products in the future.

First, let us introduce the following notations, where

0 \leq s \leq t

\begin{matrix} R (t) & = F (t, t) \end{matrix}

(3)

\begin{matrix} F^{Δ} (s, t) & = \frac{1}{Δ} \int_{t}^{t + Δ} F (s, u) d u \end{matrix}

(4)

\begin{matrix} P (s, t) & = e^{- \int_{s}^{t} F (s, u) d u} \end{matrix}

(5)

\begin{matrix} Z (s, t) & = e^{- \int_{0}^{s} R (u) d u} P (s, t) \end{matrix}

(6)

\begin{matrix} F (s) & = σ {F (u, v), 0 \leq u \leq s, u \leq v} \end{matrix}

(7)

where

R (t)

denotes the spot rate at time t,

P (s, t)

represents the price at time s of a bond paying one unit at time t.

Z (s, t)

defines the discounted price of the previously defined bond at time 0, while the information available at time s is that contained in the

F (s)

σ

-algebra, thereby implying that the whole yield curve is observed at each time point. We also introduce a new notation,

F^{Δ} (s, t)

, to the continuously compounded forward rate for the period

[t, t + Δ], (Δ > 0

), which can be interpreted as an average of the forward rate for the current period, at time s.

An important theorem is emphasized in Kennedy’s article, which states the following [2].

Theorem 1

(Kennedy (1997)). In the independent-increments case the following statements are equivalent:

(a): For each $t \geq 0$ , the discounted bond-price process ${Z (s, t), F (s), (0 \leq s \leq t)}$ is a martingale;
(b): $P (s, t) = E [e^{- \int_{s}^{t} R (u) d u} | F (s)]$ , for all $(s, t),$ $(0 \leq s \leq t)$ ; and
(c): $α (s, t) = α (0, t) + \int_{0}^{t} [c (s \land v, v, t) - c (0, v, t)] d v$ for all $(s, t)$ , $(0 \leq s \leq t)$ .

The proof of the theorem is accessible in the original article written by Kennedy [1]. Furthermore, a different derivation of the theorem can be found in the appendices appendices A.1. To complete the proof, it was necessary to include an additional statement, which formulates an equivalent form of defining the drift term with the covariance function.

Remark 1.

The two statements for the drift term in the Kennedy model are equivalent. For all

0 \leq s \leq t

\begin{matrix} α (s, t) & = α (t, t) + \int_{s}^{t} [c (s, v, t) - c (v, v, t)] d v \end{matrix}

(8)

\begin{matrix} \Leftrightarrow \end{matrix}

(9)

\begin{matrix} α (s, t) & = α (0, t) + \int_{0}^{t} [c (s \land v, v, t) - c (0, v, t)] d v . \end{matrix}

(10)

Proof of Remark 1.

The proof is given by showing that both directions are correct.

\begin{matrix} \Rightarrow & α (s, t) - α (0, t) = α (t, t) + \int_{s}^{t} [c (s, v, t) - c (v, v, t)] d v - α (t, t) - \int_{0}^{t} [c (0, v, t) - c (v, v, t)] d v = \end{matrix}

(11)

\begin{matrix} = \int_{s}^{t} [c (s, v, t) - c (0, v, t)] d v + \int_{0}^{s} [c (v, v, t) - c (0, v, t)] d v = \int_{0}^{t} [c (s \land v, v, t) - c (0, v, t)] d v \end{matrix}

(12)

\begin{matrix} \Leftarrow & α (s, t) - α (t, t) = α (0, t) + \int_{0}^{t} [c (s \land v, v, t) - c (0, v, t)] d v - α (0, t) - \int_{0}^{t} [c (t \land v, v, t) - c (0, v, t)] d v = \end{matrix}

(13)

\begin{matrix} = \int_{0}^{t} [c (s \land v, v, t) - c (v, v, t)] d v = \int_{s}^{t} [c (s, v, t) - c (v, v, t)] d v \end{matrix}

(14)

□

2.1. Connection between HJM and the Kennedy-Model

The Heath-Jarrow-Morton framework is a widely used model considered an industry standard [3]. This is also a term structure model, which creates a connection between bonds with different maturities. The HJM model is an infinite-dimensional framework. Therefore, the whole yield curve evolves in forward time instead of at a specific point.

Kennedy has stated in his article that the Kennedy model includes the Heath-Jarrow-Morton framework in the case when the coefficients,

α (s, t)

and

σ_{i} (s, t)

, in the underlying stochastic differential equations are not random and so the rates

F (s, t)

are Gaussian [2]. Therefore, in this section, we will show precisely in which cases the two models can correspond to each other.

The notations of the HJM model are written consistently with those found in the book by Shreve [6]. We first examine the case when a single Wiener process drives the forward interest rates; then, the dynamics can be written as follows:

F (s, t) = F (0, t) + \int_{0}^{s} β (u, t) d u + \int_{0}^{s} σ (u, t) d W (u)

(15)

where

F (0, t)

refers to the initial forward year curve known at time 0,

W (u)

is a Wiener process under the actual measure, and

α (s, t)

and

σ (s, t)

are deterministic processes in the variable s. Let us denote

{ξ (t)}_{t \geq 0} = {F (0, t)}_{t \geq 0}

which is independent from process

{W (t)}_{t \geq 0}

and is a Gaussian process.

The expected value and the covariance function of the Heath-Jarrow-Morton framework and the key Kennedy field conditions can be written in the following form.

The expected value function from the Heath-Jarrow-Morton model can be calculated in the following way.

$α (s, t) = E F (s, t) = E ξ (t) + \int_{0}^{s} β (u, t) d u = m (t) + \int_{0}^{s} β (u, t) d u$

(16)
Similarly to the previously calculated expected value function, the covariance function is calculated as follows. Let us denote the covariance function between $ξ (t_{1}), ξ (t_{2})$ with

$c o v (ξ (t_{1}), ξ (t_{2})) = r (t_{1}, t_{2})$

$c (s_{1}, s_{2}, t_{1}, t_{2}) = c o v (F (s_{1}, t_{1}), F (s_{2}, t_{2})) = c o v (ξ (t_{1}), ξ (t_{2})) + \int_{0}^{min (s_{1}, s_{2})} σ (u, t_{1}) σ (u, t_{2}) d u$

(17)

The covariance function is specified as a function of $s_{1} \land s_{1}$ . This ensures that the Gaussian random field $X (s, t)$ has independent increments in time s, which is also fulfilled due to point 2 in the HJM framework. This confirms that all Gaussian HJM models (where the drift and the volatility terms are deterministic) are the well-known Kennedy model.
By adding the martingale property in the Kennedy model (like in point (c) in theorem 1), which guarantees that the conditional expected value of the discounted bond-price process is a martingale under the risk-neutral measure. As a result, the model is arbitrage-free. Then, by matching the equations of the expected values to each other, we get the famous condition of the HJM model, according to which the drift term can be obtained in the form below.

$\begin{matrix} α (0, t) + \int_{0}^{s} β (u, t) d u & = α (0, t) + \int_{0}^{t} [c (s \land v, v, t) - c (0, v, t)] d v \end{matrix}$

(18)

$\begin{matrix} α (0, t) + \int_{0}^{s} β (u, t) d u & = α (0, t) + \int_{0}^{t} [r (v, t) + \int_{0}^{m i n (s, v)} σ (u, v) σ (u, t) d u - r (v, t)] d v \end{matrix}$

(19)

$\begin{matrix} \int_{0}^{s} β (u, t) d u & = \int_{0}^{t} \int_{0}^{m i n (s, v)} σ (u, v) σ (u, t) d u d v \end{matrix}$

(20)

$\begin{matrix} β (s, t) & = σ (s, t) \int_{s}^{t} σ (s, v) d v \end{matrix}$

(21)

where the last equation satisfies the famous HJM condition.
By adding the Markov property to the previous conditions, where the discounted bond price process is martingale, we get an even narrower class of models.
Definition 1
(first Markov property). The random field of instantaneous forward rates ${F (s, t) : 0 \leq s \leq t}$ satisfies the first Markov property if for all $0 \leq s_{1} \leq s_{2} < s_{3}$ , $s_{1} \leq t_{1}$ , $s_{3} \leq t_{2}$ we have $F (s_{1}, t_{1}) ⊥ F (s_{3}, t_{2}) | F (s_{2}, t_{2})$ .

Definition 2
(second Markov property). The random field of instantaneous forward rates ${F (s, t) : 0 \leq s \leq t}$ satisfies the second Markov property if for all $0 \leq s_{1} < s_{2}$ , $t_{1}$ , $t_{2}$ with $s_{2} \leq t_{1} \land t_{2}$ we have $F (s_{1}, t_{1}) ⊥ F (s_{2}, t_{2}) | F (s_{2}, t_{1})$ .

Definition 3
(Markov property). The random field of instantaneous forward rates is ${F (s, t) : 0 \leq s \leq t}$ Markov if it satisfies both the first and second Markov properties.

Definition 4
(Markov in t-direction). The random field of instantaneous forward rates ${F (s, t) : 0 \leq s \leq t}$ is Markov in the t-direction , that is, in the maturity-time coordinate, if for all $s \leq t_{1} \leq t_{2} \leq t_{3}$ then $F (s, t_{1}) ⊥ F (s, t_{3}) | F (s, t_{2})$

Definition 5
(strict Markov property). The random field of instantaneous forward rates ${F (s, t) : 0 \leq s \leq t}$ strictly Markov if it is both Markov and Markov in the t-direction.

Kennedy stated (in theorem 3.1 in [2]) that if a random field of forward rates is Markov and satisfies the independent-increments property, then the covariance function can be written in the following form.

$c (s, t_{1}, t_{2}) = f (s) g (t_{1}, t_{2}),$

(22)

where f is a monotone increasing and g is a symmetric and positive semidefinit function. This property can be written as follows for the HJM model.

$r (t_{1}, t_{2}) + \int_{0}^{s} σ (u, t_{1}) σ (u, t_{2}) d u = f (s) g (t_{1}, t_{2})$

(23)

Then by deriving (23) according to the variable s we get

$σ (s, t_{1}) σ (s, t_{2}) = f^{'} (s) g (t_{1}, t_{2})$

(24)

By setting $t_{1}$ and $t_{2}$ equal to each other $(t_{1} = t_{2} = t)$ , we obtain the following equality

$σ^{2} (s, t) = f^{'} (s) g (t, t)$

(25)

Consequently

$σ (s, t) = b (s) g (t),$

(26)

where $b (s) = \sqrt{f^{'} (s)}$ and $g (t) = \sqrt{g (t, t)}$ . Therefore, it is shown that if the HJM model is Markovian, then the $σ (s, t)$ function appears in the form of Equation (26). We thus obtained that in the Markovian case, the volatility function must be separable in the time parameters. Hence

$σ (s, t_{1}) σ (s, t_{2}) = b^{2} (s) g (t_{1}) g (t_{2})$

(27)

For $s = 0$ Equation (23) can be written in the following form

$r (t_{1}, t_{2}) = f (0) \cdot g (t_{1}, t_{2}) .$

(28)

From Equation (23), (28) and (39) it can be stated that

$\begin{matrix} r (t_{1}, t_{2}) & = f (s) g (t_{1}, t_{2}) - g (t_{1}) g (t_{2}) \int_{0}^{s} b^{2} (u) d u \end{matrix}$

(29)

$\begin{matrix} f (0) g (t_{1}, t_{2}) & = f (s) g (t_{1}, t_{2}) - g (t_{1}) g (t_{2}) \int_{0}^{s} b^{2} (u) d u \end{matrix}$

(30)

$\begin{matrix} g (t_{1}, t_{2}) & = g (t_{1}) g (t_{2}) \int_{0}^{s} f^{'} (u) d u \end{matrix}$

(31)

If the function $f (s)$ is constant, then we get the trivial case when $σ (s, t) = 0$ for all $(s, t)$ . In the non-trivial case, we get from Equation (31) that $f (s)$ is not constant. Therefore, we got

$\begin{matrix} r (t_{1}, t_{2}) & = c g (t_{1}) g (t_{2}) \end{matrix}$

(32)

Hence, we showed that if the HJM model is Markovian, then functions $σ$ and r occur in the previously derived form. Now, we show the opposite direction: if our covariance function has this shape, then the HJM model will be Markovian.

$\begin{matrix} c (s, t_{1}, t_{2}) & = c g (t_{1}) g (t_{2}) + g (t_{1}) g (t_{2}) \int_{0}^{s} b^{2} (u) d u = \end{matrix}$

(33)

$\begin{matrix} = \underset{g (t_{1}, t_{2})}{\underset{︸}{g (t_{1}) g (t_{2})}} \underset{f (s)}{\underset{︸}{(c + \int_{0}^{s} b^{2} (u) d u)}} = \end{matrix}$

(34)

$\begin{matrix} = f (s) g (t_{1}, t_{2}) \end{matrix}$

(35)

which is exactly the necessary condition (22).

In 1992, Cheyette published an article in which a restriction was applied to the Heath-Jarrow-Morton model, which forms a subset of the original HJM models to make the model Markovian. This so-called Cheyette model is an arbitrage-free term structure model, which is Markovian in a finite number of state variables and consistent with an arbitrary initial term structure. Due to these favorable properties, the Cheyette model quickly spread throughout the industry and became widely used [7].

In this case, the volatility function has to be separable into time and maturity-dependent factors given by the following structure [8].

$σ (s, t) = α (t) \frac{β (s)}{α (s)}$

(36)

However, this condition is completely identical to the previously derived condition for the volatility term in the Markov case in the Kennedy model.
Kennedy further narrowed the model class by requiring stationarity in addition to the Markov property and the independent increments property (stated in theorem 3.2 in [2]).
Definition 6
(stationary). The random field is stationary if for each $t > 0$ the joint distributions of ${F (s, t) : 0 \leq s \leq t}$ are the same as those of ${F (s + u, t + u) : 0 \leq s \leq t}$ for any fixed $u > 0$ .

Therefore, the covariance function takes the form below.:

$c (s, t_{1}, t_{2}) = e^{λ (s - (t_{1} \land t_{2}))} \cdot h (| t_{1} - t_{2} |)$

(37)

where $λ \geq 0,$ $| H (x) | \leq h (0) e^{- λ \frac{x}{2}}$ and $x \geq 0$ .

For the HJM framework, it was shown that $r (t_{1}, t_{2}) = 0$ , hence according to point 5.

$\begin{matrix} c (s, t_{1}, t_{2}) & = f (s) g (t_{1}, t_{2}) = g (t_{1}) g (t_{2}) (c + \int_{0}^{s} b^{2} (u) d u) = \end{matrix}$

(38)

$\begin{matrix} = e^{λ (s - (t_{1} \land t_{2}))} \cdot h (| t_{1} - t_{2} |) \end{matrix}$

(39)

For $s = 0$ and $t_{1} = t_{2} = t$ it can be written

$\begin{matrix} c g^{2} (t) & = e^{- λ t} h (0) \end{matrix}$

(40)

$\begin{matrix} g (t) & = \sqrt{\frac{h (0)}{c}} \cdot e^{\frac{- λ t}{2}} \end{matrix}$

(41)

Returning back to Equation (38)

$\begin{matrix} c + \int_{0}^{s} b^{2} (u) d u & = \frac{1}{g (t_{1}) g (t_{2})} e^{λ (s - (t_{1} \land t_{2}))} \cdot h (| t_{1} - t_{2} |) \end{matrix}$

(42)

$\begin{matrix} c + \int_{0}^{s} b^{2} (u) d u & = \frac{c}{h (0)} e^{\frac{λ t_{1}}{2}} e^{\frac{λ t_{2}}{2}} e^{λ (s - (t_{1} \land t_{2}))} \cdot h (| t_{1} - t_{2} |) \end{matrix}$

(43)

Now substituting $s = 0$

$\begin{matrix} c \cdot h (0) & = c exp \{\frac{λ}{2} (t_{1} + t_{2}) - λ (t_{1} \land t_{2})\} h (| t_{1} - t_{2} |) \end{matrix}$

(44)

$\begin{matrix} h (0) & = c exp \{\frac{λ}{2} | t_{1} - t_{2} |\} h (| t_{1} - t_{2} |) \end{matrix}$

(45)

$\begin{matrix} h (u) & = h (0) exp \{\frac{- λ}{2} u\} \end{matrix}$

(46)

Returning again to Equation (39) while substituting Equation (41)

$\begin{matrix} \frac{h (0)}{c} exp \{\frac{- λ}{2} (t_{1} + t_{2})\} (c + \int_{0}^{s} b^{2} (u) d u) & = e^{λ (s - (t_{1} \land t_{2}))} \cdot h (| t_{1} - t_{2} |) \end{matrix}$

(47)

$\begin{matrix} = e^{λ (s - (t_{1} \land t_{2}))} \cdot h (0) exp \{\frac{- λ}{2} | t_{1} - t_{2} |\} \end{matrix}$

(48)

$\begin{matrix} \frac{1}{c} (c + \int_{0}^{s} b^{2} (u) d u) & = e^{λ s} \end{matrix}$

(49)

$\begin{matrix} \int_{0}^{s} b^{2} (u) d u & = c e^{λ s} - c \end{matrix}$

(50)

By deriving the integral equation according to the variable s, we get the following solution

$b^{2} (u) = c λ e^{λ u}$

(51)

Therefore, the covariance function of the forward rates ${F (s, t) : 0 \leq s \leq t}$ , when the rates are stationary, strictly Markov, and satisfy the independent-increments property, can be described with the following set of four parameters ${σ, λ \geq 0, μ \geq \frac{λ}{2}, ν}$ and is of the form

$c o v [F (s_{1}, t_{1}), F (s_{2}, t_{2})] = σ^{2} e^{λ min (s_{1}, s_{2}) + (2 μ - λ) min (t_{1}, t_{2}) - μ (t_{1} + t_{2})}$

(52)

The function of the expected value of the Gaussian random field can be easily derived from the covariance function.

$\begin{matrix} α (s, t) & = ν - σ^{2} (\frac{1}{μ} - e^{- μ (t - s)} (\frac{1}{μ} + \frac{1}{λ - μ}) + e^{- λ (t - s)} \frac{1}{λ - μ}) \end{matrix}$

(53)

3. Parameter Estimation

In finance, where uncertainty reigns supreme and decisions are often made under incomplete information, accurate modeling of interest rate dynamics is paramount. This is where parameter estimation comes into play as a fundamental aspect of financial modeling, particularly in the context of Kennedy-type term structure models. While calibration is a widely adopted practice in finance, parameter estimation also holds significant importance.

The central assumption of these models is that interest rates follow stochastic processes, the parameters of which govern their behavior over time. These parameters determine the shape of the yield curve and influence the pricing of various financial instruments, such as bonds, options, and derivatives. Therefore, obtaining reliable estimates of these parameters is essential for making informed investment decisions, managing risk, and pricing financial products accurately.

Parameter estimation techniques enable practitioners to calibrate these models to observed market data, such as bond prices or interest rate derivatives. Among the most commonly used methods are maximum likelihood estimation (MLE), estimation with probability 1 and Radon-Nikodym derivatives, which allow for determining parameter values that maximize the likelihood of observing the given market data under the model assumptions. Through rigorous statistical inference, these techniques provide a systematic framework for extracting information from observed market prices and estimating the underlying dynamics of interest rates.

3.1. Maximum Likelihood Estimations

In this section, the theoretical background of the maximum likelihood estimations, in the case of Gaussian functionals, is presented based on the work of Rozanov and Arató [4,5].

Definition 7

(Gaussian functional). Let

(Ω, A, P)

be a probability space, and T is a parameter set. Then

ξ : Ω \times T \to R

is a Gaussian functional, if for any

n \in N

and

c_{1}, \dots, c_{n} \in R

t_{1}, \dots, t_{n} \in T,

\sum_{i = 1}^{n} c_{i} ξ_{t_{i}}

(54)

is normally distributed. Then P is called a Gaussian measure in

(Ω, F_{ξ})

. For simplicity, we can assume that

A = F_{ξ} .

The expected value and the standard deviation of the Gaussian functional are marked as follows

m (t) = E ξ (t), B (s, t) = c o v [ξ (s), ξ (t)]

(55)

It is well known that two Gaussian measures are either equivalent or orthogonal.

3.1.1. The Case of Different Expected Values

Let

ξ : Ω \times T \to R

be a Gaussian functional. Let the expected value of the Gaussian functional under the measure P be 0 and the expected value under the measure

P_{1}

be m.

E_{P} ξ (t) = 0, E_{P_{1}} ξ (t) = m (t), t \in T

(56)

Let U denote the linear space of the variables of the following shape

\sum_{i = 1}^{n} c_{i} ξ_{t_{i}}, n \in N, c_{1}, \dots, c_{n} \in R, t_{1}, \dots, t_{n} \in T .

(57)

Also, take the following scalar product

< u, v > = \int_{Ω} u v d P .

(58)

Finally,

\bar{U}

denotes the Hilbert space obtained by closing U.

Rozanov showed that for different expected values, the Radon-Nikodym derivative can be calculated as follows [5].

Theorem 2

(Rozanov). The P and

P_{1}

measures are equivalent if and only if there exists an

η \in \bar{U}

for which

m (t) = \int_{ω} ξ (t) η (t) d P, t \in T .

(59)

In the case of equivalence, the Radon-Nikodym derivative of the two measures are

\frac{d P_{1}}{d P} = e^{η - \frac{< η, η >}{2}}

(60)

A simple consequence of this theorem is the following statement by Arató. [4]

Theorem 3

(Arató). Let

ξ : Ω \times T \to R

be a Gaussian functional. Let the expected value of the Gaussian functional under the measure P be 0, and the expected value under the measure

P_{1}

m \cdot a (t)

. The P and

P_{1}

measures are equivalent if and only if there exists an

η \in \bar{U}

for which

a (t) = \int_{ω} ξ (t) η (t) d P, t \in T .

(61)

In the case of equivalence, the Radon-Nikodym derivative of the two measures are

\frac{d P_{1}}{d P} = e^{m η - \frac{m^{2} < η, η >}{2}}

(62)

Theorem 4

(Maximum likelihood estimation). Let

ξ (t)

be a Gaussian functional. Then, using the notations of the previous statement, the maximum likelihood estimation of m is the following

\hat{m} = \frac{η}{< η, η >} .

(63)

The estimation is normally distributed and unbiased, and the standard deviation is

D_{P_{1}}^{2} \hat{m} = \frac{1}{< η, η >}

(64)

Proof of Theorem 4.

The shape of the estimation is derived immediately from the Radon-Nikodym derivative. To determine the expected value and standard deviation, calculate the next expected value if

X \sim N (0, σ^{2})

E (X^{k} e^{m X}) = \int_{- \infty}^{\infty} x^{k} e^{m x} \frac{1}{\sqrt{2 π} σ} e^{- \frac{x^{2}}{2 σ^{2}}} d x = e^{\frac{m^{2} σ^{2}}{2}} \int_{- \infty}^{\infty} x^{k} \frac{1}{\sqrt{2 π} σ} e^{- \frac{{(x - m σ^{2})}^{2}}{2 σ^{2}}} d x

(65)

Calculating the first two moments, we get the following values

if $k = 1$ , then → $E (X e^{m X}) = m σ^{2} e^{\frac{m^{2} σ^{2}}{2}}$
if $k = 2$ , then → $E (X^{2} e^{m X}) = (σ^{2} + m^{2} σ^{4}) e^{\frac{m^{2} σ^{2}}{2}}$

For the expected value, we obtain the following

\begin{matrix} E_{P_{m}} \hat{m} & = \frac{1}{< η, η >} \int_{Ω} η d P_{m} = \frac{1}{< η, η >} \int_{Ω} η e^{m η - \frac{m^{2} < η, η >}{2}} d P = \end{matrix}

(66)

\begin{matrix} = \frac{1}{< η, η >} e^{- \frac{m^{2} < η, η >}{2}} m < η, η > e^{\frac{m^{2} < η, η >}{2}} = m \end{matrix}

(67)

Similarly to the first moment, we can derive the second moment.

\begin{matrix} E_{P_{m}} {\hat{m}}^{2} & = \frac{1}{< η, η >^{2}} \int_{Ω} η^{2} d P_{m} = \frac{1}{< η, η >^{2}} \int_{Ω} η^{2} e^{m η - \frac{m^{2} < η, η >}{2}} d P = \end{matrix}

(68)

\begin{matrix} = \frac{1}{< η, η >^{2}} e^{- \frac{m^{2} < η, η >}{2}} (< η, η > + m^{2} < η, η >^{2}) e^{\frac{m^{2} < η, η >}{2}} = \frac{1}{< η, η >} + m^{2} . \end{matrix}

(69)

The standard deviation can be deduced immediately from these derivations. Since these are Gaussian functionals, normality is evident. □

3.1.2. The Case of Constant Expected Value

If the expected value of our Gaussian process is constant, then

a (t) = 1

for every

t \in T

. Let

F = σ {(ξ (t) - ξ (s)

s, t \in T}

. Let us fix a

t_{0} \in T

point and let

h (ξ) = E_{P} [ξ (t_{0}) ∣ F)] .

Let us assume that

D^{2} [ξ (t_{0}) - h (ξ)] > 0

. Then the maximum likelihood estimation of m is

\tilde{m} = ξ (t_{0}) - h (ξ) .

(70)

Proof.

The proof uses the law of total expectation and the

E_{p} (\tilde{m} (ξ (t_{0}) - h (ξ))) = D_{P}^{2} (\tilde{m})

statement.

\begin{matrix} E_{P} (\tilde{m} ξ (t)) & = E_{P} (\tilde{m} (ξ (t) - ξ (t_{0}) + ξ (t_{0}) - h (ξ) + h (ξ))) = \end{matrix}

(71)

\begin{matrix} = E_{P} (\tilde{m} (ξ (t) - ξ (t_{0}) + h (ξ))) + D_{P}^{2} (\tilde{m}) = \end{matrix}

(72)

\begin{matrix} = E_{P} (E_{P} ((\tilde{m} (ξ (t) - ξ (t_{0}) + h (ξ)) ∣ F)) + D_{P}^{2} (\tilde{m}) = D_{P}^{2} (\tilde{m}) \end{matrix}

(73)

Based on the previous derivations, the maximum likelihood estimation is the following

\hat{m} = \frac{\tilde{m} / D_{P}^{2} (\tilde{m})}{D_{P}^{2} (\tilde{m} / D_{P}^{2} (\tilde{m}))}

(74)

□

3.1.3. Some Simple Examples

The well-known results of various stochastic processes often used to model financial processes immediately follow from the previous statements.

For example, let us observe a Gaussian process with m expected value and the same covariance as the Wiener process on the interval

[a, b]

, where

a > 0

and

a < b

. In this case, the maximum likelihood estimation of the Wiener process is the value of the process at the starting

\tilde{m} = ξ (a) .

On the other hand, a stationary Ornstein-Uhlenbeck process in the

[0, T]

interval can also be observed. We know the value of

λ > 0

in advance and the expected value and the covariance matrix of the process

\begin{matrix} E_{P_{m}} [ξ (t)] & = m \end{matrix}

(75)

\begin{matrix} c o v_{P_{m}} [(ξ (s), ξ (t))] & = σ^{2} e^{- λ | t - s |}, s, t \in [0, T] \end{matrix}

(76)

Therefore, the following covariances can be easily determined

E_{P} [ξ (0) ξ (t)] = σ^{2} e^{- λ t}, E_{P} [ξ (t) ξ (T)] = σ^{2} e^{- λ (T - t)}

(77)

E_{P} (\int_{0}^{T} ξ (s) d s \cdot ξ (t)) = σ^{2} \frac{2 - e^{- λ t} - e^{- λ (T - t)}}{λ} .

(78)

Taking advantage of the fact that, in this case, the maximum likelihood estimation is unbiased, we get the well-known Grenander formula [11]:

\hat{m} = \frac{ξ (0) + ξ (T) + λ \int_{0}^{T} ξ (s) d s}{2 + λ T} .

(79)

3.2. Parameter Estimations of the Kennedy Field

From now on, we investigate the case when the random field of forward rates

{F (s, t) : 0 \leq s \leq t}

is stationary, strictly Markov, and it satisfies the independent-increments property. Then - as we have seen before - the covariance and expected value functions have the form (52) and (53) and these functions are defined by four parameters (

ν, μ, α

and

σ

). Therefore, the expected initial forward curve is easily obtained.

\begin{matrix} α (0, t) & = ν - \frac{σ^{2}}{μ} + \frac{σ^{2}}{μ} e^{- μ t} + \frac{σ^{2}}{λ - μ} e^{- μ t} - \frac{σ^{2}}{λ - μ} e^{- λ t} \end{matrix}

(80)

\begin{matrix} = ν + \frac{σ^{2}}{μ} (e^{- μ t} - 1) + \frac{σ^{2}}{λ - μ} (e^{- μ t} - e^{- λ t}) \end{matrix}

(81)

Also, from the equation above, it can be straightforwardly seen that the parameter

ν

refers to the expected value of the spot curve.

E F (s, s) = E R (s) = α (s, s) = ν - \frac{σ^{2}}{μ} + \frac{σ^{2}}{μ} + \frac{σ^{2}}{λ - μ} - \frac{σ^{2}}{λ - μ} = ν

(82)

We can notice that the

F (s, s + t)

field is an Ornstein-Uhlenbeck process in the variable s, therefore

c o v [F (s_{1}, s_{1} + t), F (s_{2}, s_{2} + t)] = σ^{2} e^{- λ t} e^{- μ | s_{1} - s_{2} |}

(83)

This means that if we can observe the

F (s, s + t)

process on an interval according to s for some value t, then

σ^{2} e^{- λ t} μ

is determined with probability 1. If we can do this for two different t values, then

σ^{2} μ

and

λ

are defined with probability 1.

If we look at another covariance from the field

c o v [F (\frac{log s_{1}}{λ}, t), F (\frac{log s_{2}}{λ}, t)] = σ^{2} e^{- λ t} min (s_{1}, s_{2})

(84)

Which means that

σ^{2} e^{- λ t}

is defined with probability 1, therefore also

σ^{2}

and

μ

are defined with probability 1.

In the following, we observe the field on a region marked with T. The following

ξ (s, t)

auxiliary random field is introduced, where the expected value under the measure

P_{ν}

ν

ξ (s, t) = F (s, t) + σ^{2} (\frac{1}{μ} - e^{- μ (t - s)} (\frac{1}{μ} - \frac{1}{λ - μ}) + e^{- λ (t - s)} \frac{1}{λ - μ}) .

(85)

where

W (x_{i}, y_{j}) = \sum_{k = 1}^{i} \sum_{l = 1}^{j} ξ (k, l)

(86)

We demonstrate that the following estimate is the maximum likelihood estimate of this parameter.

\hat{ν} = \frac{\frac{e^{λ b_{1}}}{μ} ξ (a, b_{1}) + \frac{e^{λ b_{2}}}{μ - λ} ξ (a, b_{2}) + \int_{b_{1}}^{b_{2}} e^{λ ν} ξ (a, v) d v}{e^{λ b_{2}} (\frac{1}{λ} + \frac{1}{μ - λ}) + e^{λ b_{1}} (\frac{1}{μ} - \frac{1}{λ})} .

(87)

First, we get that

E_{P_{0}} (ξ (s, t) \hat{ν})

gives the same value for every

(s, t) \in T

. On the other hand,

E_{P_{ν}} (\hat{ν}) = ν

. Thus, based on Theorems 2 and 3,

\hat{ν}

is the maximum likelihood estimate.

4. Simulation of the Kennedy Field

In this section, we aim to simulate the Kennedy field in

n \times m

points. We can consider this as an

n \times m

normally distributed vector whose expected value and covariance matrix are known. However, for sufficiently large n and m, simulating a multidimensional, normally distributed vector is extremely slow due to the size of the covariance matrix. A much more effective, simpler, and faster way is if we notice that if

W (x, y)

is a Brownian sheet, then

α (s, t) + σ e^{- μ t} W (e^{λ s}, e^{(2 μ - λ) t})

is a Kennedy field with the appropriate covariance structure.

The question is how can we generate a Brownian sheet at the

(x_{i}, y_{j})

points

(x_{1} < \dots < x_{n}, y_{1} < \dots < y_{m})

the fastest way possible, where the division is not necessarily equidistant. Let us take independent random variables with

N (0, (x_{i} - x_{i - 1}) (y_{j} - y_{j - 1})),

(x_{0} = y_{0} = 0)

distributions and denote them with

η (i, j)

. Accordingly, the Brownian sheet can be written in the following form

W (x_{i}, y_{j}) = \sum_{k = 1}^{i} \sum_{l = 1}^{j} η (k, l)

(88)

Hence, the upcoming matrix operation should be coded in the fastest way possible to achieve the desired results.

A \to B : B (i, j) = \sum_{k = 1}^{i} \sum_{l = 1}^{j} A (k, l)

(89)

Fortunately, ready-made, fast algorithms exist for this double summation.

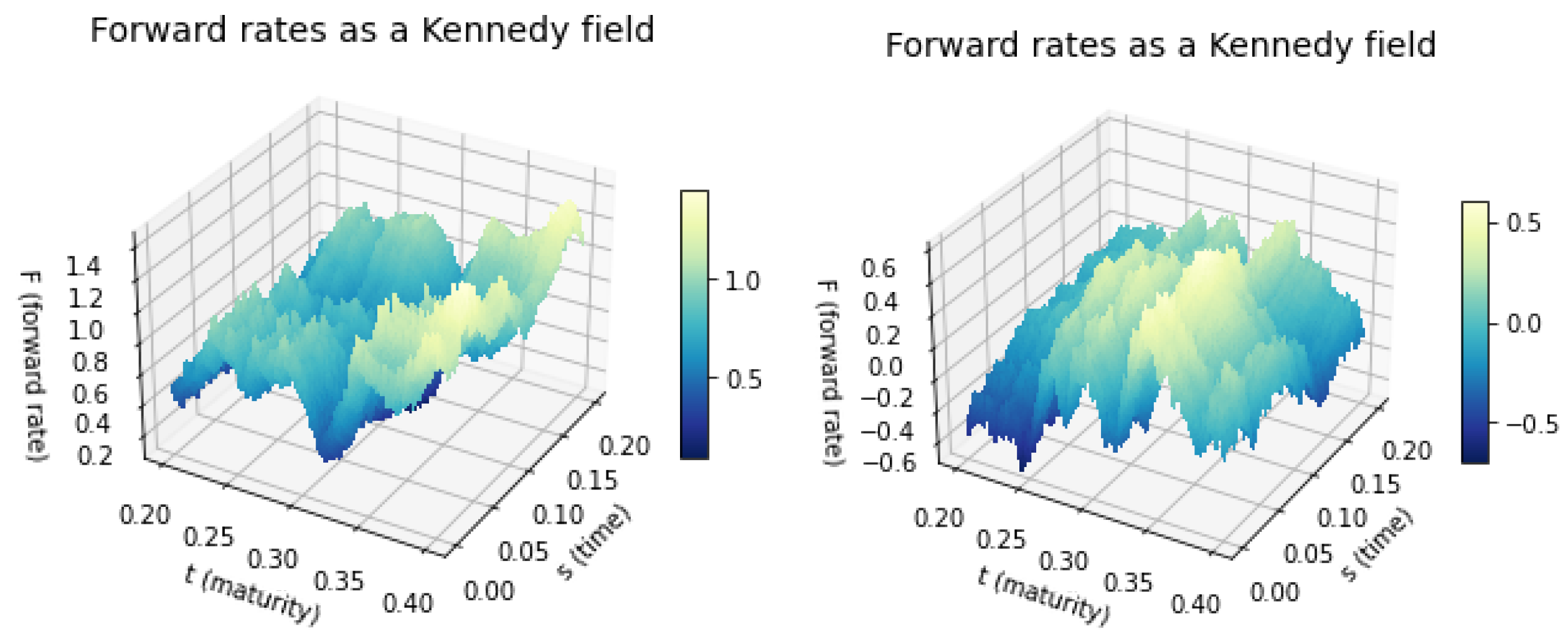
In Figure 1, we can see two different simulations where the number of simulated points is 10000.

5. Option Pricing

This section aims to show that the fair prices of various financial assets can be derived analytically if we assume that the forward rates evolve according to a Gaussian random field.

5.1. European Caplet

In the case of options, instead of using instantaneous forward rates, compounded forward rates are used. Consequently, it is necessary to transition from the instantaneous forward rate, described earlier by the Kennedy field, to a discrete forward rate for a given time period, often denoted as

L (t, T_{i})

, with reference to the LIBOR rate. Consistently with the following discretization scheme, the discretized version of the HJM framework, which is considered the industry standard, is the LIBOR Market Model (LMM).

1 + L (s, t) Δ = e^{\int_{t}^{t + Δ} F (s, u) d u} = e^{Δ F^{Δ} (s, t)}

(90)

This derivation is equivalent to the one derived by Kennedy but uses a different approach. We would like to calculate the price of an interest rate caplet at strike K for the time period t to

t + Δ

. This may be regarded as a European option on the forward rate

F^{Δ} (s, t) = \frac{1}{Δ} \int_{t}^{t + Δ} F (s, u) d u

which is exercised at time t if

f^{Δ} (t, t) > K

, yielding a payoff at time

t + Δ

. The payoff function of this transaction is shown below.

V (t, K) = {[(e^{Δ F^{Δ} (t, t)} - 1) - (e^{Δ K} - 1)]}_{+} = {[e^{Δ F^{Δ} (t, t)} - e^{Δ K}]}_{+}

(91)

The discount factor from time s to time t is defined as follows.

D (s, t) = e^{- \int_{s}^{t} r (u) d u}

(92)

A cap normally consists of a string of such options for successive time periods, but it is sufficient here to consider only one time period. The discounted payoff of the option at time s is the following

D (s, t + Δ) V (t, K) = e^{- \int_{s}^{t + Δ} r (u) d u} {(e^{Δ F^{Δ} (t, t)} - e^{Δ K})}_{+}

(93)

The price of a financial asset is obtained by taking the expected value of the discounted payoff function. The definition of the drift term guarantees that the model is under a risk-neutral measure, just like in the Heath-Jarrow-Morton framework.

P_{c a p l e t} (s) = E [e^{- \int_{s}^{t + Δ} r (u) d u} {(e^{Δ F^{Δ} (t, t)} - e^{Δ K})}_{+}]

(94)

For the sake of simplicity, two additional variables are introduced (

ξ (s, t)

and

η (s, t)

) to denote the time range over which the forward rate is integrated.

\begin{matrix} ξ (s, t) & = \int_{s}^{t} r (u) d u = \int_{s}^{t} F (u, u) d u \end{matrix}

(95)

\begin{matrix} η (s, t) & = \int_{s}^{t} F (t, u) d u \end{matrix}

(96)

Hence, in the case of caplet, we deal with the following special case of

ξ

and

η

\begin{matrix} ξ (s, t + Δ) & = \int_{s}^{t + Δ} r (u) d u = \int_{s}^{t + Δ} F (u, u) d u \end{matrix}

(97)

\begin{matrix} η (t, t + Δ) & = Δ F^{Δ} (t, t) = \int_{t}^{t + Δ} F (t, u) d u \end{matrix}

(98)

Due to the properties of the Gaussian random field

(ξ (s_{1}, t_{1}), η (s_{2}, t_{2}))

is following a multivariate normal distribution. Henceforth, except for necessary cases, we omit the corresponding time indices to indicate the expected value, standard deviation and correlation between

ξ

and

η

. Consequently let us denote them with the following notations

E ξ = μ_{1}

D^{2} (ξ) = σ_{1}^{2}

E η = μ_{2}

and

D^{2} (η) = σ_{2}^{2}

. From now on, the conditional normal distribution theorem can be used. As a result, the conditional distribution of

ξ

given

η

is the following

ξ | η \sim N (μ_{1} + ρ σ_{1} \frac{η - μ_{2}}{σ_{2}}, σ_{1}^{2} (1 - ρ^{2}))

(99)

where

c o r r (ξ (s_{1}, t_{1}), η (s_{2}, t_{2})) = ρ (s_{1}, t_{1}, s_{2}, t_{2})

. Therefore, the fair price of the European option can be calculated as follows.

\begin{matrix} E [e^{- \int_{s}^{t + Δ} r (u) d u} {(e^{Δ F^{Δ} (t, t)} - e^{Δ K})}_{+}] = E [e^{- ξ} {(e^{η} - e^{Δ K})}_{+}] = \end{matrix}

(100)

\begin{matrix} = E [E (e^{- ξ} {(e^{η} - e^{Δ K})}_{+} | η] = E [{(e^{η} - e^{Δ K})}_{+} \cdot E ((e^{- ξ}) | η)] \end{matrix}

(101)

During the derivations, the law of total expectation and the fact that

{(e^{η} - e^{Δ K})}_{+}

is measurable for

η

is used. As we can see,

ξ \sim N (μ_{1}, σ_{1})

is normally distributed, therefore

- ξ \sim N (- μ_{1}, σ_{1})

, where

c o r r (- ξ, η) = - ρ

. Therefore

- ξ | η \sim N (- μ_{1} - ρ σ_{1} \frac{η - μ_{2}}{σ_{2}}, σ_{1}^{2} (1 - ρ^{2}))

. Since the conditional distribution of

- ξ

given

η

is known, therefore

E [e^{- ξ} | η]

can be calculated as the expectation of a lognormally distributed random variable.

\begin{matrix} E [e^{- ξ} | η] = e^{- μ_{1} - ρ σ_{1} \frac{η - μ_{2}}{σ_{2}} + \frac{1}{2} σ_{1}^{2} (1 - ρ^{2})} \end{matrix}

(102)

Returning to the pricing formula

\begin{matrix} E [{(e^{η} - e^{Δ K})}_{+} \cdot & E [e^{- ξ} | η]] = E [{(e^{η} - e^{Δ K})}_{+} \cdot e^{- μ_{1} - ρ σ_{1} \frac{η - μ_{2}}{σ_{2}} + \frac{1}{2} σ_{1}^{2} (1 - ρ^{2})}] = \end{matrix}

(103)

\begin{matrix} = e^{- μ_{1} + \frac{1}{2} σ_{1}^{2} (1 - ρ^{2}) + ρ μ_{2} \frac{σ_{1}}{σ_{2}}} E [{(e^{η} - e^{Δ K})}_{+} \cdot e^{- ρ η \frac{σ_{1}}{σ_{2}}}] = \end{matrix}

(104)

\begin{matrix} = e^{- μ_{1} + \frac{1}{2} σ_{1}^{2} (1 - ρ^{2}) + ρ μ_{2} \frac{σ_{1}}{σ_{2}}} \int_{Δ K}^{\infty} (e^{x (1 - ρ μ_{2} \frac{σ_{1}}{σ_{2}})} - e^{Δ K - x ρ \frac{σ_{1}}{σ_{2}}}) \frac{1}{\sqrt{2 π} σ_{2}} e^{\frac{- {(x - μ_{2})}^{2}}{2 σ_{2}^{2}}} d x = \end{matrix}

(105)

\begin{matrix} = e^{μ_{2} - μ_{1} + \frac{σ_{1}^{2} + σ_{2}^{2}}{2} - ρ σ_{1} σ_{2}} \int_{Δ K}^{\infty} \frac{1}{\sqrt{2 π} σ_{2}} e^{\frac{- {(x - μ_{2} - σ_{2}^{2} + ρ σ_{1} σ_{2})}^{2}}{2 σ_{2}^{2}}} d x - \end{matrix}

(106)

\begin{matrix} - e^{Δ K - μ_{1} + \frac{1}{2} σ_{1}^{2}} \int_{Δ K}^{\infty} \frac{1}{\sqrt{2 π} σ_{2}} e^{\frac{- {(x - μ_{2} + ρ σ_{1} σ_{2})}^{2}}{2 σ_{2}^{2}}} d x \end{matrix}

(107)

Finally, by subtracting the values of the two integrals from each other, we get the analytical pricing formula for the European call option in the case of the Kennedy fields.

\begin{matrix} P_{c a p l e t} (s) = e^{μ_{2} - μ_{1} + \frac{1}{2} (σ_{1}^{2} + σ_{2}^{2} - 2 ρ σ_{1} σ_{2})} Φ (\frac{μ_{2} + σ_{2}^{2} - ρ σ_{1} σ_{2} - Δ K}{σ_{2}}) - e^{Δ K - μ_{1} + \frac{1}{2} σ_{1}^{2}} Φ (\frac{μ_{2} - ρ σ_{1} σ_{2} - Δ K}{σ_{2}}) \end{matrix}

(108)

5.1.1. Expected Values and Variances

Based on the calculations in Appendix A.2 for the pricing of the caplet, the expected value of

ξ

and

η

, their standard deviation, and the correlation between them are as follows.

\begin{matrix} μ_{1} = & E ξ (s, t + Δ) = (ν - \frac{σ^{2}}{μ}) (t + Δ - s) \end{matrix}

(109)

\begin{matrix} μ_{2} = & E η (t, t + Δ) = (ν - \frac{σ^{2}}{μ}) Δ - \frac{σ^{2}}{μ^{2}} (e^{- μ Δ} - 1) - \frac{σ^{2}}{μ (λ - μ)} (e^{- μ Δ} - 1) + \frac{σ^{2}}{λ (λ - μ)} (e^{- λ Δ} - 1) \end{matrix}

(110)

\begin{matrix} σ_{1}^{2} = & D^{2} ξ (s, t + Δ) = \frac{2 σ^{2}}{μ^{2}} ((t + Δ - s) μ + e^{- μ (t + Δ - s)} - 1) \end{matrix}

(111)

\begin{matrix} σ_{2}^{2} = & D^{2} η (t, t + Δ) = \end{matrix}

(112)

\begin{matrix} = & \frac{σ^{2}}{(λ - μ) λ} (e^{- λ Δ} - 1) + \frac{σ^{2}}{μ (μ - λ)} (e^{- μ Δ} - 1) + \frac{σ^{2}}{μ (μ - λ)} (e^{- μ Δ} - e^{- λ Δ}) + \frac{σ^{2}}{λ μ} (1 - e^{- λ Δ}) \end{matrix}

(113)

\begin{matrix} c o v = & c o v (ξ (s, t + Δ), η (t, t + Δ)) \end{matrix}

(114)

\begin{matrix} = & \frac{σ^{2}}{μ^{2}} (1 - e^{- μ Δ} - e^{- μ (t - s)} + e^{- μ (t + Δ - s)}) + \end{matrix}

(115)

\begin{matrix} + (\frac{σ^{2}}{λ (μ - λ)} + \frac{σ^{2}}{λ μ}) (e^{λ Δ} - 1) + \frac{2 σ^{2}}{μ (μ - λ)} (e^{λ Δ - μ Δ} - 1) \end{matrix}

(116)

\begin{matrix} ρ = & c o r r (ξ (s, t + Δ), η (t, t + Δ)) = \frac{c o v (ξ (s, t + Δ), η (t, t + Δ))}{D ξ (s, t + Δ) D η (t, t + Δ)} = \frac{c o v}{σ_{1} σ_{2}} \end{matrix}

(117)

\begin{matrix} c o v (ξ, η) = & \frac{σ^{2}}{μ^{2}} (1 - e^{- μ Δ} - e^{- μ (t - s)} + e^{- μ (t + Δ - s)}) + \end{matrix}

(118)

\begin{matrix} + (\frac{σ^{2}}{λ (μ - λ)} + \frac{σ^{2}}{λ μ}) (e^{λ Δ} - 1) + \frac{2 σ^{2}}{μ (μ - λ)} (e^{λ Δ - μ Δ} - 1) \end{matrix}

(119)

5.2. European Floorlet

Similarly to the previously derived European caplet, the price of an interest rate floorlet is now derived. Thereby, using the put-call parity, the pricing formula of the swap can be easily calculated. The payoff function of this transaction is shown below.

V (t, K) = {[(e^{Δ K} - 1) - (e^{Δ F^{Δ} (t, t)} - 1)]}_{+} = {[e^{Δ K} - e^{Δ F^{Δ} (t, t)}]}_{+}

(120)

The discount factor from time s to time t is defined just as previously:

D (s, t) = e^{- \int_{s}^{t} r (u) d u}

. A floorlet normally consists of a string of such options for successive time periods, but it is sufficient here to consider only one time period. The discounted payoff of the option at time s is the following

D (s, t + Δ) V (t, K) = e^{- \int_{s}^{t + Δ} r (u) d u} {(e^{Δ K} - e^{Δ F^{Δ} (t, t)})}_{+}

(121)

The price of a financial asset is obtained by taking the expected value of the discounted payoff function. The definition of the drift term guarantees that the model is under the risk-neutral measure, just like in the Heath-Jarrow-Morton framework.

P_{f l o o r l e t} (s) = E [e^{- \int_{s}^{t + Δ} r (u) d u} {(e^{Δ K} - e^{Δ F^{Δ} (t, t)})}_{+}]

(122)

The derivation is completely similar to the price of the caplet product presented earlier and can be found in Appendix A.3. Therefore, the analytical pricing formula for the European floorlet option in the case of Kennedy fields is as follows.

\begin{matrix} P_{f l o o r l e t} (s) = e^{- μ_{1} + \frac{1}{2} σ_{1}^{2} (1 - ρ^{2})} (e^{Δ K + \frac{1}{2} ρ^{2} σ_{1}^{2}} Φ (\frac{Δ K - μ_{2} + ρ σ_{1} σ_{2}}{σ_{2}}) - e^{μ_{2} + \frac{1}{2} {(σ_{2} - ρ σ_{1})}^{2}} Φ (\frac{Δ K - μ_{2} - σ_{2}^{2} + ρ σ_{1} σ_{2}}{σ_{2}})) = \end{matrix}

(123)

\begin{matrix} = e^{Δ K - μ_{1} + \frac{1}{2} σ_{1}^{2}} Φ (\frac{Δ K - μ_{2} + ρ σ_{1} σ_{2}}{σ_{2}}) - e^{μ_{2} - μ_{1} + \frac{1}{2} (σ_{1}^{2} + σ_{2}^{2} - 2 ρ σ_{1} σ_{2})} Φ (\frac{Δ K - μ_{2} - σ_{2}^{2} + ρ σ_{1} σ_{2}}{σ_{2}}) \end{matrix}

(124)

5.3. Swap

An interest rate swap is a forward contract exchanging a floating and fixed rate for a predetermined period. The special financial asset in which the floating versus fixed rate exchange only applies to one period is called a swaplet. In this section, the fair price, hence the conditional expected value of the discounted payoff function under the risk-neutral measure for one period, is derived. We first examine the simplest case, a one-period swap. In this case, the interest rate exchange takes place at only one point in time, T in the swap product. In this case, the swap is similar to a caplet with an extreme cap value, where the product is definitely worth calling. The price of the swaplet product at time s is as follows.

P_{s w a p l e t} (s) = E [e^{- \int_{s}^{s + Δ} F (u, u) d u} (e^{\int_{s}^{s + Δ} F (s, u) d u} - e^{Δ K})]

(125)

In this case, the previously introduced

ξ

and

η

are interpreted in the following time period.

\begin{matrix} ξ & (s, s + Δ) = \int_{s}^{s + Δ} F (u, u) d u \end{matrix}

(126)

\begin{matrix} η & (s, s + Δ) = Δ F^{Δ} (s, s) = \int_{s}^{s + Δ} F (s, u) d u \end{matrix}

(127)

As we can see, the definition of

η

is unchanged; therefore, only the value of

μ_{1}

σ_{1}

and the covariance changes.

\begin{matrix} μ_{1} = & (ν - \frac{σ^{2}}{μ}) Δ \end{matrix}

(128)

\begin{matrix} σ_{1}^{2} = & D^{2} ξ = \frac{2 σ^{2}}{μ^{2}} (Δ μ + e^{- μ Δ} - 1) \end{matrix}

(129)

\begin{matrix} c o v (ξ, η) = & \frac{σ^{2}}{(λ - μ) λ} (e^{- λ Δ} - 1) + \frac{σ^{2}}{μ (μ - λ)} (e^{- μ Δ} - 1) + \end{matrix}

(130)

\begin{matrix} + \frac{σ^{2}}{μ (μ - λ)} (e^{- μ Δ} - e^{- λ Δ}) + \frac{σ^{2}}{λ μ} (1 - e^{- λ Δ}) \end{matrix}

(131)

\begin{matrix} σ_{2}^{2} = & D^{2} η = c o v (ξ, η) = ρ σ_{1} σ_{2} \end{matrix}

(132)

As we can see, in that case, the covariance of

ξ

and

η

equals to the variance of

η

This calculation is easy to see if we use the previously introduced multidimensional normally distributed random variables (

ξ

, and

η

) because in this case,

e^{ξ}

and

e^{η}

random variables are lognormally distributed. It is well-known that the quotient of two lognormally distributed random variables with correlation

ρ

is also lognormally distributed with the following expected value and standard deviation.

ξ \sim N (μ_{1}, σ_{1}), η \sim N (μ_{2}, σ_{2}) \to (η - ξ) \sim N (μ_{2} - μ_{1}, σ_{1}^{2} + σ_{2}^{2} - 2 ρ σ_{1} σ_{2})

(133)

Hence

\begin{matrix} E (e^{- ξ}) & = e^{- μ_{1} + \frac{1}{2} σ_{1}^{2}} \end{matrix}

(134)

\begin{matrix} E (e^{- ξ} e^{η}) & = E (\frac{e^{η}}{e^{ξ}}) = E (e^{η - ξ}) = e^{μ_{2} - μ_{1} + \frac{1}{2} (σ_{1}^{2} + σ_{2}^{2} - 2 ρ σ_{1} σ_{2})} \end{matrix}

(135)

Therefore, we easily got the previously calculated result back.

P_{s w a p l e t} (s) = e^{μ_{2} - μ_{1} + \frac{1}{2} (σ_{1}^{2} + σ_{2}^{2} - 2 ρ σ_{1} σ_{2})} - e^{Δ K - μ_{1} + \frac{1}{2} σ_{1}^{2}}

(136)

Furthermore, the price of a one-period long swap, the so-called swaplet at time s, can be easily obtained using the previously derived caplet and floorlet pricing formulas and the put-call parity. Therefore, the difference between the calculated fair price of the caplet and the floorlet option.

The fair price of a fixed vs floating swap for more time periods at time 0 can be found in the Appendix A.2.

5.4. Par Swap Rate

In the previous section, we could derive the fair price of a one-period swap, the so-called swaplet.

P_{s w a p l e t} (0) = e^{μ_{2} - μ_{1} + \frac{1}{2} (σ_{1}^{2} + σ_{2}^{2} - 2 ρ σ_{1} σ_{2})} - e^{Δ K - μ_{1} + \frac{1}{2} σ_{1}^{2}}

(137)

Therefore, let us first adjust the previously defined

ξ

and

η

variables to the following time periods.

\begin{matrix} ξ & (s, s + Δ) = \int_{s}^{s + Δ} F (u, u) d u \end{matrix}

(138)

\begin{matrix} η & (s, s + Δ) = Δ F^{Δ} (s, s) = \int_{s}^{s + Δ} F (s, u) d u \end{matrix}

(139)

The so-called swap quote can be easily expressed from that equality, which equals the par swap rate. The par rate is the value of the fixed rate that gives the swap a zero present value or the fixed rate that makes the value of both legs equal. The derivation of this rate is important because, in many cases, the financial data contains par swap rates instead of swap prices; in other words, this financial product is quoted using the par swap rate.

\begin{matrix} P_{s w a p l e t} (0) = 0 & = e^{μ_{2} - μ_{1} + \frac{1}{2} (σ_{1}^{2} + σ_{2}^{2} - 2 ρ σ_{1} σ_{2})} - e^{Δ K - μ_{1} + \frac{1}{2} σ_{1}^{2}} \end{matrix}

(140)

\begin{matrix} e^{μ_{2} - μ_{1} + \frac{1}{2} (σ_{1}^{2} + σ_{2}^{2} - 2 ρ σ_{1} σ_{2})} & = e^{Δ K - μ_{1} + \frac{1}{2} σ_{1}^{2}} \end{matrix}

(141)

\begin{matrix} μ_{2} - μ_{1} + \frac{1}{2} (σ_{1}^{2} + σ_{2}^{2} - 2 ρ σ_{1} σ_{2}) & = Δ K - μ_{1} + \frac{1}{2} σ_{1}^{2} \end{matrix}

(142)

\begin{matrix} μ_{2} + \frac{1}{2} σ_{2}^{2} - ρ σ_{1} σ_{2} & = Δ K \end{matrix}

(143)

\begin{matrix} K & = \frac{1}{Δ} (μ_{2} + \frac{1}{2} σ_{2}^{2} - ρ σ_{1} σ_{2}) \end{matrix}

(144)

After that, we want to express the par swap rate with the original parameters of the Kennedy field.

\begin{matrix} Δ K = & μ_{2} + \frac{1}{2} σ_{2}^{2} - ρ σ_{1} σ_{2} = μ_{2} + \frac{1}{2} σ_{2}^{2} - σ_{2}^{2} = μ_{2} - \frac{1}{2} σ_{2}^{2} \end{matrix}

(145)

\begin{matrix} = & (ν - \frac{σ^{2}}{μ}) Δ - \frac{σ^{2}}{μ^{2}} (e^{- μ Δ} - 1) - \frac{σ^{2}}{μ (λ - μ)} (e^{- μ Δ} - 1) + \frac{σ^{2}}{λ (λ - μ)} (e^{- λ Δ} - 1) - \end{matrix}

(146)

\begin{matrix} - \frac{σ^{2}}{2 (λ - μ) λ} (e^{- λ Δ} - 1) + \frac{σ^{2}}{2 μ (λ - μ)} (e^{- μ Δ} - 1) + \frac{σ^{2}}{2 μ (λ - μ)} (e^{- μ Δ} - e^{- λ Δ}) + \frac{σ^{2}}{2 λ μ} (e^{- λ Δ} - 1) = \end{matrix}

(147)

\begin{matrix} = & (ν - \frac{σ^{2}}{μ}) Δ + (e^{- μ Δ} - 1) (- \frac{σ^{2}}{μ^{2}} - \frac{σ^{2}}{μ (λ - μ)} + \frac{σ^{2}}{2 μ (λ - μ)} + \frac{σ^{2}}{2 μ (λ - μ)}) + \end{matrix}

(148)

\begin{matrix} + (e^{- λ Δ} - 1) (\frac{σ^{2}}{λ (λ - μ)} + \frac{σ^{2}}{2 λ (λ - μ)} + \frac{σ^{2}}{2 λ μ} - \frac{σ^{2}}{2 μ (λ - μ)}) = \end{matrix}

(149)

\begin{matrix} = & (ν - \frac{σ^{2}}{μ}) Δ + \frac{σ^{2}}{μ^{2}} (1 - e^{- μ Δ}) - (\frac{σ^{2}}{2 λ (λ - μ)} + \frac{σ^{2}}{2 μ λ} - \frac{σ^{2}}{2 μ (λ - μ)}) (1 - e^{- λ Δ}) = \end{matrix}

(150)

\begin{matrix} = & (ν - \frac{σ^{2}}{μ}) Δ + \frac{σ^{2}}{μ^{2}} (1 - e^{- μ Δ}) \end{matrix}

(151)

From here, the par swap rate can be easily written with the original parameters of the Kennedy field.

K = ν - \frac{σ^{2}}{μ} + \frac{σ^{2}}{μ^{2} Δ} (1 - e^{- μ Δ})

(152)

Therefore, if the swap par rate can be observed for at least four different tenors, then three parameters of the original four (

ν, μ

, and

σ

) can be determined with a probability of 1. However, it is worth mentioning that the parameter

λ

is omitted from the description of the par swap rate.

6. Calibration on Simulated Data

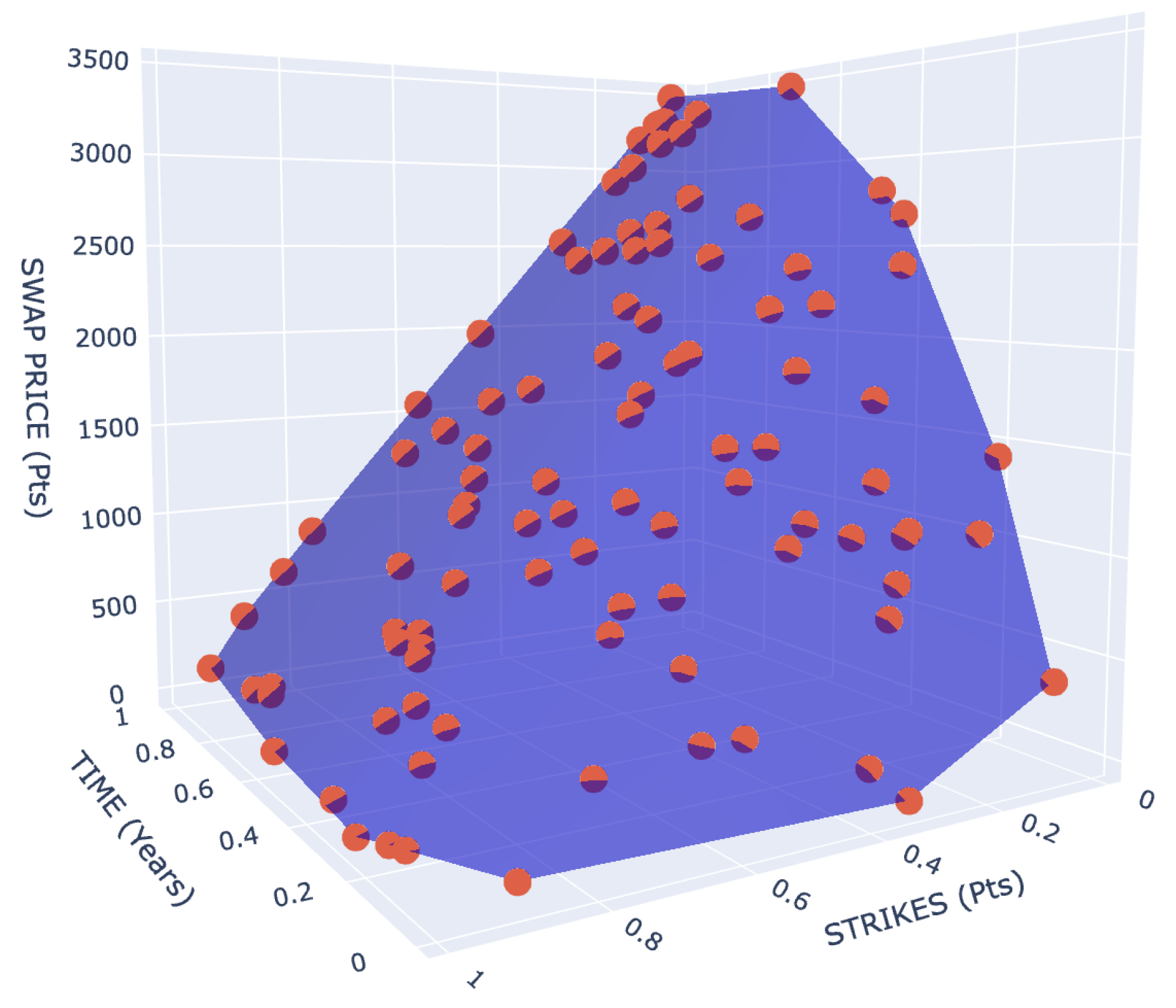
Simulated financial caplet, floorlet, and swaplet prices were generated using the previously derived analytical pricing formulas with different maturities and strikes. Therefore, first of all, we just wanted to test the punctuality of the calibration engine.

Numerical calibration is an extreme value optimization problem. The method aims to find the parameter set that minimizes the squared deviation error between the previously generated financial caplet, floorlet, and swaplet data and the analytically calculated prices with the calibrated parameters. The calibration engine is based on the stochastic gradient descent method. The extreme value optimization is based on the article of Mikhaliov and Nögel, and the implementation in Python is based on the work of Emerick and Tatsat [9,10].

Figure 2. Simulated Monte Carlo market prices (Mesh) vs Calibrated Kennedy model prices (Markers) for a caplet

The figure shows that the prices calculated with the back-estimated parameters fit our synthetic dataset almost perfectly. The calibration returns the used parameters; the difference is negligible and can be considered a numerical error.

7. Calibration on Real Data

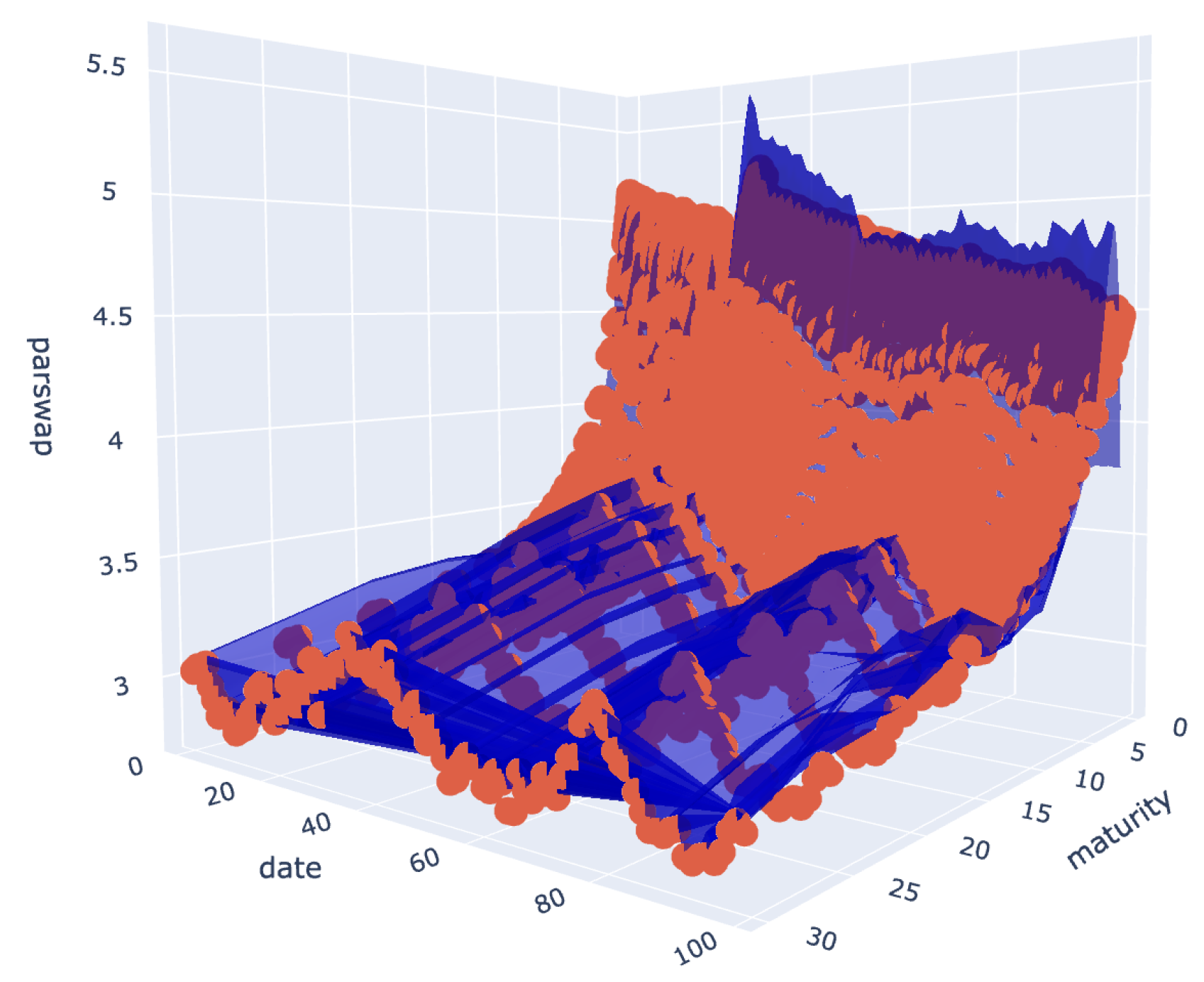
A time series of swap par rates was obtained with the help of the Bloomberg terminal. The financial dataset contains the par swap rates of the USD SOFR fixed versus floating interest rate swaplet from July 2018 to April 2023. The historical dataset includes par swap rates for 28 different maturities daily.

We calibrated the model daily for different maturities for par swap rates with the calibration algorithm 100 days back. As we can see, the Kennedy field fits the dataset nicely; however, it slightly overestimates the values for shorter maturities while slightly underestimating the par swap rates at long maturities.

Figure 3. Par swap rate market prices (Mesh) vs Calibrated Kennedy model prices (Markers)

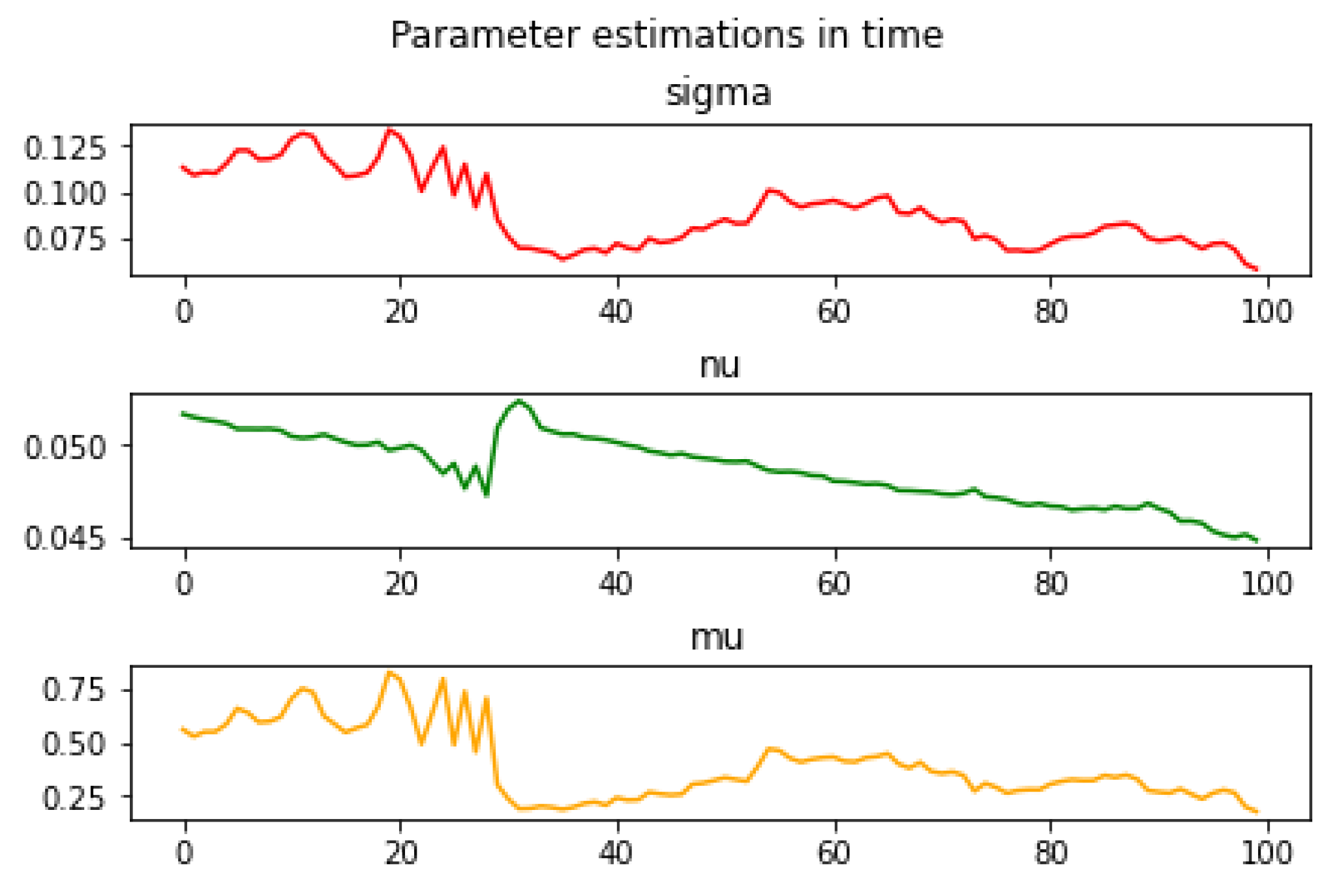
In addition to the analytical results, it can also be seen that

λ

does not play a role in the numerical implementation since this back-estimated parameter value is highly volatile. Meanwhile, the value of the other three parameters varies on a much smaller scale, and similar trends can be observed.

As a result, our guess is that the

λ

parameter, which is not included in the par swap rate, describes a temporal relationship; in other words, the term structure of the model;

σ

, greatly influences the standard deviation of the field; while

ν

is used to describe the level of the yield curves, since

ν

is the parameter that describes the expected value of the spot rate (

ν = E F (s, s))

Figure 4. Historical parameter estimations in time

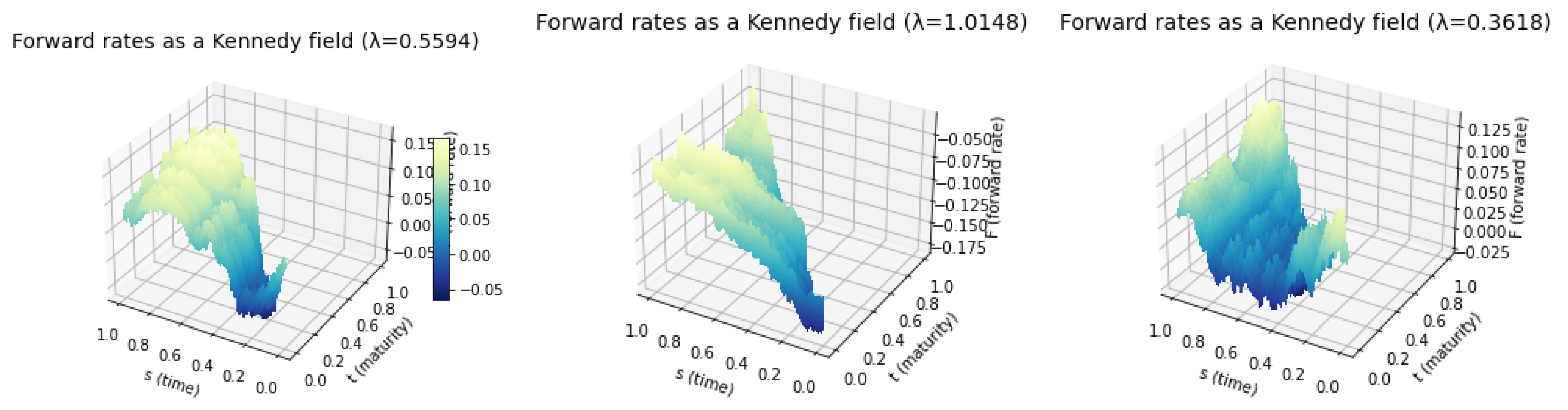
In the following, we plotted Kennedy fields for describing forward interest rates with the three parameters back-estimated from the par swap rate dataset (

ν = 0.05171817

μ = 0.56028928

and

σ = 0.11315586

) and three different

λ

values, to see what rates would be generated in a realistic case.

Figure 5. Differently parameterized Kennedy fields for describing forward rates

8. Results

Our article focuses on a mathematical model based on Gaussian random fields introduced by Kennedy to describe forward interest rates. Among other things, we provided novel proof for the equivalence of conditions regarding the martingale property of the discounted bond prices. We demonstrated the relationship between the Kennedy model and the HJM framework in special cases (Markov property, stationarity). Additionally, utilizing Radon-Nikodym derivatives, we derived maximum likelihood estimates and estimates with probability one for the original parameters of the field. We presented a new, efficient method, based on Brownian sheets, to simulate the Kennedy field.

Subsequently, we derived analytical pricing formulas resembling Black-Scholes for various financial products, including caplets, floorlets, swaplets, and swaps. Finally, we calibrated the field using a numerical extreme value search algorithm based on stochastic gradient descent on a simulated synthetic dataset to recover the original parameters. We then calibrated it on actual par swap rates to examine how our model performs in a market environment.

9. Discussion

Kennedy introduced a model based on Gaussian random fields for modeling forward interest rates in the 1990s, which, due to its normal distribution, can generate negative interest rates. At that time, this scenario was not considered feasible; however, in the interest rate environment of the 2010s, negative interest rates emerged. Since this model naturally handles them, it underscores the relevance of the model. Calibration on actual par swap rates demonstrated that our model fits well with the current interest rate environment and effectively describes the market.

Moving forward, our primary objective is to go beyond analytical pricing formulas and utilize models based on artificial intelligence, including LSTM and neural networks, for parameter estimation. We aim to compare the accuracy of parameters recovered through calibration with these AI-based models. Additionally, we plan to investigate the temporal stability of parameters and compare them with industry-standard models such as SABR.

10. Conclusions

Overall, we can conclude that a new result has been achieved in estimating the parameters of the Kennedy field, and an excellent calibrator has been built. This can be a great starting step to investigate and compare it to other, more complicated models.

Our research also aims to calibrate the parameters of the negative interest rate models with machine learning algorithms to compare them with the previously derived analytical estimations.

Funding

This work is supported by the KDP-2021 program and the ELTE TKP 2021-NKTA-62 funding scheme of the Ministry of Innovation and Technology from the source of the National Research, Development and Innovation Fund.

Data Availability Statement

Data used in this study include historical par swap rates of the USD SOFR fixed vs. floating interest rate swaps (Bloomberg ticker: USOSFR1Z BGN Curncy), obtained from Bloomberg. The data spans from April 20, 2018, to April 20, 2023, with daily frequency in USD, sourced from BGN. Due to proprietary restrictions, these data are not publicly available. Access to the data is subject to Bloomberg’s terms and conditions and is not shared openly. For more information, please contact the authors.

Acknowledgments

We would like to take this opportunity to thank my business supervisor, Csaba Kőrössy, for his help and dedication to the research. Even though he joined the research later, he spent much time understanding it, and his comments and suggestions immensely helped this article. We want to thank dr Fáth Gábor, who involved us in Risklab and since then regularly consults, gives ideas, and helps on this topic, in which he also has great expertise. Finally, we would like to thank dr András Ványolos for his help, interest, and enthusiasm with which he joined our project, who is motivated simply by his love for mathematical research. We enjoy doing math with you.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

Appendix A.1

The proof of Theorem 1 can be found in the original article by Kennedy. [1] However, we present an alternative derivation to prove the statement. To facilitate this, we first introduce an auxiliary lemma, which will be utilized in the proof of the theorem.

Lemma A1.

{X, ξ (u), u \in U}

is a Gaussian system, where

D^{2} ξ (u) > 0

for every

u \in U

. Then the following statements are equivalent:

(a): $E (e^{X} | ξ (u), u \in U) = 1$ and
(b): X and $ξ (u)$ are independent for all $u \in U$ and $E X + \frac{1}{2} D^{2} X = 0$ .

Proof of Lemma A1.

The equivalence is proven by deriving both directions from each other.

$(a)$ ⟹ $(b)$

First, we prove the (a) to (b) direction. If $E (e^{X} | ξ (u), u \in U) = e^{0} = 1$ is true then it can be stated that

$\begin{matrix} e^{E (X | ξ (v)) + \frac{1}{2} D^{2} (X | ξ (v))} = E (e^{X} | ξ (v)) = E (E (e^{X} | ξ (u), u \in U) | ξ (v)) = 1 \end{matrix}$

(A1)

Thus

$\begin{matrix} 0 & = E (X | ξ (v)) + \frac{1}{2} D^{2} (X | ξ (v)) = \end{matrix}$

(A2)

$\begin{matrix} = E X + corr (X, ξ (v)) \frac{D X}{D ξ (v)} (ξ (v) - E ξ (v)) + \frac{1}{2} D^{2} X (1 - corr {(X, ξ (v))}^{2}) \end{matrix}$

(A3)

Therefore, we can conclude that $corr (X, ξ (v)) = 0$ and $E X + \frac{1}{2} D^{2} X = 0$ .
$(b)$ ⟹ $(a)$

Then we deduce that if (b) is fulfilled, then statement (a) is also true. If X and $ξ (u)$ are independent for all $u \in U$ and $E X + \frac{1}{2} D^{2} X = 0$ then

$E (e^{X} | ξ (u), u \in U) = E (e^{X}) = e^{E X + \frac{1}{2} D^{2} X} = 1$

(A4)

□

Proof of Theorem 1.

It is obvious that

R (u)

, where

0 \leq u \leq s

, and

P (s, t)

are

F (s) -

measurable random variables, just as

Z (s, t)

. Therefore, it can be stated that there is no problem with the existence of expected values. The equivalence of the statements is proved circularly.

$(a)$ ⟹ $(b)$

Let us start with the statement that the discounted bond price is a martingale. Hence

$\begin{matrix} Z (s, t) & = E [Z (t, t) | F (s)] = E [e^{- \int_{0}^{t} R (u) d u} | F (s)] \end{matrix}$

(A5)

$\begin{matrix} ⟹ P (s, t) & = e^{\int_{0}^{s} R (u) d u} Z (s, t) = E [e^{- \int_{s}^{t} R (u) d u} | F (s)] \end{matrix}$

(A6)

From statement a, we quickly deduced that the discount factor occurs in the given form.
$(b)$ ⟹ $(c)$

Henceforth, we derive the drift term from the discount factor

$\begin{matrix} E [e^{\int_{s}^{t} (F (s, u) - R (u)) d u} | F (s)] = 1 \end{matrix}$

(A7)

According to Lemma A1, this is equivalent to the fact that $ξ (s, t)$ and $F (v_{1}, v_{2})$ are independent and $E ξ (s, t) + \frac{1}{2} D^{2} ξ (s, t) = 0$ , where $v_{1} \leq s, v_{1} \leq v_{2},$ $ξ (s, t) = \int_{s}^{t} (F (s, u) - R (u)) d u$ . Since we are dealing with Gaussian variables, it is enough to examine the covariance.

$\begin{matrix} cov (F (s, u) - R (u), F (v_{1}, v_{2})) = c (s \land v_{1}, u, v_{2}) - c (u \land v_{1}, u, v_{2}) = c (v_{1}, u, v_{2}) - c (v_{1}, u, v_{2}) = 0 \end{matrix}$

(A8)

Since $ξ (s, t)$ is equal to $\int_{s}^{t} (F (s, u) - R (u)) d u$ , therefore $ξ (s, t)$ and $F (v_{1}, v_{2})$ are independent.

$\begin{matrix} E ξ (s, t) = \int_{s}^{t} (α (s, u) - α (u, u)) d u \end{matrix}$

(A9)

The variance is a bit more complicated to calculate.

$\begin{matrix} D^{2} ξ (s, t) & = \int_{s}^{t} \int_{s}^{t} c (u \land v, u, v) d v d u + \int_{s}^{t} \int_{s}^{t} c (s, u, v) d v d u - 2 \int_{s}^{t} \int_{s}^{t} c (s, u, v) d v d u \end{matrix}$

(A10)

$\begin{matrix} = \int_{s}^{t} \int_{s}^{t} (c (u \land v, u, v) - c (s, u, v)) d v d u \end{matrix}$

(A11)

Let us apply the Leibniz integral rule to the following function.

$\begin{matrix} f (t) & = E ξ (s, t) + \frac{1}{2} D^{2} ξ (s, t) = \int_{s}^{t} (α (s, u) - α (u, u)) d u + \frac{1}{2} \int_{s}^{t} \int_{s}^{t} (c (u \land v, u, v) - c (s, u, v)) d v d u \end{matrix}$

(A12)

$\begin{matrix} \frac{d f}{d t} & = α (s, t) - α (t, t) + \frac{1}{2} (\int_{s}^{t} (c (t \land v, t, v) - c (s, t, v)) d v + \int_{s}^{t} (c (u \land t, u, t) - c (s, u, t)) d u), \end{matrix}$

(A13)

from which

$\begin{matrix} \frac{d f}{d t} = α (s, t) - α (t, t) + \int_{s}^{t} (c (v, v, t) - c (s, v, t)) d v . \end{matrix}$

(A14)

Since $f (s) = 0$ , thus

$\begin{matrix} E ξ (s, t) + \frac{1}{2} D^{2} ξ (s, t) = 0, \forall 0 \leq s \leq t \Leftrightarrow α (s, t) = α (t, t) + \int_{s}^{t} [c (s, v, t) - c (v, v, t)] d v, \end{matrix}$

(A15)

for all $0 \leq s \leq t$ . Using Remark 1, we have established the implication from (b) to (c).
$(c)$ ⟹ $(a)$

First, we show that part (b) of the theorem is satisfied, by showing that the drift term has the form of (c) and this is sufficient because part (b) immediately demonstrates that $Z (s, t)$ is a regular martingale. It can be easily seen that in Lemma A1, using the previous notations, $ξ (s, t) = \int_{s}^{t} (F (s, u) - R (u)) d u$ and $F (v_{1}, v_{2})$ are independent. During the derivations Remark 1 is used as well.

$\begin{matrix} E ξ (s, t) = & \int_{s}^{t} α (s, u) - α (u, u) d u = \int_{s}^{t} α (u, u) - \int_{s}^{u} c (s, v, u) - c (v, v, u) d v - α (u, u) d u \end{matrix}$

(A16)

$\begin{matrix} = & \int_{s}^{t} \int_{s}^{u} c (s, v, u) - c (v, v, u) d v d u \end{matrix}$

(A17)

$\begin{matrix} D^{2} ξ (s, t) = & \int_{s}^{t} \int_{s}^{t} (c (u \land v, u, v) - c (s, u, v)) d v d u = \end{matrix}$

(A18)

$\begin{matrix} = & \int_{s}^{t} \int_{s}^{u} (c (v, u, v) - c (s, u, v)) d v d u + \int_{s}^{t} \int_{u}^{t} (c (u, u, v) - c (s, u, v)) d v d u \end{matrix}$

(A19)

Let us apply the Leibniz rule again for the following

f (t)

function using the fact that the covariance function

c (s_{1} \land s_{2}, t_{1}, t_{2})

is symmetric in

t_{1}

and

t_{2}

\begin{matrix} f (t) = & E ξ (s, t) + \frac{1}{2} D^{2} ξ (s, t) = \int_{s}^{t} \int_{s}^{u} c (s, v, u) - c (v, v, u) d v d u + \end{matrix}

(A20)

\begin{matrix} + \frac{1}{2} \int_{s}^{t} \int_{s}^{u} (c (v, u, v) - c (s, u, v)) d v d u + \frac{1}{2} \int_{s}^{t} \int_{u}^{t} (c (u, u, v) - c (s, u, v)) d v d u = \end{matrix}

(A21)

\begin{matrix} = & \frac{1}{2} \int_{s}^{t} \int_{s}^{u} c (s, u, v) - c (v, u, v) d v d u + \frac{1}{2} \int_{s}^{t} \int_{u}^{t} (c (u, u, v) - c (s, u, v)) d v d u = \end{matrix}

(A22)

\begin{matrix} = & \frac{1}{2} \int_{s}^{t} \int_{s}^{t} c (s, u, v) - c (v, u, v) d v d u - \frac{1}{2} \int_{s}^{t} \int_{s}^{t} (c (u, u, v) - c (s, u, v)) d v d u = \end{matrix}

(A23)

\begin{matrix} = & \frac{1}{2} \int_{s}^{t} \int_{s}^{t} c (s, u, v) - c (v, u, v) - c (u, u, v) + c (s, u, v) d v d u = 0 \end{matrix}

(A24)

\begin{matrix}  \end{matrix}

(A25)

Finally, the theorem is proved. □

Appendix A.2

This subsection calculates the expected value and standard deviation of the expressions previously marked with

ξ (s, t)

and

η (s, t)

and their correlation.

\begin{matrix} ξ (s, t) & = \int_{s}^{t} F (u, u) d u = \int_{s}^{t} r (u) d u \end{matrix}

(A26)

\begin{matrix} μ_{1} (s, t) & = E ξ (s, t) = E \int_{s}^{t} F (u, u) d u = \int_{s}^{t} E F (u, u) d u = \end{matrix}

(A27)

\begin{matrix} = \int_{s}^{t} ν - \frac{σ^{2}}{μ} + \frac{σ^{2}}{μ} e^{- μ (u - u)} + \frac{σ^{2}}{λ - μ} e^{- μ (u - u)} - \frac{σ^{2}}{λ - μ} e^{- λ (u - u)} d u \end{matrix}

(A28)

\begin{matrix} = \int_{s}^{t} ν - \frac{σ^{2}}{μ} d u = (ν - \frac{σ^{2}}{μ}) (t - s) \end{matrix}

(A29)

Now let us move on to the expected value of

η (s, t)

. The steps of the derivation are similar to what we have seen above.

\begin{matrix} η (s, t) & = \int_{s}^{t} F (s, u) d u \end{matrix}

(A30)

\begin{matrix} μ_{2} (s, t) & = E η (s, t) = E \int_{s}^{t} F (s, u) d u = \int_{s}^{t} E F (s, u) d u = \end{matrix}

(A31)

\begin{matrix} = \int_{s}^{t} ν - \frac{σ^{2}}{μ} + \frac{σ^{2}}{μ} e^{- μ (u - s)} + \frac{σ^{2}}{λ - μ} e^{- μ (u - s)} - \frac{σ^{2}}{λ - μ} e^{- λ (u - s)} d u = \end{matrix}

(A32)

\begin{matrix} = \int_{s}^{t} ν - \frac{σ^{2}}{μ} + \frac{σ^{2}}{μ} e^{- μ u + μ s} + \frac{σ^{2}}{λ - μ} e^{- μ u + μ s} - \frac{σ^{2}}{λ - μ} e^{- λ u + λ s} d u = \end{matrix}

(A33)

\begin{matrix} = {[ν u - \frac{σ^{2}}{μ} u - \frac{σ^{2}}{μ^{2}} e^{- μ u + μ s} - \frac{σ^{2}}{μ (λ - μ)} e^{- μ u + μ s} + \frac{σ^{2}}{λ (λ - μ)} e^{- λ u + λ s}]}_{u = s}^{u = t} = \end{matrix}

(A34)

\begin{matrix} = (ν - \frac{σ^{2}}{μ}) (t - s) - \frac{σ^{2}}{μ^{2}} (e^{- μ (t - s)} - 1) - \frac{σ^{2}}{μ (λ - μ)} (e^{- μ (t - s)} - 1) + \frac{σ^{2}}{λ (λ - μ)} (e^{- λ (t - s)} - 1) \end{matrix}

(A35)

After the derivation of the expected values, the standard deviation of the expressions marked with

ξ (s, t)

and

η (s, t)

are calculated.

\begin{matrix} c o v [F (u, u), F (v, v)] & = σ^{2} exp {2 μ min (u, v) - μ (u + v)} = σ^{2} e^{- μ | v - u |} \end{matrix}

(A36)

\begin{matrix} D^{2} ξ (s, t) & = \int_{s}^{t} \int_{s}^{t} σ^{2} e^{- μ | v - u |} d u d v \end{matrix}

(A37)

At first, let us deal with the inner integral, then move on to the outer integral.

\begin{matrix} \int_{s}^{t} e^{- μ | v - u |} d u = \int_{s}^{v} e^{μ u} e^{- μ v} d u + \int_{v}^{t} e^{μ v} e^{- μ u} d u = e^{- μ v} {[\frac{e^{μ u}}{μ}]}_{u = s}^{u = v} + e^{μ v} {[\frac{e^{- μ u}}{- μ}]}_{u = v}^{u = t} = \end{matrix}

(A38)

\begin{matrix} = \frac{1}{μ} (1 - e^{- μ (v - s)} - e^{- μ (t - v)} + 1) = \frac{1}{μ} (2 - e^{- μ (v - s)} - e^{- μ (t - v)}) \end{matrix}

(A39)

\begin{matrix} \frac{σ^{2}}{μ} \int_{s}^{t} (2 - e^{- μ (v - s)} - e^{- μ (t - v)}) d v = \frac{σ^{2}}{μ} (2 (t - s) - e^{μ s} {[\frac{e^{- μ v}}{- μ}]}_{v = s}^{v = t} - e^{- μ t} {[\frac{e^{μ v}}{μ}]}_{v = s}^{v = t}) = \end{matrix}

(A40)

\begin{matrix} = \frac{σ^{2}}{μ} (2 (t - s) + \frac{1}{μ} (e^{- μ (t - s)} - 1) - \frac{1}{μ} (1 - e^{- μ (t - s)})) = \frac{σ^{2}}{μ^{2}} (2 μ (t - s) + 2 e^{- μ (t - s)} - 2) \end{matrix}

(A41)

\begin{matrix} D^{2} ξ (s, t) = \frac{2 σ^{2}}{μ^{2}} (μ (t - s) + e^{- μ (t - s)} - 1) \end{matrix}

(A42)

The variance of

η (s, t)

can be similarly derived.

\begin{matrix} c o v [F (s, u), F (s, v)] = σ^{2} exp {λ s + (2 μ - λ) min (u, v) - μ (u + v)} \end{matrix}

(A43)

\begin{matrix} D^{2} η (s, t) = \int_{s^{t}} \int_{s^{t}} σ^{2} e^{λ s + (2 μ - λ) min (u, v) - μ (u + v)} d u d v \end{matrix}

(A44)

Similarly to the previous calculation, the derivation starts by calculating the inner integral without the

σ^{2}

multiplier.

\begin{matrix} \int_{s}^{t} e^{λ s + (2 μ - λ) min (u, v) - μ (u + v)} d u = \int_{s}^{v} e^{λ s + (2 μ - λ) u - μ u - μ v} d u + \int_{v}^{t} e^{λ s + (2 μ - λ) v - μ u - μ v} d u = \end{matrix}

(A45)

\begin{matrix} = \int_{s}^{v} e^{λ s + (μ - λ) u - μ v} d u + \int_{v}^{t} e^{λ s + (μ - λ) v - μ u} d u = e^{λ s - μ v} \int_{s}^{v} e^{(μ - λ) u} d u + e^{λ s} \int_{v}^{t} e^{μ v - λ v - μ u} d u = \end{matrix}

(A46)

\begin{matrix} = e^{λ s - μ v} {[\frac{e^{(μ - λ) u}}{μ - λ}]}_{u = s}^{u = v} + e^{λ s + μ v - λ v} {[\frac{e^{- μ u}}{- μ}]}_{u = v}^{u = t} = \end{matrix}

(A47)

\begin{matrix} = e^{λ s - μ v} \frac{1}{μ - λ} (e^{μ v - λ v} - e^{μ s - λ s}) + e^{λ s + μ v - λ v} \frac{1}{μ} (e^{- μ v} - e^{- μ t}) = \end{matrix}

(A48)

\begin{matrix} = \frac{1}{μ - λ} e^{λ s - λ v} - \frac{1}{μ - λ} e^{μ s - μ v} - \frac{1}{μ} e^{λ s + (μ - λ) v - μ t} + \frac{1}{μ} e^{λ s - λ v} \end{matrix}

(A49)

Now, let us move to the outer integral per term.

\begin{matrix} ➀ & = \frac{1}{μ - λ} e^{λ s} \int_{s}^{t} e^{- λ v} d v = \frac{e^{λ s}}{μ - λ} {[\frac{e^{- λ v}}{- λ}]}_{v = s}^{t} = \frac{e^{λ s}}{(λ - μ) λ} (e^{- λ t} - e^{- λ s}) = \end{matrix}

(A50)

\begin{matrix} = \frac{1}{(λ - μ) λ} (e^{- λ (t - s)} - 1) \end{matrix}

(A51)

\begin{matrix} ➁ & = \frac{- 1}{μ - λ} e^{μ s} \int_{s}^{t} e^{- μ v} d v = \frac{- 1}{μ - λ} e^{μ s} {[\frac{e^{- μ v}}{- μ}]}_{u = s}^{t} = \frac{1}{μ (μ - λ)} e^{μ s} (e^{- μ t} - e^{- μ s}) = \end{matrix}

(A52)

\begin{matrix} = \frac{1}{μ (μ - λ)} (e^{- μ (t - s)} - 1) \end{matrix}

(A53)

\begin{matrix} ➂ & = \int_{s}^{t} \frac{- 1}{μ} e^{λ s - μ t} e^{(μ - λ) v} d v = \frac{1}{μ (μ - λ)} e^{λ s - μ t} (e^{(μ - λ) s} - e^{(μ - λ) t}) = \end{matrix}

(A54)

\begin{matrix} = \frac{1}{μ (μ - λ)} (e^{- μ (t - s)} - e^{- λ (t - s)}) \end{matrix}

(A55)

\begin{matrix} ➃ & = \int_{s}^{t} \frac{1}{μ} e^{λ s - λ v} d v = \frac{1}{μ} e^{λ s} \int_{s}^{t} e^{- λ v} d v = \frac{- 1}{λ μ} e^{λ s} (e^{- λ t} - e^{- λ s}) = \frac{1}{λ μ} (1 - e^{- λ (t - s)}) \end{matrix}

(A56)

Therefore, by adding the

σ^{2}

multiplier, we got back the variance of

η (s, t)

D^{2} η (s, t) = \frac{σ^{2}}{(λ - μ) λ} (e^{- λ (t - s)} - 1) + \frac{σ^{2}}{μ (μ - λ)} (2 e^{- μ (t - s)} - e^{- λ (t - s)} - 1) + \frac{σ^{2}}{λ μ} (1 - e^{- λ (t - s)})

(A57)

The last variable to be calculated is

ρ (s_{1}, s_{2}, t_{1}, t_{2})

, indicating the correlation between

ξ (s_{1}, t_{1}) = \int_{s_{1^{t_{1}}}} F (u, u) d u

and

η (s_{2}, t_{2}) = \int_{s_{2^{t_{2}}}} F (s_{2}, v) d v

. However, for all financial products used in the article, the values of

t_{1}

and

t_{2}

were equal, denoted by t. Furthermore, we can assume that

s_{1} \leq s_{2}

, since

s_{1}

represents the time to which we discount, the time at which we want the value of the financial product, while

s_{2}

is the starting time of the transaction, which can start now or even later. So let us suppose that

s_{1} < s_{2} < t

\begin{matrix} c o v [F (u, u), F (s_{2}, v)] & = σ^{2} exp {λ min (u, s_{2}) + (2 μ - λ) min (u, v) - μ (u + v)} \end{matrix}

(A58)

\begin{matrix} c o v (ξ (s_{1}, t), η (s_{2}, t)) & = \int_{s_{1}}^{t} \int_{s_{2}}^{t} σ^{2} exp {λ min (u, s_{2}) + (2 μ - λ) min (u, v) - μ (u + v)} d v d u = \end{matrix}

(A59)

\begin{matrix} = \int_{s_{1}}^{s_{2}} \int_{s_{2}}^{t} σ^{2} exp {λ u + (2 μ - λ) u - μ (u + v)} d v d u + \end{matrix}

(A60)

\begin{matrix} + \int_{s_{2}}^{t} \int_{s_{2}}^{t} σ^{2} exp {λ t + (2 μ - λ) min (u, v) - μ (u + v)} d v d u \end{matrix}

(A61)

The two terms of the summation are calculated separately.

\begin{matrix} ➀ = & σ^{2} \int_{s_{1}}^{s_{2}} \int_{s_{2}}^{t} exp {μ u - μ v} d v d u = σ^{2} \int_{s_{1}}^{s_{2}} e^{- μ u} d u \int_{s_{2}}^{t} e^{- μ v} d v = \end{matrix}

(A62)

\begin{matrix} = & σ^{2} {[\frac{e^{μ u}}{μ}]}_{u = s_{1}}^{s_{2}} {[\frac{e^{- μ v}}{- μ}]}_{v = s_{2}}^{t} = \frac{σ^{2}}{μ^{2}} (e^{μ s_{2}} - e^{μ s_{1}}) (e^{- μ s_{2}} - e^{- μ t}) = \end{matrix}

(A63)

\begin{matrix} = & \frac{σ^{2}}{μ^{2}} (1 - e^{- μ (t - s_{2})} - e^{- μ (s_{2} - s_{1})} + e^{- μ (t - s_{1})}) \end{matrix}

(A64)

\begin{matrix} ➁ = & σ^{2} \int_{s_{2}}^{t} \int_{s_{2}}^{t} exp {λ t + (2 μ - λ) min (u, v) - μ (u + v)} d v d u \end{matrix}

(A65)

\begin{matrix} = & σ^{2} \int_{s_{2}}^{t} \int_{s_{2}}^{u} exp {λ t + (2 μ - λ) min (u, v) - μ (u + v)} d v d u + \end{matrix}

(A66)

\begin{matrix} + σ^{2} \int_{s_{2}}^{t} \int_{u}^{t} exp {λ t + (2 μ - λ) min (u, v) - μ (u + v)} d v d u = \end{matrix}

(A67)

\begin{matrix} = & σ^{2} e^{λ t} \int_{s_{2}}^{t} e^{- μ u} \int_{s_{2}}^{u} e^{μ v - λ v} d v d u + σ^{2} e^{λ t} \int_{s_{2}}^{t} e^{μ u - λ u} \int_{u}^{t} e^{- μ v} d v d u = \end{matrix}

(A68)

\begin{matrix} = & σ^{2} e^{λ t} \int_{s_{2}}^{t} e^{- μ u} {[\frac{e^{(μ - λ) v}}{μ - λ}]}_{v = s_{2}}^{u} d u + σ^{2} e^{λ t} \int_{s_{2}}^{t} e^{(μ - λ) u} {[\frac{e^{- μ v}}{- μ}]}_{v = u}^{t} d u = \end{matrix}

(A69)

\begin{matrix} = & \frac{σ^{2}}{μ - λ} e^{λ t} \int_{s_{2}}^{t} e^{- μ u} (e^{(μ - λ) u} - e^{(μ - λ) s_{2}}) d u + \frac{σ^{2}}{μ} e^{λ t} \int_{s_{2}}^{t} e^{(μ - λ) u} (e^{- μ u} - e^{- μ t}) d u = \end{matrix}

(A70)

\begin{matrix} = & \frac{σ^{2}}{μ - λ} \int_{s_{2}}^{t} e^{λ t - λ u} - e^{λ (t - s_{2}) - μ (u - s_{2})} d u + \frac{σ^{2}}{μ} \int_{s_{2}}^{t} e^{λ (t - u)} - e^{- μ (t - u) - λ (t - u)} d u = \end{matrix}

(A71)

\begin{matrix} = & \frac{σ^{2}}{μ - λ} e^{λ t} ({[\frac{e^{- λ u}}{- λ}]}_{u = s_{2}}^{t} - {[\frac{e^{- μ u + μ s_{2} - λ s_{2}}}{- μ}]}_{u = s_{2}}^{t}) + \frac{σ^{2}}{μ} e^{λ t} ({[\frac{e^{- λ u}}{- λ}]}_{u = s_{2}}^{t} - {[\frac{e^{μ u - λ u - μ t}}{μ - λ}]}_{u = s_{2}}^{t}) = \end{matrix}

(A72)

\begin{matrix} = & \frac{σ^{2}}{λ (μ - λ)} e^{λ t} (e^{- λ s_{2}} - e^{- λ t}) + \frac{σ^{2}}{μ (μ - λ)} e^{λ t} (e^{- μ t + μ s_{2} - λ s_{2}} - e^{- μ s_{2} + μ s_{2} - λ s_{2}}) + \end{matrix}

(A73)

\begin{matrix} + \frac{σ^{2}}{λ μ} e^{λ t} (e^{- λ s_{2}} - e^{- λ t}) + \frac{σ^{2}}{μ (μ - λ)} e^{λ t} (e^{(μ - λ) s_{2} - μ t} - e^{(μ - λ) t - μ t}) = \end{matrix}

(A74)

\begin{matrix} = & \frac{σ^{2}}{λ (μ - λ)} (e^{λ (t - s_{2})} - 1) + \frac{σ^{2}}{μ (μ - λ)} (e^{λ (t - s_{2}) - μ (t - s_{2})} - 1) + \end{matrix}

(A75)

\begin{matrix} + \frac{σ^{2}}{λ μ} (e^{λ (t - s_{2})} - 1) + \frac{σ^{2}}{μ (μ - λ)} (e^{λ (t - s_{2}) - μ (t - s_{2})} - 1) = \end{matrix}

(A76)

\begin{matrix} = & (\frac{σ^{2}}{λ (μ - λ)} + \frac{σ^{2}}{λ μ}) (e^{λ (t - s_{2})} - 1) + \frac{2 σ^{2}}{μ (μ - λ)} (e^{λ (t - s_{2}) - μ (t - s_{2})} - 1) \end{matrix}

(A77)

By adding the calculated two terms back together, we got the covariance between

ξ (s_{1}, t)

and

η (s_{2}, t)

\begin{matrix} c o v (ξ (s_{1}, t), η (s_{2}, t)) = & \frac{σ^{2}}{μ^{2}} (1 - e^{- μ (t - s_{2})} - e^{- μ (s_{2} - s_{1})} + e^{- μ (t - s_{1})}) + \end{matrix}

(A78)

\begin{matrix} + (\frac{σ^{2}}{λ (μ - λ)} + \frac{σ^{2}}{λ μ}) (e^{λ (t - s_{2})} - 1) + \frac{2 σ^{2}}{μ (μ - λ)} (e^{λ (t - s_{2}) - μ (t - s_{2})} - 1) \end{matrix}

(A79)

Therefore, the correlation between

ξ

and

η

calculated as follows

c o r r (ξ, η) = \frac{c o v (ξ, η)}{D ξ D η}

(A80)

Appendix A.3

In this subsection of the appendix, the analytical fair price of the European floorlet option is also derived, similarly to the previously derived European caplet option. As we have seen before, the fair price of the floorlet is the expected value of the payoff function under the risk-neutral measure.

P_{f l o o r l e t} (s) = E [e^{- \int_{s}^{t + Δ} r (u) d u} {(e^{Δ K} - e^{Δ F^{Δ} (t, t)})}_{+}]

(A81)

We use the previously introduced variables:

ξ

and

η

\begin{matrix} ξ (s, t + Δ) & = \int_{s}^{t + Δ} r (u) d u = \int_{s}^{t + Δ} F (u, u) d u \end{matrix}

(A82)

\begin{matrix} η (t, t + Δ) & = Δ F^{Δ} (t, t) = \int_{t}^{t + Δ} F (t, u) d u \end{matrix}

(A83)

Similarly to the previously derived pricing formula for the caplet, the conditional expected value of

ξ

η

follows a normal distribution. Hence, in this case, the conditional standard distribution theorem can also be used with the previously defined parameters. Therefore, the fair price of the European floorlet can be calculated as follows.

\begin{matrix} E [e^{- \int_{s}^{t + Δ} r (u) d u} {(e^{Δ K} - e^{Δ F^{Δ} (t, t)})}_{+}] = E [e^{- ξ} {(e^{Δ K} - e^{η})}_{+}] = \end{matrix}

(A84)

\begin{matrix} = E [E (e^{- ξ} {(e^{Δ K} - e^{η})}_{+} | η] = E [{(e^{Δ K} - e^{η})}_{+} \cdot E (e^{- ξ} | η)] \end{matrix}

(A85)

During the derivations, the law of total expectation and the fact that

{(e^{Δ K} - e^{η})}_{+}

is measurable for

η

is used.

As we can see

ξ \sim N (μ_{1}, σ_{1})

is normally distributed, therefore

- ξ \sim N (- μ_{1}, σ_{1})

, where

c o r r (- ξ, η) = - ρ

. Therefore

- ξ | η \sim N (- μ_{1} - ρ σ_{1} \frac{η - μ_{2}}{σ_{2}}, σ_{1}^{2} (1 - ρ^{2}))

. Since the conditional distribution of

- ξ

given

η

is known, therefore

E [e^{- ξ} | η]

can be calculated as the expected value of a lognormal distribution.

\begin{matrix} E [e^{- ξ} | η] = e^{- μ_{1} - ρ σ_{1} \frac{η - μ_{2}}{σ_{2}} + \frac{1}{2} σ_{1}^{2} (1 - ρ^{2})} \end{matrix}

(A86)

The integral returns the expected value of a random variable that is lognormally distributed. Returning to the pricing formula

\begin{matrix} E [{(e^{Δ K} - e^{η})}_{+} \cdot E [e^{- ξ} | η]] & = E [{(e^{Δ K} - e^{η})}_{+} \cdot e^{- μ_{1} - ρ σ_{1} \frac{η - μ_{2}}{σ_{2}} + \frac{1}{2} σ_{1}^{2} (1 - ρ^{2})}] = \end{matrix}

(A87)

\begin{matrix} = e^{- μ_{1} + \frac{1}{2} σ_{1}^{2} (1 - ρ^{2})} E [{(e^{Δ K} - e^{η})}_{+} \cdot e^{- ρ σ_{1} \frac{η - μ_{2}}{σ_{2}}}] = \end{matrix}

(A88)

\begin{matrix} = e^{Δ K + \frac{1}{2} ρ^{2} σ_{1}^{2}} \int_{- \infty}^{Δ K} \frac{1}{σ_{2} \sqrt{2 π}} e^{- \frac{{(x - (μ_{2} - ρ σ_{1} σ_{2}))}^{2}}{2 σ_{2}^{2}}} d x - \end{matrix}

(A89)

\begin{matrix} - e^{μ_{2} + \frac{{(σ_{2}^{2} - ρ σ_{1} σ_{2})}^{2}}{2 σ_{2}^{2}}} \int_{- \infty}^{Δ K} \frac{1}{σ_{2} \sqrt{2 π}} e^{- \frac{{(x - (μ_{2} + σ_{2}^{2} - ρ σ_{1} σ_{2}))}^{2}}{2 σ_{2}^{2}}} d x \end{matrix}

(A90)

Therefore, the analytical pricing formula for the European floorlet option in the Kennedy fields is as follows:

\begin{matrix} P_{f l o o r l e t} (s) = e^{Δ K - μ_{1} + \frac{1}{2} σ_{1}^{2}} Φ (\frac{Δ K - μ_{2} + ρ σ_{1} σ_{2}}{σ_{2}}) - e^{μ_{2} - μ_{1} + \frac{1}{2} (σ_{1}^{2} + σ_{2}^{2} - 2 ρ σ_{1} σ_{2})} Φ (\frac{Δ K - μ_{2} - σ_{2}^{2} + ρ σ_{1} σ_{2}}{σ_{2}}) \end{matrix}

(A91)

Appendix A.4

The fair price of a fixed vs floating swap for several periods (k) at time s can be written using the formula below. Let us denote the time periods by

s < T_{0} < T_{1} < \dots < T_{k}

and

τ_{j} = T_{j} - T_{j - 1}

\begin{matrix} P_{s w a p} (s) & = E [\sum_{j = 1}^{k} e^{- \int_{s}^{T_{j}} r (u) d u} (e^{Δ F^{Δ} (T_{j - 1}, T_{j - 1})} - e^{τ_{j} K})] = \end{matrix}

(A92)

\begin{matrix} = E [\sum_{j = 1}^{k} e^{- \int_{s}^{T_{j}} r (u) d u + Δ F^{Δ} (T_{j - 1}, T_{j - 1})} - e^{- \int_{s}^{T_{j}} r (u) d u + τ_{j} K}] = \end{matrix}

(A93)

\begin{matrix} = \sum_{j = 1}^{k} E [e^{- \int_{s}^{T_{j}} r (u) d u + Δ F^{Δ} (T_{j - 1}, T_{j - 1})}] - \sum_{j = 1}^{k} E [e^{- \int_{s}^{T_{j}} r (u) d u + τ_{j} K}] = \end{matrix}

(A94)

\begin{matrix} = \sum_{j = 1}^{k} E [e^{- \int_{s}^{T_{j}} r (u) d u + Δ F^{Δ} (T_{j - 1}, T_{j - 1})}] - \sum_{j = 1}^{k} e^{τ_{j} K} E [e^{- \int_{s}^{T_{j}} r (u) d u}] \end{matrix}

(A95)

As we have done previously, more additional variables are introduced,

ξ_{j}

and

η_{j}

, the following way.

\begin{matrix} ξ_{j} (s, T_{j}) & = \int_{s}^{T_{j}} r (u) d u = \int_{s}^{T_{j}} F (u, u) d u \end{matrix}

(A96)

\begin{matrix} η_{j} (T_{j - 1}, T_{j}) & = Δ F^{Δ} (T_{j - 1}, T_{j - 1}) = \int_{T_{j - 1}}^{T_{j}} F (T_{j - 1}, u) d u \end{matrix}

(A97)

Referring to previous calculations, we know the expected value and standard deviation of

ξ

and

η

. Therefore, the expected values of the variables are the following

\begin{matrix} μ_{ξ_{j}} & = E ξ_{j} (s, T_{j}) = E \int_{s}^{T_{j}} F (u, u) d u = (ν - \frac{σ^{2}}{μ}) (T_{j} - s) \end{matrix}

(A98)

\begin{matrix} μ_{η_{j}} & = E η_{j} (T_{j - 1}, T_{j}) = E Δ F^{Δ} (T_{j - 1}, T_{j - 1}) = \int_{T_{j - 1}}^{T_{j}} E F (T_{j - 1}, u) d u = \end{matrix}

(A99)

\begin{matrix} = (ν - \frac{σ^{2}}{μ}) τ_{j} - \frac{σ^{2}}{μ^{2}} (e^{- μ τ_{j}} - 1) - \frac{σ^{2}}{μ (λ - μ)} (e^{- μ τ_{j}} - 1) + \frac{σ^{2}}{λ (λ - μ)} (e^{- λ τ_{j}} - 1) \end{matrix}

(A100)

and the covariance is

\begin{matrix} σ_{ξ_{j}}^{2} & = D^{2} ξ_{j} (s, T_{j}) = \frac{2 σ^{2}}{μ^{2}} ((T_{j} - s) μ + e^{- μ (T_{j} - s)} - 1) \end{matrix}

(A101)

\begin{matrix} σ_{η_{j}}^{2} & = D^{2} η_{j} (T_{j - 1}, T_{j}) = \frac{σ^{2}}{(λ - μ) λ} (e^{- λ τ_{j}} - 1) + \frac{σ^{2}}{μ (μ - λ)} (e^{- μ τ_{j}} - 1) + \end{matrix}

(A102)

\begin{matrix} + \frac{σ^{2}}{μ (μ - λ)} (e^{- μ τ_{j}} - e^{- λ τ_{j}}) + \frac{σ^{2}}{λ μ} (1 - e^{- λ τ_{j}}) \end{matrix}

(A103)

Due to the properties of the Gaussian random field,

(ξ_{j}, η_{j})

always follows a multivariate normal distribution, with the covariance matrix shown before.

\begin{matrix} c o v (ξ_{j}, η_{j}) = & \frac{σ^{2}}{μ^{2}} (1 - e^{- μ (T_{j} - T_{j - 1})} - e^{- μ (T_{j - 1} - s)} + e^{- μ (T_{j} - s)}) + \end{matrix}

(A104)

\begin{matrix} + (\frac{σ^{2}}{λ (μ - λ)} + \frac{σ^{2}}{λ μ}) (e^{λ (T_{j} - T_{j - 1})} - 1) + \frac{2 σ^{2}}{μ (μ - λ)} (e^{λ (T_{j} - T_{j - 1}) - μ (T_{j} - T_{j - 1})} - 1) \end{matrix}

(A105)

The correlation between

ξ_{j}

and

η_{j}

is the value of the covariance normalized with the standard deviation of

ξ_{j}

and

η_{j}

c o r r (ξ_{j}, η_{j}) = \frac{c o v (ξ_{j}, η_{j})}{D ξ_{j} D η_{j}}

(A106)

Because of the properties of the normal distribution, the distribution of

- ξ_{j} + η_{j}

is also normally distributed where the mean of the convolution is the sum of the means, and the variance is the following.

- ξ_{j} + η_{j} \sim N (- μ_{ξ_{j}} + μ_{η_{j}}, σ_{ξ_{j}}^{2} + σ_{η_{j}}^{2} - 2 ρ σ_{ξ_{j}} σ_{η_{j}})

(A107)

Therefore, the price of the interest rate swap can be easily calculated

\begin{matrix} P_{s w a p} (s) & = \sum_{j = 1}^{k} E (e^{- ξ_{j} + η_{j}}) - \sum_{j = 1}^{k} e^{τ_{j} K} E (e^{- ξ_{j}}) = \end{matrix}

(A108)

\begin{matrix} = \sum_{j = 1}^{k} e^{- μ_{ξ_{j}} + μ_{η_{j}} + \frac{1}{2} (σ_{ξ_{j}}^{2} + σ_{η_{j}}^{2} - 2 ρ σ_{ξ_{j}} σ_{η_{j}})} - \sum_{j = 1}^{k} e^{τ_{j} K} e^{- μ_{ξ_{j}} + \frac{1}{2} σ_{ξ_{j}}^{2}} = \end{matrix}

(A109)

\begin{matrix} = \sum_{j = 1}^{k} e^{- μ_{ξ_{j}} + μ_{η_{j}} + \frac{1}{2} (σ_{ξ_{j}}^{2} + σ_{η_{j}}^{2} - 2 ρ σ_{ξ_{j}} σ_{η_{j}})} - \sum_{j = 1}^{k} e^{τ_{j} K - μ_{ξ_{j}} + \frac{1}{2} σ_{ξ_{j}}^{2}} \end{matrix}

(A110)

References

Kennedy, D. P. The term structure of interest rates as a Gaussian random field. Mathematical Finance 1994, 4, 247–258. [Google Scholar] [CrossRef]
Kennedy, D. P. Characterizing Gaussian models of the term structure of interest rates. Mathematical Finance 1997, 7, 107–116. [Google Scholar] [CrossRef]
Heath, D. C.; Jarrow, R. A.; Morton, A. Bond pricing and term structure of interest rates: a new methodology for contigent claims valuation. Econometrica 1992, 60, 77–105. [Google Scholar] [CrossRef]
Arató, N. M. Mean estimation of Brownian sheet. Computers Mathematics with Applications 1997,, 33, 12–25. [Google Scholar] [CrossRef]
Rozanov, Ju. Infinite-dimensional Gaussian distributions: Proceedings (Proceedings of the Steklov Institute of Mathematics number 108 (1968)), 3rd ed.; American Mathematical Society: Providence, Rhode Island, 1971. [Google Scholar]
Shreve, S. E. Stochastic Calculus for Finance I-II., 1st ed; Springer Finance: Pittsburg, USA, 2004. [Google Scholar]
Cheyette, O. Markov representation of the Heath-Jarrow-Morton model SSRN Electronic Journal 2001. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=6073 (accessed on 13 October 2023).
Beyna, I.; Wystup, U. On the calibration of the Cheyette interest rate model PQF Working Paper Series 2010. Available online: chrome-extension://efaidnbmnnnibpcajpcglclefindmkaj/https://mathfinance.com/wp-content/uploads/2017/06/beyna-wystup-calibrationofcheyette.pdf (accessed on 26 October 2023).
Emerick, J.; Tatsat, H. Stochastic Volatility Models - Heston Model Calibration to option prices QuantPy 2022. Available online: https://quantpy.com.au/stochastic-volatility-models/heston-model-calibration-to-option-prices/ (accessed on 10 January 2023).
Mikhailov, S.; Nögel, U. Heston’s Stochastic Volatility Model Implementation, Calibration and Some Extensions. Fraunhofer Institute for Industrial Mathematics 2003. [Google Scholar]
Grenander, U. Stochastic processes and statistical inference. Ark. Mat. 1950, 1, 195–277. [Google Scholar] [CrossRef]
Norros, I.; Valkeila, E.; Virtamo, J. An Elementary Approach to a Girsanov Formula and Other Analytical Results on Fractional Brownian Motions. Bernoulli 1999, 5, 571–587. [Google Scholar] [CrossRef]

Figure 1. Simulated Kennedy-fields

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

On the Calibration of the Kennedy Model

Abstract

1. Introduction

2. Kennedy Model

2.1. Connection between HJM and the Kennedy-Model

3. Parameter Estimation

3.1. Maximum Likelihood Estimations

3.1.1. The Case of Different Expected Values

3.1.2. The Case of Constant Expected Value

3.1.3. Some Simple Examples

3.2. Parameter Estimations of the Kennedy Field

4. Simulation of the Kennedy Field

5. Option Pricing

5.1. European Caplet

5.1.1. Expected Values and Variances

5.2. European Floorlet

5.3. Swap

5.4. Par Swap Rate

6. Calibration on Simulated Data

7. Calibration on Real Data

8. Results

9. Discussion

10. Conclusions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

Appendix A

Appendix A.1

Appendix A.2

Appendix A.3

Appendix A.4

References

MDPI Initiatives

Important Links

Subscribe