Prerpints.org logo
Preprint
Article

Blind Cyclostationary Based Carrier Number and Spacing Estimation for Carrier-Aggregated Direct Sequence Spread Spectrum Cellular Signals

Altmetrics

Downloads

66

Views

31

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

04 September 2024

Posted:

05 September 2024

You are already at the latest version

Alerts
Abstract
Automatic and blind parameter estimation based on the inherent features of wireless signals is a major research area due to the fact that these techniques lead to the simplification of receivers, especially in terms of coarse synchronization, more importantly reduce down the signaling load at the control channels. Thus, in the literature many techniques are proposed to estimate a vast set of parameters including modulation types and orders, data and chip rates, phase and frequency offsets and so on. In this paper, a cyclostationary feature detection based method is proposed to estimate the carrier numbers and carrier spacing of carrier-aggregated direct sequence spread spectrum cellular signals blindly. The particular chip rate of the signal is also estimated through the process jointly. In the paper, after the proposed method is formulated, the measurement setup which is developed to collect the data for the validation of the proposed method is introduced. The measurement results are post-processed for performance analysis purposes. To that end, the method is investigated in terms of SNR values, different channel conditions, and measurement durations. Furthermore, the performance of the proposed method is compared with that of energy detection. Measurement results indicate superior performance of the proposed method under significant wireless channel impairments and in low-SNR regions.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Through the time that every generation of wireless technologies are deployed, their penetration to all other sectors or domains also increase and more complex communications topology and scenarios emerge; human to human communications evolved machine to machine communications swiftly. To be able to support diverse communications requirements of the age, wireless networks strive for becoming more adaptive, seamless, effective, robust, and intelligent. One of the main overheads and resource consuming aspects of traditional wireless communications are the signaling overheads which make sure that the right information is shared with the right point. Such overhead can be reduced down significantly if intelligent receivers are able to estimate the existence of the user in the spectrum along with its signaling parameters blindly. Therefore blind transmission parameter estimation is a critical component of modern wireless communication systems. To this end, extensive work is put on in cognitive radio (CR) domain under spectrum sensing research and techniques based on energy detection, match filtering, cyclostationary feature detection (CFD) are developed.
One of the prominent means of accessing the wireless spectrum is through direct sequence spread spectrum (DSSS) access and when the works on parameter estimation of DSSS signals are considered, CFD becomes the prominent feature. Thus, in one of the initial works [1] second order cyclostationary statistics are utilized to jointly estimate the phase, amplitude, and time delay of each uplink direct sequence code division multiple access (DS-CDMA) signals in a multi-user access setting based on minimum mean square error (MMSE) estimates of the parameters. In [2] chip rate and carrier frequency estimation is achieved by utilizing adaptive transform domain filters for phase shift keyed DSSS signals. The proposed approach works on single carrier setting and provides harmonic continuous wave and narrow band interference rejection. Air interface recognition via CFD is proposed in [3] for wireless cellular signal of single carrier time division multiple access (TDMA), orthogonal frequency division multiple access (OFDM), and single carrier code division multiple access (CDMA) signals. Simulation results based on binary hypothesis testing indicates successful separation (i.e. probability of detection above 0.9 ) of air interfaces around 7 dB of signal to noise ration (SNR) for probability of false alarm of 0.05 . A time-domain blind phase, amplitude and time delay estimation algorithm based on CFD is proposed in [4] for CDMA signals. Then, a detailed analysis of cyclostationarity for recognition of CDMA signals is provided in [5]. In this work, an explicit derivation of cyclic auto-correlation function (CAF) is provided first, then it is mathematically shown that as the number of multiplexing codes increases, cyclostationarity based on chip rate decreases. It is also revealed that the utilization of scrambling codes significantly deteriorate the cyclostationarity. Finally, simulation results illustrated that considering antenna diversity and including multiple adjacent channel CDMA signals in the decision process improves the detection probability.
CR is a technology which provides intelligence to the wireless communications networks. With many other features of CR, deployment of secondary users (SU) along with primary users (PU) in the wireless spectrum leads to the efficient utilization of resources in a dynamic manner. In this context, CFD is a spectrum sensing feature which benefits from the cyclic features of occupant signals and [6] proposes CFD to sense PU through multiple cyclic properties of symbol rate, the coding and modulation schemes, guard periods. A generalized likelihood ratio test (GLRT) is proposed for the detection of periodic statistical properties. Simulation results illustrate 1 dB detection gain per additional cycle frequency. Furthermore the study considers collaborative detection scheme with improved probability of detection. In the same context [7] utilizes autocorrelative properties of pseudorandom noise (PN) sequences for DSSS signal detection. A time domain hypothesis test is proposed to achieve the decision. Simulation results indicate successful detection in the low-SNR regime for additive white Gaussian noise ( A W G N ) channels. [8] provides a comparative analysis of performance of CFD for the separation of different wireless signals i.e., ultra wideband (UWB), OFDM, and CDMA. Extensive simulation results indicate strong detection performance when compared to other signals for CDMA, mainly due to the significant cyclic property of the spreading sequences. For the given probability of false alarm of 0.01 , CDMA signals have 5 dB performance improvement against OFDM and 10 dB against UWB for the same probability of detection. Thus CDF emerges as an advantageous technique for particular estimation of the parameters of DSSS signals.
As the multi-carrier systems emerged with the 3rd generation cellular systems, detection of number of carriers became an important issue in terms of coarse synchronization. In [9], blind estimation of number of sub-carriers of multi-carrier CDMA signals is proposed based on high order cumulants. Raw experimental results leaded to successful carrier number estimation for MC-DS-CDMA and MC-CDMA signals for 5 db SNR. Carrier frequency and symbol rate estimation via CDF for single carrier multiple phase shift keying (MPSK) signals is proposed in [10]. Cyclic spectrum is constructed based on MPSK characteristics and normalized mean square error (NMSE) estimations indicate accurate estimation of the parameters under A W G N channel conditions. In [11] cycle frequency domain profile (CDP) of single carrier analog and digital wireless modulations are fed to Hidden Markov Model (HMM) for signal classification. Again under A W G N channel conditions, the proposed classifier managed to distinguish SSB-SC-AM, BPSK, b-FSK, MSK and QPSK modulations in low-SNR regimes. As an application of online unsupervised learning machine (LEAP), principal component analysis (PCA) of a general DSSS sequence is utilized for PN sequence estimation in [12]. The proposed LEAP technique is modified for PN sequence estimation in such a way that state transition matrices are normalized before their utilization. Furthermore, instead of fixed learning states, adaptive ones are implemented. Simulation results indicate high probability of correct estimation increasing with number of iterations for the network convergence. Also in [13] an algorithm depending on turbo processing is proposed for the estimation of PN sequence and data bits of DSSS signals. The proposed method has better estimation performance when compared to eigen-value decomposition (EVD) based methods. The turbo processing algorithm is designed to achieve the estimations of these parameters blindly; which is an important requirement of advanced wireless communications systems.
As the wireless communications systems become more complex the multiplexing schemes also gets complicated. To be able to support the high data rate requirements of next generation networks, multi-carrier modes of access techniques are developed and introduced. Therefore, blind carrier frequency, carrier number and PN sequence estimation became important issues as implied by the research above. Considering the performance of CFD for DSSS signals, particularly for CDMA multiplexing [8], and ability to implement CFD for multiple cycle frequencies [6], this paper proposes blind estimation of number of carriers and carrier spacing of multi-carrier CDMA signals along with the estimation of exact chip rate, leading to joint carrier number estimation and signal identification for multi-carrier CDMA access. Through the rest of the paper first, the signal model for the carrier-Aggregated DSSS signals is provided. Second, general formulations of utilized CFD methodology are provided as a prior information. Third, the proposed method is introduced and proved through the cyclostationarity derivations over the signal model. A measurement setup is developed to validate the theoretical analysis, thus, the measurement setup is described in the following section. Fifth, in the measurement results section post-processing methodology for the measurements conducted is detailed along with the estimation method utilized. Then a parametric assessment of the proposed method based on the measurements conducted is provided considering different S N R values, wireless channel conditions,and measurement durations. Moreover the proposed method is compared with energy detection (ED). General discussion on the method along with possible future work concludes the paper.

2. Signal Model

DSSS downlink cellular systems can achieve carrier aggregation in a) intraband contiguous; b) intraband non-contiguous; c) interband non-contiguous formats [14] under multiplexing schemes of High Speed Packet Access (HSPA), Evolved High Speed Data Packet Access (HSDPA), cdma2000 Evolution-Data Optimized (EV-DO)/1X Advanced, Long Term Evolution (LTE) Advanced or 5G New Radio (NR). Derived from the preliminary models in [15,16,17], the discrete-time intra-band contiguous signal at the output of the transmitter can be written as
x c ( n ) = ∑ j = 0 J − 1 e j ∑ n = − ∞ ∞ a c , j ( n ) ∑ k = 0 P j − 1 s j ( n − k T )
where c is the carrier index, J is the number of spreading codes which is per user, e j is the amplitude of the corresponding code. a c , j ( n ) is the user symbol to be modulated to the c t h carrier, spread with the j t h code. a c , j ( n ) is normalized unity average energy i.e., E [ | a c , j ( n ) | 2 ] = 1 , s j ( n ) is the spreading sequence for the n t h symbol of the j t h code which can be written in a vector form as s j ( n ) = [ s ( n ; 0 ) , s ( n ; 1 ) … s ( n ; P j − 1 ) ] T where P j is the chip process gain. Please note that s j ( n ) is comprised of a predefined and periodic Walsh-Hadamard spreading sequence which can be represented as w j = [ w j ( 0 ) , w j ( 1 ) … w j ( P j − 1 ) ] and a base station specific scrambling sequence which is overlaid onto the Walsh-Hadamard sequence b ( n ) = [ b ( n ; 0 ) , b ( n ; 1 ) … b ( n ; P j − 1 ) ] . Thus the spreading sequence per bit becomes s j ( n ; k ) = w j ( n ) b ( n ; k ) , k ∈ 1 , … P j . In equation (1) T is the chip period which is related to the symbol period T j through the chip process gain as T j = P j T , ∀ j . Passing through dispersive multi-path wireless channel the received signal can be described as
y c ( t ) = ∑ n = − ∞ ∞ x c ( n ) h c , j ( t − n T − τ j ) e 2 j π c f 0 ( t − n T − τ j ) ,
where h c , j ( t ) represents the overall wireless channel impulse response along with τ j the propagation delay per user. The open-form received signal is defined as
y c ( t ) = ∑ j = 0 J − 1 e j ∑ n = − ∞ ∞ a c , j ( n ) ∑ k = 0 P j − 1 s j ( n − k P j ) h c , j ( t − n T − τ j ) e 2 j π c f 0 ( t − n T − τ j ) .
Since c carriers will be aggregated the complete received signal becomes
y ( t ) = ∑ c = 0 C − 1 y c ( t ) + v c ( t ) ,
where C is the number of aggregated carriers and v c ( t ) corresponds to A W G N with zero mean and variance of σ v 2 . Please note that cdma2000 EVDO Support of different RF channel bandwidths of the form N x 1.2288 MHz where C = 1 , 3 , 6 , 9 , 12 , Evolved HSDPA C = 1 , 2 , 4 . Since its initial release, LTE/LTE Advanced supports channel bandwidths of 1.4 MHz, 3 MHz, 5 MHz, 10 MHz, 15 MHz and 20 MHz, and in 5G NR, up to 16 carriers can be aggregated up-limited by 1 GHz of spectrum. The discrete form of the received signal can be obtained by y ( n ) = y ( t ) ∣ t = n T .

3. Cyclostationarity Preliminaries

In wireless random signals there are periodic processes that are not functions of time but stems from the signals statistical characteristics which vary with time. These are called as cyclostationary processes and these kinds of periodicities can be introduced due to coding, multiplexing, modulation and sampling. Especially in the field of wireless communications, these processes are wide-sense cyclostationary with the mean and the autocorrelation are time invariant. Assuming that y ( t ) defined in Section 2 is stationary over time t, and is a power signal, the mean and autocorrelation of y ( t ) can be defined as
m y ( t ) = E [ y ( t ) ] ,
r y ( t 1 , t 2 ) = E [ y ( t 1 ) y * ( t 2 ) ] ,
where E [ · ] denotes the expected value while * implies conjugation. Due to the wide-sense stationarity of y ( t ) , the mean and autocorrelation functions can be written in terms of time difference t 2 − t 1
m y ( t ) = M 0 ,
r y ( t 1 , t 2 ) = R y ( t 2 − t 1 ) .
t 2 and t 1 can be written in terms of time lags over a given time t as t 2 = t + τ / 2 and t 1 = t − τ / 2 . When these modifications are replaced on equation (8)
r y ( t 1 , t 2 ) = R y ( τ ) .
The power spectral density of the time invariant autocorrelation is given by its Fourier Transform as
S y ( f ) = ∫ − ∞ ∞ R y ( τ ) e − 2 j π f τ d τ .

3.1. Cyclic Autocorrelation Function

Since nonstationary cyclostationary signals exhibit time-varying behaviour in terms of periodic time variation, their second order moments can be represented by Fourier series as follows
R y ( t , τ ) = ∑ α R y α ( τ ) e 2 j π α t ,
where α is the cycle frequency. The periodic time variation of the cyclostationary signal is bound with the cycle frequency by α = k / T 0 , ∀ k integers, and T 0 period. Since the cyclostationary signals are extended to Fourier series through cyclic autocorrelation function, the Fourier coefficients become
R y α ( τ ) = lim T → ∞ 1 T ∫ − T / 2 T / 2 R y ( t , τ ) e − 2 j π α t d t .
Please note that for α = 0 , R y α ( τ ) converges to the autocorrelation function in equation (9). Utilizing equations (6) and (9), (12) can be written in the open form of cyclic autocorrelation function (CAF)
R y α ( τ ) = lim T → ∞ 1 T ∫ − T / 2 T / 2 x ( t + τ / 2 ) x * ( t − τ / 2 ) e − 2 j π α t d t .

3.2. Spectral Correlation Function

Similar to the Fourier analysis between autocorrelation function and its PSD, the spectral correlation function (SCF) becomes the Fourier transform for cyclic autocorrelation function
S y α ( f ) = ∫ − ∞ ∞ R y α ( τ ) e − 2 j π α τ d τ ,
and please note that SCF can also be interpreted as correlation of the complex envelopes of multiple sub-bands of a signal i.e., starting from the center frequency f, the separation between the center frequencies of the sub-bands are defined by α .

4. Proposed Method

Combining equations (6), (9), and (11), CAF can be written as
E [ y ( t ) y * ( t + τ ) ] = ∑ α R y α ( τ ) e 2 j π α t ,
furthermore, a constant estimator of equation (13) can be formulated by
R ˜ y α ( τ ) = 1 Γ ∑ t = 0 Γ − 1 y ( t ) y * ( t + τ ) e − 2 j π α t ,
where Γ is the observation time interval. Autocorrelation of the recorded signal can be computed by
[ ∑ c = 0 C − 1 ∑ j = 0 J − 1 e j ∑ n = − ∞ ∞ a c , j ( n ) ∑ k = 0 P j − 1 s j ( n − k P j ) h c , j ( t − n T − τ j ) ] e 2 j π c f 0 ( t − n T − τ j ) ∑ c = 0 C − 1 ∑ j = 0 J − 1 e j ∑ m = − ∞ ∞ a c , j ( m ) ∑ l = 0 P j − 1 s j ( m − l P j ) h c , j ( t − n T − τ j + τ ) * e − 2 j π c f 0 ( t − n T − τ j + τ ) ,
and note that since v c ( t ) is zero mean σ v 2 variance process, it is eliminated through the averaging operation. If we focus on the extensive set of summations and multiplications in equation (17) it is observed that the core subset of multiplications is
{ ∑ n = − ∞ ∞ a c , j ( n ) ∑ k = 0 P j − 1 s j ( n − k P j ) h c , j ( t − n T − τ j ) } ∑ m = − ∞ ∞ a c , j ( m ) ∑ l = 0 P j − 1 s j ( m − l P j ) h c , j ( t − n T − τ j + τ ) * .
Due to the orthogonality of the spreading codes of DSSS signals, it can be written that if a n k is the user information for the k t h user at the time of n,
E { a n k a m l * } = σ a 2 ,
if n = m and k = l , otherwise 0, since
E { s j ( n − k P j ) s j ( m − l P j ) * } = 0 ,
unless n = m and k = l . Therefore, (18) can be written for particular values of n,m,k, and l in terms of expectations of sums as
E [ { ∑ n ≠ m a c , j ( n ) ∑ k s j ( n − k P j ) h c , j ( t − n T − τ j ) } ∑ m a c , j ( m ) ∑ l s j ( m − l P j ) h c , j ( t − n T − τ j + τ ) * ] = 0 ,
E [ { ∑ n a c , j ( n ) ∑ k s j ( n − k P j ) h c , j ( t − n T − τ j ) } ∑ m a c , j ( m ) ∑ l ≠ k s j ( m − l P j ) h c , j ( t − n T − τ j + τ ) * ] = 0 ,
and it can be inferred from equations (19) and (20) that for both n ≠ m and k ≠ l , equation (21) or (22) becomes zero. Furthermore, the only case that provide non-zero can be written by
E [ { ∑ n a c , j ( n ) ∑ k s j ( n − k P j ) h c , j ( t − n T − τ j ) } ∑ m = n a c , j ( m ) ∑ l = k s j ( m − l P j ) h c , j ( t − n T − τ j + τ ) * ] ≠ 0 ,
Therefore the sums of multiplications in equation (17) reduces down to
∑ c = 0 C − 1 ∑ j = 0 J − 1 e j 2 ∑ n = m = − ∞ ∞ | a c , j ( n ) | 2 ∑ k = l = 0 P j − 1 s j 2 ( n − k P j ) h c , j ( t − n T − τ j ) h c , j ( t − n T − τ j + τ ) e − 2 j π c f 0 τ ,
and since E [ | a c , j ( n ) | 2 ] = 1 , and multiplications in the summations leads to non-zero results for a single case, equation (24) can be written as
∑ c = 0 C − 1 ∑ j = 0 J − 1 ∑ k = l = 0 P j − 1 e j 2 s j 2 ( n − k P j ) h c , j ( t − n T − τ j ) h c , j ( t − n T − τ j + τ ) e − 2 j π c f 0 τ .
Plugging equation (25) into (16) leads to
R ˜ y α ( τ ) = 1 Γ ∑ t = 0 Γ − 1 ∑ c = 0 C − 1 ∑ j = 0 J − 1 ∑ k = l = 0 P j − 1 e j 2 s j 2 ( n − k P j ) h c , j ( t − n T − τ j ) h c , j ( t − n T − τ j + τ ) e − 2 j π ( c f 0 τ + α t ) ,
which indicates that for the particular case of α = 0 and ∀ τ the constant estimator of CAF given in (16) produces Fourier coefficients for each aggregated carrier of an intra-band contiguous downlink DSSS cellular signal, starting from the zero-lag correlation point of τ = 0 for the first carrier and so on. To that end, since the SCF of the sampled signal is given by [19]
S y ( f ) = 1 T s ∑ n = − ∞ ∞ S y f − n T s ,
where T s is the spreading sequence period, spectral implications of equation (26) can be observed through the SCF based on [1] and [18] as
S y ( f ) = σ a 2 T ∑ c = 0 C − 1 G k ( f + c f 0 ) G k ( f − c f 0 ) ,
where G k ( f ) is the Fourier transform of correlation of the corresponding spreading sequences over c t h carrier.

5. Measurement Setup

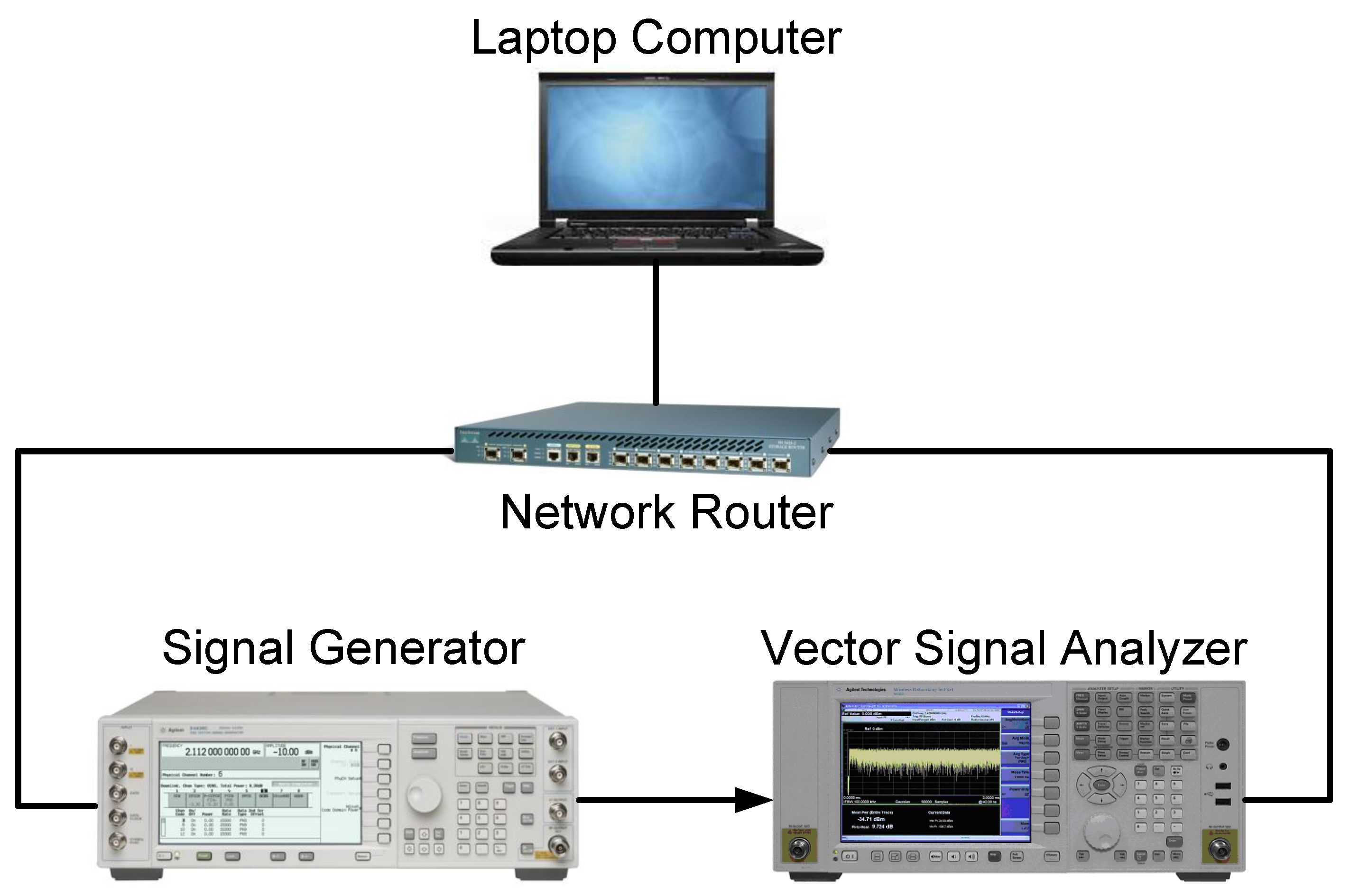
Estimation performance of the proposed method is investigated through the analysis of controlled measurements conducted on a measurement setup. The measurement system consists of an Agilent ESG E4438C signal generator to generate the standard based cellular signals, an Agilent E4440A PSA series spectrum analyzer to receive the signals along with the accompanying vector signal analyzer (VSA) software to make sure that the signals are recorded with limited distortion due to hardware impairments, and a laptop computer to implement and run the proposed method along with accompanying cables, connectors. The measurement processes are controlled by the laptop computer since all the devices are connected to each other through the network router utilizing transmission control and internet protocols. All the measurement parameters are set and controlled by the laptop computer and the recorded signals are also saved at the laptop hard disks. The setup is shown in Figure 1.
Through the measurement process, signal parameters are adjusted by the software running on the laptop. Thus, the parametric analysis which is based on the measurement parameters such as number of carriers (c), signal transmit power, signal type, protocol settings, and data length could be adjusted methodologically. Furthermore the vendor-provided VSA software ensured the signal acquisition and recording quality as indicated before. Please note that since only the transmit power of the signal can be determined by the measurement system, the S N R values of the received signal are determined by a software module developed along with implemented proposed method. Therefore, all the signal transmission loop is controlled and completed on the laptop computer while the transmitter and the receiver is allocated in the laboratory.
Table 1 depicts the list of the parameters utilized during the measurement process. The measurements are repeated for 10 times by the aid of developed software. Please note that due to the limitations of the measurement devices, only the cdma2000 intra-band contiguous carrier aggregated signals were able to be generated by the measurement setup, thus the validation of the proposed method is conducted through these recordings however the results obtained can be generalized to other cellular signals due to the fact that fundamental physical layer signal model are the same with that of other cellular intra-band carrier aggregated signals and spreading schemes are also standardized in the same way.

6. Measurement Results

After the measurements are taken, the recorded cdma2000 intra-band contiguous carrier aggregated signals are post-processed in MATLAB to adjust the S N R values of the received signals observed at the receiver side and to be able to reflect the real life impairments on the signals. The channel types utilized in this context are listed in Table 2. Please note that all the code division multiple access (CDMA) channel models deployed are 3GPP TR 25.943 V6.0.0 (2004-12) compliant.
In this setting, utilizing an extensive post-processing methodology, each measurement convoluted with random channel instances1 created from channel models listed in Table 2 and 500 measurements are obtained for each signal type,i.e., 3-carrier and 4-carrier signals ( c = 3 and c = 4 ), for each S N R value and measurement duration in Table 1. As the data set is formed, first the proposed method is implemented through (26), and (27) on a baseline case, e.g., A W G N signals with S N R = 15 dB are selected for both carrier types to observe the output of (28). 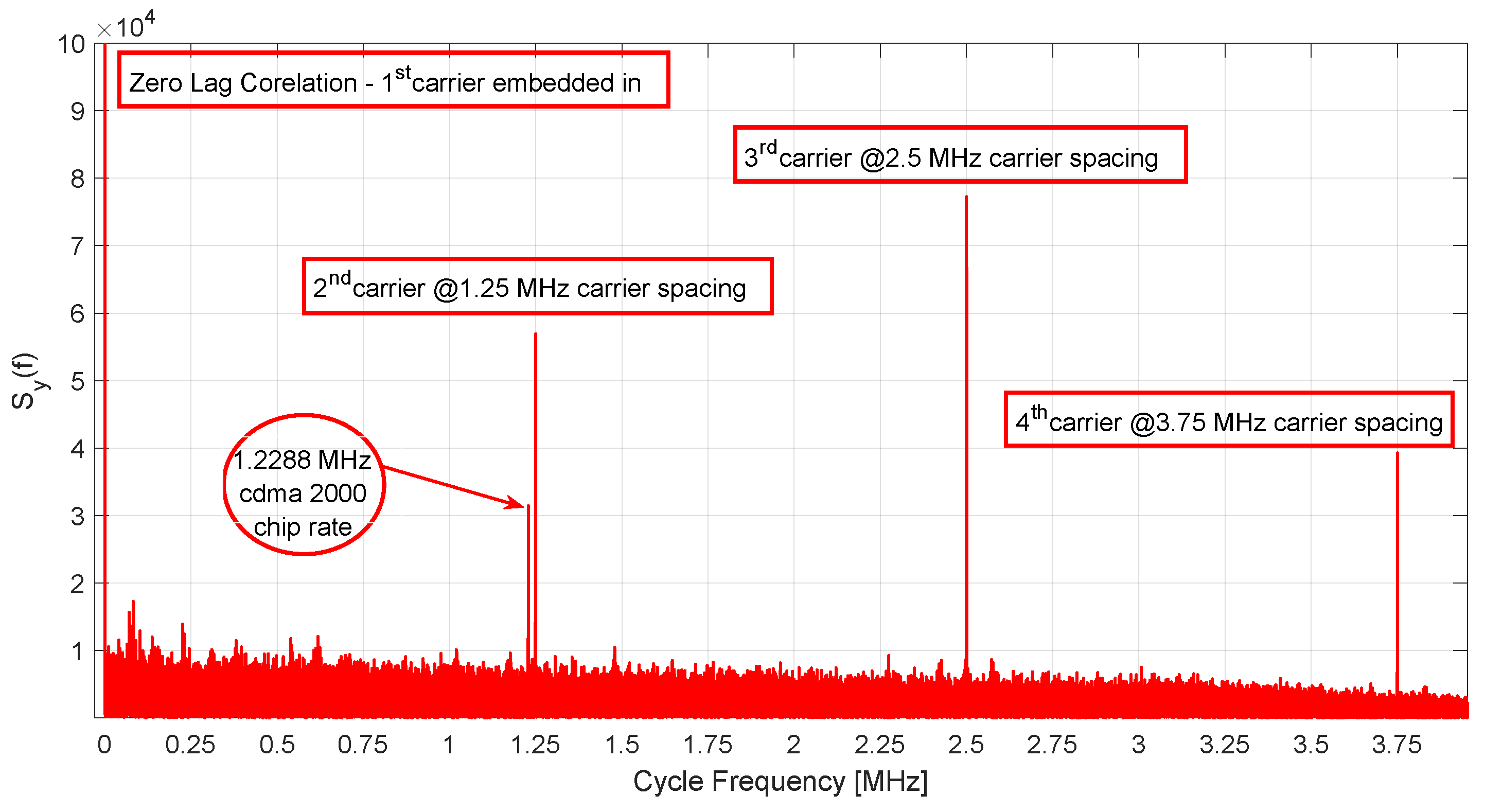Figure 2 shows the SCF spectrum for 4-carrier signal. First, it should be noted that through the derivation a specific case for α = 0 is considered and it is indicated that the first carrier will be observed at the zero-lag point in the spectrum. This outcome is consequently reflected in Figure 2 and the first carrier’s spectral components are combined with some other periodicities at τ = 0 . Since it is not possible to distinguish the components of the first-carrier from the other periodicities, in this study, it is assumed that if the signal under observation has multiple carriers, these will be observed at incriminating carrier spacings and carriers following the first carrier are selected as the focus of observation. Please also note that, if the measurement done belongs to a single carrier DSSS signal, only the chip rate which is also observed in Figure 2 would be present along with a strong zero-lag component. Thus, single carrier DSSS signal detection and multi-carrier case can be distinguished from each other in a simple way. Single carrier DSSS signal detection with cyclostationary signal analysis has been extensively studied in the literature and [20] can be consulted for detailed discussion.
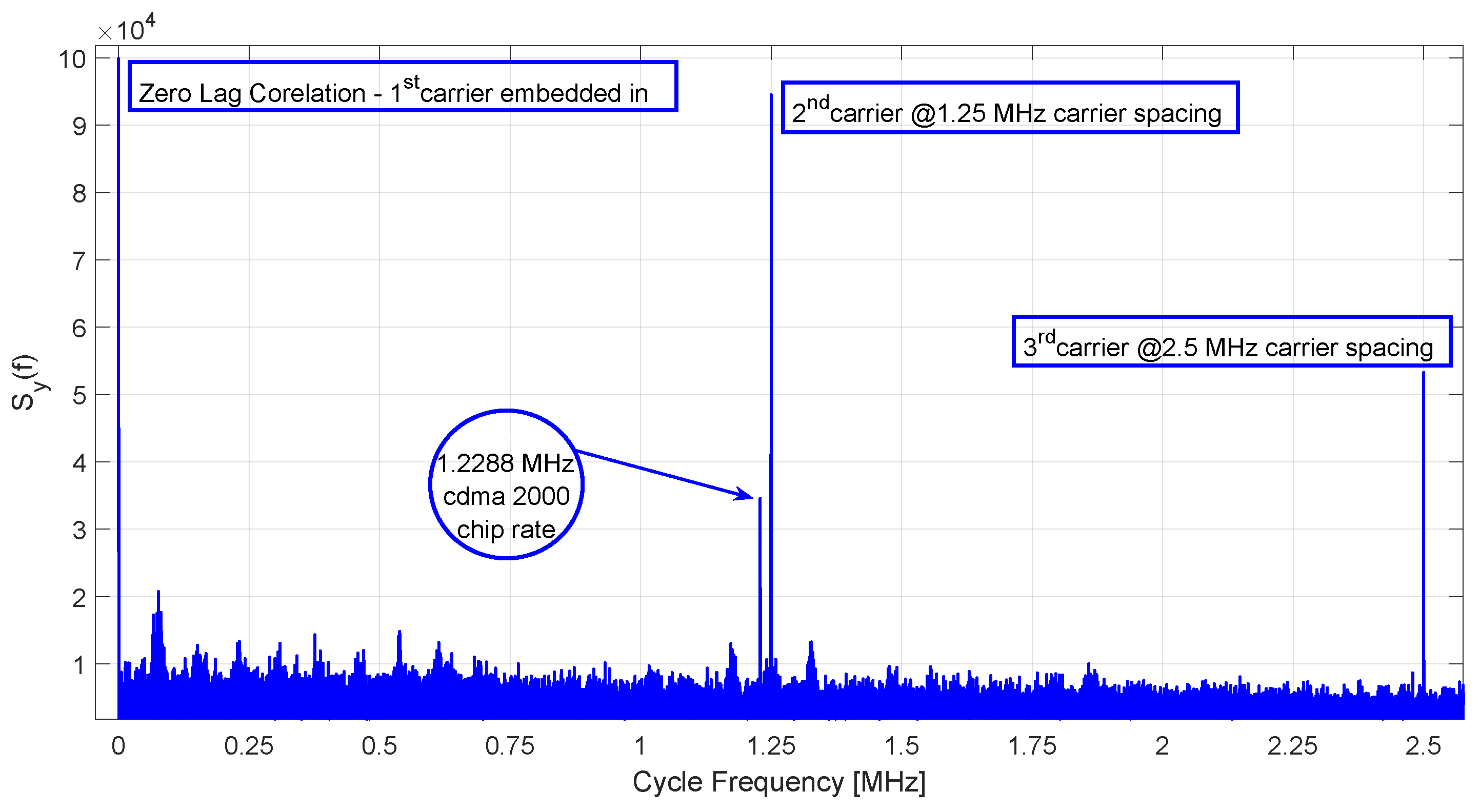
In Figure 2, cdma2000 chip rate of 1.2288 mega-chips per-second, second carrier at the 1.25 MHz carrier spacing, third carrier at the 2.5 MHz, and fourth carrier athe the 3.75 MHz are distinguished particularly as the expected results of the proposed method, beyond the zero-lag correlations. In Figure 3 same results are observed to affirm the three carrier case; besides the chip rate, only with two spectral manifolds for second and third carriers of the three carrier signal are identified.
Next, a constant false alarm rate (CFAR) detector is implemented based on method in [3] to be able to assess the performance of the proposed method. To that end, probability of detection ( P D ) rates for the values of probability of false alarm ( P F A ) rates of 0.1 , and 0.01 are provided. The estimation process is established upon the CFAR detector through the binary hypothesis testing scheme which is applied to the S ^ y ( f ) spectrum as in [6]
H 0 : ∀ { f } c = 1 c ⇒ S ^ y ( f ) = ε S y H 1 : f o r s o m e { f } c = 1 c ⇒ S ^ y ( f ) = S y ( f ) + ε S y ,
where S ^ y ( f ) is the estimate of theoretical S y ( f ) which is calculated from the measurement results and ε S y is the estimation error. The detection performance of the proposed method is investigated next, utilizing the aforementioned methodology based on the defined data set.

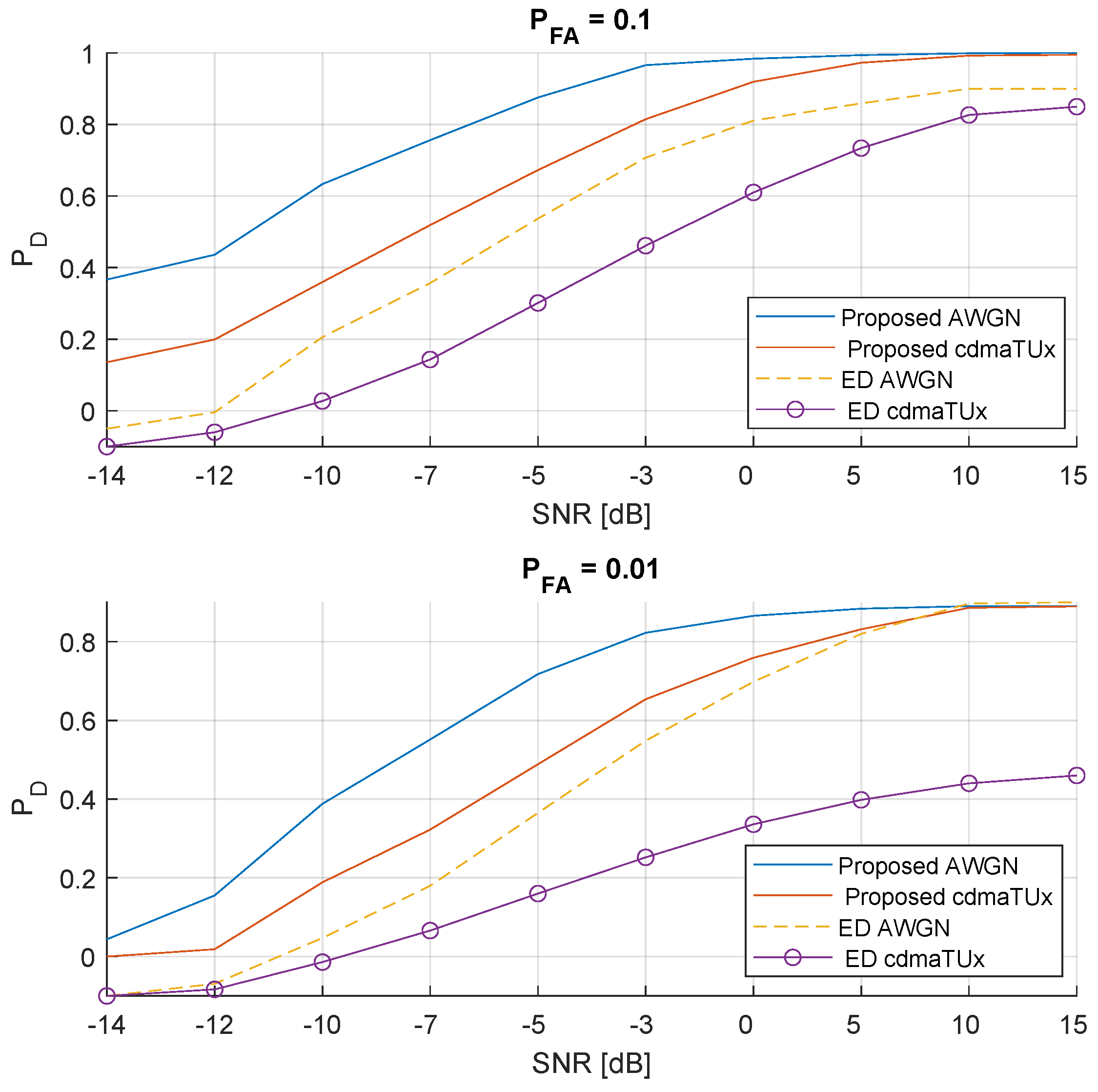
6.1. Parametric Results

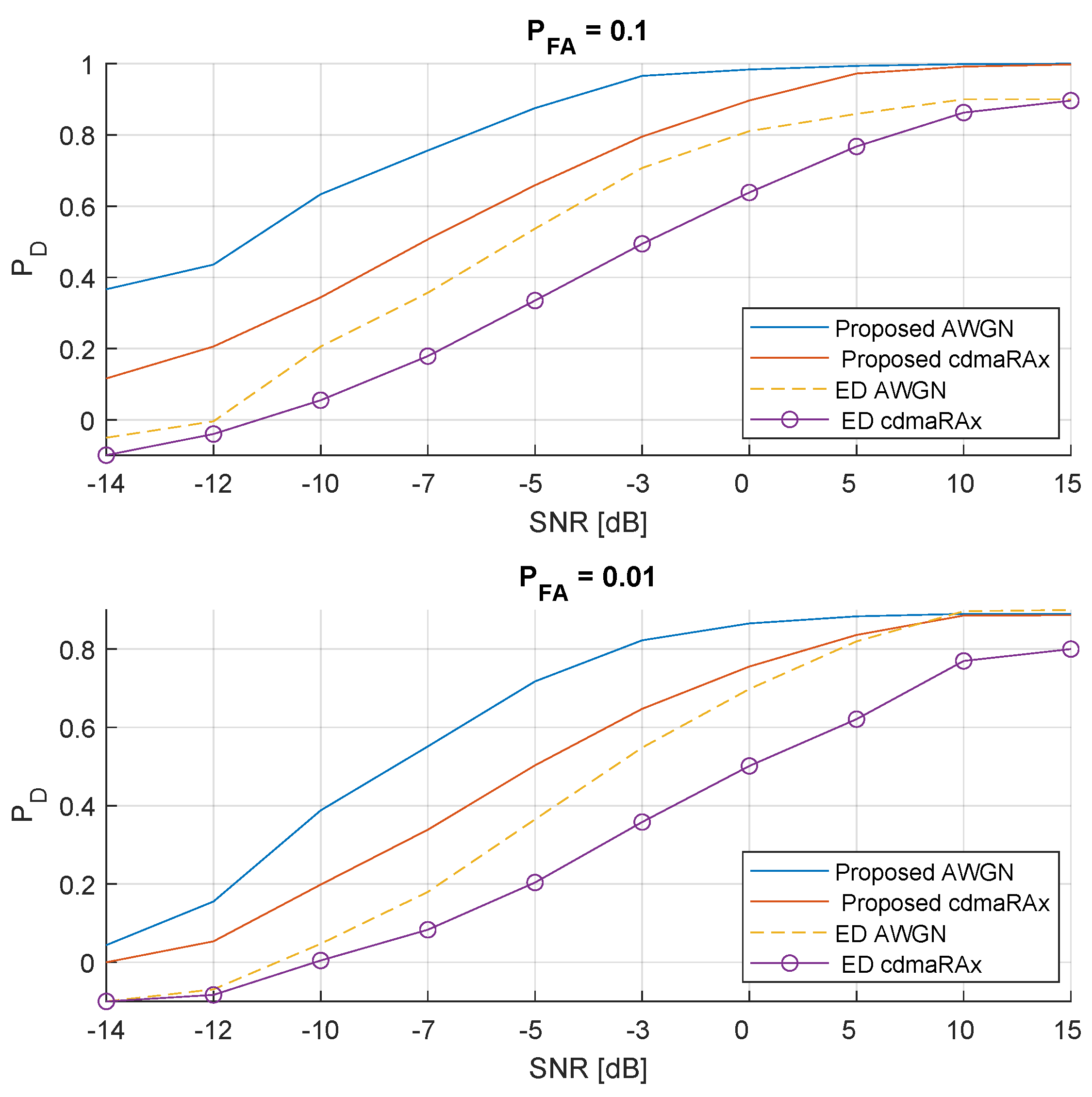
Figure 4 shows the P D performance for 4-carrier signals. The results obtained are based on implemented CFAR methodology, i.e., detection performance for varying SNR levels and P F A = 0.1 (first sub-figure), and P F A = 0.01 (second sub-figure). For the sake of simplicity, only the A W G N and typical urban CDMA ( c d m a T U x ) channels are considered in these plots. Furthermore, for the comparison purposes, classical ED developed in [21] and detailed in [22] is also implemented. Thus, ED detection performance is also plotted along with the proposed method’s outputs. From both plots it can be inferred that the proposed method is superior to ED especially in the low-SNR region, however for the P F A = 0.01 case P D deteriorates faster than P F A = 0.1 . It is notable that the proposed method provides strong statistics under scattering-rich urban environment even at the S N R = 0 region. These statistics can only be satisfied around 5dB region for P F A = 0.01 . On the other hand, while the performance gap between the proposed method and ED is similar for the A W G N and c d m a T U x cases at P F A = 0.1 , the margin increases for c d m a T U x channel in case of P F A = 0.01 .
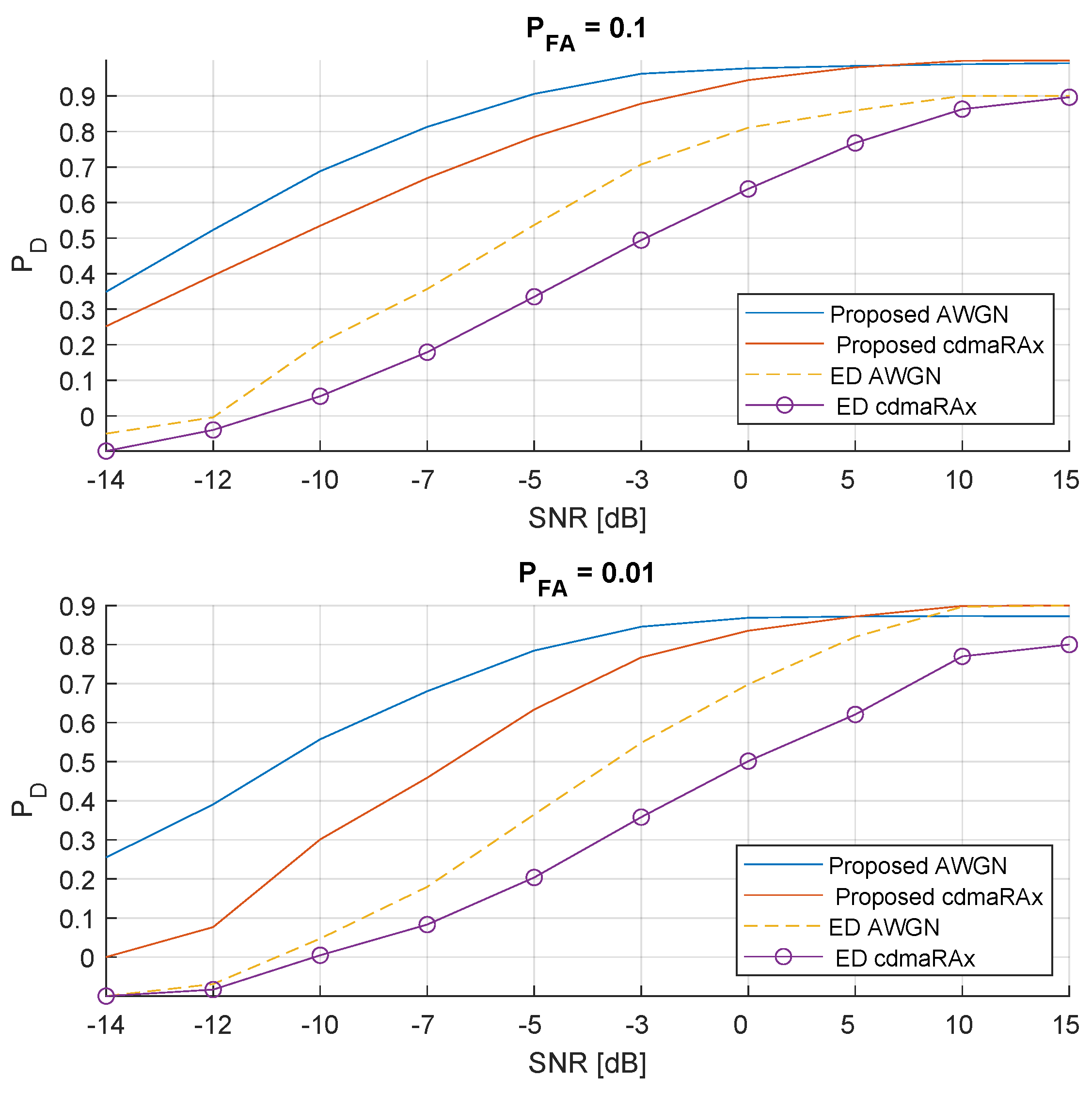
With a similar approach, in Figure 5, the performance of the proposed method is investigated particular to the rural area CDMA ( c d m a R A x ) channel conditions, again along with the reference A W G N channels and in comparison with ED method. Even though the performance of the proposed method is slightly improved, it observed that the ED performance for P F A = 0.01 has significantly improved due to the less-deteriorating channel impairments of rural environment. These results indicate that the susceptibility of the proposed method against varying channel conditions is insignificant.
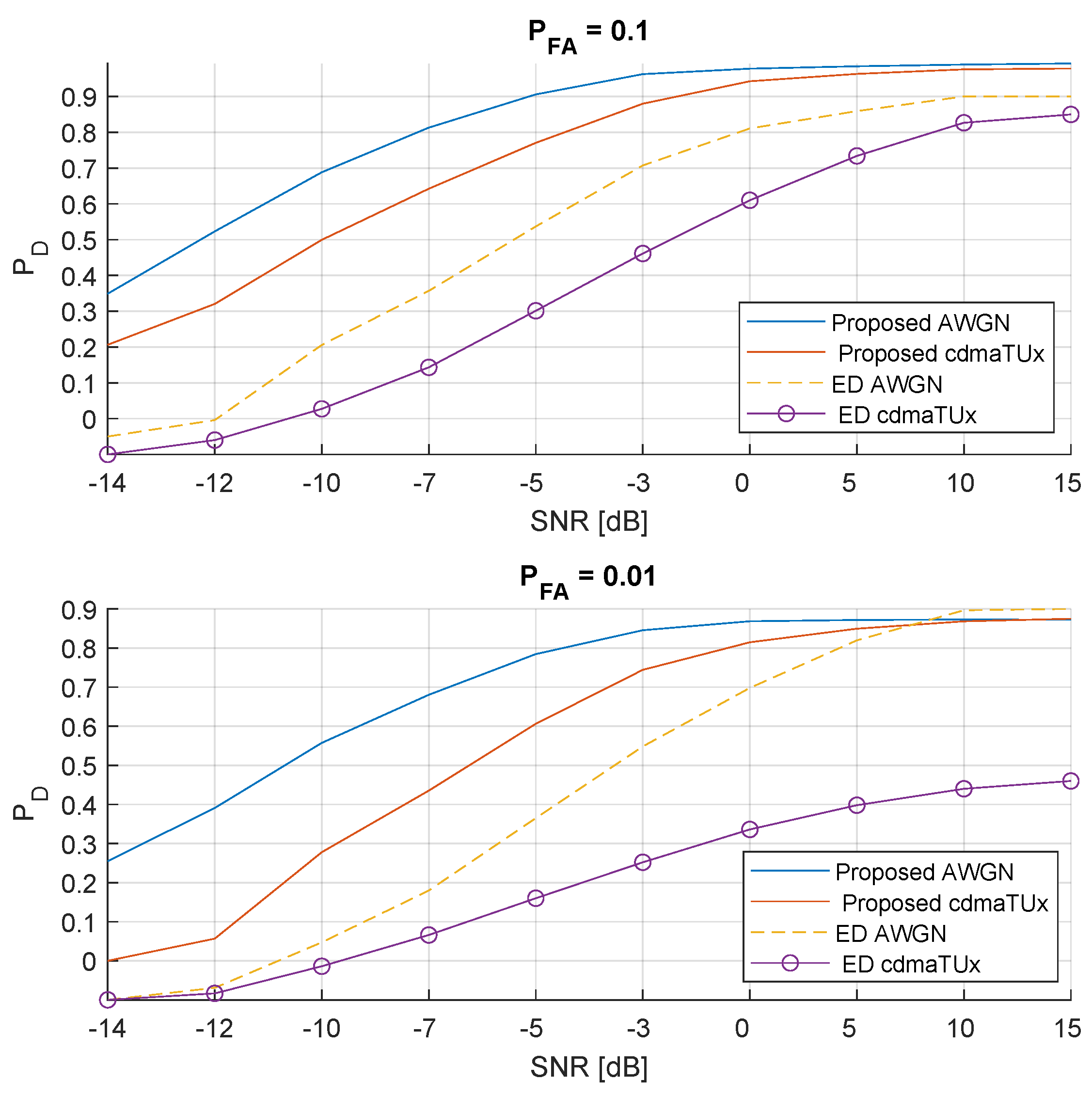
The same analysis is repeated to observe the 3-carrier signal detection performance of the proposed method. These results are illustrated in Figure 6 and Figure 7. Besides observing results which are similar to that of 4-carrier signals, in 3-carrier case it is observed that the gap between the detection performance of the proposed method for c d m a R A x and c d m a T U x channels are wider than 4-carrier signals. This result is due to the fact that wider band signals are less susceptible to the changes in the channel conditions when compared to the narrower signals.
Besides the channel characteristics and S N R values, another performance determining parameter is number of symbols, or chips in case of DSSS signals, that are involved in the process. A general analyses of the effect of sample size on ED and cyclostationary analysis can be found in [23] and in [24]. In parallel to these works, in this paper the effect of measurement duration is considered in terms of the performance analysis of the proposed method. Therefore, measurements with indicated durations in Table 1 are taken during the measurement campaign and the proposed method is implemented over these signals.
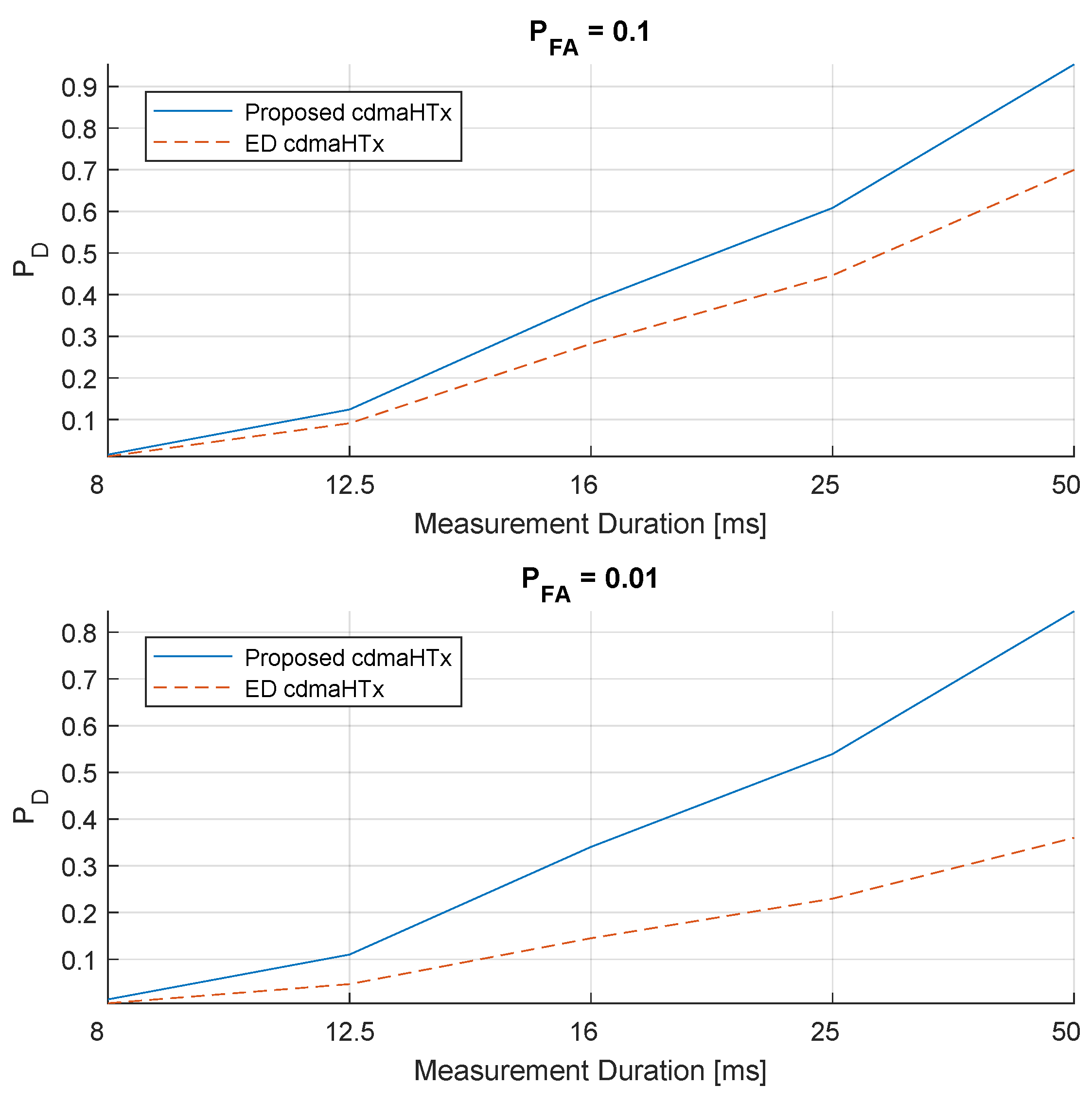
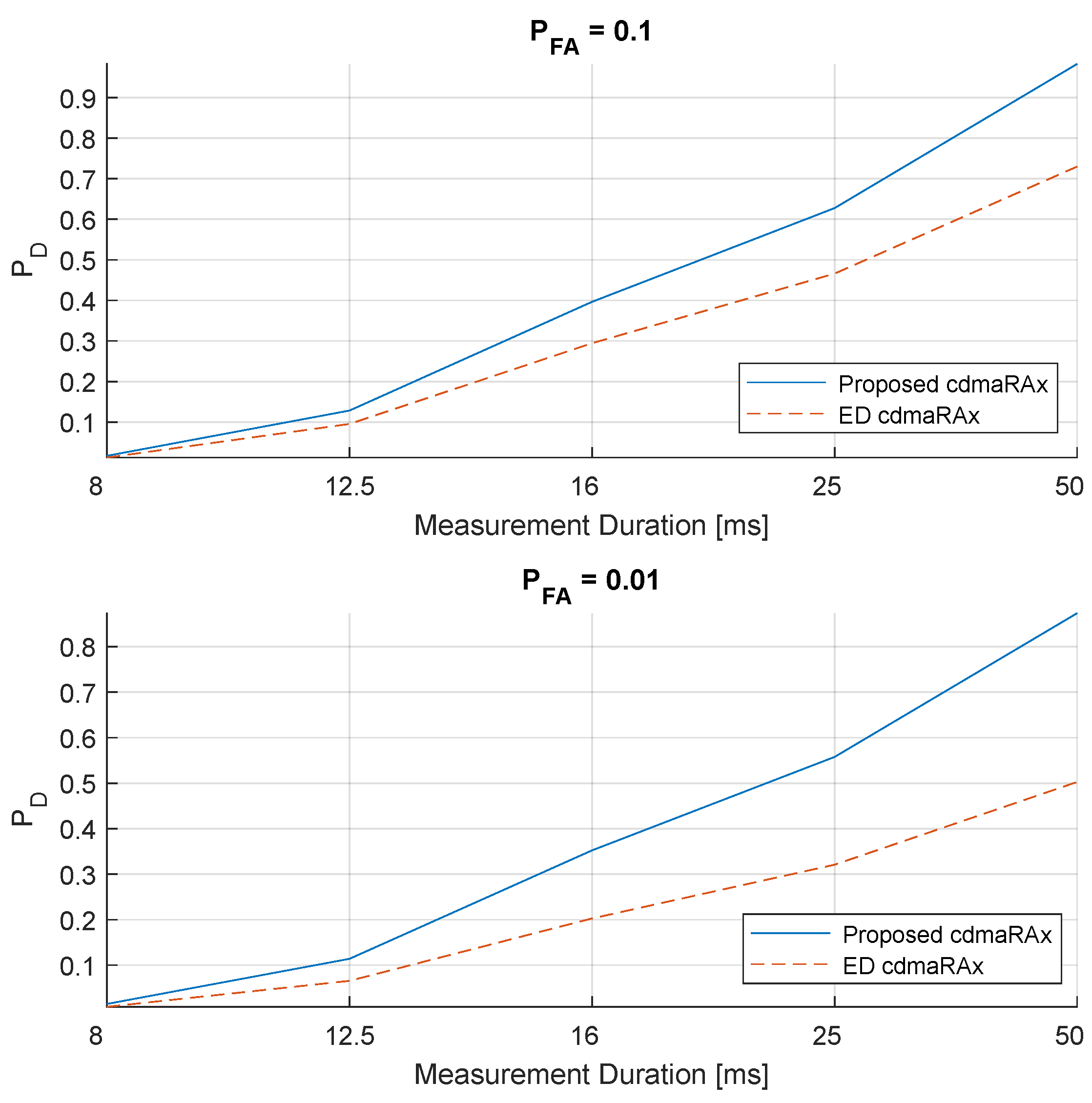
Focusing on the 4-carrier signals, in Figure 8 the performance of the proposed method and ED are considered for different measurement durations, particularly for the case of S N R = 0 and c d m a R A x channel. For each case, i.e., P F A = 0.1 , P F A = 0.01 , performance degradation is % 30 at the first halving of the data, and even more, around % 70 at the second halving which is from 25ms to 12.5 ms. ED follows a similar trend even though it performs poorer when compared to the proposed method. However particularly at the P F A = 0.01 , the performance difference becomes much more obvious. Please note that same trend with corresponding P D values are observed for other SNR levels and channel characteristics with some minor deviations. Therefore a single snapshot case is considered suffice to observe the general trend.
Similar to the previous case, second analysis in the same context focuses on 3-carrier signals. Figure 9 depicts the performance of the proposed method and ED again for different measurement durations, particularly for the case of S N R = 0 and this time hilly terrain ( c d m a H T x ) channel. For P F A = 0.1 case the similar trend to the 4-carrier case is observed, however ED performance deteriorates worse when compared to c d m a R A x in this particular case at P F A = 0.01 which is compatible with the theoretical findings of the previously mentioned works. Eventually, these results in general indicate that measurement duration or number of samples included in the process have significant influence at the performance of the proposed method and a certain number of samples should be collected to make sure that robust results are achieved.

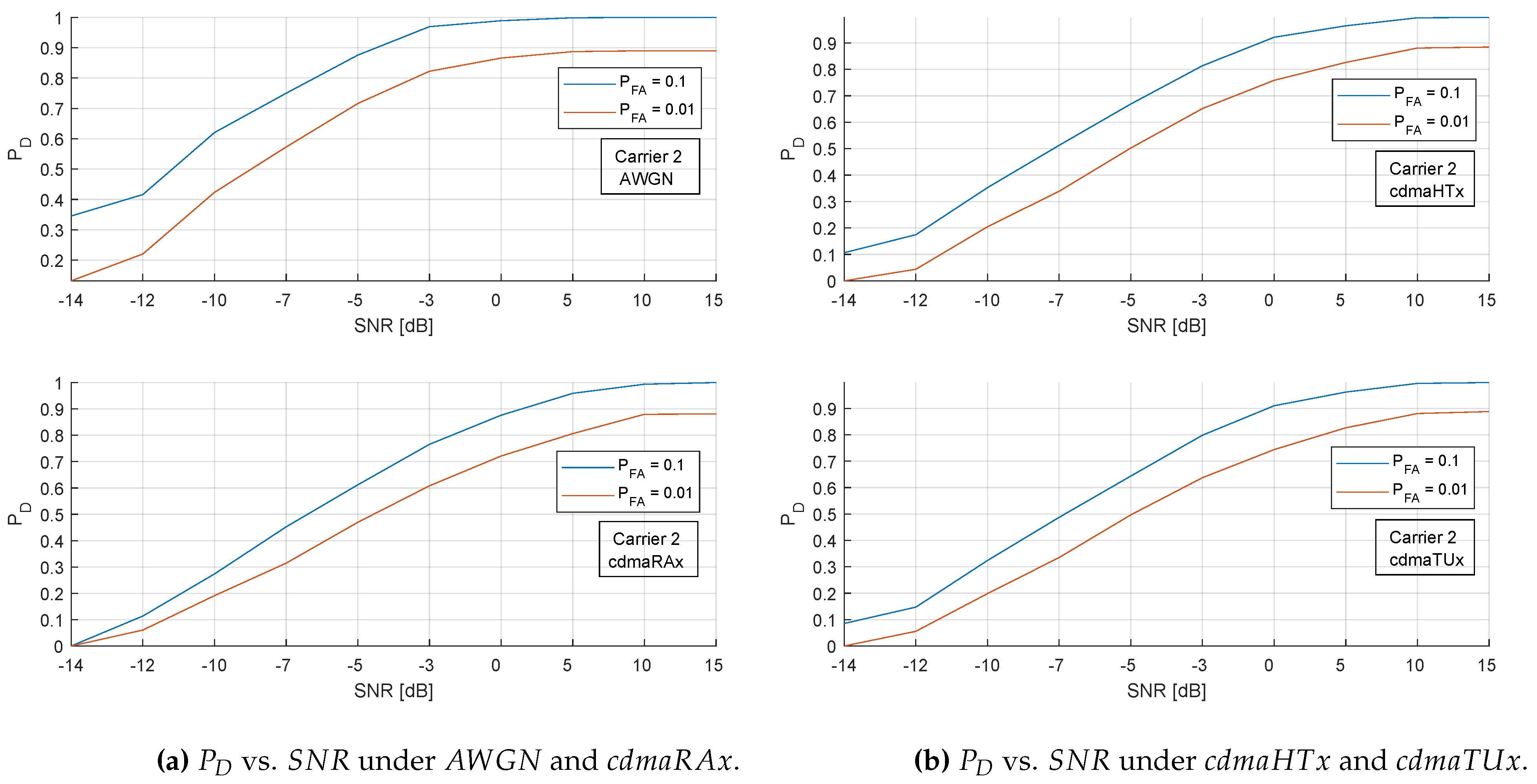
6.2. Carrier-Based Analysis

In this section carrier by carrier detection performance of the proposed method is investigated to understand how the results change in terms of carriers and under different channel conditions. To this end 4-carrier signal is selected for analysis. Leaving the zero-lag correlations aside, three carriers detected became the focus of analysis. Thus detection performance of the method is plotted for various SNR levels, under the four channel conditions listed in Table 2, again considering P D for both P F A = 0.1 , and P F A = 0.01 .
In Figure 10 four figures each with two plots provide a general overview of the P D performance of the proposed method for the second carrier. In case of P F A = 0.1 the method performs best in A W G N conditions. On the other hand, even though some local changes are observed, the method performs in a similar way for other channel models indicating robustness of the method against varying channel conditions. In case of P F A = 0.01 some level of distinction is observed in the results, meaning that under c d m a H T x the method performs marginally better when compared to c d m a R A x and c d m a T U x , meaning that in this margin of P F A channel conditions start to impose their effects.
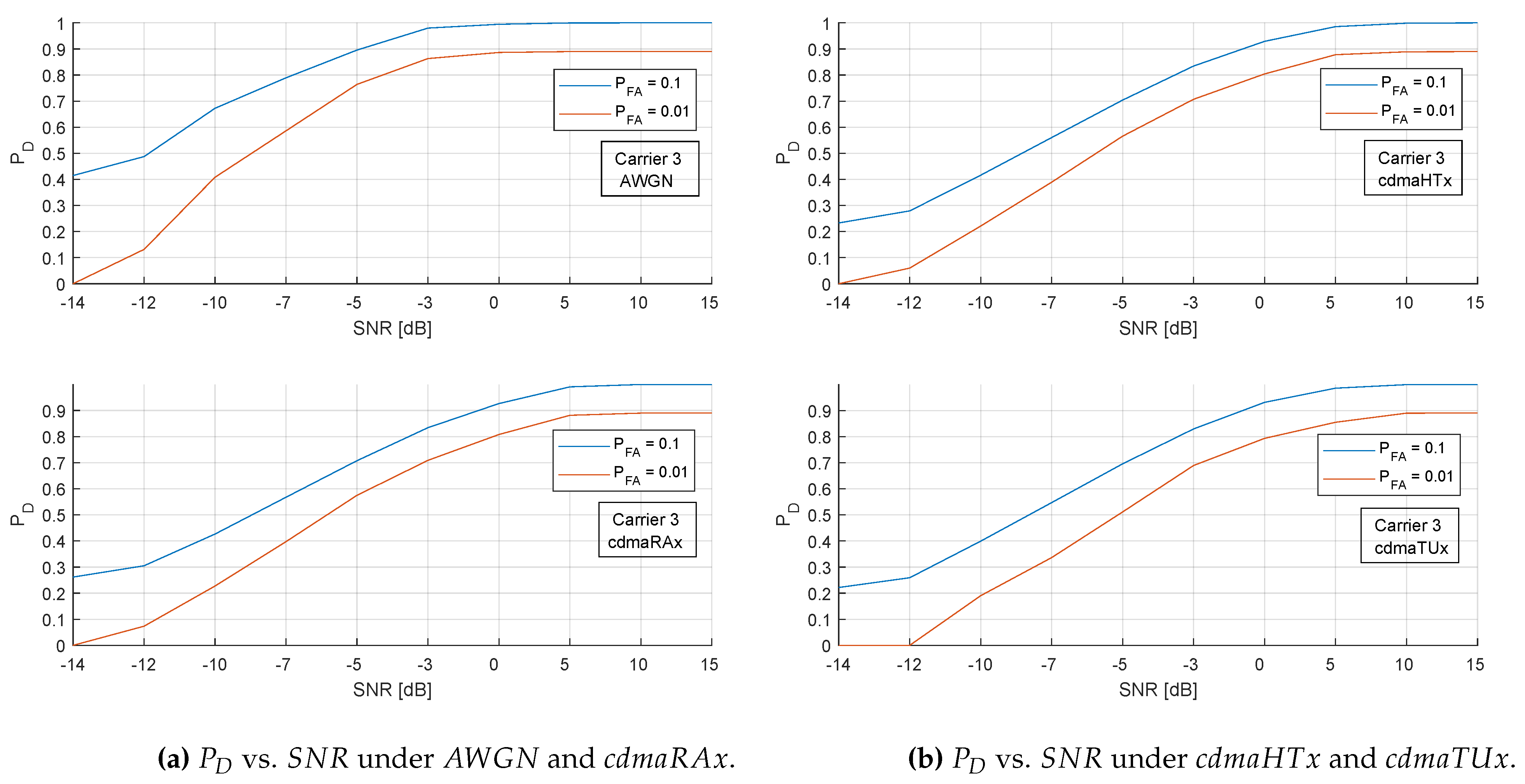
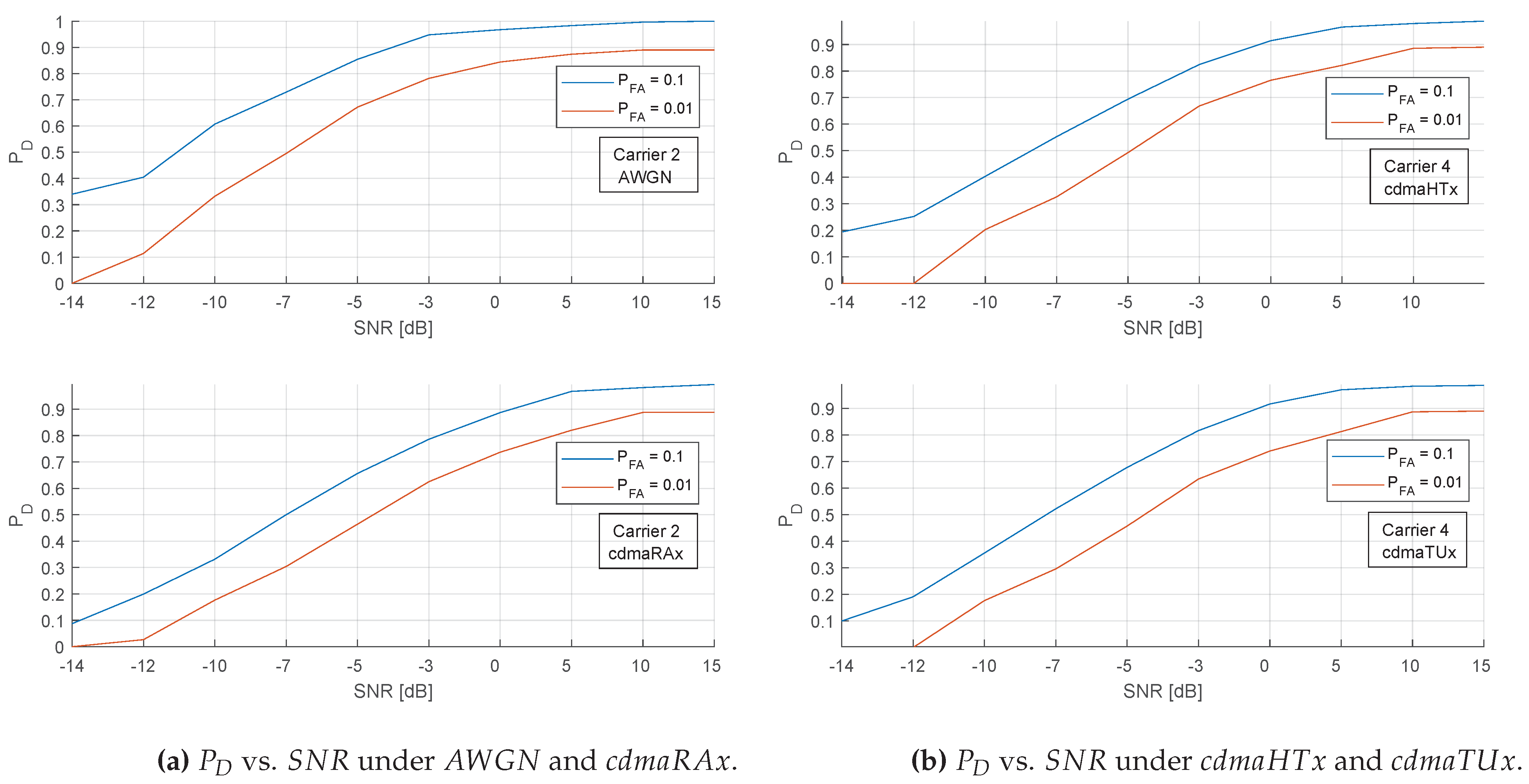
Figure 10 illustrates the same setting for the third carrier detected. It is observed that the same pattern with that of carrier two. However, in this case P D performance of P F A = 0.01 case deteriorates more when compared to the previous carrier especially in the very low-SNR region. Same trend can also be observed for the fourth carrier in Figure 11, which indicates a distinguishing feature for the second carrier. However the detection statistics in these regions are already very low and away from the significant zone of detection. In general, these results indicate that the proposed method provides strong P D performance independent of channel conditions down to the low-SNR region of 0 dB without any prior information.

7. Discussion

In this paper a blind carrier number and spacing estimation method is developed for carrier-aggregated DSSS cellular signals. The introduced method accurately and precisely provides these parameters along with the unique chip rate of the DSSS signal, which leads to the joint identification of the signal type in addition to the estimated parameters. Since chip rate estimation is vastly studied in the cyclostationary feature detection literature, this result is evaluated as a side benefit. The proposed method performs better than ED technique, which is compatible with the available literature on the subject. Please note that since the SCF is computed for α = 0 , the implementation complexity introduced is also minimal. The proposed method is robust against wireless channel impairments ranging from urban to rural and hilly terrain. However the method is susceptible to the measurement duration as also the literature indicates. In general, for a certain measurement duration, the method performs strongly even under low-SNR regimes.
In terms of future work, since artificial intelligence (AI) started to imply significant improvements especially in the area of signal estimation and detection, many new techniques based on convolutional neural networks and deep reinforcement learning methods are proposed. Therefore for the future work of this study, an advanced neural network can be developed and trained by the SCF’s that are derived in this paper. Then performance of the proposed method and that of AI-based can be compared.

Author Contributions

The idea is developed and formulated by the author. The measurements are also taken, post-processed and the results are obtained and published by the author. The paper is written by the author.

Funding

This research has not received any external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The measurement results obtained in this study is not currently available for public utilization.

References

  1. F. Mazzenga and F. Vatalaro, Parameter estimation in CDMA multiuser detection using cyclostationary statistics. Electron. Lett., 1996, 32, 179–181. [CrossRef]
  2. R. Jazdzewski, J. Lopatka, Detection of direct sequence spread spectrum signals in the presence of harmonic and narrowband interferences. In 2001 MILCOM Proceedings Communications for Network-Centric Operations: Creating the Information Force, McLean, VA, USA, 28-31 October 2001.
  3. M Oner, F Jondral, Air interface recognition for a software radio system exploiting cyclostationarity. In Proceedings of IEEE 15th International Symposium on Personal, Indoor and Mobile Radio Communications, Location of Conference, Barcelona, Spain, 05-08 September 2004.
  4. F. Mazzenga, Blind Adaptive Parameter Estimation for CDMA Systems using Cyclostationary Statistics. Signal Processing. Lett., 2000, 11, 495–500.
  5. T. Asai, A. Benjebbour, and H. Yoshino, Recognition of CDMA signals with orthogonal codes using cyclostationarity. In Proceedings of IEEE 6th Workshop on Signal Processing Advances in Wireless Communications, New York, NY, USA, 05-08 June 2005.
  6. J. Lundén, V. Koivunen, A. Huttunen, H. V. Poor, Spectrum sensing in cognitive radios based on multiple cyclic frequencies. In Proceedings of IEEE 2nd International Conference on Cognitive Radio Oriented Wireless Networks and Communications, Orlando, FL, USA, 01-03 August 2007.
  7. Zhipeng Deng, Lianfeng Shen, Nan Bao, Bailong Su, Jintao Lin, and Dayang Wang, Autocorrelation based detection of DSSS signal for cognitive radio system. In Proceedings of IEEE International Conference on Wireless Communications and Signal Processing, Location of Conference, Nanjing, China, 09-11 November 2011.
  8. Md Lushanur Rahman, Pedro Figueiredo e Silva, and Elena-Simona Lohan, Cyclostationarity-based spectrum sensing properties for signals of opportunity. In Proceedings of IEEE 10th International Conference on Wireless and Mobile Computing, Networking and Communications, Larnaca, Southern Cyprus, 08-10 October 2014.
  9. Zhiming Yu, Lili Guo, and Lin Qi, Blind estimation of multicarrier CDMA sub-carrier frequencies based on the high-order cyclic cumulants. In Proceedings of IEEE 5th International Conference on Wireless Communications, Networking and Mobile Computing, Beijing, China, 24-26 September 2009.
  10. C. A. O. Sisi, and Zhang Weiyan, Carrier frequency and symbol rate estimation based on cyclic spectrum. Journal of Systems Engineering and Electronics, 2020, 31, 37–44.
  11. K. Kim, I. A. Akbar, K. K. Bae, J. S. Um, C. M. Spooner, J. H. Reed, Cyclostationary approaches to signal detection and classification in cognitive radio. In Proceedings of 2nd IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks, Dublin, Ireland, 17-20 April 2007.
  12. Yangjie Wei, Shiliang Fang, Xiaoyan Wang, and Shuxia Huang. Blind estimation of the PN sequence of a DSSS signal using a modified online unsupervised learning machine. Sensors, 2019, 19, 354.
  13. Choi Hoesang, and Hichan Moon, Blind estimation of spreading sequence and data bits in direct-sequence spread spectrum communication systems. IEEE Access, 2020, 0, 148066–148074.
  14. M. Iwamura, K. Etemad, Mo-Han Fong, R. Nory, R. Love, Carrier aggregation framework in 3GPP LTE-advanced, IEEE Commun. Mag., 2010, 48, pp.60-67.
  15. M. K. Tsatsanis and G. B. Giannakis, Optimal decorrelating receivers for DS-CDMA systems: A signal processing framework, IEEE Trans. Signal Processing , 1996, . 44, pp. 3044–3055.
  16. I. Ghauri and D. T. M. Slock, Linear receivers for the DS-CDMA downlink exploiting orthogonality of spreading sequences. In Proceedings of 32nd Asilomar Conf. on Signals, Systems, and Computers, Pacific Grove, CA, pp. 650–654, Nov. 1998.
  17. G. E. Bottomley, Block equalization and generalized MLSE arbitration for the HSPA WCDMA uplink. In Proceedings of IEEE VTC Fall 2008, Calgary, Canada, Sep. 2008.
  18. W. A. Gardner, Statistical spectral analysis: A Nonprobabilistic Theory. Prentice Hall, Englewood Cliffs, NJ, 1987.
  19. W. A. Gardner, Exploitation of spectral redundancy in cyclostationary signals. IEEE Signal processing magazine, 1991, . 8.2 pp. 14-36.
  20. Gu, H.-Q.; Liu, X.-X.; Xu, L.; Zhang, Y. -J.; Lu, Z. -M. DSSS Signal Detection Based on CNN. Sensors 2023, 23, 6691.
  21. A.-A. A. Boulogeorgos, N. Chatzidiamantis, G. K. Karagiannidis, and L. Georgiadis Energy detection under RF impairments for cognitive radio. Proc. IEEE Int. Conf. Commun.-Workshop Cooperat. Cogn. Netw. (ICC-CoCoNet), London, U.K., Jun., 2015, pp. 955–960.
  22. Nasser, A.; Al Haj Hassan, H.; Abou Chaaya, J.; Mansour, A.; Yao, K.-C. Spectrum sensing for cognitive radio: Recent advances and future challenge. Sensors 2021, 21, 2408. [Google Scholar] [CrossRef] [PubMed]
  23. Mariani, A.; Giorgetti, A.; Chiani, A. SNR wall for energy detection with noise power estimation. In Proceedings of the IEEE International Conference on Communications, Kyoto, Japan, 5–9 June, 2011; pp. 1–6.
  24. R. Tandra and A. Sahai, B SNR walls for feature detectors, in Proc. IEEE Int. Symp. New Frontiers Dyn. Spectrum Access Netw., Apr., 2007, pp. 559–570.
1
For each channel type, the channel parameters such as tap intervals are assigned randomly.
Preprints 117266 g001
Figure 1. Measurement setup: transmitter, receiver, laptop computer, router and their connections.
Figure 1. Measurement setup: transmitter, receiver, laptop computer, router and their connections.
Preprints 117266 g001
Preprints 117266 g002
Figure 2. The raw output of the proposed algorithm; joint estimation of carrier numbers, spacing and chip rate for four-carrier DSSS signal.
Figure 2. The raw output of the proposed algorithm; joint estimation of carrier numbers, spacing and chip rate for four-carrier DSSS signal.
Preprints 117266 g002
Preprints 117266 g003
Figure 3. The raw output of the proposed algorithm; joint estimation of carrier numbers, spacing and chip rate for three-carrier DSSS signal.
Figure 3. The raw output of the proposed algorithm; joint estimation of carrier numbers, spacing and chip rate for three-carrier DSSS signal.
Preprints 117266 g003
Preprints 117266 g004
Figure 4. 4-carrier signal: The detection performance of the proposed method under A W G N and urban channel conditions. Comparison with energy detector for P F A = 0.1 , and P F A = 0.01 .
Figure 4. 4-carrier signal: The detection performance of the proposed method under A W G N and urban channel conditions. Comparison with energy detector for P F A = 0.1 , and P F A = 0.01 .
Preprints 117266 g004
Preprints 117266 g005
Figure 5. 4-carrier signal: The detection performance of the proposed method under A W G N and rural channel conditions. Comparison with energy detector for P F A = 0.1 , and P F A = 0.01 .
Figure 5. 4-carrier signal: The detection performance of the proposed method under A W G N and rural channel conditions. Comparison with energy detector for P F A = 0.1 , and P F A = 0.01 .
Preprints 117266 g005
Preprints 117266 g006
Figure 6. 3-carrier signal: The detection performance of the proposed method under A W G N and urban channel conditions. Comparison with energy detector for P F A = 0.1 , and P F A = 0.01 .
Figure 6. 3-carrier signal: The detection performance of the proposed method under A W G N and urban channel conditions. Comparison with energy detector for P F A = 0.1 , and P F A = 0.01 .
Preprints 117266 g006
Preprints 117266 g007
Figure 7. 3-carrier signal: The detection performance of the proposed method under A W G N and rural channel conditions. Comparison with energy detector for P F A = 0.1 , and P F A = 0.01 .
Figure 7. 3-carrier signal: The detection performance of the proposed method under A W G N and rural channel conditions. Comparison with energy detector for P F A = 0.1 , and P F A = 0.01 .
Preprints 117266 g007
Preprints 117266 g008
Figure 8. 4-carrier signal: The detection performance of the proposed method vs. ED for different measurement durations under hilly terrain channel conditions. S N R = 0 dB. First sub-figure is at P F A = 0.1 , and second is at P F A = 0.01 .
Figure 8. 4-carrier signal: The detection performance of the proposed method vs. ED for different measurement durations under hilly terrain channel conditions. S N R = 0 dB. First sub-figure is at P F A = 0.1 , and second is at P F A = 0.01 .
Preprints 117266 g008
Preprints 117266 g009
Figure 9. 3-carrier signal: The detection performance of the proposed method vs. ED for different measurement durations under hilly terrain channel conditions. S N R = 0 dB. First sub-figure is at P F A = 0.1 , and second is at P F A = 0.01 .
Figure 9. 3-carrier signal: The detection performance of the proposed method vs. ED for different measurement durations under hilly terrain channel conditions. S N R = 0 dB. First sub-figure is at P F A = 0.1 , and second is at P F A = 0.01 .
Preprints 117266 g009
Preprints 117266 g010
Figure 10. 4-carrier signal: Detection performance of the second carrier comparable to four different channel conditions for the cased of P F A = 0.1 , and P F A = 0.01 .
Figure 10. 4-carrier signal: Detection performance of the second carrier comparable to four different channel conditions for the cased of P F A = 0.1 , and P F A = 0.01 .
Preprints 117266 g010
Preprints 117266 g011
Figure 11. 4-carrier signal: Detection performance of the third carrier comparable to four different channel conditions for the cased of P F A = 0.1 , and P F A = 0.01 .
Figure 11. 4-carrier signal: Detection performance of the third carrier comparable to four different channel conditions for the cased of P F A = 0.1 , and P F A = 0.01 .
Preprints 117266 g011
Preprints 117266 g012
Figure 12. 4-carrier signal: Detection performance of the fourth carrier comparable to four different channel conditions for the cased of P F A = 0.1 , and P F A = 0.01 .
Figure 12. 4-carrier signal: Detection performance of the fourth carrier comparable to four different channel conditions for the cased of P F A = 0.1 , and P F A = 0.01 .
Preprints 117266 g012
Table 1. Signal Parameters Used Throughout The Measurements.
Table 1. Signal Parameters Used Throughout The Measurements.
Paramater Value
Signal Type cdma2000 Downlink (Forward) Channels
Carrier Number (C) (to be estimated) 3-4
Carrier Offset (to be estimated) 1.25 MHz
Transmit Frequencies 925 – 960 MHz Cellular Downlink
Receiver Recording Span 14 MHz
Transmit Power 10 dBm
Measurement Duration(s) 8, 12.5, 16, 25, 50 Milliseconds
Table 2. Utilized Channel Types At The Measurement Post Processing.
Table 2. Utilized Channel Types At The Measurement Post Processing.
Channel Model Description
AWGN Additive white Gaussian channel (only the measurement impairments)
cdmaRAx Rural Area channel model (RAx)
cdmaHTx Hilly Terrain channel model (HTx)
cdmaTUx Typical Urban channel model (TUx)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated