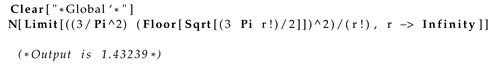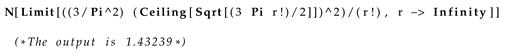1. Intro
Let and suppose function , where A and f are Borel. Let be the Hausdorff dimension, where is the Hausdorff measure in its dimension on the Borel -algebra.
1.1. First Special Case of f
If the graph of f is G, is there an explicit f where:
The function
f is everywhere surjective [
2]
1.1.1. Potential Answer
If
, using this MathOverflow post [
3], define
f such that:
Consider a Cantor set
with Hausdorff dimension 0 [
4]. Now consider a countable disjoint union
such that each
is the image of
C by some affine map and every open set
contains
for some
n. Such a countable collection can be obtained by e.g. at letting
be contained in the biggest connected component of
(with the center of
being the middle point of the component).
Note that
has Hausdorff dimension 0, so
has Hausdorff dimension one [
5].
Now, let
such that
is a bijection
for all
n (all of them can be constructed from a single bijection
, which can be obtained without choice, although it may be ugly to define) and outside
let
g be defined by
, where
has a graph with Hausdorff dimension 2 [
6] (this doesn’t require choice either).
Then the function g has a graph with Hausdorff dimension 2 and is everywhere surjective, but its graph has Lebesgue measure 0 because it is a graph (so it admits uncountably many disjoint vertical translates).
Note, we can make the construction with union of
rather explicit as follows. Split the binary expansion of
x as strings of size with a power of two, say
becomes
. If this sequence eventually contains only strings of the form
or
, say after
, then send it to
, where
. Otherwise, send it to the explicit continuous function
h given by the linked article [
6]. This will give you something from
Finally, compose an explicit (reasonable) bijection from to . In your case, the construction can be easily adapted so that the or target space is actually , then compose with .
In case this function is impossible to average, consider the following example:
1.2. Second Special Case of f
Suppose, we define
, where
, such that:
In the following sections, we shall see why we chose and this function.
1.3. Attempting to Analyze/Average f
Suppose, the expected value of
f is:
Note, using
, explicit
f is pathological since it’s everywhere surjective and difficult to meaningfully average (i.e., the most
generalized,
satisfying (
§Section 2) extension of
is non-finite).
Thus, we want the most
generalized,
satisfying extension of
on bounded
f, where the extension takes finite values for all
f defined within §
Section 1.1. Moreover, suppose:
The sequence of bounded functions is
The sequence of bounded functions converges to f: i.e.,
The generalized, satisfying extension of is : i.e., there exists a , where is finite
-
There exists
where the expected value of
and
are finite and non-equivelant: i.e.,
(Whenever (iv) is true, (iii) is non-unique.)
1.3.1. Example Proving (i)-(iv) Correct
Using the second case of
f in §
Section 1.2,
suppose:
and
where for
,
and for
Note,
and
are bounded since
f is bounded (i.e., criteria i of §
Section 1.3 is satisfied). Also, the set-theoretic limit of
and
is
: i.e.,
where:
(Not sure how to prove this; however, a mathematician that specializes in rational numbers and set-theoretic limits should be able to verify the former.)
Hence, one can see that
and
converges to
(i.e., criteria ii of §
Section 1.3 is satisfied).
Now, suppose we want to average
and
which we denote
and
. Note, this is the same as computing the following (i.e., the cardinality is
and the absolute value is
):
If we assume,
in eq.
6, then [
7]:
The integral
counts the number of fractions with even denominator and odd numerator in set
, after cancelling all possible factors of 2 in the fraction. Let’s consider the first case. We can write
, where
counts the fractions
in
that are not counted in
, i.e., for which
. This is the case when the denominator is odd after the cancellation of the factors of 2, i.e., when the numerator
c has a number of factors of 2 greater than or equal to that of
, which we will denote by
a.k.a the 2-valuation of
,
[
8]. That means,
c must be a multiple of
. The number of such
c with
is simply the length of that interval, equal to
, divided by
. Thus,
. This obviously tends to zero, proving
Since
is finite, this proves §
Section 1.3 criteria iii.
Last, we need to show
, where
proving §
Section 1.3 criteria iv.
Concerning the second case [
7], it’s again simpler to consider the complementary set of
such that the denominator is odd when all possible factors of 2 are canceled. We can see that for
, and these include obviously all those we had for smaller
j. The “new" elements in
with
are those which have denominator
when written in lowest terms. Their number is equal to the number of
,
, which is given by Euler’s
function. Since we also consider negative fractions, we have to multiply this by 2. Including
, we have
. There is no simple explicit expression for this (cf. oeis:A99957 [
9]), but we know that
[
9]. On the other hand, the total number of all elements of
is
, since each time we increase
j by 1, we have the additional fractions with the new denominator
and numerators being coprime with
d, again with + or − sign. From oeis:A002088 [
10] we know that
, so
, which finally gives
as desired.
Hence,
and
proving §
Section 1.3 criteria iv.
Therefore, in , since:
Theorem 1. The set of all Borel f, where is finite, forms a shy [11] subset of all Borel measurable functions in
Proof (Proof theorem 1 is true). We follow the argument presented in example 3.6 of this paper [
11], take
(measurable functions over
A), let
P denote the one-dimensional sub-space of
A consisting of constant functions (assuming the Lebesgue measure on
A) and let
(measurable functions over
A with no finite integral). Let
denote the Lebesgue measure over
P, for any fixed
:
Meaning P is a one-dimensional, so f is a 1-prevelant set. □
Theorem 2. The set of all Borel f, where the generalized, satisfying extension of is non-unique , , forms a prevalent [11] subset of all Borel measurable functions in
Proof (Possible method to proving theorem 2 true). Note, we first must prove that only f whose lines of symmetry intersect at one point have the same expected value for any bounded sequence of functions converging to f. Notice, the set of all symmetric Borel functions forms a shy subset of the set of all Borel measurable functions in . Hence, the set of all functions, where their lines of symmetry intersect at one point also forms a shy subset of the set of all Borel measurable functions in (i.e., a subset of a shy subset is also shy). □
Since thm. 1 and 2 are true, we need to fix the problems the theorems address with the following:
1.3.2. Blockquote
We want to find an unique,
satisfying (
§Section 3) extension of
, on bounded functions to
f which takes finite values only, such that the set of all
f with this extension forms:
a prevalent [
11] subset of
If not prevalent then a non-shy (i.e., neither prevalent [
11] nor shy [
11]) subset of
.
For the sake of clarity & precision, we describe examples of “extending
on all
A with positive & finite Hausdorff measure" (
§Section 2) and use the examples to define the terms “unique & satisfying" (
§Section 3) in the blockquote of this section.
2. Extending the Expected Value w.r.t the Hausdorff Measure
The following are two methods to determining the most generalized, satisfying extension of on all A with a positive and finite Hausdorff measure:
One way is defining a generalized, satisfying extension of the Hausdorff measure on all
A with positive & finite measure which takes positive, finite values for all Borel
A. This can theoretically be done in the paper “A Multi-Fractal Formalism for New General Fractal Measures"[
12] by taking the expected value of
f w.r.t the extended Hausdorff measure.
Another way is finding a
generalized,
satisfying average of all
A in the fractal setting. This can be done with the papers “Analogues of the Lebesgue Density Theorem for Fractal Sets of Reals and Integers" [
13] and “Ratio Geometry, Rigidity and the Scenery Process for Hyperbolic Cantor Sets" [
14] where we take the expected value of
f w.r.t the densities in [
13,
14].
(Note, the methods in these papers could be used in
§Section 3.2 to answer the blockquote of
.)
3. Attempt to Define “Unique and Satisfying” in the Blockquote of §Section 1.3
3.1. Note
“Sequences of bounded functions converging to
f" (
§Section 5.1)
“Equivalent sequences of bounded functions" (
§Section 5.3, def. 1)
“Nonequivalent sequences of bounded functions" (
§Section 5.3, def. 2)
The “measure" of a property on a sequence of bounded functions which increases at rate
linear or
super-linear to that of “non-equivelant" sequences of bounded functions (§
Section 5.4.1, §
Section 5.4.2)
The “actual" rate of expansion on a sequence of bounded sets (§
Section 5.5)
3.2. Leading Question
To define
unique and
satisfying in the blockquote of the
§Section 1.3, we take the expected value of a sequence of bounded functions chosen by a choice function. To find the choice function we ask the
leading question…
If we make sure to:
- (A)
See 3.1 and (C)-(E) when something is unclear
- (B)
Take all sequences of bounded functions which converge to f
- (C)
Define C to be chosen center point of
- (D)
Define E to be the chosen, fixed rate of expansion of a sequence on the graph of bounded functions
- (E)
Define to be actual rate of expansion of a sequence on the graph of bounded functions (5.5)
Does there exist a unique choice function which chooses a unique set of equivalent sequences of bounded functions where:
The chosen, equivelant sequences of bounded functions should satisfy (B).
The “measure" of the graph of all chosen, equivalent sequences of bounded functions which satisfy (B) should increase at a rate linear or superlinear to that of non-equivelant sequences of bounded functions satisfying (B)
The expected values, defined in the papers of
§Section 2, for all equivalent sequences of bounded functions are equivalent and finite
-
For the chosen, equivalent sequences of bounded functions satisfying (1), (2) and (3), when f is unbounded (i.e, skip when f is bounded):
-
When set is the set of all , where the choice function chooses all equivalent sequences of bounded functions satisfying (1), (2), (3) and (4), then Q is
- (a)
a prevelant [
11] subset of
- (b)
If not (5a) then a non-shy (i.e., neither prevelant [
11] nor shy [
11]) subset of
.
Out of all choice functions which satisfy (1), (2), (3), (4) and (5), we choose the one with the simplest form, meaning for each choice function fully expanded, we take the one with the fewest variables/numbers?
3.2.1. Explaining Motivation Behind
When defining “the measure" (§
Section 5.4.1,§
Section 5.4.2) of a function, we want a bounded sequence of functions with a “high" entropic density (i.e., we aren’t sure if this is infact what the “measure" measures.) For example, when
and
f is everywhere surjective [
2], the “measure" chooses bounded sequence of functions whose lines of symmetry intersect at one point rather than non-symmetrical functions §
Section 5.4.1-§
Section 6, §
Section 8.
Note, the later criteria doesn’t apply to bounded functions: e.g., using §
Section 1.3.1, when
and
, where:
depending on the sequence of bounded function chosen which converge to f: can be any number in
. Since
is bounded, we need only §
Section 3.2.1 crit. 1 to solve the blockquote of §
Section 1.3.2.
Using an unbounded function in §
Section 1.1 (i.e., an everywhere surjective
f whose graph has zero Hausdorff measure in its dimension)
depending on the sequence of bounded functionschosen which converge tof:
can be any real number (when it exists). To fix this, take all
, where the
has smallest absolute difference from the
-th coordinate of a reference point (i.e., the center point
). The problem is there exists
f, where the expected value of non-equivalent sequences (
§Section 5.3, def. 2) of bounded functions have the same minimum absolute difference from
-th coordinate of
C.
Thus, we take the sequence of functions whose actual rate of expansion
from
C (
) “diverges" [
15] at the smallest rate from the chosen, fixed rate of expansion
E from
C (i.e., the “rate of divergence of
, using the absolute value
,
is less than or equal to that of all the non-equivalent sequences of bounded functions which satisfy §
Section 3.2 criteria (1), (2), and (3)).
Finally, since there might still be non-equivalent sequences (
§Section 5.3, def. 2) of bounded functions which satisfy
criteria (1), (3) and (4), but their graphs are congruent with different
, we use equation
T in §
Section 6.3.1 eq.
144 to choose a unique set of all equivalent sequences of bounded sets with the same expected value.
I’m convinced the expected values of the sequences of bounded functions chosen by a choice function which answers the
leading question aren’t
unique nor
satisfying enough to answer the blockquote of
§Section 1.3.2. Still, adjustments are possible by changing the criteria or by adding new criteria to
the question.
4. Question Regarding My Work
Most don’t have time to address everything in my research, hence I ask the following:
Is there a research paper which already solves the ideas I’m working on? (Non-published papers, such as mine [16], don’t count.)
Using AI, papers that might answer this question are “Prediction of dynamical systems from time-delayed measurements with self-intersections" [
17] and “A Hausdorff measure boundary element method for acoustic scattering by fractal screens" [
18].
Does either of these papers solve the blockquote of ?
Suppose is a sequence of bounded functions converging to f and is a sequence of the graph of each . Let be the Hausdorff dimension and be the Hausdorff measure in its dimension on the Borel -algebra.
Is there a simpler version of the definitions below?
5.1. Defining Sequences of Bounded Functions Converging to f
The sequence of bounded functions , where and is a sequence of bounded sets, converges to function when:
For any
there exists a sequence
s.t.
and
(see [
19] for info).
Example 1 (Example of §
Section 5.1).
If and , where , then an example of , such that is:
for
Example 2 (More Complex Example). If and , where , then an example of , such that is:
5.2. Expected Value of Bounded Sequence of Functions
If
converges to
f (§
Section 5.1), the expected value of
f w.r.t
is
(when it exists), where the absolute value is
, such that
satisfies:
Note, can be extended by using .
5.2.1. Example
Using example 1, when where:
for
If we assume
:
To prove eq. is true, recall:
Since eq. is true,
. Note, if we simply took the average of
f from
, using the improper integral, the expected value:
is
(when
,
, and
) or
(when
,
, and
), making
undefined. (However, using eq.
10-, we get the
instead of an undefined value.)
5.3. Defining Equivelant and Non-Equivelant Sequences of Bounded Functions
Let
be an arbitrary set and define the following sequence of functions:
Note, the sequences of bounded functions in
converges to
f and the sequences of the graphs of all functions in each former sequence are:
Definition 1 (Equivelant Sequences of functions).
Suppose is an arbitrary set. The sequences of bounded functions in:
are equivalent, if for all , where , and are equivelant: i.e., there exists a , such for all , there is a , where:
and for all , there is a , where:
More, for each , we denote all equivalent sequences of bounded functions tousing the notation
5.3.1. Explanation
We define
and
as equivalent, where
and
are constant in
and
, such for all Borel measurable
, when both
and
exist:
Hence, consider the following:
Theorem 3.
If the sequence of functions in:
are equivalent, then for all , where :
Note, this explains criteria (3) in
5.3.2. Example of Equivalent Sequences of Bounded Functions
Suppose we define , where and , where such that:
and
Note, using def. 1, , , and . In other words, and . Now, suppose , where and . Then,
- (1)
-
For all
, there exists a
, where:
We show this with the following:
In eq.
32, since
is a 1-d interval,
. Hence,
We also show:
- (1)
-
For all
, there exists a
, where:
We show this with the following:
In eq.
38, since
:
Since crit. and (2) is true, using def. 1, we have shown and are equivalent.
Definition 2 (Non-Equivalent Sequences of functions).
Again, is an arbitrary set. Therefore, all sequences of bounded functions in:
are non-equivalent, if def. 1 is false, meaning for some , where , and are non-equivelant: there is a , where for all , there is either a , where:
or for all , there is a , where
5.3.3. Explanation
We define
and
as equivalent, where
and
are constant in
and
, such for all Borel measurable
, when either
or
exist:
Hence, consider the following:
5.3.4. Example of Non-Equivalent Bounded Sequences of Functions
Suppose we define , where and , where such that:
and
Note, using def. 1, , , and . In other words, and . Now, suppose , where and . Then,
-
For all
, there exists a
, where:
We show this with the following:
Since
is a 1-d interval,
. Hence:
Which is true, since for .
Now, considering the examples in and , here are some shortcuts to definitions of equivelant and non-equivelant sequences of bounded functions:
5.3.5. Shortcuts to Determining Equivelant and Non-Equivelant Sequences of Bounded Functions
Suppose we define , where and , where :
5.4. Defining the “Measure”
5.4.1. Preliminaries
We define the “measure” of in , where is a sequence of the graph of each . To understand this “measure", continue reading.
5.4.2. What Am I Measuring?
Suppose we define two sequences of the graph of the bounded functions converging to the graph of f: e.g., and , where for constant and cardinality
- (a)
Using (ii) and (3iiie) of
Section 5.4.1, suppose:
then (using
) we get
- (b)
Also, using (ii) and (3iiie) of
Section 5.4.1, suppose:
then (using
) we also get:
If using
and
we have:
then
what I’m measuring from increases at a rate
superlinear to that of
.
If using equations
and
(swapping
and
, in
and
, with
and
) we get:
then
what I’m measuring from increases at a rate
sublinear to that of
.
-
If using equations , , , and , we both have:
- (a)
or are equal to zero, one or
- (b)
or are equal to zero, one or
then what I’m measuring from increases at a rate linear to that of .
5.4.3. Example of The “Measure” of Increasing at Rate Super-Linear to that of
Suppose, we have function
, where
, and:
such that:
and
where for
,
and
Hence, when
is:
and
is:
Note, the following:
Since and is countably infinite, there exists minimum which is 1. Therefore, we don’t need . Also, we maximize by the following procedure:
For every
, group
into elements with an even numerator when simplified: i.e.,
which we call
, and group
into elements with an odd denominator when simplified: i.e.,
which we call
Arrange the points in from least to greatest and take the 2-d Euclidean distance between each pair of consecutive points in . In this case, since all points lie on , take the absolute difference between the x-coordinates of then call this . (Note, this is similar to step 33a).
Repeat step (3) for , then call this . (Note, all point of lie on .)
Remove any outliers from (i.e., d is the 2-d Euclidean distance between points and ). Note, in this case, and should be outliers (i.e., for any , the lengths of are more than C times the interquartile range of the lengths of ) leaving us with .
Multiply the remaining lengths in the pathway by a constant so they add up to one. (See P[r] of code for an example)
Take the entropy of the probability distribution. (See entropy[r] of code for an example.)
We can illustrate this process with the following code:
| Listing 1: Illustration of step (1)-(6) |
 |
Taking
Table[{r,entropy[r]},{r,3,8}], we get:
| Listing 2: Output of Table[{r,entropy[r]},{r,3,8}]
|
 |
and notice when:
the output of code can be defined:
Hence, since
:
and
(I need help proving this):
Hence,
entropy[r] is the same as:
Now, repeat code with:
| Listing 3: Illustration of step (1)-(6) on () |
 |
Using this post [
21], we assume an approximation of
Table[entropy[j],{j,3,Infinity}] or
is:
Hence, using §
Section 5.4.2 (ia) and §
Section 5.4.2 (ii), take
(where
is Euler’s Totient function) computing the following:
where:
For every
, we find a
, where
, but the absolute value of
is minimized. In other words, for every
, we want
where:
Finally, since
, we wish to prove
within §
Section 5.4.2 crit. ii:
where using mathematica, we get the limit is greater than one:
| Listing 4: Limit of eq. 78 |
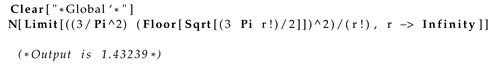 |
Also, using §
Section 5.4.2 (ib) and §
Section 5.4.2 (ii), take
(where
is Euler’s Totient function) to compute the following:
where:
-
For every , we find a , where , but the absolute value of is minimized. In other words,
for every
, we want
where:
Finally, since
, we wish to prove
within §
Section 5.4.2 crit. ii:
where using mathematica, we get the limit is greater than one:
| Listing 5: Limit of eq. 88 |
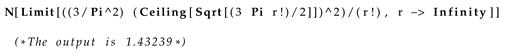 |
Hence, since the limits in eq.
77 and eq.
87 are greater than one and less than
: i.e.,
what we’re measuring from increases at a rate
superlinear to that of
(i.e.,
Section 5.4.2 crit. ii).
5.4.4. Example of The “Measure” from Increasing at a Rate Sub-Linear to that of
Using Our Previous Example, We Can Use the Following Theorem:
Theorem 4.
If what we’re measuring from increases at a rate superlinear to that of , then what we’re measuring from increases at a ratesublinearto that of
Hence, in our definition of super-linear (§
Section 5.4.2 crit. ii), swap
and
for
and
regarding
and
(i.e.,
and
) and notice thm. 4 is true when:
5.4.5. Example of The “Measure” from Increasing at a Rate Linear to that of
Suppose, we have function
, where
, and:
such that:
and
where for
,
and
Hence, when
is:
and
is:
Also, using §
Section 5.4.3 steps 2-7 on
:
| Listing 6: Illustration of step (1)-(6) on () |
 |
where the output is
| Listing 7: Output of Code 6 |
 |
Notice when:
the output of code can be defined:
Hence, since
:
since
(this is proven in [
22]):
Hence,
entropy[r] is the same as:
Therefore, using §
Section 5.4.2 (ia) and §
Section 5.4.2 (iviva), take
to compute the following:
where:
For every
, we find a
, where
, but the absolute value of
is minimized. In other words, for every
, we want
where:
To solve for
j, we try the following code:
| Listing 8: Code for j in eq. 116 |
 |
Note, the output is:
| Listing 9: Output for code 8 |
 |
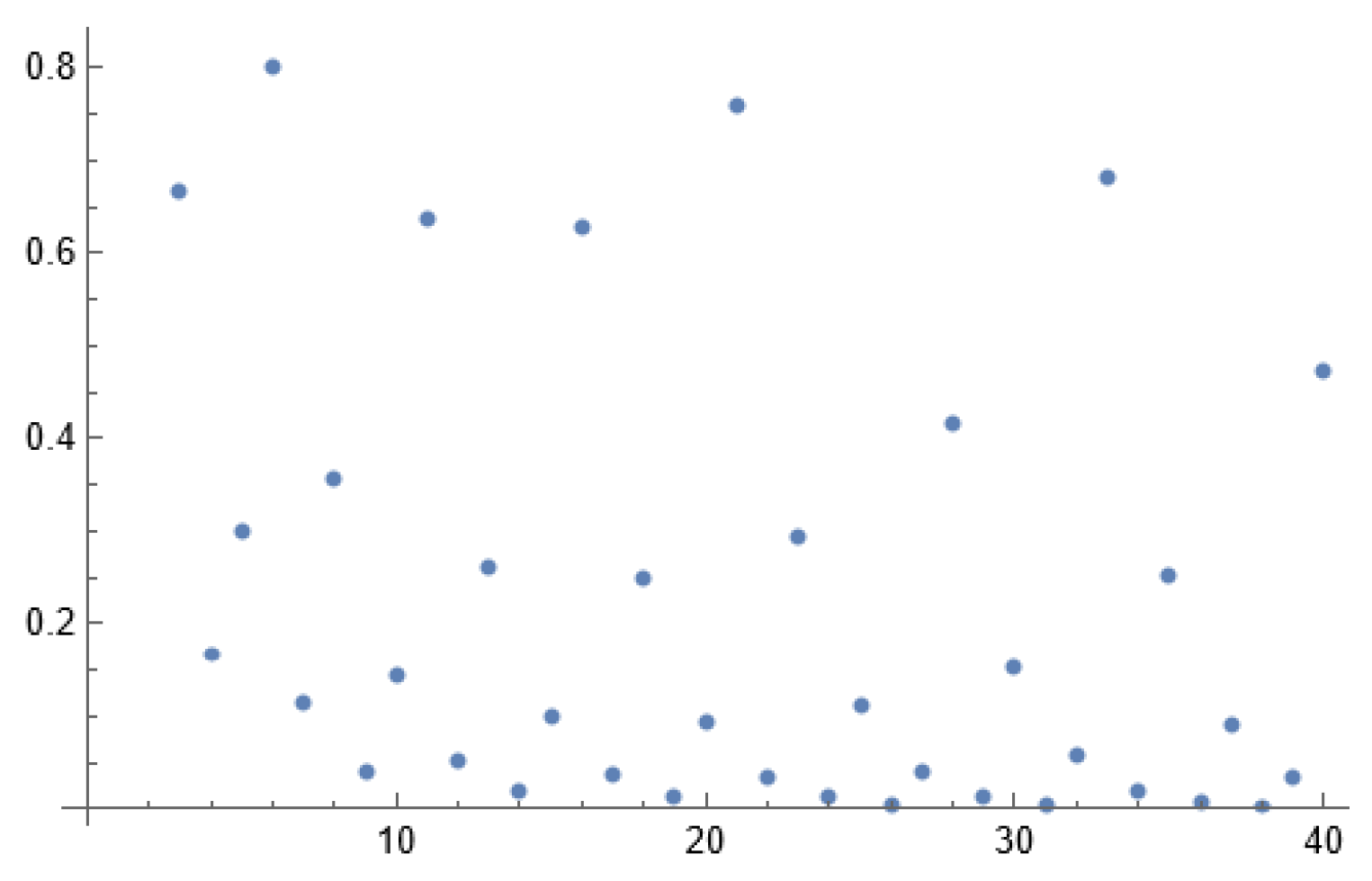
Figure 1.
Plot of loweralphr.
Figure 1.
Plot of loweralphr.
Finally, since the lower bound of
loweralphr is zero, we have shown:
Next, using §
Section 5.4.2 (ib) and §
Section 5.4.2 (ivivb), take
and swap
and
with
and
, to compute the following:
where:
For every
, we find a
, where
, but the absolute value of
is minimized. In other words, for every
, we want
where:
To solve
r, we try the following code:
| Listing 10: Code for r in eq. 123 |
 |
Note, the output is:
| Listing 11: Output for code 10 |
 |
 |
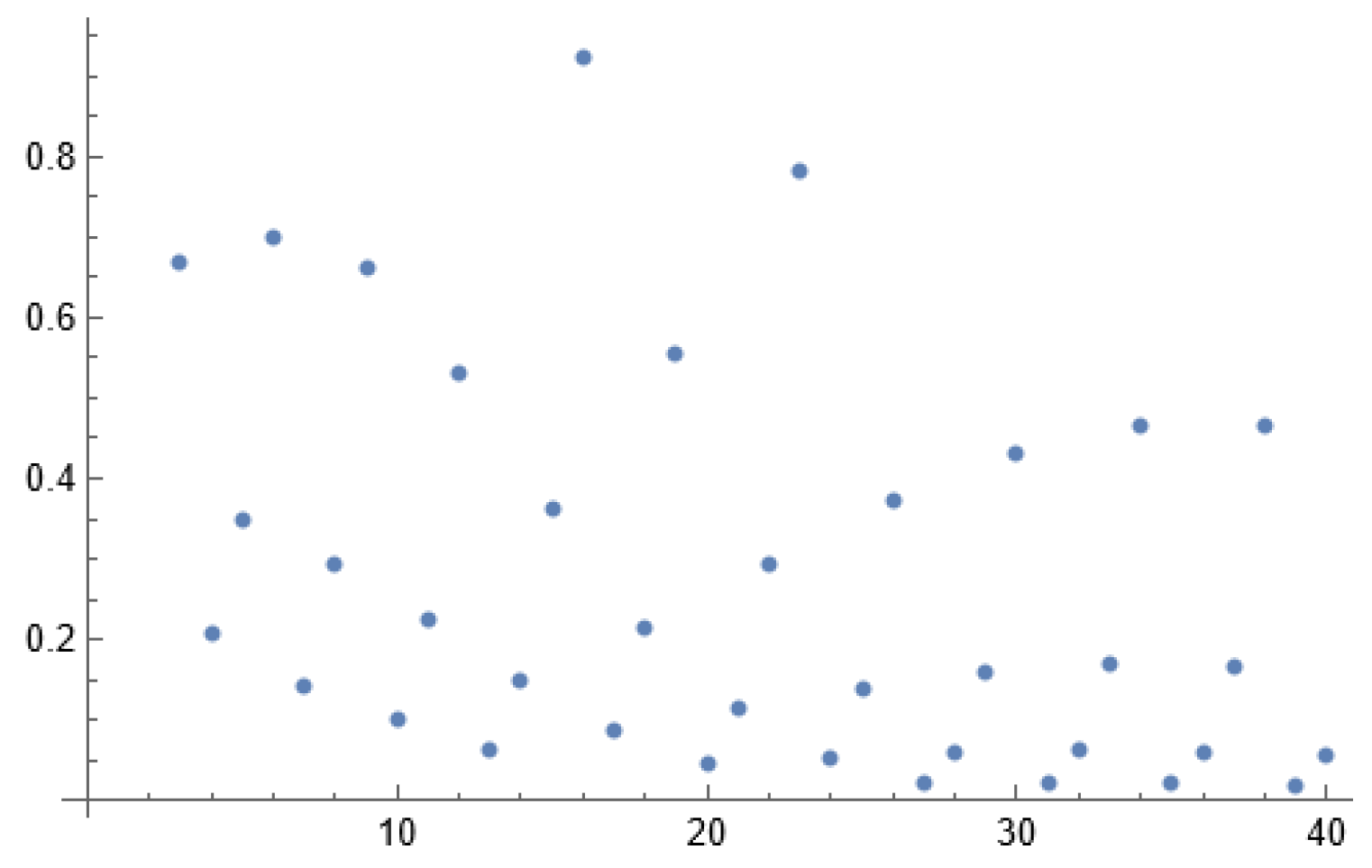
Figure 2.
Plot of loweralphj.
Figure 2.
Plot of loweralphj.
since the lower bound of
loweralphj is zero, we have shown:
Hence, using eq.
117 and
124, since
both:
or are equal to zero, one or
or are equal to zero, one or
then what I’m measuring from increases at a rate linear to that of .
5.5. Defining The Actual Rate of Expansion of Sequence of Bounded Sets
5.5.1. Definition of Actual Rate of Expansion of Sequence of Bounded Sets
Suppose
is a sequence of bounded functions converging to
f, where
is a sequence of the graph on each
, and
is the Euclidean distance between points
. Therefore, using the “chosen" center point
, when:
the
actual rate of expansion is:
Note, there are cases of when isn’t fixed and (i.e., the chosen, fixed rate of expansion).
5.5.2. Example
Suppose, we have
, where
and
, such that
and for
:
Hence, when
is:
such that
, note the farthest point of
from
C is either
or
. Hence, to compute
, we can take
or
:
and the actual rate of expansion is:
6. My Attempt at Answering the Blockquote of §Section 1.3.2
6.1. Choice Function
Suppose we define the following:
is the sequence of bounded functions which satisfies (1), (2), (3), (4) and (5) of the leading question in
is all sequences of bounded functions satisfying (1) of the leading question where the expected values, defined in the papers of , is finite.
is an element
but
not an element in the set of equivelant sequences of bounded functions to that of
(def. 1), where using the end of def. 1, we represent this criteria as:
6.2. Approach
We manipulate the definitions of
§Section 5.4.2 (ia) and
§Section 5.4.2 (ib) to solve (1), (2), (3), (4) and (5) of the
leading question in
6.3. Potential Answer
6.3.1. Preliminaries (Definition of T in Case of §Section 3.2.1 (5))
When the difference of point
and
is:
the average of
for every
is:
and
is the
n-d Euclidean distance between points
, we define an
explicit injective
such that:
If , then
If , then
If , then
where using “chosen" center point
:
6.3.2. Question
Does T Exist? If So, How Do We Define It?
Hence, using
,
,
,
E,
(§
Section 5.5), and
, such that with the absolute value function
, ceiling function
, and nearest integer function
, we define:
where
,
E, and
T are “removed" when
, the choice function which answers the
leading question in
could be the following, s.t.we explain the reason behind choosing the choice function in §
Section 6.4:
Theorem 5.
where for , we define to be the same as when swapping “" with “" (for eq. 138 & 139) and sets with (for eq. 138–145), then for constant and variable , if:
then for all (def. 1), if:
where is the ceiling function, E is the fixed rate of expansion, Γ is the gamma function, n is the dimension of , is the Hausdorff dimension of set , and is area of the smallest -dimensional box that contains , then:
the choice function is:
such that satisfies eq. 150 & eq. 151. (Note, we want , , and to answer the leading question of ) where the answer to the blockquote of is (when it exists).
6.4. Explaining the Choice Function and Evidence the Choice Function Is Credible
Notice, before reading the programming in code 12, without the “c”-terms in eq. 150 and eq. 151:
The choice function in eq.
150 and eq. is zero, when
what I’m measuring from
(§
Section 5.4.2 criteria ii) increases at a rate superlinear to that of
, where
.
The choice function in eq.
150 and eq. is zero, when for a given
and
there doesn’t exist
c where eq.
148 is satisfied or
.
-
When
c does exist, suppose:
- (a)
When
, then:
- (b)
When
, then:
Hence, for each sub-criteria under crit. (iii), if we subtract one of their limits by their limit value, then eq.
150 and eq. is zero. (We do this using the “
c”-term in eq.
150 and ). However, when the exponents of the “
c"-terms aren’t equal to
, the limits of eq.
150 and aren’t equal to zero. We want this, infact, whenever we swap
with
. Moreover, we define function
(i.e., eq.
149), where:
When
, then eq.
150 and without the “c"-terms are zero. (The “c"-terms approach zero and still allow eq.
150 and to equal zero.)
When
, then
is zero which makes eq.
150 and equal zero.
-
Here are some examples of the numerator of
(eq.
149):
When , , and , the numerator of is
When , , and , the numerator of is
When
,
, and
, the numerator of
is ceiling of constant
times the volume of an
n-dimensional ball with finite radius: i.e.,
When
,
, and
, the numerator of
is ceiling of the volume of the
n-dimensional ball: i.e.,
Now, consider the code for eq. 150 and eq. 151. (Note, the set theoretic limit of
is the graph of function
.) In this example,
, and:
such that:
the ceiling function is
, and:
such for
,
and
Hence, when
is:
and
is:
Note, the following (we leave this to mathematicians to figure LengthS1, LengthS2, Entropy1 and for other A and f in code ).
6.4.1. Evidence with Programming
| Listing 12: Code for eq. 150 and 151 to eq. 160 and eq. 161 |
 |
 |
 |
7. Questions
Does answer the in
Using thm. 5, when f is defined in , does have a finite value?
Using thm. 5, when f is defined in , does have a finite value?
If there’s no time to check questions i, ii and iii, see .
Suppose
Then one example of
, using §
Section 5.4.1 step i, (where
) is:
Note, the length of each partition is
, where the borders could be approximated as:
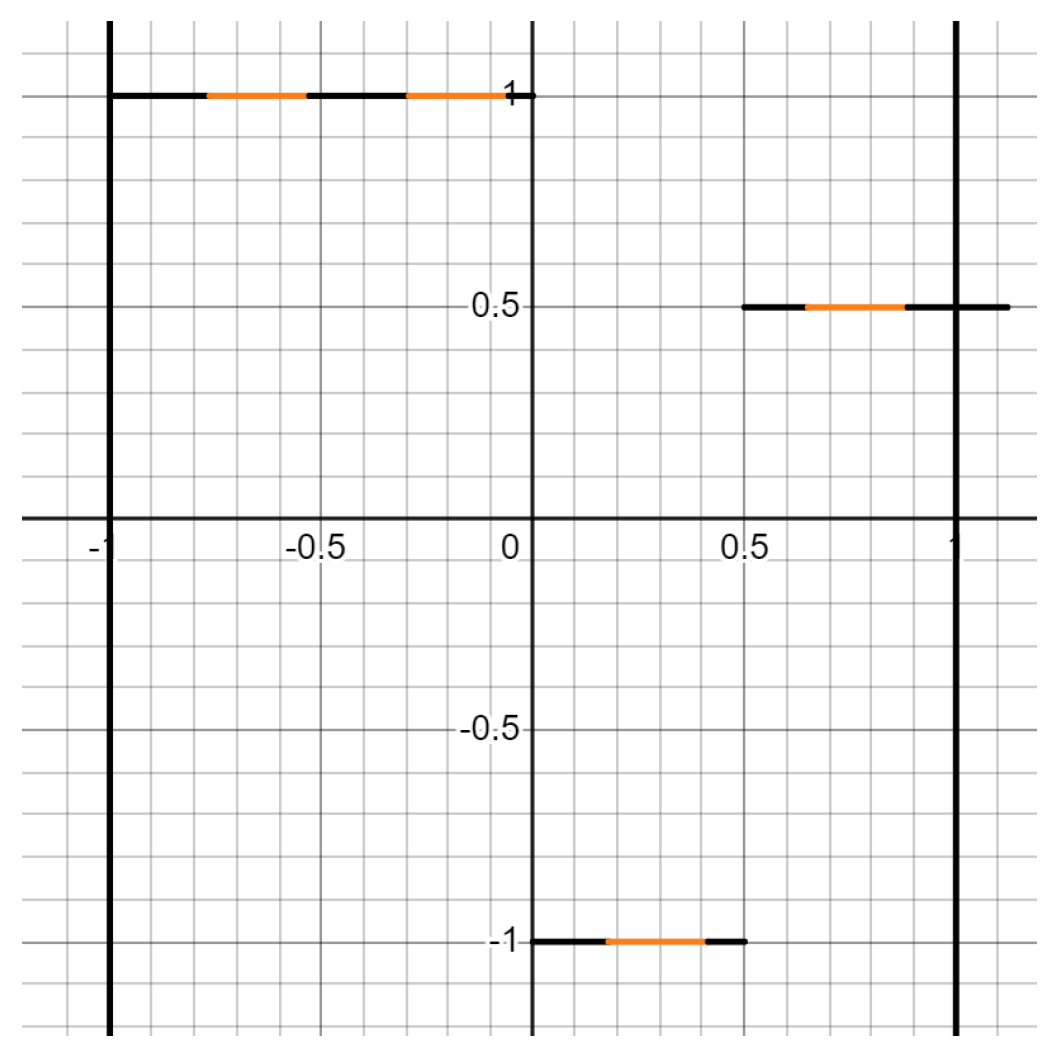
which is illustrated using
alternating orange/black lines of equal length covering
(i.e., the black vertical lines are the smallest and largest
x-cooridinates of
).
(Note, the alternating covers in
Figure 3 satisfy step (i) of §
Section 5.4.1, because the Hausdorff measure
in its dimension of the covers is
and there are 9 covers over-covering
: i.e.,
Figure 3.
The alternating orange & black lines are the “covers" and the vertical lines are the boundaries of .
Figure 3.
The alternating orange & black lines are the “covers" and the vertical lines are the boundaries of .
Definition 3 (Minimum Covers of Measure
covering
).
We can compute the minimum covers of , using the formula:
where
).
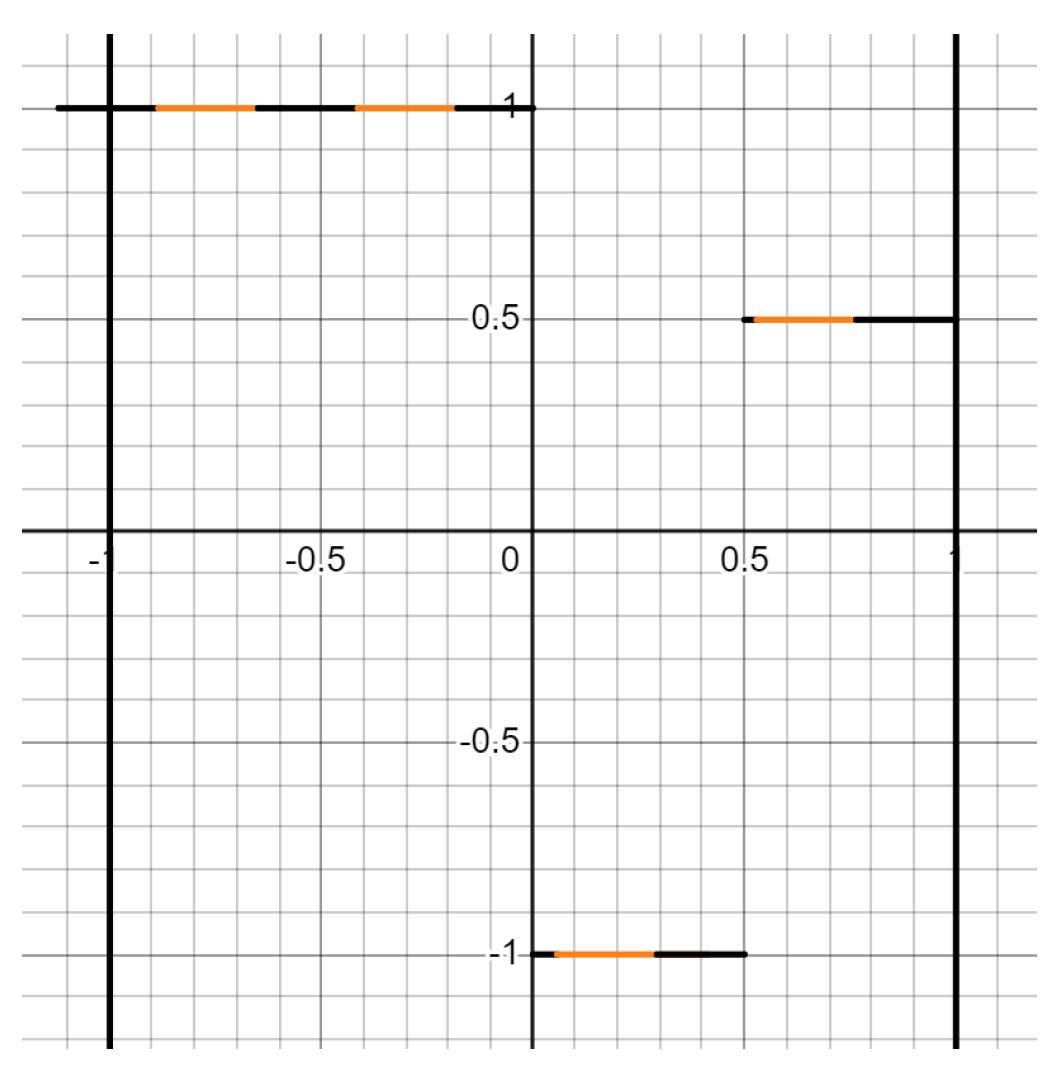
Note there are other examples of for different . Here is another case:
which can be defined (see eq.
163 for comparison):
In the case of
, there are uncountable
different covers which can be used. For instance, when
(i.e.,
) consider:
When
and
, we get
Figure 4 and when
and
, we get
Figure 3
Figure 4.
This is similar to
Figure 3, except the start-points of the covers are shifted all the way to the left.
Figure 4.
This is similar to
Figure 3, except the start-points of the covers are shifted all the way to the left.
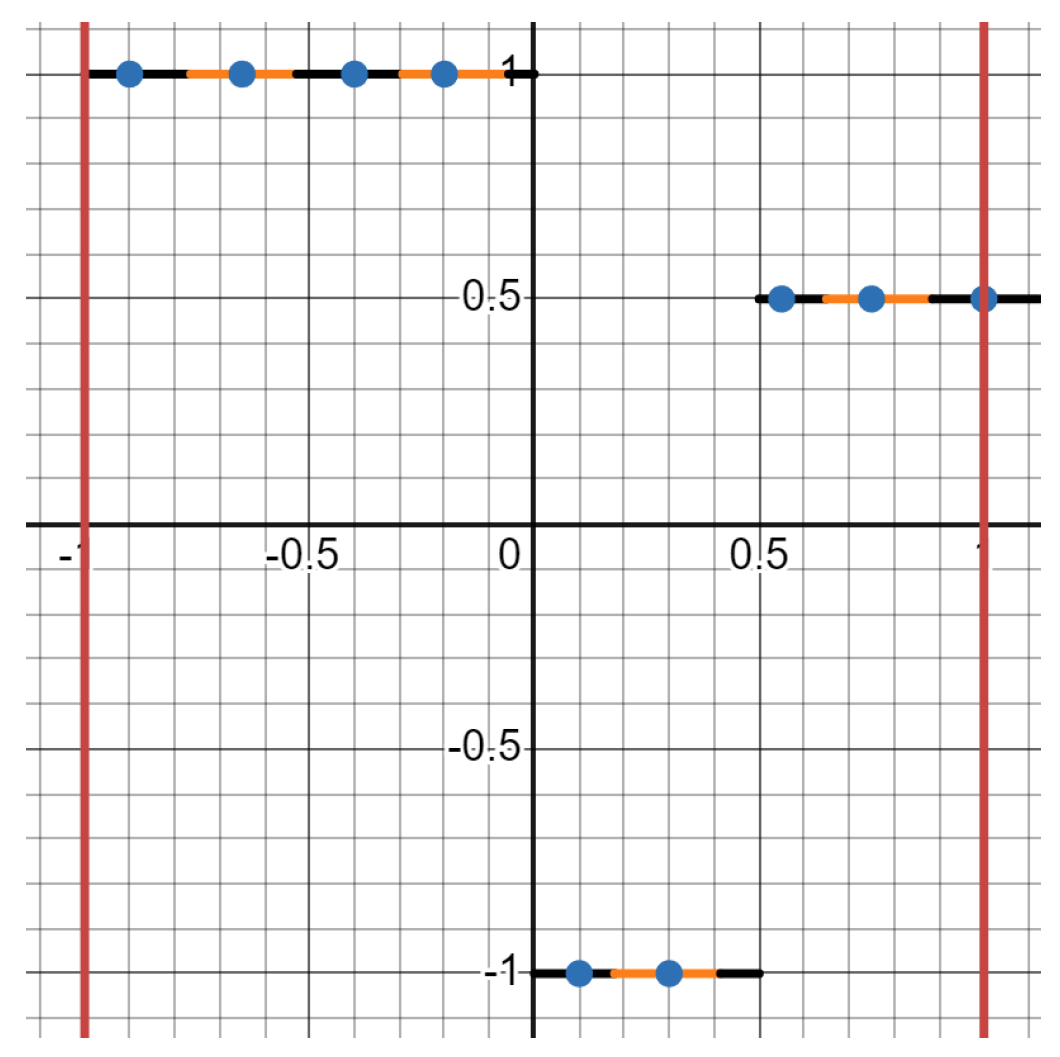
. Suppose:
When defining
: i.e.,
, using eq.
164 and
Figure 3, which is
approximately
Then, an example of
is:
Below, we illustrate the sample: i.e., the set of all blue points in each orange and black line of covering :
Figure 5.
The blue points are the “sample points", the alternative black and orange lines are the “covers", and the red lines are the smallest & largest x-coordinates .
Figure 5.
The blue points are the “sample points", the alternative black and orange lines are the “covers", and the red lines are the smallest & largest x-coordinates .
Note, there are multiple samples that can be taken, as long as one sample point is taken from each cover in .
8.3. Example of §Section 5.4.1, Step iii
Suppose
When defining
:
, using eq.
164 and
Figure 3, is approx.
, using eq.
169, is:
Therefore, consider the following process:
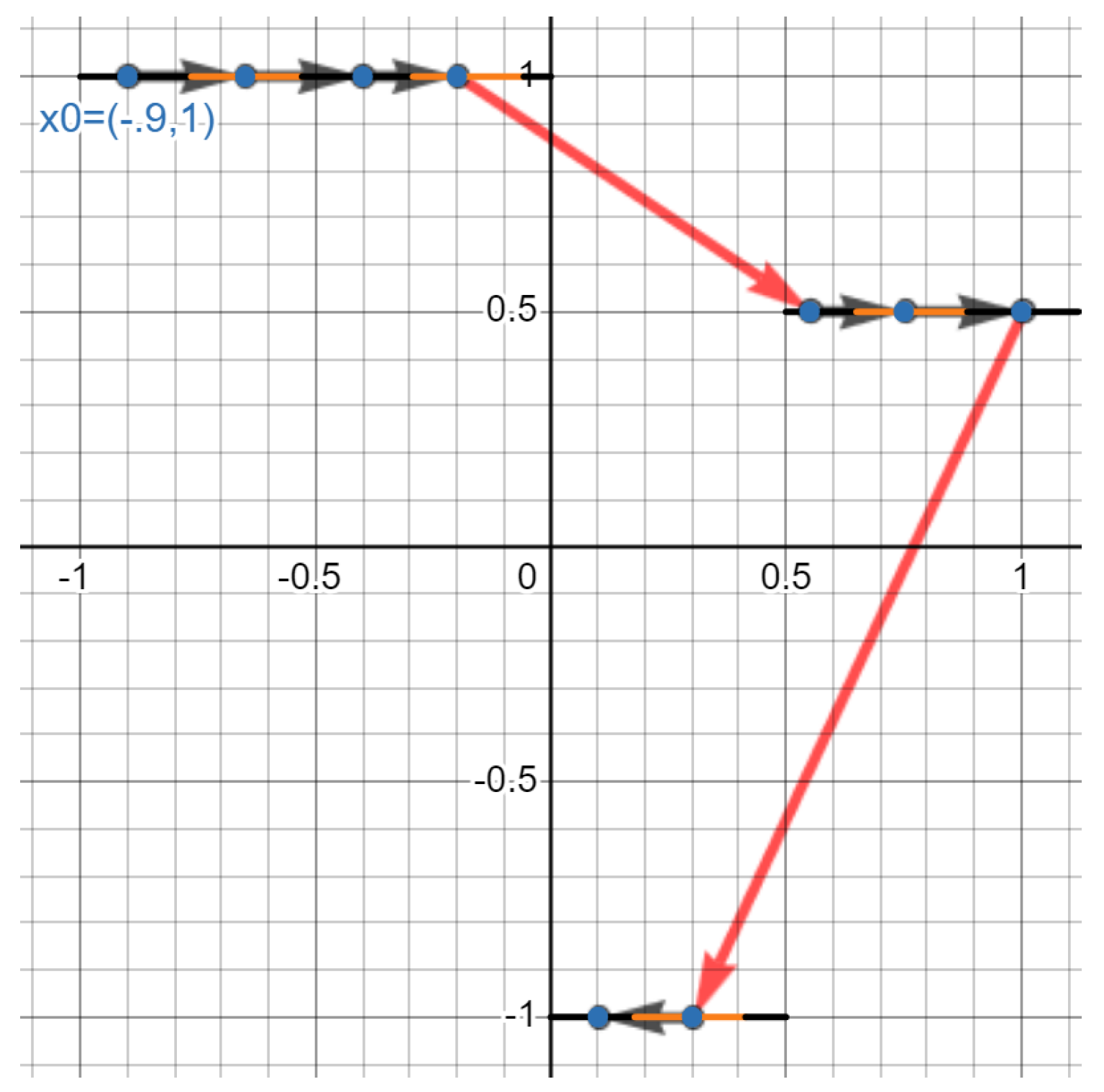
8.3.1. Step 33a
If
is:
suppose
. Note, the following:
is the next point in the “pathway" since it’s a point in with the smallest 2-d Euclidean distance to instead of .
is the third point since it’s a point in with the smallest 2-d Euclidean distance to instead of and .
is the fourth point since it’s a point in with the smallest 2-d Euclidean distance to instead of , , and .
we continue this process, where the “pathway” of is:
Proof. If more than one point has the minimum 2-d Euclidean distance from
,
,
, etc. take all potential pathways: e.g., using the sample in eq.
173, if
, then since
and
have the smallest Euclidean distance to
, take
two pathways:
and also:
□
8.3.2. Step 33b
Next, take the length of all line segments in each pathway. In other words, suppose
is the
n-th dim.Euclidean distance between points
. Using the pathway in eq.
174, we want:
Whose distances can be approximated as:
Also, we see the outliers [
23] are
and
(i.e., notice that the outliers are more prominent for
). Therefore, remove
and
from our set of lengths:
This is illustrated using:
Figure 6.
The black arrows are the “pathways" whose lengths aren’t outliers. The length of the red arrows in the pathway are outliers.
Figure 6.
The black arrows are the “pathways" whose lengths aren’t outliers. The length of the red arrows in the pathway are outliers.
Hence, when
, using §
Section 5.4.1 step 33b & eq.
173, we note:
8.3.3. Step 33c
To convert the set of distances in eq.
176 into a probability distribution, we take:
Then divide each element in
by 1.35
which gives us the probability distribution:
8.3.4. Step 33d
Take the shannon entropy of eq.
178:
We shorten
to
, giving us:
8.3.5. Step 33e
Take the entropy, w.r.t all pathways, of the sample:
In other words, we’ll compute:
Hence, since the largest value out of eq.
181- is
:
References
- Krishnan, B. Finding a Published Paper Which Meaningfully Averages The Most Pathalogical Functions, 2024. Available online: https://www.researchgate.net/publication/382557954_Finding_a_Published_Research_Paper_Which_Meaningfully_Averages_the_Most_Pathalogical_Functions. [CrossRef]
- Bernardi, C.; Rainaldi, C. Everywhere surjections and related topics: Examples and counterexamples. Le Matematiche 2018, 73, 71–88. Available online: https://www.researchgate.net/publication/325625887_Everywhere_surjections_and_related_topics_Examples_and_counterexamples.
- (https://mathoverflow.net/users/87856/arbuja), A. Is there an explicit, everywhere surjective f:R→R whose graph has zero Hausdorff measure in its dimension? MathOverflow, [https://mathoverflow.net/q /476471]. Available online: https://mathoverflow.net/q/476471.
- (https://math.stackexchange.com/users/413/jdh), J. Uncountable sets of Hausdorff dimension zero. Mathematics Stack Exchange, [https://math.stackexchange.com/q/73551]. Available online: https://math.stackexchange.com/q/73551.
- (https://mathoverflow.net/users/11009/pablo shmerkin), P.S. Hausdorff dimension of R x X. MathOverflow, [https://mathoverflow.net/q/189274]. Available online: https://mathoverflow.net/q/189274.
- Xie, T.; Zhou, S. On a class of fractal functions with graph Hausdorff dimension 2. Chaos, Solitons & Fractals 2007, 32, 1625–1630. Available online: https://www.sciencedirect.com/science/article/pii/S0960077906000129. [CrossRef]
- MFH. Prove the following limits of a sequence of sets? Mathchmaticians, 2023. Available online: https://matchmaticians.com/questions/hinaeh.
- OEIS Foundation Inc.. A011371. The On-Line Encyclopedia of Integer Sequences, 1999. Available online: https://oeis.org/A011371.
- OEIS Foundation Inc.. A099957. The On-Line Encyclopedia of Integer Sequences, 2005. Available online: https://oeis.org/A099957.
- OEIS Foundation Inc.. A002088. The On-Line Encyclopedia of Integer Sequences, 1991. Available online: https://oeis.org/A002088.
- Ott, W.; Yorke, J.A. Prevelance. Bulletin of the American Mathematical Society 2005, 42, 263–290. Available online: https://www.ams.org/journals/bull/2005-42-03/S0273-0979-05-01060-8/S0273-0979-05-01060-8.pdf. [CrossRef]
- Achour, R.; Li, Z.; Selmi, B.; Wang, T. A multifractal formalism for new general fractal measures. Chaos, Solitons & Fractals 2024, 181, 114655. Available online: https://www.sciencedirect.com/science/article/abs/pii/S0960077924002066.
- Bedford, T.; Fisher, A.M. Analogues of the Lebesgue density theorem for fractal sets of reals and integers. Proceedings of the London Mathematical Society 1992, 3, 95–124. Available online: https://www.ime.usp.br/~afisher/ps/Analogues.pdf. [CrossRef]
- Bedford, T.; Fisher, A.M. Ratio geometry, rigidity and the scenery process for hyperbolic Cantor sets. Ergodic Theory and Dynamical Systems 1997, 17, 531–564. [Google Scholar] [CrossRef]
- Sipser, M. Introduction to the Theory of Computation, 3 ed.; Cengage Learning, 2012; pp. 275–322.
- Krishnan, B. Bharath Krishnan’s ResearchGate Profile. Available online: https://www.researchgate.net/profile/Bharath-Krishnan-4.
- Barański, K.; Gutman, Y.; Śpiewak, A. Prediction of dynamical systems from time-delayed measurements with self-intersections. Journal de Mathématiques Pures et Appliquées 2024, 186, 103–149. Available online: https://www.sciencedirect.com/science/article/pii/S0021782424000345. [CrossRef]
- Caetano, A.M.; Chandler-Wilde, S.N.; Gibbs, A.; Hewett, D.P.; Moiola, A. A Hausdorff-measure boundary element method for acoustic scattering by fractal screens. Numerische Mathematik 2024, 156, 463–532. [Google Scholar] [CrossRef]
- (https://math.stackexchange.com/users/5887/sbf), S. Convergence of functions with different domain. Mathematics Stack Exchange, [https://math.stackexchange.com/q/1063261]. https://math.stackexchange.com/q/1063261. Available online: https://math.stackexchange.com/q/1063261.
- M., G. Entropy and Information Theory, 2 ed.; Springer New York: New York [America];, 2011; pp. 61–95. Available online: https://ee.stanford.edu/~gray/it.pdf. [CrossRef]
- ydd. Finding the asymptotic rate of growth of a table of value? Mathematica Stack Exchange, [https://mathematica.stackexchange.com/a/307050/34171]. Available online: https://mathematica.stackexchange.com/a/307050/34171.
- ydd. How to find a closed form for this pattern (if it exists)? Mathematica Stack Exchange, [https://mathematica.stackexchange.com/a/306951/34171]. Available online: https://mathematica.stackexchange.com/a/306951/34171.
- John, R. Outlier. Available online: https://en.m.wikipedia.org/wiki/Outlier.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).