On Duality Principles and Concerned Convex Dual Formulations Applied to a Non-Linear Plate Theory and Related Models

Preprint

Article

On Duality Principles and Concerned Convex Dual Formulations Applied to a Non-Linear Plate Theory and Related Models

Altmetrics

Downloads

115

Views

208

Comments

Fabio Botelho^*

This version is not peer-reviewed

Submitted:

16 September 2024

Posted:

17 September 2024

You are already at the latest version

Alerts

Abstract

This article develops duality principles applicable to originally non-convex primal variational formulations. More specifically, as a first application, we establish a convex dual approximate variational formulation for a non-linear Kirchhoff-Love plate model. The results are obtained through basic tools of functional analysis, calculus of variations, duality and optimization theory in infinite dimensional spaces. We emphasize such a convex dual approximate formulation obtained may be applied to a large class of similar models in the calculus of variations. Finally, in the last section, we present a duality principle and respective convex dual formulation for a Ginzburg-Landau type equation.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

MSC: 49N15

1. Introduction

This article develops a duality principle applicable to a large class of models in the calculus of variations. Specifically in this text, we present applications to the non-linear Kirchhoff-Love plate model.

We emphasize the results on duality theory here addressed and developed are inspired mainly in the approaches of J.J.Telega, W.R. Bielski and co-workers presented in the articles [1,2,3,4]. Other main reference is the article by Toland,[5].

Moreover, details on the Sobolev spaces involved may be found in [6].

Similar results and models are addressed in [7,8,9,10,11].

Basic results on convex analysis are addressed in [12]. Other similar results and approaches may be found in [13,14,15].

Now we start to describe the primal variational formulation for the plate model in question.

Let

Ω \subset R^{2}

be an open, bounded and connected set with a regular (Lipschitzian) boundary denoted by

\partial Ω .

We assume such a

Ω

set represents the middle surface of a thin plate with a constant thickness

h > 0

Moreover, we suppose such a plate is subject to a external load

(P_{α}, P) \in L^{2} (Ω; R^{3})

resulting a field of displacements denoted by

(u_{α}, w) = (u_{1}, u_{2}, w) \in W_{0}^{1, 2} (Ω; R^{2}) \times W_{0}^{2, 2} (Ω) = V .

Both the load and displacements fields refers to a cartesian system

(0, x_{1}, x_{2}, x_{3})

and related canonical basis in

R^{3} .

Finally, we denote

Y_{1} = Y_{1}^{*} = L^{2} (Ω; R^{4})

and

Y_{2} = Y_{2}^{*} = L^{2} (Ω; R^{2}) .

We also emphasize the boundary conditions in question refer to a clamped plate.

The strain tensors are defined by

γ_{α β} (u) = \frac{u_{α, β} + u_{β, α}}{2} + \frac{1}{2} w_{, α} w_{, β},

and

κ_{α β} (w) = - w_{, α β} .

The plate total energy functional is defined by

\begin{matrix} J (u) & = & \frac{1}{2} \int_{Ω} H_{α β λ μ} γ_{α β} (u) γ_{λ μ} (u) d x \\ + \frac{1}{2} \int_{Ω} h_{α β λ μ} κ_{α β} (u) κ_{λ μ} (u) d x \\ - {〈 w, P 〉}_{L^{2}} - {〈 u_{α}, P_{α} 〉}_{L^{2}} . \end{matrix}

(1)

Here

{H_{α β λ μ}}

is a fourth order positive definite symmetric constant tensor.

Moreover

{h_{α β λ μ}} = \frac{h^{2}}{12} {H_{α β λ μ}}

and we denote

\{{\bar{H}}_{α β λ μ}\} = {H_{α β λ μ}}^{- 1}

and

\{{\bar{h}}_{α β λ μ}\} = {h_{α β λ μ}}^{- 1}

in an appropriate tensor sense.

2. The Main Duality Principle and Related Convex Dual Approximate Formulation

We start by defining the approximate functional

J_{1} : V \to R

J_{1} (u) = J (u) + \sum_{α = 1}^{2} \frac{ε_{1}}{2} \int_{Ω} {(u_{α})}^{2} d x,

and considering an appropriate real constant

K > 0

, the functionals

F_{1} : V \to R

F_{2} : V \times Y_{1}^{*} \to R

F_{3} : V \to R

and

F_{4} : V \to R

, by

\begin{matrix} F_{1} (u) & = & \frac{1}{2} \int_{Ω} h_{α β λ μ} κ_{α β} (u) κ_{λ μ} (u) d x + \sum_{α = 1}^{2} \frac{K}{2} \int_{Ω} w_{, α}^{2} d x \\ + \sum_{α = 1}^{2} ε \int_{Ω} w_{, α}^{2} d x - {〈 w, P 〉}_{L^{2}} \end{matrix}

(2)

\begin{matrix} F_{2} (u, N) & = & \frac{1}{2} \int_{Ω} N_{α β} w_{, α} w_{, β} d x \\ - \sum_{α = 1}^{2} \frac{K}{2} \int_{Ω} w_{, α}^{2} d x \end{matrix}

(3)

\begin{matrix} F_{3} (u) & = & \sum_{α = 1}^{2} \frac{ε_{1}}{2} \int_{Ω} u_{α}^{2} d x \end{matrix}

(4)

\begin{matrix} F_{4} (u) & = & \sum_{α = 1}^{2} ε \int_{Ω} w_{, α}^{2} d x . \end{matrix}

(5)

Moreover, we define the polar functionals

F_{1}^{*} : {[Y_{2}^{*}]}^{2} \to R

F_{2}^{*} : {[Y_{2}^{*}]}^{2} \times Y_{1}^{*} \to R,

F_{3}^{*} : Y_{1}^{*} \to R

and

F_{4}^{*} : {[Y_{2}^{*}]}^{2} \to R

, by

\begin{matrix} F_{1}^{*} (R, L) & = & sup_{u \in V} {{〈 w_{, α}, R_{α} - L_{α} 〉}_{L^{2}} - F_{1} (u)}, \end{matrix}

(6)

\begin{matrix} F_{2}^{*} (Q, L) & = & inf_{v \in Y_{2}} \{{〈 v_{α}, Q_{α} + L_{α} 〉}_{L^{2}} - \frac{1}{2} \int_{Ω} N_{α β} v_{α} v_{β} d x \\ + \sum_{α = 1}^{2} \frac{K}{2} \int_{Ω} v_{α}^{2} d x + \frac{1}{2} \int_{Ω} {\bar{H}}_{α β λ μ} N_{α β} N_{λ μ} d x\} \\ = & \frac{1}{2} \int_{Ω} \bar{N_{α β}^{(- K)}} (Q_{α} + L_{α}) (Q_{β} + L_{β}) d x \\ + \frac{1}{2} \int_{Ω} {\bar{H}}_{α β λ μ} N_{α β} N_{λ μ} d x, \end{matrix}

(7)

N = {N_{α β}} \in B^{*}

, where

B^{*} = {N \in Y_{1}^{*} : ∥ N_{α β} ∥_{\infty} \leq K / 8, \forall α, β \in {1, 2}},

\{N_{α β}^{(- K)}\} = {N_{α β} - K δ_{α β}},

and

\{\bar{N_{α β}^{(- K)}}\} = {\{N_{α β}^{(- K)}\}}^{- 1} .

Furthermore,

\begin{matrix} F_{3}^{*} (N) & = & sup_{u \in V} {{〈 u_{α}, N_{α β, β} + P_{α} 〉}_{L_{2}} - F_{3} (u)} \\ = & \sum_{α = 1}^{2} \frac{1}{2 ε_{1}} \int_{Ω} {(N_{α β, β} + P_{α})}^{2} d x, \end{matrix}

(8)

\begin{matrix} F_{4}^{*} (R, Q) & = & sup_{(v_{1}, v_{2}) \in Y_{2}^{*}} \{{〈 {(v_{1})}_{α}, R_{α} 〉}_{L^{2}} - \frac{ε}{2} \int_{Ω} {(v_{1})}_{α}^{2} d x \\ + {〈 {(v_{2})}_{α}, Q_{α} 〉}_{L^{2}} - \frac{ε}{2} \int_{Ω} {(v_{2})}_{α}^{2} d x\} \\ = & \sum_{α = 1}^{2} (\frac{1}{2 ε} \int_{Ω} R_{α}^{2} d x + \frac{1}{2 ε} \int_{Ω} Q_{α}^{2} d x) . \end{matrix}

(9)

At this point, denoting

D^{*} = {Q = {Q_{α}} \in Y_{2}^{*} : ∥ Q_{α} ∥ \leq 5, \forall α \in {1, 2}},

we define

J_{1}^{*} : {(D^{*})}^{2} \times B^{*} \times Y_{2}^{*} \to R

J_{1}^{*} (R, Q, N, L) = - F_{1}^{*} (R, L) - F_{2}^{*} (Q, L, N) - F_{3}^{*} (N) + F_{4}^{*} (R, Q),

and

J_{2}^{*} : {(D^{*})}^{2} \times B^{*} \to R

J_{2}^{*} (R, Q, N) = {sta}_{L \in Y_{2}^{*}} J_{1}^{*} (R, Q, N, L) = J_{1}^{*} (R, Q, N, \hat{L} (R, Q, N)),

where

\hat{L} = \hat{L} (R, Q, N) \in Y_{2}^{*}

is the only solution of the linear equation in L

\frac{\partial J_{1}^{*} (R, Q, N, \hat{L})}{\partial L} = 0 .

Moreover, we define

J_{3}^{*} : {(D^{*})}^{2} \times B^{*} \to R

, by

\begin{matrix} J_{3}^{*} (R, Q, N) \\ = & J_{2}^{*} (R, Q, N) \\ - \sum_{α = 1}^{2} \sum_{β = 1}^{2} \frac{K_{1}}{2} {∥{\bar{H}}_{α β λ μ} N_{λ μ} - \frac{{(N_{α ρ, ρ} + P_{α})}_{, β} + {(N_{β ρ, ρ} + P_{α})}_{, α}}{2 ε_{1}} - \frac{1}{2} {\tilde{v}}_{α} {\tilde{v}}_{β}∥}_{0, 2}^{2}, \end{matrix}

(10)

where

{\tilde{v}}_{α} = \bar{N_{α β}^{(- K)}} (Q_{β} + L_{β} (R, Q, N)), \forall α \in {1, 2} .

Here, we assume

K_{1} ≫ max {1, K, max {{\bar{h}}_{α β λ μ}, α, β, λ, μ \in {1, 2}}},

0 < ε, ε_{1} ≪ 1

and

\frac{1}{ε} ≫ max \{K_{1}, \frac{1}{ε_{1}}\} .

Observe that

\frac{\partial^{2} J_{3}^{*} (R, Q, N)}{\partial Q_{α}^{2}} = O (\frac{1}{ε}) > 0,

\frac{\partial^{2} J_{3}^{*} (R, Q, N)}{\partial R_{α}^{2}} = O (\frac{1}{ε}) > 0,

\forall α \in {1, 2} .

Thus, considering also the remaining mixed variations in

Q_{α}

and

R_{α}

, we may infer that

det \{\frac{\partial^{2} J_{3}^{*} (R, Q, N)}{\partial Q_{α} \partial R_{β}}\} > 0,

{(D^{*})}^{2} \times B^{*}

Moreover, by direct computation, clearly

\frac{\partial^{2} J_{3}^{*} (R, Q, N)}{\partial {(N_{α β})}^{2}} < 0, \forall α, β \in {1, 2}

and considering the remaining mixed variations of

J_{3}^{*}

N_{11}

N_{22}

N_{12}

and

N_{21}

and the concerned remaining minor determinants, we may infer that

det \{\frac{\partial^{2} J_{3}^{*} (R, Q, N)}{\partial N_{α β} \partial N_{λ μ}}\} > 0,

{(D^{*})}^{2} \times B^{*}

From such results, we may also infer that

J_{3}^{*}

is convex in

(R, Q)

and concave in N in

{(D^{*})}^{2} \times B^{*}

Let

(\hat{R}, \hat{Q}, \hat{N}, \hat{L}) \in {(D^{*})}^{2} \times B^{*} \times Y_{2}^{*}

be such that

δ J_{1}^{*} (\hat{R}, \hat{Q}, \hat{N}, \hat{L}) = 0 .

Let

u_{0} = ({(u_{0})}_{α}, w_{0}) \in V

be such that

{(u_{0})}_{α} = \frac{{\hat{N}}_{α β, β} + P_{α}}{ε_{1}},

and

{(w_{0})}_{, α} = \frac{{\hat{Q}}_{α}}{ε},

\forall α \in {1, 2} .

From standard results in Duality Theory and the Legendre Transform properties, we may obtain

δ J_{1} (u_{0}) = 0,

δ J_{2}^{*} (\hat{R}, \hat{Q}, \hat{N}) = 0,

δ J_{3}^{*} (\hat{R}, \hat{Q}, \hat{N}) = 0

and

\begin{matrix} J_{1} (u_{0}) & = & J_{1}^{*} (\hat{R}, \hat{Q}, \hat{N}, \hat{L}) \\ = & J_{2}^{*} (\hat{R}, \hat{Q}, \hat{N}) \\ = & J_{3}^{*} (\hat{R}, \hat{Q}, \hat{N}) . \end{matrix}

(11)

From such results and the Min-Max Theorem, we have

J_{3}^{*} (\hat{R}, \hat{Q}, \hat{N}) = inf_{(R, Q) \in {(D^{*})}^{2}} \{sup_{N \in B^{*}} J_{3}^{*} (R, Q, N)\} .

Joining the pieces, we have got

\begin{matrix} J_{1} (u_{0}) & = & J_{1}^{*} (\hat{R}, \hat{Q}, \hat{N}, \hat{L}) \\ = & J_{2}^{*} (\hat{R}, \hat{Q}, \hat{N}) \\ = & inf_{(R, Q) \in {(D^{*})}^{2}} \{sup_{N \in B^{*}} J_{3}^{*} (R, Q, N)\} \\ = & J_{3}^{*} (\hat{R}, \hat{Q}, \hat{N}) . \end{matrix}

(12)

Remark 2.1.

Defining

J_{5}^{*} : {(D^{*})}^{2} \to R

J_{5}^{*} (R, Q) = sup_{N \in B^{*}} J_{3}^{*} (R, Q, N),

we have that such a functional

J_{5}^{*}

is convex in

{(D^{*})}^{2}

as the supremum in

N \in B^{*}

of a family of convex functionals in

(R, Q) .

In such a case, we have also obtained

\begin{matrix} J_{1} (u_{0}) & = & J_{1}^{*} (\hat{R}, \hat{Q}, \hat{N}, \hat{L}) \\ = & J_{2}^{*} (\hat{R}, \hat{Q}, \hat{N}) \\ = & inf_{(R, Q) \in {(D^{*})}^{2}} \{sup_{N \in B^{*}} J_{3}^{*} (R, Q, N)\} \\ = & J_{3}^{*} (\hat{R}, \hat{Q}, \hat{N}) \\ = & inf_{(R, Q) \in {(D^{*})}^{2}} J_{5}^{*} (R, Q) \\ = & J_{5}^{*} (\hat{R}, \hat{Q}) . \end{matrix}

(13)

3. One More Duality Principle and Related Convex Dual Formulation

In this section we develop another new duality principle with a related convex dual functional applied to a Ginzburg-Landau type equation.

Let

Ω \subset R^{3}

be an open, bounded and connected set with a regular (Lipschitzian) boundary denoted by

\partial Ω .

Consider a functional

J : V \to R

where

\begin{matrix} J (u) & = & \frac{γ}{2} \int_{Ω} \nabla u \cdot \nabla u d x \\ + \frac{α}{2} \int_{Ω} {(u^{2} - β)}^{2} d x - {〈 u, f 〉}_{L^{2}}, \end{matrix}

(14)

where

γ > 0

α > 0,

β > 0

and

f \in L^{2} (Ω) .

Here

u \in V = W_{0}^{1, 2} (Ω)

and we denote

Y = Y^{*} = L^{2} (Ω) .

Define the functionals

F_{1} : V \times Y^{*} \to R

F_{2} : V \times Y^{*} \to R

and

F_{3} : V \to R

\begin{matrix} F_{1} (u, v_{0}^{*}) & = & \frac{γ}{4} \int_{Ω} \nabla u \cdot \nabla u d x + \frac{1}{2} {〈 u^{2}, v_{0}^{*} 〉}_{L^{2}} \\ + \frac{K}{2} \int_{Ω} u^{2} d x, \end{matrix}

(15)

\begin{matrix} F_{2} (u, v_{0}^{*}) & = & \frac{γ}{4} \int_{Ω} \nabla u \cdot \nabla u d x + \frac{1}{2} {〈 u^{2}, v_{0}^{*} 〉}_{L^{2}} \\ + \frac{K}{2} \int_{Ω} u^{2} d x - {〈 u, f 〉}_{L^{2}} \\ - \frac{1}{2 α} \int_{Ω} {(v_{0}^{*})}^{2} d x - β \int_{Ω} v_{0}^{*} d x, \end{matrix}

(16)

\begin{matrix} F_{3} (u) & = & K \int_{Ω} u^{2} d x, \end{matrix}

(17)

where

K > 0

is an appropriate real constant.

Define also the polar functionals

F_{1}^{*} : {[Y^{*}]}^{3} \to R

F_{2}^{*} : {[Y^{*}]}^{3} \to R

and

F_{3}^{*} : Y^{*} \to R

\begin{matrix} F_{1}^{*} (v_{1}^{*}, v_{0}^{*}, z^{*}) & = & sup_{u \in V} {{〈 u, v_{1}^{*} + z^{*} / 2 〉}_{L^{2}} - F_{1} (u, v_{0}^{*})} \\ = & \frac{1}{2} \int_{Ω} \frac{{(v_{1}^{*} + z^{*} / 2)}^{2}}{((- γ \nabla^{2} + 2 v_{0}^{*}) / 2 + K)} d x \end{matrix}

(18)

\begin{matrix} F_{2}^{*} (v_{1}^{*}, v_{0}^{*}, z^{*}) & = & sup_{u \in V} {{〈 u, - v_{1}^{*} + z^{*} / 2 〉}_{L^{2}} - F_{2} (u, v_{0}^{*})} \\ = & \frac{1}{2} \int_{Ω} \frac{{(- v_{1}^{*} + z^{*} / 2 + f)}^{2}}{((- γ \nabla^{2} + 2 v_{0}^{*}) / 2 + K)} d x \\ + \frac{1}{2 α} \int_{Ω} {(v_{0}^{*})}^{2} d x + β \int_{Ω} v_{0}^{*} d x, \end{matrix}

(19)

v_{0}^{*} \in B^{*}

, where

B^{*} = {v_{0}^{*} \in Y^{*} : ∥ 2 v_{0}^{*} ∥ \leq K / 4},

\begin{matrix} F_{3}^{*} (z^{*}) & = & sup_{w \in L^{2}} {{〈 w, z^{*} 〉}_{L^{2}} - F_{3} (w)} \\ = & \frac{1}{4 K} \int_{Ω} {(z^{*})}^{2} d x . \end{matrix}

(20)

Moreover, define

D^{*} = {v_{1}^{*} \in Y^{*} : ∥ 2 v_{1}^{*} - f ∥_{\infty} \leq 5},

D_{1}^{+} = {z^{*} \in Y^{*} : z^{*} f \geq 0, in Ω},

and

D_{1}^{*} = {z^{*} \in D^{+} : ∥ z^{*} ∥_{\infty} \leq (5 / 2) K} .

Assuming

K_{1} ≫ max {γ, α, β, 1 / α, 1, K}

and

K ≫ α,

define

J^{*} : D^{*} \times B^{*} \times D_{1}^{*} \to R

\begin{matrix} J^{*} (v_{1}^{*}, v_{0}^{*}, z^{*}) & = & - F_{1}^{*} (v_{1}^{*}, v_{0}^{*}, z^{*}) - F_{2}^{*} (v_{1}^{*}, v_{0}^{*}, z^{*}) + F_{3}^{*} (z^{*}) . \end{matrix}

(21)

From the variation of

J^{*}

v_{1}^{*}

, we have

- \frac{v_{1}^{*} + z^{*} / 2}{((- γ \nabla^{2} + 2 v_{0}^{*}) / 2 + K)} + \frac{- v_{1}^{*} + z^{*} / 2 + f}{((- γ \nabla^{2} + 2 v_{0}^{*}) / 2 + K)} = 0, in Ω,

so that

- 2 v_{1}^{*} + f = 0, in Ω .

Moreover, denoting

u_{0} = \frac{v_{1}^{*} + z^{*} / 2}{((- γ \nabla^{2} + 2 v_{0}^{*}) / 2 + K)},

from the variation of

J^{*}

z^{*}

, we obtain

u_{0} = \frac{z^{*}}{2 K} .

From such results, we may also obtain

δ J (u_{0}) = - γ \nabla^{2} u_{0} + 2 α (u_{0}^{2} - β) u_{0} - f = 0,

so that

- γ \nabla^{2} (\frac{z^{*}}{2 K}) + 2 α ({(\frac{v_{1}^{*} + z^{*} / 2}{(- γ \nabla^{2} + 2 v_{0}^{*}) / 2 + K})}^{2} - β) (\frac{z^{*}}{2 K}) - f = 0

Ω .

With such results in mind, we define also the exactly penalized functional

J_{1}^{*} : D^{*} \times B^{*} \times D_{1}^{*} \to R

, where

\begin{matrix} J_{1}^{*} (v_{1}^{*}, v_{0}^{*}, z^{*}) \\ = & J^{*} (v_{1}^{*}, v_{0}^{*}, z^{*}) - \frac{K_{1}}{2} {∥ 2 v_{1}^{*} - f ∥}_{0, 2}^{2} \\ + 30 \frac{K}{2} {∥- γ \nabla^{2} (\frac{z^{*}}{2 K}) + 2 α ({(\frac{v_{1}^{*} + z^{*} / 2}{(- γ \nabla^{2} + 2 v_{0}^{*}) / 2 + K})}^{2} - β) (\frac{z^{*}}{2 K}) - f∥}_{0, 2}^{2} \end{matrix}

(22)

Clearly, we have

\frac{\partial^{2} J_{1}^{*} (v_{1}^{*}, v_{2}^{*}, v_{0}^{*})}{\partial {(v_{1}^{*})}^{2}} = - O (K_{1}) < 0,

and

\frac{\partial^{2} J_{1}^{*} (v_{1}^{*}, v_{2}^{*}, v_{0}^{*})}{\partial {(v_{0}^{*})}^{2}} = - O (1 / α) < 0,

so that considering also the mixed variations of

J_{1}^{*}

v_{1}^{*}

and

v_{0}^{*}

, we may infer that

det \{\frac{\partial^{2} J_{1}^{*} (v_{1}^{*}, v_{0}^{*}, z^{*})}{\partial v_{1}^{*} \partial v_{0}^{*}}\} > 0, in D^{*} \times B^{*} \times D_{1}^{*} .

Hence,

J_{1}^{*}

is concave in

(v_{1}^{*}, v_{0}^{*})

D^{*} \times B^{*} \times D_{1} .

Furthermore,

\frac{\partial^{2} J_{2}^{*} (v_{1}^{*}, v_{0}^{*}, z^{*})}{\partial {(z^{*})}^{2}} = O (30 / (4 K)) > 0,

D^{*} \times B^{*} \times D_{1}^{*}

, so that

J_{1}^{*}

is convex in

z^{*}

D^{*} \times B^{*} \times D_{1}^{*}

Let

({\hat{v}}_{1}^{*}, {\hat{v}}_{0}^{*}, {\hat{z}}^{*}) \in D^{*} \times B^{*} \times D_{1}^{*}

be such that

δ J_{1}^{*} ({\hat{v}}_{1}^{*}, {\hat{v}}_{0}^{*}, {\hat{z}}^{*}) = 0 .

From this, the last previous results and the Min-Max theorem we may infer that

J_{1}^{*} ({\hat{v}}_{1}^{*}, {\hat{v}}_{0}^{*}, {\hat{z}}^{*}) = inf_{z^{*} \in D_{1}^{*}} \{sup_{(v_{1}^{*}, v_{0}^{*}) \in D^{*} \times B^{*}} J_{1}^{*} (v_{1}^{*}, v_{0}^{*}, z^{*})\} .

Let

u_{0} \in V

be such that

u_{0} = \frac{{\hat{z}}^{*}}{2 K} .

From fundamentals of duality theory and the Legendre Transform properties, we may obtain

δ J (u_{0}) = 0,

and

J (u_{0}) = J_{1}^{*} ({\hat{v}}_{1}^{*}, {\hat{v}}_{0}^{*}, {\hat{z}}^{*}) .

Joining the pieces, we have got

\begin{matrix} J (u_{0}) & = & J_{1}^{*} ({\hat{v}}_{1}^{*}, {\hat{v}}_{0}^{*}, {\hat{z}}^{*}) \\ = & inf_{z^{*} \in D_{1}^{*}} \{sup_{(v_{1}^{*}, v_{0}^{*}) \in D^{*} \times B^{*}} J_{1}^{*} (v_{1}^{*}, v_{0}^{*}, z^{*})\} . \end{matrix}

(23)

Remark 3.1.

Defining

J_{3}^{*} : D_{1}^{*} \to R

J_{3}^{*} (z^{*}) = sup_{(v_{1}^{*}, v_{0}^{*}) \in D^{*} \times B^{*}} J_{1}^{*} (v_{1}^{*}, v_{0}^{*}, z^{*}),

we have that

J_{3}^{*}

is convex in

D_{1}^{*}

as a supremum of a family of convex functionals in

z^{*}

In such case, we have

\begin{matrix} J (u_{0}) & = & J_{1}^{*} ({\hat{v}}_{1}^{*}, {\hat{v}}_{0}^{*}, {\hat{z}}^{*}) \\ = & inf_{z^{*} \in D_{1}^{*}} \{sup_{(v_{1}^{*}, v_{0}^{*}) \in D^{*} \times B^{*}} J_{1}^{*} (v_{1}^{*}, v_{0}^{*}, z^{*})\} . \\ = & inf_{z^{*} \in D_{1}^{*}} J_{3}^{*} (z^{*}) \\ = & J_{3}^{*} ({\hat{z}}^{*}) . \end{matrix}

(24)

The objective of this section is complete.

4. An Approximate Procedure for Improving the Convexity Conditions for an Originally Non-Convex Primal Formulation

In this section we obtain an approximate procedure for improving the convexity conditions for an originally non-convex variational formulation.

In this new version we present some corrections and improvements concerning the previous one.

Let

Ω \subset R^{3}

be an open, bounded and connected set with a regular (Lipschitzian) boundary denoted by

\partial Ω .

Let

V = W_{0}^{1, 2} (Ω)

and consider a continuously twice Fréchet differentiable functional

J : V \to R

such that

- 50 I_{d} \leq \frac{\partial^{2} J (u)}{\partial u^{2}} \leq 50 I_{d},

V_{1},

where the set

V_{1}

will be specified in the next lines.

Let

K = 500000 2 π

and

K_{3} = 1.0

Define

V_{1} = {u \in V : 0 \leq u \leq K_{3}} .

and the functional

J_{2} : V_{1} \to R

J_{2} (u) = - \frac{10^{16}}{K^{3}} \int_{Ω} cos (\frac{K^{4}}{u / 10^{10} + K}) d x .

Define also the functional

J_{1} : V_{1} \to R

J_{1} (u) = J (u) + J_{2} (u) .

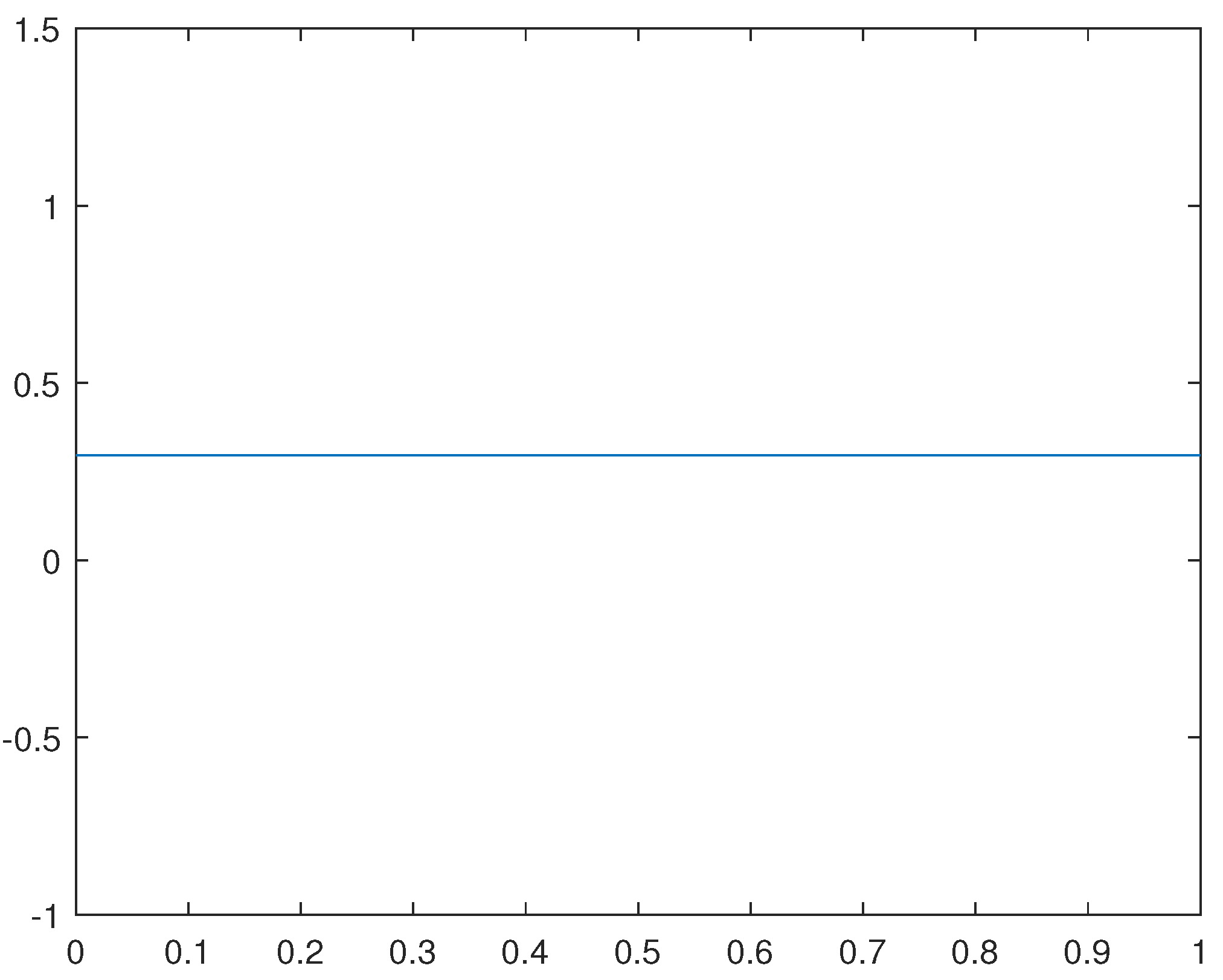
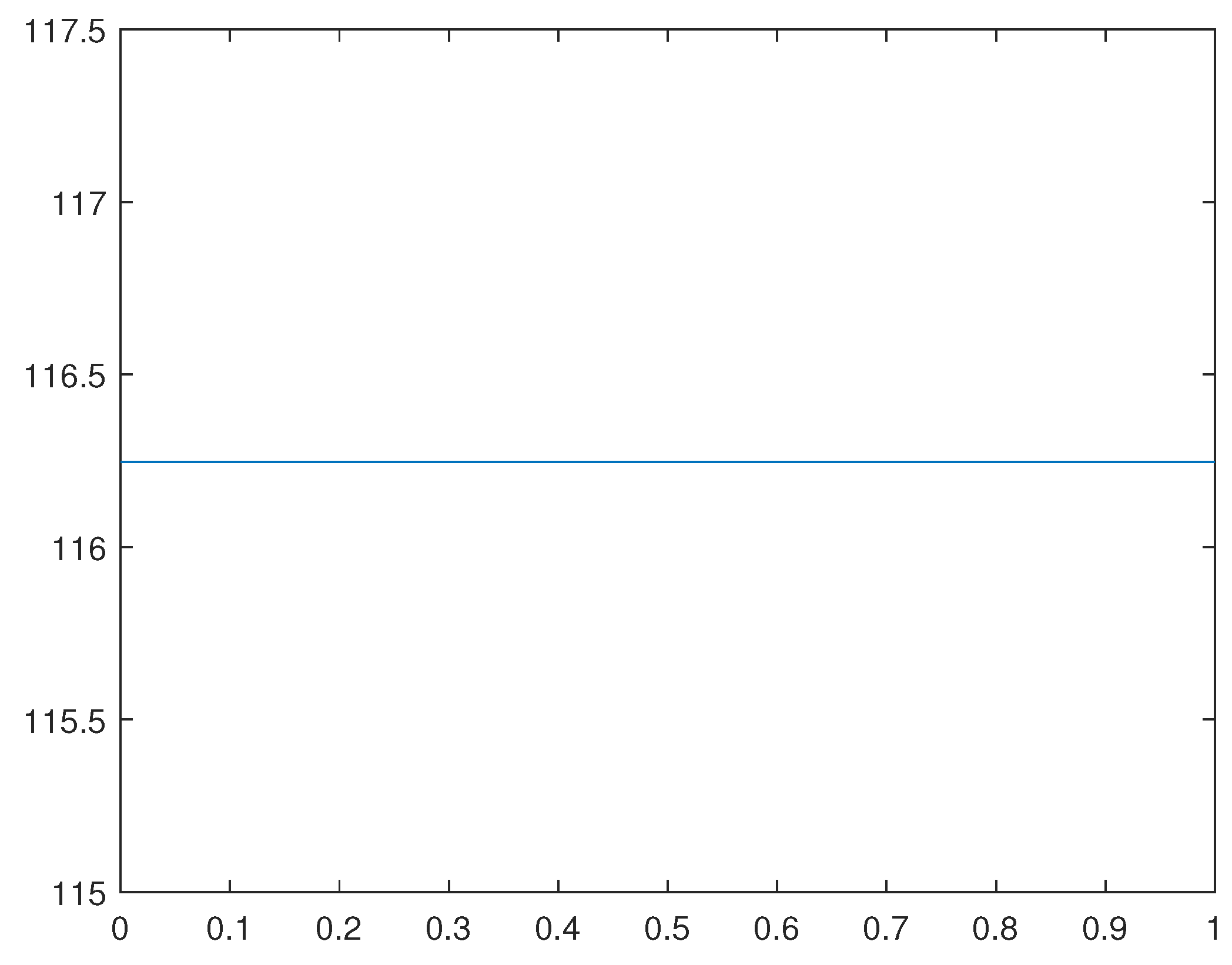
Observe that, with a help of the software MAT-LAB, we may obtain

\begin{matrix} \frac{\partial J_{1} (u)}{\partial u} & = & \frac{\partial J (u)}{\partial u} + \frac{\partial J_{2} (u)}{\partial u} \\ = & \frac{\partial J (u)}{\partial u} + O (0.3) . \end{matrix}

(25)

Moreover,

\begin{matrix} \frac{\partial^{2} J_{1} (u)}{\partial u^{2}} & = & \frac{\partial^{2} J (u)}{\partial u^{2}} + \frac{\partial^{2} J_{2} (u)}{\partial u^{2}} \\ = & \frac{\partial^{2} J (u)}{\partial u^{2}} + O (116) \\ > & 0, in V_{1} . \end{matrix}

(26)

Thus, such an approximate functional

J_{1}

is convex in

V_{1}

and its first variation results, for a large class of appropriate numerical parameters, in a very close approximation for the first variation of the original functional

J .

The functions

\frac{\partial J_{2} (x)}{\partial x}

and

\frac{\partial^{2} J_{2} (x)}{\partial x^{2}}

on the interval

[0, K_{3} = 1]

stands for

\frac{\partial J_{2} (x)}{\partial x} = \frac{10^{16}}{K^{3}} sin (\frac{K^{4}}{x / 10^{10} + K}) (\frac{- K^{4}}{{(x / 10^{10} + K)}^{2}}) (\frac{1}{10^{10}}),

\begin{matrix} \frac{\partial^{2} J_{2} (x)}{\partial x^{2}} & = & \frac{10^{16}}{K^{3}} cos (\frac{K^{4}}{x / 10^{10} + K}) {(\frac{- K^{4}}{{(x / 10^{10} + K)}^{2}})}^{2} {(\frac{1}{10^{10}})}^{2} \\ + 2 \frac{10^{16}}{K^{3}} sin (\frac{K^{4}}{x / 10^{10} + K}) (\frac{K^{4}}{{(x / 10^{10} + K)}^{3}}) (\frac{1}{10^{10}}), \end{matrix}

(27)

respectively.

For their graphs, please see Figure 1 and Figure 2, repectively.

Remark 4.1.

The reason the graphs of

J_{2}^{'} (x)

and

J_{2}^{″} (x)

are straight lines is because

\frac{x}{10^{10}}

varies very little on the interval

[0, 1] .

The objective of this section is complete.

5. Conclusion

In this article, we have developed duality principles and related convex dual variational formulations for originally non-convex primal ones.

We highlight the results here obtained are applicable to a large class of models in the calculus of variations, including other plate and shell non-linear theories, models in superconductivity, phase transition and micro-magnetism, among many others.

In a near future research we intend to apply such results to some of these mentioned related models.

Conflicts of Interest

The author declares no conflict of interest concerning this article.

References

W.R. Bielski, A. Galka, J.J. Telega, The Complementary Energy Principle and Duality for Geometrically Nonlinear Elastic Shells. I. Simple case of moderate rotations around a tangent to the middle surface. Bulletin of the Polish Academy of Sciences, Technical Sciences, Vol. 38, No. 7-9, 1988.
W.R. Bielski and J.J. Telega, A Contribution to Contact Problems for a Class of Solids and Structures, Arch. Mech., 37, 4-5, pp. 303-320, Warszawa 1985.
J.J. Telega, On the complementary energy principle in non-linear elasticity. Part I: Von Karman plates and three dimensional solids, C.R. Acad. Sci. Paris, Serie II, 308, 1193-1198; Part II: Linear elastic solid and non-convex boundary condition. Minimax approach, ibid, pp. 1313-1317 (1989).
A.Galka and J.J.Telega, Duality and the complementary energy principle for a class of geometrically non-linear structures. Part I. Five parameter shell model; Part II. Anomalous dual variational priciples for compressed elastic beams, Arch. Mech. 47 (1995) 677-698, 699-724.
J.F. Toland, A duality principle for non-convex optimisation and the calculus of variations, Arch. Rat. Mech. Anal., 71, No. 1 (1979), 41-61.
R.A. Adams and J.F. Fournier, Sobolev Spaces, 2nd edn. (Elsevier, New York, 2003).
F. Botelho, Functional Analysis and Applied Optimization in Banach Spaces, Springer Switzerland, 2014.
F.S. Botelho, Functional Analysis, Calculus of Variations and Numerical Methods for Models in Physics and Engineering, CRC Taylor and Francis, Florida, 2020.
F.S. Botelho, Variational Convex Analysis, Ph.D. thesis, Virginia Tech, Blacksburg, VA -USA, (2009).
F. Botelho, Topics on Functional Analysis, Calculus of Variations and Duality, Academic Publications, Sofia, (2011).
F. Botelho, Existence of solution for the Ginzburg-Landau system, a related optimal control problem and its computation by the generalized method of lines, Applied Mathematics and Computation, 218, 11976-11989, (2012).
R.T. Rockafellar, Convex Analysis, Princeton Univ. Press, (1970).
Botelho, F.S. Dual Variational Formulations for a Large Class of Non-Convex Models in the Calculus of Variations. Mathematics 2023, 11(1), 63. [Google Scholar] [CrossRef]
P.Ciarlet, Mathematical Elasticity, Vol. II – Theory of Plates, North Holland Elsevier (1997).
H. Attouch, G. Buttazzo and G. Michaille, Variational Analysis in Sobolev and BV Spaces, MPS-SIAM Series in Optimization, Philadelphia, 2006.

Figure 1. Graph of function

J_{2}^{'} (x)

on the interval

[0, 1]

Figure 1. Graph of function

J_{2}^{'} (x)

on the interval

[0, 1]

Figure 2. Graph of function

J_{2}^{″} (x)

on the interval

[0, 1]

Figure 2. Graph of function

J_{2}^{″} (x)

on the interval

[0, 1]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

On Duality Principles and Concerned Convex Dual Formulations Applied to a Non-Linear Plate Theory and Related Models

Abstract

1. Introduction

2. The Main Duality Principle and Related Convex Dual Approximate Formulation

3. One More Duality Principle and Related Convex Dual Formulation

4. An Approximate Procedure for Improving the Convexity Conditions for an Originally Non-Convex Primal Formulation

5. Conclusion

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe