The Distribution of Prime Numbers Based on the Proof of Riemann’s Hypothesis and the Properties of the Numbers 3, 6, and 9

Preprint

Article

The Distribution of Prime Numbers Based on the Proof of Riemann’s Hypothesis and the Properties of the Numbers 3, 6, and 9

Altmetrics

Downloads

Views

Comments

seyed kazem mousavi^*

This version is not peer-reviewed

Submitted:

11 September 2024

Posted:

11 September 2024

You are already at the latest version

Alerts

Abstract

In this paper, the distribution of prime numbers is expressed based on proving the Riemann hypothesis. The relationship between three numbers, three, six, and nine, and the modality to the distribution of prime numbers, is one of the results of Riemann's zeta function. Prime numbers are classified into six groups of single-digit numbers. There are no prime numbers in groups of three, six, and nine. The groups are made based on the sum of the internal digits. And for each set, there is an angle in the complex plane. The distance between the prime numbers in each group has a regular pattern. This pattern is a multiple of the numbers three, six, and nine. According to Euler's number, for an angle of 60 degrees, the real part of the cosine is 1/2. Accordingly, all prime numbers are related to angles greater than 60 degrees to 90 degrees. As a result, based on the relationship between the golden spiral and the complex conjugate of the zeta function, the function in The 1/2 point becomes zero based on the prime numbers.

Keywords:

Subject: Computer Science and Mathematics - Algebra and Number Theory

1. Introduction

Prime and composite numbers have been recognized for thousands of years. [1] There have been numerous methods described for studying the distribution of prime numbers. [2,3,4] Most of these studies show the complexity of the problem of the distribution of prime numbers. The distribution of prime numbers plays an important role in various scientific fields. [5] Also, the proof of the Riemann hypothesis is directly related to the distribution of prime numbers. The higher-dimensional proof of the Riemann hypothesis presents an effective method for prime number distribution. based on geometric and topological methods, defines the complex structure of prime numbers across dimensions, revealing a connection between primes and the underlying number fields. [6] The geometric approach to physics and mathematics problems, particularly in higher dimensions like general relativity, is a conventional method for explaining and solving various issues. [7,8,9]

Accordingly, in this study, we identify different groups of prime numbers. These groups have simple repeating patterns. The distribution patterns of prime numbers in each group establish a direct relationship with three numbers, three, six, and nine. Based on this, different groups of prime numbers can be identified. For example, the number 11 belongs to the number 2 group. Because the center of the field and the properties of the number are determined by the sum of its internal digits. Of course, it seems that there is no prime number in the group of six, three and nine. This paper delves into investigating the connection between the golden spiral and complex numbers within the complex plane. Furthermore, it examines distinct sets of prime numbers in the complex number plane by utilizing geometric relationships. Based on this, a method for the proof of Riemann’s hypothesis is given.

2. Golden Spiral

The equation for the eccentricity of an ellipse can be written based on trigonometric functions. (2.1)

\sin (θ) = \sin (c o s^{- 1} \frac{a}{b}) = \sqrt{1 - \frac{a^{2}}{b^{2}}}

2.1

The Fibonacci sequence causes the eccentricity. The different ratios of the sequence are directly related to the slope and growth rate of the golden spiral. (2.2) Figure 1

\sin (c o s^{- 1} \frac{8}{13}) = \frac{\sqrt{105}}{13}

\sin (c o s^{- 1} \frac{13}{21}) = \frac{4 \sqrt{17}}{21}

\sin (c o s^{- 1} \frac{21}{34}) = \frac{\sqrt{715}}{34} \dots

2.2

A Circular sector equal to the radius rotates around the circumference of the ellipse along with the spiral and ellipse rotation. (2.3)

{(\frac{1}{2})}^{2} 2 π r {(\frac{1}{2})}^{3} 4 π r^{2} {(\frac{1}{2})}^{4} 2 π^{2} r^{3} {(\frac{1}{2})}^{5} \frac{8}{3} π^{2} r^{4} {(\frac{1}{2})}^{6} π^{3} r^{5}

{(\frac{1}{2})}^{6} π^{3} r^{5} ≅ \ln (φ)

2.3

Different angles form right triangles in the area of the golden spiral. The hypotenuses of these triangles have certain ratios with each other. Figure 1

Based on eccentricity, simulations of the golden ratio can be tested. (2.4) The imaginary part of the new equation does not align with geometric rules. Naturally, this suggests the presence of higher dimensions. For instance, the eccentricity of an ellipse within a circle transforms an angle of 45 degrees into 26. Figure 2

\frac{1 + \sqrt{5}}{2} = φ \Rightarrow \frac{1 + \sqrt{- 5}}{2} = 0.5 + 1.11803398875 i

\frac{1 + \sin (c o s^{- 1} (- \frac{8}{2}))}{2} = 0.5 + 1.93649167 i \Rightarrow c o s^{- 1} (0.5) = 60 \Rightarrow

\sin (60) = \frac{\cot (45)}{\csc (60)} \Rightarrow s i n^{- 1} (1.9364..) = 90 - 73.309347 i

\sin (73.309347) = 0.95786949627

1.11803398875 i, 1.93649167 i ≢ θ, ϕ

r = a e^{b θ} \tan (α) = b \Rightarrow α = 17.032..

β = 90 - α = 73

2.4

3. Prime Numbers

We Define each prime number with an angle according to the definition of prime numbers. (3.1)

11 \times 3 = 33, 3 \times 13 = 39 \Rightarrow (c o s^{- 1} (\frac{3}{33})

(c o s^{- 1} (\frac{3}{39}) = 0.804

11 \times 5 = 55, 5 \times 13 = 65 \Rightarrow (c o s^{- 1} (\frac{5}{55})

(c o s^{- 1} (\frac{5}{65}) = 0.804

(c o s^{- 1} (\frac{7}{77}) + i (s i n^{- 1} (\frac{7}{77}))) = 84.78 + 5.215 i \Rightarrow 11 (\cos (5.215) = 10.95 = \tan (84.78)

\Rightarrow s e c^{- 1} (2) = 60

(c o s^{- 1} (\frac{1}{2}) = 60

(c o s^{- 1} (\frac{1}{3}) = 70.528779..

(c o s^{- 1} (\frac{1}{11}) = 84.784091 \dots

s e c^{- 1} (17) = 86.62771331657

s e c^{- 1} (11) = 84.78409142955

s e c^{- 1} (7) = 81.78678929826

s e c^{- 1} (\frac{180}{π}) = 1.85081571768

\sec ((c o s^{- 1} (\frac{7}{77})) = 11 \Rightarrow s e c^{- 1} (P_{μ}) = θ_{P_{μ}} μ = 1, 2, 3, 4, \dots, n

3.1

Any angle can be expressed by Euler’s number in the plane of complex numbers. (3.2)

\Rightarrow e^{i θ} = \cos (θ) + i (\frac{\tan (c o s^{- 1} (\frac{a}{b}))}{\frac{b}{a}}) \Rightarrow e^{i θ} = \cos (θ) + i (\frac{\tan (θ)}{\sec (θ)})

3.2

Based on this, according to the rotation angle of the golden spiral, and the definition of the golden ratio, we simulate the equation of the golden spiral. (3.3) This study is to investigate the connection of the eccentricity of the ellipse with the golden ratio. Figure 3

\cos (60) = 0.5 \Rightarrow e^{\tan (\frac{\ln (φ)}{\frac{π}{3}}) i} = 0.89626396199 + 0.4435210371 i

\frac{1 + \sqrt{- 5}}{2} = 0.5 + 1.11803383 i

e^{\tan (\frac{\ln (\frac{1 + s i n (c o s^{- 1} (- \frac{8}{2})}{2})}{\frac{π}{3}}) i ϕ} = ϕ (0.9782063.. + 0.0112962342 i)

3.3

4. Result

As a result of the introduction of prime numbers on the page of complex numbers, we group the numbers according to the definition of prime numbers based on different angles. First, we write each prime number based on five prime numbers in base two. (4.1)

μ

and

υ

are only counters, and also d represents the digits of prime numbers.

s e c^{- 1} (2^{υ} 2^{υ} ..) υ = 1, 2, 3, 5, 7 \Rightarrow P_{μ} = d_{1} d_{2} d_{3} \dots

(7 + 4 = 11) \to (2^{7} 2^{3} 2^{1}) \Rightarrow s e c^{- 1} (2^{2} 2^{9}) - s e c^{- 1} (2^{8} 2^{3}) = 0

17, 233 \Rightarrow

1 + 7 = 8, 2 + 3 + 3 = 8, \Rightarrow c o s^{- 1} (s e c^{- 1} (2^{2} 2^{3} 2^{3})) = c o s^{- 1} (s e c^{- 1} (2^{1} 2^{7}))

61, 151 \Rightarrow

6 + 1 = 7, 1 + 5 + 1 = 7, \Rightarrow c o s^{- 1} (s e c^{- 1} (2^{1} 2^{5} 2^{1})) = c o s^{- 1} (s e c^{- 1} (2^{6} 2^{1}))

s e c^{- 1} (x) + c s c^{- 1} (x) = 90

4.1

Accordingly, every prime number belongs to a group. The sum of the internal digits of a number shows the number’s dependence on the group. None of the prime numbers belongs to the group three six and nine. Also, the distance between the first two numbers in each group is an integer multiple of the numbers three, six and nine. (4.2) Table 1.

In groups, the distance between numbers always jumps, but all groups follow regular patterns. (4.2)

1 \Rightarrow 37 - 19 = 18, 73 - 37 = 36, 109 - 73 = 36, 127 - 109 = 18

2 \Rightarrow 29 - 11 = 18, 47 - 29 = 18, 83 - 47 = 36, 101 - 83 = 18

4 \Rightarrow 31 - 13 = 18, 67 - 31 = 36, 103 - 67 = 36,

5 \Rightarrow 41 - 23 = 18, 59 - 41 = 18, 113 - 59 = 54,

4.2

(2^{3} 2^{3} 2^{1}) = 256 \Rightarrow P_{52} = 233 \to \Rightarrow 233 + 36 = 269

36 = 6.6 \to 233 + (6) 239,

233 + (3 \times 6) = 251, 233 + (18 + 6) = 257, 233 + (18 + 12) = 263, \dots

The sum of internal figures may be one stage or several stages. (4.3) Therefore, the distance between the numbers may be different. Table 2

61 \to 6 + 1 = 7, 79 \to 7 + 9 = 16 \Rightarrow 1 + 6 = 7 \Rightarrow 79 - 61 = 18

(2^{3} 2^{3} 2^{1}) = (2^{6} 2^{1}) = 128 (2^{7} 2^{9}) = 65536 \Rightarrow 128 \times 512 = 65536

\Rightarrow (2^{7} 2^{3} 2^{3} 2^{3}) \div (2^{3} 2^{3} 2^{3}) = 128

4.3

On this basis, to study the gap between numbers, in a group, we eliminate different steps for internal summation. (4.4)

1777 \to 1 + 7 + 7 + 7 = 22 \to s e c^{- 1} (2^{1} 2^{7} 2^{7} 2^{7}) \neq s e c^{- 1} (2^{1} 2^{3})

\Rightarrow s e c^{- 1} (2^{2} 2^{2}) = s e c^{- 1} (2^{1} 2^{3})

4.4

Due to the existence of two imaginary vectors, there is an equation with internal conjugate to construct prime numbers based on five prime numbers. (4.5)

{(\tan (c o s^{- 1} (\frac{1}{\sqrt{2}})))}^{2} + {(\cot (c o s^{- 1} (\frac{1}{\sqrt{2}})))}^{2} = 2 \Rightarrow (\sqrt{2} + i) (\sqrt{2} - i) = 3

\Rightarrow (b x + (a (y + i z) (y - i z)) i) (b x - (a (y + i z) (y - i z)) i)

P_{n}

x, y, z = \sqrt{0}, \sqrt{2}, \sqrt{3}, \sqrt{5}, \sqrt{7}, a, b = 1, 2, \dots, n

4.5

Mirror numbers are specified in each group. These numbers have special properties in a group. Table 1

Based on this, it is suggested to identify and classify prime numbers in each group. There is a simple equation for each group. And also an equation to identify an N prime number is predictable.

According to the Riemann hypothesis, the zeta function is zero for the real part of 0.5. First, we rewrite the zeta function based on the defined angles. (4.6)

ζ (s) = \frac{1}{1^{e^{\pm i θ}}} + \frac{1}{2^{e^{\pm i θ}}} + \frac{1}{3^{e^{\pm i θ}}} + ..

4.6

Two types of zeta functions are introduced due to right and left rounded angles. (4.7)

ζ (e^{- i θ}), ζ (e^{i θ}) \Rightarrow ζ, ζ^{*}

4.7

Regarding the golden spiral and the golden ratio, it should be noted that the ratios are related to the ellipse’s eccentricity. (4.8)

ζ ζ^{*} = s i n^{2} (s e c^{- 1} (P_{μ})) \Rightarrow s e c^{- 1} (2^{0}) = s e c^{- 1} (e^{0})

\Rightarrow s e c^{- 1} (2^{0} 2) = 60 \Rightarrow \cos (60) = \frac{1}{2}

4.8

(\sum_{n = 1}^{\infty} \frac{1}{n^{(\frac{π}{3} + i \frac{2 π}{3})}}) (\sum_{n = 1}^{\infty} \frac{1}{n^{(\frac{π}{3} - i \frac{2 π}{3})}}) = \sum_{n = 1}^{\infty} \frac{1}{n {(ζ ((\frac{1}{3} - \frac{2}{3} i) π))}^{\frac{1}{3} π ((ζ ((\frac{1}{3} - \frac{2}{3} i) π))) + \frac{2}{3} i π ((ζ ((\frac{1}{3} - \frac{2}{3} i) π)))}} = 0

Appreciation: I appreciate L. Razzazi, H. Mousavi, and all my esteemed professors for their guidance.

References

Dickson, L.E. (1919). History of the Theory of Numbers (No. 256). Carnegie Institution of Washington.
Koukoulopoulos, D. (2020). The distribution of prime numbers. American Mathematical Soc.
De Koninck, J.M., & Luca, F. (2023). Analytic number theory: Exploring the anatomy of integers (Vol. 134). American Mathematical Society.
Zaman, B.U. New prime number theory. Annals of Mathematics and Physics 2024, 7, 158–161. [Google Scholar]
Curtis, M.; Tularam, G.A. The importance of numbers and the need to study primes: The prime questions. Journal of Mathematics and Statistics 2011, 7, 262–269. [Google Scholar]
mousavi, S.K. Six Dimension for Proof of Riemann Hypothesis. Preprints 2024, 2024081612. [Google Scholar]
Mousavi, S.K. The balance In the six dimensions of space-time description of quantum mechanics phenomena and nature of time. journal physics theories and applications 2023, 7, 95–114. [Google Scholar] [CrossRef]
mousavi, S.K. The General Balance in the Six Dimensional of Space-Time. Preprints 2023, 2023081112. [Google Scholar] [CrossRef]
Mousavi, S.K. Mousavi, S.K. Six Dimensions for Proof of Riemann Hypothesis. 2448. [Google Scholar] [CrossRef]

Figure 1. Golden spiral rotation and tangent ellipse, Also, the difference in degree in the second stage of the rotation is visible.

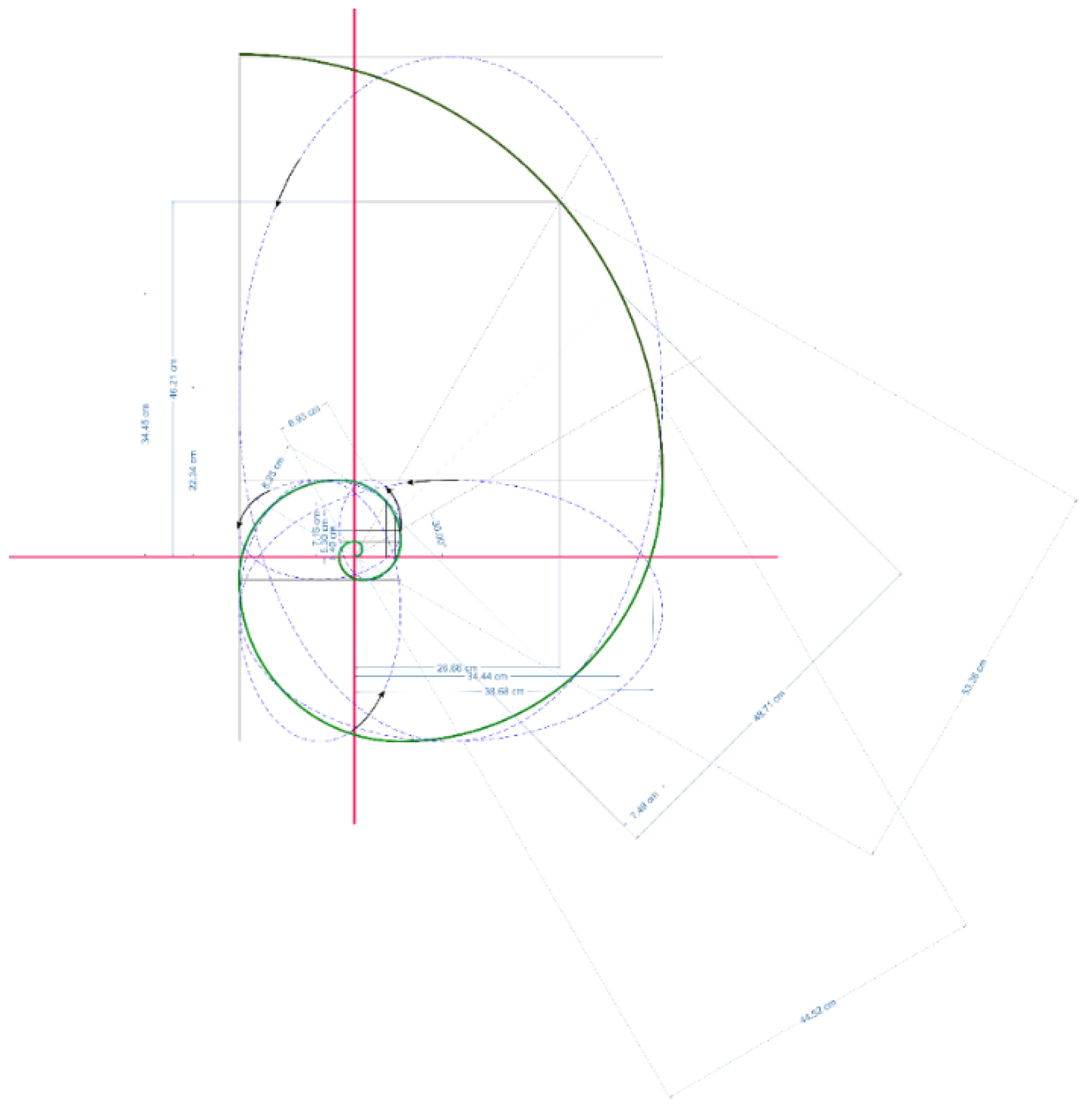
Figure 2. Creating symmetry after rotation and angle contraction in ellipse eccentricity.

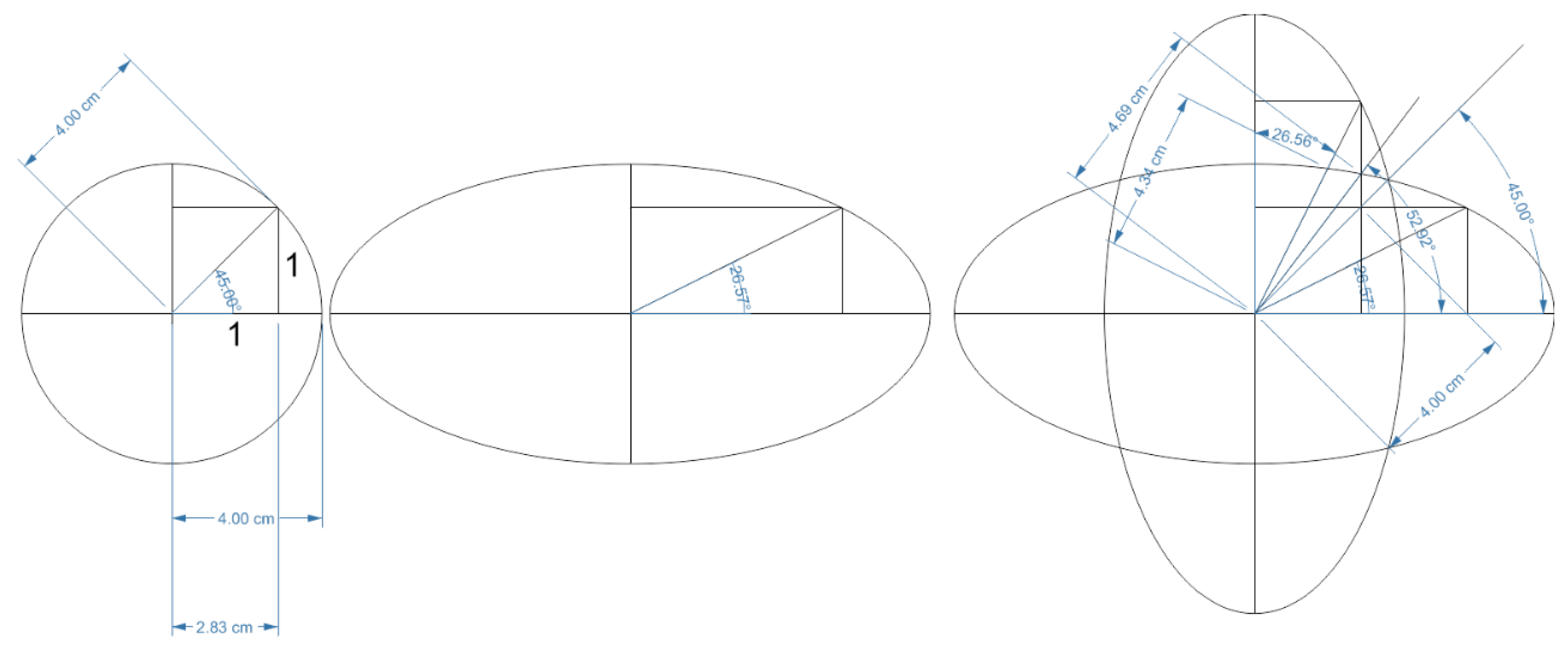
Figure 3. plot of a golden spiral in the 3D plane of the complex number.

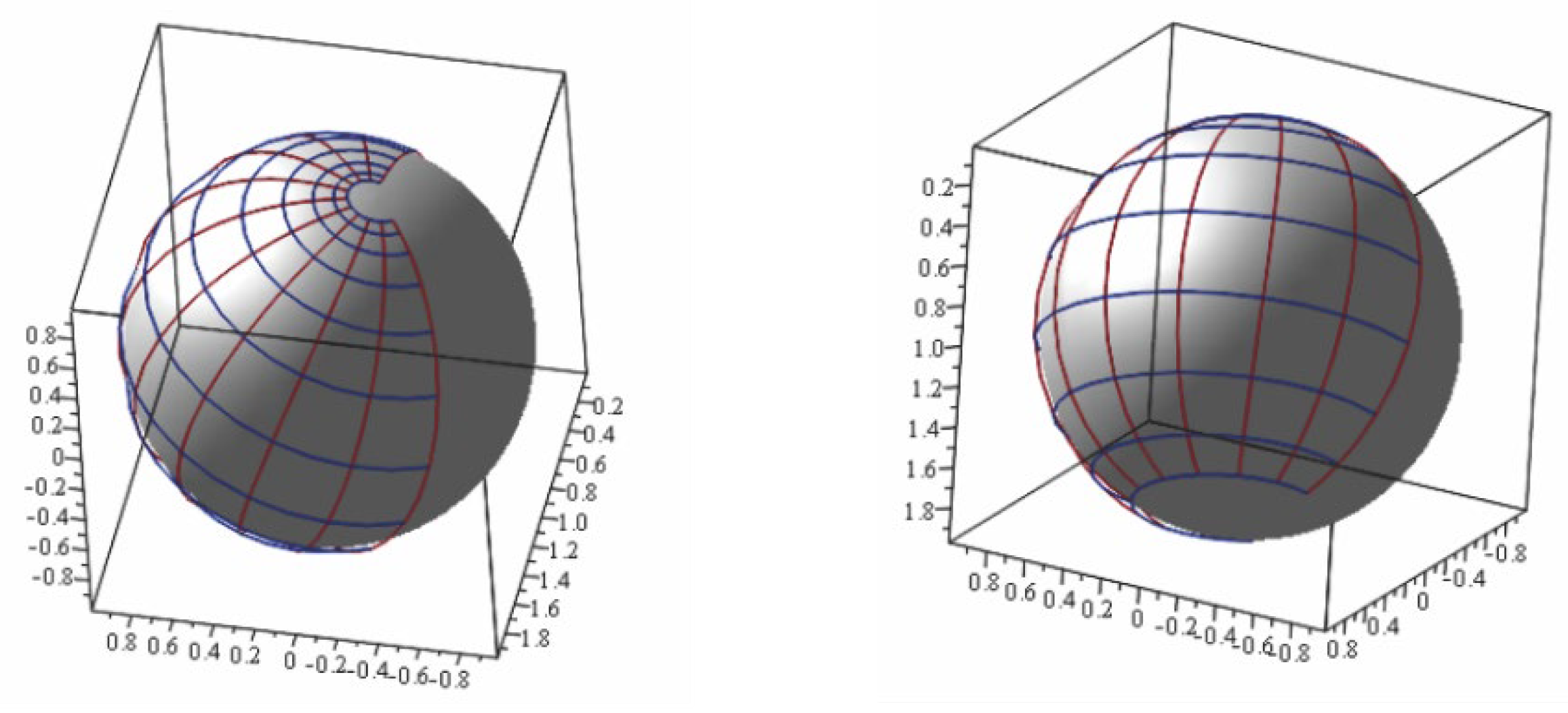
Table 1. Different groups of prime numbers, no number is a member of three, six and nine groups.

1	2	3	4	5	6	7	8	9
19	11		13	23		43	17
37	29		31	41		61	53
73	47		67	59		79	71
109	83		103	113		97	89
127	101		139	131		151	107
163	137		157	149		223	179
181	173		193	167		241	197
199	191		211	239		277	233
271	227		229	257		313	251
307	263		283	293		331	269
379	281		337	311		349	359
397	317		373	347		367	431
433	353		409	383			449
487	389-443-461-479		463-499	401-419-491		421-439-457	467

Table 2. The internal summation of the digits of a number to determine the group is one or more steps.

1	2	3	4	5	6	7	8	9
10	2		4	5		7	8
10	11		4	5		7	8
10	11		13	14		16	8
10	11		4	5		16	17
10	2		13	5		7	8
10	11		13	14		7	17
10	11		13	14		7	17
19	11		4	14		16	8
10	11		13	14		7	8
10	11		13	14		7	17
19	11		13	5		16	17
19	11		13	14		16	8
10	11		13	14		7	17

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

1	2	3	4	5	6	7	8	9
10	2		4	5		7	8
10	11		4	5		7	8
10	11		13	14		16	8
10	11		4	5		16	17
10	2		13	5		7	8
10	11		13	14		7	17
10	11		13	14		7	17
19	11		4	14		16	8
10	11		13	14		7	8
10	11		13	14		7	17
19	11		13	5		16	17
19	11		13	14		16	8
10	11		13	14		7	17

1	2	3	4	5	6	7	8	9
10	2		4	5		7	8
10	11		4	5		7	8
10	11		13	14		16	8
10	11		4	5		16	17
10	2		13	5		7	8
10	11		13	14		7	17
10	11		13	14		7	17
19	11		4	14		16	8
10	11		13	14		7	8
10	11		13	14		7	17
19	11		13	5		16	17
19	11		13	14		16	8
10	11		13	14		7	17

The Distribution of Prime Numbers Based on the Proof of Riemann’s Hypothesis and the Properties of the Numbers 3, 6, and 9

Abstract

1. Introduction

2. Golden Spiral

3. Prime Numbers

4. Result

References

MDPI Initiatives

Important Links

Subscribe

1	2	3	4	5	6	7	8	9
10	2		4	5		7	8
10	11		4	5		7	8
10	11		13	14		16	8
10	11		4	5		16	17
10	2		13	5		7	8
10	11		13	14		7	17
10	11		13	14		7	17
19	11		4	14		16	8
10	11		13	14		7	8
10	11		13	14		7	17
19	11		13	5		16	17
19	11		13	14		16	8
10	11		13	14		7	17