Solving the Transport Infrastructure Investment Projects Selection and Scheduling as a Multiple Knapsack Problem Using Genetic Algorithms

The development of transport infrastructure is a key element of economic growth, social connectivity, and sustainable development. Many countries have historically underinvested in transport infrastructure, necessitating more efficient strategic planning in transport infrastructure investment projects implementation. This article addresses the selecting and scheduling of transport infrastructure projects, specifically within the context of drawing available resources from pre-allocated funds within a multi-annual budget investment program. The current decision-making process is largely based on expert judgment, lacking quantitative decision support methods. The authors propose a genetic algorithm as a decision-support tool that frames the problem as an NP-hard 0-1 multiple knapsack problem. The proposed genetic algorithm is unique for its matrix-encoded chromosomes, specially designed genetic operators, and a customized repair operator, which is implemented to address the large number of invalid chromosomes generated during the GA computation. The goal is to maximize the impact of allocated funds over a seven-year programming period, while respecting constraints specified by the funding authorities. In computational experiments, proposed GA is compared to an exact solution and is proved to be efficient in terms of quality of obtained solutions and computational time, highlighting its potential for enhancing strategic decision-making in transport infrastructure development.

Keywords:

Subject: Computer Science and Mathematics - Discrete Mathematics and Combinatorics

1. Introduction and Literature Review

A well-developed transport infrastructure is a key element for a quality of life, sustainable socio-economic development, and international competitive position of a country, especially in relatively small countries. This case is typical for Europe and researches on this topic has been performed for example in Belgium [1] and Baltic countries [2]. Due to the importance of well-developed transport infrastructure the EU aims to help countries with neglected transport infrastructure [3] in the form of financial assistance from European funding programs. Many countries have already improved their transport infrastructure using these funds [4,5,6]. It has also been noted, that the development of transport infrastructure is different in each country, despite similar allocation of total funds for transport infrastructure development [7]. That can be caused by different strategies in allocating of the available funds to specific projects on transport infrastructure [8,9,10].

The authors of this paper have long been involved in optimizing the selection of transport infrastructure projects for implementation in the Czech Republic. Their goals is to develop a method that will support the decision making in implementation planning of transport infrastructure project to make the its development as effective as possible. As some previously mentioned European countries, the Czech Republic has also neglected transport infrastructure and therefore is fit to use the European funds. The problem of transport infrastructure development can be interpreted as a selection and scheduling of transport infrastructure investment projects, which can be presented as a modified version of multiple knapsack problem (MKP).

In the classical concept of KP the goal is to maximize the profit of selected items while being limited by the knapsack’s weight capacity. Since its high popularity as a combinatorial optimization problems, the NP-hard KP has been discussed in dozens of publications in terms of its modifications, applications and solving methods [11]. Both exact algorithms, heuristics and their combinations have been studied to solve the KP and its variations. The most important variation in case of the problem discussed in this article is the multiple knapsack problem [12,13], which extends the classical knapsack problem by adding new knapsacks into the decision process. The MKP is also often interpreted in scientific publications as multidimensional knapsack problem and while many sources [11,13,14] separates multiple knapsack problem and multidimensional knapsack problem in terms of applications, the solving algorithms are very similar and often can be used to solve both problems.

The most common methods to solve MKP can be considered branch and bound algorithm [15] and dynamic programming [16], they were also the first ones widely used [11]. The branch and bound algorithm has been used to solve many variations of MKP [17,18,19,20] and many authors have studied it’s performance in solving MKP [21,22,23]. Dynamic programming has been used to solve KMP in cases where the MKP is also multicriterial [24] or influenced by uncertainty [25,26]. Other methods used to solve MKP are for example greedy algorithm [19,27], cutting planes algorithm [28] and nature inspired algorithms [29,30,31,32].

The focus of this article is solving a very specific MKP in real-life application by another nature inspired algorithm – genetic algorithm (GA). GA is a probabilistic heuristic algorithm based on natural selection and evolution [33]. Due to its suitability for combinatorial optimization, GA has been applied to many problems, including MKP.

A GA application to a MKP problem in its basic form has been done in [34], where the authors report better results on randomly generated data than 3 other published heuristics and better performance in terms computational time while obtaining sub-optimal solution that commercial CPLEX solver. Authors also implemented a repair operator into the GA to ensure that only valid chromosomes are considered for the GA operators. In [35], authors have implemented a controlled (not probabilistic) generation of initial population to achieve a better way of exploring the feasible region and reported optimal solutions in all tested instances. A better overall performance of hybrid GA for the MKP compared to branch and bound algorithm are also presented in [36]. More complex variation of MKP solved by GA is presented in [37], where a specialized crossover operator along with two distinct mutation operators is presented to ensure validity of the chromosomes. Another complex variation of MKP is presented in [38], where the GA is modified from the classical static to the dynamic environment, where fitness function or problem constraints might change over time.

In previously mentioned publications, MKP is addressed by different approaches and concepts of genetic operators. Due to the specific constraints of the problem in this paper, the authors present a unique matrix encoding of chromosomes. While no publications have been traced where chromosomes were matrix encoded in MKP, several publications have been traced where chromosomes were matrix encoded on a different problem. A typical use of matrix-encoded chromosomes is in job shop scheduling problems [39,40,41], where chromosomes present processing of operations on individual machines. In [42], authors present a GA for a unit commitment problem, where the matrix-encoded chromosomes present a power generation schedule. Authors also present a problem-specific repair and mutation operators. Another possible use of chromosome-encoded matrices in GA is in graph-based problems, for example in [43], where chromosome represents a clustering of nodes in a graph and customized crossover and mutation operators are also presented.

2. Problem Introduction

As previously mentioned, the development of transport infrastructure is crucial element for modern countries. It contributes to economic growth, social connectivity, and sustainable development. Enhanced transport networks facilitate trade, improve access to education and healthcare, reduce travel time, and contribute to the overall quality of life. While the importance of transport infrastructure is clear, many countries have neglected transport infrastructure, and for these countries in particular, emphasis should be placed on ensuring that its development is as efficient as possible. The ability to develop transport infrastructure may be influenced, for example, by political, technological or natural aspects. This article focuses on the issue from the perspective of planning of the implementation of transport infrastructure projects already in the pipeline (ready for implementation). This implicitly includes the selection of projects for implementation and the scheduling of their funding.

The aim of the authors is to create a tool to support decision-making in the development of transport infrastructure in the context of drawing financial resources from the EU funding programs. Specifically, this is the Operational Program Transport (OPT), which is the largest in the Czech Republic in terms of the allocated volume of funds and at the same time has clearly defined rules and projects that can be supported. The financing of transport infrastructure projects within the OPT can be relatively easily formulated as an optimization task and, thanks to the amount of available funds, a greater impact on the development of transport infrastructure can be expected than with other, less voluminous funds. A similar system of financing transport infrastructure development exists also outside the EU, for example in some states in the USA [44].

The current system of financing transport infrastructure development in the Czech Republic is managed by an expert commission at the ministry of transport that meets on regular basis (usually once a year) and decides on the support of individual projects from the set of projects ready for implementation for the following year. These projects can be interpreted as projects that meet all the administrative requirements needed for its financial support and implementation. These are, for example, project documentation, construction permits, feasibility studies, environmental impact assessments, risks analysis, etc.

The current system of decision making in financial support for transport infrastructure projects is largely influenced by subjective expert opinion and is not based on any quantitative methods. The decision-making process of experts can be formulated as a 0-1 knapsack problem, where projects are selected for implementation in the following year and the selection is limited by a defined amount of available funds that cannot be exceeded when disbursed. However, given the authors' focus on the financing of transport infrastructure development in the OPT, the task can be extended to include the development of a project financing schedule. The OPT is implemented in seven-year intervals and since the Czech Republic joined the EU, two OPTs have already been implemented and a third is currently under implementation. Due to the approved budget for all 7 programming years of the OPT, it is possible to use this knowledge to extend the task of project selection to the creation of the project financing schedule, thus strengthening the possibility of effective development of transport infrastructure by taking into account all years of the programming period.

In order to finance transport infrastructure projects under the OPT, it is necessary that the projects under consideration contribute to the objectives of EU transport policy. These projects can be identified by quantitative indicators such as "Number of reconstructed or modernized railway lines – Trans-European Network". These indicators are also used by the authors to quantify the development of transport infrastructure. In terms of the allocation of funds in the OPT, in the case of projects that take more than one year to implement, the funds are released each year, not all at once. At the same time, the rule called

n + 2

by experts applies. This rule stipulates that if funds are not spent in a certain year

n

, the unspent amount of funds can be spent in years

n + 1

and

n + 2

. It is important to note that some member states have negotiated with the European Commission an additional

n + 3

option that might be implemented if the proposed solution to the problems is used in other countries.

The authors approached the problem systematically. Since their aim is to create a tool to support investment decision-making in practice, this tool can be conceived in several variants of complexity.

Variant 1 - selection of projects to be implemented from a set of transport infrastructure projects;

The mentioned variation of the KP. This simplest form of decision support tool is comparable in complexity to the current system of selecting projects for implementation by a group of experts. However, the advantage of implementing the optimization approach in practice may be its objectivity and higher quality of the solutions achieved, and consequently of the development of transport infrastructure.

Variant 2 - selection and implementation schedule of transport infrastructure projects;

In cases where an approved budget for upcoming years is known (for example in the OPT), it is possible to introduce another dimension of time into the optimization problem. In addition to selecting projects for implementation, also their specific year of implementation is decided, thus making the use of total available budget and the development of transport infrastructure more efficient. This variation is an equivalent of basic MKP.

Variant 3 - selection and implementation schedule of transport infrastructure projects with multi-year funding allocations;

This variant extends Variant 2 with the multi-year allocation of funds. This is necessary for projects that take more than one year to fully implement. This is typical for transport infrastructure projects and, given the need for a large volume of funds for their implementation, it is not appropriate to draw down the full amount of funds in the initial year of project implementation, but rather in a phased manner. At the same time, multi-year project implementation reflects the different construction phases of the project, which can vary considerably in terms of implementation phases costs (the allocation of funds for project implementation is not evenly distributed into implementation years).

Variant 4 - selection and implementation schedule of transport infrastructure projects with multi-year funding allocation and the $n + 2$ rule;

This variant is specific to the OPT and extends the Variant 3 by the

n + 2

rule. This rule is also implemented in the current system of financing transport infrastructure development and its implementation in the solution of the problem is therefore not only convenient but also necessary.

3. Mathematical Formulation of the Problem and Mathematical Model

Let

I

denote a set of transport infrastructure projects that can be implemented within the programming period years defined by elements of set

J

. Each project

i \in I

has an assigned value

a_{i}

, which determines its contribution to development of transport infrastructure. Each year

j \in J

has a specified amount of available funds

b_{j}

that can be utilized for project implementation. Additionally, each project

i \in I

is characterized by parameter

p_{i}

, indicating the number of years required for its full implementation. The costs of implementing project

i \in I

are expressed during its implementation years

t \in T

, where

T = \{1; 2; \dots; \max_{i \in I} \{p_{i}\}\}

, using parameter

n_{i t}

Table 1. Notations of sets used in the mathematical model.

Notation	Definition
$I$	set of transport infrastructure projects,
$J$	set of programming period years,
$T$	an auxiliary set of years (phases) for the implementation of projects.

Table 2. Notations of input parameters used in the mathematical model.

Notation	Definition
$m$	number of transport infrastructure projects,
$n$	number of years including years after the end of the programming period in which funds can be drawn down by the $n + 2$ rule,
$b_{j}$	the volume of funds allocated for the year $j \in J$ ,
$p_{i}$	number of phases (years of implementation) of the project $i \in I$ ,
$a_{i}$	the benefit to society achieved by the implementation of project $i \in I$ ,
$n_{i, t}$	the project implementation cost $i \in I$ in the implementation year $t \in T$ .

Table 3. Notations of decision variables used in the mathematical model.

Notation	Definition
$x_{i, j}$	binary variable indicating the start of implementation of project $i \in I$ in year $j \in J,$
$y_{i, t, j}$	auxiliary binary variable modelling for project $i \in I$ the implementation phase $t = 1, \dots, p_{i}$ in year $j \in J$ .

The mathematical model of the problem has the form:

f (x, y) = \sum_{i = 1}^{m} \sum_{j = 1}^{n - p_{i} + 1} a_{i} x_{i, j} \to m a x

(1)

subject to

\sum_{j = 1}^{n - p_{i} + 1} x_{i, j} \leq 1 i = 1, \dots, m

(2)

\sum_{i = 1}^{m} \sum_{t = 1}^{p_{i}} n_{i, t} y_{i, t, j} \leq b_{j} + (b_{j - 1} - \sum_{i = 1}^{m} \sum_{t = 1}^{p_{i}} n_{i, t} y_{i, t, j - 1}) + (b_{j - 2} - \sum_{i = 1}^{m} \sum_{t = 1}^{p_{i}} n_{i, t} y_{i, t, j - 2}) j = 3, \dots, n

(3a)

\sum_{i = 1}^{m} \sum_{t = 1}^{p_{i}} n_{i, t} y_{i, t, j} \leq b_{j} + (b_{j - 1} - \sum_{i = 1}^{m} \sum_{t = 1}^{p_{i}} n_{i, t} y_{i, t, j - 1}) j = 2

(3b)

\sum_{i = 1}^{m} \sum_{t = 1}^{p_{i}} n_{i, t} y_{i, t, j} \leq b_{j} j = 1

(3c)

p_{i} y_{i, j} = \sum_{t = 1}^{p_{i}} y_{i, t, j + t - 1} \begin{matrix} i = 1, \dots, m \\ j = 1, \dots, n - p_{i} + 1 \end{matrix}

(4)

x_{i, j} \in \{0; 1\} \begin{matrix} i = 1, \dots, m \\ j = 1, \dots, n - p_{i} + 1 \end{matrix}

(5)

y_{i, t, j} \in \{0; 1\} \begin{matrix} i = 1, \dots, m \\ j = 1, \dots, h_{i} \\ t = 1, \dots, p_{i} \end{matrix}

(6)

The objective function (1) maximizes the optimization criterion - cumulative development of transport infrastructure. The set of constraints (2) ensures that each project

i \in I

starts at most once. The set of constraints (3) ensures that the financing of projects does not exceed the use of available volume of funds allocated in year

j \in J

, taking into account the

n + 2

rule. As the

n + 2

rule can generally only be states from the 3rd year of the programming period, the group of constraints (3) is divided into (3a), (3b) and (3c). The group of constraints (4) ensures that the implementation phases

t \in T

for each project

i \in I

are executed consecutively in years

j \in J

. The group of constraints (5) and (6) defines the domains of the model variables.

4. A Proposed Genetic Algorithm Solution

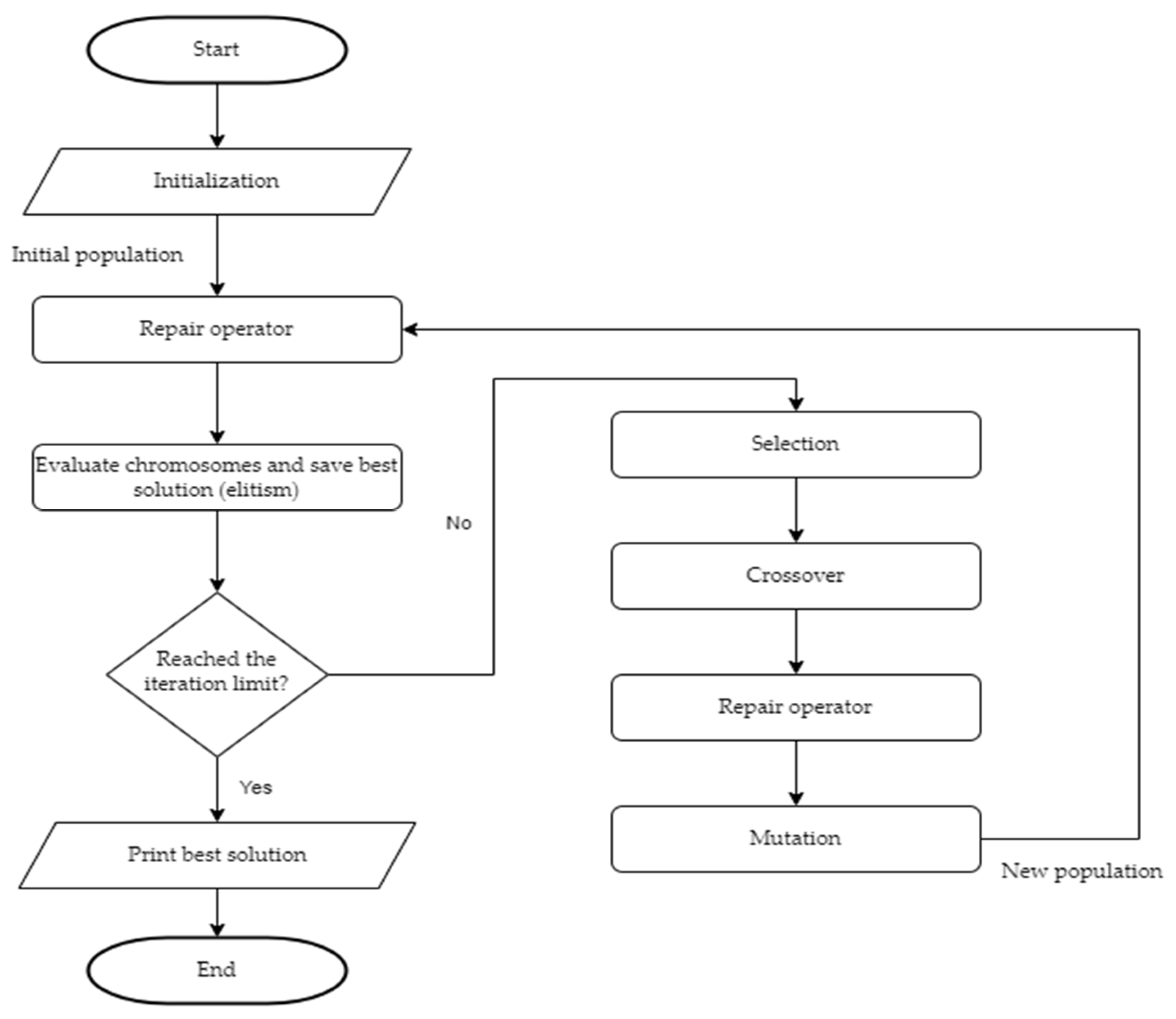
The goal of the genetic algorithm is to obtain an efficient solution to the problem in the available time. Due to the combinatorial complexity of the problem and therefore high computational time in case of implementation of an exact algorithm to solve the problem, a genetic algorithm is proposed, which is based on the classical concept of genetic algorithms with certain specifics that must be taken into account due to the nature of the problem at hand. As seen in Figure 1, in addition to the classical genetic operators, which are selection, crossover and mutation, a repair operator is introduced to ensure that the genetic algorithm works only with valid chromosomes.

In addition to the appropriate design of genetic operators, the efficiency of a genetic algorithm depends on the efficient setting of the genetic algorithm parameters. These are mainly the suitable setting of the population size

o

, crossover probability

p_{c r}

, mutation probability

p_{m}

and termination conditions. The termination conditions in the proposed GA are number of iterations

q

and number of iterations with unchanged best solution

l

Table 4. Notations of sets used in the proposed GA.

Notation	Definition
$U$	set of chromosomes in a population.

Table 5. Notations of GA parameters.

Notation	Definition
$o$	population size,
$p_{c r}$	crossover probability,
$p_{m}$	mutation probability,
$q$	maximum number of iterations,
$l$	maximum number of iterations with unchanged best solution.

The other input parameters of the proposed GA are the same as in the mathematical model (1) - (6).

4.1. The Chromosome Encoding and Fitness Function

The encoding of chromosomes reflects the principle of variables in the mathematical model (1) - (6). Since the original variable

x_{i j}

is a matrix, this concept is carried over to the chromosome encoding. In the genetic algorithm, a chromosome will be denoted by

X

and represent a matrix of dimension

m \times n

. The elements of the matrix will take the value 1 if the project

i \in I

has a start of implementation in year

j \in J

. For example, the chromosome, where

m = 6

and

n = 9

, could be in the following form

c h r o m o s o m e = X = |\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}|,

which will be further presented in the form of a table, the exemplary chromosome

X

is presented in Table 6.

The quality of a chromosome (fitness function) is calculated as follows:

f (X) = \sum_{i = 1}^{m} \sum_{j = 1}^{n} {a_{i} X}_{i, j}

(7)

4.2. The Repair Operator Concept

Due to the specifics of the problem and therefore limitation of the solution space, the probabilistic approach to solving the problem generates a large number of invalid chromosomes that must be removed to maintain the efficient function of the GA.

Before establishing a concept for dealing with invalid chromosomes in a genetic algorithm, it is necessary to determine all cases in which invalid chromosomes arise. In total, 3 different cases can occur:

Validity case I - violation of a group of constraints (2) – a project has more than one start of implementation;
Validity case II - violation of a group of constraints (3a), (3b) or (3c) - the utilization of funds for project implementation exceeds the available budget;
Validity case III - project $i \in I$ is started in year $j > n - p_{i} + 1$ - the project will not be completed within the programming period.

In the case of the chromosome shown in Table 6, it is apparent at a glance whether a violation of Validity case I occurs, and it is relatively easy to set up the concept of genetic operators in such a way that the validity of chromosomes is not violated. In Validity case II and Validity case III, the validity of chromosomes cannot be determined without knowing the values of the input parameters of the problem and additional calculations need to be implemented in the algorithm to determine the validity of chromosomes. In case of occurrence of invalid chromosomes in the GA, the authors considered 2 possible approaches for their removal:

penalization of invalid chromosomes in fitness function;
implementing repair operator into GA.

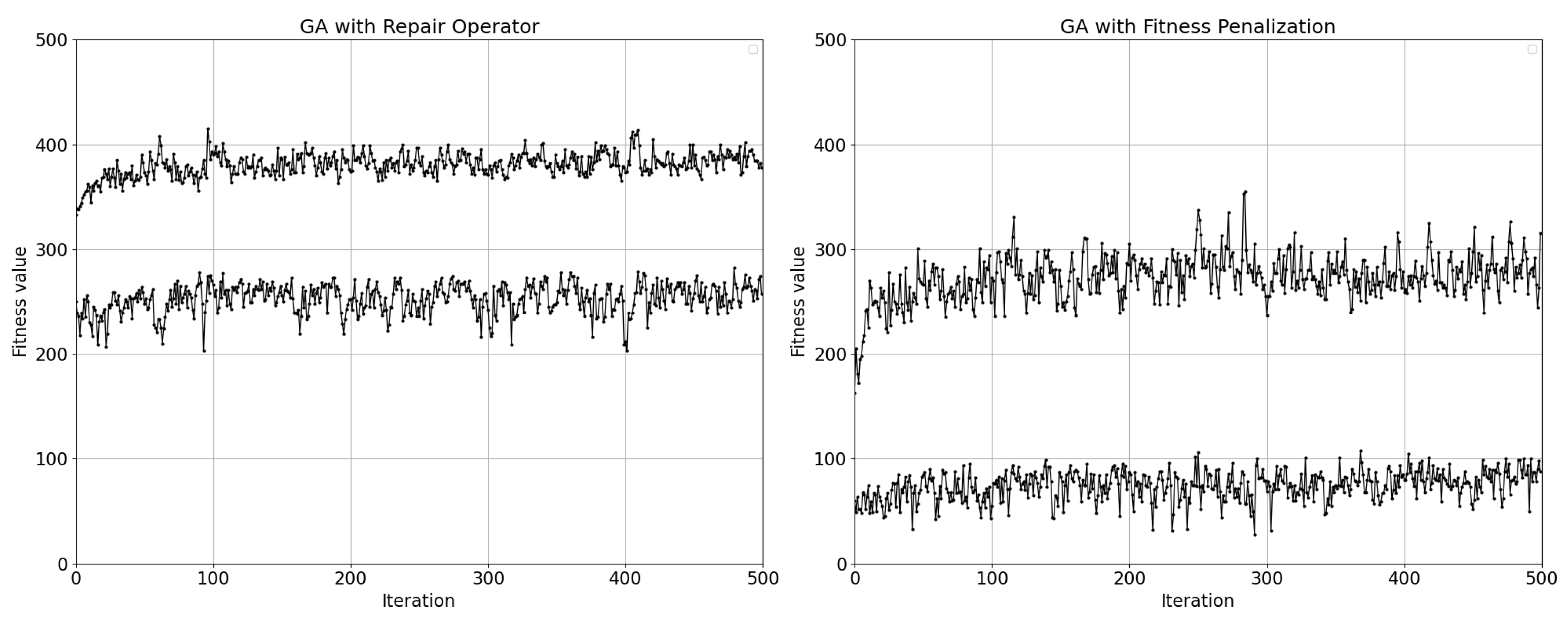
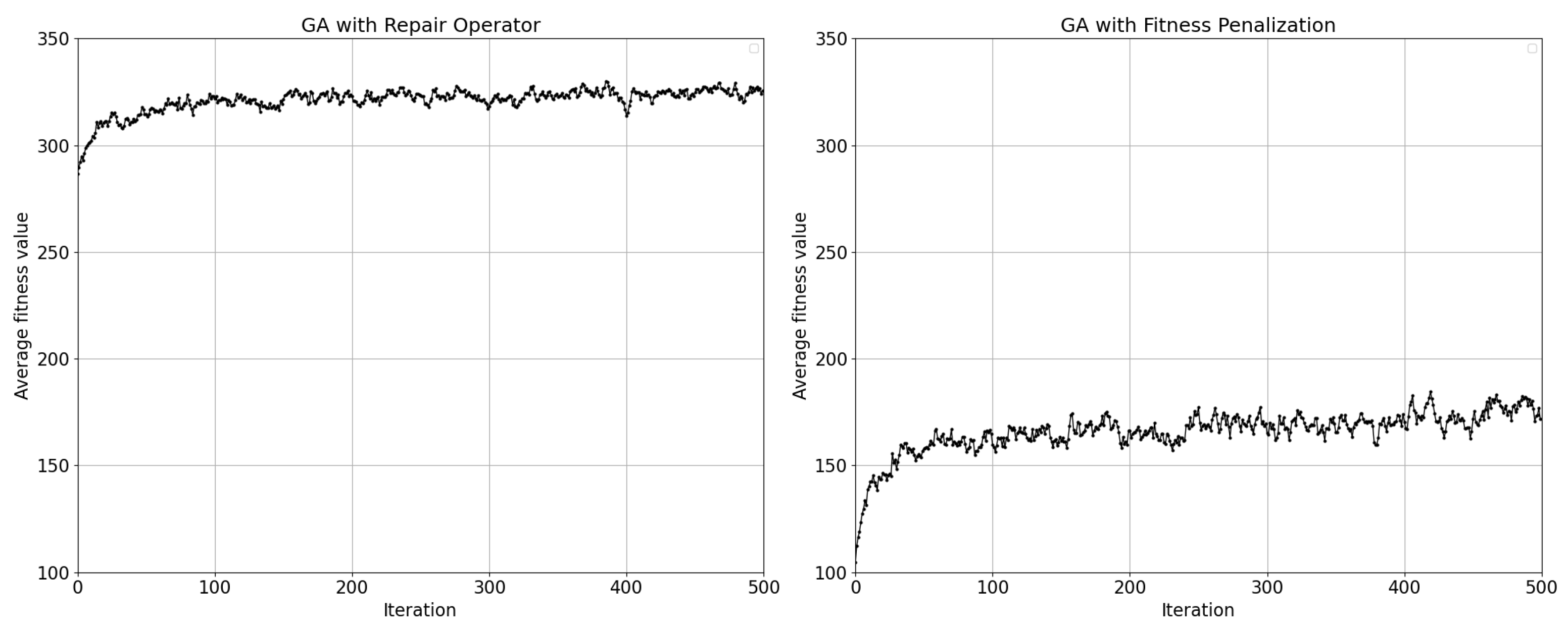
By penalizing invalid chromosomes in fitness function, the authors addressed the problem of large numbers of invalid chromosomes in their previous publication [45]. However, this method proved to be inefficient in terms of the quality of the solutions obtained, due to the large number of invalid chromosomes generated during the genetic operators. For the purpose of this article, both approaches to solving for invalid individuals were tested on generated input data. The results are based on 500 runs of the GA and presented in Figure 2 and Figure 3.

The results show that the algorithm significantly loses the quality of the solutions obtained when the repair operator is not implemented. Therefore, the authors consider only the GA using the repair operator in this article.

The purpose of the algorithm is to ensure that the chromosomes in the course of the genetic algorithm are always valid. As previously mentioned, the repair operator ensures validity in terms of Validity case II and Validity case III, since the validity of individuals in Validity case I can be ensured during the genetic operators. The algorithm is designed not to limit the probabilistic principle of the genetic algorithm in any way. The principle of the repair operator will be explained for easier understanding using the chromosome already demonstrated, supplemented with exemplary values

p_{i}

, indicating the number of implementation years of project

i \in I

C_{j}

, indicating the implementation cost of all projects in year

j \in J

, and

b_{j}

, indicating the allocated budget in year

j \in J

. The chromosome is presented in Table 7.

This chromosome is invalid because it violates Validity case II (cost of projects in year

j = 2

exceeds allocated budget) and Validity case III (project

i = 1

that takes

p_{1} = 4

years to fully implement starts in year

j = 7

). The repair operator is divided into two parts, the first part ensures the validity of the chromosomes in Validity case III and the second part in Validity case II.

4.2.1. Repair Operator for Validity Case III

Ensuring validity of chromosome in terms of Validity case III is quite simple, it is basically ensuring that each project

i \in I

does not have its start of implementation in year

j > n - p_{i} + 1

, in other words the value 1 must not occur in year

j = n - p_{i} + 2, n - p_{i} + 3, \dots, n

. The repair operator for case III can be written as follows:

Algorithm 1. Repair operator for Validity case III
Input: Chromosome $X$ $, p_{i}$ $, n$ .
for $i \in I$ :
	if $\sum_{j = n - p_{i} + 2}^{n} X_{i, j} > 0$ then
		$X_{i, j} \leftarrow 0$ for all $j \in \{n - p_{i} + 2, n - p_{i} + 3, \dots, n\}$ ;
		$X_{i, j} \leftarrow 1$ for randomly chosen $j \in \{1,2, \dots, n - p_{i} + 1\}$ ;
end
return Chromosome $X$ ;

This algorithm ensures that projects in the chromosome that violate its validity in Validity case III will be started in a year randomly chosen year

j \in \{1,2, \dots, n - p_{i} + 1\}

4.2.2. Repair Operator for Validity Case II

Repair operator for Validity case II is designed not to limit the stochastic element of the GA. First, the cost of implementing the projects

C_{j}

in year

j \in J

is calculated, and it is evaluated whether the sets of constraints (3a), (3b) and (3c) are violated. If these constraints are violated, the chromosome needs to be repaired.

Consider the chromosome demonstrated in Table 7. Since the established concept of chromosome encoding only allows to distinguish the years when a project starts its implementation, an additional calculation is needed to express the cost of project implementation in each year. Chromosome

X

can be transformed according to the following logic into a matrix

C

expressing the cost of project implementation:

C_{i, j + t - 1} = n_{i, t} \begin{matrix} i \in I, j \in J, t = 1, \dots, p_{i}, \\ X_{i, j} = 1 \end{matrix}

(8)

From this matrix, the total cost of project implementation in year

j \in J

can then be simply expressed as:

c_{j} = \sum_{i \in I} C_{i, j} j \in J

(9)

Another additional value calculated for the repair operator is the reserve

r_{j}

, which determines for each year

j \in J

the volume of funds that can be used in the following years, taking into account the

n + 2

rule. The algorithm for calculating the reserve is based on the assumption that the implementation of projects in a given year

j \in J

will be financed as a priority from unused funds from previous years

(j - 1, j - 2) .

Algorithm 2. Calculation of reserve $r_{j}$
Input: Chromosome $X$ $, n_{i, t}$ $, b_{j}$ $, n$ .
calculate $c_{j}$ $for j \in J$ ;
calculate $r_{1} \leftarrow b_{1} - c_{1}$ ;
	if $r_{1} > 0$ then
		if $r_{1} \geq c_{2}$ then
			$r_{1} \leftarrow r_{1} - c_{2}$ and $r_{2} \leftarrow b_{2}$ ;
		else
			$r_{2} \leftarrow b_{2} + r_{1} - c_{2}$ ;
			$r_{1} \leftarrow 0$ ;
	else $r_{2} \leftarrow b_{2} - c_{2}$ ;
for $j = 3, \dots, n$
if $r_{j - 2} > 0$ then
	if $r_{j - 2} > c_{j}$ then
		$r_{j - 2} \leftarrow r_{j - 2} - c_{j}$ and $r_{j} \leftarrow b_{j};$
	else if $r_{j - 1} > 0$ then
		if $r_{j - 1} \geq c_{j} - r_{j - 2}$ then
			$r_{j - 1} \leftarrow r_{j - 1} + r_{j - 2} + c_{j}$ ;
			$r_{j - 2} \leftarrow 0$ and $r_{j} \leftarrow b_{j}$ ;
		else
			$r_{j} \leftarrow b_{j} - (c_{j} - (r_{j - 2} + r_{j - 1}))$ ;
			$r_{j - 2} \leftarrow 0$ and $r_{j - 1} \leftarrow 0$ ;
	else
		$r_{j} \leftarrow b_{j} + r_{j - 2} - c_{j}$ ;
		$r_{j - 2} \leftarrow 0$ ;
else if $r_{j - 1} > 0$ then
	if $r_{j - 1} \geq c_{j}$ then
		$r_{j - 1} \leftarrow r_{j - 1} - c_{j}$ and $r_{j} \leftarrow b_{j}$ ;
	else
		$r_{j} \leftarrow b_{j} + r_{j - 1} - c_{j}$ ;
		$r_{j - 1} \leftarrow 0$ ;
else $r_{j} \leftarrow b_{j} - c_{j}$ ;
end
return $r_{j}$ $, for j \in J;$

For demonstration and easy understanding of the newly introduced values, the example chromosome

X

in Table 7, is transformed to example matrix

C

in Table 8. A reserve

r_{j}

is also calculated for each year

j \in J

into matrix

C

The repair operator for Validity case II ensures that budget utilization is not exceeded in any year of the program period

j \in J

. The concept of the operator is based on the calculated reserve

r_{j}

, which can identify the years in which budget utilization is exceeded (

r_{j} < 0

). If such years exist, projects financed in these years are either transferred and financed in other years or not financed at all. The potential for transferring the beginning of project

i \in I

to year

k \in J

is expressed by value

s_{i, k}

Algorithm 3. Repair operator for Validity case II
Input: Chromosome $X$ $, p_{i}$ $, n$ .
calculate $C_{i, j}$ ;
$r_{j} \leftarrow C a l c u l a t i o n o f r e s e r v e r_{j} (X$ $, n_{i, t}$ $, b_{j}$ $, n)$ ;
$create J^{'} \leftarrow \{j \in J \| r_{j} < 0\}$ ;
while $J^{'} \neq \emptyset$ do
	Randomly chose $j \in J^{'}$ and $i \in C_{i, j} > 0$ ;
	$X_{i, j} \leftarrow 0$ ;
	for $k = 1, \dots, n - p_{i} + 1$ and $t = 1, \dots, p_{i}$ do
		$s_{i, k} \leftarrow \sum_{t = 1}^{p_{i}} r_{k + t - 1} - n_{i, t}$ ;*
		$create S_{i} \leftarrow \{k \in 1, \dots, n - p_{i} + 1 \| s_{i, k} \geq 0\}$ ;
		if $S_{i} \neq \emptyset$ then
			$X_{i, k} \leftarrow 1$ for randomly chosen $k \in S_{i}$ ;
end
return Chromosome $X$ ;

*Note that the potential

s_{i, k}

is not always accurate in terms of the beginning of project

i \in I

being able to be transferred from year

j \in J

k \in J

. While in many cases the algorithm needs several iterations to transfer projects into feasible solution, the proposed repair operator also creates more efficient way to search solution space.

Repair operator is applied to a population as follows:

Algorithm 4. Repair operator algorithm
Input: population $U$ .
for $u = 1, \dots, o$ do
	$\{U [u]\} \leftarrow$ Repair operator for Validity case III $(\{U [u]\}, p_{i}, n)$ ;
	$\{U [u]\} \leftarrow$ Repair operator for Validity case II $(\{U [u]\}, p_{i}, n)$ ;
end
return Population $U;$

4.3. Generation of Initial Population

Considering the constraints in given problem, a high number of invalid chromosomes can be expected in the uncontrolled chromosome generation in the initial population. Due to the proposed repair operator, it is necessary to ensure the validity of individuals during the initial population generation only in terms of Validity case I. However, due to the computational complexity of the repair operator for Validity case II, it is convenient to maximize the number of valid chromosomes in the initial population to minimize the need to repair invalid ones. A suitable method for creating initial chromosomes is presented in the following algorithm:

Algorithm 5. Generation of initial chromosome
Input: $m, n$ .
create a zero matrix of size $m \times n$ ;
calculate $p_{g e n}$ ;
for $i \in I$ :
	With probability $p_{g e n}$ do:
		$X_{i, j} \leftarrow 1$ for randomly chosen $j \in J$ ;
end
return Chromosome $X;$

where

p_{g e n} = \frac{\sum_{j = 1}^{n} b_{j}}{\sum_{i = 1}^{m} \sum_{t = 1}^{p_{i}} n_{i, t}}

(10)

This algorithm ensures that the chromosome is always valid in terms of Validity case I. Validity of the chromosomes in terms of Validity case II cannot be ensured by this algorithm, but by using the

p_{g e n}

probability, the number of valid chromosomes generated will be significantly higher than in uncontrolled generation. The value of

p_{g e n}

indicates the approximate proportion of projects for implementation given the cost of implementing them and the total volume of funds available. The initial population is then generated depending on the population size

o

by the following algorithm:

Algorithm 6. Generation of initial population
Input: $o$ .
$create U = \emptyset$ ;
for $u = 1, \dots, o$ do
	$U \leftarrow U \cup \{Generation of initial chromosome (m, n)\}$ ;
end
return Initial population $U;$

4.4. Selection Operator

The selection operator is one of the three genetic operators and ensures the selection of strong chromosomes for subsequent operators and populations. The principle of evolutionary algorithms is to work with better chromosomes as the algorithm progresses (as the number of iterations increases), but to preserve the possibility of weaker chromosomes, since there are situations where crossover of two weak chromosomes can produce a stronger chromosome than crossover of two strong chromosomes. In the context of the problem at hand, Weighted Roulette Wheel Selection was chosen as it is relatively simple and suitable for problems with a maximization criterion. The probability of selecting chromosome

u \in U

by the weighted roulette wheel

p_{u}

can be calculated as the ratio of the fitness function value of chromosome

u

and the sum of the fitness function values of all chromosomes in the population, i.e.

p_{u} = \frac{f_{u}}{\sum_{u \in U} f_{u}}

(11)

In each iteration of the genetic algorithm, the selection process selects a number of chromosomes that corresponds to the population size

o

. After

o

"spins" of the roulette wheel, an intermediate population

G

is created, which corresponds to the set of chromosomes selected to proceed to subsequent genetic operators.

Algorithm 7. Selection operator algorithm
Input: population $U$ $, p_{u}$ .
$create G = \emptyset$ ;
for $u = 1, \dots, o$ do
	with probability $p_{u}$ $select u \in U$ ;
	$G \leftarrow G \cup \{U [u]\}$ ;
end
return Intermediate population $G;$

4.5. Crossover Operator

The purpose of the crossover operator is to create new chromosomes within the already existing intermediate population

G

. This allows for the combination of genetic information from chromosomes and the exploration of the solution space by diversifying chromosomes. There are several types of chromosome crossover methods, differing primarily in the way genes are exchanged between parents and their offsprings. Some of the basic crossover methods include single-point crossover, two-point crossover, uniform crossover, and probability-based crossover.

In the crossover operator a single line crossover method was chosen, where the principle is the same as in single point crossover, but due to matrix encoding of chromosomes the chromosomes are divided by line rather than a single point. Given the matrix encoding of chromosomes there are several options for setting up the crossover, the basic two being vertical line crossover and horizontal line crossover. Since it is evident that vertical line crossover could produce individuals that are invalid from Validity case I but also Validity case II, horizontal line crossover was chosen, which can produce invalid chromosomes in terms of Validity case II and Validity case III, which are covered by repair operator.

Running the crossover operator transforms 2 parent chromosomes into 2 offspring chromosomes. Offspring chromosomes are a combination of their parents via the horizontal line crossover method with probability

p_{c r}

. Hence, the population size of the GA

o

needs to be set to an even number. In terms of a GA with population size

o

, there will be

\frac{1}{2} o

runs of crossover operator to create a new set of intermediate population

G^{c r}

. The transformation of two parent chromosomes into two offspring chromosomes in case when crossover takes place is following:

Consider the interpretation of the two parent chromosomes as

P_{1} = [\begin{matrix} X_{1,1}^{P_{1}} & X_{1,2}^{P_{1}} & \dots & X_{1, n}^{P_{1}} \\ X_{2,1}^{P_{1}} & X_{2,2}^{P_{1}} & \dots & X_{2, n}^{P_{1}} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ X_{m, 1}^{P_{1}} & X_{m, 2}^{P_{1}} & \dots & X_{m, n}^{P_{1}} \end{matrix}] and P_{2} = [\begin{matrix} X_{1,1}^{P_{2}} & X_{1,2}^{P_{2}} & \dots & X_{1, n}^{P_{2}} \\ X_{2,1}^{P_{2}} & X_{2,2}^{P_{2}} & \dots & X_{2, n}^{P_{2}} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ X_{m, 1}^{P_{2}} & X_{m, 2}^{P_{2}} & \dots & X_{m, n}^{P_{2}} \end{matrix}],

then the two offspring chromosomes are created as follows.

O_{1} = [\begin{matrix} X_{1,1}^{P_{1}} & X_{1,2}^{P_{1}} & \dots & X_{1, n}^{P_{1}} \\ X_{2,1}^{P_{1}} & X_{2,2}^{P_{1}} & \dots & X_{2, n}^{P_{1}} \\ ⋮ & ⋮ & ⋮ & ⋮ \\ X_{l, 1}^{P_{1}} & X_{l, 2}^{P_{1}} & \dots & X_{l, n}^{P_{1}} \\ X_{(l + 1), 1}^{P_{2}} & X_{(l + 1), 2}^{P_{2}} & \dots & X_{(l + 1), n}^{P_{2}} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ X_{m, 1}^{P_{2}} & X_{m, 2}^{P_{2}} & \dots & X_{m, n}^{P_{2}} \end{matrix}] and O_{2} = [\begin{matrix} X_{1,1}^{P_{2}} & X_{1,2}^{P_{2}} & \dots & X_{1, n}^{P_{2}} \\ X_{2,1}^{P_{2}} & X_{2,2}^{P_{2}} & \dots & X_{2, n}^{P_{2}} \\ ⋮ & ⋮ & ⋮ & ⋮ \\ X_{l, 1}^{P_{2}} & X_{l, 2}^{P_{2}} & \dots & X_{l, n}^{P_{2}} \\ X_{(l + 1), 1}^{P_{1}} & X_{(l + 1), 2}^{P_{1}} & \dots & X_{(l + 1), n}^{P_{1}} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ X_{m, 1}^{P_{1}} & X_{m, 2}^{P_{1}} & \dots & X_{m, n}^{P_{1}} \end{matrix}],

where

X_{i, j}^{P_{1 / 2}}

represents the element of

P_{1}

P_{2}

matrix with indices

i \in I

and

j \in J

Algorithm 8. Crossover operator algorithm
Input $: Intermediate population G$ $, m$ $, o$ $, p_{c r}$ .
$create G^{c r} \leftarrow \emptyset$ ;
while $\|G^{c r}\| < o$ do
	randomly chose $P_{1}$ and $P_{2}$ chromosomes from $G$ ;
	with probability $p_{c r}$ do
		randomly chose value from interval $〈1, m - 1〉;$
		$transform chromosomes P_{1}$ and $P_{2}$ $into O_{1}$ and $O_{2}$ ;
		$G^{c r} \leftarrow G^{c r} \cup \{O_{1}, O_{2}\}$ ;
	else $G^{c r} \leftarrow G^{c r} \cup \{P_{1}, P_{2}\}$ ;
end
return Intermediate population $G^{c r};$

For better understanding is the crossover operator demonstrated by the following example in Table 9 and Table 10.

The crossover line in the example was chosen as 4 by a random choice from interval

〈1,6 - 1〉

4.5. Mutation Operator

In general, mutation is implemented in genetic algorithms to diversify the population and thus provide a larger search space of the region of solutions. In the context of the problem at hand, this is for example the formation of a population whose all chromosomes have only values 0 in a certain column. In such a population, it would not be possible for value other than zero to appear in that column by only crossover. As with crossover, the mutation must be designed so that it does not create invalid chromosomes in terms of Validity Case I.

Within the mutation, for each column

j \in J

of the chromosome

X

matrix, row

i \in I

will be selected with probability

p_{m}

. The element

X_{i, j}

will then be inverted to the opposite binary value. Three different mutation cases can occur:

Mutation case I – mutated element $X_{i, j} = 1$ ;
Mutation case II – mutated element $X_{i, j} = 0$ and $\sum_{j = 1}^{n} X_{i, j} = 0$ ;
Mutation case III – mutated element $X_{i, j} = 0$ and $\sum_{j = 1}^{n} X_{i, j} = 1$ .

While mutating an element of the chromosome matrix in Mutation case I or Mutation case II is trivial (only the binary value of the element is inverted), in Mutation case III it is necessary to ensure that after inverting the value of the element,

\sum_{j \in J} X_{i, j} \leq 1

(Validity case I) remains satisfied for a given

i \in I

. The example of all mutation cases is presented in Table 11.

The algorithm of the genetic mutation operator is as follows:

Algorithm 9. Mutation operator algorithm
Input: Intermediate population $G^{c r}$ $, p_{m}$ .
for $u = 1, \dots, o$ do
	$X \leftarrow \{G^{c r} [u]\}$ ;*
	for $j \in J$ :
		with probability $p_{m}$ do
			randomly chose $i \in I$ ;
			if $X_{i, j} = 1$ then
				$X_{i, j} \leftarrow 0$ ;
			else if $\sum_{j \in J} X_{i, j} = 0$ then
				$X_{i, j} \leftarrow 1$ ;
			else
				for $k \in J$ , where $k \neq j$ $X_{i, k} \leftarrow 0$ ;
				$X_{i, j} \leftarrow 1$ ;
end
return New population $U$ ;

*For better understanding every chromosome is expressed as matrix

X

in each iteration

u = 1, \dots, o

5. Results and Discussion

In genetic algorithms, in addition to the correct setup of genetic operators, chromosome encoding and fitness function, it is also paramount to set the input parameters correctly. GA’s parameters settings have a major impact on its efficiency, i.e. on the quality of the solutions obtained and the computational time. As stated before, the proposed GA is a support for decision-making in real-life. Since the experts meet usually once a year, the GA needs to be set up to provide a good enough solution in a short amount of time. The authors assume that several changes will be made during the meeting based on the experts' discussion and thus the calculation will need to be done repeatedly. In such cases, the solution to the problem needs to be generated quickly to minimize unproductive time. The authors aim was to achieve at least 90% of the optimal solution under 90 seconds of computation time.

All the algorithms are coded in Visual Studio using the Python Programming Language. All computations were done on the same PC with an Intel Core i5-8250U CPU @ 1.60GHz, 16 GB RAM and operating system Windows 11 Pro.

5.1. GA Parameters Calibration

Since the authors aim to implement the proposed genetic algorithm as a decision support tool in practice, computational experiments were conducted on a real-sized problem. Specifically, this involves

m = 300

transport infrastructure investment projects and a

n = 9

year program period. Calibration and computational experiments with the proposed genetic algorithm were performed on the generated input data, which correspond to reality. These are the input parameters

n_{i k}, b_{j}

and

a_{i}

. Subsequently, several variations of the GA input parameters, i.e., population size

o

, number of iterations

q

, maximum number of iterations with unchanged best solution

l

, crossover probability

p_{c r}

and mutation probability

p_{m}

were tested and then evaluated in terms of their impact on GA efficiency.

The first computational experiments were conducted to obtain effective settings for the crossover probability

p_{c r}

, mutation probability

p_{m}

and population size

o

. Since these GA parameters greatly influence the quality of the solutions obtained, it was necessary to find effective settings as a priority. The GA was run 10 times at each parameter setting combination, while maintaining

l = 300

q = 5000

While the crossover probability settings were based on fixed conventional values, the mutation probability was calculated based on the following formula:

p_{m} = \frac{1}{n \cdot h},

(12)

where the value

h

determines the period of chromosome mutation. For example, for

h = 1

, a mutation occurs in every chromosome, while for

h = 2

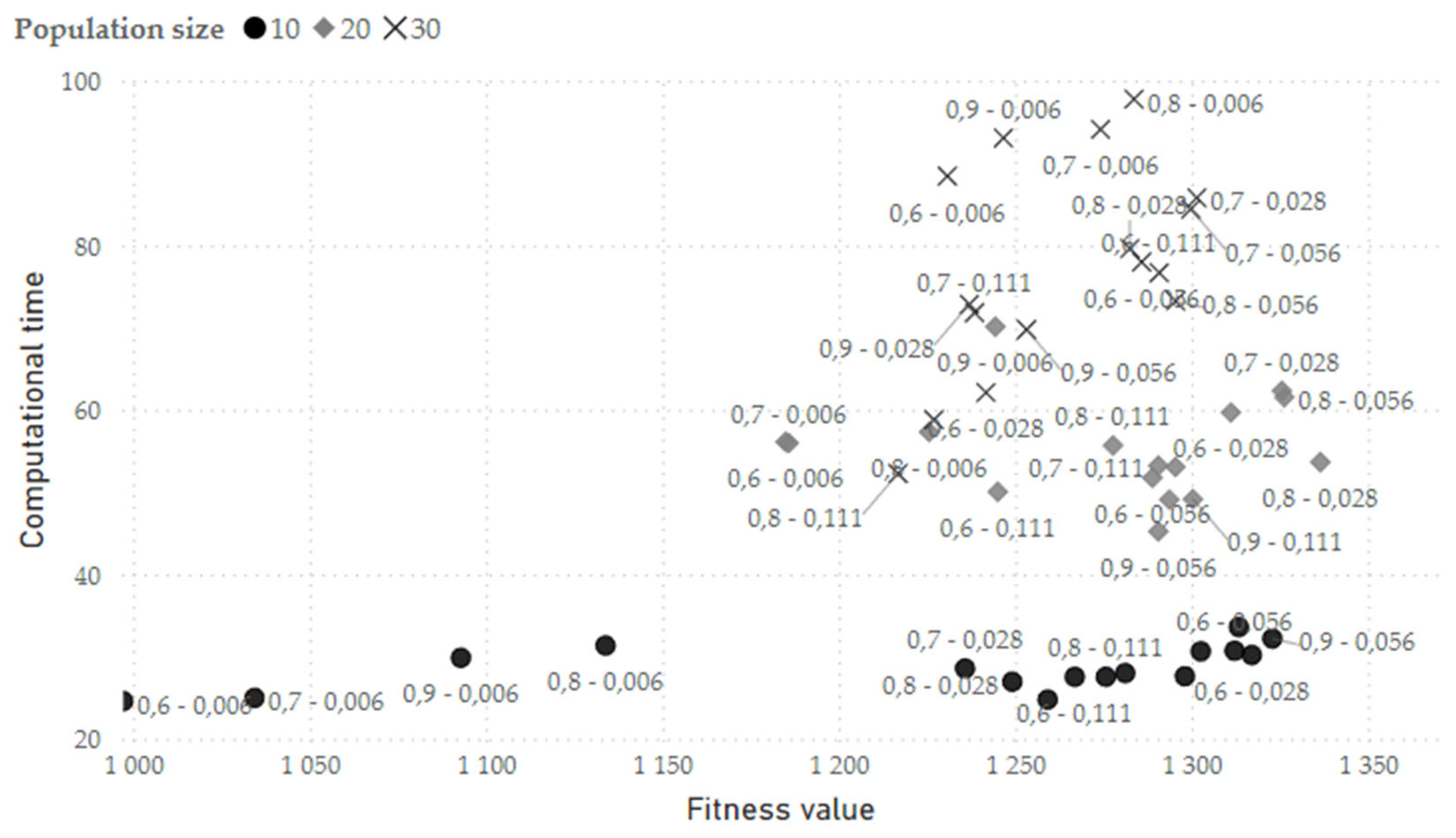
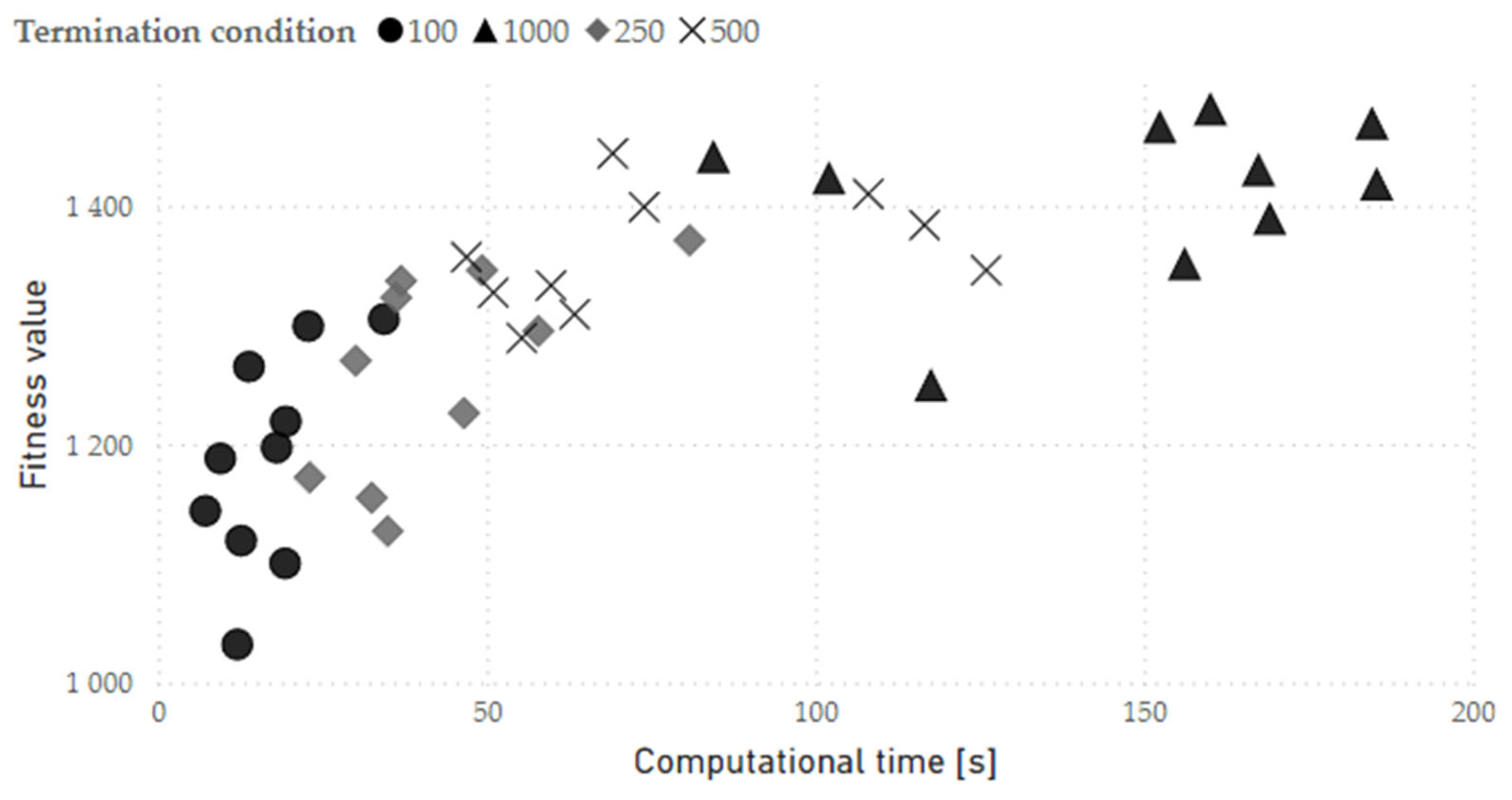
, a mutation is expected to occur once in every two chromosomes. Formula (10) was implemented to ensure the correct mutation probability setting in cases when the GA is applied to problems of varying sizes. The overall results are presented in Figure 4.

The experiments suggest that the most suitable population size setting is

o = 10

, since it provided most of the top 10 variants in terms of obtained fitness values. The results for population sizes

o = 20

and

o = 30

show more stable results in terms of average fitness values obtained by crossover and mutation probabilities variations and therefore seem to be less influenced by their settings. However, the sensitivity of population size

o = 10

to the probabilities settings suggests that with their efficient calibration, better results can be obtained and in better computational. Results of probabilities settings combinations for population size

o = 10

are shown in Table 12 and Table 13.

The results showed that the considered settings of the crossover probabilities do not differ in any significant way in terms of the quality of solutions obtained or computational time. On the contrary, the mutation probability setting has much higher impact on the GA performance due to the fact, that repair operator can nullify a lot of elements in chromosomes. Therefore, a high mutation probability increases chromosome diversity, potentially hindering efficient convergence, whereas a low mutation probability limits effective exploration of the solution space. The chosen mutation probabilities reflect setting the value

h = 1

(mutation occurs once per chromosome),

h = 2

(mutation occurs once per two chromosomes),

h = 4

(mutation occurs once per three chromosomes) and

h = 20

(mutation occurs once per twenty chromosomes). The results show a significant difference of quality of solutions obtained of the

h = 20

setting compared to the other three. In the first phase of computational experiments, the combination of crossover and mutation probabilities

p_{c r} = 0.9

and

p_{m} = 0.056

proved to be the most effective and was therefore used in further computational experiments.

The aim of the second phase of GA calibration was to figure out the efficient setting of termination condition. The authors considered two options – terminating the calculation when maximum number or iteration

q

is reached or when the best solution remains unchanged for

l

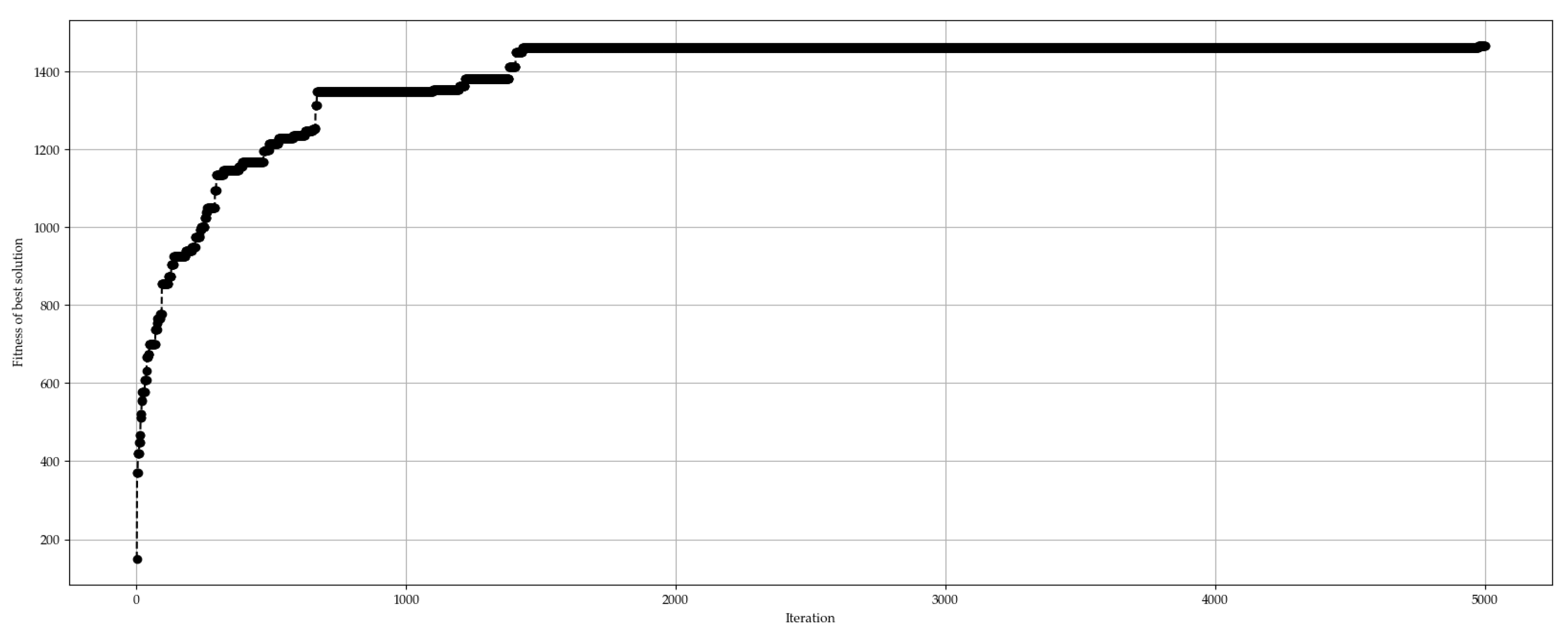
number of iterations. The preferred option is based on the convergence behavior, the example is illustrated in Figure 5.

Since the settings of termination conditions can significantly affect computational time of GA, several variations of number of iterations with unchanged best solution

l

were tested on constant number of maximum iterations

q = 5000

. The parameter

q

was set to a constant value due to GA run time limitations with the assumption that it would rarely be exceeded. The results in Figure 6 show the dependency of obtained fitness function values and computational time on the maximum number of iterations with unchanged best solution

l

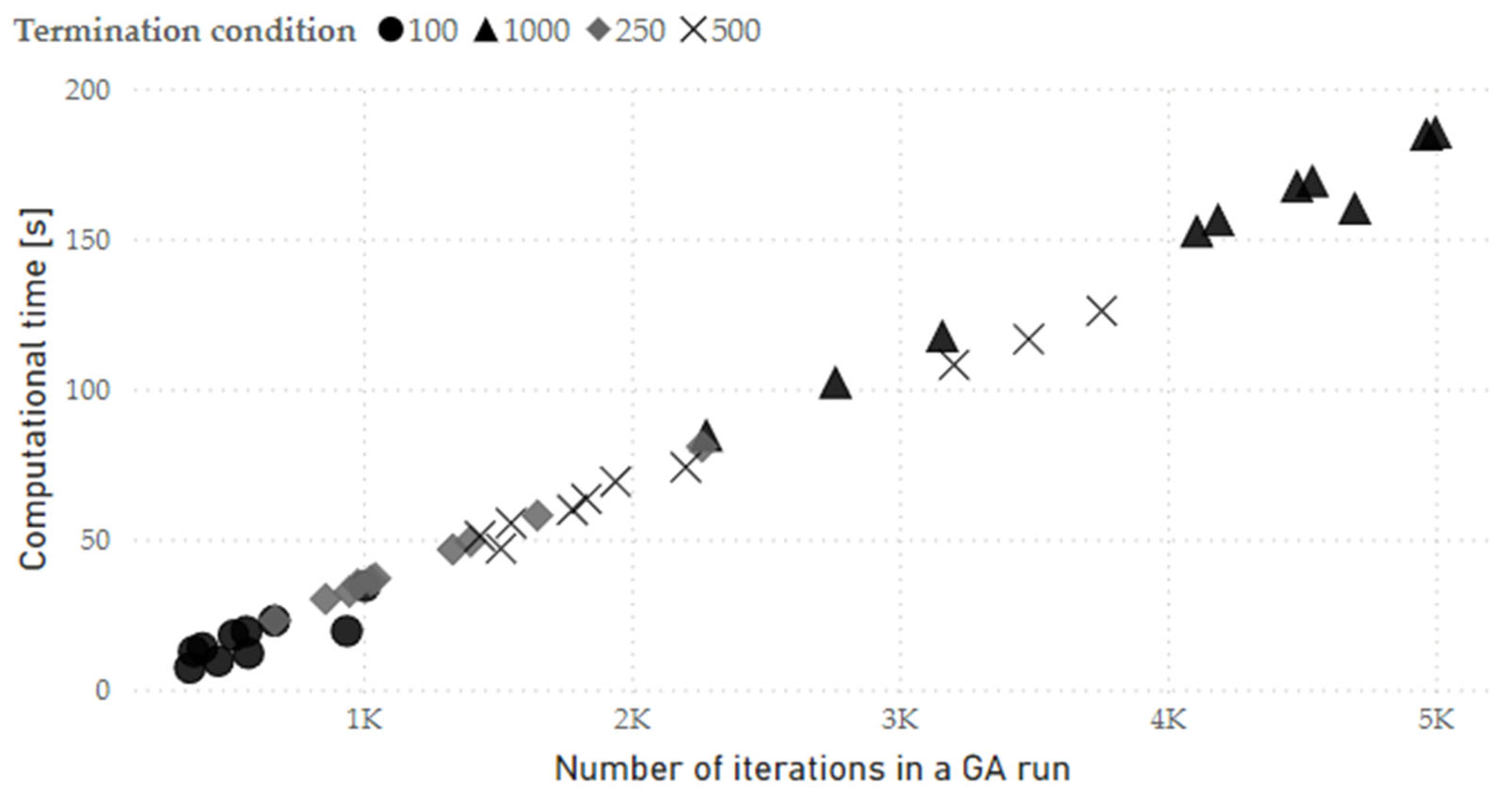
. In Figure 7, correlation between real number of iterations and computational time is presented.

Because of the computational time requirement of the genetic algorithm, the efficient setting of termination condition was determined as

l = 500

and

q = 5000

, since it provides best solutions obtained while keeping the average computation time under 90 seconds. In GA applications where maximum amount of available computational time is known, an alternative approach is to set a termination condition as a timeout. However, this approach is not generally recommended since in practical applications it is difficult to set up the correct timeout value.

5.2. GA Performance

Since the calibration provided an efficient setting of GA parameters, a comparison to an exact solution was made to justify the use of the genetic algorithm in practice and demonstrate its benefit. Since the implementation of a sophisticated decision support tool in practice is not possible to implement until its effect is substantially proven, proposed solutions are created in a freely available software. Both the genetic algorithm and the exact linear model were programmed in the Python programming language. The freely available PuLP library was used to solve the linear model, which uses the solver 'PULP_CBC_CMD' by default, The linear model was solved using the PuLP library, which uses the 'PULP_CBC_CMD' solver based on Branch and Cut algorithm.

Initially, the performance of the proposed GA was compared to an exact solution on a problem of already discussed size (

m = 300

and

n = 9

). To fully explore the possibilities of GA implementation on larger scale problems, another three scenarios were considered. The testing was performed on randomly generated data based on real data’s distribution and scaled to problem’s size. In following results in Table 14, GA was run only a single time to simulate real-life situation, calculation by 'PULP_CBC_CMD' solver was terminated after one hour of computational time.

While on medium-sized problems GA outperforms exact solution, on large problems GA loses its effectiveness. This is due to the increasing size of the matrices that encode the chromosomes. While on the size of the problem for which the GA was designed, the operators are quite efficient, for large problems the concept needs to be additionally modified. The priority should be to modify the repair operator, which takes a lot of time with the current design. The authors have considered this modification within the paper, but since the size of the problem solved in this paper was affected negatively by the modification on the quality of the solutions obtained, it was not implemented. However, in terms of time savings, it was a matter of reducing the computational time of the repair operator to roughly the same time as the crossover operator (reduction by circa 60%).

To summarize the overall performance of the proposed GA with efficient parameters calibration, additional computations were performed. The results of calibrated GA are presented in Table 15.

5.3. Discussion

Proposed GA was developed to solve a very specific version of the multiple knapsack problem, tailored for real-life decision-making process. This specific application presents unique challenges, primarily due to the constraints imposed by the problem. As a result, a significant number of chromosomes generated during the GA computation are invalid, which necessitates special handling.

Two main approaches were considered for dealing with these invalid chromosomes: penalization within the fitness function and the use of a repair operator. In the proposed GA, a repair operator was implemented to correct the invalid chromosomes. While this operator has proven effective in maintaining a viable population and searching the solution space, it is computationally demanding. In the post-computational analysis, the computational time of each phase of the GA was investigated, the results are presented in Table 16.

Since the repair operator takes about 46% of total computational time, potential area for further research is the development of a more efficient repair operator to reduce the computational time and increase overall performance of the GA, making it more suitable for practical decision-making applications. Alternatively, exploring the penalization approach, where invalid chromosomes are assigned lower fitness scores, could provide a less computationally intensive solution. This approach might allow the GA to focus on exploring the solution space more broadly, potentially leading to better overall solutions with reduced computational overhead.

Additionally, given the constraints of the problem, special crossover and mutation operators were created to preserve the feasibility of solutions. However, these custom operators may also contribute to the computational complexity of the algorithm. Future work could explore optimizing these operators to reduce their complexity, thereby improving the efficiency of the GA without sacrificing solution quality. Another consideration is the quality of the initial population. Introducing a heuristic-based method to generate a better initial population could improve the starting point for the algorithm, potentially accelerating convergence towards high-quality solutions.

In terms of the concept of the problem addressed, the authors consider several modifications for future research. Since the current article dealt only with ready-to-implement projects, it is appropriate to consider the possibility of readiness of projects in different years of the programming period. This modification also brings the possibility of introducing uncertain parameters into the problem, since in practice it very often happens that project readiness or project implementation costs changes or is hard to estimate. At the same time, the authors consider increasing the cost of project implementation in advancing years (for example, due to inflation), which would make the problem a combination of multiple and multidimensional knapsack problem.

In summary, while the proposed GA with a repair operator has demonstrated its effectiveness in solving this specific version of the multiple knapsack problem, there are several opportunities for improvement. Optimizing the repair operator, considering penalization as an alternative approach, refining crossover and mutation operators, and enhancing the initialization process through heuristics are all promising directions for future research. Addressing these areas could lead to a more efficient and robust algorithm capable of solving complex real-life decision-making problems more effectively.

5. Conclusions

The selection and scheduling of implementation of transport infrastructure investment projects, which is possible to formulate as an NP-hard multiple knapsack problem, is a real-life decision-making problem currently solved without any quantitative tools by group of experts. Since experts define the direction of transport infrastructure development for the next few years by making decisions, it is convenient to create a tool to support their decision-making. Due to the high time consumption in case of solving the problem by exact solution, the problem was solved by means of a genetic algorithm. The proposed genetic algorithm is unique in terms of encoding chromosomes and the associated genetic operators. In addition, due to the large number of invalid chromosomes appearing during genetic operators, a repair operator was introduced to ensure the validity of the chromosomes throughout the genetic algorithm computation. There are a total of 3 situations in which invalid chromosomes arise in the problem. While one of these situations can be easily secured by setting the genetic operators correctly, the rest are secured by the repair operator.

Computational experiments showed that the proposed genetic algorithm provides solutions where fitness function values range from 85% to 95% of the optimal solution value. In terms of computational time, the mean value of computational time of one run of the GA is 108 seconds, which is a small fraction of the computational time of the exact solution of a freely available solver. Detailed analysis showed that in terms of computational time of each operator, the focus in future research should be on a more efficient repair operator design or designing genetic operators that prevent the creation of invalid chromosomes. The convergence behavior of GA could possibly be improved by implementing heuristic algorithm to ensure better initial solutions.

Due to the high efficiency of the proposed genetic algorithm, it can be implemented in the current decision-making process of experts. In general, the constraints of the problem addressed are very specific, since the GA is applied to a specific decision-making process. However, the method of encoding individuals and working with them in genetic operators is universal and can be applied to both simple and complex problems.

Author Contributions

Conceptualization, K.J. and D.M.; methodology, K.J.; software, K.J.; validation, K.J. and D.M.; formal analysis, K.J.; investigation, K.J.; resources, K.J.; data curation, K.J.; writing—original draft preparation, K.J.; writing—review and editing, D.M. and D.T.; visualization, K.J.; supervision, D.M. and D.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by Czech Technical University in Prague under student grant number SGS24/069/OHK2/1T/16.

Data Availability Statement

The code of the proposed GA and LP model along with computational results are available at https://github.com/jecmekar/Genetic-algorithm-for-project-selection-and-scheduling.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Meersman, H.; Nazemzadeh, M. The Contribution of Transport Infrastructure to Economic Activity: The Case of Belgium. Case Studies on Transport Policy 2017, 5, 316–324. [Google Scholar] [CrossRef]
Kovács, G.; Spens, K.M. Transport Infrastructure in the Baltic States Post-EU Succession. Journal of Transport Geography 2006, 14, 426–436. [Google Scholar] [CrossRef]
Purwanto, A.J.; Heyndrickx, C.; Kiel, J.; Betancor, O.; Socorro, M.P.; Hernandez, A.; Eugenio-Martin, J.L.; Pawlowska, B.; Borkowski, P.; Fiedler, R. Impact of Transport Infrastructure on International Competitiveness of Europe. Transportation Research Procedia 2017, 25, 2877–2888. [Google Scholar] [CrossRef]
Pawlas, I. Cohesion Fund as an Instrument Stimulating Transport Infrastructure Development in Poland. In Proceedings of the PROCEEDINGS OF THE 16TH INTERNATIONAL SCIENTIFIC CONFERENCE FINANCE AND RISK 2014, VOL 1; Publishing House Ekonóm: Bratislava, Slovak Republic; 2014; pp. 173–181. [Google Scholar]
Warsaw University of Life, Sciences; Stawicki, M. Warsaw University of Life Sciences; Stawicki, M. Development of Transport Infrastructure in Latvia, Lithuania and Poland with Support of Structural Funds.; May 8 2018; pp. 244–251.
Crescenzi, R.; Rodríguez-Pose, A. Infrastructure and Regional Growth in the European Union*. Papers in Regional Science 2012, 91, 487–513. [Google Scholar] [CrossRef]
Kemmerling, A.; Stephan, A. Comparative Political Economy of Regional Transport Infrastructure Investment in Europe. Journal of Comparative Economics 2015, 43, 227–239. [Google Scholar] [CrossRef]
Kyriacou, A.P.; Muinelo-Gallo, L.; Roca-Sagalés, O. The Efficiency of Transport Infrastructure Investment and the Role of Government Quality: An Empirical Analysis. Transport Policy 2019, 74, 93–102. [Google Scholar] [CrossRef]
Kuzmina-Merlino, I.; Skorobogatova, O.; Schmidtke, N.; Behrendt, F. Mechanism for Investment in the Transport Infrastructure Development in Latvia. In Proceedings of the Reliability and Statistics in Transportation and Communication; Kabashkin, I., Yatskiv, I., Prentkovskis, O., Eds.; Springer International Publishing: Cham, 2018; pp. 507–518. [Google Scholar]
Zhang, Y.; Cheng, L. The Role of Transport Infrastructure in Economic Growth: Empirical Evidence in the UK. Transport Policy 2023, 133, 223–233. [Google Scholar] [CrossRef]
Assi, M.; Haraty, R.A. A Survey of the Knapsack Problem. In Proceedings of the 2018 International Arab Conference on Information Technology (ACIT); November 2018; pp. 1–6. [Google Scholar]
Kellerer, H.; Pferschy, U.; Pisinger, D. Multiple Knapsack Problems. In Knapsack Problems; Kellerer, H., Pferschy, U., Pisinger, D., Eds.; Springer: Berlin, Heidelberg, 2004; ISBN 978-3-540-24777-7. [Google Scholar]
Cacchiani, V.; Iori, M.; Locatelli, A.; Martello, S. Knapsack Problems — An Overview of Recent Advances. Part II: Multiple, Multidimensional, and Quadratic Knapsack Problems. Computers & Operations Research 2022, 143, 105693. [Google Scholar] [CrossRef]
Kellerer, H.; Pferschy, U.; Pisinger, D. Knapsack Problems; Springer: Berlin ; New York, 2004; ISBN 978-3-540-40286-2.
Morrison, D.R.; Jacobson, S.H.; Sauppe, J.J.; Sewell, E.C. Branch-and-Bound Algorithms: A Survey of Recent Advances in Searching, Branching, and Pruning. Discrete Optimization 2016, 19, 79–102. [Google Scholar] [CrossRef]
Sitarz, S. Dynamic Programming with Ordered Structures: Theory, Examples and Applications. Fuzzy Sets and Systems 2010, 161, 2623–2641. [Google Scholar] [CrossRef]
Fleszar, K. A Branch-and-Bound Algorithm for the Quadratic Multiple Knapsack Problem. European Journal of Operational Research 2022, 298, 89–98. [Google Scholar] [CrossRef]
Galli, L.; Martello, S.; Rey, C.; Toth, P. Polynomial-Size Formulations and Relaxations for the Quadratic Multiple Knapsack Problem. European Journal of Operational Research 2021, 291, 871–882. [Google Scholar] [CrossRef]
Yamada, T.; Takeoka, T. An Exact Algorithm for the Fixed-Charge Multiple Knapsack Problem. European Journal of Operational Research 2009, 192, 700–705. [Google Scholar] [CrossRef]
Dawande, M.; Kalagnanam, J.; Keskinocak, P.; Salman, F.S.; Ravi, R. Approximation Algorithms for the Multiple Knapsack Problem with Assignment Restrictions. Journal of Combinatorial Optimization 2000, 4, 171–186. [Google Scholar] [CrossRef]
Pisinger, D. An Exact Algorithm for Large Multiple Knapsack Problems. European Journal of Operational Research 1999, 114, 528–541. [Google Scholar] [CrossRef]
Lalonde, O.; Côté, J.-F.; Gendron, B. A Branch-and-Price Algorithm for the Multiple Knapsack Problem. INFORMS Journal on Computing 2022, 34, 3134–3150. [Google Scholar] [CrossRef]
Fukunaga, A. A Branch-and-Bound Algorithm for Hard Multiple Knapsack Problems. Annals OR 2011, 184, 97–119. [Google Scholar] [CrossRef]
Bazgan, C.; Hugot, H.; Vanderpooten, D. Solving Efficiently the 0–1 Multi-Objective Knapsack Problem. Computers & Operations Research 2009, 36, 260–279. [Google Scholar] [CrossRef]
Hartman, J.C.; Perry, T.C. Approximating the Solution of a Dynamic, Stochastic Multiple Knapsack Problem.
Perry, T.; Hartman, J. An Approximate Dynamic Programming Approach to Solving a Dynamic, Stochastic Multiple Knapsack Problem. International Transactions in Operational Research 2009, 16, 347–359. [Google Scholar] [CrossRef]
Hiley, A.; Julstrom, B.A. The Quadratic Multiple Knapsack Problem and Three Heuristic Approaches to It. In Proceedings of the Proceedings of the 8th annual conference on Genetic and evolutionary computation; Association for Computing Machinery: New York, NY, USA, June 8, 2006; pp. 547–552. [Google Scholar]
Ferreira, C.E.; Martin, A.; Weismantel, R. Solving Multiple Knapsack Problems by Cutting Planes. SIAM J. Optim. 1996, 6, 858–877. [Google Scholar] [CrossRef]
Sundar, S.; Singh, A. A Swarm Intelligence Approach to the Quadratic Multiple Knapsack Problem. In Proceedings of the Neural Information Processing. Theory and Algorithms; Wong, K.W., Mendis, B.S.U., Bouzerdoum, A., Eds.; Springer: Berlin, Heidelberg, 2010; pp. 626–633. [Google Scholar]
Boryczka, U. Ants and Multiple Knapsack Problem. In Proceedings of the 6th International Conference on Computer Information Systems and Industrial Management Applications (CISIM’07); June 2007; pp. 149–154. [Google Scholar]
Liu, Q.; Odaka, T.; Kuroiwa, J.; Shirai, H.; Ogura, H. A New Artificial Fish Swarm Algorithm for the Multiple Knapsack Problem. IEICE TRANSACTIONS on Information and Systems, 2014; E97-D, 455–468. [Google Scholar]
Li, S.; Cai, S.; Sun, R.; Yuan, G.; Chen, Z.; Shi, X. Improved Bat Algorithm for Multiple Knapsack Problems; 2019; p. 157; ISBN 9789811513763.
Sivanandam, S.N.; Deepa, S.N. Introduction to Genetic Algorithms; Springer: Berlin ; New York, 2007; ISBN 978-3-540-73189-4.
Chu, P.C.; Beasley, J.E. A Genetic Algorithm for the Multidimensional Knapsack Problem. Journal of Heuristics 1998, 4, 63–86. [Google Scholar] [CrossRef]
Guler, A.; Nuriyev, U.; Berberler, M. A Genetic Algorithm to Solve the Multidimensional Knapsack Problem. Mathematical and Computational Applications 2013, 18, 486–494. [Google Scholar] [CrossRef]
Cotta, C.; Troya, J.M. A Hybrid Genetic Algorithm for the 0–1 Multiple Knapsack Problem. In Proceedings of the Artificial Neural Nets and Genetic Algorithms; Smith, G.D., Steele, N.C., Albrecht, R.F., Eds.; Springer: Vienna, 1998; pp. 250–254. [Google Scholar]
Sarac, T.; Sipahioglu, A. A Genetic Algorithm for the Quadratic Multiple Knapsack Problem; 2007; p. 498; ISBN 978-3-540-75554-8.
Unal, A.N. A Genetic Algorithm for the Multiple Knapsack Problem in Dynamic Environment. In Proceedings of the WORLD CONGRESS ON ENGINEERING AND COMPUTER SCIENCE, WCECS 2013, VOL II; Ao, S.I., Douglas, C., Grundfest, W.S., Burgstone, J., Eds.; Int Assoc Engineers-Iaeng: Hong Kong, 2013; Vol. Ao, pp. 1162–1167.
Zhan, H.; Yang, J.J.; Ju, L.Y. Improved Genetic Algorithm Based on Operation Order Matrix Encoding for Job Shop Scheduling Problem. Advanced Materials Research 2011, 189–193, 4212–4215. [Google Scholar] [CrossRef]
Meng, L.; Cheng, W.; Zhang, B.; Zou, W.; Fang, W.; Duan, P. An Improved Genetic Algorithm for Solving the Multi-AGV Flexible Job Shop Scheduling Problem. Sensors 2023, 23, 3815. [Google Scholar] [CrossRef] [PubMed]
Chen, D.; Shen, Y.; Liu, S. A Two-Layer Genetic Algorithm Based on Matrix Coding for FJSP. In Proceedings of the 2018 5th IEEE International Conference on Cloud Computing and Intelligence Systems (CCIS); November 2018; pp. 507–511. [Google Scholar]
Sun, L.; Zhang, Y.; Jiang, C. A Matrix Real-Coded Genetic Algorithm to the Unit Commitment Problem. Electric Power Systems Research 2006, 76, 716–728. [Google Scholar] [CrossRef]
Chen, K.; Bi, W. A New Genetic Algorithm for Community Detection Using Matrix Representation Method. Physica A: Statistical Mechanics and its Applications 2019, 535, 122259. [Google Scholar] [CrossRef]
Capital Budgeting in the States - Nasbo. Available online: https://www.nasbo.org/reports-data/capital-budgeting-in-the-states (accessed on 14 August 2024).
Ječmen, K.; Mocková, D.; Teichmann, D.; Mertlová, O. SELECTION AND SCHEDULING OF TRANSPORT INFRASTRUCTURE PROJECTS FOR IMPLEMENTATION USING GENETIC ALGORITHMS. In Proceedings of the Proceedings of the International Scientific Conference QUANTITATIVE METHODS IN ECONOMICS Multiple Criteria Decision Making XXII; Vydavateľstvo EKONÓM: Bratislava, Slovak Republic, June, 2024; Vol. 22; pp. 70–77. [Google Scholar]

Figure 1. Scheme of the proposed genetic algorithm.

Figure 2. Min and max values achieved by GA with repair operator (left) and fitness penalization (right).

Figure 3. Average fitness value achieved by GA with repair operator (left) and fitness penalization (right).

Figure 4. representation of computational experiment results - fitness function values and time for each variation of GA parameters settings.

Figure 5. Convergence behavior of one exemplary run of the proposed GA.

Figure 6. Representation of computational experiment results - fitness function values and computational time for each termination condition settings (parameter

l

Figure 6. Representation of computational experiment results - fitness function values and computational time for each termination condition settings (parameter

l

Figure 7. Representation of computational experiment results - correlation between computation time and real number of iterations in GA run.

Table 6. Chromosome representation example.

$Project i \in I$	$Year j \in J$
$Project i \in I$	1	2	3	4	5	6	7	8	9
1	0	0	0	0	0	0	1	0	0
2	1	0	0	0	0	0	0	0	0
3	0	0	1	0	0	0	0	0	0
4	0	0	0	1	0	0	0	0	0
5	0	1	0	0	0	0	0	0	0
6	0	1	0	0	0	0	0	0	0

Table 7. Chromosome and its validity in terms of Validity case II and validity case III.

$Project i \in I$	$Year j \in J$
$Project i \in I$	1	2	3	4	5	6	7	8	9
1, $p_{i} = 4$	0	0	0	0	0	0	1	0	0
2, $p_{i} = 3$	1	0	0	0	0	0	0	0	0
3, $p_{i} = 1$	0	0	1	0	0	0	0	0	0
4, $p_{i} = 3$	0	0	0	1	0	0	0	0	0
5, $p_{i} = 1$	0	1	0	0	0	0	0	0	0
6, $p_{i} = 3$	0	1	0	0	0	0	0	0	0
$c_{j}$	10	15	7	6	8	4	4	2	1
$b_{j}$	10	10	7	8	8	8	7	0	0

Table 8. Transformed example chromosome

X

Table 8. Transformed example chromosome

X

$Project i \in I$	$Year j \in J$
$Project i \in I$	1	2	3	4	5	6	7	8	9
1, $n_{i, t} = (4,2, 1,1)$	0	0	0	0	0	0	4	2	1
2, $n_{i, t} = (10,4, 2)$	10	4	2	0	0	0	0	0	0
3, $n_{i, t} = (3)$	0	0	3	0	0	0	0	0	0
4, $n_{i, t} = (4,8, 4)$	0	0	0	4	8	4	0	0	0
5, $n_{i, t} = (5)$	0	5	0	0	0	0	0	0	0
6, $n_{i, t} = (6,2, 2)$	0	6	2	2	0	0	0	0	0
$c_{j}$	10	15	7	6	8	4	4	2	1
$b_{j}$	10	10	7	8	8	8	7	0	0
$r_{j}$	0	-5	0	0	0	2	4	0	0

Table 9. Fragments of parent chromosomes.

$Fragment of P_{1}$					$Fragment of P_{2}$
0	0	0	0	0	1	0	0	0
1	0	0	0	0	0	1	0	0
0	0	1	0	0	0	0	1	0
0	0	0	0	1	0	0	0	0
0	0	0	1	0	0	0	0	1
0	1	0	0	0	0	0	0	0

Table 10. Fragments of offspring chromosomes.

$Fragment of O_{1}$			$Fragment of O_{2}$
0	0	0	1	0	0
1	0	0	0	1	0
0	1	0	0	0	1
0	0	1	0	0	0
0	0	1	0	0	1
0	0	0	0	1	0

Table 11. Example of 3 mutation cases.

Mutation case	Initial chromosome row		Mutation
Mutation case I	0	1	$\to$	0
Mutation case II	0	0	$\to$	1
Mutation case III	1	0	$\to$	1

The mutated element is highlighted grey.

Table 12. Calibrations results - average quality of solution (10 GA runs for each combination).

Crossover probability $p_{c r}$	$Mutation probability p_{m}$
Crossover probability $p_{c r}$	0.111	0.056	0.028	0.006	Total
0.6	1 266.90	1 312.20	1 317.10	997.20	1 223.35
0.7	1 302.60	1 259.20	1 235.80	1 034.40	1 253.48
0.8	1 275.70	1 281.20	1 249.20	1 133.90	1 265.38
0.9	1 313.40	1 322.90	1 298.10	1 092.90	1 260.17
Total	1 289.65	1 293.88	1 275.05	1 064.60	-

Table 13. Calibrations results - average computational time (10 GA runs for each combination).

Crossover probability $p_{c r}$	$Mutation probability p_{m}$
Crossover probability $p_{c r}$	0.111	0.056	0.028	0.006	Total
0.6	27.56	30.72	30.20	24.60	28.27
0.7	30.66	24.80	28.58	25.00	27.26
0.8	27.57	28.02	26.97	31.36	28.48
0.9	33.60	32.20	27.63	29.87	30.83
Total	29.85	28.93	28.35	27.71	-

Table 14. Computation results of GA in comparison with LP model solution.

Problem size	GA			LP solution
Problem size	Time [s]	Solution obtained	Perc. of LP solution	Time [s]	Solution obtained
$m = 50, n = 3$	2.7	643	98.6%	0.19	652
$m = 100, n = 3$	4.8	620	90.0%	3.6	689
$m = 300, n = 9$	60.1	1 434	92.2%	3 600+	1 555
$m = 600, n = 16$	617.8	3 589	86.8%	3 600+	4 137
$m = 1200, n = 25$	1 704.4	5 943	82.1%	3 600+	7 236

Table 15. Results of 10 GA runs with calibrated parameters.

Calculation	Computational time [s]	Fitness value	Perc. of LP solution
1	144.11	1467	93.34%
2	182.03	1416	91.06%
3	121.21	1434	92.22%
4	112.43	1435	92.28%
5	63.55	1385	89.07%
6	73.13	1350	86.82%
7	120.87	1416	91.06%
8	64.92	1388	89.26%
9	81.23	1349	86.75%
10	116.01	1434	92.22%

Table 16. Computation time of GA phases (average based on 10 GA runs).

GA phase	Time [s]	Perc. of total time
Calculations	14.05	27.7%
Crossover	9.06	17.8%
Mutation	4.39	8.6%
Repair operator	23.29	45.9%

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

$Fragment of P_{1}$					$Fragment of P_{2}$
0	0	0	0	0	1	0	0	0
1	0	0	0	0	0	1	0	0
0	0	1	0	0	0	0	1	0
0	0	0	0	1	0	0	0	0
0	0	0	1	0	0	0	0	1
0	1	0	0	0	0	0	0	0

$Fragment of O_{1}$			$Fragment of O_{2}$
0	0	0	1	0	0
1	0	0	0	1	0
0	1	0	0	0	1
0	0	1	0	0	0
0	0	1	0	0	1
0	0	0	0	1	0

$Fragment of P_{1}$					$Fragment of P_{2}$
0	0	0	0	0	1	0	0	0
1	0	0	0	0	0	1	0	0
0	0	1	0	0	0	0	1	0
0	0	0	0	1	0	0	0	0
0	0	0	1	0	0	0	0	1
0	1	0	0	0	0	0	0	0

$Fragment of O_{1}$			$Fragment of O_{2}$
0	0	0	1	0	0
1	0	0	0	1	0
0	1	0	0	0	1
0	0	1	0	0	0
0	0	1	0	0	1
0	0	0	0	1	0