Preprint
Article
An Ensemble of Machine Learning Models for the Classification and Selection of Categorical Variables in Traffic Inspection Work of Importance for the Execution of Events
Altmetrics
Downloads
66
Views
43
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
06 September 2024
Posted:
06 September 2024
You are already at the latest version
Alerts
Abstract
Traffic Inspection (TI) work in this article is positioned as a specific module of road traffic with its primary function oriented towards monitoring and controlling safe traffic and the execution of significant events within a particular geographic area. Exploratory research on the significance of event execution in simple, complicated and complex traffic flow and process situations is related to the activities of monitoring and controlling functional states and performance of categorical variables, which include objects and locations of road infrastructure, communication infrastructure and networks of traffic inspection resources. It is emphasized that the words “work” and “traffic” have the semantic status as synonyms (in one world language), which is explained in the design of the Agent-based model of the complexity of content and contextual structure of TI work at the singular and plural level with 12 points of interest (POI) in the thematic research. An Event Execution Log (EEL) was created for on-site data collection with eight variables, seven of which are independent (event type, activities, objects, locations, host, duration-period and periodicity of the event) and one dependent (significance of the event) variable. The structured data set includes 10,994 input-output vectors in 970 categories collected in the EEL created by 32 human agents (traffic inspectors) over a 30-day period. An algorithmic presentation of the methodological research procedure for preprocessing and final data processing in the ensemble of machine learning models for classification and selection of TI tasks is given. Data cleaning was performed on the available dataset to increase data consistency for further processing. Vector elimination was carried out based on the Location variable, such that the total number of vectors equals the number of unique categories of this variable, which is 636. The main result of this research is the Classification modeling of the significance of events in TI work based on machine learning techniques and the Stacking ensemble. The created machine learning models for event significance classification modeling have high accuracy values. To evaluate the performance metrics of the Stacking ensemble of models, the confusion matrix, Precision, Recall, ND F1-score are used.
Keywords:
Subject: Engineering - Transportation Science and Technology
1. Introduction
Topics in which the functions, strategies, structure and methodology of executive management in traffic inspection (TI) work are the subject of research belong to a relatively new scientific problem area. This is because TI tasks have a specific status within the branched classification tree of functional areas in modern traffic systems. Traffic systems are multidimensional modular dynamic systems with processes executed with predominantly complex state configurations. As a rule, the most complex and widespread modular part of a traffic system in a country or a specific geographic area is typically road traffic, where TI work is related to identified infrastructural, predominantly construction and communication facilities and networks as well as other entities for the safe and reliable implementation of various modes of road traffic (local, urban, suburban, intercity, main roads, highways) [1,2]. The selected geographic area for this research is the Republic of Srpska (RS), Bosnia and Herzegovina (B&H), and the importance of the specificities of traffic inspection tasks positions them into a special type of management-supervisory module within the traffic system, organizationally referred to as the “Traffic Inspectorate” at the level of the RS entity. The responsibilities of this module integrate multidisciplinary domains and areas of knowledge with standardization and regulation of traffic flows through the application of entity-specific and inter-entity legal norms, international criteria and regulations, and the design of rules and implementation of other normative acts [2]. An essential function of education in TI work includes integrated areas from general system theory, traffic and transport engineering, communication engineering, traffic safety, traffic psychology, multimodal communications, traffic law, behavior of participants in real traffic situations, as well as artificial neural networks (ANNs), machine learning (ML) and artificial intelligence (AI) [2,3]. The specificity of establishing modern foundations for managing TI work can be explained by several aspects. First of all, it is a new scientific approach to the research and functional-technological execution of TI tasks. It is a new way of decision-making based on relevant information that is not final but flexible and derived from the implementation of ethical relations in multi-agent communication. Internal creativity and value are significant motivational factors for TI practitioners, who are increasingly becoming multifunctional, adaptable to content and contextual changes, and spatially-temporally flexible, with continuous learning, rather than specializing in specific activities and tasks [4].
In this research, TI tasks are viewed as hyperparameter categories with goals and strategies oriented towards continuous monitoring and supervision in establishing and maintaining full operational readiness of infrastructural, mobile and other objects within the traffic system. The subsequent goal is to improve the effective functional suitability of structural modules within a complex matrix of system interactions with the environment and reliable traffic flows. The approach used involves explaining that “traffic means work”, and this meaning of the words “work” and “traffic” as semantic synonyms derives from the Italian cultural heritage and language [5]. It is acknowledged that both “work” and “traffic” have specific semantic determinants within their content and contextual structures, which are dynamic in nature (roles, relationships, relations, interactions, space, time). From an organizational-functional perspective, TI work is a “construct of multidimensional categories of content and contextual structures at both the individual (singular) and collective (plural) levels of functioning” [6]. The main categories of the content structure of work are knowledge and skills at the individual or singular level while technology, subject and processes of work are at the collective or plural level. Consequently, in the contextual structure of work, the main categories are singular orientations and attitudes, while at the plural level, they are culture and strategies of business [4,5,6]. Many researchers point out that modern business is increasingly oriented towards the roles of individuals, as well as good interpersonal relationships, which has also been recognized by many employers.
The hypothetical assumption in this article is that TI tasks have not yet been adequately theoretically conceived, standardized or codified for the interaction of roles and the exchange of exponentially growing knowledge in open scientific communication. This is substantiated by various statistical and other data sources that need to be linked with data registers of differently complex inspection tasks, diverse physical, software and behavioral objects, types of events, locations of events, hosts or owners of inspection processes, periodicity and intervals of inspection event duration, which occur or are carried out within the context of multi-agent communication. An agent, according to the canonical definition, is “any entity that operates based on knowledge and multimodal communication within a specific context” [7]. Concepts associated with agents include action, environment, perception, sensors, effectors, while the fundamental characteristics of agents are adaptability and learning ability. “The two main classes of agents in TI roles are human and software agents”, which can operate either individually or in an ensemble of agents, i.e., as a team in a multi-agent system (MAS) fulfilling roles in TI [7]. A multi-agent system is a complex matrix of multiple agents interacting directly to achieve goals that are very difficult to accomplish through individual efforts [6,7].
Therefore, human agents (whose roles are performed by traffic inspectors) and software agents (applications and services) address individual or joint tasks related to monitoring, control, data analytics, information analysis, creation of reports and other documents, and decision-making within process structures on the multi-agent communication platform. Various communication models involve tasks related to transferring digital structured data and messages among agents within a group, ensemble or MAS, which jointly perform algorithmically defined roles, ways of presenting, exchanging and sharing data within dynamic and flexibly connected functional and process structures of TI tasks.
The following can be highlighted as significant contributions of scientific research in this article:
- Visual interpretability of the cognitive continuum of knowledge learning human agents in TI works;
- Designing an Agent-based model of the complexity of content and contextual structure of TI work in a selected geographic area;
- Constructing an Event Execution Log (EEL) for TI tasks to research categorical variables in registers of related data for a defined research geographic area;
- Creating a research procedure with algorithmization of data cleaning operations and cleaned data processing in the EEL;
- Classification modeling of the significance of events in TI work based on machine learning techniques and Stacking ensemble.
2. Related Research
The initial foundation for the scientific explanation and justification of the joint functioning of human and software agents in the execution of TI tasks includes the construct Cognitive Continuum of Knowledge (CCK) [8]. CCK contains multiple instances of knowledge aspect that exist in people’s minds. According to Polanyi [9], this is tacit knowledge that is “implicit” and utilized depending on individual cognitive potential and contextual dimensions, but cannot be measured. In contrast to tacit knowledge is explicit knowledge that has a measurable value, which is easily identified and presented in interactions, i.e., it appears on the user screens in the form of graphics, tables, text or multimodal presentations. The Information and Communication Technology (ICT) of user interfaces enables the integrated flow of tacit and explicit knowledge in discovering and solving simple, complicated and complex problems in TI work. Based on this, Davenport and Prusak [10] describe knowledge as a “fluid mix of framed experience, values, contextual information, and expert insight that provides a framework for evaluating and incorporating new experiences and information”. The interpretability of the phrase “fluid mix”, i.e., instances of knowledge aspect in the cognitive continuum, allows for indicators of cognitive and sensory learning in human-singular agents, including: the type of learning, performance focus of learning, temporal perspective of learning and the level of awareness developed through continuous learning [8]. It is concluded that instances of knowledge aspect in the cognitive continuum of human agents are not structured according to hierarchical rules, as knowledge does not have a hierarchy. In line with this, it is important to highlight the research results of Vern Allee [8], which have been adapted in this article, with visual interpretability shown in Figure 1. The following are identified:
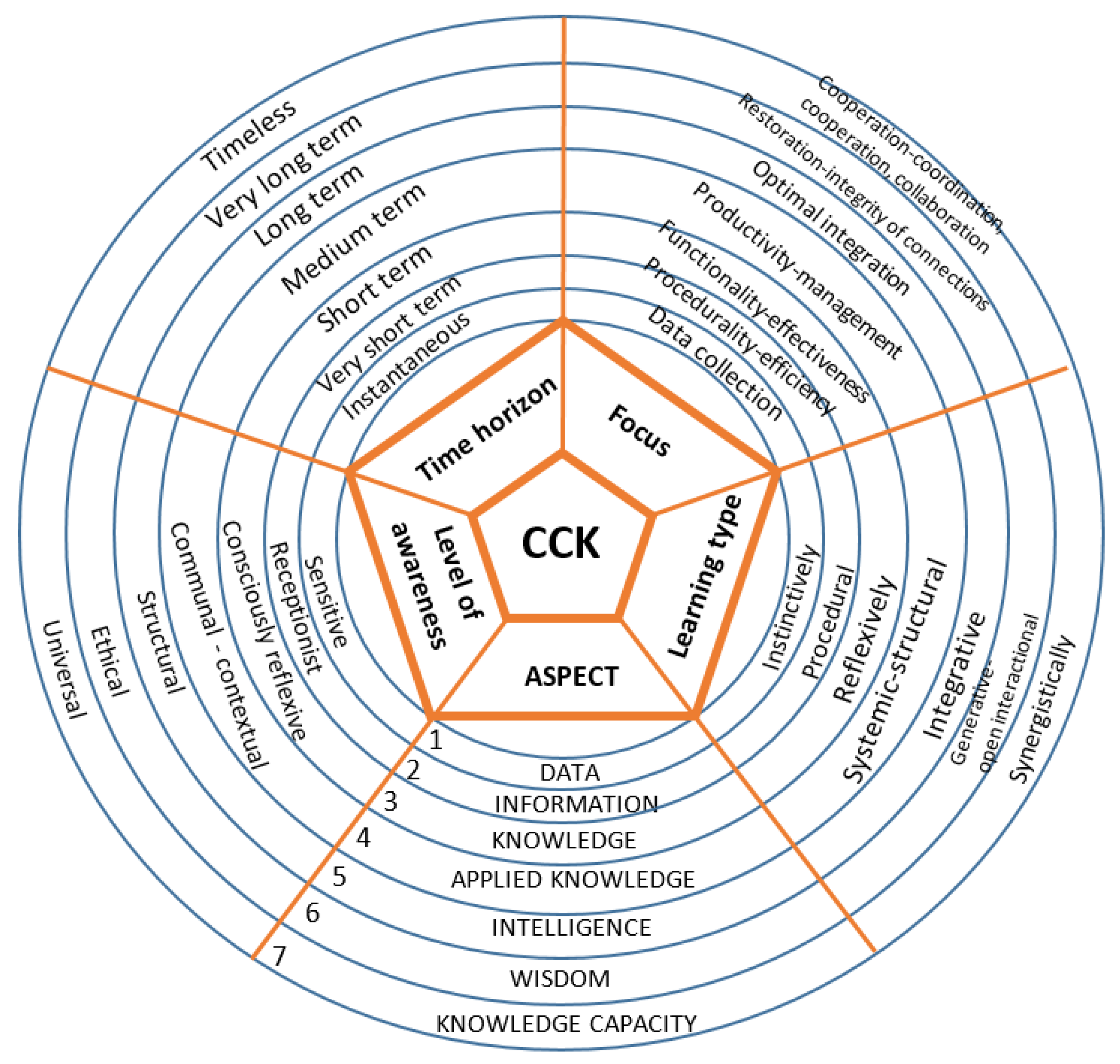
- Seven instances of knowledge aspect in the Cognitive Continuum of Knowledge (CCK), i.e., data (d), information (i), knowledge (K), applied knowledge (AK), intelligence (I), wisdom (W) and the capacity of knowledge (CK) for sharing in real situations of multimodal multi-agent communication in TI work.
- For the seven instances of knowledge aspect, the corresponding seven instances of the learning type indicator are identified as: instinctive learning, procedural learning, reflective learning, systemic-structural learning, integrative learning, generative-open interactive learning and synergistic learning [8];
- For the seven instances of knowledge aspect, the corresponding seven instances of the performance learning focus indicator are identified as: data collection (with feedback), procedurality (efficiency of information processing), functionality (effectiveness of information processing), productivity (reliability of management), optimal integration of knowledge repertoire, renewal-integrity of connections and cooperation in learning and sharing knowledge capacity in the form of 3C (3C – cooperation, coordination, collaboration) [8];
- For the seven instances of knowledge aspect, the corresponding seven instances of the learning time perspective indicator are identified as: current perspective, very short-term, short-term, medium-term, long-term, very long-term and timeless time perspective [8].
- For the seven instances of knowledge aspect, the corresponding seven instances of the indicator consciousness level, which develop through learning in different situations, are identified as: consciousness of feelings, sensory consciousness, reflective consciousness, contextual consciousness, structural consciousness, ethical and universal consciousness [8].
Instances of knowledge aspect in cognitive learning are stored in long-term and working memory in the human brain, while the overall capacity for knowledge sharing in knowledge and learning networks is enhanced by knowledge in sensory memory, which includes visual, audio and associative segments. An individual’s knowledge capacity is activated in real situations by discovering and solving problems, sharing it in the form of explicit knowledge decoded from books, brochures, graphical displays, knowledge maps, decision tables, decision trees, frames, case-based reasoning rules, intelligent software agents, knowledge repositories on disks, knowledge presentations, and various types of media suitable for offline, online and inline multi-agent communication in TI work. Awareness for understanding a situation requires the mental integration of information aligned with the user's goals and the current context. Speed, accuracy, reliability, integrity and security are expected attributes of successful ICT, which enables the delivery of knowledge to the user (on an individual or collective level) from knowledge networks. At the same time, the goal of the knowledge economy is to direct knowledge holders (knowledge agents or employees within an organization) towards greater efficiency and productivity, and improved use of knowledge at three levels of practice (operational, tactical and strategic) in TI work. Ensuring effective knowledge sharing is enhanced by communication where ICT provides unlimited opportunities for managing the integration of tacit knowledge, which resides in people’s minds, with explicit knowledge available in various repositories (databases or knowledge bases) or knowledge and learning networks.
The another foundation focuses on the learning of software agents that interactively function in a team or ensemble of agents using specific learning paradigms [11]. Currently, well-known paradigms such as Boosting, Bagging and Stacking are used to train models for classification, selection and prediction of certain target functions in real situations of TI work, which are explained in detail in Section 5 (related to research results) of this article [11].
The classification of real situations in the execution of TI tasks recognizes simple, complicated or complex situations. Problem-solving is based on the continuous learning of individual instances of knowledge in the cognitive continuum of singular human agents and interactive learning of software and cyber-physical agents [10]. These are associated with deep learning ensembles of agents in artificial neural networks and supervised machine learning models [11]. Simple situations in TI work determine a single path for solving a specific task as one action. Problem questions can be defined as closed-type questions where each question has only one correct answer leading to a solution [12]. Answers may vary depending on specific conditions of work situations, but for any given condition, there is one answer. Information requirements and changes in situation conditions can be predetermined because the situation, as a closed system, is isolated from external factors in terms of creating a solution to the situational problem [13]. The objectives of solving simple situations and information requirements in TI work are focused on the skills and activities of agents involved in locating and identifying a specific piece of information about objects, activities, locations, event types, event duration, periodicity, time perspective or event significance. The authors in [14] described cognitive processes involved in simple searches, which can be described as visual locating and recognizing the desired information that can be a word, a group of words or a phrase, an acronym, a number or a graphic symbol.
Complex situations in traffic inspection work can be fully described in terms of singular components but are perceived differently due to the large number of interactions and components in a real situation [15]. The increased number of interactive elements in a situation creates the opportunity of using various paths and methods that lead to accurate solutions for complex situations in the process structures of TI tasks. Due to the increase in multiple paths leading to accurate solutions to problem tasks, a fundamental difference arises between complex and simple situations. In complex situations [16], a hierarchical structure of all paths can be created, forming a “network of paths” with multiple feedback links” for accurately solving a specific complex problem task in TI work. The most complex situations in reality can quickly become ambiguous, so they must be treated as complex [10,11,12,13,14,15,16].
By definition, complexity is the ability of an entity (system, task, event, process) to freely choose and form an exponential set of states within the real space-time coordinates of situations. Since complex situations contain too many factors within the overall structure of tasks, it is very challenging to fully analyze and provide a complete set of information for accurately defining the path and completely solving the problem [17]. Therefore, complex situations differ from simple ones in that they are not isolated but are constantly influenced by various external factors that increase unpredictability and uncertainty in problem analysis, compromising the clarity of selecting the exact trajectory on which the solution to the problem is located [18]. Essentially, the main characteristic of complex situations is the complex relationship between input data, users or task performers, and the tasks being solved in complex work [19]. Cilliers P. in [20] described a complex situation with the following words: “The interaction among the constituents of the system and the interaction between the system and its environment, are such a nature that the system as a whole cannot be fully understood simply by analyzing its components”. This is because the relationships between system elements are not immutable, nor is there a “required piece of information” in only one place or a single correct answer or solution to the problem. In a complex situation, a “system for obtaining data from the situation” combining it with other data and presenting coherent information relevant to the situation and the user’s goals is necessary [17,18,19,20].
3. Material
3.1. Contemporary Research Frameworks for TI Work
First of all, it should be noted that classical scientific foundations for researching traffic inspection work are compatible with the application of mechanical laws and principles of system and process management in traffic and transportation engineering. Today, in modern times, quantum physics is increasingly being used instead of Newton’s, with dominant orientations towards domains of knowledge from the natural sciences and contents from the science of behavior dynamics of real traffic participants, especially in urban, increasingly dense, road traffic [18].
The other foundation is that the functional-technological TI work management, characterized by activities such as planning, forecasting flows and controlling the execution of events, should be relocated with a focus on a holistic understanding of process structures and the coherence of the entire inspection and supervision factors in road traffic. This means that the core factors of inspection and supervision activities are examined in the context of multi-agent communication dynamics, encompassing humans, i.e., people and institutional organizations, with supervision over real-world objects in road traffic, the use of operational and cyber-physical technologies, and spatial-temporal environmental impacts on a variety of TI tasks in real situations [21]. At the same time, the focus of management is on some key points of interest, including: simple, complex and intricate activities associated with various locations, multiple-positioned hosts or owners of processes, periodicity in duration intervals, and the significance of executing diverse types of events. Relevant information for decision-making in TI work is now not in a finite cognitive form but rather in domain-unlimited and infinite perspectives. This means that knowledge creation in institutionally organized traffic inspection is increasingly less singular or individual and more plural or collectively oriented towards collaboration. The known forms of collaboration are cooperative, coordinative and collaborative, provided that the desired business success is achieved in a legally determined manner within a specified geographic area [8,17,21,22].
Ethical relations in the dynamics of traffic inspection work are not established on a competitive platform of performance, rivalry and dominance of unethical influences, but rather on cooperation and the survival of a coherent network of inspection agents (management and communication agents), where the network operates within the context of trust. In contemporary times, considerable importance is given to the internal organizational life of inspection teams, ensembles or fleets of agents. Personal feelings and emotions are significant sources of understanding within this coherent whole and effective communication with dynamic content, roles, relationships and interactions between the structural components of the situational whole of traffic inspection work [17,21,23].
The source of motivation in performing TI tasks is internal creativity and value beliefs, while the sense of time, instead of being monochronic and linear (parcelized and successive), becomes polychronic and nonlinear. This implies that an increasing number of actions, activities, transactions, events and processes are executed in parallel –simultaneously within the same interval or traffic flow [2,6,13,17,18,23,24].
Performers of TI tasks are becoming less specialized and segmented by specific areas and are increasingly multifunctional, adaptable to changes and open to continuous learning [25]. This is because management is less and less driven by a “top-down” approach, and increasingly distributed and consistent with achieving consensus in a democratic functioning environment. At the same time, the creation of structural content and contextual elements of tasks and work process organization is achieved through the discovery or emergence of new ideas, new paradigms and theories, new models, algorithms and applications on the platform of developing capacity for competent problem-solving, especially in the context of digitalization of tasks and automation of specific processes in TI [26].
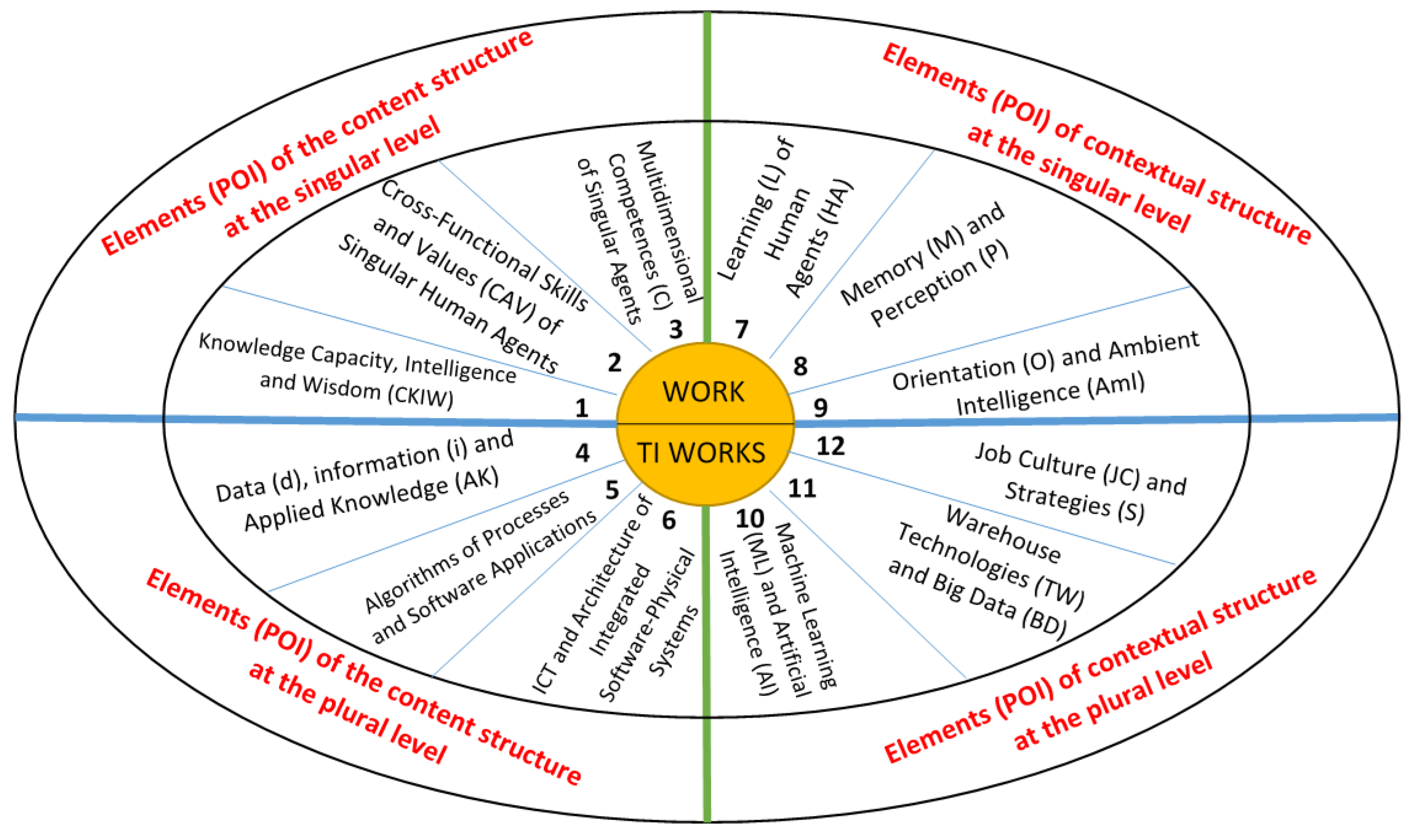
3.2. Agent-Based Model of the Complexity of Content and Contextual Structure of TI Work
Dynamics, as an inherent characteristic of the modern era, is accompanied by a much more complex and intricate environment in which TI tasks are planned, designed and implemented as activities of particular interest in the study of safe traffic as a holonic system in a defined geographic area. Therefore, in this thematic article, TI tasks are modeled as an original research outcome titled “Agent-Based Model of the Complexity of Content and Contextual Structure of TI Work”. The originality of the created TI model in the defined geographic area is structured with twelve constructs or points of interest (POI) (described in the content of the article from sections 3.2.1. to 3.2.12), as visually represented in Figure 2.
Based on the visual presentation in Figure 2, the Agent-based model of the complexity of content structure of a singular TI task consists of the following categories: 1) knowledge capacity, intelligence and wisdom (CKIW), 2) cross-functional skills and values (CAV), and multidimensional 3) business competencies (C) of singular agents. The content categories of the ensemble of agents (at the plural level of TI tasks are 4) data (d), information (i) and procedural knowledge (K) in application (piK), 5) work process algorithms and software applications, 6) information and communication technologies (ICT) and network applications (NAs). At the singular level of the contextual structural work, the categories are: 7) learning (L) of human agents, 8) memory (M) and perception (P), 9) orientation (O) and ambient of job (AmJ), while at the ensemble level of agents, the contextual categories are: 10) machine learning (ML) and artificial intelligence (AI), 11) warehouse technologies (WT) and Big Data (BD), 12) job culture (JC) and strategies (S). Each of these 12 categories of content and contextual work structure (at both the singular and plural level) of TI are explained successively.
3.2.1. Knowledge Capacity, Intelligence and Wisdom (CKIW)
These are categories of the content structure of complex and intricate situations in TI work, formed by singular-human agents through learning in an integrative, generative-interactional and synergistic manner across a temporal perspective that is long-term, very long-term and timeless. Initially, it should be noted that knowledge is one of the fundamental life resources whose potential allows it to function intelligently. The performance learning focus specified for the three instances of knowledge aspect is on optimal integration, integrity and collaborative cooperation that facilitates the development of consciousness at the structural, ethical and universal levels [8,18,24].
Intelligence is an instance of the knowledge aspect of singular human agents in TI work, which means “the global capacity” to act proactively and to think and act rationally [8,18]. This article focuses on the cognitive, social and emotional dimensions of intelligence. Cognitive intelligence develops understanding, knowledge, skills, values, and orientations for functioning in confusing states such as excitement, urgency, complexity, and chaos [8,18,24]. Social intelligence is a structure resulting from cognition, emotion, and awareness that develops and is expressed in the life context through understanding social situations in which people interact with each other. In TI work when people meet “face to face”, they “receive inputs through all senses, i.e., mechanoreceptors, thermoreceptors, and the senses of sight, hearing, smell and taste. These senses allow an individual to see, feel, hear, smell, touch (using mechanoreceptors) and exchange energy (using thermoreceptors) [27]. They assess social situations based on the inputs to their senses, which come from facial expressions (facial expression codes), body language (kinesthetic codes), gestures (sign codes), paralinguistic features of speech such as prosodic signals, and from physical contact or distance (proxemic codes) that keep people within specific communication zones (intimate-intrapersonal, personal-interpersonal, business-team, social, public) [24]. Emotional intelligence is defined as an individual’s ability to build domains of intrapersonal and interpersonal relationships, strengthen character, self-confidence, and consistent behavior within communication dynamics. Aspects of emotional intelligence behavior include: self-awareness, empathy, self-motivation, self-control, and successful interpersonal relationships [8,18,24,27].
Wisdom is an instance of knowledge aspect that defines the nuanced ability of human intelligence to adapt and self-manage functioning in the context of varying intracultural and extracultural influences on dynamic behavior.
In a unified interpretation of these three instances of knowledge aspect (intelligence, wisdom, and the capacity for knowledge sharing), they function with the cognitive continuum based on the principles of a knowledge network and a learning network.
3.2.2. Cross-Functional Skills and Values (CAV) of Singular Human Agents in TI Work
Skills and values are a set of personal qualities, habits, attitudes and social skills that enable people to effectively communicate with others and achieve their goals, both in their work and everyday life. These are soft skills, while hard skills refer to specific technical abilities or knowledge related to a particular technology, profession or activity. Soft skills can be applied in different circumstances, situations and environments. These are skills in respecting ethical principles in the knowledge and use of various technologies in multi-agent communication, where there are no disinterested agents in traffic inspection situations. Hard skills in real situations do not allow for the existence of a disinterested observer.
When considering both soft and hard skills together, the following ten skills are highlighted for individuals participating in TI work roles: 1) encoding and decoding communication skills (speaking, writing, reading and active listening); 2) digital literacy with inline and online operational interaction skills; 3) communication skills in the context of artificial intelligence; 4) skills in detecting and solving problems in real time; 5) skills in interacting with new technologies on a multi-agent communication platform; 6) intercultural reaction skills in real situations; 7) ability to address more complex situations with contextual information; 8) skills in openness in creating team culture and structure, and clarity of messages; 9) openness of mind skills; and 10) speed of action in managing time and other work resources.
3.2.3. Multidimensional Competences (C) of Singular Agents in TI Work
Eight core competences are often highlighted for individuals, including human agents in TI work: (1) effective communication in the native language including the significance of a highly inflected and morphologically rich language with the use of a large number of different word endings to express desired grammatical, syntactic or semantic functions of words, sentences and phrases; (2) communication in foreign languages; (3) mathematical, scientific and technological competences; (4) digital competences; (5) competences for learning how to learn and manage one’s own learning; (6) social and civic competencies; (7) competency to recognize the need for initiating for personal, collective and social progress; and (8) competency for developing cultural awareness and expressive abilities in symbolic interactions. In managing TI work, competencies are particularly needed for the effective and efficient creation of digital strategies, as well as for internet communication skills in the context of online, offline, inline, conversational, interactive, streaming, and background traffic in networks.
3.2.4. Data (d), Information (i) and Applied Knowledge (AK) in TI Work
Data is defined as “an attributive statement of an entity or object that does not exist as a physical object but as a coded fact that begins to exist when registered or recorded in a specific memory or database”. Learning from data involves instinctively gathering data with feedback and developing sensory awareness at the level of instinctive or spontaneous perceptual understanding. The goal of learning is focused on data collection – receiving input, recording it with possible variations based on sensation or without contemplation. The goal of learning is focused on data collection – receiving input, registering it with potential variations based on sensory perception or without thinking.
Information is a semantic representation of data organized into models with content, temporal, formal, and value meanings in information processing. The value of information is determined by the decision as the starting point for action (single-step activity). Information corresponds to procedural learning of content categories in the structure of TI work. The performance learning goals are efficient procedures with a focus on developing, monitoring, and completing defined tasks. Applied knowledge is decoded and its meaning is understood when it can be applied practically. It is important to emphasize that knowledge is a specific resource. Applied knowledge is an instance of knowledge aspect particularly significant for TI work, involving modeling and optimizing learning from data and data analysis. Models in use include Linear and Quadratic Regression and Classification, Logistic Regression, Nonlinear Regression and Classification, Feature Extraction Algorithms (such as Principal Component Analysis), Data Clustering Algorithms (such as Cluster Analysis), Stochastic Gradient Descent and other modern modifications of gradient algorithms (such as algorithms with fixed and adaptive momentum), with applications in training neural networks.
3.2.5. Algorithms of Processes and Software Applications in TI Work
According to [28,29,30,31,32], an algorithm is formally a successive set of procedures for solving specific problems. Computer algorithms are formulated in any comprehensible language and then implemented into programming languages that are understandable by all computers. In principle, an algorithm transforms data x into a result y so that it has the same role and power as calculating a function. From the aspect of mathematical objects, algorithms are sequences of finite length, and thus are countable. Since functions are not enumerable, well-defined problems cannot be solved algorithmically. For each specific problem, there is a higher number of solutions, meaning that multiple appropriate algorithms can be designed to solve it, which can vary dramatically in their efficiency [28]. This aligns with Albert Einstein’s observation that “problems cannot be solved at the same level of cognition that created them”.
A serious comparison of these algorithms can only be conducted on a reliable mathematical basis of computational complexity theory. They differ in time complexity (algorithm execution speed) and space complexity (available memory for data storage). The main parameter for evaluating the quality of an algorithm is operational time, i.e., execution time of the algorithm, which also serves as a comparative parameter for comparing or ranking algorithms against each other [29].
By definition, software is an algorithmic structure designed for interaction with the user through an appropriate interface. Interface design unconsciously influences the user’s interpretation of the display. According to the definition, “design is a complex process of synthesizing the function and form of an entity, informational object, or content of things”, so it should be emphasized that it is the form that determines whether the user perceives content as conforming or contrary [16]. Regardless of its purpose, software introduces a certain dynamism to the user’s relationship with reality by substituting symbols for things; images for bodies or construction mechanisms; statistics for estimates; and absence or intangibility for physical presence [16].
According to a relatively recent paradigm in software development, problems are solved using machine learning techniques and the formation of data set models. Consequently, tools and environments that support machine learning workflows with defined successive steps are important in TI work. Of interest is the application of automated, process-oriented (DataOps) methodologies to improve quality and minimize the duration of data analysis cycles, as well as the application of machine learning models in Big Data scenarios. Additionally, it is important to highlight the implementation of existing software tools for training standard predictive models of machine learning and deep learning (Scikit-Learn, Keras/TensorFlow) [19].
3.2.6. Information and Communication Technology (ICT) and Architecture of Integrated Software-Physical Systems in TI Work
ICT is the core of the content structure of TI tasks. As part of that, the focus is on basic terms, fundamental concepts, principles and challenges of software-physical systems (SPS) related to embedded systems, the Internet of Things (IoTs), cloud computing, cognitive computing, design principles, specifications, modeling and analysis of SPS. The examples of SPS implementation include abstractions and architectures (micro services, cloud architectures, etc.). The examples of SPS subsystem integration are Machine-to-Machine (M2M) and IoT communications. In TI work, heterogeneous data from different sources are integrated, particularly concepts related to Big Data (BD), Cloud Computing (CC) and Big Data platforms and technologies. Big Data integration in SPS and data processing algorithms involve real-time connections with real-world, industrial and critical environments, as well as package data processing for modeling and machine learning [33,34,35,36,37].
As a specific case of SPS, cyber-physical systems (CPS) emerge, consisting of physical process models and software models, computer platforms and networks. The connection between physical processes and software processes is achieved by a feedback loop with newer technologies developing in the context of artificial intelligence [38].
A specific area of the content structure of TI tasks covers Agent Communication Technology, which is developed with ANN models. The goal of ANN development is to create a technology that understands and can simulate the functioning of the human brain in terms of stimulus (signal) detection, its transmission, decision-making procedures and ways of remembering, the retention time of what is remembered, i.e., forgetting. Essentially, the application of ANN involves designing artificial systems capable of learning and making intelligent decisions like humans [39].
3.2.7. Learning of (L) Human Agents (HA) in TI Work
In a broader sense, learning is a process structure (actions, activities, events, transactions, processes) through which an individual acquires new knowledge, develops multidimensional skills, forms attitudes in different contexts in TI work. In a narrower sense, learning is a dynamic development process of knowledge, skills, orientation and behavior with the goal of discovering and solving problems in TI work. According to [40], learning is categorized into action-based, transformational, reactive, and predictive learning. Action-based learning begins with a focus on a practical problem that is assessed, discovering needs in knowledge, thinking, and creating solutions to the problem. Transformative learning uses a “root-and-branch” approach to analyzing events by asking and answering questions (who, what, where, when, how, and why) in solving problems in TI work. In reactive learning, an individual faces a specific situation and reacts to it reflexively, creating a result. Predictive learning is future-oriented focusing on selecting the best working methods in TI work. The goal is to develop a plan for future actions, and after its implementation, its effectiveness and efficiency are assessed, and the validity of solutions in IT work is determined. A system is considered to learn if it makes changes to itself [40].
From a formal aspect, learning in TI work can be explained through the theory of inverse problems. A problem can be defined as “a task that is solved without a previously known or created algorithm” [41]. To fully understand the concept of a problem, three deterministic parameters are used: f, A and g, where: A represents the “weight matrix” as the operational technology used to solve the task; f represents the inputs or input data upon which operations A are performed according to the defined method of problem-solving, and g is the direct output or solution to the problem task, i.e., the reaction to f influenced by A. Practically, A is the operator that impacts the identified input f to obtain g through a certain number of operations as a result or solution to a direct problem, which has been properly posed.
g=Af
A direct problem in TI work must be physically well or properly formulated through three attributes: stability, unambiguity and persistence [41]. The stability of a properly formulated direct problem requires that the solution sought in identifying the case or system continuously depends on the initial or input data [41]. The unambiguity for a properly formulated direct problem is satisfied when there is only one optimal or adequate solution among a series of invariant cases for the identified system. The persistence of a properly formulated direct problem meets the requirement that there is a solution for all random data from a specific domain. This is the essence of causality, which connects the causality of input or initial data (f) with the reaction (g) as the output or result of solving the deterministic problem [41].
Satisfying these three requirements for direct problems implies the context of "the constant action of Laplace's thought experiment” or “intellect” (demon) which is considered “the first instance of the publication of the articulation of causal or scientific determinism". The problem was posed by Pierre-Simon Laplace in 1814, and the laws of classical mechanics are used to calculate certain physical values [42]. In [43], a prominent example of an inverse problem is given: “Learning is an inverse problem”. In the development methods and models in TI work, the following learning strategies are implemented: cognitive strategies (e.g., note-taking, data storage, explaining), metacognitive strategies (e.g., learning planning, self-evaluation) and social strategies (e.g., collaboration with colleagues, seeking help from instructors), affective strategies (e.g., using relaxation, self-reward and risk-taking), and some communicative strategies which help agents to speak more grammatically correctly and to improve their confidence during oral presentation [44].
3.2.8. Memory (M) and Perception (P) in TI Operations
Memory is a crucial dimensional factor in the contextual structure of simple, complex and intricate TI tasks. In human cognitive architecture, sensory-perceptual, working-short-term and long-term-deep memory systems function. Sensory-perceptual memory includes visual, auditory and tactile types of memory dimensions. In the visual type, iconic memory is dimensioned; in the auditory type it is echoic memory [45]; and in the tactile dimension, the tactile memory type is important. The functions of sensory memory types are to dimension the amount of content, duration and design of the retained memorized material. From the perspective of content quantity, it is significant that the entire sensory input is retained, but only a portion is forwarded to working memory for deeper levels of processing. The researchers emphasize that in the dimension of the neural impulses received at a rate of 109 bits/sec, only 10-102 bits/s are registered, while only 10 bits/s are forwarded to working memory.
Working memory has its three subcomponents: a phonological loop that manipulates verbal material; a visual-spatial matrix that manipulates images, while the central executor controls attention, distributes cognitive resources, and initiates the recovery of retained material [46]. This model was revised by Baddeley in 2000, when the researcher introduced a component called the episodic buffer, which integrates and temporarily stores information from various modalities.
In long-term memory, all our knowledge is stored, and it has practically unlimited capacity. It contains three types of content: declarative knowledge, procedural knowledge, and experiential knowledge (autobiographical memories). Declarative and procedural knowledge belong to semantic memory, while memories are stored in episodic memory [45]. Long-term memory, which characterizes this type of memory, is determined by the formation and automation of schemas as entities of a larger number of meaningful entities, which define individual overall knowledge. In a certain way, within memory as a contextual category, the structure of the task correlates with subjective experience, which can include the state of individual subjectivity and perception upon which a person bases their own sense of reality, based on their interaction with their environment. This is associative memory. Associative memory models are called content-addressed memories, where the brain recalls events and facts through association, as a prominent feature of human memory, by retrieving items with information or with another items.
Perception is defined as a specific experience, i.e., awareness [phenomenal consciousness] and as such, it is inexplicable by algorithms, information processing levels and similar concepts [47]. Certain experts emphasize that perception is not analogous to other psychological functions of the organism but is conceived as a distinct property, an essential characteristic, or a mode of personality functioning. This indicates a certain terminological confusion in the study of perception. In terms of analogy with other concepts, such as intelligence, which has cognitive structural elements or learning that is a processing category, it is a need to establish a distinction by treating perception as access consciousness [48]. From a clinical and biological perspective, besides consciousness, “there is also a state of coma or unconsciousness in which there is no communication with the external world”. In any case, “consciousness is treated as a mode of information processing, distinct from processing that occurs without such access” [49].
Recent research into consciousness has introduced a range of terms, such as sensory consciousness, receptor consciousness, reflective consciousness, communal consciousness, structural consciousness, ethical consciousness, transcendent consciousness, meta-self-consciousness, structural consciousness. It is a result of different approaches to studying consciousness across cognitive sciences, neuropsychology, social psychology, clinical psychiatry, developmental psychology and other scientific disciplines or research paradigms. According to K. Wilber [50], in cognitive sciences, the study of consciousness is oriented as a “potential explanatory construct on a similar level as attention, a memory instance or as a ‘software’ of consciousness” [50]; In contrast, the neuropsychiatric “approach searches for the neural foundations of various constructs, including consciousness; it explores which neural structures and neurological processes form the basis of consciousness; viewing it as the ‘hardware’ of consciousness” [50]. The quantum theory of consciousness – “treats consciousness as an intrinsic property of matter; emphasizing the interaction between consciousness and matter, commonly involving quantum phenomena and microtubules – avant-garde theories in physics” [50].
3.2.9. Orientations (O) and Ambient Intelligence (AmI) in TI Work
All employees integrate content and context into their work. Context refers to the microenvironment of work, where contacts and orientations are particularly significant. In TI work, orientation is required with respect to space, time, roles and tasks, problems, goals and strategies, people and interpersonal relationships, objects, processes, or parameters of specific situations. Orientation is the primary dimension of a business vision. Orientation and vision are causally related. Without orientation, there is no vision, and a person without vision lacks the mental map necessary for navigating any situation, especially critical or crisis situations [15]. Contextual orientation analysis is based on the concept of the person or personality functioning with moral and volitional components, including response speed and typical mood [15]. Pairing orientation with intelligence as a form of cognitive continuum of knowledge in agents, which exists in people's minds, is analyzed and implemented in a multidimensional context of TI work.
3.2.10. Machine Learning (ML) and Artificial Intelligence (AI) in TI Work
AI encompasses any technique that enables computers to imitate human behavior and human decision-making to solve complex tasks either independently or with minimal human intervention [51,52,53,54,55,56,57,58]. A similar definition is provided by IBM: artificial intelligence can be defined as a set of technologies that enable computers to simulate human intelligence and problem-solving methods. In combination with other technologies, AI is becoming irreplaceable in many everyday tasks that would otherwise primarily require human intellectual engagement. The expanding use of artificial intelligence highlights the issues and importance of AI ethics and responsible AI concepts in areas like transportation, particularly in Traffic Inspection. AI ethics is a multidisciplinary field that studies how to maximize the positive effects of AI while minimizing the risks and negative consequences of its use. The goal is to ensure responsible and safe use of AI technologies in transportation, considering social, ethical, technical and legal aspects. Responsible AI refers to a set of principles that build trust in intelligent solutions that can benefit users in the transportation system and traffic inspectors [52]. Most of today’s AI systems in general, including those used in transportation, belong to Weak AI or Artificial Narrow Intelligence (ANI) systems designed for performing specific tasks. On the other hand, the concept of Strong AI is based on Artificial General Intelligence (AGI) and Artificial Super Intelligence (ASI), which implies that a machine possesses intelligence equivalent to that of a human. It is important to note that such systems still exist only at a theoretical level [52,53].
Machine learning (ML) is one of the most prominent subfields of AI and allows systems to learn from data, especially Big Data, by automating the process of creating analytical models and solving related tasks. Instead of coding knowledge into the computer, ML automatically discovers relationships and patterns in data, making it easier for people to develop intelligent systems without the need for explicit formalization of knowledge. Advances in machine learning research have enabled the development of intelligent systems with human-like cognitive capacities, which increasingly impact human life and shape networked interactions. These systems use analytical models to generate predictions, rules, recommendations, and similar outcomes [54,59].
An important feature of ML is that it facilitates the formalization of human knowledge into a machine-readable format, enabling more efficient development of AI-based systems. The learning of data-driven ML models from structured, unstructured, semi-structured and metadata is based on four paradigms: Supervised, Unsupervised, Semi-Supervised, and Reinforcement Learning. For each problem addressed by ML methods, such as classification, regression analysis, data clustering, association rule learning, feature engineering for dimensionality reduction, and deep learning, there is a range of algorithms that iteratively learn from historical data [55]. Figure 3 provides a graphical illustration of a machine learning problem. The x-axis and y-axis denote the input variables Speed and Weight, based on which the output is classified into one of two symbols, + or -. The three shown functions f1, f2 and f3 clearly separate the points on the plane that belong to these outputs, and the number of functions that can correctly separate the presented space is unlimited. Once an ML model learns the function from historical data, it is capable of autonomously classifying new, “unseen” data.
Deep learning belongs to machine learning methods and is based on the application of artificial neural networks. Artificial neural networks are among the most widespread machine learning techniques and consist of a series of processing elements – artificial neurons that are interconnected in an architecture consisting of input, hidden and output layers for learning from data. A network is typically considered deep if there is more than one hidden layer. Thus, inspired by the principle of information processing in biological systems, the flexible structure of ANN consists of mathematical representations of interconnected processing elements called artificial neurons. The first model of an artificial neuron was developed by McCulloch and Pitts, representing a logical processing element with an output function in the form of a threshold or Heaviside function. The way an artificial neuron processes signals is defined by the transfer function, which is the combination of activation and output functions. The activation function maps input signals to a single output signal of the neuron, while the output function, often sigmoid, constrains this value between 0 and 1. Each synapse has a weighting factor that adjusts during learning, enabling the network to learn to map vectors from the input space X to the output space Y = f(X). Consequently, it is said that the network learns functions, i.e., the parameters of function. Properties of the neural network, such as the number of layers and neurons in each layer, learning speed, and activation function, represent hyperparameters that cannot be learned using learning algorithms, but are adjusted manually or through optimization method.
An artificial neural network can also be defined as a graph composed of transfer functions of neurons that map vectors from an N-dimensional input space to an output space. The Universal Approximation Theorem is key to deep neural networks, stating that they can approximate any continuous nonlinear function using a sufficient number of simple linear operations and layers. The core idea is that the network decomposes complex functions into smaller, simpler components, with each neuron processing a part of the problem. As a result, deep learning can efficiently tackle high-dimensional data problems and work with various types and combinations of data within a unified model. This capability for simultaneous processing is called cross-modal learning. In contrast to deep neural networks, shallow neural networks have one hidden layer of perceptrons, with one of the common examples of shallow neural networks being collaborative filtering.
In the context of multi-agent systems (MAS), the primary goal is to develop algorithms that increase the ability of agents to link a set of inputs to corresponding outputs [56,60]. For example, let a set of examples be denoted by E. Each example e ∈ E represents a pair: e = {a,b}, where a ∈ A represents the agent’s input, and b ∈ B represents the output that the agent should produce when receiving this input. Within MAS learning, each agent must develop a function f that precisely link A to B for as many different events A as possible.
3.2.11. Warehouse Technologies (WT) and Big Data (BD) in IT Work
Big Data (BD) and Data Warehouse Technologies (DWT) represent modern ICT for processing and storing large volumes of data. The term Big Data refers to complex compilations of data and information that define various parameters (diversity, accuracy, comprehensiveness, speed, availability, constraints, relevance, location, volatility, etc.). In TI work, BD arises as a result of various digital processes in real time from sources such as administrative data, scanner data, external scanner data, satellite images, object and process tracking devices, behavioral data sources, and other different data sources. A particular significance of data sources for managing TI work includes social networks, portals, blogs, and comments from individuals and organizations in the public sector of social dynamics. In the modern treatment of BD and digital handling of TI work, special focus is on warehouse technologies such as edge computing (EC), fog computing, cloudlets, and mobile edge computing (MEC). EC is a model in which processing and storage capabilities of cloud computing are located near the data source, so the architecture of the EC model also includes small servers positioned between the data source and the cloud location [57].
3.2.12. Job Culture (JC) and Strategies (S) in TI Work
According to the canonical definition, culture is a “dynamically divided system of object and business symbols and meanings, beliefs and attitudes, experiential and creative values, expectations and norms of business and social behavior in the domain of conception, the domain of production, the domain of diffusion and the domain of communication in cultural heritage” [61]. From a broader perspective, culture is a system of knowledge that people produce and use when interpreting scientific and experiential coded knowledge in multimodal communication and intelligent behavior. The characteristics of culture are content (culture comprises heritage that is learned), divisibility (culture is disseminated everywhere and at any time to interested consumers), transmissibility (culture is transferred from one location to another in a continuous space and permanent time), symbolism (it is represented by symbols, signs and codes that are multimodal), adaptability (changes in the cultural system occur continuously and adapt in accordance with the development of knowledge and technologies, as well as the dynamic density of social situations), and structuring (an elastic integrative structure implies that changes are implemented in every part of the structure of system units [62]. In the complex structure of content and context of the cultural strategy, the domain of conception, domain of production, domain of diffusion and domain of communication are identified as integral parts of the cultural system. These domains underpin the functions, strategies and methodologies of executing TI work within a defined geographic area.
Strategy as a “creative mix of activities of an organization or other entity” was defined by Porter [63]. TI tasks are strategically oriented so that the success of the strategy depends on the successful execution of activities within the organization”. Key principles for the successful implementation of strategy within an organization are: a) Implementing business strategy into activities; b) Directing all TI tasks towards the defined strategy; c) Strategy in activities is a clear commitment from all agents in IT work; d) Strategy in activities is a continuous process in space and permanently in time; and e) The importance of strategy lies in encouraging developmental and technological changes by management agents in multi-agent communication and event execution in TI work.
4. Research Methodology
4.1. Exploratory On-Site Research of Event Execution in TI Work
In the subject of the research, a sample selected includes 32 human agents who perform traffic inspection tasks within the complexity structures of content and context in TI work on the selected geographic area. The participants in an ensemble of human agents create individual content and methods of the constructed research instrument called the Event Execution Log (EEL). The selected time period for the research is from November 1, 2023 to December, 25, 2023, conducting 31x30 + 40 working days of exploratory on-site research. The contents in the EEL include observations of particularly significant objects at locations within the geographic area, real locations of objects related to activities and types of events carried out in TI work. Certain contents are interpreted in text, maps, tables, drawings, images, records, streams, characteristic symbols and signs. In terms of factography, interesting data includes, for example, the level of developed networks of traffic signs (horizontal, vertical, and informational data and notices) across various categories of public roads (highways such as January 9 Banja Luka-Doboj, other highways, main roads or other roads for intercity traffic, urban-city traffic in major cities or municipalities – transportation lines, street intersections, roundabouts in settlements, toll booths, traffic flow control points, etc.). In the more detailed road network described within the geographic area of the research, data are collected on categories with the most important infrastructure facilities at significant locations (such as a network of bus stations, network of specific gas stations, network of significant vehicle inspection stations, network of locations with auto moto club resources, taxi stands, i.e., all facilities processed and analyzed in annual reports of completed inspections and other operations. Additionally, mobile facilities in traffic and transportation are significant from the aspect of traffic safety inspection by different categories. The main variables include vehicle speed, cargo securing on vehicle cargo boxes, accuracy of vehicle and driver documentation, the level of responsibility of authorities and organizations according to various control indicators, etc. All this is recorded and documented with specific tabular views, diagrams or other graphic forms of presentation, where data on events (processed and select by event types) are interpreted from those entered in certain reports during a period of road traffic inspection supervision.
The EEL is based on the business process model from the existing Information System of the Inspectorate of RS, which is used by traffic inspectors connected in a network model in their daily work. It creates a structured set of traffic inspection process instances (tasks, actions, activities, transactions, events) in the context of traffic inspection operations. The concept of content creation in the EEL is for individual traffic inspectors (acting as human agents) to record data daily during working hours over a period of 30 or 40 days within the previously defined research interval, resulting in a total of 970 EEL documents in the research dataset. The main variable categories registered in the EEL include traffic inspection objects in road traffic, activities in the process structures of TI work, types of events that are executed in inspection tasks, locations where events are executed, periodicity of repetition of certain types of events, duration or interval of events, the ownership or host of the process and, finally, the significance of events in real situations recorded by traffic inspectors in their results.
The goal is to organize the collected data into a more refined process of information processing, select and arrange them into process models with the aim of creating a big data basis for developing a digital platform. This platform enables the automation of traffic inspection processes within the defined geographic area of research.
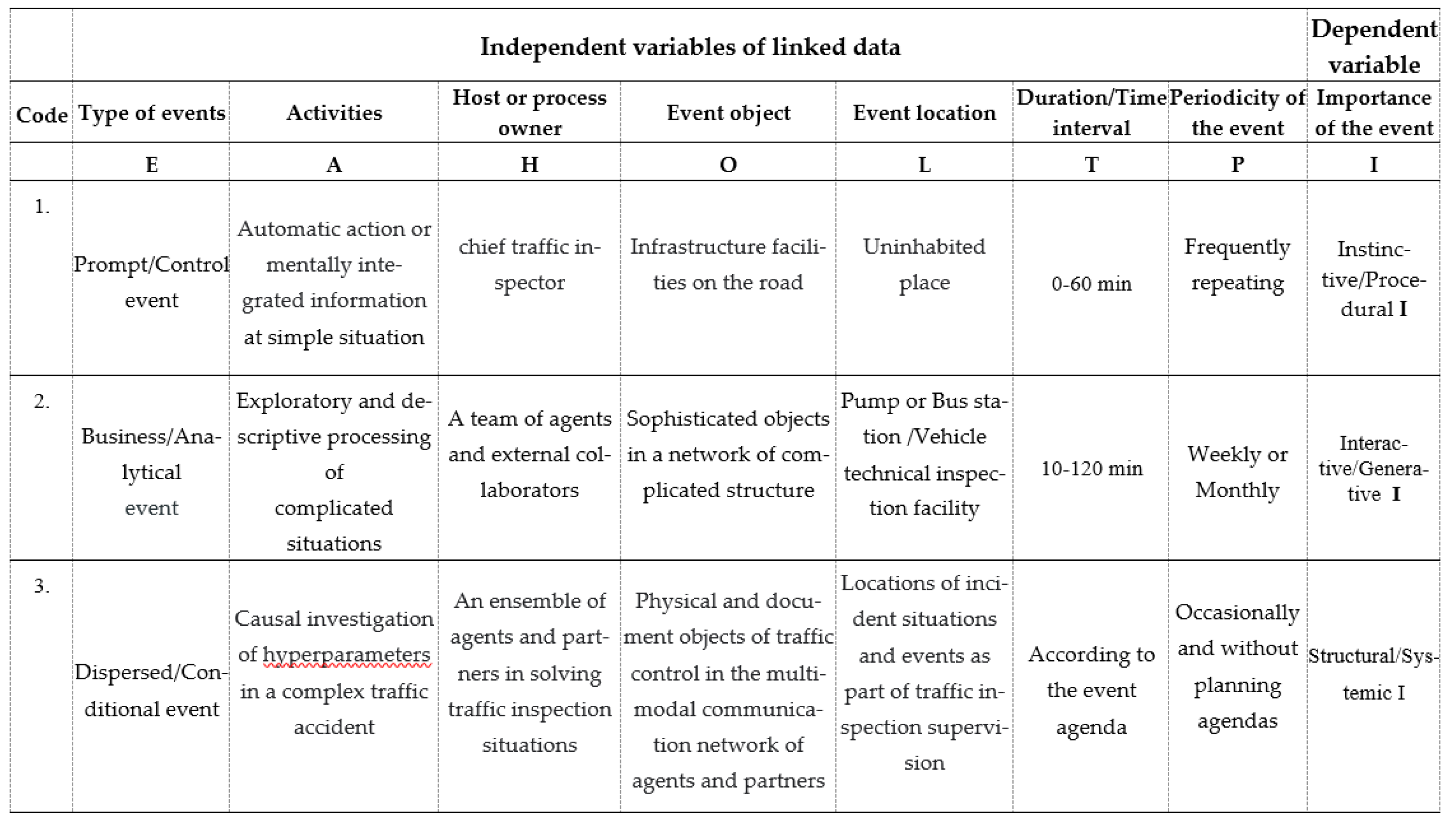
4.2. Creation of the Event Execution Log of TI Tasks
The Event Execution Log (EEL) features a matrix structure with a specific number of columns and rows, as illustrated in Figure 4. The first column is designed for the term code (event execution date), followed by columns with eight categorical variables of related data, namely: 1) type of events (E), 2) activities (A) that include two (input and output) or more events, 3) host or process owner (H), 4) event object (O), 5) event location (L), 6) duration – time interval of the event (T), 7) periodicity of the event (P) and 8) importance of the event (I). In the matrix structure, seven independent categorical variables and the eighth as a dependent research variable are named.
According to [29], an event can be represented by a relation:
where individual labels have the following meanings:
e= (E, A, H, O, L, T, P, I)
e denotes an individual event that can be defined as the perception of physical or other real facts at a certain point in the space-time continuum. A single event can be the beginning, end or any point of an activity or process in a public, business, personal or other context dimension. There are many types of events depending on the goal of on-site or experimental research activities.
E denotes the type of event in TI work that can be named as: 1) Traffic accident event, 2) Social event, 3) Prompt/Unexpected event, 4) Control event, 5) Educational event, 6) Dispersed event, 7) Business (by agenda or agent), 8) Planned/Procedural event, 9) Rigid/Conditional event, 10) Secure/Reliable event, 11) Transactional event, 12) Flexible/unconditional event, 13) Hazardous/destructive event, and 14) Structural event. A special case represents a sequence of events (e1,2,3,..n) that are executed within a single process.
A denotes an activity that can be defined as “mentally integrating information” in the processing of related data, which requires a resource of time. Generally, an activity is the main process instance in the EEL (with nuances being tasks, actions, transactions or a set of activities and events) that changes the state of one or more entities in the content and/or contextual structure of TI work. Individual activities performed by the traffic inspector during working hours are recorded (such as work planning, specification of cargo vehicle controls, procedural technical inspections, visual control of the road section, technical supervision of traffic signal maintenance, recording the behavior of taxi drivers, processing violation orders, digital processing of applications, creating reports on performed supervision of facilities on-site, creating official notes, creating inspection documents, and taking measures and actions in procedural activities). Mental integration of information implies presenting activities without redundant words, and without grammatical, syntactical or semantic errors, i.e., with substantive and formal accuracy and precise text.
H denotes the host or participant-owner of the process that can be an individual, an institution, a system, an application, a process structure or a set of objects connected to the execution of inspection tasks in a specific event, case or situation. Examples include an individual vehicle owner or city/municipal ownership, a regional chamber of commerce, bus station ownership, the authority of a technical inspection station, a tachograph calibration station controller, Public Institution “Roads of the Republic of Srpska”, Public Institution “Highways of the Republic of Srpska”, competent sector of the Ministry in RS, the Traffic Safety Agency. Thus, the host can be a person, a system, an application, a process structure, or a set of objects as a whole.
O denotes the object of the inspection activity (the object itself depends on the type of activity and the host) that can be a physical object of a certain control, an information system, a mobile object on the road, or a specific document within the jurisdiction of TI work (such as a decision, resolution, instruction, regulation, manual, guideline, etc.).
L denotes an event location that refers to the geographic location within a populated or unpopulated area with a precise address or other location parameters where the event takes place. It involves the address of the site, i.e., the determination of the spatial dimensions of the object at the location, so that each event corresponds to an individual activity, i.e., a well-defined step in the process of TI work.
T denotes duration or time interval that refers to the exact time period with the duration of a specific activity, i.e., event, regardless of how long it lasted. It can sometimes be predefined but may also depend on the fulfillment of certain conditions in the business model or event type. In further research, Period was not elaborated as an independent variable because it has no special significance.
P denotes periodicity that can be expressed with frequency such as once, occasionally, sometimes, often, every day, every week, every month, every year.
I denotes the importance of the event that indicates the complexity of the event itself, depending on the previously filled columns in the EEL. In general, the importance of the event can be simple, complex, intricate or normal. In this article, the importance of the event is coded as a dependent categorical variable according to the specifics of TI tasks.
The number of rows in the matrix structure shown in Figure 4, according to the calculated scope of the dataset, is 970 or (32x30+10). This corresponds to the number of input/output data vectors which totals 10,994 for all columns and rows in the aggregate EEL that are processed digitally. The available dataset, collected through the research instrument, Event Execution Log, is presented for each individual participant (32 sheets) in the research process via a Pivot table in Excel.
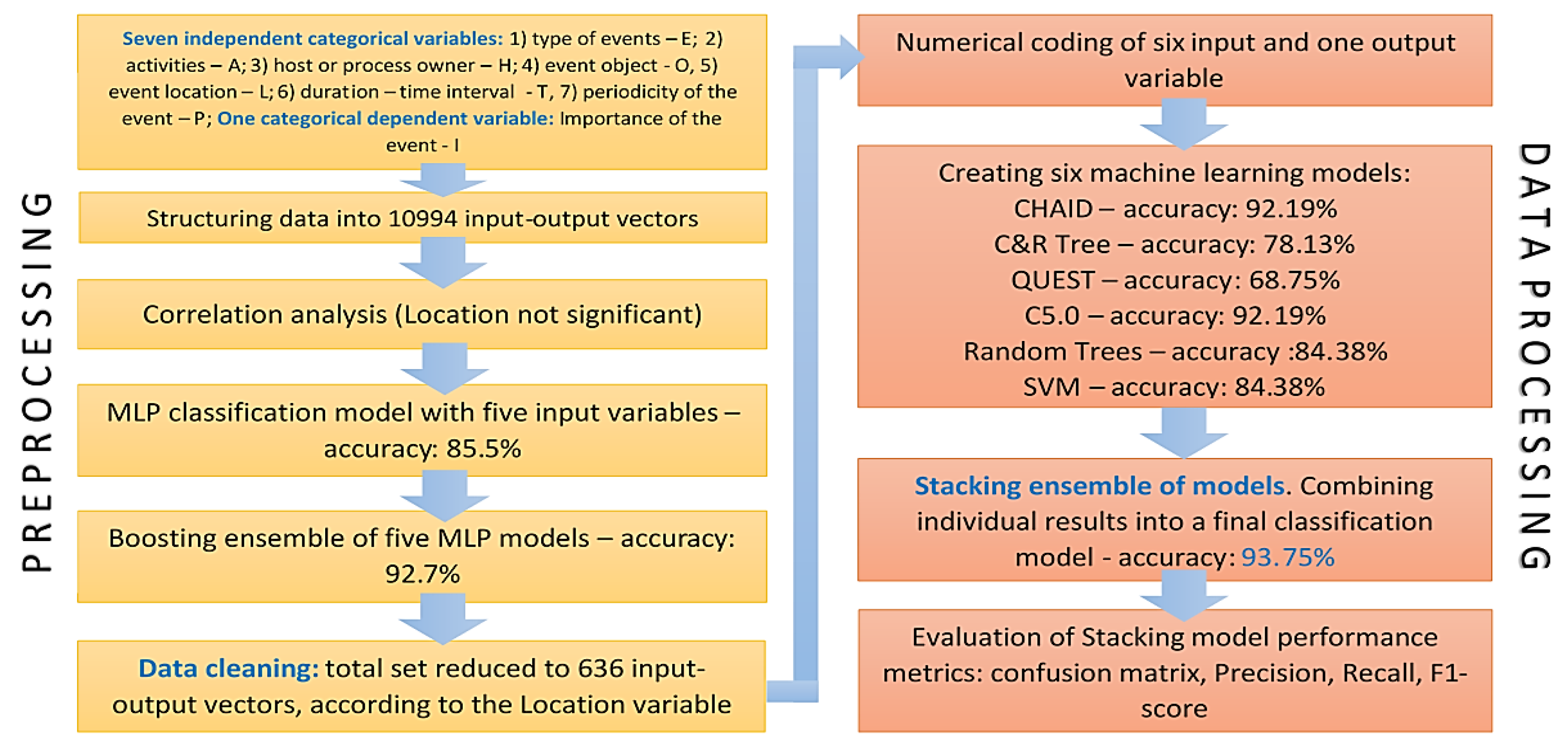
4.3. Algorithmic Overview of the Research Methodology for Data Preprocessing (Data Cleaning) and Processing in the EEL
In the process of digital treatment of collected data, preliminary processing or preprocessing of the entered dataset in the aggregate EEL is performed. The goal of preprocessing is data cleaning, which involves removing inconsistent data based on information quality criteria (content, form, location, time and interpretability value). Removed data are classified into one of five error classes in the collected dataset: conceptually unclear data, missing data, inaccurate data, imprecise data, and irrelevant data. The result of data cleaning shows that the number of data vectors was reduced from 10,994 to 636. With that number of entries, the final data processing was carried out using machine learning models, as explained in Section 5 of this article. Previously, an algorithmic representation of the research methodology for preprocessing and final processing of data by categorical variables is given in Figure 5.
4.4. Data Cleaning Procedure in the Research Dataset Collected via EEL
In the methodological procedure, data cleaning was performed on the available dataset, significantly reducing its size to enhance data consistency [16,56]. The elimination of vectors was carried out based on the categorical variable Location, such that the total number of vectors equals the number of unique categories of this variable, which is 636. Since other variables have fewer categories in their respective databases/registers, namely: Activity – 417 categories; Host – 55 categories; Object – 40 categories; Periodicity – 11 categories; Event type – 13 events, Event Significance – 12 categories, they have repeating values up to the specified number in the new, reduced dataset. The cleaned dataset exhibits greater consistency, which includes the following characteristics:
- A smaller dataset often implies higher data quality,
- Eliminating irrelevant or incorrect data reduces noise in the dataset,
- Consistent data in a smaller dataset enables a more efficient process of machine learning model training without compromising model quality,
- Focus is on representative vectors,
- Achieving reduced overfitting,
- Simplified model validation and cost reduction.
In the next step, in the SPSS Modeler software, String values were encoded into numerical values on a nominal measurement scale for all variables using the Automatic Recode method [36]. The cleaned dataset contains 8 categories of the dependent variable, i.e., Event Significance encoded as follows: 1- Instinctive event significance; 2 – Integrative event significance; 3 – Integrative/Generative event significance; 4 – Procedural event significance; 5 – Procedural/Reflexive event significance; 6 – Reflexive event significance; 7 – Reflexive/Structural event significance; 8 – Structural-systemic event significance. In this manner, the research methodology enabled further analysis and processing of data using machine learning methods.
5. Results of Creating a Machine Learning Model with Discussion
In accordance with the algorithm shown in Figure 5, the first part of the research process involves creating an MLP classification model with all seven available independent variables. Therefore, the subsequent section presents the results of this model, as well as the correlation analysis which led to the conclusion that the variable Activity has no significant impact on data classification. To increase consistency, the available dataset was cleaned, significantly reducing its size. Vector elimination was performed based on the Location variable, such that the total number of vectors equals the number of unique categories of this variable, which is 636. In addition to the numerical results of individual classification models on the cleaned dataset, which are presented later in this section, the structure/architecture of the CHAID, C&R Tree, QUEST, C5.0, Random Trees, and SVM models, as well as their hyperparameters, are thoroughly analyzed. Finally, the main focus is placed on the results of Stacking model classification.
Predictive modeling is a broad term that refers to the process of developing a mathematical tool or model that generates accurate forecasts based on existing historical data. According to [53], there are clearly defined steps in generating predictive models, with particular emphasis placed on regression and classification models. Classification models are used to predict discrete or nominal values, while regression is used to predict continuous values [55]. However, in the literature, and especially in the field of Data Mining, classification is often used as a term for predicting class labels, whereas prediction generally refers to the prediction of continuous values.
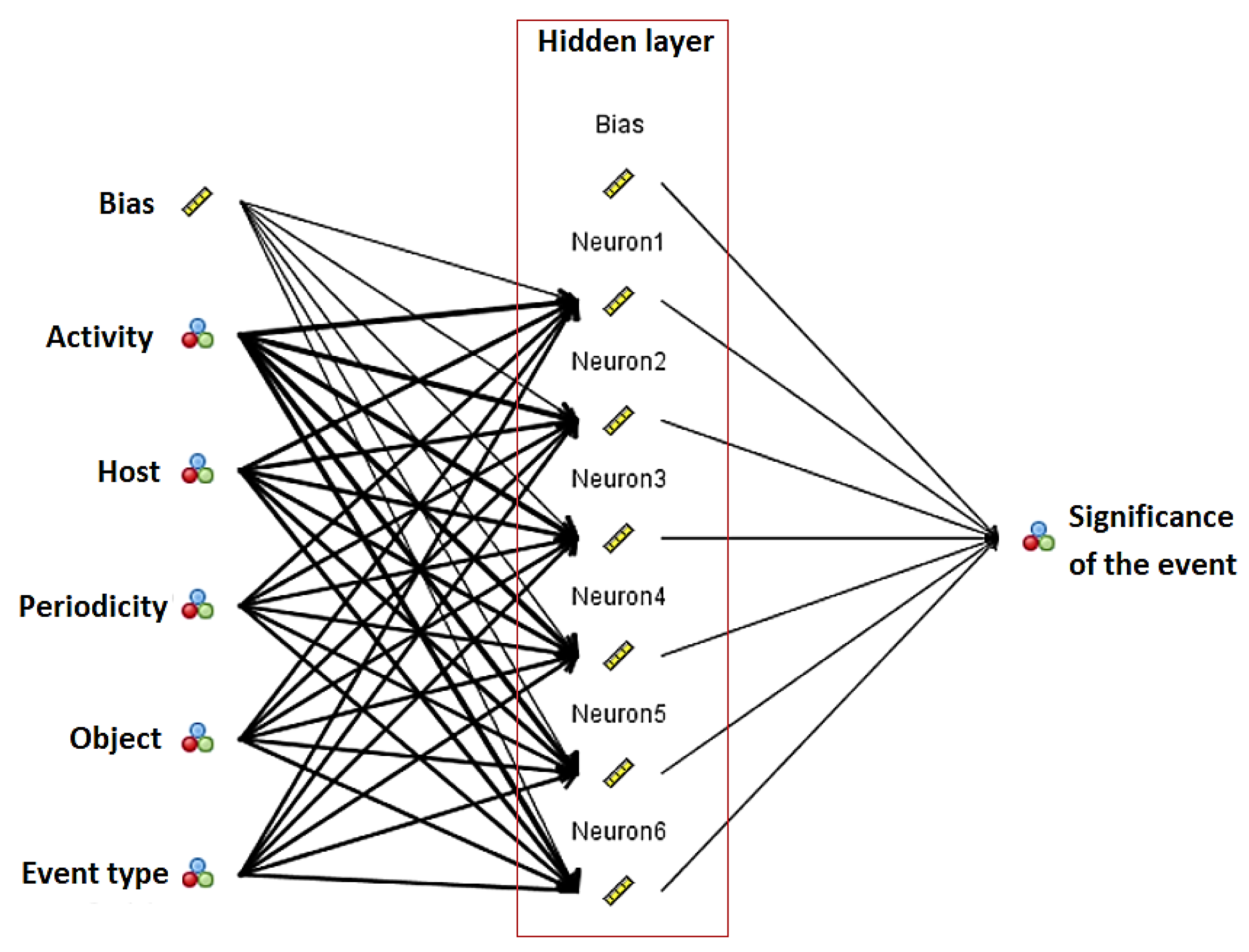
5.1. Creation of a Classification Model with all Observed Predictors
If all six predictors are considered as inputs to the ANN-MLP model, with their individual relationships to Event Significance previously modeled, the overall classification accuracy is 81.9% of the input-output vectors in the test set. At the same time, the model was trained on 90% of the total set, with the remaining portion used for testing. To improve classification performance, one possible solution is to apply variable selection techniques based on correlation. This technique involves searching for an optimal set of model inputs that are highly correlated with the dependent variable – output. Table 1 shows Spearman’s correlation coefficients between all research variables, as well as the p-value of the two-tailed test – Sig. (2-tailed). The two-tailed test checks the probability of extreme values in both directions of the distribution, i.e., it tests whether the correlation is significantly different from zero, either positively or negatively. The reason for calculating Spearman’s coefficients is that the research data set mainly consists of categorical variables, and therefore a more general approach than Pearson’s coefficients is necessary. Spearman’s correlation coefficients allow for the assessment of the strength and direction of a monotonic relationship between two variables, especially when data are ranked or linear approaches are inadequate. A negative sign in the coefficients indicates a negative monotonic relationship. As the values of one variable increase, the other variable tends to decrease.
Based on the given correlation coefficients between the six observed independent variables and the dependent variable in Table 1, it is concluded that the smallest correlation coefficient was calculated for the relationship between Location and Event Significance, which is 0.005. Additionally, the p-value for this correlation is 0.579, which is higher than the significance level of α=0.01. This indicates the insignificance of this correlation and therefore the Location variable is excluded from further analysis and classification modeling of Event Significance.
By creating a new MLP model with five independent variables, a higher classification accuracy is obtained on the test set, now reaching 85.5% of correctly classified vectors. The architecture of the model with one hidden layer and without insignificant Location variable is shown in Figure 6. The hidden layer neurons, by default, have a hyperbolic tangent activation function, while the output layer neurons use the Softmax activation function. Bias allows neural networks to better model complex relationships among data by shifting the activation function left or right on the graph along the x-axis, which is crucial in the learning and model adjustment process. Bias can be any real numerical value and is adjusted during the optimization process (e.g., using gradient descent) to minimize the network’s loss function and improve its ability to generalize to new data.
Figure 7 shows the relative importance of predictor influence on classification results. According to the graph shown, Activity has the greatest impact, while Event Type has the least.
Further improvement in the accuracy of the created model is achieved by the Boosting method. This method involves creating multiple models (components) in a sequence, i.e., creating an ensemble of models. Enhanced classification performance is achieved by creating each subsequent model in the ensemble to focus on inputs for which the previous model provided a poor class prediction. The final prediction is made by applying the entire series of models, using a weighted voting procedure. In this way, separate predictions are combined into a single resultant. The final classification accuracy achieved by the ensemble of five components, as summarized in Table 2, is 92.7%. Besides the model sequence number, each component’s classification accuracy, method or model, number of predictors, number of synapses (model size), and the number of instances on which the model was trained are provided. All five members of the ensemble are homogeneous MLP models, as defined in the Method column, and all ensemble members have five input variables each. The Records column shows the number of training vectors, which is 90% of the total set of 10,994 input-output vectors. The number of synapses, which represent connections between artificial neurons, is a crucial indicator of model size. Synapses are characterized by weights that determine the importance of signals.
Considering the obtained results and in order to improve the classification performance, the strategy for the further modeling process in this research is based on the following two points:
- The previous modeling with five predictors resulted in a model with greater interpretability. However, in many cases, a larger number of predictors can provide more information and thus enhance classification performance. Therefore, it is also necessary to model with a sixth independent variable, Location.
- To achieve better consistency, data cleaning according to the Location variable must be performed during preprocessing. It is assumed that each of the 636 categories of this variable represents key information, and reducing the total dataset to the same number of input-output vectors can help in better understanding the impact of each category on the model outcome. In addition, a smaller dataset offers certain advantages, some of which will be outlined below.
5.2. Results of Classification Modeling of Event Significance on the Cleaned Dataset
In order to further the process of classification modeling according to the supervised learning paradigm, the available set of 636 vectors is divided into a training set, a validation set and a testing set in the ratio 80%:10%:10%. Six different classification models were created, mainly based on the decision tree model with certain modifications. All model parameters and hyperparameters have default settings specified in the IBM SPSS Modeler environment.
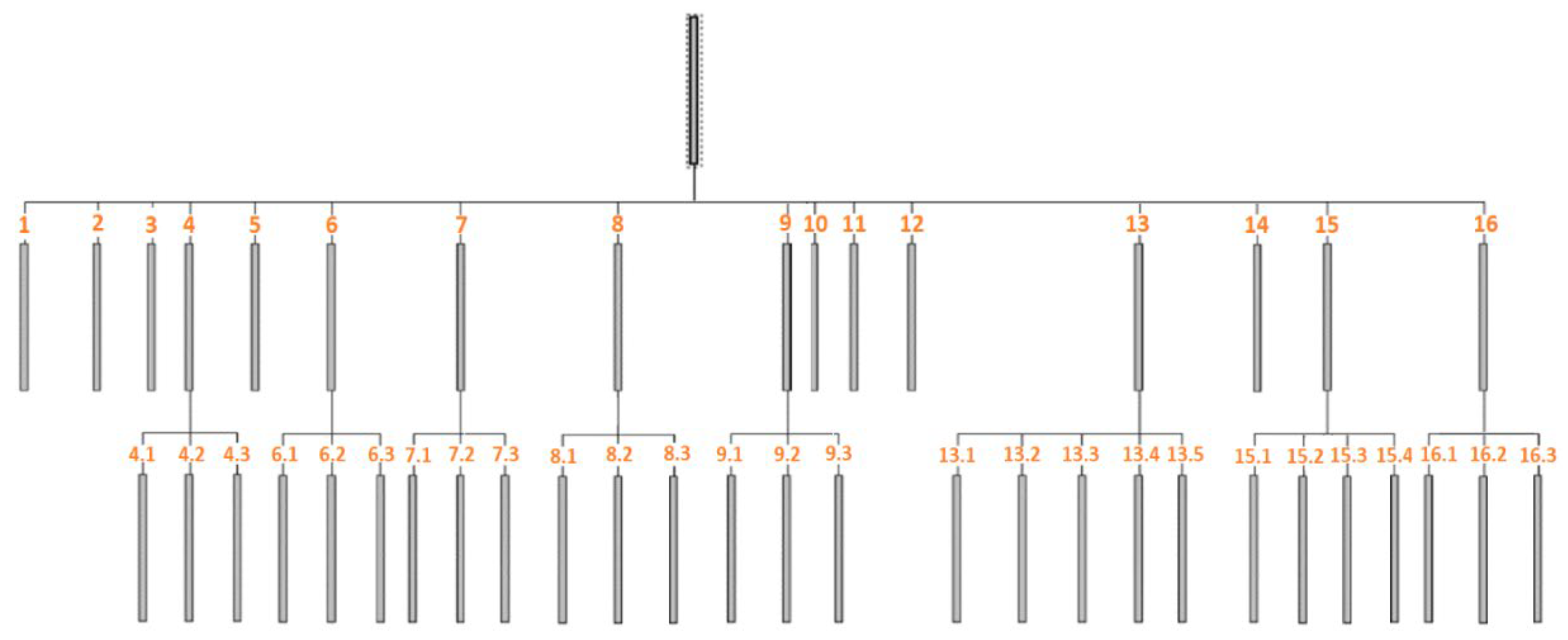
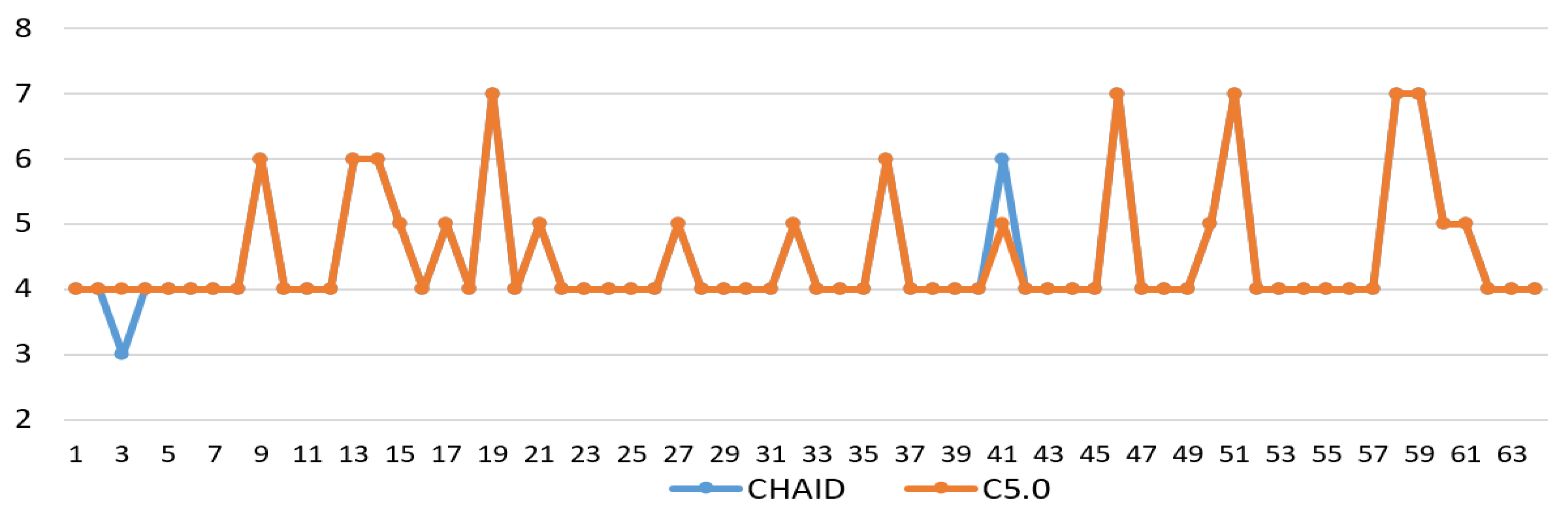
5.2.1. CHAID model
Chi-squared Automatic Interaction Detection (CHAID) is a classification method in machine learning used for creating decision trees based on Pearson Chi-square statistics. It represents one of the most popular statistically-based models for multivariate dependence, used for detecting relationships between categorical dependent and independent variables [17,35]. The CHAID model examines the chi-square test of independence to assess the significance of the relationship between independent variables and the dependent variable. When multiple relationships are statistically significant, CHAID selects the input variable with the lowest p value. For input variables with more than two categories, categories with insignificant differences in outcome are merged, starting with those with the least significant differences, until all remaining categories are significantly different. The algorithm minimizes variations in the dependent variable within groups and maximizes them between groups, achieving optimal data segmentation [35,44]. The default settings of the CHAID model in the IBM SPSS software include, among other things, two important hyperparameters: Significance level for splitting = 0.05 and Significance level for merging = 0.05. These parameters with values between 0 and 1 define thresholds for statistical significance used to decide whether a node in the tree should be split, i.e., whether multiple predictor categories should be merged. Minimum Change in Expected Cell Frequencies is another hyperparameter used in the CHAID model. It determines the smallest change in expected cell frequencies (in the contingency table) required to split or merge nodes. Maximum Iterations for Convergence sets the upper limit for the number of iterations the algorithm can perform, with the default setting for this hyperparameter being 100.
Figure 8 shows the structure of the created decision tree, i.e., the CHAID model with three layers of nodes in addition to the root node. The first layer contains nine nodes, five of which branch into terminal nodes – leaves of the second layer. Each of these nodes contains a question or test that splits the data based on certain attributes, while the leaves themselves generate predictions – classifications. Only one second-layer node is connected by a branch to two third-layer leaves.
Next to each node in Figure 1, there is a label that defines the branching rule, which is structured in two parts. The label above the node shows a set of rules for assigning individual records to child nodes based on predictor values [44]. It consists of the name of the variable according to which the branching was performed and its numerically coded categories, connected by the OR operator. The label below the node defines the classification value, which for categorical outputs, as in this case here, is expressed as a statistical parameter Mode – the most frequent category in the observed branch. For example, consider the classification of input vectors into category 5 of the Event Significance in the first node of the first layer from the left side of the tree in Figure 8, given in the following form: [Mode: 5]=>5.0. For trees with numeric dependent variables, the prediction is the average value for the branch. The created CHAID model accurately classifies 92.19% of the vectors from the test set.
5.2.2. C&R Tree model
The Classification and Regression (C&R) Tree model is a predictive classification model based on a decision tree. The C&R Tree algorithm begins by analyzing input nodes to find the best possible split, determined by the minimum Impurity Index. The Gini Index is most commonly used to measure impurity, which is related to the probability of incorrect classification of a random sample [38]. In IBM SPSS Modeler software, the default minimum impurity change is 10-4 to allow a new split in the tree. All splits are binary, meaning that each split creates two subgroups, and each of those subgroups is further split into two until one of the stopping criteria is met [38]. The stopping criteria set in the C&R Tree model are:
- Minimum records in parent branch – 2% of the total dataset,
- Minimum records in child branch – 1% of the total dataset.
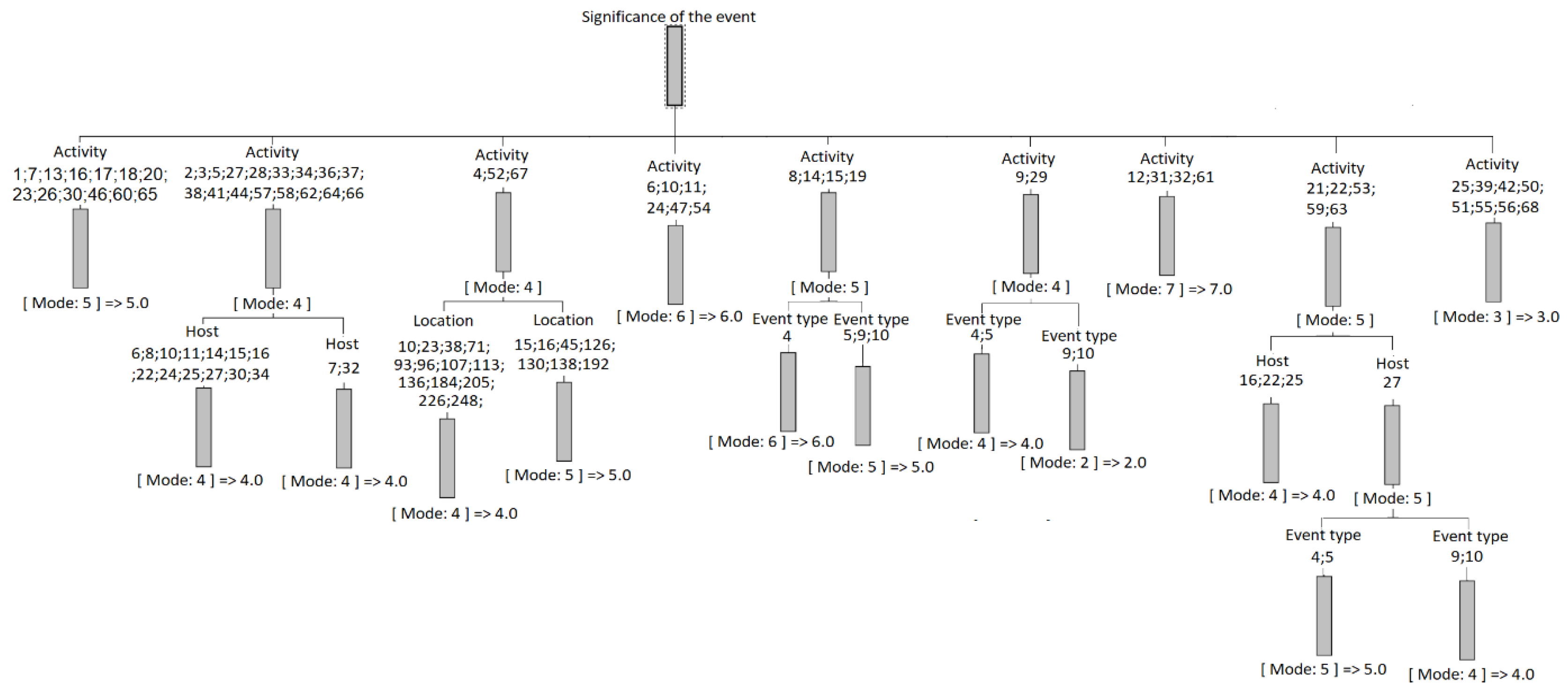
The same criteria apply to the CHAID model. In the C&R Tree model, “maximum surrogates” is an important hyperparameter that determines the maximum number of surrogate splits that can be used to split nodes if the data for the primary split variable is unavailable. By default, this hyperparameter has a value of 5.
Figure 9 shows the tree of the C&R Tree model where the best split was made according to the Event Type variable. Based on this division, the existing data set is divided into two subgroups. The final decisions or affiliations of the inputs to the categories of the dependent variable are contained in the final nodes, Node 1 and Node 2. This model showed a classification accuracy of 78.13% on the test data.
The following two inference rules define the structure of the previously shown tree:
- Event_type in [ 2.000 4.000 5.000 ] [ Mode: 5 ] => 5.0
- Event_type in [ 1.000 3.000 6.000 7.000 8.000 9.000 10.000 11.000 12.000 14.000 15.000 ] [ Mode: 4 ] => 4.0
To clarify, consider the first rule as an example: Event_type in [ 2.000 4.000 5.000 ] [ Mode: 5 ] => 5.0. The interpretation of this rule is as follows:
- Event_type in [ 2.000 4.000 5.000 ]: This means that the variable “Activity” has a value within the specified set of values: 2.000, 4.000, 5.000.
- [ Mode: 5 ]: “Mode” refers to the most frequent class in the dataset that satisfies the condition “Event_type in [ ... ]”. In this case, the most frequent class is 5.
- =>5.0: This part indicates the prediction or classification. If the “Activity” attribute has a value within the specified set of values, then the class prediction is 5.0.
Based on these rules, it can be concluded that the classification is based on the category mode of the dependent variable. For node 1 in Figure 9, the mode is 5, and for node 2 the mode is 4.
5.2.3. QUEST model
Quick, Unbiased, Efficient Statistical Tree (QUEST) represents a binary classification method for constructing decision trees. Its development was motivated by the processing time for C&R Tree models with many variables. In addition, it was necessary to reduce the tendency to favor inputs that allow more splits, such as continuous variables or those with many categories [46]. To evaluate input variables and select the best splits, QUEST uses a set of rules based on significance tests. This reduces the need to examine all possible splits and combinations of categories. This speeds up the process of analyzing and constructing decision trees, while at the same time maintaining a high level of accuracy and impartiality [46].
The created QUEST model is defined by a single rule: [Mode: 4] => 4.0, which has the following meaning:
- Left side of the rule: Mode: 4 suggests that the mode (most frequent value) for a particular node or data group is 4.
- Right side of the rule: => 4.0 indicates a prediction, i.e., if the mode is 4, the prediction or classification that the model provides is 4.0.
The accuracy of this model is 68.75%.
5.2.4. C5.0 model
The C5.0 model divides the sample based on the variable that provides the maximum information gain. Each resulting subsamples is then further split, typically based on another variable, and this process continues until the subsamples can no longer be split. The splits at the lowest level are reexamined, and those that do not significantly contribute to the classification are removed or pruned [47].
C5.0 can build two types of models: a decision tree and a rule set. The decision tree is a simple and intuitive way to represent the branching found by the algorithm. Each leaf of the decision tree describes a specific subset of the training data, where each case in the training data belongs to exactly one terminal node of the tree. In contrast, the rule set represents a simplified version of the structure that defines the branching.
The C5.0 model was created without the input variable Location due to warnings and errors reported by the software when running the algorithm. The reasons are inherent to the variable’s nature, which has a large number of unique values – categories. Figure 10 shows the structure of the resulting decision tree, which has a depth of 2. Each node of the tree is marked with a number corresponding to a specific branching rule given below. When tested, the model showed an accuracy of 92.19%, matching that of the CHAID model.
For the C5.0 model, the Training Mode hyperparameter is defined, which can have the values Simple and Expert. In Simple training, most of the C5.0 parameters are set automatically. Expert training allows for more direct control over the training parameters. By default, C5.0 attempts to generate the most accurate tree possible (Accuracy), which often can lead to overfitting and poor performance. On the other hand, Generality uses algorithm settings that are less prone to this problem [54].
The similarity with the CHAID model is also reflected in the set of rules that define the branches of the tree shown, with the position of each rule in the tree determined based on the numerical label of each node in Figure 10. In this case, the following 16 rules were generated, which can be interpreted as shown for the C&R Tree model:
1. Activity in [ 1.000 7.000 8.000 13.000 16.000 17.000 18.000 19.000 20.000 23.000 26.000 30.000 46.000 60.000 63.000 65.000 ] [ Mode: 5 ] => 5.0
2. Activity in [ 2.000 3.000 4.000 5.000 27.000 28.000 33.000 34.000 36.000 37.000 38.000 41.000 44.000 51.000 52.000 53.000 57.000 58.000 62.000 64.000 66.000 ] [ Mode: 4 ] => 4.0
3. Activity in [ 6.000 10.000 11.000 24.000 29.000 47.000 54.000 ] [ Mode: 6 ] => 6.0
4. Activity in [ 9.000 ] [ Mode: 4 ]
4.1. Event_type in [ 1.000 2.000 3.000 5.000 6.000 7.000 8.000 11.000 12.000 13.000 14.000 15.000 16.000 ] [ Mode: 2 ] => 2.0
4.2. Event_type in [ 4.000 ] [ Mode: 4 ] => 4.0
4.3. Event_type in [ 9.000 10.000 ] [ Mode: 2 ] => 2.0
5. Activity in [ 12.000 31.000 32.000 61.000 ] [ Mode: 7 ] => 7.0
6. Activity in [ 14.000 ] [ Mode: 5 ]
6.1. Periodicity in [ 1.000 2.000 3.000 6.000 7.000 8.000 9.000 10.000 ] [ Mode: 5 ] => 5.0
6.2. Periodicity in [ 4.000 ] [ Mode: 5 ] => 5.0
6.3. Periodicity in [ 5.000 ] [ Mode: 6 ] => 6.0
7. Activity in [ 15.000 ] [ Mode: 6 ]
7.1. Event_type in [ 1.000 2.000 3.000 6.000 7.000 8.000 11.000 12.000 13.000 14.000 15.000 16.000 ] [ Mode: 6 ] => 6.0
7.2. Event_type in [ 4.000 ] [ Mode: 6 ] => 6.0
7.3. Event_type in [ 5.000 9.000 10.000 ] [ Mode: 5 ] => 5.0
8. Activity in [ 21.000 ] [ Mode: 5 ]
8.1. Object in [ 1.000 2.000 3.000 4.000 5.000 7.000 8.000 9.000 10.000 11.000 12.000 13.000 14.000 15.000 16.000 17.000 18.000 19.000 20.000 21.000 22.000 24.000 25.000 26.000 27.000 28.000 29.000 ] [ Mode: 5 ] => 5.0
8.2. Object in [ 6.000 ] [ Mode: 5 ] => 5.0
8.3. Object in [ 23.000 ] [ Mode: 4 ] => 4.0
9. Activity in [ 22.000 ] [ Mode: 5 ]
9.1. Host in [ 1.000 2.000 3.000 4.000 5.000 6.000 7.000 8.000 9.000 10.000 11.000 12.000 13.000 14.000 15.000 16.000 17.000 18.000 19.000 20.000 21.000 23.000 24.000 25.000 26.000 28.000 29.000 30.000 31.000 32.000 33.000 34.000 ] [ Mode: 5 ] => 5.0
9.2. Host in [ 22.000 ] [ Mode: 4 ] => 4.0
9.3. Host in [ 27.000 ] [ Mode: 5 ] => 5.0
10. Activity in [ 25.000 ] [ Mode: 8 ] => 8.0
11. Activity in [ 35.000 40.000 43.000 45.000 48.000 49.000 ] [ Mode: 4 ] => 4.0
12. Activity in [ 39.000 50.000 56.000 68.000 ] [ Mode: 3 ] => 3.0
13. Activity in [ 42.000 ] [ Mode: 4 ]
13.1. Host in [ 1.000 2.000 3.000 4.000 5.000 6.000 8.000 10.000 11.000 13.000 14.000 15.000 16.000 19.000 20.000 21.000 22.000 23.000 24.000 26.000 28.000 29.000 30.000 32.000 33.000 34.000 ] [ Mode: 4 ] => 4.0
13.2. Host in [ 7.000 25.000 27.000 ] [ Mode: 4 ] => 4.0
13.3. Host in [ 9.000 ] [ Mode: 7 ] => 7.0
13.4. Host in [ 12.000 ] [ Mode: 3 ] => 3.0
13.5. Host in [ 17.000 18.000 31.000 ] [ Mode: 8 ] => 8.0
14. Host in [ 55.000 ] [ Mode: 1 ] => 1.0
15. Host in [ 59.000 ] [ Mode: 5 ]
15.1. Object in [ 1.000 2.000 3.000 4.000 5.000 6.000 7.000 8.000 9.000 10.000 11.000 12.000 13.000 14.000 15.000 16.000 17.000 18.000 19.000 20.000 21.000 22.000 23.000 24.000 26.000 29.000 ] [ Mode: 5 ] => 5.0
15.2. Object in [ 25.000 ] [ Mode: 7 ] => 7.0
15.3. Object in [ 27.000 ] [ Mode: 4 ] => 4.0
15.4. Object in [ 28.000 ] [ Mode: 5 ] => 5.0
16. Activity in [ 67.000 ] [ Mode: 4 ]
16.1. Event_type in [ 1.000 2.000 3.000 4.000 5.000 6.000 7.000 8.000 11.000 12.000 13.000 14.000 15.000 16.000 ] [ Mode: 4 ] => 4.0
16.2. Event_type in [ 9.000 ] [ Mode: 5 ] => 5.0
16.3. Event_type in [ 10.000 ] [ Mode: 4 ] => 4.0
The advantage of the C5.0 model is its robustness in the presence of issues such as missing data and a large number of input variables. Their training time is relatively short and, in addition, C5.0 models are more interpretable compared to a large number of other machine learning models [47].
5.2.5. Random Trees model
Random Trees represents an ensemble classification model based on a C&R tree, which has two additional characteristics:
- Bagging (Bootstrap Aggregating): Multiple copies of the training set are generated by randomly sampling with backtracking. These copies, called bootstrap samples, are of the same size as the original dataset. A separate model, a member of the ensemble, is built on each of these samples [48].
- Random selection of input variables: For each decision (split) in the tree, not all independent variables are considered. Instead, only a random subset of the input variables is considered and impurity is measured only for these variables [48].
Due to these characteristics, each tree in the forest uses different subsets of variables, which increases the variety of the trees and reduces the chance of overfitting. Additionally, since fewer variables are considered for each split, training the tree can be faster. This model achieved a classification accuracy of 84.38% on the test data. Table 3 shows the confusion matrix, which serves as a tool for evaluating the classification performance of machine learning model. For each observed category of the dependent variable, the model classification is observed by columns, with accuracy provided as a percentage. The highest percentage of correct classifications was achieved for category 4, amounting to 269 or 92% of the total test dataset.
The number of trees in the created Random Tree model is equal to 100 by default, with a maximum number of nodes being 10,000. The maximum depth of the tree is equal to 10. The Hyperparameter Minimum child node size specifies the minimum number of samples required for a node in the tree to be split or for a node to become a leaf.
5.2.6. SVM model
Support Vector Machine (SVM) represents one of the most powerful classification methods, based on statistical learning theory. The SVM training algorithm creates a model that assigns new examples to one of the categories, making it a non-probabilistic binary linear classifier. This model maps data into a multidimensional space of variables so that input data can be categorized, even when the data are not linearly separable. Therefore, it is necessary to find a separator between categories, and then the data are transformed using a Kernel function in such a way that the separator can be constructed as a hyperplane with the maximum margin between categories. By default, the Radial Basis Function (RBF) kernel is defined. The kernel has a regularization parameter C, which controls the relationship between the maximum margin and the minimum number of misclassified data. In this research, by default, its value is set to 10. The stopping criterion defines when to stop the optimization algorithm. Its value ranges from 10-1 to 10-6, and by default settings in the software, it is C=10-3. A smaller criterion value results in a more accurate model, but requires more time for training [38,39]. The RBF gamma parameter is 0.1 and can be considered as the “expansion” of the kernel and thus the decision region. SVM is particularly suitable for analyzing data with very large values of input variables. The overall classification accuracy of the created SVM model on the test data is 84.38%.
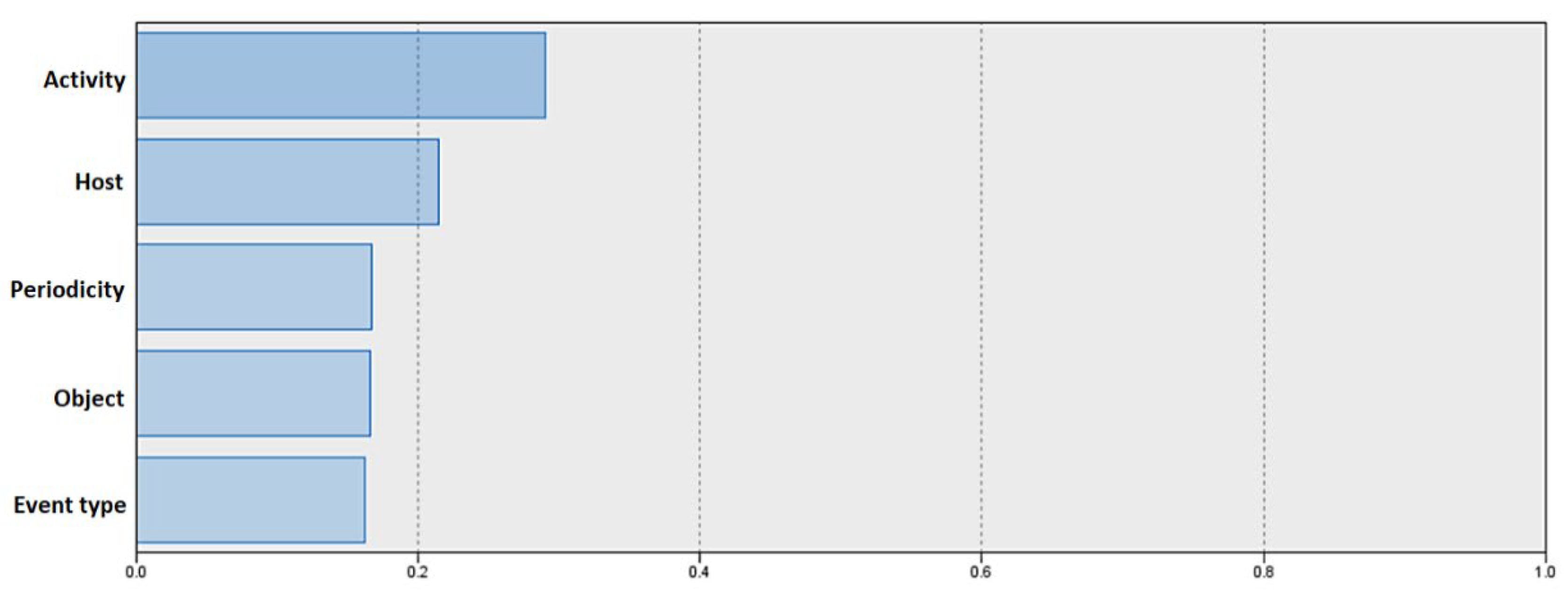
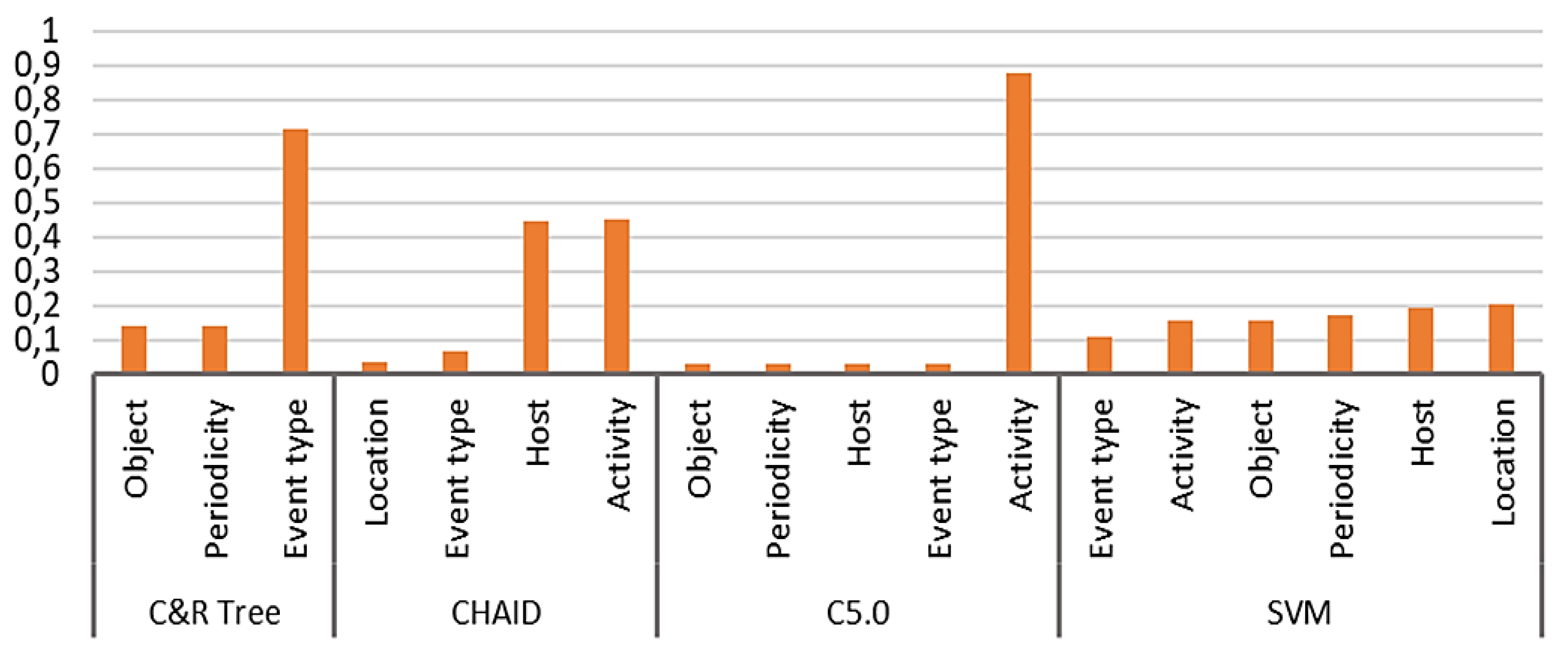
5.3. Predictor Importance Values for the Created Models
In addition to the classification performance of machine learning models, one of the most important results of model testing is the Predictor Importance value. This parameter indicates the relative importance of each predictor in model estimation. Since the values are relative, their sum across all predictors is 1. The Predictor Importance value does not refer to the model’s accuracy but to the importance of each predictor in predicting the dependent variable [49].
Predictor Importance values can serve purposes similar to those of Feature Selection techniques. Feature Selection ranks each input variable based on the strength of its relationship with a specified target, independently of other inputs. In contrast, Predictor Importance indicates the relative importance of each input specifically for the observed model. In practice, Feature Selection techniques are most useful for preliminary screening, especially with large datasets with a large number of variables, while Predictor Importance is more beneficial for fine-tuning the model [49].
Figure 11 graphically shows the Predictor importance values for four models: C&R Tree, CHAID, C5.0 and SVM. For the Random Trees and QUEST models, these values were not available in IBM SPSS Modeler. The variable Event Type has the greatest impact on classification in the C&R Tree model. The CHAID and C5.0 models are most dependent on the Activity variable, while the SVM model is most influenced by the Location variable.
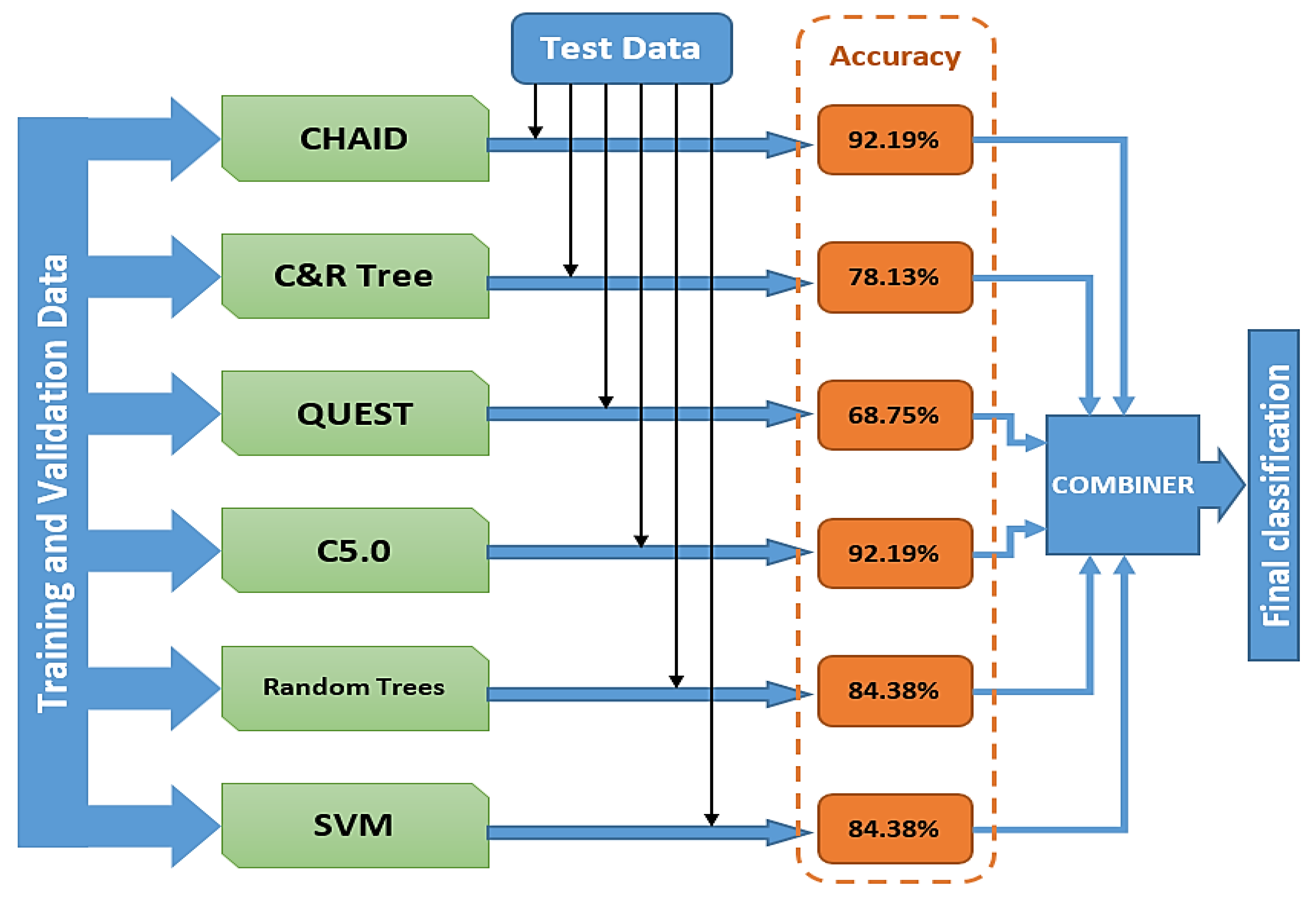
5.4. Stacking model ensemble for improving classification performance
The idea of cascading and combining models into an ensemble emerges in the 1960s and is based on one of the following types of model sets [45]:
- A set of classification models based on different algorithms,
- A set of classification models of the same type with different parameters and hyperparameters,
- A set of classification models of the same type on different samples from the dataset.
All models in the set learn the target function, and their individual classifications are then combined to classify new examples [45]. In this way, the final classification performance exceeds that of any individual model, a member of the ensemble. There are three main ensemble learning paradigms which are:
- Bagging – The high variance of available data in a dataset affects the low generalization power of the model, even if the training dataset is enlarged. Research shows that the solution to this problem lies in the Bagging method, which combines Bootstrapping and Aggregating methods [45]. Bootstrapping focuses on reducing the classifier variance and decreasing overfitting by resampling the data from the training set [45]. By using n training subsets, n training results are obtained, and the final classification results are derived using aggregation strategies such as averaging or voting [37].
- Boosting Bagging - Stacking. The main idea of this learning paradigm is that models are sequentially added to the ensemble, with each iteration requiring the new model to specifically process the data on which its predecessors or weak learners made errors [45]. The main goal of the Boosting paradigm is to reduce Bias, i.e., systematic error caused by the model itself, rather than its sensitivity to data variations. In the boosting approach, weights are implicitly assigned to models based on their performance, similar to the concept of a weighted average ensemble. Popular variants of this approach featured in research include Adaptive Boosting (AdaBoost), Gradient Boosting and Extreme Gradient Boosting (XGBoost).
- Stacking. Bagging and Boosting methods typically use homogeneous weak learners or models as ensemble members. Stacking often works with heterogeneous weak learners that learn in parallel, and their results are combined by training a meta-learner for final output classification. This means that the target learner uses model classifications as input variables [37,45]. In ensemble averaging, such as Random Forest, classifications from multiple models are combined, with each model contributing equally regardless of performance. In contrast, a weighted average ensemble measures the contribution of each member based on classification performance, thereby offering an improvement over ensemble averaging.
Based on the Stacking learning paradigm, and with the aim of improving the classification performance of individual heterogeneous models, this research proposed an ensemble model shown in Figure 12. After training, validating and testing six different models, their performance was evaluated using classification accuracy. As presented in the previous section of the research, the best performance was shown by the CHAID and C5.0 models with equal accuracy of 92.19% or 59 out of 64 correctly classified input vectors. The classification results of individual models on the input vectors from the test set were used as inputs to the Combiner. The task of the Combiner member of the ensemble is to generate the final output value or prediction for the class of the dependent variable, Event Significance, based on the inputs and the algorithm.
A summary of some of the most important hyperparameters of Stacking model ensemble members is given in Table 4. Their values are defined before the learning process begins and do not change during model training. Unlike model parameters that are learned from the data (such as weights in neural networks), hyperparameters are used to control the learning process and can significantly affect model performance.
5.5. Discussion
When generating the final classification value at the output of the Combiner, the focus is set on the most accurate models, CHAID and C5.0, and on those observations or vectors for which these two models provide different classifications. For these models, Figure 13 provides a graphical overview of the prediction class values of the dependent variable for the input vectors from the test dataset.
Based on the graphic representation, it is evident that there are differences in classification for two input vectors with serial numbers 3 and 41. In these cases, the final classification value is obtained by combining all individual models, according to an algorithm that can be described in several successive steps, as follows:
- The classifications of the first input vector from all individual models are fed to the input of the Combiner;
- If CHAID and C5.0 provide classifications, the final classification is equal to that value. If there are discrepancies between the classifications of these two models, the final classification of the input is determined by a voting method. This implies that a certain category must have a majority of votes from the six created models. For all other situations, the result of the CHAID model is taken as the final classification.
- If final classifications are not determined for all input vectors, the next input vector is fed to the input of the Combiner and the process returns to step 2;
- If final classifications are determined for the entire test dataset, the algorithm terminates.
By executing this algorithm, vector with serial number 41 was correctly classified, increasing the total number of classified vectors from 59 to 60. This means that the classification accuracy was increased from 92.19% to 93.75%. The vector with serial number 3 was incorrectly classified into category 4 of the dependent variable by the majority of individual model votes. In addition to classification accuracy, the metrics for evaluating the model’s performance – Precision, Recall and F1 score – are presented by classes/categories of Event Significance shown in Table 5 along with the confusion matrix of the Stacking model ensemble.
Precision for a given class represents the proportion of vectors correctly classified as belonging to a certain class out of all vectors for which the model predicted to belong to that class. Similarly, Recall is the proportion of vectors in a class that the model correctly classified out of all vectors in that class. The F1 score is a performance metric for classification models that takes into account both Precision and Recall and is defined as the harmonic mean of these values. Based on the calculated metrics in Table 5, and considering Good and Bad Scores [50], it is concluded that all metrics (except for classes 2 and 3) have values above 0.5, with most above 0.8, indicating good performance of the Stacking model. The Precision metric was not calculated for classes 2 and 3 due to division by zero that occurs in the calculation of these values (the model did not classify any vectors into classes 2 and 3). Due to the lack of Precision values for these classes, the F1 score metric was not calculated for them, while Recall in these cases has values of zero.
6. Conclusions
The thematic issue of traffic inspection work has not been sufficiently explored and represents a relatively new scientific field that deserves valuable attention within the modal structure of the traffic system in a specific geographic area. In addition to the introduction and review of related research, the importance of addressing the issue of researching the complexity of content and contextual structure of TI work through the design of an agent-based model with the elaboration of 12 POIs was pointed out. The Visual interpretability for seven instances of the Cognitive Continuum of Knowledge (CCK) was interestingly created, respectively associated with instances of the following indicators: learning type, performance focus, temporal perspective and the level of consciousness developed through continuous learning. Additionally, a research instrument entitled Event Execution Log (EEL) was created, investigating seven independent categorical variables (E, A, H, O, L, T, P) and one dependent variable (I), i.e., the importance of the event.
The approach to classification modeling of Event significance in TI work is divided into two parts: 1) pre-processing, during which initial models based on MLP were generated, and the results of which were used to determine the strategy for further classification modeling. In this phase, as a result, data cleaning was performed to increase the consistency of the dataset; 2) data processing, where the cleaned dataset was modeled, and a Stacking ensemble of six heterogeneous models was generated, with performance improvements compared to the initial MLP. The best individual classification results were shown by CHAID and C5.0 model with 92.19% accuracy. The final classification accuracy is 93.75%, which can be characterized as the highest model quality rating. Based on the calculated Precision, Recall and F1 score metrics, and considering Good and Bad Scores, it is concluded that all metrics (except for classes 2 and 3) have values above 0.5, with most above 0.8, indicating good performance of the Stacking model. It is obvious that thanks to data cleaning, with a large data reduction from 10,994 vectors to 636, excellent classification results can be achieved.
Author Contributions
Conceptualization, A.Đ., and T.Đ.; methodology, M.K.B., M.S., A.Đ. and T.Đ.; software, M.S. and M.K.B.; validation, M.K.B., M.S., A.Đ. and T.Đ.; formal analysis, A.Đ., T.Đ., R.Đ. and D.A.; investigation, A.Đ., R.Đ., D.A., M.K.B. and M.S.; resources, A.Đ., T.Đ. and R.Đ.; data curation, A.Đ.; T.Đ. and R.Đ.; writing—original draft preparation, A.Đ. and T.Đ.; writing—review and editing, A.Đ, T.Đ., M.K.B. and M.S.; visualization, M.S., M.K.B. and D.A.; supervision, M.K.B., M.S., T.Đ. and D.A.; project administration, A.Đ., T.Đ., M.S. and D.A.; funding acquisition, A.Đ., R.Đ., M.K.B. and T.Đ. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Statements for 32 human agents to participate in the research procedure confirm their consent, which was approved by the Chief Inspectorate for Inspectional Traffic Affairs of the Government of the Republic of Srpska, Bosnia and Herzegovina.
Data Availability Statement
Available on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Riste, R.; Slobodan, O.; Zlatko, Z.; Vasko, G.; Ivona, N.; Vlatka, K. Road safety inspection in the function of determining unsafe road locations. The 9th International Conference “CIVIL ENGINEERING – SCIENCE AND PRACTICE”, Kolašin, Montenegro, 5-9 March 2024.
- Banjanin, M.K.; Bjelošević, R.; Vasiljević, M.; Stojčić, M.; Đukić, A. The Method of the Research Loop of Teletraffic in the Structure of the System of Public Urban Passenger Transport. In Proceedings of the XIX International Symposium New Horizons 2023 of Transport and Communication; Saobraćajni fakultet Doboj, Univerzitet u Istočnom Sarajevu: Doboj, Bosnia and Herzegovina, 24-25 November 2023. (pp.4-15).
- Miller, T. Explanation in artificial intelligence: Insights from the social sciences. Artificial Intelligence 2019, 267, 1–38. [CrossRef]
- Pentland, B.T.; Liu, P.; Kremser, W.; Haerem, T. The dynamics of drift in digitized processes. MIS Quarterly 2020, 44(1), 19–47. [CrossRef]
- Iversen, V.B. Teletraffic engineering and network planning; dtu Fotonik: Copenhagen, Denmark, 2015.
- Banjanin, K.M.; Gojković, P. Analitičke Procedure u Inženjerskim Disciplinama; Saobraćajni fakultet: Doboj, Bosnia and Herzegovina, 2008.
- Pitt, J.; Mamdani, A. A Protocol-Based Semantics for an Agent Communication Language. In Proceedings of the Sixteenth International Joint Conference on Artificial Intelligence (IJCAI-99), Stockholm, Sweden, 2–6 August 1999; Volume 99, pp. 486-491.
- Alli, V. The Future of Knowledge: Increasing Prosperity through Value Networks; Butterworth-Heinemann: Amsterdam, The Netherlands, 2003. ISBN 0750675918.
- Polanyi, K. For a New West: Essays, 1919–1958; Polity Press: Cambridge, UK, 2014. ISBN-13: 978-0-7456-8443-7.
- Davenport, T.H.; Prusak, L. Working knowledge: How organizations manage what they know; Harvard Business School Press: Boston, MA, USA, 2000; pp. 1-7.
- Barna-Lipkovski, M. Konstruisanje Ličnog Identiteta Jezikom i Hronotopom Interneta: Umetničko Delo Scenskog Dizajna. Ph.D. Thesis, University of Novi Sad, Novi Sad, Serbia, 2021. Available online: https://nardus.mpn.gov.rs/handle/123456789/20928?show=full (accessed on 3 September 2024).
- Hicks, B.J.; Culley, S.J.; Allen, R.D.; Mullineux, G. A framework for the requirements of capturing, storing and reusing information and knowledge in engineering design. International Journal of Information Management 2002, 22(4), 263-280. [CrossRef]
- Hackos, J.T.; Hammar, M.; Elser, A. Customer partnering: data gathering for complex on-line documentation. IEEE Transactions on Professional Communication 1997, 40(2), 83-96. [CrossRef]
- King, W.R.; Teo, T.S.H. Key Dimensions of Facilitators and Inhibitors for the Strategic Use of Information Technology. Journal of Management 1996, 1(1), 1-25. http://www.jstor.org/stable/40398177.
- Watson, H.J.; Houdeshel, G.; Rainer, R.K. Jr. Building executive information systems and other decision support applications, 1st ed.; Wiley: Hoboken, New Jersey, United States, 1996.
- Byun, D.H.; Suh, E.H. A methodology for evaluating EIS software packages. Journal of Organizational Computing and Electronic Commerce 1996, 6(3), 195-211. [CrossRef]
- Simon, H.A. Administrative Decision Making; Carnegie Institute of Technology: Pittsburgh, PA, USA, 1996.
- Kahneman, D. Maps of Bounded Rationality: Psychology for Behavioral Economics. The American Economic Review 2003, 93(5), 1449-1475. [CrossRef]
- Benyon, D.; Murray, D. Adaptive systems: From intelligent tutoring to autonomous agents. Knowledge-Based Systems 1993, 6(4), 197-219. [CrossRef]
- Cilliers, P. Complexity and Postmodernism; Routledge: New York, NY, USA, 1998.
- Banjanin, M. Komunikacioni Inženjering; Saobraćajno tehnički fakultet: Doboj, Bosnia and Herzegovina, 2006.
- Addy, R. Effective IT Service Management – To ITIL and Beyond; Springer: New York, NY, USA, 2007.
- Banjanin, M.; Petrović, L.; Tanackov, I. Multiagent Communication Systems. In Proceedings of the XIV Međunarodna naučna konferencija Industrijski sistemi IS'08, Novi Sad, Serbia, 2-3 October 2008.
- Banjanin, M.K. Dinamika komunikacija-interkulturni poslovni kontekst; Megatrend Univerzitet primenjenih nauka: Beograd, Serbia, 2003. ISBN 86-7747-106-5.
- Michalski, R.S.; Bratko, I.; Kubat, M. Machine Learning and Data Mining, Methods and Applications; John Wiley & Sons: West Sussex, UK, 1998.
- Kurbel, K.E. The Making of Information Systems Software Engineering and Management in a Globalized World; Springer-Verlag: Berlin, Germany, 2008. [CrossRef]
- Popovic, D. Model unapređenja kvaliteta procesa životnog osiguranja. Ph.D. Thesis, University of Novi Sad, Novi Sad, Serbia, 2020. Available online: https://nardus.mpn.gov.rs/handle/123456789/10399 (Accessed on 3 September 2024).
- Banjanin, M.K.; Đukić, A.; Stojčić, M.; Vasiljević, M. Machine Learning Models in the Classification and Evaluation of Traffic Inspection Jobs in Road Traffic and Transport. In Proceedings of the 13th International Scientific Conference SED 2023, Vrnjačka Banja, Serbia, 5-8 June 2023.
- Tang, J.; Zhang, D.; Sun, X.; Qin, H. Improving Temporal Event Scheduling through STEP Perpetual Learning. Sustainability 2022, 14(23), 16178. [CrossRef]
- Fourez, T.; Verstaevel, N.; Migeon, F.; Schettini, F.; Amblard, F. An Ensemble Multi-Agent System for Non-Linear Classification. arXiv preprint 2022, arXiv:2209.06824. [CrossRef]
- Zhou, J.; Asteris, P.G.; Armaghani, D.J.; Pham, B.T. Prediction of Ground Vibration Induced by Blasting Operations through the Use of the Bayesian Network and Random Forest Models. Soil Dynamics and Earthquake Engineering 2020, 139, 106390. [CrossRef]
- Andjelković, D.; Antić, B.; Lipovac, K.; Tanackov, I. Identification of hotspots on roads using continual variance analysis. Transport 2018, 33(2), pp. 478–488. [CrossRef]
- Holdaway, M.; Rauch, M.; Flink, L. Excellent Adaptations: Managing Projects through Changing Technologies, Teams, and Clients. In Proceedings of the 2009 IEEE International Professional Communication Conference, Waikiki, HI, USA, 19-22 July 2009.
- Brown, S. M.; Santos, E.; Banks, S. B. Utility theory-based user models for intelligent interface agents. In Advances in Artificial Intelligence: 12th Biennial Conference of the Canadian Society for Computational Studies of Intelligence, AI'98 Vancouver, BC, Canada, June 18–20, 1998 Proceedings 12 (pp. 378-392). Springer Berlin Heidelberg. [CrossRef]
- Milanović, M.; Stamenković, M. CHAID Decision Tree: Methodological Frame and Application. Economic Themes 2016, 54(4), 563-586. [CrossRef]
- Potdar, K.; Pardawala, T.S.; Pai, C.D. A Comparative Study of Categorical Variable Encoding Techniques for Neural Network Classifiers. International Journal of Computer Applications 2017, 175(4), 7-9. [CrossRef]
- Wu, X.; Wang, J. Application of Bagging, Boosting and Stacking Ensemble and Easy Ensemble Methods to Landslide Susceptibility Mapping in the Three Gorges Reservoir Area of China. International Journal of Environmental Research and Public Health 2023, 20(6), 1-31. [CrossRef]
- Banjanin, M.K.; Stojčić, M.; Danilović, D.; Ćurguz, Z.; Vasiljević, M.; Puzić, G. Classification and Prediction of Sustainable Quality of Experience of Telecommunication Service Users Using Machine Learning Models. Sustainability 2022, 14(24), 17053. [CrossRef]
- Chorianopoulos, A. Effective CRM Using Predictive Analytics; Wiley: West Sussex, UK, 2015. ISBN: 978-1-119-01155-2.
- Saatçioğlu, Ö.Y. Üniversite Yönetiminde Etkinliğin Arttırılmasına Yönelik Bilgi Sistemlerinin Tasarlanması ve Uygulanması. Ph.D. Thesis, Dokuz Eylul University, Izmir, Turkey, 2024. Available online: https://avesis.deu.edu.tr/yasar.saatci/indir?languageCode=en (accessed on 3 September 2024).
- Scikit-learn. Available online: https://scikit-learn.org/stable/auto_examples/svm/plot_rbf_parameters.html (accessed on 8 November 2022).
- Laplace, P.S. A Philosophical Essay on Probabilities; Truscott, F.W., Emory, F.L., Translators; Dover Publications: New York, NY, USA, 1951.
- Neskovic, S.; Petkovic, A. The Methodology of Analysis and Assessment of Risk for Corruption in the Company Operations. Vojno Delo 2016. [CrossRef]
- IBM. https://www.ibm.com/docs/en/spss-modeler/18.5.0?topic=nodes-chaid-node (accessed on 5 July 2024).
- Twiki. Available online: https://twiki.di.uniroma1.it/pub/ApprAuto/WebHome/8.ensembles.pdf (accessed on 7 July 2024).
- IBM SPSS Modeler-help. Available online: http://127.0.0.1:50192/help/index.jsp?topic=/com.ibm.spss.modeler.help/clementine/trees_quest_fields.htm (accessed on 7 July 2024).
- IBM SPSS Modeler-help. Available online: http://127.0.0.1:55706/help/index.jsp?topic=/com.ibm.spss.modeler.help/clementine/c50_modeltab.htm (accessed on 7 July 2024).
- IBM SPSS Modeler-help. Available online: http://127.0.0.1:56089/help/index.jsp?topic=/com.ibm.spss.modeler.help/clementine/rf_fields.htm (accesed on 6 July 2024).
- IBM SPSS Modeler-help. Available online: http://127.0.0.1:57164/help/index.jsp?topic=/com.ibm.spss.modeler.help/clementine/model_nugget_variableimportance.htm (accessed on 6 July 2024).
- Klu. Available online: https://klu.ai/glossary/accuracy-precision-recall-f1 (accessed on 3 September 2024). (accessed on 3 September 2024).
- Knezevic, I. Analiza dinamičkog ponašanja kugličnih ležaja primenom veštačkih neuronskih mreža. Ph.D. Thesis, University of Novi Sad, Novi Sad, Serbia, 2021. Available online: https://nardus.mpn.gov.rs/handle/123456789/17986 (accessed on 3 September 2024).
- Petronijevic, M. Uticaj oksidacionih procesa na bazi ozona, vodonik-peroksida i UV zračenja na sadržaj i reaktivnost prirodnih organskih materija u vodi. Ph.D. Thesis, University of Novi Sad, Novi Sad, Serbia, 2020. Available online: https://nardus.mpn.gov.rs/handle/123456789/11378 (accessed on 3 September 2024).
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013. [CrossRef]
- IBM SPSS Modeler-help. Available online: http://127.0.0.1:62164/help/index.jsp?topic=/com.ibm.spss.modeler.help/clementine/c50_modeltab.htm (accesed on 6 July 2024).
- Sarker, I.H. Machine Learning: Algorithms, Real-World Applications and Research Directions. SN Computer Science 2021, 2(3), 160. [CrossRef]
- Ndung'u, R.N. Data Preparation for Machine Learning Modelling. International Journal of Computer Applications Technology and Research 2022, 11(6), 231-235. [CrossRef]
- Xu, H.; Zhou, J.; Asteris, P.G.; Armaghani, D.J.; Tahir, M.M. Supervised Machine Learning Techniques to the Prediction of Tunnel Boring Machine Penetration Rate. Applied Sciences 2019. [CrossRef]
- Russell, S.J.; Norvig, P. Artificial Intelligence: A Modern Approach; 4th ed.; Pearson: New York, NY, USA, 2021.
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016.
- Mitchell, T.M. Machine Learning; McGraw-Hill: New York, NY, USA, 1997.
- Molar, C. Kulturni Inženjering; Clio: Beograd, Serbia, 2000.
- Škorić, M. The Standard Model of Social Science and Recent Attempts to Integrate Sociology, Anthropology and Biology. Ph.D. Thesis, Filozofski Fakultet Univerziteta u Novom Sadu, Novi Sad, Serbia, 2010.
- Zelenović, D. Intelligent Business; Prometej: Novi Sad, Serbia, 2011.
Figure 1.
Visual interpretability of the seven instances of the Cognitive Continuum of Knowledge (CCK), respectively linked with instances of the following indicators: learning type, performance focus, time perspective and consciousness developed through continuous learning.
Figure 1.
Visual interpretability of the seven instances of the Cognitive Continuum of Knowledge (CCK), respectively linked with instances of the following indicators: learning type, performance focus, time perspective and consciousness developed through continuous learning.
Figure 2.
Agent-based model of the complexity of content and contextual structures of TI Work.
Figure 3.
Graphical illustration of a Machine Learning Problem.
Figure 4.
Exploratory research instrument “Event Execution Log” for constructing related data registers and automating TI Tasks.
Figure 4.
Exploratory research instrument “Event Execution Log” for constructing related data registers and automating TI Tasks.
Figure 5.
Algorithmic representation of the research methodology for data preprocessing and final processing.
Figure 5.
Algorithmic representation of the research methodology for data preprocessing and final processing.
Figure 6.
Architecture of the MLP model for classifying inputs by Event Significance.
Figure 7.
Relative importance of predictor influence on classification results.
Figure 8.
Architecture of the created CHAID model.
Figure 9.
Tree of the created C&R Tree model.
Figure 10.
Structure of the decision tree of the C5.0 model.
Figure 11.
Predictor importance values for the created classification models .
Figure 12.
Stacking model ensemble for improving classification performance .
Figure 13.
CHAID classification results and C5.0 model for input vectors from the test set.
Table 1.
Spearman’s correlation coefficients between research variables.
| Activity | Location | Host | Object | Event type | Periodicity | Event Significance |
||
|---|---|---|---|---|---|---|---|---|
| Activity | Correlation Coefficient | 1.000 | -.002 | .016 | .208** | -.015 | -.086** | -.222** |
| Sig. (2-tailed) | . | .862 | .100 | .000 | .116 | .000 | .000 | |
| Location | Correlation Coefficient | -.002 | 1.000 | -.133** | -.007 | -.059** | .034** | .005 |
| Sig. (2-tailed) | .862 | . | .000 | .439 | .000 | .000 | .579 | |
| Host | Correlation Coefficient | .016 | -.133** | 1.000 | .278** | -.221** | .135** | .158** |
| Sig. (2-tailed) | .100 | .000 | . | .000 | .000 | .000 | .000 | |
| Object | Correlation Coefficient | .208** | -.007 | .278** | 1.000 | -.112** | -.046** | -.074** |
| Sig. (2-tailed) | .000 | .439 | .000 | . | .000 | .000 | .000 | |
| Event type | Correlation Coefficient | -.015 | -.059** | -.221** | -.112** | 1.000 | -.302** | -.226** |
| Sig. (2-tailed) | .116 | .000 | .000 | .000 | . | .000 | .000 | |
| Periodicity | Correlation Coefficient | -.086** | .034** | .135** | -.046** | -.302** | 1.000 | .160** |
| Sig. (2-tailed) | .000 | .000 | .000 | .000 | .000 | . | .000 | |
| Event Significance | Correlation Coefficient | -.222** | .005 | .158** | -.074** | -.226** | .160** | 1.000 |
| Sig. (2-tailed) | .000 | .579 | .000 | .000 | .000 | .000 | . | |
Table 2.
Model ensemble members.
| Model | Accuracy | Method | Predictors | Model Size (Synapses) | Records |
|---|---|---|---|---|---|
| 1 | 92.7% | MLP | 5 | 7418 | 9,906 |
| 2 | 63.7% | MLP | 5 | 4439 | 9,906 |
| 3 | 68.6% | MLP | 5 | 3569 | 9,906 |
| 4 | 60.4% | MLP | 5 | 2853 | 9,906 |
| 5 | 37.5% | MLP | 5 | 2116 | 9,906 |
Table 3.
Confusion matrix for the Random Trees model.
| Observed categories | Classification by model | Percent correct | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 1 | 2 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 50 |
| 2 | 0 | 1 | 0 | 9 | 1 | 0 | 0 | 1 | 8 |
| 3 | 0 | 0 | 2 | 1 | 0 | 0 | 1 | 0 | 50 |
| 4 | 0 | 1 | 0 | 269 | 14 | 3 | 4 | 0 | 92 |
| 5 | 0 | 1 | 1 | 16 | 79 | 4 | 2 | 0 | 77 |
| 6 | 0 | 1 | 2 | 18 | 4 | 17 | 0 | 1 | 40 |
| 7 | 0 | 1 | 1 | 7 | 3 | 1 | 14 | 2 | 48 |
| 8 | 0 | 1 | 1 | 1 | 1 | 2 | 0 | 4 | 40 |
| Percent correct | 1 | 17 | 29 | 83 | 77 | 63 | 67 | 50 | 78 |
Table 4.
Overview of hyperparameters of Stacking model ensemble members.
| Model | Hyperparameters |
|---|---|
| CHAID | Maximum Tree Depth: 5; Minimum records in parent branch – 2% of the total dataset; Minimum records in child branch – 1% of the total dataset; Significance level for splitting = 0.05; Significance level for merging = 0.05; Minimum Change in Expected Cell Frequencies: 0.001; Maximum Iterations for Convergence: 100; Maximum surrogates: 5. |
| C&R Tree | Maximum Tree Depth: 5; Minimum records in parent branch – 2% of the total dataset; Minimum records in child branch – 1% of the total dataset; Minimal impurity change (Gini Index): 0.0001. |
| QUEST | Maximum Tree Depth: 5; Maximum surrogates: 5; Minimum records in parent branch – 2% of the total dataset; Minimum records in child branch – 1% of the total dataset; Significance level for splitting = 0.05. |
| C5.0 | Mode: Simple; Favor: Accuracy |
| Random Trees | Number of models to build: 100; Maximum number of nodes: 10000; Maximum tree depth: 10; Minimum child node size: 5. |
| SVM | Stopping criteria: 10-3; Regularization parameter (C): 10; Kernel type: RBF; RBF Gamma: 0,1; |
Table 5.
Confusion matrix and metrics of stacking model ensemble performance.
| Observed classes | Classification by model ensemble | Precision | Recall | F1 score | |||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | ||||
| 2 | 0 | 0 | 1 | 0 | 0 | 0 | - | 0 | - |
| 3 | 0 | 0 | 1 | 0 | 0 | 0 | - | 0 | - |
| 4 | 0 | 0 | 43 | 0 | 1 | 0 | 0.9348 | 0.9773 | 0.9555 |
| 5 | 0 | 0 | 1 | 9 | 1 | 0 | 1 | 0.8181 | 0.8999 |
| 6 | 0 | 0 | 0 | 0 | 2 | 0 | 0.5 | 1 | 0.6667 |
| 7 | 0 | 0 | 0 | 0 | 0 | 5 | 1 | 1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated