0. Introduction

1. Materials and Methods

2. Results

2.1. Queuing Networks with Varying Structure

Using ergodicity theorem 1, limit relations are constructed in this section for stationary distributions of discrete Markov processes with continuous time. They are used to calculate the marginal distributions of exponential queuing networks operating in a random environment. We are talking about networks whose structure (a set of operating nodes, an intensity of service and input flow, a route matrix, a number of states, transitions between nodes) or type (open, closed network) changes when some state of a system reaches some meaning. Based on the proved theorem and the choice of the functioning scheme for the models under consideration, formulas for calculating their marginal distributions are obtained and additional computational algorithms are constructed. These results are illustrated by Example 1 of switching between two different Markov processes.

2.1.1. Basic Theorems on Stationary Distributions of Markov Processes with Connecting Transient Intensities

Consider m discrete, homogeneous and irreducible (and therefore ergodic) Markov processes $X_k\left(t\right),t\ge 0,k=1,\dots ,m,$ with sets of states ${\mathcal{X}}_k,$ with transient intensities ${\lambda }_k(x_k,y_k)\ge 0,$ and stationary probabilities $P_k\left(x_k\right),x_k,y_k\in {\mathcal{X}}_k.$ From the stationary Kolmogorov-Chapman equations, the equalities follow

$$\sum _{y_k\in {\mathcal{X}}_k}{P}_k\left(x_k\right){\lambda }_k(x_k,y_k)=\sum _{y_k\in {\mathcal{X}}_k}{P}_k\left(y_k\right){\lambda }_k(y_k,x_k),x_k\in {\mathcal{X}}_k.$$

(8)

Theorem 4. 

Suppose that additional transient intensities are introduced between some states $x_k^{*}\in {\mathcal{X}}_k,k=1,\dots ,m,$ of processes $X_k\left(t\right)$ $\Lambda (x_k^{*},x_i^{*})>0,i,k=1,\dots ,m,$ satisfying for some ${\displaystyle 0<c_k,k=1,\dots ,m,\sum _{k=1}^m{c}_k=1,}$ conditions

$$\sum _{1\le i\le m,i\ne k}{c}_k{P}_k\left(x_k^{*}\right)\Lambda (x_k^{*},x_i^{*})=\sum _{1\le i\le m,i\ne k}{c}_i{P}_i\left(x_i^{*}\right)\Lambda (x_i^{*},x_k^{*}),1\le k\le m.$$

(9)

Then the process $X\left(t\right)$ with a set of states ${\displaystyle \mathcal{X}=\bigcup _{k=1}^m{\mathcal{X}}_k}$ and transient intensities

$${\lambda }_k(x_k,y_k),x_k,y_k\in {\mathcal{X}}_k;k=1,\dots ,m,\Lambda (x_k^{*},x_i^{*}),1\le k\ne i\le m,$$

is also ergodic and its stationary distribution π has the form

$$\pi \left(x_k\right)=c_k{P}_k\left(x_k\right),x_k\in {\mathcal{X}}_k;k=1,\dots ,m.$$

(10)

Proof. 

The proof of this theorem is based on the ergodicity theorem 1 and the stationary Kolmogorov-Chapman equations for the distribution of $\pi \left(x\right),x\in \mathcal{X},$ following from the formulas (8), (9).

Corollary 1. 

Let the numbers ${\alpha }_{i,k}$ satisfy the conditions

$$0\le {\alpha }_{i,k}={\alpha }_{k,i},{\alpha }_{k,k}=0,1\le k\ne i\le m,$$

(11)

and the numbers $\Lambda (x_k^{*},x_i^{*})$ satisfy the equalities

$${\alpha }_{k,i}=c_k{P}_k\left(x_k^{*}\right)\Lambda (x_k^{*},x_i^{*}),1\le k\ne i\le m.$$

(12)

Then the equalities ${\displaystyle \sum _{i=1}^m{\alpha }_{k,i}=\sum _{i=1}^m{\alpha }_{i,k}}$ imply the equalities (9). The equalities (12) allow ${\alpha }_{k,i},$ satisfying the conditions (11), to determine the transient intensities $\Lambda (x_k^{*},x_i^{*}).$ For us, the most interesting case will be when the equalities $c_k=1/m,k=1,\dots ,m,$ are fulfilled.

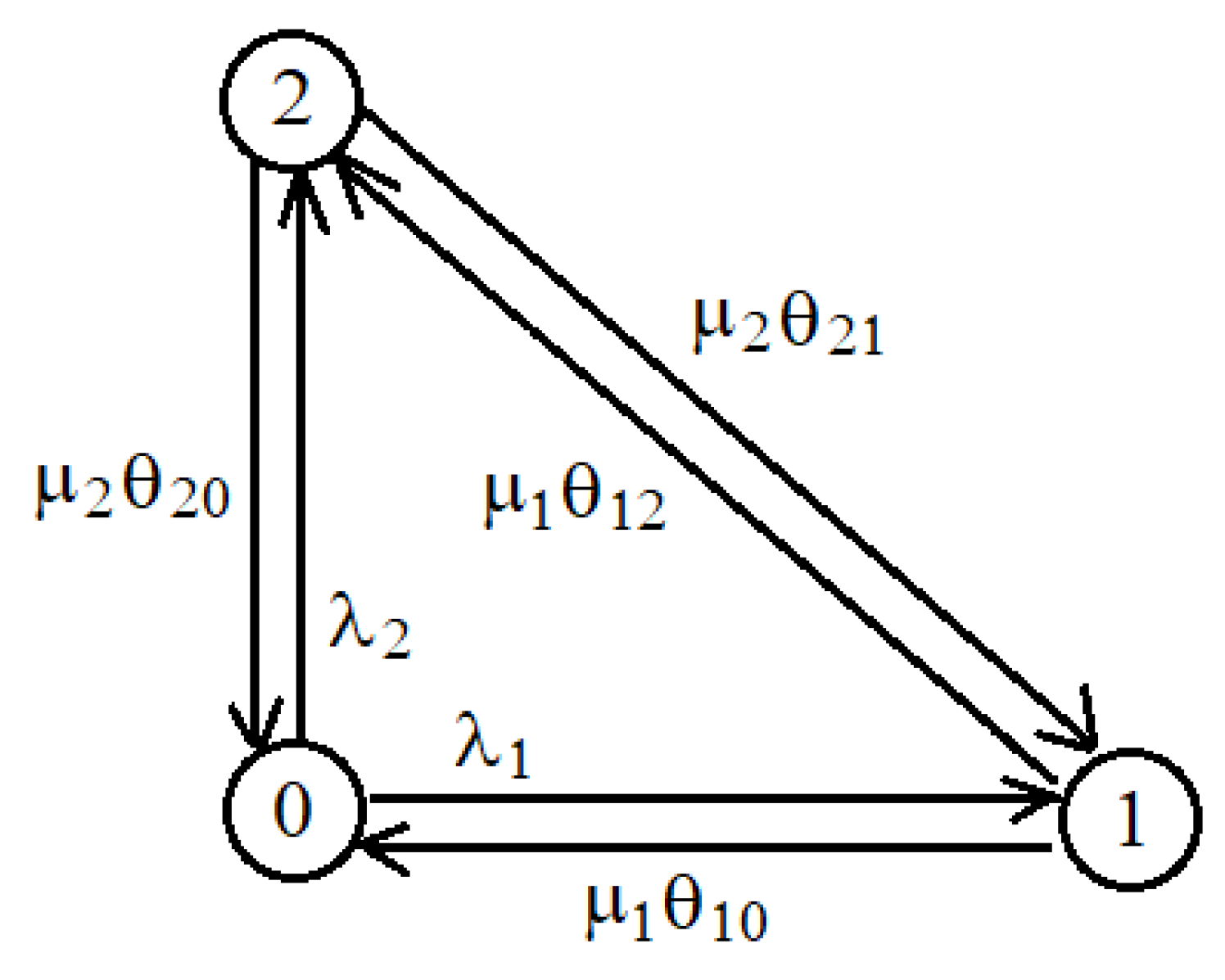
Example 1.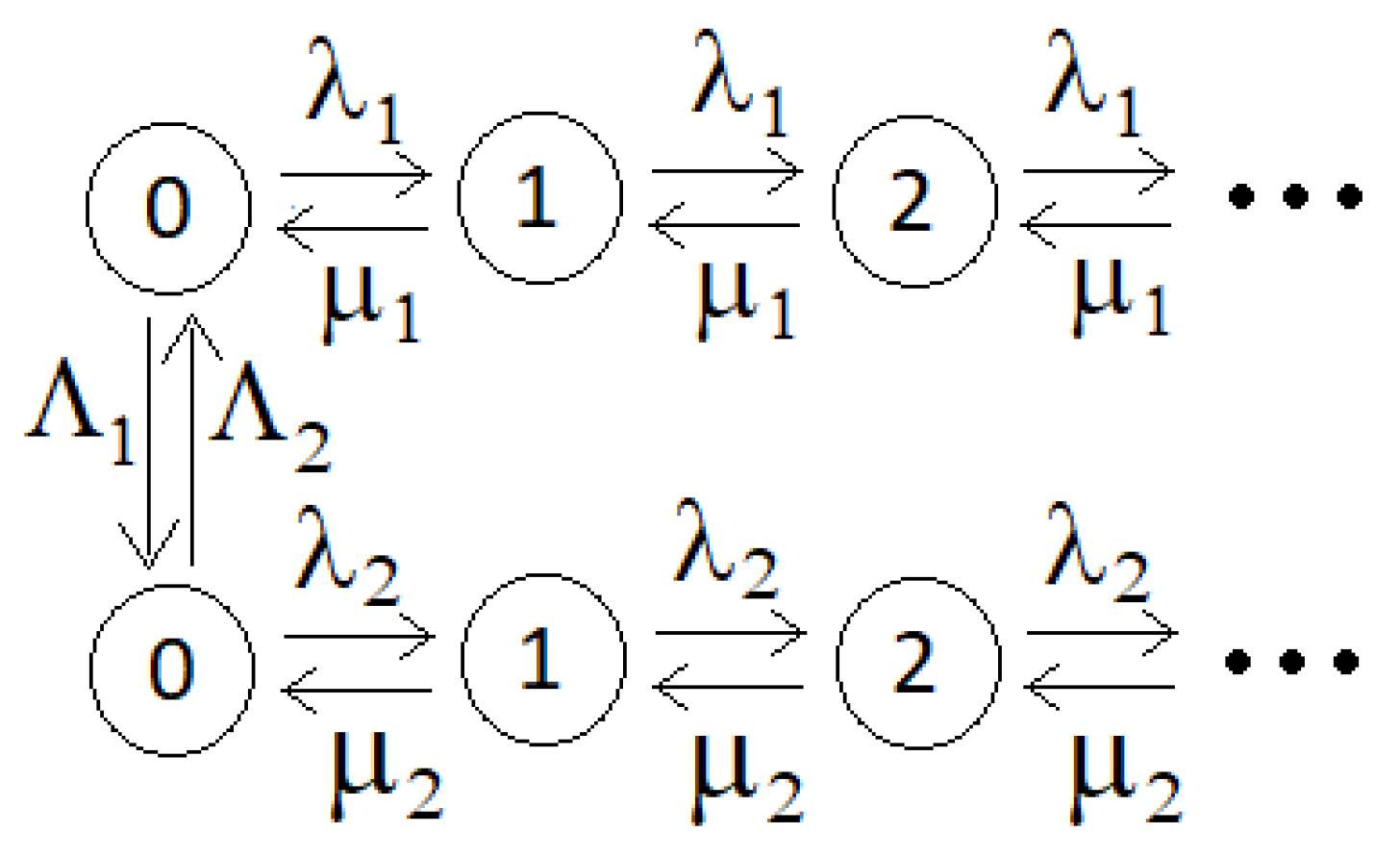 

Suppose that the discrete Markov processes $X_1\left(t\right),X_2\left(t\right),$ considered in Theorem 2 describe the number of customers in single-server queuing systems $M\left|M\right|1|\infty$ with Poisson input flows with intensities ${\lambda }_1,{\lambda }_2$ and with service intensities ${\mu }_1,{\mu }_2,{\rho }_1={\lambda }_1/{\mu }_1<1,{\rho }_2={\lambda }_2/{\mu }_2<1.$ Then discrete Markov processes $X_1\left(t\right),X_2\left(t\right),$ describing the numbers of customers in first and second queuing systems have marginal distributions $P_1(x_1=k)=(1-{\rho }_1){\rho }_1^k,P_2(x_2=l)=(1-{\rho }_2){\rho }_2^l,k,l=0,1,\dots .$ Select the states $x_1^{*}=0,x_2^{*}=0,$ select $c_1,c_2,0<c_1,c_2,c_1+c_2=1$ and determine the intensities of transitions ${\Lambda }_1=\lambda (x_1^{*}=0,x_2^{*}=0),{\Lambda }_2=\Lambda (x_2^{*}=0,x_1^{*}=0)$ from the conditions (9):

$$c_1(1-{\rho }_1)\Lambda (x_1^{*}=0,x_2^{*}=0)=c_2(1-{\rho }_2)\Lambda (x_2^{*}=0,x_1^{*}=0).$$

For this example, the positive intensities of transitions between states are described by Figure 1.

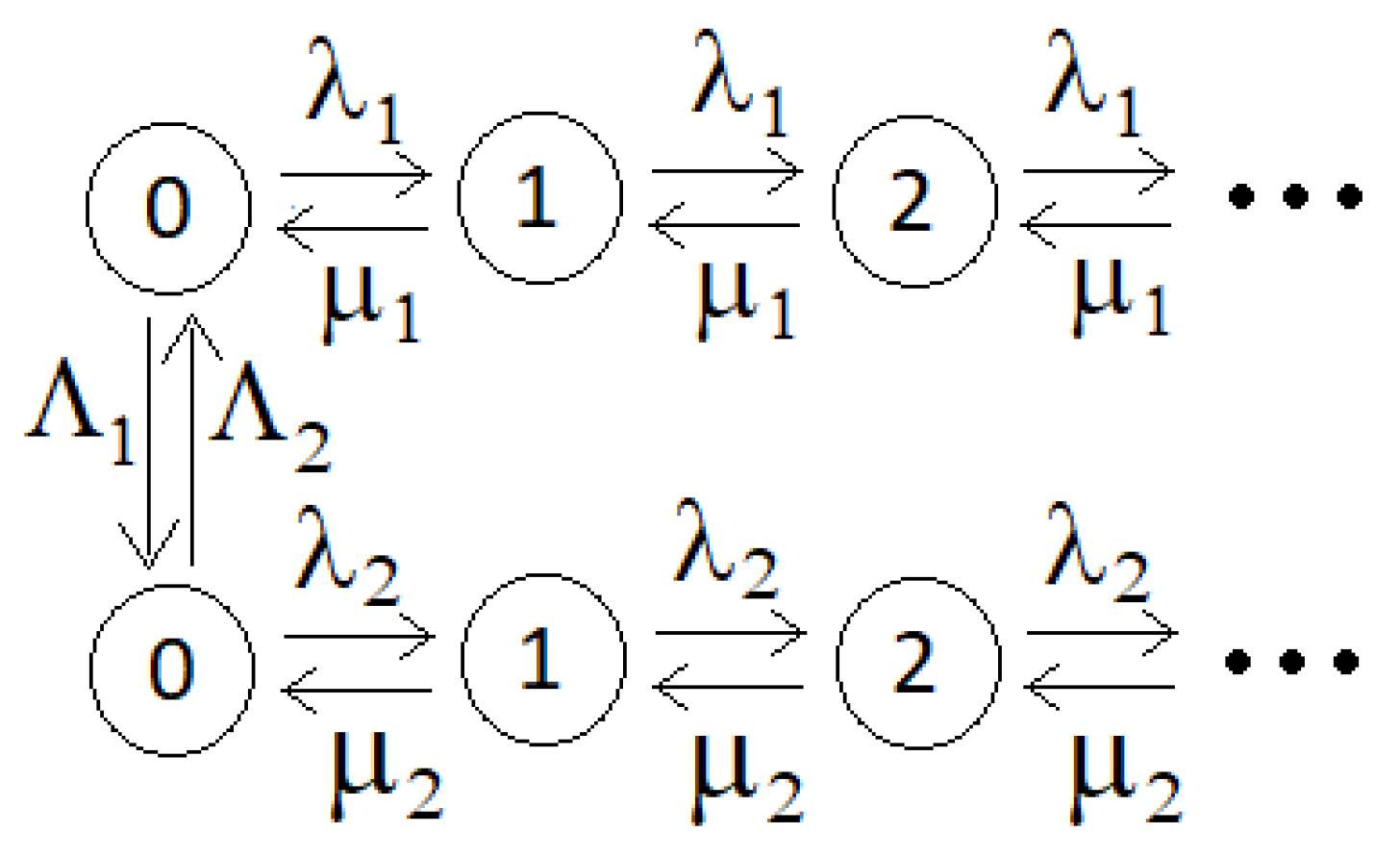
Figure 1. Transient intensities in the queuing system from Example 1.

Assume that ${\displaystyle {\lambda }_1=3,{\mu }_1=4,{\rho }_1=\frac{3}{4};{\lambda }_2=4,{\mu }_2=5,{\rho }_2=\frac{4}{5};c_1=\frac{1}{4},c_2=\frac{3}{4},}$ then ${\displaystyle \frac{\Lambda (x_1^{*},x_2^{*})}{\Lambda (x_2^{*},x_1^{*})}=\frac{12}{5}}$ and so we may take, for example, $\Lambda (x_1^{*},x_2^{*})=12,\Lambda (x_2^{*},x_1^{*})=5.$

Remark 1. 

Markov processes $X_k\left(t\right)$ may describe open/closed queuing networks. For such networks, Jackson’s/Gordon’s theorems allow to calculate both the distributions $P_k\left(x_k\right)$ and their values at points $x_k^{*}$ and to determine the transition intensities between $x_k^{*}$ using the selected $c_k,k=1,\dots ,m.$ If the distributions $P_k\left(x_k\right)$ correspond open networks, then it is convenient to choose zero vectors as $x_k^{*}.$

Remark 2. 

Analogous but more complicated models of switching from one Markov process to another Markov process (or from on to off periods of input flow) are considered in [28].

2.2. Queuing Networks with Uniform Stationary Distributions

All networks describing by Markov process with stationary uniform distribution are constructed using the following statement.

2.2.1. Main Balance Theorem

Theorem 5. 

Suppose that a discrete Markov process $X\left(t\right)$ with a finite set of states $\mathcal{X}$ and with transient intensities $\gamma (i,k),i,k\in \mathcal{X},i\ne k,$ satisfies the following condition of states connectivity. For $\forall i,k\in \mathcal{X}i\ne k\exists i_1,\dots ,i_r\in \mathcal{X},r\ge 0(i_0=i),$ so that

$$\gamma (i,i_1)>0,\gamma (i_1,i_2)>0,\dots ,\gamma (i_r,k)>0,$$

(13)

and for any $i\in \mathcal{X}$, the equalities are fulfilled

$$\sum _{k\in \mathcal{X},k\ne i}\gamma (i,k)=\sum _{k\in \mathcal{X},k\ne i}\gamma (k,i).$$

(14)

Then the Markov process $X\left(t\right)$ is ergodic and its stationary distribution $p\left(i\right)$ is uniform on the set of states $\mathcal{X}.$

Proof. 

Indeed, the relations (13), (14) and Theorem 1 imply ergodicity (and hence the existence of a single stationary distribution) for the discrete Markov process $X\left(t\right)$ [26,27]. Moreover, it follows from the equalities (14) that the uniform distribution $p\left(i\right),i\in \mathcal{X},$ satisfies the stationary Kolmogorov-Chapman equations.

Example 2.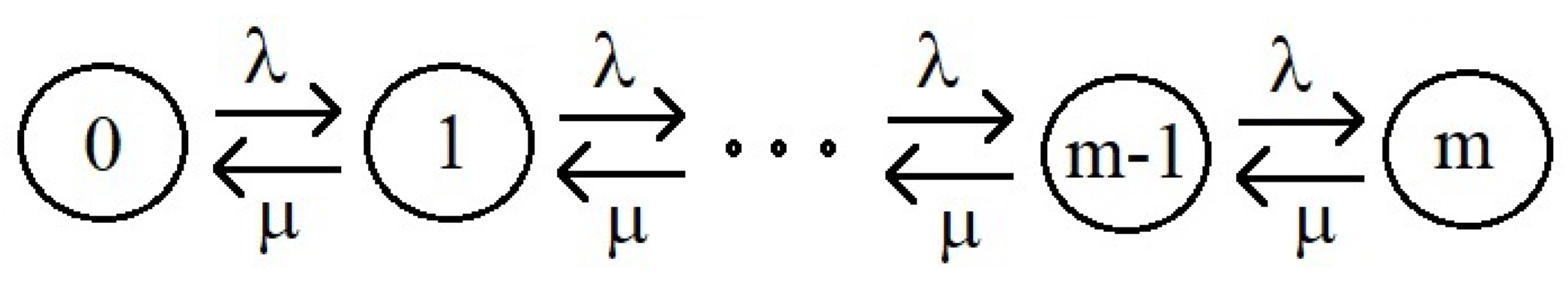 

Consider a model of a single-server queuing system with failures $M\left|M\right|1|m$ when the number of customers exceeds the upper limit $m.$ We describe this queuing system by a discrete Markov process $X\left(t\right)$ with states $0,1,\dots ,m,$ characterizing the number of customers in the system. Suppose that the Poisson input flow to this queuing system has an intensity $\lambda ,$ and the service intensity is $\mu .$ Then the transition intensities between the states of the system have the form (Figure 2)

$$\gamma (i,i+1)=\lambda ,\gamma (i+1,i)=\mu ,i=0,1,\dots ,m-1.$$

(15)

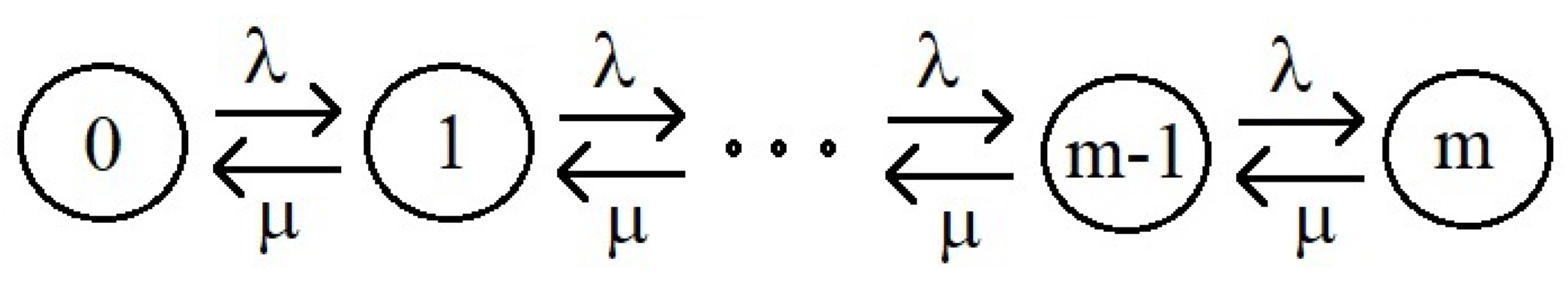
Figure 2. Transient intensities in a system with failures $M\left|M\right|1|m$.

Let’s denote $\rho =\lambda /\mu$ the system load factor, then the stationary probability $p\left(i\right)$ of finding the system in the state i satisfies the equalities

$$p_i={\displaystyle \frac{(1-\rho ){\rho }^i}{1-{\rho }^{m+1}}},\rho \ne 1;p_i={\displaystyle \frac{1}{m+1}},\rho =1;i=0,1,\dots ,m.$$

(16)

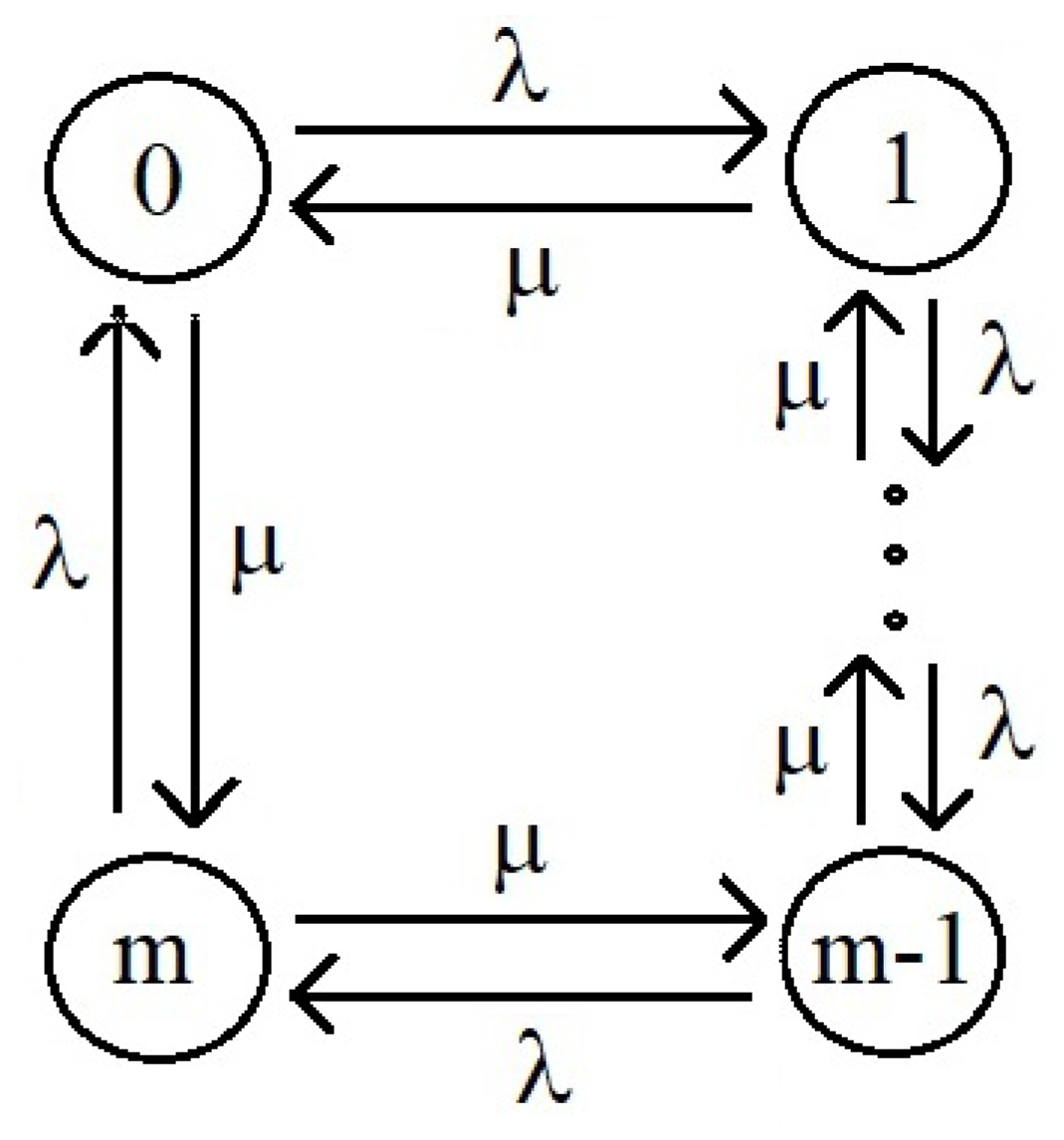
Now let’s transform the system with failures $M\left|M\right|1|m$ into a system with a uniform distribution of stationary probabilities (Figure 3). To do this, we will introduce additional transition intensities into the $M\left|M\right|1|m$ system, characterizing the cleaning of the system from customers and the replenishment of the system with deleted customers

$$\gamma (0,m)=\lambda ,\gamma (m,0)=\mu .$$

(17)

Figure 3. Transient intensities in a system with uniform stationary distribution.

An elementary calculation shows that the states $0,1,\dots ,m,0$ form a cycle in which the sum of the intensities entering the state $i,$ is equal to the sum of the intensities leaving the state (and is equal to $\lambda +\mu$). It follows that the stationary probabilities of being in the states of the extended system satisfy the equality

$$p\left(i\right)={\displaystyle \frac{1}{m+1}},i=0,1,\dots ,m,$$

(18)

and the stationary distribution itself is uniform. Thus, by introducing only two new transient intensities given in the formula (17), the stationary distribution (16) is transformed into a uniform stationary distribution (10). This change has a particularly strong effect for the state $0,$ into which the discrete Markov process $x\left(t\right),$ characterizing the number of customers in the system at the moment $t,$ passes from the state $m.$

Remark 3. 

It should be noted that the transition intensities $\gamma (0,m)=\mu ,\gamma (m,0)=\lambda$ introduced in Figure 4 may be changed. Indeed, at the vertices $1,\dots ,m-1$ of a graph depicting the states of the $M\left|M\right|1|m$ system and its transient intensities (Figure 4), the difference between the sum of the output intensities and the sum of the input intensities is zero. At the vertex 0, this difference is equal to $\lambda -\mu ,$ and at the vertex m it is equal to $\mu -\lambda .$ Therefore, introducing between the vertices $0,m$ transient intensities $\gamma (0,m)={\mu }^{\prime },\gamma (m,0)={\lambda }^{\prime },\lambda +{\mu }^{\prime }={\lambda }^{\prime }+\mu ,$ it is possible to obtain equality to zero of the corresponding differences. Moreover, with $\lambda >\mu$, we can select ${\lambda }^{\prime }=\lambda -\mu +\epsilon ,{\mu }^{\prime }=\epsilon ,\epsilon >0.$ If $\lambda =1,\mu =0,8$ then it is possible to choose ${\mu }^{\prime }=0,05,{\lambda }^{\prime }=0,25.$

Similarly, if $\mu >\lambda ,$ then the transient intensities, introducing between the vertices $0,m,$ the transient intensities $\gamma (0,m)={\lambda }^{\prime },\gamma (m,0)={\mu }^{\prime },\lambda +{\mu }^{\prime }={\lambda }^{\prime }+\mu ,$ it is possible with ${\mu }^{\prime }=\mu -\lambda +\epsilon ,{\lambda }^{\prime }=\epsilon ,\epsilon >0,$ to get the corresponding differences of incoming and outgoing intensities are equal to zero. In this case we can select $\mu =1,5,\lambda =1,2,$ then it is possible to choose ${\lambda }^{\prime }=0,05,{\mu }^{\prime }=0,35.$ It should be noted that in order to weaken the connection $0\to m,$ leading to frequent switches between these states $0,m,$ it is enough to require the condition $\epsilon \ll 1.$

2.2.2. Queuing Network Formed from a Transportation Network

Let’s now consider a queuing network composed of single-server queuing systems at the nodes of some deterministic transport network [19]. Let this transport network be represented as an oriented acyclic bipolar with a set of vertices V and a set of edges $E.$ On each edge u of the set E, the value of the flow $c_u$ is determined so that for each vertex (excluding the initial and final vertices) the sum of the flows entering it equals the sum of the outgoing ones there are flows from it. Let’s denote $\Lambda$ the amount of the flow in this deterministic transport network (the sum of flows leaving the initial vertex equal to the sum of flows entering the final vertex).

Example 3.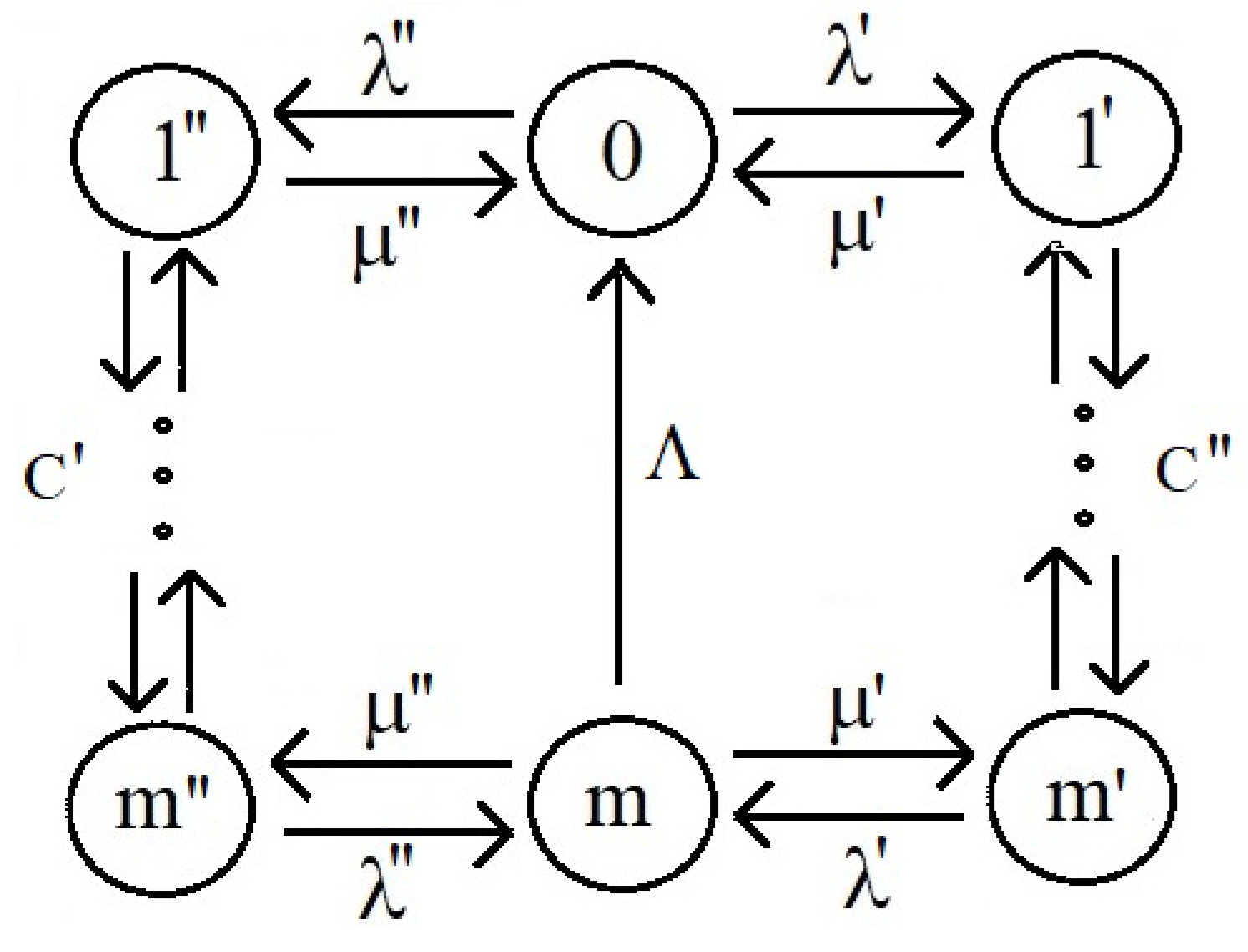 

Let us now proceed to the definition of discrete Markov process $X\left(t\right)$ describing this network. On each edge $u\in E$, we define several states of the discrete Markov process $X\left(t\right),$ indexing them $0_u,\dots ,n_u.$ Such a Markov process defines some kind of queuing network, in the nodes of which there are single-server queuing systems with failures. The states $0_u,\dots ,n_u$ characterize the number of customers in the system located on the edge $u.$ Moreover, the extreme states $0_u,n_u$ can also describe the number of customers in systems adjacent to this system if there is a transition of customers between these systems. Additionally, we introduce the transient intensity Λ from the terminal node of the bipolar to the initial node. Then all states of the process $X\left(t\right)$ will be communicating, and the process $X\left(t\right)$ will be ergodic. From the construction of the transient intensities of the process $X\left(t\right)$ (Figure 4), it follows that the sum of the input intensities is equal to the sum of the output intensities for each state. Therefore, the stationary distribution of the so-constructed process $X\left(t\right),$ defining a certain queuing network, is uniform.

Assume that ${\lambda }^{\prime }=1,{\mu }^{\prime }=0.5,C^{\prime }=1;{\lambda }^{\prime \prime }=2,{\mu }^{\prime \prime }=1,C^{\prime \prime }=2,$ then

$$\Lambda =min(C^{\prime },{\lambda }^{\prime }-{\mu }^{\prime })+min(C^{\prime \prime },{\lambda }^{\prime \prime }-{\mu }^{\prime \prime })=min(1,0.5)+min(2,1)=1.5.$$

Figure 4. Graph of the transient intensities of Markov process based on a deterministic transport network.

2.3. Some Generalizations of Product Theorems

For an open Jackson network, the graph $\Gamma$ of transient intensities consists of a set of triangles (pyramids for $m>2$) filling the entire first quadrant. In Figure 5, the graph $\Gamma$ consists of a single triangle. This subsection presents more complex graphs of transient intensities for queuing networks with a limited number of customers at different nodes.

Figure 5. Transient intensities in the simplest connected graph illustrating Formulas (2), (3).

Everywhere else, we will use the generalization of the relations (2), (3) for the case when for $\mathbf{n}\in {\mathcal{Y}}_{\mathbf{0}}$ vectors (Figure 1) $(\mathbf{n},\mathbf{n}+{\mathbf{e}}_{\mathbf{k}}),(\mathbf{n}+{\mathbf{e}}_{\mathbf{k}},\mathbf{n}+{\mathbf{e}}_{\mathbf{i}}),\mathbf{n}\in {\mathcal{Y}}_{\mathbf{0}},\mathbf{1}\le \mathbf{k}\ne \mathbf{i}\le \mathbf{m}$ create the connected graph $\Gamma .$ As examples of the set $\mathcal{Y}$ it is possible to take

$${\mathcal{Y}}_1=\{\mathbf{n}:\mathbf{0}\le \sum _{\mathbf{i}=\mathbf{1}}^{\mathbf{m}}{\mathbf{n}}_{\mathbf{i}}\le \mathbf{K}\},{\mathcal{Y}}_{\mathbf{2}}=\{\mathbf{n}:\mathbf{0}\le {\mathbf{n}}_{\mathbf{i}}\le {\mathbf{K}}_{\mathbf{i}},\mathbf{i}=\mathbf{1},\dots ,\mathbf{m}\}.$$

2.3.1. Main Product Theorem

Then the graph $\Gamma$ contains a finite number of vertices (which we will also denote $\mathcal{Y}$) and a finite number of edges. Belonging the edge $(\mathbf{n},\mathbf{n}+{\mathbf{e}}_{\mathbf{k}})$ to the graph $\Gamma$ characterizes permission for a customer to enter node k from the outside (from node 0). And the absence of the edge $(\mathbf{n},\mathbf{n}+{\mathbf{e}}_{\mathbf{k}})$ in the graph $\Gamma$ means that the customer received by the node k from the outside leaves the network. Belonging the edge $(\mathbf{n}+{\mathbf{e}}_{\mathbf{k}},\mathbf{n})$ to the graph $\Gamma$ means permission to complete the customer service in node $k,$ and the absence of the edge edge $(\mathbf{n}+{\mathbf{e}}_{\mathbf{k}},\mathbf{n})$ in the graph $\Gamma$ is a ban of a such procedure. Belonging the edge $(\mathbf{n}+{\mathbf{e}}_{\mathbf{k}},\mathbf{n}+{\mathbf{e}}_{\mathbf{i}})$ to the graph $\Gamma$ means permission to complete the service of the customer in the node i, followed by a transition to the k node and to complete the customer service at the k node, followed by a transition to the i node. On the contrary, the absence of the edge $(\mathbf{n}+{\mathbf{e}}_{\mathbf{k}},\mathbf{n}+{\mathbf{e}}_{\mathbf{i}})$ in the graph $\Gamma$ means a ban on the corresponding transitions (in both directions) (see, for example Figure 1). Such permissions and prohibitions define the protocol of the G network. Then, using the product theorem for open queuing networks [15], it is proved the following product theorem in [25]. In this subsection, the number of vertices of the corresponding graphs determines the parameter of a uniform stationary distribution.

Theorem 6. 

The Markov process $Y\left(t\right)$ defined by such graph Γ is ergodic and its stationary distribution [25] $\pi \left(\mathbf{n}\right),\mathbf{n}\in \mathcal{Y},$ is calculated by the formula

$$\pi \left(\mathbf{n}\right)=C^{-1}\Psi \left(\mathbf{n}\right),\Psi \left(\mathbf{n}\right)=\prod _{i=1}^m{a}_i\left(n_i\right),C=\sum _{\mathbf{n}\in \mathcal{Y}}\Psi \left(\mathbf{n}\right),a_i\left(n_i\right)={\left({\displaystyle \frac{{\lambda }_i}{{\mu }_i}}\right)}^{n_i}.$$

(19)

In Theorem 2 graph $\Gamma$ is connected and consists of triangles (or pyramids). Without this assumption product formula for stationary distribution can not be proved. Theorem 2 is proved by checking Kolmogorov-Chapman equalities in conditions of formula (4) for a single triangle/pyramid. Then these triangles are glued together by their vertices (not by edges). Then the obtained equalities are already fulfilled for the entire network.

Corollary 2. 

If ${\lambda }_i={\mu }_i,i=1,\dots ,m$ then limit distribution $\pi \left(\mathbf{n}\right)$ is uniform. Main parameter of uniform distribution here is a number of states.

2.3.2. Closed Queuing Network

From Theorem 3, using ergodicity theorems for Markov chains with a finite number of states [26], it is not difficult to prove the following statement. All solutions of a system of linear algebraic equations (6) consisting of positive components are representable as $a({\lambda }_1^{*},\dots ,{\lambda }_m^{*}),$ where $a>0$ and there is (single) vector $({\lambda }_1^{*},\dots ,{\lambda }_m^{*})$ satisfying the equality ${\displaystyle \sum _{k=1}^m{\lambda }_k^{*}=1.}$ Then, using the product theorem 3 for closed queuing networks with single-channel systems nodes [16], it is not difficult to establish that when the equalities ${\mu }_k=a{\lambda }_k^{*},k=1,\dots ,m,$ limit distribution $\pi \left(\mathbf{n}\right)$ of the Markov process characterizing the number of customers in the network nodes is uniform. Moreover, the uniform stationary distribution in this network has the number $M(K,m)$ of states. Here $M(K,m)$ is the number of solutions of the Diaphantine equation $n_1+\dots +n_m=K$ in non-negative integers or the number of placements of K indistinguishable particles over m distinguishable cells [29,30] equal to

$$M(n,m)=C_{n+m-1}^n$$

(20)

2.4. Open Queuing Networks with Finite Numbers of Customers

In this section, we assume that ${\lambda }_i={\mu }_i,i=1,\dots ,m,$ which ensures a uniform stationary distribution.

Example 4.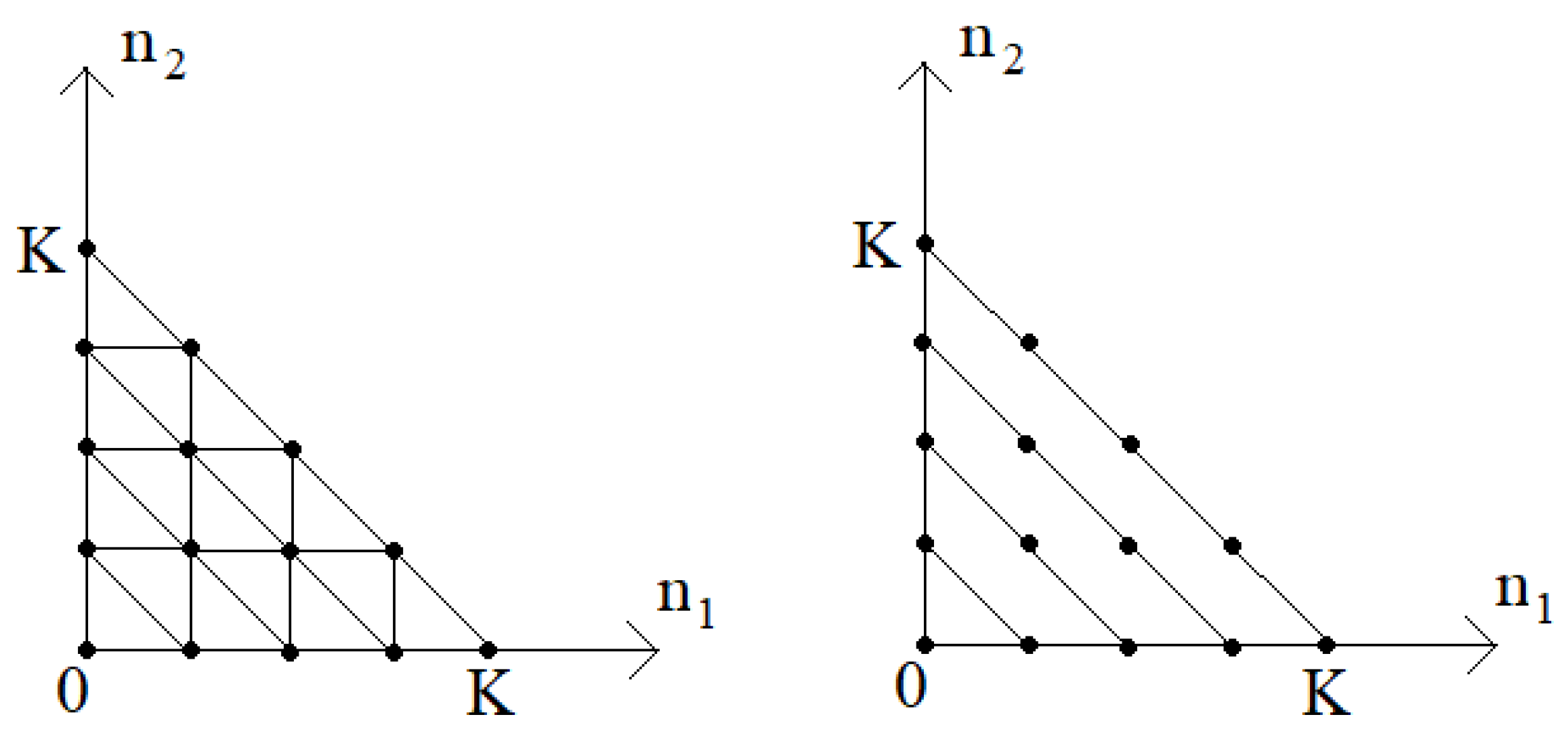 

Let’s consider an open network with a total number of customers of no more than $K,$ described in the Theorem 3. The graph characterizing the transient intensities of this network is shown in Figure 5 on the left.

Figure 5. Example of a graph defining a network with a total number of customers of no more than $K.$

The set of vertices of this graph (Figure 5, on the right)

$${\mathcal{L}}^{\prime }=\{(n_1,\dots ,n_m),0\le n_i,i=1,\dots ,m,\sum _{i=1}^m{n}_i=K\}$$

let’s imagine it as a union of disjoint subsets ${\displaystyle {\mathcal{L}}^{\prime }=\bigcup _{i=0}^K{\mathcal{L}}_i^{\prime },}$ where

$${\mathcal{L}}_i^{\prime }=\{(n_1,\dots ,n_m),0\le n_j,j=1,\dots ,m,\sum _{i=1}^m{n}_j=i\},i=0,1,\dots ,K.$$

Then from Formula (20) we find the number $M^{\prime }$ of vertices in the set ${\mathcal{L}}^{\prime }:$

$$M^{\prime }=\sum _{i=0}^K{C}_{i+m-1}^{m-1}.$$

(21)

Let’s now turn to the consideration of an open network (Figure 6) with a limited number of customers, characterized by the condition $0\le n_i\le K_i,i=1,\dots ,m.$

Example 5.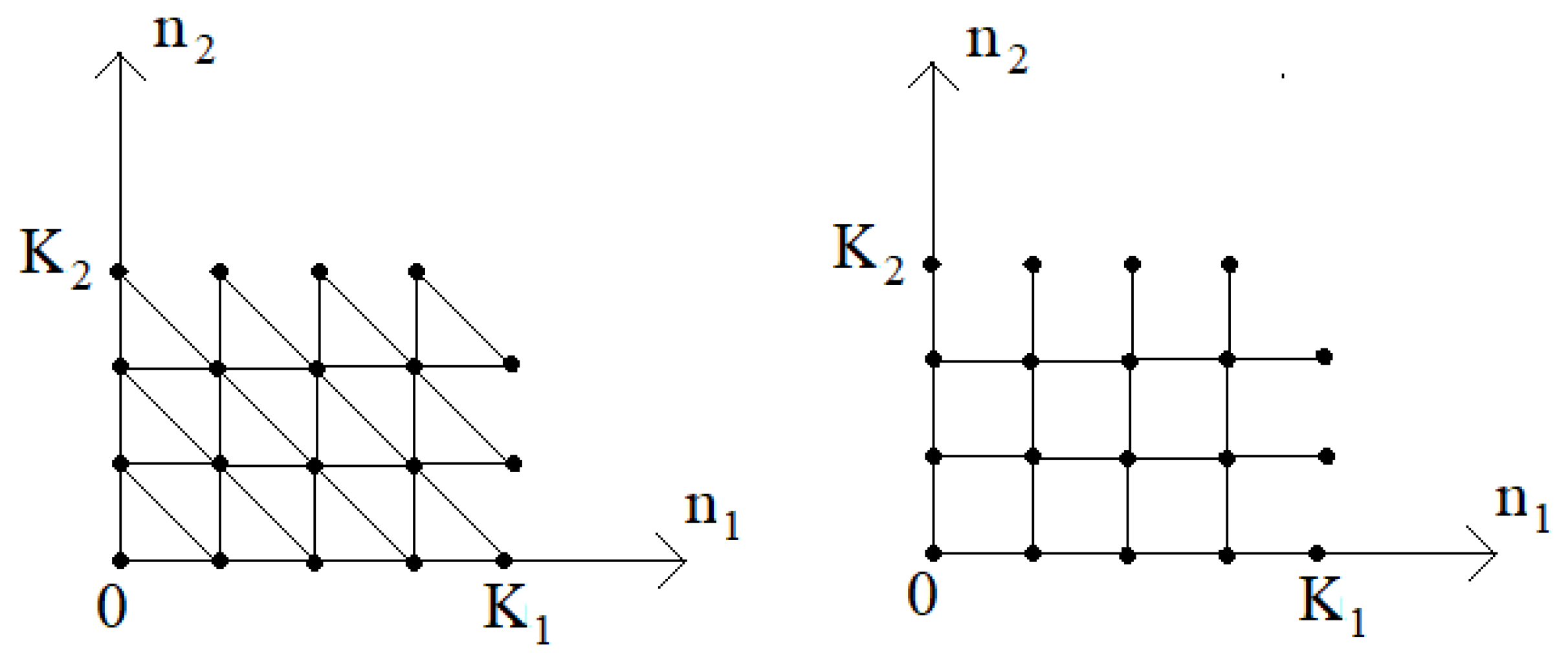 

The graph (Figure 6 on the left) has a set $\mathcal{L}$ of network states (Figure 6 on the right) which may be represented as a union of disjoint subsets ${\displaystyle \mathcal{L}=\bigcup _{j=0}^m{\mathcal{L}}_j,}$ where

$${\mathcal{L}}_0=\{(n_1,\dots ,n_m):0\le n_i\le K_i-1,i=1,\dots ,m\},$$

$${\mathcal{L}}_j=\{(n_1,\dots ,n_{j-1},K_j,n_{j+1},\dots ,n_m),0\le n_i\le K_i,i=l,\dots ,m,i\ne j\},j=1,\dots ,m.$$

Figure 6. Example of graph defining network with the number of customers $n_i\le K_i,i=1,\dots ,m.$

It follows that the number M of vertices in the set $\mathcal{L}$ satisfies the equality

$$M=\prod _{i=1}^m{K}_i\left(1+\sum _{j=1}^m{\displaystyle \frac{1}{K_j}}\right).$$

(22)

Corollary 3. 

Suppose that the graph Γ is defined by a set of vertices ${\mathcal{L}}_0.$ Replace ${\lambda }_k,{\mu }_k,k=1,\dots ,m,$ in each triangle/pyramid defined for $\mathbf{n}\in {\mathcal{L}}_0$ (see Figure 5) by $a\left(\mathbf{n}\right){\lambda }_k,a\left(\mathbf{n}\right){\mu }_k,k=1,\dots ,m.$ Then, with such a replacement, the statement of Theorem 6 and Corollary 2 will remain valid. Then parameters $a\left(\mathbf{n}\right),\mathbf{n}\in {\mathcal{L}}_0$ may be considered as queuing network management.

3. Discussion

4. Conclusions

References

1. Grimmett, G. Probability on Graphs, Second Edition, Volume 8 of the IMS Textbooks Series; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
2. Van der Hofstad, R. Random Graphs and Complex Networks. Volume 1. Cambridge Series in Statistical and Probabilistic Mathematics; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
3. Bet, G.; van der Hofstad, R.; van Leeuwaarden, J.S. Big jobs arrive early: From critical queues to random graphs. Stochastic Syst. 2020, 10, 310–334. [Google Scholar] [CrossRef]
4. Kriz, P.; Szala, L. The Combined Estimator for Stochastic Equations on Graphs with Fractional Noise. Mathematics 2020, 8. [Google Scholar] [CrossRef]
5. Overtona, Ch.E.; Broomb, M.; Hadjichrysanthouc, Ch.; Sharkeya, K.J. Methods for approximating stochastic evolutionary dynamics on graphs. J. Theor. Biol. 2019, 468, 45–59. [Google Scholar] [CrossRef] [PubMed]
6. Legros, B.; Fransoo, J.C. Production, Manufacturing, Transportation and Logistics Admission and pricing optimization of on-street parking with delivery bays. European Journal of Operational Research 2024 312 (1) 138–149.
7. Ning, R.; Wang, X.; Zhao, X.; Li, Z. Joint optimization of preventive maintenance and triggering mechanism for k-out-of-n: F systems with protective devices based on periodic inspection. Reliability Engineering and System Safety 2024, 251, 110396. [Google Scholar] [CrossRef]
8. Feng, H.; Zhang, Sh.H.; Zhang, Y. Production, Manufacturing, Transportation and Logistics Managing production-inventory-maintenance systems with condition monitoring. European Journal of Operational Research 2023 310 (2) 698–711.
9. Anokhin, P.K. Ideas and facts in the development of the theory of functional systems. Psychological Journal 1984 5 107–118. (In Russian).
10. Redko, V.G.; Prokhorov, D.V.; Burtsev, M.S. Theory of Functional Systems, Adaptive Critics and Neural Networks. Proceedings of IJCNN 2004, 1787–1792. [Google Scholar]
11. Vartanov, A.V.; Kozlovsky, S.A. et al. Human memory and anatomical features of the hippocampus. Vestn. Moscow. Univ. Ser. 14. Psychology, 2009 4, 3–16. (In Russian).
12. Lye, T.C.; Grayson, D.A. et al. Predicting memory performance in normal ageing using different measures of hippocampal size. Neuroradiology, 2006 48 (2), 90-—99.
13. Lupien, S.J.; Evans,; A.; et al. Hippocampal volume is as variable in young as in older adults: Implications for the notion of hippocampal atrophy in humans. Neuroimage, 2007 34 (2), 479-—485.
14. Squire, L.R. The legacy of patient H.M. for neuroscience. Neuron 2009 61 (1), 6-—9.
15. Jackson, J.R. Networks of Waiting Lines. Oper. Res. 1957, 5, 518–521. [Google Scholar] [CrossRef]
16. Gordon, K.D.; Newell, G.F. Closed Queuing Systems with Exponential Servers. Oper. Research 1967 15 (2) 254–265.
17. Pathria, R.K.; Beale, P.D. Statistical Mechanics, 3-rd edition. Elsevier. 2011.
18. Gyenis, B. Maxwell and the normal distribution: A coloured story of probability, independence, and tendency toward equilibrium. Studies in History and Philosophy of Science. Part B: Studies in History and Philosophy of Modern Physics. 2017 57, 53–65.
19. Ford, L.R.; Fulkerson, D.R. Maximal flow through a network. Canadian Journal of Mathematics, 1956 8, 399–404.
20. Cormen, Th.H.; Leiserson, Ch.E.; Rivest, R.L.; Stein, Cl. Algorithms: Introduction to Second Edition. The MIT Press Cambridge. Cambridge, UK, 1990.
21. Ghosh, S.; Hassin, R. Inefficiency in stochastic queueing systems with strategic customers. European J. Oper. Res. 2021, 295(1), 1–11. [Google Scholar] [CrossRef]
22. He, Q.M.; Bookbinder, J.H.; Cai, Q. Optimal policies for stochastic clearing systems with time-dependent delay penalties. Naval Res. Logist., 2020 67 (7), 487–502.
23. Kim, B.K.; Lee, D.H. The M/G/1 queue with disasters and working breakdowns. Appl. Math. Model. 2014 38 (5-6), 1788–1798.
24. Missbauer, H.; Stolletz, R.; Schneckenreither, M. Order release optimisation for time-dependent and stochastic manufacturing systems. Int. J. Prod. Res., 2023 62 (7), 2415–2434.
25. Tsitsiashvili, G.Sh.; Osipova, M.A. New multiplicative theorems for queuing networks. Problems of information transmission. 2005 41 (2), 111–122. (In Russian).
26. Ivchenko, G.I.; Kashtanov, V.A.; Kovalenko, I.N. Theory of queuing: A textbook for universities. Moscow: Higher School. Moscow, Russia, 1982. (In Russian).
27. Kovalenko, I.N.; Kuznetsov, N.Yu.; Shurenkov, V.M. Random processes. Kiev: Naukova dumka, 1983. (In Russian).
28. Mikosch, T.; Resnick, S.; Rootzen, H.; Stegeman, A. Is network traffic approximated by stable Levy motion or fractional Brownian motion? Annals of Applied Probability 2002, 12, 23–68. [Google Scholar] [CrossRef]
29. Stillwell, J. Mathematics and its History (Second ed.). Springer Science and Business Media Inc, 2004.
30. Vilenkin, N.Ya. Combinatorics. Moscow: Nauka, Moscow, Russia, 1969. (In Russian).