Definition of Optimal Time Intervals in the Queues’ Analysis: The Use of Epsilon-Entropy and Epsilon-Capacity

Preprint

Article

Definition of Optimal Time Intervals in the Queues’ Analysis: The Use of Epsilon-Entropy and Epsilon-Capacity

Altmetrics

Downloads

Views

155

Comments

This version is not peer-reviewed

Submitted:

06 September 2024

Posted:

09 September 2024

Read the latest preprint version here

Alerts

Abstract

In the paper, we suggest a method for calculating optimal time intervals in the queue analysis. The suggested method processes partitioning of the time interval and utilizes the epsilon-entropy and epsilon-capacity of the partition for finding an optimal partition. Optimality of the partition is specified based on its epsilon-information. The suggested method is illustrated by defining the intervals for histograms of differently distributed samples and demonstrated its effectiveness in comparison with the existing methods.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

MSC: 60K25; 90B22

1. Introduction

The use of queue models implies the knowledge of the arrival and departure rates, which in their turn require the well-defined time intervals [3].

For example, consider a clerk serving clients of some office during the day. Then, the arrival rate

λ

and the departure rate

μ

per day completely describe the state of the system at the end of the day but do not provide any information about the system during the day. On other hand, specification of the rates

λ

and

μ

, for example, per minute is also useless since both the clients and the clerk do not act with such rates.

The incorrect specification of the time intervals leads to incorrect consideration of the processes with unsteady arrivals or departures. In many cases, such situations are resolved using the queues with time dependent rates [5,8], but even in such considerations certain time intervals per which the rates are defined have to be specified.

Similar problem appears in statistics while plotting histograms of the data sample

X

and it is required to define the lengths

δ

of the bins. Since there is no strictly proven formula, which defines the bin length with respect to the number

n

of data counts or distribution over the sample, the heuristic formulas are used.

For example, the simplest heuristic defines the bin length as

δ_{1} = \frac{\max (X) - \min (X)}{\sqrt{n}} .

(1)

The Sturges rule [15] defines the number of bins as

⌈\log_{2} n⌉ + 1

. Then the bin length is

δ_{2} = \frac{\max (X) - \min (X)}{⌈\log_{2} n⌉ + 1} .

(2)

The Scott rule [12] defines the bin length

δ_{3} = \frac{3.49 s}{\sqrt[3]{n}}

(3)

with respect to the standard deviation

s

of the sample. Finally, the Freedman-Diaconis formula [2] uses the interquartile range instead of the standard deviation and defines the bin length

δ_{4} = \frac{2 (Q_{3} - Q_{1})}{\sqrt[3]{n}},

(4)

where

Q_{3}

is the third quartile and

Q_{1}

is the first quartile of the sample.

In general, this problem can be considered in the terms of discretization of stochastic processes [4], where it is required to build a discretization scheme, which is a sequence

t_{i}

i = 0, 1, 2, \dots

, of stopping times such that

Δ = t_{i + 1} - t_{i}

and

t_{i} = i Δ

. But if

t_{i}

is a random variable, then the length

Δ

of the time intervals is also random and depend on the distribution of the considered process. Similarly, if the discretization scheme is regular with constant interval lengths

Δ

, then the increments of the process at the times

t_{i}

are random.

For example, let

W_{t}

be a Wiener process at the time interval

T = [0, t_{m}]

starting with

W_{0} = 0

. In such a process, the increments

d W_{t}

are independent and for any

t_{i}

and

t_{j} > t_{i}

the differences

W_{t_{j}} - W_{t_{i}}

have normal distribution

N (0, σ_{t}^{2})

with the variance

σ_{t}^{2} = t_{j} - t_{i}

. Assume that the interval

T

is divided to

n

sub-intervals with the length

Δ = t_{m} / n

. Then, the stopping times are

t_{i} = i Δ

i = 0,1, 2, \dots,

and the increments

d W_{t} = W_{t_{i + 1}} - W_{t_{i}}

are normally distributed with

σ_{t}^{2} = Δ

In this paper, we seek the answer to the following question formulated by Yaakov Reis [9]. Given a total period, a sequence of clients arriving at the times

t_{0}, t_{1}, t_{2}, \dots, t_{m}

to a service point, what is an optimal length

Δ

of the time interval, on which the arrival rate

λ

and the service rate

μ

(which is a departure rate) have to be defined?

An immediate answer to this question follows the heuristics used for definition of the bin length

δ

in histogram. However, such heuristics cannot be considered as the best method and their result is not strictly proved approximation.

To find an optimal length

Δ

we follow the line of the Schwarz information criterion [11] and apply well-known concepts of

ε

-entropy and

ε

-capacity, which were introduced by Kolmogorov and Tikhomirov [6]. The calculations of the optimal interval are also based on the concept of the entropy of partition introduced by Rokhlin [10].

Initially

ε

-entropy and

ε

-capacity were used for analysis of functions and functional spaces and then, as well as the entropy of partition, were applied to the studies of dynamical systems. For many examples of application of these concepts and their relationship with the Shannon entropy [13] see the paper by Dinaburg [1] and the books by Vitushkin [16] and by Sinai [14].

2. Problem Formulation

Let

T = [t_{0}, t_{m}]

be a time interval of the length

t_{m} - t_{0} > 0

and assume that during this interval sequentially occur

m + 1

events

a_{0}, a_{1}, a_{2}, \dots, a_{m}

. The times of occurrences of these events are

t_{0} \leq t_{1} \leq t_{2} \leq \dots \leq t_{m}

, respectively.

The problem is to define a length

Δ

of the time interval or, that is the same, the stopping times

t_{i} = i Δ

i = 0, 1, 2, \dots, n

, such that

n

intervals

T_{i} = [t_{i}, t_{i + 1}]

cover the interval

T

and such that they as better as possible represent the times

t_{j}

j = 0, 1, 2, \dots, m

, when the considered events occurred.

To illustrate the problem, let us consider a simple example of a non-steady supply process. Assume that the mentioned above clerk serves the clients with the rate

μ = 5

clients/hour. During the workday of

8

hours arrive

24

clients. Then, the arrival rate of the clients defined over a workday is

λ = 24 / 8 = 3

clients/hour and the transition rate

ρ = λ / μ = 3 / 5 < 1

that should guarantee that at the end of the workday all clients will be served.

Additionally, assume that in the morning, during the first two hours of the day, arrive

12

clients. Then during the next four hours the clients do not arrive and then, in the evening, during the last two hours of the day, arrive the last

12

clients. Thus, in the morning and in the evening the arrival rate is

λ = 12 / 2 = 6

clients/hour, that means that the first

12

clients will wait in the queue and the last

12

clients will not be served until the end of the workday.

Certainly, such phenomena are well-known; in the queue theory they are solved using the state-dependent and time-dependent arrival rates [3,5,8], and in practice are overcome by adding the clerks in the morning and in the evening and by stopping the service in the midday. However, a prior definition of the appropriate time intervals can simplify further analysis and even decrease the expected number of varying rates.

Finally, note that the considered problem is essentially discrete problem, where it is required to split the discrete dataset. Together with that, since it is closely related to the discretization problems dealing with the continuous functions, below we will make some remarks on such problems as well.

3. Methods

The suggested solution of the problem is based on the concepts of

ε

-entropy and

ε

-capacity, which were introduced by Kolmogorov and Tikhomirov in the middle of 1950-s and presented in detail in their paper [6]. In addition, it uses the multiplication of partitions as it was implemented by Rokhlin [10] and by Sinai [14] in the studies of dynamical systems.

3.1. $ε$ -Entropy and $ε$ -Capacity

Let

U \subset R

be a non-empty bounded set of a metric space

R

and let

ε > 0

be a real number.

The set

α = \{A : A \subset R\}

is called

ε

-covering of the set

U

, if

U \subseteq ⋃_{A \in α} A

and the diameter of any

A \in α

is not greater than

2 ε

The set

U

is said to be

ε

-distinguishable, if any two of its distinct points are located at distance greater than

ε

Given a bounded set

U \subset R

, for any

ε > 0

there exists a finite

ε

-covering of

U

, and for any

ε > 0

any

ε

-distinguishable set

U \subset R

is finite.

Denote by

N_{ε} (U)

the minimal number of the sets in

ε

-covering

α

of the set

U

, and by

M_{ε} (U)

the maximal number of points in an

ε

-distinguishable subset of the set

U

The value

H_{ε} (U) = \log_{2} N_{ε} (U)

(5)

is called the

ε

-entropy of the set

U

, and the value

E_{ε} (U) = \log_{2} M_{ε} (U)

(6)

is called the

ε

-capacity of the set

U

These values are interpreted as follows:

ε

-entropy

H_{ε} (U)

is a minimal number of bits required to transmit the set

U

with the precision

ε

, and

ε

-capacity

E_{ε} (U)

is a maximal number of bits, which can be memorized by

U

with the precision

ε

Among the properties of

ε

-entropy

H_{ε} (U)

and

ε

-capacity

E_{ε} (U)

we will use the following fact [6]: given the bounded set

U

, both

ε

-entropy and

ε

-capacity as functions of

ε

are non-increasing with increasing

ε

Examples of calculation of the

ε

-entropy and

ε

-capacity of the sets in different metric spaces can be found in the paper by Kolmogorov and Tikhomirov [6] and in the book by Vitushkin [16].

3.2. ɛ-Entropy of Partition

Let

β = \{B : B \subset U\}

be a partition of the set

U \subset R

that is

U = ⋃_{B \in β} B

and for any two sets

B^{'}, B^{''} \in β

holds

B^{'} \cap B^{''} = \emptyset

The entropy of partition is defined as follows [10,14]. Let

μ

be a non-negative measure on the set

U

such that

μ (\emptyset) = 0

and

μ (U) = 1

. Then,

μ (B) \in [0, 1]

for any

B \in β

. The value

H_{μ} (β) = - \sum_{B \in β} μ (B) \log_{2} μ (B)

(7)

is called the entropy of partition. If

μ

is the probability measure on

U

, then the sets

B \in β

can be interpreted as events and the entropy

H_{μ}

is equivalent to the Shannon entropy [13].

Assume that the partition

β

is finite and the number of the sets in

β

N

. Define the measure

μ

on the set

U

as follows:

μ (B) = \{\begin{array}{l} 0, B = \emptyset \\ \frac{1}{N}, B \neq \emptyset, B \neq U \\ 1, B = U \end{array}

(8)

Then, the entropy of partition is reduced to the value

H_{μ} (β) = \log_{2} N

(9)

Finally, if the diameter of any set

B \in β

is not greater than

2 ε

, then the partition

β

is an

ε

-covering and called

ε

-partition. Then, the entropy

H_{μ} (β)

of partition is equivalent to the

ε

-entropy

H_{ε} (U)

of the set

U = ⋃_{B \in β} B

defined by equation (5).

Let

β = \{B : B \subset U\}

ε

-partition of the set

U

with

ε = ε_{B}

and

γ = \{C : C \subset U\}

be another

ε

-partition of the set

U

with

ε = ε_{C}

. Multiplication of the partitions

β

and

γ

is the partition

β \lor γ = \{D = B \cap C : B \in β, C \in γ\} .

(10)

Each set

D \in β \lor γ

is a subset of some set

B \in β

and of some set

C \in γ

. Then it is said that

β \lor γ

is a refinement of both

β

and

γ

; this fact is denoted by

β ≼ β \lor γ

and

γ ≼ β \lor γ

. Hence, following the properties of the entropy of partition,

H_{μ} (β) \leq H_{μ} (β \lor γ) and H_{μ} (γ) \leq H_{μ} (β \lor γ)

(11)

and

Moreover, the entropy

H_{μ} (β \lor γ)

of the multiplication

β \lor γ

of the partition

β

and

γ

is the

ε

-entropy

H_{ε} (U)

of the set

U

with any

ε \in [\min \{ε_{B}, ε_{C}\}, \max \{ε_{B}, ε_{C}\}]

For the other properties of the entropy

H_{μ}

and its application for analysis of dynamical systems see the paper [10] and the book [14].

4. Suggested Solution

Let

T = [t_{0}, t_{m}]

t_{m} > t_{0}

, be a time interval and let

T = \{t_{0}, t_{1}, t_{2}, \dots, t_{m}\}

be the set of moments in which certain events occur. We assume that the moments

t_{j}

have an increasing order such that

t_{j} < t_{j + 1}

j = 0, 1, 2, \dots, m - 1

As it follows from the formulation of the problem, in the consideration below the interval

T

plays a role of the set

U

and the intervals

[t_{j}, t_{j + 1}]

j = 0, 1, 2, \dots, m - 1

, are considered as the elements of

ε

-partitions of the interval

T

Given

ε > 0

, the minimal number of sets in the

ε

-covering

α

of the set

T

N_{ε} (T) = ⌈\frac{t_{m} - t_{0}}{2 ε}⌉ .

(12)

Then, the

ε

-entropy of the set

τ

H_{ε} (T) = \log_{2} N_{ε} (T) = \log_{2} ⌈\frac{t_{m} - t_{0}}{2 ε}⌉ .

(13)

Let

ε_{m i n} = \frac{1}{2} \frac{t_{m} - t_{0}}{m^{2}}

(14)

be a minimal value of

ε

for the set

T

. Then, the value

H_{ε_{m i n}} (T) = \log_{2} ⌈\frac{t_{m} - t_{0}}{2 ε_{m i n}}⌉ = 2 \log_{2} m

(15)

is maximal

ε

-entropy of the set

T

Finally, assume that on the interval

T

two sets

T_{1} = \{t_{1,0}, t_{1,1}, t_{1,2}, \dots, t_{1 {, m}_{1}}\}

and

T_{2} = \{t_{2,0}, t_{2,1}, t_{2,2}, \dots, t_{2, m_{2}}\}

t_{1,0} = t_{2,0}

and

t_{1, m_{1}} = t_{2, m_{2}}

, of moments are defined. Denote by

τ_{1} = \{[t_{1,0}, t_{1,1}], [t_{1,1}, t_{1,2}], \dots, [t_{1, m_{1} - 1}, t_{1, m_{1}}]\}

partition of the interval

T

corresponding to the set

T_{1}

and by

τ_{2} = \{[t_{2,0}, t_{2,1}], [t_{2,1}, t_{2,2}], \dots, [t_{2, m_{2} - 1}, t_{2, m_{2}}]\}

partition of the interval corresponding to the set

T_{2}

. The number of intervals in the partition

τ_{1}

m_{1}

and the number of intervals in the partition

τ_{2}

m_{2}

Then, since the multiplication

τ_{1} \lor τ_{2}

is a refinement of each of the partitions

τ_{1}

and

τ_{2}

of the sets, the size

m_{1 \lor 2}

of the partition

τ_{1} \lor τ_{2}

m_{1 \lor 2} \geq \max \{m_{1}, m_{2}\}

, and the entropy

H_{μ} (τ_{1} \lor τ_{2})

of the multiplication

τ_{1} \lor τ_{2}

is not smaller than the entropies

H_{μ} (τ_{1})

and

H_{μ} (τ_{2})

of the partitions

τ_{1}

and

τ_{2}

Hence, if

2 ε \geq \max_{j = 0,1, 2, \dots, m_{1} - 1} (t_{1, j + 1} - t_{1, j}) and 2 ε \geq \max_{j = 0,1, 2, \dots, m_{2} - 1} (t_{2, j + 1} - t_{2, j}),

(16)

then, following equation (11),

H_{ε} (T_{1}) \leq H_{ε} (T_{1} \lor T_{2}) and H_{ε} (T_{2}) \leq H_{ε} (T_{1} \lor T_{2}) .

(17)

Following the line of the Schwarz information criterion [11], let us define

ε

-information of the set

T

Let

τ

be a partition corresponding to the set

T

and let

τ_{ε}

be a partition corresponding to the set

T_{ε} = \{t_{ε, 0}, t_{ε, 1}, t_{ε, 2}, \dots, t_{ε {, m}_{ϵ}}\}

t_{ε, 0} = t_{0}

and

t_{ε, m_{ε}} = t_{m}

, in which

t_{ε, j + 1} - t_{ε, j} = 2 ε

j = 0, 1, 2, \dots, m - 2

. In the partition

τ_{ε}

all intervals except the last are of the length

2 ε

Denote by

T \lor T_{ε}

the set of moments corresponding to the multiplication

τ \lor τ_{ε}

of the partitions

τ

and

τ_{ε}

. Then,

ε

-information of the set

T

is defined as follows

I_{ε} (T) = H_{ε_{m i n}} (T) - H_{ε} (T) - H_{ε} (T \lor T_{ε}) .

(18)

In this formula, the first term represents the number of bits required to transmit the set

T

with maximal precision, the second term represents the number of bits required to transmit the set

T

with precision

ε

, and the last term represents the number of bits required to transmit the set

T

with precision

ε

using additional set

T_{ε}

generated with precision

ε

. Thus, the value

I_{ε} (T)

is the number of bits remained after the transmission of the set

T

with the precision

ε

. In the other words,

ε

-information of the set

T

characterizes the part of the set, which cannot be transmitted with the precision

ε

Using equations (13) and (15), formula (18) of

ε

-information can be simplified and written in the form

I_{ε} (T) = 2 \log_{2} m - \log_{2} ⌈\frac{t_{m} - t_{0}}{2 ε}⌉ - H_{ε} (T \lor T_{ε}) .

(19)

The value of the entropy

H_{ε} (T \lor T_{ε})

depends on the distribution of time moments

t_{j} \in T

j = 0, 1, 2, \dots, m

, over the interval

T

. If the moments

t_{j}

are distributed evenly, then

T \lor T_{ε} = T

and

H_{ε} (T \lor T_{ε}) = H_{ε} (T) = \log_{2} ⌈\frac{t_{m} - t_{0}}{2 ε}⌉ .

(20)

Note that in general case equation (20) does not hold and calculation of the entropy of multiplication of partitions is processed according to the algorithm presented by Function 1 (see section 5).

Similarly, the value of

ε

-capacity

E_{ε} (T)

depends on the distribution of the time moments

t_{j}

over the interval

T

. If the moments

t_{j}

are distributed evenly such that

t_{j + 1} - t_{j} = t_{j + 2} - t_{j + 1}

and

t_{j + 1} - t_{j} > ε

for any

j = 0, 1, 2, \dots, m - 2

, then

M_{ε} (T) = ⌈\frac{t_{m} - t_{0}}{ε}⌉

(21)

and

E_{ε} (T) = \log_{2} M_{ε} (T) = \log_{2} ⌈\frac{t_{m} - t_{0}}{ε}⌉ .

(22)

If the distribution of the moments

t_{i}

is such that

t_{m - 1} - t_{0} \leq ε

, which means that all the moments except

t_{m}

are located between

t_{0}

and

t_{m - 1}

, and

t_{m} - t_{0} > ε

, then

M_{ε} (T) = 2

(23)

and

E_{ε} (T) = \log_{2} 2 = 1 .

(24)

Finally, if

t_{m} - t_{0} \leq ε

, then the set

T

does not contain

ε

-distinguishable subset, and we assume that

M_{ε} (T) = 1

(25)

and

E_{ε} (T) = \log_{2} 1 = 0 .

(26)

Calculation of

ε

-capacity in general case follows the algorithm of Function 2 (see section 5).

The length

Δ

of the time interval, which defines the stopping times

t_{i} = i Δ

i = 0, 1, 2, \dots, n

, is defined as

Δ = 2 ε,

(27)

where

ε

is such a value for which

ε

-information

I_{ε} (T)

of the set

T

is as close as possible to

ε

-capacity

E_{ε} (T)

of this set.

Note that given the set

T

, the entropy

H_{ε_{m i n}} (T)

is constant and both entropies

H_{ε} (T)

and

H_{ε} (T \lor T_{ε})

as functions of

ε

are decreasing. Thus,

ε

-information

I_{ε} (T)

increases with

ε

. Along with that,

ε

-capacity

E_{ε} (T)

as function of

ε

decreases.

Hence, the problem of finding the length

Δ

is formulated as follows: given the set

T

, find the value of

ε

such that

|I_{ε} (T) - E_{ε} (T)| \to m i n .

(28)

To illustrate the calculation of the length

Δ

, let us consider a simple example. Assume that the considered time interval is

T = [t_{0}, t_{m}]

and the set

T = \{t_{0}, t_{1}, t_{2}, \dots, t_{m}\}

consists of the evenly distributed moments

t_{j}

such that

t_{j + 1} - t_{j} = t_{j + 2} - t_{j + 1}

for any

j = 0, 1, 2, \dots, m - 2

. Then (here for simplicity we omit the notion of ceiling),

I_{ε} (T) - E_{ε} (T) = 2 \log_{2} m - 2 \log_{2} \frac{t_{m} - t_{0}}{2 ε} - \log_{2} \frac{t_{m} - t_{0}}{ε} = \log_{2} m^{2} - \log_{2} \frac{{(t_{m} - t_{0})}^{3}}{4 ε^{3}} .

(29)

Hence, according to the criterion (28), it is required to specify the value

ε

such that

\frac{{(t_{m} - t_{0})}^{3}}{4 ε^{3}} = m^{2},

(30)

which is

ε = \frac{t_{m} - t_{0}}{\sqrt[3]{4 m^{2}}} .

(31)

and finally

Δ = 2 \frac{t_{m} - t_{0}}{\sqrt[3]{4 m^{2}}} .

(32)

For example, if

T = [0, 10]

and

A = \{0, 1, 2, \dots, 10\}

, then

Δ = 2 \frac{10 - 0}{\sqrt[3]{4 {\times 11}^{2}}} = 2.55 .

For comparison, the indicated above methods (1)-(4) of specifying the bin length in the histograms result in the following values:

-: the simplest rule: $δ_{1} = \frac{\max A - \min A}{\sqrt{m}} = \frac{10 - 0}{\sqrt{11}} = 3.01$ ,
-: the Sturges rule [15]: $δ_{2} = \frac{\max A - \min A}{\log_{2} m + 1} = \frac{10 - 0}{\log_{2} 11 + 1} = 2.24$ ,
-: the Scott rule [12]: $δ_{3} = \frac{3.49 s}{\sqrt[3]{m}} = \frac{3.49 \times 3.32}{\sqrt[3]{11}} = 5.20$ ,
-: the Freedman-Diaconis formula [2]: $δ_{4} = \frac{2 (Q_{3} - Q_{1})}{\sqrt[3]{m}} = \frac{2 \times (8 - 3)}{\sqrt[3]{11}} = 4.94$ .

In the considered example, the interval length calculated using the suggested method is compatible with the lengths obtained using the methods of calculating the bin lengths, but for the other distributions the interval lengths can be strongly different.

Note again that in general case the interval lengths cannot be calculated using close formulas. In the next section we summarize the suggested methods in the form of an algorithm which is applicable to arbitrary data.

5. Algorithmic Implementation

We summarize the suggested solution in the form of an algorithm which can be directly implemented in any high-level programming language. In our trials we used the MATLAB^® environment.

Algorithm 1. Computing an optimal interval length

Input:: Set $T = \{t_{0}, t_{1}, t_{2}, \dots, t_{m}\}$ of time moments, $t_{j} < t_{j + 1}$ , $j = 0, 1, 2, \dots, m - 1$ ; step $s > 0$ .
Output:: Optimal interval length $Δ$ .

1.: Calculate $ε_{m i n} = (t_{m} - t_{0}) / (2 m^{2})$ {minimal value of $ε$ , equation (14)}.
2.: Calculate $H_{ε_{m i n}} (T) = 2 \log_{2} m$ {maximal $ε$ -entropy, equation (15)}.
3.: For $ε = ε_{m i n}$ to $(t_{m} - t_{0}) / 2$ with step $s$ do:
4.: Calculate $H_{ε} (A) = \log_{2} ⌈(t_{m} - t_{0}) / 2 ε⌉$ { $ε$ -entropy, equation (13)}.
5.: Create set $T_{ε} = \{t_{ε, 0}, t_{ε, 1}, t_{ε, 2}, \dots, t_{ε, m_{ε}}\}$ such that $t_{ε, j} < t_{ε, j + 1}$ , $j = 0, 1, 2, \dots, m_{ε} - 1$ , and $t_{ε, j + 1} - t_{ε, j} = 2 ε$ , $j = 0, 1, 2, \dots, m_{ε} - 2$ .
6.: Compute $H_{ε} (T \lor T_{ε}) = e p s_e n t r o p y (T, T_{ε})$ {entropy of $T \lor T_{ε}$ , Function 1}
7.: Calculate $I_{ε} (T) = H_{ε_{m i n}} (T) - H_{ε} (T) - H_{ε} (T \lor T_{ε})$ { $ε$ -information, equation (18)}.
8.: Compute $E_{ε} (T) = e p s_c a p a c i t y (T, ε)$ { $ε$ -capacity, Function 2}.
9.: If $I_{ε} (T) > E_{ε} (T)$ then
10.: Break
11.: End if.
12.: End for.
13.: Return $Δ = 2 ε$ .

The algorithm includes two functions,

e p s_e n t r o p y (T, T_{ε})

and

e p s_c a p a c i t y (T, ε)

which are defined as follows.

Function 1.

e p s_e n t r o p y (T, T_{ε})

Input:: Set $T = \{t_{0}, t_{1}, t_{2}, \dots, t_{m}\}$ of time moments, $t_{j} < t_{j + 1}$ , $j = 0, 1, 2, \dots, m - 1$ ; set $T_{ε} = \{t_{ε, 0}, t_{ε, 1}, t_{ε, 2}, \dots, t_{ε, m_{ε}}\}$ of time moments, $t_{ε, j} < t_{ε, j + 1}$ , $j = 0, 1, 2, \dots, m_{ε} - 1$ .
Output:: $ε$ -entropy $H_{ε} (T \lor T_{ε})$ of the set $T \lor T_{ε}$ .

Join the sets $T$ and $T_{ε}$ : $T_{j o i n t} = T \cup T_{ε}$ .
Find the number $N (T_{j o i n t})$ of elements in the set $T_{j o i n t}$ .
Set $N_{ε} (T_{j o i n t}) = N (T_{j o i n t}) - 1$ .
Set $H_{ε} (T \lor T_{ε}) = \log_{2} N_{ε} (T_{j o i n t}) .$
Return $H_{ε} (T \lor T_{ε})$ .

The function

e p s_e n t r o p y

was implemented in MATLAB^® by concatenation of the sets

T

and

T_{ε}

using the function cat with further removing of the doubling elements by the function unique.

Function 2.

e p s_c a p a c i t y (T, ε)

Input:: Set $T = \{t_{0}, t_{1}, t_{2}, \dots, t_{m}\}$ of time moments, $t_{j} < t_{j + 1}$ , $j = 0, 1, 2, \dots, m - 1$ ; radius $ε > 0$ .
Output:: $ε$ -capacity $E_{ε} (T)$ of the set $T$ .

1.: If $(t_{m} - t_{0}) \leq ε$ then
2.: Set $M_{ε} (T) = 1$ .
3.: Else
4.: Set $M_{ε} (T) = 2$ .
5.: Set $j = 0$ .
6.: For $i = 1$ to $m - 1$ do:
7.: If $(t_{i} - t_{j}) \leq ε$ or $(t_{m} - t_{i}) \leq ε$ then
8.: Continue.
9.: Else
10.: Set $M_{ε} (T) = M_{ε} (T) + 1$ .
11.: Set $j = i$ .
12.: End if.
13.: End for.
14.: End if.
15.: Set $E_{ε} (T) = \log_{2} M_{ε} (T)$ .
16.: Return $E_{ε} (T)$ .

The function

e p s_c a p a c i t y

computes the number

M_{ε} (T)

ε

-distinguishable elements in the set

T

for given

ε

and then computes

E_{ε} (T)

{l o g}_{2}

of this number.

Time complexity

C

of Algorithm 1 includes the following terms:

O (1)

– complexity of the lines 1-4;

O (m)

– complexity of the line 5;

O (m \log m)

– complexity of the line 6;

O (1)

– complexity of the line 7;

O (m)

– complexity of the line 8 and

O (1)

– complexity of the lines 9-13. Then, time complexity of each iteration of the algorithm is

O (m \log m)

. The maximal number of iterations is

n = (t_{m} - t_{0}) / 2 s

; hence complexity of Algorithm 1 is

C = n \times O (m \log m) .

(33)

Convergence of Algorithm 1 is guaranteed by the indicated above fact that

ε

-information

I_{ε} (T)

increases with increasing

ε

while

ε

-capacity

E_{ε} (T)

decreases with increasing

ε

. Since the interval

T = [0, t_{m}]

is bounded, the difference between increasing

ε

-information

I_{ε} (T)

and decreasing

ε

-capacity

E_{ε} (T)

has its minimum in

T

, which is a terminating point of the algorithm.

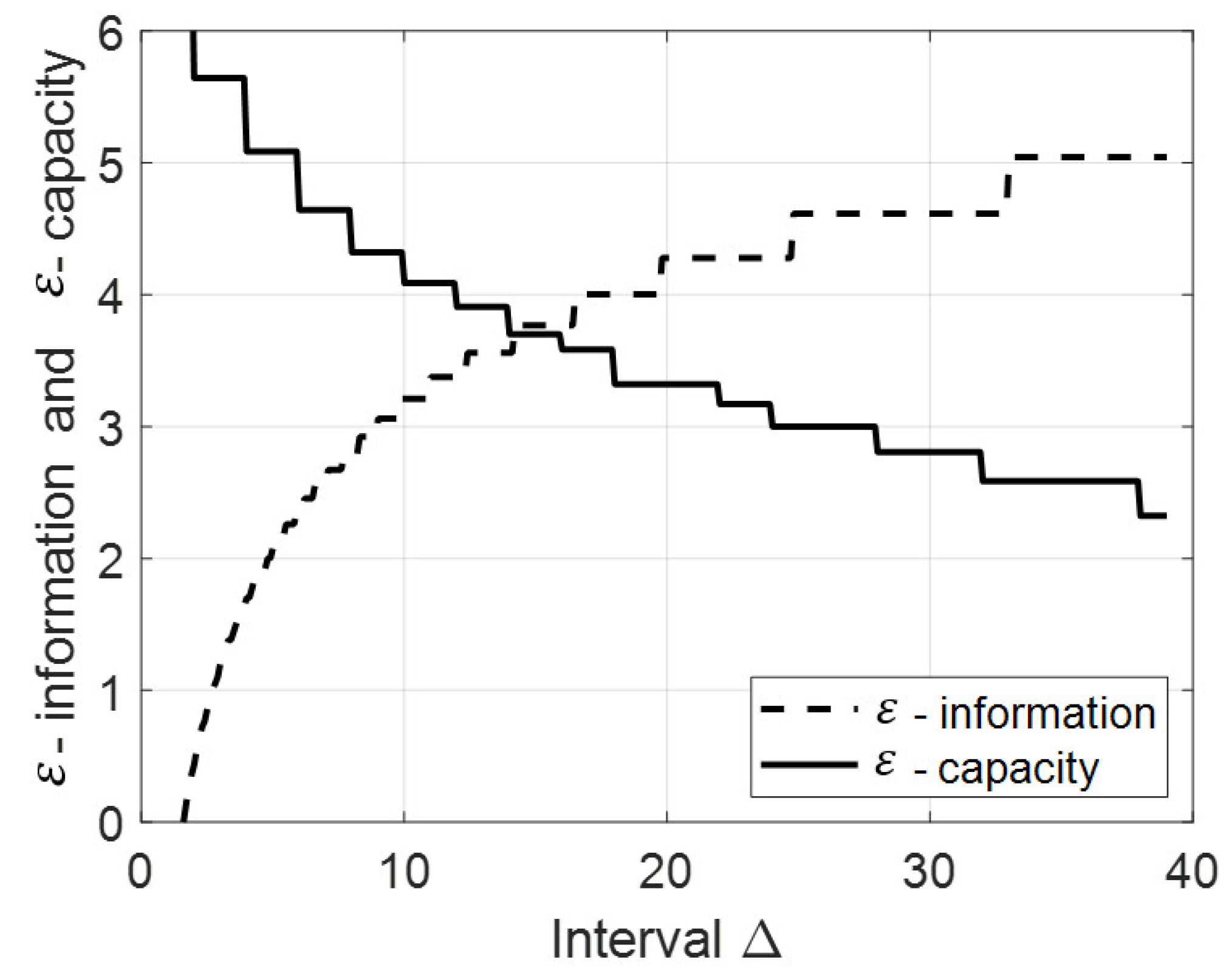
Dependence of the functions

I_{ε} (T)

and

E_{ε} (T)

on the interval length

Δ = 2 ε

is illustrated in Figure 1.

The computed interval is

Δ = 14.21

. For this interval and

ε = Δ / 2 = 7.10

, the values of

ε

-information and

ε

-capacity are

I_{ε} (T) = E_{ε} (T) \approx 3.7

bit. Note that the accuracy of computing the interval

Δ

increases with decreasing the step

s

6. Examples

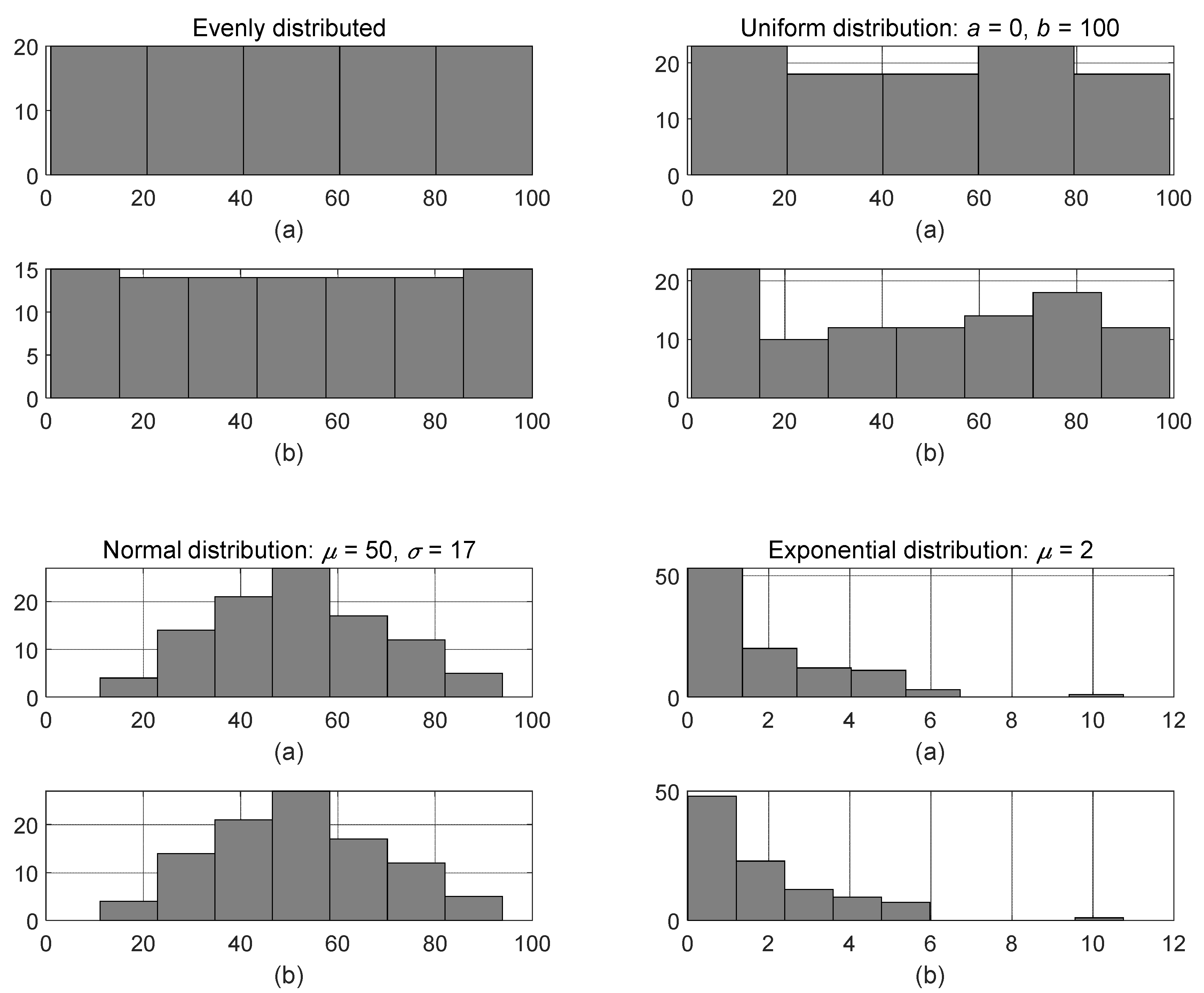
First, let us consider the examples of computing the interval lengths for different distributions of time intervals. In all considered cases we assume that the length of time interval

T = [0, t_{m}]

t_{m} = 100

and

m = 100

The data were generated by the MATLAB^® function random with respect to the distribution created by the MATLAB^® function makedist. In the examples, we used uniform distribution with

a = 0

and

b = t_{m}

, normal distribution with

μ = t_{m} / 2

and

σ = t_{m} / 6

, and exponential distribution with

μ = 2

The obtained interval lengths

Δ

were used as bin lengths

δ

in the histograms. For comparison, we present the histograms plotted with the bin lengths

δ

calculated using the Scott rule (see equation (3)), which is also used as a basis for a default method in MATLAB^®. The resulting histograms are shown in Figure 2.

The values of the interval lengths

Δ

are:

-: evenly distributed data:

Δ = 14.21, δ₁ = 9.90, δ₂ = 12.95, δ₃ = 21.81 and δ₄ = 21.54,
-: uniform distribution with $a = 0$ and $b = t_{m}$ :

Δ = 14.11, δ₁ = 9.83, δ₂ = 12.87, δ₃ = 22.69 and δ₄ = 22.65,
-: normal distribution with $μ = t_{m} / 2$ and $σ = t_{m} / 6$ :

Δ = 14.91, δ₁ = 8.27, δ₂ = 10.83, δ₃ = 13.11 and δ₄ = 10.38,
-: exponential distribution with $μ = 2$ :

Δ = 1.20, δ₁ = 1.07, δ₂ = 1.41, δ₃ = 1.35 and δ₄ = 0.91.

The suggested method results in the interval lengths

Δ

that are close to the interval lengths

δ

provided by the conventional methods with respect to the distribution of the data. In fact, for evenly and uniformly distributed data interval length

Δ

is close to the interval length

δ_{2}

resulted by the Sturges method, for normal distribution

δ_{2} < Δ < δ_{3}

and for exponential distribution

δ_{1} < Δ < δ_{2}

Now let us consider the use of the suggested algorithm for specification of the arrival rates

λ

and corresponding service rates

μ

. Assume that the office, where the mentioned above clerk works, serves

480

clients

8

hours during the day that is

T = 8 \times 60 = 480

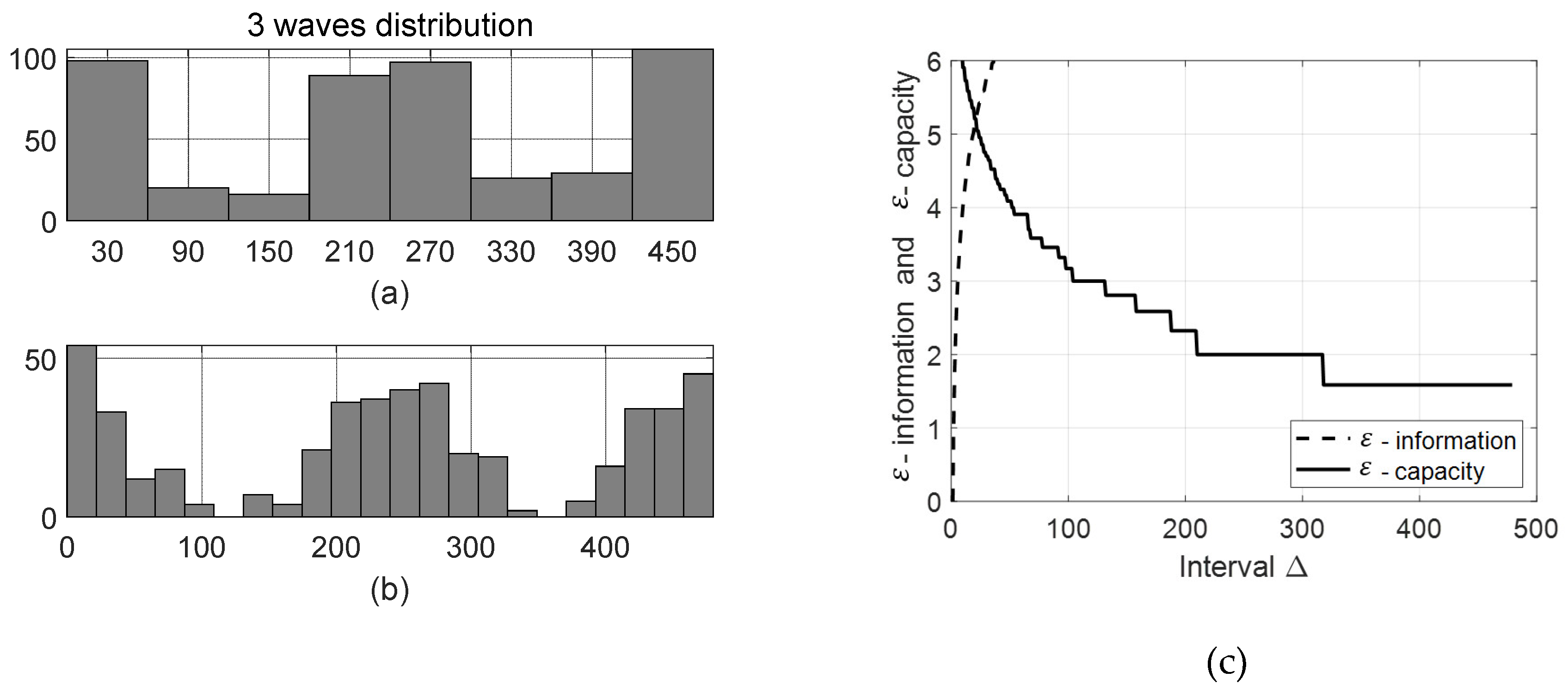
minutes. Also, assume that the clients arrive by three “waves” – in the morning, in the midday and in the evening. The histogram of the number of clients during the day is shown in Figure 3.a. In this histogram the bin length is computed by the Scott rule (value

δ_{3}

below).

The values of the interval lengths

Δ

for this distribution are:

Δ = 22.0, δ₁ = 21.91, δ₂ = 48.45, δ₃ = 67.99 and δ₄ = 66.41.

Histogram of the number of clients during the day with the bin length

δ = Δ

computed by the suggested algorithm is shown in Figure 3.b. Dependence of the functions

I_{ε} (A)

and

E_{ε} (A)

ε

for this distribution is shown in Figure 3.c.

From the results of computations of the interval length

Δ

and the bin lengths

δ

it follows that by the suggested algorithm the arrival rates during a day should be calculated each

22

minutes, while by the Scott they should be calculated each

68

minutes. Thus, for multimodal distribution the suggested algorithm results in shorter intervals that provides more exact representation of the data.

7. Conclusion

In the paper, we suggested the method of calculating optimal time intervals required for definition of arrival and departure rates. The method is useful for specification of the bin lengths in histograms, especially for the data with multimodal distributions.

The method utilizes the Kolmogorov and Tikhomirov

ε

-entropy and

ε

-capacity and the Rokhlin entropy of partition. Optimality of the partition is defined basing on the

ε

-information.

The procedure is presented in the form of a ready-to-use algorithm, which was compared with the known methods used for calculation of the interval lengths in histograms and demonstrated its robustness and correct sensitivity to the data.

Funding

This research has not received any grant from funding agencies in the public, commercial, or non-profit sectors.

Competing interests

The authors declare no competing interests.

References

Dinaburg, E.I. On the relations among various entropy characteristics of dynamical systems. Math. USSR Izvestija 1971, 5, 337–378. [Google Scholar] [CrossRef]
Freedman, D.; Diaconis, P. On the histogram as a density estimator: L₂ theory. Zeit. Wahrscheinlichkeitstheorie und Verwandte Gebiete 1981, 57, 453–476. [Google Scholar] [CrossRef]
Gross, D.; Shortle, J.F.; Thompson, J.M.; Harris, C.M. Fundamentals of Queueing Theory, 4th ed.; John Wiley & Sons: Hoboken, NJ, 2008. [Google Scholar]
Jacod, J.; Protte, P. Discretization of Processes; Springer: Berlin, 2012. [Google Scholar]
Keller, J.B. Time-dependent queues. SIAM Review 1982, 24, 401–412. [Google Scholar] [CrossRef]
Kolmogorov, A.N.; Tikhomirov, V.M. ɛ-entropy and ɛs-capacity of sets in functional spaces. Amer. Mathematical Society Translations, Ser. 2 1961, 17, 277–364. [Google Scholar]
Lawler, G.F. Introduction to Stochastic Processes; Chapman & Hall: New York, 1995. [Google Scholar]
Newell, G.F. Queues with time-dependent arrival rates (I-III). J. Applied Probability, 1968, 5(2), 436-451 (I); 5(3), 579-590 (II); 5(3), 591-606 (III).
Reis, Y. Private conversation. Ariel University, Ariel, March 2021. [Google Scholar]
Rokhlin, V.A. New progress in the theory of transformations with invariant measure. Russian Mathematical Surveys 1960, 15, 1–22. [Google Scholar] [CrossRef]
Schwarz, G. Estimating the dimension of a model. Annals of Statistics 1978, 6, 461–464. [Google Scholar] [CrossRef]
Scott, D.W. On optimal and data-based histograms. Biometrika 1979, 66, 605–610. [Google Scholar] [CrossRef]
Shannon, C. A mathematical theory of communication. The Bell System Technical Journal 1948, 27, 379–423. [Google Scholar] [CrossRef]
Sinai, Y.G. Topics in Ergodic Theory.; Princeton University Press: Princeton, 1993. [Google Scholar]
Sturges, H. The choice of a class-interval. J. Amer. Statistics Association 1926, 21, 65–66. [Google Scholar] [CrossRef]
Vitushkin, A.G. Theory of Transmission and Processing of Information; Pergamon Press: New York, 1961. [Google Scholar]

Figure 1. Dependence of

ε

-information

I_{ε} (T)

and

ε

-capacity

E_{ε} (T)

on the interval length

Δ = 2 ε

for the set

T

m = 100

evenly distributed time moments;

T = [0, t_{m}]

t_{m} = 100

and

s = 1

Figure 1. Dependence of

ε

-information

I_{ε} (T)

and

ε

-capacity

E_{ε} (T)

on the interval length

Δ = 2 ε

for the set

T

m = 100

evenly distributed time moments;

T = [0, t_{m}]

t_{m} = 100

and

s = 1

Figure 2. Histograms of the data plotted using the bin lengths computed by the Scott rule (figures (a) for each distribution) and using the bin lengths

δ = Δ

computed by the suggested algorithm (figures (b) for each distribution).

Figure 2. Histograms of the data plotted using the bin lengths computed by the Scott rule (figures (a) for each distribution) and using the bin lengths

δ = Δ

computed by the suggested algorithm (figures (b) for each distribution).

Figure 3. Arrivals of the clients during a day: (a) histogram with the bin length computed by the Scott rule; (b) histogram with the bin length

δ = Δ

computed by the suggested algorithm; (c) dependences of

ε

-information

I_{ε} (A)

and

ε

-capacity

E_{ε} (A)

ε

for the set of arrival times.

Figure 3. Arrivals of the clients during a day: (a) histogram with the bin length computed by the Scott rule; (b) histogram with the bin length

δ = Δ

computed by the suggested algorithm; (c) dependences of

ε

-information

I_{ε} (A)

and

ε

-capacity

E_{ε} (A)

ε

for the set of arrival times.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Definition of Optimal Time Intervals in the Queues’ Analysis: The Use of Epsilon-Entropy and Epsilon-Capacity

Abstract

1. Introduction

2. Problem Formulation

3. Methods

3.1. ε -Entropy and ε -Capacity

3.2. ɛ-Entropy of Partition

4. Suggested Solution

5. Algorithmic Implementation

6. Examples

7. Conclusion

Funding

Competing interests

References

MDPI Initiatives

Important Links

Subscribe

3.1. $ε$ -Entropy and $ε$ -Capacity