Prerpints.org logo
Preprint
Article

Reverse Engineering: Modeling Exhaust Emissions in Older Vehicles in the Era of New Technologies

Altmetrics

Downloads

53

Views

30

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

06 September 2024

Posted:

09 September 2024

You are already at the latest version

Alerts
Abstract
In the face of increasing environmental protection requirements, modeling emissions from older vehicles presents a significant challenge. This paper introduces an innovative methodology for developing emission models for older vehicles by employing advanced AI and machine learning techniques. The study utilized algorithms, including gradient boosting, to analyze data from road tests and the OBDII diagnostic interface, allowing the creation of precise models for CO₂, CO, THC and NOx emissions. A key achievement is the implementation of input data clustering, which significantly enhances the accuracy of emission forecasts. Model validation demonstrated high precision, with notable R² coefficients and mean squared errors. The developed models serve as a crucial tool for analyzing and managing emissions in the context of an aging vehicle fleet, providing new opportunities to shape transportation policy and strategies for pollution reduction.
Keywords: 
Subject: Engineering  -   Transportation Science and Technology

1. Introduction

In the era of rapid advancement in automotive technology, the focus has changed to achieving excellence in performance, safety, and balanced environmental development. Modern vehicles are now equipped with advanced emission control systems that significantly reduce pollutants [1,2]. However, older vehicles, which were manufactured before these innovations were introduced, still constitute a substantial part of the global vehicle fleet and continue to pose a challenge in emission management [3].
Older vehicles lacking modern emission control technologies typically emit higher levels of pollutants, complicating the precise modeling and regulation of their exhaust emissions [4,5]. Vehicles without advanced technologies such as catalytic converters or exhaust gas recirculation systems produce significantly higher levels of pollutants compared to contemporary models [6]. Historically, when emission standards were less stringent, engine designs and combustion systems were not optimized to minimize harmful emissions such as carbon dioxide (CO₂), nitrogen oxides (NOx), carbon monoxide (CO), or hydrocarbons (THC) [7]. As a result, these vehicles generate higher amounts of these pollutants, presenting a significant challenge for modeling their emissions in the context of modern environmental standards [8]. Furthermore, precise regulation of the emissions of these vehicles is problematic because the absence of advanced control technologies means that the pollutants emitted are less uniform and can vary significantly depending on the vehicle’s technical condition, operating conditions, and fuel type [9,10]. This makes it more difficult to establish accurate emission profiles and forecast their environmental impact. Additionally, older vehicles may exhibit significant variability in emissions over time [11,12], further complicating the application of standard modeling methods and the assessment of remedial measures [13,14].
From a modeling perspective, there is also a challenge associated with the lack of high-quality data for these vehicles, which could be used for precise calibration of emission models. Consequently, standard emission models developed for modern vehicles may be inappropriate or inadequate for older vehicles, leading to inaccurate forecasts and inefficient emission management. This requires the development of specific modeling methods that take into account the historical technical conditions and emission characteristics of older vehicles to effectively monitor and control their environmental impact. Artificial intelligence (AI) thus represents an opportunity to develop new emission models for older vehicles, allowing for more accurate predictions of harmful exhaust components.
Artificial intelligence (AI) and machine learning (ML) techniques have a significant impact on the emission modeling process, particularly with respect to older vehicles [15]. Traditional emission modeling methods often relied on precise but limited chemical and physical equations. In contrast, AI and ML enable a more dynamic and adaptive approach [16]. Machine learning algorithms can analyze large amounts of data from various sources, such as road tests, vehicle sensors, and historical data, allowing more accurate emission predictions in a wide range of operational conditions [17]. For older vehicles that may lack modern emission monitoring systems, ML can help create predictive models based on data collected from tests and simulations, even if these vehicles are not equipped with advanced sensors [18]. Algorithms such as neural networks and random forests can capture complex patterns and relationships that would be challenging to determine using traditional methods [19,20]. Thus, AI and ML not only improve the accuracy of emission forecasts but also facilitate the development of more effective emission reduction strategies for older vehicles that may not meet today’s environmental standards.
There is a body of work that addresses emission modeling issues for older vehicles, but focuses primarily on emissions related to the types of fuels used. For example, the study referred to as [21] develops advanced models of prediction of CO2 emissions for vehicles powered by compressed natural gas (CNG), in response to stringent global environmental regulations. Using XGBoost within the Optuna Python framework and data from chassis dynamometer and road tests, the study achieves high model precision, providing critical insights for environmental decision makers and urban transportation planning.
The application of artificial intelligence techniques to modeling emissions for older vehicles powered by LPG is presented in the work cited as [22]. This study introduces a new methodology for creating CO₂ emission models for LPG-powered vehicles based on road test data and the OBDII diagnostic interface. Using machine learning methods, the model demonstrates good precision, which proves useful for CO₂ emission analysis and creating emission maps for urban areas, achieving R2 coefficients of 0.61 and an MSE of 0.77. The need to develop new emission models in the context of an aging vehicle fleet is also highlighted in the work referenced as [23]. This study investigates the impact of aging processes on vehicle emissions, focusing on changes in aerosol pollutants resulting from these processes. Describes initial emission properties such as hygroscopicity, particle size distribution, and chemical composition, as well as changes in these properties as a result of physical actions and photochemical reactions. The study also discusses the impact of vehicle driving cycles, emission control technologies, and fuels and identifies areas for future research that could support the control of air pollution related to vehicle emissions. The increase in emissions due to the increased mileage of older vehicles is further illustrated in the study cited as [24].
A review of existing research reveals significant gaps in the literature. Many current studies focus on modeling individual exhaust components, while this study addresses groups of components. Additionally, numerous works concentrate on modeling specific vehicle fuel technologies without considering the impact of vehicle age. Furthermore, none of the existing studies has explored the issue of clustering of input data in the context of emission modeling.
In light of these gaps, this study focuses on the challenge of modeling emissions from older vehicles from a reverse engineering perspective. The emission modeling process employs modern methods, including artificial intelligence techniques using the Python programming language. For the first time, the input data has been clustered, enhancing the predictive capabilities of the models. Emissions have been classified into two main groups: for cold and warm engine conditions. This detailed approach allows for precise replication of emissions from older vehicles and can be scaled to larger vehicle groups or emission databases, facilitating the creation of more accurate predictive models. These models have been validated and their potential applications have been discussed, including their use in shaping transportation policy, particularly with respect to the fleet of aging vehicles.

2. Methods

The general outline of the work is presented in Figure 1. The study initially involved selecting a vehicle that could represent the older fleet of vehicles that did not meet the new stringent emission standards. The next step was to choose a test route and conduct road tests. These tests were performed using the Portable Emission Measurement System (PEMS), which collected emission data, vehicle location, and environmental data at a frequency of 1Hz. The data were then saved in.csv format for further processing using the Python programming language. All analyses and data processing were performed in the Google Colab programming environment. A key aspect of this process was the clustering of input data for emission modeling. This approach facilitates the creation of better and more accurate emission models. Subsequently, emission models were developed using machine learning techniques based on the appropriate clusters of input data. The final stage of the work demonstrates the potential applications of the developed models.

2.1. Research Vehicle, Route and Apparatus Used

The primary objective of this work was to develop a new methodology for creating emission models for vehicles, specifically tailored for older models. The vehicle studied is a Euro 2 class passenger car, manufactured in 1998. It is equipped with a 1598 cm3 engine that operates on spark ignition and is fueled by gasoline. The engine produces a maximum power of 88 kW at 6300 rpm and a maximum torque of 144 Nm at 4500 rpm. The car features a five-speed manual transmission. The fuel supply system is a multi-point fuel injection (MPI) system, and the emission control system is a three-way catalytic converter (TWC). The vehicle weighs 1230 kg. The vehicle studied is shown in Figure 2.
Emission data was collected using a portable emission measurement system (PEMS). PEMS employs various technologies to monitor exhaust emissions, including flame ionization detectors (FID) for hydrocarbons, NDIR spectrometers for CO and CO₂, and chemiluminescence detectors (CLD) for NO and NO₂. According to EU Regulation 2017/1151, deviations between PEMS results and stationary analyzers should not exceed 15% for HC, CO, and NOx and 10% for CO₂ [25,26]. The PEMS unit is installed in the vehicle’s trunk, with sensors connected to the exhaust pipe, and the sample extraction line must be heated to 190°C [27,28]. In addition, the system monitors air temperature and humidity and utilizes a GPS transmitter. An OBDII interface can also be connected to the ECU for a more comprehensive emission analysis.
To collect data on harmful exhaust components, a specific test route was selected for the initial phase of the work, where emission levels were recorded. The data obtained from the actual drives were subsequently used to develop emission models for the selected substances. Given the need for a large amount of input data, the test route was 40 km long, allowing the collection of sufficient information for precise modeling. The route included driving through the city of Rzeszów, the S19 expressway around Rzeszów, and a section of the A4 motorway. This varied route provided a wide range of data, reflecting different engine operating conditions and variable speeds. As a result, accurate information on harmful exhaust emissions was obtained under various driving and operational conditions.

2.2. Software Used and Data Processing

Data analysis and model execution were performed in the Google Collaboration environment. Google Colaboratory, also known as Google Colab, is a free service from Google that enables the creation and execution of interactive Jupyter notebooks in the cloud [29]. This platform provides an integrated environment that supports Python coding and documentation of results in notebooks, facilitating collaboration and project sharing. With free access to GPU and TPU units, Google Colab significantly accelerates computations related to training machine learning models [30].
A key aspect of the innovative modeling approach presented was the selection of explanatory variables to develop CO2, CO, THC, and NOx emission models. To create the most universal models, it was decided that the explanatory variables for emissions would be fundamental vehicle parameters, namely speed and acceleration. The overall process for handling emission and vehicle movement data in the context of modeling is illustrated in Figure 3.
In this context, clustering of the data was used for the first time to create the most accurate emission models possible. Vehicles operating at different speeds and acceleration dynamics generate varying levels of emissions, especially older vehicles, which may also encounter problems such as fuel system problems and higher fuel doses. Spectral clustering was used for data clustering purposes. The emissions data were further divided into categories for the cold and warmed engine states.
The use of data clustering techniques, such as Spectral Clustering, in emission modeling offers several benefits, particularly in the analysis of emissions from warm engines. Clustering allows for the identification of natural groups within the data that may correspond to different engine operating conditions and emission levels [31]. For a warm engine, different clusters may reflect various speeds and acceleration ranges, each having a different impact on the levels of harmful emissions. The application of spectral clustering in this context has several notable advantages. First, Spectral Clustering is capable of capturing complex, nonlinear structures in the data, which is particularly useful for emissions modeling, where relationships between variables can be intricate. Second, clustering facilitates a better understanding of how different engine operating conditions affect emission levels, potentially leading to more accurate predictive models and more effective emission control strategies.

3. Results

3.1. Exhaust Emissions Results from Road Tests

Figure 4 presents the THC, NOx, CO, and CO2 emission levels recorded during the tests. Notably, for THC and NOx, significantly higher emission values are observed for the cold engine, making the distinction between cold and hot emission data crucial for accurate modeling. CO emissions for the cold engine also contribute more to total emissions, whereas CO2 emissions remain at the same level as for the heated engine. The increase in THC, NOx, and CO emissions from the cold engine is closely related to the unheated exhaust emission control system of the vehicle. When the engine has not yet reached its optimal operating temperature, the combustion process is less efficient, leading to higher levels of hydrocarbons (THC) and nitrogen oxides (NOx) in the exhaust. An unheated catalyst and other components of the emission control system are not yet operating at full efficiency, increasing the emission of harmful substances [32,33]. For carbon monoxide (CO) emissions, the higher values for the cold engine also indicate inefficient combustion, typical of a cold engine, where the fuel-air mixture is not optimally burned. On the other hand, CO2 emissions, which are primarily correlated with total fuel consumption, do not show as pronounced differences between the cold and heated engines. Although fuel consumption is slightly higher for the cold engine, as it requires more fuel to reach the optimal operating temperature, differences in CO2 emissions are less noticeable. CO2 is a direct indicator of the total amount of fuel burned, and these differences are less pronounced compared to other pollutants, which are more sensitive to the technical condition of the engine and the operating temperature. Therefore, analysis of CO2 emissions may not fully reflect the impact of engine state on exhaust emissions, whereas THC, NOx, and CO are more sensitive to changes in combustion efficiency and the operation of emission control systems.
The data set of emission inputs presented in Figure 4 was used to train the model. These data were divided into “cold” and “hot” emissions. Additionally, the data were further divided based on the clusters created for the explanatory variables, namely speed (V) and acceleration (a).

3.2. Clustering of Model Learning Inputs

To analyze emissions for different engine operating conditions, the Spectral Clustering algorithm was employed. This method allows for the identification of the optimal number of clusters in the data representing emission levels, based on explanatory variables such as speed (V) and acceleration (a). The choice of this method was motivated by the need to capture complex nonlinear patterns in the data that are difficult to identify using traditional clustering methods, such as k-means. To determine the optimal number of clusters, the elbow method and silhouette coefficient analysis were used, calculated for various numbers of clusters (ranging from 2 to 9), which allowed the evaluation of cluster cohesion (Figure 5).
Figure 5 illustrates the evaluation of the silhouette score for different numbers of clusters (ranging from 2 to 9) used in the Spectral Clustering. The Silhouette Score is a measure of cluster quality, assessing how well points are grouped within a cluster and how distinct they are from points in other clusters [34]. The horizontal axis of the chart represents the number of clusters, while the vertical axis shows the Silhouette Score value. From the shape of the chart for cold emissions, it can be observed that the highest Silhouette Scores are achieved with 4 and 5 clusters, with the highest value of approximately 0.67 for 4 clusters. This suggests that 4 clusters provide the most effective clustering, indicating that it is the optimal number of clusters for the Spectral Clustering method used. The Silhouette Score for cold emissions decreases significantly with six clusters and remains at a lower level for larger numbers of clusters, indicating that a greater number of clusters leads to a less distinct and effective data partition. Thus, the optimal number of clusters for analysis using spectral clustering is 4, as it produces the highest silhouette score, indicating the best cluster quality. However, for warm emissions, the best solution is to use two clusters.
In the study, Spectral Clustering was applied to analyze emission data collected from vehicle engines. Data were initially divided into two sets according to engine temperature: cold and warm. Data for the cold engine state included the first 500 records, while the remaining records were assigned to the warm engine state.
Spectral clustering was performed on each subset, with the optimal number of clusters determined on the basis of preliminary analysis. For cold engine data, four groups were selected, while two groups were chosen for warm engine data (Figure 6). The clustering process utilized an affinity matrix based on the nearest neighbors to capture the internal structure of the data.
The results shown in Figure 6 are illustrated using scatter plots, where each data point is colored according to its assignment of clusters. These scatter plots demonstrate how the data are grouped on the basis of the explanatory variables for future emission models: speed (V) and acceleration (a), with distinct differences between clusters clearly marked. Such visualizations provide information on clustering patterns and relationships between emission characteristics under different engine operating conditions.

3.3. Emission Modeling and Validation

For the data clusters created, emission models were developed for CO2, CO, THC and NOx for both cold and hot engine states. The modeling process employed various regression techniques to assess its effectiveness in the context of different engine conditions. The simulation was carried out separately for the data from cold and hot engines, allowing for a detailed analysis of the impact of the engine state on the prediction results.
The first step was to define the target variables and the regression models to be evaluated. The models were evaluated based on their ability to predict emissions using selected features such as vehicle speed and acceleration. Different regression methods were considered to achieve a comprehensive understanding of the relationships between variables and to accurately forecast emissions for both cold and hot engines. Linear regression, as a fundamental model, was used as a starting point to evaluate the linear relationships between vehicle features and emissions [35]. Although linear regression is simple and effective, it may not suffice for more complex, nonlinear relationships. Therefore, polynomial regression was employed to model non-linear dependencies by adding polynomial terms, potentially better capturing intricate interactions between variables. Additionally, Lasso and Ridge regressions were introduced as regularization methods to address overfitting by penalizing large model coefficients. Regularization is crucial for feature selection and improving model generalization, particularly with high-dimensional data. Decision tree regression, on the other hand, introduces a hierarchical approach to data classification that handles nonlinear relationships well, but may be prone to overfitting if not properly pruned [36].
To further enhance prediction accuracy, random forest regression was used, which combines predictions from multiple decision trees, improving model stability and accuracy. Moreover, Support Vector Machines (SVM) regression was included as an advanced method that utilizes kernel functions to map input features to higher dimensions, potentially capturing more complex, non-linear relationships. The testing of various regression methods allowed the comparison of their effectiveness and the selection of the most appropriate model for the prediction of emissions, considering the specificity and complexity of the data.
For regression models such as polynomial regression, the process involved creating new features through polynomial transformation and then training a linear regression model on the processed data. The results were evaluated based on the mean squared error (MSE) and the coefficient of determination (R2), providing information on the accuracy of the prediction and the fit of the model. For each target (e.g., THC, NOx, CO, CO2) and each regression model, MSE and R2 were calculated for both cold and hot engine data. In the case of polynomial regression, the process included feature transformation, model training, and performance evaluation based on predictions and actual values. For the remaining models, the build_and_evaluate_model function was used to automatically build and assess the model, providing relevant metrics.
The results of the best prediction methods for each emission component and engine state are presented in Table 1.
Table 1 presents the evaluation results of various regression models for predicting the emissions of four chemical compounds. THC, NOx, CO, and CO2, for both cold and hot engine states. For each chemical compound, the model with the best performance is indicated, along with quality metrics such as MSE (mean squared error) and R2 (coefficient of determination).
For THC emissions in a cold engine, the best model was Random Forest Regression, achieving a low MSE of 0.00002 and a relatively high R2 of 0.74408, indicating good prediction quality. For NOx in the same engine state, polynomial regression was the best performer, with an MSE of 0.00006 and an R2 of 0.59200, suggesting moderate model fit. Gradient Boosting was the best model for CO emissions, though its MSE was 0.00291, and R2 was relatively low at 0.47986, indicating that the model may not be ideal for predicting this emission. For CO2 emissions in a cold engine, polynomial regression was also the best model, achieving an MSE close to zero (0.00321) and a very high R2 of 0.92200, indicating excellent fit of the model.
In the case of a hot engine, Gradient Boosting was the best model for THC, with a minimal MSE of 0.00001 and an R2 of 0.65674, reflecting good prediction quality. For NOx, polynomial regression was again the best model, but with lower MSE (0.00001) and R2 of 0.41565, indicating moderate fit. CO emissions in a hot engine were best predicted by polynomial regression, although its MSE was 0.00277 and R2 was relatively low at 0.21246, suggesting lower model quality compared to other emissions. Lastly, for CO2, polynomial regression was also the best model, with an MSE of 0.00221 and a very high R2 of 0.95100, indicating very good fit of the model.
These results demonstrate that different regression models exhibit varying effectiveness in predicting different types of emissions, and the choice of the best model depends on the specific chemical compound and the state of the engine. Model validation was also performed through visual interpretation of residual plots, histograms, real vs. predicted plots, and QQ plots. An example validation plot for the prediction of THC for a hot engine is presented in Figure 7.
Figure 7 presents example validation plots for THC prediction in a hot engine. The residual plot displays the differences between the actual and predicted values of the model as points. The horizontal axis represents the predicted values, while the vertical axis shows the residuals, which are the differences between actual and predicted values. Ideally, residuals should be randomly distributed around a horizontal line at zero, indicating a good fit of the model. For the THC component in Figure 7, the residual plot shows that most of the data points are clustered around the horizontal line.
The histogram of the residuals illustrates the distribution of the residuals in bar form. The horizontal axis shows the residual values, and the vertical axis represents the number of observations within each range of residual values. Ideally, the histogram should resemble a normal distribution, suggesting that the residuals are randomly distributed and the model fits the data well. The histogram of residuals presented shows a distribution similar to the normal distribution.
The real vs. predicted values plot shows how well the model predicts actual values. The horizontal axis represents the actual values, while the vertical axis represents the predicted values. Ideally, all points should be close to the diagonal line representing perfect fit (where predicted values equal actual values). The dispersion of points around this line indicates the model’s accuracy—smaller deviations suggest better model fit. For the prediction of THC, the real vs. predicted plot also indicates a good fit of the model.
The Q-Q (quantile-quantile) plot of residuals is used to assess whether the residuals follow a normal distribution [37]. The horizontal axis shows the theoretical quantiles of the residuals of a normal distribution, while the vertical axis shows the empirical quantiles of the residuals. If the points on the plot align along a straight line, it indicates that the residuals are well-fitted to a normal distribution, suggesting that the model is appropriate. Most of the THC prediction data points are located along the straight line.

3.4. Example Use of Models

The developed models can be used for new predictions simply by entering the variables V (velocity) and a (acceleration). On the basis of these inputs, emissions can be predicted for selected engine operating conditions: cold or hot. These models are applicable to new real-world data, which can be easily obtained from road tests using tools such as smartphones and GPS. They can also be used for computer simulations, for example, by generating vehicle movement data from simulation software like Vissim. The models generate emission data in grams per second (g/s) or as the total emission for the entire test route. If vehicle location data is available, it is also possible to generate emission maps.
An example of NOx emission map generation, using both real and predicted data, is presented in Figure 8. For the developed models, it is possible to adjust the engine warm-up time so that the model initially estimates emissions for a cold engine and, after a certain period, switches to estimating emissions for a hot engine. Based on Figure 8, it can be observed that for each stage of driving with new road data, the model estimates NOx emissions with very good precision.

4. Discussion

In the context of modeling emissions from older vehicles, research reveals significant gaps in the existing literature, highlighting the need for further studies and innovations. Analysis of previous work shows a tendency to focus on modeling individual pollutants, such as CO2, NOx, or CO, without considering their collective characteristics. This study addresses this gap by presenting an approach that models emissions as a group of components, contributing to a more comprehensive and accurate understanding of emissions from older vehicles.
Furthermore, existing research often focuses on specific vehicle fueling technologies, such as LPG or CNG, without considering the impact of vehicle age on emissions. This study expands this scope by incorporating aging vehicles as a critical element of emissions analysis, allowing better adaptation of models to real-world operating conditions.
Another important aspect is the use of clustering techniques in the modeling process. Previous studies have not addressed this topic, which is a notable limitation. This research introduces an innovative approach by clustering input data, significantly enhancing the predictive capabilities of emission models. Emissions were classified into two main groups: cold and hot engine conditions, enabling more accurate representation of real-world operating conditions for older vehicles. This approach can be scaled to larger vehicle groups and emission databases, potentially leading to the development of more precise predictive models and more effective emission management.
A relevant study to which the results of this research can be related is [38]. This work presents a methodology for creating models of THC and NOx emissions for vehicles with start-stop technology, considering the variability and dynamics of contemporary powertrains. Various machine learning techniques were tested, with random forests and gradient boosting demonstrating the best predictive capabilities, achieving an R2 of approximately 0.9 for engine emissions. Based on these results, recommendations for effective vehicle emission modeling were formulated. Another study that showcases the application of machine learning techniques to vehicle-related issues is [39]. This article describes the process of creating an energy consumption model for electric vehicles (EVs), which allows rapid generation of results and creation of energy maps. The best validation metrics were obtained using artificial intelligence methods, specifically neural networks, which enabled the development of two predictive models for the energy consumption of electric vehicles in winter and summer conditions, based on real driving cycles. Interesting findings concerning the emissions of internal combustion engine vehicles and their continuous impact, especially on vehicle traffic in Poland, as well as the energy consumption of BEVs, are also presented in [40]. The article compares emissions from internal combustion engine vehicles (ICEVs) and battery electric vehicles (BEVs) in the context of Poland’s coal-based energy mix, accounting for air pollutant emissions such as CO₂, NOx, SOx, CO and particulate matter (TSP). The analysis shows that replacing internal combustion engine vehicles with electric vehicles in Poland is not beneficial, as while CO, CO₂, and TSP emissions have decreased, NOx and SOx emissions have increased. The results are based on energy consumption data provided by the manufacturers and the COPERT model, as well as average vehicle mileage under Polish conditions. Aspects of emission modeling, particularly CO₂, are also addressed in [41]. This work focuses on the development of accurate emission models for hybrid and electric vehicles, especially in the context of low-emission zones, where precise mobility planning requires simulations based on updated databases. The study presents a two-dimensional CO₂ emission model for hybrid vehicles using artificial neural networks, which allows the simulation of various road scenarios and provides valuable information for future emission modeling work. The impact of fleet aging and its influence on modeling aspects is discussed in [42]. This study involves the development of a detailed inventory of air pollutant emissions from vehicles in Tianjin, a typical megacity in China, using a high-resolution time-space top-down method. The research found that light-duty passenger vehicles are the main sources of carbon monoxide and volatile organic compounds, while heavy-duty passenger and freight vehicles contribute significantly to nitrogen oxide and particulate matter emissions, with the majority of pollutants originating from vehicles meeting China III standards.
However, none of the aforementioned studies addresses the specifics of modeling older vehicles in detail. It is also important to highlight that the use of modern modeling techniques, leveraging artificial intelligence and Python programming in this study, has enabled the development of models well-suited to the characteristics of older vehicles. The application of machine learning algorithms, such as gradient boosting, allows capturing complex emission patterns that would be difficult to determine using traditional methods. Consequently, these models offer more accurate emission forecasts and can support the development of emission reduction strategies, which is particularly relevant in the context of an aging vehicle fleet.
In light of this, future research should focus on further refining modeling methods, incorporating new analytical techniques, and expanding the range of input data. It is also essential to investigate the impact of various control technologies and fuels on older vehicle emissions to develop more comprehensive and adaptive emission management strategies.

5. Conclusions

This study presents an innovative methodology for modeling older vehicle exhaust emissions, incorporating modern artificial intelligence techniques and data analysis from road and diagnostic tests. A key achievement is the development of a model for CO2, CO, THC, and NOx emissions for older vehicles, utilizing data clustering techniques and machine learning algorithms such as gradient boosting, among others. These models demonstrate high forecast accuracy.
The results of the analysis reveal that clustering of input data significantly improves the model’s ability to accurately reflect emissions under various vehicle operating conditions. The models developed in this study can be used to analyze exhaust emissions and create emission maps for urban areas, which is crucial to shaping transportation policies and emission reduction strategies in the context of an aging vehicle fleet. The application of artificial intelligence techniques has enabled the capture of complex emission patterns that are difficult to identify using traditional methods.
In summary, the results of this work confirm the effectiveness of the applied methodology in modeling emissions from older vehicles. The research conducted provides valuable insights for decision makers involved in environmental analysis and transport planning, allowing for more precise emission forecasting and more effective management of their environmental impact. Future research should focus on extending the methodology to other vehicle groups and improving emission modeling algorithms to meet the growing demands for environmental protection.

Funding

This research received no external funding.

Data Availability Statement

Data can be made available to those interested.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Agamloh, E., Von Jouanne, A., & Yokochi, A. (2020). An overview of electric machine trends in modern electric vehicles. Machines, 8(2), 20. [CrossRef]
  2. Suarez-Bertoa, R., Selleri, T., Gioria, R., Melas, A. D., Ferrarese, C., Franzetti, J.,... & Giechaskiel, B. (2022). Real-time measurements of formaldehyde emissions from modern vehicles. Energies, 15(20), 7680. [CrossRef]
  3. Sharma, R., Kumar, R., Singh, P. K., Raboaca, M. S., & Felseghi, R. A. (2020). A systematic study on the analysis of the emission of CO, CO2 and HC for four-wheelers and its impact on the sustainable ecosystem. Sustainability, 12(17), 6707. [CrossRef]
  4. Ge, J. C., Wu, G., Yoo, B. O., & Choi, N. J. (2022). Effect of injection timing on combustion, emission and particle morphology of an old diesel engine fueled with ternary blends at low idling operations. Energy, 253, 124150. [CrossRef]
  5. Gao, C., Gao, C., Song, K., Xing, Y., & Chen, W. (2020). Vehicle emissions inventory in high spatial–temporal resolution and emission reduction strategy in Harbin-Changchun Megalopolis. Process Safety and Environmental Protection, 138, 236-245.
  6. Alizadeh, H., & Sharifi, A. (2023). Analyzing urban travel behavior components in Tehran, Iran. Future transportation, 3(1), 236-253.
  7. de Meij, A., Astorga, C., Thunis, P., Crippa, M., Guizzardi, D., Pisoni, E.,... & Franco, V. (2022). Modelling the impact of the introduction of the EURO 6d-TEMP/6d regulation for light-duty vehicles on EU air quality. Applied Sciences, 12(9), 4257.
  8. Wallington, T. J., Anderson, J. E., Dolan, R. H., & Winkler, S. L. (2022). Vehicle emissions and urban air quality: 60 years of progress. Atmosphere, 13(5), 650.
  9. Singh, S., Kulshrestha, M. J., Rani, N., Kumar, K., Sharma, C., & Aswal, D. K. (2023). An overview of vehicular emission standards. Mapan, 38(1), 241-263.
  10. Zhan, T., Ruehl, C. R., Bishop, G. A., Hosseini, S., Collins, J. F., Yoon, S., & Herner, J. D. (2020). An analysis of real-world exhaust emission control deterioration in the California light-duty gasoline vehicle fleet. Atmospheric Environment, 220, 117107.
  11. Jaworski, A., Mądziel, M., Kuszewski, H., Lejda, K., Balawender, K., Jaremcio, M.,... & Ustrzycki, A. (2020). Analysis of cold start emission from light duty vehicles fueled with gasoline and LPG for selected ambient temperatures (No. 2020-01-2207). SAE Technical Paper.
  12. Wallington, T. J., Anderson, J. E., Dolan, R. H., & Winkler, S. L. (2022). Vehicle emissions and urban air quality: 60 years of progress. Atmosphere, 13(5), 650.
  13. Guno, C. S., Collera, A. A., & Agaton, C. B. (2021). Barriers and drivers of transition to sustainable public transport in the Philippines. World Electric Vehicle Journal, 12(1), 46.
  14. Guttikunda, S. K. (2024). Vehicle Stock Numbers and Survival Functions for On-Road Exhaust Emissions Analysis in India: 1993–2018. Sustainability, 16(15), 6298.
  15. Le Cornec, C. M., Molden, N., van Reeuwijk, M., & Stettler, M. E. (2020). Modelling of instantaneous emissions from diesel vehicles with a special focus on NOx: Insights from machine learning techniques. Science of The Total Environment, 737, 139625.
  16. Aliramezani, M., Koch, C. R., & Shahbakhti, M. (2022). Modeling, diagnostics, optimization, and control of internal combustion engines via modern machine learning techniques: A review and future directions. Progress in Energy and Combustion Science, 88, 100967.
  17. Zhao, B., Yu, L., Wang, C., Shuai, C., Zhu, J., Qu, S.,... & Xu, M. (2021). Urban air pollution mapping using fleet vehicles as mobile monitors and machine learning. Environmental Science & Technology, 55(8), 5579-5588.
  18. Mądziel, M. (2024). Instantaneous CO2 emission modelling for a Euro 6 start-stop vehicle based on portable emission measurement system data and artificial intelligence methods. Environmental Science and Pollution Research, 31(5), 6944-6959.
  19. Hoang, A. T., Nižetić, S., Ong, H. C., Tarelko, W., Le, T. H., Chau, M. Q., & Nguyen, X. P. (2021). A review on application of artificial neural network (ANN) for performance and emission characteristics of diesel engine fueled with biodiesel-based fuels. Sustainable Energy Technologies and Assessments, 47, 101416.
  20. Acheampong, A. O., & Boateng, E. B. (2019). Modelling carbon emission intensity: Application of artificial neural network. Journal of Cleaner Production, 225, 833-856.
  21. Mądziel, M. Modelling CO2 Emissions from Vehicles Fuelled with Compressed Natural Gas Based on On-Road and Chassis Dynamometer Tests. Energies 2024, 17, 1850. [Google Scholar] [CrossRef]
  22. Mądziel, M. Liquified Petroleum Gas-Fuelled Vehicle CO2 Emission Modelling Based on Portable Emission Measurement System, On-Board Diagnostics Data, and Gradient-Boosting Machine Learning. Energies 2023, 16, 2754. [Google Scholar] [CrossRef]
  23. Liu, H., Qi, L., Liang, C., Deng, F., Man, H., & He, K. (2020). How aging process changes characteristics of vehicle emissions? A review. Critical Reviews in Environmental Science and Technology, 50(17), 1796-1828.
  24. Kadijk, G., Elstgeest, M., Vroom, Q., Paalvast, M., Ligterink, N., & van der Mark, P. (2020). On road emissions of 38 petrol vehicles with high mileages. TNO report, 11883.
  25. Ziółkowski, A., Fuć, P., Lijewski, P., Jagielski, A., Bednarek, M., & Kusiak, W. (2022). Analysis of exhaust emissions from heavy-duty vehicles on different applications. Energies, 15(21), 7886.
  26. Pielecha, J., Skobiej, K., Gis, M., & Gis, W. (2022). Particle number emission from vehicles of various drives in the RDE tests. Energies, 15(17), 6471.
  27. Ziółkowski, A., Fuć, P., Lijewski, P., Bednarek, M., Jagielski, A., Kusiak, W., & Igielska-Kalwat, J. (2023). The Influence of the Type and Condition of Road Surfaces on the Exhaust Emissions and Fuel Consumption in the Transport of Timber. Energies, 16(21), 7257.
  28. Andrych-Zalewska, M., Chlopek, Z., Merkisz, J., & Pielecha, J. (2022). Comparison of gasoline engine exhaust emissions of a passenger car through the WLTC and RDE Type Approval Tests. Energies, 15(21), 8157.
  29. Johary, R., Révillion, C., Catry, T., Alexandre, C., Mouquet, P., Rakotoniaina, S.,... & Rakotondraompiana, S. (2023). Detection of large-scale floods using Google Earth Engine and Google Colab. Remote Sensing, 15(22), 5368.
  30. Li, Z. (2022). Forecasting weekly dengue cases by integrating google earth engine-based risk predictor generation and google colab-based deep learning modeling in fortaleza and the federal district, Brazil. International journal of environmental research and public health, 19(20), 13555.
  31. Govender, P., & Sivakumar, V. (2020). Application of k-means and hierarchical clustering techniques for analysis of air pollution: A review (1980–2019). Atmospheric pollution research, 11(1), 40-56.
  32. Teymoori, M. M., Chitsaz, I., & Zarei, A. (2023). Three-way catalyst modeling and fuel switch optimization of a natural gas bi-fuel-powered vehicle. Fuel, 341, 126979.
  33. Hamedi, M. R., Doustdar, O., Tsolakis, A., & Hartland, J. (2021). Energy-efficient heating strategies of diesel oxidation catalyst for low emissions vehicles. Energy, 230, 120819.
  34. Shutaywi, M., & Kachouie, N. N. (2021). Silhouette analysis for performance evaluation in machine learning with applications to clustering. Entropy, 23(6), 759.
  35. Kim, S. J., Bae, S. J., & Jang, M. W. (2022). Linear regression machine learning algorithms for estimating reference evapotranspiration using limited climate data. Sustainability, 14(18), 11674.
  36. Steigmann, L., Di Gianfilippo, R., Steigmann, M., & Wang, H. L. (2022). Classification based on extraction socket buccal bone morphology and related treatment decision tree. Materials, 15(3), 733.
  37. Petersen, A. H., & Ekstrøm, C. (2024). Technical Validation of Plot Designs by Use of Deep Learning. The American Statistician, 78(2), 220-228.
  38. Mądziel, M. Quantifying Emissions in Vehicles Equipped with Energy-Saving Start–Stop Technology: THC and NOx Modeling Insights. Energies 2024, 17, 2815. [Google Scholar] [CrossRef]
  39. Mądziel, M. Energy Modeling for Electric Vehicles Based on Real Driving Cycles: An Artificial Intelligence Approach for Microscale Analyses. Energies 2024, 17, 1148. [Google Scholar] [CrossRef]
  40. Zimakowska-Laskowska, M.; Laskowski, P. Emission from Internal Combustion Engines and Battery Electric Vehicles: Case Study for Poland. Atmosphere 2022, 13, 401. [Google Scholar] [CrossRef]
  41. Mądziel, M. Future Cities Carbon Emission Models: Hybrid Vehicle Emission Modelling for Low-Emission Zones. Energies 2023, 16, 6928. [Google Scholar] [CrossRef]
  42. Sun, S., Sun, L., Liu, G., Zou, C., Wang, Y., Wu, L., & Mao, H. (2021). Developing a vehicle emission inventory with high temporal-spatial resolution in Tianjin, China. Science of the Total Environment, 776, 145873.
Preprints 117532 g001
Figure 1. General scheme of work.
Figure 1. General scheme of work.
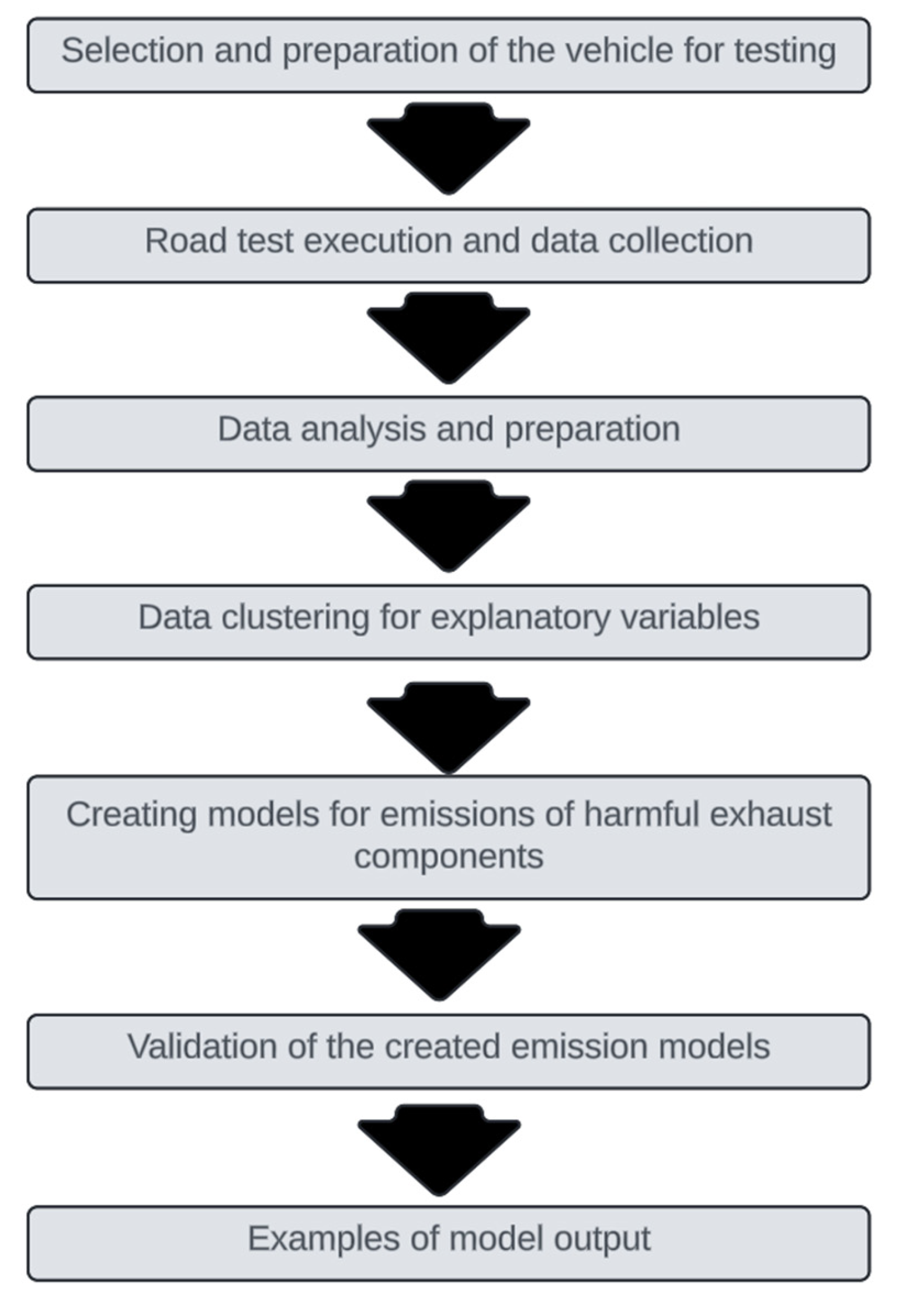
Preprints 117532 g001
Preprints 117532 g002
Figure 2. Research vehicle used for road tests.
Figure 2. Research vehicle used for road tests.
Preprints 117532 g002
Preprints 117532 g003
Figure 3. General scheme for creating emission models.
Figure 3. General scheme for creating emission models.
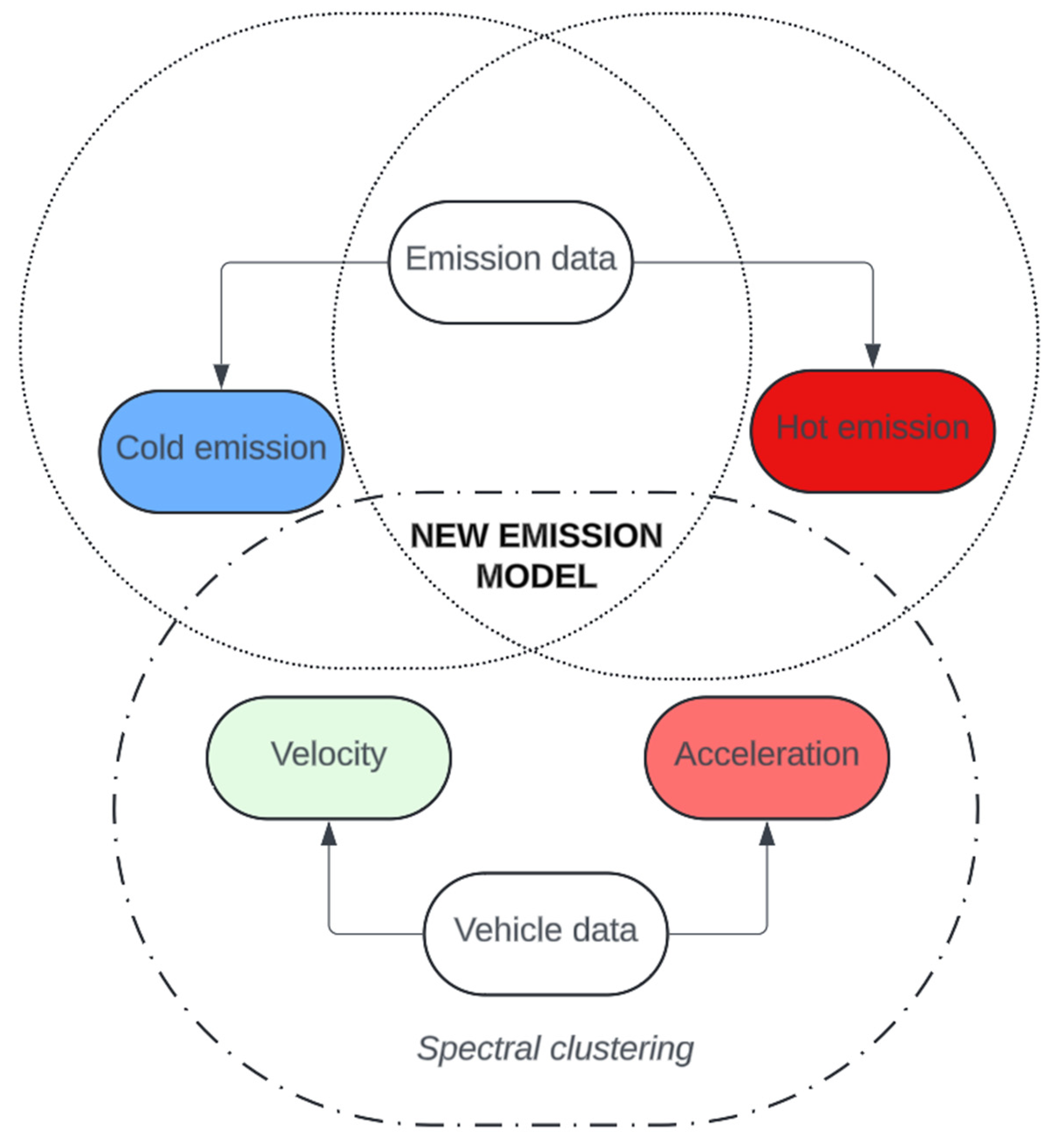
Preprints 117532 g003
Preprints 117532 g004
Figure 4. Emissions of harmful exhaust components obtained during road tests.
Figure 4. Emissions of harmful exhaust components obtained during road tests.
Preprints 117532 g004
Preprints 117532 g005
Figure 5. Silhouette score results for finding the most optimal number of clusters.
Figure 5. Silhouette score results for finding the most optimal number of clusters.
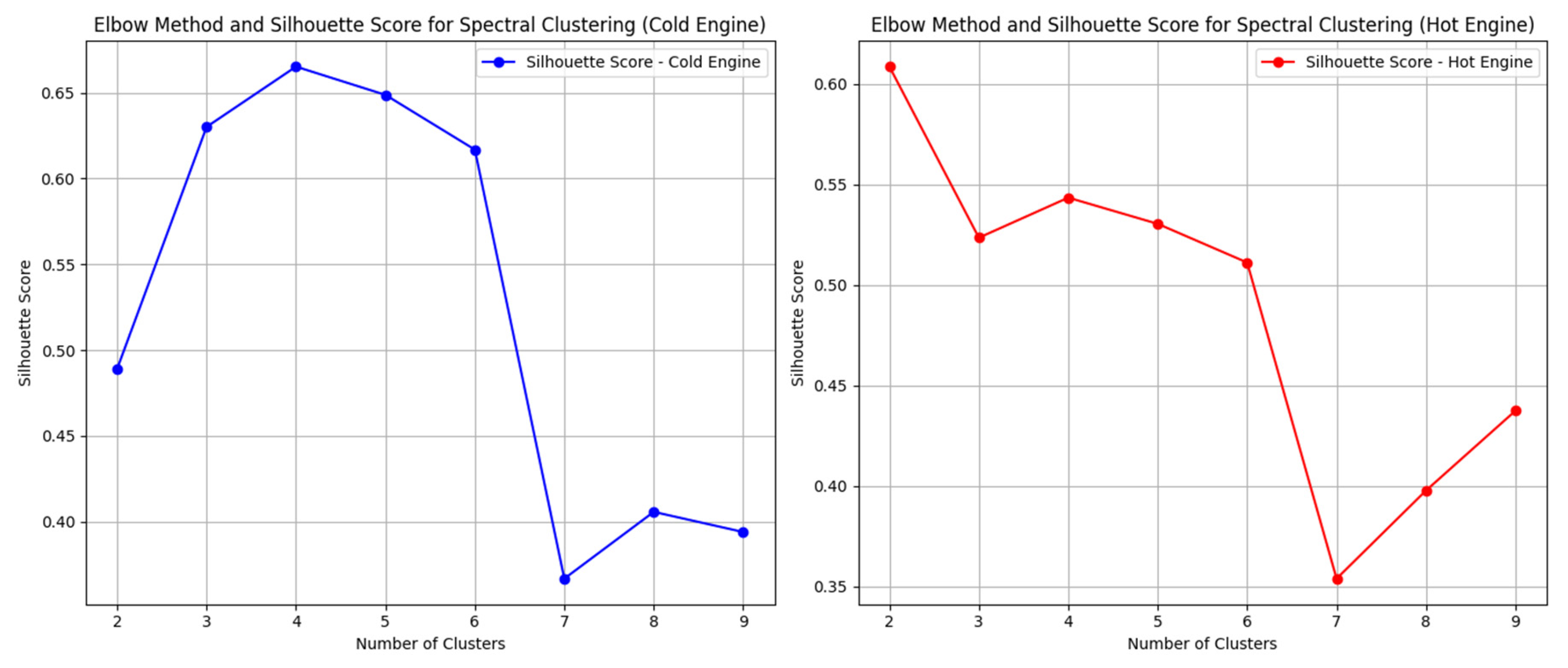
Preprints 117532 g005
Preprints 117532 g006
Figure 6. Spectral Clustering for the data obtained for cold and hot emission.
Figure 6. Spectral Clustering for the data obtained for cold and hot emission.
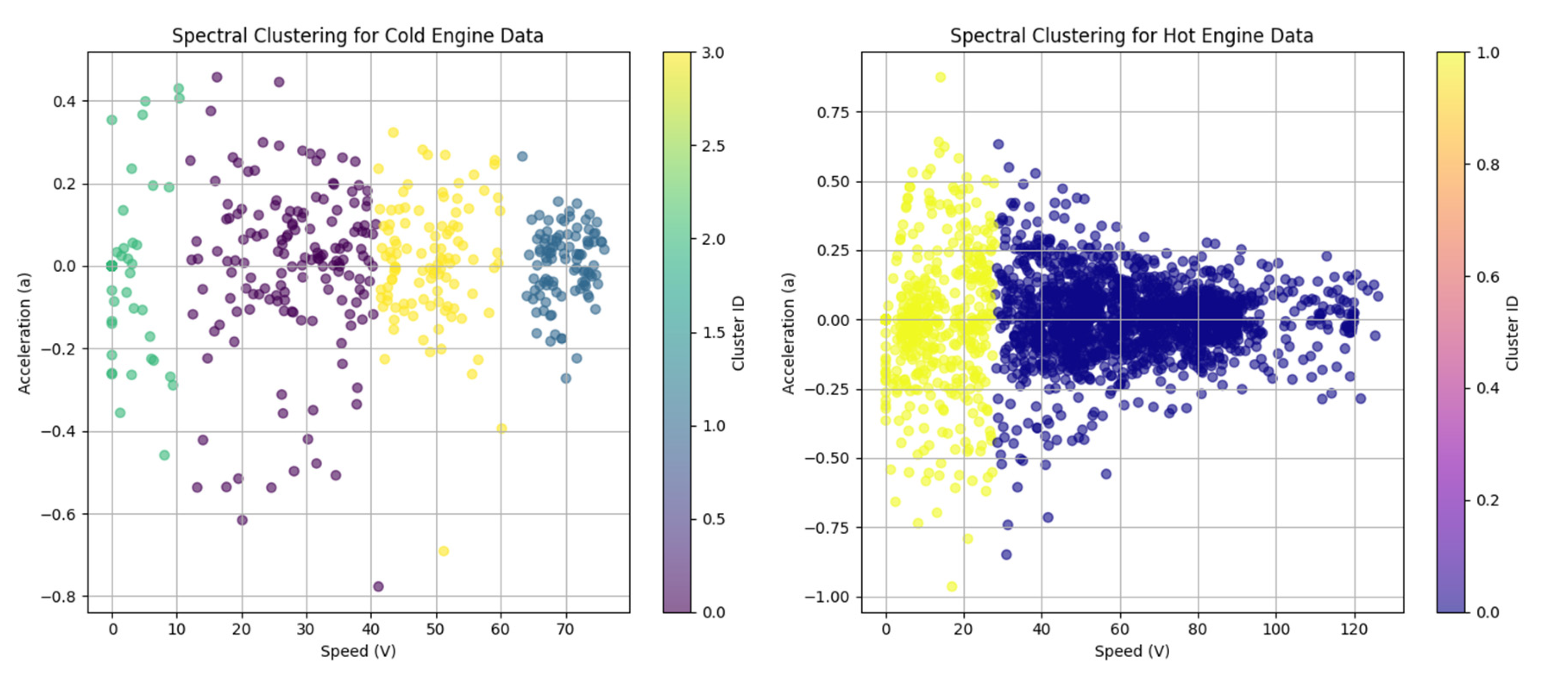
Preprints 117532 g006
Preprints 117532 g007
Figure 7. Example validation charts of THC prediction for a heated engine.
Figure 7. Example validation charts of THC prediction for a heated engine.
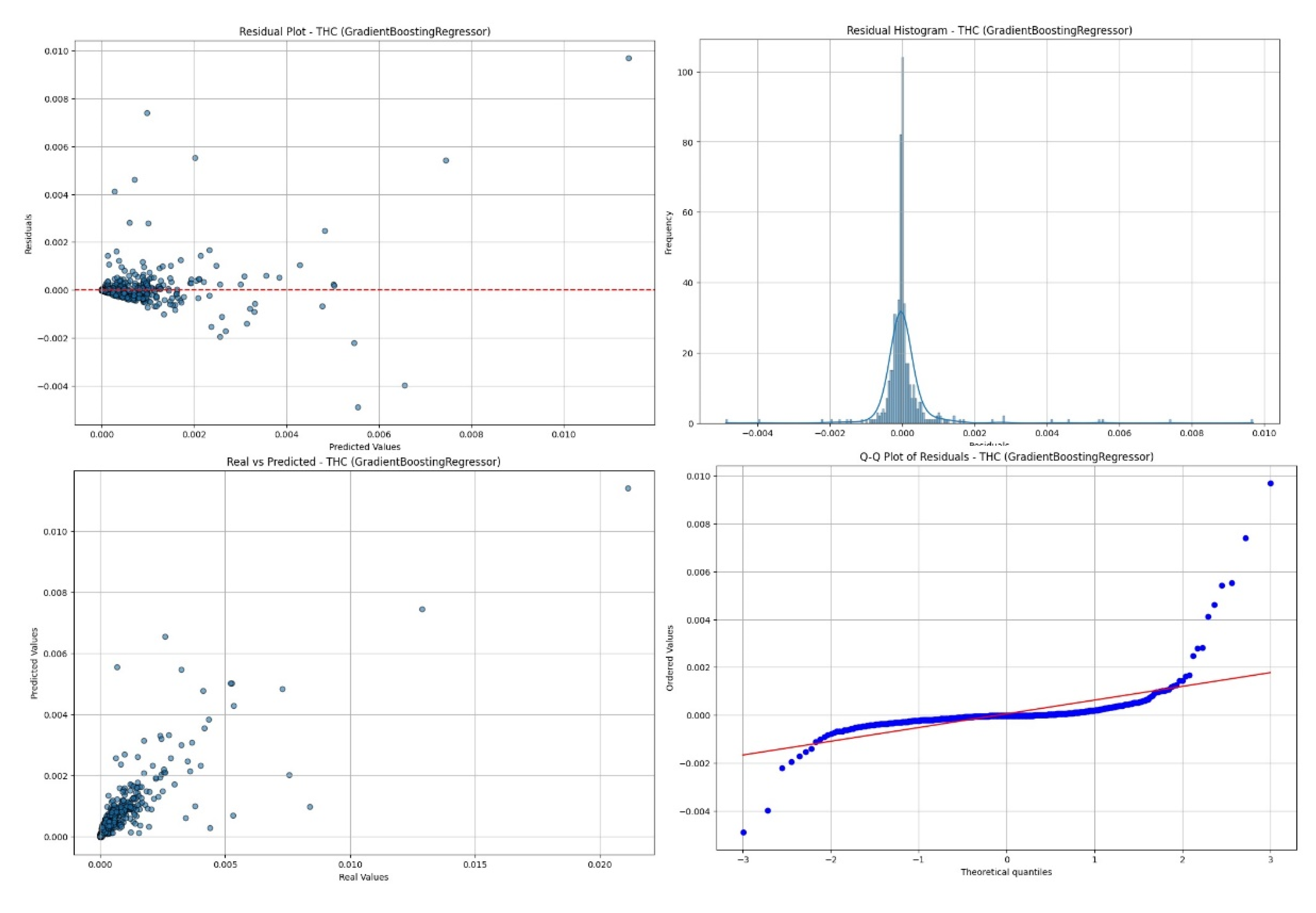
Preprints 117532 g007
Preprints 117532 g008
Figure 8. Example use of developed models for NOx prediction.
Figure 8. Example use of developed models for NOx prediction.
Preprints 117532 g008
Table 1. Results of calculations of validation rates of MSE and R2 models for a given component of combustibles with an indication for the best prediction techniques.
Table 1. Results of calculations of validation rates of MSE and R2 models for a given component of combustibles with an indication for the best prediction techniques.
Emission Compound Best Model MSE R2
THC Random Forest (Cold Engine) 0.00002 0.74408
NOx Polynomial Regression (Cold Engine) 0.00006 0.59200
CO Gradient Boosting (Cold Engine) 0.00291 0.47986
CO2 Polynomial Regression (Cold Engine) 0.00321 0.92200
THC Gradient Boosting (Warm Engine) 0.00001 0.65674
NOx Polynomial Regression (Warm Engine) 0.00001 0.41565
CO Polynomial Regression (Warm Engine) 0.00277 0.21246
CO2 Polynomial Regression (Warm Engine) 0.00221 0.95100
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated