Simulation of Polarized Light Microscopy for Multiple Analyzer Angles

Preprint

Brief Report

Simulation of Polarized Light Microscopy for Multiple Analyzer Angles

Altmetrics

Downloads

Views

Comments

Manuel Ballester^*

,Zoey Ho,Asami Odate,

Marc Walton,Aggelos Katsaggelos

Manuel Ballester^*

,Zoey Ho,Asami Odate,

Marc Walton,Aggelos Katsaggelos

This version is not peer-reviewed

Submitted:

05 September 2024

Posted:

09 September 2024

You are already at the latest version

Alerts

Abstract

We have developed an efficient simulator for polarized light microscopy experiments. It supports calculations for multiple analyzer angles across different channels of a polarized camera, enhancing imaging capabilities. Our model is publicly available here.

Keywords:

Subject: Physical Sciences - Optics and Photonics

1. Introduction

Polarized Light Microscopy (PLM) is a fundamental optical technique for analyzing the optical properties and structures of anisotropic materials. Widely applied in fields such as mineralogy and biology, PLM facilitates the study of birefringent substances, including crystals, fibers, and biological tissues. Accurately determining optical properties through PLM allows for the identification of the molecular composition of a material [1]. Additionally, PLM measurements enable for the precise determination of an object’s depth map.

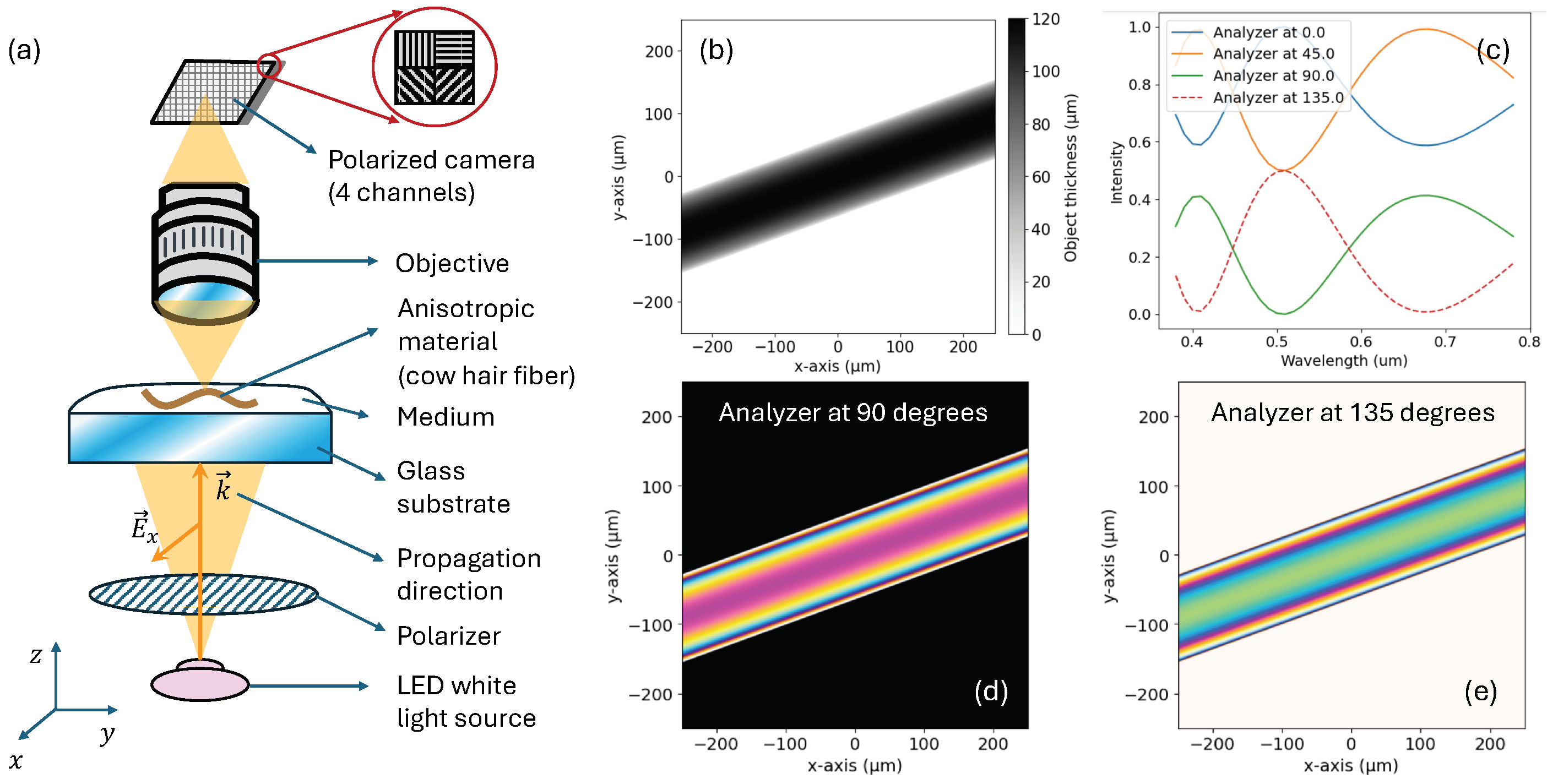
Figure 1a illustrates a basic experimental PLM setup [2]: A normal incidence white-light beam passes through a linear polarizer before reaching the material. Within the sample, ordinary and extraordinary waves propagate at different velocities. When passing through an analyzer, the interference of the two waves produces the characteristic colors images at a sensor. A polarized camera captures multiple channels for different analyzer angles (typically 0, 45, 90, and 135 degrees). This angular variation allows for a precise determination of the optical path difference (OPD) between ordinary and extraordinary waves.

This work introduces two efficient methods for simulating polarized light microscopy (PLM) experiments: numerical and analytical. These simulations can enhance the imaging capabilities of conventional PLM techniques. Future research will focus on minimizing the mean square error between simulated data and actual measurements to determine optimal material properties and the 3D shape of objects.

2. Method

Uniaxial anisotropic materials have a specific orientation defined by an optical axis

\hat{p} = (cos θ, sin θ, 0)

, where

θ

is the tilt angle of the material [3]. In this work, we assume that the optical axis is perpendicular to the wave propagation direction along the

z -

axis. This configuration can be manually set and commonly occurs in the study of many fibers, which often lie flat on the glass substrate (see Fig. 1a). This setup is particularly useful for distinguishing long hairs from different mammals.

The linear electric field

\vec{E} = E_{x} \hat{x}

entering the material can be decomposed into two orthogonal components:

{\vec{E}}_{| |} = (\vec{E} \cdot \hat{p}) \hat{p}

and

{\vec{E}}_{⊥} = \vec{E} - {\vec{E}}_{⊥}

. The component perpendicular to the optical axis generates ordinary waves, characterized by the ordinary complex refractive index

{\tilde{n}}_{o} = n_{o} + i κ_{o}

. Here,

n_{o} = c / v

represents the speed of light in the material relative to the speed of light in a vacuum, and the extinction coefficient

κ_{o}

measures light absorption. According to Lambert-Beer’s law, the intensity of a collimated beam is

I = I_{0} e^{- α_{o} z}

, where

α_{o} = \frac{4 π κ_{o}}{λ}

is the absorption coefficient [4]. For materials that are nearly transparent in the visible spectrum

κ_{o} \approx 0

. Similarly, the electric field component parallel to the optical axis propagates with the extraordinary complex refractive index

{\tilde{n}}_{e} = n_{e} + i κ_{e}

, where

κ_{e} \approx 0

for our particular case of study.

The phase difference between ordinary and extraordinary waves [5] is given by

Δ ϕ = 2 π / λ Δ n d (x, y)

, where

Δ n = n_{e} - n_{o}

represents the birefringence and

d (x, y)

the depth map at different locations. The analyzer in front of the sensor has a specific transmission axis, denoted by

\hat{a} = (cos α, sin α, 0)

. We need to consider the projection of both parallel and perpendicular electric fields along the

\hat{a} -

axis. These projections are expressed as the scalar values

E_{⊥}^{a} = (E_{⊥} \cdot \hat{a}) e^{i Δ ϕ}

and

E_{| |}^{a} = E_{| |} \cdot \hat{a}

. The final intensity at the sensor location is then calculated as

I \propto | E_{⊥}^{a} + E_{| |}^{a} |^{2}

Although all these previous operations can be performed numerically, we have derived an equivalent analytical formula that enables a more efficient computation of the resulting image:

I = {cos}^{2} (α) + 4 {sin}^{2} (\frac{Δ ϕ}{2}) cos (θ - α) cos (θ) (cos (θ - α) cos (θ) - cos (α))

(1)

3. Results and Validation

We have carried out the wave propagation through the PLM system using a simulated sample of a single cow hair fiber [6] with a certain tilt of 20 degrees with respect to the abscissas axis. Figure 1b shows the simulated depth map used as an input for our models. The refractive indices were

n_{e} = 1.55

and

n_{o} = 1.54

, which define a slight positive birefringence

Δ n = + 0.01

. The optical axis is along the longitudinal part of the fiber. The ordinary waves then occur when the E-field oscillates along the cross-wise direction of the fiber. We evaluated Equation (1) for wavelengths from 380 to 780, with a step size of 10 nm. Following the procedure described in [7], we converted a multi-wavelength intensity image into a simple sRGB image capture using a conventional sensor. Figure 1c shows the raw intensity values for different wavelengths at the location

(0, 100)

um. Two of the four output polarization channels captured at the simulated sensor are shown in Figure 1d–e.

Several computational experiments have been performed to verify the validity of our methods. First, we empirically saw the equivalence of both the numerical and analytical approaches for multiple data within a reasonable range,

(n_{o}, n_{e}, θ, α) \in {[1, 5]}^{2} \times [0, 180 °]

. Then, we evaluated our models in some particular scenarios in which the ground-truth results are theoretically known. For example, when setting an isotropic material

n_{e} = n_{o} = 1.5

, the cross-polarized channel (

α = 90 °

) correctly cancels out, the two polarized channels at

α = 45, 135 °

cancel 50% of light, and the uncrossed polarization channel (

α = 0 °

) transmits all the light, producing a uniform white constant image. If we now consider an anisotropic material with

n_{o} \neq n_{e}

and with an optical axis

θ = 0, 90 °

, the resulting images exhibit the same behavior as isotropic materials. This is expected since only ordinary or extraordinary waves propagate in these orientations. Then, setting

θ

at different angles leads to the expected interference colors.

References

Marquez, E.; Ballester, M.; Garcia, M.; Cintado, M.; Marquez, A.; Ruiz, J.; Fernández, S.; Blanco, E.; Willomitzer, F.; Katsaggelos, A. Complex dielectric function of H-free a-Si films: Photovoltaic light absorber. Materials Letters 2023, 345, 134485. [Google Scholar] [CrossRef]
Frandsen, A.F. Polarized light microscopy. Technical report, 2016.
Yeh, P.; Hendry, M. Optical waves in layered media. Physics Today 1990, 43, 77. [Google Scholar] [CrossRef]
Márquez, E.; Blanco, E.; Mánuel, J.M.; Ballester, M.; García-Gurrea, M.; Rodríguez-Tapiador, M.I.; Fernández, S.M.; Willomitzer, F.; Katsaggelos, A.K. Mid-Infrared (MIR) Complex Refractive Index Spectra of Polycrystalline Copper-Nitride Films by IR-VASE Ellipsometry and Their FIB-SEM Porosity. Coatings 2023, 14, 5. [Google Scholar] [CrossRef]
Hecht, E. Optics; Pearson Education India, 2012.
Rowe, W.F. Identification of Natural Fibers. Handbook for the analysis of micro-particles in archaeological samples.
Sørensen, B.E. A revised Michel-Lévy interference colour chart based on first-principles calculations. European Journal of Mineralogy 2013, 25, 5–10. [Google Scholar] [CrossRef]

Figure 1. (a) Diagram of the PLM experiment. (b) Simulated fiber depth map. (c) Raw intensity value for different wavelengths at image location

(0, 100)

um. (d)–(e) Output sRGB sensor image for two different angles of the analyzer.

Figure 1. (a) Diagram of the PLM experiment. (b) Simulated fiber depth map. (c) Raw intensity value for different wavelengths at image location

(0, 100)

um. (d)–(e) Output sRGB sensor image for two different angles of the analyzer.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.