Prerpints.org logo
Preprint
Article

The Synthesis of a Two-Circuit Steering Mechanism of the Ackerman Transport Mobile Robot

Altmetrics

Downloads

62

Views

49

Comments

0

Submitted:

09 September 2024

Posted:

10 September 2024

You are already at the latest version

Alerts
Abstract
In wheeled vehicles, there exists a challenge concerning the alignment of the front wheels during turns. When both wheels are turned to the same extent, the inner wheel experiences lateral slippage on the road surface, resulting in reduced steering efficiency. Such problems can be solved by using the Ackermann principle. There are two approaches: through the steering mechanism or by employing autonomous wheel control. From a technical standpoint, it is achievable to synthesize a steering mechanism that fulfills the Ackermann condition, ensuring as accurately as possible for any given turning radius. This research paper focuses on synthesizing a steering mechanism, specifically a two-circuit linkage that links the left and right wheels. The structure and kinematics of this mechanism are being investigated. Following the principles of Ackermann, an objective function for the kinematic synthesis of the mechanism has been formulated. The synthesis process of the mechanism is conducted using the analytical method of interpolation in four parameters. A dedicated method has been developed, and kinematic analysis of the mechanism using the synthesized parameters has been performed. The simulation results have demonstrated high accuracy in achieving the desired implementation of the Ackermann condition.
Keywords: 
Subject: Engineering  -   Mechanical Engineering
Annotation: In wheeled vehicles, there exists a challenge concerning the alignment of the front wheels during turns. When both wheels are turned to the same extent, the inner wheel experiences lateral slippage on the road surface, resulting in reduced steering efficiency. Such problems can be solved by using the Ackermann principle. There are two approaches: through the steering mechanism or by employing autonomous wheel control. From a technical standpoint, it is achievable to synthesize a steering mechanism that fulfills the Ackermann condition, ensuring as accurately as possible for any given turning radius. This research paper focuses on synthesizing a steering mechanism, specifically a two-circuit linkage that links the left and right wheels. The structure and kinematics of this mechanism are being investigated. Following the principles of Ackermann, an objective function for the kinematic synthesis of the mechanism has been formulated. The synthesis process of the mechanism is conducted using the analytical method of interpolation in four parameters. A dedicated method has been developed, and kinematic analysis of the mechanism using the synthesized parameters has been performed. The simulation results have demonstrated high accuracy in achieving the desired implementation of the Ackermann condition.

1. Introduction

The creation of mobile transport robots presents a wide range of challenges. The designs must incorporate various factors such as operational ease, efficiency, reliability, and safety. The development of simple wheeled mobile robots entails addressing complex tasks that demand thorough analysis and effective solutions. Practical mobile robot designs necessitate comprehensive research and enhancement of multiple components, including the design, kinematics, and dynamics of drive mechanisms, control systems, sensor systems, and artificial intelligence.
Rolling serves as the primary mode of operation for wheeled robots (machines), allowing them to function effectively. However, when both wheels are turned to the same extent, the inner wheel experiences lateral slippage on the road surface, resulting in reduced steering efficiency. This slippage not only generates undesirable heat but also leads to premature wear of the wheel. To mitigate these issues, it is necessary to turn the inner wheel at a greater angle compared to the outer wheel. The solution to this challenge is rooted in the Ackermann principle [1], which establishes the steering geometry applicable to any vehicle, ensuring the appropriate steering angle during cornering or navigating curves. Meeting this requirement necessitates a specific connection between the front wheels, typically accomplished through the utilization of the articulated four-link mechanism pioneered by the French inventor Janto. As early as 1917, Mlodzeevsky B.K. [2] demonstrated that Janto's steering mechanism approximated the principles outlined by Ackermann, asserting its practical adequacy. In contemporary times, wheeled vehicles can attain high speeds, and even a slight deviation from the Ackermann conditions (up to 1°) results in undesirable phenomena.
Contemporary wheeled vehicles have moved away from employing Janto's pure steering mechanism due to its limited consideration of crucial dynamic and compliant effects. Nevertheless, this steering principle remains applicable for low-speed maneuvers. On the other hand, certain high-speed machines adopt a reverse Ackermann geometry to address the substantial difference in slip angle between the inner and outer front tires when cornering at high velocities. Implementing this geometry assists in reducing tire temperatures during high-speed cornering situations. However, it may result in reduced performance during low-speed maneuvers. The mobile cargo transport robot, as described in the research paper by U. Joldasbekov Institute of Mechanics and Engineering scientists [3], incorporates a customized steering mechanism comprising two circuits built upon a four-bar linkage. The dimensions of the mobile transport robot are (1200×2300) mm, with a weight of 1200 kg. It is equipped with sturdy rubber-rimmed wheels capable of achieving a travel speed of 45 km/h.
The Ackermann principle has been extensively explored in numerous scientific papers. In [4], a study is conducted to assess the compliance of commonly used mechanisms in modern cars with the Ackermann principle. The analysis method employed involves the formulation and modeling of a finite-difference equation that describes the motion transmission process facilitated by a steering rack and pinion mechanism, which is essential for wheel turning. In order to enhance the accuracy of implementing the Ackermann principle, the lateral steering rods of both wheels are interconnected using a toothed rack. The control of wheels utilizing a rack and pinion mechanism is further examined in [5,6,7]. Specifically, [5] focuses on analyzing the rack and pinion tie rod for an ITS electric vehicle, providing insights into the dimensions of the steering rod and motion transmission to minimize steering errors. It is worth noting that the rack and pinion steering gear typically operates at a low speed [6], usually in the range of 10-15 rpm, resulting in less emphasis on the dynamics of these mechanisms. Zhao, etc. focuses on the synthesis of a four-link steering mechanism with the aim of achieving Ackermann steering [8]. The paper examines the precision with which a conventional four-link circuit or linkage can track a certain number of points. It then delves into the steering geometry for steerable wheels and introduces a steering mechanism featuring partial non-circular gears. The proposed mechanism aims to enhance the accuracy of meeting Ackermann's conditions for optimal steering performance. In [9], a six-link mechanism is synthesized to achieve five points of steering accuracy in automotive applications. The inner wheel is capable of turning up to 61 degrees with a satisfactory level of precision. This result is then compared to the outcomes obtained from the four-bar Ackermann steering mechanism (ASM) and the Fahey-Eight-Member-Mechanism (FEMM). The proposed mechanism demonstrates a reasonably accurate performance, falling between the two aforementioned mechanisms. Meanwhile, [10,11] focus on the optimization synthesis of a steering mechanism utilizing a two-circuit four-link configuration. The double-circuit arrangement of the four-rod mechanism enables the adjustment of errors in two stages [10]. The first circuit generates an approximate function to achieve correct steering, while the second circuit fine-tunes the function for improved accuracy. The synthesis problem of the mechanism is resolved through the utilization of the geometric optimization method.
Kinematics is a fundamental aspect in the design, analysis, synthesis, control, and simulation of robots. The effectiveness and simplicity of numerical algorithms rely on the chosen method and structure of the manipulator mechanism, emphasizing the importance of selecting an appropriate method for kinematic studies. Several methods exist for studying the kinematics of planar and spatial mechanisms, including geometric (triangle), coordinate, matrix, and vector methods. The matrix transformation method [12,13,14] is widely employed in this context. This method utilizes rotation matrices (3x3) and translation matrices (3x3) to account for the various types and classes of kinematic pairs. To consider the translational motion of a coupled coordinate system, a homogeneous transformation matrix (4x4) is utilized in place of the rotation matrix [12, 14]. Denavit and Hartenberg [13] were pioneers in utilizing matrix representation to describe the spatial geometry of manipulators. The application of screw calculus methods has proven highly effective in studying the statics, kinematics, and dynamics of parallel structure manipulators [15,16,17]. Additionally, the vector method for mechanism kinematics is presented in the form of vector recurrent formulas [12,18]. These methods offer valuable tools for analyzing and understanding the kinematic behavior of robotic systems.
The synthesis of mechanisms can be approached through various analytical methods, including algebraic, geometric, and optimization techniques. Algebraic methods, as described in [12], encompass several approaches such as the interpolation method, best fit method, method of blocked zones [18], and specific methods focused on resolving branching defects [19]. Geometric methods are rooted in the principles of differential geometry. They can be further categorized into Burmester kinematic geometry methods and approximate kinematic geometry methods [20]. Optimization methods, drawing from the theory of nonlinear optimization, involve multiple analyses of the mechanism [21,22]. They encompass a range of analytical and optimization techniques [23], wherein some parameters of the mechanism are explicitly determined using formulas, while the remaining parameters are derived through nonlinear optimization. These diverse analytical methods provide valuable tools for synthesizing mechanisms by enabling precise and efficient design optimization.
This research paper centers around the synthesis of a steering mechanism, specifically a two-circuit linkage that connects the left and right wheels. The study involves an examination of the structure and kinematics of this particular mechanism. By adhering to the principles of Ackermann steering, an objective function for the kinematic synthesis of the mechanism has been devised. The synthesis process of the mechanism employs the analytical method of interpolation in four parameters. A specialized method has been developed for this purpose, and a kinematic analysis of the mechanism utilizing the synthesized parameters has been conducted. The simulation results have indicated a high level of accuracy in achieving the desired implementation of the Ackermann condition.

2. Basic Idea

Figure 1 illustrates the kinematic diagram of the steering mechanism being examined. The mechanism comprises two circuits, namely O E 1 D 1 C 1 O and O E 2 D 2 C 2 O , responsible for driving the left and right wheels, respectively. Notably, the links within each circuit share identical dimensions. This mechanism is referred to as the two-circuit Ackermann mechanism, as it implements the Ackermann principle. The objective of this study is to develop a highly precise Ackermann steering mechanism, with a particular focus on adjusting the variable thrust E 1 E 2 . The research is conducted based on methods involving kinematic analysis and synthesis of lever mechanisms.
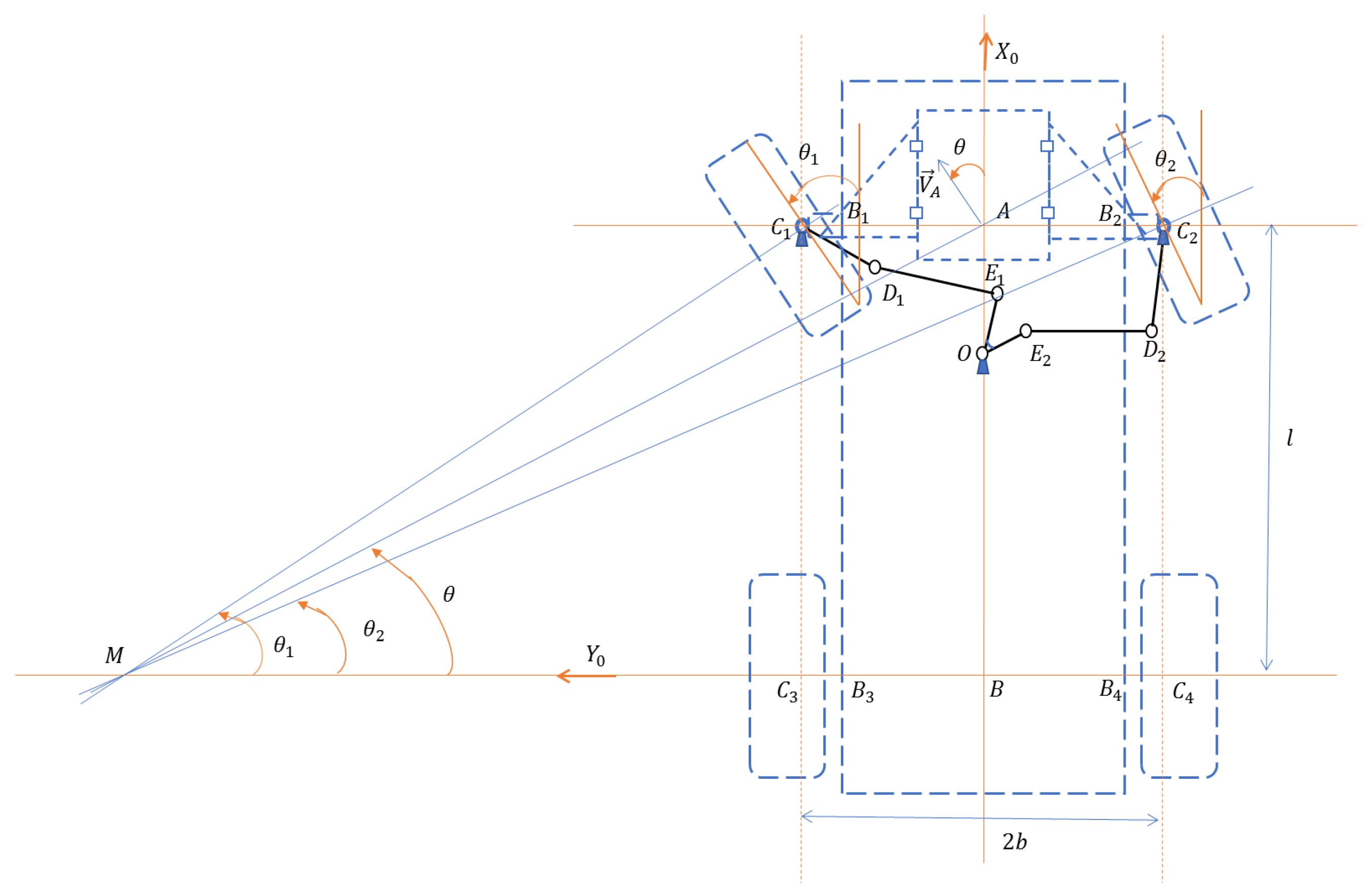
Ackermann principle. Figure 2 depicts a kinematic diagram of a mobile robot platform with four wheels and a two-circuit steering mechanism. The purpose of the two-circuit steering mechanism is to implement the Ackermann Principle, which ensures that the wheels have the correct steering angle when navigating corners or curves. This principle aims to prevent the tires from sliding sideways during curved motion. The geometric solution involves positioning the axes of all the wheels along the radii of circles that have a common central point M , which also coincides with the instantaneous center of velocities (ICV) of the mobile platform's planar motion. Since the rear wheels 3 and 4 are fixed, the central point M must lie on a line extending from the rear axle. Additionally, the front wheel axles intersect this line, which requires the inner front wheel 1 to turn through a larger angle than the outer wheel 2 during cornering. By positioning the wheels correctly in the direction of motion, stable steering is achieved without excessive wear and heat generation on each wheel. This configuration ensures that the Ackermann condition is met, promoting efficient and reliable steering performance for the mobile robot platform.
Based on the analytical representation of the Ackermann condition [1], Figure 2 also illustrates the angles involved in the steering mechanism. The angle θ 1 represents the steering angle of wheel 1, θ 2 represents the steering angle of wheel 2, and θ represents the average steering angle of the front wheels.
To create a conditional mechanism based on the two-circuit mechanism and the Ackermann condition, Figure 3 presents the kinematic diagram of this conditional mechanism. It is achieved by attaching two structural groups (TRT-type) to the kinematic chain of the Ackermann two-circuit mechanism shown in Figure 1. Group (6,8) is connected to link 1, which is rigidly connected to front wheel 1, while group (7,9) is attached to link 2, which corresponds to wheel 2. Consequently, the conditional Ackermann mechanism consists of n = 9 moving links and p 5 = 13 kinematic pairs of the 5th class type R and T [12]. The degree of freedom of the conditional mechanism can be determined using the Chebyshev formula.
W = 3 n − 2 p 5 = 3 · 9 − 2 · 13 = 1
Based on Figure 3, it is observed that
cot ⁡ θ 2 = M 2 B + b l
cot ⁡ θ 1 = M 1 B − b l
According to the Ackermann condition, the equality of M 2 B = M 1 B holds, which leads to the formation of Eq. (1). This equation represents the analytical representation of the Ackermann principle.
cot ⁡ θ 2 − cot ⁡ θ 1 = 2 b l

3. Steering Mechanism Kinematic Equations

In Figure 1, the two-circuit steering mechanism is depicted, comprising five movable links whose positions are defined relative to the reference system O Y 0 ' X 0 ' , with angular coordinates φ 1 , β 1 , ψ 1 ,   β 2 , and ψ 2 . The mechanism possesses constant geometric parameters represented by e ,   b ,   r , p , d , α ,   γ , and R (Figure 1). The vector equations governing the contours O E 1 D 1 C 1 O and O E 2 D 2 C 2 O are as follows:
d → + p → = r → + e → + b → d → + p → = r → + e → − b →
The projections on the axes of the reference system O Y 0 ' X 0 ' are given by the following expressions:
d cos ⁡ φ 1 + p cos ⁡ β 1 = r cos ⁡ ψ 1 + b , d sin ⁡ φ 1 + p sin ⁡ β 1 = r sin ⁡ ψ 1 + e ,
d cos ⁡ φ 1 − ∝ + p cos ⁡ β 2 = r cos ⁡ ψ 2 − b , d sin ⁡ φ 1 − ∝ + p sin ⁡ β 2 = r sin ⁡ ψ 2 + e ,
Taking into account the relationships ψ 1 = θ 1 + π + γ and ψ 2 = θ 2 + π − γ from Figure 1, we can rewrite Eq. (3) and Eq. (4) in the following form, where we solve them with respect to β 1 , θ 1 , β 2 , and θ 2 for a given φ 1 :
d cos ⁡ φ 1 + p cos ⁡ β 1 = − r cos ⁡ θ 1 + γ + b , d sin ⁡ φ 1 + p sin ⁡ β 1 = − r sin ⁡ θ 1 + γ + e ,
d cos ⁡ φ 1 − ∝ + p cos ⁡ β 2 = − r cos ⁡ θ 2 − γ − b , d sin ⁡ φ 1 − ∝ + p sin ⁡ β 2 = − r sin ⁡ θ 2 − γ + e ,
Assuming a relationship between the average angle of rotation of the front wheels θ and the angle φ 1 as follows:
φ 1 = π − θ + α 2
Then we can also determine
φ 2 = π − θ − α 2
The kinematic requirements for the synthesized mechanism are not contradicted by them.
Certainly, when one wheel is turned more than the other, it results in a mismatch in the direction of the wheels. However, it is crucial to ensure that both wheels are aligned in the forward direction when the robot is not turning, as depicted in Figure 4. To achieve this, the mismatch in heading angles between the wheels should gradually increase from zero (when the wheels are pointing straight ahead) to a point where there is a substantial difference in angles between the two wheels (at maximum wheel steering). This ensures both effective steering during turns and proper alignment for straight-line motion.
The rockers C i D i , where i = 1 ,   2 , are rigidly attached to wheels 1 and 2, respectively, and both rockers are inclined at an angle γ with respect to the wheel directions. In order to enable the platform to undergo translational movement, it is necessary for these rockers to intersect at a single point, namely point B . By satisfying this condition, the angle γ and the dependence of θ 1 and θ 2 through θ [1] can be determined using expressions in Eq. (7).
tan ⁡ γ = b l = λ cot ⁡ θ 1 = cot ⁡ θ − λ cot ⁡ θ 2 = cot ⁡ θ + λ
The cot ⁡ θ 1 and cot ⁡ θ 2 in Eq. (7) can be expressed using basic trigonometric functions as follows:
sin ⁡ θ i = sin ⁡ θ f i θ , λ cos ⁡ θ i = cos ⁡ θ ∓ λ sin ⁡ θ f i θ , λ ( i = 1,2 )
where f i θ , λ = 1 ∓ λ sin ⁡ 2 θ + λ 2 sin 2 ⁡ θ , i = 1,2 .
In certain cases, it is feasible to utilize approximate formulas to describe the relationship of these rotation angles [1]:
θ 1,2 = θ ± λ θ 2
whence θ ≈ θ 1 + θ 2 / 2 .
The angle θ holds a specific physical interpretation. When θ remains constant during the platform's movement, the position of ICV remains unchanged. This indicates that the robot rotates around a fixed point, causing all its points to move in a circular path. On the other hand, when θ is equal to 0, the robot moves forward in a straight line.

3. Synthesis of the Two-Circuit Ackermann Mechanism.

Let's examine the left turn of the platform, which is illustrated in Figure 2. When the IVC turns to the right, point M will shift towards the right side of the platform. In order to satisfy the requirements of the mechanism's synthesis aimed at achieving the desired trajectory of point M , the larger rotation angle θ 1 must lie within the range of θ 1 ∈ 0 ,   π 2 . Consequently, it becomes crucial to specify the values of the variable parameters including their allowable ranges and nodal points to ensure proper mechanism synthesis.
To accomplish this, we can plot graphs of θ i θ using Eq. (8). The angle θ can be determined using the formula θ k = θ k − 1 + ∆ , where k = 1 , N ¯ , θ 0 = 0 , N = 9 , and ∆ = π 18 . For the given transport robot, the parameter λ is calculated as λ = 6 20 = 0.3 , which implies γ ≈ 17.3 . The results of the calculations are summarized in Table 1. Figure 5 displays the graphs of θ i θ , for i = 1 ,   2 .
Upon analyzing the graphs of the rotation angles, it becomes evident that for small rotations, the discrepancies in θ i θ , where i = 1 ,   2 , are barely noticeable. However, as the angle approaches 90°, the mechanism can approach a special position that complicates the synthesis problem [12]. Therefore, it is advisable to select the nodal synthesis points within the region indicated by the red quadrangle on the graph. Taking these considerations into account, we can accept θ ∈ 0 0 ,   83 0 .
Let's consider the kinematic chains 1 and 2 of the hypothetical Ackerman mechanism as depicted in Figure 3. Kinematic chain 1 defines the contour O E 1 D 1 C 1 M 1 B 1 O , while kinematic chain 2 defines the contour O E 2 D 2 C 2 M 2 B 2 O . By analyzing chain 1, we can determine the coordinates of the moving point M 1 as X M 1 , Y M 1 , and by analyzing chain 2, we can determine the coordinates of M 2 as X M 2 , Y M 2 . According to the structure of the mechanism, it can be stated that X M 1 = X M 2 = − l + e , Y M 1 = B M 1 = ρ M 1 and Y M 2 = B M 2 = ρ M 2 . The latter satisfy the Ackermann condition (1). Consequently, the objective function can be expressed in the following form:
∆ = cot ⁡ θ 2 − cot ⁡ θ 1 − 2 λ → m i n
It is important to mention that if we assume the coordinates of point O to be known, and consequently X M 1 = X M 2 = − l + e to be known, then during the synthesis process, we can focus on the kinematic equations (5) and (6) specific to the real Ackermann mechanism. However, if the known coordinates are not limited to point O , we would need to formulate the synthesis equations for the entire conditional mechanism.
Let's consider the case when X M 1 = X M 2 is considered as a given value. Taking into account φ 1 = π − θ + α 2 , we can express equations (5) and (6) in relative terms as follows:
− d cos ⁡ ( θ − α 2 ) + p cos ⁡ β 1 = − r cos ⁡ θ 1 + γ + 1 , d sin ⁡ ( θ − α 2 ) + p sin ⁡ β 1 = − r sin ⁡ θ 1 + γ + e , − d cos ⁡ θ + α 2 + p cos ⁡ β 2 = − r cos ⁡ θ 2 − γ − 1 , d sin ⁡ θ + α 2 + p sin ⁡ β 2 = − r sin ⁡ θ 2 − γ + e ,
where d = d b , p = p b , r = r b , e = e b – relative parameters.
Hence, the system (11) comprises six constant parameters: d ,   p , r , α ,   γ , and e , along with variable parameters: θ , β 1 , β 2 , θ 1 , and θ 2 . The synthesis parameters are d ,   p , r , and α . In this scenario, the parameters γ and e are predetermined. Let's assume e = 0.22 .
We can represent system (11) as:
p 0 − p 1 cos ⁡ θ − e sin ⁡ θ − p 2 sin ⁡ θ + e cos ⁡ θ + p 3 cos ⁡ f 1 θ + θ + γ − − p 4 sin ⁡ f 1 θ + θ + γ = − cos ⁡ f 1 θ + γ − e sin ⁡ f 1 θ + γ , p 0 − p 1 cos ⁡ θ − e sin ⁡ θ + p 2 sin ⁡ θ + e cos ⁡ θ + p 3 cos ⁡ f 2 θ + θ − γ − − p 4 sin ⁡ f 2 θ + θ − γ = − cos ⁡ f 2 θ − γ − e sin ⁡ f 2 θ − γ ,
where
θ 1 = f 1 θ , θ 2 = f 2 θ ,
p 0 = p 2 − r 2 − d 2 − e 2 − 1 2 r , p 1 = d r cos ⁡ α 2 , p 2 = d r sin ⁡ α 2 ,
p 3 = d cos ⁡ α 2 , p 4 = d sin ⁡ α 2 .
To solve system (12) with three nodal points ( k = 1,2 , 3 ), we can set the values θ k = θ k , where k = 1,2 , 3 , within the range θ k ∈ 0 0 ,   83 0 . Let's assign the nodal point values as follows: θ 1 = 0.348 ;   θ 2 = 0.87 ;   θ 3 = 1.392 .
As a result, the system will consist of six equations:
p 0 − p 1 cos ⁡ θ k − e sin ⁡ θ k − p 2 sin ⁡ θ k + e cos ⁡ θ k + p 3 cos ⁡ f 1 θ k + θ k + γ − − p 4 sin ⁡ f 1 θ k + θ k + γ = − cos ⁡ f 1 θ k + γ − e sin ⁡ f 1 θ k + γ , ( k = 1,2 , 3 ) p 0 − p 1 cos ⁡ θ k − e sin ⁡ θ k + p 2 sin ⁡ θ k + e cos ⁡ θ k + p 3 cos ⁡ f 2 θ k + θ k − γ − − p 4 sin ⁡ f 2 θ k + θ − γ = − cos ⁡ f 2 θ k − γ − e sin ⁡ f 2 θ k − γ , ( k = 1,2 , 3 )
Since the mechanism consists of two circuits, we can determine p 0 by solving the first and fourth equations of the system (13).
p 0 = p 1 cos ⁡ θ k − e sin ⁡ θ k ± p 2 sin ⁡ θ k + e cos ⁡ θ k − p 3 cos ⁡ f i θ k + θ k + γ − − p 4 sin ⁡ f i θ k + θ k + γ − cos ⁡ f i θ k + γ − e sin ⁡ f i θ k + γ , ( k = 1,3 , i = 1,2 )
Now, let's eliminate the parameter p 0 from (13) by substituting the first equation (14) into the second and third equations, as well as substituting the second equation (14) into the fifth and sixth equations of the system. After substituting, we will have a modified system without p 0 . The θ 1 will be represented the value of θ at the first nodal point of the synthesis, corresponding to θ 1 = θ 1 . Thus, we have a system of linear equations:
A 1 p 1 + B 1 p 2 + C 1 p 3 + D 1 p 4 = F 1 A 2 p 1 + B 2 p 2 + C 2 p 3 + D 2 p 4 = F 2 A 3 p 1 + B 3 p 2 + C 3 p 3 + D 3 p 4 = F 3 A 4 p 1 + B 4 p 2 + C 4 p 3 + D 4 p 4 = F 5
where
A k − 1 = cos ⁡ θ 1 − e sin ⁡ θ 1 − cos ⁡ θ k − e sin ⁡ θ k , k = 2,3
B k − 1 = sin ⁡ θ 1 + e cos ⁡ θ 1 − sin ⁡ θ k + e cos ⁡ θ k , k = 2,3
C k − 1 = − cos ⁡ f 1 θ 1 + θ k + γ + cos ⁡ f 1 θ k + θ k + γ , k = 2,3
D k − 1 = − sin ⁡ f 1 θ 1 + θ 1 + γ − sin ⁡ θ 1 θ k + θ k + γ , k = 2,3
F k − 1 = − cos ⁡ f 1 θ 1 + γ − e sin ⁡ f 1 θ 1 + γ − cos ⁡ f 1 θ k − γ − e sin ⁡ f 1 θ k − γ , k = 2,3
A k + 1 = cos ⁡ θ 1 − e sin ⁡ θ 1 − cos ⁡ θ k − e sin ⁡ θ k , k = 2,3
B k + 1 = − sin ⁡ θ 1 + e cos ⁡ θ 1 + sin ⁡ θ k + e cos ⁡ θ k , k = 2,3
C k + 1 = − cos ⁡ f 1 θ 1 + θ k + γ + cos ⁡ f 2 θ k + θ k − γ , k = 2,3
D k = − sin ⁡ f 1 θ 1 + θ 1 + γ − sin ⁡ f 2 θ k + θ − γ , k = 2,3
F k + 1 = − cos ⁡ f 1 θ 1 + γ − e sin ⁡ f 1 θ 1 + γ − cos ⁡ f 2 θ k − γ − e sin ⁡ f 2 θ k − γ , k = 2,3
The system of linear equations (15) is solved to obtain the values of p i , where   i = 1,2 , 3,4 . The parameter p 0 can be determined using one of the equations from Equation (14). After obtaining the values of p i , the parameters d , p , r ,   and ∝ can be defined as follows:
tan ⁡ ∝ 2 = p 4 p 3 , d = ± p 3 2 + p 4 2 r = ± p 3 2 + p 4 2 p 1 2 + p 2 2 p = 2 r p 0 + r 2 + d 2 + e 2 + 1
Based on the synthesis process and calculations, the following results have been obtained for the geometric dimensions of the mechanism: α = 0,02094   r a d ;   d = 0,34   ;   r = 0,4077 ;   p = 0,97 ,   b = 1 ,   e = 0,22 . These values represent the relative geometric dimensions of the synthesized mechanism.

4. Analysis of the Two-Circuit Ackermann Mechanism and Discussion of the Results

The kinematic analysis of the two-circuit Ackermann mechanism can be performed using the algorithms implemented in the ASIAN-2014 software package [24]. This software package provides tools and functionalities specifically designed for kinematic analysis, allowing for accurate calculations and evaluation of the mechanism's motion characteristics. By utilizing the ASIAN-2014 software, detailed kinematic analysis of the two-loop Ackermann mechanism can be conducted efficiently and effectively.
Figure 6 illustrates the assembly of a two-circuit steering mechanism, accompanied by a table that specifies the dimensions of the links and the coordinates of the racks and hinges in the depicted configuration. The table utilizes designations such as L 1 - 5 and L 2 - 6 , which correspond to the links D 1 C 1 and D 2 C 2 , respectively, as shown in Figure 1. The values of the geometric parameters are determined using relative values with a given b = 246,352   m m . Figure 7 showcases the results of the mechanism's motion, including the trajectories of the characteristic hinges of the links and a table displaying the positions of the rudder (crank 1) and the two wheels (rockers 3 and 5). In this particular case, the position of crank 1 varies within the range of 0 to π .
Figure 8 presents the deviation of function Δ , which was calculated using the values of the angular positions of links 3 and 5, as indicated in the table in Figure 7. The maximum deviation of the synthesis results, based on Eq. (10), occurs at positions θ = 32,07 0 , θ 1 = 33,78 0 , and θ 2 = 33,33 0 . It is observed that the maximum deviation is less than 1.6%. It is worth noting that a deviation of less than 1.6% for the interpolation synthesis mechanism is considered relatively high. This indicates that the calculated values closely align with the desired values, demonstrating the effectiveness and accuracy of the synthesis process for the mechanism.
The successful mechanism synthesis is further supported by the graphs depicting the angular displacements of links 3 and 5 in Figure 9a. The green line represents the displacement of link 3 ( θ 1 ), while the red line represents the displacement of link 5 ( θ 2 ). The nature of these curves corresponds to their counterparts in Figure 5, which depict the complete range of motion from 0 to π / 2 . Furthermore, Figure 9c presents the angular positions of connecting rods 2 and 4 exhibiting symmetrical movements. This symmetrical behavior is indicative of the well-designed and coordinated motion of the mechanism. The consistency between the synthesized results and the graphical representations of angular displacements and positions further validates the effectiveness of the synthesis process and the accuracy of the synthesized mechanism. The graphs in Figure 9 provide visual representations of the respective components' angular displacements, showcasing the steering mechanism's motion characteristics.
The symmetry of the movements in the left and right parts of the Ackermann mechanism can be observed through the analysis of velocities and accelerations. The graphs in Figure 10 and Figure 11 show that the left and right wheels have similar velocity and acceleration profiles, indicating symmetry in their movements. The projections and absolute values of the velocities and accelerations of the hinges D i ( i = 1,2 ) of the wheels are shown in the graphs. By comparing the corresponding graphs for the left and right wheels, we can observe that the green and red lines, representing the projections of the velocities and accelerations of the left and right wheels, respectively, are almost identical in shape and magnitude, indicating symmetry. The blue lines, representing the absolute values of the velocities and accelerations, also show a high degree of symmetry between the left and right components of the mechanism.

5. Conclusions

In conclusion, the synthesis of a six-link two-circuit steering mechanism for four-wheeled mobile robots (machine) has been successfully accomplished. The mechanism has been designed to adhere to the Ackermann condition with a high level of accuracy. By determining the appropriate relative geometrical parameters of the two-circuit Ackermann mechanism, the mechanism has been optimized for efficient operation. The synthesis process involved interpolation in four different positions, leading to the achievement of the desired objective function. Through thorough kinematic analysis, the mechanism has demonstrated satisfactory performance and accuracy. Overall, the synthesized steering mechanism is a reliable and effective solution for four-wheeled mobile robots, meeting the requirements of the Ackermann condition.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Funding

This research was supported by the Funding of the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan (Project No. AP14870662).

Acknowledgments

Assistance from the U. Joldasbekov Institute of Mechanics and Engineering is gratefully acknowledged.

References

  1. Lobas, L.G. Nonholonomic models of wheeled vehicles [Russian: Negolonomnyye modeli kolesnykh ekipazhey]. - Kyiv: Nauk. dumka, 1986. - 232 p.
  2. Mlodzeevsky, B.K. On the theory of control in automobiles [Russain: K teorii upravleniya v avtomobilyakh]. - Vest. engineers, 1917. - V. 2. - P. 37-41.
  3. Report on research on grant financing (GF.2012): "Research of dynamics, development of a control system, design and creation of a mobile robot prototype" for 2012-2014 (state registration number 0112RK0206).
  4. Ioffe, M.L. Ackermann Principle and its Implementation in Modern Cars. Mech. Eng. Mach. Sci. 2021, 9, 40–47. [Google Scholar] [CrossRef]
  5. Wasiwitono U., Sidarta I., Pramono A.S., et al. Steering system kinematic and steady-state cornering analyses of the ITS electric car. J. Proc. Series, 2014, vol. 1, no. 1, pp. 58–62. 62. [CrossRef]
  6. R. Hanzaki, S. K. Saha and P. M. Rao, Modeling of a Rack and Pinion Steering Linkage Using Multibody Dynamics, Besancon (France): 12tg IFToMM World Congress, June 18-1-21, 2007.
  7. A.R. Hanzaki, P. M. Rao and S. K. Saha, Kinematic and Sensitivity Analysis and Optimization of Planar Rack and Pinion Steering Linkage, Mechanism and Machine, 44:42-56, 2009.
  8. Jing-Shan Zhao, Xiang Liu, Zhijing Feng, J. Dai. Design of an Ackermann-type steering mechanism/ Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2013, DOI:10.1177/0954406213475980.
  9. Pramanik S. Kinematic synthesis of a six-member mechanism for automotive steering. J Mech Des 2002; 124(4): 642–645. DOI: 10.1115/1.1503372.
  10. Hitesh Patel, Mitesh Mungla. Optimal synthesis of steering mechanism using double loop four bar mechanism/Australian Journal of Mechanical Engineering 20(1): 1-10, 2019. DOI:10.1080/14484846.2019.1699492.
  11. Simionescu PA, Beale D. Optimum synthesis of the four-bar function generator in its symmetric embodiment: the Ackermann steering linkage. Mech Mach Theory 2002; 37(12): 1487–1504.
  12. I.I. Wolfson, M.Z. Kolovsky, E.E. Peysakh, etc. Mechanics of machines: a textbook for HETI [Russian: Mekhanika mashin: uchebnoye posobiye dlya vtuzov]/ Edited by prof. G.A.Smirnova. - Moscow: Vysshaya shkola, 1996. - 511 p.
  13. K. S. Fu, R.C. Gonzalez, C.S.G. Lee. Robotics - Control, Sensing, Vision, and Intelligence. Mcgraw-Hill Book Company, 1987. – 594 p.
  14. Bruno Siciliano, Oussama Khatib. Springer Handbook of Robotics// Chapter 2. Kinematics (2nd edition). Verlag Berlin Heidelberg, 2016. – 2228 p.
  15. Doronin F. A. Application of the theory of screws in the statics and dynamics of spatial mechanisms of a parallel structure: [Russian: Primeneniye teorii vintov v statike i dinamike prostranstvennykh mekhanizmov parallel'noy struktury]. “Izvestiya PGUPS”, 2015, - P. 130-136. ISSN 1815-588X.
  16. Maldonado-Echegoyen, R., Castillo-Castaneda, E. & Garcia-Murillo, M.A. Kinematic and deformation analyses of a translational parallel robot for drilling tasks. J Mech Sci Technol 29, 4437–4443 (2015). [CrossRef]
  17. Jomartov A., Tuleshov A. Vector method for kinetostatic analysis of planar linkages // Journal of the Brazilian Society of Mechanical Sciences and Engineering, 40. 2018. DOI: 10.1007/s40430-018-1022-y.
  18. Peisakh E.E., Nesterov V.A. Design system for flat lever mechanisms: [Russian: Sistema proyektirovaniya ploskikh rychazhnykh mekhanizmov]. - Moscow: Mashinostroenie, 1988. - 232 p.
  19. Peisakh E.E., Pirozhkov M.A. Synthesis of transmission lever mechanisms by the method of piecewise polynomial parametric approximation, focused on the elimination of the branching defect: [Russian: Sintez peredatochnykh rychazhnykh mekhanizmov metodom kusochno-polinomial'noy parametricheskoy approksimatsii, oriyentirovannym na isklyucheniye defekta vetvleniya]. – Mashinostroenie, 1988. - V.6. - P. 48-56.
  20. Sargsyan Yu.L. Approximation synthesis of mechanisms: [Russian: Approksimatsionnyy sintez mekhanizmov]. Moscow, 1982.
  21. Levitsky, N.I. Theory of mechanisms and machines: [Russian: Teoriya mekhanizmov i mashin.]. Moscow: Nauka, 1979. - 576 p.
  22. Tuleshov, А.K., Jomartov, А.А., Ibrayev, S., Jamalov, N.K., Halicioglu, R. Optimal synthesis of planar linkages // News of the National Academy of Sciences of the Republic of Kazakhstan, Series of Geology and Technical Sciencesthis link is disabled, 2020, 1(439), p. 172–180, doi: 10.32014/2020.2518-170X.2.
  23. Tuleshov, A., Halicioglu, R., Shadymanova, A., Kuatova, M. Kinematic synthesis method and eccentricity effects of a Stephenson mechanism // Mechanical Sciences, 2021, 12(1), p. 1–8. [CrossRef]
  24. Author's certificate No. 5103 dated September 3, 2019: Software (CAD) "Complex of programs for automated design of lever load-lifting mechanisms "ATLAS.
Preprints 117666 g001
Figure 1. Modified two-circuit Ackermann steering mechanism.
Figure 1. Modified two-circuit Ackermann steering mechanism.
Preprints 117666 g001
Preprints 117666 g002
Figure 2. Ackermann principle for four-wheeled platforms.
Figure 2. Ackermann principle for four-wheeled platforms.
Preprints 117666 g002
Preprints 117666 g003
Figure 3. Conditional Ackerman mechanism.
Figure 3. Conditional Ackerman mechanism.
Preprints 117666 g003
Preprints 117666 g004
Figure 4. The diagram to determine the angle γ when the platform undergoes direct movement
Figure 4. The diagram to determine the angle γ when the platform undergoes direct movement
Preprints 117666 g004
Preprints 117666 g005
Figure 5. Graphs of the angles of rotation of the wheels and the platform when turning to the left by 90° from the vertical position of the crank (Fig. 4).
Figure 5. Graphs of the angles of rotation of the wheels and the platform when turning to the left by 90° from the vertical position of the crank (Fig. 4).
Preprints 117666 g005
Preprints 117666 g006
Figure 6. Assembly and kinematic diagram, table of steering mechanism parameters.
Figure 6. Assembly and kinematic diagram, table of steering mechanism parameters.
Preprints 117666 g006
Preprints 117666 g007
Figure 7. Kinematic diagram of the steering mechanism with a table of positions of the steering wheel (crank) and two wheels (rockers) on the ASIAN-2014.
Figure 7. Kinematic diagram of the steering mechanism with a table of positions of the steering wheel (crank) and two wheels (rockers) on the ASIAN-2014.
Preprints 117666 g007
Preprints 117666 g008
Figure 8. Deviation of the objective function Δ between the synthesis nodal points.
Figure 8. Deviation of the objective function Δ between the synthesis nodal points.
Preprints 117666 g008
Preprints 117666 g009
Figure 9. The graphs of the angular displacements of the steering mechanism links: a)the angular positions of the left (green line) and right (red line) wheels; b) the angular positions of the left (green line) and right (red line) connecting rods.
Figure 9. The graphs of the angular displacements of the steering mechanism links: a)the angular positions of the left (green line) and right (red line) wheels; b) the angular positions of the left (green line) and right (red line) connecting rods.
Preprints 117666 g009
Preprints 117666 g010
Figure 10. The velocity graphs of the wheels’ hinges D i ( i = 1,2 ) in the steering mechanism: a) the projections (green and red lines) and the absolute velocity (blue line) of the hinge D 1 of the left wheel; b) the projections (green and red lines) and the absolute velocity (blue line) of the hinge D 2 of the right wheel.
Figure 10. The velocity graphs of the wheels’ hinges D i ( i = 1,2 ) in the steering mechanism: a) the projections (green and red lines) and the absolute velocity (blue line) of the hinge D 1 of the left wheel; b) the projections (green and red lines) and the absolute velocity (blue line) of the hinge D 2 of the right wheel.
Preprints 117666 g010
Preprints 117666 g011
Figure 11. The accelerations of the wheels’ hinges D i ( i = 1,2 ) in the steering mechanism: a) the projections (green and red lines) and the absolute acceleration (blue line) of the hinge D 1 of the left wheel; b) the projections (green and red lines) and the absolute acceleration (blue line) of the hinge D 2 of the right wheel.
Figure 11. The accelerations of the wheels’ hinges D i ( i = 1,2 ) in the steering mechanism: a) the projections (green and red lines) and the absolute acceleration (blue line) of the hinge D 1 of the left wheel; b) the projections (green and red lines) and the absolute acceleration (blue line) of the hinge D 2 of the right wheel.
Preprints 117666 g011
Table 1.
N 0 1 2 3 4 5 6 7 8 9
θ 0 0,174 0,348 0,522 0,696 0,87 1,044 1,218 1,392 1,566
θ 1 0 0,18308 0,3843 0,6037 0,8413 1,097 1,371 1,663 1,9732 2,302
θ 2 0 0,1649 0,3117 0,4403 0,5507 0,643 0,717 0,773 0,8108 0,83
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated