Modeling Borehole Resistivity Logs with Exponentially Graded Multilayered Soil Inversion

In this paper, we present the application of a special soil resistivity model, the Exponentially Graded Multilayered Soil model, to the interpretation of Borehole Resistivity Logging surveys. The model, which was recently introduced by the authors, offers an alternative to the interpretation provided by constant resistivity layer models. The model is applied to synthetic soil surveys as well as to a real survey that is not satisfactorily interpreted using conventional models.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

The study of the electrical properties of soil, such as electrical resistivity, as a function of depth from the surface, is highly useful for determining the nature of the materials that compose it. The applications of this knowledge are of both scientific and technological importance. In subsurface characterization inside Geological and Geotechnical Studies, resistivity models help map subsurface structures and properties, aiding in geological surveys and engineering projects. For example, it has been used to identify different soil and rock types based on resistivity variations [1]. In Hydrogeology, the model assists in delineating aquifers and assessing groundwater quality by interpreting resistivity data to detect variations caused by water content and salinity [2]. In Mining Exploration the soil model aids in locating and evaluating mineral deposits by providing detailed resistivity profiles that help identify ore bodies [3]. The model is used in Environmental Monitoring to monitor soil conditions before and after remediation, providing insights into the effectiveness of different treatment methods [4]. In precision agriculture, helps manage irrigation and fertilization by mapping soil moisture and nutrient variations [5]. In Archaeology the model is applied to detect and map buried archaeological features by analyzing resistivity data to locate structures or artifacts [6]. In Engineering, Construction and Infrastructure Management, the soil model provides detailed resistivity profiles to assist in designing foundations and assessing soil stability for construction projects. In addition, helps plan cable and pipeline routes by providing insights into subsurface resistivity that may affect installation.[7]-[8].

The methods used to study soil electrical resistivity as a function of depth can be divided into two major groups. Non-invasive methods, where apparent soil resistivity is measured using electrodes positioned on the surface in various configurations, with Wenner and Schlumberger arrays being particularly noteworthy, are generally referred to as Vertical Electrical Sounding (VES) [9]. Invasive methods involve drilling a narrow vertical hole or well, through which a bare rod can be inserted to release current into the ground, known as the Driven-Rod method (DRM) [10]-[11], or a device with two or three electrodes can be introduced into the well, one of which releases current into the soil while the others measure the electric potential, a method known as Borehole Resistivity Logging (BRL) [12]. It can generally be said that invasive methods provide more precise and complete information than non-invasive methods. Additionally, within the invasive methods, BRL is the most effective in determining the variation of electrical resistivity with depth [13].

In an electrical survey using any of the methods described above, the electrical resistivity is not directly determined; instead, some other electrical quantity related to it is measured. In VES, the so-called apparent resistivity is measured [14]; in surveys using DRM, the electrical resistance of the rod is measured as a function of the length inserted into the ground [15], while in BRL, the electrical potential at various depths in the well or the potential difference between two nearby points is measured. Based on the information provided by the survey device, the soil resistivity as a function of depth must be determined, a procedure known in the literature as inversion. This is only possible if a soil resistivity model is available, which can be used to apply an inversion procedure to the measurement data and thus obtain the specific parameters of the model [16].

The most commonly used soil resistivity model is the Horizontal Constant Multi-Layered model (HCMS) [17], which in its simplest version involves dividing the ground into horizontal layers of constant resistivity. The soil parameters are the constant resistivities of the different layers and their thicknesses, with the exception of the deepest layer, which extends to infinity. It is a semi-analytical model in the sense that it provides calculable expressions that can be mathematically implemented numerically in the equations that determine the electrical potential in the soil, leading to more acceptable results the closer the actual soil matches the proposed model.

The HCMS is not the only possible model. It is clear that, unless we are dealing with truly stratified soils, resistivity will not be a piecewise constant function, but rather a continuous function of depth.

Recently, a multilayer model has been proposed that allows the resistivity in each layer to vary with depth according to specific functions. This is the Functionally Graded Multilayered Soil model (FGMS) [18]. This model is also semi-analytical, in the same sense as the HCMS mentioned earlier, although it is mathematically much more complex. It offers three possible modes of resistivity variation with depth: exponential, parabolic, and trigonometric, with the first being the functional mode used in this paper—the Exponentially Graded Multilayered Soil model (EGMS) [18]. Additionally, the model can be adjusted so that the resistivity is continuous at the layer interfaces, although this does not always yield suitable final results in the inversion process.

In summary, this work focuses on applying an inversion algorithm to the results of BRL measurements using an EGMS-type soil resistivity model and comparing the final results with a conventional HCMS model by directly simulating BRL with both models. To this end, after this introduction, the paper continues with a description of the mathematical foundations of the calculations to be performed. The calculation scheme is then applied to several examples to highlight the differences between the models. The paper concludes with the findings derived from the previous applications.

2. Mathematical Foundations

For the study to be conducted in this work, it is necessary to have a calculation tool capable of simulating a BRL according to a specific soil model. This is what many authors refer to as the direct or forward method. This tool is essential for applying the inversion procedure and thereby determining the parameters of the chosen model. Therefore, we will describe the mathematical foundations of both methods, direct and inversion, for the EGMS soil model.

2.1. Direct Method

The direct method, also often referred to as the forward modeling method, involves simulating how a BRL measurement would appear given a specific soil resistivity model. This method is fundamental for understanding how different soil properties influence resistivity measurements and is essential for comparing theoretical predictions with actual data.

Let us consider a point current source of strength I located at

{\vec{r}}_{P}

in a semi-infinite soil

(z \geq 0)

whose conductivity is a function

σ (\vec{r})

. The electric potential

ϕ (\vec{r})

generated at point

\vec{r}

, also called Green’s function, is the solution of the boundary value problem (BVP)

\begin{array}{l} \vec{\nabla} \cdot (σ (\vec{r}) \vec{\nabla} ϕ (\vec{r})) = - I δ (\vec{r} - {\vec{r}}_{P}) \\ \vec{\nabla} ϕ \cdot {\vec{n}}_{z} |_{z = 0} = 0 \\ ϕ (\vec{r} \to \infty) = 0 \end{array}

(1)

BVP (1) is difficult to solve in general. By the change

u = ϕ \cdot \sqrt{σ}

, (1) becomes in the following equation for the new variable

u (\vec{r})

{\vec{\nabla}}^{2} u (\vec{r}) - \frac{{\vec{\nabla}}^{2} (\sqrt{σ (\vec{r})})}{\sqrt{σ (\vec{r})}} u (\vec{r}) = - \frac{I}{\sqrt{σ (\vec{r})}} δ (\vec{r} - {\vec{r}}_{P})

(2)

When the conductivity

σ (\vec{r})

only depends on the z coordinate, the LHS second term of (2) becomes

F = \frac{1}{\sqrt{σ (z)}} \frac{d^{2} \sqrt{σ (z)}}{d z^{2}}

which will be forced to take a constant value. Among other possibilities, when the constant value F is set to

β^{2}

, it can be proof that

σ (z) = {(C_{1} \cdot e^{β \cdot z} + C_{2} \cdot e^{- β \cdot z})}^{2}

, which will be called an Exponentially Graded model and (2) becomes a modified Helmholtz equation. The solution for

u (\vec{r})

and

ϕ (\vec{r})

in an infinite medium is,

\begin{array}{l} {\vec{\nabla}}^{2} u (\vec{r}) - β^{2} u (\vec{r}) = - \frac{I}{\sqrt{σ (\vec{r})}} δ (\vec{r} - {\vec{r}}_{P}) \\ u (\vec{r}) = \frac{I \exp (- β | \vec{r} - {\vec{r}}_{P} |)}{4 π \sqrt{σ ({\vec{r}}_{P})} | \vec{r} - {\vec{r}}_{P} |} \\ ϕ (\vec{r}) = \frac{I \exp (- β | \vec{r} - {\vec{r}}_{P} |)}{4 π \sqrt{σ ({\vec{r}}_{P})} \sqrt{σ (\vec{r})} | \vec{r} - {\vec{r}}_{P} |} \end{array}

(3)

For a semi-infinite medium composed by horizontal layers where a conductivity of the type described can be defined in each layer, what in this paper is called EGMS model, a cylindrical coordinates system can be used to solve the homogeneous equations associated to (3). For a point current source located in the i layer at

{\vec{r}}_{P}

, the potential at any point

\vec{r}

of the j layer

ϕ_{i j} (\vec{r})

can be expressed as

\begin{array}{l} ϕ_{i j} (\vec{r}) = \frac{I \exp (- β | \vec{r} - {\vec{r}}_{P} |)}{4 π \sqrt{σ_{i} ({\vec{r}}_{P})} \sqrt{σ_{j} (\vec{r})} | \vec{r} - {\vec{r}}_{P} |} δ_{i j} + \\ + \int_{0}^{\infty} (f_{i j} (λ) e^{- \sqrt{λ^{2} + {β_{i}}^{2}} (z - z_{P})} + g_{i j} (λ) e^{\sqrt{λ^{2} + {β_{i}}^{2}} (z - z_{P})}) J_{0} (λ r) d λ \end{array}

(4)

where

δ_{i j}

is the Kronecker delta and the unknown functions

f_{i j}

and

g_{i j}

need to be calculated by imposing the boundary conditions at each interface, namely

\vec{\nabla} ϕ_{i 1} \cdot {\vec{n}}_{z} |_{z = 0} = 0

stands for the null electric current flux through the soil surface and

\begin{array}{l} ϕ_{i j} ({\vec{r}}_{j, j + 1}) = ϕ_{i j + 1} ({\vec{r}}_{j, j + 1}) \\ σ_{j} \cdot \vec{\nabla} ϕ_{i j} \cdot \vec{n} |_{{\vec{r}}_{j, j + 1}} = σ_{j + 1} \cdot \vec{\nabla} ϕ_{i j + 1} \cdot \vec{n} |_{{\vec{r}}_{j, j + 1}} \end{array}

(5)

guarantees continuity of potential and normal electric current flux conservation through the interface separating the layers j and j+1. In (4)-(5),

σ_{i} (z) = {(C_{i 1} \cdot e^{β_{i} \cdot z} + C_{i 2} \cdot e^{- β_{i} \cdot z})}^{2}

stands for the exponential model conductivity [18].

2.2. Inversion Method

Once the EGMS model has been defined, the calculation of the potential generated by a point current source is given by (4). In this section the inverse problem of setting the constants associated with the chosen model will be addressed. Focusing on the EGMS model, from the BRL measurements using a device as shown in Figure 1, it is possible to find the parameters associated with each layer of the model. Indeed, from BRL measurements the values

ϕ_{A, B}^{m e a s} (z)

are available so that they represent the values that must be reproduced by the proposed soil model. From the EGMS model, it is obtained

ϕ_{A, B} (z; {C_{i 1}, C_{i 2}, β_{i}}_{i = 1... N})

where

{C_{i 1}, C_{i 2}, β_{i}}_{i = 1... N}

represent the parameters associated with each layer, with N being the number of layers considered. This is sometimes referred to as the objective function. The model parameters can be found by an algorithm that minimizes

χ^{2} = {[ϕ_{A, B}^{m e a s} (z) - ϕ_{A, B} (z; {C_{i 1}, C_{i 2}, β_{i}}_{i = 1... N})]}^{2}

(6)

This procedure allows obtaining the parameters that define the function that represents the electrical conductivity in each layer. Note that conductivity is non-continuous piecewise in general since no supplementary conditions have been imposed on the interfaces. The variable conductivity model proposed here in each layer is only an approximation somewhat closer to real world than the well-known HCMS. Nevertheless, it is possible to add conditions to the parameters in the minimization process described above, to ensure that the discontinuity at the interfaces is the minimum possible. Such models will be classified as quasi-continuous models. The Lagrange multipliers method can be used to force continuity of conductivity at interfaces by expanding (6) to

\begin{array}{l} χ^{2} = {[ϕ_{A, B}^{m e a s} (z) - ϕ_{A, B} (z; {C_{i 1}, C_{i 2}, β_{i}}_{i = 1... N})]}^{2} + \\ \sum_{i = 1... N - 1} λ_{i} \cdot (σ_{i} ({C_{i 1}, C_{i 2}, β_{i}}; z_{i}) - σ_{i + 1} ({C_{i + 11}, C_{i + 12}, β_{i + 1}}; z_{i}))^{2} \end{array}

(7)

where

λ_{i}

stand for the Lagrange multipliers whose number is equal to the number of interfaces,

σ_{i}

and

σ_{i + 1}

are the conductivities on both sides of the interface i and z_i takes the value of the interface depth. This will not always improve the results obtained with the associated non-continuous model, although it is obvious that if the real conductivity behaves like a continuous EGMS model, continuity will arise by itself.

3. Applications of the Proposed Model

The mathematical foundations presented in the previous section must be implemented in calculation algorithms for both the direct and inverse processes. For simplicity, to illustrate the application of the EGMS model to BRL, only three-layer soils will be considered. This is because, given the large number of parameters required to specify the model, the calculations, particularly in the inversion method, become slower.

In this section, several simulated examples will be examined to test the differences between the HCMS and EGMS models for interpreting a BRL. Additionally, a real case will be studied with the same objective.

3.1. Direct Method

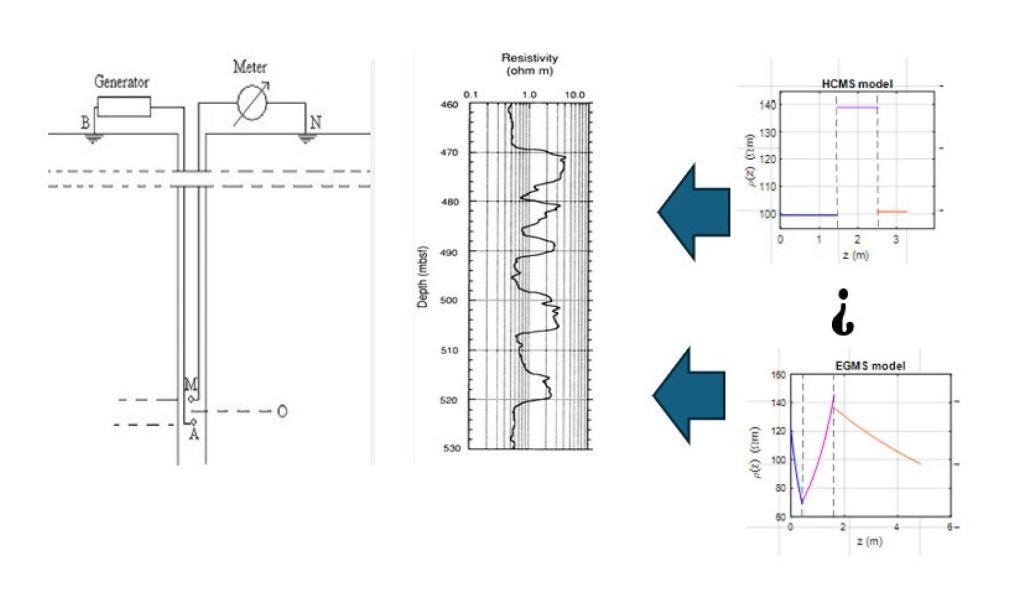
Figure 1 schematically shows the simplest device for collecting BRL data. It is the so-called Single-Point Resistance (SPR) Tool o Single-Point Log (SPL). Through contact A, a current I is injected into the ground, while contact B records the electric potential. The assembly is moved vertically along the well, probing the soil at different depths. For this device, the measured quantity is the potential at B at various depths,

ϕ_{A, B} (z)

as described by equation (4). The points M and N are considered sufficiently distant so as not to disturb the current and potential fields, ensuring that what is measured at B is the absolute electric potential generated by a current point source at A. It is also assumed that the borehole does not significantly disturb the current field associated with point A, meaning that the measurement results are not different from those associated with a point current source [19].

A typical pattern of a BRL using the device shown in an ideal multilayered soil can be seen in the right panel of Figure 1. This image was generated by simulating the survey using a conventional 5-layer HCMS model with the resistivities indicated in the figure. The horizontal distance between electrodes A and B is fixed at

d_{A B}^{h} =

5 cm, while the vertical distance is

d_{A B}^{v} =

10 cm.

It is worth noting that the SPL data acquisition device shown in Figure 1 is not the only possible configuration. Figure 2 shows a simplified schematic of another possible device used for BRL surveys. It is called Electrical Resistivity Tool (ERT) o Normal Resistivity Log (NRL). In this case, the quantity considered as the survey result is the potential difference

Δ V_{B N} (z) = ϕ_{A, B} (z) - ϕ_{A, N} (z)

. The same figure also displays the simulated survey result for the same soil used in Figure 1. In this device ERT, the potential probe N is located 10 cm above B.

Focusing on three-layer models for the reasons stated at the beginning of this section, Figure 3 shows the appearance of a BRL for two different soils using the same measuring device SPR shown in Figure 1. The left panel shows the simulated BRL in a three-layer HCMS soil with the resistivity parameters labeled on the figure itself and the widths marked with horizontal dashed lines. The right panel shows the BRL result for an EGMS model in the main plot while the functional form of the resistivity in each layer can be seen in the inscribed plot. Table 1 lists the values of the model parameters. The horizontal dashed lines in the main plot indicate the layer boundaries, as do the vertical dashed lines in the inscribed plot.

n the following example, some results from the paper [18] will be used, where the objective function is the apparent resistivity obtained from Wenner soundings. For this, we start with a three-layer stratified soil with parameters ρ₁=100 Ωm, ρ₂=50 Ωm, ρ₃=200 Ωm, h₁=3 m, h₂=2 m. A Wenner sounding is simulated over this soil, providing a defined pattern of apparent resistivity

ρ_{a p p}^{m e a s} (a)

that will be considered as the result of the sounding as a function of the electrode spacing a in the array. This sounding is then subjected to an inversion with the objective function being the apparent resistivity expression in a three-layer EGMS model

ρ_{a p p} (a; {C_{i 1}, C_{i 2}, β_{i}}_{i = 1...3})

[18], resulting in the parameter set shown in Table 2.

The graphs obtained from performing a BRL with these two models for the same soil are shown in Figure 4. The inset presents an image of the resistivity in each layer of the EGMS model. As can be seen, the BRL survey is very similar for both soil models, with the exception of the central region where the models show a discrepancy. This discrepancy arises because the central layer in the EGMS model is far from being constant, unlike in the HCMS model. It is important to note that a simulation of the sounding with the chosen objective function should closely match the sounding data obtained with the measurement device, provided that the parameters of the objective function have been well determined and the soil resistivity aligns well with the chosen model. In the described case, the objective function has been the apparent resistivity, for which the parameters of the EGMS model shown in Table 2 are optimal.

3.2. Inversión Method

As mentioned in the second item of the previous section, the task now is to determine the parameters of a specific EGMS model using the results from a BRL. For the simple device SPR shown in Figure 1, these initial data correspond to

ϕ_{A, B}^{m e a s} (z)

for a given set of depths z from the ground surface. The goal is to minimize expressions (6) or (7), where

ϕ_{A, B} (z; {C_{i 1}, C_{i 2}, β_{i}}_{i = 1...3})

represents the potential value at depth z for the three-layer EGMS model, i.e., the objective function. For the conventional HCMS model, the objective function is represented by

ϕ_{A, B} (z; {ρ_{i}, h_{i}}_{i = 1...3})

It is important to note that if the resistivity of a terrain fits well with a model, the simulation of the BRL with that model will closely resemble the BRL obtained with a direct measurement device, and expressions (6) or (7) will have very small values. However, the inverse method does not guarantee that an experimental BRL will yield a model that fits well with the data. At best, approximations may be obtained depending on the initial data. This is illustrated by Figure 3, where a stepped BRL shape suggests an HCMS soil model, while the presence of curves or slopes in the graph suggests another type of model, such as EGMS. This can also be observed in Figure 4, where two types of models are tested for the same soil. In this case, both soil models result in very similar BRL curves.

Several application examples will be analyzed next. Some of these involve simulations with synthetic soils illustrating the validity of the presented model. However, due to the high cost of BRL surveys, available data of this type are very scarce. Therefore, we are forced to use more abundant Wenner-type VES surveys. By using inversion procedures with the apparent resistivity as the objective function, we can obtain model parameters. This approach was previously used to develop the case shown in Figure 4.

Here, a new example is presented in which, starting from the apparent resistivity of a Wenner sounding applied to a synthetic soil, inversion is performed with apparent resistivity as the objective function in an EGMS model, also imposing continuity of resistivity at the interfaces. Table 3 shows the parameter values of the model, which exhibits continuity at the interfaces, as illustrated in the upper inset of Figure 5.

The equivalent HCMS model obtained through inversion is shown in the lower inset of Figure 5 and has the parameters ρ₁=569.16 Ωm, ρ₂=386.61 Ωm, ρ₃=0.71 Ωm, h₁=1.03 m, h₂=24.79 m. The main body of Figure 5 displays the BRL results using these two soil models.

As can be seen, this soil also exhibits a close equivalence between its HCMS and EGMS models for BRL surveys. However, this case, as is also the one represented in Figure 4, is quite rare. Typically, there is often incompatibility between the models considered.

Next, we will analyze the only example with measured data that we have available demonstrating the utility of the proposed model in this work. Table 5 presents the results of a BRL survey using a device similar to the one shown in Figure 1 on a site located in Yepes, Toledo (Spain).

The inversion by minimizing expression (7), enforcing the continuity of the objective function

V_{B} (z; {C_{i 1}, C_{i 2}, β_{i}}_{i = 1...3})

and using the data from Table 5 results in the EGMS model with the parameters listed in Table 6.

The inversion using the HCMS model objective function

V_{B} (z; {ρ_{i}, h_{i}}_{i = 1...3})

results in a model with parameters ρ₁=99.48 Ωm, ρ₂=138.94 Ωm, ρ₃=100.78 Ωm, h₁=1.46 m, h₂=1.06 m. Figure 6 displays the BRL data from the measurements marked with green diamond symbols. It also shows the BRL simulations for the two models obtained through inversion.

The BRL simulation for the EGMS model, using the parameters from Table 6, is shown with a red solid line, while the simulation for the HCMS model, with the previously mentioned parameters, is shown with a blue solid line. The upper right inset represents the resistivity assigned according to the EGMS model, which is nearly continuous. As seen in the main figure, this model closely reproduces the measured BRL data. The lower right inset shows the resistivity according to the HCMS model, and the main figure also displays the BRL simulation for this model with the blue solid line. It is evident that this simulation reproduces the measured BRL less accurately, highlighting the need for alternative models to HCMS for the proper interpretation of BRL soundings.

As a final comment, it is important to note that the proposed model is a layered model in which the resistivity has a defined functional form in each layer. From a technical standpoint, it represents an advancement over models with constant resistivity layers. However, real soil can be much more complex and may not fit into any of these models. Nevertheless, introducing variability with depth will always provide a better fit of the model to the actual resistivity profile.

4. Conclusions

In this work, the application of the EGMS model to the interpretation of BRL soundings has been addressed as an alternative to the more widely used HCMS models in the field of soil electrical structure research. The applicability and relevance of the EGMS model have been demonstrated, particularly in situations where conventional models do not provide an adequate result. Synthetic examples have been considered to illustrate the application of the proposed model, as well as an example from an actual BRL survey, which clearly shows the need for alternatives to conventional soil models. The EGMS model represents a significant advancement, offering a robust alternative for interpreting BRL survey when conventional models do not satisfactorily explain the soil resistivity profile based on the recorded data.

Author Contributions

Ricardo Paramo (RP), Eduardo Faleiro (EF), Gabriel Asensio (GA) and Jorge Moreno (JM). Conceptualization, RP, EF and GA.; methodology, RP, EF and GA.; software, RP and GA.; validation, JM and GA; formal analysis, RP,EF,GA and JM; investigation, RP, EF and GA; resources, GA and JM; data curation, JM and GA; writing—original draft preparation, RP, EF, GA and JM; writing—review and editing, RP and EF; visualization, JM.; supervision, RP and EF.; project administration, GA, and JM. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding

Institutional Review Board Statement

Not applicable.

Data Availability Statement

The data used and contained in this paper are in the public domain.

Acknowledgments

The authors would like to thank both the Department of Applied Mathematics and the IEEF Department of the Escuela Técnica Superior de Ingeniería y Diseño Industrial (ETSIDI) at the Universidad Politecnica de Madrid (UPM) for their support to the undertaking of the research summarized here. Furthermore, the authors appreciate the collaboration with the firm QUIBAC at Terrassa, Barcelona (Spain), for the technical support and useful advice received from the staff.

Conflicts of Interest

The authors declare no conflict of interest.

References

R.A. van Overmeeren and I.L. Ritsema. Continuous vertical electrical sounding. First Break, Volume 6, Issue 10, Oct 1988. [CrossRef]
Reynolds, J. M. (2011). An introduction to applied and environmental geophysics. John Wiley & Sons.
Kearey, P., Brooks, M., & Hill, I. (2002). An introduction to geophysical exploration (Vol. 4). John Wiley & Sons.
Loke, M. H., & Barker, R. D. (1996). Practical techniques for 3D resistivity surveys and data inversion. Geophysical Prospecting, Volume 44, Issue 3, May 1996, p. 499 – 523. [CrossRef]
Calamita, G., Perrone, A., Brocca, L., & Straface, S. (2017). Soil electrical resistivity for spatial sampling design, prediction, and uncertainty modeling of soil moisture. Vadose Zone Journal, 16(10), 1-14. [CrossRef]
Shihang, Z., Hutchinson, P., Toland, M., Floyd, J., Meehan, T., Lee, R., ... & de Smet, T. (2016, March). Archaeological Geophysics. In Symposium on the Application of Geophysics to Engineering and Environmental Problems 2015 (pp. 30-32). Society of Exploration Geophysicists and Environment and Engineering Geophysical Society.
Hossain, S., Kibria, G., & Khan, S. (2018). Site investigation using resistivity imaging. CRC Press. [CrossRef]
Lai, W. W. L., Derobert, X., & Annan, P. (2018). A review of Ground Penetrating Radar application in civil engineering: A 30-year journey from Locating and Testing to Imaging and Diagnosis. Ndt & E International, 96, 58-78. [CrossRef]
Ruan, W., Southey, R. D., Fortin, S., & Dawalibi, F. P. (2005, August). Effective sounding depths for HVDC grounding electrode design: Wenner versus Schlumberger methods. In 2005 IEEE/PES Transmission & Distribution Conference & Exposition: Asia and Pacific (pp. 1-7). IEEE. [CrossRef]
Nahman, J., & Salamon, D. (1988). A practical method for the interpretation of earth resistivity data obtained from driven rod tests. IEEE transactions on power delivery, 3(4), 1375-1379. [CrossRef]
Denche, G., Faleiro, E., Asensio, G., & Moreno, J. (2021). Grounding Electrodes with Internal Resistance: Application to Feasibility Study of the Driven-Rod Method for Modeling the Soil Electrical Resistivity Profile. Applied Sciences, 11(11), 5032. [CrossRef]
Yang, F. W., & Ward, S. H. (1984). Inversion of borehole normal resistivity logs. Geophysics, 49(9), 1541-1548. [CrossRef]
Kobr, M. (2021). Geophysical well logging. In Encyclopedia of solid earth geophysics (pp. 527-537). Cham: Springer International Publishing.
Seedher, H. R., & Arora, J. K. (1992). Estimation of two layer soil parameters using finite Wenner resistivity expressions. IEEE Transactions on Power Delivery, 7(3), 1213-1217. [CrossRef]
Takahashi, T., & Kawase, T. (1991). Calculation of earth resistance for a deep-driven rod in a multi-layer earth structure. IEEE Transactions on Power Delivery, 6(2), 608-614. [CrossRef]
Inman Jr, J. R., Ryu, J., & Ward, S. H. (1973). Resistivity inversion. Geophysics, 38(6), 1088-1108. https://. [CrossRef]
Mooney, H. M., Orellana, E., Pickett, H., & Tornheim, L. (1966). A resistivity computation method for layered earth models. Geophysics, 31(1), 192-203. [CrossRef]
Paramo, R., Faleiro, E., Asensio, G., & Moreno, J. (2021). Functionally graded multilayered soil models, an alternative to modeling the soil electrical resistivity for computing the grounding resistance. IEEE Access, 9, 55364-55372. [CrossRef]
Aweto, K.E., 2013, Resistivity Methods in Hydro-Geophysical Investigation for Groundwater in Aghalokpe, Western Niger Delta: Global Journal of Geological Sciences, v. 11, p. 47-55, . [CrossRef]

Figure 1. Simplified schematic of SPR tools for BRL surveys (left panel). The distance between A and B is fixed, while the assembly (green part) can move vertically. The right panel shows the result of the survey (see text).

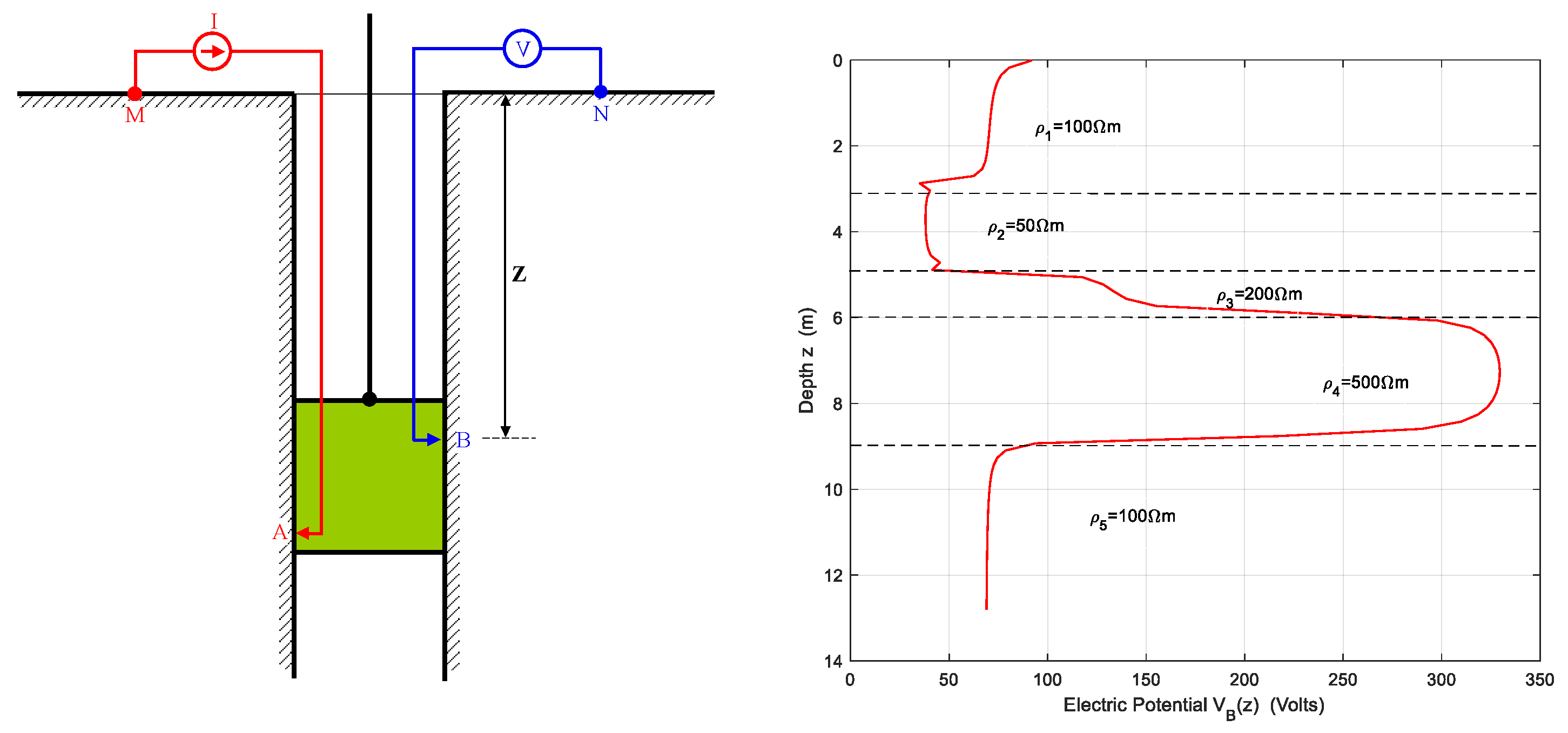
Figure 2. The NRL device for data acquisition and the simulated result image for the same 5-layer HCMS soil used in Figure 1.

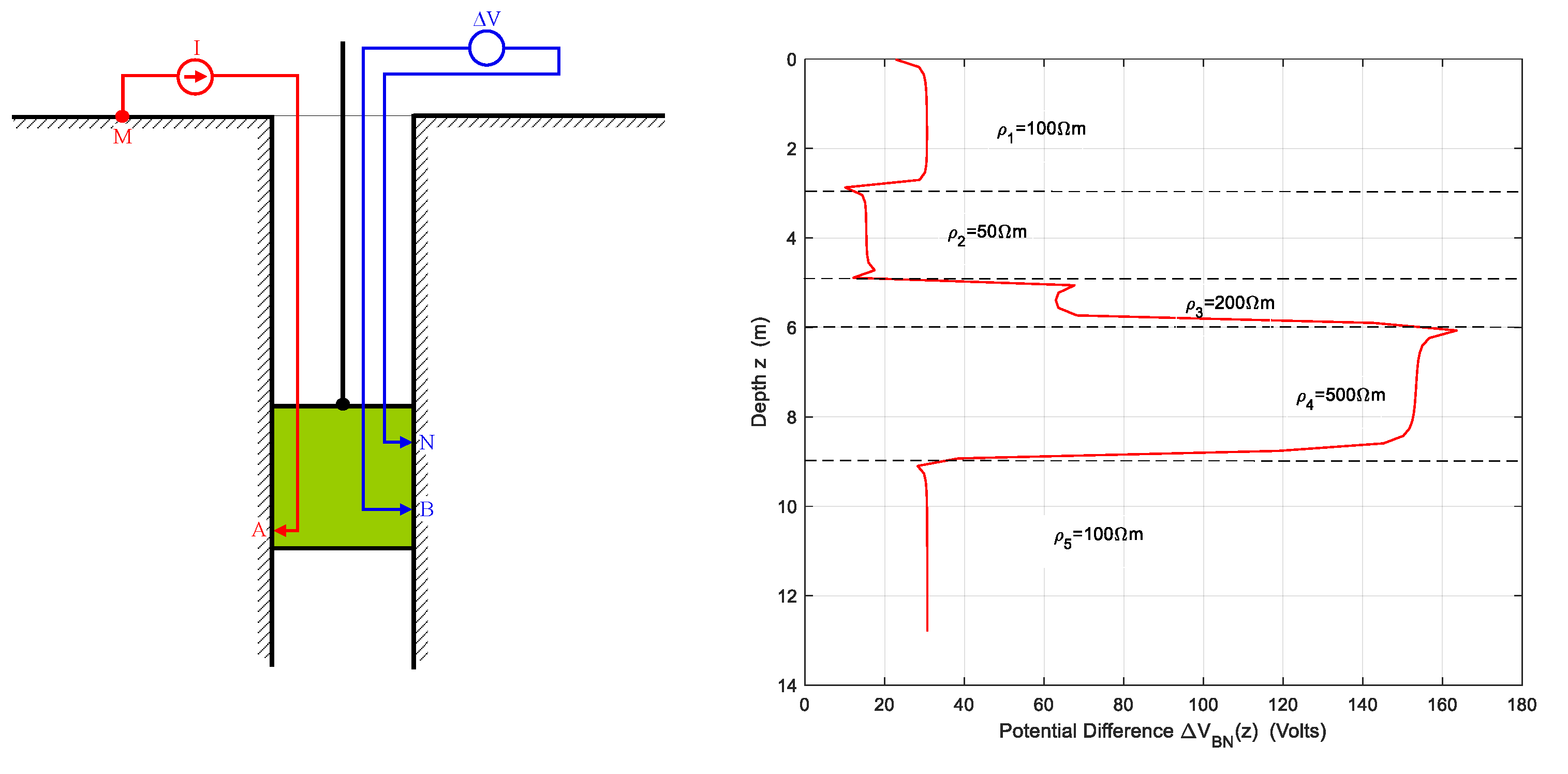
Figure 3. BRL simulations on tree-layered soil models, HCMS (left panel) and EGMS (right panel).

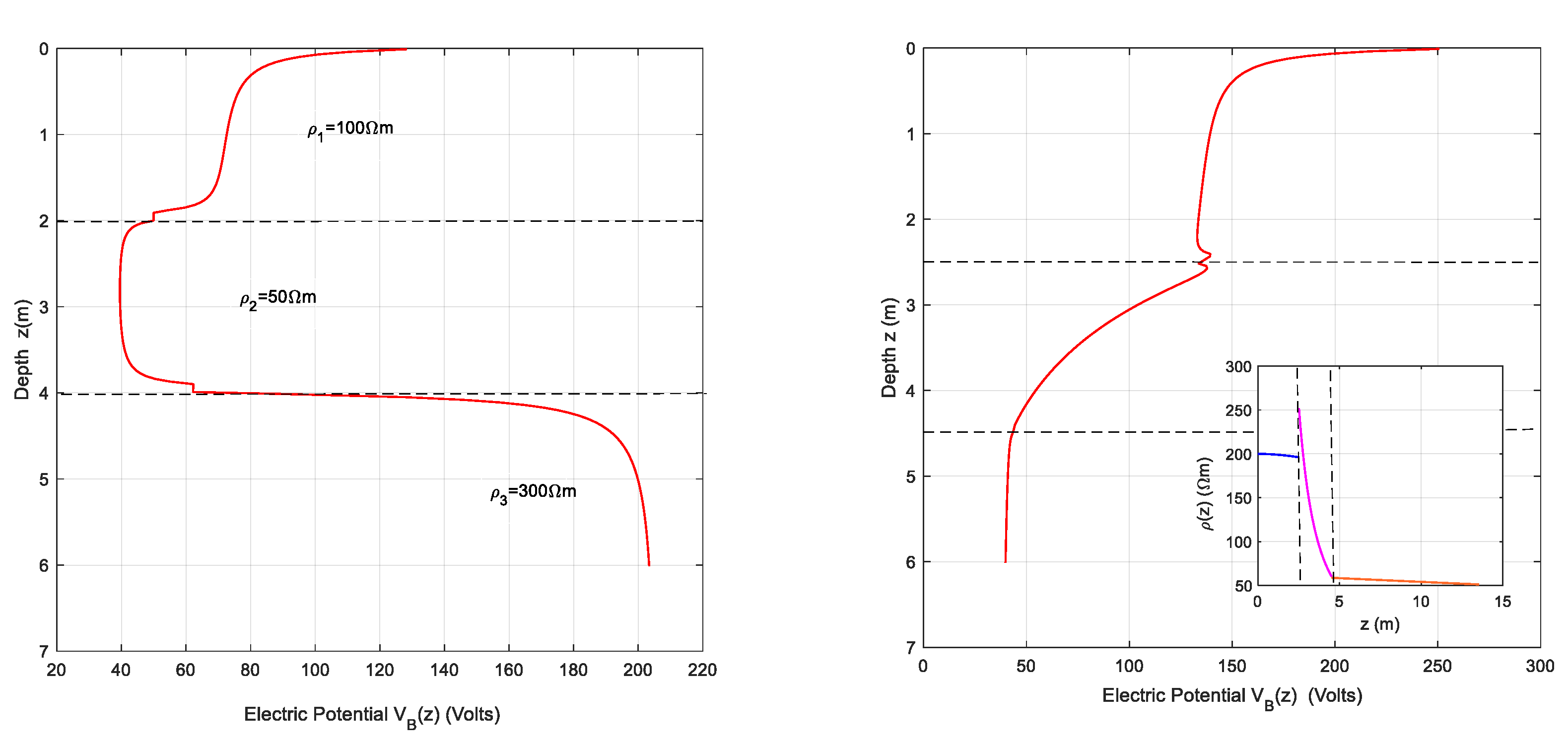
Figure 4. Result of the BRL surveys with the two models for the same soil.

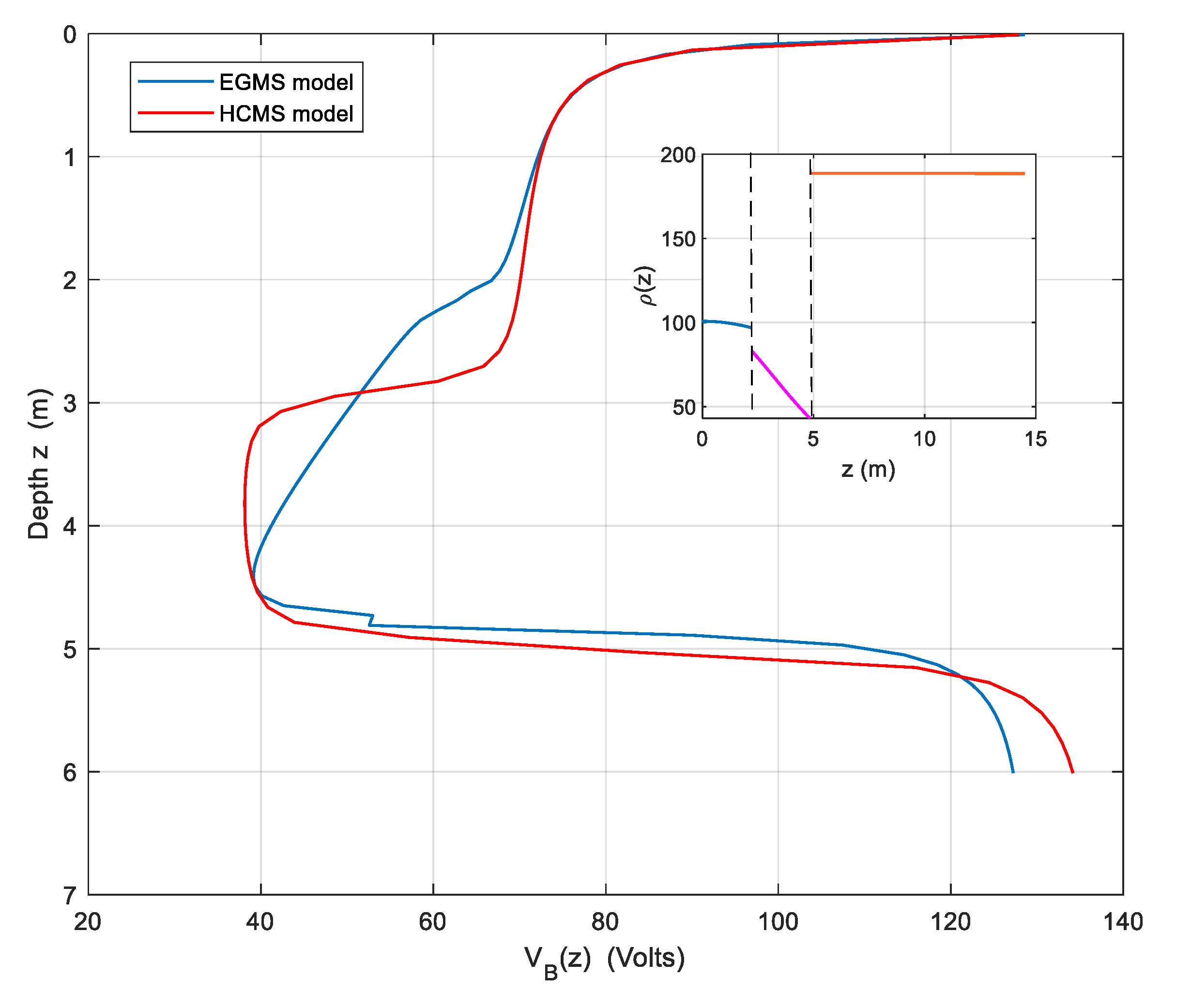
Figure 5. Result of BRL surveys with two models for the same soil.

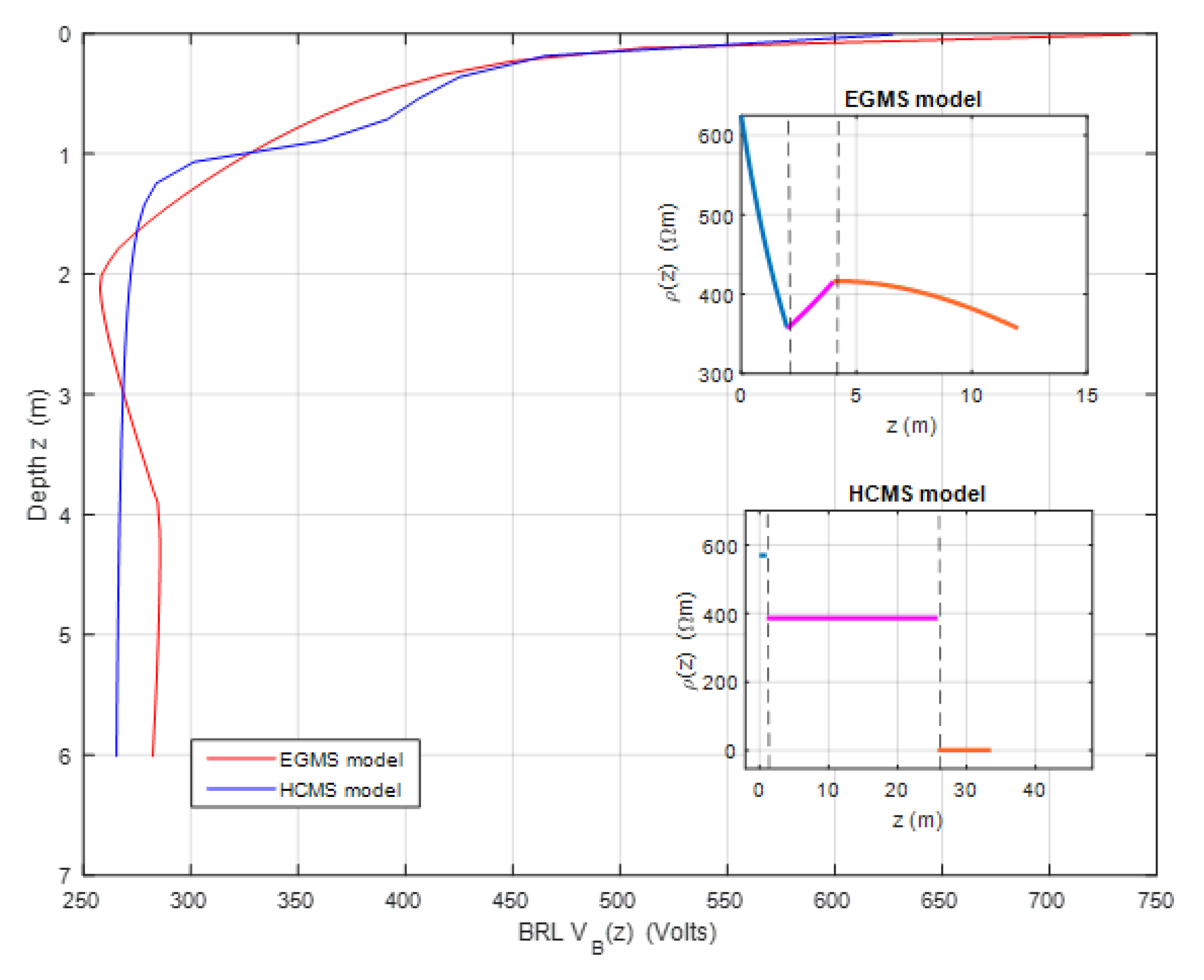
Figure 6. Measured BRL from the soil at Yepes and the simulated BRL from the two fitted models.

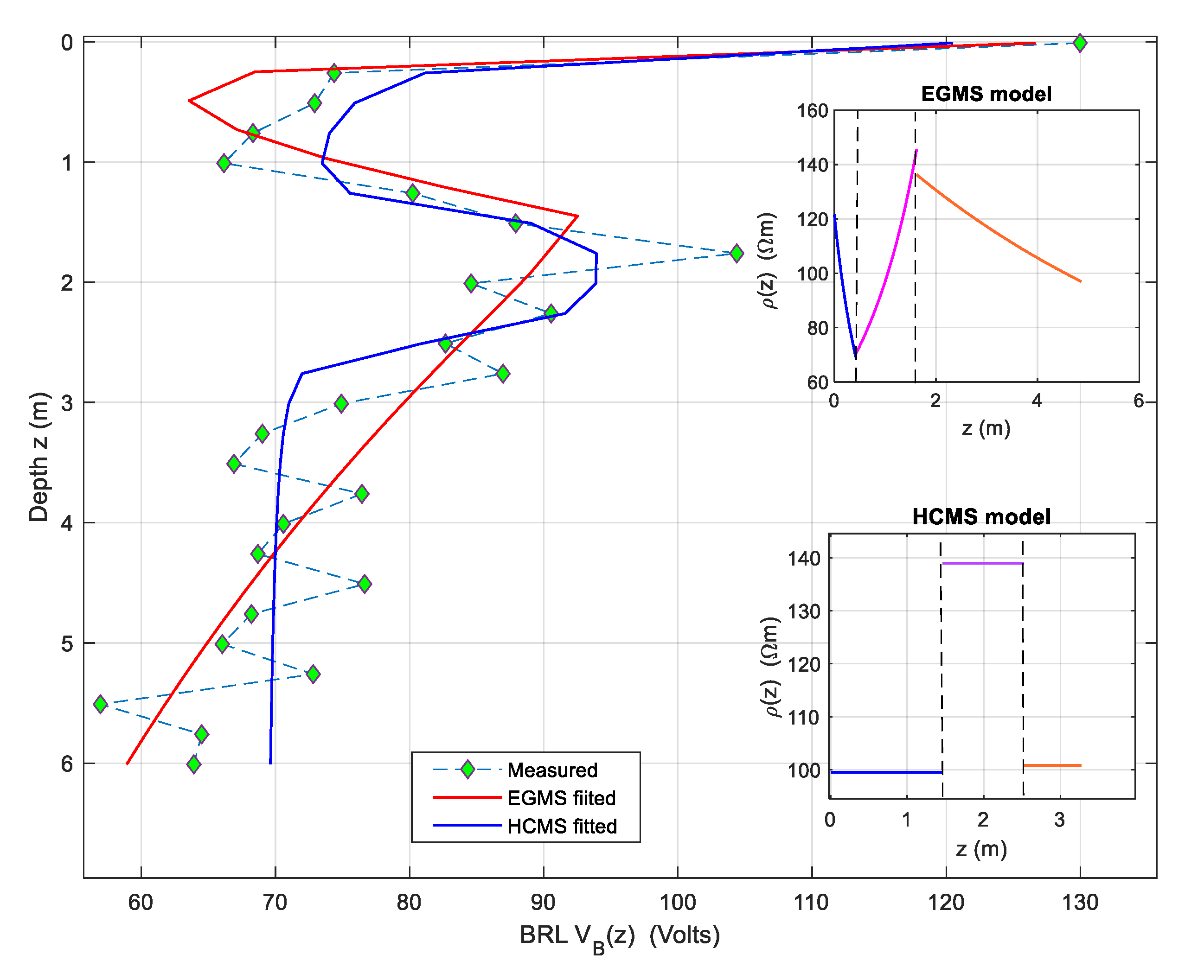
Table 1. Non-Continuous EGMS model parameters for the soil depicted in the graph shown in the right panel of Figure 2.

Params.	C₁₁	C₁₂	β₁	C₂₁	C₂₂	β₂	C₃₁	C₃₂	β₃	h₁	h₂
Values	0.0358	0.0349	0.0515	0.0861	-0.0976	0.1590	0.0995	0.0269	0.0119	2.16	1.99

Table 2. Non-Continuous EGMS model parameters for the soil depicted in the inset of Figure 4.

Params.	C₁₁	C₁₂	β₁	C₂₁	C₂₂	β₂	C₃₁	C₃₂	β₃	h₁	h₂
Values	0.0498	0.0497	0.0900	0.0496	0.0498	0.2053	0.0364	0.0365	0.0020	2.22	2.62

Table 3. Continuous EGMS model parameters for the soil depicted in the graph shown in the inset of Figure 5.

Params.	C₁₁	C₁₂	β₁	C₂₁	C₂₂	β₂	C₃₁	C₃₂	β₃	h₁	h₂
Values	0.0501	-0.0101	0.1002	-0.0218	0.0787	0.0201	0.0203	0.0310	0.0511	2,00	2.00

Table 5. Measured BRL data from the soil located at Yepes, Toledo (Spain) with a SPR Tool.

Depth z (m)	0.01	0.25	0.52	0.74	1.00
V_B(Volts)	129.98	74.38	72.92	68.32	66.16
Depth z (m)	1.25	1.51	1.74	2.00	2.25
V_B (Volts)	80.23	87.91	104.39	84.58	90.55
Depth z (m)	2.50	2.74	3.02	3.25	3.50
V_B (Volts)	82.67	86.96	74.91	69.02	66.90
Depth z (m)	3.77	3.99	4.25	4.50	4.76
V_B (Volts)	76.43	70.60	68.69	76.65	68.21
Depth z (m)	5.00	5.24	5.50	5.76	6.00
V_B (Volts)	66.03	72.81	56.95	64.50	63.92

Table 6. Continuous EGMS model parameters for the soil from Table 5 data.

Params.	C₁₁	C₁₂	β₁	C₂₁	C₂₂	β₂	C₃₁	C₃₂	β₃	h₁	h₂
Values	0.1855	-0.0948	0.2442	0.2495	-0.1172	-0.0850	0.1420	-0.0641	0.0231	0.42	1.20

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Modeling Borehole Resistivity Logs with Exponentially Graded Multilayered Soil Inversion

Abstract

1. Introduction

2. Mathematical Foundations

2.1. Direct Method

2.2. Inversion Method

3. Applications of the Proposed Model

3.1. Direct Method

3.2. Inversión Method

4. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe