Cosmic Dynamics Unveiled: A Relativistic Approach to Structure Formation and Evolution in a Friedmann Universe

1. Introduction

The homogeneity of matter distribution at large scales, known as the cosmological principle (CP), is a central assumption in the standard cosmological model (SCM). Rooted in a geometrical assumption outlined by Einstein in 1917, the cosmological principle posits that on a vast scale, the spatial distribution of matter is both homogeneous and isotropic [1]. Despite the apparent lack of homogeneity and isotropy at small scales in the distributions of celestial objects, the cosmological principle implies the existence of a homogeneity scale, beyond which the distribution becomes statistically indistinguishable from a random one bringing the argument of whether or not the universe is homogeneous or fractal in nature as the scale evolves with time [2].

In contemporary cosmological models within the framework of general relativity, the Friedmann-Lemaitre-Robertson-Walker (FLRW) metric serves as the common basis [3]. Distinctions among these models arise not from the solutions to Einstein's equations but from the selection of the stress-energy tensor ($T_{\mu \nu }$), specifically influencing the expansion factor, R(t), in the spatial line element [4].

The SCM builds upon two fundamental tenets: the consideration of General Relativity as the foundational theory of gravity and the adherence to the CP, positing statistical homogeneity and isotropy at large scales [5]. The CP, in its modern formulation, dictates that, at sufficiently large scales, the average evolution of the universe precisely adheres to the FLRW metric [6]. While the homogeneous SCM model aligns well with observations, challenges such as the fine-tuning problems, Hubble tension, and cosmic coincidence issues suggest potential deviations from the SCM [7,8,9]. Key to this discussion are the redshift-distance and light intensity-distance relations, which are fundamental tools in observational cosmology. The redshift-distance relation provides critical insights into the universe's expansion rate, serving as a direct test of cosmological models. Accurate measurements of redshift and corresponding distances allow cosmologists to map the large-scale structure of the universe, revealing patterns that either support or challenge the assumptions of homogeneity and isotropy. Similarly, the light intensity-distance relation, which describes how the observed brightness of an object diminishes with distance, is crucial for determining cosmological distances and, by extension, for understanding the universe's expansion history. Both relations are integral to testing the validity of the Friedmann model and the cosmological principle, particularly in light of the growing complexity observed in deep-space surveys.

To refine our understanding of these relations, recent studies have employed both parametric and nonparametric redshift models. Parametric models rely on predefined functional forms and assumptions about the universe’s expansion history, such as the commonly used SCM model, which assumes a specific functional form for the expansion rate and matter density[10]. Nonparametric models, on the other hand, do not assume a particular functional form and instead use data-driven approaches to infer the redshift-distance relation directly from observations [11]. These models offer greater flexibility and can capture deviations from the standard parametric assumptions, providing a more nuanced view of the universe's structure and evolution [5,12]. The integration of both parametric and nonparametric approaches allows for a more comprehensive analysis of the redshift-distance relation, potentially addressing discrepancies and refining our understanding of cosmological principle.

Compounding these theoretical challenges are the enigmatic dark matter (DM) and dark energy (DE), which together make up 95% of the universe's total mass-energy content. While DM is crucial for explaining the flat rotation curves of galaxies and the formation of large-scale structures, DE has been claimed to account for the observed acceleration in the universe's expansion—a phenomenon first detected through observations of Supernovae Type Ia [13]. Nevertheless, the physical nature of these two phenomena remains a mystery. Einstein suggested a long-forgotten solution: gravitationally repulsive negative masses, which drive cosmic expansion and cannot coalesce into light-emitting structures [14]. In addition, a type of cold dark matter in the universe is needed to explain the formation of the cosmic structure and galaxy dynamics. So far, it has been claimed that the cosmological constant is the best candidate to explain the so-called dark energy [5]. These unresolved issues further complicate the cosmological models, demanding more precise observational data and innovative theoretical approaches.

The challenge of testing the cosmological principle and the SCM is further exacerbated by the limitations of current observational methods. Three-dimensional redshift surveys, despite their sophistication, often produce limited and potentially misleading data due to inherent uncertainties in cosmic distance measurements and the complexity of interpreting large-scale structures. For instance, while observational evidence generally supports isotropy on large scales—demonstrated by the Cosmic Microwave Background Radiation (CMBR), and isotropic distributions of radio sources, gamma-ray bursts, and supernovae [15,16] findings do not unequivocally confirm large-scale homogeneity. In particular, quasar distribution studies suggest homogeneity only beyond scales of $250h^{-1}$ Mpc [17], , highlighting the need for more rigorous testing.

In light of the unsettling discoveries detailed above, there exists a pervasive sense of uncertainty regarding the accuracy of current cosmological frameworks. To this regard, we present a model describing the universe’s dynamics, structure formation and evolution by taking into account its density and geometry. The investigation centers on three astronomical parameters: number density, light intensity, and redshift. We analyze the evolution of number density and light intensity across redshift, assessing their influence from the universe’s infancy to the present, and conduct a comparative evaluation with findings from other studies. In particular, we shall make comparisons with works of Langa et al. (2017) whose model we shall refer to as ‘approximate standard Friedmann redshift model’ and Nyagisera et al. (2024) whose model we shall refer to as ‘modified standard Friedmann redshift model’. The model developed in this paper shall be referred to as the ‘standard Friedmann redshift model’. Throughout our examination, we shall account for the influence exerted by dark matter and dark energy within these theoretical constructs. In order to validate our model, a histogram plot of observational data of galactic number count against redshift extracted from NASA/IPAC Extragalactic Database shall be performed.

The paper is structured as follows: Section 2 introduces our model, Section 3 and Section 4 presents the analytical and graphical results of our study respectively, while Section 5 is devoted to discussions of our results before culminating into conclusions in Section 6.

2. Model Formulation

2.1. Parametric Model

The parametric model introduced by Bassett et al. [10] in 2015 modifies the conventional redshift framework to enhance our understanding of cosmic dynamics. By introducing parameters that adjust the redshift space, this model allows for a more refined interpretation of observational data. It also tackles intricate aspects of cosmic phenomena by incorporating these specific parameters, offering a more precise and detailed representation of redshift-related observations. In this study, we shall compare our model with the parametric model $\mathrm{f}\left(\mathrm{z}\right)={\mathsf{\alpha }}_1\mathrm{z}+{\mathsf{\alpha }}_2{\mathrm{z}}^2$ where c1 and c2 are arbitrary parameters (see details in Nyagisera et al., 2024).

2.2. Nonparametric Model

The non-parametric model developed by Wojtak and Prada [11] in 2017 adopts a different approach by avoiding predefined parameters, offering greater flexibility in modeling cosmic phenomena. Unlike parametric models, this non-parametric model does not impose fixed parameters, allowing for a more adaptive and data-driven analysis of redshift-related phenomena. In this work, we shall compare our model with the nonparametric model $f\left(z\right)=z+{\gamma \left(z\right)}^2$where γ(z) is a freely varying function of z (see details in Nyagisera et al., 2024).

2.3. The Einstein Field Equations Based on Friedmann Model

Consider the FLRW metric

$$d{s}^2=c^{2}d{t}^2-{\displaystyle \frac{R\left(t\right)}{{\left(1+\kappa r^2\right)}^2}}d{r}^2$$

(1)

where c is the speed of light, $R\left(t\right)$, denotes the scale factor governing the time-dependent evolution of the spatial portion of the metric (specifically, the surfaces corresponding to constant time, t), $\kappa =(-\mathrm{1,0},1)$ gives the geometry of the universe as open, flat, or closed respectively, and $d{r}^2=d{x}^2+d{y}^2+d{z}^2$ is the rectangular coordinate representation of the three dimensional projection space.

Straightforward calculations based on equation (1) [12,19,20] yield:

$$12\kappa c^2+3R^{\text{'}}{\left(t\right)}^2=\beta c^4\rho \left(t\right){R\left(t\right)}^2-\lambda c^2{R\left(t\right)}^2$$

(2)

$$4\kappa c^2+2R\left(t\right)R\text{'}\text{'}\left(t\right)+R^{\text{'}}{\left(t\right)}^2=\beta c^2\rho \left(t\right){R\left(t\right)}^2-\lambda c^2{R\left(t\right)}^2$$

(3)

where ${R\left(t\right)}^{\mathrm{\text{'}}}={\displaystyle \frac{dR}{dt}}$ ,${R\left(t\right)}^{\mathrm{\text{'}}\mathrm{\text{'}}}={\displaystyle \frac{d^{2}R}{d{t}^2}},$ $\rho \left(t\right)$ is the density of the observable universe and $\beta ={\displaystyle \frac{8\pi G}{c^4}}$

Equations (2) and (3) are key in describing the dynamics, formation of structures and evolution of the universe. Earlier studies [12,20] used the Noether theorem pertinent to a matter-dominated Friedmann universe;

$$\rho \left(t\right)R{\left(t\right)}^3=\alpha$$

This theorem deduced Einstein field equations relation of the form

$$\mathrm{d}\mathrm{t}={\displaystyle \frac{\mathrm{d}\mathrm{R}\left(\mathrm{t}\right)}{\sqrt{\frac{\left(\mathsf{\beta }{\mathrm{c}}^4\mathsf{\rho }\left(\mathrm{t}\right)-\mathsf{\lambda }{\mathrm{c}}^2\right)\alpha }{3\mathsf{\rho }\left(\mathrm{t}\right)\mathrm{R}\left(\mathrm{t}\right)}-4\mathsf{\kappa }{\mathrm{c}}^2}}}$$

(4)

In contrast to these studies, this work treated the density of the universe and the cosmic scale factor as variables thus rearranged equation (2) to yield;

$$dt={\displaystyle \frac{dR\left(t\right)}{\sqrt{\frac{\left(\beta c^4\rho \left(t\right)-\lambda c^2\right)R{\left(t\right)}^2}{3}-4\kappa c^2}}}$$

(5)

Equation (4) and equation (5) is the Friedmann model relation representing time taken by a light photon to travel a distance $dr,$ describing the Friedmann Universe. Equation (5) brings a clearer description of the dynamics, structure formation and evolution of the universe as compared to equation (4) obtained through conservation theorem in existing works [12,20]. Equation (5) will be applied in deriving the light intensity-redshift and the number density-redshift relations in this work.

3. Analytical solutions

3.1. Light Intensity-Redshift Relation

Considering light emanating from an astronomical object (galaxy or a star) commencing its journey at $r\left(t_e\right)$ and progressing towards the spatial origin, $r=r\left(t_o\right),$ when time$t=t_o$. In this scenario, the FLRW metric (see Equation (1)) can be formulated to capture this dynamic spatial relationship for null geodesic as;

$$0=c^2\dot{{\dot{t}}^2-}{\displaystyle \frac{{R\left(t\right)}^2}{{\left(1+\kappa r^2\right)}^2}}{\dot{r}}^2$$

(6)

where ${\displaystyle \frac{dt}{d\tau }}=\dot{t},{\displaystyle \frac{dr}{d\tau }}=\dot{r}$ implying that

$$c\dot{t}=\pm {\displaystyle \frac{R\left(t\right)}{1+\kappa r^2}}\dot{r}$$

(7)

Performing integration of equation (7) over ${(t}_e,to)$ and $(r\left(t_e\right),r(t_o\left)\right)$ and applying the reversibility of light principle while noting that $\dot{t}$ positive while $\dot{r}$ negative by our assumption,

$${\int }_{t_e}^{t_o}{\displaystyle \frac{c}{R\left(t\right)}}dt=-{\int }_{r\left(t_e\right)}^{r\left(t_o\right)}{\displaystyle \frac{1}{1+\kappa r^2}}dr$$

(8)

Substituting equation (5) into equation (8) gives :

$${\int }_{R\left(t_e\right)}^{R\left(t_o\right)}{\displaystyle \frac{dR\left(t\right)}{{R\left(t\right)}^2\sqrt{\frac{\left(\beta c^2\rho \left(t\right)-\lambda \right)}{3}-\frac{4\kappa }{{R\left(t\right)}^2}}}}=-{\int }_{r\left(t_e\right)}^{r\left(t_o\right)}{\displaystyle \frac{dr}{1+\kappa r^2}}$$

(9)

Equation (9) is more general and is suitable for describing the evolution and dynamics of the universe as it contains an extra cosmological term on its L.H.S earlier present in equation (5). Solving this equation for three different cases of $\kappa ,$ that is, for open universe$(\kappa =-1)$, flat universe$(\kappa =0)$, and for a closed universe$\left(\kappa =1\right),$ it can easily be shown that:

$$r\left(t_e\right)=\left\{\begin{array}{c}{\displaystyle \frac{z}{aR\left(t_o\right)}}fork=0,\\ {\displaystyle \frac{2\left(1+\mathrm{z}\right)\left(\mathrm{a}\mathrm{R}\left({\mathrm{t}}_{\mathrm{o}}\right)+\sqrt{(\mathrm{a}\mathrm{R}{\left({\mathrm{t}}_{\mathrm{o}}\right))}^2-4}\right)-2\left(\mathrm{a}\mathrm{R}\left({\mathrm{t}}_{\mathrm{o}}\right)+\sqrt{(\mathrm{a}\mathrm{R}{\left({\mathrm{t}}_{\mathrm{o}}\right))}^2-4{\left(1+\mathrm{z}\right)}^2}\right)}{\left(\mathrm{a}\mathrm{R}\left({\mathrm{t}}_{\mathrm{o}}\right)+\sqrt{(\mathrm{a}\mathrm{R}{\left({\mathrm{t}}_{\mathrm{o}}\right))}^2-4{\left(1+\mathrm{z}\right)}^2}\right)\left(\mathrm{a}\mathrm{R}\left({\mathrm{t}}_{\mathrm{o}}\right)+\sqrt{(\mathrm{a}\mathrm{R}{\left({\mathrm{t}}_{\mathrm{o}}\right))}^2-4}\right)+4\left(1+\mathrm{z}\right)}}fork=-1,\\ {\displaystyle \frac{2\left[\left(1+\mathrm{z}\right)\left(\mathrm{a}\mathrm{R}\left({\mathrm{t}}_{\mathrm{o}}\right)+\sqrt{{\mathrm{a}}^2\mathrm{R}{\left({\mathrm{t}}_{\mathrm{o}}\right)}^2+4}\right)-\left(\mathrm{a}\mathrm{R}\left({\mathrm{t}}_{\mathrm{o}}\right)+\sqrt{{\mathrm{a}}^2\mathrm{R}{\left({\mathrm{t}}_{\mathrm{o}}\right)}^2+4{\left(1+\mathrm{z}\right)}^2}\right)\right]}{\left(\mathrm{a}\mathrm{R}\left({\mathrm{t}}_{\mathrm{o}}\right)+\sqrt{{\mathrm{a}}^2\mathrm{R}{\left({\mathrm{t}}_{\mathrm{o}}\right)}^2+4}\right)\left(\mathrm{a}\mathrm{R}\left({\mathrm{t}}_{\mathrm{o}}\right)+\sqrt{{\mathrm{a}}^2\mathrm{R}{\left({\mathrm{t}}_{\mathrm{o}}\right)}^2+4{\left(1+\mathrm{z}\right)}^2}\right)-4\left(1+\mathrm{z}\right)}}fork=1\end{array}\right.$$

(10)

where

$a=\sqrt{{\displaystyle \frac{\left(\beta c^2\rho \left(t\right)-\lambda \right)}{3}}}$

The three cases in equation (10) can be generalized as

$$r\left(z\right)={\displaystyle \frac{2\left[\left(1+\mathrm{z}\right)\left(\mathrm{a}\mathrm{R}\left({\mathrm{t}}_{\mathrm{o}}\right)+\sqrt{{\mathrm{a}}^2\mathrm{R}{\left({\mathrm{t}}_{\mathrm{o}}\right)}^2-4\mathsf{\kappa }}\right)-\left(\mathrm{a}\mathrm{R}\left({\mathrm{t}}_{\mathrm{o}}\right)+\sqrt{{\mathrm{a}}^2\mathrm{R}{\left({\mathrm{t}}_{\mathrm{o}}\right)}^2-4\mathsf{\kappa }{\left(1+\mathrm{z}\right)}^2}\right)\right]}{\left(\mathrm{a}\mathrm{R}\left({\mathrm{t}}_{\mathrm{o}}\right)+\sqrt{{\mathrm{a}}^2\mathrm{R}{\left({\mathrm{t}}_{\mathrm{o}}\right)}^2-4\mathsf{\kappa }}\right)\left(\mathrm{a}\mathrm{R}\left({\mathrm{t}}_{\mathrm{o}}\right)+\sqrt{{\mathrm{a}}^2\mathrm{R}{\left({\mathrm{t}}_{\mathrm{o}}\right)}^2-4\mathsf{\kappa }{\left(1+\mathrm{z}\right)}^2}\right)+4\mathsf{\kappa }\left(1+\mathrm{z}\right)}}$$

(11)

where $\kappa =-\mathrm{1,0},1$, $r\left(t_e\right)=r\left(z\right)$ since $t_e$ depends on$z$,$R\left(t_e\right)=R\left(t_o\right)/(1+z$) and $\rho \left(t\right)$ is the density of the universe at observational time,$t_o.$

Equation (11) can be decomposed to;

$$\mathrm{r}\left(\mathrm{z}\right)={\displaystyle \frac{2\left(\mathrm{p}\left(1+\mathrm{z}\right)-\mathrm{q}\right)}{\mathrm{p}\mathrm{q}+4\mathsf{\kappa }\left(1+\mathrm{z}\right)}}$$

(12)

where,

$\mathrm{p}=\mathrm{a}\mathrm{R}\left({\mathrm{t}}_{\mathrm{o}}\right)+\sqrt{{\mathrm{a}}^2\mathrm{R}{\left({\mathrm{t}}_{\mathrm{o}}\right)}^2-4\mathsf{\kappa }}$

and

$$\mathrm{q}=\mathrm{a}\mathrm{R}\left({\mathrm{t}}_{\mathrm{o}}\right)+\sqrt{{\mathrm{a}}^2\mathrm{R}{\left({\mathrm{t}}_{\mathrm{o}}\right)}^2-4\mathsf{\kappa }{\left(1+\mathrm{z}\right)}^2}$$

Consider an astronomical object, whether it be a luminous star or a galaxy, positioned at the origin,$r\left(t_o\right)=0$, emitting light with absolute luminosity, L. Over a time, span of emission,$t_{e,}$ we contemplate the emission of light, each increment of which is encapsulated by$d{t}_e$. Subsequently, at a distinct moment of observation,$t_o,$ an observer gauges the intensity of the emitted light, I, which is inevitably subject to a redshift$z$. The spatial coordinates of the observer are elegantly captured by Equation (11). This intricate interplay of emission, transmission, and observation culminates in Equation (13), expressed as:

$$I={\displaystyle \frac{Ld{t}_e}{\left(1+z\right)S_{r\left(z\right)}}}$$

(13)

where $S_{r\left(z\right)}={\displaystyle \frac{4\pi r{\left(z\right)}^{2}R{\left(t_o\right)}^2}{{\left(1+\kappa r^2\right)}^2}}$ is the surface area of the sphere of radius $r=r\left(z\right)$ at time$t=t_o$ [20].

Applying equation (12) in equation (13) and the fundamental theorem of integral calculus together with the relation${\displaystyle \frac{d{t}_e}{d{t}_o}}={\displaystyle \frac{R\left(t_e\right)}{R\left(t_o\right)}}={\displaystyle \frac{1}{1+z}}$, we obtain:

$$\mathrm{I}={\displaystyle \frac{\mathrm{L}{\left[1+\mathsf{\kappa }{\left(\frac{2\left(\mathrm{p}\left(1+\mathrm{z}\right)-\mathrm{q}\right)}{\mathrm{p}\mathrm{q}+4\mathsf{\kappa }\left(1+\mathrm{z}\right)}\right)}^2\right]}^2}{4\mathsf{\pi }{\left(\frac{2\left(\mathrm{p}\left(1+\mathrm{z}\right)-\mathrm{q}\right)}{\mathrm{p}\mathrm{q}+4\mathsf{\kappa }\left(1+\mathrm{z}\right)}\right)}^2{\mathrm{R}}^2\left(t_o\right){\left(1+\mathrm{z}\right)}^2}}$$

(14)

Equation (14) unveils a profound connection between redshift z and the luminous intensity I. This equation serves as a pivotal conduit, allowing us to delve into the dynamics and evolution of the our universe.

3.2. Number Density Redshift Relation

Let us direct our focus toward celestial bodies, galaxies or supernovae for instance, which exhibit uniform distribution across the expanse of the universe within specific range of redshift. In this context, let N symbolize the number of galaxies existing per unit volume within a spatial metric denoted as$(d{r}^2+r^{2}d{\theta }^2+r^2{sin}^2\theta d\theta )/{\left(1+\kappa r^2\right)}^2$. Additionally, the volume element $r^{2}sin\theta d\theta d\phi dr/{\left(1+\kappa r^2\right)}^3$ encapsulates the spatial dimensions. This framework enables us to delineate the population of galaxies spanning the range from $r$ to $dr$, expressed as$4\pi r^{2}dr/{\left(1+\kappa r^2\right)}^3$ [19]. Subsequently, the number of galaxies between coordinate hyperspheres $r\left(z\right)$ and $r(z+dz)$ is given by

$$n\left(z\right)dz={\displaystyle \frac{4\pi r{\left(z\right)}^{2}N{r}^{\text{'}}\left(z\right)dz}{{\left(1+kr{\left(z\right)}^2\right)}^3}}$$

(15)

Differentiating Equation (11) with respect to z and using equation (12) yield;

$${\mathrm{r}}^{\mathrm{\text{'}}}\left(\mathrm{z}\right)={\displaystyle \frac{2(\mathrm{x}\left(\mathrm{x}-\mathrm{a}\mathrm{R}\left({\mathrm{t}}_{\mathrm{o}}\right)\right)-\mathrm{y}(\mathrm{y}-\mathrm{a}\mathrm{R}\left({\mathrm{t}}_{\mathrm{o}}\right))}{(\mathrm{q}-\mathrm{a}\mathrm{R}\left({\mathrm{t}}_{\mathrm{o}}\right){\mathrm{x}}^2}}$$

(16)

where $r^{\text{'}}\left(z\right)=dr/dz$, $\mathrm{x}=\mathrm{p}\mathrm{q}+4\mathsf{\kappa }\left(1+\mathrm{z}\right)$ and $\mathrm{y}=\mathrm{p}\left(1+\mathrm{z}\right)-\mathrm{q}$

Substituting Equation (12) and Equation (16) into Equation (15) gives;

$$\mathrm{n}\left(\mathrm{z}\right)={\displaystyle \frac{32\mathsf{\pi }{\left(\mathrm{p}\left(1+\mathrm{z}\right)-\mathrm{q}\right)}^2\mathrm{N}\left(\mathrm{x}\left(\mathrm{x}-\mathrm{a}\mathrm{R}\left({\mathrm{t}}_{\mathrm{o}}\right)\right)-\mathrm{y}\left(\mathrm{y}-\mathrm{a}\mathrm{R}\left({\mathrm{t}}_{\mathrm{o}}\right)\right)\right)}{{\left(\mathrm{p}\mathrm{q}+4\mathrm{k}\left(1+\mathrm{z}\right)\right)}^2{\left(\right(\mathrm{q}-\mathrm{a}\mathrm{R}\left({\mathrm{t}}_{\mathrm{o}}\right){\mathrm{x}}^2)\left(1+\mathsf{\kappa }{\left(\frac{2\left(\mathrm{p}\left(1+\mathrm{z}\right)-\mathrm{q}\right)}{\mathrm{p}\mathrm{q}+4\mathsf{\kappa }\left(1+\mathrm{z}\right)}\right)}^2\right)}^3}}$$

(17)

Equation (17) relates the evolution of the number density of astronomical objects with redshift in the Friedmann universe, which together with equation (14) constitutes the fundamental results in this paper.

4. Graphical Results

In the preceding section, we derived the interplay between galactic number density, redshift, and light intensity through analytical methods. We shall now transition to a visual exploration of our established outcomes, achieved through the development and execution of straightforward MATLAB programs. By implementing these programs, we are poised to generate graphical representations that illustrate the relationships between light intensity and redshift, as well as between number density and redshift, as dictated by equations (14) and (17) respectively. The range of redshift values employed in our MATLAB simulations spans from$z=0$ to $z=5$, a spectrum that aligns harmoniously with existing statistical data and observations. This methodology permits us to illuminate the empirical significance of our theoretical constructs and enhance our grasp of the cosmic evolution landscape.

The program encompasses a range of universe densities, spanning from $\rho \left(t\right)=3\times {10}^{-27}kg/m³$ to $\rho \left(t\right)=6.23\times {10}^{-23}kg/m³$. The velocity of light$c=3\times {10}^{8}m/s$, the cosmic scale factor,$R\left(t_o\right)=9\times {10}^{25}m$, while the gravitational constant$G=6.67\times {10}^{-11}m³/kg/s²$. The universe's curvature, $\kappa$ assumes values of $-1,0,$ and$1,$ and the cosmological constant$\lambda =1.19\times {10}^{-52}m⁻²$. To enhance accuracy, logarithms of light intensity and number density are employed. For our exploration, we assign arbitrary values of 1 to the parameters N (number of galaxies per unit volume) and L (absolute power of a galaxy or star). This approach facilitates the determination of parameter combinations$\rho$ and $R\left(t_o\right)$ that best align with experimental data without presuming assumptions about background geometry.

4.1. Light Intensity Redshift Relation

Executing our program using equation (14) for different $\mathsf{\rho }\left(\mathrm{t}\right)\left(\mathrm{k}\mathrm{g}/{\mathrm{m}}^3\right)$ and$\mathsf{\kappa }$ values yield the ensuing outcomes (refer to Figures 1 to 14) pertinent to light intensity.

Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14 show the relationship between light intensity and redshift. The Y-axis (Log I) shows the logarithm of light intensity, where lower values correspond to reduced intensity. The X-axis (Redshift, $z$) tracks the evolution of the universe from its inception at$z=0$. Different initial values of log(I) across the curves indicate varying light intensities based on the universe's density $\left(\rho \right)$ and curvature$\left(\kappa \right)$.

4.2. Number Density Redshift Relation

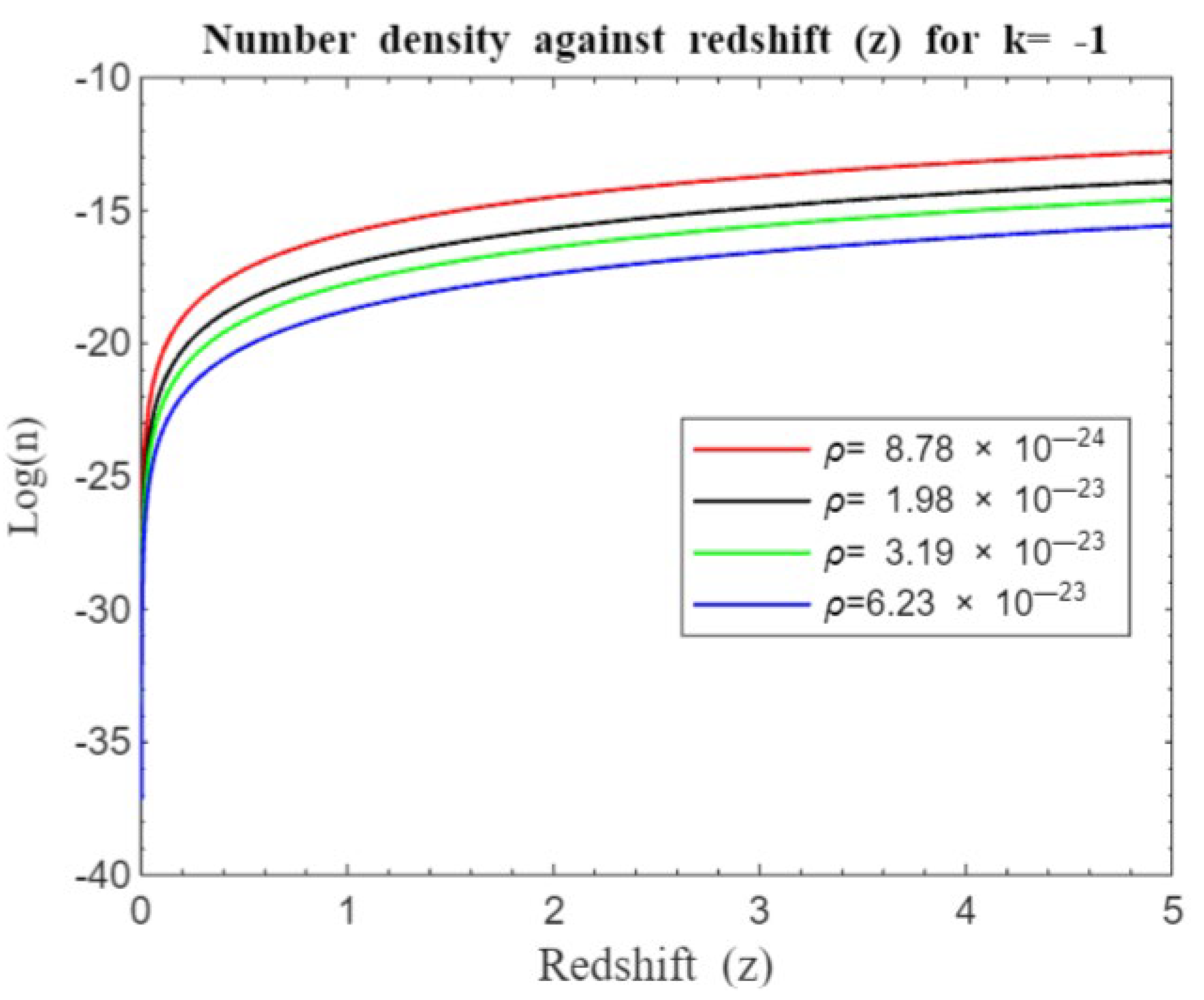
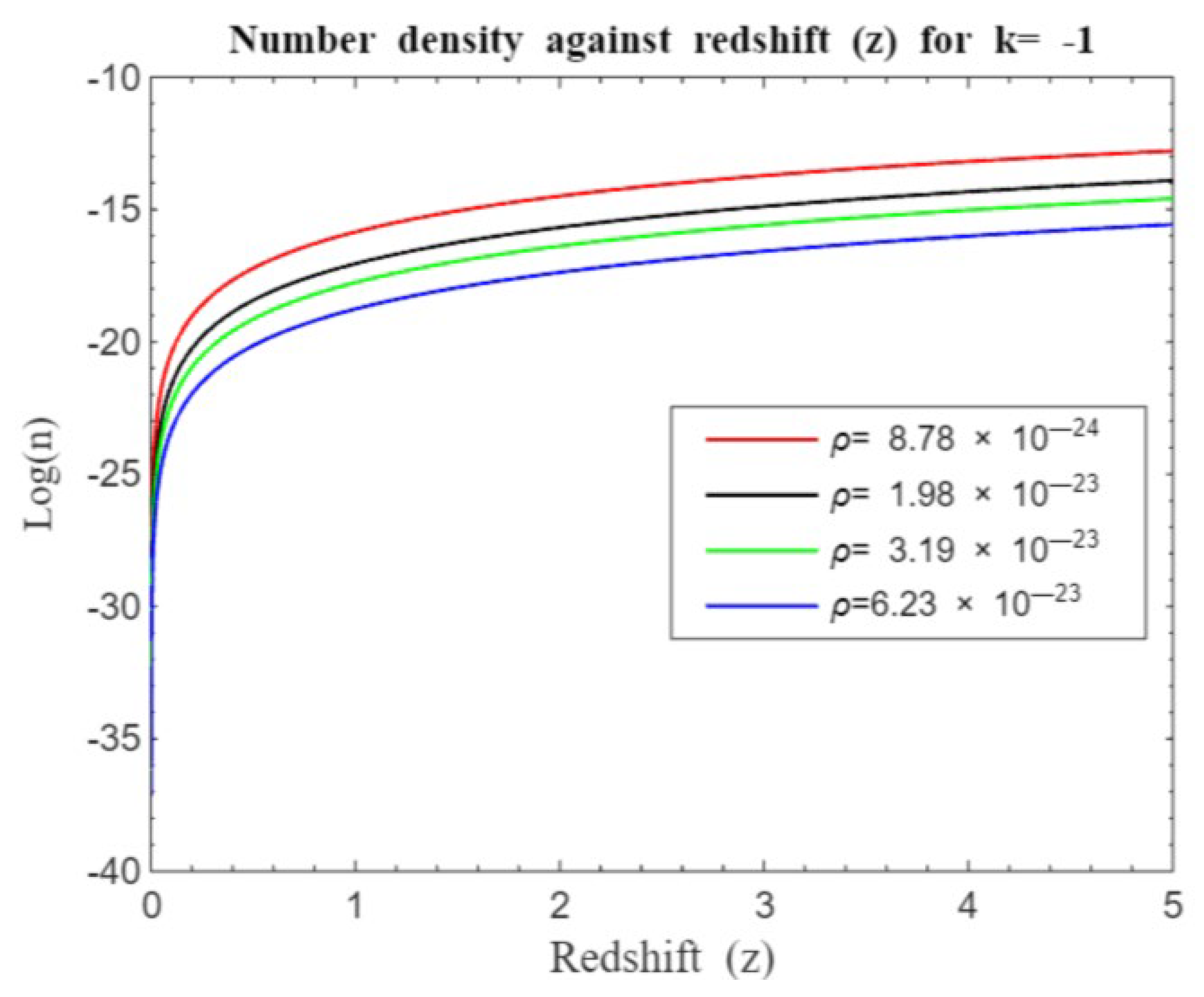
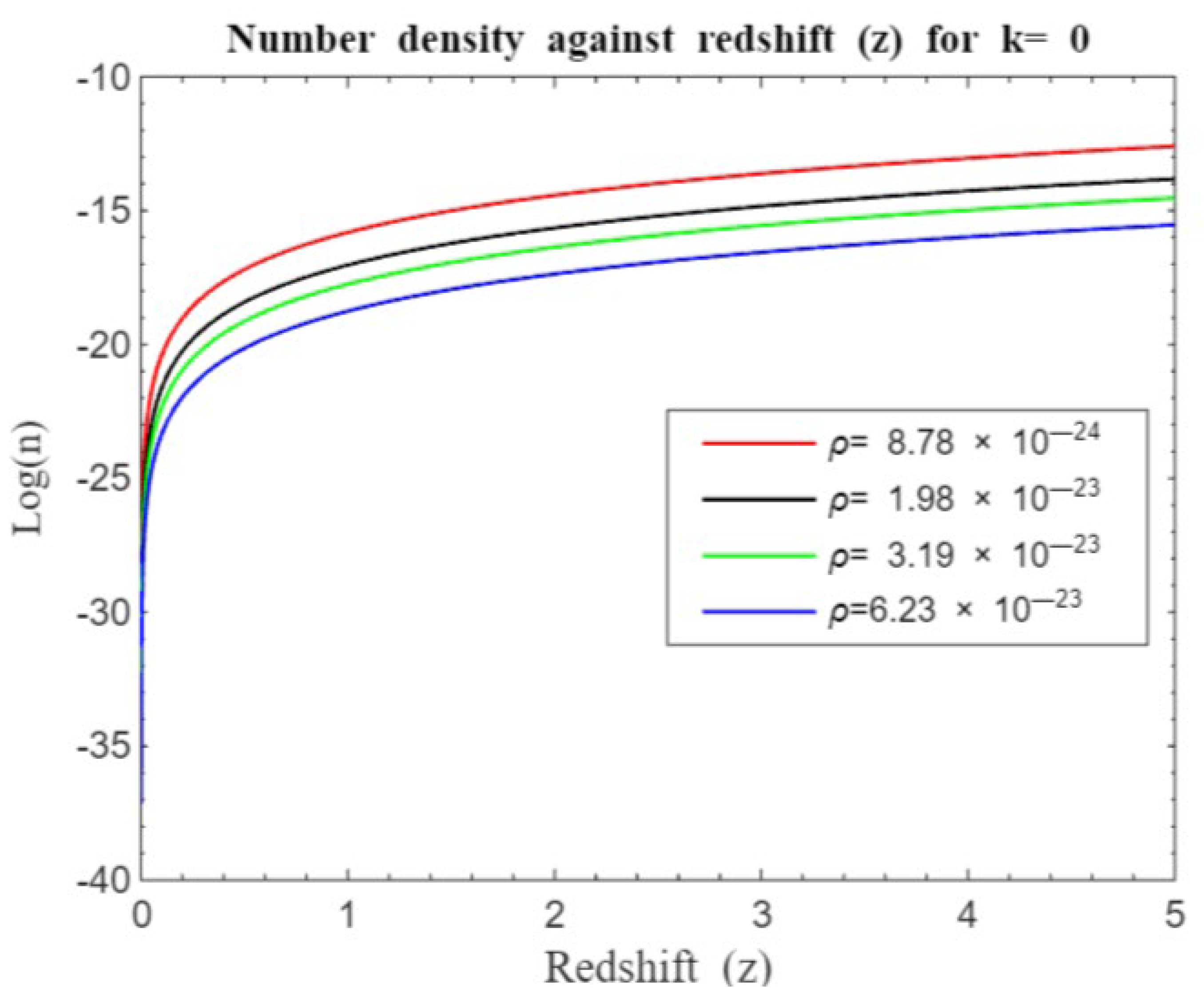
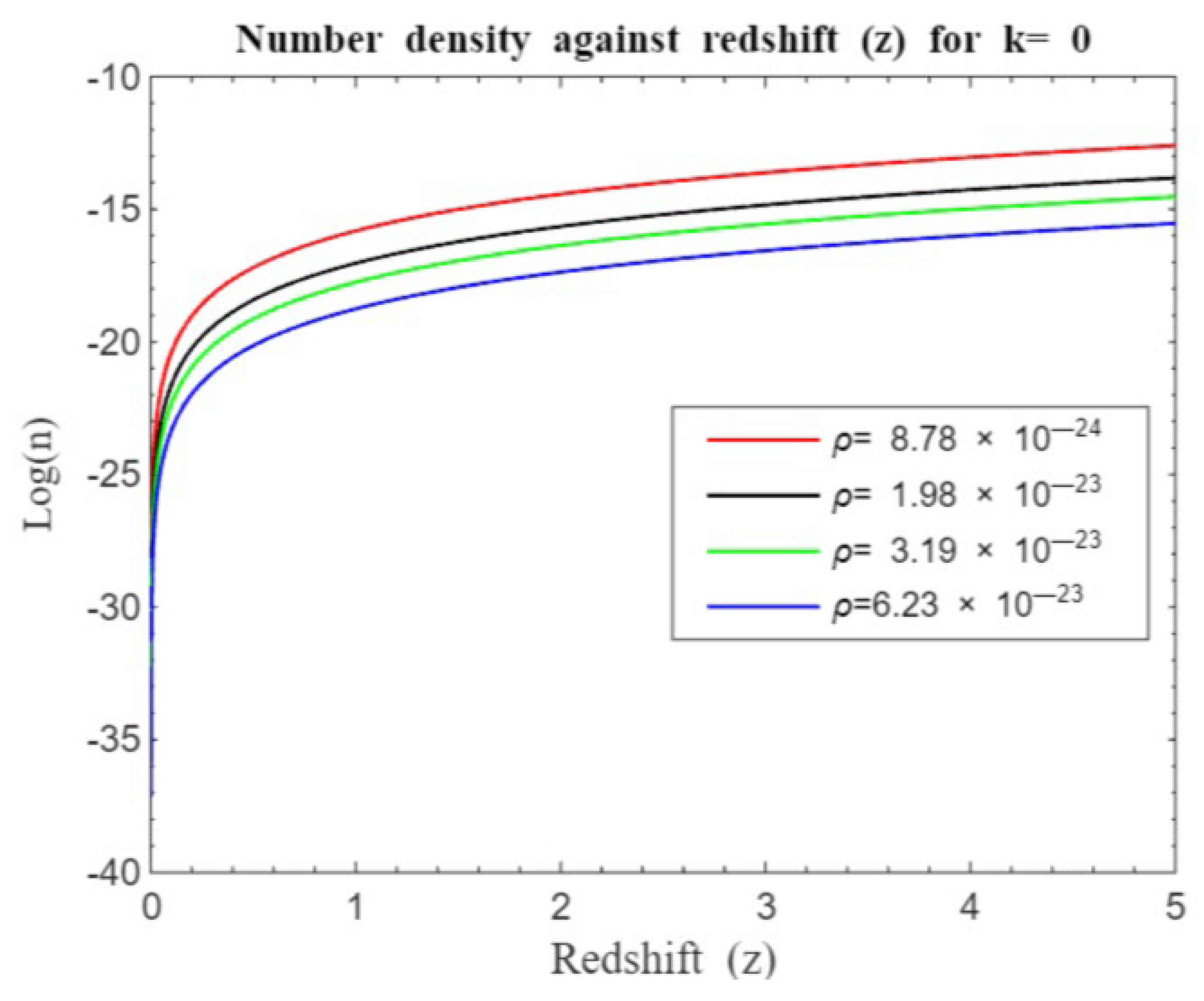
Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27 and Figure 28 show the evolution of galaxy number density, $n\left(z\right),$ in relation to redshift$z$, as described by equation (17). The Y-axis (Log n) shows the logarithm of number density, where lower values correspond to reduced density. The X-axis (Redshift,$z$) tracks the evolution of the universe from its inception at$z=0$. Different initial values of Log(n) across the curves indicate varying number densities based on the density ($\rho$) of the universe and its curvature,$\kappa$.

5. Discussion

5.1. Light Intensity Redshift Relation

In cosmological studies, the relationship between light intensity and redshift is a crucial indicator of galaxy formation and the evolution of large-scale structures. Let us consider the relationship between light intensity and redshift in light of structure formation.

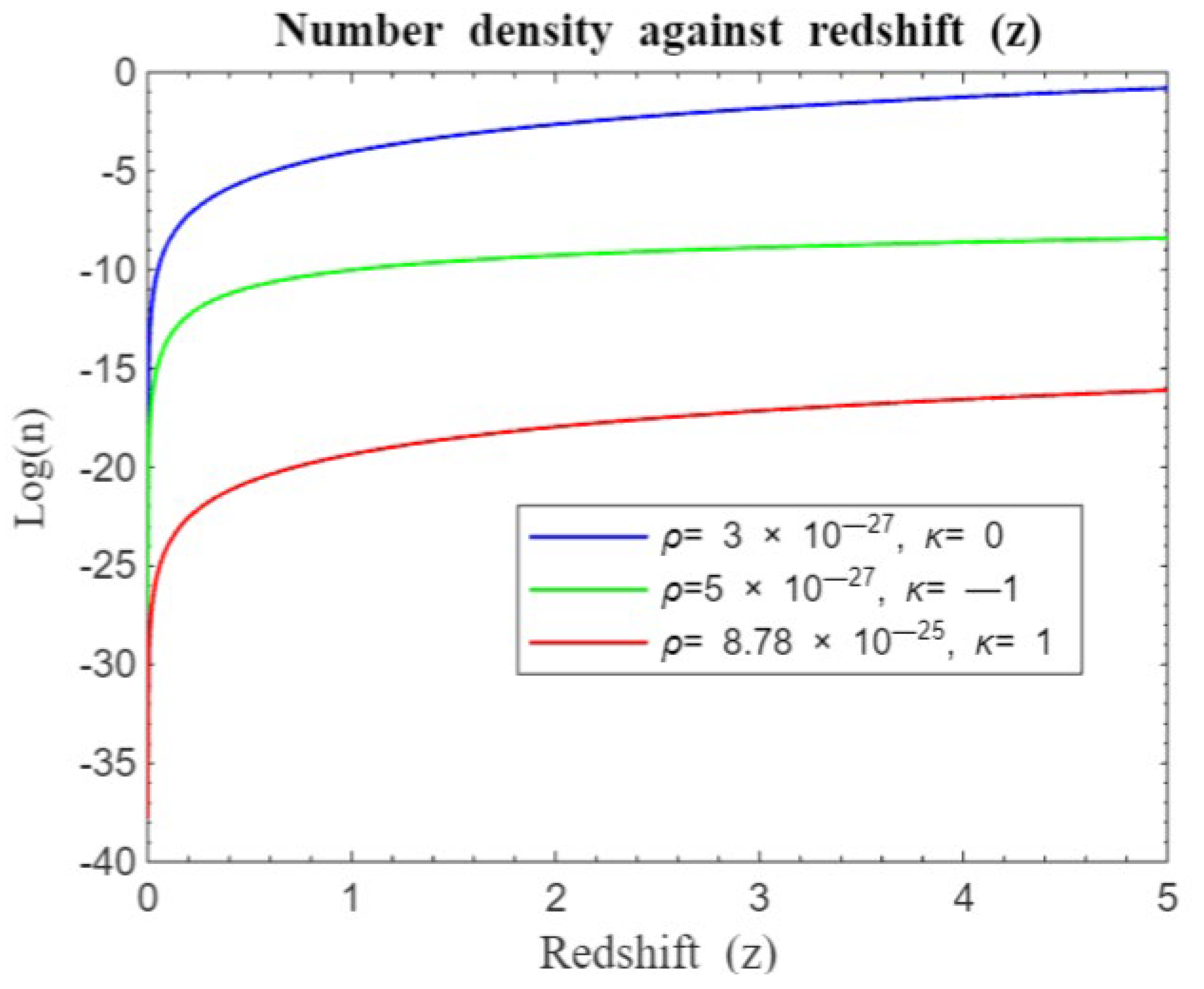
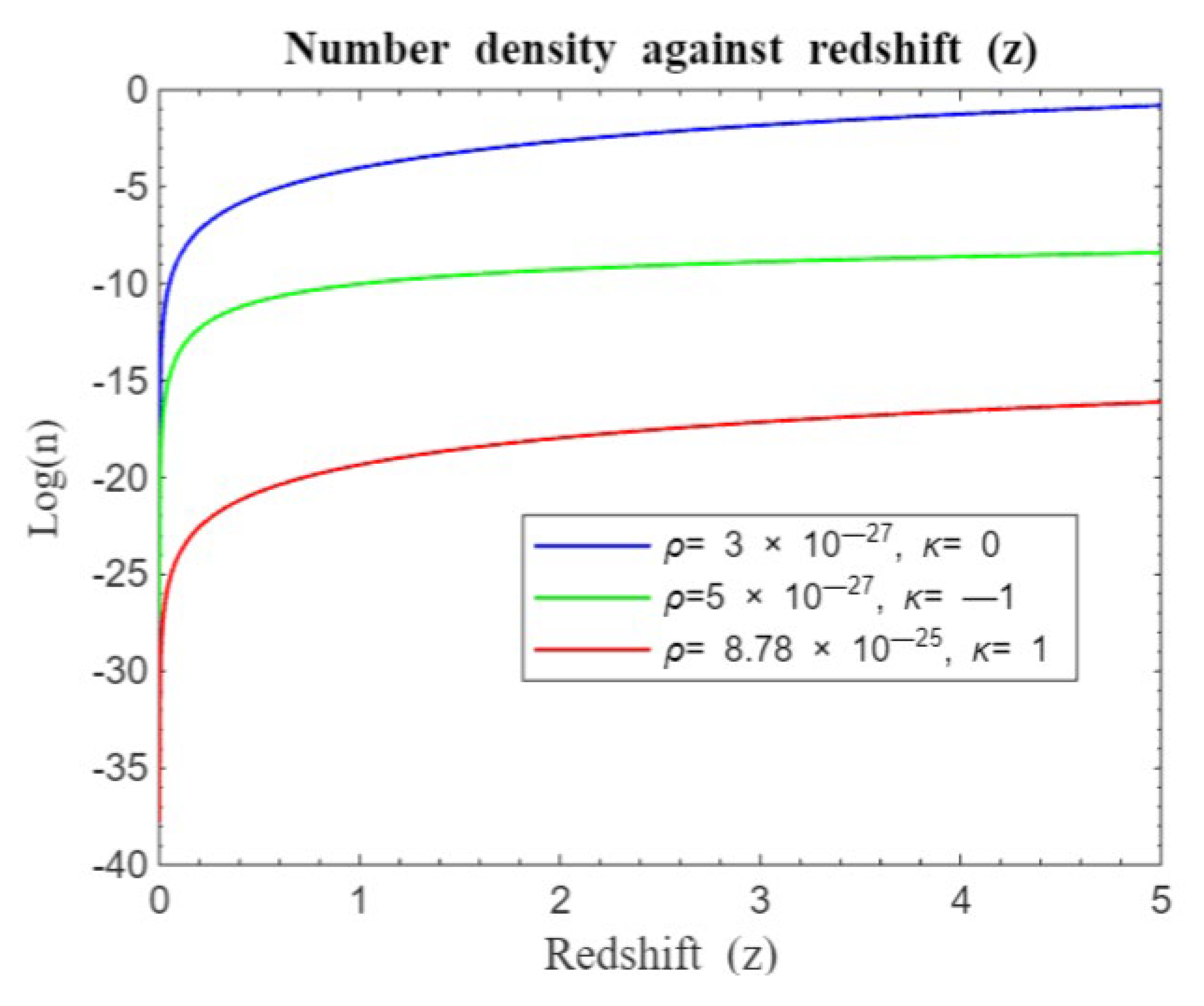
Figure 1-14 demonstrates an exponential decay in light intensity with increasing redshift, consistent with classical theory. This decay results from the dilution of photons as the universe expands. As the universe grows, the wavelengths of photons stretch, causing a decrease in their energy density. This effect arises because the number of photons remains constant while they are distributed over an increasingly larger volume [7,8,21,22].

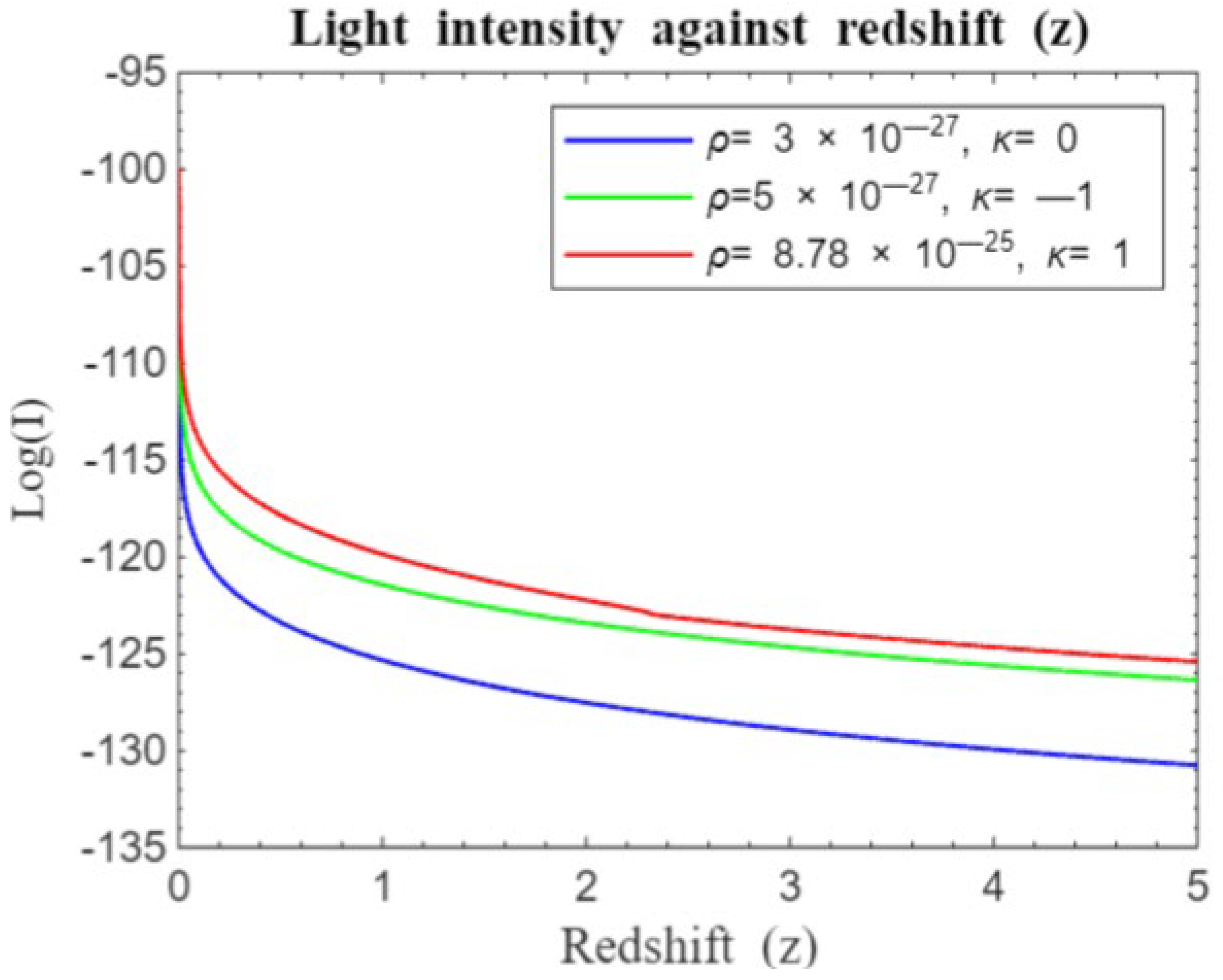
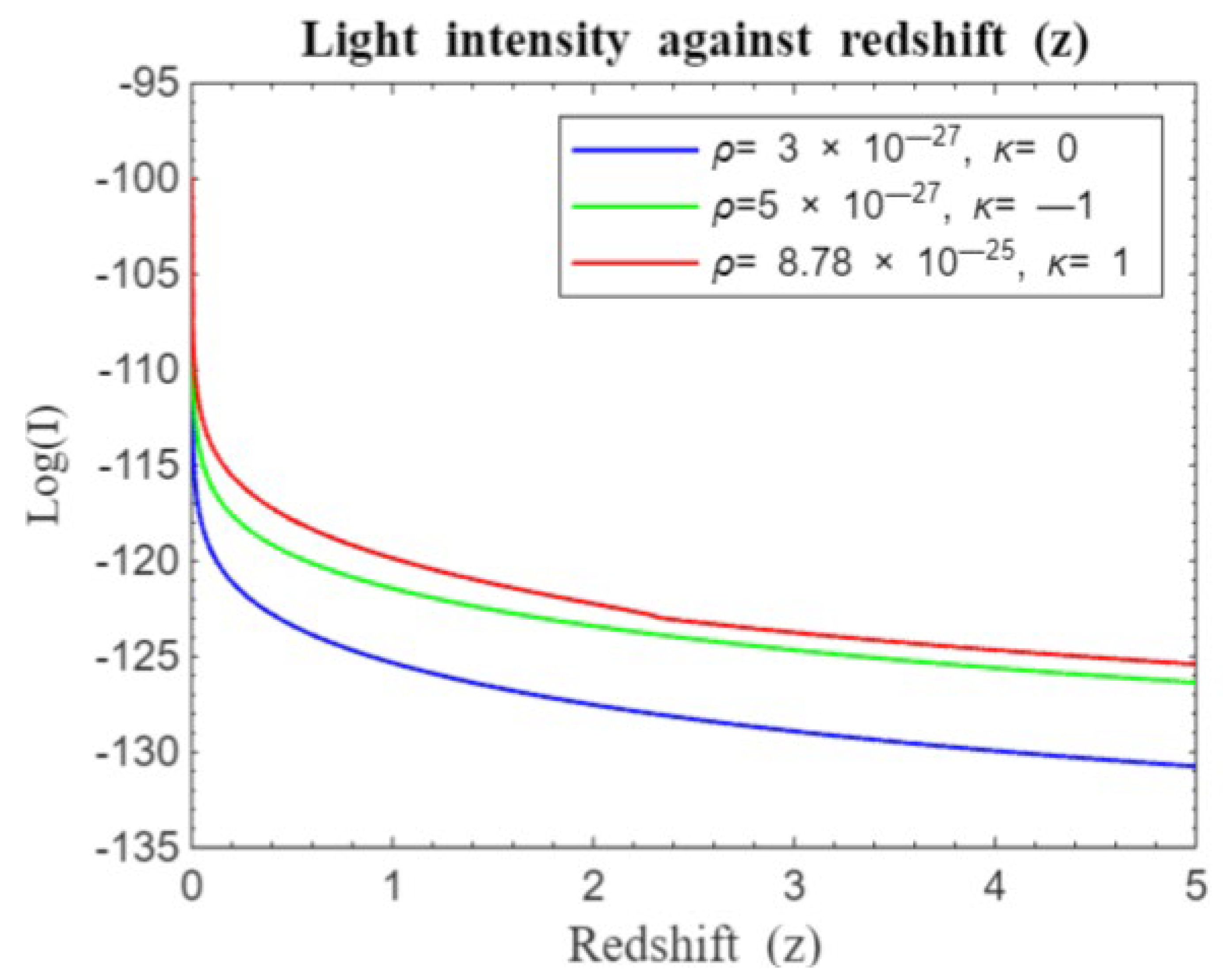
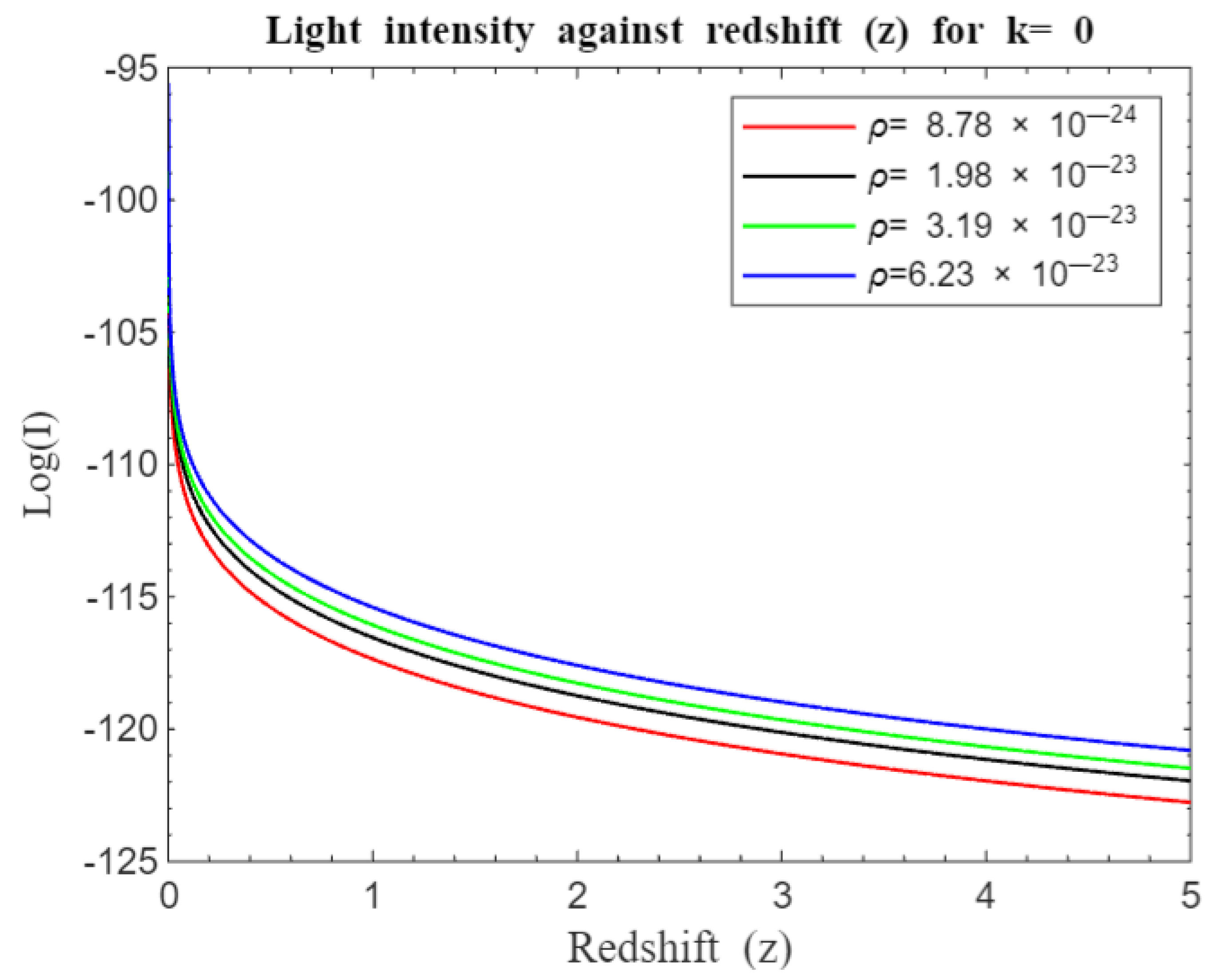
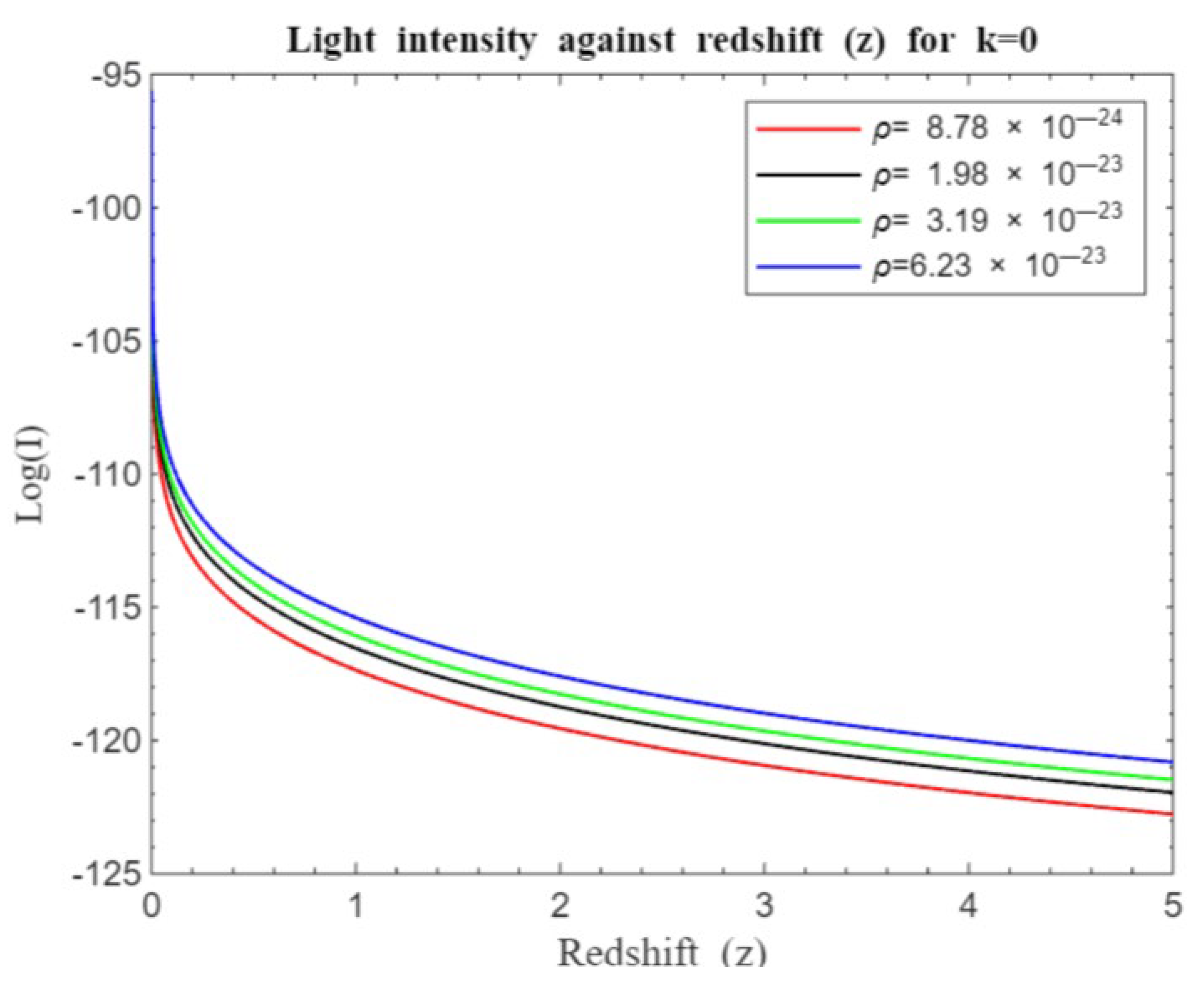
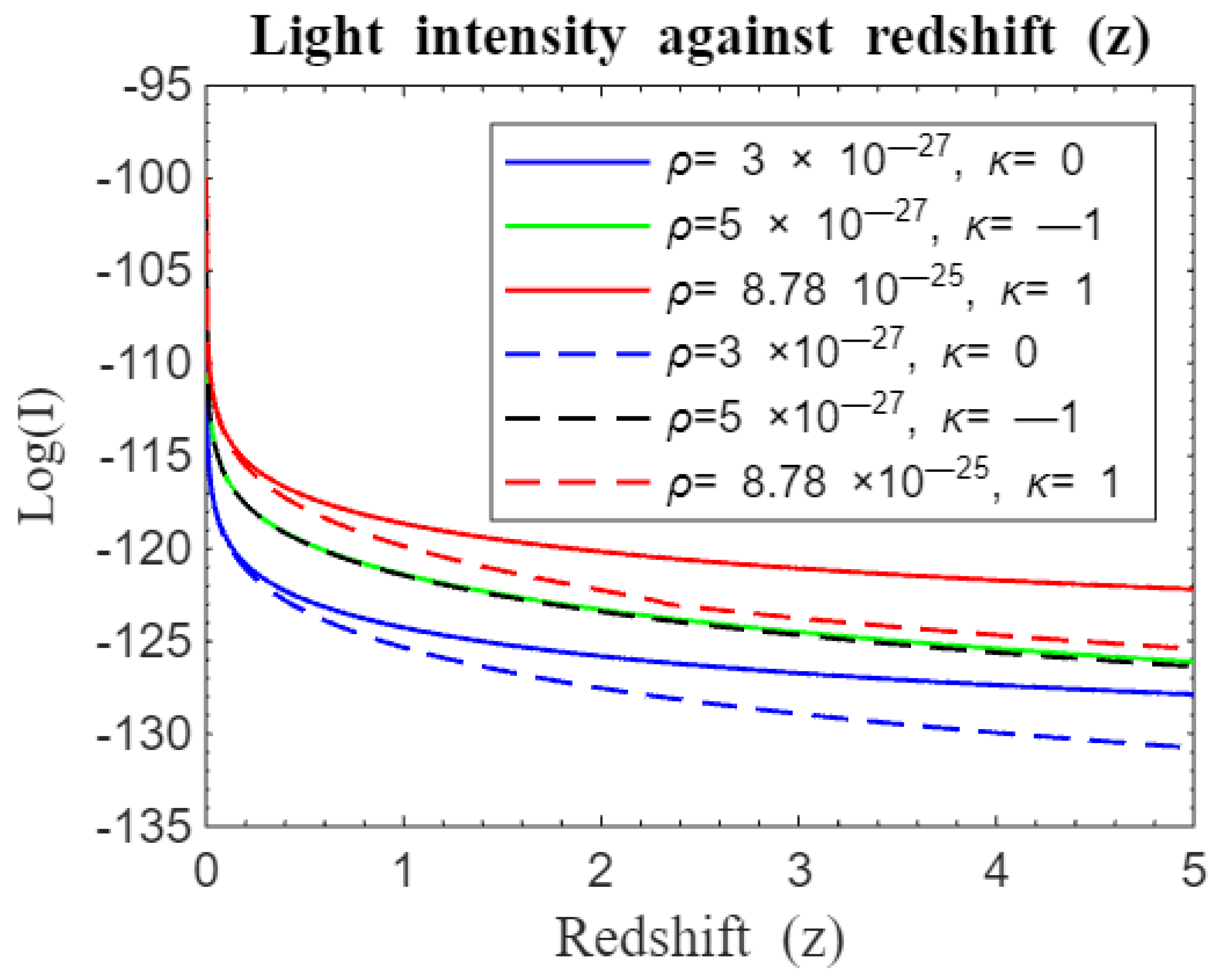
Figure 1 and Figure 2 compare light intensity-redshift relationships under different geometries, both without and with the cosmological constant. These Figures reveal that in a flat universe, light intensity decays more rapidly compared to an open or closed universe.

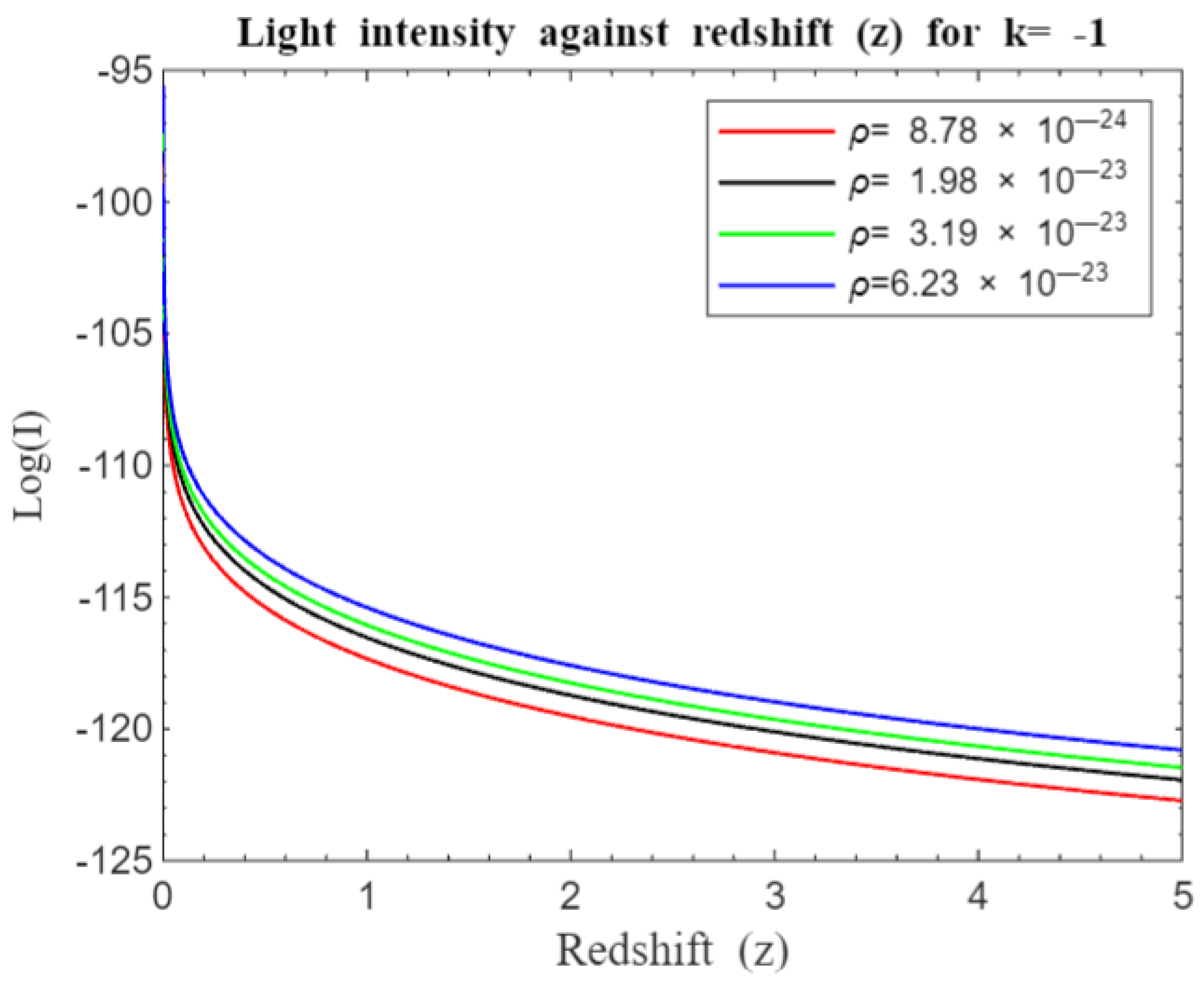
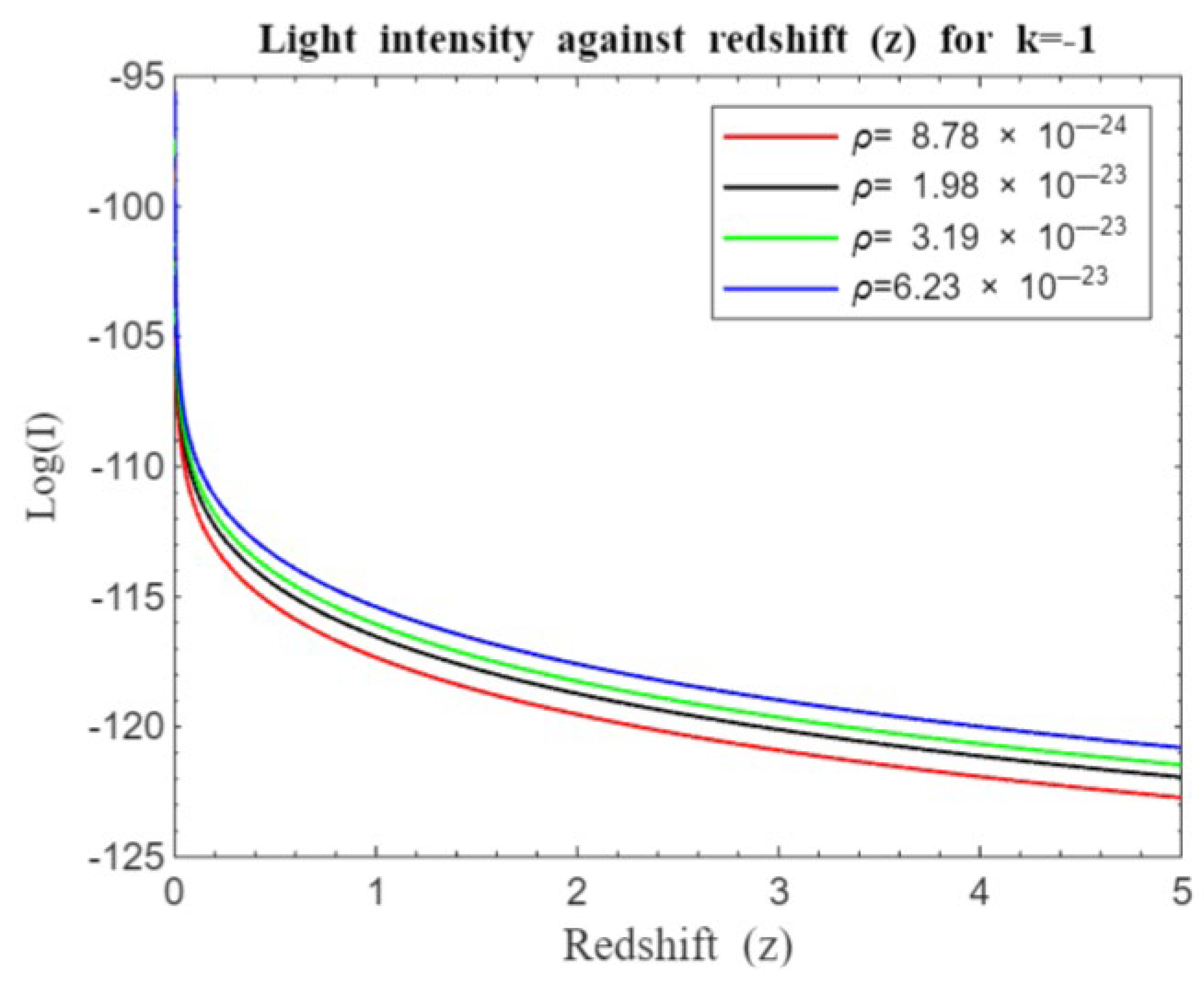
Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 illustrate how light intensity changes with redshift across various densities and curvatures. A significant drop in intensity is observed at redshifts$0<z<0.5$, with a more gradual decline at higher redshifts. At lower redshifts, the universe is relatively young, which influences intensity. As redshift increases, light comes from increasingly distant regions. The slower intensity decay at higher redshifts may result from cumulative factors like distance, cosmic expansion, and the evolving structure of the universe, reflecting the intricate interplay of spatial distance, temporal evolution, and cosmic morphology (Riess et al., 1998).

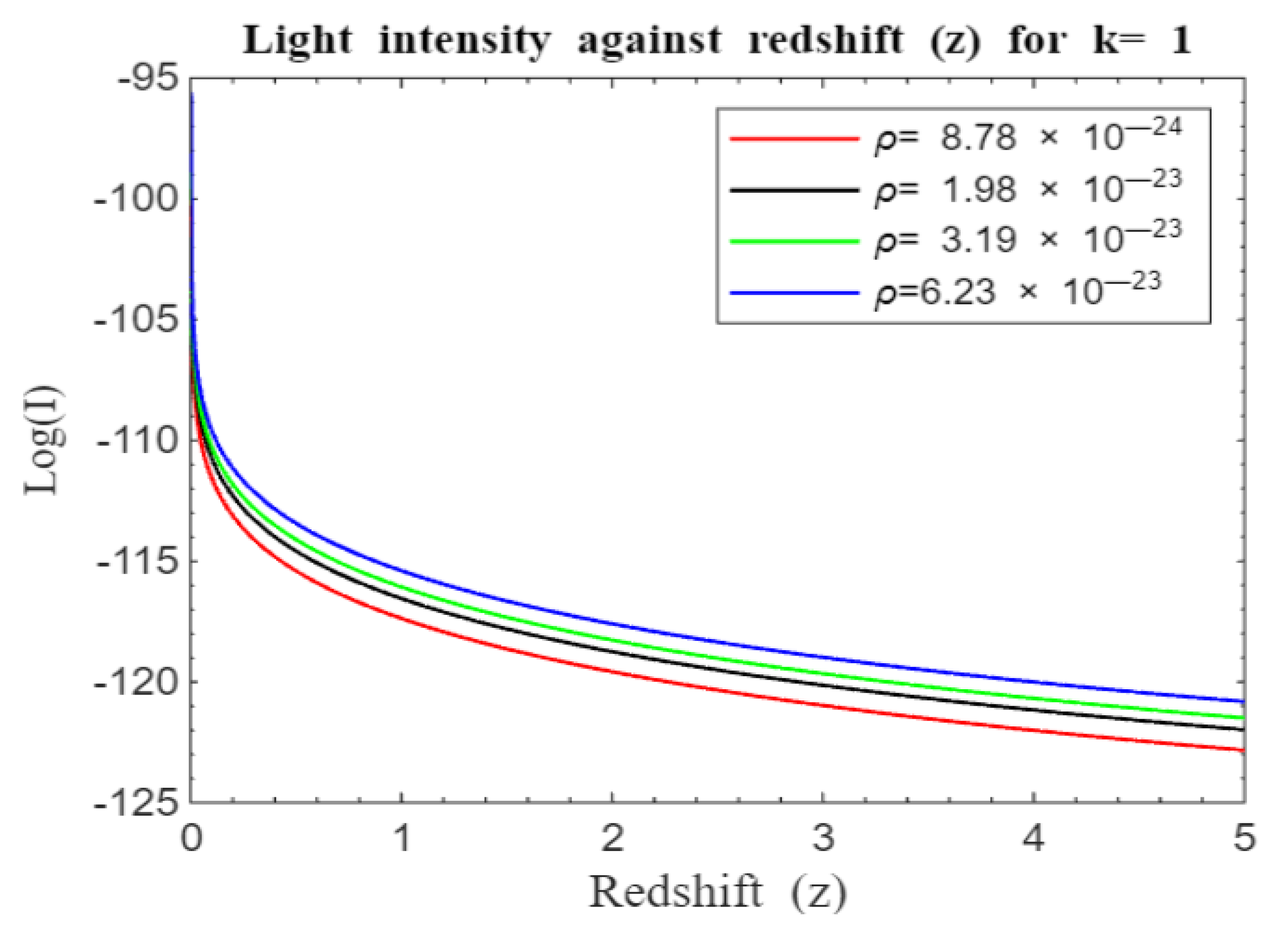
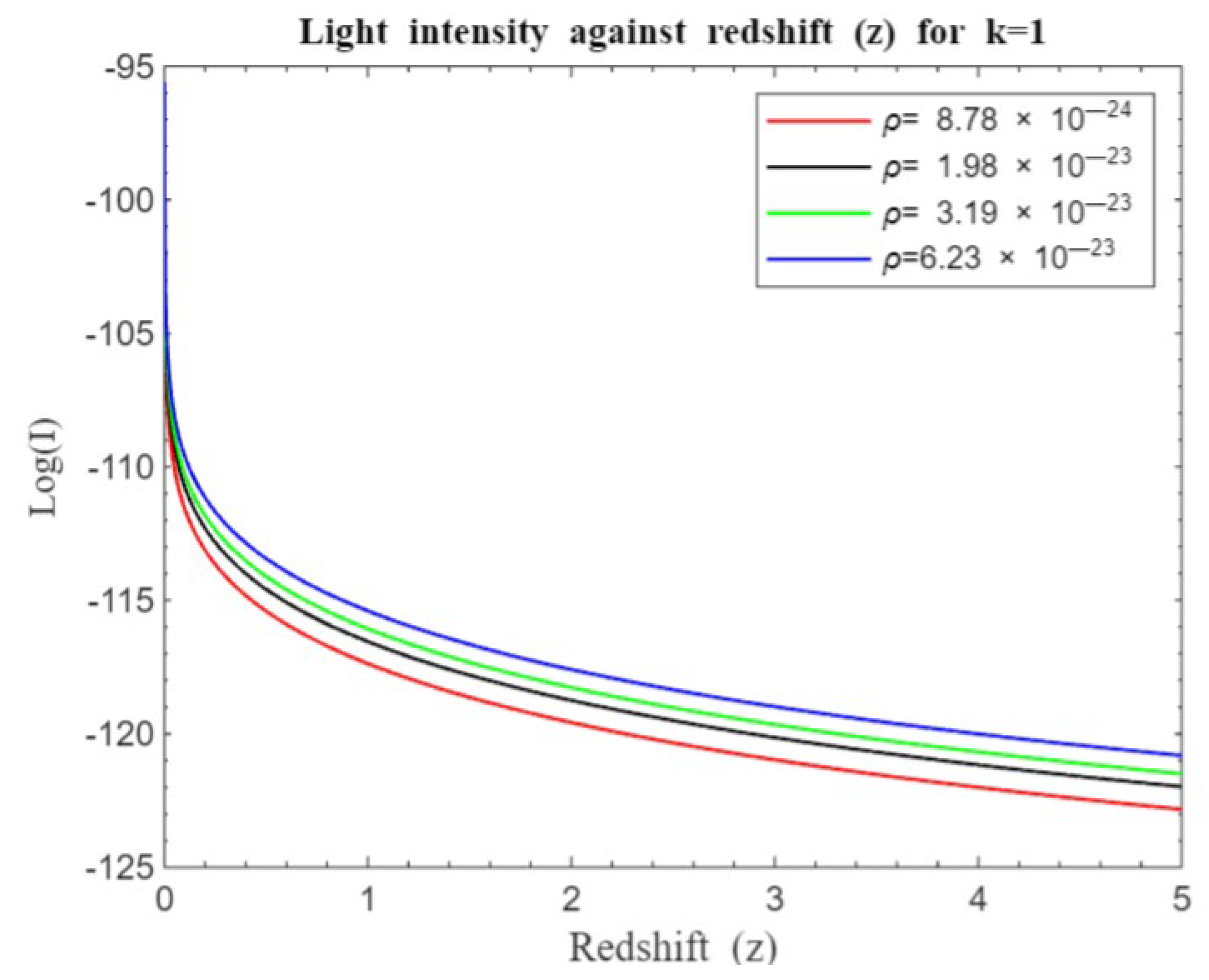
In a universe with positive curvature, a closed model akin to a spherical structure is represented. Here, we still observe light attenuation with increase in redshift. A case of positive curvature points to a closed universe whose 3-D space is similar to the surface of a sphere in which the r-sphere wipes out the entire universe leaving it unbounded as the coordinates of the sphere varies from 1 to 0. We observe that light curves seem not to converge for positive curvature according to our model in contrast to earlier works [12,20]. As the redshift parameter ($z$) increases, these geometric differences become more pronounced, showing how curvature affects light behavior. In all geometries, light intensity curves decay more rapidly at lower densities compared to higher densities.

Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14 compare our model with those from previous studies [12,20]. These Figures show that high-density universes consistently exhibit higher initial light intensity at early times, regardless of the model. This implies that a denser universe leads to stronger early cosmic structures with higher light intensity. The gradual decline over time in such models suggest that denser universes, with stronger gravitational influences, retain light longer due to slower expansion rates. In contrast, a flat universe$(\kappa =0)$ shows moderate initial intensity and a steady decrease, while an open universe $(\kappa =-1)$ exhibits a lower initial intensity and rapid decline, indicating that accelerated expansion reduces observable light intensity quickly. A closed universe $(\kappa =1)$ shows higher initial intensity and a more prolonged decline, reflecting a slower expansion rate.

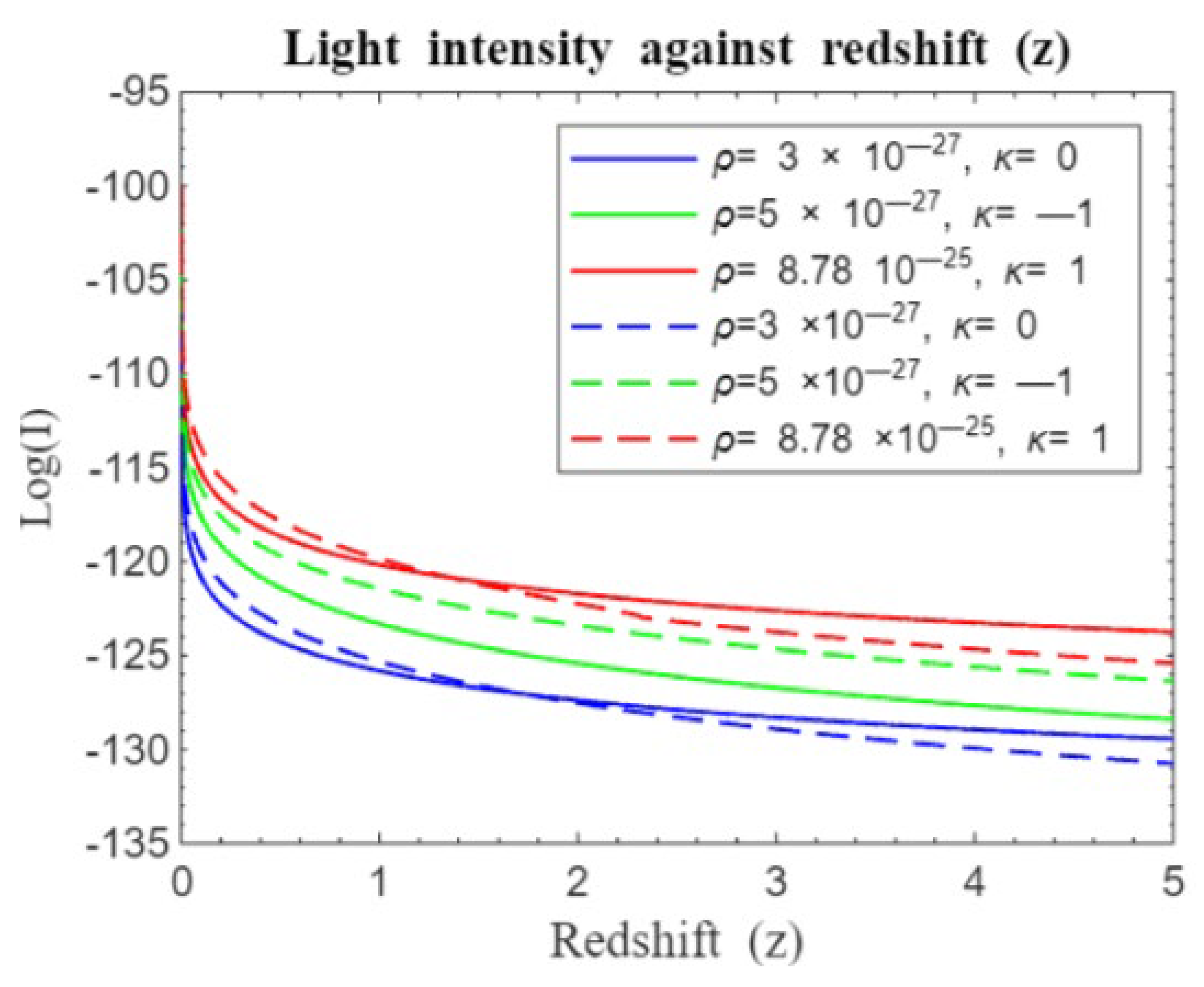
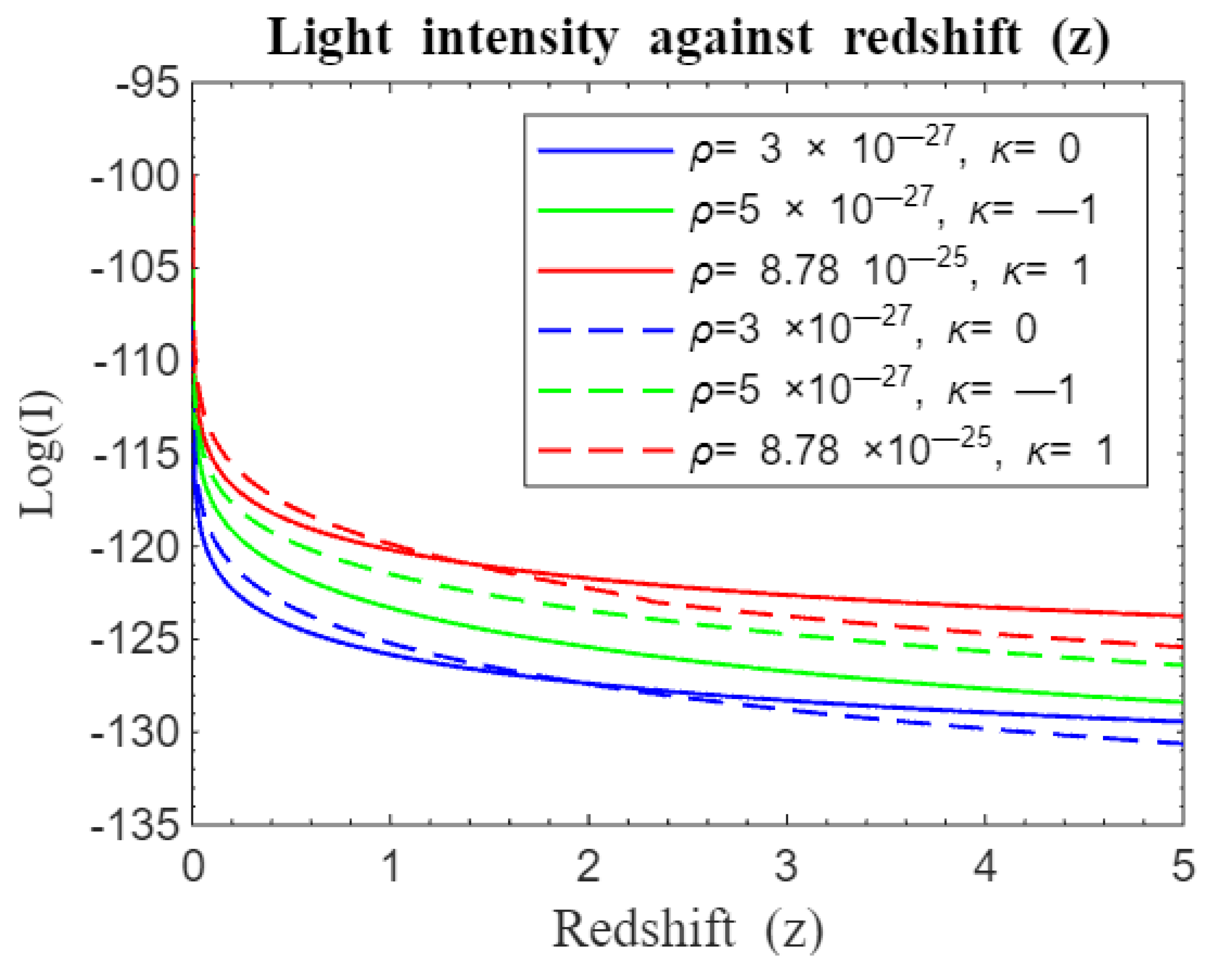
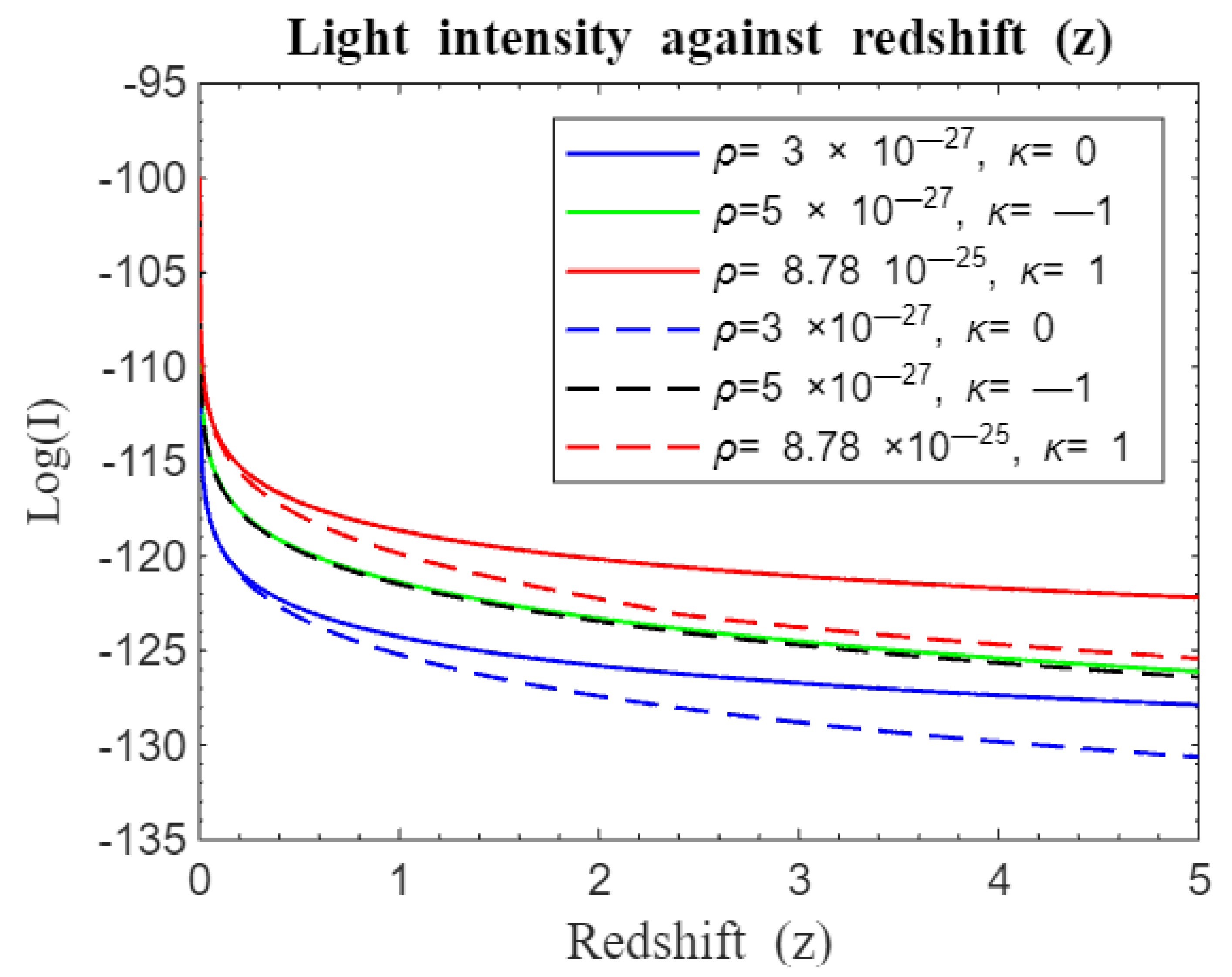
Figure 9 and Figure 10 compares our standard Friedmann redshift model with the approximate standard Friedmann redshift model proposed by Langa et al. (2017). Figure 10, which includes the cosmological constant, highlights the role of dark energy. Dark energy is known to accelerate the universe's expansion [13,14] . The approximate standard Friedmann redshift model suggests that early cosmic structures had higher initial light intensities with a slower decline, indicating that matter's gravitational influence moderate expansion and preserves light intensity. In contrast, the standard Friedmann redshift model shows lower initial light intensity and a more rapid decline, implying that insufficient matter to stabilize the expansion leads to faster reduction in light from early structures.

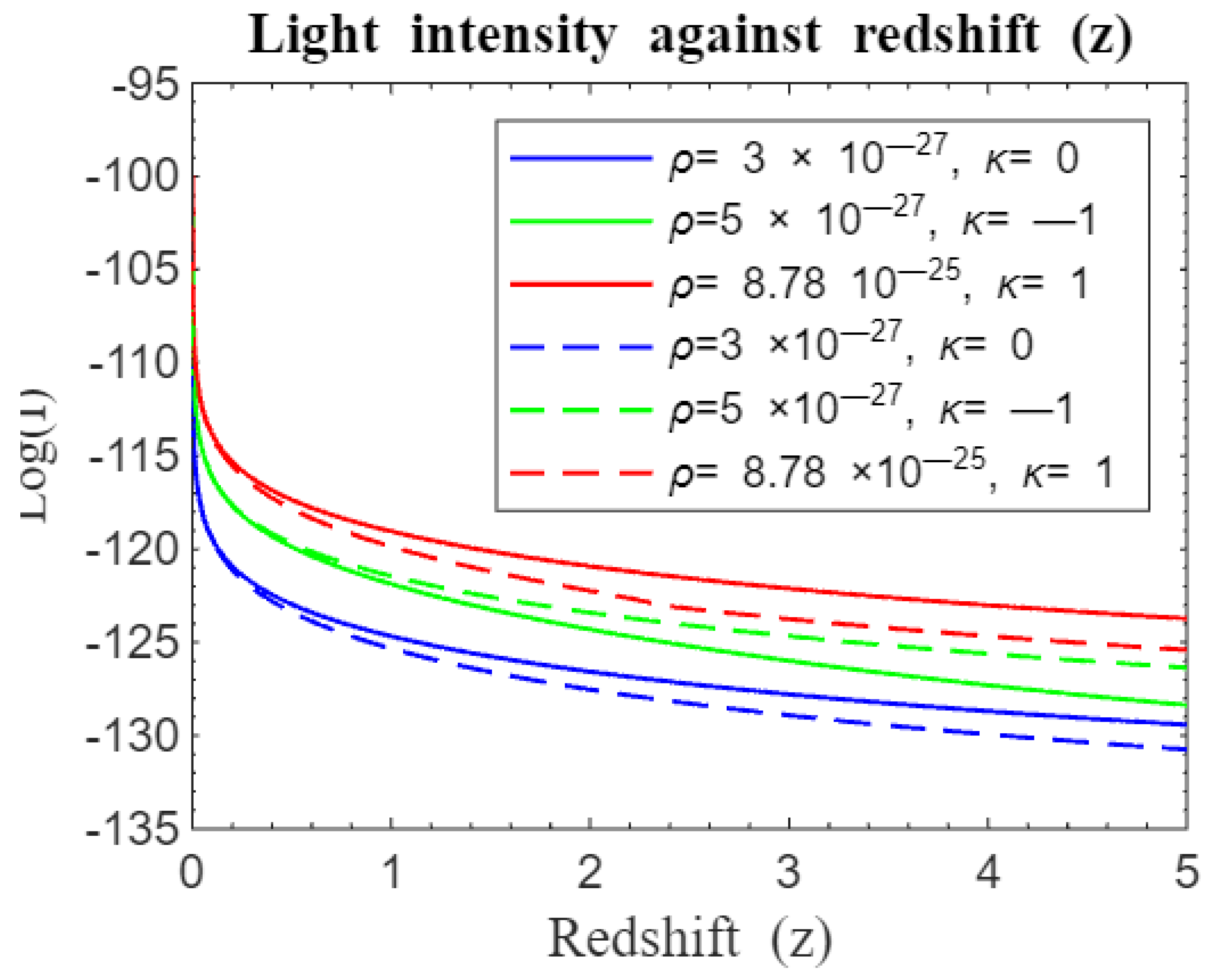
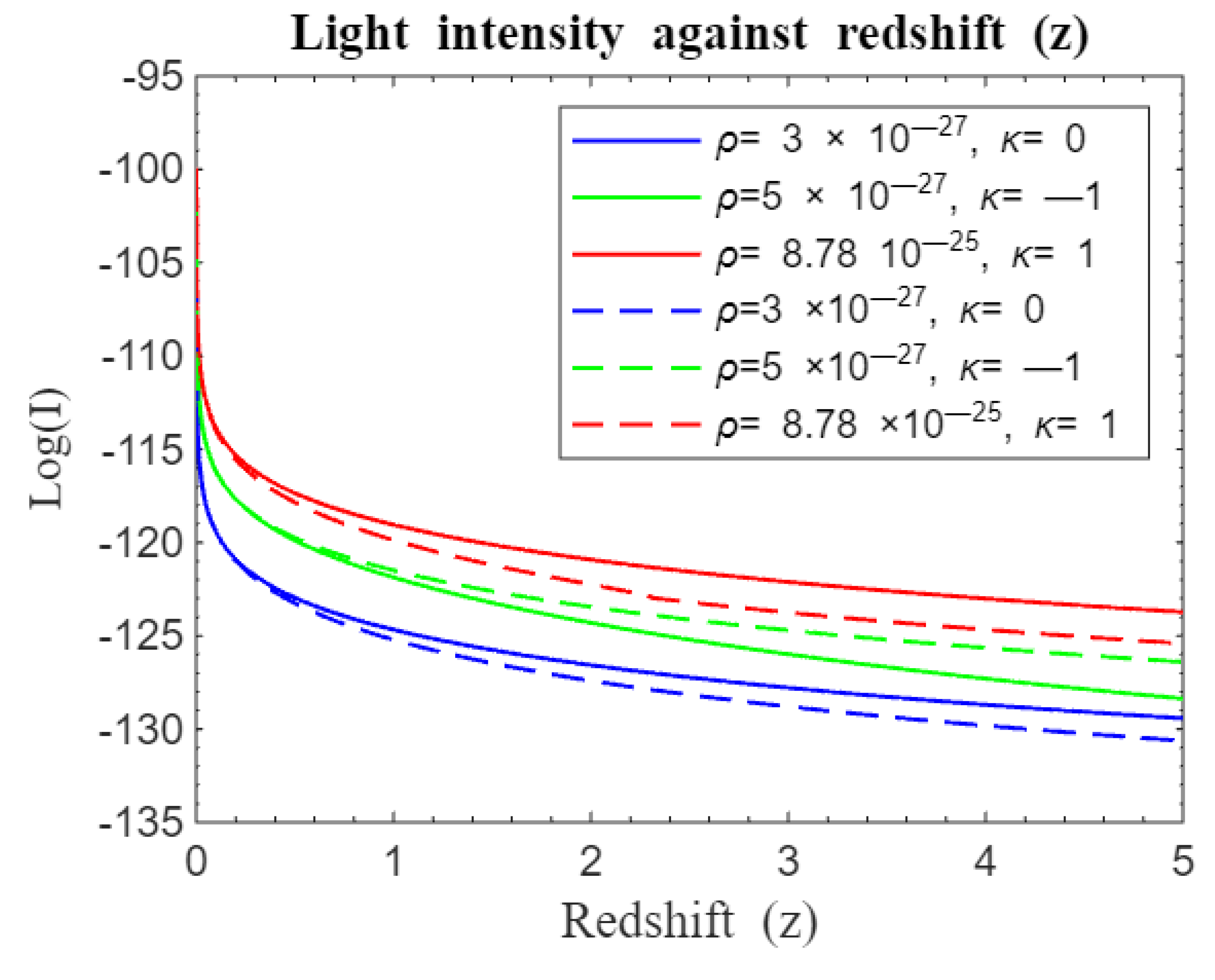
Further comparison with Nyagisera et al. (2024), who modified the approximate standard Friedmann redshift model with non-parametric (Figure 11 and Figure 12) and parametric (Figure 13 and Figure 14) redshift functions, provides additional insights. Figure 11 and Figure 12 show that light attenuation is more pronounced in the standard Friedmann redshift model compared to the modified standard Friedmann redshift nonparametric model. Even without dark energy, as indicated by the absence of a cosmological constant, the universe still experiences accelerated expansion, suggesting a significant role of dark matter in driving expansion and redshifting of light [12].

Figure 13 and Figure 14 exhibit similar trends in light attenuation with increasing redshift, particularly between redshifts 0 and 1, where attenuation is rapid for flat and closed geometries except in open geometry where our model attenuates slower than parametric model. The standard Friedmann redshift model shows faster attenuation compared to the modified standard Friedmann redshift parametric model, potentially due to factors like photon-electron recombination, Thomson scattering, or accelerated expansion. The absence of a cosmological constant in Figure 13 implies that dark matter may primarily be responsible for driving accelerated expansion, overshadowing the cosmological constant's effects.

5.2. Number Density Redshift Relation

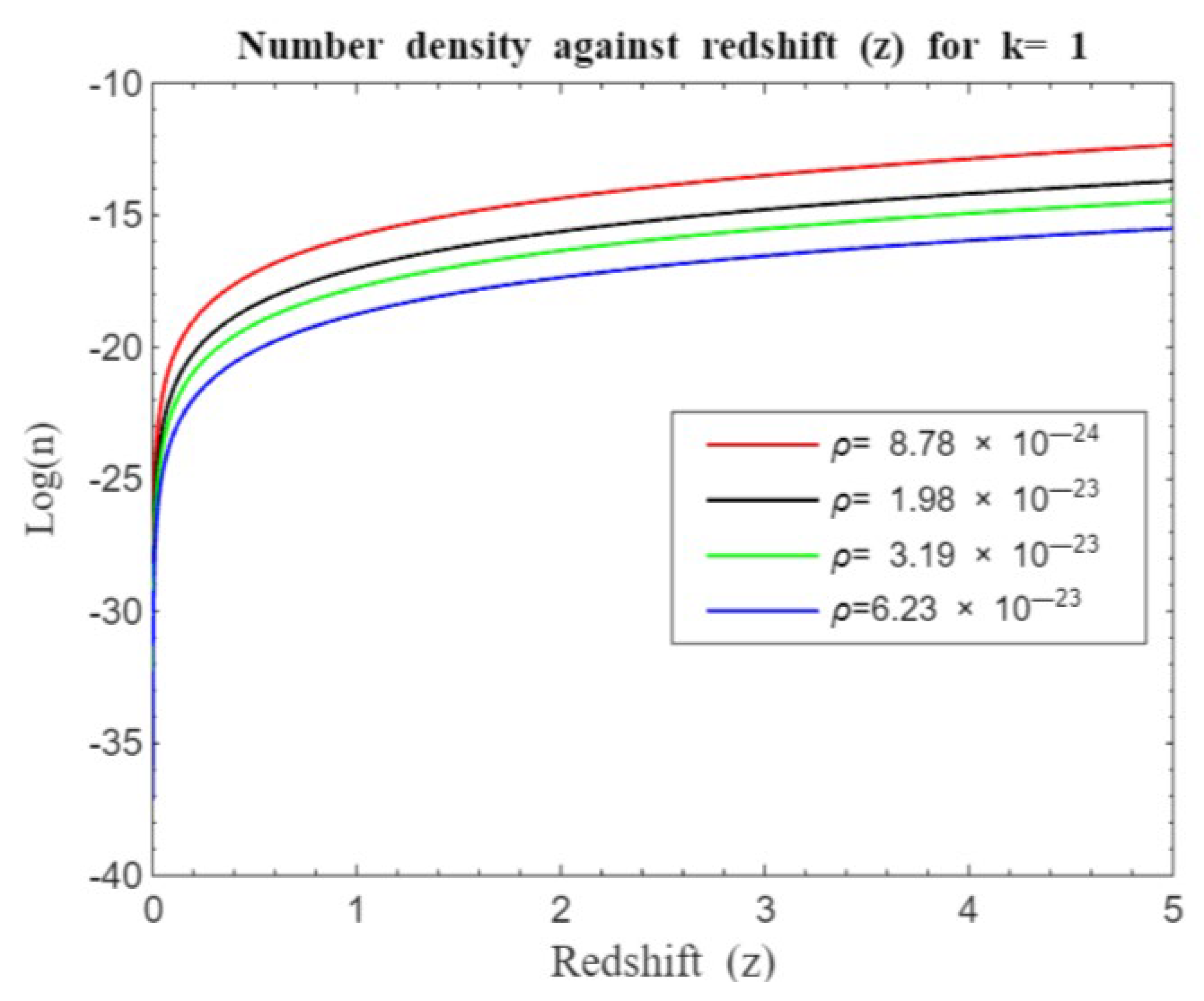
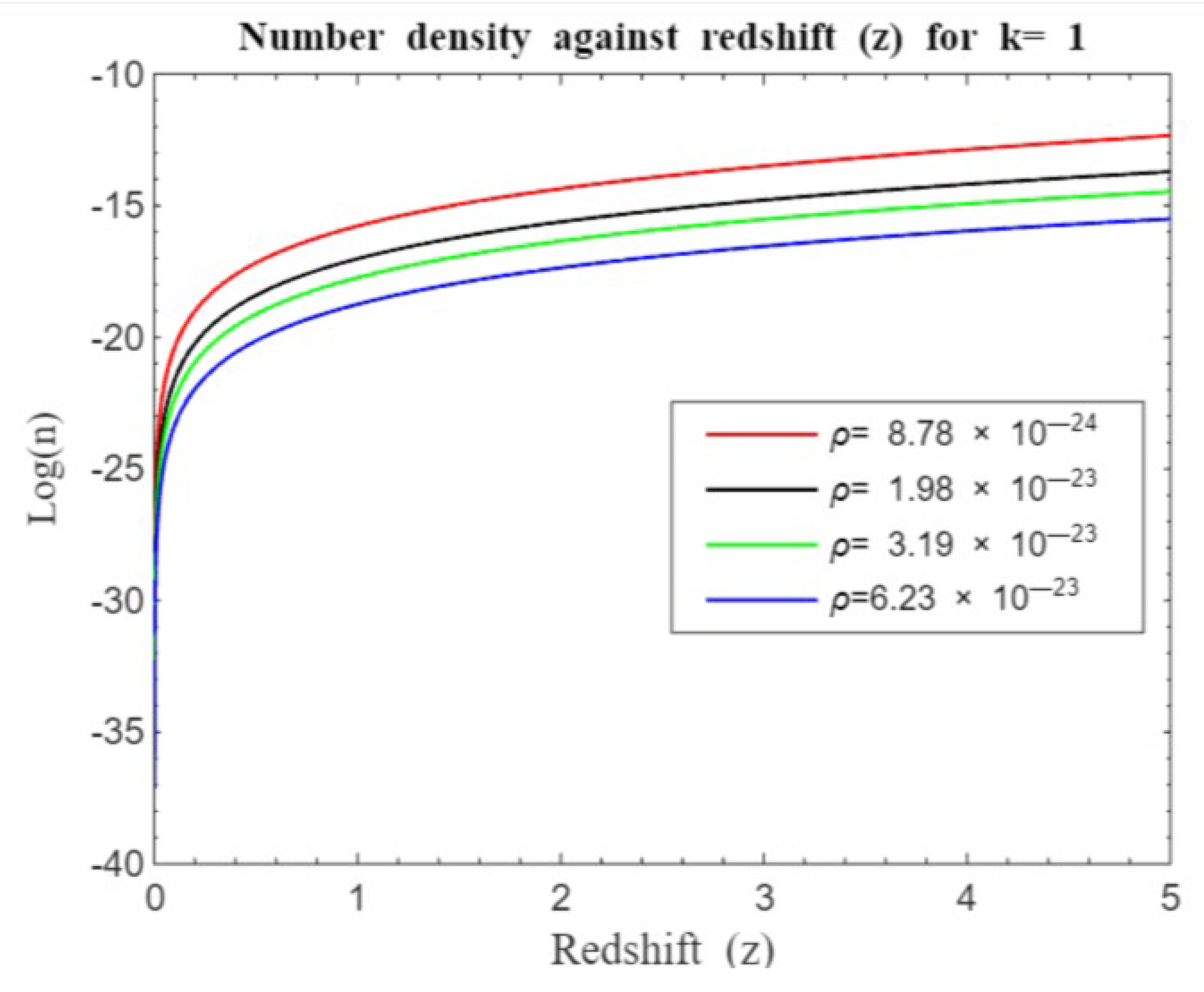
The number density redshift relation helps astronomers understand how the number of galaxies changes over time. By studying how galaxy number density evolves with redshift, scientists can infer the processes of galaxy formation, growth, and the effects of cosmic expansion on galactic structures. We shall, in particular, focus on the processes of galaxy formation and evolution. Our overall simulations (see Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27 and Figure 28) show that the number density of galaxies generally rises at the beginning from $z=0$ and grows at uneven rate until a plateau before declining, leveling or showing slight rate of increase regardless of the model used. In particular, our model in Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21 and Figure 22 show that there is rapid structure formation at the beginning of the universe for $0<z<0.5$ which gradually rises up to around$z\approx 0.8$ before structure formation proceeds at a slower rate regardless of the curvature and density of the universe. However, our standard Friedmann redshift model shows that the presence of a cosmological constant seems not to have pronounced impact on structure formation showing that dark energy presence seem to have negligible effects on galaxy formation in contrast to earlier works [20]. This may probably be because dark energy primarily affects the large-scale expansion of the universe rather than local gravitationally bound systems like galaxies or galaxy clusters. It is believed that on small scales, gravity, driven by dark matter and ordinary matter, dominates over the effects of dark energy. However, the effect of dark matter seems to go beyond small-scale influence and dominates over dark energy for all redshift ranges as far as our model investigation is concerned.

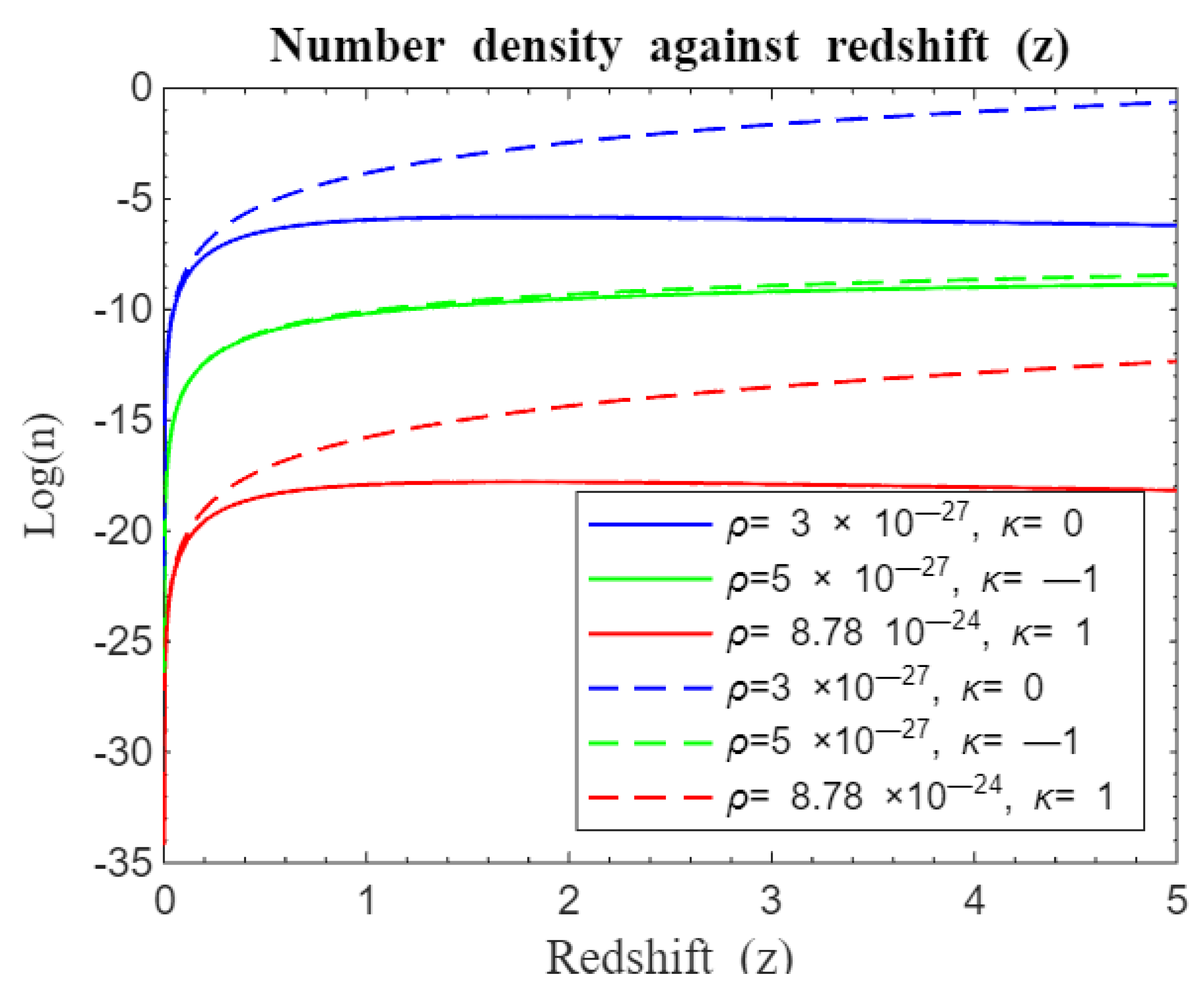
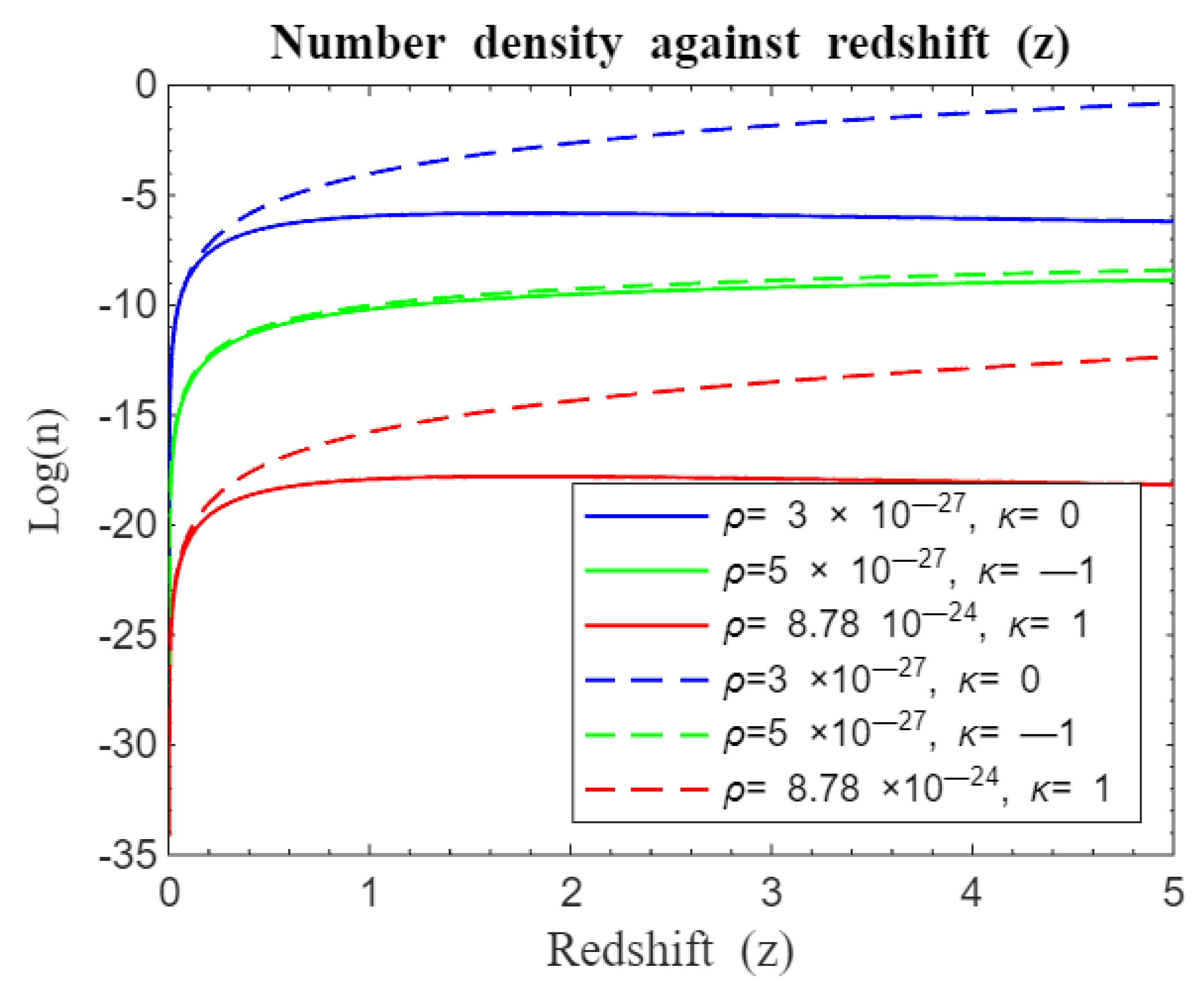
We compared our simulations on structure formation with earlier works of Langa et al. (2017) as depicted by Figure 23 and Figure 24. It is clear from these simulations that structure formation for both approximate standard Friedmann redshift model and standard Friedmann redshift model experienced similar rapid galaxy formation rate for both closed and flat universes at early times until$z\approx 0.1$ before our model (standard Friedmann redshift model) made a sharp departure from approximate standard Friedmann model [20]. It is also noted that for both models, the open universe curves do not deviate from each other at early times and tend to follow similar structure formation trajectories with our model slightly having an edge over its counterpart in terms of galaxy formation rate at late times. After the point of departure, structure formation for both closed and flat universes in our model continued steadily but at reduced rate unlike its counterpart that reached a plateau around$z\approx 0.5$ then after this, they started to decline while open universe leveled off in growth. It is also clear that the effect of a cosmological constant associated with dark energy is less impactful as demonstrated by results of Figure 23 and Figure 24. This shows that structural growth of galaxies is influenced by dark Matter much more than dark energy. This emphasizes the fact that dark matter is associated with accelerated expansion of the universe and arises as an emergent phenomenon as posited by phenomenological models [10,11,12,23] .

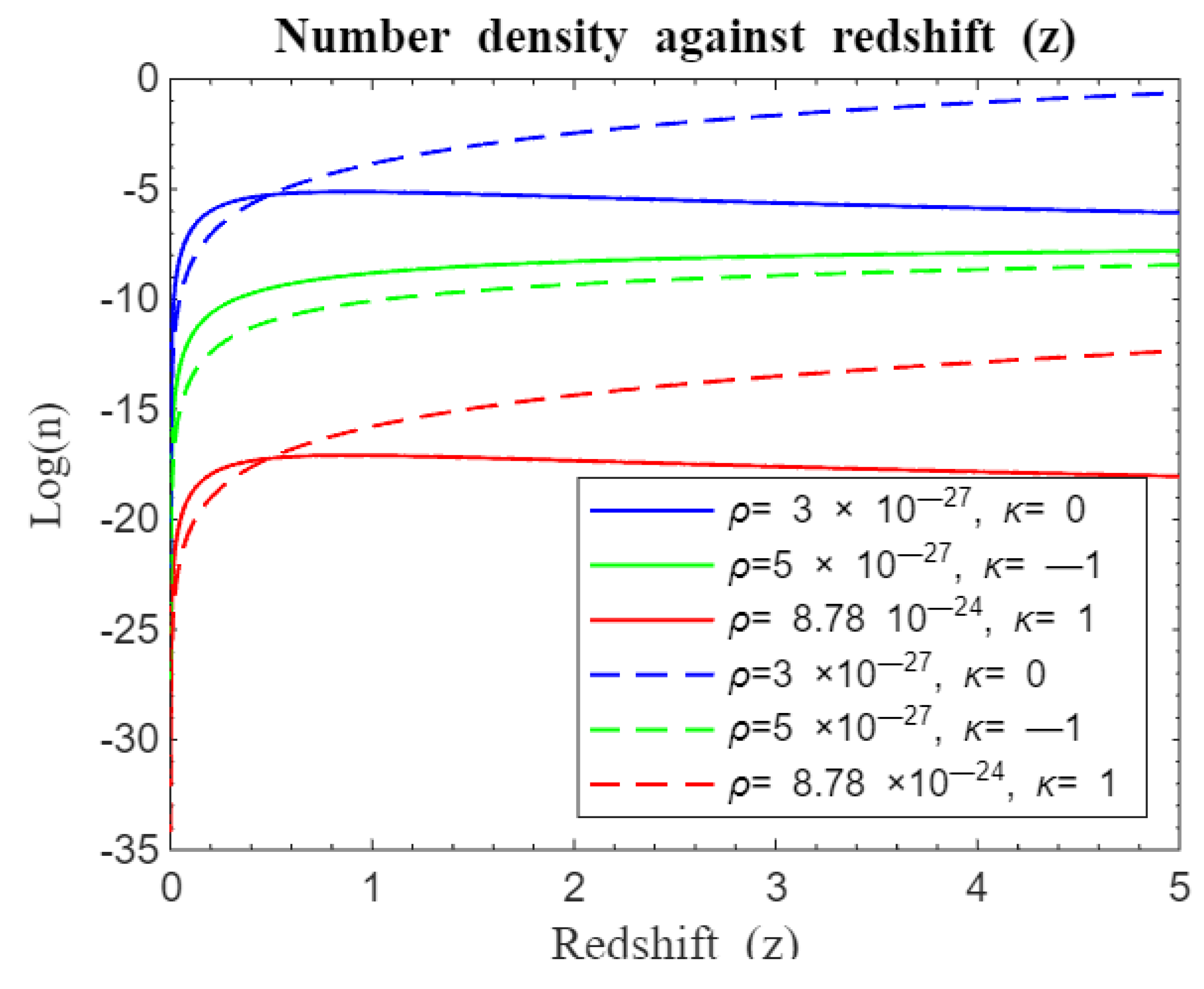
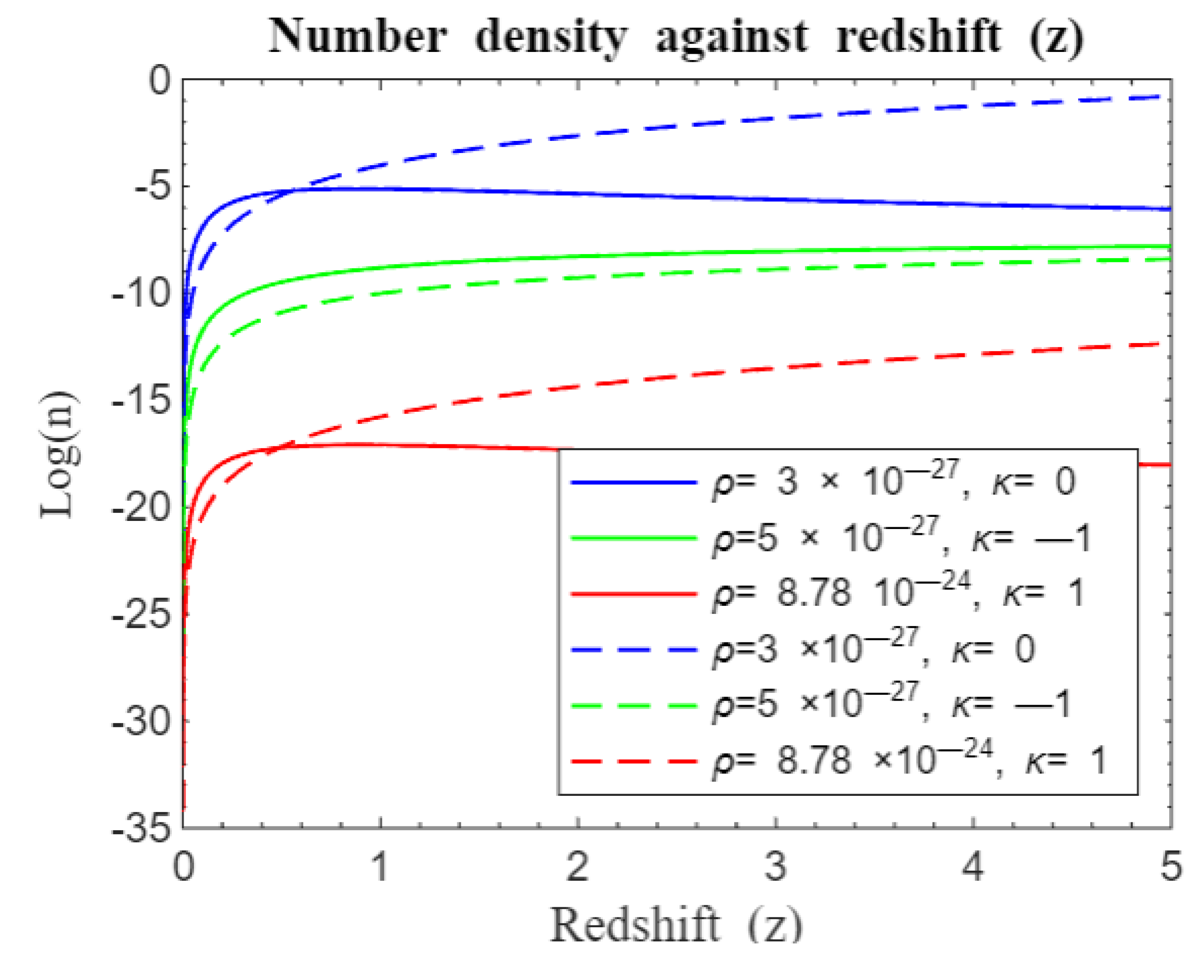
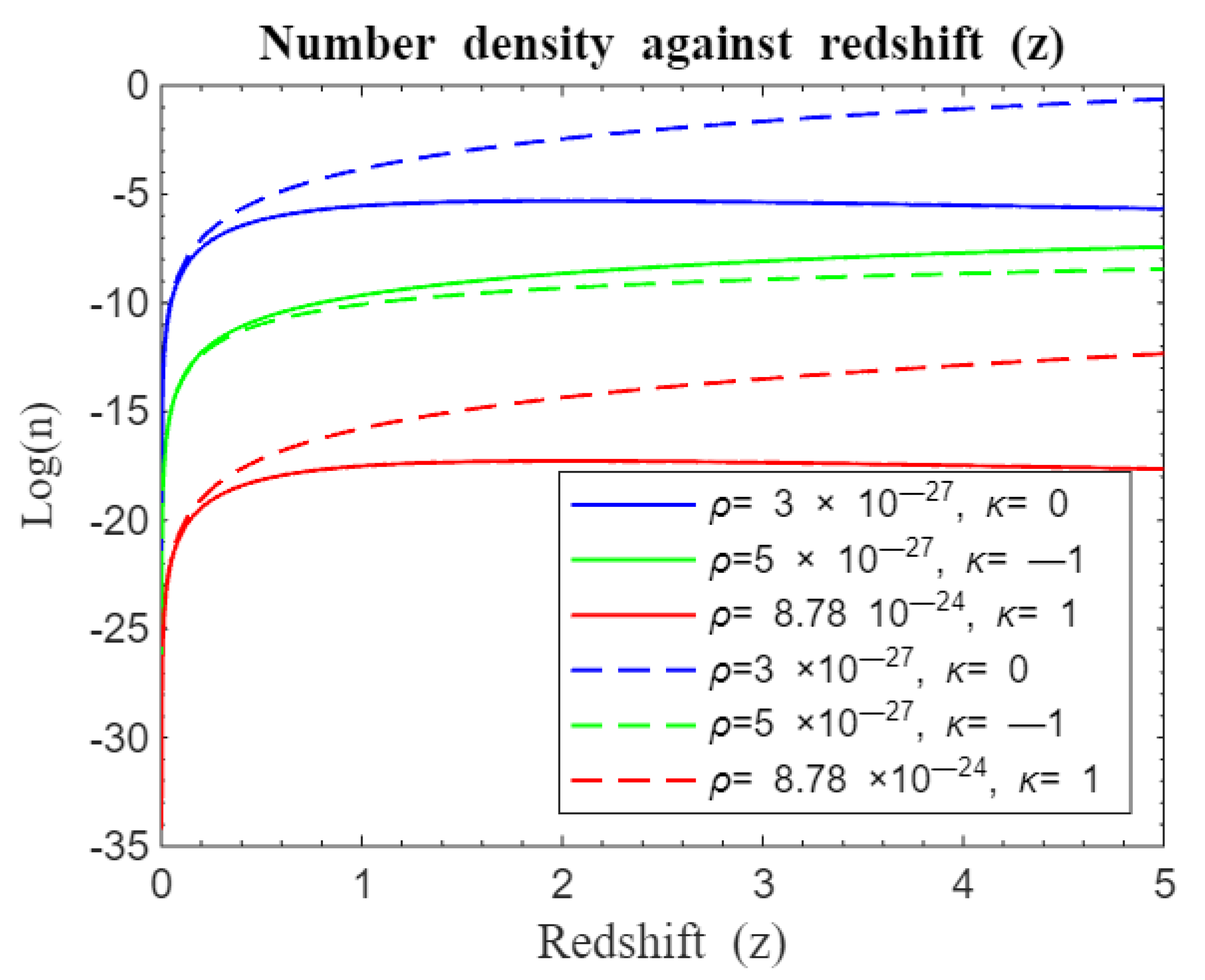
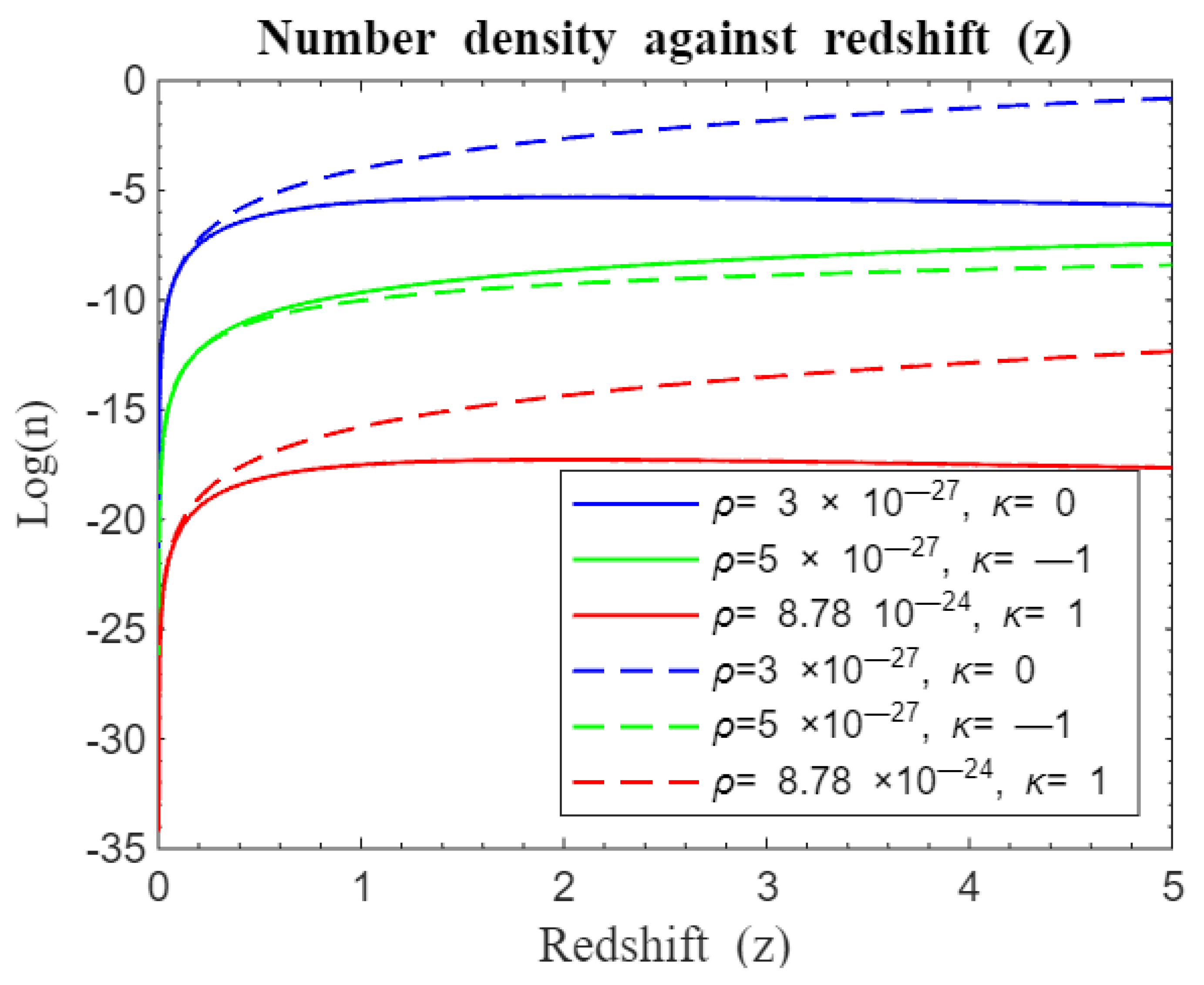
We again proceeded to compare our model with Nyagisera et al. (2024) as depicted by simulation results in Figure 25, Figure 26, Figure 27 and Figure 28. Our model was compared with the modified standard Friedmann redshift model for parametric and nonparametric functions as shown in Figure 25 and Figure 26 and 27-28 respectively. It is evident from Figure 25 and Figure 26 that there was rapid structure formation at the beginning of the universe for the modified standard Friedmann redshift parametric models than our standard Friedmann redshift model until redshift$z\approx 0.5$ when formation rate was now same and divergent of curves followed hereafter. Structure formation consequently changed with our model maintaining a stead but less rapid galaxy formation for both closed and flat universe after$z\approx 0.5$. However, there is obvious departure for curves of open universe right from the onset of structure formation with our model trailing in number density at early epoch but trying to catch up at later times. On the other hand, modified standard Friedmann redshift nonparametric model in Figure 27 and Figure 28 compares with our standard Friedmann redshift model in such a way that structure formation rate is similar at the beginning of the universe for both closed and flat universe only diverging after$z\approx 0.2$. Hereafter, curves from our model depict steady galaxy formation for both closed and flat universe. However, the green curves depicting an open universe follow a similar trajectory to the modified parametric curves, starting together and only differing infinitesimally at later times with ours slightly below the modified parametric green curve. The two universes reach a plateau at$z\approx 0.5$ before structure formation proceeds at a constant rate. From Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27 and Figure 28, we observe high activity in galaxy formation rate at the beginning of the universe than at later times. Formation of cosmic structures seem to have been faster at redshifts up to $0<z<0.5$ after which it slowed down. Galaxy formation is influenced by a variety of factors including the density fluctuations in the early universe and the nature of dark matter. In the early universe, density fluctuations provided the seeds for the formation of structures like galaxies. These fluctuations were more pronounced at smaller redshifts, corresponding to earlier times in the universe's history. As the universe expanded, the density of matter decreased, leading to slower galaxy formation over time [24]. Dark matter, which constitutes a significant portion of the universe's mass, plays a crucial role in galaxy formation by gravitationally attracting ordinary matter. Studies have shown that dark matter halos, which host galaxies, grow more rapidly at smaller redshifts due to the higher density of matter in the early universe [13,25]. This observation is in agreement with our results. Also, feedback processes, including supernova explosions and black hole activity, regulate the rate of star formation within galaxies. As the universe ages and galaxies evolve, these feedback mechanisms become more efficient, leading to a slowdown in the formation of new stars or galaxies. This observation well aligns with our findings where we observed that galaxy formation slowed time at later times when $z>0.8$. Observations and simulations, like those conducted by Péroux et al. [26], highlight the importance of feedback in shaping galaxy properties over cosmic time. Recent observational studies, such as those analyzed by Huterer & Shafer [27], indicate that as the universe expands, the gravitational pull between galaxies weakens, contributing to a slowdown in the formation of new galaxies at higher redshifts in tandem with our findings. These factors collectively contribute to the observed trend of faster galaxy formation at smaller redshifts and a gradual decrease in the rate of formation as redshifts increase or as the universe expands. This balanced expansion results in a relatively stable number density of objects over cosmic time [28]. In an open universe with negative curvature, the spatial geometry is hyperbolic, and the expansion continues indefinitely without a collapse. Similarly, in the flat universe, the expansion may decelerate due to matter density, but the presence of dark matter again may lead to an accelerated expansion. This continuous expansion results in a gradual decrease in the growth rate of large-scale structure, leading to a flattening of the number density vs redshift curve [6,29]. In a universe with positive curvature, the spatial geometry resembles that of a hypersphere. As the universe evolves, the gravitational attraction due to the matter density eventually overcomes the expansion driven by dark energy, leading to a collapse of the universe. This collapse results in a rapid decrease in the observed number density of objects (such as galaxies) as redshift increases [30]. In our case, we did not observe substantial impact of dark energy so that its effect may have been overshadowed by dark matter effects.

5.3. Comparison with Observational Data

The study of redshift in galaxies stands as a cornerstone in our quest to understand the processes of structure formation, and evolutionary in the universe.

Central to our task, we embarked on the utilization of vast and accurate astronomical datasets of our present time, teeming with measurements of redshift and number density. These datasets are curated to ensure accuracy and freedom from the effects of background geometry or cosmic distance measurement anomalies as much as possible. Leveraging on these datasets, we embarked on comparative analysis, extracting plots that mirrored the parameters of our analytical models. This alignment in scale facilitates a direct comparison between the theoretical constructs delineated by our model and the empirical realities captured by observational data.

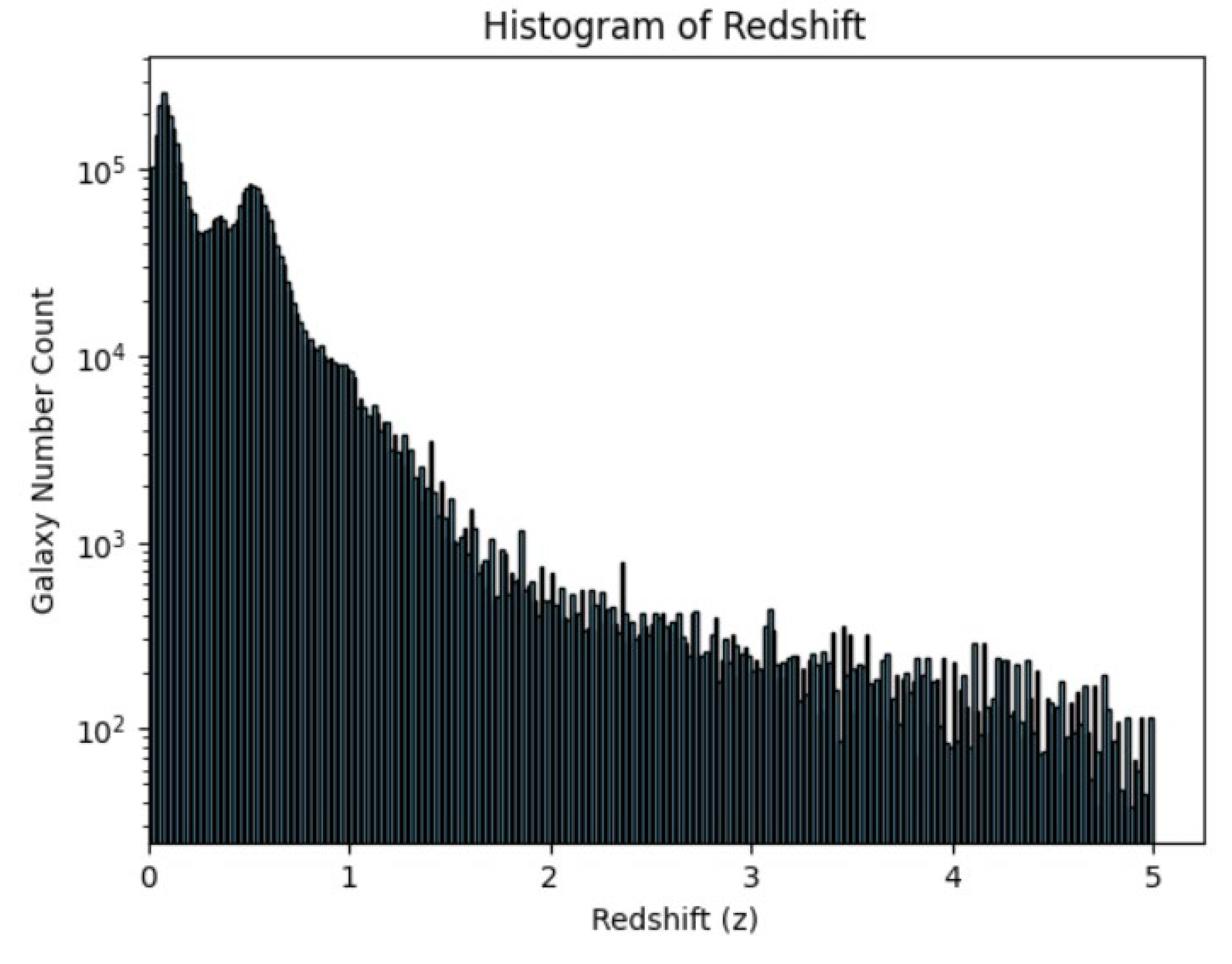
We collected observed redshifts between 0 and 5, specifically, for extragalactic galaxies in the infrared spectral region, using Planck 2015 cosmological parameters from the NASA/IPAC Extragalactic Database (NED) (https://ned.ipac.caltech.edu/; [31]. The distribution of these retrieved redshifts was plotted, with the bin heights indicating the number of galaxies observed at each redshift, as shown in Figure 29.

In Figure 29, an exponential decrease in the distribution of observed galaxies with increase in redshift was observed. Clearly, there was high activity of galaxy formation in the redshift range $0<z<1.5$ with a burst of galaxies forming between$0<z<0.8$ and presenting two characteristic peaks at $z\approx 0.1$ and $z\approx 0.5.$ This indicated that galaxies were formed at a faster rate in the beginning of the universe $z<1$than at later time. It is interesting to note that this observational data exactly coincides with our theoretical model predictions of galaxy formation peaks at $z\approx 0.5$ and $z\approx 0.1$ as presented by Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21 and Figure 22 and Figure 23 and Figure 24 respectively. This alignment therefore, validates our Friedmann model adopted in this work as a correct cosmological framework for accounting of structure formation and evolution in the universe.

6. Summary and Conclusions

The cosmological principle, a fundamental assumption in the standard cosmological model, posits that the universe is homogeneous and isotropic at large scales, though this is not evident on smaller scales. The Friedmann-Lemaitre-Robertson-Walker metric serves as the foundation of modern cosmology, with deviations from the standard model addressing challenges such as the Hubble tension and cosmic coincidence problems. Redshift-distance and light intensity-distance relations are critical tools for testing the validity of cosmological models, especially with the rise of both parametric and nonparametric redshift models.

Dark matter and dark energy play significant roles in explaining galaxy formation and cosmic expansion, though their nature remains largely unknown. Observational methods, such as three-dimensional redshift surveys, present challenges in affirming large-scale homogeneity. Discrepancies between observations, such as quasar distribution studies, and the expected homogeneity, indicate that further analysis is needed.

This study aims to refine our understanding of the universe’s structure by focusing on three key astronomical parameters: number density, light intensity, and redshift. It examines the evolution of these quantities from the early universe to the present and compares findings with both the ‘approximate standard Friedmann redshift model’ by Langa et al. (2017) and the ‘modified standard Friedmann redshift model’ by Nyagisera et al. (2024). The study introduces the 'standard Friedmann redshift model,' which incorporates the effects of dark matter and dark energy.

The study establishes that light intensity decays exponentially with increasing redshift due to the universe's expansion. This relationship, confirmed by Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14, is in agreement with our classical expectation that attribute the decrease in energy density to photon dilution as the universe expands.

The results highlight that the geometry of the universe significantly impacts light intensity. In a flat universe, light intensity decays more rapidly compared to an open or closed universe, as shown in Figure 1 and Figure 2. For example, a closed universe$(\kappa =1)$ displays higher initial intensity with a slower decline, while an open universe$(\kappa =-1)$ shows a faster drop in light intensity. Comparative analysis of models reveals that high-density universes exhibit higher initial light intensities during early times.

Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21 and Figure 22 indicate that dark energy has negligible effects on structure formation, contrasting with earlier works of Langa et al (2017) and Nyagisera et al (2024). This emphasizes the fact that dark matter, rather than dark energy, drives galaxy formation by influencing local gravitationally bound systems and even beyond.

Furthermore, the study shows that galaxy formation occurred more rapidly at early times, particularly within the redshift range$0<z<0.5$, as illustrated by Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27 and Figure 28. This aligns with the idea that density fluctuations in the early universe, amplified by dark matter, were key in facilitating early galaxy formation.

Observational data from the NASA/IPAC Extragalactic Database, presented in Figure 29, reinforces these findings by showing that there was a galaxy burst between redshifts 0 and 1, which peaked around$z\approx 0.1$ and $z\approx 0.5.$ These characteristic redshift peak values are consistent with our theoretical predictions of the standard Friedmann redshift model used in this work (see Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21 and Figure 22 and Figure 23 and Figure 24 respectively), validating its accuracy in explaining the formation and evolution of cosmic structures.

In conclusion, this work therefore, presents a formidable understanding of the relationship between light intensity, redshift, and structure formation in the universe, while emphasizing the pivotal role of dark matter and cosmic geometry in shaping the universe's evolution.

The implications of this work extend into several key areas for future research. First, a more subtle approach is needed to model the structure and evolution of the universe, one that better accounts for the complexities of dark energy’s and dark matter's influence on galaxy formation. Second, our results call for more detailed observational campaigns targeting the redshift ranges identified in this study to further investigate the underlying mechanisms driving these processes.

Furthermore, the growing challenges to the cosmological principle suggest that alternative models of the universe, potentially those that allow for more variation on large scales, should be considered.

Lastly, the evidence of rapid galaxy formation at specific redshifts and the crucial role of dark matter in shaping cosmic structures point to gaps in our current understanding that require further exploration.