Prerpints.org logo
Preprint
Article

Networking 3 K Logic Gate Quantum Processors to Approach 1 Billion Logic Gate Performance

Altmetrics

Downloads

70

Views

27

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

09 September 2024

Posted:

10 September 2024

You are already at the latest version

Alerts
Abstract
Outlined is a proposal designed to culminate in the foundry fabrication of arrays of singly addressable quantum dot sources deterministically emitting single pairs of energy-time entangled photons at C-band wavelengths; each pair having negligible spin-orbit fine structure splitting; each pair being channeled into single mode pig-tail optical fibers. Entangled photons carry quantum state information among distributed quantum servers via I/O ports having two functions; the unconditionally secure distribution of decryption keys to decrypt publicly distributed, encrypted classical bit streams as input to generate corresponding qubit excitations, and to convert a stream of quantum nondemolition measurements of qubit states into a classical bit stream. Outlined are key steps necessary to fabricate arrays of on-demand quantum dot sources of entangled photon pairs, principal among are 1) foundry fabrication of arrays of isolated quantum dots, 2) generation of localized sub-surface shear strain in a semiconductor stack, 3) a cryogenic anvil cell, 4) channeling entangled photons into single mode optical fibers, 5) unconditionally secure decryption key distribution over the fiber network, 6) resonant excitation of a Josephson tunnel junction qubits from classical bits, and 7) conversion of a quantum nondemolition measurements of a qubit states into a classical bit.
Keywords: 
Subject: Engineering  -   Telecommunications

1. Introduction

There are numerous approaches to the development of physical qubits that constitute a quantum processor, for example, those based on neutral atoms, trapped ions or most commonly superconducting charge tunneling across a pair of Josephson junctions, sometimes referred to as a Transmon. Here we consider only the latter based on its decades of research and development but note that the common challenge to all physical qubits is their fragility of the entanglement among them in the ever present vacuum noise and local interference requiring various error correction strategies that generally involve mapping many physical qubits into fewer logical qubits or logic gates [1,2].
Consistent with the classical computer paradigm that a “bigger” mainframe equals greater computing power at higher speeds, according to its revised quantum technology roadmap, IBM plans, by 2033, to link together multiple of its “System Two” quantum processors to form a single multi-platform system, named Blue Jay, that will include 16,632 logical qubits, 1 billion entangling gates between physical qubits and error correction modularity [3]. For reference, one logical qubit commonly requires 1,000 physical qubits, but this depends on several factors, for instance, the error correction algorithm and the error rate.
Historically, classical computing pivoted from a mainframes-centric roadmap to one based on networked servers in the 1990’s. This led to classical supercomputers and classical data centers comprising networks of task-specific servers after the brief advent of the Cray-1 supercomputer which was essentially a highly integrated mainframe. In the present age one should expect the quantum computing paradigm to evolve from one based on large quantum processor, or cooperative multiples thereof linked internally into a single super quantum computer reminiscent of the Cray-1, to a quantum network of externally linked quantum servers. After initially exploring “more is better” as did previous generations of classical mainframe computing, a number of barriers to quantum computer scaling are becoming apparent.
Barrier 1. Quantum decoherence is a fundamental barrier in quantum computing as it refers to the loss of entanglement fidelity when a system inevitably interacts with vacuum fluctuations or thermal noise or interference in its immediate environment.
Barrier 2. Quantum Error Correction (QEC) is a vital natural response to Barrier 1 as quantum states are inherently fragile. The price for implementing QEC is an inevitable drain on qubit resources as QEC is bound by the rules of quantum mechanics.
  • Error detection in quantum systems must obey the quantum no-cloning theorem, which states that it is impossible to create an identical copy of an arbitrary, unknown quantum state. This rule contrasts with classical error correction, where information can be duplicated and checked for errors.
  • Quantum errors can occur in more ways than classical bit errors due to the nature of the qubit. For instance, a qubit error could be due to one-flip of state or a double flip to return to the original state but out of phase. This is more subtle and requires more complex error correction codes.
Barrier 3. Physical qubit number scaling does indeed scale the computational power of the processor but not in the same way as adding more transistors to a classical silicon processor. In a quantum processor, every qubit must interact with every other qubit to maximize computational power. This requirement becomes increasingly difficult to meet as the number of qubits increases. As the number of qubits increases, so does the probability for error. Errors can be introduced by anything from environmental noise to imperfections resulting from the manufacturing process, at least for qubits based on Josephson tunnel junction charge current.
Barrier 4. Formfactor of the external Input/Output (I/O) microwave links (cabling) to the outside world, [4,5] at least for qubits based on charge current tunneling in Josephson tunnel junction. Present packaging technology cannot scale formfactor to accommodate increasing number of output links.
Barrier 5. Six-sigma refers to the degree of control over defects and variations that a manufacturing process produces during Josephson junction qubit production and packaging. The six-sigma standard is important to achieve high manufacturing yield, reduce overhead of error correction and relax fault tolerance measures. However, six sigma scalability is limited by (1) the availability and cost of suitable materials and hardware, (2) the difficulty of controlling and connecting qubits to minimize cross talk noise, (3) the trade-off between coherence time, (roughly the half-life of a qubit) and gate speed, (generally, a fast Transmon gate is preferred as it spends less time in a noisy environment).
Barrier 6. Complexity in designing and utilizing quantum algorithms and protocols to solve a problem on a quantum computer. Complexity depends on the structure of the physical qubit, the optimization of quantum gates, the encoding and decoding of quantum information, the communication and synchronization of qubits, the verification of quantum computations and their input/output to classical bits.
Given the foregoing qualitative benefit/cost considerations of scaling the number of logical qubits per quantum processor, or the linking several quantum processors on the same platform, as indicated by the IBM quantum technology roadmap [3], in the spirit of the “chip multiprocessor (CMP) concept prevalent in the late 20th Century,” we here propose the concept of quantum server networks in the spirit of classical server networks that comprise classical supercomputers and classical data centers.
In this paper we propose means and methods for constructing a quantum secure network of quantum servers.
A quantum server network, as described here, comprises five basic functions.
1) Distributed small formfactor, deterministic sources of entangled photon pairs.
2) An optical fiber network over which entangled photons and encrypted classical bits streams propagate.
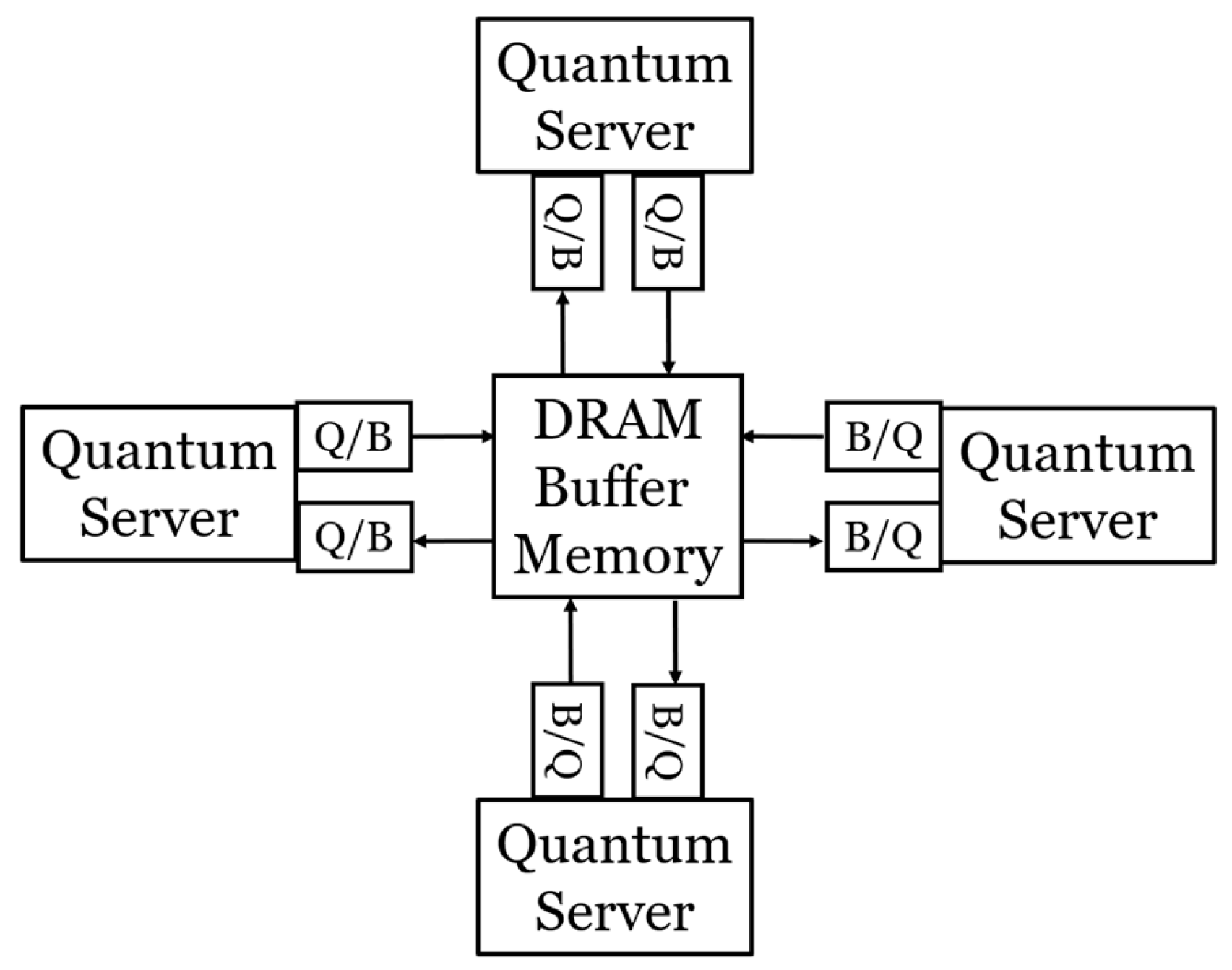
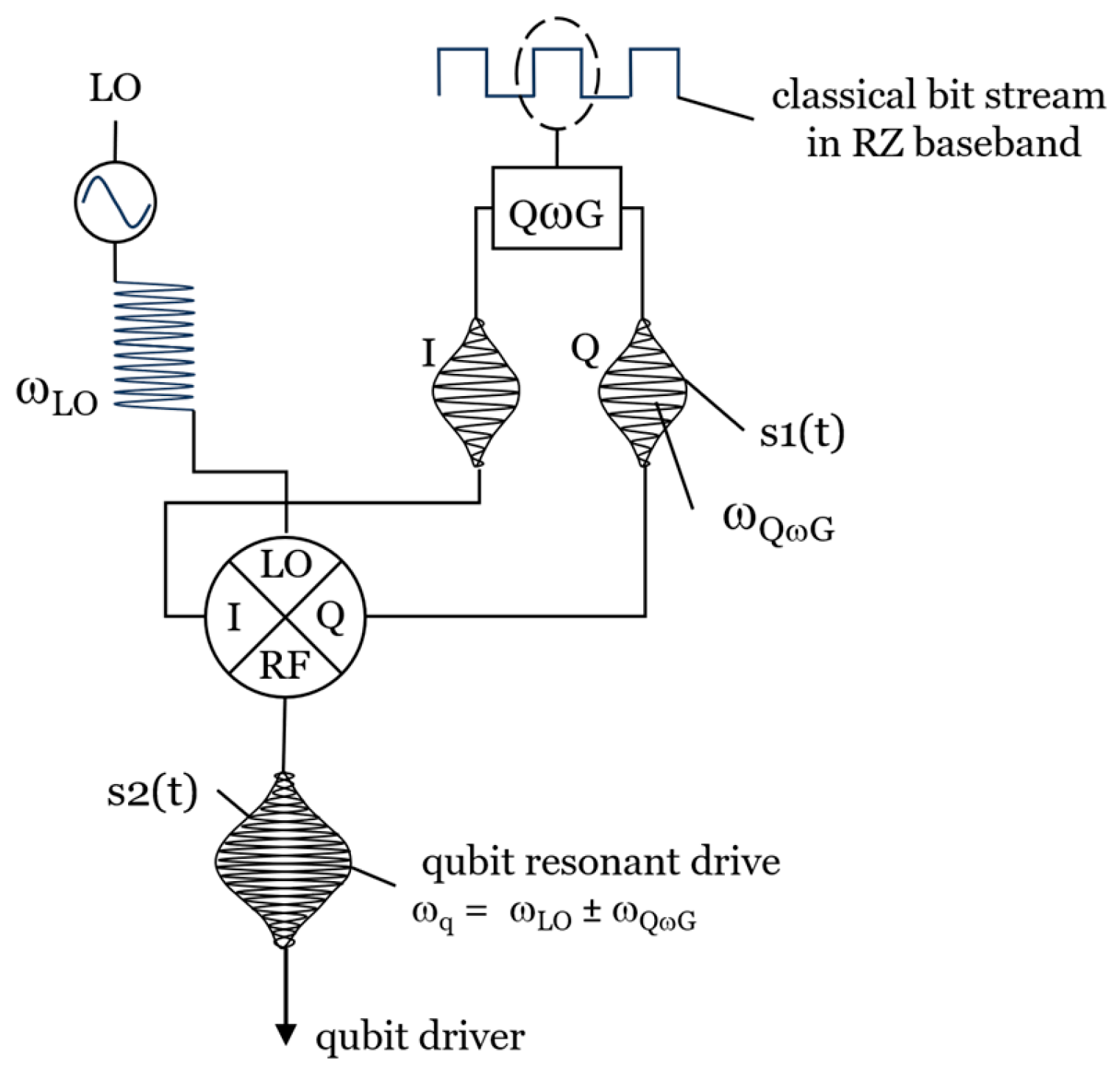
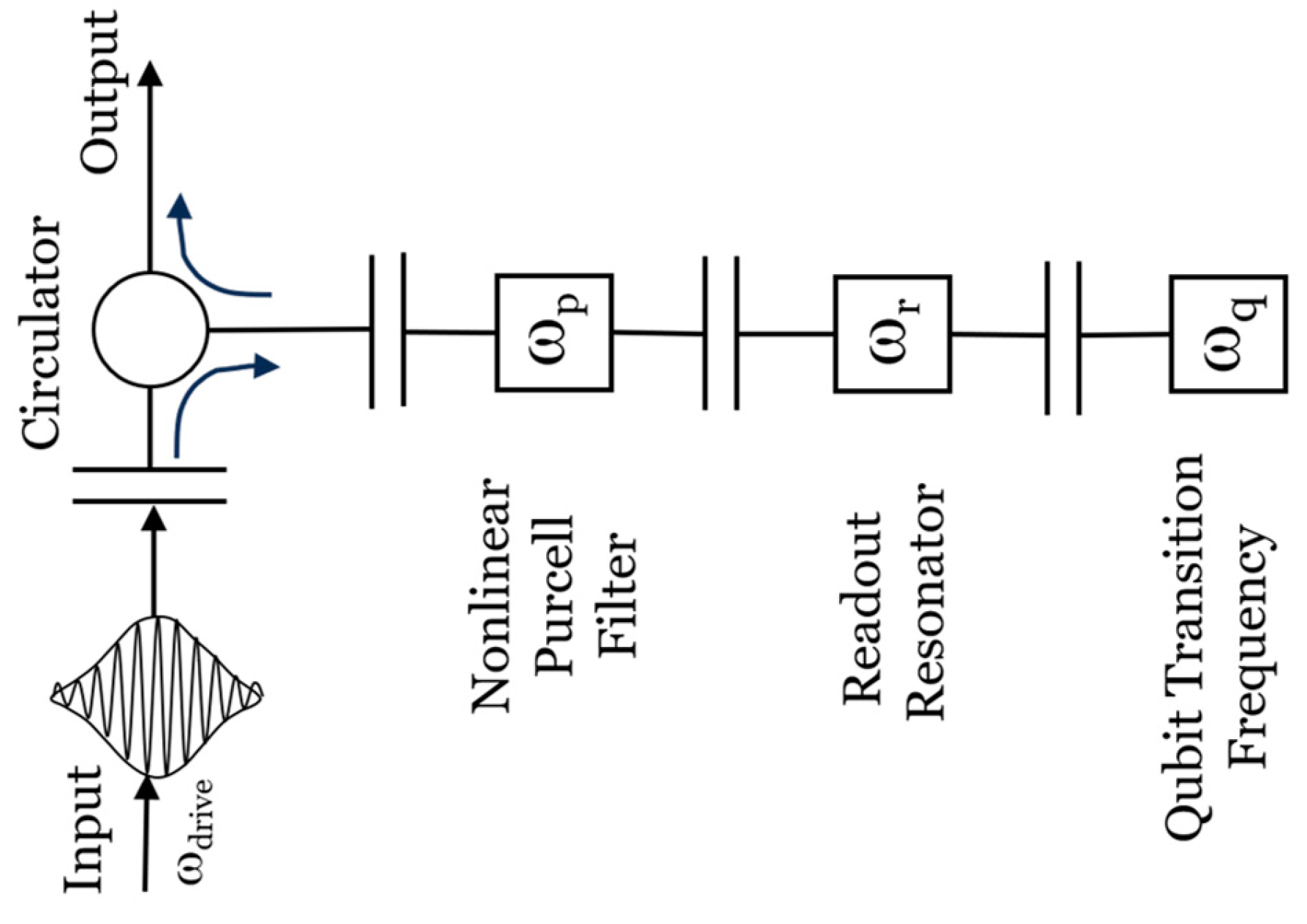
3) Classical bit to qubit (B/Q) interfaces by which classical bit streams generate streams of Transmon qubit states via a resonant qubit drive circuit as shown in Figures 8 and 9.
4) Qubit to classical bit (Q/B) interfaces by which streams of Transmon nondemolition readouts generate classical bit streams.
5) A quantum key distribution protocol, for example, the E 91 [6], and its security analysis [7].
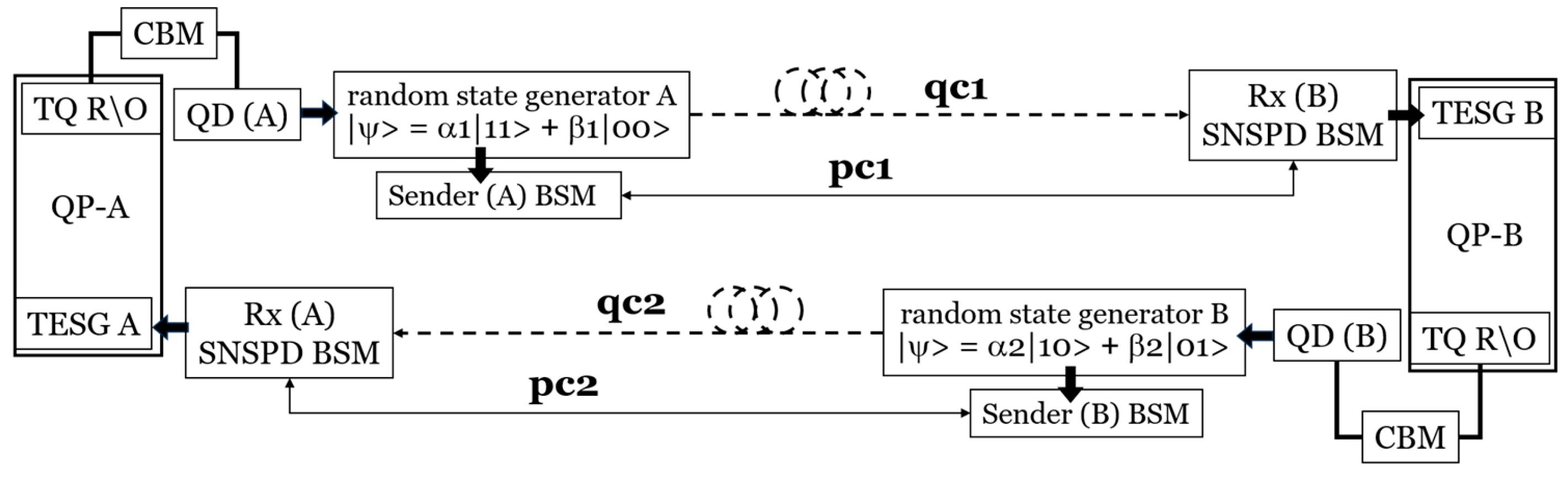
The E 91 protocol of step 5) is very briefly summarized:
i) quantum dot sources that generates pairs of entangled photons on demand.
ii) sending station that prepare the entangled photons in a random superposition of two orthogonal states of polarization.
iii) sending station sends the first of two entangled photons to a receiving station.
iv) the receiving station measured the state of the received photon and records the results.
v) the sending station measures and records the quantum state of the second of the two entangled photons.
Upon the completion of several similar exchanges,
vi) the two sets of measurements are shared and compared over an insecure channel to generate the decryption key.
Compositions of InxGa(1-x)As quantum dots are thought to make good sources with which to generate on-demand entangled pairs of photons in the Telecom spectrum. The outstanding obstacle to this goal is the fine structure energy splitting attributed to the valence band spin-orbit coupling of the intermediate exciton level in the biexciton recombination cascade which makes the two photons correlated but not entangled because of their energy difference; see, for example [8,9,10,11]. The fine structure splitting must be sufficiently minimized to produce entangled photons having sufficiently high entanglement finesse compared to the four maximally entangled wave functions (Bell states) of two maximally entangled photon polarizations. A way to minimize the effects of spin-orbit splitting in semiconductor excitons has been theoretically understood [12] and experimentally demonstrated in a few publications [13,14].

Organization of the Proposal

SECTION I describes the fabrication of deterministic semiconductor sources of entangled photons based on InxGa(1-x)As quantum dots comprising: (1) an optical resonator cavity to maximize photon production [11], (2) means to locate an individual QD source sufficiently isolated from neighboring QD sources [15,16], (3) an anvil cell construction and operation designed to generate a shear strain in a subsurface volume that contains one and only one quantum dot source, (4) efficiently channel the entangled photon pairs generated by a specific quantum dot into a single mode Telecom optical fiber and (5) means to cryogenically cool the subject QDs to about 10 K while applying the necessary external stress.
Based on the reasonable assumption that quantum servers having just a few hundred logical qubits have a higher manufacturing yield and simpler error correction tasks, and that their coordinated problem solving may hasten the goal of reaching the ‘Practical Quantum Advantage,’ sometimes defined as the point at which quantum processors can solve problems of practical interest that cannot be solved by traditional supercomputers.
SECTION II describes a basic architecture leading to a synchronized, unconditionally secure network of modest quantum servers:
1) Secure optical fiber network for the distribution of encryption keys based on one of many quantum key distraction protocols, for example the E 91 protocol [6] and its security analysis [7], used “only once” for decrypting the encrypted classical bit stream sent over an unsecure channel.
2) Synchronization between quantum servers and the secure optical fiber network is possible only by the deterministic nature of the source that generates entangled photon pairs on demand.
SECTION III describes one input/output (I/O) interface scheme between a qubit and a classical bit (Q/B) and vice versa, (B/Q). A quantum server networks can be characterized by a set of separate and smaller quantum processors comprising about 100 physical qubits and about 3 k logic gates and, therefore, should have higher manufacturing yields. When judiciously linked by a quantum secure optical fiber network, a sufficiently large set of quantum servers, operating in concert, should be able to potentially achieve a performance approaching that of a large single machine endowed with a much higher qubit count but may be encumbered by massive error correction complexity. Smaller quantum processors linked in a quantum network is a concept reminiscent of classical supercomputers or classical data center networks.
By 2033, according to its revised roadmap [3] IBM has projected that it will link together multiple System Two processors; the integrated super quantum processor will then be capable of executing 1 G gates over 2 k logical qubits. The super quantum computer ion a single platform has been given the name “Blue Jay” by its creator.
Quantum server networks can only be enabled by the development of deterministic, “on-demand,” sources of entangled pairs of photons. These sources enable photon synchronization and networking. In contrast, quantum networking and photon synchronization are not possible with probabilistic legacy sources of entangled photon pairs such as spontaneous parametric downconversion (SPDC) in various nonlinear crystals [17] or spontaneous four wave mixing (SFWM) in a Si3N4 ring resonator [18], for example. These sources exhibit entangled pair production gated by Poisson statistics.

SECTION I.

A. Constructing Arrays of InxGa(1-x)As Semiconductor Quantum Dot Sources of Entangled Photons

A source of entangled photons should have at least the following attributes:
  • The production of entangled photon pairs should be deterministic. This is necessary for quantum network synchronization.
  • The entanglement fidelity of the emitted photon pairs should be at least 95% compared with the four maximally entangled two-photon (Bell) states.
  • The generated pair of entangled photons should be spectrally indistinguishable and be orthogonally polarized.
  • The energy of entangled photon pairs should fall withing the Telecom C-band to minimize optical fiber propagation loss.
  • The emerging photon pairs should be entangled in the energy-time or energy-momentum degrees of freedom within the Heisenberg uncertainty limit and their provenance should be indeterminate; (there should be no “which path” information).
Manufacturing of semiconductor quantum dot sources should provide for:
  • Efficient harvesting of quantum entangled photon pairs into optical fiber channels.
  • Arrays of sources should be manufacturable at commercial semiconductor foundries.
  • The separation between quantum dots in an array should be of the order of 1000 – 10,000 Å to individualize a specific single quantum dot. Further separation leads to long search times.
  • Each source, including its cryogenic anvil cell, should have a “small” formfactor.
Several publications can be found that report work on semiconductor quantum dot sources emitting polarized pairs of photons in the optical C-band. However, while the emerging photons are often correlated to a degree, they are far from being entangled because of the influence that spin-orbit coupling has on exciton states at the valence band edge, causing differences in the energy of excitons depending on electron spin. This energy difference is seen in the exciton recombination cascade to the ground state and is termed “fine structure splitting” (FSS). FSS varies with the composition of compound semiconductor quantum dots, and is particularly large in InxGa(1-x)As. Non-degeneracy of light emitted during the recombination cascade will violate one of the conditions for entanglement, to wit, energy indistinguishability.
The spin–orbit interaction is a relativistic interaction of the electron spin with its orbital angular momentum. Spin-orbit coupling has a significant effect on the band structure, particularly at the valance band edges where the exciton energy levels reside.
Cumulative internal strain stemming from naturally occurring or designed lattice mismatch, for example, designed metamorphic strain as part of bandgap engineering, or an externally applied stress introduces additional coupling between the heavy-hole (HH) bands, light-hole (LH) bands, and the spin-orbit split-off (SO) bands. Such coupling can be useful, for example, in partially or wholly negating the effects of sub-band exciton energy splitting in cascade recombination emission. This is the case for excitons in metamorphic lattice-matched systems such as AlxGa(1-x)As/GaAs and InxGa(1-x)As/GaAs, the latter being of interest here.
The theory of the effects of shear strain on spin-orbit valence band edge energy levels, and experimental verification as it applies to exciton level splitting can be found in part in [12,13,14].
Fabrication practices by which to control the density of quantum dots can be found, for example, in publications [15,16].
The construction of an optical resonator cavity suitable to produce efficient emitters of entangled photon pairs from a semiconductor quantum dot may be found, for example, in publication [11].
Significant early results on the effect which an externally applied stress has on the fine structure splitting in the exciton emission cascade from InGaAs quantum dots is reported in [19].
In addition to the attributes listed above, a deterministic quantum dot source of entangled photons, must be based on:
  • An optical resonator cavity to maximize photon production [11].
  • Means to locate the individual QD source, isolated from neighboring QD sources, [15,16].
  • An anvil cell with which to generate a shear strain in a subsurface volume of a quantum layer that contains the quantum dot source
  • Efficient channeling of entangled photon pairs generated by a specific quantum dot into a single mode Telecom optical fiber, and
  • Means to cryogenically cool arrays of anvil cells containing quantum dot sources to about 10K.

B. Optical Resonator Source Fabrication

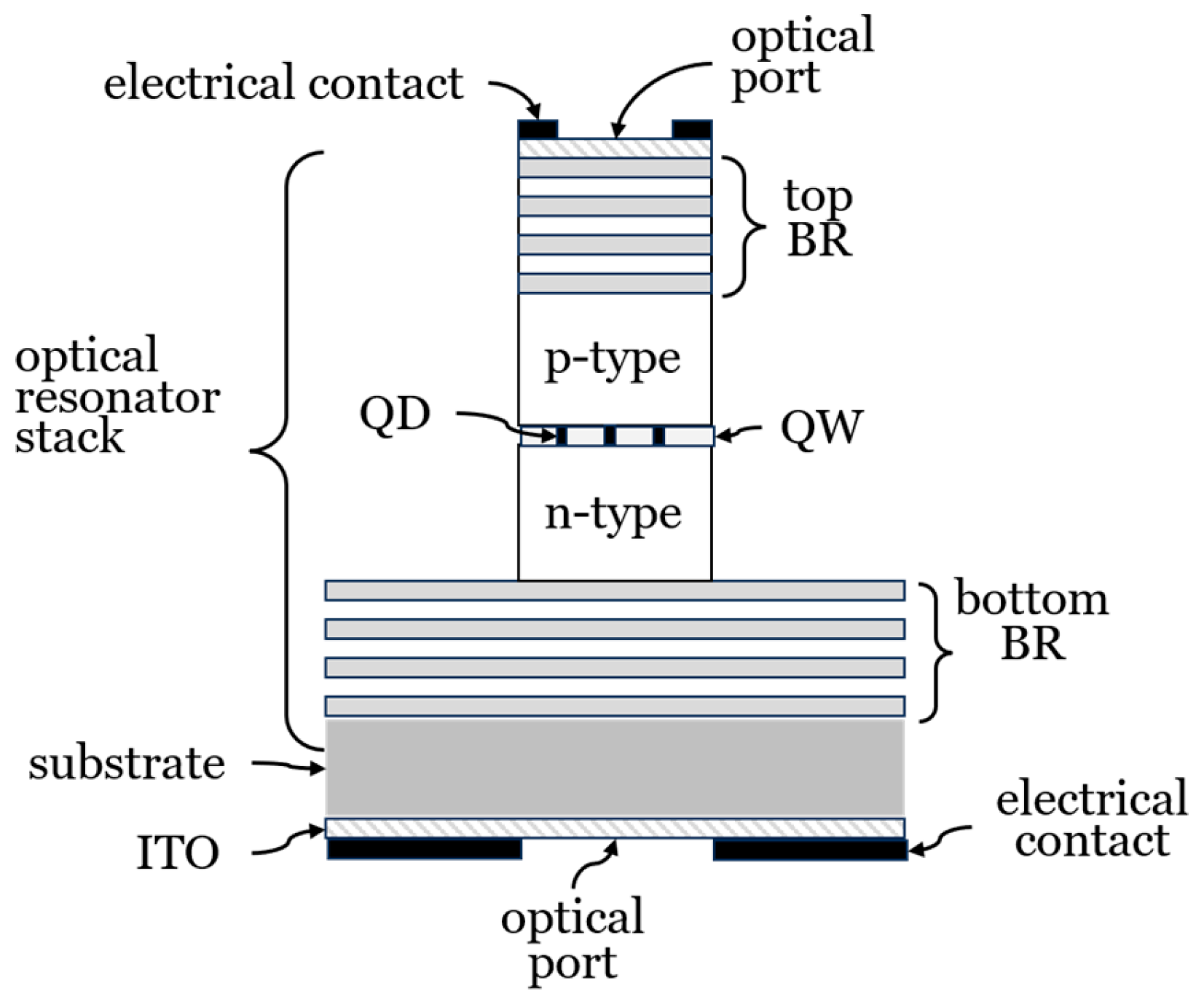
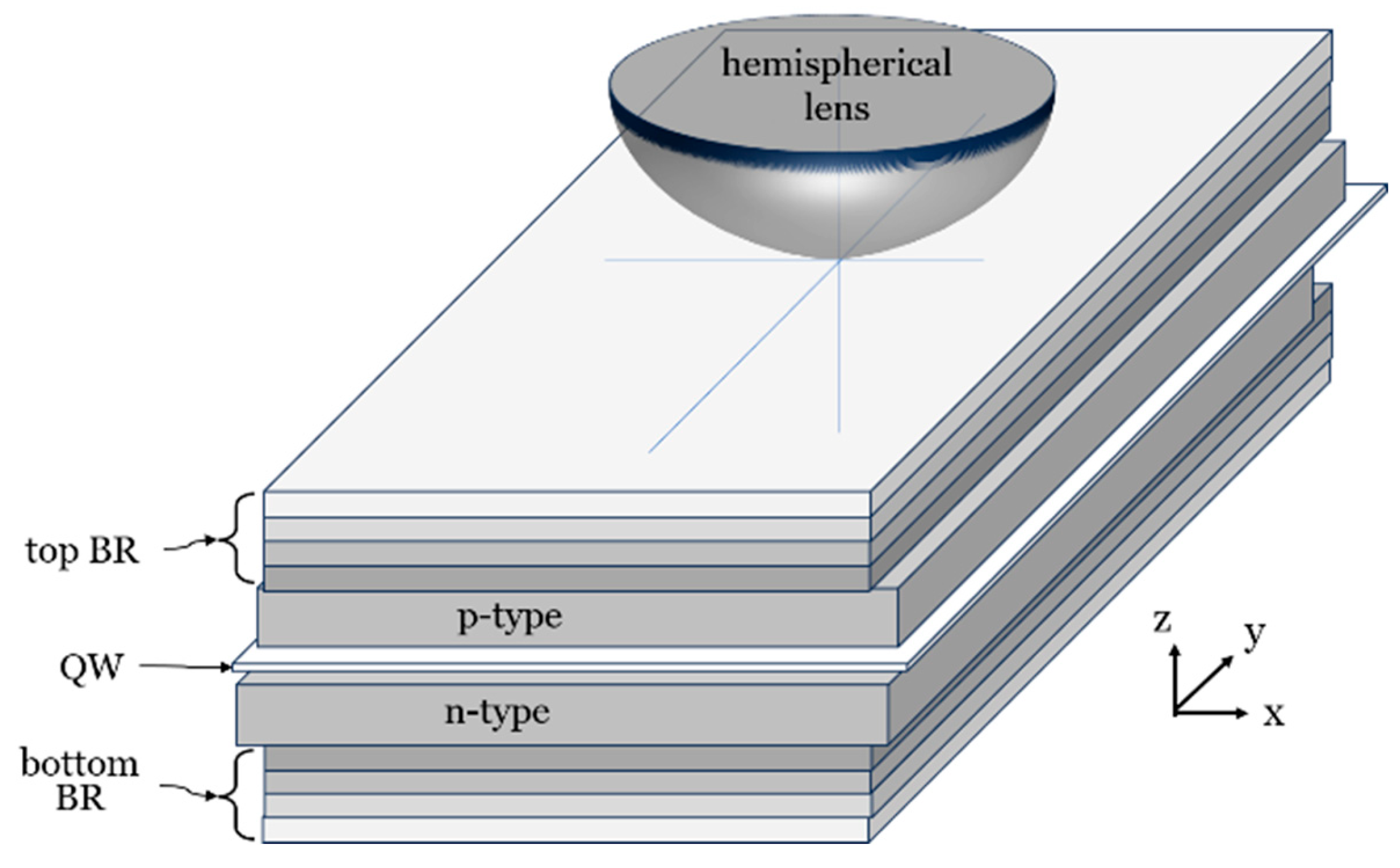
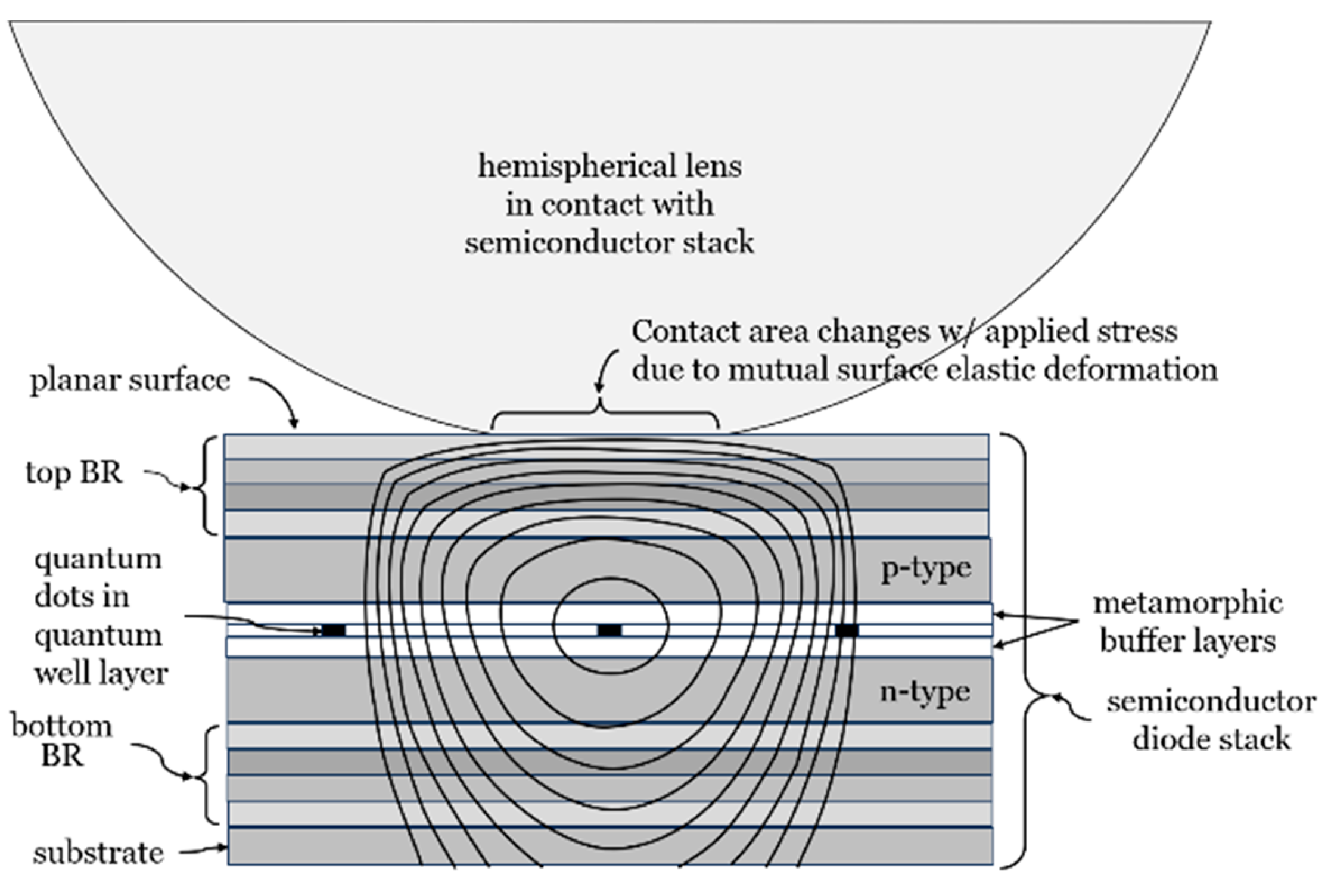
Depicted in Figure 1 is a stack of compound semiconductor layers comprising an optical field micro-cavity resonator substantially similar to those commonly found in ubiquitous Vertical Cavity Surface Emitting Lasers (VCSELs) and discussed in reference [11]. It is noted that VCSELs are generally used in short distance optical communications over multimode optical fibers and generally operate at wavelengths in the 850 nm range where semiconductor compound compositions can be found to simultaneously offer 1) good lattice matching and 2) indices of refraction with sufficiently high contrast so that the number of layers in the top and bottom Bragg grating reflectors, that define the optical resonance cavity, can be kept to a minimum and still achieve a resonator cavity with sufficiently high quality factor.
Unfortunately, these fortuitous advantages are greatly diminished in the optical C-band where a substantially larger number of Bragg grating reflector layers, top BR and bottom BR, are needed to achieve a substantially adequate resonance finesse.
Quantum dots (QD) are fabricated in a semiconductor quantum well (QW) layer between a p-type and an n-type cladding layers, generally built on a GaAs substrate. It is noted that the structure is, in fact, a semiconductor diode having top and bottom electrical contacts.
A top and bottom thin layer of optically transparent Indium Tin Oxide (ITO) alloy of composition In(2-x)SnxO3, may be added to promote uniformity in the applied electric bias field. A bottom optical pump port is added to facilitate optical excitation of quantum dots whose fluorescence emission may be used to locate a single quantum dot in a sparse quantum dot field. A system designed to generate and align entangled photon emissions from a specific quantum dot for the purpose of deterministically generating, entangled photon pairs and channeling them into output optical fibers is shown in Figure 2, Figure 3 and Figure 4 and 7.

C. Anvil Cell and Entangled Photon Harvesting

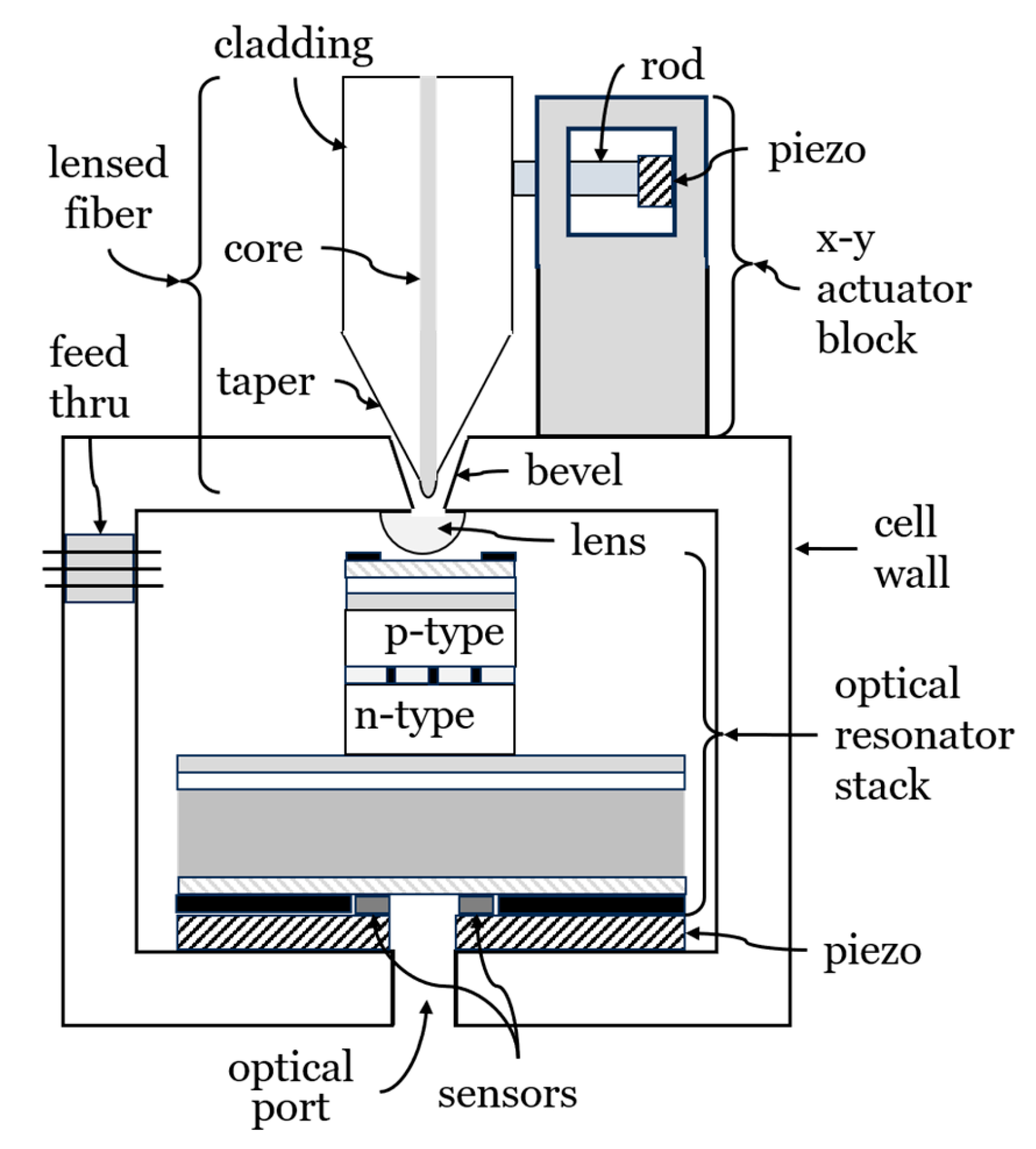
The primary purpose of the anvil cell is to generate a shear strain in a subsurface volume that contains the quantum dot source. The magnitude of the shear volume must be sufficient to sufficiently reduce the indistinguishability of the emitted entangled photon pairs. The cell wall enclosure provides the elastic spring constant restoring force that opposes the compressive stress produced by the piezoelectric actuator that pushes the semiconductor stack, shown in Figure 1, against the hemispherical lens. Emitted photons exit the top port and are channeled into an optical fiber by the hemispherical lens into the core of a lensed optical fiber. An x-y actuator block is used to align the lensed fiber while feed-thru electrodes provide diode electrical bias, piezoelectric actuator power and sensor I/O.
Depicted in Figure 2 is an anvil cell design whose purpose is to produce subsurface shear strain in a small volume v, that includes the target quantum dot located at a distance d, below the surface of the semiconductor stack shown in Figure 1. The volume v and subsurface distance d, are nonlinear functions of the radius of the hemispherical lens, the applied force generated by the piezoelectric actuator (piezo), the effective spring constant of the anvil cell enclosure, the moduli of elasticity and Poisson ratios of each the hemispherical lens and the optical resonator stack. These determine the diameter, 2r, of the contact area shown in more detail in Figure 6. In the elastic limit the contact area should reversibly deform with applied stress whose magnitude can be monitored with stress sensors.
It is noted that the key parameters 2r, d and v can be computed quasi analytically and is the subject of the theory of Hertzian contact stress, an excellent review of which may be found beginning with page 1658 in publication [20].
Emitted entangled photon pairs can be channeled into an external output optical fiber by a lensed optical fiber. Figure 4 shows, in more details the role of components directly related to coupling emitted photons to an external optical fiber through a bevel access port in the anvil cell; in particular the role of the internal hemispherical lens which also serves to generate the subsurface shear strain field. The purpose of the bottom optical access port is explained in conjunction with Figure 1.
The hemispherical optical lens has the dual purpose of aiding in channeling the emitted entangled photon pairs into the external optical fiber and to provide subsurface shear strain. Lens materials having sufficient mechanical hardness, vis a vis the semiconductor stack and high transparency in the optical C-band are, for example, fused silica and Al2O3.
The electrical feed thru provides low bias voltage to the optical resonator cavity diode stack, high bias voltage to drive the piezoelectric actuator providing external stress and I/O signal/power to the calibrated force sensors. The beveled access hole on the anvil cell top wall provides lensed fiber access.
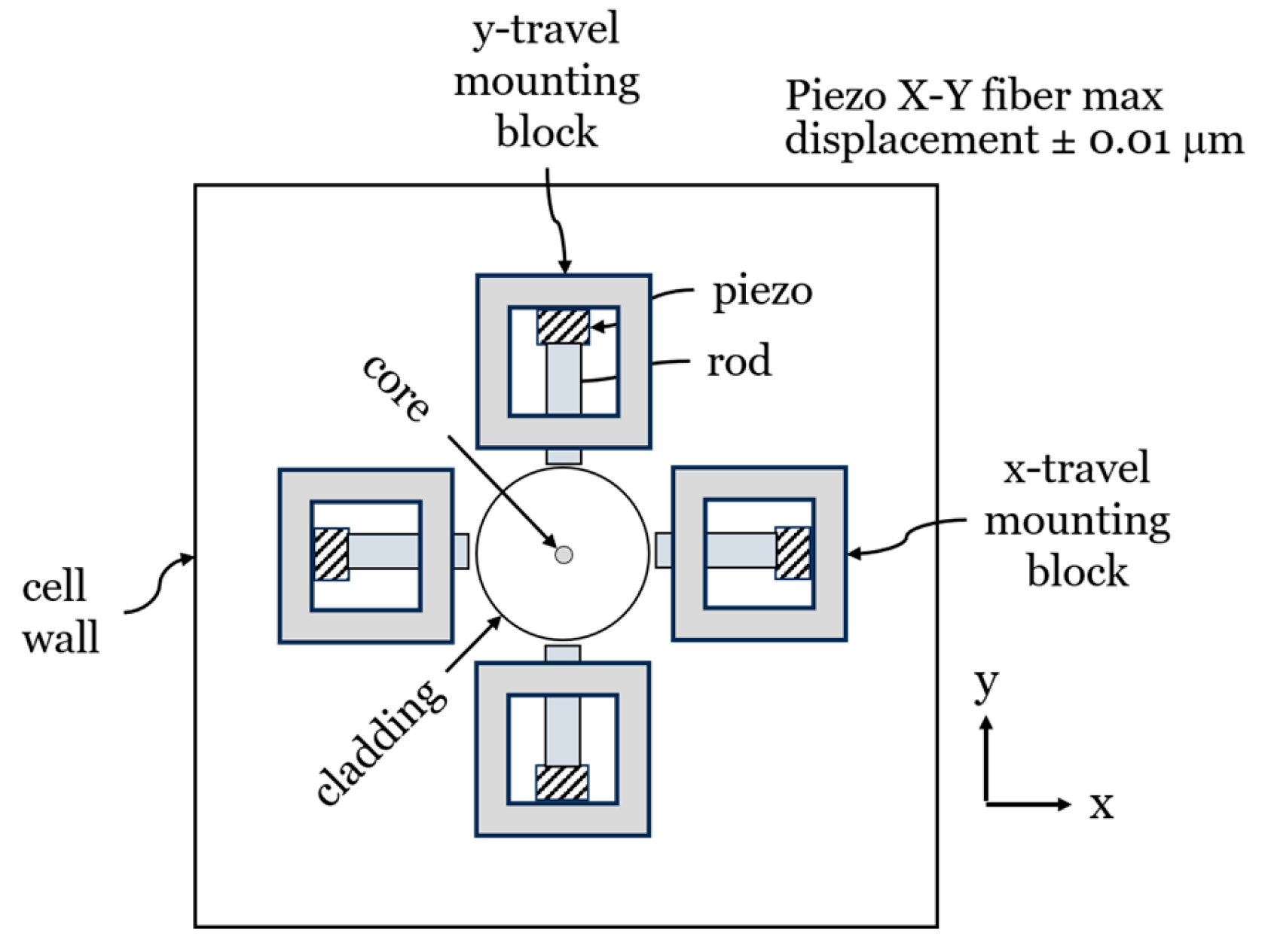
The x-y actuator block attached to the top wall of anvil cell provides fine optical fiber alignment in the x-y plane to locate a specific quantum dot and optimize the collection of entangled photon pairs therefrom.

D. Lensed Fiber Fine Positioning

Once a quantum dot is selected, for example, by locating its fluorescence emission under optical pumping through the bottom optical port in the anvil cell, its location is more precisely ascertained by moving the lensed optical fiber in the x-y plane orthogonal to the quantum well layer containing the quantum dot. This is accomplished by the piezoelectric actuators mounted on the anvil cell top wall used to minimally translate the lensed optical fiber.

E. Quantum Dot Source to Optical Fiber Photon Channeling

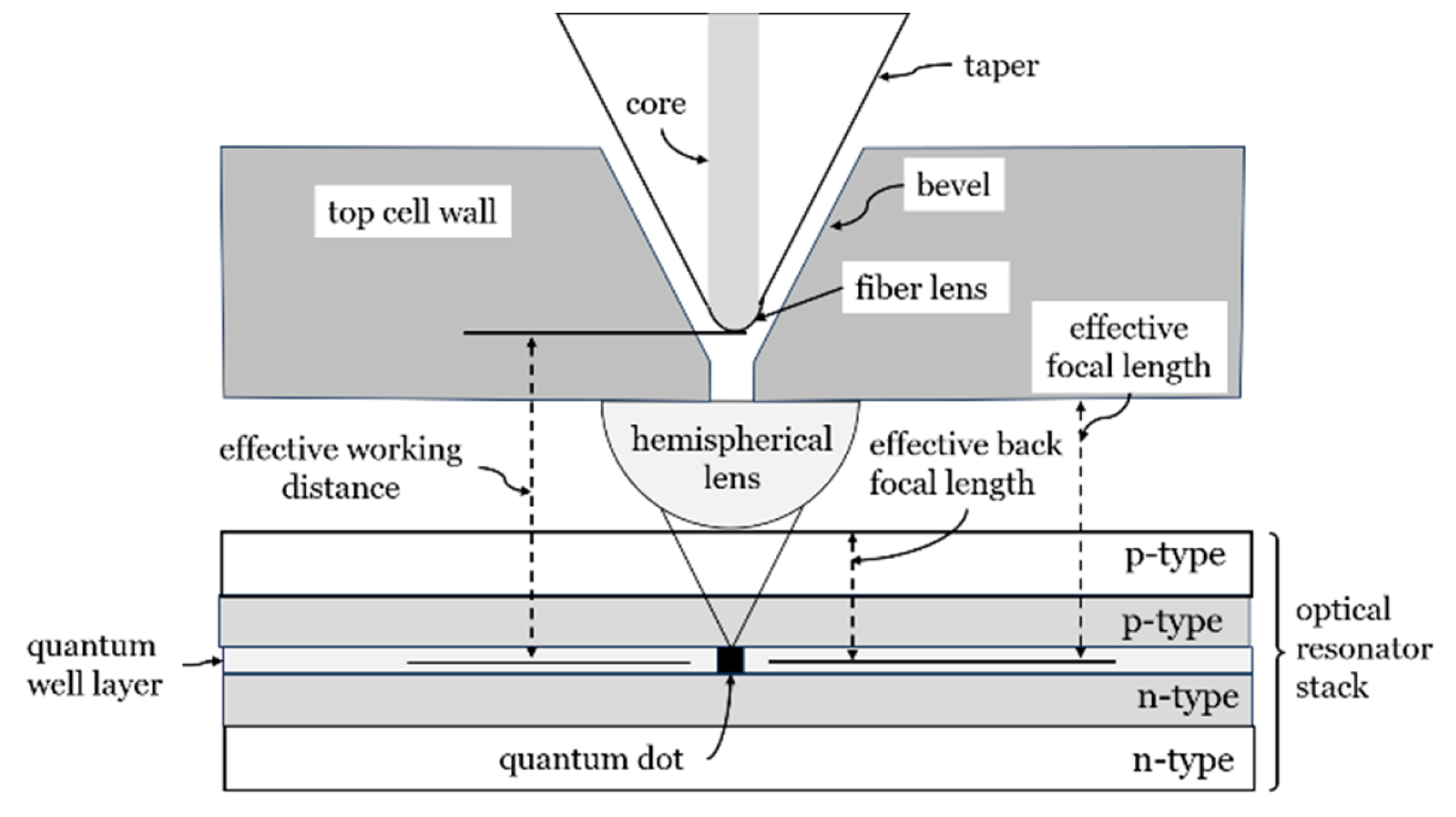
In Figure 4 only that portion of the top wall of the anvil cell that contains the bevel access port that enables access to the lensed optical fiber is shown. The clearance between the bevel cut and lensed fiber enables alignment of the lensed fiber in the x-y plane by means shown in Figure 3 and intended to optimize the collection efficiency between a quantum dot emitter and the collecting optical fiber core with the aid of a hemispherical lens which is also used to generate the subsurface shear strain. Important distances to consider in a first order optical simulation are shown as 1) the effective working distance from the plane of the quantum dot to the tip of the lensed fiber, 2) the effective focal length from the planar surface of the hemispherical lens to the plane of the quantum dot, and 3) the effective back focal length from the tangent to the hemispherical lenses’ curved surface to the plane of the quantum dot.
Several optical simulators are commercially available with which to simulate the light collection efficiency of combinations of the various parameters. For example, Ansys Optics and Photonics Simulation Software.

F. Subsurface Generation of Maximum Shear Strain

Figure 5 is a less detailed perspective representation of the structure depicted in Figure 1.
Contours in Figure 6 are meant to represent surfaces of constant shear strain. Contained smaller contour area correspond to higher in magnitude in a smaller volume under conditions of applied constant external stress. The volume of maximum shear strain can be designed to coincide with a volume that contains a single quantum dot by means summarized in conjunction with Figure 2 and Figure 4. It should be noted that the formalism used to describe the shear strain generated during the application of an external compressive stress between two objects whose surfaces are in mechanical contact is based on the elastic limit of all components. For example, the depth, d, of maximum shear train below the flat surface is estimated as
d = (contact area)2 / (lens radius) [20–22].
Preprints 117747 g006
Figure 6. Hertzian theory of contacting surface. Depicted is a side view of the drawing in Figure 5 emphasizing a rendition of subsurface shear strain contours resulting when a spherical surface is in compressive contact with a planar surface [20,21,22].
Figure 6. Hertzian theory of contacting surface. Depicted is a side view of the drawing in Figure 5 emphasizing a rendition of subsurface shear strain contours resulting when a spherical surface is in compressive contact with a planar surface [20,21,22].
Preprints 117747 g006

G. Cryogenic Assembly of Quantum Dot Sources of Entangled Photons

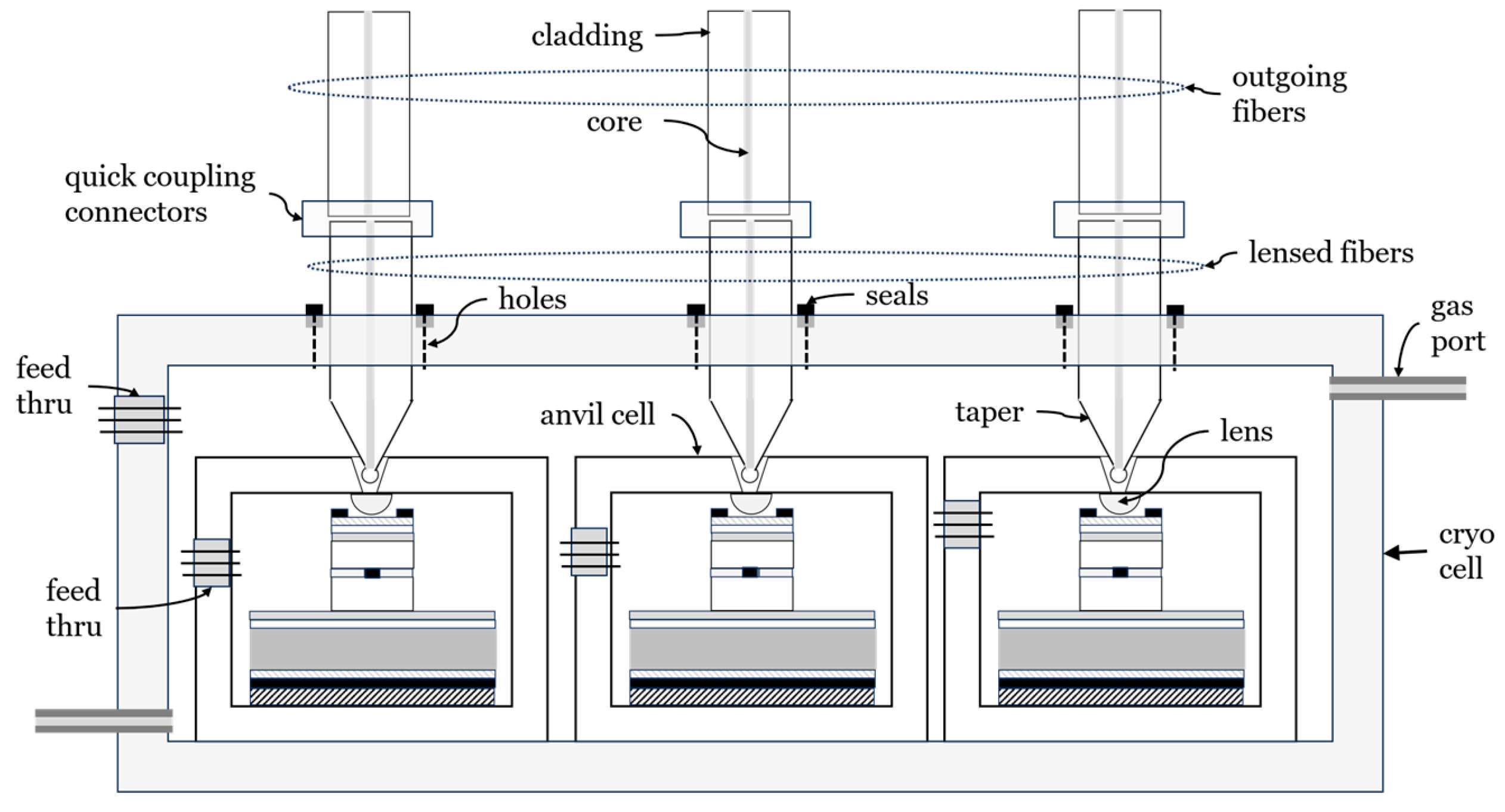
Figure 7 depicts one approach for increasing the throughput of a quantum information network by taking advantage of plural deterministic and synchronized sources of entangled pairs of photons. In the figure is shown an array of anvil cells each hosting an activated quantum dot in a quantum well layer while being coupled to a lensed optical fiber. A cryogenic enclosure keeps all anvil cells contained therein within a desired range of temperature by continuously flowing cold gases through I/O gas ports. A closed-cycle cryostat may provide cooling gases at about 10 K. Lensed optical fiber arrays couple streams of entangled photon pairs from quantum dots sources to matching outgoing optical fiber arrays by means of standard single mode optical fiber quick couplers/decouplers. Cryogenic seals minimize loss of cooling gas through optical fiber access holes. Electrical feedthroughs provide power and sensor I/Os as needed.

SECTION II.

A. Development of Quantum Server Networks

Here we only consider superconducting quantum processors that are based on the Josephson charge tunnel junction and operate at a few mK. This is because the science, technology and error correction algorithms have been developed over the past 40 or so years of experience and because quantum processor platforms are currently at an advanced stage of hardware development. Lessons learned so far tell us to expect significant scaling challenges due to quantum decoherence owing to vacuum energy fluctuations, local sources of noise and Transmon manufacturing variations, all of which draw on error correction resources which, in turn draw on the pool of qubit arrays and physical qubits.
As pointed out in the introduction, lessons learned during the evolution of classical computing systems should be re-examined for relevance and lessons to be learned in the evolution of classical quantum computing systems. For example, might not several smaller quantum processors be networked by a secure optical fiber network and exchanges classical bits so as to share problem solving tasks among them in the spirit of a classical supercomputer?

B. Definitions

1. Quantum servers here refers to currently manufactured prototypes having about 100 physical qubits and about 3k logic gates. Future systems capable of executing 1G gates over 2k physical qubits are expected by 2033 as projected by a revised roadmap announced by IBM [3] in 2024.
2. “Unconditionally secure” quantum channel in the present context, relates to the mathematically provable detection against classical and quantum mechanical attacks in nearly real time. Mathematical proofs are based on the concepts of photon entanglement, entanglement swapping, teleportation and incorporates the “no-cloning” theorem [7]. This does not, however, exclude vulnerabilities associated with implementation.
3. The protocol of choice for the secure transfer of classical data among quantum servers may be used as one of the many “Key Distribution Protocols” based on the transmission of entangled photons over terrestrial Telecom optical fiber channels used to secretly and securely transfers a Key to an encrypted string of classical bits.
4. Classical bit-to-qubit resonant drive excitation is a way in which one classical bit, coded in a “return-to-zero” format may be used to excite one qubit state comprising one superconducting charge tunneling occurrence across a pair of Josephson junctions that define a Transmon [23]
5. Qubit readout by a “Quantum nondemolition measurement” is required to probe the state of a qubit in a Josephson processor without disturbing its entanglement “too much” and yet discern the state of the qubit. This raises fundamental questions in quantum mechanics and is discussed further in SECTION III C.
6. Measrement fidelity is a measure of how close a measurement of a quantum state is to the “actual” or intended quantum state. If |ψ> is the measured quantum state and |φ> is the “actual” quantum state, the measurement fidelity is given by F = |<ψ|φ>|2. F = 1 suggests that the measured quantum state is identical to the “actual” quantum state. F = 0 suggests that the two states are orthogonal. Clearly, readout fidelity is a measure of the degree of “demolition” that a nondemolition measurement causes on the “actual” quantum state.
7. Quantum nondemolition fidelity. This concept is related to the previous two. When measuring a qubit that is nominally prepared in state |x>, the readout fidelity is defined by Fx = 1−p(t,x) where p(t,x) is the sum of all probabilities that add to NOT finding the qubit in the quantum state |x>, and could be interpreted as representing the sum of all possible errors that can occur during the process of measuring the qubit state. The question then is: what is the actual state|φ> of a quantum system and how do we measure it without changing it “too much” and how can we verify that the measurement caused negligible change, at least within the Eisenberg uncertainty? The only answer seems to be that one can only assume “nondemolition” until evidence suggests otherwise.

C. Conceptual Network Comprising Two Quantum Servers

A block diagram that exemplifies the concept of a quantum secure optical fiber network linking two quantum servers is shown in Figure 8. Two medium capacity quantum processors, QP-A and QP-B, exchange a string of encrypted classical bits over public domain optical fibers. The encryption key is transmitted by means of entangled photons over unconditionally secure channels utilizing either a separate or a common optical fiber.
Figure 8 and Figure 9 depict examples of bi-directional external links between two or more quantum servers. For simplicity, the secure exchange between two designated quantum servers of a secret decryption key to an encrypted classical bit stream may be based on any of the well-known key distribution protocols. Generally, these protocols employ one secure channel for key distribution and public channel to transmit the classical bit stream. Alternatively, a single optical fiber can be time multiplexed to carry both a secure and a public channels. There are numerous protocols for secretly distributing a decryption key of which the E 91 key distribution protocol [6] and proof of its security [7] is one of the earliest.
Operational example: quantum processor-A (QP-A) wants to send a classical bit to quantum processor-B (QP-B). QP-A initiate a qubit readout TQ R\O, see Figure 11 and the discussion on quantum nondemolition measurements that follows. TQ R\O sends the resulting classical bit to buffer memory CBM. At some point CBM sends one classical bit to quantum dot source QD (A) which generates a pair of entangled photons that is sent to a “random quantum state generator A” that churns out an entangled pair of photon states, for example, |ψ> = α1|11> + β1|00>, where α1 and β1 are probability amplitudes and |α1|2 +|β1|2 = 1. One of the pair is sent to the receiving station of quantum processor-B (QP-B), Rx (B) SNSPD BSM, which may include superconducting nanowire single photon detectors (SNSPDs) and a Bell state measurement (BSM) station. At the receiving station of quantum processor-B, the classical bit is converted into a Transmon excitation signal, e.g., ~ 5 GHz, by Transmon signal generator TESG B, as discussed in conjunction with Figure 10. Quantum processor-B (QP-B) may similarly communicate classical bits to quantum processor-A (QP-A). Secure key distribution occurs over quantum channels qc1, qc2 while encrypted bit streams are openly transmitted over public channels, pc1, pc2.
Figure 9 is a straightforward extrapolation of Figure 8.
It is noted that a 2-Transmon CNOT gate has a minimum switching time of about 100 ns [24] which is not too much longer than the 30 ns access time to transfer a single memory bit in or out of dynamic random-access memory (DRAM). Therefore, a DRAM buffer has a reasonable timing match for a network of quantum processors [25]. DRAM access times are measured in nanoseconds and are typically between 20 and 35 nanoseconds [25].
Central to the creation of a quantum server network is the qubit-to-bit (Q/B) interface by which a qubit is interpreted as a classical bit and vice versa. The rudimentary requirements for a Q/B interface have been explored since the mid 1970’s. A remaining central question is:
How much energy can be used to probe a quantum system without causing degradation of entanglement fidelity?
This question dates as far back as the concept of the Heisenberg uncertainty principle and has evolved from philosophical discussion to experimental practice [26,27,28,29].

SECTION III.

A. Classical Bit Energy Converted to Qubit Excitation: The Bit / Qubit Interface

A classical bit, represented by the circled return-to-zero pulse in Figure 10, is converted, by a Quadrature frequency Generator (QωG), to a time-limited envelope, S1(t), quadrature microwave signal at a first frequency, ω1, comprising Sin (ω1t) and Cos (ω1t) components. A second microwave frequency, ωLO, is generated by a local oscillator (LO). A quadrature mixer combines the two signals to generate a second pulse envelope, S2(t), temporally limiting the mixer output frequency ωq = ωLO ± ωQωG in resonance with the target qubit.
A microwave source supplies a first reference frequency (ωLO), and a Quadrature frequency Generator (QωG) supplies a second frequency limited in time by envelope S1(t). Mixing the QωG output with the reference frequency, ωLO, in a quadrature mixer creates the oscillating drive in resonance with the qubit tunneling frequency. The IQ-mixer combines the two signals to generate a time-limited second pulse envelope S2(t) with a frequency, ωq = ωLO ± ωQωG, tuned to the transition frequency of the qubit. The local oscillator (LO) is used for fine tuning.

B. Qubit Energy Converted to a Classical Bit Pulse: The Qubit / Bit Interface

While classical bit-to-qubit conversion is rather straight forward (Figure 10), probing the qubit without compromising its entanglement has become known as the “qubit non-demolition readout” and poses fundamental, quantum philosophical concerns when attempts are made toward implementation.
Quantum non-demolition (QND) measurement refers to a measurement of the state of a quantum system in which the uncertainty of the measured observable does not change subsequent to the measurement, nor does that of any other state of the measured system. The working question is:
“How much energy can be used to gain knowledge of a particular state of a quantum system?”
The upper limit must surely be bounded by the Eisenberg uncertainty principle.
Input probe frequency, ωdrive; Purcell filter, ωp; readout resonator ωr; qubit energy ωq,; circulator input/output. Adapted from Figure 1 of reference [30].
In Figure 11 it is assumed that the qubit transition frequency is ωq and is capacitively coupled to a readout resonator of frequency ωr which, in turn, is coupled to a nonlinear Purcell filter of frequency ωp. The state of the qubit is interpreted from the phase shift observed in the output probe frequency. Qbit states |1> and |0> cause different phase shifts of the probe frequency.
It is noted that a small phase shift angle can be interpreted as a small frequency shift or a small inverse time interval.
In superconducting circuits based on Josephson junction charge tunneling circuits, the state of a qubit is generally determined by a readout measurement of the dispersive frequency shift in a resonator coupled to the qubit, as sketched in Figure 11. The predominant source of error is the relaxation of the qubit from the excited state to the ground state during the readout. On short time scales, this error grows almost linearly with the ratio of readout time, Tr, to the qubit relaxation time, Tx, and can be mitigated by a reduction of the readout time.
A challenge is how to reduce the initialization and measurement times to take advantage of fast quantum error correction (QEC) algorithms. Fast measurement will decrease readout error and, more importantly, reduce decoherence associated with long cycle times. A problem is that in Josephson junction quantum systems, the measurement time is typically orders of magnitude longer than the qubit gate transition time so that if the measurement time is too long, the measurement delays the quantum error correction (QEC) cycle and increases qubit decoherence. A compromise is found in the “dispersive readout” sketched in Figure 11 and discussed in more detailed in [30,31].
Dispersive readout refers to a measurement of the state of a qubit as seen by a dispersively coupled resonator as a result of a frequency transitions between the qubit states |1> and |0>. The dispersive readout measurement is a technique to quickly and accurately measure the state of a superconducting qubit. However, the resonator introduces additional channels by which the qubit can lose coherency. One such channel is the energy relaxation of the qubit through the resonator. This can be suppressed using a “Purcell filter” [31,32] or large qubit-resonator detuning [33]. Another decoherence process is the dephasing due to residual noise photons in the resonator. This can be reduced by minimizing the influx of noise from the readout waveguide [34].
It is noted that a nonlinear Purcell filter has been shown to suppresses the photon-noise-induced dephasing of the qubit without sacrificing the readout performance [34]. A readout fidelity of 99.4% and a quantum nondemolition fidelity of 99.2% are achieved using a 40-ns readout pulse. The nonlinear Purcell filter should be an effective tool for realizing a fast, high-fidelity readout without compromising the coherence time of the qubit [31,32,34].

C. Quantum Nondemolition Readout Measurements

Gard, et al., [26] Braginsky and Khalili [27] and Daria Gusenkova [28] provide an excellent summary of the history and philosophy leading to the state of quantum nondemolition measurements near the end of the 20th century.
The history of how to probe a fragile quantum state to discover some of its properties but not thereto cause a change in the Heisenberg uncertainty sense, is as long as the discipline of quantum mechanics. In the 21st century, with the advent of quantum processors, the question has acquired added urgency and relevance. How to rapidly and reliably probe a Transmon qubit within the limits prescribed by Heisenberg so as not to “disturb” its quantum state “too much” and how to know when the probing is “too much” aside from the observation of manifest errors and added application of error correction? The poorly defined notion of quantum nondemolition (QND) has emerged over time, see for example, [26,27,28,29].
It is assumed without proof, that a QND measurement should, in principle, provide information about a qubit’s state without disturbing the qubit thus maintaining the fidelity of the qubit. In the case of a Transmon, the present state-of the-art QND measurement involves coupling the qubit to a dispersive readout cavity waveguide coupled to a nonlinear Purcell filter [31,32,34] as discussed in the previous section. Of course, alternative QND measurement techniques have been and will always be suggested. What is lacking is a proof that a QND measurement poses a disturbance to the quantum state at least as weak as allowed by the Heisenberg uncertainty principle. One could start with the premise that certain non-zero energy is needed to tickle a quantum state so that, by its reaction, ascertain the actual quantum state within a certain probability predicted by a given model. The proof should establish the upper limit of the tickle energy so as to leave the quantum state as near to its original state as possible, with a finesse of, let’s say, 0.95.
For example, the energy of a Transmon is about 5 GHz ~ 250 mK. It is kept at a working temperature of about 10-20 mK or about 10% of its internal energy. Is a tickle energy of 10 MHz ~ 0.5 mK sufficiently high to determine its quantum state but, simultaneously, sufficiently low to leave it in an energy state that is only altered by ± 0.05%? A somewhat early book may be worth reading on the subject [29] for philosophical interest.
In practice, Sunada, et al., [35] report a readout fidelity of 99.4% and a quantum nondemolition fidelity of 99.2% in a 40-ns readout pulse without compromising the coherence time of the qubit by using a nonlinear Purcell filter. See Figure 10 for a generic readout set-up. However, the authors do not define or say what they mean by “nondemolition fidelity.” Often readout fidelity simply refers to the number of readout deviations over a number of repeated measurements?

CONTRIBUTIONS of this Work to the Evolution of Quantum Server Networks and Quantum Information Networks

1. This work outlines the technology development steps necessary in the foundry manufacturing a semiconductor quantum dot source that deterministically generates pairs of entangled photons. It is generally acknowledged that small formfactor quantum dot source will enable the development of quantum secure networks in quantum data centers and provide unconditionally secure terrestrial metropolitan area communication over Telecom optical fibers. We have outlined the necessary steps to remove the fine structure splitting that naturally occurs in the exciton recombination cascade process in III-V semiconductors by the application of calibrated subsurface shear strain in the volume occupied by a single, isolated semiconductor quantum dot, thereby enabling high fidelity photon entanglement.
2. On-demand quantum dot sources of fresh ancillary photons are necessary for the forwarding of quantum state information in a daisy chain scenario in which repeater nodes are used in long distance terrestrial optical fiber secure networks. Deterministic sources replace the long-standing notion of volatile quantum memory whose use has been shown to degrade entanglement fidelity.
3. A secure quantum network, based on deterministic InGaAs quantum dot sources that emit entangled pairs of photons will enable the establishment of network of quantum servers. A secure network comprising quantum servers each having just a few thousand logic gates may approach the performance of stand-alone quantum computers having 109 logic gates when working cooperatively and therefore enable the emergence of quantum server networks and quantum data centers.
4. We outline the construction and use of parallel arrays of cryogenic anvil cells, each housing an active quantum dot sources of entangled photon pairs coupled to pigtail optical fiber.
5. ‘Practical Quantum Advantage’ is sometimes defined as the point at which quantum processors can solve problems of practical interest that cannot be solved by legacy supercomputers. This is the long awaited inflection point of stand-alone quantum processing platforms. In this paper it is proposed that a judicious mix of early, more modest quantum processors that are currently manufacturable with some yield, when linked by a secure quantum fiber network, in conjunction with classical buffer memory, can demonstrate the first practical use of a secure quantum data center.

Conclusions

Hindsight enables one to understand the evolutionary outcome of events that could not have been imagined, foretold, or understand at the time.
This paper represents an attempt to design a plausible evolution of some aspects of quantum computing toward its goal toward achieving demonstrable ‘Practical Quantum Advantage’ before 2033.
We affirm our conviction that an important step toward this goal is to develop a source that can provide entangled photon pairs, “on-demand,” vital for entanglement swapping and synchronization in secure quantum data center or metropolitan area networks.

Author Contributions

conceptualization, Daniel Guidotti and Gee-Kung Chang; partial resources, Xioali Ma; writing – original draft preparation, Daniel Guidotti; writing review and editing, Gee-kung Chang. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Gambetta, J.M.; Chow, J.M.; Steffen, M. Building logical qubits in a superconducting quantum computing system. npj Quantum Information 2017 3. [CrossRef]
  2. Erhard, A.; Nautrup, H.P.; Meth, M; Postler, L.; Stricker, R; Ringbauer, M; Schindler, P.; Briegel, H.J.; Blatt, R.; Friis, F.; Monz, T. Entangling logical qubits with lattice surgery. Nature 2021 589, 220–224. [CrossRef]
  3. IBM Quantum Development and Innovation Roadmap: https://www.ibm.com/quantum/assets/IBM_Quantum_Development_&_Innovation_Roadmap.pdf.
  4. Kuitenbrouwer, D.; Bos, W.; Vermeulen, K.; Lindeborg, K.; Sorgedrager, R.; Vivien, T.; Kammhuber, J.; Bosman, S. Scaling the input/output architecture of quantum processors to kQbit, and beyond, size in the NISQ era abstract id: V26.012. APS March Meeting 2019.
  5. Monarkha, V. Y.; Simbierowicz, S.; Borrelli, M.; van Gulik, R.; Drobotun, N.; Kuitenbrouwer, D.N.; Bouman, D.; Datta, D.; Eskelinen, P.; Mannila, E.; Kaikkonen, J.; Vesterinen, V.; Govenius J.; Lake, R. E. Equivalence of flexible stripline and coaxial cables for superconducting qubit control and readout pulses. App. Phys. Lett. 2024 124, 224001. [CrossRef]
  6. Ekert, A.K. Quantum cryptography based on Bell’s theorem Phys. Rev. Lett. 1991 67, 661-663.
  7. Li, L.; Li, H.; Li, C.; Chen, X.; Chang Y.; Yang Y.; Li, J. The security analysis of E91 protocol in collective-rotation noise channel International Journal of Distributed Sensor Networks, 2018 14, 15501477187. [CrossRef]
  8. Olbrich, F.; Jonatan Höschele, J.; Müller, M.; Kettler, J.; Portalupi, L.P.; Paul, M.; Jetter, M; Michler, P. Polarization-entangled photons from an InGaAs-based quantum dot emitting in the telecom C-band Appl. Phys. Lett., 2017 111, 133106. [CrossRef]
  9. Vajner, D.A.; Holewa, P.; Zięba-Ostój, E.; Wasiluk, M.; von Helversen, M.; Sakanas, A.; Huck, A.; Yvind, K.; Gregersen, N.; Musiał, A.; Syperek, M.; Semenova, E.; Heindel, T. On-demand generation of idistinguishable Photons in the telecom C-Band using quantum dot devices ACS Photonics 2024 11, 339-347. [CrossRef]
  10. Benson, O.; Santori, C.; Pelton M.; Yamamoto, Y. Regulated and entangled photons from a single quantum dot Phys. Rev. Let., 2000 84, 2513-2516. [CrossRef]
  11. Dousse, A.; Suffczyn’ski, J.; Beveratos, A.; Krebs, O.; Lemaître, A.; Sagnes, I.; Bloch, J.; Voisin, P; Senellart, P. Ultrabright source of entangled photon pairs Nature 2010 466, 217–220. [CrossRef]
  12. Chao, C. Y.-P..; Chuang, S. L. Spin-orbit-coupling effects on the valence-band structure of strained semiconductor quantum wells Phys. Rev. 1992 46, 4110-4122.
  13. Guidotti, D.; Lai, S.; Klein, M.V.; Wolfe, J.P. Electronic Raman scattering and antiresonance behavior in highly stressed photoexcited silicon Phys. Rev. Lett. 1979, 43, 1950–1953. [Google Scholar] [CrossRef]
  14. Markiewicz, R.S.; Wolfe, J.P.; Jeffries, C.D. Strain-confined electron-hole liquid in germanium. Phys. Rev. B 1977, 15, 1988–2005. [Google Scholar] [CrossRef]
  15. Seravalli, L Metamorphic InAs/InGaAs quantum dots for optoelectronic devices: a review, Microelectronic Engineering 2023 276 111996. [CrossRef]
  16. Seravalli, L.; Trevisi, G.; Frigeri, P.; Rivas, D.; Muñoz-Matutano, G.; Suárez, I.; Alén, B.; Canet-Ferrer, J.; Martínez-Pastor, J.P. Single quantum dot emission at telecom wavelengths from metamorphic InAs/InGaAs nanostructures grown on GaAs substrates Appl. Phys. Lett. 2011, 98, 173112. [Google Scholar] [CrossRef]
  17. Zhang, C.; Huang, Y.-F.; Liu, B.-H.; Li, C.-F.; Guo, G.-C. Spontaneous parametric down-conversion sources for multiphoton experiments Adv. Quantum Technol., 2021 4 2000132. [CrossRef]
  18. Samara, F.; Maring, N.; Martin, A.; Raja, A.S.; Kippenberg, T.J.; Zbinden, H.; Thew, R. Entanglement swapping between independent and asynchronous integrated photon-pair sources Quantum Science and Technology 2021 6 045024. [CrossRef]
  19. Lettner, T. Gyger, S.; Zeuner, K.D.; Schweickert, L.; Steinhauer, S.; Hedlund, C.R.; Stroj, S.; Rastelli, A.; Hammar, M.; Trotta, R.; Jöns, K.D.; Zwiller, V. Strain-controlled quantum dot fine structure for entangled photon generation at 1550 nm Nano Lett. 2021 21, 10501−10506. [CrossRef]
  20. Wang, Q.J.; Zhu, D. Hertz theory: contact of spherical surfaces. In: Wang, Q.J., Chung, Y.W. (eds), Encyclopedia of Tribology, 2013 Springer, Boston, MA. [CrossRef]
  21. https://www.abbottaerospace.com/aa-sb-001/12-joints/12-3-general-treatment-of-contact-stresses/12-3-1-formulas-for-stress-and-deformations-due-to-pressure-between-elastic-bodies/.
  22. https://wp.optics.arizona.edu/optomech/wp-content/uploads/sites/53/2016/10/OPTI-521-Tutorial-on-Hertz-contact-stress-Xiaoyin-Zhu.pdf.
  23. Krantz, P.; Kjaergaard, M.; Yan, F.; Orlando, T.P.; Gustavsson, S.; W. D. Oliver, W.D. A quantum engineer’s guide to superconducting qubits,” Appl. Phys. Rev. 2019 6, 021318. [CrossRef]
  24. Howard, J.; Lidiak, A.; Jameson, C.; Basyildiz, B.; Clark, K.; Zhao, T.; Bal, M.; Long, J.; Pappas, D.P.; Singh, M.; Gong, Z. Implementing two-qubit gates at the quantum speed limit,” Phys. Rev. Research 2023, 5, 043194. [Google Scholar] [CrossRef]
  25. Eyerman, S.; Heirman, W.; Hur, I. DRAM bandwidth and latency stacks: visualizing DRAM bottlenecks IEEE International Symposium on Performance Analysis of Systems and Software (ISPASS), 2022 Singapore, 322-331. [CrossRef]
  26. Gard, B.T.; Parrott, Z.; Jacobs, K.; Aumentado, J.; Simmonds, R.W. Fast high-fidelity quantum nondemolition readout of a superconducting qubit with tunable transverse couplings Phys. Rev. Applied 2024, 21, 024008. [Google Scholar] [CrossRef]
  27. Braginsky, V.B.; Khalili, F.Ya. Quantum nondemolition measurements: the route from toys to tools Rev. Mod. Phys. 1996 68 1. [CrossRef]
  28. Gusenkova, D.; Spiecker, M.; Gebauer, R.; Willsch, M.; Willsch, D.; Valenti, F.; Karcher, N.; Grünhaupt, L.; Takmakov, I.; Winkel, P.; Rieger, D.; Ustinov, A.V.; Roch, N.; Wernsdorfer, W.; Michielsen, K.; Oliver Sander, O.; Pop, I.M. Quantum nondemolition dispersive readout of a superconducting artificial atom using large photon numbers. Phys. Rev. Appl. 2021, 15, 064030. [Google Scholar] [CrossRef]
  29. Jacobs, K. An introduction to quantum measurement theory and its applications, 1st Ed.; Cambridge University, Press: 2014. [CrossRef]
  30. Swiadek, F.; Shillito, R.; Magnard, P.; Remm, A.; Hellings, C.; Lacroix, N.; Ficheux, Q.; Zanuz, D.C.; Norris, G.J.; Blais, A.; Krinner, S.; Wallraff, A. Enhancing dispersive readout of superconducting qubits through dynamic control of the dispersive shift: experiment and theory,” 2023. [CrossRef]
  31. Yan, H.; Wu, X.; Lingenfelter, A.; Joshi, Y.J.; Andersson, G; Conner, C.R.; Chou, M-H; Grebel J.; Miller, J.M.; Povey, R.G.; Qiao, H.; Clerk, A.A.; Cleland, A.N. Broadband bandpass Purcell filter for circuit quantum eectrodynamics,” Appl. Phys. Lett. 2023 123, 134001. [CrossRef]
  32. Abdo, B.; Jinka, O.; Bronn, N.T.; Olivadese, S.; Brink, M. High-fidelity qubit readout using interferometric directional Josephson devices PRX Quantum 2021 2, 040360. [CrossRef]
  33. Yan, F.; Campbell, D.; Krantz, P.; Kjaergaard, M.; Kim, D.; Yoder, J.L.; Hover, D.; Sears, A.; Kerman, A.J.; Orlando, T.P.; Gustavsson, S.; Oliver, W.D. Distinguishing coherent and thermal photon noise in a circuit quantum electrodynamical system Phys. Rev. Lett. 2018, 120, 260504. [Google Scholar] [CrossRef] [PubMed]
  34. Sunada, Y.; Yuki, K.; Wang, Z.; Miyamura, T.; Ilves, J.; Matsuura, K.; Spring, P.A.; Tamate, S.; Kono, S.; Nakamura, Y. Photon-noise-tolerant dispersive readout of a superconducting qubit using a nonlinear Purcell filter PRX Quantum 2024 5, 010307. [CrossRef]
Preprints 117747 g001
Figure 1. A semiconductor optical resonator typically comprises two opposing semiconductor Bragg reflectors enclosing a source of light, in this case one or more semiconductor quantum dots. When the source is electrically biased the structure functions as a semiconductor diode generating currents thought the quantum dot that initiate a relaxation process to the ground state with the emission of light out of the upper port. Entangled photon pairs emanate from the top optical port. A bottom optical port may be used as an alternative means to optically pump the quantum dot. Optically transparent and electrically conducting Indium tin oxide (ITO) films may be used to aid in forming more uniform electric fields initiated at the optical contacts.
Figure 1. A semiconductor optical resonator typically comprises two opposing semiconductor Bragg reflectors enclosing a source of light, in this case one or more semiconductor quantum dots. When the source is electrically biased the structure functions as a semiconductor diode generating currents thought the quantum dot that initiate a relaxation process to the ground state with the emission of light out of the upper port. Entangled photon pairs emanate from the top optical port. A bottom optical port may be used as an alternative means to optically pump the quantum dot. Optically transparent and electrically conducting Indium tin oxide (ITO) films may be used to aid in forming more uniform electric fields initiated at the optical contacts.
Preprints 117747 g001
Preprints 117747 g002
Figure 2. The anvil cell comprises 1) a cell wall having a tapered top access port to channel entangled photons into a lensed optical fiber, 2) a bottom optical access port, 3) an electrical I/O port, and an means to translate the lensed optical fiber in a horizontal plane provided by an x-y actuator block mounted externally to the upper cell wall. Compressive stress is provided by the action of a piezoelectric actuator and the elastic response to the anvil cell. The lens is used to provide localized subsurface shear strain and to channel entangled photons into the lensed optical fiber.
Figure 2. The anvil cell comprises 1) a cell wall having a tapered top access port to channel entangled photons into a lensed optical fiber, 2) a bottom optical access port, 3) an electrical I/O port, and an means to translate the lensed optical fiber in a horizontal plane provided by an x-y actuator block mounted externally to the upper cell wall. Compressive stress is provided by the action of a piezoelectric actuator and the elastic response to the anvil cell. The lens is used to provide localized subsurface shear strain and to channel entangled photons into the lensed optical fiber.
Preprints 117747 g002
Preprints 117747 g003
Figure 3. Lensed optical fiber fine alignment. The optical fiber is represented by the core and cladding. x- and y- mounting blocks, fixed to the upper wall exterior, enable piezoelectric actuation of push rods to translate the optical fiber so as to maximize photon collection efficiency.
Figure 3. Lensed optical fiber fine alignment. The optical fiber is represented by the core and cladding. x- and y- mounting blocks, fixed to the upper wall exterior, enable piezoelectric actuation of push rods to translate the optical fiber so as to maximize photon collection efficiency.
Preprints 117747 g003
Preprints 117747 g004
Figure 4. Simplified side view of the optical system designed to optimize the channeling of entangled photon pairs emanating from a quantum dot in a quantum well layer formed between a p-type, and an n-type, compound semiconductor stack that comprises an optical field resonator shown in detail in Figure 1 and Figure 2. The tip of the lensed optical fiber is represented the tapered cladding and core fitting in a beveled access port in the top wall of the anvil cell.
Figure 4. Simplified side view of the optical system designed to optimize the channeling of entangled photon pairs emanating from a quantum dot in a quantum well layer formed between a p-type, and an n-type, compound semiconductor stack that comprises an optical field resonator shown in detail in Figure 1 and Figure 2. The tip of the lensed optical fiber is represented the tapered cladding and core fitting in a beveled access port in the top wall of the anvil cell.
Preprints 117747 g004
Preprints 117747 g005
Figure 5. Perspective view of a quantum well (QW) layer fabricated between n-type and p-type semiconductor top Bragg reflectors (BR) and bottom Bragg reflector (BR) that form the optical resonator cavity as shown in Figure 1. In the interest of clarity, the quantum dot distribution in the quantum well (QW) layer is not show here.
Figure 5. Perspective view of a quantum well (QW) layer fabricated between n-type and p-type semiconductor top Bragg reflectors (BR) and bottom Bragg reflector (BR) that form the optical resonator cavity as shown in Figure 1. In the interest of clarity, the quantum dot distribution in the quantum well (QW) layer is not show here.
Preprints 117747 g005
Preprints 117747 g007
Figure 7. Shown is a gas flow cryogenic cell containing three anvil cells some features of which are also depicted in Figure 2, Figure 3 and Figure 4. Gas ports allow for continuous gas flow, feed thru ports allow for current flow while holes and seals enable sealed lensed optical fiber access. Quick release connectors couple to outgoing optical fibers.
Figure 7. Shown is a gas flow cryogenic cell containing three anvil cells some features of which are also depicted in Figure 2, Figure 3 and Figure 4. Gas ports allow for continuous gas flow, feed thru ports allow for current flow while holes and seals enable sealed lensed optical fiber access. Quick release connectors couple to outgoing optical fibers.
Preprints 117747 g007
Preprints 117747 g008
Figure 8. Concept diagram for a secure external optical network enabling exchange of classical bits between two quantum servers. QP-A, QP-B quantum processors; TQ R\O Transmon qubit read\out; CBM classical DRAM buffer; QD (A), QD (B) quantum dot transmitter; Rx (B) SNSPD BSM, Rx (A) SNSPD BSM are photon receivers and Bell state measurement stations; Sender (A) BSM and Sender (B) BSM are Bell state measurement (BSM) stations; TESG A and TESG B are Transmon excitation signal generators that generate Transmon qubit of generic frequency 5 GHz from a classical bit waveform. qc1, qc2 are quantum channels and pc1, pc2 are public channels.
Figure 8. Concept diagram for a secure external optical network enabling exchange of classical bits between two quantum servers. QP-A, QP-B quantum processors; TQ R\O Transmon qubit read\out; CBM classical DRAM buffer; QD (A), QD (B) quantum dot transmitter; Rx (B) SNSPD BSM, Rx (A) SNSPD BSM are photon receivers and Bell state measurement stations; Sender (A) BSM and Sender (B) BSM are Bell state measurement (BSM) stations; TESG A and TESG B are Transmon excitation signal generators that generate Transmon qubit of generic frequency 5 GHz from a classical bit waveform. qc1, qc2 are quantum channels and pc1, pc2 are public channels.
Preprints 117747 g008
Preprints 117747 g009
Figure 9. Concept drawing of networked quantum servers linked to a classical buffer memory via unconditionally secure quantum channels. Direction of arrow indicate directions of flow of classical bits, B. Q denoted a qubit and B/Q denotes classical bit-to-qubit interface while Q/B denotes a qubit-to-classical bit interface.
Figure 9. Concept drawing of networked quantum servers linked to a classical buffer memory via unconditionally secure quantum channels. Direction of arrow indicate directions of flow of classical bits, B. Q denoted a qubit and B/Q denotes classical bit-to-qubit interface while Q/B denotes a qubit-to-classical bit interface.
Preprints 117747 g009
Preprints 117747 g010
Figure 10. The Bit / Qubit Interface. A quantum server receiving a classical bit stream with return-to-zero (RZ) coding is shown in the figure. The frequency spectrum of the classical bit (circled) is mixed with the frequency output of a local oscillator to generate a microwave frequency that is in resonance with the target Transmon qubit microwave energy. Adapted from Figure 13 in reference [23].
Figure 10. The Bit / Qubit Interface. A quantum server receiving a classical bit stream with return-to-zero (RZ) coding is shown in the figure. The frequency spectrum of the classical bit (circled) is mixed with the frequency output of a local oscillator to generate a microwave frequency that is in resonance with the target Transmon qubit microwave energy. Adapted from Figure 13 in reference [23].
Preprints 117747 g010
Preprints 117747 g011
Figure 11. Simplified schematic of a qubit readout through a nonlinear Purcell-filter [30].
Figure 11. Simplified schematic of a qubit readout through a nonlinear Purcell-filter [30].
Preprints 117747 g011
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated