Monitoring and Modeling Urban Heat Patterns in the State of Iowa, USA Utilizing Mobile Sensors and Geospatial Data

With cities experiencing faster warming rates than their surroundings and two-thirds of the global population projected to be living in urban areas by 2050, studies that help to describe in detail the spatial temperature patterns in the urban environment have the potential to address concerns regarding cities’ livability. The goal of this research was to examine the spatial pattern of temperature across multiple small to medium-sized cities in the state of Iowa, a relatively rural state. The study utilized mobile temperature sensors to collect air temperature data at a high temporal and spatial resolution in ten urban areas in Iowa during the afternoon, evening, and night on days exceeding 32°C from June to September 2022. Using a Random forest algorithm, and independent variables derived from aerial imagery and LiDAR data, we created predicted surface temperature models that demonstrated R² coefficients ranging from 0.879 to 0.997 with a majority of the temperature models reaching a R² higher than 0.95. These strong modeling results and derived highly detailed raster spatial data supports recent research which help explain the influence of morphometric features on temperature patterns in the urban environment. This study expands on previous research by investigating multiple small to medium sized cities in Iowa.

Keywords:

Subject: Environmental and Earth Sciences - Geography

1. Introduction

Rising temperatures and extreme heat events have been recorded across the globe in recent decades [1]. Urban areas specifically, home to a majority of the world’s population, have experienced higher temperatures caused by the morphology of the built environment [2], and the high probability of future extreme heat events has been brought up in many studies. Fischer et al. [3] revealed that week-long heat extremes that break records by three or more standard deviations are predicted to be two to seven times more likely to happen in 2021–2050 and three to 21 times more in 2051–2080 when compared to the last three decades. With cities experiencing faster warming rates than rural areas [4], serious public health problems (e.g., chronic diseases, death) can arise, affecting a larger portion of the global population, including those with higher socioeconomic vulnerability. Research has indicated that more casualties have resulted from heat waves than other hazardous weather events such as hurricanes, floods, and tornadoes combined [5]. In the United States, average daytime temperatures in urban areas are up to 4°C higher than those in outlying areas [2] and in extreme cases can be up to 10°C higher compared to the rural countryside [6].

An important part of understanding the intensity of urban heat is how the surrounding landscape features and processes influence the magnitude of heat. Paravantis et al. [7] summarized that components critical to the variation of temperature within the urban environment include cloud cover, vegetation, wind speed, albedo of impervious surface and road traffic intensity. Other urban characteristics such as surface roughness [8], pavement composition [9] and anthropogenic heat flux generated by cultural activities [10] have also been shown to be associated with higher urban temperatures.

Studies evaluating urban temperatures using remote sensing analysis techniques [11,12,13] have been common over the last couple of decades. While leveraging satellite imagery provides the most affordable way to collect data covering large areas and across multiple urban areas, these techniques suffer from limited spatial resolutions (e.g., 30 m for Landsat, 250 m for MODIS). Moderate resolution imagery is unable to capture the highly detailed structures of complicated urban matrices. To address this shortcoming, advances in lower-cost sensor technologies and high-resolution geospatial data have been used in conjunction to provide highly detailed spatial data capturing spatial heterogeneity across urban areas. The use of vehicle mounted mobile devices, either mounted on cars [11,14,15,16], motorbikes [17], or bicycles [16] offers the benefit of enabling very high-resolution temperature data collection, thus allowing for a better understanding of small variations of the temperature found within an urban area [18]. Voelkel and Shandas [15] successfully demonstrated the use of these mobile sensor systems to map detailed temperatures multiple times on a very hot day in Portland, Oregon and expanded this methodology to a study Washington D.C, Baltimore, Maryland, and Richmond, Virginia [16].

Advances in the technology of remote sensing such as improvements in spatial resolution from satellite and airborne-based imagery and the increasing availability of other geospatial data have allowed researchers to examine the influence of urban features on air temperatures including the shape of tree canopy [19] and tree shade [13]. Chun and Guhathakurta [20] proposed that the type of vegetation could also play a role in regulating urban temperatures, and the study conducted by Stone and Norman [21] pointed out that if the suburban areas of Atlanta, Georgia were able to reduce their lawn areas by 25% and replace them with trees, the contribution of latent heat to the increase of temperatures would be reduced by 13%.

More recent studies have investigated detailed urban morphometric features (vegetation and building metrics) through Light Detection and Ranging (LiDAR) data (e.g., [12,16]). With the capability of generating detailed three-dimensional information about the shape of the Earth and its surface characteristics, LiDAR is widely used to map the urban landscape and can produce an array of data, ranging from the spatial distribution of land cover, tree canopy, and information on building structure such as height or volume. Chun and Guldmann [22], for example, used LiDAR data paired with land surface temperature (LST) to delineate the urban characteristics and factors that enhance or mitigate urban heat.

Studies like the ones conducted by Voelkel and Shandas [15] used mobile traverse data collection methods to build extensive datasets of temperature measurements that were subsequently used to study and model temperature variation across different areas of the urban environment making use of statistical techniques such as multiple linear regression (MLR), classification regression tree (CART) combined with multiple linear regression, and random forest (RF). Independent variables derived from LiDAR, building footprint vector files, and imagery data helped to feed the predictive models. They found the random forest to produce the highest predictive power, varying from R²=0.8199 for temperature data collected in the afternoon (3 p.m.) to R²=0.9793 for temperature data collected in the morning (6 a.m.). For temperature collections that took place in the evening (7 p.m.), the model presented a predictive power of R²=0.9715.

Shandas et al. [16] published a similar study by employing a satellite pixel-based modeling approach for the creation of a continuous surface of predicted temperatures across three different US cities: Richmond, Washington D.C., and Baltimore. Using a combination of ground-based measurements, spectral data from the Sentinel-2 constellation, spatial analysis, and machine learning techniques (random forest algorithm) they demonstrated a high predictive power of no less than R²=0.9644 for all nine models (morning, afternoon, and night for each of the 3 study areas). In a study in southern Brazil, Oukawa et al. [23] compared two different modeling approaches (multiple linear regression and random forest) to analyze and predict the spatiotemporal occurrence of the UHI intensity using air temperature as the dependent variable. To do that, urban temperature was measured at 12 different sites in the city of Londrina using HOBO sensors (U23-001, Onset) with built-in data loggers, and were complemented with data from two more permanent weather stations. Results showed that random forest performed considerably better than multiple linear regression, with explanatory power of over 96% in both, daytime and nighttime (compared to 64% and 34% respectively).

In a study conducted by Chen et al. [24], three canopy and three height were used as independent variables to explain the variation in land surface temperature using multiple linear regression, while the same author considered the proportion of impervious surface, albedo, and anthropogenic parameters to derive a model for land surface temperature and meteorological stations using Random forest algorithms in a study published two years later [25]. Examining several instances in the literature reveals variability in the methods used to measure urban heat, as well as in the selection of independent variables and statistical tools for deriving predictive models or understanding the influences of natural and built-up features on urban heat. Nonetheless, results consistently demonstrated high statistical confidence, particularly in studies employing random forest as a modeling algorithm.

While recent progress has been made in understanding urban heat spatial heterogeneity, more research in a variety of urban settings would be useful. The majority of previous studies have focused on larger urban areas (e.g., [15,16]) and often have only considered one study area at a time. While there have been studies conducted in the U.S. Midwest [26,27,28], no studies have examined the pattern of temperature in urban areas using high spatial and temporal resolution methods across multiple different sized cities. This study aims to contribute to the existent literature on urban heat patterns while providing a high-resolution model in numerous cities across the state of Iowa. This study attempted to examine heat patterns across urbanized areas of various sizes including investigating whether smaller cities with comparable highly local urban structures (e.g. tree canopy, building density) experience urban heat similarly (with the same proportional variation in temperature) to larger cities. This heterogeneity of the urban division in Iowa provides an interesting scenario for this study to be conducted.

2. Materials and Methods

2.1. Study Area

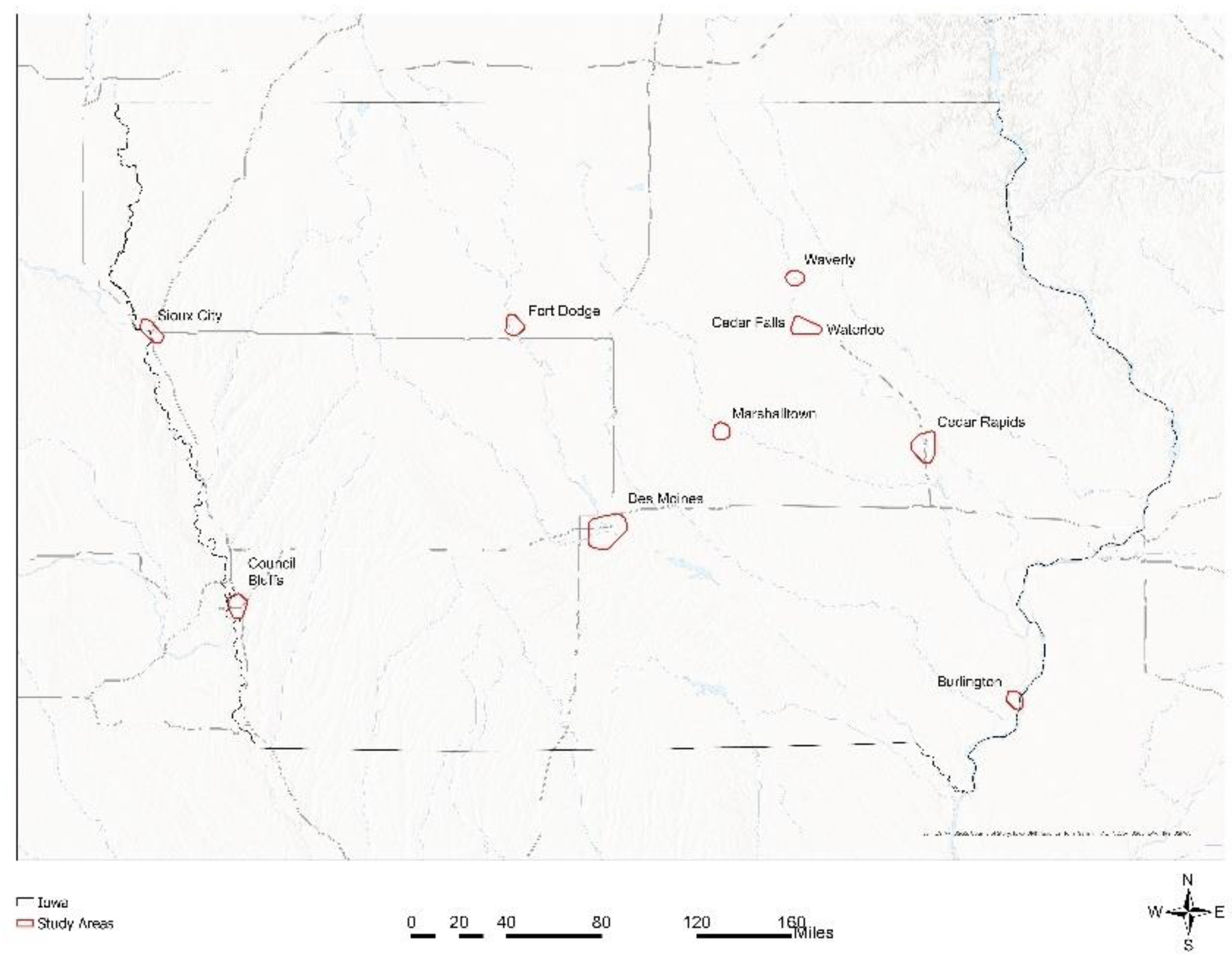
Iowa is one of the 12 states in the Midwest region of the United States, located in the center of the region between 40°35’N - 43°30’N latitude and 90°8’W - 96°38’W longitude (Figure 1). Surrounded by the Mississippi River (east) and Missouri River (west), it borders six other states: Minnesota (north), Wisconsin (northeast), Illinois (southeast), Missouri (south), Nebraska (southwest), and South Dakota (northwest). With an area of 55,857 square miles, Iowa figures as the 9th largest state by area in the region, its highest elevation is in Osceola County at 509 meters and the lowest elevation point is in Lee County at 146 meters [29]. According to Köppen Climate Types, Iowa is in a hot-summer humid continental climate area (Dfa) and in the past decade (2012 – 2022) had an average temperature of 9.1°C and a precipitation of 902.2 mm per year. The maximum average temperature for the same period was 14.8°C and the minimum average temperature was 3.4°C [30]. Iowa has no urban area with a population over one million inhabitants with Des Moines having the largest by population with approximately 210,000 inhabitants (approximately 700,000 in the metro area).

2.2. Temperature Data Collection

This study collected temperature data from urban areas with populations ranging from approximately 10,000 to 210,000 inhabitants across the state on days when the temperature was forecasted to exceed 32 °C during the day between June and September 2022. The cities in which data were collected included Burlington, Cedar Falls (CF), Cedar Rapids, Council Bluffs, Des Moines, Fort Dodge, Marshalltown, Sioux City, Waterloo, and Waverly (Figure 1).

A total of 9 custom multi-function mobile sensor systems were built by author J. Dietrich. The systems were comprised of a small microcontroller (Adafruit QTPy RP2040), a Global Navigation Satellite Systems receiver (Adafruit Mini GPS PA1010D) and sensors that recorded air temperature and humidity (Sensirion SHT40) as well as surface temperature (Melexis MLX90614) and ambient light (Rohm BH1750) all within the Adafruit Stemma ecosystem. The precision of the thermometers is two decimals’ Celsius degrees, and the accuracy is up to 0.2°C [31].

Figure 2. Temperature Sensor Devices (Adafruit Sensirion SHT40).

The sensors were housed in a custom, white 3D printed semi-enclosure to protect the sensors from direct exposure to the sun and mounted on the vehicles with an large suction cup. Preliminary testing indicated mounting the mobile system on three different positions (driver’s window, passenger front window, and passenger’s back window on the driver’s side) showed negligible difference (and within the accuracy of the devices) on air temperature measurements. Hence, devices were mounted on the driver’s side windows of all vehicles that performed the measurements. Python-based scripts were developed to allow sensor communication and data collection and for post-processing of the raw data collected by the sensors.

Temperatures were collected during three rime periods on selected days (afternoon - 4 to 5 p.m., evening – 9 to 10 p.m., and night – 4 to 5 a.m.). The chosen times of the day were selected to capture the differences and intensity of air temperature in the urban environment while taking into consideration the stability of the temperature commonly seen throughout the day. The study by Oke [32] established that urban areas experience their highest air temperatures between 2 p.m. and 5 p.m., (corresponding to the afternoon data collection), and densely urban areas exhibit the most significant air temperature differences compared to non-built-up regions a few hours after sunset (corresponding to our evening data collection). Moreover, the nighttime period, known to worsen health issues related to heat exposure, has been emphasized in studies [6,33,34], providing justification for air temperature data collection during nighttime (4 a.m. to 5 a.m.) in the current research.

2.3. Urban Landscape Data Collection and Processing

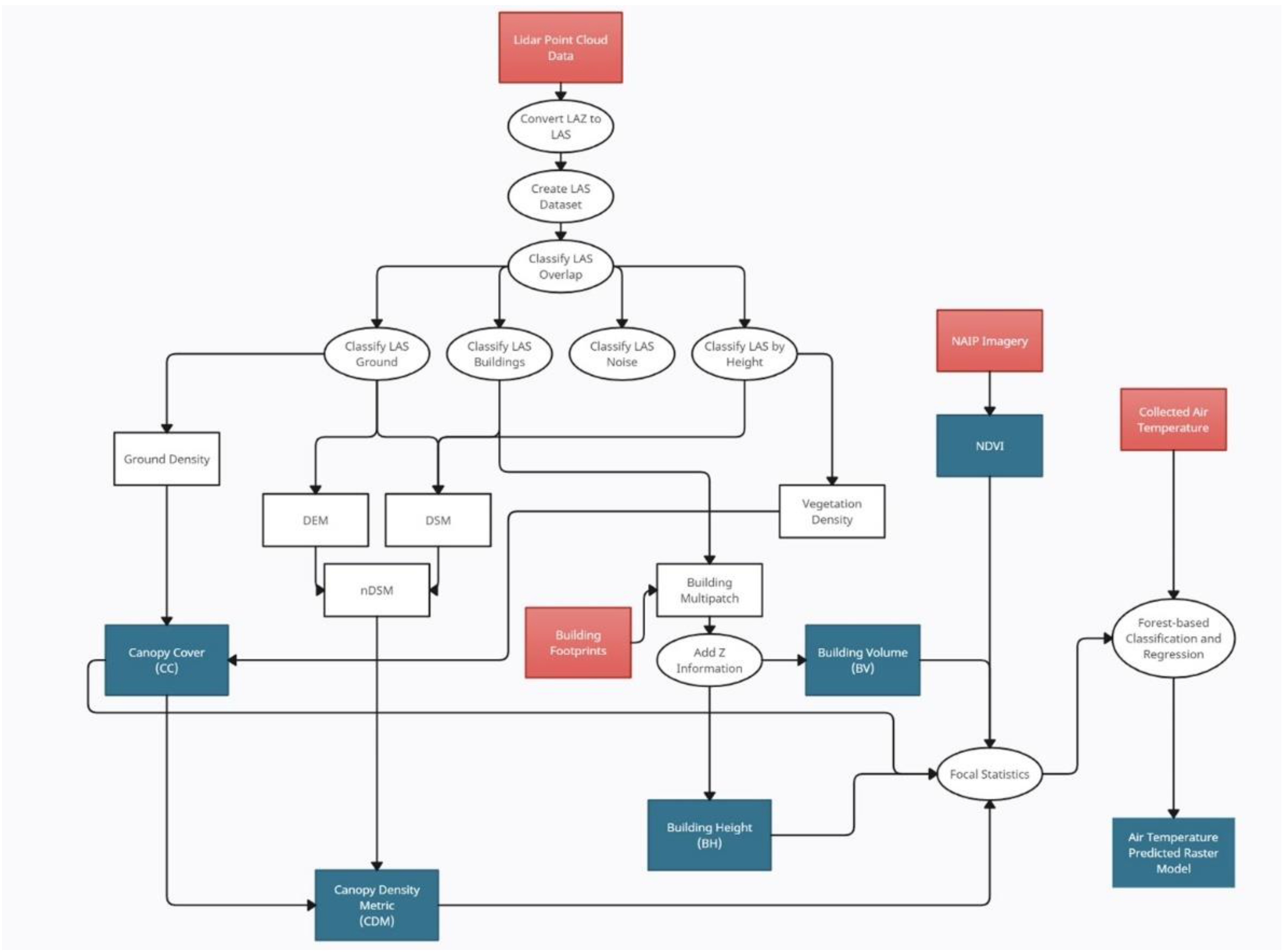
This study considered urban morphometric features such as vegetation coverage and built-up characteristic (building height and building volume) that were derived from a variety of geospatial datasets and used for later spatial modeling. LiDAR point cloud data collected in the state of Iowa during the years 2019–2022 were used to estimate urban vegetation and building morphology. The original data have a minimum of 2 points per square meter with a vertical and horizontal accuracy of 95% [35].

Using ArcGIS Pro (3D Analyst tools) and arcpy/Python automation, the LiDAR point cloud data were classified into ground points, vegetation points, and building points, which were then rasterized to represent ground density, vegetation density, and buildings; leading to the creation of models representing the bare-earth (digital elevation models), and above ground features existent in the study areas (digital surface models). In addition, in order to accurately represent the shape and surface area of buildings, the LiDAR point cloud data were also processed along with building vector polygons obtained from individual counties and cities GIS departments, to construct the final building multi-patch volumetric feature classes. Finally, according to the literature, an important component in explaining urban heat patterns is vegetation. For that reason, the 60-centimeter 2021 Iowa NAIP imagery downloaded from the National Oceanic and Atmospheric Administration [36] was used to create individual Normalized Difference Vegetation Index (NDVI) raster files for each urban area. Other studies have used NDVI also either from aerial imagery (e.g., [15]) or satellite imagery (e.g. [24]).

A total of five main independent variables were created from LiDAR point cloud data, and NAIP Imagery: Canopy Cover (CC): the proportion of vegetation compared to the amount of bare-earth and built-up structure in a given area (derived from LiDAR point cloud data classified as bare-earth and as vegetation points). The results are expressed in pixel values ranging from 0 to 1, where 0 represents no vegetation, and 1 represents fully vegetated area; Canopy Density Metric (CDM): the result of pixel values of CC multiplied by pixel values found in the normalized digital surface model (nDSM) which represents the relative height of features from the digital surface models; Building Height (BH): the average height of buildings expressed in meters for each individual structure; Building Volume (BV): the volume of buildings expressed in cubic meters; Normalized Difference Vegetation Index (NDVI): the value per pixel ranging from minus one (-1) to plus one (+1) representing the density, intensity of vegetation as well as vegetation health. The Focal Statistics tool in ArcGIS Pro Spatial Analyst Extension was used to derive neighborhood raster datasets for the natural and built-up structures (e.g., canopy cover, building height, building volume) independent variables. Neighborhood statistics (mean and standard deviation) were derived per 1 m² cell with fixed neighborhood distances of 50, 100, 200, 400, and 800 meters. This methodology has been utilized previously when using RF for modeling to investigate the surrounding urban conditions effect on the variation of air temperature [15,23,25].

To model the temperature patterns over various Iowa cities, the measured temperature was used as the dependent variable while neighborhood statistics for each of the independent variables was derived as a raster dataset (described below) after being resampled to be 1-meter resolution.

2.4. Modeling Development Using Random Forest Technique

Data from the temperature collection and the urban landscape metrics derived through geoprocessing of primary sources were organized based on location to create comprehensive an ESRI File Geodatabases per urban area. The geodatabases allowed the development of spatial models, which were applied on a spatial resolution of one square meter per study area and time period (afternoon, evening, and night). The models basically took the collected temperature point data as the dependent variable while using the derived urban morphometric data surrounding (multiple neighborhood distances) the points as independent variables to develop spatial models that estimated urban temperatures at those urban locations where no temperatures were recorded. Although several techniques can be used to create such models and to analyze and predict urban heat patterns, the most common methods found in the reviewed literature were MLR, CART, RF, and sometimes a combination of multiple methods in the same study. However, recent studies utilizing mobile devices for temperature data collection showed that RF significantly outperformed MLR and CART [15,16,23,25].

Recent advances in spatial statistical modeling techniques have been built into embedded tools in the software ArcGIS Pro (3.0.1). Thus, for this study, ArcGIS Pro was used for most of the steps in both the pre-processing of dependent and independent variables and also in spatial modeling. The Forest-based Classification and Regression (nomenclature utilized by ArcGIS Pro for RF algorithm) model built into the Spatial Statistics toolbox in ArcGIS Pro was chosen for air temperature modeling. Random forest is a supervised machine learning method developed by Leo Breiman and Adele Cutler [37]. Random forests are a non-parametric and nonlinear machine learning technique and are a “combination of tree predictors such that each tree depends on the values of a random vector sampled independently and with the same distribution for all trees in the forest” [38] (p.1). Models generated using a random forest algorithm not only provided the predicted temperature in areas where temperature data was not collected but also indicated the most influential independent variables that explain temperature patterns throughout each individual study area.

A workflow of the process to derive the necessary raster datasets used as independent variables used in the random forest model can be seen in Figure 3. Ellipsoids represent functions and geoprocessing tools, rectangular red-filled objects represent the input datasets, rectangular white-filled objects represent the outcome files necessary to generate the final independent variables used in the Random forest modeling, and rectangular blue-filled objects represent the generated independent variables and final outcome (predictive models).

The parameters set in RF for all models consisted of 1000 randomized trees built from all effective focal distance raster datasets to predict the air temperature in each urban area in the afternoon, evening, and pre-dawn. A 70/30 hold-out method for model evaluation was used to assess the accuracy of all models. This technique separates the temperature measurements into two sets (training set and testing set) and was set as the percentage of data excluded for validation (=30%) before running each one of the models. Finally, only one number of runs was used as a validation option. The ArcGIS Pro Forest-based Classification and Regression tool accepted the inputted dependent variable as a Geodatabase Feature Class with each point holding the measured air temperature while each independent variable came in the form of a 1m² rasters (39 independent variables described below).

The RF model originally considered 50 different independent variables based on five variables (CC, CDM, BH, BV, NDVI) each calculated with two different statistical measurements (mean and standard deviation) at five different neighborhood distances (50 meters, 100 meters, 200 meters, 400 meters, and 800 meters). However, Building Volume (BV) calculated at all neighbor distances as standard deviation (BV_STD) showed noticeable signs of banding (straight lines across the whole area of interest) with no calculated values, and thus was excluded from the modeling. Two other variables, Canopy Cover (CC), and Canopy Density Metric (CDM) presented the same banding issue using standard deviation at distances under 400 meters ((CC_STD<400m) and (CDM_STD<400m)). Their standard deviations computed at 50 meters, 100 meters, and 200 meters were also discarded from the model for all urban areas. Therefore, only 39 different independent variables were used for the final model in all urban areas.

Temperature data were collected in seven different urban areas at three times of the day (afternoon, evening, and night): Burlington, Cedar Falls, Cedar Rapids, Council Bluffs, Des Moines, Sioux City, and Waterloo. In three other cities, data were collected only in two periods, either due to personnel or logistical constraints (Waverly and Fort Dodge), or extreme weather conditions (thunderstorm) during the time of collection (Marshalltown).

3. Results

Analyzing the temperatures collected in each urban area and comparing them to the surrounding morphometric features along each respective route revealed observations consistent with the literature. The lowest temperatures were usually collected close to or in highly vegetated areas, while the highest temperatures were often collected in areas such as downtown or with a large number of built-up structures (e.g., industrial parks). The amplitude of temperature was higher during afternoon collection (Burlington, Council Bluffs, Des Moines, Marshalltown, and Waverly), followed by evening (Cedar Rapids, Fort Dodge, and Waterloo/CF), and night (Sioux City). 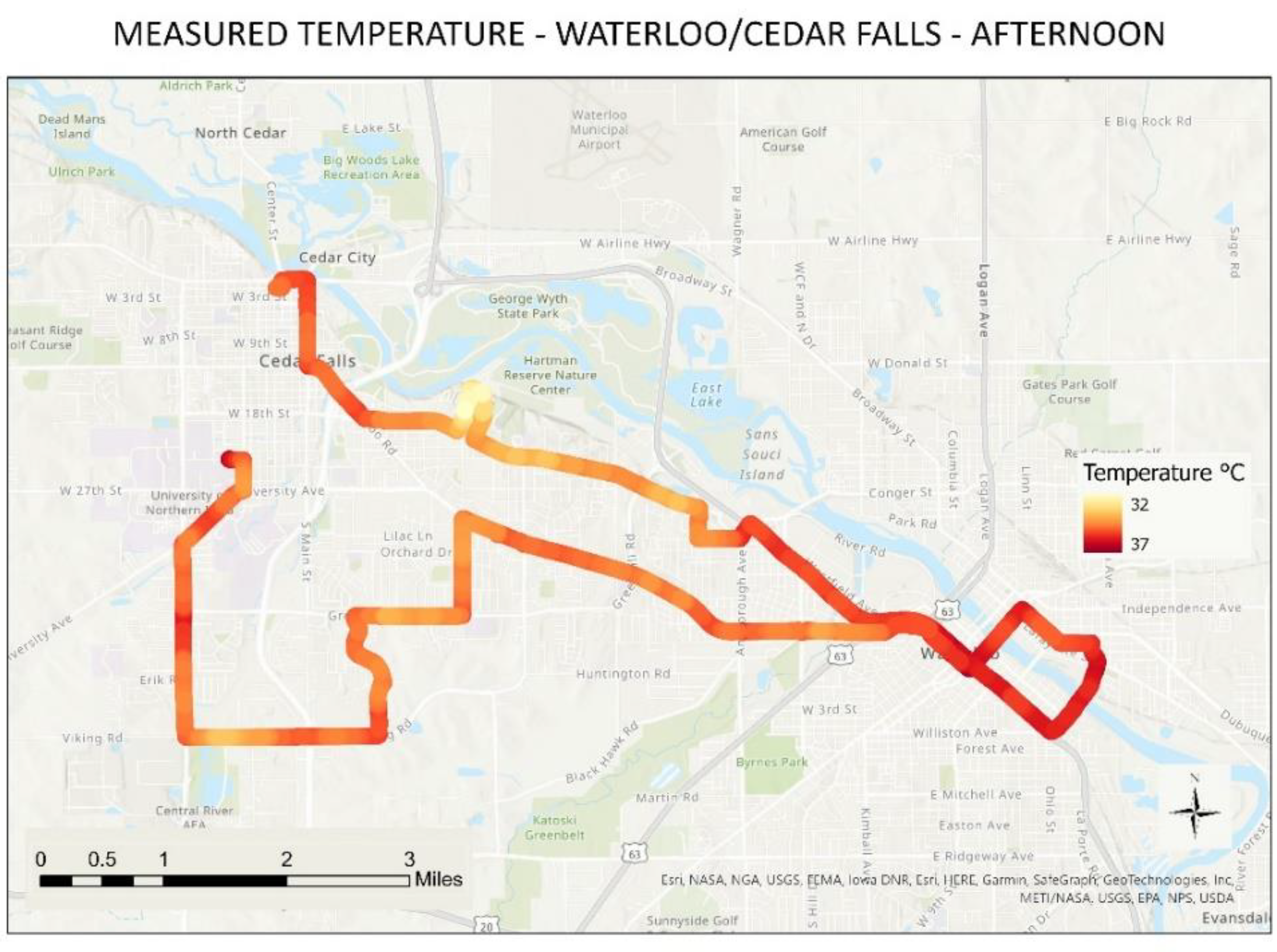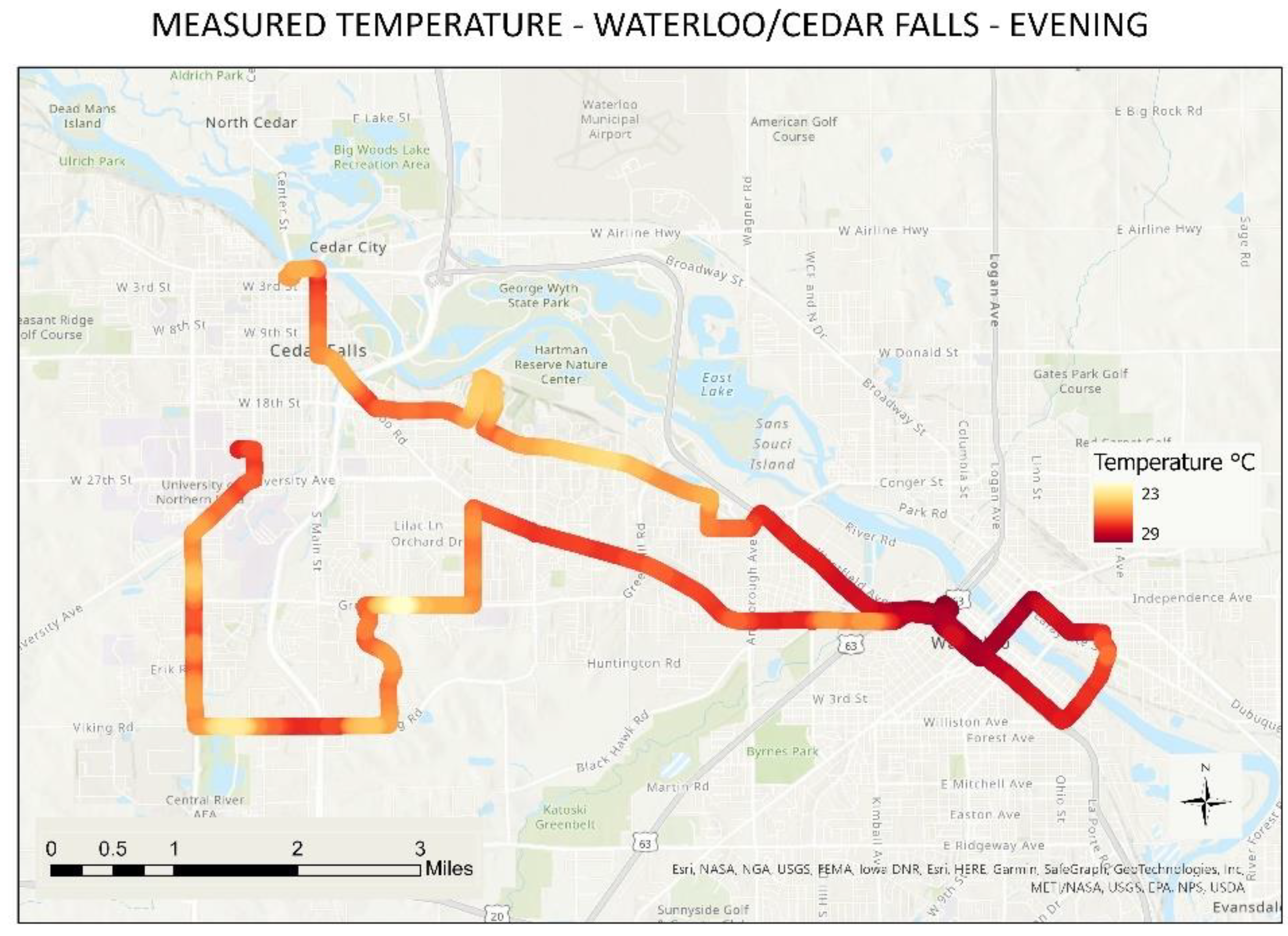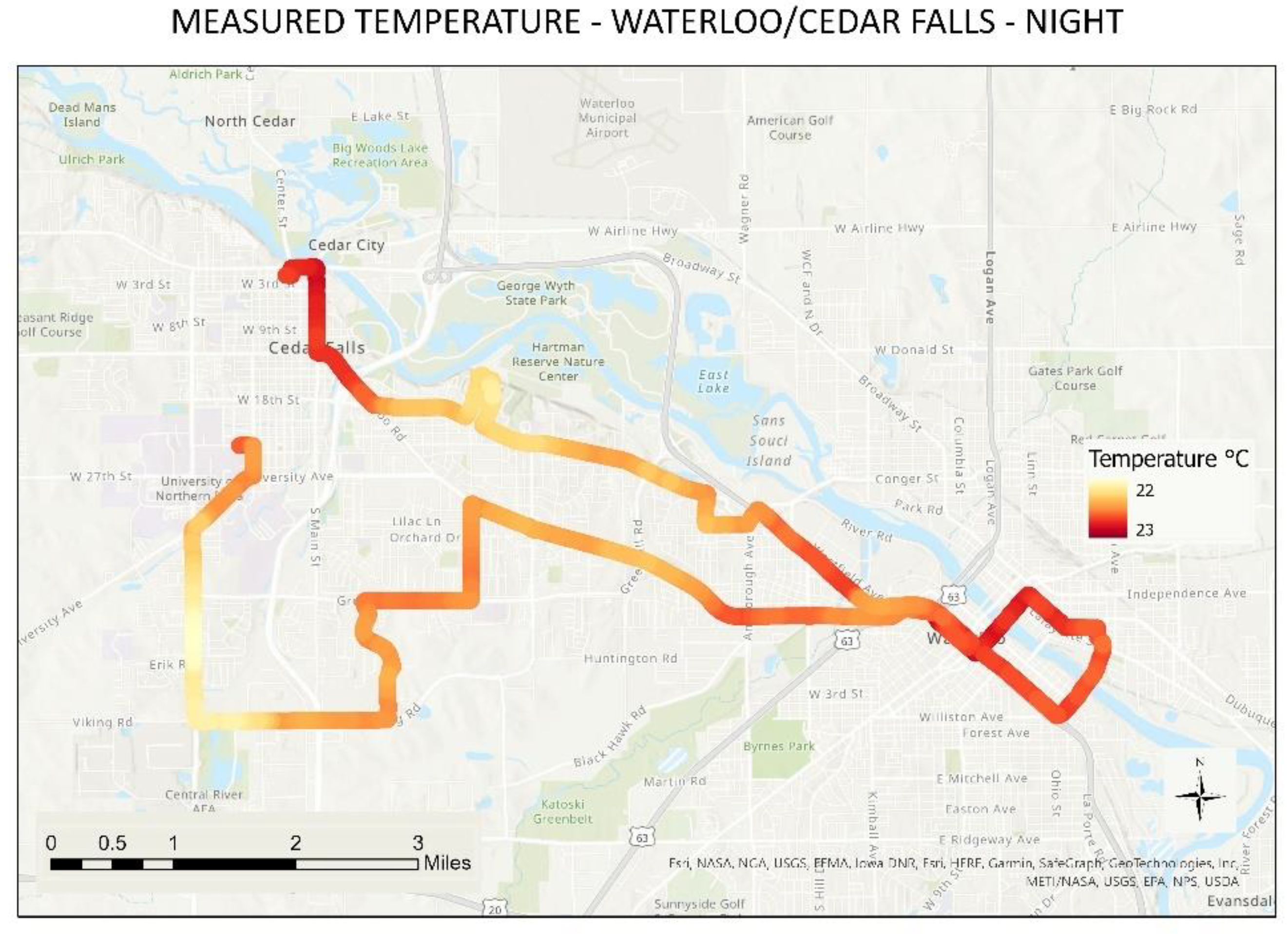Table 1 depicts the summary of dates, number of routes, time of collection, and number of measurements taken in each one of the study areas. The number of routes was dictated by the size of the study area and indicates how many individual vehicles were used on that given date/time. Waterloo-Cedar Falls is used to provide an example of one urban area with Figure 4, Figure 5 and Figure 6 demonstrating the temperature patterns throughout all times of collection.

Predictive models for all 24 areas (Table 2) showed an average R² of 0.947 for the afternoon models, R² of 0.973 for the evening models, and R² of 0.987 for the nighttime. Most study areas had models of over R² 0.95 (20 out of 24 models). These high R² values were comparable to or stronger than other studies that made use either of random forest (e.g., [15,16]), or other statistic algorithms/techniques (e.g., [17,24]). Taking into account all predictive surface raster models generated by the Forest-based Classification and Regression algorithm, results varied from an R² of 0.879 (p-value < 0.00, standard error of 0.011) to an R² of 0.997 (p-value of 0.00, and standard error of 0.002). These results were respectively Sioux City in the afternoon, and Council Bluffs in the night. Analyzing p-values and standard errors for each result showed that all results are very statistically significant, with p-values of <0.000, and standard errors not higher than 0.011.

Among the independent variables describing urban morphometric features, NDVI, regardless of the statistic used or neighborhood distance, appeared as the most important in explaining the variation in temperature in 14 out of 24 models, followed by BH (6 out of 24 models), CDM (3 out of 24), and CC (1 out of 24 models). Among the five neighbor distances being considered, the 800-meter distance accounted for 52.5% of all variables, followed by 400 meters (20%), 200 meters (15.83%), 100 meters (8.33%), and 50 meters (3.33%). These results indicated that the morphometric feature influence (natural and built-up) in small neighbor distances has a smaller statistical influence on urban temperatures when compared to larger neighbor distances (e.g., the average building height in a 50 meters radius seems to have considerably less statistical significance/influence in generating the predictive models than the average for building height in 800 meters radius). Considering the statistical method of central tendency (mean vs. standard deviation) being computed, the mean seems to have a higher statistical influence on the predictive models than standard deviation, appearing in 72.5% as one of the five most important independent variables per model.

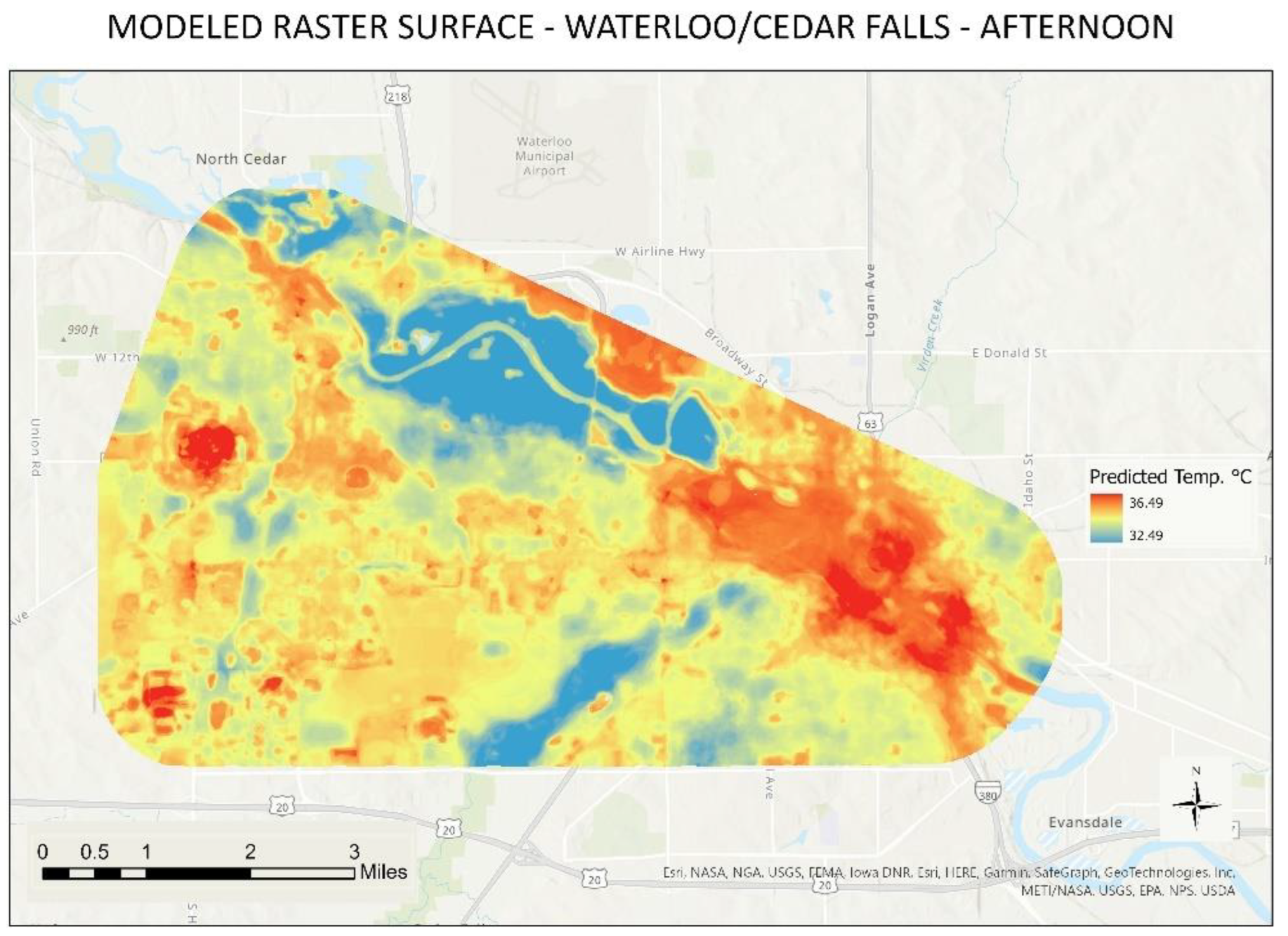
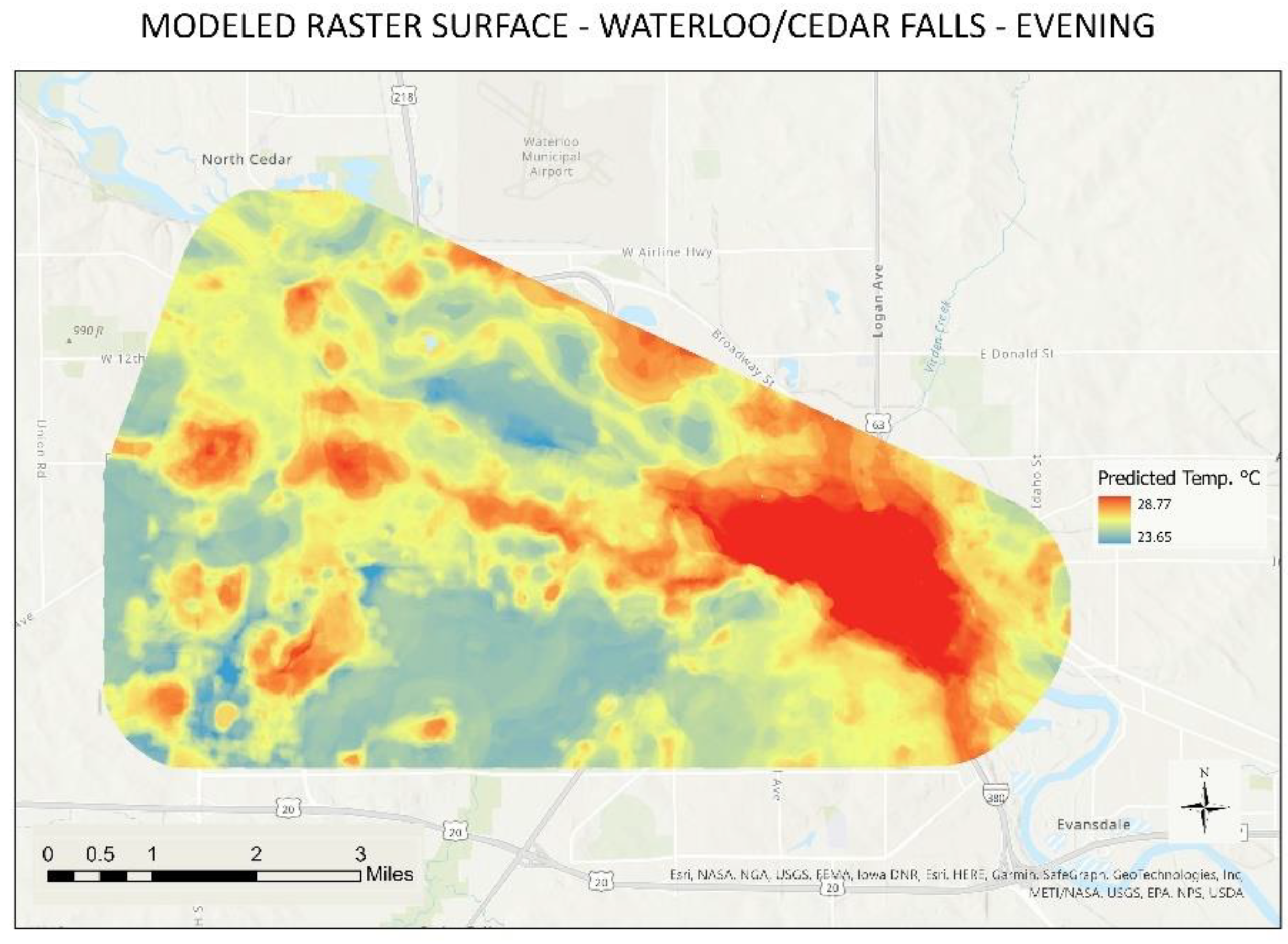
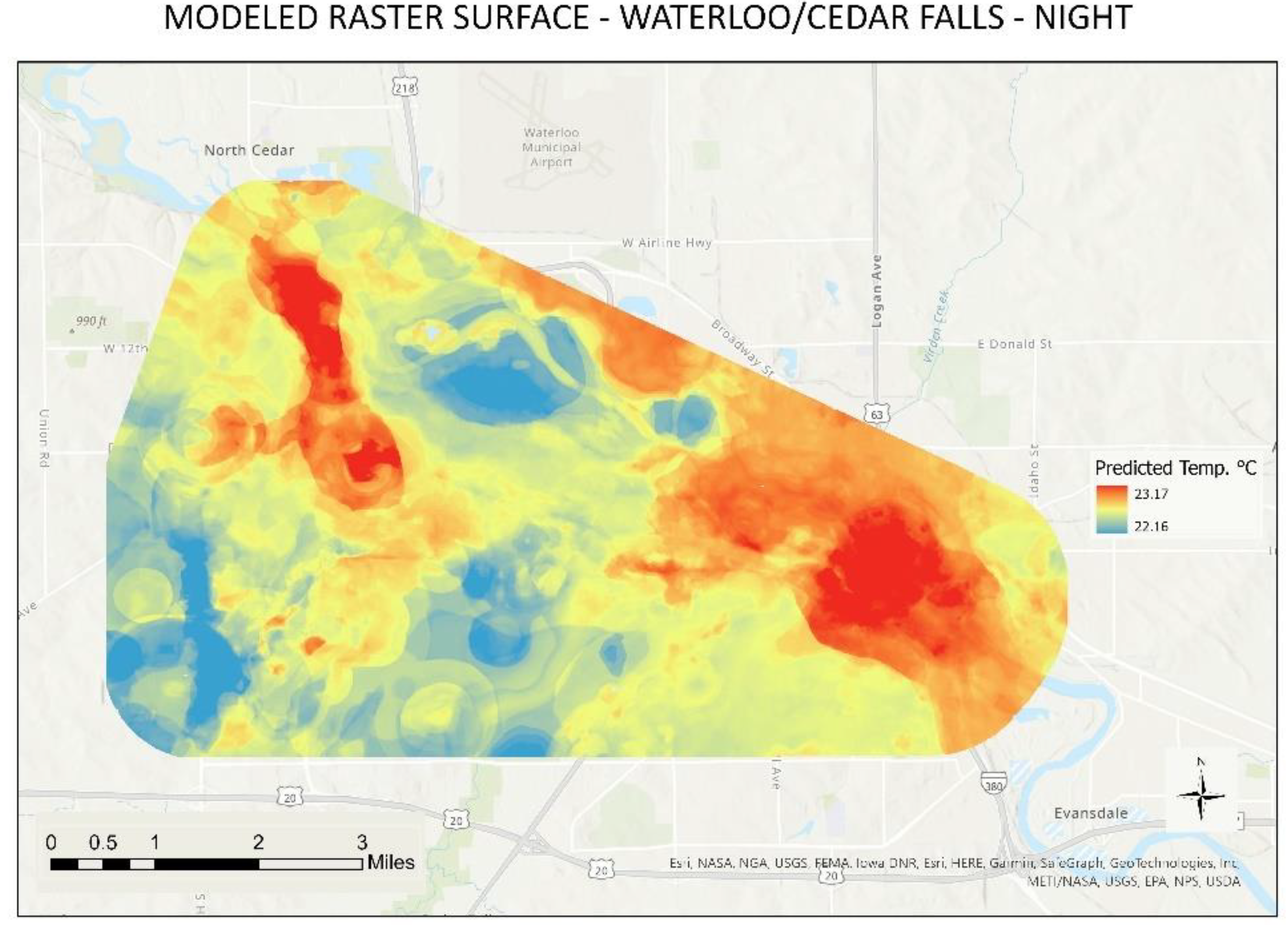
Analyzing the predictive raster surface models generated for each study area, most of the high predictive results (based on the coefficient R²) resembled findings from other studies [15]. Evaluating the models by study area and time of the day against the collected temperature show similar minimum and maximum temperatures, an expected outcome given the high coefficients (R²) produced by random forest. Utilizing as an example, the urban area of Waterloo/Cedar Falls, predictive raster models showed modeled temperature rasters consistent with the temperature collected at all times of the day (Figure 7, Figure 8 and Figure 9). The proportion of buildings in areas such as downtown Waterloo (eastern part of the map where high temperatures are shown) downtown Cedar Falls (north-center west of the map and southwest of the north cold area seeing on the map), and the University of Northern Iowa campus (west-central area of the map presenting high temperatures) influenced the high temperatures seen in those areas, especially during the nighttime, which is supported by the most important variables for that model (NDVI and BV).

In addition to the statistics output by the modeling, when comparing the values from the predicted raster surface models with coincident measured temperatures in each study area by the time of the day, values were presented with differences no higher than 0.5°C degrees for minimum temperatures (Waterloo/Cedar Falls - Evening) and no lower than 0.46°C degrees for maximum temperatures (Council Bluffs – Afternoon). Table 3 shows all cities and the time of collection with the difference of measured and predicted temperature for minimum and maximum temperatures.

4. Discussion

This study carried out a systematic examination of temperature patterns across a variety of urban areas in Iowa based on extensive in-field temperature monitoring in afternoon, evening, and night times and highly detailed spatial statistical modeling. The three selected times for data collection were based on similar studies from the existing literature. This sampling effort led to a unique and robust dataset of air temperature measurements (more than 110,000 temperature points were collected) in ten different areas of diverse urban features. Even though methods of air temperature collection measured by mobile devices have been researched in previous studies, this study represents a novel effort to collect data across multiple urban areas in a single state. Temperature collection routes were designed to capture temperature data across a variety of urban land uses thus providing the necessary data required for the development of geospatial models with high predictive power throughout most, if not all urban areas.

Modeled results generated by random forest algorithms resulted in coefficients that varied from an R² of 0.879 to 0.997 (all statistically significant), with most coefficients resulting in R² higher than 0.95, which seemed consistent with other studies utilizing mobile sensors for temperature data collection, LiDAR data and/or aerial imagery to derive independent variables, and the use of RF as a machine learning algorithm [15,16,23]. The results indicate that the chosen independent variables and neighborhood distances were effective in generating detailed and accurate temperature raster surfaces in urban environments. Predicted surface temperatures in this study were found to be within a very similar range of collected air temperature, showing the expected consistency between collected air temperature and predicted air temperature. Regarding the time of day when air temperature was modeled and predicted in each urban area, the results exhibited similarities with previous studies [16,34], which found the highest predictive power during the evening or night periods.

Surprisingly, the consistency of certain independent variables, such as NDVI, as the most significant factors in explaining the variation in the models across different study areas suggests that, theoretically, even fewer independent variables could have been employed. NDVI not only appears as the most important variable, it also appears as the most reoccurring important variable for the second, fourth, and fifth most important variable across all 24 models. In comparison to the study conducted by Voelkel and Shandas [15], the most important variable for the three models provided (morning, afternoon, and evening), was building height, while in studies such as Oukawa et al. [23] and Shandas et al. [16] found the most important variables in explaining the modeled temperature were relative humidity and NDVI.

Regarding the five neighbor distances employed in this research, 800 meters is the one that appeared the most frequently as the first, second, third, fourth, and fifth most important variable. Out of all neighbor distances, 50 meters had the least common appearance as the most important variable, regardless of the position (1st, 2nd, 3rd, 4th, or 5th most important variable), with only 4 appearances. These results are somewhat similar to other studies [15] in which neighborhood distances between 800 and 1000 were most commonly shown to be the most important overall (53.3% of all 5 most important variables of all models), especially for morning and evening data collections.

The use of the RF algorithm in predicting temperature across all urban areas resulted in significant R² coefficients, where 83% of the models exhibited values higher than 0.95, and 62.5% showed values over 0.97, all being statistically significant (p-value <0.01). This indicates that the approach of creating detailed geospatial temperature patterns by incorporating a diverse range of morphometric and natural features as independent variables (Canopy Cover, Canopy Density Metric, Building Height, Building Volume, and Normalized Difference Vegetation Index) in the urban environment proved to be effective. The highly statistically significant predictive power of the multiple developed models also offered valuable insights on the impacts that man-made and natural features (the foundation to derive most independent variables) have in contributing or preventing urban heat across the state of Iowa.

Moreover, continuous investment in understanding urban heat patterns will certainly allow for preventive measures to be taken at different scales, as well as mitigative actions that can lead to the development novel techniques, potentially reducing deleterious public health effects and significantly enhancing the overall quality of life for both individuals and the community as a whole. The results of the modeling efforts provide highly detailed spatial data and maps that could be used in a variety of public health mitigation efforts (e.g., location of cooling centers) and urban planning efforts. Urban planners, landscape architects, zoning specialists, and public health experts are just a few of the professionals that can potentially make use of the content provided in this study to develop ways of mitigating urban heat (e.g., by implementing highly vegetated areas) and establishing or improving environmentally equitable housing to prevent and respond to heat-related health issues.

Even though the goal of this study was to collect air temperature data during hot days in different study areas, temperature patterns for urban areas during cold days are seldom explored by existing literature. While extensive research has been conducted on temperature patterns in urban environments, the focus has predominantly been on urban heat during extremely hot weather conditions. The lack of research in areas where temperatures frequently drop to sub-zero temperatures during winter warrants the need for additional studies. While the derived spatial independent variables and neighborhood distances used in this study produced strong results, other variables and distances could potentially be explored. For example, considering different variables that can portray the heterogeneity of the urban fabric and meteorological conditions (e.g., sky view factor, humidity, the proportion of impervious surfaces, albedo of built-up structures), or reducing to a fewer number of variables that presented higher statistic influence in the air temperature models (e.g., NDVI at certain neighbor distances).

Author Contributions

Conceptualization of the study: John DeGroote, Dr. James Dietrich, and Dr. Bingqing Liang; methodology: all authors contributed to the development of the methodology; software: Dr. James Dietrich developed sensor Python scripts and post-processing temperature data Python scripts while Clemir Coproski, with assistance from John DeGroote, was primarily responsible for the development of automated GIS processing (Python, arcpy) scripts; validation, Clemir Coproski was primarily responsible for spatial modeling and testing with input from all authors.; formal analysis, Clemir Coproski was primarily responsible for spatial modeling and testing with input from all authors: original draft preparation was carried out by Clemir Coproski; writing—review and editing has been carried out by all authors; supervision was led by John DeGroote; project administration – was the primary project lead; funding acquisition – John DeGroote wrote the proposal that led to the funding that allowed this study. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Iowa Economic Development Authority Iowa Energy Center Grant Program (agreement number 21-IEC-012).

Data Availability Statement

The full datasets containing the collected dataset as well as the output files can be found at https://www.geotree.uni.edu/web/IowaUrbanHeatProject_IowaEnergyCenter/IowaUrbanHeat_MonitoringModeling.zip. As this article was originated from a master’s degree thesis carrying the same title, the full detailed version of this study can be found at https://www.geotree.uni.edu/web/IowaUrbanHeatProject_IowaEnergyCenter/IowaUrbanHeatThesis.pdf or through University of Northern Iowa Library services database at https://scholarworks.uni.edu.

Acknowledgments

A special thank you to the University of Northern Iowa Geography Department, and staff; Dr. Alex Oberle, and Dr. Kamyar Enshayan, whose significant contributions were instrumental in concluding this study.

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

Vicedo-Cabrera, A. M., Scovronick, N., Sera, F., Royé, D., Schneider, R., Tobias, A., Astrom, C., Guo, Y., Honda, Y., Hondula, D. M., Abrutzky, R., Tong, S., de Sousa Zanotti Stagliorio Coelho, M., Saldiva, P., Lavigne, E., Correa, P. M., Ortega, N. V., Kan, H., Osorio, S., Kyselý, J., … Gasparrini, A. 2021. The burden of heat-related mortality attributable to recent human-induced climate change. Nature climate change, 11(6), 492–500. [CrossRef]
Environmental Protection Agency. Heat Island Effect. 2022. Available online: https://www.epa.gov/heatislands (accessed on 10 May 2022).
Fischer, E. M., S. Sippel, and R. Knutti. 2021. “Increasing Probability of Record-Shattering Climate Extremes.” Nature Climate Change 11, no. 8: 689–95. [CrossRef]
Stone, Brian. 2007. “Urban and Rural Temperature Trends in Proximity to Large US Cities: 1951–2000.” International Journal of Climatology 27, no. 13 (2007): 1801–7. [CrossRef]
Wong, Kaufui V., Andrew Paddon, and Alfredo Jimenez. 2013. “Review of World Urban Heat Islands: Many Linked to Increased Mortality.” Journal of Energy Resources Technology 135, no. 2. [CrossRef]
Heaviside, Clare, Helen Macintyre, and Sotiris Vardoulakis. 2017. “The Urban Heat Island: Implications for Health in a Changing Environment.” Current Environmental Health Reports 4, no. 3: 296–305. [CrossRef]
Paravantis, John & Tzavali, A. & Mihalakakou, Giouli & Fotiadi, Aleksandr & Stigka, Eleni. 2015. Urban heat island intensity: A literature review. 24. 4537–4554.
Oke, T.R. 1987. Boundary Layer Climates. London England: Routledge.
Gartland, Lisa. 2011. Heat Islands: Understanding and Mitigating Heat in Urban Areas. London: Earthscan.
Oke, T. 2009. Classifying urban climate field sites by “local climate zones”: The case of Nagano, Japan.
Balázs, Bernadett, János Unger, Tamás Gál, Zoltán Sümeghy, János Geiger, and Sándor Szegedi. 2009. “Simulation of the Mean Urban Heat Island Using 2D Surface Parameters: Empirical Modelling, Verification and Extension.” Meteorological Applications 16, no. 3: 275–87. [CrossRef]
Saydelles, A.P. 2005. ‘Estudo do campo térmico das ilhas de calor urbano em Santa Maria-RS’ Dissertação (mestrado) – Universidade Federal de Santa Maria, 2005.
Yu, Qiuyan, Wenjie Ji, Ruiliang Pu, Shawn Landry, Michael Acheampong, Jarlath O’ Neil-Dunne, Zhibin Ren, and Shakhawat Hosen Tanim. 2020. “A Preliminary Exploration of the Cooling Effect of Tree Shade in Urban Landscapes.” International Journal of Applied Earth Observation and Geoinformation 92: 102161. [CrossRef]
Saaroni, Hadas, Eyal Ben-Dor, Arieh Bitan, and Oded Potchter. 2000. “Spatial Distribution and Microscale Characteristics of the Urban Heat Island in Tel-Aviv, Israel.” Landscape and Urban Planning 48, no. 1–2 (2000): 1–18. [CrossRef]
Voelkel, Jackson, and Vivek Shandas. 2017. “Towards Systematic Prediction of Urban Heat Islands: Grounding Measurements, Assessing Modeling Techniques.” Climate 5, no. 2: 41. [CrossRef]
Shandas, Vivek, Jackson Voelkel, Joseph Williams, and Jeremy Hoffman. 2019. “Integrating Satellite and Ground Measurements for Predicting Locations of Extreme Urban Heat.” Climate 7, no. 1: 5. [CrossRef]
Yokobori, T, and S Ohta. 2009. “Effect of Land Cover on Air Temperatures Involved in the Development of an Intra-Urban Heat Island.” Climate Research 39: 61–73. [CrossRef]
Szymanowski, Mariusz, and Maciej Kryza. 2011. “Local Regression Models for Spatial Interpolation of Urban Heat Island—an Example from Wrocław, SW Poland.” Theoretical and Applied Climatology 108, no. 1–2: 53–71. [CrossRef]
Gkatsopoulos, Panagiotis. 2017. “A Methodology for Calculating Cooling from Vegetation Evapotranspiration for Use in Urban Space Microclimate Simulations.” Procedia Environmental Sciences 38: 477–84. [CrossRef]
Chun, Bumseok, and Subhrajit Guhathakurta. 2016. “The Impacts of Three-Dimensional Surface Characteristics on Urban Heat Islands over the Diurnal Cycle.” The Professional Geographer 69, no. 2: 191–202. [CrossRef]
Stone, Brian, and John M. Norman. 2006. “Land Use Planning and Surface Heat Island Formation: A Parcel-Based Radiation Flux Approach.” Atmospheric Environment 40, no. 19: 3561–3573. [CrossRef]
Chun, Bumseok and Guldmann, Jean-Michel. 2012. Spatial Analysis of the Urban Heat Island Using a 3-D City Model. Journal of Geographic Information System Association of Korea. 20. 1–16. [CrossRef]
Oukawa, Gabriel Yoshikazu, Patricia Krecl, and Admir Créso Targino. 2022. “Fine-Scale Modeling of the Urban Heat Island: A Comparison of Multiple Linear Regression and Random forest Approaches.” Science of The Total Environment 815: 152836. [CrossRef]
Chen, Jike, Shuangen Jin, and Peijun Du. 2020. “Roles of Horizontal and Vertical Tree Canopy Structure in Mitigating Daytime and Nighttime Urban Heat Island Effects.” International Journal of Applied Earth Observation and Geoinformation 89: 102060. [CrossRef]
Chen, Jike, Peijun Du, Shuangen Jin, Haiyong Ding, Cheng Chen, Yongming Xu, Li Feng, Guanhua Guo, Hongrui Zheng, and Minmin Huang. 2022. “Unravelling the Multilevel and Multi-Dimensional Impacts of Building and Tree on Surface Urban Heat Islands.” Energy and Buildings 259 (March 2022): 111843. [CrossRef]
Kunkel, K. E., Changnon, S. A., Reinke, B. C., & Arritt, R. W. 1996. The July 1995 Heat Wave in the Midwest: A Climatic Perspective and Critical Weather Factors, Bulletin of the American Meteorological Society, 77(7), 1507–1518.
Rajasekar, Umamaheshwaran, and Qihao Weng. “Urban Heat Island Monitoring and Analysis Using a Non-Parametric Model: A Case Study of Indianapolis.” ISPRS Journal of Photogrammetry and Remote Sensing 64, no. 1 (2009): 86–96. [CrossRef]
Gallo, K. P., A. L. McNab, T. R. Karl, J. F . Brown, J. J. Hood, and J. D. Tarpley. 1993. “The use of NOAA AVHRR data for assessment of the urban heat island effect”. Journal of Applied Meteorology 32 (5): 899–908.
U.S. Geological Survey (USGS). Highest and Lowest Elevations. 2022. Available online: https://www.usgs.gov/educational-resources/highest-and-lowest-elevations (accessed on 24 September 2022).
National Centers for Environmental Information (NCEI)—National Oceanic and Atmospheric Administration (NOAA). 2022; Accessed on 24 September 2022.
Adafruit. “Adafruit Sensirion SHT40 Temperature & Humidity Sensor.” adafruit industries blog RSS. 2022. Available online: https://www.adafruit.com/product/4885 (accessed on 2 November 2022).
Oke, T.R. 1982. “The energetic basis of the urban heat island.” Quarterly Journal of the Royal Meteorological Society, 108, pp. 1–24.
Basu, Rupa. 2009. “High Ambient Temperature and Mortality: A Review of Epidemiologic Studies from 2001 to 2008” Environmental Health 8, no. 1. [CrossRef]
Voelkel, Jackson, Dana Hellman, Ryu Sakuma, and Vivek Shandas. 2018. “Assessing Vulnerability to Urban Heat: A Study of Disproportionate Heat Exposure and Access to Refuge by Socio-Demographic Status in Portland, Oregon.” International Journal of Environmental Research and Public Health 15, no. 4: 640. [CrossRef]
US Geological Survey (USGS). Base Specification Online. Lidar Base Specification Online | U.S. Geological Survey. 2024. Available online: https://www.usgs.gov/ngp-standards-and-specifications/lidar-base-specification-online (accessed on 5 August 2024).
NOAA. 2021 Iowa NAIP 4-Band 8 Bit Imagery. 2022. Available online: https://www.fisheries.noaa.gov/inport/item/68084 (accessed on 22 June 2023).
ESRI. “Forest-Based Classification and Regression (Spatial Statistics).” Forest-based Classification and Regression (Spatial Statistics)-ArcGIS Pro | Documentation. 2022. Available online: https://pro.arcgis.com/en/pro-app/latest/tool-reference/spatial-statistics/forestbasedclassificationregression.htm (accessed on 1 November 2022).
Breiman, Leo. 2001. Machine Learning 45, no. 1:5–32. [CrossRef]

Figure 1. Cities for which temperature data was collected.

Figure 3. Workflow to derive the final air temperature predicted raster models using random forest algorithm.

Figure 4. Measured temperature in Waterloo/Cedar Falls During the Afternoon.

Figure 5. Measured temperature in Waterloo/Cedar Falls During the Evening.

Figure 6. Measured temperature in Waterloo/Cedar Falls during the night.

Figure 7. Modeled raster surface for Waterloo/Cedar Falls afternoon.

Figure 8. Modeled raster surface for Waterloo/Cedar Falls evening.

Figure 9. Modeled raster surface for Waterloo/Cedar Falls night.

Table 1. Summary of Runs for Air Temperature Collection.

Urban Area	Date	Number of Routes	Times of Collection	Total Measurements
Waverly	14-Jun	1	Afternoon, Evening	7,160
Cedar Rapids	20-Jun, 21-Jun	3	Afternoon, Evening, Night	23,918
Marshalltown	05-Jul, 06-Jul	1	Afternoon, Night	4,114
Sioux City	18-Jul, 19-Jul	2	Afternoon, Evening, Night	9,647
Fort Dodge	19-Jul	2	Afternoon, Evening	5,151
Des Moines	02-Aug, 03-Aug	3	Afternoon, Evening, Night	29,817
Burlington	05-Aug, 06-Aug	1	Afternoon, Evening, Night	10,315
Council Bluffs	13-Aug, 14-Aug	1	Afternoon, Evening, Night	11,805
WaterlooCF	20-Sep, 21-Sep	1	Afternoon, Evening, Night	11,299

Table 2. Random forest Results for every Urban Area/Time of the Day.

Urban Area	Afternoon R²	Evening R²	Night R²
Burlington	0.978	0.995	0.994
Cedar Rapids	0.982	0.989	0.997
Council Bluffs	0.952	0.984	0.988
Des Moines	0.952	0.974	-
Fort Dodge	0.956	-	0.963
Marshalltown	0.879	0.974	0.987
Sioux City	0.975	0.994	0.99
WaterlooCF	0.923	0.956	0.987
Waverly	0.93	0.915	-

Table 3. Measured vs. Predicted Temperature by Urban Area/Time of the Day.

Urban Area	Time of the Day	Minimum Measured Temperature (°C)	Maximum Measured Temperature (°C)	Minimum Predicted Temperature (°C)	Maximum Predicted Temperature (°C)	Difference in Minimum Temperature (°C)	Difference in Maximum Temperature (°C)
Burlington	Afternoon	31.41	35.12	31.48	35.03	0.07	-0.09
Burlington	Evening	28.47	30.99	28.51	30.97	0.04	-0.02
Burlington	Night	25.92	27.82	25.96	27.8	0.04	-0.02
Cedar Rapids	Afternoon	32.5	35.97	32.62	35.62	0.12	-0.35
Cedar Rapids	Evening	25.95	29.47	26.04	29.38	0.09	-0.09
Cedar Rapids	Night	22.36	25.57	22.54	25.47	0.18	-0.1
Council Bluffs	Afternoon	27.84	32.64	27.88	32.18	0.04	-0.46
Council Bluffs	Evening	23.4	26.6	23.42	26.38	0.02	-0.22
Council Bluffs	Night	18.66	21.59	18.72	21.5	0.06	-0.09
Des Moines	Afternoon	35.62	39.77	35.76	39.5	0.14	-0.27
Des Moines	Evening	29.75	32.91	29.8	32.78	0.05	-0.13
Des Moines	Night	26.95	29.3	27.09	29.26	0.14	-0.04
Fort Dodge	Afternoon	30.34	34.6	30.49	34.38	0.15	-0.22
Fort Dodge	Evening	22.09	27.6	22.33	27.49	0.24	-0.11
Marshalltown	Afternoon	32.79	36.9	32.89	36.58	0.1	-0.32
Marshalltown	Night	21.33	22.42	21.36	22.37	0.03	-0.05
Sioux City	Afternoon	32.75	35.85	32.84	35.64	0.09	-0.21
Sioux City	Evening	27.15	30.4	27.29	30.22	0.14	-0.18
Sioux City	Night	22.04	26.05	22.06	25.95	0.02	-0.1
WaterlooCF	Afternoon	32.35	36.57	32.49	36.49	0.14	-0.08
WaterlooCF	Evening	23.15	28.81	23.65	28.77	0.5	-0.04
WaterlooCF	Night	22.14	23.19	22.16	23.17	0.02	-0.02
Waverly	Afternoon	34.73	37.66	34.8	37.37	0.07	-0.29
Waverly	Evening	28.27	30.52	28.49	30.48	0.22	-0.04

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer