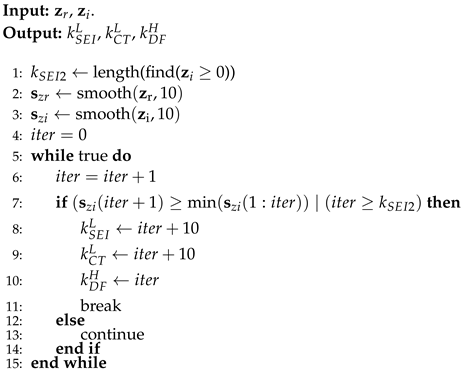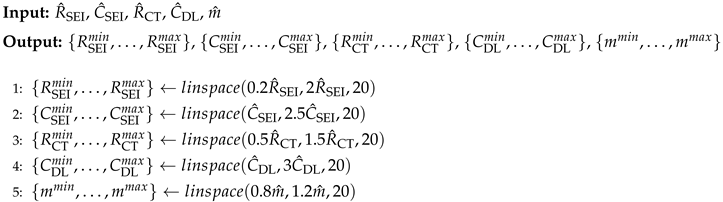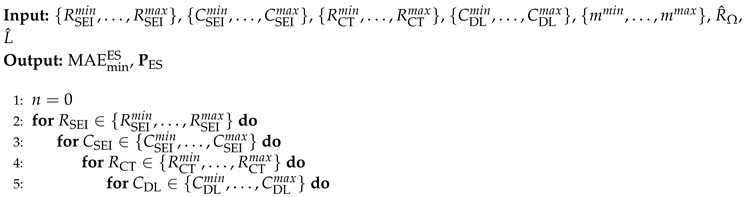1. Introduction
Battery Management System (BMS) is a crucial component in electric vehicles (EVs), renewable energy systems, and other applications that use rechargeable batteries to ensure safe and efficient operation. The primary function of a BMS is to monitor the battery’s state of charge (SOC) and state of health (SOH) [
1]. Electrochemical impedance spectroscopy (EIS) was proposed by Heaviside 1894 [
2], it has become an essential tool in the study and development of batteries, this allows researchers to better understand the fundamental electrochemical mechanisms such that correct strategies can be implemented in BMS for improving battery performance and lifespan.
EIS has been used to study the ion transport properties and electrode/electrolyte interfacial behavior of Li-ion batteries, providing insights into their performance and potential avenues for improvement [
3]. In a typical EIS experiment, a small amplitude sinusoidal current/voltage signal is applied to the battery, and the resulting voltage/current response is measured over a range of frequencies [
4]. The resulting impedance data can be analyzed using equivalent electrical circuit models to extract information on the underlying electrochemical behavior [
5]. EIS can provide detailed information on the electrochemical processes occurring within the battery, including the charge transfer kinetics, ion transport properties, and electrode/electrolyte interfacial behavior [
6]. Pastor-Fernández et al. [
7] conducted the battery aging identification and quantification research by analyzing the EIS of four parallel Li-ion cells.
The EIS can be characterized using an equivalent circuit model (ECM), which represents the battery as a combination of resistive, inductive, and capacitive components; then, the ECM parameters can be identified by fitting the ECM to the measured EIS data [
8]. There are different ECM models relevant to different types of batteries, this requires prior knowledge of the battery chemistry [
9]; furthermore, by iteratively adjusting the ECM parameters, the best fit can be obtained.
There are various approaches to fit the ECM model to the measured EIS data. For instance, nonlinear least squares (NLS) approach can be used to estimate the parameters of a nonlinear model; this aims to optimize the nonlinear function such that the difference between experimental data and the estimations based on the ECM model can be minimized [
10]. Xu et al. [
11] applied a NLS approach to fit the EIS data of a supercapacitor using the ECM model, this approach can identify the ECM parameters by minimizing the error between measurements and predictions.
Besides, Genetic Algorithm (GA) is a population-based optimization approach that can also be used in fitting the ECM to EIS data; however, the computational complexity of this approach will increase significantly with the number of ECM parameters, which means that a large number of iterations are needed; furthermore, the selection of population size, mutation rate, and crossover rate requires continuous tuning to reach the optimal estimation [
12].
The complex nonlinear least squares (CNLS) approach is widely used to fit the ECM model to EIS data. Pastor-Fernández et al. [
7] applied the CNLS algorithm to fit ECM to the EIS data measured from four Lion-ion batteries. Feng et al. [
13] applied CNLS approach to estimate ECM parameters using the EIS data collected from a battery cell at different SOC level and temperature. The drawback of this approach is that the fitting accuracy can easily be affected by the initial guess of the ECM parameters; for instance, the optimization algorithm may converge to a local minimum instead of converging to a global minimum if the initial guess is selected inappropriately; this will lead to inaccurate ECM parameter estimation. Also, CNLS approach requires the specification of ECM models, such as the number of components and the arrangement of RC circuits, which leads to extra work being done before the fitting process; furthermore, CNLS is a computationally expensive approach, especially when the size of EIS measurements are large [
14].
Ghadi [
15] applied the least squares (LS) approach to fit the EIS data to identify ECM parameters by assuming the solid electrolyte interphase (SEI) arc and charge transfer (CT) arc as semicircle, and the solid electrolyte interphase resistance
and charge transfer resistance
is the diameter of the SEI arc and the CT arc, respectively; the merit of this approach is that the estimation of the parameters can be expressed in closed form; however, the main drawback is that the accuracy of this approach is not sufficient. One of the improvements is to apply the exhaustive search (ES) approach to identify more accurate estimations of ECM parameters with the assistance of LS approach, in this paper, the ES approach will be explained in detail.
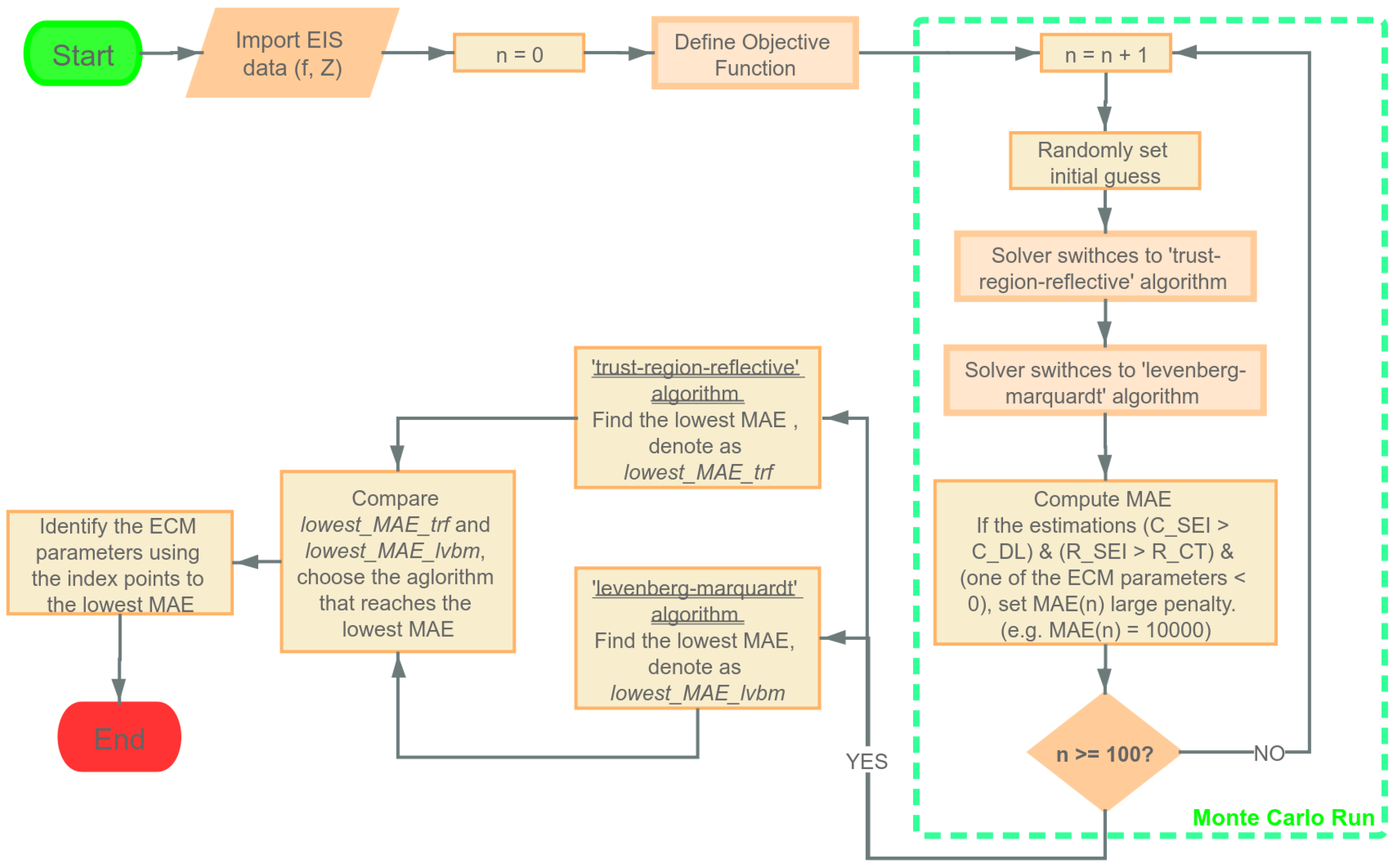
Furthermore, we proposed a novel NLS approach which only needs to define the objective function, then, randomly choose the initial guess in each Monte-Carlo Run and the estimated parameters that can reach the lowest fitting error will be selected. While the ES approach can somewhat reach a better fitting accuracy compared with the LS approach, the computational time is still very slow. Besides, the computational time of the NLS approach is much faster than that of the ES approach; in addition, compared to LS and ES approach, NLS shows higher fitting accuracy.
The contributions of this paper can be summarized as follows:
This paper compares the performance of the LS, ES, and Monte-Carlo-based NLS approaches to identifying battery ECM parameters.
Compared to the LS approach presented in [
15], the ES and the NLS approach can significantly boost the fitting accuracy of EIS measurements.
This paper presents a novel approach to implementing NLS through Monte Carlo runs. At each Monte Carlo run, the initial parameters required for the NLS approach are selected randomly. This approach results in better accuracy and much faster computation time than the ES approach.
All the methods are validated using both simulated EIS data with different noise levels and real EIS data collected from two different types of Li-ion batteries; the fitting performance of the NLS approach outweighs other approaches in all cases.
The remainder of the paper is organized as follows:
Section 2 describes the analysis of battery ECM parameters via EIS in the frequency domain.
Section 3 describes the algorithms to estimate ECM parameters using the least squares approach.
Section 4 describes algorithms of exhaustive search, the Monte-Carlo-based nonlinear least squares approach is explained in
Section 5. Implementation procedure is explained in
Section 6. Results are discussed in
Section 7.
Section 8 concludes the paper.
2. Analysis of ECM Parameters in Frequency Domain
EIS is a widely used technique to investigate the impedance response of the battery. To measure the EIS, a small perturbation current with a wide range of frequencies (0.01 Hz to 10 kHz) is injected to the battery; then, by using the discrete Fourier transform (DFT), the measured voltage and current in the time domain can be converted to the frequency domain; thus, the impedance in the frequency domain can be analyzed [
16,
17]. The battery EIS can then be represented by the real and imaginary part of the impedance on the complex plane to form the Nyquist plot [
18,
19]. This plot represents the impedance spectrum of the battery at a range of frequencies; the ECM parameters can be estimated by fitting the EIS data with suitable fitting algorithms.
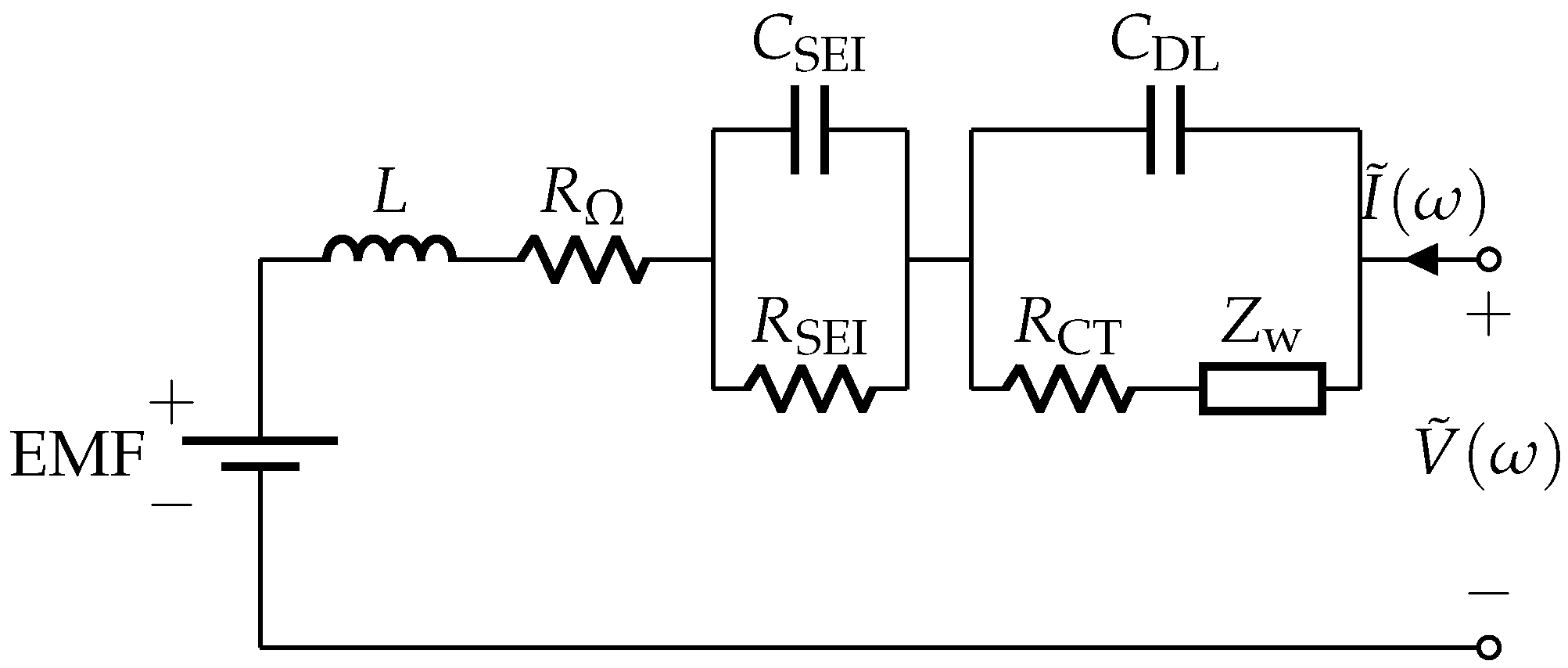
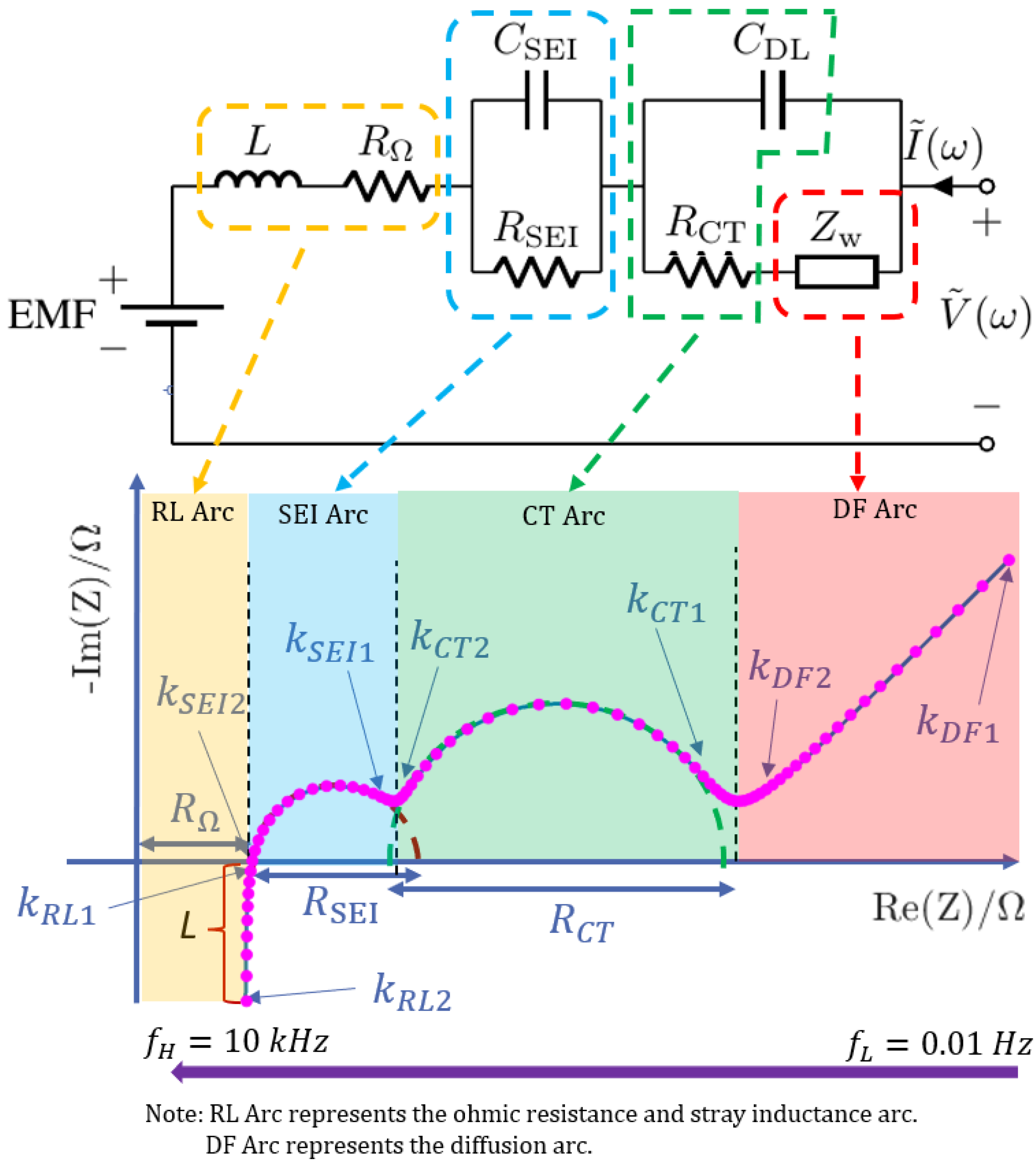
The frequency domain approach uses the Adaptive Randles (AR) ECM shown in
Figure 1. The AR-ECM consists of the following components [
17]:
Voltage Source,
Stray Inductance, L
Ohmic Resistance,
Solid Electrolytic Interface (SEI) Resistance,
SEI Capacitance,
Charge Transfer (CT) resistance,
Double Layer (DL) Capacitance,
Warburg Impedance,
Figure 1 shows the Nyquist plot relevant to the AR-ECM. According to this figure, the AC impedance
corresponding to the AR-ECM can be written as [
15]
Where
denotes the impedance in the RL arc,
denotes the impedance in the SEI arc, and
denotes the impedance in the CT arc and DF arc.
3. Least Squares Approach
To solve the problem of ECM parameter estimation, Ghadi [
15] applied the LS algorithm to fit the EIS measurements; furthermore, this approach can express the estimation of ECM parameters in closed form. In this section, an improved LS approach to AR-ECM parameter estimation is presented.
Figure 2 shows the impedance spectrum/Nyquist plot corresponding to the AR-ECM shown in
Figure 1. Each data point in the Nyquist plot is obtained through the procedure as shown in
Figure 3, where
and
are the measured voltage and current in the time domain while injecting sinusoidal current to the battery at different frequencies;
and
are the Fourier transform of the corresponding voltage and current measurements; and the real part and imaginary part of the measured impedance can be defined as:
where,
.
It can be observed that the Nyquist plot needs to be divided into four parts to see how it is directly related to the AR-ECM. The feature points of the Nyquist plot are indicated by index
and
in the DF arc; are indicated by
and
in the CT arc; are indicated by
and
in the SEI arc; and are indicated by
and
in the RL arc. Different parts of the Nyquist plot represent the battery’s impedance at different frequencies [
20]. In this paper, to keep the consistency of nomenclature, we define:
is the index of the first data point in the DF arc, in this paper, we define .
is selected such that the data points from to follows the linear line.
is selected at the beginning of the CT arc such that the data points start to follow the arc.
is selected at the end of the CT arc such that data points between follow the CT arc.
Similarly, is selected at the beginning of the SEI arc.
is selected at the end of the SEI arc such that data points between follow the SEI arc.
is selected at the beginning of the RL arc.
is selected at the end of the RL arc.
3.1. Estimation of Ohmic Resistance and Stray Inductance
As shown in
Figure 2, based on the impedance measurements in the RL arc, the estimation of ohmic resistance
can be estimated as
and stray inductance
L can be estimated using the improved method:
3.2. Estimation of Diffusion Arc’s Gradient m
Considering the imaginary part of the measured impedance
and the real part of the measured impedance
in the Diffusion arc, it can be represented with a linear model [
21]:
Assuming the measurements are from
to
as shown in
Figure 2, the following can be written as
Equation (
6) can be written in the matrix form
m and
a can be estimated using the LS approach:
Algorithm 1 estimates quantities (list) based on the following impedance values:
In this paper, the uppermost bound of the DF arc is denoted as
, the lowest bound of the CT arc is denoted as
, and the lowest bound of the SEI arc is denoted as
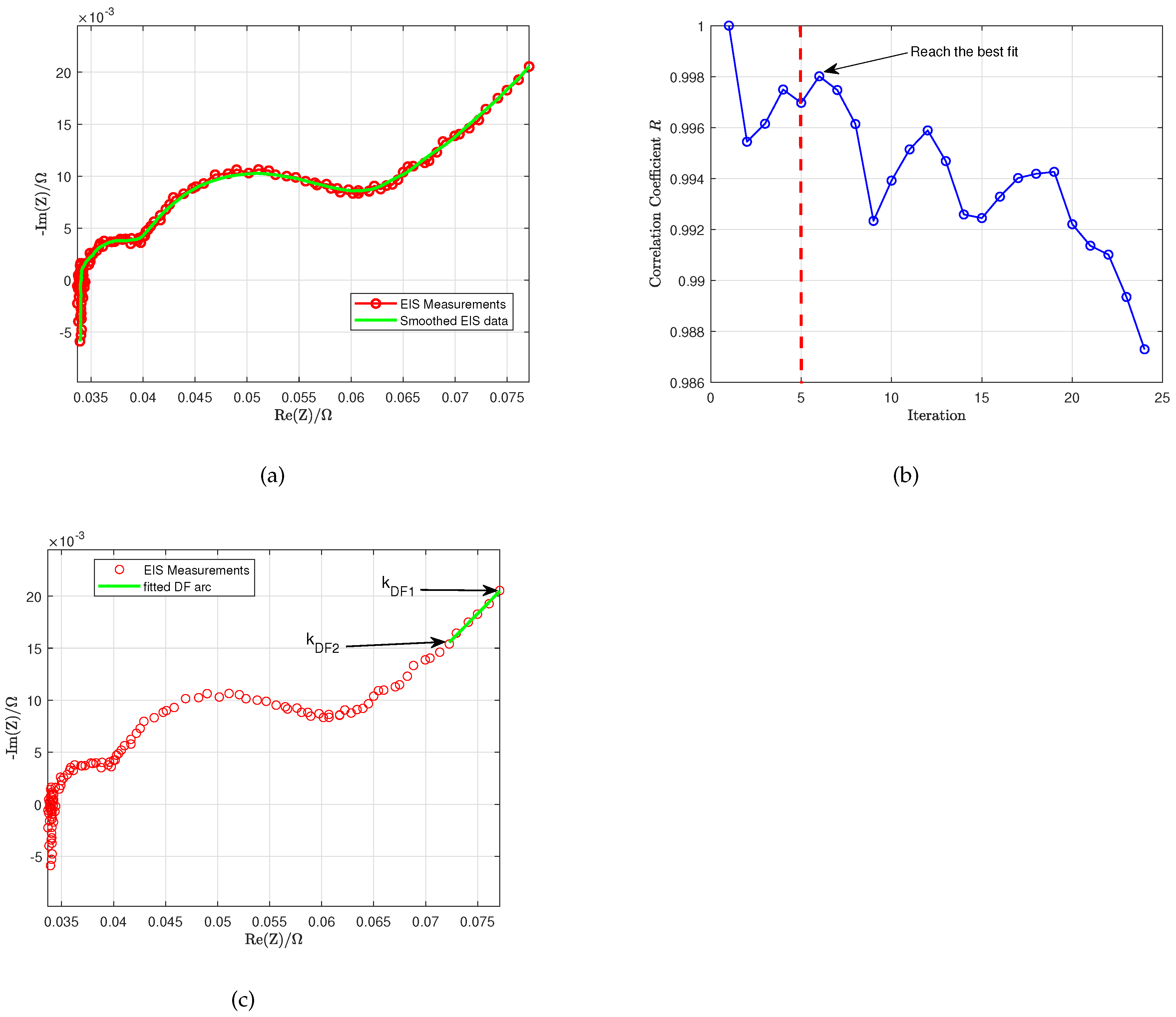
, these boundaries can be identified by applying moving average filter (MAF) to process the measured impedance data via Algorithm 1, the filtered EIS data is shown in
Figure 4a. The algorithms presented in this paper are written by utilizing MATLAB syntax. Algorithm 1 uses the following MATLAB commands: ’smooth’, ’length’, ’find’,’min’, ’break’, and ’continue’.
Figure 3.
The procedure to obtain battery EIS [
22].
Figure 3.
The procedure to obtain battery EIS [
22].
|
Algorithm 1 Boundary identification. |
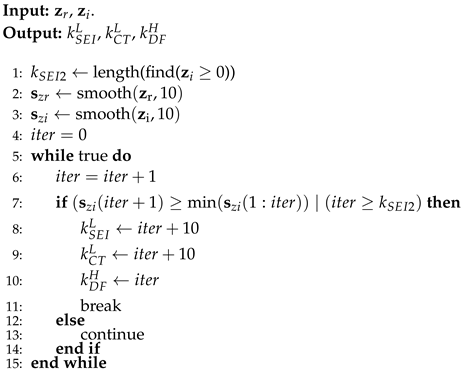 |
The gradient
m of the Diffusion arc can be estimated by fitting the Diffusion arc with the linear model mentioned in (
5) and searching out the best fit using Algorithm 2. The fitting process is also demonstrated in
Figure 4b,c. Algorithm 2 uses the following MATLAB commands: ’mean’, ’find’, and ’max’.
|
Algorithm 2 Diffusion arc fitting. |
 |
3.3. First Estimation of Warburg Coefficient
From the observation of EIS measurements in [
20], it was found that the gradient of the Diffusion arc varies with the SOC level; in addition, gradients may be different even at the same SOC level of batteries from two different manufacturers; therefore, an improved method to represent Warburg impedance is defined mathematically as
where
is the Warburg coefficient,
m is the gradient of fitted DF arc, and
j is
.
It must be emphasized here that in [
15] the gradient was assumed to be
. In this paper, it is proposed to estimate the gradient m to achieve better EIS fitting.
It can be shown based on (
1) that the Warburg impedance is significant only at lower frequencies. In
Figure 2, impedance measurements from
to
are selected to estimate the Warburg coefficient (we define
, and
is obtained via Algorithm 2). Considering the real part of the impedance
in the diffusion arc:
where
.
The observation model corresponding to (
13) is
where
and the LS estimate of
is
3.4. Estimation of and
As shown in
Figure 2, to fit the SEI arc precisely, we select feature points that lie between
and
. Let us denote the impedance measurements in the SEI arc as
The estimation of
is to fit the SEI arc using a semicircle with its centre lying on the real axis; the coordinate of this semicircle’s center can be denoted as (
, 0); the radius of the semicircle can be denoted as
; thus, the measurements in (
16) should satisfy the equation of the semicircle [
20]:
Let
and
, thus
And (18) can be rewritten as
In the matrix form, (
21) can be written as
Using LS algorithm, the estimate of
will be given by
The estimates of
c and
d are:
From
Figure 2,
is the diameter of the SEI arc; thus, by substituting the values of
c and
d in (20), the estimate of
is
The estimated centre of the semicircle can then be expressed as
The fitting accuracy of the SEI arc can be evaluated as [
23]
Where
is the geometrical distance between the actual EIS data point and predicted EIS data point, which is defined as
It can be shown in (
1) that when the frequency is very high, the impedance in CT arc and Diffusion arc will be minimal so that it is negligible; thus, we assume the
term will be zero, that is
Therefore, the impedance in SEI arc can be expressed as:
Take the imaginary part on both sides of the above equation,
Substituting the expression for
and
L from (
3) and (
4), respectively, in (36) at
:
Finally, average all the estimates
to obtain the final estimate
Using the LS approach to identify
and
via the automatic selection of feature points are fully described in Algorithm 3. In addition,
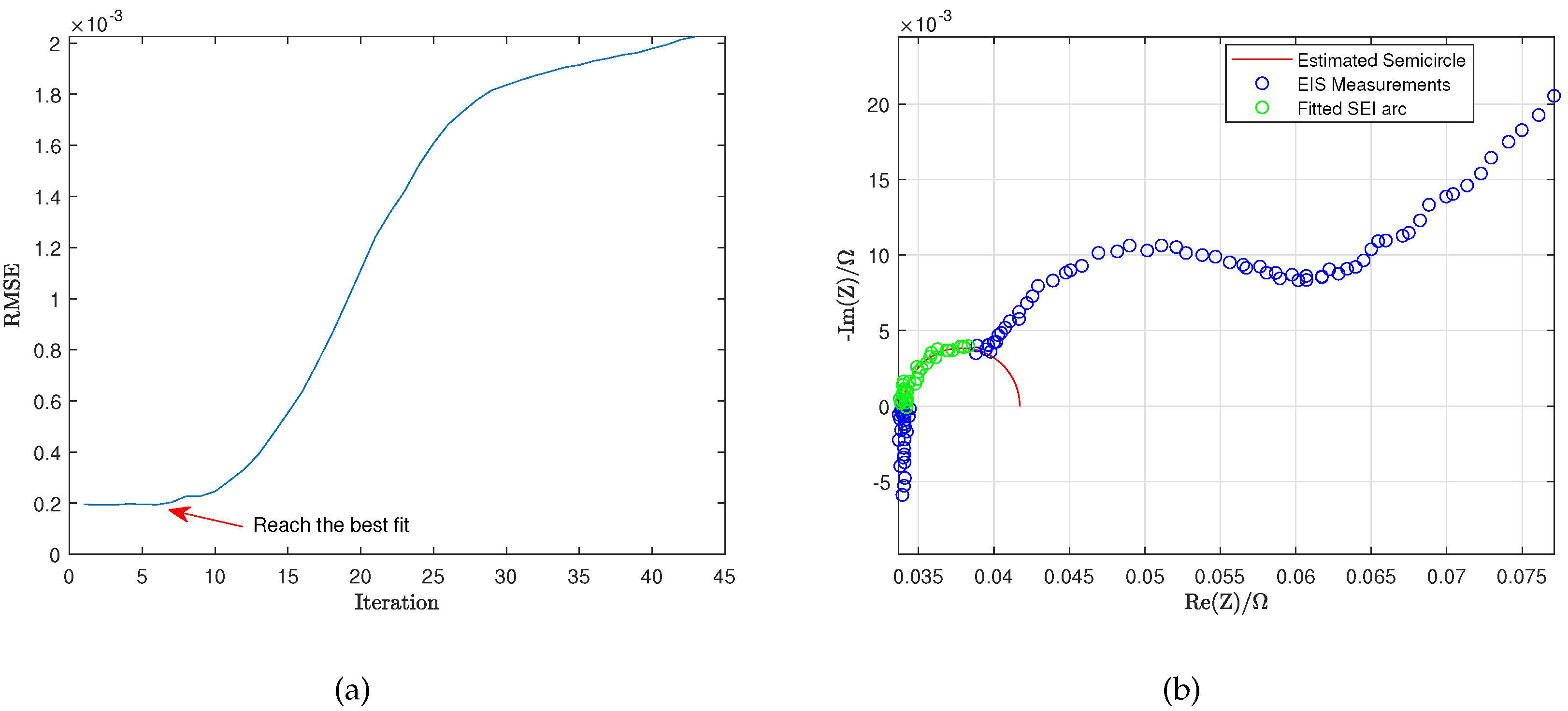
Figure 5a shows the RMSE of the fitted SEI arc in each iteration and
Figure 5b shows the SEI arc, which is selected since it can reach the best fit. Algorithm 3 uses the following MATLAB commands: ’floor’, ’length’.
|
Algorithm 3 Estimate and via automatic feature detection. |
 |
3.5. Estimation of and
It can be observed in
Figure 2 that to fit the CT arc using a semicircle precisely, we need to select feature points that lie between
to
; therefore, the impedance measurements in the CT arc can be denoted as:
Assuming that the centre of the semicircle lies on the real axis, which is noted as (
, 0), the radius of the semicircle can be noted as
; thus, the measurements in (
39) should satisfy the equation of the semicircle [
20]:
Let
and
, thus
And (41) can be rewritten as
In the matrix form, (
44) can be written as
From (
45),
can be estimated using LS algorithm
Thus, the estimates of
a and
b are:
As shown in
Figure 2,
is the diameter of the CT arc; thus, by substituting the values of
a and
b in (43), the estimate of
is
The estimated centre of the semicircle can then be expressed as
The fitting accuracy of the CT arc can be evaluated as [
23]
Where
is the geometrical distance between the actual EIS data point and predicted EIS data point, which is defined as [
23]
Therefore, the impedance in CT arc and DF arc can be expressed as:
Take the imaginary part on both sides of (
56), and substitute
with the expression given in (
13), we obtain
Substituting
L,
,
,
,
and
with the estimations given in (
4), (
3), (
25), (
38), (
48) and (
15) respectively, in the above equation at
:
Finally, average all the estimates
to obtain the final estimate
Using the LS approach to identify
and
via the automatic selection of feature points is shown in Algorithm 4. Furthermore,
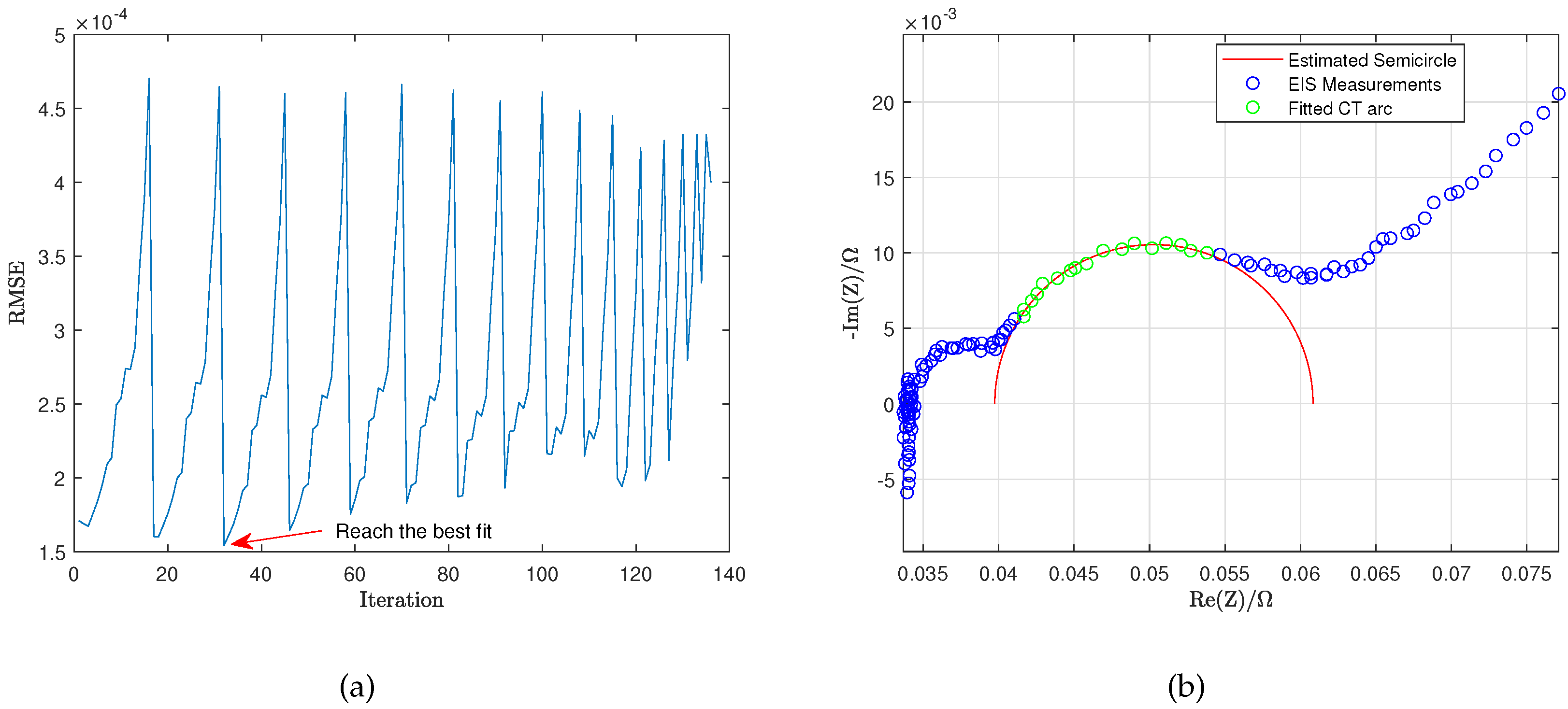
Figure 6a shows the RMSE of the fitted CT arc in each iteration, and
Figure 6b shows the CT arc selected since it can reach the best fit. Algorithm 4 uses the following MATLAB commands: ’floor’ and ’round’.
|
Algorithm 4 Estimate and via automatic feature detection. |
 |
3.6. Evaluation of the General Fitting Accuracy
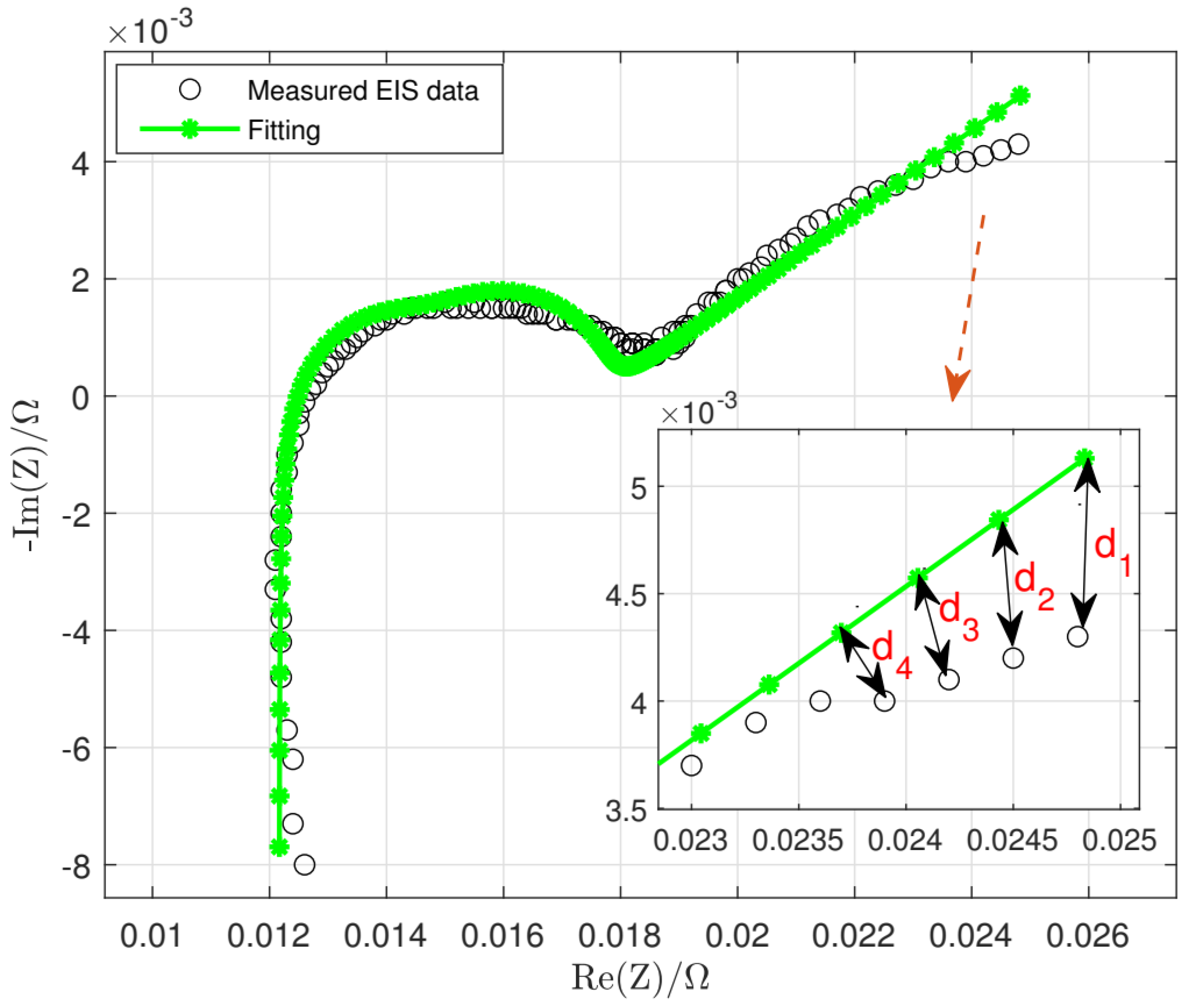
In the complex plane, the absolute value of the error between the measured EIS and estimated EIS is actually the distance between measured EIS data points and estimated EIS data points as shown in
Figure 7,
, where
, ...
are the distances between measured EIS data point
and estimated EIS data point
, which can be used to evaluate the fitting accuracy, the distance
is represented as.
where
n is the number of measurements,
.
Therefore, the evaluation of EIS fitting can be expressed as
where
is the measured impedance at
,
is the impedance estimation at
, which is computed based on (
1) with the estimated ECM parameters,
N is the total number of measurements,
denotes the absolute value of the complex number.
The goal is to fit the EIS measurements such that the fitted EIS can achieve the lowest MAE.
The percentage error of the estimated parameters can be expressed as:
8. Conclusions and Discussions
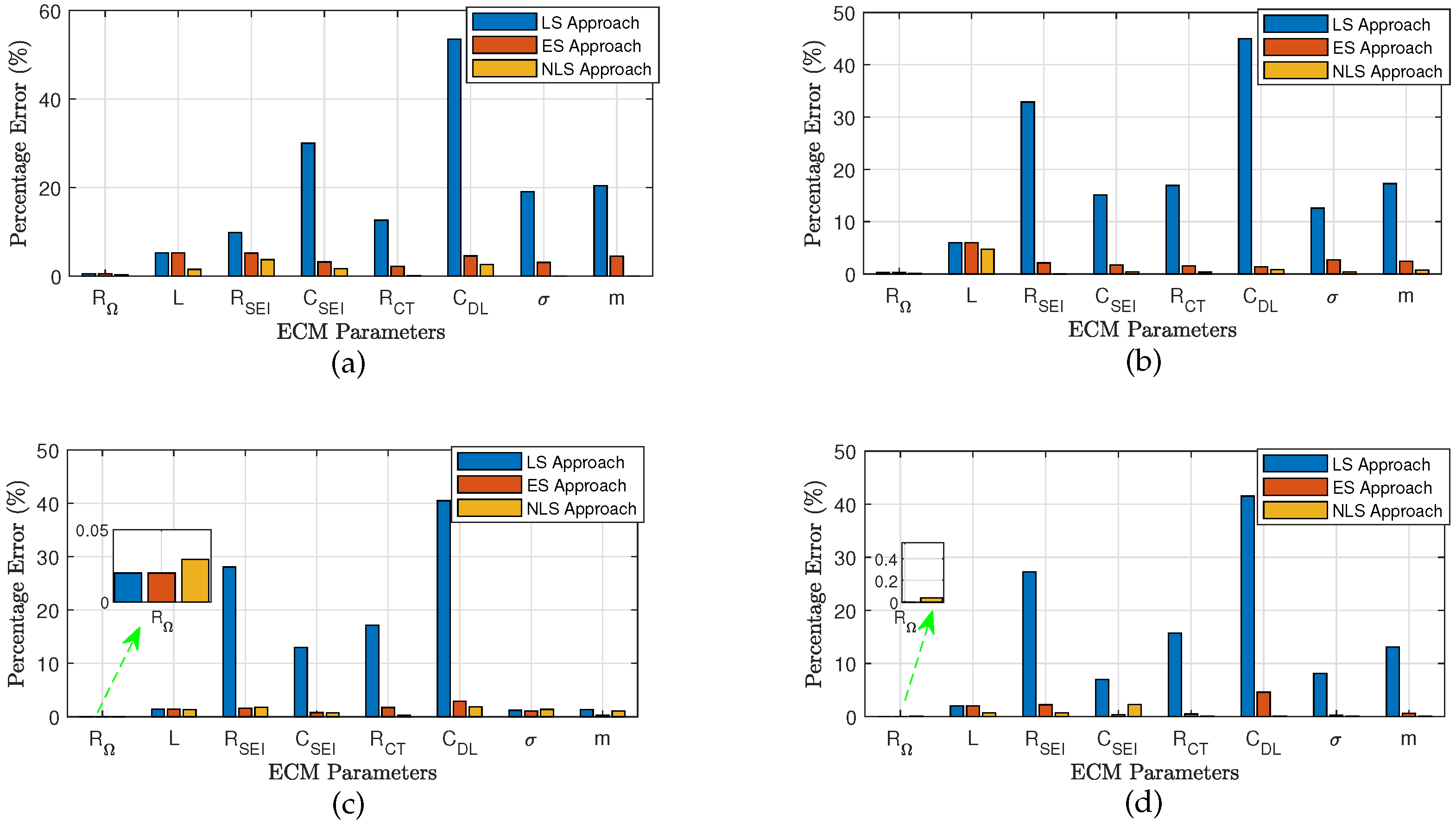
This paper presented the LS, ES, and NLS approaches to extract ECM parameters through battery impedance measurements. Compared to the LS approach, the ES and NLS approach can extract ECM parameters more accurately. Though the LS approach shows insufficient goodness of fitting at various noise levels, it can boost the fitting accuracy of the ES approach by offering initial estimations; however, it is worth mentioning that while the ECM contains more than two RC components, the computation time will increase significantly such that this approach will be infeasible.
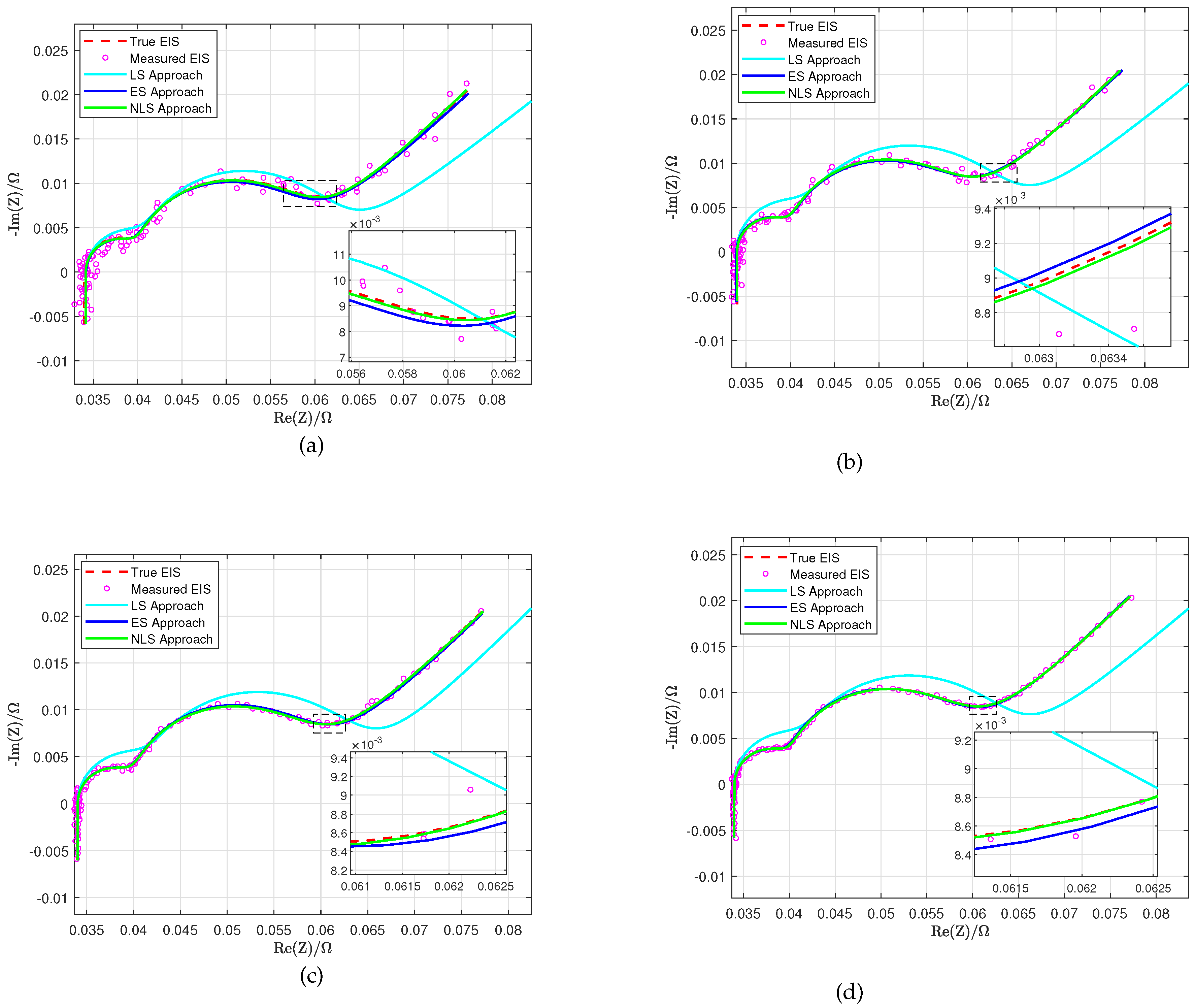
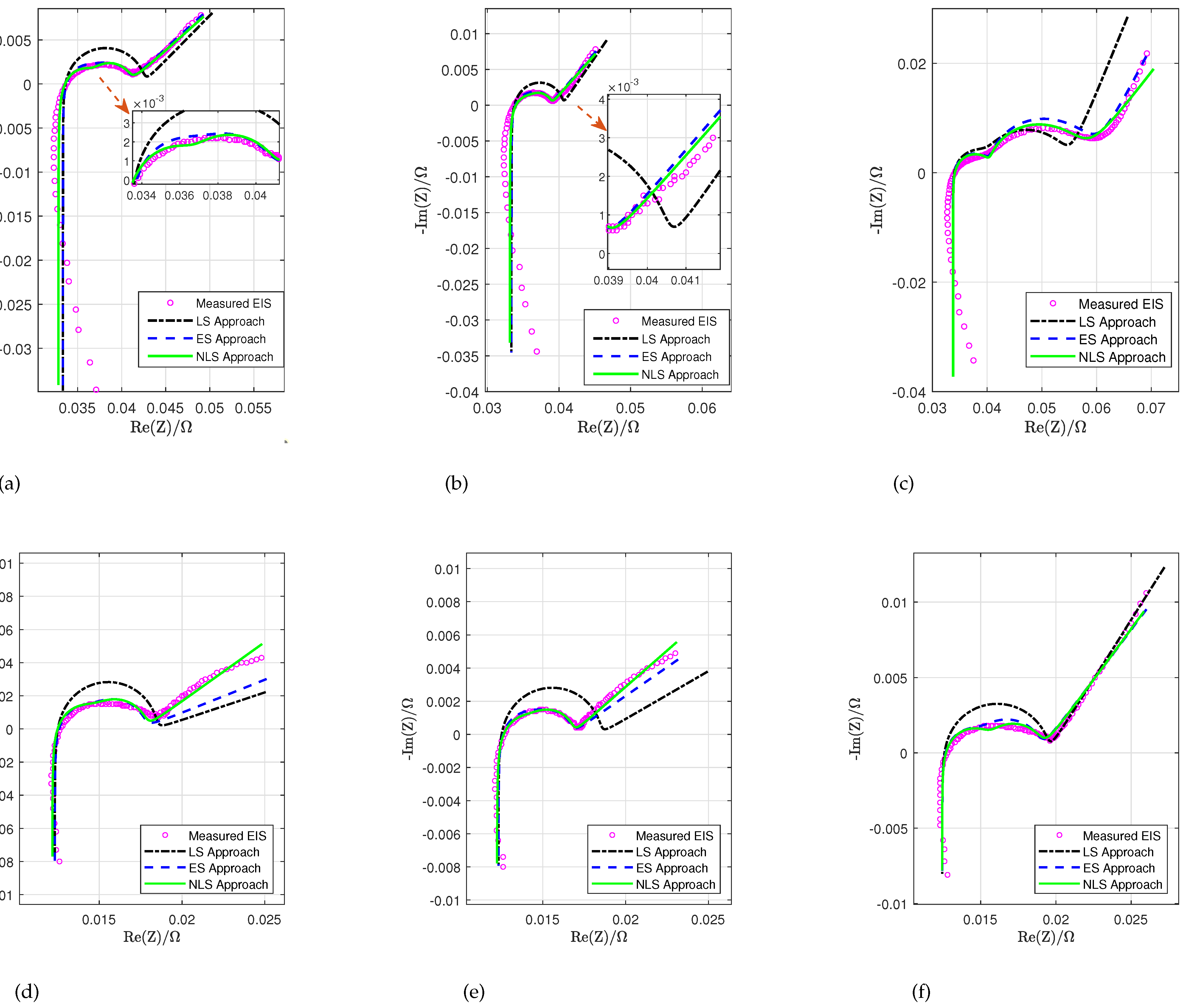
When fitting the simulated EIS data, both ES and NLS approaches show considerably high accuracy at each noise level, and the fitting accuracy increases as the noise decreases. When fitting the battery EIS measurements, the NLS approach still shows faster and more accurate fitting performance than the ES approach; this result is validated in simulated EIS data.
In future works, we will investigate deploying the NLS approach to the BMS board combined with the rapid EIS measurement hardware to improve the accuracy and computational time for ECM parameters estimation; the BMS can then adopt these precisely estimated ECM parameters for more accurate online SOC/SOH estimation.
Figure 1.
Adaptive Randles equivalent circuit model (AR-ECM) of a battery.
Figure 1.
Adaptive Randles equivalent circuit model (AR-ECM) of a battery.
Figure 2.
The theoretical Nyquist plot corresponding to the AR-ECM.
Figure 2.
The theoretical Nyquist plot corresponding to the AR-ECM.
Figure 4.
DF arc fitting process. (a) Smooth the EIS using MAF. (b) Find the highest correlation coefficient r when fitting the DF arc. (c) Fitted DF arc.
Figure 4.
DF arc fitting process. (a) Smooth the EIS using MAF. (b) Find the highest correlation coefficient r when fitting the DF arc. (c) Fitted DF arc.
Figure 5.
Fitted SEI arc using LS approach. (a) RMSE of the fitted SEI arc. (b) Best fitting of SEI arc.
Figure 5.
Fitted SEI arc using LS approach. (a) RMSE of the fitted SEI arc. (b) Best fitting of SEI arc.
Figure 6.
Fitted CT arc using LS approach. (a) RMSE of the fitted CT arc. (b) Best fitting of CT arc.
Figure 6.
Fitted CT arc using LS approach. (a) RMSE of the fitted CT arc. (b) Best fitting of CT arc.
Figure 7.
Geometrical distance between measured EIS data point and predicted EIS data point.
Figure 7.
Geometrical distance between measured EIS data point and predicted EIS data point.
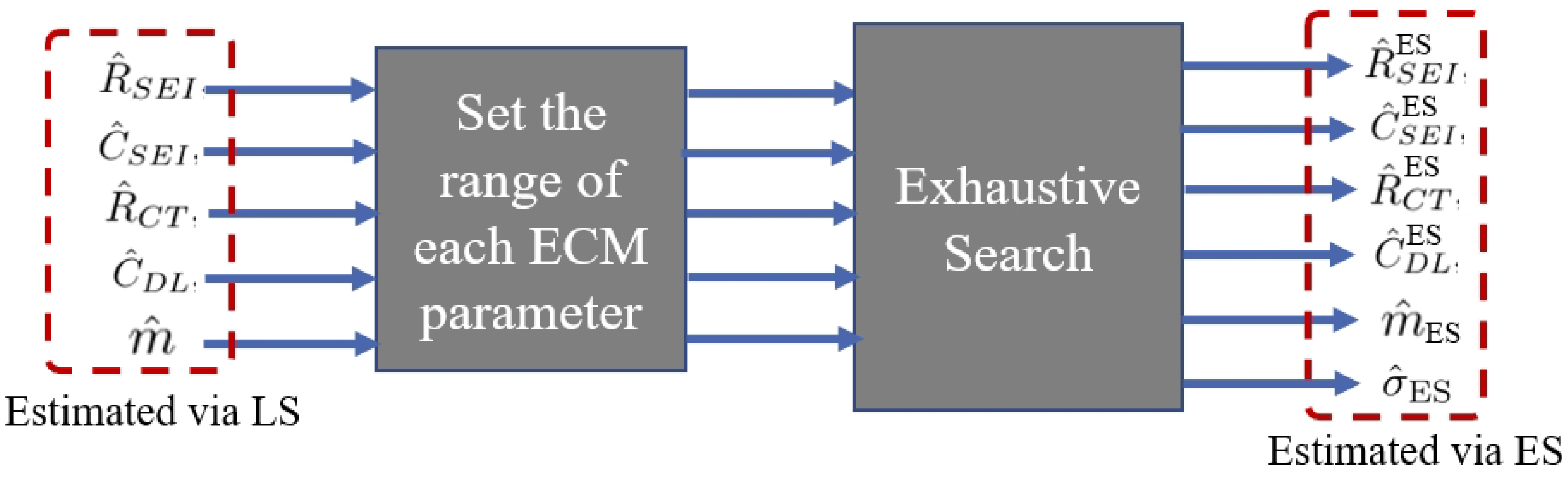
Figure 8.
The principle of ES approach.
Figure 8.
The principle of ES approach.
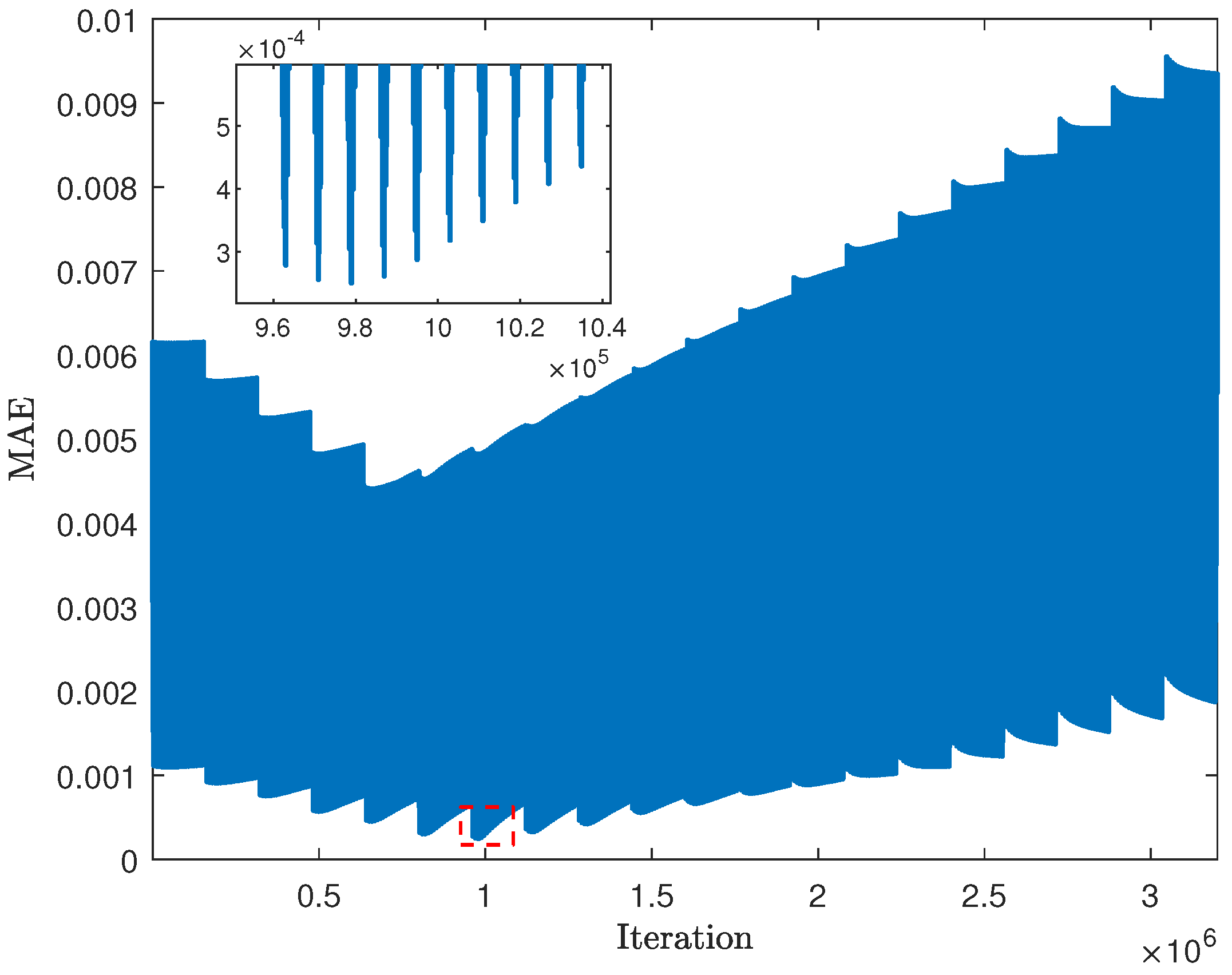
Figure 9.
Find the lowest MAE of ES approach .
Figure 9.
Find the lowest MAE of ES approach .
Figure 10.
Monte-Carlo based Nonlinear Least Sqaures Approach.
Figure 10.
Monte-Carlo based Nonlinear Least Sqaures Approach.
Figure 11.
Fitting simulated EIS measurements via LS, ES, and NLS approaches at different noise levels. (a) = 0.6046 . (b) = 0.3400 . (c) = 0.1912 . (d) = 0.1075 .
Figure 11.
Fitting simulated EIS measurements via LS, ES, and NLS approaches at different noise levels. (a) = 0.6046 . (b) = 0.3400 . (c) = 0.1912 . (d) = 0.1075 .
Figure 12.
Percentage difference between true and estimated ECM parameters at different noise levels. (a) = 0.6046 . (b) = 0.3400 . (c) = 0.1912 . (d) = 0.1075 .
Figure 12.
Percentage difference between true and estimated ECM parameters at different noise levels. (a) = 0.6046 . (b) = 0.3400 . (c) = 0.1912 . (d) = 0.1075 .
Figure 13.
Fitting real EIS measurements of LG and Molicel batteries at different SOC levels via LS, ES, and NLS approaches. (a) LG battery at 90% SOC. (b) LG battery at 50% SOC. (c) LG battery at 10% SOC. (d) Molicel battery at 90% SOC. (e) Molicel battery at 50% SOC. (f) Molicel battery at 10% SOC.
Figure 13.
Fitting real EIS measurements of LG and Molicel batteries at different SOC levels via LS, ES, and NLS approaches. (a) LG battery at 90% SOC. (b) LG battery at 50% SOC. (c) LG battery at 10% SOC. (d) Molicel battery at 90% SOC. (e) Molicel battery at 50% SOC. (f) Molicel battery at 10% SOC.
Table 1.
True ECM parameters used for EIS simulation.
Table 1.
True ECM parameters used for EIS simulation.
|
L
|
|
|
|
|
|
m |
| 34 |
95 |
6 |
1 |
18 |
8 |
5 |
1 |
Table 2.
Esitmated ECM parameters, computational time, and accuracy of using LS, ES and NLS approaches to fit simulated EIS data
Table 2.
Esitmated ECM parameters, computational time, and accuracy of using LS, ES and NLS approaches to fit simulated EIS data
|
|
|
L
|
|
|
|
|
|
m
|
|
|
| |
LS |
34.1732 |
90.0059 |
6.5913 |
0.7001 |
20.2695 |
3.7199 |
5.9541 |
0.7955 |
0.8179 |
36 |
| 0.6046 |
ES |
34.1732 |
90.0059 |
5.6893 |
1.0318 |
17.6020 |
7.6356 |
5.1542 |
0.9546 |
132.5195 |
7.7635 |
| |
NLS |
34.1513 |
94.9926 |
5.8394 |
0.9940 |
17.9632 |
7.9505 |
4.9704 |
1.0083 |
2.4578 |
7.5761 |
| |
LS |
33.9115 |
89.3443 |
7.9729 |
0.8487 |
21.0450 |
4.4013 |
5.6291 |
0.8273 |
1.3832 |
37 |
| 0.3400 |
ES |
33.9115 |
89.3443 |
6.1266 |
0.9827 |
17.7220 |
8.1076 |
5.1341 |
0.9754 |
150.6105 |
4.3921 |
| |
NLS |
33.9639 |
91.2816 |
5.9986 |
0.9877 |
18.0590 |
7.9177 |
4.9947 |
1.0035 |
2.4566 |
4.2861 |
| |
LS |
34.0076 |
93.6538 |
7.6838 |
0.8704 |
21.0861 |
4.7606 |
5.0606 |
1.0132 |
0.8481 |
31 |
| 0.1912 |
ES |
34.0076 |
93.6538 |
5.9044 |
1.0078 |
18.3116 |
7.7674 |
4.9456 |
1.0025 |
133.6487 |
2.5021 |
| |
NLS |
34.0100 |
96.2899 |
5.8936 |
1.0074 |
17.9556 |
7.8518 |
5.0690 |
0.9891 |
2.0977 |
2.2978 |
| |
LS |
33.9983 |
93.1031 |
7.6353 |
0.9300 |
20.8236 |
4.6782 |
5.4055 |
0.8688 |
0.7761 |
32 |
| 0.1075 |
ES |
33.9983 |
93.1031 |
5.8671 |
1.0034 |
18.0840 |
7.6328 |
4.9885 |
1.0060 |
134.4532 |
1.6276 |
| |
NLS |
33.9979 |
93.9546 |
5.9664 |
1.0366 |
17.9481 |
7.9246 |
5.0128 |
0.9960 |
2.0583 |
1.3904 |
Table 3.
Esitmated ECM parameters, computational time, and accuracy of using LS, ES and NLS approaches to fit real EIS data collected from LG 18650 battery while discharging
Table 3.
Esitmated ECM parameters, computational time, and accuracy of using LS, ES and NLS approaches to fit real EIS data collected from LG 18650 battery while discharging
|
|
|
L
|
|
|
|
|
|
m
|
|
|
| |
LS |
33.3308 |
555.2298 |
4.8670 |
0.3253 |
4.1876 |
0.7179 |
1.9801 |
1.0186 |
0.729 |
16 |
| 90 |
ES |
33.3308 |
555.2298 |
3.7399 |
0.3253 |
3.6366 |
2.1536 |
2.1423 |
0.9221 |
133.9269 |
4.8733 |
| |
NLS |
32.8162 |
544.9949 |
3.9102 |
0.1691 |
4.0532 |
1.9840 |
2.1418 |
0.8933 |
1.8634 |
3.9978 |
| |
LS |
33.3500 |
550.4295 |
3.9987 |
0.2971 |
3.0794 |
0.4795 |
1.5624 |
1.4540 |
0.7036 |
16 |
| 50 |
ES |
33.3500 |
550.4295 |
2.6938 |
0.2971 |
2.6742 |
1.2366 |
1.6223 |
1.1632 |
131.8468 |
4.1756 |
| |
NLS |
33.1436 |
529.4929 |
2.8149 |
0.1890 |
2.8303 |
1.2932 |
1.5826 |
1.1364 |
1.7841 |
4.012 |
| |
LS |
33.7480 |
548.8295 |
6.3127 |
0.2972 |
14.3045 |
1.7628 |
2.8718 |
2.4868 |
0.7296 |
31 |
| 10 |
ES |
33.7480 |
548.8295 |
6.6449 |
0.2972 |
18.4450 |
5.1029 |
2.6614 |
1.9894 |
133.3339 |
12 |
| |
NLS |
33.7766 |
593.9607 |
6.6475 |
0.2611 |
16.1871 |
5.2409 |
3.5550 |
1.3235 |
2.1813 |
9.3198 |
Table 4.
Esitmated ECM parameters, computational time, and accuracy of using LS, ES and NLS approaches to fit real EIS data collected from Molicel 21700 battery while discharging
Table 4.
Esitmated ECM parameters, computational time, and accuracy of using LS, ES and NLS approaches to fit real EIS data collected from Molicel 21700 battery while discharging
|
|
|
L
|
|
|
|
|
|
m
|
|
|
| |
LS |
12.3167 |
128.0069 |
3.4751 |
0.1814 |
2.5873 |
0.3466 |
1.6716 |
0.3333 |
0.763 |
12 |
| 90 |
ES |
12.3167 |
128.0069 |
2.3411 |
0.1814 |
2.9278 |
1.0399 |
1.8852 |
0.4000 |
137.6328 |
5.8928 |
| |
NLS |
12.1632 |
124.6571 |
2.5830 |
0.1318 |
2.9435 |
0.9523 |
1.7920 |
0.7169 |
1.8859 |
3.2337 |
| |
LS |
12.3167 |
128.0069 |
3.2931 |
0.1772 |
2.7962 |
0.3224 |
1.6401 |
0.5792 |
0.7237 |
15 |
| 50 |
ES |
12.3167 |
128.0069 |
2.2185 |
0.1772 |
2.1339 |
0.8994 |
1.6279 |
0.6950 |
135.3571 |
2.7111 |
| |
NLS |
12.2259 |
126.3043 |
2.0331 |
0.1294 |
2.4749 |
0.7420 |
1.5924 |
0.8763 |
1.891 |
1.3862 |
| |
LS |
12.4444 |
129.6070 |
3.8936 |
0.1900 |
3.0673 |
0.3903 |
1.9573 |
1.5757 |
0.7366 |
12 |
| 10 |
ES |
12.4444 |
129.6070 |
2.6230 |
0.1900 |
3.7937 |
1.1708 |
1.7966 |
1.3269 |
134.0528 |
3.3286 |
| |
NLS |
12.4349 |
126.2317 |
3.1777 |
0.1418 |
3.3352 |
1.9094 |
1.7361 |
1.3533 |
1.9071 |
2.7548 |