Preprint
Article
Two-Step Fifth-Order Efficient Jacobian-Free Iterative Method for Solving Nonlinear Systems
Altmetrics
Downloads
94
Views
37
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
10 September 2024
Posted:
11 September 2024
You are already at the latest version
Alerts
Abstract
This article introduces a novel two-step fifth-order Jacobian-free iterative method aimed at efficiently solving systems of nonlinear equations. The method leverages the benefits of Jacobian-free approaches, utilizing divided differences to circumvent the computationally intensive calculation of Jacobian matrices. This adaptation significantly reduces computational overhead and simplifies the implementation process while maintaining high convergence rates. We demonstrate that this method achieves fifth-order convergence under specific parameter settings, with a broad applicability across various types of nonlinear systems. The effectiveness of the proposed method is validated through a series of numerical experiments which confirm its superior performance in terms of accuracy and computational efficiency compared to existing methods.
Keywords:
Subject: Computer Science and Mathematics - Computational Mathematics
1. Introduction
Let be a nonlinear system of equations, , and the functions for , are the coordinate components of F, expressed as . Solving nonlinear systems is generally challenging, and solutions are typically found by linearizing the problem or employing a fixed-point iteration function , leading to an iterative fixed-point method. Among the various root-finding techniques for nonlinear systems, Newton’s method is the most well-known, which follows the second-order iterative procedure:
being the Jacobian matrix of F at the k-th iterate.
Recenty, many researchers have focused on developing iterative methods that outperform Newton’s method in terms of both efficiency and order of convergence. Numerous approaches need the computation of at different points along each iteration. Nevertheless, calculating the Jacobian poses significant challenges, particularly in high-dimensional problems, where its computation can be costly or even impractical. In some instances, the Jacobian may not exist at all.
To address this issue, alternative approaches have been proposed, such as replacing the Jacobian matrix with a divided difference operator. One of the simplest alternatives is the multidimensional version of Steffensen’s method, attributed to Samanskii [1,2], which substitutes the Jacobian in Newton’s procedure with a first-order operator of divided differences:
being , and is the operator of divided differences related to F [3],
This substitution retains the 2-nd order of convergence while bypassing the calculation of the .
Although both Steffensen and Newton methods exhibit quadratic convergence, it has been shown that Steffensen’s scheme is less stable than Newton’s method, with stability depending more on the initial guess. This has been thoroughly analyzed in [4,5], where it was found that, for scalar cases , derivative-free iterative methods become more stable when selecting for small real values of .
However, substituting the Jacobian with divided differences can result in lower convergence order for some iterative methods. For example, the multidimensional version of Ostrowski’s fourth-order method (see [6,13]):
achieves only cubic convergence if is replaced by , as follows:
Other fourth-order methods also loose their convergence order when the Jacobian is replaced with divided differences, such as Jarratt’s scheme [7], Sharma’s method [8], Montazeri’s method [9], Ostrowski’s vectorial extension ([13,15]), and Sharma-Arora’s fifth-order scheme [10]. In all these cases, Jacobian-free versions of the methods reduce to lower orders of convergence.
Nevertheless, Amiri et al. [11] demonstrated that using a specialized divided difference operator of the form , where , , as an approximation of the Jacobian matrix, may preserve the convergence order. By selecting an appropriate parameter m, the original fourth-order convergence of these methods can be maintained.
Despite the reduction in performance observed in some Jacobian-free methods, it is important to highlight that there are iterative methods that are successfully modified in their iterative expressions to preserve the order of convergence, even after fully transitioning to Jacobian-free formulations. This is the case of a combination of the Traub-Steffensen family of methods and a second step with divided differences operators, proposed by Behl et al. in [12]
where . The iterative schemes have a fourth order of convergence for every , , for our purposes we choose and this be called .
Now, we consider several efficient vectorial iterative schemes existing in the literature to transform them in their Jacobian-free versions following the idea of Amiri et al. [11]. In the following sections, we compare these later schemes with our proposed procedures, in terms of efficiency and numerical performance. The first one is the vectorial extension of Ostrowski’s scheme (see [13–15], for instance),
whose Jacobian-free version obtained by substituting the Jacobian matrix by the divided difference operator (with Amiri et al. approach [11], ) is
where , and (with ), . We denote this method as .
Another fourth-order method proposed by Sharma in [16] using Jacobian matrices is
to which we apply the same Amiri’s procedure performed for (2), getting its Jacobian-free partner
that we denote by , where and , , firstly appeared in [11].
We finish with a sixth-order scheme [16], which is obtained by adding a step to the previous method (4),
Similarly, its Jacobian-free version was constructed in [11] and denoted by ,
where again and , . It should be noticed that in schemes (3), (5) and (7), we employed a quadratic element-by-element power of in the divided differences. This adjustment was essential for preserving the convergence order of the original method (see [11]). However, in our proposal, the order of convergence of the original schemes is held avoiding the computational cost of this element-by-element power.
Therefore, to avoid the calculation of Jacobian matrices, which can be a bottleneck in terms of computational efficiency especially for large systems, this article presents a two-step fifth-order efficient Jacobian-free iterative method that addresses these challenges by eliminating the need for direct Jacobian computation. Our approach is grounded in the use of divided differences and scalar accelerators recently developed in some very efficient schemes (using Jacobian matrices), [17,18]. This not only reduces the computational costs, but also accelerates the convergence with simpler iterative expressions. The proposed method’s design and theoretical underpinnings are discussed, emphasizing its ability to achieve high-order convergence without the Jacobian calculations typically required.
In the Section 2, we develop a new parametric class of Jacobian-free iterative methods using scalar accelerators and demonstrate its theoretical order of convergence, depending on the values of the parameters involved. Subsequently, in Section 3 we carry out an efficiency analysis in which we compare our proposed method with the Jacobian-free versions of others previously cited in the literature. Finally, Section 4 presents practical results of these iterative methods applied to different nonlinear systems of equations.
2. Construction and Convergence of New Jacobian-Free Iterative Method
In 2023, Singh, Sharma and Kumar [18] proposed a family of iterative methods,
where is a scalar accelerator that can be interpreted as , and , respectively. The real parameters and make the order of convergence of the method five if =, order four if and arbitrary and order two if and arbitrary. It is known that in many practical applications, computing the Jacobian matrix can be very resource-intensive and time-consuming, therefore, Jacobian-free methods are often preferred.
Making a modification to the scheme (8) by replacing the Jacobian matrices by specific divided differences, we obtain the following family:
where , , and . From now on, we will refer to our modified scheme as .
The following result shows the error equations arising from method (9) for the possible parameter values, thereby demonstrating that the convergence results of the family (8) hold.
Theorem 1.
Let F be a differentiable enough function defined in the open convex neighbourhood Ω of ξ, solution of . Let us also consider an initial seed near enough to ξ and let be continuous and invertible at ξ. Then, the parametric class of iterative schemes presented in (9) locally converges for all , with the order of convergence given by:
- (a)
- Fifth-order convergence if , being the corresponding error equation
- (b)
- Fourth-order convergence if , being the corresponding error equation
- (c)
- Second-order convergence if , being the corresponding error equation
being , , and , , are combinations of , and denoting the error at iteration k by .
Proof.
Let be the error at the k-th iteration and let be a solution of . Then, expanding in the neighborhood of , we have
Then, based on the formula of Genochi and Hermite (see [3]) we have
Taking into account that , and performing a series expansion up to fifth-order, we get
Next, we expand the inverse of the divided difference operator , forcing it to satisfy ,
where
By using the Taylor expansions of defined in (13) and obtained in (17), we get the error equation for the first step:
where
Now, we find the error equation for the second step,
from which arises
Then, following the process seen in (14), the expansion of the second difference operator is given by
that can be expressed as
being
Again, we get in a similar way as in (17),
Now, we proceed to calculate the expansion of , obtaining
According to Theorem 1 proven by Singh, Sharma and Kurmar in [18], we have
where
and
Finally, fitting (19), (27) and the last result obtained in (30), we have
In this last result, it is easy to observe that when is different from one () the iterative method has order of convergence equal to two, since the term would not cancel out. However, when both terms with and cancel out while the term is as follows
Let us remember that , so that
but since , then , so . Also, . Given that , replacing in equation (32), we get
resulting in the error equation
From the above it is clear to see that if but only order four is reached. □
3. Efficiency Analysis
We have demonstrated the order of convergence of the proposed class of the iterative method for the different values of the parameters . In this section, we perform a computational effort study considering the effort of solving the involved linear systems per iteration and the other computational cost (functional evaluations, amount of product/quotients,...), not only for the proposed class but also for some Jacobian-free schemes presented in the introductory section.
In order to get this aim, it is known that the needed operations (products/quotients) of solving a linear system is
However, if other linear systems with the same coefficient matrix are solved, then the cost upgrades only in operations each; for each divided difference we calculate quotients; for each functional evaluation of F at different points, a cost of n real evaluations; for each evaluation of a divided differences, scalar evaluations; Indeed, a matrix–vector product needs product/quotients. Based on the above, the computational cost for each method appears in Table 1. From family (9), which we call , we consider the fifth-order member and its fourth-order partner . They have the same computational cost, which will be reflected, along with the others, in Table 1.
The results presented in Table 1 show that the method with the highest computational cost is , while those with intermediate costs are and , with the latter being slightly better. The ones that offer the lowest cost are and , although the latter has sixth-order convergence, which is a factor to consider when obtaining the efficiency index.
In order to show more clearly how computational cost influences the efficiency index , where p is the convergence order of the corresponding scheme (see [20]), we present Figure 1 and Figure 2 for different sizes of the nonlinear system to be solved.
In Figure 1, we observe that for systems with dimensions , the proposed class of vectorial iterative methods (9) shows a better computational efficiency than the other schemes, for both members of the family. On the other hand, as the system grows to sizes it becomes apparent that methods and yield better results. Let us notice that for sizes of , our method has better efficiency than , and for sizes , it has better efficiency compared to (see Figure 2).
In the next section, we check the theoretical convergence order of our proposed method and assess the efficiency of different schemes on nonlinear systems of various sizes.
4. Numerical Results
In this section, we test numerically that the theoretical order holds for practical purposes in the proposed Jacobian-free class (9). Moreover, we compare it with the methods appearing in the efficiency section to show their accuracy and computational performance.
Below we show some nonlinear problems, including one whose related nonlinear function is not differentiable, in order to test the applicability of the methods on different kind of problems.
- We consider , wherewhose solution is .
- We also have , wherebeing its solution.
- We also consider , wherewhere the solution is .
- We test also , wherewhose solution is .
- , wherebeing it solution .
- , whereand there exist two solutions, , and .
- , wherebeing .
- We also test , wherewith solutions and .
Numerical results have been obtained with Matlab2022b version, using 8000 digits in variable precision arithmetics, a processor AMD RADEON R7, 12 COMPUTE CORES 4C, +8G-Ram, 2.70 GHz. These results are shown in Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12 and Table 13, including the following information, where the appearing norms are Euclidean:
- k: amount of iterations needed ("-" appears when the scheme does not converge or it needs more iterations than the maximum allowed).
- : obtained solution.
- Cpu-time: average time in seconds required by the iterative method to reach the solution of the problem when executed ten times.
-
: approximated computational order of convergence, ACOC, firstly appeaaring in [19](if is not stable, then "-" appears in the table).
- .
- . If or are very far from zero or we get infinity or NAN, then "-" appears in the table.
Regarding the stopping criterium, the iterative process ends when one of the following conditions is fulfilled:
- (i)
- ,
- (ii)
- ,
- (iii)
- 50 iterations are reached.
In Table 2, method reached the maximum number of iterations without converging to the solution, while the most notable scheme is in almost all aspects such as errors, iterations and computational time. On the other hand, although exhibits a lower computational time than , the latter has an additional iteration, a relatively similar time, and better errors, proving that it might even be superior in terms of efficiency.
In Table 3, we observe that our proposed schemes yield the best computational times, with method standing out for having the smallest error norm among all schemes. The method, while showing good overall performance in terms of errors, is more computationally expensive as it takes one iteration longer to reach the solution to the system and slightly more time compared to methods, indicating that the program takes more time to generate each iteration.
The results in Table 4 and Table 5 are very balanced, with the method showing the best errors while the shortest computational time is achieved by the method. However, this last one takes more effort to generate an iteration because, despite producing one less iteration than the other iterative methods, their execution times are very similar.
For Table 6, we note that the best computational times are obtained by the methods . On the other hand, the best errors are obtained by scheme, which has a competitive computational time considering it requires four iterations, similar to . The latter has shown to be the one that requires the most time to converge.
In Table 7, the best errors were obtained by and , which converged to different solutions, while in terms of performance, and appeared to be better.
In Table 8, method could not converge to the solution because it reached the maximum number of iterations, whereas the and methods showed better overall behavior.
In the Table 9, method stands out with the lowest computational time, being more efficient than the others, despite requiring a similar number of iterations and showing a convergence order of , close to the other methods. The method is less efficient, with a computational time of but with a larger errors. , is competitive only falling slightly behind in computational time. The methods and are the most expensive in terms of computational time, requiring 7 and 6 iterations respectively, with the highest time recorded for . Despite their higher orders of convergence, both methods show lower overall efficiency compared to the and methods.
In Table 10, method stands out as the one with the lowest computational time, requiring fewer iterations compared to the other methods and showing a convergence order of 4.05. The method, despite having the same convergence order as , shows a slightly higher computational time and larger errors in the difference between iterates. , which requires more iterations, falls only slightly behind in computational time but remains competitive overall. Methods and do not converge to the solution, as division by zero occurred when calculating divided differences.
Method stands out as the one with the lowest computational time, requiring fewer iterations compared to the other methods and showing a convergence order of . scheme, although it has the same convergence order as , shows a significantly higher computational time but better results in terms of errors. , while requiring more iterations than , still maintains a competitive time compared to . Division by zero is the reason why the other methods could not reach the solution.
In Table 12, it is observed that only the members of our proposed class converge, and they do it to different solutions. stands out as the most efficient in terms of time and iterations, while yields the best errors. The method do not converge because it exceeded the maximum number of iterations, while the other methods could not reach the solution due to division by zero during the computation of divided differences.
The observations for Table 13 are the same as those in the previous one, but now method does not converge to the solution due to a division by zero, just like the other methods that do not converge.
5. Conclusions
The fifth-order Jacobian-Free iterative method with scalar accelerators developed in this study (along with its fourth-order partners) has proven to be an efficient tool for solving nonlinear systems of equations. It preserves the convergence order of the original scheme, despite the elimination of Jacobian matrix calculations, with low computational cost. The substitution of these matrices with divided differences not only reduces computational complexity but also facilitates implementation, maintaining high precision and efficiency. The numerical results highlight its superiority in terms of performance compared to conventional methods, especially for not-so-large systems.
Author Contributions
Conceptualization, J.R.T. and A.C.; software, A.R.-C.; methodology, J.G.M.; validation, J.G.M., A.C. and J.R.T.; investigation, A.C.; formal analysis, J.R.; resources, A.R.-C.; writing—original draft preparation, A.R.-C.; visualization, J.G.M.; writing—review and editing, J.R.T. and A.C.; supervision, J.R.T. and A.C. All the authors have read and agreed to the published version of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Samanskii, V.: On a modification of the Newton method. Ukr. Math. J. 19, 133–138 (1967).
- Steffensen, J.F.: Remarks on iteration. Skand. Aktuarietidskr. 1, 64–72 (1933). [CrossRef]
- Ortega, J.M.; Rheinboldt, W.C. Iterative Solution of Nonlinear Equations in Several Variables; Academic Press: Cambridge, MA, USA, 1970. [CrossRef]
- Chicharro, F.I., Cordero, A., Gutiérrez, J.M., Torregrosa, J.R.: Complex dynamics of derivative-free methods for nonlinear equations. Appl. Math. Comput. 219, 7023–7035 (2013). [CrossRef]
- Cordero, A., Soleymani, F., Torregrosa, J.R., Shateyi, S.: Basins of attraction for various Steffensen-type methods. Appl. Math. 2014, Article ID 539707 1–17 (2014). [CrossRef]
- Cordero, A., García-Maimó, J., Torregrosa, J.R., Vassileva, M.P.: Solving nonlinear problems by Ostrowski–Chun type parametric families. Math. Chem. 53, 430–449 (2015). [CrossRef]
- Jarratt, P.: Some fourth order multipoint iterative methods for solving equations. Math. Comp. 20, 434–437 (1966). [CrossRef]
- Sharma, J.R., Arora, H.: On efficient weighted-Newton methods for solving systems of nonlinear equations. Appl. Math. Comput. 222, 497–506 (2013). [CrossRef]
- Montazeri, H., Soleymani, F., Shateyi, S., Motsa, S.S.: On a new method for computing the numerical solution of systems of nonlinear equations. Appl. Math. 2012 ID. 751975, 1–15 (2012). [CrossRef]
- Sharma, J.R., Arora, H.: Efficient derivative-free numerical methods for solving systems of nonlinear equations. Comp. Appl. Math. 35, 269–284 (2016). [CrossRef]
- Amiri, A.R., Cordero, A., Darvishi, M.T., Torregrosa, J.R.: Preserving the order of convergence: Low-complexity Jacobian-free iterative schemes for solving nonlinear systems. Comput. Appl. Math. 337, 87–97 (2018). [CrossRef]
- Behl, R., Cordero, A., Torregrosa, J. R., Bhalla, S., A New High-Order Jacobian-Free Iterative Method with Memory for Solving Nonlinear Systems. Mathematics 9(17), 2122 (2021). [CrossRef]
- Ostrowski, A.M., Solutions of Equations and Systems of Equations, Academic Press, New York, London, 1966.
- Abad, M.F., Cordero, A., Torregrosa, J.R., A family of seventh-order schemes for solving nonlinear systems, Bull. Math. Soc. Sci. Math. Roumanie 57(105)(2), 133–145 (2014).
- Cordero, A. , Maimó, J.G. ,Torregrosa, J.R., Vassileva, M.P., Solving nonlinear problems by Ostrowski-Chun type parametric families, Math. Chem. 53, 430–449 (2015). [CrossRef]
- Sharma, J.R., Arora, H., On efficient weighted-Newton methods for solving systems of nonlinear equations, Applied Mathematics and Computation 222, 497–506 (2013). [CrossRef]
- Cordero, A, Rojas–Hiciano, R. V., Torregrosa, J. R., Vassileva, M. P: A highly efficient class of optimal fourth-order methods for solving nonlinear systems. Numerical Algorithms 95, 1879–1904 (2024). [CrossRef]
- Singh, H., Sharma, J. R., Kumar, S.: A simple yet efficient two-step fifth-order weighted-Newton method for nonlinear models. Numerical Algorithms 93, 203–225 (2023). [CrossRef]
- Cordero, A., Torregrosa, J.R., Variants of Newton’s method using fifth order quadrature formulas. Appl. Math. Comput. 190, 686–698 (2007). [CrossRef]
- Traub, I.F. Iterative Methods for the Solution of Equations; Prentice-Hall: Englewood Cliffs, NJ, USA, 1964. [CrossRef]
Figure 1.
I indices for and comparison methods
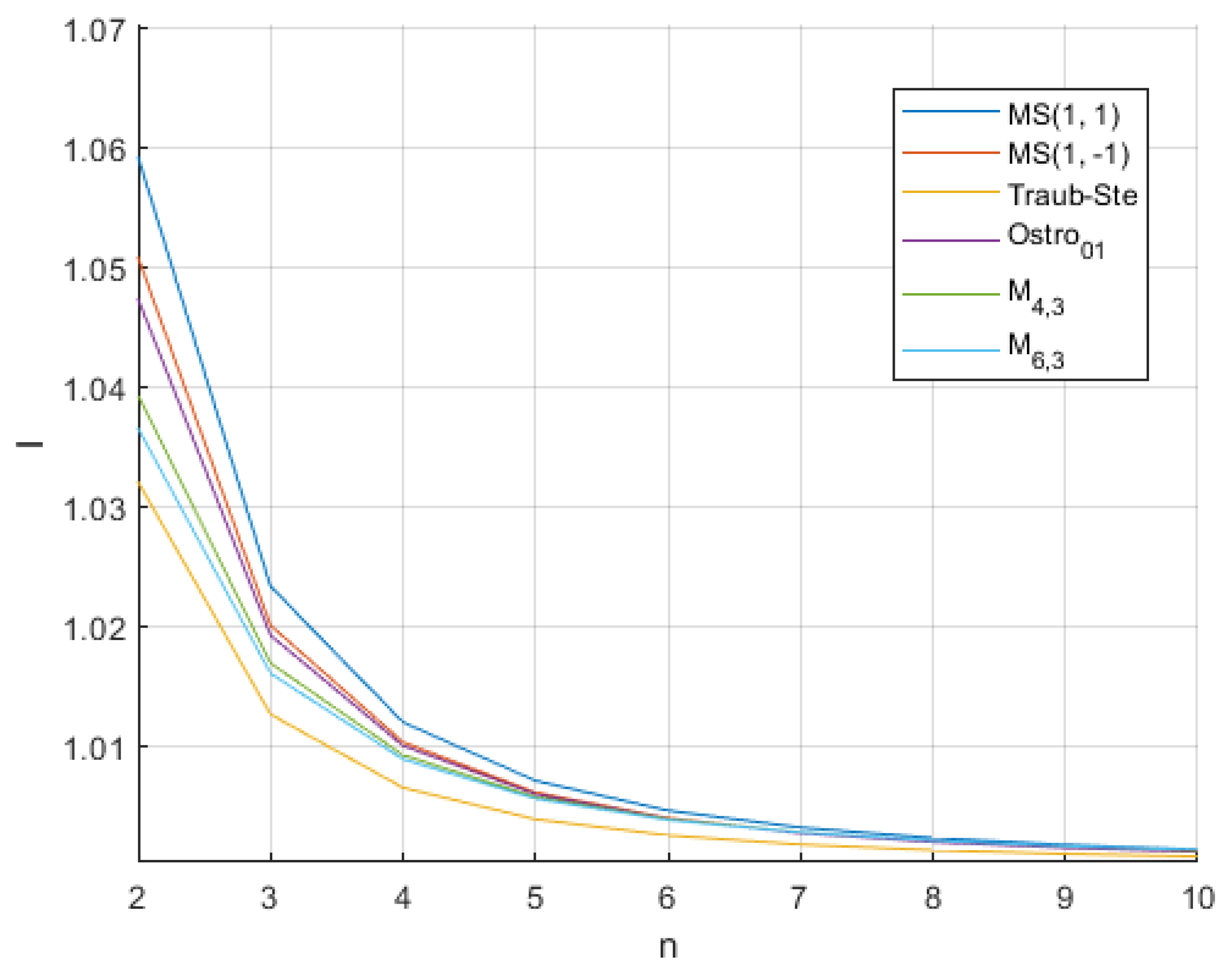
Figure 2.
I indices for and comparison schemes
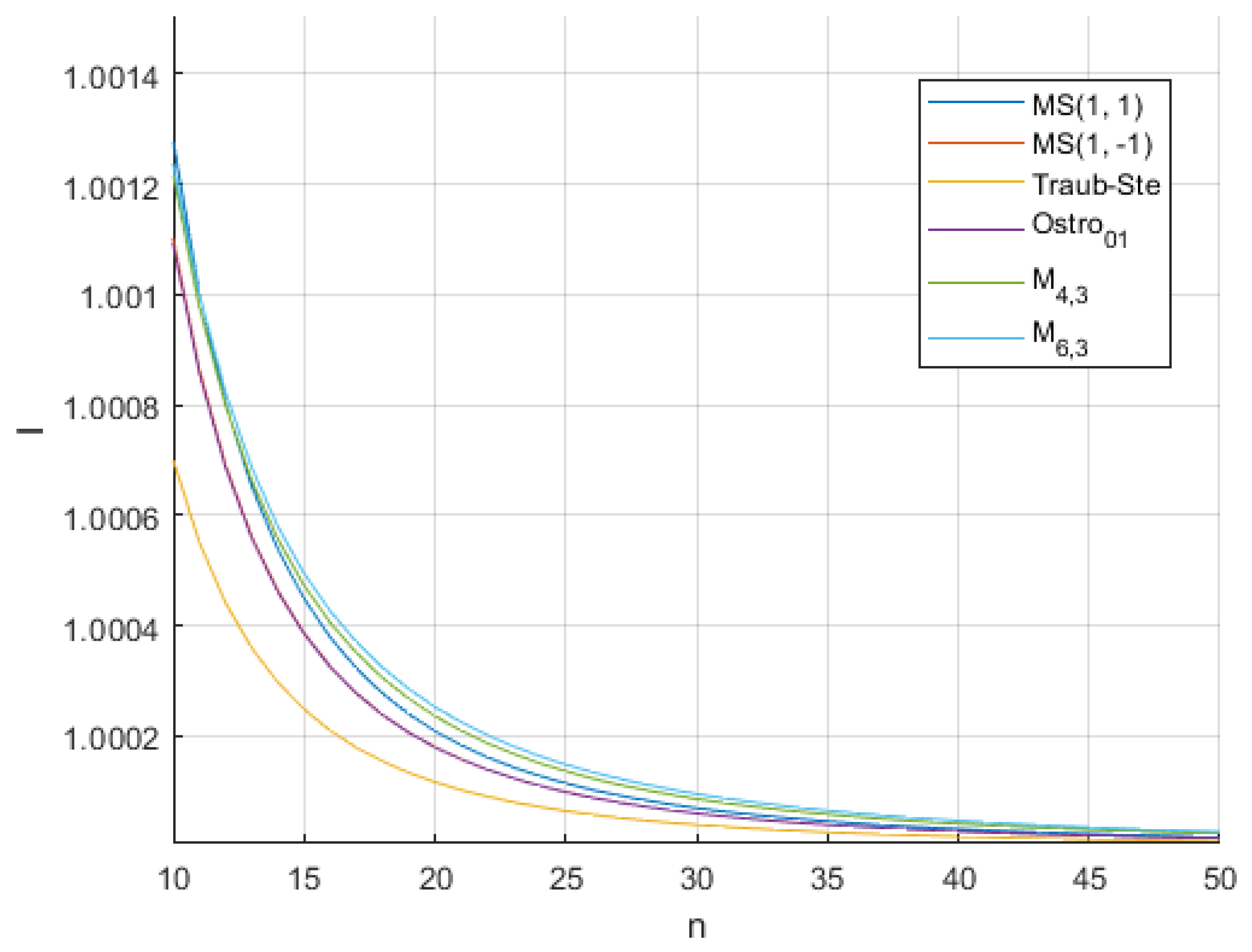
Table 1.
Computational effort of new and comparison schemes
| Method | Complexity C |
|---|---|
Table 2.
Results for function , using as seed
| Iterative method | k | Cpu-time | ||||
| 7 | 4.00 | 1.108e-51 | 4.624e-204 | 191.7242 | ||
| 5 | 4.97 | 4.904e-24 | 3.995e-117 | 143.1027 | ||
| 5 | 4.00 | 1.241e-35 | 1.517e-140 | 227.8747 | ||
| - | - | - | - | - | - | |
| 6 | 4.00 | 7.338e-40 | 3.015e-158 | 163.9808 | ||
| 5 | 5.96 | 1.336e-47 | 7.876e-284 | 142.6446 |
Table 3.
Numerical results for ,
| Iterative method | k | Cpu-time | ||||
| 8 | 3.99 | 2.794e-29 | 4.092e-115 | 73.3126 | ||
| 8 | 5.00 | 7.534e-74 | 2.162e-366 | 72.6143 | ||
| 16 | 4.00 | 9.389e-68 | 3.459e-269 | 317.9304 | ||
| 15 | 4.00 | 6.341e-70 | 1.641e-278 | 139.3808 | ||
| 7 | 4.00 | 8.510e-87 | 3.949e-346 | 76.9114 | ||
| 6 | 6.02 | 4.223e-47 | 8.063e-281 | 79.7898 |
Table 4.
Numerical results for ,
| Iterative method | k | Cpu-time | ||||
| 4 | 4.00 | 1.305e-55 | 2.980e-221 | 12.8166 | ||
| 4 | 5.00 | 4.997e-101 | 1.143e-503 | 12.6105 | ||
| 4 | 4.00 | 9.461e-68 | 1.372e-270 | 18.9457 | ||
| 4 | 4.00 | 1.420e-47 | 2.882e-189 | 12.4768 | ||
| 4 | 4.00 | 3.440e-44 | 1.007e-175 | 12.8707 | ||
| 3 | 6.07 | 1.482e-21 | 3.012e-127 | 10.5536 |
Table 5.
Numerical results for ,
| Iterative method | k | Cpu-time | ||||
| 4 | 3.99 | 7.838e-31 | 4.801e-121 | 14.6365 | ||
| 4 | 5.00 | 2.864e-52 | 2.514e-258 | 14.6532 | ||
| 4 | 4.00 | 8.656e-34 | 3.124e-133 | 21.7138 | ||
| 4 | 4.00 | 2.268e-35 | 6.443e-140 | 14.0140 | ||
| 4 | 4.00 | 2.594e-47 | 9.227e-188 | 14.8093 | ||
| 3 | 5.32 | 6.593e-26 | 7.254e-153 | 12.0667 |
Table 6.
Numerical results for ,
| Iterative method | k | Cpu-time | ||||
| 3 | 4.03 | 1.343e-24 | 1.076e-101 | 58.6649 | ||
| 3 | 5.03 | 5.715e-36 | 1.098e-183 | 58.6010 | ||
| 4 | 4.00 | 2.252e-97 | 1.397e-392 | 138.3238 | ||
| 4 | 4.00 | 1.317e-99 | 1.705e-401 | 76.6871 | ||
| 3 | 4.00 | 1.490e-24 | 2.175e-101 | 64.3101 | ||
| 3 | 6.01 | 1.565e-53 | 4.782e-326 | 69.4223 |
Table 7.
Numerical results for
| Iterative method | k | Cpu-time | ||||
| 6 | 4.00 | 5.425e-88 | 5.270e-349 | 20.2517 | ||
| 5 | 4.97 | 5.922e-39 | 1.965e-190 | 16.9191 | ||
| 20 | 4.00 | 9.536e-99 | 4.618e-391 | 154.5691 | ||
| 5 | 4.00 | 1.050e-33 | 2.164e-132 | 16.5869 | ||
| 10 | 4.01 | 3.127e-35 | 1.500e-138 | 51.2143 | ||
| 17 | 5.90 | 6.480e-23 | 2.076e-132 | 105.4212 |
Table 8.
Numerical results for ,
| Iterative method | k | Cpu-time | ||||
| 5 | 4.00 | 5.203e-41 | 6.322e-161 | 3.6588 | ||
| 4 | 5.00 | 5.282e-73 | 6.419e-362 | 3.0030 | ||
| 6 | 4.00 | 6.615e-81 | 7.658e-321 | 4.6891 | ||
| - | - | - | - | - | - | |
| 6 | 4.00 | 5.613e-98 | 3.787e-389 | 3.7011 | ||
| 7 | 5.92 | 2.032e-32 | 5.723e-190 | 4.4699 |
Table 9.
Numerical results for ,
| Iterative method | k | Cpu-time | ||||
| 4 | 4.00 | 1.139e-54 | 9.420e-217 | 2.9146 | ||
| 4 | 4.20 | 1.415e-72 | 2.272e-301 | 2.8907 | ||
| 4 | 4.11 | 4.417e-48 | 1.391e-191 | 3.1954 | ||
| 6 | 4.00 | 2.520e-78 | 1.241e-310 | 3.4855 | ||
| 7 | 4.02 | 1.401e-72 | 3.093e-288 | 4.0501 | ||
| 6 | 6.27 | 4.634e-58 | 7.902e-346 | 3.6475 |
Table 10.
Numerical results for ,
| Iterative method | k | Cpu-time | ||||
| 6 | 4.00 | 1.019e-65 | 6.029e-261 | 4.1403 | ||
| 5 | 4.05 | 2.474e-42 | 4.929e-177 | 3.3999 | ||
| 6 | 4.00 | 8.946e-86 | 2.341e-342 | 4.4433 | ||
| 8 | 4.00 | 2.050e-55 | 5.429e-219 | 4.4246 | ||
| - | - | - | - | - | - | |
| - | - | - | - | - | - |
Table 11.
Numerical results for ,
| Iterative method | k | Cpu-time | ||||
| 10 | 4.00 | 6.679e-71 | 1.113e-281 | 6.9568 | ||
| 8 | 4.28 | 4.387e-77 | 3.113e-321 | 5.4126 | ||
| 15 | 4.00 | 4.978e-100 | 2.442e-397 | 10.6624 | ||
| - | - | - | - | - | - | |
| - | - | - | - | - | - | |
| - | - | - | - | - | - |
Table 12.
Numerical results for ,
| Iterative method | k | Cpu-time | ||||
| 16 | 4.00 | 2.821e-94 | 3.543e-375 | 10.5084 | ||
| 6 | 4.19 | 8.959e-45 | 1.550e-184 | 4.2948 | ||
| - | - | - | - | - | - | |
| - | - | - | - | - | ||
| - | - | - | - | - | - | |
| - | - | - | - | - | - |
Table 13.
Numerical results for ,
| Iterative method | k | Cpu-time | ||||
| 10 | 4.00 | 2.063e-86 | 6.071e-344 | 6.8361 | ||
| 7 | 4.17 | 3.281e-52 | 6.327e-218 | 4.7535 | ||
| - | - | - | - | - | - | |
| - | - | - | - | - | - | |
| - | - | - | - | - | - | |
| - | - | - | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








