Area-Time Efficient High-Radix Modular Inversion Algorithm and Hardware Implementation for ECC over Prime Fields

Preprint

Article

Area-Time Efficient High-Radix Modular Inversion Algorithm and Hardware Implementation for ECC over Prime Fields

Altmetrics

Downloads

Views

178

Comments

A peer-reviewed article of this preprint also exists.

Yamin Li^*

This version is not peer-reviewed

Submitted:

12 September 2024

Posted:

12 September 2024

You are already at the latest version

Alerts

Abstract

Modular inversion on large operands is a time-consuming calculation used in elliptic curve cryptography. Its hardware implementation requires extensive hardware resources such as lookup tables and registers. We investigate state-of-the-art modular inversion algorithms and evaluate the performance and cost of the algorithms and their hardware implementations. We then propose a high-radix modular inversion algorithm aimed at short execution time and low hardware cost. We present a detailed radix-8 hardware implementation based on 256-bit primes in Verilog HDL and compare its cost performance with other implementations. Our implementation on the Altera Cyclone V FPGA chip uses 1227 ALMs (Adaptive logic modules) and 1037 registers. The modular inversion calculation takes 3.67 microseconds. The AT (Area time) factor is 8.30, outperforming other implementations. We also present an implementation of elliptic curve cryptography using the proposed radix-8 modular inversion algorithm. The implementation results also show that our modular inversion algorithm is more efficient in area time than other algorithms.

Keywords:

Subject: Computer Science and Mathematics - Computer Science

1. Introduction

Modular inversion is an important computation in elliptic curve cryptography (ECC). ECC provides a secure key agreement between two parties over an insecure network. It calculates points on an elliptic curve over a finite field (such as a field of prime numbers) based on point addition (PA) and point doubling (PD) computations. In affine coordinates, PA and PD must calculate the slope of a line. Such calculations involve costly modular inversions. In projective or Jacobian coordinates, PA and PD do not require such calculations, but a modular inversion is still required to transform the points to affine coordinates to obtain the same key for the two parties.

Given a prime number m, the inverse r of a number a with

a < m

is defined as

r = a^{- 1} m o d m

. There are mainly two popular methods for calculating modular inversion:

(1): Extended Euclidean Algorithm (EEA) without using divisions.
(2): Using Fermat’s Little Theorem $a^{m - 1} = 1 m o d m$ [1]: $r = a^{m - 2} m o d m = a^{- 1} m o d m$ .

We will see that the method using Fermat’s Little Theorem takes longer time and requires more registers than EEA. Therefore, we will focus our design on using the EEA.

The EEA inherently needs divisions. It calculates the largest integer quotient and calculates the remainder based on the quotient. The divisions can be replaced by addition, subtraction, and shift operations. For simplicity, we will also refer to EEA which does not use divisions as EEA.

For calculating

r = a^{- 1} m o d m

, EEA first initializes

u, v, x, y

with

a, m, 1, 0

, respectively. Then EEA repeats calculations containing only addition, subtraction, and shift operations on

u, v, x, y

until

u = 1

v = 1

. Finally, the modular inversion result is available by adjusting x or y, corresponding to

u = 1

v = 1

. A modular inversion algorithm is said to be fast if u or v reaches 1 quickly.

The widely used modular inversion algorithm is Algorithm 2.22, proposed by Hankerson, Menezes, and Vanstone [2]. It repeatedly shifts u or v to the right when u or v is even. Correspondingly, x is also shifted to the right with the shift of u; y is also shifted to the right with the shift of v. Note that when x or y is odd, m will be added before shift. This guarantees that the value to be right-shifted is even, since the prime m is odd. Next, if

u \geq v

, u and x will be replaced by

u - v

and

x - y

, respectively. Otherwise, v and y will be replaced by

v - u

and

y - x

, respectively. Finally, the result is

x m o d m

u = 1

and

y m o d m

otherwise. Hossain and Kong [3] revised Algorithm 2.22 by adding m to x or y if it is negative. This ensures that x and y are non-negative. Daly, Marnane, Kerins, and Popovici [4] revised Algorithm 2.22 by dividing

u - v

v - u

by two because the subtraction result is even (both u and v are odd before the subtraction). Correspondingly,

x - y

y - x

needs also to be divided by two: If

x - y

y - x

is odd, m is added before the division. Division by two is done by shifting one bit to the right. Mrabet, El-Mrabet, Bouallegue, Mesnager, and Machhout proposed a modular inversion algorithm [5] with

u + v

. Instead of

u - v

v - u

, as Algorithm 2.22 does, they perform

u + v

for new u or v. This operation slows down the speed at which u or v reaches 1, increasing execution time. Chen and Qin proposed a modular inversion algorithm [6] that uses only adders. Subtractions are performed by addition with inversion and addition by 1. Choi, Lee, Kong, and Kim proposed a modular inversion algorithm [7] that replaces the repeated shift of u or v and the corresponding shift of x or y in Algorithm 2.22 by a selection of

u, x

0, 0

, or a selection of

v, y

0, 0

, based on the even/odd of v or u. This simplifies the circuit by replacing adders with multiplexers, reducing the circuit delay. Also, they use

- v

and

- y

, instead of v and y, during the calculation. This merges

u - v

and

v - u

into

u + v

and merges

x - y

and

y - x

into

x + y

, reducing the circuit cost. Mixed radix-4 modular inversion algorithms are investigated in [7,8,9,10]. If u or v is divisible by four, u or v is shifted to the right by two bits. Otherwise, if u or v is even (divisible by two), u or v is shifted to the right by one bit. Otherwise (both u and v are odd),

u - v

v - u

is shifted to the right by one bit and assigned to u or v. Correspondingly, x or y is adjusted by adding

- m

, m, or

2 m

and shifted to the right by two bits or one bit. [8] proposed a radix-4 modular inversion algorithm that uses a sequential condition checking for the calculations of u, v, x, and y. [9] implemented the SM2 ECC protocol. The iterations of the modular inversion are controlled by the bit counter

ρ

, resulting in unnecessary iterations. Using u and v to control the iterations will finish the calculation quickly. [10] gave a radix-4 version of Algorithm 2.22. Dong, Zhang, and Gao proposed a mixed radix-8 modular inversion algorithm [11] that uses extensive hardware resources.

The AT (Area time) factor is often used for comparisons between implementations. It is defined as the execution time in milliseconds multiplied by the required hardware resources consisting of registers and lookup tables or ALMs (Adaptive logic modules).

In this paper, we implement and evaluate all the algorithms mentioned above. We then propose a mixed radix-8 modular inversion algorithm aimed at short execution time and small hardware resources. We give its detailed hardware implementation in Verilog HDL based on 256-bit primes. It has lower hardware costs for ALMs and registers and has better performance than other algorithms. The implementation on the Altera Cyclone V FPGA chip uses 1227 ALMs and 1037 registers and takes 3.67 microseconds for the modular inversion computation. It achieves an AT factor of 8.30, lower than all other implementations. We also implement ECC using different modular inversion algorithms and compare their cost performance.

The rest of the paper is organized as follows. Section 2 introduces ECC and modular inversion algorithms. Instead of pseudocodes, all modular inversion algorithms are provided in Python code. Section 3 proposes a mixed radix-8 modular inversion algorithm, gives its hardware implementation in Verilog HDL, and compares its cost performance with other algorithms. Section 4 provides an ECC implementation using the proposed algorithm and compares its cost performance with the ECC implementations using other modular inversion algorithms. And Section 5 concludes the paper.

2. ECC and Modular Inversion Algorithms

This section briefly introduces elliptic curve cryptography and modular inversion algorithms based on the extended Euclidean algorithm.

2.1. Elliptic Curve Cryptography

ECC [12,13] relies on the fact that scalar point multiplication

Q = d P

can be computed, but it is almost impossible to compute d given only the original point P and the point of the product Q. An ECC over the finite field of an n-bit prime number m can use the equation:

y^{2} = x^{3} + a x + b m o d m

(1)

For example, Secp256k1 [14] elliptic curve used in Ethereum Blockchain uses a 256-bit

m = 2^{256} - 2^{32} - 2^{9} - 2^{8} - 2^{7} - 2^{6} - 2^{4} - 1

. Secp256k1 defines

y^{2} = x^{3} + a x + b = x^{3} + 7

and gives a point

P = [x, y]

on the elliptic curve as follows.

a = 0x0000000000000000000000000000000000000000000000000000000000000000

b = 0x0000000000000000000000000000000000000000000000000000000000000007

m = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f

x = 0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798

y = 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8

The elliptic curve Diffie–Hellman (ECDH) key exchange protocol can be used by two parties, Alice and Bob for example, to establish a shared secret key over an insecure network [14,15]. The ECDH protocol is shown in Table 1.

Because

Q_{a b} = d_{a} Q_{b} = d_{a} d_{b} P

Q_{b a} = d_{b} Q_{a} = d_{b} d_{a} P

, and

d_{a} d_{b} = d_{b} d_{a}

, we have

Q_{b a} = Q_{a b}

. Below is an ECDH key exchange example using Secp256k1. We can see that the two parties, Alice and Bob, have the same shared secret key (Qabx = Qbax).

Alice keeps

d_{a}

secret and exposes

Q_{a} = d_{a} P

da = 0x0e26233af432c34fa2523e72b64ebcf5abb4f7cb07d8f25909160a50f584f461

Qax = 0x672751a7b8ec03f4610c364d3776fc5200f401aa26074b10d33c2c202fc63330

Qay = 0xdbf4a0758d81414d2ee049a07c3d8288428235dec9dbfb7fb15d6f478cb4ccf6

Bob keeps

d_{b}

secret and exposes

Q_{b} = d_{b} P

db = 0xbbb481621f91b8e9225649109919a7962cec4225c981b6b68b4f8d8a356cc6d9

Qbx = 0x09aff71612598a88d5299ae81e3161a2c9045f343315da8cfabb4dc55253041f

Qby = 0x736b118369583448c0b77eed11ac26af31450d406130d82a1bc56cc3a1835b1d

Alice obtains

Q_{b}

and calculates

Q_{a b} = d_{a} Q_{b}

Qabx = 0x0f675b3195fd6a6f06c9a6960ff2a4f647f637f513c8bb7bedc8a89311f62df2

Qaby = 0x79de922da4db277fe0c674277243c1dfd0653913d037fb07e955c3cdf21e69c7

Bob obtains

Q_{a}

and calculates

Q_{b a} = d_{b} Q_{a}

Qbax = 0x0f675b3195fd6a6f06c9a6960ff2a4f647f637f513c8bb7bedc8a89311f62df2

Qbay = 0x79de922da4db277fe0c674277243c1dfd0653913d037fb07e955c3cdf21e69c7

Now, Alice and Bob have the same secret key (Qabx = Qbax). They can use symmetric-key cryptography for subsequent communications. A third party, Eve for example, knows

y^{2} = x^{3} + a x + b m o d m

, P,

Q_{a}

, and

Q_{b}

, but cannot calculate the same secret key.

2.2. Point Addition and Point Doubling

Scalar point multiplication

Q = d P

calls point addition (PA) and point doubling (PD).

2.2.1. Point Addition

Given

P = [x_{p}, y_{p}]

and

Q = [x_{q}, y_{q}]

, the formulas for point addition

R = [x_{r}, y_{r}] = P + Q

on elliptic curve

y^{2} = x^{3} + a x + b m o d m

are shown as follows, where

λ

is the slope of the line through points P and Q.

\begin{matrix} \{\begin{matrix} λ & = \frac{y_{q} - y_{p}}{x_{q} - x_{p}} m o d m \\ x_{r} & = (λ^{2} - x_{p} - x_{q}) m o d m \\ y_{r} & = (λ (x_{p} - x_{r}) - y_{p}) m o d m \end{matrix} \end{matrix}

(2)

The point at infinity, denoted

O

, is included in the group of elliptic curves and is defined as

P + (- P) = O

for

Q = - P

. By this definition,

P + O = P

. In our implementation,

O

is represented as

[- 1, - 1]

. In the case of

P = O

R = P + Q = O + Q = Q

. In the case of

Q = O

R = P + Q = P + O = P

. We give the point addition

R = P + Q

algorithm over the finite field of

F_{m}

in Algorithm 1. In the case of

Q = - P

R = P + Q = P + (- P) = O

(line 5 in the algorithm). In the case of

Q = P

R = P + Q = P + P = 2 P

, we perform the point doubling

R = 2 P

(line 6 in the algorithm).

Algorithm 1 PA (P, Q, m, a) (Point Addition in Affine Coordinates).

inputs: Points

P = [P_{x}, P_{y}]

and

Q = [Q_{x}, Q_{y}]

; m and a in

y^{2} = x^{3} + a x + b \mod m

output:

R = P + Q = [R_{x}, R_{y}] = [x_{r}, y_{r}]

begin

x_{p} = P_{x}

y_{p} = P_{y}

x_{q} = Q_{x}

y_{q} = Q_{y}

O = [- 1, - 1]

2 if

P = O

return Q /*

O + Q = Q

3 if

Q = O

return P /*

P + O = P

4 if

x_{p} = x_{q}

5 if

(y_{p} + y_{q}) \mod m = 0

return

O

P + (- P) = O

6 else return PD (P, m, a) /*

P + P = 2 P

λ = ((y_{q} - y_{p}) / (x_{q} - x_{p})) \mod m

x_{r} = (λ^{2} - x_{p} - x_{q}) \mod m

y_{r} = (λ (x_{p} - x_{r}) - y_{p}) \mod m

10 return

[x_{r}, y_{r}]

R = P + Q

end

An example of point addition

R = P + Q

on the Secp256k1 curve is shown below where

[P_{x}, P_{y}] = P

[Q_{x}, Q_{y}] = Q

, and

[R_{x}, R_{y}] = R

in affine coordinates.

Px = 0xfc7dafb820a20da1a73c36465f2fe37bfd98ce4ef3a10a5df110abda03b20a3d

Py = 0xa442a2d1b8bde4a09e45725add5daae89e726b56f0e8fe6609dacaf5279b2564

Qx = 0xe106c069450b2663febb83e29b67fa93c4c48a45d5fbe7ce4ddb8ceb601fcc1d

Qy = 0xc9da9bd440909c8862c06a44d432d2dd45284636b7049b9bf4695f9e4018d2f2

Rx = 0xfd52a0334e16f8cf45a6b0820887a9e8b1b180516a76c8adfef95df98aeef376

Ry = 0xb0fe3f04cc4c64fd66a133b8c97b4905771238f8ba89631efb85a8059e969a49

2.2.2. Point Doubling

Given

P = [x_{p}, y_{p}]

, the formulas for point doubling

R = [x_{r}, y_{r}] = 2 P

on elliptic curve

y^{2} = x^{3} + a x + b m o d m

are shown as follows, where

λ

is the slope of the tangent line of the elliptic curve at point P.

\begin{matrix} \{\begin{matrix} λ & = \frac{3 x_{p}^{2} + a}{2 y_{p}} m o d m \\ x_{r} & = (λ^{2} - 2 x_{p}) m o d m \\ y_{r} & = (λ (x_{p} - x_{r}) - y_{p}) m o d m \end{matrix} \end{matrix}

(3)

We give the point doubling

R = 2 P

algorithm over the finite field of

F_{m}

in Algorithm 2. In the case of

P_{y} = 0

(vertical tangent line),

R = 2 P = O

(line 2 in the algorithm).

Algorithm 2 PD (P, m, a) (Point Doubling in Affine Coordinates).

inputs: Point

P = [P_{x}, P_{y}]

; m and a in

y^{2} = x^{3} + a x + b \mod m

output:

R = 2 P = [R_{x}, R_{y}] = [x_{r}, y_{r}]

begin

x_{p} = P_{x}

y_{p} = P_{y}

O = [- 1, - 1]

2 if

y_{p} = 0

return

O

/* vertical tangent */

λ = ((3 x_{p}^{2} + a) / (2 y_{p})) m o d m

x_{r} = (λ^{2} - 2 x_{p}) \mod m

y_{r} = (λ (x_{p} - x_{r}) - y_{p}) \mod m

6 return

[x_{r}, y_{r}]

R = 2 P

end

An example of point doubling

R = 2 P

on the Secp256k1 curve is shown below where

[P_{x}, P_{y}] = P

and

[R_{x}, R_{y}] = R

in affine coordinates.

Px = 0x6034b56424fb31ea6ec5483b52ae5d07d6f3ef80264d769ae2714abb83fb279a

Py = 0xfe4cde1ff7546a87f906f50ab1002fda7811828ea6fc467a44d1c6c11aa65a37

Rx = 0x5491ee8b73a4ed9713ed32e467de5100b80861babf8ffd09fd595ab457d042c9

Ry = 0xf91e6a4e132a1bdf4f5c846559431ec7373de8872b719f188b5902932f0a2b30

The computation of

λ

in PA and PD requires modular division, which can be realized by a modular inversion algorithm based on the extended Euclidean algorithm.

2.3. Modular Inversion Algorithms

Given a prime number m, the inverse r of a number a with

a < m

is defined as

r = a^{- 1} m o d m

(4)

That is,

r a = 1 \mod m

. The Python code below implements the modular inversion calculation using Fermat’s Little Theorem. When executed, it outputs 4 4 4. The first output value is calculated by the code, and the rest are for checking. This calculation consists of costly modular multiply and modular squaring, very similar to RSA exponentiation [16].

The extended Euclidean algorithm can be used for the modular inversion calculation. Below is the fundamental extended Euclidean algorithm given in Python code (modinv_algo_1.py), where q is the integer quotient of u divided by v.

Considering

b = 1

. u and x are initialized with a and 1, respectively. At each iteration, u and x are modified with similar calculations. Therefore, when u reaches 1 from a, x reaches the reciprocal of a from 1. If m is a prime number, the greatest common divisor of a and m is guaranteed to be 1, and we can always get the inverse result of a. With the initialization of x with b, the algorithm performs the modular division

r = b a^{- 1} m o d m

An example of running modinv_algo_1.py using modinv(1, 3, 11) is shown in Table 2 (

b = 1

a = 3

, and

m = 11

). The calculation finishes when

v = 0

. Because

u = 1

, the result

a^{- 1} m o d m = x m o d m = 4 m o d 11 = 4

. We can check the correctness as follows:

r a m o d m = 4 \times 3 m o d 11 = 12 m o d 11 = 1 m o d 11

The algorithm requires division, which is expensive. We can remove division by setting the quotient to 0 or 1, as shown below (modinv_algo_2.py).

The algorithm yields a quotient of 0 or 1 based on the comparison of u and v. If the quotient is a 1, a subtraction is performed. Otherwise, no calculation is performed, resulting in a slow calculation speed. The calculation of modinv (1, 3, 11) will require 9 iterations. We can modify the algorithm as follows (modinv_algo_3.py). This reduces the number of iterations by about half.

We can check u first before the subtractions. If it is even, we can shift it to the right by one bit (the least significant bit 0 is shifted out). Correspondingly, x must also be shifted. To ensure that the value to be right-shifted is even, m will be added to x before the shift if x is odd. Note that m is odd because it is a prime number. This shift of u and x can be performed repeatedly until u becomes an odd number. Similar actions can be applied to v and y. Then we can have an algorithm as follows (modinv_algo_4.py). In fact, this is Algorithm 2.22 provided in [2] and implemented in Verilog HDL in [17].

When the two inner while loops finish, u and v are both odd numbers. Therefore

u - v

v - u

is even. Then we can shift it to the right by one bit. Correspondingly,

x - y

y - x

must also be shifted. If

x - y

y - x

is odd, m must be added before the shift so that the bit being shifted out is 0. The algorithm is shown below (modinv_algo_5.py).

The two inner while loops can be replaced by assigning u, x, v, y, or 0 to the temporary variables

t u

t x

t v

, and

t y

. The following assignments make

t u - t v

even, so we can shift it to the right by one bit: (1) If both u and v are odd, those temporary variables are assigned with u, x, v, y, respectively. (2) If u is even and v is odd, those temporary variables are assigned with u, x, 0, 0, respectively. (3) If u is odd and v is even, those temporary variables are assigned with 0, 0, v, y, respectively. Such replacements reduce the latency from the carry propagate adder to the multiplexer and speed up the calculation. The algorithm is shown below (modinv_algo_6.py).

The algorithm above requires calculations of

t u - t v

t v - t u

t x - t y

, and

t y - t x

. We can unify these calculations with negative assignments

- v

and

- y

to v and y, respectively. That is,

u = u - v = u + (- v)

becomes

u = u + v

, and

x = x - y = x + (- y)

becomes

x = x + y

with the negative assignments to v and y. Similarly,

v = - (u - v)

becomes

v = u + v

, and

y = - (x - y)

becomes

y = x + y

with the negative assignments to v and y. Therefore,

u + v

and

x + y

are sufficient for the calculation. The algorithm is given below (modinv_algo_7.py). Because of the negative assignments to v and y, v is initialized with

- m

and y is initialized with

- 0 = 0

. Note that x is never greater than or equal to m. Therefore, no adjustment of

x = x - m

x = x m o d m

is required.

A modular inversion algorithm is said to be good when u reaches 1 quickly (high performance) and the algorithm uses a small number of adders and subtractors (low cost).

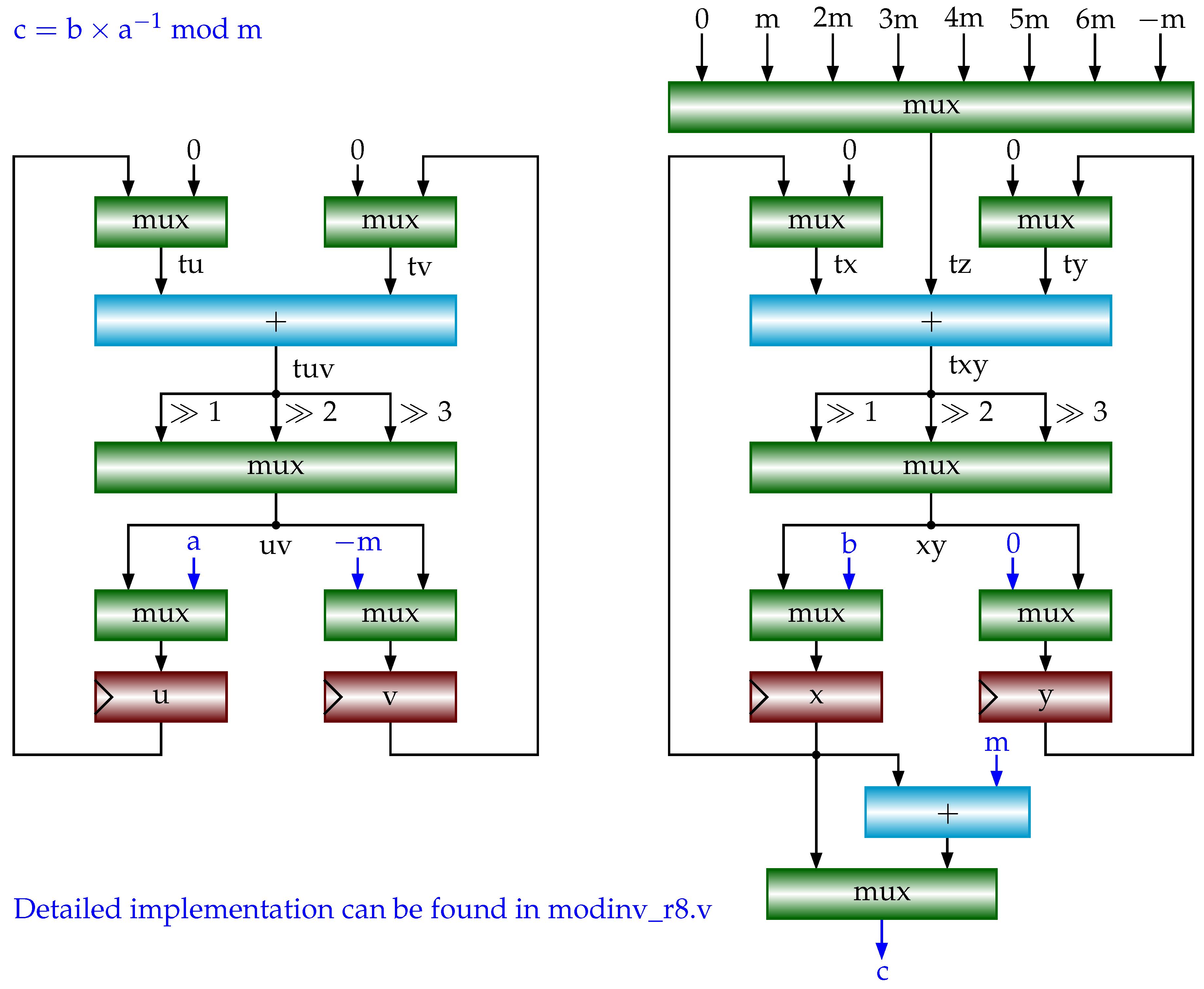
3. Proposed Radix-8 Modular Inversion Algorithm and its Performance

The proposed mixed radix-8 modular inversion algorithm is shown below (modinv_radix_8.py). To calculate

r = a^{- 1} m o d m

, we initialize

u = a

and

v = - m

with the negative assignment to v and y. The temporary variable

t u

is assigned with u or 0 and the temporary variable

t v

is assigned with v or 0 so that

t u v = t u + t v

is even. If the three least significant bits of

t u v

are 000, it is shifted to the right by three bits (radix-8). Otherwise, if the two least significant bits of

t u v

are 00, it is shifted to the right by two bits (radix-4). Otherwise, it is shifted to the right by one bit (radix-2), because

t u v

is even.

Correspondingly,

t x

and

t y

are arranged and

t x y = t x + t y

is also shifted to the right by three bits, two bits, or one bit. The bits being shifted out must be 0. Therefore, we need to adjust

t x y

using the prime number m before shifting. Table 3 lists such adjustments based on the three least significant bits of

t x y

and the three least significant bits of m for the radix-8 operations, where x represents a don’t care. The three least significant bits of the adjusted value are 000, as shown in the comment column of the table.

Similarly, Table 4 lists the adjustments based on the two least significant bits of

t x y

and the two least significant bits of m for the radix-4 operations. The two least significant bits of the adjusted value are 00, as shown in the comment column of the table.

An example of

c = b \times a^{- 1} m o d m

is shown below. The modinv_radix_8 algorithm takes 206 iterations to reach

u = 1

and

v = - 1

. In contrast, the modinv_radix_4 and modinv_radix_2 algorithms require 243 and 356 iterations, respectively.

b = 0x9cfa1c993911914be0f15bd74a878abe0079c6254b961b82e1abda76387d1d85

a = 0xd5076ae274e874c2eb0f7778717c39460236549ddd9fc651e68a0c0e787b4ce8

m = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f

c = 0xe8e5ac2e1d3358894ce1b3342737b38c39b89059dd55d3c4741626de8270228e

To reduce the number of adders, we use multiplexers to select an appropriate value and assign it to the temporary variable

t z

. And then we perform

t x y = t x + t y + t z

. Based on the three least significant bits of

t u v

, we assign

t x y ≫ 1

t x y ≫ 2

, or

t x y ≫ 3

(shift right) to

x y

. Figure 1 shows the block diagram of the proposed mixed radix-8 modular inversion circuit. Because we perform addition for

t x y = t x + t y + t z

- 2 m

and

- 3 m

are replaced by

+ 6 m

and

+ 5 m

, respectively. Also, for the addition, we prepare

- m

that can be obtained by inverting all the bits of m and setting the right-most bit to 1 because m is odd. The registers u, v, x, and y are shown with red rectangles. The multiplexers are drawn with green rectangles. The blue rectangles are adders. The Verilog HDL implementation uses continuous assignment to compute

u v

and

x y

and writes them to the corresponding registers on the rising edge of the clock signal. Note that we have to use adders for generating

3 m

5 m

, and

6 m

, which are not shown in the figure.

Below we give the hardware implementation code in Verilog HDL for the proposed mixed radix-8 modular inversion algorithm (modinv_r8.v). The signals start and ready indicate the start of the modular inversion calculation and the availability of the calculation result, respectively. Because we use Secp256k1 elliptic curve, the input and output signals b, a, m, and c are 256 bits. During the calculations, we use 260 bits for the internal signals.

Below is the testbench Verilog HDL code used to simulate modinv_r8.v.

Figure 2 shows the functional simulation waveform, generated with ModelSim. The result c is available at 416ns. That is, the calculation takes 208 clock cycles.

We have implemented the modular inversion algorithms on the Altera Cyclone V 5CGXFC9E7F35C8 FPGA chip. Table 5 lists the cost performance of the modular inversion algorithms. The column of Cycles shows the required number of clock cycles when executing the modular inversion algorithm. The column of Freq.(MHz) shows the clock frequency in MHz at which the circuit can work. The column of Latency(

μ

s) shows the execution time in microseconds calculated by dividing the clock cycles by the clock frequency. The column of ALMs shows the required number of adaptive logic modules. The column of Registers shows the required number of flip-flops. The flip-flops are mainly used to store u, v, x, and y. Their contents are updated on every clock cycle. The last column shows the AT factor, which is the product of the Latency in milliseconds and the sum of ALMs and Registers.

The row of [1] in the table shows the performance and cost of modular inversion using Fermat’s Little Theorem

r = a^{m - 2} m o d m = a^{- 1} m o d m

. It consists of costly modular multiply and modular squaring, very similar to RSA exponentiation [16]. Its AT factor is much higher than others. The remaining rows show the performance and cost of the EEA-based modular inversion algorithms. The number of registers used by [2,3,8], and [10] is larger than others. This is because extra registers are used to adjust the value of x or y so that the modular inversion result is within the range of 0 and m. Our algorithm implementation achieves an execution time of 3.67

μ

s and an AT factor of 8.30, outperforming all other implementations. Figure 3 shows an intuitive view of latency and AT histograms.

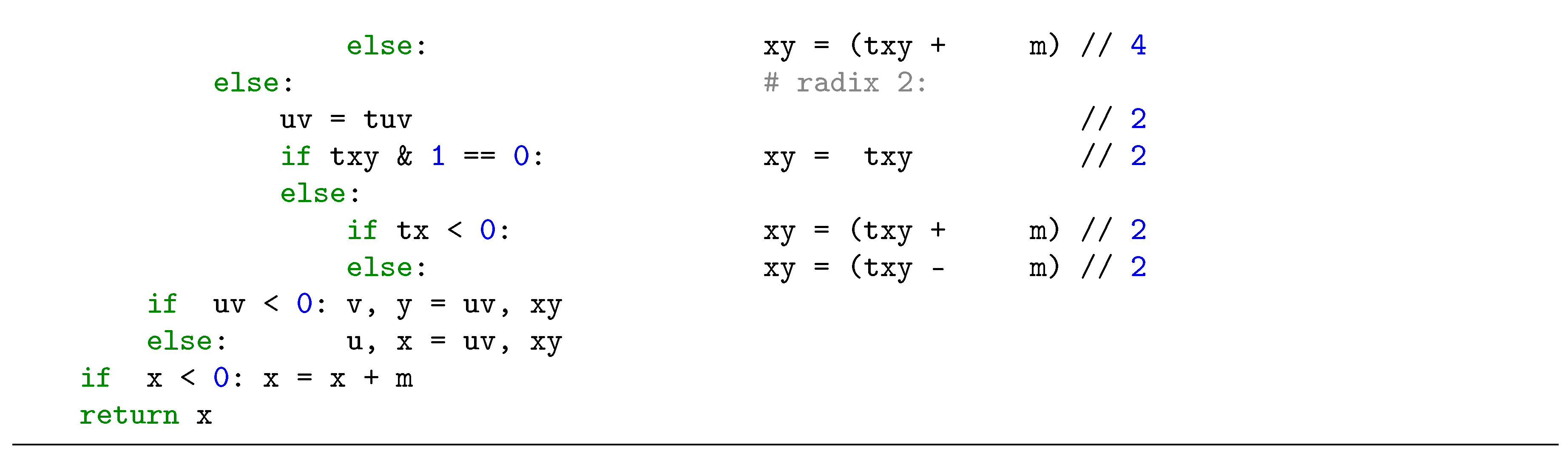
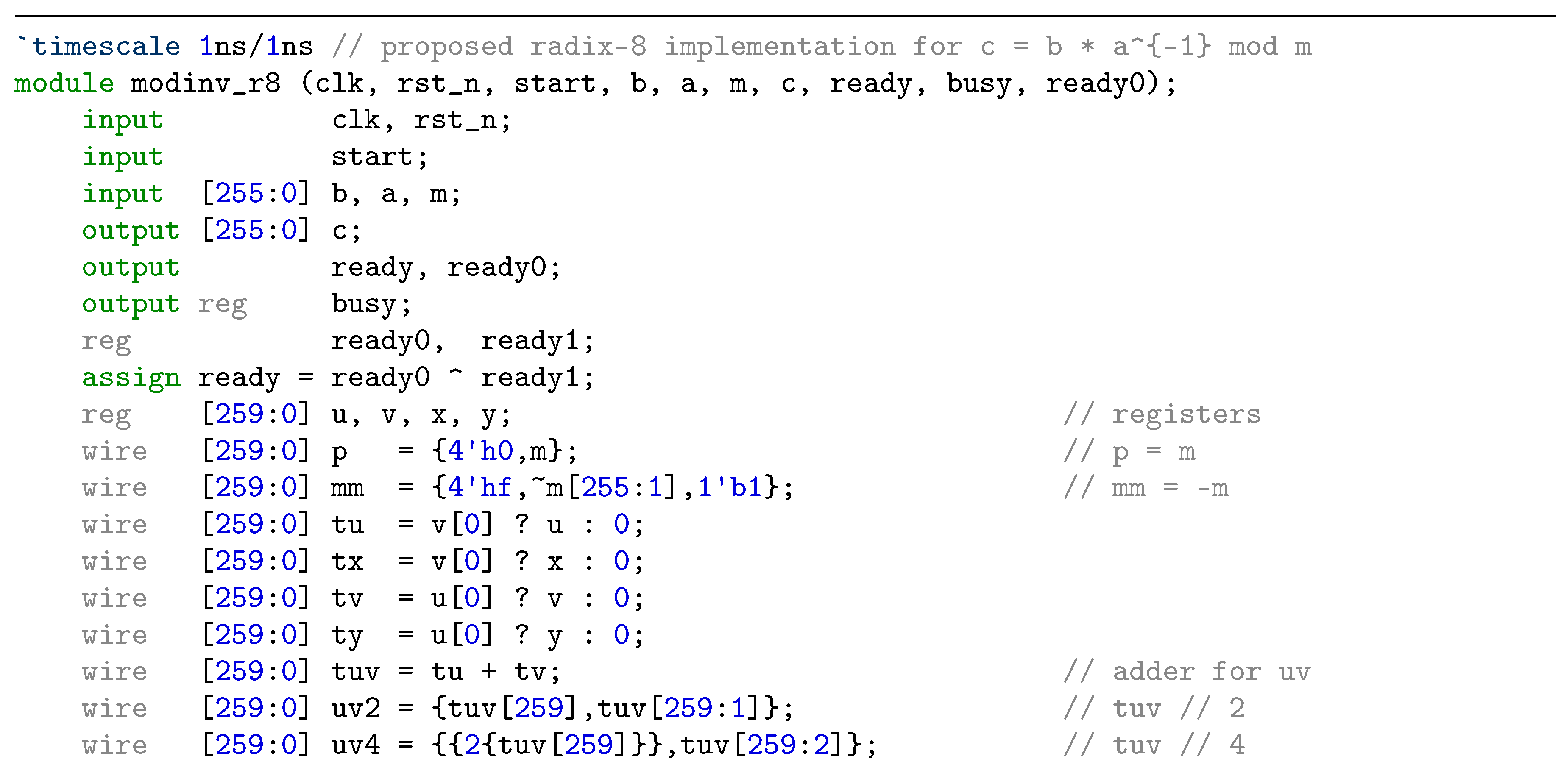
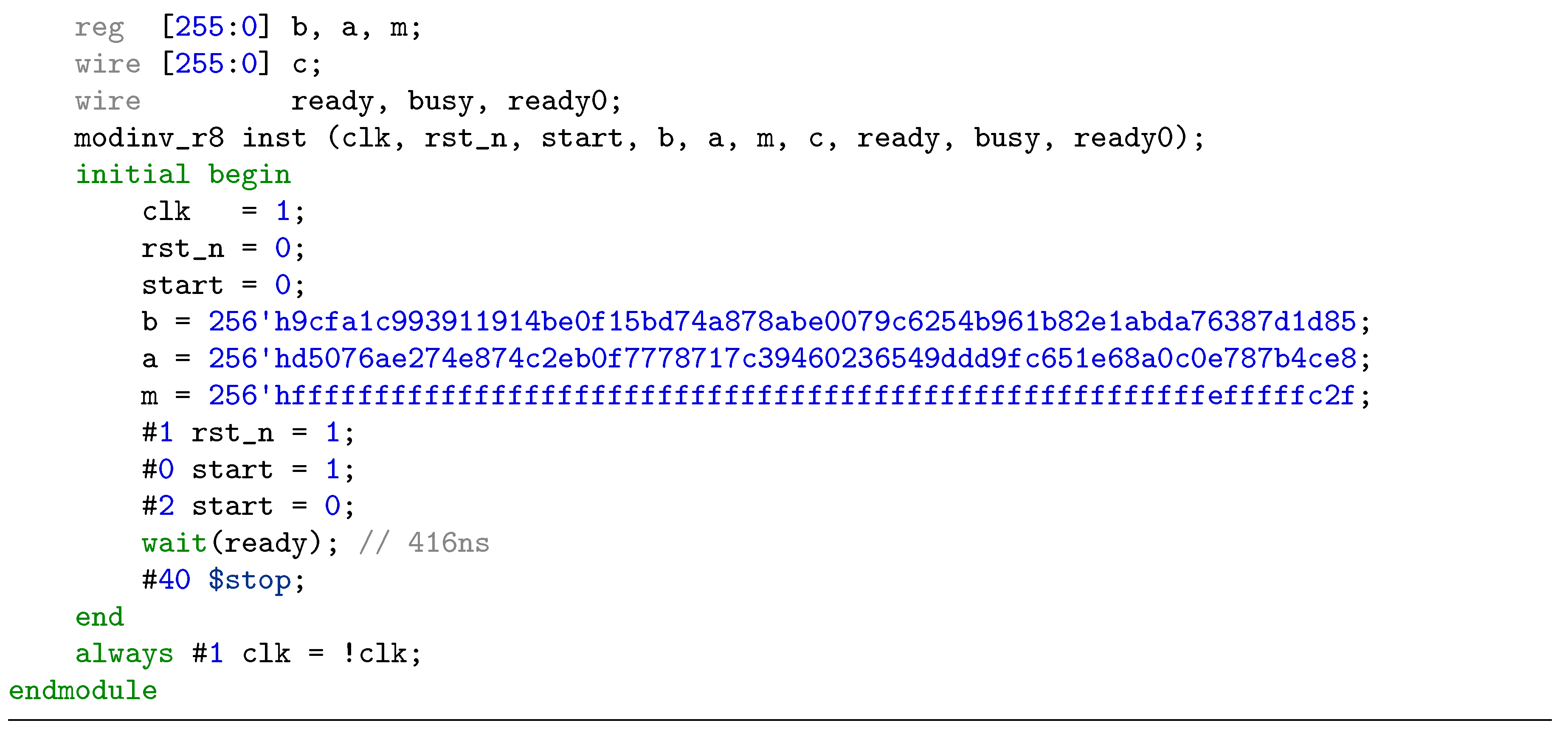
4. ECC Implementation with Proposed Modular Inversion Algorithm

ECC relies on scalar point multiplication. Suppose

P = [x_{p}, y_{p}]

is a point on the curve, the scalar point multiplication

Q = d P

gets the

Q = [x_{q}, y_{q}]

that is also on the curve, where

d = 〈 d_{n - 1} \dots d_{1} d_{0} 〉

is an n-bit scalar. Scalar point multiplication can be conducted with point addition (adding two points) and point doubling, as shown in Algorithm 3.

Algorithm 3 ScaMul (d, P, m, a) (Scalar Point Multiplication in Affine Coordinates).

inputs:

d = 〈 d_{n - 1} \dots d_{1} d_{0} 〉

and point

P = [P_{x}, P_{y}]

; m and a in

y^{2} = x^{3} + a x + b m o d m

output:

Q = d P

begin

Q = O

R = P

k = d

Q = O

and

R = P

2 while

k \neq 0

3 if

k & 1 = 1

Q =

PA (Q, R, m, a) /*

Q = Q + R

(Algorithm 1) */

R =

PD (R, m, a) /*

R = 2 R

(Algorithm 2) */

k = k ≫ 1

7 endwhile

8 return Q /*

Q = d P

end

The algorithm calls point addition PA (P, Q, m, a) and point doubling PD (P, m, a). Table 6 gives an example to show the calculation steps of the scalar point multiplication. For a 5-bit

d = 10101_{2} = 21

, we calculate

Q = d P

in 5 steps to obtain

Q = 21 P

. We can see that the algorithm is similar to RSA exponentiation [16].

The ECDH algorithm is shown below in Python code that invokes scalar point multiplication four times. The code is hardware oriented. For code integrity, we listed our radix-8 code again but here

+ 6 m

and

+ 5 m

are used instead of

- 2 m

and

- 3 m

, respectively.

Based on the above Python code, we implemented ECC using our radix-8 modular inversion algorithm for calculating

λ

in PA and PD. Figure 4 shows the functional simulation waveform of scalar point multiplication

Q = d P

with

P = [x, y]

and

Q = [q x, q y]

. The result is available at 635362ns. That is, the calculation takes 317681 clock cycles.

The ECC cost performance comparison is given in Table 7 when implementing on the Altera Cyclone V 5CGXFC9E7F35C8 FPGA chip. All ECC implementations use the same circuit except for the modular inversion part. Figure 5 shows the latency and AT histogram. The ECC latency using our proposed radix-8 modular inversion algorithm is 0.02007 second and its AT factor is 401237.93. From the table and histogram, we can see that our ECC implementation achieves a lower latency and a lower AT factor than all others.

5. Conclusions

In this paper, we proposed a mixed radix-8 modular inversion algorithm and hardware implementation based on 256-bit primes in Verilog HDL and compared its cost performance with other implementations on the Altera Cyclone V FPGA chip. The algorithm and its hardware implementation are area-time efficient with an AT factor of 8.30, which outperforms other algorithms and implementations. We also presented the cost performance of an elliptic curve cryptography implementation using the proposed modular inversion algorithm. Implementation results also show that our algorithm reduces execution time and requires fewer hardware resources than all other investigated algorithms.

Future research could include shortening the critical path and using carry-select adders and carry-save adders to speed up additions of large operands. Also, using a fixed prime m, Secp256k1 for example, we can simplify the circuit by considering only the case where the lower three bits are equal to 111 and using precomputations of

3 m

5 m

, and

6 m

to speed up the radix-8 modular inversion calculations.

References

Burton, D. The History of Mathematics / An Introduction (7th ed.); McGraw-Hill, 2011. [CrossRef]
Hankerson, D.; Menezes, A.; Vanstone, S. Guide to Elliptic Curve Cryptography; Springer-Verlag: New York Inc, 2004. [Google Scholar] [CrossRef]
Hossain, M.S.; Kong, Y. High-Performance FPGA Implementation of Modular Inversion over F_256 for Elliptic Curve Cryptography. 2015 IEEE International Conference on Data Science and Data Intensive Systems, 2015, pp. 169–174. [CrossRef]
Daly, A.; Marnane, W.; Kerins, T.; Popovici, E. Division in GF(p) for Application in Elliptic Curve Cryptosystems on Field Programmable Logic. In New Algorithms, Architectures and Applications for Reconfigurable Computing; Springer US: Boston, MA, 2005; pp. 219–229. [CrossRef]
Mrabet, A.; El-Mrabet, N.; Bouallegue, B.; Mesnager, S.; Machhout, M. An efficient and scalable modular inversion/division for public key cryptosystems. 2017 International Conference on Engineering & MIS (ICEMIS), 2017, pp. 1–6. [CrossRef]
Chen, C.; Qin, Z. Fast Algorithm and Hardware Architecture for Modular Inversion in GF(p). 2009 Second International Conference on Intelligent Networks and Intelligent Systems, 2009, pp. 43–45. [CrossRef]
Choi, P.; Lee, M.K.; Kong, J.T.; Kim, D.K. Efficient Design and Performance Analysis of a Hardware Right-shift Binary Modular Inversion Algorithm in GF(p). Journal of Semiconductor Technology and Science 2017, 17, 425–437. [Google Scholar] [CrossRef]
Wang, D.; Lin, Y.; Hu, J.; Zhang, C.; Zhong, Q. FPGA Implementation for Elliptic Curve Cryptography Algorithm and Circuit with High Efficiency and Low Delay for IoT Applications. Micromachines 2023, 14, 1–15, https://www.mdpi.com/2072-666X/14/5/1037, doi:10.3390/mi14051037. [Google Scholar] [CrossRef] [PubMed]
Yang, D.; Dai, Z.; Li, W.; Chen, T. An Efficient ASIC Implementation of Public Key Cryptography Algorithm SM2 Based on Module Arithmetic Logic Unit. 2019 IEEE 13th International Conference on ASIC (ASICON), 2019, pp. 1–4. [CrossRef]
Yan, X.; Li, S. Modified modular inversion algorithm for VLSI implementation. 2007 7th International Conference on ASIC, 2007, pp. 90–93. [CrossRef]
Dong, X.; Zhang, L.; Gao, X. An Efficient FPGA Implementation of ECC Modular Inversion over F256. Proceedings of the 2nd International Conference on Cryptography, Security and Privacy, 2018, pp. 29–33. [CrossRef]
Koblitz, N. Elliptic curve cryptosystems. Mathematics of Computation 1987, 48, 203–209, https://www.ams.org/journals/mcom/1987-48-177/S0025-5718-1987-0866109-5/S0025-5718-1987-0866109-5.pdf. [Google Scholar] [CrossRef]
Miller, V.S. Use of Elliptic Curves in Cryptography. Advances in Cryptology — CRYPTO ’85 Proceedings; Springer Berlin Heidelberg: Berlin, Heidelberg, 1986; pp. 417–426, https://link.springer.com/content/pdf/10.1007/3-540-39799-X_31.pdf?pdf=inline%20link. [Google Scholar]
Certicom_Corp. Standards for Efficient Cryptography. SEC 2: Recommended Elliptic Curve Domain Parameters; http://www.secg.org/sec2-v2.pdf, 2010.
Barker, E.; Chen, L.; Roginsky, A.; Vassilev, A.; Davis, R. SP 800-56A Rev. 3, Recommendation for Pair-Wise Key-Establishment Schemes Using Discrete Logarithm Cryptography; National Institute of Standards and Technology, 2018. https://nvlpubs.nist.gov/nistpubs/SpecialPublications/NIST.SP.800-56Ar3.pdf.
Li, Y.; Chu, W. Shift-Sub Modular Multiplication Algorithm and Hardware Implementation for RSA Cryptography. 17th International Conference on Information Assurance and Security, Lecture Notes in Networks and Systems; Springer: Cham, 2021; pp. 541–552. [Google Scholar] [CrossRef]
Li, Y. Hardware Implementations of Elliptic Curve Cryptography Using Shift-Sub Based Modular Multiplication Algorithms. Cryptography 2023, 7, 1–29. [Google Scholar] [CrossRef]

Figure 1. Block diagram of the proposed mixed radix-8 modular inversion circuit.

Figure 2. Waveform of modular inversion that calculates

c = b a^{- 1} m o d m

Figure 2. Waveform of modular inversion that calculates

c = b a^{- 1} m o d m

Figure 3. Latency and AT comparison of modular inversion algorithms.

Figure 4. Waveform of scalar point multiplication

Q = d P

with

P = [x, y]

and

Q = [q x, q y]

Figure 4. Waveform of scalar point multiplication

Q = d P

with

P = [x, y]

and

Q = [q x, q y]

Figure 5. ECC Latency and AT comparison of modular inversion algorithms.

Table 1. Elliptic curve Diffie–Hellman key exchange.

Expose an elliptic curve $y^{2} = x^{3} + a x + b m o d m$ and a point P on the elliptic curve to the world
Alice	Bob
Generate a secret $d_{a}$	Generate a secret $d_{b}$
Calculate $Q_{a} = d_{a} P$	Calculate $Q_{b} = d_{b} P$
Expose $Q_{a}$	Expose $Q_{b}$
Get $Q_{b}$ from Bob	Get $Q_{a}$ from Alice
Calculate $Q_{a b} = d_{a} Q_{b}$	Calculate $Q_{b a} = d_{b} Q_{a}$
Use x of $Q_{a b}$ as the key	Use x of $Q_{b a}$ as the key

Table 2. Execution example of modinv_algo_1.py: print(modinv(1, 3, 11)). It calculates

r = 3^{- 1} m o d 11

. The result is

x m o d 11 = 4

Table 2. Execution example of modinv_algo_1.py: print(modinv(1, 3, 11)). It calculates

r = 3^{- 1} m o d 11

. The result is

x m o d 11 = 4

i	u			v			x			y			q
0	3	=	a	11	=	m	1	=	b	0			q	=	$u / v$
0	u	=	v	v	=	$u - q * v$	x	=	y	y	=	$x - q * y$
1													0	=	$3 / 11$
1	11	=	v	3	=	$3 - 0 * 11$	0	=	y	1	=	$1 - 0 * 0$
2													3	=	$11 / 3$
2	3	=	v	2	=	$11 - 3 * 3$	1	=	y	$- 3$	=	$0 - 3 * 1$
3													1	=	$3 / 2$
3	2	=	v	1	=	$3 - 1 * 2$	$- 3$	=	y	4	=	$1 - 1 * (- 3)$
4													2	=	$2 / 1$
4	1	=	v	0	=	$2 - 2 * 1$	4	=	y	$- 11$	=	$(- 3) - 2 * 4$
End	u	=	1	v	=	0	x	=	4

Table 3. XY adjustment for shift right by three-bit in the proposed modular inversion algorithm.

$txy$	m	$2 m$	$3 m$	$4 m$	$xy$	Comment
000	xx1				$t x y / / 8$	$0 + 0 = 0$
100	xx1			100	$(t x y + 4 m) / / 8$	$4 + 4 = 8$
010	x01	010			$(t x y - 2 m) / / 8$	$2 - 2 = 0$
110	x11	110			$(t x y - 2 m) / / 8$	$6 - 6 = 0$
010	x11	110			$(t x y + 2 m) / / 8$	$2 + 6 = 8$
110	x01	010			$(t x y + 2 m) / / 8$	$6 + 2 = 8$
001	001				$(t x y - m) / / 8$	$1 - 1 = 0$
011	011				$(t x y - m) / / 8$	$3 - 3 = 0$
101	101				$(t x y - m) / / 8$	$5 - 5 = 0$
111	111				$(t x y - m) / / 8$	$7 - 7 = 0$
001	101	010	111		$(t x y + 3 m) / / 8$	$1 + 7 = 8$
011	111	110	101		$(t x y + 3 m) / / 8$	$3 + 5 = 8$
101	001	010	011		$(t x y + 3 m) / / 8$	$5 + 3 = 8$
111	011	110	001		$(t x y + 3 m) / / 8$	$7 + 1 = 8$
001	111				$(t x y + m) / / 8$	$1 + 7 = 8$
011	101				$(t x y + m) / / 8$	$3 + 5 = 8$
101	011				$(t x y + m) / / 8$	$5 + 3 = 8$
111	001				$(t x y + m) / / 8$	$7 + 1 = 8$
001	011	110	001		$(t x y - 3 m) / / 8$	$1 - 1 = 0$
011	001	010	011		$(t x y - 3 m) / / 8$	$3 - 3 = 0$
101	111	110	101		$(t x y - 3 m) / / 8$	$5 - 5 = 0$
111	101	010	111		$(t x y - 3 m) / / 8$	$7 - 7 = 0$

Table 4. XY adjustment for shift right by two-bit in the proposed modular inversion algorithm.

$txy$	m	$2 m$	$xy$	Comment
00	x1		$t x y / / 4$	$0 + 0 = 0$
10	x1	10	$(t x y + 2 m) / / 4$	$2 + 2 = 4$
01	01		$(t x y - m) / / 4$	$1 - 1 = 0$
11	11		$(t x y - m) / / 4$	$3 - 3 = 0$
01	11		$(t x y + m) / / 4$	$1 + 3 = 4$
11	01		$(t x y + m) / / 4$	$3 + 1 = 4$

Table 5. Comparison of modular inversion algorithms (on Altera Cyclone V FPGA chip).

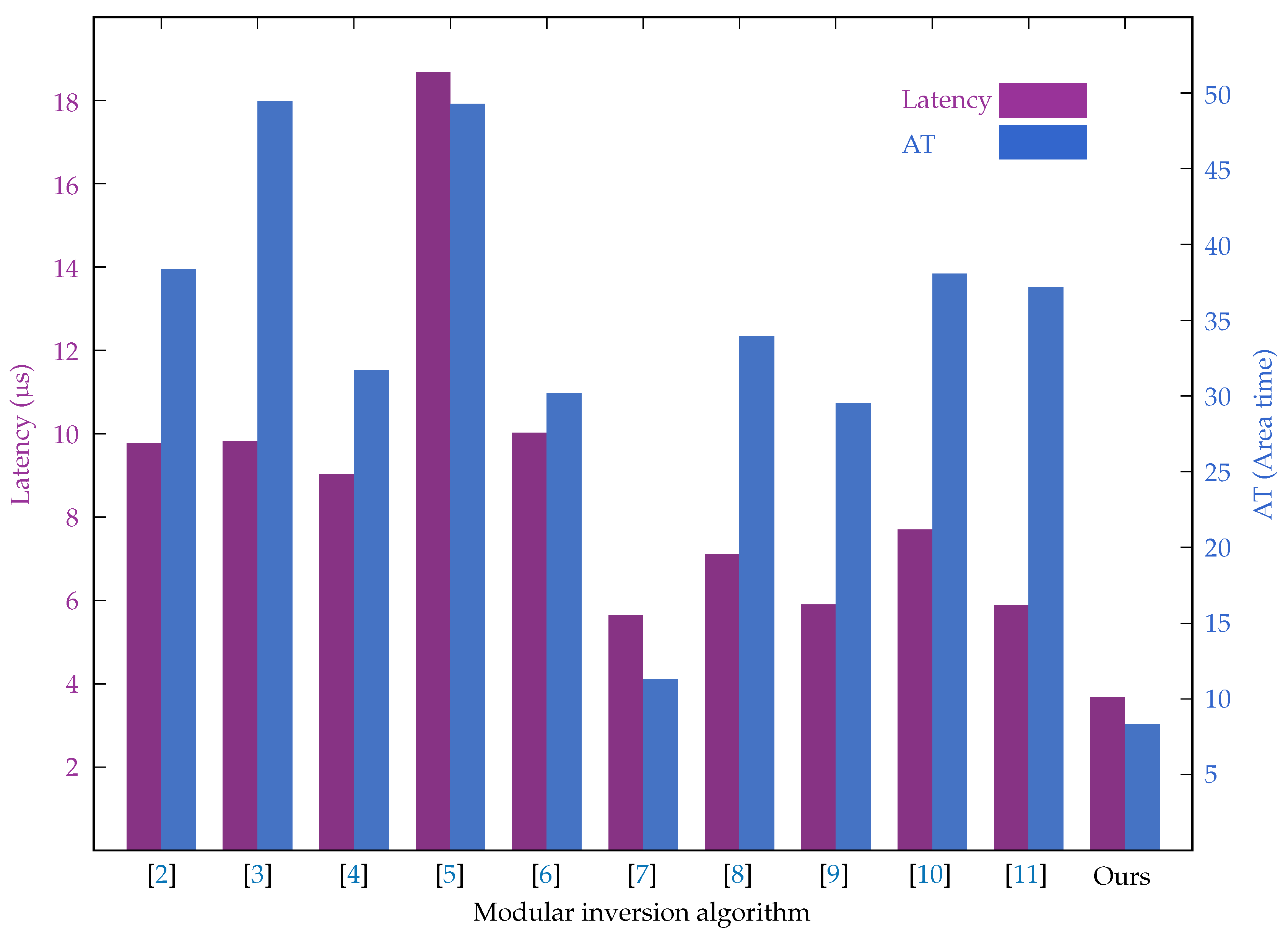
Algorithm	Cycles	Freq.(MHz)	Latency( $μ$ s)	ALMs	Registers	AT
[1]	66264	57.54	1151.63	2004	2775	5503.66
[2]	534	54.66	9.77	2619	1302	38.31
[3]	535	54.52	9.81	3735	1303	49.42
[4]	358	39.73	9.01	2474	1038	31.64
[5]	1205	64.55	18.67	1596	1043	49.26
[6]	723	72.21	10.01	1968	1042	30.13
[7]	358	63.60	5.63	959	1037	11.24
[8]	423	59.56	7.10	3475	1303	33.92
[9]	356	60.43	5.89	3950	1057	29.50
[10]	423	54.99	7.69	3644	1303	38.05
[11]	334	56.93	5.87	5276	1057	37.15
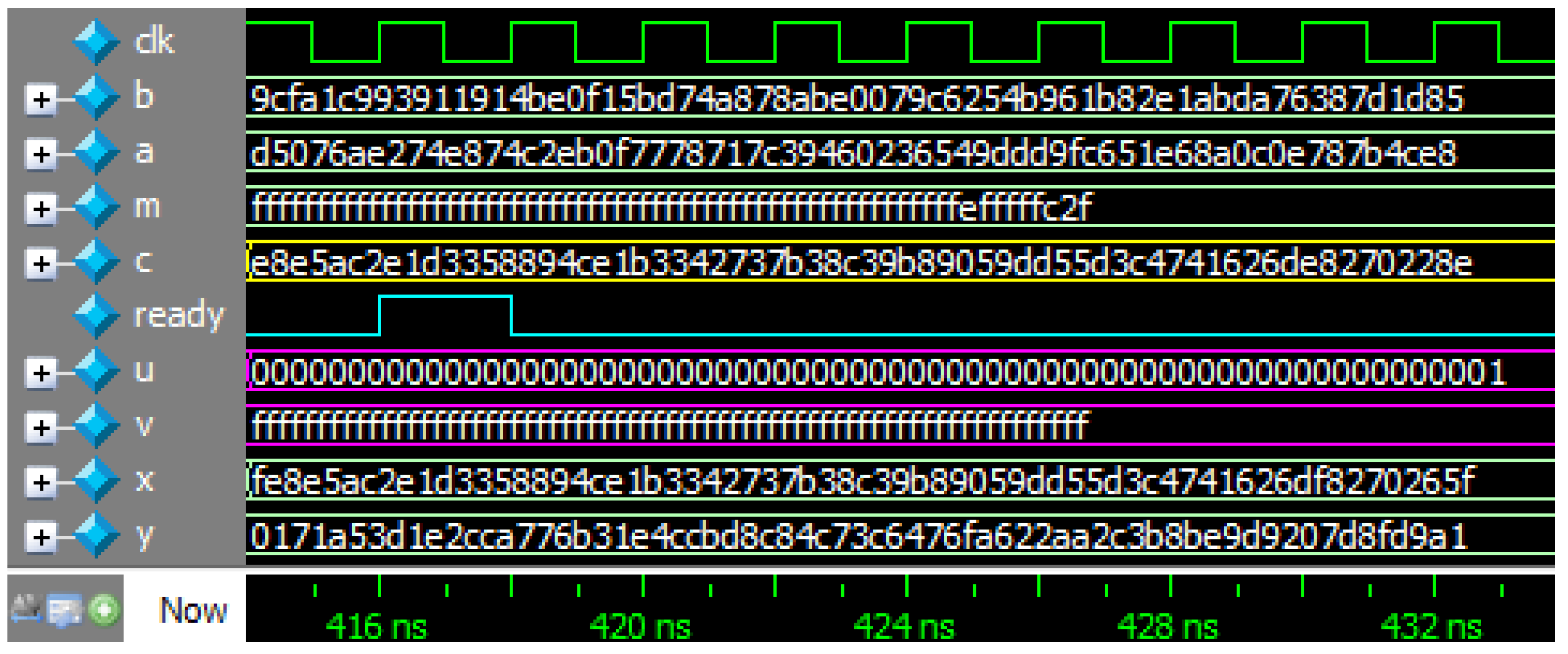
Ours	208	56.71	3.67	1227	1037	8.30

Table 6. Execution example of

Q = d P

with

d = 10101_{2} = 21

Table 6. Execution example of

Q = d P

with

d = 10101_{2} = 21

	Weight	Point addition	Point doubling
Initial		$Q = O$	$R = P$
$d_{0} = 1$	1	$Q = Q + R = O + P = P$	$R = 2 R = 2 P$
$d_{1} = 0$	2		$R = 2 R = 4 P$
$d_{2} = 1$	4	$Q = Q + R = P + 4 P = 5 P$	$R = 2 R = 8 P$
$d_{3} = 0$	8		$R = 2 R = 16 P$
$d_{4} = 1$	16	$Q = Q + R = 5 P + 16 P = 21 P$	$R = 2 R = 32 P$

Table 7. ECC comparison using modular inversion algorithms (on Altera Cyclone V FPGA chip).

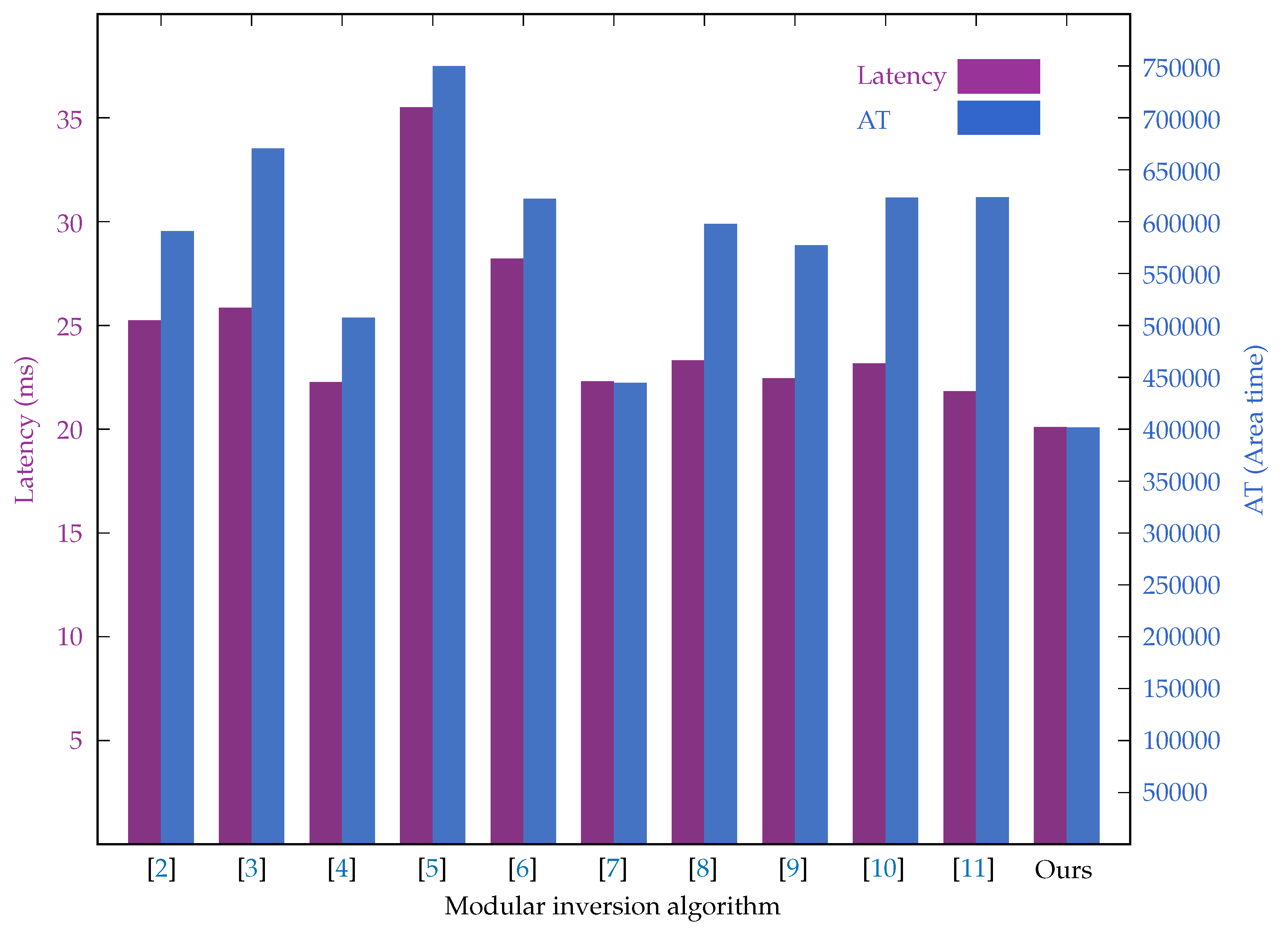
Algorithm	Cycles	Freq.(MHz)	Latency(ms)	ALMs	Registers	AT
[2]	402145	15.94	25.23	15043	8355	590300.42
[3]	402400	15.58	25.83	17585	8355	669977.92
[4]	357262	16.06	22.25	14975	7821	507107.38
[5]	570142	16.07	35.48	13292	7834	749522.08
[6]	455425	16.15	28.20	14211	7831	621577.58
[7]	356878	16.01	22.29	12114	7820	444347.67
[8]	372127	15.98	23.29	17292	8353	597196.30
[9]	352761	15.72	22.44	17841	7860	576737.31
[10]	372127	16.08	23.14	18548	8355	622595.32
[11]	346194	15.88	21.80	20716	7859	622952.99
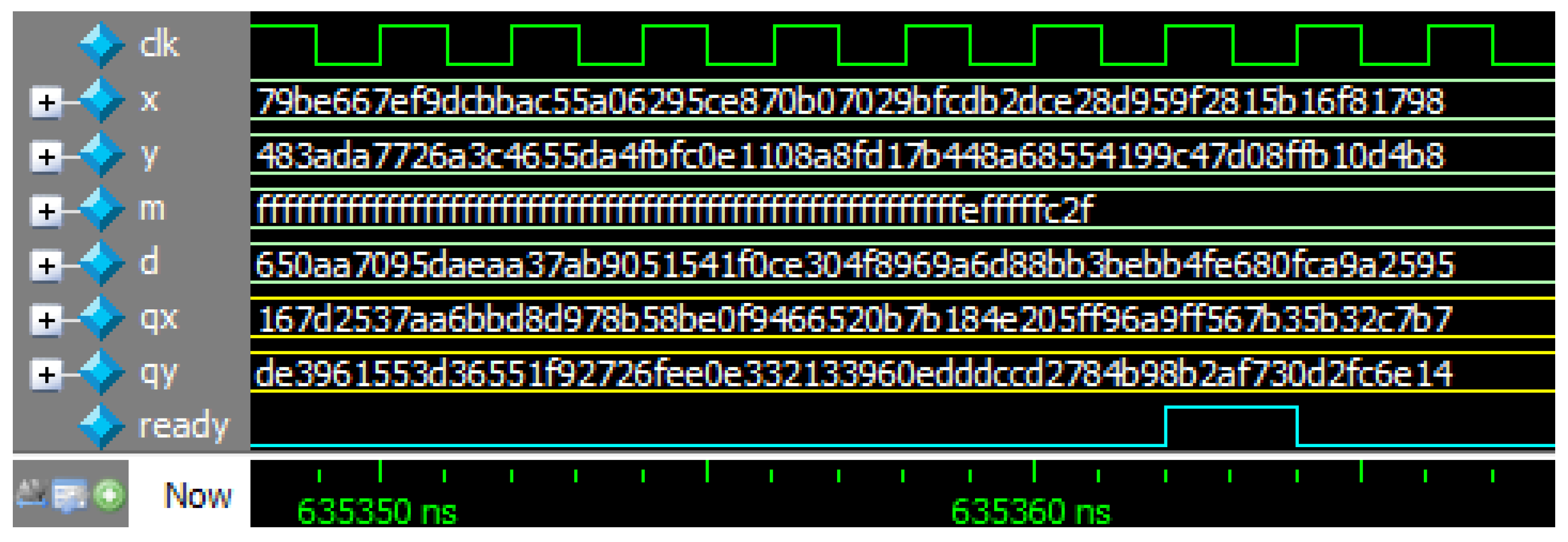
Ours	317681	15.82	20.08	12157	7824	401237.93

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Area-Time Efficient High-Radix Modular Inversion Algorithm and Hardware Implementation for ECC over Prime Fields

Abstract

1. Introduction

2. ECC and Modular Inversion Algorithms

2.1. Elliptic Curve Cryptography

2.2. Point Addition and Point Doubling

2.2.1. Point Addition

2.2.2. Point Doubling

2.3. Modular Inversion Algorithms

3. Proposed Radix-8 Modular Inversion Algorithm and its Performance

4. ECC Implementation with Proposed Modular Inversion Algorithm

5. Conclusions

References

MDPI Initiatives

Important Links

Subscribe