1. Introduction
The development of agriculture, as the economic foundation of China, holds a significant position in the national economy. The yield and quality of crops receive considerable attention. High yields and good quality undoubtedly bring enormous benefits to China's economy and the quality of people's lives. The growth of crops from planting to maturity is a cyclical process, during which crops may be affected by pests and diseases. Therefore, achieving non-destructive detection of crop pests and diseases is crucial. Additionally, the classification of agricultural products is a key step in ensuring their quality. How to achieve non-destructive classification and identification of agricultural products is a critical issue for ensuring quality.
In the above-mentioned issues, using traditional methods for detection and classification may lead to crop damage and low classification accuracy. Compared to traditional detection and classification methods, using hyperspectral imaging technology can effectively address this problem. Hyperspectral imaging technology mainly integrates multiple techniques to achieve detection and classification of targets. In agricultural development, it can realize non-destructive rapid detection of crops and improve the accuracy of crop product classification.
Hyperspectral imaging (HSI) technology originated from hyperspectral remote sensing technology and, together with laser radar technology and synthetic aperture radar technology, is known as the three core technologies for obtaining Earth observation information. The research on hyperspectral imaging technology was pioneered by the Jet Propulsion Laboratory (JPL) in the United States, starting in the 1980s [
1]. In 1983, with strong support from the National Aeronautics and Space Administration (NASA), JPL developed the first airborne imaging spectrometer (AIS) internationally [
2]. China's research on hyperspectral imaging technology began slightly later, at the beginning of the 1990s [
3]. The Shanghai Institute of Technical Physics was the first to successfully develop the airborne imaging spectrometer OMIS and the wide-field push-broom hyperspectral imaging instrument PHI [
4].
Hyperspectral imaging technology has been widely applied in various fields such as agriculture [
5,
6,
7], environmental protection [
8,
9,
10], medical diagnosis [
11,
12,
13], and cultural heritage research [
14,
15,
16] since its development. In agricultural production, it is commonly used for non-destructive rapid detection of crop pests and diseases and the classification and identification of agricultural products. With the continuous development of this technology, the methods of acquiring original image data of detection objects using hyperspectral cameras have become more diversified and efficient, including indoor collection methods and UAV-based methods. The collected hyperspectral original image data is susceptible to environmental factors, equipment-related factors, and other influences, containing rich information and multidimensional data. Therefore, preprocessing is necessary before conducting data analysis. During data analysis, machine learning algorithms and deep learning algorithms are typically used to build recognition and classification models. After extensive data training, these models can effectively achieve the detection and identification of crop pests and diseases, as well as the classification of agricultural products.
2. Development of Hyperspectral Imaging Applications
2.1. Crop Pest and Disease Detection and Identification Application Development
Since the successful implementation of hyperspectral imaging technology, it has gradually commercialized, leading to a large number of hyperspectral imaging instrument manufacturers emerging both domestically and internationally. The production of hyperspectral imaging instruments by these manufacturers is progressively applied in fields such as agriculture, forestry, and healthcare. Particularly in recent years, with the rapid development of agriculture and artificial intelligence, this technology combined with AI algorithms has been widely used in the agricultural production sector. It has found extensive applications in the detection of crop pests and diseases and the classification and identification of agricultural products.
Hyperspectral imagers can capture spectral characteristic changes in crops when affected by pests and diseases, enabling detection and early warning before or at the onset of pests and diseases [
17]. This assists farmers in promptly implementing preventive measures to reduce losses caused by pests and diseases. By analyzing spectral information from different bands, it can identify and classify various types of pests and diseases, including viruses, bacteria, fungi, and insects [
18]. This helps farmers accurately determine the type and severity of pests and diseases, providing a basis for precise control measures.
Researchers have conducted extensive studies using hyperspectral imaging technology to address the issue of crop pest and disease detection. By conducting detailed spectral sampling of crops, this technology can acquire continuous spectral curves of crops, analyze subtle spectral features, and thereby achieve pest and disease detection in crops.
In reference [
19], Yu Jiajia et al. proposed the independent soft modeling method (SIMCA) for early detection of gray mold on tomato leaves. They extracted characteristic spectral band images of gray mold on tomato leaves and fused the bands using multiple linear regression (MLR) to obtain a merged image, establishing a technical route to obtain disease information using the minimum distance method. The results indicated that the proposed method exhibited excellent predictive capabilities, providing a new approach to early detection of gray mold on tomatoes.
In reference [
20], Zhang Jingyi et al. aimed to detect Alternaria leaf spot disease in melons. They utilized hyperspectral imaging technology to acquire raw spectral images, preprocessed the raw data using principal component analysis and minimum noise fraction methods, and established leaf lesion discrimination models using the K-nearest neighbors and support vector machine methods. The study demonstrated the effectiveness of this method in detecting Alternaria leaf spot disease in melons.
In reference [
21], as Sclerotinia stem rot in rapeseed is a soil-borne disease with no visible early symptoms on leaves, Liang Wenjie et al. employed hyperspectral imaging technology combined with deep learning models to construct an early identification model for Sclerotinia stem rot in rapeseed, achieving good recognition results.
In reference [
22], Li Yang et al. sought to achieve rapid online identification of cucumber diseases and pests. They used hyperspectral imaging and machine learning to study the rapid identification of cucumber downy mildew and two-spotted spider mite infestation. The model built using full-band spectral data preprocessed with the MA method showed the best identification performance, with the MA-RF model achieving an overall classification accuracy (OA) of 97.89% and a Kappa coefficient of 0.97. Research results indicated that using hyperspectral imaging technology for identifying cucumber downy mildew and two-spotted spider mite infestation yielded excellent results.
In conclusion, the application of hyperspectral imaging technology in crop pest and disease detection can more efficiently assist farmers in managing their crops, promoting the rapid development of smart agriculture. This technology can make crop growth more intelligent and precise.
2.2. Development of Applications for Classification and Identification of Agricultural Products
Before the successful implementation of hyperspectral imaging technology, traditional methods were primarily utilized for agricultural product classification. These conventional techniques often require extensive manual intervention, are time-consuming, labor-intensive, and prone to errors. Hyperspectral imaging technology can capture multispectral information of the target, enabling the identification of distinct features of different agricultural products based on subtle spectral differences, thus achieving precise and non-destructive classification of agricultural products [
23].
Hyperspectral imaging technology enables rapid, non-contact detection of agricultural products, allowing for the identification of potential contaminants and harmful substances such as pesticide residues, thereby ensuring food safety [
24]. Moreover, hyperspectral imaging technology plays a vital role in agricultural intelligence, facilitating the transformation of agricultural production methods and enhancing both the efficiency and quality of agricultural production.
Many researchers have effectively addressed the time-consuming, labor-intensive, and inefficient issues encountered in agricultural product classification and identification by utilizing hyperspectral imaging technology in conjunction with machine learning and deep learning methods. This technological approach enables efficient and non-destructive identification of agricultural products.
In reference [
25], Zhang Fu et al. proposed a support vector machine (SVM) classification model based on hyperspectral imaging technology to achieve efficient and non-destructive identification of Ginkgo biloba varieties. They optimized model parameters using genetic algorithms (GA) and particle swarm optimization algorithms (PSO) to enhance the accuracy of variety identification. Experimental results indicated that the SNV-CARS-PSO-SVM model had the best identification performance, with a classification accuracy of 96.67%. This suggests that CARS feature wavelength variables can represent all wavelength information, and the PSO-SVM model demonstrates good variety identification performance, enabling the identification of Ginkgo biloba varieties.
In reference [
26], Ma Lingkai et al. used hyperspectral imaging technology to differentiate between organic eggs and conventional eggs. They established egg category identification models using partial least squares discriminant analysis (PLS-DA) and support vector machines (SVM). Due to the large volume of hyperspectral data and the presence of significant redundant information, they applied the successive projection algorithm (SPA) and competitive adaptive reweighted sampling (CARS) to reduce the dimensionality of the egg yolk ROI data, eliminating redundant information to build the classification models. The experimental results showed that the SPA-SVM identification model achieved a highest accuracy rate of 94.2% on the test set.
In reference [
27], Li Guohou et al. collected hyperspectral images of the front and back of wheat seeds from eight varieties using a hyperspectral imaging device. They proposed a hyperspectral wheat variety identification method based on an attention mechanism mixed convolutional neural network using this dataset. Experimental results demonstrated that the proposed method outperformed other methods with a classification accuracy of 97.92%.
In reference [
28], Zhang Long et al. utilized hyperspectral imaging technology in combination with Savitzky-Golay smoothing filter (SG), multiplicative scatter correction (MSC), and support vector machine (SVM) to establish a classification method for tobacco leaves and contaminants. The experimental results indicated an overall classification accuracy of 99.92% for tobacco leaves and contaminants, with a Kappa coefficient of 0.998.
In conclusion, the application of hyperspectral imaging technology in agricultural product classification and identification holds significant importance, as it can enhance classification accuracy, reduce manual costs, improve work efficiency, ensure food safety, and drive the development of intelligent agriculture.
3. Hyperspectral Data Acquisition
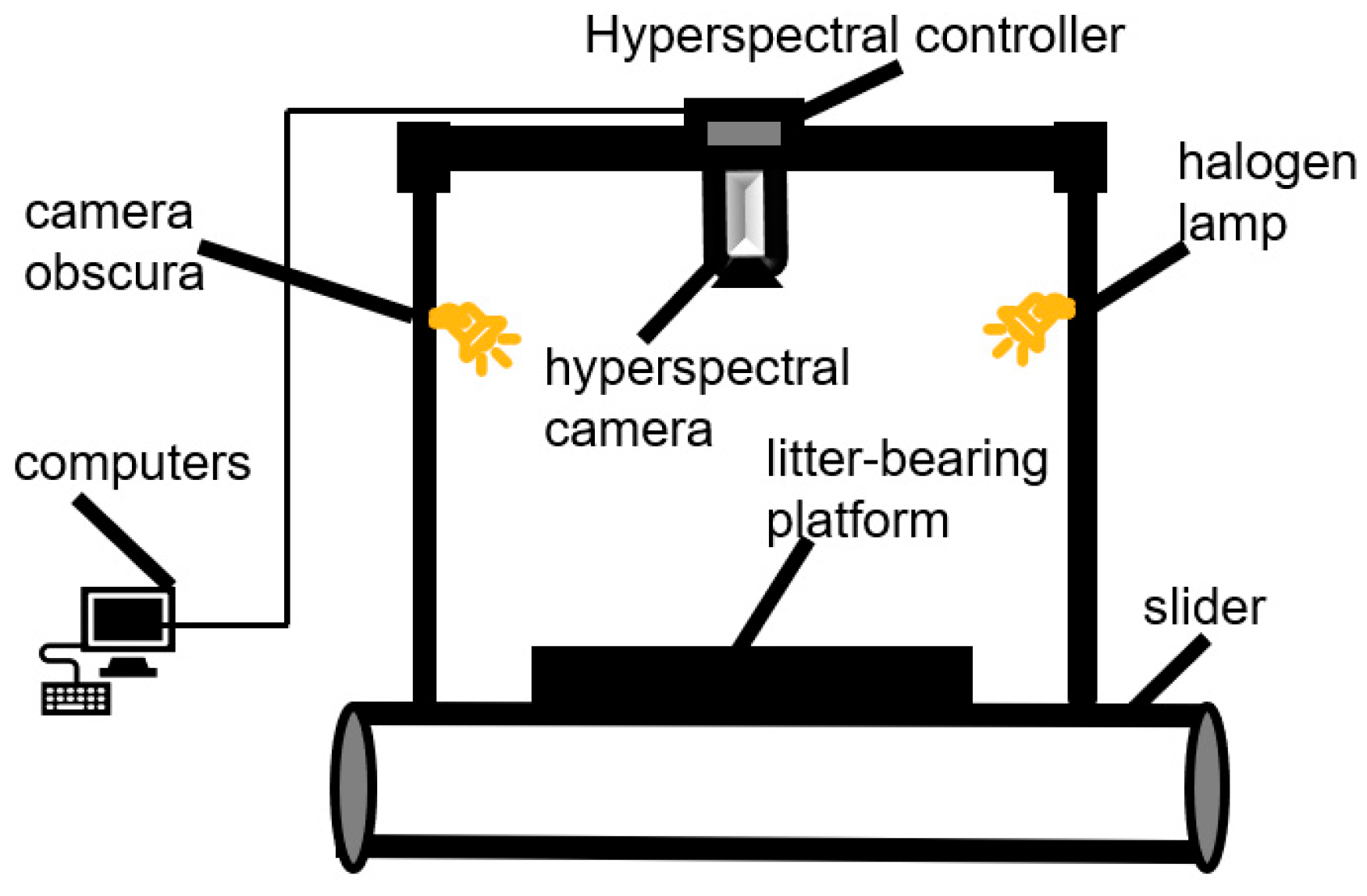
Nowadays, according to different application requirements in the field of agriculture, spectral data acquisition can be divided into two types: indoor acquisition and outdoor acquisition. The indoor acquisition system consists mainly of a hyperspectral camera, halogen lamp, camera obscura, and slider. The advantage of this acquisition system is primarily to reduce the impact of environmental factors, thereby improving the final recognition accuracy and classification precision. In order to achieve the classification and identification of sorghum varieties, Song Shaozhong et al. built an indoor spectral acquisition system based on hyperspectral imaging technology. By employing various preprocessing and data analysis methods, they achieved a classification accuracy of 97.16% [
29]. The schematic diagram of the indoor acquisition system is shown in
Figure 1.
Due to limitations in conditions, indoor acquisition is generally used for small-scale and limited sample testing. When there is a need to collect data on a large scale with multiple samples, outdoor acquisition methods are required. Outdoor acquisition methods mainly involve using drones equipped with hyperspectral cameras to collect spectral data. The outdoor acquisition system primarily consists of a drone, a gimbal, and a hyperspectral camera. The advantage of this method is the ability to collect data over large areas and to increase the collection rate. Feng Haikuan et al. utilized a drone equipped with a hyperspectral imager to monitor nitrogen levels in winter wheat [
30].
Hyperspectral imaging is commonly done using outdoor acquisition methods for detecting crop pests and diseases and monitoring their growth conditions. This method allows for the acquisition of a large amount of data, enabling the training of a significant dataset during data analysis, which can help reduce measurement errors.
4. Hyperspectral Data Acquisition
4.1. The Need for Hyperspectral Data Preprocessing
Hyperspectral raw data cannot be directly used for data analysis because various sources of noise may exist during the collection of raw hyperspectral data of crops and agricultural products, such as atmospheric interference, instrument noise, and disturbances during the data acquisition process [
31]. The hyperspectral raw data can also be influenced by factors like lighting conditions and sensor responses. By applying correction processes to the data, these influencing factors can be eliminated, making the data more accurate and comparable [
32].
Hyperspectral raw data typically have high dimensions, containing a large amount of spectral information [
33]. To enhance the efficiency of data processing and analysis, it is necessary to perform dimensionality reduction on the data, mapping the data from a high-dimensional space to a lower-dimensional space while retaining the most representative information [
34]. The raw hyperspectral data contains rich spectral information, and extracting useful features from it is a critical issue. Feature extraction transforms the data into more representative and discriminative feature vectors, laying the foundation for subsequent modeling and analysis [
35,
36].
In summary, processing hyperspectral raw data involves noise removal, data correction, dimensionality reduction, and feature extraction. These preprocessing steps can enhance the quality and reliability of the data, reduce the impact of interfering factors, and provide a more reliable and effective basis for subsequent data analysis and applications, ultimately improving the accuracy of data analysis.
4.2. Hyperspectral Data Processing Flow
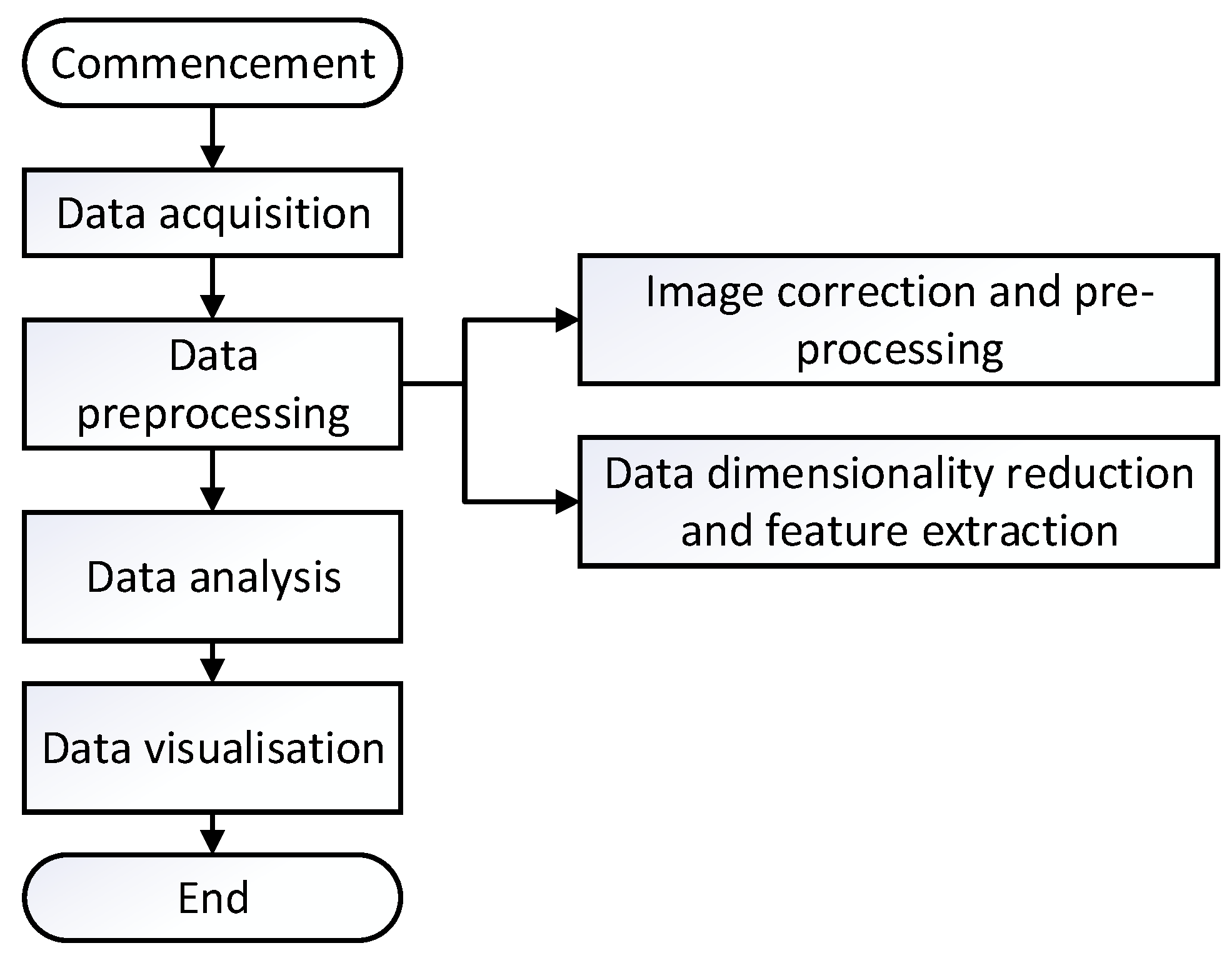
Hyperspectral raw data possesses characteristics such as high dimensionality and diversity. Utilizing raw data directly for data analysis may lead to compromised detection results and classification accuracy. Therefore, it is crucial to process hyperspectral raw data, with the main aim being to extract meaningful data, filter out irrelevant information, and eliminate various environmental influences [
37]. The general data processing workflow is illustrated in
Figure 2 below.
4.3. Hyperspectral Data Preprocessing Methods
4.3.1. Data Calibration and Pre-Processing
During the process of image data acquisition by a hyperspectral camera, the acquired images are raw and uncorrected, necessitating post-acquisition correction of the image data. The primary reasons for this are as follows: on one hand, during image acquisition, the hyperspectral camera can be affected by dark current and the surrounding environment, potentially impacting the stability of the acquired hyperspectral images [
38]; on the other hand, since the raw hyperspectral image data consists of photon intensity information, it requires reflectance correction to obtain relative reflectance. Therefore, black and white correction of hyperspectral raw data is a necessary step before data analysis [
39,
40]. Additionally, factors such as light scattering, irregularities in the detected object images, and random noise during spectral information acquisition can lead to issues like non-smooth spectral curves and low signal-to-noise ratio. Hence, preprocessing of the data is typically conducted before any data analysis, with common preprocessing methods including smoothing, normalization, derivative methods, multiscatter correction, standard normal variate transformation, wavelet transformation, etc. [
41,
42,
43,
44]. The data processed through these methods not only enhance curve smoothness and signal-to-noise ratio but also contribute to improved accuracy in subsequent modeling steps.
Smoothing Processing;
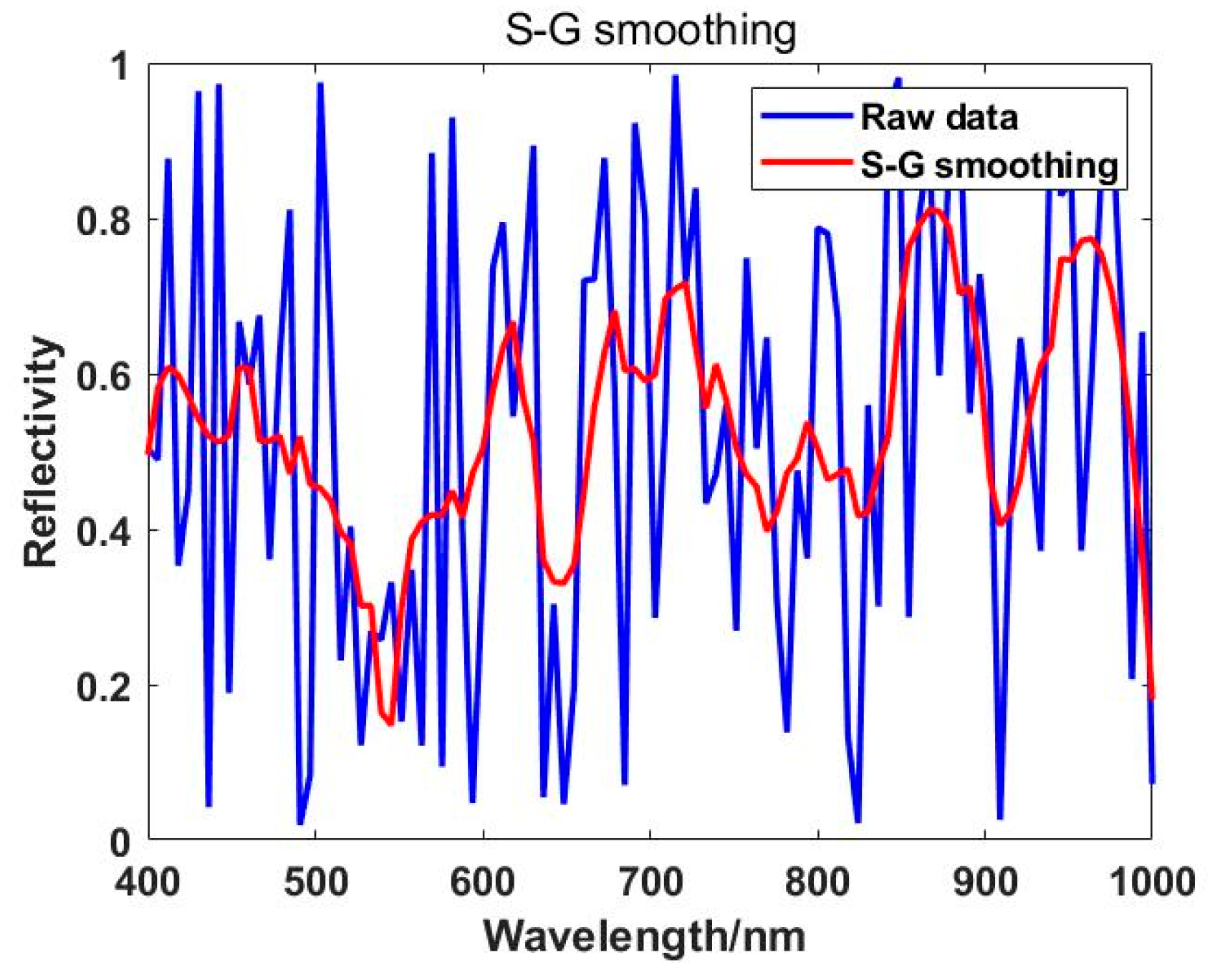
The spectral raw data collected is influenced by external factors such as noise and jitter, resulting in irregular and jagged spectral curves that are not conducive to later data analysis. After smoothing, the spectral curve not only eliminates the salient points in the original data but also makes the spectral curve more continuous and smooth. Common smoothing methods include median smoothing, mean smoothing, and Savitzky-Golay (S-G) smoothing. The S-G smoothing filtering method [
45] is a commonly used filtering technique in spectral preprocessing, initially proposed by Savitzky and Golay in 1964. This method is widely applied for data smoothing and noise reduction, utilizing local polynomial least squares fitting in the time domain [
46,
47].
The core idea of the Savitzky-Golay (S-G) smoothing method is to perform weighted filtering on all data within a window, with the weights obtained through least squares fitting of a given high-order polynomial. The main feature of this filtering method is that it can remove noise while ensuring that the shape and width of the signal remain unchanged. The key to this smoothing method lies in finding appropriate parameters: the window width (N) and the order of the polynomial fit (K). The primary approach to implementing S-G smoothing is as follows: first, for the i-th reference point and its 2N+1 neighboring points (N points on each side), conduct a least squares fit on the spectral data, obtaining polynomial coefficients (k). After solving for the coefficients a0, a1, ..., ak-1, replace the original intensity value of the reference point with the fitted value Fi [
48].
where (X=-N,-N+1,…,N). After iterating through the entire data band using this method,the smoothed spectral curve can be obtained, as shown in
Figure 3 below.
In spectral analysis, the intensity values of spectral data may vary due to factors such as concentration, temperature, and pressure of different samples. To eliminate the interference of these factors, it is necessary to normalize the spectral data for a more accurate comparison and analysis of the spectral characteristics of different samples [
49]. The basic principle of spectral normalization is to standardize the intensity values of each wavelength point in the spectral data, ensuring that they fluctuate within a certain range without being influenced by external factors. Common normalization methods include Min-Max normalization, Z-score normalization, etc. [
50,
51]. Min-Max normalization involves linearly transforming the values of each feature dimension so that they are mapped to the range [0, 1] (interval scaling), with the transformation function as follows:
The Z-score normalization method standardizes the values of each feature dimension using the mean and standard deviation of each dimension. Its transformation function is as follows:
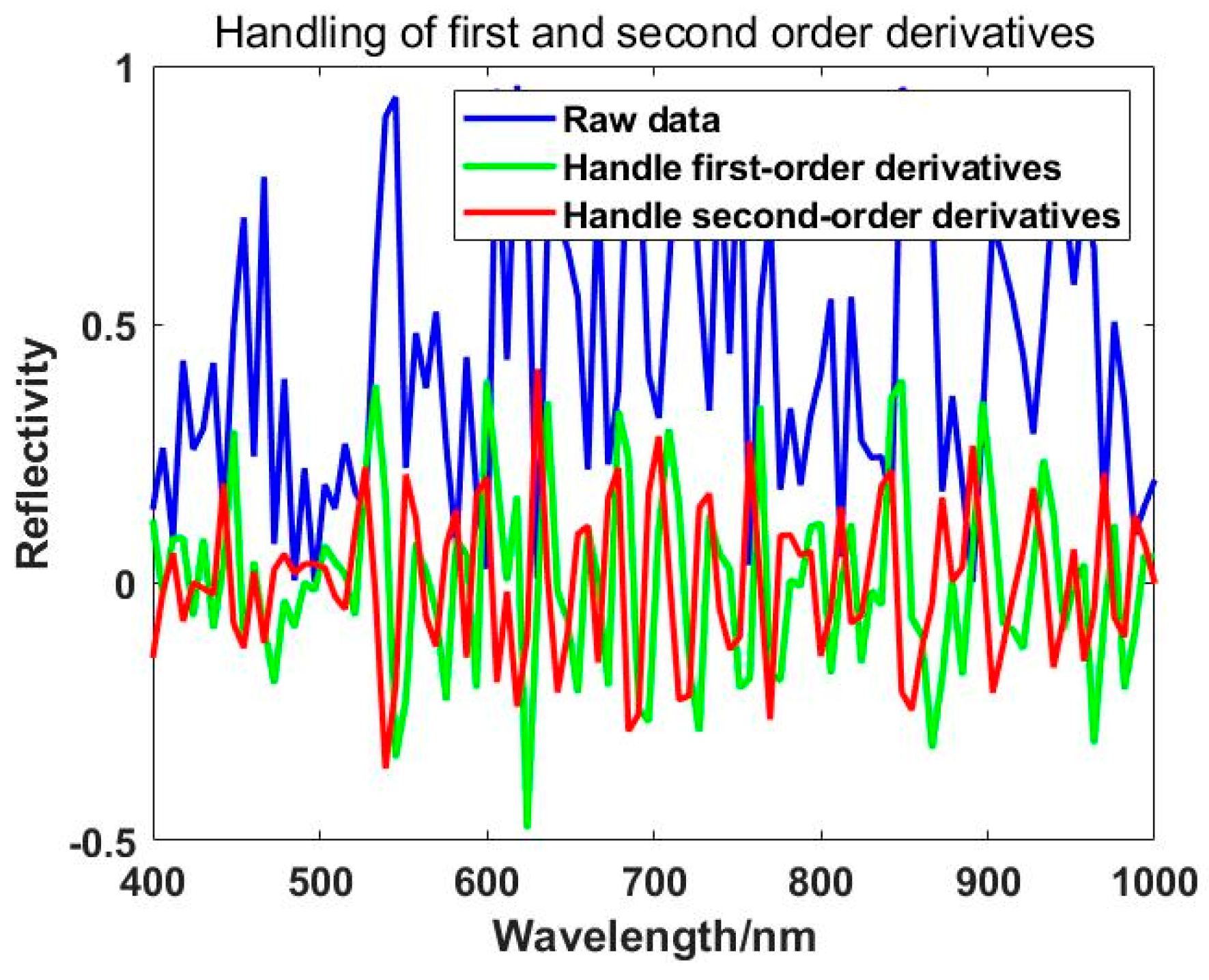
The derivative method can reduce baseline drift caused by instrumental interference, uneven sample surfaces, lighting variations, and other factors. It partially addresses the issue of spectral signal overlap, amplifies hidden weak but effective spectral information, and enhances spectral changes and resolution [
52]. The spectral derivative method is commonly used in the identification of absorption peaks and valleys in near-infrared spectra and in the extraction of characteristic wavelengths. Derivative spectra include first-order derivative spectra, second-order derivative spectra, and higher-order derivative spectra, with practical applications often requiring only first and second-order derivative spectra to meet requirements [
53,
54]. The application of first and second-order derivative processing on spectra is illustrated in
Figure 4.
Multiple scattering correction (MSC) is a linearization process applied to spectra. Uneven sample distribution or variations in sample size can lead to light scattering, resulting in the inability to obtain an "ideal" spectrum [
55]. This algorithm assumes that the actual spectrum is linearly related to the "ideal" spectrum. In most cases, the "ideal" spectrum is unattainable, so during spectral data preprocessing, the average spectrum of the sample data set is often used as a replacement [
56]. Multiple scattering correction can eliminate random variations, and the corrected spectrum differs from the original spectrum. When the spectrum is highly correlated with the chemical properties of the substance being measured, multiple scattering correction yields better results [
57,
58]. In practical applications, it is common to use the average value of all data as the ideal spectrum/standard spectrum, which is expressed as:
Next, perform a univariate linear regression on the spectrum of each sample with the standard spectrum to determine the baseline shift (ki) and offset (bi):
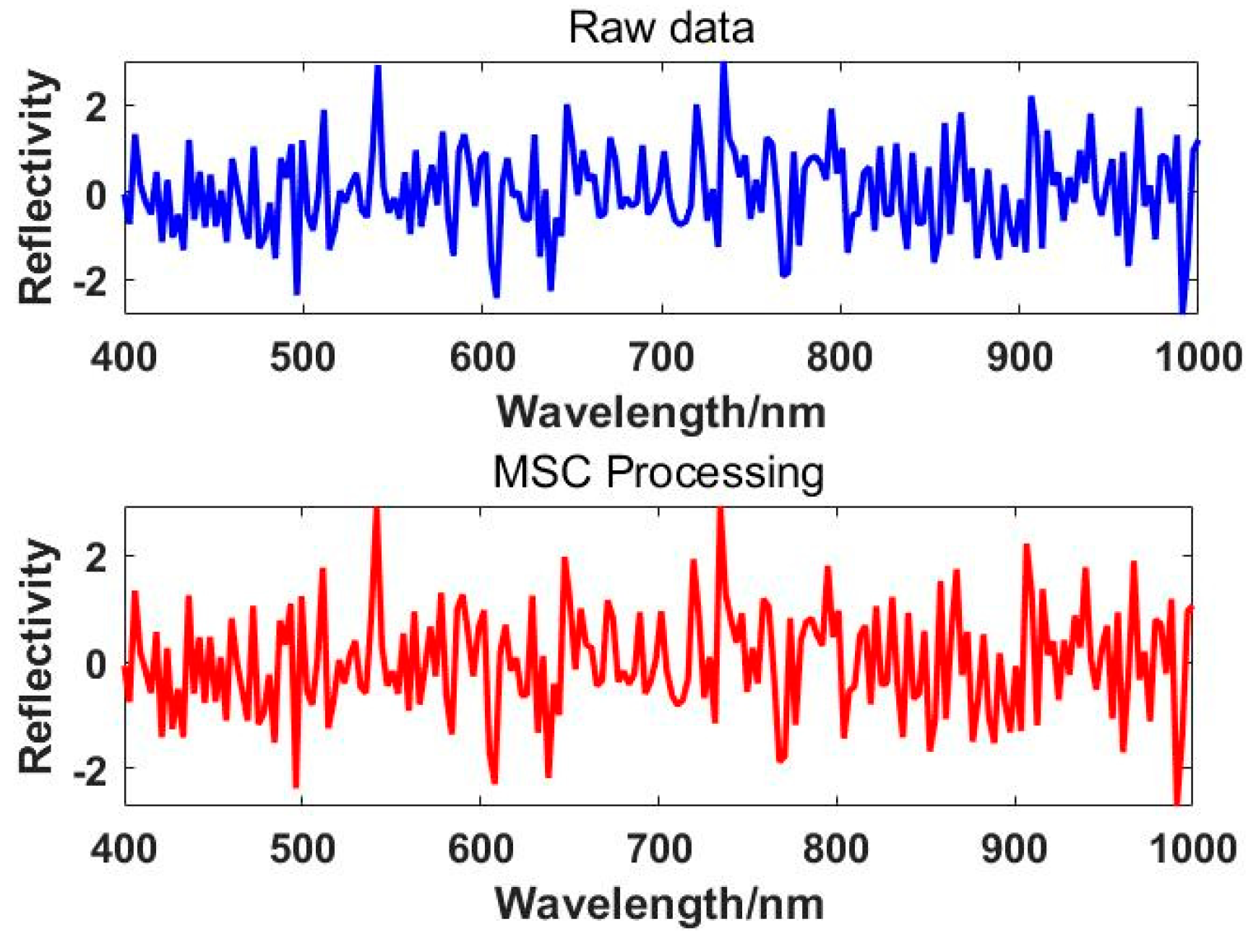
The effect plot of the MSC correction is shown in
Figure 5.
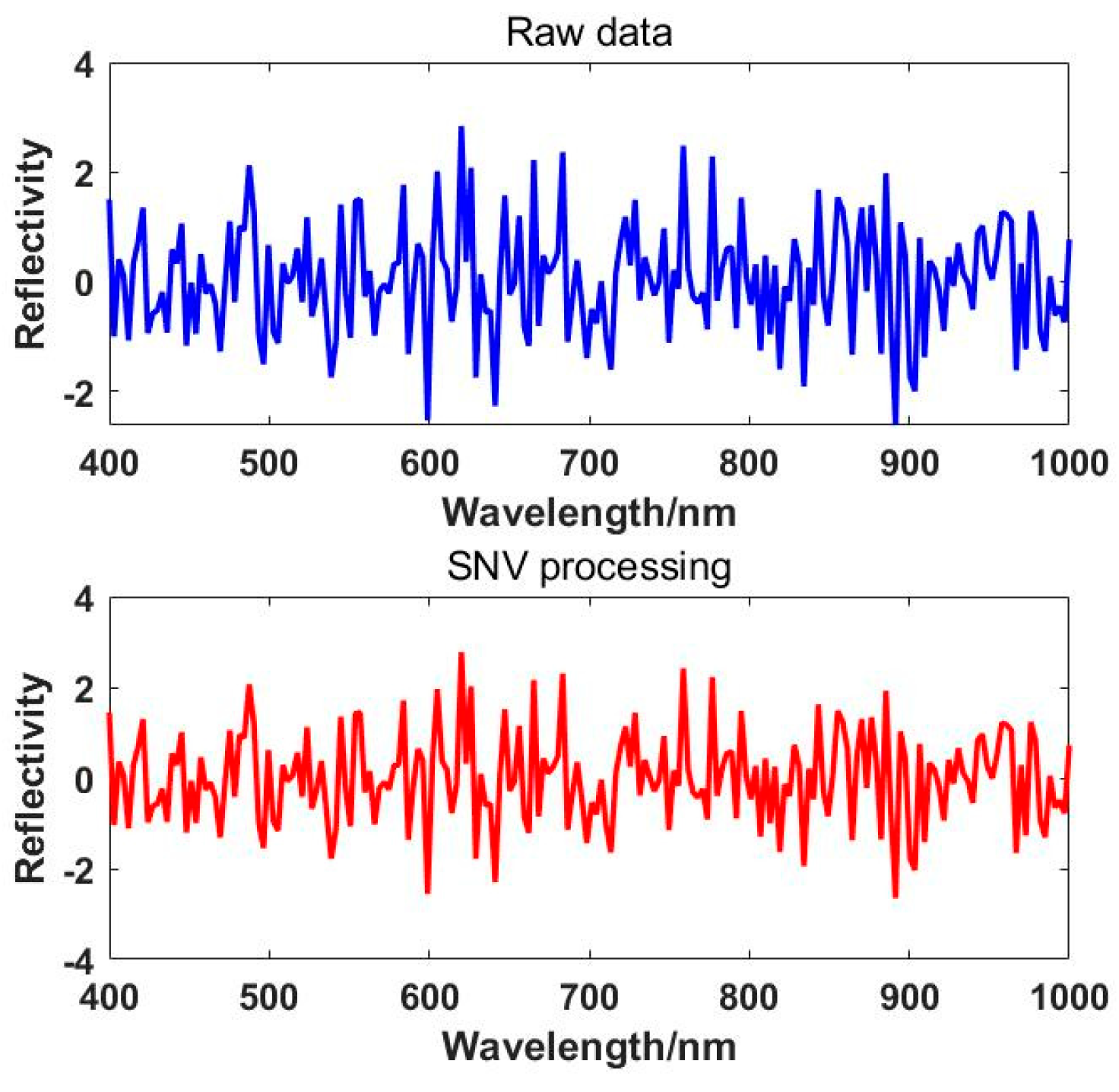
Standard Normal Variate (SNV) transformation, similar to multiple scattering correction, can be used to eliminate scattering errors and path length variations [
59]. However, the two methods have different processing principles. This method does not require an "ideal" spectrum; instead, it assumes that the spectral absorbance values at each wavelength in every spectrum satisfy certain conditions, such as following a normal distribution. The SNV transformation involves standardizing each spectrum [
60,
61]. In practical processing, this method involves subtracting the original spectrum from the mean spectrum and then dividing by the standard deviation, effectively normalizing the original spectral data, satisfying the equation:
where i is the number of samples, j is the number of spectral channels, and Z
ij is the SNV-transformed data. The effect plot of the SNV correction is shown in
Figure 6.
Wavelet Transform (WT) is a newly developed time/frequency transformation analysis method used for spectral data compression and noise reduction [
62]. Wavelet Transform inherits the localized idea of Fourier Transform, where the window size in the transformation varies with frequency. Moreover, when the time/frequency localization and multi-resolution properties are good, Wavelet Transform decomposes the spectral signal into multiple scale components at different frequencies. It selects the appropriate sampling step based on the size of the scale component, allowing it to focus on any spectral signal [
63].
Wavelet Transform typically includes Continuous Wavelet Transform (CWT) and Discrete Wavelet Transform (DWT) [
64]. The multi-scale resolution characteristics of Wavelet Transform enable it to quickly extract the original spectral signal from noisy signals. Utilizing wavelet analysis, it can eliminate spectral signals with significant noise, making it a crucial application in hyperspectral analysis [
65].
Basic formula for Continuous Wavelet Transform;
where W(a,b) is the wavelet coefficient, x(t) is the original signal, ψ(t) is the wavelet basis function, a is the scale parameter, and b is the shift parameter.
Basic formula for Discrete Wavelet Transform.
where W(j,k) is the discrete wavelet coefficient, and ψj,k(t) is the wavelet basis function.
4.3.2. Data Calibration and Pre-Processing
Due to the high number of spectral bands, often hundreds or even thousands, in the raw data captured by hyperspectral cameras, there exists high-dimensional spectral information and significant data redundancy. This not only complicates the computation process but also diminishes the accuracy of non-destructive detection models [
66]. Therefore, it is an important step in data analysis to perform dimensionality reduction and extract spectral feature wavelengths from hyperspectral raw data before modeling. The most commonly used methods for dimensionality reduction and feature wavelength extraction include Principal Component Analysis, Independent Component Analysis, Genetic Algorithms, and Minimum Noise Fraction transformation [
67,
68]. After processing with the corresponding dimensionality reduction algorithms, a significant amount of redundant information is eliminated. By extracting feature wavelengths, the most distinctive and information-rich wavelengths can be selected to better understand the data and perform target identification or classification [
69]. These processes play a crucial role in simplifying the computation process and enhancing the accuracy of models.
Principal Component Analysis (PCA) is a commonly used dimensionality reduction method in statistics and mathematics. It transforms multiple possibly correlated variables into a set of linearly uncorrelated variables through orthogonal transformation, known as principal components. It aims to convert high-dimensional features into a few key components that are mutually uncorrelated and contain the maximum amount of information [
70].
The basic idea behind PCA is to recombine several originally correlated indicators into a new set of composite indicators that are mutually independent, while retaining as much information from the original variables as possible [
71]. This method is highly effective in handling multivariable problems as it reduces data dimensionality, decreases computational complexity, eliminates noise, and irrelevant features, making the dataset more user-friendly and interpretable. The computational steps of PCA typically involve standardizing the samples, calculating the covariance matrix of the standardized samples, determining the eigenvalues and eigenvectors of the covariance matrix, computing the contribution rate and cumulative contribution rate of the principal components, and selecting principal components that achieve a certain level of cumulative contribution rate [
72]. These principal components can be utilized for subsequent data analyses such as cluster analysis, regression analysis, etc. [
73].
For hyperspectral data represented as an i×j matrix:
where i is the number of samples, and j is the number of spectral channels.The main steps of the PCA method are as follows:
Standardize the matrix X with a mean of x̅ and a standard deviation of Sn;
Whereby, the original matrix is standardized to obtain matrix X1=(X1,…,Xj).
Calculate the correlation matrix along with its eigenvalues and eigenvectors;
Compute the variance contribution rates and determine the principal components Typically, select the top k principal components whose cumulative contribution rate exceeds 90% for data analysis.
Independent Component Analysis (ICA) is a statistical method used for separating multivariate signals, aimed at decomposing multiple mixed signals into independent components [
74]. Unlike other linear transformation methods (such as PCA), ICA assumes that the original signals are mutually independent rather than simply having low correlation. Its core idea is based on the assumption of independence, positing that the observed multivariate signals are linear mixtures of multiple independent components, each with its own statistical distribution [
75]. The assumption of independence is crucial to ICA, enabling the decomposition of mixed signals into independent components through appropriate transformations. This algorithm is currently widely applied in fields such as signal processing, image processing, and other domains [
76].
Assuming that the observed mixed signal X is a linear combination of unknown independent signals S, satisfying:
In this case, X is the observed signal matrix, A is the unknown mixing matrix, and S is the source signal matrix.
The goal of ICA is to estimate the inverse or pseudo-inverse of the mixing matrix A in order to recover the source signal S. The main steps of ICA are:
Minimum Noise Fraction (MNF) is a method used to determine the intrinsic dimensionality (i.e., number of spectral bands) of image data [
77]. This method can separate noise in the data, reducing computational demands in subsequent processing. MNF is essentially a two-stage stacked principal component transformation. The first transformation (based on the estimated noise covariance matrix) is used to separate and readjust noise in the data, ensuring that the transformed noise data has minimal variance and no inter-band correlation. The second step involves a standard principal component transformation of noise-whitened data. To further conduct spectral processing, the intrinsic dimension of the data is determined by examining the final eigenvalues and associated images [
78]. The data space can be divided into two parts: one part is related to larger eigenvalues and corresponding feature images, while the remaining part is related to approximately equal eigenvalues and images dominated by noise [
79,
80].Main Steps of MNF:
Utilize a high-pass filter template to filter the entire image or image data blocks with the same characteristics, obtaining the noise covariance matrix (C
N). Diagonalize it into a matrix (D
N);
where D
N is the diagonal matrix of eigenvalues of C
N arranged in descending order; U is an orthogonal matrix composed of eigenvectors. Further transformation formulas can be derived as follows:
where I is the identity matrix, P is the transformation matrix. When P is applied to image data X, through the transformation Y = PX, the original image is projected into a new space, generating transformed data where the noise has unit variance and is uncorrelated between bands.
Conduct standard principal component transformation on the noise data, with the formula.
where C
D is the covariance matrix of image X. C
D-adj is the matrix after transformation by P, further diagonalized into matrix D
D-adj.
where D
D-adj is a diagonal matrix of eigenvalues of C
D-adj arranged in descending order, V is an orthogonal matrix composed of eigenvectors.
After the MNF transformation, the resulting components are uncorrelated with each other, arranged in descending order of signal-to-noise ratio. MNF transformation separates the noise and ensures inter-band decorrelation, making it superior to PCA transformation. Currently, it is widely used in image denoising, image fusion, image enhancement, and feature extraction, among other applications.
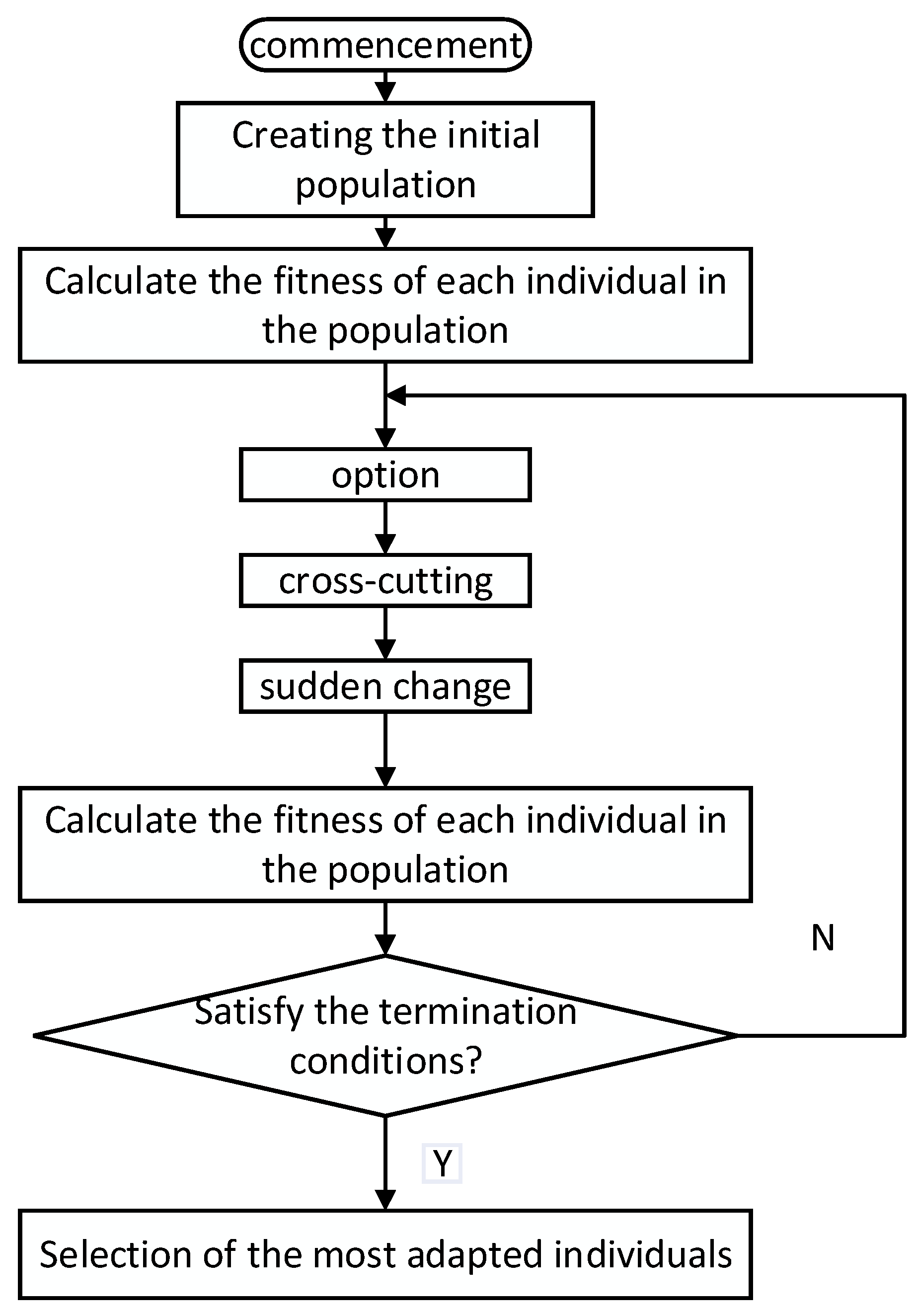
The Genetic Algorithm (GA) is an optimization algorithm that simulates the evolutionary process in nature. By mimicking genetic, crossover, and mutation operations in biology, it progressively searches for the optimal solution [
81]. The principle of genetic algorithm dimensionality reduction is an effective method of high-dimensional data analysis, through the simulation of the biological evolution process in nature to extract the most representative combination of features from high-dimensional data, to achieve the optimisation of data reduction and peacekeeping [
82]. The core idea of genetic algorithm dimensionality reduction is to select the most representative features from high-dimensional data through the optimization process of genetic algorithms and reduce the high-dimensional data to a lower-dimensional space [
83]. The main stages of the genetic algorithm process are illustrated in
Figure 7. The specific steps are as follows:
Generate a set of solutions with random feature combinations;
Evaluate the quality of each solution using an evaluation function such as information gain, variance, etc;
Choose excellent solutions based on fitness evaluation results as parents for the next generation of the population;
Exchange and recombine chromosomes in parents, such as single-point crossover, multi-point crossover.;
Introduce randomness by mutating some solutions to increase population diversity, like bit flips, bit swaps;
Determine which solutions to retain based on a replacement strategy like elitism, randomness;
Set stopping conditions for the algorithm, such as maximum number of iterations, fitness function reaching a threshold value.
4.4. Hyperspectral Data Analysis Methods
4.4.1. Machine Learning Methods
Support Vector Machine (SVM) is a commonly used supervised learning algorithm that is applicable to both binary and multiclass problems [
84]. Its principle is based on the minimization of structural risk in statistical learning theory by finding an optimal hyperplane for classification. The basic principle of SVM is as follows:
Assuming the training dataset is linearly separable, meaning there exists a hyperplane that can completely separate samples from different classes. The hyperplane can be represented by the following equation;
where w is the normal vector, x is the sample feature, and b is the bias term.
The goal of SVM is to find an optimal hyperplane that maximizes the margin between the sample points and the hyperplane. The margin refers to the distance from the sample points to the hyperplane, and maximizing this margin helps improve the generalization ability of SVM [
85]. The margin can be expressed as;
where y
i is the label of the sample (1 or -1), ||w|| is the norm of the normal vector w.
During the process of maximizing the margin, only a subset of sample points have an impact on the position of the hyperplane, and these points are called support vectors. Support vectors are the sample points closest to the hyperplane, determining the position and orientation of the hyperplane;
Transforming the goal of maximizing the geometric margin into a convex optimization problem can be solved using the Lagrange multiplier method. By maximizing the margin, the optimization problem can be reformulated in its dual form, where the objective is to minimize a function involving Lagrange multipliers;
In practical applications, many problems cannot be perfectly separated by a linear hyperplane. To address this issue, SVM introduces the concept of kernel functions, mapping nonlinear problems from low-dimensional spaces to high-dimensional spaces to make them linearly separable. Common kernel functions include linear kernel, polynomial kernel, Gaussian kernel, etc [
86];
In real-world scenarios, data often contain noise and outliers. To enhance the robustness of the model, SVM introduces the concepts of soft margin and penalty terms. Soft margin allows some sample points to fall within the margin by introducing slack variables to control this. The penalty term balances maximizing the margin and penalizing misclassifications through regularization [
87];
For multi-class problems, one can use the one-vs-one or one-vs-rest methods to con-struct multiple binary classifiers, then combine them for multiclass classification.
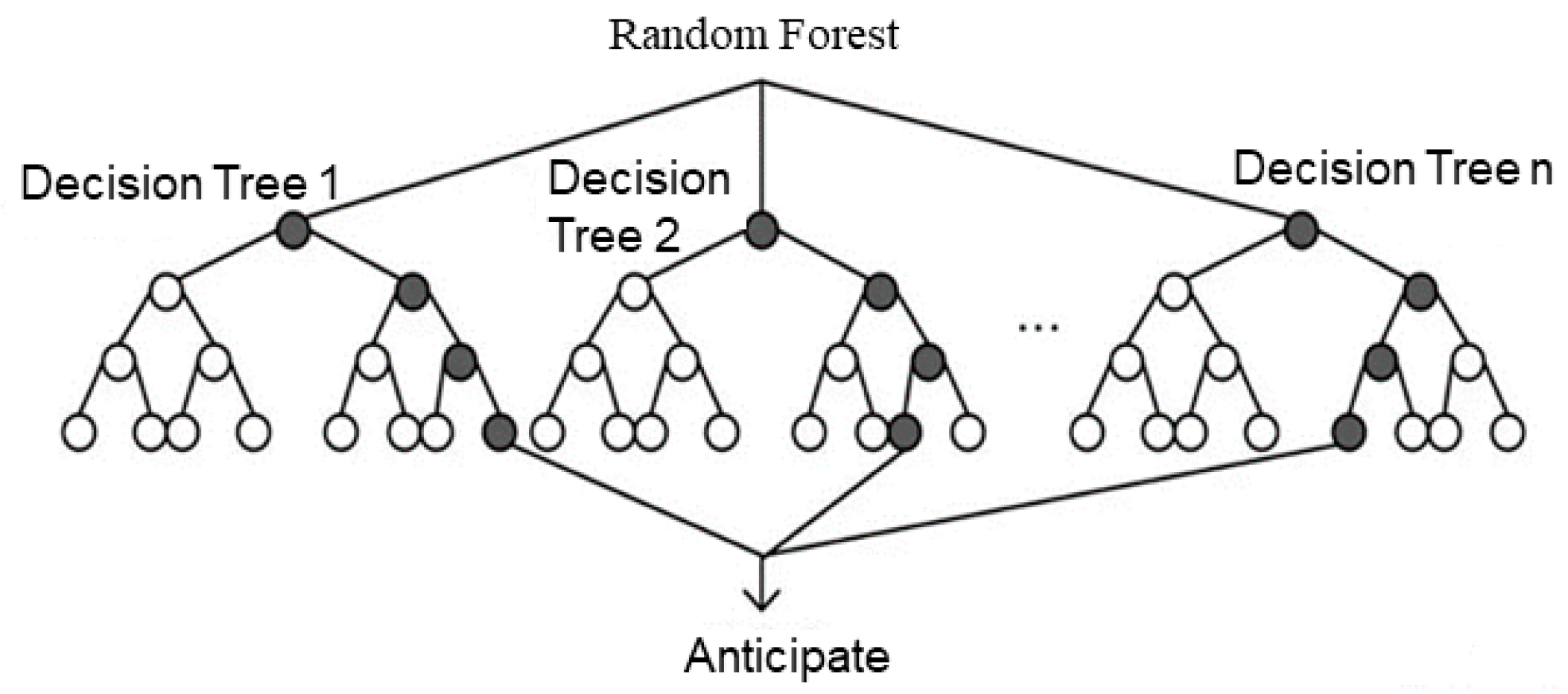
The Random Forest (RF) algorithm is a classification and regression method based on ensemble learning [
88]. Its core idea is to improve prediction performance by constructing multiple decision trees and combining them. Specifically, when building each decision tree, the Random Forest algorithm uses random sampling to extract samples from the original dataset, and randomly selects a subset of features at each node to split the decision tree [
89]. This randomness helps reduce the correlation between models, increase model diversity, prevent overfitting, and enhance generalization capability. The main steps of RF are as follows:
First, assuming there are T samples and M features available for a classification task, each sample is associated with a corresponding label yi. Next, n decision trees are built, where each tree is constructed on a randomly selected subset of samples, considering only a subset of all features during the tree-building process [
90]. Each feature is referred to as a predictor variable, and all predictor variables can be denoted as {X1, X2, ..., Xm}. For each tree, the Random Forest algorithm defines the following steps:
Sample training set samples from the sample set using sampling with replacement;
Randomly select k variables without replacement from all predictor variables, where k is much less than m. The selected set of variables can be represented as {f1, f2, ..., fk};
Build a decision tree based on the training samples and the generated subset of variables, using a certain criterion to measure the importance of features to determine the feature for the first split node in the tree.
Repeat step (3) n times to generate n decision trees.
An example diagram is shown in
Figure 8.
The K-Nearest Neighbors (KNN) algorithm is a classification method based on Euclidean distance to infer the category of items. It is used to accomplish hyperspectral classification by computing distances between two targets [
91,
92].
The distance calculation method is as follows:
where x and y represent two targets, xk and yk denote the coordinates of the two targets in the k-th dimension, and n is the dimension of the target coordinates. The main implementation steps of the K-Nearest Neighbors algorithm are as follows:
Collect and prepare a dataset for training and testing. Each sample should include a set of features and corresponding labels (for classification) or target values (for regression);
Determine the value of K, which represents the number of nearest neighbor samples to consider. The choice of K value affects the algorithm's performance and is typically selected through methods like cross-validation;
For a given test sample, calculate the distance between it and each sample in the training set. Common distance metrics include Euclidean distance, Manhattan distance, etc;
Based on the calculated distances, select the K nearest training samples to the test sample as its nearest neighbors;
For classification problems, determine the category of the test sample using a majority voting approach. Predict based on the most frequently occurring category among the labels of the K nearest neighbors. For regression problems, average the target values of the K nearest neighbors to obtain the predicted value for the test sample;
Based on the results of the majority voting or averaging operation, consider it as the final prediction result for the test sample.
When selecting the value of K, it is essential to balance the sensitivity and complexity of the model. A small K value is susceptible to noise interference, leading to underfitting and missing data features. On the other hand, a large K value may result in over-smoothing, potentially causing overfitting and reduced generalization. In imbalanced data, an inappropriate K value can bias towards the majority class. The appropriate K value affects the smoothness of boundaries; a smaller K value results in complexity and high variability, while a larger K value leads to smoother results but may lose detail [
93].
Linear Discriminant Analysis (LDA) is a supervised classification method, which requires prior knowledge of the sample classification results in the training set. This method linearly transforms high-dimensional feature vectors into low-dimensional feature vectors. This transformation ensures that the data features of samples belonging to the same class are close to each other, while the features of samples from different classes are significantly different [
94,
95].
LDA primarily constructs a low-dimensional "boundary" to project each sample, such that after projection, the within-class variance is minimized, and the between-class variance is maximized [
96]. This boundary is obtained under supervised classification samples and can be used for classifying test sets and unknown samples. The basic steps of LDA are as follows:
Compute the within-class scatter matrix and between-class scatter matrix: The within-class scatter matrix (S
W) represents the dispersion of data points within the same class, while the between-class scatter matrix (S
B) represents the dispersion between different classes;
where c is the number of classes, Di is the dataset of the ith class, and mi is the mean vector of the ith class.
where Ni is the number of samples in the ith class, and m is the global mean vector of all samples.
Calculate the eigenvalues and eigenvectors of matrix : The eigenvalues of matrix represent the ratio of between-class scatter to within-class scatter in the direction defined by the corresponding eigenvectors after projecting the data. These eigenvectors define the projection directions from the original high-dimensional space to the new low-dimensional space. The purpose of this step is to find a matrix that, when multiplied by the data points, maximizes between-class scatter while minimizing within-class scatter;
Select eigenvectors with the largest eigenvalues: Choose the eigenvectors corresponding to the largest eigenvalues. These eigenvectors determine the optimal new coordinate axes;
Project the data onto the new coordinate axes: Project the original data onto the new coordinate system using the selected eigenvectors to achieve dimensionality reduction.
4.4.2. Machine Learning Methods
Deep Learning is a type of machine learning method based on artificial neural networks that utilizes multiple layers of neural networks to perform nonlinear transformations and feature extraction, enabling the modeling and processing of complex data [
97]. Common deep learning algorithms used for hyperspectral data analysis include Convolutional Neural Networks, Deep Neural Networks, and Residual Networks, among others [
98,
99].
Convolutional Neural Networks (CNNs) are a type of feedforward neural network that includes convolutional computations and are particularly well-suited for tasks such as image processing [
100]. CNNs have the capability of learning representations and can perform translation-invariant classification of input information based on their hierarchical structure, hence also known as "translation-invariant artificial neural networks".
The working principle involves first extracting various features from the input using convolutional and pooling layers, and then combining these features using fully connected layers to obtain the final output [
101]. The convolution operation involves moving a small window (data window) over the image, multiplying and summing elements element-wise. This window essentially consists of a set of fixed weights and can be viewed as a specific filter or convolutional kernel.
The convolutional layer is the core component of convolutional neural networks, enabling feature extraction from input images through convolutional operations. In the convolution operation, each neuron in the convolutional layer performs convolution operations with a portion of pixels in the input image, resulting in a feature map [
102]. Convolution operations help capture local features in the input image, such as edges, textures, and other image characteristics.
The pooling layer is another essential part of convolutional neural networks, reducing the complexity of the model by downsampling the feature maps. Pooling operations typically include max pooling and average pooling, where max pooling involves selecting the maximum value within a specific region, while average pooling involves computing the average value within a specific region. Pooling operations help reduce the number of parameters in the model, thereby enhancing the model's generalization ability.
Deep Neural Networks (DNNs) are recursive functions composed of multiple layers, each consisting of multiple neurons. Each neuron receives outputs from all neurons in the previous layer, calculates outputs based on input data, and passes them to neurons in the next layer, ultimately completing prediction or classification tasks [
103,
104].The basic steps of Deep Neural Networks are as follows:
Data preprocessing: Transforming raw data into a format acceptable by the model. Common preprocessing methods include normalization, standardization, encoding, etc;
Building network structure: Deep neural networks consist of multiple layers, including input layers, hidden layers, and output layers. The input layer receives input data, hidden layers can contain multiple levels based on the model's complexity, and the output layer is responsible for outputting the model's prediction results;
Defining the loss function: The loss function measures the gap between the model's prediction results and the ground truth. Common loss functions include Mean Squared Error (MSE), Cross Entropy, etc;
Backpropagation: Through the backpropagation algorithm, the model's parameters are updated layer by layer based on the gradient information of the loss function to minimize the loss function;
Model training: Input training data into the model, continuously update parameters through the backpropagation algorithm until the model converges or reaches a predefined stopping condition;
Model evaluation: Evaluate the model's performance using an independent test dataset, including metrics such as accuracy, precision, recall, etc.
Residual Networks (ResNets) make deep neural networks easier to optimize and improve accuracy by introducing residual blocks and skip connections. In traditional neural networks, the output of each layer comes from the output of the previous layer [
105]. However, in Residual Networks, the output of each layer is obtained by adding the output of the previous layer to the input of that layer. This residual connection can be viewed as a skip connection that directly passes information from one layer to the next. Each residual block consists of several convolutional layers and a skip connection that adds the input directly to the output of the convolutional layers, forming a residual connection [
106]. This design aims to enable the network to learn residual functions, the differences between inputs and outputs, rather than directly learning the mapping from inputs to outputs. This residual learning concept helps alleviate the vanishing gradient problem and makes the network easier to optimize.
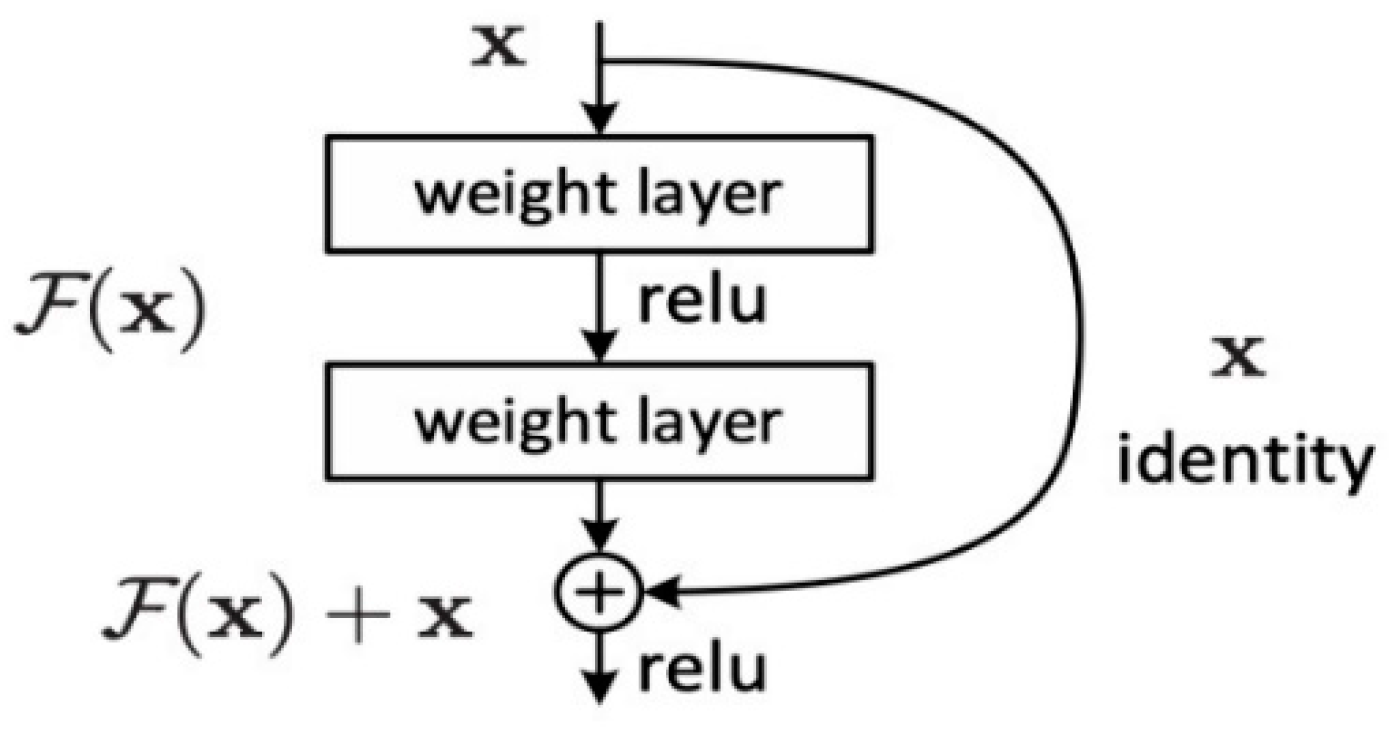
The basic unit of Residual Networks is the residual module, which includes two or more convolutional layers and a skip connection [
107]. The skip connection adds the input directly to the output of the convolutional layers, forming a residual connection. An example of a residual block is shown in
Figure 9.
5. Specific Applications and Analyses
Taking the example of Zhang Fan et al. in 2024, who utilized hyperspectral technology combined with convolutional neural networks to identify the latent period of potato dry rot, let's briefly explain the process of hyperspectral technology in detecting crop diseases and pests. During hyperspectral data acquisition, they used healthy potatoes and potatoes with different degrees of decay as experimental subjects to obtain hyperspectral images of healthy potatoes and potatoes with various disease levels. Subsequently, based on ENVI, they manually selected the healthy parts and diseased spots of samples with different degrees of decay as Regions of Interest (ROIs) and calculated the average spectral values of ROIs as the final spectral information of the sample.
In the data preprocessing stage, they employed the S-G smoothing filter algorithm and the second derivative method for spectral preprocessing. The second derivative can eliminate high-frequency noise and mutual interference between components, but it may also introduce unnecessary noise, reducing the signal-to-noise ratio. Therefore, in data preprocessing, they first used the S-G smoothing filter to remove random noise and then applied the second derivative preprocessing. The second derivative processing enhanced tiny feature peaks hidden in wider absorption bands in the original spectrum, improving resolution and sensitivity [
108].
For data analysis, spectral data were primarily used as input variables, and disease levels were used as output variables to build a Convolutional Neural Network (CNN) model. They optimized the network structure, compared the prediction results of different models, and selected the optimal network layer model as Model-3-3. The test results of nine different network layer models are shown in
Table 1: through a comparison of nine different experimental designs, the optimal network layer model, Model-3-3, was determined.
Based on the optimal network structure Model-3-3 mentioned above, five learning rate optimization experimental schemes were designed, and the optimal learning rate was determined to be 0.0001. The prediction results of models with different learning rates are shown in
Table 2:
To compare the recognition results of the convolutional neural network model, diagnostic models for potato dry rot using LS-SVM, RF, KNN, and LDA as classifiers were established. The comparison of their prediction results is shown in
Table 3.
By combining hyperspectral imaging technology with CNN, successful identification and classification of samples in the latent period of potato dry rot were achieved. Classification models including CNN, LS-SVM, RF, KNN, and LDA were established, and their classification effectiveness was compared. The overall accuracies of the five algorithms were 99.68%, 90.77%, 92.30%, 93.10%, and 92.34% respectively. The CNN model performed the best, with precision, sensitivity, and specificity reaching 99.76%, 98.82%, and 99.54% respectively. The identification rate of latent period samples reached as high as 99.73%, which was 5.55% to 14.15% higher than other methods.
This case demonstrates that when applying hyperspectral technology to solve real-world problems, it is essential to flexibly utilize various preprocessing methods to eliminate interference. By employing machine learning and deep learning algorithms for data analysis and optimizing model parameters, the accuracy of the model can be enhanced, leading to better predictive outcomes. Hyperspectral technology exhibits significant advantages in the detection of crop diseases and pests as well as agricultural product classification.
6. Concluding Remarks
With the rapid development of hyperspectral imaging technology and artificial intelligence, their integration will expand into a wide range of application areas. With technological innovation and hardware performance improvements, hyperspectral data acquisition will become more efficient and convenient. The use of unmanned aerial vehicles equipped with hyperspectral cameras for data collection systems has been widely applied in various fields. Many researchers have focused on preprocessing and data analysis issues related to hyperspectral data, improving and designing more algorithms to enhance data processing capabilities and analysis results.
Agriculture holds a significant position globally, and the shift from traditional agriculture to smart agriculture reflects its rapid development. The rise of smart agriculture, combined with advanced sensing technologies, communication, artificial intelligence, and other technologies, is propelling agriculture into an era of rapid advancement. Hyperspectral imaging technology is increasingly being applied in agriculture, especially in the identification of crop diseases and pests and product classification and authentication. By integrating artificial intelligence, communication, and networking technologies, multiple parameters of crops and products can be simultaneously detected, enabling real-time online dynamic monitoring.
In terms of agricultural product quality classification and authentication, simultaneous internal and external quality inspections will enhance classification accuracy. In the future, the integration of the Internet of Things, cloud services, and artificial intelligence will become the development direction of hyperspectral imaging technology in agricultural production.
Author Contributions
For Conceptualization, J.W., P.H. and Y.Z.; methodology, J.W., P.H.and Y.W.; Investigation, Y.W. andY.Z.; validation, J.W., P.H. and Y.Z.; writing—original draft preparation, Y.Z.; writing—review and editing, J.W., P.H. and Y.W.; supervision, J.W., P.H., and Y.W. All authors have read and agreed tothe published version of the manuscript.
Funding
This study was supported by Natural Science Foundation of Guizhou Minzu University (No. GZMUZK[2022]YB01); Doctoralfunding project of Guizhou Minzu University GZMUZK[2024]QD72 and Guizhou Provincial Department of Education supports the scientific research platform [2022]014.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, J.Y.; Li, C.L. Development and Prospect of Hyperspectral Remote Sensing Imaging Technology [J]. Journal of Space Science 2021, 41, 22–33. [Google Scholar]
- Vane, G.; Goetz, A.F.H.; Wellman, J.B. Airborne imaging spectrometer: a new tool for remote sensing [J]. IEEE Transactions on Geoscience and Remote Sensing 1984, 22, 546–54. [Google Scholar] [CrossRef]
- Liu, Y.N.; Xue, Y.Q.; Wang, J.Y.; et al. Practical Modular Imaging Spectrometer [J]. Journal of Infrared and Millimeter Waves 2002, 21, 9–13. [Google Scholar]
- Dong, G.J.; Zhang, Y.S.; Fan, Y.H. Research on Fusion Technology of PHI Hyperspectral Data and High Spatial Resolution Remote Sensing Images [J]. Journal of Infrared and Millimeter Waves 2006, 25, 123–126. [Google Scholar]
- Liu, Y.D.; Zhang, G.W. Application of Hyperspectral Imaging Technology in Agricultural Product Detection [J]. Food and Machinery 2012, 28, 223–226+242. [Google Scholar]
- Gui, J.S.; Wu, Z.X.; Gu, M.; et al. Overview of the Application of Hyperspectral Imaging Technology in Agriculture [J]. Journal of Zhejiang Agricultural Sciences 2017, 58, 1101–1105. [Google Scholar]
- Wang, D.; Wang, K.; Wu, J.Z.; et al. Research Progress on Non-destructive Rapid Measurement of Seed Quality Based on Spectral and Imaging Technology [J]. Spectroscopy and Spectral Analysis 2021, 41, 52–59. [Google Scholar]
- Xiu, L.C.; Zheng, Z.Z.; Yang, B.; et al. Application of Airborne Hyperspectral Imaging Technology in Ecological Environment Protection in the Jiangsu, Anhui, and Zhejiang Regions of the Yangtze River Economic Belt [J]. Geology of China 2021, 48, 1334–1356. [Google Scholar]
- Tao, H.H.; Yao, Y.T.; Lin, W.J. Research on the Application of UAV Technology in Monitoring Water Quality Pollution in Rivers and Lakes [J]. China Water Power and Electrification 2021, 42–45+10. [Google Scholar]
- Zhao, S.H.; Zhang, F.; Wang, Q.; et al. Application of Hyperspectral Remote Sensing Technology in the National Environmental Protection Field [J]. Spectroscopy and Spectral Analysis 2013, 33, 3343–3348. [Google Scholar]
- Yu, C.R.; Wang, T.R.; Li, S.; et al. Application of Hyperspectral Imaging Technology for Extracting Cancerous Information from Liver Slices [J]. Science Technology and Engineering 2015, 15, 106–109. [Google Scholar]
- Jiang, H.M.; Mei, J.; Hu, X.X.; et al. Exploration of Hyperspectral Imaging in Medical Diagnosis [J]. Chinese Journal of Medical Physics 2013, 30, 4148–4152, 4158. [Google Scholar]
- Liu, L.X.; Li, M.Z.; Zhao, Z.G.; et al. Advances in the Application of Hyperspectral Imaging Technology in Biomedicine [J]. Chinese Laser 2018, 45, 214–223. [Google Scholar]
- Shi, N.C.; Li, G.H.; Lei, Y.; et al. Application of Hyperspectral Imaging Technology in the Protection of Palace Museum Calligraphy and Painting Cultural Relics [J]. Cultural Relics Protection and Archaeology Science 2017, 29, 23–29. [Google Scholar]
- Li, G.H.; Chen, Y.; Sun, X.J.; et al. Application of Large-format Hyperspectral Scanning System in Cultural Relics Research [J]. Infrared 2024, 45, 42–52. [Google Scholar]
- Ding, L.; Yang, Q.; Jiang, P. Comprehensive Review of the Application of Hyperspectral Imaging Technology in the Analysis of Ancient Chinese Calligraphy and Painting [J]. Cultural Relics Protection and Archaeology Science 2023, 35, 128–141. [Google Scholar]
- Qiao, S.C.; Tian, Y.W.; He, K.; et al. Research Progress on Non-destructive Detection Techniques for Fruit Diseases and Pests [J]. Food Science 2019, 40, 227–234. [Google Scholar]
- Yang, X.; Liu, W.; Ma, M.J.; et al. Research Progress on the Application of Hyperspectral Imaging Technology in Tea Production [J]. Journal of South Central Agricultural Science and Technology 2023, 44, 238–242+252. [Google Scholar]
- Yu, J.J.; He, Y. Early Detection of Tomato Leaf Gray Mold Disease Based on Hyperspectral Imaging Technology [J]. Spectroscopy and Spectral Analysis 2013, 33, 2168–2171. [Google Scholar]
- Zhang, J.Y.; Chen, J.C.; Fu, X.P.; et al. Hyperspectral Imaging Detection of Fusarium Wilt in Melon Leaves [J]. Spectroscopy and Spectral Analysis 2019, 39, 3184–3188. [Google Scholar]
- Liang, W.J.; Feng, H.; Jiang, D.; et al. Early Identification of Sclerotinia Stem Rot in Rapeseed Using Hyperspectral Images Combined with Deep Learning [J]. Spectroscopy and Spectral Analysis 2023, 43, 2220–2225. [Google Scholar]
- Li, Y.; Li, C.L.; Wang, X.; et al. Identification of Cucumber Diseases and Pests Using Hyperspectral Imaging and Extraction of Feature Wavelengths Method [J]. Spectroscopy and Spectral Analysis 2024, 44, 301–309. [Google Scholar]
- Li, B.X.; Zhou, B.; He, X.; et al. Current Status and Prospects of Target Classification Methods for Hyperspectral Images [J]. Laser & Infrared 2020, 50, 259–265. [Google Scholar]
- Wang, D.; Luan, Y.Q.; Tan, Z.J.; et al. Detection of Pesticide Residues in Broccoli Based on Hyperspectral Imaging and Convolutional Neural Network [J/OL]. Food Industry and Technology 2024, 1–15. [Google Scholar]
- Zhang, F.; Zhang, F.Y.; Cui, X.H.; et al. Discrimination of Ginkgo Varieties Using Hyperspectral Imaging Combined with PSO-SVM [J]. Spectroscopy and Spectral Analysis 2024, 44, 859–864. [Google Scholar]
- Ma, L.K.; Zhu, S.P.; Miao, Y.J.; et al. Discrimination between Organic Eggs and Conventional Eggs Based on Hyperspectral Technology [J]. Spectroscopy and Spectral Analysis 2022, 42, 1222–1228. [Google Scholar]
- Li, G.H.; Li, Z.X.; Jin, S.L.; et al. Hybrid Convolutional Neural Network for Wheat Variety Discrimination using Hyperspectral Imaging [J]. Spectroscopy and Spectral Analysis 2024, 44, 807–813. [Google Scholar]
- Zhang, L.; Ma, X.Y.; Wang, R.L.; et al. Application of Hyperspectral Imaging Technology in the Classification of Tobacco Leaves and Foreign Matter [J]. Tobacco Science & Technology 2020, 53, 72–78. [Google Scholar]
- Song, S.Z.; Liu, Y.Y.; Zhou, Z.Y.; et al. Research on Sorghum Variety Identification Based on Hyperspectral Image Technology [J]. Spectroscopy and Spectral Analysis 2024, 44, 1392–1397. [Google Scholar]
- Feng, H.K.; Fan, Y.G.; Tao, H.L.; et al. Monitoring Nitrogen Content in Winter Wheat Using UAV-based Hyperspectral Imaging [J]. Spectroscopy and Spectral Analysis 2023, 43, 3239–3246. [Google Scholar]
- Wu, C.Q.; Tong, Q.X.; Zheng, L.F. Preprocessing of Ground and Image Spectral Data [J]. Remote Sensing Technology and Application 2005, 50–55. [Google Scholar]
- Fan, N.N.; Li, Z.Y.; Fan, W.Y.; et al. Preprocessing of PHI-3 Hyperspectral Data [J]. Research of Soil and Water Conservation 2007, 283–286+290. [Google Scholar]
- Liu, P.P.; Lin, H.; Sun, H.; et al. Research on Dimensionality Reduction Methods for Hyperspectral Data [J]. Journal of Central South University of Forestry & Technology 2011, 31, 34–38. [Google Scholar]
- Wang, X.H.; Xiao, P.; Guo, J.M. Research on Hyperspectral Data Dimensionality Reduction Techniques [J]. Bulletin of Soil and Water Conservation 2006, 89–91. [Google Scholar]
- Su, H.J.; Du, P.J. Research on Feature Selection and Feature Extraction of Hyperspectral Data [J]. Remote Sensing Technology and Application 2006, 288–293. [Google Scholar]
- Lv, J.; Hao, N.Y.; Shi, X.L. Research on Feature Extraction of Soil Hyperspectral Data Based on Manifold Learning [J]. Arid Zone Research and Environment 2015, 29, 176–180. [Google Scholar]
- Zhang, B. Advances in Hyperspectral Image Processing and Information Extraction [J]. Journal of Remote Sensing 2016, 20, 1062–1090. [Google Scholar]
- Zhou, X.M.; Wang, N.; Wu, H. Analysis and Comparison of Two Atmospheric Correction Methods for Hyperspectral Thermal Infrared Data [J]. Journal of Remote Sensing 2012, 16, 796–808. [Google Scholar]
- Ma, L.L.; Wang, X.H.; Tang, L.L. Preliminary Exploration of Efficient Atmospheric Correction and Application Potential of HJ-1A Hyperspectral Data [J]. Remote Sensing Technology and Application 2010, 25, 525–531. [Google Scholar]
- Wu, B.; Miao, F.; Ye, C.M.; et al. Application of Atmospheric Correction for Hyperspectral Remote Sensing Data Based on FLAASH [J]. Computational Techniques in Geophysical and Geochemical Exploration 2010, 32, 442–445+340. [Google Scholar]
- Li, X.; Tang, W.R.; Zhang, Y.H.; et al. Discrimination Model of Tobacco Leaf Field Maturity Based on Hyperspectral Imaging Technology [J]. Tobacco Science and Technology 2022, 55, 17–24. [Google Scholar]
- Li, M.; Hu, C.L.; Tao, G.L. Research on Hyperspectral Remote Sensing Estimation of SPAD Value of Camellia Oleifera Leaves Based on Different Preprocessing Methods [J]. Jiangsu Forestry Science and Technology 2022, 49, 1–5. [Google Scholar]
- Ding, Z.; Chang, B.S. Preprocessing Methods of Near-Infrared Reflectance Spectral Data for Coal Gangue Identification [J]. Industrial and Mine Automation 2021, 47, 93–97. [Google Scholar]
- Wen, P.; Li, H.J.; Lei, H.Y.; et al. Research on Hyperspectral Data Acquisition and Preprocessing Methods of Water-Injected Lamb [J]. Journal of Inner Mongolia Agricultural University (Natural Science Edition) 2021, 42, 79–84. [Google Scholar]
- Cai, T.J.; Tang, H. Overview of the Least Squares Fitting Principle of Savitzky-Golay Smoothing Filters [J]. Digital Communications 2011, 38, 63–68+82. [Google Scholar]
- Zhao, A.X.; Tang, X.J.; Zhang, Z.H.; et al. Optimization of Parameters of Savitzky-Golay Filters and Their Application in Smoothing Preprocessing of Fourier Transform Infrared Gas Spectral Data [J]. Spectroscopy and Spectral Analysis 2016, 36, 1340–1344. [Google Scholar]
- Gao, N.; Du, Z.H.; Qi, R.B.; et al. Research on Data Preprocessing of Broadband Tunable Diode Laser Absorption Spectroscopy [J]. Acta Optica Sinica 2012, 32, 304–309. [Google Scholar]
- Zhang, B.; Sun, Y.S.; Li, X.J.; et al. Development and Prospects of Hyperspectral Target Classification Technology [J]. Infrared 2023, 44, 1–12. [Google Scholar]
- Lian, M.R.; Zhang, S.J.; Ren, R.; et al. Non-destructive Detection of Moisture Content in Fresh Sweet Corn Based on Hyperspectral Technology [J]. Food and Machinery 2021, 37, 127–132. [Google Scholar]
- Deng, J.M.; Wang, H.J.; Li, Z.Z.; et al. External Quality Detection of Potatoes Based on Hyperspectral Technology [J]. Food and Machinery 2016, 32, 122–125+211. [Google Scholar]
- Chi, J.T.; Zhang, S.J.; Ren, R.; et al. External Defect Detection of Eggplants Based on Hyperspectral Imaging [J]. Modern Food Science and Technology 2021, 37, 279–284+178. [Google Scholar]
- Wang, B.N. Derivative Spectrophotometry Method [J]. Analytical Chemistry 1983, 149–158. [Google Scholar]
- Liang, L.; Zhang, L.P.; Lin, H.; et al. Estimation of Wheat Canopy Leaf Water Content Based on Derivative Spectroscopy [J]. Chinese Agricultural Science 2013, 46, 18–29. [Google Scholar]
- Liu, W.; Chang, Q.R.; Guo, M.; et al. Wavelet Denoising of Soil Derivative Spectra and Extraction of Organic Matter Absorption Features [J]. Spectroscopy and Spectral Analysis 2011, 31, 100–104. [Google Scholar]
- Ni, Z.; Hu, C.Q.; Feng, F. The Role and Development of Spectral Preprocessing Methods in Near-Infrared Spectral Analysis [J]. Journal of Pharmaceutical Analysis 2008, 28, 824–829. [Google Scholar]
- DiWu, P.Y.; Bian, X.H.; Wang, Z.F.; et al. Study on the Selection of Spectral Preprocessing Methods [J]. Spectroscopy and Spectral Analysis 2019, 39, 2800–2806. [Google Scholar]
- Chen, H.Z.; Pan, T.; Chen, J.M. Optimal Application of Combined Multiple Scattering Correction and Savitzky-Golay Smoothing Model in Near-Infrared Spectral Analysis of Soil Organic Matter [J]. Computer and Applied Chemistry 2011, 28, 518–522. [Google Scholar]
- Lu, Y.J.; Qu, Y.L.; Song, M. Study on Multiscattering Correction Processing of Near-Infrared Correlated Spectra [J]. Spectroscopy and Spectral Analysis 2007, 877–880. [Google Scholar]
- Li, J.; Li, S.K.; Jiang, L.W.; et al. Study on Non-destructive Discrimination Method of Green Tea Based on Near-Infrared Spectroscopy Technology and Chemometrics [J]. Journal of Instrumental Analysis 2020, 39, 1344–1350. [Google Scholar]
- Li, S.K.; Du, G.R.; Li, P.; et al. Non-destructive Discrimination Study of Soy Milk Powder Based on Near-Infrared Spectroscopy Technology and Optimized Preprocessing Methods [J]. Food Research and Development 2020, 41, 144–150. [Google Scholar]
- Wu, Y.R.; Jin, X.K.; Feng, J.Q.; et al. Impurity Detection of Cotton Based on Hyperspectral Imaging Technology [J/OL]. Modern Textile Technology 2024, 1–11. [Google Scholar]
- Wang, X.S.; Qi, D.W.; Huang, A.M. Research on Denoising of Near-Infrared Spectra of Wood Based on Wavelet Transform [J]. Spectroscopy and Spectral Analysis 2009, 29, 2059–2062. [Google Scholar]
- Xie, J.C.; Zhang, D.L.; Xu, W.L. A Review on Wavelet Image Denoising [J]. Journal of Image and Graphics 2002, 3–11. [Google Scholar]
- Wen, L.; Liu, Z.S.; Ge, Y.J. Several Methods of Wavelet Denoising [J]. Journal of Hefei University of Technology (Natural Science Edition) 2002, 167–172. [Google Scholar]
- Qin, X.; Shen, L.S. Wavelet Analysis and Its Applications in Spectral Analysis [J]. Spectroscopy and Spectral Analysis 2000, 892–897. [Google Scholar]
- Su, H.J. Dimensionality Reduction of Hyperspectral Remote Sensing Images: Progress, Challenges, and Prospects [J]. Journal of Remote Sensing 2022, 26, 1504–1529. [Google Scholar]
- Liu, P.P.; Lin, H.; Sun, H.; et al. Research on Dimensionality Reduction Methods for Hyperspectral Data [J]. Journal of Central South University of Forestry and Technology 2011, 31, 34–38. [Google Scholar]
- Jiang, Y.H.; Wang, T.; Chang, H.W. A Review of Hyperspectral Image Feature Extraction Methods. Electric Light & Control 2020, 27, 73–77. [Google Scholar]
- Xiao, P.; Wang, X.H. Hyperspectral Data Classification Based on Feature Extraction [J]. Geomatics and Information Science 2006, 45–47. [Google Scholar]
- Wang, Y.F.; Tang, Z.N. Dimensionality Reduction Method for Multispectral Data Based on PCA and ICA [J]. Optical Technique 2014, 40, 180–183. [Google Scholar] [CrossRef]
- Li, B.; Liu, Z.Y.; Huang, J.F.; et al. Hyperspectral Identification of Rice Diseases and Insect Pests Based on PCA and PNN [J]. Transactions of the Chinese Society of Agricultural Engineering 2009, 25, 143–147. [Google Scholar]
- Zhang, L. Research on Hyperspectral Remote Sensing Image Classification Based on PCA and SVM [J]. Optical Technique 2008, 34, 184–187.
- Tian, Y.; Zhao, C.H.; Ji, Y.X. Application of Principal Component Analysis in Dimensionality Reduction of Hyperspectral Remote Sensing Images [J]. Journal of Harbin Normal University (Natural Science Edition) 2007, 58–60. [Google Scholar]
- Feng, Y.; He, M.Y.; Song, J.; et al. Dimensionality Reduction and Compression of Hyperspectral Image Data Based on Independent Component Analysis [J]. Journal of Electronics & Information Technology 2007, 2871–2875. [Google Scholar]
- Liang, L.; Yang, M.H.; Li, Y. Classification of Hyperspectral Remote Sensing Images Based on ICA and SVM Algorithm [J]. Spectroscopy and Spectral Analysis 2010, 30, 2724–2728. [Google Scholar]
- Luo, W.F.; Zhong, L.; Zhang, B.; et al. Independent Component Analysis Technique for Spectral Unmixing of Hyperspectral Remote Sensing Images [J]. Spectroscopy and Spectral Analysis 2010, 30, 1628–1633. [Google Scholar]
- Li, H.T.; Gu, H.Y.; Zhang, B.; et al. Research on Hyperspectral Remote Sensing Image Classification Based on MNF and SVM [J]. Remote Sensing Information 2007, 12–15+25+103. [Google Scholar]
- Lin, N.; Yang, W.N.; Wang, B. Feature Extraction of Hyperspectral Remote Sensing Image Based on Kernel Minimum Noise Fraction Transformation [J]. Journal of Wuhan University (Information Science Edition) 2013, 38, 988–992. [Google Scholar]
- Liu, B.X.; Zhang, Z.D.; Li, Y.; et al. Oil Spill Information Extraction Method Based on Airborne Hyperspectral Remote Sensing Data [J]. Journal of Dalian Maritime University 2014, 40, 89–92. [Google Scholar]
- Bai, L.; Hui, M. Feature Extraction and Classification Based on Improved Minimum Noise Fraction Transformation [J]. Computer Engineering and Science 2015, 37, 1344–1348. [Google Scholar]
- Liu, Y.D.; Zhang, G.W.; Cai, L.J. Quantitative Analysis of Chlorophyll in Navel Orange Leaves in Southern Jiangxi Based on Hyperspectral GA and SPA Algorithms [J]. Spectroscopy and Spectral Analysis 2012, 32, 3377–3380. [Google Scholar] [PubMed]
- Wang, L.G.; Wei, F.J. Band Selection of Hyperspectral Images Combining Genetic Algorithm and Ant Colony Algorithm [J]. Journal of Image and Graphics in China 2013, 18, 235–242. [Google Scholar]
- Zhang, T.T.; Zhao, B.; Yang, L.M.; et al. Determination of Sweet Corn Seed Electrical Conductivity Using Hyperspectral Imaging Technology Combined with SPA and GA Algorithms [J]. Spectroscopy and Spectral Analysis 2019, 39, 2608–2613. [Google Scholar]
- Tan, K.; Du, P.J. Hyperspectral Remote Sensing Image Classification Based on Support Vector Machine [J]. Journal of Infrared and Millimeter Waves 2008, 123–128. [Google Scholar] [CrossRef]
- Zhao, P.; Tang, Y.H.; Li, Z.Y. Wood Species Classification of Hyperspectral Microscopic Imaging Based on Support Vector Machine with Composite Kernel Function [J]. Spectroscopy and Spectral Analysis 2019, 39, 3776–3782. [Google Scholar]
- Sun, J.T.; Ma, B.X.; Dong, J.; et al. Research on Muskmelon Ripeness Discrimination Using Hyperspectral Technology Combined with Feature Wavelength Selection and Support Vector Machine [J]. Spectroscopy and Spectral Analysis 2017, 37, 2184–2191. [Google Scholar]
- Lin, H.; Liang, L.; Zhang, L.P.; et al. Estimation of Wheat Leaf Area Index by Hyperspectral Remote Sensing Based on Support Vector Machine Regression Algorithm [J]. Transactions of the Chinese Society of Agricultural Engineering 2013, 29, 139–146. [Google Scholar]
- Dong, J.J.; Tian, Y.; Zhang, J.X.; et al. Research on Classification Method of Benthic Organisms Hyperspectral Data Based on Random Forest Algorithm [J]. Spectroscopy and Spectral Analysis 2023, 43, 3015–3022. [Google Scholar]
- Ke, Y.C.; Shi, Z.K.; Li, P.J.; et al. Lithology Classification and Analysis Based on Hyperion Hyperspectral Data and Random Forest Method [J]. Acta Petrologica Sinica 2018, 34, 2181–2188. [Google Scholar]
- Cheng, S.X.; Kong, W.W.; Zhang, C.; et al. Research on Variety Identification of Chinese Cabbage Seeds Using Hyperspectral Imaging Combined with Machine Learning [J]. Spectroscopy and Spectral Analysis 2014, 34, 2519–2522. [Google Scholar]
- Zhao, J.L.; Hu, L.; Yan, H.; et al. Hyperspectral Image Classification Method Combining Local Binary Pattern and K-Nearest Neighbors Algorithm [J]. Journal of Infrared and Millimeter Waves 2021, 40, 400–412. [Google Scholar]
- Tu, B.; Zhang, X.F.; Zhang, G.Y.; et al. Hyperspectral Remote Sensing Image Classification Method Using Recursive Filtering and K-Nearest Neighbors (KNN) [J]. Remote Sensing of Land and Resources 2019, 31, 22–32. [Google Scholar]
- Huang, H.; Zheng, X.L. Hyperspectral Image Classification Combining Weighted Space-Spectral Features with Nearest Neighbor Classifier [J]. Optics and Precision Engineering 2016, 24, 873–881. [Google Scholar] [CrossRef]
- Wang, L.; Qin, H.; Li, J.; et al. Origin Discrimination of Ningxia Goji Berry Based on Near-Infrared Hyperspectral Imaging [J]. Spectroscopy and Spectral Analysis 2020, 40, 1270–1275. [Google Scholar]
- Ji, H.Y.; Ren, Z.Q.; Rao, Z.H. Discriminant Analysis of Millet from Different Origins Based on Hyperspectral Imaging Technology [J]. Spectroscopy and Spectral Analysis 2019, 39, 2271–2277. [Google Scholar]
- Zhu, M.Y.; Yang, H.B.; Li, Z.W. Early Detection and Identification of Rice Sheath Blight Based on Hyperspectral Images and Chlorophyll Content [J]. Spectroscopy and Spectral Analysis 2019, 39, 1898–1904. [Google Scholar]
- Zheng, Y.P.; Li, G.Y.; Li, Y. A Review of the Application of Deep Learning in Image Recognition [J]. Computer Engineering and Applications 2019, 55, 20–36. [Google Scholar]
- Jia, S.P.; Gao, H.J.; Hang, X. Research Progress on Crop Disease and Pest Image Recognition Technology Based on Deep Learning [J]. Transactions of the Chinese Society for Agricultural Machinery 2019, 50, 313–317. [Google Scholar]
- Wang, B.; Fan, D.L. A Review of Research Progress on Remote Sensing Image Classification and Recognition Based on Deep Learning [J]. Bulletin of Surveying and Mapping 2019, 99–102+136. [Google Scholar]
- Liu, J.X.; Ban, W.; Chen, Y.; et al. Hyperspectral Remote Sensing Image Classification Algorithm Based on Multi-Dimensional CNN Fusion [J]. Chinese Journal of Lasers 2021, 48, 159–169. [Google Scholar]
- Wei, X.P.; Yu, X.C.; Zhang, P.Q.; et al. Hyperspectral Image Classification Using CNN with Joint Local Binary Pattern [J]. Journal of Remote Sensing 2020, 24, 1000–1009. [Google Scholar]
- Yu, C.C.; Zhou, L.; Wang, X.; et al. Hyperspectral Detection of Wheat Shrunken Grains Based on CNN Neural Network [J]. Food Science 2017, 38, 283–287. [Google Scholar]
- Huang, S.P.; Sun, C.; Qi, L.; et al. Detection Method of Rice Panicle Blight Based on Deep Convolutional Neural Network [J]. Transactions of the Chinese Society of Agricultural Engineering 2017, 33, 169–176. [Google Scholar]
- Luo, J.H.; Li, M.Q.; Zheng, Z.Z.; et al. Hyperspectral Remote Sensing Image Classification Based on Deep Convolutional Neural Network [J]. Journal of Xihua University (Natural Science Edition) 2017, 36, 13–20. [Google Scholar]
- Yan, M.J.; Su, X.Y. Hyperspectral Image Classification Method Based on Three-Dimensional Dilated Convolution Residual Neural Network [J]. Acta Optica Sinica 2020, 40, 163–172. [Google Scholar]
- Zhang, X.D.; Wang, T.J.; Yang, Y. Small Sample Hyperspectral Image Classification Based on Multi-Scale Residual Network [J]. Laser & Optoelectronics Progress 2020, 57, 348–355. [Google Scholar]
- Lu, Y.S.; Li, Y.X.; Liu, B.; et al. Haze Monitoring of Hyperspectral Remote Sensing Data Based on Deep Residual Network [J]. Acta Optica Sinica 2017, 37, 314–324. [Google Scholar]
- Zhang, F.; Wang, W.X.; Wang, C.S.; et al. Identification of Potato Late Blight Incubation Period Using Hyperspectral Images Combined with Convolutional Neural Network [J]. Spectroscopy and Spectral Analysis 2024, 44, 480–489. [Google Scholar]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).