Prerpints.org logo
Preprint
Article

Jaya-Based Optimization of Active Elements for Hybrid Relay-Reflecting Intelligent Surface-Assisted Secrecy Wireless Communications

Altmetrics

Downloads

43

Views

21

Comments

0

This version is not peer-reviewed

Submitted:

11 September 2024

Posted:

12 September 2024

You are already at the latest version

Alerts
Abstract
In this work, we investigate how to obtain the optimal active elements in Hybrid Relay-Reflecting Intelligent Surface (HR-RIS) systems while considering enhancing the sum rate of the communication system in the presence of malevolent eavesdropper. Therefore, when dealing with numerous elements in the HR-RIS, the complicated optimization task of activating and deactivating the active elements of RIS renders typical exhaustive search methods impracticable. Standard techniques, such as alternating optimization, often frequently converge and unfortunately become trapped in local optima, leading to less-than-ideal results. To address these issues, we suggest performing the Jaya algorithm, which modifies its search strategy in response to historical data to find a compromise between investigating novel avenues and taking advantage of well-established answers. Our simulation findings demonstrate that this strategy outperforms the most recent techniques, yielding higher sum rates with the best possible user location and robust security against eavesdropping. It’s interesting to observe that even at lower total power levels, the Jaya algorithm performs incredibly well and efficiently identifies the optimal amount of active elements. This demonstrates how it can decrease interference, increase signal quality, improve Signal-to-Interference-plus-Noise Ratio (SINR), and increase secrecy rates, opening the door for more efficient and secure wireless communication systems.
Keywords: 
Subject: Engineering  -   Telecommunications

1. Introduction

Reconfigurable Intelligent Surfaces (RIS) have emerged as a key area of interest for improving wireless communications secrecy. RIS can be used to intelligently control the wireless environment because it is made up of several inexpensive, passive reflecting elements. Through the optimization of reflected signal phase and amplitude, RIS can improve data security during transmission by preventing illegal access and eavesdropping [1,2]. This feature is especially helpful in situations when protecting the privacy of data is essential, notably in financial and military applications [3]. The secrecy capacity of wireless communication networks can be increased by using RIS to successfully generate favourable conditions for authorised users while simultaneously preventing signals intended for prospective eavesdroppers, as evidenced by recent studies [4,5]. Furthermore, RIS can facilitate the adoption of sophisticated physical layer security strategies in addition to improving secrecy.
In order to establish a more secure communication environment, researchers have investigated a number of strategies that leverage RIS, including beamforming and signal jamming [6,7]. By optimizing reflecting element configurations in real-time network conditions, the integration of machine learning approaches has significantly enhanced the performance of RIS in communications security [8,9]. In addition, operators seeking to improve security without incurring unavoidable expenditures find RIS technologies to be a compelling alternative due to their cost-effectiveness [10,11]. A revolutionary change in the design of wireless systems is heralded by the creative application of RIS in secret communications, which offers improved security and adaptability for the transfer of sensitive data.

1.1. Related Works

A noteworthy development in the field of wireless communication technologies is the HR-RIS. These devices enable more secrecy and control over signal propagation in wireless communications by combining passive reflecting elements with active components. The available literature offers significant insights into the strategies used to maximize secrecy by employing alternating optimization techniques to optimize the active aspects of HR-RIS. One of the first studies in this field investigated the idea of HR-RIS as a way to improve concealment by utilising signal configurations that are carefully thought out. A new framework was presented by Wu et al. (2020), in which the active and passive components are optimized to maximize the signal strength of individuals with authorisation while minimizing the possibility of eavesdropping [6].
Several researchers have built upon this basic concept by concentrating on alternating optimization techniques. Subsequent research has turned to certain alternating optimization methods that modify the active components of HR-RIS in an iterative fashion. The secret capacity of the communication channel was successfully increased by Liu et al. (2021) with their dual optimization framework, which uses alternating projections to modify the phases of both active and passive elements [12]. The authors used numerical simulations to validate the effectiveness of their approach and showed notable improvements in secrecy rate performance. Yang et al. (2022) made a substantial further contribution by investigating a multi-objective optimization framework that uses alternating techniques to control interference between authorised users and eavesdroppers. Their method demonstrated a balanced resource allocation strategy by enabling the simultaneous improvement of user fairness and secrecy rate [13]. HR-RIS demonstrated its adaptability in various operational circumstances by implementing the alternating optimization on both spatial and temporal signal resources. The influence of channel knowledge on the optimization procedure was also investigated in [14] for example shown that incomplete channel state information (CSI) might be successfully integrated into the alternating optimization framework to modify the HR-RIS active components. According to their findings, a reliable method for preserving high secrecy rates even in the face of variable channel uncertainty might be used. The authors in [15] highlighted more developments in the application of alternating optimization for HR-RIS, focusing on the trade-offs between secrecy and energy efficiency in wireless systems using HR-RIS. They achieved acceptable performance in both metrics by putting forth particular criteria for choosing active elements based on the alternating optimization strategy.
Game theory concepts included into the HR-RIS alternating optimization framework in [16]. Their results emphasise the need of users and database accessibility working together to maximize secrecy rates and reduce the possibility of eavesdropping. Combining alternating optimization technique with game theory is an innovative way to use HR-RIS for secret communication. Further research on the financial feasibility of HR-RIS-based secrecy systems was done by Ma et al. (2023), who used alternating optimization to balance the costs and performance variables related to the implementation of both active and passive parts [17]. The vital information from this study will help to improve the accessibility of HR-RIS technology for wider use.

1.2. Motivation and Contributions

HR-RIS optimization of active elements has gained considerable amount of attention considering to the pursuit of secure wireless communication networks. In dynamic situations, traditional optimization methods including alternating optimization frequently suffer from rapid convergence and trapped into local optima, producing less-than-ideal results. These constraints are efficiently addressed by the Jaya algorithm, which balances exploration and exploitation in an effective and simple way [18]. It does this by navigating the search space depending on success and failure. This is important in secret communications because it allows for quick parameter changes in response to possible eavesdropping risks [13]. To the best of our knowledge, no other works consider the Jaya optimization technique in the HR-RIS approach for secrecy wireless communication systems. The main contributions of this paper are summarized as follows:
  • In order to maximize the secrecy communication rate, we propose an efficient method of allocating active relay elements by repeatedly varying a number of parameters, including power levels, user positions, and relay numbers. It ensures optimal performance in a variety of contexts by taking into account several effects, including path loss and channel uncertainty, to adapt to changing channel conditions. Furthermore, the Jaya algorithm’s population-based search mechanism facilitates varied solution space exploration, raising the possibility of obtaining optimal configurations and removing the difficulties associated with local optima that are frequently encountered in conventional optimization techniques. Therefore, the proposed method is compared with the state-of-the-art schemes.
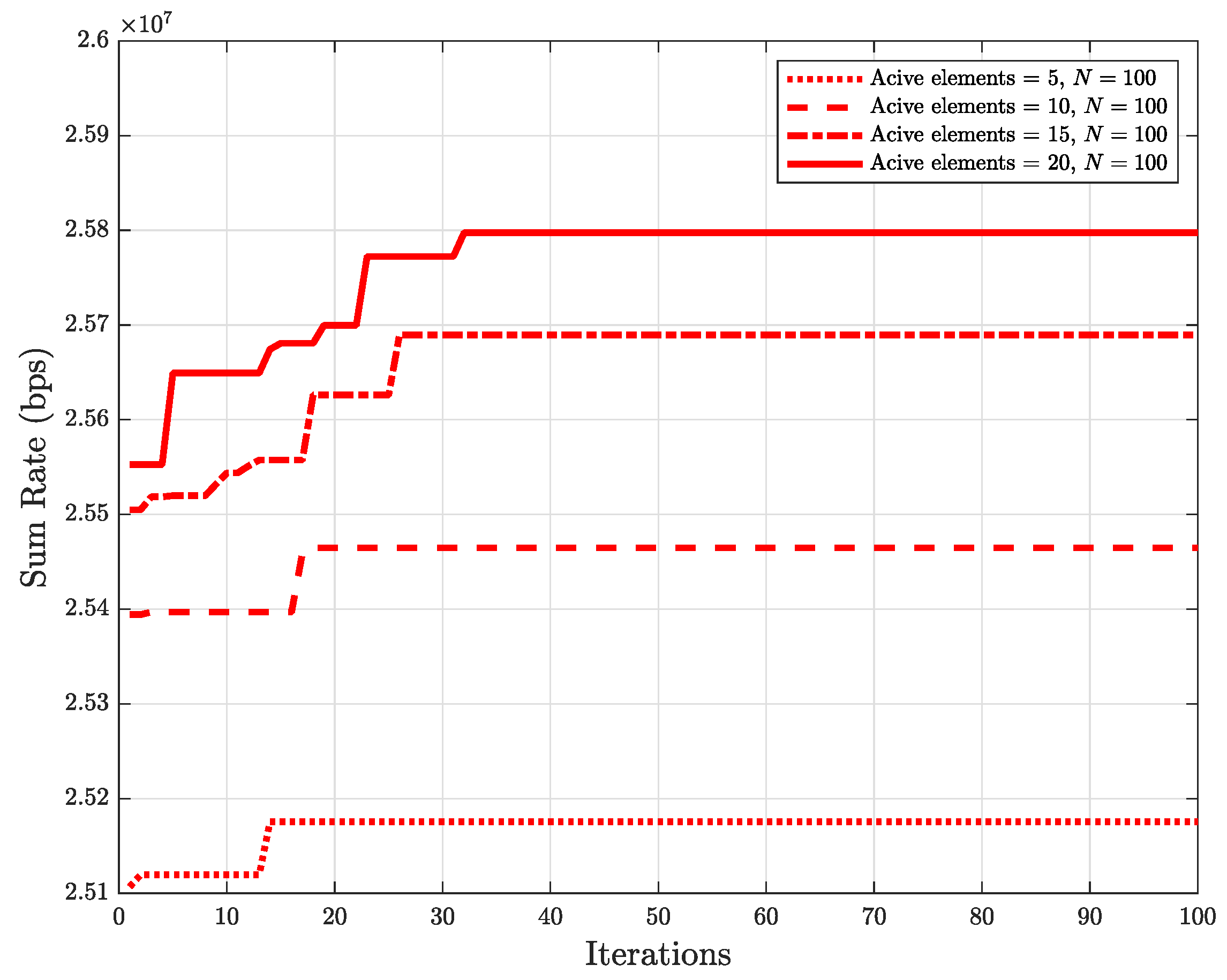
  • The proposed method’s effectiveness in obtaining the best aspects active elements of HR-RIS under an extensive variety of scenarios is demonstrated by the simulation results. In particular, the number of RIS elements in the RIS, the number of antennas equipped with the edge node (EN), the user’s various locations, and the eavesdropper’s various locations are all investigated in terms of sum rate.

1.3. Paper Organization

The rest of this paper is structured as follows. The system model including the HR-RIS architecture and channel model is presented in Section 2. Section 3 and Section 4 give the problem formulation and the proposed solution for this work, respectively. Simulation results and discussions are provided in Section 5. The conclusions for this paper is presented in Section 6.

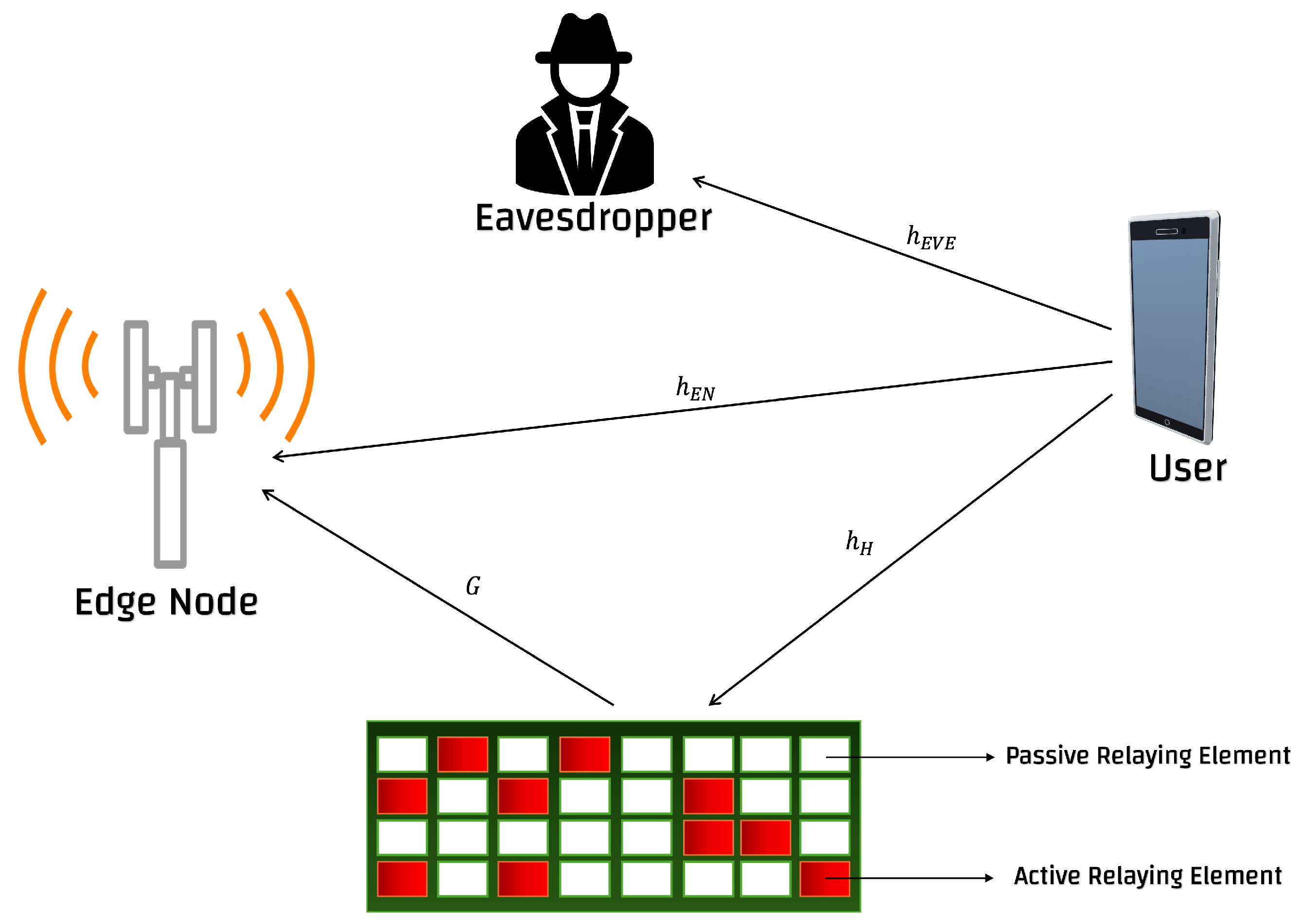
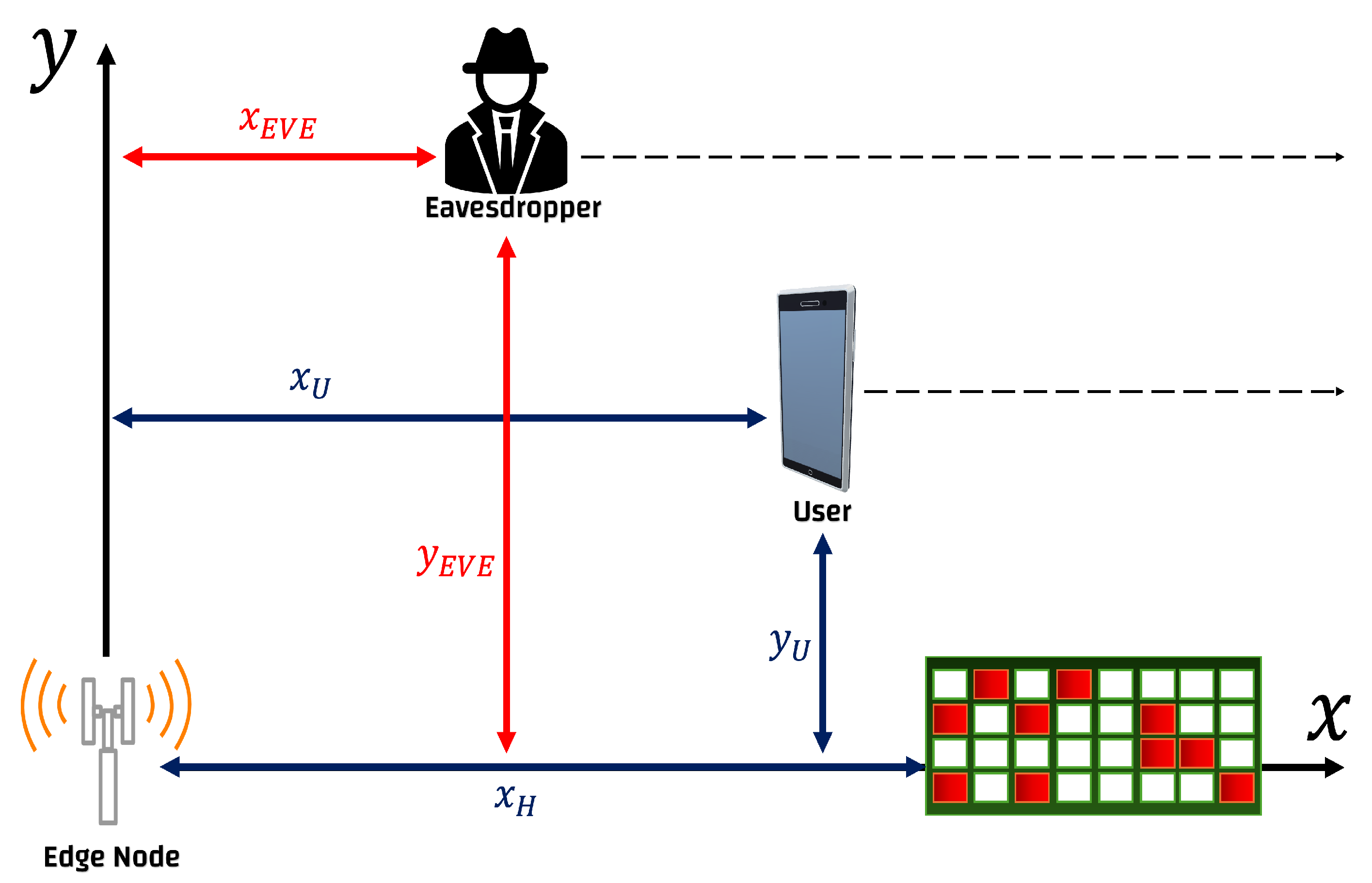
2. System Model

In this paper, we investigate a single-user system that is under attack from a malevolent eavesdropper, as shown in Figure 1. Assumed to have a single antenna, K antennas, and J antennas, respectively, are the user, edge node (EN), and eavesdropper. The N elements, which include  K  active relaying elements and  N − K  passive reflecting elements, compose the HR-RIS. Furthermore, the next subsection provides in details the HR-RIS architecture.

2.1. HR-RIS Architecture

It is significant to take into account that the optimum amplitude of a passive reflecting coefficient is unity, enhancing the power of the received signal [19]. As a result, a passive device simply modifies the incident signal’s phase. In contrast, an active element has the ability to both modify the phase and increase the power of the signal [20]. The index of set of active elements can be defined as K ⊂ [ N ] ≜ { 1 , 2 , . . . , N } . Let the relay/reflection coefficient for the n -th element are expressed as α n = α n e j θ n where α n and θ n ∈ [ π , 2 π ) correspond to the amplitude and the phase shift, respectively. It should be noted that α n = 1 ∀ n ∉ K  [20,21]. We define α ≜ [ α 1 , . . . , α N ] T and introduce Y as
Υ ≜ α 1 α 2 ⋱ α N .
We decompose Υ as Υ = Φ + Ψ , where
Φ = ϕ 1 ϕ 2 ⋱ ϕ N
and
Ψ = ψ 1 2 ⋱ ψ N
with
ϕ n = 0 , if n ∈ K α n = e j θ n , otherwise
where ϕ n gives the passive coefficients, and
ψ n = α n = α n e j θ n , if n ∈ K 0 , otherwise
where ψ n gives the active coefficients.

2.2. Channel Model

h EN ∈ C K , h H ∈ C N and h EVE ∈ C J are considered as the channels between the user and the EN, the user and the HR-RIS, and the user and the eavesdropper, respectively. It is assumed that these channels are quasi-static [21]. h EVE is known by the eavesdropper, while h EN and h H are also known by the EN. However, the EN only knows the estimated h EVE which is symbolized by h ^ EVE . In addition, ∥ h EVE − h ^ EVE ∥ h EVE ≤ ν , where ν gives the upper bound of the estimation error [21,24,25]. Hence, the previous assumption is for deterministic uncertainty model. The channels between the HR-RIS and the EN is denoted by G which can be perfectly known by the EN. The user, the EN, and the eavesdropper implement uniform linear arrays (ULAs), and the HR-RIS imposes uniform polar arrays (UPAs) with N elements. All nodes are assumed to have half-wavelength separations between array elements. Figure 2 shows the nodes’ locations in a two-dimensional coordinate system. To be more precise, the EN is located at ( 0 , 0 ) , the eavesdropper at ( x EVE , y EVE ) , the user at x H , y H , and the HR-RIS at ( x H , 0 ) . The Pythagorean theorem makes it easy to determine the distances between the nodes using these coordinates. β ( d ) = β o ( d d o ) − η , where β o gives the path loss at d o which is the reference distance and the path loss exponent is denoted by η . Thus, β ( d ) is provided in order to obtain the path loss of a link distance ( d ) for the large-scale fading [20,22,23]. Regarding to small-scale fading, the Rician fading channel model is proposed between the HR-RIS and EN and is expressed as [22,23]
G ^ = ϰ 1 + ϰ G ^ LoS + 1 1 + ϰ G ^ NLoS ,
where the line of sight (LoS) and non line of sight (NLoS) components are denoted by G ^ LoS , and G ^ NLoS , respectively. ϰ gives the Rician factor. Furthermore, G ^ approaches to the Rayleigh fading channel when ( ϰ → 0 ) , while G ^ provides LoS channel with ( ϰ → ∞ ) . Based on the azimuth and elevation angles of departure (AoD) and angles of arrival (AoA), the array response vectors are multiplied to determine the LoS component. Thus, G ^ LoS is given as
G ^ LoS = a H ( θ H , ϕ H ) a EN H ( θ EN ) ,
where a EN H ( θ EN ) denotes the array response vectors at the EN, while the array response vectors at the HR-RIS are denoted by a H ( θ H , ϕ H ) . Therefore, n th element of a EN H ( θ EN ) and a H ( θ H , ϕ H ) can be expressed as [22]
a EN , n H ( θ EN ) = e j π ( n − 1 ) sin θ EN , k = 1 , 2 , . . . , K ,
and
a H ( θ H , ϕ H ) = e j π [ n N x ] sin θ H sin ϕ H + ( n − [ n N x ] N x ) sin θ H cos ϕ H , n = 1 , . . . , N .
It is worthy noting that ϕ H ∈ [ − π 2 , π 2 ) denotes the elevation AoD from the HR-RIS. In addition, θ EN ∈ [ 0 , 2 π ) denotes the AoA at the EN, and θ H ∈ [ 0 , 2 π ) denotes the AoD from the HR-RIS. Following CN ( 0.1 ) , the Rayleigh fading with independent entries models the NLoS component. Therefore, the channel between the user and the EN is presented as h EN ∈ C K , whereas the channel between the user and the HR-RIS and the channel between the user and the eavesdropper are h H ∈ C N and h EVE ∈ C J , respectively. The channel between the EN and the HR-RIS is symbolized by G ∈ C K × N and obtained by [20,21]
G = β ( x H ) G ^ .
Similar way can be utilized to model the channels between other links.

3. Problem Formulation

P and s represent the user’s transmit power and transmitted signal, respectively. At the HR-RIS, the incident signal is P h H s + z H , where the noise vecor is expressed as z ∽ CN ( 0 , σ H 2 I N ) . The HR-RIS active elements’ transmit power is given as P a ( α ) ≜ tr ( Ψ ( P h H h H H + σ H 2 I N ) Ψ H ) . The signal that the EN received is expressed as [20,21]
r = P ( h EN + G Υ h H ) s k + G Ψ z H + z EN ,
where ( h EN + G Υ h H ) gives the effective channel between the user and the EN. z EN ∽ CN ( 0 , σ EN 2 I K ) provides the additive noise at the EN, whereas G Ψ z H + z EN is considered as the total effective noise. For simplicity, it is assumed that σ EN 2 = σ H 2 = σ 2 [21]. Therefore, G Ψ z H + z EN ∽ CN ( 0 , σ 2 I K + G Ψ Ψ H G H ) .
Linear combining vector for the EN is symbolized by F ∈ C K . Therefore, the transmitted signal at the EN is expressed as s ^ = F H r . The effective SINR is expressed as
SIN R ( F , α ) = P | F H ( h EN + G Υ h H ) | 2 σ 2 F H ( I K + G Ψ Ψ H G H ) F .
As a consequence, the maximum achievable rate is provided as
R ( F , α ) = B log 2 ( 1 + SIN R ( F , α ) ) ,
where B gives the bandwidth for the uplink transmission.
The eavesdropper intercepts the user’s signal and tries to decode the data, assuming it does not receive the signal from HR-RIS. The rate at which the eavesdropper can decode the user’s signal, known as the leakage rate, is defined as
R EVE = B log 2 ( 1 + P ∥ h ^ EVE ∥ 2 σ EVE 2 ) ,
where σ EVE 2 denotes the the eavesdropper’s noise variance. The secrecy rate is symbolized as R s and obtained by R ( F , α ) − R EVE . When the EN knows h ^ EVE , the upper bound of the R EVE on the leakage rate is expressed as
R EVE ≜ log 2 ( 1 + P ( 1 + ε ) 2 ∥ h ^ EVE ∥ 2 σ EVE 2 ) .
Thus, the user in informed by the EN to transmit at lower bound on the secrecy rate in order to guarantee the secrecy which is given as
R s ( F , α ) = R ( F , α ) − R EVE .
The main aim of this work is to maximize the secrecy rate by taking into account the joint optimization of the combining vector ( F ), the coefficients of HR-RIS ( α ), and the positions of the active elements (K). Thus, the formulated optimization problem is written as [21]
maximize F , α R s ( F , α ) subject to α n = 1 ∀ n ∉ K , P a ( α ) ≤ P a max , | K | ≤ K ⊂ [ N ] ≜ { 1 , 2 , . . . , N } .
R s ( F , α ) is maximized in the same way as the optimization of F and α based on similar constraints, which are α n = 1 ∀ n ∉ K , P a ( α ) ≤ P a max , and | K | ≤ K ⊂ [ N ] ≜ { 1 , 2 , . . . , N } . Furthermore, it is observed that the leakage rate R EVE does not depend on F and α . The optimal solution is anticipated to satisfy R ( F , α ) > R EVE . Therefore, R s ( F , α ) can be replaced by R ( F , α ) which results in maximizing the SIN R ( F , α ) . The optimization problem in (17) can be rewritten as
maximize F , α SIN R ( F , α ) = P | F H ( h EN + G Υ h H ) | 2 σ 2 F H ( I K + G Ψ Ψ H G H ) F subject to α n = 1 ∀ n ∉ K , P a ( α ) ≤ P a max , | K | ≤ K ⊂ [ N ] ≜ { 1 , 2 , . . . , N } .
α phases can be optimized when there are no active elements. In particular, the SINR becomes into
P | F H ( h EN + G Υ h H ) | 2 σ 2 ∥ F ∥ 2 ≤ P ( | F H ( h EN ) + ∑ n = 1 N | h H , n F H g n | σ 2 ∥ F ∥ 2 ,
where g n and h H , n denote the n-th column of G and n-th entry of h H , respectively. Thus, the equality of (19) is obtained when arg { | F H h EN | } = arg { | F H G Υ h H | } . Hence, the phases of the HR-RIS coefficients are espressed as
θ * = arg { F H h EN } − arg { diag { F H G } h H } ,
where arg { . } returns the element-wise phases of a complex number or vector. Optimizing both phases, as mentioned in (20) and amplitudes is necessary when there is at least one active element. Moreover, this works forces on how to obtain { α i } i ∈ K corresponding to each valid set of  K  because both   K  and  { α i } i ∈ K  are available in the numerator and denominator in SIN R ( F , α ) as expressed as
P | F H ( h EN + G Υ h H ) | 2 σ 2 F H ( I K + G Ψ Ψ H G H ) F ≤ P ( | F H ( h EN ) + ∑ n = 1 N | h H , n F H g n | σ 2 ∥ F ∥ 2 = P ( | a n | 2 a n + | a n b n | + c n ) σ 2 ∥ F ∥ 2 ,
where
a n ≜ | h H , n | 2 | F H g n | 2 ,
c n = ( | F H h EN | + ∑ i = 1 , i ≠ n N | α i h H , i F H g i | ) 2 ,
and
b n ≜ 2 | h H , n F H g n | c n .
In order to simplify the optimization to maximize P ( | F H ( h EN ) + ∑ n = 1 N | h H , n F H g n | σ 2 ∥ F ∥ 2 , it is noted that σ 2 F H ( G Ψ Ψ H G H ) F is small when the noise variance is small, the path loss is large and the number of active elements is small. An active element has the ability to enhance the system performance when | α n | > 1 . Because of that, the reformulated optimization problem takes into account only the second-order term as expressed as
maximize K , | α n | n ∈ K ∑ n ∈ K log 2 ( 1 + P ( | a n | 2 a n ) subject to ∑ n ∈ K | α n | 2 ( σ 2 + P | h H , n | 2 ) ≤ P a max , | K | ≤ K ⊂ [ N ] ≜ { 1 , 2 , . . . , N } .

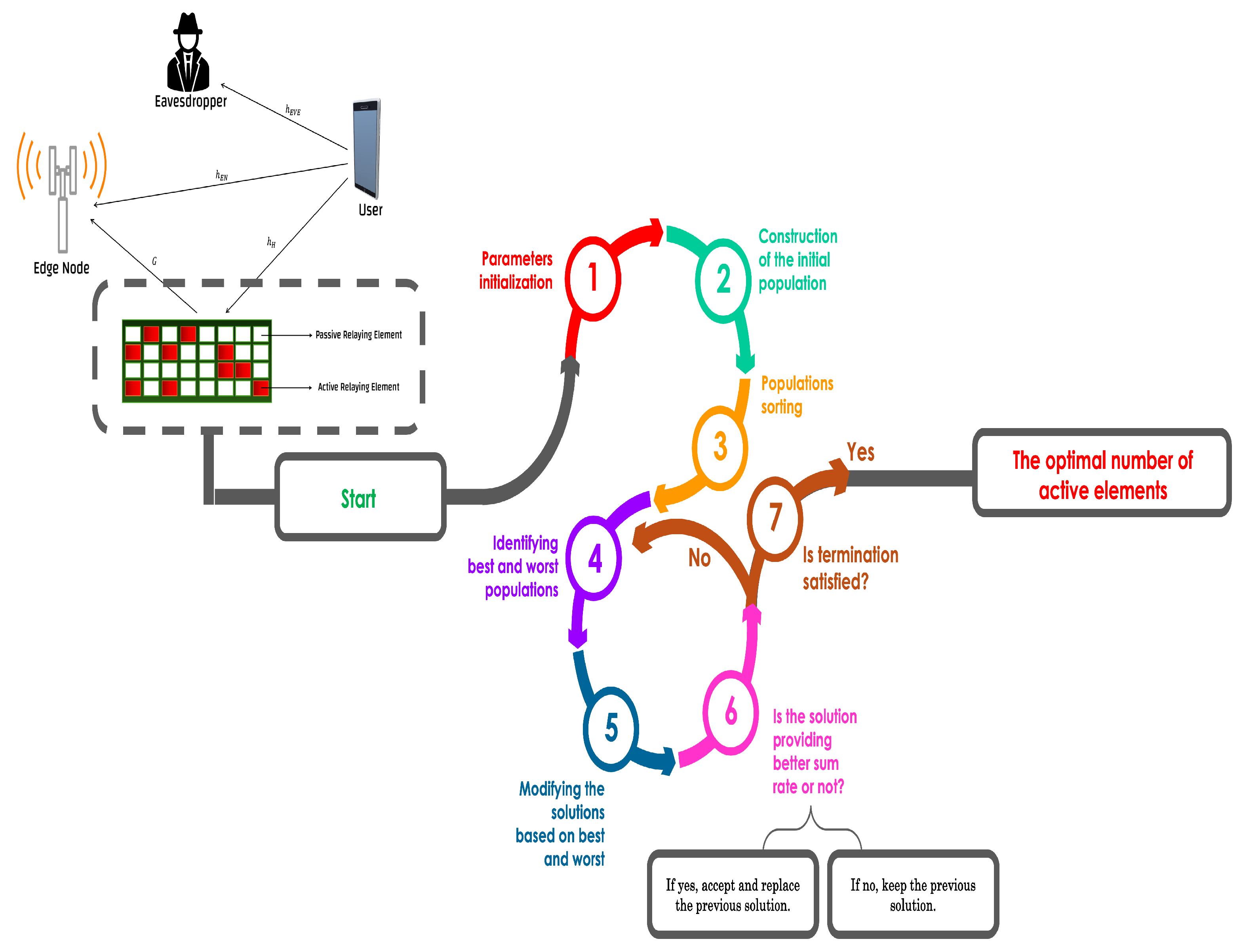
4. Proposed Solution

As mentioned in the previous section, the formulated problem in (22) is NP-hard and the exhaustive searching approach is considered as a solution to obtain the optimal set  K  to maximize the total secrecy rate of the HR-RIS system. However, this method is computationally complex due to the large number of possible combinations, i.e., the number of possible active elements for HR-RIS is expressed as N K . A novel approach based on the Jaya optimization technique is proposed in this work in order to solve this issue as well as taking into account ∑ n ∈ K | α n | 2 ( σ 2 + P | h H , n | 2 ) ≤ P a max as shown in Figure 3.

4.1. Background of Jaya Optimization Approach

In 2016, Professor Ravipudi Venkata Rao presented the Jaya algorithm [18], a simple and efficient optimization method. It differs from previous evolutionary algorithms in that it is intended to address both continuous and discrete optimization issues without requiring algorithm-specific control factors, such crossover or mutation rates. The basic idea behind the algorithm’s operation is to iteratively enhance a population of solutions by directing each candidate away from the poorest solution in the current population and towards the best one. This focused motion helps the optimal solution to swiftly converge. Jaya is a straightforward tool to use in a variety of fields, such as network optimization, engineering design, and scheduling, because of its simplicity and parameter-free structure. The Jaya algorithm effectively looks for global optima by iteratively improving upon previous solutions while weighing the pros and cons of exploring and exploiting the solution space.

4.2. Proposed Jaya Optimization Procedures

4.2.1. Parameters Initialization

Set up the parameters for both the Jaya algorithm and the optimization problem. At the start of execution, the Jaya algorithm’s parameters are defined. Notably, the Jaya algorithm does not require any control parameters; it only utilizes two algorithmic parameters: the population size J , and the number of iterations Λ . Thus, the populations is expressed as
U = [ K 1 , K 2 , . . . , K J ] T .

4.2.2. Building up the Initial Populations for Jaya Approach

The Jaya memory ( Δ ) is utilized to build and store the initial solutions, also known as the population, of the Jaya algorithm. Moreover, δ is considered as an augmented matrix of size of size J × E , where E denotes the solution dimension. As indicated in the equation below [26]
Δ i , j = K j min + ( K j min − K j max ) × r a n d ,
where i ∈ { 1 , 2 , . . . , J } and j ∈ { 1 , 2 , . . . , E } . In addition, r a n d is considered as random values between 0 and 1 that can be generated by an uniform function.

4.2.3. Evaluation Process

the initial populations are considered as the possible solutions to find the optimal active elements of HR-RIS. Moreover, as mentioned previously, each population is assumed to be the active elements of the HR-RIS. Thus, it is required to the corresponding position and amplitude, and its corresponding P = ∑ n ∈ K | α n | 2 ( σ 2 + P | h H , n | 2 ) ≤ P a max . Given population K J , P n is obtained by utilizing water-filling technique as expressed as
P = ∑ n ∈ K J ( 1 ϱ − σ 2 + P | h H , n | 2 P α n ) ,
where ϱ is used in order to satisfy P ≤ P a max . Furthermore, α n for n ∈ K J is given as
α n = max 1 ϱ σ 2 + P | h H , n | 2 − 1 P a n , 1 .
Then, the fitness function that can be used to evaluate each population is expressed as
ξ = ∑ n ∈ K J log 2 ( 1 + P α n ( 1 ϱ − σ 2 + P | h H , n | 2 P α n ) σ 2 + P | h H , n | 2 ) .
The decision variables of all solutions in Δ undergoes changes using Jaya operator as expressed as
K j ′ i = K j i + λ 1 × ( K j 1 − | K j i | ) − λ 2 × ( K j J − | K j i | ) ,
where the new updated solution K j ′ i and the present solution K j i are denoted, respectively. The uniform function generates the random values λ 1 and λ 2 , which are employed to determine the ideal balance between the exploration and exploitation processes in the range of [ 0 , 1 ] . It is important to note that the decision variable j in the best solution is K j 1 , whereas the decision variable j in the worst solution is K j J . The Jaya algorithm’s diversity control is determined by the separation between the decision variables of the best solution and the current one, as well as the separation between the decision variables of the wort solution and the current one. Greater exploration occurs at greater distances, and greater exploitation occurs at closer ranges.

4.2.4. Updating Δ

As stated previously, δ is considered as an augmented matrix of size of size J × E and given as [18,26]
Δ = K 1 1 K 2 1 . . . K Λ 1 K 1 2 K 2 2 . . . K Λ 2 . . . . . . . . . . . . K 1 J K 2 J . . . K Λ J .
Updating at each iteration is reflected to Δ , whereas ξ is determined. When the new solution’s fitness function exceeds the present one, it takes the place of the existing one.
[1]Require:  h EVE , h EN , h H and G. Ensure:  K * . Initialize the parameters of both Jaya algorithm and optimization problem based on Equation (23). Initialize a population of J solutions randomly based on Equation (24). Compute F = P σ 2 ( I K + G Ψ Ψ H G H ) − 1 ( ( h EN + G Υ h H ) ) . Compute θ * based on Equation(20). Calculate the fitness function ξ ( K i ) ∀ i = 1 , 2 , . . . , J based on Equation (29). Sort the population: ( K 1 and K J are the best and the worst solutions respectively.).  t = 1   t ≤ Λ   i = 1 , . . . , J  j = 1,..., E  Set λ 1 ∈ [ 0 , 1 ]  Set λ 2 ∈ [ 0 , 1 ]  Compute K j ′ i based on Equation (28)  ξ ( K j ′ i ) ≤ ξ ( K i )   K i = K ′ i  Update Δ based on Equation (29)  t = t + 1
The entire process of the proposed Jaya optimization to determine the optimum vital elements of HR-RIS will be outlined by Algorithm 4.2.4. The total rate for the secrecy HR-RIS system is maximised by this procedure. The first two steps are used to define the parameters J , Λ , h EVE , h EN , h H , and G, respectively, for the Jaya algorithm and the optimization problem. Based on Equation(20), F and θ * are computed in the third and fourth phases, respectively. Next, using Equation (29) to find the fitness function ξ ( K i ) ∀ i = 1 , 2 , . . . , J , all populations are sorted according to the best and worst solutions, K 1 and K J . The Jaya algorithm is used to to obtain the optimal active elements from step 10 till step 22. As a result, we can be confident that we progress toward our goal of identifying the best active elements of HR-RIS with each iteration.

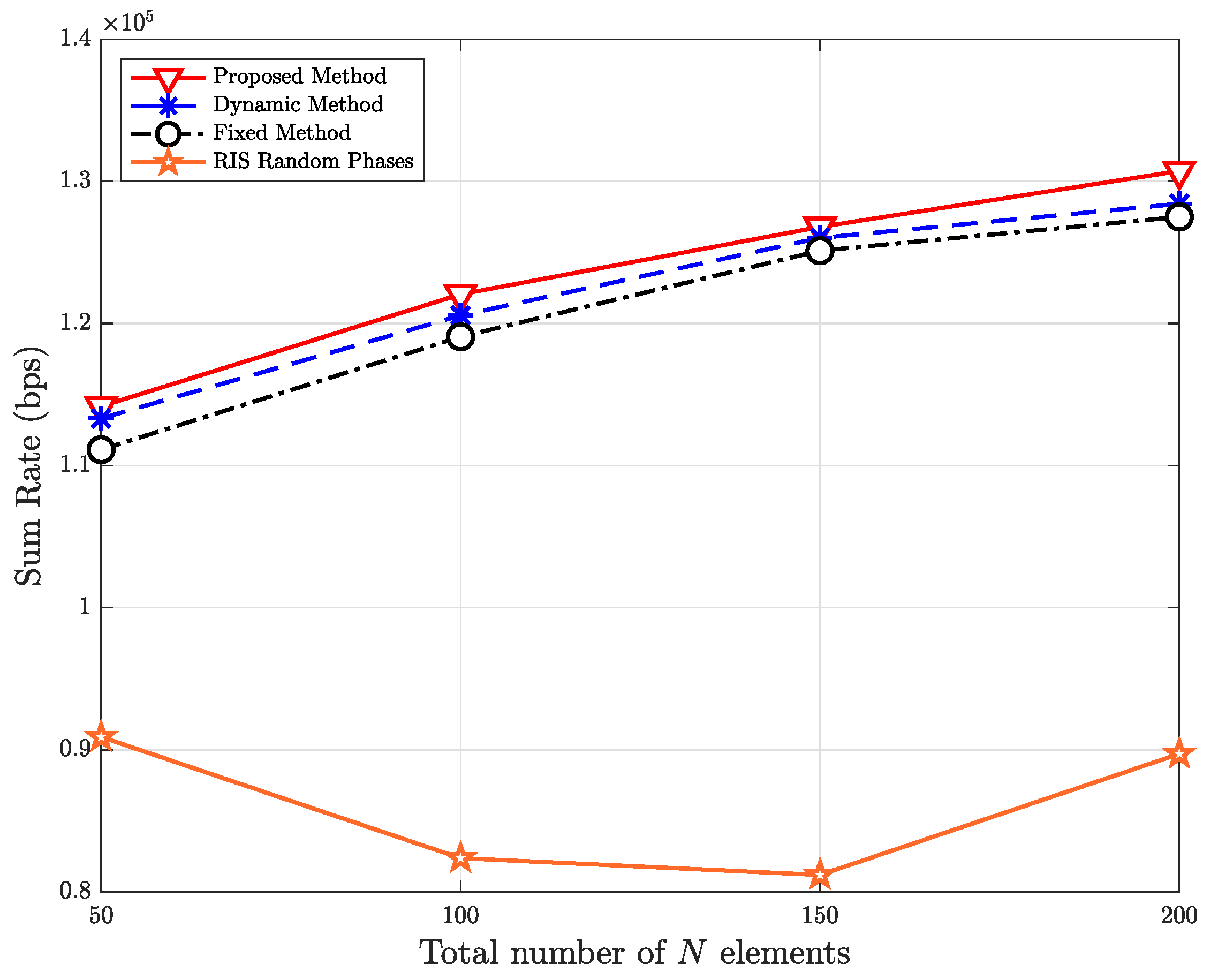
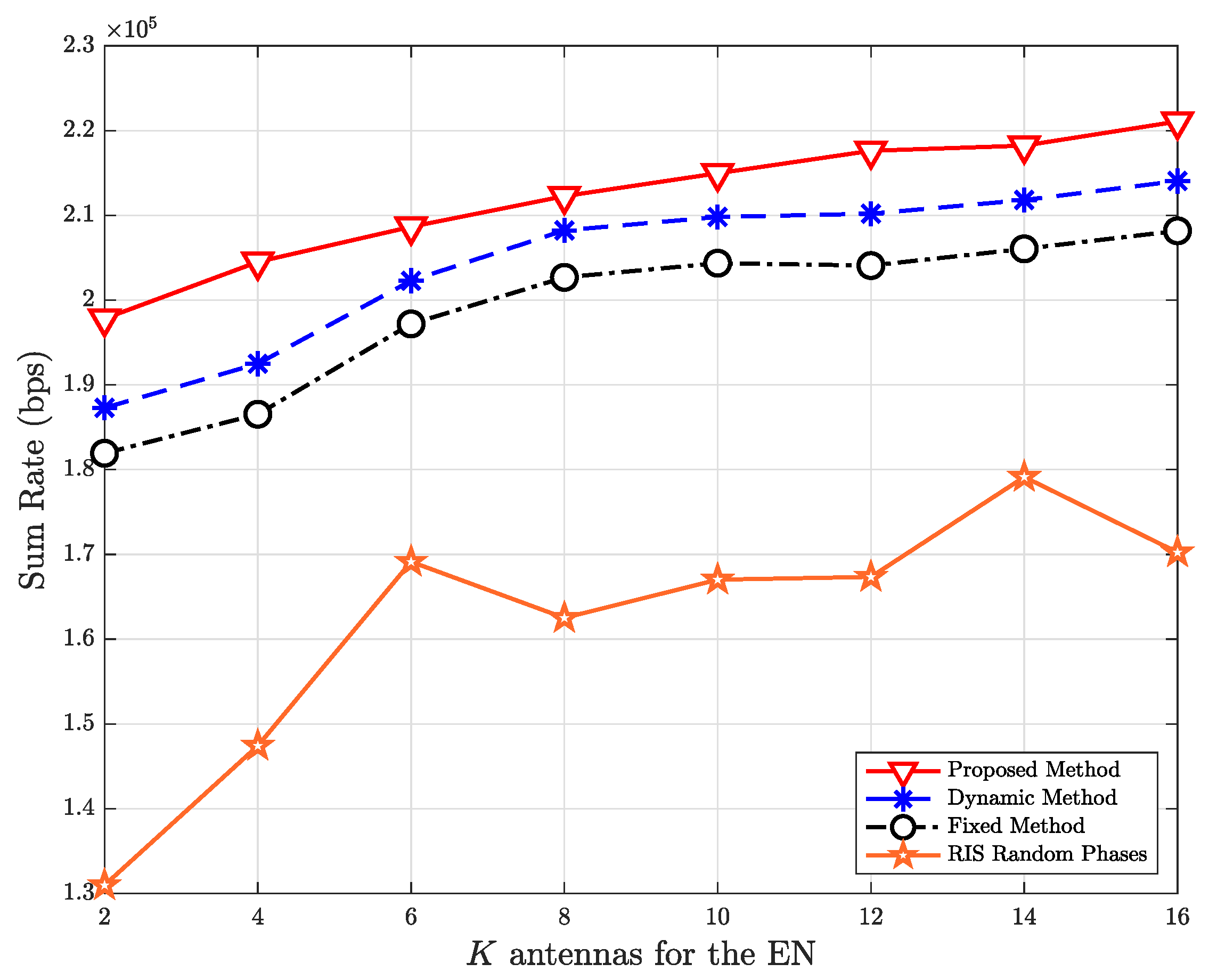
5. Simulation Results and Discussions

We conduct a numerical evaluation of the performance of the proposed approach in comparison to the state-of-the-art HR-RIS schemes in this section. We study the conventional passive RIS with random phases [22] and the optimized fixed and dynamic HR-RIS [20,21] as comparison approaches. The fact that active elements contribute to the power consumption of all systems is worth being noted. Thus, we maintain the total power of all of schemes constant in order to provide an equitable comparison same as [21]. Monte-Carlo simulation is utilized in this work for channel realizations. Table 1 contains the parameters used in all simulations based on [20,21,22,23] in this section.
The sum rate attained by the strategies presented when the user’s position changes is shown in Figure 5. To be more precise, we move x U in the interval [ 10 , 100 ] m to ensure the user is able to pivot along the x-axis, as Figure 2 illustrates. It is clear that when the user is closer to the EN or the HR-RIS, the sum rate rises significantly. Furthermore, the stronger direct user-EU or user-HR-RIS link, which permits the user to transmit at higher secrecy rates, is the cause of this improvement. Better channel conditions are made possible by the enhanced connection quality brought about by a stronger line-of-sight component and decreased path loss, which allows for enhanced sum rates.
The sum rate attained by the proposed approach and other the latest schemes at different eavesdropper locations are shown in Figure 6. Specifically, as the eavesdropper moves along the (x)-axis shown in Figure 2, x EVE is varied within the range [ 10 , 100 ] m. It is noteworthy that when compared to current approaches, the proposed approach regularly delivers the highest sum rate. The enhanced functionality of the HR-RIS is due to its sophisticated active element optimization, which dynamically adjusts to reduce the effect of the eavesdropper by maximising system secrecy through the direction of signal routes. The technique effectively increases data transmission security and efficiency by limiting the signal intensity that can be intercepted by the eavesdropper and increasing constructive interference towards the authorised user. Furthermore, improved overall system sum rate and optimal signal management are further ensured by the HR-RIS’s ability to reconfigure in response to the movements of the eavesdropper. This flexibility also reduces the risk of eavesdropping. Its flexibility also enables the proposed approach to continue operating with strong performance, highlighting its capacity to offer better security and effectiveness in changing circumstances, irrespective of the location of the eavesdropper.
The enhanced sum rate performance of the proposed approach, as a function of total power, P Total , is shown in Figure 7 when compared to state-of-the-art approaches. It proved that the HR-RIS system performs better when the Jaya technique is integrated, even at reduced power levels. The Jaya algorithm’s ability to identify the optimal number of active elements within the HR-RIS is mostly responsible for this improvement. This method guarantees optimal power allocation by optimizing the layout of active elements, hence maximizing signal reflection towards the intended user and minimizing interference. By strategically allocating power, the system is able to achieve higher performance without using more power, while simultaneously improving the overall sum rate and signal quality.
In Figure 8, we show the sum rate performance improvement of the proposed scheme compared to the sate-of-the-art schemes against the P a max when N = 50 , K = 3 , K = 4 , and J = 1 for the number of HR-RIS elements, the active elements of HR-RIS, the EN and eavesdropper antennas, respectively. It is observed that the proposed Jaya optimization technique with HR-RIS system can attain a higher performance at a lower value of P Total .
In Figure 9, we plot the sum rate as a function of the active elements of the HR-RIS system when N = 50 , K = 4 , and J = 1 for the number of HR-RIS elements, the EN and eavesdropper antennas, respectively. It is noted that the sum rate of the proposed method, the dynamic and fixed methods saturate as the number of active elements increases, but the proposed method outcomes the other mentioned schemes because the powerful of the proposed algorithm to obtain the optimal number of the active elements. Figure 10 presents that the sum rate increases when N increases when K = 3 , K = 4 , and J = 1 for the active elements of HR-RIS, the EN and eavesdropper antennas, respectively. Furthermore, it is noted that the sum rate of the proposed method can attain better results compared to the mentioned schemes.
Figure 11 demonstrates the impact of K antennas for the EN on the sum rate of the HR-RIS system when N = 50 , K = 3 and J = 4 for the number of HR-RIS elements, the number of active elements the eavesdropper antennas, respectively. It is obvious that the sum rate increases as K increases. This is because the strong link between the EN and the user or the strong link between the HR-RIS and the EN link. In particular, it indicates that large K antennas in the proposed Jaya algorithm perform better than other schemes in terms of sum rate. This is because the chance that the optimal number of elements at the HR-RIS are activated and the proposed method can attain the global optimum. This will enhance the preservation of the system from significant loss in sum rate. For example, when K = 6 antennas, the proposed method can attain approximately 4.53 % , 6.15 % , and 22.7 % sum rate improvement compared to the dynamic method, fixed method, and RIS random phases, respectively.
A comprehensive evaluation of the proposed approach using HR-RIS and the Jaya algorithm demonstrates notable improvements in system performance in a number of scenarios. When the user is positioned favourably, the Jaya algorithm efficiently finds the optimal number of active elements, increasing sum rates and providing strong security by adjusting to different eavesdropper positions. Interestingly, the scheme performs better even at lower total power levels, proving the effective power allocation capabilities of the Jaya algorithm. These benefits highlight the algorithm’s potential to enhance signal reflection, improving SINR, reducing interference, and increasing secrecy rates.

6. Conclusions

This study addressed how to determine the optimal active elements HR-RIS system while taking into account how to increase the communication system’s sum rate when a threatening eavesdropper is involved. A novel approach for the activation of HR-RIS elements has been introduced, based on the Jaya optimization process. Significant gains in system performance were demonstrated in numerous instances by an extensive investigation of the proposed approach employing HR-RIS and the Jaya algorithm. By adapting to various eavesdropper positions, the Jaya algorithm effectively determines the ideal number of active elements when the user is positioned favorably. This results in enhanced sum rates and robust security. Looking ahead to future works, it will be utilized the proposed scheme for multiple users’ scenario. Also, this proposed scheme can be used when the HR-RIS attached to the drone scenario. Another possible future direction is to use the proposed method in this work with multi-RIS scenario.

Author Contributions

Conceptualization, A.A.A.; methodology, A.A.A.; software, A.A.A.; validation, A.A.A.; formal analysis, A.A.A.; investigation, A.A.A.; resources, A.A.A.; data curation, A.A.A.; writing—original draft preparation, A.A.A.; writing—review and editing, A.A.A.; visualization, A.A.A.; The author has read and agreed to the published version of the manuscript.

Funding

This research was fully funded by the Deanship of Scientific Research at King Khalid University Fund - RGP 2/594/44.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable for studies not involving humans.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Huang, C.; Wu, Q.; Zhang, L. Reconfigurable Intelligent Surface (RIS)-Assisted Wireless Systems: A Review. IEEE Trans. Wirel. Commun. 2020, 20, 3902–3919. [Google Scholar]
  2. Wu, Q.; Zhang, L.; Yang, H. Towards Smart Wireless Communication Environments: An Overview of Reconfigurable Intelligent Surfaces. IEEE Commun. Mag. 2021, 59, 98–105. [Google Scholar]
  3. Li, Y.; et al. Physical Layer Security with Reconfigurable Intelligent Surface: A New Paradigm in Wireless Communications. IEEE Trans. Inf. Forensics Secur. 2021, 16, 1389–1404. [Google Scholar]
  4. Zhang, S.; et al. Securing Wireless Communication with Reconfigurable Intelligent Surfaces: Strategies and Applications. IEEE Trans. Wirel. Commun. 2022, 21, 1202–1213. [Google Scholar]
  5. Liu, H.; et al. Rethinking Wireless Communication: Towards Secure and Energy-Efficient Systems with Intelligent Surfaces. IEEE J. Sel. Areas Commun. 2021, 39, 2375–2390. [Google Scholar]
  6. Wu, Q.; et al. Physical Layer Security in Wireless Networks with Reconfigurable Intelligent Surfaces. IEEE Access 2020, 8, 71127–71139. [Google Scholar]
  7. Kammoun, A.; et al. Secrecy Analysis of RIS-Assisted Caching Wireless Networks. IEEE Trans. Wirel. Commun. 2021, 20, 5901–5916. [Google Scholar]
  8. Zhang, J.; et al. Machine Learning for Secrecy Communications with Flat and Adaptive Reconfigurable Intelligent Surfaces. IEEE Trans. Cybern. 2022, 52, 2452–2463. [Google Scholar]
  9. Xiong, Z.; et al. A Machine Learning Approach for Secure Wireless Communications using Reconfigurable Intelligent Surfaces. IEEE Trans. Commun. 2021, 69, 3334–3347. [Google Scholar]
  10. Di Renzo, M.; et al. Economic Feasibility and Efficiency of Reconfigurable Intelligent Surfaces for Wireless Communications. IEEE Wirel. Commun. Lett. 2020, 9, 88–91. [Google Scholar]
  11. Basar, E. Transmit Designs for Energy-Efficient and Secure Deployments of Reconfigurable Intelligent Surfaces. In Proceedings of the 2020 IEEE International Conference on Communications (ICC); 2020; pp. 1–6. [Google Scholar]
  12. Liu, H.; et al. Secrecy Rate Maximization for Hybrid Reconfigurable Intelligent Surface-Aided Wireless Networks. IEEE J. Sel. Areas Commun. 2021, 39, 3296–3315. [Google Scholar]
  13. Yang, K.; et al. Multi-Objective Optimization for Secrecy Communication with Hybrid Reconfigurable Intelligent Surfaces. IEEE Trans. Commun. 2022, 70, 6000–6015. [Google Scholar]
  14. Chen, G.; et al. Secrecy Communications with Active and Passive Reconfigurable Intelligent Surfaces Under Imperfect Channel State Information. IEEE Trans. Inf. Forensics Secur. 2021, 16, 1390–1403. [Google Scholar]
  15. Qiu, J.; et al. Energy-Efficient and Secure Hybrid Reconfigurable Intelligent Surface Systems: An Alternating Optimization Approach. IEEE Trans. Wirel. Commun. 2021, 20, 4323–4336. [Google Scholar]
  16. Alghamdi, A.; et al. Game Theory-Based Active Elements Optimization in HR-RIS for Secrecy Communication. IEEE Access 2022, 10, 34567–34578. [Google Scholar]
  17. Ma, Y.; et al. Cost-Effective Secrecy Communication via Hybrid Reconfigurable Intelligent Surfaces. IEEE Trans. Wirel. Commun. 2023, 22, 789–802. [Google Scholar]
  18. Rao, R.V. Jaya: A New Optimization Algorithm. Adv. Comput. Sci. Eng. 2016, 2016, 1–14. [Google Scholar]
  19. Wu, Q.; Zhang, R. Intelligent reflecting surface enhanced wireless network: Joint active and passive beamforming design. In Proceedings of the IEEE Global Commun. Conf. 2018; pp. 1–6. [Google Scholar]
  20. Nguyen, N.T.; Vu, Q.-D.; Lee, K.; Juntti, M. Hybrid Relay-Reflecting Intelligent Surface-Assisted Wireless Communications. IEEE Trans. Veh. Technol. 2022, 71, 6228–6244. [Google Scholar] [CrossRef]
  21. Ngo, K.-H.; Nguyen, N.T.; Dinh, T.Q.; Hoang, T.-M.; Juntti, M. Low-Latency and Secure Computation Offloading Assisted by Hybrid Relay-Reflecting Intelligent Surface. In Proceedings of the 2021 International Conference on Advanced Technologies for Communications (ATC), Ho Chi Minh City, Vietnam; 2021; pp. 306–311. [Google Scholar]
  22. Zhang, S.; Zhang, R. Capacity Characterization for Intelligent Reflecting Surface Aided MIMO Communication. IEEE J. Sel. Areas Commun. 2020, 38, 1823–1838. [Google Scholar] [CrossRef]
  23. Jung, M.; Saad, W.; Debbah, M.; Hong, C.S. Asymptotic Optimality of Reconfigurable Intelligent Surfaces: Passive Beamforming and Achievable Rate. In Proceedings of the IEEE International Conference on Communications (ICC); 2020; pp. 1–6. [Google Scholar]
  24. Khandaker, M.R.A.; Masouros, C.; Wong, K.-K. Constructive Interference Based Secure Precoding: A New Dimension in Physical Layer Security. IEEE Trans. Inf. Forensics Secur. 2018, 13, 2256–2268. [Google Scholar] [CrossRef]
  25. He, X.; Jin, R.; Dai, H. Physical-Layer Assisted Secure Offloading in Mobile-Edge Computing. IEEE Trans. Wirel. Commun. 2020, 19, 4054–4066. [Google Scholar] [CrossRef]
  26. Zitar, R.A.; Al-Betar, M.A.; Awadallah, M.A.; et al. An Intensive and Comprehensive Overview of JAYA Algorithm, Its Versions and Applications. Arch. Comput. Methods Eng. 2022, 29, 763–792. [Google Scholar] [CrossRef] [PubMed]
Preprints 117928 g001
Figure 1. Illustration of HR-RIS structure in the presence of the eavesdropper.
Figure 1. Illustration of HR-RIS structure in the presence of the eavesdropper.
Preprints 117928 g001
Preprints 117928 g002
Figure 2. Illustration of the positions for the EN, the eavesdropper and the user in the proposed HR-RIS structure.
Figure 2. Illustration of the positions for the EN, the eavesdropper and the user in the proposed HR-RIS structure.
Preprints 117928 g002
Preprints 117928 g003
Figure 3. Flow chart of the proposed method to obtain the optimal number of active elements of HR-RIS based on Jaya algorithm.
Figure 3. Flow chart of the proposed method to obtain the optimal number of active elements of HR-RIS based on Jaya algorithm.
Preprints 117928 g003
Preprints 117928 g004
Figure 4. Sum rate in (bps) versus number of iterations for the proposed method, where K = 4 , and J = 1 for the EN and eavesdropper antennas, respectively.
Figure 4. Sum rate in (bps) versus number of iterations for the proposed method, where K = 4 , and J = 1 for the EN and eavesdropper antennas, respectively.
Preprints 117928 g004
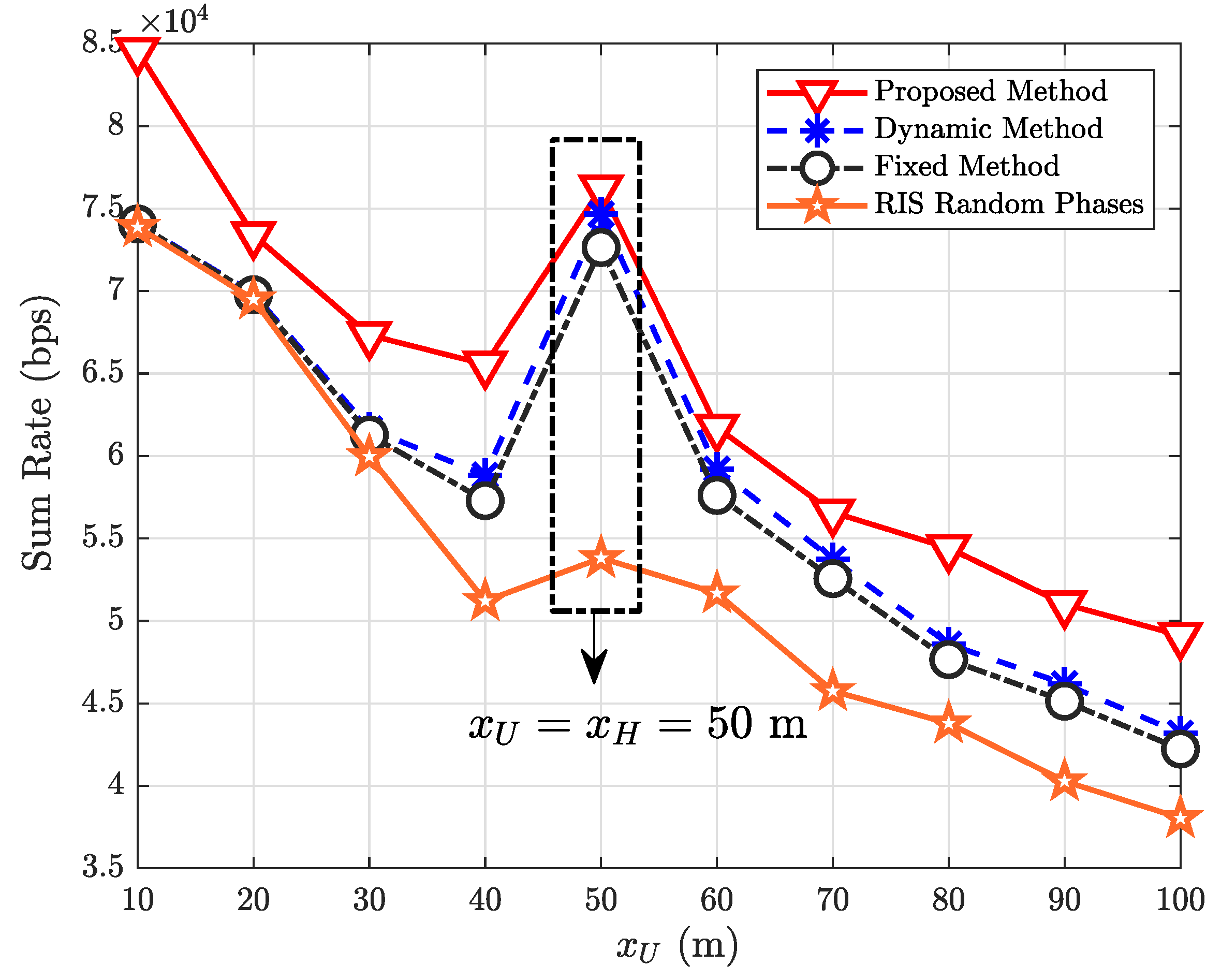
Preprints 117928 g005
Figure 5. Sum rate in (bps) versus different locations for the user, where N = 50 , K = 3 , K = 4 , and J = 1 for the number of HR-RIS elements, the active elements of HR-RIS, the EN and eavesdropper antennas, respectively.
Figure 5. Sum rate in (bps) versus different locations for the user, where N = 50 , K = 3 , K = 4 , and J = 1 for the number of HR-RIS elements, the active elements of HR-RIS, the EN and eavesdropper antennas, respectively.
Preprints 117928 g005
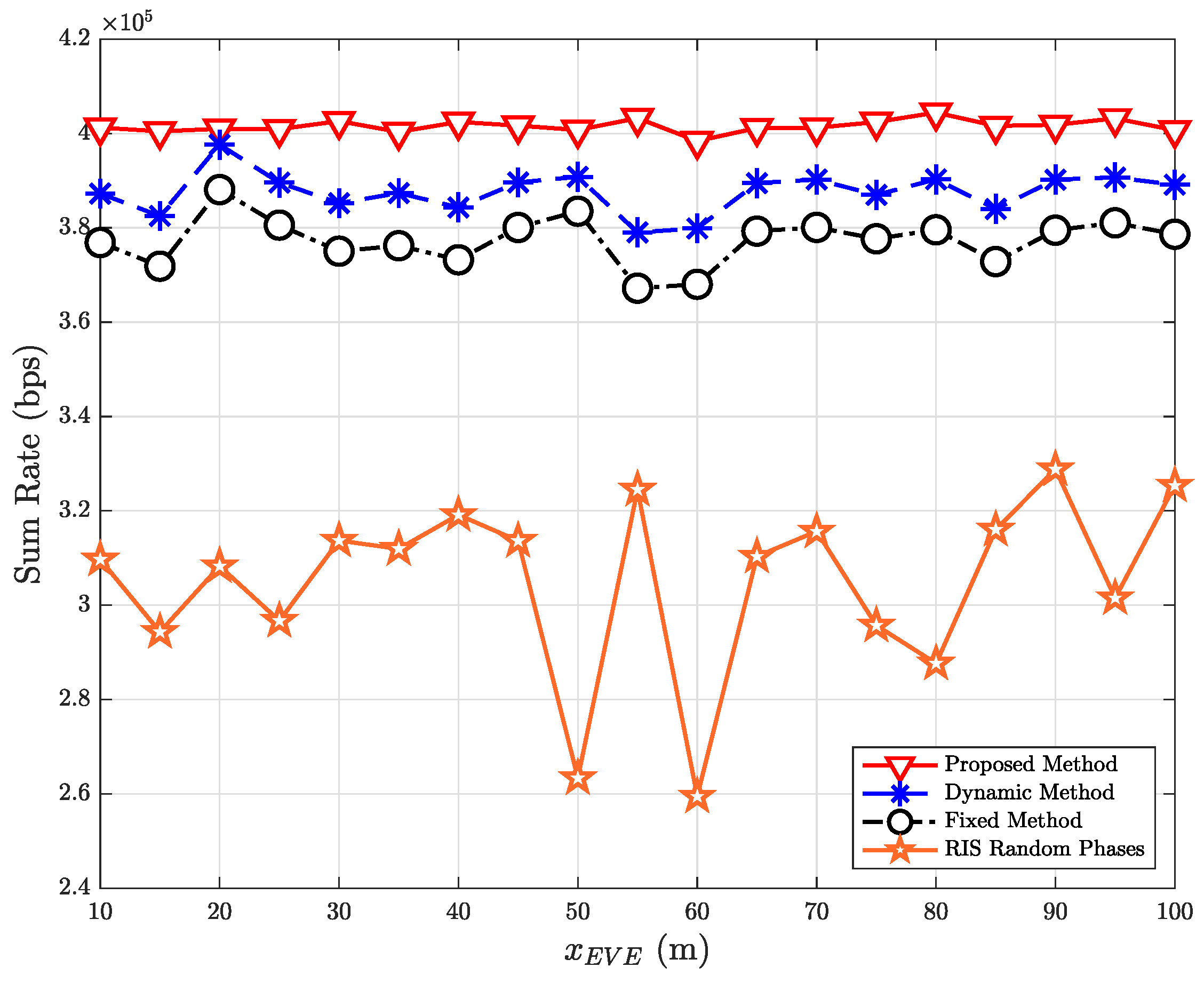
Preprints 117928 g006
Figure 6. Sum rate in (bps) versus different locations for the eavesdropper, where x U = 50 m, N = 50 , K = 3 , K = 4 , and J = 1 for the user’s location, the number of HR-RIS elements, the active elements of HR-RIS, the EN and eavesdropper antennas, respectively.
Figure 6. Sum rate in (bps) versus different locations for the eavesdropper, where x U = 50 m, N = 50 , K = 3 , K = 4 , and J = 1 for the user’s location, the number of HR-RIS elements, the active elements of HR-RIS, the EN and eavesdropper antennas, respectively.
Preprints 117928 g006
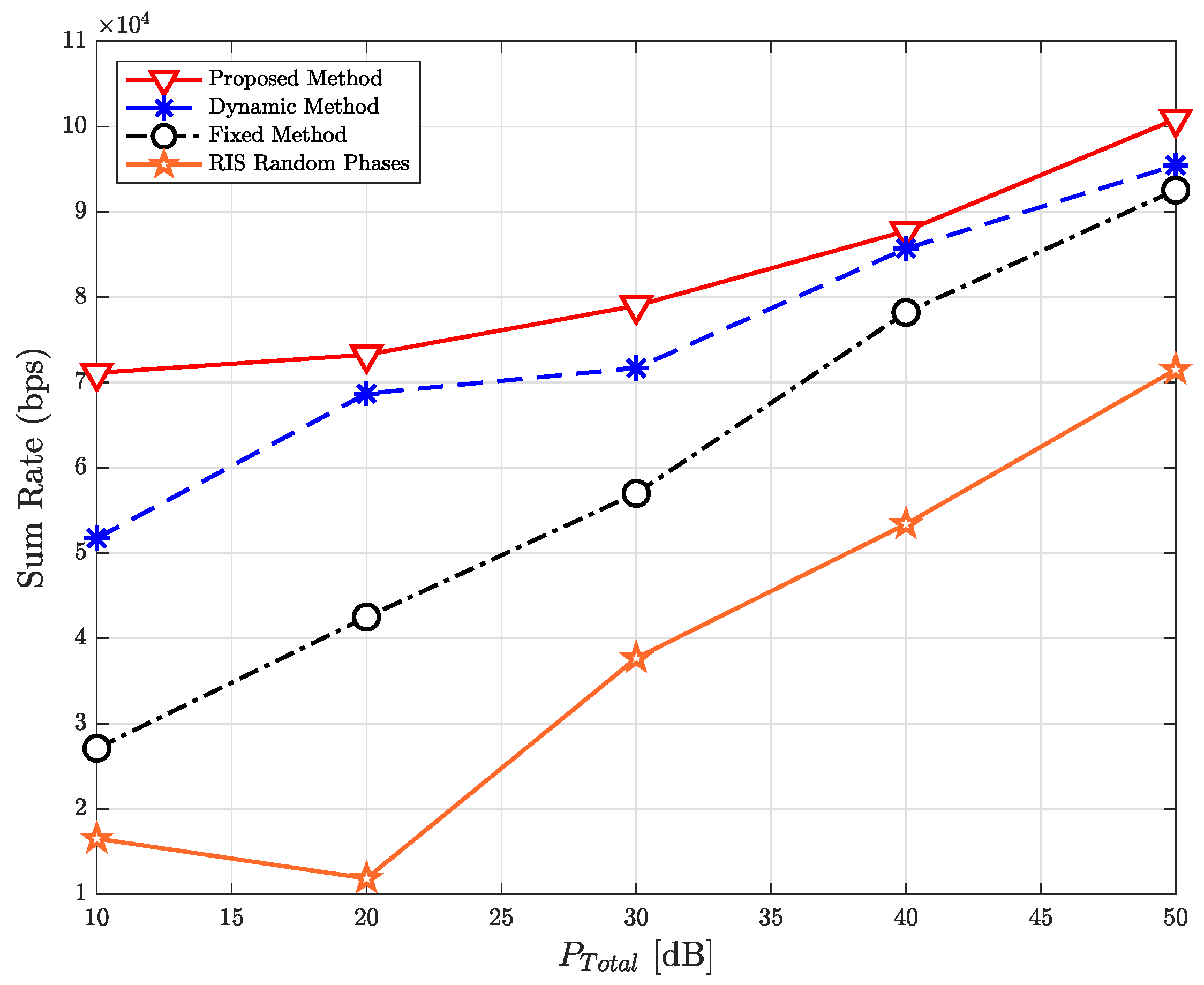
Preprints 117928 g007
Figure 7. Sum rate in (bps) versus total power consumption, where N = 50 , K = 3 , K = 4 , and J = 1 for the number of HR-RIS elements, the active elements of HR-RIS, the EN and eavesdropper antennas, respectively.
Figure 7. Sum rate in (bps) versus total power consumption, where N = 50 , K = 3 , K = 4 , and J = 1 for the number of HR-RIS elements, the active elements of HR-RIS, the EN and eavesdropper antennas, respectively.
Preprints 117928 g007
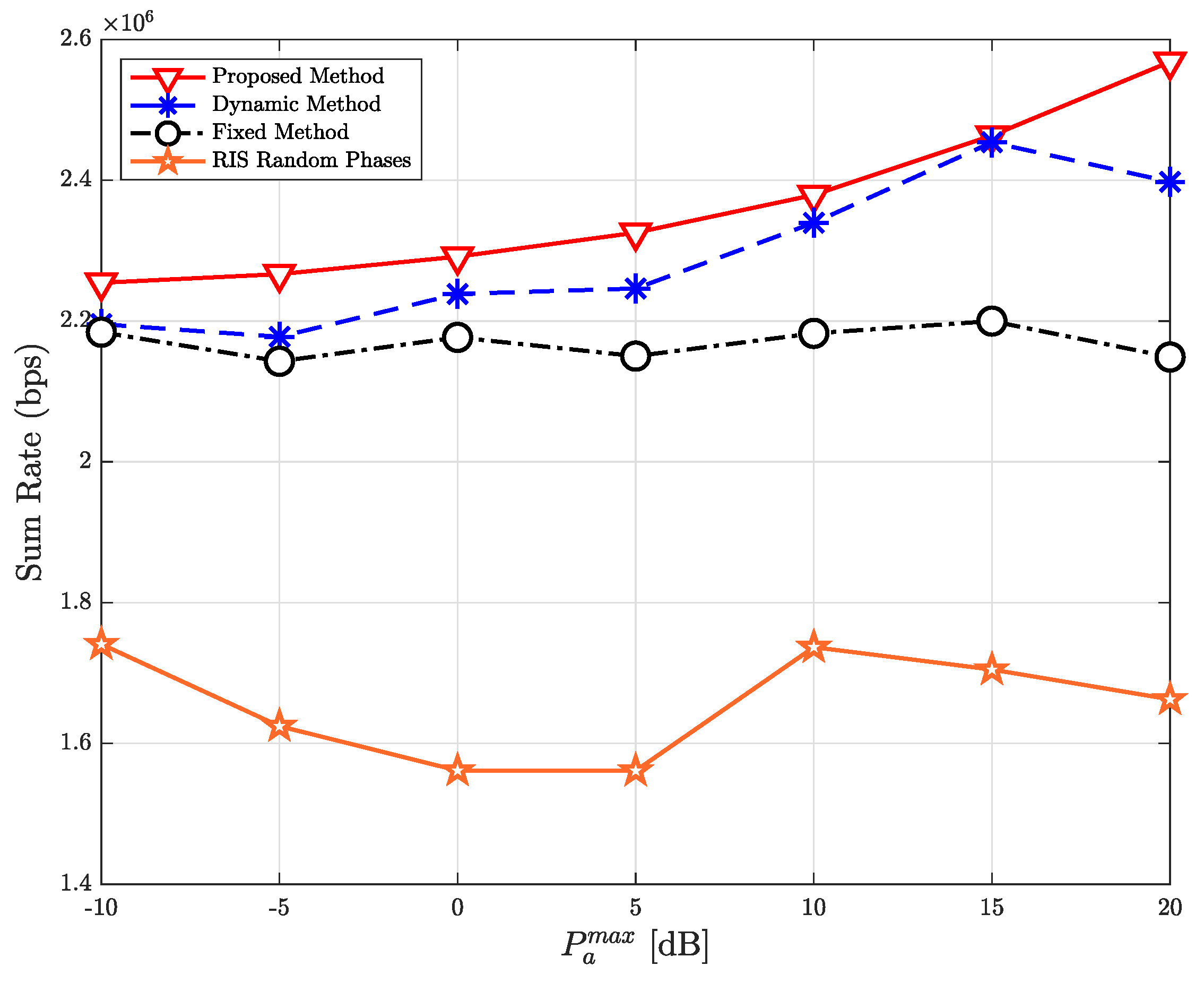
Preprints 117928 g008
Figure 8. Sum rate in (bps) versus P a max , where N = 50 , K = 3 , K = 4 , and J = 1 for the number of HR-RIS elements, the active elements of HR-RIS, the EN and eavesdropper antennas, respectively.
Figure 8. Sum rate in (bps) versus P a max , where N = 50 , K = 3 , K = 4 , and J = 1 for the number of HR-RIS elements, the active elements of HR-RIS, the EN and eavesdropper antennas, respectively.
Preprints 117928 g008
Preprints 117928 g009
Figure 9. Sum rate in (bps) versus  K  active elements, where N = 50 , K = 4 , and J = 1 for the number of HR-RIS elements, the EN and eavesdropper antennas, respectively.
Figure 9. Sum rate in (bps) versus  K  active elements, where N = 50 , K = 4 , and J = 1 for the number of HR-RIS elements, the EN and eavesdropper antennas, respectively.
Preprints 117928 g009
Preprints 117928 g010
Figure 10. Sum rate in (bps) versus N elements of HR-RIS, where K = 3 , K = 4 , and J = 1 for the active elements of HR-RIS, the EN and eavesdropper antennas, respectively.
Figure 10. Sum rate in (bps) versus N elements of HR-RIS, where K = 3 , K = 4 , and J = 1 for the active elements of HR-RIS, the EN and eavesdropper antennas, respectively.
Preprints 117928 g010
Preprints 117928 g011
Figure 11. Sum rate in (bps) versus K antennas for the EN, where N = 50 , K = 3 and J = 4 for the number of HR-RIS elements, the number of active elements the eavesdropper antennas, respectively.
Figure 11. Sum rate in (bps) versus K antennas for the EN, where N = 50 , K = 3 and J = 4 for the number of HR-RIS elements, the number of active elements the eavesdropper antennas, respectively.
Preprints 117928 g011
Table 1. Simulation parameters.
Table 1. Simulation parameters.
Parameter Value
Upper bound of the estimation error ( ν ) 0.1
Bandwidth (B) 1 MHz
The path loss at d o ( β o ) -30 dBm
σ EN 2 = σ H 2 = σ 2 -80 dBm
( x H , x U , y U , x EVE , y EVE ) ( 50 , 45 , 2 , 30 , 9 ) m
Power components: P Total = 30 dBm, and P a max = 0 dBm
The effectiveness and efficacy of the proposed algorithm in identifying the optimum number of active elements in HR-RIS scenario is demonstrated by its convergence behaviour, which is depicted in the Figure 4. The approach involves 100 iterations in total, and when the system has N = 100 elements and the main aim is to optimize K = 5 active elements, it converges satisfactorily at the 23rd iteration. In addition, when the system has N = 100 elements and the main aim is to optimize K = 20 active elements, it converges satisfactorily at the 34th iteration. This fast convergence implies that the proposed Jaya algorithm efficiently searches the solution space to find the best configurations in the shortest amount of time and with the least amount of computational complexity. Thus, this characteristic is particularly valuable for real-time or adaptive systems, where quick decision-making and adjustments are required. Overall, the convergence pattern displayed attests to the robustness and suitability of the Jaya optimization method for active element selection in complex RIS scenarios.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated