3D FEM Modeling of Polish Apple ‘Chopin’: Elastic vs. Elastoplastic Behavior Across Maturity Stages

1. Introduction

Fruits consist of various structural elements with differing mechanical properties, but the majority of their composition comprises edible parenchymatous tissue. It is precisely the quality of this tissue that primarily determines the suitability of fruits for consumption. The primary factors influencing the mechanical properties of apple parenchyma, which change during their ripening process, are the content of pectin and cellulose compounds. From a mechanical perspective, the plant cell wall can be regarded as a robust fibrous network that imparts a stable shape to each cell: a cellulose network resistant to tensile forces, a hemicellulose network resistant to shearing forces, and a pectin network resistant to compressive forces [1,2,3,4,5,6,7,8,9]. Moreover, the preservation of fruit freshness is significantly influenced by the content of malic and citric acids, with citric acid serving as a natural antioxidant that safeguards apples against the oxidation process, which results in a loss of quality. Moreover, the sugar degradation and water loss also contribute to the [10,11,12,13,14,15,16,17,18]. Hence, it is of paramount importance to be aware of the physiological stage of the examined fruits when determining their mechanical properties for the construction and validation of FEM models. The most prevalent, straightforward, and cost-effective method for assessing the fruit’s maturity stage of apples is the Streif Index, although it is gradually being replaced by the examination of ethylene concentration in seed chambers.

Numerical modelling is becoming increasingly popular tool in the field of fruit research. The Finite Element Method (FEM) is a numerical technique that enables the analysis of the fruit behaviour under variable loads and also to predict their damage. Numerical models are based on physical models that take into account various factors such as fruit geometry and the mechanical properties. [19] calculated the average elastic modulus, yield stress, and ultimate stress of apples by conducting compression tests. Unfortunately, the authors didn’t present the model validation. Celik, (2017) presented an approach for identifying bruises through the application of a dynamic Finite Element Analysis (FEA) model, demonstrated using a pear as an example. The material data for the model were based on elastic modulus, Poisson’s ratio, the yield point, and ultimate stress. The model results obtained by the authors were not subjected to a proper validation process. On the other hand, Du et al., (2019) conducted an analysis for predicting bruising in kiwi fruit using a numerical method. They validated their results based on initial velocity, maximum deformation length, contact surface area, and simulated bruise volumes. [22] developed a dynamic model of an apple with material properties resembling crushable foam (typically used for modelling low-density polymer foams). Furthermore, they opted to employ a volume-based material reinforcement procedure. In the material stiffening process, they set the yield point at 3 MPa with a deformation value of 1. The values for elastic modulus and Poisson’s ratio were adapted from a study published by [23]. The authors subjected the models to drop tests on various types of surfaces. The model results underwent validation based on empirical data, including surface pressures, and force measurements.

To summarize, the Finite Element Method (FEM) enables the identification of factors influencing the mechanical properties of fruits, such as their shape, size, density, or stiffness, which is highly valuable in the process of designing new fruit processing equipment. However, it is essential to bear in mind that simulation results can be considered reliable only after their validation. Additionally, it is crucial to be aware of the ripeness stage of the fruits subjected to the study or to create models for multiple ripeness stages commonly found in the market right from the outset.

2. Materials and Methods

2.1. Material

The research material consisted of Chopin variety apples bred and harvested by the Experimental Orchards of the Warsaw University of Life Sciences in Wilanów. Both the description of the variety, its physicochemical properties, as well as the description of the method and the results of determining its strength properties, are provided in another scientific article dedicated to studying the impact of fruit maturity stages on the mechanical properties of fruit for the purpose of building FEM models [24].

2.2. MES Modelling

Using the Abaqus CAE program, a model of the apple compression process in quasi-static conditions was designed.

2.2.1. Geometry

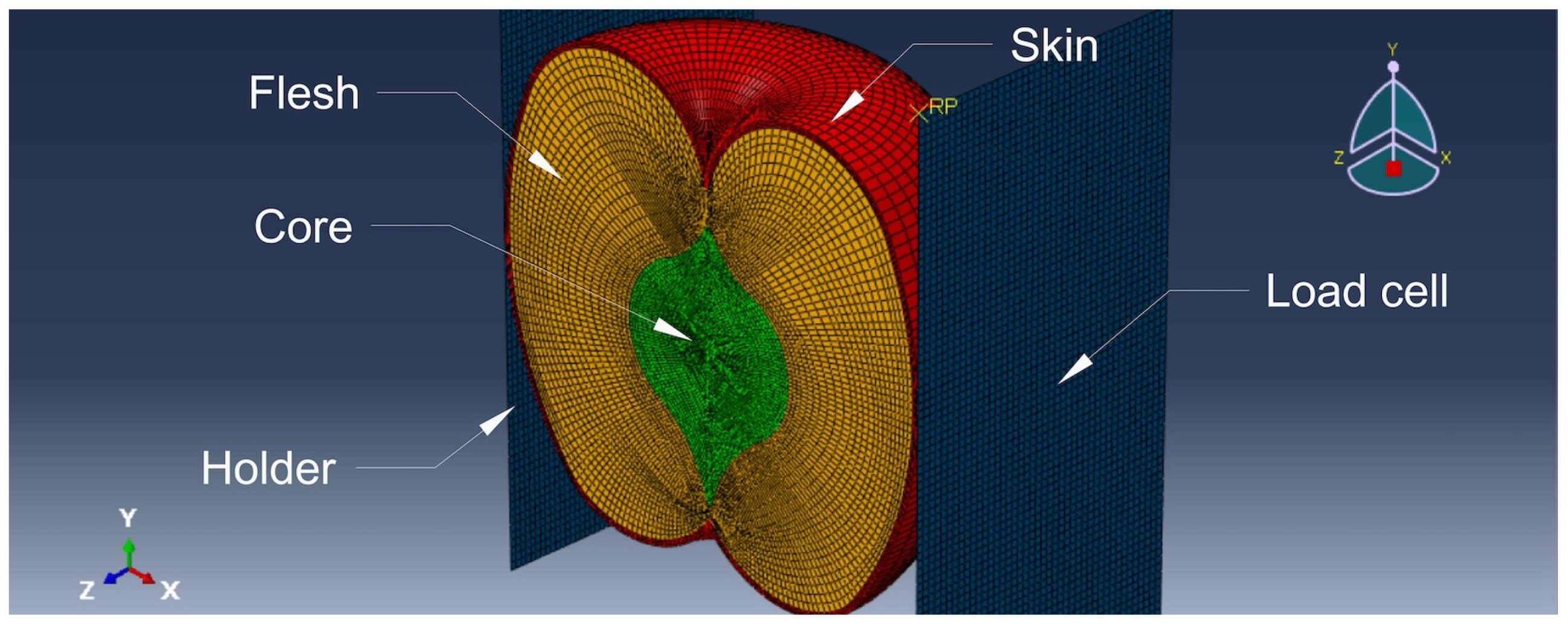
Based on the averaged measurements of apple geometry, a fruit model consisting of three 3D geometric elements was designed - the core, flesh, and skin. The fruit had a diameter of 77.5 mm, a height of 64 mm, skin thickness of 0.6 mm, core diameter of 32 mm, and a core height of 39 mm. The model also included two steel plates, which served as a holder and a load cell. Both plates had dimensions of 100 × 50 mm and were 3D shell-type components with a thickness of 2 mm. The aforementioned elements of the model are described in Figure 1.

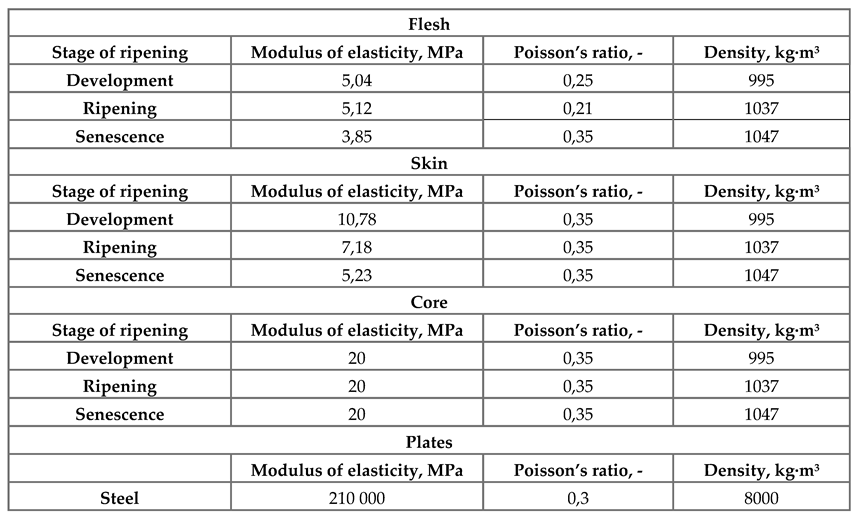
2.2.2. Elastic Properties

The Young Modulus’ values of the flesh and skin were determined through strength tests, the same as Poisson’s Ratio values of the flesh. The mechanical testing methodology has been described in detail in another publication [24]. Due to the choice of a static method and, consequently, the lack of significant impact of the difference in the density of the peel and core on the model results, the density of whole fruits determined in the tests was assumed for both the peel, core and flesh. The elastic properties of the core were adopted from the article of [25], the same as value of Poisson’s ratio for skin. For the holder and the load cell, material properties characteristic of steel was adopted to reflect real measurement conditions. The elastic properties of both elastic and elastoplastic models are presented in Table 1.

2.2.3. Elastic Plastic Isotropic Behaviour of Flesh

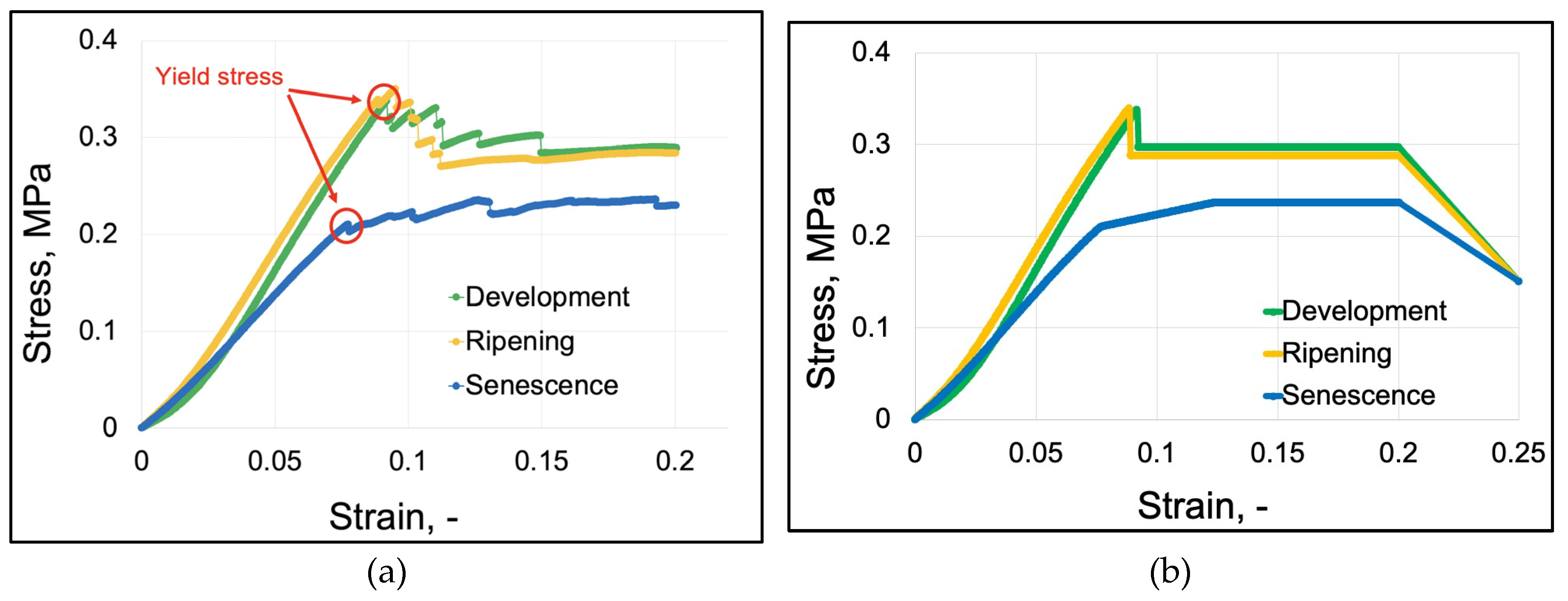
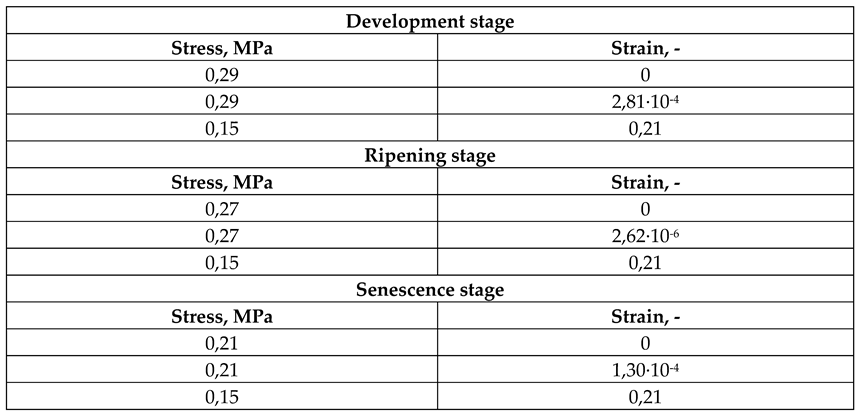
Elastic-plastic models required the use of calibration of stress-strain curves obtained in the empirical research on the flesh (Figure 2). Then, the graphs calibrated (Figure 2b) in Abaqus CAE, based on the original stress-strain plots (Figure 2a), were used to determine the plastic points, using the Elastic Plastic Isotropic behaviour. The plastic points determined by the program are presented in Table 2. The results of elastic properties obtained during this procedure coincided with the values determined in tests with an accuracy of thousandths.

2.2.4. Step

The model analysis type was set to Static General; the properties were as follows Time period: 1, NIgeom: on, Initial increment size: 0.01, Minimum increment size: 1·10^-8, Maximum increment size: 0.01, Maximum number of increments 15,000.

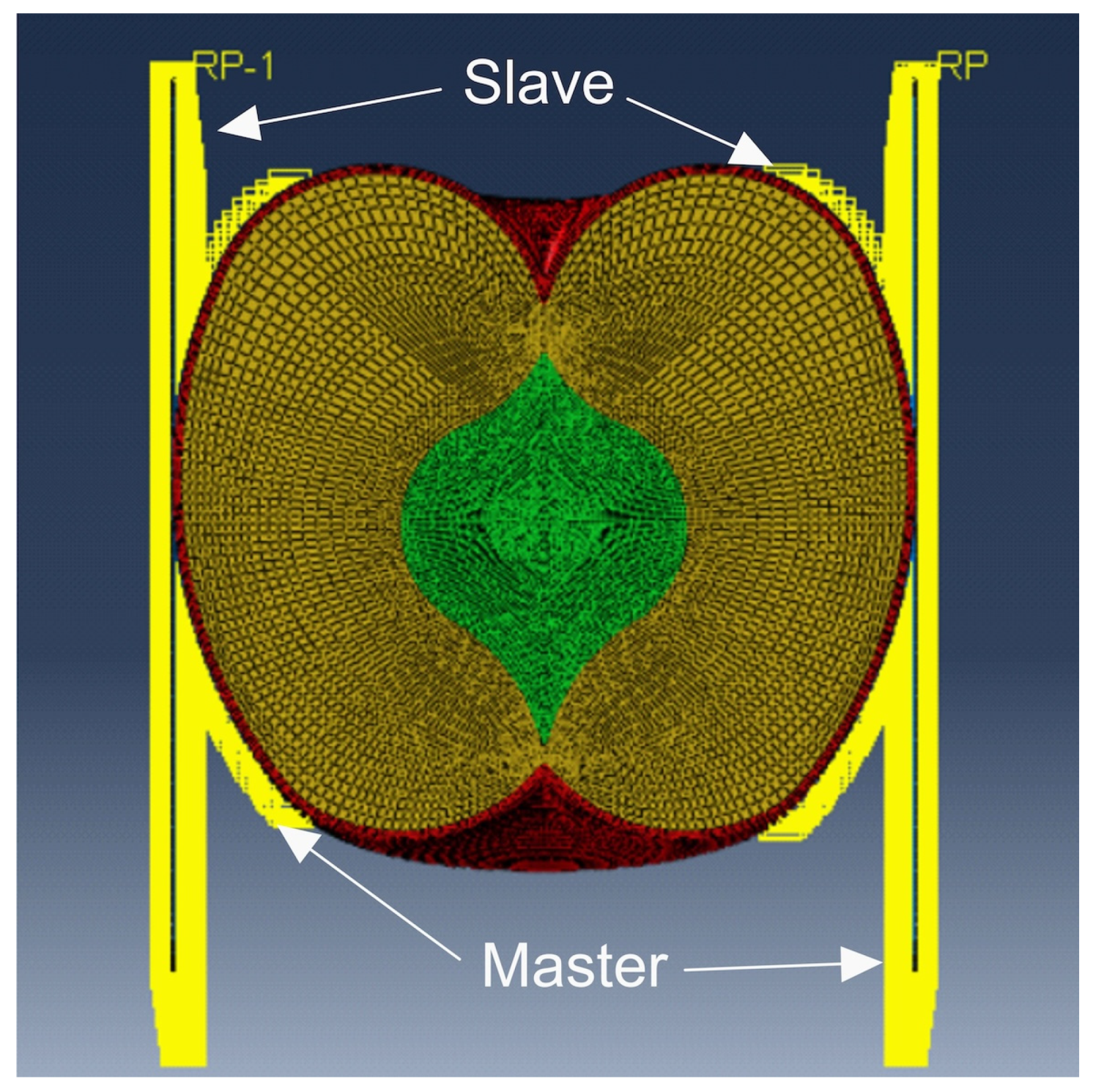
2.2.5. Interaction

In the Interaction module, the contact between steel plates and the fruit was determined. The interaction type was defined as “surface-to-surface contact (Standard)”, while the discretization method was set as “node-to-surface”. On the loading side, the plate surface was defined as the Master surface, while the fruit surface was defined as the Slave surface. On the passive side, the skin was assigned the Master surface, while the base was assigned the Slave surface (Figure 3). A value of 0.2 was assumed for the degree of smoothing for master surface. For tangential behaviour, a friction coefficient of 0.7 was set. Normal behaviour was defined as hard contact.

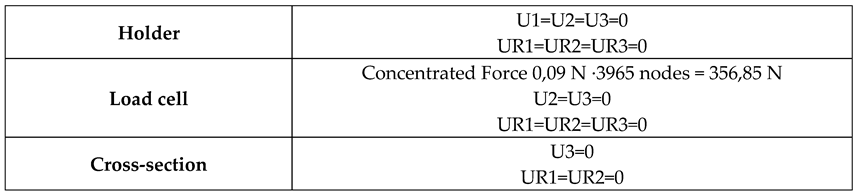
2.2.6. Boundary Conditions

Figure 4 contains a description of the sets to which boundary conditions have been assigned, while Table 3 contains their parameters.

• Figure 4. Description of the sets used to model the boundary conditions.

The base was fixed in all directions. A concentrated force of 0.09 N was assigned to each node of the working element, allowing displacement only in the X-axis direction. The cross-section of the fruit was restricted from moving in the Z-axis direction and from rotating around the X and Y axes (Table 3).

2.2.7. Mesh

The parenchyma tissue consisted of 91,908 elements of the C3D8 type and 1,656 elements of the C3D6 type. The epidermal tissue consisted of 11,983 elements of the C3D8 type and 216 elements of the C3D6 type. The seed nest consisted of 50,256 elements of the C3D8 type, 3,528 elements of the C3D6 type and 3,024 elements of the C3D4 type. To discretize both plates, 3,444 S4 elements were used.

2.3. Models’ Validation

2.3.1. Validation Based on Force vs. Displacement Graphs

The static analysis provided data that allowed for generating displacement and force vs. time curves (for individual frames representing increments of the analysis) at specified model nodes. The curves were then combined by eliminating the X variable (time) and replacing it with displacement, while force was assigned to the Y-axis. The data from the resulting curves were copied into Excel sheets for comparison with test data.

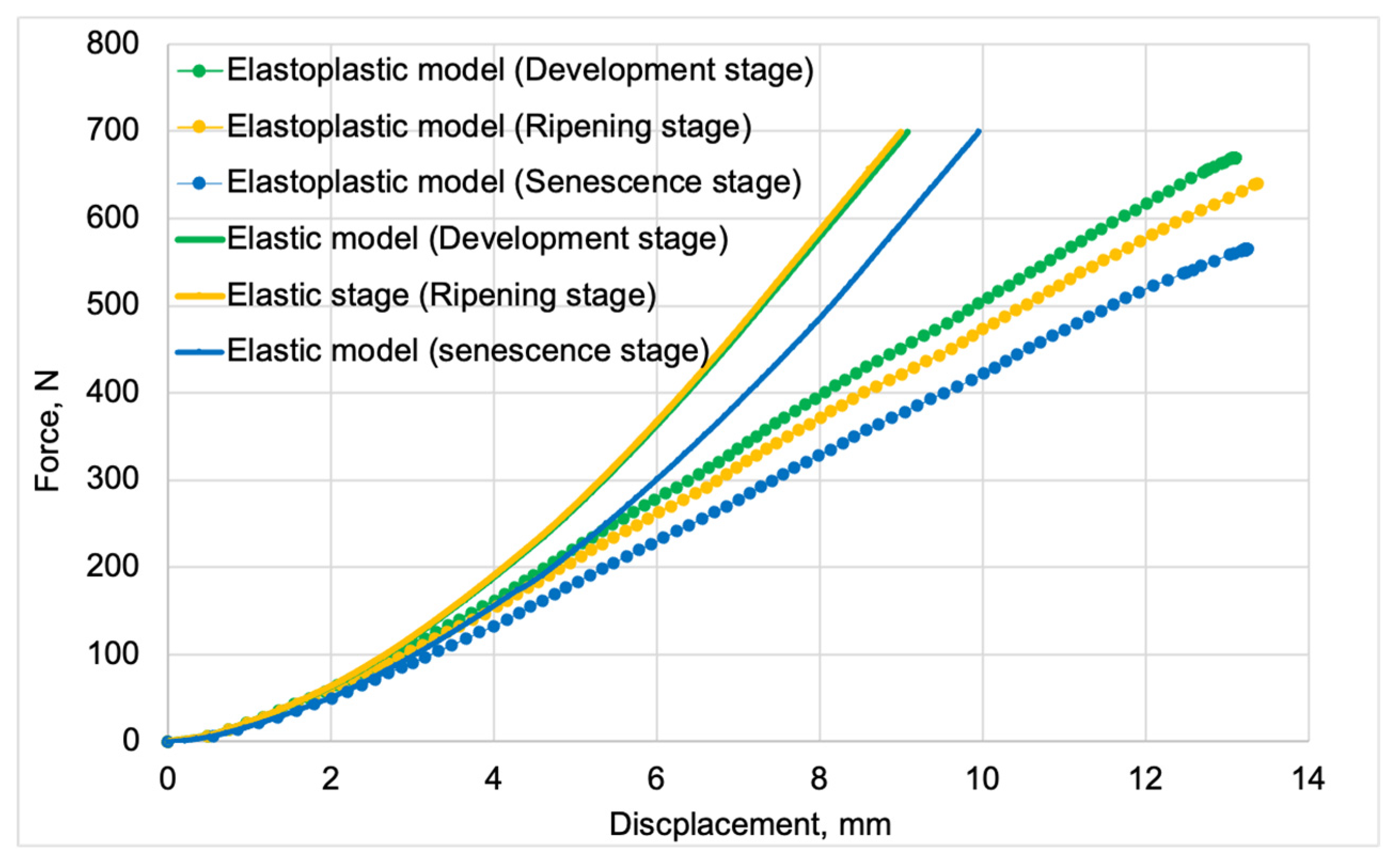
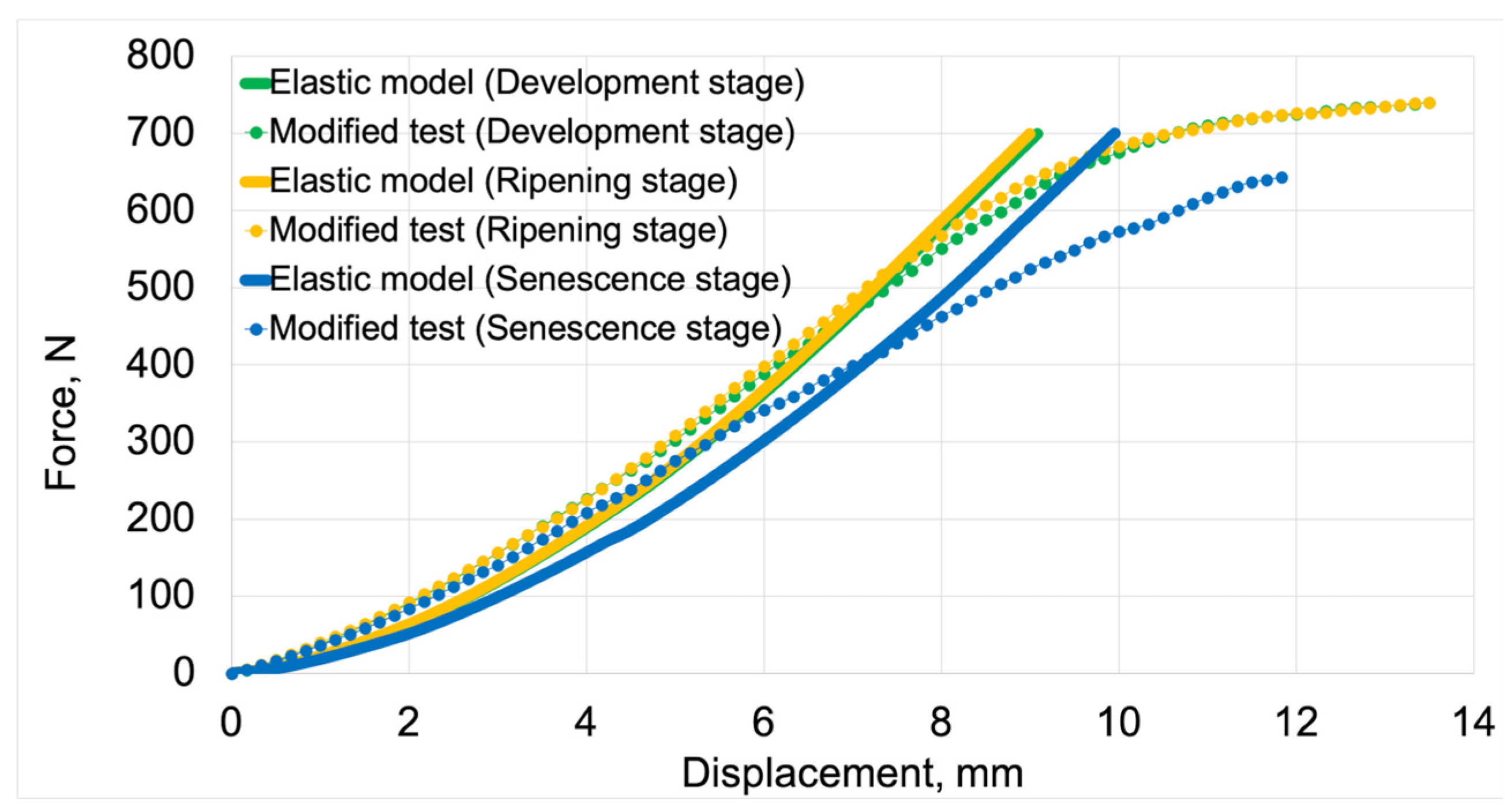
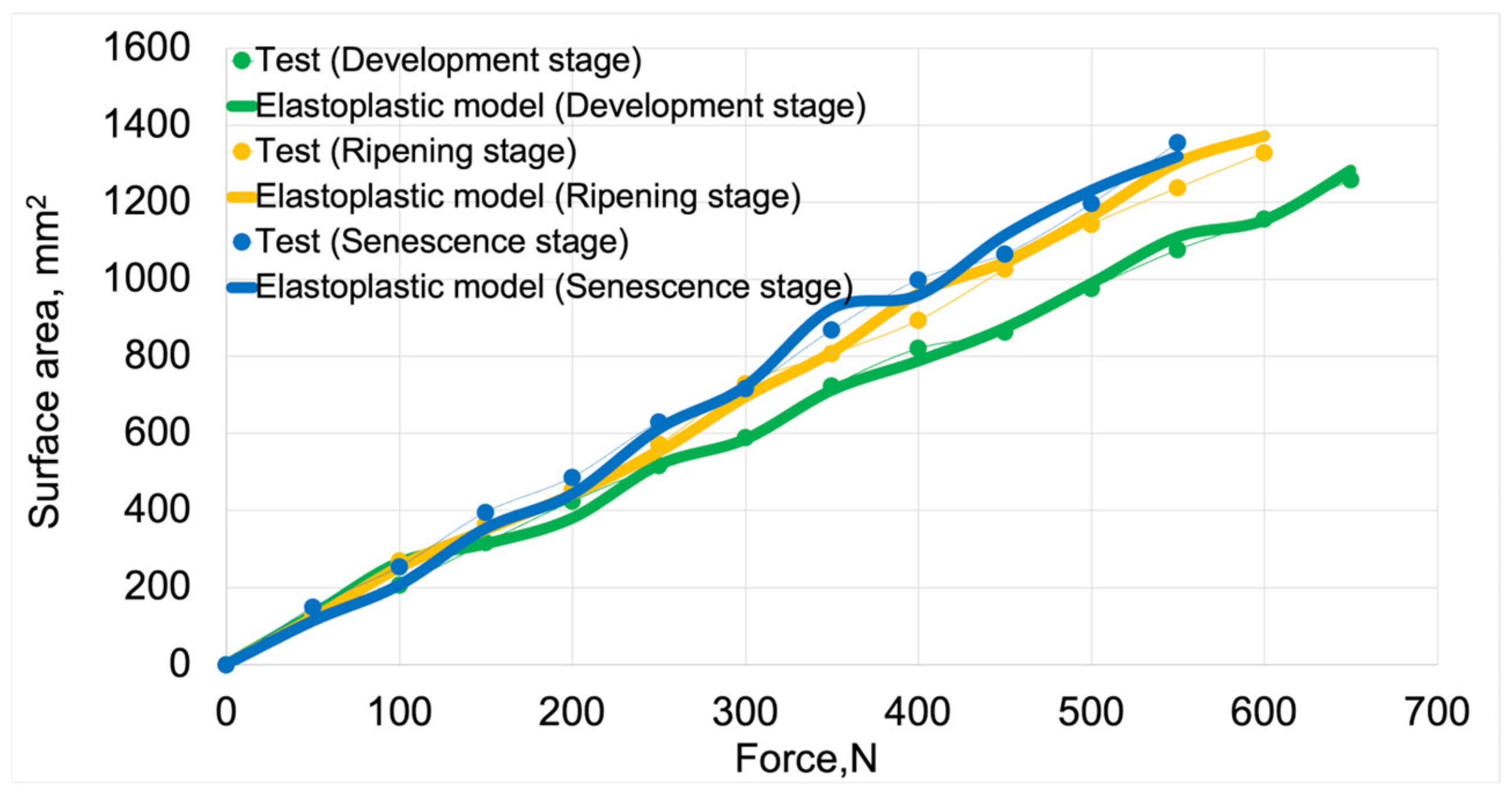
Figure 5 presents the force vs. displacement curves for elastic and elastoplastic models at all stages of fruit maturity. These curves were used for validating the discrete models.

Elastic models were compared with both test data and modified data (generated according to the methodology described in previous article [24]). Elastoplastic models were validated solely based on unprocessed test data.

2.3.2. Validation Based on the Change of Contact Area as a Function of Load

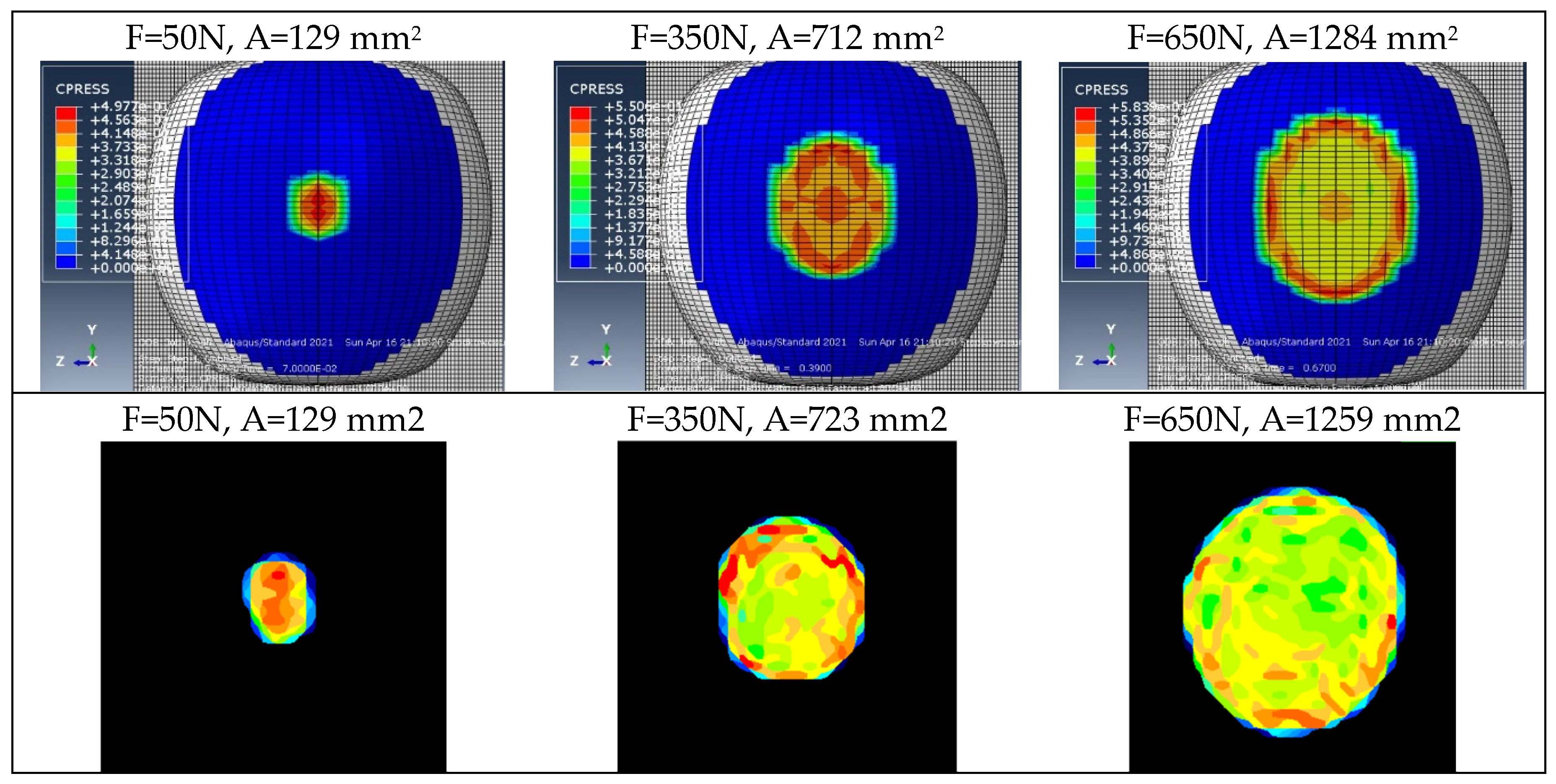
Pressure contours were determined at intervals of 50 N (± 2.5 N). This process required prior verification of the frame number assigned to a specific force. Due to the elliptical shape of the contours, pressure radii were measured along the Y and Z axes. The area was calculated using the formula for the area of an ellipse.

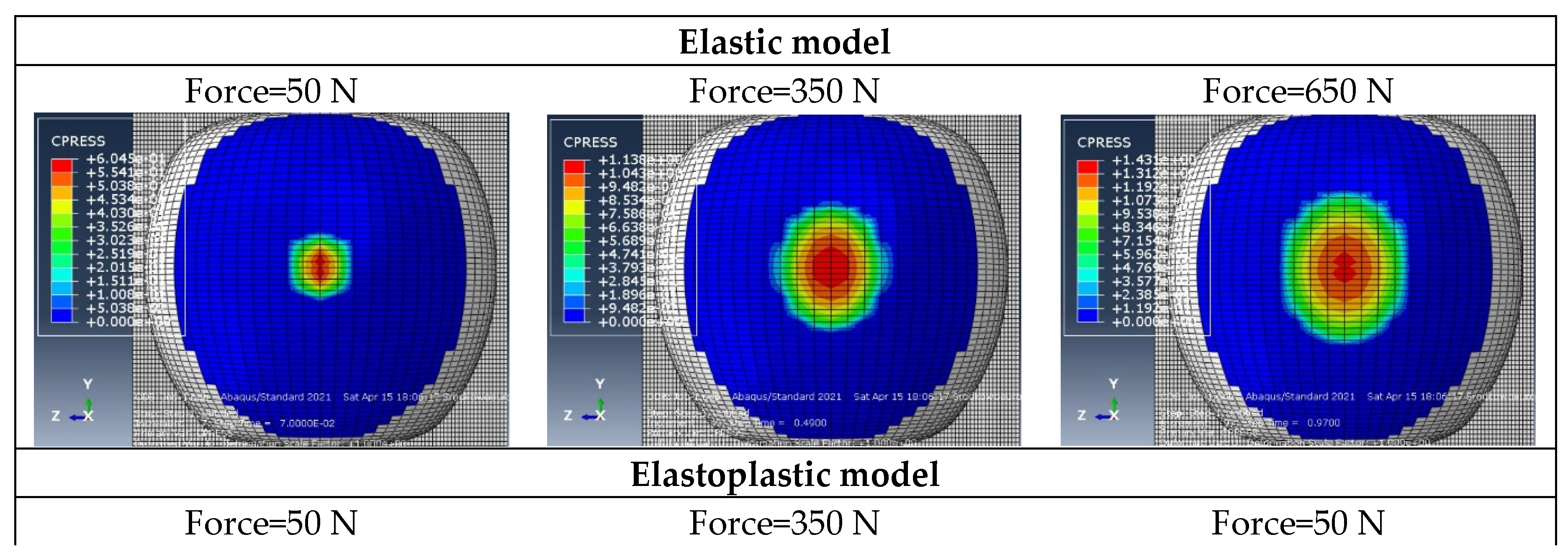
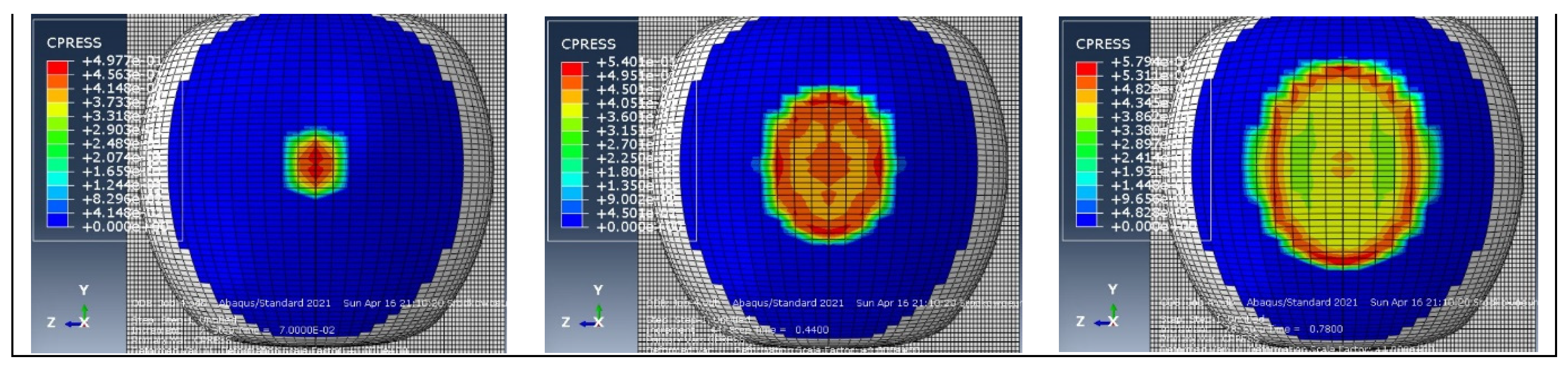
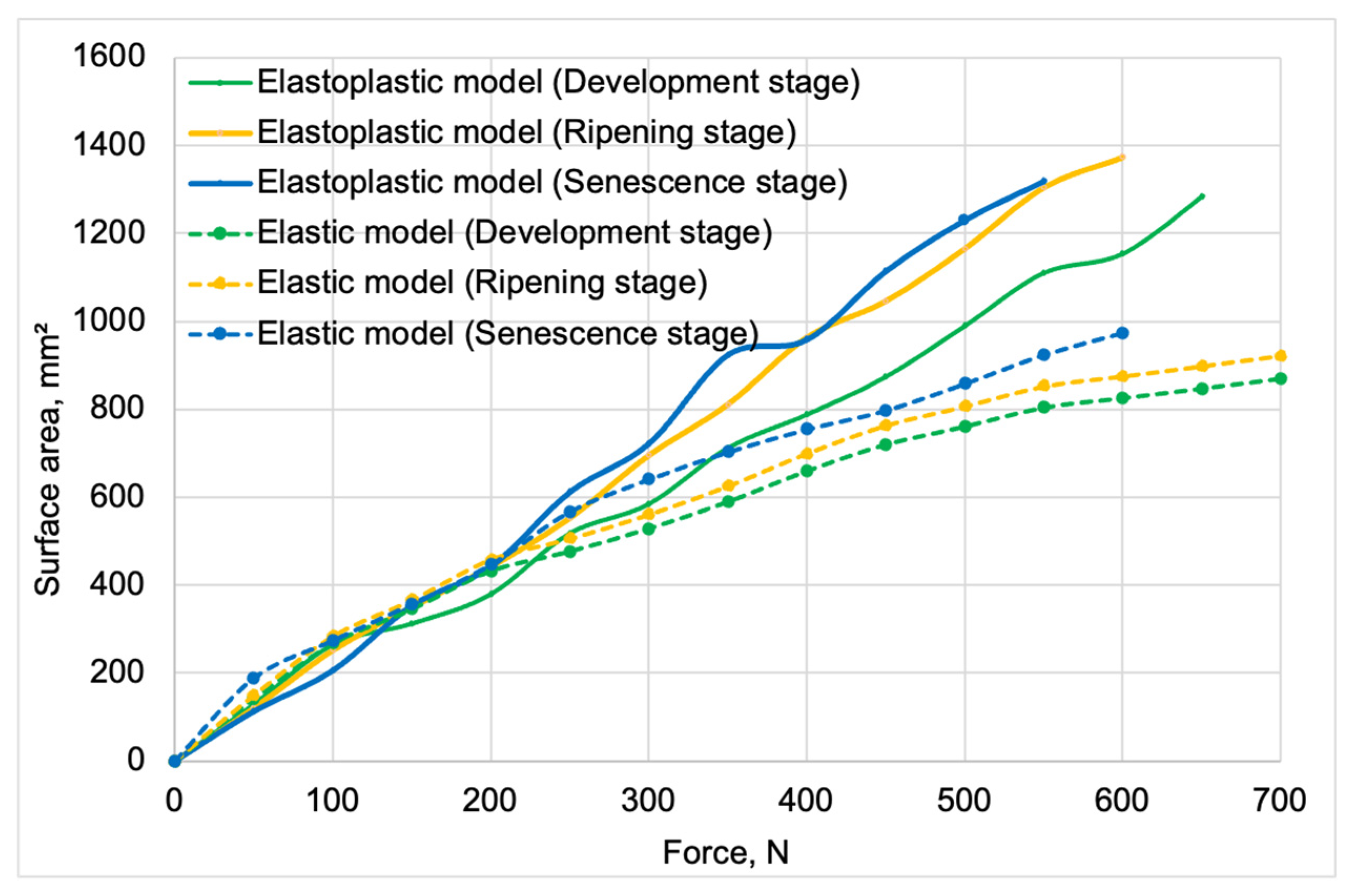
Figure 6 presents example pressure contours for elastic and elastoplastic models used to determine the contact areas of the models during loading. Figure 7 shows the measurement results of contours obtained for all variants of discrete models, which were used for their validation.

3. Results

3.1. Validation Based on Force vs. Displacement Graphs

As a result of the static analysis, data was obtained that allowed for the generation of displacement and force graphs as a function of time (for individual frames representing analysis increments) at the specified nodes of the model. Next, the graphs were combined by eliminating the X variable (time) and replacing it with displacement, while force was assigned to the Y axis. The data from the resulting graphs was copied into Excel sheets to compare it with test data.

3.1.1. Elastic Models

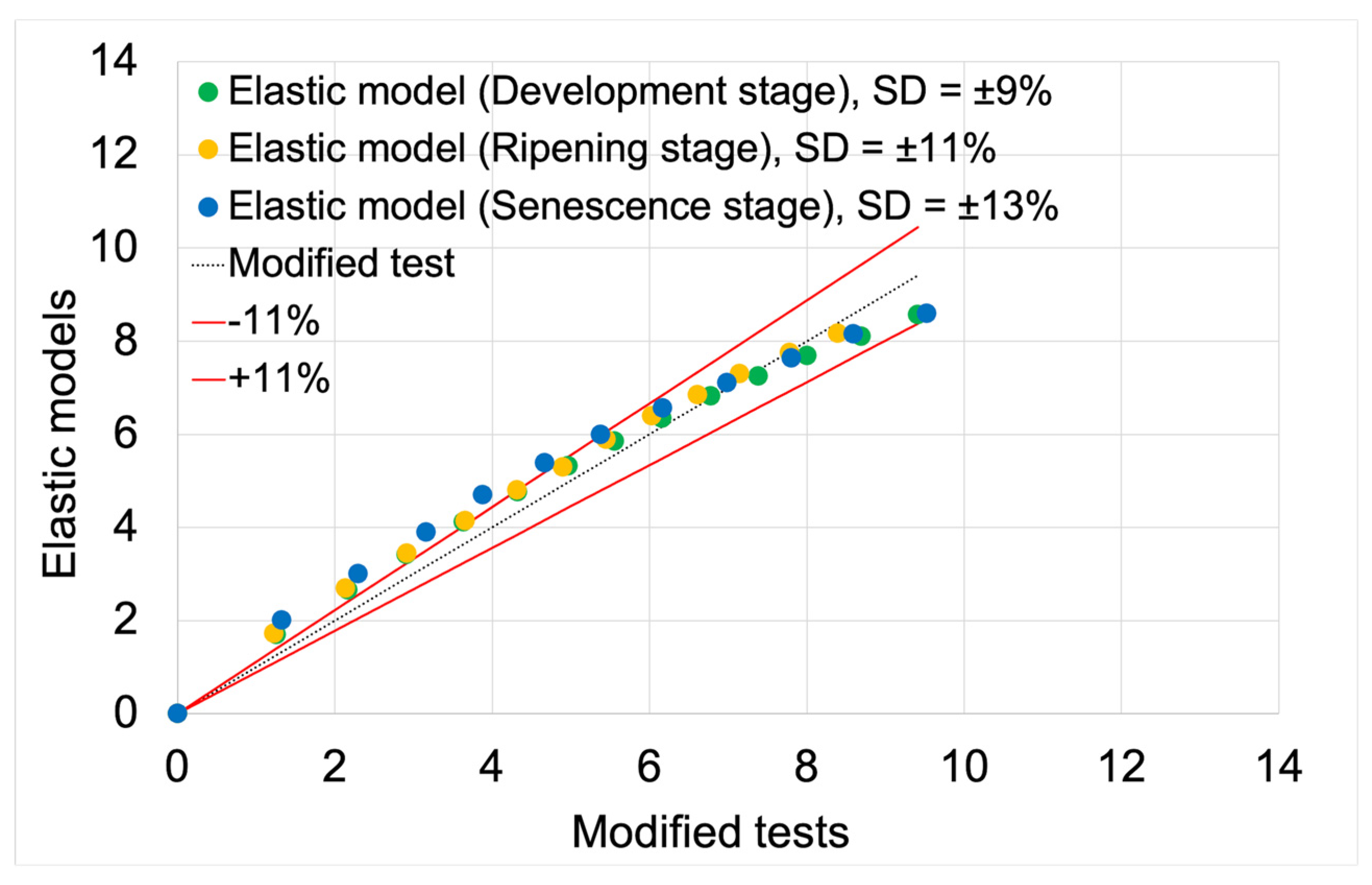
Figure 8 presents force-displacement graphs used in the initial validation process of elastic models. Solid lines represent the graphs obtained from model tests, while the dotted line represents the modified load-displacement graphs. The numerical calculation results for the elastic models were compared with the elastic properties of the material derived from the modified graphs. For both model data and processed test results, the development maturity stage is marked in green, the ripening maturity stage in orange, and the senescence maturity stage in blue. The processed graphs are labeled as “Modified test”.

The correlation analysis between the processed test data and the model results obtained for elastic models was conducted based on a scatter plot for displacement as a function of force (Figure 9). Force was the independent variable, while displacement was the dependent variable. The grouping variable was the individual stages of fruit maturity. The fit analysis of the models was based on the average deviation ranges of the model data from the test data, calculated in Excel. The averages of the deviations for all maturity stages were plotted on the scatter plots, while the average deviation values and model fit values for each maturity stage are presented in Table 4.

The average fit of the elastic models to the modified test results was 89%. The elastic model for the development maturity stage achieved the highest fit value (91%). The model for the senescence maturity stage achieved the lowest value (87%). The model for the ripening maturity stage achieved a fit value of 89%.

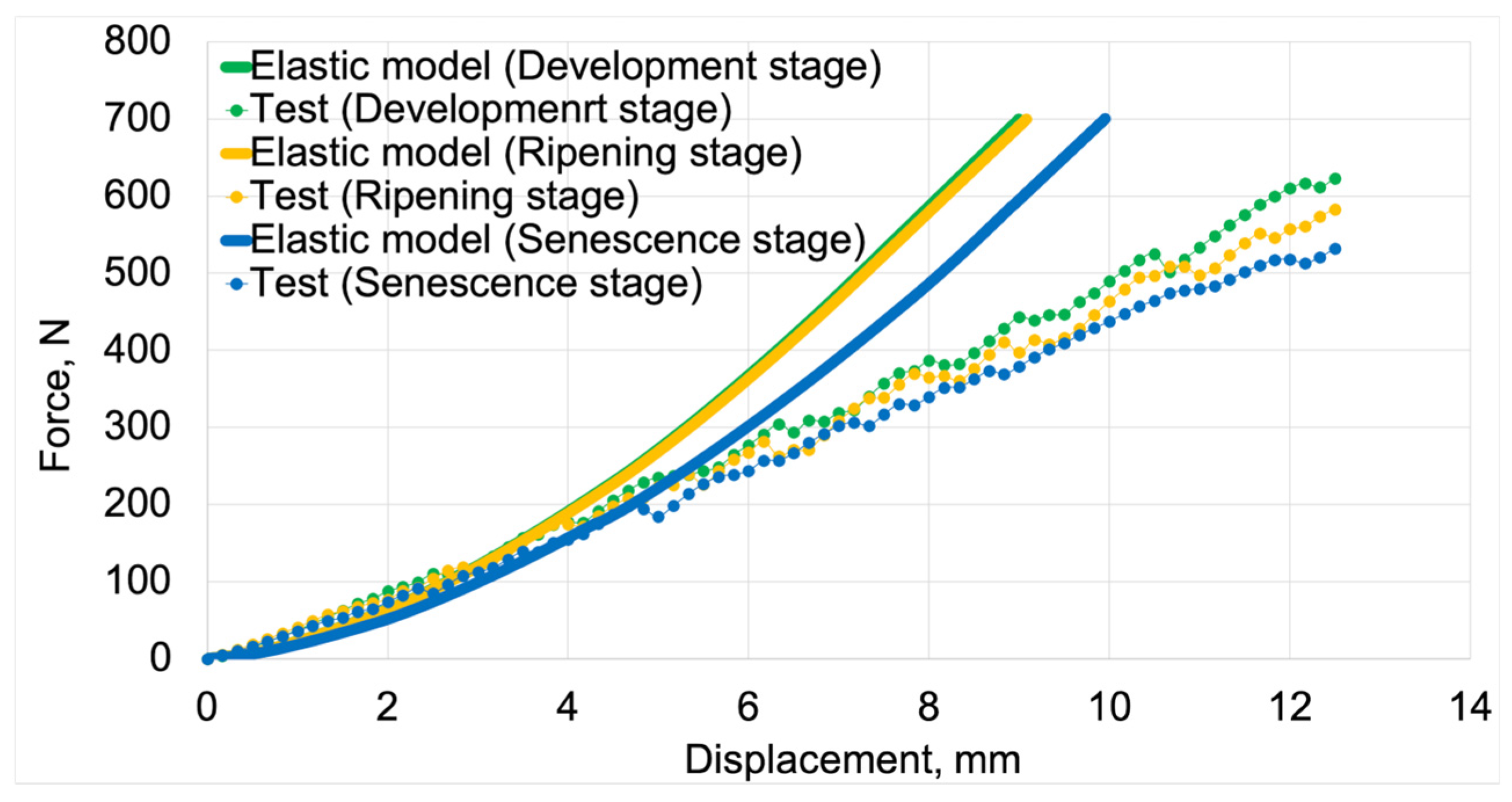
Figure 10 presents the force vs. displacement curves used for the second validation process of elastic models. Solid lines represent curves obtained from model studies, while markers indicate actual data from tests. For both model data and empirical results, green denotes the development maturity stage, orange represents the consumptive maturity stage, and blue denotes the physiological maturity stage.

Figure 11 shows the validation of elastic models based on empirical data, with the validation results summarized in Table 5.

The average fit of the elastic models to the actual test results was 80%. The highest fit value (81%) was achieved by the elastic model for the senescence maturity stage. The lowest fit value (79%) was achieved by the model for the ripening maturity stage. The model for the development maturity stage achieved a fit value of 80%.

3.1.2. Elastoplastic Models

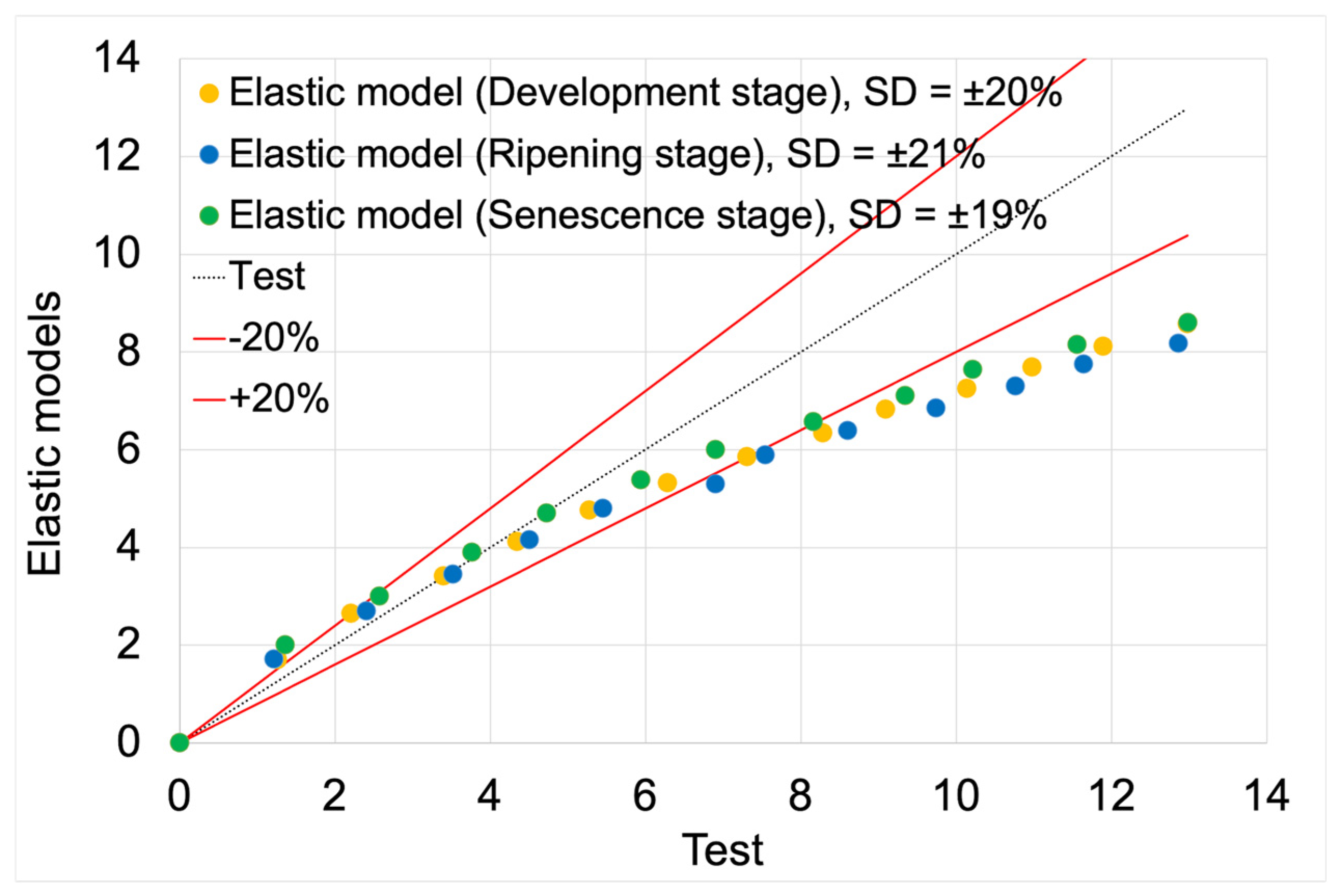
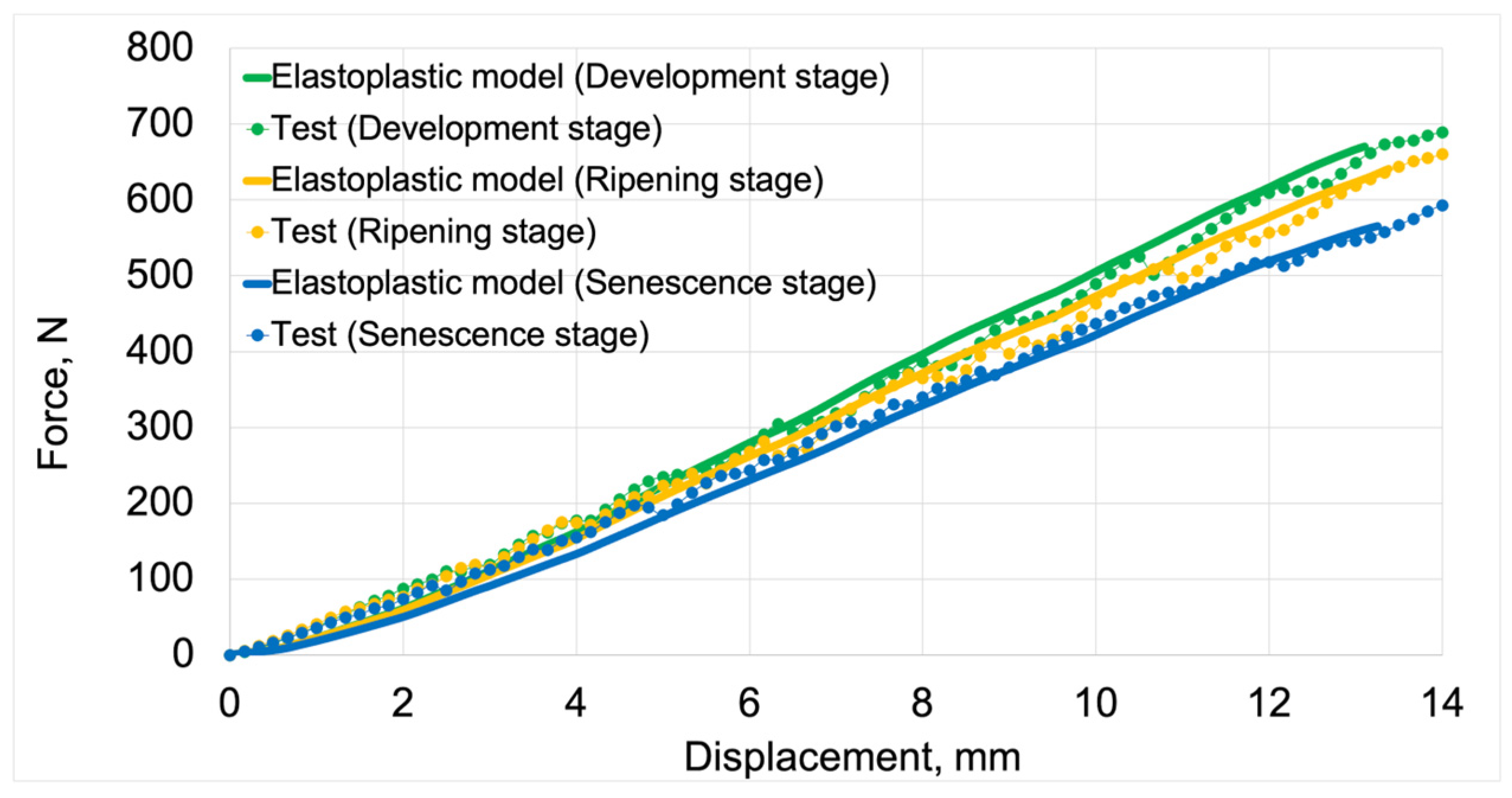
Figure 12 presents force vs. displacement curves used in the validation process of elastoplastic models. Solid lines represent the curves obtained from model studies, while markers denote data from tests. For both model data and empirical results, the green color indicates the stage of development maturity, orange represents the stage of ripening maturity, and blue denotes the stage of senescence maturity.

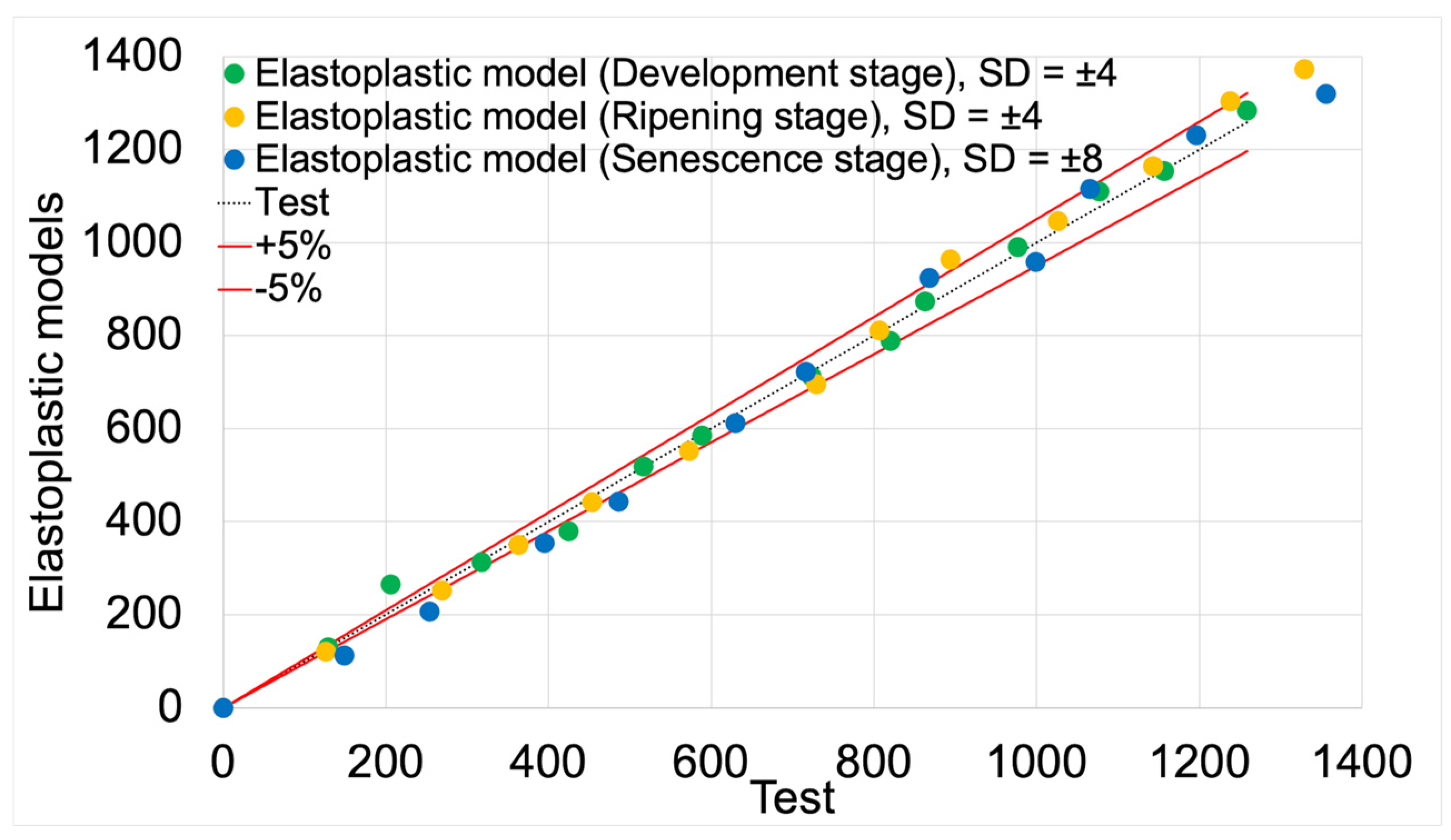
Figure 13 presents the validation of elastoplastic models based on test data. The validation results, including average deviation values and model fit values, are summarized in Table 6.

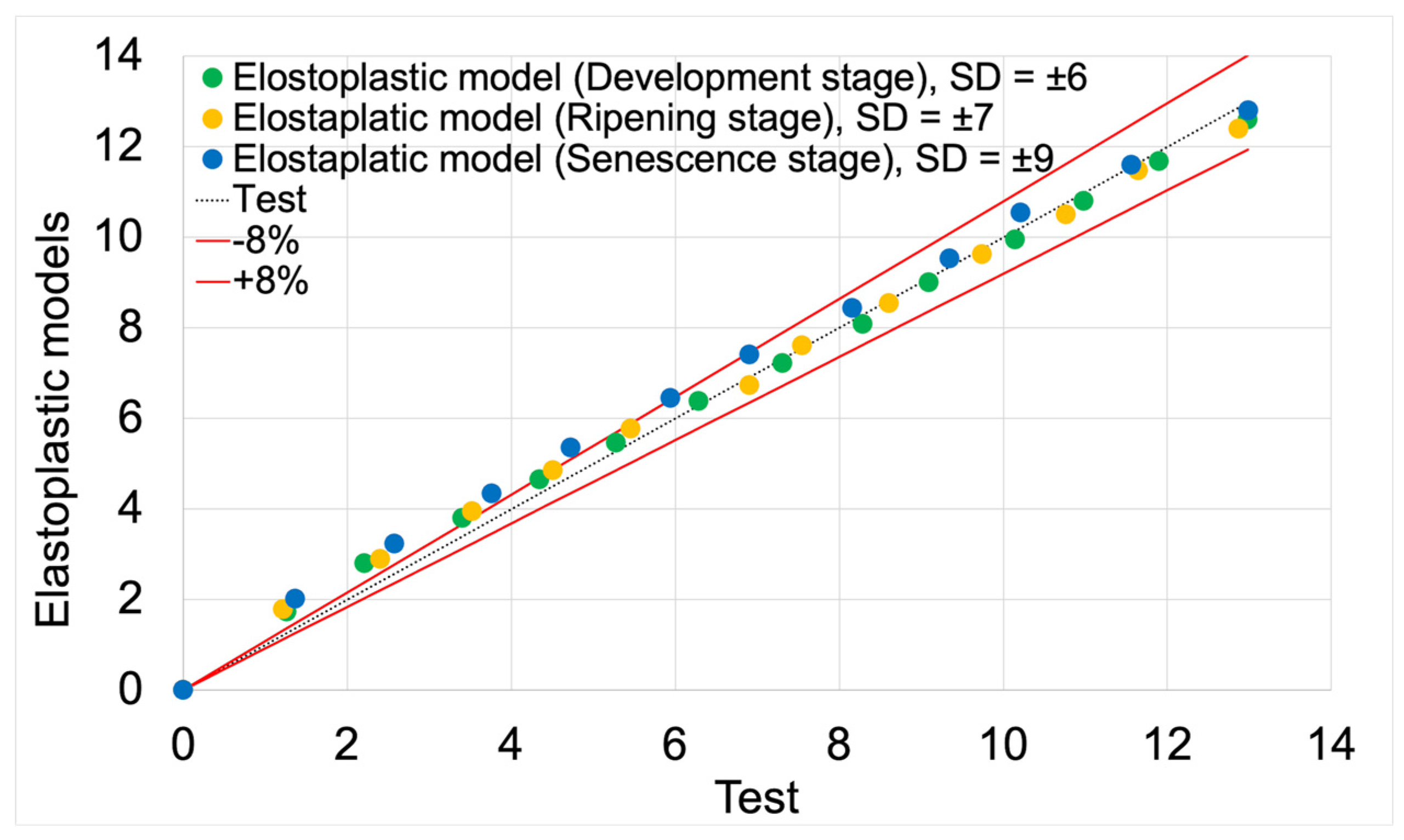
The average fit of the elastoplastic models to the test results was 92%. The highest fit value (94%) was achieved by the elastoplastic model for the development maturity stage. The lowest value (91%) was achieved by the model for the senescence maturity stage. The model for the ripening maturity stage achieved a fit value of 93%.

3.2. Validation Based on the Change of Contact Area as a Function of Load

3.2.1. Elastic Models

Figure 14 shows example contour plots of pressures for both model results and empirical data.

Based on Figure 14, it can be concluded that the pressure distribution for elastic models does not match the test results. In empirical studies, at the initial stage of compression, the highest stress values were observed in the center of the contact area. In the subsequent stage (which followed the first local decrease in force, indicating the first permanent damage to the material), the highest stress values were observed at the edges of the contact area. This trend continued until the end of the test and was observed for all stages of fruit maturity. Figure 15 shows the contact area vs. force curves used in the validation process of elastic models. Solid lines represent curves obtained from model studies, while markers indicate empirical test results. For both model data and empirical results, green denotes the development maturity stage, orange represents the ripening maturity stage, and blue denotes the senescence maturity stage. Figure 16 presents the validation of elastic models based on test data. The validation results, including average deviation values and model fit values, are summarized in Table 7.

In Figure 15, it can be observed that the contact area results for models corresponding to development and ripening maturity stages were similar.

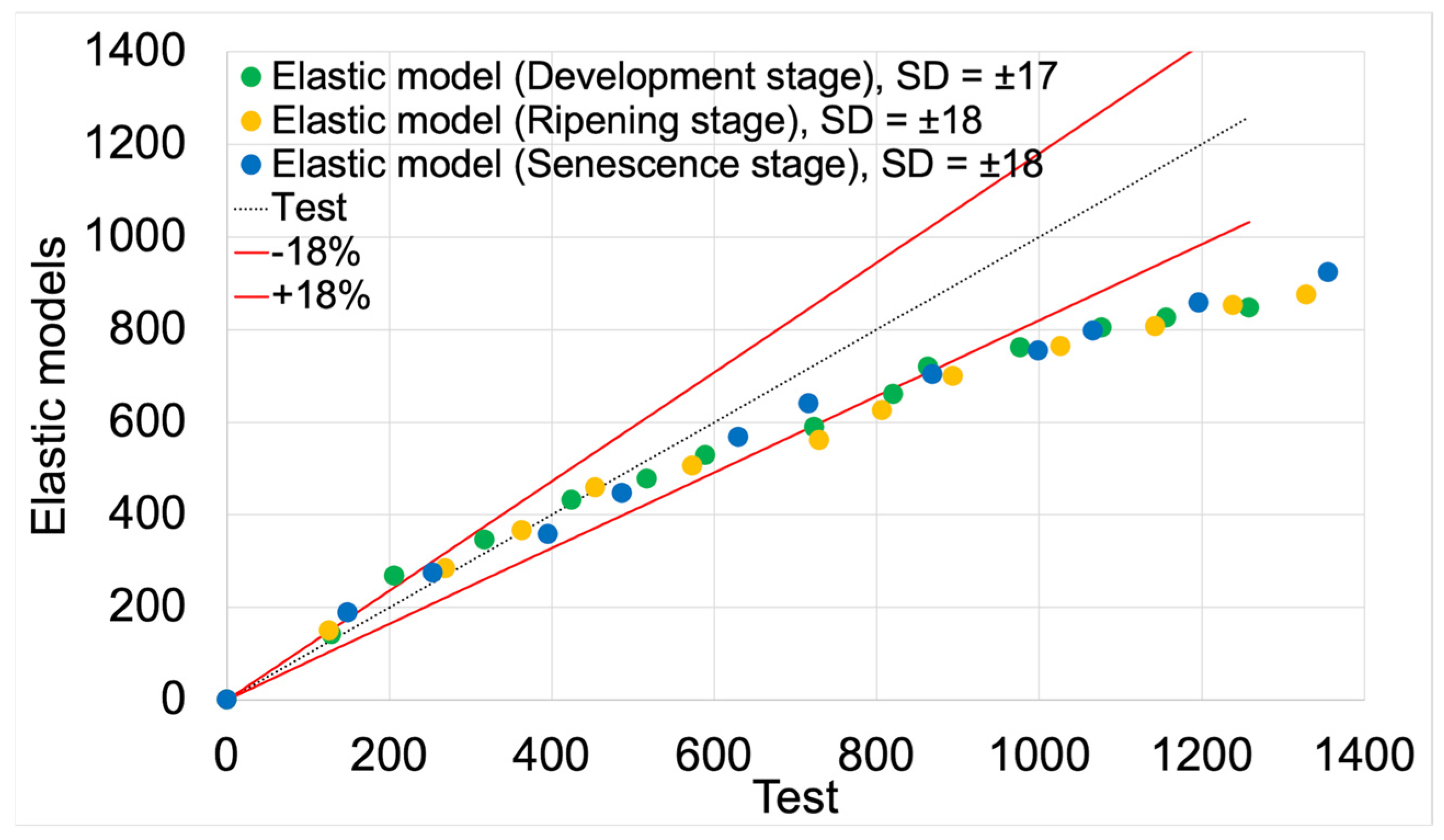
The average fit of the elastic models to the test results was 82%. The highest fit value (83%) was achieved by the elastic model for the development maturity stage. The models for the ripening and senescence maturity stages achieved a fit value of 82% (Figure 16 and Table 7).

3.2.2. Elastoplastic Models

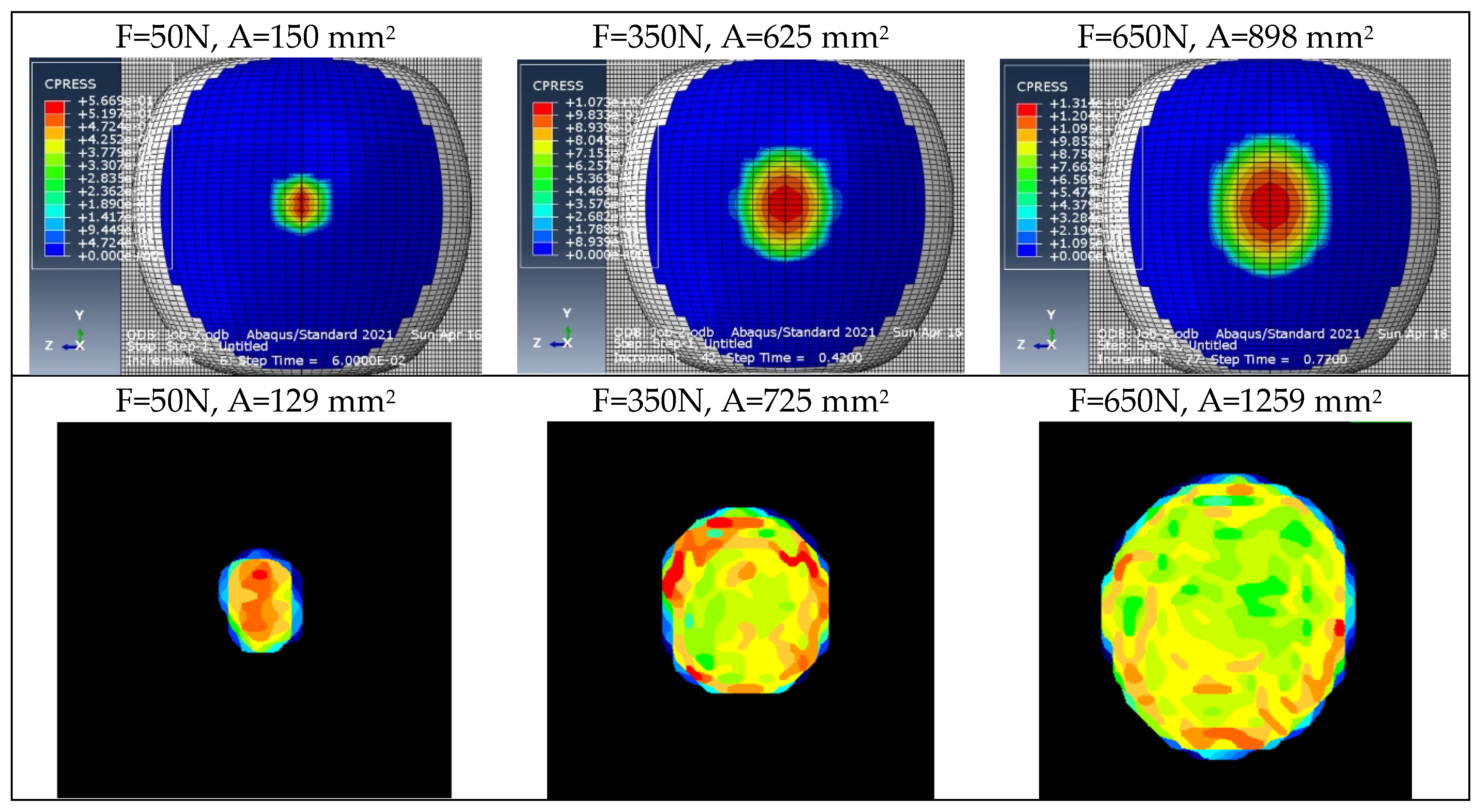
Figure 17 presents example contour plots of pressures for both model and empirical results.

Based on Figure 17, it can be concluded that the contour plots of pressures for elastoplastic models align much better with the test results. Similar to the empirical studies, at the initial stage of compression, the highest stress values are observed in the center of the contact area, while in the subsequent stage, the highest stress values are observed at the edges of the contact area. This trend continued until the end of the test and was observed for all stages of fruit maturity.

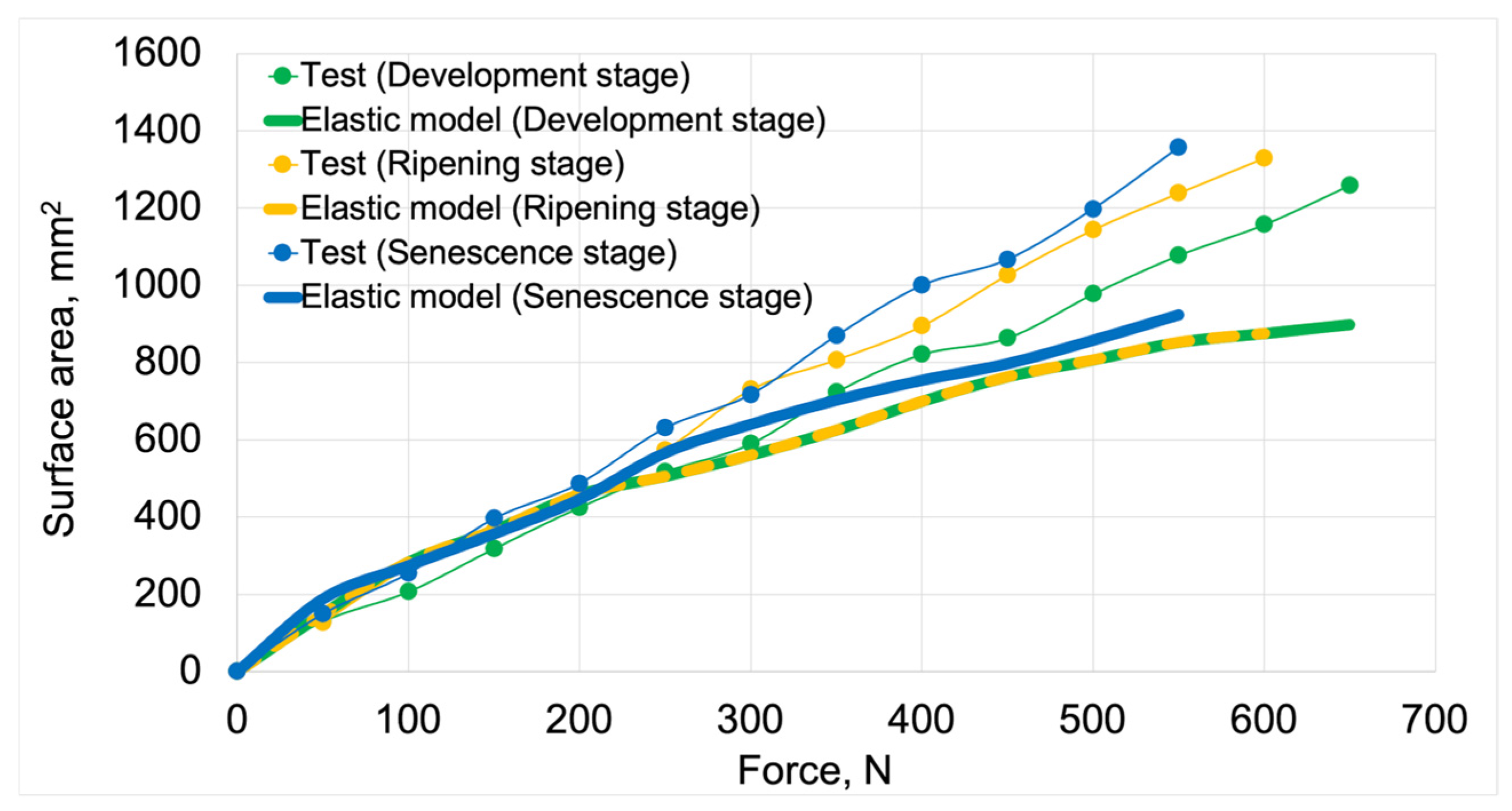
Figure 18 shows the contact area vs. force curves used for the validation process of elastoplastic models. Solid lines represent curves obtained from model studies, while markers indicate empirical test results. Figure 19 presents the validation of elastoplastic models based on test data. The validation results, including average deviation values and model fit values, are summarized in Table 8.

The average fit of the elastoplastic models to the test results was 95%. The highest fit value (96%) was achieved by the elastoplastic models for the development and ripening maturity stages. The lowest fit value (82%) was achieved by the model for the senescence maturity stage.

4. Conclusions

• Elastoplastic models reflect empirical studies much better. The fit of the elastic models, based on force vs. displacement curves, ranged from 79% to 83%, while the fit of the elastoplastic models to empirical data ranged from 91% to 96%.
• Elastic models, on the other hand, are well-suited to the modified force vs. displacement values, which reflect the elastic behavior of apples during compression. The fit values for these models, based on force vs. displacement curves, ranged from 87% to 91%.
• Contour plots of pressures for elastoplastic models align much better with the test results than those for elastic models.
• Similarly, in the case of contact area values, the elastoplastic models outperformed the elastic models, achieving a fit between 92% and 96%, while the elastic models reached only 82% to 83% compliance.