Prerpints.org logo
Preprint
Article

Environmental Impact Minimization Model for Storage Yard of In-Situ Produced PC Components: Comparison of Dung Beetle Algorithm and Improved Dung Beetle Algorithm

Altmetrics

Downloads

47

Views

20

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

11 September 2024

Posted:

14 September 2024

You are already at the latest version

Alerts
Abstract
In-situ production of PC components is the same process as in a factory, with the order of installing processed rebar, pouring concrete, curing, and storage. In-situ production not only reduces environmental impact by more than 14.58% compared to factory production, but also reduces costs by up to 39.4% compared to factory production when increasing the number of in-situ produced PC components. The stock yard area is more than 5 times larger than the production area, which accounts for a significantly higher proportion. Research on in-situ production of PC components is mainly focused on the production area. PC component yard layout planning for in-situ production can effectively reduce carbon dioxide emissions and improve construction efficiency. Therefore, the purpose of this study is to develop an environmental impact minimization model for in-situ production of PC components. As a result of applying the developed model, the improved dung beetle optimization algorithm optimization improved the adjacent correlation by 22.79% and reduced carbon dioxide emissions by 18.33% compared to the dung beetle optimization algorithm, which verifies its efficiency. The proposed environmental impact minimization model can support the construction, reconstruction, and functional upgrade of logistics centers, contributing to low carbon dioxide in the logistics industry.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

The in-situ production of PC components is the same process as that of a factory, in which the processed rebar is installed, concrete is poured, cured, and stacked. In-situ production can reduce environmental impact by more than 14.58% compared to factory production [1,2,3,4], and cost savings of up to 39.4% compared to factory production can be achieved by increasing the number of in-situ produced PC components [5,6,7]. Under the same conditions, in-situ production of PC components can achieve the same or better quality than factory production [8,9,10,11,12]. Therefore, studies have been conducted on the in-situ production of PC components that are competitive in terms of convenience, quality, cost, and time [13,14,15,16].
The stock yard area is more than five times larger than the production area, which is a significant proportion [17,18]. at the research on in-situ production of PC components, the main focus is on the production area [19,20,21], and there are no studies on the risk management of stock yard. In the construction storage yard studies, there is no study on the stock yard of PC component in-situ production, as it is mainly focused on the production area [22,23,24,25,26], and there is no study on storage yard management.
PC component yard layout planning for in-situ production can effectively reduce carbon dioxide emissions and improve construction efficiency. In the context of improving the logistics service system and the “double carbon” goal, how to adjust the layout planning of logistics centers is crucial to achieve the green development of the logistics industry [27]. However, most existing research focuses on optimizing the layout of logistics centers, and relatively little attention has been paid to PC member yard layout for in-situ production.
Meta-heuristic optimization algorithms are being applied to more nonlinear, large-scale, high-dimensional, and complex constrained problems [27,28]. Meta-heuristic optimization algorithms are effective for complex problems because they are based on simple principles and better avoid local optima [29,30]. Meta-heuristic optimization algorithms do not require a derivation of the optimization problem and are only interested in the input and output data. This process is considered a black box, which allows meta-heuristic optimization algorithms to be used for optimization in a wide variety of fields [31]. Meta-heuristic optimization algorithms perform an iterative “trial and error” procedure, which means that the meta-heuristic algorithm can update a new solution at each iteration to find the optimal value. Furthermore, the new solution is compared to the optimal solution obtained so far [32].
Various models have been established in the research area of distribution center layout planning. Jiang et al. [33] designed a multi-objective simulated annealing algorithm to address the dual objectives of material handling cost and transportation facility cost, and validated the proposed method in experimental cases of different scales. Geng et al. [34] proposed a logistics park layout optimization method incorporating an extended environmental impact model, and validated it with a case study to obtain satisfactory results. Hu et al. [35] constructed a nonlinear programming model and solved it using a genetic algorithm to minimize the overall processing cost and maximize the comprehensive relationship to reduce the processing cost of the enterprise.
Optimization algorithms have attracted considerable attention in the scientific community to solve data clustering problems. These methods are considered more efficient than existing techniques and provide more compelling solutions to data clustering tasks [36]. Meta-heuristic algorithms consist of a unique mechanism that explores both global and local search spaces to improve promising solutions. These algorithms are self-sustaining, distributed, and exhibit habitual behavior, which gives them greater potential to solve a variety of problems compared to existing algorithms. The basic principles of meta-heuristics are based on exploitation and exploration. Exploitation involves discovering candidate solutions that are close to the current solution, while exploration involves searching for new candidate solutions that are farther away from the current solution location. High-quality solutions to optimization problems require a balanced interaction between the exploitation and exploration processes.
When dealing with the optimization of layout models using meta-heuristics, it has been proven that layout optimization is non-deterministic polynomial-time hard [37] and traditional optimization algorithms are insufficient to solve this problem. Therefore, recently, scholars often use intelligent optimization algorithms such as Genetic Algorithm (GA) [38], Particle Swarm Optimization (PSO) [39], and Hybrid algorithms [40] to solve these problems. However, as model complexity increases and the search space expands in layout problems, these algorithms tend to get stuck in local optima, converge slowly, and face exponentially increasing difficulty in finding solutions. The DBO algorithm proposed by Xue et al. [41] has strong optimization capabilities compared to other algorithms and is widely applied across different domains. For example, Zhu et al. [42] introduced an improved DBO algorithm that integrates quantum computing and multiple strategies and applies them to solve several real-world engineering problems.
Li et al. [43] used an improved DBO algorithm to optimize the parameters of a bidirectional long- and short-term memory network model to improve the accuracy and stability of a wind speed prediction model. Li et al. [43] used the improved DBO algorithm to solve a nonlinear optimization problem with multiple constraints in the manufacturing industry and demonstrated the robustness of the improved algorithm. Overall, intelligent optimization algorithms can effectively solve layout optimization problems. However, as models become increasingly complex, algorithmic improvements tailored to the specific problem at hand are essential for optimal solutions. Based on this, this study develops a layout optimization model for in-situ production of PC components that aims to maximize adjacent correlation, and minimize carbon dioxide emissions. In other words, the purpose of this study is to develop an environmental impact minimization model for in-situ production of PC components.
The sequence of this study is as follows.
1) To review the appropriateness of the methodology of this study, the meta-heuristic algorithm is reviewed and categorized.
2) After analyzing the storage layout process of in-situ produced PC component, the stock yard problems are identified.
3) The objective function and constraints of stock yard are presented to build an optimization model.
4) Based on the standard DBO algorithm, a multi-objective optimization model for carbon dioxide emission minimization is built.
5) To improve the algorithm, it is proposed the IDBO algorithm by introducing Chebyshev chaos mapping and adaptive Gaussian Cauchy mixed mutation perturbation strategy.
6) The results of this study are verified by comparing the optimized layouts obtained by applying the DBO and IDBO algorithms to a real logistics center site.

2. Literature review

2.1 Classification of Meta-heuristic Algorithms

Meta-heuristic algorithms are divided into four classes: evolutionary algorithms (EA), physics-based algorithms (PhA), human-based algorithms (HBA), and swarm intelligence (SI) algorithms [44,45]. Genetic algorithm (GA), a representative EA, was proposed by Holland, inspired by Darwin's evolution [46]. GAs mainly perform crossover and mutation strategies to obtain better solutions to replace worse ones. Other well-known EAs such as differential evolution (DE) [47], evolutionary programming (EP) [48], genetic programming (GP) [49], and evolutionary strategies (ES) [50] all involve mutation, crossover, and recombination. Biogeography-based optimization (BBO) algorithms focus primarily on migration and information exchange [51].
PhA was proposed inspired by the natural laws of physics, and Simulated Annealing (SA) is one of the classical representatives of PhA [52]. Inspired by the physical concept of annealing, the performance of SA is affected by temperature. The probability that the optimal solution obtained so far is replaced by a bad solution is reduced by gradually decreasing the temperature until the SA converges to or approaches the optimal solution. Other examples of PhAs include Atom Search Optimization (ASO) [53], based on basic molecular dynamics; Charged System Search (CSS) [54], based on Coulomb's law and the laws of Newtonian mechanics; Flow Direction Algorithm (FDA) [55], inspired by the direction of flow towards the outlet of a drainage basin; and Fick's Law Algorithm (FLA) [56], inspired by Fick's first diffusion rule, Gravitational Search Algorithm (GSA) [57], inspired by the law of the interaction of gravity and mass; Lichtenberg Algorithm (LA) [58], inspired by the Lichtenberg geometry pattern; Light Spectrum Optimizer (LSO) [59], inspired by the dispersion of light through raindrops; Multi-Verse Optimizer (MVO) [60], based on black holes, white holes, and wormholes in the universe; and Nuclear Reaction Optimization (NRO) [61], inspired by the nuclear reaction process. The Kepler Optimization Algorithm (KOA) [62], inspired by Kepler's laws of planetary motion, and the Snow Ablation Optimizer (SAO) [63], inspired by the sublimation and recording of snow.
Human-based algorithms are proposed inspired by human production and life behaviors. One of the most well-known algorithms is Teaching-Learning-Based Optimization (TLBO), which uses two phases, a “teacher phase” and a “learner phase,” to search for optimal solutions [64,65,66]. Other examples include Collision Body Optimization (CBO) [67], inspired by collisions between bodies; Chef-Based Optimization Algorithm (CBOA) [68], inspired by the process of learning to cook; Collective Decision Optimization (CSO) [69], based on the five decision-making characteristics of humans; Equilibrium Optimizer (EO) [70], based on controlled volume mass balance; Knowledge Sharing Gain (GSK)-based algorithms [71], inspired by knowledge acquisition and sharing behavior; and Human Happiness Algorithm (HFA) [70], League Championship Algorithm (LCA) [72], based on competition between sports teams in sports leagues; Mountain Climbing Team-Based Optimization (MTBO) [73], inspired by human cooperative behavior to reach the top of a mountain; Poor and Rich Optimization (PRO) [74], based on the efforts of poor and rich people to achieve a better life; and Past Present Future (PPF) [75], inspired by what successful people learn to improve their lives. The collective intelligence of humans is used to obtain the appropriateness of hyper-parameterization [76].
Currently, many SI algorithms have also been proposed. Aquila Optimizer (AO) is a novel SI algorithm inspired by the hunting behavior of Aquila, which uses four different hunting methods [77]. Artificial Rabbits Optimization (ARO) is inspired by survival methods that use detouring and random hiding for exploration and exploitation, and exploit energy conservation to switch between exploration and exploitation [78]. The Nutcracker Optimization Algorithm (NOA) was proposed based on the two behaviors of Clark's nutcracker: storing seeds in summer and fall and searching for previously stored seeds in winter and spring [79]. The Shrimp and Goby Association (SGA) search algorithm, inspired by the cooperation between shrimp and goby, was proposed and applied to damage identification of the Canton Tower in Guangzhou, China [80]. Snake Optimizer (SO) simulates the mating behavior of snakes, whose exploration and utilization depends on food and environmental temperature [81].
Meta-heuristic optimization algorithms have been effectively applied to complex layout optimization problems. Due to their simple principles and great flexibility, these algorithms are suitable for solving a variety of high-dimensional and nonlinear optimization problems. In particular, the DBO, one of the SI algorithms, is a meta-heuristic algorithm with powerful optimization capabilities and has been used effectively in various domains. While the DBO performs well in terms of exploration and convergence speed, it can fall into local optima in problems with complex constraints. To solve this, the IDBO is designed to enhance the global exploration capability by introducing chaos mapping and adaptive mutation strategies, and to derive more stable optimal solutions. Therefore, in this study, the DBO and IDBO are applied to develop a yard layout environmental impact minimization model for in-situ production of PC components.

2.2 Analyzing the Process of Stock Yard Layout PC Components Produced on Site

When PC components are actually constructed in the field, they are produced in the order of in-situ production, stock yard, and erection, and the process is as shown in Figure 1 [82,83]. As shown in Figure 1(a), the in-situ production of PC components is carried out in the order of installing processed rebar, pouring concrete, and curing. As the production, stock yard, and erection quantities are the same, it is necessary to check PC components to be erected.
As shown in Figure 1(b), the number of stock yard components and stock yard area based on one storage yard are calculated for yard layout, and the required yard area is calculated as the product of the number of yard components. By calculating the available area for production and storage yard by process, it should simulate the yarding and production layout plan by month, week, day, etc. according to the reviewed area. If the stock yard and production are not satisfied, the batch simulation is completed through repeated modification (feedback routine). For yard simulation, the crane movement is analyzed and the possibility of utilizing the yard space is reviewed. The stock yard space is determined by dividing it into before and during PC member erection. it is necessary to determine the order of utilization of the stock yard and arrange the storage yard by reviewing the possibility of utilizing the yard space according to the in-situ production schedule.
Then, as shown in Figure 1(c), PC components are erected. For this, the number of cranes is determined according to the in-situ production time for the erection of PC components, and the crane specifications are determined by considering the crane working radius and working capacity [84]. A zoning plan is established according to the number of cranes. Through the analysis of design drawings, the location of columns, beams, and slab components by zone is analyzed, and the erection volume of each member is calculated. After that, the erection order of PC components is determined in consideration of the crane movement by zone, and the erection time for each member such as columns, beams, and slabs is calculated. The erection process is simulated according to the erection process plan on the basis of month, week and day according to the construction plan. In other words, the in-situ produced PC components are placed at the stock yard and installed in the order of erection.
The storage yard layout for in-situ produced PC components is a hybrid layout problem that requires consideration of both the layout of the stock yard and the routing of transportation lines, which is the same as the layout of a general logistics facility. The layout of a logistics center can be simplified by how to arrange the positional relationships between each functional area in the plane to achieve the set goals and ensure the connectivity and efficiency of operational processes. According to the assumptions, a schematic diagram of the center plane coordinates is shown in Figure 2. In Figure 2, the x-axis and y-axis represent the length and width directions of the large logistics center, respectively, and the safety distance from the stock yard to the boundary of the logistics center is represented by the x-axis and y-axis, respectively. In addition, the assumptions for this are as shown in Table 1.
where, L: total length of the logistics center, W: total width of the logistics center, li: length of production area i, wi: he width of production area i, lj: length of stock yard j, wj: width of stock yard j, hij: distance to be maintained between production zone i and stock yard j along the X-axis, vij: distance to be maintained between production zone i and stock yard j along the Y-axis, vjk: distance to be maintained between stock yard j and erection zone k along the Y-axis, ai: Safety clearance along the X-axis from zone i to the boundary of the distribution center, bi: Safety clearance along the Y-axis from zone i to the boundary of the distribution center, i: i-th production zone (1, … , n), j: j-th stock yard zone (1, … , m), k: k-th erection zone (1, … , n)
Hence, the in-situ production and erection of PC components are affected by each other. The problems can be categorized as follows: 1) Space constraints, 2) Increased environmental impact: Space constraints are the limited PC member stock yard space, which makes stock yard inefficient. When space is insufficient, it becomes difficult to properly arrange the components, which can result in reduced moving distance and time, and reduced work efficiency. In addition, misplacement can result in the need for additional component yardage or component movement, which can negatively impact the entire production process. Environmental impact is caused by the increased travel distance of PC components, and inefficient stock yard increases the travel distance between components. This can lead to increased energy consumption and carbon dioxide emissions. In particular, if the components are moved repeatedly, the environmental impact increases significantly. Therefore, it is important to reduce the energy consumption of the equipment and vehicles used in the transportation process and to reduce this environmental impact through efficient layout. Therefore, in this study, it is developed an environmental impact minimization model for the stock yard layout of in-situ produced PC components shown in Figure 1(b).

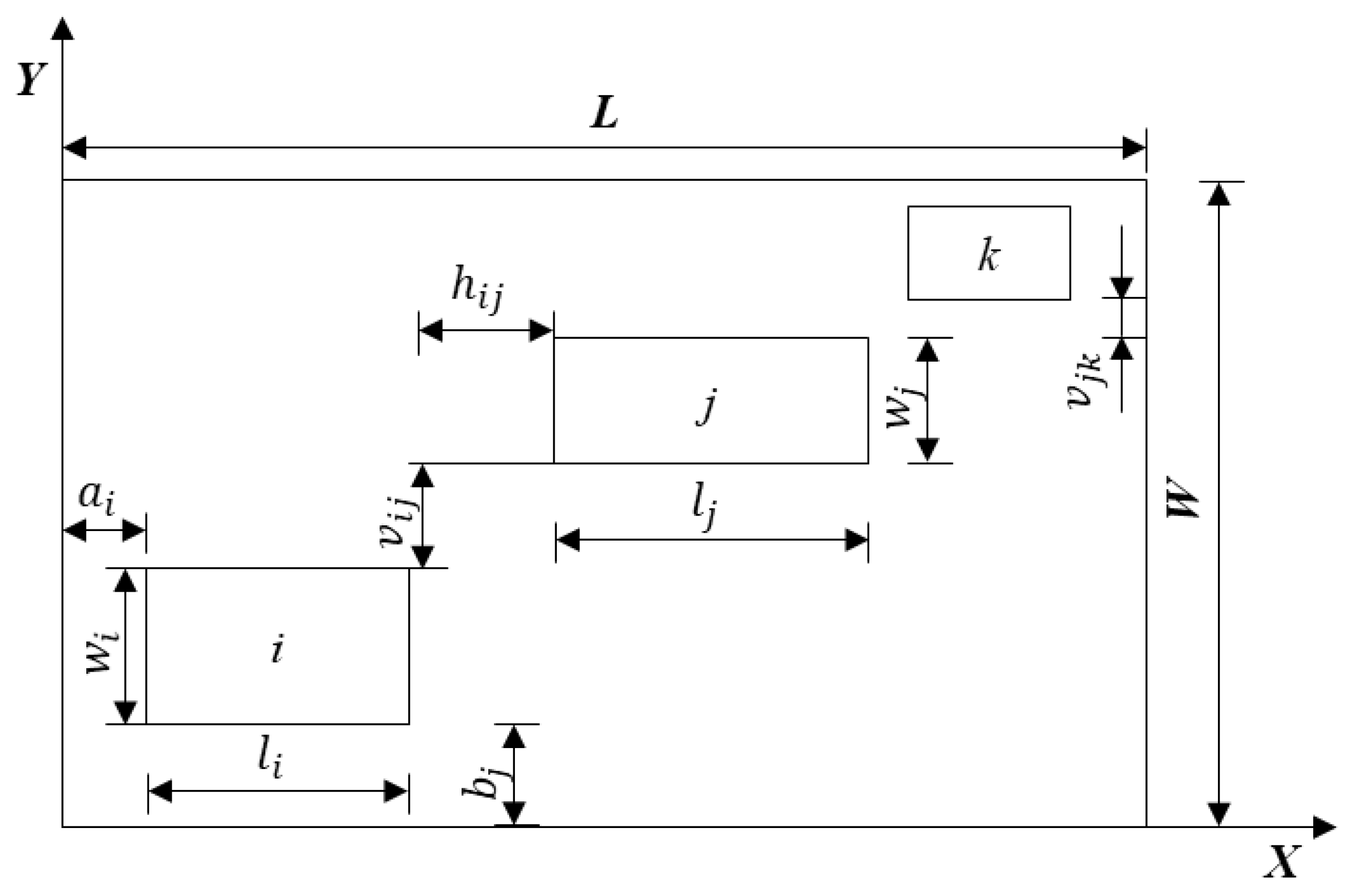
3. Modeling Layout Optimization

3.1 Objective Function

The Paris Agreement, the centerpiece of international action on climate change, was adopted in 2015 [85]. The Paris Agreement includes Article 6, which is the rule underlying the formation of an international carbon market. Article 6 sets out market and non-market approaches for Parties to voluntarily collaborate in implementing their nationally determined contributions (NDCs), making mitigation and adaptation efforts more flexible and cost-effective. Article 6 of the Paris Agreement includes two principles: environmental integrity and the promotion of sustainable development (PA 2015, Article 6.1). In particular, Parties engaging in cooperative approaches under Article 6.2 of the Paris Agreement can use internationally transferred mitigation outcomes to achieve the mitigation targets in their NDCs, provided that they promote sustainable development and ensure environmental integrity and transparency in the process. This study focuses on the concept of “environmental soundness” as a guiding principle for a collaborative approach.
Environmental soundness has two major meanings. One is that in international greenhouse gas emission reduction projects, the produced reduction results are not over-credited. In other words, the carbon dioxide emission reduction results must clearly reflect the reduction efforts equivalent to the actual carbon dioxide emissions. The other means that international greenhouse gas emissions do not increase due to the international transfer process through the use of carbon market mechanisms. Minimizing carbon dioxide emissions during construction site operation is essential to achieving high efficiency and low carbon goals [86]. The arrangement of PC components in the storage yard should be designed to minimize energy usage, carbon dioxide emissions, and resource consumption. The problem of arranging in-situ produced PC components can be modeled that minimizes environmental impact. For this, this study defines objective functions and constraints through mathematical modeling and applies an algorithm to solve them. In this section, it is defined objective functions, constraints, and key variables and parameters for constructing a mathematical model of the arranging problem. Carbon emission calculation is mainly divided into two categories: fixed source carbon dioxide emissions and mobile source carbon dioxide emissions, and the objective function is as in equation (1).
M i n i m i z e   C = C F + C M  
where, C: carbon dioxide emissions of in-situ produced PC components, CF: fixed source carbon dioxide emissions, CM: mobile source carbon dioxide emissions
① Fixed source carbon dioxide emissions refer to the carbon dioxide emissions generated by the storage yard in the logistics center and increase as the stock yard period increases. Therefore, the calculation of fixed source carbon dioxide emissions can be related to the number of PCs as well as the space occupied by the stock yard. However, in this study, it is assumed that the fixed source carbon dioxide emissions are calculated by the number of stock yards, which means that the fixed source carbon dioxide emissions can be smaller than the value calculated by the number of PC components due to economies of scale. The fixed source carbon dioxide emissions are calculated by summing the fixed source carbon dioxide emissions of labor, electricity, lighting, and heating use. Then, the carbon dioxide emissions of labor, electricity, lighting, and heating use are calculated by multiplying the space occupied by storage yard j (m3), the consumption per m3 of space, and the unit fixed source carbon dioxide emission factor. The equations (2)-(5) are as follows.
C F = C F L + C F E + C F L H
C F L = ∑ j = 1 m ( S j L F j N L F c )
C F E = ∑ j = 1 m S j E F j N E F c
C F L H = ∑ j = 1 n ( S j L H F j N L H F c )  
where, CF: fixed source carbon dioxide emissions, CFL: fixed source carbon dioxide emissions from labor, CFE: fixed source carbon dioxide emissions from electricity, CFLH: fixed source carbon dioxide emissions from lighting and heating use, Sj: space (man/m3) occupied by storage yard j in m3, L F j N : labor consumption of space (man/m3) when there are PC components N in storage yard j, LFC: fixed source carbon dioxide emission factor (kg/kWh) of labor, E F j N : Electricity consumption of space (kWh/m3) when the number of PC components in stock yard area j is N, EFC: fixed source carbon dioxide emission factor (kg-CO2/kWh) of electricity, L H F j N : lighting and heating usage (kWh/m3) of space when the number of PCs in storage yard j is N, LHFC: Fixed source carbon dioxide emission factor (kg-CO2/kWh) of lighting and heating, j: j-th stock yard zone (1, … , m), k: k-th erection zone (1, … , n)
② mobile source carbon dioxide emissions are caused by fuel or electricity consumption during transportation, loading and unloading activities between different storage yards. The energy consumption of these processes is affected by various factors such as the use of mobile cranes, changes in worker behavior, and environmental conditions. Therefore, this paper considers the impact of travel distance and crane load on energy consumption by considering actual operating conditions. Therefore, mobile source carbon dioxide emissions are calculated as the total travel distance of PC components from the storage yard to the erection area. The mobile source carbon dioxide emissions are calculated by summing the mobile source carbon dioxide emissions of labor, oil, electricity, lighting, and heating use. Then, the carbon dioxide emissions of labor, electricity, lighting, and heating use are calculated by multiplying the distance calculated using the Manhattan distance formula, a binary variable indicating whether the PC components are moved between the stock yard and the erection area, the consumption per PC components, and the mobile source carbon dioxide emission factor. The equations (6)-(13) are as follows.
C M = C M L + C M O + C M E + C M L H
C M L = ∑ j = 1 m ( M j k D j k L M j N L M c )
C M O = ∑ j = 1 m ( M j k D j k O M j N O M c )
C M E = ∑ j = 1 m ( M j k D j k E M j N E M c )  
C M L H = ∑ j = 1 m ( M j k D j k L H M j N L H M c )
M j k = 0 ,   t h e r e   i s   n o   f l o w   o f   g o o d s   b e t w e e n   j   a n d   k . 1 ,   o t h e r w i s e
D j k = x j + x k + y j + y k
O M j N = O l + O u
where, CM: mobile source carbon dioxide emissions, CML: mobile source carbon dioxide emissions of labor, CMO: mobile source carbon dioxide emissions of oil, CME: mobile source carbon dioxide emissions of electricity, CMLH: mobile source carbon dioxide emissions of lighting and heating use, Mjk: binary variable (0-1) indicating whether there is a movement of PC components between storage yard j and erection area k, Djk: distance between storage yard j and erection area k calculated using the Manhattan distance formula, L M j N : labor consumption (man/ea) when the number of PC components in storage yard j is N, LMC: mobile source carbon dioxide emission factor (kg/kWh) of labor, O M j N : oil consumption (l/ea) when there are N PCs in storage yard j, OMC: mobile source carbon dioxide emission factor (kg/l) of oil, E M j N : electricity consumption (kWh/ea) when there are N PC components in storage yard j, EMC: mobile source carbon dioxide emission factor (kg-CO2/kWh) of electricity, L H F j N : Light and heating usage (kWh/ea) when the number of PC components in storage yard j is N, LHMC: mobile source carbon dioxide emission factor (kg-CO2/kWh) of light and heating, x j : x-axis of storage yard j, x k : x-axis of erection zone k , y j : y-axis of storage yard j, y k : y-axis of erection area , Ol: Oil use (l/ea) for loading of mobile crane, Ou: Oil use (l/ea) for unloading of mobile crane, j: j-th stock yard zone (1, … , m), k: k-th erection zone (1, … , n)

3.2 Constraint

Layout planning mainly involves the following constraints.
① Boundary constraint
Each storage yard cannot exceed the boundary of the planning area and must maintain a specified safety distance from the boundary. In addition, PC components must be placed within the space of a given stock yard, and the coordinates of PC member placement must not exceed the allowed range within each zone. The equations (14)-(17) are as follows.
x i + a i + l i 2 ≤ L x i − a i − l i 2 ≥ 0
y i + b i + w i 2 ≤ W y i − b i − w i 2 ≥ 0
x i   ∈   [ x m i n ,   x m a x ]
y i   ∈   [ y m i n ,   y m a x ]
where, x i : x-axis of zone , y i : y- axis of zone i, ai: x-axis clearance from zone i to the logistics center boundary, bi: y-axis clearance from zone i to the logistics center boundary, li: length of zone i, wi: width of zone i, L: total length of the logistics center, W: total width of the logistics center, x m i n : x- axis of the minimum boundary of the zone , x m a x : x- axis of the maximum boundary of the zone , y m i n : y- axis of the minimum boundary of the zone , y m a x : y- axis of the maximum boundary of the zone
② Non-overlapping constraints
Each production area, stock yard area, and erection area of a PC components cannot overlap each other, and a minimum distance must be maintained between each area, i.e., enough distance must be maintained between each area to provide workspace for PC components quality inspection and verification, equipment and material movement, etc. The equations (18) are as follows. However, the completed erection area can partially overlap with the stock yard area.
l i + l j 2 + h i j ≤ x i − x j w i + w j 2 + v i j ≥ y i − y j   ,   ∀ i   ≠ j
where, li: length of zone i, wi: width of stock yard, hij: distance maintained between zones i and j along the x-axis, vij: distance maintained between zones i and j along the y-axis, x i : x- axis of zone , y i : y- axis of zone i
③ Work procedure constraints
PC components must be moved according to the order of work, and the order of placement of certain PC components can be fixed or restricted. This is a constraint to maintain a specific work flow, which is necessary to maximize work efficiency. The equation (19) for this is as follows.
i f   i   p r e c e d e s   j ,   x i < x i + 1   o r   y i < y i + 1
④ Stacking height constraints
The stacking height of PC components must not exceed the allowed height limit. This model provides the basic mathematical modeling for optimizing the stock yard arrangement of PC components. Based on this model, the DBO and IDBO can be applied to solve the optimization problem.
H i < H m a x
H i = W A W l × H P C j
where, H i :   stacking height of storage yard i, H m a x : maximum allowable height of PC member, W A : allowable weight per area, W l : weight of one layer, H P C j : height of PC member j

4. Solving Algorithms

3.1. Standard DBO Algorithm

Inspired by the activities of dung beetles, the DBO algorithm divides the population into four subpopulations based on the dung beetles' behaviors of rolling, dancing, reproducing, foraging, and stealing. It then executes various search methods and adopts a dynamic boundary search strategy to improve the efficiency of the algorithm's search.
(1) Rolling Behavior
Rolling behavior is divided into scenarios without obstacles and scenarios with obstacles. When there are no obstacles along the winding path, dung beetles use sunlight as a navigational aid. Therefore, the intensity of the light source affects the path of the dung beetles. In this case, the position update equations (22)-(23) for the rolling dung beetles is as follows.
X i n + 1 = X i n + α × b × X i n − 1 + B × ∆ x
∆ x = X i n − X W
where, X i n : location information of the i-th generation of dung beetles after the nth iteration, a: -1 or 1 to represent various effects of nature, b: a random number in [0, 0.2] to represent the defect factor, B: A constant taking values from [1, 0] (used to simulate the change in light intensity), X W : global worst location.
When there is no light in the environment or the road is rough, the direction of travel cannot be identified, and the dung beetles must dance and change direction to find a new path. To determine their next direction of travel, the dung beetles' position update equations (24)-(25) are.
X i n + 1 = X i n + t a n ⁡ β X i n − X i n − 1
0 ≤ β ≤ π
where, X i n : position information of the i-th generation of dung beetles after the n-th iteration, X i n − X i n − 1 : distance between the i-th generation and the (n-1)th iteration position at the n-th iteration position, β : Deflection angle belonging to [0,π] (position remains unchanged when 0, π 2 ).
(2) Reproduction Behavior
In nature, dung beetles reproduce by rolling dung balls to a safe place and hiding them. On the other hand, it is important for dung beetles to choose a suitable location in a pile of dung balls to lay eggs. Therefore, the formula for determining the spawning boundary is defined by the following equations (26)-(28).
L B 1 = m a x ⁡ X r × 1 − T , L B
U B 1 = m i n ⁡ X r × 1 + T , U B
T = 1 − n N m a x
where, X r : current local optimal position, L B 1 : lower bounds of the optimization issues, U B 1 : upper bounds of the optimization issues, N m a x : Maximum number of repetitions
When the boundaries of the dung beetles spawning area are determined, females lay eggs only in the area determined by the above formula, and only one egg is laid per generation. When the spawning area changes, female dung beetles can clearly sense the change in boundaries and dynamically adjust their spawning location. The formula for selecting a spawning site for dung beetles is given by the following equation (29). The boundary range of the spawning area changes dynamically, mainly depending on the R value. Therefore, the position of the generated balls is dynamic even during the iteration process for.
X i n + 1 = X r + B 1 × ( X i n − L B 1 ) + B 2 × ( X i n − U B 1 )
where, X i n : position of the i-th generation after the nth iteration, B 1 , B 2 : two random matrices of (1×Dim), L B 1 : lower bounds of the optimization issues, U B 1 : upper bounds of the optimization issues, Dim: dimensional size of the algorithm
(3) Foraging Behavior
After successful hatching, small dung beetles must forage independently, and the optimal foraging area is shown in equations (30)-(31).
L B 2 = m a x ⁡ X − × 1 − T , L B
U B 2 = m i n ⁡ X − × 1 + T , U B
where, L B 2 : lower boundaries of the dung beetle’s search area for food, U B 2 : upper boundaries of the dung beetle’s search area for food, X − : global optimal position, T: boundary selection strategy of dung beetles when laying eggs
X − denotes the best location globally, L B 2 and U B 2 denote the lower and upper bounds of the optimal foraging area, respectively, and the location update of the dung beetles is given by the following equation (32).
X i n + 1 = X i n + K 1 × ( X i n − L B 2 ) + K 2 × ( X i n − U B 2 )
where, X i n : position of the i-th generation of small dung beetles at the n-th iteration, K 1 : a number obeying gaussian distribution, K 2 : a set belonging to [0, 1].
(4) Theft Behavior
In a colony of dung beetles, there are thieves who steal dung balls from other dung beetles, called theft dung beetles. Theft dung beetles steal dung balls from other dung beetles. The equation (33) for updating the location of the thief dung beetles is.
X i n + 1 = X s + P × f × ( X i n − X r + X i n − X − )
where, X i n : the position of the i-th burglar at the n-th iteration, f: a stochastic set obeying a normal distribution with size (1 × Dim), P: a constant value
(5) DBO algorithm implementation steps
Preprints 117942 i001

3.2. IDBO Algorithm

In the standard DBO algorithm, the initial population is randomly generated, but this does not guarantee a high level of chaos. In later iterations, the dung beetles population tends to congregate near the currently obtained optimal location and extend the search, which easily leads to a local optimal solution. Therefore, improvements will be made to overcome this drawback.
(1) Chebyshev Chaos Initialization Population
In the early stages, the quality of the initial population has a significant impact on the convergence speed of the algorithm. Improving the quality of the initial population usually involves using chaotic mapping functions for initialization. Among these, Chebyshev Mapping stands out due to its good chaotic properties and promotes a more uniform distribution of the population within the search space. Agrawal et al. [20] tested and compared several common chaotic mapping functions and demonstrated the superiority of Chebyshev chaotic mapping over other mapping functions. In addition, Zhang et al. and Pan and Xu [87,88] applied Chebyshev Mapping to improve other intelligent optimization algorithms and obtained better results. Therefore, in this paper, it is utilized Chebyshev chaotic mapping to optimize the initial population of DBO algorithm, and the iteration process is as follows.
x n + 1 = c o s k × arccos ⁡ ( x n , x n ∈ − 1,1
k: order (value 4), x n : the position at the n-th iteration
(2) Adaptive Gaussian-Cauchy Hybrid Mutation Disturbance Strategy
Mutational perturbations are commonly applied to enhance the diversity of the population and encourage the algorithm to move away from local optima to better explore the solution space. In intelligent optimization algorithms, Gaussian mutation and Cauchy mutation are frequently used mutation operators, each of which has its own characteristics. Gaussian mutation exhibits good search ability within a small range [89] and provides a relatively controllable degree of mutation. In contrast, the Cauchy distribution produces larger mutations compared to the Gaussian distribution, resulting in overly decentralized search. This study adopts an adaptive Gaussian-Cauchy hybrid mutation perturbation strategy [90], which integrates the advantages of Cauchy mutation and Gaussian mutation to mutate the optimal individuals. The fitness values before and after perturbation are compared to select a better solution for the next iteration. The specific equations (35)-(37) are as follows. The coefficients of the mutation operators δ a and δ b are gradually adjusted in a one-dimensional linear fashion to ensure a smooth and balanced perturbation in each iteration. After many tests, a value of 1 was chosen for the parameter σ 에 to achieve better results in this study.
M b ( n ) = X b ( n ) × ( 1 + δ a × G a u s s ( σ ) + δ b × C a u c h y ( σ ) )
δ 1 = n T m a x
δ 2 = 1 − n T m a x
where, X b ( n ) : optimal position of individual X at n-th iteration, M b ( n ) : position of X b ( n ) perturbed by Gaussian-Cauchy hybrid mutation at n-th iteration, δ 1 , δ 2 : mutation operator coefficients, Gauss (σ) is Gaussian mutation operator, Cauchy(σ) is Cauchy mutation operator
After applying this strategy to change the solution, the fitness of the changed solution must be reevaluated against the current optimal solution. Therefore, a Griddy rule is introduced to determine whether the optimal solution should be updated.
X − = M b n , f M b n < f [ X − ( n ) ] X b n , f M b n ≥ f [ X − ( n ) ]
X − : global optimal position, M b ( n ) : position of X b ( n ) perturbed by Gaussian-Cauchy hybrid mutation at the n-th iteration
(3) IDBO algorithm implementation steps
Preprints 117942 i002

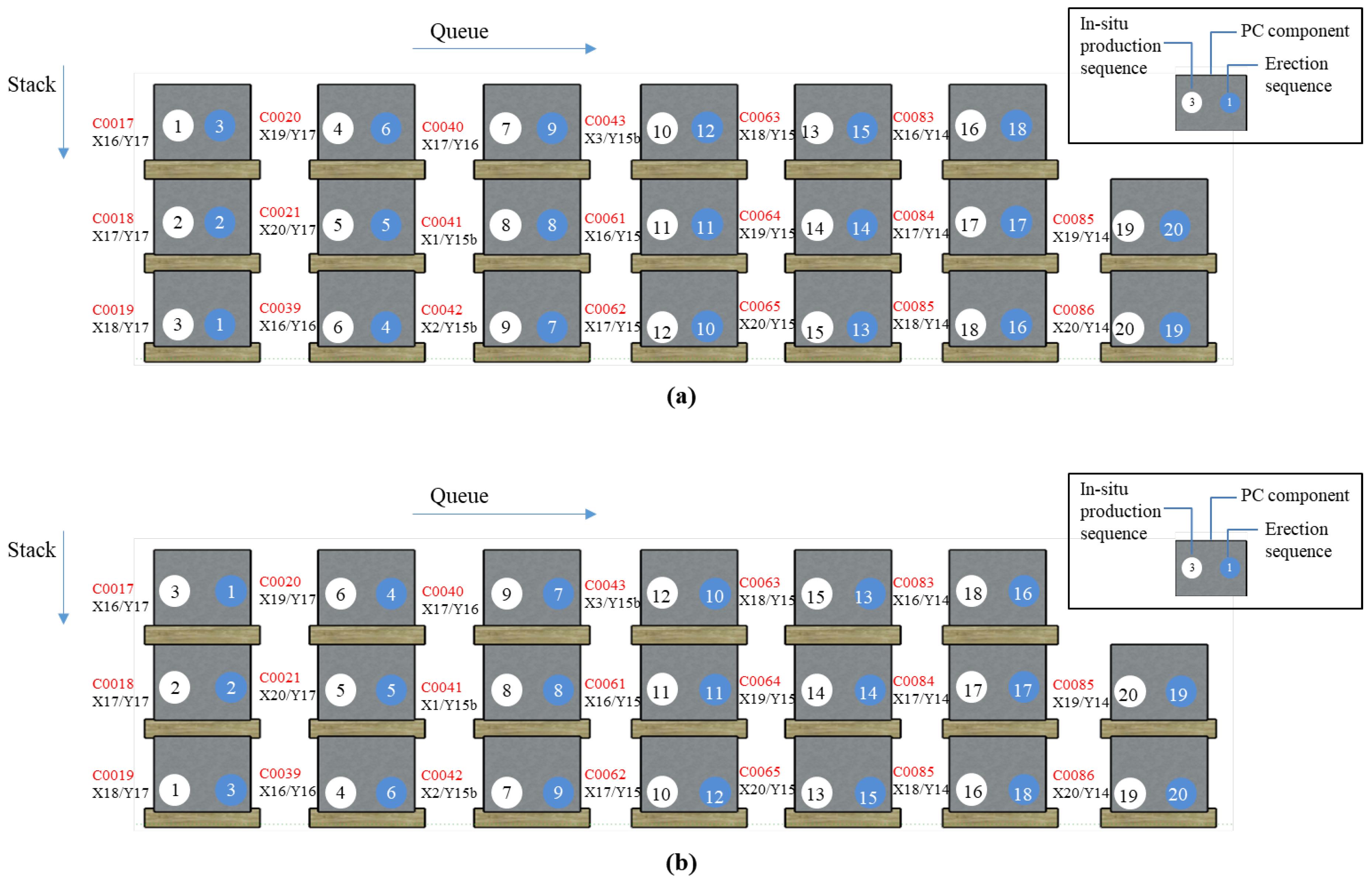
5. Case Project Application

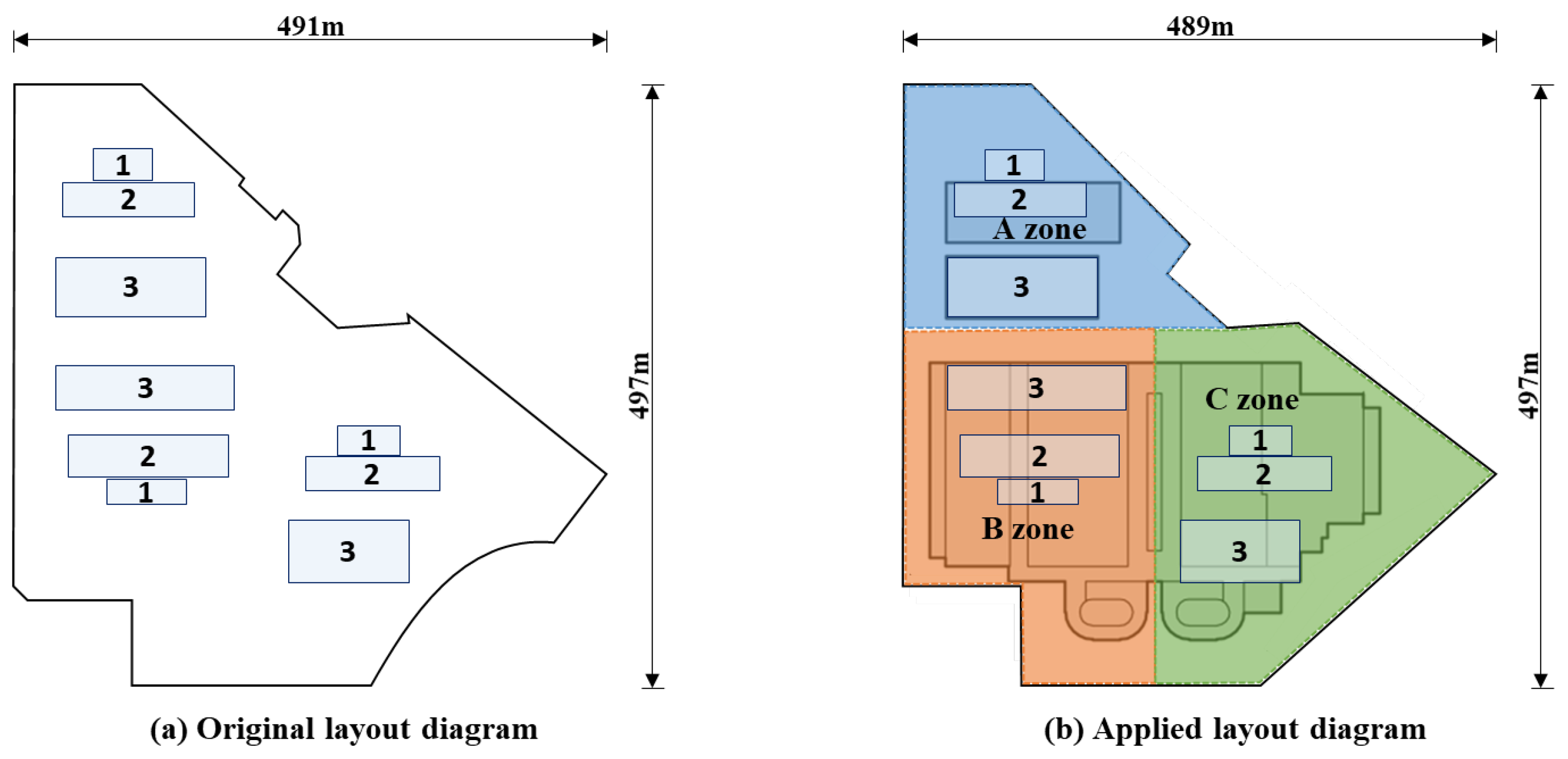
5.1. Case Overview

In order to derive the optimal stock yard layout for minimizing the environmental impact of in-situ production of PC components, a case site was selected and then components for in-situ production were selected. The outline of the case project, a large logistics center building, is shown in Table 2. The case project consists of a RC core, steel reinforced concrete structure of one building, mainly a PC structure with 5 floors above ground and 2 floors below ground (6 buildings). It should be noted that the case building has a floor height of 8.7-12.2 m and a heavy loaded building of 2.4 t/m2.
In this study, the case sites applied in this study are columns, girders, and slabs that are manufactured and constructed with PC. However, the components that can be in-situ produced are limited to columns and girders, which require less production area. In other words, columns and girders are long and thin, so the production space is narrow, but slabs require a large production and stock yard space, so it is difficult to produce on-site in a limited area. Therefore, this study calculates the quantity of columns and girders that are subject to optimal stock yard layout. The actual project layout is modified for the efficiency of the stock yard layout simulation, which is defined as the original layout and the applied layout as shown in Figure 3. Figure 3(a) 84,413m2, Figure 3(b) 84,140m2, and divided into A, B, and C zones according to the number of cranes used. According to the functional attributes, PC components can be divided into four zones: production zone (1), stock yard zone (2), erection zone (3), and other work zone (4), and the other work area is not separately indicated because it is an area to be calculated. In this case, the stock yard area is the total site area excluding production, erection, and other work zone (including free space for transportation, etc.). This can be expressed as equation (39).
A S i j = ∑ ∑ ( A T i j − A P i j − A E i j − A O i j )
where, A S i j : stock yard area of i-zone j-period, A T i j : total site area of i-zone j-period, A P i j : production area of i-zone j-period, A E i j : erection area of i-zone j-period, A O i j : other operations area of i-zone j-period, i: i-th zone (1, ... , n), j: j-th period (1, ... , m)

5.2. Optimization Result

It is necessary to calculate the movement distance of the crane used in the stacking stage of the in-situ production PC components and the erection stage of the stacked components. The crane movement distance can be calculated as the rotation distance. The rotation distance can be divided into the crane horizontal (Figure 4a) and vertical (Figure 4b) rotation distances, and is calculated by calculating each distance and then adding them up [91]. That is, the horizontal rotation of the crane means the movement from ⓐ to ⓑ in Figure 6a, and the vertical rotation means the movement from ⓑ to ⓒ in Figure 6b. The horizontal rotation angle of the boom is calculated as the relative coordinate value of the installation part with the crane position coordinate as the origin, as in Equation (40). The horizontal distance of the crane can be calculated as in Equation (41) using the distance from the crane to the trailer and the horizontal rotation angle of the boom. The boom head position must be defined to calculate the horizontal rotation distance. The vertical rotation angle of the boom is calculated using the boom length and the straight-line distance during vertical rotation, as in Equation (42). The vertical distance of the crane can be calculated using the boom length and the vertical rotation angle, as in Equation (43). Finally, the boom trajectory distance D t   is calculated as the sum of the horizontal rotation distance and the vertical rotation distance, as in Equation (44). The vertical rotation angle of the boom is calculated using Equations (40)-(44), and the vertical rotation distance of the crane is derived.
θ i = π − arctan ⁡ x i − 0 y i − 0
r ( θ i ) = l T × θ i
φ i = 2 ∗ arcsin ⁡ A / 2 L B
r φ i = L B × φ i
D t = ∑ i = 1 n ( r ( θ i ) + r φ i )
where, M c i : column member position coordinate, x c i : erection column member x- axis, y c i : erection column member y- axis, z c i : erection column member z- axis, C: Crane position axis, T: Trailer position axis, x t : x- axis of the trailer, y t : y- axis of the trailer, z t : z- axis of the trailer, θ i : Horizontal rotation angle of the boom in radians, r( θ i ) : Horizontal rotation distance, l T : Distance from the crane to the trailer, l c m c i : Distance from the crane to the erection member, L B : Boom length, A: Straight line distance in vertical rotation, φ i : Vertical rotation angle of the boom in radians, r( φ i ) : Vertical rotation distance, D t : Boom trajectory distance, i: Number of i-th erection member at crane position (1, ... , n)
Create rules utilizing the queue and stack methods to stack PC components. The simulation is performed accordingly, and if there is an error in the order of utilization of the storage yard and the order of loading in the stock yard, the simulation is corrected (feedback routine). If there are no errors, the simulation is completed. Since the order of erection in three-layer yarding is different from the order of in-situ production, stock yard rules are required for simulation. To manage the order of erection and production, Rule 1 is established as shown in Figure 5. PC components in all stock yards are based on sequentially loading from the 1st storage yard to the n-th storage yard.
This rule utilizes the queue method to produce and load First In First Out (FIFO) from left to right, and the stack method to produce and load First In Last Out (FILO) from top to bottom [92,93]. In addition, since the loading of PC beams and the loading of the 4th floor are single-layer loading, no separate loading plan is required. Storage yard consisting of a n×m matrix can be represented as the following equation (45), and the stock yard rule 1 can be formulated as the following equation (46). The total number of components in storage yard is given by the product of the rows and columns of the stock yard. If the storage yard is organized as a n×m matrix with rows in the stack method and columns in the queue method, the positions of the stacking order and production order can be expressed as a matrix.
f x = n × m
X a i j , b i j = ( a 11 , b 11 ) ⋯ ( a 1 j , b 1 j ) ⋮ ⋱ ⋮ ( a i 1 , b i 1 ) ⋯ ( a i j , b i j ) = ( n , 1 ) ⋯ ( n m − ( n − n ) , n m − ( n − 1 ) ) ⋮ ⋱ ⋮ ( 1 , n ) ⋯ ( n m − ( n − 1 ) , n m − ( n − n ) )
where, f x : Total number of components in 1 storage yard, P 1 : Production order, a function of stock yard order, X ( a i j , b i j ) : Production rule of the 1st stock yard rule, a i j : Production order of the member in the i-th row, column j-th, and b i j : stock yard order of the member in the i-th row, column j-th.
PC columns are based on stacking 10 PC columns in 3 tiers, and an area of 125.5㎡ is required for PC columns as shown in Figure 6. In addition, if it is stacked on the bottom floor of the 5th floor, it will be stacked in one layer, so an area of 376.5㎡ is required for 30 pieces. The production and stock yard area for PC beam can be calculated in the same way. In addition, the following rules have been established to minimize the risk of PC components when loading and unloading as shown in Table 3.
After in-situ production of PC components, the details of the loading rules are as follows.
① PC components are in-situ produced and erected by driving cranes in each zone. Therefore, the basic rule is that the in-situ produced components are stacked outside the building corresponding to the area of each zone. However, if the space is limited, it is possible to utilize the site of a neighboring zone, a site outside the zone, or a building slab.
② PC components should be stacked in consideration of the erection location, i.e., stacked close to the erection location so that the travel distance of the components is short. Also, the components must be stacked within the crane working radius.
③ To minimize the risk, it is important to ensure that the loading plan is not affected by the erection schedule of PC components. Therefore, in this project, which is a PC structure up to the 5th floor, the 5th floor can be utilized as stock yard space after the construction of the 5th floor is completed. In other words, the 5th floor is the roof level of the building, and there is no interference with the erection of PC components, so there is no need to move the stock yard space.
④ The in-situ produced components are basically stacked in three columns and one beam after installing steel plates at GL. The reason for installing steel plates is that there is a problem of damage to the components due to ground subsidence caused by the weight of the components due to insufficient compaction. In addition, the number of loading units is based on the characteristics of the components, and columns that can be loaded in multiple units are loaded in three units, and beams that cannot be loaded in multiple units are loaded in one unit.
⑤ This case project is a logistics center facility, and the building is designed with a load of 2.4 tons/㎡ to reflect the movement of large vehicles transporting loaded cargo. Therefore, when the bottom floors of the 2nd-5th floors of the building are utilized as stock yard space, the number of stacks of components is limited to one in consideration of the load of the components.
⑥ When stacking components, establish a stacking plan by zone, by type of column and beam member, and by the nth stock yard.
⑦ Storage yard is based on sequential loading. However, if the space is limited, the stock yard and erection can be carried out simultaneously at one stock yard.
⑧ Each storage yard is based on loading 30 components for the convenience of stock yard management. In addition, the stock yard area is calculated by considering the basic unit of the stock yard.
The total construction time was 20 months, and the erection time was 12 months. Through time series analysis, the area derived by each zone corresponding to the erection time is as shown in Table 4. It is necessary to calculate the stock yard area corresponding to the number of stock yard components per zone and per member type. This should be calculated on a weekly or monthly basis during the period of simultaneous production and erection. To perform the production and erection simulation, the production and stock yard area is calculated according to the calculated number of molds and the number of stock yard components.

5.3 Result Comparison

In this study, the DBO and IDBO algorithms were applied to minimize the environmental impact of in-situ produced PC components, with the number of iterations being 300, the initial population size being 30, and the number of ball-rolling dung beetles, reproduction of dung beetles, foraging of dung beetles, and stealing of dung beetles being 6, 6, 7, and 11, respectively. Since each algorithm produced different results each time, it was simulated each algorithm 30 times to avoid differences due to random factors. The optimal solutions obtained by the two algorithms are compared and the fitness iteration curves are shown in Figure 7.
Figure 5 shows that the DBO algorithm reached the optimum at the 45th iteration and then entered a plateau phase. On the other hand, the IDBO algorithm showed relatively fast convergence in the early stages, indicating that the introduction of Chebyshev mapping facilitated the generation of a diverse initial population, which accelerated convergence. Despite the stagnation that occurred in the later stages, the IDBO algorithm continued to move away from the local optimum after a short period of stagnation. After 300 iterations, there was still room for improvement, indicating the effectiveness of the adaptive Gaussian-Cauchy mixed mutation perturbation strategy in improving the global exploration ability of the algorithm.
Figure 8 shows the optimal layout derived from the two algorithms. Analyzing Figure 8, it can be seen that the DBO layout shows cross logistics routes that are detrimental to efficient system operation. On the other hand, after the IDBO optimized layout, there are no detours or intersections, making the logistics flow paths between stock yards more reasonable and ensuring the continuity of system operation. Therefore, it was concluded that the IDBO algorithm is more suitable than the DBO algorithm for the environmental impact optimization problem for the stock yard of in-situ produced PC components.
The optimization effect of each layout method on the random simulation results is compared as shown in Table 6. This table shows that after optimization, the DBO algorithm reduces the overall logistics cost by 14.47%. The adjacent correlations of the DBO and IDBO algorithms are 29.93 and 36.75, respectively, and the carbon dioxide emissions are 2,765 and 2,258. In other words, the IDBO algorithm improves the adjacent correlation by 22.79% and reduces the carbon dioxide emissions by 18.33% compared to the DBO algorithm. This confirms that the IDBO algorithm can improve adjacent correlation and reduce carbon dioxide emissions based on the DBO algorithm.
The DBO algorithm applied in this study solves the stock yard layout optimization problem through the basic exploration and exploitation mechanism. The DBO algorithm can generally perform adequately in optimization problems, especially in the initial exploration, which has a good global exploration ability and can explore a variety of solutions. In the initial stage of this study, the environmental impact optimization for the stock yard of in-situ produced PC components was simulated in two parts because the convergence speed was slowed down during the simulation process and the final solution was not close to the optimal solution. The reason for the slow convergence was that the DBO algorithm was likely to fall into a local optimum due to the large number of complex constraints and the large problem space. In other words, the DBO algorithm can have poor solution quality for problems with complex constraints.
The IDBO algorithm, on the other hand, is an algorithm designed to improve the performance of the DBO algorithm. By introducing chaos mapping and mutation strategies, the IDBO algorithm was able to enhance its exploration capabilities and better balance global exploration and local exploitation. It was found that the IDBO algorithm is more likely to outperform the DBO algorithm in problems with complex constraints or multi-objective optimization problems, which means that the IDBO algorithm is more likely to outperform the DBO algorithm. It was also found that the IDBO algorithm produces higher quality solutions compared to the DBO algorithm. This is because the IDBO algorithm is able to use different search strategies to search for the global optimum and converge more precisely. Therefore, the solution produced by IDBO is more likely to be an optimal arrangement that satisfies the constraints while minimizing the environmental footprint.

6. Discussion

When stock yard space is limited, it is sometimes necessary to move stacked components to storage yard in a different space. This is the same as the default for odd-order reloading, but different for even-order reloading. This is defined as yard storage rule 2 and is illustrated in Figure 9. If a PC member needs to be installed in storage yard that is stacked with components on the ground floor, the storage yard must be moved to another room for erection. The calculation of the number of storage yard movements is expressed as equation (47). However, it is assumed that reloading is not done because it increases environmental impact, cost, and time.
N S = M i n ∑ f ( x i )
where, Ns: Total number of storage yard moves for PC components, xi: storage yard moves
Modern societies are facing a variety of environmental challenges due to rapid industrialization and urbanization. These challenges can be described by the concept of environmental impact, which refers to the negative impact of human activities on the natural environment. Environmental impact is primarily related to resource consumption, energy use, emissions generation, and waste disposal, which can lead to a number of environmental problems such as air pollution, water pollution, ecosystem degradation, and climate change.
Effective management of environmental footprint in construction projects is an essential component of realizing sustainable construction. It goes beyond simply complying with legal regulations and extends to a strategic approach related to corporate social responsibility. Reducing environmental footprint can also provide economic benefits in the long run, leading to cost savings and efficiency gains. For these reasons, innovative methodologies are needed to minimize the environmental footprint and enhance sustainability. Optimizing stock yard layout in PC member in-situ production is part of this effort, and is an important strategy to minimize the environmental impact of construction sites and promote sustainable development.

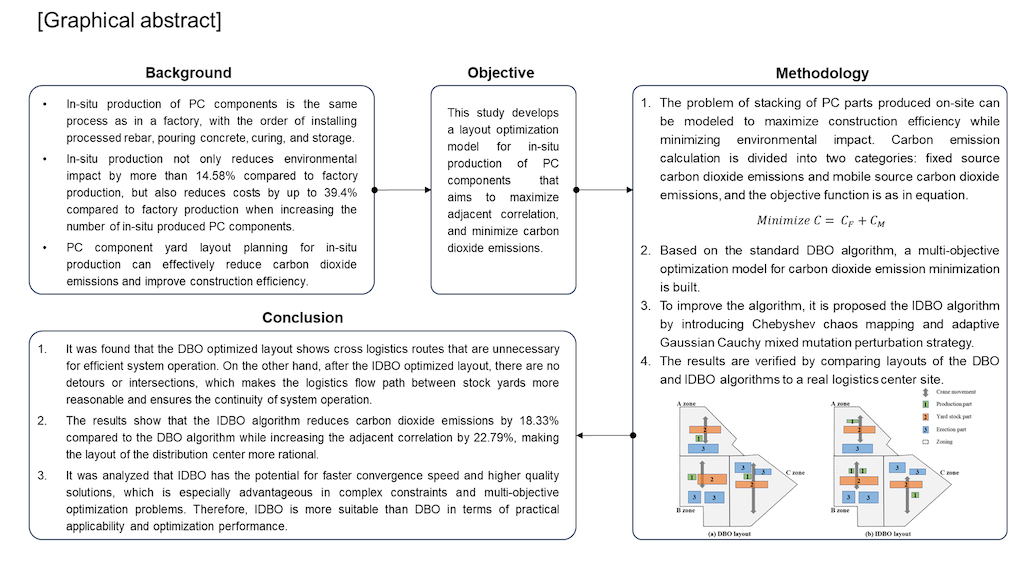
7. Conclusion

In this study, DBO algorithm and IDBO algorithm were applied to develop an environmental impact minimization model for in-situ production of PC components. For this, after analyzing the existing in-situ production process of PC components, the problems of in-situ production were identified, and the objective function and constraints of in-situ production were presented to build the optimization model. And the DBO algorithm and IDBO algorithm were compared and analyzed. The following conclusions were derived from this study.
1) Considering the impact of characteristics of the large logistics center and internal layout on carbon emissions, a carbon dioxide emission factor was introduced. And the layout optimization model was formulated with the goal of maximizing adjacency correlation and minimizing carbon dioxide emissions. It was found that the DBO optimized layout shows cross logistics routes that are unnecessary for efficient system operation. On the other hand, after the IDBO optimized layout, there are no detours or intersections, which makes the logistics flow path between stock yards more reasonable and ensures the continuity of system operation. In other words, it was confirmed that the IDBO algorithm is more suitable than the DBO algorithm for the environmental impact optimization problem.
2) Based on the DBO algorithm, Chebyshev Chaotic Mapping was introduced in the initial stage to improve the quality of the initial population; an adaptive Gaussian-Cauchy hybrid mutation perturbation strategy was introduced in the subsequent iterations to prevent the population from falling into a local optimum state and improve the global exploration capability of the algorithm. The IDBO algorithm was applied to solve the layout problem of the distribution center. The results showed that the IDBO algorithm reduces carbon dioxide emissions by 18.33% compared to the DBO algorithm while increasing the adjacent correlation by 22.79%, making the layout of the distribution center more rational.
3) For the environmental impact optimization for the stock yard of in-situ produced PC components, the DBO algorithm slowed down the convergence speed during the simulation process and the final solution was not close to the optimal solution. However, the IDBO algorithm performed well even when the number of complex constraints and the problem space of the stock yard optimization problem increased. It was analyzed that IDBO has the potential for faster convergence speed and higher quality solutions, which is especially advantageous in complex constraints and multi-objective optimization problems. Therefore, IDBO is more suitable than DBO in terms of practical applicability and optimization performance.
Using the IDBO algorithm, the proposed method is applied to a real logistics center and verified to provide reference for the development of large logistics centers. The proposed environmental impact minimization model can support the construction, reconstruction, and functional upgrade of logistics centers, contributing to the low-carbon development of the logistics industry. The results of this study can be used as a basis for further research on stock yards, stock yard area, and supply chain management of various materials in limited construction sites. Furthermore, it is necessary to apply the results to various meta-heuristic algorithms and compare the results in the future.

Author Contributions

Conceptualization, S.K. and J.L.; methodology, S.K. and J.L.; validation, J.L.; formal analysis, S.K. and J.L.; investigation, J.L.; data curation, J.L.; writing—original draft preparation, J.L.; writing—review and editing, S.K. and J.L.; visualization, J.L.; supervision, S.K. and J.L.; project administration, S.K. and J.L.; funding acquisition, J.L. and S.K. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MOE) (No. 2021R1C1C2094527 and No. 2022R1A2C2005276).

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Na Y, Han B, Son S. Analysis of CO2 Emission Reduction Effect of On-Site Production Precast Concrete Member according to Factory Production Environment. Advances in Civil Engineering. 2021;2021(1):4569651. [CrossRef]
  2. Lim J, Kim DY. Integrated management model of production and yard stock for in-situ precast concrete production. Journal of Asian Architecture and Building Engineering. 2023 Jan 2;22(1):286-302. [CrossRef]
  3. Lim J, Kim JJ. Dynamic optimization model for estimating in-situ production quantity of PC members to minimize environmental loads. Sustainability. 2020 Oct 5;12(19):8202. [CrossRef]
  4. Lim J, Son CB, Kim S. Scenario-based 4D dynamic simulation model for in-situ production and yard stock of precast concrete members. Journal of Asian Architecture and Building Engineering. 2023 Jul 4;22(4):2320-34. [CrossRef]
  5. Hong WK, Lee G, Lee S, Kim S. Algorithms for in-situ production layout of composite precast concrete members. Automation in Construction. 2014 May 1;41:50-9. [CrossRef]
  6. Na YJ, Kim SK. A process for the efficient in-situ production of precast concrete members. Journal of the Regional Association of Architectural Institute of Korea. 2017 Oct;19(4):153-61.
  7. Lim, C. 2016. “Construction Planning Model for In-situ Production and Installation of Composite Precast Concrete Frame.” PhD diss., Kyung Hee University.
  8. Lim, C, Joo, J. K., Lee, G. J., and Kim, S. K. 2011a. “Basic Analysis for Form System of In-situ Production of Precast Concrete Members.” In Proceeding of the 2011 Autumn Annual Conference of Construction Engineering and Management, 12(1), 137-138. Seoul, Korea.
  9. Lim, C. Y., Joo, J. K., Lee, G. J., and Kim, S. K. 2011b. “In-Situ Production Analysis of Composite Precast Concrete Members of Green Frame.” Journal of the Korea Institute of Building Construction 11 (5): 501–514. [CrossRef]
  10. Lee, G. J., Lee, S. H., Joo, J. K., and Kim, S. K. 2011a. “A Basic Study of In-Situ Production Process of PC Members.” In Proceeding of the 2011 Autumn Annual Conference of the Architectural Institute of Korea, 31(2), 263-264. Seoul, Korea.
  11. Lee, G. J., Joo, J. K., Lee, S. H., and Kim, S. K. 2011b. “A Basic Study on the Arrangement of In-situ Production Module of the Composite PC Members.” In Proceeding of the 2011 Autumn Annual Conference of the Korea Institute of Building Construction, 11(2), 29-30. Seoul, Korea.
  12. Jung, H. T., and Lee, M. S. 1992. “A Study on the Site-production Possibility of the Prefabricated PC Components.” In Proceeding of the 1992 Autumn Annual Conference of the Architectural Institute of Korea, 12(2), 629-636. Seoul, Korea.
  13. Li H, Love PE. Genetic search for solving construction site-level unequal-area facility layout problems. Automation in construction. 2000 Mar 1;9(2):217-26. [CrossRef]
  14. Osman HM, Georgy ME, Ibrahim ME. A hybrid CAD-based construction site layout planning system using genetic algorithms. Automation in construction. 2003 Nov 1;12(6):749-64. [CrossRef]
  15. Ning X, Lam KC, Lam MC. Dynamic construction site layout planning using max-min ant system. Automation in construction. 2010 Jan 1;19(1):55-65. [CrossRef]
  16. Abdul-Rahman H, Wang C, Eng KS. Repertory grid technique in the development of Tacit-based Decision Support System (TDSS) for sustainable site layout planning. Automation in Construction. 2011 Nov 1;20(7):818-29. 829, . [CrossRef]
  17. Lee, G. J. 2012. “A Study of In-situ Production Management Model of Composite Precast Concrete Members.” PhD diss., Kyung Hee University.
  18. Won I, Na Y, Kim JT, Kim S. Energy-efficient algorithms of the steam curing for the in situ production of precast concrete members. Energy and buildings. 2013 Sep 1;64:275-84. [CrossRef]
  19. Lim J, Park K, Son S, Kim S. Cost reduction effects of in-situ PC production for heavily loaded long-span buildings. Journal of Asian Architecture and Building Engineering. 2020 May 3;19(3):242-53. [CrossRef]
  20. Kim SH, Kim GH, Kang KI. A study on the effective inventory management by optimizing lot size in building construction. Journal of the Korea Institute of Building Construction. 2004;4(2):73-80. [CrossRef]
  21. Lee JM, Yu JH, Kim CD. A Economic Order Quantity (EOQ) Determination Method considering Stock Yard Size. InProceedings of the Korean Institute Of Construction Engineering and Management 2007 (pp. 549-552). Korea Institute of Construction Engineering and Management.
  22. Lee JM, Yu JH, Kim CD, Lee KJ, Lim BS. Order Point Determination Method considering Materials Demand Variation of Construction Site. Journal of the Architectural Institute of Korea. 2008;24(10):117-25.
  23. Thomas HR, Horman MJ, Minchin Jr RE, Chen D. Improving labor flow reliability for better productivity as lean construction principle. Journal of construction engineering and management. 2003 Jun;129(3):251-61. [CrossRef]
  24. Yun JS, Yu JH, Kim CD. Economic Order Quantity (EOQ) Determination Process for Construction Material considering Demand Variation and Stockyard Availability. Korean Journal of Construction Engineering and Management. 2011;12(1):33-42. [CrossRef]
  25. Lim, J., and Kim, S. 2020a. “Evaluation of CO2 Emission Reduction Effect Using In-situ Production of Precast Concrete Components.” Journal of Asian Architecture and Building Engineering 19: 176–186. [CrossRef]
  26. Lim, J., Kim, S., and Kim, J. J. 2020a. “Dynamic Simulation Model for Estimating In-situ Production Quantity of PC Members.” International Journal of Civil Engineering 18: 935–950. [CrossRef]
  27. Yang, B.; Han, J.W.; Yang, L.; Ren, Q.S.; Yang, X.T. Evaluation system of China’s low-carbon cold chain logistics development level. Smart Agric. 2023, 5(01), 44-51. [CrossRef]
  28. Bai J, Li Y, Zheng M, Khatir S, Benaissa B, Abualigah L, Wahab MA. A sinh cosh optimizer. Knowledge-Based Systems. 2023 Dec 20;282:111081. [CrossRef]
  29. Wehrens R, Buydens LM. Classical and nonclassical optimization methods. Encyclopedia of analytical chemistry. 2000:9678-89.
  30. YiFei L, MaoSen C, Tran-Ngoc H, Khatir S, Wahab MA. Multi-parameter identification of concrete dam using polynomial chaos expansion and slime mould algorithm. Computers & Structures. 2023 Jun 1;281:107018. [CrossRef]
  31. Khishe M, Mosavi MR. Chimp optimization algorithm. Expert systems with applications. 2020 Jul 1;149:113338. [CrossRef]
  32. Minh HL, Sang-To T, Theraulaz G, Wahab MA, Cuong-Le T. Termite life cycle optimizer. Expert Systems with Applications. 2023 Mar 1;213:119211. [CrossRef]
  33. Jiang, F.; Li, L.; Tang, Y.M.; Zhang, H.L.; Liu, X.P. A Facility Layout Algorithm for Logistics Scenarios Driven by Transport Lines. Appl. Sci. 2023, 13(12), 7215. [CrossRef]
  34. Geng, Q.Q.; Jia, Y.H.; Wu, J.; Sun, D.Y. Research on layout optimization of logistics parks considering impact of carbon emissions. J. Beijing Jiaotong. Univ. 2023, 47(01), 115-125.
  35. Hu, X.; Chuang, Y.F. E-commerce warehouse layout optimization: systematic layout planning using a genetic algorithm. Electron. Comm. Res. 2023, 23(1), 97-114. [CrossRef]
  36. Nanda SJ, Panda G. A survey on nature inspired metaheuristic algorithms for partitional clustering. Swarm and Evolutionary computation. 2014 Jun 1;16:1-8. [CrossRef]
  37. Amaral, A.R.S. On the exact solution of a facility layout problem. Eur. J. Oper. Res. 2006, 173(2), 508-518. [CrossRef]
  38. Wang, N.A. Planning and layout of intelligent logistics park based on improved genetic algorithm. Mobi. Informa. Syst. 2022, 2022. [CrossRef]
  39. Eswaran, M.; Inkulu, A.K.; Tamilarasan, K.; Bahubalendruni, M.V.A.R.; Jaideep, R. Faris, M.S.; Jacob, N. Optimal layout planning for human robot collaborative assembly systems and visualization through immersive technologies. Expert Syst. Appl.2024, 241, 122465. [CrossRef]
  40. Zhang, M.Y.; Zhu, Y.J.; Zhang, X.Y.L. Layout optimization of forging plant based on systematic layout planning and mixed algorithm. Sci. Technol. Eng. 2024, 24(01), 170-176.
  41. Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79(7), 7305-7336. [CrossRef]
  42. Zhu, F.; Li, G.; Tang, H.; Li, Y.B.; Lv, X.M.; Wang, X. Dung beetle optimization algorithm based on quantum computing and multi-strategy fusion for solving engineering problems. Expert Syst. Appl. 2024, 236, 121219. [CrossRef]
  43. Li, Y.; Sun, K.; Yao, Q.; Wang, L. A dual-optimization wind speed forecasting model based on deep learning and improved dung beetle optimization algorithm. Energy. 2024, 286, 129604. [CrossRef]
  44. Rajakumar R, Dhavachelvan P, Vengattaraman T. A survey on nature inspired meta-heuristic algorithms with its domain specifications. In2016 international conference on communication and electronics systems (ICCES) 2016 Oct 21 (pp. 1-6). IEEE.
  45. YiFei L, Minh HL, Khatir S, Sang-To T, Cuong-Le T, MaoSen C, Wahab MA. Structure damage identification in dams using sparse polynomial chaos expansion combined with hybrid K-means clustering optimizer and genetic algorithm. Engineering Structures. 2023 May 15;283:115891. [CrossRef]
  46. De Jong K. Learning with genetic algorithms: An overview. Machine learning. 1988 Oct;3:121-38. [CrossRef]
  47. Storn R, Price K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. Journal of global optimization. 1997 Dec;11:341-59. [CrossRef]
  48. Juste KA, Kita H, Tanaka E, Hasegawa J. An evolutionary programming solution to the unit commitment problem. IEEE Transactions on Power systems. 1999 Nov;14(4):1452-9. [CrossRef]
  49. Koza JR. On the programming of computers by means of natural selection. Genetic programming. 1992.
  50. Beyer HG, Schwefel HP. Evolution strategies–a comprehensive introduction. Natural computing. 2002 Mar;1:3-52. [CrossRef]
  51. Simon D. Biogeography-based optimization. IEEE transactions on evolutionary computation. 2008 Mar 21;12(6):702-13. [CrossRef]
  52. Kirkpatrick S, Gelatt Jr CD, Vecchi MP. Optimization by simulated annealing. science. 1983 May 13;220(4598):671-80. [CrossRef]
  53. Zhao W, Wang L, Zhang Z. Atom search optimization and its application to solve a hydrogeologic parameter estimation problem. Knowledge-Based Systems. 2019 Jan 1;163:283-304. [CrossRef]
  54. Zhao W, Wang L, Zhang Z. Atom search optimization and its application to solve a hydrogeologic parameter estimation problem. Knowledge-Based Systems. 2019 Jan 1;163:283-304. [CrossRef]
  55. Karami H, Anaraki MV, Farzin S, Mirjalili S. Flow direction algorithm (FDA): a novel optimization approach for solving optimization problems. Computers & Industrial Engineering. 2021 Jun 1;156:107224. [CrossRef]
  56. Hashim FA, Mostafa RR, Hussien AG, Mirjalili S, Sallam KM. Fick’s Law Algorithm: A physical law-based algorithm for numerical optimization. Knowledge-Based Systems. 2023 Jan 25;260:110146. [CrossRef]
  57. Rashedi E, Nezamabadi-Pour H, Saryazdi S. GSA: a gravitational search algorithm. Information sciences. 2009 Jun 13;179(13):2232-48. [CrossRef]
  58. Pereira JL, Francisco MB, Diniz CA, Oliver GA, Cunha Jr SS, Gomes GF. Lichtenberg algorithm: A novel hybrid physics-based meta-heuristic for global optimization. Expert Systems with Applications. 2021 May 15;170:114522. [CrossRef]
  59. Abdel-Basset M, Mohamed R, Sallam KM, Chakrabortty RK. Light spectrum optimizer: a novel physics-inspired metaheuristic optimization algorithm. Mathematics. 2022 Sep 23;10(19):3466. [CrossRef]
  60. Mirjalili S, Mirjalili SM, Hatamlou A. Multi-verse optimizer: a nature-inspired algorithm for global optimization. Neural Computing and Applications. 2016 Feb;27:495-513. [CrossRef]
  61. Wei Z, Huang C, Wang X, Han T, Li Y. Nuclear reaction optimization: A novel and powerful physics-based algorithm for global optimization. IEEE Access. 2019 May 22;7:66084-109. [CrossRef]
  62. Abdel-Basset M, Mohamed R, Azeem SA, Jameel M, Abouhawwash M. Kepler optimization algorithm: A new metaheuristic algorithm inspired by Kepler’s laws of planetary motion. Knowledge-based systems. 2023 May 23;268:110454. [CrossRef]
  63. Deng L, Liu S. Snow ablation optimizer: A novel metaheuristic technique for numerical optimization and engineering design. Expert Systems with Applications. 2023 Sep 1;225:120069. [CrossRef]
  64. Rao RV, Savsani VJ, Vakharia DP. Teaching–learning-based optimization: a novel method for constrained mechanical design optimization problems. Computer-aided design. 2011 Mar 1;43(3):303-15. [CrossRef]
  65. Xu Y, Peng Y, Su X, Yang Z, Ding C, Yang X. Improving teaching–learning-based-optimization algorithm by a distance-fitness learning strategy. Knowledge-Based Systems. 2022 Dec 5;257:108271. [CrossRef]
  66. Kumar S, Tejani GG, Pholdee N, Bureerat S, Jangir P. Multi-objective teaching-learning-based optimization for structure optimization. Smart Science. 2022 Jan 2;10(1):56-67. [CrossRef]
  67. Kaveh A, Mahdavi VR. Colliding bodies optimization: a novel meta-heuristic method. Computers & Structures. 2014 Jul 15;139:18-27. [CrossRef]
  68. Trojovská E, Dehghani M. A new human-based metahurestic optimization method based on mimicking cooking training. Scientific Reports. 2022 Sep 1;12(1):14861. [CrossRef]
  69. Zhang Q, Wang R, Yang J, Ding K, Li Y, Hu J. Collective decision optimization algorithm: A new heuristic optimization method. Neurocomputing. 2017 Jan 19;221:123-37. [CrossRef]
  70. Faramarzi A, Heidarinejad M, Stephens B, Mirjalili S. Equilibrium optimizer: A novel optimization algorithm. Knowledge-based systems. 2020 Mar 5;191:105190. [CrossRef]
  71. Mohamed AW, Hadi AA, Mohamed AK. Gaining-sharing knowledge based algorithm for solving optimization problems: a novel nature-inspired algorithm. International Journal of Machine Learning and Cybernetics. 2020 Jul;11(7):1501-29. [CrossRef]
  72. Kashan AH. League championship algorithm: a new algorithm for numerical function optimization. In2009 international conference of soft computing and pattern recognition 2009 Dec 4 (pp. 43-48). IEEE.
  73. Faridmehr I, Nehdi ML, Davoudkhani IF, Poolad A. Mountaineering team-based optimization: A novel human-based metaheuristic algorithm. Mathematics. 2023 Mar 6;11(5):1273. [CrossRef]
  74. Moosavi SH, Bardsiri VK. Poor and rich optimization algorithm: A new human-based and multi populations algorithm. Engineering applications of artificial intelligence. 2019 Nov 1;86:165-81. [CrossRef]
  75. Naik A, Satapathy SC. Past present future: a new human-based algorithm for stochastic optimization. Soft Computing. 2021 Oct;25(20):12915-76. [CrossRef]
  76. Veysari EF. A new optimization algorithm inspired by the quest for the evolution of human society: human felicity algorithm. Expert Systems with Applications. 2022 May 1;193:116468. [CrossRef]
  77. Abualigah L, Yousri D, Abd Elaziz M, Ewees AA, Al-Qaness MA, Gandomi AH. Aquila optimizer: a novel meta-heuristic optimization algorithm. Computers & Industrial Engineering. 2021 Jul 1;157:107250. [CrossRef]
  78. Wang L, Cao Q, Zhang Z, Mirjalili S, Zhao W. Artificial rabbits optimization: A new bio-inspired meta-heuristic algorithm for solving engineering optimization problems. Engineering Applications of Artificial Intelligence. 2022 Sep 1;114:105082. [CrossRef]
  79. Abdel-Basset M, Mohamed R, Jameel M, Abouhawwash M. Nutcracker optimizer: A novel nature-inspired metaheuristic algorithm for global optimization and engineering design problems. Knowledge-Based Systems. 2023 Feb 28;262:110248. [CrossRef]
  80. Sang-To T, Le-Minh H, Wahab MA, Thanh CL. A new metaheuristic algorithm: Shrimp and Goby association search algorithm and its application for damage identification in large-scale and complex structures. Advances in Engineering Software. 2023 Feb 1;176:103363. [CrossRef]
  81. Hashim FA, Hussien AG. Snake Optimizer: A novel meta-heuristic optimization algorithm. Knowledge-Based Systems. 2022 Apr 22;242:108320. [CrossRef]
  82. Lim, J.; Kim, S. Evaluation of CO2 emission reduction effect using in-situ production of precast concrete components. J. Asian Archit. Build. Eng. 2020, 19, 176–186. [CrossRef]
  83. Lim, J.; Kim, S.; Kim, J.J. Dynamic simulation model for estimating in-situ production quantity of PC members. Int. J. Civ. Eng. 2020, 18, 935–950. [CrossRef]
  84. Lee H, Lee C, Han H, Lee J. A Study on Development of Construction Standard Production Rates and Cost Analysis for Off-Site Construction (OSC)-Based PC Structure Construction Costs: Comparison with RC Method. Korean Journal of Construction Engineering and Management. 2024 Mar 31;25(2):56–68. [CrossRef]
  85. Park J, Choa S. A Study on Variation of Economic Value of Overseas Carbon Reduction Projects with Risk Factors. Korean Journal of Construction Engineering and Management. 2023 Nov 30;24(6):45–52. [CrossRef]
  86. Jiang X.H.; Chen, S.; Zhang, Y. Calculation method of total carbon emission and efficiency of logistics enterprises. Journal of Transp. Syst. Eng. Informa. Technol. 2022, 22(02), 313-321.
  87. Chen, X.R.; Wu, L.F. Yang, X.Z. Fractional order PID parameter tuning based on improved sparrow search algorithm. Contro.Decis. 2024, 39(04),1177-1184.
  88. Zhang, C.; Liang, Y.; Tavares, A.; Wang, L.D. Gomes, T.; Pinto, S. An Improved Public Key Cryptographic Algorithm Based on Chebyshev Polynomials and RSA. Symmetry, 2024, 16(3), 263. [CrossRef]
  89. Pan, G.; Xu, Y. Chaotic glowworm swarm optimization algorithm based on Gauss mutation. Proceedings of the 2016 12th International Conference on Natural Computation, Changsha, China, 30, 11, 2016.
  90. Chen, Y.; Li, X.; Zhao, S. A Novel Photovoltaic Power Prediction Method Based on a Long Short-Term Memory Network Optimized by an Improved Sparrow Search Algorithm. Electronics. 2024, 13(5). 993. [CrossRef]
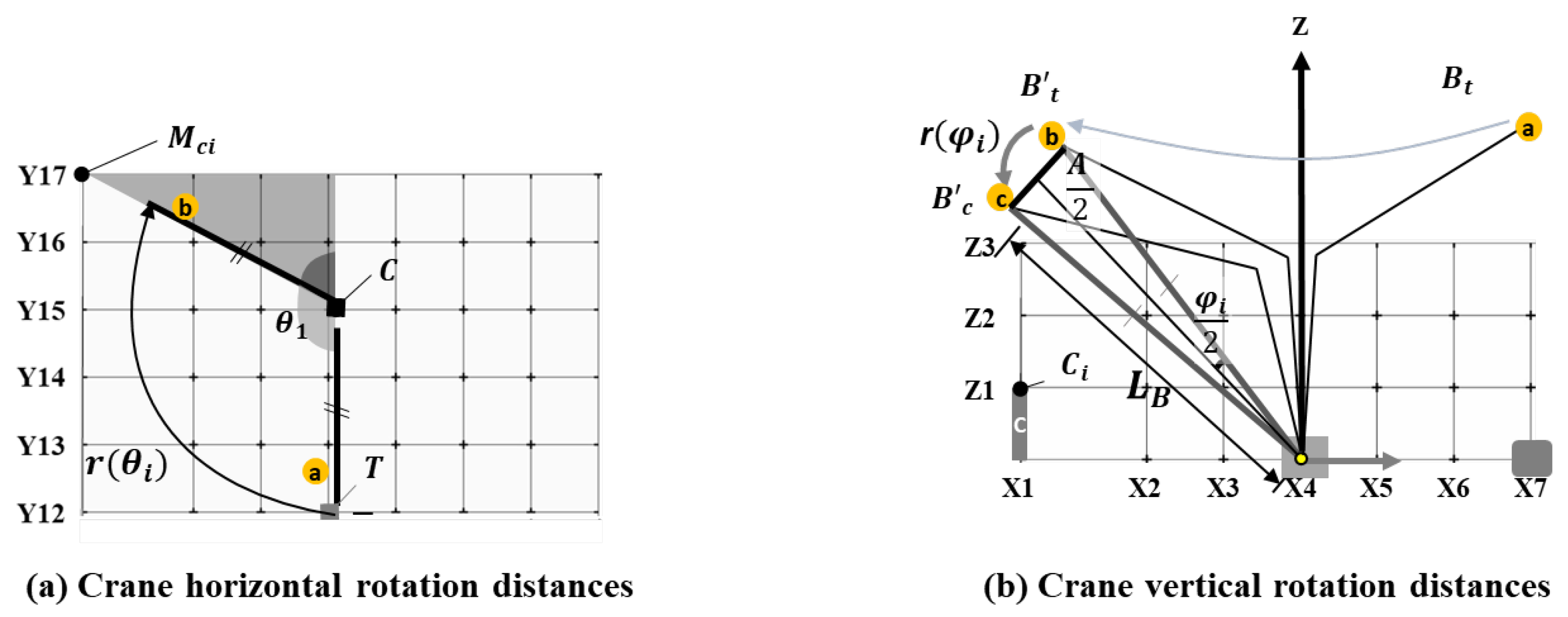
  91. Kim S, Oh J, Lim J. Development of an Algorithm for Crane Trajectory Distance Calculation for Erection of Precast Concrete Members. Buildings. 2023 Dec 20;14(1):11. [CrossRef]
  92. Yoon, S. 1997. Inventory Management Methods and Applications, Sigongsa, 25-29.
  93. Kim, K. Y. 2005. Inventory Management for Logistics Bases. Hyomin.
Preprints 117942 g001
Figure 1. Production-stock yard-erection process of PC components
Figure 1. Production-stock yard-erection process of PC components
Preprints 117942 g001
Preprints 117942 g002
Figure 2. Stock Yard Plane Coordinate Diagram
Figure 2. Stock Yard Plane Coordinate Diagram
Preprints 117942 g002
Preprints 117942 g003
Figure 3. Layout diagram
Figure 3. Layout diagram
Preprints 117942 g003
Preprints 117942 g004
Figure 4. Calculate Crane Vertical and Horizontal Rotation Distance
Figure 4. Calculate Crane Vertical and Horizontal Rotation Distance
Preprints 117942 g004
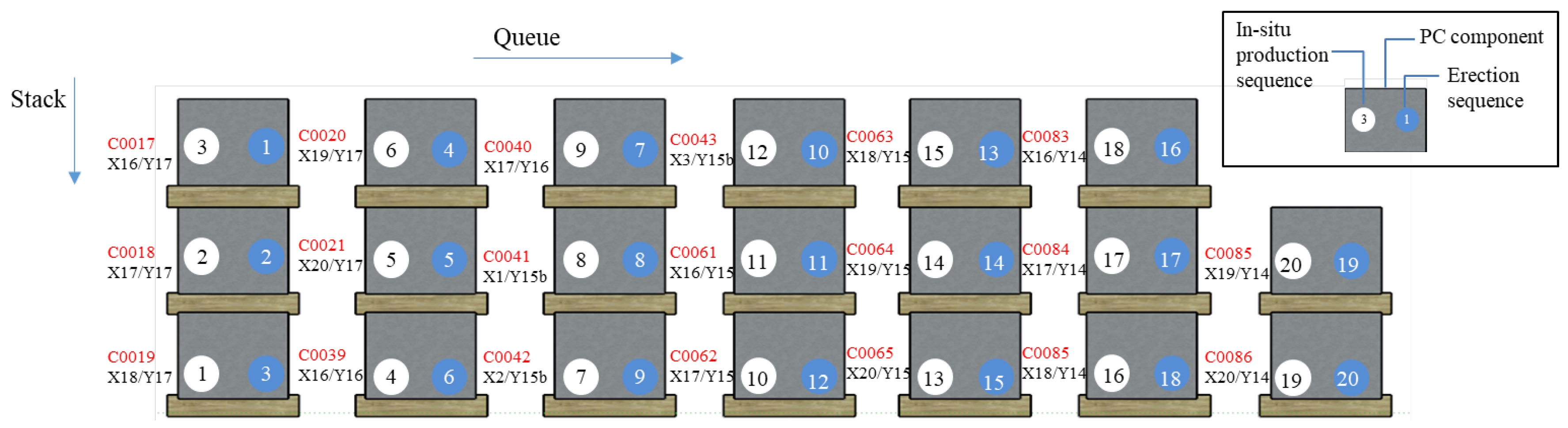
Preprints 117942 g005
Figure 5. Stock yard rules 1 for in-situ produced PC components
Figure 5. Stock yard rules 1 for in-situ produced PC components
Preprints 117942 g005
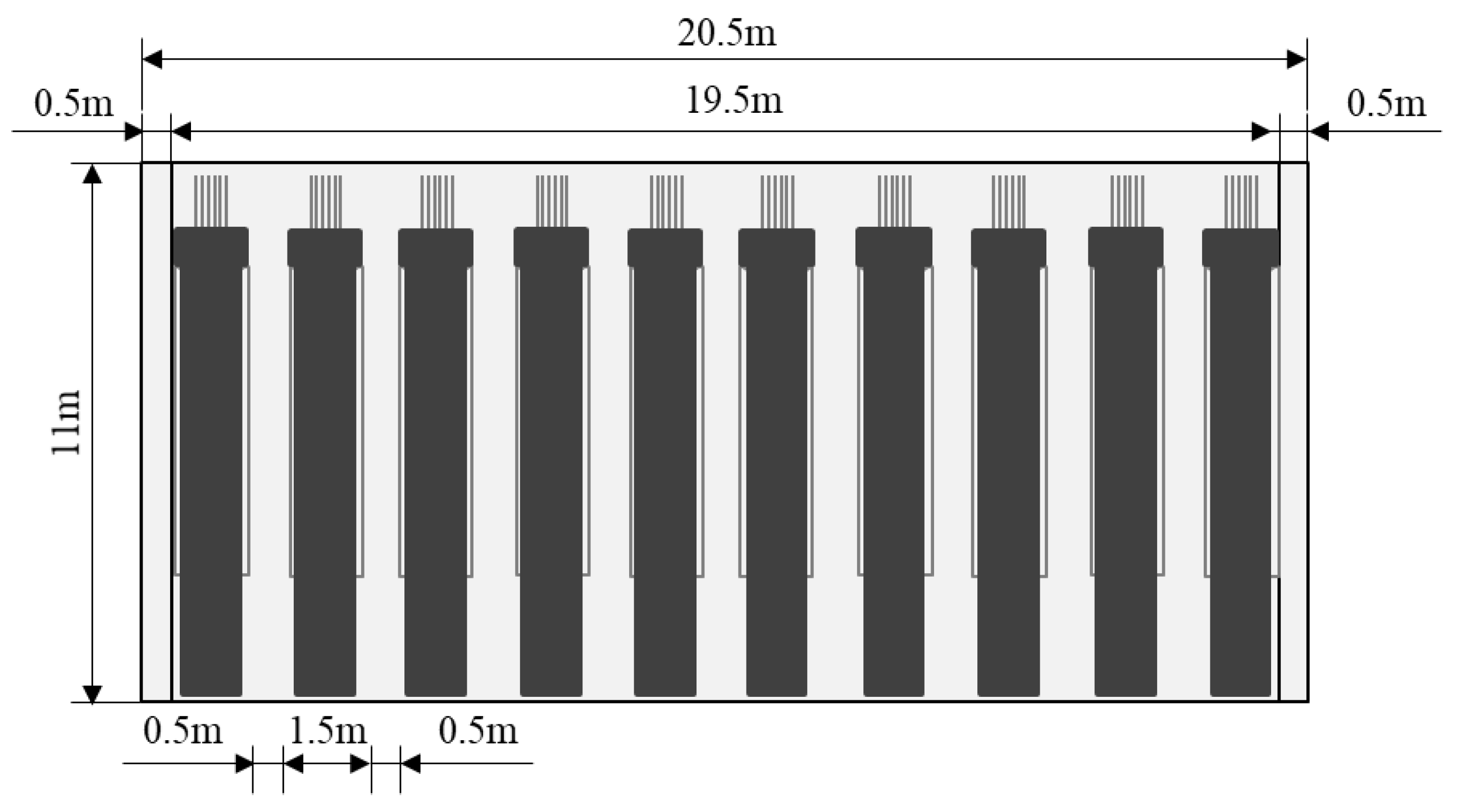
Preprints 117942 g006
Figure 6. Calculation of the outdoor storage area of PC column
Figure 6. Calculation of the outdoor storage area of PC column
Preprints 117942 g006
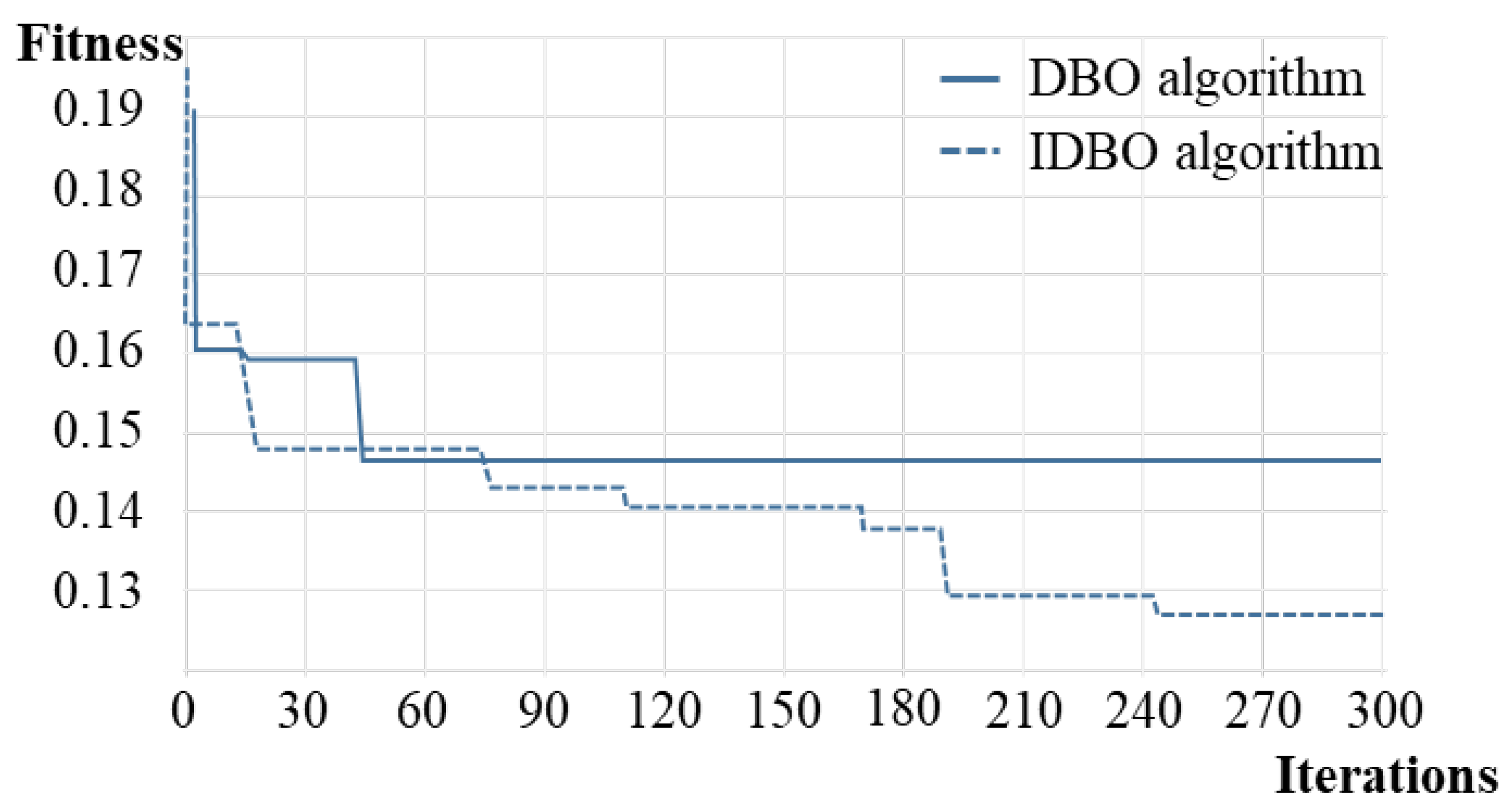
Preprints 117942 g007
Figure 7. Comparison of fitness iteration curves for DBO and IDBO algorithm
Figure 7. Comparison of fitness iteration curves for DBO and IDBO algorithm
Preprints 117942 g007
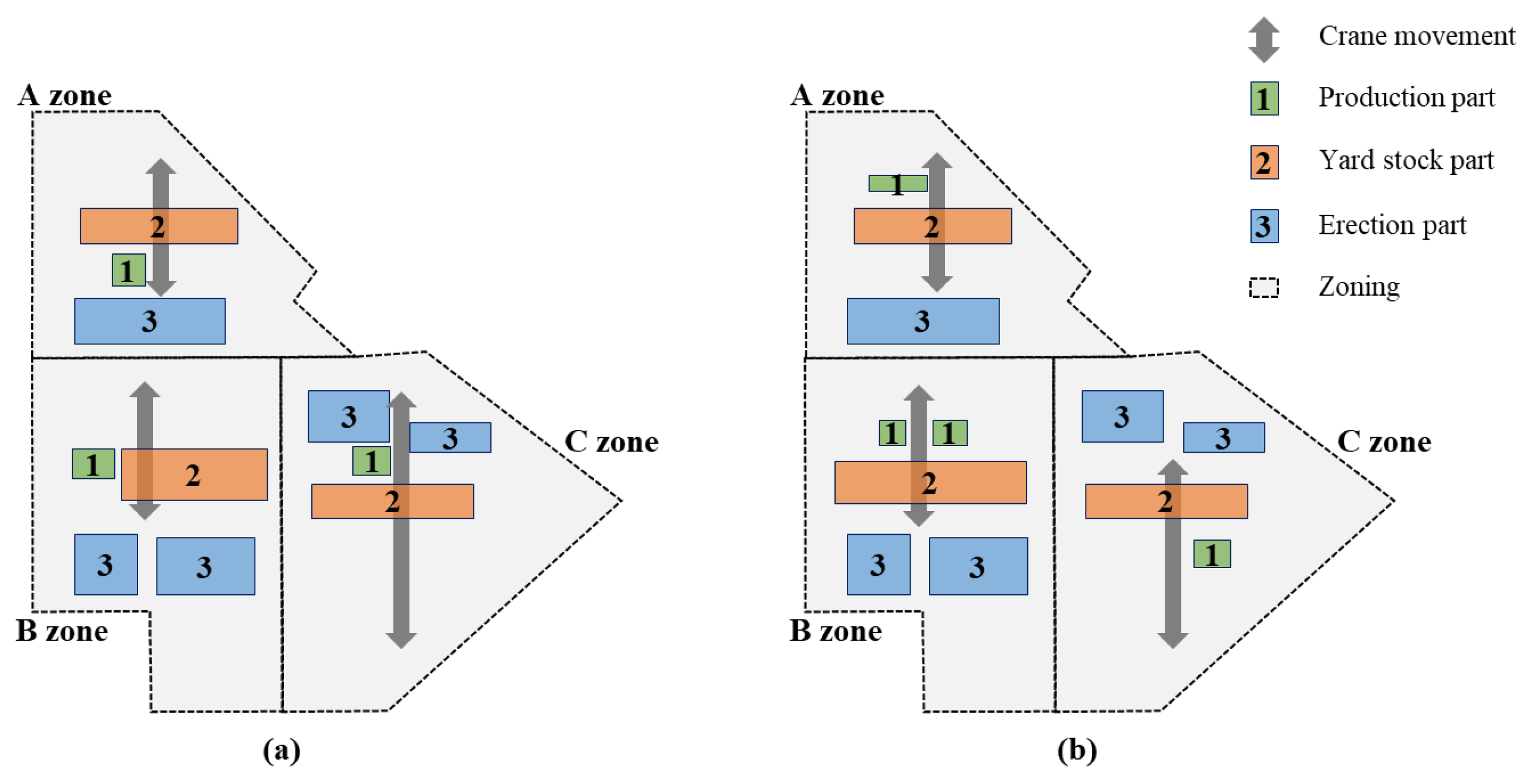
Preprints 117942 g008
Figure 8. Optimization layout on M+1: (a) DBO layout, (b) IDBO layout
Figure 8. Optimization layout on M+1: (a) DBO layout, (b) IDBO layout
Preprints 117942 g008
Preprints 117942 g009
Figure 9. Stock yard rules 2 for in-situ produced PC components: a) 1st storage yard, (b) 2nd storage yard (movement)
Figure 9. Stock yard rules 2 for in-situ produced PC components: a) 1st storage yard, (b) 2nd storage yard (movement)
Preprints 117942 g009
Table 1. Assumptions for Layout Optimization Modeling
Table 1. Assumptions for Layout Optimization Modeling
No. Assumption
1 The entire area and each stock yard are simplified as rectangles with boundaries parallel to the X and Y axes.
2 The orientation of the function zone is categorized into four types: up, down, left and right, and they cannot be placed at an inclined angle.
3 The sum of the areas of all stock yards must be less than the total site area.
4 A safe distance must be maintained between stock yards and PC components.
5 Transportation lines are restricted to extend only in the horizontal or vertical direction.
6 Transportation efficiency and unit costs are available for material transportation routes and each individual transportation line.
7 The entrances and exits within the logistics facility are not considered, but only the actual PC component loading and erection.
Table 2. Brief description of case project
Table 2. Brief description of case project
Description Contents
Location Seoul-si, Republic of Korea
Site area 147,112m2
Building area 84,413m2 (491m long x 497m width)
Total floor area 420,991m2
No. of floors B2 – 5F (6 buildings, floor height 8.7-12.2m)
Structure Columns, Girders, Slabs: Precast concrete structure,
Cores: Reinforced concrete structure
One building: Steel reinforced concrete structure
Table 3. PC member yard storage rules
Table 3. PC member yard storage rules
No. Assumption
1 In-situ produced components in each zone are basically stacked outside the building of each zone.
2 PC components are stacked within the crane working radius.
3 When the construction of the 5th floor is completed, the 5th floor is prioritized as the stock yard space.
4 In-situ produced components are based on the erection of steel plates at + GL (Ground Level) and then stacked in 3 columns and 2 beams.
5 As the load of the building is designed to be 2.4 tons/㎡, the PC components are stacked in 1-layer on the 2nd, 3rd, 4th, and 5th floors.
6 i-th storage yard is divided by zone and member.
7 i-th storage yard is based on sequential loading.
8 Each storage yard is based on stacking 30 components.
Table 4. PC absence area for 12 months by time series analysis (unit: m2).
Table 4. PC absence area for 12 months by time series analysis (unit: m2).
Area M+1 M+2 M+3 M+4 M+5 M+6 M+7 M+8 M+9 M+10 M+11 M+12
Erection 36603 35574 36058 37994 30976 15972 19844 12100 7502 2420 2420 2178
Other work 4350 4682 3025 3120 2925 2543 2432 2210 2100 1468 1055 831
Production 3220 3220 3220 2240 2240 1120 1120 1120 0 0 0 0
Stock 49581 49168 43454 37626 33421 29660 16915 10753 9702 9580 8883 0
Table 6. Layout optimization comparison of DBO and IDBO algorithm
Table 6. Layout optimization comparison of DBO and IDBO algorithm
Layout plan Adjacent correlation Carbon dioxide emissions (T-CO2)
DBO optimization layout 29.93 2,765
IDBO optimization layout 36.75 2,258
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated