Rare Visual Token Enhancement Improves Registration and Few-Shot Change Detection in Remote Sensing Data

Preprint

Article

Rare Visual Token Enhancement Improves Registration and Few-Shot Change Detection in Remote Sensing Data

Altmetrics

Downloads

Views

Comments

Adrien CHAN-HON-TONG^*

This version is not peer-reviewed

Submitted:

12 September 2024

Posted:

13 September 2024

You are already at the latest version

Alerts

Abstract

This paper introduces the self-supervised pretext task of rare visual token enhancement: given an image, the model is trained to push the rarest visual tokens far from all the others. This pretext task slightly-but-consistently improves baseline performances for both registration and few-shot change detection on OSCD, LEVIR-CD and S2looking.

Keywords:

Subject: Computer Science and Mathematics - Computer Science

1. Introduction

Self-supervision consists in selecting a label-free pretext task whose resolution eventually forces the model to organize an underlying representation of the datum / data. Two classical pretext tasks are contrastive learning (e.g. [1]) which aims to make all image representations distant from each other while grouping representations of an single image under data augmentations, or, masked prediction (e.g. [2,3]) where the model should predicts parts of the datum (or related features) that are voluntary removed.

If those two pretext tasks have been successfully used to train very large foundation models (e.g. [4,5]), they may have two limitations. First, those approach are mainly global: they help to embed the datum but not the different parts of it. Thus, one can wonder if related features are relevant for tasks requiring fine spatial information like registration. Then, those pretext task may struggle when trained on smaller models [1]. Yet, both frugality at server level to save energy and frugality at edge level to run on limited hardware require lighter models for many industrial applications. And, despite that pruning [6], distillation [7] and/or quantization [8] of large models have allowed a rapid spread of large-made-light models on smartphone, considering more frugal approaches should be investigated independently from compression of large networks.

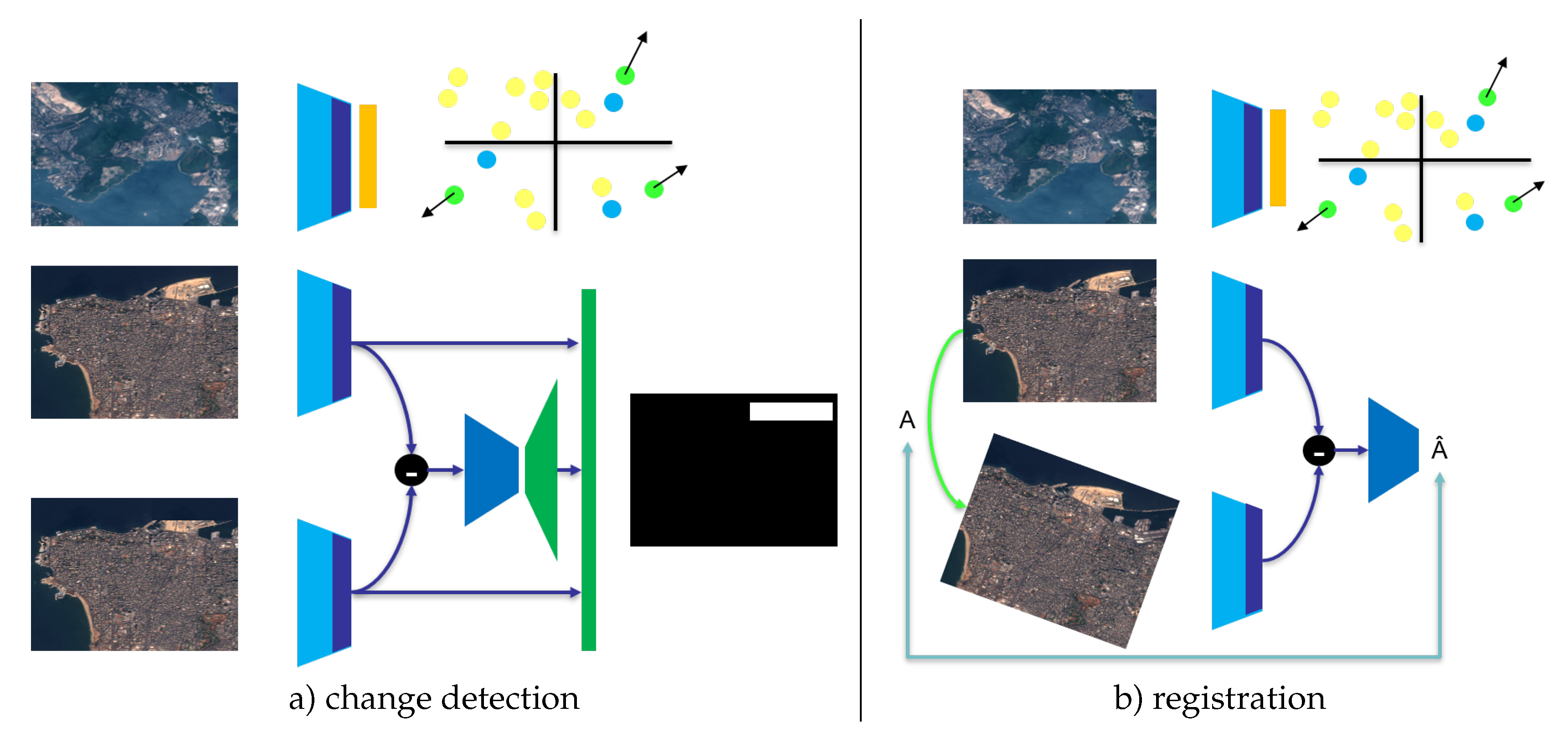
This paper considers a label-free task which may be relevant for frugality purpose: extracting from a datum only the rare tokens. Obviously, it is not true that rare tokens always capture the global information of the entire datum. In some situation, proportion of different banal tokens may encode the main information. Yet, when information is carried by rare tokens, getting rid of all banal ones may allow an interesting speedup. More precisely, this paper focuses on self-supervised rare visual token enhancement: the model is trained to make the most distant visual tokens of an image to be distant to all others forcing both features to align with Euclidean distance and rarity to align to distance to others (see overview Figure 1).

It is worth noticing that standard contrastive loss on tokens rather than image can not work: a lot of tokens are duplicated in an image (e.g. all ocean tokens may be very close), thus they can not be made distant to the others. So making all tokens distant to each other can not work. This is why the offered task is to make rare tokens distant from the others.

This idea seems relevant for change detection and registration where it is common to focus on some part of the images, as recalled in related works in section 2. Indeed, the offered framework, described in section 3, slightly-but-consistently improves baseline for both registration and change detection on several remote sensing datasets. These results presented in section 4 and potential limits are discussed with a general conclusion in section 5.

2. Related Works and Datasets

2.1. Sparsity in Image Classification

The idea of selecting rare areas in image was somehow common before deep learning rising. Indeed, trend in bag-of-features approaches just before Alexnet [9] was about selecting relevant words or features from the codebook [10] i.e. processing the image using only the most relevant features. Since then, image classification is overwhelmingly performed in dense manner using deep network. Despite network efficiency is improved using somehow sparser architectures (e.g. introduction of block removing the need to improve the width of the layers in Resnet [11], grouped convolution and separation between spatial and spectral operation in state of the art ConvNext[12]), deep network tends to process the image entirely.

Recent transformer approaches [13] which perform tokenization of the images could easily reintroduce the idea of token selection. Yet, current trends mostly focuses on training larger networks on larger databases.

2.2. Sparsity for vision based geometry

The closer works to this paper are related to vision based geometry. Indeed, simultaneous localization and mapping (SLAM [14]), 3D reconstruction[15], or image registration [16] still mostly rely on points: salient points are extracted from multiple images, then, points are matched across images based on their neighborhood to recover corresponding 3D points (1 3D point is associated to 1 2D point in each image).

This process requires the ability to select one salient point and the ability to describe it in such way a same 3D points will be described similarly in multiple images i.e. such process should enhance visual rarity. Yet, only few works have considered this task with deep learning approaches. For example, it worth notices that even recent advanced vision language mapping like [17] relies on hand crafted 2D point extractions to generate 3D point cloud (then processing the point cloud with large transformer and language model).

Currently, almost only [18] tries to select the salient point in end-to-end fashion. However, [18] relies on a geometric-based pre-training: geometric strong-corner solids are used to generated image on which corresponding 2D points should be extracted. Thus, this approaches is completely relevant for extracting geometric points, but, it does not directly tackle the task of enhancing rare visual token that may not be salient geometric points. Inversely, this paper tries a more general approach which should include both salient geometric points and salient textures and more generally rare tokens. For example, in a remote sensing image that contains a single small pond, then it is possible that the pond matches a token that becomes a rare token despite the pond is neither geometrically or textually salient.

2.3. Datasets

This paper offers to consider pair of images based semantic change segmentation and synthetic registration (on the same data). EuroSAT [19] (a standard remote sensing image classification dataset) and Imagenet [20] are also considered in discussion but main experiments are performed on change detection datasets.

2.3.1. Change Detection

This paper considers classical change segmentation datasets:

OSCD [21] is a set of 24 pairs of Sentinel2 image-crops with binary mask of change. In this paper, only RGB images are used resulting in around 24 image pairs of size around 400x400. Each pair is annotated with changes which are mostly related to land-use change e.g. new road or building.
LEVIR-CD [22] is a set of pairs of very high resolution images (extracted from google earth - hence being straightforwardly RGB). They are annotated with change mask focusing on urban change (mostly building).
S2looking [23] is a Sentinel2 image dataset like OSCD (from which only RGB is used in this paper like for OSCD) but with a much larger scale: it contains 5000 pairs of images of size 1024x1024 annotated with change mask.

For all those datasets, this paper focuses on few annotation settings: only 25% of each dataset is considered as labeled for training while the remaining is considered as unlabeled i.e. useful for self/semi-supervised approaches only.

2.3.2. Synthetic Registration

As OSCD, LEVIR and S2looking provides registered pair of images, they can be used to evaluate synthetic registration: from a pair of registered images, one can select an affine transformation and create a pair of unregistered images by performing the transformation on image two. As the affine transformation has been selected, it is known. Thus, one can train a model to regress the homography matrix corresponding to the affine transformation.

Thus, this paper considers the same setting as for few-shot change detection: 25% of each dataset is considered as labeled for training registration models - i.e. pairs are given registered - while the remaining images are randomly transformed or not provided by pair. During testing phase, homography matrix should be retrieved from a pair of images.

In order to avoid transformation artifact, only the rectangular crop of size 256x256 from the image center is kept for both original image 1 and transformed image 2. This ensures that the crop is filled by real pixel.

3. Methodology

3.1. Overview

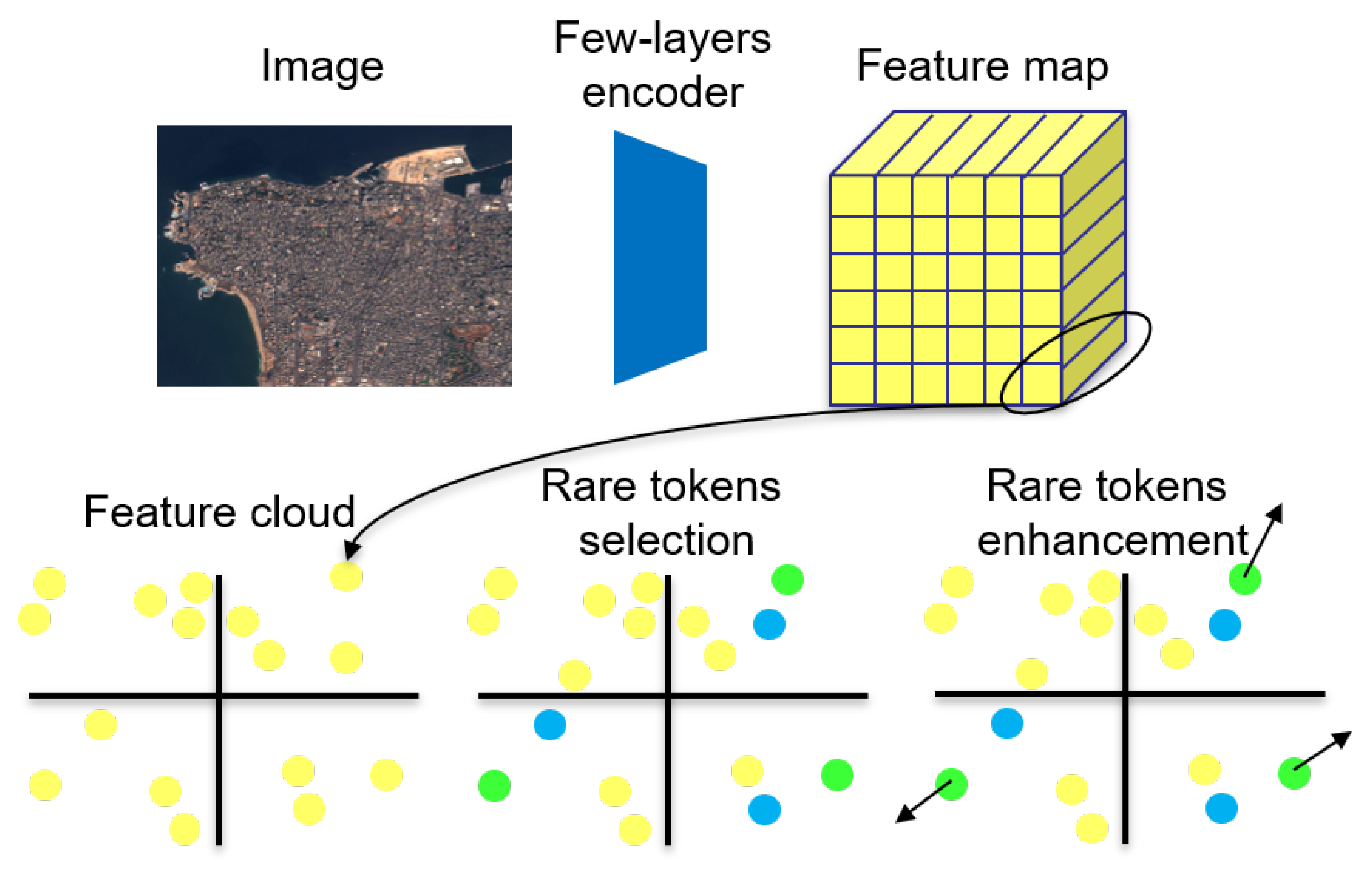
The pretext task considered in this paper is to force a small part of the tokens to be far from all other tokens. As the geometry of a token cloud is independent from the distance unit, all token clouds are scaled to be included in the unit hyper-sphere (by dividing by the maximal token norm).

Formally is

f_{1} (θ), . . ., f_{N} (θ)

are N tokens in dimension D (included in the D-sphere) extracted from one image by a few-layers encoder with weights

θ

, then, the related objective of making some tokens are distant to all others is described by eq(1):

max_{θ, \forall n, | | f_{n} (θ) | | \leq 1} max_{(i_{1} \neq . . . \neq i_{K}) \in {1, . . ., N}} \sum_{k \in {1, . . ., K}} min_{n \neq i_{k}} | | f_{i_{k}} (θ) - f_{n} (θ) {| |}^{2}

(1)

One important point is the selection of K features

i_{1}, . . ., i_{K}

with

K ≪ N

(typically

K = 10

), such that

f_{i_{k}}

is distant to all

f_{n}

(except himself i.e.

n \neq i_{k}

). Thus, all

f_{i_{k}}

f_{i_{k}^{'}}

have to be distant from each other and from all other

f_{n}

. But not-selected n can be close together. This last point (that banal token are not constrained) is a critical difference with classical contrastive learning: similar parts of the image have to lead to similar features and can not be made different - but rare tokens can be made distant to all others.

3.2. Greedy Strategy

This problem is not convex as one wants to optimize a distance between some points that should be selected. Yet, a greedy approach is to consider, for a given image, the currently most distant

i_{1}, . . ., i_{K}

, and, to enhance their distance to others. Indeed, for a frozen

θ

max_{(i_{1} \neq . . . \neq i_{K}) \in {1, . . ., N}} \sum_{k \in {1, . . ., K}} min_{n \neq i_{k}} | | f_{i_{k}} - f_{n} {| |}^{2}

can be trivially solved by:

computing $| | f_{i} - f_{j} {| |}^{2}$ $\forall i \neq j \in {1, . . ., N}$
computing $d_{i} = {min}_{j \neq i} | | f_{i} - f_{j} {| |}^{2}$ $\forall i \in {1, . . ., N}$
sorting ${1, . . ., N}$ decreasingly according to $d_{i}$
selecting the top-K

As, stochastic gradient descent will introduce a lot of noise in the selection of the next batch of images and in the optimization process, this greedy approach of enhancing the distance of the current most-far-points may in practice allows to enhance the rarity of all possible candidates.

Thus, in practice given

f_{1} (θ), . . ., f_{N} (θ)

, one will first compute I the set of size K of currently most distant features and J the corresponding closer neighbor, then,

max_{(i_{1} \neq . . . \neq i_{K}) \in {1, . . ., N}} \sum_{k \in {1, . . ., K}} min_{n \neq i_{k}} | | f_{i_{k}} - f_{n} {| |}^{2} = \sum | | f_{I} - f_{J} {| |}^{2}

Importantly, the computation of

I, J

can be done without retaining the gradient flow, only the computation of

\sum | | f_{I} - f_{J} {| |}^{2}

should kept the gradient. Yet, this last step only considers K tokens while computing I naively requires

N \times N

operations to compute the distance between each pair of tokens (despite some recent works claim to approximate efficiently those operations like Linformer [24]).

Algorithm 1:Compute_metric

(F, K)

1:: $N \leftarrow len (F)$
2:: $F \leftarrow \frac{F}{{max}_{n \in {1, . . ., N}} | | F_{n} | |}$
3:: $\forall i, j \in {1, . . ., N}, D_{i, j} \leftarrow | | F_{i} - F_{j} {| |}^{2}$
4:: $\forall i, j \in {1, . . ., N}, J_{i} \leftarrow sorting_permutation (D_{i})$
5:: $J \leftarrow J [:, 1]$ #remove distance to itself
6:: $D_{min} \leftarrow | | F - F_{J} {| |}^{2}$
7:: $I \leftarrow inverse_sorting_permutation (D_{min})$
8:: $I \leftarrow I_{{1, . . ., K}}$
9:: $J \leftarrow J_{I}$
10:: compute with gradient $L = 4 - \sum {(F_{I} - F_{J})}^{2}$
11:: return L

3.3. Loss

As the metric of the task is already smooth, the offered task can be trained with stochastic gradient descent just by considering loss of equation2

L (x, θ) = 4 - \sum | | F_{I_{x}} (x, θ) - F_{J_{x}} (x, θ) {| |}^{2}

(2)

where x is the current image, F the few-layers encoder and

I_{x}, J_{x}

are computed as pointed in subsection 3.2. The 4 in equation2 comes from the fact that the distances are computed after linear normalization of the features to force them to be in the unit disk, so the maximal square distance between two points is 4. The global flow for computing the main metric is provided in pseudo-code1.

This loss can be used either alone or following semi-supervised framework: given

x_{1}, x_{2}, y

a batch of pairs of images and their corresponding targets and

χ

a batch of unlabeled images, the final loss is

L (x_{1}, x_{2}, y, χ, θ) = L (x_{1}, x_{2}, y, θ) + L (χ, θ)

where L is the offered rarity loss and

L

is a task-specific loss e.g. change detection or homography matrix regression.

3.4. Implementations Detail

Experiments are performed with small frozen encoders being the 2 first block of EfficientNet-b5 or EfficientNetV2-s. A first linear layer is used to project the frozen encoder output into an useful embedding directly used by a task-specific head. Independently, an other linear layer prepares the feature map from the embedding for rarity loss (see Figure 2 for the semi-supervised framework or Figure 1 for detail on rarity loss):

For change detection, the head is inspired from deeplab architecture [25] applied on the difference of the features from the pair of images to highlight the areas with change (see Figure 1.a).
For registration, the task is homography matrix regression. For this purpose, an encoder used the difference of features from the pair of images to predict the homography matrix. Precisely, if $x_{1}$ is the feature map of image 1 with dimension $C \times H \times W$ and $x_{2}$ the one of image 2, then, the network computes $| | x_{1} [i] [j] - x_{2} [i + d i] [j + d j] | |$ for $d i, d j \in {- 1, 0, 1}$ in 9 independent channels, then, those 9 channels $Δ$ are normalized with $Δ = \frac{1}{Δ} \times \frac{1}{\sum \frac{1}{Δ}}$ resulting in a 9 channel $L_{1}$ normalized and independent from the scale of $x_{1}, x_{2}$ . The encoder which predicts $\hat{A}$ mainly considers those $9 \times 2$ channels ( $x_{1}$ over $x_{2}$ and $x_{2}$ over $x_{1}$ ).

Figure 2. Selected architecture for semi-supervised experiments: in both case a frozen encoder (sky blue) followed by a linear (blue) create a feature map. This feature map can be projected by a linear layer for rare token enhancement, or, used directly for change (a) or registration (b). Best seen in color.

4. Experiments

Except for S2Looking which is a larger dataset, experiments are performed at least 10 times and averaged over the best half. This best-half-mean makes sense in the way that a validation process may detect a poor convergence inviting to retry the training rather then to send a model for deployment. Thus, this metric prevents to focus on a very specific seed (value is at least the mean of 5 experiments) but discard bad models which will never really be considered as converged.

4.1. Registration

The Table 1 shows the mean square error (mse) of baseline vs baseline+rarity loss on homography matrix regression on OSCD, LEVIR and S2Looking.

The error reached are slightly lower for the offered semi-supervised method compared to the baseline. Considering that 0.01 of MSE on the affine matrix on 256x256 crops coarsely leads to 4 pixel errors, the difference of MSE is slight but relevant for fine registration.

4.2. Change detection

The Table 2 shows the intersection over union (IoU) metric of baseline vs baseline+rarity loss on change segmentation on OSCD and LEVIR. IoU is computed from confusion matrix by considering for each class the ratio of the true positive (i.e. pixels from the class correctly predicted for this class) over all pixels from the class + false alarm (all pixels not from the class but predicted as this class). Both mean IoU and IoU for class change are reported.

Due to unbalance, it is known that reaching a high change IoU is challenging. However, using the additional loss, change IoU increases slightly but consistently in all experiments with a peak of +4% with EfficientNet encoder on LEVIR. EfficientNet-b5 seems to perform better than EfficientNetV2-s. Yet, this may be explained by the fact that only the first layers of both are kept, hence cutting a more significant part of EfficientNetV2-s.

IoU is not reported on S2Looking as all methods performs poorly on this dataset: change IoU does not exceed 9% even with the addition of rarity loss. S2Looking contains many pairs of images with large color changes, making it challenging to extract semantic change with few layers only even if the size of the dataset is interesting for deep models.

4.3. Auxiliary results

4.3.1. EuroSAT

The offered framework has also been tested on EuroSAT for image classification. However, it under-performs the baseline on this task as pointed in Table 3: rarity loss leads to around 1% of accuracy drop.

Despite this result is not in favor of the offered task, it is understandable: the offered task only constraint the rare tokens. Thus, the representation of all banal tokens may collapse. Yet, to decide if an image is a forest, one needs a lot of banal forest tokens and not just 1 rare token of a specific tree close to a specific rock. For this reason, this result does not degrade the relevancy of the offered framework for registration or change detection.

4.3.2. Imagenet

Despite the offered pretext task has been proven useful for remote sensing data, it could be interesting to compare with very textured images. For this purpose, an experiment has been performed on rare token enhancement only: for this experiment there is no longer target task and the only goal is to seen how much the pretext task is correctly realized. Table 4 compares the distance between rare and banal tokens on both LEVIR, S2Looking and Imagenet (OSCD is not considered due to it small size allowing over-fitting of the pretext task).

Tokens are more easily separated on Imagenet than LEVIR or S2 while Imagenet is larger. This indicates that natural images (more textured than remote sensing ones) tends to contain more rare tokens. This is consistent with the fact that the offered self-supervised loss work better on LEVIR compare to S2Looking. This point invites to consider the offered pretext task on very high resolution remote sensing data (or natural image). Yet, this idea is not trivial as it would require to consider multi-scale tokens (despite some backbone like SWIN [26] may provide relevant encoding for such purpose).

Interestingly, qualitative visualization shows that the resulting rare tokens are more humanly understandable on Imagenet and match to some extend Harris corners (see example in Figure 3).

5. Conclusion

5.1. Summary

This paper presents a new pretext task which enhances the distance of rare visual tokens to other tokens in images. This framework is evaluated for both registration and change detection on OSCD, LEVIR and S2Looking datasets. While adding this task improves slightly the baselines, the improvement is consistent with a peak of +4% on LEVIR change IoU.

Future works would be required to explore more deeply this idea of rare token enhancement or derived version. However, this pretext task should be considered as it is frugal-friendly by design, and, it allows to advance on closing the gap between dense processing of images and salient point extraction.

5.2. Limits

One clear limit of the offered pretext task is that it seems not universal regarding the targeted task: by focusing on rare token only, this task may lead to a collapse of all banal tokens as pointed in EuroSAT image classification experiment where accuracy drop by 1%.

Future works should try to combine both token level and image level pretext tasks to offer self-supervised framework useful for all usages from classification to segmentation or registration.

Funding

This research received no external funding

Data Availability Statement

All datasets used in this paper are public. All details (like optimizer, learning rate) can be found in the source code which is available at github.com/delta-onera/delta_tb/tree/master/RARE_TOKEN_ENHANCEMENT. All experiments have been done on a A5000 nvidia GPU card, yet a GeForce RTX 4070 Ti should be enough.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. International conference on machine learning. PMLR, 2020, pp. 1597–1607.
Oquab, M.; Darcet, T.; Moutakanni, T.; Vo, H.; Szafraniec, M.; Khalidov, V.; Fernandez, P.; Haziza, D.; Massa, F.; El-Nouby, A.; others. Dinov2: Learning robust visual features without supervision. arXiv preprint arXiv:2304.07193 2023. [CrossRef]
Bardes, A.; Garrido, Q.; Ponce, J.; Chen, X.; Rabbat, M.; LeCun, Y.; Assran, M.; Ballas, N. V-jepa: Latent video prediction for visual representation learning. arXiv 2023.
Touvron, H.; Martin, L.; Stone, K.; Albert, P.; Almahairi, A.; Babaei, Y.; Bashlykov, N.; Batra, S.; Bhargava, P.; Bhosale, S.; others. Llama 2: Open foundation and fine-tuned chat models. arXiv preprint arXiv:2307.09288 2023. [CrossRef]
Ravi, N.; Gabeur, V.; Hu, Y.T.; Hu, R.; Ryali, C.; Ma, T.; Khedr, H.; Rädle, R.; Rolland, C.; Gustafson, L.; others. Sam 2: Segment anything in images and videos. arXiv preprint arXiv:2408.00714 2024. [CrossRef]
Li, H.; Kadav, A.; Durdanovic, I.; Samet, H.; Graf, H.P. Pruning filters for efficient convnets. arXiv preprint arXiv:1608.08710 2016. [CrossRef]
Sanh, V.; Debut, L.; Chaumond, J.; Wolf, T. DistilBERT, a distilled version of BERT: smaller, faster, cheaper and lighter. arXiv preprint arXiv:1910.01108 2019. [CrossRef]
Hu, Q.; Wang, P.; Cheng, J. From hashing to cnns: Training binary weight networks via hashing. Proceedings of the AAAI Conference on Artificial Intelligence, 2018, Vol. 32.
Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Advances in neural information processing systems 2012, 25.
Zhang, L.; Chen, C.; Bu, J.; Chen, Z.; Tan, S.; He, X. Discriminative codeword selection for image representation. Proceedings of the 18th ACM international conference on Multimedia, 2010, pp. 173–182.
He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778.
Liu, Z.; Mao, H.; Wu, C.Y.; Feichtenhofer, C.; Darrell, T.; Xie, S. A convnet for the 2020s. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2022, pp. 11976–11986.
Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; others. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv preprint arXiv:2010.11929 2020. [CrossRef]
Durrant-Whyte, H.; Bailey, T. Simultaneous localization and mapping: part I. IEEE robotics & automation magazine 2006, 13, 99–110. [CrossRef]
Labatut, P.; Pons, J.P.; Keriven, R. Efficient multi-view reconstruction of large-scale scenes using interest points, delaunay triangulation and graph cuts. 2007 IEEE 11th international conference on computer vision. IEEE, 2007, pp. 1–8.
Fitzpatrick, J.M.; Hill, D.L.; Maurer, C.R.; others. Image registration. Handbook of medical imaging 2000, 2, 447–513.
Avetisyan, A.; Xie, C.; Howard-Jenkins, H.; Yang, T.Y.; Aroudj, S.; Patra, S.; Zhang, F.; Frost, D.; Holland, L.; Orme, C.; others. SceneScript: Reconstructing Scenes With An Autoregressive Structured Language Model. arXiv preprint arXiv:2403.13064 2024.
DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superpoint: Self-supervised interest point detection and description. Proceedings of the IEEE conference on computer vision and pattern recognition workshops, 2018, pp. 224–236.
Helber, P.; Bischke, B.; Dengel, A.; Borth, D. Introducing EuroSAT: A Novel Dataset and Deep Learning Benchmark for Land Use and Land Cover Classification. IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium. IEEE, 2018, pp. 204–207.
Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. 2009 IEEE conference on computer vision and pattern recognition. Ieee, 2009, pp. 248–255.
Caye Daudt, R.; Le Saux, B.; Boulch, A.; Gousseau, Y. Urban Change Detection for Multispectral Earth Observation Using Convolutional Neural Networks. IEEE International Geoscience and Remote Sensing Symposium (IGARSS), 2018.
Chen, H.; Shi, Z. A spatial-temporal attention-based method and a new dataset for remote sensing image change detection. Remote Sensing 2020, 12, 1662. [CrossRef]
Shen, L.; Lu, Y.; Chen, H.; Wei, H.; Xie, D.; Yue, J.; Chen, R.; Lv, S.; Jiang, B. S2Looking: A satellite side-looking dataset for building change detection. Remote Sensing 2021, 13, 5094. [CrossRef]
Wang, S.; Li, B.Z.; Khabsa, M.; Fang, H.; Ma, H. Linformer: Self-attention with linear complexity. arXiv preprint arXiv:2006.04768 2020.
Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE transactions on pattern analysis and machine intelligence 2017, 40, 834–848.
Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. Proceedings of the IEEE/CVF international conference on computer vision, 2021, pp. 10012–10022.

Figure 1. Overview of the offered framework (best see in color): each image is converted into a feature cloud by a few-layers encoder, then, rare visual tokens are selected (green) and the loss tends to move them far from their nearest neighbors (in blue). Illustration image is from OSCD.

Figure 3. Example of outputs on Imagenet images. Boxes are the top-7 selected tokens, green point are Harris corners extracted with default scikit-image params. Best seen when not printed.

Table 1. Mean square error on OSCD, LEVIR and S2Looking of the registration baseline (EfficienNet or EfficientNetV2) vs the same baseline with an additional head performing rare token enhancement from a common embedding (see Figure 2b).

%	OSCD	LEVIR	S2Looking
Baseline	0.02642196	0.009819713	0.00814459
Baseline + rarity loss	0.024850774	0.00957441	0.0076796
Baseline V2	0.025716013	0.009981078	0.0096835742
Baseline V2 + rarity loss	0.023570214	0.009831453	0.009405145

Table 2. Mean IoU and change IoU on OSCD and LEVIR for the baseline (EfficientNet or EfficientNetV2) and for the same baseline with rare token enhancement from a common embedding (see Figure 2a).

	OSCD		LEVIR
%	mIoU	IoU1	mIoU	IoU1
Baseline	57.39	22.35	53.13	12.38
Baseline + rarity loss	58.38	25.38	55.47	17.28
Baseline V2	57.54	22.21	54.19	14.61
Baseline V2 + rarity loss	59.07	25.31	54.60	16.15

Table 3. Accuracy on Eurosat for both baseline and baseline+rarity loss (with both EfficientNet and EfficientNetV2 encoder).

%	EfficientNet	EfficientNetV2
Baseline	77.54	72.14
Baseline + rarity loss	76.51	71.02

Table 4. Mean square distance between rare tokens and other tokens on LEVIR, S2Looking and Imagenet (after projection on the unit hyper-sphere).

Encoder	LEVIR	S2Looking	Imagenet
EfficientNet	0.6869364	0.6563601	0.797317505
EfficientNetV2	0.6720152	0.64909315	0.7725842

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Rare Visual Token Enhancement Improves Registration and Few-Shot Change Detection in Remote Sensing Data

Abstract

1. Introduction

2. Related Works and Datasets

2.1. Sparsity in Image Classification

2.2. Sparsity for vision based geometry

2.3. Datasets

2.3.1. Change Detection

2.3.2. Synthetic Registration

3. Methodology

3.1. Overview

3.2. Greedy Strategy

3.3. Loss

3.4. Implementations Detail

4. Experiments

4.1. Registration

4.2. Change detection

4.3. Auxiliary results

4.3.1. EuroSAT

4.3.2. Imagenet

5. Conclusion

5.1. Summary

5.2. Limits

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe