Prerpints.org logo
Preprint
Article

Multi-UAV Escape Target Search: A Multi-Agent Reinforce-ment Learning Method

Altmetrics

Downloads

74

Views

40

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

13 September 2024

Posted:

14 September 2024

You are already at the latest version

Alerts
Abstract
The multi-UAV target search problem is crucial in the field of autonomous Unmanned Aerial Vehicle (UAV) decision-making. The algorithm design of Multi-agent Reinforcement Learning (MARL) methods has become integral to research on multi-UAV target search, due to its adaptability to the rapid online decision-making required by UAVs in complex, uncertain environments. In non-cooperative target search scenarios, targets may have the ability to escape, complicating UAVs' search efforts and hindering the convergence of the MARL algorithm training. This paper investigates the multi-UAV target search problem in scenarios involving static obstacles and dynamic escape targets, modeling the problem within the framework of Decentralized Partially Observable Markov Decision Process. Based on this model, a Spatio-Temporal Efficient Exploration network and a Global Convolutional Local Ascent mechanism are proposed. Subsequently,we introduce a Multi-UAV Escape Target Search Algorithm Based on MAPPO(ETS-MAPPO) for addressing the escape target search difficulty problem. Simulation results demonstrate that the ETS-MAPPO algorithm outperforms five classical MARL algorithms in terms of the number of target searches,the area coverage rate, and other metrics.
Keywords: 
Subject: Engineering  -   Transportation Science and Technology

1. Introduction

In recent years, unmanned aerial vehicles (UAVs) have found applications in various military and civilian domains due to their advantages, such as high mobility, accessibility, convenient deployment, and low cost. They have gradually become indispensable in modern society, with roles in civil sectors such as agriculture [1,2], mineral exploration [3], and forest rescue [4], as well as in military reconnaissance [5] and strikes [6]. Multi-UAV target search problem is a significant issue in autonomous UAV decision-making and has garnered extensive academic attention recently. Multi-UAV target search involves UAVs using on-board detection equipment to reconnoiter designated areas and share information via a communication network, thereby jointly capturing targets. Currently, three primary methods are used for multi-UAV target search. The first category is pre-planning methods, such as partition search [7] and formation search [8]. These methods essentially transform the target search problem into a planning problem with area coverage, offering high reliability and easy evaluation of the solution results. However, they require a known mission area model in advance, involve longer planning times, and are not highly adaptive to dynamic environmental changes. The second category is online optimization methods, which approximate the search problem as a real-time objective function optimization problem and typically employ traditional or heuristic algorithms, such as ant colony algorithms [9] and genetic algorithms [10]. These methods are better adapted to environmental dynamics than pre-planning approaches, but depend on a central node for decision-making and exhibit low adaptability in distributed environments. The third category is Multi-Agent Reinforcement Learning (MARL) methods, which model the problem as a Partially Observable Markov Decision Process (POMDP) and use algorithms based on the MARL framework. These methods enable agents to learn and optimize behavior through interaction with the environment and other agents, allowing adaptation to dynamic changes and rapid decision-making [11,12]. The primary challenge lies in designing the algorithm training architecture, agent exploration mechanism, and reward function tailored to specific task requirements.
Currently, the design of MARL methods is a prominent focus in multi-UAV target search research. Within the MARL framework, Shen et al. [13] proposed the DNQMIX algorithm, which enhances search rate and coverage. Lu et al. [14] proposed the MUICTSTP algorithm, demonstrating superior performance in terms of anti-interference and collision avoidance. Yu et al. [15] proposed the Multi-Agent Proximal Policy Optimization (MAPPO) algorithm, which has exhibited excellent performance in multi-agent testing environments and is regarded as one of the most advanced algorithms available. Wei et al. [16] combined the MAPPO algorithm with optimal control (OC) and GPU parallelization to propose the OC-MAPPO algorithm, which accelerates UAV learning.
To better describe environmental uncertainty, Bertuccelli et al. [17] proposed a probabilistic approach that divides the task area into units, each associated with the probability of target presence, establishing a target probability graph. This method has achieved good results in target search and is widely recognized. Building on the MARL framework and the target probability graph, Zhang et al. [18] designed a confidence probability graph using evidence theory and proposed a Double Critic DDPG algorithm. This approach effectively balances the bias in action-value function estimation and the variance in strategy updates. Hou et al. [19] converted the probability function into a grid-based goal probability graph and proposed a MADDPG-based search algorithm, improving search speed and avoiding collisions and duplications.
Multi-UAV target search has made some progress at this stage, but two challenges remain. Firstly, the utilization of sample data remains inefficient, and balancing utilization and exploration presents a challenge. Existing MARL algorithms primarily employ neural networks such as fully connected networks and convolutional networks, which fail to simultaneously achieve efficient utilization of temporal and spatial information in the sample data, and also lack effective environmental exploration. Secondly, the behavioral modeling of dynamic targets is relatively simple, and existing work primarily considers changes in the target's position over time, often transforming the target search problem into a target tracking problem. In actual non-cooperative target search scenarios, targets may exhibit escape behavior, actively changing their position to evade detection and potentially using environmental blind spots to hide, preventing real-time tracking by UAVs. Addressing the challenges identified above, this paper investigates the Multi-UAV Escape Target Search (METS) problem in complex environments. The contributions of this paper are summarized as follows:
  • The simulation environment for the METS problem is constructed, introducing a Target Existence Probability Map (TEPM), and an appropriate probability update method is employed for the escaping target. Based on the TEPM, a Local State Field of View is designed, with local state values obtained through entropy calculation. Additionally, a new state space, action space, and reward function are devised within the framework of Decentralized Partially Observable Markov Decision process (DEC-POMDP). Ultimately, a model that addresses the METS problem is established.
  • To enhance the MARL algorithm's ability to process spatio-temporal sequence information and improve environmental exploration, this paper propose the Spatio-Temporal Efficient Exploration (STEE) network, constructed using a Convolutional Long Short-Term Memory network and a Noise network. This network is integrated into the MAPPO algorithm, and its impact on the overall performance of the MAPPO algorithm is validated.
  • For searching the escape target in the METS problem, the Global Convolutional Local Ascent (GCLA) mechanism is proposed. A Multi-UAV Escape Target Search Algorithm Based on MAPPO (ETS-MAPPO) is introduced by combining the STEE network. This algorithm effectively addresses the challenges of searching for escape target, and experimental comparisons with five classical MARL algorithms show significant improvements in the number of target searches, the area coverage rate, and other metrics.
The remaining chapters of this paper are organized as follows: Section 2 defines the system model and provides a mathematical formulation of the METS problem. Section 3 introduces the ETS-MAPPO algorithm within the MARL framework and describes it in detail. In Section 4, experiment results are presented to validate the effectiveness of ETS-MAPPO. Section 5 concludes the paper and outlooks the future research.

2. System Model and Problem Formulation

2.1. System Model

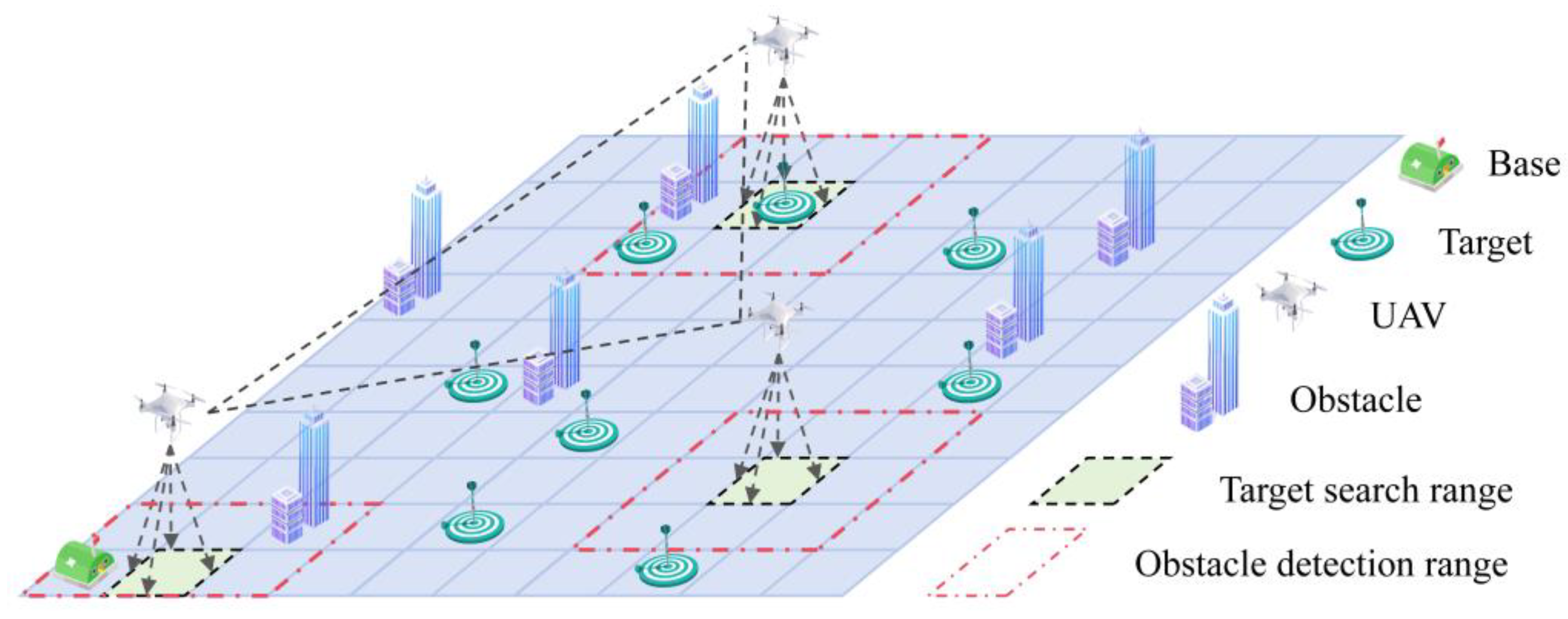
A typical multi-UAV escape target search mission scenario is shown in Figure 1. Assuming that several escape targets and fixed obstacles are distributed within an unknown mission area Ω , N u UAVs depart from the base and cooperatively search the area. The mission requires UAVs to capture as many escape targets as possible, maximize coverage of mission area Ω , and avoid collisions with obstacles to the greatest extent possible.

2.1.1. Mission Area Model

Considering the need for relative stability in the operation of the UAV detection payload, the UAV is set to maintain a constant flight altitude during target search operations in the mission area Ω [20]. In this scenario, the mission area Ω is conceptualized as a two-dimensional plane with two layers, where the UAV operates in the upper layer. Escape targets are positioned on the ground in the lower layer of the mission area. Obstacles are distributed across both the upper and lower layers.
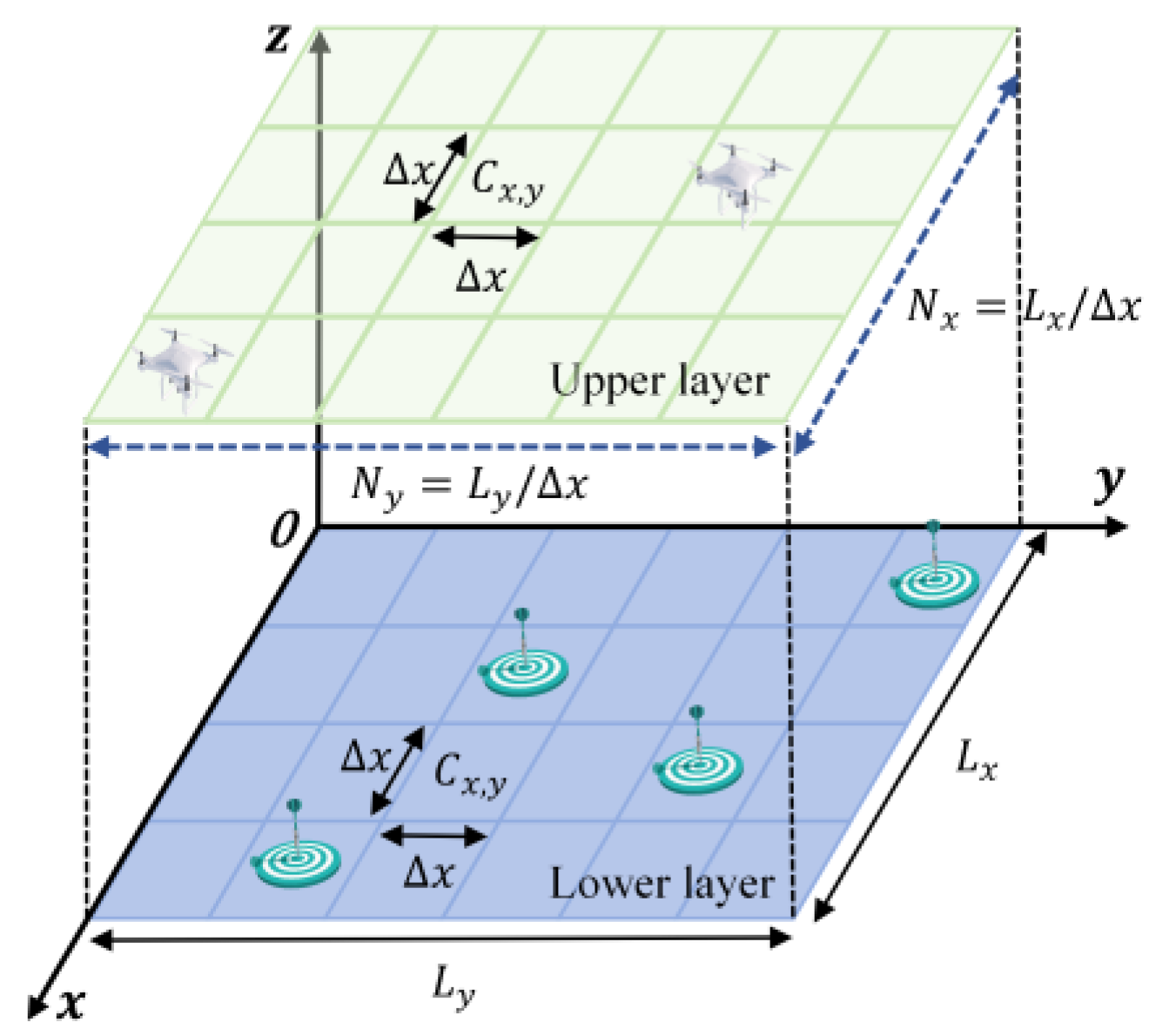
In Figure 2, each layer is a rectangular region L x × L y , which is rasterized into a cellular grid N x × N y , with each cell having an area of S = Δ x × Δ x . The positional coordinates of any cell C x , y in the Cartesian coordinate system are denoted by Equation (1).
C ( x , y ) = { ( x , y ) | x ∈ [ 1 , ​   N x ] , y ∈ [ 1 , ​   N y ] }

2.1.2. Unmanned Aerial Vehicle Model

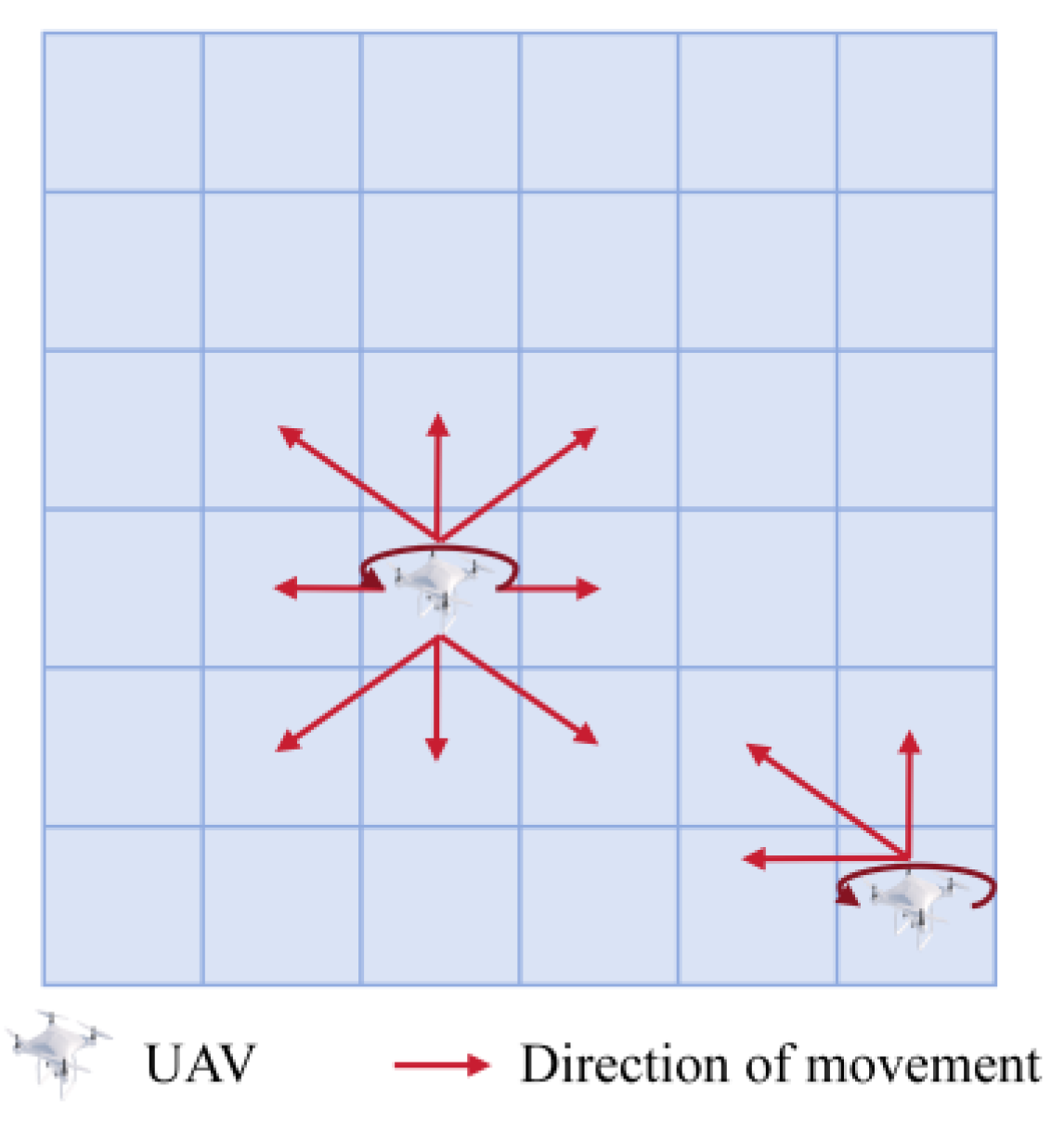
To facilitate the study, the motions of N u identical quadrotor UAVs are modeled as depicted in Figure 3. The UAVs are capable of discrete movements with a total of 9 degrees of freedom: left up, up, right up, left down, down, right down, left, right, and stationary.
The UAVs are equipped with a detection payload for target identification, with a detection range of L t a r g e t . In the rasterized mission area model, this detection range is mapped to n u = L t a r g e t / S cells. Assuming no omissions or false detections by the detection payload, it is considered that the UAVs can correctly identify a target within a cell at time t with a probability p . The UAVs'detection range for stationary obstacles is L o b s t a c l e , which is mapped to n o = L o b s t a c l e / S cells.

2.1.3. Escape Target Model

In the METS mission, the mission area contains N t escape targets, each of which can be in one of two states: stationary or escaping. These targets can detect UAVs within a detectable range of L u a v , which is mapped to cells n t = L u a v / S . Initially, each escape target remains stationary, meaning it maintains its current position while detecting UAVs. When a UAV enters the detection range of an escape target, the escape target transitions from the stationary state to the escaping state. In the escaping state, the escape target engages in active concealment, releases false information to the UAV, and chooses a movement distance L c h a n g e in a random direction with probability P c , mapped to n c = L c h a n g e / S cells, or remains stationary with probability 1 − P c , within the escape time step T c h a n g e . The escape target returns to the stationary state at the end of the escaping state.

2.1.4. Target Existence Probability Map Model

In the METS problem, at the start of each search cycle, a probability distribution function is employed to model the target's location information. In the rasterized mission area, the probability function is transformed into a cell-based Target Existence Probability Map (TEPM), with each cell having an associated target existence probability b x , y ∈ [ 0 , 1 ] . The initial target existence probability for all cells in the TEPM is set to b x , y ( 0 ) = 0.5 , indicating that the UAVs lack any a priori information about target presence in the mission area.
As the UAVs continuously search the mission area, their detection payload scan for target information along the path, and the TEPM is probabilistically updated based on this detection information. We use a Bayesian update model to update the TEPM. When the UAV scans cell C x , y at time t , the probability update for the target appearing in cell C x , y is given by Equation (2) [21]. If multiple UAVs scan cell b x , y simultaneously, the probability value is updated correspondingly for each scan.
b x , y ( t ) = p s b x , y ( t − 1 ) p s b x , y ( t − 1 ) + ( 1 − p s ) ( 1 − b x , y ( t − 1 ) )
where p s is the correct probability p of the UAV's detection payload in detecting a target in cell C x , y . If no targets exist, p s is substituted with 1 − p .

2.2. Formulation of the Problem

In the METS mission, the UAVs begin at a base position and make operational decisions based on state information, aiming to explore the unknown mission area and search for the escape targets as extensively as possible. Consequently, the objective function is defined to maximize the exploration degree f 1 of the entire region while also maximizing the number of target searches f 2 , as represented in Equation (3).
f 1 = ∑ x = 1 N x ∑ y = 1 N y b x , y ( t ) − p max f 2 = ∑ x = 1 N x ∑ y = 1 N y 1 , b x , y ( t ) > ε
where ε is the confidence level of the target's existence in a cell, and p max is the maximum uncertainty value.
Considering the UAV's motion is constrained by the mission area's boundaries, the boundary condition for the UAV at position u i , t ( x , y ) is expressed in Equation (4).
1 ≤ u i , t ( x ) ≤ N x , ∀ u ∈ U 1 ≤ u i , t ( y ) ≤ N y , ∀ u ∈ U
Additionally, it is essential to consider that the UAV should avoid collisions with obstacles, with the collision constraint expressed in Equation (5).
B k ( x , y ) − u i , t ( x , y ) > d s a f e , k ∈ { 1 , 2 , ... , N B }
where B k ( x , y ) is the position of obstacles k , d s a f e is the safety distance, and N B is the number of obstacles.
The collision constraint is subsequently transformed into the optimization objective of the objective function f 3 , as expressed in Equation (6).
f 3 = ∑ i = 1 N u ∑ k = 1 N B 1 , B k ( x , y ) − u i , t ( x , y ) ≤ d s a f e
Finally, the METS problem is formulated as an optimization problem with an objective function, as represented in Equation (7).
max   f 1 +   f 2 −   f 3 s . t .   1 ≤ u i , x ( t ) ≤ N x , ∀ u ∈ U           1 ≤ u i , y ( t ) ≤ N y , ∀ u ∈ U

3. Multi-UAV Escape Target Search Approach on MARL

In this section, the optimization problem presented in Equation. 7 is firstly reformulated within the framework of DEC-POMDP based on MARL methods. The state space of UAVs and the reward function are then defined according to the TEPM. Finally, the ETS-MAPPO algorithm is proposed, and its framework is detailed.

3.1. Decentralized Partially Observable Markov Decision Process

In the METS, an extended form of the POMDP is presented as the DEC-POMDP to model the optimization problem [22], considering multiple UAVs and decentralized decision-making. The DEC-POMDP is defined by the tuple ( N , O , A , S , F s , F o , R , γ ) .
  • N is the number of UAVs.
  • O = { O 1 , … , O N } is the joint observation space, which consists of the observation state space O i of all UAVs.
Based on the UAV modeling in Section II, it is assumed that each UAV has a Local State Field of View (LSFV) that corresponds to the obstacle detection range, i.e., n o cells. By extracting the target probability information of n o cells near the UAV's location on the TEPM, the local state value of the LSFV is calculated at each time step t. The extracted cell uncertainty ux,y(t) is calculated as the Shannon entropy, serving as the local state value of the LSFV, as defined in Equation (8). Additionally, the local state value of the cell where an obstacle is detected is set to -1.
u x , y ( t ) = H [ b x , y ( t ) ] = − b x , y ( t ) log 2 b x , y ( t ) − ( 1 − b x , y ( t ) ) log 2 ( 1 − b x , y ( t ) )
In the METS mission, it is considered that the communication between individual UAVs is unrestricted, and individual UAVs are able to obtain the current position information of other UAVs and TEPM for assisting decision-making at the moment of decision-making. Therefore, the observation state space o i , t of UAV i consists of four parts, as defined in Equation (9).
o i , t = { P t , D t , l o c t , u , l o c t , u ¯ }
where P t is the TEPM at time t , D t is the LSFV of the UAV, l o c t , u is the position of the UAV, and l o c t , u ¯ is the position of the other UAVs.
3.
A = { A 1 , … , A N } is the joint action space, which consists of each UAV i choosing action a i , t ∈ A i based on its own observed state space o i , t .
4.
S is the state space of the environment, s t ∈ S is the state of time slot t .
5.
F o ( s t , a t − 1 ) = P ( o t = o | s t , a t − 1 ) is the observation probability function.
6.
F s ( s t , a t ) = P ( s t + 1 = s | s t , a t ) is the state transition probability function.
7.
R is the reward function, consisting of three components: a escape target search reward J T ( t ) , a environment search reward J E ( t ) , and a collision prevention reward J C ( t ) . Weighting coefficients ω 1 , ω 2 , and ω 3 are applied to balance these three components, as defined in Equation (10).
R ( t ) = ω 1 J T ( t ) + ω 2 J E ( t ) + ω 3 J C ( t )
The escape target search reward J T ( t ) is rewarded based on both the initial discovery of targets and the subsequent rediscovery of these targets. The search for an escape target in cell C x , y at time step t is evaluated as described in Equation (11). If the probability of a target's existence in cell C x , y exceeds a threshold ε, the target is considered to be present in that cell
β x , y ( t ) = 1   , b x , y ( t ) > ε 0   ,   e l s e  
The evaluation process for determining the existence of an escape target in a cell, initially and in subsequent evaluations, is represented by β x , y 1 ( t ) and β x , y 2 ( t ) . Therefore, the escape target search reward is calculated as shown in Equation (12).
J T ( t ) = ∑ x , y ∈ T 1 β x , y 1 ( t ) ∗ r t 1 + ∑ x , y ∈ T 2 β x , y 2 ( t ) ∗ r t 2
where T 1 and T 2 are the sets of locations where the escape target was initially discovered and subsequently rediscovered, respectively. r t 1 and r t 2 are the reward factors for the initial discovery and subsequent rediscovery of the escape target, respectively.
The environment search reward J E ( t ) quantifies the extent of environmental exploration and is determined by the change in cell uncertainty ux,y(t) over time, as represented in Equation (13).
J E ( t ) = ∑ x = 1 N x ∑ y = 1 N y u x , y ( t ) − u x , y ( t + 1 )
The collision prevention reward J C ( t ) is defined as the condition in which the distance between the UAV and an obstacle falls below a safe threshold, as represented in Equation (14).
J C ( t ) = r c * ∑ i = 1 N u ∑ k = 1 N B 1 , B k − u i , t ( x , y ) ≤ d s a f e
where r c is the collision penalty factor.
8.
γ ∈ ( 0 , 1 ] is the reward discount factor.

3.2. Multi-UAV Escape Target Search Algorithm Based on MAPPO

In a Multi-agent environment, the MAPPO algorithm [15] demonstrates superior adaptability and stability in strategy optimization compared to other MARL algorithms. To address the METS problem, we propose the Multi-UAV Escape Target Search Algorithm Based on MAPPO (ETS-MAPPO), which includes two key components: First, the Spatio-Temporal Efficient Exploration Network (STEE) to enhance the MAPPO algorithm's capability in processing spatio-temporal sequence information and exploring the environment. Second, the Global Convolution and Local Ascent Mechanism (GCLA) to overcome challenges posed by the variability of the escape target and the weak directionality of state inputs.

3.2.1. Spatio-Temporal Efficient Exploration Network

The MARL algorithm focuses on both data utilization and environmental exploration when solving search problems. Utilization refers to the agent selecting the action that maximizes the reward from previous actions, while exploration involves the agent choosing a new, untested action in anticipation of a higher reward. Balancing utilization and exploration poses a significant challenge in reinforcement learning [23], particularly in complex environments with multiple state inputs and sparse rewards.
In the MARL, empirical data contains both temporal and spatial information. Temporal information includes state dynamics, action continuity, and reward latency, while spatial information encompasses environmental complexity, relative UAV positions, and target distribution. Current approaches to data utilization commonly employ recurrent neural networks, such as LSTM [24] and GRU [25], for temporal data processing. Spatial data is primarily processed using convolutional neural networks, such as GCN [26] and HGCN [27]. These networks face challenges in efficiently processing both temporal and spatial information. 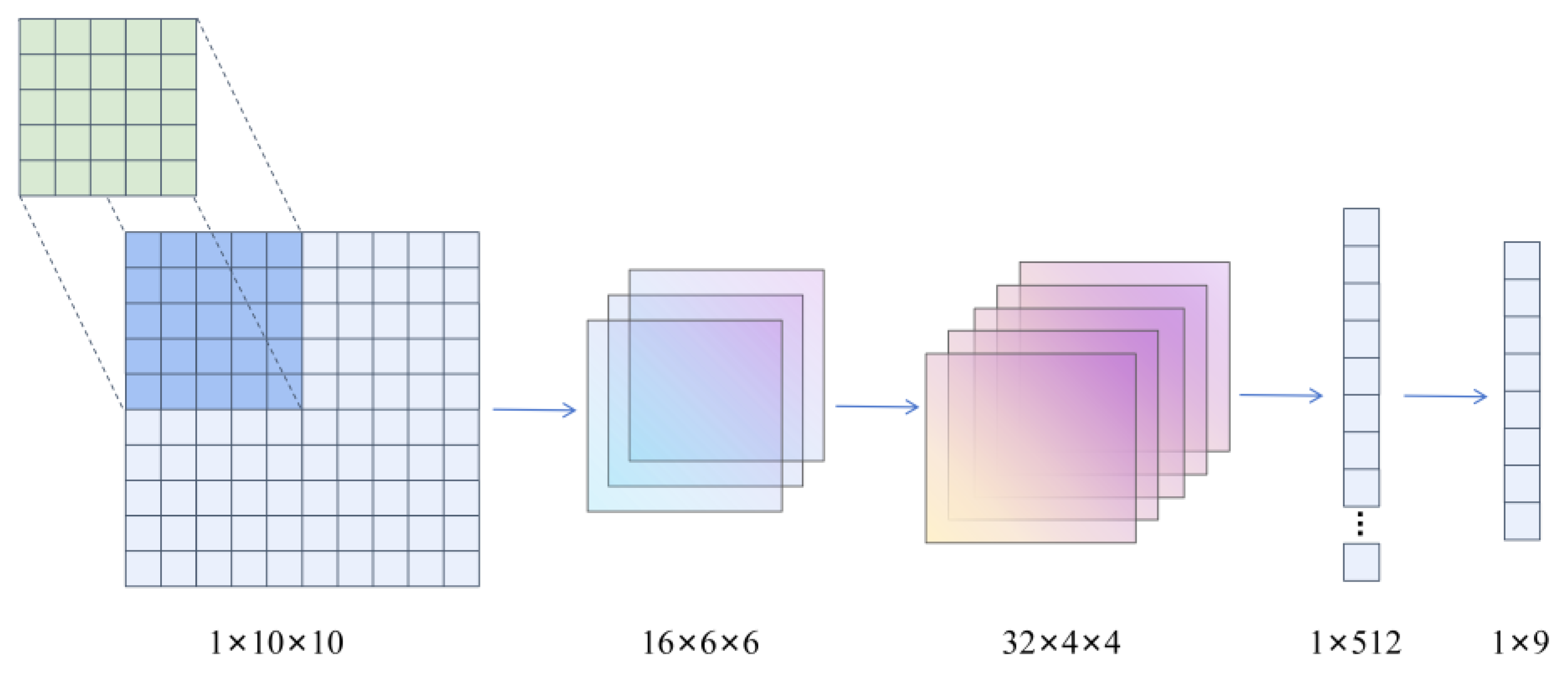As a solution, Convolutional Long Short-Term Memory Network (ConvLSTM) [28], which combine convolutional operations with memory networks, were introduced.The ConvLSTM network can capture both spatial and temporal features, thereby enhancing the performance of MARL algorithms. However, the ConvLSTM network lacks strong environment exploration capabilities, necessitating improvements in this area. Currently, MARL algorithms employ epsilon-greedy and entropy regularization strategies for exploration, which introduce noise to agents' actions, but often result in low exploration efficiency. This paper proposes using the Noise Network, which adds parameterized noise to the neural network, thereby improving the exploration efficiency of MARL algorithms and preventing them from converging to local optima.
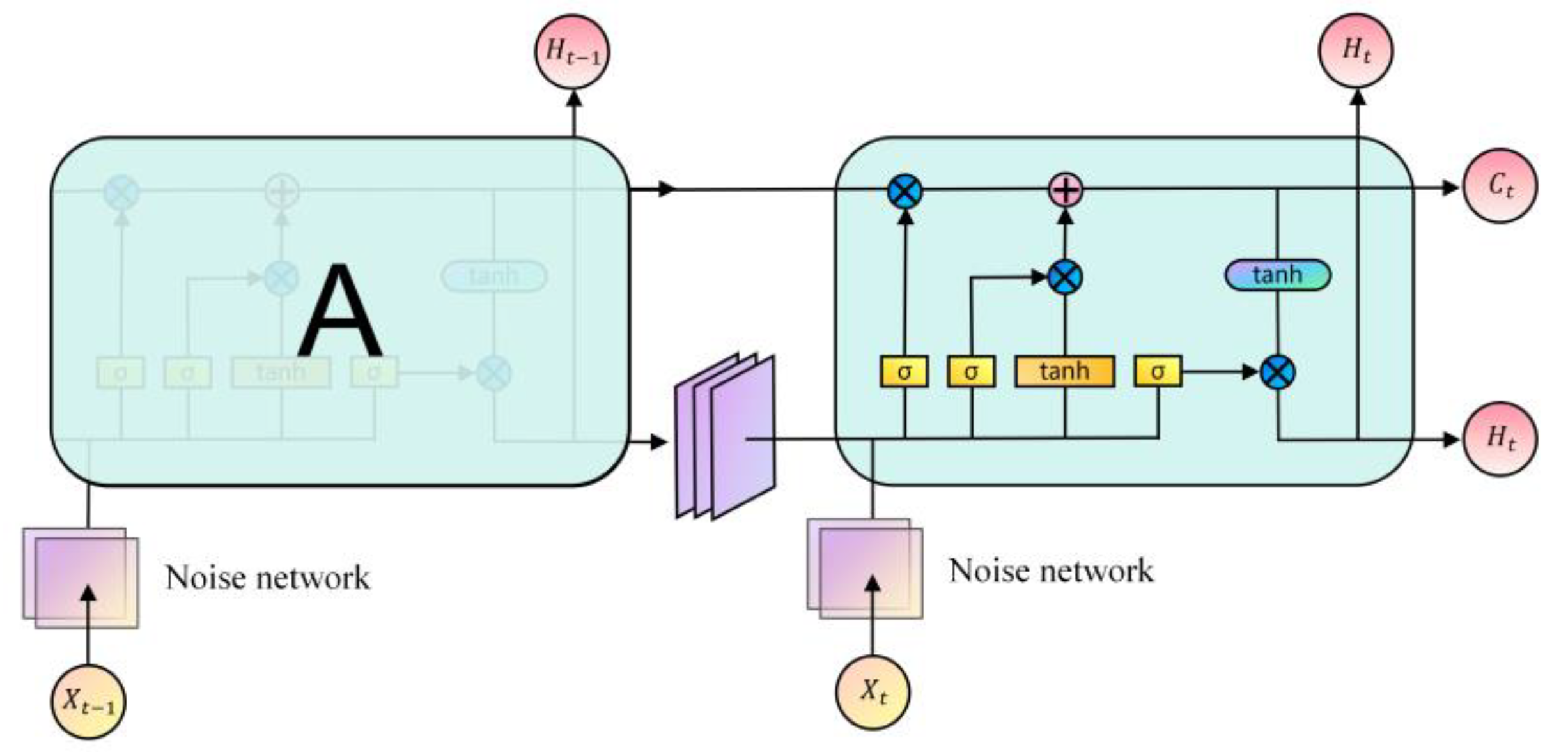
This paper proposes the STEE network architecture, which integrates the ConvLSTM network's efficient processing of spatio-temporal sequential information with the Noise network's effective environmental exploration. The STEE network architecture is illustrated in Figure 4. Data is first normalized with features and then fed into the Noise network to process state data features. The output from the Noise network is then used as the input for the ConvLSTM network unit, and the final output of the STEE network is obtained through a multi-layer ConvLSTM network unit.
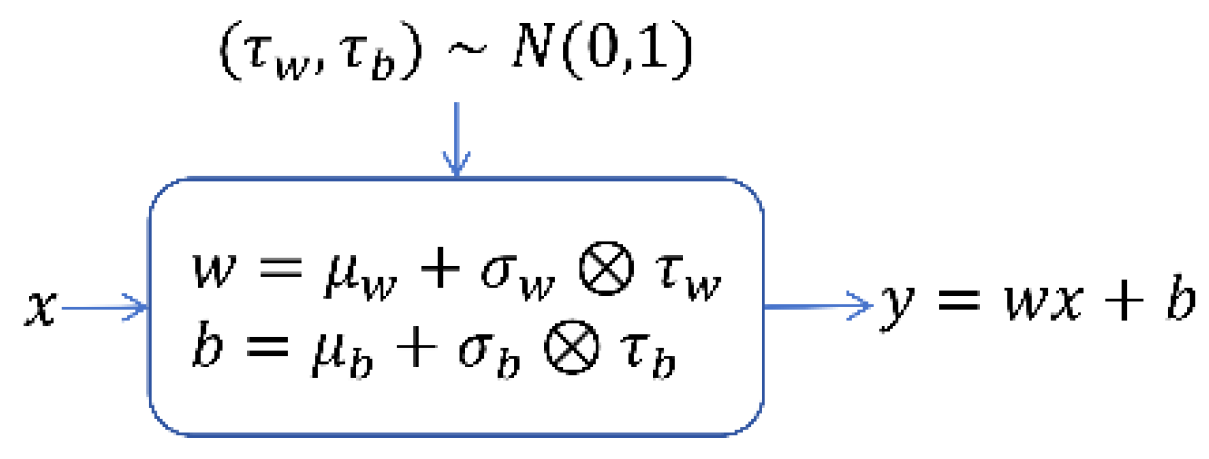
The ConvLSTM network unit is used to capture spatio-temporal data, enabling the modeling of dynamic environmental changes and long-term dependencies on historical information. The ConvLSTM network unit structure primarily comprises forget gate, input gate, memory cell, and output gate.The Noise network is a fully connected neural network that incorporates parameterized noise, as depicted in Figure 5, allowing the STEE network to continuously learn the mean μ and variance σ of w , b during the training process.

3.2.2. Global Convolution Local Ascent Mechanism

In the METS problem, the escape target initially remains stationary and only enters the escaping state after detecting the UAV. During the escaping state, the target takes random actions, leading to positional changes and increased environmental instability. Under the existing mechanism, each UAV observes a larger number of state space parameters than the TEPM's N x × N y , but these state parameters are sparse and lack clear directionality, offering no advantage in searching for the escape target. The UAV's limited ability to capture changes in the escape target's location hinders its ability to relocate the target, resulting in poor network convergence.
Currently, there is insufficient research on the poor convergence of networks due to target escape. This paper proposes the GCLA mechanism, which employs a global TEPM convolution operation and a target local area uncertain probability ascent operation to enhance both the capability to capture escaping targets and the convergence of the algorithmic network.
The global TEPM convolution operation optimizes the state parameters of the TEPM's N x × N y into a set of values 1 × 9 through convolution and inputs them into the network. This operation aims to divide the entire task area into nine orientation zones to capture global direction guidance information. The TEPM convolution operation for the state parameters 10 × 10 is illustrated in Figure 6.
The target local area uncertain probability ascent operation involves increasing the uncertain probability of the target local area, accounting for its escape behavior ,after the initial search of the escape target. To enhance the UAV's ability to re-search the area of location from which the target may have escaped, the operation increases the uncertain probability p ( t ) at a specific rate within the escaped area, defined as the area spanning n c cells around cell C x , y , as calculated in Equation (15). Subsequently, the TEPM is updated based on this revised uncertain probability within the escaped area.
C ( x ′ , y ′ ) = C ( x + i , y + i ) , i = [ − n c , n c ] p x ′ , y ′ ( t ) = p max + p x ′ , y ′ ( t − 1 ) e − τ t
where p x ′ , y ′ ( t ) is the uncertain probability of target existence at C x ′ , y ′ at time t , and τ is the ascent rate.
After processing with the GCLA mechanism, the UAV's observation state space o i , t is reformulated as shown in Equation (16).
o i , t = { P ′ t , D t , C t , l o c t , u , l o c t , u ¯ }
where C t is the result following the convolution operation on the TEPM and P ′ t is the updated TEPM.

3.3. ETS-MAPPO Algorithmic Framework

The ETS-MAPPO algorithm builds upon the foundational architecture of MAPPO, incorporating the STEE network and the GCLA mechanism.
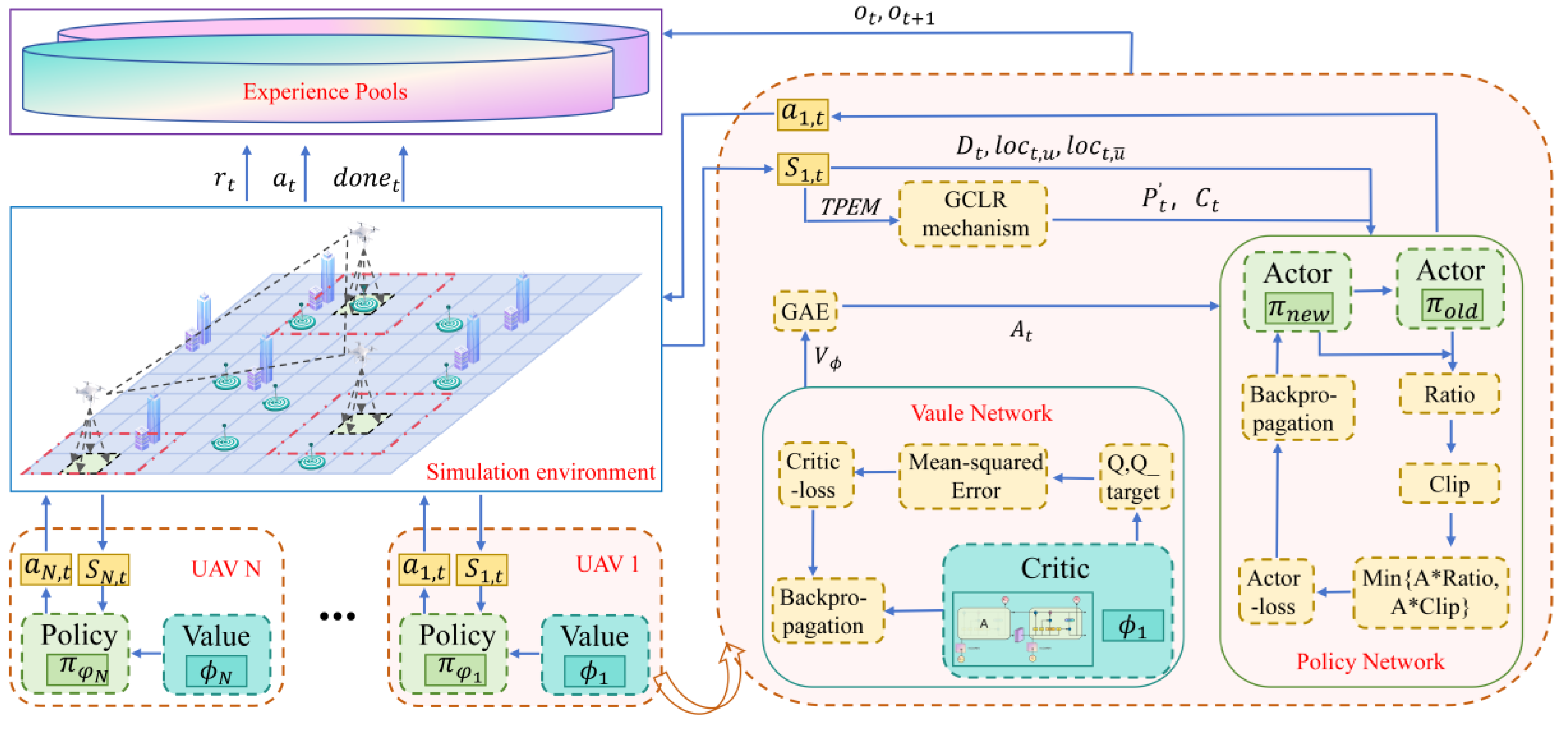
As shown in Figure 7, the algorithm adopts the Actor-Critic network architecture and applies the Centralized Training and Decentralized Execution framework to solve the DEC-POMDP. Through interaction between the UAV and the simulation environment, empirical data is generated and stored in experience pools, from which the UAV extracts data to calculate the Actor and Critic network losses. The Backpropagation algorithm is then employed to update these networks, enabling centralized training. Each UAV obtains observation state data from the environment and processes it through the GCLA mechanism. Based on the current Actor network, these UAVs then select actions to interact with the simulation environment, thereby enabling decentralized execution.
The pseudocode for the ETS-MAPPO algorithm is provided in Algorithm 1. This algorithm primarily focuses on optimizing the Actor and Critic networks. The Actor network is designed to learn mapping function π φ from the observed state space O t to the action a t , and is constructed using a fully connected neural network. To avoid over-modification of the objective values, the Actor network is implemented by optimizing a cropped alternative objective function L t ( θ ) as shown in Equation (17).
L t ( θ ) = E { min [ r t ( θ ) A t , c l i p ( r t ( θ ) , 1 − ε , 1 + ε ) A t ] + σ S [ π θ ( O t ) ] }
where θ is the parameter of the Actor network, r t ( θ ) is the ratio of the new strategy to the old one, A t is General Advantage Estimation (GAE), c l i p ( ⋅ ) is the cropping function, ε ∈ [ 0 , 1 ] is the truncation factor, S [ π θ ( O t ) ] is the entropy of the strategy π θ ( O t ) , and σ is the hyper-parameter controlling the entropy coefficient.
The calculation of GAE is based on Temporal Difference (TD) error δ t , as defined in Equation (18).
δ t = r t + γ V ϕ ( s t + 1 ) − V ϕ ( s t )
where r t is the reward, γ is the discount factor, and V ϕ ( s t ) is the value function of the Critic network at time step t .
The GAE estimates the dominance function A t G A E ( λ ) by considering the TD errors for k time steps forward from the current time step t and performing a weighted summation of them. The specific weighted summation expression is provided in Equation (19).
A t G A E ( λ ) = 1 − λ δ t + λ δ t + 1 + ⋯ + λ k − 1 δ t + k − 1
where B is the hyperparameter of TD error weights at different time steps.
The purpose of the Critic network is to learn the mapping function V ϕ from the state space S t to real values, constructed using the STEE network. The Critic network optimizes the network parameters using the mean square error loss function L t ( ϕ ) , with its expression provided in Equation (20).
L t ( ϕ ) = E { max [ ( V ϕ ( s t ) − R ^ t ) 2 , ( c l i p ( V ϕ ( s t ) , V ϕ o l d ( s t ) − ε , V ϕ o l d ( s t ) + ε , ) − R ^ t ) 2 ] }
where ϕ is the Critic network parameters and R ^ t is the discount reward.
Algorithm 1: ETS-MAPPO
Initialization: The Actor network parameters and the Critic network parameters for each UAV, and other relevant parameters
1.For episode = 1,2,…,M do.
2.Reset environment state：x ← env.reset()
3. For time step = 1,2,…,T do
4.  For UAV i = 1,2,…,N do
5.   eceive P t , D t , l o c t , u , l o c t , u ¯
6.   Obtain o i , t = { P ′ t , D t , C t , l o c t , u , l o c t , u ¯ } by the GCLA mechanism
7.   Obtain the UAV action a i , t through π i , θ ( a i , t | o i , t )
8.  End
9.  Execute actions a t and update the environment
10.  eceive the environment reward r t and next state o t + 1
11.  Store trajectory τ + = [ o t , r t , a t , o t + 1 ]
12. End
13. Compute advantage estimate A t via GAE on τ
14. Compute the discount reward R ^ t and normalize
15. Split trajectory τ into chunks of length Y and store in experience pools
16. For mini-batch = 1,2,…,H do
17.  b ← random sample mini-batch from experience pools with all UAV data
18.  Compute loss functions L t ( θ ) 、 L t ( ϕ ) with data b
19.  Adam to update θ on L t ( θ )
20.  Adam to update ϕ on L t ( ϕ )
21. End
22.End

4. Experiments

To verify the effectiveness of the proposed ETS-MAPPO algorithm, it was compared against five classical MARL algorithms: MAPPO [15], MADDPG [29], MATD3 [30], QMIX [31], and IQL [32]. Ablation experiments were also conducted to demonstrate the contributions of the STEE network and the GCLA mechanism.

4.1. Simulation Environment and Parameter Settings

In the multi-UAV escape target search simulation scenario established, the environment is divided into two layers with a size of 2000 m × 2000 m . There are 3 UAVs, with a detection range for targets of 200 m and a detection range for stationary obstacles of 400 m .There are 10 escape targets, with a detection range for UAVs of 200 m , an escape range of 400 m , and a single escape attempt. The number of obstacles is 15. The simulation environment and network parameters are detailed in Table 1.
The simulation experiments were conducted using the following computer hardware and software: an Intel i5-12400F CPU, 32 GB RAM, an NVIDIA GeForce RTX 4060Ti GPU, Python 3.11.5, and Pytorch 2.1.0.

4.2. Model Performance Analysis

The analysis of model performance begins with evaluating the training results of each model, focusing on convergence and the performance metrics of six algorithm models: ETS-MAPPO, MAPPO, MADDPG, MATD3, QMIX, and IQL. Subsequently, the test results are analyzed to assess the generalization performance of the ETS-MAPPO algorithm model. Finally, the operational state of the ETS-MAPPO algorithm in the simulation environment at different time step is presented. To ensure the reliability of the experiments, the number of network layers and neurons in each algorithm is kept consistent, and the algorithm parameters were appropriately tuned. All experiments were conducted three times under random seeds of 1, 2, and 3, and the average value of the three experiments was taken as the final experimental result.

4.2.1. Analysis of Model Training Results

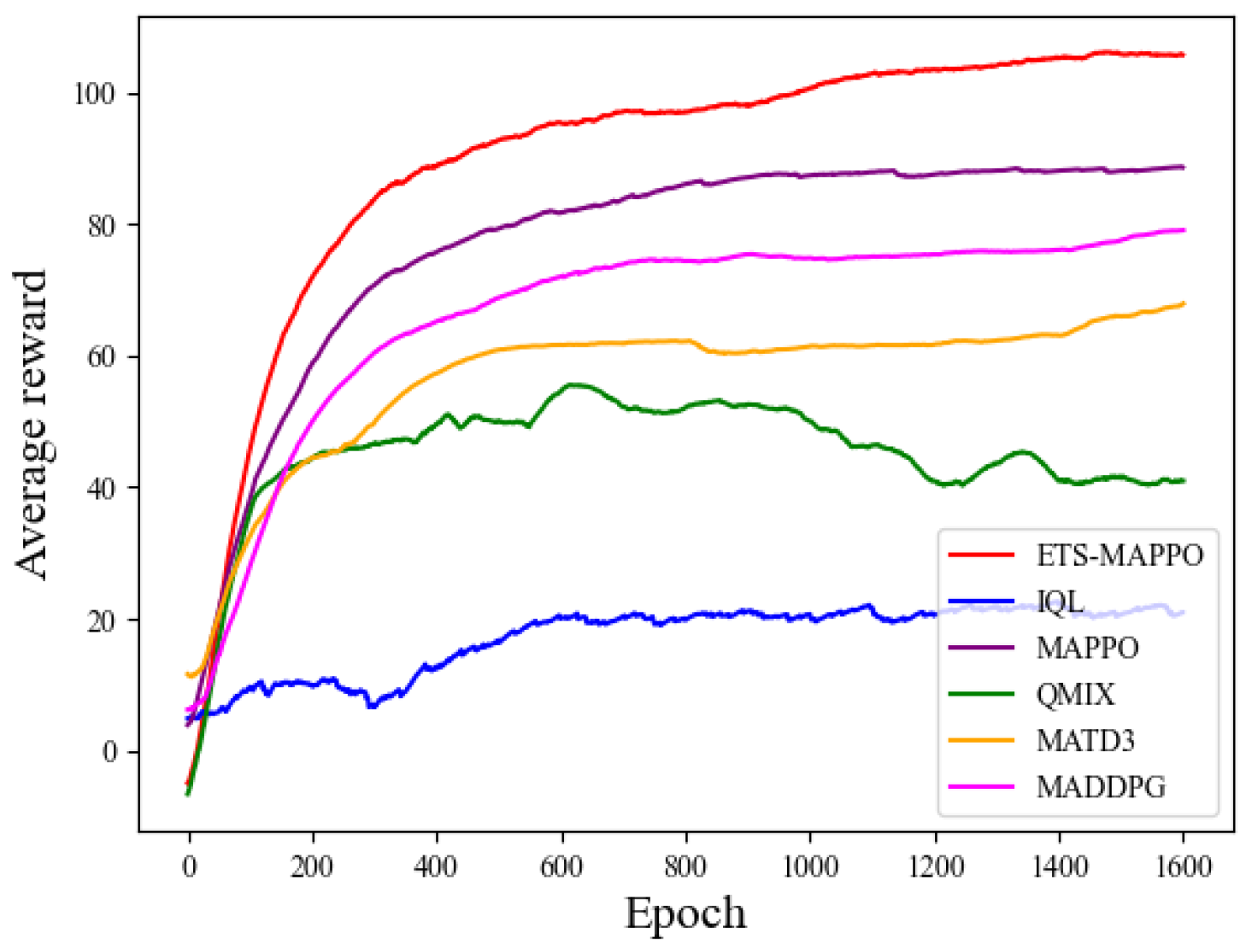
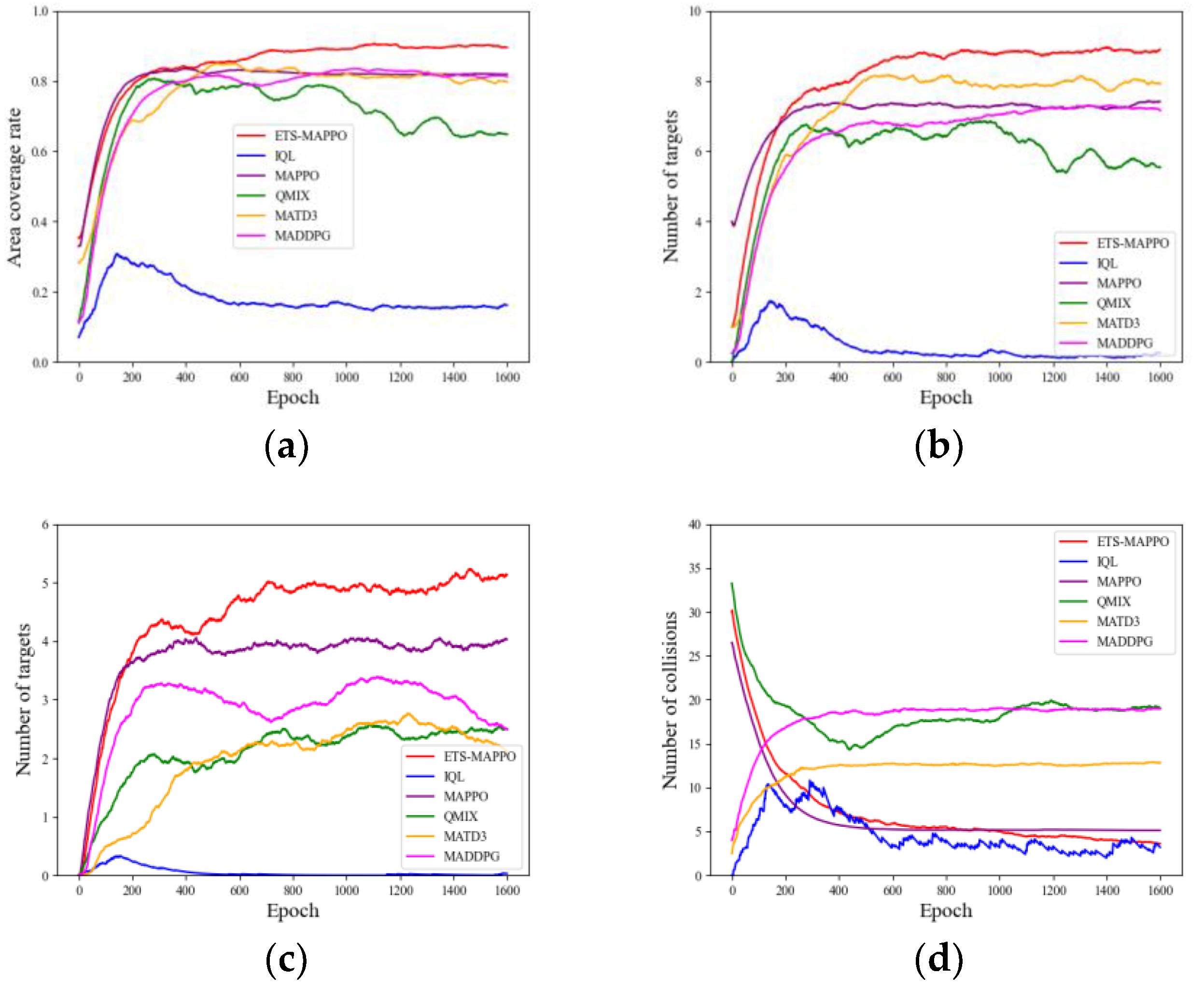
Model training was conducted according to the experimental setup described above, with the convergence curves of six algorithms—ETS-MAPPO, MAPPO, MAD-DPG, MATD3, QMIX, and IQL—presented in Figure 8. As the number of training rounds increased, the UAV average reward value gradually rises and converges. The average reward value curve of the ETS-MAPPO algorithm demonstrates a significant advantage over the other five classical algorithms.
Besides the average reward results representing the combined effect of multiple metrics, the specific parameter metrics that measure the actual performance in the METS problem include the area coverage rate, the number of collisions, the number of initial target searches, and the number of target re-searches. As shown in Figure 9a–c, the ETS-MAPPO algorithm is compared with the other five algorithms in terms of area coverage, the number of initial target searches, and the number of target re-searches. Although the convergence curves are intertwined in the early stages, the results after convergence display clear advantages.
On the indicator of the number of collisions shown in Figure 9(d), the convergence trend of MADDPG and MATD3 differs from the downward convergence observed in the ETS-MAPPO, MAPPO, QMIX, and IQL algorithms by exhibiting upward convergence, leading to poorer results. Additionally, the results of the ETS-MAPPO, MAPPO, and IQL algorithms are similar.
The observed results can be attributed to the adoption of the STEE network and the GCLA mechanism within the ETS-MAPPO algorithm. These components enhance the processing of spatio-temporal sequence data and environmental exploration, strengthen the network state parameters, improve the algorithm's learning efficiency, accelerate network convergence, and optimize the search for the escape target, ultimately yielding higher reward values, as reflected in the specific parameter metrics.

4.2.2. Analysis of Model Testing Results

In order to further validate the experimental results, six algorithms, ETS-MAPPO, MAPPO, MADDPG, MATD3, QMIX and IQL, were tested. The model with random seed of 1 was chosen for model testing, and each algorithm was tested for 20 rounds to take the average value as the test result, and other environmental parameters were consistent with the model training above; then the number of targets and time steps were changed to verify the generalization performance of the ETS-MAPPO algorithm.
The model test results are shown in Table 2, which compares the performance of the six algorithms across five metrics. The ETS-MAPPO algorithm outperforms the others on four of these metrics: the average reward, the area coverage rate, the number of initial target searches, and the number of target re-searches. In terms of obstacle collisions, comparison of the training curves and other indicators reveals that the IQL algorithm experiences fewer obstacle collisions, likely due to its limited UAV exploration of the environment, rendering it less comparable. Therefore, excluding the IQL algorithm, the ETS-MAPPO algorithm surpasses the remaining four algorithms in this metric. To summarize, the ETS-MAPPO algorithm outperforms the other five classical algorithms across all five performance metrics and demonstrates superior performance overall.
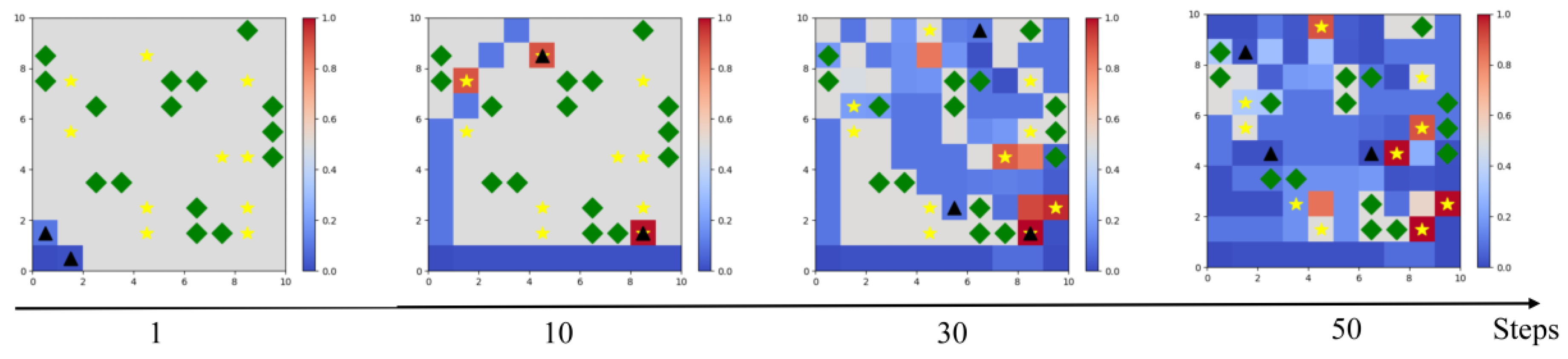
Figure 10 gives the results of the environment operation under 50 consecutive time steps in the test phase, at time step 1, time step 10, time step 30, and time step 50. At the beginning of the simulation, the UAV departed from the base and was divided into two paths for searching. From time step 1 to time step 10, it can be found that the UAV is trying to avoid collision with obstacles. From time step 10 to time step 30, it can be observed that the UAVs take a decentralized search and start searching for targets in full range, many targets are successfully searched for the first time, and it can be observed that some of the escaped targets have already escaped and there is a movement of their position. At the 30th time to 50th time step, some targets have been successfully searched again; at the same time, it can be found that the UAV has covered and searched most of the mission area. The above test results show that the ETS-MAPPO algorithm can reasonably and efficiently complete the area reconnaissance and escape target search.
To verify the generalization performance of the ETS-MAPPO algorithm, we varied the number of time steps and targets during testing. From Table 3 and Table 4, it can be seen that the average reward, the number of initial target searches, and the number of target re-searches increase with the increase in time steps and target count. The area coverage ratio remains near 0.9, and the percentage of initial-repeat target searches ratio stays around 0.5. This demonstrates that the ETS-MAPPO algorithm remains effective across different the number of time steps and targets.

4.3. Ablation Experiment

To investigate the impact of the STEE network and the GCLA mechanism on the ETS-MAPPO algorithm's performance, two variants were constructed: GCLA-MAPPO, by removing the STEE network, and STEE-MAPPO, by removing the GCLA mechanism. The test results for these algorithms across five performance metrics were analyzed. The specific configurations of the four algorithms in the ablation experiments are presented in Table 5, where “√” indicates inclusion and “×” indicates exclusion.
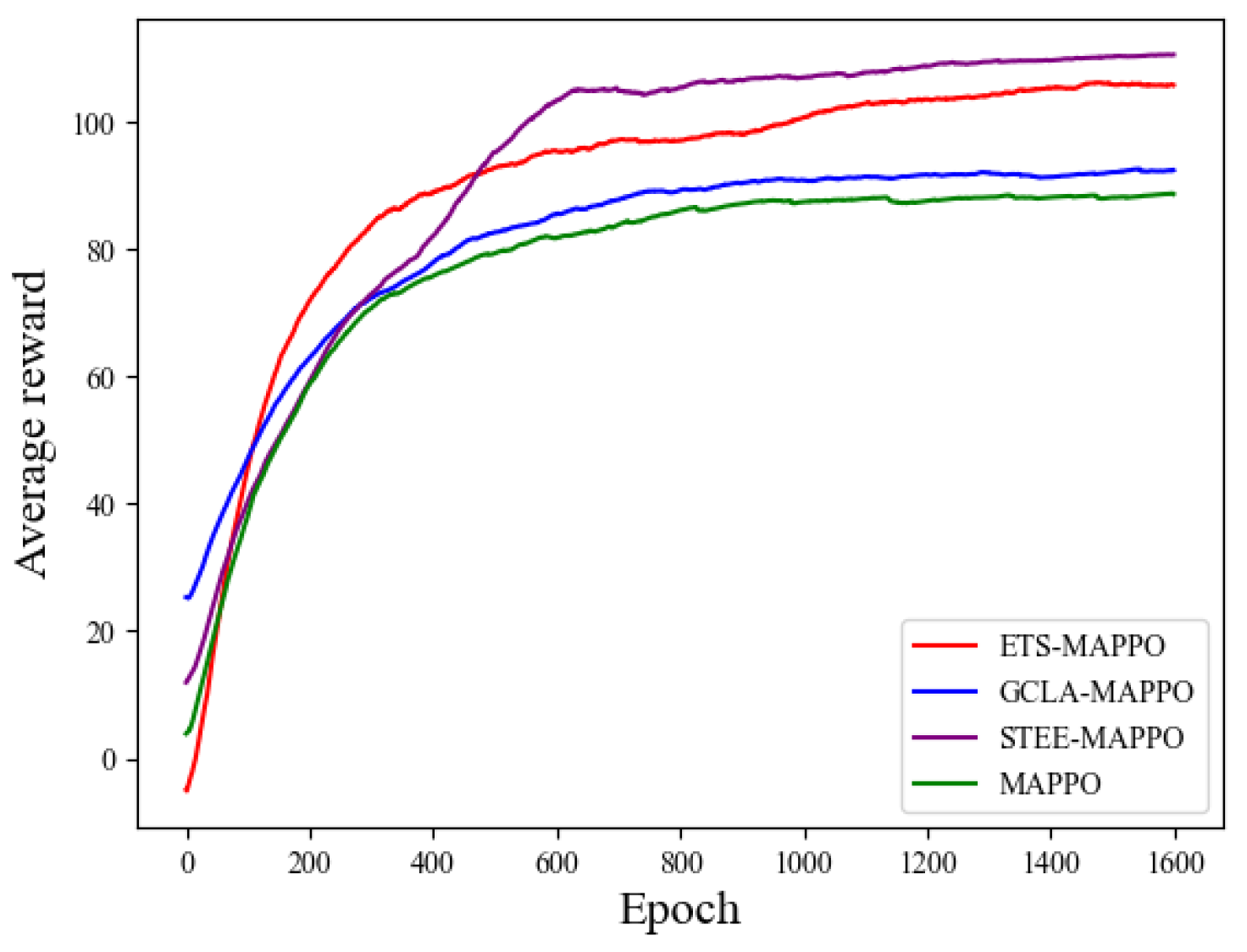
Figure 11 presents the training results of each ablation experiment algorithm in terms of average reward. From these results, the GCLA-MAPPO and MAPPO algorithms have similar reward values, while the ETS-MAPPO and STEE-MAPPO algorithms demonstrate higher reward values, with the ETS-MAPPO algorithm being slightly lower than the STEE-MAPPO algorithm.
Table 6 shows the test results of the four ablation experimental algorithms across five performance metrics. The results demonstrate that the ETS-MAPPO, STEE-MAPPO, and GCLA-MAPPO algorithms show improvements over the MAPPO algorithm in four metrics: the average reward, the number of collisions, the number of initial target searches, and the number of target re-searches. However, on the area coverage rate metric, the GCLA-MAPPO algorithm is slightly lower than the MAPPO algorithm.
These results can be attributed to the STEE network's ability to efficiently process spatio-temporal sequence data and enhance environmental exploration, thereby improving the overall performance of the algorithms. Consequently, algorithms utilizing the STEE network achieve higher reward values. The GCLA mechanism causes the UAV to focus its search near the initial target discovery area, which often includes regions that have already been explored. Given the limited number of time steps, the UAV lacks sufficient time to search unexplored areas after repeatedly scanning near the initial target area. This leads to a decrease in the area coverage rate and an increase in the number of target re-searches. These findings suggest that the STEE network and the GCLA mechanism effectively enhance the performance of the ETS-MAPPO algorithm in the METS problem.

5. Conclusions

This paper proposes a multi-UAV escape target search algorithm that combines the STEE network with the GCLA mechanism, built upon the MAPPO algorithm and applied to the multi-UAV escape target search task. Experimental results demonstrate that the ETS-MAPPO algorithm excels in addressing the METS problem, outperforming the other five MARL algorithms across all metrics. Ablation experiments confirm that the STEE network enhances the utilization of spatio-temporal sequence data while effectively balancing environmental exploration, thereby improving the algorithm's overall performance. Additionally, the GCLA mechanism significantly improves performance in the escape target search problem.
Future work will focus on optimizing the training efficiency of the algorithmic network model and reducing computational costs. Additionally, we will explore the generalization capability of the STEE network in other domains.

Author Contributions

G.L. completed the main experiment and wrote the initial paper; J.W. gave the experimental guidance and revised the initial article; D.Y. and J.Y. guided the revision of the article. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Francesco, T.; Costanza, F.; Nicola, C. Unmanned Aerial Vehicle for Precision Agriculture: A Review. IEEE Access 2024, 12, 69188–69205. [Google Scholar]
  2. Dimosthenis, C. ; Tsouros.; Stamatia, B. A Review on UAV-Based Applications for Precision Agriculture. Information 2019, 10, 349. [Google Scholar]
  3. Su, Z.N.; Jiao, J.; Lin, T. Integrated development of aeromagnetic system based on UAV platform and its application in mineral resources exploration. IOP Conf. Ser.: Earth Environ. Sci 2021, 660, 012103. [Google Scholar] [CrossRef]
  4. Yang, H.Y.; Wang, J.; Wang, J.C. Efficient Detection of Forest Fire Smoke in UAV Aerial Imagery Based on an Improved Yolov5 Model and Transfer Learning. Remote Sensing 2023, 15, 5527. [Google Scholar] [CrossRef]
  5. Tang, J.Z.; Liu, D.; Wang, Q.S. Probabilistic Chain-Enhanced Parallel Genetic Algorithm for UAV Reconnaissance Task Assignment. Drones 2024, 8, 213. [Google Scholar] [CrossRef]
  6. Hu, J.Q.; Wu, H.S.; Zhan, R.J. Self-organized search-attack mission planning for UAV swarm based on wolf pack hunting behavior. J. Syst. Eng. Electron. 2021, 32, 1463–1476. [Google Scholar]
  7. Vitaly, A.; Magnus, S. Optimal search for a moving target - A geometric approach. AIAA Guid., Contro; Conf. Exhib., Dever, CO, USA, 14-17 8 2000.
  8. Howie, C. Coverage for robotics – A survey of recent results. Ann. Math. Artif. Intell. 2001, 31, 113–126. [Google Scholar]
  9. Liang, Z.B.; Li, Q.; Fu, G.D. Multi-UAV Collaborative Search and Attack Mission Decision-Making in Unknown Environments. Sensors 2023, 23, 7398. [Google Scholar] [CrossRef]
  10. Mohammed, A.; Houssem, B.; Tijani, A. Dynamic Target Search Using Multi-UAVs Based on Motion-Encoded Genetic Algorithm With Multiple Parents. IEEE Access 2022, 10, 77922–77939. [Google Scholar]
  11. Chen, R.L.; Chen, J.L.; Li, S.Q. A review of multi-agent reinforcement learning methods. Inf. Countermeas. Technol. 2024, 3, 18–32. [Google Scholar]
  12. Littman, M.L. Markov Games as a Framework for Multi-Agent Reinforcement Learning. In Machine Learning Proceedings 1994, Elsevier, 157–163. [Google Scholar]
  13. Shen, G.Q.; Lei, L.; Zhang, X.T. Multi-UAV Cooperative Search Based on Reinforcement Learning with a Digital Twin Driven Training Framework. IEEE Trans. Veh. Technol. 2023, 72, 1–15. [Google Scholar] [CrossRef]
  14. Lu, Z.A.; Wu, Q.H.; Zhou, F.H. Algorithm for intelligent collaborative target search and trajectory planning of MAv/UAv. J. Commun. 2024, 45, 31–40. [Google Scholar]
  15. Yu, C.; Velu, A.; Vinitsky, E. The Surprising Effectiveness of PPO in Cooperative Multi-Agent Games. Adv. Neural Inf. Process. Syst. 2022, 35, 24611–24624. [Google Scholar]
  16. Wei, D.X.; Zhang, L.; Liu, Q. UAV Swarm Cooperative Dynamic Target Search: A MAPPO-Based Discrete Optimal Control Method. Drones 2024, 8, 214. [Google Scholar] [CrossRef]
  17. Bertuccelli, L.F.; How, J.P. Robust UAV search for environments with imprecise probability maps. 44th IEEE Conference on CCD-ECC, Seville, Spain, 12-15 12 2005.
  18. Zhang, B.Q.; Lin, X.; Zhu, Y.F.; Tian, J. Enhancing Multi-UAV Reconnaissance and Search Through Double Critic DDPG With Belief Probability Maps. IEEE Trans. Intell. Veh. 2024, 9, 1–16. [Google Scholar] [CrossRef]
  19. Hou, Y.K.; Zhao, J.; Zhang, R.Q. UAV Swarm Cooperative Target Search: A Multi-Agent Reinforcement Learning Approach. J. Cloud Comput 2024, 9, 568–578. [Google Scholar] [CrossRef]
  20. Vinh, K. Gebreyohannes, S.; Karimoddini, A. An Area-Decomposition Based Approach for Cooperative Tasking and Coordination of UAVs in a Search and Coverage Mission. 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 02-09 3 2019.
  21. Chung, T.H.; Burdick, J.W. Analysis of search decision making using probabilistic search strategies. IEEE Trans. Robot 2012, 28, 132–144. [Google Scholar] [CrossRef]
  22. Frans, A.O.; Matthijs, T.S.; Nikos, V. Optimal and Approximate Q-value Functions for Decentralized POMDPs. J. Artif. Intell. Res. 2011, 32, 289–353. [Google Scholar]
  23. Mahajan, A.; Rashid, T.; Samvelyan, M. Maven: Multi-agent variational exploration. 33rd Conference on NeurIPS, Vancouver, Canada, 08-14 12 2019.
  24. Zhang, B.; Hu, W.H.; Cao, D. Novel Data-Driven decentralized coordination model for electric vehicle aggregator and energy hub entities in multi-energy system using an improved multi-agent DRL approach. Applied Energy 2023, 339, 120902. [Google Scholar] [CrossRef]
  25. Shi, D.X.; Peng, Y.X.; Yang, H. A DQN-based deep reinforcement learning motion planning method for multiple agents. Computer Science 2024, 51, 268–277. [Google Scholar]
  26. Sun, D.M.; Chen, Y.M.; Li, H. Intelligent Vehicle Computation Offloading in Vehicular Ad Hoc Networks: A Multi-Agent LSTM Approach with Deep Reinforcement Learning. Mathematics 2024, 12, 424. [Google Scholar] [CrossRef]
  27. He, H.R.; Zhou, F.Q.; Zhao, Y.K. Hypergraph convolution mix DDPG for multi-aerial base station deployment. J. Cloud Comput. 2023, 12, 1–11. [Google Scholar] [CrossRef]
  28. Shi, X.J.; Chen, Z.R.; Wang, H. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. Computer Science. 29th Annual Conference on NIPS, Montreal, Canada, 07-12 12 2015.
  29. Lowe, R.; Wu, Y.; Tamar, A. Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments. 31st Annual Conference on NIPS, Long Beach, CA, USA, 04-09 12 2017.
  30. Fujimoto, S.; van Hoof, H.; Meger, D. Addressing Function Approximation Error in Actor-Critic Methods. 35th ICML, Stockholm, Sweden, 10-15 7 2018.
  31. Rashid, T.; Samvelyan, M.; Farquhar, G. Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning. J. Mach. Learn. Res. 2020, 21, 178. [Google Scholar]
  32. Tampuu, A.; Matiisen, T.; Kodelja, D. Multiagent cooperation and competition with deep reinforcement learning. PLoS One 2017, 12, 1–15. [Google Scholar] [CrossRef]
Preprints 118137 g001
Figure 1. Typical scenario diagram for a multi-UAV escape target search mission.
Figure 1. Typical scenario diagram for a multi-UAV escape target search mission.
Preprints 118137 g001
Preprints 118137 g002
Figure 2. Rasterized model map of the task area.
Figure 2. Rasterized model map of the task area.
Preprints 118137 g002
Preprints 118137 g003
Figure 3. UAV action space model.
Figure 3. UAV action space model.
Preprints 118137 g003
Preprints 118137 g004
Figure 4. The STEE network architecture.
Figure 4. The STEE network architecture.
Preprints 118137 g004
Preprints 118137 g005
Figure 5. Network parameterized noise.
Figure 5. Network parameterized noise.
Preprints 118137 g005
Preprints 118137 g006
Figure 6. Processing of TEPM convolutional operations for 10 × 10 state parameters.
Figure 6. Processing of TEPM convolutional operations for 10 × 10 state parameters.
Preprints 118137 g006
Preprints 118137 g007
Figure 7. The ETS-MAPPO algorithmic framework.
Figure 7. The ETS-MAPPO algorithmic framework.
Preprints 118137 g007
Preprints 118137 g008
Figure 8. Comparison of the average reward values of the six algorithms.
Figure 8. Comparison of the average reward values of the six algorithms.
Preprints 118137 g008
Preprints 118137 g009
Figure 9. The specific parameter metrics train results. (a) Area coverage rate, (b) The number of initial target searches; (c) The number of target re-searches; (d) The number of collisions.
Figure 9. The specific parameter metrics train results. (a) Area coverage rate, (b) The number of initial target searches; (c) The number of target re-searches; (d) The number of collisions.
Preprints 118137 g009
Preprints 118137 g010
Figure 10. Results of UAV operation under 50 consecutive time steps in the simulation environment testing phase.
Figure 10. Results of UAV operation under 50 consecutive time steps in the simulation environment testing phase.
Preprints 118137 g010
Preprints 118137 g011
Figure 11. Comparison of average reward results from ablation experiment.
Figure 11. Comparison of average reward results from ablation experiment.
Preprints 118137 g011
Table 1. The simulation environment and network parameter settings.
Table 1. The simulation environment and network parameter settings.
Parameter Value
Total running steps 2000000
Time step per round 50
Actor network learning rate 5e-4
Critic network learning rate 5e-4
Hidden layer size 64
Discount factor 0.99
Detection payload correct rate 0.90
Table 2. Six algorithms test results.
Table 2. Six algorithms test results.
Algorithms Average reward Area coverage rate Number of collisions Number of target initial searches Number of target re-searches
IQL 24.85 0.15 2.68* 0.55 0.09
QMIX 41.95 0.63 18.11 5.25 2.43
MADDPG 79.73 0.80 18.95 6.93 2.18
MATD3 71.11 0.78 12.67 7.87 1.80
MAPPO 88.86 0.82 5.12 7.45 2.75
ETS-MAPPO 106.21 0.89 3.18 9.09 5.11
Table 3. Experimental test results for changing the number of time steps.
Table 3. Experimental test results for changing the number of time steps.
Time steps Average reward Area coverage rete Number of collisions Number of target initial searches Number of target re-searches
50 106.21 0.89 3.18 9.09 5.11
60 111.65 0.96 9.7 9.55 5.65
80 124.86 0.99 16.2 9.73 7.05
100 129.76 1.00 18.4 9.82 7.10
Table 4. Experimental test results of changing the number of targets.
Table 4. Experimental test results of changing the number of targets.
Target numbers Average reward Area coverage rate Percentage of initial-repeat target searches Number of target initial searches Number of target re-searches
5 102.26 0.94 0.51 4.55 2.33
10 106.21 0.89 0.57 9.09 5.11
15 107.51 0.92 0.48 13.05 6.35
Table 5. Ablation experimental setup.
Table 5. Ablation experimental setup.
Algorithms STEE network GCLA mechanism
ETS-MAPPO √ √
STEE-MAPPO √ ×
GCLA-MAPPO × √
MAPPO × ×
Table 6. Results of ablation experiment.
Table 6. Results of ablation experiment.
Algorithms Average reward Area coverage rete Number of collisions Number of target initial searches Number of target re-searches
MAPPO 88.86 0.82 5.12 7.45 2.75
STEE-MAPPO 109.28 0.93 0.36 9.85 3.05
GCLA-MAPPO 89.98 0.77 0.84 8.89 4.23
ETS-MAPPO 106.21 0.89 3.18 9.09 5.11
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated